🎲 [ICLR 2025] DICE: Data Influence Cascade in Decentralized Learning

Tongtian Zhu

TongtianZhu

Follow

Tags: Data_Influence, Decentralized_Learning

Authors:   Tongtian Zhu¹    Wenhao Li¹    Can Wang¹    Fengxiang He²

¹Zhejiang University      ²The University of Edinburgh

📄 Openreview • 💻 Code • 📚 arXiv • 🔗 Twitter • 🖼️ Poster • 📊 Slides • 🎥 Video (Chinese)

Updates in progress. More coming soon! 😉

🗓️ 2025-07-17 — Updated main results

Main Results

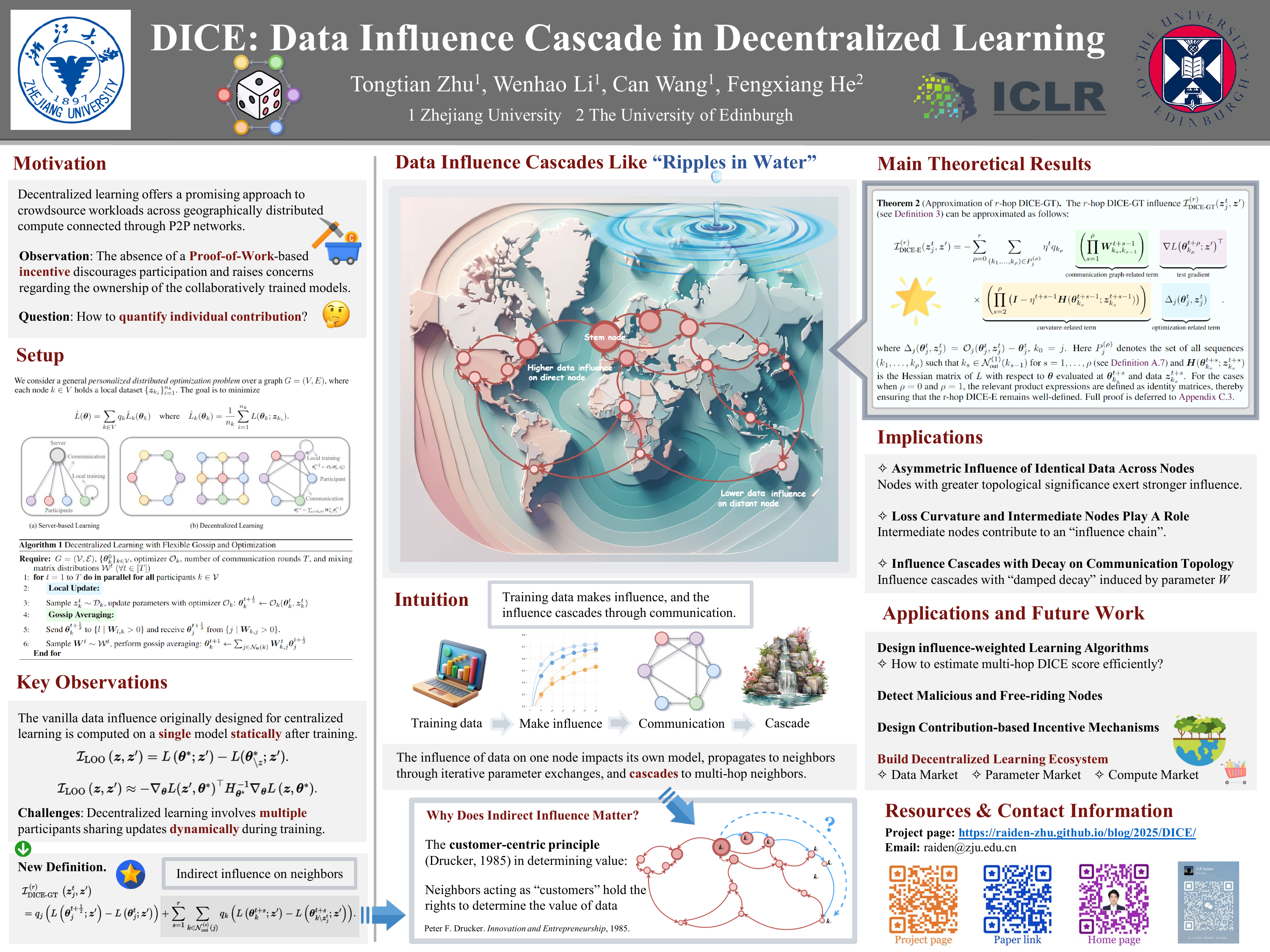
Theorem (Approximation of r-hop DICE-GT)

The r-hop DICE-GT influence ${\mathcal{I}}_{\mathrm{D}\mathrm{I}\mathrm{C}\mathrm{E}-\mathrm{G}\mathrm{T}}^{(r)}({\mathit{z}}_j^t,{\mathit{z}}^{\mathrm{\prime }})\backslash mathcal\{I\}\_\{\backslash mathrm\{DICE-GT\}\}^\{(r)\}(\backslash boldsymbol\{z\}\_j^t,\; \backslash boldsymbol\{z\}^\{\backslash prime\})$ can be approximated as follows:

where ${\mathrm{\Delta }}_j({\mathit{\theta }}_j^t,{\mathit{z}}_j^t)={\mathcal{O}}_j({\mathit{\theta }}_j^t,{\mathit{z}}_j^t)-{\mathit{\theta }}_j^t\backslash Delta\_j(\backslash boldsymbol\{\backslash theta\}\_j^t,\backslash boldsymbol\{z\}\_j^t)\; =\; \backslash mathcal\{O\}\_j(\backslash boldsymbol\{\backslash theta\}\_j^t,\backslash boldsymbol\{z\}\_j^t)-\backslash boldsymbol\{\backslash theta\}\_j^t$, $k_0=jk\_0\; =\; j$. Here $P_j^{(\rho )}P\_j^\{(\backslash rho)\}$ denotes the set of all sequences $(k_1,\dots ,k_{\rho })(k\_1,\; \backslash dots,\; k\_\{\backslash rho\})$ such that $k_s\in {\mathcal{N}}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{(1)}(k_{s-1})k\_s\; \backslash in\; \backslash mathcal\{N\}\_\{\backslash mathrm\{out\}\}^\{(1)\}(k\_\{s-1\})$ for $s=1,\dots ,\rho s=1,\backslash dots,\backslash rho$ and $\mathit{H}({\mathit{\theta }}_{k_s}^{t+s};{\mathit{z}}_{k_s}^{t+s})\backslash boldsymbol\{H\}(\backslash boldsymbol\{\backslash theta\}\_\{k\_s\}^\{t+s\};\; \backslash boldsymbol\{z\}\_\{k\_s\}^\{t+s\})$ is the Hessian matrix of $LL$ with respect to $\mathit{\theta }\backslash boldsymbol\{\backslash theta\}$ evaluated at ${\mathit{\theta }}_{k_s}^{t+s}\backslash boldsymbol\{\backslash theta\}\_\{k\_s\}^\{t+s\}$ and data ${\mathit{z}}_{k_s}^{t+s}\backslash boldsymbol\{z\}\_\{k\_s\}^\{t+s\}$.

For the cases when $\rho =0\backslash rho\; =\; 0$ and $\rho =1\backslash rho\; =\; 1$, the relevant product expressions are defined as identity matrices, thereby ensuring that the r-hop DICE-E remains well-defined.

Citation

@inproceedings{zhu2025dice,
  title="{DICE: Data Influence Cascade in Decentralized Learning}",
  author="Tongtian Zhu and Wenhao Li and Can Wang and Fengxiang He",
  booktitle="The Thirteenth International Conference on Learning Representations",
  year="2025",
  url="[https://openreview.net/forum?id=2TIYkqieKw](https://openreview.net/forum?id=2TIYkqieKw)"
}