problem
stringlengths 18
4.46k
| answer
stringlengths 1
942
| pass_at_n
float64 0.08
0.92
|
|---|---|---|
Given positive numbers \( a, b, c, x, y, z \) such that \( cy + bz = a \), \( az + cx = b \), and \( bx + ay = c \), find the minimum value of the function \( f(x, y, z) = \frac{x^2}{1+x} + \frac{y^2}{1+y} + \frac{z^2}{1+z} \).
|
\frac{1}{2}
| 0.75 |
Calculate the integral
$$
\int_{0}^{0.1} \cos \left(100 x^{2}\right) d x
$$
with an accuracy of $\alpha=0.001$.
|
0.090
| 0.5 |
Let \( l \) and \( m \) be two skew lines. On \( l \), there are three points \( A, B, \) and \( C \), such that \( AB = BC \). From points \( A, B, \) and \( C \), perpendiculars \( AD, BE, \) and \( CF \) are respectively drawn to \( m \), with feet of the perpendiculars at \( D, E, \) and \( F \). Given \( AD = \sqrt{15}, BE = \frac{7}{2}, CF = \sqrt{10} \), find the distance between lines \( l \) and \( m \).
|
\sqrt{6}
| 0.5 |
Given natural numbers \( M \) and \( N \), both greater than ten, consisting of the same number of digits, and such that \( M = 3N \). To obtain the number \( M \), one of the digits in \( N \) is increased by 2, and each of the remaining digits is increased by an odd digit. What digit could the number \( N \) end with? Find all possible answers.
(N. Agahanov)
|
6
| 0.625 |
Given that four integers \( a, b, c, d \) are all even numbers, and \( 0 < a < b < c < d \), with \( d - a = 90 \). If \( a, b, c \) form an arithmetic sequence and \( b, c, d \) form a geometric sequence, then find the value of \( a + b + c + d \).
|
194
| 0.75 |
Let \( m = 999 \ldots 99 \) be the number formed by 77 digits all equal to 9 and let \( n = 777 \ldots 77 \) be the number formed by 99 digits all equal to 7. What is the number of digits of \( m \cdot n \)?
|
176
| 0.625 |
In the expression \((x+y+z)^{2032}+(x-y-z)^{2032}\), the parentheses were expanded and like terms were combined. How many monomials \(x^{a} y^{b} z^{c}\) with a nonzero coefficient are obtained?
|
1034289
| 0.5 |
The probability of failure for each device during testing is 0.2. How many such devices need to be tested so that, with a probability not less than 0.9, it can be stated that at least two devices will fail?
|
18
| 0.375 |
Given a natural number \( n \), the polynomial
\[ P(x) = \sum_{h=0}^{n} \binom{n}{h} x^{n-h}(x-1)^{h} \]
can be expanded into an ascending order of \( x \) as \( a_{0} + a_{1} x + a_{2} x^{2} + \cdots + a_{n} x^{n} \). Find
\[ \left| a_{0} \right| + \left| a_{1} \right| + \left| a_{2} \right| + \cdots + \left| a_{n} \right|. \]
|
3^n
| 0.5 |
Given fifty distinct natural numbers, twenty-five of which do not exceed 50, and the remaining are greater than 50 but do not exceed 100. Additionally, no two of these numbers differ by exactly 50. Find the sum of these numbers.
|
2525
| 0.75 |
Vanya goes to the swimming pool every Wednesday and Friday. After his latest visit, he noticed that he had already gone 10 times this month. What will be the date of his third visit next month if he continues going on Wednesdays and Fridays?
|
12
| 0.375 |
Calculate \(\sqrt{31 \times 30 \times 29 \times 28 + 1}\).
|
869
| 0.875 |
Determine the mass fraction of potassium sulfate in the original solution:
$$
\omega\left(K_{2} \mathrm{SO}_{4}\right)=\frac{m\left(K_{2} \mathrm{SO}_{4}\right) \cdot 100 \%}{m_{\mathrm{p}-\mathrm{pa}}\left(K_{2} \mathrm{SO}_{4}\right)}=\frac{2,61 \cdot 100 \%}{160}=1,63 \%
$$
|
1.63\%
| 0.375 |
Let \( A B C \) be a right triangle with \(\angle BAC = 90^{\circ}\) and \(I\) the intersection point of its angle bisectors. A line through \(I\) intersects the sides \(AB\) and \(AC\) at \(P\) and \(Q\) respectively. The distance from \(I\) to the side \(BC\) is \(1 \, \text{cm}\).
a) Find the value of \( PM \cdot NQ \).
b) Determine the minimum possible value for the area of triangle \(APQ\).
Hint: If \(x\) and \(y\) are two non-negative real numbers, then \(x + y \geq 2 \sqrt{xy}\).
|
2
| 0.875 |
Vanya thought of two natural numbers whose product is 7200. What is the greatest possible value of the greatest common divisor (GCD) of these numbers?
|
60
| 0.875 |
Lucas writes two distinct positive integers on a whiteboard. He decreases the smaller number by 20 and increases the larger number by 23, only to discover the product of the two original numbers is equal to the product of the two altered numbers. Compute the minimum possible sum of the original two numbers on the board.
|
321
| 0.875 |
An 8 by 6 grid is placed in the first quadrant with its edges along the axes. A total of 32 of the squares in the grid are shaded. A line is drawn through (0,0) and (8, c) cutting the shaded region into two equal areas. What is the value of c?
|
c = 4
| 0.25 |
Calculate the definite integral:
$$
\int_{0}^{\pi} 2^{4} \cdot \sin ^{6} x \cos ^{2} x \, dx
$$
|
\frac{5\pi}{8}
| 0.75 |
The sum of the elements of all subsets of a set \( S \) of 4 real numbers is 2008 (here, the sum of the elements of the empty set is considered to be 0). Find the sum of all elements in \( S \).
|
251
| 0.875 |
Let \(a\) and \(b\) be strictly positive integers such that \(a^n\) divides \(b^{n+1}\) for all integers \(n \geq 1\). Show that \(a\) divides \(b\).
|
a \mid b
| 0.5 |
For each pair of real numbers \((x, y)\) with \(0 \leq x \leq y \leq 1\), consider the set
\[ A = \{ x y, x y - x - y + 1, x + y - 2 x y \}. \]
Let the maximum value of the elements in set \(A\) be \(M(x, y)\). Find the minimum value of \(M(x, y)\).
|
\frac{4}{9}
| 0.625 |
Calculate the sum of the cubes of two numbers if their sum and product are 11 and 21, respectively.
|
638
| 0.875 |
\(\frac{\left(\frac{1}{a}+\frac{1}{b}-\frac{2c}{ab}\right)(a+b+2c)}{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{2}{ab}-\frac{4c^{2}}{a^{2}b^{2}}} ; \quad a = 7.4 , b = \frac{5}{37}\).
|
1
| 0.875 |
For what smallest natural number \( a \) are there exactly 50 perfect squares in the numerical interval \( (a, 3a) \)?
|
4486
| 0.125 |
Points \( A, B, C \) lie on a circle \(\omega\) such that \( BC \) is a diameter. \( AB \) is extended past \( B \) to point \( B' \) and \( AC \) is extended past \( C \) to point \( C' \) such that line \( B'C' \) is parallel to \( BC \) and tangent to \(\omega\) at point \( D \). If \( B'D = 4 \) and \( C'D = 6 \), compute \( BC \).
|
\frac{24}{5}
| 0.25 |
Suppose that \((a_1, b_1), (a_2, b_2), \ldots, (a_{100}, b_{100})\) are distinct ordered pairs of nonnegative integers. Let \(N\) denote the number of pairs of integers \((i, j)\) satisfying \(1 \leq i < j \leq 100\) and \(\left|a_i b_j - a_j b_i\right| = 1\). Determine the largest possible value of \(N\) over all possible choices of the 100 ordered pairs.
|
197
| 0.875 |
The positive numbers \( x \) and \( y \) change such that \( x > y \) and \( x^{2} + y^{2} = 18xy \). Show that the following expression is constant:
\[
\log (x - y) - \frac{1}{2} (\log x + \log y)
\]
The base of the logarithms is \( \sqrt{2} \).
|
4
| 0.75 |
In a right triangle \(ABC\) with legs \(AB = 10\) and \(AC = 24\), medians \(AM\) and \(CN\) are drawn, where \(M\) and \(N\) are the midpoints of the sides \(BC\) and \(AB\), respectively. Point \(I\) lies on the side \(AC\), and \(BI\) is the angle bisector. Find the area of triangle \(MNI\).
|
30
| 0.625 |
Arrange all proper fractions in a sequence $\left\{a_{n}\right\}: \frac{1}{2}, \frac{1}{3}, \frac{2}{3}, \frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \cdots$. The sorting method is: from left to right, the denominators are arranged in ascending order, and for fractions with the same denominator, the numerators are arranged in ascending order. What is the 2017th term $a_{2017}$ of this sequence?
|
\frac{1}{65}
| 0.875 |
Given a sequence \(\{a_n\}\) which satisfies \(a_n = a_{n-1} - a_{n-2}\) for \(n \geqslant 3\), if the sum of its first 1492 terms is 1985 and the sum of its first 1985 terms is 1492, find the sum of its first 2001 terms.
|
986
| 0.125 |
The decimal representation of a natural number \( N \) contains 1580 digits. Among these digits, there are threes, fives, and sevens, and there are no other digits. It is known that the number of sevens is 20 less than the number of threes. Find the remainder when \( N \) is divided by 3.
|
0
| 0.75 |
A box contains 10 identical balls. Among them, 3 balls are labeled with the number 1, 4 balls are labeled with the number 2, and 3 balls are labeled with the number 5. One ball is randomly selected from the box, recorded, and then placed back into the box. Another ball is then randomly selected. Let the sum of the numbers on the balls from the first and second selections be denoted as $\xi$.
(I) Find the distribution of the random variable $\xi$.
(II) Find the expected value $E(\xi)$ of the random variable $\xi$.
|
5.20
| 0.25 |
There are functions \( f(x) \) with the following properties:
- \( f(x) = a x^2 + b x + c \) for some integers \( a, b \) and \( c \) with \( a > 0 \), and
- \( f(p) = f(q) = 17 \) and \( f(p+q) = 47 \) for some prime numbers \( p \) and \( q \) with \( p < q \).
For each such function, the value of \( f(p q) \) is calculated. The sum of all possible values of \( f(p q) \) is \( S \). What are the rightmost two digits of \( S \)?
|
71
| 0.875 |
Given plane vectors $\boldsymbol{a}$ and $\boldsymbol{b}$ such that $|\boldsymbol{a}+\boldsymbol{b}|=3$, find the maximum value of $\boldsymbol{a} \cdot \boldsymbol{b}$.
|
\frac{9}{4}
| 0.25 |
Calculate the limit of the function:
$$\lim _{x \rightarrow a} \frac{\operatorname{tg} x-\operatorname{tg} a}{\ln x-\ln a}$$
|
\frac{a}{\cos^2 a}
| 0.125 |
Yaw yaw and her father are discussing the upcoming year 2016. Yaw yaw says: "I find the number 2016 interesting because the last digit 6 is exactly twice the sum of the preceding digits 2, 0, and 1." Her father says that they can define a year that meets this condition as a "lucky double year." Yaw yaw quickly calculates and says: "After 2016, the next 'lucky double year' will be when I am 17 years old." How old is Yaw yaw in 2016?
|
5
| 0.5 |
A circle passes through the intersection points of any two of the lines \( y = x \), \( y = 2x \), and \( y = 15 - 0.5x \). What is the length of the chord of the circle that lies on the line \( x + y = 16 \)?
|
8\sqrt{2}
| 0.875 |
How many triangles exist in which the measures of the angles, measured in degrees, are whole numbers?
|
2700
| 0.625 |
Given the function \( f(x)=\sqrt{3} \sin 2x + 2 \cos^2 x + a \), if the minimum value of \( f(x) \) on the interval \(\left[ 0, \frac{\pi}{2} \right] \) is \(-1\), find the value of \( a \).
|
-1
| 0.75 |
From the three-digit numbers \(100, 101, 102, \ldots, 699, 700\), choose \(n\) different numbers such that you can always find three of them with the same sum of digits. What is the minimum value of \(n\)?
|
47
| 0.375 |
If \( n \) is a positive integer, and \( a(n) \) is the smallest positive integer such that \( (a(n))! \) is divisible by \( n \), find all positive integers \( n \) such that \( \frac{a(n)}{n} = \frac{2}{3} \). (2003 German Math Olympiad)
|
9
| 0.375 |
If from point $P$ two perpendicular chords are drawn to a given circle, then the sum of the squares of the resulting four segments is constant.
|
4r^2
| 0.5 |
Find the smallest two-digit number \( N \) such that the sum of digits of \( 10^N - N \) is divisible by 170.
|
20
| 0.375 |
The three different points \(A(x_1, y_1)\), \(B\left(4, \frac{9}{5}\right)\), and \(C(x_2, y_2)\) on the ellipse \(\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1\), along with the focus \(F(4,0)\) have distances that form an arithmetic sequence. If the perpendicular bisector of line segment \(AC\) intersects the x-axis at point \(T\), find the slope \(k\) of the line \(BT\).
|
\frac{5}{4}
| 0.5 |
Suppose that \(x_{1}, x_{2}\), and \(x_{3}\) are the three roots of \((11-x)^{3}+(13-x)^{3}=(24-2x)^{3}\). Find the value of \(x_{1}+x_{2}+x_{3}\).
|
36
| 0.875 |
In $\triangle ABC$, the side lengths opposite to the angles $\angle A$, $\angle B$, and $\angle C$ are $a$, $b$, and $c$ respectively, and it is given that
$$
\begin{array}{l}
\sin C \cdot \cos \frac{A}{2}=(2-\cos C) \sin \frac{A}{2}, \\
\cos A=\frac{3}{5}, \quad a=4.
\end{array}
$$
Then the area of $\triangle ABC$ is ___.
|
6
| 0.875 |
A few natural numbers were multiplied together to get 224, and the smallest number was exactly half of the largest number.
How many numbers were multiplied?
|
3
| 0.75 |
What is the integer part of the following number:
$$
\sqrt{6+\sqrt{6+\ldots+\sqrt{6}}}+\sqrt[3]{6+\sqrt[3]{6+\cdots+\sqrt[3]{6}}}
$$
where both the number of square roots and cube roots is 100?
|
4
| 0.75 |
The function \( y = f(t) \) is such that the sum of the roots of the equation \( f(\sin x) = 0 \) in the interval \([3 \pi / 2, 2 \pi]\) is \( 33 \pi \), and the sum of the roots of the equation \( f(\cos x) = 0 \) in the interval \([\pi, 3 \pi / 2]\) is \( 23 \pi \). What is the sum of the roots of the second equation in the interval \([\pi / 2, \pi]?\)
|
17 \pi
| 0.375 |
How many different combinations of 4 marbles can be made from 5 indistinguishable red marbles, 4 indistinguishable blue marbles, and 2 indistinguishable black marbles?
|
12
| 0.625 |
Given the sets \(A=\{x \mid x^{2}-4x+3<0, x \in \mathbf{R}\}\) and \(B=\{x \mid 2^{1-x}+a \leq 0, x^{2}-2(a+7)x+5 \leq 0, x \in \mathbf{R}\}\). If \(A \subset B\), find the range of values for the real number \(a\).
|
[-4, -1]
| 0.625 |
Starting from 1, there are n consecutive natural numbers. If one of these numbers is removed, the average of the remaining numbers is $\frac{152}{7}$. What is the number that was removed?
|
34
| 0.625 |
The parabola \(C_{1}: x^{2}=2 py\) has its focus at \(F\). The hyperbola \(C_{2}: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) has its left and right foci at \(F_{1}\) and \(F_{2}\). Point \(P\) is a common point of the two curves in the first quadrant. If points \(P\), \(F\), and \(F_{1}\) are collinear and \(C_{1}\) and \(C_{2}\) share a common tangent at \(P\), find the eccentricity of \(C_{2}\).
|
e = \sqrt{2}
| 0.875 |
A cone has a height of $12 \mathrm{~cm}$. When the lateral surface is unwrapped, we obtain a circular sector with a central angle of $100^{\circ} 48^{\prime}$. What is the surface area and the volume of the cone?
|
49 \pi \text{ cm}^3
| 0.125 |
The area of trapezoid $ABCD$ is 90. The diagonals intersect at point $O$. Segments connecting the midpoint $P$ of the base $AD$ with vertices $B$ and $C$ intersect with the diagonals of the trapezoid at points $M$ and $N$. Find the area of quadrilateral $OMPN$ if one of the bases of the trapezoid is twice as long as the other.
|
10
| 0.5 |
Given a sequence \( a_{1}, a_{2}, a_{3}, \cdots, a_{n}, \cdots \) that satisfies \( a_{1}=a_{2}=1 \), \( a_{3}=2 \), and for any positive integer \( n \), \( a_{n} \cdot a_{n+1} \cdot a_{n+2} \neq 1 \). Additionally, \( a_{n} \cdot a_{n+1} \cdot a_{n+2} \cdot a_{n+3} = a_{n} + a_{n+1} + a_{n+2} + a_{n+3} \). Find the value of \( a_{1} + a_{2} + \cdots + a_{100} \).
|
200
| 0.125 |
An equilateral triangle with side length \( n \) is divided into \( n^2 \) smaller equilateral triangles each with side length 1 by lines parallel to its sides. This creates a network of nodes connected by line segments of length 1. What is the maximum number of segments that can be chosen such that no three chosen segments form a triangle?
|
n(n+1)
| 0.75 |
Solve the equation:
$$(x+1)^{63}+(x+1)^{62}(x-1)+(x+1)^{61}(x-1)^{2}+\ldots+(x-1)^{63}=0$$
|
0
| 0.375 |
Three friends play the following game. They position themselves at the points with coordinates $(0,0),(1,0)$, and $(0,1)$. Every minute, one of the three friends moves somewhere along the line parallel to the line passing through the positions of the other two friends. Can they reach the coordinates $(0,0),(1,1),(0,2)$?
|
\text{No}
| 0.75 |
\(ABCD\) is a square with side length 2. \(E\) is the midpoint of \(AB\), \(F\) is the midpoint of \(BC\), \(AF\) and \(DE\) intersect at \(I\), and \(BD\) and \(AF\) intersect at \(H\). Find the area of quadrilateral \(BEIH\).
|
\frac{7}{15}
| 0.875 |
Find the largest real number \( p \) such that all three roots of the equation below are positive integers:
\[
5x^{3} - 5(p+1)x^{2} + (71p-1)x + 1 = 66p .
\]
|
76
| 0.375 |
Natural numbers \(a, b, c\) are such that \(\gcd(\operatorname{lcm}(a, b), c) \cdot \operatorname{lcm}(\gcd(a, b), c) = 200\).
What is the maximum value of \(\gcd(\operatorname{lcm}(a, b), c) ?\)
|
10
| 0.375 |
Let $G$ be a graph with $n$ vertices that does not contain any triangles (cycles of length 3). Show that $G$ has at most $n^{2} / 4$ edges.
|
\frac{n^2}{4}
| 0.5 |
Find the number of ways to color all natural numbers from 1 to 20 in blue and red so that both colors are used and the product of all red numbers is relatively prime to the product of all blue numbers.
|
62
| 0.25 |
Find the smallest positive integer \( n \) such that the set \( \{1, 2, 3, \cdots, 3n-1, 3n\} \) can be divided into \( n \) disjoint triples \( \{x, y, z\} \) where \( x + y = 3z \).
|
5
| 0.25 |
The set of positive even numbers $\{2, 4, 6, \cdots\}$ is grouped in increasing order such that the $n$-th group has $3n-2$ numbers:
\[
\{2\}, \{4, 6, 8, 10\}, \{12, 14, 16, 18, 20, 22, 24\}, \cdots
\]
Determine which group contains the number 2018.
|
27
| 0.75 |
In the Rhind Papyrus (Ancient Egypt), among other information, there are decompositions of fractions into a sum of fractions with numerator 1. For example,
\[
\frac{2}{73} = \frac{1}{60} + \frac{1}{219} + \frac{1}{292} + \frac{1}{x}
\]
One of the denominators is replaced by the letter \( x \). Find this denominator.
|
365
| 0.5 |
What is the exact value of the product $\sin 10^{\circ} \sin 30^{\circ} \sin 50^{\circ} \sin 70^{\circ}$?
|
\frac{1}{16}
| 0.75 |
Find the range of the function
$$
f(x)=\sqrt{g^{2}(x)-245}, \text { where } g(x)=15-2 \cos 2x-4 \sin x
$$
|
[0, 14]
| 0.375 |
Robinson had 200,000 strands of hair when he ended up on the deserted island. At that time, his hair strands were $5 \mathrm{~cm}$ long. The hair strands grew $0.5 \mathrm{~mm}$ per day, but Robinson did not cut his hair because he did not have the proper tools, and he lost 50 strands of hair each day without replacement.
How many days passed until the total length of the hair strands on Robinson's head reached its maximum?
|
1950
| 0.625 |
In how many ways can the numbers from 1 to 100 be rearranged so that neighboring numbers differ by no more than 1?
|
2
| 0.625 |
What is the smallest positive integer that leaves a remainder of 2 when divided by 5, a remainder of 3 when divided by 7, and a remainder of 4 when divided by 9?
|
157
| 0.75 |
Given \(a, b > 0\), satisfy the equation for \(x\):
\[
\sqrt{|x|} + \sqrt{|x + a|} = b
\]
There are exactly three distinct real solutions \(x_1, x_2, x_3\), where \(x_1 < x_2 < x_3 = b\). Find the value of \(a + b\).
|
144
| 0.5 |
Determine all pairs of positive integers \((a, n)\) such that
$$
3^{n} = a^{2} - 16
$$
|
(5, 2)
| 0.75 |
a) Show that for any \(a \in \mathbb{N}\), the equation \(x^{2} + y^{2} + z^{2} = 8a + 7\) has no solutions in \(\mathbb{Q}^{3}\).
b) Find all natural numbers \(n\) such that \(7^{n} + 8\) is a perfect square.
|
0
| 0.125 |
Find all integers \( x, y \geq 1 \) such that \( 7^x = 3^y + 4 \).
|
(1, 1)
| 0.625 |
The area of an isosceles trapezoid circumscribed around a circle is $S$. Determine the radius of this circle if the angle at the base of the trapezoid is $30^{\circ}$.
|
\frac{\sqrt{2S}}{4}
| 0.75 |
In the figure below, triangle \( \triangle ABC \) is right-angled at \( C \), and both \( BCDE \) and \( CAFG \) are squares. If the product of the areas of triangles \( EAB \) and \( BFA \) is 64, determine the area of triangle \( \triangle ABC \).
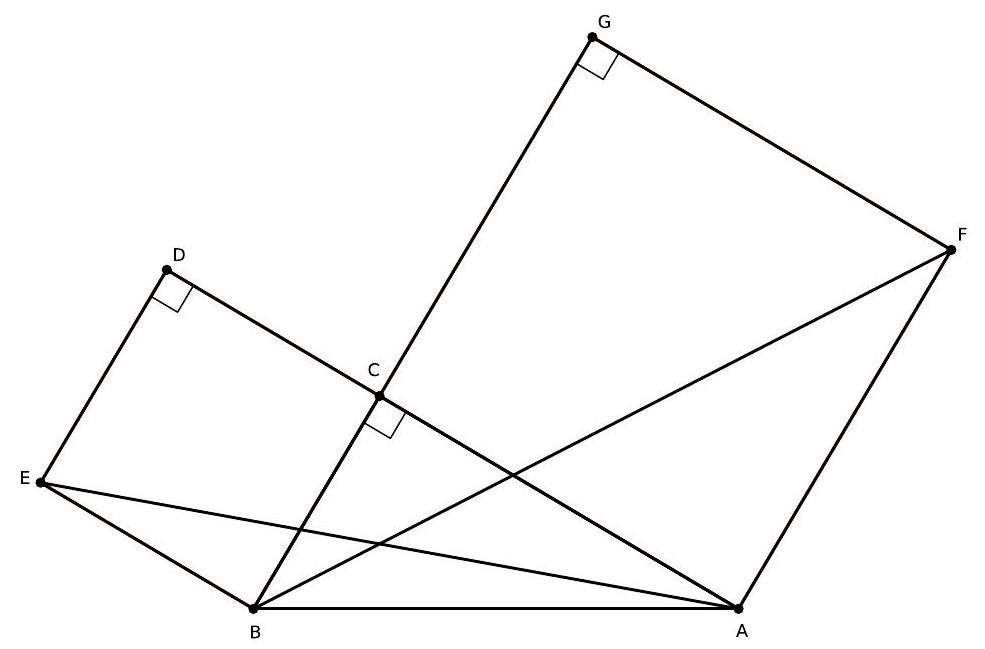
|
8
| 0.375 |
The focus of the parabola \( y^{2} = 2px \) (with \( p > 0 \)) is \( F \), and the directrix is \( l \). Points \( A \) and \( B \) are points on the parabola such that \( \angle AFB = \frac{\pi}{3} \). Let \( M \) be the midpoint of the line segment \( AB \), and let \( N \) be the projection of \( M \) onto \( l \). What is the maximum value of \( \frac{|MN|}{|AB|} \)?
|
1
| 0.125 |
How many 100-digit natural numbers are there, each digit of which is even and the difference between any two adjacent digits is $2$?
|
7 \cdot 3^{49}
| 0.25 |
Vasya added the same natural number, which is less than both the numerator and the denominator, to the numerator and the denominator of a proper fraction. As a result, the fraction increased by more than 50%. Vasya claims that if he subtracts this number from the numerator and the denominator of the original fraction, the fraction will decrease by less than 50%. Is this possible?
|
\text{No}
| 0.875 |
Given a function \( f: \mathbf{N}^{*} \rightarrow \mathbf{N}^{*} \) satisfying \( f(f(m) + f(n)) = m + n \) for all \( m, n \in \mathbf{N}^{*} \), find \( f(2005) \).
|
2005
| 0.75 |
Find the smallest positive real t such that
\[ x_1 + x_3 = 2tx_2, \]
\[ x_2 + x_4 = 2tx_3, \]
\[ x_3 + x_5 = 2tx_4 \]
has a solution \( x_1, x_2, x_3, x_4, x_5 \) in non-negative reals, not all zero.
|
\frac{1}{\sqrt{2}}
| 0.125 |
In the quadrilateral \(ABCD\), it is known that \(AB = BD\), \(\angle ABD = \angle DBC\), and \(\angle BCD = 90^\circ\). On the segment \(BC\), there is a point \(E\) such that \(AD = DE\). What is the length of segment \(BD\) if it is known that \(BE = 7\) and \(EC = 5\)?
|
17
| 0.25 |
\[
\left(\sqrt[3]{\frac{8 z^{3}+24 z^{2}+18 z}{2 z-3}}-\sqrt[3]{\frac{8 z^{2}-24 z^{2}+18 z}{2 z+3}}\right)-\left(\frac{1}{2} \sqrt[3]{\frac{2 z}{27}-\frac{1}{6 z}}\right)^{-1}
\]
|
0
| 0.25 |
In trapezoid \(A B C D\), the bases \(A D\) and \(B C\) are 8 and 18, respectively. It is known that the circumscribed circle of triangle \(A B D\) is tangent to lines \(B C\) and \(C D\). Find the perimeter of the trapezoid.
|
56
| 0.125 |
If a class of 30 students is seated in a movie theater, then in any case at least two classmates will be in the same row. If the same is done with a class of 26 students, then at least three rows will be empty. How many rows are in the theater?
|
29
| 0.875 |
Suppose that \(\log _{a} 125 = \log _{5} 3\) and \(\log _{b} 16 = \log _{4} 7\). Find the value of \(a^{\left(\log _{5} 3\right)^{2}} - b^{\left(\log _{4} 7\right)^{2}}\).
|
-22
| 0.875 |
What is the maximum number of \(4 \times 1\) rectangles that can be placed inside a \(6 \times 6\) square (without breaking cell boundaries)?
|
8
| 0.25 |
Let \(a, b, c\) be three distinct real numbers, and let \(p(x)\) be a polynomial with real coefficients. Given that:
1. The remainder when \(p(x)\) is divided by \(x - a\) is \(a\).
2. The remainder when \(p(x)\) is divided by \(x - b\) is \(b\).
3. The remainder when \(p(x)\) is divided by \(x - c\) is \(c\).
Find the remainder when \(p(x)\) is divided by \((x - a)(x - b)(x - c)\). (Problem from the 1990 Italian competition)
|
x
| 0.75 |
Define \( a \star = \frac{a-1}{a+1} \) for \( a \neq -1 \). Determine all real values \( N \) for which \( (N \star) \star = \tan 15^\circ \).
|
-2 - \sqrt{3}
| 0.5 |
Let \( a, b \), and \( c \) be complex numbers such that \( |a|=|b|=|c|=1 \). If
\[ \frac{a^{2}}{b c}+\frac{b^{2}}{c a}+\frac{c^{2}}{a b}=1 \]
as well, determine the product of all possible values of \( |a+b+c| \).
|
2
| 0.25 |
Let $ABCD$ be a convex quadrilateral, with $E$ on $[AB]$ and $F$ on $[CD]$. Assume $AE = BE = CF = DF = EF$. The diagonals of $BCFE$ intersect at $K$ and those of $ADFE$ at $L$. The perpendicular to $[AD]$ passing through $K$ and the perpendicular to $[BC]$ passing through $L$ intersect at $T$.
Show that $TE = TF$.
|
TE = TF
| 0.875 |
Due to the reconstruction of equipment, a worker's productivity increased twice during the year by the same percentage each time. By what percentage did the worker's productivity increase each time if, in the same amount of time, the worker used to produce goods worth 2500 rubles, and now produces goods worth 2809 rubles?
|
6 \%
| 0.875 |
Given that \( n \) is a positive integer, \( P \) is a prime number, and \( pn \) has exactly 8 positive divisors, arrange them in ascending order as \( 1=d_{1}<d_{2}< \cdots <d_{8}=pn \). Additionally, let \( d_{17p-d_{3}}=\left(d_{1}+d_{2}+d_{3}\right)\left(d_{3}+d_{4}+13p\right) \). Find \( n \).
|
2021
| 0.625 |
In triangle \(ABC\), lines parallel to the sides of the triangle are drawn through an arbitrary point \(O\). As a result, triangle \(ABC\) is divided into three parallelograms and three triangles. The areas of the resulting triangles are \(6 \, \text{cm}^2\), \(24 \, \text{cm}^2\), and \(54 \, \text{cm}^2\). Find the area of triangle \(ABC\).
|
216
| 0.75 |
Find all positive integers \( n \) for which all positive divisors of \( n \) can be put into the cells of a rectangular table under the following constraints:
- each cell contains a distinct divisor;
- the sums of all rows are equal; and
- the sums of all columns are equal.
|
1
| 0.625 |
Let the sequence $\left\{a_{n}\right\}$ be defined as $a_{n}=(2 n-1)(2 n+1)(2 n+3)$. Determine the greatest common divisor $d$ of the terms $a_{1}, a_{2}, \cdots, a_{2008}$.
|
3
| 0.375 |
In triangle \( ABC \), angle \( B \) is \( 80^\circ \). On side \( BC \), point \( D \) is marked such that \( AB = AD = CD \). On side \( AB \), point \( F \) is marked such that \( AF = BD \). On segment \( AC \), point \( E \) is marked such that \( AB = AE \). Find angle \( AEF \).
|
20^\circ
| 0.125 |
Vasya has three cans of paint of different colors. In how many different ways can he paint a fence of 10 boards such that any two adjacent boards are of different colors, and all three colors are used?
|
1530
| 0.75 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.