code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
```
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
import seaborn as sns
austin_311_df = pd.read_csv("Final_City_Comparison_Datasets/Final_City_Comparison_Datasets/Austin_TX_311.csv")
WA_311_df = pd.read_csv("Final_City_Comparison_Datasets/Final_City_Comparison_Datasets/Washington_DC_311_2021_2022.csv")
NYC_311_df = pd.read_csv("Final_City_Comparison_Datasets/Final_City_Comparison_Datasets/New_York_NY_311.csv")
austin_311_df.head(100)
WA_311_df.head(100)
NYC_311_df.head(100)
austin_311_df['SR Description'].unique()
WA_311_df['SERVICECODEDESC'].unique()
NYC_311_df['Complaint Type'].unique()
traffic_issues = ['Pothole Repair', 'Austin Code - Signs/Billboards', 'Sign - Traffic Sign Emergency', 'Traffic Signal - Maintenance', 'Traffic Signal - Dig Tess Request', 'Lane/Road Closure Notification', 'Debris in Street', 'Traffic Calming', 'Traffic Signal - New/Change', 'Street Light Issue- Address', 'Sign - New', 'Street Lights New',
'Sign - Traffic Sign Maintenance', 'Speed Management', 'Speed Limit - Changes/Signs', 'Street Light Issue- Multiple poles/multiple streets', 'Traffic Engineering - Jurisdiction Issue']
traffic_issues_WA = ['Streetlight Repair Investigation', 'Roadway Signs', 'Pothole', 'Traffic Signal Issue', 'Roadway Striping / Markings', 'Roadway Repair', 'How Is My Driving - Complaint', 'Traffic Safety Investigation', 'DMV - Drivers License/ID Reinstatement', 'Snow/Ice Removal (Roadways AND Bridge walkways ONLY)', 'Snow Removal Complaints for Sidewalks', 'Snow Other (Snow Vehicle / Property Damage)', 'Snow Towing', 'How Is My Driving - Compliment']
traffic_issues_NYC = ['Traffic Signal Condition', 'Highway Condition', 'Street Sign - Dangling', 'Traffic', 'Highway Sign - Damaged', 'Highway Sign - Missing', 'Snow Removal', 'DEP Bridge Condition']
austin_traffic = austin_311_df[austin_311_df['SR Description'].isin(traffic_issues)]
WA_traffic = WA_311_df[WA_311_df['SERVICECODEDESC'].isin(traffic_issues_WA)]
NYC_traffic = NYC_311_df[NYC_311_df['Complaint Type'].isin(traffic_issues_NYC)]
fig = px.histogram(austin_traffic, x="SR Description")
fig.update_layout(
title="311 Calls - Frequency of Traffic Related Issues - Austin, TX",
xaxis_title="Issues Related to Traffic",
yaxis_title="Frequency",
font=dict(
size=12,
color="RebeccaPurple"
)
)
fig.show()
fig = px.histogram(WA_traffic, x="SERVICECODEDESC")
fig.update_layout(
title="311 Calls - Frequency of Traffic Related Issues - Washington, DC",
xaxis_title="Issues Related to Traffic",
yaxis_title="Frequency",
font=dict(
size=12,
color="RebeccaPurple"
)
)
fig.show()
fig = px.histogram(NYC_traffic, x="Complaint Type")
fig.update_layout(
title="311 Calls - Frequency of Traffic Related Issues - New York, NY",
xaxis_title="Issues Related to Traffic",
yaxis_title="Frequency",
font=dict(
size=12,
color="RebeccaPurple"
)
)
fig.show()
len_traffic_Issues_AU = len(austin_traffic)
len_traffic_Issues_WA = len(WA_traffic)
len_traffic_Issues_NYC = len(NYC_traffic)
len_AU = len(austin_311_df)
len_WA = len(WA_311_df)
len_NYC = len(NYC_311_df)
d = {'City': ["Austin, TX", "Washington, DC", "New York, NY"], 'Traffic Issues': [len_traffic_Issues_AU, len_traffic_Issues_WA, len_traffic_Issues_NYC], 'Total Length': [len_AU, len_WA, len_NYC], 'Non-traffic Length': [len_AU - len_traffic_Issues_AU, len_WA - len_traffic_Issues_WA, len_NYC - len_traffic_Issues_NYC]}
Traffic_data = pd.DataFrame(data=d)
Traffic_data
import plotly.graph_objects as go
city=Traffic_data['City']
fig = go.Figure(data=[
go.Bar(name='Traffic Issues', x=city, y=Traffic_data["Traffic Issues"]),
go.Bar(name='Other Issues', x=city, y=Traffic_data["Non-traffic Length"])
])
# Change the bar mode
fig.update_layout(barmode='group')
fig.update_layout(
title="Frequency of Traffic Related Issues vs Other Issues",
xaxis_title="City",
yaxis_title="Frequency",
font=dict(
size=12,
color="RebeccaPurple"
)
)
fig.show()
#Clean Data
NYC_311_df = NYC_311_df[["Unique Key", "Complaint Type", "Borough"]]
NYC_311_df = NYC_311_df.dropna(axis = 0)
# TODO: Filter Data based on Complaint Type
# Plot
sns.set(rc = {'figure.figsize':(15,8)})
plot = sns.countplot(x = "Borough", data = NYC_311_df, hue = "Borough", palette = ["red", "blue", "green", "orange", "brown"])
plot.set_xticklabels(plot.get_xticklabels(), size = 10)
plot.set(title = 'Traffic 311 Calls per Burough in NY')
Traffic_data['Non-traffic Length'] / Traffic_data['Total Length']
Traffic_data['Traffic Issues'] / Traffic_data['Total Length']
#Clean Data
NYC_traffic = NYC_traffic[["Unique Key", "Complaint Type", "Borough"]]
NYC_traffic = NYC_traffic.dropna(axis = 0)
NYC_traffic = NYC_traffic.sort_values(axis = 0, by = "Borough")
# TODO: Filter Data based on Complaint Type
# Plot
sns.set(rc = {'figure.figsize':(15,8)})
sns.set(font_scale = 1)
plot = sns.countplot(x = "Borough", data = NYC_traffic, hue = "Borough", palette = ["red", "blue", "black", "orange", "brown", "black"])plot.set_xticklabels(plot.get_xticklabels())
plot.set(title = 'Traffic 311 Calls per Burough in NY')
```
|
github_jupyter
|
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
import seaborn as sns
austin_311_df = pd.read_csv("Final_City_Comparison_Datasets/Final_City_Comparison_Datasets/Austin_TX_311.csv")
WA_311_df = pd.read_csv("Final_City_Comparison_Datasets/Final_City_Comparison_Datasets/Washington_DC_311_2021_2022.csv")
NYC_311_df = pd.read_csv("Final_City_Comparison_Datasets/Final_City_Comparison_Datasets/New_York_NY_311.csv")
austin_311_df.head(100)
WA_311_df.head(100)
NYC_311_df.head(100)
austin_311_df['SR Description'].unique()
WA_311_df['SERVICECODEDESC'].unique()
NYC_311_df['Complaint Type'].unique()
traffic_issues = ['Pothole Repair', 'Austin Code - Signs/Billboards', 'Sign - Traffic Sign Emergency', 'Traffic Signal - Maintenance', 'Traffic Signal - Dig Tess Request', 'Lane/Road Closure Notification', 'Debris in Street', 'Traffic Calming', 'Traffic Signal - New/Change', 'Street Light Issue- Address', 'Sign - New', 'Street Lights New',
'Sign - Traffic Sign Maintenance', 'Speed Management', 'Speed Limit - Changes/Signs', 'Street Light Issue- Multiple poles/multiple streets', 'Traffic Engineering - Jurisdiction Issue']
traffic_issues_WA = ['Streetlight Repair Investigation', 'Roadway Signs', 'Pothole', 'Traffic Signal Issue', 'Roadway Striping / Markings', 'Roadway Repair', 'How Is My Driving - Complaint', 'Traffic Safety Investigation', 'DMV - Drivers License/ID Reinstatement', 'Snow/Ice Removal (Roadways AND Bridge walkways ONLY)', 'Snow Removal Complaints for Sidewalks', 'Snow Other (Snow Vehicle / Property Damage)', 'Snow Towing', 'How Is My Driving - Compliment']
traffic_issues_NYC = ['Traffic Signal Condition', 'Highway Condition', 'Street Sign - Dangling', 'Traffic', 'Highway Sign - Damaged', 'Highway Sign - Missing', 'Snow Removal', 'DEP Bridge Condition']
austin_traffic = austin_311_df[austin_311_df['SR Description'].isin(traffic_issues)]
WA_traffic = WA_311_df[WA_311_df['SERVICECODEDESC'].isin(traffic_issues_WA)]
NYC_traffic = NYC_311_df[NYC_311_df['Complaint Type'].isin(traffic_issues_NYC)]
fig = px.histogram(austin_traffic, x="SR Description")
fig.update_layout(
title="311 Calls - Frequency of Traffic Related Issues - Austin, TX",
xaxis_title="Issues Related to Traffic",
yaxis_title="Frequency",
font=dict(
size=12,
color="RebeccaPurple"
)
)
fig.show()
fig = px.histogram(WA_traffic, x="SERVICECODEDESC")
fig.update_layout(
title="311 Calls - Frequency of Traffic Related Issues - Washington, DC",
xaxis_title="Issues Related to Traffic",
yaxis_title="Frequency",
font=dict(
size=12,
color="RebeccaPurple"
)
)
fig.show()
fig = px.histogram(NYC_traffic, x="Complaint Type")
fig.update_layout(
title="311 Calls - Frequency of Traffic Related Issues - New York, NY",
xaxis_title="Issues Related to Traffic",
yaxis_title="Frequency",
font=dict(
size=12,
color="RebeccaPurple"
)
)
fig.show()
len_traffic_Issues_AU = len(austin_traffic)
len_traffic_Issues_WA = len(WA_traffic)
len_traffic_Issues_NYC = len(NYC_traffic)
len_AU = len(austin_311_df)
len_WA = len(WA_311_df)
len_NYC = len(NYC_311_df)
d = {'City': ["Austin, TX", "Washington, DC", "New York, NY"], 'Traffic Issues': [len_traffic_Issues_AU, len_traffic_Issues_WA, len_traffic_Issues_NYC], 'Total Length': [len_AU, len_WA, len_NYC], 'Non-traffic Length': [len_AU - len_traffic_Issues_AU, len_WA - len_traffic_Issues_WA, len_NYC - len_traffic_Issues_NYC]}
Traffic_data = pd.DataFrame(data=d)
Traffic_data
import plotly.graph_objects as go
city=Traffic_data['City']
fig = go.Figure(data=[
go.Bar(name='Traffic Issues', x=city, y=Traffic_data["Traffic Issues"]),
go.Bar(name='Other Issues', x=city, y=Traffic_data["Non-traffic Length"])
])
# Change the bar mode
fig.update_layout(barmode='group')
fig.update_layout(
title="Frequency of Traffic Related Issues vs Other Issues",
xaxis_title="City",
yaxis_title="Frequency",
font=dict(
size=12,
color="RebeccaPurple"
)
)
fig.show()
#Clean Data
NYC_311_df = NYC_311_df[["Unique Key", "Complaint Type", "Borough"]]
NYC_311_df = NYC_311_df.dropna(axis = 0)
# TODO: Filter Data based on Complaint Type
# Plot
sns.set(rc = {'figure.figsize':(15,8)})
plot = sns.countplot(x = "Borough", data = NYC_311_df, hue = "Borough", palette = ["red", "blue", "green", "orange", "brown"])
plot.set_xticklabels(plot.get_xticklabels(), size = 10)
plot.set(title = 'Traffic 311 Calls per Burough in NY')
Traffic_data['Non-traffic Length'] / Traffic_data['Total Length']
Traffic_data['Traffic Issues'] / Traffic_data['Total Length']
#Clean Data
NYC_traffic = NYC_traffic[["Unique Key", "Complaint Type", "Borough"]]
NYC_traffic = NYC_traffic.dropna(axis = 0)
NYC_traffic = NYC_traffic.sort_values(axis = 0, by = "Borough")
# TODO: Filter Data based on Complaint Type
# Plot
sns.set(rc = {'figure.figsize':(15,8)})
sns.set(font_scale = 1)
plot = sns.countplot(x = "Borough", data = NYC_traffic, hue = "Borough", palette = ["red", "blue", "black", "orange", "brown", "black"])plot.set_xticklabels(plot.get_xticklabels())
plot.set(title = 'Traffic 311 Calls per Burough in NY')
| 0.462473 | 0.23131 |
# **G.G.: Good Game?**
## **Introduction**
In the modern age, video games have become a modern past time enjoyed by many people of various ages. A now lucrative industry, video games come in a variety of genres, experiences, and platforms. When asked about successful video games, a handful of titles might come to mind. Ones that are iconic because of their characters, revolutionary because of the way they engage with storytelling, or perhaps nostalgic because of how long they have been around.
This project seeks to define top performing video games and the traits that may have contributed to the success of these titles. Subsequently, I would like to conduct a more qualitative investigation on these titles, mainly examining reviews to paint a clearer picture of what consumers like about top games.
## **The Data**
Initial exploration of defining what makes a good game will be conducted using the Video Games CORGIS dataset which can be accessed [here.](https://corgis-edu.github.io/corgis/python/video_games/) This data was originally collected by Dr. Joe Cox who conducted an empirical investigation of U.S. sales data of video games. Dr. Cox concluded that the major factors that predict for a title's ability to attain "blockbuster" status were threefold: the company that produced the title, the console, and the critic reviews.
I would like to use the data that Dr. Cox collected, which spans thousands of titles that were released between 2004 and 2010, and conduct my own analysis agnostic to his fidnings.
The categoies that I am interested in and their possible effects on the success of a game are:
1. Maximum number of players: how many people can play this game at one time?
2. Online Features: does the game support online play?
3. Genre: what genre does this game belong to?
Within these categories, I would like to measure success of a game using:
1. Review score: the typical review score out of 100
2. Sales: the total sales made on the game measured in millions of dollars
3. Completionist: players reported completing everything in the game
## **Data Exploration**
```
#hide
import pandas as pd
import seaborn as sns
#hide
import video_games
#hide
video_game = video_games.get_video_game()
#hide
df = pd.read_csv('video_games.csv')
#hide-input
df.head()
```
### 1. What are the top games by critic reviews?
```
#hide-input
df[['Title','Metrics.Review Score']].sort_values('Metrics.Review Score', ascending = False )
```
### 2. What are the top games by sales?
```
#hide-input
df[['Title', 'Metrics.Sales']].sort_values('Metrics.Sales', ascending = False)
```
### 3. What games have the most number of people who report completing the game?
* will be skewed based on how many people played the game
```
#hide-input
df[['Title', 'Length.Completionists.Polled']].sort_values ('Length.Completionists.Polled', ascending = False)
```
### 4. What genre of game was popular on the market during this time period (2004-2010)?
```
#collapse-output
df['Metadata.Genres'].value_counts()
```
### I would like to take the "top games" from questions 1-3 and get a closer look at these titles, since they are considered "top performing" in their respective categories.
```
#collapse-output
df.iloc[837]
#collapse-output
df.iloc[156]
#collapse-output
df.iloc[442]
#hide-input
df.iloc[[837,156,442]]
```
Observed similarities and differences:
1. Action as one of the genres, though none fall exclusively into action only.
2. All 3 were a sequel of some kind, and based off of a previously licensed entity.
3. Max players do not go above 2, two of the three games are only single-player.
4. All games came from different publishers.
5. All released for different consoles.
Because I am interested in the intersection of video games and pedagogy, I wanted to see the games that were considered "Educational."
* These were only the titles exclusively listed as 'Educational' as the genre
```
#hide-input
df[df['Metadata.Genres'] == 'Educational']
#collapse-output
df.iloc[549]
#collapse-output
df.iloc[1000]
```
Takeaways from initial data exploration:
1. Because of the saturation of Action games, I would like to take a closer look at the metrics for success in that specific genre, as well as the other genres that are well-represented in the market.
2. Because the games that were successful in these categories were all sequels of some kind, I think it would be interested to investigate if there are any titles that were successful without being a sequel, which would speak to the degree to which a factor like nostalgia or investment in a story/ universe contribute to a title's success.
3. Because these three games did not have a max player capacity above 2, are there any titles that support multiplayer that are also finding success?
4. Are there certain publishers or consoles that are finding more general success with their titles than others?
## **Further Exploration**
Based on the preliminary findings from my first data exploration, I would like to take a closer look at the data in certain places.
### Defining Success
Using the metrics I established previously, I would like to examine the top-performing games in the categories of critic reviews, sales, and number of completionists.
### 1. Critic Reviews
```
#hide
df_reviews = df[['Title','Metrics.Review Score']]
#hide
df_reviews_top = df_reviews[df_reviews['Metrics.Review Score'] > 90].sort_values('Metrics.Review Score', ascending = False)
#hide
df_reviews_top.index
#hide
df2 = df.iloc[df_reviews_top.index]
#hide-input
sns.regplot(x = df2['Metrics.Review Score'], y = df2['Metrics.Sales'])
```
Here, a sucessful game by critic review was defined as having a critic review score of over 90, of which there were 29 games. It does not seem to be the case, however, that a high critic score correlates very strongly to commercial success in sales. In fact, the games that received the highest critic scores were not the ones which had the most number of sales, with a handfull of games receiving more commercial sucess, and the highest seller (in this group) having the lowest critics score...
```
#hide-input
sns.regplot(x = df2['Metrics.Review Score'], y = df2['Length.Completionists.Polled'])
```
I observed an even weaker relationship between critic review scores and number of completionists in for the games.
This could however be because the games which received the highest critic review scores, such as Grand Theft Auto IV, are known for being "open-world" games in which the player can freely navigate the world without the story being a main part of interacting with the game.
```
#collapse-output
df2[['Title', 'Metrics.Review Score', 'Metrics.Sales', 'Length.Completionists.Polled', 'Metadata.Genres']].sort_values('Metrics.Sales', ascending = False)
```
Notably, 27 out of the 29 titles that were considered top-performers as described by their critic review scores had Action as one of their genre descriptors. The two games that did not belong to this genre were considered as Role-Playing and Racing/ Driving games.
### 2. Commercial Sales
```
#hide
df_sales = df[['Title', 'Metrics.Sales']]
#hide
df['Metrics.Sales'].mean
#hide
df_sales_top = df_sales[df_sales['Metrics.Sales'] > 4.69]
#hide
len(df_sales_top.index)
#hide
df3 = df.iloc[df_sales_top.index]
#hide-input
sns.regplot(x = df3['Metrics.Sales'], y =df3['Metrics.Review Score'] )
```
Very interestingly, for the top-performing games in terms if sales, being 14 games, there was actually a negative correlation between sales and critic scores. Shockingly, the game with the most sales had the lowest (sub-60) score of the group of games! However, the games with the highest critic scores in this set still had sales that were above the mean of the entire set, so these games were by no means unsuccessful.
```
#hide-input
sns.regplot(x = df3['Metrics.Sales'], y =df3['Length.Completionists.Polled'])
```
A similar negative relationship was observed between sales and number of completionist players. For similar reasons as the to critic scores grouping, the top game, Wii Play, is not a game that is well-known for having a definitive plot that players follow, but rather is a game that is often played socially with family and friends.
```
#hide-input
df3[['Title', 'Metrics.Review Score', 'Metrics.Sales', 'Length.Completionists.Polled', 'Metadata.Genres']].sort_values('Metrics.Sales', ascending = False)
```
The distribution of genres in this group were slightly more diverse than that of the critic scores group. While Action games still held a slight majority at 8 out 14 games being part of the Action genre, Role-Playing, sports, and Driving games made up the remainder of this group.
### 3. Completionists (or not?)
Following my analysis of the top-performing games under critic scores and commercial sales, I have decided not to continue with using number of completionists as a measure of success for a variety of reasons. Firstly, this number would already be skewed because of how the number of players would affect this figure, and completionist data as such would require standardization. While the additional work of standardizing this data is not very much work, I also chose not to use number of completionists in the remainder of my analysis because of how easily this number could be affected by the type of game. There are many games that are made simply to be enjoyed, and do not have the aspect of following a story or plot that other games have. In the former case, players would not be as motivated to "complete" the game, which would skew how the number of com
### Action Games and Reviews?
Because of the overrepresentation of Action games in the games with high critic reviews, I wanted to explore the idea that critics tend to favor games that are of the Action genre.
```
#hide
df_action = df[df['Metadata.Genres'] == 'Action']
#collapse-output
df_action['Metrics.Review Score'].mean
#hide
df_sports = df[df['Metadata.Genres'] == 'Sports']
#collapse-output
df_sports['Metrics.Review Score'].mean
#hide
df_strategy = df[df['Metadata.Genres'] == 'Strategy']
#collapse-output
df_strategy['Metrics.Review Score'].mean
```
Looking at the 3 most common genres and examining the mean critic review scores, it seems that there does not seem to be an inherent bias for Action games amonst critics, since strategy games had a higher mean score, though I think this is one area of analysis that could benefit from more investigation.
## **Who's at the Top?**
From both my own personal perspective, as well as how I assume businesses and consumers would define success, I think commerical sales is the best way to mesure the success of a game. However, because I think critic reviews may encapsulate some measure of the quality of a game, I think it would be beneficial to include critics reviews as a measure of success in some way. Therefore, I decided that when choosing the "top games," I would choose those games that were present in both categories or top-performers in critic scores and sales. That is, games that received both above a 90 on critic scores and had sales above 4.69.
To account for any phenomenon that goes beyond any conventional measure of success I would like to include those titles that had extremely high sales, but perhaps were not deemed a "good game" by critics. These three games would be: Wii Play, Mario Kart Wii, and New Super Mario Bros, all titles that had commericial sales greater that 10 million dollars.
```
#hide
top_reviews = df2['Title'].tolist()
top_sales = df3['Title'].tolist()
#collapse-output
top_sales
#collapse-output
top_reviews
#collapse-output
print(set(top_sales).intersection(set(top_reviews)))
#hide
top_games = set(top_sales).intersection(set(top_reviews))
#hide
top_games_dict = {'Grand Theft Auto IV' : 837,
'Mario Kart DS' : 22,
'Halo 3' : 420,
'Call of Duty 4: Modern Warfare' : 421,
'Super Mario Galaxy' : 422,
'Super Smash Bros.: Brawl' : 835
}
#hide
target_indices = [837, 22, 420, 421, 422, 835, 156, 833, 157]
top_games = df.iloc[target_indices]
#hide
top_games = top_games[['Title', 'Metrics.Review Score', 'Metrics.Sales', 'Metadata.Genres', 'Metadata.Sequel?', 'Metadata.Publishers', 'Features.Max Players', 'Release.Console', 'Release.Year']]
#hide-input
top_games.sort_values('Metrics.Sales', ascending = False)
#hide-input
sns.countplot(x = top_games['Metadata.Genres'], palette = 'ch:.25')
#hide-input
sns.countplot(x = top_games['Metadata.Publishers'], palette = 'ch:.25')
#hide-input
sns.countplot(x = top_games['Features.Max Players'], palette = 'ch:.25')
#hide-input
sns.countplot(x = top_games['Release.Console'], palette = 'ch:.25')
```
## **Discussion**
Examining the commonalities among the top performing games, it is clear that Nintendo games have the highest sales. They make up 6 of the 9 games that I identified as top-performing games, and represent the 6 highest-earning games in the entire dataset. This seems to operate independently of critic reviews, as the three highest selling games did not receive scores above 90 from critics.
I think that there are factors, especially metadata about each game beyond the scope of information that was included in this dataset, that contributes to why games from Nintendo, and especially those that came out at the top of this dataset were considered top-performers by sales.
Three of the top four games- Wii Play, Mario Kart Wii, and Mario Kart DS- are titles that do not have a strong storyline for the player to follow. Rather, they are multiplayer games that are centered around gaming as a social aspect. With family or friends, players can compete on teams with or against each other. Because you are constantly playing with real people in a competitive environment, the gaming experience is kept dynamic and engaging, rather then relying on a progressing in a story line.
When considering what kinds of games are successful in the market, it may be helpful to consider whether a game is player-versus-player (PVP) or player-vs-everyone (PVE). Wii Play, Mario Kart Wii, and Mario Kart DS, are examples of PVP games, that is, players do not play by the themselves against computers, but rather against other real players, and these kinds of games inherently carry with them a competitive aspect. In terms of motivation, players are motivated to constantly return to the game in order to hone their skills in the game. In many PVE games, players are instead motivated by the desire to progress in the game itself.
The other game that was represented in the top-performing game, despite not having the same PVP quality as the others, was New Super Mario Bros. I think the reason that this title in particular was so successful is because of its recognisability. Just the name Mario in the gaming sphere is already enough for people, gamer or not, to have a mental image of what the game will entail. As a game that has had many remakes and interations, I think that this game's successful largely comes from its capacity to combine the nostalgia of players with the refreshing nature of a game remake or sequel. A game beloved by many, the Super Mario series of games is one that people are invested in because of their emotional attatchment to the games and characters.
When it comes to learning, motivation is a crucial part of pedagogy. In both the conventional sense and in the realm of possibly gamifying learning, I think that it would be helpful to incoroporate a healthy amount of competition, whether it be against the self or against others. I think it is also important for students to have the ability to engage with other students as well, as this social aspect to learning and gaming is something that motivates students additionally.
## **Nintendo: A Closer Look**
Looking at the top-performing games, it is clear to see that Nintendo has a clear group on the gaming market when it comes to sales. As such, I would like to examine just what about these games makes them so desirable to players, and as such I would like to look to Nintendo themselves to see how they would market and describe these games.
```
#hide
from wordcloud import WordCloud, ImageColorGenerator
from PIL import Image
import matplotlib.pyplot as plt
#hide
myStopWords = list(punctuation) + stopwords.words('english')
#hide
super_mario_describe = '''
Bowser has taken over the Mushroom Kingdom, and it's up to Mario to put an end to his sinister reign! Battle Bowser's vile henchmen through 32 levels in the Original 1985 game mode. Move on to collecting special Red Coins and Yoshi Eggs in Challenge mode. Then, try to unlock a secret mode that's waiting to be found by super players like you! Every mode will give you the chance to beat your own score, and there's a lot more to do than just saving a princess. So get ready for a brick-smashin', pipe-warpin', turtle-stompin' good time!
Mario™ and Luigi™ star in their first ever Mushroom Kingdom adventure! Find out why Super Mario Bros. is instantly recognizable to millions of people across the globe, and what made it the best-selling game in the world for three decades straight. Jump over obstacles, grab coins, kick shells, and throw fireballs through eight action-packed worlds in this iconic NES classic. Only you and the Mario Bros. can rescue Princess Toadstool from the clutches of the evil Bowser.
Pick up items and throw them at your adversaries to clear levels in seven fantastical worlds. Even enemies can be picked up and tossed across the screen. Each character has a unique set of abilities: Luigi can jump higher and farther than any of the other characters, Toad can dig extremely fast and pull items out of the ground quicker than anyone, and the princess is the only one who can jump and hover temporarily. This unique installment in the Mario series will keep you coming back for more!
Relive the classic that brought renowned power-ups such as the Tanooki Suit to the world of Super Mario Bros.!
Bowser™ and the Koopalings are causing chaos yet again, but this time they’re going beyond the Mushroom Kingdom into the seven worlds that neighbor it. Now Mario™ and Luigi™ must battle a variety of enemies, including a Koopaling in each unique and distinctive world, on their way to ultimately taking on Bowser himself. Lucky for the brothers, they have more power-ups available than ever before. Fly above the action using the Super Leaf, swim faster by donning the Frog Suit, or defeat enemies using the Hammer Bros. Suit. Use the brand-new overworld map to take the chance to play a minigame in hopes of gaining extra lives or to find a Toad’s House where you can pick up additional items. All this (and more) combines into one of gaming’s most well-known and beloved titles—are you ready to experience gaming bliss?
'''
#hide-input
wc = WordCloud().generate_from_text(super_mario_describe)
#Use matplotlib.pyplot to display the fitted wordcloud
#Turn axis off to get rid of axis numbers
plt.imshow(wc)
plt.axis('off')
plt.show()
#hide
mario_kart_describe = '''
Select one of eight characters from the Mario™ series—offering a variety of driving styles—and take on three championship cups in three different kart classes. Win enough, and you'll unlock a fourth circuit: the ultra-tough Special Cup. Crossing the finish line in first place isn't an easy task, though, as each track has unique obstacles to conquer and racers can obtain special power-ups that boost them to victory. With more than 15 tracks to master and nearly endless replay value, Super Mario Kart is classic gaming…with some banana peels thrown in for good measure!
The newest installment of the fan-favorite Mario Kart™ franchise brings Mushroom Kingdom racing fun into glorious 3D. For the first time, drivers explore new competitive kart possibilities, such as soaring through the skies or plunging into the depths of the sea. New courses, strategic new abilities and customizable karts bring the racing excitement to new heights.
FEATURES:
The Mario Kart franchise continues to evolve. New kart abilities add to the wild fun that the games are known for. On big jumps, a kart deploys a wing to let it glide over the track shortcut. When underwater, a propeller pops out to help the kart cruise across the sea floor.
Players can show their own style by customizing their vehicles with accessories that give them a competitive advantage. For instance, giant tires help a kart drive off-road, while smaller tires accelerate quickly on paved courses.
People can choose to race as one of their favorite Mushroom Kingdom characters or even as their Mii™ character.
New courses take players on wild rides over mountains, on city streets and through a dusty desert. Nintendo fans will recognize new courses on Wuhu Island and in the jungles from Donkey Kong Country™ Returns.
The game supports both SpotPass™ and StreetPass™ features.
Players can compete in local wireless matches or online over a broadband Internet connection.
The newest installment of the fan-favorite Mario Kart™ franchise brings Mushroom Kingdom racing fun into glorious 3D. For the first time, drivers explore new competitive kart possibilities, such as soaring through the skies or plunging into the depths of the sea. New courses, strategic new abilities and customizable karts bring the racing excitement to new heights.
FEATURES:
The Mario Kart franchise continues to evolve. New kart abilities add to the wild fun that the games are known for. On big jumps, a kart deploys a wing to let it glide over the track shortcut. When underwater, a propeller pops out to help the kart cruise across the sea floor.
Players can show their own style by customizing their vehicles with accessories that give them a competitive advantage. For instance, giant tires help a kart drive off-road, while smaller tires accelerate quickly on paved courses.
People can choose to race as one of their favorite Mushroom Kingdom characters or even as their Mii™ character.
New courses take players on wild rides over mountains, on city streets and through a dusty desert. Nintendo fans will recognize new courses on Wuhu Island and in the jungles from Donkey Kong Country™ Returns.
The game supports both SpotPass™ and StreetPass™ features.
Players can compete in local wireless matches or online over a broadband Internet connection.
'''
#hide-input
wc2 = WordCloud().generate_from_text(mario_kart_describe)
#Use matplotlib.pyplot to display the fitted wordcloud
#Turn axis off to get rid of axis numbers
plt.imshow(wc2)
plt.axis('off')
plt.show()
#hide
smash_bros_describe = '''
Super Smash Bros. for Nintendo 3DS is the first portable entry in the renowned series, in which game worlds collide. Up to four players battle each other locally or online using some of Nintendo’s most well-known and iconic characters across beautifully designed stages inspired by classic portable Nintendo games. It’s a genuine, massive Super Smash Bros. experience that’s available to play on the go, anytime, anywhere.
FEATURES:
Smash and crash through “Smash Run” mode, a new mode exclusive to the Nintendo 3DS version that gives up to four players five minutes to fight solo through a huge battlefield while taking down recognizable enemies from almost every major Nintendo franchise and multiple third-party partners. Defeated enemies leave behind power-ups to collect. Players who collect more power-ups have an advantage once time runs out and the battle with opponents begins.
Compete with classic characters from the Super Smash Bros. series like Mario, Link, Samus and Pikachu, along with new challengers like Mega Man, Little Mac and newly announced Palutena, the Goddess of Light from the Kid Icarus games. For the first time players can even compete as their own Mii characters.
Customize different aspects of your character when playing locally or online with friends in a variety of multiplayer modes.
View most elements of the high-energy action at silky-smooth 60 frames per second and in eye-popping stereoscopic 3D.
Fight against friends and family locally or online, or battle random challengers all over the world online in “For Fun” or “For Glory” modes.
Gaming icons clash in the ultimate brawl you can play anytime, anywhere! Smash rivals off the stage as new characters Simon Belmont and King K. Rool join Inkling, Ridley, and every fighter in Super Smash Bros. history. Enjoy enhanced speed and combat at new stages based on the Castlevania series, Super Mario Odyssey, and more!
Having trouble choosing a stage? Then select the Stage Morph option to transform one stage into another while battling—a series first! Plus, new echo fighters Dark Samus, Richter Belmont, and Chrom join the battle. Whether you play locally or online, savor the faster combat, new attacks, and new defensive options, like a perfect shield. Jam out to 900 different music compositions and go 1-on-1 with a friend, hold a 4-player free-for-all, kick it up to 8-player battles and more! Feel free to bust out your GameCube controllers—legendary couch competitions await—or play together anytime, anywhere!
'''
#hide-input
wc3 = WordCloud().generate_from_text(smash_bros_describe)
#Use matplotlib.pyplot to display the fitted wordcloud
#Turn axis off to get rid of axis numbers
plt.imshow(wc3)
plt.axis('off')
plt.show()
```
### It's Mario's World and We're Just Playing in It
After creating word clouds from Nintendo's descriptions of its highest selling titles from 2004-2010, there are some recurring themes that we see when Nintendo describes its games to players and potential customers. Words unique to the game, such as "stage," "kart", and "world" are combined with descriptors such as "new," "fun," and "unique," as well as familiar terms such as "Nintendo," "Mario," and "Bowser," to create a sense that the player will be buying into a refreshing, updated, and modernized version of a product that they know and love. I think that much of Nintendo's success in the gaming market comes from the so-called empire that it has created both with its consistency of creating modern versions of its classic titles and capitalizing off of the nostalgia for these titles as well.
For developers that are not Nintendo, I think that it is important to create characters that people will love, and create a universe around these characters, incorporating them into different games and genres. While Mario is one character that definitely become a poster-child for Nintendo, I think that other characters such as Link and Zelda, or the Pokemon franchise in general have also achieved a similar status of recognizability for the company, and would likely be top-performing games in a more modern dataset.
## **Conclusion**
Through conducting this analysis of the video games dataset from CORGIS, I was able to learn a lot about the market in general, and what makes a "successful" game. My findings constrasted my expectations, but I was able to come to conclusions that I believe would be helpful for both game developers, and my own interests in gamifying learning.
In my exploration of both this project, and the course Digital Humanities 140, I learned many Python tools and became more comfortable working with new libraries as well as datasets. Although I used pandas for the majority of my analysis, the two libraries that I found helpful as well were seaborn and wordcloud for data visualization. Seaborn allowed me to combine aesthetic graphical information with statistical information, and wordcloud allowed me to create easy-to-understand visualizations, both of which reminded me of the importance of being able to tell a story with your data.
In the future, it would be fascinating to conduct a similar study with the modern video game market. Nowadays, gaming has been expanded to PC and mobile platforms, which were not represented in the CORGIS dataset. Additionally, many games are now free-to-play, so I think the metrics that are used for success may be a bit different that they were in my investigation. With the rise of e-sports and streaming, gaming is consumed in ways outside of simply playing the game, and has become a form of entertainment that is similar to movies, sporting, and YouTube.
I would like to acknowledge Professor Winjum for his dedication to instruction this quarter, and his continual understanding. Thank you!
|
github_jupyter
|
#hide
import pandas as pd
import seaborn as sns
#hide
import video_games
#hide
video_game = video_games.get_video_game()
#hide
df = pd.read_csv('video_games.csv')
#hide-input
df.head()
#hide-input
df[['Title','Metrics.Review Score']].sort_values('Metrics.Review Score', ascending = False )
#hide-input
df[['Title', 'Metrics.Sales']].sort_values('Metrics.Sales', ascending = False)
#hide-input
df[['Title', 'Length.Completionists.Polled']].sort_values ('Length.Completionists.Polled', ascending = False)
#collapse-output
df['Metadata.Genres'].value_counts()
#collapse-output
df.iloc[837]
#collapse-output
df.iloc[156]
#collapse-output
df.iloc[442]
#hide-input
df.iloc[[837,156,442]]
#hide-input
df[df['Metadata.Genres'] == 'Educational']
#collapse-output
df.iloc[549]
#collapse-output
df.iloc[1000]
#hide
df_reviews = df[['Title','Metrics.Review Score']]
#hide
df_reviews_top = df_reviews[df_reviews['Metrics.Review Score'] > 90].sort_values('Metrics.Review Score', ascending = False)
#hide
df_reviews_top.index
#hide
df2 = df.iloc[df_reviews_top.index]
#hide-input
sns.regplot(x = df2['Metrics.Review Score'], y = df2['Metrics.Sales'])
#hide-input
sns.regplot(x = df2['Metrics.Review Score'], y = df2['Length.Completionists.Polled'])
#collapse-output
df2[['Title', 'Metrics.Review Score', 'Metrics.Sales', 'Length.Completionists.Polled', 'Metadata.Genres']].sort_values('Metrics.Sales', ascending = False)
#hide
df_sales = df[['Title', 'Metrics.Sales']]
#hide
df['Metrics.Sales'].mean
#hide
df_sales_top = df_sales[df_sales['Metrics.Sales'] > 4.69]
#hide
len(df_sales_top.index)
#hide
df3 = df.iloc[df_sales_top.index]
#hide-input
sns.regplot(x = df3['Metrics.Sales'], y =df3['Metrics.Review Score'] )
#hide-input
sns.regplot(x = df3['Metrics.Sales'], y =df3['Length.Completionists.Polled'])
#hide-input
df3[['Title', 'Metrics.Review Score', 'Metrics.Sales', 'Length.Completionists.Polled', 'Metadata.Genres']].sort_values('Metrics.Sales', ascending = False)
#hide
df_action = df[df['Metadata.Genres'] == 'Action']
#collapse-output
df_action['Metrics.Review Score'].mean
#hide
df_sports = df[df['Metadata.Genres'] == 'Sports']
#collapse-output
df_sports['Metrics.Review Score'].mean
#hide
df_strategy = df[df['Metadata.Genres'] == 'Strategy']
#collapse-output
df_strategy['Metrics.Review Score'].mean
#hide
top_reviews = df2['Title'].tolist()
top_sales = df3['Title'].tolist()
#collapse-output
top_sales
#collapse-output
top_reviews
#collapse-output
print(set(top_sales).intersection(set(top_reviews)))
#hide
top_games = set(top_sales).intersection(set(top_reviews))
#hide
top_games_dict = {'Grand Theft Auto IV' : 837,
'Mario Kart DS' : 22,
'Halo 3' : 420,
'Call of Duty 4: Modern Warfare' : 421,
'Super Mario Galaxy' : 422,
'Super Smash Bros.: Brawl' : 835
}
#hide
target_indices = [837, 22, 420, 421, 422, 835, 156, 833, 157]
top_games = df.iloc[target_indices]
#hide
top_games = top_games[['Title', 'Metrics.Review Score', 'Metrics.Sales', 'Metadata.Genres', 'Metadata.Sequel?', 'Metadata.Publishers', 'Features.Max Players', 'Release.Console', 'Release.Year']]
#hide-input
top_games.sort_values('Metrics.Sales', ascending = False)
#hide-input
sns.countplot(x = top_games['Metadata.Genres'], palette = 'ch:.25')
#hide-input
sns.countplot(x = top_games['Metadata.Publishers'], palette = 'ch:.25')
#hide-input
sns.countplot(x = top_games['Features.Max Players'], palette = 'ch:.25')
#hide-input
sns.countplot(x = top_games['Release.Console'], palette = 'ch:.25')
#hide
from wordcloud import WordCloud, ImageColorGenerator
from PIL import Image
import matplotlib.pyplot as plt
#hide
myStopWords = list(punctuation) + stopwords.words('english')
#hide
super_mario_describe = '''
Bowser has taken over the Mushroom Kingdom, and it's up to Mario to put an end to his sinister reign! Battle Bowser's vile henchmen through 32 levels in the Original 1985 game mode. Move on to collecting special Red Coins and Yoshi Eggs in Challenge mode. Then, try to unlock a secret mode that's waiting to be found by super players like you! Every mode will give you the chance to beat your own score, and there's a lot more to do than just saving a princess. So get ready for a brick-smashin', pipe-warpin', turtle-stompin' good time!
Mario™ and Luigi™ star in their first ever Mushroom Kingdom adventure! Find out why Super Mario Bros. is instantly recognizable to millions of people across the globe, and what made it the best-selling game in the world for three decades straight. Jump over obstacles, grab coins, kick shells, and throw fireballs through eight action-packed worlds in this iconic NES classic. Only you and the Mario Bros. can rescue Princess Toadstool from the clutches of the evil Bowser.
Pick up items and throw them at your adversaries to clear levels in seven fantastical worlds. Even enemies can be picked up and tossed across the screen. Each character has a unique set of abilities: Luigi can jump higher and farther than any of the other characters, Toad can dig extremely fast and pull items out of the ground quicker than anyone, and the princess is the only one who can jump and hover temporarily. This unique installment in the Mario series will keep you coming back for more!
Relive the classic that brought renowned power-ups such as the Tanooki Suit to the world of Super Mario Bros.!
Bowser™ and the Koopalings are causing chaos yet again, but this time they’re going beyond the Mushroom Kingdom into the seven worlds that neighbor it. Now Mario™ and Luigi™ must battle a variety of enemies, including a Koopaling in each unique and distinctive world, on their way to ultimately taking on Bowser himself. Lucky for the brothers, they have more power-ups available than ever before. Fly above the action using the Super Leaf, swim faster by donning the Frog Suit, or defeat enemies using the Hammer Bros. Suit. Use the brand-new overworld map to take the chance to play a minigame in hopes of gaining extra lives or to find a Toad’s House where you can pick up additional items. All this (and more) combines into one of gaming’s most well-known and beloved titles—are you ready to experience gaming bliss?
'''
#hide-input
wc = WordCloud().generate_from_text(super_mario_describe)
#Use matplotlib.pyplot to display the fitted wordcloud
#Turn axis off to get rid of axis numbers
plt.imshow(wc)
plt.axis('off')
plt.show()
#hide
mario_kart_describe = '''
Select one of eight characters from the Mario™ series—offering a variety of driving styles—and take on three championship cups in three different kart classes. Win enough, and you'll unlock a fourth circuit: the ultra-tough Special Cup. Crossing the finish line in first place isn't an easy task, though, as each track has unique obstacles to conquer and racers can obtain special power-ups that boost them to victory. With more than 15 tracks to master and nearly endless replay value, Super Mario Kart is classic gaming…with some banana peels thrown in for good measure!
The newest installment of the fan-favorite Mario Kart™ franchise brings Mushroom Kingdom racing fun into glorious 3D. For the first time, drivers explore new competitive kart possibilities, such as soaring through the skies or plunging into the depths of the sea. New courses, strategic new abilities and customizable karts bring the racing excitement to new heights.
FEATURES:
The Mario Kart franchise continues to evolve. New kart abilities add to the wild fun that the games are known for. On big jumps, a kart deploys a wing to let it glide over the track shortcut. When underwater, a propeller pops out to help the kart cruise across the sea floor.
Players can show their own style by customizing their vehicles with accessories that give them a competitive advantage. For instance, giant tires help a kart drive off-road, while smaller tires accelerate quickly on paved courses.
People can choose to race as one of their favorite Mushroom Kingdom characters or even as their Mii™ character.
New courses take players on wild rides over mountains, on city streets and through a dusty desert. Nintendo fans will recognize new courses on Wuhu Island and in the jungles from Donkey Kong Country™ Returns.
The game supports both SpotPass™ and StreetPass™ features.
Players can compete in local wireless matches or online over a broadband Internet connection.
The newest installment of the fan-favorite Mario Kart™ franchise brings Mushroom Kingdom racing fun into glorious 3D. For the first time, drivers explore new competitive kart possibilities, such as soaring through the skies or plunging into the depths of the sea. New courses, strategic new abilities and customizable karts bring the racing excitement to new heights.
FEATURES:
The Mario Kart franchise continues to evolve. New kart abilities add to the wild fun that the games are known for. On big jumps, a kart deploys a wing to let it glide over the track shortcut. When underwater, a propeller pops out to help the kart cruise across the sea floor.
Players can show their own style by customizing their vehicles with accessories that give them a competitive advantage. For instance, giant tires help a kart drive off-road, while smaller tires accelerate quickly on paved courses.
People can choose to race as one of their favorite Mushroom Kingdom characters or even as their Mii™ character.
New courses take players on wild rides over mountains, on city streets and through a dusty desert. Nintendo fans will recognize new courses on Wuhu Island and in the jungles from Donkey Kong Country™ Returns.
The game supports both SpotPass™ and StreetPass™ features.
Players can compete in local wireless matches or online over a broadband Internet connection.
'''
#hide-input
wc2 = WordCloud().generate_from_text(mario_kart_describe)
#Use matplotlib.pyplot to display the fitted wordcloud
#Turn axis off to get rid of axis numbers
plt.imshow(wc2)
plt.axis('off')
plt.show()
#hide
smash_bros_describe = '''
Super Smash Bros. for Nintendo 3DS is the first portable entry in the renowned series, in which game worlds collide. Up to four players battle each other locally or online using some of Nintendo’s most well-known and iconic characters across beautifully designed stages inspired by classic portable Nintendo games. It’s a genuine, massive Super Smash Bros. experience that’s available to play on the go, anytime, anywhere.
FEATURES:
Smash and crash through “Smash Run” mode, a new mode exclusive to the Nintendo 3DS version that gives up to four players five minutes to fight solo through a huge battlefield while taking down recognizable enemies from almost every major Nintendo franchise and multiple third-party partners. Defeated enemies leave behind power-ups to collect. Players who collect more power-ups have an advantage once time runs out and the battle with opponents begins.
Compete with classic characters from the Super Smash Bros. series like Mario, Link, Samus and Pikachu, along with new challengers like Mega Man, Little Mac and newly announced Palutena, the Goddess of Light from the Kid Icarus games. For the first time players can even compete as their own Mii characters.
Customize different aspects of your character when playing locally or online with friends in a variety of multiplayer modes.
View most elements of the high-energy action at silky-smooth 60 frames per second and in eye-popping stereoscopic 3D.
Fight against friends and family locally or online, or battle random challengers all over the world online in “For Fun” or “For Glory” modes.
Gaming icons clash in the ultimate brawl you can play anytime, anywhere! Smash rivals off the stage as new characters Simon Belmont and King K. Rool join Inkling, Ridley, and every fighter in Super Smash Bros. history. Enjoy enhanced speed and combat at new stages based on the Castlevania series, Super Mario Odyssey, and more!
Having trouble choosing a stage? Then select the Stage Morph option to transform one stage into another while battling—a series first! Plus, new echo fighters Dark Samus, Richter Belmont, and Chrom join the battle. Whether you play locally or online, savor the faster combat, new attacks, and new defensive options, like a perfect shield. Jam out to 900 different music compositions and go 1-on-1 with a friend, hold a 4-player free-for-all, kick it up to 8-player battles and more! Feel free to bust out your GameCube controllers—legendary couch competitions await—or play together anytime, anywhere!
'''
#hide-input
wc3 = WordCloud().generate_from_text(smash_bros_describe)
#Use matplotlib.pyplot to display the fitted wordcloud
#Turn axis off to get rid of axis numbers
plt.imshow(wc3)
plt.axis('off')
plt.show()
| 0.260672 | 0.986071 |
<a href="https://colab.research.google.com/github/andrecianflone/policy_value_iteration/blob/master/Policy_Value_Iteration.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Policy Iteration
The state-value function for any given policy $\pi$ can be evaluated as:
$$
\newcommand{\given}{|}
\newcommand{\states}{S}
\newcommand{\E}{\mathbb{E}}
\newcommand{\actions}{A}
\newcommand{\argmax}{\text{argmax}}
\newcommand{\R}{\mathbb{R}}
V_\pi (s) = \sum_a \pi(a\given s) \left[r(s,a) + \gamma P(s^\prime \given s,a) V_\pi (s^\prime)\right]
$$
for all $s \in \states$
Equivalently, we can write the above as a function of state-action values:
$$
V_\pi (s) = \sum_a \pi(a \given s) q_\pi(s,a)
$$
Which must be less than or equal to the max q-value:
$$
V_\pi (s) = \sum_a \pi(a \given s) q_\pi(s,a) \leq \max_a q_\pi(s,a)
$$
We perform a policy step improvement to get new policy $\pi^\prime$:
$$
\pi^\prime(a|s) = \argmax_a q_\pi (s,a)
$$
Then the following is true:
$$
V_\pi (s) = \sum_a \pi(a \given s) q_\pi(s,a) \leq \sum_a \pi^\prime(a \given s) q_\pi(s,a)
$$
And if we improve again:
$$
\pi^{\prime\prime} = (a|s) = \argmax_a q_{\pi^\prime} (s,a)
$$
Then the following is also true:
$$
V_\pi (s) = \sum_a \pi(a \given s) q_\pi(s,a) \leq \sum_a \pi^\prime(a \given s) q_\pi(s,a) \leq \sum_a \pi^{\prime\prime}(a \given s) q_{\pi^\prime}(s,a)
$$
And so on for all $s\in \states$. Since every application of policy iteration must result in a better policy, as evaluated by the value function, successive policies are nondecreasing. And, since the MDP is finite, therefore there is a finite set of policies, policy iteration *must* terminate. If such new policy results in state values equal to the states values under the previous policy, then the optimal policy must have been found.
# Track 1: Policy Iteration and Value Iteration
# Policy Iteration
Policy iteration alternates between evaluating a policy and improving a policy. Policy evaluation is defined as the expected future reward, defined as the expectation for the infinite sum of discounted rewards:
$$
\begin{aligned}
v_\pi(s) &= \E_\pi\left[ \sum_{t=0}^\infty \gamma^t r(S_t, A_t) \given S_0 = s\right] \\
&=\E_\pi\left[ r(S_0, A_0) + \sum_{t=1}^\infty \gamma^t r(S_t, A_t) \given S_0 = s\right] \\
&=\E_\pi\left[ r(S_0, A_0) + \sum_{t=0}^\infty \gamma^{t+1} r(S_{t+1}, A_{t+1}) \given S_0 = s\right] \\
&=\E_\pi\left[ r(S_0, A_0) + \gamma \sum_{t=0}^\infty \gamma^{t} r(S_{t+1}, A_{t+1}) \given S_0 = s\right] \\
&=\E_\pi\left[ r(S_0, A_0) + \gamma v_\pi(S_1) \given S_0 = s\right] \\
\end{aligned}
$$
Replacing the definition of the expectation with policy $\pi$ and transition probability matrix $P$, we get:
$$
v_\pi(s) = \sum_{a \in \actions} \pi\left(a \given s\right)\left( r(s, a) + \gamma \sum_{s'} P\left(s' \given s, a\right) v_\pi(s')\right)
$$
Note this definition is slightly different, but equivalent to the notation in S&B, page 58:
$$
\begin{aligned}
v_\pi (s) &= \E_\pi \left[ G_t \given S_t = s\right]\\
&= \E_\pi \left[ R_{t+1} + \gamma G_{t+1} \given S_t = s\right]\\
&= \E_\pi \left[ R_{t+1} + \gamma v_\pi ( S_{t+1}) \mid S_t = s \right]\\
&= \sum_a \pi(a|s) \sum_{s^\prime, r} p(s^\prime, r \mid s,a) \left[r + \gamma v_\pi (s^\prime)\right]
\end{aligned}
$$
The pseudo code uses the latter notation, but we implement the algorithm with the former notation.
We implement policy evaluation in matrix form. To do so, we define the following:
$$
\begin{align*}
r_\pi(s) \defeq \sum_{a} \pi\left(a \given s\right) r(s,a) \hspace{2em}P_\pi(s, s') \defeq \sum_{a} \pi\left(a \given s\right) P\left(s' \given s, a\right)\enspace ,
\end{align*}
$$
where $r_\pi \in \R^{|\states|}$, $P_\pi \in \R^{|\states|\times|\states|}, v_\pi \in \R^{\states}$. In this form, $v_\pi$ is defined as:
$$
v_\pi = r_\pi + \gamma P_\pi v_\pi
$$
Since we are solving for $v_\pi$ iteratively, as opposed to closed form, we must keep track of our changing policy, and stationary reward functions. These are represented as matrices, where $\pi(a \given s) \in \R^{|\states| \times|\actions|}$ and $r(s,a) \in \R^{|\states| \times |\actions|}$.
Pseudo code for policy iteration, which includes policy evaluation and improvement, from S&B p.63

## Policy and Value Iteration
$$
\def\E{\mathbb{E}}
\def\R{\mathbb{R}}
\def\given{\mid}
\def\actions{\mathcal{A}}
\def\states{\mathcal{S}}
\def\defeq{\dot=}
\def\argmax{\text{argmax}}
$$
## Bellman Optimality Equation
The Bellman Optimality Equation is defined as:
$$
V_* = \max_a [r(s,a) + \gamma \sum_{s^\prime} P(s^\prime \given s,a) V_* (s^\prime)]
$$
For each step $k$, The Bellman Optimality Operator updates an estimate of $V_*$, that is $V_{k+1}$ based on previous estimate $V_{k}$:
$$
V_{k+1} = \max_a [r(s,a) + \gamma \sum_{s^\prime} P(s^\prime \given s,a) V_k (s^\prime)]
$$
Let the error in our estimate be defined as the absolute distance between the estimate and the true value:
$$
\epsilon_{k} = \mid V_k - V_*|
$$
In the worst case, our error is upper bounded by the infinity norm:
$$
\lVert V_k - V_* \rVert_\infty = \max_s\left| V_k (s) - V_*(s) \right|
$$
Using these equations, let's apply the Bellman Optimality operator and show that with our error function it is a contraction operator:
$$
\begin{aligned}
V_{k+1} - V_* &= \left| \max_a \left[r(s,a) + \gamma \sum_{s^\prime}P(s^\prime \given s,a)V_k(s^\prime)\right] - \max_a \left[r(s,a) + \gamma \sum_{s^\prime}P(s^\prime \given s,a)V_*(s^\prime)\right] \right| \\
&\leq \max_a\left| r(s,a) + \gamma \sum_{s^\prime}P(s^\prime \given s,a)V_k(s^\prime) - r(s,a) + \gamma \sum_{s^\prime}P(s^\prime \given s,a)V_*(s^\prime)\right| \\
&= \max_a\left|\gamma \sum_{s^\prime}P(s^\prime \given s,a)V_k(s^\prime) - \gamma \sum_{s^\prime}P(s^\prime \given s,a)V_*(s^\prime)\right| \\
&= \gamma \max_a\left|\sum_{s^\prime}P(s^\prime \given s,a)\left[V_k(s^\prime) - V_*(s^\prime)\right]\right| \\
&\leq \gamma \max_a\left|\max_{s}\left[V_k(s) - V_*(s)\right]\right| \\
&= \gamma \max_{s}\left|V_k(s) - V_*(s)\right| \\
&= \gamma \lVert V_k - V_* \rVert_\infty
\end{aligned}
$$
Since applying one iteration of the operator must result in a decreasing error for all states $s \in \states$, with error equal to zero in the limit, the Bellman optimality operator is a contraction mapping.
# Value Iteration
One downside to policy iteration, which is clear from the pseudo code, is that after every stage of policy improvement we must re-evaluate our policy in a full sweep. We can combine policy improvement and evaluation into *value iteration*. For all $s \in \states$, value iteration is defined by the update rule:
$$
\begin{aligned}
v_{k+1}(s) \defeq &\max_a \E \left[R_{t+1} + \gamma v_k (S_{t+1}) \given S_t = s, A_t = a\right]\\
= &\max_a \sum_{s^\prime, r} p(s^\prime, r \given s, a)[r+ \gamma v_k (s^\prime)]
\end{aligned}
$$
After convergence, the optimal policy is derived from the state values, for all $s \in \states$:
$$
\pi (s) = \argmax_a \sum_{s^\prime, r} p(s^\prime, r \given s, a) [r + \gamma v(s)]
$$
Pseudo code for value iteration from S&B p.65

# Implementation
### Einstein Notation
**Note on implementation**: The class `MDPAgent` implements two algorithms: policy iteration and value iteration. In both cases, the algorithms are implemented in matrix form, specifically using [Einstein summation convention](https://en.wikipedia.org/wiki/Einstein_notation) with the help of `numpy.einsum`. This notation is used to make the code more succinct and computationally efficient. If you are unfamiliar with Einstein notation, continue reading, otherwise skip to the section **MDP Agent**. Consider the following common operation. Given the 3-d array $A \in \R^{4 \times 3 \times 4}$, and vector $b \in \R^4$, we wish to compute the element-wise product of $A$ and $b$, with $b$ broadcast in the second and third dimension, followed by a summation over the second and third dimension resulting in vector $c \in \R^4$. This can be accomplished in `Numpy` the following way:
```
import numpy as np
a = np.random.randint(0,5,(3,2,2))
b = np.random.randint(0,5,3)
c = a*b[:, None, None] # explicit broadcasting
c = np.sum(c, axis=2) # sum 3rd dimension
c = np.sum(c, axis=1) # sum 2nd
print(c)
```
The first issue is that the equation must be split into multiple lines. Secondly, Python creates temporary arrays, requiring more memory than necessary. We can compute the three lines above with a single function:
```
c = np.einsum('ijk, i->i',a,b)
print(c)
```
The operation is interpreted by the string argument. The first part, `ijk, i` labels the dimensions of the arrays `a` and `b` respectively. Array `b` has a single dimension, which is identified as `i`, meaning it matches the orientation of dimension `i` of array `a`. Since `b` is a vector, it must be multiplied by broadcasting to match the shape of `a`. The second part of the string, `->i`, tells `numpy` which dimension to return, and therefore how to sum along axes. If we write `->ij`, `numpy` returns a matrix matching the first two dimensions of `a`, and so must sum along dimension `k`. Since we wrote `->i`, `numpy` must sum along dimension `j` and `k`. Einstein notation can be used for dot-products or element-wise multiplication with broadcasting and summation, all in a single numpy function. See [`numpy.einsum`](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.einsum.html) documentation for more details.
## MDP Agent
The `MDPAgent` class implements both policy iteration (class method `policy_iteration`) and value iteration (class method `value_iteration`). In the policy iteration case, the policy can be evaluated in closed form with a matrix inverse (class method `_policy_evaluation_exact`) or by iteration until convergence (class method `_policy_evaluation_modified`). Please read comments in the code for details of each function.
```
import numpy as np
from numpy.linalg import inv
from pdb import set_trace
import numpy.ma as ma
!pip install PTable
from prettytable import PrettyTable, ALL
from datetime import datetime
import matplotlib.pyplot as plt
def table_print(arr, headers="",decimals=6):
x = PrettyTable()
x.field_names = headers
a = np.around(arr, decimals)
rows = a.shape[0]
if rows > 1 and a.ndim > 1:
for i in range(rows):
x.add_row([i, *a[i]])
else:
x.add_row(arr)
print(x)
def print_values(v,decimals):
table_print(np.expand_dims(v,1), headers=["states", "values"],decimals=decimals)
def print_policy(pi, decimals):
headers = ["states"]
#set_trace()
for i in range(pi.shape[1]):
headers.append("action " + str(i))
table_print(pi, headers=headers, decimals=decimals)
class MDPAgent():
def __init__(self, gamma):
"""
Basic MDP agent, can do policy iteration and value iteration
"""
self.gamma = gamma # discount rate
self.theta = 0.000001 # convergence threshold
def _initialize_deterministic(self, p, n_states, n_actions):
""" Initial policy """
# Random deterministic policy, array of shape |S| x |A|
r_actions = np.random.randint(0,n_actions,n_states)
pi = np.zeros((r_actions.size, n_actions))
pi[np.arange(r_actions.size), r_actions] = 1
return pi
def _initialize_uniform(self, p, n_states, n_actions):
""" Initial policy """
# Begin with uniform policy: array of shape |S| x |A|
pi = np.full((n_states, n_actions), 1)
pi = pi*np.sum(p, axis=2) # remove invalid actions
base = np.sum(pi, axis=1) # get number of valid actions per state
np.seterr(divide='ignore')
pi = np.nan_to_num(pi/base[:,None]) # divide by number of actions, broadcast
#np.seterr(divide='raise')
return pi
def _policy_evaluation_exact(self, pi, v, r, p):
"""
Evaluate policy by taking the inverse
Args:
pi: policy, array of shape |S| x |A|
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
Return:
v: 1D array with updated state values
"""
# Rewards according to policy: Hadamard product and row-wise sum
r_pi = np.einsum('ij,ij->i', pi, r)
# Policy-weighted transitions:
# multiply p by pi by broadcasting pi, then sum second axis
# result is an array of shape |S| x |S|
p_pi = np.einsum('ijk, ij->ik', p, pi)
v = np.dot(inv((np.eye(p_pi.shape[0]) - self.gamma*p_pi)), r_pi)
return v
def _policy_evaluation_modified(self, pi, v, r, p):
"""
Evaluate pi using an initial v estimate and iterate
Args:
pi: policy, array of shape |S| x |A|
v: state values, array of shape |S|
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
Return:
v: 1D array with updated state values
"""
max_iteration = 10000 # avoid core meltdown
for i in range(max_iteration):
# Rewards according to policy: Hadamard product and row-wise sum
r_pi = np.einsum('ij,ij->i', pi, r)
# Policy-weighted transitions:
# multiply p by pi by broadcasting pi, then sum second axis
# result is an array of shape |S| x |S|
p_pi = np.einsum('ijk, ij->ik', p, pi)
# New values
v_new = r_pi + self.gamma*np.dot(p_pi,v)
# Stop condition
if np.max(np.absolute(v - v_new)) < self.theta:
v = v_new
break;
v = v_new
return v
def _policy_improvement(self, v, r, p):
"""
Args:
v: state values, array of shape |S|
p: state transition probabilities, array of shape |S| x |A| x |S|
"""
# Get value for each action
#set_trace()
q = r + self.gamma*np.einsum('ijk, k->ij', p, v) # get q values
# If a 3rd dimension vector sums to 0, invalid action, so mask
q = ma.masked_array(q, mask=(np.sum(p,axis=2)-1)*(-1))
# New policy is max action (masked elements automatically ignored)
pi = (q == q.max(axis=1)[:,None]).astype(int)
pi = pi.filled(0)
# np.sum(p,axis=2)
# Break ties randomly
if pi.sum()>pi.shape[0]:
for i in range(pi.shape[0]):
if np.sum(pi[i]) == 0: continue
id = np.random.choice(np.where(pi[i] == pi[i].max())[0])
temp = np.zeros_like(pi[i])
temp[id] = 1
pi[i] = temp
return pi
def policy_iteration(self, r, p, method, initial='deterministic'):
"""
Args:
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
method: `exact` or `modified` (iterative)
initial: if `uniform`, policy is uniformly distributed at the start,
otherwise a deterministic policy is randomly generated
"""
t1 = datetime.now()
if method == 'exact':
policy_evaluation = self._policy_evaluation_exact
elif method =='modified':
policy_evaluation = self._policy_evaluation_modified
else:
raise ValueError("method must be 'exact' or 'modified'")
n_states, n_actions = p.shape[:2]
# Initial policy estimates
if initial=='uniform':
pi = self._initialize_uniform(p, n_states, n_actions)
else:
pi = self._initialize_deterministic(p, n_states, n_actions)
v = np.zeros(n_states)
# Main loop
policy_stable = False
it = 0
while policy_stable == False:
v = policy_evaluation(pi, v, r, p)
old_actions = pi
pi = self._policy_improvement(v, r, p)
if np.array_equal(pi, old_actions): policy_stable = True
it += 1
# Evaluate final policy
v = policy_evaluation(pi, v, r, p)
t2 = datetime.now()
seconds = (t2 - t1).total_seconds()
return pi, v, it, seconds
def value_iteration(self, r, p):
"""
Args:
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
Return;
pi: policy, |S| x |A|
v: state values, |S|
it: number of iterations
"""
t1 = datetime.now()
n_states, n_actions = p.shape[:2]
v = np.zeros(n_states)
max_iteration = 10000
for it in range(max_iteration):
q = r + self.gamma*np.einsum('ijk, k->ij', p, v) # get q values
q = ma.masked_array(q, mask=(np.sum(p,axis=2)-1)*(-1)) #mask invalid actions
v_new = np.max(q, axis=1) # state-values equal max possible values
v_new = v_new.filled(0) # Masked states should have value 0
if np.max(np.absolute(v - v_new)) < self.theta:
v = v_new
break;
v = v_new
# Derive new policy
pi = (q == q.max(axis=1)[:,None]).astype(int)
pi = pi.filled(0)
t2 = datetime.now()
seconds = (t2 - t1).total_seconds()
return pi, v, it+1, seconds
def policy_eval(self, pi, v, r, p):
"""
Evaluate policy by taking the inverse
Args:
pi: policy, array of shape |S| x |A|
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
Return:
v: 1D array with updated state values
"""
# Rewards according to policy: Hadamard product and row-wise sum
r_pi = np.einsum('ij,ij->i', pi, r)
# Policy-weighted transitions:
# multiply p by pi by broadcasting pi, then sum second axis
# result is an array of shape |S| x |S|
p_pi = np.einsum('ijk, ij->ik', p, pi)
v = np.dot(inv((np.eye(p_pi.shape[0]) - self.gamma*p_pi)), r_pi)
return v
gamma = 0.5
policy = np.array(
[[1,0],
[0,1],
[1,0]])
p_pi = np.array(
[[0.8, 0.4, 0],
[0.15, 0.5, 0],
[0.05, 0.1, 1]])
r_pi = np.array(
[[2,1,0]])
v = np.dot(inv((np.eye(p_pi.shape[0]) - gamma*p_pi)), r_pi)
```
## Basic MDP Experiment
The first MDP is a basic MDP which consists of two states and three actions, with the following transition probabilities and rewards:
**Transition Probabilities**:
- P(s_0 | s_0, a_0) = 0.5
- P(s_1 | s_0, a_0) = 0.5
- P(s_0 | s_0, a_1) = 0
- P(s_1 | s_0, a_1) = 1
- P(s_1 | s_0, a_2) = 0
- P(s_1 | s_1, a_2) = 1
**Rewards**:
- r(s_0, a_0) = 5
- r(s_0, a_1) = 10
- r(s_1, a_2) = -1
The above MDP is implemented below as a class environment with transitions as array `p` and rewards as array `r`
```
class BasicMDP():
def __init__(self):
"""Very basic MDP to test policy/value iteration"""
# Transition probabilities is a 3D array of shape |S| x |A| x |S|
# the
self.p = np.array(
[[[0.5, 0.5],[0,1],[0,0]],
[[0.0, 0.0],[0,0],[0,1]]])
# Rewards is a function of state and action, i.e. r(s,a), shape |S| x |A|
self.r = np.array(
[[5, 10, 0],
[0, 0, -1]])
```
Let's solve this MDP and see if we arrive at the same solution using policy iteration, modified policy iteration, value iteration, and their compute time.
```
def print_info(pi, v, it, sec, title):
print("="*79)
print(title)
print("Final Policy:")
print_policy(pi,2)
print("Values:")
print_values(v,6)
print("compute seconds: ", sec)
print("iterations: ", it)
print()
def experiment_1():
gamma = 0.95
agent = MDPAgent(gamma)
env = BasicMDP()
title = "Policy Iteration with closed form policy evaluation"
pi1, v, it, sec = agent.policy_iteration(env.r, env.p, method='exact', initial='deterministic')
print_info(pi1,v,it,sec,title)
title = "Modified Policy Iteration with partial policy evaluation"
pi2, v, it, sec = agent.policy_iteration(env.r, env.p, method='modified', initial='deterministic')
print_info(pi2,v,it,sec,title)
title = "Value Iteration"
pi3, v, it, sec = agent.value_iteration(env.r, env.p)
print_info(pi3,v,it,sec,title)
if (np.array_equal(pi1,pi2) and np.array_equal(pi2, pi3)):
print("all policies are equal")
else:
print("policies not equal")
experiment_1()
```
All 3 methods arrive at the same policy and values. It seems, however, that on this trivial MDP the policy iteration with the closed form version of policy evaluation is the fastest method, while only marginally faster than modified policy iteration. This may be due to the random initialization of our policy, and so it would be prudent to repeat the exercise and average the results:
```
def experiment_2():
gamma = 0.95
agent = MDPAgent(gamma)
env = BasicMDP()
trials = 100
pol_it = np.zeros(trials)
mod_it = np.zeros(trials)
val_it = np.zeros(trials)
pol_time = np.zeros(trials)
mod_time = np.zeros(trials)
val_time = np.zeros(trials)
for i in range(trials):
_, _, pol_it[i], pol_time[i] = agent.policy_iteration(env.r, env.p, method='exact', initial='deterministic')
_, _, mod_it[i], mod_time[i] = agent.policy_iteration(env.r, env.p, method='modified', initial='deterministic')
_, _, val_it[i], val_time[i] = agent.value_iteration(env.r, env.p)
print("Policy iteration: {:.4f} seconds, {:.2f} iterations".format(np.sum(pol_time)/trials, np.sum(pol_it)/trials))
print("Modified policy : {:.4f} seconds, {:.2f} iterations".format(np.sum(mod_time)/trials, np.sum(mod_it)/trials))
print("Value iteration : {:.4f} seconds, {:.2f} iterations".format(np.sum(val_time)/trials, np.sum(val_it)/trials))
experiment_2()
```
Value iteration may seem more elegant mathematically, since it does not alternate between policy evaluation and policy improvement, it takes much longer to converge on this MDP as it requires a large number of iterations to converge. Policy iteration converges much faster than other methods, although this might not be feasible in a realistic MDP where taking a matrix inverse may not be feasible. Next, we test these algorithms in a Grid World setup.
## Grid World Experiment
To experiment with a more elaborate MDP, the GridWorld class is implemented below. The class will automatically create transition and reward arrays for an arbitrary sized grid and any number of terminal states. Rewards are -1 for all transitions, while terminal states have 0 reward.
```
class GridWorld():
def __init__(self, rows, cols, terminal_states, reward_value):
"""
Creates a GridWorld of size `rows` X `cols` with the listed terminal states
Args:
rows: int
cols: int
terminal_states: list of int where each element is the grid index of the
terminal state. The grid's cells are numbered left to right, top to
bottom, starting with index 0.
"""
self.rows, self.cols = rows, cols
self.terminal_states = terminal_states
self.n_states = rows * cols # number of states
self.n_actions = 4 # left, up, right, down
self.p = self._init_dynamics(rows, cols, self.n_states, self.n_actions, terminal_states)
self.r = self._init_rewards(self.n_states, self.n_actions, reward_value, terminal_states)
def _init_dynamics(self, rows, cols, n_states, n_actions, terminal_states):
""" Returns model dynamics array of shape |S| x |A| x |S| """
# Empty transition array
p = np.zeros((n_states,n_actions,n_states))
# Add deterministic transitions by traversing an imaginary grid
for r in range(rows):
for c in range(cols):
cur_s = rows*r + c # current state
# left?
left_s = rows*r + c -1 # left state id
if (c-1) >= 0: p[cur_s,0, left_s] = 1
# up?
up_s = rows*(r - 1) + c # up state id
if (r-1) >= 0: p[cur_s, 1, up_s] = 1;
# right?
right_s = rows*r + c + 1 # right state id
if (c+1) < cols: p[cur_s, 2, right_s] = 1;
# down?
down_s = rows*(r + 1) + c # down state id
if (r+1) < rows: p[cur_s, 3, down_s] = 1;
# Terminal states have no actions
for t in terminal_states:
p[t] = 0
return p
def _init_rewards(self, n_states, n_actions, reward_value, terminal_states):
""" Returns reward matrix, shape |S| x |A| """
# Rewards are -1 on all actions. No rewards for terminal since no action
r = np.full((n_states, n_actions), reward_value)
for t in terminal_states:
r[t] = 0
return r
def render_policy(self, pi):
pass
def __str__(self):
""" Print the grid """
x = PrettyTable()
x.header = False
for r in range(self.rows):
row = []
for c in range(self.cols):
cur_s = self.rows*r + c # current state
if cur_s in self.terminal_states:
row.append('#')
else:
row.append('-')
x.add_row(row)
x.hrules = ALL
return x.get_string()
```
We first start with a simple 4 x 4 grid with 3 terminal states and visualize it. Note the hash symbol stands for terminal states.
```
rows = cols = 4
terminal_states = [0,6,15]
env = GridWorld(rows, cols, terminal_states, reward_value=-1)
print(env)
```
### Baseline
Let's first test if all methods arrive at the same policy, and their compute time.
```
def experiment_3():
rows = cols = 4
terminal_states = [0,6,15]
env = GridWorld(rows, cols, terminal_states, reward_value=-1)
gamma = 0.95
agent = MDPAgent(gamma)
title = "Policy Iteration with closed form policy evaluation"
pi1, v, it, sec = agent.policy_iteration(env.r, env.p, method='exact', initial='deterministic')
print(title)
print(sec)
title = "Modified Policy Iteration with partial policy evaluation"
pi2, v, it, sec = agent.policy_iteration(env.r, env.p, method='modified', initial='deterministic')
print(title)
print(sec)
title = "Value Iteration"
pi3, v, it, sec = agent.value_iteration(env.r, env.p)
print(title)
print(sec)
if (np.array_equal(pi1,pi2) and np.array_equal(pi2, pi3)):
print("all policies are equal")
else:
print("policies not equal")
experiment_3()
```
### Varying discount rate
They all converge once again to the same solution. If we vary gamma, how does this affect convergence time?
```
def multi_plot_data(x, data, names, xlabel):
""" data, names are lists of vectors """
for i, y in enumerate(data):
plt.plot(x, y, 'o', markersize=3, label=names[i])
plt.legend(loc='upper left', prop={'size': 16}, numpoints=10)
plt.xlabel(xlabel)
plt.ylabel("milliseconds")
plt.show()
def experiment_4():
rows = cols = 4
terminal_states = [0,6,15]
env = GridWorld(rows, cols, terminal_states, reward_value=-1)
trials = 10
samples = 200
gammas = np.linspace(0.001,1,endpoint=False,num=samples)
pol_time = np.zeros((trials, samples))
mod_time = np.zeros((trials, samples))
val_time = np.zeros((trials, samples))
for t in range(trials):
for i in range(samples):
agent = MDPAgent(gammas[i])
_, _, _, pol_time[t,i] = agent.policy_iteration(env.r, env.p, method='exact', initial='uniform')
_, _, _, mod_time[t,i] = agent.policy_iteration(env.r, env.p, method='modified', initial='uniform')
_, _, _, val_time[t,i] = agent.value_iteration(env.r, env.p)
# Plot data
pol_time = np.average(pol_time, axis=0)*1000
mod_time = np.average(mod_time, axis=0)*1000
val_time = np.average(val_time, axis=0)*1000
data = [pol_time, mod_time, val_time]
names = ["Policy Iteration", "Modified PI", "Value Iteration"]
multi_plot_data(gammas, data, names, xlabel="gamma")
experiment_4()
```
In this setup, value iteration computes faster than either policy iteration or modified policy iteration, with modified policy iteration increasing exponentially with gamma. Value iteration is quite robust varying gamma.
### Varying MDP Complexity
Let's see if increasing the model complexity has an large impact on the algorithms
```
def experiment_5():
gamma = 0.95
agent = MDPAgent(gamma)
terminal_states = [0,6]
rows = cols = 5
env = GridWorld(rows, cols, terminal_states, reward_value=-1)
_, _, pol_it, pol_time = agent.policy_iteration(env.r, env.p, method='exact', initial='deterministic')
_, _, mod_it, mod_time = agent.policy_iteration(env.r, env.p, method='modified', initial='deterministic')
_, _, val_it, val_time = agent.value_iteration(env.r, env.p)
print("Policy iteration: {:.4f} seconds, {:.2f} iterations".format(pol_time, pol_it))
print("Modified policy : {:.4f} seconds, {:.2f} iterations".format(mod_time, mod_it))
print("Value iteration : {:.4f} seconds, {:.2f} iterations".format(val_time, val_it))
experiment_5()
```
Increasing the grid size by a single column and row makes computation time explode for Policy Iteration and much worse for Modified Policy Iteration. Quite surprisingly, it's no sweat for Value Iteration. Value Iteration converges a fraction of a second, compared to 307 in the case of modified policy iteration. It only required 7 iterations compared to 216,967 for modified policy. Outstanding!
|
github_jupyter
|
import numpy as np
a = np.random.randint(0,5,(3,2,2))
b = np.random.randint(0,5,3)
c = a*b[:, None, None] # explicit broadcasting
c = np.sum(c, axis=2) # sum 3rd dimension
c = np.sum(c, axis=1) # sum 2nd
print(c)
c = np.einsum('ijk, i->i',a,b)
print(c)
import numpy as np
from numpy.linalg import inv
from pdb import set_trace
import numpy.ma as ma
!pip install PTable
from prettytable import PrettyTable, ALL
from datetime import datetime
import matplotlib.pyplot as plt
def table_print(arr, headers="",decimals=6):
x = PrettyTable()
x.field_names = headers
a = np.around(arr, decimals)
rows = a.shape[0]
if rows > 1 and a.ndim > 1:
for i in range(rows):
x.add_row([i, *a[i]])
else:
x.add_row(arr)
print(x)
def print_values(v,decimals):
table_print(np.expand_dims(v,1), headers=["states", "values"],decimals=decimals)
def print_policy(pi, decimals):
headers = ["states"]
#set_trace()
for i in range(pi.shape[1]):
headers.append("action " + str(i))
table_print(pi, headers=headers, decimals=decimals)
class MDPAgent():
def __init__(self, gamma):
"""
Basic MDP agent, can do policy iteration and value iteration
"""
self.gamma = gamma # discount rate
self.theta = 0.000001 # convergence threshold
def _initialize_deterministic(self, p, n_states, n_actions):
""" Initial policy """
# Random deterministic policy, array of shape |S| x |A|
r_actions = np.random.randint(0,n_actions,n_states)
pi = np.zeros((r_actions.size, n_actions))
pi[np.arange(r_actions.size), r_actions] = 1
return pi
def _initialize_uniform(self, p, n_states, n_actions):
""" Initial policy """
# Begin with uniform policy: array of shape |S| x |A|
pi = np.full((n_states, n_actions), 1)
pi = pi*np.sum(p, axis=2) # remove invalid actions
base = np.sum(pi, axis=1) # get number of valid actions per state
np.seterr(divide='ignore')
pi = np.nan_to_num(pi/base[:,None]) # divide by number of actions, broadcast
#np.seterr(divide='raise')
return pi
def _policy_evaluation_exact(self, pi, v, r, p):
"""
Evaluate policy by taking the inverse
Args:
pi: policy, array of shape |S| x |A|
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
Return:
v: 1D array with updated state values
"""
# Rewards according to policy: Hadamard product and row-wise sum
r_pi = np.einsum('ij,ij->i', pi, r)
# Policy-weighted transitions:
# multiply p by pi by broadcasting pi, then sum second axis
# result is an array of shape |S| x |S|
p_pi = np.einsum('ijk, ij->ik', p, pi)
v = np.dot(inv((np.eye(p_pi.shape[0]) - self.gamma*p_pi)), r_pi)
return v
def _policy_evaluation_modified(self, pi, v, r, p):
"""
Evaluate pi using an initial v estimate and iterate
Args:
pi: policy, array of shape |S| x |A|
v: state values, array of shape |S|
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
Return:
v: 1D array with updated state values
"""
max_iteration = 10000 # avoid core meltdown
for i in range(max_iteration):
# Rewards according to policy: Hadamard product and row-wise sum
r_pi = np.einsum('ij,ij->i', pi, r)
# Policy-weighted transitions:
# multiply p by pi by broadcasting pi, then sum second axis
# result is an array of shape |S| x |S|
p_pi = np.einsum('ijk, ij->ik', p, pi)
# New values
v_new = r_pi + self.gamma*np.dot(p_pi,v)
# Stop condition
if np.max(np.absolute(v - v_new)) < self.theta:
v = v_new
break;
v = v_new
return v
def _policy_improvement(self, v, r, p):
"""
Args:
v: state values, array of shape |S|
p: state transition probabilities, array of shape |S| x |A| x |S|
"""
# Get value for each action
#set_trace()
q = r + self.gamma*np.einsum('ijk, k->ij', p, v) # get q values
# If a 3rd dimension vector sums to 0, invalid action, so mask
q = ma.masked_array(q, mask=(np.sum(p,axis=2)-1)*(-1))
# New policy is max action (masked elements automatically ignored)
pi = (q == q.max(axis=1)[:,None]).astype(int)
pi = pi.filled(0)
# np.sum(p,axis=2)
# Break ties randomly
if pi.sum()>pi.shape[0]:
for i in range(pi.shape[0]):
if np.sum(pi[i]) == 0: continue
id = np.random.choice(np.where(pi[i] == pi[i].max())[0])
temp = np.zeros_like(pi[i])
temp[id] = 1
pi[i] = temp
return pi
def policy_iteration(self, r, p, method, initial='deterministic'):
"""
Args:
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
method: `exact` or `modified` (iterative)
initial: if `uniform`, policy is uniformly distributed at the start,
otherwise a deterministic policy is randomly generated
"""
t1 = datetime.now()
if method == 'exact':
policy_evaluation = self._policy_evaluation_exact
elif method =='modified':
policy_evaluation = self._policy_evaluation_modified
else:
raise ValueError("method must be 'exact' or 'modified'")
n_states, n_actions = p.shape[:2]
# Initial policy estimates
if initial=='uniform':
pi = self._initialize_uniform(p, n_states, n_actions)
else:
pi = self._initialize_deterministic(p, n_states, n_actions)
v = np.zeros(n_states)
# Main loop
policy_stable = False
it = 0
while policy_stable == False:
v = policy_evaluation(pi, v, r, p)
old_actions = pi
pi = self._policy_improvement(v, r, p)
if np.array_equal(pi, old_actions): policy_stable = True
it += 1
# Evaluate final policy
v = policy_evaluation(pi, v, r, p)
t2 = datetime.now()
seconds = (t2 - t1).total_seconds()
return pi, v, it, seconds
def value_iteration(self, r, p):
"""
Args:
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
Return;
pi: policy, |S| x |A|
v: state values, |S|
it: number of iterations
"""
t1 = datetime.now()
n_states, n_actions = p.shape[:2]
v = np.zeros(n_states)
max_iteration = 10000
for it in range(max_iteration):
q = r + self.gamma*np.einsum('ijk, k->ij', p, v) # get q values
q = ma.masked_array(q, mask=(np.sum(p,axis=2)-1)*(-1)) #mask invalid actions
v_new = np.max(q, axis=1) # state-values equal max possible values
v_new = v_new.filled(0) # Masked states should have value 0
if np.max(np.absolute(v - v_new)) < self.theta:
v = v_new
break;
v = v_new
# Derive new policy
pi = (q == q.max(axis=1)[:,None]).astype(int)
pi = pi.filled(0)
t2 = datetime.now()
seconds = (t2 - t1).total_seconds()
return pi, v, it+1, seconds
def policy_eval(self, pi, v, r, p):
"""
Evaluate policy by taking the inverse
Args:
pi: policy, array of shape |S| x |A|
r: rewards, array of shape |S| x |A|
p: state transition probabilities, array of shape |S| x |A| x |S|
Return:
v: 1D array with updated state values
"""
# Rewards according to policy: Hadamard product and row-wise sum
r_pi = np.einsum('ij,ij->i', pi, r)
# Policy-weighted transitions:
# multiply p by pi by broadcasting pi, then sum second axis
# result is an array of shape |S| x |S|
p_pi = np.einsum('ijk, ij->ik', p, pi)
v = np.dot(inv((np.eye(p_pi.shape[0]) - self.gamma*p_pi)), r_pi)
return v
gamma = 0.5
policy = np.array(
[[1,0],
[0,1],
[1,0]])
p_pi = np.array(
[[0.8, 0.4, 0],
[0.15, 0.5, 0],
[0.05, 0.1, 1]])
r_pi = np.array(
[[2,1,0]])
v = np.dot(inv((np.eye(p_pi.shape[0]) - gamma*p_pi)), r_pi)
class BasicMDP():
def __init__(self):
"""Very basic MDP to test policy/value iteration"""
# Transition probabilities is a 3D array of shape |S| x |A| x |S|
# the
self.p = np.array(
[[[0.5, 0.5],[0,1],[0,0]],
[[0.0, 0.0],[0,0],[0,1]]])
# Rewards is a function of state and action, i.e. r(s,a), shape |S| x |A|
self.r = np.array(
[[5, 10, 0],
[0, 0, -1]])
def print_info(pi, v, it, sec, title):
print("="*79)
print(title)
print("Final Policy:")
print_policy(pi,2)
print("Values:")
print_values(v,6)
print("compute seconds: ", sec)
print("iterations: ", it)
print()
def experiment_1():
gamma = 0.95
agent = MDPAgent(gamma)
env = BasicMDP()
title = "Policy Iteration with closed form policy evaluation"
pi1, v, it, sec = agent.policy_iteration(env.r, env.p, method='exact', initial='deterministic')
print_info(pi1,v,it,sec,title)
title = "Modified Policy Iteration with partial policy evaluation"
pi2, v, it, sec = agent.policy_iteration(env.r, env.p, method='modified', initial='deterministic')
print_info(pi2,v,it,sec,title)
title = "Value Iteration"
pi3, v, it, sec = agent.value_iteration(env.r, env.p)
print_info(pi3,v,it,sec,title)
if (np.array_equal(pi1,pi2) and np.array_equal(pi2, pi3)):
print("all policies are equal")
else:
print("policies not equal")
experiment_1()
def experiment_2():
gamma = 0.95
agent = MDPAgent(gamma)
env = BasicMDP()
trials = 100
pol_it = np.zeros(trials)
mod_it = np.zeros(trials)
val_it = np.zeros(trials)
pol_time = np.zeros(trials)
mod_time = np.zeros(trials)
val_time = np.zeros(trials)
for i in range(trials):
_, _, pol_it[i], pol_time[i] = agent.policy_iteration(env.r, env.p, method='exact', initial='deterministic')
_, _, mod_it[i], mod_time[i] = agent.policy_iteration(env.r, env.p, method='modified', initial='deterministic')
_, _, val_it[i], val_time[i] = agent.value_iteration(env.r, env.p)
print("Policy iteration: {:.4f} seconds, {:.2f} iterations".format(np.sum(pol_time)/trials, np.sum(pol_it)/trials))
print("Modified policy : {:.4f} seconds, {:.2f} iterations".format(np.sum(mod_time)/trials, np.sum(mod_it)/trials))
print("Value iteration : {:.4f} seconds, {:.2f} iterations".format(np.sum(val_time)/trials, np.sum(val_it)/trials))
experiment_2()
class GridWorld():
def __init__(self, rows, cols, terminal_states, reward_value):
"""
Creates a GridWorld of size `rows` X `cols` with the listed terminal states
Args:
rows: int
cols: int
terminal_states: list of int where each element is the grid index of the
terminal state. The grid's cells are numbered left to right, top to
bottom, starting with index 0.
"""
self.rows, self.cols = rows, cols
self.terminal_states = terminal_states
self.n_states = rows * cols # number of states
self.n_actions = 4 # left, up, right, down
self.p = self._init_dynamics(rows, cols, self.n_states, self.n_actions, terminal_states)
self.r = self._init_rewards(self.n_states, self.n_actions, reward_value, terminal_states)
def _init_dynamics(self, rows, cols, n_states, n_actions, terminal_states):
""" Returns model dynamics array of shape |S| x |A| x |S| """
# Empty transition array
p = np.zeros((n_states,n_actions,n_states))
# Add deterministic transitions by traversing an imaginary grid
for r in range(rows):
for c in range(cols):
cur_s = rows*r + c # current state
# left?
left_s = rows*r + c -1 # left state id
if (c-1) >= 0: p[cur_s,0, left_s] = 1
# up?
up_s = rows*(r - 1) + c # up state id
if (r-1) >= 0: p[cur_s, 1, up_s] = 1;
# right?
right_s = rows*r + c + 1 # right state id
if (c+1) < cols: p[cur_s, 2, right_s] = 1;
# down?
down_s = rows*(r + 1) + c # down state id
if (r+1) < rows: p[cur_s, 3, down_s] = 1;
# Terminal states have no actions
for t in terminal_states:
p[t] = 0
return p
def _init_rewards(self, n_states, n_actions, reward_value, terminal_states):
""" Returns reward matrix, shape |S| x |A| """
# Rewards are -1 on all actions. No rewards for terminal since no action
r = np.full((n_states, n_actions), reward_value)
for t in terminal_states:
r[t] = 0
return r
def render_policy(self, pi):
pass
def __str__(self):
""" Print the grid """
x = PrettyTable()
x.header = False
for r in range(self.rows):
row = []
for c in range(self.cols):
cur_s = self.rows*r + c # current state
if cur_s in self.terminal_states:
row.append('#')
else:
row.append('-')
x.add_row(row)
x.hrules = ALL
return x.get_string()
rows = cols = 4
terminal_states = [0,6,15]
env = GridWorld(rows, cols, terminal_states, reward_value=-1)
print(env)
def experiment_3():
rows = cols = 4
terminal_states = [0,6,15]
env = GridWorld(rows, cols, terminal_states, reward_value=-1)
gamma = 0.95
agent = MDPAgent(gamma)
title = "Policy Iteration with closed form policy evaluation"
pi1, v, it, sec = agent.policy_iteration(env.r, env.p, method='exact', initial='deterministic')
print(title)
print(sec)
title = "Modified Policy Iteration with partial policy evaluation"
pi2, v, it, sec = agent.policy_iteration(env.r, env.p, method='modified', initial='deterministic')
print(title)
print(sec)
title = "Value Iteration"
pi3, v, it, sec = agent.value_iteration(env.r, env.p)
print(title)
print(sec)
if (np.array_equal(pi1,pi2) and np.array_equal(pi2, pi3)):
print("all policies are equal")
else:
print("policies not equal")
experiment_3()
def multi_plot_data(x, data, names, xlabel):
""" data, names are lists of vectors """
for i, y in enumerate(data):
plt.plot(x, y, 'o', markersize=3, label=names[i])
plt.legend(loc='upper left', prop={'size': 16}, numpoints=10)
plt.xlabel(xlabel)
plt.ylabel("milliseconds")
plt.show()
def experiment_4():
rows = cols = 4
terminal_states = [0,6,15]
env = GridWorld(rows, cols, terminal_states, reward_value=-1)
trials = 10
samples = 200
gammas = np.linspace(0.001,1,endpoint=False,num=samples)
pol_time = np.zeros((trials, samples))
mod_time = np.zeros((trials, samples))
val_time = np.zeros((trials, samples))
for t in range(trials):
for i in range(samples):
agent = MDPAgent(gammas[i])
_, _, _, pol_time[t,i] = agent.policy_iteration(env.r, env.p, method='exact', initial='uniform')
_, _, _, mod_time[t,i] = agent.policy_iteration(env.r, env.p, method='modified', initial='uniform')
_, _, _, val_time[t,i] = agent.value_iteration(env.r, env.p)
# Plot data
pol_time = np.average(pol_time, axis=0)*1000
mod_time = np.average(mod_time, axis=0)*1000
val_time = np.average(val_time, axis=0)*1000
data = [pol_time, mod_time, val_time]
names = ["Policy Iteration", "Modified PI", "Value Iteration"]
multi_plot_data(gammas, data, names, xlabel="gamma")
experiment_4()
def experiment_5():
gamma = 0.95
agent = MDPAgent(gamma)
terminal_states = [0,6]
rows = cols = 5
env = GridWorld(rows, cols, terminal_states, reward_value=-1)
_, _, pol_it, pol_time = agent.policy_iteration(env.r, env.p, method='exact', initial='deterministic')
_, _, mod_it, mod_time = agent.policy_iteration(env.r, env.p, method='modified', initial='deterministic')
_, _, val_it, val_time = agent.value_iteration(env.r, env.p)
print("Policy iteration: {:.4f} seconds, {:.2f} iterations".format(pol_time, pol_it))
print("Modified policy : {:.4f} seconds, {:.2f} iterations".format(mod_time, mod_it))
print("Value iteration : {:.4f} seconds, {:.2f} iterations".format(val_time, val_it))
experiment_5()
| 0.652906 | 0.988992 |
<a href="https://colab.research.google.com/github/dvschultz/stylegan3/blob/main/SG3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# StyleGAN3
By [Derrick Schultz](https://twitter.com/dvsch), with contributions from [crimeacs](https://twitter.com/EarthML1)
Just starting this...expect more updates soon.
If you find this helpful, please consider backing me on [Patreon](https://www.patreon.com/bustbright) or becoming a [YouTube channel member](https://www.youtube.com/channel/UCaZuPdmZ380SFUMKHVsv_AA/join).
## Setup
```
!nvidia-smi -L
from google.colab import drive
drive.mount('/content/drive')
import os
if os.path.isdir("/content/drive/MyDrive/colab-sg3"):
%cd "/content/drive/MyDrive/colab-sg3/stylegan3/"
elif os.path.isdir("/content/drive/"):
#install script
%cd "/content/drive/MyDrive/"
!mkdir colab-sg3
%cd colab-sg3
!git clone https://github.com/dvschultz/stylegan3
%cd stylegan3
!mkdir downloads
!mkdir datasets
!mkdir pretrained
!gdown --id 1-5xZkD8ajXw1DdopTkH_rAoCsD72LhKU -O /content/drive/MyDrive/colab-sg2-ada-pytorch/stylegan2-ada-pytorch/pretrained/wikiart.pkl
else:
!git clone https://github.com/dvschultz/stylegan3
%cd stylegan3
!mkdir downloads
!mkdir datasets
!mkdir pretrained
%cd pretrained
!gdown --id 1-5xZkD8ajXw1DdopTkH_rAoCsD72LhKU
%cd ../
!pip install Ninja opensimplex
```
This cell will update to the latest repo. Git and Drive/Colab don’t play as nicely as I’d like so 🤞. The other option is to delete your folder in Drive (after saving out `/results` and `/datasets`!) and running the script above to replace the entire folder.
```
%cd "/content/drive/My Drive/colab-sg2-ada-pytorch/stylegan2-ada-pytorch"
!git config --global user.name "test"
!git config --global user.email "test@test.com"
!git fetch origin
!git pull
!git stash
!git checkout origin/main -- train.py gen_images.py gen_video.py README.md training/training_loop.py
```
## Convert/Create Dataset
Pass a folder of images (just .pngs? TK) to create a zip file.
```
!python dataset_tool.py --source=/content/tmp/drawn-gems-1024 --dest=./datasets/drawn-gems-1024.zip
```
## Training
Before you start training, read [this](https://github.com/dvschultz/stylegan3/blob/main/docs/configs.md).
Working Notes:
- It appears that you must use an SG3 pre-trained model for transfer learning. I _think_ you also want to match config to the pretrained model (`t` with `t`, `r` with `r`).
- For an `A100` I’ve found you can use a `--batch-gpu=8`. For other GPUs I recommend `--batch-gpu=4`.
- I see `~205 sec/kimg` on A100s, and `~325 sec/kimg` on V100s (1024, `r` config). This seems slightly slower than what [NVIDIA reports.](https://github.com/dvschultz/stylegan3/blob/main/docs/configs.md)
```
!python train.py --help
!python train.py --outdir=./results --cfg=stylegan3-r --data=./datasets/drawn-gems-1024.zip \
--gpus=1 --batch=32 --batch-gpu=4 --gamma=10.0 --mirror=1 --kimg=5000 --snap=1 \
--resume=/content/drive/MyDrive/colab-sg3/stylegan3/results/00014-stylegan3-r-drawn-gems-1024-gpus1-batch32-gamma10/network-snapshot-000104.pkl --metrics=None
```
## Image Generation
```
!python gen_images.py --help
!python gen_images.py --outdir=out --trunc=1 --seeds=2 \
--network=https://api.ngc.nvidia.com/v2/models/nvidia/research/stylegan3/versions/1/files/stylegan3-r-afhqv2-512x512.pkl
```
## Video Generation
```
!python gen_video.py --help
!python gen_video.py --output=/content/lerp.mp4 --trunc=1 --seeds=100-124 --grid=1x1 --w-frames=72 \
--network=/content/drive/MyDrive/colab-sg3/stylegan3/results/00014-stylegan3-r-drawn-gems-1024-gpus1-batch32-gamma10/network-snapshot-000104.pkl
```
|
github_jupyter
|
!nvidia-smi -L
from google.colab import drive
drive.mount('/content/drive')
import os
if os.path.isdir("/content/drive/MyDrive/colab-sg3"):
%cd "/content/drive/MyDrive/colab-sg3/stylegan3/"
elif os.path.isdir("/content/drive/"):
#install script
%cd "/content/drive/MyDrive/"
!mkdir colab-sg3
%cd colab-sg3
!git clone https://github.com/dvschultz/stylegan3
%cd stylegan3
!mkdir downloads
!mkdir datasets
!mkdir pretrained
!gdown --id 1-5xZkD8ajXw1DdopTkH_rAoCsD72LhKU -O /content/drive/MyDrive/colab-sg2-ada-pytorch/stylegan2-ada-pytorch/pretrained/wikiart.pkl
else:
!git clone https://github.com/dvschultz/stylegan3
%cd stylegan3
!mkdir downloads
!mkdir datasets
!mkdir pretrained
%cd pretrained
!gdown --id 1-5xZkD8ajXw1DdopTkH_rAoCsD72LhKU
%cd ../
!pip install Ninja opensimplex
%cd "/content/drive/My Drive/colab-sg2-ada-pytorch/stylegan2-ada-pytorch"
!git config --global user.name "test"
!git config --global user.email "test@test.com"
!git fetch origin
!git pull
!git stash
!git checkout origin/main -- train.py gen_images.py gen_video.py README.md training/training_loop.py
!python dataset_tool.py --source=/content/tmp/drawn-gems-1024 --dest=./datasets/drawn-gems-1024.zip
!python train.py --help
!python train.py --outdir=./results --cfg=stylegan3-r --data=./datasets/drawn-gems-1024.zip \
--gpus=1 --batch=32 --batch-gpu=4 --gamma=10.0 --mirror=1 --kimg=5000 --snap=1 \
--resume=/content/drive/MyDrive/colab-sg3/stylegan3/results/00014-stylegan3-r-drawn-gems-1024-gpus1-batch32-gamma10/network-snapshot-000104.pkl --metrics=None
!python gen_images.py --help
!python gen_images.py --outdir=out --trunc=1 --seeds=2 \
--network=https://api.ngc.nvidia.com/v2/models/nvidia/research/stylegan3/versions/1/files/stylegan3-r-afhqv2-512x512.pkl
!python gen_video.py --help
!python gen_video.py --output=/content/lerp.mp4 --trunc=1 --seeds=100-124 --grid=1x1 --w-frames=72 \
--network=/content/drive/MyDrive/colab-sg3/stylegan3/results/00014-stylegan3-r-drawn-gems-1024-gpus1-batch32-gamma10/network-snapshot-000104.pkl
| 0.238994 | 0.757593 |
```
import copy
import numpy
from numpy import exp, square
na = numpy.newaxis
imag = numpy.imag
import scipy
import scipy.special
from scipy.special import erfc, exp1
import cryspy
f_name = "tof.rcif"
rhochi_obj = cryspy.file_to_globaln(f_name)
def calc_y_z_u_v(alpha, beta, sigma, delta_2d):
"""Calculate y, z, u, v
y = (alpha * sigma**2 + delta)/(sigma * 2**0.5)
z = (beta * sigma**2 - delta)/(sigma * 2**0.5)
u = 0.5 * alpha * (alpha*sigma**2 + 2 delta)
v = 0.5 * beta * (beta*sigma**2 - 2 delta)
"""
sigma_sq = square(sigma)
y = (alpha * sigma/(2.**0.5))[:, na] + delta_2d/(sigma*2.**0.5)[:, na]
z = (beta * sigma/(2.**0.5))[:, na] - delta_2d/(sigma*2.**0.5)[:, na]
u = (0.5*square(alpha)*sigma_sq)[:, na] + delta_2d*alpha[:, na]
v = (0.5*square(beta)*sigma_sq)[:, na] - delta_2d*beta[:, na]
return y, z, u, v
def calc_hpv_eta(h_g, h_l):
"""pseudo-Voight function
calculate h_pV and eta based on Gauss and Lorentz Size
"""
h_g_2, h_l_2 = h_g**2, h_l**2
h_g_3, h_l_3 = h_g_2*h_g, h_l_2*h_l
h_g_4, h_l_4 = h_g_3*h_g, h_l_3*h_l
h_g_5, h_l_5 = h_g_4*h_g, h_l_4*h_l
c_2, c_3, c_4, c_5 = 2.69269, 2.42843, 4.47163, 0.07842
h_pv = (h_g_5 + c_2*h_g_4*h_l + c_3*h_g_3*h_l_2 +
c_4*h_g_2*h_l_3 + c_5*h_g*h_l_4 + h_l_5)**0.2
hh = h_l*1./h_pv
eta = 1.36603*hh - 0.47719*hh**2 + 0.11116*hh**3
return h_pv, eta
def calc_sigma_gamma(
d, sigma0, sigma1, sigma2, gamma0, gamma1, gamma2,
size_g: float = 0., size_l: float = 0., strain_g: float = 0.,
strain_l: float = 0.):
"""Calculate H_G (sigma) and H_L (gamma)
H_G**2 = (sigma2+size_g)*d**4 + (sigma1+strain_g)*d**2 + sigma0
H_L = (gamma2+size_l)*d**2 + (sigma1+strain_l)*d + sigma0
"""
d_sq = numpy.square(d)
d_sq_sq = numpy.square(d_sq)
h_g_sq = (sigma2+size_g) * d_sq_sq + (sigma1+strain_l) * d_sq + sigma0
h_l = (gamma2+size_l) * d_sq + (gamma1+strain_l) * d + gamma0
h_g = numpy.sqrt(h_g_sq)
return h_g, h_l
def calc_hpv_eta(h_g, h_l):
"""pseudo-Voight function
calculate h_pV and eta based on Gauss and Lorentz Size
"""
h_g_2, h_l_2 = h_g**2, h_l**2
h_g_3, h_l_3 = h_g_2*h_g, h_l_2*h_l
h_g_4, h_l_4 = h_g_3*h_g, h_l_3*h_l
h_g_5, h_l_5 = h_g_4*h_g, h_l_4*h_l
c_2, c_3, c_4, c_5 = 2.69269, 2.42843, 4.47163, 0.07842
h_pv = (h_g_5 + c_2*h_g_4*h_l + c_3*h_g_3*h_l_2 +
c_4*h_g_2*h_l_3 + c_5*h_g*h_l_4 + h_l_5)**0.2
hh = h_l*1./h_pv
eta = 1.36603*hh - 0.47719*hh**2 + 0.11116*hh**3
return h_pv, eta
tof_obj = rhochi_obj.tof_tof
crystal = rhochi_obj.crystal_cecual
tof_meas = tof_obj.tof_meas
tof_parameters = tof_obj.tof_parameters
tof_profile = tof_obj.tof_profile
cell = crystal.cell
time = tof_meas.numpy_time
d = tof_parameters.calc_d_by_time(time)
d_min, d_max = tof_parameters.calc_d_min_max(time)
sthovl_min = 0.5/d_max
sthovl_max = 0.5/d_min
index_h, index_k, index_l, mult = crystal.calc_hkl(sthovl_min, sthovl_max)
sthovl_hkl = cell.calc_sthovl(index_h, index_k, index_l)
d_hkl = 0.5/sthovl_hkl
time_hkl = tof_parameters.calc_time_by_d(d_hkl)
np_shape_2d = tof_profile.calc_peak_shape_function(
d, time, time_hkl, size_g=0., strain_g=0.,
size_l=0., strain_l=0.)
np_shape_2d.max()
alpha = tof_profile.alpha0 + tof_profile.alpha1 / d
beta = tof_profile.beta0 + tof_profile.beta1 / d**4
sigma, gamma = calc_sigma_gamma(
d, tof_profile.sigma0, tof_profile.sigma1, tof_profile.sigma2, tof_profile.gamma0,
tof_profile.gamma1, tof_profile.gamma2, size_g=0, size_l=0,
strain_g=0, strain_l=0)
two_over_pi = 2.*numpy.pi
norm = 0.5*alpha*beta/(alpha+beta)
time_2d, time_hkl_2d = numpy.meshgrid(time, time_hkl, indexing="ij")
delta_2d = time_2d-time_hkl_2d
# FIXME: it has to be checked
# sigma = gamma*(inv_8ln2)**0.5
h_pv, eta = calc_hpv_eta(sigma, gamma)
y, z, u, v = calc_y_z_u_v(alpha, beta, sigma, delta_2d)
exp_u = exp(u)
exp_v = exp(v)
exp_u[numpy.isinf(exp_u)] = 1e200
exp_v[numpy.isinf(exp_v)] = 1e200
profile_g_2d = norm[:, na] * (exp_u * erfc(y) + exp_v * erfc(z))
delta_sec_2d = copy.deepcopy(delta_2d)
delta_sec_2d[delta_2d_sec < -10] = -10
delta_sec_2d[delta_2d_sec > 10] = 10
z1_2d = alpha[:, na]*delta_sec_2d + (1j*0.5*alpha*gamma)[:, na]
z2_2d = -beta[:, na]*delta_sec_2d + (1j*0.5*beta*gamma)[:, na]
imag_fz1_2d = imag(exp1(z1_2d))
imag_fz2_2d = imag(exp1(z2_2d))
# imag_fz1_2d[numpy.isnan(imag_fz1_2d)]=0.
# imag_fz1_2d[numpy.isinf(imag_fz1_2d)]=0.
# imag_fz1_2d[numpy.isneginf(imag_fz1_2d)]=0.
# imag_fz2_2d[numpy.isnan(imag_fz2_2d)]=0.
# imag_fz2_2d[numpy.isinf(imag_fz2_2d)]=0.
# imag_fz2_2d[numpy.isneginf(imag_fz2_2d)]=0.
oml_a_2d = -imag_fz1_2d * two_over_pi
oml_b_2d = -imag_fz2_2d * two_over_pi
profile_l_2d = norm[:, na] * (oml_a_2d + oml_b_2d)
profile_l_2d.min()
norm = 0.5*alpha*beta/(alpha+beta)
time_2d, time_hkl_2d = numpy.meshgrid(time, time_hkl, indexing="ij")
delta_2d = time_2d-time_hkl_2d
y, z, u, v = calc_y_z_u_v(alpha, beta, sigma, delta_2d)
exp_u = exp(u)
exp_v = exp(v)
exp_u[numpy.isinf(exp_u)] = 1e200
exp_v[numpy.isinf(exp_v)] = 1e200
res_2d = norm[:, na] * (exp_u * erfc(y) + exp_v * erfc(z))
(exp_u * erfc(y)).max()
(exp_v * erfc(z)).max()
norm.max()
res_2d.max()
```
|
github_jupyter
|
import copy
import numpy
from numpy import exp, square
na = numpy.newaxis
imag = numpy.imag
import scipy
import scipy.special
from scipy.special import erfc, exp1
import cryspy
f_name = "tof.rcif"
rhochi_obj = cryspy.file_to_globaln(f_name)
def calc_y_z_u_v(alpha, beta, sigma, delta_2d):
"""Calculate y, z, u, v
y = (alpha * sigma**2 + delta)/(sigma * 2**0.5)
z = (beta * sigma**2 - delta)/(sigma * 2**0.5)
u = 0.5 * alpha * (alpha*sigma**2 + 2 delta)
v = 0.5 * beta * (beta*sigma**2 - 2 delta)
"""
sigma_sq = square(sigma)
y = (alpha * sigma/(2.**0.5))[:, na] + delta_2d/(sigma*2.**0.5)[:, na]
z = (beta * sigma/(2.**0.5))[:, na] - delta_2d/(sigma*2.**0.5)[:, na]
u = (0.5*square(alpha)*sigma_sq)[:, na] + delta_2d*alpha[:, na]
v = (0.5*square(beta)*sigma_sq)[:, na] - delta_2d*beta[:, na]
return y, z, u, v
def calc_hpv_eta(h_g, h_l):
"""pseudo-Voight function
calculate h_pV and eta based on Gauss and Lorentz Size
"""
h_g_2, h_l_2 = h_g**2, h_l**2
h_g_3, h_l_3 = h_g_2*h_g, h_l_2*h_l
h_g_4, h_l_4 = h_g_3*h_g, h_l_3*h_l
h_g_5, h_l_5 = h_g_4*h_g, h_l_4*h_l
c_2, c_3, c_4, c_5 = 2.69269, 2.42843, 4.47163, 0.07842
h_pv = (h_g_5 + c_2*h_g_4*h_l + c_3*h_g_3*h_l_2 +
c_4*h_g_2*h_l_3 + c_5*h_g*h_l_4 + h_l_5)**0.2
hh = h_l*1./h_pv
eta = 1.36603*hh - 0.47719*hh**2 + 0.11116*hh**3
return h_pv, eta
def calc_sigma_gamma(
d, sigma0, sigma1, sigma2, gamma0, gamma1, gamma2,
size_g: float = 0., size_l: float = 0., strain_g: float = 0.,
strain_l: float = 0.):
"""Calculate H_G (sigma) and H_L (gamma)
H_G**2 = (sigma2+size_g)*d**4 + (sigma1+strain_g)*d**2 + sigma0
H_L = (gamma2+size_l)*d**2 + (sigma1+strain_l)*d + sigma0
"""
d_sq = numpy.square(d)
d_sq_sq = numpy.square(d_sq)
h_g_sq = (sigma2+size_g) * d_sq_sq + (sigma1+strain_l) * d_sq + sigma0
h_l = (gamma2+size_l) * d_sq + (gamma1+strain_l) * d + gamma0
h_g = numpy.sqrt(h_g_sq)
return h_g, h_l
def calc_hpv_eta(h_g, h_l):
"""pseudo-Voight function
calculate h_pV and eta based on Gauss and Lorentz Size
"""
h_g_2, h_l_2 = h_g**2, h_l**2
h_g_3, h_l_3 = h_g_2*h_g, h_l_2*h_l
h_g_4, h_l_4 = h_g_3*h_g, h_l_3*h_l
h_g_5, h_l_5 = h_g_4*h_g, h_l_4*h_l
c_2, c_3, c_4, c_5 = 2.69269, 2.42843, 4.47163, 0.07842
h_pv = (h_g_5 + c_2*h_g_4*h_l + c_3*h_g_3*h_l_2 +
c_4*h_g_2*h_l_3 + c_5*h_g*h_l_4 + h_l_5)**0.2
hh = h_l*1./h_pv
eta = 1.36603*hh - 0.47719*hh**2 + 0.11116*hh**3
return h_pv, eta
tof_obj = rhochi_obj.tof_tof
crystal = rhochi_obj.crystal_cecual
tof_meas = tof_obj.tof_meas
tof_parameters = tof_obj.tof_parameters
tof_profile = tof_obj.tof_profile
cell = crystal.cell
time = tof_meas.numpy_time
d = tof_parameters.calc_d_by_time(time)
d_min, d_max = tof_parameters.calc_d_min_max(time)
sthovl_min = 0.5/d_max
sthovl_max = 0.5/d_min
index_h, index_k, index_l, mult = crystal.calc_hkl(sthovl_min, sthovl_max)
sthovl_hkl = cell.calc_sthovl(index_h, index_k, index_l)
d_hkl = 0.5/sthovl_hkl
time_hkl = tof_parameters.calc_time_by_d(d_hkl)
np_shape_2d = tof_profile.calc_peak_shape_function(
d, time, time_hkl, size_g=0., strain_g=0.,
size_l=0., strain_l=0.)
np_shape_2d.max()
alpha = tof_profile.alpha0 + tof_profile.alpha1 / d
beta = tof_profile.beta0 + tof_profile.beta1 / d**4
sigma, gamma = calc_sigma_gamma(
d, tof_profile.sigma0, tof_profile.sigma1, tof_profile.sigma2, tof_profile.gamma0,
tof_profile.gamma1, tof_profile.gamma2, size_g=0, size_l=0,
strain_g=0, strain_l=0)
two_over_pi = 2.*numpy.pi
norm = 0.5*alpha*beta/(alpha+beta)
time_2d, time_hkl_2d = numpy.meshgrid(time, time_hkl, indexing="ij")
delta_2d = time_2d-time_hkl_2d
# FIXME: it has to be checked
# sigma = gamma*(inv_8ln2)**0.5
h_pv, eta = calc_hpv_eta(sigma, gamma)
y, z, u, v = calc_y_z_u_v(alpha, beta, sigma, delta_2d)
exp_u = exp(u)
exp_v = exp(v)
exp_u[numpy.isinf(exp_u)] = 1e200
exp_v[numpy.isinf(exp_v)] = 1e200
profile_g_2d = norm[:, na] * (exp_u * erfc(y) + exp_v * erfc(z))
delta_sec_2d = copy.deepcopy(delta_2d)
delta_sec_2d[delta_2d_sec < -10] = -10
delta_sec_2d[delta_2d_sec > 10] = 10
z1_2d = alpha[:, na]*delta_sec_2d + (1j*0.5*alpha*gamma)[:, na]
z2_2d = -beta[:, na]*delta_sec_2d + (1j*0.5*beta*gamma)[:, na]
imag_fz1_2d = imag(exp1(z1_2d))
imag_fz2_2d = imag(exp1(z2_2d))
# imag_fz1_2d[numpy.isnan(imag_fz1_2d)]=0.
# imag_fz1_2d[numpy.isinf(imag_fz1_2d)]=0.
# imag_fz1_2d[numpy.isneginf(imag_fz1_2d)]=0.
# imag_fz2_2d[numpy.isnan(imag_fz2_2d)]=0.
# imag_fz2_2d[numpy.isinf(imag_fz2_2d)]=0.
# imag_fz2_2d[numpy.isneginf(imag_fz2_2d)]=0.
oml_a_2d = -imag_fz1_2d * two_over_pi
oml_b_2d = -imag_fz2_2d * two_over_pi
profile_l_2d = norm[:, na] * (oml_a_2d + oml_b_2d)
profile_l_2d.min()
norm = 0.5*alpha*beta/(alpha+beta)
time_2d, time_hkl_2d = numpy.meshgrid(time, time_hkl, indexing="ij")
delta_2d = time_2d-time_hkl_2d
y, z, u, v = calc_y_z_u_v(alpha, beta, sigma, delta_2d)
exp_u = exp(u)
exp_v = exp(v)
exp_u[numpy.isinf(exp_u)] = 1e200
exp_v[numpy.isinf(exp_v)] = 1e200
res_2d = norm[:, na] * (exp_u * erfc(y) + exp_v * erfc(z))
(exp_u * erfc(y)).max()
(exp_v * erfc(z)).max()
norm.max()
res_2d.max()
| 0.425367 | 0.523542 |
# Machine Learning Engineer Nanodegree
## Unsupervised Learning
## Project 3: Creating Customer Segments
Welcome to the third project of the Machine Learning Engineer Nanodegree! In this notebook, some template code has already been provided for you, and it will be your job to implement the additional functionality necessary to successfully complete this project. Sections that begin with **'Implementation'** in the header indicate that the following block of code will require additional functionality which you must provide. Instructions will be provided for each section and the specifics of the implementation are marked in the code block with a `'TODO'` statement. Please be sure to read the instructions carefully!
In addition to implementing code, there will be questions that you must answer which relate to the project and your implementation. Each section where you will answer a question is preceded by a **'Question X'** header. Carefully read each question and provide thorough answers in the following text boxes that begin with **'Answer:'**. Your project submission will be evaluated based on your answers to each of the questions and the implementation you provide.
>**Note:** Code and Markdown cells can be executed using the **Shift + Enter** keyboard shortcut. In addition, Markdown cells can be edited by typically double-clicking the cell to enter edit mode.
## Getting Started
In this project, you will analyze a dataset containing data on various customers' annual spending amounts (reported in *monetary units*) of diverse product categories for internal structure. One goal of this project is to best describe the variation in the different types of customers that a wholesale distributor interacts with. Doing so would equip the distributor with insight into how to best structure their delivery service to meet the needs of each customer.
The dataset for this project can be found on the [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Wholesale+customers). For the purposes of this project, the features `'Channel'` and `'Region'` will be excluded in the analysis — with focus instead on the six product categories recorded for customers.
Run the code block below to load the wholesale customers dataset, along with a few of the necessary Python libraries required for this project. You will know the dataset loaded successfully if the size of the dataset is reported.
```
# Import libraries necessary for this project
import numpy as np
import pandas as pd
import renders as rs
from IPython.display import display # Allows the use of display() for DataFrames
# Show matplotlib plots inline (nicely formatted in the notebook)
%matplotlib inline
# Load the wholesale customers dataset
try:
data = pd.read_csv("customers.csv")
data.drop(['Region', 'Channel'], axis = 1, inplace = True)
print "Wholesale customers dataset has {} samples with {} features each.".format(*data.shape)
except:
print "Dataset could not be loaded. Is the dataset missing?"
```
## Data Exploration
In this section, you will begin exploring the data through visualizations and code to understand how each feature is related to the others. You will observe a statistical description of the dataset, consider the relevance of each feature, and select a few sample data points from the dataset which you will track through the course of this project.
Run the code block below to observe a statistical description of the dataset. Note that the dataset is composed of six important product categories: **'Fresh'**, **'Milk'**, **'Grocery'**, **'Frozen'**, **'Detergents_Paper'**, and **'Delicatessen'**. Consider what each category represents in terms of products you could purchase.
```
# Display a description of the dataset
display(data.describe())
# XING: Gaussian distribution fitting used in Question 3
from scipy.stats import norm
def gaussian_func(x, *p):
A, mu, sigma = p
return A * np.exp(-(x-mu)**2 / (2.*sigma**2))
# run gaussian fits for all features
gaussian_fits = []
for column in data:
feature = data[column]
mu, sigma = norm.fit(feature)
feature_fit = gaussian_func(feature, 1, mu, sigma)
error = np.linalg.norm(feature - feature_fit)
gaussian_fits.append([mu, sigma, error / (len(feature) * feature.std())])
print "\n Gaussian distribution fitting of features"
gaussian_fits = pd.DataFrame(np.array(gaussian_fits).T,
columns = data.columns,
index = ['mean', 'var', 'error/(N * std)'])
display(gaussian_fits)
```
### Implementation: Selecting Samples
To get a better understanding of the customers and how their data will transform through the analysis, it would be best to select a few sample data points and explore them in more detail. In the code block below, add **three** indices of your choice to the `indices` list which will represent the customers to track. It is suggested to try different sets of samples until you obtain customers that vary significantly from one another.
```
# TODO: Select three indices of your choice you wish to sample from the dataset
indices = [23, 27, 412]
# Create a DataFrame of the chosen samples
samples = pd.DataFrame(data.loc[indices], columns = data.keys()).reset_index(drop = True)
print "Chosen samples of wholesale customers dataset:"
display(samples)
# XING: show devations of each feature from its mean measured by std
mean_data = np.mean(data)
std_data = np.std(data)
deviation_samples = (samples - mean_data) / std_data
print "\nDeviation of chosen samples of wholesale customers dataset in mean+deviation*std:"
display(deviation_samples)
```
### Question 1
Consider the total purchase cost of each product category and the statistical description of the dataset above for your sample customers.
*What kind of establishment (customer) could each of the three samples you've chosen represent?*
**Hint:** Examples of establishments include places like markets, cafes, and retailers, among many others. Avoid using names for establishments, such as saying *"McDonalds"* when describing a sample customer as a restaurant.
**Answer:**
Patterns that may help identify the types of wholesale distributer:
1. total value of produces being sold indicates the scale of distributer
2. the statistics of produces sold, especially those deviate a lot (+-1.0 std value) from mean value, implies the type of the distributer
Sample | Type | Reason
--- | --- | --- | ---
0 | Supermarket | all kinds of produces are sold much more than average value
1 | Greengrocer | the main produce being sold is fresh produce, while the total amount of produces is below average
2 | Convenience store | the main produce being sold is grocery, while the total amount of produces is below average
- Reference: [wikipedia](https://en.wikipedia.org/wiki/Grocery_store#Types)
### Implementation: Feature Relevance
One interesting thought to consider is if one (or more) of the six product categories is actually relevant for understanding customer purchasing. That is to say, is it possible to determine whether customers purchasing some amount of one category of products will necessarily purchase some proportional amount of another category of products? We can make this determination quite easily by training a supervised regression learner on a subset of the data with one feature removed, and then score how well that model can predict the removed feature.
In the code block below, you will need to implement the following:
- Assign `new_data` a copy of the data by removing a feature of your choice using the `DataFrame.drop` function.
- Use `sklearn.cross_validation.train_test_split` to split the dataset into training and testing sets.
- Use the removed feature as your target label. Set a `test_size` of `0.25` and set a `random_state`.
- Import a decision tree regressor, set a `random_state`, and fit the learner to the training data.
- Report the prediction score of the testing set using the regressor's `score` function.
```
from sklearn.cross_validation import train_test_split
from sklearn.tree import DecisionTreeRegressor
# TODO: Make a copy of the DataFrame, using the 'drop' function to drop the given feature
new_data = data.copy()
names = ['Fresh', 'Milk', 'Grocery', 'Frozen', 'Detergents_Paper', 'Delicatessen']
# XING: train and evaluate for each feature
scores = []
for name in names:
label = new_data[name]
features = new_data.drop([name], axis=1)
# TODO: Split the data into training and testing sets using the given feature as the target
X_train, X_test, y_train, y_test = train_test_split(features, label, test_size=0.25, random_state=1)
# TODO: Create a decision tree regressor and fit it to the training set
regressor = DecisionTreeRegressor(random_state=1)
regressor.fit(X_train, y_train)
# TODO: Report the score of the prediction using the testing set
score = regressor.score(X_test, y_test)
scores.append(score)
# display features and scores
result = pd.DataFrame(np.array([names, scores]).T, columns=['Feature', 'Score'])
display(result)
```
### Question 2
*Which feature did you attempt to predict? What was the reported prediction score? Is this feature is necessary for identifying customers' spending habits?*
**Hint:** The coefficient of determination, `R^2`, is scored between 0 and 1, with 1 being a perfect fit. A negative `R^2` implies the model fails to fit the data.
**Answer:**
As shown above, are features are predicated.
1. Predication with **higher score** (close to 1.0) means the training features are likely to predicate the label feature, namely, the label feature is more **dependent on** the other features, which makes it **unnecessary** for identifying customer's spending habits.
2. In contrast, predication with **lower score** (negative value) indicates the labeling feature is **necessary** for learning algorithm.
3. Thus at least one of `Detergents_Paper` or `Grocery` tends to be redundant.
### Visualize Feature Distributions
To get a better understanding of the dataset, we can construct a scatter matrix of each of the six product features present in the data. If you found that the feature you attempted to predict above is relevant for identifying a specific customer, then the scatter matrix below may not show any correlation between that feature and the others. Conversely, if you believe that feature is not relevant for identifying a specific customer, the scatter matrix might show a correlation between that feature and another feature in the data. Run the code block below to produce a scatter matrix.
```
# Produce a scatter matrix for each pair of features in the data
pd.scatter_matrix(data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');
```
### Question 3
*Are there any pairs of features which exhibit some degree of correlation? Does this confirm or deny your suspicions about the relevance of the feature you attempted to predict? How is the data for those features distributed?*
**Hint:** Is the data normally distributed? Where do most of the data points lie?
**Answer:**
1. **Are there any pairs of features which exhibit some degree of correlation?**
There is obvious correlation between `Detergents_Paper` and `Grocery`.
There may be correlation between `Detergents_Paper` and `Milk`, `Grocery` and `Milk`.
2. **Does this confirm or deny your suspicions about the relevance of the feature you attempted to predict?**
It confirms my suspicions about the relevance of the feature in Question 2.
3. **How is the data for those features distributed?**
The data distributes plot looks more like a lognormal or F distribution.
## Data Preprocessing
In this section, you will preprocess the data to create a better representation of customers by performing a scaling on the data and detecting (and optionally removing) outliers. Preprocessing data is often times a critical step in assuring that results you obtain from your analysis are significant and meaningful.
### Implementation: Feature Scaling
If data is not normally distributed, especially if the mean and median vary significantly (indicating a large skew), it is most [often appropriate](http://econbrowser.com/archives/2014/02/use-of-logarithms-in-economics) to apply a non-linear scaling — particularly for financial data. One way to achieve this scaling is by using a [Box-Cox test](http://scipy.github.io/devdocs/generated/scipy.stats.boxcox.html), which calculates the best power transformation of the data that reduces skewness. A simpler approach which can work in most cases would be applying the natural logarithm.
In the code block below, you will need to implement the following:
- Assign a copy of the data to `log_data` after applying a logarithm scaling. Use the `np.log` function for this.
- Assign a copy of the sample data to `log_samples` after applying a logrithm scaling. Again, use `np.log`.
```
# TODO: Scale the data using the natural logarithm
log_data = np.log(data)
# TODO: Scale the sample data using the natural logarithm
log_samples = np.log(samples)
# Produce a scatter matrix for each pair of newly-transformed features
pd.scatter_matrix(log_data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');
```
### Observation
After applying a natural logarithm scaling to the data, the distribution of each feature should appear much more normal. For any pairs of features you may have identified earlier as being correlated, observe here whether that correlation is still present (and whether it is now stronger or weaker than before).
Run the code below to see how the sample data has changed after having the natural logarithm applied to it.
```
# Display the log-transformed sample data
display(log_samples)
```
### Implementation: Outlier Detection
Detecting outliers in the data is extremely important in the data preprocessing step of any analysis. The presence of outliers can often skew results which take into consideration these data points. There are many "rules of thumb" for what constitutes an outlier in a dataset. Here, we will use [Tukey's Method for identfying outliers](http://datapigtechnologies.com/blog/index.php/highlighting-outliers-in-your-data-with-the-tukey-method/): An *outlier step* is calculated as 1.5 times the interquartile range (IQR). A data point with a feature that is beyond an outlier step outside of the IQR for that feature is considered abnormal.
In the code block below, you will need to implement the following:
- Assign the value of the 25th percentile for the given feature to `Q1`. Use `np.percentile` for this.
- Assign the value of the 75th percentile for the given feature to `Q3`. Again, use `np.percentile`.
- Assign the calculation of an outlier step for the given feature to `step`.
- Optionally remove data points from the dataset by adding indices to the `outliers` list.
**NOTE:** If you choose to remove any outliers, ensure that the sample data does not contain any of these points!
Once you have performed this implementation, the dataset will be stored in the variable `good_data`.
```
bad_indexes = {}
# For each feature find the data points with extreme high or low values
for feature in log_data.keys():
feature_data = log_data[feature]
# TODO: Calculate Q1 (25th percentile of the data) for the given feature
Q1 = np.percentile(feature_data, 25)
# TODO: Calculate Q3 (75th percentile of the data) for the given feature
Q3 = np.percentile(feature_data, 75)
# TODO: Use the interquartile range to calculate an outlier step (1.5 times the interquartile range)
step = 1.5 * (Q3 - Q1)
feature_outliers = log_data[~((feature_data >= Q1 - step) & (feature_data <= Q3 + step))]
for i, r in feature_data.iteritems():
if not (Q1 - step <= r <= Q3 + step):
if i not in bad_indexes:
bad_indexes[i] = 1
else:
bad_indexes[i] += 1
# Display the outliers
print "Data points considered outliers for the feature '{}':".format(feature)
display(feature_outliers)
# OPTIONAL: Select the indices for data points you wish to remove
# remove features with more than one outliers
outliers = [i for i, n in bad_indexes.items() if n > 1]
# Remove the outliers, if any were specified
good_data = log_data.drop(log_data.index[outliers]).reset_index(drop = True)
# XING: display data points with more than one outlier features
print "\nData points with more than one outlier features"
print sorted(outliers)
```
### Question 4
*Are there any data points considered outliers for more than one feature based on the definition above? Should these data points be removed from the dataset? If any data points were added to the `outliers` list to be removed, explain why.*
**Answer:**
Yes.
Data points at row [65, 66, 142, 154] has more than one outlier features, they should be romoved from the dataset, because they are more likely to be true outliers than others.
For ones with one feature outlier, I decided to keep them as single outlier feature may be the desirable pattern in the datasets. Removing them could cause underfitting.
## Feature Transformation
In this section you will use principal component analysis (PCA) to draw conclusions about the underlying structure of the wholesale customer data. Since using PCA on a dataset calculates the dimensions which best maximize variance, we will find which compound combinations of features best describe customers.
### Implementation: PCA
Now that the data has been scaled to a more normal distribution and has had any necessary outliers removed, we can now apply PCA to the `good_data` to discover which dimensions about the data best maximize the variance of features involved. In addition to finding these dimensions, PCA will also report the *explained variance ratio* of each dimension — how much variance within the data is explained by that dimension alone. Note that a component (dimension) from PCA can be considered a new "feature" of the space, however it is a composition of the original features present in the data.
In the code block below, you will need to implement the following:
- Import `sklearn.decomposition.PCA` and assign the results of fitting PCA in six dimensions with `good_data` to `pca`.
- Apply a PCA transformation of the sample log-data `log_samples` using `pca.transform`, and assign the results to `pca_samples`.
```
from sklearn.decomposition import PCA
# TODO: Apply PCA by fitting the good data with the same number of dimensions as features
pca = PCA()
pca.fit(good_data)
# TODO: Transform the sample log-data using the PCA fit above
pca_samples = pca.transform(log_samples)
# Generate PCA results plot
pca_results = rs.pca_results(good_data, pca)
# XING: cumulative variance
print pca_results['Explained Variance'].cumsum()
```
### Question 5
*How much variance in the data is explained* ***in total*** *by the first and second principal component? What about the first four principal components? Using the visualization provided above, discuss what the first four dimensions best represent in terms of customer spending.*
**Hint:** A positive increase in a specific dimension corresponds with an *increase* of the *positive-weighted* features and a *decrease* of the *negative-weighted* features. The rate of increase or decrease is based on the indivdual feature weights.
**Answer:**
1. **How much variance in the data is explained in total by the first and second principal component?**
0.7068
2. **What about the first four principal components?**
0.9311
3. **Using the visualization provided above, discuss what the first four dimensions best represent in terms of customer spending.**
Dimension 1 has large increases for features Milk, Grocery and Detergents_Paper, a small increase for Delicatessen, and small decreases for features Fresh and Frozen.
Dimension 2 has large increases for Fresh, Frozen and Delicatessen, and small increase for Milk, Grocery and Detergents_Paper.
Dimension 3 has large increases for Frozen and Delicatessen, and large decreases for Fresh and Detergents_Paper.
Dimension 4 has large increases for Frozen and Detergents_Paper, and large a decrease for Fish and Delicatessen.
### Observation
Run the code below to see how the log-transformed sample data has changed after having a PCA transformation applied to it in six dimensions. Observe the numerical value for the first four dimensions of the sample points. Consider if this is consistent with your initial interpretation of the sample points.
```
# Display sample log-data after having a PCA transformation applied
display(pd.DataFrame(np.round(pca_samples, 4), columns = pca_results.index.values))
```
### Implementation: Dimensionality Reduction
When using principal component analysis, one of the main goals is to reduce the dimensionality of the data — in effect, reducing the complexity of the problem. Dimensionality reduction comes at a cost: Fewer dimensions used implies less of the total variance in the data is being explained. Because of this, the *cumulative explained variance ratio* is extremely important for knowing how many dimensions are necessary for the problem. Additionally, if a signifiant amount of variance is explained by only two or three dimensions, the reduced data can be visualized afterwards.
In the code block below, you will need to implement the following:
- Assign the results of fitting PCA in two dimensions with `good_data` to `pca`.
- Apply a PCA transformation of `good_data` using `pca.transform`, and assign the reuslts to `reduced_data`.
- Apply a PCA transformation of the sample log-data `log_samples` using `pca.transform`, and assign the results to `pca_samples`.
```
# TODO: Apply PCA by fitting the good data with only two dimensions
pca = PCA(n_components=2)
pca.fit(good_data)
# TODO: Transform the good data using the PCA fit above
reduced_data = pca.transform(good_data)
# TODO: Transform the sample log-data using the PCA fit above
pca_samples = pca.transform(log_samples)
# Create a DataFrame for the reduced data
reduced_data = pd.DataFrame(reduced_data, columns = ['Dimension 1', 'Dimension 2'])
```
### Observation
Run the code below to see how the log-transformed sample data has changed after having a PCA transformation applied to it using only two dimensions. Observe how the values for the first two dimensions remains unchanged when compared to a PCA transformation in six dimensions.
```
# Display sample log-data after applying PCA transformation in two dimensions
#display(pd.DataFrame(np.round(pca_samples, 4), columns = ['Dimension 1', 'Dimension 2']))
# Display sample log-data after applying PCA transformation in two dimensions
display(pd.DataFrame(np.round(pca_samples, 4), columns = ['Dimension 1', 'Dimension 2']))
# scatter plot of reduced features
pd.scatter_matrix(reduced_data, alpha = 0.3, figsize = (10,10), diagonal = 'kde');
```
## Clustering
In this section, you will choose to use either a K-Means clustering algorithm or a Gaussian Mixture Model clustering algorithm to identify the various customer segments hidden in the data. You will then recover specific data points from the clusters to understand their significance by transforming them back into their original dimension and scale.
### Question 6
*What are the advantages to using a K-Means clustering algorithm? What are the advantages to using a Gaussian Mixture Model clustering algorithm? Given your observations about the wholesale customer data so far, which of the two algorithms will you use and why?*
**Answer:**
1. **What are the advantages to using a K-Means clustering algorithm?**
It's simple and easy to implement, fast to run and always converge.
It's suitable for searching convex clusters.
2. **What are the advantages to using a Gaussian Mixture Model clustering algorithm?**
A "soft" classification is available allowing it to handle overlapping clusters. There are well-studied statistical inference techniques available. It is the fastest algorithm for learning mixture models.
3. **Given your observations about the wholesale customer data so far, which of the two algorithms will you use and why?**
From preious scatter graph of data sets with reduced features, there are two clusters that overlap with each other. So Gaussian Mixture Model clustering algorithm would be more appropriate.
### Implementation: Creating Clusters
Depending on the problem, the number of clusters that you expect to be in the data may already be known. When the number of clusters is not known *a priori*, there is no guarantee that a given number of clusters best segments the data, since it is unclear what structure exists in the data — if any. However, we can quantify the "goodness" of a clustering by calculating each data point's *silhouette coefficient*. The [silhouette coefficient](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.silhouette_score.html) for a data point measures how similar it is to its assigned cluster from -1 (dissimilar) to 1 (similar). Calculating the *mean* silhouette coefficient provides for a simple scoring method of a given clustering.
In the code block below, you will need to implement the following:
- Fit a clustering algorithm to the `reduced_data` and assign it to `clusterer`.
- Predict the cluster for each data point in `reduced_data` using `clusterer.predict` and assign them to `preds`.
- Find the cluster centers using the algorithm's respective attribute and assign them to `centers`.
- Predict the cluster for each sample data point in `pca_samples` and assign them `sample_preds`.
- Import sklearn.metrics.silhouette_score and calculate the silhouette score of `reduced_data` against `preds`.
- Assign the silhouette score to `score` and print the result.
```
from sklearn.mixture import GMM
from sklearn.metrics import silhouette_score
# XING: method to find the best n_components
def score_cluster(data, num_components):
clusterer = GMM(n_components=num_components)
clusterer.fit(data)
preds = clusterer.predict(data)
score = silhouette_score(data, preds)
return score
print "Silhouette Score for different sizes"
silhouette_scores_matrix = pd.DataFrame(index=['Score'])
for size in range(2,11):
silhouette_scores_matrix[size] = pd.Series(score_cluster(reduced_data, size), index = silhouette_scores_matrix.index)
display(silhouette_scores_matrix)
best_n_components = 2
# Apply the selected clustering algorithm to the reduced data
clusterer = GMM(n_components=best_n_components)
clusterer.fit(reduced_data)
# Predict the cluster for each data point
preds = clusterer.predict(reduced_data)
# Find the cluster centers
centers = clusterer.means_
# Predict the cluster for each transformed sample data point
sample_preds = clusterer.predict(pca_samples)
# Calculate the mean silhouette coefficient for the number of clusters chosen
score = silhouette_score(reduced_data, preds)
print "Best Score: {}, n_components={}".format(score, best_n_components)
```
### Question 7
*Report the silhouette score for several cluster numbers you tried. Of these, which number of clusters has the best silhouette score?*
**Answer:**
As shown in previous output of "**Implementation: Creating Clusters**".
### Cluster Visualization
Once you've chosen the optimal number of clusters for your clustering algorithm using the scoring metric above, you can now visualize the results by executing the code block below. Note that, for experimentation purposes, you are welcome to adjust the number of clusters for your clustering algorithm to see various visualizations. The final visualization provided should, however, correspond with the optimal number of clusters.
```
# Display the results of the clustering from implementation
rs.cluster_results(reduced_data, preds, centers, pca_samples)
```
### Implementation: Data Recovery
Each cluster present in the visualization above has a central point. These centers (or means) are not specifically data points from the data, but rather the *averages* of all the data points predicted in the respective clusters. For the problem of creating customer segments, a cluster's center point corresponds to *the average customer of that segment*. Since the data is currently reduced in dimension and scaled by a logarithm, we can recover the representative customer spending from these data points by applying the inverse transformations.
In the code block below, you will need to implement the following:
- Apply the inverse transform to `centers` using `pca.inverse_transform` and assign the new centers to `log_centers`.
- Apply the inverse function of `np.log` to `log_centers` using `np.exp` and assign the true centers to `true_centers`.
```
# TODO: Inverse transform the centers
log_centers = pca.inverse_transform(centers)
# TODO: Exponentiate the centers
true_centers = np.exp(log_centers)
# Display the true centers
segments = ['Segment {}'.format(i) for i in range(0,len(centers))]
true_centers = pd.DataFrame(np.round(true_centers), columns = data.keys())
true_centers.index = segments
display(true_centers)
# XING: show segments in percentile
newdata = data.append(true_centers)
print "Percentiles of the centers"
percent_centers = 100.0 * newdata.rank(axis=0, pct=True).loc[['Segment 0', 'Segment 1']].round(decimals=3)
display(percent_centers)
```
### Question 8
Consider the total purchase cost of each product category for the representative data points above, and reference the statistical description of the dataset at the beginning of this project. *What set of establishments could each of the customer segments represent?*
**Hint:** A customer who is assigned to `'Cluster X'` should best identify with the establishments represented by the feature set of `'Segment X'`.
**Answer:**
- **Segment 0** customers buy most Fresh, Frozen (> %50) and much Delicatessen (40%), it's mostly likely to be a **convinence store or greegrocery**.
- **Segment 1** customers buy lots of Grocery, Milk and Detergents_Paper (~ 70%), following by Delicatessen (%50), it indicates it's a **supermarket**.
### Question 9
*For each sample point, which customer segment from* ***Question 8*** *best represents it? Are the predictions for each sample point consistent with this?*
Run the code block below to find which cluster each sample point is predicted to be.
```
# Display the predictions
for i, pred in enumerate(sample_preds):
print "Sample point", i, "predicted to be in Cluster", pred
```
**Answer:**
1. **For each sample point, which customer segment from Question 8 best represents it?**
As shown in output of **Question 9**.
2. **Are the predictions for each sample point consistent with this?**
Yes, partly. The prediction agrees with previous guess that samples are Supermarket, Greengrocer, except for sample 3 as Convenience store.
Sample 1 customers buy lots of produces in all category, which is close to Segment 1.
Sample 2 customers buy mostly Fresh and Delicatessen, which makes it close to Segment 0.
Sample 3 customers buy mostly Grocery and Detergents_Paper, which makes it close to Segment 1.
- Samples
| Fresh| Milk | Grocery | Frozen | Detergents_Paper | Delicatessen
--- | --- | --- | --- | --- | ---
0|1.137716|4.154476|1.482005|0.429367|0.305623|5.324340
1|0.180140|-0.677330|-0.516866|-0.533481|-0.584049|-0.357439
2|-0.942242|-0.297242|0.468664|-0.613289|0.018584|-0.519319
## Conclusion
In this final section, you will investigate ways that you can make use of the clustered data. First, you will consider how the different groups of customers, the ***customer segments***, may be affected differently by a specific delivery scheme. Next, you will consider how giving a label to each customer (which *segment* that customer belongs to) can provide for additional features about the customer data. Finally, you will compare the ***customer segments*** to a hidden variable present in the data, to see whether the clustering identified certain relationships.
### Question 10
Companies will often run [A/B tests](https://en.wikipedia.org/wiki/A/B_testing) when making small changes to their products or services to determine whether making that change will affect its customers positively or negatively. The wholesale distributor is considering changing its delivery service from currently 5 days a week to 3 days a week. However, the distributor will only make this change in delivery service for customers that react positively. *How can the wholesale distributor use the customer segments to determine which customers, if any, would react positively to the change in delivery service?*
**Hint:** Can we assume the change affects all customers equally? How can we determine which group of customers it affects the most?
**Answer:**
Customers who buy lots of Fresh, Milk and Frozen may prefer faster dilivery. So the distributor can try to do clustering focusing on these three features.
1. One way to do the A/B test is selecting a random sample from each cluster and reducing the delivery frequency for each of them (and with some form of compensation). Then make a suvey of customer satisfaction. An equally sized control group (with same shopping conditions except the delivery time) selected from the remaining customers should be used for comparison.
2. Once the A/B test data is ready, it can be interpreated and cross-validated by changing the delivery service to certain amount of test customers.
3. The process can be iterated until certain model is verified or market goals are met.
### Question 11
Additional structure is derived from originally unlabeled data when using clustering techniques. Since each customer has a ***customer segment*** it best identifies with (depending on the clustering algorithm applied), we can consider *'customer segment'* as an **engineered feature** for the data. Assume the wholesale distributor recently acquired ten new customers and each provided estimates for anticipated annual spending of each product category. Knowing these estimates, the wholesale distributor wants to classify each new customer to a ***customer segment*** to determine the most appropriate delivery service.
*How can the wholesale distributor label the new customers using only their estimated product spending and the* ***customer segment*** *data?*
**Hint:** A supervised learner could be used to train on the original customers. What would be the target variable?
**Answer:**
It can use the customer segment (cluster prediction) as a new feature and train a supervised learning model using this feature as target.
### Visualizing Underlying Distributions
At the beginning of this project, it was discussed that the `'Channel'` and `'Region'` features would be excluded from the dataset so that the customer product categories were emphasized in the analysis. By reintroducing the `'Channel'` feature to the dataset, an interesting structure emerges when considering the same PCA dimensionality reduction applied earlier to the original dataset.
Run the code block below to see how each data point is labeled either `'HoReCa'` (Hotel/Restaurant/Cafe) or `'Retail'` the reduced space. In addition, you will find the sample points are circled in the plot, which will identify their labeling.
```
# Display the clustering results based on 'Channel' data
rs.channel_results(reduced_data, outliers, pca_samples)
```
### Question 12
*How well does the clustering algorithm and number of clusters you've chosen compare to this underlying distribution of Hotel/Restaurant/Cafe customers to Retailer customers? Are there customer segments that would be classified as purely 'Retailers' or 'Hotels/Restaurants/Cafes' by this distribution? Would you consider these classifications as consistent with your previous definition of the customer segments?*
**Answer:**
1. How well does the clustering algorithm and number of clusters you've chosen compare to this underlying distribution of Hotel/Restaurant/Cafe customers to Retailer customers?
The algorithm and the number of clusters chosen is consistent with the underlying distribution, by tuning the numbers of centers.
2. Are there customer segments that would be classified as purely 'Retailers' or 'Hotels/Restaurants/Cafes' by this distribution?
No, there will be overlap areas for two clusters.
3. Would you consider these classifications as consistent with your previous definition of the customer segments?
I consider that the previous definition of customer segments is consistent with the classification using the Channel feature.
> **Note**: Once you have completed all of the code implementations and successfully answered each question above, you may finalize your work by exporting the iPython Notebook as an HTML document. You can do this by using the menu above and navigating to
**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
|
github_jupyter
|
# Import libraries necessary for this project
import numpy as np
import pandas as pd
import renders as rs
from IPython.display import display # Allows the use of display() for DataFrames
# Show matplotlib plots inline (nicely formatted in the notebook)
%matplotlib inline
# Load the wholesale customers dataset
try:
data = pd.read_csv("customers.csv")
data.drop(['Region', 'Channel'], axis = 1, inplace = True)
print "Wholesale customers dataset has {} samples with {} features each.".format(*data.shape)
except:
print "Dataset could not be loaded. Is the dataset missing?"
# Display a description of the dataset
display(data.describe())
# XING: Gaussian distribution fitting used in Question 3
from scipy.stats import norm
def gaussian_func(x, *p):
A, mu, sigma = p
return A * np.exp(-(x-mu)**2 / (2.*sigma**2))
# run gaussian fits for all features
gaussian_fits = []
for column in data:
feature = data[column]
mu, sigma = norm.fit(feature)
feature_fit = gaussian_func(feature, 1, mu, sigma)
error = np.linalg.norm(feature - feature_fit)
gaussian_fits.append([mu, sigma, error / (len(feature) * feature.std())])
print "\n Gaussian distribution fitting of features"
gaussian_fits = pd.DataFrame(np.array(gaussian_fits).T,
columns = data.columns,
index = ['mean', 'var', 'error/(N * std)'])
display(gaussian_fits)
# TODO: Select three indices of your choice you wish to sample from the dataset
indices = [23, 27, 412]
# Create a DataFrame of the chosen samples
samples = pd.DataFrame(data.loc[indices], columns = data.keys()).reset_index(drop = True)
print "Chosen samples of wholesale customers dataset:"
display(samples)
# XING: show devations of each feature from its mean measured by std
mean_data = np.mean(data)
std_data = np.std(data)
deviation_samples = (samples - mean_data) / std_data
print "\nDeviation of chosen samples of wholesale customers dataset in mean+deviation*std:"
display(deviation_samples)
from sklearn.cross_validation import train_test_split
from sklearn.tree import DecisionTreeRegressor
# TODO: Make a copy of the DataFrame, using the 'drop' function to drop the given feature
new_data = data.copy()
names = ['Fresh', 'Milk', 'Grocery', 'Frozen', 'Detergents_Paper', 'Delicatessen']
# XING: train and evaluate for each feature
scores = []
for name in names:
label = new_data[name]
features = new_data.drop([name], axis=1)
# TODO: Split the data into training and testing sets using the given feature as the target
X_train, X_test, y_train, y_test = train_test_split(features, label, test_size=0.25, random_state=1)
# TODO: Create a decision tree regressor and fit it to the training set
regressor = DecisionTreeRegressor(random_state=1)
regressor.fit(X_train, y_train)
# TODO: Report the score of the prediction using the testing set
score = regressor.score(X_test, y_test)
scores.append(score)
# display features and scores
result = pd.DataFrame(np.array([names, scores]).T, columns=['Feature', 'Score'])
display(result)
# Produce a scatter matrix for each pair of features in the data
pd.scatter_matrix(data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');
# TODO: Scale the data using the natural logarithm
log_data = np.log(data)
# TODO: Scale the sample data using the natural logarithm
log_samples = np.log(samples)
# Produce a scatter matrix for each pair of newly-transformed features
pd.scatter_matrix(log_data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');
# Display the log-transformed sample data
display(log_samples)
bad_indexes = {}
# For each feature find the data points with extreme high or low values
for feature in log_data.keys():
feature_data = log_data[feature]
# TODO: Calculate Q1 (25th percentile of the data) for the given feature
Q1 = np.percentile(feature_data, 25)
# TODO: Calculate Q3 (75th percentile of the data) for the given feature
Q3 = np.percentile(feature_data, 75)
# TODO: Use the interquartile range to calculate an outlier step (1.5 times the interquartile range)
step = 1.5 * (Q3 - Q1)
feature_outliers = log_data[~((feature_data >= Q1 - step) & (feature_data <= Q3 + step))]
for i, r in feature_data.iteritems():
if not (Q1 - step <= r <= Q3 + step):
if i not in bad_indexes:
bad_indexes[i] = 1
else:
bad_indexes[i] += 1
# Display the outliers
print "Data points considered outliers for the feature '{}':".format(feature)
display(feature_outliers)
# OPTIONAL: Select the indices for data points you wish to remove
# remove features with more than one outliers
outliers = [i for i, n in bad_indexes.items() if n > 1]
# Remove the outliers, if any were specified
good_data = log_data.drop(log_data.index[outliers]).reset_index(drop = True)
# XING: display data points with more than one outlier features
print "\nData points with more than one outlier features"
print sorted(outliers)
from sklearn.decomposition import PCA
# TODO: Apply PCA by fitting the good data with the same number of dimensions as features
pca = PCA()
pca.fit(good_data)
# TODO: Transform the sample log-data using the PCA fit above
pca_samples = pca.transform(log_samples)
# Generate PCA results plot
pca_results = rs.pca_results(good_data, pca)
# XING: cumulative variance
print pca_results['Explained Variance'].cumsum()
# Display sample log-data after having a PCA transformation applied
display(pd.DataFrame(np.round(pca_samples, 4), columns = pca_results.index.values))
# TODO: Apply PCA by fitting the good data with only two dimensions
pca = PCA(n_components=2)
pca.fit(good_data)
# TODO: Transform the good data using the PCA fit above
reduced_data = pca.transform(good_data)
# TODO: Transform the sample log-data using the PCA fit above
pca_samples = pca.transform(log_samples)
# Create a DataFrame for the reduced data
reduced_data = pd.DataFrame(reduced_data, columns = ['Dimension 1', 'Dimension 2'])
# Display sample log-data after applying PCA transformation in two dimensions
#display(pd.DataFrame(np.round(pca_samples, 4), columns = ['Dimension 1', 'Dimension 2']))
# Display sample log-data after applying PCA transformation in two dimensions
display(pd.DataFrame(np.round(pca_samples, 4), columns = ['Dimension 1', 'Dimension 2']))
# scatter plot of reduced features
pd.scatter_matrix(reduced_data, alpha = 0.3, figsize = (10,10), diagonal = 'kde');
from sklearn.mixture import GMM
from sklearn.metrics import silhouette_score
# XING: method to find the best n_components
def score_cluster(data, num_components):
clusterer = GMM(n_components=num_components)
clusterer.fit(data)
preds = clusterer.predict(data)
score = silhouette_score(data, preds)
return score
print "Silhouette Score for different sizes"
silhouette_scores_matrix = pd.DataFrame(index=['Score'])
for size in range(2,11):
silhouette_scores_matrix[size] = pd.Series(score_cluster(reduced_data, size), index = silhouette_scores_matrix.index)
display(silhouette_scores_matrix)
best_n_components = 2
# Apply the selected clustering algorithm to the reduced data
clusterer = GMM(n_components=best_n_components)
clusterer.fit(reduced_data)
# Predict the cluster for each data point
preds = clusterer.predict(reduced_data)
# Find the cluster centers
centers = clusterer.means_
# Predict the cluster for each transformed sample data point
sample_preds = clusterer.predict(pca_samples)
# Calculate the mean silhouette coefficient for the number of clusters chosen
score = silhouette_score(reduced_data, preds)
print "Best Score: {}, n_components={}".format(score, best_n_components)
# Display the results of the clustering from implementation
rs.cluster_results(reduced_data, preds, centers, pca_samples)
# TODO: Inverse transform the centers
log_centers = pca.inverse_transform(centers)
# TODO: Exponentiate the centers
true_centers = np.exp(log_centers)
# Display the true centers
segments = ['Segment {}'.format(i) for i in range(0,len(centers))]
true_centers = pd.DataFrame(np.round(true_centers), columns = data.keys())
true_centers.index = segments
display(true_centers)
# XING: show segments in percentile
newdata = data.append(true_centers)
print "Percentiles of the centers"
percent_centers = 100.0 * newdata.rank(axis=0, pct=True).loc[['Segment 0', 'Segment 1']].round(decimals=3)
display(percent_centers)
# Display the predictions
for i, pred in enumerate(sample_preds):
print "Sample point", i, "predicted to be in Cluster", pred
# Display the clustering results based on 'Channel' data
rs.channel_results(reduced_data, outliers, pca_samples)
| 0.610686 | 0.995497 |
```
# Use this javascript to scrub links from a google page
urls=Array.from(document.querySelectorAll('.rg_i')).map(el=> el.hasAttribute('data-src')?el.getAttribute('data-src'):el.getAttribute('data-iurl'));
window.open('data:text/csv;charset=utf-8,' + escape(urls.join('\n')));
from fastai.vision import *
from IPython.display import display
from PIL import Image
from IPython.display import clear_output
import os # Use this to make folders (For Data) in Windows
# The class names of all the data files.
classes = ['vietnam_war'] # 'ww2', Removed Classes 'gulf_war', 'lebonon_war', 'civil_war', 'afghan_war', 'korean_war', 'vietnam_war', 'ww1'
# Download all the files into the respective repositories.
path_links = './data_links/'
path_dest = './data/'
# Only need to run this once
for i in classes:
file_name = path_links + i + '.txt' # Get the textfile containing the links to the images.
file_name = Path(file_name)
dest = path_dest + i # Download the images into a folder resembling the class name.
dest = Path(dest)
if not os.path.exists(dest): # Create a folder if it does not exist. (Only for Windows)
os.makedirs(dest)
download_images(file_name, dest, max_pics=10000)
print(i + ": Successfully Downloaded.")
# Perform light clean on images.
for c in classes:
print("Verifying Images In: {}".format(c))
final_dest = Path(path_dest + c)
verify_images(final_dest, delete=True, max_pics=10000)
# Loop through a folder and remove underiable images.
path_to_scrub = Path('./data_links/vietnam_war.txt')
loc_of_imgs = path_dest + 'vietnam_war/'
old_links = []
new_links = []
images_kept = 0
with open(path_to_scrub) as f:
old_links = f.read().splitlines()
user_input = None
counter = 0
for filename in os.listdir(loc_of_imgs):
print(filename)
img = Path(loc_of_imgs + filename)
display(Image.open(img))
user_input = input("Keep Image (y or n): ") # Determine whether the users wishes to keep the image or not.
while (user_input != 'n' and user_input != 'y'):
if user_input == 'END': break
print("Invalid Answer (y or n)")
user_input = input("Keep Image (y or n): ")
if user_input == 'END': break
if user_input == 'y': # Ensure the image link is kept
new_links.append(old_links[counter])
images_kept += 1
else: os.remove(img) # Remove the file from your dataset
counter += 1
clear_output(wait=True)
print("The amount of images kept: {}".format(images_kept))
with open('./data_links/ww2NEW.txt', 'a+') as f:
f.write("--------------------------------\n")
for item in new_links:
f.write("%s\n" % item)
# Organise the data into proper folders.
np.random.seed(42)
data = ImageDataBunch.from_folder(path_dest, train=".", valid_pct=0.2,
ds_tfms=get_transforms(), size=224, num_workers=4, bs=12).normalize(imagenet_stats)
# Display some of the data... looks like it will require some scrubbing.
data.show_batch(rows=3, figsize=(7,8))
# Display additional parameters. Is this enough data?
data.classes, data.c, len(data.train_ds), len(data.valid_ds)
# Train with resnet34
learn = cnn_learner(data, models.resnet34, metrics=error_rate)
learn.fit_one_cycle(4)
# Interpret the losses
interp = ClassificationInterpretation.from_learner(learn)
losses,idxs = interp.top_losses()
len(data.valid_ds)==len(losses)==len(idxs)
interp.plot_top_losses(9, figsize=(15,11))
#(Prediction, actual, loss, probability)
# Time to train the entire model. Plot the learing curve.
learn.lr_find()
learn.recorder.plot()
# Train the entire model with adjusted learning rate.
learn.unfreeze()
learn.fit_one_cycle(2, max_lr=slice(1e-6, 1e-2))
# Attempt to use Resnet50
learn = cnn_learner(data, models.resnet50, metrics=error_rate)
# Fit the model
learn.fit_one_cycle(4)
# Save the model and print the learning function
learn.save("res50")
learn.lr_find()
learn.recorder.plot()
# Unfreeze and fit once more.
learn.unfreeze()
learn.fit_one_cycle(3, max_lr=slice(1e-5,1e-2))
```
|
github_jupyter
|
# Use this javascript to scrub links from a google page
urls=Array.from(document.querySelectorAll('.rg_i')).map(el=> el.hasAttribute('data-src')?el.getAttribute('data-src'):el.getAttribute('data-iurl'));
window.open('data:text/csv;charset=utf-8,' + escape(urls.join('\n')));
from fastai.vision import *
from IPython.display import display
from PIL import Image
from IPython.display import clear_output
import os # Use this to make folders (For Data) in Windows
# The class names of all the data files.
classes = ['vietnam_war'] # 'ww2', Removed Classes 'gulf_war', 'lebonon_war', 'civil_war', 'afghan_war', 'korean_war', 'vietnam_war', 'ww1'
# Download all the files into the respective repositories.
path_links = './data_links/'
path_dest = './data/'
# Only need to run this once
for i in classes:
file_name = path_links + i + '.txt' # Get the textfile containing the links to the images.
file_name = Path(file_name)
dest = path_dest + i # Download the images into a folder resembling the class name.
dest = Path(dest)
if not os.path.exists(dest): # Create a folder if it does not exist. (Only for Windows)
os.makedirs(dest)
download_images(file_name, dest, max_pics=10000)
print(i + ": Successfully Downloaded.")
# Perform light clean on images.
for c in classes:
print("Verifying Images In: {}".format(c))
final_dest = Path(path_dest + c)
verify_images(final_dest, delete=True, max_pics=10000)
# Loop through a folder and remove underiable images.
path_to_scrub = Path('./data_links/vietnam_war.txt')
loc_of_imgs = path_dest + 'vietnam_war/'
old_links = []
new_links = []
images_kept = 0
with open(path_to_scrub) as f:
old_links = f.read().splitlines()
user_input = None
counter = 0
for filename in os.listdir(loc_of_imgs):
print(filename)
img = Path(loc_of_imgs + filename)
display(Image.open(img))
user_input = input("Keep Image (y or n): ") # Determine whether the users wishes to keep the image or not.
while (user_input != 'n' and user_input != 'y'):
if user_input == 'END': break
print("Invalid Answer (y or n)")
user_input = input("Keep Image (y or n): ")
if user_input == 'END': break
if user_input == 'y': # Ensure the image link is kept
new_links.append(old_links[counter])
images_kept += 1
else: os.remove(img) # Remove the file from your dataset
counter += 1
clear_output(wait=True)
print("The amount of images kept: {}".format(images_kept))
with open('./data_links/ww2NEW.txt', 'a+') as f:
f.write("--------------------------------\n")
for item in new_links:
f.write("%s\n" % item)
# Organise the data into proper folders.
np.random.seed(42)
data = ImageDataBunch.from_folder(path_dest, train=".", valid_pct=0.2,
ds_tfms=get_transforms(), size=224, num_workers=4, bs=12).normalize(imagenet_stats)
# Display some of the data... looks like it will require some scrubbing.
data.show_batch(rows=3, figsize=(7,8))
# Display additional parameters. Is this enough data?
data.classes, data.c, len(data.train_ds), len(data.valid_ds)
# Train with resnet34
learn = cnn_learner(data, models.resnet34, metrics=error_rate)
learn.fit_one_cycle(4)
# Interpret the losses
interp = ClassificationInterpretation.from_learner(learn)
losses,idxs = interp.top_losses()
len(data.valid_ds)==len(losses)==len(idxs)
interp.plot_top_losses(9, figsize=(15,11))
#(Prediction, actual, loss, probability)
# Time to train the entire model. Plot the learing curve.
learn.lr_find()
learn.recorder.plot()
# Train the entire model with adjusted learning rate.
learn.unfreeze()
learn.fit_one_cycle(2, max_lr=slice(1e-6, 1e-2))
# Attempt to use Resnet50
learn = cnn_learner(data, models.resnet50, metrics=error_rate)
# Fit the model
learn.fit_one_cycle(4)
# Save the model and print the learning function
learn.save("res50")
learn.lr_find()
learn.recorder.plot()
# Unfreeze and fit once more.
learn.unfreeze()
learn.fit_one_cycle(3, max_lr=slice(1e-5,1e-2))
| 0.521227 | 0.20949 |
# Statistics from Stock Data
In this lab we will load stock data into a Pandas Dataframe and calculate some statistics on it. We will be working with stock data from Google, Apple, and Amazon. All the stock data was downloaded from yahoo finance in CSV format. In your workspace you should have a file named GOOG.csv containing the Google stock data, a file named AAPL.csv containing the Apple stock data, and a file named AMZN.csv containing the Amazon stock data. All the files contain 7 columns of data:
**Date Open High Low Close Adj_Close Volume**
We will start by reading in any of the above CSV files into a DataFrame and see what the data looks like.
```
# We import pandas into Python
import pandas as pd
# We read in a stock data data file into a data frame and see what it looks like
aapl = pd.read_csv('AAPL.csv')
# We display the first 5 rows of the DataFrame
print(aapl.head(5))
```
We clearly see that the Dataframe is has automatically labeled the row indices using integers and has labeled the columns of the DataFrame using the names of the columns in the CSV files.
# To Do
You will now load the stock data from Google, Apple, and Amazon into separte DataFrames. However, for each stock data you will only be interested in loading the `Date` and `Adj Close` columns into the Dataframe. In addtion, you want to use the `Date` column as your row index. Finally, you want the DataFrame to recognize the dates as actual dates (year/month/day) and not as strings. For each stock, you can accomplish all theses things in just one line of code by using the appropiate keywords in the `pd.read_csv()` function. Here are a few hints:
* Use the `index_col` keyword to indicate which column you want to use as an index. For example `index_col = ['Open']`
* Set the `parse_dates` keyword equal to `True` to convert the Dates into real dates of the form year/month/day
* Use the `usecols` keyword to select which columns you want to load into the DataFrame. For example `usecols = ['Open', 'High']`
Fill in the code below:
```
# We load the Google stock data into a DataFrame
google_stock = pd.read_csv('GOOG.csv', index_col = ['Date'], parse_dates = True, usecols = ['Date', 'Adj Close'])
# We load the Apple stock data into a DataFrame
apple_stock = pd.read_csv('AAPL.csv', index_col = ['Date'], parse_dates = True, usecols = ['Date', 'Adj Close'])
# We load the Amazon stock data into a DataFrame
amazon_stock = pd.read_csv('AMZN.csv', index_col = ['Date'], parse_dates = True, usecols = ['Date', 'Adj Close'])
```
You can check that you have loaded the data correctly by displaying the head of the DataFrames.
```
# We display the google_stock DataFrame
print(google_stock.head(5))
```
You will now join the three DataFrames above to create a single new DataFrame that contains all the `Adj Close` for all the stocks. Let's start by creating an empty DataFrame that has as row indices calendar days between `2000-01-01` and `2016-12-31`. We will use the `pd.date_range()` function to create the calendar dates first and then we will create a DataFrame that uses those dates as row indices:
```
# We create calendar dates between '2000-01-01' and '2016-12-31'
dates = pd.date_range('2000-01-01', '2016-12-31')
# We create and empty DataFrame that uses the above dates as indices
all_stocks = pd.DataFrame(index = dates)
```
# To Do
You will now join the the individual DataFrames, `google_stock`, `apple_stock`, and `amazon_stock`, to the `all_stocks` DataFrame. However, before you do this, it is necessary that you change the name of the columns in each of the three dataframes. This is because the column labels in the `all_stocks` dataframe must be unique. Since all the columns in the individual dataframes have the same name, `Adj Close`, we must change them to the stock name before joining them. In the space below change the column label `Adj Close` of each individual dataframe to the name of the corresponding stock. You can do this by using the `pd.DataFrame.rename()` function.
```
# Change the Adj Close column label to Google
google_stock = google_stock.rename(columns = { 'Adj Close' : 'Google' })
# Change the Adj Close column label to Apple
apple_stock = apple_stock.rename(columns = { 'Adj Close' : 'Apple' })
# Change the Adj Close column label to Amazon
amazon_stock = amazon_stock.rename(columns = { 'Adj Close' : 'Amazon' })
```
You can check that the column labels have been changed correctly by displaying the datadrames
```
# We display the google_stock DataFrame
print(google_stock.head(5))
# We display the apple_stock DataFrame
print(apple_stock.head(5))
# We display the amazon_stock DataFrame
print(amazon_stock.head(5))
```
Now that we have unique column labels, we can join the individual DataFrames to the `all_stocks` DataFrame. For this we will use the `dataframe.join()` function. The function `dataframe1.join(dataframe2)` joins `dataframe1` with `dataframe2`. We will join each dataframe one by one to the `all_stocks` dataframe. Fill in the code below to join the dataframes, the first join has been made for you:
```
# We join the Google stock to all_stocks
all_stocks = all_stocks.join(google_stock)
# We join the Apple stock to all_stocks
all_stocks = all_stocks.join(apple_stock)
# We join the Amazon stock to all_stocks
all_stocks = all_stocks.join(amazon_stock)
```
You can check that the dataframes have been joined correctly by displaying the `all_stocks` dataframe
```
# We display the all_stocks DataFrame
print(all_stocks.head(5))
```
# To Do
Before we proceed to get some statistics on the stock data, let's first check that we don't have any *NaN* values. In the space below check if there are any *NaN* values in the `all_stocks` dataframe. If there are any, remove any rows that have *NaN* values:
```
# Check if there are any NaN values in the all_stocks dataframe
print(all_stocks.isnull().any())
# Remove any rows that contain NaN values
all_stocks = all_stocks.dropna()
```
You can check that the *NaN* values have been eliminated by displaying the `all_stocks` dataframe
```
# Check if there are any NaN values in the all_stocks dataframe
print(all_stocks.isnull().any())
```
Display the `all_stocks` dataframe and verify that there are no *NaN* values
```
# We display the all_stocks DataFrame
print(all_stocks)
```
Now that you have eliminated any *NaN* values we can now calculate some basic statistics on the stock prices. Fill in the code below
```
# Print the average stock price for each stock
print(all_stocks.mean(axis=0))
# Print the median stock price for each stock
print(all_stocks.median(axis=0))
# Print the standard deviation of the stock price for each stock
print(all_stocks.std(axis=0))
# Print the correlation between stocks
print(all_stocks.corr())
```
We will now look at how we can compute some rolling statistics, also known as moving statistics. We can calculate for example the rolling mean (moving average) of the Google stock price by using the Pandas `dataframe.rolling().mean()` method. The `dataframe.rolling(N).mean()` calculates the rolling mean over an `N`-day window. In other words, we can take a look at the average stock price every `N` days using the above method. Fill in the code below to calculate the average stock price every 150 days for Google stock
```
# We compute the rolling mean using a 150-Day window for Google stock
rollingMean = google_stock.rolling(150).mean()
```
We can also visualize the rolling mean by plotting the data in our dataframe. In the following lessons you will learn how to use **Matplotlib** to visualize data. For now I will just import matplotlib and plot the Google stock data on top of the rolling mean. You can play around by changing the rolling mean window and see how the plot changes.
```
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Google stock data
plt.plot(all_stocks['Google'])
# We plot the rolling mean ontop of our Google stock data
plt.plot(rollingMean)
plt.legend(['Google Stock Price', 'Rolling Mean'])
plt.show()
```
|
github_jupyter
|
# We import pandas into Python
import pandas as pd
# We read in a stock data data file into a data frame and see what it looks like
aapl = pd.read_csv('AAPL.csv')
# We display the first 5 rows of the DataFrame
print(aapl.head(5))
# We load the Google stock data into a DataFrame
google_stock = pd.read_csv('GOOG.csv', index_col = ['Date'], parse_dates = True, usecols = ['Date', 'Adj Close'])
# We load the Apple stock data into a DataFrame
apple_stock = pd.read_csv('AAPL.csv', index_col = ['Date'], parse_dates = True, usecols = ['Date', 'Adj Close'])
# We load the Amazon stock data into a DataFrame
amazon_stock = pd.read_csv('AMZN.csv', index_col = ['Date'], parse_dates = True, usecols = ['Date', 'Adj Close'])
# We display the google_stock DataFrame
print(google_stock.head(5))
# We create calendar dates between '2000-01-01' and '2016-12-31'
dates = pd.date_range('2000-01-01', '2016-12-31')
# We create and empty DataFrame that uses the above dates as indices
all_stocks = pd.DataFrame(index = dates)
# Change the Adj Close column label to Google
google_stock = google_stock.rename(columns = { 'Adj Close' : 'Google' })
# Change the Adj Close column label to Apple
apple_stock = apple_stock.rename(columns = { 'Adj Close' : 'Apple' })
# Change the Adj Close column label to Amazon
amazon_stock = amazon_stock.rename(columns = { 'Adj Close' : 'Amazon' })
# We display the google_stock DataFrame
print(google_stock.head(5))
# We display the apple_stock DataFrame
print(apple_stock.head(5))
# We display the amazon_stock DataFrame
print(amazon_stock.head(5))
# We join the Google stock to all_stocks
all_stocks = all_stocks.join(google_stock)
# We join the Apple stock to all_stocks
all_stocks = all_stocks.join(apple_stock)
# We join the Amazon stock to all_stocks
all_stocks = all_stocks.join(amazon_stock)
# We display the all_stocks DataFrame
print(all_stocks.head(5))
# Check if there are any NaN values in the all_stocks dataframe
print(all_stocks.isnull().any())
# Remove any rows that contain NaN values
all_stocks = all_stocks.dropna()
# Check if there are any NaN values in the all_stocks dataframe
print(all_stocks.isnull().any())
# We display the all_stocks DataFrame
print(all_stocks)
# Print the average stock price for each stock
print(all_stocks.mean(axis=0))
# Print the median stock price for each stock
print(all_stocks.median(axis=0))
# Print the standard deviation of the stock price for each stock
print(all_stocks.std(axis=0))
# Print the correlation between stocks
print(all_stocks.corr())
# We compute the rolling mean using a 150-Day window for Google stock
rollingMean = google_stock.rolling(150).mean()
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Google stock data
plt.plot(all_stocks['Google'])
# We plot the rolling mean ontop of our Google stock data
plt.plot(rollingMean)
plt.legend(['Google Stock Price', 'Rolling Mean'])
plt.show()
| 0.515376 | 0.993248 |

# Callysto’s Weekly Data Visualization
## Climate Change Evidence - CO2 Emissions
### Recommended grade levels: 7-12¶
### Instructions
#### “Run” the cells to see the graphs
Click “Cell” and select “Run All”. <br>This will import the data and run all the code, so you can see this week's data visualizations (scroll to the top after you’ve run the cells). <br>**You don’t need to do any coding**.

### About The Notebook
Callysto's Weekly Data Visualization is a learning resource that aims to develop data literacy skills. We provide grades 5-12 teachers and students with a data visualization, like a graph, to interpret. This companion resource walks learners through how the data visualization is created and interpreted by a data scientist.
The steps of the data analysis process are listed below and applied to each weekly topic.
1. Question - What are we trying to answer?
2. Gather - Find the data source(s) you will need.
3. Organize - Arrange the data so that you can easily explore it.
4. Explore - Examine the data to look for evidence to answer our question. This includes creating visualizations.
5. Interpret - Explain how the evidence answers our question.
6. Communicate - Reflect on the interpretation.
## 1. Question
C02 is a [greenhouse gas](https://en.wikipedia.org/wiki/Greenhouse_gas#:~:text=The%20primary%20greenhouse%20gases%20in,and%20ozone%20(O3).). It is found throughout the atmosphere and has dramatically increased in atmospheric concentration since industrialization. Have you ever wondered how Canada's CO2 emissions compare to other countries?
### Goal
We want to see how Canada's per capita CO2 emissions compare with those of our partner [G7](https://en.wikipedia.org/wiki/Group_of_Seven) nations. To do this we will create a figure with a line of per capita CO2 emissions using [World Bank](https://data.worldbank.org/) data. We will also create other plots that may be of interest.
## 2. Gather
The code below will import the Python programming libraries we need to gather and organize the data to answer our question.
```
import wbdata # API to grab world bank data
import pandas as pd # library to work with data
import plotly.express as px #library to plot the data
```
The code below will grab our data from "data.worldbank".
```
#indicators maps WB codes to meaningful names
indicators = {'EN.ATM.CO2E.KT': 'Total CO2 Emissions(kt)',
'EN.ATM.CO2E.KD.GD': 'kg CO2 Per 10 Dollars USD GDP', 'EN.ATM.CO2E.PC': "CO2 Tons Per Capita"}
#country codes for the 7 G7 nations
g7 = ['CAN', 'GBR', 'USA', 'FRA', 'ITA', 'DEU', 'JPN']
#create our dataframe using wbdata
df = wbdata.get_dataframe(indicators, country=g7, convert_date=True)
#Show the data
df
```
## 3. Organize
To organize the data we will make each weight unit grams. Using grams instead of kilograms is helpful in this case since our plots x-axis will use si-prefixes such as k for kilo.
```
#create new index and have country and date be columns of the dataframe
df.reset_index(level=['country', 'date'], inplace=True)
# convert metric tons to g
df["CO2 Tons Per Capita"] = df.apply(lambda x: x["CO2 Tons Per Capita"]*1000000, axis=1)
#convert metric kt to g
df["Total CO2 Emissions(kt)"] = df.apply(lambda x: x["Total CO2 Emissions(kt)"]*1000000000 , axis=1)
#convert kg to g
df["kg CO2 Per 10 Dollars USD GDP"] = df.apply(lambda x: x["kg CO2 Per 10 Dollars USD GDP"]*1000, axis=1)
#rename columns
df = df.rename(columns={"CO2 Tons Per Capita": "CO2 g Per Capita",
"Total CO2 Emissions(kt)":"Total CO2 Emissions(g)",
"kg CO2 Per 10 Dollars USD GDP":"g CO2 Per 10 Dollars USD GDP",
"date": "Date", 'country': 'Country'})
#show the dataframe
df
```
## 4. Explore
We will examine CO2 emissions by creating a few line graphs showing CO2 emissions in G7 countries.
```
# Create Figures
fig1 = px.line(df, x="Date", y="Total CO2 Emissions(g)", color='Country',
title="G7 Nations Total CO2 Emissions")
fig2 = px.line(df, x="Date", y="g CO2 Per 10 Dollars USD GDP", color='Country',
title="G7 Nations CO2 Emissions In Grams Per $10 USD GDP")
fig3 = px.line(df, x="Date", y="CO2 g Per Capita", color='Country',
title='G7 Nations CO2 Emissions Per Capita')
#Show figures
fig1.show()
fig2.show()
fig3.show()
```
## 5. Interpret
Below, we will discuss the plot we created and how to examine it.
Starting with the top most plot, we see that the USA produces more CO2 emissions relative to other G7 nations. However, the next two plots tell a slightly different story. If we look at CO2 emissions by GDP, Canada actually produced the most CO2 out of G7 nations in 2016. When looking at carbon emissions per capita (third plot), we see that Canada is just below the US, and the gap seems to be lessening.
To look more closely at these plots, hover your mouse over data points or click on legend items to remove or add lines to the plot
**Make meaning from the data visualization**
- What do you notice about the line graph?
- What do you wonder about the data?
- Are all the plots clear to you? If not, why?
- Which plot do you think is the most fair in explaining national CO2 emissions? Why?
## 6. Communicate
Below, we will reflect on the new information that is presented from the data. When we look at the evidence, think about what you perceive about the information. Is this perception based on what the evidence shows? If others were to view it, what perceptions might they have? These writing prompts can help you reflect.
Cause and effect
- What human activities affect CO2 emissions?
- How can people contribute to solutions for changing CO2 emissions?
Ethics
- How can personal and societal choices impact change?
- How might CO2 emissions impact society or the economy?
[](https://github.com/callysto/curriculum-notebooks/blob/master/LICENSE.md)
|
github_jupyter
|
import wbdata # API to grab world bank data
import pandas as pd # library to work with data
import plotly.express as px #library to plot the data
#indicators maps WB codes to meaningful names
indicators = {'EN.ATM.CO2E.KT': 'Total CO2 Emissions(kt)',
'EN.ATM.CO2E.KD.GD': 'kg CO2 Per 10 Dollars USD GDP', 'EN.ATM.CO2E.PC': "CO2 Tons Per Capita"}
#country codes for the 7 G7 nations
g7 = ['CAN', 'GBR', 'USA', 'FRA', 'ITA', 'DEU', 'JPN']
#create our dataframe using wbdata
df = wbdata.get_dataframe(indicators, country=g7, convert_date=True)
#Show the data
df
#create new index and have country and date be columns of the dataframe
df.reset_index(level=['country', 'date'], inplace=True)
# convert metric tons to g
df["CO2 Tons Per Capita"] = df.apply(lambda x: x["CO2 Tons Per Capita"]*1000000, axis=1)
#convert metric kt to g
df["Total CO2 Emissions(kt)"] = df.apply(lambda x: x["Total CO2 Emissions(kt)"]*1000000000 , axis=1)
#convert kg to g
df["kg CO2 Per 10 Dollars USD GDP"] = df.apply(lambda x: x["kg CO2 Per 10 Dollars USD GDP"]*1000, axis=1)
#rename columns
df = df.rename(columns={"CO2 Tons Per Capita": "CO2 g Per Capita",
"Total CO2 Emissions(kt)":"Total CO2 Emissions(g)",
"kg CO2 Per 10 Dollars USD GDP":"g CO2 Per 10 Dollars USD GDP",
"date": "Date", 'country': 'Country'})
#show the dataframe
df
# Create Figures
fig1 = px.line(df, x="Date", y="Total CO2 Emissions(g)", color='Country',
title="G7 Nations Total CO2 Emissions")
fig2 = px.line(df, x="Date", y="g CO2 Per 10 Dollars USD GDP", color='Country',
title="G7 Nations CO2 Emissions In Grams Per $10 USD GDP")
fig3 = px.line(df, x="Date", y="CO2 g Per Capita", color='Country',
title='G7 Nations CO2 Emissions Per Capita')
#Show figures
fig1.show()
fig2.show()
fig3.show()
| 0.554229 | 0.992732 |
# Notebook Visualization
This notebook demonstrates a number of ways to visualize OmniSci data in a notebook.
However **if you are looking to create interactive visualizations, please use the [`ibis-vega-transform`](https://github.com/quansight/ibis-vega-transform) package instead of these approaches**.
## Establishing a connection
pymapd allows us to connect to a OmniSci server using the following code:
```
import pymapd
import jupyterlab_omnisci
connection_data = dict(
user='mapd',
password='HyperInteractive',
host='metis.mapd.com',
port='443',
dbname='mapd',
protocol='https'
)
con = pymapd.connect(**connection_data)
```
Once we have a connection, we can try to send vega data to the backend and render it.
Both the Jupyter notebook client (typically a browser), and the kernel (in this case
a python process) have the ability to make this request. There are a number of different
ways we can try to proceed in the notebook.
## Generate vega in Python, request in the browser, render in notebook
The following cell magic parses yaml data into JSON. This JSON is then sent *to the browser*,
along with the relevant connection data. The browser then makes the request using
the OmniSci browser client, and renders the resulting image in the notebook:
```
connection_data = dict(
username='mapd',
password='HyperInteractive',
host='metis.mapd.com',
port='443',
database='mapd',
protocol='https'
)
%%omnisci_vega $connection_data
width: 384
height: 564
config:
ticks: false
data:
- name: 'tweets'
sql: 'SELECT goog_x as x, goog_y as y, tweets_nov_feb.rowid FROM tweets_nov_feb'
scales:
- name: 'x'
type: 'linear'
domain:
- -3650484.1235206556
- 7413325.514451755
range: 'width'
- name: 'y'
type: 'linear'
domain:
- -5778161.9183506705
- 10471808.487466192
range: 'height'
marks:
- type: 'points'
from:
data: 'tweets'
properties:
x:
scale: 'x'
field: 'x'
y:
scale: 'y'
field: 'y'
fillColor: 'green'
size:
value: 1
```
You can also do the same but for vega lite, which will get translated to vega in the browser before being executed with the omnisci browser client
```
%%omnisci_vegalite $connection_data
width: 384
height: 564
data:
sql: 'SELECT goog_x as x, goog_y as y, tweets_nov_feb.rowid FROM tweets_nov_feb'
mark:
type: circle
color: green
size: 1
encoding:
x:
field: x
type: quantitative
scale:
range: width
domain:
- -3650484.1235206556
- 7413325.514451755
y:
field: y
type: quantitative
scale:
range: height
domain:
- -5778161.9183506705
- 10471808.487466192
```
## Write vega directly, request in the browser, render in notebook
We don't necessarily need to use yaml as the input format. The following takes a JSON
string and sends it to the browser, along with the connection data:
```
import json
# TODO: Fix connection information and enalbe this
connection_data = dict(
user='mapd',
password='HyperInteractive',
host='vega-demo.omnisci.com',
port='9092',
dbname='mapd',
protocol='http'
)
# con = pymapd.connect(**connection_data)
# vega1 = """ {
# "width": 733,
# "height": 530,
# "data": [
# {
# "name": "heatmap_query",
# "sql": "SELECT rect_pixel_bin(conv_4326_900913_x(lon), -13847031.457875465, -7451726.712679257, 733, 733) as x,
# rect_pixel_bin(conv_4326_900913_y(lat), 2346114.147993467, 6970277.197053557, 530, 530) as y,
# SUM(amount) as cnt
# FROM fec_contributions_oct
# WHERE (lon >= -124.39000000000038 AND lon <= -66.93999999999943) AND
# (lat >= 20.61570573311549 AND lat <= 52.93117449504004) AND
# amount > 0 AND
# recipient_party = 'R'
# GROUP BY x, y"
# }
# ],
# "scales": [
# {
# "name": "heat_color",
# "type": "quantize",
# "domain": [
# 10000.0,
# 1000000.0
# ],
# "range": [ "#0d0887", "#2a0593", "#41049d", "#5601a4", "#6a00a8",
# "#7e03a8", "#8f0da4", "#a11b9b", "#b12a90", "#bf3984",
# "#cb4679", "#d6556d", "#e16462", "#ea7457", "#f2844b",
# "#f89540", "#fca636", "#feba2c", "#fcce25", "#f7e425", "#f0f921"
# ],
# "default": "#0d0887",
# "nullValue": "#0d0887"
# }
# ],
# "marks": [
# {
# "type": "symbol",
# "from": {
# "data": "heatmap_query"
# },
# "properties": {
# "shape": "square",
# "x": {
# "field": "x"
# },
# "y": {
# "field": "y"
# },
# "width": 1,
# "height": 1,
# "fillColor": {
# "scale": "heat_color",
# "field": "cnt"
# }
# }
# }
# ]
# }""".replace('\n', '')
# im = jupyterlab_omnisci.OmniSciVegaRenderer(con, json.loads(vega1))
# display(im)
```
## Requesting in Python
Making the omnisci request in the browser has a major drawback, in that the image data is not
easily available to the python kernel. Instead, we can make the request on the Python side:
```
# con.render_vega(vega1)
```
|
github_jupyter
|
import pymapd
import jupyterlab_omnisci
connection_data = dict(
user='mapd',
password='HyperInteractive',
host='metis.mapd.com',
port='443',
dbname='mapd',
protocol='https'
)
con = pymapd.connect(**connection_data)
connection_data = dict(
username='mapd',
password='HyperInteractive',
host='metis.mapd.com',
port='443',
database='mapd',
protocol='https'
)
%%omnisci_vega $connection_data
width: 384
height: 564
config:
ticks: false
data:
- name: 'tweets'
sql: 'SELECT goog_x as x, goog_y as y, tweets_nov_feb.rowid FROM tweets_nov_feb'
scales:
- name: 'x'
type: 'linear'
domain:
- -3650484.1235206556
- 7413325.514451755
range: 'width'
- name: 'y'
type: 'linear'
domain:
- -5778161.9183506705
- 10471808.487466192
range: 'height'
marks:
- type: 'points'
from:
data: 'tweets'
properties:
x:
scale: 'x'
field: 'x'
y:
scale: 'y'
field: 'y'
fillColor: 'green'
size:
value: 1
%%omnisci_vegalite $connection_data
width: 384
height: 564
data:
sql: 'SELECT goog_x as x, goog_y as y, tweets_nov_feb.rowid FROM tweets_nov_feb'
mark:
type: circle
color: green
size: 1
encoding:
x:
field: x
type: quantitative
scale:
range: width
domain:
- -3650484.1235206556
- 7413325.514451755
y:
field: y
type: quantitative
scale:
range: height
domain:
- -5778161.9183506705
- 10471808.487466192
import json
# TODO: Fix connection information and enalbe this
connection_data = dict(
user='mapd',
password='HyperInteractive',
host='vega-demo.omnisci.com',
port='9092',
dbname='mapd',
protocol='http'
)
# con = pymapd.connect(**connection_data)
# vega1 = """ {
# "width": 733,
# "height": 530,
# "data": [
# {
# "name": "heatmap_query",
# "sql": "SELECT rect_pixel_bin(conv_4326_900913_x(lon), -13847031.457875465, -7451726.712679257, 733, 733) as x,
# rect_pixel_bin(conv_4326_900913_y(lat), 2346114.147993467, 6970277.197053557, 530, 530) as y,
# SUM(amount) as cnt
# FROM fec_contributions_oct
# WHERE (lon >= -124.39000000000038 AND lon <= -66.93999999999943) AND
# (lat >= 20.61570573311549 AND lat <= 52.93117449504004) AND
# amount > 0 AND
# recipient_party = 'R'
# GROUP BY x, y"
# }
# ],
# "scales": [
# {
# "name": "heat_color",
# "type": "quantize",
# "domain": [
# 10000.0,
# 1000000.0
# ],
# "range": [ "#0d0887", "#2a0593", "#41049d", "#5601a4", "#6a00a8",
# "#7e03a8", "#8f0da4", "#a11b9b", "#b12a90", "#bf3984",
# "#cb4679", "#d6556d", "#e16462", "#ea7457", "#f2844b",
# "#f89540", "#fca636", "#feba2c", "#fcce25", "#f7e425", "#f0f921"
# ],
# "default": "#0d0887",
# "nullValue": "#0d0887"
# }
# ],
# "marks": [
# {
# "type": "symbol",
# "from": {
# "data": "heatmap_query"
# },
# "properties": {
# "shape": "square",
# "x": {
# "field": "x"
# },
# "y": {
# "field": "y"
# },
# "width": 1,
# "height": 1,
# "fillColor": {
# "scale": "heat_color",
# "field": "cnt"
# }
# }
# }
# ]
# }""".replace('\n', '')
# im = jupyterlab_omnisci.OmniSciVegaRenderer(con, json.loads(vega1))
# display(im)
# con.render_vega(vega1)
| 0.19787 | 0.913291 |
### 3.6 Softmax回归的从零开始实现
```
import torch
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
import sys
import os, sys
sys.path.append("..")
import d2lzh_pytorch.utils as d2l
np.random.seed(666)
cur_path = os.path.abspath(os.path.dirname('__file__'))
data_path = cur_path.replace('dl\dive-into-dl\chapter03-dl-basics', 'data\\')
data_path
```
### 3.6.1 获取和读取数据
```
batch_size = 256
if sys.platform.startswith('win'):
cur_path = os.path.abspath(os.path.dirname('__file__'))
data_path = cur_path.replace('dl\dive-into-dl\chapter03-dl-basics', 'data\\')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, root=data_path)
else:
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
```
### 3.6.2 初始化模型参数
```
num_inputs = 784
num_outputs = 10
# W [784, 10]
# b [1, 10]
W = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_outputs)), dtype=torch.float, requires_grad=True)
b = torch.zeros(num_outputs, dtype=torch.float, requires_grad=True)
X = torch.tensor([[1, 2, 3], [4, 5, 6]])
# 按行或者按列求和,并保持维度
print(X.sum(dim=0, keepdim=True))
print(X.sum(dim=1, keepdim=True))
```
### 3.6.3 实现softmax运算
```
def softmax(X):
# 求每个元素的exp
X_exp = X.exp()
partition = X_exp.sum(dim=1, keepdim=True)
return X_exp / partition
```
### 3.6.4 定义模型
```
def net(X):
# 将X转为(-1, 784),这样 X * W + b
return softmax(torch.mm(X.view((-1, num_inputs)), W) + b)
```
### 3.6.5 定义损失函数
```
# out[i][j][k] = input[index[i][j][k]][j][k] # dim=0
# out[i][j][k] = input[i][index[i][j][k]][k] # dim=1
# out[i][j][k] = input[i][j][index[i][j][k]] # dim=2
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = torch.LongTensor([0, 2])
y_hat.gather(1, y.view(-1, 1))
def cross_entropy(y_hat, y):
return - torch.log(y_hat.gather(1, y.view(-1, 1)))
```
### 3.6.6 计算分类准确率
```
def accuracy(y_hat, y):
return (y_hat.argmax(dim=1) == y).float().mean().item()
print(accuracy(y_hat, y))
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
print(evaluate_accuracy(test_iter, net))
```
### 3.6.7 训练模型
```
num_epochs, lr = 5, 0.1
def train_ch3(net, train_iter, test_iter, loss, num_epochs,
batch_size, params=None, lr=None, optimizer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
# 梯度清零
if optimizer:
optimizer.zero_grad()
elif params and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
d2l.sgd(params, lr, batch_size)
else:
optimizer.step()
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %3.f, test acc %.3f' %
(epoch+1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)
```
### 预测
```
X, y = iter(test_iter).next()
true_labels = d2l.get_fashion_mnist_labels(y.numpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])
```
|
github_jupyter
|
import torch
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
import sys
import os, sys
sys.path.append("..")
import d2lzh_pytorch.utils as d2l
np.random.seed(666)
cur_path = os.path.abspath(os.path.dirname('__file__'))
data_path = cur_path.replace('dl\dive-into-dl\chapter03-dl-basics', 'data\\')
data_path
batch_size = 256
if sys.platform.startswith('win'):
cur_path = os.path.abspath(os.path.dirname('__file__'))
data_path = cur_path.replace('dl\dive-into-dl\chapter03-dl-basics', 'data\\')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, root=data_path)
else:
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
num_inputs = 784
num_outputs = 10
# W [784, 10]
# b [1, 10]
W = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_outputs)), dtype=torch.float, requires_grad=True)
b = torch.zeros(num_outputs, dtype=torch.float, requires_grad=True)
X = torch.tensor([[1, 2, 3], [4, 5, 6]])
# 按行或者按列求和,并保持维度
print(X.sum(dim=0, keepdim=True))
print(X.sum(dim=1, keepdim=True))
def softmax(X):
# 求每个元素的exp
X_exp = X.exp()
partition = X_exp.sum(dim=1, keepdim=True)
return X_exp / partition
def net(X):
# 将X转为(-1, 784),这样 X * W + b
return softmax(torch.mm(X.view((-1, num_inputs)), W) + b)
# out[i][j][k] = input[index[i][j][k]][j][k] # dim=0
# out[i][j][k] = input[i][index[i][j][k]][k] # dim=1
# out[i][j][k] = input[i][j][index[i][j][k]] # dim=2
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = torch.LongTensor([0, 2])
y_hat.gather(1, y.view(-1, 1))
def cross_entropy(y_hat, y):
return - torch.log(y_hat.gather(1, y.view(-1, 1)))
def accuracy(y_hat, y):
return (y_hat.argmax(dim=1) == y).float().mean().item()
print(accuracy(y_hat, y))
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
print(evaluate_accuracy(test_iter, net))
num_epochs, lr = 5, 0.1
def train_ch3(net, train_iter, test_iter, loss, num_epochs,
batch_size, params=None, lr=None, optimizer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
# 梯度清零
if optimizer:
optimizer.zero_grad()
elif params and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
d2l.sgd(params, lr, batch_size)
else:
optimizer.step()
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %3.f, test acc %.3f' %
(epoch+1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)
X, y = iter(test_iter).next()
true_labels = d2l.get_fashion_mnist_labels(y.numpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])
| 0.375248 | 0.856932 |
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
```
# Causal Inference in `ktrain`
## What is the causal impact of having a PhD on making over 50K/year?
As of v0.27.x, ktrain supports causal inference using [meta-learners](https://arxiv.org/abs/1706.03461). We will use the well-studied [Adults Census](https://raw.githubusercontent.com/amaiya/ktrain/master/ktrain/tests/tabular_data/adults.csv) dataset from the UCI ML repository, which is census data from the early to mid 1990s. The objective is to estimate how much earning a PhD increases the probability of making over $50K in salary. (Note that this dataset is simply being used as a simple demonstration example of estimation. In a real-world scenario, you would spend more time on identifying which variables you should control for and which variables you should not control for.) Unlike conventional supervised machine learning, there is typically no ground truth for causal inference models, unless you're using a simulated dataset. So, we will simply check our estimates to see if they agree with intuition for illustration purposes in addition to inspecting robustness.
Let's begin by loading the dataset and creating a binary treatment (1 for PhD and 0 for no PhD).
```
!wget https://raw.githubusercontent.com/amaiya/ktrain/master/ktrain/tests/tabular_data/adults.csv -O /tmp/adults.csv
import pandas as pd
df = pd.read_csv('/tmp/adults.csv')
df = df.rename(columns=lambda x: x.strip())
df = df.applymap(lambda x: x.strip() if isinstance(x, str) else x)
filter_set = 'Doctorate'
df['treatment'] = df['education'].apply(lambda x: 1 if x in filter_set else 0)
df.head()
```
Next, let's invoke the `causal_inference_model` function to create a `CausalInferenceModel` instance and invoke `fit` to estimate the individualized treatment effect for each row in this dataset. By default, a [T-Learner](https://arxiv.org/abs/1706.03461) metalearner is used with LightGBM models as base learners. These can be adjusted using the `method` and `learner` parameters. Since this example is simply being used for illustration purposes, we will ignore the `fnlwgt` column, which represents the number of people the census believes the entry represents. In practice, one might incorporate domain knowledge when choosing which variables to include and ignore. For instance, variables thought to be common effects of both the treatment and outcome might be excluded as [colliders](https://en.wikipedia.org/wiki/Collider_(statistics)). Finally, we will also exclude the education-related columns as they are already captured in the treatment.
```
from ktrain.tabular.causalinference import causal_inference_model
cm = causal_inference_model(df,
treatment_col='treatment',
outcome_col='class',
ignore_cols=['fnlwgt', 'education','education-num']).fit()
```
As shown above, the dataset is automatically preprocessed and fitted very quickly.
### Average Treatment Effect (ATE)
The overall average treatment effect for all examples is 0.20. That is, having a PhD increases your probability of making over $50K by 20 percentage points.
```
cm.estimate_ate()
```
### Conditional Average Treatment Effects (CATE)
We also compute treatment effects after conditioning on attributes.
For those with Master's degrees, we find that it is lower than the overall population as expected but still positive (which is qualitatively [consistent with studies by the Census Bureau](https://www.wes.org/advisor-blog/salary-difference-masters-phd)):
```
cm.estimate_ate(cm.df['education'] == 'Masters')
```
For those that dropped out of school, we find that it is higher (also as expected):
```
cm.estimate_ate(cm.df['education'].isin(['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th', '10th', '12th']))
```
### Invidividualized Treatment Effects (ITE)
The CATEs above illustrate how causal effects vary across different subpopulations in the dataset. In fact, `CausalInferenceModel.df` stores a DataFrame representation of your dataset that has been augmented with a column called `treatment_effect` that stores the **individualized** treatment effect for each row in your dataset.
For instance, these individuals are predicted to benefit the most from a PhD with an increase of nearly 100 percentage points in the probability (see the **treatment_effect** column).
```
drop_cols = ['fnlwgt', 'education-num', 'capital-gain', 'capital-loss'] # omitted for readability
cm.df.sort_values('treatment_effect', ascending=False).drop(drop_cols, axis=1).head()
```
Examining how the treatment effect varies across units in the population can be useful for variety of different applications. [Uplift modeling](https://en.wikipedia.org/wiki/Uplift_modelling) is often used by companies for targeted promotions by identifying those individuals with the highest estimated treatment effects. Assessing the impact after such campaigns is yet another way to assess the model.
### Making Predictions on New Examples
Finally, we can predict treatment effects on new examples, as long as they are formatted like the original DataFrame. For instance, let's make a prediction for one of the rows we already examined:
```
df_example = cm.df.sort_values('treatment_effect', ascending=False).iloc[[0]]
df_example
cm.predict(df_example)
```
### Evaluating Robustness
As mentioned above, there is no ground truth for this problem to validate our estimates. In the cells above, we simply inspected the estimates to see if they correspond to our intuition on what should happen. Another approach to validating causal estimates is to evaluate robustness to various data manipulations (i.e., sensitivity analysis). For instance, the Placebo Treatment test replaces the treatment with a random covariate. We see below that this causes our estimate to drop to near zero, which is expected and exactly what we want. Such tests might be used to compare different models.
```
cm.evaluate_robustness()
```
**ktrain** uses the **CausalNLP** package for inferring causality. For more information, see the [CausalNLP documentation](https://amaiya.github.io/causalnlp).
|
github_jupyter
|
%reload_ext autoreload
%autoreload 2
%matplotlib inline
!wget https://raw.githubusercontent.com/amaiya/ktrain/master/ktrain/tests/tabular_data/adults.csv -O /tmp/adults.csv
import pandas as pd
df = pd.read_csv('/tmp/adults.csv')
df = df.rename(columns=lambda x: x.strip())
df = df.applymap(lambda x: x.strip() if isinstance(x, str) else x)
filter_set = 'Doctorate'
df['treatment'] = df['education'].apply(lambda x: 1 if x in filter_set else 0)
df.head()
from ktrain.tabular.causalinference import causal_inference_model
cm = causal_inference_model(df,
treatment_col='treatment',
outcome_col='class',
ignore_cols=['fnlwgt', 'education','education-num']).fit()
cm.estimate_ate()
cm.estimate_ate(cm.df['education'] == 'Masters')
cm.estimate_ate(cm.df['education'].isin(['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th', '10th', '12th']))
drop_cols = ['fnlwgt', 'education-num', 'capital-gain', 'capital-loss'] # omitted for readability
cm.df.sort_values('treatment_effect', ascending=False).drop(drop_cols, axis=1).head()
df_example = cm.df.sort_values('treatment_effect', ascending=False).iloc[[0]]
df_example
cm.predict(df_example)
cm.evaluate_robustness()
| 0.403097 | 0.987876 |
# Generative Adversarial Networks
```
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
%matplotlib inline
mu, sigma = -1,1
xs = np.linspace(-5,5,1000)
plt.plot(xs, norm.pdf(xs, loc=mu, scale=sigma))
TRAIN_ITERS=10000
M=200 # minibatch size
# MLP - used for D_pre, D1, D2, G networks
def mlp(input, output_dim):
# construct learnable parameters within local scope
w1=tf.get_variable("w0", [input.get_shape()[1], 6], initializer=tf.random_normal_initializer())
b1=tf.get_variable("b0", [6], initializer=tf.constant_initializer(0.0))
w2=tf.get_variable("w1", [6, 5], initializer=tf.random_normal_initializer())
b2=tf.get_variable("b1", [5], initializer=tf.constant_initializer(0.0))
w3=tf.get_variable("w2", [5,output_dim], initializer=tf.random_normal_initializer())
b3=tf.get_variable("b2", [output_dim], initializer=tf.constant_initializer(0.0))
# nn operators
fc1=tf.nn.tanh(tf.matmul(input,w1)+b1)
fc2=tf.nn.tanh(tf.matmul(fc1,w2)+b2)
fc3=tf.nn.tanh(tf.matmul(fc2,w3)+b3)
return fc3, [w1,b1,w2,b2,w3,b3]
# re-used for optimizing all networks
def momentum_optimizer(loss,var_list):
batch = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
0.001, # Base learning rate.
batch, # Current index into the dataset.
TRAIN_ITERS // 4, # Decay step - this decays 4 times throughout training process.
0.95, # Decay rate.
staircase=True)
#optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step=batch,var_list=var_list)
optimizer=tf.train.MomentumOptimizer(learning_rate,0.6).minimize(loss,global_step=batch,var_list=var_list)
return optimizer
with tf.variable_scope("D_pre"):
input_node=tf.placeholder(tf.float32, shape=(M,1))
train_labels=tf.placeholder(tf.float32,shape=(M,1))
D,theta=mlp(input_node,1)
loss=tf.reduce_mean(tf.square(D-train_labels))
optimizer = momentum_optimizer(loss, None)
sess = tf.InteractiveSession()
tf.initialize_all_variables().run()
# plot decision surface
def plot_d0(D,input_node):
f,ax=plt.subplots(1)
# p_data
xs=np.linspace(-5,5,1000)
ax.plot(xs, norm.pdf(xs,loc=mu,scale=sigma), label='p_data')
# decision boundary
r=1000 # resolution (number of points)
xs=np.linspace(-5,5,r)
ds=np.zeros((r,1)) # decision surface
# process multiple points in parallel in a minibatch
for i in range(r/M):
x=np.reshape(xs[M*i:M*(i+1)],(M,1))
ds[M*i:M*(i+1)]=sess.run(D,{input_node: x})
ax.plot(xs, ds, label='decision boundary')
ax.set_ylim(0,1.1)
plt.legend()
plot_d0(D,input_node)
plt.title('Initial Decision Boundary')
#plt.savefig('fig1.png')
lh=np.zeros(1000)
for i in range(1000):
#d=np.random.normal(mu,sigma,M)
d=(np.random.random(M)-0.5) * 10.0 # instead of sampling only from gaussian, want the domain to be covered as uniformly as possible
labels=norm.pdf(d,loc=mu,scale=sigma)
lh[i],_=sess.run([loss,optimizer], {input_node: np.reshape(d,(M,1)), train_labels: np.reshape(labels,(M,1))})
# training loss
plt.plot(lh)
plt.title('Training Loss')
plot_d0(D,input_node)
#plt.savefig('fig2.png')
weightsD = sess.run(theta)
sess.close()
```
### Building the Network
```
with tf.variable_scope("G"):
z_node=tf.placeholder(tf.float32, shape=(M,1)) # M uniform01 floats
G,theta_g=mlp(z_node,1) # generate normal transformation of Z
G=tf.mul(5.0,G) # scale up by 5 to match range
with tf.variable_scope("D") as scope:
# D(x)
x_node=tf.placeholder(tf.float32, shape=(M,1)) # input M normally distributed floats
fc,theta_d=mlp(x_node,1) # output likelihood of being normally distributed
D1=tf.maximum(tf.minimum(fc,.99), 0.01) # clamp as a probability
# make a copy of D that uses the same variables, but takes in G as input
scope.reuse_variables()
fc,theta_d=mlp(G,1)
D2=tf.maximum(tf.minimum(fc,.99), 0.01)
obj_d=tf.reduce_mean(tf.log(D1)+tf.log(1-D2))
obj_g=tf.reduce_mean(tf.log(D2))
# set up optimizer for G,D
opt_d=momentum_optimizer(1-obj_d, theta_d)
opt_g=momentum_optimizer(1-obj_g, theta_g) # maximize log(D(G(z)))
sess=tf.InteractiveSession()
tf.initialize_all_variables().run()
def plot_fig():
# plots pg, pdata, decision boundary
f,ax=plt.subplots(1)
# p_data
xs=np.linspace(-5,5,1000)
ax.plot(xs, norm.pdf(xs,loc=mu,scale=sigma), label='p_data')
# decision boundary
r=5000 # resolution (number of points)
xs=np.linspace(-5,5,r)
ds=np.zeros((r,1)) # decision surface
# process multiple points in parallel in same minibatch
for i in range(r/M):
x=np.reshape(xs[M*i:M*(i+1)],(M,1))
ds[M*i:M*(i+1)]=sess.run(D1,{x_node: x})
ax.plot(xs, ds, label='decision boundary')
# distribution of inverse-mapped points
zs=np.linspace(-5,5,r)
gs=np.zeros((r,1)) # generator function
for i in range(r/M):
z=np.reshape(zs[M*i:M*(i+1)],(M,1))
gs[M*i:M*(i+1)]=sess.run(G,{z_node: z})
histc, edges = np.histogram(gs, bins = 10)
ax.plot(np.linspace(-5,5,10), histc/float(r), label='p_g')
# ylim, legend
ax.set_ylim(0,1.1)
plt.legend()
# initial conditions
plot_fig()
plt.title('Before Training')
#plt.savefig('fig3.png')
# Algorithm 1 of Goodfellow et al 2014
k=1
histd, histg= np.zeros(TRAIN_ITERS), np.zeros(TRAIN_ITERS)
for i in range(TRAIN_ITERS):
for j in range(k):
x= np.random.normal(mu,sigma,M) # sampled m-batch from p_data
x.sort()
z= np.linspace(-5.0,5.0,M)+np.random.random(M)*0.01 # sample m-batch from noise prior
histd[i],_=sess.run([obj_d,opt_d], {x_node: np.reshape(x,(M,1)), z_node: np.reshape(z,(M,1))})
z= np.linspace(-5.0,5.0,M)+np.random.random(M)*0.01 # sample noise prior
histg[i],_=sess.run([obj_g,opt_g], {z_node: np.reshape(z,(M,1))}) # update generator
if i % (TRAIN_ITERS//10) == 0:
print(float(i)/float(TRAIN_ITERS))
plt.plot(range(TRAIN_ITERS),histd, label='obj_d')
plt.plot(range(TRAIN_ITERS), 1-histg, label='obj_g')
plt.legend()
#plt.savefig('fig4.png')
plot_fig()
```
|
github_jupyter
|
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
%matplotlib inline
mu, sigma = -1,1
xs = np.linspace(-5,5,1000)
plt.plot(xs, norm.pdf(xs, loc=mu, scale=sigma))
TRAIN_ITERS=10000
M=200 # minibatch size
# MLP - used for D_pre, D1, D2, G networks
def mlp(input, output_dim):
# construct learnable parameters within local scope
w1=tf.get_variable("w0", [input.get_shape()[1], 6], initializer=tf.random_normal_initializer())
b1=tf.get_variable("b0", [6], initializer=tf.constant_initializer(0.0))
w2=tf.get_variable("w1", [6, 5], initializer=tf.random_normal_initializer())
b2=tf.get_variable("b1", [5], initializer=tf.constant_initializer(0.0))
w3=tf.get_variable("w2", [5,output_dim], initializer=tf.random_normal_initializer())
b3=tf.get_variable("b2", [output_dim], initializer=tf.constant_initializer(0.0))
# nn operators
fc1=tf.nn.tanh(tf.matmul(input,w1)+b1)
fc2=tf.nn.tanh(tf.matmul(fc1,w2)+b2)
fc3=tf.nn.tanh(tf.matmul(fc2,w3)+b3)
return fc3, [w1,b1,w2,b2,w3,b3]
# re-used for optimizing all networks
def momentum_optimizer(loss,var_list):
batch = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
0.001, # Base learning rate.
batch, # Current index into the dataset.
TRAIN_ITERS // 4, # Decay step - this decays 4 times throughout training process.
0.95, # Decay rate.
staircase=True)
#optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step=batch,var_list=var_list)
optimizer=tf.train.MomentumOptimizer(learning_rate,0.6).minimize(loss,global_step=batch,var_list=var_list)
return optimizer
with tf.variable_scope("D_pre"):
input_node=tf.placeholder(tf.float32, shape=(M,1))
train_labels=tf.placeholder(tf.float32,shape=(M,1))
D,theta=mlp(input_node,1)
loss=tf.reduce_mean(tf.square(D-train_labels))
optimizer = momentum_optimizer(loss, None)
sess = tf.InteractiveSession()
tf.initialize_all_variables().run()
# plot decision surface
def plot_d0(D,input_node):
f,ax=plt.subplots(1)
# p_data
xs=np.linspace(-5,5,1000)
ax.plot(xs, norm.pdf(xs,loc=mu,scale=sigma), label='p_data')
# decision boundary
r=1000 # resolution (number of points)
xs=np.linspace(-5,5,r)
ds=np.zeros((r,1)) # decision surface
# process multiple points in parallel in a minibatch
for i in range(r/M):
x=np.reshape(xs[M*i:M*(i+1)],(M,1))
ds[M*i:M*(i+1)]=sess.run(D,{input_node: x})
ax.plot(xs, ds, label='decision boundary')
ax.set_ylim(0,1.1)
plt.legend()
plot_d0(D,input_node)
plt.title('Initial Decision Boundary')
#plt.savefig('fig1.png')
lh=np.zeros(1000)
for i in range(1000):
#d=np.random.normal(mu,sigma,M)
d=(np.random.random(M)-0.5) * 10.0 # instead of sampling only from gaussian, want the domain to be covered as uniformly as possible
labels=norm.pdf(d,loc=mu,scale=sigma)
lh[i],_=sess.run([loss,optimizer], {input_node: np.reshape(d,(M,1)), train_labels: np.reshape(labels,(M,1))})
# training loss
plt.plot(lh)
plt.title('Training Loss')
plot_d0(D,input_node)
#plt.savefig('fig2.png')
weightsD = sess.run(theta)
sess.close()
with tf.variable_scope("G"):
z_node=tf.placeholder(tf.float32, shape=(M,1)) # M uniform01 floats
G,theta_g=mlp(z_node,1) # generate normal transformation of Z
G=tf.mul(5.0,G) # scale up by 5 to match range
with tf.variable_scope("D") as scope:
# D(x)
x_node=tf.placeholder(tf.float32, shape=(M,1)) # input M normally distributed floats
fc,theta_d=mlp(x_node,1) # output likelihood of being normally distributed
D1=tf.maximum(tf.minimum(fc,.99), 0.01) # clamp as a probability
# make a copy of D that uses the same variables, but takes in G as input
scope.reuse_variables()
fc,theta_d=mlp(G,1)
D2=tf.maximum(tf.minimum(fc,.99), 0.01)
obj_d=tf.reduce_mean(tf.log(D1)+tf.log(1-D2))
obj_g=tf.reduce_mean(tf.log(D2))
# set up optimizer for G,D
opt_d=momentum_optimizer(1-obj_d, theta_d)
opt_g=momentum_optimizer(1-obj_g, theta_g) # maximize log(D(G(z)))
sess=tf.InteractiveSession()
tf.initialize_all_variables().run()
def plot_fig():
# plots pg, pdata, decision boundary
f,ax=plt.subplots(1)
# p_data
xs=np.linspace(-5,5,1000)
ax.plot(xs, norm.pdf(xs,loc=mu,scale=sigma), label='p_data')
# decision boundary
r=5000 # resolution (number of points)
xs=np.linspace(-5,5,r)
ds=np.zeros((r,1)) # decision surface
# process multiple points in parallel in same minibatch
for i in range(r/M):
x=np.reshape(xs[M*i:M*(i+1)],(M,1))
ds[M*i:M*(i+1)]=sess.run(D1,{x_node: x})
ax.plot(xs, ds, label='decision boundary')
# distribution of inverse-mapped points
zs=np.linspace(-5,5,r)
gs=np.zeros((r,1)) # generator function
for i in range(r/M):
z=np.reshape(zs[M*i:M*(i+1)],(M,1))
gs[M*i:M*(i+1)]=sess.run(G,{z_node: z})
histc, edges = np.histogram(gs, bins = 10)
ax.plot(np.linspace(-5,5,10), histc/float(r), label='p_g')
# ylim, legend
ax.set_ylim(0,1.1)
plt.legend()
# initial conditions
plot_fig()
plt.title('Before Training')
#plt.savefig('fig3.png')
# Algorithm 1 of Goodfellow et al 2014
k=1
histd, histg= np.zeros(TRAIN_ITERS), np.zeros(TRAIN_ITERS)
for i in range(TRAIN_ITERS):
for j in range(k):
x= np.random.normal(mu,sigma,M) # sampled m-batch from p_data
x.sort()
z= np.linspace(-5.0,5.0,M)+np.random.random(M)*0.01 # sample m-batch from noise prior
histd[i],_=sess.run([obj_d,opt_d], {x_node: np.reshape(x,(M,1)), z_node: np.reshape(z,(M,1))})
z= np.linspace(-5.0,5.0,M)+np.random.random(M)*0.01 # sample noise prior
histg[i],_=sess.run([obj_g,opt_g], {z_node: np.reshape(z,(M,1))}) # update generator
if i % (TRAIN_ITERS//10) == 0:
print(float(i)/float(TRAIN_ITERS))
plt.plot(range(TRAIN_ITERS),histd, label='obj_d')
plt.plot(range(TRAIN_ITERS), 1-histg, label='obj_g')
plt.legend()
#plt.savefig('fig4.png')
plot_fig()
| 0.743634 | 0.885928 |
# Quantum Key Distribution
## 1. Introduction
When Alice and Bob want to communicate a secret message (such as Bob’s online banking details) over an insecure channel (such as the internet), it is essential to encrypt the message. Since cryptography is a large area and almost all of it is outside the scope of this textbook, we will have to believe that Alice and Bob having a secret key that no one else knows is useful and allows them to communicate using symmetric-key cryptography.
If Alice and Bob want to use Eve’s classical communication channel to share their key, it is impossible to tell if Eve has made a copy of this key for herself- they must place complete trust in Eve that she is not listening. If, however, Eve provides a quantum communication channel, Alice and Bob no longer need to trust Eve at all- they will know if she tries to read Bob’s message before it gets to Alice.
For some readers, it may be useful to give an idea of how a quantum channel may be physically implemented. An example of a classical channel could be a telephone line; we send electric signals through the line that represent our message (or bits). A proposed example of a quantum communication channel could be some kind of fiber-optic cable, through which we can send individual photons (particles of light). Photons have a property called _polarisation,_ and this polarisation can be one of two states. We can use this to represent a qubit.
## 2. Protocol Overview
The protocol makes use of the fact that measuring a qubit can change its state. If Alice sends Bob a qubit, and an eavesdropper (Eve) tries to measure it before Bob does, there is a chance that Eve’s measurement will change the state of the qubit and Bob will not receive the qubit state Alice sent.
```
from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from numpy.random import randint
import numpy as np
```
If Alice prepares a qubit in the state $|+\rangle$ (`0` in the $X$-basis), and Bob measures it in the $X$-basis, Bob is sure to measure `0`:
```
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
qc.barrier()
# Alice now sends the qubit to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())
```
But if Eve tries to measure this qubit in the $Z$-basis before it reaches Bob, she will change the qubit's state from $|+\rangle$ to either $|0\rangle$ or $|1\rangle$, and Bob is no longer certain to measure `0`:
```
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
# Alice now sends the qubit to Bob
# but Eve intercepts and tries to read it
qc.measure(0, 0)
qc.barrier()
# Eve then passes this on to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())
```
We can see here that Bob now has a 50% chance of measuring `1`, and if he does, he and Alice will know there is something wrong with their channel.
The quantum key distribution protocol involves repeating this process enough times that an eavesdropper has a negligible chance of getting away with this interception. It is roughly as follows:
**- Step 1**
Alice chooses a string of random bits, e.g.:
`1000101011010100`
And a random choice of basis for each bit:
`ZZXZXXXZXZXXXXXX`
Alice keeps these two pieces of information private to herself.
**- Step 2**
Alice then encodes each bit onto a string of qubits using the basis she chose; this means each qubit is in one of the states $|0\rangle$, $|1\rangle$, $|+\rangle$ or $|-\rangle$, chosen at random. In this case, the string of qubits would look like this:
$$ |1\rangle|0\rangle|+\rangle|0\rangle|-\rangle|+\rangle|-\rangle|0\rangle|-\rangle|1\rangle|+\rangle|-\rangle|+\rangle|-\rangle|+\rangle|+\rangle
$$
This is the message she sends to Bob.
**- Step 3**
Bob then measures each qubit at random, for example, he might use the bases:
`XZZZXZXZXZXZZZXZ`
And Bob keeps the measurement results private.
**- Step 4**
Bob and Alice then publicly share which basis they used for each qubit. If Bob measured a qubit in the same basis Alice prepared it in, they use this to form part of their shared secret key, otherwise they discard the information for that bit.
**- Step 5**
Finally, Bob and Alice share a random sample of their keys, and if the samples match, they can be sure (to a small margin of error) that their transmission is successful.
## 3. Qiskit Example: Without Interception
Let’s first see how the protocol works when no one is listening in, then we can see how Alice and Bob are able to detect an eavesdropper. As always, let's start by importing everything we need:
To generate pseudo-random keys, we will use the `randint` function from numpy. To make sure you can reproduce the results on this page, we will set the seed to 0:
```
np.random.seed(seed=0)
```
We will call the length of Alice's initial message `n`. In this example, Alice will send a message 100 qubits long:
```
n = 100
```
### 3.1 Step 1:
Alice generates her random set of bits:
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
print(alice_bits)
```
At the moment, the set of bits '`alice_bits`' is only known to Alice. We will keep track of what information is only known to Alice, what information is only known to Bob, and what has been sent over Eve's channel in a table like this:
| Alice's Knowledge |Over Eve's Channel| Bob's Knowledge |
|:-----------------:|:----------------:|:---------------:|
| alice_bits | | |
### 3.2 Step 2:
Alice chooses to encode each bit on qubit in the $X$ or $Z$-basis at random, and stores the choice for each qubit in `alice_bases`. In this case, a `0` means "prepare in the $Z$-basis", and a `1` means "prepare in the $X$-basis":
```
np.random.seed(seed=0)
n = 100
## Step 1
#Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
print(alice_bases)
```
Alice also keeps this knowledge private:
| Alice's Knowledge |Over Eve's Channel| Bob's Knowledge |
|:-----------------:|:----------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
The function `encode_message` below, creates a list of `QuantumCircuit`s, each representing a single qubit in Alice's message:
```
def encode_message(bits, bases):
message = []
for i in range(n):
qc = QuantumCircuit(1,1)
if bases[i] == 0: # Prepare qubit in Z-basis
if bits[i] == 0:
pass
else:
qc.x(0)
else: # Prepare qubit in X-basis
if bits[i] == 0:
qc.h(0)
else:
qc.x(0)
qc.h(0)
qc.barrier()
message.append(qc)
return message
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
```
We can see that the first bit in `alices_bits` is `0`, and the basis she encodes this in is the $X$-basis (represented by `1`):
```
print('bit = %i' % alice_bits[0])
print('basis = %i' % alice_bases[0])
```
And if we view the first circuit in `message` (representing the first qubit in Alice's message), we can verify that Alice has prepared a qubit in the state $|+\rangle$:
```
message[0].draw()
```
As another example, we can see that the fourth bit in `alice_bits` is `1`, and it is encoded in the $Z$-basis, Alice prepares the corresponding qubit in the state $|1\rangle$:
```
print('bit = %i' % alice_bits[4])
print('basis = %i' % alice_bases[4])
message[4].draw()
```
This message of qubits is then sent to Bob over Eve's quantum channel:
| Alice's Knowledge |Over Eve's Channel| Bob's Knowledge |
|:-----------------:|:----------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
### 3.3 Step 3:
Bob then measures each qubit in the $X$ or $Z$-basis at random and stores this information:
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
print(bob_bases)
```
`bob_bases` stores Bob's choice for which basis he measures each qubit in.
| Alice's Knowledge |Over Eve's Channel| Bob's Knowledge |
|:-----------------:|:----------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
Below, the function `measure_message` applies the corresponding measurement and simulates the result of measuring each qubit. We store the measurement results in `bob_results`.
```
def measure_message(message, bases):
backend = Aer.get_backend('aer_simulator')
measurements = []
for q in range(n):
if bases[q] == 0: # measuring in Z-basis
message[q].measure(0,0)
if bases[q] == 1: # measuring in X-basis
message[q].h(0)
message[q].measure(0,0)
aer_sim = Aer.get_backend('aer_simulator')
result = aer_sim.run(message[q], shots=1, memory=True).result()
measured_bit = int(result.get_memory()[0])
measurements.append(measured_bit)
return measurements
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
```
We can see that the circuit in `message[0]` (representing the 0th qubit) has had an $X$-measurement added to it by Bob:
```
message[0].draw()
```
Since Bob has by chance chosen to measure in the same basis Alice encoded the qubit in, Bob is guaranteed to get the result `0`. For the 6th qubit (shown below), Bob's random choice of measurement is not the same as Alice's, and Bob's result has only a 50% chance of matching Alices'.
```
message[6].draw()
print(bob_results)
```
Bob keeps his results private.
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
### 3.4 Step 4:
After this, Alice reveals (through Eve's channel) which qubits were encoded in which basis:
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
And Bob reveals which basis he measured each qubit in:
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
If Bob happened to measure a bit in the same basis Alice prepared it in, this means the entry in `bob_results` will match the corresponding entry in `alice_bits`, and they can use that bit as part of their key. If they measured in different bases, Bob's result is random, and they both throw that entry away. Here is a function `remove_garbage` that does this for us:
```
def remove_garbage(a_bases, b_bases, bits):
good_bits = []
for q in range(n):
if a_bases[q] == b_bases[q]:
# If both used the same basis, add
# this to the list of 'good' bits
good_bits.append(bits[q])
return good_bits
```
Alice and Bob both discard the useless bits, and use the remaining bits to form their secret keys:
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
print(alice_key)
```
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
| alice_key | | |
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
print(bob_key)
```
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
| alice_key | | bob_key |
### 3.5 Step 5:
Finally, Bob and Alice compare a random selection of the bits in their keys to make sure the protocol has worked correctly:
```
def sample_bits(bits, selection):
sample = []
for i in selection:
# use np.mod to make sure the
# bit we sample is always in
# the list range
i = np.mod(i, len(bits))
# pop(i) removes the element of the
# list at index 'i'
sample.append(bits.pop(i))
return sample
```
Alice and Bob both broadcast these publicly, and remove them from their keys as they are no longer secret:
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
```
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
| alice_key | | bob_key |
| bob_sample | bob_sample | bob_sample |
| alice_sample | alice_sample | alice_sample |
If the protocol has worked correctly without interference, their samples should match:
```
bob_sample == alice_sample
```
If their samples match, it means (with high probability) `alice_key == bob_key`. They now share a secret key they can use to encrypt their messages!
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
| alice_key | | bob_key |
| bob_sample | bob_sample | bob_sample |
| alice_sample | alice_sample | alice_sample |
| shared_key | | shared_key |
```
print(bob_key)
print(alice_key)
print("key length = %i" % len(alice_key))
```
## 4. Qiskit Example: *With* Interception
Let’s now see how Alice and Bob can tell if Eve has been trying to listen in on their quantum message. We repeat the same steps as without interference, but before Bob receives his qubits, Eve will try and extract some information from them. Let's set a different seed so we get a specific set of reproducible 'random' results:
```
np.random.seed(seed=3)
```
### 4.1 Step 1:
Alice generates her set of random bits:
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
print(alice_bits)
```
### 4.2 Step 2:
Alice encodes these in the $Z$ and $X$-bases at random, and sends these to Bob through Eve's quantum channel:
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
print(alice_bases)
```
In this case, the first qubit in Alice's message is in the state $|+\rangle$:
```
message[0].draw()
```
### Interception!
Oh no! Eve intercepts the message as it passes through her channel. She tries to measure the qubits in a random selection of bases, in the same way Bob will later.
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
print(intercepted_message)
```
We can see the case of qubit 0 below; Eve's random choice of basis is not the same as Alice's, and this will change the qubit state from $|+\rangle$, to a random state in the $Z$-basis, with 50% probability of $|0\rangle$ or $|1\rangle$:
```
message[0].draw()
```
### 4.3 Step 3:
Eve then passes on the qubits to Bob, who measures them at random. In this case, Bob chose (by chance) to measure in the same basis Alice prepared the qubit in. Without interception, Bob would be guaranteed to measure `0`, but because Eve tried to read the message he now has a 50% chance of measuring `1` instead.
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
message[0].draw()
```
### 4.4 Step 4:
Bob and Alice reveal their basis choices, and discard the useless bits:
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
```
### 4.5 Step 5:
Bob and Alice compare the same random selection of their keys to see if the qubits were intercepted:
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
bob_sample == alice_sample
```
Oh no! Bob's key and Alice's key do not match. We know this is because Eve tried to read the message between steps 2 and 3, and changed the qubits' states. For all Alice and Bob know, this could be due to noise in the channel, but either way they must throw away all their results and try again- Eve's interception attempt has failed.
## 5. Risk Analysis
For this type of interception, in which Eve measures all the qubits, there is a small chance that Bob and Alice's samples could match, and Alice sends her vulnerable message through Eve's channel. Let's calculate that chance and see how risky quantum key distribution is.
- For Alice and Bob to use a qubit's result, they must both have chosen the same basis. If Eve chooses this basis too, she will successfully intercept this bit without introducing any error. There is a 50% chance of this happening.
- If Eve chooses the *wrong* basis, i.e. a different basis to Alice and Bob, there is still a 50% chance Bob will measure the value Alice was trying to send. In this case, the interception also goes undetected.
- But if Eve chooses the *wrong* basis, i.e. a different basis to Alice and Bob, there is a 50% chance Bob will not measure the value Alice was trying to send, and this *will* introduce an error into their keys.

If Alice and Bob compare 1 bit from their keys, the probability the bits will match is $0.75$, and if so they will not notice Eve's interception. If they measure 2 bits, there is a $0.75^2 = 0.5625$ chance of the interception not being noticed. We can see that the probability of Eve going undetected can be calculated from the number of bits ($x$) Alice and Bob chose to compare:
$$ P(\text{undetected}) = 0.75^x $$
If we decide to compare 15 bits as we did above, there is a 1.3% chance Eve will be undetected. If this is too risky for us, we could compare 50 bits instead, and have a 0.00006% chance of being spied upon unknowingly.
You can retry the protocol again by running the cell below. Try changing `sample_size` to something low and see how easy it is for Eve to intercept Alice and Bob's keys.
```
n = 100
# Step 1
alice_bits = randint(2, size=n)
alice_bases = randint(2, size=n)
# Step 2
message = encode_message(alice_bits, alice_bases)
# Interception!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
# Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
# Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
# Step 5
sample_size = 15 # Change this to something lower and see if
# Eve can intercept the message without Alice
# and Bob finding out
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
alice_sample = sample_bits(alice_key, bit_selection)
if bob_sample != alice_sample:
print("Eve's interference was detected.")
else:
print("Eve went undetected!")
import qiskit.tools.jupyter
%qiskit_version_table
```
|
github_jupyter
|
from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from numpy.random import randint
import numpy as np
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
qc.barrier()
# Alice now sends the qubit to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
# Alice now sends the qubit to Bob
# but Eve intercepts and tries to read it
qc.measure(0, 0)
qc.barrier()
# Eve then passes this on to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())
np.random.seed(seed=0)
n = 100
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
print(alice_bits)
np.random.seed(seed=0)
n = 100
## Step 1
#Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
print(alice_bases)
def encode_message(bits, bases):
message = []
for i in range(n):
qc = QuantumCircuit(1,1)
if bases[i] == 0: # Prepare qubit in Z-basis
if bits[i] == 0:
pass
else:
qc.x(0)
else: # Prepare qubit in X-basis
if bits[i] == 0:
qc.h(0)
else:
qc.x(0)
qc.h(0)
qc.barrier()
message.append(qc)
return message
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
print('bit = %i' % alice_bits[0])
print('basis = %i' % alice_bases[0])
message[0].draw()
print('bit = %i' % alice_bits[4])
print('basis = %i' % alice_bases[4])
message[4].draw()
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
print(bob_bases)
def measure_message(message, bases):
backend = Aer.get_backend('aer_simulator')
measurements = []
for q in range(n):
if bases[q] == 0: # measuring in Z-basis
message[q].measure(0,0)
if bases[q] == 1: # measuring in X-basis
message[q].h(0)
message[q].measure(0,0)
aer_sim = Aer.get_backend('aer_simulator')
result = aer_sim.run(message[q], shots=1, memory=True).result()
measured_bit = int(result.get_memory()[0])
measurements.append(measured_bit)
return measurements
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
message[0].draw()
message[6].draw()
print(bob_results)
def remove_garbage(a_bases, b_bases, bits):
good_bits = []
for q in range(n):
if a_bases[q] == b_bases[q]:
# If both used the same basis, add
# this to the list of 'good' bits
good_bits.append(bits[q])
return good_bits
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
print(alice_key)
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
print(bob_key)
def sample_bits(bits, selection):
sample = []
for i in selection:
# use np.mod to make sure the
# bit we sample is always in
# the list range
i = np.mod(i, len(bits))
# pop(i) removes the element of the
# list at index 'i'
sample.append(bits.pop(i))
return sample
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
bob_sample == alice_sample
print(bob_key)
print(alice_key)
print("key length = %i" % len(alice_key))
np.random.seed(seed=3)
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
print(alice_bits)
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
print(alice_bases)
message[0].draw()
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
print(intercepted_message)
message[0].draw()
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
message[0].draw()
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
bob_sample == alice_sample
n = 100
# Step 1
alice_bits = randint(2, size=n)
alice_bases = randint(2, size=n)
# Step 2
message = encode_message(alice_bits, alice_bases)
# Interception!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
# Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
# Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
# Step 5
sample_size = 15 # Change this to something lower and see if
# Eve can intercept the message without Alice
# and Bob finding out
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
alice_sample = sample_bits(alice_key, bit_selection)
if bob_sample != alice_sample:
print("Eve's interference was detected.")
else:
print("Eve went undetected!")
import qiskit.tools.jupyter
%qiskit_version_table
| 0.555435 | 0.990404 |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Gena/map_set_zoom.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Gena/map_set_zoom.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Gena/map_set_zoom.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Gena/map_set_zoom.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geehydro](https://github.com/giswqs/geehydro). The **geehydro** Python package builds on the [folium](https://github.com/python-visualization/folium) package and implements several methods for displaying Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, `Map.centerObject()`, and `Map.setOptions()`.
The magic command `%%capture` can be used to hide output from a specific cell.
```
# %%capture
# !pip install earthengine-api
# !pip install geehydro
```
Import libraries
```
import ee
import folium
import geehydro
```
Authenticate and initialize Earth Engine API. You only need to authenticate the Earth Engine API once. Uncomment the line `ee.Authenticate()`
if you are running this notebook for this first time or if you are getting an authentication error.
```
# ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
This step creates an interactive map using [folium](https://github.com/python-visualization/folium). The default basemap is the OpenStreetMap. Additional basemaps can be added using the `Map.setOptions()` function.
The optional basemaps can be `ROADMAP`, `SATELLITE`, `HYBRID`, `TERRAIN`, or `ESRI`.
```
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
```
## Add Earth Engine Python script
```
# add some data to the Map
dem = ee.Image("AHN/AHN2_05M_RUW")
Map.addLayer(dem, {'min': -5, 'max': 50, 'palette': ['000000', 'ffffff'] }, 'DEM', True)
# zoom in somewhere
Map.setCenter(4.4585, 52.0774, 15)
# TEST
Map.setZoom(10)
```
## Display Earth Engine data layers
```
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
```
|
github_jupyter
|
# %%capture
# !pip install earthengine-api
# !pip install geehydro
import ee
import folium
import geehydro
# ee.Authenticate()
ee.Initialize()
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
# add some data to the Map
dem = ee.Image("AHN/AHN2_05M_RUW")
Map.addLayer(dem, {'min': -5, 'max': 50, 'palette': ['000000', 'ffffff'] }, 'DEM', True)
# zoom in somewhere
Map.setCenter(4.4585, 52.0774, 15)
# TEST
Map.setZoom(10)
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
| 0.376165 | 0.949763 |
# Chapter 9: Electrostatics for Salty Solutions
(c) 2018 Manuel Razo. This work is licensed under a [Creative Commons Attribution License CC-BY 4.0](https://creativecommons.org/licenses/by/4.0/). All code contained herein is licensed under an [MIT license](https://opensource.org/licenses/MIT).
---
```
# Our numerical workhorses
import numpy as np
import scipy as sp
import scipy.signal
import pandas as pd
import mpmath
# Import matplotlib stuff for plotting
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from mpl_toolkits.mplot3d import Axes3D # For 3D plots
# Seaborn, useful for graphics
import seaborn as sns
# Import the default plotting style
import plotting_style as pstyle
# Function to import and display images from the Garland website
from IPython.display import Image
# Magic function to make matplotlib inline
%matplotlib inline
# This enables SVG graphics inline.
%config InlineBackend.figure_formats = {'png', 'retina'}
# Define directories
figdir = '../fig/'
# Set plotting style
pstyle.set_plotting_style()
```
## 9.5 A simple model for viral capsid assembly
(c) Carry out a numerical solution for $\phi_n$, $n = 1,2,\ldots,12$, as a function of $\phi_T$ and $\Delta\varepsilon$. Plot $\phi_n$ as a function of $n$ for
$\phi_T = \phi_C$ and $\Delta\varepsilon = -1, -5,$ and $-10 \; k_BT$. How are the capsomers distributed among the 12 different structures in each of these cases? What happens to the fraction of capsomers in complete capsids as the total volume fraction is varied from below to above $\phi_C$, in the case $\Delta\varepsilon = -5 \; k_BT?$
### Solution
As derived earlier in the problem the volume fraction of the partially assembled capsid with $n$ capsomers is of the form
$$
\phi_n = \left( \phi_1 \right)^n e^{- \varepsilon_n / k_BT},
\label{eq_vol_frac}
$$
where $\varepsilon_n$ is the total energy of the interactions between $n$ of the capsomers. This energy is of the form
$$
\varepsilon_n = \sum_{m = 1}^n f_m \Delta\varepsilon,
$$
where $f_m$ is the number of additional contacts between capsomers created when a capsomer binds a structure of size $n - 1$ to form a structure of size $n$. These contacts are listed as
$$
f_n = \begin{cases}
1 \; (n = 2),\\
2 \; (3 \leq n \leq 7),\\
3 \; (8 \leq n \leq 10),\\
4 \; (n = 11),\\
5 \; (n = 12).
\end{cases}
$$
To make things simpler further down let's define a function that computes this energy given a number of capsomers and a value for $\Delta\varepsilon$.
```
def epsilon_n(Depsilon, n=1):
'''
Function that returns the energy of a structure of size n viral capsomers
in kBT by adding the number of contacts between capsomers with energy
Depsilon.
Parameters
----------
Depsilon: float.
Energy of interaction between contacts
n : int. Default 1
Number of capsomers in structure
Returns
-------
Energy of interactions between capsomers in kBT
'''
# Create dictionary with number of contacts when adding a new capsomer to
# a structure of size n - 1 to form a structure of size n
fn = {1: 0,
2: 1, 3: 2, 4: 2, 5: 2, 6: 2, 7: 2,
8: 3, 9: 3, 10: 3,
11: 4,
12: 5}
# Extract the energy of each capsomer contribution
return np.sum([fn[x] * Depsilon for x in range(1, n + 1)])
```
In the problem we also derived a relationship for $\phi_C$ the critical volume fraction in which, if we assume that there are only two structures contributing significantly to the volume fraction, these being the single capsomers and the fully assembled dodecahedron, then at this volume fraction half of the capsomers are forming fully formed capsids. This function was found to be of the form
$$
\ln \left( {\phi_C \over 2} \right) = {\varepsilon_{12} \over 11 k_BT}.
$$
Solving for $\phi_C$ this gives
$$
\phi_C = 2 e^{\varepsilon_{12} \over 11 k_BT}.
$$
By assumption at this critical concentration the individual capsomers volume fraction $\phi_1$ and the fully assembled capsids $\phi_{12}$ occupy half of the total volume fraction. Therefore we can use $\phi_C / 2 = \phi_1$ along Eq. \ref{eq_vol_frac} to compute the volume fraction for the other partially assembled capsids. Let's first define a function that computes the volume fraction as given by Eq. \ref{eq_vol_frac}.
```
def phi_n(Depsilon, n, phi_1):
'''
Function that computes the volume fraction occupied by a structure formed
out of n capsomers given the volume fraction occupied by the single
monomers in solution.
Parameters
----------
Depsilon: float.
Energy of interaction between contacts
n : int. Default 1
Number of capsomers in structure
phi_1 : float [0, 1]
Volume fraction of individual capsomers
Returns
-------
Volume fraction of structure with n capsomers
'''
# Compute and return the volume fraction
return phi_1**n * np.exp(- epsilon_n(Depsilon, n))
```
With these functions in hand and a value of $\phi_1 = \phi_C / 2$ let's compute the volume fraction for each partially assembled structure.
```
# Define energies for individual contacts
Depsilon = [-1, -5, -10]
# Define names for columns of tidy data frame
names = ['n', 'Depsilon', 'phi_n', 'phi_c']
# Initialize dataframe
df = pd.DataFrame(columns=names)
# Loop through each binding energy computing the volume fraction of each
# structure
for de in Depsilon:
# Define fraction of monomers
phi_1 = np.exp(epsilon_n(de, 12) / 11)
# Loop through each individual capsomer
for n in range(1, 13):
# Compute the volume fraction
phi = phi_n(de, n, phi_1)
# Save results in Series to append to dataframe
series = pd.Series([n, de, phi, phi_1 * 2], index=names)
# Append to data frame
df = df.append(series, ignore_index=True)
# Let's look at the dataframe
df.head()
```
Let's now plot these fractions
```
# Group dataframe by energy of single contact
df_group = df.groupby('Depsilon')
# Define markers for each group
markers = ['o', 'v', 's']
# Initialize figure
# Loop through groups plotting volume fraction
for i, (group, data) in enumerate(df_group):
plt.plot(data.n, data.phi_n / data.phi_c,
lw=0, marker=markers[i], markersize=4,
label=group)
# Set y scale to be log
plt.yscale('log')
# Label axis
plt.xlabel(r'number of capsomers $n$')
plt.ylabel(r'$\phi_n / \phi_T$')
# set legend
plt.legend(title=r'$\Delta\varepsilon \; (k_BT)$')
# save figure
plt.tight_layout()
plt.savefig(figdir + 'problem_09_05_01.png', bbox_inches='tight')
```
Let's now explore for the case of $\Delta\varepsilon = -5 \; k_BT$ how the volume fraction of complete capsids changes as we go below and above the critical volume fraction $\phi_C$.
```
# Compute the critical volume fraction for -5 kBT
phi_c = 2 * np.exp(epsilon_n(-5, 12) / 11)
# Print critical volume fraction
print('phi_C(-5 kBT) = ', phi_c)
```
Given that it is a small number we can vary this critical volume fraction to be 100 times larger and smaller.
```
# Define range of fractions to be used for phi_1
phi_1_array = np.logspace(-2, 2, 100) * phi_c / 2
# Compute the volume fraction of the complete capsids
phi_n_array = phi_n(-5, 12, phi_1_array)
# Plot result
plt.loglog(phi_1_array / (phi_c / 2), phi_n_array / (phi_c / 2))
# Label axis
plt.xlabel(r'$\phi_1 \; / \; \phi_1^C$')
plt.ylabel(r'$\phi_{12} \; / \; \phi_1^C $')
# Save figure
plt.tight_layout()
plt.savefig(figdir + 'problem_09_05_02.png', bbox_inches='tight')
```
## 9.7 Poisson–Boltzmann revisited
(b) Plot the electric potential and the concentrations of positive and negative charges as functions of the distance from the charged plane, assuming that the charge on the plane is one electron per 100 nm$^2$ , and $c_\infty$ = 100 mM.
### Solution
On part (a) we found out that the solution of the linearized Poission-Boltzmann equation for the potential $V(x)$ is given by
$$
V(x) = {\sigma \lambda_D \over \varepsilon_o D} e^{-x / \lambda_D},
$$
where $x$ is the distance from the charged plane, $\sigma \equiv e/a$ is the charge per unit area of the plane, $\lambda_D$ is the Debye length, $\varepsilon_o$ is the permittivity of free space, $D$ is the dielectric constant. We also found that the Debye length is given by
$$
\lambda_D = \sqrt{\varepsilon_o D k_BT \over 2 (ze)^2 c_\infty}.
$$
Under this linear regime the positive and negative charge concentrations as a function of the distance from the charged plane is given by
$$
c_{\pm}(x) \approx c_\infty \left( 1 \mp {z e \over k_BT}
{\sigma \lambda_D \over \varepsilon_o D} e^{-x / \lambda_D} \right),
$$
where $c_\infty$ represents the ion concentration far away from the charged plane. Let's define all these quantities.
```
# Define parameters to plot ion concentration
c_inf = 100E-3 * 6.022E23 * 1000 # number / m**3
eps_D = 80 * 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
z = 1 # monovalent ions
e_charge = 1.6E-19 # C
```
Having defined these variables let's estimate the Debye length $\lambda_D$
```
lam_D = np.sqrt(eps_D * kBT / 2 / (z * e_charge)**2 / c_inf)
print('lambda_D ≈ {:.2f} nm'.format(lam_D * 1E9))
```
Also on part (a) we found that the area must satisfy the condition
$$
a \gg {z e^2 \over k_BT}{\lambda_D \over \varepsilon_o D}.
$$
Using the values that we just define this gives
```
a_condition = z * e_charge**2 / kBT * lam_D / eps_D
print('area >> {:.2f} nm**2'.format(a_condition * (1E9)**2))
```
Having defined the condition for the linear approximation to be valid let us choose an area of $100 \;nm^2$ for our computation. With that we now have all of the necessary elements to compute the ion concentration as a function of the distance from the charged plate.
```
# Define range of x values
x_range = np.linspace(0, 5, 50) / 1E9 # m
# Compute ion concentration
c_plus = 100 * (1 - z * e_charge / kBT *
(e_charge / 100 * 1E9**2) * lam_D / eps_D *
np.exp(-x_range / lam_D))
c_minus = 100 * (1 + z * e_charge / kBT *
(e_charge / 100 * 1E9**2) * lam_D / eps_D *
np.exp(-x_range / lam_D))
# Plot ion concentrations
plt.plot(x_range * 1E9, c_plus, label=r'$c_+$')
plt.plot(x_range * 1E9 , c_minus, label=r'$c_-$')
# Label axis
plt.xlabel(r'distance $x$ (nM)')
plt.ylabel(r'concentration (mM)')
# Add legend
plt.legend(title='ion')
# Save figure
plt.savefig(figdir + 'problem_09_07_01.png', bbox_inches='tight', dpi=300)
```
## 9.8 Potential near a protein
Consider a protein sphere with a radius of 1.8 nm, and charge $Q = −10e$, in an aqueous solution of $c_\infty = 0.05$ M NaCl at 25$^\circ$C. Consider the small ions as point charges and use the linear approximation to the Poisson–Boltzmann equation.
(b) What is the surface potential of the protein in units $k_BT / e$?
### Solution
On part (a) we derived the functional form of the potential $V(r)$ to be
$$
V(r) = {Q \over r} {e^{R - r \over \lambda_D} \over
4 \pi \varepsilon_o D \left( 1 + {R \over \lambda_D}\right)},
$$
where $Q$ is the charge of the protein, $R$ is the radius of the protein as well, $r$ is the distance at which the potential is measured, $\epsilon_o$ is the permitivity of free space, $D$ is the water's dielectric constant, and $\lambda_D$ the Debye length, just as before is given by
$$
\lambda_D = \sqrt{\varepsilon_o D k_BT \over 2 (ze)^2 c_\infty}.
$$
At the surface of the protein we have that $r = R$, therefore the potential is given by
$$
V(R) = {Q \over R} {1 \over 4 \pi \epsilon_o D \left( 1 + {R \over \lambda_D} \right)}.
$$
Evaluating this numerically gives
```
# Define parameters to plot ion concentration
c_inf = 0.05 * 6.022E23 * 1000 # converted from M to number / m**3
eps_D = 80 * 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
e_charge = 1.6E-19 # Coulombs
Q = -10 * e_charge #Charge of the protein
R = 1.8E-9 # Protein size (m)
# Compute lambda_D
lam_D = np.sqrt(eps_D * kBT / 2 / (z * e_charge)**2 / c_inf)
# Evaluate potential
V_R = (Q / R) * (1 / (4 * np.pi * eps_D * (1 + R / lam_D)))
# Convert to kBT/e
print('potential at protein surface:')
print('V(R) = {:.1f} kBT / e'.format(V_R / kBT * e_charge))
```
This numerical value does not satisfy the condition of the linearization of the Debye-Hückle equation since $\vert V(R) \vert$ is not much less than $k_BT / e$. Having said that we'll continue with the numerical evaluation of the requested results.
(c) What is the concentration of Na$^+$ ions and of Cl$^−$ ions at the surface of the protein?
### Solution
Given that the ion concentration is given by
$$
c_\pm (r) = c_\infty e^{\mp \beta z e V(r)},
$$
we can evaluate this numerically, obtaining
```
# Positive ions
c_plus = 0.05 * np.exp(-V_R / kBT * e_charge)
# Negative ions
c_minus = 0.05 * np.exp(V_R / kBT * e_charge)
print('Positive ions:')
print('c_+(R) = {:.3f} M'.format(c_plus))
print('Negative ions:')
print('c_-(R) = {:.3f} M'.format(c_minus))
```
(d) What is the concentration of Na$^+$ and Cl$^−$ ions at a distance of 0.3 nm from the protein surface?
### Solution
In order to evaluate this result we use the full form of the potential $V(r)$ given by
$$
V(r) = {Q \over r} {e^{R - r \over \lambda_D} \over
4 \pi \varepsilon_o D \left( 1 + {R \over \lambda_D}\right)}.
$$
Evaluating this numerically at 0.3 nm gives
```
# Define distance to evaluate potential at
dist = 0.3E-9 # nm converted to m
r = dist + R # add radius of the protein to distance to be evaluated
# Evaluating potential at distance 0.3 nm gives
V_zerothree = (Q / r) * np.exp((R - r) / lam_D) / (4 * np.pi * eps_D *
(1 + R / lam_D))
# Evaluate concentrations
# Positive ions
c_plus = 0.05 * np.exp(-V_zerothree / kBT * e_charge)
# Negative ions
c_minus = 0.05 * np.exp(V_zerothree / kBT * e_charge)
print('potential at 0.3 nm')
print('V(0.3 nm) = {:.2f} kBT/e'.format(V_zerothree / kBT * e_charge))
print('Positive ions:')
print('c_+(0.3 nm) = {:.3f} M'.format(c_plus))
print('Negative ions:')
print('c_-(0.3 nm) = {:.3f} M'.format(c_minus))
```
## 9.9 Charging energy of proteins in salty water
In the toy model of a protein described in Section 9.3.2, we assumed that a protein can be thought of as a charged sphere in water. Here, we consider the effect of salt on its electrical energy.
(b) Redo the calculation leading to the plot in Figure 9.14. Plot the electrical energy of the protein as a function of its radius for different salt concentrations, ranging between
1 mM and 100 mM. What conclusion do you draw about the effect of salt on the charged state of a protein?
### Solution
On part (a) we derived the energy to be
$$
U = {\lambda_D l_B \over (\lambda_D + R)} \left( 8 {R^3 \over r^4} \right) k_BT,
$$
where $\lambda_D$ is the now familiar Debye length, $l_B$ is the Bjerrum length, i.e. the length where the electric potential $V$ equals the thermal energy $k_BT$, $R$ is the radius of the protein and $r$ the radius of a single amino acid.
Let's now numerically evaluate these results for different salt concentrations.
```
# Define parameters to plot ion concentration
eps_D = 80 * 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
e_charge = 1.6E-19 # Coulombs
lB = 0.7E-9 # m
r = 0.5E-9 # m
# Define range of protein radius to consider
R = np.linspace(0, 10, 50) * 1E-9 # Protein size (m)
# Define concentrations to utilize
c_range = np.array([1, 3, 10, 30, 100]) # mM
c_inf = c_range * 1E-3 * 6.022E23 * 1000 # converted from mM to number / m**3
# Define colors for plot
colors = sns.color_palette('Blues', n_colors=len(c_range) + 1)[1::]
# Loop through concentrations and evaluate the energy
for i, c in enumerate(c_inf):
# Compute lambda_D
lam_D = np.sqrt(eps_D * kBT / 2 / e_charge**2 / c)
# Evaluate energy
U_R = lam_D * lB / (lam_D + R) * (8 * R**3 / r**4) * kBT
# Plot protein size vs energy
plt.plot(R * 1E9, U_R / kBT, label=str(c_range[i]), color=colors[i])
# Label axis
plt.xlabel('protein radius $R$ (nm)')
plt.ylabel('energy $U \; (k_BT)$')
# Add legend
plt.legend(title=r'$c_\infty$ (mM)')
# Save figure
plt.tight_layout()
plt.savefig(figdir + 'problem_09_09_01.png', bbox_inches='tight', dpi=300)
```
## 9.10 Binding to a membrane
Consider a phospholipid bilayer membrane consisting of a mixture of 90% uncharged lipid and 10% singly charged acid lipid. Assume 0.68 nm$^2$ surface area per lipid head group, and assume further that the charged lipids are uniformly distributed and immobile. The membrane is in contact with an aqueous solution of NaCl at 25ºC. The salt concentration is $c_\infty$ = 100 mM.
(b) Calculate the surface potential of the membrane.
### Solution
As derived for problem 9.7, the potenetial at the surface is given by
$$
V(x) = {\sigma \lambda_D \over \varepsilon_o D} e^{-x/\lambda_D},
$$
where $\sigma$ is the charge per area, and $\lambda_D$ is the Debye length.
At the surface ($x=0$) we have a potential of the form
$$
V(0) = {\sigma \lambda_D \over \varepsilon_o D}.
$$
Let's evaluate this quantity numerically.
```
# Define parameters to plot ion concentration
c_inf = 100E-3 * 6.022E23 * 1000 # number / m**3
eps_D = 80 * 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
z = 1 # monovalent ions
e_charge = 1.6E-19 # C
sigma = -e_charge / 6.8 * (1E9)**2 # m
```
Let's evaluate the Debye length for a trivalent ion.
```
lam_D = np.sqrt(eps_D * kBT / 2 / (z * 3 * e_charge)**2 / c_inf)
print('lambda_D ≈ {:.2f} nm'.format(lam_D * 1E9))
```
The potential at the surface is then given by
```
# Debye length for single charge
lam_D = np.sqrt(eps_D * kBT / 2 / (z * e_charge)**2 / c_inf)
# Potential
V_o = sigma * lam_D / eps_D
print('surface potential of the membrane')
print('V(x=0) = {:.3f} volts'.format(V_o))
```
What is the electrostatic energy (in kBT units) of binding to
the membrane of a trivalent positive ion such as spermidine
(a biologically active polyamine) assuming that:
(c) Binding occurs at the membrane surface?
(d) Owing to steric factors, the charges of the bound spermidine stay in the water 0.5 nm distant from the membrane surface?
### Solution
(c) The electrostatic energy of a trivalent ion bound to the membrane surface is given by
```
U_o = (3 * e_charge) * V_o
print('electrostatic energy')
print('U(x=0) = {:.2f} kBT'.format(U_o / kBT))
```
If the ion binds 0.5 nm away from the membrane we have
(c) The electrostatic energy of a trivalent ion bound to the membrane surface is given by
```
# Potential
V_05 = sigma * lam_D / eps_D * np.exp(-0.5E-9 / lam_D)
# Energy
U_05 = (3 * e_charge) * V_05
print('electrostatic energy')
print('U(x=0.5 nm) = {:.2f} kBT'.format(U_05 / kBT))
```
## 9.12 Membrane pores
A neutral protein “carrier” may help an ion to transfer into
and cross a lipid membrane.
(a) What is the electrostatic free-energy change when a monovalent ion is transferred from water at 25ºC to a hydrocarbon solvent with dielectric constant $D = 2$? The radius of the ion is 0.2 nm.
### Solution
For a monovalent ion modeled as a charged sphere the electrostatic energy is of the form
$$
U = {1 \over 4 \pi \varepsilon_o D}{e^2 \over 2 R},
$$
where $R$ is the radius of the ion.
The change in energy is then of the form
$$
\Delta U = {1 \over 4 \pi \varepsilon_o }{e^2 \over 2 R}
\left( {1 \over D^c} - {1 \over D^{H_2O}} \right),
$$
where $D^c = 2$ and $D^{H_2O} = 80$.
Evaluating this numerically gives
```
# Define parameters to plot ion concentration
eps = 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
e_charge = 1.6E-19 # Coulombs
R = 0.2E-9 # m
# Compute free energy ∆U
delta_U = (1 / (4 * np.pi * eps)) * (e_charge**2 / (2 * R)) * (1 / 2 - 1 / 80)
# Print energy in kBTs
print('free energy')
print('∆U = {:.1f} kBT'.format(delta_U / kBT))
```
|
github_jupyter
|
# Our numerical workhorses
import numpy as np
import scipy as sp
import scipy.signal
import pandas as pd
import mpmath
# Import matplotlib stuff for plotting
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from mpl_toolkits.mplot3d import Axes3D # For 3D plots
# Seaborn, useful for graphics
import seaborn as sns
# Import the default plotting style
import plotting_style as pstyle
# Function to import and display images from the Garland website
from IPython.display import Image
# Magic function to make matplotlib inline
%matplotlib inline
# This enables SVG graphics inline.
%config InlineBackend.figure_formats = {'png', 'retina'}
# Define directories
figdir = '../fig/'
# Set plotting style
pstyle.set_plotting_style()
def epsilon_n(Depsilon, n=1):
'''
Function that returns the energy of a structure of size n viral capsomers
in kBT by adding the number of contacts between capsomers with energy
Depsilon.
Parameters
----------
Depsilon: float.
Energy of interaction between contacts
n : int. Default 1
Number of capsomers in structure
Returns
-------
Energy of interactions between capsomers in kBT
'''
# Create dictionary with number of contacts when adding a new capsomer to
# a structure of size n - 1 to form a structure of size n
fn = {1: 0,
2: 1, 3: 2, 4: 2, 5: 2, 6: 2, 7: 2,
8: 3, 9: 3, 10: 3,
11: 4,
12: 5}
# Extract the energy of each capsomer contribution
return np.sum([fn[x] * Depsilon for x in range(1, n + 1)])
def phi_n(Depsilon, n, phi_1):
'''
Function that computes the volume fraction occupied by a structure formed
out of n capsomers given the volume fraction occupied by the single
monomers in solution.
Parameters
----------
Depsilon: float.
Energy of interaction between contacts
n : int. Default 1
Number of capsomers in structure
phi_1 : float [0, 1]
Volume fraction of individual capsomers
Returns
-------
Volume fraction of structure with n capsomers
'''
# Compute and return the volume fraction
return phi_1**n * np.exp(- epsilon_n(Depsilon, n))
# Define energies for individual contacts
Depsilon = [-1, -5, -10]
# Define names for columns of tidy data frame
names = ['n', 'Depsilon', 'phi_n', 'phi_c']
# Initialize dataframe
df = pd.DataFrame(columns=names)
# Loop through each binding energy computing the volume fraction of each
# structure
for de in Depsilon:
# Define fraction of monomers
phi_1 = np.exp(epsilon_n(de, 12) / 11)
# Loop through each individual capsomer
for n in range(1, 13):
# Compute the volume fraction
phi = phi_n(de, n, phi_1)
# Save results in Series to append to dataframe
series = pd.Series([n, de, phi, phi_1 * 2], index=names)
# Append to data frame
df = df.append(series, ignore_index=True)
# Let's look at the dataframe
df.head()
# Group dataframe by energy of single contact
df_group = df.groupby('Depsilon')
# Define markers for each group
markers = ['o', 'v', 's']
# Initialize figure
# Loop through groups plotting volume fraction
for i, (group, data) in enumerate(df_group):
plt.plot(data.n, data.phi_n / data.phi_c,
lw=0, marker=markers[i], markersize=4,
label=group)
# Set y scale to be log
plt.yscale('log')
# Label axis
plt.xlabel(r'number of capsomers $n$')
plt.ylabel(r'$\phi_n / \phi_T$')
# set legend
plt.legend(title=r'$\Delta\varepsilon \; (k_BT)$')
# save figure
plt.tight_layout()
plt.savefig(figdir + 'problem_09_05_01.png', bbox_inches='tight')
# Compute the critical volume fraction for -5 kBT
phi_c = 2 * np.exp(epsilon_n(-5, 12) / 11)
# Print critical volume fraction
print('phi_C(-5 kBT) = ', phi_c)
# Define range of fractions to be used for phi_1
phi_1_array = np.logspace(-2, 2, 100) * phi_c / 2
# Compute the volume fraction of the complete capsids
phi_n_array = phi_n(-5, 12, phi_1_array)
# Plot result
plt.loglog(phi_1_array / (phi_c / 2), phi_n_array / (phi_c / 2))
# Label axis
plt.xlabel(r'$\phi_1 \; / \; \phi_1^C$')
plt.ylabel(r'$\phi_{12} \; / \; \phi_1^C $')
# Save figure
plt.tight_layout()
plt.savefig(figdir + 'problem_09_05_02.png', bbox_inches='tight')
# Define parameters to plot ion concentration
c_inf = 100E-3 * 6.022E23 * 1000 # number / m**3
eps_D = 80 * 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
z = 1 # monovalent ions
e_charge = 1.6E-19 # C
lam_D = np.sqrt(eps_D * kBT / 2 / (z * e_charge)**2 / c_inf)
print('lambda_D ≈ {:.2f} nm'.format(lam_D * 1E9))
a_condition = z * e_charge**2 / kBT * lam_D / eps_D
print('area >> {:.2f} nm**2'.format(a_condition * (1E9)**2))
# Define range of x values
x_range = np.linspace(0, 5, 50) / 1E9 # m
# Compute ion concentration
c_plus = 100 * (1 - z * e_charge / kBT *
(e_charge / 100 * 1E9**2) * lam_D / eps_D *
np.exp(-x_range / lam_D))
c_minus = 100 * (1 + z * e_charge / kBT *
(e_charge / 100 * 1E9**2) * lam_D / eps_D *
np.exp(-x_range / lam_D))
# Plot ion concentrations
plt.plot(x_range * 1E9, c_plus, label=r'$c_+$')
plt.plot(x_range * 1E9 , c_minus, label=r'$c_-$')
# Label axis
plt.xlabel(r'distance $x$ (nM)')
plt.ylabel(r'concentration (mM)')
# Add legend
plt.legend(title='ion')
# Save figure
plt.savefig(figdir + 'problem_09_07_01.png', bbox_inches='tight', dpi=300)
# Define parameters to plot ion concentration
c_inf = 0.05 * 6.022E23 * 1000 # converted from M to number / m**3
eps_D = 80 * 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
e_charge = 1.6E-19 # Coulombs
Q = -10 * e_charge #Charge of the protein
R = 1.8E-9 # Protein size (m)
# Compute lambda_D
lam_D = np.sqrt(eps_D * kBT / 2 / (z * e_charge)**2 / c_inf)
# Evaluate potential
V_R = (Q / R) * (1 / (4 * np.pi * eps_D * (1 + R / lam_D)))
# Convert to kBT/e
print('potential at protein surface:')
print('V(R) = {:.1f} kBT / e'.format(V_R / kBT * e_charge))
# Positive ions
c_plus = 0.05 * np.exp(-V_R / kBT * e_charge)
# Negative ions
c_minus = 0.05 * np.exp(V_R / kBT * e_charge)
print('Positive ions:')
print('c_+(R) = {:.3f} M'.format(c_plus))
print('Negative ions:')
print('c_-(R) = {:.3f} M'.format(c_minus))
# Define distance to evaluate potential at
dist = 0.3E-9 # nm converted to m
r = dist + R # add radius of the protein to distance to be evaluated
# Evaluating potential at distance 0.3 nm gives
V_zerothree = (Q / r) * np.exp((R - r) / lam_D) / (4 * np.pi * eps_D *
(1 + R / lam_D))
# Evaluate concentrations
# Positive ions
c_plus = 0.05 * np.exp(-V_zerothree / kBT * e_charge)
# Negative ions
c_minus = 0.05 * np.exp(V_zerothree / kBT * e_charge)
print('potential at 0.3 nm')
print('V(0.3 nm) = {:.2f} kBT/e'.format(V_zerothree / kBT * e_charge))
print('Positive ions:')
print('c_+(0.3 nm) = {:.3f} M'.format(c_plus))
print('Negative ions:')
print('c_-(0.3 nm) = {:.3f} M'.format(c_minus))
# Define parameters to plot ion concentration
eps_D = 80 * 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
e_charge = 1.6E-19 # Coulombs
lB = 0.7E-9 # m
r = 0.5E-9 # m
# Define range of protein radius to consider
R = np.linspace(0, 10, 50) * 1E-9 # Protein size (m)
# Define concentrations to utilize
c_range = np.array([1, 3, 10, 30, 100]) # mM
c_inf = c_range * 1E-3 * 6.022E23 * 1000 # converted from mM to number / m**3
# Define colors for plot
colors = sns.color_palette('Blues', n_colors=len(c_range) + 1)[1::]
# Loop through concentrations and evaluate the energy
for i, c in enumerate(c_inf):
# Compute lambda_D
lam_D = np.sqrt(eps_D * kBT / 2 / e_charge**2 / c)
# Evaluate energy
U_R = lam_D * lB / (lam_D + R) * (8 * R**3 / r**4) * kBT
# Plot protein size vs energy
plt.plot(R * 1E9, U_R / kBT, label=str(c_range[i]), color=colors[i])
# Label axis
plt.xlabel('protein radius $R$ (nm)')
plt.ylabel('energy $U \; (k_BT)$')
# Add legend
plt.legend(title=r'$c_\infty$ (mM)')
# Save figure
plt.tight_layout()
plt.savefig(figdir + 'problem_09_09_01.png', bbox_inches='tight', dpi=300)
# Define parameters to plot ion concentration
c_inf = 100E-3 * 6.022E23 * 1000 # number / m**3
eps_D = 80 * 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
z = 1 # monovalent ions
e_charge = 1.6E-19 # C
sigma = -e_charge / 6.8 * (1E9)**2 # m
lam_D = np.sqrt(eps_D * kBT / 2 / (z * 3 * e_charge)**2 / c_inf)
print('lambda_D ≈ {:.2f} nm'.format(lam_D * 1E9))
# Debye length for single charge
lam_D = np.sqrt(eps_D * kBT / 2 / (z * e_charge)**2 / c_inf)
# Potential
V_o = sigma * lam_D / eps_D
print('surface potential of the membrane')
print('V(x=0) = {:.3f} volts'.format(V_o))
U_o = (3 * e_charge) * V_o
print('electrostatic energy')
print('U(x=0) = {:.2f} kBT'.format(U_o / kBT))
# Potential
V_05 = sigma * lam_D / eps_D * np.exp(-0.5E-9 / lam_D)
# Energy
U_05 = (3 * e_charge) * V_05
print('electrostatic energy')
print('U(x=0.5 nm) = {:.2f} kBT'.format(U_05 / kBT))
# Define parameters to plot ion concentration
eps = 8.85E-12 # C**2 / N m**2
kBT = 4E-21 # J = N * m
e_charge = 1.6E-19 # Coulombs
R = 0.2E-9 # m
# Compute free energy ∆U
delta_U = (1 / (4 * np.pi * eps)) * (e_charge**2 / (2 * R)) * (1 / 2 - 1 / 80)
# Print energy in kBTs
print('free energy')
print('∆U = {:.1f} kBT'.format(delta_U / kBT))
| 0.819857 | 0.974362 |
# Merge Sort
Known to [John von Neumann](https://www.wikiwand.com/en/John_von_Neumann) in 1945, 70+ years ago
### Step 0- Testing utilities
Take a look at `resources/utils.py` if you're curious.
```
import random
random.seed(0)
from resources.utils import run_tests
```
### Step 1- split
Given a list let's split it into two lists right down the middle
```
def split(input_list):
"""
Splits a list into two pieces
:param input_list: list
:return: left and right lists (list, list)
"""
input_list_len = len(input_list)
midpoint = input_list_len // 2
return input_list[:midpoint], input_list[midpoint:]
tests_split = [
({'input_list': [1, 2, 3]}, ([1], [2, 3])),
({'input_list': [1, 2, 3, 4]}, ([1, 2], [3, 4])),
({'input_list': [1, 2, 3, 4, 5]}, ([1, 2], [3, 4, 5])),
({'input_list': [1]}, ([], [1])),
({'input_list': []}, ([], []))
]
run_tests(tests_split, split)
```
### Step 2- merge sorted lists
Given two sorted lists we should be able to "merge" them into a single list as a linear operation
```
def merge_sorted_lists(list_left, list_right):
"""
Merge two sorted lists
This is a linear operation
O(len(list_right) + len(list_right))
:param left_list: list
:param right_list: list
:return merged list
"""
# Special case: one or both of lists are empty
if len(list_left) == 0:
return list_right
elif len(list_right) == 0:
return list_left
# General case
index_left = index_right = 0
list_merged = [] # list to build and return
list_len_target = len(list_left) + len(list_right)
while len(list_merged) < list_len_target:
if list_left[index_left] <= list_right[index_right]:
# Value on the left list is smaller (or equal so it should be selected)
list_merged.append(list_left[index_left])
index_left += 1
else:
# Right value bigger
list_merged.append(list_right[index_right])
index_right += 1
# If we are at the end of one of the lists we can take a shortcut
if index_right == len(list_right):
# Reached the end of right
# Append the remainder of left and break
list_merged += list_left[index_left:]
break
elif index_left == len(list_left):
# Reached the end of left
# Append the remainder of right and break
list_merged += list_right[index_right:]
break
return list_merged
tests_merged_sorted_lists = [
({'list_left': [1, 5], 'list_right': [3, 4]}, [1, 3, 4, 5]),
({'list_left': [5], 'list_right': [1]}, [1, 5]),
({'list_left': [], 'list_right': []}, []),
({'list_left': [1, 2, 3, 5], 'list_right': [4]}, [1, 2, 3, 4, 5]),
({'list_left': [1, 2, 3], 'list_right': []}, [1, 2, 3]),
({'list_left': [1], 'list_right': [1, 2, 3]}, [1, 1, 2, 3]),
({'list_left': [1, 1], 'list_right': [1, 1]}, [1, 1, 1, 1]),
({'list_left': [1, 1], 'list_right': [1, 2]}, [1, 1, 1, 2]),
({'list_left': [3, 3], 'list_right': [1, 4]}, [1, 3, 3, 4]),
]
run_tests(tests_merged_sorted_lists, merge_sorted_lists)
```
### Step 3- merge sort
- Merge sort only needs to utilize the previous 2 functions
- We need to split the lists until they have a single element
- A list with a single element is sorted (duh)
- Now we can merge these single-element (or empty) lists
```
def merge_sort(input_list):
if len(input_list) <= 1:
return input_list
else:
left, right = split(input_list)
# The following line is the most important piece in this whole thing
return merge_sorted_lists(merge_sort(left), merge_sort(right))
random_list = [random.randint(1, 1000) for _ in range(100)]
tests_merge_sort = [
({'input_list': [1, 2]}, [1, 2]),
({'input_list': [2, 1]}, [1, 2]),
({'input_list': []}, []),
({'input_list': [1]}, [1]),
({'input_list': [5, 1, 1]}, [1, 1, 5]),
({'input_list': [9, 1, 10, 2]}, [1, 2, 9, 10]),
({'input_list': range(10)[::-1]}, list(range(10))),
({'input_list': random_list}, sorted(random_list))
]
run_tests(tests_merge_sort, merge_sort)
```
## Example walk through
`merge_sort` keeps splitting until we get to single-element lists. Once we're there (the base case of recursion) the callers can start applying `merge_sorted_list`. For the following example here's what's going on:
- `input_list=[9, 1, 10, 2]`
- `left=[9, 1]` and `right=[10, 2]`
- `merge_sort([9, 1])` is responsible for sorting `[9, 1]`, let's call it `L1`.
- `merge_sort([10, 2])` is reponsible for sorting `[10, 2]`, let's call it `R1`.
For `L1`:
- `left=[9]` and `right=[1]`
- `merge_sort([9])` returns `[9]` since it's the base case and `merge_sort([1])` returns `[1]`
- `merge_sorted_lists([9], [1])` returns `[1, 9]` which is sorted
Same thing happens for `R1` and the result is `[2, 10]`. Now `merge_sorted_lists(L1, R1)` returns the final answer.
<img src="resources/mergesort.png">
|
github_jupyter
|
import random
random.seed(0)
from resources.utils import run_tests
def split(input_list):
"""
Splits a list into two pieces
:param input_list: list
:return: left and right lists (list, list)
"""
input_list_len = len(input_list)
midpoint = input_list_len // 2
return input_list[:midpoint], input_list[midpoint:]
tests_split = [
({'input_list': [1, 2, 3]}, ([1], [2, 3])),
({'input_list': [1, 2, 3, 4]}, ([1, 2], [3, 4])),
({'input_list': [1, 2, 3, 4, 5]}, ([1, 2], [3, 4, 5])),
({'input_list': [1]}, ([], [1])),
({'input_list': []}, ([], []))
]
run_tests(tests_split, split)
def merge_sorted_lists(list_left, list_right):
"""
Merge two sorted lists
This is a linear operation
O(len(list_right) + len(list_right))
:param left_list: list
:param right_list: list
:return merged list
"""
# Special case: one or both of lists are empty
if len(list_left) == 0:
return list_right
elif len(list_right) == 0:
return list_left
# General case
index_left = index_right = 0
list_merged = [] # list to build and return
list_len_target = len(list_left) + len(list_right)
while len(list_merged) < list_len_target:
if list_left[index_left] <= list_right[index_right]:
# Value on the left list is smaller (or equal so it should be selected)
list_merged.append(list_left[index_left])
index_left += 1
else:
# Right value bigger
list_merged.append(list_right[index_right])
index_right += 1
# If we are at the end of one of the lists we can take a shortcut
if index_right == len(list_right):
# Reached the end of right
# Append the remainder of left and break
list_merged += list_left[index_left:]
break
elif index_left == len(list_left):
# Reached the end of left
# Append the remainder of right and break
list_merged += list_right[index_right:]
break
return list_merged
tests_merged_sorted_lists = [
({'list_left': [1, 5], 'list_right': [3, 4]}, [1, 3, 4, 5]),
({'list_left': [5], 'list_right': [1]}, [1, 5]),
({'list_left': [], 'list_right': []}, []),
({'list_left': [1, 2, 3, 5], 'list_right': [4]}, [1, 2, 3, 4, 5]),
({'list_left': [1, 2, 3], 'list_right': []}, [1, 2, 3]),
({'list_left': [1], 'list_right': [1, 2, 3]}, [1, 1, 2, 3]),
({'list_left': [1, 1], 'list_right': [1, 1]}, [1, 1, 1, 1]),
({'list_left': [1, 1], 'list_right': [1, 2]}, [1, 1, 1, 2]),
({'list_left': [3, 3], 'list_right': [1, 4]}, [1, 3, 3, 4]),
]
run_tests(tests_merged_sorted_lists, merge_sorted_lists)
def merge_sort(input_list):
if len(input_list) <= 1:
return input_list
else:
left, right = split(input_list)
# The following line is the most important piece in this whole thing
return merge_sorted_lists(merge_sort(left), merge_sort(right))
random_list = [random.randint(1, 1000) for _ in range(100)]
tests_merge_sort = [
({'input_list': [1, 2]}, [1, 2]),
({'input_list': [2, 1]}, [1, 2]),
({'input_list': []}, []),
({'input_list': [1]}, [1]),
({'input_list': [5, 1, 1]}, [1, 1, 5]),
({'input_list': [9, 1, 10, 2]}, [1, 2, 9, 10]),
({'input_list': range(10)[::-1]}, list(range(10))),
({'input_list': random_list}, sorted(random_list))
]
run_tests(tests_merge_sort, merge_sort)
| 0.488283 | 0.948822 |
# Machine learning using scikit-learn
There are two kinds of machine learning algorithms: *supervised* and *unsupervised* learning.
Examples for supervised algorithms: classification, regression, etc.
Examples for unsupervised algorithms: clustering, dimension reduction, etc.
## scikit-learn estimators
Scikit-learn strives to have a uniform interface across all objects. Given a scikit-learn *estimator* named `model`, the following methods are available:
- Available in **all estimators**
+ `model.fit()` : Fit training data. For supervised learning applications,
this accepts two arguments: the data `X` and the labels `y` (e.g., `model.fit(X, y)`).
For unsupervised learning applications, ``fit`` takes only a single argument,
the data `X` (e.g. `model.fit(X)`).
- Available in **supervised estimators**
+ `model.predict()` : Given a trained model, predict the label of a new set of data.
This method accepts one argument, the new data `X_new` (e.g., `model.predict(X_new)`),
and returns the learned label for each object in the array.
+ `model.fit_predict()`: Fits and predicts at the same time.
+ `model.predict_proba()` : For classification problems, some estimators also provide
this method, which returns the probability that a new observation has each categorical label.
In this case, the label with the highest probability is returned by `model.predict()`.
+ `model.score()` : An indication of how well the model fits the training data. Scores are between 0 and 1, with a larger score indicating a better fit.
## Data in scikit-learn
Data in scikit-learn, with very few exceptions, is assumed to be stored as a
**two-dimensional array** of size `[n_samples, n_features]`. Many algorithms also accept ``scipy.sparse`` matrices of the same shape.
- **n_samples:** The number of samples: each sample is an item to process (e.g., classify).
A sample can be a document, a picture, a sound, a video, an astronomical object,
a row in database or CSV file, or whatever you can describe with a fixed set of quantitative traits.
- **n_features:** The number of features or distinct traits that can be used to describe each
item in a quantitative manner. Features are generally real-valued, but may be boolean or
discrete-valued in some cases.
### Numerical vs. categorical
What if you have categorical features? For example, imagine there is dataset containing the color of the
iris:
color in [red, blue, purple]
You might be tempted to assign numbers to these features, i.e. *red=1, blue=2, purple=3*
but in general **this is a bad idea**. Estimators tend to operate under the assumption that
numerical features lie on some continuous scale, so, for example, 1 and 2 are more alike
than 1 and 3, and this is often not the case for categorical features.
A better strategy is to give each category its own dimension.
The enriched iris feature set would hence be in this case:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- color=purple (1.0 or 0.0)
- color=blue (1.0 or 0.0)
- color=red (1.0 or 0.0)
Note that using many of these categorical features may result in data which is better
represented as a **sparse matrix**, as we'll see with the text classification example
below.
#### Using the DictVectorizer to encode categorical features
When the source data has a list of dicts where the values are either string names of categories or numerical values, you can use the `DictVectorizer` class to compute the boolean expansion of the categorical features while leaving the numerical features unimpacted:
```
measurements = [
{'city': 'Dubai', 'temperature': 33.},
{'city': 'London', 'temperature': 12.},
{'city': 'San Francisco', 'temperature': 18.},
]
from sklearn.feature_extraction import DictVectorizer
vec = DictVectorizer()
tf_measurements = vec.fit_transform(measurements)
tf_measurements.toarray()
vec.get_feature_names()
```
## Unsupervised Clustering using K-Means
```
#disable some annoying warning
import warnings
warnings.filterwarnings('ignore', category=FutureWarning)
%matplotlib inline
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
#load the iris datasets
import sklearn.datasets
data = sklearn.datasets.load_iris()
data.data.shape
from sklearn.cluster import KMeans
iris_pred = KMeans(n_clusters=3, random_state = 102).fit_predict(data.data)
plt.figure(figsize=(12, 12))
colors = sns.color_palette()
plt.subplot(211)
plt.scatter(data.data[:, 0], data.data[:, 1], c=[colors[i] for i in iris_pred], s=40)
plt.title('KMeans-3 clusterer')
plt.xlabel(data.feature_names[0])
plt.ylabel(data.feature_names[1])
plt.subplot(212)
plt.scatter(data.data[:, 0], data.data[:, 1], c=[colors[i] for i in data.target],s=40)
plt.title('Ground Truth')
plt.xlabel(data.feature_names[0])
plt.ylabel(data.feature_names[1])
```
## Supervised classification using decision trees
Well, the result is not that great. Let's use a supervised classifier.
First, split our data into training and test set.
```
import sklearn.model_selection
data_train, data_test, target_train, target_test = sklearn.model_selection.train_test_split(
data.data, data.target, test_size=0.20, random_state = 5)
print(data.data.shape, data_train.shape, data_test.shape)
```
Now, we use a *DecisionTree* to learn a model and test our result.
```
from sklearn.tree import DecisionTreeClassifier
instance = DecisionTreeClassifier()
r = instance.fit(data_train, target_train)
target_predict = instance.predict(data_test)
from sklearn.metrics import accuracy_score
print('Prediction accuracy: ', accuracy_score(target_predict, target_test))
```
Pretty good, isn't it?
## Dimension reduction using MDS and PCA
If we go back to our K-Means example, the clustering doesn't really make sense. However, we are just looking at two out of four dimensions. So, we can't really see the real distances/similarities between items. Dimension reduction techniques reduce the number of dimensions, while preserving the inner structure of the higher dimensions. We take a look at two of them: Multi Dimensional Scaling (MDS) and Principal Component Analysis (PCA).
```
from sklearn import manifold
#create mds instance
mds = manifold.MDS(n_components=2, random_state=5)
#fit the model and get the embedded coordinates
pos = mds.fit(data.data).embedding_
plt.scatter(pos[:, 0], pos[:, 1], s=20, c=[colors[i] for i in data.target])
#create a legend since we just have one plot and not three fake the legend using patches
import matplotlib.patches as mpatches
patches = [ mpatches.Patch(color=colors[i], label=data.target_names[i]) for i in range(3) ]
plt.legend(handles=patches)
#compare with PCA
from sklearn import decomposition
pca = decomposition.PCA(n_components=2)
pca_pos = pca.fit(data.data).transform(data.data)
mds_pos = mds.fit(data.data).embedding_
plt.figure(figsize=[20,7])
plt.subplot(121)
plt.scatter(mds_pos[:, 0], mds_pos[:, 1], s=30, c=[colors[i] for i in data.target])
plt.title('MDS')
plt.subplot(122)
plt.scatter(pca_pos[:, 0], pca_pos[:, 1], s=30, c=[colors[i] for i in data.target])
plt.title('PCA')
```
Seems like versicolor and virginicia are more similar than setosa.
## TASK
> Create an interactive colored plot of the Iris dataset projected in 2D using MDS. The color should correspong to the result of a K-Means clusterin alrogithm where the user can interactivly define the number of clusters between 1 and 10.
Thanks!
|
github_jupyter
|
measurements = [
{'city': 'Dubai', 'temperature': 33.},
{'city': 'London', 'temperature': 12.},
{'city': 'San Francisco', 'temperature': 18.},
]
from sklearn.feature_extraction import DictVectorizer
vec = DictVectorizer()
tf_measurements = vec.fit_transform(measurements)
tf_measurements.toarray()
vec.get_feature_names()
#disable some annoying warning
import warnings
warnings.filterwarnings('ignore', category=FutureWarning)
%matplotlib inline
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
#load the iris datasets
import sklearn.datasets
data = sklearn.datasets.load_iris()
data.data.shape
from sklearn.cluster import KMeans
iris_pred = KMeans(n_clusters=3, random_state = 102).fit_predict(data.data)
plt.figure(figsize=(12, 12))
colors = sns.color_palette()
plt.subplot(211)
plt.scatter(data.data[:, 0], data.data[:, 1], c=[colors[i] for i in iris_pred], s=40)
plt.title('KMeans-3 clusterer')
plt.xlabel(data.feature_names[0])
plt.ylabel(data.feature_names[1])
plt.subplot(212)
plt.scatter(data.data[:, 0], data.data[:, 1], c=[colors[i] for i in data.target],s=40)
plt.title('Ground Truth')
plt.xlabel(data.feature_names[0])
plt.ylabel(data.feature_names[1])
import sklearn.model_selection
data_train, data_test, target_train, target_test = sklearn.model_selection.train_test_split(
data.data, data.target, test_size=0.20, random_state = 5)
print(data.data.shape, data_train.shape, data_test.shape)
from sklearn.tree import DecisionTreeClassifier
instance = DecisionTreeClassifier()
r = instance.fit(data_train, target_train)
target_predict = instance.predict(data_test)
from sklearn.metrics import accuracy_score
print('Prediction accuracy: ', accuracy_score(target_predict, target_test))
from sklearn import manifold
#create mds instance
mds = manifold.MDS(n_components=2, random_state=5)
#fit the model and get the embedded coordinates
pos = mds.fit(data.data).embedding_
plt.scatter(pos[:, 0], pos[:, 1], s=20, c=[colors[i] for i in data.target])
#create a legend since we just have one plot and not three fake the legend using patches
import matplotlib.patches as mpatches
patches = [ mpatches.Patch(color=colors[i], label=data.target_names[i]) for i in range(3) ]
plt.legend(handles=patches)
#compare with PCA
from sklearn import decomposition
pca = decomposition.PCA(n_components=2)
pca_pos = pca.fit(data.data).transform(data.data)
mds_pos = mds.fit(data.data).embedding_
plt.figure(figsize=[20,7])
plt.subplot(121)
plt.scatter(mds_pos[:, 0], mds_pos[:, 1], s=30, c=[colors[i] for i in data.target])
plt.title('MDS')
plt.subplot(122)
plt.scatter(pca_pos[:, 0], pca_pos[:, 1], s=30, c=[colors[i] for i in data.target])
plt.title('PCA')
| 0.768907 | 0.993618 |
First, we import pandas and set two options we learnt about last week.
```
import pandas as pd
pd.options.mode.chained_assignment = None
%matplotlib inline
```
# 2. Pandas advanced
### Documentation
Check out the ```read_csv()``` documentation: https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_csv.html
There are many other functions to read different file formats as Pandas dataframes:
- ```read_excel()``` https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_excel.html
- ```read_sql()``` https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_sql.html
- ```read_sas()``` https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_sas.html
and many more. They are all working in a similar way. Just check out the Pandas documentation:
https://pandas.pydata.org/pandas-docs/stable/reference/io.html
### Bad lines
Sometimes files you want to read are formatted in a bad way. This may prevent you from reading it (Pandas will show you errors). You may skip these lines by passing a ```error_bad_lines=False``` like that: ```read_csv(filepath, sep=",", error_bad_lines=False)```
### Separators
Not all files are separated by ```,```. Oftetimes tabs, semicolons or even whitespaces are used. Sometimes its crazy stuff like ```:::```.
Just pass the separator as a string to the Pandas ```read_csv(filepath, sep=",")``` function. Here are some important special symbols you may want to use:
- tab: ```"\t"```
- newline: ```"\n"```
So if you want to read a file that is tab delimited, pass ```read_csv(filepath, sep="\t")```.
### Importing large files
If you read data from your hard drive to a Pandas dataframe, your computer's memory (RAM) needs to be large enough to hold all of that data. Sometimes you may want to work with data files that are larger than your memory. There are several ways to deal with that issue.
First, we can use the ```nrows=``` parameter to read only a certain number of lines from the top of the file we are loading.
```
pd.read_csv("../data/times_university_data.csv", sep=",", nrows=2)
```
We may also load only certain columns by passing a list with their names.
```
pd.read_csv("../data/times_university_data.csv", sep=",", nrows=2, usecols=["world_rank", "university_name"])
```
Lastly there is a way to read files in small chunks by passing the ```chunksize=``` parameter and the number of lines each chunk should contain, for example ```read_csv(filepath, sep=",", chunksize=1000)```. However this will not directly return a single dataframe, but an object ```pandas.io.parsers.TextFileReader``` that is ready to read you file chunk by chunk.
```
chunks = pd.read_csv("../data/times_university_data.csv", sep=",", chunksize=1000)
chunks
```
We can either call ```.get_chunk()``` on this reader to retrieve chunk after chunk...
```
chunks.get_chunk()
```
... or, we use a for loop to read the file chunk by chunk.
```
for chunk in chunks:
print(chunk[["world_rank", "university_name"]].head(1))
print("############")
for index, chunk in enumerate(chunks):
one_obs = chunk.sample(1)
if index == 0:
collecter = one_obs
else:
collecter = pd.concat([collecter, one_obs])
```
### Format columns
Last week we had this issue that some columns in our university ranking data were not properly formatted. The columns "international", "income", "total_score", and "num_students" should be numbers (float or integer), but they are objects (text).
```
df = pd.read_csv("../data/times_university_data.csv", sep=",")
print(df.dtypes)
df.head(2)
```
Because of that we cannot do basic mathematical operations on these columns because these cannot handle the text values that cannot be casted to float. Python will show us an error like this:
```
TypeError: unsupported operand type(s) for /: 'str' and 'float'
```
It will work on a column with float datatype.
```
df["teaching"] / 10
```
But not on one with datatype "object".
```
df["international"] / 10.0
```
Python will raise the same "TypeError" when we do something like this.
```
"ten" / 2.0
```
Let's use Pandas ```to_numeric()``` function to transfer the column to numeric. This time the error message is more helpful, because it tells us that it cannot parse string ```-``` at postion (line) 16.
```
pd.to_numeric(df["international"])
```
Let's have a look at that line with position 16 by using the ```.loc``` method on our dataframe and passing the location we are looking for as an index in squared brackets ```[16]```.
```
df.loc[16]
```
Maybe there are more ```-``` in the "international" column (Python stops when the first error occurs which was at position 16 and will only show this first error).
```
df[df["international"] == "-"]
df.head(2)
```
Now we have several options to get rid of these ```-``` which the creators of the dataset have used instead of inserting proper "NaN" (nulls) for missing values.
First, we may use Pandas ```to_numeric()``` function and pass the ```errors="coerce"``` parameter to tell it to return "NaN" values for data that cannot be transfered to numeric.
```
pd.to_numeric(df["international"], errors="coerce")
```
Let's overwrite the original column with a numeric copy. After this step, the datatype of the "international" column should have changed to float.
```
df["international"] = pd.to_numeric(df["international"], errors="coerce")
df.dtypes
```
Now mathematical operations are possible.
```
df["international"] / 10.0
```
### Use of the ```apply()``` method
The ```apply()``` method can be used to apply any kind of function while iterating through the observations in a dataframe.
Let's say we want to replace the ```-``` values in the "income" column with a random number based on the distribution of the "income" values in our dataset.
Let's first have a look at the income distribution of our dataset. For that we (again) use ```pd.to_numeric(errors="coerce")``` to transfer the values in the "income" column to numeric while replacing values that cannot be transferred to NaNs.
```
income_distribution = pd.to_numeric(df["income"], errors="coerce")
income_distribution.plot(kind="hist")
```
The mean is 48.97 and the standard deviation is 21.7 as we can see using the ```describe()``` method we learned about last week.
```
income_distribution.describe()
```
We can use these parameters to define a normal distribution just for demonstration purposes. For that we use the numpy Python package which includes a lot of scientific computing stuff.
Let's import numpy and use the ```random.normal()``` function to generate 100 random numbers using a normal distribution defined by the mean and standard deviation from the observed income distribution of our dataset.
```
import numpy as np
random_values = np.random.normal(income_distribution.mean(), income_distribution.std(), size=100)
random_values
```
We can also plot these numbers by transferring them to a Pandas Series.
```
pd.Series(random_values).plot(kind="hist", bins=25)
```
To draw a single observation from the distribution, we pass ```size=1``` to the function and use indexing ```[0]``` to get the first element from the returned array (remember, Python starts counting indexes at 0 and not at 1).
```
np.random.normal(income_distribution.mean(), income_distribution.std(), size=1)[0]
np.random.normal(income_distribution.mean(), income_distribution.std())
```
Okay, now let us use the ```apply()``` function on the "income" column. The ```lambda x:``` tells Python to create a temporary variable x for each observation in the "income" column. Now we can draw a single number from our normal distribution and relace x if x equals ```-```, otherwise we just return x (the temporary variable which holds the original value of the current observation from "income").
```
mean = income_distribution.mean()
std = income_distribution.std()
print(df.loc[4])
df["income"] = df["income"].apply(lambda x: np.random.normal(mean, std, size=1)[0] if x == "-" else x)
print("----------------------------------------")
print(df.loc[4])
```
After this operation, "income" will still be an object column.
```
df.dtypes
```
But now all values contained in "income" should be transferable to numeric without any problems.
```
df["income"] = pd.to_numeric(df["income"])
df.dtypes
df["country"].replace({"United States of America": "USA", "United Kingdom": "UK", "Germany": "Deutschland"})
```
### replace()
Another option is to use the ```replace()``` method, if you know exactly what values you want to replace with another specific value.
```
df["country_renamed"] = df["country"].replace({"United States of America": "USA", "United Kingdom": "UK", "Germany": "Deutschland"})
df.head(2)
```
# 3. Seaborn
We will now use the Python package Seaborn, which is based on the very popular matplotlib libary. Seaborn provides a high-level interface for drawing attractive and informative statistical graphics. Check out the seaborn gallery for some awesome examples:
```
from IPython.display import IFrame
display(IFrame("https://seaborn.pydata.org/examples/index.html", width=800, height=400))
```
First install seaborn using pip.
```pip install seaborn```
Import seaborn
```
import seaborn as sns
```
It is very easy to use seaborn functions to plot something because we can just pass our dataframe:
```
sns.scatterplot(x="income", y="student_staff_ratio", data=df)
```
There is also another way to create seaborn (and matplot) plots that give us more control over the indiviual elements of the plot. First we create an empty figure with one or more subplots. For that we need the matplot libary which runs "under the hood" of seaborn.
```
import matplotlib.pyplot as plt
```
Now we can create emtpy plots.
```
plt.subplots(1, figsize=(5, 5))
```
One row with two subplots.
```
plt.subplots(1, 2, figsize=(10, 5))
```
Two rows with two sublots.
```
plt.subplots(2, 2, figsize=(5, 5))
```
The ```subplot()``` function returns two objects (one "figure" object and a number of "axis" objects). Let's assign these to two variables.
```
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
```
We can now fill these empty subplots with seaborn plots by passing the axes object togehter with an index (remember Python starts counting with 0, so when we want to reference the first axis, we pass ```[0]```).
```
sns.scatterplot(x="income", y="student_staff_ratio", data=df, ax=axes[0])
fig
```
Let's fill the second subplot with a histogram of the "year" column. The seaborn ```distplot()``` takes as input the column, we want to plot.
```
sns.distplot(df["year"], ax=axes[1])
fig
```
Let's get rid of that kernel density estimate and tell the function to use a number of bins that correspond to the number of years present in our dataset. Check out the documentation for more options:
https://seaborn.pydata.org/generated/seaborn.distplot.html#seaborn.distplot
```
df["year"].nunique()
df["year"].unique()
```
When you overwrite a subplot, make sure to ```clear()``` the axis and the contained plot you previously put there (otherwise the new content will overlap the old content).
```
axes[1].clear()
sns.distplot(df["year"], ax=axes[1], kde=False, bins=df["year"].nunique())
fig
```
We can also control the elements of the subplots.
```
axes[0].set_xlabel("Income of university")
axes[0].set_ylabel("Student to staff ratio")
axes[0].set_xlim(0,100)
axes[0].set_ylim(0,100)
axes[0].set_title("Scatterplot")
fig
axes[1].set_xlabel("Year")
axes[1].set_ylabel("Frequency")
axes[1].set_ylim(0,1000)
axes[1].set_title("Year distribution")
fig
```
Usually you want to do put all the plot related code into a single cell. But first let's select and prepare some data.
```
# get ivy league universities
ivy = df[df["university_name"].isin(["Harvard University", "Stanford University", "Massachusetts Institute of Technology"])]
# world rank to numeric
ivy["world_rank"] = pd.to_numeric(ivy["world_rank"])
# change uni names
ivy["university_name"] = ivy["university_name"].replace({"Harvard University": "Harvard", "Stanford University": "Stanford", "Massachusetts Institute of Technology": "MIT"})
# clean and cast to numeric international_student and num_students
ivy["international_students"] = pd.to_numeric(ivy["international_students"].apply(lambda x: x.replace("%", "")))
ivy["num_students"] = pd.to_numeric(ivy["num_students"].apply(lambda x: x.replace(",", "")))
```
First we set some general styling options.
Also check out the seaborn color palettes: https://seaborn.pydata.org/tutorial/color_palettes.html
```
sns.set(font_scale=1.2)
sns.set_style("ticks")
fig, axes = plt.subplots(2,2, figsize=(10,10))
# Ranking plot axis [0,0] first row, first column
ranking = sns.lineplot(x="year", y="world_rank", hue="university_name", style="university_name", data=ivy, markers=True, palette="Paired", ax=axes[0,0])
ranking.set_ylim(0,10)
ranking.set_yticks([1,2,3,4,5,6,7,8,9,10])
ranking.set_ylabel("Ranking")
ranking.invert_yaxis()
ranking.set_xlabel("Year")
ranking.legend(loc=4).texts[0].set_text("University")
# Income plot axis [0,1] first row, second column
income = sns.barplot(x="year", y="income", hue="university_name", data=ivy, palette="Paired", ax=axes[0,1])
income.set_xlabel("Year")
income.set_ylabel("Income")
income.legend(loc=4).set_title("University")
# Citations plot axis [1,0] second row, first column
citations = sns.stripplot(x="university_name", y="citations", hue="year", palette="Paired", data=ivy, size=10, ax=axes[1,0])
citations.set_ylabel("Citations")
citations.set_xlabel("")
citations.set_ylim(95.0,100)
citations.legend(loc=4).set_title("Year")
citations.grid(linestyle="dotted")
# Remove last subplot [1,1] second row, second column
fig.delaxes(axes[1,1])
# Final adjustments
fig.tight_layout() #tidy up the figure
plt.savefig("../misc/my_nice_plot.png", dpi=150) #save the figure
```
Documentation legend: https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.legend.html
|
github_jupyter
|
import pandas as pd
pd.options.mode.chained_assignment = None
%matplotlib inline
### Separators
Not all files are separated by ```,```. Oftetimes tabs, semicolons or even whitespaces are used. Sometimes its crazy stuff like ```:::```.
Just pass the separator as a string to the Pandas ```read_csv(filepath, sep=",")``` function. Here are some important special symbols you may want to use:
- tab: ```"\t"```
- newline: ```"\n"```
So if you want to read a file that is tab delimited, pass ```read_csv(filepath, sep="\t")```.
### Importing large files
If you read data from your hard drive to a Pandas dataframe, your computer's memory (RAM) needs to be large enough to hold all of that data. Sometimes you may want to work with data files that are larger than your memory. There are several ways to deal with that issue.
First, we can use the ```nrows=``` parameter to read only a certain number of lines from the top of the file we are loading.
We may also load only certain columns by passing a list with their names.
Lastly there is a way to read files in small chunks by passing the ```chunksize=``` parameter and the number of lines each chunk should contain, for example ```read_csv(filepath, sep=",", chunksize=1000)```. However this will not directly return a single dataframe, but an object ```pandas.io.parsers.TextFileReader``` that is ready to read you file chunk by chunk.
We can either call ```.get_chunk()``` on this reader to retrieve chunk after chunk...
... or, we use a for loop to read the file chunk by chunk.
### Format columns
Last week we had this issue that some columns in our university ranking data were not properly formatted. The columns "international", "income", "total_score", and "num_students" should be numbers (float or integer), but they are objects (text).
Because of that we cannot do basic mathematical operations on these columns because these cannot handle the text values that cannot be casted to float. Python will show us an error like this:
It will work on a column with float datatype.
But not on one with datatype "object".
Python will raise the same "TypeError" when we do something like this.
Let's use Pandas ```to_numeric()``` function to transfer the column to numeric. This time the error message is more helpful, because it tells us that it cannot parse string ```-``` at postion (line) 16.
Let's have a look at that line with position 16 by using the ```.loc``` method on our dataframe and passing the location we are looking for as an index in squared brackets ```[16]```.
Maybe there are more ```-``` in the "international" column (Python stops when the first error occurs which was at position 16 and will only show this first error).
Now we have several options to get rid of these ```-``` which the creators of the dataset have used instead of inserting proper "NaN" (nulls) for missing values.
First, we may use Pandas ```to_numeric()``` function and pass the ```errors="coerce"``` parameter to tell it to return "NaN" values for data that cannot be transfered to numeric.
Let's overwrite the original column with a numeric copy. After this step, the datatype of the "international" column should have changed to float.
Now mathematical operations are possible.
### Use of the ```apply()``` method
The ```apply()``` method can be used to apply any kind of function while iterating through the observations in a dataframe.
Let's say we want to replace the ```-``` values in the "income" column with a random number based on the distribution of the "income" values in our dataset.
Let's first have a look at the income distribution of our dataset. For that we (again) use ```pd.to_numeric(errors="coerce")``` to transfer the values in the "income" column to numeric while replacing values that cannot be transferred to NaNs.
The mean is 48.97 and the standard deviation is 21.7 as we can see using the ```describe()``` method we learned about last week.
We can use these parameters to define a normal distribution just for demonstration purposes. For that we use the numpy Python package which includes a lot of scientific computing stuff.
Let's import numpy and use the ```random.normal()``` function to generate 100 random numbers using a normal distribution defined by the mean and standard deviation from the observed income distribution of our dataset.
We can also plot these numbers by transferring them to a Pandas Series.
To draw a single observation from the distribution, we pass ```size=1``` to the function and use indexing ```[0]``` to get the first element from the returned array (remember, Python starts counting indexes at 0 and not at 1).
Okay, now let us use the ```apply()``` function on the "income" column. The ```lambda x:``` tells Python to create a temporary variable x for each observation in the "income" column. Now we can draw a single number from our normal distribution and relace x if x equals ```-```, otherwise we just return x (the temporary variable which holds the original value of the current observation from "income").
After this operation, "income" will still be an object column.
But now all values contained in "income" should be transferable to numeric without any problems.
### replace()
Another option is to use the ```replace()``` method, if you know exactly what values you want to replace with another specific value.
# 3. Seaborn
We will now use the Python package Seaborn, which is based on the very popular matplotlib libary. Seaborn provides a high-level interface for drawing attractive and informative statistical graphics. Check out the seaborn gallery for some awesome examples:
First install seaborn using pip.
Import seaborn
It is very easy to use seaborn functions to plot something because we can just pass our dataframe:
There is also another way to create seaborn (and matplot) plots that give us more control over the indiviual elements of the plot. First we create an empty figure with one or more subplots. For that we need the matplot libary which runs "under the hood" of seaborn.
Now we can create emtpy plots.
One row with two subplots.
Two rows with two sublots.
The ```subplot()``` function returns two objects (one "figure" object and a number of "axis" objects). Let's assign these to two variables.
We can now fill these empty subplots with seaborn plots by passing the axes object togehter with an index (remember Python starts counting with 0, so when we want to reference the first axis, we pass ```[0]```).
Let's fill the second subplot with a histogram of the "year" column. The seaborn ```distplot()``` takes as input the column, we want to plot.
Let's get rid of that kernel density estimate and tell the function to use a number of bins that correspond to the number of years present in our dataset. Check out the documentation for more options:
https://seaborn.pydata.org/generated/seaborn.distplot.html#seaborn.distplot
When you overwrite a subplot, make sure to ```clear()``` the axis and the contained plot you previously put there (otherwise the new content will overlap the old content).
We can also control the elements of the subplots.
Usually you want to do put all the plot related code into a single cell. But first let's select and prepare some data.
First we set some general styling options.
Also check out the seaborn color palettes: https://seaborn.pydata.org/tutorial/color_palettes.html
| 0.835618 | 0.976802 |
# CutMix data augmentation for image classification
**Author:** [Sayan Nath](https://twitter.com/SayanNa20204009)<br>
**Date created:** 2021/03/25<br>
**Last modified:** 2021/03/25<br>
**Description:** Data augmentation with CutMix for image classification on CIFAR-10.
## Introduction
_CutMix_ is a data augmentation technique that addresses the issue of
information loss and inefficiency present in regional dropout strategies.
Instead of removing pixels and filling them with black or grey pixels or
Gaussian noise, you replace the removed regions with a patch from another image,
while the ground truth labels are mixed proportionally to the number of pixels
of combined images. CutMix was proposed in
[CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features](https://arxiv.org/pdf/1905.04899.pdf)
(Yun et al., 2019)
It's implemented with the following formulas:

where M is the binary mask which indicates the cutout and the fill-in regions from the two randomly drawn images and λ is drawn from [Beta(α,α) distribution](https://en.wikipedia.org/wiki/Beta_distribution) and `λ ∈ [0, 1]`
The coordinates of bounding boxes are  which indicates the cutout and fill-in regions in case of the images.
The bounding box sampling is represented by:

where `rx,ry` are randomly drawn from a uniform distribution with upper bound
This example requires TensorFlow 2.4 or higher.
## Import the necessary packages
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import mixed_precision
np.random.seed(42)
tf.random.set_seed(42)
```
## Load the CIFAR-10 dataset
In this example, we will use the
[CIFAR- 10 dataset](https://www.cs.toronto.edu/~kriz/cifar.html).
```
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
y_train = tf.keras.utils.to_categorical(y_train, num_classes=10)
y_test = tf.keras.utils.to_categorical(y_test, num_classes=10)
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
class_names = ["Airplane", "Automobile", "Bird", "Cat", "Deer", "Dog", "Frog", "Horse", "Ship", "Truck"]
```
## Define hyperparameters
```
AUTO = tf.data.experimental.AUTOTUNE
BATCH_SIZE = 32
IMG_SHAPE = 32
```
## Define the image preprocessing function
```
def preprocess_image(image, label):
image = tf.image.resize(image, (IMG_SHAPE, IMG_SHAPE))
image = tf.image.convert_image_dtype(image, tf.float32) / 255.
return image, label
```
## Convert the data into TensorFlow `Dataset` objects
```
train_ds_one = tf.data.Dataset.from_tensor_slices((x_train, y_train)).shuffle(1024).map(preprocess_image, num_parallel_calls=AUTO)
train_ds_two = tf.data.Dataset.from_tensor_slices((x_train, y_train)).shuffle(1024).map(preprocess_image, num_parallel_calls=AUTO)
train_ds_simple = tf.data.Dataset.from_tensor_slices((x_train, y_train))
test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
train_ds_simple = (train_ds_simple.map(preprocess_image, num_parallel_calls=AUTO).batch(BATCH_SIZE).prefetch(AUTO))
# Combine two shuffled datasets from the same training data.
train_ds = tf.data.Dataset.zip((train_ds_one, train_ds_two))
test_ds = (test_ds.map(preprocess_image, num_parallel_calls=AUTO).batch(BATCH_SIZE).prefetch(AUTO))
```
## Define the CutMix data augmentation function
The CutMix function takes two `image` and `label` pairs to perform the
augmentation. It samples `λ(l)` from the
[Beta distribution](https://en.wikipedia.org/wiki/Beta_distribution) and returns
a bounding box from `get_box` function. We then crop the second image (`image2`)
and pad this image in the final padded image at the same location.
```
def sample_beta_distribution(size, concentration_0=0.2, concentration_1=0.2):
gamma_1_sample = tf.random.gamma(shape=[size], alpha=concentration_1)
gamma_2_sample = tf.random.gamma(shape=[size], alpha=concentration_0)
return gamma_1_sample / (gamma_1_sample + gamma_2_sample)
@tf.function
def get_box(lambda_value):
cut_rat = tf.math.sqrt(1.0 - lambda_value)
cut_w = IMG_SHAPE * cut_rat # rw
cut_w = tf.cast(cut_w, tf.int32)
cut_h = IMG_SHAPE * cut_rat # rh
cut_h = tf.cast(cut_h, tf.int32)
cut_x = tf.random.uniform((1,), minval=0, maxval=IMG_SHAPE, dtype=tf.int32) # rx
cut_y = tf.random.uniform((1,), minval=0, maxval=IMG_SHAPE, dtype=tf.int32) # ry
boundaryx1 = tf.clip_by_value(cut_x[0] - cut_w // 2, 0, IMG_SHAPE)
boundaryy1 = tf.clip_by_value(cut_y[0] - cut_h // 2, 0, IMG_SHAPE)
bbx2 = tf.clip_by_value(cut_x[0] + cut_w // 2, 0, IMG_SHAPE)
bby2 = tf.clip_by_value(cut_y[0] + cut_h // 2, 0, IMG_SHAPE)
target_h = bby2 - boundaryy1
if target_h == 0:
target_h += 1
target_w = bbx2 - boundaryx1
if target_w == 0:
target_w += 1
return boundaryx1, boundaryy1, target_h, target_w
@tf.function
def cutmix(train_ds_one, train_ds_two):
(image1, label1), (image2, label2) = train_ds_one, train_ds_two
alpha = [0.25]
beta = [0.25]
# Get a sample from the Beta distribution
lambda_value = sample_beta_distribution(1, alpha, beta)
# Define Lambda
lambda_value = lambda_value[0][0]
# Get the bounding box offsets, heights and widths
boundaryx1, boundaryy1, target_h, target_w = get_box(lambda_value)
# Get a patch from the second image (`image2`)
crop2 = tf.image.crop_to_bounding_box(image2, boundaryy1, boundaryx1, target_h, target_w)
# Pad the `image2` patch (`crop2`) with the same offset
image2 = tf.image.pad_to_bounding_box(crop2, boundaryy1, boundaryx1, IMG_SHAPE, IMG_SHAPE)
# Get a patch from the first image (`image1`)
crop1 = tf.image.crop_to_bounding_box(image1, boundaryy1, boundaryx1, target_h, target_w)
# Pad the `image1` patch (`crop1`) with the same offset
img1 = tf.image.pad_to_bounding_box(crop1, boundaryy1, boundaryx1, IMG_SHAPE, IMG_SHAPE)
# Modify the first image by subtracting the patch from `image1`
# (before applying the `image2` patch)
image1 = image1 - img1
# Add the modified `image1` and `image2` together to get the CutMix image
image = image1 + image2
# Adjust Lambda in accordance to the pixel ration
lambda_value = 1 - (target_w * target_h) / (IMG_SHAPE * IMG_SHAPE)
lambda_value = tf.cast(lambda_value, tf.float32)
# Combine the labels of both images
label = lambda_value * label1 + (1 - lambda_value) * label2
return image, label
```
**Note**: we are combining two images to create a single one.
## Visualize the new dataset after applying the CutMix augmentation
```
# Create the new dataset using our `cutmix` utility
train_ds_cmu = (train_ds.shuffle(1024).map(cutmix, num_parallel_calls=AUTO).batch(BATCH_SIZE).prefetch(AUTO))
# Let's preview 9 samples from the dataset
image_batch, label_batch = next(iter(train_ds_cmu))
plt.figure(figsize=(10,10))
for i in range(9):
ax = plt.subplot(3 ,3 ,i + 1)
plt.title(class_names[np.argmax(label_batch[i])])
plt.imshow(image_batch[i])
plt.axis('off')
```
## Define the model using ResNet-20
```
def resnet_layer(inputs,
num_filters=16,
kernel_size=3,
strides=1,
activation='relu',
batch_normalization=True,
conv_first=True):
conv = keras.layers.Conv2D(num_filters,
kernel_size=kernel_size,
strides=strides,
padding='same',
kernel_initializer='he_normal',
kernel_regularizer=keras.regularizers.l2(1e-4))
x = inputs
if conv_first:
x = conv(x)
if batch_normalization:
x = keras.layers.BatchNormalization()(x)
if activation is not None:
x = keras.layers.Activation(activation)(x)
else:
if batch_normalization:
x = keras.layers.BatchNormalization()(x)
if activation is not None:
x = keras.layers.Activation(activation)(x)
x = conv(x)
return x
def resnet_v20(input_shape, depth, num_classes=10):
if (depth - 2) % 6 != 0:
raise ValueError('depth should be 6n+2 (eg 20, 32, 44 in [a])')
# Start model definition.
num_filters = 16
num_res_blocks = int((depth - 2) / 6)
inputs = keras.layers.Input(shape=input_shape)
x = resnet_layer(inputs=inputs)
# Instantiate the stack of residual units
for stack in range(3):
for res_block in range(num_res_blocks):
strides = 1
if stack > 0 and res_block == 0: # first layer but not first stack
strides = 2 # downsample
y = resnet_layer(inputs=x,
num_filters=num_filters,
strides=strides)
y = resnet_layer(inputs=y,
num_filters=num_filters,
activation=None)
if stack > 0 and res_block == 0: # first layer but not first stack
# linear projection residual shortcut connection to match
# changed dims
x = resnet_layer(inputs=x,
num_filters=num_filters,
kernel_size=1,
strides=strides,
activation=None,
batch_normalization=False)
x = keras.layers.add([x, y])
x = keras.layers.Activation('relu')(x)
num_filters *= 2
# Add classifier on top.
# v1 does not use BN after last shortcut connection-ReLU
x = keras.layers.AveragePooling2D(pool_size=8)(x)
y = keras.layers.Flatten()(x)
outputs = keras.layers.Dense(num_classes,
activation='softmax',
kernel_initializer='he_normal')(y)
# Instantiate model.
model = keras.models.Model(inputs=inputs, outputs=outputs)
return model
def training_model():
return resnet_v20((32,32,3), 20)
initial_model = training_model()
initial_model.save_weights("initial_weights.h5")
```
## 1. Train the model with the dataset augmented by CutMix
```
model = training_model()
model.load_weights("initial_weights.h5")
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
model.fit(train_ds_cmu,validation_data=test_ds, epochs=15)
test_loss, test_accuracy = model.evaluate(test_ds)
print("Test accuracy: {:.2f}%".format(test_accuracy * 100))
```
## 2. Train the model using the original non-augmented dataset
```
model = training_model()
model.load_weights("initial_weights.h5")
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
model.fit(train_ds_simple,validation_data=test_ds, epochs=15)
test_loss, test_accuracy = model.evaluate(test_ds)
print("Test accuracy: {:.2f}%".format(test_accuracy * 100))
```
## Notes
In this example, we trained our model for 15 epochs. In our experiment, the
model with CutMix achieves a better accuracy on the CIFAR-10 dataset (80.36% in
our experiment) compared to the model that doesn't use the augmentation
(72.70%).
You may notice it takes less time to train the model with the CutMix augmentation.
You can experiment further with the CutMix technique by following the
[original paper](https://arxiv.org/pdf/1905.04899.pdf).
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import mixed_precision
np.random.seed(42)
tf.random.set_seed(42)
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
y_train = tf.keras.utils.to_categorical(y_train, num_classes=10)
y_test = tf.keras.utils.to_categorical(y_test, num_classes=10)
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
class_names = ["Airplane", "Automobile", "Bird", "Cat", "Deer", "Dog", "Frog", "Horse", "Ship", "Truck"]
AUTO = tf.data.experimental.AUTOTUNE
BATCH_SIZE = 32
IMG_SHAPE = 32
def preprocess_image(image, label):
image = tf.image.resize(image, (IMG_SHAPE, IMG_SHAPE))
image = tf.image.convert_image_dtype(image, tf.float32) / 255.
return image, label
train_ds_one = tf.data.Dataset.from_tensor_slices((x_train, y_train)).shuffle(1024).map(preprocess_image, num_parallel_calls=AUTO)
train_ds_two = tf.data.Dataset.from_tensor_slices((x_train, y_train)).shuffle(1024).map(preprocess_image, num_parallel_calls=AUTO)
train_ds_simple = tf.data.Dataset.from_tensor_slices((x_train, y_train))
test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
train_ds_simple = (train_ds_simple.map(preprocess_image, num_parallel_calls=AUTO).batch(BATCH_SIZE).prefetch(AUTO))
# Combine two shuffled datasets from the same training data.
train_ds = tf.data.Dataset.zip((train_ds_one, train_ds_two))
test_ds = (test_ds.map(preprocess_image, num_parallel_calls=AUTO).batch(BATCH_SIZE).prefetch(AUTO))
def sample_beta_distribution(size, concentration_0=0.2, concentration_1=0.2):
gamma_1_sample = tf.random.gamma(shape=[size], alpha=concentration_1)
gamma_2_sample = tf.random.gamma(shape=[size], alpha=concentration_0)
return gamma_1_sample / (gamma_1_sample + gamma_2_sample)
@tf.function
def get_box(lambda_value):
cut_rat = tf.math.sqrt(1.0 - lambda_value)
cut_w = IMG_SHAPE * cut_rat # rw
cut_w = tf.cast(cut_w, tf.int32)
cut_h = IMG_SHAPE * cut_rat # rh
cut_h = tf.cast(cut_h, tf.int32)
cut_x = tf.random.uniform((1,), minval=0, maxval=IMG_SHAPE, dtype=tf.int32) # rx
cut_y = tf.random.uniform((1,), minval=0, maxval=IMG_SHAPE, dtype=tf.int32) # ry
boundaryx1 = tf.clip_by_value(cut_x[0] - cut_w // 2, 0, IMG_SHAPE)
boundaryy1 = tf.clip_by_value(cut_y[0] - cut_h // 2, 0, IMG_SHAPE)
bbx2 = tf.clip_by_value(cut_x[0] + cut_w // 2, 0, IMG_SHAPE)
bby2 = tf.clip_by_value(cut_y[0] + cut_h // 2, 0, IMG_SHAPE)
target_h = bby2 - boundaryy1
if target_h == 0:
target_h += 1
target_w = bbx2 - boundaryx1
if target_w == 0:
target_w += 1
return boundaryx1, boundaryy1, target_h, target_w
@tf.function
def cutmix(train_ds_one, train_ds_two):
(image1, label1), (image2, label2) = train_ds_one, train_ds_two
alpha = [0.25]
beta = [0.25]
# Get a sample from the Beta distribution
lambda_value = sample_beta_distribution(1, alpha, beta)
# Define Lambda
lambda_value = lambda_value[0][0]
# Get the bounding box offsets, heights and widths
boundaryx1, boundaryy1, target_h, target_w = get_box(lambda_value)
# Get a patch from the second image (`image2`)
crop2 = tf.image.crop_to_bounding_box(image2, boundaryy1, boundaryx1, target_h, target_w)
# Pad the `image2` patch (`crop2`) with the same offset
image2 = tf.image.pad_to_bounding_box(crop2, boundaryy1, boundaryx1, IMG_SHAPE, IMG_SHAPE)
# Get a patch from the first image (`image1`)
crop1 = tf.image.crop_to_bounding_box(image1, boundaryy1, boundaryx1, target_h, target_w)
# Pad the `image1` patch (`crop1`) with the same offset
img1 = tf.image.pad_to_bounding_box(crop1, boundaryy1, boundaryx1, IMG_SHAPE, IMG_SHAPE)
# Modify the first image by subtracting the patch from `image1`
# (before applying the `image2` patch)
image1 = image1 - img1
# Add the modified `image1` and `image2` together to get the CutMix image
image = image1 + image2
# Adjust Lambda in accordance to the pixel ration
lambda_value = 1 - (target_w * target_h) / (IMG_SHAPE * IMG_SHAPE)
lambda_value = tf.cast(lambda_value, tf.float32)
# Combine the labels of both images
label = lambda_value * label1 + (1 - lambda_value) * label2
return image, label
# Create the new dataset using our `cutmix` utility
train_ds_cmu = (train_ds.shuffle(1024).map(cutmix, num_parallel_calls=AUTO).batch(BATCH_SIZE).prefetch(AUTO))
# Let's preview 9 samples from the dataset
image_batch, label_batch = next(iter(train_ds_cmu))
plt.figure(figsize=(10,10))
for i in range(9):
ax = plt.subplot(3 ,3 ,i + 1)
plt.title(class_names[np.argmax(label_batch[i])])
plt.imshow(image_batch[i])
plt.axis('off')
def resnet_layer(inputs,
num_filters=16,
kernel_size=3,
strides=1,
activation='relu',
batch_normalization=True,
conv_first=True):
conv = keras.layers.Conv2D(num_filters,
kernel_size=kernel_size,
strides=strides,
padding='same',
kernel_initializer='he_normal',
kernel_regularizer=keras.regularizers.l2(1e-4))
x = inputs
if conv_first:
x = conv(x)
if batch_normalization:
x = keras.layers.BatchNormalization()(x)
if activation is not None:
x = keras.layers.Activation(activation)(x)
else:
if batch_normalization:
x = keras.layers.BatchNormalization()(x)
if activation is not None:
x = keras.layers.Activation(activation)(x)
x = conv(x)
return x
def resnet_v20(input_shape, depth, num_classes=10):
if (depth - 2) % 6 != 0:
raise ValueError('depth should be 6n+2 (eg 20, 32, 44 in [a])')
# Start model definition.
num_filters = 16
num_res_blocks = int((depth - 2) / 6)
inputs = keras.layers.Input(shape=input_shape)
x = resnet_layer(inputs=inputs)
# Instantiate the stack of residual units
for stack in range(3):
for res_block in range(num_res_blocks):
strides = 1
if stack > 0 and res_block == 0: # first layer but not first stack
strides = 2 # downsample
y = resnet_layer(inputs=x,
num_filters=num_filters,
strides=strides)
y = resnet_layer(inputs=y,
num_filters=num_filters,
activation=None)
if stack > 0 and res_block == 0: # first layer but not first stack
# linear projection residual shortcut connection to match
# changed dims
x = resnet_layer(inputs=x,
num_filters=num_filters,
kernel_size=1,
strides=strides,
activation=None,
batch_normalization=False)
x = keras.layers.add([x, y])
x = keras.layers.Activation('relu')(x)
num_filters *= 2
# Add classifier on top.
# v1 does not use BN after last shortcut connection-ReLU
x = keras.layers.AveragePooling2D(pool_size=8)(x)
y = keras.layers.Flatten()(x)
outputs = keras.layers.Dense(num_classes,
activation='softmax',
kernel_initializer='he_normal')(y)
# Instantiate model.
model = keras.models.Model(inputs=inputs, outputs=outputs)
return model
def training_model():
return resnet_v20((32,32,3), 20)
initial_model = training_model()
initial_model.save_weights("initial_weights.h5")
model = training_model()
model.load_weights("initial_weights.h5")
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
model.fit(train_ds_cmu,validation_data=test_ds, epochs=15)
test_loss, test_accuracy = model.evaluate(test_ds)
print("Test accuracy: {:.2f}%".format(test_accuracy * 100))
model = training_model()
model.load_weights("initial_weights.h5")
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
model.fit(train_ds_simple,validation_data=test_ds, epochs=15)
test_loss, test_accuracy = model.evaluate(test_ds)
print("Test accuracy: {:.2f}%".format(test_accuracy * 100))
| 0.84916 | 0.989034 |
<a href="https://colab.research.google.com/github/ibnuhajar/TrainingMachineLearning/blob/main/TraineKerasTensorflow.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import tensorflow as tf
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.image import ImageDataGenerator
print(tf.__version__)
!wget --no-check-certificate \
https://dicodingacademy.blob.core.windows.net/picodiploma/ml_pemula_academy/messy-vs-clean-room.zip \
-O /tmp/messy_vs_clean_room.zip
# melakukan ekstraksi pada file zip
import zipfile,os
local_zip = '/tmp/messy_vs_clean_room.zip'
zip_ref = zipfile.ZipFile(local_zip,'r')
zip_ref.extractall('/tmp')
zip_ref.close()
base_dir = '/tmp/images'
train_dir = os.path.join(base_dir,'train')
validation_dir = os.path.join(base_dir, 'val')
os.listdir('/tmp/images/train')
os.listdir('/tmp/images/val')
# membuat direktori ruangan rapi pada direktori data training
train_clean_dir = os.path.join(train_dir,'clean')
# membuat direktori ruangan berantakan pada direktori data training
train_messy_dir = os.path.join(train_dir, 'messy')
# membuat direktori ruangan rapi pada direktori data validasi
validation_clean_dir = os.path.join(validation_dir, 'clean')
# membuat direktori ruangan berantakan pada direktori data validasi
validation_messy_dir = os.path.join(validation_dir, 'messy')
train_datagen = ImageDataGenerator(
rescale = 1./255,
rotation_range = 20,
horizontal_flip = True,
shear_range = 0.2,
fill_mode = 'nearest'
)
test_datagen = ImageDataGenerator(
rescale = 1./255,
rotation_range = 20,
horizontal_flip = True,
shear_range = 0.2,
fill_mode = 'nearest'
)
train_generator = train_datagen.flow_from_directory(
train_dir, # direktori data latih
target_size = (150,150), # mengubah resolusi seluruh gambar menjadi 150x150 piksel
batch_size = 4, # karena kita merupakan masalah klasifikasi 2 kelas maka menggunakan class_mode = 'binary
class_mode = 'binary'
)
validation_generator = test_datagen.flow_from_directory(
validation_dir, # direktori data validasi
target_size = (150,150), # mengubah resulusi seluruh gambar menjadi 150x150 piksel
batch_size = 4, # karena kita merupakan masalah klasifikasi 2 kelas maka menggunakan class_mode = 'binary'
class_mode = 'binary'
)
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32,(3,3),activation='relu', input_shape=(150,150,3)),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512,activation='relu'),
tf.keras.layers.Dense(1,activation='sigmoid')
])
# compile model dengan 'adam' optimizzer loss function 'binary_crossentropy'
model.compile(loss='binary_crossentropy',
optimizer=tf.optimizers.Adam(),
metrics = ['accuracy'])
# latih model dengan model.fit
model.fit(
train_generator,
steps_per_epoch = 25,
epochs = 20,
validation_data = validation_generator,
validation_steps= 5,
verbose=2
)
import numpy as np
from google.colab import files
from keras.preprocessing import image
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
%matplotlib inline
uploaded = files.upload()
for fn in uploaded.keys():
path = fn
img = image.load_img(path,target_size =(150,150))
imgplot = plt.imshow(img)
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x])
classes = model.predict(images,batch_size=10)
print(fn)
if classes==0:
print('clean')
else:
print('messy')
```
|
github_jupyter
|
import tensorflow as tf
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.image import ImageDataGenerator
print(tf.__version__)
!wget --no-check-certificate \
https://dicodingacademy.blob.core.windows.net/picodiploma/ml_pemula_academy/messy-vs-clean-room.zip \
-O /tmp/messy_vs_clean_room.zip
# melakukan ekstraksi pada file zip
import zipfile,os
local_zip = '/tmp/messy_vs_clean_room.zip'
zip_ref = zipfile.ZipFile(local_zip,'r')
zip_ref.extractall('/tmp')
zip_ref.close()
base_dir = '/tmp/images'
train_dir = os.path.join(base_dir,'train')
validation_dir = os.path.join(base_dir, 'val')
os.listdir('/tmp/images/train')
os.listdir('/tmp/images/val')
# membuat direktori ruangan rapi pada direktori data training
train_clean_dir = os.path.join(train_dir,'clean')
# membuat direktori ruangan berantakan pada direktori data training
train_messy_dir = os.path.join(train_dir, 'messy')
# membuat direktori ruangan rapi pada direktori data validasi
validation_clean_dir = os.path.join(validation_dir, 'clean')
# membuat direktori ruangan berantakan pada direktori data validasi
validation_messy_dir = os.path.join(validation_dir, 'messy')
train_datagen = ImageDataGenerator(
rescale = 1./255,
rotation_range = 20,
horizontal_flip = True,
shear_range = 0.2,
fill_mode = 'nearest'
)
test_datagen = ImageDataGenerator(
rescale = 1./255,
rotation_range = 20,
horizontal_flip = True,
shear_range = 0.2,
fill_mode = 'nearest'
)
train_generator = train_datagen.flow_from_directory(
train_dir, # direktori data latih
target_size = (150,150), # mengubah resolusi seluruh gambar menjadi 150x150 piksel
batch_size = 4, # karena kita merupakan masalah klasifikasi 2 kelas maka menggunakan class_mode = 'binary
class_mode = 'binary'
)
validation_generator = test_datagen.flow_from_directory(
validation_dir, # direktori data validasi
target_size = (150,150), # mengubah resulusi seluruh gambar menjadi 150x150 piksel
batch_size = 4, # karena kita merupakan masalah klasifikasi 2 kelas maka menggunakan class_mode = 'binary'
class_mode = 'binary'
)
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32,(3,3),activation='relu', input_shape=(150,150,3)),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512,activation='relu'),
tf.keras.layers.Dense(1,activation='sigmoid')
])
# compile model dengan 'adam' optimizzer loss function 'binary_crossentropy'
model.compile(loss='binary_crossentropy',
optimizer=tf.optimizers.Adam(),
metrics = ['accuracy'])
# latih model dengan model.fit
model.fit(
train_generator,
steps_per_epoch = 25,
epochs = 20,
validation_data = validation_generator,
validation_steps= 5,
verbose=2
)
import numpy as np
from google.colab import files
from keras.preprocessing import image
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
%matplotlib inline
uploaded = files.upload()
for fn in uploaded.keys():
path = fn
img = image.load_img(path,target_size =(150,150))
imgplot = plt.imshow(img)
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x])
classes = model.predict(images,batch_size=10)
print(fn)
if classes==0:
print('clean')
else:
print('messy')
| 0.519034 | 0.844473 |
(ECNL)=
# 3.4 Ecuaciones no lineales
```{admonition} Notas para contenedor de docker:
Comando de docker para ejecución de la nota de forma local:
nota: cambiar `<ruta a mi directorio>` por la ruta de directorio que se desea mapear a `/datos` dentro del contenedor de docker.
`docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion -p 8888:8888 -d palmoreck/jupyterlab_optimizacion:2.1.4`
password para jupyterlab: `qwerty`
Detener el contenedor de docker:
`docker stop jupyterlab_optimizacion`
Documentación de la imagen de docker `palmoreck/jupyterlab_optimizacion:2.1.4` en [liga](https://github.com/palmoreck/dockerfiles/tree/master/jupyterlab/optimizacion).
```
---
Nota generada a partir de [liga1](https://www.dropbox.com/s/dfwk0y04ksgfilv/3.5.Aplicaciones_del_algebra_lineal_numerica.pdf?dl=0), [liga2](https://www.dropbox.com/s/6zree47e1u3p5wx/Ecuaciones_no_lineales.pdf?dl=0).
```{admonition} Al final de esta nota el y la lectora:
:class: tip
* Distinguirá la diferencia entre métodos abiertos y cerrados a partir del método de bisección y método de Newton.
* Conocerá algunos criterios de paro utilizados en métodos iterativos y la importancia de considerar la escala de las variables y la función a la que se le desea calcular sus raíces o ceros.
```
## Sistemas de ecuaciones lineales
Las ecuaciones lineales tienen importantes aplicaciones en todas las áreas de la ciencia. La teoría del álgebra lineal nos permite tener resultados universales de las mismas y son una herramienta importante para aproximaciones a ecuaciones no lineales. Por ejemplo, al considerar pequeñas perturbaciones en un punto, un sistema no lineal puede típicamente aproximarse por un sistema lineal en una vecindad local del punto. Sin embargo, la linearización sólo describe propiedades locales y para un análisis global de problemas no lineales otras técnicas se requieren. Tales métodos comúnmente utilizan esquemas iterativos para gradualmente aproximar la solución.
```{admonition} Definición
En general un sistema de ecuaciones lineal es de la forma:
$$
\begin{array}{ccc}
a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n &= & b_1 \\
a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n &= & b_2 \\
\vdots & & \\
a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n &=& b_m
\end{array}
$$
donde: las $x_i$'s son las incógnitas y las $a_i$'s y $b_i$'s son constantes conocidas.
Las entradas $a_{ij}$'s son nombradas **coeficientes del sistema** y forman a la **matriz del sistema** $A \in \mathbb{R}^{m \times n}$. El conjunto de $b_i$'s se le nombra **lado derecho del sistema** y forma al **vector de lado derecho** $b \in \mathbb{R}^{m}$. Así, el sistema se escribe como $Ax = b$.
Si todas las $b_i$'s son iguales a $0$ el sistema se le nombra **homogéneo** si no se cumple esto se le nombra **no homogéneo**.
```
La teoría del álgebra lineal nos ayuda a determinar que existen solamente **3 posibilidades para solución del sistema anterior:**
* **Una única solución:** sólo existe uno y sólo un conjunto de valores de $x_i$'s que satisfacen todas las ecuaciones simultáneamente.
* **Ninguna solución:** no existe ningún conjunto de valores de $x_i$'s que satisfacen todas las ecuaciones simultáneamente (el conjunto solución es vacío).
* **Infinitas soluciones:** hay una infinidad de valores distintos de las $x_i$'s que satisfacen todas las ecuaciones simultáneamente.
```{admonition} Definición
En el caso de una o infinitas soluciones el sistema de ecuaciones lineales se nombra consistente o no singular, si no existe solución se nombra inconsistente o singular.
```
```{admonition} Observación
:class: tip
Es sencillo probar que si un sistema tiene más de una solución entonces tiene una infinidad de soluciones. Esto contrasta con sistemas de ecuaciones no lineales donde pueden existir para tales sistemas un número finito de soluciones mayor a uno.
```
### Interpretación geométrica
Resolver un sistema de ecuaciones lineales equivale a encontrar la intersección entre rectas, planos o hiperplanos (2,3 o n dimensiones respectivamente). Por ejemplo para un caso de dos dimensiones se tiene:
<img src="https://dl.dropboxusercontent.com/s/p92z7zlquo1adbm/algebra_lineal_1.jpg?dl=0" heigth="700" width="700">
El inciso a) representa un sistema de ecuaciones lineales sin solución, el inciso b) infinitas soluciones (en el dibujo ligeramente se desplazó hacia abajo una de las rectas para mostrar ambas) y el inciso c) una única solución.
### Algoritmos
Existen una gran cantidad de algoritmos para resolver los sistemas de ecuaciones. Típicamente se elige el algoritmo de acuerdo a las características de los coeficientes de la matriz del sistema y sus dimensiones.
### Algoritmos para sistemas triangulares
Son sistemas cuya matriz del sistema es triangular inferior o superior. Un sistema triangular inferior se resuelve con el **método de sustitución hacia delante**. Si es triangular superior se resuelve con el **método de sustitución hacia atrás**.
### Algoritmos para sistemas no triangulares
Para sistemas de ecuaciones lineales más generales (no tienen estructura identificable) se tienen los **métodos iterativos** y **directos o basados en factorizaciones matriciales**.
Entre los directos o basados en factorizaciones matriciales se encuentran:
```{margin}
Ver {ref}`definición <MATRIZSDPOSITIVA>` de una matriz simétrica definida positiva.
```
* Eliminación Gaussiana o factorización LU.
* Factorización de Cholesky (la matriz del sistema debe ser un elemento en $\mathbb{S}^n_{++}$ simétrica positiva definida)
* Factorización QR.
* Descomposición en valores singulares o SVD.
y como ejemplo de los iterativos están:
* Jacobi.
* Gauss-Seidel.
* Gradiente conjugado (la versión que se aplica a matrices del sistema simétricas requiere que tales matrices estén en $\mathbb{S}^n_{++}$).
Ambos métodos: iterativos y directos o basados en factorizaciones matriciales encuentran sistemas de ecuaciones equivalentes a partir de operaciones básicas del álgebra lineal.
```{admonition} Definición
Dos sistemas de ecuaciones lineales son equivalentes si tienen el mismo conjunto solución.
```
### Sistemas de ecuaciones lineales *square*, *underdetermined*, *overdetermined*
Entre las características que definen el problema a resolver y el tipo de algoritmo a usar se encuentran las dimensiones de una matriz.
```{admonition} Definición
Si la matriz del sistema tiene más renglones que columnas, $m > n$, se tiene un sistema ***overdetermined***, si tiene más columnas que renglones, $m < n$, se nombra ***underdetermined*** y si tiene el mismo número de renglones y columnas, $m=n$, se nombra ***square***.
```
Los sistemas de ecuaciones lineales *overdetermined* en general no tienen solución si $b \notin \text{Im}(A)$ con $\text{Im}(A)$ espacio columna de $A$. Por esto se busca resolver un **problema de mínimos cuadrados** de la forma:
$$\displaystyle \min_{x \in \mathbb{R}^n} ||Ax-b||_2$$
con única solución si $A$ es de *rank* completo.
Los sistemas de ecuaciones lineales *underdetermined* pueden tener infinitas soluciones o ninguna solución. En el caso que $A$ sea de *rank* completo el sistema es consistente y se busca resolver el **problema de optimización de mínima norma** :
$$\displaystyle \min_{x \in \mathcal{K}} ||x||_2$$
donde: $\mathcal{K} = \{x \in \mathbb{R}^n | Ax = b\}$ que es interesante para $b \neq 0$ y tiene única solución.
```{margin}
Recuérdese que el producto $x^T Ax$ con $A$ simétrica se le nombra forma cuadrática y es un número en $\mathbb{R}$.
```
```{admonition} Comentarios
* El problema de mínimos cuadrados es un problema convexo no importando si $A$ es o no de *rank* completo pues la forma cuadrática involucra a la expresión $x^TA^TAx$ y $A^TA \in \mathbb{S}^n_+$.
* El problema de optimización a resolver para el caso de sistemas de ecuaciones lineales *underdetermined* y matriz del sistema de *rank* completo también puede escribirse como:
$$\min_{x \in \mathbb{R}^n} ||x||_2$$
$$\text{sujeto a:} Ax = b$$
el cual es un problema de optimización convexa con restricciones (no importando si $A$ es o no de *rank* completo).
```
## Ecuaciones no lineales
El problema que queremos resolver es el siguiente: dada $f: \mathbb{R} \rightarrow \mathbb{R}$ encontrar $x^*$ que resuelva la ecuación no lineal $f(x) = 0$. Nos interesa al menos una solución de la ecuación anterior.
```{admonition} Definición
$x^*$ se nombra raíz o cero de $f$.
```
Algunos ejemplos son:
* $e^x+1=0$
* $e^{-x}-x =0$
* $x^2 -4\sin(x)=0$
* $x^3+6x^2+11x-6=0$
* $\sin(x) = 0$.
**Resolvamos con [scipy.optimize.fsolve](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fsolve.html#scipy.optimize.fsolve) algunas de las ecuaciones no lineales anteriores.**
```
from matplotlib import pyplot as plt
from scipy.optimize import fsolve
import math
import numpy as np
np.set_printoptions(precision=3, suppress=True)
```
La ecuación no lineal $e^x + 1 = 0$ no tiene solución, su gráfica es la siguiente
```
t = np.linspace(-1,1,100)
eqn = np.exp(t) + 1
plt.plot(t, eqn)
plt.axhline(color="black")
plt.title("$f(x) = e^x + 1$")
plt.grid()
plt.show()
```
La ecuación no lineal $e^{-x} - x = 0$ tiene una solución
```
t = np.linspace(-.25,1,100)
eqn = lambda x: np.exp(-x) - x
```
```{margin}
Elegimos un punto inicial por ejemplo el $0$.
```
```
root = fsolve(eqn, 0)
print(root)
plt.plot(t, eqn(t))
plt.scatter(root, 0, color = "red")
plt.axhline(color="black")
plt.title("$f(x) = e^{-x}-x$")
plt.grid()
plt.show()
```
La ecuación no lineal $x^2 -4\sin(x)=0$ tiene dos soluciones
```
t = np.linspace(-5,5,100)
eqn = lambda x: x**2-4*np.sin(x)
```
```{margin}
Elegimos un punto inicial por ejemplo el $-2$.
```
```
root = fsolve(eqn, -2)
print(root)
```
```{margin}
Observamos que tenemos dos raíces de $f$.
```
```
plt.plot(t, eqn(t))
plt.scatter(root, 0, color = "red")
plt.axhline(color="black")
plt.title("$f(x) = x^2-4\sin(x)$")
plt.grid()
plt.show()
```
```{margin}
Elegimos un punto inicial por ejemplo el $3$.
```
```
root2 = fsolve(eqn, 3)
print(root2)
plt.plot(t, eqn(t))
plt.scatter(root, 0, color = "red")
plt.scatter(root2, 0, color = "red")
plt.axhline(color="black")
plt.title("$f(x) = x^2-4\sin(x)$")
plt.grid()
plt.show()
```
```{margin}
Como ejemplo que no es posible expresar las raíces o ceros por una fórmula cerrada que involucren a los coeficientes, operaciones aritméticas y raíces $\sqrt[n]{\cdot}$, considérese la ecuación no lineal $x^5 - x^2 + 1 = 0$.
```
```{admonition} Comentarios
* En el caso de una ecuación o un sistema de ecuaciones no lineales no tenemos resultados que determinen la existencia o unicidad de soluciones a diferencia de un sistema lineal. Sin embargo, en muchas situaciones en la práctica se resuelven ecuaciones no lineales que sí tienen solución y se desea aproximar una solución o varias soluciones en una región de interés por lo que determinar la existencia o unicidad de la solución no es primordial.
* La mayoría de los métodos para calcular raíces o ceros de $f$ vía la ecuación no lineal $f(x) = 0$ nos devuelven aproximaciones y no fórmulas cerradas. Son métodos **iterativos** que en el caso de $1$ dimensión los podemos dividir en $2$ tipos: **cerrados** y **abiertos**. Los cerrados inician sus iteraciones en un intervalo que encierra a la raíz y conforme avanzan las iteraciones hacen subdivisiones del intervalo inicial por lo que su longitud se reduce y **siempre** convergen. Los abiertos no requieren encerrar a la raíz, en general tienen mejor desempeño que los cerrados en cuanto al número de iteraciones pero **no siempre convergen**.
* Es conveniente comentar que si bien quisiéramos tener algoritmos que calculasen todas las raíces o ceros de $f$ esto no es posible, es un hecho que los métodos nos darán una solución aproximada o un mensaje del tipo "no se encontró solución".
```
## Sistema de ecuaciones no linales
El caso de sistema de ecuaciones no lineales es una generalización del caso de una dimensión en el que tenemos $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$ y debemos encontrar una raíz o cero de $f$ que resuelva el sistema de ecuaciones no lineales $f(x) = 0$.
```{admonition} Observación
:class: tip
$f$ tiene $n$ funciones componentes:
$$
f(x) = \left [ \begin{array}{c}
f_1(x) \\
f_2(x) \\
\vdots \\
f_n(x)
\end{array}
\right ]
$$
y su derivada es la matriz de $n \times n$, la Jacobiana $(\mathcal{J}_f(x))_{ij} = \frac{\partial f_i(x)}{\partial x_j}$, ver {ref}`Definición de función, continuidad y derivada <FCD>`.
```
Algunos ejemplos son:
1) $$
\begin{eqnarray}
x_1^2+x_1x_2&=&10 \nonumber \\
x_2 + 3x_1x_2^2&=&57 \nonumber
\end{eqnarray}
$$
2) $$
\begin{eqnarray}
2=\displaystyle \int_{-1}^{1}1dx &=& w_0 \cdot 1 + w_1\cdot1 \nonumber \\
0 = \displaystyle \int_{-1}^1xdx &=& w_0x_0 + w_1x_1 \nonumber \\
\frac{2}{3} = \displaystyle \int_{-1}^1x^2dx &=& w_0x_0^2 + w_1x_1^2 \nonumber \\
0 = \displaystyle \int_{-1}^1x^3dx &=& w_0x_0^3 + w_1x_1^3 \nonumber \\
\end{eqnarray}
$$
## Criterios de paro, escala de la variable $x$ y de la función $f$
Un tema importante en la implementación de algoritmos es la escala del problema tanto en la variable $x$ como en la función $f$. Por ejemplo, si $x_1$ está en el rango $[10^2, 10^3]$ de metros y $x_2$ está en el rango $[10^{-7}, 10^{-6}]$ de segundos entonces tenemos que realizar un reescalamiento para tener evaluaciones de $f$, criterios de paro y actualizaciones en esquemas iterativos, por ejemplo, independientes de las escalas de las variables o de la función. Asimismo, los criterios de paro en un método iterativo ayudan a contestar preguntas del tipo ¿hemos resuelto el problema de forma aproximada? ¿en las últimas dos (o un poco más) iteraciones nos hemos quedado virtualmente en el mismo punto?
```{margin}
El reescalamiento en el ejemplo de kilómetros y microsegundos puede describirse como la multiplicación de una matriz diagonal por las variables $x_1$ y $x_2$ en la que las entradas de la diagonal son $\frac{1}{10^3}$ y $\frac{1}{10^{-6}}$ para las variables $x_1$ y $x_2$ respectivamente.
```
Muchos algoritmos cumplen que son invariantes ante escala de las variables, el método de Newton en la variable $x$ es uno de ellos por ejemplo, pero otros no, por lo que al implementar un algoritmo se debe revisar los reescalamientos a realizar. En el ejemplo anterior de los metros y segundos si se cambian las unidades de $x_1$ a kilómetros y las de $x_2$ a microsegundos entonces tanto $x_1$ como $x_2$ se encontrarán en el rango $[10^{-1}, 1]$. Si en dos dimensiones $x_1 \in [10^{6}, 10^{7}]$ y $x_2 \in [10^{-1}, 1]$ entonces una prueba del tipo $||\nabla f(x)|| < 10^{-3}$ no será equilibrada para ambas variables si se desea por ejemplo minimizar $f$ ($x_1$ tendería a ser lo más pequeña posible si por ejemplo tenemos una alta contribución de esta variable en $f$).
En el caso de la función $f$, es común requerir que $f$ o la magnitud de $f$ sea cero (o su derivada). Si consideramos $f(x) = 0$ es muy probable que los errores por redondeo no permitan que se satisfaga esto para ningún punto $x$ por lo que modificamos la condición anterior a $f(x) \approx 0$. También si $f$ no está escalada apropiadamente la condición $|f(x)| < tol$ es probable que siempre o nunca se satisfaga. Por ejemplo si $tol = 10^{-3}$ y $f$ siempre está en $[10^{-7}, 10^{-5}]$ entonces cualquier $x$ satisface $|f(x)| < 10^{-3}$.
Considerando $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$, dentro de los criterios de paro que se utilizan en los métodos iterativos para resolver ecuaciones no lineales que apuntan a tener una evaluación independiente de la escala se encuentran:
```{margin}
En los criterios de paro que revisan la norma de la derivada de $f$, una opción independiente de la escala de $f$ y $x$ es la cantidad $\frac{||Df(x)||||x||}{||f(x)||}$.
```
* Medir diferencia entre iteraciones. Por ejemplo:
* $||x^{(k+1)} - x^{(k)}|| < tol(||x^{(k)}|| +1)$
* $||x^{(k+1)} - x^{(k)}|| < tol\max\{||x_{k+1}||, ||x_k||\}$
* $||x^{(k+1)} - x^{(k)}|| < tol\max\{||x_{k+1}||, \text{user_defined_value}\}$.
con `user_defined_value` un valor positivo proporcionado por *user* que mide la magnitud típica de $x$ y $|| \cdot ||$ norma.
* Medir la norma de $f$ reescalándola por ejemplo:
$$||Diag f|| < tol$$
con $Diag$ matriz diagonal tal que $Diagf$ tenga norma alrededor de $1$ en puntos no cercanos a la raíz y también puede proveerse sus valores con un `user_defined_value`.
* Máximo número de iteraciones.
## Métodos para resolver ecuaciones no lineales de funciones $f: \mathbb{R} \rightarrow \mathbb{R}$
### Método de bisección
Es un método cerrado que requiere $f \in \mathbb{R} \rightarrow \mathbb{R}$ con $f \in \mathcal{C}([a,b])$ tal que $f(a) f(b) <0$, esto es, que $f$ tenga un cambio de signo. Por el **teorema del valor intermedio** se cumple que $f$ tiene una raíz en $[a,b]$.
### Algoritmo: método de bisección
> **Dados** $x_i, x_s$ límite inferior y superior respectivamente tales que $x^* \in [x_i, x_s]$ con $f(x_i)f(x_s)<0$ y $tol >0$
>
> **Repetir** el siguiente bloque para $k=1,2,\dots$
>> 1. $x^{(k)} = \frac{x_i + x_s}{2}$
>>
>> 2. Si $f(x_i)f(x^{(k)}) < 0$ entonces $x^* \in [x_i, x^{(k)}]$ por lo tanto $x_s = x^{(k)}$.
>>
>> 3. Si $f(x_i)f(x^{(k)}) > 0$ entonces $x^* \in [x^{(k)}, x_s]$ por lo tanto $x_i = x^{(k)}$.
>
> **hasta** convergencia: satisfacer criterio de paro en el que se utiliza $tol$ y $maxiter$.
````{admonition} Comentarios
En el método de bisección:
* Se garantiza que el error relativo en cada iteración se reduce por la mitad y se obtiene una cantidad constante de dígitos por cada iteración, lo cual es representativo de una convergencia lineal.
* Siempre tenemos convergencia pero es lenta.
* No es posible extenderlo a más dimensiones de forma natural pues tendríamos que definir metodologías para elegir puntos en regiones como rectángulos, cubos,... para evaluar a la función $f$ y determinar cambios de signo.
* La evaluación de los pasos 2 y 3 del algoritmo anterior se visualizan respectivamente como sigue:
<img src="https://dl.dropboxusercontent.com/s/sl9m30qmy8cf4rr/bisection_method.png?dl=0" heigth="600" width="600">
* La implementación del método utiliza lo siguiente:
* El punto medio se calcula con la expresión: $x^{(k)} = x_i + \frac{x_s - x_i}{2}$
* Se revisan los signos de $f(x_i)$, $f(x^{(k)})$ para determinar si $f(x_i)f(x^{(k)}) < 0$ o $f(x_i)f(x^{(k)}) > 0$.
````
```{admonition} Ejercicio
:class: tip
Con el método de bisección aproxima la raíz $x^* \approx 0.56714329$ de la ecuación no lineal $f(x) = e^{-x}-x$ tomando como intervalo inicial $[0,2]$ y un valor de $tol = 10^{-8}$. Crea una tabla de la forma:
|Iter | $x_i$ | $x_s$ | $x^{(k)}$ | Err_rel$(x^{(k)})$|
|:---:|:---:|:---:|:---:|:---:|
|1|0|2|1|1.5 e-2|
|2|0|1|0.5|1.3 e-2|
(valores ejemplo)
```
### Método de Newton o Newton-Raphson
Es un método abierto que sigue un esquema iterativo de la forma:
$$x^{(k+1)} = x^{(k)} - \frac{f(x^{(k)})}{f'(x^{(k)})}$$
requiere un punto inicial $x^{(0)}$ y converge si se cumplen condiciones descritas en {ref}`comentarios del método de Newton-Raphson <COMENTMETNEWTONRAPSHON>`.
Existen varias formas de obtener tal esquema iterativo, la que se presenta a continuación **define un modelo afín local que aproxima a nuestra función $f$ y encuentra la raíz de tal modelo**, gráficamente:
<img src="https://dl.dropboxusercontent.com/s/hw6fluifowjnpdo/Newton-Raphson_method.png?dl=0" heigth="600" width="600">
El modelo afín en el dibujo anterior es de la forma:
$$M(x) = f(x^{(k)}) + f'(x^{(k)})(x-x^{(k)})$$
E igualando a cero el modelo se tiene:
$$
\begin{eqnarray}
0 &=& M(x) = f(x^{(k)}) + f'(x^{(k)})(x-x^{(k)}) \nonumber \\
&\therefore& x = x^{(k)} - \frac{f(x^{(k)})}{f'(x^{(k)})} \nonumber
\end{eqnarray}
$$
```{admonition} Observación
:class: tip
Obsérvese que el modelo afín anterior $M(x)$ es la aproximación a primer orden dada por el teorema de Taylor.
```
### Ejemplo
Encontrar la raíz de $f(x) = 4x + 5$ con el método de Newton.
```
import sympy
```
```{margin}
Elección del punto inicial.
```
```
x_0 = -2
```
```{margin}
Definición de función.
```
```
x = sympy.Symbol('x')
f = 4*x + 5
```
```{margin}
Derivada de $f$.
```
```
df = f.diff()
sympy.pprint(df)
```
```{margin}
Actualización por el método de Newton: $x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}$.
```
```
x_1 = x_0 - f.subs(x, x_0)/df.subs(x, x_0)
sympy.pprint(x_1)
```
### Ejemplo
Aproximar el valor $\sqrt{3}$ con el método de Newton
```{margin}
Elección del punto inicial. ¿Qué pasa si elegimos $x_0 = -10$?
```
```
x_0 = 10
```
```{margin}
Definimos la función $f(x) = x^2 - 3$
```
```
x_sym = sympy.Symbol('x')
f = x_sym**2 - 3
```
```{margin}
Derivada de $f$.
```
```
df = f.diff()
sympy.pprint(df)
```
**Primera iteración**
```{margin}
Actualización por el método de Newton: $x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}$.
```
```
x = x_0 - f.subs(x_sym, x_0)/df.subs(x_sym, x_0)
sympy.pprint(x)
sympy.pprint(x.evalf())
```
**Segunda iteración**
```{margin}
Actualización por el método de Newton: $x_2 = x_1 - \frac{f(x_1)}{f'(x_1)}$.
```
```
x = x - f.subs(x_sym, x)/df.subs(x_sym, x)
sympy.pprint(x)
sympy.pprint(x.evalf())
```
**Tercera iteración**
```{margin}
Actualización por el método de Newton: $x_3 = x_2 - \frac{f(x_2)}{f'(x_2)}$.
```
```
x = x - f.subs(x_sym, x)/df.subs(x_sym, x)
sympy.pprint(x)
sympy.pprint(x.evalf())
```
**...**
**Séptima iteración**
```
x_7 = 1.73205080756888
from pytest import approx
import math
print(x_7 == approx(math.sqrt(3)))
```
(COMENTMETNEWTONRAPSHON)=
```{admonition} Comentarios
* El modelo afín anterior $M(x) = f(x^{(k)}) + f'(x^{(k)})(x-x^{(k)})$ es también nombrado **modelo lineal**.
* Si la función $f$ es lineal el método de Newton converge en una iteración.
* La convergencia del método de Newton en una dimensión converge de forma cuadrática, esto es, el número de dígitos de precisión en cada iteración se duplica si se satisfacen las siguientes condiciones:
* El punto inicial $x^{(0)}$ es cercano a la raíz $x^*$ de $f$.
* $f'(x^*) \neq 0$ y existe un conjunto abierto $\mathcal{D}$ en el que $f'(x) \neq 0$ $\forall x \in \mathcal{D}$, $x^* \in \mathcal{D}$ y la segunda derivada de $f$ es acotada en $\mathcal{D}$ \*.
\* La segunda condición referente a la segunda derivada puede ser sustituida por la condición que la primera derivada sea *Lipschitz* continua en $\mathcal{D}$, ver [Lipschitz_continuity](https://en.wikipedia.org/wiki/Lipschitz_continuity). Esto ayuda a acotar la diferencia entre $f$ y el modelo afín $M$. Además evitamos calcular la segunda derivada (que en más dimensiones puede ser complicada de describir) para verificar convergencia.
```
```{admonition} Observaciones
:class: tip
* Si la derivada de $f$ es cero en la raíz no podemos concluir si el método de Newton converge o no y si converge podría o no hacerlo de forma cuadrática.
* Si elegimos un punto inicial lejos de $x^*$ no podemos concluir, el método de Newton podría o no converger.
```
```{admonition} Ejercicio
:class: tip
Para revisar la hipótesis que la derivada de $f$ sea diferente de cero en la raíz y garantice que el método de Newton tenga convergencia cuadrática considérese aproximar la raíz $1$ para las ecuaciones no lineales:
1.$x^2-1=0$
2.$x^2-2x+1=0$
Realícense $6$ iteraciones del método de Newton para cada ecuación no lineal y háganse conclusiones.
```
```{admonition} Ejercicio
:class: tip
Para revisar la hipótesis que el punto inicial $x^{(0)}$ sea "cercano" a la raíz y garantice que el método de Newton tenga convergencia cuadrática considérese aproximar la raíz $0$ para la ecuación no lineal $\arctan(x) = 0$. Realícense $6$ iteraciones del método de Newton eligiendo un punto $x^{(0)}$ en tres casos:
1.tal que sea en valor absoluto menor a un punto cualquiera en $[1.39, 1.40]$,
2.tal que esté en $[1.39, 1.40]$,
3.tal que en valor absoluto sea mayor a un punto en el intervalo $[1.39, 1.40]$.
y háganse conclusiones.
```
Concerniente a la dependencia de un punto inicial, la convergencia del método de Newton se robustece al incorporar metodologías que permiten su convergencia a una solución **local** desde prácticamente cualquier punto inicial. Tales metodologías resultan en **algoritmos híbridos** en los que se utiliza el método de Newton siempre que funcione bien pero se utiliza otro método (quizás más lento) que garantice convergencia. Uno de éstos es el método de bisección en el que una vez se encuentre "cerca" de una solución se utilice el método de Newton. Otra metodología consiste en que en cada iteración se reduzca una medida de cercanía a la solución como una forma de *backtracking*, ver por ejemplo el {ref}`método de búsqueda de línea por backtracking <MBUSLINBACK>` en el contexto de minimización de una función.
El siguiente es un algoritmo en una forma general de algoritmos híbridos [quasi-Newton](https://en.wikipedia.org/wiki/Quasi-Newton_method) para resolver una ecuación no lineal.
(ALGMGCNHEN)=
### Algoritmo: método general cuasi-Newton híbrido para resolver una ecuación no lineal
> **Dados** $x^{(0)}$ punto inicial, $f: \mathbb{R} \rightarrow \mathbb{R}$ y $tol >0$
>
> **Repetir** el siguiente bloque para $k=1,2,\dots$
>> 1. Construir un modelo local de $f$ alrededor de $x^{(k)}$ y encontrar el punto $x_N$ que resuelva (o cercanamente resuelva) el modelo del problema.
>>
>> 2. Realizar alguno de los dos pasos siguientes:
>>>
>>> a. Decidir si $x^{(k+1)} = x_N$ si no,
>>>
>>> b. Elegir $x^{(k+1)}$ usando una estrategia global (usar $x_N$ del inciso a. de forma más conservadora).
>
> **hasta** convergencia: satisfacer criterio de paro en el que se utiliza $tol$ y $maxiter$.
```{admonition} Comentario
Además de estrategias globales es común que no se tengan disponibles las derivadas de $f$, en este caso las metodologías de diferenciación finita son útiles, ver {ref}`diferenciación numérica por diferencias finitas <DIFNUMDIFFINITAS>`.
```
## Una nota sobre problemas *Unconstrained Optimization* (UO)
En esta sección utilizamos la notación para un problema de optimización sin restricciones de la forma:
$$\displaystyle \min_{x^\in \mathbb{R}^n} f_o(x)$$
y $f_o: \mathbb{R}^n \rightarrow \mathbb{R}$ es una función objetivo en general que asumimos es de clase $\mathcal{C}^2$ en su dominio.
Así como en ecuaciones no lineales no tenemos resultados que determinen la existencia o unicidad de soluciones, en problemas de optimización sin restricciones esto es similar al plantear la búsqueda de mínimos globales de las funciones objetivo. Lo mejor que podemos obtener son aproximaciones a minimos locales y es prácticamente imposible saber si se ha aproximado un mínimo global.
```{margin}
Por condición necesaria de primer orden recuérdese que si $x^*$ es óptimo entonces $\nabla f_o(x^*) = 0$ que establece un sistema de ecuaciones no lineales en general.
```
Además, en la nota de {ref}`algoritmos de descenso y búsqueda de línea en Unconstrained Convex Optimization (UCO) <ADBLUCO>` se mostró la relación que existe entre resolver problemas tipo UO y ecuaciones no lineales. Es natural entonces aplicar el algoritmo de {ref}`método general cuasi-Newton híbrido para resolver una ecuación no lineal <ALGMGCNHEN>` a la ecuación no lineal de una variable $f_o'(x) = 0$. El esquema iterativo entonces es de la forma:
$$x^{(k+1)} = x^{(k)} - \frac{f_o'(x^{(k)})}{f_o''(x^{(k)})}$$
Recuérdese que tal esquema iterativo se obtiene mediante un modelo afín de $f_o'(x)$ alrededor de $x^{(k)}$, lo cual es equivalente en términos de la función $f_o$ a definir un modelo cuadrático alrededor de $x^{(k)}$ que aproxime a nuestra función $f_o$ y que encuentre la raíz de tal modelo:
$$m(x) = f(x^{(k)}) + f'(x^{(k)})(x-x^{(k)}) + \frac{1}{2} f''(x^{(k)})(x-x^{(k)})^2,$$
con lo que obtendremos el esquema iterativo anterior.
```{admonition} Comentarios
* Un modelo cuadrático es más apropiado que un modelo afín para $f_o$ ya sea para maximización o minimización pues tiene a lo más un punto extremo.
* Si la función $f_o$ es una función cuadrática el método de Newton converge en una iteración.
* Así como se revisaron las condiciones bajo las cuales el método de Newton converge de forma cuadrática, en el caso de un problema UO se requiere:
* El punto inicial $x^{(0)}$ sea cercano a la raíz $x^*$ de $f'$.
* $f''(x^*) \neq 0$ y existe un conjunto abierto $\mathcal{D}$ en el que $f''(x) \neq 0$ $\forall x \in \mathcal{D}$, $x^* \in \mathcal{D}$ y la segunda derivada sea *Lipschitz* continua en $\mathcal{D}$, ver [Lipschitz_continuity](https://en.wikipedia.org/wiki/Lipschitz_continuity). Esto ayuda a acotar la diferencia entre $f$ y el modelo cuadrático $m$. Además evitamos calcular la tercera derivada (que en más dimensiones puede ser complicada de describir) para verificar convergencia.
```
## Método de Newton para ecuaciones no lineales de funciones $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$
(en proceso de realización)
### Ejemplo
El problema de optimización:
$$\displaystyle \max_{v \in \mathbb{R}^n - \{0\}} \frac{1}{2} v^TX^TXv$$
$$\text{sujeto a: } \frac{1}{2}v^Tv =1$$
donde: $X \in \mathbb{R}^{m \times n}$ cuyas columnas tienen una observación de un **vector aleatorio** (tenemos $n$ vectores aleatorios de mediciones) tiene solución cerrada dada por: $\sigma_1^2 = \displaystyle \max_{v \in \mathbb{R}^n - \{0\}} \frac{v^TX^TXv}{v^Tv}$.
Utilizando las condiciones de [Karush-Kuhn-Tucker](https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions) (KKT) de optimalidad se tiene que resolver el siguiente sistema de ecuaciones no lineales:
$$\nabla f_o(v,\lambda) =
\left[
\begin{array}{c}
X^TX v + \lambda v \\
v^Tv-1
\end{array}
\right] = 0.
$$
```{admonition} Observación
Obsérvese que la variable de optimización es el vector $(v, \lambda) \in \mathbb{R}^{n+1}$.
```
```{admonition} Ejercicios
:class: tip
1.Resuelve los ejercicios y preguntas de la nota.
```
**Preguntas de comprehensión.**
1)
**Referencias:**
1. C. Meyer, Matrix Analysis and Applied Linear Algebra, SIAM, 2000.
2. J. Dennis, R. B. Schnabel, Numerical Methods for Unconstrained Optimization and Nonlinear Equations, SIAM, 1996.
3. R. Johansson, Numerical Python, Scientific Computing and Data Science Applications with Numpy, SciPy and Matplotlib, Apress, 2015.
|
github_jupyter
|
---
Nota generada a partir de [liga1](https://www.dropbox.com/s/dfwk0y04ksgfilv/3.5.Aplicaciones_del_algebra_lineal_numerica.pdf?dl=0), [liga2](https://www.dropbox.com/s/6zree47e1u3p5wx/Ecuaciones_no_lineales.pdf?dl=0).
## Sistemas de ecuaciones lineales
Las ecuaciones lineales tienen importantes aplicaciones en todas las áreas de la ciencia. La teoría del álgebra lineal nos permite tener resultados universales de las mismas y son una herramienta importante para aproximaciones a ecuaciones no lineales. Por ejemplo, al considerar pequeñas perturbaciones en un punto, un sistema no lineal puede típicamente aproximarse por un sistema lineal en una vecindad local del punto. Sin embargo, la linearización sólo describe propiedades locales y para un análisis global de problemas no lineales otras técnicas se requieren. Tales métodos comúnmente utilizan esquemas iterativos para gradualmente aproximar la solución.
La teoría del álgebra lineal nos ayuda a determinar que existen solamente **3 posibilidades para solución del sistema anterior:**
* **Una única solución:** sólo existe uno y sólo un conjunto de valores de $x_i$'s que satisfacen todas las ecuaciones simultáneamente.
* **Ninguna solución:** no existe ningún conjunto de valores de $x_i$'s que satisfacen todas las ecuaciones simultáneamente (el conjunto solución es vacío).
* **Infinitas soluciones:** hay una infinidad de valores distintos de las $x_i$'s que satisfacen todas las ecuaciones simultáneamente.
### Interpretación geométrica
Resolver un sistema de ecuaciones lineales equivale a encontrar la intersección entre rectas, planos o hiperplanos (2,3 o n dimensiones respectivamente). Por ejemplo para un caso de dos dimensiones se tiene:
<img src="https://dl.dropboxusercontent.com/s/p92z7zlquo1adbm/algebra_lineal_1.jpg?dl=0" heigth="700" width="700">
El inciso a) representa un sistema de ecuaciones lineales sin solución, el inciso b) infinitas soluciones (en el dibujo ligeramente se desplazó hacia abajo una de las rectas para mostrar ambas) y el inciso c) una única solución.
### Algoritmos
Existen una gran cantidad de algoritmos para resolver los sistemas de ecuaciones. Típicamente se elige el algoritmo de acuerdo a las características de los coeficientes de la matriz del sistema y sus dimensiones.
### Algoritmos para sistemas triangulares
Son sistemas cuya matriz del sistema es triangular inferior o superior. Un sistema triangular inferior se resuelve con el **método de sustitución hacia delante**. Si es triangular superior se resuelve con el **método de sustitución hacia atrás**.
### Algoritmos para sistemas no triangulares
Para sistemas de ecuaciones lineales más generales (no tienen estructura identificable) se tienen los **métodos iterativos** y **directos o basados en factorizaciones matriciales**.
Entre los directos o basados en factorizaciones matriciales se encuentran:
* Eliminación Gaussiana o factorización LU.
* Factorización de Cholesky (la matriz del sistema debe ser un elemento en $\mathbb{S}^n_{++}$ simétrica positiva definida)
* Factorización QR.
* Descomposición en valores singulares o SVD.
y como ejemplo de los iterativos están:
* Jacobi.
* Gauss-Seidel.
* Gradiente conjugado (la versión que se aplica a matrices del sistema simétricas requiere que tales matrices estén en $\mathbb{S}^n_{++}$).
Ambos métodos: iterativos y directos o basados en factorizaciones matriciales encuentran sistemas de ecuaciones equivalentes a partir de operaciones básicas del álgebra lineal.
### Sistemas de ecuaciones lineales *square*, *underdetermined*, *overdetermined*
Entre las características que definen el problema a resolver y el tipo de algoritmo a usar se encuentran las dimensiones de una matriz.
Los sistemas de ecuaciones lineales *overdetermined* en general no tienen solución si $b \notin \text{Im}(A)$ con $\text{Im}(A)$ espacio columna de $A$. Por esto se busca resolver un **problema de mínimos cuadrados** de la forma:
$$\displaystyle \min_{x \in \mathbb{R}^n} ||Ax-b||_2$$
con única solución si $A$ es de *rank* completo.
Los sistemas de ecuaciones lineales *underdetermined* pueden tener infinitas soluciones o ninguna solución. En el caso que $A$ sea de *rank* completo el sistema es consistente y se busca resolver el **problema de optimización de mínima norma** :
$$\displaystyle \min_{x \in \mathcal{K}} ||x||_2$$
donde: $\mathcal{K} = \{x \in \mathbb{R}^n | Ax = b\}$ que es interesante para $b \neq 0$ y tiene única solución.
## Ecuaciones no lineales
El problema que queremos resolver es el siguiente: dada $f: \mathbb{R} \rightarrow \mathbb{R}$ encontrar $x^*$ que resuelva la ecuación no lineal $f(x) = 0$. Nos interesa al menos una solución de la ecuación anterior.
Algunos ejemplos son:
* $e^x+1=0$
* $e^{-x}-x =0$
* $x^2 -4\sin(x)=0$
* $x^3+6x^2+11x-6=0$
* $\sin(x) = 0$.
**Resolvamos con [scipy.optimize.fsolve](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fsolve.html#scipy.optimize.fsolve) algunas de las ecuaciones no lineales anteriores.**
La ecuación no lineal $e^x + 1 = 0$ no tiene solución, su gráfica es la siguiente
La ecuación no lineal $e^{-x} - x = 0$ tiene una solución
La ecuación no lineal $x^2 -4\sin(x)=0$ tiene dos soluciones
## Sistema de ecuaciones no linales
El caso de sistema de ecuaciones no lineales es una generalización del caso de una dimensión en el que tenemos $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$ y debemos encontrar una raíz o cero de $f$ que resuelva el sistema de ecuaciones no lineales $f(x) = 0$.
Algunos ejemplos son:
1) $$
\begin{eqnarray}
x_1^2+x_1x_2&=&10 \nonumber \\
x_2 + 3x_1x_2^2&=&57 \nonumber
\end{eqnarray}
$$
2) $$
\begin{eqnarray}
2=\displaystyle \int_{-1}^{1}1dx &=& w_0 \cdot 1 + w_1\cdot1 \nonumber \\
0 = \displaystyle \int_{-1}^1xdx &=& w_0x_0 + w_1x_1 \nonumber \\
\frac{2}{3} = \displaystyle \int_{-1}^1x^2dx &=& w_0x_0^2 + w_1x_1^2 \nonumber \\
0 = \displaystyle \int_{-1}^1x^3dx &=& w_0x_0^3 + w_1x_1^3 \nonumber \\
\end{eqnarray}
$$
## Criterios de paro, escala de la variable $x$ y de la función $f$
Un tema importante en la implementación de algoritmos es la escala del problema tanto en la variable $x$ como en la función $f$. Por ejemplo, si $x_1$ está en el rango $[10^2, 10^3]$ de metros y $x_2$ está en el rango $[10^{-7}, 10^{-6}]$ de segundos entonces tenemos que realizar un reescalamiento para tener evaluaciones de $f$, criterios de paro y actualizaciones en esquemas iterativos, por ejemplo, independientes de las escalas de las variables o de la función. Asimismo, los criterios de paro en un método iterativo ayudan a contestar preguntas del tipo ¿hemos resuelto el problema de forma aproximada? ¿en las últimas dos (o un poco más) iteraciones nos hemos quedado virtualmente en el mismo punto?
Muchos algoritmos cumplen que son invariantes ante escala de las variables, el método de Newton en la variable $x$ es uno de ellos por ejemplo, pero otros no, por lo que al implementar un algoritmo se debe revisar los reescalamientos a realizar. En el ejemplo anterior de los metros y segundos si se cambian las unidades de $x_1$ a kilómetros y las de $x_2$ a microsegundos entonces tanto $x_1$ como $x_2$ se encontrarán en el rango $[10^{-1}, 1]$. Si en dos dimensiones $x_1 \in [10^{6}, 10^{7}]$ y $x_2 \in [10^{-1}, 1]$ entonces una prueba del tipo $||\nabla f(x)|| < 10^{-3}$ no será equilibrada para ambas variables si se desea por ejemplo minimizar $f$ ($x_1$ tendería a ser lo más pequeña posible si por ejemplo tenemos una alta contribución de esta variable en $f$).
En el caso de la función $f$, es común requerir que $f$ o la magnitud de $f$ sea cero (o su derivada). Si consideramos $f(x) = 0$ es muy probable que los errores por redondeo no permitan que se satisfaga esto para ningún punto $x$ por lo que modificamos la condición anterior a $f(x) \approx 0$. También si $f$ no está escalada apropiadamente la condición $|f(x)| < tol$ es probable que siempre o nunca se satisfaga. Por ejemplo si $tol = 10^{-3}$ y $f$ siempre está en $[10^{-7}, 10^{-5}]$ entonces cualquier $x$ satisface $|f(x)| < 10^{-3}$.
Considerando $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$, dentro de los criterios de paro que se utilizan en los métodos iterativos para resolver ecuaciones no lineales que apuntan a tener una evaluación independiente de la escala se encuentran:
* Medir diferencia entre iteraciones. Por ejemplo:
* $||x^{(k+1)} - x^{(k)}|| < tol(||x^{(k)}|| +1)$
* $||x^{(k+1)} - x^{(k)}|| < tol\max\{||x_{k+1}||, ||x_k||\}$
* $||x^{(k+1)} - x^{(k)}|| < tol\max\{||x_{k+1}||, \text{user_defined_value}\}$.
con `user_defined_value` un valor positivo proporcionado por *user* que mide la magnitud típica de $x$ y $|| \cdot ||$ norma.
* Medir la norma de $f$ reescalándola por ejemplo:
$$||Diag f|| < tol$$
con $Diag$ matriz diagonal tal que $Diagf$ tenga norma alrededor de $1$ en puntos no cercanos a la raíz y también puede proveerse sus valores con un `user_defined_value`.
* Máximo número de iteraciones.
## Métodos para resolver ecuaciones no lineales de funciones $f: \mathbb{R} \rightarrow \mathbb{R}$
### Método de bisección
Es un método cerrado que requiere $f \in \mathbb{R} \rightarrow \mathbb{R}$ con $f \in \mathcal{C}([a,b])$ tal que $f(a) f(b) <0$, esto es, que $f$ tenga un cambio de signo. Por el **teorema del valor intermedio** se cumple que $f$ tiene una raíz en $[a,b]$.
### Algoritmo: método de bisección
> **Dados** $x_i, x_s$ límite inferior y superior respectivamente tales que $x^* \in [x_i, x_s]$ con $f(x_i)f(x_s)<0$ y $tol >0$
>
> **Repetir** el siguiente bloque para $k=1,2,\dots$
>> 1. $x^{(k)} = \frac{x_i + x_s}{2}$
>>
>> 2. Si $f(x_i)f(x^{(k)}) < 0$ entonces $x^* \in [x_i, x^{(k)}]$ por lo tanto $x_s = x^{(k)}$.
>>
>> 3. Si $f(x_i)f(x^{(k)}) > 0$ entonces $x^* \in [x^{(k)}, x_s]$ por lo tanto $x_i = x^{(k)}$.
>
> **hasta** convergencia: satisfacer criterio de paro en el que se utiliza $tol$ y $maxiter$.
### Método de Newton o Newton-Raphson
Es un método abierto que sigue un esquema iterativo de la forma:
$$x^{(k+1)} = x^{(k)} - \frac{f(x^{(k)})}{f'(x^{(k)})}$$
requiere un punto inicial $x^{(0)}$ y converge si se cumplen condiciones descritas en {ref}`comentarios del método de Newton-Raphson <COMENTMETNEWTONRAPSHON>`.
Existen varias formas de obtener tal esquema iterativo, la que se presenta a continuación **define un modelo afín local que aproxima a nuestra función $f$ y encuentra la raíz de tal modelo**, gráficamente:
<img src="https://dl.dropboxusercontent.com/s/hw6fluifowjnpdo/Newton-Raphson_method.png?dl=0" heigth="600" width="600">
El modelo afín en el dibujo anterior es de la forma:
$$M(x) = f(x^{(k)}) + f'(x^{(k)})(x-x^{(k)})$$
E igualando a cero el modelo se tiene:
$$
\begin{eqnarray}
0 &=& M(x) = f(x^{(k)}) + f'(x^{(k)})(x-x^{(k)}) \nonumber \\
&\therefore& x = x^{(k)} - \frac{f(x^{(k)})}{f'(x^{(k)})} \nonumber
\end{eqnarray}
$$
### Ejemplo
Encontrar la raíz de $f(x) = 4x + 5$ con el método de Newton.
### Ejemplo
Aproximar el valor $\sqrt{3}$ con el método de Newton
**Primera iteración**
**Segunda iteración**
**Tercera iteración**
**...**
**Séptima iteración**
(COMENTMETNEWTONRAPSHON)=
Concerniente a la dependencia de un punto inicial, la convergencia del método de Newton se robustece al incorporar metodologías que permiten su convergencia a una solución **local** desde prácticamente cualquier punto inicial. Tales metodologías resultan en **algoritmos híbridos** en los que se utiliza el método de Newton siempre que funcione bien pero se utiliza otro método (quizás más lento) que garantice convergencia. Uno de éstos es el método de bisección en el que una vez se encuentre "cerca" de una solución se utilice el método de Newton. Otra metodología consiste en que en cada iteración se reduzca una medida de cercanía a la solución como una forma de *backtracking*, ver por ejemplo el {ref}`método de búsqueda de línea por backtracking <MBUSLINBACK>` en el contexto de minimización de una función.
El siguiente es un algoritmo en una forma general de algoritmos híbridos [quasi-Newton](https://en.wikipedia.org/wiki/Quasi-Newton_method) para resolver una ecuación no lineal.
(ALGMGCNHEN)=
### Algoritmo: método general cuasi-Newton híbrido para resolver una ecuación no lineal
> **Dados** $x^{(0)}$ punto inicial, $f: \mathbb{R} \rightarrow \mathbb{R}$ y $tol >0$
>
> **Repetir** el siguiente bloque para $k=1,2,\dots$
>> 1. Construir un modelo local de $f$ alrededor de $x^{(k)}$ y encontrar el punto $x_N$ que resuelva (o cercanamente resuelva) el modelo del problema.
>>
>> 2. Realizar alguno de los dos pasos siguientes:
>>>
>>> a. Decidir si $x^{(k+1)} = x_N$ si no,
>>>
>>> b. Elegir $x^{(k+1)}$ usando una estrategia global (usar $x_N$ del inciso a. de forma más conservadora).
>
> **hasta** convergencia: satisfacer criterio de paro en el que se utiliza $tol$ y $maxiter$.
## Una nota sobre problemas *Unconstrained Optimization* (UO)
En esta sección utilizamos la notación para un problema de optimización sin restricciones de la forma:
$$\displaystyle \min_{x^\in \mathbb{R}^n} f_o(x)$$
y $f_o: \mathbb{R}^n \rightarrow \mathbb{R}$ es una función objetivo en general que asumimos es de clase $\mathcal{C}^2$ en su dominio.
Así como en ecuaciones no lineales no tenemos resultados que determinen la existencia o unicidad de soluciones, en problemas de optimización sin restricciones esto es similar al plantear la búsqueda de mínimos globales de las funciones objetivo. Lo mejor que podemos obtener son aproximaciones a minimos locales y es prácticamente imposible saber si se ha aproximado un mínimo global.
Además, en la nota de {ref}`algoritmos de descenso y búsqueda de línea en Unconstrained Convex Optimization (UCO) <ADBLUCO>` se mostró la relación que existe entre resolver problemas tipo UO y ecuaciones no lineales. Es natural entonces aplicar el algoritmo de {ref}`método general cuasi-Newton híbrido para resolver una ecuación no lineal <ALGMGCNHEN>` a la ecuación no lineal de una variable $f_o'(x) = 0$. El esquema iterativo entonces es de la forma:
$$x^{(k+1)} = x^{(k)} - \frac{f_o'(x^{(k)})}{f_o''(x^{(k)})}$$
Recuérdese que tal esquema iterativo se obtiene mediante un modelo afín de $f_o'(x)$ alrededor de $x^{(k)}$, lo cual es equivalente en términos de la función $f_o$ a definir un modelo cuadrático alrededor de $x^{(k)}$ que aproxime a nuestra función $f_o$ y que encuentre la raíz de tal modelo:
$$m(x) = f(x^{(k)}) + f'(x^{(k)})(x-x^{(k)}) + \frac{1}{2} f''(x^{(k)})(x-x^{(k)})^2,$$
con lo que obtendremos el esquema iterativo anterior.
## Método de Newton para ecuaciones no lineales de funciones $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$
(en proceso de realización)
### Ejemplo
El problema de optimización:
$$\displaystyle \max_{v \in \mathbb{R}^n - \{0\}} \frac{1}{2} v^TX^TXv$$
$$\text{sujeto a: } \frac{1}{2}v^Tv =1$$
donde: $X \in \mathbb{R}^{m \times n}$ cuyas columnas tienen una observación de un **vector aleatorio** (tenemos $n$ vectores aleatorios de mediciones) tiene solución cerrada dada por: $\sigma_1^2 = \displaystyle \max_{v \in \mathbb{R}^n - \{0\}} \frac{v^TX^TXv}{v^Tv}$.
Utilizando las condiciones de [Karush-Kuhn-Tucker](https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions) (KKT) de optimalidad se tiene que resolver el siguiente sistema de ecuaciones no lineales:
$$\nabla f_o(v,\lambda) =
\left[
\begin{array}{c}
X^TX v + \lambda v \\
v^Tv-1
\end{array}
\right] = 0.
$$
| 0.61231 | 0.897785 |
<a href="https://colab.research.google.com/github/EduardoML7200/daa_2021_1/blob/master/20Enero2021.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
class NodoArbol:
def __init__( self , dato , left = None , right = None ):
self.data = dato
self.left = left
self.right = right
```
#Árbol Binario de búsqueda
Los nodos a la izquierda son menores a la raiz y los nodos a la derecha son mayores a la raiz.
Pueden ser recorridos en: pre-orden, in-orden y post-orden.
```
class BinarySearchTree:
def __init__( self ):
self.__root = None
def insert( self , value ):
if self.__root == None:
self.__root = NodoArbol( value , None , None )
else:
self.__insert_nodo__( self.__root , value )
def __insert_nodo__( self , nodo , value ):
if nodo.data == value:
pass
elif value < nodo.data: #True va a la IZQ
if nodo.left == None: #Si hay espacio en la IZQ, ahí va
nodo.left = NodoArbol( value , None , None ) #Insertamos nodo derecha
else:
self.__insert_nodo__( nodo.left , value ) #Buscar en su arbol IZQ
else:
if nodo.right == None:
nodo.right = NodoArbol( value , None , None )
else:
self.__insert_nodo__( nodo.right , value ) #Buscar en sub arbol derecho
def buscar( self , value ):
if self.__root == None:
return None
else:
#Haremos busqueda recursiva
return self.__busca_nodo( self.__root , value )
def __busca_nodo( self , nodo , value ):
if nodo == None:
return None
elif nodo.data == value:
return nodo.data
elif value < nodo.data:
return self.__busca_nodo( nodo.left , value )
else:
return self.__busca_nodo( nodo.right , value )
def transversal( self , format = "inOrden"):
if format == "inOrden":
self.__recorrido_in( self.__root )
elif format == "preOrden":
self.__recorrido_pre( self.__root)
elif format == "posOrden":
self.__recorrido_pos( self.__root )
else:
print("Fomato de recorrido no válido")
def __recorrido_pre( self , nodo ):
if nodo != None:
print( nodo.data , end = ",")
self.__recorrido_pre( nodo.left )
self.__recorrido_pre( nodo.right )
def __recorrido_in( self , nodo ):
if nodo != None:
self.__recorrido_in( nodo.left )
print( nodo.data , end = ",")
self.__recorrido_in( nodo.right )
def __recorrido_pos( self , nodo ):
if nodo != None:
self.__recorrido_pos( nodo.left )
self.__recorrido_pos( nodo.right )
print( nodo.data , end = ",")
bst = BinarySearchTree()
bst.insert( 50 )
bst.insert( 30 )
bst.insert( 20 )
res = bst.buscar( 30 ) #True o False
print("Dato : " , res)
print( bst.buscar(40) )
print("\nRecorrido preOrden:")
bst.transversal(format = "preOrden")
print("\nRecorrido inOrden:")
bst.transversal(format = "inOrden")
print("\nRecorrido posOrden:")
bst.transversal(format = "posOrden")
```
|
github_jupyter
|
class NodoArbol:
def __init__( self , dato , left = None , right = None ):
self.data = dato
self.left = left
self.right = right
class BinarySearchTree:
def __init__( self ):
self.__root = None
def insert( self , value ):
if self.__root == None:
self.__root = NodoArbol( value , None , None )
else:
self.__insert_nodo__( self.__root , value )
def __insert_nodo__( self , nodo , value ):
if nodo.data == value:
pass
elif value < nodo.data: #True va a la IZQ
if nodo.left == None: #Si hay espacio en la IZQ, ahí va
nodo.left = NodoArbol( value , None , None ) #Insertamos nodo derecha
else:
self.__insert_nodo__( nodo.left , value ) #Buscar en su arbol IZQ
else:
if nodo.right == None:
nodo.right = NodoArbol( value , None , None )
else:
self.__insert_nodo__( nodo.right , value ) #Buscar en sub arbol derecho
def buscar( self , value ):
if self.__root == None:
return None
else:
#Haremos busqueda recursiva
return self.__busca_nodo( self.__root , value )
def __busca_nodo( self , nodo , value ):
if nodo == None:
return None
elif nodo.data == value:
return nodo.data
elif value < nodo.data:
return self.__busca_nodo( nodo.left , value )
else:
return self.__busca_nodo( nodo.right , value )
def transversal( self , format = "inOrden"):
if format == "inOrden":
self.__recorrido_in( self.__root )
elif format == "preOrden":
self.__recorrido_pre( self.__root)
elif format == "posOrden":
self.__recorrido_pos( self.__root )
else:
print("Fomato de recorrido no válido")
def __recorrido_pre( self , nodo ):
if nodo != None:
print( nodo.data , end = ",")
self.__recorrido_pre( nodo.left )
self.__recorrido_pre( nodo.right )
def __recorrido_in( self , nodo ):
if nodo != None:
self.__recorrido_in( nodo.left )
print( nodo.data , end = ",")
self.__recorrido_in( nodo.right )
def __recorrido_pos( self , nodo ):
if nodo != None:
self.__recorrido_pos( nodo.left )
self.__recorrido_pos( nodo.right )
print( nodo.data , end = ",")
bst = BinarySearchTree()
bst.insert( 50 )
bst.insert( 30 )
bst.insert( 20 )
res = bst.buscar( 30 ) #True o False
print("Dato : " , res)
print( bst.buscar(40) )
print("\nRecorrido preOrden:")
bst.transversal(format = "preOrden")
print("\nRecorrido inOrden:")
bst.transversal(format = "inOrden")
print("\nRecorrido posOrden:")
bst.transversal(format = "posOrden")
| 0.488771 | 0.782372 |
```
%load_ext watermark
%watermark -d -u -a 'Andreas Mueller, Kyle Kastner, Sebastian Raschka' -v -p numpy,scipy,matplotlib,scikit-learn
```
# SciPy 2016 Scikit-learn Tutorial
# Case Study - Titanic Survival
# Feature Extraction
Here we will talk about an important piece of machine learning: the extraction of
quantitative features from data. By the end of this section you will
- Know how features are extracted from real-world data.
- See an example of extracting numerical features from textual data
In addition, we will go over several basic tools within scikit-learn which can be used to accomplish the above tasks.
## What Are Features?
### Numerical Features
Recall that data in scikit-learn is expected to be in two-dimensional arrays, of size
**n_samples** $\times$ **n_features**.
Previously, we looked at the iris dataset, which has 150 samples and 4 features
```
from sklearn.datasets import load_iris
iris = load_iris()
print(iris.data.shape)
```
These features are:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
Numerical features such as these are pretty straightforward: each sample contains a list
of floating-point numbers corresponding to the features
### Categorical Features
What if you have categorical features? For example, imagine there is data on the color of each
iris:
color in [red, blue, purple]
You might be tempted to assign numbers to these features, i.e. *red=1, blue=2, purple=3*
but in general **this is a bad idea**. Estimators tend to operate under the assumption that
numerical features lie on some continuous scale, so, for example, 1 and 2 are more alike
than 1 and 3, and this is often not the case for categorical features.
In fact, the example above is a subcategory of "categorical" features, namely, "nominal" features. Nominal features don't imply an order, whereas "ordinal" features are categorical features that do imply an order. An example of ordinal features would be T-shirt sizes, e.g., XL > L > M > S.
One work-around for parsing nominal features into a format that prevents the classification algorithm from asserting an order is the so-called one-hot encoding representation. Here, we give each category its own dimension.
The enriched iris feature set would hence be in this case:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- color=purple (1.0 or 0.0)
- color=blue (1.0 or 0.0)
- color=red (1.0 or 0.0)
Note that using many of these categorical features may result in data which is better
represented as a **sparse matrix**, as we'll see with the text classification example
below.
#### Using the DictVectorizer to encode categorical features
When the source data is encoded has a list of dicts where the values are either strings names for categories or numerical values, you can use the `DictVectorizer` class to compute the boolean expansion of the categorical features while leaving the numerical features unimpacted:
```
measurements = [
{'city': 'Dubai', 'temperature': 33.},
{'city': 'London', 'temperature': 12.},
{'city': 'San Francisco', 'temperature': 18.},
]
from sklearn.feature_extraction import DictVectorizer
vec = DictVectorizer()
print vec
print vec.fit_transform(measurements).toarray()
vec.fit_transform(measurements).toarray()
vec.get_feature_names()
```
### Derived Features
Another common feature type are **derived features**, where some pre-processing step is
applied to the data to generate features that are somehow more informative. Derived
features may be based in **feature extraction** and **dimensionality reduction** (such as PCA or manifold learning),
may be linear or nonlinear combinations of features (such as in polynomial regression),
or may be some more sophisticated transform of the features.
### Combining Numerical and Categorical Features
As an example of how to work with both categorical and numerical data, we will perform survival predicition for the passengers of the HMS Titanic.
We will use a version of the Titanic (titanic3.xls) from [here](http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic3.xls). We converted the .xls to .csv for easier manipulation but left the data is otherwise unchanged.
We need to read in all the lines from the (titanic3.csv) file, set aside the keys from the first line, and find our labels (who survived or died) and data (attributes of that person). Let's look at the keys and some corresponding example lines.
```
import os
import pandas as pd
titanic = pd.read_csv(os.path.join('datasets', 'titanic3.csv'))
print(titanic.columns)
```
Here is a broad description of the keys and what they mean:
```
pclass Passenger Class
(1 = 1st; 2 = 2nd; 3 = 3rd)
survival Survival
(0 = No; 1 = Yes)
name Name
sex Sex
age Age
sibsp Number of Siblings/Spouses Aboard
parch Number of Parents/Children Aboard
ticket Ticket Number
fare Passenger Fare
cabin Cabin
embarked Port of Embarkation
(C = Cherbourg; Q = Queenstown; S = Southampton)
boat Lifeboat
body Body Identification Number
home.dest Home/Destination
```
In general, it looks like `name`, `sex`, `cabin`, `embarked`, `boat`, `body`, and `homedest` may be candidates for categorical features, while the rest appear to be numerical features. We can also look at the first couple of rows in the dataset to get a better understanding:
```
titanic.head()
```
We clearly want to discard the "boat" and "body" columns for any classification into survived vs not survived as they already contain this information. The name is unique to each person (probably) and also non-informative. For a first try, we will use "pclass", "sibsp", "parch", "fare" and "embarked" as our features:
```
labels = titanic.survived.values
features = titanic[['pclass', 'sex', 'age', 'sibsp', 'parch', 'fare', 'embarked']]
features.head()
```
The data now contains only useful features, but they are not in a format that the machine learning algorithms can understand. We need to transform the strings "male" and "female" into binary variables that indicate the gender, and similarly for "embarked".
We can do that using the pandas ``get_dummies`` function:
```
pd.get_dummies(features).head()
```
This transformation successfully encoded the string columns. However, one might argue that the class is also a categorical variable. We can explicitly list the columns to encode using the ``columns`` parameter, and include ``pclass``:
```
features_dummies = pd.get_dummies(features, columns=['pclass', 'sex', 'embarked'])
features_dummies.head(n=16)
data = features_dummies.values
data.shape
import numpy as np
np.isnan(data).any()
```
With all of the hard data loading work out of the way, evaluating a classifier on this data becomes straightforward. Setting up the simplest possible model, we want to see what the simplest score can be with `DummyClassifier`.
```
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import Imputer
train_data, test_data, train_labels, test_labels = train_test_split(data, labels, random_state=0)
imp = Imputer()
imp.fit(train_data)
train_data_finite = imp.transform(train_data)
test_data_finite = imp.transform(test_data)
train_data_finite[0]
from sklearn.dummy import DummyClassifier
clf = DummyClassifier('most_frequent')
clf.fit(train_data_finite, train_labels)
print("Prediction accuracy: %f" % clf.score(test_data_finite, test_labels))
```
Exercise
=====
Try executing the above classification, using LogisticRegression and RandomForestClassifier instead of DummyClassifier
Does selecting a different subset of features help?
```
# %load solutions/10_titanic.py
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
lr_score = LogisticRegression().fit(train_data_finite,train_labels).score(test_data_finite,test_labels)
rfc = RandomForestClassifier().fit(train_data_finite,train_labels).score(test_data_finite,test_labels)
print lr_score
print rfc
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression().fit(train_data_finite, train_labels)
print("logistic regression score: %f" % lr.score(test_data_finite, test_labels))
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=500, random_state=0).fit(train_data_finite, train_labels)
print("random forest score: %f" % rf.score(test_data_finite, test_labels))
features_dummies_sub = pd.get_dummies(features[['pclass', 'sex', 'age', 'sibsp', 'fare']])
data_sub = features_dummies_sub.values
train_data_sub, test_data_sub, train_labels, test_labels = train_test_split(data_sub, labels, random_state=0)
imp = Imputer()
imp.fit(train_data_sub)
train_data_finite_sub = imp.transform(train_data_sub)
test_data_finite_sub = imp.transform(test_data_sub)
lr = LogisticRegression().fit(train_data_finite_sub, train_labels)
print("logistic regression score w/o embark, parch: %f" % lr.score(test_data_finite_sub, test_labels))
rf = RandomForestClassifier(n_estimators=500, random_state=0).fit(train_data_finite_sub, train_labels)
print("random forest score w/o embark, parch: %f" % rf.score(test_data_finite_sub, test_labels))
```
|
github_jupyter
|
%load_ext watermark
%watermark -d -u -a 'Andreas Mueller, Kyle Kastner, Sebastian Raschka' -v -p numpy,scipy,matplotlib,scikit-learn
from sklearn.datasets import load_iris
iris = load_iris()
print(iris.data.shape)
measurements = [
{'city': 'Dubai', 'temperature': 33.},
{'city': 'London', 'temperature': 12.},
{'city': 'San Francisco', 'temperature': 18.},
]
from sklearn.feature_extraction import DictVectorizer
vec = DictVectorizer()
print vec
print vec.fit_transform(measurements).toarray()
vec.fit_transform(measurements).toarray()
vec.get_feature_names()
import os
import pandas as pd
titanic = pd.read_csv(os.path.join('datasets', 'titanic3.csv'))
print(titanic.columns)
pclass Passenger Class
(1 = 1st; 2 = 2nd; 3 = 3rd)
survival Survival
(0 = No; 1 = Yes)
name Name
sex Sex
age Age
sibsp Number of Siblings/Spouses Aboard
parch Number of Parents/Children Aboard
ticket Ticket Number
fare Passenger Fare
cabin Cabin
embarked Port of Embarkation
(C = Cherbourg; Q = Queenstown; S = Southampton)
boat Lifeboat
body Body Identification Number
home.dest Home/Destination
titanic.head()
labels = titanic.survived.values
features = titanic[['pclass', 'sex', 'age', 'sibsp', 'parch', 'fare', 'embarked']]
features.head()
pd.get_dummies(features).head()
features_dummies = pd.get_dummies(features, columns=['pclass', 'sex', 'embarked'])
features_dummies.head(n=16)
data = features_dummies.values
data.shape
import numpy as np
np.isnan(data).any()
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import Imputer
train_data, test_data, train_labels, test_labels = train_test_split(data, labels, random_state=0)
imp = Imputer()
imp.fit(train_data)
train_data_finite = imp.transform(train_data)
test_data_finite = imp.transform(test_data)
train_data_finite[0]
from sklearn.dummy import DummyClassifier
clf = DummyClassifier('most_frequent')
clf.fit(train_data_finite, train_labels)
print("Prediction accuracy: %f" % clf.score(test_data_finite, test_labels))
# %load solutions/10_titanic.py
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
lr_score = LogisticRegression().fit(train_data_finite,train_labels).score(test_data_finite,test_labels)
rfc = RandomForestClassifier().fit(train_data_finite,train_labels).score(test_data_finite,test_labels)
print lr_score
print rfc
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression().fit(train_data_finite, train_labels)
print("logistic regression score: %f" % lr.score(test_data_finite, test_labels))
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=500, random_state=0).fit(train_data_finite, train_labels)
print("random forest score: %f" % rf.score(test_data_finite, test_labels))
features_dummies_sub = pd.get_dummies(features[['pclass', 'sex', 'age', 'sibsp', 'fare']])
data_sub = features_dummies_sub.values
train_data_sub, test_data_sub, train_labels, test_labels = train_test_split(data_sub, labels, random_state=0)
imp = Imputer()
imp.fit(train_data_sub)
train_data_finite_sub = imp.transform(train_data_sub)
test_data_finite_sub = imp.transform(test_data_sub)
lr = LogisticRegression().fit(train_data_finite_sub, train_labels)
print("logistic regression score w/o embark, parch: %f" % lr.score(test_data_finite_sub, test_labels))
rf = RandomForestClassifier(n_estimators=500, random_state=0).fit(train_data_finite_sub, train_labels)
print("random forest score w/o embark, parch: %f" % rf.score(test_data_finite_sub, test_labels))
| 0.545044 | 0.977241 |
```
import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#reading the data set from the github link
insurance = pd.read_csv("https://raw.githubusercontent.com/stedy/Machine-Learning-with-R-datasets/master/insurance.csv")
insurance
insurance['sex'].dtype, insurance['smoker'].dtype, insurance['age'].dtype
```
There are some chategorical variables, so lets convert them into numbers using One-Hot Encoding or Pandas's get_dummies method
```
insurance_one_hot = pd.get_dummies(insurance)
insurance_one_hot
insurance_one_hot.head()
```
Splitting our data set
```
X = insurance_one_hot.drop("charges",axis=1)
y = insurance_one_hot['charges']
X.head()
y.head()
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=42)
X_train.shape, X_test.shape
y_train.shape, y_test.shape
```
Building a Neural Network
```
tf.random.set_seed(42)
insurance_model = tf.keras.Sequential([
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])
insurance_model.compile(loss = tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=['mae'])
insurance_model.fit(X_train,y_train,epochs=100)
tf.random.set_seed(42)
insurance_model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(100),
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])
insurance_model_2.compile(loss = tf.keras.losses.mae,
optimizer = tf.keras.optimizers.SGD())
insurance_model.fit(X_train,y_train,epochs=100)
insurance_model_2.evaluate(X_test,y_test)
insurance_model.evaluate(X_test,y_test)
tf.random.set_seed(42)
insurance_model_3 = tf.keras.Sequential([
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])
insurance_model_3.compile(loss = tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=['mae'])
history = insurance_model_3.fit(X_train,y_train,epochs=100)
insurance_model_3.evaluate(X_test,y_test)
pd.DataFrame(history.history).plot()
plt.ylabel("loss")
plt.xlabel("epochs");
# Set random seed
tf.random.set_seed(42)
# Add an extra layer and increase number of units
insurance_model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(100), # 100 units
tf.keras.layers.Dense(10), # 10 units
tf.keras.layers.Dense(1) # 1 unit (important for output layer)
])
# Compile the model
insurance_model_2.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(), # Adam works but SGD doesn't
metrics=['mae'])
# Fit the model and save the history (we can plot this)
history = insurance_model_2.fit(X_train, y_train, epochs=100, verbose=0)
insurance_model_2.evaluate(X_test, y_test)
pd.DataFrame(history.history).plot()
plt.ylabel("loss")
plt.xlabel("epochs");
```
Preprocessing data (normalisation and standardisation)
```
insurance
from sklearn.compose import make_column_transformer
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder, StandardScaler
ct = make_column_transformer(
(MinMaxScaler(), ['age','bmi','children']),
(OneHotEncoder(handle_unknown="ignore"),['sex','smoker','region'])
)
X = insurance.drop('charges', axis=1)
y = insurance['charges']
X_train , X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,
random_state=42)
ct.fit(X_train)
X_train_normal = ct.transform(X_train)
X_test_normal = ct.transform(X_test)
X_train_normal.shape, X_train.shape
tf.random.set_seed(42)
# Build the model (3 layers, 100, 10, 1 units)
insurance_model_3 = tf.keras.Sequential([
tf.keras.layers.Dense(100),
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])
# Compile the model
insurance_model_3.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(),
metrics=['mae'])
# Fit the model for 200 epochs (same as insurance_model_2)
insurance_model_3.fit(X_train_normal, y_train, epochs=200)
insurance_model_3.evaluate(X_test_normal,y_test)
```
|
github_jupyter
|
import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#reading the data set from the github link
insurance = pd.read_csv("https://raw.githubusercontent.com/stedy/Machine-Learning-with-R-datasets/master/insurance.csv")
insurance
insurance['sex'].dtype, insurance['smoker'].dtype, insurance['age'].dtype
insurance_one_hot = pd.get_dummies(insurance)
insurance_one_hot
insurance_one_hot.head()
X = insurance_one_hot.drop("charges",axis=1)
y = insurance_one_hot['charges']
X.head()
y.head()
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=42)
X_train.shape, X_test.shape
y_train.shape, y_test.shape
tf.random.set_seed(42)
insurance_model = tf.keras.Sequential([
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])
insurance_model.compile(loss = tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=['mae'])
insurance_model.fit(X_train,y_train,epochs=100)
tf.random.set_seed(42)
insurance_model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(100),
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])
insurance_model_2.compile(loss = tf.keras.losses.mae,
optimizer = tf.keras.optimizers.SGD())
insurance_model.fit(X_train,y_train,epochs=100)
insurance_model_2.evaluate(X_test,y_test)
insurance_model.evaluate(X_test,y_test)
tf.random.set_seed(42)
insurance_model_3 = tf.keras.Sequential([
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])
insurance_model_3.compile(loss = tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=['mae'])
history = insurance_model_3.fit(X_train,y_train,epochs=100)
insurance_model_3.evaluate(X_test,y_test)
pd.DataFrame(history.history).plot()
plt.ylabel("loss")
plt.xlabel("epochs");
# Set random seed
tf.random.set_seed(42)
# Add an extra layer and increase number of units
insurance_model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(100), # 100 units
tf.keras.layers.Dense(10), # 10 units
tf.keras.layers.Dense(1) # 1 unit (important for output layer)
])
# Compile the model
insurance_model_2.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(), # Adam works but SGD doesn't
metrics=['mae'])
# Fit the model and save the history (we can plot this)
history = insurance_model_2.fit(X_train, y_train, epochs=100, verbose=0)
insurance_model_2.evaluate(X_test, y_test)
pd.DataFrame(history.history).plot()
plt.ylabel("loss")
plt.xlabel("epochs");
insurance
from sklearn.compose import make_column_transformer
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder, StandardScaler
ct = make_column_transformer(
(MinMaxScaler(), ['age','bmi','children']),
(OneHotEncoder(handle_unknown="ignore"),['sex','smoker','region'])
)
X = insurance.drop('charges', axis=1)
y = insurance['charges']
X_train , X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,
random_state=42)
ct.fit(X_train)
X_train_normal = ct.transform(X_train)
X_test_normal = ct.transform(X_test)
X_train_normal.shape, X_train.shape
tf.random.set_seed(42)
# Build the model (3 layers, 100, 10, 1 units)
insurance_model_3 = tf.keras.Sequential([
tf.keras.layers.Dense(100),
tf.keras.layers.Dense(10),
tf.keras.layers.Dense(1)
])
# Compile the model
insurance_model_3.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(),
metrics=['mae'])
# Fit the model for 200 epochs (same as insurance_model_2)
insurance_model_3.fit(X_train_normal, y_train, epochs=200)
insurance_model_3.evaluate(X_test_normal,y_test)
| 0.724773 | 0.877056 |
# Using numerical and categorical variables together
In the previous notebooks, we showed the required preprocessing to apply
when dealing with numerical and categorical variables. However, we decoupled
the process to treat each type individually. In this notebook, we will show
how to combine these preprocessing steps.
We will first load the entire adult census dataset.
```
import pandas as pd
adult_census = pd.read_csv("../datasets/adult-census.csv")
# drop the duplicated column `"education-num"` as stated in the first notebook
adult_census = adult_census.drop(columns="education-num")
target_name = "class"
target = adult_census[target_name]
data = adult_census.drop(columns=[target_name])
```
## Selection based on data types
We will separate categorical and numerical variables using their data
types to identify them, as we saw previously that `object` corresponds
to categorical columns (strings). We make use of `make_column_selector`
helper to select the corresponding columns.
```
from sklearn.compose import make_column_selector as selector
numerical_columns_selector = selector(dtype_exclude=object)
categorical_columns_selector = selector(dtype_include=object)
numerical_columns = numerical_columns_selector(data)
categorical_columns = categorical_columns_selector(data)
categorical_columns
```
## Dispatch columns to a specific processor
In the previous sections, we saw that we need to treat data differently
depending on their nature (i.e. numerical or categorical).
Scikit-learn provides a `ColumnTransformer` class which will send specific
columns to a specific transformer, making it easy to fit a single predictive
model on a dataset that combines both kinds of variables together
(heterogeneously typed tabular data).
We first define the columns depending on their data type:
* **one-hot encoding** will be applied to categorical columns. Besides, we
use `handle_unknown="ignore"` to solve the potential issues due to rare
categories.
* **numerical scaling** numerical features which will be standardized.
Now, we create our `ColumnTransfomer` by specifying three values:
the preprocessor name, the transformer, and the columns.
First, let's create the preprocessors for the numerical and categorical
parts.
```
from sklearn.preprocessing import OneHotEncoder, StandardScaler
categorical_preprocessor = OneHotEncoder(handle_unknown="ignore")
numerical_preprocessor = StandardScaler()
```
Now, we create the transformer and associate each of these preprocessors
with their respective columns.
```
from sklearn.compose import ColumnTransformer
preprocessor = ColumnTransformer([
('one-hot-encoder', categorical_preprocessor, categorical_columns),
('standard-scaler', numerical_preprocessor, numerical_columns)])
```
We can take a minute to represent graphically the structure of a
`ColumnTransformer`:

A `ColumnTransformer` does the following:
* It **splits the columns** of the original dataset based on the column names
or indices provided. We will obtain as many subsets as the number of
transformers passed into the `ColumnTransformer`.
* It **transforms each subsets**. A specific transformer is applied to
each subset: it will internally call `fit_transform` or `transform`. The
output of this step is a set of transformed datasets.
* It then **concatenate the transformed datasets** into a single dataset.
The important thing is that `ColumnTransformer` is like any other
scikit-learn transformer. In particular it can be combined with a classifier
in a `Pipeline`:
```
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
model = make_pipeline(preprocessor, LogisticRegression(max_iter=500))
```
We can display an interactive diagram with the following command:
```
from sklearn import set_config
set_config(display='diagram')
model
```
The final model is more complex than the previous models but still follows
the same API (the same set of methods that can be called by the user):
- the `fit` method is called to preprocess the data and then train the
classifier of the preprocessed data;
- the `predict` method makes predictions on new data;
- the `score` method is used to predict on the test data and compare the
predictions to the expected test labels to compute the accuracy.
Let's start by splitting our data into train and test sets.
```
from sklearn.model_selection import train_test_split
data_train, data_test, target_train, target_test = train_test_split(
data, target, random_state=42)
```
<div class="admonition caution alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Caution!</p>
<p class="last">Be aware that we use <tt class="docutils literal">train_test_split</tt> here for didactic purposes, to show
the scikit-learn API.</p>
</div>
Now, we can train the model on the train set.
```
_ = model.fit(data_train, target_train)
```
Then, we can send the raw dataset straight to the pipeline. Indeed, we do not
need to make any manual preprocessing (calling the `transform` or
`fit_transform` methods) as it will be handled when calling the `predict`
method. As an example, we predict on the five first samples from the test
set.
```
data_test.head()
model.predict(data_test)[:5]
target_test[:5]
```
To get directly the accuracy score, we need to call the `score` method. Let's
compute the accuracy score on the entire test set.
```
model.score(data_test, target_test)
```
## Evaluation of the model with cross-validation
As previously stated, a predictive model should be evaluated by
cross-validation. Our model is usable with the cross-validation tools of
scikit-learn as any other predictors:
```
from sklearn.model_selection import cross_validate
cv_results = cross_validate(model, data, target, cv=5)
cv_results
scores = cv_results["test_score"]
print("The mean cross-validation accuracy is: "
f"{scores.mean():.3f} +/- {scores.std():.3f}")
```
The compound model has a higher predictive accuracy than the two models that
used numerical and categorical variables in isolation.
## Fitting a more powerful model
**Linear models** are nice because they are usually cheap to train,
**small** to deploy, **fast** to predict and give a **good baseline**.
However, it is often useful to check whether more complex models such as an
ensemble of decision trees can lead to higher predictive performance. In this
section we will use such a model called **gradient-boosting trees** and
evaluate its statistical performance. More precisely, the scikit-learn model
we will use is called `HistGradientBoostingClassifier`. Note that boosting
models will be covered in more details in a future module.
For tree-based models, the handling of numerical and categorical variables is
simpler than for linear models:
* we do **not need to scale the numerical features**
* using an **ordinal encoding for the categorical variables** is fine even if
the encoding results in an arbitrary ordering
Therefore, for `HistGradientBoostingClassifier`, the preprocessing pipeline
is slightly simpler than the one we saw earlier for the `LogisticRegression`:
```
from sklearn.experimental import enable_hist_gradient_boosting
from sklearn.ensemble import HistGradientBoostingClassifier
from sklearn.preprocessing import OrdinalEncoder
categorical_preprocessor = OrdinalEncoder(handle_unknown="use_encoded_value",
unknown_value=-1)
preprocessor = ColumnTransformer([
('categorical', categorical_preprocessor, categorical_columns)],
remainder="passthrough")
model = make_pipeline(preprocessor, HistGradientBoostingClassifier())
```
Now that we created our model, we can check its statistical performance.
```
%%time
_ = model.fit(data_train, target_train)
model.score(data_test, target_test)
```
We can observe that we get significantly higher accuracies with the Gradient
Boosting model. This is often what we observe whenever the dataset has a
large number of samples and limited number of informative features (e.g. less
than 1000) with a mix of numerical and categorical variables.
This explains why Gradient Boosted Machines are very popular among
datascience practitioners who work with tabular data.
In this notebook we:
* used a `ColumnTransformer` to apply different preprocessing for
categorical and numerical variables;
* used a pipeline to chain the `ColumnTransformer` preprocessing and
logistic regression fitting;
* seen that **gradient boosting methods** can outperform **linear
models**.
|
github_jupyter
|
import pandas as pd
adult_census = pd.read_csv("../datasets/adult-census.csv")
# drop the duplicated column `"education-num"` as stated in the first notebook
adult_census = adult_census.drop(columns="education-num")
target_name = "class"
target = adult_census[target_name]
data = adult_census.drop(columns=[target_name])
from sklearn.compose import make_column_selector as selector
numerical_columns_selector = selector(dtype_exclude=object)
categorical_columns_selector = selector(dtype_include=object)
numerical_columns = numerical_columns_selector(data)
categorical_columns = categorical_columns_selector(data)
categorical_columns
from sklearn.preprocessing import OneHotEncoder, StandardScaler
categorical_preprocessor = OneHotEncoder(handle_unknown="ignore")
numerical_preprocessor = StandardScaler()
from sklearn.compose import ColumnTransformer
preprocessor = ColumnTransformer([
('one-hot-encoder', categorical_preprocessor, categorical_columns),
('standard-scaler', numerical_preprocessor, numerical_columns)])
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
model = make_pipeline(preprocessor, LogisticRegression(max_iter=500))
from sklearn import set_config
set_config(display='diagram')
model
from sklearn.model_selection import train_test_split
data_train, data_test, target_train, target_test = train_test_split(
data, target, random_state=42)
_ = model.fit(data_train, target_train)
data_test.head()
model.predict(data_test)[:5]
target_test[:5]
model.score(data_test, target_test)
from sklearn.model_selection import cross_validate
cv_results = cross_validate(model, data, target, cv=5)
cv_results
scores = cv_results["test_score"]
print("The mean cross-validation accuracy is: "
f"{scores.mean():.3f} +/- {scores.std():.3f}")
from sklearn.experimental import enable_hist_gradient_boosting
from sklearn.ensemble import HistGradientBoostingClassifier
from sklearn.preprocessing import OrdinalEncoder
categorical_preprocessor = OrdinalEncoder(handle_unknown="use_encoded_value",
unknown_value=-1)
preprocessor = ColumnTransformer([
('categorical', categorical_preprocessor, categorical_columns)],
remainder="passthrough")
model = make_pipeline(preprocessor, HistGradientBoostingClassifier())
%%time
_ = model.fit(data_train, target_train)
model.score(data_test, target_test)
| 0.67662 | 0.991938 |
```
%matplotlib inline
```
How to optimize GEMM on CPU
===========================
**Author**: `Jian Weng <https://github.com/were>`_, `Ruofei Yu <https://github.com/yuruofeifei>`_
(TL;DR) TVM provides abstract interfaces which allows users to depict an algorithm and the
algorithm's implementing organization (the so-called schedule) separately. Typically, writing
algorithm in high-performance schedule breaks the algorithm's readability and modularity. Also,
trying various seemingly promising schedules is time-consuming. With the help of TVM, we can
try these schedules efficiently to enhance the performance.
In this tutorial, we will demonstrate how to use TVM to optimize square matrix multiplication
and achieve 200 times faster than baseline by simply adding 18 extra lines of code.
There are two important optimizations on intense computation applications executed on CPU:
1. Increase the cache hit rate of memory access. Both complex numerical computation and hot-spot
memory access can be accelerated from high cache hit rate. This requires us to transform the
origin memory access pattern to the pattern fits the cache policy.
2. SIMD (Single instruction multi-data), or we call it vector processing unit. Every time, a
small batch of data, rather than a single grid, will be processed. This requires us to
transform the data access pattern in the loop body in uniform pattern so that the LLVM
backend can lower it to SIMD.
Actually, all the methodologies used in this tutorial is a subset of tricks mentioned in this
`repo <https://github.com/flame/how-to-optimize-gemm>`_. Some of them have been applied by TVM
abstraction automatically, but some of them cannot be simply applied due to TVM constraints.
All the experiment results mentioned below, are executed on 2015's 15' MacBook equipped with
Intel i7-4770HQ CPU. The cache line size should be 64 bytes for all the x86 CPUs.
Preparation and Baseline
------------------------
In this tutorial, we will demo how to use TVM to optimize matrix multiplication.
Before actually demonstrating, we first define these variables.
Then we write a baseline implementation, the simplest way to write a matrix multiplication in TVM.
```
import tvm
import tvm.testing
from tvm import te
import numpy
import timeit
# The size of the matrix
# (M, K) x (K, N)
# You are free to try out different shapes, sometimes TVM optimization outperforms numpy with MKL.
M = 1024
K = 1024
N = 1024
# The default tensor type in tvm
dtype = "float32"
# using Intel AVX2(Advanced Vector Extensions) ISA for SIMD
# To get the best performance, please change the following line
# to llvm -mcpu=core-avx2, or specific type of CPU you use
target = "llvm"
ctx = tvm.context(target, 0)
# Random generated tensor for testing
a = tvm.nd.array(numpy.random.rand(M, K).astype(dtype), ctx)
b = tvm.nd.array(numpy.random.rand(K, N).astype(dtype), ctx)
np_repeat = 100
np_runing_time = timeit.timeit(
setup="import numpy\n"
"M = " + str(M) + "\n"
"K = " + str(K) + "\n"
"N = " + str(N) + "\n"
'dtype = "float32"\n'
"a = numpy.random.rand(M, K).astype(dtype)\n"
"b = numpy.random.rand(K, N).astype(dtype)\n",
stmt="answer = numpy.dot(a, b)",
number=np_repeat,
)
print("Numpy running time: %f" % (np_runing_time / np_repeat))
answer = numpy.dot(a.asnumpy(), b.asnumpy())
# Algorithm
k = te.reduce_axis((0, K), "k")
A = te.placeholder((M, K), name="A")
B = te.placeholder((K, N), name="B")
C = te.compute((M, N), lambda x, y: te.sum(A[x, k] * B[k, y], axis=k), name="C")
# Default schedule
s = te.create_schedule(C.op)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=1)
print("Baseline: %f" % evaluator(a, b, c).mean)
```
In TVM, we can always inspect lower level IR to debug or optimize our schedule.
Here is the generated IR using our baseline schedule.
```
print(tvm.lower(s, [A, B, C], simple_mode=True))
```
Blocking
--------
A important trick to enhance the cache hit rate is blocking --- data chunk will be computed
block by block. The memory access inside the block is a small neighbourhood which is with high
memory locality. In this tutorial, I picked up 32 as the blocking factor. So the block will
fill 32 * 32 * sizeof(float) which is 4KB in the cache whose total size is 32KB (L1 data cache)
```
bn = 32
s = te.create_schedule(C.op)
# Blocking by loop tiling
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
# Hoist reduction domain outside the blocking loop
s[C].reorder(xo, yo, ko, ki, xi, yi)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
# By simply tiling the loop 32x32, and hoisting ko, ki outside the blocking loops,
# we can see big speedup compared with the baseline.
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt1: %f" % evaluator(a, b, c).mean)
```
Here is the generated IR after blocking.
```
print(tvm.lower(s, [A, B, C], simple_mode=True))
```
Vectorization
-------------
Another important trick is vectorization. When the memory access pattern is uniform,
the compiler can detect this pattern and pass the continuous memory to vector processor. In TVM,
we can use `vectorize` interface to hint the compiler this pattern, so that we can accelerate it vastly.
In this tutorial, we chose to vectorize the inner loop row data since it is cache friendly.
```
s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
s[C].reorder(xo, yo, ko, ki, xi, yi)
# Vectorization
s[C].vectorize(yi)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt2: %f" % evaluator(a, b, c).mean)
```
Here is the generated IR after vectorization.
```
print(tvm.lower(s, [A, B, C], simple_mode=True))
```
Loop Permutation
----------------
If we look at the above IR, we can see the inner loop row data is vectorized and
B is transformed into PackedB. The traversal of PackedB is sequential now.
So we will look at the access pattern of A. In current schedule, A is accessed column by column
which is not cache friendly. If we change the nested loop order of ki and inner axes xi,
the access pattern for A matrix is more cache friendly.
```
s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
# re-ordering
s[C].reorder(xo, yo, ko, xi, ki, yi)
s[C].vectorize(yi)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt3: %f" % evaluator(a, b, c).mean)
```
Here is the generated IR after loop permutation.
```
print(tvm.lower(s, [A, B, C], simple_mode=True))
```
Array Packing
-------------
Another important trick is array packing. This trick is to reorder the storage dimension of the
array to convert the continuous access pattern on certain dimension to a sequential pattern after
flattening.

:align: center
Just as it is shown in the figure above, after blocking the computations, we can observe the array
access pattern of B (after flattening), which is regular but discontinuous. We expect that after
some transformation we can get continuous access pattern. We can reorder a [16][16] array to
a [16/4][16][4] array, so that the access pattern of B will be sequential when grabing
the corresponding value from the packed array.
```
# We have to re-write the algorithm slightly.
packedB = te.compute((N / bn, K, bn), lambda x, y, z: B[y, x * bn + z], name="packedB")
C = te.compute(
(M, N),
lambda x, y: te.sum(A[x, k] * packedB[y // bn, k, tvm.tir.indexmod(y, bn)], axis=k),
name="C",
)
s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
s[C].reorder(xo, yo, ko, xi, ki, yi)
s[C].vectorize(yi)
x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt4: %f" % evaluator(a, b, c).mean)
```
Here is the generated IR after array packing.
```
print(tvm.lower(s, [A, B, C], simple_mode=True))
```
Write cache for blocks
----------------------
After blocking, the program will write result to C block by block, the access pattern
is not sequential. So we can use a sequential cache array to hold the block results and
write to C when all the block results are ready.
```
s = te.create_schedule(C.op)
# Allocate write cache
CC = s.cache_write(C, "global")
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
# Write cache is computed at yo
s[CC].compute_at(s[C], yo)
# New inner axes
xc, yc = s[CC].op.axis
(k,) = s[CC].op.reduce_axis
ko, ki = s[CC].split(k, factor=4)
s[CC].reorder(ko, xc, ki, yc)
s[CC].unroll(ki)
s[CC].vectorize(yc)
x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt5: %f" % evaluator(a, b, c).mean)
```
Here is the generated IR after blocking.
```
print(tvm.lower(s, [A, B, C], simple_mode=True))
```
Parallel
--------
Futhermore, we can also utilize multi-core processors to do the thread-level parallelization.
```
s = te.create_schedule(C.op)
CC = s.cache_write(C, "global")
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
s[CC].compute_at(s[C], yo)
xc, yc = s[CC].op.axis
(k,) = s[CC].op.reduce_axis
ko, ki = s[CC].split(k, factor=4)
s[CC].reorder(ko, xc, ki, yc)
s[CC].unroll(ki)
s[CC].vectorize(yc)
# parallel
s[C].parallel(xo)
x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=50)
opt6_time = evaluator(a, b, c).mean
print("Opt6: %f" % opt6_time)
```
Here is the generated IR after parallelization.
```
print(tvm.lower(s, [A, B, C], simple_mode=True))
```
Summary
-------
After applying the above simple optimizations with only 18 lines of code,
our generated code can achieve 60% of the `numpy` performance with MKL.
Note that the outputs on the web page reflect the running times on a non-exclusive
Docker container, thereby they are *unreliable*. It is highly encouraged to run the
tutorial by yourself to observe the performance gain acheived by TVM.
|
github_jupyter
|
%matplotlib inline
import tvm
import tvm.testing
from tvm import te
import numpy
import timeit
# The size of the matrix
# (M, K) x (K, N)
# You are free to try out different shapes, sometimes TVM optimization outperforms numpy with MKL.
M = 1024
K = 1024
N = 1024
# The default tensor type in tvm
dtype = "float32"
# using Intel AVX2(Advanced Vector Extensions) ISA for SIMD
# To get the best performance, please change the following line
# to llvm -mcpu=core-avx2, or specific type of CPU you use
target = "llvm"
ctx = tvm.context(target, 0)
# Random generated tensor for testing
a = tvm.nd.array(numpy.random.rand(M, K).astype(dtype), ctx)
b = tvm.nd.array(numpy.random.rand(K, N).astype(dtype), ctx)
np_repeat = 100
np_runing_time = timeit.timeit(
setup="import numpy\n"
"M = " + str(M) + "\n"
"K = " + str(K) + "\n"
"N = " + str(N) + "\n"
'dtype = "float32"\n'
"a = numpy.random.rand(M, K).astype(dtype)\n"
"b = numpy.random.rand(K, N).astype(dtype)\n",
stmt="answer = numpy.dot(a, b)",
number=np_repeat,
)
print("Numpy running time: %f" % (np_runing_time / np_repeat))
answer = numpy.dot(a.asnumpy(), b.asnumpy())
# Algorithm
k = te.reduce_axis((0, K), "k")
A = te.placeholder((M, K), name="A")
B = te.placeholder((K, N), name="B")
C = te.compute((M, N), lambda x, y: te.sum(A[x, k] * B[k, y], axis=k), name="C")
# Default schedule
s = te.create_schedule(C.op)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=1)
print("Baseline: %f" % evaluator(a, b, c).mean)
print(tvm.lower(s, [A, B, C], simple_mode=True))
bn = 32
s = te.create_schedule(C.op)
# Blocking by loop tiling
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
# Hoist reduction domain outside the blocking loop
s[C].reorder(xo, yo, ko, ki, xi, yi)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
# By simply tiling the loop 32x32, and hoisting ko, ki outside the blocking loops,
# we can see big speedup compared with the baseline.
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt1: %f" % evaluator(a, b, c).mean)
print(tvm.lower(s, [A, B, C], simple_mode=True))
s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
s[C].reorder(xo, yo, ko, ki, xi, yi)
# Vectorization
s[C].vectorize(yi)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt2: %f" % evaluator(a, b, c).mean)
print(tvm.lower(s, [A, B, C], simple_mode=True))
s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
# re-ordering
s[C].reorder(xo, yo, ko, xi, ki, yi)
s[C].vectorize(yi)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt3: %f" % evaluator(a, b, c).mean)
print(tvm.lower(s, [A, B, C], simple_mode=True))
# We have to re-write the algorithm slightly.
packedB = te.compute((N / bn, K, bn), lambda x, y, z: B[y, x * bn + z], name="packedB")
C = te.compute(
(M, N),
lambda x, y: te.sum(A[x, k] * packedB[y // bn, k, tvm.tir.indexmod(y, bn)], axis=k),
name="C",
)
s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
s[C].reorder(xo, yo, ko, xi, ki, yi)
s[C].vectorize(yi)
x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt4: %f" % evaluator(a, b, c).mean)
print(tvm.lower(s, [A, B, C], simple_mode=True))
s = te.create_schedule(C.op)
# Allocate write cache
CC = s.cache_write(C, "global")
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
# Write cache is computed at yo
s[CC].compute_at(s[C], yo)
# New inner axes
xc, yc = s[CC].op.axis
(k,) = s[CC].op.reduce_axis
ko, ki = s[CC].split(k, factor=4)
s[CC].reorder(ko, xc, ki, yc)
s[CC].unroll(ki)
s[CC].vectorize(yc)
x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=10)
print("Opt5: %f" % evaluator(a, b, c).mean)
print(tvm.lower(s, [A, B, C], simple_mode=True))
s = te.create_schedule(C.op)
CC = s.cache_write(C, "global")
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
s[CC].compute_at(s[C], yo)
xc, yc = s[CC].op.axis
(k,) = s[CC].op.reduce_axis
ko, ki = s[CC].split(k, factor=4)
s[CC].reorder(ko, xc, ki, yc)
s[CC].unroll(ki)
s[CC].vectorize(yc)
# parallel
s[C].parallel(xo)
x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), ctx)
func(a, b, c)
tvm.testing.assert_allclose(c.asnumpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, ctx, number=50)
opt6_time = evaluator(a, b, c).mean
print("Opt6: %f" % opt6_time)
print(tvm.lower(s, [A, B, C], simple_mode=True))
| 0.562417 | 0.962356 |
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# You can write up to 5GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
df = pd.read_csv("/kaggle/input/amazon-fine-food-reviews/Reviews.csv")
df
df.isna().sum()
df.Text.fillna("",inplace = True)
del df['Id']
del df['ProductId']
del df['UserId']
del df['ProfileName']
del df['HelpfulnessNumerator']
del df['HelpfulnessDenominator']
del df['Time']
df
df['text'] = df['Text'] + ' ' + df['Summary']
del df['Text']
del df['Summary']
df.head()
def sentiment_rating(rating):
if(int(rating) == 1 or int(rating) == 2 or int(rating) == 3):
return 0
else:
return 1
df.Score = df.Score.apply(sentiment_rating)
df.head()
df.Score.value_counts()
df.columns = ['Liked','Review']
df
X=df.Review.astype('str')
y=df.Liked
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
vocab=1000
tokenizer=Tokenizer(vocab,oov_token="<oov>")
tokenizer.fit_on_texts(X_train)
train_sequence=tokenizer.texts_to_sequences(X_train)
test_sequence=tokenizer.texts_to_sequences(X_test)
padded_train=pad_sequences(train_sequence,maxlen=500)
padded_test=pad_sequences(test_sequence,maxlen=500)
from keras.models import Sequential
from keras.layers import Dense,LSTM,Embedding,GlobalAveragePooling1D
from keras.optimizers import Adam
model=Sequential()
model.add(Embedding(vocab,1000))
model.add(GlobalAveragePooling1D())
model.add(Dense(128,activation='relu'))
model.add(Dense(128,activation='relu'))
model.add(Dense(128,activation='relu'))
model.add(Dense(128,activation='relu'))
model.add(Dense(1,activation='sigmoid'))
model.compile(optimizer=Adam(lr=0.001),loss='binary_crossentropy',metrics=['accuracy'])
model.summary()
history = model.fit(padded_train,y_train,validation_data=(padded_test,y_test),epochs=10)
import matplotlib.pyplot as plt
# summarize history for accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
```
|
github_jupyter
|
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# You can write up to 5GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
df = pd.read_csv("/kaggle/input/amazon-fine-food-reviews/Reviews.csv")
df
df.isna().sum()
df.Text.fillna("",inplace = True)
del df['Id']
del df['ProductId']
del df['UserId']
del df['ProfileName']
del df['HelpfulnessNumerator']
del df['HelpfulnessDenominator']
del df['Time']
df
df['text'] = df['Text'] + ' ' + df['Summary']
del df['Text']
del df['Summary']
df.head()
def sentiment_rating(rating):
if(int(rating) == 1 or int(rating) == 2 or int(rating) == 3):
return 0
else:
return 1
df.Score = df.Score.apply(sentiment_rating)
df.head()
df.Score.value_counts()
df.columns = ['Liked','Review']
df
X=df.Review.astype('str')
y=df.Liked
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
vocab=1000
tokenizer=Tokenizer(vocab,oov_token="<oov>")
tokenizer.fit_on_texts(X_train)
train_sequence=tokenizer.texts_to_sequences(X_train)
test_sequence=tokenizer.texts_to_sequences(X_test)
padded_train=pad_sequences(train_sequence,maxlen=500)
padded_test=pad_sequences(test_sequence,maxlen=500)
from keras.models import Sequential
from keras.layers import Dense,LSTM,Embedding,GlobalAveragePooling1D
from keras.optimizers import Adam
model=Sequential()
model.add(Embedding(vocab,1000))
model.add(GlobalAveragePooling1D())
model.add(Dense(128,activation='relu'))
model.add(Dense(128,activation='relu'))
model.add(Dense(128,activation='relu'))
model.add(Dense(128,activation='relu'))
model.add(Dense(1,activation='sigmoid'))
model.compile(optimizer=Adam(lr=0.001),loss='binary_crossentropy',metrics=['accuracy'])
model.summary()
history = model.fit(padded_train,y_train,validation_data=(padded_test,y_test),epochs=10)
import matplotlib.pyplot as plt
# summarize history for accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
| 0.737347 | 0.23001 |
# Webscraping the following websites for news on upcoming mission to mars:
https://redplanetscience.com/
https://spaceimages-mars.com
https://galaxyfacts-mars.com
https://marshemispheres.com/
```
# Import modules for use in webscraping:
import pandas as pd
from bs4 import BeautifulSoup as bs
from splinter import Browser
from webdriver_manager.chrome import ChromeDriverManager
# Setup for working with Browser:
executable_path = {'executable_path': ChromeDriverManager().install()}
browser = Browser('chrome', **executable_path, headless=False)
```
## Latest News - Mars Mission
```
# URL for news on Mars Mission
rps_url = "https://redplanetscience.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(rps_url)
rps_html = browser.html
rps_soup = bs(rps_html, "html.parser")
# Search parsed soup file for latest news title and snippet
news_title = rps_soup.find("div", class_="content_title").text
news_teaser = rps_soup.find("div", class_ = "article_teaser_body").text
print(news_title)
print(news_teaser)
```
## Capture Mars image
```
# URL for JPL site housing image of Mars
jpl_url = "https://spaceimages-mars.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(jpl_url)
jpl_html = browser.html
jpl_soup = bs(jpl_html, "html.parser")
# Search parsed soup file for html containing Mars image
jpl_find_img = jpl_soup.find_all("img", "headerimage")
# Loop through header data to find the url link of of the image
for img in jpl_find_img:
jpl_img = img["src"]
# Establish variable to hold the image url
featured_image_url = jpl_url + jpl_img
print(featured_image_url)
```
## Mars Facts
```
# URL for facts about Mars
facts_url = "https://galaxyfacts-mars.com"
# Read html from url into variable
table = pd.read_html(facts_url)
# Create data frame from html data
facts_df = table[0]
# Convert first row to column headers
header_row = 0
facts_df.columns = facts_df.iloc[header_row]
facts_df = facts_df.drop(header_row)
# Rename first column
facts_df=facts_df.rename(columns = {'Mars - Earth Comparison':'Description'})
# Set index to first column
facts_df.set_index("Description", inplace = True)
# Convert dataframe to html
facts_table = facts_df.to_html()
# Remove new line code from table
facts_table = facts_table.replace("\n", " ")
# Create html file from dataframe:
facts_df.to_html("facts_html", index=False)
facts_df
```
## Mars Hemispheres
```
# URL for images of Mars hemispheres
hem_url = "https://marshemispheres.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(hem_url)
hem_html = browser.html
hem_soup = bs(hem_html, "html.parser")
# Search soup file for section containing hemisphere titles and html's for images
hem_find = hem_soup.find_all("div", class_ = "item")
# Setup for loop to pull the hemisphere titles from H3 header data
# For loop pulls html links for each hemisphere's page
# Image link from each hemisphere page is pulled
# Hemisphere title and image url are stored in a dictionary
hemisphere_image_urls = []
for item in hem_find:
title = item.find("h3").text
link = item.find("a", class_ = "itemLink")["href"]
hemi_url = hem_url + link
browser.visit(hemi_url)
hemi_url_html = browser.html
hemi_soup = bs(hemi_url_html, "html.parser")
img = hem_url + hemi_soup.find("img", class_ = "wide-image")["src"]
hemisphere_image_urls.append({"img_url": img, "title": title})
print(hemisphere_image_urls)
browser.quit()
```
|
github_jupyter
|
# Import modules for use in webscraping:
import pandas as pd
from bs4 import BeautifulSoup as bs
from splinter import Browser
from webdriver_manager.chrome import ChromeDriverManager
# Setup for working with Browser:
executable_path = {'executable_path': ChromeDriverManager().install()}
browser = Browser('chrome', **executable_path, headless=False)
# URL for news on Mars Mission
rps_url = "https://redplanetscience.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(rps_url)
rps_html = browser.html
rps_soup = bs(rps_html, "html.parser")
# Search parsed soup file for latest news title and snippet
news_title = rps_soup.find("div", class_="content_title").text
news_teaser = rps_soup.find("div", class_ = "article_teaser_body").text
print(news_title)
print(news_teaser)
# URL for JPL site housing image of Mars
jpl_url = "https://spaceimages-mars.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(jpl_url)
jpl_html = browser.html
jpl_soup = bs(jpl_html, "html.parser")
# Search parsed soup file for html containing Mars image
jpl_find_img = jpl_soup.find_all("img", "headerimage")
# Loop through header data to find the url link of of the image
for img in jpl_find_img:
jpl_img = img["src"]
# Establish variable to hold the image url
featured_image_url = jpl_url + jpl_img
print(featured_image_url)
# URL for facts about Mars
facts_url = "https://galaxyfacts-mars.com"
# Read html from url into variable
table = pd.read_html(facts_url)
# Create data frame from html data
facts_df = table[0]
# Convert first row to column headers
header_row = 0
facts_df.columns = facts_df.iloc[header_row]
facts_df = facts_df.drop(header_row)
# Rename first column
facts_df=facts_df.rename(columns = {'Mars - Earth Comparison':'Description'})
# Set index to first column
facts_df.set_index("Description", inplace = True)
# Convert dataframe to html
facts_table = facts_df.to_html()
# Remove new line code from table
facts_table = facts_table.replace("\n", " ")
# Create html file from dataframe:
facts_df.to_html("facts_html", index=False)
facts_df
# URL for images of Mars hemispheres
hem_url = "https://marshemispheres.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(hem_url)
hem_html = browser.html
hem_soup = bs(hem_html, "html.parser")
# Search soup file for section containing hemisphere titles and html's for images
hem_find = hem_soup.find_all("div", class_ = "item")
# Setup for loop to pull the hemisphere titles from H3 header data
# For loop pulls html links for each hemisphere's page
# Image link from each hemisphere page is pulled
# Hemisphere title and image url are stored in a dictionary
hemisphere_image_urls = []
for item in hem_find:
title = item.find("h3").text
link = item.find("a", class_ = "itemLink")["href"]
hemi_url = hem_url + link
browser.visit(hemi_url)
hemi_url_html = browser.html
hemi_soup = bs(hemi_url_html, "html.parser")
img = hem_url + hemi_soup.find("img", class_ = "wide-image")["src"]
hemisphere_image_urls.append({"img_url": img, "title": title})
print(hemisphere_image_urls)
browser.quit()
| 0.270673 | 0.845113 |
# Code snippets
A collection of small code snippets that can be helpful for some parts of the lab.
```
import numpy as np
```
## Spark
```
import json
from operator import itemgetter
# Each line can be transformed into a Python dict using `json.loads`.
data = sc.textFile("/ix/ml-20m/movies.txt").map(json.loads)
datum = data.take(1)[0]
print(datum)
print(datum["title"])
print(datum["genres"][2])
# `itemgetter` can be useful to extract certain fields.
datum = data.map(itemgetter("movieId", "title")).take(1)[0]
print(datum)
```
It is easy to append additional data to an RDD using `union`.
```
data = sc.textFile("/ix/ml-20m/ratings.txt").map(json.loads)
# `parallelize` transforms a Python list into an RDD.
additional = sc.parallelize([
{"movieId": 1, "userId": 1, "timestamp": 98765, "rating": 5.0},
{"movieId": 2, "userId": 1, "timestamp": 98765, "rating": 5.0},
])
# This will simply extend the `data` RDD with the `additional` RDD.
combined = data.union(additional)
```
The method `join` can be used to "merge" two RDDs based on the key.
```
ratings1 = sc.parallelize([
(("user1", "movie7"), 3),
(("user2", "movie4"), 4),
])
ratings2 = sc.parallelize([
(("user1", "movie7"), 2.75),
(("user2", "movie4"), 4.17),
])
joined = ratings1.join(ratings2).collect()
for key, val in joined:
print(key, val)
```
## Visualization
Matplotlib can be used for simple static plots.
```
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use("ggplot")
ys1 = np.random.randn(100)
ys2 = np.sort(ys1)
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 3), sharey=True)
ax1.plot(ys1)
ax1.set_title("Unsorted")
ax2.plot(ys2)
ax2.set_title("Sorted")
```
Bokeh is another library that can be used for interactive plots.
```
from bokeh.io import show, output_notebook
from bokeh.plotting import figure, ColumnDataSource
from bokeh.models import HoverTool, ResetTool, PanTool, WheelZoomTool, SaveTool
output_notebook()
data = (
(0.7, -0.3, "car", 0.1, 0),
(-0.1, -0.5, "train", 0.3, 1),
(-0.5, 0.7, "plane", 0.6, 2),
(0.2, 0.2, "bike", 0.9, 3),
)
# Continuous colors
from matplotlib.colors import rgb2hex
cmap = plt.get_cmap('viridis')
def val2rgb(val):
return rgb2hex(cmap(val)[:3])
source = ColumnDataSource(
data={
"x": [x[0] for x in data],
"y": [x[1] for x in data],
"name": [x[2] for x in data],
"color": [val2rgb(x[3]) for x in data],
})
hover = HoverTool(
tooltips=[
("Name", "@name"),
])
tools = [hover, ResetTool(), PanTool(), WheelZoomTool(), SaveTool()]
p = figure(plot_width=960, plot_height=360, tools=tools, title="Mouse over the dots")
p.circle("x", "y", source=source, size=20, color="color", alpha=0.5)
show(p, notebook_handle=True)
# Categorial colors
from bokeh.palettes import Dark2_8
source = ColumnDataSource(
data={
"x": [x[0] for x in data],
"y": [x[1] for x in data],
"name": [x[2] for x in data],
"color": [Dark2_8[x[4]] for x in data],
})
hover = HoverTool(
tooltips=[
("Name", "@name"),
])
tools = [hover, ResetTool(), PanTool(), WheelZoomTool(), SaveTool()]
p = figure(plot_width=960, plot_height=360, tools=tools, title="Mouse over the dots")
p.circle("x", "y", source=source, size=20, color="color", alpha=0.5)
show(p, notebook_handle=True)
```
## Serialization
The `pickle` module can be used to read and write Python objects from / to disk.
```
import pickle
# Reading an object from disk.
with open("selected-movies.pickle", "rb") as f:
movies = pickle.load(f, encoding="utf-8")
for movie in movies[:3]:
print(movie)
# Writing an object to disk.
data = {"a": np.arange(10), "b": np.random.randn(10)}
with open("sample-file.pickle", "wb") as f:
pickle.dump(data, f)
```
|
github_jupyter
|
import numpy as np
import json
from operator import itemgetter
# Each line can be transformed into a Python dict using `json.loads`.
data = sc.textFile("/ix/ml-20m/movies.txt").map(json.loads)
datum = data.take(1)[0]
print(datum)
print(datum["title"])
print(datum["genres"][2])
# `itemgetter` can be useful to extract certain fields.
datum = data.map(itemgetter("movieId", "title")).take(1)[0]
print(datum)
data = sc.textFile("/ix/ml-20m/ratings.txt").map(json.loads)
# `parallelize` transforms a Python list into an RDD.
additional = sc.parallelize([
{"movieId": 1, "userId": 1, "timestamp": 98765, "rating": 5.0},
{"movieId": 2, "userId": 1, "timestamp": 98765, "rating": 5.0},
])
# This will simply extend the `data` RDD with the `additional` RDD.
combined = data.union(additional)
ratings1 = sc.parallelize([
(("user1", "movie7"), 3),
(("user2", "movie4"), 4),
])
ratings2 = sc.parallelize([
(("user1", "movie7"), 2.75),
(("user2", "movie4"), 4.17),
])
joined = ratings1.join(ratings2).collect()
for key, val in joined:
print(key, val)
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use("ggplot")
ys1 = np.random.randn(100)
ys2 = np.sort(ys1)
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 3), sharey=True)
ax1.plot(ys1)
ax1.set_title("Unsorted")
ax2.plot(ys2)
ax2.set_title("Sorted")
from bokeh.io import show, output_notebook
from bokeh.plotting import figure, ColumnDataSource
from bokeh.models import HoverTool, ResetTool, PanTool, WheelZoomTool, SaveTool
output_notebook()
data = (
(0.7, -0.3, "car", 0.1, 0),
(-0.1, -0.5, "train", 0.3, 1),
(-0.5, 0.7, "plane", 0.6, 2),
(0.2, 0.2, "bike", 0.9, 3),
)
# Continuous colors
from matplotlib.colors import rgb2hex
cmap = plt.get_cmap('viridis')
def val2rgb(val):
return rgb2hex(cmap(val)[:3])
source = ColumnDataSource(
data={
"x": [x[0] for x in data],
"y": [x[1] for x in data],
"name": [x[2] for x in data],
"color": [val2rgb(x[3]) for x in data],
})
hover = HoverTool(
tooltips=[
("Name", "@name"),
])
tools = [hover, ResetTool(), PanTool(), WheelZoomTool(), SaveTool()]
p = figure(plot_width=960, plot_height=360, tools=tools, title="Mouse over the dots")
p.circle("x", "y", source=source, size=20, color="color", alpha=0.5)
show(p, notebook_handle=True)
# Categorial colors
from bokeh.palettes import Dark2_8
source = ColumnDataSource(
data={
"x": [x[0] for x in data],
"y": [x[1] for x in data],
"name": [x[2] for x in data],
"color": [Dark2_8[x[4]] for x in data],
})
hover = HoverTool(
tooltips=[
("Name", "@name"),
])
tools = [hover, ResetTool(), PanTool(), WheelZoomTool(), SaveTool()]
p = figure(plot_width=960, plot_height=360, tools=tools, title="Mouse over the dots")
p.circle("x", "y", source=source, size=20, color="color", alpha=0.5)
show(p, notebook_handle=True)
import pickle
# Reading an object from disk.
with open("selected-movies.pickle", "rb") as f:
movies = pickle.load(f, encoding="utf-8")
for movie in movies[:3]:
print(movie)
# Writing an object to disk.
data = {"a": np.arange(10), "b": np.random.randn(10)}
with open("sample-file.pickle", "wb") as f:
pickle.dump(data, f)
| 0.723895 | 0.903635 |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from sklearn.preprocessing import OneHotEncoder
nhis = pd.read_csv('../data/nhis_clean.csv') # Using cleaned NHIS dataset from Stanford CARE SRI
nhis1 = nhis.drop(['PPSU', 'PSTRAT', 'WTFA_SA', 'AHCSYR1', 'MD', 'RACE', 'MARITAL'], axis=1) # dropping unnecessary columns
nhis2 = nhis.loc[:, ['RACE', 'MARITAL']]
nhis.head()
```
## Preprocessing
```
def encode_binary(x):
if x == 'Yes' or x == 'Male' or x == 'Covered':
return 1
else:
return 0
binary_vars = [
'SEX',
'ASSIST',
'COVERAGE',
'LIMIT',
'HEART',
'STROKE',
'CANCER',
'LUNG',
'DIABETES',
'HYPERTENSION',
'GMC',
'PLBORN'
]
for var in binary_vars:
nhis1[var] = nhis1[var].map(encode_binary)
nhis2 = pd.get_dummies(nhis2)
age_dict = {
'18 ~ 25': 1,
'26 ~ 44': 2,
'45 ~ 64': 3,
'+65': 4
}
educ_dict = {
'Less Than High School': 1,
'High School Graduate/GED/Some College': 2,
'College Degree': 3
}
faminc_dict = {
'<10K': 1,
'<25K': 2,
'<45K': 3,
'<75K': 4,
'+75K': 5
}
bmi_dict = {
'Underweight': 1,
'Normal': 2,
'Overweight': 3,
'Obese': 4
}
phstat_dict = {
'Poor': 1,
'Fair': 2,
'Good': 3,
'Very good': 4,
'Excellent': 5
}
drink_dict = {
'Current': 1,
'Former': 2,
'Never': 3
}
smoke_dict = {
'Current Daily': 1,
'Current Occasional': 2,
'Former': 3,
'Never': 4
}
nhis1['AGE'] = nhis['AGE'].map(age_dict)
nhis1['EDUC'] = nhis['EDUC'].map(educ_dict)
nhis1['FAMINC'] = nhis['FAMINC'].map(faminc_dict)
nhis1['BMI_CAT'] = nhis['BMI_CAT'].map(bmi_dict)
nhis1['PHSTAT'] = nhis['PHSTAT'].map(phstat_dict)
nhis1['DRINK'] = nhis['DRINK'].map(drink_dict)
nhis1['SMOKE'] = nhis['SMOKE'].map(smoke_dict)
nhis1.describe()
nhis = pd.concat([nhis1, nhis2], axis=1)
X = (nhis.drop('K6', axis=1)
.fillna(0)
.to_numpy())
y = pd.get_dummies(nhis['K6']).fillna(0).to_numpy()
X.shape
y.shape
```
## Model to Training
```
model = keras.models.Sequential()
model.add(keras.layers.Dense(64, activation='relu', input_shape=(33, )))
model.add(keras.layers.Dense(64, activation='relu'))
model.add(keras.layers.Dense(25, activation='softmax'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=123)
history = model.fit(X_train,
y_train,
epochs=20,
batch_size=516,
validation_data=(X_test, y_test))
```
## Results
```
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.legend()
acc = history.history['acc']
val_acc = history.history['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.legend()
```
## Consideration
The validation loss is all over the place. There could be several reasons for this.
* Not enough features i.e. not enough information is embedded
* Inappropriate feature encoding
* Inappropriate network architecture
* Inappropriate loss function
**Next Steps**
* Search for academic literature using NHIS and Neural Networks
* Extract more features from the NHIS dataset
* Find appropriate loss function
**Notes**
* Instead of trying to predict the K6 scale itself, try to predict none, mild, moderate, or severe
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from sklearn.preprocessing import OneHotEncoder
nhis = pd.read_csv('../data/nhis_clean.csv') # Using cleaned NHIS dataset from Stanford CARE SRI
nhis1 = nhis.drop(['PPSU', 'PSTRAT', 'WTFA_SA', 'AHCSYR1', 'MD', 'RACE', 'MARITAL'], axis=1) # dropping unnecessary columns
nhis2 = nhis.loc[:, ['RACE', 'MARITAL']]
nhis.head()
def encode_binary(x):
if x == 'Yes' or x == 'Male' or x == 'Covered':
return 1
else:
return 0
binary_vars = [
'SEX',
'ASSIST',
'COVERAGE',
'LIMIT',
'HEART',
'STROKE',
'CANCER',
'LUNG',
'DIABETES',
'HYPERTENSION',
'GMC',
'PLBORN'
]
for var in binary_vars:
nhis1[var] = nhis1[var].map(encode_binary)
nhis2 = pd.get_dummies(nhis2)
age_dict = {
'18 ~ 25': 1,
'26 ~ 44': 2,
'45 ~ 64': 3,
'+65': 4
}
educ_dict = {
'Less Than High School': 1,
'High School Graduate/GED/Some College': 2,
'College Degree': 3
}
faminc_dict = {
'<10K': 1,
'<25K': 2,
'<45K': 3,
'<75K': 4,
'+75K': 5
}
bmi_dict = {
'Underweight': 1,
'Normal': 2,
'Overweight': 3,
'Obese': 4
}
phstat_dict = {
'Poor': 1,
'Fair': 2,
'Good': 3,
'Very good': 4,
'Excellent': 5
}
drink_dict = {
'Current': 1,
'Former': 2,
'Never': 3
}
smoke_dict = {
'Current Daily': 1,
'Current Occasional': 2,
'Former': 3,
'Never': 4
}
nhis1['AGE'] = nhis['AGE'].map(age_dict)
nhis1['EDUC'] = nhis['EDUC'].map(educ_dict)
nhis1['FAMINC'] = nhis['FAMINC'].map(faminc_dict)
nhis1['BMI_CAT'] = nhis['BMI_CAT'].map(bmi_dict)
nhis1['PHSTAT'] = nhis['PHSTAT'].map(phstat_dict)
nhis1['DRINK'] = nhis['DRINK'].map(drink_dict)
nhis1['SMOKE'] = nhis['SMOKE'].map(smoke_dict)
nhis1.describe()
nhis = pd.concat([nhis1, nhis2], axis=1)
X = (nhis.drop('K6', axis=1)
.fillna(0)
.to_numpy())
y = pd.get_dummies(nhis['K6']).fillna(0).to_numpy()
X.shape
y.shape
model = keras.models.Sequential()
model.add(keras.layers.Dense(64, activation='relu', input_shape=(33, )))
model.add(keras.layers.Dense(64, activation='relu'))
model.add(keras.layers.Dense(25, activation='softmax'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=123)
history = model.fit(X_train,
y_train,
epochs=20,
batch_size=516,
validation_data=(X_test, y_test))
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.legend()
acc = history.history['acc']
val_acc = history.history['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.legend()
| 0.539954 | 0.776199 |
<h1> 1. Exploring natality dataset </h1>
This notebook illustrates:
<ol>
<li> Exploring a BigQuery dataset using Datalab
</ol>
```
# change these to try this notebook out
BUCKET = 'cloud-training-demos-ml'
PROJECT = 'cloud-training-demos'
REGION = 'us-central1'
import os
os.environ['BUCKET'] = BUCKET
os.environ['PROJECT'] = PROJECT
os.environ['REGION'] = REGION
%%bash
if ! gsutil ls | grep -q gs://${BUCKET}/; then
gsutil mb -l ${REGION} gs://${BUCKET}
fi
```
<h2> Explore data </h2>
The data is natality data (record of births in the US). My goal is to predict the baby's weight given a number of factors about the pregnancy and the baby's mother. Later, we will want to split the data into training and eval datasets. The hash of the year-month will be used for that -- this way, twins born on the same day won't end up in different cuts of the data.
```
# Create SQL query using natality data after the year 2000
query = """
SELECT
weight_pounds,
is_male,
mother_age,
plurality,
gestation_weeks,
ABS(FARM_FINGERPRINT(CONCAT(CAST(YEAR AS STRING), CAST(month AS STRING)))) AS hashmonth
FROM
publicdata.samples.natality
WHERE year > 2000
"""
# Call BigQuery and examine in dataframe
import google.datalab.bigquery as bq
df = bq.Query(query + " LIMIT 100").execute().result().to_dataframe()
df.head()
```
Let's write a query to find the unique values for each of the columns and the count of those values.
This is important to ensure that we have enough examples of each data value, and to verify our hunch that the parameter has predictive value.
```
# Create function that finds the number of records and the average weight for each value of the chosen column
def get_distinct_values(column_name):
sql = """
SELECT
{0},
COUNT(1) AS num_babies,
AVG(weight_pounds) AS avg_wt
FROM
publicdata.samples.natality
WHERE
year > 2000
GROUP BY
{0}
""".format(column_name)
return bq.Query(sql).execute().result().to_dataframe()
# Bar plot to see is_male with avg_wt linear and num_babies logarithmic
df = get_distinct_values('is_male')
df.plot(x='is_male', y='num_babies', logy=True, kind='bar');
df.plot(x='is_male', y='avg_wt', kind='bar');
# Line plots to see mother_age with avg_wt linear and num_babies logarithmic
df = get_distinct_values('mother_age')
df = df.sort_values('mother_age')
df.plot(x='mother_age', y='num_babies');
df.plot(x='mother_age', y='avg_wt');
# Bar plot to see plurality(singleton, twins, etc.) with avg_wt linear and num_babies logarithmic
df = get_distinct_values('plurality')
df = df.sort_values('plurality')
df.plot(x='plurality', y='num_babies', logy=True, kind='bar');
df.plot(x='plurality', y='avg_wt', kind='bar');
# Bar plot to see gestation_weeks with avg_wt linear and num_babies logarithmic
df = get_distinct_values('gestation_weeks')
df = df.sort_values('gestation_weeks')
df.plot(x='gestation_weeks', y='num_babies', logy=True, kind='bar');
df.plot(x='gestation_weeks', y='avg_wt', kind='bar');
```
All these factors seem to play a part in the baby's weight. Male babies are heavier on average than female babies. Teenaged and older moms tend to have lower-weight babies. Twins, triplets, etc. are lower weight than single births. Preemies weigh in lower as do babies born to single moms. In addition, it is important to check whether you have enough data (number of babies) for each input value. Otherwise, the model prediction against input values that doesn't have enough data may not be reliable.
<p>
In the next notebook, I will develop a machine learning model to combine all of these factors to come up with a prediction of a baby's weight.
Copyright 2017-2018 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
|
github_jupyter
|
# change these to try this notebook out
BUCKET = 'cloud-training-demos-ml'
PROJECT = 'cloud-training-demos'
REGION = 'us-central1'
import os
os.environ['BUCKET'] = BUCKET
os.environ['PROJECT'] = PROJECT
os.environ['REGION'] = REGION
%%bash
if ! gsutil ls | grep -q gs://${BUCKET}/; then
gsutil mb -l ${REGION} gs://${BUCKET}
fi
# Create SQL query using natality data after the year 2000
query = """
SELECT
weight_pounds,
is_male,
mother_age,
plurality,
gestation_weeks,
ABS(FARM_FINGERPRINT(CONCAT(CAST(YEAR AS STRING), CAST(month AS STRING)))) AS hashmonth
FROM
publicdata.samples.natality
WHERE year > 2000
"""
# Call BigQuery and examine in dataframe
import google.datalab.bigquery as bq
df = bq.Query(query + " LIMIT 100").execute().result().to_dataframe()
df.head()
# Create function that finds the number of records and the average weight for each value of the chosen column
def get_distinct_values(column_name):
sql = """
SELECT
{0},
COUNT(1) AS num_babies,
AVG(weight_pounds) AS avg_wt
FROM
publicdata.samples.natality
WHERE
year > 2000
GROUP BY
{0}
""".format(column_name)
return bq.Query(sql).execute().result().to_dataframe()
# Bar plot to see is_male with avg_wt linear and num_babies logarithmic
df = get_distinct_values('is_male')
df.plot(x='is_male', y='num_babies', logy=True, kind='bar');
df.plot(x='is_male', y='avg_wt', kind='bar');
# Line plots to see mother_age with avg_wt linear and num_babies logarithmic
df = get_distinct_values('mother_age')
df = df.sort_values('mother_age')
df.plot(x='mother_age', y='num_babies');
df.plot(x='mother_age', y='avg_wt');
# Bar plot to see plurality(singleton, twins, etc.) with avg_wt linear and num_babies logarithmic
df = get_distinct_values('plurality')
df = df.sort_values('plurality')
df.plot(x='plurality', y='num_babies', logy=True, kind='bar');
df.plot(x='plurality', y='avg_wt', kind='bar');
# Bar plot to see gestation_weeks with avg_wt linear and num_babies logarithmic
df = get_distinct_values('gestation_weeks')
df = df.sort_values('gestation_weeks')
df.plot(x='gestation_weeks', y='num_babies', logy=True, kind='bar');
df.plot(x='gestation_weeks', y='avg_wt', kind='bar');
| 0.55929 | 0.97296 |
```
%matplotlib inline
import yt
import numpy as np
```
This notebook shows how to use yt to make plots and examine FITS X-ray images and events files.
## Sloshing, Shocks, and Bubbles in Abell 2052
This example uses data provided by [Scott Randall](http://hea-www.cfa.harvard.edu/~srandall/), presented originally in [Blanton, E.L., Randall, S.W., Clarke, T.E., et al. 2011, ApJ, 737, 99](https://ui.adsabs.harvard.edu/abs/2011ApJ...737...99B). They consist of two files, a "flux map" in counts/s/pixel between 0.3 and 2 keV, and a spectroscopic temperature map in keV.
```
ds = yt.load("xray_fits/A2052_merged_0.3-2_match-core_tmap_bgecorr.fits",
auxiliary_files=["xray_fits/A2052_core_tmap_b1_m2000_.fits"])
```
Since the flux and projected temperature images are in two different files, we had to use one of them (in this case the "flux" file) as a master file, and pass in the "temperature" file with the `auxiliary_files` keyword to `load`.
Next, let's derive some new fields for the number of counts, the "pseudo-pressure", and the "pseudo-entropy":
```
def _counts(field, data):
exposure_time = data.get_field_parameter("exposure_time")
return data["flux"]*data["pixel"]*exposure_time
ds.add_field(("gas","counts"), function=_counts, sampling_type="cell", units="counts", take_log=False)
def _pp(field, data):
return np.sqrt(data["counts"])*data["projected_temperature"]
ds.add_field(("gas","pseudo_pressure"), function=_pp, sampling_type="cell", units="sqrt(counts)*keV", take_log=False)
def _pe(field, data):
return data["projected_temperature"]*data["counts"]**(-1./3.)
ds.add_field(("gas","pseudo_entropy"), function=_pe, sampling_type="cell", units="keV*(counts)**(-1/3)", take_log=False)
```
Here, we're deriving a "counts" field from the "flux" field by passing it a `field_parameter` for the exposure time of the time and multiplying by the pixel scale. Second, we use the fact that the surface brightness is strongly dependent on density ($S_X \propto \rho^2$) to use the counts in each pixel as a "stand-in". Next, we'll grab the exposure time from the primary FITS header of the flux file and create a `YTQuantity` from it, to be used as a `field_parameter`:
```
exposure_time = ds.quan(ds.primary_header["exposure"], "s")
```
Now, we can make the `SlicePlot` object of the fields we want, passing in the `exposure_time` as a `field_parameter`. We'll also set the width of the image to 250 pixels.
```
slc = yt.SlicePlot(ds, "z",
["flux","projected_temperature","pseudo_pressure","pseudo_entropy"],
origin="native", field_parameters={"exposure_time":exposure_time})
slc.set_log("flux",True)
slc.set_log("pseudo_pressure",False)
slc.set_log("pseudo_entropy",False)
slc.set_width(250.)
slc.show()
```
To add the celestial coordinates to the image, we can use `PlotWindowWCS`, if you have a recent version of AstroPy (>= 1.3) installed:
```
from yt.frontends.fits.misc import PlotWindowWCS
wcs_slc = PlotWindowWCS(slc)
wcs_slc.show()
```
We can make use of yt's facilities for profile plotting as well.
```
v, c = ds.find_max("flux") # Find the maximum flux and its center
my_sphere = ds.sphere(c, (100.,"code_length")) # Radius of 150 pixels
my_sphere.set_field_parameter("exposure_time", exposure_time)
```
Such as a radial profile plot:
```
radial_profile = yt.ProfilePlot(my_sphere, "radius",
["counts","pseudo_pressure","pseudo_entropy"],
n_bins=30, weight_field="ones")
radial_profile.set_log("counts", True)
radial_profile.set_log("pseudo_pressure", True)
radial_profile.set_log("pseudo_entropy", True)
radial_profile.set_xlim(3,100.)
radial_profile.show()
```
Or a phase plot:
```
phase_plot = yt.PhasePlot(my_sphere, "pseudo_pressure", "pseudo_entropy", ["counts"], weight_field=None)
phase_plot.show()
```
Finally, we can also take an existing [ds9](http://ds9.si.edu/site/Home.html) region and use it to create a "cut region", using `ds9_region` (the [pyregion](https://pyregion.readthedocs.io) package needs to be installed for this):
```
from yt.frontends.fits.misc import ds9_region
reg_file = ["# Region file format: DS9 version 4.1\n",
"global color=green dashlist=8 3 width=3 include=1 source=1 fk5\n",
"circle(15:16:44.817,+7:01:19.62,34.6256\")"]
f = open("circle.reg","w")
f.writelines(reg_file)
f.close()
circle_reg = ds9_region(ds, "circle.reg", field_parameters={"exposure_time":exposure_time})
```
This region may now be used to compute derived quantities:
```
print (circle_reg.quantities.weighted_average_quantity("projected_temperature", "counts"))
```
Or used in projections:
```
prj = yt.ProjectionPlot(ds, "z",
["flux","projected_temperature","pseudo_pressure","pseudo_entropy"],
origin="native", field_parameters={"exposure_time":exposure_time},
data_source=circle_reg,
method="sum")
prj.set_log("flux",True)
prj.set_log("pseudo_pressure",False)
prj.set_log("pseudo_entropy",False)
prj.set_width(250.)
prj.show()
```
## The Bullet Cluster
This example uses an events table file from a ~100 ks exposure of the "Bullet Cluster" from the [Chandra Data Archive](http://cxc.harvard.edu/cda/). In this case, the individual photon events are treated as particle fields in yt. However, you can make images of the object in different energy bands using the `setup_counts_fields` function.
```
from yt.frontends.fits.api import setup_counts_fields
```
`load` will handle the events file as FITS image files, and will set up a grid using the WCS information in the file. Optionally, the events may be reblocked to a new resolution. by setting the `"reblock"` parameter in the `parameters` dictionary in `load`. `"reblock"` must be a power of 2.
```
ds2 = yt.load("xray_fits/acisf05356N003_evt2.fits.gz", parameters={"reblock":2})
```
`setup_counts_fields` will take a list of energy bounds (emin, emax) in keV and create a new field from each where the photons in that energy range will be deposited onto the image grid.
```
ebounds = [(0.1,2.0),(2.0,5.0)]
setup_counts_fields(ds2, ebounds)
```
The "x", "y", "energy", and "time" fields in the events table are loaded as particle fields. Each one has a name given by "event\_" plus the name of the field:
```
dd = ds2.all_data()
print (dd["event_x"])
print (dd["event_y"])
```
Now, we'll make a plot of the two counts fields we made, and pan and zoom to the bullet:
```
slc = yt.SlicePlot(ds2, "z", ["counts_0.1-2.0","counts_2.0-5.0"], origin="native")
slc.pan((100.,100.))
slc.set_width(500.)
slc.show()
```
The counts fields can take the field parameter `"sigma"` and use [AstroPy's convolution routines](https://astropy.readthedocs.io/en/latest/convolution/) to smooth the data with a Gaussian:
```
slc = yt.SlicePlot(ds2, "z", ["counts_0.1-2.0","counts_2.0-5.0"], origin="native",
field_parameters={"sigma":2.}) # This value is in pixel scale
slc.pan((100.,100.))
slc.set_width(500.)
slc.set_zlim("counts_0.1-2.0", 0.01, 100.)
slc.set_zlim("counts_2.0-5.0", 0.01, 50.)
slc.show()
```
|
github_jupyter
|
%matplotlib inline
import yt
import numpy as np
ds = yt.load("xray_fits/A2052_merged_0.3-2_match-core_tmap_bgecorr.fits",
auxiliary_files=["xray_fits/A2052_core_tmap_b1_m2000_.fits"])
def _counts(field, data):
exposure_time = data.get_field_parameter("exposure_time")
return data["flux"]*data["pixel"]*exposure_time
ds.add_field(("gas","counts"), function=_counts, sampling_type="cell", units="counts", take_log=False)
def _pp(field, data):
return np.sqrt(data["counts"])*data["projected_temperature"]
ds.add_field(("gas","pseudo_pressure"), function=_pp, sampling_type="cell", units="sqrt(counts)*keV", take_log=False)
def _pe(field, data):
return data["projected_temperature"]*data["counts"]**(-1./3.)
ds.add_field(("gas","pseudo_entropy"), function=_pe, sampling_type="cell", units="keV*(counts)**(-1/3)", take_log=False)
exposure_time = ds.quan(ds.primary_header["exposure"], "s")
slc = yt.SlicePlot(ds, "z",
["flux","projected_temperature","pseudo_pressure","pseudo_entropy"],
origin="native", field_parameters={"exposure_time":exposure_time})
slc.set_log("flux",True)
slc.set_log("pseudo_pressure",False)
slc.set_log("pseudo_entropy",False)
slc.set_width(250.)
slc.show()
from yt.frontends.fits.misc import PlotWindowWCS
wcs_slc = PlotWindowWCS(slc)
wcs_slc.show()
v, c = ds.find_max("flux") # Find the maximum flux and its center
my_sphere = ds.sphere(c, (100.,"code_length")) # Radius of 150 pixels
my_sphere.set_field_parameter("exposure_time", exposure_time)
radial_profile = yt.ProfilePlot(my_sphere, "radius",
["counts","pseudo_pressure","pseudo_entropy"],
n_bins=30, weight_field="ones")
radial_profile.set_log("counts", True)
radial_profile.set_log("pseudo_pressure", True)
radial_profile.set_log("pseudo_entropy", True)
radial_profile.set_xlim(3,100.)
radial_profile.show()
phase_plot = yt.PhasePlot(my_sphere, "pseudo_pressure", "pseudo_entropy", ["counts"], weight_field=None)
phase_plot.show()
from yt.frontends.fits.misc import ds9_region
reg_file = ["# Region file format: DS9 version 4.1\n",
"global color=green dashlist=8 3 width=3 include=1 source=1 fk5\n",
"circle(15:16:44.817,+7:01:19.62,34.6256\")"]
f = open("circle.reg","w")
f.writelines(reg_file)
f.close()
circle_reg = ds9_region(ds, "circle.reg", field_parameters={"exposure_time":exposure_time})
print (circle_reg.quantities.weighted_average_quantity("projected_temperature", "counts"))
prj = yt.ProjectionPlot(ds, "z",
["flux","projected_temperature","pseudo_pressure","pseudo_entropy"],
origin="native", field_parameters={"exposure_time":exposure_time},
data_source=circle_reg,
method="sum")
prj.set_log("flux",True)
prj.set_log("pseudo_pressure",False)
prj.set_log("pseudo_entropy",False)
prj.set_width(250.)
prj.show()
from yt.frontends.fits.api import setup_counts_fields
ds2 = yt.load("xray_fits/acisf05356N003_evt2.fits.gz", parameters={"reblock":2})
ebounds = [(0.1,2.0),(2.0,5.0)]
setup_counts_fields(ds2, ebounds)
dd = ds2.all_data()
print (dd["event_x"])
print (dd["event_y"])
slc = yt.SlicePlot(ds2, "z", ["counts_0.1-2.0","counts_2.0-5.0"], origin="native")
slc.pan((100.,100.))
slc.set_width(500.)
slc.show()
slc = yt.SlicePlot(ds2, "z", ["counts_0.1-2.0","counts_2.0-5.0"], origin="native",
field_parameters={"sigma":2.}) # This value is in pixel scale
slc.pan((100.,100.))
slc.set_width(500.)
slc.set_zlim("counts_0.1-2.0", 0.01, 100.)
slc.set_zlim("counts_2.0-5.0", 0.01, 50.)
slc.show()
| 0.658198 | 0.977607 |
===================================================================
Determining and plotting the altitude/azimuth of the Canopus and Sun
In this notebook I an going to calculate the altitude/azimuth of the Canopus and Sun
seen from an observer in Tai Mountain from -3000BC to 2000AD.
The main procedures are listed as follow:
(1) Calculate the time-dependent position of the Canopus in the ICRF2, using the position
and proper motion data in Hipparcus catalog (Hipparcos, the New Reduction (van Leeuwen, 2007) );
(2) Calculate the tim
e-dependent position of the Sun in the ICRF2, using the ephemeris DE431;
(3) Calculate the transformation metrix between ICRF2 and ITRF, only considering the effect of Precession;
(4) Determine the altitude/azimuth of the Canopus and Sun
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from astropy.visualization import astropy_mpl_style
plt.style.use(astropy_mpl_style)
import astropy.units as u
from astropy.time import Time
from astropy.coordinates import SkyCoord, EarthLocation, AltAz, ICRS
# Time system
time0 = Time("J2000.0")
print(time0.utc)
# Input the position and proper motion information of the Canopus from Hiparcus
hip30438 = SkyCoord(ra=95.98787790*u.deg, dec=-52.69571787*u.deg,
frame="icrs")
shangqiu = EarthLocation(lat=36.2*u.deg, lon=117.1*u.deg, height=1500*u.m)
utcoffset = + 8*u.hour # Daylight Time
time = Time("2018-9-22 23:00:00") - utcoffset
hip30438altaz = hip30438.transform_to(AltAz(obstime=time, location=shangqiu))
print("HIP 30438's Altitude = {0.alt:.2}".format(hip30438altaz))
midnight = Time("2018-9-23 00:00:00") - utcoffset
delta_midnight = np.linspace(-2, 10, 100) * u.hour
frame_July13night = AltAz(obstime=midnight + delta_midnight,
location=shangqiu)
m33altazs_July13night = hip30438.transform_to(frame_July13night)
m33airmasss_July13night = m33altazs_July13night.secz
from astropy.coordinates import get_sun
delta_midnight = np.linspace(-12, 12, 1000)*u.hour
times_July12_to_13 = midnight + delta_midnight
frame_July12_to_13 = AltAz(obstime=times_July12_to_13, location=shangqiu)
sunaltazs_July12_to_13 = get_sun(times_July12_to_13).transform_to(frame_July12_to_13)
hip30438altazs_July12_to_13 = hip30438.transform_to(frame_July12_to_13)
plt.plot(delta_midnight, sunaltazs_July12_to_13.alt, color='r', label='Sun')
plt.scatter(delta_midnight, hip30438altazs_July12_to_13.alt,
label='Canopus', lw=0, s=8)
plt.fill_between(delta_midnight.to('hr').value, 0, 90,
sunaltazs_July12_to_13.alt < -0*u.deg, color='0.5', zorder=0)
plt.fill_between(delta_midnight.to('hr').value, 0, 90,
sunaltazs_July12_to_13.alt < -18*u.deg, color='k', zorder=0)
plt.legend(loc='upper left')
plt.xlim(-12, 12)
plt.xticks(np.arange(13)*2 -12)
plt.ylim(0, 90)
plt.xlabel('Hours from Midnigt (2018-09-23)')
plt.ylabel('Altitude [deg]')
# plt.savefig("/Users/Neo/Desktop/temp1.png", dpi=100)
mask = (sunaltazs_July12_to_13.alt < -0*u.deg) & (hip30438altazs_July12_to_13.alt>0)
observable_time = delta_midnight[mask]
# observable_time
beg_time, end_time = observable_time.min(), observable_time.max()
print(beg_time, end_time)
print(end_time - beg_time)
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from astropy.visualization import astropy_mpl_style
plt.style.use(astropy_mpl_style)
import astropy.units as u
from astropy.time import Time
from astropy.coordinates import SkyCoord, EarthLocation, AltAz, ICRS
# Time system
time0 = Time("J2000.0")
print(time0.utc)
# Input the position and proper motion information of the Canopus from Hiparcus
hip30438 = SkyCoord(ra=95.98787790*u.deg, dec=-52.69571787*u.deg,
frame="icrs")
shangqiu = EarthLocation(lat=36.2*u.deg, lon=117.1*u.deg, height=1500*u.m)
utcoffset = + 8*u.hour # Daylight Time
time = Time("2018-9-22 23:00:00") - utcoffset
hip30438altaz = hip30438.transform_to(AltAz(obstime=time, location=shangqiu))
print("HIP 30438's Altitude = {0.alt:.2}".format(hip30438altaz))
midnight = Time("2018-9-23 00:00:00") - utcoffset
delta_midnight = np.linspace(-2, 10, 100) * u.hour
frame_July13night = AltAz(obstime=midnight + delta_midnight,
location=shangqiu)
m33altazs_July13night = hip30438.transform_to(frame_July13night)
m33airmasss_July13night = m33altazs_July13night.secz
from astropy.coordinates import get_sun
delta_midnight = np.linspace(-12, 12, 1000)*u.hour
times_July12_to_13 = midnight + delta_midnight
frame_July12_to_13 = AltAz(obstime=times_July12_to_13, location=shangqiu)
sunaltazs_July12_to_13 = get_sun(times_July12_to_13).transform_to(frame_July12_to_13)
hip30438altazs_July12_to_13 = hip30438.transform_to(frame_July12_to_13)
plt.plot(delta_midnight, sunaltazs_July12_to_13.alt, color='r', label='Sun')
plt.scatter(delta_midnight, hip30438altazs_July12_to_13.alt,
label='Canopus', lw=0, s=8)
plt.fill_between(delta_midnight.to('hr').value, 0, 90,
sunaltazs_July12_to_13.alt < -0*u.deg, color='0.5', zorder=0)
plt.fill_between(delta_midnight.to('hr').value, 0, 90,
sunaltazs_July12_to_13.alt < -18*u.deg, color='k', zorder=0)
plt.legend(loc='upper left')
plt.xlim(-12, 12)
plt.xticks(np.arange(13)*2 -12)
plt.ylim(0, 90)
plt.xlabel('Hours from Midnigt (2018-09-23)')
plt.ylabel('Altitude [deg]')
# plt.savefig("/Users/Neo/Desktop/temp1.png", dpi=100)
mask = (sunaltazs_July12_to_13.alt < -0*u.deg) & (hip30438altazs_July12_to_13.alt>0)
observable_time = delta_midnight[mask]
# observable_time
beg_time, end_time = observable_time.min(), observable_time.max()
print(beg_time, end_time)
print(end_time - beg_time)
| 0.587943 | 0.96051 |
# SQL Joins: TMDb Database
© Explore Data Science Academy
## Instructions to Students
This challenge is designed to determine how much you have learned so far and will test your knowledge on join SQL statements.
The answers for this challenge should be selected on Athena for each corresponding Multiple Choice Question. The questions are included in this notebook and are numbered according to the Athena Questions, the options to choose from for each question have also been included.
Do not add or remove cells in this notebook. Do not edit or remove the `%%sql` comment as it is required to run each cell.
**_Good Luck!_**
## Honour Code
I YOUR NAME, YOUR SURNAME, confirm - by submitting this document - that the solutions in this notebook are a result of my own work and that I abide by the EDSA honour code (https://drive.google.com/file/d/1QDCjGZJ8-FmJE3bZdIQNwnJyQKPhHZBn/view?usp=sharing).
Non-compliance with the honour code constitutes a material breach of contract.
## The TMDb Database
In this challenge you will be exploring the [The Movie Database](https://www.themoviedb.org/) - an online movie and TV show database, which houses some of the most popular movies and TV shows at your finger tips. The TMDb database supports 39 official languages used in over 180 countries daily and dates all the way back to 2008.
<img src="https://github.com/Explore-AI/Pictures/blob/master/sql_tmdb.jpg?raw=true" width=80%/>
Below is an Entity Relationship diagram(ERD) of the TMDb database:
<img src="https://github.com/Explore-AI/Pictures/blob/master/TMDB_ER_diagram.png?raw=true" width=70%/>
As can be seen from the ER diagram, the TMDb database consists of `12 tables` containing information about movies, cast, genre and so much more.
Let's get started!
## Loading the database
To begin and start making use of SQL queries you need to prepare your SQL environment you can do this by loading in the magic command `%load_ext sql`, next you can go ahead and load in your database. To do this you will need to ensure you have downloaded the `TMDB.db`sqlite file from Athena and have stored it in a known location. Now that you have all the prerequisites you can go ahead and load it into the notebook.
```
%load_ext sql
%%sql
sqlite:///TMDB.db
```
## Questions on SQL Join Statements
Use the given cell below each question to execute your SQL queries to find the correct input from the options provided for the multiple choice questions on Athena.
**Question 1**
What is the primary key for the table “movies”?
**Options:**
- title
- movie_key
- film_id
- movie_id
**Solution**
```
%%sql
PRAGMA table_info(movies);
```
**Question 2**
How many foreign keys does the “LanguageMap” table have?
**Options:**
- 0
- 2
- 3
- 1
**Solution**
```
%%sql
--PRAGMA table_info(LanguageMap);
EXEC sp_fkeys LanguageMap
```
**Question 3**
How many movies in the database were produced by Pixar Animation Studios?
**Options:**
- 16
- 14
- 18
- 20
**Solution**
```
%%sql
SELECT count(*)
FROM movies m
INNER JOIN productioncompanymap pcm
ON m.movie_id=pcm.movie_id
INNER JOIN productioncompanies pc
ON (pc.production_company_name="Pixar Animation Studios" AND pc.production_company_id=pcm.production_company_id)
```
**Question 4**
What is the most popular action movie that has some German in it? (Hint: The German word for German is Deutsch)
**Options:**
- The Bourne Identity
- Mission: Impossible - Rogue Nation
- Captain America: Civil War
- Quantum of Solace
**Solution**
```
%%sql
SELECT title, popularity
FROM movies m
INNER JOIN languagemap lm
ON m.movie_id=lm.movie_id
INNER JOIN languages ls
ON (ls.language_name="Deutsch" AND ls.iso_639_1=lm.iso_639_1)
ORDER BY popularity DESC
LIMIT 1
```
**Question 5**
In how many movies did Tom Cruise portray the character Ethan Hunt? (Hint: Characters are listed in the Casts table.)
**Options:**
- 4
- 3
- 6
- 5
**Solution**
```
%%sql
SELECT count(*)
FROM movies m
INNER JOIN casts c
ON m.movie_id=c.movie_id
INNER JOIN actors a
ON c.actor_id=a.actor_id
WHERE (c.characters="Ethan Hunt" AND a.actor_name="Tom Cruise")
```
**Question 6**
How many times was the actress Cate Blanchett nominated for an Oscar?
**Options:**
- 7
- 4
- 5
- 2
**Solution**
```
%%sql
SELECT count(*)
FROM oscars
WHERE name="Cate Blanchett"
```
**Question 7**
How many movies were nominated for the Best Picture award at the Oscars?
**Options:**
- 12
- 16
- 8
- 18
**Solution**
```
%%sql
SELECT count(*)
FROM movies m
INNER JOIN oscars os
ON (os.award="Best Picture" AND m.title=os.name)
LIMIT 10
```
**Question 8**
How many movies contain at least one of the languages, Afrikaans or Zulu?
**Options:**
- 10
- 8
- 12
- 15
**Solution**
```
%%sql
SELECT count(*)
FROM movies m
INNER JOIN languagemap lm
ON m.movie_id=lm.movie_id
INNER JOIN languages ls
ON (ls.language_name LIKE "%Zulu%" OR ls.language_name LIKE "%Afrikaans%")
AND ls.iso_639_1=lm.iso_639_1
```
**Question 9**
In which country was the movie “Star Wars” produced?
**Options:**
- Canada
- United Kingdom
- France
- United States of America
**Solution**
```
%%sql
SELECT production_country_name
FROM movies m
INNER JOIN productioncountrymap pcm
ON m.movie_id=pcm.movie_id AND m.title="Star Wars"
INNER JOIN productioncountries pc
ON pcm.iso_3166_1=pc.iso_3166_1
```
**Question 10**
How many movies are in the database that are both a Romance and a Comedy?
**Options:**
- 373
- 484
- 262
- 595
**Solution**
```
%%sql
SELECT count(*)
FROM movies m
INNER JOIN genremap gm
ON m.movie_id=gm.movie_id
INNER JOIN genres g
ON g.genre_id=gm.genre_id AND g.genre_name LIKE "%Romance%" OR g.genre_name LIKE "%Comedy%"
INNER JOIN keywordmap kmp
ON m.movie_id=kmp.movie_id
INNER JOIN keywords kw
ON kmp.keyword_id=kw.keyword_id AND (kw.keyword_name LIKE "%Comedy%" OR kw.keyword_name LIKE "%Romance%")
LIMIT 10
%%sql
SELECT count(*)
FROM keywords
where keyword_name like "%romantic comedy%"
LIMIT 20
```
|
github_jupyter
|
%load_ext sql
%%sql
sqlite:///TMDB.db
%%sql
PRAGMA table_info(movies);
%%sql
--PRAGMA table_info(LanguageMap);
EXEC sp_fkeys LanguageMap
%%sql
SELECT count(*)
FROM movies m
INNER JOIN productioncompanymap pcm
ON m.movie_id=pcm.movie_id
INNER JOIN productioncompanies pc
ON (pc.production_company_name="Pixar Animation Studios" AND pc.production_company_id=pcm.production_company_id)
%%sql
SELECT title, popularity
FROM movies m
INNER JOIN languagemap lm
ON m.movie_id=lm.movie_id
INNER JOIN languages ls
ON (ls.language_name="Deutsch" AND ls.iso_639_1=lm.iso_639_1)
ORDER BY popularity DESC
LIMIT 1
%%sql
SELECT count(*)
FROM movies m
INNER JOIN casts c
ON m.movie_id=c.movie_id
INNER JOIN actors a
ON c.actor_id=a.actor_id
WHERE (c.characters="Ethan Hunt" AND a.actor_name="Tom Cruise")
%%sql
SELECT count(*)
FROM oscars
WHERE name="Cate Blanchett"
%%sql
SELECT count(*)
FROM movies m
INNER JOIN oscars os
ON (os.award="Best Picture" AND m.title=os.name)
LIMIT 10
%%sql
SELECT count(*)
FROM movies m
INNER JOIN languagemap lm
ON m.movie_id=lm.movie_id
INNER JOIN languages ls
ON (ls.language_name LIKE "%Zulu%" OR ls.language_name LIKE "%Afrikaans%")
AND ls.iso_639_1=lm.iso_639_1
%%sql
SELECT production_country_name
FROM movies m
INNER JOIN productioncountrymap pcm
ON m.movie_id=pcm.movie_id AND m.title="Star Wars"
INNER JOIN productioncountries pc
ON pcm.iso_3166_1=pc.iso_3166_1
%%sql
SELECT count(*)
FROM movies m
INNER JOIN genremap gm
ON m.movie_id=gm.movie_id
INNER JOIN genres g
ON g.genre_id=gm.genre_id AND g.genre_name LIKE "%Romance%" OR g.genre_name LIKE "%Comedy%"
INNER JOIN keywordmap kmp
ON m.movie_id=kmp.movie_id
INNER JOIN keywords kw
ON kmp.keyword_id=kw.keyword_id AND (kw.keyword_name LIKE "%Comedy%" OR kw.keyword_name LIKE "%Romance%")
LIMIT 10
%%sql
SELECT count(*)
FROM keywords
where keyword_name like "%romantic comedy%"
LIMIT 20
| 0.137967 | 0.938463 |
```
from matplotlib import pyplot
from sklearn.model_selection import train_test_split
import numpy as np
from skimage.transform import resize
import cv2, skimage
import matplotlib.pyplot as plt
import os
from google.colab import drive
drive.mount("/content/drive")
!cp "/content/drive/My Drive/RWTHFingerSpelling.zip" .
#!echo 'A' | unzip -q asl-alphabet.zip
!unzip -q RWTHFingerSpelling.zip
imageWidth = 320
imageHeight = 240
imageSize = 64
labels = [i for i in range(1, 36) if i not in [10, 26, 27, 28, 29]]
def prepare_train_validation():
folder = "train/"
X = []
y = []
for label in labels:
folderName = str(label)
for imageFileName in os.listdir(folder + folderName):
imgFile = cv2.imread(folder + folderName + '/' + imageFileName)
imgFile = cv2.cvtColor(imgFile, cv2.COLOR_BGR2RGB)
imgFile = skimage.transform.resize(imgFile, (imageSize, imageSize, 3))
imgArr = np.asarray(imgFile).reshape((-1, imageSize, imageSize, 3))
attributes = imageFileName.split("_")
person = attributes[0]
session = attributes[2]
camera = attributes[3]
X.append(imgArr)
y.append((label, person, session, camera))
return np.array(X, dtype=np.float32),np.array(y)
def prepare_test():
folder = "test/"
totalImage = 20*11*2*30
X = []
y = []
for folderName in os.listdir(folder):
if not folderName.startswith('.'):
label = folderName
for imageFileName in os.listdir(folder + folderName):
imgFile = cv2.imread(folder + folderName + '/' + imageFileName)
imgFile = cv2.cvtColor(imgFile, cv2.COLOR_BGR2RGB)
if imgFile is not None:
imgFile = skimage.transform.resize(imgFile, (imageSize, imageSize, 3))
imgArr = np.asarray(imgFile).reshape((-1, imageSize, imageSize, 3))
attributes = imageFileName.split("_")
person = attributes[0]
session = attributes[2]
camera = attributes[3]
X.append(imgArr)
y.append((label, person, session, camera))
return np.array(X, dtype=np.float32),np.array(y)
trainX, trainY = prepare_train_validation()
np.save('/content/drive/My Drive/datasetRWTH/trainFeatures',trainX)
np.save('/content/drive/My Drive/datasetRWTH/trainLabels',trainY)
testX, testY = prepare_test()
testY
np.save('/content/drive/My Drive/datasetRWTH/testFeatures',testX)
np.save('/content/drive/My Drive/datasetRWTH/testLabels',testY)
imgFile = cv2.imread("test/4/5_4_2_cam2_00000033.jpg")
imgFile = cv2.cvtColor(imgFile, cv2.COLOR_BGR2RGB)
imgFile = skimage.transform.resize(imgFile, (imageSize, imageSize, 3))
plt.imshow(testX[0].reshape(64,64,3))
imgArr = np.asarray(imgFile).reshape((-1, imageSize, imageSize, 3))
imgArr
imgFile1.shape
!du -hs '/content/drive/My Drive/datasetRWTH/'
```
|
github_jupyter
|
from matplotlib import pyplot
from sklearn.model_selection import train_test_split
import numpy as np
from skimage.transform import resize
import cv2, skimage
import matplotlib.pyplot as plt
import os
from google.colab import drive
drive.mount("/content/drive")
!cp "/content/drive/My Drive/RWTHFingerSpelling.zip" .
#!echo 'A' | unzip -q asl-alphabet.zip
!unzip -q RWTHFingerSpelling.zip
imageWidth = 320
imageHeight = 240
imageSize = 64
labels = [i for i in range(1, 36) if i not in [10, 26, 27, 28, 29]]
def prepare_train_validation():
folder = "train/"
X = []
y = []
for label in labels:
folderName = str(label)
for imageFileName in os.listdir(folder + folderName):
imgFile = cv2.imread(folder + folderName + '/' + imageFileName)
imgFile = cv2.cvtColor(imgFile, cv2.COLOR_BGR2RGB)
imgFile = skimage.transform.resize(imgFile, (imageSize, imageSize, 3))
imgArr = np.asarray(imgFile).reshape((-1, imageSize, imageSize, 3))
attributes = imageFileName.split("_")
person = attributes[0]
session = attributes[2]
camera = attributes[3]
X.append(imgArr)
y.append((label, person, session, camera))
return np.array(X, dtype=np.float32),np.array(y)
def prepare_test():
folder = "test/"
totalImage = 20*11*2*30
X = []
y = []
for folderName in os.listdir(folder):
if not folderName.startswith('.'):
label = folderName
for imageFileName in os.listdir(folder + folderName):
imgFile = cv2.imread(folder + folderName + '/' + imageFileName)
imgFile = cv2.cvtColor(imgFile, cv2.COLOR_BGR2RGB)
if imgFile is not None:
imgFile = skimage.transform.resize(imgFile, (imageSize, imageSize, 3))
imgArr = np.asarray(imgFile).reshape((-1, imageSize, imageSize, 3))
attributes = imageFileName.split("_")
person = attributes[0]
session = attributes[2]
camera = attributes[3]
X.append(imgArr)
y.append((label, person, session, camera))
return np.array(X, dtype=np.float32),np.array(y)
trainX, trainY = prepare_train_validation()
np.save('/content/drive/My Drive/datasetRWTH/trainFeatures',trainX)
np.save('/content/drive/My Drive/datasetRWTH/trainLabels',trainY)
testX, testY = prepare_test()
testY
np.save('/content/drive/My Drive/datasetRWTH/testFeatures',testX)
np.save('/content/drive/My Drive/datasetRWTH/testLabels',testY)
imgFile = cv2.imread("test/4/5_4_2_cam2_00000033.jpg")
imgFile = cv2.cvtColor(imgFile, cv2.COLOR_BGR2RGB)
imgFile = skimage.transform.resize(imgFile, (imageSize, imageSize, 3))
plt.imshow(testX[0].reshape(64,64,3))
imgArr = np.asarray(imgFile).reshape((-1, imageSize, imageSize, 3))
imgArr
imgFile1.shape
!du -hs '/content/drive/My Drive/datasetRWTH/'
| 0.236604 | 0.286069 |
```
from time import time
import pickle
import os
import numpy as np
from adaptive.experiment import run_mab_experiment
from adaptive.compute import fill_up, collect
from adaptive.inference import aw_scores, sample_mean
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set(font_scale=1.2)
%matplotlib inline
%reload_ext autoreload
%autoreload 2
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
```
# Introduction Example
DGP: run a contextual bandit experiment with a Thompson sampling agent, collecting $1000$ observations for one simulation.
- context space $\{x_0, x_1, x_2, x_3, x_4\}$ with probability $[0.6, 0.1, 0.1, 0.1]$.
- arms: $\{w_0, w_1, w_2, w_3, w_4\}$
- potential outcomes of $x_i$ assigned to $w_j$: $0.5\cdot 1_{i=j} + \mathcal{N}(0,1)$
- agent: Thompson sampling with floor $0.2t^{-0.7}$
Target policy: always assigning treatment $W_t=w_0$.
Compared estimators: Direct Method (DM) and Doubly Robust (DR).
```
K = 5 # number of arms
N = 5 # number of different context
initial = 2 # initial number of samples of each arm to do pure exploration
floor_start = 1/K
floor_decay = 0.7
noise_scale = 1.0
signal = 0.5
T = 1000
p_X = [0.6, 0.1, 0.1, 0.1, 0.1]
truth = np.eye(K) * signal
w_optimal_X = np.eye(K)
mu_K = np.transpose(truth).dot(p_X)
arm=0
sim = 1000
DM = []
AIPW = []
```
## Run simulations
```
Probs = []
for _ in range(sim):
""" Generate data """
xs = np.random.choice(a=N, size=T, p=p_X)
noise = np.random.normal(loc=0.0, scale=noise_scale, size=(T, K))
#noise = np.random.uniform(-noise_scale, noise_scale, size=(T, K))
#R = noise_scale * 2
ys = truth[xs] + noise
""" Run experiment """
probs = np.zeros((T, N, K))
rewards = np.zeros(T)
arms = np.zeros(T, dtype=np.int)
muhat = np.zeros((T, K))
for n in range(N):
idx = xs == n
data = run_mab_experiment(
ys[idx],
initial=initial,
floor_start=floor_start,
floor_decay=floor_decay)
P = data['probs']
idx_a = np.where(xs == n)[0]
if idx_a[-1] < T-1:
idx_a = np.concatenate([idx_a, [T-1]])
P = np.concatenate([P, [data['future_p']]], axis=0)
probs[:, n, :] = fill_up(T, idx_a, P)
rewards[idx] = data['rewards']
arms[idx] = data['arms']
muhat[idx] = sample_mean(rewards[idx], arms[idx], K)[-1]
balwts = 1 / collect(probs[np.arange(T), xs], arms)
scores = aw_scores(rewards, arms, balwts, K, muhat)
# add best arm policy
Probs.append(probs[:, :, arm])
best_mtx = np.zeros((T, K))
best_mtx[:, arm] = 1
qx = truth[:, arm] * p_X
DM.append(np.mean(np.sum(muhat * best_mtx, axis=1)))
AIPW.append(np.mean(np.sum(scores * best_mtx, axis=1)))
```
## Boxplot of estimates of DM and DR
```
print(f"DM bias: {np.mean(DM) - mu_K[arm]}, std: {np.std(DM)}")
print(f"AIPW bias: {np.mean(AIPW) - mu_K[arm]}, std: {np.std(AIPW)}")
dataset_1 = pd.DataFrame({'method':['DM']*len(DM), 'eval': np.array(DM)})
dataset_2 = pd.DataFrame({'method':['DR']*len(AIPW), 'eval': np.array(AIPW)})
dataset = pd.concat([dataset_1, dataset_2])
sns.set(style='white', font_scale=1.5)
f, ax = plt.subplots()
ax.axhline(y=mu_K[arm], color='k', linestyle='--', label='truth')
sns.boxplot(x='method', y='eval', data=dataset)
ax.set_xlabel('')
ax.legend()
ax.set_ylabel('Estimate')
plt.tight_layout()
plt.savefig('intro.pdf')
```
## Evolution of variance proxy over time with different covariates
```
sns.set_context(font_scale=2)
cond_var = 1 / np.array(Probs)
idx = np.arange(0,T,T//100)
df = []
for i in range(K):
df.append(pd.DataFrame({'$1/e_t$': np.concatenate(cond_var[:, idx, i], axis=0), 't': np.tile(idx, sim),
'Value':[str(i)]*(len(idx)*sim), 'Style':[0]*(len(idx)*sim)}))
df.append(pd.DataFrame({'$1/e_t$': np.concatenate(cond_var[:, idx, :], axis=0).dot(p_X), 't': np.tile(idx, sim),
'Value':['E']*(len(idx)*sim), 'Style':[1]*(len(idx)*sim)}))
df = pd.concat(df)
hue_order = [str(i) for i in range(K)]
hue_order.append('E')
g = sns.relplot(data=df, kind='line', x='t', y='$1/e_t$', hue='Value',
aspect=1.0,
hue_order=hue_order,
palette=[*sns.color_palette()[:K], 'k'],
style='Style',
)
for ax in g.axes.flat:
#ax.set_yscale('log')
handles, labels = ax.get_legend_handles_labels()
g.set_ylabels("Variance proxy")
g.set_xlabels("t")
handles = [*handles[1:(K+1)], handles[-1]]
labels_X = [f'$x_{i}$' for i in range(K)]
labels = [
*labels_X,
'$E_x$']
g._legend.remove()
g.fig.tight_layout()
g.fig.legend(labels=labels, handles=handles, fontsize=18, loc='center left', frameon=False, bbox_to_anchor=(0.95, 0.5) )
plt.savefig('motivation_contextual.pdf', bbox_inches='tight')
```
|
github_jupyter
|
from time import time
import pickle
import os
import numpy as np
from adaptive.experiment import run_mab_experiment
from adaptive.compute import fill_up, collect
from adaptive.inference import aw_scores, sample_mean
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set(font_scale=1.2)
%matplotlib inline
%reload_ext autoreload
%autoreload 2
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
K = 5 # number of arms
N = 5 # number of different context
initial = 2 # initial number of samples of each arm to do pure exploration
floor_start = 1/K
floor_decay = 0.7
noise_scale = 1.0
signal = 0.5
T = 1000
p_X = [0.6, 0.1, 0.1, 0.1, 0.1]
truth = np.eye(K) * signal
w_optimal_X = np.eye(K)
mu_K = np.transpose(truth).dot(p_X)
arm=0
sim = 1000
DM = []
AIPW = []
Probs = []
for _ in range(sim):
""" Generate data """
xs = np.random.choice(a=N, size=T, p=p_X)
noise = np.random.normal(loc=0.0, scale=noise_scale, size=(T, K))
#noise = np.random.uniform(-noise_scale, noise_scale, size=(T, K))
#R = noise_scale * 2
ys = truth[xs] + noise
""" Run experiment """
probs = np.zeros((T, N, K))
rewards = np.zeros(T)
arms = np.zeros(T, dtype=np.int)
muhat = np.zeros((T, K))
for n in range(N):
idx = xs == n
data = run_mab_experiment(
ys[idx],
initial=initial,
floor_start=floor_start,
floor_decay=floor_decay)
P = data['probs']
idx_a = np.where(xs == n)[0]
if idx_a[-1] < T-1:
idx_a = np.concatenate([idx_a, [T-1]])
P = np.concatenate([P, [data['future_p']]], axis=0)
probs[:, n, :] = fill_up(T, idx_a, P)
rewards[idx] = data['rewards']
arms[idx] = data['arms']
muhat[idx] = sample_mean(rewards[idx], arms[idx], K)[-1]
balwts = 1 / collect(probs[np.arange(T), xs], arms)
scores = aw_scores(rewards, arms, balwts, K, muhat)
# add best arm policy
Probs.append(probs[:, :, arm])
best_mtx = np.zeros((T, K))
best_mtx[:, arm] = 1
qx = truth[:, arm] * p_X
DM.append(np.mean(np.sum(muhat * best_mtx, axis=1)))
AIPW.append(np.mean(np.sum(scores * best_mtx, axis=1)))
print(f"DM bias: {np.mean(DM) - mu_K[arm]}, std: {np.std(DM)}")
print(f"AIPW bias: {np.mean(AIPW) - mu_K[arm]}, std: {np.std(AIPW)}")
dataset_1 = pd.DataFrame({'method':['DM']*len(DM), 'eval': np.array(DM)})
dataset_2 = pd.DataFrame({'method':['DR']*len(AIPW), 'eval': np.array(AIPW)})
dataset = pd.concat([dataset_1, dataset_2])
sns.set(style='white', font_scale=1.5)
f, ax = plt.subplots()
ax.axhline(y=mu_K[arm], color='k', linestyle='--', label='truth')
sns.boxplot(x='method', y='eval', data=dataset)
ax.set_xlabel('')
ax.legend()
ax.set_ylabel('Estimate')
plt.tight_layout()
plt.savefig('intro.pdf')
sns.set_context(font_scale=2)
cond_var = 1 / np.array(Probs)
idx = np.arange(0,T,T//100)
df = []
for i in range(K):
df.append(pd.DataFrame({'$1/e_t$': np.concatenate(cond_var[:, idx, i], axis=0), 't': np.tile(idx, sim),
'Value':[str(i)]*(len(idx)*sim), 'Style':[0]*(len(idx)*sim)}))
df.append(pd.DataFrame({'$1/e_t$': np.concatenate(cond_var[:, idx, :], axis=0).dot(p_X), 't': np.tile(idx, sim),
'Value':['E']*(len(idx)*sim), 'Style':[1]*(len(idx)*sim)}))
df = pd.concat(df)
hue_order = [str(i) for i in range(K)]
hue_order.append('E')
g = sns.relplot(data=df, kind='line', x='t', y='$1/e_t$', hue='Value',
aspect=1.0,
hue_order=hue_order,
palette=[*sns.color_palette()[:K], 'k'],
style='Style',
)
for ax in g.axes.flat:
#ax.set_yscale('log')
handles, labels = ax.get_legend_handles_labels()
g.set_ylabels("Variance proxy")
g.set_xlabels("t")
handles = [*handles[1:(K+1)], handles[-1]]
labels_X = [f'$x_{i}$' for i in range(K)]
labels = [
*labels_X,
'$E_x$']
g._legend.remove()
g.fig.tight_layout()
g.fig.legend(labels=labels, handles=handles, fontsize=18, loc='center left', frameon=False, bbox_to_anchor=(0.95, 0.5) )
plt.savefig('motivation_contextual.pdf', bbox_inches='tight')
| 0.474144 | 0.720909 |
# ***tensors* Tutorial**
The simplest object we can create is a vector.
```
import torch
x = torch.arange(12)
print (x)
```
We can ge the *tensor* shape through its *shape* attribute or *size()* function
```
x.shape
x.size()
```
The reshape function change the shape of the vector $x$ to a matrix of 3 rows and 4 columns.
```
x = x.reshape((3, 4))
print(x)
```
Call *empty* to allocate some memory for a tensor filled with uninitialized data
```
torch.empty(2, 3)
```
Usually, we initialize a tensor with all zeros. For example, an all zero matrix at size (2, 3, 4)
```
torch.zeros((2,3,4))
```
We can also intialize a tensor with all ones.
```
torch.ones((2,3,4))
```
We can also specify the value of each element to initialize a tensor (But it is rarely done bucause usually we may either have a quite large tensor to feed the model or we want it to be initialized with a certain distribution).
```
y = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(y)
```
In some cases, we need to randomly generate the value of each element. This is especially common when we intend to use the array as a parameter in a neural network.
The following code creates a tensor with the shape of (3,4), and each elements of it is randomly sampled in a normal distribution with zero mean and unit variance.
```
torch.normal(mean=0.0, std=1.0, size=(3, 4))
```
# **Operations**
```
x = torch.tensor([1, 2, 4, 8], dtype=torch.float32)
y = torch.ones_like(x) * 2
print('x = ', x)
print('x + y = ', x + y)
print('x - y = ', x - y)
print('x * y = ', x * y)
print('x / y = ', x / y)
print('Element-wise exponentation: ', x.exp())
```
We can also concatenate tensors at the dimension we want.
```
x = torch.arange(12).reshape((3,4))
y = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(torch.cat((x, y), dim=0))
print(torch.cat((x, y), dim=1))
```
Like in Numpy, we can construct binary tensors by a logical statement.
```
x == y
```
Personally, I don't like broadcast mechanism. I'd rather use *torch.repeat* to modify the tensor to desired shape and then add two tensors.
```
a = torch.arange(3, dtype=torch.float32).reshape((3, 1))
b = torch.arange(2, dtype=torch.float32).reshape((1, 2))
print('a, b: ', a, b)
print('Boardcast mechanism of a+b shoule be equvalent to: \n', a.repeat(1, 2) + b.repeat(3,1))
```
# **Indexing and Slicing**
Indexing and Slicing in Pytorch tensors are the same as what we do in Python.
# **Transformation between Pytorch tensors and Numpy array**
Note that according to PyTorch document, **UNLIKE** MxNet, the torch Tensor and numpy array will **SHARE** their underlying memory locations, and changing one will change the other.
```
import numpy as np
a = x.numpy()
print(type(a))
b = torch.tensor(a)
print(type(b))
t = torch.ones((3, 2))
n = t.numpy()
print("Before change tensor value: {} \n {}.".format(t, n))
t[0,0] = 100
print("After change tensor value: {} \n {}.\n\n".format(t, n))
!pip install mxnet
import mxnet as mx
from mxnet import nd
mx_nd = nd.ones((3,2))
mx_n = mx_nd.asnumpy()
print("Before change NDArray value: {} \n {}.".format(mx_nd, mx_n))
mx_nd[0,0] = 100
print("After change NDArray value: {} \n {}.".format(mx_nd, mx_n))
```
|
github_jupyter
|
import torch
x = torch.arange(12)
print (x)
x.shape
x.size()
x = x.reshape((3, 4))
print(x)
torch.empty(2, 3)
torch.zeros((2,3,4))
torch.ones((2,3,4))
y = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(y)
torch.normal(mean=0.0, std=1.0, size=(3, 4))
x = torch.tensor([1, 2, 4, 8], dtype=torch.float32)
y = torch.ones_like(x) * 2
print('x = ', x)
print('x + y = ', x + y)
print('x - y = ', x - y)
print('x * y = ', x * y)
print('x / y = ', x / y)
print('Element-wise exponentation: ', x.exp())
x = torch.arange(12).reshape((3,4))
y = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(torch.cat((x, y), dim=0))
print(torch.cat((x, y), dim=1))
x == y
a = torch.arange(3, dtype=torch.float32).reshape((3, 1))
b = torch.arange(2, dtype=torch.float32).reshape((1, 2))
print('a, b: ', a, b)
print('Boardcast mechanism of a+b shoule be equvalent to: \n', a.repeat(1, 2) + b.repeat(3,1))
import numpy as np
a = x.numpy()
print(type(a))
b = torch.tensor(a)
print(type(b))
t = torch.ones((3, 2))
n = t.numpy()
print("Before change tensor value: {} \n {}.".format(t, n))
t[0,0] = 100
print("After change tensor value: {} \n {}.\n\n".format(t, n))
!pip install mxnet
import mxnet as mx
from mxnet import nd
mx_nd = nd.ones((3,2))
mx_n = mx_nd.asnumpy()
print("Before change NDArray value: {} \n {}.".format(mx_nd, mx_n))
mx_nd[0,0] = 100
print("After change NDArray value: {} \n {}.".format(mx_nd, mx_n))
| 0.473414 | 0.98869 |
```
from math import hypot, pi, cos, sin
from PIL import Image
import numpy as np
import cv2
import math
from matplotlib import pyplot as plt
img = cv2.imread('road.jpg', cv2.IMREAD_COLOR) # road.png is the filename
img_copy=img.copy()
# Convert the image to gray-scale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Find the edges in the image using canny detector
edges = cv2.Canny(gray, 50, 200)
# Detect points that form a line
lines = cv2.HoughLinesP(edges, 1, np.pi/180, 69, minLineLength=10, maxLineGap=250)
for line in lines:
x1, y1, x2, y2 = line[0]
cv2.line(img, (x1, y1), (x2, y2), (255, 0, 0), 3)
# Show result
plt.figure(figsize=(20,10))
plt.subplot(1,2,1)
plt.imshow(img_copy)
plt.subplot(1,2,2)
plt.imshow(img)
thresh = 235
plt.figure(figsize=(20,10))
img=cv2.imread('road.jpg',0)
BW = cv2.threshold(img, thresh, 255, cv2.THRESH_BINARY)[1]
edges = cv2.Canny(img,100,200)
plt.subplot(131),plt.imshow(img,cmap='gray')
plt.title('Original Image')
plt.subplot(132),plt.imshow(edges,cmap = 'gray')
plt.title('Edge Image')
plt.subplot(133),plt.imshow(BW,cmap='gray')
plt.title('Binary Image')
plt.show()
def hough(img):
thetaAxisSize = 460 #Width of the hough space image
rAxisSize = 360 #Height of the hough space image
rAxisSize= int(rAxisSize/2)*2 #we make sure that this number is even
#img = edges.load()
w, h = edges.shape
print(w,h)
#plt.imshow(img)
houghed_img = Image.new("L", (thetaAxisSize, rAxisSize), 0)
pixel_houghed_img = houghed_img.load()
max_radius = hypot(w, h)
d_theta = pi / thetaAxisSize
d_rho = max_radius / (rAxisSize/2)
#Accumulator
for x in range(0, w):
for y in range(0, h):
threshold = 255
col = img[x, y]
if col >= threshold: #determines for each pixel at (x,y) if there is enough evidence of a straight line at that pixel.
for vx in range(0, thetaAxisSize):
theta = d_theta * vx #angle between the x axis and the line connecting the origin with that closest point.
rho = x*cos(theta) + y*sin(theta) #distance from the origin to the closest point on the straight line
vy = rAxisSize/2 + int(rho/d_rho+0.5)
pixel_houghed_img[vx, vy] += 1 #voting
return houghed_img, rAxisSize, d_rho, d_theta
houghed_img, rAxisSize, d_rho, d_theta = hough(edges)
plt.imshow(houghed_img, cmap='hot')
def find_maxima(houghed_img, rAxisSize, d_rho, d_theta):
w, h = houghed_img.size
pixel_houghed_img = houghed_img.load()
maxNumbers = 9
ignoreRadius = 10
maxima = [0] * maxNumbers
rhos = [0] * maxNumbers
thetas = [0] * maxNumbers
for u in range(0, maxNumbers):
value = 0
xposition = 0
yposition = 0
#find maxima in the image
for x in range(0, w):
for y in range(0, h):
if(pixel_houghed_img[x,y] > value):
value = pixel_houghed_img[x, y]
xposition = x
yposition = y
#Save Maxima, rhos and thetas
maxima[u] = value
rhos[u] = (yposition - rAxisSize/2) * d_rho
thetas[u] = xposition * d_theta
pixel_houghed_img[xposition, yposition] = 0
#Delete the values around the found maxima
radius = ignoreRadius
for vx2 in range (-radius, radius): #checks the values around the center
for vy2 in range (-radius, radius): #checks the values around the center
x2 = xposition + vx2 #sets the spectated position on the shifted value
y2 = yposition + vy2
if not(x2 < 0 or x2 >= w):
if not(y2 < 0 or y2 >= h):
pixel_houghed_img[x2, y2] = 0
return maxima, rhos, thetas
img_copy = np.ones(edges.shape)
maxima, rhos, thetas = find_maxima(houghed_img, rAxisSize, d_rho, d_theta)
for t in range(0, len(maxima)):
a = math.cos(thetas[t])
b = math.sin(thetas[t])
x = a * rhos[t]
y = b * rhos[t]
pt1 = (int(x + 500*(-b)), int(y + 500*(a)))
pt2 = (int(x - 500*(-b)), int(y - 500*(a)))
cv2.line(img_copy, pt1, pt2, (0,0,255), 3)
plt.imshow(img_copy,cmap='gray')
plt.title('lines')
```
|
github_jupyter
|
from math import hypot, pi, cos, sin
from PIL import Image
import numpy as np
import cv2
import math
from matplotlib import pyplot as plt
img = cv2.imread('road.jpg', cv2.IMREAD_COLOR) # road.png is the filename
img_copy=img.copy()
# Convert the image to gray-scale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Find the edges in the image using canny detector
edges = cv2.Canny(gray, 50, 200)
# Detect points that form a line
lines = cv2.HoughLinesP(edges, 1, np.pi/180, 69, minLineLength=10, maxLineGap=250)
for line in lines:
x1, y1, x2, y2 = line[0]
cv2.line(img, (x1, y1), (x2, y2), (255, 0, 0), 3)
# Show result
plt.figure(figsize=(20,10))
plt.subplot(1,2,1)
plt.imshow(img_copy)
plt.subplot(1,2,2)
plt.imshow(img)
thresh = 235
plt.figure(figsize=(20,10))
img=cv2.imread('road.jpg',0)
BW = cv2.threshold(img, thresh, 255, cv2.THRESH_BINARY)[1]
edges = cv2.Canny(img,100,200)
plt.subplot(131),plt.imshow(img,cmap='gray')
plt.title('Original Image')
plt.subplot(132),plt.imshow(edges,cmap = 'gray')
plt.title('Edge Image')
plt.subplot(133),plt.imshow(BW,cmap='gray')
plt.title('Binary Image')
plt.show()
def hough(img):
thetaAxisSize = 460 #Width of the hough space image
rAxisSize = 360 #Height of the hough space image
rAxisSize= int(rAxisSize/2)*2 #we make sure that this number is even
#img = edges.load()
w, h = edges.shape
print(w,h)
#plt.imshow(img)
houghed_img = Image.new("L", (thetaAxisSize, rAxisSize), 0)
pixel_houghed_img = houghed_img.load()
max_radius = hypot(w, h)
d_theta = pi / thetaAxisSize
d_rho = max_radius / (rAxisSize/2)
#Accumulator
for x in range(0, w):
for y in range(0, h):
threshold = 255
col = img[x, y]
if col >= threshold: #determines for each pixel at (x,y) if there is enough evidence of a straight line at that pixel.
for vx in range(0, thetaAxisSize):
theta = d_theta * vx #angle between the x axis and the line connecting the origin with that closest point.
rho = x*cos(theta) + y*sin(theta) #distance from the origin to the closest point on the straight line
vy = rAxisSize/2 + int(rho/d_rho+0.5)
pixel_houghed_img[vx, vy] += 1 #voting
return houghed_img, rAxisSize, d_rho, d_theta
houghed_img, rAxisSize, d_rho, d_theta = hough(edges)
plt.imshow(houghed_img, cmap='hot')
def find_maxima(houghed_img, rAxisSize, d_rho, d_theta):
w, h = houghed_img.size
pixel_houghed_img = houghed_img.load()
maxNumbers = 9
ignoreRadius = 10
maxima = [0] * maxNumbers
rhos = [0] * maxNumbers
thetas = [0] * maxNumbers
for u in range(0, maxNumbers):
value = 0
xposition = 0
yposition = 0
#find maxima in the image
for x in range(0, w):
for y in range(0, h):
if(pixel_houghed_img[x,y] > value):
value = pixel_houghed_img[x, y]
xposition = x
yposition = y
#Save Maxima, rhos and thetas
maxima[u] = value
rhos[u] = (yposition - rAxisSize/2) * d_rho
thetas[u] = xposition * d_theta
pixel_houghed_img[xposition, yposition] = 0
#Delete the values around the found maxima
radius = ignoreRadius
for vx2 in range (-radius, radius): #checks the values around the center
for vy2 in range (-radius, radius): #checks the values around the center
x2 = xposition + vx2 #sets the spectated position on the shifted value
y2 = yposition + vy2
if not(x2 < 0 or x2 >= w):
if not(y2 < 0 or y2 >= h):
pixel_houghed_img[x2, y2] = 0
return maxima, rhos, thetas
img_copy = np.ones(edges.shape)
maxima, rhos, thetas = find_maxima(houghed_img, rAxisSize, d_rho, d_theta)
for t in range(0, len(maxima)):
a = math.cos(thetas[t])
b = math.sin(thetas[t])
x = a * rhos[t]
y = b * rhos[t]
pt1 = (int(x + 500*(-b)), int(y + 500*(a)))
pt2 = (int(x - 500*(-b)), int(y - 500*(a)))
cv2.line(img_copy, pt1, pt2, (0,0,255), 3)
plt.imshow(img_copy,cmap='gray')
plt.title('lines')
| 0.674372 | 0.757099 |
# Webscraping the following websites for news on upcoming mission to mars:
https://redplanetscience.com/
https://spaceimages-mars.com
https://galaxyfacts-mars.com
https://marshemispheres.com/
```
# Import modules for use in webscraping:
import pandas as pd
from bs4 import BeautifulSoup as bs
from splinter import Browser
from webdriver_manager.chrome import ChromeDriverManager
# Setup for working with Browser:
executable_path = {'executable_path': ChromeDriverManager().install()}
browser = Browser('chrome', **executable_path, headless=False)
```
## Latest News - Mars Mission
```
# URL for news on Mars Mission
rps_url = "https://redplanetscience.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(rps_url)
rps_html = browser.html
rps_soup = bs(rps_html, "html.parser")
# Search parsed soup file for latest news title and snippet
news_title = rps_soup.find("div", class_="content_title").text
news_teaser = rps_soup.find("div", class_ = "article_teaser_body").text
print(news_title)
print(news_teaser)
```
## Capture Mars image
```
# URL for JPL site housing image of Mars
jpl_url = "https://spaceimages-mars.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(jpl_url)
jpl_html = browser.html
jpl_soup = bs(jpl_html, "html.parser")
# Search parsed soup file for html containing Mars Featured Image
jpl_find = jpl_soup.find_all("div", class_="floating_text_area")
# Find image url within jpl_find
for item in jpl_find:
a = item.find("a")
href = a["href"]
# Establish variable to hold the image url
featured_image_url = jpl_url + href
print(featured_image_url)
```
## Mars Facts
```
# URL for facts about Mars
facts_url = "https://galaxyfacts-mars.com"
# Read html from url into variable
table = pd.read_html(facts_url)
# Create data frame from html data
facts_df = table[0]
# Convert first row to column headers
header_row = 0
facts_df.columns = facts_df.iloc[header_row]
facts_df = facts_df.drop(header_row)
# Rename first column
facts_df=facts_df.rename(columns = {'Mars - Earth Comparison':'Description'})
# Set index to first column
facts_df.set_index("Description", inplace = True)
# Convert dataframe to html
facts_table = facts_df.to_html()
# Remove new line code from table
facts_table = facts_table.replace("\n", " ")
# Create html file from dataframe:
facts_df.to_html("facts_html", index=False)
facts_df
```
## Mars Hemispheres
```
# URL for images of Mars hemispheres
hem_url = "https://marshemispheres.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(hem_url)
hem_html = browser.html
hem_soup = bs(hem_html, "html.parser")
# Search soup file for section containing hemisphere titles and html's for images
hem_find = hem_soup.find_all("div", class_ = "item")
# Setup for loop to pull the hemisphere titles from H3 header data
# For loop pulls html links for each hemisphere's page
# Image link from each hemisphere page is pulled
# Hemisphere title and image url are stored in a dictionary
hemisphere_image_urls = []
for item in hem_find:
title = item.find("h3").text
link = item.find("a", class_ = "itemLink")["href"]
hemi_url = hem_url + link
browser.visit(hemi_url)
hemi_url_html = browser.html
hemi_soup = bs(hemi_url_html, "html.parser")
img = hem_url + hemi_soup.find("img", class_ = "wide-image")["src"]
hemisphere_image_urls.append({"img_url": img, "title": title})
print(hemisphere_image_urls)
browser.quit()
```
|
github_jupyter
|
# Import modules for use in webscraping:
import pandas as pd
from bs4 import BeautifulSoup as bs
from splinter import Browser
from webdriver_manager.chrome import ChromeDriverManager
# Setup for working with Browser:
executable_path = {'executable_path': ChromeDriverManager().install()}
browser = Browser('chrome', **executable_path, headless=False)
# URL for news on Mars Mission
rps_url = "https://redplanetscience.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(rps_url)
rps_html = browser.html
rps_soup = bs(rps_html, "html.parser")
# Search parsed soup file for latest news title and snippet
news_title = rps_soup.find("div", class_="content_title").text
news_teaser = rps_soup.find("div", class_ = "article_teaser_body").text
print(news_title)
print(news_teaser)
# URL for JPL site housing image of Mars
jpl_url = "https://spaceimages-mars.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(jpl_url)
jpl_html = browser.html
jpl_soup = bs(jpl_html, "html.parser")
# Search parsed soup file for html containing Mars Featured Image
jpl_find = jpl_soup.find_all("div", class_="floating_text_area")
# Find image url within jpl_find
for item in jpl_find:
a = item.find("a")
href = a["href"]
# Establish variable to hold the image url
featured_image_url = jpl_url + href
print(featured_image_url)
# URL for facts about Mars
facts_url = "https://galaxyfacts-mars.com"
# Read html from url into variable
table = pd.read_html(facts_url)
# Create data frame from html data
facts_df = table[0]
# Convert first row to column headers
header_row = 0
facts_df.columns = facts_df.iloc[header_row]
facts_df = facts_df.drop(header_row)
# Rename first column
facts_df=facts_df.rename(columns = {'Mars - Earth Comparison':'Description'})
# Set index to first column
facts_df.set_index("Description", inplace = True)
# Convert dataframe to html
facts_table = facts_df.to_html()
# Remove new line code from table
facts_table = facts_table.replace("\n", " ")
# Create html file from dataframe:
facts_df.to_html("facts_html", index=False)
facts_df
# URL for images of Mars hemispheres
hem_url = "https://marshemispheres.com/"
# Use Browser to pull html data and use beautiful soup to parse the data
browser.visit(hem_url)
hem_html = browser.html
hem_soup = bs(hem_html, "html.parser")
# Search soup file for section containing hemisphere titles and html's for images
hem_find = hem_soup.find_all("div", class_ = "item")
# Setup for loop to pull the hemisphere titles from H3 header data
# For loop pulls html links for each hemisphere's page
# Image link from each hemisphere page is pulled
# Hemisphere title and image url are stored in a dictionary
hemisphere_image_urls = []
for item in hem_find:
title = item.find("h3").text
link = item.find("a", class_ = "itemLink")["href"]
hemi_url = hem_url + link
browser.visit(hemi_url)
hemi_url_html = browser.html
hemi_soup = bs(hemi_url_html, "html.parser")
img = hem_url + hemi_soup.find("img", class_ = "wide-image")["src"]
hemisphere_image_urls.append({"img_url": img, "title": title})
print(hemisphere_image_urls)
browser.quit()
| 0.26588 | 0.836154 |
# Part 5 - Intro to Encrypted Programs
Believe it or not, it is possible to compute with encrypted data. In other words, it's possible to run a program where **ALL of the variables** in the program are **encrypted**!
In this tutorial, we're going to walk through very basic tools of encrypted computation. In particular, we're going to focus on one popular approach called Secure Multi-Party Computation. In this lesson, we'll learn how to build an encrypted calculator which can perform calculations on encrypted numbers.
Authors:
- Andrew Trask - Twitter: [@iamtrask](https://twitter.com/iamtrask)
- Théo Ryffel - GitHub: [@LaRiffle](https://github.com/LaRiffle)
References:
- Morten Dahl - [Blog](https://mortendahl.github.io) - Twitter: [@mortendahlcs](https://twitter.com/mortendahlcs)
# Step 1: Encryption Using Secure Multi-Party Computation
SMPC is at first glance a rather strange form of "encryption". Instead of using a public/private key to encrypt a variable, each value is split into multiple `shares`, each of which operate like a private key. Typically, these `shares` will be distributed amongst 2 or more _owners_. Thus, in order to decrypt the variable, all owners must agree to allow the decryption. In essence, everyone has a private key.
### Encrypt()
So, let's say we wanted to "encrypt" a variable `x`, we could do so in the following way.
> Encryption doesn't use floats or real numbers but happens in a mathematical space called [integer quotient ring](http://mathworld.wolfram.com/QuotientRing.html) which is basically the integers between `0` and `Q-1`, where `Q` is prime and "big enough" so that the space can contain all the numbers that we use in our experiments. In practice, given a value `x` integer, we do `x % Q` to fit in the ring. (That's why we avoid using number `x' > Q`).
```
Q = 1234567891011
x = 25
import random
def encrypt(x):
share_a = random.randint(0,Q)
share_b = random.randint(0,Q)
share_c = (x - share_a - share_b) % Q
return (share_a, share_b, share_c)
encrypt(x)
```
As you can see here, we have split our variable `x` into 3 different shares, which could be sent to 3 different owners.
### Decrypt()
If we wanted to decrypt these 3 shares, we could simply sum them together and take the modulus of the result (mod Q)
```
def decrypt(*shares):
return sum(shares) % Q
a,b,c = encrypt(25)
decrypt(a, b, c)
```
Importantly, notice that if we try to decrypt with only two shares, the decryption does not work!
```
decrypt(a, b)
```
Thus, we need all of the owners to participate in order to decrypt the value. It is in this way that the `shares` act like private keys, all of which must be present in order to decrypt a value.
# Step 2: Basic Arithmetic Using SMPC
However, the truly extraordinary property of Secure Multi-Party Computation is the ability to perform computation **while the variables are still encrypted**. Let's demonstrate simple addition below.
```
x = encrypt(25)
y = encrypt(5)
def add(x, y):
z = list()
# the first worker adds their shares together
z.append((x[0] + y[0]) % Q)
# the second worker adds their shares together
z.append((x[1] + y[1]) % Q)
# the third worker adds their shares together
z.append((x[2] + y[2]) % Q)
return z
decrypt(*add(x,y))
```
### Success!!!
And there you have it! If each worker (separately) adds their shares together, then the resulting shares will decrypt to the correct value (25 + 5 == 30).
As it turns out, SMPC protocols exist which can allow this encrypted computation for the following operations:
- addition (which we've just seen)
- multiplication
- comparison
and using these basic underlying primitives, we can perform arbitrary computation!!!
In the next section, we're going to learn how to use the PySyft library to perform these operations!
# Step 3: SMPC Using PySyft
In the previous sections, we outlined some basic intuitions around SMPC is supposed to work. However, in practice we don't want to have to hand-write all of the primitive operations ourselves when writing our encrypted programs. So, in this section we're going to walk through the basics of how to do encrypted computation using PySyft. In particular, we're going to focus on how to do the 3 primitives previously mentioned: addition, multiplication, and comparison.
First, we need to create a few Virtual Workers (which hopefully you're now familiar with given our previous tutorials).
```
import torch
import syft as sy
hook = sy.TorchHook(torch)
bob = sy.VirtualWorker(hook, id="bob")
alice = sy.VirtualWorker(hook, id="alice")
bill = sy.VirtualWorker(hook, id="bill")
```
### Basic Encryption/Decryption
Encryption is as simple as taking any PySyft tensor and calling .share(). Decryption is as simple as calling .get() on the shared variable
```
x = torch.tensor([25])
encrypted_x = x.share(bob, alice, bill)
encrypted_x.get()
```
### Introspecting the Encrypted Values
If we look closer at Bob, Alice, and Bill's workers, we can see the shares that get created!
```
bob._objects
x = torch.tensor([25]).share(bob, alice, bill)
# Bob's share
bobs_share = list(bob._objects.values())[0]
bobs_share
# Alice's share
alices_share = list(alice._objects.values())[0]
alices_share
# Bill's share
bills_share = list(bill._objects.values())[0]
bills_share
```
And if we wanted to, we could decrypt these values using the SAME approach we talked about earlier!!!
```
Q = x.child.field
(bobs_share + alices_share + bills_share) % Q
```
As you can see, when we called `.share()` it simply split the value into 3 shares and sent one share to each of the parties!
# Encrypted Arithmetic
And now you see that we can perform arithmetic on the underlying values! The API is constructed so that we can simply perform arithmetic like we would normal PyTorch tensors.
```
x = torch.tensor([25]).share(bob,alice)
y = torch.tensor([5]).share(bob,alice)
z = x + y
z.get()
z = x - y
z.get()
# TODO: finish
# z = x * y
# z.get()
# TODO: finish
# z = x > y
# z.get()
# TODO: finish
# z = x < y
# z.get()
# TODO: finish
# z = x == y
# z.get()
# TODO: finish
# z = x == y + 20
# z.get()
```
# Congratulations!!! - Time to Join the Community!
Congratulations on completing this notebook tutorial! If you enjoyed this and would like to join the movement toward privacy preserving, decentralized ownership of AI and the AI supply chain (data), you can do so in the following ways!
### Star PySyft on GitHub
The easiest way to help our community is just by starring the Repos! This helps raise awareness of the cool tools we're building.
- [Star PySyft](https://github.com/OpenMined/PySyft)
### Join our Slack!
The best way to keep up to date on the latest advancements is to join our community! You can do so by filling out the form at [http://slack.openmined.org](http://slack.openmined.org)
### Join a Code Project!
The best way to contribute to our community is to become a code contributor! At any time you can go to PySyft GitHub Issues page and filter for "Projects". This will show you all the top level Tickets giving an overview of what projects you can join! If you don't want to join a project, but you would like to do a bit of coding, you can also look for more "one off" mini-projects by searching for GitHub issues marked "good first issue".
- [PySyft Projects](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3AProject)
- [Good First Issue Tickets](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
### Donate
If you don't have time to contribute to our codebase, but would still like to lend support, you can also become a Backer on our Open Collective. All donations go toward our web hosting and other community expenses such as hackathons and meetups!
[OpenMined's Open Collective Page](https://opencollective.com/openmined)
|
github_jupyter
|
Q = 1234567891011
x = 25
import random
def encrypt(x):
share_a = random.randint(0,Q)
share_b = random.randint(0,Q)
share_c = (x - share_a - share_b) % Q
return (share_a, share_b, share_c)
encrypt(x)
def decrypt(*shares):
return sum(shares) % Q
a,b,c = encrypt(25)
decrypt(a, b, c)
decrypt(a, b)
x = encrypt(25)
y = encrypt(5)
def add(x, y):
z = list()
# the first worker adds their shares together
z.append((x[0] + y[0]) % Q)
# the second worker adds their shares together
z.append((x[1] + y[1]) % Q)
# the third worker adds their shares together
z.append((x[2] + y[2]) % Q)
return z
decrypt(*add(x,y))
import torch
import syft as sy
hook = sy.TorchHook(torch)
bob = sy.VirtualWorker(hook, id="bob")
alice = sy.VirtualWorker(hook, id="alice")
bill = sy.VirtualWorker(hook, id="bill")
x = torch.tensor([25])
encrypted_x = x.share(bob, alice, bill)
encrypted_x.get()
bob._objects
x = torch.tensor([25]).share(bob, alice, bill)
# Bob's share
bobs_share = list(bob._objects.values())[0]
bobs_share
# Alice's share
alices_share = list(alice._objects.values())[0]
alices_share
# Bill's share
bills_share = list(bill._objects.values())[0]
bills_share
Q = x.child.field
(bobs_share + alices_share + bills_share) % Q
x = torch.tensor([25]).share(bob,alice)
y = torch.tensor([5]).share(bob,alice)
z = x + y
z.get()
z = x - y
z.get()
# TODO: finish
# z = x * y
# z.get()
# TODO: finish
# z = x > y
# z.get()
# TODO: finish
# z = x < y
# z.get()
# TODO: finish
# z = x == y
# z.get()
# TODO: finish
# z = x == y + 20
# z.get()
| 0.281702 | 0.990169 |
# 9. Operations with Pandas objects
```
import pandas as pd
import numpy as np
```
One of the great advantages of using Pandas to handle tabular data is how simple it is to extract valuable information from them. Here we are going to see various types of operations that are available for this.
## 9.1 Matrix types of operations
The strength of Numpy is its natural way of handling matrix operations, and Pandas reuses a lot of these features. For example one can use simple mathematical operations to operate at the cell level:
```
compo_pd = pd.read_excel('Data/composers.xlsx')
compo_pd
compo_pd['birth']*2
np.log(compo_pd['birth'])
```
Here we applied functions only to series. Indeed, since our Dataframe contains e.g. strings, no operation can be done on it:
```
#compo_pd+1
```
If however we have a homogenous Dataframe, this is possible:
```
compo_pd[['birth','death']]
compo_pd[['birth','death']]*2
```
## 9.2 Column operations
There are other types of functions whose purpose is to summarize the data. For example the mean or standard deviation. Pandas by default applies such functions column-wise and returns a series containing e.g. the mean of each column:
```
np.mean(compo_pd)
```
Note that columns for which a mean does not make sense, like the city are discarded.
A series of common functions like mean or standard deviation are directly implemented as methods and can be accessed in the alternative form:
```
compo_pd.describe()
compo_pd.std()
```
If you need the mean of only a single column you can of course chains operations:
```
compo_pd.birth.mean()
```
## 9.3 Operations between Series
We can also do computations with multiple series as we would do with Numpy arrays:
```
compo_pd['death']-compo_pd['birth']
```
We can even use the result of this computation to create a new column in our Dataframe:
```
compo_pd
compo_pd['age'] = compo_pd['death']-compo_pd['birth']
compo_pd
```
## 9.4 Other functions
Sometimes one needs to apply to a column a very specific function that is not provided by default. In that case we can use one of the different ```apply``` methods of Pandas.
The simplest case is to apply a function to a column, or Series of a DataFrame. Let's say for example that we want to define the the age >60 as 'old' and <60 as 'young'. We can define the following general function:
```
def define_age(x):
if x>60:
return 'old'
else:
return 'young'
define_age(30)
define_age(70)
```
We can now apply this function on an entire Series:
```
compo_pd.age.apply(define_age)
compo_pd.age.apply(lambda x: x**2)
```
And again, if we want, we can directly use this output to create a new column:
```
compo_pd['age_def'] = compo_pd.age.apply(define_age)
compo_pd
```
We can also apply a function to an entire DataFrame. For example we can ask how many composers have birth and death dates within the XIXth century:
```
def nineteen_century_count(x):
return np.sum((x>=1800)&(x<1900))
compo_pd[['birth','death']].apply(nineteen_century_count)
```
The function is applied column-wise and returns a single number for each in the form of a series.
```
def nineteen_century_true(x):
return (x>=1800)&(x<1900)
compo_pd[['birth','death']].apply(nineteen_century_true)
```
Here the operation is again applied column-wise but the output is a Series.
There are more combinations of what can be the in- and output of the apply function and in what order (column- or row-wise) they are applied that cannot be covered here.
## 9.5 Logical indexing
Just like with Numpy, it is possible to subselect parts of a Dataframe using logical indexing. Let's have a look again at an example:
```
compo_pd
```
If we use a logical comparison on a series, this yields a **logical Series**:
```
compo_pd['birth']
compo_pd['birth'] > 1859
```
Just like in Numpy we can use this logical Series as an index to select elements in the Dataframe:
```
log_indexer = compo_pd['birth'] > 1859
log_indexer
compo_pd
~log_indexer
compo_pd[~log_indexer]
```
We can also create more complex logical indexings:
```
(compo_pd['birth'] > 1859)&(compo_pd['age']>60)
compo_pd[(compo_pd['birth'] > 1859)&(compo_pd['age']>60)]
```
And we can create new arrays containing only these subselections:
```
compos_sub = compo_pd[compo_pd['birth'] > 1859]
compos_sub
```
We can then modify the new array:
```
compos_sub.loc[0,'birth'] = 3000
```
Note that we get this SettingWithCopyWarning warning. This is a very common problem hand has to do with how new arrays are created when making subselections. Simply stated, did we create an entirely new array or a "view" of the old one? This will be very case-dependent and to avoid this, if we want to create a new array we can just enforce it using the ```copy()``` method (for more information on the topic see for example this [explanation](https://www.dataquest.io/blog/settingwithcopywarning/):
```
compos_sub2 = compo_pd[compo_pd['birth'] > 1859].copy()
compos_sub2.loc[0,'birth'] = 3000
compos_sub2
```
|
github_jupyter
|
import pandas as pd
import numpy as np
compo_pd = pd.read_excel('Data/composers.xlsx')
compo_pd
compo_pd['birth']*2
np.log(compo_pd['birth'])
#compo_pd+1
compo_pd[['birth','death']]
compo_pd[['birth','death']]*2
np.mean(compo_pd)
compo_pd.describe()
compo_pd.std()
compo_pd.birth.mean()
compo_pd['death']-compo_pd['birth']
compo_pd
compo_pd['age'] = compo_pd['death']-compo_pd['birth']
compo_pd
def define_age(x):
if x>60:
return 'old'
else:
return 'young'
define_age(30)
define_age(70)
compo_pd.age.apply(define_age)
compo_pd.age.apply(lambda x: x**2)
compo_pd['age_def'] = compo_pd.age.apply(define_age)
compo_pd
def nineteen_century_count(x):
return np.sum((x>=1800)&(x<1900))
compo_pd[['birth','death']].apply(nineteen_century_count)
def nineteen_century_true(x):
return (x>=1800)&(x<1900)
compo_pd[['birth','death']].apply(nineteen_century_true)
compo_pd
compo_pd['birth']
compo_pd['birth'] > 1859
log_indexer = compo_pd['birth'] > 1859
log_indexer
compo_pd
~log_indexer
compo_pd[~log_indexer]
(compo_pd['birth'] > 1859)&(compo_pd['age']>60)
compo_pd[(compo_pd['birth'] > 1859)&(compo_pd['age']>60)]
compos_sub = compo_pd[compo_pd['birth'] > 1859]
compos_sub
compos_sub.loc[0,'birth'] = 3000
compos_sub2 = compo_pd[compo_pd['birth'] > 1859].copy()
compos_sub2.loc[0,'birth'] = 3000
compos_sub2
| 0.134151 | 0.989066 |
# "COVID-19 Recovery Scores"
> "See the progression of COVID-19 and understand the state of recovery in a single glance"
- toc: false
- branch: master
- badges: false
- hide_binder_badge: true
- comments: false
- categories: [fastpages, jupyter]
- hide: false
- search_exclude: true
## The following Recovery Scores show the progression of fatalities due to COVID-19 for countries with more than 200 deaths to date.
They're based on the rate of change of fatalities. As the rate of fatalities increases or decreases, it supplies evidence that can help us compute the position of the recovery.
## The vertical axis represents the magnitude of the fatalities.
## The horizontal axis represents the progression of time.
There are a lot of assumptions that went into making these models. Populations change very dynamically. For that reason, these are only estimates of the actual progression. For the countries with many fatailties, they are a good approximation of the recoveries of each country.
References:
- https://towardsdatascience.com/modeling-exponential-growth-49a2b6f22e1f
- https://towardsdatascience.com/modeling-logistic-growth-1367dc971de2
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5348083/
- https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series
- Us-Only Data: https://github.com/nytimes/covid-19-data
```
#hide_input
%matplotlib inline
import pandas as pd
import numpy as np
from csaps import csaps
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
import matplotlib.patches as patches
#hide_input
# dfconf = pd.read_csv("https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv")
# dfrcvd = pd.read_csv("https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv")
dfdied = pd.read_csv("https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv")
#hide_input
def logistic(t, a, b, c):
return c/(1 + a * np.exp(-b*t))
def smoother(df_in, col="Deaths", smooth_amount=0.2):
y = df_in[col]
x = y.index
fit_x = np.arange(len(y))
fit_y = csaps(fit_x, y, fit_x, smooth=smooth_amount)
# Add to dataframe and save
temp = pd.DataFrame(index=x)
temp['Smoother'] = fit_y.astype(int)
return df_in.join(temp, how="left")
def local_max(data, thresh=None, x=[], min_peak_separation=None):
'''Find local maxima
Input:
data - Amplitude data for peak searching
thresh - Finds peaks in data ABOVE this level
x - x-axis data, or []
dx - Minimum x-axis peak separation, or []
plots - 1 = plots, 0 = no plots (optional)
Output:
mxInds - Indices of maxima
mxVals - Amplitudes of correspondin maxima
Notes:
1. When dx = [], or omitted, ALL peaks above threshold will be found.
2. When the x = [], or omitted, equispaced data are assumed
# Example
data = np.array([1,2,3,4,5,4,3,4,5,4,3,2,1])
x = np.arange(len(data))
x[3] = x[3] = x[2]
min_peak_separation = 2
print(local_max(data, min_peak_separation=2, x=x))
>>> ([4, 8], [5, 5])
'''
y = data.copy()
if thresh != None:
y[y < thresh] = -1e-50
dy = np.diff(y)
d2y = np.diff(dy)
# Find the maxima
dyChSign = [int(x) for x in (dy <= 0)] # Find where dy changes sign
temp1 = np.diff(dyChSign) # Find where dy changes sign form pos to neg
mxInds = np.intersect1d(np.where(temp1 > 0), np.where(d2y < 0)) + 1; # +1 accounts for the diff
mxVals = y[mxInds]
if min_peak_separation is not None:
if len(x) == 0:
xMaxVals = mxInds
else:
xMaxVals = x[mxInds]
df = np.diff(xMaxVals);
fd = np.where(np.abs(df) > min_peak_separation)[0]; # find large separations --> next sh2 region
intervals = len(fd)+1; # Number of regions
inds = [-1] + list(fd) + [len(mxInds)-1]; # Set up indices of intervals
pkVals2 = []
pkInds2 = []
for i in range(intervals):
indx = np.arange(inds[i]+1, inds[i+1]+1); # The intervals in Times y array
windLo = mxInds[indx[0]];
windHi = mxInds[indx[-1]]; # Window the intervals
temp = y[windLo:windHi+1]
d1 = max(temp)
d2 = np.argmax(temp) # Take max in interval
pkVals2.append(d1)
pkInds2.append(windLo + d2);
mxInds = pkInds2;
mxVals = pkVals2;
return mxInds, mxVals
#hide_input
def plot_status(fraction_to_midpoint, title_text='', plot_size=(8, 4)):
n_pts = 200
ylim_bounds = 7
x = np.linspace(-ylim_bounds, ylim_bounds, n_pts)
y = logistic(x, 1, 1, 1)
dx = np.diff(y, prepend = 0)
d2x = np.diff(dx, prepend = 0)
maxInds, maxVals = local_max(d2x, min_peak_separation=100)
maxInds2, maxVals2 = local_max(-d2x, min_peak_separation=100)
fig = plt.figure(figsize=plot_size)
ax = fig.add_subplot(111)
# Plot Logistic
ax.plot(x, y, '#cdcdcd', lw=10)
ax2 = ax.twinx()
# ax2.plot(x, dx, 'orange', alpha=1)
# ax2.plot(x, d2x, 'blue', alpha=1)
# ax2.axhline(y=0, color='w', linestyle='-', alpha=0.2)
pt_A = x[maxInds[0]-2]
pt_B = x[maxInds2[0]-1]
ax.vlines(0, ymin=0, ymax=1, linewidth=1, color='gray', alpha=0.2)
# ax.vlines(pt_A, ymin=0, ymax=1, linewidth=2, color='r')
# ax.vlines(pt_B, ymin=0, ymax=1, linewidth=2, color='r')
active_point = pt_A + np.abs(pt_A)*fraction_to_midpoint
active_x = x[x <= active_point]
active_y = y[:len(active_x)]
# Plot logistic progress
ax.plot(active_x, active_y, 'b', lw=8)
# ax.vlines(active_point, ymin=0, ymax=1, linewidth=2, color='r')
# Plot rectangle colors
red = '#e03531'
yellow = '#f0bd27'
green = '#51b364'
alpha = 0.65
rect_1 = patches.Rectangle((-ylim_bounds, 0), pt_A - -ylim_bounds, 1, color=red, alpha=alpha)
rect_2 = patches.Rectangle((pt_A, 0), -2*pt_A, 1, color=yellow, alpha=alpha)
rect_3 = patches.Rectangle((pt_A-2*pt_A, 0), pt_A - -ylim_bounds, 1, color=green, alpha=alpha)
ax.add_patch(rect_1)
ax.add_patch(rect_2)
ax.add_patch(rect_3)
plt.xlim([-ylim_bounds, ylim_bounds])
plt.ylim([0, 1])
ax.axis('off')
ax2.axis('off')
plt.title(title_text, weight='bold', fontsize=14)
txt="Slow Start"
y_point = 0.05
plt.figtext(.28, y_point, txt, wrap=True, horizontalalignment='center', fontsize=14)
txt="Fast Growth"
plt.figtext(.51, y_point, txt, wrap=True, horizontalalignment='center', fontsize=14)
txt="Flattening"
plt.figtext(.71, y_point, txt, wrap=True, horizontalalignment='left', fontsize=14)
# txt="Time -->"
# plt.figtext(.51, -0.05, txt, wrap=True, horizontalalignment='center', fontsize=14)
txt="Deaths -->"
plt.figtext(.115, 0.5, txt, wrap=True, horizontalalignment='center', fontsize=14, rotation=90)
plt.show()
def find_fraction_to_midpoint(data):
"""
# If there's a max:
# 1. Find last zero of neg before max if a max exists
# 2. Find max
# 3. Find any non-positive value after max
"""
data[data < 0] = 0 # No need for negative values
# Find maxima
maxInds, maxVals = local_max(data, min_peak_separation=100)
if maxInds != []:
# Did it cross zero on the right yet?
# Find first zero-crossing (if any) beyond maxInds
delta_to_pt_B = np.where(data[maxInds[0]:] <= 0)[0]
if len(delta_to_pt_B):
pts_to_end = (len(data) - (delta_to_pt_B[0] + maxInds[0]))
# Percentage of mid-region
fraction_to_midpoint = 1 + pts_to_end / delta_to_pt_B[0]
else:
# Find early zero crossing
idx_last_early_zero = np.where(data == 0)[0][-1]
# Inds from last early zero to point A
inds_to_A = maxInds[0] - idx_last_early_zero
days_beyond_pt_A = len(data) - maxInds[0]
fraction_to_midpoint = days_beyond_pt_A / inds_to_A
return fraction_to_midpoint
def plot_slopes(d, country, offset=40, plot_size=(8, 3)):
fig = plt.figure(figsize=plot_size)
ax = fig.add_subplot(111)
d[offset:].Smoother.plot(ax=ax, color='red', lw=5, alpha=1)
plt.legend(loc=2)
ax2 = ax.twinx()
d[offset:].dx.plot(ax=ax2, color='orange', lw=4, alpha=0.8)
d[offset:].d2x.plot(ax=ax2, color='blue', lw=2, alpha=0.7)
maxInds, maxVals = local_max(d[offset:].d2x.values, min_peak_separation=100)
d[offset:].d2x[maxInds].plot(ax=ax2, marker='o', ms=12)
ax2.axhline(y=0, color='g', linestyle='--')
ax2.set_ylabel('Number of Deaths')
ax2.set_ylabel('Number of New Deaths Per Day')
plt.legend(loc=9)
plt.title(country)
plt.show();
NON_DATE_COLS = ["Province/State", "Country/Region", "Lat", "Long", "Country"]
def prepare_data(df):
date_cols = [c for c in df.columns if c not in NON_DATE_COLS]
# Collapse by country in the case where there are multiple
# regions in a country
df_plot = dfdied.groupby(by="Country/Region").sum()
# Sort to position highest numberss first
df_plot.sort_values(by=date_cols[-1], inplace=True, ascending=False)
threshold_for_total_events = 200
df_plot = df_plot[df_plot[date_cols[-1]] > threshold_for_total_events].reset_index()#[date_cols]
df_plot = df_plot.rename(columns={"Country/Region": "Country"})[["Country"] + date_cols]
return df_plot
def make_dervatives(df, country):
date_cols = [c for c in df.columns if c not in NON_DATE_COLS]
data = df[df.Country == country][date_cols].T
data.index = pd.to_datetime(data.index)
d = pd.DataFrame(index=pd.to_datetime(pd.date_range(data.index.values[0], periods=len(data)+7, freq='d').strftime('%m/%d/%Y')))
d = d.join(data)
d.columns = ['Deaths']
# Add new column, "Smoother", to dataframe
d = smoother(d.loc[d['Deaths'].notnull()], smooth_amount=.26)
d['Smoother'] = d.Smoother.round().astype(int)
d['dx'] = np.diff(d.Smoother, prepend=d.Deaths[0])
d['d2x'] = np.diff(d.dx, prepend=d.Smoother[0])
return d
#hide_input
# Create the data
df = prepare_data(dfdied)
dfd = make_dervatives(df, 'Italy')
countries = df.Country.values
last_date = dfd.tail(1).columns[-1]
country_data = {}
for country in countries:
country_data[country] = {}
dfd = make_dervatives(df, country)
country_data[country]['deaths'] = int(dfd.Deaths[-1])
country_data[country]['date'] = str(dfd.index[-1])[:10]
country_data[country]['fraction_to_midpoint'] = np.round(find_fraction_to_midpoint(dfd.d2x.values), 3)
#hide_input
plot_size=(8, 3)
for country in country_data:
title_text = "{:}\nTotal Deaths: {:,} as of {:}".format(
country, country_data[country]['deaths'], country_data[country]['date'])
fraction_to_midpoint = country_data[country]['fraction_to_midpoint']
plot_status(fraction_to_midpoint, title_text, plot_size=plot_size)
# Show the slope plots for verification/investigation
# plot_slopes(make_dervatives(df, country), country)
```
|
github_jupyter
|
#hide_input
%matplotlib inline
import pandas as pd
import numpy as np
from csaps import csaps
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
import matplotlib.patches as patches
#hide_input
# dfconf = pd.read_csv("https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv")
# dfrcvd = pd.read_csv("https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv")
dfdied = pd.read_csv("https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv")
#hide_input
def logistic(t, a, b, c):
return c/(1 + a * np.exp(-b*t))
def smoother(df_in, col="Deaths", smooth_amount=0.2):
y = df_in[col]
x = y.index
fit_x = np.arange(len(y))
fit_y = csaps(fit_x, y, fit_x, smooth=smooth_amount)
# Add to dataframe and save
temp = pd.DataFrame(index=x)
temp['Smoother'] = fit_y.astype(int)
return df_in.join(temp, how="left")
def local_max(data, thresh=None, x=[], min_peak_separation=None):
'''Find local maxima
Input:
data - Amplitude data for peak searching
thresh - Finds peaks in data ABOVE this level
x - x-axis data, or []
dx - Minimum x-axis peak separation, or []
plots - 1 = plots, 0 = no plots (optional)
Output:
mxInds - Indices of maxima
mxVals - Amplitudes of correspondin maxima
Notes:
1. When dx = [], or omitted, ALL peaks above threshold will be found.
2. When the x = [], or omitted, equispaced data are assumed
# Example
data = np.array([1,2,3,4,5,4,3,4,5,4,3,2,1])
x = np.arange(len(data))
x[3] = x[3] = x[2]
min_peak_separation = 2
print(local_max(data, min_peak_separation=2, x=x))
>>> ([4, 8], [5, 5])
'''
y = data.copy()
if thresh != None:
y[y < thresh] = -1e-50
dy = np.diff(y)
d2y = np.diff(dy)
# Find the maxima
dyChSign = [int(x) for x in (dy <= 0)] # Find where dy changes sign
temp1 = np.diff(dyChSign) # Find where dy changes sign form pos to neg
mxInds = np.intersect1d(np.where(temp1 > 0), np.where(d2y < 0)) + 1; # +1 accounts for the diff
mxVals = y[mxInds]
if min_peak_separation is not None:
if len(x) == 0:
xMaxVals = mxInds
else:
xMaxVals = x[mxInds]
df = np.diff(xMaxVals);
fd = np.where(np.abs(df) > min_peak_separation)[0]; # find large separations --> next sh2 region
intervals = len(fd)+1; # Number of regions
inds = [-1] + list(fd) + [len(mxInds)-1]; # Set up indices of intervals
pkVals2 = []
pkInds2 = []
for i in range(intervals):
indx = np.arange(inds[i]+1, inds[i+1]+1); # The intervals in Times y array
windLo = mxInds[indx[0]];
windHi = mxInds[indx[-1]]; # Window the intervals
temp = y[windLo:windHi+1]
d1 = max(temp)
d2 = np.argmax(temp) # Take max in interval
pkVals2.append(d1)
pkInds2.append(windLo + d2);
mxInds = pkInds2;
mxVals = pkVals2;
return mxInds, mxVals
#hide_input
def plot_status(fraction_to_midpoint, title_text='', plot_size=(8, 4)):
n_pts = 200
ylim_bounds = 7
x = np.linspace(-ylim_bounds, ylim_bounds, n_pts)
y = logistic(x, 1, 1, 1)
dx = np.diff(y, prepend = 0)
d2x = np.diff(dx, prepend = 0)
maxInds, maxVals = local_max(d2x, min_peak_separation=100)
maxInds2, maxVals2 = local_max(-d2x, min_peak_separation=100)
fig = plt.figure(figsize=plot_size)
ax = fig.add_subplot(111)
# Plot Logistic
ax.plot(x, y, '#cdcdcd', lw=10)
ax2 = ax.twinx()
# ax2.plot(x, dx, 'orange', alpha=1)
# ax2.plot(x, d2x, 'blue', alpha=1)
# ax2.axhline(y=0, color='w', linestyle='-', alpha=0.2)
pt_A = x[maxInds[0]-2]
pt_B = x[maxInds2[0]-1]
ax.vlines(0, ymin=0, ymax=1, linewidth=1, color='gray', alpha=0.2)
# ax.vlines(pt_A, ymin=0, ymax=1, linewidth=2, color='r')
# ax.vlines(pt_B, ymin=0, ymax=1, linewidth=2, color='r')
active_point = pt_A + np.abs(pt_A)*fraction_to_midpoint
active_x = x[x <= active_point]
active_y = y[:len(active_x)]
# Plot logistic progress
ax.plot(active_x, active_y, 'b', lw=8)
# ax.vlines(active_point, ymin=0, ymax=1, linewidth=2, color='r')
# Plot rectangle colors
red = '#e03531'
yellow = '#f0bd27'
green = '#51b364'
alpha = 0.65
rect_1 = patches.Rectangle((-ylim_bounds, 0), pt_A - -ylim_bounds, 1, color=red, alpha=alpha)
rect_2 = patches.Rectangle((pt_A, 0), -2*pt_A, 1, color=yellow, alpha=alpha)
rect_3 = patches.Rectangle((pt_A-2*pt_A, 0), pt_A - -ylim_bounds, 1, color=green, alpha=alpha)
ax.add_patch(rect_1)
ax.add_patch(rect_2)
ax.add_patch(rect_3)
plt.xlim([-ylim_bounds, ylim_bounds])
plt.ylim([0, 1])
ax.axis('off')
ax2.axis('off')
plt.title(title_text, weight='bold', fontsize=14)
txt="Slow Start"
y_point = 0.05
plt.figtext(.28, y_point, txt, wrap=True, horizontalalignment='center', fontsize=14)
txt="Fast Growth"
plt.figtext(.51, y_point, txt, wrap=True, horizontalalignment='center', fontsize=14)
txt="Flattening"
plt.figtext(.71, y_point, txt, wrap=True, horizontalalignment='left', fontsize=14)
# txt="Time -->"
# plt.figtext(.51, -0.05, txt, wrap=True, horizontalalignment='center', fontsize=14)
txt="Deaths -->"
plt.figtext(.115, 0.5, txt, wrap=True, horizontalalignment='center', fontsize=14, rotation=90)
plt.show()
def find_fraction_to_midpoint(data):
"""
# If there's a max:
# 1. Find last zero of neg before max if a max exists
# 2. Find max
# 3. Find any non-positive value after max
"""
data[data < 0] = 0 # No need for negative values
# Find maxima
maxInds, maxVals = local_max(data, min_peak_separation=100)
if maxInds != []:
# Did it cross zero on the right yet?
# Find first zero-crossing (if any) beyond maxInds
delta_to_pt_B = np.where(data[maxInds[0]:] <= 0)[0]
if len(delta_to_pt_B):
pts_to_end = (len(data) - (delta_to_pt_B[0] + maxInds[0]))
# Percentage of mid-region
fraction_to_midpoint = 1 + pts_to_end / delta_to_pt_B[0]
else:
# Find early zero crossing
idx_last_early_zero = np.where(data == 0)[0][-1]
# Inds from last early zero to point A
inds_to_A = maxInds[0] - idx_last_early_zero
days_beyond_pt_A = len(data) - maxInds[0]
fraction_to_midpoint = days_beyond_pt_A / inds_to_A
return fraction_to_midpoint
def plot_slopes(d, country, offset=40, plot_size=(8, 3)):
fig = plt.figure(figsize=plot_size)
ax = fig.add_subplot(111)
d[offset:].Smoother.plot(ax=ax, color='red', lw=5, alpha=1)
plt.legend(loc=2)
ax2 = ax.twinx()
d[offset:].dx.plot(ax=ax2, color='orange', lw=4, alpha=0.8)
d[offset:].d2x.plot(ax=ax2, color='blue', lw=2, alpha=0.7)
maxInds, maxVals = local_max(d[offset:].d2x.values, min_peak_separation=100)
d[offset:].d2x[maxInds].plot(ax=ax2, marker='o', ms=12)
ax2.axhline(y=0, color='g', linestyle='--')
ax2.set_ylabel('Number of Deaths')
ax2.set_ylabel('Number of New Deaths Per Day')
plt.legend(loc=9)
plt.title(country)
plt.show();
NON_DATE_COLS = ["Province/State", "Country/Region", "Lat", "Long", "Country"]
def prepare_data(df):
date_cols = [c for c in df.columns if c not in NON_DATE_COLS]
# Collapse by country in the case where there are multiple
# regions in a country
df_plot = dfdied.groupby(by="Country/Region").sum()
# Sort to position highest numberss first
df_plot.sort_values(by=date_cols[-1], inplace=True, ascending=False)
threshold_for_total_events = 200
df_plot = df_plot[df_plot[date_cols[-1]] > threshold_for_total_events].reset_index()#[date_cols]
df_plot = df_plot.rename(columns={"Country/Region": "Country"})[["Country"] + date_cols]
return df_plot
def make_dervatives(df, country):
date_cols = [c for c in df.columns if c not in NON_DATE_COLS]
data = df[df.Country == country][date_cols].T
data.index = pd.to_datetime(data.index)
d = pd.DataFrame(index=pd.to_datetime(pd.date_range(data.index.values[0], periods=len(data)+7, freq='d').strftime('%m/%d/%Y')))
d = d.join(data)
d.columns = ['Deaths']
# Add new column, "Smoother", to dataframe
d = smoother(d.loc[d['Deaths'].notnull()], smooth_amount=.26)
d['Smoother'] = d.Smoother.round().astype(int)
d['dx'] = np.diff(d.Smoother, prepend=d.Deaths[0])
d['d2x'] = np.diff(d.dx, prepend=d.Smoother[0])
return d
#hide_input
# Create the data
df = prepare_data(dfdied)
dfd = make_dervatives(df, 'Italy')
countries = df.Country.values
last_date = dfd.tail(1).columns[-1]
country_data = {}
for country in countries:
country_data[country] = {}
dfd = make_dervatives(df, country)
country_data[country]['deaths'] = int(dfd.Deaths[-1])
country_data[country]['date'] = str(dfd.index[-1])[:10]
country_data[country]['fraction_to_midpoint'] = np.round(find_fraction_to_midpoint(dfd.d2x.values), 3)
#hide_input
plot_size=(8, 3)
for country in country_data:
title_text = "{:}\nTotal Deaths: {:,} as of {:}".format(
country, country_data[country]['deaths'], country_data[country]['date'])
fraction_to_midpoint = country_data[country]['fraction_to_midpoint']
plot_status(fraction_to_midpoint, title_text, plot_size=plot_size)
# Show the slope plots for verification/investigation
# plot_slopes(make_dervatives(df, country), country)
| 0.540924 | 0.82176 |
This article is a continuation of [this previous post](https://www.python-graph-gallery.com/custom-legend-with-matplotlib) on how to customize Matplotlib legends.
## Problem
For various reasons you may want to add a legend with handles that consist of squares or rectangles. For some plots, such as the ones obtained with `plt.fill_between()` the legend handle is going to be a rectangle by default (see [this example](https://www.python-graph-gallery.com/area-fill-between-two-lines-in-matplotlib)).
However, for other types of charts, you will have to build them up from scratch.
## Example
Let's see this problem live with a scatterplot:
```
import palmerpenguins
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Patch
```
Load the data:
```
penguins = palmerpenguins.load_penguins().dropna()
FLIPPER_LENGTH = penguins["flipper_length_mm"].values
BILL_LENGTH = penguins["bill_length_mm"].values
SPECIES = penguins["species"].values
SPECIES_ = np.unique(SPECIES)
COLORS = ["#1B9E77", "#D95F02", "#7570B3"]
```
The following code is extracted from the mentioned post on custom legends. Let's see what is the default legend we get for a scatterplot
```
fig, ax = plt.subplots(figsize=(9, 6))
for species, color in zip(SPECIES_, COLORS):
idxs = np.where(SPECIES == species)
ax.scatter(
FLIPPER_LENGTH[idxs], BILL_LENGTH[idxs], label=species,
s=50, color=color, alpha=0.7
)
legend = ax.legend();
```
Here we are, a scatterplot with circles used in the legend. How to use rectangles instead?
## Using rectangles in legend
Let's see how we can override this default behavior and use a rectangle instead. The following function is created to make it simpler to replicate the same plot several times.
```
def scatterplot():
fig, ax = plt.subplots(figsize=(9, 6))
for species, color in zip(SPECIES_, COLORS):
idxs = np.where(SPECIES == species)
ax.scatter(
FLIPPER_LENGTH[idxs], BILL_LENGTH[idxs],
s=50, color=color, alpha=0.7
)
return fig, ax
```
Let's generate the chart and create the handles for the legend. This is as simple as using `matplotlib.patches.Patch`.
```
fig, ax = scatterplot()
handles = [
Patch(facecolor=color, label=label)
for label, color in zip(SPECIES_, COLORS)
]
ax.legend(handles=handles);
```
## Customizing the rectangle
It's also possible to remove the fill and just leave the color of the borders.
```
fig, ax = scatterplot()
handles = [
Patch(edgecolor=color, label=label, fill=False)
for label, color in zip(SPECIES_, COLORS)
]
ax.legend(handles=handles);
```
Or use one color for the fill, and another for the border:
```
fig, ax = scatterplot()
handles = [
Patch(facecolor=color, edgecolor="k", label=label)
for label, color in zip(SPECIES_, COLORS)
]
ax.legend(handles=handles);
```
And if you want to make them squared, you only need to set both `handlelength` and `handleheight` to the same value when creating the legend.
```
fig, ax = scatterplot()
handles = [
Patch(facecolor=color, edgecolor="k", label=label, alpha=0.7)
for label, color in zip(SPECIES_, COLORS)
]
legend = ax.legend(handles=handles, handlelength=1.4, handleheight=1.4);
```
<!-- ## Using FancyBboxPatch and BoxStyle
Some differences worth remark:
* The first three arguments are `xy`, `width` and `height`. These are not too important here because they're used for the legend. But they are relevant when including the `FancyBboxPatch` within the plot region.
* The edge has a black color by default, which is not the case with `Patch`.
Let's make the borders rounded:
TURNS OUT IT'S NOT POSSIBLE TO MAKE THEM ROUNDED -->
|
github_jupyter
|
import palmerpenguins
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Patch
penguins = palmerpenguins.load_penguins().dropna()
FLIPPER_LENGTH = penguins["flipper_length_mm"].values
BILL_LENGTH = penguins["bill_length_mm"].values
SPECIES = penguins["species"].values
SPECIES_ = np.unique(SPECIES)
COLORS = ["#1B9E77", "#D95F02", "#7570B3"]
fig, ax = plt.subplots(figsize=(9, 6))
for species, color in zip(SPECIES_, COLORS):
idxs = np.where(SPECIES == species)
ax.scatter(
FLIPPER_LENGTH[idxs], BILL_LENGTH[idxs], label=species,
s=50, color=color, alpha=0.7
)
legend = ax.legend();
def scatterplot():
fig, ax = plt.subplots(figsize=(9, 6))
for species, color in zip(SPECIES_, COLORS):
idxs = np.where(SPECIES == species)
ax.scatter(
FLIPPER_LENGTH[idxs], BILL_LENGTH[idxs],
s=50, color=color, alpha=0.7
)
return fig, ax
fig, ax = scatterplot()
handles = [
Patch(facecolor=color, label=label)
for label, color in zip(SPECIES_, COLORS)
]
ax.legend(handles=handles);
fig, ax = scatterplot()
handles = [
Patch(edgecolor=color, label=label, fill=False)
for label, color in zip(SPECIES_, COLORS)
]
ax.legend(handles=handles);
fig, ax = scatterplot()
handles = [
Patch(facecolor=color, edgecolor="k", label=label)
for label, color in zip(SPECIES_, COLORS)
]
ax.legend(handles=handles);
fig, ax = scatterplot()
handles = [
Patch(facecolor=color, edgecolor="k", label=label, alpha=0.7)
for label, color in zip(SPECIES_, COLORS)
]
legend = ax.legend(handles=handles, handlelength=1.4, handleheight=1.4);
| 0.586049 | 0.983455 |
# Лекция 14. Тензоры и тензорные разложения
## На прошлой лекции
- Матричные функции
- Алгоритм Шура-Парлетта
- Аппроксимация Паде
- Крыловские методы для вычисления действия матричной экспоненты на вектор
- Матричные уравнения: уравнение Сильвестра и уравнение Ляпунова
## План на сегодня
- Тензоры
- Тензорные разложения
- Приложения тензорных разложений
## Тензоры
Будем называть тензором многомерный массив:
$$
A(i_1, \dots, i_d), \quad 1\leq i_k\leq n_k,
$$
где $d$ называется размерностью, а $n_k$ количеством мод.
Это стандартное определение в сообществе прикладных математиков, более подробно смотрите в [[1]](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.153.2059&rep=rep1&type=pdf), [[2]](http://arxiv.org/pdf/1302.7121.pdf) и [[3]](http://epubs.siam.org/doi/abs/10.1137/090752286).
* $d=2$ (матрицы) $\Rightarrow$ классическая теория (SVD, LU, QR, $\dots$)
* $d\geq 3$ (тензоры) $\Rightarrow$ в стадии разработки. Обобщение стандартных результатов для матриц не является **прямолинейным**.
<img src="./tensor_dogs.png">
Изображение из [этой презентации](http://users.cecs.anu.edu.au/~koniusz/tensors-cvpr17/present/anandkumar_anima_tmcv2017.pdf)
## Более формальное определение
- Тензор - это мультилинейная форма.
- Когда вы фиксируете базис, то получаете $d$-мерный массив.
## Проклятие размерности
Проблема в работе с многомерными данными в том, что число параметров растёт <font color='red'> экспоненциально </font> с ростом $d$:
$$
\text{storage} = n^d.
$$
Например, для $n=2$ и $d=500$
$$
n^d = 2^{500} \gg 10^{83} - \text{ число атомов во вселенной}
$$
- Почему нас это волнует? Кажется, что мы живём в трёхмерном мире :)
## Приложения
#### Квантовая химия
Стационарное уравнение Шрёдингера для системы с $N_{el}$ электронами
$$
\hat H \Psi = E \Psi,
$$
где
$$
\Psi = \Psi(\{{\bf r_1},\sigma_1\},\dots, \{{\bf r_{N_{el}}},\sigma_{N_{el}}\})
$$
3$N_{el}$ пространственных переменных и $N_{el}$ спиновых переменных.
<img src="./large_mol.jpg" width=600>
* Создание новых матриеалов и лекарств
* Предсказание результатов физических экспериментов
#### Работа в условиях неопределённости (uncertainty quantification)
Пример: моделирование нефтяного месторождения. Модель может зависеть от параметров $p_1,\dots,p_d$ (измеренных в эксперименте, например температуре, пористость), известными неточно
$$
u = u(t,{\bf r},\,{p_1,\dots,p_d})
$$
#### И многие другие
* Обработка сигналов
* Рекомендательные системы: [обзор](https://arxiv.org/pdf/1603.06038.pdf)
* Нейронные сети: сжатие слоёв с использования тензорных разложений (например [статья 1](https://arxiv.org/pdf/1412.6553) и [статья 2](https://papers.nips.cc/paper/2015/file/6855456e2fe46a9d49d3d3af4f57443d-Paper.pdf))
* Языковые модели
* Финансовая математика
* ...
## Как работать с большим числом размерностей?
- **Монте-Карло**: класс методов, основанный на сэмплировании. Есть проблемы со сходимостью
- **Разреженные сетки**: специальный тип сеток с малым количеством параметров. Сильные условия регулярности
- **Лучшая аппроксимация N слагаемыми** : разреженное представление в заданном базисе.
- Подход <font color='red'>**тензорных разложений** </font>
## Тензорные разложения
## 2D
Скелетное разложение:
$$ A = UV^T $$
или поэлементно:
$$ a_{ij} = \sum_{\alpha=1}^r u_{i\alpha} v_{j\alpha} $$
приводит нас к идее **разделения переменных**
**Свойства:**
* Неединственно: $A = U V^T = UBB^{-1}V^T = \tilde U \tilde V^T$
* Может бысть вычислена устойчиво с помощью **SVD**
## Каноническое разложение
Наиболее прямолинейное обобщение идеи разделения переменных на несколько размерностей - это **каноническое разложение**: (альтернативные названия CP/CANDECOMP/PARAFAC)
$$
a_{ijk} = \sum_{\alpha=1}^r u_{i\alpha} v_{j\alpha} w_{k\alpha},
$$
минимально возможное $r$ называется **каноническим рангом**. Матрицы $U$, $V$ и $W$ называются **каноническими факторами**. Это разложение было предложено в 1927 Hitchcock'ом, [link](https://onlinelibrary.wiley.com/doi/abs/10.1002/sapm192761164).
### Свойства:
* Память: для $d$-мерного тензора требуется хранить $nrd$ элементов
* Единственно при условии несильных ограничений
* Множество тензоров ранга $\leq r$ не замкнуто (в отличии от матриц): <br>
$a_{ijk} = i+j+k$, $\text{rank}(A) = 3$, но
$$a^\epsilon_{ijk} = \frac{(1+\epsilon i)(1+\epsilon j)(1+\epsilon k) - 1}{\epsilon}\to i+j+k=a_{ijk},\quad \epsilon\to 0 $$
и $\text{rank}(A^{\epsilon}) = 2$
* Отсутствует устойчивый алгоритм для вычисления наилучшей аппроксимации ранга $r$
### Алгоритм попеременных наименьших квадратов
0. Инициализировать $U,V,W$
1. Фиксировать $V,W$, решить задачу наименьших квадратов для $U$
2. Фиксировать $U,W$, решить задачу наименьших квадратов для $V$
3. Фиксировать $U,V$, решить задачу наименьших квадратов для $W$
4. Возвращаемся на шаг 1.
### Сжатие глубоких свёрточных сетей ([Lebedev, et. al 2015](https://arxiv.org/pdf/1412.6553.pdf))
- Свёртки выячисляются с помощью 4-мерного тензора (также называется ядро)
- Применим CP-разложение в этому тензору
- Применим последовательно свёртки с меньшими ядрами, задаными факторами в CP разложении
- Дообучим полученную модель
<img src="./cp_compress_dnn.png" width=600>
```
import tensorly as tl
import tensorly.decomposition as tldec
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
tensor = tl.tensor(np.arange(24).reshape((3, 4, 2)))
# tensor = tl.random.cp_tensor(shape=(3,3,3), rank=3, full=True)
print(tensor)
rank_range = [1, 2, 3, 4, 5, 6]
error_rec = []
for r in rank_range:
factors = tldec.parafac(tensor.astype("f"), rank=r)
error_rec.append(np.linalg.norm(tl.kruskal_to_tensor(factors) - tensor))
plt.semilogy(rank_range, error_rec)
plt.xlabel("CP rank")
plt.ylabel("Approximation error")
```
## Разложение Таккера
Следующая тнзорное разложение было предложено в работе ([Tucker, 1963](https://link.springer.com/content/pdf/10.1007/BF02289464.pdf)) в журнале [Psychometrika](https://link.springer.com/journal/11336):
$$
a_{ijk} = \sum_{\alpha_1,\alpha_2,\alpha_3=1}^{r_1,r_2,r_3}g_{\alpha_1\alpha_2\alpha_3} u_{i\alpha_1} v_{j\alpha_2} w_{k\alpha_3}.
$$
В этом случае у нас несколько различных рангов. Минимально возможные $r_1,r_2,r_3$ называются **рангами Таккера**.
**Свойства**:
* Для $d$-мерного массива нужна <font color='red'>$r^d$</font> $+ nrd$ памяти, по-прежнему есть экспоненциальный рост!
* Устойчивый алгоритм, основанный на SVD:
1. $U =$ главные компоненты развёртки `A.reshape(n1, n2*n3)`
2. $V =$ главные компоненты развёртки `A.transpose([1,0,2]).reshape(n2, n1*n3)`
3. $W =$ главные компоненты развёртки `A.transpose([2,0,1]).reshape(n3, n1*n2)`
4. $g_{\alpha_1\alpha_2\alpha_3} = \sum_{i,j,k=1}^{n_1,n_2,n_3} a_{ijk} u_{i\alpha_1} v_{j\alpha_2} w_{k\alpha_3}$.
```
tensor = tl.tensor(np.arange(24).reshape((3, 4, 2)))
core, factors = tldec.tucker(tensor, ranks=[3, 4, 2])
print("Shape of core = {}".format(core.shape))
for f in factors:
print("Shape of factors = {}".format(f.shape))
print("Approximation error = {}".format(np.linalg.norm(tensor - tl.tucker_to_tensor(core, factors))))
```
### Применение в рекомендательных системах [(Frolov, Oseledets 2016)](https://dl.acm.org/citation.cfm?id=2959170)
- Представим матрицу **пользователей-товаров** как бинарный тензор **пользователей-товаров-рейтингов**
- После разложения Таккера этого тензора у нас будут три фактора
- Два из них являются проекциями на пространство рейтингов и пространство товаров
- Этот подход позволяет принять во внимание негативные оценки товаров некоторыми пользователями
## Реализации разложений CP и Таккера
- Matlab: [Tensorlab](https://www.tensorlab.net/) и [Tensor Toolbox](https://www.sandia.gov/~tgkolda/TensorToolbox/index-2.5.html)
- Python: [TensorLy](http://tensorly.org/stable/home.html) и [Scikit-tensor](https://github.com/mnick/scikit-tensor)
## Разложение тензорного поезда (Tensor Train decomposition)
* Вычисление канонического разложения неустойчиво
* Разложение Таккера не решает проблему экспоненциального роста параметров
Разложение тензорного поезда (**TT**-разложение) ([Oseledets, Tyrtyshnikov 2009](http://www.mat.uniroma2.it/~tvmsscho/papers/Tyrtyshnikov4.pdf) и [Oseledets, 2011](https://epubs.siam.org/doi/abs/10.1137/090752286)) одновременно и устойчиво и содержит линейное по количеству размерностей число параметров:
$$
a_{i_1 i_2 \dots i_d} = \sum_{\alpha_1,\dots,\alpha_{d-1}}
g_{i_1\alpha_1} g_{\alpha_1 i_2\alpha_2}\dots g_{\alpha_{d-2} i_{d-1}\alpha_{d-1}} g_{\alpha_{d-1} i_{d}}
$$
или в матричной форме
$$
a_{i_1 i_2 \dots i_d} = G_1 (i_1)G_2 (i_2)\dots G_d(i_d)
$$
* Требуется памяти $\mathcal{O}(dnr^2)$
* Устойчивый TT-SVD алгоритм
**Пример**
$$a_{i_1\dots i_d} = i_1 + \dots + i_d$$
Канонический ранг равен $d$. В то же время TT-ранги равны $2$:
$$
i_1 + \dots + i_d = \begin{pmatrix} i_1 & 1 \end{pmatrix}
\begin{pmatrix} 1 & 0 \\ i_2 & 1 \end{pmatrix}
\dots
\begin{pmatrix} 1 & 0 \\ i_{d-1} & 1 \end{pmatrix}
\begin{pmatrix} 1 \\ i_d \end{pmatrix}
$$
### Реализации
- Matlab: [TT Toolbox](https://github.com/oseledets/TT-Toolbox)
- Python: [ttpy](https://github.com/oseledets/ttpy)
- TensorFlow: [t3f](https://github.com/Bihaqo/t3f)
- PyTorch: [tt-pytorch](https://github.com/KhrulkovV/tt-pytorch) and [tntorch](https://github.com/rballester/tntorch)
## Использование TT-разложения в римановой оптимизации
- Пусть дан тензор $A$ в ТТ формате с большими tt-рангами
- Хотим найти такой тензор $X$ (с малым заданным tt-рангом $r$), который наиболее близок к $A$ по Фробениусовой норме:
\begin{equation*}
\begin{aligned}
& \underset{X}{\text{minimize}}
& & \frac{1}{2}\|X - A\|_F^2 \\
& \text{subject to}
& & \text{tt_rank}(X) = r
\end{aligned}
\end{equation*}
- Известно, что множество тензоров в ТТ формате с поэлементно фиксированными TT рангами образует многообразие
- Поэтому мы можем решать эту задачу используя так называемый риманов градиентный спуск.
### Риманов градиентный спуск
- Пусть дана некоторая функция $F$ на многообразии $\mathcal{M}$. Римановым градиентным спуском называется следующая процедура
$$\hat{x}_{k+1} = x_{k} - \alpha P_{T_{x_k}\mathcal{M}} \nabla F(x_k),$$
$$x_{k+1} = \mathcal{R}(\hat{x}_{k+1})$$
где $P_{T_{x_k}\mathcal{M}}$ проекция на касательное пространство к $\mathcal{M}$ в точке $x_k$, а $\mathcal{R}$ называется ретракция - операция проекции точки с касательного пространства на многообразие и $\alpha > 0$ размер шага
- Далее показана реализация с помощью библиотеки `t3f`. В качестве ретракции используется процедура отсечения по tt-рангу (`t3f.round`).
```
import t3f
import tensorflow as tf
tf.set_random_seed(0)
np.random.seed(0)
sess = tf.InteractiveSession()
# Initialize A randomly, with large tt-ranks
shape = 10 * [2]
init_A = t3f.random_tensor(shape, tt_rank=16)
A = t3f.get_variable('A', initializer=init_A, trainable=False)
# Create an X variable and compute the gradient of the functional. Note that it is simply X - A.
init_X = t3f.random_tensor(shape, tt_rank=2)
X = t3f.get_variable('X', initializer=init_X)
gradF = X - A
# Let us compute the projection of the gradient onto the tangent space at X
riemannian_grad = t3f.riemannian.project(gradF, X)
# Compute the update by subtracting the Riemannian gradient
# and retracting back to the manifold
alpha = 1.0
train_step = t3f.assign(X, t3f.round(X - alpha * riemannian_grad, max_tt_rank=2))
# let us also compute the value of the functional
# to see if it is decreasing
F = 0.5 * t3f.frobenius_norm_squared(X - A)
sess.run(tf.global_variables_initializer())
log = []
for i in range(100):
F_v, _ = sess.run([F, train_step.op])
if i % 10 == 0:
print (F_v)
log.append(F_v)
```
Сравним полученный результат с квазиоптимальным решением, полученным с помощью отсечения по tt-рангу исходного тензора $A$.
```
quasi_sol = t3f.round(A, max_tt_rank=2)
val = sess.run(0.5 * t3f.frobenius_norm_squared(quasi_sol - A))
print (val)
```
Видно, что найденное значение немного больше, чем значение найденное римановым градиентным спуском, но процедура tt-round быстрее и потому часто используется на практике.
```
plt.semilogy(log, label='Riemannian gradient descent')
plt.axhline(y=val, lw=1, ls='--', color='gray', label='TT-round(A)')
plt.xlabel('Iteration')
plt.ylabel('Value of the functional')
plt.legend()
```
## Квантизованное разложение тензорного поезда (QTT)
Рассмотрим одномерный массив $a_k = f(x_k)$, $k=1,\dots,2^d$ где $f$ некоторая одномерная функция, вычисленная в точках сетки $x_k$.
Пусть $$k = {2^{d-1} i_1 + 2^{d-2} i_2 + \dots + 2^0 i_{d}}\quad i_1,\dots,i_d = 0,1 $$
двоичное представление $k$, тогда
$$
a_k = a_{2^{d-1} i_1 + 2^{d-2} i_2 + \dots + 2^0 i_{d}} \equiv \tilde a_{i_1,\dots,i_d},
$$
где $\tilde a$ не что иное как тензор $a$ с изменёнными размерами. TT-разложение $\tilde a$ называется **квантизованным TT-разложением (QTT)**.
- Интересный факт, что QTT-разложение связано с вейвлетами, более подробно смотрите [тут](https://epubs.siam.org/doi/abs/10.1137/100811647).
- Такое разложение содержит <font color='red'>$\mathcal{O}(\log n r^2)$</font> элементов!
## Метод крестовой аппроксимации
- Если дано разложение тензора, то нет проблем с быстрым выполнением базовых операций
- Однако, неясно, как получить разложение, когда тензор не может быть сохранён в памяти целиком
- **[Метод крестовой аппроксимации](https://ac.els-cdn.com/S0024379509003747/1-s2.0-S0024379509003747-main.pdf?_tid=0739e049-650f-4fed-8087-61563927f6ac&acdnat=1544040611_b7cd24f6dd7a48d85665d6b562129ab4)** позволяет получить тензорное разложение на основе лишь небольшого числа элементов тензора.
## Тензорные сети
- Универсальный способ записи тензорных разложений
- Могут быть интерпретированы как специальная арзхитектура нейронной сети
- Некоторые теоретические результаты о выразительной силе глубкоих нейронных сетей могут быть получены с использованием аппарата тензорных сетей, пример такого использования можно найти [тут](https://arxiv.org/pdf/1711.00811.pdf)
- [tntorch](https://github.com/rballester/tntorch) объединяет тензорные сети и PyTorch
- Более подробно можно прочитать [здесь](https://arxiv.org/pdf/1609.00893.pdf) и [здесь](https://arxiv.org/abs/1708.09165)
## Резюме
* Тензорные разложения - полезный инструмент для работы с многомерными данными
* Примеры тензорных разложений: каноническое, Таккера, ТТ и QTT
* Идея крестовой аппроксимации
## На следующей неделе
- Презентация проектов
```
from IPython.core.display import HTML
def css_styling():
styles = open("./styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
|
github_jupyter
|
import tensorly as tl
import tensorly.decomposition as tldec
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
tensor = tl.tensor(np.arange(24).reshape((3, 4, 2)))
# tensor = tl.random.cp_tensor(shape=(3,3,3), rank=3, full=True)
print(tensor)
rank_range = [1, 2, 3, 4, 5, 6]
error_rec = []
for r in rank_range:
factors = tldec.parafac(tensor.astype("f"), rank=r)
error_rec.append(np.linalg.norm(tl.kruskal_to_tensor(factors) - tensor))
plt.semilogy(rank_range, error_rec)
plt.xlabel("CP rank")
plt.ylabel("Approximation error")
tensor = tl.tensor(np.arange(24).reshape((3, 4, 2)))
core, factors = tldec.tucker(tensor, ranks=[3, 4, 2])
print("Shape of core = {}".format(core.shape))
for f in factors:
print("Shape of factors = {}".format(f.shape))
print("Approximation error = {}".format(np.linalg.norm(tensor - tl.tucker_to_tensor(core, factors))))
import t3f
import tensorflow as tf
tf.set_random_seed(0)
np.random.seed(0)
sess = tf.InteractiveSession()
# Initialize A randomly, with large tt-ranks
shape = 10 * [2]
init_A = t3f.random_tensor(shape, tt_rank=16)
A = t3f.get_variable('A', initializer=init_A, trainable=False)
# Create an X variable and compute the gradient of the functional. Note that it is simply X - A.
init_X = t3f.random_tensor(shape, tt_rank=2)
X = t3f.get_variable('X', initializer=init_X)
gradF = X - A
# Let us compute the projection of the gradient onto the tangent space at X
riemannian_grad = t3f.riemannian.project(gradF, X)
# Compute the update by subtracting the Riemannian gradient
# and retracting back to the manifold
alpha = 1.0
train_step = t3f.assign(X, t3f.round(X - alpha * riemannian_grad, max_tt_rank=2))
# let us also compute the value of the functional
# to see if it is decreasing
F = 0.5 * t3f.frobenius_norm_squared(X - A)
sess.run(tf.global_variables_initializer())
log = []
for i in range(100):
F_v, _ = sess.run([F, train_step.op])
if i % 10 == 0:
print (F_v)
log.append(F_v)
quasi_sol = t3f.round(A, max_tt_rank=2)
val = sess.run(0.5 * t3f.frobenius_norm_squared(quasi_sol - A))
print (val)
plt.semilogy(log, label='Riemannian gradient descent')
plt.axhline(y=val, lw=1, ls='--', color='gray', label='TT-round(A)')
plt.xlabel('Iteration')
plt.ylabel('Value of the functional')
plt.legend()
from IPython.core.display import HTML
def css_styling():
styles = open("./styles/custom.css", "r").read()
return HTML(styles)
css_styling()
| 0.661048 | 0.957557 |
##### Welcome to ECE 594n
### Geometric Machine Learning for Biomedical Imaging and Shape Analysis
$\color{#003660}{\text{Nina Miolane - Assistant Professor}}$
BioShape Lab @ UCSB ECE
<center><img src="figs/00_bioshape.jpg" width=650px alt="default"/></center>
# Instructor: Nina Miolane (me)
<img src="figs/00_nina.jpg" width=200px alt="default"/>
<img src="figs/00_brains.jpg" width=200px alt="default"/>
$\color{#047C91}{\text{Research}}$: Exploring the geometries of life:
- how proteins, cells, organs adopt specific shapes to function,
- and how pathologies arise from abnormal shapes.
$\color{#047C91}{\text{Office Hours}}$: Fridays 3 - 4 PM (starting week 3)
https://ucsb.zoom.us/my/nmiolane
# Classes
- Phelps 1431, Tue and Thu 04:00 PM - 5:50 PM (remote next week)
- Slides: [ECE 594n's GitHub](https://github.com/bioshape-lab/ece594n)
Notes:
- Do not enroll in other courses whose schedule is conflicting with this class.
- If you cannot attend/watch all lectures, please drop this class.
# Slack
Join the class Slack workspace via this link:
https://join.slack.com/t/ucsbece594n/shared_invite/zt-15rs9b4k2-chv_p0c9I6NfKbPNVfb~pw
- Slack is our prefered communication channel.
- Do not email me, write on slack instead.
# Python and Jupyter Notebooks
We will use:
- Python version 3.7 or higher as our programming language,
- Jupyter notebooks to run Python interactively in a web browser.
You should download Anaconda which will install everything you need to run Python 3.7+ and Jupyter notebooks:
- Anaconda: https://www.anaconda.com/download
# DataCamp: Learn Python
Join the group with your @ucsb.edu address [via this link](https://www.datacamp.com/groups/shared_links/11e534b5d9eb74d03754278bffca47ef91322a6a3cd3f3180cbfe980e25ec930).
If you are not familiar with Python, we recommend these assignments:
- Introduction to Python
- Intermediate Python
- Biological Imaging in Python
- Image Processing in Python
None of these are graded. These assignments are here to help you learn Python if you need to.
# Outline
- **Unit 1 (Geometry - Math!)**: Differential Geometry for Engineers
- **Unit 2 (Shapes)**: Computational Representations of Biomedical Shapes
- **Unit 3 (Machine Learning)**: Geometric Machine Learning for Shape Analysis
- **Unit 4 (Deep Learning)**: Geometric Deep Learning for Shape Analysis
<center><img src="figs/00_bioshape.jpg" width=350px alt="default"/></center>
Examples and applications will be taken from cutting-edge research in the **biomedical field**.
# Resources
- **Unit 1**: Guigui, Miolane, Pennec (2022). Introduction to Riemannian Geometry and Geometric Statistics. Ch. 1 - 4.
- **Unit 2**: See references in corresponding lecture notes.
- **Unit 3**: Guigui, Miolane, Pennec (2022). Introduction to Riemannian Geometry and Geometric Statistics. Ch. 5.
- **Unit 4**: Bronstein et al. Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges.
<center><img src="figs/00_book.jpeg" width=550px alt="default"/></center>
# Computational Resources
- Miolane et al (2020). Geomstats: a Python package for Geometry in Machine Learning.
- https://github.com/geomstats/geomstats
- Fey, Lenssen (2019). Fast Graph Representation Learning with PyTorch Geometric.
- https://github.com/pyg-team/pytorch_geometric
- Myers (2022). Tutorials of Riemannian Geometry and Geometric Statistics.
- https://github.com/geomstats/geomstats/tree/master/notebooks
<center><img src="figs/00_github.png" width=350px alt="default"/></center>
# Grading
- **Geometry** $\color{#EF5645}{\text{(20%)}}$: Visualizing differential geometry with Geomstats
- **Shapes** $\color{#EF5645}{\text{(20%)}}$: Reproducing the findings of a research paper (DDB)
- **Final project** $\color{#EF5645}{\text{(20%)}}$: Geometric Learning for Biomedical Shape Analysis
- **Machine Learning** $\color{#EF5645}{\text{(40%)}}$: Review of Geometric Learning
- **Extra-credits**:
- Tackle Geomstats GitHub issues (up to +10%)
No midterm exam, no final exam, no homeworks: only projects (/research papers !).
<center><img src="figs/00_aplus.png" width=300px alt="default"/></center>
# Geometry: Visualizations (Math!)
$\color{#EF5645}{\text{Goal}}$: Get intuition on Differential Geometry by visualizing manifolds.
- Deadline: Thursday 04/21/2022.
- Team of 2-3 students.
Steps:
- Read guidelines in the [`geomviz` folder](https://github.com/bioshape-lab/ece594n/tree/main/geomviz), we will explain them in class in ~2 weeks.
- Register your team on the README.md of the [`geomviz` folder](https://github.com/bioshape-lab/ece594n/tree/main/geomviz).
- Submit your visualization as a Jupyter notebook to the [`geomviz` folder](https://github.com/bioshape-lab/ece594n/tree/main/geomviz) by Thursday 04/21/2022.
- Present in class on Thursday 04/21/2022 (5 min per team).
# Shapes: Reproducing the findings of a research paper
$\color{#EF5645}{\text{Goal}}$: Determine if it is easy to reproduce the findings of a research paper on biomedical shape analysis.
- Deadline: Tuesday 05/03/2022.
- Teams of 2-3 students.
- Paper: Cell states beyond transcriptomics (https://pubmed.ncbi.nlm.nih.gov/34043964/).
Steps:
- Read guidelines in the README.md of the [`reproducibility` folder](https://github.com/bioshape-lab/ece594n/blob/main/reproducibility/README.md).
- Try reproducing the figures of the paper using their published data and code.
- Write report (1 page per student) on whether it was easy to reproduce the results.
- Present in class on Thursday 05/03/2022 (5 min per team).
# Final project: Geometric Learning for Biomedical Shape Analysis
$\color{#EF5645}{\text{Goal}}$: Put your skills in practice to tackle a project of your choice: perform geometric machine learning analysis on a biomedical dataset.
- Deadline: Tuesday 05/31/2022 and Thursday 06/02/2022
- Presentations in class: Tuesday 05/31/2022 and Thursday 06/02/2022
- Teams of 2-3 students.
Steps:
- Read guidelines in the README.md of the [`projects` folder](https://github.com/bioshape-lab/ece594n/blob/main/projects/README.md).
- Register your team on the README.md of the `projects` folder.
- Submit your project as a Jupyter notebook in the `projects` folder.
- Present your work in class: 5 min per student, i.e. 10 min or 15 min presentations per team.
# Machine Learning: Review of Geometric Learning
$\color{#EF5645}{\text{Goal}}$: Review the published papers in Geometric Machine Learning
- Deadline: Tuesday 06/07/2022
- Teams of 1 student.
Steps:
- Read guidelines in the README.md of the [`reviews` folder](https://github.com/bioshape-lab/ece594n/tree/main/reviews).
- Register on the README.md of the `reviews` folder starting April 15th.
- Send your review (2 pages) as a zip file from overleaf to Nina.
# Extra-Credits: Tackle Geomstats GitHub Issues
- Deadline: Tuesday 06/07/2022
<center><img src="figs/00_geomstats.png" width=1100px alt="default"/></center>
# Questions?
|
github_jupyter
|
##### Welcome to ECE 594n
### Geometric Machine Learning for Biomedical Imaging and Shape Analysis
$\color{#003660}{\text{Nina Miolane - Assistant Professor}}$
BioShape Lab @ UCSB ECE
<center><img src="figs/00_bioshape.jpg" width=650px alt="default"/></center>
# Instructor: Nina Miolane (me)
<img src="figs/00_nina.jpg" width=200px alt="default"/>
<img src="figs/00_brains.jpg" width=200px alt="default"/>
$\color{#047C91}{\text{Research}}$: Exploring the geometries of life:
- how proteins, cells, organs adopt specific shapes to function,
- and how pathologies arise from abnormal shapes.
$\color{#047C91}{\text{Office Hours}}$: Fridays 3 - 4 PM (starting week 3)
https://ucsb.zoom.us/my/nmiolane
# Classes
- Phelps 1431, Tue and Thu 04:00 PM - 5:50 PM (remote next week)
- Slides: [ECE 594n's GitHub](https://github.com/bioshape-lab/ece594n)
Notes:
- Do not enroll in other courses whose schedule is conflicting with this class.
- If you cannot attend/watch all lectures, please drop this class.
# Slack
Join the class Slack workspace via this link:
https://join.slack.com/t/ucsbece594n/shared_invite/zt-15rs9b4k2-chv_p0c9I6NfKbPNVfb~pw
- Slack is our prefered communication channel.
- Do not email me, write on slack instead.
# Python and Jupyter Notebooks
We will use:
- Python version 3.7 or higher as our programming language,
- Jupyter notebooks to run Python interactively in a web browser.
You should download Anaconda which will install everything you need to run Python 3.7+ and Jupyter notebooks:
- Anaconda: https://www.anaconda.com/download
# DataCamp: Learn Python
Join the group with your @ucsb.edu address [via this link](https://www.datacamp.com/groups/shared_links/11e534b5d9eb74d03754278bffca47ef91322a6a3cd3f3180cbfe980e25ec930).
If you are not familiar with Python, we recommend these assignments:
- Introduction to Python
- Intermediate Python
- Biological Imaging in Python
- Image Processing in Python
None of these are graded. These assignments are here to help you learn Python if you need to.
# Outline
- **Unit 1 (Geometry - Math!)**: Differential Geometry for Engineers
- **Unit 2 (Shapes)**: Computational Representations of Biomedical Shapes
- **Unit 3 (Machine Learning)**: Geometric Machine Learning for Shape Analysis
- **Unit 4 (Deep Learning)**: Geometric Deep Learning for Shape Analysis
<center><img src="figs/00_bioshape.jpg" width=350px alt="default"/></center>
Examples and applications will be taken from cutting-edge research in the **biomedical field**.
# Resources
- **Unit 1**: Guigui, Miolane, Pennec (2022). Introduction to Riemannian Geometry and Geometric Statistics. Ch. 1 - 4.
- **Unit 2**: See references in corresponding lecture notes.
- **Unit 3**: Guigui, Miolane, Pennec (2022). Introduction to Riemannian Geometry and Geometric Statistics. Ch. 5.
- **Unit 4**: Bronstein et al. Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges.
<center><img src="figs/00_book.jpeg" width=550px alt="default"/></center>
# Computational Resources
- Miolane et al (2020). Geomstats: a Python package for Geometry in Machine Learning.
- https://github.com/geomstats/geomstats
- Fey, Lenssen (2019). Fast Graph Representation Learning with PyTorch Geometric.
- https://github.com/pyg-team/pytorch_geometric
- Myers (2022). Tutorials of Riemannian Geometry and Geometric Statistics.
- https://github.com/geomstats/geomstats/tree/master/notebooks
<center><img src="figs/00_github.png" width=350px alt="default"/></center>
# Grading
- **Geometry** $\color{#EF5645}{\text{(20%)}}$: Visualizing differential geometry with Geomstats
- **Shapes** $\color{#EF5645}{\text{(20%)}}$: Reproducing the findings of a research paper (DDB)
- **Final project** $\color{#EF5645}{\text{(20%)}}$: Geometric Learning for Biomedical Shape Analysis
- **Machine Learning** $\color{#EF5645}{\text{(40%)}}$: Review of Geometric Learning
- **Extra-credits**:
- Tackle Geomstats GitHub issues (up to +10%)
No midterm exam, no final exam, no homeworks: only projects (/research papers !).
<center><img src="figs/00_aplus.png" width=300px alt="default"/></center>
# Geometry: Visualizations (Math!)
$\color{#EF5645}{\text{Goal}}$: Get intuition on Differential Geometry by visualizing manifolds.
- Deadline: Thursday 04/21/2022.
- Team of 2-3 students.
Steps:
- Read guidelines in the [`geomviz` folder](https://github.com/bioshape-lab/ece594n/tree/main/geomviz), we will explain them in class in ~2 weeks.
- Register your team on the README.md of the [`geomviz` folder](https://github.com/bioshape-lab/ece594n/tree/main/geomviz).
- Submit your visualization as a Jupyter notebook to the [`geomviz` folder](https://github.com/bioshape-lab/ece594n/tree/main/geomviz) by Thursday 04/21/2022.
- Present in class on Thursday 04/21/2022 (5 min per team).
# Shapes: Reproducing the findings of a research paper
$\color{#EF5645}{\text{Goal}}$: Determine if it is easy to reproduce the findings of a research paper on biomedical shape analysis.
- Deadline: Tuesday 05/03/2022.
- Teams of 2-3 students.
- Paper: Cell states beyond transcriptomics (https://pubmed.ncbi.nlm.nih.gov/34043964/).
Steps:
- Read guidelines in the README.md of the [`reproducibility` folder](https://github.com/bioshape-lab/ece594n/blob/main/reproducibility/README.md).
- Try reproducing the figures of the paper using their published data and code.
- Write report (1 page per student) on whether it was easy to reproduce the results.
- Present in class on Thursday 05/03/2022 (5 min per team).
# Final project: Geometric Learning for Biomedical Shape Analysis
$\color{#EF5645}{\text{Goal}}$: Put your skills in practice to tackle a project of your choice: perform geometric machine learning analysis on a biomedical dataset.
- Deadline: Tuesday 05/31/2022 and Thursday 06/02/2022
- Presentations in class: Tuesday 05/31/2022 and Thursday 06/02/2022
- Teams of 2-3 students.
Steps:
- Read guidelines in the README.md of the [`projects` folder](https://github.com/bioshape-lab/ece594n/blob/main/projects/README.md).
- Register your team on the README.md of the `projects` folder.
- Submit your project as a Jupyter notebook in the `projects` folder.
- Present your work in class: 5 min per student, i.e. 10 min or 15 min presentations per team.
# Machine Learning: Review of Geometric Learning
$\color{#EF5645}{\text{Goal}}$: Review the published papers in Geometric Machine Learning
- Deadline: Tuesday 06/07/2022
- Teams of 1 student.
Steps:
- Read guidelines in the README.md of the [`reviews` folder](https://github.com/bioshape-lab/ece594n/tree/main/reviews).
- Register on the README.md of the `reviews` folder starting April 15th.
- Send your review (2 pages) as a zip file from overleaf to Nina.
# Extra-Credits: Tackle Geomstats GitHub Issues
- Deadline: Tuesday 06/07/2022
<center><img src="figs/00_geomstats.png" width=1100px alt="default"/></center>
# Questions?
| 0.711531 | 0.94887 |
<a href="https://colab.research.google.com/github/SrinithiSrinivasan/Local-Binary-Patterns-based-Criminal-Identification-System/blob/master/Login_UI.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#Loginflask.py
from flask import Flask, render_template, redirect, url_for, request
from werkzeug import secure_filename
import os
app = Flask(__name__)
@app.route('/login', methods=['GET', 'POST'])
def login():
error = None
if request.method == 'POST':
error = None
if request.method == 'POST':
if request.form['username'] != 'admin' or request.form['password'] != 'admin':
error = 'Invalid Credentials. Please try again.'
else:
return redirect(url_for('upload_file'))
return render_template('login.html', error=error)
@app.route('/upload_file')
def upload_file():
return render_template('upload.html')
@app.route('/uploader', methods = ['GET', 'POST'])
def upload_file1():
if request.method == 'POST':
f = request.files['file']
f.save(secure_filename(f.filename))
os.system('python integrate.py')
return 'file uploaded successfully'
if __name__ == '__main__':
app.run(debug = True)
Login.html
<html>
<head>
<link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/font-awesome/4.7.0/css/font-awesome.min.css">
<style>
body{
background-image:url("alvaro-pinot-502465-unsplash.jpg");
margin: 0;
font-family: Arial, Helvetica, sans-serif;
}
.topnav {
overflow: hidden;
background-color: #000000;
}
.topnav a {
float: left;
color: lime;
text-align: center;
padding: 14px 16px;
text-decoration: none;
font-size: 17px;
}
.topnav a:hover {
color:white;
transform: scale(1.3);
}
.topnav a.active {
background-color: #ff0080;
color:white;
}
div.transbox {
margin-left: 300px;
margin-top:20px;
background-color:#ffffff;
border: 1px solid black;
opacity: 0.7;
filter: alpha(opacity=60); /* For IE8 and earlier */
border-radius: 50px 50px;
padding: 20px;
width: 700px;
height: 700px;
}
div.trans{
opacity:0.9;
background-color:#ffff00;
height: 50px;
color:#400080;
font-weight:bold;
}
input[type=text], input[type=password] {
width: 60%;
padding: 12px 20px;
margin: 8px 0;
display: inline-block;
border: 1px solid #ccc;
box-sizing: border-box;
background-color:#000000;
border-radius:15 px;
color:#ffffff;
font-size:"7";
font-family: Arial, Helvetica, sans-serif;
font-weight:bold;
}
input:hover{
opacity:0.9;
}
button {
background-color:lime;
color: white;
padding: 14px 20px;
margin: 8px 0;
border: none;
cursor: pointer;
border-radius: 12px;
width: 50%;
}
button:hover {
opacity: 0.8;
}
.cancelbtn {
width: auto;
padding: 10px 18px;
background-color: #ff0000;
}
.imgcontainer {
text-align: center;
margin: 24px 0 12px 0;
}
img.avatar {
width: 40%;
border-radius: 50%;
}
.container {
padding: 16px;
width: 50 px;
height:50 px;
}
span.psw {
float: right;
padding-top: 16px;
}
p{color:#000000;
font-family: Arial, Helvetica, sans-serif;
font-size:"7";
}
</style>
</head>
<body>
<div class="topnav">
</div>
<div class="transbox">
<div class="trans">
<h1 align="center">LOGIN PAGE</h1>
</div>
</hr>
<form id="members" method="post">
<div class="imgcontainer">
<!img src="" alt="Avatar" class="avatar">
</div>
<div class="container">
<i class="fa fa-address-book-o" style="font-size:36px;color:black"></i>
<label for="uname"><b>USERNAME</b></label>
<br>
<input type="text" placeholder="Enter username" name="username" value="{{
request.form.username }}">
<br> <br>
<i class="fa fa-expeditedssl" style="font-size:36px;color:black"></i>
<label for="psw"><b>PASSWORD</b></label>
<br>
<input type="password" placeholder="Enter Password" name="password" value="{{
request.form.password }}">
<br><br><br><br>
<input class="btn btn-default" type="submit" value="Login">
<br>
</div>
<div class="container" style="background-color:#f1f1f1">
</div>
</form>
{% if error %}
<p class="error"><strong>Error:</strong> {{ error }}
{% endif %}
</div>
</body>
</html>
Upload.html
<html>
<style>
.button {
background-color: #4CAF50;
border: none;
color: white;
padding: 15px 32px;
text-align: center;
text-decoration: none;
display: inline-block;
font-size: 16px;
margin: 4px 2px;
cursor: pointer;
}
.modal {
display: none; /* Hidden by default */
position: fixed; /* Stay in place */
z-index: 1; /* Sit on top */
left: 0;
top: 0;
width: 50%; /* Full width */
height: 100%; /* Full height */
overflow: auto; /* Enable scroll if needed */
background-color: #474e5d;
padding-top: 50px;
border-radius: 25px;
}
/* Modal Content/Box */
.modal-content {
background: #f6f1d3;
//background: linear-gradient(to right, , #648880 85%, #293f50);
margin: 5% auto 15% auto; /* 5% from the top, 15% from the bottom and centered */
border: 1px solid #888;
border-radius: 25px;
width: 30%; /* Could be more or less, depending on screen size */
height:30%;
}
.container {
padding: 16px;
}
</style>
<body background="download.jpg">
<center><h1 style="color:white" font-family:"Georgia">CRIMINAL INVESTIGATION SYSTEM</H1></center>
<br><br><br>
<form class="modal-content" action = "http://localhost:5000/uploader" method = "POST"
enctype = "multipart/form-data">
<div class="container"> <br><br>
<center><input type = "file" name = "file" />
<input class="button" type = "submit"/>
</form>
</body>
</html>
```
|
github_jupyter
|
#Loginflask.py
from flask import Flask, render_template, redirect, url_for, request
from werkzeug import secure_filename
import os
app = Flask(__name__)
@app.route('/login', methods=['GET', 'POST'])
def login():
error = None
if request.method == 'POST':
error = None
if request.method == 'POST':
if request.form['username'] != 'admin' or request.form['password'] != 'admin':
error = 'Invalid Credentials. Please try again.'
else:
return redirect(url_for('upload_file'))
return render_template('login.html', error=error)
@app.route('/upload_file')
def upload_file():
return render_template('upload.html')
@app.route('/uploader', methods = ['GET', 'POST'])
def upload_file1():
if request.method == 'POST':
f = request.files['file']
f.save(secure_filename(f.filename))
os.system('python integrate.py')
return 'file uploaded successfully'
if __name__ == '__main__':
app.run(debug = True)
Login.html
<html>
<head>
<link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/font-awesome/4.7.0/css/font-awesome.min.css">
<style>
body{
background-image:url("alvaro-pinot-502465-unsplash.jpg");
margin: 0;
font-family: Arial, Helvetica, sans-serif;
}
.topnav {
overflow: hidden;
background-color: #000000;
}
.topnav a {
float: left;
color: lime;
text-align: center;
padding: 14px 16px;
text-decoration: none;
font-size: 17px;
}
.topnav a:hover {
color:white;
transform: scale(1.3);
}
.topnav a.active {
background-color: #ff0080;
color:white;
}
div.transbox {
margin-left: 300px;
margin-top:20px;
background-color:#ffffff;
border: 1px solid black;
opacity: 0.7;
filter: alpha(opacity=60); /* For IE8 and earlier */
border-radius: 50px 50px;
padding: 20px;
width: 700px;
height: 700px;
}
div.trans{
opacity:0.9;
background-color:#ffff00;
height: 50px;
color:#400080;
font-weight:bold;
}
input[type=text], input[type=password] {
width: 60%;
padding: 12px 20px;
margin: 8px 0;
display: inline-block;
border: 1px solid #ccc;
box-sizing: border-box;
background-color:#000000;
border-radius:15 px;
color:#ffffff;
font-size:"7";
font-family: Arial, Helvetica, sans-serif;
font-weight:bold;
}
input:hover{
opacity:0.9;
}
button {
background-color:lime;
color: white;
padding: 14px 20px;
margin: 8px 0;
border: none;
cursor: pointer;
border-radius: 12px;
width: 50%;
}
button:hover {
opacity: 0.8;
}
.cancelbtn {
width: auto;
padding: 10px 18px;
background-color: #ff0000;
}
.imgcontainer {
text-align: center;
margin: 24px 0 12px 0;
}
img.avatar {
width: 40%;
border-radius: 50%;
}
.container {
padding: 16px;
width: 50 px;
height:50 px;
}
span.psw {
float: right;
padding-top: 16px;
}
p{color:#000000;
font-family: Arial, Helvetica, sans-serif;
font-size:"7";
}
</style>
</head>
<body>
<div class="topnav">
</div>
<div class="transbox">
<div class="trans">
<h1 align="center">LOGIN PAGE</h1>
</div>
</hr>
<form id="members" method="post">
<div class="imgcontainer">
<!img src="" alt="Avatar" class="avatar">
</div>
<div class="container">
<i class="fa fa-address-book-o" style="font-size:36px;color:black"></i>
<label for="uname"><b>USERNAME</b></label>
<br>
<input type="text" placeholder="Enter username" name="username" value="{{
request.form.username }}">
<br> <br>
<i class="fa fa-expeditedssl" style="font-size:36px;color:black"></i>
<label for="psw"><b>PASSWORD</b></label>
<br>
<input type="password" placeholder="Enter Password" name="password" value="{{
request.form.password }}">
<br><br><br><br>
<input class="btn btn-default" type="submit" value="Login">
<br>
</div>
<div class="container" style="background-color:#f1f1f1">
</div>
</form>
{% if error %}
<p class="error"><strong>Error:</strong> {{ error }}
{% endif %}
</div>
</body>
</html>
Upload.html
<html>
<style>
.button {
background-color: #4CAF50;
border: none;
color: white;
padding: 15px 32px;
text-align: center;
text-decoration: none;
display: inline-block;
font-size: 16px;
margin: 4px 2px;
cursor: pointer;
}
.modal {
display: none; /* Hidden by default */
position: fixed; /* Stay in place */
z-index: 1; /* Sit on top */
left: 0;
top: 0;
width: 50%; /* Full width */
height: 100%; /* Full height */
overflow: auto; /* Enable scroll if needed */
background-color: #474e5d;
padding-top: 50px;
border-radius: 25px;
}
/* Modal Content/Box */
.modal-content {
background: #f6f1d3;
//background: linear-gradient(to right, , #648880 85%, #293f50);
margin: 5% auto 15% auto; /* 5% from the top, 15% from the bottom and centered */
border: 1px solid #888;
border-radius: 25px;
width: 30%; /* Could be more or less, depending on screen size */
height:30%;
}
.container {
padding: 16px;
}
</style>
<body background="download.jpg">
<center><h1 style="color:white" font-family:"Georgia">CRIMINAL INVESTIGATION SYSTEM</H1></center>
<br><br><br>
<form class="modal-content" action = "http://localhost:5000/uploader" method = "POST"
enctype = "multipart/form-data">
<div class="container"> <br><br>
<center><input type = "file" name = "file" />
<input class="button" type = "submit"/>
</form>
</body>
</html>
| 0.342132 | 0.457561 |
```
# hide
%load_ext autoreload
%autoreload 2
%load_ext nb_black
%load_ext lab_black
# default_exp model_pipeline
```
# ModelPipeline
> Putting it all together.
## Overview
The functionality below uses the `NumerFrame`, `PreProcessor`, `Model` and `PostProcessor` objects to easily propagate
data, generate predictions and postprocess them in one go.
Specifically, this section introduces two objects:
1. `ModelPipeline`: Run all preprocessing, models and postprocessing that you define and return a `NumerFrame`.
2. `ModelPipelineCollection`: Manage and run multiple `ModelPipeline` objects.
```
# hide
from nbdev.showdoc import *
#export
import uuid
import pandas as pd
from tqdm.auto import tqdm
from typeguard import typechecked
from typing import List, Union, Dict
from rich import print as rich_print
from numerblox.numerframe import NumerFrame, create_numerframe
from numerblox.preprocessing import BaseProcessor, CopyPreProcessor, GroupStatsPreProcessor, FeatureSelectionPreProcessor
from numerblox.model import BaseModel, ConstantModel, RandomModel
from numerblox.postprocessing import Standardizer, MeanEnsembler, FeatureNeutralizer
```
## 1. ModelPipeline
`ModelPipeline` handles all preprocessing, model prediction and postprocessing. It returns a `NumerFrame` with the preprocessed data, metadata and postprocessed prediction columns.
```
#export
@typechecked
class ModelPipeline:
"""
Execute all preprocessing, prediction and postprocessing for a given setup.
:param models: Initiliazed numerai-blocks Models (Objects inheriting from BaseModel) \n
:param preprocessors: List of initialized Preprocessors. \n
:param postprocessors: List of initialized Postprocessors. \n
:param copy_first: Whether to copy the NumerFrame as a first preprocessing step. \n
Highly recommended in order to avoid surprise behaviour by manipulating the original dataset. \n
:param pipeline_name: Unique name for pipeline. Only used for display purposes.
"""
def __init__(self,
models: List[BaseModel],
preprocessors: List[BaseProcessor] = [],
postprocessors: List[BaseProcessor] = [],
copy_first = True,
standardize = True,
pipeline_name: str = None):
self.pipeline_name = pipeline_name if pipeline_name else uuid.uuid4().hex
self.models = models
self.copy_first = copy_first
self.standardize = standardize
self.preprocessors = preprocessors
self.postprocessors = postprocessors
def preprocess(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
""" Run all preprocessing steps. Copies input by default. """
if self.copy_first:
dataf = CopyPreProcessor()(dataf)
for preprocessor in tqdm(self.preprocessors,
desc=f"{self.pipeline_name} Preprocessing:",
position=0):
rich_print(f":construction: Applying preprocessing: '[bold]{preprocessor.__class__.__name__}[/bold]' :construction:")
dataf = preprocessor(dataf)
return NumerFrame(dataf)
def postprocess(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
""" Run all postprocessing steps. Standardizes model prediction by default. """
if self.standardize:
dataf = Standardizer()(dataf)
for postprocessor in tqdm(self.postprocessors,
desc=f"{self.pipeline_name} Postprocessing: ",
position=0):
rich_print(f":construction: Applying postprocessing: '[bold]{postprocessor.__class__.__name__}[/bold]' :construction:")
dataf = postprocessor(dataf)
return NumerFrame(dataf)
def process_models(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
""" Run all models. """
for model in tqdm(self.models,
desc=f"{self.pipeline_name} Model prediction: ",
position=0):
rich_print(f":robot: Generating model predictions with '[bold]{model.__class__.__name__}[/bold]'. :robot:")
dataf = model(dataf)
return NumerFrame(dataf)
def pipeline(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
""" Process full pipeline and return resulting NumerFrame. """
preprocessed_dataf = self.preprocess(dataf)
prediction_dataf = self.process_models(preprocessed_dataf)
processed_prediction_dataf = self.postprocess(prediction_dataf)
rich_print(f":checkered_flag: [green]Finished pipeline:[green] [bold blue]'{self.pipeline_name}'[bold blue]! :checkered_flag:")
return processed_prediction_dataf
def __call__(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
return self.pipeline(dataf)
```
Example using several preprocessor, dummy models and postprocessors
```
model_names = ["test_0.5", "test_0.8"]
dataf = create_numerframe("test_assets/mini_numerai_version_1_data.csv", metadata={'version': 1})
preprocessors = [GroupStatsPreProcessor(), FeatureSelectionPreProcessor(feature_cols=['feature_intelligence_mean', 'feature_intelligence_std'])]
models = [ConstantModel(constant=0.5, model_name=model_names[0]), ConstantModel(constant=0.8, model_name=model_names[1])]
postprocessors = [MeanEnsembler(cols=[f"prediction_{name}" for name in model_names], final_col_name='prediction_ensembled'),
FeatureNeutralizer(feature_names=['feature_intelligence_mean', 'feature_intelligence_std'],
pred_name='prediction_ensembled', proportion=0.8)]
test_pipeline = ModelPipeline(preprocessors=preprocessors, models=models,
postprocessors=postprocessors, pipeline_name="test_pipeline",
standardize=False)
processed_dataf = test_pipeline(dataf)
assert processed_dataf.meta == dataf.meta
assert isinstance(processed_dataf, NumerFrame)
processed_dataf.head(2)
```
## 2. ModelPipelineCollection
`ModelPipelineCollection` can be used to manage and run multiple `ModelPipeline` objects.
`ModelPipelineCollection` simply takes a list of `ModelPipeline` objects as input.
```
#export
@typechecked
class ModelPipelineCollection:
"""
Execute multiple initialized ModelPipelines in a sequence.
:param pipelines: List of initialized ModelPipelines.
"""
def __init__(self, pipelines: List[ModelPipeline]):
self.pipelines = {pipe.pipeline_name: pipe for pipe in pipelines}
self.pipeline_names = list(self.pipelines.keys())
def process_all_pipelines(self, dataf: Union[pd.DataFrame, NumerFrame]) -> Dict[str, NumerFrame]:
""" Process all pipelines and return Dictionary mapping pipeline names to resulting NumerFrames. """
result_datafs = dict()
for name, pipeline in tqdm(self.pipelines.items(),
desc="Processing Pipeline Collection"):
result_datafs[name] = self.process_single_pipeline(dataf, name)
return result_datafs
def process_single_pipeline(self, dataf: Union[pd.DataFrame, NumerFrame], pipeline_name: str) -> NumerFrame:
""" Run full model pipeline for given name in collection. """
rich_print(f":construction_worker: [bold green]Processing model pipeline:[/bold green] '{pipeline_name}' :construction_worker:")
pipeline = self.get_pipeline(pipeline_name)
dataf = pipeline(dataf)
return NumerFrame(dataf)
def get_pipeline(self, pipeline_name: str) -> ModelPipeline:
""" Retrieve model pipeline for given name. """
available_pipelines = self.pipeline_names
assert pipeline_name in available_pipelines, f"Requested pipeline '{pipeline_name}', but only the following models are in the collection: '{available_pipelines}'."
return self.pipelines[pipeline_name]
def __call__(self, dataf: Union[pd.DataFrame, NumerFrame]) -> Dict[str, NumerFrame]:
return self.process_all_pipelines(dataf=dataf)
```
We introduce a different pipeline with no preprocessing or postprocessing. Only a `RandomModel`.
```
test_pipeline2 = ModelPipeline(models=[RandomModel()], pipeline_name="test_pipeline2")
```
We process two `ModelPipeline`s with different characteristics on the same data.
```
collection = ModelPipelineCollection([test_pipeline, test_pipeline2])
assert collection.get_pipeline("test_pipeline2").pipeline_name == 'test_pipeline2'
result_datasets = collection(dataf=dataf)
```
The `ModelPipelineCollection` returns a dictionary mapping pipeline names to `NumerFrame` objects, retaining all metadata and added prediction columns for each. Note that in this example, the 1st `NumerFrame` had a feature selection step, so it did not retain all columns. However, the second dataset retained all feature columns, because no preprocessing was done.
```
result_datasets.keys()
result_datasets['test_pipeline'].head(2)
result_datasets['test_pipeline2'].head(2)
```
Since metadata is not manipulated in these pipelines, metadata should be the same as the original `NumerFrame` for all resulting `NumerFrame` objects.
```
for _, result in result_datasets.items():
assert dataf.meta == result.meta
result_datasets['test_pipeline'].meta
```
-----------------------------------------------------------------------------
```
# hide
# Run this cell to sync all changes with library
from nbdev.export import notebook2script
notebook2script()
```
|
github_jupyter
|
# hide
%load_ext autoreload
%autoreload 2
%load_ext nb_black
%load_ext lab_black
# default_exp model_pipeline
# hide
from nbdev.showdoc import *
#export
import uuid
import pandas as pd
from tqdm.auto import tqdm
from typeguard import typechecked
from typing import List, Union, Dict
from rich import print as rich_print
from numerblox.numerframe import NumerFrame, create_numerframe
from numerblox.preprocessing import BaseProcessor, CopyPreProcessor, GroupStatsPreProcessor, FeatureSelectionPreProcessor
from numerblox.model import BaseModel, ConstantModel, RandomModel
from numerblox.postprocessing import Standardizer, MeanEnsembler, FeatureNeutralizer
#export
@typechecked
class ModelPipeline:
"""
Execute all preprocessing, prediction and postprocessing for a given setup.
:param models: Initiliazed numerai-blocks Models (Objects inheriting from BaseModel) \n
:param preprocessors: List of initialized Preprocessors. \n
:param postprocessors: List of initialized Postprocessors. \n
:param copy_first: Whether to copy the NumerFrame as a first preprocessing step. \n
Highly recommended in order to avoid surprise behaviour by manipulating the original dataset. \n
:param pipeline_name: Unique name for pipeline. Only used for display purposes.
"""
def __init__(self,
models: List[BaseModel],
preprocessors: List[BaseProcessor] = [],
postprocessors: List[BaseProcessor] = [],
copy_first = True,
standardize = True,
pipeline_name: str = None):
self.pipeline_name = pipeline_name if pipeline_name else uuid.uuid4().hex
self.models = models
self.copy_first = copy_first
self.standardize = standardize
self.preprocessors = preprocessors
self.postprocessors = postprocessors
def preprocess(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
""" Run all preprocessing steps. Copies input by default. """
if self.copy_first:
dataf = CopyPreProcessor()(dataf)
for preprocessor in tqdm(self.preprocessors,
desc=f"{self.pipeline_name} Preprocessing:",
position=0):
rich_print(f":construction: Applying preprocessing: '[bold]{preprocessor.__class__.__name__}[/bold]' :construction:")
dataf = preprocessor(dataf)
return NumerFrame(dataf)
def postprocess(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
""" Run all postprocessing steps. Standardizes model prediction by default. """
if self.standardize:
dataf = Standardizer()(dataf)
for postprocessor in tqdm(self.postprocessors,
desc=f"{self.pipeline_name} Postprocessing: ",
position=0):
rich_print(f":construction: Applying postprocessing: '[bold]{postprocessor.__class__.__name__}[/bold]' :construction:")
dataf = postprocessor(dataf)
return NumerFrame(dataf)
def process_models(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
""" Run all models. """
for model in tqdm(self.models,
desc=f"{self.pipeline_name} Model prediction: ",
position=0):
rich_print(f":robot: Generating model predictions with '[bold]{model.__class__.__name__}[/bold]'. :robot:")
dataf = model(dataf)
return NumerFrame(dataf)
def pipeline(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
""" Process full pipeline and return resulting NumerFrame. """
preprocessed_dataf = self.preprocess(dataf)
prediction_dataf = self.process_models(preprocessed_dataf)
processed_prediction_dataf = self.postprocess(prediction_dataf)
rich_print(f":checkered_flag: [green]Finished pipeline:[green] [bold blue]'{self.pipeline_name}'[bold blue]! :checkered_flag:")
return processed_prediction_dataf
def __call__(self, dataf: Union[pd.DataFrame, NumerFrame]) -> NumerFrame:
return self.pipeline(dataf)
model_names = ["test_0.5", "test_0.8"]
dataf = create_numerframe("test_assets/mini_numerai_version_1_data.csv", metadata={'version': 1})
preprocessors = [GroupStatsPreProcessor(), FeatureSelectionPreProcessor(feature_cols=['feature_intelligence_mean', 'feature_intelligence_std'])]
models = [ConstantModel(constant=0.5, model_name=model_names[0]), ConstantModel(constant=0.8, model_name=model_names[1])]
postprocessors = [MeanEnsembler(cols=[f"prediction_{name}" for name in model_names], final_col_name='prediction_ensembled'),
FeatureNeutralizer(feature_names=['feature_intelligence_mean', 'feature_intelligence_std'],
pred_name='prediction_ensembled', proportion=0.8)]
test_pipeline = ModelPipeline(preprocessors=preprocessors, models=models,
postprocessors=postprocessors, pipeline_name="test_pipeline",
standardize=False)
processed_dataf = test_pipeline(dataf)
assert processed_dataf.meta == dataf.meta
assert isinstance(processed_dataf, NumerFrame)
processed_dataf.head(2)
#export
@typechecked
class ModelPipelineCollection:
"""
Execute multiple initialized ModelPipelines in a sequence.
:param pipelines: List of initialized ModelPipelines.
"""
def __init__(self, pipelines: List[ModelPipeline]):
self.pipelines = {pipe.pipeline_name: pipe for pipe in pipelines}
self.pipeline_names = list(self.pipelines.keys())
def process_all_pipelines(self, dataf: Union[pd.DataFrame, NumerFrame]) -> Dict[str, NumerFrame]:
""" Process all pipelines and return Dictionary mapping pipeline names to resulting NumerFrames. """
result_datafs = dict()
for name, pipeline in tqdm(self.pipelines.items(),
desc="Processing Pipeline Collection"):
result_datafs[name] = self.process_single_pipeline(dataf, name)
return result_datafs
def process_single_pipeline(self, dataf: Union[pd.DataFrame, NumerFrame], pipeline_name: str) -> NumerFrame:
""" Run full model pipeline for given name in collection. """
rich_print(f":construction_worker: [bold green]Processing model pipeline:[/bold green] '{pipeline_name}' :construction_worker:")
pipeline = self.get_pipeline(pipeline_name)
dataf = pipeline(dataf)
return NumerFrame(dataf)
def get_pipeline(self, pipeline_name: str) -> ModelPipeline:
""" Retrieve model pipeline for given name. """
available_pipelines = self.pipeline_names
assert pipeline_name in available_pipelines, f"Requested pipeline '{pipeline_name}', but only the following models are in the collection: '{available_pipelines}'."
return self.pipelines[pipeline_name]
def __call__(self, dataf: Union[pd.DataFrame, NumerFrame]) -> Dict[str, NumerFrame]:
return self.process_all_pipelines(dataf=dataf)
test_pipeline2 = ModelPipeline(models=[RandomModel()], pipeline_name="test_pipeline2")
collection = ModelPipelineCollection([test_pipeline, test_pipeline2])
assert collection.get_pipeline("test_pipeline2").pipeline_name == 'test_pipeline2'
result_datasets = collection(dataf=dataf)
result_datasets.keys()
result_datasets['test_pipeline'].head(2)
result_datasets['test_pipeline2'].head(2)
for _, result in result_datasets.items():
assert dataf.meta == result.meta
result_datasets['test_pipeline'].meta
# hide
# Run this cell to sync all changes with library
from nbdev.export import notebook2script
notebook2script()
| 0.809502 | 0.84759 |
<a href="https://colab.research.google.com/github/athenian-ct-projects/Fortnite-AA/blob/master/Adrian.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#FORTNITE
#FORTNITE
#FORTNITE
#FORTNITE
print("Welcome to Fortnite Battle Royale *Fortnite music theme now cues*")
print("which fortnite skin to you desire to be? ")
costume=input("Brite Bomber, Skull Trooper, Renegade Raider, Dark Knight, Twitch Prime Skin, or Default? ")
print("What pickaxe do you fancy")
pickaxe=input("shovel, omega, pick squeak, default, or daddy whacker? ")
print("Which back bling do you crave? ")
back_bling=input("Royale Shield, Rust Bucket, Black Shield, Red Shield, or an Alpine backpack? ")
print("Your selection " + costume + " " + pickaxe + " "+ back_bling + " is ready for use ;)")
print("Click next block to drop into the Fortnite Map")
import random
print(costume + " where do you want to drop")
location1=input("Anarchy Acres, Greasy Grove, Pleasant Park, Lonely Lodge, Retail Row, Salty Springs, Moisty Mire, Fatal Fields, Dusty Depot")
droppers=random.randint(0,20)
print(location1 + " is a nice choice " + str(droppers) + " people have landed there")
print("Which weapon do you want?" )
weapon1=input("legendary scar, grey tactical submachine gun, the papi artale, or the rocket propeller grenade? ")
def fighting_time ():
print("You have encountered an enemy. What do you do? ")
enemy1=input("Team, dance, shoot at, or build? ")
while enemy1 != "team" and enemy1 != "dance" and enemy1 != "shoot at" and enemy1 != "build":
enemy1=input("Team, dance, shoot at, or build? ")
if enemy1 == 'team':
print("epic games has banned you. NEVER TEAM AGAIN CHEATER")
quit()
if enemy1 == 'dance':
print("enemy shoots at you and your dead. NEXT TIME WHEN YOU SEE AN EMEMY DONT BE DUMB")
quit()
if enemy1 == 'shoot at':
print("good job you have eleminated your enemy with your " + weapon1)
if enemy1 == 'build':
print("good job. You have blocked their shots and have allowed time to escape from the enemy")
if enemy1 == 'build' or 'shoot at':
print("congratulations. You have beaten your first enemy now you may continue your match. ")
import random
print("You are currently still in " + location1 + " where do you desire to go next?")
place1=input("Where do you desire to go to next? Retail Row, Dusty Depot, or Anarchy Acres?")
people_in_game1= random.randint(0,10)
choice1=input("there are currently " + str(people_in_game1)+ " people there. Do you still desire to go?")
if choice1 == "yes":
location2=print("You will be transported on the next block")
if choice1 == "no":
place2=input("Where do you desire to go to next? Retail Row, Dusty Depot, or Anarchy Acres?")
people_in_game2= random.randint(0,10)
choice2=input("There are currently " + str(people_in_game2)+ " people there. Do you still desire to go?")
if choice2 == "yes":
location2=print("You will be transported on the next block")
if choice2 == "no":
print("Too bad your going there whether you like it or not. Click the nect block to continue.")
import random
def hunterer_gatherer ():
material1 = random.randint(150,500)
choice3=input("Which matertial do you want? Wood, Brick, or Steel? ")
if choice3 == "wood":
for x in range(5):
print("chop")
print("you have gathered " + str(material1) + " wood")
if choice3 == "brick":
for x in range(5):
print("plip plop")
print("you have gathered " + str(material1) + " brick")
if choice3 == "steel":
for x in range(5):
print("ding")
print("you have gathered " + str(material1) + " steel")
hunterer_gatherer()
import random
people_in_game3= random.randint (3,10)
print("There are now " + str(people_in_game3) + " left in the game.")
print("You are now in " + place1 or place2 + "What would you like to do now? ")
choice4=input("Would you like to gather more materials, or fight? ")
if choice4 == "materials":
hunterer_gatherer()
if choice4 == "fight":
fighting_time()
print("You are in the endgame. It is a 1v1.")
guerr_bears=(random.choice(["shooting you","building"]))
choice5=input("Your opponent is " + guerr_bears + " . What do you desire to do? Build, or shoot?")
if choice5 == "build":
print("Nice. You are now well protected. You have earned yourself a VICTORY ROYALE!!!!!!")
if choice5 == "shoot":
print("Your shoots are useless and they have obliterated you. Better luck next time.")
quit()
```
|
github_jupyter
|
#FORTNITE
#FORTNITE
#FORTNITE
#FORTNITE
print("Welcome to Fortnite Battle Royale *Fortnite music theme now cues*")
print("which fortnite skin to you desire to be? ")
costume=input("Brite Bomber, Skull Trooper, Renegade Raider, Dark Knight, Twitch Prime Skin, or Default? ")
print("What pickaxe do you fancy")
pickaxe=input("shovel, omega, pick squeak, default, or daddy whacker? ")
print("Which back bling do you crave? ")
back_bling=input("Royale Shield, Rust Bucket, Black Shield, Red Shield, or an Alpine backpack? ")
print("Your selection " + costume + " " + pickaxe + " "+ back_bling + " is ready for use ;)")
print("Click next block to drop into the Fortnite Map")
import random
print(costume + " where do you want to drop")
location1=input("Anarchy Acres, Greasy Grove, Pleasant Park, Lonely Lodge, Retail Row, Salty Springs, Moisty Mire, Fatal Fields, Dusty Depot")
droppers=random.randint(0,20)
print(location1 + " is a nice choice " + str(droppers) + " people have landed there")
print("Which weapon do you want?" )
weapon1=input("legendary scar, grey tactical submachine gun, the papi artale, or the rocket propeller grenade? ")
def fighting_time ():
print("You have encountered an enemy. What do you do? ")
enemy1=input("Team, dance, shoot at, or build? ")
while enemy1 != "team" and enemy1 != "dance" and enemy1 != "shoot at" and enemy1 != "build":
enemy1=input("Team, dance, shoot at, or build? ")
if enemy1 == 'team':
print("epic games has banned you. NEVER TEAM AGAIN CHEATER")
quit()
if enemy1 == 'dance':
print("enemy shoots at you and your dead. NEXT TIME WHEN YOU SEE AN EMEMY DONT BE DUMB")
quit()
if enemy1 == 'shoot at':
print("good job you have eleminated your enemy with your " + weapon1)
if enemy1 == 'build':
print("good job. You have blocked their shots and have allowed time to escape from the enemy")
if enemy1 == 'build' or 'shoot at':
print("congratulations. You have beaten your first enemy now you may continue your match. ")
import random
print("You are currently still in " + location1 + " where do you desire to go next?")
place1=input("Where do you desire to go to next? Retail Row, Dusty Depot, or Anarchy Acres?")
people_in_game1= random.randint(0,10)
choice1=input("there are currently " + str(people_in_game1)+ " people there. Do you still desire to go?")
if choice1 == "yes":
location2=print("You will be transported on the next block")
if choice1 == "no":
place2=input("Where do you desire to go to next? Retail Row, Dusty Depot, or Anarchy Acres?")
people_in_game2= random.randint(0,10)
choice2=input("There are currently " + str(people_in_game2)+ " people there. Do you still desire to go?")
if choice2 == "yes":
location2=print("You will be transported on the next block")
if choice2 == "no":
print("Too bad your going there whether you like it or not. Click the nect block to continue.")
import random
def hunterer_gatherer ():
material1 = random.randint(150,500)
choice3=input("Which matertial do you want? Wood, Brick, or Steel? ")
if choice3 == "wood":
for x in range(5):
print("chop")
print("you have gathered " + str(material1) + " wood")
if choice3 == "brick":
for x in range(5):
print("plip plop")
print("you have gathered " + str(material1) + " brick")
if choice3 == "steel":
for x in range(5):
print("ding")
print("you have gathered " + str(material1) + " steel")
hunterer_gatherer()
import random
people_in_game3= random.randint (3,10)
print("There are now " + str(people_in_game3) + " left in the game.")
print("You are now in " + place1 or place2 + "What would you like to do now? ")
choice4=input("Would you like to gather more materials, or fight? ")
if choice4 == "materials":
hunterer_gatherer()
if choice4 == "fight":
fighting_time()
print("You are in the endgame. It is a 1v1.")
guerr_bears=(random.choice(["shooting you","building"]))
choice5=input("Your opponent is " + guerr_bears + " . What do you desire to do? Build, or shoot?")
if choice5 == "build":
print("Nice. You are now well protected. You have earned yourself a VICTORY ROYALE!!!!!!")
if choice5 == "shoot":
print("Your shoots are useless and they have obliterated you. Better luck next time.")
quit()
| 0.094678 | 0.637327 |
# Average Perceptron Algorithm
1 point possible (graded)
The average perceptron will add a modification to the original perceptron algorithm: since the basic algorithm continues updating as the algorithm runs, nudging parameters in possibly conflicting directions, it is better to take an average of those parameters as the final answer. Every update of the algorithm is the same as before. The returned parameters θ, however, are an average of the θs across the nT steps:
θfinal=1nT(θ(1)+θ(2)+...+θ(nT))
You will now implement the average perceptron algorithm. This function should be constructed similarly to the Full Perceptron Algorithm above, except that it should return the average values of θ and
```
##Function used instructed by the exercise.. craaazy stuff bro
from string import punctuation, digits
import numpy as np
import random
from matplotlib import pyplot as plt
%matplotlib inline
def get_order(n_samples):
try:
with open(str(n_samples) + '.txt') as fp:
line = fp.readline()
return list(map(int, line.split(',')))
except FileNotFoundError:
random.seed(1)
indices = list(range(n_samples))
random.shuffle(indices)
return indices
def perceptron_single_step_update(feature_vector,label,current_theta, current_theta_0):
if (label*(np.dot(feature_vector, current_theta) + current_theta_0)) <= 0:
current_theta= current_theta + (np.dot(label, feature_vector))
current_theta_0= (current_theta_0 + label)
else:
current_theta_0= current_theta_0
current_theta= current_theta
return (current_theta, current_theta_0)
def average_perceptron(feature_matrix, labels, T):
theta = np.ones(feature_matrix.shape[1])
theta_0 = np.zeros(1)
sum_theta = np.zeros(feature_matrix.shape[1])
sum_theta_0 = np.zeros(1)
update_counter = 0
for t in range(T):
for i in get_order(feature_matrix.shape[0]):
theta, theta_0 = perceptron_single_step_update(feature_matrix[i],
labels[i],
theta,
theta_0)
sum_theta += theta
sum_theta_0 += theta_0
n_samples= T * feature_matrix.shape[0]
return((sum_theta/n_samples, sum_theta_0/n_samples))
#Example
feature_matrix= np.array([
[-1.85954975e-01, -5.09014576e-02, 3.18341925e-01, -4.92494361e-01, 1.17290142e-01],
[-2.67159545e-01, 1.58003187e-01, -3.07128547e-01, 1.52733302e-01, -9.28785729e-02],
[-1.68852441e-01, 2.13241036e-01, 1.05168850e-01, 3.86352473e-02, 8.45188135e-02],
[-3.27003047e-01, 4.30601481e-01, -3.22000933e-02, -2.95024675e-01, 1.05874501e-01],
[9.11263652e-02, -4.07725654e-01, 4.85931682e-02, -3.60755570e-01, 2.86148788e-02],
[-3.74836722e-01, 2.37854783e-01, 2.64549662e-01, -1.40486303e-01, -3.52008461e-01],
[-5.07496929e-02, 3.09763446e-01, -1.81890428e-01, 2.16650758e-01, 1.52858451e-01],
[1.30719418e-01, -2.57653578e-01, -4.92338668e-01, 4.50303583e-01, -1.06309065e-01],
[4.34751868e-01, 1.82111419e-02, 3.76404633e-01, 2.93951357e-01, 3.13608230e-01],
[1.48316020e-01, 3.95543188e-04, -3.14938610e-01, 4.55522298e-01, -1.66514414e-01]])
labels= np.array([-1, 1 , 1 ,-1 ,-1 , 1 ,-1 ,-1 , 1 , 1])
T= 5
average_perceptron(feature_matrix, labels, T)
average_perceptron(feature_matrix, labels, T)
def perceptron_single_step_update(
feature_vector,
label,
current_theta,
current_theta_0):
if label*(feature_vector@current_theta + current_theta_0) <= 0:
current_theta += label*feature_vector
current_theta_0 += label
return (current_theta, current_theta_0)
def average_perceptron(feature_matrix, labels, T):
theta = np.ones(feature_matrix.shape[1])
theta_0 = np.zeros(1)
sum_theta = np.zeros(feature_matrix.shape[1])
sum_theta_0 = np.zeros(1)
update_counter = 0
for t in range(T):
for i in get_order(feature_matrix.shape[0]):
update_counter += 1
theta, theta_0 = perceptron_single_step_update(feature_matrix[i],
labels[i],
theta,
theta_0)
sum_theta += theta
sum_theta_0 += theta_0
total= len(feature_matrix.shape[0])
return((sum_theta/update_counter, sum_theta_0/update_counter))
#Example
feature_matrix= np.array([[-0.11286146, -0.22198953, -0.14659728, 0.14990055, 0.34362585, 0.29124364, 0.36645741, -0.38395815, 0.48403646, -0.42986177],
[-0.19900484, 0.13816285, 0.17549319, -0.06134774, -0.14103174, 0.38151342, -0.21006459, 0.40763644, 0.43762875, -0.21409213],
[ 0.16840433, 0.24093196, 0.41094187, -0.13137612, 0.1754318, -0.24527301, 0.38110738, 0.4539427, -0.15527533, 0.12831007],
[ 0.02549292, 0.44185929, 0.15622804, 0.47588618, 0.48284325, 0.02557214, 0.02240127, -0.14858076 ,-0.14493135, 0.4540024 ],
[ 0.45530607, 0.36479921, 0.41953732, 0.2119896, -0.12570394, -0.24385637, -0.25120552, 0.44586771, -0.03470791, 0.16483698],
[ 0.42528185, 0.32090971, 0.48880699, 0.45960949, -0.01070594, -0.45291631, 0.39311651, 0.08046444, -0.35589567, -0.35737133],
[-0.2120859,-0.33509341, 0.05469693, 0.2267908, -0.31843438, -0.45843391, -0.01369163, -0.19757312, -0.01284696, -0.46651944],
[-0.2120859, -0.33509341, 0.05469693, 0.2267908, -0.31843438, -0.45843391, -0.01369163, -0.19757312, -0.01284696, -0.46651944],
[-0.36050136, 0.00698636, 0.42998158, -0.06502174, 0.18412658, -0.28876618, -0.11885911, -0.38759219, 0.39600346, 0.47586519],
[ 0.36094748, -0.33641301, -0.28465536, -0.28115422, 0.25607074, 0.27662758,0.27289085, -0.42365394, -0.02593193, -0.4825735]])
labels= np.array([-1 ,-1 ,1 ,-1 ,-1 ,-1 ,-1 , 1 , 1, -1])
T= 1
average_perceptron(feature_matrix, labels, T)
```
|
github_jupyter
|
##Function used instructed by the exercise.. craaazy stuff bro
from string import punctuation, digits
import numpy as np
import random
from matplotlib import pyplot as plt
%matplotlib inline
def get_order(n_samples):
try:
with open(str(n_samples) + '.txt') as fp:
line = fp.readline()
return list(map(int, line.split(',')))
except FileNotFoundError:
random.seed(1)
indices = list(range(n_samples))
random.shuffle(indices)
return indices
def perceptron_single_step_update(feature_vector,label,current_theta, current_theta_0):
if (label*(np.dot(feature_vector, current_theta) + current_theta_0)) <= 0:
current_theta= current_theta + (np.dot(label, feature_vector))
current_theta_0= (current_theta_0 + label)
else:
current_theta_0= current_theta_0
current_theta= current_theta
return (current_theta, current_theta_0)
def average_perceptron(feature_matrix, labels, T):
theta = np.ones(feature_matrix.shape[1])
theta_0 = np.zeros(1)
sum_theta = np.zeros(feature_matrix.shape[1])
sum_theta_0 = np.zeros(1)
update_counter = 0
for t in range(T):
for i in get_order(feature_matrix.shape[0]):
theta, theta_0 = perceptron_single_step_update(feature_matrix[i],
labels[i],
theta,
theta_0)
sum_theta += theta
sum_theta_0 += theta_0
n_samples= T * feature_matrix.shape[0]
return((sum_theta/n_samples, sum_theta_0/n_samples))
#Example
feature_matrix= np.array([
[-1.85954975e-01, -5.09014576e-02, 3.18341925e-01, -4.92494361e-01, 1.17290142e-01],
[-2.67159545e-01, 1.58003187e-01, -3.07128547e-01, 1.52733302e-01, -9.28785729e-02],
[-1.68852441e-01, 2.13241036e-01, 1.05168850e-01, 3.86352473e-02, 8.45188135e-02],
[-3.27003047e-01, 4.30601481e-01, -3.22000933e-02, -2.95024675e-01, 1.05874501e-01],
[9.11263652e-02, -4.07725654e-01, 4.85931682e-02, -3.60755570e-01, 2.86148788e-02],
[-3.74836722e-01, 2.37854783e-01, 2.64549662e-01, -1.40486303e-01, -3.52008461e-01],
[-5.07496929e-02, 3.09763446e-01, -1.81890428e-01, 2.16650758e-01, 1.52858451e-01],
[1.30719418e-01, -2.57653578e-01, -4.92338668e-01, 4.50303583e-01, -1.06309065e-01],
[4.34751868e-01, 1.82111419e-02, 3.76404633e-01, 2.93951357e-01, 3.13608230e-01],
[1.48316020e-01, 3.95543188e-04, -3.14938610e-01, 4.55522298e-01, -1.66514414e-01]])
labels= np.array([-1, 1 , 1 ,-1 ,-1 , 1 ,-1 ,-1 , 1 , 1])
T= 5
average_perceptron(feature_matrix, labels, T)
average_perceptron(feature_matrix, labels, T)
def perceptron_single_step_update(
feature_vector,
label,
current_theta,
current_theta_0):
if label*(feature_vector@current_theta + current_theta_0) <= 0:
current_theta += label*feature_vector
current_theta_0 += label
return (current_theta, current_theta_0)
def average_perceptron(feature_matrix, labels, T):
theta = np.ones(feature_matrix.shape[1])
theta_0 = np.zeros(1)
sum_theta = np.zeros(feature_matrix.shape[1])
sum_theta_0 = np.zeros(1)
update_counter = 0
for t in range(T):
for i in get_order(feature_matrix.shape[0]):
update_counter += 1
theta, theta_0 = perceptron_single_step_update(feature_matrix[i],
labels[i],
theta,
theta_0)
sum_theta += theta
sum_theta_0 += theta_0
total= len(feature_matrix.shape[0])
return((sum_theta/update_counter, sum_theta_0/update_counter))
#Example
feature_matrix= np.array([[-0.11286146, -0.22198953, -0.14659728, 0.14990055, 0.34362585, 0.29124364, 0.36645741, -0.38395815, 0.48403646, -0.42986177],
[-0.19900484, 0.13816285, 0.17549319, -0.06134774, -0.14103174, 0.38151342, -0.21006459, 0.40763644, 0.43762875, -0.21409213],
[ 0.16840433, 0.24093196, 0.41094187, -0.13137612, 0.1754318, -0.24527301, 0.38110738, 0.4539427, -0.15527533, 0.12831007],
[ 0.02549292, 0.44185929, 0.15622804, 0.47588618, 0.48284325, 0.02557214, 0.02240127, -0.14858076 ,-0.14493135, 0.4540024 ],
[ 0.45530607, 0.36479921, 0.41953732, 0.2119896, -0.12570394, -0.24385637, -0.25120552, 0.44586771, -0.03470791, 0.16483698],
[ 0.42528185, 0.32090971, 0.48880699, 0.45960949, -0.01070594, -0.45291631, 0.39311651, 0.08046444, -0.35589567, -0.35737133],
[-0.2120859,-0.33509341, 0.05469693, 0.2267908, -0.31843438, -0.45843391, -0.01369163, -0.19757312, -0.01284696, -0.46651944],
[-0.2120859, -0.33509341, 0.05469693, 0.2267908, -0.31843438, -0.45843391, -0.01369163, -0.19757312, -0.01284696, -0.46651944],
[-0.36050136, 0.00698636, 0.42998158, -0.06502174, 0.18412658, -0.28876618, -0.11885911, -0.38759219, 0.39600346, 0.47586519],
[ 0.36094748, -0.33641301, -0.28465536, -0.28115422, 0.25607074, 0.27662758,0.27289085, -0.42365394, -0.02593193, -0.4825735]])
labels= np.array([-1 ,-1 ,1 ,-1 ,-1 ,-1 ,-1 , 1 , 1, -1])
T= 1
average_perceptron(feature_matrix, labels, T)
| 0.310694 | 0.876793 |
## Review Rating Prediction
### Imports
```
import numpy as np
import pandas as pd
import seaborn as sns
from scipy import sparse
import matplotlib.pyplot as plt
%matplotlib inline
print('Libraries imported')
```
## Data Import
```
df = pd.read_csv('full_merge.csv')
data = df.loc[:, ('Reviews', 'Rating')]
data.Reviews = data.Reviews.astype(str)
data.Rating = data.Rating.astype(float)
data
```
### Splitting among test/train
```
n = data.shape[0] #337354
split_ratio = 0.8
sample_size = int(n*split_ratio)
rev_samp = data.sample(n = n, random_state = 42)
train = rev_samp[0:sample_size]
test = rev_samp[sample_size:]
train.shape, test.shape
```
## Label Exploration
```
print(train.head())
sns.countplot(data['Rating']).set_title('Rating Distribution')
plt.show()
```
## One-hot Encoding
```
print('One-Hot Encoding')
train = pd.get_dummies(train, columns = ['Rating'])
print('On Train')
train.head()
test = pd.get_dummies(test, columns = ['Rating'])
print('Train and test shape')
train.shape, test.shape
```
### Setting train, test fractions
```
# set frac = 1 to use the entire sample
train_samp = train.sample(frac = 1, random_state = 42)
test_samp = test.sample(frac = 1, random_state = 42)
print(train_samp.shape, test_samp.shape)
print(train_samp.head())
```
## Long Short Term Memory - LSTM Model
```
# Defining parameters
# max number of unique words
max_features = 20000
# max number of words from review to use
maxlen = 200
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
class_names = ['Rating_1.0','Rating_2.0','Rating_3.0','Rating_4.0','Rating_5.0',\
'Rating_6.0','Rating_7.0','Rating_8.0','Rating_9.0','Rating_10.0']
# Splitting off my y variable
print('Y data')
y = train_samp[class_names].values
print(y.shape)
print(y)
# Train test split
tokenizer = Tokenizer(num_words=max_features)
tokenizer.fit_on_texts(list(train_samp['Reviews'].values))
X_train = tokenizer.texts_to_sequences(train_samp['Reviews'].values)
X_test = tokenizer.texts_to_sequences(test_samp['Reviews'].values)
x_train = pad_sequences(X_train, maxlen = maxlen)
x_test = pad_sequences(X_test, maxlen = maxlen)
print('X test data')
print(x_test)
print(x_test.shape)
```
### Saving tokenizer
```
import pickle
# saving tokenizer
with open('./ml_model/tokenizer/tokenizer.pkl', 'wb') as handle:
pickle.dump(tokenizer, handle)
print('tokenizer saved')
```
### Saving reviews for embedding
```
review_df = df.loc[:, ('Reviews')]
np.savetxt(r'./ml_model/reviews/review.txt', review_df.values, fmt='%s')
print('text file created')
```
## Training LSTM Model
```
from keras.models import Model
from keras.callbacks import EarlyStopping, ModelCheckpoint
from keras.layers import Bidirectional, GlobalAveragePooling1D, GlobalMaxPooling1D, concatenate
from keras.layers import Dense, Input, LSTM, Embedding, Dropout, Activation, SpatialDropout1D, GRU
embed_size = 20
inp = Input(shape = (maxlen,))
x = Embedding(max_features, embed_size, trainable = True)(inp)
x = SpatialDropout1D(0.5)(x)
x = Bidirectional(LSTM(40, return_sequences=True))(x)
x = Bidirectional(GRU(40, return_sequences=True))(x)
avg_pool = GlobalAveragePooling1D()(x)
max_pool = GlobalMaxPooling1D()(x)
conc = concatenate([avg_pool, max_pool])
outp = Dense(10, activation = 'sigmoid')(conc)
model = Model(inputs = inp, outputs = outp)
# patience is how many epochs to wait to see if val_loss will improve again
earlystop = EarlyStopping(monitor = 'val_loss', min_delta = 0, patience = 5)
checkpoint = ModelCheckpoint(monitor = 'val_loss', save_best_only = True,\
filepath = './ml_model/weights/lstm_gru_weights.hdf5')
model.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
```
## Model Training
```
print('Model Training Initiated')
epoch = 10
model.fit(x_train, y, batch_size = 512, epochs = epoch, validation_split = .2, callbacks=[earlystop, checkpoint])
print('Model Training Completed')
```
### Model Evaluation
```
y_test = model.predict([x_test], batch_size=1024, verbose = 1)
y_test
```
### Model Accuracy
```
from sklearn import metrics
v = metrics.classification_report(np.argmax(test_samp[class_names].values, axis = 1),np.argmax(y_test, axis = 1))
print(v)
```
### Saving model
```
model.save('./ml_model/model/review_rating_pred.h5')
print('Model Saved')
```
### Model Testing
```
from keras.models import load_model
lstm = load_model('./ml_model/model/review_rating_pred.h5')
tokenizer_test = pd.read_pickle('./ml_model/tokenizer/tokenizer.pkl')
print('Model Loaded')
```
#### Sample review prediction
```
# Sample Reviews (Bad, moderate(less bad), Good)
# 'Intunive did not work for my son; he was bouncing off the walls while he was taking it, and having major issues in class! It seems to work the opposite on him!'
# 'Increased dose from 1mg to 2 mg now urinating in bed every night, bad effect'
# 'Good experience, it has worked well for my son for about 2 months now.. For some that say they can no longer afford because of insurance. Some places sell generic for under 10$ a month'
s = 1
review_list = []
rating = [1, 3, 8]
review1 = ['Intunive did not work for my son; he was bouncing off the walls while he was taking it, and having major issues in class! It seems to work the opposite on him!']
review2 = ['Increased dose from 1mg to 2 mg now urinating in bed every night, bad effect, worse, major pain']
review3 = ['Good experience, it has worked well for my son for about 2 months now.. For some that say they can no longer afford because of insurance. Some places sell generic for under 10$ a month']
review_list.append(review1)
print(review2)
review_list.append(review2)
review_list.append(review3)
for sample in review_list:
X_sample = tokenizer_test.texts_to_sequences(sample)
print('Review ', s)
print('Original Rating', rating[s-1])
x_sample = pad_sequences(X_sample, maxlen = 200)
y_sample = lstm.predict([x_sample], batch_size = 512, verbose = 1)
y_max = np.argmax(y_sample, axis = 1)
print('Predicted Rating',y_max + 1)
s += 1
print('')
```
### Predicting for entire sample
```
print('Read csv')
df = pd.read_csv('full_merge_emotion_sentiment.csv')
data = df.loc[:, ('Reviews', 'Rating')]
data.Reviews = data.Reviews.astype(str)
print('Tokenizing')
X_sample = tokenizer_test.texts_to_sequences(data['Reviews'].values)
x_sample = pad_sequences(X_sample, maxlen = 200)
print('Sample Prediction')
y_sample = lstm.predict([x_sample], batch_size=512, verbose = 1)
print('')
df['Predicted_rating'] = np.argmax(y_sample, axis=1)
print(df)
df.to_csv('full_merge_model_predictions.csv', index=False)
print('new dataframe saved as csv')
# %match 15% 66% 81% 89%
# new_rating Exact nearest 1 nearest 2 nearest 3
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import seaborn as sns
from scipy import sparse
import matplotlib.pyplot as plt
%matplotlib inline
print('Libraries imported')
df = pd.read_csv('full_merge.csv')
data = df.loc[:, ('Reviews', 'Rating')]
data.Reviews = data.Reviews.astype(str)
data.Rating = data.Rating.astype(float)
data
n = data.shape[0] #337354
split_ratio = 0.8
sample_size = int(n*split_ratio)
rev_samp = data.sample(n = n, random_state = 42)
train = rev_samp[0:sample_size]
test = rev_samp[sample_size:]
train.shape, test.shape
print(train.head())
sns.countplot(data['Rating']).set_title('Rating Distribution')
plt.show()
print('One-Hot Encoding')
train = pd.get_dummies(train, columns = ['Rating'])
print('On Train')
train.head()
test = pd.get_dummies(test, columns = ['Rating'])
print('Train and test shape')
train.shape, test.shape
# set frac = 1 to use the entire sample
train_samp = train.sample(frac = 1, random_state = 42)
test_samp = test.sample(frac = 1, random_state = 42)
print(train_samp.shape, test_samp.shape)
print(train_samp.head())
# Defining parameters
# max number of unique words
max_features = 20000
# max number of words from review to use
maxlen = 200
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
class_names = ['Rating_1.0','Rating_2.0','Rating_3.0','Rating_4.0','Rating_5.0',\
'Rating_6.0','Rating_7.0','Rating_8.0','Rating_9.0','Rating_10.0']
# Splitting off my y variable
print('Y data')
y = train_samp[class_names].values
print(y.shape)
print(y)
# Train test split
tokenizer = Tokenizer(num_words=max_features)
tokenizer.fit_on_texts(list(train_samp['Reviews'].values))
X_train = tokenizer.texts_to_sequences(train_samp['Reviews'].values)
X_test = tokenizer.texts_to_sequences(test_samp['Reviews'].values)
x_train = pad_sequences(X_train, maxlen = maxlen)
x_test = pad_sequences(X_test, maxlen = maxlen)
print('X test data')
print(x_test)
print(x_test.shape)
import pickle
# saving tokenizer
with open('./ml_model/tokenizer/tokenizer.pkl', 'wb') as handle:
pickle.dump(tokenizer, handle)
print('tokenizer saved')
review_df = df.loc[:, ('Reviews')]
np.savetxt(r'./ml_model/reviews/review.txt', review_df.values, fmt='%s')
print('text file created')
from keras.models import Model
from keras.callbacks import EarlyStopping, ModelCheckpoint
from keras.layers import Bidirectional, GlobalAveragePooling1D, GlobalMaxPooling1D, concatenate
from keras.layers import Dense, Input, LSTM, Embedding, Dropout, Activation, SpatialDropout1D, GRU
embed_size = 20
inp = Input(shape = (maxlen,))
x = Embedding(max_features, embed_size, trainable = True)(inp)
x = SpatialDropout1D(0.5)(x)
x = Bidirectional(LSTM(40, return_sequences=True))(x)
x = Bidirectional(GRU(40, return_sequences=True))(x)
avg_pool = GlobalAveragePooling1D()(x)
max_pool = GlobalMaxPooling1D()(x)
conc = concatenate([avg_pool, max_pool])
outp = Dense(10, activation = 'sigmoid')(conc)
model = Model(inputs = inp, outputs = outp)
# patience is how many epochs to wait to see if val_loss will improve again
earlystop = EarlyStopping(monitor = 'val_loss', min_delta = 0, patience = 5)
checkpoint = ModelCheckpoint(monitor = 'val_loss', save_best_only = True,\
filepath = './ml_model/weights/lstm_gru_weights.hdf5')
model.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
print('Model Training Initiated')
epoch = 10
model.fit(x_train, y, batch_size = 512, epochs = epoch, validation_split = .2, callbacks=[earlystop, checkpoint])
print('Model Training Completed')
y_test = model.predict([x_test], batch_size=1024, verbose = 1)
y_test
from sklearn import metrics
v = metrics.classification_report(np.argmax(test_samp[class_names].values, axis = 1),np.argmax(y_test, axis = 1))
print(v)
model.save('./ml_model/model/review_rating_pred.h5')
print('Model Saved')
from keras.models import load_model
lstm = load_model('./ml_model/model/review_rating_pred.h5')
tokenizer_test = pd.read_pickle('./ml_model/tokenizer/tokenizer.pkl')
print('Model Loaded')
# Sample Reviews (Bad, moderate(less bad), Good)
# 'Intunive did not work for my son; he was bouncing off the walls while he was taking it, and having major issues in class! It seems to work the opposite on him!'
# 'Increased dose from 1mg to 2 mg now urinating in bed every night, bad effect'
# 'Good experience, it has worked well for my son for about 2 months now.. For some that say they can no longer afford because of insurance. Some places sell generic for under 10$ a month'
s = 1
review_list = []
rating = [1, 3, 8]
review1 = ['Intunive did not work for my son; he was bouncing off the walls while he was taking it, and having major issues in class! It seems to work the opposite on him!']
review2 = ['Increased dose from 1mg to 2 mg now urinating in bed every night, bad effect, worse, major pain']
review3 = ['Good experience, it has worked well for my son for about 2 months now.. For some that say they can no longer afford because of insurance. Some places sell generic for under 10$ a month']
review_list.append(review1)
print(review2)
review_list.append(review2)
review_list.append(review3)
for sample in review_list:
X_sample = tokenizer_test.texts_to_sequences(sample)
print('Review ', s)
print('Original Rating', rating[s-1])
x_sample = pad_sequences(X_sample, maxlen = 200)
y_sample = lstm.predict([x_sample], batch_size = 512, verbose = 1)
y_max = np.argmax(y_sample, axis = 1)
print('Predicted Rating',y_max + 1)
s += 1
print('')
print('Read csv')
df = pd.read_csv('full_merge_emotion_sentiment.csv')
data = df.loc[:, ('Reviews', 'Rating')]
data.Reviews = data.Reviews.astype(str)
print('Tokenizing')
X_sample = tokenizer_test.texts_to_sequences(data['Reviews'].values)
x_sample = pad_sequences(X_sample, maxlen = 200)
print('Sample Prediction')
y_sample = lstm.predict([x_sample], batch_size=512, verbose = 1)
print('')
df['Predicted_rating'] = np.argmax(y_sample, axis=1)
print(df)
df.to_csv('full_merge_model_predictions.csv', index=False)
print('new dataframe saved as csv')
# %match 15% 66% 81% 89%
# new_rating Exact nearest 1 nearest 2 nearest 3
| 0.535584 | 0.829975 |
```
import numpy as np
import pandas as pd
from scipy.spatial.distance import pdist, squareform
import seaborn as sns
import json
import networkx as nx
from networkx.readwrite import json_graph
# Import SNP data
data = pd.read_csv(
'./patient_snps_ci99.txt',
sep='\t',
index_col=0
)
# Code nucleotide values to numbers
data = data.replace("A", 0)
data = data.replace("T", 1)
data = data.replace("C", 2)
data = data.replace("G", 3)
data = data.replace("R", 4)
data = data.replace("K", 5)
data = data.replace("M", 6)
data = data.replace("Y", 7)
data = data.replace("S", 8)
data = data.replace("W", 9)
# Measure similarity between samples based on SNPs
data_comparisons = squareform(
pdist(
data.T,
metric='hamming'
)
)
# Convert data to table
table = pd.DataFrame(
data_comparisons,
columns=data.columns.tolist(),
index=data.columns.tolist()
)
# Visualize similarity matrix
sns.clustermap(
table,
figsize=(17,17)
)
# Create temporal metadata dictionary
meta = pd.read_csv(
'./patient_metadata.txt',
sep='\t')
meta_dict = pd.Series(
meta['normalized_time'].values,
index=meta['sample']
).to_dict()
meta
# Progress through time, if sample is introduced, add its node and edges
G = nx.DiGraph()
# Ignore list (refs and outliers)
#used = ['mt-5543-Patient2-A', 'ref_mt-0080', 'mt-0080', '68995']
#used2 = ['mt-5543-Patient2-A', 'ref_mt-0080', 'mt-0080', '68995']
used = ['ref_mt-0080']
used2 = ['ref_mt-0080']
#used = []
#used2 = []
# Add nodes
for sample in table.columns.tolist():
if sample not in used:
G.add_node(sample)
G.nodes()[sample]['time'] = meta_dict[sample]
# Add edges
for x in range(0, max(meta.normalized_time.tolist())):
time = []
for k, v in meta_dict.items():
if v == x and k not in used:
time.append(k)
for y in time:
if y not in used:
used.append(y)
smallest = list(np.unique(table[[y]].sort_values(by=y).values))
added = False
for x in range(len(smallest) - 2):
# Get samples in this relationship neighborhood
closest = table.loc[
((table[y] == smallest[x]) | (table[y] == smallest[x + 1]) | (table[y] == smallest[x + 2]))
][y].index.tolist()
for z in closest:
if y != z and not G.has_edge(y,z) and z not in used2 and z != used[0] and z != used[1]:
G.add_edges_from([
(y, z)
])
added = True
used2.append(z)
if added == True:
break
list(G.degree)
# Export network
data = json_graph.node_link_data(G)
with open("./tuberculosis_network.json", 'w') as f:
json.dump(data, f, indent=4)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
from scipy.spatial.distance import pdist, squareform
import seaborn as sns
import json
import networkx as nx
from networkx.readwrite import json_graph
# Import SNP data
data = pd.read_csv(
'./patient_snps_ci99.txt',
sep='\t',
index_col=0
)
# Code nucleotide values to numbers
data = data.replace("A", 0)
data = data.replace("T", 1)
data = data.replace("C", 2)
data = data.replace("G", 3)
data = data.replace("R", 4)
data = data.replace("K", 5)
data = data.replace("M", 6)
data = data.replace("Y", 7)
data = data.replace("S", 8)
data = data.replace("W", 9)
# Measure similarity between samples based on SNPs
data_comparisons = squareform(
pdist(
data.T,
metric='hamming'
)
)
# Convert data to table
table = pd.DataFrame(
data_comparisons,
columns=data.columns.tolist(),
index=data.columns.tolist()
)
# Visualize similarity matrix
sns.clustermap(
table,
figsize=(17,17)
)
# Create temporal metadata dictionary
meta = pd.read_csv(
'./patient_metadata.txt',
sep='\t')
meta_dict = pd.Series(
meta['normalized_time'].values,
index=meta['sample']
).to_dict()
meta
# Progress through time, if sample is introduced, add its node and edges
G = nx.DiGraph()
# Ignore list (refs and outliers)
#used = ['mt-5543-Patient2-A', 'ref_mt-0080', 'mt-0080', '68995']
#used2 = ['mt-5543-Patient2-A', 'ref_mt-0080', 'mt-0080', '68995']
used = ['ref_mt-0080']
used2 = ['ref_mt-0080']
#used = []
#used2 = []
# Add nodes
for sample in table.columns.tolist():
if sample not in used:
G.add_node(sample)
G.nodes()[sample]['time'] = meta_dict[sample]
# Add edges
for x in range(0, max(meta.normalized_time.tolist())):
time = []
for k, v in meta_dict.items():
if v == x and k not in used:
time.append(k)
for y in time:
if y not in used:
used.append(y)
smallest = list(np.unique(table[[y]].sort_values(by=y).values))
added = False
for x in range(len(smallest) - 2):
# Get samples in this relationship neighborhood
closest = table.loc[
((table[y] == smallest[x]) | (table[y] == smallest[x + 1]) | (table[y] == smallest[x + 2]))
][y].index.tolist()
for z in closest:
if y != z and not G.has_edge(y,z) and z not in used2 and z != used[0] and z != used[1]:
G.add_edges_from([
(y, z)
])
added = True
used2.append(z)
if added == True:
break
list(G.degree)
# Export network
data = json_graph.node_link_data(G)
with open("./tuberculosis_network.json", 'w') as f:
json.dump(data, f, indent=4)
| 0.319758 | 0.497131 |
## Omega and Xi
To implement Graph SLAM, a matrix and a vector (omega and xi, respectively) are introduced. The matrix is square and labelled with all the robot poses (xi) and all the landmarks (Li). Every time you make an observation, for example, as you move between two poses by some distance `dx` and can relate those two positions, you can represent this as a numerical relationship in these matrices.
It's easiest to see how these work in an example. Below you can see a matrix representation of omega and a vector representation of xi.
<img src='images/omega_xi.png' width=20% height=20% />
Next, let's look at a simple example that relates 3 poses to one another.
* When you start out in the world most of these values are zeros or contain only values from the initial robot position
* In this example, you have been given constraints, which relate these poses to one another
* Constraints translate into matrix values
<img src='images/omega_xi_constraints.png' width=70% height=70% />
If you have ever solved linear systems of equations before, this may look familiar, and if not, let's keep going!
### Solving for x
To "solve" for all these x values, we can use linear algebra; all the values of x are in the vector `mu` which can be calculated as a product of the inverse of omega times xi.
<img src='images/solution.png' width=30% height=30% />
---
**You can confirm this result for yourself by executing the math in the cell below.**
```
import numpy as np
# define omega and xi as in the example
omega = np.array([[1,0,0],
[-1,1,0],
[0,-1,1]])
xi = np.array([[-3],
[5],
[3]])
# calculate the inverse of omega
omega_inv = np.linalg.inv(np.matrix(omega))
# calculate the solution, mu
mu = omega_inv*xi
# print out the values of mu (x0, x1, x2)
print(mu)
```
## Motion Constraints and Landmarks
In the last example, the constraint equations, relating one pose to another were given to you. In this next example, let's look at how motion (and similarly, sensor measurements) can be used to create constraints and fill up the constraint matrices, omega and xi. Let's start with empty/zero matrices.
<img src='images/initial_constraints.png' width=35% height=35% />
This example also includes relationships between poses and landmarks. Say we move from x0 to x1 with a displacement `dx` of 5. Then we have created a motion constraint that relates x0 to x1, and we can start to fill up these matrices.
<img src='images/motion_constraint.png' width=50% height=50% />
In fact, the one constraint equation can be written in two ways. So, the motion constraint that relates x0 and x1 by the motion of 5 has affected the matrix, adding values for *all* elements that correspond to x0 and x1.
### 2D case
In these examples, we've been showing you change in only one dimension, the x-dimension. In the project, it will be up to you to represent x and y positional values in omega and xi. One solution could be to create an omega and xi that are 2x larger, so that they can hold both x and y values for poses. I might suggest drawing out a rough solution to graph slam as you read the instructions in the next notebook; that always helps me organize my thoughts. Good luck!
|
github_jupyter
|
import numpy as np
# define omega and xi as in the example
omega = np.array([[1,0,0],
[-1,1,0],
[0,-1,1]])
xi = np.array([[-3],
[5],
[3]])
# calculate the inverse of omega
omega_inv = np.linalg.inv(np.matrix(omega))
# calculate the solution, mu
mu = omega_inv*xi
# print out the values of mu (x0, x1, x2)
print(mu)
| 0.322633 | 0.992704 |
# Differential poly(A) tail lengths
In this notebook we plot the poly(A) tail length (estimate) distribution for CAB1
```
import sys
import os
from glob import glob
import random
from collections import Counter
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
import matplotlib_venn as vn
from matplotlib.colors import ListedColormap
import seaborn as sns
import pysam
## Default plotting params
%matplotlib inline
sns.set(font='Arial')
plt.rcParams['svg.fonttype'] = 'none'
style = sns.axes_style('white')
style.update(sns.axes_style('ticks'))
style['xtick.major.size'] = 2
style['ytick.major.size'] = 2
sns.set(font_scale=1.5, style=style)
pal = sns.color_palette(['#0072b2', '#d55e00', '#009e73', '#f0e442', '#cc79a7'])
cmap = ListedColormap(pal.as_hex())
sns.set_palette(pal)
sns.palplot(pal)
plt.show()
vir1_pa_dists = pd.read_csv(
'../pooled/vir1_vs_col0_differential_polya_dists.tsv',
sep='\t',
names=['chrom', 'start', 'end', 'gene_id',
'score', 'strand', 'nreads_vir1', 'nreads_col0',
'median_vir1', 'ci_lower_vir1', 'ci_upper_vir1',
'median_col0', 'ci_lower_col0', 'ci_upper_col0',
'ks', 'ks_p_val', 'ks_fdr',
'mwu', 'mwu_p_val', 'mwu_fdr']
)
vir1_pa_dists.head()
plt.hist(vir1_pa_dists.ks_p_val, bins=25)
plt.show()
def bam_cigar_to_invs(aln):
invs = []
start = aln.reference_start
end = aln.reference_end
strand = '-' if aln.is_reverse else '+'
left = start
right = left
aln_length = 0
for op, ln in aln.cigar:
if op in (1, 4, 5):
# does not consume reference
continue
elif op in (0, 2, 7, 8):
# consume reference but do not add to invs yet
right += ln
elif op == 3:
invs.append([left, right])
aln_length += right - left
left = right + ln
right = left
if right > left:
invs.append([left, right])
assert invs[0][0] == start
assert invs[-1][1] == end
return invs, start, end, strand
def parse_pysam_aln(aln):
chrom = aln.reference_name
read_id = aln.query_name
invs, start, end, strand = bam_cigar_to_invs(aln)
is_secondary = aln.is_secondary
mapq = aln.mapping_quality
return chrom, start, end, read_id, strand, invs, is_secondary, mapq
def get_gtf_gene_id(attrs):
return re.search('gene_id \"(.*?)\";', attrs).group(1)
def get_gtf_exons(gtf_fn):
with open(gtf_fn) as gtf:
for record in gtf:
record = record.strip().split('\t')
if record[2] == 'exon':
gene_id = get_gtf_gene_id(record[8])
yield record[0], int(record[3]) - 1, int(record[4]), gene_id, record[6]
def parse_gtf_flat_exon_invs(gtf_fn):
gene_cluster = []
gtf_iter = get_gtf_exons(gtf_fn)
curr_chrom, start, end, curr_gene_id, curr_strand = next(gtf_iter)
gene_cluster.append([[start, end]])
for chrom, start, end, gene_id, strand in gtf_iter:
if gene_id != curr_gene_id:
yield curr_gene_id, curr_chrom, curr_strand, flatten(gene_cluster)
curr_gene_id, curr_chrom, curr_strand = gene_id, chrom, strand
gene_cluster = []
gene_cluster.append([[start, end]])
else:
gene_cluster.append([[start, end]])
if gene_cluster:
yield curr_gene_id, curr_chrom, curr_strand, flatten(gene_cluster)
def flatten(bundle):
flattened = []
all_invs = iter(sorted(it.chain(*bundle)))
inv_start, inv_end = next(all_invs)
for start, end in all_invs:
if start <= inv_end:
inv_end = max(inv_end, end)
else:
flattened.append([inv_start, inv_end])
inv_start, inv_end = start, end
if not flattened or flattened[-1] != [inv_start, inv_end]:
flattened.append([inv_start, inv_end])
return flattened
def intersect(inv_a, inv_b):
a_start, a_end = inv_a
b_start, b_end = inv_b
if a_end < b_start or a_start > b_end:
return 0
else:
s = max(a_start, b_start)
e = min(a_end, b_end)
return e - s
def intersect_spliced_invs(invs_a, invs_b):
score = 0
invs_a = iter(invs_a)
invs_b = iter(invs_b)
a_start, a_end = next(invs_a)
b_start, b_end = next(invs_b)
while True:
if a_end < b_start:
try:
a_start, a_end = next(invs_a)
except StopIteration:
break
elif a_start > b_end:
try:
b_start, b_end = next(invs_b)
except StopIteration:
break
else:
score += intersect([a_start, a_end], [b_start, b_end])
if a_end > b_end:
try:
b_start, b_end = next(invs_b)
except StopIteration:
break
else:
try:
a_start, a_end = next(invs_a)
except StopIteration:
break
return score
def get_polya_dist(chrom, start, end, strand, bam, gene_invs=None,
overlap_thresh=200, gene_frac_thresh=0.2,
read_frac_thresh=0.25):
if gene_invs is None:
gene_invs = [[start, end]]
gene_ln = sum([e - s for s, e in gene_invs])
polya_lengths = []
for aln in bam.fetch(chrom, start, end):
*_, read_id, read_strand, read_invs, _, _ = parse_pysam_aln(aln)
if strand != read_strand:
continue
read_ln = sum([e - s for s, e in read_invs])
abs_overlap = intersect_spliced_invs(gene_invs, read_invs)
read_frac = abs_overlap / read_ln
gene_frac = abs_overlap / gene_ln
if abs_overlap >= overlap_thresh and \
read_frac >= read_frac_thresh and \
gene_frac >= gene_frac_thresh:
pa = aln.get_tag('pA')
polya_lengths.append(pa)
return np.array(polya_lengths)
def plot_overlayed_dists(*args, query, bins, clip, colors, title, lw=1, log=True, ax=None):
if ax is None:
fig, ax = plt.subplots(figsize=(6, 5))
groups = []
for i, group in enumerate(args):
group_p_a = []
for bam_fn in group:
with pysam.AlignmentFile(bam_fn) as bam:
p_a = get_polya_dist(*query, bam)
group_p_a.append(p_a)
group_p_a = np.concatenate(group_p_a)
groups.append(group_p_a)
if log:
group_p_a = np.log10(group_p_a)
sns.distplot(group_p_a, bins=bins, kde_kws=dict(clip=clip, lw=lw), hist_kws=dict(alpha=0.2), color=colors[i], ax=ax)
ax.set_xlabel('polyA length')
ax.set_title(title)
return ax, groups
fig, ax = plt.subplots(figsize=(8, 5))
_, g = plot_overlayed_dists(
glob('../*Col*/aligned_data/*.with_pA_tag.bam'),
glob('../*VIR*/aligned_data/*.with_pA_tag.bam'),
glob('../*/aligned_data/*_vir1_*.with_pA_tag.bam'),
query=('1', 10477885, 10479114, '+'),
log=False,
bins=np.linspace(0, 120, 50),
clip=(0, 120),
colors=[pal[0], pal[2], pal[1]],
lw=3,
title='CAB1 (AT1G29930)',
ax=ax
)
ax.plot([], [], color=pal[0], label='Col-0')
ax.plot([], [], color=pal[2], label='VIRc')
ax.plot([], [], color=pal[1], label='vir-1')
ax.legend()
ax.set_xlim(0, 120)
ax.set_xlabel('Poly(A) tail length')
ax.set_ylabel('Density')
plt.tight_layout()
plt.savefig('cab1_polya_tail_length_distribution.svg')
plt.show()
```
|
github_jupyter
|
import sys
import os
from glob import glob
import random
from collections import Counter
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
import matplotlib_venn as vn
from matplotlib.colors import ListedColormap
import seaborn as sns
import pysam
## Default plotting params
%matplotlib inline
sns.set(font='Arial')
plt.rcParams['svg.fonttype'] = 'none'
style = sns.axes_style('white')
style.update(sns.axes_style('ticks'))
style['xtick.major.size'] = 2
style['ytick.major.size'] = 2
sns.set(font_scale=1.5, style=style)
pal = sns.color_palette(['#0072b2', '#d55e00', '#009e73', '#f0e442', '#cc79a7'])
cmap = ListedColormap(pal.as_hex())
sns.set_palette(pal)
sns.palplot(pal)
plt.show()
vir1_pa_dists = pd.read_csv(
'../pooled/vir1_vs_col0_differential_polya_dists.tsv',
sep='\t',
names=['chrom', 'start', 'end', 'gene_id',
'score', 'strand', 'nreads_vir1', 'nreads_col0',
'median_vir1', 'ci_lower_vir1', 'ci_upper_vir1',
'median_col0', 'ci_lower_col0', 'ci_upper_col0',
'ks', 'ks_p_val', 'ks_fdr',
'mwu', 'mwu_p_val', 'mwu_fdr']
)
vir1_pa_dists.head()
plt.hist(vir1_pa_dists.ks_p_val, bins=25)
plt.show()
def bam_cigar_to_invs(aln):
invs = []
start = aln.reference_start
end = aln.reference_end
strand = '-' if aln.is_reverse else '+'
left = start
right = left
aln_length = 0
for op, ln in aln.cigar:
if op in (1, 4, 5):
# does not consume reference
continue
elif op in (0, 2, 7, 8):
# consume reference but do not add to invs yet
right += ln
elif op == 3:
invs.append([left, right])
aln_length += right - left
left = right + ln
right = left
if right > left:
invs.append([left, right])
assert invs[0][0] == start
assert invs[-1][1] == end
return invs, start, end, strand
def parse_pysam_aln(aln):
chrom = aln.reference_name
read_id = aln.query_name
invs, start, end, strand = bam_cigar_to_invs(aln)
is_secondary = aln.is_secondary
mapq = aln.mapping_quality
return chrom, start, end, read_id, strand, invs, is_secondary, mapq
def get_gtf_gene_id(attrs):
return re.search('gene_id \"(.*?)\";', attrs).group(1)
def get_gtf_exons(gtf_fn):
with open(gtf_fn) as gtf:
for record in gtf:
record = record.strip().split('\t')
if record[2] == 'exon':
gene_id = get_gtf_gene_id(record[8])
yield record[0], int(record[3]) - 1, int(record[4]), gene_id, record[6]
def parse_gtf_flat_exon_invs(gtf_fn):
gene_cluster = []
gtf_iter = get_gtf_exons(gtf_fn)
curr_chrom, start, end, curr_gene_id, curr_strand = next(gtf_iter)
gene_cluster.append([[start, end]])
for chrom, start, end, gene_id, strand in gtf_iter:
if gene_id != curr_gene_id:
yield curr_gene_id, curr_chrom, curr_strand, flatten(gene_cluster)
curr_gene_id, curr_chrom, curr_strand = gene_id, chrom, strand
gene_cluster = []
gene_cluster.append([[start, end]])
else:
gene_cluster.append([[start, end]])
if gene_cluster:
yield curr_gene_id, curr_chrom, curr_strand, flatten(gene_cluster)
def flatten(bundle):
flattened = []
all_invs = iter(sorted(it.chain(*bundle)))
inv_start, inv_end = next(all_invs)
for start, end in all_invs:
if start <= inv_end:
inv_end = max(inv_end, end)
else:
flattened.append([inv_start, inv_end])
inv_start, inv_end = start, end
if not flattened or flattened[-1] != [inv_start, inv_end]:
flattened.append([inv_start, inv_end])
return flattened
def intersect(inv_a, inv_b):
a_start, a_end = inv_a
b_start, b_end = inv_b
if a_end < b_start or a_start > b_end:
return 0
else:
s = max(a_start, b_start)
e = min(a_end, b_end)
return e - s
def intersect_spliced_invs(invs_a, invs_b):
score = 0
invs_a = iter(invs_a)
invs_b = iter(invs_b)
a_start, a_end = next(invs_a)
b_start, b_end = next(invs_b)
while True:
if a_end < b_start:
try:
a_start, a_end = next(invs_a)
except StopIteration:
break
elif a_start > b_end:
try:
b_start, b_end = next(invs_b)
except StopIteration:
break
else:
score += intersect([a_start, a_end], [b_start, b_end])
if a_end > b_end:
try:
b_start, b_end = next(invs_b)
except StopIteration:
break
else:
try:
a_start, a_end = next(invs_a)
except StopIteration:
break
return score
def get_polya_dist(chrom, start, end, strand, bam, gene_invs=None,
overlap_thresh=200, gene_frac_thresh=0.2,
read_frac_thresh=0.25):
if gene_invs is None:
gene_invs = [[start, end]]
gene_ln = sum([e - s for s, e in gene_invs])
polya_lengths = []
for aln in bam.fetch(chrom, start, end):
*_, read_id, read_strand, read_invs, _, _ = parse_pysam_aln(aln)
if strand != read_strand:
continue
read_ln = sum([e - s for s, e in read_invs])
abs_overlap = intersect_spliced_invs(gene_invs, read_invs)
read_frac = abs_overlap / read_ln
gene_frac = abs_overlap / gene_ln
if abs_overlap >= overlap_thresh and \
read_frac >= read_frac_thresh and \
gene_frac >= gene_frac_thresh:
pa = aln.get_tag('pA')
polya_lengths.append(pa)
return np.array(polya_lengths)
def plot_overlayed_dists(*args, query, bins, clip, colors, title, lw=1, log=True, ax=None):
if ax is None:
fig, ax = plt.subplots(figsize=(6, 5))
groups = []
for i, group in enumerate(args):
group_p_a = []
for bam_fn in group:
with pysam.AlignmentFile(bam_fn) as bam:
p_a = get_polya_dist(*query, bam)
group_p_a.append(p_a)
group_p_a = np.concatenate(group_p_a)
groups.append(group_p_a)
if log:
group_p_a = np.log10(group_p_a)
sns.distplot(group_p_a, bins=bins, kde_kws=dict(clip=clip, lw=lw), hist_kws=dict(alpha=0.2), color=colors[i], ax=ax)
ax.set_xlabel('polyA length')
ax.set_title(title)
return ax, groups
fig, ax = plt.subplots(figsize=(8, 5))
_, g = plot_overlayed_dists(
glob('../*Col*/aligned_data/*.with_pA_tag.bam'),
glob('../*VIR*/aligned_data/*.with_pA_tag.bam'),
glob('../*/aligned_data/*_vir1_*.with_pA_tag.bam'),
query=('1', 10477885, 10479114, '+'),
log=False,
bins=np.linspace(0, 120, 50),
clip=(0, 120),
colors=[pal[0], pal[2], pal[1]],
lw=3,
title='CAB1 (AT1G29930)',
ax=ax
)
ax.plot([], [], color=pal[0], label='Col-0')
ax.plot([], [], color=pal[2], label='VIRc')
ax.plot([], [], color=pal[1], label='vir-1')
ax.legend()
ax.set_xlim(0, 120)
ax.set_xlabel('Poly(A) tail length')
ax.set_ylabel('Density')
plt.tight_layout()
plt.savefig('cab1_polya_tail_length_distribution.svg')
plt.show()
| 0.264263 | 0.701266 |
```
import codecs
import glob
import logging
import os
import re
import scipy
import spacy
import logging
import sys
import string
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import mode
from time import time
from string import punctuation
from nltk.corpus import stopwords
from nltk.stem.wordnet import WordNetLemmatizer
from nltk.stem import PorterStemmer
from collections import Counter
from sklearn import ensemble
from sklearn.pipeline import Pipeline
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer, TfidfTransformer
from nltk.tokenize import sent_tokenize
from sklearn.model_selection import train_test_split,cross_val_score, KFold, cross_val_predict, GridSearchCV, StratifiedKFold
from sklearn.svm import LinearSVC
from sklearn.linear_model.stochastic_gradient import SGDClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.decomposition import TruncatedSVD
from sklearn.pipeline import make_pipeline
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.preprocessing import Normalizer, normalize
from sklearn.manifold import TSNE
from sklearn.naive_bayes import BernoulliNB, MultinomialNB
from sklearn.neural_network import MLPClassifier
%matplotlib inline
get_ipython().magic('pylab inline')
```
### Introduction ###
The purpose of this challenge is to classify authors using different novels that they have written. In this case supervised techniques have been used and compared to see which one is giving better results using tfidf and bag of words in all of them. Regarding the corpus, then authors have been chosen randomly from Gutenberg Project and 7 novels from those authors. Although initially ten novesl were picked, due to computing restrictions only seven have been left for the classification purposes. The authors that have been picked are:
1. Jane Austen
2. Chesterton
3. Conan Doyle
4. Charles Dickens
5. Elliot
In this notebook we will see the following steps:
1. Retreive and store the data creating the dataset
2. Cleanse and parse and tokenize texts
3. Generate features and select the most appropiate for the models
4. Supervised models
5. Increase the performance of one of the models by 5 percentage points
To run the supervised parts of this challenge a new virtual machine has been set up to improve the computational performance. After initial trials on the machine with increased RAM 12GB, the conditions of the challenge were too resource intensive reasing why a virtual machine 8 vCPUs, 30 GB memory was set using Google Compute Engine.
### 1. Retreive and store the data creating the dataset ###
Ten novels from four different authors have been retreived form Gutenberg project and a list of all the book files is created.
```
# Create a list of all of our book files.
book_filenames_austen = sorted(glob.glob("/home/borjaregueral/challengesuper2/austen/*.txt"))
book_filenames_chesterton = sorted(glob.glob("/home/borjaregueral/challengesuper2/chesterton/*.txt"))
book_filenames_conandoyle = sorted(glob.glob("/home/borjaregueral/challengesuper2/conandoyle/*.txt"))
book_filenames_elliot = sorted(glob.glob("/home/borjaregueral/challengesuper2/elliot/*.txt"))
```
The information is added to the copus and stored as raw books so that they can be cleansed
```
#Read and add the text of each book to corpus_raw.
corpus_raw_austen = u""
for book_filename in book_filenames_austen:
print("Reading '{0}'...".format(book_filename))
with codecs.open(book_filename, "r", "utf-8") as book_file:
corpus_raw_austen += book_file.read()
print("Corpus is now {0} characters long".format(len(corpus_raw_austen)))
print()
#Read and add the text of each book to corpus_raw.
corpus_raw_chesterton = u""
for book_filename in book_filenames_chesterton:
print("Reading '{0}'...".format(book_filename))
with codecs.open(book_filename, "r", "utf-8") as book_file:
corpus_raw_chesterton += book_file.read()
print("Corpus is now {0} characters long".format(len(corpus_raw_chesterton)))
print()
#Read and add the text of each book to corpus_raw.
corpus_raw_conandoyle = u""
for book_filename in book_filenames_conandoyle:
print("Reading '{0}'...".format(book_filename))
with codecs.open(book_filename, "r", "utf-8") as book_file:
corpus_raw_conandoyle += book_file.read()
print("Corpus is now {0} characters long".format(len(corpus_raw_conandoyle)))
print()
#Read and add the text of each book to corpus_raw.
corpus_raw_elliot = u""
for book_filename in book_filenames_elliot:
print("Reading '{0}'...".format(book_filename))
with codecs.open(book_filename, "r", "utf-8") as book_file:
corpus_raw_elliot += book_file.read()
print("Corpus is now {0} characters long".format(len(corpus_raw_elliot)))
print()
doc_complete = [corpus_raw_austen, corpus_raw_chesterton, corpus_raw_conandoyle,
corpus_raw_elliot]
book_file.close()
```
### 2. Cleanse and parse and tokenize text###
Before generating the features, and to increase the explanatory power of them, text has been cleaned and parsed accordingly. The books have gone through an initial set of cleansing actions before been parsed using Spacy, to reduce the computing effort required by the latter and then have been cleaned again before the feature generation.
The initial cleansing action has had three steps. The first step consisted on deleting all references to the Gutenberg Project from every book. This way, it has been avoided that words like “Gutenberg” and “Gutenberg Project” appear as features and distort the clustering of the authors.
As described below, cleaning actions have gone from removing all references to chapters, digits double whitespaces and references to numbers like dates and ordinal numbers. This has been followed by removing punctuation and common stop words that will only add noise to the features that are generated afterwards.
The remaining words, considered to have the most explanatory power regarding each of the titles from the authors, have been lemmatized and stemmed reducing up to 60% the computing resources needed. In the first case words from the same family are reduced to their lemmas and in the second case, additional prefixes and suffixes are removed. All cleaning operations have been carried out in a way that remaining sentences are stored in a list of lists.
```
#Create a set of stopwords in english from nltk
stop = set(stopwords.words('english'))
# Create a set of punctuation marks to exclude them from the text
exclude = set(string.punctuation)
# Call the lemmatizer
lemma = WordNetLemmatizer()
#Define a cleaning function that incorporates the different steps in the pipeline to clean the texts
def clean(doc):
doc = re.sub(r'--',' ',doc)
doc = re.sub("[\[].*?[\]]", "", doc)
doc = re.sub(r'Chapter \d+', '', doc)
doc = re.sub(r'CHAPTER .*', '', doc)
doc = re.sub('[0-9]+', '', doc)
doc = re.sub("^\d+\s|\s\d+\s|\s\d+$", " ", doc)
stop_free = " ".join([i for i in doc.lower().split() if i not in stop])
punc_free = ''.join(ch for ch in stop_free if ch not in exclude)
normalized = " ".join(lemma.lemmatize(word) for word in punc_free.split())
return normalized
#Create a list of lists with all the documents
doc_clean = [clean(doc) for doc in doc_complete]
# Parse the cleaned novels
#load spacy for english language as all novels are in english
nlp = spacy.load('en')
#Parse novels one by one to maintain the author tagging
austen_doc = nlp(doc_clean[0])
chesterton_doc = nlp(doc_clean[1])
conandoyle_doc = nlp(doc_clean[2])
elliot_doc = nlp(doc_clean[3])
# Group into sentences.
austen_sents = [[str(sent), "Austen"] for sent in austen_doc.sents]
chesterton_sents = [[str(sent), "Chesterton"] for sent in chesterton_doc.sents]
conandoyle_sents = [[str(sent), "Conandoyle"] for sent in conandoyle_doc.sents]
elliot_sents = [[str(sent), "elliot"] for sent in elliot_doc.sents]
# Combine the sentences from the two novels into one data frame.
names = ['Sentences','Author']
sent = pd.DataFrame(austen_sents + chesterton_sents +
conandoyle_sents +
elliot_sents, columns = names)
#Plot the contribution of each author to the corpus (sentences)
sent.Author.value_counts().plot(kind='bar', grid=False, figsize=(16, 9))
#Aadd numerical column to tag the authors for supervised classification
sent.loc[sent['Author'] == 'Austen', 'Target'] = 0
sent.loc[sent['Author'] == 'Chesterton', 'Target'] = 1
sent.loc[sent['Author'] == 'Conandoyle', 'Target'] = 2
sent.loc[sent['Author'] == 'elliot', 'Target'] = 3
```
### 3. Generate features and select the most appropiate for the models ###
***Features using BoW***
Texts have been vectorized using bag of words. In this case the algorithm counts the numnber of times a word appears in a certain text. During the creation of the bag of words space, ngrams up to 4 components have been considered and stop words in english to remove noise from the dataset. Due to the authors that have been chosen, this method will bias the models towards the authors that have longer texts being Elliot and Austen compared to Conan Doyle and Chesterton. The total number of features is 52k.
```
#Transform into Bag of Words
vec = CountVectorizer(max_df = 0.75 , min_df = 2 , ngram_range = (1,4), stop_words = 'english')
#Build the predictors and the predicted variable applying BoW.
X = vec.fit_transform(sent['Sentences'])
y = sent['Target']
#Split the data set into train and test 70/30
X_train_bow, X_test_bow, y_train_bow, y_test_bow = train_test_split(X,y, test_size=0.30, random_state=1234)
X_train_bow.shape
```
***Features using Tf-idf***
When using tfidf, the frequency of appearance is normalized and also considered the ones that appear in less than 75% of the documents. With this method, the value counts are smoothen considering additional features of the word such as the amount of information it adds to describe the novel. As in the case of the ba og words, ngamrs up to four have been considered, stop words removed and thesublinear_tf used. It Apply scales the word count obtained and smoothened by the frequency of appearence in the document and whithin a document.
```
#Transform into Tf-idf considering the relative frequency
vect = TfidfVectorizer(norm = 'l2', max_df = 0.75 , min_df = 2 , ngram_range = (1,4), stop_words = 'english',
use_idf = True, sublinear_tf = True)
#Build the predictors and the predicted variable applying BoW.
X_tfidf = vect.fit_transform(sent['Sentences'])
y_tfidf = sent['Target']
#Split the data set into train and test 70/30
X_train_tfidf, X_test_tfidf, y_train_tfidf, y_test_tfidf = train_test_split(X_tfidf,y_tfidf, test_size=0.30, random_state=1234)
```
Five folds have been defined and will be used to tune and evaluate the models
```
#KFold for cross validation analysis
kf = KFold(n_splits=5, shuffle=True, random_state=123)
```
### 4. Supervised models ###
All models have been run using the features obtained through bag of words and tfidf. In this case results are compared to see which one gives a better overall accuracy as it has been used as the score function. In all cases cross validation over five folds is applied.
#### Logistic Regression Classifier ####
*** Bag of Words***
A Logistic Regression Classifier is trained using the features obtained through tfidf. Additionally, using fridsearch the parameters are tunned. As length of texts and therefore the features per author are not balanced, the class weight is set up so that is consideres unbalanced classes.
```
# Initialize and fit the model.
log_reg_bow = LogisticRegression(class_weight='balanced', penalty = 'l2', multi_class= 'multinomial', max_iter = 1000)
#Tune parameters: C parameter
c_param = [ 0.1, 0.5, 1 ]
#Tune the type of penalty used between l1 and l2
solver_param = ['newton-cg', 'lbfgs']
parameters = {'C': c_param, 'solver': solver_param}
#Fit parameters
log_reg_tuned_bow = GridSearchCV(log_reg_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
log_reg_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters logistic regression BoW:\n {}\n').format(log_reg_tuned_bow.best_params_))
```
After the parameters are tunned, the model is fit in the test dataset. As a measurement of the computing effort it requires 3.6 min to fit the test set.
```
#Once the model has been trained test it on the test dataset
log_reg_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = log_reg_tuned_bow.predict(X_test_bow)
```
The model is evaluated on the test set. In this case the solver has been chosen between the different options that support multiclass classification. As it can be seen in the classification report the model presents overfitting being the precision and recall close to one in all classes expect for class five (Huxley) which is the one that reduces the overall accuracy of the model.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}')
.format(classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print(('Confusion Matrix BoW: \n\n {}\n'
).format(confusion_bow))
print(('Logistic Regression set accuracy BoW: {0:.2f} % \n'
).format(cross_val_score(log_reg_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100
))
```
The logistic regression model is computationally efficient as it fits the dataset with over 50k in less than two minutes making it a string candidate to move intro production. The overall accuracy is nearly 77% which is roughly five percentage points more than in the challenge for this unit. The accuracy is higher than the one obainted by undsupervised methdos using clustering as is much more stable. In this case, the introduction of the test set, unseen by the model is not provoking unstable classifications.
***TF-idf***
A Logistic Regression Classifier is trained using the features obtained through tfidf. Additionally, using fridsearch the parameters are tunned. As length of texts and therefore the features per author are not balanced, the class weight is set up so that is consideres unbalanced classes. In this case the parameter of the model C is higher than the one used with the bag of words.
```
# Initialize and fit the model.
log_reg_tfidf = LogisticRegression(class_weight='balanced', penalty = 'l2', multi_class= 'multinomial', max_iter = 600)
#Tune parameters
#C parameter
c_param = [ 0.1, 0.5, 1 ]
#Tune the type of penalty used between l1 and l2
solver_param = ['newton-cg','lbfgs']
parameters = {'C': c_param, 'solver': solver_param}
#Fit parameters
log_reg_tuned_tfidf = GridSearchCV(log_reg_tfidf, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
log_reg_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters logistic regression Tfidf: \n{}\n'
).format(log_reg_tuned_tfidf.best_params_))
```
After the parameters are tunned, the model is fit in the test dataset. As a measurement of the computing effort it requires less than one min to fit the test set.
```
#Once the model has been trained test it on the test dataset
log_reg_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = log_reg_tuned_tfidf.predict(X_test_tfidf)
```
The model is evaluated on the test set. In this case the solver has been chosen between the different options that support multiclass classification. As it can be seen in the classification report the model presents overfitting being the precision and recall close to one in all classes expect for class five (Huxley) which is the one that reduces the overall accuracy of the model.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tf-idf: \n {}')
.format(classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print(('Confusion Matrix Tf-idf: \n\n {}\n'
).format(confusion_tfidf))
print(('Logistic Regression set accuracy Tf-idf: {0:.2f} % \n'
).format(cross_val_score(log_reg_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100
))
```
The logistic regression model is computationally efficient as it fits the dataset with over 80k in less than two minutes making it a string candidate to move intro production. The overall accuracy is nearly 80% which is roughly five percentage points more than in the challenge for this unit. The accuracy is higher than the one obainted by undsupervised methdos using clustering as is much more stable. In this case, the introduction of the test set, unseen by the model is not provoking unstable classifications.
#### Naive-Bayes Classifiers ####
***Bernoulli Classifier***
***Bag of Words ***
A Bernoulli classifier has been tunned and trained in the feautures obtained through Tf-idf. In this case the simplicity of the model added to the good classification results make of this model a good candidate to move into production. The time required to train it is lower than the time required to train the logistic regression one.
```
# Initialize and fit the model.
naive_bayes_bernoulli_bow = BernoulliNB()
#Tune hyperparameters
#Create range of values to fit parameters
alpha = [0.0001, 0.001, 0.01]
parameters = {'alpha': alpha}
#Fit parameters using gridsearch
naive_bayes_bernoulli_tuned_bow = GridSearchCV(naive_bayes_bernoulli_bow, n_jobs = -1, param_grid=parameters, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
naive_bayes_bernoulli_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters logistic Naive-Bayes Bernoulli BoW: \n{}\n').format(naive_bayes_bernoulli_tuned_bow.best_params_))
```
After several runs, with different extremes in the values of the alpha parameter, the parameter chosen is always the one closer to zero. This means that the smoothing parameter is very low so the additive smoothing required is low. The model is fit within seconds which makes it a strong candidate (the best one from a computational and speed standpoint) to move intro production.
```
#Once the model has been trained test it on the test dataset
naive_bayes_bernoulli_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = naive_bayes_bernoulli_tuned_bow.predict(X_test_bow)
```
The model is evaluated using cross validation and five folds. In this case as in the case of logistic regression the model presents overfitting as it can be seen from the classification report. Both precision and recall is one for this reason.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print(('Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print(('Bernoulli Classifier set accuracy BoW: {0:.2f} %\n').format(cross_val_score(naive_bayes_bernoulli_tuned_bow,
X_test_bow,
y_test_bow,cv=kf).mean()*100))
```
The overall accuracy of the model is slightly lower than the accuracy obtained with the logistic regression classifier. However, the time required to fit the model is at least one tenth of the time required for the logistic regression presenting both overfitting. Hence, if overall accuracy is what is tried to be improved, this is the best model with a very small loss of accuracy scoring 81.75%.
*** Tf-idf***
A Bernoulli classifier has been tunned and trained in the feautures obtained through Tf-idf. In this case the simplicity of the model added to the good classification results make of this model a good candidate to move into production. The time required to train it is lower than the time required to train the logistic regression one.
```
# Initialize and fit the model.
naive_bayes_bernoulli_tfidf = BernoulliNB()
#Tune hyperparameters
#Create range of values to fit parameters
alpha = [0.001, 0.01,0.1]
parameters = {'alpha': alpha}
#Fit parameters using gridsearch
naive_bayes_bernoulli_tuned_tfidf = GridSearchCV(naive_bayes_bernoulli_tfidf,
n_jobs = -1,
param_grid=parameters,
cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
naive_bayes_bernoulli_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters logistic Naive-Bayes Bernoulli Tfidf: \n{}\n').format(naive_bayes_bernoulli_tuned_tfidf.best_params_))
```
After several runs, with different extremes in the values of the alpha parameter, the parameter chosen is always the one closer to zero. This means that the smoothing parameter is very low so the additive smoothing required is low. The model is fit within seconds which makes it a strong candidate (the best one from a computational and speed standpoint) to move intro production.
```
#Once the model has been trained test it on the test dataset
naive_bayes_bernoulli_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = naive_bayes_bernoulli_tuned_tfidf.predict(X_test_tfidf)
```
he model is evaluated using cross validation and five folds. In this case as in the case of logistic regression the model presents overfitting as it can be seen from the classification report. Both precision and recall is one for this reason.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}').format(classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print(('Confusion Matrix Tf-idf: \n\n {}\n').format(confusion_tfidf))
print(('Bernoulli Classifier Tf-Idf set accuracy Tf-idf: {0:.2f} % \n').format(cross_val_score(naive_bayes_bernoulli_tuned_tfidf,
X_test_tfidf,
y_test_tfidf,
cv=kf).mean()*100))
```
The overall accuracy of the model is slightly higher than the accuracy obtained with the logistic regression classifier (81.58%). However, the time required to fit the model is at least one tenth of the time required for the logistic regression presenting both overfitting. In this case is class seven (Shaw) the one that shows the lowest precision being the one that determines the lower value of the overall accuracy when compared to the Bernoulli model. Hence, if overall accuracy is what is tried to be improved, this is the best model with a very small loss of accuracy
***Multinomial Classifier***
***BoW***
A multinomial classifier is trained on the features obtained using tfidf and evaluated on the holdout. In this case, as in the previous Navy Bayes classification used, alpha always gets the value cloaer to zero, therefore there is no additive smoothing used in this classifier. From a compuational effort standpoint, as in the previous case, this is the one that requires less time to fit making it a strong candidate to move into production.
```
# Initialize and fit the model.
naive_bayes_multinomial_bow = MultinomialNB()
#Tune hyperparameters
#Create range of values to fit parameters
alpha = [0.01,0.1,0.5]
parameters = {'alpha': alpha}
#Fit parameters using gridsearch
naive_bayes_multinomial_tuned_bow = GridSearchCV(naive_bayes_multinomial_bow,
n_jobs = -1,
param_grid=parameters,
cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
naive_bayes_multinomial_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters Naive-Bayes Multinomial BoW:\n {}\n').format(
naive_bayes_multinomial_tuned_bow.best_params_))
```
The value of alpha is in all trials the closest one to zero being the additive smoothing lose. In this case the time required for fitting is less than one minute. The model is then evaluated on the test set. For that, the first step is to fit the test hodout of the dataset.
```
#Once the model has been trained test it on the test dataset
naive_bayes_multinomial_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = naive_bayes_multinomial_tuned_bow.predict(X_test_bow)
```
The model presents overfitting and the accuracy is slightly higher than in the previous case 3% more. The confusion matrix presents a lower number of false positives and negatives for all categories, taking into account that the size of each of them is different results are consistent across all of them.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'Multinomial Classifier set accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(naive_bayes_multinomial_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
```
The time required to fit the model is lower than in any other case presenting a higher accuracy. In this case, the accuracy is close to 84.12% while the classification report shows values close to one, showing that there is overfitting. Hence, from the classifiers evaluated until now this is the one that presents better results, from an accuracy and a computational effort perspective. This is the best candidate to move into production for the moment.
***Tf-idf***
A multinomial classifier is trained on the features obtained using tfidf and evaluated on the holdout. In this case, as in the previous Navy Bayes classification used, alpha always gets the value cloaer to zero, therefore there is no additive smoothing used in this classifier. From a compuational effort standpoint, as in the previous case, this is the one that requires less time to fit making it a strong candidate to move into production.
```
# Initialize and fit the model.
naive_bayes_multinomial_tfidf = MultinomialNB()
#Tune hyperparameters
#Create range of values to fit parameters
alpha = [0.01,0.1,0.5,1]
parameters = {'alpha': alpha}
#Fit parameters using gridsearch
naive_bayes_multinomial_tuned_tfidf = GridSearchCV(naive_bayes_multinomial_tfidf,
n_jobs = -1,
param_grid=parameters,
cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
naive_bayes_multinomial_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters Naive-Bayes Multinomial BoW:\n {}\n').format(
naive_bayes_multinomial_tuned_tfidf.best_params_))
```
he value of alpha is in all trials the closest one to zero being the additive smoothing lose. In this case the time required for fitting is less than one minute. The model is then evaluated on the test set. For that, the first step is to fit the test hodout of the dataset.
```
#Once the model has been trained test it on the test dataset
naive_bayes_multinomial_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = naive_bayes_multinomial_tuned_tfidf.predict(X_test_tfidf)
```
The model presents overfitting and the accuracy is slightly higher than in the previous case 3% more. The confusion matrix presents a lower number of false positives and negatives for all categories, taking into account that the size of each of them is different results are consistent across all of them.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report tfidf: \n {}').format(classification_report(y_test_tfidf,
predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print(('Confusion Matrix Tf-idf: \n\n {}\n').format(confusion_tfidf))
print(('Multinomial Classifier set accuracy Tf-idf: {0:.2f} % \n').format(cross_val_score(naive_bayes_multinomial_tuned_tfidf,
X_test_tfidf,
y_test_tfidf,
cv=kf).mean()*100))
```
The time required to fit the model is lower than in any other case presenting a higher accuracy. In this case, the accuracy is close to 83.67% while the classification report shows values close to one, showing that there is overfitting. Hence, from the classifiers evaluated until now this is the one that presents better results, from an accuracy and a computational effort perspective. This is the best candidate to move into production for the moment.
#### KNN Classifier ####
***Bag of Words***
The KNN classifier has been fit using bag of words. In this case during the gridsearch, five neighbors have been selected as the optimumm number of neighbors when using bag of words
```
# Initialize and fit the model.
KNN_bow = KNeighborsClassifier(weights = 'distance')
#Tune hyperparameters
#Create range of values to fit parameters
neighbors = [3, 5, 7,9]
#Fit parameters
parameters = {'n_neighbors': neighbors}
#Fit parameters using gridsearch
KNN_tuned_bow = GridSearchCV(KNN_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
KNN_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters KNN BoW:\n {}\n').format(
KNN_tuned_bow.best_params_))
```
Once the model has been tuned, it is fit in the test holdout
```
#Once the model has been trained test it on the test dataset
KNN_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = KNN_tuned_bow.predict(X_test_bow)
```
The evaluation of the model is done using the classification report, confusion matrix and overall accuracy. In this case KNN works worse than other models as it does not have enough data. From the classification report it can be seen that the model is not overfitting having a high but not equal to one precision and recall. Author two is the one that is scoring the worst results.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'KNN accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(KNN_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
```
The model is scoring really low from the accuracy that is normally achieved when using KNN. One of the reaons is the amount of data used to fit the model.
***Tf- idf***
The model is fit on the training set using the features obtained using tfidf. In this case the tuning of the model give lower parameters as the features have been already smoothened being the number of neighbors equal to three.
```
# Initialize and fit the model.
KNN_tfidf = KNeighborsClassifier(weights = 'distance')
#Tune hyperparameters
#Create range of values to fit parameters
neighbors = [3, 5, 7,9]
#Fit parameters
parameters = {'n_neighbors': neighbors}
#Fit parameters using gridsearch
KNN_tuned_tfidf = GridSearchCV(KNN_tfidf,
param_grid=parameters,
n_jobs = -1,
cv=kf,
verbose = 1)
#Fit the tunned classifier in the training space
KNN_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters KNN Tfidf:\n {}\n').format(KNN_tuned_tfidf.best_params_))
```
Once the parameters are tuned the model is fit on the test set.
```
#Once the model has been trained test it on the test dataset
KNN_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = KNN_tuned_tfidf.predict(X_test_tfidf)
```
In this case, the accuracy obtained with tfidf is not very different from the accuracy obtained with the bag of words. Better results would be obtained if more data is used to run the model
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}\n').format(
classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print((
'Confusion Matrix Tfidf: \n\n {}\n\n').format(confusion_tfidf))
print((
'KNN accuracy Tfidf: {0:.2f} %\n'
).format(cross_val_score(KNN_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100))
```
Regarding the time used by this model, it is unexpectedly low as it runs over a small dataset. This is the reason why the values obtained are so low when compared to the results obtained through the bag of words.
#### SDG Classifier ####
***Bag of Words***
The SDG classifier is fit on the training set. The SGD Classifier uses regularized linear models with stochastic gradient descendent learning. The model is updated in its learning rate after the gradient of the loss is estaimated for each sample. This classifier can work with sparse data se the one obtained from bag of words. In this case from the types of penalties the algorithm accepts, it uses L2 instead of a combination of L! and L2 implemented through Elastic Net.
```
# Initialize and fit the model.
SGD_bow = SGDClassifier(class_weight = 'balanced', max_iter=1000)
#Tune hyperparameters
#Create range of values to fit parameters
loss_param = ['hinge', 'squared_hinge']
penalty_param = ['l2', 'elasticnet']
alpha_param = [0.1, 1, 10, 100]
#Fit parameters
parameters = {'loss': loss_param,
'penalty': penalty_param,
'alpha': alpha_param}
#Fit parameters using gridsearch
SGD_tuned_bow = GridSearchCV(SGD_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
SGD_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters SGD BoW:\n {}\n').format(
SGD_tuned_bow.best_params_))
```
The parameters show that the smooting continues to be loose as a first option as it is a regression with a gradient descendent algorithm. Regarding the loss, the hinge loss is used which means that the real loss, in case it is not convergent due to the sparse data used is replaced by the upper bond forcing its convergence. Time required is significanlty higher than in the case of the Naive Bayes classifiers
```
#Once the model has been trained test it on the test dataset
SGD_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = SGD_tuned_bow.predict(X_test_bow)
```
This model presents overfitting as all precision and recall are equal to one for every class. The confusion matrix shows a lower number of false negatives and positives per class being more or less evenly represented except for class three.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'SGD accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(SGD_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
```
In this case, the overall accuracy is 72.57%, very similar to the overall accuracy obtained using the multinomial classifier. The computational effort required by this model to achieve this accuracy is much higher than in the case of the multinomial classifier. Hence, from a production perspective, this model would not be recommended to move into production despite of its high accuracy.
***Tf- idf ***
The SGD Classifier uses regularized linear models with stochastic gradient descendent learning. The model is updated in its learning rate after the gradient of the loss is estaimated for each sample. This classifier can work with sparse data se the one obtained from tfidf. In this case from the types of penalties the algorithm accepts, it uses L2 instead of a combination of L! and L2 implemented through Elastic Net.
```
# Initialize and fit the model.
SGD_tfidf = SGDClassifier(class_weight = 'balanced', max_iter=1000)
#Tune hyperparameters
#Create range of values to fit parameters
loss_param = ['hinge', 'squared_hinge']
penalty_param = ['elasticnet', 'l2' ]
alpha_param = [1, 0.0001, 0.001, 0.01, 0.1]
#Fit parameters
parameters = {'loss': loss_param,
'penalty': penalty_param,
'alpha': alpha_param}
#Fit parameters using gridsearch
SGD_tuned_tfidf = GridSearchCV(SGD_tfidf, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
SGD_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters SDG Tfidf:\n {}\n').format(
SGD_tuned_tfidf.best_params_))
```
The parameters show that the smooting continues to be loose as a first option as it is a regression with a gradient descendent algorithm. Regarding the loss, the hinge loss is used which means that the real loss, in case it is not convergent due to the sparse data used is replaced by the upper bond forcing its convergence. Time required is significanlty higher than in the case of the Naive Bayes classifiers
```
#Once the model has been trained test it on the test dataset
SGD_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = SGD_tuned_tfidf.predict(X_test_tfidf)
```
This model presents overfitting as all precision and recall are equal to one for every class. The confusion matrix shows a lower number of false negatives and positives per class being more or less evenly represented except for class one.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}\n').format(
classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print((
'Confusion Matrix Tfidf: \n\n {}\n\n').format(confusion_tfidf))
print((
'SGD accuracy Tfidf: {0:.2f} %\n'
).format(cross_val_score(SGD_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100))
```
In this case, the overall accuracy is 80.78%, very similar to the overall accuracy obtained using the multinomial classifier. The computational effort required by this model to achieve this accuracy is much higher than in the case of the multinomial classifier . Hence, from a production perspective, this model would not be recommended to move into production despite of its high accuracy.
#### Random Forest ####
*** Bag of Words***
The hyperparamters of the random forest model have been tuned one by one. After trying to tune them all at once, a significant increase of the overall performance of the classifier was obtained with the proposed method (one by one). The parameters to be tuned are (in the same order as the hyperparameter tuning has been performed):
N_estimators determining the number of trees that will be part of the algorithm.
Max depth determining the size of the tree.
```
# Initialize and fit the model.
rf_bow = RandomForestClassifier(class_weight = 'balanced')
#Tune hyperparameters
#Create range of values to fit parameters
n_estimators_param = np.arange(250,401,20)
max_depth_param = np.arange(46,63,2)
#Fit parameters
parameters = {'n_estimators': n_estimators_param,
'max_depth': max_depth_param}
#Fit parameters using gridsearch
rf_tuned_bow = GridSearchCV(rf_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
rf_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters Random Forest BoW:\n {}\n').format(rf_tuned_bow.best_params_))
```
The tuned model is fit and run on the test set
```
#Once the model has been trained test it on the test dataset
rf_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = rf_tuned_bow.predict(X_test_bow)
```
The overall accuracy of the model has significantly increase compared to the previous classifiers achieving 73%. This result is low for the type of classifier used. Additionally it is lower than the results obtained with other classifiers. In this case, author seven is the one that is decreasig the overall accuracy.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'Random Forest accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(rf_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
```
This classifier requires more time to run than the Naive Bayes ones and throws poorer results than them. Author three is the one that is reducing the overall accuracy.
*** Tf-idf***
The hyperparamters of the random forest model have been tuned one by one. After trying to tune them all at once, a significant increase of the overall performance of the classifier was obtained with the proposed method (one by one). The parameters to be tuned are (in the same order as the hyperparameter tuning has been performed):
N_estimators determining the number of trees that will be part of the algorithm.
Max depth determining the size of the tree.
```
# Initialize and fit the model.
rf_tfidf = RandomForestClassifier(class_weight = 'balanced')
#Tune hyperparameters
#Create range of values to fit parameters
n_estimators_param = np.arange(100,201,10)
max_depth_param = np.arange(50,71,5)
#Fit parameters
parameters = {'n_estimators': n_estimators_param,
'max_depth': max_depth_param}
#Fit parameters using gridsearch
rf_tuned_tfidf = GridSearchCV(rf_tfidf, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
rf_tuned_tfidf.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters Random Forest Tfidf:\n {}\n').format(
rf_tuned_tfidf.best_params_))
```
The tuned model is fit and run on the test set
```
#Once the model has been trained test it on the test dataset
rf_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = rf_tuned_tfidf.predict(X_test_tfidf)
```
The overall accuracy of the model has significantly increase compared to the previous classifiers achieving 73%. This result is low for the type of classifier used. Additionally it is lower than the results obtained with other classifiers. In this case, author seven is the one that is decreasig the overall accuracy.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}\n').format(
classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print((
'Confusion Matrix Tfidf: \n\n {}\n\n').format(confusion_tfidf))
print((
'Random Forest accuracy Tfidf: {0:.2f} %\n'
).format(cross_val_score(rf_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100))
```
This classifier requires more time to run than the Naive Bayes ones and throws poorer results than them. Author three is the one that is reducing the overall accuracy.
#### SVC ####
***Bag of Words ***
A linear support vector classifier has been set up and tuned on the training data and run on the test set. The hyperparameters that have been tuned are:
C parameter, acting on the margin hyperplane having a bigger margin when C is smaller. (The value of C will tell the SVM how much misclassification is to be avoided).
The loss parameter.
In this case the crammer singer algorithm is used to solve the multiclass classification problem. This algorithm optimizes the joint objective over all classes but it is not interesting from a production standpoint as it rarely leads to better accuracy and is more expensive to compute. Due to the size of the feature´s space the linear SVC has been used instead of the SVC due to computational restrictions.
```
# Initialize and fit the model.
LSVC_bow = LinearSVC(class_weight='balanced', multi_class = 'crammer_singer')
#Tune hyperparameters
#Create range of values to fit parameters
loss_param = ['hinge','squared_hinge']
C_param = [1, 10, 100, 100000]
#Fit parameters
parameters = { 'loss': loss_param,
'C': C_param}
#Fit parameters using gridsearch
LSVC_tuned_bow = GridSearchCV(LSVC_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
LSVC_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters LinearSVC BoW:\n {}\n').format(
LSVC_tuned_bow.best_params_))
```
Once the parameters have been tunned the model is fit in the testing dataset
```
#Once the model has been trained test it on the test dataset
LSVC_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = LSVC_tuned_bow.predict(X_test_bow)
```
Although from a computational perspective it requires more effort, it presents better results than the previous algorithms. In this case, nearly 73% has been achieved competing agasint the multiclass algorithm in terms of accuracy but not in terms of computational effort.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'Linear SVC accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(LSVC_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
```
The algorithm presents overfitting as it can be seen from the classification report. Although recall and precision are one, in reality they are lower than one having an overall accuracy of 79.37%. Furthermore, the time required to fit the dataset is higher than the one required wuth the Naive Bayes algorithms.
***Tf-idf***
A linear support vector classifier has been set up and tuned on the training data and run on the test set. The hyperparameters that have been tuned are:
C parameter, acting on the margin hyperplane having a bigger margin when C is smaller. (The value of C will tell the SVM how much misclassification is to be avoided).
The loss parameter.
In this case the crammer singer algorithm is used to solve the multiclass classification problem. This algorithm optimizes the joint objective over all classes but it is not interesting from a production standpoint as it rarely leads to better accuracy and is more expensive to compute. Due to the size of the feature´s space the linear SVC has been used instead of the SVC due to computational restrictions.
```
# Initialize and fit the model.
LSVC_tfidf = LinearSVC(class_weight='balanced', multi_class = 'crammer_singer')
#Tune hyperparameters
#Create range of values to fit parameters
loss_param = ['hinge','squared_hinge']
C_param = [0.1, 1, 10, 100]
#Fit parameters
parameters = {
'loss': loss_param,
'C': C_param}
#Fit parameters using gridsearch
LSVC_tuned_tfidf = GridSearchCV(LSVC_tfidf, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
LSVC_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters Linear SVC Tfidf:\n {}\n').format(LSVC_tuned_tfidf.best_params_))
```
Once the parameters have been tunned the model is fit in the testing dataset
```
#Once the model has been trained test it on the test dataset
LSVC_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = LSVC_tuned_tfidf.predict(X_test_tfidf)
```
Although from a computational perspective it requires more effort, it presents better results than the previous algorithms. In this case, nearly 79% has been achieved competing agasint the multiclass algorithm in terms of accuracy but not in terms of computational effort.
```
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}\n').format(
classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print((
'Confusion Matrix Tfidf: \n\n {}\n\n').format(confusion_tfidf))
print((
'Linear SVC accuracy Tfidf: {0:.2f} %\n'
).format(cross_val_score(LSVC_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100))
```
The algorithm presents overfitting as it can be seen from the classification report. Although recall and precision are one, in reality they are lower than one having an overall accuracy of 79.37%. Furthermore, the time required to fit the dataset is higher than the one required wuth the Naive Bayes algorithms.
### 5. Improve accuracy of one of the models ###
The accuracy improvement of all of the models has been done in the capstone project. To achieve this improvement the steps that have been taken have been:
1. Increase the dataset per author
2. Increase the steps and the cleansing of the texts.
3. Improve the feature generation and selection using tf-idf
The results obtained once all the stepst have been taken are:
1. SGD Classifier: 87.12%
2. Multinomial Classifier: 87.02%
3. Linear Support Vector Machine: 86.48%
4. Logistic Regression: 84.88%
5. Bernouilli Classifier: 82.53%
6. Random Forest: 73.34%
7. KNN: 68.05%.
From the initial set of results obtained in this challenge:
1. Multinomial Classifier: 84.13% (BoW) & 83.46 (Tfidf)
2. Bernoulli Classifier: 81.75% (BoW) & 81.58% (Tfidf)
3. Random Forest: 77.64 (Bow) & 76.93% (Tfidf)
3. Logistic Regression: 77.54 (Bow) & 80.43% (Tfidf)
4. SGD Clasifier: 72.57% (BoW) & 80.78% (Tfidf)
5. Support Vector Machine: 72.27% (BoW) & 79.37% (Tfidf)
6. KNN: 59.72% (Bow) & 51,75 (Tfidf)
From all the improvements made, I pick up the one made in the SGD classifier that goes from 80.78% to 87.12%. The changes made in the model can be seen in the capstone project.
|
github_jupyter
|
import codecs
import glob
import logging
import os
import re
import scipy
import spacy
import logging
import sys
import string
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import mode
from time import time
from string import punctuation
from nltk.corpus import stopwords
from nltk.stem.wordnet import WordNetLemmatizer
from nltk.stem import PorterStemmer
from collections import Counter
from sklearn import ensemble
from sklearn.pipeline import Pipeline
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer, TfidfTransformer
from nltk.tokenize import sent_tokenize
from sklearn.model_selection import train_test_split,cross_val_score, KFold, cross_val_predict, GridSearchCV, StratifiedKFold
from sklearn.svm import LinearSVC
from sklearn.linear_model.stochastic_gradient import SGDClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.decomposition import TruncatedSVD
from sklearn.pipeline import make_pipeline
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.preprocessing import Normalizer, normalize
from sklearn.manifold import TSNE
from sklearn.naive_bayes import BernoulliNB, MultinomialNB
from sklearn.neural_network import MLPClassifier
%matplotlib inline
get_ipython().magic('pylab inline')
# Create a list of all of our book files.
book_filenames_austen = sorted(glob.glob("/home/borjaregueral/challengesuper2/austen/*.txt"))
book_filenames_chesterton = sorted(glob.glob("/home/borjaregueral/challengesuper2/chesterton/*.txt"))
book_filenames_conandoyle = sorted(glob.glob("/home/borjaregueral/challengesuper2/conandoyle/*.txt"))
book_filenames_elliot = sorted(glob.glob("/home/borjaregueral/challengesuper2/elliot/*.txt"))
#Read and add the text of each book to corpus_raw.
corpus_raw_austen = u""
for book_filename in book_filenames_austen:
print("Reading '{0}'...".format(book_filename))
with codecs.open(book_filename, "r", "utf-8") as book_file:
corpus_raw_austen += book_file.read()
print("Corpus is now {0} characters long".format(len(corpus_raw_austen)))
print()
#Read and add the text of each book to corpus_raw.
corpus_raw_chesterton = u""
for book_filename in book_filenames_chesterton:
print("Reading '{0}'...".format(book_filename))
with codecs.open(book_filename, "r", "utf-8") as book_file:
corpus_raw_chesterton += book_file.read()
print("Corpus is now {0} characters long".format(len(corpus_raw_chesterton)))
print()
#Read and add the text of each book to corpus_raw.
corpus_raw_conandoyle = u""
for book_filename in book_filenames_conandoyle:
print("Reading '{0}'...".format(book_filename))
with codecs.open(book_filename, "r", "utf-8") as book_file:
corpus_raw_conandoyle += book_file.read()
print("Corpus is now {0} characters long".format(len(corpus_raw_conandoyle)))
print()
#Read and add the text of each book to corpus_raw.
corpus_raw_elliot = u""
for book_filename in book_filenames_elliot:
print("Reading '{0}'...".format(book_filename))
with codecs.open(book_filename, "r", "utf-8") as book_file:
corpus_raw_elliot += book_file.read()
print("Corpus is now {0} characters long".format(len(corpus_raw_elliot)))
print()
doc_complete = [corpus_raw_austen, corpus_raw_chesterton, corpus_raw_conandoyle,
corpus_raw_elliot]
book_file.close()
#Create a set of stopwords in english from nltk
stop = set(stopwords.words('english'))
# Create a set of punctuation marks to exclude them from the text
exclude = set(string.punctuation)
# Call the lemmatizer
lemma = WordNetLemmatizer()
#Define a cleaning function that incorporates the different steps in the pipeline to clean the texts
def clean(doc):
doc = re.sub(r'--',' ',doc)
doc = re.sub("[\[].*?[\]]", "", doc)
doc = re.sub(r'Chapter \d+', '', doc)
doc = re.sub(r'CHAPTER .*', '', doc)
doc = re.sub('[0-9]+', '', doc)
doc = re.sub("^\d+\s|\s\d+\s|\s\d+$", " ", doc)
stop_free = " ".join([i for i in doc.lower().split() if i not in stop])
punc_free = ''.join(ch for ch in stop_free if ch not in exclude)
normalized = " ".join(lemma.lemmatize(word) for word in punc_free.split())
return normalized
#Create a list of lists with all the documents
doc_clean = [clean(doc) for doc in doc_complete]
# Parse the cleaned novels
#load spacy for english language as all novels are in english
nlp = spacy.load('en')
#Parse novels one by one to maintain the author tagging
austen_doc = nlp(doc_clean[0])
chesterton_doc = nlp(doc_clean[1])
conandoyle_doc = nlp(doc_clean[2])
elliot_doc = nlp(doc_clean[3])
# Group into sentences.
austen_sents = [[str(sent), "Austen"] for sent in austen_doc.sents]
chesterton_sents = [[str(sent), "Chesterton"] for sent in chesterton_doc.sents]
conandoyle_sents = [[str(sent), "Conandoyle"] for sent in conandoyle_doc.sents]
elliot_sents = [[str(sent), "elliot"] for sent in elliot_doc.sents]
# Combine the sentences from the two novels into one data frame.
names = ['Sentences','Author']
sent = pd.DataFrame(austen_sents + chesterton_sents +
conandoyle_sents +
elliot_sents, columns = names)
#Plot the contribution of each author to the corpus (sentences)
sent.Author.value_counts().plot(kind='bar', grid=False, figsize=(16, 9))
#Aadd numerical column to tag the authors for supervised classification
sent.loc[sent['Author'] == 'Austen', 'Target'] = 0
sent.loc[sent['Author'] == 'Chesterton', 'Target'] = 1
sent.loc[sent['Author'] == 'Conandoyle', 'Target'] = 2
sent.loc[sent['Author'] == 'elliot', 'Target'] = 3
#Transform into Bag of Words
vec = CountVectorizer(max_df = 0.75 , min_df = 2 , ngram_range = (1,4), stop_words = 'english')
#Build the predictors and the predicted variable applying BoW.
X = vec.fit_transform(sent['Sentences'])
y = sent['Target']
#Split the data set into train and test 70/30
X_train_bow, X_test_bow, y_train_bow, y_test_bow = train_test_split(X,y, test_size=0.30, random_state=1234)
X_train_bow.shape
#Transform into Tf-idf considering the relative frequency
vect = TfidfVectorizer(norm = 'l2', max_df = 0.75 , min_df = 2 , ngram_range = (1,4), stop_words = 'english',
use_idf = True, sublinear_tf = True)
#Build the predictors and the predicted variable applying BoW.
X_tfidf = vect.fit_transform(sent['Sentences'])
y_tfidf = sent['Target']
#Split the data set into train and test 70/30
X_train_tfidf, X_test_tfidf, y_train_tfidf, y_test_tfidf = train_test_split(X_tfidf,y_tfidf, test_size=0.30, random_state=1234)
#KFold for cross validation analysis
kf = KFold(n_splits=5, shuffle=True, random_state=123)
# Initialize and fit the model.
log_reg_bow = LogisticRegression(class_weight='balanced', penalty = 'l2', multi_class= 'multinomial', max_iter = 1000)
#Tune parameters: C parameter
c_param = [ 0.1, 0.5, 1 ]
#Tune the type of penalty used between l1 and l2
solver_param = ['newton-cg', 'lbfgs']
parameters = {'C': c_param, 'solver': solver_param}
#Fit parameters
log_reg_tuned_bow = GridSearchCV(log_reg_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
log_reg_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters logistic regression BoW:\n {}\n').format(log_reg_tuned_bow.best_params_))
#Once the model has been trained test it on the test dataset
log_reg_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = log_reg_tuned_bow.predict(X_test_bow)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}')
.format(classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print(('Confusion Matrix BoW: \n\n {}\n'
).format(confusion_bow))
print(('Logistic Regression set accuracy BoW: {0:.2f} % \n'
).format(cross_val_score(log_reg_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100
))
# Initialize and fit the model.
log_reg_tfidf = LogisticRegression(class_weight='balanced', penalty = 'l2', multi_class= 'multinomial', max_iter = 600)
#Tune parameters
#C parameter
c_param = [ 0.1, 0.5, 1 ]
#Tune the type of penalty used between l1 and l2
solver_param = ['newton-cg','lbfgs']
parameters = {'C': c_param, 'solver': solver_param}
#Fit parameters
log_reg_tuned_tfidf = GridSearchCV(log_reg_tfidf, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
log_reg_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters logistic regression Tfidf: \n{}\n'
).format(log_reg_tuned_tfidf.best_params_))
#Once the model has been trained test it on the test dataset
log_reg_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = log_reg_tuned_tfidf.predict(X_test_tfidf)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tf-idf: \n {}')
.format(classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print(('Confusion Matrix Tf-idf: \n\n {}\n'
).format(confusion_tfidf))
print(('Logistic Regression set accuracy Tf-idf: {0:.2f} % \n'
).format(cross_val_score(log_reg_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100
))
# Initialize and fit the model.
naive_bayes_bernoulli_bow = BernoulliNB()
#Tune hyperparameters
#Create range of values to fit parameters
alpha = [0.0001, 0.001, 0.01]
parameters = {'alpha': alpha}
#Fit parameters using gridsearch
naive_bayes_bernoulli_tuned_bow = GridSearchCV(naive_bayes_bernoulli_bow, n_jobs = -1, param_grid=parameters, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
naive_bayes_bernoulli_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters logistic Naive-Bayes Bernoulli BoW: \n{}\n').format(naive_bayes_bernoulli_tuned_bow.best_params_))
#Once the model has been trained test it on the test dataset
naive_bayes_bernoulli_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = naive_bayes_bernoulli_tuned_bow.predict(X_test_bow)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print(('Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print(('Bernoulli Classifier set accuracy BoW: {0:.2f} %\n').format(cross_val_score(naive_bayes_bernoulli_tuned_bow,
X_test_bow,
y_test_bow,cv=kf).mean()*100))
# Initialize and fit the model.
naive_bayes_bernoulli_tfidf = BernoulliNB()
#Tune hyperparameters
#Create range of values to fit parameters
alpha = [0.001, 0.01,0.1]
parameters = {'alpha': alpha}
#Fit parameters using gridsearch
naive_bayes_bernoulli_tuned_tfidf = GridSearchCV(naive_bayes_bernoulli_tfidf,
n_jobs = -1,
param_grid=parameters,
cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
naive_bayes_bernoulli_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters logistic Naive-Bayes Bernoulli Tfidf: \n{}\n').format(naive_bayes_bernoulli_tuned_tfidf.best_params_))
#Once the model has been trained test it on the test dataset
naive_bayes_bernoulli_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = naive_bayes_bernoulli_tuned_tfidf.predict(X_test_tfidf)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}').format(classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print(('Confusion Matrix Tf-idf: \n\n {}\n').format(confusion_tfidf))
print(('Bernoulli Classifier Tf-Idf set accuracy Tf-idf: {0:.2f} % \n').format(cross_val_score(naive_bayes_bernoulli_tuned_tfidf,
X_test_tfidf,
y_test_tfidf,
cv=kf).mean()*100))
# Initialize and fit the model.
naive_bayes_multinomial_bow = MultinomialNB()
#Tune hyperparameters
#Create range of values to fit parameters
alpha = [0.01,0.1,0.5]
parameters = {'alpha': alpha}
#Fit parameters using gridsearch
naive_bayes_multinomial_tuned_bow = GridSearchCV(naive_bayes_multinomial_bow,
n_jobs = -1,
param_grid=parameters,
cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
naive_bayes_multinomial_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters Naive-Bayes Multinomial BoW:\n {}\n').format(
naive_bayes_multinomial_tuned_bow.best_params_))
#Once the model has been trained test it on the test dataset
naive_bayes_multinomial_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = naive_bayes_multinomial_tuned_bow.predict(X_test_bow)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'Multinomial Classifier set accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(naive_bayes_multinomial_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
# Initialize and fit the model.
naive_bayes_multinomial_tfidf = MultinomialNB()
#Tune hyperparameters
#Create range of values to fit parameters
alpha = [0.01,0.1,0.5,1]
parameters = {'alpha': alpha}
#Fit parameters using gridsearch
naive_bayes_multinomial_tuned_tfidf = GridSearchCV(naive_bayes_multinomial_tfidf,
n_jobs = -1,
param_grid=parameters,
cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
naive_bayes_multinomial_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters Naive-Bayes Multinomial BoW:\n {}\n').format(
naive_bayes_multinomial_tuned_tfidf.best_params_))
#Once the model has been trained test it on the test dataset
naive_bayes_multinomial_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = naive_bayes_multinomial_tuned_tfidf.predict(X_test_tfidf)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report tfidf: \n {}').format(classification_report(y_test_tfidf,
predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print(('Confusion Matrix Tf-idf: \n\n {}\n').format(confusion_tfidf))
print(('Multinomial Classifier set accuracy Tf-idf: {0:.2f} % \n').format(cross_val_score(naive_bayes_multinomial_tuned_tfidf,
X_test_tfidf,
y_test_tfidf,
cv=kf).mean()*100))
# Initialize and fit the model.
KNN_bow = KNeighborsClassifier(weights = 'distance')
#Tune hyperparameters
#Create range of values to fit parameters
neighbors = [3, 5, 7,9]
#Fit parameters
parameters = {'n_neighbors': neighbors}
#Fit parameters using gridsearch
KNN_tuned_bow = GridSearchCV(KNN_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
KNN_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters KNN BoW:\n {}\n').format(
KNN_tuned_bow.best_params_))
#Once the model has been trained test it on the test dataset
KNN_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = KNN_tuned_bow.predict(X_test_bow)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'KNN accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(KNN_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
# Initialize and fit the model.
KNN_tfidf = KNeighborsClassifier(weights = 'distance')
#Tune hyperparameters
#Create range of values to fit parameters
neighbors = [3, 5, 7,9]
#Fit parameters
parameters = {'n_neighbors': neighbors}
#Fit parameters using gridsearch
KNN_tuned_tfidf = GridSearchCV(KNN_tfidf,
param_grid=parameters,
n_jobs = -1,
cv=kf,
verbose = 1)
#Fit the tunned classifier in the training space
KNN_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters KNN Tfidf:\n {}\n').format(KNN_tuned_tfidf.best_params_))
#Once the model has been trained test it on the test dataset
KNN_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = KNN_tuned_tfidf.predict(X_test_tfidf)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}\n').format(
classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print((
'Confusion Matrix Tfidf: \n\n {}\n\n').format(confusion_tfidf))
print((
'KNN accuracy Tfidf: {0:.2f} %\n'
).format(cross_val_score(KNN_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100))
# Initialize and fit the model.
SGD_bow = SGDClassifier(class_weight = 'balanced', max_iter=1000)
#Tune hyperparameters
#Create range of values to fit parameters
loss_param = ['hinge', 'squared_hinge']
penalty_param = ['l2', 'elasticnet']
alpha_param = [0.1, 1, 10, 100]
#Fit parameters
parameters = {'loss': loss_param,
'penalty': penalty_param,
'alpha': alpha_param}
#Fit parameters using gridsearch
SGD_tuned_bow = GridSearchCV(SGD_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
SGD_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters SGD BoW:\n {}\n').format(
SGD_tuned_bow.best_params_))
#Once the model has been trained test it on the test dataset
SGD_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = SGD_tuned_bow.predict(X_test_bow)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'SGD accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(SGD_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
# Initialize and fit the model.
SGD_tfidf = SGDClassifier(class_weight = 'balanced', max_iter=1000)
#Tune hyperparameters
#Create range of values to fit parameters
loss_param = ['hinge', 'squared_hinge']
penalty_param = ['elasticnet', 'l2' ]
alpha_param = [1, 0.0001, 0.001, 0.01, 0.1]
#Fit parameters
parameters = {'loss': loss_param,
'penalty': penalty_param,
'alpha': alpha_param}
#Fit parameters using gridsearch
SGD_tuned_tfidf = GridSearchCV(SGD_tfidf, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
SGD_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters SDG Tfidf:\n {}\n').format(
SGD_tuned_tfidf.best_params_))
#Once the model has been trained test it on the test dataset
SGD_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = SGD_tuned_tfidf.predict(X_test_tfidf)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}\n').format(
classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print((
'Confusion Matrix Tfidf: \n\n {}\n\n').format(confusion_tfidf))
print((
'SGD accuracy Tfidf: {0:.2f} %\n'
).format(cross_val_score(SGD_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100))
# Initialize and fit the model.
rf_bow = RandomForestClassifier(class_weight = 'balanced')
#Tune hyperparameters
#Create range of values to fit parameters
n_estimators_param = np.arange(250,401,20)
max_depth_param = np.arange(46,63,2)
#Fit parameters
parameters = {'n_estimators': n_estimators_param,
'max_depth': max_depth_param}
#Fit parameters using gridsearch
rf_tuned_bow = GridSearchCV(rf_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
rf_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters Random Forest BoW:\n {}\n').format(rf_tuned_bow.best_params_))
#Once the model has been trained test it on the test dataset
rf_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = rf_tuned_bow.predict(X_test_bow)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'Random Forest accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(rf_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
# Initialize and fit the model.
rf_tfidf = RandomForestClassifier(class_weight = 'balanced')
#Tune hyperparameters
#Create range of values to fit parameters
n_estimators_param = np.arange(100,201,10)
max_depth_param = np.arange(50,71,5)
#Fit parameters
parameters = {'n_estimators': n_estimators_param,
'max_depth': max_depth_param}
#Fit parameters using gridsearch
rf_tuned_tfidf = GridSearchCV(rf_tfidf, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
rf_tuned_tfidf.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters Random Forest Tfidf:\n {}\n').format(
rf_tuned_tfidf.best_params_))
#Once the model has been trained test it on the test dataset
rf_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = rf_tuned_tfidf.predict(X_test_tfidf)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}\n').format(
classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print((
'Confusion Matrix Tfidf: \n\n {}\n\n').format(confusion_tfidf))
print((
'Random Forest accuracy Tfidf: {0:.2f} %\n'
).format(cross_val_score(rf_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100))
# Initialize and fit the model.
LSVC_bow = LinearSVC(class_weight='balanced', multi_class = 'crammer_singer')
#Tune hyperparameters
#Create range of values to fit parameters
loss_param = ['hinge','squared_hinge']
C_param = [1, 10, 100, 100000]
#Fit parameters
parameters = { 'loss': loss_param,
'C': C_param}
#Fit parameters using gridsearch
LSVC_tuned_bow = GridSearchCV(LSVC_bow, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
LSVC_tuned_bow.fit(X_train_bow, y_train_bow)
#Print the best parameters
print(('Best paramenters LinearSVC BoW:\n {}\n').format(
LSVC_tuned_bow.best_params_))
#Once the model has been trained test it on the test dataset
LSVC_tuned_bow.fit(X_test_bow, y_test_bow)
# Predict on test set
predtest_y_bow = LSVC_tuned_bow.predict(X_test_bow)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report BoW: \n {}\n').format(
classification_report(y_test_bow, predtest_y_bow,
target_names=target_names)))
confusion_bow = confusion_matrix(y_test_bow, predtest_y_bow)
print((
'Confusion Matrix BoW: \n\n {}\n\n').format(confusion_bow))
print((
'Linear SVC accuracy BoW: {0:.2f} %\n'
).format(cross_val_score(LSVC_tuned_bow, X_test_bow, y_test_bow,cv=kf).mean()*100))
# Initialize and fit the model.
LSVC_tfidf = LinearSVC(class_weight='balanced', multi_class = 'crammer_singer')
#Tune hyperparameters
#Create range of values to fit parameters
loss_param = ['hinge','squared_hinge']
C_param = [0.1, 1, 10, 100]
#Fit parameters
parameters = {
'loss': loss_param,
'C': C_param}
#Fit parameters using gridsearch
LSVC_tuned_tfidf = GridSearchCV(LSVC_tfidf, param_grid=parameters, n_jobs = -1, cv=kf, verbose = 1)
#Fit the tunned classifier in the training space
LSVC_tuned_tfidf.fit(X_train_tfidf, y_train_tfidf)
#Print the best parameters
print(('Best paramenters Linear SVC Tfidf:\n {}\n').format(LSVC_tuned_tfidf.best_params_))
#Once the model has been trained test it on the test dataset
LSVC_tuned_tfidf.fit(X_test_tfidf, y_test_tfidf)
# Predict on test set
predtest_y_tfidf = LSVC_tuned_tfidf.predict(X_test_tfidf)
#Evaluation of the model (testing)
target_names = ['0.0', '1.0', '2.0', '3.0']
print(('Classification Report Tfidf: \n {}\n').format(
classification_report(y_test_tfidf, predtest_y_tfidf,
target_names=target_names)))
confusion_tfidf = confusion_matrix(y_test_tfidf, predtest_y_tfidf)
print((
'Confusion Matrix Tfidf: \n\n {}\n\n').format(confusion_tfidf))
print((
'Linear SVC accuracy Tfidf: {0:.2f} %\n'
).format(cross_val_score(LSVC_tuned_tfidf, X_test_tfidf, y_test_tfidf,cv=kf).mean()*100))
| 0.410638 | 0.741709 |
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import plotly.express as px
data = pd.read_csv('https://raw.githubusercontent.com/Develop-Packt/Predicting-the-Energy-Usage-of-Household-Appliances/master/Datasets/energydata_complete.csv')
data.head()
data.isnull().sum()
df1 = data.rename(columns = {
'date' : 'date_time',
'Appliances' : 'a_energy',
'lights' : 'l_energy',
'T1' : 'kitchen_temp',
'RH_1' : 'kitchen_hum',
'T2' : 'liv_temp',
'RH_2' : 'liv_hum',
'T3' : 'laun_temp',
'RH_3' : 'laun_hum',
'T4' : 'off_temp',
'RH_4' : 'off_hum',
'T5' : 'bath_temp',
'RH_5' : 'bath_hum',
'T6' : 'out_b_temp',
'RH_6' : 'out_b_hum',
'T7' : 'iron_temp',
'RH_7' : 'iron_hum',
'T8' : 'teen_temp',
'RH_8' : 'teen_hum',
'T9' : 'par_temp',
'RH_9' : 'par_hum',
'T_out' : 'out_temp',
'Press_mm_hg' : 'out_press',
'RH_out' : 'out_hum',
'Windspeed' : 'wind',
'Visibility' : 'visibility',
'Tdewpoint' : 'dew_point',
'rv1' : 'rv1',
'rv2' : 'rv2'
})
df1.head()
df1.tail()
df1.describe()
lights_box = sns.boxplot(df1.l_energy)
l = [0, 10, 20, 30, 40, 50, 60, 70]
counts = []
for i in l:
a = (df1.l_energy == i).sum()
counts.append(a)
counts
lights = sns.barplot(x = l, y = counts)
lights.set_xlabel('Energy Consumed by Lights')
lights.set_ylabel('Number of Lights')
lights.set_title('Distribution of Energy Consumed by Lights')
((df1.l_energy == 0).sum() / (df1.shape[0])) * 100
new_data = df1
new_data.drop(['l_energy'], axis = 1, inplace = True)
new_data.head()
app_box = sns.boxplot(new_data.a_energy)
out = (new_data['a_energy'] > 200).sum()
out
(out/19735) * 100
out_e = (new_data['a_energy'] > 950).sum()
out_e
(out_e/19735) * 100
energy = new_data[(new_data['a_energy'] <= 200)]
energy.describe()
new_en = energy
new_en['date_time'] = pd.to_datetime(new_en.date_time, format = '%Y-%m-%d %H:%M:%S')
new_en.head()
new_en.insert(loc = 1, column = 'month', value = new_en.date_time.dt.month)
new_en.insert(loc = 2, column = 'day', value = (new_en.date_time.dt.dayofweek)+1)
new_en.head()
import plotly.graph_objs as go
app_date = go.Scatter(x = new_en.date_time, mode = "lines", y = new_en.a_energy)
layout = go.Layout(title = 'Appliance Energy Consumed by Date', xaxis = dict(title='Date'), yaxis = dict(title='Wh'))
fig = go.Figure(data = [app_date], layout = layout)
fig.show()
app_mon = new_en.groupby(by = ['month'], as_index = False)['a_energy'].sum()
app_mon
app_mon.sort_values(by = 'a_energy', ascending = False).head()
plt.subplots(figsize = (15, 6))
am = sns.barplot(app_mon.month, app_mon.a_energy)
plt.xlabel('Month')
plt.ylabel('Energy Consumed by Appliances')
plt.title('Total Energy Consumed by Appliances per Month')
plt.show()
```
**Activity 02**
```
app_day = new_en.groupby(by = ['day'], as_index = False)['a_energy'].sum()
app_day
app_day.sort_values(by = 'a_energy', ascending = False)
plt.subplots(figsize = (15, 6))
ad = sns.barplot(app_day.day, app_day.a_energy)
plt.xlabel('Day of the Week')
plt.ylabel('Energy Consumed by Appliances')
plt.title('Total Energy Consumed by Appliances')
plt.show()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import plotly.express as px
data = pd.read_csv('https://raw.githubusercontent.com/Develop-Packt/Predicting-the-Energy-Usage-of-Household-Appliances/master/Datasets/energydata_complete.csv')
data.head()
data.isnull().sum()
df1 = data.rename(columns = {
'date' : 'date_time',
'Appliances' : 'a_energy',
'lights' : 'l_energy',
'T1' : 'kitchen_temp',
'RH_1' : 'kitchen_hum',
'T2' : 'liv_temp',
'RH_2' : 'liv_hum',
'T3' : 'laun_temp',
'RH_3' : 'laun_hum',
'T4' : 'off_temp',
'RH_4' : 'off_hum',
'T5' : 'bath_temp',
'RH_5' : 'bath_hum',
'T6' : 'out_b_temp',
'RH_6' : 'out_b_hum',
'T7' : 'iron_temp',
'RH_7' : 'iron_hum',
'T8' : 'teen_temp',
'RH_8' : 'teen_hum',
'T9' : 'par_temp',
'RH_9' : 'par_hum',
'T_out' : 'out_temp',
'Press_mm_hg' : 'out_press',
'RH_out' : 'out_hum',
'Windspeed' : 'wind',
'Visibility' : 'visibility',
'Tdewpoint' : 'dew_point',
'rv1' : 'rv1',
'rv2' : 'rv2'
})
df1.head()
df1.tail()
df1.describe()
lights_box = sns.boxplot(df1.l_energy)
l = [0, 10, 20, 30, 40, 50, 60, 70]
counts = []
for i in l:
a = (df1.l_energy == i).sum()
counts.append(a)
counts
lights = sns.barplot(x = l, y = counts)
lights.set_xlabel('Energy Consumed by Lights')
lights.set_ylabel('Number of Lights')
lights.set_title('Distribution of Energy Consumed by Lights')
((df1.l_energy == 0).sum() / (df1.shape[0])) * 100
new_data = df1
new_data.drop(['l_energy'], axis = 1, inplace = True)
new_data.head()
app_box = sns.boxplot(new_data.a_energy)
out = (new_data['a_energy'] > 200).sum()
out
(out/19735) * 100
out_e = (new_data['a_energy'] > 950).sum()
out_e
(out_e/19735) * 100
energy = new_data[(new_data['a_energy'] <= 200)]
energy.describe()
new_en = energy
new_en['date_time'] = pd.to_datetime(new_en.date_time, format = '%Y-%m-%d %H:%M:%S')
new_en.head()
new_en.insert(loc = 1, column = 'month', value = new_en.date_time.dt.month)
new_en.insert(loc = 2, column = 'day', value = (new_en.date_time.dt.dayofweek)+1)
new_en.head()
import plotly.graph_objs as go
app_date = go.Scatter(x = new_en.date_time, mode = "lines", y = new_en.a_energy)
layout = go.Layout(title = 'Appliance Energy Consumed by Date', xaxis = dict(title='Date'), yaxis = dict(title='Wh'))
fig = go.Figure(data = [app_date], layout = layout)
fig.show()
app_mon = new_en.groupby(by = ['month'], as_index = False)['a_energy'].sum()
app_mon
app_mon.sort_values(by = 'a_energy', ascending = False).head()
plt.subplots(figsize = (15, 6))
am = sns.barplot(app_mon.month, app_mon.a_energy)
plt.xlabel('Month')
plt.ylabel('Energy Consumed by Appliances')
plt.title('Total Energy Consumed by Appliances per Month')
plt.show()
app_day = new_en.groupby(by = ['day'], as_index = False)['a_energy'].sum()
app_day
app_day.sort_values(by = 'a_energy', ascending = False)
plt.subplots(figsize = (15, 6))
ad = sns.barplot(app_day.day, app_day.a_energy)
plt.xlabel('Day of the Week')
plt.ylabel('Energy Consumed by Appliances')
plt.title('Total Energy Consumed by Appliances')
plt.show()
| 0.416322 | 0.531027 |
# Assignment 1: Workspace Configuration
In this assignment I configure your machine learning environment needed to run the Jupyter Notebooks from Geron Text
https://github.com/ageron/handson-ml
Here, I will illustrating the basic python packages needed to run a Juypter notebook.
## Introduction
First, import a few common modules like numpy etc.
```
# Common imports
import numpy as np
import os
from sklearn.datasets import *
import pandas as pd
import matplotlib.pyplot as plt
```
## NumPy Array
Here we see how to create and generate Arrays
```
arr = np.array([1,3,5,8,9,17,5,6,9,7,1,3,22,12,10])
print('arr:', arr)
print('arr plus 5:', arr + 5)
print('first 5th element of arr:', arr[:5])
print('sum of arr:', np.sum(arr))
print('max value in arr:', np.max(arr))
print('index of max value in arr:', np.argmax(arr))
print('std of arr:', np.std(arr))
print('arr sorted:', np.sort(arr))
print()
arr_even = np.arange(2,20,2)
print('arr_even:', arr_even)
```
## NumPy Random
Here we see how to generate random numbers
```
# to make this notebook's output stable across runs
np.random.seed(13)
rnd = np.random.rand(4)
print(rnd)
```
## Pandas and Dataset
Now lets use the saved csv dataset from local storage
```
quakes = pd.read_csv("datasets/quakes.csv")
print(quakes.info())
print()
print(quakes.head(5))
print()
print(quakes.tail(5))
```
## Matplotlib and Histogram
Lets draw Histogram to represent the data from the csv
```
quakes.hist(figsize=(16,12))
plt.show()
```
## Matplotlib and Density Graph
Lets plot Density Graph to represent the data from the csv
```
quakes.plot(kind='density', subplots=True, layout=(3,2), figsize=(16,12), sharex=False)
plt.show()
```
## Dataset Information
Get information from csv and represent it
```
print(quakes["magnitude"].describe())
print()
print(quakes[["latitude", "longitude"]].describe())
```
## Sklearn
Playing around with sklearn
```
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(quakes, test_size=0.2, random_state=42)
print(train_set.describe())
print()
print("Training Percentages:")
print()
print(train_set.count() / quakes.count())
train_set.plot(kind="scatter", x="depth", y="magnitude", alpha=0.3)
plt.show()
train_set.plot(kind="scatter", x="longitude", y="latitude", alpha=0.3, s=quakes["depth"], label="depth",
figsize=(10,8), c="magnitude", cmap=plt.get_cmap("jet"), colorbar=True, sharex=False)
plt.legend()
plt.show()
```
### Examine Correlation between features and label
```
corr_matrix = train_set.corr()
corr_matrix["magnitude"].sort_values(ascending=False)
```
### Draw scatter matrix of Depth and Madniture
```
from pandas.plotting import scatter_matrix
attributes = ["magnitude", "depth"]
scatter_matrix(train_set[attributes], figsize=(12, 8))
plt.show()
```
## Prepare the data for Machine Learning algorithms
Here we use train_set to make data ready for Machine Learning algorithms
```
earthquakes = train_set.drop("magnitude", axis=1) # drop labels for training set
earthquakes_labels = train_set["magnitude"].copy()
print (earthquakes_labels.describe())
print (earthquakes.describe())
earthquakes_m = earthquakes["depth"].copy()
print(type(earthquakes_m))
print (earthquakes_m.describe())
print (earthquakes_m.iloc[:5])
```
Check for Null values
```
nulls = earthquakes_m.isnull()
print(nulls.loc[nulls.iloc[0:]==True])
```
## Checking out LinearRegression from sklearn
```
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
print(earthquakes_m.shape)
train_m = earthquakes_m.values
train_m = train_m.reshape(-1, 1)
print(train_m.shape)
train_labels = earthquakes_labels.values
lin_reg.fit(train_m, train_labels)
example_data = earthquakes_m.iloc[:5].values.reshape(-1,1)
example_labels = earthquakes_labels.iloc[:5]
print("Predictions:", lin_reg.predict(example_data))
print("Labels:", list(example_labels))
columns = ["magnitude","depth"]
earthquakes_m = quakes[columns].copy()
print(type(earthquakes_m))
earthquakes_m.describe()
print (earthquakes_m.iloc[:5])
print (earthquakes_labels.describe())
print (earthquakes.describe())
```
|
github_jupyter
|
# Common imports
import numpy as np
import os
from sklearn.datasets import *
import pandas as pd
import matplotlib.pyplot as plt
arr = np.array([1,3,5,8,9,17,5,6,9,7,1,3,22,12,10])
print('arr:', arr)
print('arr plus 5:', arr + 5)
print('first 5th element of arr:', arr[:5])
print('sum of arr:', np.sum(arr))
print('max value in arr:', np.max(arr))
print('index of max value in arr:', np.argmax(arr))
print('std of arr:', np.std(arr))
print('arr sorted:', np.sort(arr))
print()
arr_even = np.arange(2,20,2)
print('arr_even:', arr_even)
# to make this notebook's output stable across runs
np.random.seed(13)
rnd = np.random.rand(4)
print(rnd)
quakes = pd.read_csv("datasets/quakes.csv")
print(quakes.info())
print()
print(quakes.head(5))
print()
print(quakes.tail(5))
quakes.hist(figsize=(16,12))
plt.show()
quakes.plot(kind='density', subplots=True, layout=(3,2), figsize=(16,12), sharex=False)
plt.show()
print(quakes["magnitude"].describe())
print()
print(quakes[["latitude", "longitude"]].describe())
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(quakes, test_size=0.2, random_state=42)
print(train_set.describe())
print()
print("Training Percentages:")
print()
print(train_set.count() / quakes.count())
train_set.plot(kind="scatter", x="depth", y="magnitude", alpha=0.3)
plt.show()
train_set.plot(kind="scatter", x="longitude", y="latitude", alpha=0.3, s=quakes["depth"], label="depth",
figsize=(10,8), c="magnitude", cmap=plt.get_cmap("jet"), colorbar=True, sharex=False)
plt.legend()
plt.show()
corr_matrix = train_set.corr()
corr_matrix["magnitude"].sort_values(ascending=False)
from pandas.plotting import scatter_matrix
attributes = ["magnitude", "depth"]
scatter_matrix(train_set[attributes], figsize=(12, 8))
plt.show()
earthquakes = train_set.drop("magnitude", axis=1) # drop labels for training set
earthquakes_labels = train_set["magnitude"].copy()
print (earthquakes_labels.describe())
print (earthquakes.describe())
earthquakes_m = earthquakes["depth"].copy()
print(type(earthquakes_m))
print (earthquakes_m.describe())
print (earthquakes_m.iloc[:5])
nulls = earthquakes_m.isnull()
print(nulls.loc[nulls.iloc[0:]==True])
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
print(earthquakes_m.shape)
train_m = earthquakes_m.values
train_m = train_m.reshape(-1, 1)
print(train_m.shape)
train_labels = earthquakes_labels.values
lin_reg.fit(train_m, train_labels)
example_data = earthquakes_m.iloc[:5].values.reshape(-1,1)
example_labels = earthquakes_labels.iloc[:5]
print("Predictions:", lin_reg.predict(example_data))
print("Labels:", list(example_labels))
columns = ["magnitude","depth"]
earthquakes_m = quakes[columns].copy()
print(type(earthquakes_m))
earthquakes_m.describe()
print (earthquakes_m.iloc[:5])
print (earthquakes_labels.describe())
print (earthquakes.describe())
| 0.455925 | 0.979823 |
# NumPy Arrays
## 1. Creating Arrays
| command | description |
|---------|-------------|
| np.array( ) | create an array from list-like type |
| np.arange( ) | create an array with sequential numbers |
| np.linspace( ) | create an array by interpolation |
| np.zeros( ) | create an array full of zeros |
| np.ones( ) | create an array full of ones |
| np.meshgrid( ) | create a tuple of x/y gradients |
### Creating Arrays from scratch
```
import numpy as np
a = np.array([1,1, 2, 2, 3, 3])
a
```
- **Two dimensions, also specifying data type:**
```
# this will return floating point numbers e.g. 1., 1. ...
b = np.array([[1,1], [2, 2], [3, 3]], dtype=np.float64)
b
```
### Create an array with sequential numbers
```
np.arange(10)
```
### Create an array by linear interpolation
```
# 1 is starting number, 4 is final number
# 7 is the length of the array!
np.linspace(1, 4, 7)
```
### Create a null vector
```
np.zeros(10)
```
### Create a two-dimensional vector
```
np.ones((3, 3))
```
### Create an identity matrix
```
np.eye(3)
```
### Create random arrays
```
np.random.random((3,3))
# normal distribution
np.random.normal(0.0, 1.0, 100)
import matplotlib.pyplot as plt
%matplotlib inline
plt.hist(np.random.normal(0.0, 1.0, 100))
```
### Create x/y gradients
```
np.meshgrid([0, 1, 2], [0, 1, 2])
```
## 2. Selecting and modifying arrays
### Replace values in an array
```
a = np.zeros(10)
a[4] = 1
a
```
### Reverse a vector
```
a = np.arange(10)
a[::-1]
```
### Change the shape of arrays
```
np.arange(9)
np.arange(9).reshape(3,3)
```
### Find indices of non-zero elements
```
np.nonzero([1, 2, 0, 0, 4, 0])
```
### Apply mathematical functions
```
a = np.arange(5)
a
np.exp(a)
```
### Find the maximum value
- a[a.argmax()]
```
a = np.random.random(10)
a
a[a.argmax()]
#equivalent of doing this:
a.max()
a[a.argmax()] = 0
a
```
## 3. NumPy Arrays Exercises
```
from sklearn.datasets import make_moons
X, y = make_moons(noise=0.3)
```
### 1. Examine the size of X
- nparray.shape
Gives tuple of array dimensions.
```
X.shape
```
### 2. Convert X to a one-dimensional vector
- Use .reshape( )
#### CAN ALSO USE .flatten( )!!
```
xvector = X.reshape(-1)
xvector.shape
X.flatten().shape
```
### 3. Select the first 3 data points from X
```
X[:3]
xvector[:3]
```
### 4. Select the second column from X
**X[ : , 1 ]** - Selects every row from column index position 1
**X[ 2 : , 1 ]** - Selects every row starting from the 3rd row from column index pos. 1
**X[ 2 : 10, 0 ]** - Selects row 3 to 9 for column 0!
**X[ 2 : 10: 2, : ]** - Selects every 2nd row from the 3rd row to the 10th row for ALL columns - selects row 3, 5, 7, 9!
```
X[:,1][:40]
X[2:10:2, :]
```
### 5. Select every second row from X
```
X[::2,]
```
### 6. Calculate the sum of X
```
X.sum()
X[:,0].sum()
X[:,1].sum()
X.max()
X.min()
```
### 7. Convert X to a DataFrame
```
import pandas as pd
df = pd.DataFrame(X)
df.head()
```
## Exercises
### 1. Convert the 1D array to a 2D array with 3x4 dimensions.
```
ex1 = np.arange(12)
ex1
ex1.reshape(3,4)
```
### 2. Replace odd numbers by -1
```
ex2 = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
ex2
for n in ex2:
if n%2 != 0:
ex2[n] = -1
ex2
```
### 3. Retrieve the positions (indices) where the elements of a and b match
```
ex3a = np.array([1,2,3,2,3,4,3,4,5,6])
ex3b = np.array([7,2,10,2,7,4,9,4,9,8])
```
### 4. Drop all missing values from a numpy array
```
ex4 = np.array([1,2,3,np.nan,5,6,7,np.nan])
ex4
ex4 = ex4[np.logical_not(np.isnan(ex4))]
ex4
```
### 5. Append a new column of ones to the matrix below
```
ex5 = np.random.random((5, 2))
ex5
ones = np.ones((5, 1))
ones
```
#### Use np.append( )!
```
np.append(ex5, ones, axis=1)
```
|
github_jupyter
|
import numpy as np
a = np.array([1,1, 2, 2, 3, 3])
a
# this will return floating point numbers e.g. 1., 1. ...
b = np.array([[1,1], [2, 2], [3, 3]], dtype=np.float64)
b
np.arange(10)
# 1 is starting number, 4 is final number
# 7 is the length of the array!
np.linspace(1, 4, 7)
np.zeros(10)
np.ones((3, 3))
np.eye(3)
np.random.random((3,3))
# normal distribution
np.random.normal(0.0, 1.0, 100)
import matplotlib.pyplot as plt
%matplotlib inline
plt.hist(np.random.normal(0.0, 1.0, 100))
np.meshgrid([0, 1, 2], [0, 1, 2])
a = np.zeros(10)
a[4] = 1
a
a = np.arange(10)
a[::-1]
np.arange(9)
np.arange(9).reshape(3,3)
np.nonzero([1, 2, 0, 0, 4, 0])
a = np.arange(5)
a
np.exp(a)
a = np.random.random(10)
a
a[a.argmax()]
#equivalent of doing this:
a.max()
a[a.argmax()] = 0
a
from sklearn.datasets import make_moons
X, y = make_moons(noise=0.3)
X.shape
xvector = X.reshape(-1)
xvector.shape
X.flatten().shape
X[:3]
xvector[:3]
X[:,1][:40]
X[2:10:2, :]
X[::2,]
X.sum()
X[:,0].sum()
X[:,1].sum()
X.max()
X.min()
import pandas as pd
df = pd.DataFrame(X)
df.head()
ex1 = np.arange(12)
ex1
ex1.reshape(3,4)
ex2 = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
ex2
for n in ex2:
if n%2 != 0:
ex2[n] = -1
ex2
ex3a = np.array([1,2,3,2,3,4,3,4,5,6])
ex3b = np.array([7,2,10,2,7,4,9,4,9,8])
ex4 = np.array([1,2,3,np.nan,5,6,7,np.nan])
ex4
ex4 = ex4[np.logical_not(np.isnan(ex4))]
ex4
ex5 = np.random.random((5, 2))
ex5
ones = np.ones((5, 1))
ones
np.append(ex5, ones, axis=1)
| 0.439266 | 0.987841 |
<center>
<img src="https://gitlab.com/ibm/skills-network/courses/placeholder101/-/raw/master/labs/module%201/images/IDSNlogo.png" width="300" alt="cognitiveclass.ai logo" />
</center>
# **SpaceX Falcon 9 First Stage Landing Prediction**
## Assignment: Exploring and Preparing Data
Estimated time needed: **70** minutes
In this assignment, we will predict if the Falcon 9 first stage will land successfully. SpaceX advertises Falcon 9 rocket launches on its website with a cost of 62 million dollars; other providers cost upward of 165 million dollars each, much of the savings is due to the fact that SpaceX can reuse the first stage.
In this lab, you will perform Exploratory Data Analysis and Feature Engineering.
Falcon 9 first stage will land successfully

Several examples of an unsuccessful landing are shown here:

Most unsuccessful landings are planned. Space X performs a controlled landing in the oceans.
## Objectives
Perform exploratory Data Analysis and Feature Engineering using `Pandas` and `Matplotlib`
* Exploratory Data Analysis
* Preparing Data Feature Engineering
***
### Import Libraries and Define Auxiliary Functions
We will import the following libraries the lab
```
# andas is a software library written for the Python programming language for data manipulation and analysis.
import pandas as pd
#NumPy is a library for the Python programming language, adding support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays
import numpy as np
# Matplotlib is a plotting library for python and pyplot gives us a MatLab like plotting framework. We will use this in our plotter function to plot data.
import matplotlib.pyplot as plt
#Seaborn is a Python data visualization library based on matplotlib. It provides a high-level interface for drawing attractive and informative statistical graphics
import seaborn as sns
```
## Exploratory Data Analysis
First, let's read the SpaceX dataset into a Pandas dataframe and print its summary
```
df=pd.read_csv("https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/datasets/dataset_part_2.csv")
# If you were unable to complete the previous lab correctly you can uncomment and load this csv
# df = pd.read_csv('https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DS0701EN-SkillsNetwork/api/dataset_part_2.csv')
df.head(5)
```
First, let's try to see how the `FlightNumber` (indicating the continuous launch attempts.) and `Payload` variables would affect the launch outcome.
We can plot out the <code>FlightNumber</code> vs. <code>PayloadMass</code>and overlay the outcome of the launch. We see that as the flight number increases, the first stage is more likely to land successfully. The payload mass is also important; it seems the more massive the payload, the less likely the first stage will return.
```
sns.catplot(y="PayloadMass", x="FlightNumber", hue="Class", data=df, aspect = 5)
plt.xlabel("Flight Number",fontsize=20)
plt.ylabel("Pay load Mass (kg)",fontsize=20)
plt.show()
```
We see that different launch sites have different success rates. <code>CCAFS LC-40</code>, has a success rate of 60 %, while <code>KSC LC-39A</code> and <code>VAFB SLC 4E</code> has a success rate of 77%.
Next, let's drill down to each site visualize its detailed launch records.
### TASK 1: Visualize the relationship between Flight Number and Launch Site
Use the function <code>catplot</code> to plot <code>FlightNumber</code> vs <code>LaunchSite</code>, set the parameter <code>x</code> parameter to <code>FlightNumber</code>,set the <code>y</code> to <code>Launch Site</code> and set the parameter <code>hue</code> to <code>'class'</code>
```
# Plot a scatter point chart with x axis to be Flight Number and y axis to be the launch site, and hue to be the class value
sns.catplot(y="LaunchSite", x="FlightNumber", hue="Class", data=df, aspect = 5)
plt.xlabel("Flight Number",fontsize=20)
plt.ylabel("Launch Site",fontsize=20)
plt.show()
```
Now try to explain the patterns you found in the Flight Number vs. Launch Site scatter point plots.
### TASK 2: Visualize the relationship between Payload and Launch Site
We also want to observe if there is any relationship between launch sites and their payload mass.
```
# Plot a scatter point chart with x axis to be Pay Load Mass (kg) and y axis to be the launch site, and hue to be the class value
sns.catplot(y="LaunchSite", x="PayloadMass", hue="Class", data=df, aspect = 5)
plt.xlabel("Pay load Mass (kg)",fontsize=20)
plt.ylabel("Launch Site",fontsize=20)
plt.show()
```
Now if you observe Payload Vs. Launch Site scatter point chart you will find for the VAFB-SLC launchsite there are no rockets launched for heavypayload mass(greater than 10000).
### TASK 3: Visualize the relationship between success rate of each orbit type
Next, we want to visually check if there are any relationship between success rate and orbit type.
Let's create a `bar chart` for the sucess rate of each orbit
```
# HINT use groupby method on Orbit column and get the mean of Class column
# find mean for Class grouping by Orbit
success_rate_df = df[['Orbit','Class']]
success_rate_df.groupby(['Orbit']).mean()
# create bar plot
sns.barplot(y="Class", x="Orbit", data=success_rate_df)
plt.xlabel("Orbit", fontsize=20)
plt.ylabel("Class", fontsize=20)
plt.show()
```
Analyze the ploted bar chart try to find which orbits have high sucess rate.
### TASK 4: Visualize the relationship between FlightNumber and Orbit type
For each orbit, we want to see if there is any relationship between FlightNumber and Orbit type.
```
# Plot a scatter point chart with x axis to be FlightNumber and y axis to be the Orbit, and hue to be the class value
sns.scatterplot(y="Orbit", x="FlightNumber", hue='Class', data=df)
plt.xlabel("Flight Number", fontsize=20)
plt.ylabel("Orbit", fontsize=20)
plt.show()
```
You should see that in the LEO orbit the Success appears related to the number of flights; on the other hand, there seems to be no relationship between flight number when in GTO orbit.
### TASK 5: Visualize the relationship between Payload and Orbit type
Similarly, we can plot the Payload vs. Orbit scatter point charts to reveal the relationship between Payload and Orbit type
```
# Plot a scatter point chart with x axis to be Payload and y axis to be the Orbit, and hue to be the class value
sns.scatterplot(y="Orbit", x="PayloadMass", hue='Class', data=df)
plt.xlabel("Payload Mass (kg)", fontsize=20)
plt.ylabel("Orbit", fontsize=20)
plt.show()
```
With heavy payloads the successful landing or positive landing rate are more for Polar,LEO and ISS.
However for GTO we cannot distinguish this well as both positive landing rate and negative landing(unsuccessful mission) are both there here.
### TASK 6: Visualize the launch success yearly trend
You can plot a line chart with x axis to be <code>Year</code> and y axis to be average success rate, to get the average launch success trend.
The function will help you get the year from the date:
```
# A function to Extract years from the date
year=[]
def Extract_year(date):
for i in df["Date"]:
year.append(i.split("-")[0])
return year
# create Year column from Date column
date_class_df = df[['Date','Class']]
df['Year'] = pd.DatetimeIndex(df['Date']).year
yearly_df = pd.concat([date_class_df, df['Year']], axis=1)
yearly_df
# Plot a line chart with x axis to be the extracted year and y axis to be the success rate
sns.lineplot(y="Class", x="Year", data=yearly_df)
plt.xlabel("Year", fontsize=20)
plt.ylabel("Avg Class", fontsize=20)
plt.show()
```
you can observe that the sucess rate since 2013 kept increasing till 2020
## Features Engineering
By now, you should obtain some preliminary insights about how each important variable would affect the success rate, we will select the features that will be used in success prediction in the future module.
```
features = df[['FlightNumber', 'PayloadMass', 'Orbit', 'LaunchSite', 'Flights', 'GridFins', 'Reused', 'Legs', 'LandingPad', 'Block', 'ReusedCount', 'Serial']]
features.head()
```
### TASK 7: Create dummy variables to categorical columns
Use the function <code>get_dummies</code> and <code>features</code> dataframe to apply OneHotEncoder to the column <code>Orbits</code>, <code>LaunchSite</code>, <code>LandingPad</code>, and <code>Serial</code>. Assign the value to the variable <code>features_one_hot</code>, display the results using the method head. Your result dataframe must include all features including the encoded ones.
```
# HINT: Use get_dummies() function on the categorical columns
features_one_hot = pd.get_dummies(data=features, columns=['Orbit','LaunchSite','LandingPad','Serial'])
features_one_hot.head()
```
### TASK 8: Cast all numeric columns to `float64`
Now that our <code>features_one_hot</code> dataframe only contains numbers cast the entire dataframe to variable type <code>float64</code>
```
# HINT: use astype function
features_one_hot.astype('float64')
```
We can now export it to a <b>CSV</b> for the next section,but to make the answers consistent, in the next lab we will provide data in a pre-selected date range.
<code>features_one_hot.to_csv('dataset_part\_3.csv', index=False)</code>
## Authors
<a href="https://www.linkedin.com/in/joseph-s-50398b136/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDS0321ENSkillsNetwork26802033-2021-01-01">Joseph Santarcangelo</a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
<a href="https://www.linkedin.com/in/nayefaboutayoun/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDS0321ENSkillsNetwork26802033-2021-01-01">Nayef Abou Tayoun</a> is a Data Scientist at IBM and pursuing a Master of Management in Artificial intelligence degree at Queen's University.
## Change Log
| Date (YYYY-MM-DD) | Version | Changed By | Change Description |
| ----------------- | ------- | ------------- | ----------------------- |
| 2021-10-12 | 1.1 | Lakshmi Holla | Modified markdown |
| 2020-09-20 | 1.0 | Joseph | Modified Multiple Areas |
| 2020-11-10 | 1.1 | Nayef | updating the input data |
Copyright © 2020 IBM Corporation. All rights reserved.
|
github_jupyter
|
# andas is a software library written for the Python programming language for data manipulation and analysis.
import pandas as pd
#NumPy is a library for the Python programming language, adding support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays
import numpy as np
# Matplotlib is a plotting library for python and pyplot gives us a MatLab like plotting framework. We will use this in our plotter function to plot data.
import matplotlib.pyplot as plt
#Seaborn is a Python data visualization library based on matplotlib. It provides a high-level interface for drawing attractive and informative statistical graphics
import seaborn as sns
df=pd.read_csv("https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/datasets/dataset_part_2.csv")
# If you were unable to complete the previous lab correctly you can uncomment and load this csv
# df = pd.read_csv('https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DS0701EN-SkillsNetwork/api/dataset_part_2.csv')
df.head(5)
sns.catplot(y="PayloadMass", x="FlightNumber", hue="Class", data=df, aspect = 5)
plt.xlabel("Flight Number",fontsize=20)
plt.ylabel("Pay load Mass (kg)",fontsize=20)
plt.show()
# Plot a scatter point chart with x axis to be Flight Number and y axis to be the launch site, and hue to be the class value
sns.catplot(y="LaunchSite", x="FlightNumber", hue="Class", data=df, aspect = 5)
plt.xlabel("Flight Number",fontsize=20)
plt.ylabel("Launch Site",fontsize=20)
plt.show()
# Plot a scatter point chart with x axis to be Pay Load Mass (kg) and y axis to be the launch site, and hue to be the class value
sns.catplot(y="LaunchSite", x="PayloadMass", hue="Class", data=df, aspect = 5)
plt.xlabel("Pay load Mass (kg)",fontsize=20)
plt.ylabel("Launch Site",fontsize=20)
plt.show()
# HINT use groupby method on Orbit column and get the mean of Class column
# find mean for Class grouping by Orbit
success_rate_df = df[['Orbit','Class']]
success_rate_df.groupby(['Orbit']).mean()
# create bar plot
sns.barplot(y="Class", x="Orbit", data=success_rate_df)
plt.xlabel("Orbit", fontsize=20)
plt.ylabel("Class", fontsize=20)
plt.show()
# Plot a scatter point chart with x axis to be FlightNumber and y axis to be the Orbit, and hue to be the class value
sns.scatterplot(y="Orbit", x="FlightNumber", hue='Class', data=df)
plt.xlabel("Flight Number", fontsize=20)
plt.ylabel("Orbit", fontsize=20)
plt.show()
# Plot a scatter point chart with x axis to be Payload and y axis to be the Orbit, and hue to be the class value
sns.scatterplot(y="Orbit", x="PayloadMass", hue='Class', data=df)
plt.xlabel("Payload Mass (kg)", fontsize=20)
plt.ylabel("Orbit", fontsize=20)
plt.show()
# A function to Extract years from the date
year=[]
def Extract_year(date):
for i in df["Date"]:
year.append(i.split("-")[0])
return year
# create Year column from Date column
date_class_df = df[['Date','Class']]
df['Year'] = pd.DatetimeIndex(df['Date']).year
yearly_df = pd.concat([date_class_df, df['Year']], axis=1)
yearly_df
# Plot a line chart with x axis to be the extracted year and y axis to be the success rate
sns.lineplot(y="Class", x="Year", data=yearly_df)
plt.xlabel("Year", fontsize=20)
plt.ylabel("Avg Class", fontsize=20)
plt.show()
features = df[['FlightNumber', 'PayloadMass', 'Orbit', 'LaunchSite', 'Flights', 'GridFins', 'Reused', 'Legs', 'LandingPad', 'Block', 'ReusedCount', 'Serial']]
features.head()
# HINT: Use get_dummies() function on the categorical columns
features_one_hot = pd.get_dummies(data=features, columns=['Orbit','LaunchSite','LandingPad','Serial'])
features_one_hot.head()
# HINT: use astype function
features_one_hot.astype('float64')
| 0.73077 | 0.991844 |
```
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150, n_features=2, centers=3, cluster_std=0.5, shuffle=True, random_state=0)
import matplotlib.pyplot as plt
plt.scatter(X[:,0], X[:,1], c='white', marker='o', edgecolor='black', s=50)
plt.grid()
plt.show()
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, init='random', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km.fit_predict(X)
import matplotlib.pyplot as plt
plt.scatter(X[y_km == 0, 0], X[y_km == 0, 1], s=50, c='lightgreen', marker='s', edgecolor='black', label='cluster 1')
plt.scatter(X[y_km == 1, 0], X[y_km == 1, 1], s=50, c='orange', marker='o', edgecolor='black', label='cluster 2')
plt.scatter(X[y_km == 2, 0], X[y_km == 2, 1], s=50, c='lightblue', marker='v', edgecolor='black', label='cluster 3')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], s=250, marker='*', c='red', edgecolor='black', label='centroids')
plt.legend(scatterpoints=1)
plt.grid()
plt.show()
print('Distortion: %.2f' % km.inertia_)
distortions = []
for i in range(1, 11):
km = KMeans(n_clusters=i, init='k-means++', n_init=10, max_iter=300, random_state=0)
km.fit(X)
distortions.append(km.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()
km = KMeans(n_clusters=3, init='k-means++', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km.fit_predict(X)
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0, edgecolor='none', color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.show()
km = KMeans(n_clusters=2, init='k-means++', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km.fit_predict(X)
plt.scatter(X[y_km==0, 0], X[y_km==0, 1], s=50, c='lightgreen', edgecolor='black', marker='s', label='cluster 1')
plt.scatter(X[y_km==1, 0], X[y_km==1, 1], s=50, c='orange', edgecolor='black', marker='o', label='cluster 2')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], s=250, marker='*', c='red', label='centroids')
plt.legend()
plt.grid()
plt.show()
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0, edgecolor='none', color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.show()
```
|
github_jupyter
|
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150, n_features=2, centers=3, cluster_std=0.5, shuffle=True, random_state=0)
import matplotlib.pyplot as plt
plt.scatter(X[:,0], X[:,1], c='white', marker='o', edgecolor='black', s=50)
plt.grid()
plt.show()
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, init='random', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km.fit_predict(X)
import matplotlib.pyplot as plt
plt.scatter(X[y_km == 0, 0], X[y_km == 0, 1], s=50, c='lightgreen', marker='s', edgecolor='black', label='cluster 1')
plt.scatter(X[y_km == 1, 0], X[y_km == 1, 1], s=50, c='orange', marker='o', edgecolor='black', label='cluster 2')
plt.scatter(X[y_km == 2, 0], X[y_km == 2, 1], s=50, c='lightblue', marker='v', edgecolor='black', label='cluster 3')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], s=250, marker='*', c='red', edgecolor='black', label='centroids')
plt.legend(scatterpoints=1)
plt.grid()
plt.show()
print('Distortion: %.2f' % km.inertia_)
distortions = []
for i in range(1, 11):
km = KMeans(n_clusters=i, init='k-means++', n_init=10, max_iter=300, random_state=0)
km.fit(X)
distortions.append(km.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()
km = KMeans(n_clusters=3, init='k-means++', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km.fit_predict(X)
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0, edgecolor='none', color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.show()
km = KMeans(n_clusters=2, init='k-means++', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km.fit_predict(X)
plt.scatter(X[y_km==0, 0], X[y_km==0, 1], s=50, c='lightgreen', edgecolor='black', marker='s', label='cluster 1')
plt.scatter(X[y_km==1, 0], X[y_km==1, 1], s=50, c='orange', edgecolor='black', marker='o', label='cluster 2')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], s=250, marker='*', c='red', label='centroids')
plt.legend()
plt.grid()
plt.show()
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0, edgecolor='none', color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.show()
| 0.806129 | 0.76145 |
<a href="https://colab.research.google.com/github/sardarmonsoorsait/Crossroad/blob/master/asaiTech_predictfuturesales.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
path ='/content/drive/My Drive/predictfuturesales/sales_train.csv'
df_sale = pd.read_csv(path)
path_1 = '/content/drive/My Drive/predictfuturesales/item_categories.csv'
df_item_catagories =pd.read_csv(path_1)
path_2 = '/content/drive/My Drive/predictfuturesales/items.csv'
df_item = pd.read_csv(path_2)
path_3 = '/content/drive/My Drive/predictfuturesales/shops.csv'
df_shops = pd.read_csv(path_3)
path_test = '/content/drive/My Drive/predictfuturesales/test.csv'
df_test = pd.read_csv(path_test)
df_sales = df_sale.copy()
df_item_catagories
df_item
df_shops.head()
df_sales = df_sales.join(df_item,on='item_id',rsuffix='_').join(df_shops,on='shop_id',rsuffix='_').join(df_item_catagories,on='item_category_id',rsuffix="_")
df_sales.head()
df_sales.drop(['shop_id_','item_category_id_','item_id_'],axis=1,inplace=True)
df_sales.keys()
df_sales.dtypes
df_sales.shape
df_sales.describe()
df_sales['date_block_num'].value_counts()
df_sales['shop_id'].value_counts()
df_sales['date_block_num'].nunique()
df_sales['date_block_num'].unique()
df_sales[df_sales['item_price']<0]
df_sales[df_sales['item_cnt_day']<0]
df_sales.isnull().sum()
pd.to_datetime(df_sales['date'])
df_sales['date_block_num'].hist(bins=5)
df_sales['date'].hist()
plt.figure(figsize=(44,8))
plt.figure(figsize=(22,8))
print(df_sales.boxplot(column='item_price',by='shop_id'))
sns.boxplot(df_sales['item_cnt_day'])
plt.figure(figsize=(44,16))
sns.countplot(df_sales['shop_name'])
df_sales = df_sales[df_sales['item_price']>0]
df_sales.shape
df_sales = df_sales[df_sales['item_cnt_day']>0]
df_sales.shape
df_sales['item_price'].mean()
monthly_sales = df_sales.groupby(['date_block_num','shop_id','item_id','item_price'],as_index=False).agg({'item_cnt_day':['sum','mean','count']})
monthly_sales
monthly_sales.columns = ['date_block_num','shop_id','item_id','item_price','item_cnt_month','item_cnt_mean','transaction']
monthly_sales.dtypes
monthly_sales.shape
test_item_ids = df_test['item_id'].unique()
test_shop_ids = df_test['shop_id'].unique()
lk_sales = monthly_sales[monthly_sales['shop_id'].isin(test_shop_ids)]
monthly_sales_n= lk_sales[lk_sales['item_id'].isin(test_item_ids)]
monthly_sales_n.columns=['date_block_num','shop_id','item_id','item_price','item_cnt_month','item_cnt_mean','transaction']
monthly_sales_n
monthly_sales_n['item_cnt_month']=monthly_sales_n['item_cnt_month'] .shift(-1,axis=0)
monthly_sales_n
plt.figure(figsize=(22,30))
plt.subplot(7,1,1)
axe[0]=sns.boxplot(monthly_sales_n['date_block_num'])
plt.subplot(7,1,2)
axe[1]=sns.boxplot(monthly_sales_n['shop_id'])
plt.subplot(7,1,3)
axe[2]=sns.boxplot(monthly_sales_n['item_id'])
plt.subplot(7,1,4)
axe[3]=sns.boxplot(monthly_sales_n['item_price'])
plt.subplot(7,1,5)
axe[4]=sns.boxplot(monthly_sales_n['item_cnt_month'])
plt.subplot(7,1,6)
axe[5]=sns.boxplot(monthly_sales_n['item_cnt_mean'])
plt.subplot(7,1,7)
axe[6]=sns.boxplot(monthly_sales_n['transaction'])
plt.show()
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
path ='/content/drive/My Drive/predictfuturesales/sales_train.csv'
df_sale = pd.read_csv(path)
path_1 = '/content/drive/My Drive/predictfuturesales/item_categories.csv'
df_item_catagories =pd.read_csv(path_1)
path_2 = '/content/drive/My Drive/predictfuturesales/items.csv'
df_item = pd.read_csv(path_2)
path_3 = '/content/drive/My Drive/predictfuturesales/shops.csv'
df_shops = pd.read_csv(path_3)
path_test = '/content/drive/My Drive/predictfuturesales/test.csv'
df_test = pd.read_csv(path_test)
df_sales = df_sale.copy()
df_item_catagories
df_item
df_shops.head()
df_sales = df_sales.join(df_item,on='item_id',rsuffix='_').join(df_shops,on='shop_id',rsuffix='_').join(df_item_catagories,on='item_category_id',rsuffix="_")
df_sales.head()
df_sales.drop(['shop_id_','item_category_id_','item_id_'],axis=1,inplace=True)
df_sales.keys()
df_sales.dtypes
df_sales.shape
df_sales.describe()
df_sales['date_block_num'].value_counts()
df_sales['shop_id'].value_counts()
df_sales['date_block_num'].nunique()
df_sales['date_block_num'].unique()
df_sales[df_sales['item_price']<0]
df_sales[df_sales['item_cnt_day']<0]
df_sales.isnull().sum()
pd.to_datetime(df_sales['date'])
df_sales['date_block_num'].hist(bins=5)
df_sales['date'].hist()
plt.figure(figsize=(44,8))
plt.figure(figsize=(22,8))
print(df_sales.boxplot(column='item_price',by='shop_id'))
sns.boxplot(df_sales['item_cnt_day'])
plt.figure(figsize=(44,16))
sns.countplot(df_sales['shop_name'])
df_sales = df_sales[df_sales['item_price']>0]
df_sales.shape
df_sales = df_sales[df_sales['item_cnt_day']>0]
df_sales.shape
df_sales['item_price'].mean()
monthly_sales = df_sales.groupby(['date_block_num','shop_id','item_id','item_price'],as_index=False).agg({'item_cnt_day':['sum','mean','count']})
monthly_sales
monthly_sales.columns = ['date_block_num','shop_id','item_id','item_price','item_cnt_month','item_cnt_mean','transaction']
monthly_sales.dtypes
monthly_sales.shape
test_item_ids = df_test['item_id'].unique()
test_shop_ids = df_test['shop_id'].unique()
lk_sales = monthly_sales[monthly_sales['shop_id'].isin(test_shop_ids)]
monthly_sales_n= lk_sales[lk_sales['item_id'].isin(test_item_ids)]
monthly_sales_n.columns=['date_block_num','shop_id','item_id','item_price','item_cnt_month','item_cnt_mean','transaction']
monthly_sales_n
monthly_sales_n['item_cnt_month']=monthly_sales_n['item_cnt_month'] .shift(-1,axis=0)
monthly_sales_n
plt.figure(figsize=(22,30))
plt.subplot(7,1,1)
axe[0]=sns.boxplot(monthly_sales_n['date_block_num'])
plt.subplot(7,1,2)
axe[1]=sns.boxplot(monthly_sales_n['shop_id'])
plt.subplot(7,1,3)
axe[2]=sns.boxplot(monthly_sales_n['item_id'])
plt.subplot(7,1,4)
axe[3]=sns.boxplot(monthly_sales_n['item_price'])
plt.subplot(7,1,5)
axe[4]=sns.boxplot(monthly_sales_n['item_cnt_month'])
plt.subplot(7,1,6)
axe[5]=sns.boxplot(monthly_sales_n['item_cnt_mean'])
plt.subplot(7,1,7)
axe[6]=sns.boxplot(monthly_sales_n['transaction'])
plt.show()
| 0.08469 | 0.6677 |
### IMPORTANT: matplotlib.pyplot conflicts with garbage collection of peppercorns' objects.
Whenever you enumerate multiple systems that use same-named domains, complexes, etc., make sure to import plotting libraries only after all your data has been generated. (You have to restart the kernel in order to modify your data once a plotting library has been importet, even if it is e.g. a shell script in the background importing that library. Yes, it's terrible.)
```
import numpy as np
from pandas import DataFrame
from yin2008 import data; y08 = data()
```
# Generate the data
```
%%timeit
y08 = data()
for fig in y08:
fig.eval(verbose = 0, enumprofile = True)
Table1 = DataFrame()
for fig in y08:
display(fig.pepperargs['default'])
fig.eval('default', verbose = 0, cmpfig=True)
for df in fig.get_dataframes():
df['name'] = fig.name
#display(df)
Table1 = Table1.append(df)
import matplotlib.pyplot as plt
from numpy import log10
import seaborn as sns
sns.set(style="darkgrid")
tmpfig = Table1.copy()
tmpfig['Time (experiment)'] = log10(tmpfig['Time (experiment)'])
tmpfig['Time (simulation)'] = log10(tmpfig['Time (simulation)'])
tmpfig = tmpfig.loc[tmpfig['Semantics'].isin(['default'])]
#display(tmpfig)
sns.lmplot(x = "Time (experiment)",
y = "Time (simulation)",
hue = "Metric",
fit_reg = False,
data = tmpfig)
(mi, ma)=(1, 4)
plt.plot([mi, ma], [mi, ma], linewidth=1, color='white',zorder=0)
#plt.gcf().set_size_inches(3.5,2.5)
# Get Data from File
F3 = y08[0]
nxy = np.loadtxt(F3.cmpfig['default'], skiprows=1)
print(F3.cmpfig['default'])
time = nxy[:,0] / 60
ys = nxy[:,1:]
legend = ['20 nM', '6 nM', '2 nM', '1 nM', '0.6 nM', '0.4 nM', '0.2 nM', '0.1 nM', '0.06 nM', '0.02 nM', '0.01 nM']#, '0 nM']
legend = list(map(lambda x: '{}{}'.format('I = ', x), legend))
assert ys.shape[1] == len(legend)
# Customize plot using Yin 2008 color scheme, etc.
mycolors = ['#882486',
'#ffbb11',
'#ea0081',
'#eb1c22',
'#f68a1d',
'#0faa44',
'#87398e',
'#2b2d89',
'#016667',
'#027ac5',
'#eb125b']
#'#211e1f']
plt.figure(figsize=(3.5,2.5))
plt.gca().set_prop_cycle(color=mycolors)
#sns.set(rc={'figure.figsize':(3.5,2.5)})
#plt.gca().invert_yaxis()
# Plot the data
plt.plot(time, ys)
plt.xlim(-0.5,20.5)
plt.xticks(np.arange(0, 21, step=5))
plt.ylim(21,-1)
plt.yticks(np.arange(0, 21, step=5))
plt.legend(legend, ncol=1, loc='center right', fontsize=7);
plt.gca().set_xlabel('Time [min]', fontsize=10)
plt.gca().set_ylabel('Concentration A [nM]', fontsize=10)
plt.gca().axhline(y=10, linewidth=1, color='black', linestyle='--')
#plt.savefig('yinF3.pdf', bbox_inches='tight')
#plt.savefig('yinF3.svg', bbox_inches='tight')
```
|
github_jupyter
|
import numpy as np
from pandas import DataFrame
from yin2008 import data; y08 = data()
%%timeit
y08 = data()
for fig in y08:
fig.eval(verbose = 0, enumprofile = True)
Table1 = DataFrame()
for fig in y08:
display(fig.pepperargs['default'])
fig.eval('default', verbose = 0, cmpfig=True)
for df in fig.get_dataframes():
df['name'] = fig.name
#display(df)
Table1 = Table1.append(df)
import matplotlib.pyplot as plt
from numpy import log10
import seaborn as sns
sns.set(style="darkgrid")
tmpfig = Table1.copy()
tmpfig['Time (experiment)'] = log10(tmpfig['Time (experiment)'])
tmpfig['Time (simulation)'] = log10(tmpfig['Time (simulation)'])
tmpfig = tmpfig.loc[tmpfig['Semantics'].isin(['default'])]
#display(tmpfig)
sns.lmplot(x = "Time (experiment)",
y = "Time (simulation)",
hue = "Metric",
fit_reg = False,
data = tmpfig)
(mi, ma)=(1, 4)
plt.plot([mi, ma], [mi, ma], linewidth=1, color='white',zorder=0)
#plt.gcf().set_size_inches(3.5,2.5)
# Get Data from File
F3 = y08[0]
nxy = np.loadtxt(F3.cmpfig['default'], skiprows=1)
print(F3.cmpfig['default'])
time = nxy[:,0] / 60
ys = nxy[:,1:]
legend = ['20 nM', '6 nM', '2 nM', '1 nM', '0.6 nM', '0.4 nM', '0.2 nM', '0.1 nM', '0.06 nM', '0.02 nM', '0.01 nM']#, '0 nM']
legend = list(map(lambda x: '{}{}'.format('I = ', x), legend))
assert ys.shape[1] == len(legend)
# Customize plot using Yin 2008 color scheme, etc.
mycolors = ['#882486',
'#ffbb11',
'#ea0081',
'#eb1c22',
'#f68a1d',
'#0faa44',
'#87398e',
'#2b2d89',
'#016667',
'#027ac5',
'#eb125b']
#'#211e1f']
plt.figure(figsize=(3.5,2.5))
plt.gca().set_prop_cycle(color=mycolors)
#sns.set(rc={'figure.figsize':(3.5,2.5)})
#plt.gca().invert_yaxis()
# Plot the data
plt.plot(time, ys)
plt.xlim(-0.5,20.5)
plt.xticks(np.arange(0, 21, step=5))
plt.ylim(21,-1)
plt.yticks(np.arange(0, 21, step=5))
plt.legend(legend, ncol=1, loc='center right', fontsize=7);
plt.gca().set_xlabel('Time [min]', fontsize=10)
plt.gca().set_ylabel('Concentration A [nM]', fontsize=10)
plt.gca().axhline(y=10, linewidth=1, color='black', linestyle='--')
#plt.savefig('yinF3.pdf', bbox_inches='tight')
#plt.savefig('yinF3.svg', bbox_inches='tight')
| 0.499512 | 0.85022 |
# Considering the Environment
So far, we have worked through a number of hands-on implementations
fitting machine learning models to a variety of datasets.
And yet, until now we skated over the matter
of where are data comes from in the first place,
and what we plan to ultimately *do* with the outputs from our models.
Too often in the practice of machine learning,
developers rush ahead with the development of models
tossing these fundamental considerations aside.
Many failed machine learning deployments can be traced back to this situation.
Sometimes the model does well as evaluated by test accuracy
only to fail catastrophically in the real world
when the distribution of data suddenly shifts.
More insidiously, sometimes the very deployment of a model
can be the catalyst which perturbs the data distribution.
Say for example that we trained a model to predict loan defaults,
finding that the choice of footware was associated with risk of default
(Oxfords indicate repayment, sneakers indicate default).
We might be inclined to thereafter grant loans
to all applicants wearing Oxfords
and to deny all applicants wearing sneakers.
But our ill-conceived leap from pattern recognition to decision-making
and our failure to think critically about the environment
might have disastrous consequences.
For starters, as soon as we began making decisions based on footware,
customers would catch on and change their behavior.
Before long, all applicants would be wearing Oxfords,
and yet there would be no coinciding improvement in credit-worthiness.
Think about this deeply because similar issues abound in the application of machine learning: by introducing our model-based decisions to the environment,
we might break the model.
In this chapter, we describe some common concerns
and aim to get you started acquiring the critical thinking
that you will need in order to detect these situations early,
mitigate the damage, and use machine learning responsibly.
Some of the solutions are simple (ask for the 'right' data)
some are technically difficult (implement a reinforcement learning system),
and others require that we entre the realm of philosophy
and grapple with difficult questions concerning ethics and informed consent.
## Distribution Shift
To begin, we return to the observational setting,
putting aside for now the impacts of our actions
on the environment.
In the following sections, we take a deeper look
at the various ways that data distributions might shift,
and what might be done to salvage model performance.
From the outset, we should warn that if
the data-generating distribution $p(\mathbf{x},y)$
can shift in arbitrary ways at any point in time,
then learning a robust classifier is impossible.
In the most pathological case, if the label definitions themselves
can change at a moments notice: if suddenly
what we called "cats" are now dogs
and what we previously called "dogs" are now in fact cats,
without any perceptible change in the distribution of inputs $p(\mathbf{x})$,
then there is nothing we could do to detect the change
or to correct our classifier at test time.
Fortunately, under some restricted assumptions
on the ways our data might change in the future,
principled algorithms can detect shift and possibly even
adapt, achieving higher accuracy
than if we naively continued to rely on our original classifier.
### Covariate Shift
One of the best-studied forms of distribution shift is *covariate shift*.
Here we assume that although the distribution of inputs may change over time,
the labeling function, i.e., the conditional distribution $p(y|\mathbf{x})$
does not change.
While this problem is easy to understand
its also easy to overlook it in practice.
Consider the challenge of distinguishing cats and dogs.
Our training data consists of images of the following kind:
|cat|cat|dog|dog|
|:---------------:|:---------------:|:---------------:|:---------------:|
|||||
At test time we are asked to classify the following images:
|cat|cat|dog|dog|
|:---------------:|:---------------:|:---------------:|:---------------:|
|||||
Obviously this is unlikely to work well.
The training set consists of photos,
while the test set contains only cartoons.
The colors aren't even realistic.
Training on a dataset that looks substantially different from the test set
without some plan for how to adapt to the new domain is a bad idea.
Unfortunately, this is a very common pitfall.
Statisticians call this *covariate shift*
because the root of the problem owed to
a shift in the distribution of features (i.e., of *covariates*).
Mathematically, we could say that $p(\mathbf{x})$ changes
but that $p(y|\mathbf{x})$ remains unchanged.
Although its usefulness is not restricted to this setting,
when we believe $\mathbf{x}$ causes $y$, covariate shift is usually
the right assumption to be working with.
### Label Shift
The converse problem emerges when we believe that what drives the shift
is a change in the marginal distribution over the labels $p(y)$
but that the class-conditional distributions are invariant $p(\mathbf{x}|y)$.
Label shift is a reasonable assumption to make
when we believe that $y$ causes $\mathbf{x}$.
For example, commonly we want to predict a diagnosis given its manifestations.
In this case we believe that the diagnosis causes the manifestations,
i.e., diseases cause symptoms.
Sometimes the label shift and covariate shift assumptions
can hold simultaneously.
For example, when the true labeling function is deterministic and unchanging,
then covariate shift will always hold,
including if label shift holds too.
Interestingly, when we expect both label shift and covariate shift hold,
it's often advantageous to work with the methods
that flow from the label shift assumption.
That's because these methods tend to involve manipulating objects
that look like the label,
which (in deep learning) tends to be comparatively easy
compared to working with the objects that look like the input,
which tends (in deep learning) to be a high-dimensional object.
### Concept Shift
One more related problem arises in *concept shift*,
the situation in which the very label definitions change.
This sounds weird—after all, a *cat* is a *cat*.
Indeed the definition of a cat might not change,
but can we say the same about soft drinks?
It turns out that if we navigate around the United States,
shifting the source of our data by geography,
we'll find considerable concept shift regarding
the definition of even this simple term:

If we were to build a machine translation system,
the distribution $p(y|x)$ might be different
depending on our location.
This problem can be tricky to spot.
A saving grace is that often the $p(y|x)$ only shifts gradually.
Before we go into further detail and discuss remedies,
we can discuss a number of situations where covariate and concept shift
may not be so obvious.
### Examples
#### Medical Diagnostics
Imagine that you want to design an algorithm to detect cancer.
You collect data from healthy and sick people and you train your algorithm.
It works fine, giving you high accuracy
and you conclude that you’re ready
for a successful career in medical diagnostics.
Not so fast...
Many things could go wrong.
In particular, the distributions that you work with
for training and those that you encounter in the wild
might differ considerably.
This happened to an unfortunate startup,
that Alex had the opportunity to consult for many years ago.
They were developing a blood test for a disease
that affects mainly older men and they’d managed to obtain
a fair amount of blood samples from patients.
It is considerably more difficult, though,
to obtain blood samples from healthy men (mainly for ethical reasons).
To compensate for that, they asked a large number of students on campus
to donate blood and they performed their test.
Then they asked me whether I could help them
build a classifier to detect the disease.
I told them that it would be very easy to distinguish
between both datasets with near-perfect accuracy.
After all, the test subjects differed in age, hormone levels,
physical activity, diet, alcohol consumption,
and many more factors unrelated to the disease.
This was unlikely to be the case with real patients:
Their sampling procedure made it likely that
an extreme case of covariate shift would arise
between the *source* and *target* distributions,
and at that, one that could not be corrected by conventional means.
In other words, training and test data were so different
that nothing useful could be done
and they had wasted significant amounts of money.
#### Self Driving Cars
Say a company wanted to build a machine learning system for self-driving cars.
One of the key components is a roadside detector.
Since real annotated data is expensive to get,
they had the (smart and questionable) idea
to use synthetic data from a game rendering engine
as additional training data.
This worked really well on 'test data' drawn from the rendering engine.
Alas, inside a real car it was a disaster.
As it turned out, the roadside had been rendered
with a very simplistic texture.
More importantly, *all* the roadside had been rendered
with the *same* texture and the roadside detector
learned about this 'feature' very quickly.
A similar thing happened to the US Army
when they first tried to detect tanks in the forest.
They took aerial photographs of the forest without tanks,
then drove the tanks into the forest and took another set of pictures.
The so-trained classifier worked 'perfectly'.
Unfortunately, all it had learned was to distinguish trees
with shadows from trees without shadows—the
first set of pictures was taken in the early morning, the second one at noon.
#### Nonstationary distributions
A much more subtle situation arises when the distribution changes slowly
and the model is not updated adequately.
Here are some typical cases:
* We train a computational advertising model and then fail to update it frequently (e.g. we forget to incorporate that an obscure new device called an iPad was just launched).
* We build a spam filter. It works well at detecting all spam that we've seen so far. But then the spammers wisen up and craft new messages that look unlike anything we've seen before.
* We build a product recommendation system. It works throughout the winter... but then it keeps on recommending Santa hats long after Christmas.
#### More Anecdotes
* We build a face detector. It works well on all benchmarks. Unfortunately it fails on test data - the offending examples are close-ups where the face fills the entire image (no such data was in the training set).
* We build a web search engine for the USA market and want to deploy it in the UK.
* We train an image classifier by compiling a large dataset where each among a large set of classes is equally represented in the dataset, say 1000 categories, represented by 1000 images each. Then we deploy the system in the real world, where the actual label distribution of photographs is decidedly non-uniform.
In short, there are many cases where training and test distributions
$p(\mathbf{x}, y)$ are different.
In some cases, we get lucky and the models work
despite covariate, label, or concept shift.
In other cases, we can do better by employing
principled strategies to cope with the shift.
The remainder of this section grows considerably more technical.
The impatient reader could continue on to the next section
as this material is not prerequisite to subsequent concepts.
### Covariate Shift Correction
Assume that we want to estimate some dependency $p(y|\mathbf{x})$
for which we have labeled data $(\mathbf{x}_i,y_i)$.
Unfortunately, the observations $x_i$ are drawn
from some *target* distribution $q(\mathbf{x})$
rather than the *source* distribution $p(\mathbf{x})$.
To make progress, we need to reflect about what exactly
is happening during training:
we iterate over training data and associated labels
$\{(\mathbf{x}_1, y_1), \ldots (\mathbf{x}_n, y_n)\}$
and update the weight vectors of the model after every minibatch.
We sometimes additionally apply some penalty to the parameters,
using weight decay, dropout, or some other related technique.
This means that we largely minimize the loss on the training.
$$
\mathop{\mathrm{minimize}}_w \frac{1}{n} \sum_{i=1}^n l(x_i, y_i, f(x_i)) + \mathrm{some~penalty}(w)
$$
Statisticians call the first term an *empirical average*,
i.e., an average computed over the data drawn from $p(x) p(y|x)$.
If the data is drawn from the 'wrong' distribution $q$,
we can correct for that by using the following simple identity:
$$
\begin{aligned}
\int p(\mathbf{x}) f(\mathbf{x}) dx & = \int p(\mathbf{x}) f(\mathbf{x}) \frac{q(\mathbf{x})}{q(\mathbf{x})} dx \\
& = \int q(\mathbf{x}) f(\mathbf{x}) \frac{p(\mathbf{x})}{q(\mathbf{x})} dx
\end{aligned}
$$
In other words, we need to re-weight each instance
by the ratio of probabilities
that it would have been drawn from the correct distribution
$\beta(\mathbf{x}) := p(\mathbf{x})/q(\mathbf{x})$.
Alas, we do not know that ratio,
so before we can do anything useful we need to estimate it.
Many methods are available,
including some fancy operator-theoretic approaches
that attempt to recalibrate the expectation operator directly
using a minimum-norm or a maximum entropy principle.
Note that for any such approach, we need samples
drawn from both distributions—the 'true' $p$, e.g.,
by access to training data, and the one used
for generating the training set $q$ (the latter is trivially available).
Note however, that we only need samples $\mathbf{x} \sim q(\mathbf{x})$;
we do not to access labels $y \sim q(y)$.
In this case, there exists a very effective approach
that will give almost as good results: logistic regression.
This is all that is needed to compute estimate probability ratios.
We learn a classifier to distinguish between data drawn from $p(\mathbf{x})$
and data drawn from $q(x)$.
If it is impossible to distinguish between the two distributions
then it means that the associated instances are equally likely
to come from either one of the two distributions.
On the other hand, any instances that can be well discriminated
should be significantly over/underweighted accordingly.
For simplicity’s sake assume that we have an equal number of instances
from both distributions, denoted by $\mathbf{x}_i \sim p(\mathbf{x})$ and $\mathbf{x}_i' \sim q(\mathbf{x})$ respectively.
Now denote by $z_i$ labels which are 1
for data drawn from $p$ and -1 for data drawn from $q$.
Then the probability in a mixed dataset is given by
$$p(z=1|\mathbf{x}) = \frac{p(\mathbf{x})}{p(\mathbf{x})+q(\mathbf{x})} \text{ and hence } \frac{p(z=1|\mathbf{x})}{p(z=-1|\mathbf{x})} = \frac{p(\mathbf{x})}{q(\mathbf{x})}$$
Hence, if we use a logistic regression approach where $p(z=1|\mathbf{x})=\frac{1}{1+\exp(-f(\mathbf{x}))}$ it follows that
$$
\beta(\mathbf{x}) = \frac{1/(1 + \exp(-f(\mathbf{x})))}{\exp(-f(\mathbf{x})/(1 + \exp(-f(\mathbf{x})))} = \exp(f(\mathbf{x}))
$$
As a result, we need to solve two problems:
first one to distinguish between data drawn from both distributions,
and then a reweighted minimization problem
where we weigh terms by $\beta$, e.g. via the head gradients.
Here's a prototypical algorithm for that purpose
which uses an unlabeled training set $X$ and test set $Z$:
1. Generate training set with $\{(\mathbf{x}_i, -1) ... (\mathbf{z}_j, 1)\}$
1. Train binary classifier using logistic regression to get function $f$
1. Weigh training data using $\beta_i = \exp(f(\mathbf{x}_i))$ or better $\beta_i = \min(\exp(f(\mathbf{x}_i)), c)$
1. Use weights $\beta_i$ for training on $X$ with labels $Y$
Note that this method relies on a crucial assumption.
For this scheme to work, we need that each data point
in the target (test time) distribution
had nonzero probability of occurring at training time.
If we find a point where $q(\mathbf{x}) > 0$ but $p(\mathbf{x}) = 0$,
then the corresponding importance weight should be infinity.
**Generative Adversarial Networks**
use a very similar idea to that described above
to engineer a *data generator* that outputs data
that cannot be distinguished
from examples sampled from a reference dataset.
In these approaches, we use one network, $f$
to distinguish real versus fake data
and a second network $g$ that tries to fool the discriminator $f$
into accepting fake data as real.
We will discuss this in much more detail later.
### Label Shift Correction
For the discussion of label shift,
we'll assume for now that we are dealing
with a $k$-way multiclass classification task.
When the distribution of labels shifts over time $p(y) \neq q(y)$
but the class-conditional distributions stay the same
$p(\mathbf{x})=q(\mathbf{x})$,
our importance weights will correspond to the
label likelihood ratios $q(y)/p(y)$.
One nice thing about label shift is that
if we have a reasonably good model (on the source distribution)
then we can get consistent estimates of these weights
without ever having to deal with the ambient dimension
(in deep learning, the inputs are often high-dimensional perceptual objects like images, while the labels are often easier to work,
say vectors whose length corresponds to the number of classes).
To estimate calculate the target label distribution,
we first take our reasonably good off the shelf classifier
(typically trained on the training data)
and compute its confusion matrix using the validation set
(also from the training distribution).
The confusion matrix C, is simply a $k \times k$ matrix
where each column corresponds to the *actual* label
and each row corresponds to our model's predicted label.
Each cell's value $c_{ij}$ is the fraction of predictions
where the true label was $j$ *and* our model predicted $y$.
Now we can't calculate the confusion matrix
on the target data directly,
because we don't get to see the labels for the examples
that we see in the wild,
unless we invest in a complex real-time annotation pipeline.
What we can do, however, is average all of our models predictions
at test time together, yielding the mean model output $\mu_y$.
It turns out that under some mild conditions—
if our classifier was reasonably accurate in the first place,
if the target data contains only classes of images that we've seen before,
and if the label shift assumption holds in the first place
(far the strongest assumption here),
then we can recover the test set label distribution by solving
a simple linear system $C \cdot q(y) = \mu_y$.
If our classifier is sufficiently accurate to begin with,
then the confusion C will be invertible,
and we get a solution $q(y) = C^{-1} \mu_y$.
Here we abuse notation a bit, using $q(y)$
to denote the vector of label frequencies.
Because we observe the labels on the source data,
it's easy to estimate the distribution $p(y)$.
Then for any training example $i$ with label $y$,
we can take the ratio of our estimates $\hat{q}(y)/\hat{p}(y)$
to calculate the weight $w_i$,
and plug this into the weighted risk minimization algorithm above.
### Concept Shift Correction
Concept shift is much harder to fix in a principled manner.
For instance, in a situation where suddenly the problem changes
from distinguishing cats from dogs to one of
distinguishing white from black animals,
it will be unreasonable to assume
that we can do much better than just collecting new labels
and training from scratch.
Fortunately, in practice, such extreme shifts are rare.
Instead, what usually happens is that the task keeps on changing slowly.
To make things more concrete, here are some examples:
* In computational advertising, new products are launched, old products become less popular. This means that the distribution over ads and their popularity changes gradually and any click-through rate predictor needs to change gradually with it.
* Traffic cameras lenses degrade gradually due to environmental wear, affecting image quality progressively.
* News content changes gradually (i.e. most of the news remains unchanged but new stories appear).
In such cases, we can use the same approach that we used for training networks to make them adapt to the change in the data. In other words, we use the existing network weights and simply perform a few update steps with the new data rather than training from scratch.
## A Taxonomy of Learning Problems
Armed with knowledge about how to deal with changes in $p(x)$ and in $p(y|x)$, we can now consider some other aspects of machine learning problems formulation.
* **Batch Learning.** Here we have access to training data and labels $\{(x_1, y_1), \ldots (x_n, y_n)\}$, which we use to train a network $f(x,w)$. Later on, we deploy this network to score new data $(x,y)$ drawn from the same distribution. This is the default assumption for any of the problems that we discuss here. For instance, we might train a cat detector based on lots of pictures of cats and dogs. Once we trained it, we ship it as part of a smart catdoor computer vision system that lets only cats in. This is then installed in a customer's home and is never updated again (barring extreme circumstances).
* **Online Learning.** Now imagine that the data $(x_i, y_i)$ arrives one sample at a time. More specifically, assume that we first observe $x_i$, then we need to come up with an estimate $f(x_i,w)$ and only once we've done this, we observe $y_i$ and with it, we receive a reward (or incur a loss), given our decision. Many real problems fall into this category. E.g. we need to predict tomorrow's stock price, this allows us to trade based on that estimate and at the end of the day we find out whether our estimate allowed us to make a profit. In other words, we have the following cycle where we are continuously improving our model given new observations.
$$
\mathrm{model} ~ f_t \longrightarrow
\mathrm{data} ~ x_t \longrightarrow
\mathrm{estimate} ~ f_t(x_t) \longrightarrow
\mathrm{observation} ~ y_t \longrightarrow
\mathrm{loss} ~ l(y_t, f_t(x_t)) \longrightarrow
\mathrm{model} ~ f_{t+1}
$$
* **Bandits.** They are a *special case* of the problem above. While in most learning problems we have a continuously parametrized function $f$ where we want to learn its parameters (e.g. a deep network), in a bandit problem we only have a finite number of arms that we can pull (i.e. a finite number of actions that we can take). It is not very surprising that for this simpler problem stronger theoretical guarantees in terms of optimality can be obtained. We list it mainly since this problem is often (confusingly) treated as if it were a distinct learning setting.
* **Control (and nonadversarial Reinforcement Learning).** In many cases the environment remembers what we did. Not necessarily in an adversarial manner but it'll just remember and the response will depend on what happened before. E.g. a coffee boiler controller will observe different temperatures depending on whether it was heating the boiler previously. PID (proportional integral derivative) controller algorithms are a popular choice there. Likewise, a user's behavior on a news site will depend on what we showed him previously (e.g. he will read most news only once). Many such algorithms form a model of the environment in which they act such as to make their decisions appear less random (i.e. to reduce variance).
* **Reinforcement Learning.** In the more general case of an environment with memory, we may encounter situations where the environment is trying to *cooperate* with us (cooperative games, in particular for non-zero-sum games), or others where the environment will try to *win*. Chess, Go, Backgammon or StarCraft are some of the cases. Likewise, we might want to build a good controller for autonomous cars. The other cars are likely to respond to the autonomous car's driving style in nontrivial ways, e.g. trying to avoid it, trying to cause an accident, trying to cooperate with it, etc.
One key distinction between the different situations above is that the same strategy that might have worked throughout in the case of a stationary environment, might not work throughout when the environment can adapt. For instance, an arbitrage opportunity discovered by a trader is likely to disappear once he starts exploiting it. The speed and manner at which the environment changes determines to a large extent the type of algorithms that we can bring to bear. For instance, if we *know* that things may only change slowly, we can force any estimate to change only slowly, too. If we know that the environment might change instantaneously, but only very infrequently, we can make allowances for that. These types of knowledge are crucial for the aspiring data scientist to deal with concept shift, i.e. when the problem that he is trying to solve changes over time.
## Fairness, Accountability, and Transparency in machine Learning
Finally, it's important to remember
that when you deploy machine learning systems
you aren't simply minimizing negative log likelihood
or maximizing accuracy—you are automating some kind of decision process.
Often the automated decision-making systems that we deploy
can have consequences for those subject to its decisions.
If we are deploying a medical diagnostic system,
we need to know for which populations it may work and which it may not.
Overlooking foreseeable risks to the welfare of a subpopulation
would run afoul of basic ethical principles.
Moreover, "accuracy" is seldom the right metric.
When translating predictions into actions
we'll often want to take into account the potential cost sensitivity
of erring in various ways.
If one way that you might classify an image could be perceived as a racial sleight, while misclassification to a different category
would be harmless, then you might want to adjust your thresholds
accordingly, accounting for societal values
in designing the decision-making protocol.
We also want to be careful about how prediction systems
can lead to feedback loops.
For example, if prediction systems are applied naively to predictive policing,
allocating patrol officers accordingly, a vicious cycle might emerge.
Neighborhoods that have more crimes, get more patrols, get more crimes discovered, get more training data, get yet more confident predictions, leading to even more patrols, even more crimes discovered, etc.
Additionally, we want to be careful about whether we are addressing the right problem in the first place. Predictive algorithms now play an outsize role in mediating the dissemination of information.
Should what news someone is exposed to be determined by which Facebook pages they have *Liked*? These are just a few among the many profound ethical dilemmas that you might encounter in a career in machine learning.
## Summary
* In many cases training and test set do not come from the same distribution. This is called covariate shift.
* Covariate shift can be detected and corrected if the shift isn't too severe. Failure to do so leads to nasty surprises at test time.
* In some cases the environment *remembers* what we did and will respond in unexpected ways. We need to account for that when building models.
## Exercises
1. What could happen when we change the behavior of a search engine? What might the users do? What about the advertisers?
1. Implement a covariate shift detector. Hint - build a classifier.
1. Implement a covariate shift corrector.
1. What could go wrong if training and test set are very different? What would happen to the sample weights?
## Scan the QR Code to [Discuss](https://discuss.mxnet.io/t/2347)

|
github_jupyter
|
# Considering the Environment
So far, we have worked through a number of hands-on implementations
fitting machine learning models to a variety of datasets.
And yet, until now we skated over the matter
of where are data comes from in the first place,
and what we plan to ultimately *do* with the outputs from our models.
Too often in the practice of machine learning,
developers rush ahead with the development of models
tossing these fundamental considerations aside.
Many failed machine learning deployments can be traced back to this situation.
Sometimes the model does well as evaluated by test accuracy
only to fail catastrophically in the real world
when the distribution of data suddenly shifts.
More insidiously, sometimes the very deployment of a model
can be the catalyst which perturbs the data distribution.
Say for example that we trained a model to predict loan defaults,
finding that the choice of footware was associated with risk of default
(Oxfords indicate repayment, sneakers indicate default).
We might be inclined to thereafter grant loans
to all applicants wearing Oxfords
and to deny all applicants wearing sneakers.
But our ill-conceived leap from pattern recognition to decision-making
and our failure to think critically about the environment
might have disastrous consequences.
For starters, as soon as we began making decisions based on footware,
customers would catch on and change their behavior.
Before long, all applicants would be wearing Oxfords,
and yet there would be no coinciding improvement in credit-worthiness.
Think about this deeply because similar issues abound in the application of machine learning: by introducing our model-based decisions to the environment,
we might break the model.
In this chapter, we describe some common concerns
and aim to get you started acquiring the critical thinking
that you will need in order to detect these situations early,
mitigate the damage, and use machine learning responsibly.
Some of the solutions are simple (ask for the 'right' data)
some are technically difficult (implement a reinforcement learning system),
and others require that we entre the realm of philosophy
and grapple with difficult questions concerning ethics and informed consent.
## Distribution Shift
To begin, we return to the observational setting,
putting aside for now the impacts of our actions
on the environment.
In the following sections, we take a deeper look
at the various ways that data distributions might shift,
and what might be done to salvage model performance.
From the outset, we should warn that if
the data-generating distribution $p(\mathbf{x},y)$
can shift in arbitrary ways at any point in time,
then learning a robust classifier is impossible.
In the most pathological case, if the label definitions themselves
can change at a moments notice: if suddenly
what we called "cats" are now dogs
and what we previously called "dogs" are now in fact cats,
without any perceptible change in the distribution of inputs $p(\mathbf{x})$,
then there is nothing we could do to detect the change
or to correct our classifier at test time.
Fortunately, under some restricted assumptions
on the ways our data might change in the future,
principled algorithms can detect shift and possibly even
adapt, achieving higher accuracy
than if we naively continued to rely on our original classifier.
### Covariate Shift
One of the best-studied forms of distribution shift is *covariate shift*.
Here we assume that although the distribution of inputs may change over time,
the labeling function, i.e., the conditional distribution $p(y|\mathbf{x})$
does not change.
While this problem is easy to understand
its also easy to overlook it in practice.
Consider the challenge of distinguishing cats and dogs.
Our training data consists of images of the following kind:
|cat|cat|dog|dog|
|:---------------:|:---------------:|:---------------:|:---------------:|
|||||
At test time we are asked to classify the following images:
|cat|cat|dog|dog|
|:---------------:|:---------------:|:---------------:|:---------------:|
|||||
Obviously this is unlikely to work well.
The training set consists of photos,
while the test set contains only cartoons.
The colors aren't even realistic.
Training on a dataset that looks substantially different from the test set
without some plan for how to adapt to the new domain is a bad idea.
Unfortunately, this is a very common pitfall.
Statisticians call this *covariate shift*
because the root of the problem owed to
a shift in the distribution of features (i.e., of *covariates*).
Mathematically, we could say that $p(\mathbf{x})$ changes
but that $p(y|\mathbf{x})$ remains unchanged.
Although its usefulness is not restricted to this setting,
when we believe $\mathbf{x}$ causes $y$, covariate shift is usually
the right assumption to be working with.
### Label Shift
The converse problem emerges when we believe that what drives the shift
is a change in the marginal distribution over the labels $p(y)$
but that the class-conditional distributions are invariant $p(\mathbf{x}|y)$.
Label shift is a reasonable assumption to make
when we believe that $y$ causes $\mathbf{x}$.
For example, commonly we want to predict a diagnosis given its manifestations.
In this case we believe that the diagnosis causes the manifestations,
i.e., diseases cause symptoms.
Sometimes the label shift and covariate shift assumptions
can hold simultaneously.
For example, when the true labeling function is deterministic and unchanging,
then covariate shift will always hold,
including if label shift holds too.
Interestingly, when we expect both label shift and covariate shift hold,
it's often advantageous to work with the methods
that flow from the label shift assumption.
That's because these methods tend to involve manipulating objects
that look like the label,
which (in deep learning) tends to be comparatively easy
compared to working with the objects that look like the input,
which tends (in deep learning) to be a high-dimensional object.
### Concept Shift
One more related problem arises in *concept shift*,
the situation in which the very label definitions change.
This sounds weird—after all, a *cat* is a *cat*.
Indeed the definition of a cat might not change,
but can we say the same about soft drinks?
It turns out that if we navigate around the United States,
shifting the source of our data by geography,
we'll find considerable concept shift regarding
the definition of even this simple term:

If we were to build a machine translation system,
the distribution $p(y|x)$ might be different
depending on our location.
This problem can be tricky to spot.
A saving grace is that often the $p(y|x)$ only shifts gradually.
Before we go into further detail and discuss remedies,
we can discuss a number of situations where covariate and concept shift
may not be so obvious.
### Examples
#### Medical Diagnostics
Imagine that you want to design an algorithm to detect cancer.
You collect data from healthy and sick people and you train your algorithm.
It works fine, giving you high accuracy
and you conclude that you’re ready
for a successful career in medical diagnostics.
Not so fast...
Many things could go wrong.
In particular, the distributions that you work with
for training and those that you encounter in the wild
might differ considerably.
This happened to an unfortunate startup,
that Alex had the opportunity to consult for many years ago.
They were developing a blood test for a disease
that affects mainly older men and they’d managed to obtain
a fair amount of blood samples from patients.
It is considerably more difficult, though,
to obtain blood samples from healthy men (mainly for ethical reasons).
To compensate for that, they asked a large number of students on campus
to donate blood and they performed their test.
Then they asked me whether I could help them
build a classifier to detect the disease.
I told them that it would be very easy to distinguish
between both datasets with near-perfect accuracy.
After all, the test subjects differed in age, hormone levels,
physical activity, diet, alcohol consumption,
and many more factors unrelated to the disease.
This was unlikely to be the case with real patients:
Their sampling procedure made it likely that
an extreme case of covariate shift would arise
between the *source* and *target* distributions,
and at that, one that could not be corrected by conventional means.
In other words, training and test data were so different
that nothing useful could be done
and they had wasted significant amounts of money.
#### Self Driving Cars
Say a company wanted to build a machine learning system for self-driving cars.
One of the key components is a roadside detector.
Since real annotated data is expensive to get,
they had the (smart and questionable) idea
to use synthetic data from a game rendering engine
as additional training data.
This worked really well on 'test data' drawn from the rendering engine.
Alas, inside a real car it was a disaster.
As it turned out, the roadside had been rendered
with a very simplistic texture.
More importantly, *all* the roadside had been rendered
with the *same* texture and the roadside detector
learned about this 'feature' very quickly.
A similar thing happened to the US Army
when they first tried to detect tanks in the forest.
They took aerial photographs of the forest without tanks,
then drove the tanks into the forest and took another set of pictures.
The so-trained classifier worked 'perfectly'.
Unfortunately, all it had learned was to distinguish trees
with shadows from trees without shadows—the
first set of pictures was taken in the early morning, the second one at noon.
#### Nonstationary distributions
A much more subtle situation arises when the distribution changes slowly
and the model is not updated adequately.
Here are some typical cases:
* We train a computational advertising model and then fail to update it frequently (e.g. we forget to incorporate that an obscure new device called an iPad was just launched).
* We build a spam filter. It works well at detecting all spam that we've seen so far. But then the spammers wisen up and craft new messages that look unlike anything we've seen before.
* We build a product recommendation system. It works throughout the winter... but then it keeps on recommending Santa hats long after Christmas.
#### More Anecdotes
* We build a face detector. It works well on all benchmarks. Unfortunately it fails on test data - the offending examples are close-ups where the face fills the entire image (no such data was in the training set).
* We build a web search engine for the USA market and want to deploy it in the UK.
* We train an image classifier by compiling a large dataset where each among a large set of classes is equally represented in the dataset, say 1000 categories, represented by 1000 images each. Then we deploy the system in the real world, where the actual label distribution of photographs is decidedly non-uniform.
In short, there are many cases where training and test distributions
$p(\mathbf{x}, y)$ are different.
In some cases, we get lucky and the models work
despite covariate, label, or concept shift.
In other cases, we can do better by employing
principled strategies to cope with the shift.
The remainder of this section grows considerably more technical.
The impatient reader could continue on to the next section
as this material is not prerequisite to subsequent concepts.
### Covariate Shift Correction
Assume that we want to estimate some dependency $p(y|\mathbf{x})$
for which we have labeled data $(\mathbf{x}_i,y_i)$.
Unfortunately, the observations $x_i$ are drawn
from some *target* distribution $q(\mathbf{x})$
rather than the *source* distribution $p(\mathbf{x})$.
To make progress, we need to reflect about what exactly
is happening during training:
we iterate over training data and associated labels
$\{(\mathbf{x}_1, y_1), \ldots (\mathbf{x}_n, y_n)\}$
and update the weight vectors of the model after every minibatch.
We sometimes additionally apply some penalty to the parameters,
using weight decay, dropout, or some other related technique.
This means that we largely minimize the loss on the training.
$$
\mathop{\mathrm{minimize}}_w \frac{1}{n} \sum_{i=1}^n l(x_i, y_i, f(x_i)) + \mathrm{some~penalty}(w)
$$
Statisticians call the first term an *empirical average*,
i.e., an average computed over the data drawn from $p(x) p(y|x)$.
If the data is drawn from the 'wrong' distribution $q$,
we can correct for that by using the following simple identity:
$$
\begin{aligned}
\int p(\mathbf{x}) f(\mathbf{x}) dx & = \int p(\mathbf{x}) f(\mathbf{x}) \frac{q(\mathbf{x})}{q(\mathbf{x})} dx \\
& = \int q(\mathbf{x}) f(\mathbf{x}) \frac{p(\mathbf{x})}{q(\mathbf{x})} dx
\end{aligned}
$$
In other words, we need to re-weight each instance
by the ratio of probabilities
that it would have been drawn from the correct distribution
$\beta(\mathbf{x}) := p(\mathbf{x})/q(\mathbf{x})$.
Alas, we do not know that ratio,
so before we can do anything useful we need to estimate it.
Many methods are available,
including some fancy operator-theoretic approaches
that attempt to recalibrate the expectation operator directly
using a minimum-norm or a maximum entropy principle.
Note that for any such approach, we need samples
drawn from both distributions—the 'true' $p$, e.g.,
by access to training data, and the one used
for generating the training set $q$ (the latter is trivially available).
Note however, that we only need samples $\mathbf{x} \sim q(\mathbf{x})$;
we do not to access labels $y \sim q(y)$.
In this case, there exists a very effective approach
that will give almost as good results: logistic regression.
This is all that is needed to compute estimate probability ratios.
We learn a classifier to distinguish between data drawn from $p(\mathbf{x})$
and data drawn from $q(x)$.
If it is impossible to distinguish between the two distributions
then it means that the associated instances are equally likely
to come from either one of the two distributions.
On the other hand, any instances that can be well discriminated
should be significantly over/underweighted accordingly.
For simplicity’s sake assume that we have an equal number of instances
from both distributions, denoted by $\mathbf{x}_i \sim p(\mathbf{x})$ and $\mathbf{x}_i' \sim q(\mathbf{x})$ respectively.
Now denote by $z_i$ labels which are 1
for data drawn from $p$ and -1 for data drawn from $q$.
Then the probability in a mixed dataset is given by
$$p(z=1|\mathbf{x}) = \frac{p(\mathbf{x})}{p(\mathbf{x})+q(\mathbf{x})} \text{ and hence } \frac{p(z=1|\mathbf{x})}{p(z=-1|\mathbf{x})} = \frac{p(\mathbf{x})}{q(\mathbf{x})}$$
Hence, if we use a logistic regression approach where $p(z=1|\mathbf{x})=\frac{1}{1+\exp(-f(\mathbf{x}))}$ it follows that
$$
\beta(\mathbf{x}) = \frac{1/(1 + \exp(-f(\mathbf{x})))}{\exp(-f(\mathbf{x})/(1 + \exp(-f(\mathbf{x})))} = \exp(f(\mathbf{x}))
$$
As a result, we need to solve two problems:
first one to distinguish between data drawn from both distributions,
and then a reweighted minimization problem
where we weigh terms by $\beta$, e.g. via the head gradients.
Here's a prototypical algorithm for that purpose
which uses an unlabeled training set $X$ and test set $Z$:
1. Generate training set with $\{(\mathbf{x}_i, -1) ... (\mathbf{z}_j, 1)\}$
1. Train binary classifier using logistic regression to get function $f$
1. Weigh training data using $\beta_i = \exp(f(\mathbf{x}_i))$ or better $\beta_i = \min(\exp(f(\mathbf{x}_i)), c)$
1. Use weights $\beta_i$ for training on $X$ with labels $Y$
Note that this method relies on a crucial assumption.
For this scheme to work, we need that each data point
in the target (test time) distribution
had nonzero probability of occurring at training time.
If we find a point where $q(\mathbf{x}) > 0$ but $p(\mathbf{x}) = 0$,
then the corresponding importance weight should be infinity.
**Generative Adversarial Networks**
use a very similar idea to that described above
to engineer a *data generator* that outputs data
that cannot be distinguished
from examples sampled from a reference dataset.
In these approaches, we use one network, $f$
to distinguish real versus fake data
and a second network $g$ that tries to fool the discriminator $f$
into accepting fake data as real.
We will discuss this in much more detail later.
### Label Shift Correction
For the discussion of label shift,
we'll assume for now that we are dealing
with a $k$-way multiclass classification task.
When the distribution of labels shifts over time $p(y) \neq q(y)$
but the class-conditional distributions stay the same
$p(\mathbf{x})=q(\mathbf{x})$,
our importance weights will correspond to the
label likelihood ratios $q(y)/p(y)$.
One nice thing about label shift is that
if we have a reasonably good model (on the source distribution)
then we can get consistent estimates of these weights
without ever having to deal with the ambient dimension
(in deep learning, the inputs are often high-dimensional perceptual objects like images, while the labels are often easier to work,
say vectors whose length corresponds to the number of classes).
To estimate calculate the target label distribution,
we first take our reasonably good off the shelf classifier
(typically trained on the training data)
and compute its confusion matrix using the validation set
(also from the training distribution).
The confusion matrix C, is simply a $k \times k$ matrix
where each column corresponds to the *actual* label
and each row corresponds to our model's predicted label.
Each cell's value $c_{ij}$ is the fraction of predictions
where the true label was $j$ *and* our model predicted $y$.
Now we can't calculate the confusion matrix
on the target data directly,
because we don't get to see the labels for the examples
that we see in the wild,
unless we invest in a complex real-time annotation pipeline.
What we can do, however, is average all of our models predictions
at test time together, yielding the mean model output $\mu_y$.
It turns out that under some mild conditions—
if our classifier was reasonably accurate in the first place,
if the target data contains only classes of images that we've seen before,
and if the label shift assumption holds in the first place
(far the strongest assumption here),
then we can recover the test set label distribution by solving
a simple linear system $C \cdot q(y) = \mu_y$.
If our classifier is sufficiently accurate to begin with,
then the confusion C will be invertible,
and we get a solution $q(y) = C^{-1} \mu_y$.
Here we abuse notation a bit, using $q(y)$
to denote the vector of label frequencies.
Because we observe the labels on the source data,
it's easy to estimate the distribution $p(y)$.
Then for any training example $i$ with label $y$,
we can take the ratio of our estimates $\hat{q}(y)/\hat{p}(y)$
to calculate the weight $w_i$,
and plug this into the weighted risk minimization algorithm above.
### Concept Shift Correction
Concept shift is much harder to fix in a principled manner.
For instance, in a situation where suddenly the problem changes
from distinguishing cats from dogs to one of
distinguishing white from black animals,
it will be unreasonable to assume
that we can do much better than just collecting new labels
and training from scratch.
Fortunately, in practice, such extreme shifts are rare.
Instead, what usually happens is that the task keeps on changing slowly.
To make things more concrete, here are some examples:
* In computational advertising, new products are launched, old products become less popular. This means that the distribution over ads and their popularity changes gradually and any click-through rate predictor needs to change gradually with it.
* Traffic cameras lenses degrade gradually due to environmental wear, affecting image quality progressively.
* News content changes gradually (i.e. most of the news remains unchanged but new stories appear).
In such cases, we can use the same approach that we used for training networks to make them adapt to the change in the data. In other words, we use the existing network weights and simply perform a few update steps with the new data rather than training from scratch.
## A Taxonomy of Learning Problems
Armed with knowledge about how to deal with changes in $p(x)$ and in $p(y|x)$, we can now consider some other aspects of machine learning problems formulation.
* **Batch Learning.** Here we have access to training data and labels $\{(x_1, y_1), \ldots (x_n, y_n)\}$, which we use to train a network $f(x,w)$. Later on, we deploy this network to score new data $(x,y)$ drawn from the same distribution. This is the default assumption for any of the problems that we discuss here. For instance, we might train a cat detector based on lots of pictures of cats and dogs. Once we trained it, we ship it as part of a smart catdoor computer vision system that lets only cats in. This is then installed in a customer's home and is never updated again (barring extreme circumstances).
* **Online Learning.** Now imagine that the data $(x_i, y_i)$ arrives one sample at a time. More specifically, assume that we first observe $x_i$, then we need to come up with an estimate $f(x_i,w)$ and only once we've done this, we observe $y_i$ and with it, we receive a reward (or incur a loss), given our decision. Many real problems fall into this category. E.g. we need to predict tomorrow's stock price, this allows us to trade based on that estimate and at the end of the day we find out whether our estimate allowed us to make a profit. In other words, we have the following cycle where we are continuously improving our model given new observations.
$$
\mathrm{model} ~ f_t \longrightarrow
\mathrm{data} ~ x_t \longrightarrow
\mathrm{estimate} ~ f_t(x_t) \longrightarrow
\mathrm{observation} ~ y_t \longrightarrow
\mathrm{loss} ~ l(y_t, f_t(x_t)) \longrightarrow
\mathrm{model} ~ f_{t+1}
$$
* **Bandits.** They are a *special case* of the problem above. While in most learning problems we have a continuously parametrized function $f$ where we want to learn its parameters (e.g. a deep network), in a bandit problem we only have a finite number of arms that we can pull (i.e. a finite number of actions that we can take). It is not very surprising that for this simpler problem stronger theoretical guarantees in terms of optimality can be obtained. We list it mainly since this problem is often (confusingly) treated as if it were a distinct learning setting.
* **Control (and nonadversarial Reinforcement Learning).** In many cases the environment remembers what we did. Not necessarily in an adversarial manner but it'll just remember and the response will depend on what happened before. E.g. a coffee boiler controller will observe different temperatures depending on whether it was heating the boiler previously. PID (proportional integral derivative) controller algorithms are a popular choice there. Likewise, a user's behavior on a news site will depend on what we showed him previously (e.g. he will read most news only once). Many such algorithms form a model of the environment in which they act such as to make their decisions appear less random (i.e. to reduce variance).
* **Reinforcement Learning.** In the more general case of an environment with memory, we may encounter situations where the environment is trying to *cooperate* with us (cooperative games, in particular for non-zero-sum games), or others where the environment will try to *win*. Chess, Go, Backgammon or StarCraft are some of the cases. Likewise, we might want to build a good controller for autonomous cars. The other cars are likely to respond to the autonomous car's driving style in nontrivial ways, e.g. trying to avoid it, trying to cause an accident, trying to cooperate with it, etc.
One key distinction between the different situations above is that the same strategy that might have worked throughout in the case of a stationary environment, might not work throughout when the environment can adapt. For instance, an arbitrage opportunity discovered by a trader is likely to disappear once he starts exploiting it. The speed and manner at which the environment changes determines to a large extent the type of algorithms that we can bring to bear. For instance, if we *know* that things may only change slowly, we can force any estimate to change only slowly, too. If we know that the environment might change instantaneously, but only very infrequently, we can make allowances for that. These types of knowledge are crucial for the aspiring data scientist to deal with concept shift, i.e. when the problem that he is trying to solve changes over time.
## Fairness, Accountability, and Transparency in machine Learning
Finally, it's important to remember
that when you deploy machine learning systems
you aren't simply minimizing negative log likelihood
or maximizing accuracy—you are automating some kind of decision process.
Often the automated decision-making systems that we deploy
can have consequences for those subject to its decisions.
If we are deploying a medical diagnostic system,
we need to know for which populations it may work and which it may not.
Overlooking foreseeable risks to the welfare of a subpopulation
would run afoul of basic ethical principles.
Moreover, "accuracy" is seldom the right metric.
When translating predictions into actions
we'll often want to take into account the potential cost sensitivity
of erring in various ways.
If one way that you might classify an image could be perceived as a racial sleight, while misclassification to a different category
would be harmless, then you might want to adjust your thresholds
accordingly, accounting for societal values
in designing the decision-making protocol.
We also want to be careful about how prediction systems
can lead to feedback loops.
For example, if prediction systems are applied naively to predictive policing,
allocating patrol officers accordingly, a vicious cycle might emerge.
Neighborhoods that have more crimes, get more patrols, get more crimes discovered, get more training data, get yet more confident predictions, leading to even more patrols, even more crimes discovered, etc.
Additionally, we want to be careful about whether we are addressing the right problem in the first place. Predictive algorithms now play an outsize role in mediating the dissemination of information.
Should what news someone is exposed to be determined by which Facebook pages they have *Liked*? These are just a few among the many profound ethical dilemmas that you might encounter in a career in machine learning.
## Summary
* In many cases training and test set do not come from the same distribution. This is called covariate shift.
* Covariate shift can be detected and corrected if the shift isn't too severe. Failure to do so leads to nasty surprises at test time.
* In some cases the environment *remembers* what we did and will respond in unexpected ways. We need to account for that when building models.
## Exercises
1. What could happen when we change the behavior of a search engine? What might the users do? What about the advertisers?
1. Implement a covariate shift detector. Hint - build a classifier.
1. Implement a covariate shift corrector.
1. What could go wrong if training and test set are very different? What would happen to the sample weights?
## Scan the QR Code to [Discuss](https://discuss.mxnet.io/t/2347)

| 0.705582 | 0.987735 |
```
%%capture
!pip install tensorboardX simpletransformers sklearn
!cat /usr/local/cuda/version.txt
!pip install pydash
!pip install torch==1.6.0
#conda install pytorch==1.1.0 torchvision==0.3.0 cudatoolkit=10.0 -c pytorch
#https://pytorch.org/get-started/previous-versions/
!rm -rf outputs
from simpletransformers.classification import ClassificationModel, ClassificationArgs
import pandas as pd
import logging
import sklearn
from tqdm import tqdm
import pandas as pd
df = pd.read_csv("downloads/47k_train.csv")
len(df)
blacklist=["abstract", "discussion", "background", "summary", "rationale", "introduction", "purpose", "objective" ]
blacklist += [t + ":" for t in blacklist]
def remove_special_words(text, blacklist=blacklist ):
words = text.split(" ")
try:
first=words[0]
except:
return text
if any(first.strip().lower() in string for string in blacklist):
return " ".join(words[1:]).strip()
return text
remove_special_words("ABSTRACT The northern corn rootworm")
df["text"] = df["text"].map(remove_special_words)
df= df[["text", "labels"]]
df =df.dropna()
df = df.rename(columns={"labels": "label"})
df= df[["text", "label"]]
df.label = df.label.map(int)
df
logging.basicConfig(level=logging.INFO)
transformers_logger = logging.getLogger("transformers")
transformers_logger.setLevel(logging.WARNING)
df2 = df.sample(frac=1)
# Train and Evaluation data needs to be in a Pandas Dataframe of two columns.
#The first column is the text with type str, and the second column is the label with type int.
size = len(df2)
train_cutoff = round(size*0.8)
train_df= df2[:train_cutoff]
eval_df = df2[train_cutoff:]
model_args = ClassificationArgs(save_steps=-1, save_model_every_epoch=False, sliding_window=True)
model = ClassificationModel('distilbert', 'distilbert-base-uncased',args=model_args, use_cuda=True) # You can set class weights by using the optional weight argument
# Train the model
model.train_model(train_df, overwrite_output_dir=True)
# Evaluate the model, u
result, model_outputs, wrong_predictions = model.eval_model(eval_df, acc=sklearn.metrics.accuracy_score)
result
import pandas as pd
dfx = pd.read_csv("downloads/s2c_5M_bioadjacent.csv", lineterminator='\n', error_bad_lines=False)
dfx = dfx.dropna(subset=["text"])
dfx=dfx[dfx["text"].str.len() > 15]
dfx.head()
dfx = dfx[dfx.fields.isin(["Medicine", 'Environmental Science', 'Sociology', 'Psychology', 'Geology', 'Biology', 'Materials Science', 'Chemistry'])]
dfx["text"] = dfx["text"].map(remove_special_words)
len(dfx)
dfx["text"] = dfx["text"].astype(str)
len(dfx)
def stepwise(step, df, f):
l = []
for idx in range(step, len(df)+step-1, step):
print(idx-step, idx)# dataframe[idx-step:idx])
sl = df[idx-step:idx]
batch = model.predict(list(sl))
l = l + list(batch[0])
with open('predicts_backup.txt', 'w') as f:
for item in l:
f.write("%s\n" % item)
return l
predicts = stepwise(20000, dfx["text"], model.predict)
with open('downloads/predicts_backup.txt', 'r') as f:
preds = f.read().split()#f.write("%s\n" % item)
len(preds)
preds = [int(p) for p in preds]
preds[:4]
preds[:5]
dfx
dfx = dfx[:3000000]
dfx["predicts"] = preds
dfx = dfx[dfx["predicts"]==1]
dfx = dfx[dfx["text"] != "nan"]
dfx = dfx[dfx["text"].str.len() > 14]
len(dfx)
dfx.to_csv("downloads/pos_preds_15052022.csv", index = False, header=True)
dt = pd.read_csv("core_pos.csv")
#d[d["first_sent"].str.contains(re.escape("|".join(d["authors"][2:-2].replace("'", "").split(","))).strip().replace('\\', ''))]
def formatStr (x):
x = eval(x)
x = [re.escape(v) for v in x]
return "|".join(x)
regexs = d.authors.apply(formatStr)
matches = pd.Series()
for i, r in tqdm(d.iterrows()):
matches.loc[i] = len(re.findall(regexs.loc[i], d.first_sent.loc[i])) > 0
dc["authors"] = dc["authors"].map(eval)
dc = dc.drop(columns=["fullText"])
dc.to_csv("core_pos_parsed.csv", index = False, header=True)
tt.to_csv("core_pos_min.csv", index = False, header=True)
```
distilbert
'mcc': 0.7621432780395265, 'tp': 167, 'tn': 480, 'fp': 39, 'fn': 30, 'acc': 0.9036312849162011, 'eval_loss': 0.24669100075132316}
|
github_jupyter
|
%%capture
!pip install tensorboardX simpletransformers sklearn
!cat /usr/local/cuda/version.txt
!pip install pydash
!pip install torch==1.6.0
#conda install pytorch==1.1.0 torchvision==0.3.0 cudatoolkit=10.0 -c pytorch
#https://pytorch.org/get-started/previous-versions/
!rm -rf outputs
from simpletransformers.classification import ClassificationModel, ClassificationArgs
import pandas as pd
import logging
import sklearn
from tqdm import tqdm
import pandas as pd
df = pd.read_csv("downloads/47k_train.csv")
len(df)
blacklist=["abstract", "discussion", "background", "summary", "rationale", "introduction", "purpose", "objective" ]
blacklist += [t + ":" for t in blacklist]
def remove_special_words(text, blacklist=blacklist ):
words = text.split(" ")
try:
first=words[0]
except:
return text
if any(first.strip().lower() in string for string in blacklist):
return " ".join(words[1:]).strip()
return text
remove_special_words("ABSTRACT The northern corn rootworm")
df["text"] = df["text"].map(remove_special_words)
df= df[["text", "labels"]]
df =df.dropna()
df = df.rename(columns={"labels": "label"})
df= df[["text", "label"]]
df.label = df.label.map(int)
df
logging.basicConfig(level=logging.INFO)
transformers_logger = logging.getLogger("transformers")
transformers_logger.setLevel(logging.WARNING)
df2 = df.sample(frac=1)
# Train and Evaluation data needs to be in a Pandas Dataframe of two columns.
#The first column is the text with type str, and the second column is the label with type int.
size = len(df2)
train_cutoff = round(size*0.8)
train_df= df2[:train_cutoff]
eval_df = df2[train_cutoff:]
model_args = ClassificationArgs(save_steps=-1, save_model_every_epoch=False, sliding_window=True)
model = ClassificationModel('distilbert', 'distilbert-base-uncased',args=model_args, use_cuda=True) # You can set class weights by using the optional weight argument
# Train the model
model.train_model(train_df, overwrite_output_dir=True)
# Evaluate the model, u
result, model_outputs, wrong_predictions = model.eval_model(eval_df, acc=sklearn.metrics.accuracy_score)
result
import pandas as pd
dfx = pd.read_csv("downloads/s2c_5M_bioadjacent.csv", lineterminator='\n', error_bad_lines=False)
dfx = dfx.dropna(subset=["text"])
dfx=dfx[dfx["text"].str.len() > 15]
dfx.head()
dfx = dfx[dfx.fields.isin(["Medicine", 'Environmental Science', 'Sociology', 'Psychology', 'Geology', 'Biology', 'Materials Science', 'Chemistry'])]
dfx["text"] = dfx["text"].map(remove_special_words)
len(dfx)
dfx["text"] = dfx["text"].astype(str)
len(dfx)
def stepwise(step, df, f):
l = []
for idx in range(step, len(df)+step-1, step):
print(idx-step, idx)# dataframe[idx-step:idx])
sl = df[idx-step:idx]
batch = model.predict(list(sl))
l = l + list(batch[0])
with open('predicts_backup.txt', 'w') as f:
for item in l:
f.write("%s\n" % item)
return l
predicts = stepwise(20000, dfx["text"], model.predict)
with open('downloads/predicts_backup.txt', 'r') as f:
preds = f.read().split()#f.write("%s\n" % item)
len(preds)
preds = [int(p) for p in preds]
preds[:4]
preds[:5]
dfx
dfx = dfx[:3000000]
dfx["predicts"] = preds
dfx = dfx[dfx["predicts"]==1]
dfx = dfx[dfx["text"] != "nan"]
dfx = dfx[dfx["text"].str.len() > 14]
len(dfx)
dfx.to_csv("downloads/pos_preds_15052022.csv", index = False, header=True)
dt = pd.read_csv("core_pos.csv")
#d[d["first_sent"].str.contains(re.escape("|".join(d["authors"][2:-2].replace("'", "").split(","))).strip().replace('\\', ''))]
def formatStr (x):
x = eval(x)
x = [re.escape(v) for v in x]
return "|".join(x)
regexs = d.authors.apply(formatStr)
matches = pd.Series()
for i, r in tqdm(d.iterrows()):
matches.loc[i] = len(re.findall(regexs.loc[i], d.first_sent.loc[i])) > 0
dc["authors"] = dc["authors"].map(eval)
dc = dc.drop(columns=["fullText"])
dc.to_csv("core_pos_parsed.csv", index = False, header=True)
tt.to_csv("core_pos_min.csv", index = False, header=True)
| 0.481454 | 0.330876 |
```
import numpy as np
import pandas as pd
from sklearn.metrics import roc_auc_score
import math
import os
import gc
import sys
import pickle
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import f1_score, plot_confusion_matrix, classification_report, confusion_matrix, ConfusionMatrixDisplay
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import StratifiedKFold
import statsmodels.api as sm
from sklearn.model_selection import train_test_split
from catboost import CatBoostClassifier, CatBoostRegressor, Pool, cv, sum_models
import lightgbm as lgb
import xgboost as xgb
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.utils.class_weight import compute_class_weight
from six.moves import xrange
from sklearn import preprocessing
from matplotlib import pyplot as plt
import seaborn as sns
%matplotlib inline
def reduce_mem_usage(df):
"""
iterate through all the columns of a dataframe and
modify the data type to reduce memory usage.
"""
start_mem = df.memory_usage().sum() / 1024**2
print(('Memory usage of dataframe is {:.2f}'
'MB').format(start_mem))
for col in df.columns:
col_type = df[col].dtype
if col_type != object:
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == 'int':
if c_min > np.iinfo(np.int8).min and c_max <\
np.iinfo(np.int8).max:
df[col] = df[col].astype(np.int8)
elif c_min > np.iinfo(np.int16).min and c_max <\
np.iinfo(np.int16).max:
df[col] = df[col].astype(np.int16)
elif c_min > np.iinfo(np.int32).min and c_max <\
np.iinfo(np.int32).max:
df[col] = df[col].astype(np.int32)
elif c_min > np.iinfo(np.int64).min and c_max <\
np.iinfo(np.int64).max:
df[col] = df[col].astype(np.int64)
else:
if c_min > np.finfo(np.float16).min and c_max <\
np.finfo(np.float16).max:
df[col] = df[col].astype(np.float16)
elif c_min > np.finfo(np.float32).min and c_max <\
np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
else:
df[col] = df[col].astype('category')
end_mem = df.memory_usage().sum() / 1024**2
print(('Memory usage after optimization is: {:.2f}'
'MB').format(end_mem))
print('Decreased by {:.1f}%'.format(100 * (start_mem - end_mem)
/ start_mem))
return df
df_train = pd.read_csv("alfa1_df_train6.csv")
df_valid = pd.read_csv("alfa1_df_valid6.csv")
df_train.fillna('nothing', inplace=True)
df_valid.fillna('nothing', inplace=True)
df_train = reduce_mem_usage(df_train)
df_valid = reduce_mem_usage(df_valid)
df_train_exp = pd.read_csv("alfa1_df_train10.csv")
df_valid_exp = pd.read_csv("alfa1_df_valid10.csv")
df_train_exp = reduce_mem_usage(df_train_exp)
df_valid_exp = reduce_mem_usage(df_valid_exp)
df_train_exp1 = pd.read_csv("alfa1_df_train11.csv")
df_valid_exp1 = pd.read_csv("alfa1_df_valid11.csv")
df_train_exp1 = reduce_mem_usage(df_train_exp1)
df_valid_exp1 = reduce_mem_usage(df_valid_exp1)
df_train_exp2 = pd.read_csv("alfa1_df_train12.csv")
df_valid_exp2 = pd.read_csv("alfa1_df_valid12.csv")
df_train_exp2 = reduce_mem_usage(df_train_exp2)
df_valid_exp2 = reduce_mem_usage(df_valid_exp2)
aug = df_train_exp.drop(['client_pin', 'lag_1', 'lag_2', 'weight'], axis=1).columns
aug1 = df_train_exp1.drop(['client_pin', 'lag_1', 'lag_2', 'weight'], axis=1).columns
aug2 = df_train_exp2.drop(['client_pin', 'lag_1', 'lag_2', 'weight'], axis=1).columns
df_train[aug] = df_train_exp[aug]
df_valid[aug] = df_valid_exp[aug]
df_train[aug1] = df_train_exp1[aug1]
df_valid[aug1] = df_valid_exp1[aug1]
df_train[aug2] = df_train_exp2[aug2]
df_valid[aug2] = df_valid_exp2[aug2]
from_parq = ['application_id', 'event_type', 'event_category', 'event_name', 'device_screen_name', 'timezone', 'net_connection_type', 'net_connection_tech']
trn_input_lag_cols = []
for i in range(2, 36):
trn_input_lag_cols.append(f'lag_{i}')
to_drop = []
to_drop.append('lag_1')
to_drop.append('client_pin')
to_drop.append('weight')
to_drop.append('class_weight')
categorical = trn_input_lag_cols + from_parq + ['most_popular']
df_weight = pd.DataFrame()
df_weight['lag_1'] = df_train['lag_1'].unique()
df_weight['class_weight'] = compute_class_weight(classes=df_train['lag_1'].unique(), y=df_train['lag_1'], class_weight='balanced')**0.5
df_train = df_train.merge(df_weight, how='left', on='lag_1')
df_valid = df_valid.merge(df_weight, how='left', on='lag_1')
weights = np.array(df_train['weight'])**2 * np.array(df_train['class_weight'])
weights_val = np.array(df_valid['weight'])**2 * np.array(df_valid['class_weight'])
le1 = preprocessing.LabelEncoder()
le1.fit(df_valid['lag_1'].unique())
df_train['lag_1'] = le1.transform(df_train['lag_1'])
df_valid['lag_1'] = le1.transform(df_valid['lag_1'])
X, y = pd.DataFrame(pd.concat((df_valid.drop(to_drop, axis=1), df_train.drop(to_drop, axis=1))).reset_index(drop=True)), pd.concat((df_valid['lag_1'], df_train['lag_1'])).reset_index(drop=True)
weights = np.concatenate([weights_val,weights])
X['event_type'] = X['event_type'].astype('category')
X['net_connection_tech'] = X['net_connection_tech'].astype('category')
n_splits = 8
folds = StratifiedKFold(n_splits=n_splits, shuffle=True, random_state=777)
trn_idx, val_idx = list(folds.split(X, y))[4]
X, y = X.iloc[trn_idx], y.iloc[trn_idx]
weights = weights[trn_idx, ]
lgb_train = lgb.Dataset(X, y, weight=weights)
lgb_eval = lgb.Dataset(df_valid.drop(to_drop, axis=1), df_valid['lag_1'], reference=lgb_train, weight=weights_val)
def evalerror(preds, dtrain):
labels = dtrain.get_label()
preds = preds.reshape(10, -1).T
preds = preds.argmax(axis = 1)
f_score = f1_score(labels , preds, average = 'macro')
return 'f1_score', f_score, True
tree_params = {
"objective" : "multiclass",
'metric':'custom',
"num_class" : 10,
'learning_rate': 0.12,
'max_depth': 5,
'n_jobs': 5,
"num_leaves" : 24,
'boosting':'dart',
"bagging_fraction" : 0.9, # subsample
"feature_fraction" : 0.9, # colsample_bytree
"bagging_freq" : 5, # subsample_freq
"bagging_seed" : 2020,
'n_estimators': 1000
}
model = lgb.train(tree_params,
lgb_train,
feval = evalerror,
valid_sets=[lgb_eval],
early_stopping_rounds=250)
with open('lgb_model8_fold4.pkl', 'wb') as fout:
pickle.dump(model, fout)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
from sklearn.metrics import roc_auc_score
import math
import os
import gc
import sys
import pickle
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import f1_score, plot_confusion_matrix, classification_report, confusion_matrix, ConfusionMatrixDisplay
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import StratifiedKFold
import statsmodels.api as sm
from sklearn.model_selection import train_test_split
from catboost import CatBoostClassifier, CatBoostRegressor, Pool, cv, sum_models
import lightgbm as lgb
import xgboost as xgb
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.utils.class_weight import compute_class_weight
from six.moves import xrange
from sklearn import preprocessing
from matplotlib import pyplot as plt
import seaborn as sns
%matplotlib inline
def reduce_mem_usage(df):
"""
iterate through all the columns of a dataframe and
modify the data type to reduce memory usage.
"""
start_mem = df.memory_usage().sum() / 1024**2
print(('Memory usage of dataframe is {:.2f}'
'MB').format(start_mem))
for col in df.columns:
col_type = df[col].dtype
if col_type != object:
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == 'int':
if c_min > np.iinfo(np.int8).min and c_max <\
np.iinfo(np.int8).max:
df[col] = df[col].astype(np.int8)
elif c_min > np.iinfo(np.int16).min and c_max <\
np.iinfo(np.int16).max:
df[col] = df[col].astype(np.int16)
elif c_min > np.iinfo(np.int32).min and c_max <\
np.iinfo(np.int32).max:
df[col] = df[col].astype(np.int32)
elif c_min > np.iinfo(np.int64).min and c_max <\
np.iinfo(np.int64).max:
df[col] = df[col].astype(np.int64)
else:
if c_min > np.finfo(np.float16).min and c_max <\
np.finfo(np.float16).max:
df[col] = df[col].astype(np.float16)
elif c_min > np.finfo(np.float32).min and c_max <\
np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
else:
df[col] = df[col].astype('category')
end_mem = df.memory_usage().sum() / 1024**2
print(('Memory usage after optimization is: {:.2f}'
'MB').format(end_mem))
print('Decreased by {:.1f}%'.format(100 * (start_mem - end_mem)
/ start_mem))
return df
df_train = pd.read_csv("alfa1_df_train6.csv")
df_valid = pd.read_csv("alfa1_df_valid6.csv")
df_train.fillna('nothing', inplace=True)
df_valid.fillna('nothing', inplace=True)
df_train = reduce_mem_usage(df_train)
df_valid = reduce_mem_usage(df_valid)
df_train_exp = pd.read_csv("alfa1_df_train10.csv")
df_valid_exp = pd.read_csv("alfa1_df_valid10.csv")
df_train_exp = reduce_mem_usage(df_train_exp)
df_valid_exp = reduce_mem_usage(df_valid_exp)
df_train_exp1 = pd.read_csv("alfa1_df_train11.csv")
df_valid_exp1 = pd.read_csv("alfa1_df_valid11.csv")
df_train_exp1 = reduce_mem_usage(df_train_exp1)
df_valid_exp1 = reduce_mem_usage(df_valid_exp1)
df_train_exp2 = pd.read_csv("alfa1_df_train12.csv")
df_valid_exp2 = pd.read_csv("alfa1_df_valid12.csv")
df_train_exp2 = reduce_mem_usage(df_train_exp2)
df_valid_exp2 = reduce_mem_usage(df_valid_exp2)
aug = df_train_exp.drop(['client_pin', 'lag_1', 'lag_2', 'weight'], axis=1).columns
aug1 = df_train_exp1.drop(['client_pin', 'lag_1', 'lag_2', 'weight'], axis=1).columns
aug2 = df_train_exp2.drop(['client_pin', 'lag_1', 'lag_2', 'weight'], axis=1).columns
df_train[aug] = df_train_exp[aug]
df_valid[aug] = df_valid_exp[aug]
df_train[aug1] = df_train_exp1[aug1]
df_valid[aug1] = df_valid_exp1[aug1]
df_train[aug2] = df_train_exp2[aug2]
df_valid[aug2] = df_valid_exp2[aug2]
from_parq = ['application_id', 'event_type', 'event_category', 'event_name', 'device_screen_name', 'timezone', 'net_connection_type', 'net_connection_tech']
trn_input_lag_cols = []
for i in range(2, 36):
trn_input_lag_cols.append(f'lag_{i}')
to_drop = []
to_drop.append('lag_1')
to_drop.append('client_pin')
to_drop.append('weight')
to_drop.append('class_weight')
categorical = trn_input_lag_cols + from_parq + ['most_popular']
df_weight = pd.DataFrame()
df_weight['lag_1'] = df_train['lag_1'].unique()
df_weight['class_weight'] = compute_class_weight(classes=df_train['lag_1'].unique(), y=df_train['lag_1'], class_weight='balanced')**0.5
df_train = df_train.merge(df_weight, how='left', on='lag_1')
df_valid = df_valid.merge(df_weight, how='left', on='lag_1')
weights = np.array(df_train['weight'])**2 * np.array(df_train['class_weight'])
weights_val = np.array(df_valid['weight'])**2 * np.array(df_valid['class_weight'])
le1 = preprocessing.LabelEncoder()
le1.fit(df_valid['lag_1'].unique())
df_train['lag_1'] = le1.transform(df_train['lag_1'])
df_valid['lag_1'] = le1.transform(df_valid['lag_1'])
X, y = pd.DataFrame(pd.concat((df_valid.drop(to_drop, axis=1), df_train.drop(to_drop, axis=1))).reset_index(drop=True)), pd.concat((df_valid['lag_1'], df_train['lag_1'])).reset_index(drop=True)
weights = np.concatenate([weights_val,weights])
X['event_type'] = X['event_type'].astype('category')
X['net_connection_tech'] = X['net_connection_tech'].astype('category')
n_splits = 8
folds = StratifiedKFold(n_splits=n_splits, shuffle=True, random_state=777)
trn_idx, val_idx = list(folds.split(X, y))[4]
X, y = X.iloc[trn_idx], y.iloc[trn_idx]
weights = weights[trn_idx, ]
lgb_train = lgb.Dataset(X, y, weight=weights)
lgb_eval = lgb.Dataset(df_valid.drop(to_drop, axis=1), df_valid['lag_1'], reference=lgb_train, weight=weights_val)
def evalerror(preds, dtrain):
labels = dtrain.get_label()
preds = preds.reshape(10, -1).T
preds = preds.argmax(axis = 1)
f_score = f1_score(labels , preds, average = 'macro')
return 'f1_score', f_score, True
tree_params = {
"objective" : "multiclass",
'metric':'custom',
"num_class" : 10,
'learning_rate': 0.12,
'max_depth': 5,
'n_jobs': 5,
"num_leaves" : 24,
'boosting':'dart',
"bagging_fraction" : 0.9, # subsample
"feature_fraction" : 0.9, # colsample_bytree
"bagging_freq" : 5, # subsample_freq
"bagging_seed" : 2020,
'n_estimators': 1000
}
model = lgb.train(tree_params,
lgb_train,
feval = evalerror,
valid_sets=[lgb_eval],
early_stopping_rounds=250)
with open('lgb_model8_fold4.pkl', 'wb') as fout:
pickle.dump(model, fout)
| 0.325735 | 0.346293 |
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="images/book_cover.jpg" width="120">
*This notebook contains an excerpt from the [Python Programming and Numerical Methods - A Guide for Engineers and Scientists](https://www.elsevier.com/books/python-programming-and-numerical-methods/kong/978-0-12-819549-9), the content is also available at [Berkeley Python Numerical Methods](https://pythonnumericalmethods.berkeley.edu/notebooks/Index.html).*
*The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work on [Elsevier](https://www.elsevier.com/books/python-programming-and-numerical-methods/kong/978-0-12-819549-9) or [Amazon](https://www.amazon.com/Python-Programming-Numerical-Methods-Scientists/dp/0128195495/ref=sr_1_1?dchild=1&keywords=Python+Programming+and+Numerical+Methods+-+A+Guide+for+Engineers+and+Scientists&qid=1604761352&sr=8-1)!*
<!--NAVIGATION-->
< [14.2 Linear Transformations](chapter14.02-Linear-Transformations.ipynb) | [Contents](Index.ipynb) | [14.4 Solutions to Systems of Linear Equations](chapter14.04-Solutions-to-Systems-of-Linear-Equations.ipynb) >
# Systems of Linear Equations
A $\textbf{linear equation}$ is an equality of the form
$$
\sum_{i = 1}^{n} (a_i x_i) = y,
$$
where $a_i$ are scalars, $x_i$ are unknown variables in $\mathbb{R}$, and $y$ is a scalar.
**TRY IT!** Determine which of the following equations is linear and which is not. For the ones that are not linear, can you manipulate them so that they are?
1. $3x_1 + 4x_2 - 3 = -5x_3$
2. $\frac{-x_1 + x_2}{x_3} = 2$
3. $x_1x_2 + x_3 = 5$
Equation 1 can be rearranged to be $3x_1 + 4x_2 + 5x_3= 3$, which
clearly has the form of a linear equation. Equation 2 is not linear
but can be rearranged to be $-x_1 + x_2 - 2x_3 = 0$, which is
linear. Equation 3 is not linear.
A $\textbf{system of linear equations}$ is a set of linear equations that share the same variables. Consider the following system of linear equations:
\begin{eqnarray*}
\begin{array}{rcrcccccrcc}
a_{1,1} x_1 &+& a_{1,2} x_2 &+& {\ldots}& +& a_{1,n-1} x_{n-1} &+&a_{1,n} x_n &=& y_1,\\
a_{2,1} x_1 &+& a_{2,2} x_2 &+&{\ldots}& +& a_{2,n-1} x_{n-1} &+& a_{2,n} x_n &=& y_2, \\
&&&&{\ldots} &&{\ldots}&&&& \\
a_{m-1,1}x_1 &+& a_{m-1,2}x_2&+ &{\ldots}& +& a_{m-1,n-1} x_{n-1} &+& a_{m-1,n} x_n &=& y_{m-1},\\
a_{m,1} x_1 &+& a_{m,2}x_2 &+ &{\ldots}& +& a_{m,n-1} x_{n-1} &+& a_{m,n} x_n &=& y_{m}.
\end{array}
\end{eqnarray*}
where $a_{i,j}$ and $y_i$ are real numbers. The $\textbf{matrix form}$ of a system of linear equations is $\textbf{$Ax = y$}$ where $A$ is a ${m} \times {n}$ matrix, $A(i,j) = a_{i,j}, y$ is a vector in ${\mathbb{R}}^m$, and $x$ is an unknown vector in ${\mathbb{R}}^n$. The matrix form is showing as below:
$$\begin{bmatrix}
a_{1,1} & a_{1,2} & ... & a_{1,n}\\
a_{2,1} & a_{2,2} & ... & a_{2,n}\\
... & ... & ... & ... \\
a_{m,1} & a_{m,2} & ... & a_{m,n}
\end{bmatrix}\left[\begin{array}{c} x_1 \\x_2 \\ ... \\x_n \end{array}\right] =
\left[\begin{array}{c} y_1 \\y_2 \\ ... \\y_m \end{array}\right]$$
If you carry out the matrix multiplication, you will see that you arrive back at the original system of equations.
**TRY IT!** Put the following system of equations into matrix form.
\begin{eqnarray*}
4x + 3y - 5z &=& 2 \\
-2x - 4y + 5z &=& 5 \\
7x + 8y &=& -3 \\
x + 2z &=& 1 \\
9 + y - 6z &=& 6 \\
\end{eqnarray*}
$$\begin{bmatrix}
4 & 3 & -5\\
-2 & -4 & 5\\
7 & 8 & 0\\
1 & 0 & 2\\
9 & 1 & -6
\end{bmatrix}\left[\begin{array}{c} x \\y \\z \end{array}\right] =
\left[\begin{array}{c} 2 \\5 \\-3 \\1 \\6 \end{array}\right]$$
<!--NAVIGATION-->
< [14.2 Linear Transformations](chapter14.02-Linear-Transformations.ipynb) | [Contents](Index.ipynb) | [14.4 Solutions to Systems of Linear Equations](chapter14.04-Solutions-to-Systems-of-Linear-Equations.ipynb) >
|
github_jupyter
|
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="images/book_cover.jpg" width="120">
*This notebook contains an excerpt from the [Python Programming and Numerical Methods - A Guide for Engineers and Scientists](https://www.elsevier.com/books/python-programming-and-numerical-methods/kong/978-0-12-819549-9), the content is also available at [Berkeley Python Numerical Methods](https://pythonnumericalmethods.berkeley.edu/notebooks/Index.html).*
*The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work on [Elsevier](https://www.elsevier.com/books/python-programming-and-numerical-methods/kong/978-0-12-819549-9) or [Amazon](https://www.amazon.com/Python-Programming-Numerical-Methods-Scientists/dp/0128195495/ref=sr_1_1?dchild=1&keywords=Python+Programming+and+Numerical+Methods+-+A+Guide+for+Engineers+and+Scientists&qid=1604761352&sr=8-1)!*
<!--NAVIGATION-->
< [14.2 Linear Transformations](chapter14.02-Linear-Transformations.ipynb) | [Contents](Index.ipynb) | [14.4 Solutions to Systems of Linear Equations](chapter14.04-Solutions-to-Systems-of-Linear-Equations.ipynb) >
# Systems of Linear Equations
A $\textbf{linear equation}$ is an equality of the form
$$
\sum_{i = 1}^{n} (a_i x_i) = y,
$$
where $a_i$ are scalars, $x_i$ are unknown variables in $\mathbb{R}$, and $y$ is a scalar.
**TRY IT!** Determine which of the following equations is linear and which is not. For the ones that are not linear, can you manipulate them so that they are?
1. $3x_1 + 4x_2 - 3 = -5x_3$
2. $\frac{-x_1 + x_2}{x_3} = 2$
3. $x_1x_2 + x_3 = 5$
Equation 1 can be rearranged to be $3x_1 + 4x_2 + 5x_3= 3$, which
clearly has the form of a linear equation. Equation 2 is not linear
but can be rearranged to be $-x_1 + x_2 - 2x_3 = 0$, which is
linear. Equation 3 is not linear.
A $\textbf{system of linear equations}$ is a set of linear equations that share the same variables. Consider the following system of linear equations:
\begin{eqnarray*}
\begin{array}{rcrcccccrcc}
a_{1,1} x_1 &+& a_{1,2} x_2 &+& {\ldots}& +& a_{1,n-1} x_{n-1} &+&a_{1,n} x_n &=& y_1,\\
a_{2,1} x_1 &+& a_{2,2} x_2 &+&{\ldots}& +& a_{2,n-1} x_{n-1} &+& a_{2,n} x_n &=& y_2, \\
&&&&{\ldots} &&{\ldots}&&&& \\
a_{m-1,1}x_1 &+& a_{m-1,2}x_2&+ &{\ldots}& +& a_{m-1,n-1} x_{n-1} &+& a_{m-1,n} x_n &=& y_{m-1},\\
a_{m,1} x_1 &+& a_{m,2}x_2 &+ &{\ldots}& +& a_{m,n-1} x_{n-1} &+& a_{m,n} x_n &=& y_{m}.
\end{array}
\end{eqnarray*}
where $a_{i,j}$ and $y_i$ are real numbers. The $\textbf{matrix form}$ of a system of linear equations is $\textbf{$Ax = y$}$ where $A$ is a ${m} \times {n}$ matrix, $A(i,j) = a_{i,j}, y$ is a vector in ${\mathbb{R}}^m$, and $x$ is an unknown vector in ${\mathbb{R}}^n$. The matrix form is showing as below:
$$\begin{bmatrix}
a_{1,1} & a_{1,2} & ... & a_{1,n}\\
a_{2,1} & a_{2,2} & ... & a_{2,n}\\
... & ... & ... & ... \\
a_{m,1} & a_{m,2} & ... & a_{m,n}
\end{bmatrix}\left[\begin{array}{c} x_1 \\x_2 \\ ... \\x_n \end{array}\right] =
\left[\begin{array}{c} y_1 \\y_2 \\ ... \\y_m \end{array}\right]$$
If you carry out the matrix multiplication, you will see that you arrive back at the original system of equations.
**TRY IT!** Put the following system of equations into matrix form.
\begin{eqnarray*}
4x + 3y - 5z &=& 2 \\
-2x - 4y + 5z &=& 5 \\
7x + 8y &=& -3 \\
x + 2z &=& 1 \\
9 + y - 6z &=& 6 \\
\end{eqnarray*}
$$\begin{bmatrix}
4 & 3 & -5\\
-2 & -4 & 5\\
7 & 8 & 0\\
1 & 0 & 2\\
9 & 1 & -6
\end{bmatrix}\left[\begin{array}{c} x \\y \\z \end{array}\right] =
\left[\begin{array}{c} 2 \\5 \\-3 \\1 \\6 \end{array}\right]$$
<!--NAVIGATION-->
< [14.2 Linear Transformations](chapter14.02-Linear-Transformations.ipynb) | [Contents](Index.ipynb) | [14.4 Solutions to Systems of Linear Equations](chapter14.04-Solutions-to-Systems-of-Linear-Equations.ipynb) >
| 0.831554 | 0.971779 |
```
# coding: utf-8
# python2.7
from __future__ import division, print_function
from parsers import CitationWindowParser
from context_parsing_functions import create_context_parsers
import subprocess
import re
# functions to make indexing param files
def index_collections(window_specs, index_dir, collection_dir):
""" Takes window specs {'Sentence': [(0,0)], 'Word': [(0,0)}
Args:
window_specs = dict with lists of tuples
"""
parsers = create_context_parsers(window_specs)
index_names = []
for parser in parsers:
index_name = parser.get_stringy_name()
citation_field = parser.get_field_name()
write_param_file(citation_field, index_name, index_dir, collection_dir)
index_names.append(index_name) # add index_name to list of index_names
build_indexes(index_names)
return
def write_param_file(citation_field, index_name, index_dir, collection_dir):
"""Writes param files for building Indri indexes from each document collection.
Args:
"""
stop_stem_list = ['ss','sn','ns','nn']
for stop_stem in stop_stem_list:
filename = "param-I.{}.{}.xml".format(index_name, stop_stem)
print("...writing index param file: {}".format(filename))
with open("{}Param_Files/{}".format(index_dir, filename), 'w') as param:
param.write(param_text(citation_field, index_name, stop_stem, index_dir, collection_dir))
return
def param_text(citation_field, index_name, stop_stem, index_dir, collection_dir):
if re.search('[ns]s', stop_stem):
param_text = """<parameters>
<index>{}I.{}.{}</index>
<memory>2G</memory>
<storeDocs>false</storeDocs>
<stemmer>
<name>krovetz</name>
</stemmer>
<field>
<name>isearchdoc</name>
</field>
<field>
<name>author</name>
</field>
<field>
<name>category</name>
</field>
<field>
<name>description</name>
</field>
<field>
<name>docno</name>
</field>
<field>
<name>documentlink</name>
</field>
<field>
<name>fulltext</name>
</field>
<field>
<name>subject</name>
</field>
<field>
<name>title</name>
</field>
<field>
<name>type</name>
</field>
<field>
<name>venue</name>
</field>
<field>
<name>citations</name>
</field>
<field>
<name>{}</name>
</field>
<corpus>
<path>{}PF+PN+C.{}/</path>
<class>xml</class>
</corpus>
</parameters>
""".format(index_dir, index_name, stop_stem, citation_field, collection_dir, index_name)
else:
param_text = """<parameters>
<index>{}I.{}.{}</index>
<memory>2G</memory>
<storeDocs>false</storeDocs>
<field>
<name>isearchdoc</name>
</field>
<field>
<name>author</name>
</field>
<field>
<name>category</name>
</field>
<field>
<name>description</name>
</field>
<field>
<name>docno</name>
</field>
<field>
<name>documentlink</name>
</field>
<field>
<name>fulltext</name>
</field>
<field>
<name>subject</name>
</field>
<field>
<name>title</name>
</field>
<field>
<name>type</name>
</field>
<field>
<name>venue</name>
</field>
<field>
<name>citations</name>
</field>
<field>
<name>{}</name>
</field>
<corpus>
<path>{}PF+PN+C.{}/</path>
<class>xml</class>
</corpus>
</parameters>
""".format(index_dir, index_name, stop_stem, citation_field, collection_dir, index_name)
return param_text
# functions to build Indri indexes
def build_indexes(index_names):
for index_name in index_names:
subprocess.call(["./build_indri_index.bash", str(index_name)])
return
index_names = []
index_name = 'a'
index_names.append(index_name)
index_names
```
|
github_jupyter
|
# coding: utf-8
# python2.7
from __future__ import division, print_function
from parsers import CitationWindowParser
from context_parsing_functions import create_context_parsers
import subprocess
import re
# functions to make indexing param files
def index_collections(window_specs, index_dir, collection_dir):
""" Takes window specs {'Sentence': [(0,0)], 'Word': [(0,0)}
Args:
window_specs = dict with lists of tuples
"""
parsers = create_context_parsers(window_specs)
index_names = []
for parser in parsers:
index_name = parser.get_stringy_name()
citation_field = parser.get_field_name()
write_param_file(citation_field, index_name, index_dir, collection_dir)
index_names.append(index_name) # add index_name to list of index_names
build_indexes(index_names)
return
def write_param_file(citation_field, index_name, index_dir, collection_dir):
"""Writes param files for building Indri indexes from each document collection.
Args:
"""
stop_stem_list = ['ss','sn','ns','nn']
for stop_stem in stop_stem_list:
filename = "param-I.{}.{}.xml".format(index_name, stop_stem)
print("...writing index param file: {}".format(filename))
with open("{}Param_Files/{}".format(index_dir, filename), 'w') as param:
param.write(param_text(citation_field, index_name, stop_stem, index_dir, collection_dir))
return
def param_text(citation_field, index_name, stop_stem, index_dir, collection_dir):
if re.search('[ns]s', stop_stem):
param_text = """<parameters>
<index>{}I.{}.{}</index>
<memory>2G</memory>
<storeDocs>false</storeDocs>
<stemmer>
<name>krovetz</name>
</stemmer>
<field>
<name>isearchdoc</name>
</field>
<field>
<name>author</name>
</field>
<field>
<name>category</name>
</field>
<field>
<name>description</name>
</field>
<field>
<name>docno</name>
</field>
<field>
<name>documentlink</name>
</field>
<field>
<name>fulltext</name>
</field>
<field>
<name>subject</name>
</field>
<field>
<name>title</name>
</field>
<field>
<name>type</name>
</field>
<field>
<name>venue</name>
</field>
<field>
<name>citations</name>
</field>
<field>
<name>{}</name>
</field>
<corpus>
<path>{}PF+PN+C.{}/</path>
<class>xml</class>
</corpus>
</parameters>
""".format(index_dir, index_name, stop_stem, citation_field, collection_dir, index_name)
else:
param_text = """<parameters>
<index>{}I.{}.{}</index>
<memory>2G</memory>
<storeDocs>false</storeDocs>
<field>
<name>isearchdoc</name>
</field>
<field>
<name>author</name>
</field>
<field>
<name>category</name>
</field>
<field>
<name>description</name>
</field>
<field>
<name>docno</name>
</field>
<field>
<name>documentlink</name>
</field>
<field>
<name>fulltext</name>
</field>
<field>
<name>subject</name>
</field>
<field>
<name>title</name>
</field>
<field>
<name>type</name>
</field>
<field>
<name>venue</name>
</field>
<field>
<name>citations</name>
</field>
<field>
<name>{}</name>
</field>
<corpus>
<path>{}PF+PN+C.{}/</path>
<class>xml</class>
</corpus>
</parameters>
""".format(index_dir, index_name, stop_stem, citation_field, collection_dir, index_name)
return param_text
# functions to build Indri indexes
def build_indexes(index_names):
for index_name in index_names:
subprocess.call(["./build_indri_index.bash", str(index_name)])
return
index_names = []
index_name = 'a'
index_names.append(index_name)
index_names
| 0.24817 | 0.164248 |
```
import numpy as np
import pandas as pd
captions = np.load('data/mscoco/all_captions.npy')
captions = [c[:5] for c in captions]
sentences = []
for c in captions:
sentences += c
# "GOOGLE ELMO" sentence embeddings
import tensorflow as tf
import tensorflow_hub as hub
# ELMO
elmo = hub.Module("https://tfhub.dev/google/elmo/1", trainable=False)
elmo_input = tf.placeholder(tf.string)
elmo_embeddings = elmo(elmo_input, signature="default", as_dict=True)["default"]
def get_elmo_emb(sentences):
batch_size = 64
ix = 0
result = []
while ix < len(sentences):
result.append(session.run(elmo_embeddings,
feed_dict={elmo_input: sentences[ix: min(ix + batch_size, len(sentences))]}))
ix += batch_size
return np.concatenate(result, axis=0)
# USE
unsent = hub.Module("https://tfhub.dev/google/universal-sentence-encoder/1")
unsent_input = tf.placeholder(tf.string)
unsent_embeddings = unsent(unsent_input)
def get_unsent_emb(sentences):
return session.run(unsent_embeddings, feed_dict={unsent_input: sentences})
#SESSION
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
session = tf.Session(config=config)
session.run([tf.global_variables_initializer(), tf.tables_initializer()])
get_elmo_emb(["the cat is on the mat", "dogs are in the fog"])
get_unsent_emb(["The quick brown fox jumps over the lazy dog.",
"I am a sentence for which I would like to get its embedding"])
import torch as t
import utils
from utils.batch_loader import BatchLoader
from model.parameters import Parameters
from model.paraphraser import Paraphraser
class Args(object):
pass
args = Args()
args.batch_size = 32
args.seq_len=30
args.use_cuda = True
args.use_cuda = True
args.model_name = 'snli_200kit_600_800'
datasets = set()
datasets.add('snli')
sentences = np.array([utils.batch_loader.clean_str(s) for s in sentences])
captions = [[utils.batch_loader.clean_str(s) for s in bucket] for bucket in captions]
batch_loader = BatchLoader(path='', datasets=datasets)
batch_loader.build_input_vocab(sentences)
# PARAPHRASER
parameters = Parameters(batch_loader.max_seq_len, batch_loader.vocab_size)
paraphraser = Paraphraser(parameters)
paraphraser.load_state_dict(t.load('saved_models/trained_paraphraser_' + args.model_name))
if args.use_cuda:
paraphraser = paraphraser.cuda()
# PARAPHRASER EXPAND
def paraphrases_from_sources(sources, use_mean=True):
result = []
for s1,s2 in zip(sources[0], sources[1]):
input = batch_loader.input_from_sentences([[s1],[s2]])
input = [var.cuda() if args.use_cuda else var for var in input]
result += [paraphraser.sample_with_input(batch_loader, args.seq_len, args.use_cuda, use_mean, input)]
return result
def paraphrase_expand(X, y, n_paraphrases, pure_paraphrases):
if n_paraphrases <= 0:
return X,y
X_gen, y_gen = [], []
y = np.array(y)
X = np.array(X)
for class_id in np.unique(y):
X_class = X[y == class_id]
idx = []
for i in range(len(X_class)):
for j in range(len(X_class)):
if i == j and len(X_class) != 1:
continue
idx.append((i,j))
idx = np.array(idx)
idx = idx[np.random.choice(list(range(len(idx))), n_paraphrases, replace=False)]
sources = [X_class[idx[:,0]], X_class[idx[:,1]]]
X_gen += [paraphrases_from_sources(sources)]
y_gen += [[class_id] * n_paraphrases]
if pure_paraphrases:
return np.concatenate(X_gen), np.concatenate(y_gen)
X_result = np.concatenate([X] + X_gen)
y_result = np.concatenate([y] + y_gen)
return X_result, y_result
```
### infersent
```
# build infersent
import torch as t
import sys
sys.path.append('../InferSent/encoder')
INFERSENT_PATH = '../InferSent/encoder/'
GLOVE_PATH = '/home/aleksey.zotov/InferSent/dataset/GloVe/glove.840B.300d.txt'
infersent_model = t.load(INFERSENT_PATH + 'infersent.allnli.pickle', map_location=lambda storage, loc: storage)
# infersent_model = t.load(INFERSENT_PATH + 'infersent.allnli.pickle', map_location={'cuda:1' : 'cuda:0', 'cuda:2' : 'cuda:0'})
# infersent_model = t.load(INFERSENT_PATH + 'infersent.allnli.pickle')
infersent_model.set_glove_path(GLOVE_PATH)
infersent_model.build_vocab(sentences, tokenize=False)
# infersent_model.build_vocab_k_words(K=200000)
# infersent embs
def get_infersent_emb(X):
embeddings = infersent_model.encode(X, bsize=64, tokenize=False, verbose=False)
return embeddings
```
# Some paraphrasing samples
```
paraphrases_from_sources([
['Woman sits near the table with her dog'],
['Very old woman is sitting with her child on the table']], use_mean=False)
paraphrases_from_sources([
['Woman sits near the table with her dog'],
['Very old woman is sitting with her child on the table']], use_mean=False)
paraphrases_from_sources([
['man is chopping old wood with an axe'],
['very old man is outside']], use_mean=True)
cid = 0
captions[cid][0], captions[cid][1], paraphrases_from_sources([[captions[cid][0]], [captions[cid][1]]], use_mean=True)[0]
cid = 1
captions[cid][0], captions[cid][1], paraphrases_from_sources([[captions[cid][0]], [captions[cid][1]]], use_mean=True)[0]
cid = 1337
captions[cid][0], captions[cid][1], paraphrases_from_sources([[captions[cid][0]], [captions[cid][1]]], use_mean=True)[0]
# GLOVE EMB using batch loader
def get_glove_emb(sentence):
emb_size = 300
embed = np.zeros((len(sentence), emb_size))
for i, s in enumerate(sentence.strip().split()):
if s in batch_loader.word_vec.keys():
embed[i, :] = batch_loader.word_vec[s]
else:
embed[i, :] = batch_loader.word_vec['null']
return embed
# Build ONEHOT model embeddings
from collections import Counter
vocab_size = 10000
word_counter = Counter((' '.join(sentences)).split())
idx_to_word = [x[0] for x in word_counter.most_common(vocab_size - 1)]
word_to_idx = {v : i for i,v in enumerate(idx_to_word)}
def get_idx_by_word(w):
if w in word_to_idx:
return word_to_idx[w]
return vocab_size - 1
def get_simple_onehot_embs(X):
embed = []
for sentence in X:
result = np.zeros(vocab_size)
result[[get_idx_by_word(w) for w in sentence.split()]] = 1.0
embed.append(result)
return np.array(embed)
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_recall_fscore_support
def get_f1_score(y_true, y_pred):
return precision_recall_fscore_support(y_true=np.array(y_true), y_pred=y_pred)[2]
def split_and_test(classifier, model_function, X_all, y_all, n_samples, n_paraphrases, pure_paraphrases=False):
n_classes = len(np.unique(y_all))
X_train, X_test, y_train, y_test = train_test_split(X_all, y_all, stratify=y_all, train_size=n_samples * n_classes)
X_train, y_train = paraphrase_expand(X_train, y_train, n_paraphrases, pure_paraphrases)
predicted_proba = model_function(classifier, X_train, X_test, y_train)
return np.mean(get_f1_score(y_test, predicted_proba))
def with_embs(emb_function, classifier, X_train, X_test, y_train):
X_train = emb_function(X_train)
X_test = emb_function(X_test)
classifier.fit(X_train, y_train)
return classifier.predict(X_test)
def onehot_embs_function(classifier, X_train, X_test, y_train):
return with_embs(get_simple_onehot_embs, classifier, X_train, X_test, y_train)
def infersent_embs_function(classifier, X_train, X_test, y_train):
return with_embs(get_infersent_emb, classifier, X_train, X_test, y_train)
def bag_of_words_function(classifier, X_train, X_test, y_train):
get_avg_glove_emb = lambda X: np.array([get_glove_emb(x).mean(axis=0) for x in X])
return with_embs(get_avg_glove_emb, classifier, X_train, X_test, y_train)
def elmo_embs_function(classifier, X_train, X_test, y_train):
return with_embs(get_elmo_emb, classifier, X_train, X_test, y_train)
def unsent_embs_function(classifier, X_train, X_test, y_train):
return with_embs(get_unsent_emb, classifier, X_train, X_test, y_train)
def build_xy_sampled(n_classes):
assert n_classes <= len(captions)
sampled_captions_id = np.random.choice(list(range(len(captions))), size=n_classes, replace=False)
x_all, y_all = [], []
for i in sampled_captions_id:
y_all += [i] * len(captions[i])
for s in captions[i]:
x_all.append(s)
return x_all, y_all
import warnings
warnings.filterwarnings('ignore')
from tqdm import tqdm
def run(classifier, function, n_samples, n_paraphrases, n_classes, averaging_order, pure_paraphrases):
result_f1 = []
for i in tqdm(range(averaging_order), position=0):
X,y = build_xy_sampled(n_classes)
result_f1.append(split_and_test(classifier, function, X, y, n_samples, n_paraphrases, pure_paraphrases))
return np.mean(result_f1), np.std(result_f1)
```
# paraphrasing VS no-paraphrasing
```
from sklearn.linear_model import LogisticRegression
logreg_classifier = LogisticRegression(multi_class='multinomial', solver='saga', max_iter=500, C=100, n_jobs=-1)
```
## 1 sample
```
run(logreg_classifier,
bag_of_words_function,
n_samples=1,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=1,
n_paraphrases=1,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
```
## 2 samples
```
run(logreg_classifier,
bag_of_words_function,
n_samples=2,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=2,
n_paraphrases=1,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
```
## 3 samples
```
run(logreg_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=3,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
```
## 4 samples
```
run(logreg_classifier,
bag_of_words_function,
n_samples=4,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=4,
n_paraphrases=6,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
paraphrases_from_sources([['a table with a quesadilla salad and drinks'],['a sliced pizza a salad and two milk shakes on a table']], use_mean=True)
# !export CUDA_VISIBLE_DEVICES=1
!echo $CUDA_VISIBLE_DEVICES
```
# GLOVE BAG vs USE vs ELMO vs InferSent
```
from sklearn.linear_model import LogisticRegression
logreg_classifier = LogisticRegression(multi_class='multinomial', solver='saga', max_iter=500, C=100, n_jobs=-1)
# GLOVE BAG
run(logreg_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# %%time
run(logreg_classifier,
elmo_embs_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
%%time
run(logreg_classifier,
unsent_embs_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
%%time
run(logreg_classifier,
infersent_embs_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
(0.896825396825397, 0.046513606386423476)
```
# RANDOM FOREST
```
from sklearn.ensemble import RandomForestClassifier
# GLOVE BAG
rf_classifier = RandomForestClassifier(n_estimators=2000, max_depth=7, n_jobs=-1)
run(rf_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# GLOVE BAG
rf_classifier = RandomForestClassifier(n_estimators=3000, n_jobs=-1)
run(rf_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# GLOVE BAG
rf_classifier = RandomForestClassifier(n_estimators=3000, n_jobs=-1)
run(rf_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# 13.1s/it:CPU , 8.5s/it:GPU
# %%time
classifier = RandomForestClassifier(n_estimators=2000, n_jobs=-1)
run(rf_classifier,
elmo_embs_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# session.close()
```
# Plots
```
import matplotlib.pyplot as plt
%matplotlib inline
colors = ['b', 'g', 'r', 'orange', 'black']
def plots_for_nsources_range(title, names, scores, stds, n_samples):
plt.figure()
fig, ax = plt.subplots(figsize=(12,9))
ax.grid(True)
plt.title(title, fontsize=14)
for i in range(len(scores)):
ax.plot(n_samples, scores[i],'-o', label = names[i], color=colors[i])
ax.fill_between(n_samples, scores[i] - stds[i], scores[i] + stds[i],alpha=0.10, color=colors[i])
ax.set_ylabel('F1')
ax.legend(loc=(0.8,0.1), fontsize=12)
ax.set_ylabel('between y1 and 0')
plt.xlabel('number of training samples per class', fontsize=12)
plt.ylabel('F1', fontsize=12)
plt.savefig('logs/nsources_{}.png'.format(title))
plt.show()
```
# EMBS
```
AVERAGING_ORDER = 50
def process_for_sources_range(name, classifier, function , n_sources_range, n_paraphrases = 0):
mean = []
std = []
for n_sources in tqdm(n_sources_range, position=0):
cur_mean, cur_std = results = run(classifier,
function,
n_samples=n_sources,
n_paraphrases=n_paraphrases,
n_classes=30,
averaging_order=AVERAGING_ORDER,
pure_paraphrases=False)
mean.append(cur_mean)
std.append(cur_std)
mean = np.array(mean)
std = np.array(std)
n_sources_range = np.array(n_sources_range)
np.save('logs/mscoco_score_{}.npy'.format(name), [mean, std, n_sources_range])
return mean, std, n_sources_range
from sklearn.linear_model import LogisticRegression
logreg_classifier = LogisticRegression(multi_class='multinomial', solver='saga', max_iter=1000, n_jobs=-1, C=100)
n_sources_range = [1,2,3,4]
%%time
name = 'glove_logreg'
process_for_sources_range(name, logreg_classifier, bag_of_words_function, n_sources_range, n_paraphrases=0)
%%time
name = 'elmo_logreg'
process_for_sources_range(name, logreg_classifier, elmo_embs_function, n_sources_range, n_paraphrases=0)
%%time
name = 'unsent_logreg'
process_for_sources_range(name, logreg_classifier, unsent_embs_function, n_sources_range, n_paraphrases=0)
%%time
name = 'infersent_logreg'
process_for_sources_range(name, logreg_classifier, infersent_embs_function, n_sources_range, n_paraphrases=0)
%%time
name = 'onehot_logreg_50'
logreg_classifier = LogisticRegression(multi_class='multinomial', solver='saga', max_iter=50, n_jobs=-1, C=50)
process_for_sources_range(name,logreg_classifier, onehot_embs_function, n_sources_range, n_paraphrases=0)
glove = np.load('logs/mscoco_score_glove_logreg.npy')
elmo = np.load('logs/mscoco_score_elmo_logreg.npy')
unsent = np.load('logs/mscoco_score_unsent_logreg.npy')
infersent = np.load('logs/mscoco_score_infersent_logreg.npy')
onehot = np.load('logs/mscoco_score_onehot_logreg_50.npy')
names = ['glove','elmo','unsent','infersent','onehot']
data = [glove , elmo , unsent , infersent , onehot]
scores = [d[0] for d in data]
stds = [d[1] for d in data]
ranges = data[0][2]
plots_for_nsources_range('MSCOCO LogReg with Embeddings', names, scores, stds, ranges)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
captions = np.load('data/mscoco/all_captions.npy')
captions = [c[:5] for c in captions]
sentences = []
for c in captions:
sentences += c
# "GOOGLE ELMO" sentence embeddings
import tensorflow as tf
import tensorflow_hub as hub
# ELMO
elmo = hub.Module("https://tfhub.dev/google/elmo/1", trainable=False)
elmo_input = tf.placeholder(tf.string)
elmo_embeddings = elmo(elmo_input, signature="default", as_dict=True)["default"]
def get_elmo_emb(sentences):
batch_size = 64
ix = 0
result = []
while ix < len(sentences):
result.append(session.run(elmo_embeddings,
feed_dict={elmo_input: sentences[ix: min(ix + batch_size, len(sentences))]}))
ix += batch_size
return np.concatenate(result, axis=0)
# USE
unsent = hub.Module("https://tfhub.dev/google/universal-sentence-encoder/1")
unsent_input = tf.placeholder(tf.string)
unsent_embeddings = unsent(unsent_input)
def get_unsent_emb(sentences):
return session.run(unsent_embeddings, feed_dict={unsent_input: sentences})
#SESSION
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
session = tf.Session(config=config)
session.run([tf.global_variables_initializer(), tf.tables_initializer()])
get_elmo_emb(["the cat is on the mat", "dogs are in the fog"])
get_unsent_emb(["The quick brown fox jumps over the lazy dog.",
"I am a sentence for which I would like to get its embedding"])
import torch as t
import utils
from utils.batch_loader import BatchLoader
from model.parameters import Parameters
from model.paraphraser import Paraphraser
class Args(object):
pass
args = Args()
args.batch_size = 32
args.seq_len=30
args.use_cuda = True
args.use_cuda = True
args.model_name = 'snli_200kit_600_800'
datasets = set()
datasets.add('snli')
sentences = np.array([utils.batch_loader.clean_str(s) for s in sentences])
captions = [[utils.batch_loader.clean_str(s) for s in bucket] for bucket in captions]
batch_loader = BatchLoader(path='', datasets=datasets)
batch_loader.build_input_vocab(sentences)
# PARAPHRASER
parameters = Parameters(batch_loader.max_seq_len, batch_loader.vocab_size)
paraphraser = Paraphraser(parameters)
paraphraser.load_state_dict(t.load('saved_models/trained_paraphraser_' + args.model_name))
if args.use_cuda:
paraphraser = paraphraser.cuda()
# PARAPHRASER EXPAND
def paraphrases_from_sources(sources, use_mean=True):
result = []
for s1,s2 in zip(sources[0], sources[1]):
input = batch_loader.input_from_sentences([[s1],[s2]])
input = [var.cuda() if args.use_cuda else var for var in input]
result += [paraphraser.sample_with_input(batch_loader, args.seq_len, args.use_cuda, use_mean, input)]
return result
def paraphrase_expand(X, y, n_paraphrases, pure_paraphrases):
if n_paraphrases <= 0:
return X,y
X_gen, y_gen = [], []
y = np.array(y)
X = np.array(X)
for class_id in np.unique(y):
X_class = X[y == class_id]
idx = []
for i in range(len(X_class)):
for j in range(len(X_class)):
if i == j and len(X_class) != 1:
continue
idx.append((i,j))
idx = np.array(idx)
idx = idx[np.random.choice(list(range(len(idx))), n_paraphrases, replace=False)]
sources = [X_class[idx[:,0]], X_class[idx[:,1]]]
X_gen += [paraphrases_from_sources(sources)]
y_gen += [[class_id] * n_paraphrases]
if pure_paraphrases:
return np.concatenate(X_gen), np.concatenate(y_gen)
X_result = np.concatenate([X] + X_gen)
y_result = np.concatenate([y] + y_gen)
return X_result, y_result
# build infersent
import torch as t
import sys
sys.path.append('../InferSent/encoder')
INFERSENT_PATH = '../InferSent/encoder/'
GLOVE_PATH = '/home/aleksey.zotov/InferSent/dataset/GloVe/glove.840B.300d.txt'
infersent_model = t.load(INFERSENT_PATH + 'infersent.allnli.pickle', map_location=lambda storage, loc: storage)
# infersent_model = t.load(INFERSENT_PATH + 'infersent.allnli.pickle', map_location={'cuda:1' : 'cuda:0', 'cuda:2' : 'cuda:0'})
# infersent_model = t.load(INFERSENT_PATH + 'infersent.allnli.pickle')
infersent_model.set_glove_path(GLOVE_PATH)
infersent_model.build_vocab(sentences, tokenize=False)
# infersent_model.build_vocab_k_words(K=200000)
# infersent embs
def get_infersent_emb(X):
embeddings = infersent_model.encode(X, bsize=64, tokenize=False, verbose=False)
return embeddings
paraphrases_from_sources([
['Woman sits near the table with her dog'],
['Very old woman is sitting with her child on the table']], use_mean=False)
paraphrases_from_sources([
['Woman sits near the table with her dog'],
['Very old woman is sitting with her child on the table']], use_mean=False)
paraphrases_from_sources([
['man is chopping old wood with an axe'],
['very old man is outside']], use_mean=True)
cid = 0
captions[cid][0], captions[cid][1], paraphrases_from_sources([[captions[cid][0]], [captions[cid][1]]], use_mean=True)[0]
cid = 1
captions[cid][0], captions[cid][1], paraphrases_from_sources([[captions[cid][0]], [captions[cid][1]]], use_mean=True)[0]
cid = 1337
captions[cid][0], captions[cid][1], paraphrases_from_sources([[captions[cid][0]], [captions[cid][1]]], use_mean=True)[0]
# GLOVE EMB using batch loader
def get_glove_emb(sentence):
emb_size = 300
embed = np.zeros((len(sentence), emb_size))
for i, s in enumerate(sentence.strip().split()):
if s in batch_loader.word_vec.keys():
embed[i, :] = batch_loader.word_vec[s]
else:
embed[i, :] = batch_loader.word_vec['null']
return embed
# Build ONEHOT model embeddings
from collections import Counter
vocab_size = 10000
word_counter = Counter((' '.join(sentences)).split())
idx_to_word = [x[0] for x in word_counter.most_common(vocab_size - 1)]
word_to_idx = {v : i for i,v in enumerate(idx_to_word)}
def get_idx_by_word(w):
if w in word_to_idx:
return word_to_idx[w]
return vocab_size - 1
def get_simple_onehot_embs(X):
embed = []
for sentence in X:
result = np.zeros(vocab_size)
result[[get_idx_by_word(w) for w in sentence.split()]] = 1.0
embed.append(result)
return np.array(embed)
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_recall_fscore_support
def get_f1_score(y_true, y_pred):
return precision_recall_fscore_support(y_true=np.array(y_true), y_pred=y_pred)[2]
def split_and_test(classifier, model_function, X_all, y_all, n_samples, n_paraphrases, pure_paraphrases=False):
n_classes = len(np.unique(y_all))
X_train, X_test, y_train, y_test = train_test_split(X_all, y_all, stratify=y_all, train_size=n_samples * n_classes)
X_train, y_train = paraphrase_expand(X_train, y_train, n_paraphrases, pure_paraphrases)
predicted_proba = model_function(classifier, X_train, X_test, y_train)
return np.mean(get_f1_score(y_test, predicted_proba))
def with_embs(emb_function, classifier, X_train, X_test, y_train):
X_train = emb_function(X_train)
X_test = emb_function(X_test)
classifier.fit(X_train, y_train)
return classifier.predict(X_test)
def onehot_embs_function(classifier, X_train, X_test, y_train):
return with_embs(get_simple_onehot_embs, classifier, X_train, X_test, y_train)
def infersent_embs_function(classifier, X_train, X_test, y_train):
return with_embs(get_infersent_emb, classifier, X_train, X_test, y_train)
def bag_of_words_function(classifier, X_train, X_test, y_train):
get_avg_glove_emb = lambda X: np.array([get_glove_emb(x).mean(axis=0) for x in X])
return with_embs(get_avg_glove_emb, classifier, X_train, X_test, y_train)
def elmo_embs_function(classifier, X_train, X_test, y_train):
return with_embs(get_elmo_emb, classifier, X_train, X_test, y_train)
def unsent_embs_function(classifier, X_train, X_test, y_train):
return with_embs(get_unsent_emb, classifier, X_train, X_test, y_train)
def build_xy_sampled(n_classes):
assert n_classes <= len(captions)
sampled_captions_id = np.random.choice(list(range(len(captions))), size=n_classes, replace=False)
x_all, y_all = [], []
for i in sampled_captions_id:
y_all += [i] * len(captions[i])
for s in captions[i]:
x_all.append(s)
return x_all, y_all
import warnings
warnings.filterwarnings('ignore')
from tqdm import tqdm
def run(classifier, function, n_samples, n_paraphrases, n_classes, averaging_order, pure_paraphrases):
result_f1 = []
for i in tqdm(range(averaging_order), position=0):
X,y = build_xy_sampled(n_classes)
result_f1.append(split_and_test(classifier, function, X, y, n_samples, n_paraphrases, pure_paraphrases))
return np.mean(result_f1), np.std(result_f1)
from sklearn.linear_model import LogisticRegression
logreg_classifier = LogisticRegression(multi_class='multinomial', solver='saga', max_iter=500, C=100, n_jobs=-1)
run(logreg_classifier,
bag_of_words_function,
n_samples=1,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=1,
n_paraphrases=1,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=2,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=2,
n_paraphrases=1,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=3,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=4,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
run(logreg_classifier,
bag_of_words_function,
n_samples=4,
n_paraphrases=6,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
paraphrases_from_sources([['a table with a quesadilla salad and drinks'],['a sliced pizza a salad and two milk shakes on a table']], use_mean=True)
# !export CUDA_VISIBLE_DEVICES=1
!echo $CUDA_VISIBLE_DEVICES
from sklearn.linear_model import LogisticRegression
logreg_classifier = LogisticRegression(multi_class='multinomial', solver='saga', max_iter=500, C=100, n_jobs=-1)
# GLOVE BAG
run(logreg_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# %%time
run(logreg_classifier,
elmo_embs_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
%%time
run(logreg_classifier,
unsent_embs_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
%%time
run(logreg_classifier,
infersent_embs_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
(0.896825396825397, 0.046513606386423476)
from sklearn.ensemble import RandomForestClassifier
# GLOVE BAG
rf_classifier = RandomForestClassifier(n_estimators=2000, max_depth=7, n_jobs=-1)
run(rf_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# GLOVE BAG
rf_classifier = RandomForestClassifier(n_estimators=3000, n_jobs=-1)
run(rf_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# GLOVE BAG
rf_classifier = RandomForestClassifier(n_estimators=3000, n_jobs=-1)
run(rf_classifier,
bag_of_words_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# 13.1s/it:CPU , 8.5s/it:GPU
# %%time
classifier = RandomForestClassifier(n_estimators=2000, n_jobs=-1)
run(rf_classifier,
elmo_embs_function,
n_samples=3,
n_paraphrases=0,
n_classes=30,
averaging_order=30,
pure_paraphrases=False)
# session.close()
import matplotlib.pyplot as plt
%matplotlib inline
colors = ['b', 'g', 'r', 'orange', 'black']
def plots_for_nsources_range(title, names, scores, stds, n_samples):
plt.figure()
fig, ax = plt.subplots(figsize=(12,9))
ax.grid(True)
plt.title(title, fontsize=14)
for i in range(len(scores)):
ax.plot(n_samples, scores[i],'-o', label = names[i], color=colors[i])
ax.fill_between(n_samples, scores[i] - stds[i], scores[i] + stds[i],alpha=0.10, color=colors[i])
ax.set_ylabel('F1')
ax.legend(loc=(0.8,0.1), fontsize=12)
ax.set_ylabel('between y1 and 0')
plt.xlabel('number of training samples per class', fontsize=12)
plt.ylabel('F1', fontsize=12)
plt.savefig('logs/nsources_{}.png'.format(title))
plt.show()
AVERAGING_ORDER = 50
def process_for_sources_range(name, classifier, function , n_sources_range, n_paraphrases = 0):
mean = []
std = []
for n_sources in tqdm(n_sources_range, position=0):
cur_mean, cur_std = results = run(classifier,
function,
n_samples=n_sources,
n_paraphrases=n_paraphrases,
n_classes=30,
averaging_order=AVERAGING_ORDER,
pure_paraphrases=False)
mean.append(cur_mean)
std.append(cur_std)
mean = np.array(mean)
std = np.array(std)
n_sources_range = np.array(n_sources_range)
np.save('logs/mscoco_score_{}.npy'.format(name), [mean, std, n_sources_range])
return mean, std, n_sources_range
from sklearn.linear_model import LogisticRegression
logreg_classifier = LogisticRegression(multi_class='multinomial', solver='saga', max_iter=1000, n_jobs=-1, C=100)
n_sources_range = [1,2,3,4]
%%time
name = 'glove_logreg'
process_for_sources_range(name, logreg_classifier, bag_of_words_function, n_sources_range, n_paraphrases=0)
%%time
name = 'elmo_logreg'
process_for_sources_range(name, logreg_classifier, elmo_embs_function, n_sources_range, n_paraphrases=0)
%%time
name = 'unsent_logreg'
process_for_sources_range(name, logreg_classifier, unsent_embs_function, n_sources_range, n_paraphrases=0)
%%time
name = 'infersent_logreg'
process_for_sources_range(name, logreg_classifier, infersent_embs_function, n_sources_range, n_paraphrases=0)
%%time
name = 'onehot_logreg_50'
logreg_classifier = LogisticRegression(multi_class='multinomial', solver='saga', max_iter=50, n_jobs=-1, C=50)
process_for_sources_range(name,logreg_classifier, onehot_embs_function, n_sources_range, n_paraphrases=0)
glove = np.load('logs/mscoco_score_glove_logreg.npy')
elmo = np.load('logs/mscoco_score_elmo_logreg.npy')
unsent = np.load('logs/mscoco_score_unsent_logreg.npy')
infersent = np.load('logs/mscoco_score_infersent_logreg.npy')
onehot = np.load('logs/mscoco_score_onehot_logreg_50.npy')
names = ['glove','elmo','unsent','infersent','onehot']
data = [glove , elmo , unsent , infersent , onehot]
scores = [d[0] for d in data]
stds = [d[1] for d in data]
ranges = data[0][2]
plots_for_nsources_range('MSCOCO LogReg with Embeddings', names, scores, stds, ranges)
| 0.529993 | 0.461684 |
```
import numpy as np
import tensorflow as tf
from tensorflow import keras
```
### 1. 手动求导
**一元函数求导**
```
def f(x):
return 3. * x ** 2 + 2. * x -1
def approximate_derivative(f, x, eps = 1e-3):
"""函数 f 对 x 求导"""
return (f(x + eps) - f(x - eps)) / (2. * eps)
print(approximate_derivative(f, 1.))
```
**多元函数求导**
```
def g(x1, x2):
return (x1 + 5) * (x2 ** 2)
def approximate_gredient(g, x1, x2, eps=1e-3):
gred_x1 = approximate_derivative(lambda x: g(x, x2), x1, eps)
gred_x2 = approximate_derivative(lambda x: g(x1, x), x2, eps)
return gred_x1, gred_x2
print(approximate_gredient(g, 2., 3.))
```
### 2. 自动求导
```
x1 = tf.Variable(2.0)
x2 = tf.Variable(3.0)
with tf.GradientTape() as tape:
z = g(x1, x2) # 定义函数
dz_x1 = tape.gradient(z, x1)
print(dz_x1)
try:
dz_x2 = tape.gradient(z, x2)
except RuntimeError as ex:
print(ex)
x1 = tf.Variable(2.0)
x2 = tf.Variable(3.0)
with tf.GradientTape(persistent=True) as tape:
z = g(x1, x2) # 定义函数
dz_x1 = tape.gradient(z, x1)
dz_x2 = tape.gradient(z, x2)
print(dz_x1)
print(dz_x2)
del tape
x1 = tf.Variable(2.0)
x2 = tf.Variable(3.0)
with tf.GradientTape() as tape:
z = g(x1, x2)
dz_x1x2 = tape.gradient(z, [x1, x2])
print(dz_x1x2)
```
**对常量求偏导**
```
x1 = tf.constant(2.0)
x2 = tf.constant(3.0)
with tf.GradientTape() as tape:
z = g(x1, x2)
dz_x1x2 = tape.gradient(z, [x1, x2])
print(dz_x1x2)
x1 = tf.constant(2.0)
x2 = tf.constant(3.0)
with tf.GradientTape() as tape:
tape.watch(x1)
tape.watch(x2)
z = g(x1, x2)
dz_x1x2 = tape.gradient(z, [x1, x2])
print(dz_x1x2)
```
**两个函数对一个变量求导**
```
x = tf.Variable(5.0)
with tf.GradientTape() as tape:
z1 = 3 * x
z2 = x ** 2
tape.gradient([z1, z2], x)
# 13 = 3 + 10
```
**二阶导数**
```
x1 = tf.Variable(2.0)
x2 = tf.Variable(3.0)
with tf.GradientTape(persistent=True) as outer_tape:
with tf.GradientTape(persistent=True) as inner_tape:
z = g(x1, x2)
inner_grads = inner_tape.gradient(z, [x1, x2])
outer_grads = [outer_tape.gradient(inner_grad, [x1, x2])
for inner_grad in inner_grads]
print(outer_grads)
del inner_tape
del outer_tape
```
### 3. 梯度下降
```
learning_rate = 0.1
x = tf.Variable(0.0)
for _ in range(100):
with tf.GradientTape() as tape:
z = f(x)
dz_dx = tape.gradient(z, x)
x.assign_sub(learning_rate * dz_dx)
print(x)
learning_rate = 0.1
x = tf.Variable(0.0)
optimizer = keras.optimizers.SGD(learning_rate = learning_rate)
for _ in range(100):
with tf.GradientTape() as tape:
z = f(x)
dz_dx = tape.gradient(z, x)
optimizer.apply_gradients([(dz_dx, x)])
print(x)
```
|
github_jupyter
|
import numpy as np
import tensorflow as tf
from tensorflow import keras
def f(x):
return 3. * x ** 2 + 2. * x -1
def approximate_derivative(f, x, eps = 1e-3):
"""函数 f 对 x 求导"""
return (f(x + eps) - f(x - eps)) / (2. * eps)
print(approximate_derivative(f, 1.))
def g(x1, x2):
return (x1 + 5) * (x2 ** 2)
def approximate_gredient(g, x1, x2, eps=1e-3):
gred_x1 = approximate_derivative(lambda x: g(x, x2), x1, eps)
gred_x2 = approximate_derivative(lambda x: g(x1, x), x2, eps)
return gred_x1, gred_x2
print(approximate_gredient(g, 2., 3.))
x1 = tf.Variable(2.0)
x2 = tf.Variable(3.0)
with tf.GradientTape() as tape:
z = g(x1, x2) # 定义函数
dz_x1 = tape.gradient(z, x1)
print(dz_x1)
try:
dz_x2 = tape.gradient(z, x2)
except RuntimeError as ex:
print(ex)
x1 = tf.Variable(2.0)
x2 = tf.Variable(3.0)
with tf.GradientTape(persistent=True) as tape:
z = g(x1, x2) # 定义函数
dz_x1 = tape.gradient(z, x1)
dz_x2 = tape.gradient(z, x2)
print(dz_x1)
print(dz_x2)
del tape
x1 = tf.Variable(2.0)
x2 = tf.Variable(3.0)
with tf.GradientTape() as tape:
z = g(x1, x2)
dz_x1x2 = tape.gradient(z, [x1, x2])
print(dz_x1x2)
x1 = tf.constant(2.0)
x2 = tf.constant(3.0)
with tf.GradientTape() as tape:
z = g(x1, x2)
dz_x1x2 = tape.gradient(z, [x1, x2])
print(dz_x1x2)
x1 = tf.constant(2.0)
x2 = tf.constant(3.0)
with tf.GradientTape() as tape:
tape.watch(x1)
tape.watch(x2)
z = g(x1, x2)
dz_x1x2 = tape.gradient(z, [x1, x2])
print(dz_x1x2)
x = tf.Variable(5.0)
with tf.GradientTape() as tape:
z1 = 3 * x
z2 = x ** 2
tape.gradient([z1, z2], x)
# 13 = 3 + 10
x1 = tf.Variable(2.0)
x2 = tf.Variable(3.0)
with tf.GradientTape(persistent=True) as outer_tape:
with tf.GradientTape(persistent=True) as inner_tape:
z = g(x1, x2)
inner_grads = inner_tape.gradient(z, [x1, x2])
outer_grads = [outer_tape.gradient(inner_grad, [x1, x2])
for inner_grad in inner_grads]
print(outer_grads)
del inner_tape
del outer_tape
learning_rate = 0.1
x = tf.Variable(0.0)
for _ in range(100):
with tf.GradientTape() as tape:
z = f(x)
dz_dx = tape.gradient(z, x)
x.assign_sub(learning_rate * dz_dx)
print(x)
learning_rate = 0.1
x = tf.Variable(0.0)
optimizer = keras.optimizers.SGD(learning_rate = learning_rate)
for _ in range(100):
with tf.GradientTape() as tape:
z = f(x)
dz_dx = tape.gradient(z, x)
optimizer.apply_gradients([(dz_dx, x)])
print(x)
| 0.542136 | 0.940572 |
```
%pylab inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
pwd
def order_book(month,day):
data = []
datapath = '/home/rory/Demo/Data_Transformation/Train_Test_Builder/order_book_3_2014'\
+ '_' + str(month) + '_' + str(day) + '.csv'
order_book = pd.read_csv(datapath,sep=',')
bid_price_1 = np.array(map(float,order_book['Bid'][1::4]))/100.0
bid_price_2 = np.array(map(float,order_book['Bid'][2::4]))/100.0
bid_price_3 = np.array(map(float,order_book['Bid'][3::4]))/100.0
timestamp = np.array(order_book['Bid_Quantity'][0::4])
bid_quantity_1 = np.array(map(float,order_book['Bid_Quantity'][1::4]))
bid_quantity_2 = np.array(map(float,order_book['Bid_Quantity'][2::4]))
bid_quantity_3 = np.array(map(float,order_book['Bid_Quantity'][3::4]))
ask_price_1 = np.array(map(float,order_book['Ask'][1::4]))/100.0
ask_price_2 = np.array(map(float,order_book['Ask'][2::4]))/100.0
ask_price_3 = np.array(map(float,order_book['Ask'][3::4]))/100.0
ask_quantity_1 = np.array(map(float,order_book['Ask_Quantity'][1::4]))
ask_quantity_2 = np.array(map(float,order_book['Ask_Quantity'][2::4]))
ask_quantity_3 = np.array(map(float,order_book['Ask_Quantity'][3::4]))
bid_quantity_1[isnan(bid_quantity_1)] = 0
bid_quantity_2[isnan(bid_quantity_2)] = 0
bid_quantity_3[isnan(bid_quantity_3)] = 0
ask_quantity_1[isnan(ask_quantity_1)] = 0
ask_quantity_2[isnan(ask_quantity_2)] = 0
ask_quantity_3[isnan(ask_quantity_3)] = 0
return timestamp,order_book,bid_price_1,bid_price_2,bid_price_3,bid_quantity_1,\
bid_quantity_2,bid_quantity_3,ask_price_1,ask_price_2,ask_price_3,ask_quantity_1,\
ask_quantity_2,ask_quantity_3
def time_transform(timestamp_time):
time_second_basic = []
time_second = []
for i in range(0,len(timestamp_time),1):
second = float(timestamp_time[i][11])*36000 + float(timestamp_time[i][12])*3600+\
float(timestamp_time[i][14])*600 + float(timestamp_time[i][15])*60+\
float(timestamp_time[i][17])*10 + float(timestamp_time[i][18])
time_second_basic.append(second - 32400.0)
time_second.append(second)
return np.array(time_second),np.array(time_second_basic)
def weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3):
Weight_Ask = (w1 * ask_quantity_1 + w2 * ask_quantity_2 + w3 * ask_quantity_3)
Weight_Bid = (w1 * bid_quantity_1 + w2 * bid_quantity_2 + w3 * bid_quantity_3)
W_AB = Weight_Ask/Weight_Bid
W_A_B = (Weight_Ask - Weight_Bid)/(Weight_Ask + Weight_Bid)
return W_AB, W_A_B
def Feature_DataFrame_UP(traded_time,time_second_basic,bid_price_1,ask_price_1,rise_ratio_ask_1,\
rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,rise_ratio_ask_5,\
rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,rise_ratio_ask_9,\
rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,rise_ratio_ask_13,\
rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,rise_ratio_ask_17,\
rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,rise_ratio_ask_21,\
rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,rise_ratio_ask_25,\
rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,rise_ratio_ask_29,\
rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010, W_AB_001,\
W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730 , W_A_B_730,\
W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721, W_AB_532,\
W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280 , W_A_B_280,\
W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127, W_AB_235, W_A_B_235):
# 09:00 ~ 11:30
time1 = 0
time2 = 9000
print len(W_AB_910)
traded,index_,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235=\
traded_label_one_second(time1,time2,time_second_basic,bid_price_1,ask_price_1,traded_time,\
rise_ratio_ask_1,rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,\
rise_ratio_ask_5,rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,\
rise_ratio_ask_9,rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,\
rise_ratio_ask_13,rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,\
rise_ratio_ask_17,rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,\
rise_ratio_ask_21,rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,\
rise_ratio_ask_25,rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,\
rise_ratio_ask_29,rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010,\
W_AB_001,W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730,\
W_A_B_730,W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721,\
W_AB_532,W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280,\
W_A_B_280,W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127,\
W_AB_235, W_A_B_235)
data = np.array([traded,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235]).T
return pd.DataFrame(data)#,traded_1 #, columns = ['label', 'rise', 'depth_divid', 'depth_diff'])
def Feature_DataFrame_DOWN(traded_time,time_second_basic,bid_price_1,ask_price_1,rise_ratio_ask_1,\
rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,rise_ratio_ask_5,\
rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,rise_ratio_ask_9,\
rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,rise_ratio_ask_13,\
rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,rise_ratio_ask_17,\
rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,rise_ratio_ask_21,\
rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,rise_ratio_ask_25,\
rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,rise_ratio_ask_29,\
rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010, W_AB_001,\
W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730 , W_A_B_730,\
W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721, W_AB_532,\
W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280 , W_A_B_280,\
W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127, W_AB_235, W_A_B_235):
# 13:00 ~ 16:00
time1 = 14400
time2 = 25200
traded,index_,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235 =\
traded_label_one_second(time1,time2,time_second_basic,bid_price_1,ask_price_1,traded_time,\
rise_ratio_ask_1,rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,\
rise_ratio_ask_5,rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,\
rise_ratio_ask_9,rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,\
rise_ratio_ask_13,rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,\
rise_ratio_ask_17,rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,\
rise_ratio_ask_21,rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,\
rise_ratio_ask_25,rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,\
rise_ratio_ask_29,rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010,\
W_AB_001,W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730,\
W_A_B_730,W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721,\
W_AB_532,W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280,\
W_A_B_280,W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127,\
W_AB_235, W_A_B_235)
data = np.array([traded,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235]).T
return pd.DataFrame(data)#,traded_2 #, columns = ['label', 'rise', 'depth_divid', 'depth_diff'])
def rise_ask(Ask1,timestamp_time_second,before_time):
Ask1[Ask1 == 0] = mean(Ask1)
rise_ratio = []
index = np.where(timestamp_time_second >= before_time)[0][0]
#open first before_time mins
for i in range(0,index,1):
rise_ratio_ = round((Ask1[i] - Ask1[0])*(1.0)/Ask1[0]*100,5)
rise_ratio.append(rise_ratio_)
for i in range(index,len(Ask1),1):
#print np.where(timestamp_time_second[:i] >= timestamp_time_second[i] - before_time)
#print timestamp_time_second[i],timestamp_time_second[i] - before_time
index_start = np.where(timestamp_time_second[:i] >= timestamp_time_second[i] - before_time)[0][0]
rise_ratio_ = round((Ask1[i] - Ask1[index_start])*(1.0)/Ask1[index_start]*100,5)
rise_ratio.append(rise_ratio_)
return np.array(rise_ratio)
def traded_label_one_second(time1,time2,time_second_basic,bid_price_1,ask_price_1,traded_time,\
rise_ratio_ask_1,rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,\
rise_ratio_ask_5,rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,\
rise_ratio_ask_9,rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,\
rise_ratio_ask_13,rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,\
rise_ratio_ask_17,rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,\
rise_ratio_ask_21,rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,\
rise_ratio_ask_25,rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,\
rise_ratio_ask_29,rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010,\
W_AB_001,W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730,\
W_A_B_730,W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721,\
W_AB_532,W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280,\
W_A_B_280,W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127,\
W_AB_235, W_A_B_235):
global index
traded = []
index_ = []
rise_ratio_second_1 = []
rise_ratio_second_2 = []
rise_ratio_second_3 = []
rise_ratio_second_4 = []
rise_ratio_second_5 = []
rise_ratio_second_6 = []
rise_ratio_second_7 = []
rise_ratio_second_8 = []
rise_ratio_second_9 = []
rise_ratio_second_10 = []
rise_ratio_second_11 = []
rise_ratio_second_12 = []
rise_ratio_second_13 = []
rise_ratio_second_14 = []
rise_ratio_second_15 = []
rise_ratio_second_16 = []
rise_ratio_second_17 = []
rise_ratio_second_18 = []
rise_ratio_second_19 = []
rise_ratio_second_20 = []
rise_ratio_second_21 = []
rise_ratio_second_22 = []
rise_ratio_second_23 = []
rise_ratio_second_24 = []
rise_ratio_second_25 = []
rise_ratio_second_26 = []
rise_ratio_second_27 = []
rise_ratio_second_28 = []
rise_ratio_second_29 = []
rise_ratio_second_30 = []
w_divid_100 = []
w_diff_100 = []
w_divid_010 = []
w_diff_010 = []
w_divid_001 = []
w_diff_001 = []
w_divid_910 = []
w_diff_910 = []
w_divid_820 = []
w_diff_820 = []
w_divid_730 = []
w_diff_730 = []
w_divid_640 = []
w_diff_640 = []
w_divid_550 = []
w_diff_550 = []
w_divid_721 = []
w_diff_721 = []
w_divid_532 = []
w_diff_532 = []
w_divid_111 = []
w_diff_111 = []
w_divid_190 = []
w_diff_190 = []
w_divid_280 = []
w_diff_280 = []
w_divid_370 = []
w_diff_370 = []
w_divid_460 = []
w_diff_460 = []
w_divid_127 = []
w_diff_127 = []
w_divid_235 = []
w_diff_235 = []
if time1 == 0:
index_one = np.where(time_second_basic <= 0)[0][-1]
elif time1 == 14400:
index_one = np.where(time_second_basic <= 14400)[0][-1]
for i in range(time1, time2, 1):
if i == 0 or i == 14400:
index_array = np.where(time_second_basic <= i)[-1]
else:
index_array = np.where((time_second_basic < i+1) & (time_second_basic >= i))[-1]
if len(index_array) > 0:
index = index_array[-1]
if i == time1:
index_.append(index)
if i == time2 - 1:
index_.append(index)
if i < 25200 - traded_time:
index_min = np.where(time_second_basic <= i + traded_time)[0][-1]
traded_min = ask_price_1[index:index_min]
if bid_price_1[index] > min(traded_min):
traded.append(1)
else:
traded.append(0)
elif i >= 25200 - traded_time:
if bid_price_1[index] > ask_price_1[-1]:
traded.append(1)
else:
traded.append(0)
rise_ratio_second_1.append(rise_ratio_ask_1[(index - index_one)])
rise_ratio_second_2.append(rise_ratio_ask_2[(index - index_one)])
rise_ratio_second_3.append(rise_ratio_ask_3[(index - index_one)])
rise_ratio_second_4.append(rise_ratio_ask_4[(index - index_one)])
rise_ratio_second_5.append(rise_ratio_ask_5[(index - index_one)])
rise_ratio_second_6.append(rise_ratio_ask_6[(index - index_one)])
rise_ratio_second_7.append(rise_ratio_ask_7[(index - index_one)])
rise_ratio_second_8.append(rise_ratio_ask_8[(index - index_one)])
rise_ratio_second_9.append(rise_ratio_ask_9[(index - index_one)])
rise_ratio_second_10.append(rise_ratio_ask_10[(index - index_one)])
rise_ratio_second_11.append(rise_ratio_ask_11[(index - index_one)])
rise_ratio_second_12.append(rise_ratio_ask_12[(index - index_one)])
rise_ratio_second_13.append(rise_ratio_ask_13[(index - index_one)])
rise_ratio_second_14.append(rise_ratio_ask_14[(index - index_one)])
rise_ratio_second_15.append(rise_ratio_ask_15[(index - index_one)])
rise_ratio_second_16.append(rise_ratio_ask_16[(index - index_one)])
rise_ratio_second_17.append(rise_ratio_ask_17[(index - index_one)])
rise_ratio_second_18.append(rise_ratio_ask_18[(index - index_one)])
rise_ratio_second_19.append(rise_ratio_ask_19[(index - index_one)])
rise_ratio_second_20.append(rise_ratio_ask_20[(index - index_one)])
rise_ratio_second_21.append(rise_ratio_ask_21[(index - index_one)])
rise_ratio_second_22.append(rise_ratio_ask_22[(index - index_one)])
rise_ratio_second_23.append(rise_ratio_ask_23[(index - index_one)])
rise_ratio_second_24.append(rise_ratio_ask_24[(index - index_one)])
rise_ratio_second_25.append(rise_ratio_ask_25[(index - index_one)])
rise_ratio_second_26.append(rise_ratio_ask_26[(index - index_one)])
rise_ratio_second_27.append(rise_ratio_ask_27[(index - index_one)])
rise_ratio_second_28.append(rise_ratio_ask_28[(index - index_one)])
rise_ratio_second_29.append(rise_ratio_ask_29[(index - index_one)])
rise_ratio_second_30.append(rise_ratio_ask_30[(index - index_one)])
w_divid_100.append(W_AB_100[index_one + (index - index_one)])
w_diff_100.append(W_A_B_100[index_one + (index - index_one)])
w_divid_010.append(W_AB_010[index_one + (index - index_one)])
w_diff_010.append(W_A_B_010[index_one + (index - index_one)])
w_divid_001.append(W_AB_001[index_one + (index - index_one)])
w_diff_001.append(W_A_B_001[index_one + (index - index_one)])
w_divid_910.append(W_AB_910[index_one + (index - index_one)])
w_diff_910.append(W_A_B_910[index_one + (index - index_one)])
w_divid_820.append(W_AB_820[index_one + (index - index_one)])
w_diff_820.append(W_A_B_820[index_one + (index - index_one)])
w_divid_730.append(W_AB_730[index_one + (index - index_one)])
w_diff_730.append(W_A_B_730[index_one + (index - index_one)])
w_divid_640.append(W_AB_640[index_one + (index - index_one)])
w_diff_640.append(W_A_B_640[index_one + (index - index_one)])
w_divid_550.append(W_AB_550[index_one + (index - index_one)])
w_diff_550.append(W_A_B_550[index_one + (index - index_one)])
w_divid_721.append(W_AB_721[index_one + (index - index_one)])
w_diff_721.append(W_A_B_721[index_one + (index - index_one)])
w_divid_532.append(W_AB_532[index_one + (index - index_one)])
w_diff_532.append(W_A_B_532[index_one + (index - index_one)])
w_divid_111.append(W_AB_111[index_one + (index - index_one)])
w_diff_111.append(W_A_B_111[index_one + (index - index_one)])
w_divid_190.append(W_AB_190[index_one + (index - index_one)])
w_diff_190.append(W_A_B_190[index_one + (index - index_one)])
w_divid_280.append(W_AB_280[index_one + (index - index_one)])
w_diff_280.append(W_A_B_280[index_one + (index - index_one)])
w_divid_370.append(W_AB_370[index_one + (index - index_one)])
w_diff_370.append(W_A_B_370[index_one + (index - index_one)])
w_divid_460.append(W_AB_460[index_one + (index - index_one)])
w_diff_460.append(W_A_B_460[index_one + (index - index_one)])
w_divid_127.append(W_AB_127[index_one + (index - index_one)])
w_diff_127.append(W_A_B_127[index_one + (index - index_one)])
w_divid_235.append(W_AB_235[index_one + (index - index_one)])
w_diff_235.append(W_A_B_235[index_one + (index - index_one)])
elif len(index_array) == 0:
if i < 25200 - traded_time:
index_min = np.where(time_second_basic <= i + traded_time)[0][-1]
traded_min = ask_price_1[index:index_min]
if bid_price_1[index] > min(traded_min):
traded.append(1)
else:
traded.append(0)
elif i >= 25200 - traded_time:
if bid_price_1[index] > ask_price_1[-1]:
traded.append(1)
else:
traded.append(0)
rise_ratio_second_1.append(rise_ratio_second_1[-1])
rise_ratio_second_2.append(rise_ratio_second_2[-1])
rise_ratio_second_3.append(rise_ratio_second_3[-1])
rise_ratio_second_4.append(rise_ratio_second_4[-1])
rise_ratio_second_5.append(rise_ratio_second_5[-1])
rise_ratio_second_6.append(rise_ratio_second_6[-1])
rise_ratio_second_7.append(rise_ratio_second_7[-1])
rise_ratio_second_8.append(rise_ratio_second_8[-1])
rise_ratio_second_9.append(rise_ratio_second_9[-1])
rise_ratio_second_10.append(rise_ratio_second_10[-1])
rise_ratio_second_11.append(rise_ratio_second_11[-1])
rise_ratio_second_12.append(rise_ratio_second_12[-1])
rise_ratio_second_13.append(rise_ratio_second_13[-1])
rise_ratio_second_14.append(rise_ratio_second_14[-1])
rise_ratio_second_15.append(rise_ratio_second_15[-1])
rise_ratio_second_16.append(rise_ratio_second_16[-1])
rise_ratio_second_17.append(rise_ratio_second_17[-1])
rise_ratio_second_18.append(rise_ratio_second_18[-1])
rise_ratio_second_19.append(rise_ratio_second_19[-1])
rise_ratio_second_20.append(rise_ratio_second_20[-1])
rise_ratio_second_21.append(rise_ratio_second_21[-1])
rise_ratio_second_22.append(rise_ratio_second_22[-1])
rise_ratio_second_23.append(rise_ratio_second_23[-1])
rise_ratio_second_24.append(rise_ratio_second_24[-1])
rise_ratio_second_25.append(rise_ratio_second_25[-1])
rise_ratio_second_26.append(rise_ratio_second_26[-1])
rise_ratio_second_27.append(rise_ratio_second_27[-1])
rise_ratio_second_28.append(rise_ratio_second_28[-1])
rise_ratio_second_29.append(rise_ratio_second_29[-1])
rise_ratio_second_30.append(rise_ratio_second_30[-1])
w_divid_100.append(w_divid_100[-1])
w_diff_100.append(w_diff_100[-1])
w_divid_010.append(w_divid_010[-1])
w_diff_010.append(w_diff_010[-1])
w_divid_001.append(w_divid_001[-1])
w_diff_001.append(w_diff_001[-1])
w_divid_910.append(w_divid_910[-1])
w_diff_910.append(w_diff_910[-1])
w_divid_820.append(w_divid_820[-1])
w_diff_820.append(w_diff_820[-1])
w_divid_730.append(w_divid_730[-1])
w_diff_730.append(w_diff_730[-1])
w_divid_640.append(w_divid_640[-1])
w_diff_640.append(w_diff_640[-1])
w_divid_550.append(w_divid_550[-1])
w_diff_550.append(w_diff_550[-1])
w_divid_721.append(w_divid_721[-1])
w_diff_721.append(w_diff_721[-1])
w_divid_532.append(w_divid_532[-1])
w_diff_532.append(w_diff_532[-1])
w_divid_111.append(w_divid_111[-1])
w_diff_111.append(w_diff_111[-1])
w_divid_190.append(w_divid_190[-1])
w_diff_190.append(w_diff_190[-1])
w_divid_280.append(w_divid_280[-1])
w_diff_280.append(w_diff_280[-1])
w_divid_370.append(w_divid_370[-1])
w_diff_370.append(w_diff_370[-1])
w_divid_460.append(w_divid_460[-1])
w_diff_460.append(w_diff_460[-1])
w_divid_127.append(w_divid_127[-1])
w_diff_127.append(w_diff_127[-1])
w_divid_235.append(w_divid_235[-1])
w_diff_235.append(w_diff_235[-1])
return traded,index_,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235
def data(month,day,traded_time):
timestamp,order_book_ ,bid_price_1, bid_price_2, bid_price_3,\
bid_quantity_1, bid_quantity_2, bid_quantity_3,\
ask_price_1, ask_price_2, ask_price_3,ask_quantity_1,\
ask_quantity_2, ask_quantity_3 = order_book(month,day)
time_second,time_second_basic = time_transform(timestamp)
Ask1 = ask_price_1[np.where(time_second_basic <= 0.0)[0][-1]:]
before_time = 60.0 * 6
rise_ratio_ask_1 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 6 + 30
rise_ratio_ask_2 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 7
rise_ratio_ask_3 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 7 + 30
rise_ratio_ask_4 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 8
rise_ratio_ask_5 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 8 + 30
rise_ratio_ask_6 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 9
rise_ratio_ask_7 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 9 + 30
rise_ratio_ask_8 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 10
rise_ratio_ask_9 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 10 + 30
rise_ratio_ask_10 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 11
rise_ratio_ask_11 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 11 + 30
rise_ratio_ask_12 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 12
rise_ratio_ask_13 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 12 + 30
rise_ratio_ask_14 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 13
rise_ratio_ask_15 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 13 + 30
rise_ratio_ask_16 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 14
rise_ratio_ask_17 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 14 + 30
rise_ratio_ask_18 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 15
rise_ratio_ask_19 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 15 + 30
rise_ratio_ask_20 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 16
rise_ratio_ask_21 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 16 + 30
rise_ratio_ask_22 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 17
rise_ratio_ask_23 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 17 + 30
rise_ratio_ask_24 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 18
rise_ratio_ask_25 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 18 + 30
rise_ratio_ask_26 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 19
rise_ratio_ask_27 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 19 + 30
rise_ratio_ask_28 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 20
rise_ratio_ask_29 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 20 + 30
rise_ratio_ask_30 = rise_ask(Ask1, time_second_basic, before_time)
#Weight Depth
w1,w2,w3 = [100.0, 0.0, 0.0]
W_AB_100 , W_A_B_100 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [0.0, 100.0, 0.0]
W_AB_010 , W_A_B_010 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [0.0, 0.0, 100.0]
W_AB_001 , W_A_B_001 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [90.0, 10.0, 0.0]
W_AB_910 , W_A_B_910 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [80.0, 20.0, 0.0]
W_AB_820 , W_A_B_820 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [70.0, 30.0, 0.0]
W_AB_730 , W_A_B_730 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [60.0, 40.0, 0.0]
W_AB_640 , W_A_B_640 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [50.0, 50.0, 0.0]
W_AB_550 , W_A_B_550 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [70.0, 20.0, 10.0]
W_AB_721 , W_A_B_721 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [50.0, 30.0, 20.0]
W_AB_532 , W_A_B_532 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [1.0, 1.0, 1.0]
W_AB_111 , W_A_B_111 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [10.0, 90.0, 1.0]
W_AB_190 , W_A_B_190 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [20.0, 80.0, 0.0]
W_AB_280 , W_A_B_280 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [30.0, 70.0, 0.0]
W_AB_370 , W_A_B_370 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [40.0, 60.0, 0.0]
W_AB_460 , W_A_B_460 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [10.0, 20.0, 70.0]
W_AB_127 , W_A_B_127 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [20.0, 30.0, 50.0]
W_AB_235 , W_A_B_235 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
data_2014_UP =\
Feature_DataFrame_UP(traded_time,time_second_basic,bid_price_1,ask_price_1,rise_ratio_ask_1,\
rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,rise_ratio_ask_5,\
rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,rise_ratio_ask_9,\
rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,rise_ratio_ask_13,\
rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,rise_ratio_ask_17,\
rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,rise_ratio_ask_21,\
rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,rise_ratio_ask_25,\
rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,rise_ratio_ask_29,\
rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010, W_AB_001,\
W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730 , W_A_B_730,\
W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721, W_AB_532,\
W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280 , W_A_B_280,\
W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127, W_AB_235, W_A_B_235)
data_2014_DOWN =\
Feature_DataFrame_DOWN(traded_time,time_second_basic,bid_price_1,ask_price_1,rise_ratio_ask_1,\
rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,rise_ratio_ask_5,\
rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,rise_ratio_ask_9,\
rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,rise_ratio_ask_13,\
rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,rise_ratio_ask_17,\
rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,rise_ratio_ask_21,\
rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,rise_ratio_ask_25,\
rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,rise_ratio_ask_29,\
rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010, W_AB_001,\
W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730 , W_A_B_730,\
W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721, W_AB_532,\
W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280 , W_A_B_280,\
W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127, W_AB_235, W_A_B_235)
return data_2014_UP,data_2014_DOWN,len(W_AB_111)#,trade_1,trade_2#,timestamp
def train_test_to_csv(month,day,traded_time):
data_UP,data_DOWN,len_ = data(month,day,traded_time)
path_up = '/home/rory/Demo/Data_Transformation/Train_Test_Builder/order_book_3_2014'\
+'_'+str(month)+'_'+str(day)+'_'+'UP'+'.csv'
path_down = '/home/rory/Demo/Data_Transformation/Train_Test_Builder/order_book_3_2014'\
+'_'+str(month)+'_'+str(day)+'_'+'DOWN'+'.csv'
data_UP.to_csv(path_up, index = False)
data_DOWN.to_csv(path_down, index = False)
month = 1
day_ = [2]
traded_time = 600
for i in day_:
print i
train_test_to_csv(month,i,600)
```
|
github_jupyter
|
%pylab inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
pwd
def order_book(month,day):
data = []
datapath = '/home/rory/Demo/Data_Transformation/Train_Test_Builder/order_book_3_2014'\
+ '_' + str(month) + '_' + str(day) + '.csv'
order_book = pd.read_csv(datapath,sep=',')
bid_price_1 = np.array(map(float,order_book['Bid'][1::4]))/100.0
bid_price_2 = np.array(map(float,order_book['Bid'][2::4]))/100.0
bid_price_3 = np.array(map(float,order_book['Bid'][3::4]))/100.0
timestamp = np.array(order_book['Bid_Quantity'][0::4])
bid_quantity_1 = np.array(map(float,order_book['Bid_Quantity'][1::4]))
bid_quantity_2 = np.array(map(float,order_book['Bid_Quantity'][2::4]))
bid_quantity_3 = np.array(map(float,order_book['Bid_Quantity'][3::4]))
ask_price_1 = np.array(map(float,order_book['Ask'][1::4]))/100.0
ask_price_2 = np.array(map(float,order_book['Ask'][2::4]))/100.0
ask_price_3 = np.array(map(float,order_book['Ask'][3::4]))/100.0
ask_quantity_1 = np.array(map(float,order_book['Ask_Quantity'][1::4]))
ask_quantity_2 = np.array(map(float,order_book['Ask_Quantity'][2::4]))
ask_quantity_3 = np.array(map(float,order_book['Ask_Quantity'][3::4]))
bid_quantity_1[isnan(bid_quantity_1)] = 0
bid_quantity_2[isnan(bid_quantity_2)] = 0
bid_quantity_3[isnan(bid_quantity_3)] = 0
ask_quantity_1[isnan(ask_quantity_1)] = 0
ask_quantity_2[isnan(ask_quantity_2)] = 0
ask_quantity_3[isnan(ask_quantity_3)] = 0
return timestamp,order_book,bid_price_1,bid_price_2,bid_price_3,bid_quantity_1,\
bid_quantity_2,bid_quantity_3,ask_price_1,ask_price_2,ask_price_3,ask_quantity_1,\
ask_quantity_2,ask_quantity_3
def time_transform(timestamp_time):
time_second_basic = []
time_second = []
for i in range(0,len(timestamp_time),1):
second = float(timestamp_time[i][11])*36000 + float(timestamp_time[i][12])*3600+\
float(timestamp_time[i][14])*600 + float(timestamp_time[i][15])*60+\
float(timestamp_time[i][17])*10 + float(timestamp_time[i][18])
time_second_basic.append(second - 32400.0)
time_second.append(second)
return np.array(time_second),np.array(time_second_basic)
def weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3):
Weight_Ask = (w1 * ask_quantity_1 + w2 * ask_quantity_2 + w3 * ask_quantity_3)
Weight_Bid = (w1 * bid_quantity_1 + w2 * bid_quantity_2 + w3 * bid_quantity_3)
W_AB = Weight_Ask/Weight_Bid
W_A_B = (Weight_Ask - Weight_Bid)/(Weight_Ask + Weight_Bid)
return W_AB, W_A_B
def Feature_DataFrame_UP(traded_time,time_second_basic,bid_price_1,ask_price_1,rise_ratio_ask_1,\
rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,rise_ratio_ask_5,\
rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,rise_ratio_ask_9,\
rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,rise_ratio_ask_13,\
rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,rise_ratio_ask_17,\
rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,rise_ratio_ask_21,\
rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,rise_ratio_ask_25,\
rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,rise_ratio_ask_29,\
rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010, W_AB_001,\
W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730 , W_A_B_730,\
W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721, W_AB_532,\
W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280 , W_A_B_280,\
W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127, W_AB_235, W_A_B_235):
# 09:00 ~ 11:30
time1 = 0
time2 = 9000
print len(W_AB_910)
traded,index_,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235=\
traded_label_one_second(time1,time2,time_second_basic,bid_price_1,ask_price_1,traded_time,\
rise_ratio_ask_1,rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,\
rise_ratio_ask_5,rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,\
rise_ratio_ask_9,rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,\
rise_ratio_ask_13,rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,\
rise_ratio_ask_17,rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,\
rise_ratio_ask_21,rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,\
rise_ratio_ask_25,rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,\
rise_ratio_ask_29,rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010,\
W_AB_001,W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730,\
W_A_B_730,W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721,\
W_AB_532,W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280,\
W_A_B_280,W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127,\
W_AB_235, W_A_B_235)
data = np.array([traded,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235]).T
return pd.DataFrame(data)#,traded_1 #, columns = ['label', 'rise', 'depth_divid', 'depth_diff'])
def Feature_DataFrame_DOWN(traded_time,time_second_basic,bid_price_1,ask_price_1,rise_ratio_ask_1,\
rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,rise_ratio_ask_5,\
rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,rise_ratio_ask_9,\
rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,rise_ratio_ask_13,\
rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,rise_ratio_ask_17,\
rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,rise_ratio_ask_21,\
rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,rise_ratio_ask_25,\
rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,rise_ratio_ask_29,\
rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010, W_AB_001,\
W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730 , W_A_B_730,\
W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721, W_AB_532,\
W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280 , W_A_B_280,\
W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127, W_AB_235, W_A_B_235):
# 13:00 ~ 16:00
time1 = 14400
time2 = 25200
traded,index_,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235 =\
traded_label_one_second(time1,time2,time_second_basic,bid_price_1,ask_price_1,traded_time,\
rise_ratio_ask_1,rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,\
rise_ratio_ask_5,rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,\
rise_ratio_ask_9,rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,\
rise_ratio_ask_13,rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,\
rise_ratio_ask_17,rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,\
rise_ratio_ask_21,rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,\
rise_ratio_ask_25,rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,\
rise_ratio_ask_29,rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010,\
W_AB_001,W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730,\
W_A_B_730,W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721,\
W_AB_532,W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280,\
W_A_B_280,W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127,\
W_AB_235, W_A_B_235)
data = np.array([traded,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235]).T
return pd.DataFrame(data)#,traded_2 #, columns = ['label', 'rise', 'depth_divid', 'depth_diff'])
def rise_ask(Ask1,timestamp_time_second,before_time):
Ask1[Ask1 == 0] = mean(Ask1)
rise_ratio = []
index = np.where(timestamp_time_second >= before_time)[0][0]
#open first before_time mins
for i in range(0,index,1):
rise_ratio_ = round((Ask1[i] - Ask1[0])*(1.0)/Ask1[0]*100,5)
rise_ratio.append(rise_ratio_)
for i in range(index,len(Ask1),1):
#print np.where(timestamp_time_second[:i] >= timestamp_time_second[i] - before_time)
#print timestamp_time_second[i],timestamp_time_second[i] - before_time
index_start = np.where(timestamp_time_second[:i] >= timestamp_time_second[i] - before_time)[0][0]
rise_ratio_ = round((Ask1[i] - Ask1[index_start])*(1.0)/Ask1[index_start]*100,5)
rise_ratio.append(rise_ratio_)
return np.array(rise_ratio)
def traded_label_one_second(time1,time2,time_second_basic,bid_price_1,ask_price_1,traded_time,\
rise_ratio_ask_1,rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,\
rise_ratio_ask_5,rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,\
rise_ratio_ask_9,rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,\
rise_ratio_ask_13,rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,\
rise_ratio_ask_17,rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,\
rise_ratio_ask_21,rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,\
rise_ratio_ask_25,rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,\
rise_ratio_ask_29,rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010,\
W_AB_001,W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730,\
W_A_B_730,W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721,\
W_AB_532,W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280,\
W_A_B_280,W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127,\
W_AB_235, W_A_B_235):
global index
traded = []
index_ = []
rise_ratio_second_1 = []
rise_ratio_second_2 = []
rise_ratio_second_3 = []
rise_ratio_second_4 = []
rise_ratio_second_5 = []
rise_ratio_second_6 = []
rise_ratio_second_7 = []
rise_ratio_second_8 = []
rise_ratio_second_9 = []
rise_ratio_second_10 = []
rise_ratio_second_11 = []
rise_ratio_second_12 = []
rise_ratio_second_13 = []
rise_ratio_second_14 = []
rise_ratio_second_15 = []
rise_ratio_second_16 = []
rise_ratio_second_17 = []
rise_ratio_second_18 = []
rise_ratio_second_19 = []
rise_ratio_second_20 = []
rise_ratio_second_21 = []
rise_ratio_second_22 = []
rise_ratio_second_23 = []
rise_ratio_second_24 = []
rise_ratio_second_25 = []
rise_ratio_second_26 = []
rise_ratio_second_27 = []
rise_ratio_second_28 = []
rise_ratio_second_29 = []
rise_ratio_second_30 = []
w_divid_100 = []
w_diff_100 = []
w_divid_010 = []
w_diff_010 = []
w_divid_001 = []
w_diff_001 = []
w_divid_910 = []
w_diff_910 = []
w_divid_820 = []
w_diff_820 = []
w_divid_730 = []
w_diff_730 = []
w_divid_640 = []
w_diff_640 = []
w_divid_550 = []
w_diff_550 = []
w_divid_721 = []
w_diff_721 = []
w_divid_532 = []
w_diff_532 = []
w_divid_111 = []
w_diff_111 = []
w_divid_190 = []
w_diff_190 = []
w_divid_280 = []
w_diff_280 = []
w_divid_370 = []
w_diff_370 = []
w_divid_460 = []
w_diff_460 = []
w_divid_127 = []
w_diff_127 = []
w_divid_235 = []
w_diff_235 = []
if time1 == 0:
index_one = np.where(time_second_basic <= 0)[0][-1]
elif time1 == 14400:
index_one = np.where(time_second_basic <= 14400)[0][-1]
for i in range(time1, time2, 1):
if i == 0 or i == 14400:
index_array = np.where(time_second_basic <= i)[-1]
else:
index_array = np.where((time_second_basic < i+1) & (time_second_basic >= i))[-1]
if len(index_array) > 0:
index = index_array[-1]
if i == time1:
index_.append(index)
if i == time2 - 1:
index_.append(index)
if i < 25200 - traded_time:
index_min = np.where(time_second_basic <= i + traded_time)[0][-1]
traded_min = ask_price_1[index:index_min]
if bid_price_1[index] > min(traded_min):
traded.append(1)
else:
traded.append(0)
elif i >= 25200 - traded_time:
if bid_price_1[index] > ask_price_1[-1]:
traded.append(1)
else:
traded.append(0)
rise_ratio_second_1.append(rise_ratio_ask_1[(index - index_one)])
rise_ratio_second_2.append(rise_ratio_ask_2[(index - index_one)])
rise_ratio_second_3.append(rise_ratio_ask_3[(index - index_one)])
rise_ratio_second_4.append(rise_ratio_ask_4[(index - index_one)])
rise_ratio_second_5.append(rise_ratio_ask_5[(index - index_one)])
rise_ratio_second_6.append(rise_ratio_ask_6[(index - index_one)])
rise_ratio_second_7.append(rise_ratio_ask_7[(index - index_one)])
rise_ratio_second_8.append(rise_ratio_ask_8[(index - index_one)])
rise_ratio_second_9.append(rise_ratio_ask_9[(index - index_one)])
rise_ratio_second_10.append(rise_ratio_ask_10[(index - index_one)])
rise_ratio_second_11.append(rise_ratio_ask_11[(index - index_one)])
rise_ratio_second_12.append(rise_ratio_ask_12[(index - index_one)])
rise_ratio_second_13.append(rise_ratio_ask_13[(index - index_one)])
rise_ratio_second_14.append(rise_ratio_ask_14[(index - index_one)])
rise_ratio_second_15.append(rise_ratio_ask_15[(index - index_one)])
rise_ratio_second_16.append(rise_ratio_ask_16[(index - index_one)])
rise_ratio_second_17.append(rise_ratio_ask_17[(index - index_one)])
rise_ratio_second_18.append(rise_ratio_ask_18[(index - index_one)])
rise_ratio_second_19.append(rise_ratio_ask_19[(index - index_one)])
rise_ratio_second_20.append(rise_ratio_ask_20[(index - index_one)])
rise_ratio_second_21.append(rise_ratio_ask_21[(index - index_one)])
rise_ratio_second_22.append(rise_ratio_ask_22[(index - index_one)])
rise_ratio_second_23.append(rise_ratio_ask_23[(index - index_one)])
rise_ratio_second_24.append(rise_ratio_ask_24[(index - index_one)])
rise_ratio_second_25.append(rise_ratio_ask_25[(index - index_one)])
rise_ratio_second_26.append(rise_ratio_ask_26[(index - index_one)])
rise_ratio_second_27.append(rise_ratio_ask_27[(index - index_one)])
rise_ratio_second_28.append(rise_ratio_ask_28[(index - index_one)])
rise_ratio_second_29.append(rise_ratio_ask_29[(index - index_one)])
rise_ratio_second_30.append(rise_ratio_ask_30[(index - index_one)])
w_divid_100.append(W_AB_100[index_one + (index - index_one)])
w_diff_100.append(W_A_B_100[index_one + (index - index_one)])
w_divid_010.append(W_AB_010[index_one + (index - index_one)])
w_diff_010.append(W_A_B_010[index_one + (index - index_one)])
w_divid_001.append(W_AB_001[index_one + (index - index_one)])
w_diff_001.append(W_A_B_001[index_one + (index - index_one)])
w_divid_910.append(W_AB_910[index_one + (index - index_one)])
w_diff_910.append(W_A_B_910[index_one + (index - index_one)])
w_divid_820.append(W_AB_820[index_one + (index - index_one)])
w_diff_820.append(W_A_B_820[index_one + (index - index_one)])
w_divid_730.append(W_AB_730[index_one + (index - index_one)])
w_diff_730.append(W_A_B_730[index_one + (index - index_one)])
w_divid_640.append(W_AB_640[index_one + (index - index_one)])
w_diff_640.append(W_A_B_640[index_one + (index - index_one)])
w_divid_550.append(W_AB_550[index_one + (index - index_one)])
w_diff_550.append(W_A_B_550[index_one + (index - index_one)])
w_divid_721.append(W_AB_721[index_one + (index - index_one)])
w_diff_721.append(W_A_B_721[index_one + (index - index_one)])
w_divid_532.append(W_AB_532[index_one + (index - index_one)])
w_diff_532.append(W_A_B_532[index_one + (index - index_one)])
w_divid_111.append(W_AB_111[index_one + (index - index_one)])
w_diff_111.append(W_A_B_111[index_one + (index - index_one)])
w_divid_190.append(W_AB_190[index_one + (index - index_one)])
w_diff_190.append(W_A_B_190[index_one + (index - index_one)])
w_divid_280.append(W_AB_280[index_one + (index - index_one)])
w_diff_280.append(W_A_B_280[index_one + (index - index_one)])
w_divid_370.append(W_AB_370[index_one + (index - index_one)])
w_diff_370.append(W_A_B_370[index_one + (index - index_one)])
w_divid_460.append(W_AB_460[index_one + (index - index_one)])
w_diff_460.append(W_A_B_460[index_one + (index - index_one)])
w_divid_127.append(W_AB_127[index_one + (index - index_one)])
w_diff_127.append(W_A_B_127[index_one + (index - index_one)])
w_divid_235.append(W_AB_235[index_one + (index - index_one)])
w_diff_235.append(W_A_B_235[index_one + (index - index_one)])
elif len(index_array) == 0:
if i < 25200 - traded_time:
index_min = np.where(time_second_basic <= i + traded_time)[0][-1]
traded_min = ask_price_1[index:index_min]
if bid_price_1[index] > min(traded_min):
traded.append(1)
else:
traded.append(0)
elif i >= 25200 - traded_time:
if bid_price_1[index] > ask_price_1[-1]:
traded.append(1)
else:
traded.append(0)
rise_ratio_second_1.append(rise_ratio_second_1[-1])
rise_ratio_second_2.append(rise_ratio_second_2[-1])
rise_ratio_second_3.append(rise_ratio_second_3[-1])
rise_ratio_second_4.append(rise_ratio_second_4[-1])
rise_ratio_second_5.append(rise_ratio_second_5[-1])
rise_ratio_second_6.append(rise_ratio_second_6[-1])
rise_ratio_second_7.append(rise_ratio_second_7[-1])
rise_ratio_second_8.append(rise_ratio_second_8[-1])
rise_ratio_second_9.append(rise_ratio_second_9[-1])
rise_ratio_second_10.append(rise_ratio_second_10[-1])
rise_ratio_second_11.append(rise_ratio_second_11[-1])
rise_ratio_second_12.append(rise_ratio_second_12[-1])
rise_ratio_second_13.append(rise_ratio_second_13[-1])
rise_ratio_second_14.append(rise_ratio_second_14[-1])
rise_ratio_second_15.append(rise_ratio_second_15[-1])
rise_ratio_second_16.append(rise_ratio_second_16[-1])
rise_ratio_second_17.append(rise_ratio_second_17[-1])
rise_ratio_second_18.append(rise_ratio_second_18[-1])
rise_ratio_second_19.append(rise_ratio_second_19[-1])
rise_ratio_second_20.append(rise_ratio_second_20[-1])
rise_ratio_second_21.append(rise_ratio_second_21[-1])
rise_ratio_second_22.append(rise_ratio_second_22[-1])
rise_ratio_second_23.append(rise_ratio_second_23[-1])
rise_ratio_second_24.append(rise_ratio_second_24[-1])
rise_ratio_second_25.append(rise_ratio_second_25[-1])
rise_ratio_second_26.append(rise_ratio_second_26[-1])
rise_ratio_second_27.append(rise_ratio_second_27[-1])
rise_ratio_second_28.append(rise_ratio_second_28[-1])
rise_ratio_second_29.append(rise_ratio_second_29[-1])
rise_ratio_second_30.append(rise_ratio_second_30[-1])
w_divid_100.append(w_divid_100[-1])
w_diff_100.append(w_diff_100[-1])
w_divid_010.append(w_divid_010[-1])
w_diff_010.append(w_diff_010[-1])
w_divid_001.append(w_divid_001[-1])
w_diff_001.append(w_diff_001[-1])
w_divid_910.append(w_divid_910[-1])
w_diff_910.append(w_diff_910[-1])
w_divid_820.append(w_divid_820[-1])
w_diff_820.append(w_diff_820[-1])
w_divid_730.append(w_divid_730[-1])
w_diff_730.append(w_diff_730[-1])
w_divid_640.append(w_divid_640[-1])
w_diff_640.append(w_diff_640[-1])
w_divid_550.append(w_divid_550[-1])
w_diff_550.append(w_diff_550[-1])
w_divid_721.append(w_divid_721[-1])
w_diff_721.append(w_diff_721[-1])
w_divid_532.append(w_divid_532[-1])
w_diff_532.append(w_diff_532[-1])
w_divid_111.append(w_divid_111[-1])
w_diff_111.append(w_diff_111[-1])
w_divid_190.append(w_divid_190[-1])
w_diff_190.append(w_diff_190[-1])
w_divid_280.append(w_divid_280[-1])
w_diff_280.append(w_diff_280[-1])
w_divid_370.append(w_divid_370[-1])
w_diff_370.append(w_diff_370[-1])
w_divid_460.append(w_divid_460[-1])
w_diff_460.append(w_diff_460[-1])
w_divid_127.append(w_divid_127[-1])
w_diff_127.append(w_diff_127[-1])
w_divid_235.append(w_divid_235[-1])
w_diff_235.append(w_diff_235[-1])
return traded,index_,rise_ratio_second_1,rise_ratio_second_2,rise_ratio_second_3,\
rise_ratio_second_4,rise_ratio_second_5,rise_ratio_second_6,rise_ratio_second_7,\
rise_ratio_second_8,rise_ratio_second_9,rise_ratio_second_10,rise_ratio_second_11,\
rise_ratio_second_12,rise_ratio_second_13,rise_ratio_second_14,rise_ratio_second_15,\
rise_ratio_second_16,rise_ratio_second_17,rise_ratio_second_18,rise_ratio_second_19,\
rise_ratio_second_20,rise_ratio_second_21,rise_ratio_second_22,rise_ratio_second_23,\
rise_ratio_second_24,rise_ratio_second_25,rise_ratio_second_26,rise_ratio_second_27,\
rise_ratio_second_28,rise_ratio_second_29,rise_ratio_second_30,w_divid_100,w_diff_100,\
w_divid_010,w_diff_010,w_divid_001,w_diff_001,w_divid_910,w_diff_910,w_divid_820,w_diff_820,\
w_divid_730,w_diff_730,w_divid_640,w_diff_640,w_divid_550,w_diff_550,w_divid_721,w_diff_721,\
w_divid_532,w_diff_532,w_divid_111,w_diff_111,w_divid_190,w_diff_190,w_divid_280,w_diff_280,\
w_divid_370,w_diff_370,w_divid_460,w_diff_460,w_divid_127,w_diff_127,w_divid_235,w_diff_235
def data(month,day,traded_time):
timestamp,order_book_ ,bid_price_1, bid_price_2, bid_price_3,\
bid_quantity_1, bid_quantity_2, bid_quantity_3,\
ask_price_1, ask_price_2, ask_price_3,ask_quantity_1,\
ask_quantity_2, ask_quantity_3 = order_book(month,day)
time_second,time_second_basic = time_transform(timestamp)
Ask1 = ask_price_1[np.where(time_second_basic <= 0.0)[0][-1]:]
before_time = 60.0 * 6
rise_ratio_ask_1 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 6 + 30
rise_ratio_ask_2 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 7
rise_ratio_ask_3 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 7 + 30
rise_ratio_ask_4 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 8
rise_ratio_ask_5 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 8 + 30
rise_ratio_ask_6 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 9
rise_ratio_ask_7 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 9 + 30
rise_ratio_ask_8 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 10
rise_ratio_ask_9 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 10 + 30
rise_ratio_ask_10 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 11
rise_ratio_ask_11 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 11 + 30
rise_ratio_ask_12 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 12
rise_ratio_ask_13 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 12 + 30
rise_ratio_ask_14 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 13
rise_ratio_ask_15 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 13 + 30
rise_ratio_ask_16 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 14
rise_ratio_ask_17 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 14 + 30
rise_ratio_ask_18 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 15
rise_ratio_ask_19 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 15 + 30
rise_ratio_ask_20 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 16
rise_ratio_ask_21 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 16 + 30
rise_ratio_ask_22 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 17
rise_ratio_ask_23 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 17 + 30
rise_ratio_ask_24 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 18
rise_ratio_ask_25 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 18 + 30
rise_ratio_ask_26 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 19
rise_ratio_ask_27 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 19 + 30
rise_ratio_ask_28 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 20
rise_ratio_ask_29 = rise_ask(Ask1, time_second_basic, before_time)
before_time = 60.0 * 20 + 30
rise_ratio_ask_30 = rise_ask(Ask1, time_second_basic, before_time)
#Weight Depth
w1,w2,w3 = [100.0, 0.0, 0.0]
W_AB_100 , W_A_B_100 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [0.0, 100.0, 0.0]
W_AB_010 , W_A_B_010 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [0.0, 0.0, 100.0]
W_AB_001 , W_A_B_001 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [90.0, 10.0, 0.0]
W_AB_910 , W_A_B_910 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [80.0, 20.0, 0.0]
W_AB_820 , W_A_B_820 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [70.0, 30.0, 0.0]
W_AB_730 , W_A_B_730 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [60.0, 40.0, 0.0]
W_AB_640 , W_A_B_640 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [50.0, 50.0, 0.0]
W_AB_550 , W_A_B_550 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [70.0, 20.0, 10.0]
W_AB_721 , W_A_B_721 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [50.0, 30.0, 20.0]
W_AB_532 , W_A_B_532 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [1.0, 1.0, 1.0]
W_AB_111 , W_A_B_111 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [10.0, 90.0, 1.0]
W_AB_190 , W_A_B_190 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [20.0, 80.0, 0.0]
W_AB_280 , W_A_B_280 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [30.0, 70.0, 0.0]
W_AB_370 , W_A_B_370 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [40.0, 60.0, 0.0]
W_AB_460 , W_A_B_460 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [10.0, 20.0, 70.0]
W_AB_127 , W_A_B_127 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
w1,w2,w3 = [20.0, 30.0, 50.0]
W_AB_235 , W_A_B_235 = weight_pecentage(w1,w2,w3,ask_quantity_1,ask_quantity_2,ask_quantity_3,\
bid_quantity_1,bid_quantity_2,bid_quantity_3)
data_2014_UP =\
Feature_DataFrame_UP(traded_time,time_second_basic,bid_price_1,ask_price_1,rise_ratio_ask_1,\
rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,rise_ratio_ask_5,\
rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,rise_ratio_ask_9,\
rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,rise_ratio_ask_13,\
rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,rise_ratio_ask_17,\
rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,rise_ratio_ask_21,\
rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,rise_ratio_ask_25,\
rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,rise_ratio_ask_29,\
rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010, W_AB_001,\
W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730 , W_A_B_730,\
W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721, W_AB_532,\
W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280 , W_A_B_280,\
W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127, W_AB_235, W_A_B_235)
data_2014_DOWN =\
Feature_DataFrame_DOWN(traded_time,time_second_basic,bid_price_1,ask_price_1,rise_ratio_ask_1,\
rise_ratio_ask_2,rise_ratio_ask_3,rise_ratio_ask_4,rise_ratio_ask_5,\
rise_ratio_ask_6,rise_ratio_ask_7,rise_ratio_ask_8,rise_ratio_ask_9,\
rise_ratio_ask_10,rise_ratio_ask_11,rise_ratio_ask_12,rise_ratio_ask_13,\
rise_ratio_ask_14,rise_ratio_ask_15,rise_ratio_ask_16,rise_ratio_ask_17,\
rise_ratio_ask_18,rise_ratio_ask_19,rise_ratio_ask_20,rise_ratio_ask_21,\
rise_ratio_ask_22,rise_ratio_ask_23,rise_ratio_ask_24,rise_ratio_ask_25,\
rise_ratio_ask_26,rise_ratio_ask_27,rise_ratio_ask_28,rise_ratio_ask_29,\
rise_ratio_ask_30,W_AB_100, W_A_B_100, W_AB_010, W_A_B_010, W_AB_001,\
W_A_B_001, W_AB_910, W_A_B_910, W_AB_820, W_A_B_820, W_AB_730 , W_A_B_730,\
W_AB_640, W_A_B_640, W_AB_550, W_A_B_550,W_AB_721, W_A_B_721, W_AB_532,\
W_A_B_532, W_AB_111, W_A_B_111, W_AB_190, W_A_B_190, W_AB_280 , W_A_B_280,\
W_AB_370, W_A_B_370, W_AB_460, W_A_B_460, W_AB_127, W_A_B_127, W_AB_235, W_A_B_235)
return data_2014_UP,data_2014_DOWN,len(W_AB_111)#,trade_1,trade_2#,timestamp
def train_test_to_csv(month,day,traded_time):
data_UP,data_DOWN,len_ = data(month,day,traded_time)
path_up = '/home/rory/Demo/Data_Transformation/Train_Test_Builder/order_book_3_2014'\
+'_'+str(month)+'_'+str(day)+'_'+'UP'+'.csv'
path_down = '/home/rory/Demo/Data_Transformation/Train_Test_Builder/order_book_3_2014'\
+'_'+str(month)+'_'+str(day)+'_'+'DOWN'+'.csv'
data_UP.to_csv(path_up, index = False)
data_DOWN.to_csv(path_down, index = False)
month = 1
day_ = [2]
traded_time = 600
for i in day_:
print i
train_test_to_csv(month,i,600)
| 0.295738 | 0.415788 |
# Inference with Discrete Latent Variables
This tutorial describes Pyro's enumeration strategy for discrete latent variable models.
This tutorial assumes the reader is already familiar with the [Tensor Shapes Tutorial](http://pyro.ai/examples/tensor_shapes.html).
#### Summary
- Pyro implements automatic enumeration over discrete latent variables.
- This strategy can be used alone or inside SVI (via [TraceEnum_ELBO](http://docs.pyro.ai/en/dev/inference_algos.html#pyro.infer.traceenum_elbo.TraceEnum_ELBO)), HMC, or NUTS.
- The standalone [infer_discrete](http://docs.pyro.ai/en/dev/inference_algos.html#pyro.infer.discrete.infer_discrete) can generate samples or MAP estimates.
- Annotate a sample site `infer={"enumerate": "parallel"}` to trigger enumeration.
- If a sample site determines downstream structure, instead use `{"enumerate": "sequential"}`.
- Write your models to allow arbitrarily deep batching on the left, e.g. use broadcasting.
- Inference cost is exponential in treewidth, so try to write models with narrow treewidth.
- If you have trouble, ask for help on [forum.pyro.ai](https://forum.pyro.ai)!
#### Table of contents
- [Overview](#Overview)
- [Mechanics of enumeration](#Mechanics-of-enumeration)
- [Multiple latent variables](#Multiple-latent-variables)
- [Examining discrete latent states](#Examining-discrete-latent-states)
- [Plates and enumeration](#Plates-and-enumeration)
- [Dependencies among plates](#Dependencies-among-plates)
- [Time series example](#Time-series-example)
- [How to enumerate more than 25 variables](#How-to-enumerate-more-than-25-variables)
```
import os
import torch
import pyro
import pyro.distributions as dist
from torch.distributions import constraints
from pyro import poutine
from pyro.infer import SVI, Trace_ELBO, TraceEnum_ELBO, config_enumerate, infer_discrete
from pyro.contrib.autoguide import AutoDiagonalNormal
smoke_test = ('CI' in os.environ)
assert pyro.__version__.startswith('0.3.0')
pyro.enable_validation()
pyro.set_rng_seed(0)
```
## Overview <a class="anchor" id="Overview"></a>
Pyro's enumeration strategy encompasses popular algorithms including variable elimination, exact message passing, forward-filter-backward-sample, inside-out, Baum-Welch, and many other special-case algorithms. Aside from enumeration, Pyro implements a number of inference strategies including variational inference ([SVI](http://docs.pyro.ai/en/dev/inference_algos.html)) and monte carlo ([HMC](http://docs.pyro.ai/en/dev/mcmc.html#pyro.infer.mcmc.HMC) and [NUTS](http://docs.pyro.ai/en/dev/mcmc.html#pyro.infer.mcmc.NUTS)). Enumeration can be used either as a stand-alone strategy via [infer_discrete](http://docs.pyro.ai/en/dev/inference_algos.html#pyro.infer.discrete.infer_discrete), or as a component of other strategies. Thus enumeration allows Pyro to marginalize out discrete latent variables in HMC and SVI models, and to use variational enumeration of discrete variables in SVI guides.
## Mechanics of enumeration <a class="anchor" id="Mechanics-of-enumeration"></a>
The core idea of enumeration is to interpret discrete [pyro.sample](http://docs.pyro.ai/en/dev/primitives.html#pyro.sample) statements as full enumeration rather than random sampling. Other inference algorithms can then sum out the enumerated values. For example a sample statement might return a tensor of scalar shape under the standard "sample" interpretation (we'll illustrate with trivial model and guide):
```
def model():
z = pyro.sample("z", dist.Categorical(torch.ones(5)))
print('model z = {}'.format(z))
def guide():
z = pyro.sample("z", dist.Categorical(torch.ones(5)))
print('guide z = {}'.format(z))
elbo = Trace_ELBO()
elbo.loss(model, guide);
```
However under the enumeration interpretation, the same sample site will return a fully enumerated set of values, based on its distribution's [.enumerate_support()](https://pytorch.org/docs/stable/distributions.html#torch.distributions.distribution.Distribution.enumerate_support) method.
```
elbo = TraceEnum_ELBO(max_plate_nesting=0)
elbo.loss(model, config_enumerate(guide, "parallel"));
```
Note that we've used "parallel" enumeration to enumerate along a new tensor dimension. This is cheap and allows Pyro to parallelize computation, but requires downstream program structure to avoid branching on the value of `z`. To support dynamic program structure, you can instead use "sequential" enumeration, which runs the entire model,guide pair once per sample value, but requires running the model multiple times.
```
elbo = TraceEnum_ELBO(max_plate_nesting=0)
elbo.loss(model, config_enumerate(guide, "sequential"));
```
Parallel enumeration is cheaper but more complex than sequential enumeration, so we'll focus the rest of this tutorial on the parallel variant. Note that both forms can be interleaved.
### Multiple latent variables <a class="anchor" id="Multiple-latent-variables"></a>
We just saw that a single discrete sample site can be enumerated via nonstandard interpretation. A model with a single discrete latent variable is a mixture model. Models with multiple discrete latent variables can be more complex, including HMMs, CRFs, DBNs, and other structured models. In models with multiple discrete latent variables, Pyro enumerates each variable in a different tensor dimension (counting from the right; see [Tensor Shapes Tutorial](http://pyro.ai/examples/tensor_shapes.html)). This allows Pyro to determine the dependency graph among variables and then perform cheap exact inference using variable elimination algorithms.
To understand enumeration dimension allocation, consider the following model, where here we collapse variables out of the model, rather than enumerate them in the guide.
```
@config_enumerate
def model():
p = pyro.param("p", torch.randn(3, 3).exp(), constraint=constraints.simplex)
x = pyro.sample("x", dist.Categorical(p[0]))
y = pyro.sample("y", dist.Categorical(p[x]))
z = pyro.sample("z", dist.Categorical(p[y]))
print('model x.shape = {}'.format(x.shape))
print('model y.shape = {}'.format(y.shape))
print('model z.shape = {}'.format(z.shape))
return x, y, z
def guide():
pass
pyro.clear_param_store()
elbo = TraceEnum_ELBO(max_plate_nesting=0)
elbo.loss(model, guide);
```
### Examining discrete latent states <a class="anchor" id="Examining-discrete-latent-states"></a>
While enumeration in SVI allows fast learning of parameters like `p` above, it does not give access to predicted values of the discrete latent variables like `x,y,z` above. We can access these using a standalone [infer_discrete](http://docs.pyro.ai/en/dev/inference_algos.html#pyro.infer.discrete.infer_discrete) handler. In this case the guide was trivial, so we can simply wrap the model in `infer_discrete`. We need to pass a `first_available_dim` argument to tell `infer_discrete` which dimensions are available for enumeration; this is related to the `max_plate_nesting` arg of `TraceEnum_ELBO` via
```
first_available_dim = -1 - max_plate_nesting
```
```
serving_model = infer_discrete(model, first_available_dim=-1)
x, y, z = serving_model() # takes the same args as model(), here no args
print("x = {}".format(x))
print("y = {}".format(y))
print("z = {}".format(z))
```
Notice that under the hood `infer_discrete` runs the model twice: first in forward-filter mode where sites are enumerated, then in replay-backward-sample model where sites are sampled. `infer_discrete` can also perform MAP inference by passing `temperature=0`. Note that while `infer_discrete` produces correct posterior samples, it does not currently produce correct logprobs, and should not be used in other gradient-based inference algorthms.
## Plates and enumeration <a class="anchor" id="Plates-and-enumeration"></a>
Pyro [plates](http://docs.pyro.ai/en/dev/primitives.html#pyro.plate) express conditional independence among random variables. Pyro's enumeration strategy can take advantage of plates to reduce the high cost (exponential in the size of the plate) of enumerating a cartesian product down to a low cost (linear in the size of the plate) of enumerating conditionally independent random variables in lock-step. This is especially important for e.g. minibatched data.
To illustrate, consider a gaussian mixture model with shared variance and different mean.
```
@config_enumerate
def model(data, num_components=3):
print('Running model with {} data points'.format(len(data)))
p = pyro.sample("p", dist.Dirichlet(0.5 * torch.ones(3)))
scale = pyro.sample("scale", dist.LogNormal(0, num_components))
with pyro.plate("components", num_components):
loc = pyro.sample("loc", dist.Normal(0, 10))
with pyro.plate("data", len(data)):
x = pyro.sample("x", dist.Categorical(p))
print("x.shape = {}".format(x.shape))
pyro.sample("obs", dist.Normal(loc[x], scale), obs=data)
print("dist.Normal(loc[x], scale).batch_shape = {}".format(
dist.Normal(loc[x], scale).batch_shape))
guide = AutoDiagonalNormal(poutine.block(model, hide=["x", "data"]))
data = torch.randn(10)
pyro.clear_param_store()
elbo = TraceEnum_ELBO(max_plate_nesting=1)
elbo.loss(model, guide, data);
```
Observe that the model is run twice, first by the `AutoDiagonalNormal` to trace sample sites, and second by `elbo` to compute loss. In the first run, `x` has the standard interpretation of one sample per datum, hence shape `(10,)`. In the second run enumeration can use the same three values `(3,1)` for all data points, and relies on broadcasting for any dependent sample or observe sites that depend on data. For example, in the `pyro.sample("obs",...)` statement, the distribution has shape `(3,1)`, the data has shape`(10,)`, and the broadcasted log probability tensor has shape `(3,10)`.
For a more in-depth treatment of enumeration in mixture models, see the [Gaussian Mixture Model Tutorial](http://pyro.ai/examples/gmm.html) and the.
### Dependencies among plates <a class="anchor" id="Dependencies-among-plates"></a>
The computational savings of enumerating in vectorized plates comes with restrictions on the dependency structure of models. These restrictions are in addition to the usual restrictions of conditional independence. The enumeration restrictions are checked by `TraceEnum_ELBO` and will result in an error if violated (however the usual conditional independence restriction cannot be generally verified by Pyro). For completeness we list all three restrictions:
#### Restriction 1: conditional independence
Variables within a plate may not depend on each other (along the plate dimension). This applies to any variable, whether or not it is enumerated. This applies to both sequential plates and vectorized plates. For example the following model is invalid:
```py
def invalid_model():
x = 0
for i in pyro.plate("invalid", 10):
x = pyro.sample("x_{}".format(i), dist.Normal(x, 1.))
```
#### Restriction 2: no downstream coupling
No variable outside of a vectorized plate can depend on an enumerated variable inside of that plate. This would violate Pyro's exponential speedup assumption. For example the following model is invalid:
```py
@config_enumerate
def invalid_model(data):
with pyro.plate("plate", 10): # <--- invalid vectorized plate
x = pyro.sample("x", dist.Bernoulli(0.5))
assert x.shape == (10,)
pyro.sample("obs", dist.Normal(x.sum(), 1.), data)
```
To work around this restriction, you can convert the vectorized plate to a sequential plate:
```py
@config_enumerate
def valid_model(data):
x = []
for i in pyro.plate("plate", 10): # <--- valid sequential plate
x.append(pyro.sample("x_{}".format(i), dist.Bernoulli(0.5)))
assert len(x) == 10
pyro.sample("obs", dist.Normal(sum(x), 1.), data)
```
#### Restriction 3: single path leaving each plate
The final restriction is subtle, but is required to enable Pyro's exponential speedup
> For any enumerated variable `x`, the set of all enumerated variables on which `x` depends must be linearly orderable in their vectorized plate nesting.
This requirement only applies when there are at least two plates and at least three variables in different plate contexts. The simplest counterexample is a Boltzmann machine
```py
@config_enumerate
def invalid_model(data):
plate_1 = pyro.plate("plate_1", 10, dim=-1) # vectorized
plate_2 = pyro.plate("plate_2", 10, dim=-2) # vectorized
with plate_1:
x = pyro.sample("y", dist.Bernoulli(0.5))
with plate_2:
y = pyro.sample("x", dist.Bernoulli(0.5))
with plate_1, plate2:
z = pyro.sample("z", dist.Bernoulli((1. + x + y) / 4.))
...
```
Here we see that the variable `z` depends on variable `x` (which is in `plate_1` but not `plate_2`) and depends on variable `y` (which is in `plate_2` but not `plate_1`). This model is invalid because there is no way to linearly order `x` and `y` such that one's plate nesting is less than the other.
To work around this restriction, you can convert one of the plates to a sequential plate:
```py
@config_enumerate
def valid_model(data):
plate_1 = pyro.plate("plate_1", 10, dim=-1) # vectorized
plate_2 = pyro.plate("plate_2", 10) # sequential
with plate_1:
x = pyro.sample("y", dist.Bernoulli(0.5))
for i in plate_2:
y = pyro.sample("x_{}".format(i), dist.Bernoulli(0.5))
with plate_1:
z = pyro.sample("z_{}".format(i), dist.Bernoulli((1. + x + y) / 4.))
...
```
but beware that this increases the computational complexity, which may be exponential in the size of the sequential plate.
## Time series example <a class="anchor" id="Time-series-example"></a>
Consider a discrete HMM with latent states $x_t$ and observations $y_t$. Suppose we want to learn the transition and emission probabilities.
```
data_dim = 4
num_steps = 10
data = dist.Categorical(torch.ones(num_steps, data_dim)).sample()
def hmm_model(data, data_dim, hidden_dim=10):
print('Running for {} time steps'.format(len(data)))
# Sample global matrices wrt a Jeffreys prior.
with pyro.plate("hidden_state", hidden_dim):
transition = pyro.sample("transition", dist.Dirichlet(0.5 * torch.ones(hidden_dim)))
emission = pyro.sample("emission", dist.Dirichlet(0.5 * torch.ones(data_dim)))
x = 0 # initial state
for t, y in enumerate(data):
x = pyro.sample("x_{}".format(t), dist.Categorical(transition[x]),
infer={"enumerate": "parallel"})
pyro.sample("y_{}".format(t), dist.Categorical(emission[x]), obs=y)
print("x_{}.shape = {}".format(t, x.shape))
```
We can learn the global parameters using SVI with an autoguide.
```
hmm_guide = AutoDiagonalNormal(poutine.block(hmm_model, expose=["transition", "emission"]))
pyro.clear_param_store()
elbo = TraceEnum_ELBO(max_plate_nesting=1)
elbo.loss(hmm_model, hmm_guide, data, data_dim=data_dim);
```
Notice that the model was run twice here: first it was run without enumeration by `AutoDiagonalNormal`, so that the autoguide can record all sample sites; then second it is run by `TraceEnum_ELBO` with enumeration enabled. We see in the first run that samples have the standard interpretation, whereas in the second run samples have the enumeration interpretation.
For more complex examples, including minibatching and multiple plates, see the [HMM tutorial](https://github.com/uber/pyro/blob/dev/examples/hmm.py).
### How to enumerate more than 25 variables <a class="anchor" id="How-to-enumerate-more-than-25-variables"></a>
PyTorch tensors have a dimension limit of 25 in CUDA and 64 in CPU. By default Pyro enumerates each sample site in a new dimension. If you need more sample sites, you can annotate your model with [pyro.markov](http://docs.pyro.ai/en/dev/poutine.html#pyro.poutine.markov) to tell Pyro when it is safe to recycle tensor dimensions. Let's see how that works with the HMM model from above. The only change we need is to annotate the for loop with `pyro.markov`, informing Pyro that the variables in each step of the loop depend only on variables outside of the loop and variables at this step and the previous step of the loop:
```diff
- for t, y in enumerate(data):
+ for t, y in pyro.markov(enumerate(data)):
```
```
def hmm_model(data, data_dim, hidden_dim=10):
with pyro.plate("hidden_state", hidden_dim):
transition = pyro.sample("transition", dist.Dirichlet(0.5 * torch.ones(hidden_dim)))
emission = pyro.sample("emission", dist.Dirichlet(0.5 * torch.ones(data_dim)))
x = 0 # initial state
for t, y in pyro.markov(enumerate(data)):
x = pyro.sample("x_{}".format(t), dist.Categorical(transition[x]),
infer={"enumerate": "parallel"})
pyro.sample("y_{}".format(t), dist.Categorical(emission[x]), obs=y)
print("x_{}.shape = {}".format(t, x.shape))
# We'll reuse the same guide and elbo.
elbo.loss(hmm_model, hmm_guide, data, data_dim=data_dim);
```
Notice that this model now only needs three tensor dimensions: one for the plate, one for even states, and one for odd states. For more complex examples, see the Dynamic Bayes Net model in the [HMM example](https://github.com/uber/pyro/blob/dev/examples/hmm.py).
|
github_jupyter
|
import os
import torch
import pyro
import pyro.distributions as dist
from torch.distributions import constraints
from pyro import poutine
from pyro.infer import SVI, Trace_ELBO, TraceEnum_ELBO, config_enumerate, infer_discrete
from pyro.contrib.autoguide import AutoDiagonalNormal
smoke_test = ('CI' in os.environ)
assert pyro.__version__.startswith('0.3.0')
pyro.enable_validation()
pyro.set_rng_seed(0)
def model():
z = pyro.sample("z", dist.Categorical(torch.ones(5)))
print('model z = {}'.format(z))
def guide():
z = pyro.sample("z", dist.Categorical(torch.ones(5)))
print('guide z = {}'.format(z))
elbo = Trace_ELBO()
elbo.loss(model, guide);
elbo = TraceEnum_ELBO(max_plate_nesting=0)
elbo.loss(model, config_enumerate(guide, "parallel"));
elbo = TraceEnum_ELBO(max_plate_nesting=0)
elbo.loss(model, config_enumerate(guide, "sequential"));
@config_enumerate
def model():
p = pyro.param("p", torch.randn(3, 3).exp(), constraint=constraints.simplex)
x = pyro.sample("x", dist.Categorical(p[0]))
y = pyro.sample("y", dist.Categorical(p[x]))
z = pyro.sample("z", dist.Categorical(p[y]))
print('model x.shape = {}'.format(x.shape))
print('model y.shape = {}'.format(y.shape))
print('model z.shape = {}'.format(z.shape))
return x, y, z
def guide():
pass
pyro.clear_param_store()
elbo = TraceEnum_ELBO(max_plate_nesting=0)
elbo.loss(model, guide);
first_available_dim = -1 - max_plate_nesting
serving_model = infer_discrete(model, first_available_dim=-1)
x, y, z = serving_model() # takes the same args as model(), here no args
print("x = {}".format(x))
print("y = {}".format(y))
print("z = {}".format(z))
@config_enumerate
def model(data, num_components=3):
print('Running model with {} data points'.format(len(data)))
p = pyro.sample("p", dist.Dirichlet(0.5 * torch.ones(3)))
scale = pyro.sample("scale", dist.LogNormal(0, num_components))
with pyro.plate("components", num_components):
loc = pyro.sample("loc", dist.Normal(0, 10))
with pyro.plate("data", len(data)):
x = pyro.sample("x", dist.Categorical(p))
print("x.shape = {}".format(x.shape))
pyro.sample("obs", dist.Normal(loc[x], scale), obs=data)
print("dist.Normal(loc[x], scale).batch_shape = {}".format(
dist.Normal(loc[x], scale).batch_shape))
guide = AutoDiagonalNormal(poutine.block(model, hide=["x", "data"]))
data = torch.randn(10)
pyro.clear_param_store()
elbo = TraceEnum_ELBO(max_plate_nesting=1)
elbo.loss(model, guide, data);
def invalid_model():
x = 0
for i in pyro.plate("invalid", 10):
x = pyro.sample("x_{}".format(i), dist.Normal(x, 1.))
@config_enumerate
def invalid_model(data):
with pyro.plate("plate", 10): # <--- invalid vectorized plate
x = pyro.sample("x", dist.Bernoulli(0.5))
assert x.shape == (10,)
pyro.sample("obs", dist.Normal(x.sum(), 1.), data)
@config_enumerate
def valid_model(data):
x = []
for i in pyro.plate("plate", 10): # <--- valid sequential plate
x.append(pyro.sample("x_{}".format(i), dist.Bernoulli(0.5)))
assert len(x) == 10
pyro.sample("obs", dist.Normal(sum(x), 1.), data)
@config_enumerate
def invalid_model(data):
plate_1 = pyro.plate("plate_1", 10, dim=-1) # vectorized
plate_2 = pyro.plate("plate_2", 10, dim=-2) # vectorized
with plate_1:
x = pyro.sample("y", dist.Bernoulli(0.5))
with plate_2:
y = pyro.sample("x", dist.Bernoulli(0.5))
with plate_1, plate2:
z = pyro.sample("z", dist.Bernoulli((1. + x + y) / 4.))
...
@config_enumerate
def valid_model(data):
plate_1 = pyro.plate("plate_1", 10, dim=-1) # vectorized
plate_2 = pyro.plate("plate_2", 10) # sequential
with plate_1:
x = pyro.sample("y", dist.Bernoulli(0.5))
for i in plate_2:
y = pyro.sample("x_{}".format(i), dist.Bernoulli(0.5))
with plate_1:
z = pyro.sample("z_{}".format(i), dist.Bernoulli((1. + x + y) / 4.))
...
data_dim = 4
num_steps = 10
data = dist.Categorical(torch.ones(num_steps, data_dim)).sample()
def hmm_model(data, data_dim, hidden_dim=10):
print('Running for {} time steps'.format(len(data)))
# Sample global matrices wrt a Jeffreys prior.
with pyro.plate("hidden_state", hidden_dim):
transition = pyro.sample("transition", dist.Dirichlet(0.5 * torch.ones(hidden_dim)))
emission = pyro.sample("emission", dist.Dirichlet(0.5 * torch.ones(data_dim)))
x = 0 # initial state
for t, y in enumerate(data):
x = pyro.sample("x_{}".format(t), dist.Categorical(transition[x]),
infer={"enumerate": "parallel"})
pyro.sample("y_{}".format(t), dist.Categorical(emission[x]), obs=y)
print("x_{}.shape = {}".format(t, x.shape))
hmm_guide = AutoDiagonalNormal(poutine.block(hmm_model, expose=["transition", "emission"]))
pyro.clear_param_store()
elbo = TraceEnum_ELBO(max_plate_nesting=1)
elbo.loss(hmm_model, hmm_guide, data, data_dim=data_dim);
- for t, y in enumerate(data):
+ for t, y in pyro.markov(enumerate(data)):
def hmm_model(data, data_dim, hidden_dim=10):
with pyro.plate("hidden_state", hidden_dim):
transition = pyro.sample("transition", dist.Dirichlet(0.5 * torch.ones(hidden_dim)))
emission = pyro.sample("emission", dist.Dirichlet(0.5 * torch.ones(data_dim)))
x = 0 # initial state
for t, y in pyro.markov(enumerate(data)):
x = pyro.sample("x_{}".format(t), dist.Categorical(transition[x]),
infer={"enumerate": "parallel"})
pyro.sample("y_{}".format(t), dist.Categorical(emission[x]), obs=y)
print("x_{}.shape = {}".format(t, x.shape))
# We'll reuse the same guide and elbo.
elbo.loss(hmm_model, hmm_guide, data, data_dim=data_dim);
| 0.680029 | 0.959001 |
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Automated Machine Learning
_**Prepare Data using `azureml.dataprep` for Remote Execution (DSVM)**_
## Contents
1. [Introduction](#Introduction)
1. [Setup](#Setup)
1. [Data](#Data)
1. [Train](#Train)
1. [Results](#Results)
1. [Test](#Test)
## Introduction
In this example we showcase how you can use the `azureml.dataprep` SDK to load and prepare data for AutoML. `azureml.dataprep` can also be used standalone; full documentation can be found [here](https://github.com/Microsoft/PendletonDocs).
Make sure you have executed the [configuration](../../../configuration.ipynb) before running this notebook.
In this notebook you will learn how to:
1. Define data loading and preparation steps in a `Dataflow` using `azureml.dataprep`.
2. Pass the `Dataflow` to AutoML for a local run.
3. Pass the `Dataflow` to AutoML for a remote run.
## Setup
Currently, Data Prep only supports __Ubuntu 16__ and __Red Hat Enterprise Linux 7__. We are working on supporting more linux distros.
As part of the setup you have already created an Azure ML `Workspace` object. For AutoML you will need to create an `Experiment` object, which is a named object in a `Workspace` used to run experiments.
```
import logging
import time
import pandas as pd
import azureml.core
from azureml.core.compute import DsvmCompute
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
import azureml.dataprep as dprep
from azureml.train.automl import AutoMLConfig
ws = Workspace.from_config()
# choose a name for experiment
experiment_name = 'automl-dataprep-remote-dsvm'
# project folder
project_folder = './sample_projects/automl-dataprep-remote-dsvm'
experiment = Experiment(ws, experiment_name)
output = {}
output['SDK version'] = azureml.core.VERSION
output['Subscription ID'] = ws.subscription_id
output['Workspace Name'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Project Directory'] = project_folder
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## Data
```
# You can use `auto_read_file` which intelligently figures out delimiters and datatypes of a file.
# The data referenced here was pulled from `sklearn.datasets.load_digits()`.
simple_example_data_root = 'https://dprepdata.blob.core.windows.net/automl-notebook-data/'
X = dprep.auto_read_file(simple_example_data_root + 'X.csv').skip(1) # Remove the header row.
# You can also use `read_csv` and `to_*` transformations to read (with overridable delimiter)
# and convert column types manually.
# Here we read a comma delimited file and convert all columns to integers.
y = dprep.read_csv(simple_example_data_root + 'y.csv').to_long(dprep.ColumnSelector(term='.*', use_regex = True))
```
You can peek the result of a Dataflow at any range using `skip(i)` and `head(j)`. Doing so evaluates only `j` records for all the steps in the Dataflow, which makes it fast even against large datasets.
```
X.skip(1).head(5)
```
## Train
This creates a general AutoML settings object applicable for both local and remote runs.
```
automl_settings = {
"iteration_timeout_minutes" : 10,
"iterations" : 2,
"primary_metric" : 'AUC_weighted',
"preprocess" : False,
"verbosity" : logging.INFO,
"n_cross_validations": 3
}
```
### Create or Attach a Remote Linux DSVM
```
dsvm_name = 'mydsvmc'
try:
while ws.compute_targets[dsvm_name].provisioning_state == 'Creating':
time.sleep(1)
dsvm_compute = DsvmCompute(ws, dsvm_name)
print('Found existing DVSM.')
except:
print('Creating a new DSVM.')
dsvm_config = DsvmCompute.provisioning_configuration(vm_size = "Standard_D2_v2")
dsvm_compute = DsvmCompute.create(ws, name = dsvm_name, provisioning_configuration = dsvm_config)
dsvm_compute.wait_for_completion(show_output = True)
print("Waiting one minute for ssh to be accessible")
time.sleep(90) # Wait for ssh to be accessible
from azureml.core.runconfig import RunConfiguration
from azureml.core.conda_dependencies import CondaDependencies
conda_run_config = RunConfiguration(framework="python")
conda_run_config.target = dsvm_compute
cd = CondaDependencies.create(pip_packages=['azureml-sdk[automl]'], conda_packages=['numpy','py-xgboost<=0.80'])
conda_run_config.environment.python.conda_dependencies = cd
```
### Pass Data with `Dataflow` Objects
The `Dataflow` objects captured above can also be passed to the `submit` method for a remote run. AutoML will serialize the `Dataflow` object and send it to the remote compute target. The `Dataflow` will not be evaluated locally.
```
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
path = project_folder,
run_configuration=conda_run_config,
X = X,
y = y,
**automl_settings)
remote_run = experiment.submit(automl_config, show_output = True)
remote_run
```
## Results
#### Widget for Monitoring Runs
The widget will first report a "loading" status while running the first iteration. After completing the first iteration, an auto-updating graph and table will be shown. The widget will refresh once per minute, so you should see the graph update as child runs complete.
**Note:** The widget displays a link at the bottom. Use this link to open a web interface to explore the individual run details.
```
from azureml.widgets import RunDetails
RunDetails(remote_run).show()
```
#### Retrieve All Child Runs
You can also use SDK methods to fetch all the child runs and see individual metrics that we log.
```
children = list(remote_run.get_children())
metricslist = {}
for run in children:
properties = run.get_properties()
metrics = {k: v for k, v in run.get_metrics().items() if isinstance(v, float)}
metricslist[int(properties['iteration'])] = metrics
rundata = pd.DataFrame(metricslist).sort_index(1)
rundata
```
### Retrieve the Best Model
Below we select the best pipeline from our iterations. The `get_output` method returns the best run and the fitted model. Overloads on `get_output` allow you to retrieve the best run and fitted model for *any* logged metric or for a particular *iteration*.
```
best_run, fitted_model = remote_run.get_output()
print(best_run)
print(fitted_model)
```
#### Best Model Based on Any Other Metric
Show the run and the model that has the smallest `log_loss` value:
```
lookup_metric = "log_loss"
best_run, fitted_model = remote_run.get_output(metric = lookup_metric)
print(best_run)
print(fitted_model)
```
#### Model from a Specific Iteration
Show the run and the model from the first iteration:
```
iteration = 0
best_run, fitted_model = remote_run.get_output(iteration = iteration)
print(best_run)
print(fitted_model)
```
## Test
#### Load Test Data
```
from sklearn import datasets
digits = datasets.load_digits()
X_test = digits.data[:10, :]
y_test = digits.target[:10]
images = digits.images[:10]
```
#### Testing Our Best Fitted Model
We will try to predict 2 digits and see how our model works.
```
#Randomly select digits and test
from matplotlib import pyplot as plt
import numpy as np
for index in np.random.choice(len(y_test), 2, replace = False):
print(index)
predicted = fitted_model.predict(X_test[index:index + 1])[0]
label = y_test[index]
title = "Label value = %d Predicted value = %d " % (label, predicted)
fig = plt.figure(1, figsize=(3,3))
ax1 = fig.add_axes((0,0,.8,.8))
ax1.set_title(title)
plt.imshow(images[index], cmap = plt.cm.gray_r, interpolation = 'nearest')
plt.show()
```
## Appendix
### Capture the `Dataflow` Objects for Later Use in AutoML
`Dataflow` objects are immutable and are composed of a list of data preparation steps. A `Dataflow` object can be branched at any point for further usage.
```
# sklearn.digits.data + target
digits_complete = dprep.auto_read_file('https://dprepdata.blob.core.windows.net/automl-notebook-data/digits-complete.csv')
```
`digits_complete` (sourced from `sklearn.datasets.load_digits()`) is forked into `dflow_X` to capture all the feature columns and `dflow_y` to capture the label column.
```
print(digits_complete.to_pandas_dataframe().shape)
labels_column = 'Column64'
dflow_X = digits_complete.drop_columns(columns = [labels_column])
dflow_y = digits_complete.keep_columns(columns = [labels_column])
```
|
github_jupyter
|
import logging
import time
import pandas as pd
import azureml.core
from azureml.core.compute import DsvmCompute
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
import azureml.dataprep as dprep
from azureml.train.automl import AutoMLConfig
ws = Workspace.from_config()
# choose a name for experiment
experiment_name = 'automl-dataprep-remote-dsvm'
# project folder
project_folder = './sample_projects/automl-dataprep-remote-dsvm'
experiment = Experiment(ws, experiment_name)
output = {}
output['SDK version'] = azureml.core.VERSION
output['Subscription ID'] = ws.subscription_id
output['Workspace Name'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Project Directory'] = project_folder
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
# You can use `auto_read_file` which intelligently figures out delimiters and datatypes of a file.
# The data referenced here was pulled from `sklearn.datasets.load_digits()`.
simple_example_data_root = 'https://dprepdata.blob.core.windows.net/automl-notebook-data/'
X = dprep.auto_read_file(simple_example_data_root + 'X.csv').skip(1) # Remove the header row.
# You can also use `read_csv` and `to_*` transformations to read (with overridable delimiter)
# and convert column types manually.
# Here we read a comma delimited file and convert all columns to integers.
y = dprep.read_csv(simple_example_data_root + 'y.csv').to_long(dprep.ColumnSelector(term='.*', use_regex = True))
X.skip(1).head(5)
automl_settings = {
"iteration_timeout_minutes" : 10,
"iterations" : 2,
"primary_metric" : 'AUC_weighted',
"preprocess" : False,
"verbosity" : logging.INFO,
"n_cross_validations": 3
}
dsvm_name = 'mydsvmc'
try:
while ws.compute_targets[dsvm_name].provisioning_state == 'Creating':
time.sleep(1)
dsvm_compute = DsvmCompute(ws, dsvm_name)
print('Found existing DVSM.')
except:
print('Creating a new DSVM.')
dsvm_config = DsvmCompute.provisioning_configuration(vm_size = "Standard_D2_v2")
dsvm_compute = DsvmCompute.create(ws, name = dsvm_name, provisioning_configuration = dsvm_config)
dsvm_compute.wait_for_completion(show_output = True)
print("Waiting one minute for ssh to be accessible")
time.sleep(90) # Wait for ssh to be accessible
from azureml.core.runconfig import RunConfiguration
from azureml.core.conda_dependencies import CondaDependencies
conda_run_config = RunConfiguration(framework="python")
conda_run_config.target = dsvm_compute
cd = CondaDependencies.create(pip_packages=['azureml-sdk[automl]'], conda_packages=['numpy','py-xgboost<=0.80'])
conda_run_config.environment.python.conda_dependencies = cd
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
path = project_folder,
run_configuration=conda_run_config,
X = X,
y = y,
**automl_settings)
remote_run = experiment.submit(automl_config, show_output = True)
remote_run
from azureml.widgets import RunDetails
RunDetails(remote_run).show()
children = list(remote_run.get_children())
metricslist = {}
for run in children:
properties = run.get_properties()
metrics = {k: v for k, v in run.get_metrics().items() if isinstance(v, float)}
metricslist[int(properties['iteration'])] = metrics
rundata = pd.DataFrame(metricslist).sort_index(1)
rundata
best_run, fitted_model = remote_run.get_output()
print(best_run)
print(fitted_model)
lookup_metric = "log_loss"
best_run, fitted_model = remote_run.get_output(metric = lookup_metric)
print(best_run)
print(fitted_model)
iteration = 0
best_run, fitted_model = remote_run.get_output(iteration = iteration)
print(best_run)
print(fitted_model)
from sklearn import datasets
digits = datasets.load_digits()
X_test = digits.data[:10, :]
y_test = digits.target[:10]
images = digits.images[:10]
#Randomly select digits and test
from matplotlib import pyplot as plt
import numpy as np
for index in np.random.choice(len(y_test), 2, replace = False):
print(index)
predicted = fitted_model.predict(X_test[index:index + 1])[0]
label = y_test[index]
title = "Label value = %d Predicted value = %d " % (label, predicted)
fig = plt.figure(1, figsize=(3,3))
ax1 = fig.add_axes((0,0,.8,.8))
ax1.set_title(title)
plt.imshow(images[index], cmap = plt.cm.gray_r, interpolation = 'nearest')
plt.show()
# sklearn.digits.data + target
digits_complete = dprep.auto_read_file('https://dprepdata.blob.core.windows.net/automl-notebook-data/digits-complete.csv')
print(digits_complete.to_pandas_dataframe().shape)
labels_column = 'Column64'
dflow_X = digits_complete.drop_columns(columns = [labels_column])
dflow_y = digits_complete.keep_columns(columns = [labels_column])
| 0.677901 | 0.931463 |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import re
import nltk # wonderful tutorial can be found here https://pythonprogramming.net/tokenizing-words-sentences-nltk-tutorial/
%matplotlib inline
df = pd.read_csv('amazon_alexa.tsv', sep='\t')
```
# Initial data exploration
```
df.head(10)
df.describe()
```
It seems unreasonable to use any data except for the reviews and their rating. We could have product variation categorized and then create chart which one is the best, but it is outside the scope of the problem. Feedback and date are also unnecessary.
Second, the distribution of ratings in dataset is way off. 25-th percentile already has value of 4, and 50-th - of 5. If there is enough data for different ratings, it would seem reasonable to construct a subset with better distribution.
```
#omitting unnecessary columns
cdf = df[['rating', 'verified_reviews']]
print(cdf['rating'].value_counts())
cdf = pd.concat([cdf[cdf['rating'] < 5], cdf[cdf['rating'] == 5].sample(frac=1).iloc[:300]])
cdf['rating'].describe()
```
Perfect dataset supposed to have equal amount of items with every rating, and their mean should be 3.0. Constructing such dataset would shrink dataset to 480 entries. Instead we can have dataset with 1164 entries with a mean of 3.5. That could create a shift in models predictions, but more data will help prevent overfitting and help model generalize data better.
```
cdf['rating'].hist(bins=5)
```
# Assessing word vectors data
One of the most precise method when analysing natural language is to use word2vec approach. Let's check how many different words there is and create a full set of all used words in review. That would be useful later when chosing pre-trained word vectors.
```
text_body = ''
for row in cdf.iterrows():
text_body += row[1]['verified_reviews'] + ' '
cleaned_text_body = re.sub('[^a-zA-Z]', ' ', text_body)
word_list = nltk.tokenize.word_tokenize(cleaned_text_body.lower())
word_set = set(word_list)
len(word_set)
```
Now that we got complete set of words used in dataset we can estimate how good or bad a certain vectorization of words could serve.
```
embeddings = {}
f = open('glove.6B/glove.6B.100d.txt', 'r', encoding='utf-8')
for line in f:
values = line.split()
word = values[0]
vector = np.asarray(values[1:], dtype='float32')
embeddings[word] = vector
f.close()
def assess_embeddings(set_of_words):
c = 0
missing_embeddings = []
for word in set_of_words:
if word in embeddings:
c+=1
else:
missing_embeddings.append(word)
print(c/len(set_of_words)*100, 'percents of words in reviews are covered in embeddings')
return missing_embeddings
missing_embeddings = assess_embeddings(word_set)
print(sorted(missing_embeddings))
```
Embeddings successfully cover almost all word set, except for some typos. Since typos are only ~3% of words, we can ignore the problem unless we would want to improve accuracy.
We will use the Keras library to solve the problem
```
import keras
```
# Preparing data
```
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
tokenizer = Tokenizer(num_words=len(word_set))
tokenizer.fit_on_texts([cleaned_text_body])
print('Words in word_index:', len(tokenizer.word_index))
```
As we could expect, keras' tokenizer uses an algorithm that is somewhat different from the one we chose earlier. However, the amount of words in created word_index is bigger only by 1. Generally, it is better to use already made solutions than to create something from scratch. Let's quickly assess this word_index and make a decision whether it is reasonable to use it.
```
_ = assess_embeddings(set([kvp for kvp in tokenizer.word_index]))
```
The results are just as good, so the tokenizer's word_index stays.
```
cdf['cleaned_text'] = cdf['verified_reviews'].apply(lambda x: re.sub('[^a-zA-Z]', ' ', x))
cdf['cleaned_text'] = cdf['cleaned_text'].apply(lambda x: re.sub(' +',' ', x)) #remove consecutive spacing
cdf['sequences'] = cdf['cleaned_text'].apply(lambda x: tokenizer.texts_to_sequences([x])[0])
cdf['sequences'].head(10)
# Need to know max_sequence_length to pad other sequences
max_sequence_length = cdf['sequences'].apply(lambda x: len(x)).max()
cdf['padded_sequences'] = cdf['sequences'].apply(lambda x: pad_sequences([x], max_sequence_length)[0])
print(cdf['padded_sequences'][2])
```
Now split into train, validation and test subsets
```
train = cdf.sample(frac=0.8)
test_and_validation = cdf.loc[~cdf.index.isin(train.index)]
validation = test_and_validation.sample(frac=0.5)
test = test_and_validation.loc[~test_and_validation.index.isin(validation.index)]
print(train.shape, validation.shape, test.shape)
def get_arrayed_data(df_set):
setX = np.stack(df_set['padded_sequences'].values, axis=0)
setY = pd.get_dummies(df_set['rating']).values #using one-hot encoding
return (setX, setY)
trainX, trainY = get_arrayed_data(train)
validationX, validationY = get_arrayed_data(validation)
testX, testY = get_arrayed_data(test)
```
# Building the model
```
from keras.layers import Embedding
embedding_matrix = np.zeros((len(tokenizer.word_index) + 1, 100))
for word, i in tokenizer.word_index.items():
# words that are not in pretrained embedding will be zero vectors.
if word in embeddings:
embedding_matrix[i] = embeddings[word]
embedding_layer = Embedding(len(tokenizer.word_index) + 1, 100,
weights=[embedding_matrix],
input_length=max_sequence_length,
trainable=False)
from keras.models import Sequential
from keras.layers import Dense, Input, LSTM, Flatten, Dropout
def simple_reccurent_model(input_shape, output_shape):
model = Sequential()
model.add(embedding_layer)
model.add(LSTM(64, dropout=0.2))
#model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(output_shape, activation='softmax'))
return model
model = simple_reccurent_model(trainX.shape[1], trainY.shape[1])
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
model.summary()
model.fit(trainX, trainY, batch_size=64, epochs=100)
```
Let's evaluate this simple model on validation set:
```
score, accuracy = model.evaluate(validationX, validationY, batch_size=64)
print(accuracy)
```
### 58% of accuracy
It is much better than random guessing, though. Let's check the failed predictions manually.
```
reverse_word_map = dict(map(reversed, tokenizer.word_index.items()))
for i, y in enumerate(validationY):
#p = model.predict(np.array([validationX[i]])).round()[0].astype('int32')
prediction = model.predict(np.array([validationX[i]])).argmax()
actual = y.argmax()
if prediction != actual:
print("Validation", i)
print("Predicted review:", prediction + 1, ", actual review:", actual + 1)
#print(validationX[i])
text = []
for word_i in validationX[i]:
if word_i in reverse_word_map:
text.append(reverse_word_map[word_i])
print(' '.join(text))
print()
```
## First try conclusion
While in some cases the model cannot be really guilty for misunderstanding (validation example 1, validation example 13), in many cases there could be some improvement. Time to tune model.
```
def tunable_reccurent_model(input_shape, output_shape, hyperparams):
model = Sequential()
model.add(embedding_layer)
for i, lstm_size in enumerate(hyperparams['lstm_sizes']):
model.add(LSTM(lstm_size, dropout=hyperparams['dp']))
for i, dense_size in enumerate(hyperparams['dense_sizes']):
model.add(Dense(dense_size, activation=hyperparams['dense_activation']))
model.add(Dropout(hyperparams['dp']))
model.add(Dense(output_shape, activation='softmax'))
return model
def evaluate_model(input_shape, output_shape,
hyperparams, train_set, validation_set,
train_epochs=100):
model = simple_reccurent_model(trainX.shape[1], trainY.shape[1])
model.compile(loss='categorical_crossentropy',
optimizer=hyperparams['optimizer'],
metrics=['accuracy'])
model.fit(train_set[0], train_set[1], batch_size=hyperparams['batch_size'], epochs=train_epochs, verbose=0)
_, train_accuracy = model.evaluate(train_set[0], train_set[1])
_, validation_accuracy = model.evaluate(validation_set[0], validation_set[1])
print("Train accuaracy:", train_accuracy, "Validation Accuracy:", validation_accuracy)
return validation_accuracy
lstm_sizes = [[32], [64], [128], [64, 32]]
dense_sizes = [[32], [64], [128], [64, 32]]
dense_activations = ['relu', 'tanh', 'sigmoid']
dps = [0.1, 0.2, 0.3]
optimizers = ['Adam', 'SGD', 'RMSprop']
epochs = [100, 125, 150]
batch_sizes = [32, 64, 128]
results = []
counter=1
# all hyperparameters here are enumerated not in random order - the least important are closer to outer cycle
for ep in epochs:
for optimizer in optimizers:
for dense_activation in dense_activations:
for batch_size in batch_sizes:
for dp in dps:
for dense_size in dense_sizes:
for lstm_size in lstm_sizes:
hyperparams = {
'lstm_sizes': lstm_size,
'dp': dp,
'dense_sizes': dense_size,
'dense_activation': dense_activation,
'optimizer': optimizer,
'batch_size': batch_size
}
#print("Interation", counter)
#acc = evaluate_model(trainX.shape[1], trainY.shape[1],
# hyperparams, (trainX, trainY), (validationX, validationY),
# ep)
#results.append((acc, hyperparams, {'ep': ep, 'batch_size': batch_size}))
#counter+=1
#print()
```
This method would find the best model among all the combinations, but it will take a lot of time. If every training would take similar amount of time that the original simple model took (about 10 minutes on 100 epochs), trying only the combinations of lstm_sizes and dense_sizes would take 6 * 6 * 10 = 360 minutes = 6 hours, and we got combinations of other hyperparameters. The required time would be enourmous.
Alternative is to try every hyperparameter with default model, measure the impact on accuracy and then, judging on how good model performed with certain parameter, try to manually find the required combination.
Pros of the second tactics are that it is much more computationally efficient. Cons are that some hyperparameters might improve performance only with combination with others, and we are likely to miss it.
Nevertheless, we have to choose the computationally efficient path.
Additional time optimization is to cut the amount of epochs here. On 25 epochs the results probably would not be very much impressive, but it could be enough for us to determine if those hyperparameters are comparatively work or not.
We will not try here total grid search of hyperparameters. Instead we focus on how each hyperparameter changes performance individually, and then try to finish tuning manually.
```
import copy
lstm_sizes = [[32], [64], [64, 32]]
dense_sizes = [[32], [64], [64, 32]]
dense_activations = ['relu', 'tanh', 'sigmoid']
dps = [0.1, 0.2, 0.3]
optimizers = ['Adam', 'SGD', 'RMSprop']
epochs = 25
batch_sizes = [32, 64, 128]
hyperparams = {
'lstm_size': lstm_sizes,
'dense_size': dense_sizes,
'dense_activation': dense_activations,
'dp': dps,
'optimizer': optimizers,
'batch_size': batch_sizes
}
default_hyperparams = {
'lstm_size': [64],
'dp': 0.2,
'dense_size': [64],
'dense_activation': 'relu',
'optimizer': 'adam',
'batch_size': 64
}
counter = 1
validation_results = []
for hp_name, hp_list in hyperparams.items():
accs = []
for hp_val in hp_list:
hp = copy.deepcopy(default_hyperparams)
hp[hp_name] = hp_val
print("Interation", counter)
acc = evaluate_model(trainX.shape[1], trainY.shape[1],
hp, (trainX, trainY), (validationX, validationY), epochs)
counter+=1
accs.append(acc)
print()
validation_results.append((hp_name, accs))
fig = plt.figure(figsize=(6, 18))
for i, result in enumerate(validation_results):
ax = fig.add_subplot(len(validation_results), 1, i+1)
hp_name = result[0]
hp_errors = result[1]
ax.set_title(hp_name)
ax.plot(range(0, len(hp_errors)), hp_errors)
plt.sca(ax)
x_labels = hyperparams[hp_name]
plt.xticks(range(0, len(hp_errors)), x_labels)
fig.tight_layout()
plt.show()
# edited function to return model
def evaluate_model(input_shape, output_shape,
hyperparams, train_set, validation_set,
train_epochs=100, verbose=0):
model = simple_reccurent_model(trainX.shape[1], trainY.shape[1])
model.compile(loss='categorical_crossentropy',
optimizer=hyperparams['optimizer'],
metrics=['accuracy'])
model.fit(train_set[0], train_set[1], batch_size=hyperparams['batch_size'], epochs=train_epochs, verbose=verbose)
_, train_accuracy = model.evaluate(train_set[0], train_set[1])
_, validation_accuracy = model.evaluate(validation_set[0], validation_set[1])
print("Train accuaracy:", train_accuracy, "Validation Accuracy:", validation_accuracy)
return validation_accuracy, model
tuned_hyperparams = {
'lstm_size': [32],
'dp': 0.2,
'dense_size': [64],
'dense_activation': 'relu',
'optimizer': 'adam',
'batch_size': 32
}
acc, model = evaluate_model(trainX.shape[1], trainY.shape[1],
tuned_hyperparams, (trainX, trainY), (validationX, validationY), 100, 1)
tuned_hyperparams = {
'lstm_size': [32],
'dp': 0.5,
'dense_size': [64],
'dense_activation': 'relu',
'optimizer': 'adam',
'batch_size': 32
}
acc, model2 = evaluate_model(trainX.shape[1], trainY.shape[1],
tuned_hyperparams, (trainX, trainY), (validationX, validationY), 50, 1)
```
Third model and id didn't improve accuracy on validation set. We have a huge overfitting. Small dataset is the main suspect in that.
We have to reconsider the problem. Choosing the rating on 1-5 scale is quite arbitrary proccess. As we saw earlier when we inspected errors, there are misleading samples.
This time let's assume that rating of 1-3 is bad and of 4-5 is good. What is percentage of error in that case?
```
error_count = 0
for i, y in enumerate(validationY):
#p = model.predict(np.array([validationX[i]])).round()[0].astype('int32')
prediction = model2.predict(np.array([validationX[i]])).argmax() > 3
actual = y.argmax() > 3
if prediction != actual:
print("Validation", i)
print("Predicted review is good:", prediction, ", actual review is good:", actual)
#print(validationX[i])
text = []
for word_i in validationX[i]:
if word_i in reverse_word_map:
text.append(reverse_word_map[word_i])
print(' '.join(text))
print()
error_count+=1
print("Accuracy of prediction whether review was good:",(validationY.shape[0] - error_count)/validationY.shape[0] * 100)
```
That's more like it! 84% accuracy in prediction whether the review was good or bad.
The other helpful thing to use when analizing results is confucion matrix.
```
predicted = [x > 3 for x in model2.predict(validationX).argmax(axis=1)]
actual = [x > 3 for x in validationY.argmax(axis=1)]
from sklearn.metrics import confusion_matrix
cnf_matrix = confusion_matrix(actual, predicted)
sns.heatmap(cnf_matrix)
tn, fp, fn, tp = cnf_matrix.ravel()
print("True positive:", tp, ", True negative:", tn,
", False positive:", fp, ", False negative:", fn)
```
It seems like the validation set is severely unbalanced - it contains far more negative reviews than positive.
Regardless the confusion matrix results, in our case, for Amazon it would be worse to have False positive review than False negative, so our model's errors are rather acceptable.
Now let's check our model against the test data. If it is not as unbalanced as validation set, there are good chances that model will perform better.
```
test_accuracy = model2.evaluate(testX, testY)
print(test_accuracy)
```
## 55% of accuracy in precise predicitons.
Now let's check how model generally predicts whether reviews are good or not.
```
def check_general_accuracy(model, setX, setY):
predicted = [x > 3 for x in model.predict(setX).argmax(axis=1)]
actual = [x > 3 for x in setY.argmax(axis=1)]
cnf_matrix = confusion_matrix(actual, predicted)
sns.heatmap(cnf_matrix)
tn, fp, fn, tp = cnf_matrix.ravel()
print("True positive:", tp, ", True negative:", tn,
", False positive:", fp, ", False negative:", fn)
print("Total accuracy:", (tp+tn)/testX.shape[0]*100)
check_general_accuracy(model2, testX, testY)
```
We didn't get improvements in performing on test set, sadly. Nevertheless, **79,5%** of accuracy in predicting general moods of reviews.
Possible ways to improve model:
* get bigger dataset
* balance dataset better
* perform more diligent search for optimal hyperparameters
* try other models
# Convolutional model
Before wrapping up, let's try to solve this problem using another architecture of model.
We had a choice to treat each word in sentence as just another value and feed it into plain neural network, or treat it as a sequence in RNN, and we used it as such.
Now, we can try a somewhat middleground at this. Convolutional neural network, due to it's nature will have an effect of a sequence model with rolling window of chosen width.
```
from keras.layers import Conv1D, MaxPooling1D
def simple_conv_model(input_shape, output_shape):
model = Sequential()
model.add(embedding_layer)
model.add(Conv1D(32, 5, activation='relu'))
model.add(Conv1D(64, 5, activation='relu'))
model.add(MaxPooling1D(5))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.4))
model.add(Dense(output_shape, activation='softmax'))
return model
model = simple_conv_model(trainX.shape[1], trainY.shape[1])
model.compile(loss='categorical_crossentropy', optimizer='rmsprop',metrics=['accuracy'])
model.summary()
from keras.callbacks import ModelCheckpoint
checkpoint = ModelCheckpoint("weights-improvements.hdf5",
monitor='val_acc', verbose=1, save_best_only=True, mode='max')
model.fit(trainX, trainY, validation_data=(validationX, validationY),
batch_size=64, callbacks=[checkpoint], epochs=10)
model.load_weights("weights-improvements.hdf5")
```
Not too great in precise rating predictions.
```
check_general_accuracy(model, testX, testY)
```
# 74% of general accuracy for convolutional network
Convolutional neural network predictions was slightly less accurate comparing to LSTM-based network, but no major tuning was performed.
Possible improvements stay same as for LSTM-based network:
* get bigger dataset
* balance dataset better
* perform more diligent search for optimal hyperparameters
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import re
import nltk # wonderful tutorial can be found here https://pythonprogramming.net/tokenizing-words-sentences-nltk-tutorial/
%matplotlib inline
df = pd.read_csv('amazon_alexa.tsv', sep='\t')
df.head(10)
df.describe()
#omitting unnecessary columns
cdf = df[['rating', 'verified_reviews']]
print(cdf['rating'].value_counts())
cdf = pd.concat([cdf[cdf['rating'] < 5], cdf[cdf['rating'] == 5].sample(frac=1).iloc[:300]])
cdf['rating'].describe()
cdf['rating'].hist(bins=5)
text_body = ''
for row in cdf.iterrows():
text_body += row[1]['verified_reviews'] + ' '
cleaned_text_body = re.sub('[^a-zA-Z]', ' ', text_body)
word_list = nltk.tokenize.word_tokenize(cleaned_text_body.lower())
word_set = set(word_list)
len(word_set)
embeddings = {}
f = open('glove.6B/glove.6B.100d.txt', 'r', encoding='utf-8')
for line in f:
values = line.split()
word = values[0]
vector = np.asarray(values[1:], dtype='float32')
embeddings[word] = vector
f.close()
def assess_embeddings(set_of_words):
c = 0
missing_embeddings = []
for word in set_of_words:
if word in embeddings:
c+=1
else:
missing_embeddings.append(word)
print(c/len(set_of_words)*100, 'percents of words in reviews are covered in embeddings')
return missing_embeddings
missing_embeddings = assess_embeddings(word_set)
print(sorted(missing_embeddings))
import keras
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
tokenizer = Tokenizer(num_words=len(word_set))
tokenizer.fit_on_texts([cleaned_text_body])
print('Words in word_index:', len(tokenizer.word_index))
_ = assess_embeddings(set([kvp for kvp in tokenizer.word_index]))
cdf['cleaned_text'] = cdf['verified_reviews'].apply(lambda x: re.sub('[^a-zA-Z]', ' ', x))
cdf['cleaned_text'] = cdf['cleaned_text'].apply(lambda x: re.sub(' +',' ', x)) #remove consecutive spacing
cdf['sequences'] = cdf['cleaned_text'].apply(lambda x: tokenizer.texts_to_sequences([x])[0])
cdf['sequences'].head(10)
# Need to know max_sequence_length to pad other sequences
max_sequence_length = cdf['sequences'].apply(lambda x: len(x)).max()
cdf['padded_sequences'] = cdf['sequences'].apply(lambda x: pad_sequences([x], max_sequence_length)[0])
print(cdf['padded_sequences'][2])
train = cdf.sample(frac=0.8)
test_and_validation = cdf.loc[~cdf.index.isin(train.index)]
validation = test_and_validation.sample(frac=0.5)
test = test_and_validation.loc[~test_and_validation.index.isin(validation.index)]
print(train.shape, validation.shape, test.shape)
def get_arrayed_data(df_set):
setX = np.stack(df_set['padded_sequences'].values, axis=0)
setY = pd.get_dummies(df_set['rating']).values #using one-hot encoding
return (setX, setY)
trainX, trainY = get_arrayed_data(train)
validationX, validationY = get_arrayed_data(validation)
testX, testY = get_arrayed_data(test)
from keras.layers import Embedding
embedding_matrix = np.zeros((len(tokenizer.word_index) + 1, 100))
for word, i in tokenizer.word_index.items():
# words that are not in pretrained embedding will be zero vectors.
if word in embeddings:
embedding_matrix[i] = embeddings[word]
embedding_layer = Embedding(len(tokenizer.word_index) + 1, 100,
weights=[embedding_matrix],
input_length=max_sequence_length,
trainable=False)
from keras.models import Sequential
from keras.layers import Dense, Input, LSTM, Flatten, Dropout
def simple_reccurent_model(input_shape, output_shape):
model = Sequential()
model.add(embedding_layer)
model.add(LSTM(64, dropout=0.2))
#model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(output_shape, activation='softmax'))
return model
model = simple_reccurent_model(trainX.shape[1], trainY.shape[1])
model.compile(loss='categorical_crossentropy', optimizer='adam',metrics=['accuracy'])
model.summary()
model.fit(trainX, trainY, batch_size=64, epochs=100)
score, accuracy = model.evaluate(validationX, validationY, batch_size=64)
print(accuracy)
reverse_word_map = dict(map(reversed, tokenizer.word_index.items()))
for i, y in enumerate(validationY):
#p = model.predict(np.array([validationX[i]])).round()[0].astype('int32')
prediction = model.predict(np.array([validationX[i]])).argmax()
actual = y.argmax()
if prediction != actual:
print("Validation", i)
print("Predicted review:", prediction + 1, ", actual review:", actual + 1)
#print(validationX[i])
text = []
for word_i in validationX[i]:
if word_i in reverse_word_map:
text.append(reverse_word_map[word_i])
print(' '.join(text))
print()
def tunable_reccurent_model(input_shape, output_shape, hyperparams):
model = Sequential()
model.add(embedding_layer)
for i, lstm_size in enumerate(hyperparams['lstm_sizes']):
model.add(LSTM(lstm_size, dropout=hyperparams['dp']))
for i, dense_size in enumerate(hyperparams['dense_sizes']):
model.add(Dense(dense_size, activation=hyperparams['dense_activation']))
model.add(Dropout(hyperparams['dp']))
model.add(Dense(output_shape, activation='softmax'))
return model
def evaluate_model(input_shape, output_shape,
hyperparams, train_set, validation_set,
train_epochs=100):
model = simple_reccurent_model(trainX.shape[1], trainY.shape[1])
model.compile(loss='categorical_crossentropy',
optimizer=hyperparams['optimizer'],
metrics=['accuracy'])
model.fit(train_set[0], train_set[1], batch_size=hyperparams['batch_size'], epochs=train_epochs, verbose=0)
_, train_accuracy = model.evaluate(train_set[0], train_set[1])
_, validation_accuracy = model.evaluate(validation_set[0], validation_set[1])
print("Train accuaracy:", train_accuracy, "Validation Accuracy:", validation_accuracy)
return validation_accuracy
lstm_sizes = [[32], [64], [128], [64, 32]]
dense_sizes = [[32], [64], [128], [64, 32]]
dense_activations = ['relu', 'tanh', 'sigmoid']
dps = [0.1, 0.2, 0.3]
optimizers = ['Adam', 'SGD', 'RMSprop']
epochs = [100, 125, 150]
batch_sizes = [32, 64, 128]
results = []
counter=1
# all hyperparameters here are enumerated not in random order - the least important are closer to outer cycle
for ep in epochs:
for optimizer in optimizers:
for dense_activation in dense_activations:
for batch_size in batch_sizes:
for dp in dps:
for dense_size in dense_sizes:
for lstm_size in lstm_sizes:
hyperparams = {
'lstm_sizes': lstm_size,
'dp': dp,
'dense_sizes': dense_size,
'dense_activation': dense_activation,
'optimizer': optimizer,
'batch_size': batch_size
}
#print("Interation", counter)
#acc = evaluate_model(trainX.shape[1], trainY.shape[1],
# hyperparams, (trainX, trainY), (validationX, validationY),
# ep)
#results.append((acc, hyperparams, {'ep': ep, 'batch_size': batch_size}))
#counter+=1
#print()
import copy
lstm_sizes = [[32], [64], [64, 32]]
dense_sizes = [[32], [64], [64, 32]]
dense_activations = ['relu', 'tanh', 'sigmoid']
dps = [0.1, 0.2, 0.3]
optimizers = ['Adam', 'SGD', 'RMSprop']
epochs = 25
batch_sizes = [32, 64, 128]
hyperparams = {
'lstm_size': lstm_sizes,
'dense_size': dense_sizes,
'dense_activation': dense_activations,
'dp': dps,
'optimizer': optimizers,
'batch_size': batch_sizes
}
default_hyperparams = {
'lstm_size': [64],
'dp': 0.2,
'dense_size': [64],
'dense_activation': 'relu',
'optimizer': 'adam',
'batch_size': 64
}
counter = 1
validation_results = []
for hp_name, hp_list in hyperparams.items():
accs = []
for hp_val in hp_list:
hp = copy.deepcopy(default_hyperparams)
hp[hp_name] = hp_val
print("Interation", counter)
acc = evaluate_model(trainX.shape[1], trainY.shape[1],
hp, (trainX, trainY), (validationX, validationY), epochs)
counter+=1
accs.append(acc)
print()
validation_results.append((hp_name, accs))
fig = plt.figure(figsize=(6, 18))
for i, result in enumerate(validation_results):
ax = fig.add_subplot(len(validation_results), 1, i+1)
hp_name = result[0]
hp_errors = result[1]
ax.set_title(hp_name)
ax.plot(range(0, len(hp_errors)), hp_errors)
plt.sca(ax)
x_labels = hyperparams[hp_name]
plt.xticks(range(0, len(hp_errors)), x_labels)
fig.tight_layout()
plt.show()
# edited function to return model
def evaluate_model(input_shape, output_shape,
hyperparams, train_set, validation_set,
train_epochs=100, verbose=0):
model = simple_reccurent_model(trainX.shape[1], trainY.shape[1])
model.compile(loss='categorical_crossentropy',
optimizer=hyperparams['optimizer'],
metrics=['accuracy'])
model.fit(train_set[0], train_set[1], batch_size=hyperparams['batch_size'], epochs=train_epochs, verbose=verbose)
_, train_accuracy = model.evaluate(train_set[0], train_set[1])
_, validation_accuracy = model.evaluate(validation_set[0], validation_set[1])
print("Train accuaracy:", train_accuracy, "Validation Accuracy:", validation_accuracy)
return validation_accuracy, model
tuned_hyperparams = {
'lstm_size': [32],
'dp': 0.2,
'dense_size': [64],
'dense_activation': 'relu',
'optimizer': 'adam',
'batch_size': 32
}
acc, model = evaluate_model(trainX.shape[1], trainY.shape[1],
tuned_hyperparams, (trainX, trainY), (validationX, validationY), 100, 1)
tuned_hyperparams = {
'lstm_size': [32],
'dp': 0.5,
'dense_size': [64],
'dense_activation': 'relu',
'optimizer': 'adam',
'batch_size': 32
}
acc, model2 = evaluate_model(trainX.shape[1], trainY.shape[1],
tuned_hyperparams, (trainX, trainY), (validationX, validationY), 50, 1)
error_count = 0
for i, y in enumerate(validationY):
#p = model.predict(np.array([validationX[i]])).round()[0].astype('int32')
prediction = model2.predict(np.array([validationX[i]])).argmax() > 3
actual = y.argmax() > 3
if prediction != actual:
print("Validation", i)
print("Predicted review is good:", prediction, ", actual review is good:", actual)
#print(validationX[i])
text = []
for word_i in validationX[i]:
if word_i in reverse_word_map:
text.append(reverse_word_map[word_i])
print(' '.join(text))
print()
error_count+=1
print("Accuracy of prediction whether review was good:",(validationY.shape[0] - error_count)/validationY.shape[0] * 100)
predicted = [x > 3 for x in model2.predict(validationX).argmax(axis=1)]
actual = [x > 3 for x in validationY.argmax(axis=1)]
from sklearn.metrics import confusion_matrix
cnf_matrix = confusion_matrix(actual, predicted)
sns.heatmap(cnf_matrix)
tn, fp, fn, tp = cnf_matrix.ravel()
print("True positive:", tp, ", True negative:", tn,
", False positive:", fp, ", False negative:", fn)
test_accuracy = model2.evaluate(testX, testY)
print(test_accuracy)
def check_general_accuracy(model, setX, setY):
predicted = [x > 3 for x in model.predict(setX).argmax(axis=1)]
actual = [x > 3 for x in setY.argmax(axis=1)]
cnf_matrix = confusion_matrix(actual, predicted)
sns.heatmap(cnf_matrix)
tn, fp, fn, tp = cnf_matrix.ravel()
print("True positive:", tp, ", True negative:", tn,
", False positive:", fp, ", False negative:", fn)
print("Total accuracy:", (tp+tn)/testX.shape[0]*100)
check_general_accuracy(model2, testX, testY)
from keras.layers import Conv1D, MaxPooling1D
def simple_conv_model(input_shape, output_shape):
model = Sequential()
model.add(embedding_layer)
model.add(Conv1D(32, 5, activation='relu'))
model.add(Conv1D(64, 5, activation='relu'))
model.add(MaxPooling1D(5))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.4))
model.add(Dense(output_shape, activation='softmax'))
return model
model = simple_conv_model(trainX.shape[1], trainY.shape[1])
model.compile(loss='categorical_crossentropy', optimizer='rmsprop',metrics=['accuracy'])
model.summary()
from keras.callbacks import ModelCheckpoint
checkpoint = ModelCheckpoint("weights-improvements.hdf5",
monitor='val_acc', verbose=1, save_best_only=True, mode='max')
model.fit(trainX, trainY, validation_data=(validationX, validationY),
batch_size=64, callbacks=[checkpoint], epochs=10)
model.load_weights("weights-improvements.hdf5")
check_general_accuracy(model, testX, testY)
| 0.410638 | 0.842604 |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
import tensorflow as tf
from tensorflow.keras.layers import Input, Dense, Flatten
from tensorflow.keras.applications.vgg16 import VGG16 as PretrainedModel, preprocess_input
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import SGD, Adam
from tensorflow.keras.preprocessing import image
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from glob import glob
from PIL import Image
import sys, os
```
Downloaded data set from kaggle onto D: (no space on C:)
I ran these in bash from DL location. Can be run in notebook if space on C: and downloaded directly from notebook
!mkdir data
!mkdir data/train
!mkdir data/test
!mkdir data/train/nonfood
!mkdir data/train/food
!mkdir data/test/nonfood
!mkdir data/test/food
!mv training/0*.jpg data/train/nonfood
!mv training 1*.jpg data/train/food
!mv validation/0*.jpg data/train/nonfood
!mv validation/1*.jpg data/train/food
```
train_path = r"D:\DataSets\Food-5K\data\train"
valid_path = r"D:\DataSets\Food-5K\data\test"
IMAGE_SIZE = [200,200]
image_files = glob(train_path + '/*/*.jpg')
valid_image_files = glob(valid_path + '/*/*.jpg')
folders = glob(train_path + '/*')
folders
plt.imshow(image.load_img(np.random.choice(image_files)))
ptm = PretrainedModel(
input_shape = IMAGE_SIZE + [3],
weights = 'imagenet',
include_top=False
)
ptm.trainable =False
K = len(folders)
x = Flatten()(ptm.output)
x = Dense(K, activation='softmax')(x)
model = Model(inputs=ptm.input, outputs=x)
model.summary()
gen = ImageDataGenerator(
rotation_range =20,
width_shift_range =0.1,
height_shift_range=0.1,
shear_range=0.1,
zoom_range=0.1,
horizontal_flip=True,
preprocessing_function=preprocess_input
)
batch_size =128
train_generator = gen.flow_from_directory(
train_path,
shuffle=True,
target_size = IMAGE_SIZE,
batch_size = batch_size
)
valid_generator = gen.flow_from_directory(
valid_path,
target_size = IMAGE_SIZE,
batch_size = batch_size
)
model.compile(
loss= 'categorical_crossentropy',
optimizer='adam',
metrics = ['accuracy']
)
r = model.fit_generator(
train_generator,
validation_data = valid_generator,
epochs=5,
steps_per_epoch = int(np.ceil(len(image_files)/batch_size)),
validation_steps = int(np.ceil(len(valid_image_files)/batch_size))
)
#Cannot train due to hardware limitations
plt.plot(r.history['loss'],label='loss')
plt.plot(r.history['val_loss'],label='val_loss')
plt.plot(r.history['accuracy'],label='accuracy')
plt.plot(r.history['val_accuracy'],label='val_accuracy')
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
import tensorflow as tf
from tensorflow.keras.layers import Input, Dense, Flatten
from tensorflow.keras.applications.vgg16 import VGG16 as PretrainedModel, preprocess_input
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import SGD, Adam
from tensorflow.keras.preprocessing import image
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from glob import glob
from PIL import Image
import sys, os
train_path = r"D:\DataSets\Food-5K\data\train"
valid_path = r"D:\DataSets\Food-5K\data\test"
IMAGE_SIZE = [200,200]
image_files = glob(train_path + '/*/*.jpg')
valid_image_files = glob(valid_path + '/*/*.jpg')
folders = glob(train_path + '/*')
folders
plt.imshow(image.load_img(np.random.choice(image_files)))
ptm = PretrainedModel(
input_shape = IMAGE_SIZE + [3],
weights = 'imagenet',
include_top=False
)
ptm.trainable =False
K = len(folders)
x = Flatten()(ptm.output)
x = Dense(K, activation='softmax')(x)
model = Model(inputs=ptm.input, outputs=x)
model.summary()
gen = ImageDataGenerator(
rotation_range =20,
width_shift_range =0.1,
height_shift_range=0.1,
shear_range=0.1,
zoom_range=0.1,
horizontal_flip=True,
preprocessing_function=preprocess_input
)
batch_size =128
train_generator = gen.flow_from_directory(
train_path,
shuffle=True,
target_size = IMAGE_SIZE,
batch_size = batch_size
)
valid_generator = gen.flow_from_directory(
valid_path,
target_size = IMAGE_SIZE,
batch_size = batch_size
)
model.compile(
loss= 'categorical_crossentropy',
optimizer='adam',
metrics = ['accuracy']
)
r = model.fit_generator(
train_generator,
validation_data = valid_generator,
epochs=5,
steps_per_epoch = int(np.ceil(len(image_files)/batch_size)),
validation_steps = int(np.ceil(len(valid_image_files)/batch_size))
)
#Cannot train due to hardware limitations
plt.plot(r.history['loss'],label='loss')
plt.plot(r.history['val_loss'],label='val_loss')
plt.plot(r.history['accuracy'],label='accuracy')
plt.plot(r.history['val_accuracy'],label='val_accuracy')
| 0.55447 | 0.630358 |
# Environment and tools setup
This short lesson will teach you the basics of the work environments needed for this course.
# Installing Python
What is python?
https://docs.python.org/3/tutorial/index.html
Python is an easy to learn, powerful programming language. It has efficient high-level data structures and a simple but effective approach to object-oriented programming. Python’s elegant syntax and dynamic typing, together with its interpreted nature, make it an ideal language for scripting and rapid application development in many areas on most platforms.
The Python interpreter and the extensive standard library are freely available in source or binary form for all major platforms from the Python Web site, https://www.python.org/, and may be freely distributed. The same site also contains distributions of and pointers to many free third party Python modules, programs and tools, and additional documentation.
The Python interpreter is easily extended with new functions and data types implemented in C or C++ (or other languages callable from C). Python is also suitable as an extension language for customizable applications.
What can you do with Python? Just about anything, and most things quite easily. Topics like data analysis, machine learning, web development, desktop applications, robotics, and more are all things that you can immediately begin doing with Python without much effort. Personally, I've used Python to train some AI, to help companies detect diseases, to help detect fraud and abuse against servers, to create games, to trade stocks, and I've built and helped to build multiple businesses with Python.
Python and programming is life-changing, and it's my honor to share it with you!
https://pythonprogramming.net/introduction-learn-python-3-tutorials/
If you want to install python on your machine, you can download from here: https://www.python.org/downloads/
The python version used in this course is the python 3.6 because it's more versatile for all Data Science libraries used in this course.
In some machines (mac, linux) will be installed by default version 2.7 of python, we ask you not to use version 2.x for incompatibility issues.
Install the basic version from the website if you want to start playing with python!
## Anaconda
- What is anaconda
- Install
- GUI vs Command Line
Anaconda is a an open source distribution of the Python and R programming languages and it is used in data science, machine learning, deep learning-related applications aiming at simplifying package management and deployment.
Anaconda Distribution is used by over 7 million users, and it includes more than 300 data science packages suitable for Windows, Linux, and MacOS.
It contains all the packages that you need to start developing with Python and it's the distribution that we recommend because it's very easy to learn and to use.
If you want to install Anaconda download the 3.X version from here: https://www.anaconda.com/distribution/
Anaconda has two type of interaction:
- Graphical approach
- Terminal based approach
The graphical approach is with the Anaconda Navigator a GUI that can you help to use the tools
<img src="resources/anaconda_navigator.png">
In the immage above you can see some different parts:
- The blue part: is where you can manage some different python-conda environments (we talk about this in the next cpt.)
- The red part: is where you can change the installed environments and related apps
- The yellow part: are the apps installed in a specific environment that you can use
If you open the blue part (enviroments) you can find all the environments, all the packages and you can create new environments, packages and libraries or uninstall and manage the others already in
<img src="resources/anaconda_environments.png">
The best way to use anaconda is with the terminal, after the installation open CMD (or your terminal app) and you can interactive with Anaconda using the command: conda
<img src="resources/conda-terminal.png">
Here some useful command:
- Conda installation info
- To see your environments
- List of packages in your environments
- Update anaconda
### Virtual Environments
- What is an virtual environment
- Create a new virtual environment
- Install python packages into libreries and packages (conda vs pip)
- Change environment and use different environments
The main purpose of Python virtual environments (also called venv) is to create an isolated environment for Python projects.
This means that each project can have its own dependencies, regardless of what dependencies every other project has.
In our little example above, we’d just need to create a separate virtual environment for both ProjectA and ProjectB, and we’d be good to go.
Each environment, in turn, would be able to depend on whatever version of ProjectC they choose, independent of the other.
The great thing about this is that there are no limits to the number of environments you can have since they’re just directories containing a few scripts.
Plus, they’re easily created using the virtualenv or pyenv command line tools.
It's possibile to create a virtual environment with default python, but we use environments with Anaconda.
For standard python info about the virtual environments, see this link below:
https://realpython.com/python-virtual-environments-a-primer/
Here some useful command to use with Anaconda to create, check, validate and update a Conda Venv
WARNING: if you are on windows, use CMD (as an admin if possibile) and try to avoid Powershell until you are confident with this technology
__To visualize Conda information about your installation__
```bash
conda -v
```
__Check conda is up to date__
```bash
conda update conda
```
__Create a new virtual environment (venv) with a specific python version__
Remember to replace x.x with your python version (we use principally the 3.6 version) and "yourenvname" with your environment name
```bash
conda create -n yourenvname python=x.x anaconda
```
If you want to create an empty environment without the default conda libraries you can do:
```bash
conda create -n yourenvname python=x.x
```
without the anaconda label
__Now you have to activate your conda environment__
```bash
conda activate yourenvname
```
__To install a new package in your new environment you can...__
```bash
conda install -n yourenvname [package]
```
but if you are already in your conda environment you can do simply:
```bash
conda install [package]
```
*always without the [ ] parenthesis
__To exit from your virtual environment__
```bash
conda deactivate
```
__If you want to delete your anaconda virtual environment__
```bash
conda remove -n yourenvname -all
```
__If you want to see your installed anaconda virtual environments__
```bash
conda env list
```
__If you want remove your conda environment__
```bash
conda remove --name yourenvname --all
```
__If you want to have some info about your conda venv or if an environment is deleted launch:__
```bash
conda info --envs
```
There are 2 types of scenario that you can use to install new python packages or libraries in Conda:
- Using pip
- Using conda
both are two library managers, the first one is the default python manager and the second is the anaconda default manager.
The available libraries that have both can be the same or different, so we suggest to use both manager but prioritising the use of Conda.
WARNING: If you are using pip, you must have your environment activated and be inside it.
If you want some other informations see this article (expecially if you want to use a custom requirements.yml file for your python libraries)
https://towardsdatascience.com/getting-started-with-python-environments-using-conda-32e9f2779307
## Jupyter
The Jupyter Notebook is an open-source web application that allows you to create and share documents that contain live code, equations, visualizations and narrative text.
Uses include: data cleaning and transformation, numerical simulation, statistical modeling, data visualization, machine learning, and much more.
Is the default tool for this lab and it's one of the common tools for Data Science used worldwide.
Jupyter is installed by default inside the base conda environment, but if you want to use inside your new conda virtual environment you have to install on it.
To install jupyter inside conda you have to:
1. activate your conda venv
2. launch `conda install jupyter`
3. run jupyter typing `jupyter notebook`
Everytime you want to launch Jupyter notebook with your custom conda virtual environment you have to:
1. activate your conda env
2. run: `jupyter notebook` inside the terminal
then a new browser window will appear and you can use Jupyter from there with your venv.
If you want to close jupyter
1. save your work
2. close the browser tabs
3. press: CRTL + C inside the console windows to kill all the kernels and jupyter server
#### Set Jupyter default project folder
You can set the default Jupyter home main folder with this simple guide
Use the jupyter notebook config file:
After you have installed Anaconda..
1. Open cmd (or Anaconda Prompt) and run jupyter notebook --generate-config.
2. This writes a file to C:\Users\username\.jupyter\jupyter_notebook_config.py.
3. Browse to the file location and open it in an Editor
4. Search for the following line in the file: #c.NotebookApp.notebook_dir = ''
5. Replace by c.NotebookApp.notebook_dir = '/the/path/to/home/folder/'
6. Make sure you use forward slashes in your path and use /home/user/ instead of ~/ for your home directory, backslashes could be used if placed in double quotes even if folder name contains spaces as such : "D:\yourUserName\Any Folder\More Folders\"
7. Remove the # at the beginning of the line to allow the line to execute
If you want to extend and upgrade Jupyter with new features, you can follow this guide:
https://ndres.me/post/best-jupyter-notebook-extensions/
### Jupyter Lab
JupyterLab is a web-based interactive development environment for Jupyter notebooks, code, and data.
JupyterLab is flexible: configure and arrange the user interface to support a wide range of workflows in data science, scientific computing, and machine learning.
JupyterLab is extensible and modular: write plugins that add new components and integrate with existing ones.
Compared to jupyter notebooks, jupyter lab is a single web page with much more functionalities and extended interface, it's almost an IDE more complex.
To install jupyter lab inside conda you have to:
1. activate your conda venv
2. launch `conda install jupyterlab`
3. run jupyter typing `jupyter lab`
Everytime you want to launch Jupyter notebook with your custom conda virtual environment you have to:
1. activate your conda env
2. run: `jupyter lab` inside the terminal
#### Problemi noti
Utilizzando jupyter su un environment creato a mano è possibile che non vi trovi i pacchetti installati, questo perchè si sta utilizzando jupyter installato nell'environment di default oppure in un altro ambiente, ma non nell'ambiente di riferimento della libreria installata.
Quando questo si verifica ricordate di installare jupyter all'interno del vostro nuovo ambiente (environment) di lavoro.
## Visual Studio Code
https://code.visualstudio.com/
Visual Studio Code is a source-code editor developed by Microsoft for Windows, Linux and macOS. It includes support for debugging, embedded Git control and GitHub, syntax highlighting, intelligent code completion, snippets, and code refactoring.
It's a useful IDE to develop powerful and complex applications with python and it's suggested when you want to create, design, engineer and build large application or production code.
Visual Studio Code is compatible with Python and you can follow this guide to use with:
https://code.visualstudio.com/docs/python/python-tutorial
With visual studio code you can also use code cells like jupyter notebook.
They are not the same, but the use it's quite similar thanks to IPython that is the base package on which Jupyter was built.
To use notebooks follow this guide:
https://code.visualstudio.com/docs/python/jupyter-support
Here a list of useful extension for visual studio code that we use:
- Anaconda extension pack
- Code Runner
- Git History
- Git Lens
- Live share
- Powershell
- Python
- Project manager
- Shell launcher
- vscode-icons
# Git
- What's Git?
- Why Git?
- How to use it
- Suggested course for GIT
- Using Github
Git is a distributed version control software
Created by Linus Torvalds in 2005 to manage Linux code
Can be used from the command line
Also available on Windows
It may have a more important "central" repository than the others
It's the basic foundamental tool to cooperate in a team, sharing code and "programming thing" with each others.
The purpose of Git is to manage a project, or a set of files, as they change over time.
Git stores this information in a data structure called a repository. A git repository contains, among other things, the following: A set of commit objects.
There are also companies that extends and use git for many purpose, two examples are: Github and GitLab.
GitHub is a Git repository hosting service, but it adds many of its own features. While Git is a command line tool, GitHub provides a Web-based graphical interface.
It also provides access control and several collaboration features, such as a wikis and basic task management tools for every project.
Version Control repository management services like Github and GitLab are a key component in the software development workflow. In the last few years, GitHub and GitLab positioned themselves as handy assistants for developers, particularly when working in large teams.
Both, GitLab and GitHub are web-based Git repositories.
The aim of Git is to manage software development projects and its files, as they are changing over time. Git stores this information in a data structure called a repository.
Such a git repository contains a set of commit objects and a set of references to commit objects.
A git repository is a central place where developers store, share, test and collaborate on web projects.
There are some differences beetween Gitlab and Github, but the key points are the same.
#### Install Git
Download git from here: https://git-scm.com/downloads using POSIX emulation in windows.
Or for geeks, you can follow this guide for windows with Linux Subsytem:
https://docs.microsoft.com/en-us/windows/wsl/about
#### Git the simple guide
http://rogerdudler.github.io/git-guide/
#### Git Interactive Tutorial
https://learngitbranching.js.org/
#### Using Github
Using GitHub is absolutely suggested and recommended to familiarize yourself with these tools for this course.
We recommend that you create an account on GitHub and use it for the projects and code that you will build in this lab and path.
Use this tutorial to understand how to use GitHub
https://product.hubspot.com/blog/git-and-github-tutorial-for-beginners
|
github_jupyter
|
conda -v
conda update conda
conda create -n yourenvname python=x.x anaconda
conda create -n yourenvname python=x.x
conda activate yourenvname
conda install -n yourenvname [package]
conda install [package]
conda deactivate
conda remove -n yourenvname -all
conda env list
conda remove --name yourenvname --all
conda info --envs
| 0.273963 | 0.977349 |
# Exercise 3.3 for CGT assignment 1
## Student info
- **Name**: Bontinck Lennert
- **StudentID**: 568702
- **Affiliation**: VUB - Master Computer Science: AI
```
import random
import numpy as np
```
### Moran_step function
```
def moran_step(current_state, beta, mu, Z, A):
"""
This function returns the next state of the population where
* current_state, is the current state of the population
* beta is the intensity of selection
* mu is the mutation probability
* Z is the population size
* A is the matrix that contains the payoffs of each strategy against each other.
"""
def select_random_player_from_population():
return random.randint(0, Z-1)
def get_player_payoff(player, opponent):
return A[player,opponent]
def get_random_strategy():
return random.randint(0, 1)
def should_do_random_value():
return random.random() <= mu
def fermi_prob(fitness_difference):
return np.clip(1. / (1. + np.exp(beta * fitness_difference, dtype=np.float64)), 0., 1.)
#Select 2 random players
selected=[select_random_player_from_population(), select_random_player_from_population()]
#Init fitness var
fitness = np.zeros(2)
#Calculate avg fitness for both players
for i, player in enumerate(selected):
for j in range(Z):
if j == player: continue #Skip playing against himself
players_payoff = get_player_payoff(current_state[player],current_state[j])
fitness[i] += players_payoff
fitness[i] = fitness[i] / (Z-1)
fitness_difference = fitness[0] - fitness[1]
#Assign mutation with fermi prob or adopt random strategy with mu probability
if random.random() < fermi_prob(fitness_difference):
if should_do_random_value():
current_state[selected[0]] = get_random_strategy()
else:
current_state[selected[0]] = current_state[selected[1]]
else:
if should_do_random_value():
current_state[selected[0]] = get_random_strategy()
else:
current_state[selected[1]] = current_state[selected[0]]
#Return new state
return current_state
```
### Estimate_stationary_distribution function
```
def estimate_stationary_distribution(nb_runs, transitory, nb_generations, beta, mu, Z, A) :
"""
This function returns the stationary distribution of the population as a vector of floats
containing the fraction of time the population spends in each possible state where
* nb_runs, is number of independent realizations of the Monte Carlo simulation
* transitory is the transitory period
* nb_generations is the number of generations to run the moran process
* beta is the intensity of selection, mu is the mutation probability
* Z is the population size
* A is the matrix that contains the payoffs of each strategy against each other.
"""
#make an array to count how many times a certain state occurs (O and Z possible so Z+1)
state_count = np.zeros(Z+1)
#Repeat the simulation nb_runs times
for nb_run_index in range(nb_runs):
#Generate a random population state
current_state = np.random.randint(2, size=Z)
#Run the Moran process for a transitory period.
#No logging required
for transitory_loop_index in range(transitory):
moran_step(current_state, beta, mu, Z, A)
#Run the process for nb_generations and count how often
#the population passes through each possible state.
for nb_generation_index in range(nb_generations):
###get new current state
current_state = moran_step(current_state, beta, mu, Z, A)
###count amount of hawk players and save an extra instance of this state
state = (current_state == 0).sum()
state_count[state] += 1
#avg state_count
state_count = state_count/nb_runs
#scale state_count
state_count = state_count/nb_generations
return state_count
```
### Main loop
```
#Main loop
"""
we assume that 𝛽=10, 𝜇=10^−3, 𝑍=50, 𝑉=2, 𝐷=3 and 𝑇 = 1.
We assume that transitory = 10^3, nb_generations = 10^5 and the nb_runs = 10.
This main loop executes my code and produces the appropiate results for these assumptions.
It is possible to execute it as: python moran_process.py.
"""
#Setting the parameters for ease of use
beta = 10
mu = 0.001
Z = 50
V = 2
D = 3
T = 1
transitory = 1000
nb_generations = 100000
nb_runs = 10
# Payoff matrix
A = np.array([
[ (V-D)/2, V],
[ 0 , (V/2) - T],
])
#get results
result = estimate_stationary_distribution(nb_runs, transitory, nb_generations, beta, mu, Z, A)
result
```
### plotting the results
```
# Plotting libraries
import matplotlib.pylab as plt
# Magic function to make matplotlib inline; other style specs must come AFTER
%matplotlib inline
# This enables high resolution PNGs.
%config InlineBackend.figure_formats = {'png', 'svg'}
fig, ax = plt.subplots(figsize=(5, 4))
fig.patch.set_facecolor('white')
lines = ax.plot(np.arange(0, Z+1)/Z, result)
plt.setp(lines, linewidth=2.0)
ax.set_ylabel('stationary distribution',size=16)
ax.set_xlabel('$k/Z$',size=16)
ax.set_xlim(0, 1)
plt.show()
```
|
github_jupyter
|
import random
import numpy as np
def moran_step(current_state, beta, mu, Z, A):
"""
This function returns the next state of the population where
* current_state, is the current state of the population
* beta is the intensity of selection
* mu is the mutation probability
* Z is the population size
* A is the matrix that contains the payoffs of each strategy against each other.
"""
def select_random_player_from_population():
return random.randint(0, Z-1)
def get_player_payoff(player, opponent):
return A[player,opponent]
def get_random_strategy():
return random.randint(0, 1)
def should_do_random_value():
return random.random() <= mu
def fermi_prob(fitness_difference):
return np.clip(1. / (1. + np.exp(beta * fitness_difference, dtype=np.float64)), 0., 1.)
#Select 2 random players
selected=[select_random_player_from_population(), select_random_player_from_population()]
#Init fitness var
fitness = np.zeros(2)
#Calculate avg fitness for both players
for i, player in enumerate(selected):
for j in range(Z):
if j == player: continue #Skip playing against himself
players_payoff = get_player_payoff(current_state[player],current_state[j])
fitness[i] += players_payoff
fitness[i] = fitness[i] / (Z-1)
fitness_difference = fitness[0] - fitness[1]
#Assign mutation with fermi prob or adopt random strategy with mu probability
if random.random() < fermi_prob(fitness_difference):
if should_do_random_value():
current_state[selected[0]] = get_random_strategy()
else:
current_state[selected[0]] = current_state[selected[1]]
else:
if should_do_random_value():
current_state[selected[0]] = get_random_strategy()
else:
current_state[selected[1]] = current_state[selected[0]]
#Return new state
return current_state
def estimate_stationary_distribution(nb_runs, transitory, nb_generations, beta, mu, Z, A) :
"""
This function returns the stationary distribution of the population as a vector of floats
containing the fraction of time the population spends in each possible state where
* nb_runs, is number of independent realizations of the Monte Carlo simulation
* transitory is the transitory period
* nb_generations is the number of generations to run the moran process
* beta is the intensity of selection, mu is the mutation probability
* Z is the population size
* A is the matrix that contains the payoffs of each strategy against each other.
"""
#make an array to count how many times a certain state occurs (O and Z possible so Z+1)
state_count = np.zeros(Z+1)
#Repeat the simulation nb_runs times
for nb_run_index in range(nb_runs):
#Generate a random population state
current_state = np.random.randint(2, size=Z)
#Run the Moran process for a transitory period.
#No logging required
for transitory_loop_index in range(transitory):
moran_step(current_state, beta, mu, Z, A)
#Run the process for nb_generations and count how often
#the population passes through each possible state.
for nb_generation_index in range(nb_generations):
###get new current state
current_state = moran_step(current_state, beta, mu, Z, A)
###count amount of hawk players and save an extra instance of this state
state = (current_state == 0).sum()
state_count[state] += 1
#avg state_count
state_count = state_count/nb_runs
#scale state_count
state_count = state_count/nb_generations
return state_count
#Main loop
"""
we assume that 𝛽=10, 𝜇=10^−3, 𝑍=50, 𝑉=2, 𝐷=3 and 𝑇 = 1.
We assume that transitory = 10^3, nb_generations = 10^5 and the nb_runs = 10.
This main loop executes my code and produces the appropiate results for these assumptions.
It is possible to execute it as: python moran_process.py.
"""
#Setting the parameters for ease of use
beta = 10
mu = 0.001
Z = 50
V = 2
D = 3
T = 1
transitory = 1000
nb_generations = 100000
nb_runs = 10
# Payoff matrix
A = np.array([
[ (V-D)/2, V],
[ 0 , (V/2) - T],
])
#get results
result = estimate_stationary_distribution(nb_runs, transitory, nb_generations, beta, mu, Z, A)
result
# Plotting libraries
import matplotlib.pylab as plt
# Magic function to make matplotlib inline; other style specs must come AFTER
%matplotlib inline
# This enables high resolution PNGs.
%config InlineBackend.figure_formats = {'png', 'svg'}
fig, ax = plt.subplots(figsize=(5, 4))
fig.patch.set_facecolor('white')
lines = ax.plot(np.arange(0, Z+1)/Z, result)
plt.setp(lines, linewidth=2.0)
ax.set_ylabel('stationary distribution',size=16)
ax.set_xlabel('$k/Z$',size=16)
ax.set_xlim(0, 1)
plt.show()
| 0.618435 | 0.936285 |
# Web-site Demo
http://myweatherproject.s3-website-us-east-1.amazonaws.com/
#### If viewing on github, here is a sample of the index web-page and Chicago city web-page
[index.html](https://htmlpreview.github.io/?https://github.com/mike-seeber/Weather/blob/master/web-page_sample/index.html)
[chicago.html](https://htmlpreview.github.io/?https://raw.githubusercontent.com/mike-seeber/Weather/master/web-page_sample/chicago.html)
# Architecture

# EC2
- Hourly cronjob (meets api data restrictions)
- [weather_api.py](code/weather_api.py)
### Weather API
- Obtains data from Weather Underground
- Creates a list of tuples: (city, current_weather), for speed layer
- Ships raw data to Firehose
### Speed Layer
- Pulls in web-site HTML as String
- Updates Current Weather for each City using Regular Expressions
### E-mail
- Sends completion e-mail that Weather API and Speed Layer are Complete
- Indicates number of cities updated (expecting all)
# Kinesis
### Firehose
- Packages raw data from all cities together into a single file
- Ships raw data to S3
# S3
### Raw Data
- Stores raw data
### Web Host
- Hosts web-site
# EMR Spark Cluster
### Normalize

- city: Data about the city
- nearby: Nearby locations for each city
- cityDay: Data about the city on the given date
- weather: Weather data for the given city, date, and time
- forecast: Forecasted weather for the city retrieved at the given date and time about the forecast date and forecast time
- path: All S3 paths that have been loaded into the tables
- stats: Output from analyze job discussed below
### Normalize Process
- Hourly cronjob following EC2 API job
- [weather_normalize.py](code/weather_normalize.py)
- Load each table from parquet\*
- Check S3 for any/all new files that are not in "path" table
- For each new file:
- Normalize the file's data
- Add filepath "source" data for each record (track lineage)
- Append new data to full tables
- Enforce keys (see below)
- Write back to parquet
- Send Job Completion E-mail
\* Self-healing mechanism recreates tables from raw data if issues encountered with parquet files. This was used during development but hasn't been encountered in production.
#### Forecast Problem/Solution
Problem - can't explode multiple columns
Solution - switch to RDD
DataFrame:
City, Date, Time, [forecast date/times], [forecast temperatures], [forecast humidity], [ ]...
RDD:
Zip:
City, Date, Time, zip(forecast date/times, forecast temps, hum etc.)
City, Date, Time, [(dt, temp, hum, ...), (dt, temp, hum, ...), (dt, temp, hum...), ...)
Reshape:
[(city, date, time, dt, temp, hum, ...), (city, date, time, dt, temp, hum, ...), ...]
FlatMap:
(city, date, time, dt, temp, hum, ...)
Switch Back to DF
#### Enforce Keys
- I noticed that Weather Underground shipped me 2 different historical temperatures for the same city/day (they were different by 1 degree).
- If I simply append the new data, weather underground may not live up to my keys.
- To enforce my keys, I will use the most recent data provided by Weather Underground for each key.
- Because I tracked the data lineage (source) of each piece of information, I can accomplish this as follows:
select *
from
(select *
,row_number() over(partition by city, date order by source desc) as rk
from cityDay2V)
where rk=1').drop('rk')
- I enforce keys for every table
### Analyze

- Hourly cronjob following Web Update job (we discuss it first since the previously analyzed data is used in the web update)
- [weather_analyze.py](code/weather_analyze.py)
- Load tables from Parquet
- Join Actual Weather that occured back onto the Previous Forecasts that were made
- I truncated minutes and joined to the nearest hour (reasonable since most data was between xx:00 and xx:02)
- Calculate the number of hours between forecast and actual weather (call it "forecast hours")
- For example, at 11:00 we forecast weather for 2:00, the forecast hours are 3
- Calculate the difference between the forecast weather features and the actual weather features
- Calculate counts, means, and standard deviations for the differences by "forecast hours"
- Write Stats to Parquet
- Send Job Completion E-mail
### Web Update
- Hourly cronjob following Normalize process
- [weather_report.py](code/weather_report.py)
- Load tables from Parquet
- Phase 1: Preprocess DataFrames to filter on the Current Data needed and Cache the smaller tables
- Phase 2: For each city:
- Query all the different tables for the current data for each section of the html report
- Create city web-page html using both strings and pandas DataFrame.to_html()
- Create plots by joining stats with forecast, calculating confidence intervals, using DataFrame.plot(), and saving each image to S3
- Create index and error web-pages.
- Send Job Completion E-mail
# Hourly E-mails

# Appendix - Big Data System Properties
### Robustness and fault tolerance
How does my system have this property?
- The system is broken down into 4 self-contained parts with e-mail notifications for the successful completion of each part. If one of these parts break, I will immediately know which part broke and can run the code for that part directly to identify the exact error within the code.
- The normalize job incorporates self-healing code where if it encounters issues loading the needed parquet files, it will rebuild them from scratch from the source data.
- Everything downstream from the S3 raw data can be easily reconstructed or moved to another server should any part of the system go down.
- The enforce_keys function in the normalize process ensures that the keys for each table are respected by using the most recent data if duplicates are accidently sent from the external API.
How does my system fall short and how could it be improved?
- The system is dependent on the EC2 machine connecting to the data api and the firehose to stream new data into S3. If this part of the system goes down, the weather for that timeframe would be lost forever.
- The successful job completion e-mail serves as one measure to limit the amount of time that would pass before this situation would be caught.
- The system is dependent on the weather underground api being available.
- Potentially, I could source weather data from a second source in case weather underground ever failed, but the development and maintenance for this may be prohibitive.
### Low latency reads and updates
How does my system have this property?
- The speed layer gets the current weather directly to the web-site immediately when it is obtained.
- The rest of the data is not urgent and is updated 9 minutes later (which is plenty soon enough).
- The web-site is hosted on S3 and loads immediately upon request.
How does my system fall short and how could it be improved?
- The weather conditions are updated hourly. This is a constraint of the number of api calls we are allowed to make on our budget.
- The system could be improved by reading new weather data more frequently into our system.
- The system could also get all of the data to the web-site with a quicker turnaround if we piped the stream directly into Spark Streaming and cut out the time delay from Firehose.
### Scalability
How does my system have this property?
- The EC2 API is only performing 15 requests per hour. There is a ton of room to scale if we paid weather underground for more requests.
- Firehose will automatically scale to handle an increased load.
- S3 is infinitely scalable for both raw data and web hosting of html pages.
- Spark can also be scaled by easily adding more machines to increase capacity.
How does my system fall short and how could it be improved?
- The self-healing recreation of parquet files from scratch would become more expensive if our data volume increased.
- Instead, I would probably store the parquet files in a backup location and load from the backup if the primary load failed.
### Generalization
How does my system have this property?
- We store all raw data in S3 so any changes that we want to make downstream can be ran to incorporate all of the data that we have accumulated into the change. This makes our system quite flexible and adaptible.
How does my system fall short and how could it be improved?
- There is a short lag (few minutes) in between the api call and firehose packaging and shipping the data to S3. This limits our ability to serve all the data downstream with no delay. This is being overcome with the speed layer for current temperature but not for the other pieces of data. There are potentially some other future applications that would want other real-time data that we aren't serving real-time today.
- As mentioned above, we could improve this by using Spark Streaming instead of firehose to essentially cut out the time delay.
### Extensibility
How does my system have this property?
- It would be very easy to update the Weather Underground API to add a new weather feature that we want to collect and the data would automatically flow into S3.
- The normalize process stores the data in 3NF, so the new feature would only need to belong to the single approrpriate table. There is some development required to pull in a new feature, but the system is extensible.
- The web-site could also be extended to display new features.
- If, for example, we wanted to add additional cities, we would only have to update the EC2 weather API. The Spark Cluster would automatically incorporate the new data. The new city would be auto-detected and a new web-page for the city would automatically be built and incorporated!
### Ad hoc Queries
How does my system have this property?
- The data tables are stored in Parquet on the cluster. It is super easy to open a new Jupyter Notebook, point to the tables, and begin querying. The data is already in 3NF, so it easy and obvious to join tables and create exactly what is needed.
How does my system fall short and how could it be improved?
- There were some data elements in the Raw Data json structure that didn't seem useful, and that I didn't bring into the normalized format. I could normalize those additional features as well so they would also be available for querying in case of future use cases.
### Minimal maintenance
How does my system have this property?
- Every part of the system scales very easily, with many parts that will scale automatically. The cluster size we are using is more than sufficient to last months before we would need to add additional nodes.
- The data system has already run from end-to-end (producing all 4 job complete e-mails) hundreds of times without ever encountering a single error.
How does my system fall short and how could it be improved?
- The size of the spark cluster would need to be updated periodically. Maybe I could create a job that would measure utilization and notfiy me when we reached a certain capacity and it was time to update.
### Debuggability
How does my system have this property?
- As discussed above, the 4 discrete phases with e-mail completions makes it easy to find where the error started. From there, it is easy to run the single failing script ad hoc and retrieve the exact line number where the error is occurring.
- S3 stores all raw data and the normalize process has a function that can be swapped in/out on demand to re-build from scratch whenever needed or desired.
- The analyze and report jobs run on all of the data, so they will continue to work even without ever caring if we reload from scratch.
How does my system fall short and how could it be improved?
- I could write it in additional checks throughout each of the 4 phases and report out on each, so that failures would be isolated to specific portions of the code within each phase.
|
github_jupyter
|
# Web-site Demo
http://myweatherproject.s3-website-us-east-1.amazonaws.com/
#### If viewing on github, here is a sample of the index web-page and Chicago city web-page
[index.html](https://htmlpreview.github.io/?https://github.com/mike-seeber/Weather/blob/master/web-page_sample/index.html)
[chicago.html](https://htmlpreview.github.io/?https://raw.githubusercontent.com/mike-seeber/Weather/master/web-page_sample/chicago.html)
# Architecture

# EC2
- Hourly cronjob (meets api data restrictions)
- [weather_api.py](code/weather_api.py)
### Weather API
- Obtains data from Weather Underground
- Creates a list of tuples: (city, current_weather), for speed layer
- Ships raw data to Firehose
### Speed Layer
- Pulls in web-site HTML as String
- Updates Current Weather for each City using Regular Expressions
### E-mail
- Sends completion e-mail that Weather API and Speed Layer are Complete
- Indicates number of cities updated (expecting all)
# Kinesis
### Firehose
- Packages raw data from all cities together into a single file
- Ships raw data to S3
# S3
### Raw Data
- Stores raw data
### Web Host
- Hosts web-site
# EMR Spark Cluster
### Normalize

- city: Data about the city
- nearby: Nearby locations for each city
- cityDay: Data about the city on the given date
- weather: Weather data for the given city, date, and time
- forecast: Forecasted weather for the city retrieved at the given date and time about the forecast date and forecast time
- path: All S3 paths that have been loaded into the tables
- stats: Output from analyze job discussed below
### Normalize Process
- Hourly cronjob following EC2 API job
- [weather_normalize.py](code/weather_normalize.py)
- Load each table from parquet\*
- Check S3 for any/all new files that are not in "path" table
- For each new file:
- Normalize the file's data
- Add filepath "source" data for each record (track lineage)
- Append new data to full tables
- Enforce keys (see below)
- Write back to parquet
- Send Job Completion E-mail
\* Self-healing mechanism recreates tables from raw data if issues encountered with parquet files. This was used during development but hasn't been encountered in production.
#### Forecast Problem/Solution
Problem - can't explode multiple columns
Solution - switch to RDD
DataFrame:
City, Date, Time, [forecast date/times], [forecast temperatures], [forecast humidity], [ ]...
RDD:
Zip:
City, Date, Time, zip(forecast date/times, forecast temps, hum etc.)
City, Date, Time, [(dt, temp, hum, ...), (dt, temp, hum, ...), (dt, temp, hum...), ...)
Reshape:
[(city, date, time, dt, temp, hum, ...), (city, date, time, dt, temp, hum, ...), ...]
FlatMap:
(city, date, time, dt, temp, hum, ...)
Switch Back to DF
#### Enforce Keys
- I noticed that Weather Underground shipped me 2 different historical temperatures for the same city/day (they were different by 1 degree).
- If I simply append the new data, weather underground may not live up to my keys.
- To enforce my keys, I will use the most recent data provided by Weather Underground for each key.
- Because I tracked the data lineage (source) of each piece of information, I can accomplish this as follows:
select *
from
(select *
,row_number() over(partition by city, date order by source desc) as rk
from cityDay2V)
where rk=1').drop('rk')
- I enforce keys for every table
### Analyze

- Hourly cronjob following Web Update job (we discuss it first since the previously analyzed data is used in the web update)
- [weather_analyze.py](code/weather_analyze.py)
- Load tables from Parquet
- Join Actual Weather that occured back onto the Previous Forecasts that were made
- I truncated minutes and joined to the nearest hour (reasonable since most data was between xx:00 and xx:02)
- Calculate the number of hours between forecast and actual weather (call it "forecast hours")
- For example, at 11:00 we forecast weather for 2:00, the forecast hours are 3
- Calculate the difference between the forecast weather features and the actual weather features
- Calculate counts, means, and standard deviations for the differences by "forecast hours"
- Write Stats to Parquet
- Send Job Completion E-mail
### Web Update
- Hourly cronjob following Normalize process
- [weather_report.py](code/weather_report.py)
- Load tables from Parquet
- Phase 1: Preprocess DataFrames to filter on the Current Data needed and Cache the smaller tables
- Phase 2: For each city:
- Query all the different tables for the current data for each section of the html report
- Create city web-page html using both strings and pandas DataFrame.to_html()
- Create plots by joining stats with forecast, calculating confidence intervals, using DataFrame.plot(), and saving each image to S3
- Create index and error web-pages.
- Send Job Completion E-mail
# Hourly E-mails

# Appendix - Big Data System Properties
### Robustness and fault tolerance
How does my system have this property?
- The system is broken down into 4 self-contained parts with e-mail notifications for the successful completion of each part. If one of these parts break, I will immediately know which part broke and can run the code for that part directly to identify the exact error within the code.
- The normalize job incorporates self-healing code where if it encounters issues loading the needed parquet files, it will rebuild them from scratch from the source data.
- Everything downstream from the S3 raw data can be easily reconstructed or moved to another server should any part of the system go down.
- The enforce_keys function in the normalize process ensures that the keys for each table are respected by using the most recent data if duplicates are accidently sent from the external API.
How does my system fall short and how could it be improved?
- The system is dependent on the EC2 machine connecting to the data api and the firehose to stream new data into S3. If this part of the system goes down, the weather for that timeframe would be lost forever.
- The successful job completion e-mail serves as one measure to limit the amount of time that would pass before this situation would be caught.
- The system is dependent on the weather underground api being available.
- Potentially, I could source weather data from a second source in case weather underground ever failed, but the development and maintenance for this may be prohibitive.
### Low latency reads and updates
How does my system have this property?
- The speed layer gets the current weather directly to the web-site immediately when it is obtained.
- The rest of the data is not urgent and is updated 9 minutes later (which is plenty soon enough).
- The web-site is hosted on S3 and loads immediately upon request.
How does my system fall short and how could it be improved?
- The weather conditions are updated hourly. This is a constraint of the number of api calls we are allowed to make on our budget.
- The system could be improved by reading new weather data more frequently into our system.
- The system could also get all of the data to the web-site with a quicker turnaround if we piped the stream directly into Spark Streaming and cut out the time delay from Firehose.
### Scalability
How does my system have this property?
- The EC2 API is only performing 15 requests per hour. There is a ton of room to scale if we paid weather underground for more requests.
- Firehose will automatically scale to handle an increased load.
- S3 is infinitely scalable for both raw data and web hosting of html pages.
- Spark can also be scaled by easily adding more machines to increase capacity.
How does my system fall short and how could it be improved?
- The self-healing recreation of parquet files from scratch would become more expensive if our data volume increased.
- Instead, I would probably store the parquet files in a backup location and load from the backup if the primary load failed.
### Generalization
How does my system have this property?
- We store all raw data in S3 so any changes that we want to make downstream can be ran to incorporate all of the data that we have accumulated into the change. This makes our system quite flexible and adaptible.
How does my system fall short and how could it be improved?
- There is a short lag (few minutes) in between the api call and firehose packaging and shipping the data to S3. This limits our ability to serve all the data downstream with no delay. This is being overcome with the speed layer for current temperature but not for the other pieces of data. There are potentially some other future applications that would want other real-time data that we aren't serving real-time today.
- As mentioned above, we could improve this by using Spark Streaming instead of firehose to essentially cut out the time delay.
### Extensibility
How does my system have this property?
- It would be very easy to update the Weather Underground API to add a new weather feature that we want to collect and the data would automatically flow into S3.
- The normalize process stores the data in 3NF, so the new feature would only need to belong to the single approrpriate table. There is some development required to pull in a new feature, but the system is extensible.
- The web-site could also be extended to display new features.
- If, for example, we wanted to add additional cities, we would only have to update the EC2 weather API. The Spark Cluster would automatically incorporate the new data. The new city would be auto-detected and a new web-page for the city would automatically be built and incorporated!
### Ad hoc Queries
How does my system have this property?
- The data tables are stored in Parquet on the cluster. It is super easy to open a new Jupyter Notebook, point to the tables, and begin querying. The data is already in 3NF, so it easy and obvious to join tables and create exactly what is needed.
How does my system fall short and how could it be improved?
- There were some data elements in the Raw Data json structure that didn't seem useful, and that I didn't bring into the normalized format. I could normalize those additional features as well so they would also be available for querying in case of future use cases.
### Minimal maintenance
How does my system have this property?
- Every part of the system scales very easily, with many parts that will scale automatically. The cluster size we are using is more than sufficient to last months before we would need to add additional nodes.
- The data system has already run from end-to-end (producing all 4 job complete e-mails) hundreds of times without ever encountering a single error.
How does my system fall short and how could it be improved?
- The size of the spark cluster would need to be updated periodically. Maybe I could create a job that would measure utilization and notfiy me when we reached a certain capacity and it was time to update.
### Debuggability
How does my system have this property?
- As discussed above, the 4 discrete phases with e-mail completions makes it easy to find where the error started. From there, it is easy to run the single failing script ad hoc and retrieve the exact line number where the error is occurring.
- S3 stores all raw data and the normalize process has a function that can be swapped in/out on demand to re-build from scratch whenever needed or desired.
- The analyze and report jobs run on all of the data, so they will continue to work even without ever caring if we reload from scratch.
How does my system fall short and how could it be improved?
- I could write it in additional checks throughout each of the 4 phases and report out on each, so that failures would be isolated to specific portions of the code within each phase.
| 0.807537 | 0.730001 |
```
%matplotlib inline
from matplotlib import rcParams
rcParams['font.family'] = 'sans-serif'
import pandas as pd
file = '/Users/quartz/data/collabo/adult.csv'
data_raw = pd.read_csv(file)
data_raw.tail()
```
### EDA
```
# dependent variable(y) <=50K = 1, >50K = 0
data_raw.income.value_counts()
# age
data_raw.age.value_counts()
# workclass
data_raw.workclass.value_counts()
data_raw.education.value_counts()
data_revise = data_raw[['age', 'income']]
data_revise.sort_values(by='age', inplace=True)
data_revise = data_revise.reset_index(drop=True)
data_revise.income = data_revise.income.apply(lambda x : 0 if x == '<=50K' else 1)
data_revise.tail()
x = data_revise.age
y = data_revise.income
plt.scatter(x, y)
```
### preprocessing
```
data_revise.tail()
data = data_revise.age
def seq2dataset(seq, window_size):
dataset = []
for i in range(len(seq)-window_size):
subset = seq[i:(i+window_size+1)]
dataset.append(subset)
return np.array(dataset)
dataset = seq2dataset(data, window_size=4)
dataset.shape, dataset
# scaling
min_value = min(data)
max_value = max(data)
min_value, max_value
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
dataset = scaler.fit_transform(dataset)
X_train = dataset.copy()
from keras.utils import np_utils
import keras
y_train = data_revise.income
y_train = y_train[:-4]
y_train = np_utils.to_categorical(y_train)
X_train.shape, y_train.shape
```
### modeling
```
# 손실 이력 클래스 정의
class LossHistory(keras.callbacks.Callback):
def init(self):
self.losses = []
def on_epoch_end(self, batch, logs={}):
self.losses.append(logs.get('loss'))
history = LossHistory()
history.init()
import numpy as np
from keras.models import Sequential
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
from keras.layers import Flatten
from keras.layers import Dense,LSTM
model = Sequential()
model.add(Dense(128, input_dim=5, activation='relu'))
model.add(Dense(128, activation='relu'))
model.add(Dense(2, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=100, batch_size=30, verbose=2, callbacks=[history])
# loss function graph
plt.plot(history.losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
scores = model.evaluate(X_train, y_train)
print("%s: %.2f%%" %(model.metrics_names[1], scores[1]*100))
```
### 결론
- sequence하지 않은 데이터를 RNN 모델에 넣고 돌리니 제대로 학습이 이루어지지 않는다.
- 데이터에 따라 걸맞는 알고리즘을 사용해야 퍼포먼스도 좋고, 비용(시간, 파워)도 줄일 수 있다.
|
github_jupyter
|
%matplotlib inline
from matplotlib import rcParams
rcParams['font.family'] = 'sans-serif'
import pandas as pd
file = '/Users/quartz/data/collabo/adult.csv'
data_raw = pd.read_csv(file)
data_raw.tail()
# dependent variable(y) <=50K = 1, >50K = 0
data_raw.income.value_counts()
# age
data_raw.age.value_counts()
# workclass
data_raw.workclass.value_counts()
data_raw.education.value_counts()
data_revise = data_raw[['age', 'income']]
data_revise.sort_values(by='age', inplace=True)
data_revise = data_revise.reset_index(drop=True)
data_revise.income = data_revise.income.apply(lambda x : 0 if x == '<=50K' else 1)
data_revise.tail()
x = data_revise.age
y = data_revise.income
plt.scatter(x, y)
data_revise.tail()
data = data_revise.age
def seq2dataset(seq, window_size):
dataset = []
for i in range(len(seq)-window_size):
subset = seq[i:(i+window_size+1)]
dataset.append(subset)
return np.array(dataset)
dataset = seq2dataset(data, window_size=4)
dataset.shape, dataset
# scaling
min_value = min(data)
max_value = max(data)
min_value, max_value
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
dataset = scaler.fit_transform(dataset)
X_train = dataset.copy()
from keras.utils import np_utils
import keras
y_train = data_revise.income
y_train = y_train[:-4]
y_train = np_utils.to_categorical(y_train)
X_train.shape, y_train.shape
# 손실 이력 클래스 정의
class LossHistory(keras.callbacks.Callback):
def init(self):
self.losses = []
def on_epoch_end(self, batch, logs={}):
self.losses.append(logs.get('loss'))
history = LossHistory()
history.init()
import numpy as np
from keras.models import Sequential
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
from keras.layers import Flatten
from keras.layers import Dense,LSTM
model = Sequential()
model.add(Dense(128, input_dim=5, activation='relu'))
model.add(Dense(128, activation='relu'))
model.add(Dense(2, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=100, batch_size=30, verbose=2, callbacks=[history])
# loss function graph
plt.plot(history.losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
scores = model.evaluate(X_train, y_train)
print("%s: %.2f%%" %(model.metrics_names[1], scores[1]*100))
| 0.609059 | 0.788176 |
```
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
from numpy.random import randint
from numpy.random import rand
# objective function
def objective(x):
out = x[0]**2.0 + x[1]**2.0
return out
# decode bitstring to numbers
def decode(bounds, n_bits, bitstring):
decoded = list()
largest = 2**n_bits
for i in range(len(bounds)):
# extract the substring
start, end = i * n_bits, (i * n_bits)+n_bits
substring = bitstring[start:end]
# convert bitstring to a string of chars
chars = ''.join([str(s) for s in substring])
# convert string to integer
integer = int(chars, 2)
# scale integer to desired range
value = bounds[i][0] + (integer/largest) * (bounds[i][1] - bounds[i][0])
# store
decoded.append(value)
return decoded
# tournament selection
def selection(pop, scores, k=3):
# first random selection
selection_ix = randint(len(pop))
for ix in randint(0, len(pop), k-1):
# check if better (e.g. perform a tournament)
if scores[ix] < scores[selection_ix]:
selection_ix = ix
return pop[selection_ix]
# crossover two parents to create two children
def crossover(p1, p2, r_cross):
# children are copies of parents by default
c1, c2 = p1.copy(), p2.copy()
# check for recombination
if rand() < r_cross:
# select crossover point that is not on the end of the string
pt = randint(1, len(p1)-2)
# perform crossover
c1 = p1[:pt] + p2[pt:]
c2 = p2[:pt] + p1[pt:]
return [c1, c2]
# mutation operator
def mutation(bitstring, r_mut):
for i in range(len(bitstring)):
# check for a mutation
if rand() < r_mut:
# flip the bit
bitstring[i] = 1 - bitstring[i]
# genetic algorithm
def genetic_algorithm(objective, bounds, n_bits, n_iter, n_pop, r_cross, r_mut):
# initial population of random bitstring
pop = [randint(0, 2, n_bits*len(bounds)).tolist() for _ in range(n_pop)]
# keep track of best solution
best, best_eval = 0, objective(decode(bounds, n_bits, pop[0]))
# enumerate generations
for gen in range(n_iter):
# decode population
decoded = [decode(bounds, n_bits, p) for p in pop]
# evaluate all candidates in the population
scores = [objective(d) for d in decoded]
# check for new best solution
for i in range(n_pop):
if scores[i] < best_eval:
best, best_eval = pop[i], scores[i]
print(">%d, new best f(%s) = %f" % (gen, decoded[i], scores[i]))
# select parents
selected = [selection(pop, scores) for _ in range(n_pop)]
# create the next generation
children = list()
for i in range(0, n_pop, 2):
# get selected parents in pairs
p1, p2 = selected[i], selected[i+1]
# crossover and mutation
for c in crossover(p1, p2, r_cross):
# mutation
mutation(c, r_mut)
# store for next generation
children.append(c)
# replace population
pop = children
return [best, best_eval]
# define range for input
bounds = [[-5.0, 5.0], [-5.0, 5.0]]
# define the total iterations
n_iter = 100
# bits per variable
n_bits = 16
# define the population size
n_pop = 100
# crossover rate
r_cross = 0.9
# mutation rate
r_mut = 1.0 / (float(n_bits) * len(bounds)) #0.03125
# perform the genetic algorithm search
best, score = genetic_algorithm(objective, bounds, n_bits, n_iter, n_pop, r_cross, r_mut)
print('Done!')
decoded = decode(bounds, n_bits, best)
print('f(%s) = %f' % (decoded, score))
# testing over breast cancer data
# define range for input
bounds = cancer.data
# define the total iterations
n_iter = 100
# bits per variable
n_bits = 16
# define the population size
n_pop = 100
# crossover rate
r_cross = 0.9
# mutation rate
r_mut = 1.0 / (float(n_bits) * len(bounds)) #0.00010984182776801405
# perform the genetic algorithm search
best, score = genetic_algorithm(objective, bounds, n_bits, n_iter, n_pop, r_cross, r_mut)
print('Done!')
decoded = decode(bounds, n_bits, best)
print('f(%s) = %f' % (decoded, score))
print(decoded[len(decoded)-30:-1])
print(best)
print(r_mut)
print(bounds)
print(len(bounds))
print(len(bounds[1]))
print(cancer.feature_names)
print(len(cancer.feature_names))
```
|
github_jupyter
|
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
from numpy.random import randint
from numpy.random import rand
# objective function
def objective(x):
out = x[0]**2.0 + x[1]**2.0
return out
# decode bitstring to numbers
def decode(bounds, n_bits, bitstring):
decoded = list()
largest = 2**n_bits
for i in range(len(bounds)):
# extract the substring
start, end = i * n_bits, (i * n_bits)+n_bits
substring = bitstring[start:end]
# convert bitstring to a string of chars
chars = ''.join([str(s) for s in substring])
# convert string to integer
integer = int(chars, 2)
# scale integer to desired range
value = bounds[i][0] + (integer/largest) * (bounds[i][1] - bounds[i][0])
# store
decoded.append(value)
return decoded
# tournament selection
def selection(pop, scores, k=3):
# first random selection
selection_ix = randint(len(pop))
for ix in randint(0, len(pop), k-1):
# check if better (e.g. perform a tournament)
if scores[ix] < scores[selection_ix]:
selection_ix = ix
return pop[selection_ix]
# crossover two parents to create two children
def crossover(p1, p2, r_cross):
# children are copies of parents by default
c1, c2 = p1.copy(), p2.copy()
# check for recombination
if rand() < r_cross:
# select crossover point that is not on the end of the string
pt = randint(1, len(p1)-2)
# perform crossover
c1 = p1[:pt] + p2[pt:]
c2 = p2[:pt] + p1[pt:]
return [c1, c2]
# mutation operator
def mutation(bitstring, r_mut):
for i in range(len(bitstring)):
# check for a mutation
if rand() < r_mut:
# flip the bit
bitstring[i] = 1 - bitstring[i]
# genetic algorithm
def genetic_algorithm(objective, bounds, n_bits, n_iter, n_pop, r_cross, r_mut):
# initial population of random bitstring
pop = [randint(0, 2, n_bits*len(bounds)).tolist() for _ in range(n_pop)]
# keep track of best solution
best, best_eval = 0, objective(decode(bounds, n_bits, pop[0]))
# enumerate generations
for gen in range(n_iter):
# decode population
decoded = [decode(bounds, n_bits, p) for p in pop]
# evaluate all candidates in the population
scores = [objective(d) for d in decoded]
# check for new best solution
for i in range(n_pop):
if scores[i] < best_eval:
best, best_eval = pop[i], scores[i]
print(">%d, new best f(%s) = %f" % (gen, decoded[i], scores[i]))
# select parents
selected = [selection(pop, scores) for _ in range(n_pop)]
# create the next generation
children = list()
for i in range(0, n_pop, 2):
# get selected parents in pairs
p1, p2 = selected[i], selected[i+1]
# crossover and mutation
for c in crossover(p1, p2, r_cross):
# mutation
mutation(c, r_mut)
# store for next generation
children.append(c)
# replace population
pop = children
return [best, best_eval]
# define range for input
bounds = [[-5.0, 5.0], [-5.0, 5.0]]
# define the total iterations
n_iter = 100
# bits per variable
n_bits = 16
# define the population size
n_pop = 100
# crossover rate
r_cross = 0.9
# mutation rate
r_mut = 1.0 / (float(n_bits) * len(bounds)) #0.03125
# perform the genetic algorithm search
best, score = genetic_algorithm(objective, bounds, n_bits, n_iter, n_pop, r_cross, r_mut)
print('Done!')
decoded = decode(bounds, n_bits, best)
print('f(%s) = %f' % (decoded, score))
# testing over breast cancer data
# define range for input
bounds = cancer.data
# define the total iterations
n_iter = 100
# bits per variable
n_bits = 16
# define the population size
n_pop = 100
# crossover rate
r_cross = 0.9
# mutation rate
r_mut = 1.0 / (float(n_bits) * len(bounds)) #0.00010984182776801405
# perform the genetic algorithm search
best, score = genetic_algorithm(objective, bounds, n_bits, n_iter, n_pop, r_cross, r_mut)
print('Done!')
decoded = decode(bounds, n_bits, best)
print('f(%s) = %f' % (decoded, score))
print(decoded[len(decoded)-30:-1])
print(best)
print(r_mut)
print(bounds)
print(len(bounds))
print(len(bounds[1]))
print(cancer.feature_names)
print(len(cancer.feature_names))
| 0.547222 | 0.596609 |
### Decision trees – Classification and Visualization
```
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y)
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier() #Instantiate tree class
dtc.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
y_pred = dtc.predict(X_test)
accuracy_score(y_test, y_pred)
import numpy as np
from sklearn import tree
from sklearn.externals.six import StringIO
import pydot
from IPython.display import Image
dot_iris = StringIO()
tree.export_graphviz(dtc, out_file = dot_iris, feature_names = iris.feature_names)
graph = pydot.graph_from_dot_data(dot_iris.getvalue())
Image(graph.create_png())
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier(criterion='entropy')
dtc.fit(X_train, y_train)
dot_iris = StringIO()
tree.export_graphviz(dtc, out_file = dot_iris, feature_names = iris.feature_names)
graph = pydot.graph_from_dot_data(dot_iris.getvalue())
Image(graph.create_png())
```
### Tuning a decision tree
```
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:,:2]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y)
import pandas as pd
pd.DataFrame(X,columns=iris.feature_names[:2])
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier() #Instantiate tree with default parameters
dtc.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
y_pred = dtc.predict(X_test)
accuracy_score(y_test, y_pred)
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=((12,6)))
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train)
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier()
from sklearn.model_selection import GridSearchCV, cross_val_score
param_grid = {'criterion':['gini','entropy'], 'max_depth' : [3,5,7,20]}
gs_inst = GridSearchCV(dtc,param_grid=param_grid,cv=5)
gs_inst.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
y_pred_gs = gs_inst.predict(X_test)
accuracy_score(y_test, y_pred_gs)
gs_inst.grid_scores_
gs_inst.best_estimator_
import numpy as np
from sklearn import tree
from sklearn.externals.six import StringIO
import pydot
from IPython.display import Image
dot_iris = StringIO()
tree.export_graphviz(gs_inst.best_estimator_, out_file = dot_iris, feature_names = iris.feature_names[:2])
graph = pydot.graph_from_dot_data(dot_iris.getvalue())
Image(graph.create_png())
rid_interval = 0.02
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xmin, xmax = np.percentile(X[:, 0], [0, 100])
ymin, ymax = np.percentile(X[:, 1], [0, 100])
xmin_plot, xmax_plot = xmin - .5, xmax + .5
ymin_plot, ymax_plot = ymin - .5, ymax + .5
xx, yy = np.meshgrid(np.arange(xmin_plot, xmax_plot, grid_interval),
np.arange(ymin_plot, ymax_plot, grid_interval))
import matplotlib.pyplot as plt
%matplotlib inline
X_0 = X[y == 0]
X_1 = X[y == 1]
X_2 = X[y == 2]
plt.figure(figsize=(15,8)) #change figure-size for easier viewing
plt.scatter(X_0[:,0],X_0[:,1], color = 'red')
plt.scatter(X_1[:,0],X_1[:,1], color = 'blue')
plt.scatter(X_2[:,0],X_2[:,1], color = 'green')
test_preds = gs_inst.best_estimator_.predict(list(zip(xx.ravel(), yy.ravel())))
colors = np.array(['r', 'b','g'])
plt.scatter(xx.ravel(), yy.ravel(), color=colors[test_preds], alpha=0.15)
plt.scatter(X[:, 0], X[:, 1], color=colors[y])
plt.title("Decision Tree Visualization")
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.axvline(x = 5.45,color='black')
plt.axvline(x = 5.45, color='black')
plt.axvline(x = 6.2, color='black')
plt.plot((xmin_plot, 5.45), (2.8, 2.8), color='black')
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier()
from sklearn.model_selection import GridSearchCV, cross_val_score
max_depths = range(2,51)
param_grid = {'max_depth' : max_depths}
gs_inst = GridSearchCV(dtc, param_grid=param_grid,cv=5)
gs_inst.fit(X_train, y_train)
plt.plot(max_depths,gs_inst.cv_results_['mean_test_score'])
plt.xlabel('Max Depth')
plt.ylabel("Cross-validation Score")
```
### Using decision trees for regression
```
#Use within an Jupyter notebook
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
X_feature_names = ['age', 'gender', 'body mass index', 'average blood pressure','bl_0','bl_1','bl_2','bl_3','bl_4','bl_5']
pd.Series(y).hist(bins=50)
bins = 50*np.arange(8)
bins
binned_y = np.digitize(y, bins)
pd.Series(binned_y).hist(bins=50)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,stratify=binned_y)
from sklearn.tree import DecisionTreeRegressor
dtr = DecisionTreeRegressor()
dtr.fit(X_train, y_train)
y_pred = dtr.predict(X_test)
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)
(np.abs(y_test - y_pred)/(y_test)).mean()
pd.Series((y_test - y_pred)).hist(bins=50)
pd.Series((y_test - y_pred)/(y_test)).hist(bins=50)
```
### Reducing overfitting with cross-validation
```
#Use within an Jupyter notebook
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
X_feature_names = ['age', 'gender', 'body mass index', 'average blood pressure','bl_0','bl_1','bl_2','bl_3','bl_4','bl_5']
bins = 50*np.arange(8)
binned_y = np.digitize(y, bins)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,stratify=binned_y)
from sklearn.tree import DecisionTreeRegressor
dtr = DecisionTreeRegressor()
from sklearn.model_selection import GridSearchCV
gs_inst = GridSearchCV(dtr, param_grid = {'max_depth': [3,5,7,9,20]},cv=10)
gs_inst.fit(X_train, y_train)
gs_inst.best_estimator_
y_pred = gs_inst.predict(X_test)
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)
(np.abs(y_test - y_pred)/(y_test)).mean()
import numpy as np
from sklearn import tree
from sklearn.externals.six import StringIO
import pydot
from IPython.display import Image
dot_diabetes = StringIO()
tree.export_graphviz(gs_inst.best_estimator_, out_file = dot_diabetes, feature_names = X_feature_names)
graph = pydot.graph_from_dot_data(dot_diabetes.getvalue())
Image(graph.create_png())
```
|
github_jupyter
|
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y)
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier() #Instantiate tree class
dtc.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
y_pred = dtc.predict(X_test)
accuracy_score(y_test, y_pred)
import numpy as np
from sklearn import tree
from sklearn.externals.six import StringIO
import pydot
from IPython.display import Image
dot_iris = StringIO()
tree.export_graphviz(dtc, out_file = dot_iris, feature_names = iris.feature_names)
graph = pydot.graph_from_dot_data(dot_iris.getvalue())
Image(graph.create_png())
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier(criterion='entropy')
dtc.fit(X_train, y_train)
dot_iris = StringIO()
tree.export_graphviz(dtc, out_file = dot_iris, feature_names = iris.feature_names)
graph = pydot.graph_from_dot_data(dot_iris.getvalue())
Image(graph.create_png())
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:,:2]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y)
import pandas as pd
pd.DataFrame(X,columns=iris.feature_names[:2])
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier() #Instantiate tree with default parameters
dtc.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
y_pred = dtc.predict(X_test)
accuracy_score(y_test, y_pred)
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=((12,6)))
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train)
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier()
from sklearn.model_selection import GridSearchCV, cross_val_score
param_grid = {'criterion':['gini','entropy'], 'max_depth' : [3,5,7,20]}
gs_inst = GridSearchCV(dtc,param_grid=param_grid,cv=5)
gs_inst.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
y_pred_gs = gs_inst.predict(X_test)
accuracy_score(y_test, y_pred_gs)
gs_inst.grid_scores_
gs_inst.best_estimator_
import numpy as np
from sklearn import tree
from sklearn.externals.six import StringIO
import pydot
from IPython.display import Image
dot_iris = StringIO()
tree.export_graphviz(gs_inst.best_estimator_, out_file = dot_iris, feature_names = iris.feature_names[:2])
graph = pydot.graph_from_dot_data(dot_iris.getvalue())
Image(graph.create_png())
rid_interval = 0.02
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xmin, xmax = np.percentile(X[:, 0], [0, 100])
ymin, ymax = np.percentile(X[:, 1], [0, 100])
xmin_plot, xmax_plot = xmin - .5, xmax + .5
ymin_plot, ymax_plot = ymin - .5, ymax + .5
xx, yy = np.meshgrid(np.arange(xmin_plot, xmax_plot, grid_interval),
np.arange(ymin_plot, ymax_plot, grid_interval))
import matplotlib.pyplot as plt
%matplotlib inline
X_0 = X[y == 0]
X_1 = X[y == 1]
X_2 = X[y == 2]
plt.figure(figsize=(15,8)) #change figure-size for easier viewing
plt.scatter(X_0[:,0],X_0[:,1], color = 'red')
plt.scatter(X_1[:,0],X_1[:,1], color = 'blue')
plt.scatter(X_2[:,0],X_2[:,1], color = 'green')
test_preds = gs_inst.best_estimator_.predict(list(zip(xx.ravel(), yy.ravel())))
colors = np.array(['r', 'b','g'])
plt.scatter(xx.ravel(), yy.ravel(), color=colors[test_preds], alpha=0.15)
plt.scatter(X[:, 0], X[:, 1], color=colors[y])
plt.title("Decision Tree Visualization")
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.axvline(x = 5.45,color='black')
plt.axvline(x = 5.45, color='black')
plt.axvline(x = 6.2, color='black')
plt.plot((xmin_plot, 5.45), (2.8, 2.8), color='black')
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier()
from sklearn.model_selection import GridSearchCV, cross_val_score
max_depths = range(2,51)
param_grid = {'max_depth' : max_depths}
gs_inst = GridSearchCV(dtc, param_grid=param_grid,cv=5)
gs_inst.fit(X_train, y_train)
plt.plot(max_depths,gs_inst.cv_results_['mean_test_score'])
plt.xlabel('Max Depth')
plt.ylabel("Cross-validation Score")
#Use within an Jupyter notebook
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
X_feature_names = ['age', 'gender', 'body mass index', 'average blood pressure','bl_0','bl_1','bl_2','bl_3','bl_4','bl_5']
pd.Series(y).hist(bins=50)
bins = 50*np.arange(8)
bins
binned_y = np.digitize(y, bins)
pd.Series(binned_y).hist(bins=50)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,stratify=binned_y)
from sklearn.tree import DecisionTreeRegressor
dtr = DecisionTreeRegressor()
dtr.fit(X_train, y_train)
y_pred = dtr.predict(X_test)
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)
(np.abs(y_test - y_pred)/(y_test)).mean()
pd.Series((y_test - y_pred)).hist(bins=50)
pd.Series((y_test - y_pred)/(y_test)).hist(bins=50)
#Use within an Jupyter notebook
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
X_feature_names = ['age', 'gender', 'body mass index', 'average blood pressure','bl_0','bl_1','bl_2','bl_3','bl_4','bl_5']
bins = 50*np.arange(8)
binned_y = np.digitize(y, bins)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,stratify=binned_y)
from sklearn.tree import DecisionTreeRegressor
dtr = DecisionTreeRegressor()
from sklearn.model_selection import GridSearchCV
gs_inst = GridSearchCV(dtr, param_grid = {'max_depth': [3,5,7,9,20]},cv=10)
gs_inst.fit(X_train, y_train)
gs_inst.best_estimator_
y_pred = gs_inst.predict(X_test)
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)
(np.abs(y_test - y_pred)/(y_test)).mean()
import numpy as np
from sklearn import tree
from sklearn.externals.six import StringIO
import pydot
from IPython.display import Image
dot_diabetes = StringIO()
tree.export_graphviz(gs_inst.best_estimator_, out_file = dot_diabetes, feature_names = X_feature_names)
graph = pydot.graph_from_dot_data(dot_diabetes.getvalue())
Image(graph.create_png())
| 0.792504 | 0.871693 |
# SIT742: Modern Data Science
**(Week 03: Data Wrangling)**
---
- Materials in this module include resources collected from various open-source online repositories.
- You are free to use, change and distribute this package.
- If you found any issue/bug for this document, please submit an issue at [tulip-lab/sit742](https://github.com/tulip-lab/sit742/issues)
Prepared by **SIT742 Teaching Team**
---
# Session 3A - Data Wrangling with Pandas
## Table of Content
* Part 1. Scraping data from the web
* Part 2. States and Territories of Australia
* Part 3. Parsing XML files with BeautifulSoup
**Note**: The data available on those service might be changing, so you need to adjust the code to accommodate those changes.
---
## Part 1. Scraping data from the web
Many of you will probably be interested in scraping data from the web for your projects. For example, what if we were interested in working with some historical Canadian weather data? Well, we can get that from: http://climate.weather.gc.ca using their API. Requests are going to be formatted like this:
```
import pandas as pd
url_template = "http://climate.weather.gc.ca/climate_data/bulk_data_e.html?format=csv&stationID=5415&Year={year}&Month={month}&timeframe=1&submit=Download+Data"
```
Note that we've requested the data be returned as a CSV, and that we're going to supply the month and year as inputs when we fire off the query. To get the data for March 2012, we need to format it with month=3, year=2012:
```
url = url_template.format(month=3, year=2012)
url
```
This is great! We can just use the same `read_csv` function as before, and just give it a URL as a filename. Awesome.
Upon inspection, we find out that there are 0 rows (as in 03/2020) of metadata at the top of this CSV, but pandas knows CSVs are weird, so there's a `skiprows` options. We parse the dates again, and set 'Date/Time' to be the index column. Here's the resulting dataframe.
```
weather_mar2012 = pd.read_csv(url, skiprows=0, index_col='Date/Time (LST)', parse_dates=True, encoding='latin1')
weather_mar2012.head()
```
As before, we can get rid of any columns that don't contain real data using ${\tt .dropna()}$
```
weather_mar2012 = weather_mar2012.dropna(axis=1, how='any')
weather_mar2012.head()
```
Getting better! The Year/Month/Day/Time columns are redundant, though, and the Data Quality column doesn't look too useful. Let's get rid of those.
```
weather_mar2012 = weather_mar2012.drop(['Year', 'Month', 'Day', 'Time (LST)'], axis=1)
weather_mar2012[:5]
```
Great! Now let's figure out how to download the whole year? It would be nice if we could just send that as a single request, but like many APIs this one is limited to prevent people from hogging bandwidth. No problem: we can write a function!
```
def download_weather_month(year, month):
url = url_template.format(year=year, month=month)
weather_data = pd.read_csv(url, skiprows=0, index_col='Date/Time (LST)', parse_dates=True)
weather_data = weather_data.dropna(axis=1)
weather_data.columns = [col.replace('\xb0', '') for col in weather_data.columns]
weather_data = weather_data.drop(['Year', 'Day', 'Month', 'Time (LST)'], axis=1)
return weather_data
```
Now to test that this function does the right thing:
```
download_weather_month(2020, 1).head()
```
Woohoo! Now we can iteratively request all the months using a single line. This will take a little while to run.
```
data_by_month = [download_weather_month(2012, i) for i in range(1, 12)]
```
Once that's done, it's easy to concatenate all the dataframes together into one big dataframe using ${\tt pandas.concat()}$. And now we have the whole year's data!
```
weather_2012 = pd.concat(data_by_month)
```
This thing is long, so instead of printing out the whole thing, I'm just going to print a quick summary of the ${\tt DataFrame}$ by calling ${\tt .info()}$:
```
weather_2012.info()
```
And a quick reminder, if we wanted to save that data to a file:
```
weather_2012.to_csv('weather_2012.csv')
!ls
```
And finally, something you should do early on in the wrangling process, plot data:
```
# plot that data
import matplotlib.pyplot as plt
# so now 'plt' means matplotlib.pyplot
dateRange = weather_2012.index
temperature = weather_2012['Temp (C)']
df1 = pd.DataFrame({'Temperature' : temperature}, index=dateRange)
plt.plot(df1.index.to_pydatetime(), df1.Temperature)
plt.title("The 2012 annual temperature in Canada")
plt.xlabel("Month")
plt.ylabel("Temperature")
# nothing to see... in iPython you need to specify where the chart will display, usually it's in a new window
# to see them 'inline' use:
%matplotlib inline
#If you add the %matplotlib inline, then you can skip the plt.show() function.
#How to close python warnings
import warnings
warnings.filterwarnings('ignore')
# that's better, try other plots, scatter is popular, also boxplot
df1 = pd.read_csv('weather_2012.csv', low_memory=False)
df1.plot(kind='scatter',x='Dew Point Temp (C)',y='Rel Hum (%)',color='red')
df1.plot(kind='scatter',x='Temp (C)',y='Wind Spd (km/h)',color='yellow')
# show first several 'weather' columns value
weather_2012['Weather'].head()
#Boxplot sample
climategroup1 = df1[df1['Weather']=='Fog']['Temp (C)']
climategroup2 = df1[df1['Weather']=='Rain']['Temp (C)']
climategroup3 = df1[df1['Weather']=='Clear']['Temp (C)']
climategroup4 = df1[df1['Weather']=='Cloudy']['Temp (C)']
data =[climategroup1,climategroup2,climategroup3,climategroup4]
fig1, ax1 = plt.subplots()
ax1.set_title('Temperature Boxplot based on the Climate group')
ax1.set_ylabel('Temperature')
ax1.set_xlabel('Climate Group')
boxplot=ax1.boxplot(data,
notch=True,
patch_artist=True,
labels=['Fog','Rain','Clear','Cloudy'],
boxprops=dict(linestyle='--', linewidth=2, color='black'))
colors = ['cyan', 'pink', 'lightgreen', 'tan', 'pink']
for patch, color in zip(boxplot['boxes'], colors):
patch.set_facecolor(color)
plt.show()
```
## Part 2. States and Territories of Australia
We are interested in getting State and Territory information from Wikipedia, however we do not want to copy and paste the table : )
Here is the URL
https://en.wikipedia.org/wiki/States_and_territories_of_Australia
We need two libraries to do the task:
Check documentations here:
* [urllib](https://docs.python.org/2/library/urllib.html)
* [BeautifulSoup](https://www.crummy.com/software/BeautifulSoup/bs4/doc/)
```
import sys
if sys.version_info[0] == 3:
from urllib.request import urlopen
else:
from urllib import urlopen
from bs4 import BeautifulSoup
```
We first save the link in wiki
```
wiki = "https://en.wikipedia.org/wiki/States_and_territories_of_Australia"
```
Then use ulropen to open the page.
If you get "SSL: CERTIFICATE_VERIFY_FAILED", what you need to do is find where "Install Certificates.command" file is, and click it to upgrade the certificate. Then, you should be able to solve the problem.
```
page = urlopen(wiki)
if sys.version_info[0] == 3:
page = page.read()
```
You will meet BeautifulSoup later in this subject, so don't worry if you feel uncomfortable with it now. You can always revisit.
We begin by reading in the source code and creating a Beautiful Soup object with the BeautifulSoup function.
```
soup = BeautifulSoup(page, "lxml")
```
Then we print and see.
```
print(soup.prettify())
```
For who do not know much about HTML, this might be a bit overwhelming, but essentially it contains lots of tags in the angled brackets providing structural and formatting information that we don't care so much here. What we need is the table.
Let's first check the title.
```
soup.title.string
```
It looks fine, then we would like to find the table.
Let's have a try to extract all contents within the 'table' tag.
```
all_tables = soup.findAll('table')
print(all_tables)
```
This returns a collection of tag objects. It seems that most of the information are useless and it's getting hard to hunt for the table. So searched online and found an instruction here:
https://adesquared.wordpress.com/2013/06/16/using-python-beautifulsoup-to-scrape-a-wikipedia-table/
The class is "wikitable sortable"!! Have a try then.
```
right_table = soup.find('table', class_='wikitable sortable')
print(right_table)
```
Next we need to extract table header row by find the first 'tr'>
```
head_row = right_table.find('tr')
print(head_row)
```
Then we extract header row name via iterate through each row and extract text.
The `.findAll` function in Python returns a list containing all the elements, which you can iterate through.
```
header_list = []
headers = head_row.findAll('th')
for header in headers:
#print header.find(text = True)
header_list.append(header.find(text = True).strip())
header_list
```
We can probably iterate through this list and then extract contents. But let's take a simple approach of extracting each column separately.
```
flag = []
state = []
abbrev = []
ISO = []
Capital = []
Population = []
Area = []
Seats = []
Gov = []
Premier = []
for row in right_table.findAll("tr"):
cells = row.findAll('td')
if len(cells) > 0 : # and len(cells) < 10:
flag.append(cells[0].find(text=True))
state.append(cells[1].find(text=True).strip())
abbrev.append(cells[2].find(text=True).strip())
ISO.append(cells[3].find(text=True).strip())
Capital.append(cells[4].find(text=True).strip())
Population.append(cells[5].find(text=True).strip())
Area.append(cells[6].find(text=True).strip())
Seats.append(cells[7].find(text=True).strip())
Gov.append(cells[8].find(text=True).strip())
Premier.append(cells[10].find(text=True).strip())
```
Next we can append all list to the dataframe.
```
df_au = pd.DataFrame()
df_au[header_list[0]] = flag
df_au[header_list[1]] = state
df_au[header_list[2]] = abbrev
df_au[header_list[3]] = ISO
df_au[header_list[4]] = Capital
df_au[header_list[5]] = Population
df_au[header_list[6]] = Area
df_au[header_list[7]] = Seats
df_au[header_list[8]] = Gov
df_au[header_list[9]] = Premier
```
Done !
```
df_au
```
## Part 3. Parsing XML files with BeautifulSoup
Now, we are going to demonstrate how to use BeautifulSoup to extract information from the XML file, called "Melbourne_bike_share.xml".
For the documentation of BeautifulSoup, please refer to it <a href="https://www.crummy.com/software/BeautifulSoup/bs4/doc/#find-all">official website</a>.
```
!pip install wget
import wget
link_to_data = 'https://github.com/tulip-lab/sit742/raw/master/Jupyter/data/Melbourne_bike_share.xml'
DataSet = wget.download(link_to_data)
!ls
from bs4 import BeautifulSoup
btree = BeautifulSoup(open("Melbourne_bike_share.xml"),"lxml-xml")
```
You can also print out the BeautifulSoup object by calling the <font color="blue">prettify()</font> function.
```
print(btree.prettify())
```
It is easy to figure out information we would like to extract is stored in the following tags
<ul>
<li>id </li>
<li>featurename </li>
<li>terminalname </li>
<li>nbbikes </li>
<li>nbemptydoc </li>
<li>uploaddate </li>
<li>coordinates </li>
</ul>
Each record is stored in "<row> </row>". To extract information from those tags, except for "coordinates", we use the <font color="blue">find_all()</font> function. Its documentation can be found <a href="https://www.crummy.com/software/BeautifulSoup/bs4/doc/#find-all">here</a>.
```
featuretags = btree.find_all("featurename")
featuretags
```
The output shows that the <font color="blue"> find_all() </font> returns all the 50 station names. Now, we need to exclude the tags and just keep the text stored between the tags.
```
for feature in featuretags:
print (feature.string)
```
Now, we can put all the above code together using list comprehensions.
```
featurenames = [feature.string for feature in btree.find_all("featurename")]
featurenames
```
Similarly, we can use the <font color = "blue">find_all()</font> function to extract the other information.
```
nbbikes = [feature.string for feature in btree.find_all("nbbikes")]
nbbikes
NBEmptydoc = [feature.string for feature in btree.find_all("nbemptydoc")]
NBEmptydoc
TerminalNames = [feature.string for feature in btree.find_all("terminalname")]
TerminalNames
UploadDate = [feature.string for feature in btree.find_all("uploaddate")]
UploadDate
ids = [feature.string for feature in btree.find_all("id")]
ids
```
Now, how can we extract the attribute values from the tags called "coordinates"?
```
latitudes = [coord["latitude"] for coord in btree.find_all("coordinates")]
latitudes
longitudes = [coord["longitude"] for coord in btree.find_all("coordinates")]
longitudes
```
After the extraction, we can put all the information in a Pandas DataFrame.
```
import pandas as pd
dataDict = {}
dataDict['Featurename'] = featurenames
dataDict['TerminalName'] = TerminalNames
dataDict['NBBikes'] = nbbikes
dataDict['NBEmptydoc'] = NBEmptydoc
dataDict['UploadDate'] = UploadDate
dataDict['lat'] = latitudes
dataDict['lon'] = longitudes
df = pd.DataFrame(dataDict, index = ids)
df.index.name = 'ID'
df.head()
```
|
github_jupyter
|
import pandas as pd
url_template = "http://climate.weather.gc.ca/climate_data/bulk_data_e.html?format=csv&stationID=5415&Year={year}&Month={month}&timeframe=1&submit=Download+Data"
url = url_template.format(month=3, year=2012)
url
weather_mar2012 = pd.read_csv(url, skiprows=0, index_col='Date/Time (LST)', parse_dates=True, encoding='latin1')
weather_mar2012.head()
weather_mar2012 = weather_mar2012.dropna(axis=1, how='any')
weather_mar2012.head()
weather_mar2012 = weather_mar2012.drop(['Year', 'Month', 'Day', 'Time (LST)'], axis=1)
weather_mar2012[:5]
def download_weather_month(year, month):
url = url_template.format(year=year, month=month)
weather_data = pd.read_csv(url, skiprows=0, index_col='Date/Time (LST)', parse_dates=True)
weather_data = weather_data.dropna(axis=1)
weather_data.columns = [col.replace('\xb0', '') for col in weather_data.columns]
weather_data = weather_data.drop(['Year', 'Day', 'Month', 'Time (LST)'], axis=1)
return weather_data
download_weather_month(2020, 1).head()
data_by_month = [download_weather_month(2012, i) for i in range(1, 12)]
weather_2012 = pd.concat(data_by_month)
weather_2012.info()
weather_2012.to_csv('weather_2012.csv')
!ls
# plot that data
import matplotlib.pyplot as plt
# so now 'plt' means matplotlib.pyplot
dateRange = weather_2012.index
temperature = weather_2012['Temp (C)']
df1 = pd.DataFrame({'Temperature' : temperature}, index=dateRange)
plt.plot(df1.index.to_pydatetime(), df1.Temperature)
plt.title("The 2012 annual temperature in Canada")
plt.xlabel("Month")
plt.ylabel("Temperature")
# nothing to see... in iPython you need to specify where the chart will display, usually it's in a new window
# to see them 'inline' use:
%matplotlib inline
#If you add the %matplotlib inline, then you can skip the plt.show() function.
#How to close python warnings
import warnings
warnings.filterwarnings('ignore')
# that's better, try other plots, scatter is popular, also boxplot
df1 = pd.read_csv('weather_2012.csv', low_memory=False)
df1.plot(kind='scatter',x='Dew Point Temp (C)',y='Rel Hum (%)',color='red')
df1.plot(kind='scatter',x='Temp (C)',y='Wind Spd (km/h)',color='yellow')
# show first several 'weather' columns value
weather_2012['Weather'].head()
#Boxplot sample
climategroup1 = df1[df1['Weather']=='Fog']['Temp (C)']
climategroup2 = df1[df1['Weather']=='Rain']['Temp (C)']
climategroup3 = df1[df1['Weather']=='Clear']['Temp (C)']
climategroup4 = df1[df1['Weather']=='Cloudy']['Temp (C)']
data =[climategroup1,climategroup2,climategroup3,climategroup4]
fig1, ax1 = plt.subplots()
ax1.set_title('Temperature Boxplot based on the Climate group')
ax1.set_ylabel('Temperature')
ax1.set_xlabel('Climate Group')
boxplot=ax1.boxplot(data,
notch=True,
patch_artist=True,
labels=['Fog','Rain','Clear','Cloudy'],
boxprops=dict(linestyle='--', linewidth=2, color='black'))
colors = ['cyan', 'pink', 'lightgreen', 'tan', 'pink']
for patch, color in zip(boxplot['boxes'], colors):
patch.set_facecolor(color)
plt.show()
import sys
if sys.version_info[0] == 3:
from urllib.request import urlopen
else:
from urllib import urlopen
from bs4 import BeautifulSoup
wiki = "https://en.wikipedia.org/wiki/States_and_territories_of_Australia"
page = urlopen(wiki)
if sys.version_info[0] == 3:
page = page.read()
soup = BeautifulSoup(page, "lxml")
print(soup.prettify())
soup.title.string
all_tables = soup.findAll('table')
print(all_tables)
right_table = soup.find('table', class_='wikitable sortable')
print(right_table)
head_row = right_table.find('tr')
print(head_row)
header_list = []
headers = head_row.findAll('th')
for header in headers:
#print header.find(text = True)
header_list.append(header.find(text = True).strip())
header_list
flag = []
state = []
abbrev = []
ISO = []
Capital = []
Population = []
Area = []
Seats = []
Gov = []
Premier = []
for row in right_table.findAll("tr"):
cells = row.findAll('td')
if len(cells) > 0 : # and len(cells) < 10:
flag.append(cells[0].find(text=True))
state.append(cells[1].find(text=True).strip())
abbrev.append(cells[2].find(text=True).strip())
ISO.append(cells[3].find(text=True).strip())
Capital.append(cells[4].find(text=True).strip())
Population.append(cells[5].find(text=True).strip())
Area.append(cells[6].find(text=True).strip())
Seats.append(cells[7].find(text=True).strip())
Gov.append(cells[8].find(text=True).strip())
Premier.append(cells[10].find(text=True).strip())
df_au = pd.DataFrame()
df_au[header_list[0]] = flag
df_au[header_list[1]] = state
df_au[header_list[2]] = abbrev
df_au[header_list[3]] = ISO
df_au[header_list[4]] = Capital
df_au[header_list[5]] = Population
df_au[header_list[6]] = Area
df_au[header_list[7]] = Seats
df_au[header_list[8]] = Gov
df_au[header_list[9]] = Premier
df_au
!pip install wget
import wget
link_to_data = 'https://github.com/tulip-lab/sit742/raw/master/Jupyter/data/Melbourne_bike_share.xml'
DataSet = wget.download(link_to_data)
!ls
from bs4 import BeautifulSoup
btree = BeautifulSoup(open("Melbourne_bike_share.xml"),"lxml-xml")
print(btree.prettify())
featuretags = btree.find_all("featurename")
featuretags
for feature in featuretags:
print (feature.string)
featurenames = [feature.string for feature in btree.find_all("featurename")]
featurenames
nbbikes = [feature.string for feature in btree.find_all("nbbikes")]
nbbikes
NBEmptydoc = [feature.string for feature in btree.find_all("nbemptydoc")]
NBEmptydoc
TerminalNames = [feature.string for feature in btree.find_all("terminalname")]
TerminalNames
UploadDate = [feature.string for feature in btree.find_all("uploaddate")]
UploadDate
ids = [feature.string for feature in btree.find_all("id")]
ids
latitudes = [coord["latitude"] for coord in btree.find_all("coordinates")]
latitudes
longitudes = [coord["longitude"] for coord in btree.find_all("coordinates")]
longitudes
import pandas as pd
dataDict = {}
dataDict['Featurename'] = featurenames
dataDict['TerminalName'] = TerminalNames
dataDict['NBBikes'] = nbbikes
dataDict['NBEmptydoc'] = NBEmptydoc
dataDict['UploadDate'] = UploadDate
dataDict['lat'] = latitudes
dataDict['lon'] = longitudes
df = pd.DataFrame(dataDict, index = ids)
df.index.name = 'ID'
df.head()
| 0.265214 | 0.963746 |
# Node Classification with Graph Neural Networks
Here, we are given the ground-truth labels of only a small subset of nodes, and want to infer the labels for all the remaining nodes (*transductive learning*).
To demonstrate, we make use of the `Cora` dataset, which is a **citation network** where nodes represent documents.
- Each node is described by a 1433-dimensional bag-of-words feature vector.
- Two documents are connected if there exists a citation link between them.
- The task is to infer the category of each document (7 in total).
> This dataset was first introduced by [Yang et al. (2016)](https://arxiv.org/abs/1603.08861) as one of the datasets of the `Planetoid` benchmark suite.
```
# # Install required packages.
# !pip install -q torch-scatter -f https://pytorch-geometric.com/whl/torch-1.8.0+cu101.html
# !pip install -q torch-sparse -f https://pytorch-geometric.com/whl/torch-1.8.0+cu101.html
# !pip install -q torch-geometric
import matplotlib.pyplot as plt
import torch
import torch.nn.functional as F
from sklearn.manifold import TSNE
from torch.nn import Linear
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import GCNConv
from torch_geometric.transforms import NormalizeFeatures
torch.manual_seed(43)
print(f"pytorch: {torch.__version__}")
# OUT???? out.detach().cpu().numpy()
def visualize(h, color):
z = TSNE(n_components=2).fit_transform(out.detach().cpu().numpy())
plt.figure(figsize=(10, 10))
plt.xticks([])
plt.yticks([])
plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
plt.show()
```
## Dataset
Overall, this dataset is quite similar to the previously used [`KarateClub`](https://pytorch-geometric.readthedocs.io/en/latest/modules/datasets.html#torch_geometric.datasets.KarateClub) network.
We can see that the `Cora` network holds 2,708 nodes and 10,556 edges, resulting in an average node degree of 3.9.
For training this dataset, we are given the ground-truth categories of 140 nodes (20 for each class).
This results in a training node label rate of only 5%.
In contrast to `KarateClub`, this graph holds the additional attributes `val_mask` and `test_mask`, which denotes which nodes should be used for validation and testing.
Furthermore, we make use of **[data transformations](https://pytorch-geometric.readthedocs.io/en/latest/notes/introduction.html#data-transforms) via `transform=NormalizeFeatures()`**.
Transforms can be used to modify your input data before inputting them into a neural network, *e.g.*, for normalization or data augmentation????.
Here, we [row-normalize](https://pytorch-geometric.readthedocs.io/en/latest/modules/transforms.html#torch_geometric.transforms.NormalizeFeatures) the bag-of-words input feature vectors.
We can further see that this network is undirected, and that there exists no isolated nodes (each document has at least one citation).
```
dataset = Planetoid(root="data/Planetoid", name="Cora", transform=NormalizeFeatures())
print()
print(f"Dataset: {dataset}:")
print("======================")
print(f"Number of graphs: {len(dataset)}")
print(f"Number of features: {dataset.num_features}")
print(f"Number of classes: {dataset.num_classes}")
data = dataset[0] # Get the first graph object.
print()
print(data)
print("======================")
# Gather some statistics about the graph.
print(f"Number of nodes: {data.num_nodes}")
print(f"Number of edges: {data.num_edges}")
print(f"Average node degree: {data.num_edges / data.num_nodes:.2f}")
print(f"Number of training nodes: {data.train_mask.sum()}")
print(f"Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}")
print(f"Contains isolated nodes: {data.contains_isolated_nodes()}")
print(f"Contains self-loops: {data.contains_self_loops()}")
print(f"Is undirected: {data.is_undirected()}")
```
## Baseline MLP
In theory, we should be able to infer the category of a document solely based on its content, *i.e.* its bag-of-words feature representation, without taking any relational information into account.
Let's verify that by constructing a simple MLP that solely operates on input node features (using shared weights across all nodes):
```
class MLP(torch.nn.Module):
def __init__(self, hidden_channels, num_features, num_classes):
super(MLP, self).__init__()
self.lin1 = Linear(num_features, hidden_channels)
self.lin2 = Linear(hidden_channels, num_classes)
def forward(self, x):
x = self.lin1(x)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.lin2(x)
return x
mlp_model = MLP(16, dataset.num_features, dataset.num_classes)
mlp_model
```
Our MLP is defined by two linear layers and enhanced by `ReLU` non-linearity and `dropout`.
Here, we first reduce the 1433-dimensional feature vector to a low-dimensional embedding (`hidden_channels=16`), while the second linear layer acts as a classifier that should map each low-dimensional node embedding to one of the 7 classes.
Let's train our simple MLP model making use of the **cross entropy loss** and **Adam optimizer**.
```
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(mlp_model.parameters(), lr=0.01, weight_decay=5e-4)
def train():
mlp_model.train()
optimizer.zero_grad()
out = mlp_model(data.x)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss
def test():
mlp_model.eval()
out = mlp_model(data.x)
pred = out.argmax(dim=1)
test_correct = pred[data.test_mask] == data.y[data.test_mask]
test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
return test_acc
for epoch in range(1, 201):
loss = train()
if epoch % 25 == 0:
print(f"Epoch: {epoch:03d}, Loss: {loss:.4f}")
```
After training the model, we can call the `test` function to see how well our model performs on unseen labels.
Here, we are interested in the accuracy of the model, *i.e.*, the ratio of correctly classified nodes:
```
test_acc = test()
print(f"Test Accuracy: {test_acc:.4f}")
```
As one can see, our MLP performs rather bad with only about 59% test accuracy.
But why does the MLP do not perform better?
The main reason for that is that this model suffers from heavy overfitting due to only a **small amount of training nodes**, and therefore generalizes poorly to unseen node representations.
>It also fails to incorporate an important bias into the model: **Cited papers are very likely related to the category of a document**.
That is exactly where Graph Neural Networks come into play and can help to boost the performance of our model.
## Training a Graph Neural Network (GNN)
We can easily convert our MLP to a GNN by swapping the `torch.nn.Linear` layers with PyG's GNN operators.
The **GCN layer** ([Kipf et al. (2017)](https://arxiv.org/abs/1609.02907)) is defined as
$$
\mathbf{x}_v^{(\ell + 1)} = \mathbf{W}^{(\ell + 1)} \sum_{w \in \mathcal{N}(v) \, \cup \, \{ v \}} \frac{1}{c_{w,v}} \cdot \mathbf{x}_w^{(\ell)}
$$
where $\mathbf{W}^{(\ell + 1)}$ denotes a trainable weight matrix of shape `[num_output_features, num_input_features]` and $c_{w,v}$ refers to a fixed normalization coefficient for each edge.
In contrast, a single linear layer is defined as
$$
\mathbf{x}_v^{(\ell + 1)} = \mathbf{W}^{(\ell + 1)} \mathbf{x}_v^{(\ell)}
$$
which does not make use of neighboring node information.
```
class GCN(torch.nn.Module):
def __init__(self, hidden_channels, num_features, num_classes):
super(GCN, self).__init__()
self.conv1 = GCNConv(num_features, hidden_channels)
self.conv2 = GCNConv(hidden_channels, num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
model = GCN(16, dataset.num_features, dataset.num_classes)
model
```
Let's visualize the node embeddings of our **untrained** GCN network.
For visualization, we make use of [**TSNE**](https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html) to embed our 7-dimensional node embeddings onto a 2D plane.
```
model = GCN(16, dataset.num_features, dataset.num_classes)
model.eval()
out = model(data.x, data.edge_index)
visualize(out, color=data.y)
```
As one can see, there is at least *some kind* of clustering (*e.g.*, for the "blue" nodes), but we certainly can do better by training our model.
The training and testing procedure is once again the same, but this time we make use of the node features `x` **and** the graph connectivity `edge_index` as input to our GCN model.
```
model = GCN(16, dataset.num_features, dataset.num_classes)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
def train():
model.train()
optimizer.zero_grad()
out = model(data.x, data.edge_index)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss
def test():
model.eval()
out = model(data.x, data.edge_index)
pred = out.argmax(dim=1)
test_correct = pred[data.test_mask] == data.y[data.test_mask]
test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
return test_acc
for epoch in range(1, 201):
loss = train()
if epoch % 25 == 0:
print(f"Epoch: {epoch:03d}, Loss: {loss:.4f}")
test_acc = test()
print(f"Test Accuracy: {test_acc:.4f}")
```
**There it is!**
By simply swapping the linear layers with GNN layers, we can reach **79.9% of test accuracy**!
This is in stark contrast to the 59% of test accuracy obtained by our MLP, indicating that relational information plays a crucial role in obtaining better performance.
We can also verify that once again by looking at the output embeddings of our **trained** model, which now produces a far better clustering of nodes of the same category.
```
model.eval()
out = model(data.x, data.edge_index)
visualize(out, color=data.y)
```
|
github_jupyter
|
# # Install required packages.
# !pip install -q torch-scatter -f https://pytorch-geometric.com/whl/torch-1.8.0+cu101.html
# !pip install -q torch-sparse -f https://pytorch-geometric.com/whl/torch-1.8.0+cu101.html
# !pip install -q torch-geometric
import matplotlib.pyplot as plt
import torch
import torch.nn.functional as F
from sklearn.manifold import TSNE
from torch.nn import Linear
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import GCNConv
from torch_geometric.transforms import NormalizeFeatures
torch.manual_seed(43)
print(f"pytorch: {torch.__version__}")
# OUT???? out.detach().cpu().numpy()
def visualize(h, color):
z = TSNE(n_components=2).fit_transform(out.detach().cpu().numpy())
plt.figure(figsize=(10, 10))
plt.xticks([])
plt.yticks([])
plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
plt.show()
dataset = Planetoid(root="data/Planetoid", name="Cora", transform=NormalizeFeatures())
print()
print(f"Dataset: {dataset}:")
print("======================")
print(f"Number of graphs: {len(dataset)}")
print(f"Number of features: {dataset.num_features}")
print(f"Number of classes: {dataset.num_classes}")
data = dataset[0] # Get the first graph object.
print()
print(data)
print("======================")
# Gather some statistics about the graph.
print(f"Number of nodes: {data.num_nodes}")
print(f"Number of edges: {data.num_edges}")
print(f"Average node degree: {data.num_edges / data.num_nodes:.2f}")
print(f"Number of training nodes: {data.train_mask.sum()}")
print(f"Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}")
print(f"Contains isolated nodes: {data.contains_isolated_nodes()}")
print(f"Contains self-loops: {data.contains_self_loops()}")
print(f"Is undirected: {data.is_undirected()}")
class MLP(torch.nn.Module):
def __init__(self, hidden_channels, num_features, num_classes):
super(MLP, self).__init__()
self.lin1 = Linear(num_features, hidden_channels)
self.lin2 = Linear(hidden_channels, num_classes)
def forward(self, x):
x = self.lin1(x)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.lin2(x)
return x
mlp_model = MLP(16, dataset.num_features, dataset.num_classes)
mlp_model
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(mlp_model.parameters(), lr=0.01, weight_decay=5e-4)
def train():
mlp_model.train()
optimizer.zero_grad()
out = mlp_model(data.x)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss
def test():
mlp_model.eval()
out = mlp_model(data.x)
pred = out.argmax(dim=1)
test_correct = pred[data.test_mask] == data.y[data.test_mask]
test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
return test_acc
for epoch in range(1, 201):
loss = train()
if epoch % 25 == 0:
print(f"Epoch: {epoch:03d}, Loss: {loss:.4f}")
test_acc = test()
print(f"Test Accuracy: {test_acc:.4f}")
class GCN(torch.nn.Module):
def __init__(self, hidden_channels, num_features, num_classes):
super(GCN, self).__init__()
self.conv1 = GCNConv(num_features, hidden_channels)
self.conv2 = GCNConv(hidden_channels, num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
model = GCN(16, dataset.num_features, dataset.num_classes)
model
model = GCN(16, dataset.num_features, dataset.num_classes)
model.eval()
out = model(data.x, data.edge_index)
visualize(out, color=data.y)
model = GCN(16, dataset.num_features, dataset.num_classes)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
def train():
model.train()
optimizer.zero_grad()
out = model(data.x, data.edge_index)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss
def test():
model.eval()
out = model(data.x, data.edge_index)
pred = out.argmax(dim=1)
test_correct = pred[data.test_mask] == data.y[data.test_mask]
test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
return test_acc
for epoch in range(1, 201):
loss = train()
if epoch % 25 == 0:
print(f"Epoch: {epoch:03d}, Loss: {loss:.4f}")
test_acc = test()
print(f"Test Accuracy: {test_acc:.4f}")
model.eval()
out = model(data.x, data.edge_index)
visualize(out, color=data.y)
| 0.907166 | 0.991764 |
# Here's what we're going to do on missing value treatment:
### 1) Take a first look at the data
### 2) See how many missing data points we have
### 3) Figure out why the data is missing
### 4) Drop missing values
### 5) Filling in missing values
### Take a first look at the data
#### We will use a python library called pandas which is a datastructure and data analysis tool. More on pandas in the A11 course
#### Few other libraries we will use are seaborn, matplotlib for visualisation
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
```
### load the data
```
data = pd.read_csv("data/scraped_data.csv")
data.dtypes
data.head()
```
### Cleaning
```
dataCopy = data.copy()
dataCopy = dataCopy.replace('-', np.NaN)
dataCopy.head()
#missingno is a python library for nice visulaisation of missing number in the data
import missingno as msno
# Nullity or missing values by columns
msno.matrix(df=dataCopy.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
```
# So how many missing datapoints we have
```
# get the number of missing data points per column
missing_values_count = dataCopy.isnull().sum()
# look at the # of missing points in the first ten columns
missing_values_count[0:17]
```
## Remove incomplete rows
```
#Dropping all rows with any NA values is easy
dataCopyDropAll = dataCopy.copy()
dataCopyDropAll.dropna(inplace=True)
msno.matrix(df=dataCopyDropAll.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
# This might drop a lot of rows which might hamper our analysis
# We can drop rows with all NULLs, thats not the case here
dataCopyDropRowWithAllNA = dataCopy.copy()
dataCopyDropRowWithAllNA.dropna(how='all',inplace=True)
msno.matrix(df=dataCopyDropRowWithAllNA.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
#We also can remove rows with a threshold value
dataCopyDropRowWithThres = dataCopy.copy()
dataCopyDropRowWithThres.dropna(thresh=10,inplace=True)
msno.matrix(df=dataCopyDropRowWithThres.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
#Sometimes it makes sense to drop
# Drop the columns with that are all NA values
dataCopyDropColAllNA = dataCopy.copy()
dataCopyDropColAllNA.dropna(axis=1, how='all', inplace=True)
msno.matrix(df=dataCopyDropColAllNA.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
# Drop all columns with any NA values:
dataCopyDropColAnyNA = dataCopy.copy()
dataCopyDropColAnyNA.dropna(axis=1, how='any', inplace=True)
msno.matrix(df=dataCopyDropColAnyNA.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
#The threshold thing also can be applied here
dataCopyDropColWithThres = dataCopy.copy()
dataCopyDropColWithThres.dropna(axis=1, thresh=5, inplace=True)
msno.matrix(df=dataCopyDropColWithThres.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
```
## Imputation of missing values
##### This is the point at which we get into the part of data science that I like to call "data intution", by which I mean "really looking at your data and trying to figure out why it is the way it is and how that will affect your analysis". It can be a frustrating part of data science, especially if you're newer to the field and don't have a lot of experience. For dealing with missing values, you'll need to use your intution to figure out why the value is missing. One of the most important question you can ask yourself to help figure this out is this:
Is this value missing becuase it wasn't recorded or becuase it dosen't exist?
If a value is missing becuase it doens't exist (like the height of the oldest child of someone who doesn't have any children) then it doesn't make sense to try and guess what it might be. These values you probalby do want to keep as NaN. On the other hand, if a value is missing becuase it wasn't recorded, then you can try to guess what it might have been based on the other values in that column and row. (This is called "imputation" and we'll learn how to do it next! :)
### Mean, median, mode
### Frequent values
```
# A simple imputation to make the nan values 0, but not a good idea always
dataCopyFillNAZero = dataCopy.copy()
dataCopyFillNAZero = dataCopyFillNAZero.fillna(0)
dataCopyFillNAZero.head()
# The values can also be replace with mean, media, mode or frquent values in the column
dataCopyFillNAMean = dataCopy.copy()
dataCopyFillNAMean["first_class.average"] = pd.to_numeric(dataCopyFillNAMean["first_class.average"])
dataCopyFillNAMean = dataCopyFillNAMean.fillna(dataCopyFillNAMean.mean())
dataCopyFillNAMean.head()
```
### A simple imputer from sklearn cane be used, Detailed sklearn will be covered in the next module
class sklearn.impute.SimpleImputer(missing_values=nan, strategy=’mean’, fill_value=None, verbose=0, copy=True, add_indicator=False)
missing_values : number, string, np.nan (default) or None
The placeholder for the missing values. All occurrences of missing_values will be imputed.
strategy : string, optional (default=”mean”)
The imputation strategy.
If “mean”, then replace missing values using the mean along each column. Can only be used with numeric data.
If “median”, then replace missing values using the median along each column. Can only be used with numeric data.
If “most_frequent”, then replace missing using the most frequent value along each column. Can be used with strings or numeric data.
If “constant”, then replace missing values with fill_value. Can be used with strings or numeric data.
New in version 0.20: strategy=”constant” for fixed value imputation.
fill_value : string or numerical value, optional (default=None)
When strategy == “constant”, fill_value is used to replace all occurrences of missing_values. If left to the default, fill_value will be 0 when imputing numerical data and “missing_value” for strings or object data types.
erbose : integer, optional (default=0)
Controls the verbosity of the imputer.
copy : boolean, optional (default=True)
If True, a copy of X will be created. If False, imputation will be done in-place whenever possible. Note that, in the following cases, a new copy will always be made, even if copy=False:
If X is not an array of floating values;
If X is encoded as a CSR matrix;
If add_indicator=True.
add_indicator : boolean, optional (default=False)
If True, a MissingIndicator transform will stack onto output of the imputer’s transform. This allows a predictive estimator to account for missingness despite imputation. If a feature has no missing values at fit/train time, the feature won’t appear on the missing indicator even if there are missing values at transform/test time.
```
from sklearn.impute import SimpleImputer
dataCopyImputation = dataCopy.copy()
my_imputer = SimpleImputer()
dataCopyImputation['first_class.average'] = dataCopyImputation['first_class.average'].astype('float')
dataCopyImputation['first_class.strike_rate'] = dataCopyImputation['first_class.strike_rate'].astype('float')
data_with_imputed_values = my_imputer.fit_transform(dataCopyImputation[['first_class.average','first_class.strike_rate']])
```
# Assignment: Predicting Missing values
KNN is an algorithm that is useful for matching a point with its closest k neighbors in a multi-dimensional space. It can be used for data that are continuous, discrete, ordinal and categorical which makes it particularly useful for dealing with all kind of missing data.
The assumption behind using KNN for missing values is that a point value can be approximated by the values of the points that are closest to it, based on other variables.
https://towardsdatascience.com/the-use-of-knn-for-missing-values-cf33d935c637
```
# Assignment: Use KNN Impute library to fill up the missing data from data/scrapped_data_large.csv
import knnimpute
```
### missForest
Nonparametric Missing Value Imputation Using Random Forest
'missForest' is used to impute missing values particularly in the case of mixed-type data. It can be used to impute continuous and/or categorical data including complex interactions and nonlinear relations.
## Noisy data removal
```
import re
def clean_data(s):
s = s.replace('u', '')
s = s.replace('\'', '')
s = s.upper()
s = s.replace(',', ' ')
s = s.replace('[', '')
s = s.replace(']', '')
# Isolate punctuation
s = re.sub(r'([\'\"\.\(\)\!\?\-\\\/\,\$%])', r' \1 ', s)
# Remove some special characters
s = re.sub(r'([\;\:\|"«\n])', ' ', s)
return s
import re
dataCopyNoisyData = dataCopy.copy()
dataCopyNoisyData['born_new'] = dataCopyNoisyData['born'].apply(clean_data)
dataCopyNoisyData.head()
```
# Inconsistent data removal
### Use fuzzy matching to correct inconsistent data entry
I'm going to use the fuzzywuzzy package to help identify which string are closest to each other. This dataset is small enough that we could probably could correct errors by hand, but that approach doesn't scale well. (Would you want to correct a thousand errors by hand? What about ten thousand? Automating things as early as possible is generally a good idea. Plus, it’s fun! :)
Fuzzy matching: The process of automatically finding text strings that are very similar to the target string. In general, a string is considered "closer" to another one the fewer characters you'd need to change if you were transforming one string into another. So "apple" and "snapple" are two changes away from each other (add "s" and "n") while "in" and "on" and one change away (rplace "i" with "o"). You won't always be able to rely on fuzzy matching 100%, but it will usually end up saving you at least a little time.
Fuzzywuzzy returns a ratio given two strings. The closer the ratio is to 100, the smaller the edit distance between the two strings.
```
# fuzz is used to compare TWO strings
from fuzzywuzzy import fuzz
# process is used to compare a string to MULTIPLE other strings
from fuzzywuzzy import process
#fuzz.ratio compares the entire string, in order
print(fuzz.ratio("this is a test", "this is a fun"))
#fuzz.partial_ratio compares subsections of the string
print(fuzz.partial_ratio("this is a test", "test a is this"))
#fuzz.token_sort_ratio ignores word order
print(fuzz.token_sort_ratio("fuzzy wuzzy was a bear", "wuzzy fuzzy was a bear"))
print(fuzz.token_sort_ratio("fuzzy was a bear", "fuzzy fuzzy was a bear"))
#fuzz.token_set_ratio ignores duplicate words
print(fuzz.token_set_ratio("fuzzy was a bear", "fuzzy fuzzy was a bear"))
# replace data with one consistent version if match score is higher than a pre-determined threshold
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
data = pd.read_csv("data/scraped_data.csv")
data.dtypes
data.head()
dataCopy = data.copy()
dataCopy = dataCopy.replace('-', np.NaN)
dataCopy.head()
#missingno is a python library for nice visulaisation of missing number in the data
import missingno as msno
# Nullity or missing values by columns
msno.matrix(df=dataCopy.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
# get the number of missing data points per column
missing_values_count = dataCopy.isnull().sum()
# look at the # of missing points in the first ten columns
missing_values_count[0:17]
#Dropping all rows with any NA values is easy
dataCopyDropAll = dataCopy.copy()
dataCopyDropAll.dropna(inplace=True)
msno.matrix(df=dataCopyDropAll.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
# This might drop a lot of rows which might hamper our analysis
# We can drop rows with all NULLs, thats not the case here
dataCopyDropRowWithAllNA = dataCopy.copy()
dataCopyDropRowWithAllNA.dropna(how='all',inplace=True)
msno.matrix(df=dataCopyDropRowWithAllNA.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
#We also can remove rows with a threshold value
dataCopyDropRowWithThres = dataCopy.copy()
dataCopyDropRowWithThres.dropna(thresh=10,inplace=True)
msno.matrix(df=dataCopyDropRowWithThres.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
#Sometimes it makes sense to drop
# Drop the columns with that are all NA values
dataCopyDropColAllNA = dataCopy.copy()
dataCopyDropColAllNA.dropna(axis=1, how='all', inplace=True)
msno.matrix(df=dataCopyDropColAllNA.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
# Drop all columns with any NA values:
dataCopyDropColAnyNA = dataCopy.copy()
dataCopyDropColAnyNA.dropna(axis=1, how='any', inplace=True)
msno.matrix(df=dataCopyDropColAnyNA.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
#The threshold thing also can be applied here
dataCopyDropColWithThres = dataCopy.copy()
dataCopyDropColWithThres.dropna(axis=1, thresh=5, inplace=True)
msno.matrix(df=dataCopyDropColWithThres.iloc[:,2:39], figsize=(20, 14), color=(0.42, 0.1, 0.05))
# A simple imputation to make the nan values 0, but not a good idea always
dataCopyFillNAZero = dataCopy.copy()
dataCopyFillNAZero = dataCopyFillNAZero.fillna(0)
dataCopyFillNAZero.head()
# The values can also be replace with mean, media, mode or frquent values in the column
dataCopyFillNAMean = dataCopy.copy()
dataCopyFillNAMean["first_class.average"] = pd.to_numeric(dataCopyFillNAMean["first_class.average"])
dataCopyFillNAMean = dataCopyFillNAMean.fillna(dataCopyFillNAMean.mean())
dataCopyFillNAMean.head()
from sklearn.impute import SimpleImputer
dataCopyImputation = dataCopy.copy()
my_imputer = SimpleImputer()
dataCopyImputation['first_class.average'] = dataCopyImputation['first_class.average'].astype('float')
dataCopyImputation['first_class.strike_rate'] = dataCopyImputation['first_class.strike_rate'].astype('float')
data_with_imputed_values = my_imputer.fit_transform(dataCopyImputation[['first_class.average','first_class.strike_rate']])
# Assignment: Use KNN Impute library to fill up the missing data from data/scrapped_data_large.csv
import knnimpute
import re
def clean_data(s):
s = s.replace('u', '')
s = s.replace('\'', '')
s = s.upper()
s = s.replace(',', ' ')
s = s.replace('[', '')
s = s.replace(']', '')
# Isolate punctuation
s = re.sub(r'([\'\"\.\(\)\!\?\-\\\/\,\$%])', r' \1 ', s)
# Remove some special characters
s = re.sub(r'([\;\:\|"«\n])', ' ', s)
return s
import re
dataCopyNoisyData = dataCopy.copy()
dataCopyNoisyData['born_new'] = dataCopyNoisyData['born'].apply(clean_data)
dataCopyNoisyData.head()
# fuzz is used to compare TWO strings
from fuzzywuzzy import fuzz
# process is used to compare a string to MULTIPLE other strings
from fuzzywuzzy import process
#fuzz.ratio compares the entire string, in order
print(fuzz.ratio("this is a test", "this is a fun"))
#fuzz.partial_ratio compares subsections of the string
print(fuzz.partial_ratio("this is a test", "test a is this"))
#fuzz.token_sort_ratio ignores word order
print(fuzz.token_sort_ratio("fuzzy wuzzy was a bear", "wuzzy fuzzy was a bear"))
print(fuzz.token_sort_ratio("fuzzy was a bear", "fuzzy fuzzy was a bear"))
#fuzz.token_set_ratio ignores duplicate words
print(fuzz.token_set_ratio("fuzzy was a bear", "fuzzy fuzzy was a bear"))
# replace data with one consistent version if match score is higher than a pre-determined threshold
| 0.53048 | 0.972598 |
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
from fastai.nlp import *
from sklearn.linear_model import LogisticRegression
```
## IMDB dataset and the sentiment classification task
The [large movie review dataset](http://ai.stanford.edu/~amaas/data/sentiment/) contains a collection of 50,000 reviews from IMDB. The dataset contains an even number of positive and negative reviews. The authors considered only highly polarized reviews. A negative review has a score ≤ 4 out of 10, and a positive review has a score ≥ 7 out of 10. Neutral reviews are not included in the dataset. The dataset is divided into training and test sets. The training set is the same 25,000 labeled reviews.
The **sentiment classification task** consists of predicting the polarity (positive or negative) of a given text.
To get the dataset, in your terminal run the following commands:
`wget http://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz`
`gunzip aclImdb_v1.tar.gz`
`tar -xvf aclImdb_v1.tar`
### Tokenizing and term document matrix creation
```
PATH='data/aclImdb/'
names = ['neg','pos']
%ls {PATH}
%ls {PATH}train
%ls {PATH}train/pos | head
trn,trn_y = texts_labels_from_folders(f'{PATH}train',names)
val,val_y = texts_labels_from_folders(f'{PATH}test',names)
```
Here is the text of the first review
```
trn[0]
trn_y[0]
```
[`CountVectorizer`](http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.CountVectorizer.html) converts a collection of text documents to a matrix of token counts (part of `sklearn.feature_extraction.text`).
```
veczr = CountVectorizer(tokenizer=tokenize)
```
`fit_transform(trn)` finds the vocabulary in the training set. It also transforms the training set into a term-document matrix. Since we have to apply the *same transformation* to your validation set, the second line uses just the method `transform(val)`. `trn_term_doc` and `val_term_doc` are sparse matrices. `trn_term_doc[i]` represents training document i and it contains a count of words for each document for each word in the vocabulary.
```
trn_term_doc = veczr.fit_transform(trn)
val_term_doc = veczr.transform(val)
trn_term_doc
trn_term_doc[0]
vocab = veczr.get_feature_names(); vocab[5000:5005]
w0 = set([o.lower() for o in trn[0].split(' ')]); w0
len(w0)
veczr.vocabulary_['absurd']
trn_term_doc[0,1297]
trn_term_doc[0,5000]
```
## Naive Bayes
We define the **log-count ratio** $r$ for each word $f$:
$r = \log \frac{\text{ratio of feature $f$ in positive documents}}{\text{ratio of feature $f$ in negative documents}}$
where ratio of feature $f$ in positive documents is the number of times a positive document has a feature divided by the number of positive documents.
```
def pr(y_i):
p = x[y==y_i].sum(0)
return (p+1) / ((y==y_i).sum()+1)
x=trn_term_doc
y=trn_y
r = np.log(pr(1)/pr(0))
b = np.log((y==1).mean() / (y==0).mean())
```
Here is the formula for Naive Bayes.
```
pre_preds = val_term_doc @ r.T + b
preds = pre_preds.T>0
(preds==val_y).mean()
```
...and binarized Naive Bayes.
```
x=trn_term_doc.sign()
r = np.log(pr(1)/pr(0))
pre_preds = val_term_doc.sign() @ r.T + b
preds = pre_preds.T>0
(preds==val_y).mean()
```
### Logistic regression
Here is how we can fit logistic regression where the features are the unigrams.
```
m = LogisticRegression(C=1e8, dual=True)
m.fit(x, y)
preds = m.predict(val_term_doc)
(preds==val_y).mean()
m = LogisticRegression(C=1e8, dual=True)
m.fit(trn_term_doc.sign(), y)
preds = m.predict(val_term_doc.sign())
(preds==val_y).mean()
```
...and the regularized version
```
m = LogisticRegression(C=0.1, dual=True)
m.fit(x, y)
preds = m.predict(val_term_doc)
(preds==val_y).mean()
m = LogisticRegression(C=0.1, dual=True)
m.fit(trn_term_doc.sign(), y)
preds = m.predict(val_term_doc.sign())
(preds==val_y).mean()
```
### Trigram with NB features
Our next model is a version of logistic regression with Naive Bayes features described [here](https://www.aclweb.org/anthology/P12-2018). For every document we compute binarized features as described above, but this time we use bigrams and trigrams too. Each feature is a log-count ratio. A logistic regression model is then trained to predict sentiment.
```
veczr = CountVectorizer(ngram_range=(1,3), tokenizer=tokenize, max_features=800000)
trn_term_doc = veczr.fit_transform(trn)
val_term_doc = veczr.transform(val)
trn_term_doc.shape
vocab = veczr.get_feature_names()
vocab[200000:200005]
y=trn_y
x=trn_term_doc.sign()
val_x = val_term_doc.sign()
r = np.log(pr(1) / pr(0))
b = np.log((y==1).mean() / (y==0).mean())
```
Here we fit regularized logistic regression where the features are the trigrams.
```
m = LogisticRegression(C=0.1, dual=True)
m.fit(x, y);
preds = m.predict(val_x)
(preds.T==val_y).mean()
```
Here is the $\text{log-count ratio}$ `r`.
```
r.shape, r
np.exp(r)
```
Here we fit regularized logistic regression where the features are the trigrams' log-count ratios.
```
x_nb = x.multiply(r)
m = LogisticRegression(dual=True, C=0.1)
m.fit(x_nb, y);
val_x_nb = val_x.multiply(r)
preds = m.predict(val_x_nb)
(preds.T==val_y).mean()
```
## fastai NBSVM++
```
sl=2000
# Here is how we get a model from a bag of words
md = TextClassifierData.from_bow(trn_term_doc, trn_y, val_term_doc, val_y, sl)
learner = md.dotprod_nb_learner()
learner.fit(0.02, 1, wds=1e-6, cycle_len=1)
learner.fit(0.02, 2, wds=1e-6, cycle_len=1)
learner.fit(0.02, 2, wds=1e-6, cycle_len=1)
```
## References
* Baselines and Bigrams: Simple, Good Sentiment and Topic Classification. Sida Wang and Christopher D. Manning [pdf](https://www.aclweb.org/anthology/P12-2018)
|
github_jupyter
|
%reload_ext autoreload
%autoreload 2
%matplotlib inline
from fastai.nlp import *
from sklearn.linear_model import LogisticRegression
PATH='data/aclImdb/'
names = ['neg','pos']
%ls {PATH}
%ls {PATH}train
%ls {PATH}train/pos | head
trn,trn_y = texts_labels_from_folders(f'{PATH}train',names)
val,val_y = texts_labels_from_folders(f'{PATH}test',names)
trn[0]
trn_y[0]
veczr = CountVectorizer(tokenizer=tokenize)
trn_term_doc = veczr.fit_transform(trn)
val_term_doc = veczr.transform(val)
trn_term_doc
trn_term_doc[0]
vocab = veczr.get_feature_names(); vocab[5000:5005]
w0 = set([o.lower() for o in trn[0].split(' ')]); w0
len(w0)
veczr.vocabulary_['absurd']
trn_term_doc[0,1297]
trn_term_doc[0,5000]
def pr(y_i):
p = x[y==y_i].sum(0)
return (p+1) / ((y==y_i).sum()+1)
x=trn_term_doc
y=trn_y
r = np.log(pr(1)/pr(0))
b = np.log((y==1).mean() / (y==0).mean())
pre_preds = val_term_doc @ r.T + b
preds = pre_preds.T>0
(preds==val_y).mean()
x=trn_term_doc.sign()
r = np.log(pr(1)/pr(0))
pre_preds = val_term_doc.sign() @ r.T + b
preds = pre_preds.T>0
(preds==val_y).mean()
m = LogisticRegression(C=1e8, dual=True)
m.fit(x, y)
preds = m.predict(val_term_doc)
(preds==val_y).mean()
m = LogisticRegression(C=1e8, dual=True)
m.fit(trn_term_doc.sign(), y)
preds = m.predict(val_term_doc.sign())
(preds==val_y).mean()
m = LogisticRegression(C=0.1, dual=True)
m.fit(x, y)
preds = m.predict(val_term_doc)
(preds==val_y).mean()
m = LogisticRegression(C=0.1, dual=True)
m.fit(trn_term_doc.sign(), y)
preds = m.predict(val_term_doc.sign())
(preds==val_y).mean()
veczr = CountVectorizer(ngram_range=(1,3), tokenizer=tokenize, max_features=800000)
trn_term_doc = veczr.fit_transform(trn)
val_term_doc = veczr.transform(val)
trn_term_doc.shape
vocab = veczr.get_feature_names()
vocab[200000:200005]
y=trn_y
x=trn_term_doc.sign()
val_x = val_term_doc.sign()
r = np.log(pr(1) / pr(0))
b = np.log((y==1).mean() / (y==0).mean())
m = LogisticRegression(C=0.1, dual=True)
m.fit(x, y);
preds = m.predict(val_x)
(preds.T==val_y).mean()
r.shape, r
np.exp(r)
x_nb = x.multiply(r)
m = LogisticRegression(dual=True, C=0.1)
m.fit(x_nb, y);
val_x_nb = val_x.multiply(r)
preds = m.predict(val_x_nb)
(preds.T==val_y).mean()
sl=2000
# Here is how we get a model from a bag of words
md = TextClassifierData.from_bow(trn_term_doc, trn_y, val_term_doc, val_y, sl)
learner = md.dotprod_nb_learner()
learner.fit(0.02, 1, wds=1e-6, cycle_len=1)
learner.fit(0.02, 2, wds=1e-6, cycle_len=1)
learner.fit(0.02, 2, wds=1e-6, cycle_len=1)
| 0.380183 | 0.9659 |
## Sentinel-1 feature tracking
ethz-02-02-01
This application takes a pair of Sentinel-1 products and perform feature tracking using the run_dic package
### <a name="service">Service definition
```
service = dict([('title', 'Sentinel-1 feature tracking'),
('abstract', 'Sentinel-1 feature tracking'),
('id', 'ewf-ethz-02-02-01')])
max_velocity = dict([('id', 'max_velocity'),
('value', '8'),
('title', 'Max velocity'),
('abstract', 'Max velocity (m/day)')])
aoi = dict([('id', 'area_of_interest'),
('value', 'POLYGON((-107.3010512293226 37.96041091059219, -107.196442762009 37.96256467405659, -107.1949566934473 38.02435737739832, -107.306338874926 38.02130079875337, -107.3010512293226 37.96041091059219))'),
('title', 'Area of interest in WKT'),
('abstract', 'Area of interest in WKT')])
dem = dict([('id', 'dem'),
('value', 'SRTM 3Sec'),
('title', 'Area of interest in WKT'),
('abstract', 'Area of interest in WKT'),
('options', 'SRTM 3Sec,ACE30')])
utm_zone = dict([('id', 'utm_zone'),
('title', 'UTM zone'),
('abstract', 'UTM zone'),
('value', 'EPSG:32715')])
resolution = dict([("id", "resolution"),
("title", "Spatial resolution"),
("value", "40"),
("abstract", "Spatial resolution in meters (10 or 40)"),
('options', '10,40')])
window_size = dict([('id', 'window_size'),
('title', 'window_size'),
('abstract', 'window size in pixels'),
('value', '512')])
oversampling_factor = dict([('id', 'oversampling_factor'),
('title', 'oversampling_factor'),
('abstract', 'oversampling factor'),
('value', '2')])
color_scale_limits = dict([('id', 'color_scale_limits'),
('title', 'color_scale_limits'),
('abstract', 'color_scale_limits'),
('value', '0,10')])
```
### <a name="runtime">Runtime parameter definition
**Input identifiers**
These are the Sentinel-1 product identifiers
```
input_identifiers = ['S1A_IW_GRDH_1SDV_20190925T131011_20190925T131036_029178_035034_002F',
'S1A_IW_GRDH_1SDV_20191007T131011_20191007T131036_029353_035643_ACAE']
```
**Input references**
These are the Sentinel-1 catalogue references
```
input_references = ('https://catalog.terradue.com/sentinel1/search?uid=S1A_IW_GRDH_1SDV_20190925T131011_20190925T131036_029178_035034_002F',
'https://catalog.terradue.com/sentinel1/search?uid=S1A_IW_GRDH_1SDV_20191007T131011_20191007T131036_029353_035643_ACAE')
```
**Data path**
This path defines where the data is staged-in.
```
data_path = '/workspace/data'
```
### <a name="workflow">Workflow
#### Import the packages required for processing the data
```
%load_ext autoreload
%autoreload 2
import sys
import os
sys.path.append('/application/notebook/libexec/')
sys.path.append(os.getcwd())
import ellip_snap_helpers
from ellip_snap_helpers import create_metadata
import xml.etree.ElementTree as ET
from snappy import jpy
from snappy import ProductIO
from snappy import GPF
from snappy import HashMap
import dateutil.parser as parser
import geopandas as gpd
from datetime import datetime
import matplotlib.pyplot as plt
from shapely.geos import ReadingError
import gdal
import time
import exifread
import lxml.etree as etree
from shapely.wkt import loads
from shapely.geometry import mapping
from shapely.geometry import box
import numpy as np
import warnings
warnings.filterwarnings("ignore")
sys.path.append('/opt/anaconda/bin/')
import numpy as np
import subprocess
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.colors as colors
from osgeo.gdalconst import GA_ReadOnly
from struct import unpack
from PIL import Image
from PIL import ImageDraw
import cioppy
ciop = cioppy.Cioppy()
```
### AOI
```
if aoi['value'] == 'Full':
aoi_wkt = cascaded_union(search.geometry.values).wkt
min_lon, min_lat, max_lon, max_lat = cascaded_union(search.geometry.values).bounds
else:
try:
aoi_wkt = loads(aoi['value']).wkt
min_lon, min_lat, max_lon, max_lat = loads(aoi['value']).bounds
except ReadingError:
aoi_wkt = box(*[float(i) for i in aoi['value'].split(',')]).wkt
min_lon, min_lat, max_lon, max_lat = [float(i) for i in aoi['value'].split(',')]
print aoi_wkt
```
## Read the products
### check if all the products have the same track number
```
product_TR = [None]*len(input_references)
for index,product_ref in enumerate(input_references):
result_prod = ciop.search(end_point=product_ref,
params=[],
output_fields='startdate,track',
model='EOP')
product_TR[index] = result_prod[0]['track']
if index==0:
slave_date = result_prod[0]['startdate'][:10]
elif result_prod[0]['startdate'][:10] > slave_date:
slave_date = result_prod[0]['startdate'][:10]
if not all(x == product_TR[0] for x in product_TR):
raise ValueError('Not all products pertain the same track!')
slave_date
```
#### Read the products
```
s1meta = "manifest.safe"
slave_products = []
master_products = []
slave_prefix = []
master_prefix = []
dates = []
for index, identifier in enumerate(input_identifiers):
s1_zip_file = os.path.join(data_path, identifier + '.zip')
s1_meta_file = os.path.join(data_path, identifier, identifier + '.SAFE', 'manifest.safe')
if os.path.isfile(s1_zip_file):
s1prd = s1_zip_file
elif os.path.isfile(s1_meta_file):
s1prd = s1_meta_file
print identifier, s1prd
reader = ProductIO.getProductReader("SENTINEL-1")
product = reader.readProductNodes(s1prd, None)
width = product.getSceneRasterWidth()
height = product.getSceneRasterHeight()
name = product.getName()
start_date = parser.parse(product.getStartTime().toString()).isoformat()
dates.append(start_date[:19])
if start_date[:10] == slave_date:
slave_products.append(s1prd)
print("\nProduct: %s, %d x %d pixels of %s assigned as slave" % (name, width, height, start_date))
slave_prefix.append(identifier.split('_')[-1])
slave_data_take = identifier.split('_')[-2]
else:
master_products.append(s1prd)
print("\nProduct: %s, %d x %d pixels of %s assigned as master" % (name, width, height, start_date))
master_data_take = identifier.split('_')[-2]
master_prefix.append(identifier.split('_')[-1])
output_name = 'S1_OFFSET_TRACKING_%s_%s' % (parser.parse(min(dates)).strftime('%Y%m%d%H%M%S'),
parser.parse(max(dates)).strftime('%Y%m%d%H%M%S'))
print("\nco-registered OUTPUT Img name is %s"%output_name)
mygraph = ellip_snap_helpers.GraphProcessor()
```
#### Read and if need assemble the products
```
operator = 'Read'
node_id = 'Read'
source_node_id = ''
if len(slave_products) > 1:
slave_read_nodes = []
# Read
for index, slave_identifier in enumerate(slave_products):
operator = 'Read'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
node_id = 'Read-S(%s)' % index
source_node_id = ''
parameters['file'] = slave_identifier
mygraph.add_node(node_id, operator, parameters, source_node_id)
slave_read_nodes.append(node_id)
source_nodes_id = slave_read_nodes
operator = 'SliceAssembly'
node_id = 'SliceAssembly-S'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
#parameters['selectedPolarisations'] = polarisation['value']
mygraph.add_node(node_id, operator, parameters, source_nodes_id)
source_slave_orbit = node_id
else:
operator = 'Read'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
node_id = 'Read-S'
source_node_id = ''
parameters['file'] = slave_products[0]
mygraph.add_node(node_id, operator, parameters, source_node_id)
source_slave_orbit = node_id
if len(master_products) > 1:
master_read_nodes = []
# Read
for index, master_identifer in enumerate(master_products):
operator = 'Read'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
node_id = 'Read-M(%s)' % index
source_node_id = ''
parameters['file'] = master_identifer
mygraph.add_node(node_id, operator, parameters, source_node_id)
master_read_nodes.append(node_id)
source_nodes_id = master_read_nodes
operator = 'SliceAssembly'
node_id = 'SliceAssembly-M'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
#parameters['selectedPolarisations'] = polarisation['value']
mygraph.add_node(node_id, operator, parameters, source_nodes_id)
source_master_orbit = node_id
else:
operator = 'Read'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
node_id = 'Read-M'
source_node_id = ''
parameters['file'] = master_products[0]
mygraph.add_node(node_id, operator, parameters, source_node_id)
source_master_orbit = node_id
mygraph.view_graph()
```
### Apply orbit file
```
operator = 'Apply-Orbit-File'
node_id = 'Apply-Orbit-File-S'
source_node_id = source_slave_orbit
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['orbitType'] = 'Sentinel Restituted (Auto Download)'
mygraph.add_node(node_id, operator, parameters, source_node_id)
operator = 'Apply-Orbit-File'
node_id = 'Apply-Orbit-File-M'
source_node_id = source_master_orbit
mygraph.add_node(node_id, operator, parameters, source_node_id)
mygraph.view_graph()
```
### Land/sea mask
```
operator = 'Land-Sea-Mask'
node_id = 'Land-Sea-Mask-S'
source_node_id = 'Apply-Orbit-File-S'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['landMask'] = 'false'
mygraph.add_node(node_id, operator, parameters, source_node_id)
operator = 'Land-Sea-Mask'
node_id = 'Land-Sea-Mask-M'
source_node_id = 'Apply-Orbit-File-M'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['landMask'] = 'false'
mygraph.add_node(node_id, operator, parameters, source_node_id)
```
### DEM assisted coregistration
```
operator = 'DEM-Assisted-Coregistration'
node_id = 'DEM-Assisted-Coregistration'
source_node_id = ['Land-Sea-Mask-S',
'Land-Sea-Mask-M']
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
mygraph.add_node(node_id, operator, parameters, source_node_id)
```
### Subset
```
operator = 'Subset'
node_id = 'Subset'
source_node_id = 'DEM-Assisted-Coregistration'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['geoRegion'] = aoi_wkt
parameters['copyMetadata'] = 'true'
mygraph.add_node(node_id, operator, parameters, source_node_id)
```
### Terrain correction
```
operator = 'Terrain-Correction'
source_node_id = 'Subset'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['demName'] = dem['value']
parameters['pixelSpacingInMeter'] = resolution['value']
parameters['mapProjection'] = utm_zone['value']
node_id = 'Terrain-Correction'
parameters
mygraph.add_node(node_id, operator, parameters, source_node_id)
```
### Write
```
operator = 'Write'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['file'] = output_name
parameters['formatName'] = 'GeoTIFF-BigTIFF'
node_id = 'Write'
source_node_id = 'Terrain-Correction'
mygraph.add_node(node_id, operator, parameters, source_node_id)
mygraph.view_graph()
print os.listdir(data_path)
print os.listdir(os.getcwd())
mygraph.run()
print os.listdir(data_path)
print os.listdir(os.getcwd())
```
### Separate tiffs
```
output_tif = '{}.tif'.format(output_name)
f = open(output_tif, 'rb')
tags = exifread.process_file(f)
xml_data = tags['Image OwnerName'].values
tree = ET.XML(xml_data)
input_list = dict()
for child in tree.find('Image_Interpretation'):
band_index = child.find('BAND_INDEX').text
name = child.find('BAND_NAME').text
input_list[band_index] = name
input_list
src = gdal.Open(output_tif)
geo_transform = src.GetGeoTransform()
projection = src.GetProjection()
for band_number in range(1, src.RasterCount+1):
band_data = src.GetRasterBand(band_number).ReadAsArray()
band_description = input_list[str(band_number-1)]
#band_data = np.where(band_data==0, np.nan, band_data)
print band_description
drv = gdal.GetDriverByName('GTiff')
ds = drv.Create('{}.tif'.format(band_description), band_data.shape[1], band_data.shape[0], 1, gdal.GDT_Float64)
ds.SetGeoTransform(geo_transform)
ds.SetProjection(projection)
ds.FlushCache()
ds = gdal.Open('{}.tif'.format(band_description), gdal.OF_UPDATE)
ds.GetRasterBand(1).WriteArray(band_data)
new_data = ds.GetRasterBand(1).ReadAsArray()
imgplot = plt.imshow(new_data)
plt.show()
ds.FlushCache()
```
#### deleting the inputs
```
os.remove(output_tif)
print os.listdir(os.getcwd())
```
#### List of geotiffs produced
```
master_list = list()
slave_list = list()
for element in input_list.values():
if 'mst' in element:
master_list.append(element)
if 'slv' in element:
slave_list.append(element)
print master_list
print slave_list
```
### run_dic
#### writing the input_dic.txt
```
input_list = list()
for idx, master_tif in enumerate(sorted(master_list)):
if 'VV' in master_tif:
pol = 'VV'
elif 'VH' in master_tif:
pol = 'VH'
input_list.append('input_dic_{}.txt'.format(pol))
with open('input_dic_{}.txt'.format(pol), 'wb') as file:
file.write('{}.tif\n'.format(master_tif))
file.write('{}.tif\n'.format(sorted(slave_list)[idx]))
file.write('{} {} {}\n'.format(window_size['value'],oversampling_factor['value'], resolution['value']))
file.write('{} {}\n'.format(color_scale_limits['value'].split(',')[0], color_scale_limits['value'].split(',')[1]))
for file in input_list:
print file
with open(file) as f:
print f.read()
input_list
```
#### running the package
```
if 'LD_LIBRARY_PATH' not in os.environ.keys():
os.environ['LD_LIBRARY_PATH'] = '/opt/v94/runtime/glnxa64:/opt/v94/bin/glnxa64:/opt/v94/sys/os/glnxa64:/opt/v94/extern/bin/glnxa64'
else:
os.environ['LD_LIBRARY_PATH'] = '/opt/v94/runtime/glnxa64:/opt/v94/bin/glnxa64:/opt/v94/sys/os/glnxa64:/opt/v94/extern/bin/glnxa64:' + os.environ['LD_LIBRARY_PATH']
import run_dic
print os.environ['LD_LIBRARY_PATH']
dir(run_dic)
for input_file in input_list:
print input_file
command = 'import run_dic; mr = run_dic.initialize(); mr.run_dic(\"{}\", nargout=0)'.format(input_file)
options = ['python', '-c', command]
p = subprocess.Popen(options,
stdout=subprocess.PIPE,
stdin=subprocess.PIPE,
stderr=subprocess.PIPE)
res, err = p.communicate()
if res:
print 'RESULTS:\n'
for el in res.split('\n'):
print el
if err:
print 'ERRORS:\n'
for el in res.split('\n'):
print el
print
output_check = list()
for file in os.listdir('./'):
if '.txt' in file:
if file not in input_list:
output_check.append(file)
assert(output_check), Exception("no output produced")
print os.listdir(os.getcwd())
```
#### adding geotransform and projection to the output geotiffs
for file in os.listdir('./'):
if '.tif' in file:
print file
"""old code that converts png into geotiff"""
#with rasterio.open(file, 'r') as ds:
# arr = ds.read()
#drv = gdal.GetDriverByName('GTiff')
#ds = drv.Create('{}.tif'.format(os.path.splitext(os.path.basename(file))[0]), arr.shape[2], arr.shape[1], arr.shape[0], gdal.GDT_Byte)
ds = gdal.Open(file, gdal.OF_UPDATE)
ds.SetGeoTransform(geo_transform)
ds.SetProjection(projection)
#for band_number in range(arr.shape[0]):
# ds.GetRasterBand(band_number+1).WriteArray(arr[band_number])
ds.FlushCache()
print gdal.Info(file)
```
output_file = list()
for file in os.listdir('./'):
if '.txt' in file:
print file
if file not in input_list:
os.rename(file, '{}_{}'.format('output', file))
output_file.append('{}_{}'.format('output', file))
else:
output_file.append(file)
output_file
metadata = {'geo_transform' : geo_transform,
'projection' : projection}
with open('metadata.txt', 'wb') as file:
file.write(str(metadata))
file.close()
with open('metadata.txt') as f:
print f.read()
print os.listdir(os.getcwd())
```
#### Properties file
```
metadata = dict()
try:
input_reference = input_references[0]
search0 = ciop.search(end_point=input_reference,
params=dict(),
output_fields='identifier, startdate, enddate, wkt',
model='GeoTime')[0]
input_reference = input_references[1]
search1 = ciop.search(end_point=input_reference,
params=dict(),
output_fields='identifier, startdate, enddate, wkt',
model='GeoTime')[0]
if search0['startdate'] > search1['startdate']:
master_date = search1['startdate']
slave_date = search0['startdate']
else:
master_date = search0['startdate']
slave_date = search1['startdate']
metadata['startdate'] = master_date
metadata['enddate'] = slave_date
metadata['wkt'] = aoi_wkt
print metadata
for file in os.listdir(os.getcwd()):
if '.txt' in file or '.tif' in file:
print os.path.splitext(file)[0]
metadata['identifier'] = os.path.splitext(file)[0]
metadata['title'] = os.path.splitext(file)[0]
create_metadata(metadata, metadata['identifier'])
except Exception as e:
print('ERROR: could not retrieve product metadata {}. {}'.format(input_reference, e))
print os.listdir(os.getcwd())
```
### License
This work is licenced under a [Attribution-ShareAlike 4.0 International License (CC BY-SA 4.0)](http://creativecommons.org/licenses/by-sa/4.0/)
YOU ARE FREE TO:
* Share - copy and redistribute the material in any medium or format.
* Adapt - remix, transform, and built upon the material for any purpose, even commercially.
UNDER THE FOLLOWING TERMS:
* Attribution - You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
* ShareAlike - If you remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.
|
github_jupyter
|
service = dict([('title', 'Sentinel-1 feature tracking'),
('abstract', 'Sentinel-1 feature tracking'),
('id', 'ewf-ethz-02-02-01')])
max_velocity = dict([('id', 'max_velocity'),
('value', '8'),
('title', 'Max velocity'),
('abstract', 'Max velocity (m/day)')])
aoi = dict([('id', 'area_of_interest'),
('value', 'POLYGON((-107.3010512293226 37.96041091059219, -107.196442762009 37.96256467405659, -107.1949566934473 38.02435737739832, -107.306338874926 38.02130079875337, -107.3010512293226 37.96041091059219))'),
('title', 'Area of interest in WKT'),
('abstract', 'Area of interest in WKT')])
dem = dict([('id', 'dem'),
('value', 'SRTM 3Sec'),
('title', 'Area of interest in WKT'),
('abstract', 'Area of interest in WKT'),
('options', 'SRTM 3Sec,ACE30')])
utm_zone = dict([('id', 'utm_zone'),
('title', 'UTM zone'),
('abstract', 'UTM zone'),
('value', 'EPSG:32715')])
resolution = dict([("id", "resolution"),
("title", "Spatial resolution"),
("value", "40"),
("abstract", "Spatial resolution in meters (10 or 40)"),
('options', '10,40')])
window_size = dict([('id', 'window_size'),
('title', 'window_size'),
('abstract', 'window size in pixels'),
('value', '512')])
oversampling_factor = dict([('id', 'oversampling_factor'),
('title', 'oversampling_factor'),
('abstract', 'oversampling factor'),
('value', '2')])
color_scale_limits = dict([('id', 'color_scale_limits'),
('title', 'color_scale_limits'),
('abstract', 'color_scale_limits'),
('value', '0,10')])
input_identifiers = ['S1A_IW_GRDH_1SDV_20190925T131011_20190925T131036_029178_035034_002F',
'S1A_IW_GRDH_1SDV_20191007T131011_20191007T131036_029353_035643_ACAE']
input_references = ('https://catalog.terradue.com/sentinel1/search?uid=S1A_IW_GRDH_1SDV_20190925T131011_20190925T131036_029178_035034_002F',
'https://catalog.terradue.com/sentinel1/search?uid=S1A_IW_GRDH_1SDV_20191007T131011_20191007T131036_029353_035643_ACAE')
data_path = '/workspace/data'
%load_ext autoreload
%autoreload 2
import sys
import os
sys.path.append('/application/notebook/libexec/')
sys.path.append(os.getcwd())
import ellip_snap_helpers
from ellip_snap_helpers import create_metadata
import xml.etree.ElementTree as ET
from snappy import jpy
from snappy import ProductIO
from snappy import GPF
from snappy import HashMap
import dateutil.parser as parser
import geopandas as gpd
from datetime import datetime
import matplotlib.pyplot as plt
from shapely.geos import ReadingError
import gdal
import time
import exifread
import lxml.etree as etree
from shapely.wkt import loads
from shapely.geometry import mapping
from shapely.geometry import box
import numpy as np
import warnings
warnings.filterwarnings("ignore")
sys.path.append('/opt/anaconda/bin/')
import numpy as np
import subprocess
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.colors as colors
from osgeo.gdalconst import GA_ReadOnly
from struct import unpack
from PIL import Image
from PIL import ImageDraw
import cioppy
ciop = cioppy.Cioppy()
if aoi['value'] == 'Full':
aoi_wkt = cascaded_union(search.geometry.values).wkt
min_lon, min_lat, max_lon, max_lat = cascaded_union(search.geometry.values).bounds
else:
try:
aoi_wkt = loads(aoi['value']).wkt
min_lon, min_lat, max_lon, max_lat = loads(aoi['value']).bounds
except ReadingError:
aoi_wkt = box(*[float(i) for i in aoi['value'].split(',')]).wkt
min_lon, min_lat, max_lon, max_lat = [float(i) for i in aoi['value'].split(',')]
print aoi_wkt
product_TR = [None]*len(input_references)
for index,product_ref in enumerate(input_references):
result_prod = ciop.search(end_point=product_ref,
params=[],
output_fields='startdate,track',
model='EOP')
product_TR[index] = result_prod[0]['track']
if index==0:
slave_date = result_prod[0]['startdate'][:10]
elif result_prod[0]['startdate'][:10] > slave_date:
slave_date = result_prod[0]['startdate'][:10]
if not all(x == product_TR[0] for x in product_TR):
raise ValueError('Not all products pertain the same track!')
slave_date
s1meta = "manifest.safe"
slave_products = []
master_products = []
slave_prefix = []
master_prefix = []
dates = []
for index, identifier in enumerate(input_identifiers):
s1_zip_file = os.path.join(data_path, identifier + '.zip')
s1_meta_file = os.path.join(data_path, identifier, identifier + '.SAFE', 'manifest.safe')
if os.path.isfile(s1_zip_file):
s1prd = s1_zip_file
elif os.path.isfile(s1_meta_file):
s1prd = s1_meta_file
print identifier, s1prd
reader = ProductIO.getProductReader("SENTINEL-1")
product = reader.readProductNodes(s1prd, None)
width = product.getSceneRasterWidth()
height = product.getSceneRasterHeight()
name = product.getName()
start_date = parser.parse(product.getStartTime().toString()).isoformat()
dates.append(start_date[:19])
if start_date[:10] == slave_date:
slave_products.append(s1prd)
print("\nProduct: %s, %d x %d pixels of %s assigned as slave" % (name, width, height, start_date))
slave_prefix.append(identifier.split('_')[-1])
slave_data_take = identifier.split('_')[-2]
else:
master_products.append(s1prd)
print("\nProduct: %s, %d x %d pixels of %s assigned as master" % (name, width, height, start_date))
master_data_take = identifier.split('_')[-2]
master_prefix.append(identifier.split('_')[-1])
output_name = 'S1_OFFSET_TRACKING_%s_%s' % (parser.parse(min(dates)).strftime('%Y%m%d%H%M%S'),
parser.parse(max(dates)).strftime('%Y%m%d%H%M%S'))
print("\nco-registered OUTPUT Img name is %s"%output_name)
mygraph = ellip_snap_helpers.GraphProcessor()
operator = 'Read'
node_id = 'Read'
source_node_id = ''
if len(slave_products) > 1:
slave_read_nodes = []
# Read
for index, slave_identifier in enumerate(slave_products):
operator = 'Read'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
node_id = 'Read-S(%s)' % index
source_node_id = ''
parameters['file'] = slave_identifier
mygraph.add_node(node_id, operator, parameters, source_node_id)
slave_read_nodes.append(node_id)
source_nodes_id = slave_read_nodes
operator = 'SliceAssembly'
node_id = 'SliceAssembly-S'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
#parameters['selectedPolarisations'] = polarisation['value']
mygraph.add_node(node_id, operator, parameters, source_nodes_id)
source_slave_orbit = node_id
else:
operator = 'Read'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
node_id = 'Read-S'
source_node_id = ''
parameters['file'] = slave_products[0]
mygraph.add_node(node_id, operator, parameters, source_node_id)
source_slave_orbit = node_id
if len(master_products) > 1:
master_read_nodes = []
# Read
for index, master_identifer in enumerate(master_products):
operator = 'Read'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
node_id = 'Read-M(%s)' % index
source_node_id = ''
parameters['file'] = master_identifer
mygraph.add_node(node_id, operator, parameters, source_node_id)
master_read_nodes.append(node_id)
source_nodes_id = master_read_nodes
operator = 'SliceAssembly'
node_id = 'SliceAssembly-M'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
#parameters['selectedPolarisations'] = polarisation['value']
mygraph.add_node(node_id, operator, parameters, source_nodes_id)
source_master_orbit = node_id
else:
operator = 'Read'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
node_id = 'Read-M'
source_node_id = ''
parameters['file'] = master_products[0]
mygraph.add_node(node_id, operator, parameters, source_node_id)
source_master_orbit = node_id
mygraph.view_graph()
operator = 'Apply-Orbit-File'
node_id = 'Apply-Orbit-File-S'
source_node_id = source_slave_orbit
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['orbitType'] = 'Sentinel Restituted (Auto Download)'
mygraph.add_node(node_id, operator, parameters, source_node_id)
operator = 'Apply-Orbit-File'
node_id = 'Apply-Orbit-File-M'
source_node_id = source_master_orbit
mygraph.add_node(node_id, operator, parameters, source_node_id)
mygraph.view_graph()
operator = 'Land-Sea-Mask'
node_id = 'Land-Sea-Mask-S'
source_node_id = 'Apply-Orbit-File-S'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['landMask'] = 'false'
mygraph.add_node(node_id, operator, parameters, source_node_id)
operator = 'Land-Sea-Mask'
node_id = 'Land-Sea-Mask-M'
source_node_id = 'Apply-Orbit-File-M'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['landMask'] = 'false'
mygraph.add_node(node_id, operator, parameters, source_node_id)
operator = 'DEM-Assisted-Coregistration'
node_id = 'DEM-Assisted-Coregistration'
source_node_id = ['Land-Sea-Mask-S',
'Land-Sea-Mask-M']
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
mygraph.add_node(node_id, operator, parameters, source_node_id)
operator = 'Subset'
node_id = 'Subset'
source_node_id = 'DEM-Assisted-Coregistration'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['geoRegion'] = aoi_wkt
parameters['copyMetadata'] = 'true'
mygraph.add_node(node_id, operator, parameters, source_node_id)
operator = 'Terrain-Correction'
source_node_id = 'Subset'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['demName'] = dem['value']
parameters['pixelSpacingInMeter'] = resolution['value']
parameters['mapProjection'] = utm_zone['value']
node_id = 'Terrain-Correction'
parameters
mygraph.add_node(node_id, operator, parameters, source_node_id)
operator = 'Write'
parameters = ellip_snap_helpers.get_operator_default_parameters(operator)
parameters['file'] = output_name
parameters['formatName'] = 'GeoTIFF-BigTIFF'
node_id = 'Write'
source_node_id = 'Terrain-Correction'
mygraph.add_node(node_id, operator, parameters, source_node_id)
mygraph.view_graph()
print os.listdir(data_path)
print os.listdir(os.getcwd())
mygraph.run()
print os.listdir(data_path)
print os.listdir(os.getcwd())
output_tif = '{}.tif'.format(output_name)
f = open(output_tif, 'rb')
tags = exifread.process_file(f)
xml_data = tags['Image OwnerName'].values
tree = ET.XML(xml_data)
input_list = dict()
for child in tree.find('Image_Interpretation'):
band_index = child.find('BAND_INDEX').text
name = child.find('BAND_NAME').text
input_list[band_index] = name
input_list
src = gdal.Open(output_tif)
geo_transform = src.GetGeoTransform()
projection = src.GetProjection()
for band_number in range(1, src.RasterCount+1):
band_data = src.GetRasterBand(band_number).ReadAsArray()
band_description = input_list[str(band_number-1)]
#band_data = np.where(band_data==0, np.nan, band_data)
print band_description
drv = gdal.GetDriverByName('GTiff')
ds = drv.Create('{}.tif'.format(band_description), band_data.shape[1], band_data.shape[0], 1, gdal.GDT_Float64)
ds.SetGeoTransform(geo_transform)
ds.SetProjection(projection)
ds.FlushCache()
ds = gdal.Open('{}.tif'.format(band_description), gdal.OF_UPDATE)
ds.GetRasterBand(1).WriteArray(band_data)
new_data = ds.GetRasterBand(1).ReadAsArray()
imgplot = plt.imshow(new_data)
plt.show()
ds.FlushCache()
os.remove(output_tif)
print os.listdir(os.getcwd())
master_list = list()
slave_list = list()
for element in input_list.values():
if 'mst' in element:
master_list.append(element)
if 'slv' in element:
slave_list.append(element)
print master_list
print slave_list
input_list = list()
for idx, master_tif in enumerate(sorted(master_list)):
if 'VV' in master_tif:
pol = 'VV'
elif 'VH' in master_tif:
pol = 'VH'
input_list.append('input_dic_{}.txt'.format(pol))
with open('input_dic_{}.txt'.format(pol), 'wb') as file:
file.write('{}.tif\n'.format(master_tif))
file.write('{}.tif\n'.format(sorted(slave_list)[idx]))
file.write('{} {} {}\n'.format(window_size['value'],oversampling_factor['value'], resolution['value']))
file.write('{} {}\n'.format(color_scale_limits['value'].split(',')[0], color_scale_limits['value'].split(',')[1]))
for file in input_list:
print file
with open(file) as f:
print f.read()
input_list
if 'LD_LIBRARY_PATH' not in os.environ.keys():
os.environ['LD_LIBRARY_PATH'] = '/opt/v94/runtime/glnxa64:/opt/v94/bin/glnxa64:/opt/v94/sys/os/glnxa64:/opt/v94/extern/bin/glnxa64'
else:
os.environ['LD_LIBRARY_PATH'] = '/opt/v94/runtime/glnxa64:/opt/v94/bin/glnxa64:/opt/v94/sys/os/glnxa64:/opt/v94/extern/bin/glnxa64:' + os.environ['LD_LIBRARY_PATH']
import run_dic
print os.environ['LD_LIBRARY_PATH']
dir(run_dic)
for input_file in input_list:
print input_file
command = 'import run_dic; mr = run_dic.initialize(); mr.run_dic(\"{}\", nargout=0)'.format(input_file)
options = ['python', '-c', command]
p = subprocess.Popen(options,
stdout=subprocess.PIPE,
stdin=subprocess.PIPE,
stderr=subprocess.PIPE)
res, err = p.communicate()
if res:
print 'RESULTS:\n'
for el in res.split('\n'):
print el
if err:
print 'ERRORS:\n'
for el in res.split('\n'):
print el
print
output_check = list()
for file in os.listdir('./'):
if '.txt' in file:
if file not in input_list:
output_check.append(file)
assert(output_check), Exception("no output produced")
print os.listdir(os.getcwd())
output_file = list()
for file in os.listdir('./'):
if '.txt' in file:
print file
if file not in input_list:
os.rename(file, '{}_{}'.format('output', file))
output_file.append('{}_{}'.format('output', file))
else:
output_file.append(file)
output_file
metadata = {'geo_transform' : geo_transform,
'projection' : projection}
with open('metadata.txt', 'wb') as file:
file.write(str(metadata))
file.close()
with open('metadata.txt') as f:
print f.read()
print os.listdir(os.getcwd())
metadata = dict()
try:
input_reference = input_references[0]
search0 = ciop.search(end_point=input_reference,
params=dict(),
output_fields='identifier, startdate, enddate, wkt',
model='GeoTime')[0]
input_reference = input_references[1]
search1 = ciop.search(end_point=input_reference,
params=dict(),
output_fields='identifier, startdate, enddate, wkt',
model='GeoTime')[0]
if search0['startdate'] > search1['startdate']:
master_date = search1['startdate']
slave_date = search0['startdate']
else:
master_date = search0['startdate']
slave_date = search1['startdate']
metadata['startdate'] = master_date
metadata['enddate'] = slave_date
metadata['wkt'] = aoi_wkt
print metadata
for file in os.listdir(os.getcwd()):
if '.txt' in file or '.tif' in file:
print os.path.splitext(file)[0]
metadata['identifier'] = os.path.splitext(file)[0]
metadata['title'] = os.path.splitext(file)[0]
create_metadata(metadata, metadata['identifier'])
except Exception as e:
print('ERROR: could not retrieve product metadata {}. {}'.format(input_reference, e))
print os.listdir(os.getcwd())
| 0.370339 | 0.805823 |
```
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split,cross_val_score,GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier,GradientBoostingClassifier,AdaBoostClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from xgboost import XGBClassifier
from sklearn.preprocessing import StandardScaler,MinMaxScaler
from sklearn.naive_bayes import GaussianNB
from imblearn.under_sampling import NearMiss
from keras.models import Sequential
from keras.layers import Dense
from sklearn import metrics
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from pandas_profiling import ProfileReport
data=pd.read_csv("train_ctrUa4K.csv")
for column in ('Gender','Married','Dependents','Self_Employed'):
data[column].fillna(data[column].mode()[0],inplace=True)
for column in ('LoanAmount','Loan_Amount_Term','Credit_History'):
data[column].fillna(data[column].mean(),inplace=True)
for variable in ('Gender','Married','Dependents','Education','Self_Employed','Property_Area'):
data[variable].fillna("Missing",inplace=True)
dummies=pd.get_dummies(data[variable],prefix=variable)
data=pd.concat([data,dummies],axis=1)
data.drop([variable],axis=1,inplace=True)
data['Loan_Status']=data.Loan_Status.map({'Y':0,'N':1})
Y=data['Loan_Status']
data.drop(['Loan_Status'],axis=1,inplace=True)
X=data[data.iloc[:,1:23].columns]
X_train,X_test,Y_train,Y_test=train_test_split(X,Y,random_state=100,test_size=0.2)
scaler=StandardScaler()
scaled_X_train=scaler.fit_transform(X_train)
scaled_X_test=scaler.transform(X_test)
def xg_param(X, y, nfolds):
n_estimators=[150,200,500,1000,1500,2000]
max_features=[1,2,3]
max_depth=[1,2,3,4,5,6,7,8,9,10]
gammas = [0.001, 0.01, 0.1, 1]
param_grid = {'n_estimators': n_estimators,'max_features':max_features,'max_depth':max_depth,'gamma':gammas}
grid_search_xg = GridSearchCV(XGBClassifier(learning_rate= 0.05), param_grid, cv=nfolds)
grid_search_xg.fit(X,y)
return grid_search_xg.best_params_
xg_param(scaled_X_train,Y_train,2)
XG_model=XGBClassifier(n_estimators=150, learning_rate = 0.05, max_features=1, max_depth = 1,gamma=0.001)
XG_model.fit(scaled_X_train,Y_train)
XG_pred=XG_model.predict(scaled_X_test)
print("Recall for XGBoost model:",metrics.recall_score(Y_test,XG_pred))
print("Precision for XGBoost model:",metrics.precision_score(Y_test,XG_pred))
print("Accuracy for XGBoost model:",metrics.accuracy_score(Y_test,XG_pred))
print("F-score for XGBoost model:",metrics.f1_score(Y_test,XG_pred))
print("Log-loss for XGBoost model:",metrics.log_loss(Y_test,XG_pred))
```
|
github_jupyter
|
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split,cross_val_score,GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier,GradientBoostingClassifier,AdaBoostClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from xgboost import XGBClassifier
from sklearn.preprocessing import StandardScaler,MinMaxScaler
from sklearn.naive_bayes import GaussianNB
from imblearn.under_sampling import NearMiss
from keras.models import Sequential
from keras.layers import Dense
from sklearn import metrics
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from pandas_profiling import ProfileReport
data=pd.read_csv("train_ctrUa4K.csv")
for column in ('Gender','Married','Dependents','Self_Employed'):
data[column].fillna(data[column].mode()[0],inplace=True)
for column in ('LoanAmount','Loan_Amount_Term','Credit_History'):
data[column].fillna(data[column].mean(),inplace=True)
for variable in ('Gender','Married','Dependents','Education','Self_Employed','Property_Area'):
data[variable].fillna("Missing",inplace=True)
dummies=pd.get_dummies(data[variable],prefix=variable)
data=pd.concat([data,dummies],axis=1)
data.drop([variable],axis=1,inplace=True)
data['Loan_Status']=data.Loan_Status.map({'Y':0,'N':1})
Y=data['Loan_Status']
data.drop(['Loan_Status'],axis=1,inplace=True)
X=data[data.iloc[:,1:23].columns]
X_train,X_test,Y_train,Y_test=train_test_split(X,Y,random_state=100,test_size=0.2)
scaler=StandardScaler()
scaled_X_train=scaler.fit_transform(X_train)
scaled_X_test=scaler.transform(X_test)
def xg_param(X, y, nfolds):
n_estimators=[150,200,500,1000,1500,2000]
max_features=[1,2,3]
max_depth=[1,2,3,4,5,6,7,8,9,10]
gammas = [0.001, 0.01, 0.1, 1]
param_grid = {'n_estimators': n_estimators,'max_features':max_features,'max_depth':max_depth,'gamma':gammas}
grid_search_xg = GridSearchCV(XGBClassifier(learning_rate= 0.05), param_grid, cv=nfolds)
grid_search_xg.fit(X,y)
return grid_search_xg.best_params_
xg_param(scaled_X_train,Y_train,2)
XG_model=XGBClassifier(n_estimators=150, learning_rate = 0.05, max_features=1, max_depth = 1,gamma=0.001)
XG_model.fit(scaled_X_train,Y_train)
XG_pred=XG_model.predict(scaled_X_test)
print("Recall for XGBoost model:",metrics.recall_score(Y_test,XG_pred))
print("Precision for XGBoost model:",metrics.precision_score(Y_test,XG_pred))
print("Accuracy for XGBoost model:",metrics.accuracy_score(Y_test,XG_pred))
print("F-score for XGBoost model:",metrics.f1_score(Y_test,XG_pred))
print("Log-loss for XGBoost model:",metrics.log_loss(Y_test,XG_pred))
| 0.418222 | 0.40248 |
**Diplomatura en Ciencia de Datos, Aprendizaje Automático y sus Aplicaciones**
**Edición 2022**
---
# Aplicaciones en Python
La idea de esta notebook es poder introducir algunos conceptos básicos de estadistica descriptiva y sus aplicaciones en Python. Intentaremos familiarizarnos con algunos
conceptos (librerias, paquetes y funciones) que nos facilitaran el camino hacia la manipulacion y procesamiento de los datos.
## Herramientas de trabajo
En esta oportunidad vamos a utilizar el lenguaje de programación Python junto con Google Colab para realizar nuestro primer analisis de la encuesta de sueldos. Recorda que Colab es un servicio cloud basado en los Notebooks de Jupyter, por lo tanto no es necesario descargar nada. A su vez, nos iniciaremos en un primer uso de herramientas de software libre, es decir no necesitas una licencia para porder utilizarlas.
<center>
<img src="https://i.imgur.com/Cq52LcH.png" height="150" />
</center>
## Pero primero: ¡Hola mundo!
Si es tu primer experiencia con Python, usá la celda de acá abajo para probar tu primer línea de código. Para imprimirlo en pantalla escribimos print("Hola mundo!")
```
print("hola mundo! bienvenidos a la Diplo!!") # Probá acá
```
## ¿Que es "EDA"?
En sus siglas en inglés hace referencia al **Análisis Exploratorio de Datos**. Este es el primer paso que debemos realizar como Data Scientists y consta de una primera revisión del estado de los datos y los consecuentes pasos necesarios para una correcta transformación.
La ciencia de datos es una disciplina que te permite convertir datos crudos en entendimiento, comprensión y conocimiento.
<center>
<img src="https://i.imgur.com/jclXnDS.png" height="200" />
</center>
En este sentido, el primer objetivo radica en preguntarnos **¿De qué se trata este dataset?**
## Importación de librerías
El concepto correcto en español es "biblioteca". Una biblioteca es básicamente un componente de software que nos brinda acceso a distintas funcionalidades.
Existen librerías con funciones para leer un archivo excel o csv y trabajar los datos como tablas (librería Pandas, por ejemplo), otras con funciones para graficar nuestros datos (como Seaborn), para trabajar con cálculo numérico (como Numpy).
Cualquiera sea el lenguaje con el que se decida programar, será útil conocer mediante la página oficial del lenguaje cuáles son las librerías disponibles, que nos facilitarán, en éste caso, el análisis de datos.
```
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
sns.set(rc={'figure.figsize':(10,6)})
```
# Leer dataset Encuesta Sysarmy en formato csv
En esta primera notebook, aprendemos cómo cargar un conjunto de datos utilizando pandas y cómo ver su contenido.
Durante la materia, se trabajará con la Encuesta Sysarmy del año 2022 versión 1. Se trata de una encuesta personal y voluntaria que busca relevar información sobre salarios y condiciones de trabajo de programadores, que se realiza anualmente.
Se analizarán sólo los datos provenientes de Argentina
[Link a los datos](https://sysarmy.com/blog/posts/resultados-de-la-encuesta-de-sueldos-2022-1/)
## ¿Cómo leer datos desde un archivo utilizando pandas?
```
import io
import pandas as pd
pd.set_option('display.max_rows', 4)
```
### Subiendo el archivo al entorno de Colaboratory
Colaboratory no tiene acceso a nuestro sistema de archivos local (¡menos mal!). Por ello, para poder leer un archivo, primero debemos subirlo a la nube. Eso se logra con:
```
from google.colab import files
uploaded = files.upload()
```
En la salida de la celda anterior, verán el texto
```
Saving 2020.2 - sysarmy - Encuesta de remuneración salarial Argentina - Argentina.csv to XXX
```
El texto XXX será la clave del archivo, que se utiliza para identificarlo entre todos los archivos subidos. Tener en cuenta que esta clave no necesariamente es el nombre del archivo.
```
file_key = '2022.1 - sysarmy - Encuesta de remuneración salarial Argentina - Argentina.csv' # Replace for correspoing key
df = pd.read_csv(io.StringIO(uploaded[file_key].decode('utf-8')))
```
Con esta operación, hemos creado un DataFrame de pandas en base al archivo de respuestas. Un DataFrame no es más que una tabla sobre la cual podemos aplicar un montón de operaciones similares a las de Excel o a las SQL. En esta notebook no pretendemos hacer un tutorial de pandas, el Internet está lleno de ellos, pero sí iremos explicando cómo implementar determinadas operaciones necesarias para el análisis de este conjunto de datos.
Veamos qué valoir tiene la variable `df`.
```
df[:10]
```
## Selección de filas
¡No es lo que esperamos! Si vemos el conjunto de datos, efectivamente tiene celdas en blanco en la parte superior, y el nombre de las columnas aparece en la fila 9. Con Pandas podemos manejar estas situaciones pasando argumentos específicos a la función `pd.read_csv`
```
df_fixed = pd.read_csv(
io.StringIO(uploaded[file_key].decode('utf-8')),
skiprows=range(9), header=1)
df_fixed[:3]
```
## Renombrar columnas
Para trabajar más cómodamente, renombraremos las columnas de DataFrame. Tengan cuidado de que el orden de los nombres nuevos se corresponda con el contenido de cada columna.
```
df_fixed.columns
new_columns = {
'profile': {
'Me identifico (género)': 'gender', 'Tengo (edad)': 'age', 'Años de experiencia': 'years_experience',
'Nivel de estudios alcanzado': 'studies_level',
'Estado': 'studies_level_state', 'Carrera': 'career', 'Universidad': 'university',
'Realizaste cursos de especialización': 'specialization_courses',
'¿Contribuís a proyectos open source?': 'open_source_contributions',
'¿Programás como hobbie?': 'programming_as_hobby',
'Orientación sexual': 'sexual_orientation',
'¿Tenés algún tipo de discapacidad?': 'has_disabilities',
'¿Sentís que alguna vez los prejuicios culturales/sociales sobre tu orientación, género, etnia o discapacidad pudieron obstaculizar el que consigas un trabajo?': 'has_disabilities_hiring_difficulties',
},
'work' : {
'Estoy trabajando en': 'country',
'Dónde estás trabajando': 'province', 'Años en la empresa actual': 'years_in_company',
'Años en el puesto actual': 'years_in_current_position', '¿Gente a cargo?': 'people_in_charge_of',
'Trabajo de': 'role', '¿Tenés guardias?': 'on_call_duty',
'¿Porcentaje, bruto o neto?': 'on_call_duty_charge_type', 'Tipo de contrato': 'contract_type',
'Sufriste o presenciaste situaciones de violencia y/o acoso por motivo de': 'has_violence_situations',
'¿Considerás que tenés oportunidades de crecimiento siendo quien sos dentro de tu organización?':'listen_more_men',
'¿Sentís que podés ser vos en tu trabajo?': 'yourself_in_your_work',
'En el último año, en tu trabajo ¿recibiste o escuchaste comentarios que considerás inapropiados, subidos de tono y/o discriminatorios?':'lastyear_discrimination',
},
'tools': {
'Plataformas': 'platform', 'Lenguajes de programación': 'programming_languages',
'Frameworks, herramientas y librerías': 'frameworks', 'Bases de datos': 'data_bases',
'QA / Testing': 'qa_testing', 'IDEs': 'IDEs',
'¿Qué SO usás en tu laptop/PC para trabajar?': 'work_pc_os', '¿Y en tu celular?': 'cellphone_os'
},
'salary': {
'Cuánto cobrás por guardia': 'on_call_duty_charge',
'Salario mensual o retiro BRUTO (en tu moneda local)': 'monthly_BRUTO',
'Salario mensual o retiro NETO (en tu moneda local)': 'monthly_NETO',
'Pagos en dólares': 'in_usd', '¿Cuál fue el último valor de dólar que tomaron?':'last_dollar_value','¿Qué tan conforme estás con tu sueldo?': 'satisfaction',
'Cómo creés que está tu sueldo con respecto al último semestre': 'comparison_last_semester',
'Recibís algún tipo de bono': 'has_bonus', 'A qué está atado el bono': 'bonus_tied_to',
'¿Tuviste ajustes por inflación durante 2021?': 'inflation_adjustment_2021',
'¿De qué % fue el ajuste total?': 'percentage_inflation_adjustment_2021',
'¿En qué mes fue el último ajuste?': 'month_last_inflation_adjustment',
},
'company' : {
'Cantidad de empleados': 'employee_number', 'Actividad principal': 'main_activity',
'¿La recomendás como un buen lugar para trabajar?': 'recommended',
'¿Cuál es el compromiso que tiene tu empresa con la diversidad, la equidad y la inclusión?': 'diversity_policies',
'Beneficios extra': 'extra_benefits', '¿Instauraron algún beneficio nuevo?': 'new_benefits',
'¿Qué tanto sentís que te está apoyando tu empresa/organización durante la pandemia?': 'pandemic_support',
'¿Cuántas veces a la semana vas a trabajar a la oficina?':'days_in_the_office',
}
}
def replace_columns(df, new_columns):
new_col_names = {
original_name: category + '_' + new_name
for category, cols in new_columns.items()
for original_name, new_name in cols.items()
}
return df.rename(columns=new_col_names)
df_renamed = replace_columns(df_fixed, new_columns)
df_renamed[:2]
```
### Leer archivo desde URL
Como realizar estas operaciones es un poco tedioso y requiere intervención manual, hemos subido el dataset a un servidor local de FaMAF para poder accederlos directamente a través de consultas HTTP (por ejemplo, desde un navegador).
Otra forma de disponibilizar un conjunto de datos pequeño es creando un archivo en un repositorio de github o un gist.
Primero, es necesario descargar el archivo ya procesado. El procedimiento es similar a leer el archivo.
1. Se guarda el DataFrame en un archivo en el servidor remoto.
2. Se descarga ese archivo.
```
df_renamed.to_csv("sysarmy_survey_2022_processed.csv", index=False)
from google.colab import files
files.download("sysarmy_survey_2022_processed.csv")
```
Subiremos este archivo con el dataset procesado a un servidor de la universidad.
Pandas permite leer archivos `.csv` desde una URL, sin necesidad de descargarlos en el sistema de archivos local. La siguiente celda funcionará tanto en Colaboratory como en Jupyter, y será el método por defecto de acceder a los datos en las notebooks siguientes.
```
url = 'https://cs.famaf.unc.edu.ar/~mteruel/datasets/diplodatos/sysarmy_survey_2020_processed.csv'
df2 = pd.read_csv(url)
df2[:3]
```
|
github_jupyter
|
print("hola mundo! bienvenidos a la Diplo!!") # Probá acá
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
sns.set(rc={'figure.figsize':(10,6)})
import io
import pandas as pd
pd.set_option('display.max_rows', 4)
from google.colab import files
uploaded = files.upload()
Saving 2020.2 - sysarmy - Encuesta de remuneración salarial Argentina - Argentina.csv to XXX
file_key = '2022.1 - sysarmy - Encuesta de remuneración salarial Argentina - Argentina.csv' # Replace for correspoing key
df = pd.read_csv(io.StringIO(uploaded[file_key].decode('utf-8')))
df[:10]
df_fixed = pd.read_csv(
io.StringIO(uploaded[file_key].decode('utf-8')),
skiprows=range(9), header=1)
df_fixed[:3]
df_fixed.columns
new_columns = {
'profile': {
'Me identifico (género)': 'gender', 'Tengo (edad)': 'age', 'Años de experiencia': 'years_experience',
'Nivel de estudios alcanzado': 'studies_level',
'Estado': 'studies_level_state', 'Carrera': 'career', 'Universidad': 'university',
'Realizaste cursos de especialización': 'specialization_courses',
'¿Contribuís a proyectos open source?': 'open_source_contributions',
'¿Programás como hobbie?': 'programming_as_hobby',
'Orientación sexual': 'sexual_orientation',
'¿Tenés algún tipo de discapacidad?': 'has_disabilities',
'¿Sentís que alguna vez los prejuicios culturales/sociales sobre tu orientación, género, etnia o discapacidad pudieron obstaculizar el que consigas un trabajo?': 'has_disabilities_hiring_difficulties',
},
'work' : {
'Estoy trabajando en': 'country',
'Dónde estás trabajando': 'province', 'Años en la empresa actual': 'years_in_company',
'Años en el puesto actual': 'years_in_current_position', '¿Gente a cargo?': 'people_in_charge_of',
'Trabajo de': 'role', '¿Tenés guardias?': 'on_call_duty',
'¿Porcentaje, bruto o neto?': 'on_call_duty_charge_type', 'Tipo de contrato': 'contract_type',
'Sufriste o presenciaste situaciones de violencia y/o acoso por motivo de': 'has_violence_situations',
'¿Considerás que tenés oportunidades de crecimiento siendo quien sos dentro de tu organización?':'listen_more_men',
'¿Sentís que podés ser vos en tu trabajo?': 'yourself_in_your_work',
'En el último año, en tu trabajo ¿recibiste o escuchaste comentarios que considerás inapropiados, subidos de tono y/o discriminatorios?':'lastyear_discrimination',
},
'tools': {
'Plataformas': 'platform', 'Lenguajes de programación': 'programming_languages',
'Frameworks, herramientas y librerías': 'frameworks', 'Bases de datos': 'data_bases',
'QA / Testing': 'qa_testing', 'IDEs': 'IDEs',
'¿Qué SO usás en tu laptop/PC para trabajar?': 'work_pc_os', '¿Y en tu celular?': 'cellphone_os'
},
'salary': {
'Cuánto cobrás por guardia': 'on_call_duty_charge',
'Salario mensual o retiro BRUTO (en tu moneda local)': 'monthly_BRUTO',
'Salario mensual o retiro NETO (en tu moneda local)': 'monthly_NETO',
'Pagos en dólares': 'in_usd', '¿Cuál fue el último valor de dólar que tomaron?':'last_dollar_value','¿Qué tan conforme estás con tu sueldo?': 'satisfaction',
'Cómo creés que está tu sueldo con respecto al último semestre': 'comparison_last_semester',
'Recibís algún tipo de bono': 'has_bonus', 'A qué está atado el bono': 'bonus_tied_to',
'¿Tuviste ajustes por inflación durante 2021?': 'inflation_adjustment_2021',
'¿De qué % fue el ajuste total?': 'percentage_inflation_adjustment_2021',
'¿En qué mes fue el último ajuste?': 'month_last_inflation_adjustment',
},
'company' : {
'Cantidad de empleados': 'employee_number', 'Actividad principal': 'main_activity',
'¿La recomendás como un buen lugar para trabajar?': 'recommended',
'¿Cuál es el compromiso que tiene tu empresa con la diversidad, la equidad y la inclusión?': 'diversity_policies',
'Beneficios extra': 'extra_benefits', '¿Instauraron algún beneficio nuevo?': 'new_benefits',
'¿Qué tanto sentís que te está apoyando tu empresa/organización durante la pandemia?': 'pandemic_support',
'¿Cuántas veces a la semana vas a trabajar a la oficina?':'days_in_the_office',
}
}
def replace_columns(df, new_columns):
new_col_names = {
original_name: category + '_' + new_name
for category, cols in new_columns.items()
for original_name, new_name in cols.items()
}
return df.rename(columns=new_col_names)
df_renamed = replace_columns(df_fixed, new_columns)
df_renamed[:2]
df_renamed.to_csv("sysarmy_survey_2022_processed.csv", index=False)
from google.colab import files
files.download("sysarmy_survey_2022_processed.csv")
url = 'https://cs.famaf.unc.edu.ar/~mteruel/datasets/diplodatos/sysarmy_survey_2020_processed.csv'
df2 = pd.read_csv(url)
df2[:3]
| 0.246352 | 0.953837 |
<a href="https://colab.research.google.com/github/Kira8045/ColorizedMNIST_GAN/blob/master/ColorizedMNIST.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive')
import tensorflow as tf
tf.get_logger().setLevel('WARNING')
import tensorflow as tf
tf.disable_v2_behavior()
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image as img
from IPython.display import clear_output, Image
from tensorflow.examples.tutorials.mnist import input_data
from keras.models import Sequential
from keras.layers import Dense, Flatten, Activation, Reshape
from keras.layers import Conv2D, Conv2DTranspose, UpSampling2D
from keras.layers import LeakyReLU,Dropout
from keras.optimizers import Adam, RMSprop
from keras.layers import BatchNormalization
x_train = input_data.read_data_sets( "mnist",one_hot = True ).train.images
x_train = x_train.reshape((-1,28,28,1)).astype(np.float32)
ref_image = img.open("/content/drive/My Drive/Colab Notebooks/mnist_colorized_GAN/Low Poly Colorful Background Preview.jpg")
plt.imshow(ref_image)
plt.axis("off")
plt.show()
import scipy.ndimage
def get_mnist_batch_sample(batch_size = 256, change_colors = False):
idx = np.random.choice(x_train.shape[0], batch_size)
batch_raw = x_train[idx,:,:,0].reshape((batch_size,28,28,1))
batch_resized = np.asarray([ scipy.ndimage.zoom( image, (2.3,2.3,1), order = 1 ) for image in batch_raw ])
batch_rgb = np.concatenate([batch_resized, batch_resized, batch_resized], axis = 3)
batch_binary = (batch_rgb > 0.5)
batch = np.zeros((batch_size, 64,64,3))
for i in range(batch_size):
x_c = np.random.randint( 0, ref_image.size[0]-64 )
y_c = np.random.randint( 0, ref_image.size[1]-64 )
image = ref_image.crop( (x_c,y_c, x_c+64, y_c+64) )
image = (np.array(image))/255.0
if change_colors :
for j in range(3):
image[:,:,j] = image[:,:,j] + np.random.uniform(0, 1)/2.0
image[batch_binary[i]] = 1- image[batch_binary[i]]
batch[i] = image
return batch
count = 20
examples = get_mnist_batch_sample(count, True)
plt.figure(figsize = (15,3) )
for i in range(count):
plt.subplot( 2, count//2 , i+1 )
plt.imshow(examples[i])
plt.axis("off")
plt.tight_layout()
plt.show()
def create_discriminator():
net = Sequential()
input_shape = (64,64,3)
dropout_prob = 0.4
net.add( Conv2D( 64 , 5 ,strides=2, input_shape = input_shape, padding = "same" ) )
net.add( LeakyReLU() )
net.add( Conv2D(128, 5, strides = 2, padding = "same") )
net.add(LeakyReLU())
net.add(Dropout(dropout_prob))
net.add( Conv2D( 256, 5, strides = 2, padding = "same" ) )
net.add(LeakyReLU())
net.add(Dropout(dropout_prob))
net.add( Conv2D( 512, 5, strides = 2, padding = "same" ) )
net.add(LeakyReLU())
net.add(Dropout(dropout_prob))
net.add(Flatten())
net.add(Dense(1))
net.add(Activation("sigmoid"))
return net
net_discriminator = create_discriminator()
net_discriminator.summary()
def create_generator():
net = Sequential()
dropout_prob = 0.4
net.add( Dense( 8*8*256, input_dim = 100 ) )
net.add(BatchNormalization( momentum= 0.9 ))
net.add( Activation("relu") )
net.add(Reshape((8,8,256)))
net.add(Dropout(dropout_prob))
net.add( UpSampling2D() )
net.add(Conv2D( 128, 5, padding = "same" ))
net.add(BatchNormalization(momentum= 0.9))
net.add(Activation("relu"))
net.add( UpSampling2D() )
net.add(Conv2D( 128, 5, padding = "same" ))
net.add(BatchNormalization(momentum= 0.9))
net.add(Activation("relu"))
net.add(UpSampling2D())
net.add(Conv2D( 64, 5, padding = "same" ))
net.add(BatchNormalization(momentum= 0.9))
net.add(Activation("relu"))
net.add(Conv2D( 32, 5, padding = "same" ))
net.add(BatchNormalization(momentum= 0.9))
net.add(Activation("relu"))
net.add(Conv2D(3, 5, padding = "same"))
net.add(Activation("tanh"))
return net
net_generator = create_generator()
net_generator.summary()
optim_discriminator = RMSprop( lr = 0.0002, clipvalue = 1.0, decay= 6e-8 )
model_discriminator = Sequential()
model_discriminator.add( net_discriminator )
model_discriminator.compile( loss = "binary_crossentropy", optimizer = optim_discriminator, metrics = ["accuracy"] )
model_discriminator.summary()
optim_adversarial = Adam( lr = 0.0001, clipvalue = 1.0, decay = 3e-8 )
model_adversarial = Sequential()
model_adversarial.add(net_generator)
for layer in net_discriminator.layers:
layer.trainable = False
model_adversarial.add(net_discriminator)
model_adversarial.compile( loss = "binary_crossentropy", optimizer = optim_adversarial , metrics = ["accuracy"] )
model_adversarial.summary()
batch_size = 128
epochs = 20000
vis_noise = np.random.uniform(-1,1 , [16,100])
loss_adv = []
loss_dis = []
acc_adv = []
acc_dis = []
plot_iteration = []
for epoch in range(epochs):
images_train = get_mnist_batch_sample(batch_size, True)
noise = np.random.uniform(-1, 1, size = [batch_size, 100])
images_fake = net_generator.predict(noise)
x = np.concatenate([images_train, images_fake])
y = np.ones([2*batch_size, 1])
y[batch_size:, :] = 0
model_discriminator.train_on_batch(x ,y)
d_stats = model_discriminator.train_on_batch(x ,y)
y = np.ones([batch_size, 1])
noise = np.random.uniform(-1, 1, [batch_size, 100])
a_stats = model_adversarial.train_on_batch(noise, y)
if epoch%50==0:
plot_iteration.append(i)
loss_adv.append(a_stats[0])
loss_dis.append(d_stats[0])
acc_adv.append(a_stats[1])
acc_dis.append(d_stats[1])
print(loss_adv)
clear_output( wait = True )
fig,(ax1, ax2) = plt.subplots(1,2)
fig.set_size_inches(16,8)
ax1.plot( plot_iteration, loss_adv, label = "loss_adversarial" )
ax1.plot( plot_iteration, loss_dis, label = "loss_discriminator" )
ax1.legend()
ax2.plot( plot_iteration, acc_adv, label = "acc_adversarial" )
ax2.plot( plot_iteration, acc_dis, label = "acc_discriminator" )
ax2.legend()
plt.show()
if (epoch < 1000 and epoch%50 == 0) or (epoch % 100 == 0):
images = net_generator.predict(vis_noise)
# Map back to original range
#images = (images + 1 ) * 0.5
plt.figure(figsize=(10,10))
for im in range(images.shape[0]):
plt.subplot(4, 4, im+1)
image = images[im, :, :, :]
image = np.reshape(image, [64,64,3])
plt.imshow(image)
plt.axis('off')
plt.tight_layout()
plt.savefig(r'/content/drive/My Drive/Colab Notebooks/mnist_colorized_GAN/output/mnist-color/{}.png'.format(epoch))
plt.close('all')
plt.figure(figsize=(15,4))
for i in range(10):
noise = np.zeros([1,100]) - 1 + (i * 0.2) + 0.1
images = net_generator.predict(noise)
image = images[0, :, :, :]
image = np.reshape(image, [64, 64, 3])
plt.subplot(1, 10, i+1)
plt.imshow(image)
plt.axis('off')
plt.tight_layout()
plt.show()
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/drive')
import tensorflow as tf
tf.get_logger().setLevel('WARNING')
import tensorflow as tf
tf.disable_v2_behavior()
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image as img
from IPython.display import clear_output, Image
from tensorflow.examples.tutorials.mnist import input_data
from keras.models import Sequential
from keras.layers import Dense, Flatten, Activation, Reshape
from keras.layers import Conv2D, Conv2DTranspose, UpSampling2D
from keras.layers import LeakyReLU,Dropout
from keras.optimizers import Adam, RMSprop
from keras.layers import BatchNormalization
x_train = input_data.read_data_sets( "mnist",one_hot = True ).train.images
x_train = x_train.reshape((-1,28,28,1)).astype(np.float32)
ref_image = img.open("/content/drive/My Drive/Colab Notebooks/mnist_colorized_GAN/Low Poly Colorful Background Preview.jpg")
plt.imshow(ref_image)
plt.axis("off")
plt.show()
import scipy.ndimage
def get_mnist_batch_sample(batch_size = 256, change_colors = False):
idx = np.random.choice(x_train.shape[0], batch_size)
batch_raw = x_train[idx,:,:,0].reshape((batch_size,28,28,1))
batch_resized = np.asarray([ scipy.ndimage.zoom( image, (2.3,2.3,1), order = 1 ) for image in batch_raw ])
batch_rgb = np.concatenate([batch_resized, batch_resized, batch_resized], axis = 3)
batch_binary = (batch_rgb > 0.5)
batch = np.zeros((batch_size, 64,64,3))
for i in range(batch_size):
x_c = np.random.randint( 0, ref_image.size[0]-64 )
y_c = np.random.randint( 0, ref_image.size[1]-64 )
image = ref_image.crop( (x_c,y_c, x_c+64, y_c+64) )
image = (np.array(image))/255.0
if change_colors :
for j in range(3):
image[:,:,j] = image[:,:,j] + np.random.uniform(0, 1)/2.0
image[batch_binary[i]] = 1- image[batch_binary[i]]
batch[i] = image
return batch
count = 20
examples = get_mnist_batch_sample(count, True)
plt.figure(figsize = (15,3) )
for i in range(count):
plt.subplot( 2, count//2 , i+1 )
plt.imshow(examples[i])
plt.axis("off")
plt.tight_layout()
plt.show()
def create_discriminator():
net = Sequential()
input_shape = (64,64,3)
dropout_prob = 0.4
net.add( Conv2D( 64 , 5 ,strides=2, input_shape = input_shape, padding = "same" ) )
net.add( LeakyReLU() )
net.add( Conv2D(128, 5, strides = 2, padding = "same") )
net.add(LeakyReLU())
net.add(Dropout(dropout_prob))
net.add( Conv2D( 256, 5, strides = 2, padding = "same" ) )
net.add(LeakyReLU())
net.add(Dropout(dropout_prob))
net.add( Conv2D( 512, 5, strides = 2, padding = "same" ) )
net.add(LeakyReLU())
net.add(Dropout(dropout_prob))
net.add(Flatten())
net.add(Dense(1))
net.add(Activation("sigmoid"))
return net
net_discriminator = create_discriminator()
net_discriminator.summary()
def create_generator():
net = Sequential()
dropout_prob = 0.4
net.add( Dense( 8*8*256, input_dim = 100 ) )
net.add(BatchNormalization( momentum= 0.9 ))
net.add( Activation("relu") )
net.add(Reshape((8,8,256)))
net.add(Dropout(dropout_prob))
net.add( UpSampling2D() )
net.add(Conv2D( 128, 5, padding = "same" ))
net.add(BatchNormalization(momentum= 0.9))
net.add(Activation("relu"))
net.add( UpSampling2D() )
net.add(Conv2D( 128, 5, padding = "same" ))
net.add(BatchNormalization(momentum= 0.9))
net.add(Activation("relu"))
net.add(UpSampling2D())
net.add(Conv2D( 64, 5, padding = "same" ))
net.add(BatchNormalization(momentum= 0.9))
net.add(Activation("relu"))
net.add(Conv2D( 32, 5, padding = "same" ))
net.add(BatchNormalization(momentum= 0.9))
net.add(Activation("relu"))
net.add(Conv2D(3, 5, padding = "same"))
net.add(Activation("tanh"))
return net
net_generator = create_generator()
net_generator.summary()
optim_discriminator = RMSprop( lr = 0.0002, clipvalue = 1.0, decay= 6e-8 )
model_discriminator = Sequential()
model_discriminator.add( net_discriminator )
model_discriminator.compile( loss = "binary_crossentropy", optimizer = optim_discriminator, metrics = ["accuracy"] )
model_discriminator.summary()
optim_adversarial = Adam( lr = 0.0001, clipvalue = 1.0, decay = 3e-8 )
model_adversarial = Sequential()
model_adversarial.add(net_generator)
for layer in net_discriminator.layers:
layer.trainable = False
model_adversarial.add(net_discriminator)
model_adversarial.compile( loss = "binary_crossentropy", optimizer = optim_adversarial , metrics = ["accuracy"] )
model_adversarial.summary()
batch_size = 128
epochs = 20000
vis_noise = np.random.uniform(-1,1 , [16,100])
loss_adv = []
loss_dis = []
acc_adv = []
acc_dis = []
plot_iteration = []
for epoch in range(epochs):
images_train = get_mnist_batch_sample(batch_size, True)
noise = np.random.uniform(-1, 1, size = [batch_size, 100])
images_fake = net_generator.predict(noise)
x = np.concatenate([images_train, images_fake])
y = np.ones([2*batch_size, 1])
y[batch_size:, :] = 0
model_discriminator.train_on_batch(x ,y)
d_stats = model_discriminator.train_on_batch(x ,y)
y = np.ones([batch_size, 1])
noise = np.random.uniform(-1, 1, [batch_size, 100])
a_stats = model_adversarial.train_on_batch(noise, y)
if epoch%50==0:
plot_iteration.append(i)
loss_adv.append(a_stats[0])
loss_dis.append(d_stats[0])
acc_adv.append(a_stats[1])
acc_dis.append(d_stats[1])
print(loss_adv)
clear_output( wait = True )
fig,(ax1, ax2) = plt.subplots(1,2)
fig.set_size_inches(16,8)
ax1.plot( plot_iteration, loss_adv, label = "loss_adversarial" )
ax1.plot( plot_iteration, loss_dis, label = "loss_discriminator" )
ax1.legend()
ax2.plot( plot_iteration, acc_adv, label = "acc_adversarial" )
ax2.plot( plot_iteration, acc_dis, label = "acc_discriminator" )
ax2.legend()
plt.show()
if (epoch < 1000 and epoch%50 == 0) or (epoch % 100 == 0):
images = net_generator.predict(vis_noise)
# Map back to original range
#images = (images + 1 ) * 0.5
plt.figure(figsize=(10,10))
for im in range(images.shape[0]):
plt.subplot(4, 4, im+1)
image = images[im, :, :, :]
image = np.reshape(image, [64,64,3])
plt.imshow(image)
plt.axis('off')
plt.tight_layout()
plt.savefig(r'/content/drive/My Drive/Colab Notebooks/mnist_colorized_GAN/output/mnist-color/{}.png'.format(epoch))
plt.close('all')
plt.figure(figsize=(15,4))
for i in range(10):
noise = np.zeros([1,100]) - 1 + (i * 0.2) + 0.1
images = net_generator.predict(noise)
image = images[0, :, :, :]
image = np.reshape(image, [64, 64, 3])
plt.subplot(1, 10, i+1)
plt.imshow(image)
plt.axis('off')
plt.tight_layout()
plt.show()
| 0.739893 | 0.842863 |
<table>
<tr align=left><td><img align=left src="./images/CC-BY.png">
<td>Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved MIT license. (c) Kyle T. Mandli</td>
</table>
```
from __future__ import print_function
from __future__ import absolute_import
%matplotlib inline
import numpy
import matplotlib.pyplot as plt
```
# Interpolation
Interpolation is a fundamental numerical problem that is central to many other numerical algorithms. Simply put, given a finite number of points where values are known, find an *interpolant*, a (usually) continuous function that returns values everywhere and is guaranteed to pass through the known data.
## Objectives:
* Define an interpolant
* Understand **Polynomial** Interpolation
* Define the interpolating polynomial $P_N(x)$ that exactly interpolates $N+1$ points
* Calculation (in the monomial basis)
* Uniqueness
* Other bases (Lagrange, Newton?)
* Error Analysis
* Chebyshev Polynomials and optimal interpolation
* Understand Other interpolants
* Piecewise Polynomial interpolation
* Overlapping Polynomial interpolation
* Cubic Splines and other smooth interpolants
* Higher dimensional Interpolation schemes and scipy.interpolate
### Interpolation (vs Fitting)
**Definition:** Given a discrete set of values $y_i$ at locations $x_i$, an **interpolant** is a (piece-wise) continuous function $f(x)$ that passes exactly through the data (*i.e.* $f(x_i) = y_i$).
A visual example for 3 random points
```
from scipy.interpolate import pchip_interpolate
N= 3
x = [ 1, 2.3, 4.8 ]
y = [ 1., 0.5, 5.0]
p2 = numpy.polyfit(x,y,2)
p1 = numpy.polyfit(x,y,1)
xa = numpy.linspace(0.,5)
xs = numpy.linspace(x[0],x[-1])
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1,1,1)
axes.plot(x,y,'ro',markersize=10,label='data')
axes.plot(xa,numpy.polyval(p2, xa), label='quadratic interpolant')
axes.plot(x,y,'g', label='Piecewise linear interpolant')
axes.plot(xs,pchip_interpolate(x,y,xs),'k', label='Piecewise cubic interpolant')
axes.plot(xa,numpy.polyval(p1, xa), label='best fit line')
axes.legend(loc='best')
axes.set_xlim(min(x) - 0.5,max(x) + 0.5)
axes.set_xlabel('x',fontsize=16)
axes.set_ylabel('f(x)',fontsize=16)
axes.grid()
plt.show()
```
**Comment**:
In general a polynomial of degree $N$ can be used to interpolate $N+1$ data points. There are many choices of functions to use to interpolate values, but here we focus on polynomials.
## Applications
- Data filling
- Function approximation
- Fundamental component of other algorithms
- Root finding (secant method)
- Optimization, minima/maxima (successive parabolic interpolation)
- Numerical integration and differentiation
- The Finite Element Method
## Polynomial Interpolation
**Theorem:** There is a *unique* polynomial of degree $N$, $P_N(x)$, that passes exactly through $N + 1$ values $y_0, y_1, \ldots, y_N $ at *distinct* points $x_0, x_1, \ldots, x_N$.
Consequence of the number of unknowns in $P_N(x)$.
#### Example 1: 2 Points
Given two points $(x_0, y_0)$ and $(x_1, y_1)$, There is a unique line
$$P_1(x) = p_0 + p_1 x$$
that connects them. We simply need to use the data to find $p_0$ and $p_1$:
We first note that we have two equations and two unknowns. The two equations can be found by assuming the function $P_1(x)$ interpolates the two data points
$$
\begin{matrix}
P_1(x_0) = & p_0 + p_1 x_0 =& y_0 \\
P_1(x_1) =& p_0 + p_1 x_1 = & y_1 \\
\end{matrix}
$$
We can also (and should) write this problem as a small $2\times2$ linear algebra problem $A\mathbf{x}=\mathbf{b}$
$$
\begin{bmatrix}
1 & x_0 \\
1 & x_1 \\
\end{bmatrix}
\begin{bmatrix}
p_0 \\
p_1 \\
\end{bmatrix}=\begin{bmatrix}
y_0 \\
y_1 \\
\end{bmatrix}
$$
**Question:** What are the unknowns, and where does the data sit in $A$ and $\mathbf{b}$?
With a bit of algebra you should be able to show that the solution of this problem is
$$
p_1 = \frac{y_1 - y_0}{x_1 - x_0}, \quad\quad
p_0 = y_0 - \frac{y_1 - y_0}{x_1 - x_0} x_0
$$
and
$$P_1(x) = \frac{y_1 - y_0}{x_1 - x_0} (x - x_0) + y_0$$
which is just the equation of the straight line with slope $p_1$, that connects the two points.
#### Example 2: 3 Points
Given three points $(x_0, y_0)$, $(x_1, y_1)$, and $(x_2, y_2)$ leads to a quadratic polynomial:
$$P_2(x) = p_0 + p_1 x + p_2x^2$$
Again, setting $P_2(x_i) = y_i$ yields 3 equations in 3 unknowns
$$ p_0 + p_1 x_0 + p_2 x_0^2 = y_0$$
$$ p_0 + p_1 x_1 + p_2 x_1^2 = y_1$$
$$ p_0 + p_1 x_2 + p_2 x_2^2 = y_2$$
Which reduces to the $3\times3$ linear system
$
A(\mathbf{x})\mathbf{p} = \mathbf{y}
$
A more general approach to solving the system will be explored later, but first it is important to determine whether or not the system even has a solution.
### Proof - Uniqueness of Polynomial Interpolants
Let
$$\mathcal{P}_N(x) = \sum^N_{n=0} p_n x^n $$
or
$$\mathcal{P}_N(x) = p_0 + p_1 x + \cdots + p_{N - 1} x^{N - 1} + p_{N} x^N$$
and require $\mathcal{P}_N(x_i) = y_i$ for $i=0,1,\ldots,N$ and $x_i \neq x_j ~~~ \forall i,j$.
### Preliminaries: Monomial Basis
We can think of $\mathcal{P}_N(x) = \sum^N_{n=0} p_n x^n$ as a polynomial, or more fundamentally as a *linear combination* of a set of simpler functions, the monomials
$$1, x, x^2, x^3, \ldots, x^{N-1}, x^N$$
with weights
$$p_0, p_1, p_2, p_3, \ldots, p_{N-1}, \text{and } p_N$$
respectively.
### Linear independence of the Monomials
The monomials, form a *linearly independent* set of functions such that no monomial $x^n$ can be written as a linear combination of any other monomial. We can see this graphically, for the first few monomials
```
x = numpy.linspace(-1,1,100)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1,1,1)
for n in range(4):
axes.plot(x,x**n,label='$x^{}$'.format(n))
axes.set_xlabel('x')
axes.grid()
axes.legend(loc='best')
axes.set_title('The First 4 Monomials')
plt.show()
```
But more fundamentally. A set of functions is **linearly independent** if the only linear combination that add to form the zero function, e.g.
$$
P_N(x) = p_0 1 + p_1 x + p_2 x^2 + \ldots + p_n x^n = 0
$$
is if all the coefficients $p_i = 0$, $\forall i=0,\ldots N$
**Theorem**: The monomials $x^0,\ldots, x^n$ are linear independent.
**Proof**: consider $P_N(x) = 0$ for all $x$. Since the polynomials (and monomials) are differentiable at least $n$ times, differentiate $n$ times to yield
$$
P^{(n)}_N(x) = n!p_n = 0
$$
which implies $p_n=0$.
Using this result and differentiating $n-1$ times shows $p_{n-1}=0$, which by induction gives all $p_i = 0$.
Put another way, the only $n$th degree polynomial that is zero everywhere is if all coefficients are zero.
#### The Fundamental theorem of algebra
Every $n$th degree polynomial has exactly $n$ complex roots, i.e.
$$
P_N(x) = (x - a_1)(x - a_2)\ldots(x - a_n)
$$
for $a_i\in \mathbb{C}$. Therefore, a _non-trivial_ $n$th order polynomial can only be zero at at most $n$ points.
### Proof - Uniqueness of Polynomial Interpolants
Let
$$\mathcal{P}_N(x) = \sum^N_{n=0} p_n x^n $$
**interpolate** the $N+1$ points $y_i$ at $x_i$.
i.e.
$$
\mathcal{P}_N(x_i) = y_i,\quad \mathrm{for}\quad i=0,1,\ldots,N
$$
and $x_i \neq x_j ~~~ \forall i,j$.
Assume there exists another polynomial
$$Q_N(x) = \sum^N_{n=0} q_n x^n$$
that passes through the same set of points such that $Q_N(x_i) = y_i$. Now compute $T_N(x) = \mathcal{P}_N(x) - Q_N(x)$:
Now, by construction, $T_N(x_i) = 0$ which implies that it is equal to zero at $n+1$ points. However,
$$T_N(x) = \mathcal{P}_N(x) - Q_N(x) = \sum^N_{n=0} p_n x^n - q_n x^n = \sum^N_{n=0} (p_n - q_n) x^n$$
is a $n$th order polynomial which has at most $n$ real roots. The only way to reconcile this is if $T_n(x) = 0$, *for all* $x$, and therefore $p_n - q_n = 0$ individually and therefore $\mathcal{P}_N(x) = Q_N(x)$.
#### Example 3: Monomial Basis
Consider $\mathcal{P}_3(x) = p_0 + p_1 x + p_2 x^2 + p_3 x^3$ with the four data points $(x_i, y_i), ~~ i = 0,1,2,3$. We have four equations and four unknowns as expected:
$$\mathcal{P}_3(x_0) = p_0 + p_1 x_0 + p_2 x_0^2 + p_3 x_0^3 = y_0$$
$$\mathcal{P}_3(x_1) = p_0 + p_1 x_1 + p_2 x_1^2 + p_3 x_1^3 = y_1$$
$$\mathcal{P}_3(x_2) = p_0 + p_1 x_2 + p_2 x_2^2 + p_3 x_2^3 = y_2$$
$$\mathcal{P}_3(x_3) = p_0 + p_1 x_3 + p_2 x_3^2 + p_3 x_3^3 = y_3$$
Lets rewrite these as a matrix equation: First define the following vectors
$$\mathbf{x} = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix} \quad \mathbf{y} = \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \end{bmatrix} \quad \mathbf{p} = \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \end{bmatrix}$$
When we write the system in matrix/vector form the matrix that arises is called *Vandermonde* matrix:
$$
V = \begin{bmatrix}
1 & x_0 & x_0^2 & x_0^3 \\
1 & x_1 & x_1^2 & x_1^3 \\
1 & x_2 & x_2^2 & x_2^3 \\
1 & x_3 & x_3^2 & x_3^3
\end{bmatrix}.
$$
We can now write the system of linear equations
$$\mathcal{P}_3(x_0) = p_0 + p_1 x_0 + p_2 x_0^2 + p_3 x_0^3 = y_0$$
$$\mathcal{P}_3(x_1) = p_0 + p_1 x_1 + p_2 x_1^2 + p_3 x_1^3 = y_1$$
$$\mathcal{P}_3(x_2) = p_0 + p_1 x_2 + p_2 x_2^2 + p_3 x_2^3 = y_2$$
$$\mathcal{P}_3(x_3) = p_0 + p_1 x_3 + p_2 x_3^2 + p_3 x_3^3 = y_3$$
as $V(\mathbf{x}) \mathbf{p} = \mathbf{y}$:
$$\begin{bmatrix}
1 & x_0 & x_0^2 & x_0^3 \\
1 & x_1 & x_1^2 & x_1^3 \\
1 & x_2 & x_2^2 & x_2^3 \\
1 & x_3 & x_3^2 & x_3^3
\end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \end{bmatrix}.$$
**Note**: the columns of $V$ are simply the monomial functions sampled at the discrete points $x_i$. i.e $V_j = \mathbf{x}^j$.
Because the monomials are linearly independent, so are the columns of $V$
$$\begin{bmatrix}
1 & x_0 & x_0^2 & x_0^3 \\
1 & x_1 & x_1^2 & x_1^3 \\
1 & x_2 & x_2^2 & x_2^3 \\
1 & x_3 & x_3^2 & x_3^3
\end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \end{bmatrix}$$
- What happens if we have redundant data? Either $(x_i, y_i)$ is repeated or for one $i$ we have two values of $y$.
- What if we have more points then the order of polynomial we want?
- How does this relate to solving the above linear system of equations?
Vandermonde matrices in general are defined as
$$V = \begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^N \\
1 & x_1 & x_1^2 & \cdots & x_1^N \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_m & x_m^2 & \cdots & x_m^N \\
\end{bmatrix}
$$
where $V$ is a $m \times n$ matrix with points $(x_i, y_i)$ for $i = 0, 1, 2, 3, \ldots m$ and for an order $N$ polynomial $\mathcal{P}_N(x)$.
### Finding $p_i$
Finding the coefficients of $\mathcal{P}_N(x)$ can be done by solving the system outlined above. There are functions in `numpy` that can do this for us such as:
- `numpy.polyfit(x, y, x.shape[0] - 1)`
- `numpy.vander(x, N=None)` to construct the matrix and use a linear solver routine.
We can also use a different **basis** that might be easier to use.
### Basis
**Def:** A basis for a $N$ dimensional vector space is a set of linearly independent vectors that span the space.
The monomials, $1,x,\ldots, x^n$, form the usual basis for the vector space of $n$th degree polynomials $P_N(x)$.
**Example** $P_2(x)$ is the space of all quadratic functions. i.e. $P_2(x) = \mathrm{span}< 1,x,x^2>$
$$
P_2(x) = p_0 + p_1 x + p_2 x^2
$$
i.e for every vector $\mathbf{p}\in\mathbb{R}^3$, there is a unique quadratic function in $P_2(x)$. (we say $P_2$ is *isomorphic* to $\mathbb{R}^3$ and is a three dimensional function space).
**However**, the monomials are not the only basis for $P_N$
### Lagrange Basis
Given $N+1$ points $(x_0,y_0), (x_1,y_1), \ldots, (x_{N},y_{N})$ again assuming the $x_i$ are all unique, the interpolating polynomial $\mathcal{P}_N(x)$ can be written as
$$\mathcal{P}_N(x) = \sum^{N}_{i=0} y_i \ell_i(x)$$
where
$$\ell_i(x) = \prod^{N}_{j=0, j \neq i} \frac{x - x_j}{x_i - x_j} = \frac{x - x_0}{x_i - x_0} \frac{x - x_1}{x_i - x_1} \cdots \frac{x - x_{i-1}}{x_i - x_{i-1}}\frac{x - x_{i+1}}{x_i - x_{i+1}} \cdots \frac{x - x_{N}}{x_i - x_{N}}$$
are the **Lagrange Polynomials**
### Lagrange Polynomials
$$\ell_i(x) = \prod^{N}_{j=0, j \neq i} \frac{x - x_j}{x_i - x_j} $$
A Key property of the Lagrange polynomials is that
$$
\ell_i(x_j) = \delta_{ij} = \left\{\begin{matrix}
0 & i\neq j \\
1 & i=j\\
\end{matrix}\right.
$$
which is why the weights in $P_N(x)$ are simply the $y$ values of the interpolant
### Visualizing the Lagrange Polynomials
```
# ====================================================
# Compute the Lagrange basis (\ell_i(x))
def lagrange_basis(x, data):
"""Compute Lagrange basis at x given N data points
params:
-------
x: ndarray
1-d Array of floats
data: ndarray of shape (N,2)
2-d Array of data where each row is [ x_i, y_i ]
returns:
--------
basis: ndarray of shape (N, x.shape)
: 2-D array of lagrange basis functions evaluated at x
"""
basis = numpy.ones((data.shape[0], x.shape[0]))
for i in range(data.shape[0]):
for j in range(data.shape[0]):
if i != j:
basis[i, :] *= (x - data[j, 0]) / (data[i, 0] - data[j, 0])
return basis
# ====================================================
# Calculate full polynomial
def poly_interpolant(x, data):
"""Compute polynomial interpolant of (x,y) using Lagrange basis"""
P = numpy.zeros(x.shape[0])
basis = lagrange_basis(x, data)
for n in range(data.shape[0]):
P += basis[n, :] * data[n, 1]
return P
# ====================================================
x_data = numpy.array([0., 1., 2., 3.])
x_data = numpy.array([0., 1., 2.])
y_data = numpy.ones(x_data.shape)
data = numpy.array([x_data, y_data]).T
x = numpy.linspace(x_data.min(),x_data.max(),100)
basis = lagrange_basis(x, data)
# ====================================================
# Plot individual basis functions
fig = plt.figure(figsize=(8, 6))
axes = fig.add_subplot(1, 1, 1)
basis = lagrange_basis(x, data)
for i in range(len(x_data)):
axes.plot(x, basis[i, :], label="$\ell_{%s}(x)$" % i)
axes.plot(x_data,numpy.zeros(x_data.shape),'ko')
axes.plot(x_data,y_data,'k+',markersize=10)
axes.set_title("Lagrange Basis $\ell_i(x)$")
axes.set_xlabel("x")
axes.set_ylabel("$\ell_i(x)$")
axes.grid()
axes.legend(loc='best')
plt.show()
```
### Solving for the coefficients of $P_N(x)$
In general, if
$$
P_N(x) = \sum_{j=0}^N w_j\phi_j(x)
$$
where $\phi_j(x)$ is any basis function for $P_N$ (i.e. monomial, Lagrange, and there are many more). Then finding the unique set of weights for the interpolating polynomial through $N+1$ distinct data points $(x_i, y_i)$, just reduces to solving $N+1$ linear equations $P_N(x_i) = y_i$.
For the monomial basis this reduces to the linear system
$$
V(\mathbf{x})\mathbf{w} = \mathbf{y}
$$
What is the matrix $V$, for the Lagrange Basis? What are the weights $\mathbf{w}$?
A little pen-and-paper work here can be instructive$\ldots$
### Linear Independence of the Lagrange Polynomials
Because the weights of each basis function in the Lagrange basis is just the $y$ value at the interpolation points, it is straightforward to show that the Lagrange polynomials are linearly independent. I.e. the statement
$$
\sum_{n=0}^N w_j\phi_j(x) =0
$$
is equivalent to interpolating the zero function, where all the $w_j =0$
#### Example : $N = 1$ 1st order general Lagrange Polynomial as linear interpolant
Given 2 points $(x_0, y_0)$ and $(x_1, y_1)$ the Lagrange form of $\mathcal{P}_N(x)$ is given by
$$\ell_0(x) = \frac{x - x_1}{x_0 - x_1}$$
and
$$\ell_1(x) = \frac{x - x_0}{x_1 - x_0}$$
and the 1st order interpolating Polynomial is simply
$$\mathcal{P}_1(x) = y_0\ell_0(x)+ y_1\ell_1(x)$$
The behavior of $\mathcal{P}_1(x)$ becomes clearer if we note that on the interval $x\in[x_0,x_1]$ that
$$
\ell_1(x) = \frac{x- x_0}{x_1 - x_0} = s
$$
is simply the fractional distance across the interval.
We should also note that
$$
\begin{align}
\ell_0(x) &= \frac{x - x_1}{x_0 - x_1}\\
&= 1-\ell_1(x) \\
&= 1-s\\
\end{align}
$$
(show this)
Then the interpolating polynomial is simply
$$
\begin{align}
\mathcal{P}_1(s) &= y_0(1-s) + y_1 s \\&= y_0 + s(y_1 - y_0)
\end{align}
$$
for $s\in[0,1]$ which is just the linear line segment that connects points $y_0$ and $y_1$
As a specific example we will plot $\ell_0(x)$, $\ell_1(x)$ and $\mathcal{P}_1$ for the interval
$x=[1,3]$ and $y_0=2$, $y_1=3$
```
x0, y0 = (1., 2.)
x1, y1 = (3., 3.)
ell0 = lambda x: (x - x1)/(x0 - x1)
ell1 = lambda x: (x - x0)/(x1 - x0)
P1 = lambda x: y0*ell0(x) + y1*ell1(x)
x = numpy.linspace(x0,x1)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1,1,1)
axes.plot(x,ell0(x),'r',label='$\ell_0$')
axes.plot(x,ell1(x),'b',label='$\ell_1$')
axes.plot(x,P1(x),'g',label='$P_1(x)$')
axes.plot((x0,x1),(y0,y1),'go')
axes.set_xlabel('x')
axes.grid()
axes.legend(loc='best',fontsize=16)
plt.show()
```
#### Example: Interpolate four points from $\sin(2\pi x)$
Use four evenly spaced points to approximate $\sin$ on the interval $x \in [-1, 1]$. What is the behavior as $N \rightarrow \infty$? Also plot the absolute error between $f(x)$ and the interpolant $P_N(x)$.
```
num_points = 6
# num_points = 5
# num_points = 6
# num_points = 20
data = numpy.empty((num_points, 2))
data[:, 0] = numpy.linspace(-1, 1, num_points)
data[:, 1] = numpy.sin(2.0 * numpy.pi * data[:, 0])
N = data.shape[0] - 1 # Degree of polynomial
M = data.shape[0]
x = numpy.linspace(-1.0, 1.0, 100)
px = poly_interpolant(x, data)
f = numpy.sin(2.0 * numpy.pi * x)
err = numpy.abs(f - px)
# ====================================================
# Plot individual basis functions
fig = plt.figure(figsize=(16,6))
axes = fig.add_subplot(1, 2, 1)
basis = lagrange_basis(x, data)
for i in range(N + 1):
axes.plot(x, basis[i, :], label="$\ell_{%s}(x)$" % i)
axes.set_title("Lagrange Basis $\ell_i(x)$",fontsize=16)
axes.set_xlabel("x")
axes.set_ylabel("$\ell_i(x)$")
axes.legend(loc='best',fontsize=14)
axes.grid()
# Plot full polynomial P_N(x)
axes = fig.add_subplot(1, 2, 2)
axes.plot(x, px , label="$P_{%s}(x)$" % N)
axes.plot(x, numpy.sin(2.0 * numpy.pi * x), 'r--', label="True $f(x)$")
axes.plot(x, err, 'k', linestyle='dotted',label='abs error')
for point in data:
axes.plot(point[0], point[1], 'ko')
axes.set_title("$P_N(x)$",fontsize=16)
axes.set_xlabel("x")
axes.set_ylabel("$P_N(x)$")
axes.legend(loc='best',fontsize=14)
axes.grid()
plt.show()
```
#### Example 6: Runge's Function
Interpolate $f(x) = \frac{1}{1 + 25 x^2}$ using 6 points of your choosing on $x \in [-1, 1]$.
Try it with 11 points.
Keep increasing the number of points and see what happens.
```
def f(x):
return 1.0 / (1.0 + 25.0 * x**2)
x = numpy.linspace(-1., 1., 100)
num_points = 6
data = numpy.empty((num_points, 2))
data[:, 0] = numpy.linspace(-1, 1, num_points)
data[:, 1] = f(data[:, 0])
N = data.shape[0] - 1
# Plot the results
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, poly_interpolant(x, data), 'b', label="$P_{{{name}}}(x)$".format(name=num_points-1))
axes.plot(x, f(x), 'k', label="True $f(x)$")
axes.plot(data[:, 0], data[:, 1], 'ro', label="data")
axes.set_title("Interpolation of Runge's function",fontsize=18)
axes.set_xlabel("x")
axes.set_ylabel("y")
axes.legend(loc='best',fontsize=14)
axes.grid()
plt.show()
```
#### Example 7: Weierstrass "Monster" Function
Defined as
$$
f(x) = \sum^\infty_{n=0} a^n \cos(b^n \pi x)
$$
such that
$$
0 < a < 1 \quad \text{and} \quad a b > 1 + \frac{3\pi}{2}.
$$
This function is continuous everywhere but not differentiable anywhere.
```
def f(x, a=0.9, N=100):
summation = 0.0
b = (1.0 + 3.0 / 2.0 * numpy.pi) / a + 0.01
print(b)
for n in range(N + 1):
summation += a**n * numpy.cos(b**n * numpy.pi * x)
return summation
x = numpy.linspace(-1, 1, 1000)
# x = numpy.linspace(-2, 2, 100)
num_points = 10
data = numpy.empty((num_points, 2))
data[:, 0] = numpy.linspace(-1, 1, num_points)
data[:, 1] = f(data[:, 0])
N = data.shape[0] - 1
# Plot the results
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, poly_interpolant(x, data), 'b', label="$P_6(x)$")
axes.plot(x, f(x), 'k', label="True $f(x)$")
axes.plot(data[:, 0], data[:, 1], 'ro', label="data")
axes.set_title("Interpolation of Runge's function")
axes.set_xlabel("x")
axes.set_ylabel("y")
axes.legend(loc=1)
plt.show()
```
### Rules of Thumb
- Avoid high-order interpolants when possible! Keep increasing the number of points and see what happens.
- Avoid extrapolation - Increase the range of $x$ in the above example and check how good the approximation is beyond our sampling interval
### Error Analysis
**Theorem:** Lagrange Remainder Theorem - Let $f(x) \in C^{N+1}[-1, 1]$, then
$$
f(x) = \mathcal{P}_N(x) + R_N(x)
$$
where $\mathcal{P}_N(x)$ is the interpolating polynomial and
$$
R_N(x) = Q(x) \frac{f^{(N+1)}(c)}{(N+1)!} \quad \text{with} \quad c \in [-1,1]
$$
where
$$
Q(x) = \prod^N_{i=0} (x - x_i) = (x-x_0)(x-x_1)\cdots(x-x_N) .
$$
is a *monic* polynomial of order $N+1$ with exactly $N+1$ roots at the nodes $x_i$
A few things to note:
- For Taylor's theorem note that $Q(x) = (x - x_0)^{N+1}$ and the error only vanishes at $x_0$.
- For Lagrange's theorem the error vanishes at all $x_i$.
- To minimize $R_N(x)$ requires minimizing $|Q(x)|$ for $x \in [-1, 1]$.
#### Minimizing $R_N(x)$
Minimizing the error $R_N(x)$ in Lagrange's theorem is equivalent to minimizing $|Q(x)|$ for $x \in [-1, 1]$.
Minimizing error $\Leftrightarrow$ picking roots of $Q(x)$ or picking the points where the interpolant data is located. How do we this?
### Chebyshev Polynomials
*Chebyshev polynomials* $T_N(x)$ are another basis that can be used for interpolation.
First 5 polynomials
$$T_0(x) = 1$$
$$T_1(x) = x$$
$$T_2(x) = 2 x^2 - 1$$
$$T_3(x) = 4 x^3 - 3 x$$
$$T_4(x) = 8x^4 - 8x^2 + 1$$
In general, the Chebyshev polynomials are generated by a recurrence relation
$$T_k(x) = 2 x T_{k-1}(x) - T_{k-2}(x)$$
```
def cheb_poly(x, N):
"""Compute the *N*th Chebyshev polynomial and evaluate it at *x*"""
T = numpy.empty((3, x.shape[0]))
T[0, :] = numpy.ones(x.shape)
T[1, :] = x
if N == 0:
return T[0, :]
elif N == 1:
return T[1, :]
else:
for k in range(2, N + 1):
T[2, :] = 2.0 * x * T[1, :] - T[0, :]
T[0, :] = T[1, :]
T[1, :] = T[2, :]
return T[2, :]
x = numpy.linspace(-1, 1, 100)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
for n in range(5):
axes.plot(x, cheb_poly(x, n), label="$T_%s$" % n)
axes.set_ylim((-1.1, 1.1))
axes.set_title("Chebyshev Polynomials")
axes.set_xlabel("x")
axes.set_ylabel("$T_N(x)$")
axes.legend(loc='best')
axes.grid()
plt.show()
```
#### Chebyshev nodes
Chebyshev polynomials have many special properties and locations including the location of their roots and extrema known as Chebyshev nodes
* Chebyshev nodes of the 1st kind (roots)
$$
x_k = \cos \left (\frac{(2 k - 1) \pi}{2 N} \right ) \quad k = 1, \ldots, N
$$
* Chebyshev nodes of the 2nd kind (extrema)
$$
x_k = \cos \left( \frac{k \pi}{N} \right) \quad k = 0, \ldots, N
$$
```
N = 4
x_extrema = numpy.cos(numpy.arange(N + 1) * numpy.pi / N)
x_nodes = numpy.cos((2.0 * numpy.arange(1, N + 1) - 1.0) / (2.0 * N) * numpy.pi)
fig = plt.figure()
# fig.set_figwidth(fig.get_figwidth() * 2)
axes = fig.add_subplot(1, 1, 1)
# Plot points
axes.plot(x_extrema, numpy.zeros(N+1), 'ro')
axes.plot(x_nodes, numpy.zeros(N), 'bo')
# Plot some helpful lines
axes.plot((-1.0, -1.0), (-1.1, 1.1), 'k--')
axes.plot((1.0, 1.0), (-1.1, 1.1), 'k--')
axes.plot((-1.0, 1.0), (0.0, 0.0), 'k--')
for i in range(x_extrema.shape[0]):
axes.plot((x_extrema[i], x_extrema[i]), (-1.1, 1.1), 'r--')
axes.plot(x_extrema[i], cheb_poly(x_extrema, N)[i], 'ro')
print('Nodes = {}'.format(numpy.sort(x_nodes)))
print('Extrema = {}'.format(numpy.sort(x_extrema)))
#print(numpy.cos(x_extrema))
# Plot Chebyshev polynomial
x_hat = numpy.linspace(-1, 1, 1000)
axes.plot(x_hat, cheb_poly(x_hat, N), 'k')
axes.set_xlim((-1.1, 1.1))
axes.set_ylim((-1.1, 1.1))
# Labels
axes.set_title("Chebyshev Nodes and Extrema, N={}".format(N), fontsize="20")
axes.set_xlabel("x", fontsize="15")
axes.set_ylabel("$T_{N+1}(x)$", fontsize="15")
plt.show()
# First-kind Nesting (3 x)
fig = plt.figure()
# fig.set_figwidth(fig.get_figwidth() * 2)
axes = fig.add_subplot(1, 1, 1)
N = 5
factor = 3
x_1 = numpy.cos((2.0 * numpy.arange(1, N + 1) - 1.0) / (2.0 * N) * numpy.pi)
x_2 = numpy.cos((2.0 * numpy.arange(1, factor * N + 1) - 1.0) / (2.0 * factor * N) * numpy.pi)
axes.plot(x_1, numpy.zeros(N), "o", color="r", markerfacecolor="lightgray", markersize="15")
axes.plot(x_2, numpy.zeros(N * factor), 'kx', markersize="10")
x_hat = numpy.linspace(-1, 1, 1000)
axes.plot(x_hat, cheb_poly(x_hat, N), 'k')
axes.plot(x_hat, cheb_poly(x_hat, factor * N), 'k')
axes.set_xlim((-1.1, 1.1))
axes.set_ylim((-1.1, 1.1))
axes.set_title("Nesting of 1st and 2nd Kind Chebyshev Polynomials")
axes.set_xlabel("$x$")
axes.set_ylabel("$T_N(x)$")
plt.show()
```
#### Properties of Chebyshev Polynomials
1. Defined by a recurrence relation
$$T_k(x) = 2 x T_{k-1}(x) - T_{k-2}(x)$$
2. Leading coefficient of $x^N$ in $T_N(x)$ is $2^{N-1}$ for $N \geq 1$
3. Extreme values:
$$|T_N(x)| \leq 1 \quad \text{for} \quad -1 \leq x \leq 1$$
#### Properties of Chebyshev Polynomials
4. Minimax principle: The polynomial
$$T(x) = \frac{T_{N+1}(x)}{2^N}$$
is a *monic polynomial*, a univariate function with the leading coefficient equal to 1, with the property that
$$
\max |T(x)| \leq \max |Q(X)| \quad \text{for} \quad x \in [-1, 1], \quad \text{and}
$$
$$
\max |T(x)| = \frac{1}{2^N}
$$
Recall that the remainder term in the Lagrange Remainder Theorem was
$$
R_N(x) = Q(x) \frac{f^{(N+1)}(c)}{(N+1)!} \quad \text{with} \quad c \in [-1,1]
$$
with
$$
Q(x) = \prod^N_{i=0} (x - x_i) = (x-x_0)(x-x_1)\cdots(x-x_N) .
$$
#### Error Analysis Redux
Given that the Chebyshev polynomials are a minimum on the interval $[-1, 1]$ we would like $Q(x) = T(x)$.
Since we only know the roots of $Q(x)$ (the points where the interpolant data is located) we require these points to be the roots of the Chebyshev polynomial $T_{N+1}(x)$ therefore enforcing $T(x) = Q(x)$.
The zeros of $T_N(x)$ in the interval $[-1, 1]$ can be shown to satisfy
$$
x_k = \cos\left( \frac{(2k - 1) \pi}{2 N} \right ) \quad \text{for} \quad k=1, \ldots, N
$$
These nodal points (sampling the function at these points) can be shown to minimize interpolation error.
```
x = numpy.linspace(0, numpy.pi, 100)
N = 15
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1, aspect="equal")
axes.plot(numpy.cos(x), numpy.sin(x), 'r--')
axes.plot(numpy.linspace(-1.1, 1.1, 100), numpy.zeros(x.shape), 'r')
for k in range(1, N + 1):
location = [numpy.cos((2.0 * k - 1.0) * numpy.pi / (2.0 * N)),
numpy.sin((2.0 * k - 1.0) * numpy.pi / (2.0 * N))]
axes.plot(location[0], location[1], 'ko')
axes.plot(location[0], 0.0, 'ko')
axes.plot([location[0], location[0]], [0.0, location[1]], 'k--')
axes.set_xlim((-1.1, 1.1))
axes.set_ylim((-0.1, 1.1))
plt.show()
```
#### Summary
1. Minimizing the error in Lagrange's theorem is equivalent to minimizing
$$
|Q(x)| \quad \text{for} \quad x \in [-1, 1].
$$
1. We know Chebyshev polynomials are a minimum on the interval $[-1, 1]$ so we would like to have $Q(x)=T(x)$.
1. Since we only know the roots of $Q(x)$ (the points where the interpolant data is located) we require these points to be the roots of the Chebyshev polynomial $T_{N+1}(x)$ therefore enforcing $T(x) = Q(x)$.
1. The zeros of $T_N(x)$ in the interval $[-1, 1]$ can be shown to satisfy
$$
x_k = \cos\left( \frac{(2k - 1) \pi}{2 N} \right ) \quad \text{for} \quad k=1, \ldots, N
$$
These nodal points (sampling the function at these points) can be shown to minimize interpolation error.
#### Notes
- The Chebyshev nodes minimize interpolation error for any polynomial basis (due to uniqueness of the interpolating polynomial, any polynomial that interpolates these points are identical regardless of the basis).
- Chebyshev nodes uniquely define the Chebyshev polynomials.
- The boundedness properties of Chebyshev polynomials are what lead us to the roots as a minimization but there are other uses for these orthogonal polynomials.
- There are two kinds of Chebyshev nodes and therefore two definitions.
### Example: Chebyshev Interpolation of Runge's function
Comparison between interpolation at Chebyshev Nodes vs equally spaced points
```
# Runge's function again
def f(x):
return 1.0 / (1.0 + 25.0 * x**2)
# Parameters
x = numpy.linspace(-1., 1., 100)
num_points = 6
# ============================================================
# Equidistant nodes
equidistant_data = numpy.empty((num_points, 2))
equidistant_data[:, 0] = numpy.linspace(-1, 1, num_points)
equidistant_data[:, 1] = f(equidistant_data[:, 0])
N = equidistant_data.shape[0] - 1
P_lagrange = poly_interpolant(x, equidistant_data)
# ============================================================
# Chebyshev nodes
chebyshev_data = numpy.empty((num_points, 2))
chebyshev_data[:, 0] = numpy.cos((2.0 * numpy.arange(1, num_points + 1) - 1.0) * numpy.pi / (2.0 * num_points))
chebyshev_data[:, 1] = f(chebyshev_data[:, 0])
P_cheby1 = poly_interpolant(x, chebyshev_data)
# Fit directly with Chebyshev polynomials
coeff = numpy.polynomial.chebyshev.chebfit(chebyshev_data[:, 0], chebyshev_data[:, 1], N)
P_cheby2 = numpy.polynomial.chebyshev.chebval(x, coeff)
# Check on unique polynomials
#print(numpy.allclose(P_cheby1, P_cheby2))
# calculate errornorms for different interpolants
equidistant_err = numpy.linalg.norm(P_lagrange - f(x))
cheb_err = numpy.linalg.norm(P_cheby1 - f(x))
# ============================================================
# Plot the results
fig = plt.figure(figsize=(16,6))
fig.subplots_adjust(hspace=.5)
axes = fig.add_subplot(1, 2, 1)
axes.plot(x, P_lagrange, 'b', label="$P_%s(x)$" % N)
axes.plot(x, f(x), 'k', label="True $f(x)$")
axes.plot(equidistant_data[:, 0], equidistant_data[:, 1], 'ro', label="data")
axes.set_title("Equispaced Points: err = {:5.5g}".format(equidistant_err),fontsize=18)
axes.set_xlabel("x",fontsize=16)
axes.set_ylabel("y",fontsize=16)
axes.grid()
axes.legend(loc=8,fontsize=16)
#print('Equispaced error = {}'.format(numpy.linalg.norm(P_lagrange - f(x))))
axes = fig.add_subplot(1, 2, 2)
axes.plot(x, f(x), 'k', label="True $f(x)$")
axes.plot(x, P_cheby1, 'b', label="$P_%s(x)$" % N)
axes.plot(chebyshev_data[:, 0], chebyshev_data[:, 1], 'ro', label="data")
axes.set_title("Chebyshev Points: err = {:5.5g}".format(cheb_err),fontsize=18)
axes.set_xlabel("x",fontsize=16)
axes.set_ylabel("y",fontsize=16)
axes.legend(loc=1,fontsize=16)
axes.grid()
#print('Chebyshev error = {}'.format(numpy.linalg.norm(P_cheby1 - f(x))))
plt.show()
```
## Piece-Wise Polynomial Interpolation
Given $N$ points, use lower order polynomial interpolation to fit the function in pieces. We can choose the order of the polynomials and the continuity.
- $C^0$: Interpolant is continuous
- Linear interpolation
- Quadratic interpolation
- $C^1$: Interpolation and 1st derivative are continuous
- Cubic Hermite polynomials (PCHiP)
- $C^2$: Interpolation, 1st and 2nd derivatives are continuous
- Cubic splines
### Piece-Wise Linear
Given a segment between point $(x_k, y_k)$a nd $(x_{k+1}, y_{k+1})$ define the segment as
$$\mathcal{P}_k(x) = \frac{y_{k+1} - y_k}{x_{k+1} - x_k} (x - x_k) + y_k$$
The final interpolant $\mathcal{P}(x)$ is then defined on $[x_k, x_{k+1}]$ using this function.
```
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
N = data.shape[0] - 1
# Lagrange Basis
P_lagrange = poly_interpolant(x, data)
# C^0 Piece-wise linear
# P_pw_linear = numpy.interp(x, data[:, 0], data[:, 1])
P_linear = numpy.zeros(x.shape)
for n in range(1, N + 1):
P_linear += ((data[n, 1] - data[n - 1, 1]) / (data[n, 0] - data[n - 1, 0]) * (x - data[n - 1, 0])
+ data[n - 1, 1]) * (x > data[n - 1, 0]) * (x <= data[n, 0])
# Add end points for continuity
P_linear += numpy.ones(x.shape) * data[0, 1] * (x < data[0, 0])
P_linear += numpy.ones(x.shape) * data[-1, 1] * (x >= data[-1, 0])
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ko')
axes.plot(x, P_lagrange, 'b--',label='$P_{{{name}}}$'.format(name=N))
axes.plot(x, P_linear, 'r',label='Piecewise Linear')
axes.set_title("Interpolated Data - $C^0$ Linear",fontsize=18)
axes.set_xlabel("x",fontsize=16)
axes.set_ylabel("$P_1(x)$",fontsize=16)
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
axes.legend(loc='best',fontsize=14)
axes.grid()
plt.show()
```
### Piece-Wise Quadratic $C^0$ Polynomials
Use every three points $(x_{k+1}, y_{k+1})$, $(x_{k}, y_{k})$, and $(x_{k-1}, y_{k-1})$, to find quadratic interpolant and define final interpolant $P(x)$ using the quadratic interpolant $\mathcal{P}_k(x)$ on $[x_{k-1}, x_{k+1}]$.
```
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
N = data.shape[0] - 1
# This isn't overlapping, it's more like C_0 P_2
# C^0 Piece-wise quadratic
P_quadratic = numpy.zeros(x.shape)
for k in range(1, N + 1, 2):
p = numpy.polyfit(data[k - 1:k + 2, 0], data[k - 1:k + 2, 1], 2)
P_quadratic += numpy.polyval(p, x) * (x > data[k - 1, 0]) * (x <= data[k + 1, 0])
# Add end points for continuity
P_quadratic += numpy.ones(x.shape) * data[0, 1] * (x < data[0, 0])
P_quadratic += numpy.ones(x.shape) * data[-1, 1] * (x >= data[-1, 0])
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ko')
axes.plot(x, P_lagrange, 'b--',label='$P_{{{name}}}$'.format(name=N))
axes.plot(x, P_quadratic, 'r',label='Piecewise quadratic')
axes.set_title("Interpolated Data - $C^0$ Quadratic",fontsize=18)
axes.set_xlabel("x",fontsize=16)
axes.set_ylabel("$P_2(x)$",fontsize=16)
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
axes.legend(loc='best',fontsize=14)
axes.grid()
plt.show()
```
### Transformation of intervals
The previous algorithms are quite direct but can look a bit messy because every interval (or set of points) appears different...An important trick that is used in finite-element analysis is to to transform each interval (or element)
$$
x \in[x_k, x_{k+1}]
$$
to the unit interval
$$
s \in [0,1]
$$
by the affine transformation
$$ x(s) = x_k + s(x_{k+1} - x_k)$$
and do all the interpolation in the transformed frame.
### Example: Linear Interpolation
for Linear interpolation over an arbitrary interval $[x_k, x_{k+1}]$ we can use a Lagrange interpolant
$$
P_k(x) = y_k\ell_0(x) + y_{k+1}\ell_1(x)
$$
where
$$
\ell_0(x) = \frac{x - x_{k+1}}{x_k - x_{k+1}},~\quad~ \ell_1(x) = \frac{x - x_{k}}{x_{k+1} - x_{k}}
$$
and do all the interpolation in the transformed frame.
Substituting
$$ x(s) = x_k + s(x_{k+1} - x_k)$$
into the definitions of $\ell_0(x)$ and $\ell_1(x)$ show that within this element
$$
\ell_0(s) = 1-s,~\quad~\ell_1(s) = s
$$
and
$$
P_k(s) = y_k(1-s) + y_{k+1}s
$$
```
xk = [ .5, 1., 3., 5.]
yk = [ .5, 2., 2.5, 1. ]
ell0 = lambda x: (x - x1)/(x0 - x1)
ell1 = lambda x: (x - x0)/(x1 - x0)
P1 = lambda x: y0*ell0(x) + y1*ell1(x)
x = numpy.linspace(x0,x1)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1,1,1)
axes.plot(x,ell0(x),'r',label='$\ell_0$')
axes.plot(x,ell1(x),'b',label='$\ell_1$')
axes.plot(x,P1(x),'g',label='$P_1(x)$')
axes.plot((x0,x1),(y0,y1),'go')
axes.set_xlabel('x')
axes.set_xlim(0.,5.)
axes.grid()
axes.legend(loc='best',fontsize=16)
plt.show()
```
### Piece-Wise $C^1$ Cubic Interpolation
For the previous two cases we had discontinous 1st derivatives! We can make this better by constraining the polynomials to be continuous at the boundaries of the piece-wise intervals.
Given a segment between points $(x_k, y_k)$ and $(x_{k+1}, y_{k+1})$ we want to fit a cubic function between the two points.
$$\mathcal{P}_k(x) = p_0 + p_1 x + p_2 x^2 + p_3 x^3$$
$$\mathcal{P}_k(x_k) = y_k, \quad \mathcal{P}_k(x_{k+1}) = y_{k+1}$$
Now we have 4 unknowns but only two data points! Constraining the derivative at each interval end will lead to two new equations and therefore we can solve for the interpolant.
$$\frac{\text{d}}{\text{dx}} \mathcal{P}_k(x_k) = d_k, \quad \frac{\text{d}}{\text{dx}} \mathcal{P}_k(x_{k+1}) = d_{k+1}$$
where we need to prescribe the $d_k$s. Since we know the polynomial we can write these 4 equations as
$$\begin{aligned}
p_0 + p_1 x_k + p_2 x_k^2 + p_3 x_k^3 &= y_k \\
p_0 + p_1 x_{k+1} + p_2 x_{k+1}^2 + p_3 x_{k+1}^3 &= y_{k+1} \\
p_1 + 2p_2 x_k + 3 p_3 x_k^2 &= d_k \\
p_1 + 2 p_2 x_{k+1} + 3 p_3 x_{k+1}^2 &= d_{k+1}
\end{aligned}$$
Rewriting this as a system we get
$$\begin{bmatrix}
1 & x_k & x_k^2 & x_k^3 \\
1 & x_{k+1} & x_{k+1}^2 & x_{k+1}^3 \\
0 & 1 & 2 x_k & 3 x_k^2 \\
0 & 1 & 2 x_{k+1} & 3 x_{k+1}^2
\end{bmatrix} \begin{bmatrix}
p_0 \\ p_1 \\ p_2 \\ p_3
\end{bmatrix} = \begin{bmatrix}
y_k \\ y_{k+1} \\ d_k \\ d_{k+1}
\end{bmatrix}$$
A common simplification to the problem description re-parameterizes the locations of the points such that $s \in [0, 1]$ and recast the problem with $(0, y_k)$ and $(1, y_{k+1})$. This simplifies the above system to
$$\begin{bmatrix}
1 & 0 & 0 & 0 \\
1 & 1 & 1 & 1 \\
0 & 1 & 0 & 0 \\
0 & 1 & 2 & 3
\end{bmatrix} \begin{bmatrix}
p_0 \\ p_1 \\ p_2 \\ p_3
\end{bmatrix} = \begin{bmatrix}
y_k \\ y_{k+1} \\ d_k \\ d_{k+1}
\end{bmatrix}$$
which can be solved to find
$$\begin{aligned}
\mathcal{P}(s) &= (1-s)^2 (1 + 2s) y_k + s^2 (3 - 2 s) y_{k+1} + s (1 - s)^2 d_k - s^2 (1 - s)d_{k+1}\\
\mathcal{P}'(s) &= 6s(s-1) y_k + 6s(1-s) y_{k+1} + (s-1)(3s-1) d_k - s(3s-2) d_{k+1}\\
\mathcal{P}''(s) &= 6 (1-2s)(y_{k+1} - y_k) + (6s - 4) d_k + (6s-2) d_{k+1}
\end{aligned}$$
#### 2 Questions
* is $d_k$ in the transformed frame $P(s)$ the same as in the original frame $P(x)$?
* how to choose $d_k$ in general?
#### PCHIP
Piecewise Cubic Hermite Interpolation Polynomial
- Picks the slope that preserves monotonicity
- Also tried to preserve the shape of the data
- Note that in general this interpolant is $\mathcal{P}_k(x) \in C^1$
```
from scipy.interpolate import pchip_interpolate
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
# C^1 Piece-wise PCHIP
P_pchip = pchip_interpolate(data[:, 0], data[:, 1], x)
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ro')
axes.plot(x, P_pchip, 'r')
axes.set_title("Interpolated Data - $C^1$ Cubic PCHIP")
axes.set_xlabel("x")
axes.set_ylabel("$P_3(x)$")
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
axes.grid()
plt.show()
```
#### Cubic Splines
Enforces continuity on second derivatives as well:
$$\mathcal{P}''_{k}(x_{k}) = \mathcal{P}''_{k-1}(x_k)$$
From our generalization before we know
$$\mathcal{P}''(s) = 6 (1-2s)(y_{k+1} - y_k) + (6s - 4) d_k + (6s-2) d_{k+1}$$
and our constraint now becomes
$$\mathcal{P}''_{k}(0) = \mathcal{P}''_{k-1}(1)$$
$$\mathcal{P}''_{k-1}(1) = 6 (1-2 \cdot 1)(y_{k} - y_{k-1}) + (6\cdot 1 - 4) d_{k-1} + (6\cdot 1-2) d_{k}$$
$$\mathcal{P}''_{k}(0) = 6 (1-2 \cdot 0)(y_{k+1} - y_k) + (6\cdot 0 - 4) d_k + (6\cdot 0-2) d_{k+1}$$
$$-6(y_{k} - y_{k-1}) + 2 d_{k-1} + 4 d_{k} = 6 (y_{k+1} - y_k) - 4 d_k -2 d_{k+1}$$
or rearrange knowns and unknowns to get.
$$
2 d_{k-1} + 8 d_k + 2 d_{k+1} = 6 (y_{k+1} - y_{k-1})
$$
We now have constraints on choosing the $d_k$ values for all interior values of $k$. Note that we still need to prescribe them at the boundaries of the full interval.
This forms a linear set of equations for the $d_k$s based on the $y_k$ values and can be reformulated into a tri-diagonal linear system
$$\begin{bmatrix}
& \ddots & \ddots & \ddots & & &\\
& 0 & 2 & 8 & 2 & 0 & & \\
& & 0 & 2 & 8 & 2 & 0 & & & \\
& & & 0 & 2 & 8 & 2 & 0 & & \\
& & & & & \ddots & \ddots & \ddots &
\end{bmatrix}\begin{bmatrix}
\vdots \\ d_{k-1} \\ d_{k} \\ d_{k+1} \\ \vdots
\end{bmatrix} = \begin{bmatrix}
\vdots \\ 6 (y_{k} - y_{k-2}) \\ 6 (y_{k+1} - y_{k-1}) \\ 6 (y_{k+2} - y_{k}) \\\vdots
\end{bmatrix}$$
The boundaries are still left unconstrained and we must pick some rule to specify the derivatives there.
```
from scipy.interpolate import UnivariateSpline
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
# C^2 Piece-wise Splines
# Note that to get an interpolant we need to set the smoothing
# parameters *s* to 0
P_spline = UnivariateSpline(data[:, 0], data[:, 1], s=0)
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ro')
axes.plot(x, P_spline(x), 'r', label = '$C^2$')
axes.plot(x, P_pchip, 'b--', label = 'Pchip')
axes.set_title("Interpolated Data - $C^2$ Cubic Splines")
axes.set_xlabel("x")
axes.set_ylabel("$P_3(x)$")
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
axes.grid()
axes.legend(loc='best')
plt.show()
```
### Let's compare all of these methods
```
import scipy.interpolate as interpolate
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
# Lagrange Basis
N = data.shape[0] - 1
lagrange_basis = numpy.ones((N + 1, x.shape[0]))
for i in range(N + 1):
for j in range(N + 1):
if i != j:
lagrange_basis[i, :] *= (x - data[j, 0]) / (data[i, 0] - data[j, 0])
# Calculate full polynomial
P_lagrange = numpy.zeros(x.shape[0])
for n in range(N + 1):
P_lagrange += lagrange_basis[n, :] * data[n, 1]
# C^0 Piece-wise linear
# P_pw_linear = numpy.interp(x, data[:, 0], data[:, 1])
P_linear = numpy.zeros(x.shape)
for n in range(1, N + 1):
P_linear += ((data[n, 1] - data[n - 1, 1]) / (data[n, 0] - data[n - 1, 0]) * (x - data[n - 1, 0])
+ data[n - 1, 1]) * (x > data[n - 1, 0]) * (x <= data[n, 0])
# Add end points for continuity
P_linear += numpy.ones(x.shape) * data[0, 1] * (x < data[0, 0])
P_linear += numpy.ones(x.shape) * data[-1, 1] * (x >= data[-1, 0])
# C^0 Piece-wise quadratic
P_quadratic = numpy.zeros(x.shape)
for k in range(1, N + 1, 2):
p = numpy.polyfit(data[k - 1:k + 2, 0], data[k - 1:k + 2, 1], 2)
P_quadratic += numpy.polyval(p, x) * (x > data[k - 1, 0]) * (x <= data[k + 1, 0])
# Add end points for continuity
P_quadratic += numpy.ones(x.shape) * data[0, 1] * (x < data[0, 0])
P_quadratic += numpy.ones(x.shape) * data[-1, 1] * (x >= data[-1, 0])
# C^1 Piece-wise PCHIP
P_pchip = interpolate.pchip_interpolate(data[:, 0], data[:, 1], x)
# C^2 Piece-wise Splines
P_spline = interpolate.UnivariateSpline(data[:, 0], data[:, 1], s=0)
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ko', label="Data")
axes.plot(x, P_lagrange, 'y', label="Lagrange")
axes.plot(x, P_linear, 'g', label="PW Linear")
axes.plot(x, P_quadratic, 'r', label="PW Quadratic")
axes.plot(x, P_pchip, 'c', label="PW Cubic - PCHIP")
axes.plot(x, P_spline(x), 'b', label="PW Cubic - Spline")
axes.grid()
axes.set_title("Interpolated Data - Method Comparisons")
axes.set_xlabel("x")
axes.set_ylabel("$P(x)$")
axes.legend(loc='best')
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
plt.show()
```
## Relationship to Regression
What if we have more data and want a lower degree polynomial but do not want to use a piece-wise defined interpolant?
Regression techniques are often used to minimize a form of error between the data points $y_i$ at $x_i$ with an approximating function $f(x_i)$. Note that this is NOT interpolation anymore!
### Least-Squares
One way of doing this is to require that we minimize the least-squares error
$$
E = \left( \sum^m_{i=1} |y_i - f(x_i)|^2 \right )^{1/2}.
$$
where as before we have data $y_i$ at locations $x_i$ and an approximating function $f(x_i)$.
From the beginning of our discussion we know we can write the interpolant as a system of linear equations which we can then solve for the coefficients of a monomial basis. If we wanted to fit a line
$$
\mathcal{P}_1(x) = p_0 + p_1 x
$$
to $N$ data points we would have
$$
\begin{bmatrix}
1 & x_1 \\
1 & x_2 \\
\vdots & \vdots \\
1 & x_N
\end{bmatrix} \begin{bmatrix}
p_0 \\ p_1
\end{bmatrix} = \begin{bmatrix}
y_1 \\ y_2 \\ \vdots \\ y_N
\end{bmatrix}
$$
or
$$
A p = y
$$
What's wrong with this system?
This leads to the likelihood that there is no solution to the system as
$$
A \in \mathbb{R}^{N \times 2}, p \in \mathbb{R}^{2 \times 1}, \text{ and } y \in \mathbb{R}^{N \times 1}.
$$
Instead we can solve the related least-squares system
$$
A^T A p = A^T y
$$
whose solution minimizes the least-square error defined before as $E$.
Note: In general, this is not the most stable way to solve least squares problems, in general, using an orthogonalization technique like $QR$ factorization is better numerically.
```
# Linear Least Squares Problem
N = 50
x = numpy.linspace(-1.0, 1.0, N)
y = x + numpy.random.random((N))
A = numpy.ones((x.shape[0], 2))
A[:, 1] = x
p = numpy.linalg.solve(numpy.dot(A.transpose(), A), numpy.dot(A.transpose(), y))
print('Normal Equations: p = {}'.format(p))
p = numpy.linalg.lstsq(A, y, rcond=None)[0]
print('Numpy Lstsq : p = {}'.format(p))
f = lambda x: p[0] + p[1] * x
E = numpy.linalg.norm(y - f(x), ord=2)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, y, 'ko')
axes.plot(x, f(x), 'r')
axes.set_title("Least Squares Fit to Data, err={}".format(E))
axes.set_xlabel("$x$")
axes.set_ylabel("$f(x)$ and $y_i$")
axes.grid()
plt.show()
```
### Themes and variations
You can play all sorts of games, whether they are justified by the data or not, for example we can fit the same random data with a function like
$$
f(x) = p_0 + p_1\tanh(x)
$$
which is still a linear problem for the coefficients $p_0$ and $p_1$, however the vandermonde matrix now has columns of $\mathbf{1}$ and $\tanh\mathbf{x}$.
```
# Linear Least Squares Problem
A = numpy.ones((x.shape[0], 2))
A[:, 1] = numpy.tanh(x)
#p = numpy.linalg.solve(numpy.dot(A.transpose(), A), numpy.dot(A.transpose(), y))
p = numpy.linalg.lstsq(A, y,rcond=None)[0]
f = lambda x: p[0] + p[1] * numpy.tanh(x)
E = numpy.linalg.norm(y - f(x), ord=2)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, y, 'ko')
axes.plot(x, f(x), 'r')
axes.set_title("Least Squares Fit to Data, err = {}".format(E))
axes.set_xlabel("$x$")
axes.set_ylabel("$f(x)$ and $y_i$")
axes.grid()
plt.show()
```
### Let ye be warned...
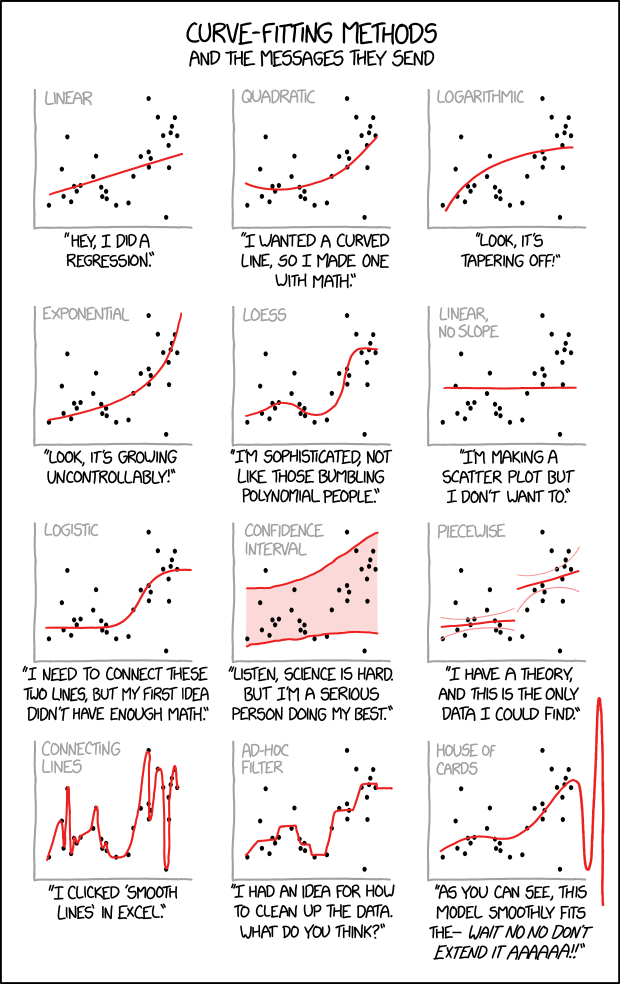
(Original image can be found at [Curve Fitting](https://xkcd.com/2048/).)
|
github_jupyter
|
from __future__ import print_function
from __future__ import absolute_import
%matplotlib inline
import numpy
import matplotlib.pyplot as plt
from scipy.interpolate import pchip_interpolate
N= 3
x = [ 1, 2.3, 4.8 ]
y = [ 1., 0.5, 5.0]
p2 = numpy.polyfit(x,y,2)
p1 = numpy.polyfit(x,y,1)
xa = numpy.linspace(0.,5)
xs = numpy.linspace(x[0],x[-1])
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1,1,1)
axes.plot(x,y,'ro',markersize=10,label='data')
axes.plot(xa,numpy.polyval(p2, xa), label='quadratic interpolant')
axes.plot(x,y,'g', label='Piecewise linear interpolant')
axes.plot(xs,pchip_interpolate(x,y,xs),'k', label='Piecewise cubic interpolant')
axes.plot(xa,numpy.polyval(p1, xa), label='best fit line')
axes.legend(loc='best')
axes.set_xlim(min(x) - 0.5,max(x) + 0.5)
axes.set_xlabel('x',fontsize=16)
axes.set_ylabel('f(x)',fontsize=16)
axes.grid()
plt.show()
x = numpy.linspace(-1,1,100)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1,1,1)
for n in range(4):
axes.plot(x,x**n,label='$x^{}$'.format(n))
axes.set_xlabel('x')
axes.grid()
axes.legend(loc='best')
axes.set_title('The First 4 Monomials')
plt.show()
# ====================================================
# Compute the Lagrange basis (\ell_i(x))
def lagrange_basis(x, data):
"""Compute Lagrange basis at x given N data points
params:
-------
x: ndarray
1-d Array of floats
data: ndarray of shape (N,2)
2-d Array of data where each row is [ x_i, y_i ]
returns:
--------
basis: ndarray of shape (N, x.shape)
: 2-D array of lagrange basis functions evaluated at x
"""
basis = numpy.ones((data.shape[0], x.shape[0]))
for i in range(data.shape[0]):
for j in range(data.shape[0]):
if i != j:
basis[i, :] *= (x - data[j, 0]) / (data[i, 0] - data[j, 0])
return basis
# ====================================================
# Calculate full polynomial
def poly_interpolant(x, data):
"""Compute polynomial interpolant of (x,y) using Lagrange basis"""
P = numpy.zeros(x.shape[0])
basis = lagrange_basis(x, data)
for n in range(data.shape[0]):
P += basis[n, :] * data[n, 1]
return P
# ====================================================
x_data = numpy.array([0., 1., 2., 3.])
x_data = numpy.array([0., 1., 2.])
y_data = numpy.ones(x_data.shape)
data = numpy.array([x_data, y_data]).T
x = numpy.linspace(x_data.min(),x_data.max(),100)
basis = lagrange_basis(x, data)
# ====================================================
# Plot individual basis functions
fig = plt.figure(figsize=(8, 6))
axes = fig.add_subplot(1, 1, 1)
basis = lagrange_basis(x, data)
for i in range(len(x_data)):
axes.plot(x, basis[i, :], label="$\ell_{%s}(x)$" % i)
axes.plot(x_data,numpy.zeros(x_data.shape),'ko')
axes.plot(x_data,y_data,'k+',markersize=10)
axes.set_title("Lagrange Basis $\ell_i(x)$")
axes.set_xlabel("x")
axes.set_ylabel("$\ell_i(x)$")
axes.grid()
axes.legend(loc='best')
plt.show()
x0, y0 = (1., 2.)
x1, y1 = (3., 3.)
ell0 = lambda x: (x - x1)/(x0 - x1)
ell1 = lambda x: (x - x0)/(x1 - x0)
P1 = lambda x: y0*ell0(x) + y1*ell1(x)
x = numpy.linspace(x0,x1)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1,1,1)
axes.plot(x,ell0(x),'r',label='$\ell_0$')
axes.plot(x,ell1(x),'b',label='$\ell_1$')
axes.plot(x,P1(x),'g',label='$P_1(x)$')
axes.plot((x0,x1),(y0,y1),'go')
axes.set_xlabel('x')
axes.grid()
axes.legend(loc='best',fontsize=16)
plt.show()
num_points = 6
# num_points = 5
# num_points = 6
# num_points = 20
data = numpy.empty((num_points, 2))
data[:, 0] = numpy.linspace(-1, 1, num_points)
data[:, 1] = numpy.sin(2.0 * numpy.pi * data[:, 0])
N = data.shape[0] - 1 # Degree of polynomial
M = data.shape[0]
x = numpy.linspace(-1.0, 1.0, 100)
px = poly_interpolant(x, data)
f = numpy.sin(2.0 * numpy.pi * x)
err = numpy.abs(f - px)
# ====================================================
# Plot individual basis functions
fig = plt.figure(figsize=(16,6))
axes = fig.add_subplot(1, 2, 1)
basis = lagrange_basis(x, data)
for i in range(N + 1):
axes.plot(x, basis[i, :], label="$\ell_{%s}(x)$" % i)
axes.set_title("Lagrange Basis $\ell_i(x)$",fontsize=16)
axes.set_xlabel("x")
axes.set_ylabel("$\ell_i(x)$")
axes.legend(loc='best',fontsize=14)
axes.grid()
# Plot full polynomial P_N(x)
axes = fig.add_subplot(1, 2, 2)
axes.plot(x, px , label="$P_{%s}(x)$" % N)
axes.plot(x, numpy.sin(2.0 * numpy.pi * x), 'r--', label="True $f(x)$")
axes.plot(x, err, 'k', linestyle='dotted',label='abs error')
for point in data:
axes.plot(point[0], point[1], 'ko')
axes.set_title("$P_N(x)$",fontsize=16)
axes.set_xlabel("x")
axes.set_ylabel("$P_N(x)$")
axes.legend(loc='best',fontsize=14)
axes.grid()
plt.show()
def f(x):
return 1.0 / (1.0 + 25.0 * x**2)
x = numpy.linspace(-1., 1., 100)
num_points = 6
data = numpy.empty((num_points, 2))
data[:, 0] = numpy.linspace(-1, 1, num_points)
data[:, 1] = f(data[:, 0])
N = data.shape[0] - 1
# Plot the results
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, poly_interpolant(x, data), 'b', label="$P_{{{name}}}(x)$".format(name=num_points-1))
axes.plot(x, f(x), 'k', label="True $f(x)$")
axes.plot(data[:, 0], data[:, 1], 'ro', label="data")
axes.set_title("Interpolation of Runge's function",fontsize=18)
axes.set_xlabel("x")
axes.set_ylabel("y")
axes.legend(loc='best',fontsize=14)
axes.grid()
plt.show()
def f(x, a=0.9, N=100):
summation = 0.0
b = (1.0 + 3.0 / 2.0 * numpy.pi) / a + 0.01
print(b)
for n in range(N + 1):
summation += a**n * numpy.cos(b**n * numpy.pi * x)
return summation
x = numpy.linspace(-1, 1, 1000)
# x = numpy.linspace(-2, 2, 100)
num_points = 10
data = numpy.empty((num_points, 2))
data[:, 0] = numpy.linspace(-1, 1, num_points)
data[:, 1] = f(data[:, 0])
N = data.shape[0] - 1
# Plot the results
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, poly_interpolant(x, data), 'b', label="$P_6(x)$")
axes.plot(x, f(x), 'k', label="True $f(x)$")
axes.plot(data[:, 0], data[:, 1], 'ro', label="data")
axes.set_title("Interpolation of Runge's function")
axes.set_xlabel("x")
axes.set_ylabel("y")
axes.legend(loc=1)
plt.show()
def cheb_poly(x, N):
"""Compute the *N*th Chebyshev polynomial and evaluate it at *x*"""
T = numpy.empty((3, x.shape[0]))
T[0, :] = numpy.ones(x.shape)
T[1, :] = x
if N == 0:
return T[0, :]
elif N == 1:
return T[1, :]
else:
for k in range(2, N + 1):
T[2, :] = 2.0 * x * T[1, :] - T[0, :]
T[0, :] = T[1, :]
T[1, :] = T[2, :]
return T[2, :]
x = numpy.linspace(-1, 1, 100)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
for n in range(5):
axes.plot(x, cheb_poly(x, n), label="$T_%s$" % n)
axes.set_ylim((-1.1, 1.1))
axes.set_title("Chebyshev Polynomials")
axes.set_xlabel("x")
axes.set_ylabel("$T_N(x)$")
axes.legend(loc='best')
axes.grid()
plt.show()
N = 4
x_extrema = numpy.cos(numpy.arange(N + 1) * numpy.pi / N)
x_nodes = numpy.cos((2.0 * numpy.arange(1, N + 1) - 1.0) / (2.0 * N) * numpy.pi)
fig = plt.figure()
# fig.set_figwidth(fig.get_figwidth() * 2)
axes = fig.add_subplot(1, 1, 1)
# Plot points
axes.plot(x_extrema, numpy.zeros(N+1), 'ro')
axes.plot(x_nodes, numpy.zeros(N), 'bo')
# Plot some helpful lines
axes.plot((-1.0, -1.0), (-1.1, 1.1), 'k--')
axes.plot((1.0, 1.0), (-1.1, 1.1), 'k--')
axes.plot((-1.0, 1.0), (0.0, 0.0), 'k--')
for i in range(x_extrema.shape[0]):
axes.plot((x_extrema[i], x_extrema[i]), (-1.1, 1.1), 'r--')
axes.plot(x_extrema[i], cheb_poly(x_extrema, N)[i], 'ro')
print('Nodes = {}'.format(numpy.sort(x_nodes)))
print('Extrema = {}'.format(numpy.sort(x_extrema)))
#print(numpy.cos(x_extrema))
# Plot Chebyshev polynomial
x_hat = numpy.linspace(-1, 1, 1000)
axes.plot(x_hat, cheb_poly(x_hat, N), 'k')
axes.set_xlim((-1.1, 1.1))
axes.set_ylim((-1.1, 1.1))
# Labels
axes.set_title("Chebyshev Nodes and Extrema, N={}".format(N), fontsize="20")
axes.set_xlabel("x", fontsize="15")
axes.set_ylabel("$T_{N+1}(x)$", fontsize="15")
plt.show()
# First-kind Nesting (3 x)
fig = plt.figure()
# fig.set_figwidth(fig.get_figwidth() * 2)
axes = fig.add_subplot(1, 1, 1)
N = 5
factor = 3
x_1 = numpy.cos((2.0 * numpy.arange(1, N + 1) - 1.0) / (2.0 * N) * numpy.pi)
x_2 = numpy.cos((2.0 * numpy.arange(1, factor * N + 1) - 1.0) / (2.0 * factor * N) * numpy.pi)
axes.plot(x_1, numpy.zeros(N), "o", color="r", markerfacecolor="lightgray", markersize="15")
axes.plot(x_2, numpy.zeros(N * factor), 'kx', markersize="10")
x_hat = numpy.linspace(-1, 1, 1000)
axes.plot(x_hat, cheb_poly(x_hat, N), 'k')
axes.plot(x_hat, cheb_poly(x_hat, factor * N), 'k')
axes.set_xlim((-1.1, 1.1))
axes.set_ylim((-1.1, 1.1))
axes.set_title("Nesting of 1st and 2nd Kind Chebyshev Polynomials")
axes.set_xlabel("$x$")
axes.set_ylabel("$T_N(x)$")
plt.show()
x = numpy.linspace(0, numpy.pi, 100)
N = 15
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1, aspect="equal")
axes.plot(numpy.cos(x), numpy.sin(x), 'r--')
axes.plot(numpy.linspace(-1.1, 1.1, 100), numpy.zeros(x.shape), 'r')
for k in range(1, N + 1):
location = [numpy.cos((2.0 * k - 1.0) * numpy.pi / (2.0 * N)),
numpy.sin((2.0 * k - 1.0) * numpy.pi / (2.0 * N))]
axes.plot(location[0], location[1], 'ko')
axes.plot(location[0], 0.0, 'ko')
axes.plot([location[0], location[0]], [0.0, location[1]], 'k--')
axes.set_xlim((-1.1, 1.1))
axes.set_ylim((-0.1, 1.1))
plt.show()
# Runge's function again
def f(x):
return 1.0 / (1.0 + 25.0 * x**2)
# Parameters
x = numpy.linspace(-1., 1., 100)
num_points = 6
# ============================================================
# Equidistant nodes
equidistant_data = numpy.empty((num_points, 2))
equidistant_data[:, 0] = numpy.linspace(-1, 1, num_points)
equidistant_data[:, 1] = f(equidistant_data[:, 0])
N = equidistant_data.shape[0] - 1
P_lagrange = poly_interpolant(x, equidistant_data)
# ============================================================
# Chebyshev nodes
chebyshev_data = numpy.empty((num_points, 2))
chebyshev_data[:, 0] = numpy.cos((2.0 * numpy.arange(1, num_points + 1) - 1.0) * numpy.pi / (2.0 * num_points))
chebyshev_data[:, 1] = f(chebyshev_data[:, 0])
P_cheby1 = poly_interpolant(x, chebyshev_data)
# Fit directly with Chebyshev polynomials
coeff = numpy.polynomial.chebyshev.chebfit(chebyshev_data[:, 0], chebyshev_data[:, 1], N)
P_cheby2 = numpy.polynomial.chebyshev.chebval(x, coeff)
# Check on unique polynomials
#print(numpy.allclose(P_cheby1, P_cheby2))
# calculate errornorms for different interpolants
equidistant_err = numpy.linalg.norm(P_lagrange - f(x))
cheb_err = numpy.linalg.norm(P_cheby1 - f(x))
# ============================================================
# Plot the results
fig = plt.figure(figsize=(16,6))
fig.subplots_adjust(hspace=.5)
axes = fig.add_subplot(1, 2, 1)
axes.plot(x, P_lagrange, 'b', label="$P_%s(x)$" % N)
axes.plot(x, f(x), 'k', label="True $f(x)$")
axes.plot(equidistant_data[:, 0], equidistant_data[:, 1], 'ro', label="data")
axes.set_title("Equispaced Points: err = {:5.5g}".format(equidistant_err),fontsize=18)
axes.set_xlabel("x",fontsize=16)
axes.set_ylabel("y",fontsize=16)
axes.grid()
axes.legend(loc=8,fontsize=16)
#print('Equispaced error = {}'.format(numpy.linalg.norm(P_lagrange - f(x))))
axes = fig.add_subplot(1, 2, 2)
axes.plot(x, f(x), 'k', label="True $f(x)$")
axes.plot(x, P_cheby1, 'b', label="$P_%s(x)$" % N)
axes.plot(chebyshev_data[:, 0], chebyshev_data[:, 1], 'ro', label="data")
axes.set_title("Chebyshev Points: err = {:5.5g}".format(cheb_err),fontsize=18)
axes.set_xlabel("x",fontsize=16)
axes.set_ylabel("y",fontsize=16)
axes.legend(loc=1,fontsize=16)
axes.grid()
#print('Chebyshev error = {}'.format(numpy.linalg.norm(P_cheby1 - f(x))))
plt.show()
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
N = data.shape[0] - 1
# Lagrange Basis
P_lagrange = poly_interpolant(x, data)
# C^0 Piece-wise linear
# P_pw_linear = numpy.interp(x, data[:, 0], data[:, 1])
P_linear = numpy.zeros(x.shape)
for n in range(1, N + 1):
P_linear += ((data[n, 1] - data[n - 1, 1]) / (data[n, 0] - data[n - 1, 0]) * (x - data[n - 1, 0])
+ data[n - 1, 1]) * (x > data[n - 1, 0]) * (x <= data[n, 0])
# Add end points for continuity
P_linear += numpy.ones(x.shape) * data[0, 1] * (x < data[0, 0])
P_linear += numpy.ones(x.shape) * data[-1, 1] * (x >= data[-1, 0])
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ko')
axes.plot(x, P_lagrange, 'b--',label='$P_{{{name}}}$'.format(name=N))
axes.plot(x, P_linear, 'r',label='Piecewise Linear')
axes.set_title("Interpolated Data - $C^0$ Linear",fontsize=18)
axes.set_xlabel("x",fontsize=16)
axes.set_ylabel("$P_1(x)$",fontsize=16)
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
axes.legend(loc='best',fontsize=14)
axes.grid()
plt.show()
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
N = data.shape[0] - 1
# This isn't overlapping, it's more like C_0 P_2
# C^0 Piece-wise quadratic
P_quadratic = numpy.zeros(x.shape)
for k in range(1, N + 1, 2):
p = numpy.polyfit(data[k - 1:k + 2, 0], data[k - 1:k + 2, 1], 2)
P_quadratic += numpy.polyval(p, x) * (x > data[k - 1, 0]) * (x <= data[k + 1, 0])
# Add end points for continuity
P_quadratic += numpy.ones(x.shape) * data[0, 1] * (x < data[0, 0])
P_quadratic += numpy.ones(x.shape) * data[-1, 1] * (x >= data[-1, 0])
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ko')
axes.plot(x, P_lagrange, 'b--',label='$P_{{{name}}}$'.format(name=N))
axes.plot(x, P_quadratic, 'r',label='Piecewise quadratic')
axes.set_title("Interpolated Data - $C^0$ Quadratic",fontsize=18)
axes.set_xlabel("x",fontsize=16)
axes.set_ylabel("$P_2(x)$",fontsize=16)
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
axes.legend(loc='best',fontsize=14)
axes.grid()
plt.show()
xk = [ .5, 1., 3., 5.]
yk = [ .5, 2., 2.5, 1. ]
ell0 = lambda x: (x - x1)/(x0 - x1)
ell1 = lambda x: (x - x0)/(x1 - x0)
P1 = lambda x: y0*ell0(x) + y1*ell1(x)
x = numpy.linspace(x0,x1)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1,1,1)
axes.plot(x,ell0(x),'r',label='$\ell_0$')
axes.plot(x,ell1(x),'b',label='$\ell_1$')
axes.plot(x,P1(x),'g',label='$P_1(x)$')
axes.plot((x0,x1),(y0,y1),'go')
axes.set_xlabel('x')
axes.set_xlim(0.,5.)
axes.grid()
axes.legend(loc='best',fontsize=16)
plt.show()
from scipy.interpolate import pchip_interpolate
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
# C^1 Piece-wise PCHIP
P_pchip = pchip_interpolate(data[:, 0], data[:, 1], x)
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ro')
axes.plot(x, P_pchip, 'r')
axes.set_title("Interpolated Data - $C^1$ Cubic PCHIP")
axes.set_xlabel("x")
axes.set_ylabel("$P_3(x)$")
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
axes.grid()
plt.show()
from scipy.interpolate import UnivariateSpline
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
# C^2 Piece-wise Splines
# Note that to get an interpolant we need to set the smoothing
# parameters *s* to 0
P_spline = UnivariateSpline(data[:, 0], data[:, 1], s=0)
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ro')
axes.plot(x, P_spline(x), 'r', label = '$C^2$')
axes.plot(x, P_pchip, 'b--', label = 'Pchip')
axes.set_title("Interpolated Data - $C^2$ Cubic Splines")
axes.set_xlabel("x")
axes.set_ylabel("$P_3(x)$")
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
axes.grid()
axes.legend(loc='best')
plt.show()
import scipy.interpolate as interpolate
data = numpy.array([[1.0, 3.0], [2.0, 1.0], [3.5, 4.0], [5.0, 0.0], [6.0, 0.5], [9.0, -2.0], [9.5, -3.0]])
x = numpy.linspace(0.0, 10, 100)
# Lagrange Basis
N = data.shape[0] - 1
lagrange_basis = numpy.ones((N + 1, x.shape[0]))
for i in range(N + 1):
for j in range(N + 1):
if i != j:
lagrange_basis[i, :] *= (x - data[j, 0]) / (data[i, 0] - data[j, 0])
# Calculate full polynomial
P_lagrange = numpy.zeros(x.shape[0])
for n in range(N + 1):
P_lagrange += lagrange_basis[n, :] * data[n, 1]
# C^0 Piece-wise linear
# P_pw_linear = numpy.interp(x, data[:, 0], data[:, 1])
P_linear = numpy.zeros(x.shape)
for n in range(1, N + 1):
P_linear += ((data[n, 1] - data[n - 1, 1]) / (data[n, 0] - data[n - 1, 0]) * (x - data[n - 1, 0])
+ data[n - 1, 1]) * (x > data[n - 1, 0]) * (x <= data[n, 0])
# Add end points for continuity
P_linear += numpy.ones(x.shape) * data[0, 1] * (x < data[0, 0])
P_linear += numpy.ones(x.shape) * data[-1, 1] * (x >= data[-1, 0])
# C^0 Piece-wise quadratic
P_quadratic = numpy.zeros(x.shape)
for k in range(1, N + 1, 2):
p = numpy.polyfit(data[k - 1:k + 2, 0], data[k - 1:k + 2, 1], 2)
P_quadratic += numpy.polyval(p, x) * (x > data[k - 1, 0]) * (x <= data[k + 1, 0])
# Add end points for continuity
P_quadratic += numpy.ones(x.shape) * data[0, 1] * (x < data[0, 0])
P_quadratic += numpy.ones(x.shape) * data[-1, 1] * (x >= data[-1, 0])
# C^1 Piece-wise PCHIP
P_pchip = interpolate.pchip_interpolate(data[:, 0], data[:, 1], x)
# C^2 Piece-wise Splines
P_spline = interpolate.UnivariateSpline(data[:, 0], data[:, 1], s=0)
# Plot
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(data[:,0], data[:,1], 'ko', label="Data")
axes.plot(x, P_lagrange, 'y', label="Lagrange")
axes.plot(x, P_linear, 'g', label="PW Linear")
axes.plot(x, P_quadratic, 'r', label="PW Quadratic")
axes.plot(x, P_pchip, 'c', label="PW Cubic - PCHIP")
axes.plot(x, P_spline(x), 'b', label="PW Cubic - Spline")
axes.grid()
axes.set_title("Interpolated Data - Method Comparisons")
axes.set_xlabel("x")
axes.set_ylabel("$P(x)$")
axes.legend(loc='best')
axes.set_xlim([0.0, 10.0])
axes.set_ylim([-4.0, 15.0])
plt.show()
# Linear Least Squares Problem
N = 50
x = numpy.linspace(-1.0, 1.0, N)
y = x + numpy.random.random((N))
A = numpy.ones((x.shape[0], 2))
A[:, 1] = x
p = numpy.linalg.solve(numpy.dot(A.transpose(), A), numpy.dot(A.transpose(), y))
print('Normal Equations: p = {}'.format(p))
p = numpy.linalg.lstsq(A, y, rcond=None)[0]
print('Numpy Lstsq : p = {}'.format(p))
f = lambda x: p[0] + p[1] * x
E = numpy.linalg.norm(y - f(x), ord=2)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, y, 'ko')
axes.plot(x, f(x), 'r')
axes.set_title("Least Squares Fit to Data, err={}".format(E))
axes.set_xlabel("$x$")
axes.set_ylabel("$f(x)$ and $y_i$")
axes.grid()
plt.show()
# Linear Least Squares Problem
A = numpy.ones((x.shape[0], 2))
A[:, 1] = numpy.tanh(x)
#p = numpy.linalg.solve(numpy.dot(A.transpose(), A), numpy.dot(A.transpose(), y))
p = numpy.linalg.lstsq(A, y,rcond=None)[0]
f = lambda x: p[0] + p[1] * numpy.tanh(x)
E = numpy.linalg.norm(y - f(x), ord=2)
fig = plt.figure(figsize=(8,6))
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, y, 'ko')
axes.plot(x, f(x), 'r')
axes.set_title("Least Squares Fit to Data, err = {}".format(E))
axes.set_xlabel("$x$")
axes.set_ylabel("$f(x)$ and $y_i$")
axes.grid()
plt.show()
| 0.802942 | 0.984956 |
When we fit a linear regression model to a particular data set, many problems may occur. Most common among these are the following:
1. Non-linearity of the response-predictor relationships.
2. Correlation of error terms.
3. Non-constant variance of error terms.
4. Outliers.
5. High-leverage points.
6. Collinearity
# <div align="center">1. Non-linearity of the Data</div>
---------------------------------------------------------------------
The linear regression model assumes that there is a straight-line relationship between the predictors and the response. If the true relationship is far from linear, then virtually all of the conclusions that we draw from the fit are suspect. In addition, the prediction accuracy of the model can be significantly reduced.
**Residual plots** are a useful graphical tool for identifying non-linearity. Given a simple linear regression model, we can plot the residuals, $e_{i}=y_{i} - \hat{y_{i}}$ , versus the predictor $x_{i}$. In the case of a multiple regression model, since there are multiple predictors, we instead plot the residuals versus the predicted (or fitted) values $\hat{y_{i}}$. Ideally, the residual plot will show no fitted discernible pattern. The presence of a pattern may indicate a problem with some aspect of the linear model.
<img src="pics/40.png"/>
If the residual plot indicates that there are non-linear associations in the data, then a simple approach is to use non-linear transformations of the predictors, such as $\log{X}$, $\sqrt{X}$, and $X^2$, in the regression model. In the later chapters of this book, we will discuss other more advanced non-linear approaches for addressing this issue.
# <div align="center">2. Correlation of Error Terms</div>
---------------------------------------------------------------------
An important assumption of the linear regression model is that the error terms, $\epsilon_{1}, \epsilon_{2}, ... \epsilon_{n}$, are uncorrelated. What does this mean? For instance, if the errors are uncorrelated, then the fact that $\epsilon_{i}$ is positive provides little or no information about the sign of $\epsilon_{i+1}$. The standard errors that are computed for the estimated regression coefficients or the fitted values are based on the assumption of uncorrelated error terms. If in fact there is correlation among the error terms, then the estimated standard errors will tend to underestimate the true standard errors. As a result, confidence and prediction intervals will be narrower than they should be. For example, a 95% confidence interval may in reality have a much lower probability than 0.95 of containing the true value of the parameter. In addition, p-values associated with the model will be lower than they should be; this could cause us to erroneously conclude that a parameter is statistically significant. In short, if the error terms are correlated, we may have an unwarranted sense of confidence in our model.
Why might correlations among the error terms occur? Such correlations frequently occur in the context of time series data, which consists of observations for which measurements are obtained at discrete points in time. In many cases, observations that are obtained at adjacent time points will have positively correlated errors. In order to determine if this is the case for
a given data set, we can plot the residuals from our model as a function of time. If the errors are uncorrelated, then there should be no discernible pattern. On the other hand, if the error terms are positively correlated, then we may see tracking in the residuals—that is, adjacent residuals may have similar values. In the top panel, we see the residuals from a linear regression fit to data generated with uncorrelated errors. There is no evidence of a time-related trend in the residuals.In contrast, the residuals in the bottom panel are from a data set in which adjacent errors had a correlation of 0.9. Now there is a clear pattern in the residuals—adjacent residuals tend to take on similar values. Finally, the center panel illustrates a more moderate case in which the residuals had a correlation of 0.5. There is still evidence of tracking, but the pattern is less clear.
Many methods have been developed to properly take account of correlations in the error terms in time series data. Correlation among the error terms can also occur outside of time series data. For instance, consider a study in which individuals’ heights are predicted from their weights. The assumption of uncorrelated errors could be violated if some of the individuals in the study are members of the same family, or eat the same diet, or have been exposed to the same environmental factors. In general, the assumption of uncorrelated errors is extremely important for linear regression as well as for other statistical methods, and good experimental design is crucial in order to mitigate the risk of such correlations.
<img src="pics/41.png"/>
# <div align="center">3. Non-constant Variance of Error Terms</div>
---------------------------------------------------------------------
Another important assumption of the linear regression model is that the error terms have a constant variance, $Var(\epsilon_{i})=\sigma^2$. The standard errors, confidence intervals, and hypothesis tests associated with the linear model rely upon this assumption.
Unfortunately, it is often the case that the variances of the error terms are non-constant. For instance, the variances of the error terms may increase with the value of the response. One can identify non-constant variances in the errors, or heteroscedasticity, from the presence of a funnel shape in residual plot. An example is shown in the left-hand panel of Figure in which the magnitude of the residuals tends to increase with the fitted values. When faced with this problem, one possible solution is to transform the response $Y$ using a concave function such as $\log(Y)$ or $\sart{Y}$. Such a transformation results in a greater amount of shrinkage of the larger responses, leading to a reduction in heteroscedasticity. The right-hand panel of Figure displays the residual plot after transforming the response using $\log(Y)$ . The residuals now appear to have constant variance, though there is some evidence of a slight non-linear relationship in the data.
<img src="pics/43.png"/>
Sometimes we have a good idea of the variance of each response. For example, the $i$th response could be an average of $n_{i}$ raw observations. If each of these raw observations is uncorrelated with variance $\sigma^2$, then their average has variance $\sigma_{i}^2 = \sigma^2/n_{i}$. In this case a simple remedy is to fit our model by weighted least squares, with weights proportional to the inverse variances—i.e. $w_{i} = n_{i}$ in this case. Most linear regression software allows for observation weights.
# <div align="center">4. Outliers</div>
---------------------------------------------------------------------
An outlier is a point for which yi is far from the value predicted by the model. Outliers can arise for a variety of reasons, such as incorrect recording of an observation during data collection.
The red point (observation 20) in the left-hand panel of Figure illustrates a typical outlier. The red solid line is the least squares regression fit, while the blue dashed line is the least squares fit after removal of the outlier. In this case, removing the outlier has little effect on the least squares line: it leads to almost no change in the slope, and a miniscule reduction in the intercept. It is typical for an outlier that does not have an unusual predictor value to have little effect on the least squares fit. However, even if an outlier does not have much effect on the least squares fit, it can cause other problems. For instance, in this example, the RSE is 1.09 when the outlier is included in the regression, but it is only 0.77 when the outlier is removed. Since the RSE is used to compute all confidence intervals and p-values, such a dramatic increase caused by a single data point can have implications for the interpretation of the fit. Similarly, inclusion of the outlier causes the $R^2$ to decline from 0.892 to 0.805.
<img src="pics/44.png"/>
Residual plots can be used to identify outliers. In this example, the outlier is clearly visible in the residual plot illustrated in the center panel of Figure. But in practice, it can be difficult to decide how large a residual needs to be before we consider the point to be an outlier. To address this problem, instead of plotting the residuals, we can plot the studentized residuals, computed by dividing each residual $e_{i}$ by its estimated standard error. Observations whose studentized residuals are greater than 3 in absolute value are possible outliers. In the right-hand panel of Figure, the outlier’s studentized residual exceeds 6, while all other observations have studentized residuals between −2 and 2.
# <div align="center">5. High Leverage Points</div>
---------------------------------------------------------------------
We just saw that outliers are observations for which the response yi is unusual given the predictor xi. In contrast, observations with high leverage have an unusual value for xi. For example, observation 41 in the left-hand panel of Figure has high leverage, in that the predictor value for this observation is large relative to the other observations. (Note that the data displayed in Figure are the same as the data displayed in previous Figure, but with the addition of a single high leverage observation.) The red solid line is the least squares fit to the data, while the blue dashed line is the fit produced when observation 41 is removed. Comparing the left-hand panels of previous Figure and this Figure, we observe that removing the high leverage observation has a much more substantial impact on the least squares line than removing the outlier. In fact, high leverage observations tend to have a sizable impact on the estimated regression line. It is cause for concern if the least squares line is heavily affected by just a couple of observations, because any problems with these points may invalidate the entire fit. For this reason, it is important to identify high leverage observations.
<img src="pics/45.png"/>
In a simple linear regression, high leverage observations are fairly easy to identify, since we can simply look for observations for which the predictor value is outside of the normal range of the observations. But in a multiple linear regression with many predictors, it is possible to have an observation that is well within the range of each individual predictor’s values, but that is unusual in terms of the full set of predictors. An example is shown in the center panel of Figure, for a data set with two predictors, $X_{1}$ and $X_{2}$. Most of the observations’ predictor values fall within the blue dashed ellipse, but the red observation is well outside of this range. But neither its value for X1 nor its value for X2 is unusual. So if we examine just X1 or just X2, we will fail to notice this high leverage point. This problem is more pronounced in multiple regression settings with more than two predictors, because then there is no simple way to plot all dimensions of the data simultaneously.
In order to quantify an observation’s leverage, we compute the leverage statistic. A large value of this statistic indicates an observation with highleverage.
# <div align="center">6. Collinearity (Multicollinearity)</div>
---------------------------------------------------------------------
Multicollinearity occurs when independent variables in a regression model are correlated. This correlation is a problem because independent variables should be independent. If the degree of correlation between variables is high enough, it can cause problems when you fit the model and interpret the results.
A key goal of regression analysis is to isolate the relationship between each independent variable and the dependent variable. The interpretation of a regression coefficient is that it represents the mean change in the dependent variable for each 1 unit change in an independent variable when you hold all of the other independent variables constant. That last portion is crucial for our discussion about multicollinearity.
The idea is that you can change the value of one independent variable and not the others. However, when independent variables are correlated, it indicates that changes in one variable are associated with shifts in another variable. The stronger the correlation, the more difficult it is to change one variable without changing another. It becomes difficult for the model to estimate the relationship between each independent variable and the dependent variable independently because the independent variables tend to change in unison.
There are two basic kinds of multicollinearity:
1. Structural multicollinearity: This type occurs when we create a model term using other terms. In other words, it’s a byproduct of the model that we specify rather than being present in the data itself. For example, if you square term $X$ to model curvature, clearly there is a correlation between $X$ and $X^2$.
2. Data multicollinearity: This type of multicollinearity is present in the data itself rather than being an artifact of our model. Observational experiments are more likely to exhibit this kind of multicollinearity.
### <div align="center">Testing for Multicollinearity with Variance Inflation Factors (VIF)</div>
---------------------------------------------------------------------
If you can identify which variables are affected by multicollinearity and the strength of the correlation, you’re well on your way to determining whether you need to fix it. Fortunately, there is a very simple test to assess multicollinearity in your regression model. The variance inflation factor (VIF) identifies correlation between independent variables and the strength of that correlation.
Statistical software calculates a VIF for each independent variable. VIFs start at 1 and have no upper limit. A value of 1 indicates that there is no correlation between this independent variable and any others. VIFs between 1 and 5 suggest that there is a moderate correlation, but it is not severe enough to warrant corrective measures. VIFs greater than 5 represent critical levels of multicollinearity where the coefficients are poorly estimated, and the p-values are questionable.
Use VIFs to identify correlations between variables and determine the strength of the relationships. Most statistical software can display VIFs for you. Assessing VIFs is particularly important for observational studies because these studies are more prone to having multicollinearity.
|
github_jupyter
|
When we fit a linear regression model to a particular data set, many problems may occur. Most common among these are the following:
1. Non-linearity of the response-predictor relationships.
2. Correlation of error terms.
3. Non-constant variance of error terms.
4. Outliers.
5. High-leverage points.
6. Collinearity
# <div align="center">1. Non-linearity of the Data</div>
---------------------------------------------------------------------
The linear regression model assumes that there is a straight-line relationship between the predictors and the response. If the true relationship is far from linear, then virtually all of the conclusions that we draw from the fit are suspect. In addition, the prediction accuracy of the model can be significantly reduced.
**Residual plots** are a useful graphical tool for identifying non-linearity. Given a simple linear regression model, we can plot the residuals, $e_{i}=y_{i} - \hat{y_{i}}$ , versus the predictor $x_{i}$. In the case of a multiple regression model, since there are multiple predictors, we instead plot the residuals versus the predicted (or fitted) values $\hat{y_{i}}$. Ideally, the residual plot will show no fitted discernible pattern. The presence of a pattern may indicate a problem with some aspect of the linear model.
<img src="pics/40.png"/>
If the residual plot indicates that there are non-linear associations in the data, then a simple approach is to use non-linear transformations of the predictors, such as $\log{X}$, $\sqrt{X}$, and $X^2$, in the regression model. In the later chapters of this book, we will discuss other more advanced non-linear approaches for addressing this issue.
# <div align="center">2. Correlation of Error Terms</div>
---------------------------------------------------------------------
An important assumption of the linear regression model is that the error terms, $\epsilon_{1}, \epsilon_{2}, ... \epsilon_{n}$, are uncorrelated. What does this mean? For instance, if the errors are uncorrelated, then the fact that $\epsilon_{i}$ is positive provides little or no information about the sign of $\epsilon_{i+1}$. The standard errors that are computed for the estimated regression coefficients or the fitted values are based on the assumption of uncorrelated error terms. If in fact there is correlation among the error terms, then the estimated standard errors will tend to underestimate the true standard errors. As a result, confidence and prediction intervals will be narrower than they should be. For example, a 95% confidence interval may in reality have a much lower probability than 0.95 of containing the true value of the parameter. In addition, p-values associated with the model will be lower than they should be; this could cause us to erroneously conclude that a parameter is statistically significant. In short, if the error terms are correlated, we may have an unwarranted sense of confidence in our model.
Why might correlations among the error terms occur? Such correlations frequently occur in the context of time series data, which consists of observations for which measurements are obtained at discrete points in time. In many cases, observations that are obtained at adjacent time points will have positively correlated errors. In order to determine if this is the case for
a given data set, we can plot the residuals from our model as a function of time. If the errors are uncorrelated, then there should be no discernible pattern. On the other hand, if the error terms are positively correlated, then we may see tracking in the residuals—that is, adjacent residuals may have similar values. In the top panel, we see the residuals from a linear regression fit to data generated with uncorrelated errors. There is no evidence of a time-related trend in the residuals.In contrast, the residuals in the bottom panel are from a data set in which adjacent errors had a correlation of 0.9. Now there is a clear pattern in the residuals—adjacent residuals tend to take on similar values. Finally, the center panel illustrates a more moderate case in which the residuals had a correlation of 0.5. There is still evidence of tracking, but the pattern is less clear.
Many methods have been developed to properly take account of correlations in the error terms in time series data. Correlation among the error terms can also occur outside of time series data. For instance, consider a study in which individuals’ heights are predicted from their weights. The assumption of uncorrelated errors could be violated if some of the individuals in the study are members of the same family, or eat the same diet, or have been exposed to the same environmental factors. In general, the assumption of uncorrelated errors is extremely important for linear regression as well as for other statistical methods, and good experimental design is crucial in order to mitigate the risk of such correlations.
<img src="pics/41.png"/>
# <div align="center">3. Non-constant Variance of Error Terms</div>
---------------------------------------------------------------------
Another important assumption of the linear regression model is that the error terms have a constant variance, $Var(\epsilon_{i})=\sigma^2$. The standard errors, confidence intervals, and hypothesis tests associated with the linear model rely upon this assumption.
Unfortunately, it is often the case that the variances of the error terms are non-constant. For instance, the variances of the error terms may increase with the value of the response. One can identify non-constant variances in the errors, or heteroscedasticity, from the presence of a funnel shape in residual plot. An example is shown in the left-hand panel of Figure in which the magnitude of the residuals tends to increase with the fitted values. When faced with this problem, one possible solution is to transform the response $Y$ using a concave function such as $\log(Y)$ or $\sart{Y}$. Such a transformation results in a greater amount of shrinkage of the larger responses, leading to a reduction in heteroscedasticity. The right-hand panel of Figure displays the residual plot after transforming the response using $\log(Y)$ . The residuals now appear to have constant variance, though there is some evidence of a slight non-linear relationship in the data.
<img src="pics/43.png"/>
Sometimes we have a good idea of the variance of each response. For example, the $i$th response could be an average of $n_{i}$ raw observations. If each of these raw observations is uncorrelated with variance $\sigma^2$, then their average has variance $\sigma_{i}^2 = \sigma^2/n_{i}$. In this case a simple remedy is to fit our model by weighted least squares, with weights proportional to the inverse variances—i.e. $w_{i} = n_{i}$ in this case. Most linear regression software allows for observation weights.
# <div align="center">4. Outliers</div>
---------------------------------------------------------------------
An outlier is a point for which yi is far from the value predicted by the model. Outliers can arise for a variety of reasons, such as incorrect recording of an observation during data collection.
The red point (observation 20) in the left-hand panel of Figure illustrates a typical outlier. The red solid line is the least squares regression fit, while the blue dashed line is the least squares fit after removal of the outlier. In this case, removing the outlier has little effect on the least squares line: it leads to almost no change in the slope, and a miniscule reduction in the intercept. It is typical for an outlier that does not have an unusual predictor value to have little effect on the least squares fit. However, even if an outlier does not have much effect on the least squares fit, it can cause other problems. For instance, in this example, the RSE is 1.09 when the outlier is included in the regression, but it is only 0.77 when the outlier is removed. Since the RSE is used to compute all confidence intervals and p-values, such a dramatic increase caused by a single data point can have implications for the interpretation of the fit. Similarly, inclusion of the outlier causes the $R^2$ to decline from 0.892 to 0.805.
<img src="pics/44.png"/>
Residual plots can be used to identify outliers. In this example, the outlier is clearly visible in the residual plot illustrated in the center panel of Figure. But in practice, it can be difficult to decide how large a residual needs to be before we consider the point to be an outlier. To address this problem, instead of plotting the residuals, we can plot the studentized residuals, computed by dividing each residual $e_{i}$ by its estimated standard error. Observations whose studentized residuals are greater than 3 in absolute value are possible outliers. In the right-hand panel of Figure, the outlier’s studentized residual exceeds 6, while all other observations have studentized residuals between −2 and 2.
# <div align="center">5. High Leverage Points</div>
---------------------------------------------------------------------
We just saw that outliers are observations for which the response yi is unusual given the predictor xi. In contrast, observations with high leverage have an unusual value for xi. For example, observation 41 in the left-hand panel of Figure has high leverage, in that the predictor value for this observation is large relative to the other observations. (Note that the data displayed in Figure are the same as the data displayed in previous Figure, but with the addition of a single high leverage observation.) The red solid line is the least squares fit to the data, while the blue dashed line is the fit produced when observation 41 is removed. Comparing the left-hand panels of previous Figure and this Figure, we observe that removing the high leverage observation has a much more substantial impact on the least squares line than removing the outlier. In fact, high leverage observations tend to have a sizable impact on the estimated regression line. It is cause for concern if the least squares line is heavily affected by just a couple of observations, because any problems with these points may invalidate the entire fit. For this reason, it is important to identify high leverage observations.
<img src="pics/45.png"/>
In a simple linear regression, high leverage observations are fairly easy to identify, since we can simply look for observations for which the predictor value is outside of the normal range of the observations. But in a multiple linear regression with many predictors, it is possible to have an observation that is well within the range of each individual predictor’s values, but that is unusual in terms of the full set of predictors. An example is shown in the center panel of Figure, for a data set with two predictors, $X_{1}$ and $X_{2}$. Most of the observations’ predictor values fall within the blue dashed ellipse, but the red observation is well outside of this range. But neither its value for X1 nor its value for X2 is unusual. So if we examine just X1 or just X2, we will fail to notice this high leverage point. This problem is more pronounced in multiple regression settings with more than two predictors, because then there is no simple way to plot all dimensions of the data simultaneously.
In order to quantify an observation’s leverage, we compute the leverage statistic. A large value of this statistic indicates an observation with highleverage.
# <div align="center">6. Collinearity (Multicollinearity)</div>
---------------------------------------------------------------------
Multicollinearity occurs when independent variables in a regression model are correlated. This correlation is a problem because independent variables should be independent. If the degree of correlation between variables is high enough, it can cause problems when you fit the model and interpret the results.
A key goal of regression analysis is to isolate the relationship between each independent variable and the dependent variable. The interpretation of a regression coefficient is that it represents the mean change in the dependent variable for each 1 unit change in an independent variable when you hold all of the other independent variables constant. That last portion is crucial for our discussion about multicollinearity.
The idea is that you can change the value of one independent variable and not the others. However, when independent variables are correlated, it indicates that changes in one variable are associated with shifts in another variable. The stronger the correlation, the more difficult it is to change one variable without changing another. It becomes difficult for the model to estimate the relationship between each independent variable and the dependent variable independently because the independent variables tend to change in unison.
There are two basic kinds of multicollinearity:
1. Structural multicollinearity: This type occurs when we create a model term using other terms. In other words, it’s a byproduct of the model that we specify rather than being present in the data itself. For example, if you square term $X$ to model curvature, clearly there is a correlation between $X$ and $X^2$.
2. Data multicollinearity: This type of multicollinearity is present in the data itself rather than being an artifact of our model. Observational experiments are more likely to exhibit this kind of multicollinearity.
### <div align="center">Testing for Multicollinearity with Variance Inflation Factors (VIF)</div>
---------------------------------------------------------------------
If you can identify which variables are affected by multicollinearity and the strength of the correlation, you’re well on your way to determining whether you need to fix it. Fortunately, there is a very simple test to assess multicollinearity in your regression model. The variance inflation factor (VIF) identifies correlation between independent variables and the strength of that correlation.
Statistical software calculates a VIF for each independent variable. VIFs start at 1 and have no upper limit. A value of 1 indicates that there is no correlation between this independent variable and any others. VIFs between 1 and 5 suggest that there is a moderate correlation, but it is not severe enough to warrant corrective measures. VIFs greater than 5 represent critical levels of multicollinearity where the coefficients are poorly estimated, and the p-values are questionable.
Use VIFs to identify correlations between variables and determine the strength of the relationships. Most statistical software can display VIFs for you. Assessing VIFs is particularly important for observational studies because these studies are more prone to having multicollinearity.
| 0.961307 | 0.995566 |
# Matthew Hansen
## What statistics are required to have an MVP level season? Does winning an MVP mean the player will have a good career?
I am interested in analyzing the statistics of NHL MVPs to find similar stats to understand what is needed to be an MVP. In addition I want to see what type of careers an MVP has.
### Step 1: Import the the data
```
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
import seaborn as sns
nhl_stats = pd.read_csv("../data/raw/NHL_Players_Statistics.csv", sep=';')
nhl_stats
```
## Task 1: Conduct an exploratory data analysis (EDA)
```
print("Number of rows and columns respectively:", nhl_stats.shape)
print("Columns in the dataset:", nhl_stats.columns)
nhl_stats.describe(include=['float64', 'int64'])
```
**Analysis:** By looking at the mean we can see the average player in the NHL. 44 games played, 8 goals, 13 assists, and 21 points per season.
```
sns.displot(nhl_stats["Goals"])
sns.displot(nhl_stats["Points"])
```
These graphs show how rare it is for a player to score 40 goals or have 100 points
## Task 2-3: Setting up an analysis pipeline
### To complete step 3, I will import my functions
```
import project_functions2 as pf
```
The first function imports the dataset and loads it as a pandas dataframe
```
data = pf.unprocessed("../data/raw/NHL_Players_Statistics.csv")
data
```
The second function is to complete task 2 of creating the analysis pipeline. It starts to load, clean, process and wrangle the data.
It drops all of the columns that will not be used in my analysis. In addition, it removes all data of the years before 1988. This is so that I can look at the career stats of each MVP winner from 2001-2018.
```
initial_clean = pf.intial_process("../data/raw/NHL_Players_Statistics.csv")
initial_clean
```
This final function is the most important for my analysis. I need to identify which player won the MVP in each year. In order to do this I created a list of the player that won the award and the season they won it in.
It then merges the new list with the original datafile. This drops every row except the season statistics for an MVP.
One player was traded mid season so he had two rows for himself. This function adds up his two seperate columns to give his season total.
```
mvp_skaters = pf.mvp_seasons("../data/raw/NHL_Players_Statistics.csv")
mvp_skaters
```
**This list excludes goalies because comparing their stats to skaters is implausible**
```
mvp_skaters[["Age","Goals","Points","PlusMinus_Ratings"]].describe()
```
There is some key information that can be identified from this. Firstly, the mean of each players stats provides an idea of what is needed to be an MVP.
Second, the average age hints towards when a player is at peak performance. A common idea in sports is that a player is at their prime at the age of 27. This analysis agrees with that
The average total age for an MVP is: **26.9**
The average total goals for an MVP is: **42.1**
The average total points for an MVP is: **104.5**
The average total +/- for an MVP is: **+23**
**By using a series of scatterplots we can compare the MVPs on each statistical element**
```
mvp_skaters.plot(kind='scatter', x='Goals', y='Name')
mvp_skaters.plot(kind='scatter', x='Assists', y='Name')
mvp_skaters.plot(kind='scatter', x='Points', y='Name')
mvp_skaters.plot(kind='scatter', x='PlusMinus_Ratings', y='Name')
mvp_skaters.plot(kind='scatter', x='Game_Winning_Goals', y='Name')
```
We can see that there are also lower thresholds for specific statistics. In addition, we can see that there is a variety in performance from player to player.
One thing to point out is the outliers of Alex Ovechkin on the bottom row. The 2015 season missed half of the games due to a lockout.
```
mvp_careers = {
'Name': ['Taylor Hall', 'Connor McDavid', 'Patrick Kane', 'Sidney Crosby', 'Alex Ovechkin', 'Evgeni Malkin', 'Corey Perry', 'Henrik Sedin', 'Joe Thornton', 'Martin St. Louis', 'Peter Forsberg', 'Joe Sakic'],
}
pd.DataFrame.from_dict(mvp_careers)
```
**Now I am creating a new dataframe that shows the career numbers of each player that has won an MVP**
```
mvp_df = pd.DataFrame(mvp_careers)
nhl_analysis_merged_careers = pd.merge(data, mvp_df)
nhl_analysis_merged_careers2 = nhl_analysis_merged_careers.groupby(["Name"],as_index=False)[["Games_Played","Goals", "Assists","Points", "PlusMinus_Ratings", "Game_Winning_Goals"]].sum()
nhl_analysis_merged_careers2
nhl_analysis_merged_careers2[["Goals","Assists","Points","PlusMinus_Ratings"]].describe()
```
Again we can look at the mean for each column to find the average career for an MVP.
```
games_total = nhl_analysis_merged_careers2["Games_Played"].sum()
goals_total = nhl_analysis_merged_careers2["Goals"].sum()
assists_total = nhl_analysis_merged_careers2["Assists"].sum()
points_total = nhl_analysis_merged_careers2["Points"].sum()
goals_per_game = goals_total/games_total
assists_per_game = assists_total/games_total
points_per_game = points_total/games_total
print("Average goals per game is: {:.3f}".format(goals_per_game))
print("Average assists per game is: {:.3f}".format(assists_per_game))
print("Average points per game is: {:.3f}".format(points_per_game))
```
We can see that over the course of the career of an MVP, on average they will score more than one point every game.
In addition, we can see from the dataframe that all but one player is a career positive when on the ice.
70% of the players reached the significant 1000 point mark as well.
```
nhl_analysis_merged_careers2.plot(kind='scatter', x='Goals', y='Name')
nhl_analysis_merged_careers2.plot(kind='scatter', x='Assists', y='Name')
nhl_analysis_merged_careers2.plot(kind='scatter', x='Points', y='Name')
nhl_analysis_merged_careers2.plot(kind='scatter', x='PlusMinus_Ratings', y='Name')
nhl_analysis_merged_careers2.plot(kind='scatter', x='Game_Winning_Goals', y='Name')
```
Another set of scatterplots compares the career statistics of each player
```
mvp_df = pd.DataFrame(mvp_careers)
nhl_analysis_merged_seasons = pd.merge(data, mvp_df)
a4_dims = (15, 12)
fig, ax = plt.subplots(figsize=a4_dims)
ax = sns.boxplot(x="Points", y="Name", data=nhl_analysis_merged_seasons)
ax.set_title('BoxPlot of Weighted Scores by Genre')
ax.set_xlabel("Points")
ax.set_ylabel("Genre")
ax
```
Finally, by using a histogram the average points of each player are shown more clearly.
This visual shows the most common point totals and identifies any outliers.
It is important to note that the outlier for Taylor Hall is the season that he won MVP. This implies that his MVP season was a fluke and that he is unlikely to repeat that season or compare equally with the other players
## Concluding my analysis
By analysing the statistics of each MVP winner and using an assortment of graphing tools I have determined a framework of what is required to be an MVP. The average goals and points for an MVP are 42 and 105 respectively. In addition, from the plus minus statistic it is easy to tell that MVPs contribute to more goals for their team than the amount they give up.
After that first analysis, I then observed the overall careers of each player that won the award. A winner of the award is expected to have a fruitful career. By looking at the career statistics I found that each player finishes with well over 1000 points and 400 goals. These are massive milestones for any player.
Finally, the histogram shows the consistency of each player. It provides a range of points that the player usually scores in a season. The main thing out of this visual is that Taylor Hall has not consistently performed at his MVP level. This implies that he will not live up to the careers of other MVPs.
In conclusion, MVP is a difficult award to achieve and that is clear from this analysis. Each of these players are some of the best of all time.
```
nhl_analysis_merged_careers2.to_csv("analysis2_processed.csv", index = False)
mvp_skaters.to_csv("analysis2_processed_part2.csv", index = False)
initial_clean.to_csv("cleaned_data.csv", index = False)
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
import seaborn as sns
nhl_stats = pd.read_csv("../data/raw/NHL_Players_Statistics.csv", sep=';')
nhl_stats
print("Number of rows and columns respectively:", nhl_stats.shape)
print("Columns in the dataset:", nhl_stats.columns)
nhl_stats.describe(include=['float64', 'int64'])
sns.displot(nhl_stats["Goals"])
sns.displot(nhl_stats["Points"])
import project_functions2 as pf
data = pf.unprocessed("../data/raw/NHL_Players_Statistics.csv")
data
initial_clean = pf.intial_process("../data/raw/NHL_Players_Statistics.csv")
initial_clean
mvp_skaters = pf.mvp_seasons("../data/raw/NHL_Players_Statistics.csv")
mvp_skaters
mvp_skaters[["Age","Goals","Points","PlusMinus_Ratings"]].describe()
mvp_skaters.plot(kind='scatter', x='Goals', y='Name')
mvp_skaters.plot(kind='scatter', x='Assists', y='Name')
mvp_skaters.plot(kind='scatter', x='Points', y='Name')
mvp_skaters.plot(kind='scatter', x='PlusMinus_Ratings', y='Name')
mvp_skaters.plot(kind='scatter', x='Game_Winning_Goals', y='Name')
mvp_careers = {
'Name': ['Taylor Hall', 'Connor McDavid', 'Patrick Kane', 'Sidney Crosby', 'Alex Ovechkin', 'Evgeni Malkin', 'Corey Perry', 'Henrik Sedin', 'Joe Thornton', 'Martin St. Louis', 'Peter Forsberg', 'Joe Sakic'],
}
pd.DataFrame.from_dict(mvp_careers)
mvp_df = pd.DataFrame(mvp_careers)
nhl_analysis_merged_careers = pd.merge(data, mvp_df)
nhl_analysis_merged_careers2 = nhl_analysis_merged_careers.groupby(["Name"],as_index=False)[["Games_Played","Goals", "Assists","Points", "PlusMinus_Ratings", "Game_Winning_Goals"]].sum()
nhl_analysis_merged_careers2
nhl_analysis_merged_careers2[["Goals","Assists","Points","PlusMinus_Ratings"]].describe()
games_total = nhl_analysis_merged_careers2["Games_Played"].sum()
goals_total = nhl_analysis_merged_careers2["Goals"].sum()
assists_total = nhl_analysis_merged_careers2["Assists"].sum()
points_total = nhl_analysis_merged_careers2["Points"].sum()
goals_per_game = goals_total/games_total
assists_per_game = assists_total/games_total
points_per_game = points_total/games_total
print("Average goals per game is: {:.3f}".format(goals_per_game))
print("Average assists per game is: {:.3f}".format(assists_per_game))
print("Average points per game is: {:.3f}".format(points_per_game))
nhl_analysis_merged_careers2.plot(kind='scatter', x='Goals', y='Name')
nhl_analysis_merged_careers2.plot(kind='scatter', x='Assists', y='Name')
nhl_analysis_merged_careers2.plot(kind='scatter', x='Points', y='Name')
nhl_analysis_merged_careers2.plot(kind='scatter', x='PlusMinus_Ratings', y='Name')
nhl_analysis_merged_careers2.plot(kind='scatter', x='Game_Winning_Goals', y='Name')
mvp_df = pd.DataFrame(mvp_careers)
nhl_analysis_merged_seasons = pd.merge(data, mvp_df)
a4_dims = (15, 12)
fig, ax = plt.subplots(figsize=a4_dims)
ax = sns.boxplot(x="Points", y="Name", data=nhl_analysis_merged_seasons)
ax.set_title('BoxPlot of Weighted Scores by Genre')
ax.set_xlabel("Points")
ax.set_ylabel("Genre")
ax
nhl_analysis_merged_careers2.to_csv("analysis2_processed.csv", index = False)
mvp_skaters.to_csv("analysis2_processed_part2.csv", index = False)
initial_clean.to_csv("cleaned_data.csv", index = False)
| 0.318591 | 0.983738 |
# Header
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math as math
import janitor
from sklearn.linear_model import LinearRegression
import os
exec(open("../header.py").read())
```
# Import
```
threshold = 40
data_folder = processed_root("02-train-validation-test-split/threshold-"+str(threshold)+"/")
data_folder
train_data = pd.read_csv(data_folder+"train_data.csv")
val_data = pd.read_csv(data_folder+"val_data.csv")
test_data = pd.read_csv(data_folder+"test_data.csv")
```
# Clean
## Bag of words functions
```
def extract_words_from_text(texts):
'''
Purpose: Helper function for bag_of_words
Input: texts
Output: list of words that occur in more than threshold texts
'''
threshold = 5
word_counts = {}
for text in texts:
for word in text:
if word in word_counts:
word_counts[word] += 1
else:
word_counts[word] = 1
filtered_word_counts = word_counts.copy()
for i in word_counts:
if filtered_word_counts[i] < threshold:
filtered_word_counts.pop(i)
return list(filtered_word_counts.keys())
def extract_text(data, text_column):
'''
Purpose: Helper function for bag_of_words
Input: Dataset
Output: array of email sets of words (sets don't allow duplicates)
'''
return(data.apply(lambda x:set(x[text_column].split(' ')), axis = 1))
extract_text(train_data, 'clean_content')
def bag_of_words(data, content_column, word_data = None):
'''
Purpose: Converts a dataset to bag of words format.
Input: Dataset
Output: Bag of words version of the data
'''
texts = extract_text(data, content_column)
if word_data is None:
bag = extract_words_from_text(texts)
else:
bag = extract_words_from_text(extract_text(word_data, content_column))
word_occurence = words_in_texts(bag, texts)
data = data.reset_index(drop = True)
new_data = pd.DataFrame(data = word_occurence, columns = bag)
new_data.insert(0, 'poetry_text', data[content_column])
new_data['poetry_author'] = data['author']
return(new_data)
def words_in_texts(words, texts):
'''
Args:
words (list-like): words to find
texts (Series): sets of words to search in
Returns:
NumPy array of 0s and 1s with shape (n, p) where n is the
number of texts and p is the number of words.
Only considers whole words, not partial.
'''
indicator_array = np.array([texts.map(lambda x:word in x) for word in words]).T
return indicator_array.astype('int32')
```
# Run bag of words for each threshold
```
def save_datasets(df_dict, save_folder):
for i in df_dict:
try:
df_dict[i].to_csv(save_folder + "/" + i, index = False)
except FileNotFoundError:
os.mkdir(save_folder)
df_dict[i].to_csv(save_folder + "/" + i, index = False)
def bag_of_words_for_threshold(threshold):
data_folder = processed_root("02-train-validation-test-split/threshold-"+str(threshold)+"/")
train_data = pd.read_csv(data_folder+"train_data.csv")
val_data = pd.read_csv(data_folder+"val_data.csv")
test_data = pd.read_csv(data_folder+"test_data.csv")
bag_train_data = bag_of_words(train_data, content_column = 'clean_content')
bag_val_data = bag_of_words(val_data,
content_column = 'clean_content',
word_data = train_data)
bag_test_data = bag_of_words(test_data,
content_column = 'clean_content',
word_data = train_data)
print("Threshold:", threshold)
print("Bag Train:", bag_train_data.shape)
print("Bag Val:", bag_val_data.shape)
print("Bag Test:", bag_test_data.shape)
dfs_to_save = {'bow_train_data.csv':bag_train_data,
'bow_val_data.csv':bag_val_data,
'bow_test_data.csv':bag_test_data}
save_datasets(dfs_to_save, save_folder = processed_root("03-bag-of-words/threshold-"+str(threshold)))
bag_of_words_for_threshold(30)
bag_of_words_for_threshold(40)
bag_of_words_for_threshold(50)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math as math
import janitor
from sklearn.linear_model import LinearRegression
import os
exec(open("../header.py").read())
threshold = 40
data_folder = processed_root("02-train-validation-test-split/threshold-"+str(threshold)+"/")
data_folder
train_data = pd.read_csv(data_folder+"train_data.csv")
val_data = pd.read_csv(data_folder+"val_data.csv")
test_data = pd.read_csv(data_folder+"test_data.csv")
def extract_words_from_text(texts):
'''
Purpose: Helper function for bag_of_words
Input: texts
Output: list of words that occur in more than threshold texts
'''
threshold = 5
word_counts = {}
for text in texts:
for word in text:
if word in word_counts:
word_counts[word] += 1
else:
word_counts[word] = 1
filtered_word_counts = word_counts.copy()
for i in word_counts:
if filtered_word_counts[i] < threshold:
filtered_word_counts.pop(i)
return list(filtered_word_counts.keys())
def extract_text(data, text_column):
'''
Purpose: Helper function for bag_of_words
Input: Dataset
Output: array of email sets of words (sets don't allow duplicates)
'''
return(data.apply(lambda x:set(x[text_column].split(' ')), axis = 1))
extract_text(train_data, 'clean_content')
def bag_of_words(data, content_column, word_data = None):
'''
Purpose: Converts a dataset to bag of words format.
Input: Dataset
Output: Bag of words version of the data
'''
texts = extract_text(data, content_column)
if word_data is None:
bag = extract_words_from_text(texts)
else:
bag = extract_words_from_text(extract_text(word_data, content_column))
word_occurence = words_in_texts(bag, texts)
data = data.reset_index(drop = True)
new_data = pd.DataFrame(data = word_occurence, columns = bag)
new_data.insert(0, 'poetry_text', data[content_column])
new_data['poetry_author'] = data['author']
return(new_data)
def words_in_texts(words, texts):
'''
Args:
words (list-like): words to find
texts (Series): sets of words to search in
Returns:
NumPy array of 0s and 1s with shape (n, p) where n is the
number of texts and p is the number of words.
Only considers whole words, not partial.
'''
indicator_array = np.array([texts.map(lambda x:word in x) for word in words]).T
return indicator_array.astype('int32')
def save_datasets(df_dict, save_folder):
for i in df_dict:
try:
df_dict[i].to_csv(save_folder + "/" + i, index = False)
except FileNotFoundError:
os.mkdir(save_folder)
df_dict[i].to_csv(save_folder + "/" + i, index = False)
def bag_of_words_for_threshold(threshold):
data_folder = processed_root("02-train-validation-test-split/threshold-"+str(threshold)+"/")
train_data = pd.read_csv(data_folder+"train_data.csv")
val_data = pd.read_csv(data_folder+"val_data.csv")
test_data = pd.read_csv(data_folder+"test_data.csv")
bag_train_data = bag_of_words(train_data, content_column = 'clean_content')
bag_val_data = bag_of_words(val_data,
content_column = 'clean_content',
word_data = train_data)
bag_test_data = bag_of_words(test_data,
content_column = 'clean_content',
word_data = train_data)
print("Threshold:", threshold)
print("Bag Train:", bag_train_data.shape)
print("Bag Val:", bag_val_data.shape)
print("Bag Test:", bag_test_data.shape)
dfs_to_save = {'bow_train_data.csv':bag_train_data,
'bow_val_data.csv':bag_val_data,
'bow_test_data.csv':bag_test_data}
save_datasets(dfs_to_save, save_folder = processed_root("03-bag-of-words/threshold-"+str(threshold)))
bag_of_words_for_threshold(30)
bag_of_words_for_threshold(40)
bag_of_words_for_threshold(50)
| 0.318485 | 0.738174 |
<a href="https://colab.research.google.com/github/SotaYoshida/Lecture_DataScience/blob/2021/notebooks/Python_chapter6_Regression.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 相関・回帰分析
*相関関係は因果関係を含意しない (Correlation does not imply causation)*
[この章の目的]
初歩的な相関分析と回帰分析がPythonで出来るようになる。
補足資料: [講義ノート](https://drive.google.com/file/d/1ZKi8DJFSg00xir1IoEQiw3z9vxmejeCv/view)
今回使用するライブラリをインポートしておきましょう。
```
from matplotlib import pyplot as plt
!pip install japanize-matplotlib
import japanize_matplotlib
import numpy as np
```
## 相関分析 (復習)
1年生前期の必修科目[DS入門]でも(多くの学科で)[相関分析]を学習しました。
解析したいデータが2種類だけなら、プログラムを使うありがたみはそれほど感じられないと思いますが
「多くのデータ間の相関関係を系統的に調べたい」
あるいは「複数年度に渡るデータを解析したい」となると、
Excelはデータが大きくなるとすぐに挙動が重くなってしまうため
精神によくありません(私見)ので、Pythonで扱うのがオススメです。
以下では、復習を兼ねて簡単な例の相関分析を扱って、
時間に余裕があれば前章のおまけの詳細を扱うことにします。
まずは簡単な例から初めましょう。
```
x= [3.1, 4.3, 6.6, 13.2, 19.1, 20.9, 26.4, 25.1, 21.9, 15.7, 9.6, 3.8]
y= [568, 572, 804, 833, 930, 965, 1213, 1120, 835, 540, 451, 502]
```
上に示したのは、2017年の宇都宮市における月別の平均気温$x$と
世帯ごとのアイスクリーム・シャーベットの平均消費金額$y$です。
散布図にすると↓こんな感じ
```
plt.figure(figsize=(6,6))
plt.title("宇都宮市")
plt.xlabel("平均気温 (℃)")
plt.ylabel("世帯あたりのアイスクリム・シャーベットの消費金額 (円)")
plt.scatter(x,y)
plt.show()
plt.close()
```
「平均気温とアイスの消費には相関がありそう」という直感の通り、
正の相関があることが見て取れます。
では"どれほどの"相関を持つかを表す量として相関係数を算出してみましょう。
相関係数$r$は以下のように定義されます。
$r= \frac{ \sum^n_i (x_i-\bar{x})(y_i-\bar{y})}{ \sqrt{\sum^n_i (x_i-\bar{x})^2 \sum^n_i (y_i-\bar{y})^2} }$
$\bar{x},\bar{y}$はそれぞれ$x,y$の平均値で、数式で書くと$\bar{x} \equiv \frac{1}{n} \sum^n_i x_i $, $\bar{y} \equiv \frac{1}{n} \sum^n_i y_i $
という感じです。
ここで$\equiv$は[定義]を表し、下付き添字$i$は$x$の$i$番目の要素であることを表します。
(つまり$x$をn次元ベクトルとみなしたときの$i$成分が$x_i$とも言えますね)
今考えているデータの場合、$\sum$の和記号は$i$は1から12までの値を取り
対応する値を足し上げることを意味します。
("$i$の和が1から12までを走る"といったりもする)
この$r$の定義では、$r$は必ず-1から1までの値を取り※
1.0(-1.0)に近づくにつれて強い正(負)の相関を持ちます。
(強いというのは曖昧な表現で絶対的な線引がある訳ではありません)
>$|r|\leq1$は、コーシーシュワルツの不等式を用いるか
上の$r$の定義と$n$次元ベクトル同士の内積の定義とを見比べると示すことが出来ます(暇があればやってみましょう)。
では```x``` ,``` y```2つのリストを引数に持ち、この相関係数$r$を返す関数を作成してみましょう。
にらめっこするために式を再掲しておきます:
$r= \frac{ \sum^n_i (x_i-\bar{x})(y_i-\bar{y})}{ \sqrt{\sum^n_i (x_i-\bar{x})^2 \sum^n_i (y_i-\bar{y})^2} }$
```
### ライブラリを一切使わない方法
# ※1 xとyの長さが違う場合、長さ0の場合はエラーとし、返り値Noneを返す。
# ※2 Pythonではwarning(警告)を返す機能などもあるが、授業では扱わないのでNoneを返す関数とした。
def cor_coeff(x,y):
if len(x) != len(y) or len(x)==len(y)==0:
print("Error: x&y must satisfy len(x) = len(y) != 0") # ※1
return None # ※2
n = len(x)
## 平均を計算
xbar = sum(x)/n; ybar = sum(y)/n
##分子(numerator)の和を計算 (初期値を0に)
s_n = 0.0
for i in range(n):
s_n += (x[i]-xbar)*(y[i]-ybar)
##分母(denominator)の計算 (和を先に計算して積を取り、最後にsquare rootをとる)
s_x = 0.0; s_y = 0.0
for i in range(n):
s_x += (x[i]-xbar)**2
s_y += (y[i]-ybar)**2
s_d = (s_x * s_y)**0.5
# 一行で書くなら
#s_d = ( sum([(x[i]-xbar)**2 for i in range(n)]) * sum([(y[i]-ybar)**2 for i in range(n)]) )**0.5
return s_n/s_d # 分子/分母の値を返す
cor_coeff(x,y)
```
という風に、$r$が約0.83で、非常に強い正の相関を示すことがわかりました.
numpyライブラリを使うともう少しシンプルに書けるので、それもやっておきましょう.
```
def cor_coeff_np(x,y):
xbar = np.mean(x); ybar=np.mean(y) #np.mean()は整数・実数値が入ったリスト(やnumpy array)の平均を計算
return np.dot(x - xbar,y-ybar) / np.sqrt( np.dot(x-xbar,x-xbar) * np.dot(y-ybar,y-ybar) )
cor_coeff_np(x,y)
```
とすると、関数自体は数行で書けてしまいました。
さらに$\bar{x},\bar{y}$をいちいち定義しないように書き換えれば、関数の中身自体は一行でかけてしまいます。
上のコードを少し補足しておくと...分子や分母に現れる
$\sum^n_i (x_i-\bar{x})(y_i-\bar{y})$や$\sum^n_i (x_i-\bar{x})^2 $といった項は、
$i$番目の成分に$x_i-\bar{x}$を持つベクトル$\tilde{x}$と
$i$番目の成分に$y_i-\bar{y}$を持つベクトル$\tilde{y}$を定義しておくと、
$\tilde{x}\cdot\tilde{y}$, $\tilde{x}\cdot\tilde{x}$, $\tilde{y}\cdot\tilde{y}$といったように、
ベクトルの内積の形でいずれも表すことができます。
numpyにはブロードキャスト機能(Numpyのノートを参照)や
ベクトル積を計算する関数```dot```が備わっているので、
それらを活用することで短く実装することができました。
実はnumpyには相関係数を計算する関数```corrcoef()```が予め用意されていて
```
print(np.corrcoef(x,y))
print("r(x,y)=", np.corrcoef(x,y)[0,1])
```
を使えば
[ xとxの相関(=1.0), xとyの相関;
yとxの相関, yとyの相関(=1.0)]
といった2行2列の相関行列を取得することが出来ます。
確かに上の相関行列の[0,1]成分は、
さっき計算した$r$の値と一致しています。
「初めからそれを教えろ!」と思うかもしれませんが、
**考えたい量を数式として定義してそれをプログラムに変換し、
値が正しいかどうかを確かめておくのは、式(考え方)とプログラミング
双方の理解を深める上で非常に重要なプロセスです**
### 相関分析と因果関係
前章のファイル操作では、エクセルファイルからデータを読み込んで
系統的に相関分析を行うコードを紹介しました。
以下では、そのうちの一つのグラフを見ながら、
冒頭の*相関関係は因果関係を含意しない (Correlation does not imply causation)*
に関して説明します。
下の図は、2017年の家計調査・気候データから作成した散布図で、
千葉市での平均気温と、しめじの消費支出の間の相関を示しています。
<img src="https://drive.google.com/uc?export=view&id=1P4bYyfUDHMXOtGRrDBBLszVNijDqGv6H" width = 40%>
生産量と平均気温の間に、強い負の相関が見て取れますが、これはどうしてでしょうか?
「寒い季節には鍋が食べたくなるから」と言われるとふむふむと感じる一方で
「そもそも生産量が冬に多く、市場に出回る量が多いから」と考えることもできます。
したがって、このデータを見ただけでは、しめじが冬によく売れる理由までははっきりとは分かりません。
事実、しめじの旬はGoogle検索によると9月下旬から11月初旬とのことで、
最も売れている時期(12月1月)とは少し時期にズレがあり、
購買意欲は必ずしも"旬"によって決まっている訳ではなさそうな印象を受けます。
気温と特定の野菜の購買意欲の真の関係を知りたければ、
「その野菜はビニールハウスなどの生産設備の向上で年中、安定した味で生産ができる」
「比較的新しい品種で〇〇といえば秋、のような固定観念がない」
「季節ごとの生産量がほぼ同じ」
など、他の条件が揃った状況下で比較しなければ確度の高い議論は難しいでしょう。
このように、因果関係を紐解くことは、我々が思うほど容易ではなく、
それ自体が一つの学問体系になっています。
気になる方は、たとえば[因果推論]で調べてみましょう。
「我々が見ている相関関係は2次元よりも遥かに高次元の空間での関係
を低次元へ射影した影を見ているに過ぎない」とも言えるでしょう。
疑似相関に関するその他の話題は以下を参照してください
* [講義ノート](https://drive.google.com/file/d/1ZKi8DJFSg00xir1IoEQiw3z9vxmejeCv/view)の3.2章
* [疑似相関をまとめたおもしろいサイトはこちら](https://www.tylervigen.com/spurious-correlations)
## 回帰分析
以下では自分が立てたモデルを表現する関数のことを*モデル関数*、
モデル関数とデータとの齟齬を最小化するようにモデル関数の係数を決定することを**回帰**、
そして回帰に基づく分析を指して**回帰分析**と呼ぶことにします。
データとモデル間の齟齬を表現する方法はいくつかありますが、
以下では最もポピュラーな誤差の二乗和を採用することとし、
その最小化を考えていきましょう(最小二乗法とも呼びます)。
$D$個の点$\{x_1,x_2,...,x_D\}$でのyの値$\{y_1,y_2,...,y_D\}$が観測されているとき、
最小二乗法とは、ある決められたモデル関数$f(x)$との齟齬$\chi^2 = \sum^D_{i=1} (y_i - f(x_i))^2$を
最小化するように関数$f$の係数を調整することとも言いかえられます。
$f$自体をどう決める/設計するかも重要な話題ですが、授業では深入りしません。
たとえば回帰を行う関数として、ニューラルネットワークを採用する立場を採ることも可能です。
参照: [おまけのノートブック: ニューラルネットワークによる回帰](https://colab.research.google.com/github/SotaYoshida/Lecture_DataScience/blob/2021/notebooks/Python_chapter_ArtificialNeuralNetwork.ipynb)
以下では、$f(x)$として単純な多項式のみを考えることにします。
まず回帰を学ぶために、適当なデータを生成しておきましょう
```
# sample_size: データの数
# std: standard deviation (標準偏差σ)
def create_toy_data(sample_size, std):
x = np.linspace(0, 1, sample_size)
t = np.sin(2*np.pi*x) + np.random.normal(scale=std, size=x.shape)
return x, t
np.random.seed(1234) #私と皆さんで結果が変わらないよう乱数のseedを固定, 詳しくは8章で
x,y = create_toy_data(10,1.e-1)
```
これをグラフにしてみると...
```
fig = plt.figure(figsize=(10,4))
ax = fig.add_subplot(111)
ax.set_xlabel("x"); ax.set_ylabel("y")
ax.scatter(x, y, facecolor="none", edgecolor="b", s=50, label="Data")
ax.legend()
plt.show()
plt.close()
```
こんな感じ。
このデータを、$p$次元の多項式(p=0,1,2,...)でフィッティングすることを考えてみましょう。
$p$次式($p$次元多項式)は、$p+1$個の係数, $a_0$から$a_p$を使って
$a_0 + a_1x + a_2x^2\cdots +a_p x^p $と書くことが出来ます。
$p$次元のフィッティングは、実はnumpyにある関数```polyfit()```を利用すれば一瞬で行えます。
(全学部向けの授業なのでとりあえずライブラリを利用することにします。
他にもscikit-learnなどのライブラリもより高度な関数のフィッティングが可能です。
第2回のレポートでは、ごく簡単な場合にもう少し自分の手で愚直にフィッティングをすることを考えてもらう予定です。)
> $\clubsuit$進んだ注:
多項式で回帰を行う場合には、実はパラメータの最適解は"閉じた形"で与えられます。
この辺りのことは、おまけのノートブック[ベイズ線形回帰](https://colab.research.google.com/github/SotaYoshida/Lecture_DataScience/blob/2021/notebooks/Python_chapter_Bayesian_linear_regression.ipynb)で詳しく書いています。
なお"閉じた形"というのは、数学や物理をやっていると出てくる表現で、
答えが具体的な形で書き下せる、程度の意味です。
たとえば 行列$A$、ベクトル$\vec{x},\vec{y}$,スカラー$\lambda$について方程式$A\vec{x}=\lambda \vec{y}$が成り立つとき、
$A$の逆行列をどうやって求めるか(数値的にやるのか解析的に求めるのか)はさておき、
$\vec{x} = \lambda A^{-1}\vec{y}$と書き直せるので
「$\vec{x}$は閉じた形で与えられる」と言ったりします。
### polyfit/poly1d関数
たとえば今のデータを3次式でフィットしたければ、以下のようにします
```
## 多項式をplotするためのxの値を準備(グラフをなめらかにするために、0から1までの間の500点を等間隔に取る)
xp = np.linspace(0, 1, 500)
p=3 #多項式の次元を決める. 今は3次式.
coeff = np.polyfit(x, y, p)
yp = np.poly1d( coeff )(xp)
print("係数",coeff)
```
```np.polyfit(x, y, p)```では、データのx,yの値と多項式の次元pを引数として与え、
$p$次の多項式でデータ$(x,y)$をfitしなさい
(つまり、$p$次までの係数を関数がデータと整合するように"最適化"しなさい)
という指令を与えています.
```np.poly1d( np.polyfit(x, y, p) )(xp)```では、
fitしたp次元の係数をもつ多項式に```xp```(今は500点)を代入して、対応する```y```の値を返します。
上のコードはこの返り値をypという変数に格納しています。
最後に、調整(最適化)された3次式の係数を表示してみました。
ちなみに、表示される係数は次数が高いところから$a_3,a_2,a_1,a_0$です(ややこしい...)。
グラフを描いてみるとこんな感じ。
```
#お絵かき
fig = plt.figure(figsize=(10,4))
ax = fig.add_subplot(111)
ax.set_xlabel("x"); ax.set_ylabel("y")
ax.scatter(x, y, facecolor="none", edgecolor="b", s=50, label="Data")
ax.plot(xp, yp,label="p=3")
ax.legend()
plt.show()
plt.close()
```
さて、$p$次の多項式は$p-1$次の多項式を特別な場合として含むため、
一般に$p$(多項式の次元)を増やせば、より複雑な関数を表現することができます。
(2次式は3次式の$a_3=0$の場合ですよね?)
$p$を複数変えながら比較した図を作ってみましょう。
方法は$p$に関するループを回すだけです。
```
ps = [0,1,3,6,9]
ys = []
xp = np.linspace(0, 1, 500) ## 多項式をplotするためのxの値を準備
for p in ps:
ys += [np.poly1d(np.polyfit(x, y, p))(xp)]
ytrue = np.sin(2*np.pi*xp)
fig = plt.figure(figsize=(12,5))
ax = fig.add_subplot(111)
ax.set_xlabel("x"); ax.set_ylabel("y")
ax.scatter(x, y, facecolor="none", edgecolor="b", s=80, label="Data")
for i in range(len(ps)):
ax.plot(xp, ys[i],label="p="+str(ps[i]),alpha=0.8)
ax.plot(xp,ytrue,linestyle="dotted", label="True",color="k")
ax.legend(loc="upper right")
plt.show()
plt.close()
```
> 注: 今の場合、コードをよく見るとデータはsin関数に適当なノイズを足したものだということが分かります。
解析の手法を学ぶ際には、このように答えを知っている状態からはじめて、手法がうまくデータを説明しているかどうかを検証したりします。一見ズルっぽいですが、重要なプロセスです。
現実のデータ解析の状況では、背後にある"真の関数"が分かっていることは非常に稀ですし、
「興味のあるデータが、人間がよく知っている単純な式(有限次元の多項式や指数関数)で
完全に表現できる道理はない」ということも抑えておくべき重要な点です.
真の関数というのは一般に[神のみぞ知る]で、
人間ができることは出来るだけ尤もらしい関数を見つけ、
その背後にあるメカニズム(の主要部分)を解明することです.
一般に、関数をどんどん複雑なものにしていくにつれて、表現できるデータの幅は大きく拡がります。
その一方で、用意した関数がデータに過度に適合するあまり、
**未知の点での値の予測精度(汎化性能)が著しく損なわれている危険性があります**。
このことを予言能力がない(データに過適合している) と言ったりします。
データの背後にあるメカニズムが何かを考えたり理論的な解析をして初めて、
回帰に用いる関数の妥当性が検証できるという点に注意しましょう。
### $\clubsuit$ モデルの複雑さとモデル選択
上の多項式回帰では、たとえば9次式はデータをピッタリと再現している一方で
真の関数(sin関数)の振る舞いよりもむしろ、測定誤差のようなものにまで過適合してしまっています。
ここで過適合を防ぐためにデータとの整合性(二乗誤差)だけでなく
**モデルの複雑さ**も定量化して勘定することを考える。
ここではこのモデルの複雑さ$C$として多項式の係数の絶対値の2乗和:
$C= \sum_i |a_i|^2$を採用することにしよう。
さらに、"モデルを選択するための基準$L$"を
$L = $(二乗誤差) + $\lambda$ log10(モデルの複雑さ$C$)で定量化し
この$L$が最小になる多項式を採用することにしよう。
(この選択はあくまで例であることに注意)
各次数での多項式のモデルの複雑さ$C$と二乗誤差、そしてモデル選択基準量$L$を表示してみると...
```
def complexity(r):
return np.sqrt(np.dot(r,r))
def my_criteria(comp,err,lam=1.0): #lambda=1.0
return err + lam * np.log10(comp)
for p in ps:
coeff = np.polyfit(x, y, p)
diff = np.poly1d(np.polyfit(x, y, p))(x) - y
chi2 = np.dot(diff,diff)
comp = complexity(coeff)
print("p",p, "モデルの複雑さ(log10)→", np.log10(comp),
"二乗誤差", chi2, "モデル選択基準量", my_criteria(comp,chi2))
```
9次式は、データをよく説明する一方で、非常に複雑なモデルになっている。
上記のモデル選択基準量$L$は$p=3$で最小となるため
この$L$の定義のもとでは3次式が選ばれることになる。
このように実際のデータ分析や機械学習などのモデル選択では、
データの説明(たとえば二乗誤差)と複雑さのトレードオフで
できるだけ過適合を避けるようなモデルを選択することを目指す。
上の$L$の定義中の$\lambda$の大きさを変えることは
データとの整合性を高める/モデルの複雑さを抑える
のどちらを重視するかの"度合い"を決めることに相当する。
($\lambda$を適当に変えてみよう)
参考→正則化でググってみよう.
### (余談1) 100メートル走のタイム
上記のことに関連して、こういう例を考えてみましょう。
```
y = [ 10.06, 10.03,10.02, 9.95,9.93, 9.92,9.9, 9.86,9.85, 9.84, 9.79, 9.78, 9.77, 9.74,9.72,9.69,9.58 ]
x = [1964, 1968,1968,1968,1983,1988,1991,1991,1994,1996,1999,2002,2005,2007,2008,2008,2009 ]
fig = plt.figure(figsize=(12,3))
ax = fig.add_subplot(111)
ax.set_xlabel("year"); ax.set_ylabel("Mens 100m")
ax.scatter(x,y,marker="o",color="red")
plt.show()
plt.close()
```
図にしたのは、男子100mの世界記録の推移です。
このデータに対して「$p=3$の多項式でフィットして予測する」という立場をとってみましょう。
```
xp = np.arange(2020,2101,1)
fig = plt.figure(figsize=(12,6))
ax = fig.add_subplot(111)
ax.set_xlabel("year"); ax.set_ylabel("Mens 100m")
ax.set_xlim(1960,2100)
ax.set_ylim(0,12)
for p in [3]:
yp = np.poly1d(np.polyfit(x, y, p))(xp)
ax.plot(xp,yp,marker="x",label="p="+str(p))
ax.scatter(x,y,marker="x",color="red")
ax.legend(loc="upper right")
plt.show()
plt.close()
```
当然おかしな予測だと気がつくはずです。
なぜなら、2080年代には100m走のタイムがゼロになってしまうからです。
今の場合、我々はこのデータが100走の世界記録のタイムの推移であること、つまり
* 非増加関数であること
* 必ず正の値であること
など、データが持つべき性質を予め知っているので、
「このデータに対して単純な多項式回帰を当てはめるのはおかしい」
と気がつくことが出来ます。
**でも、他のデータではどうでしょうか?**
データを分析するためには、データの値だけをみて闇雲に分析するだけではダメで、
データの背景やドメイン知識が不可欠である、という好例です。
### (余談2) 新型コロナウイルス感染症の陽性者数の推移に関して
回帰分析に関連して、この話題も取り上げておきましょう。
我々が現実世界で観測することのできる種々の[値]というのは、
何らかの関数$f(x)$の、ある$x$での(実現)値と言えるかと思います。
テレビで見るコロナウイルスの感染者数の推移も日付に対する関数になっていたりします。
ただし一般に物事の背景にある"真の関数"というのは多次元の変数に対する複雑な関数になっているはずで、
コロナウイルスの感染者数の推移も単なる時間に対する1変数の関数であるはずなどがありません。
日付に対して陽性者数の推移をプロットして「このままだと指数関数的に増加する」
という予想を立てることは簡単ですが、一般に物事は多様な要素が絡み合っています。
たとえば検査数や我々の外出自粛や国・都道府県ごとの取り組み・政策,
ウイルスの変異,その他様々な要素に左右されるはずです。
我々人間がグラフにして理解できるのはたかだか3次元(3つの変数がある状況)までです。
言い換えれば、人間は物事を理解するときに本来D次元(D>>3, Dは3よりずっと大きい)
の変数で定義される関数を、3次元以下に射影した「影」をみて理解しようとする生き物だということは、
意識しておくべきでしょう。
一度目の感染ピークが訪れて緊急事態宣言が出され、
報道が加熱していた頃には、「ぼく(わたし)が考えた最強のモデル」
を使って感染者数を予測して危険を煽ったり、あるいは逆に
「過度に心配する必要がない」などと主張したりする専門家・非専門家が数多くいました。
また事態が収束したあとに「私のモデルはこんなに正しかった」という人も現れることでしょう。
ですが、それは極めて高い蓋然性で偶然です。
無限の数の関数を考えれば、データに適合するものが存在してもおかしくはありません。
何にでも言えることですが、モデルを立てて終わり、ではなく検証する姿勢が重要です。
# LICENSE
Copyright (C) 2021 Sota Yoshida
[ライセンス:クリエイティブ・コモンズ 4.0 表示 (CC-BY 4.0)](https://creativecommons.org/licenses/by/4.0/deed.ja)
|
github_jupyter
|
from matplotlib import pyplot as plt
!pip install japanize-matplotlib
import japanize_matplotlib
import numpy as np
x= [3.1, 4.3, 6.6, 13.2, 19.1, 20.9, 26.4, 25.1, 21.9, 15.7, 9.6, 3.8]
y= [568, 572, 804, 833, 930, 965, 1213, 1120, 835, 540, 451, 502]
plt.figure(figsize=(6,6))
plt.title("宇都宮市")
plt.xlabel("平均気温 (℃)")
plt.ylabel("世帯あたりのアイスクリム・シャーベットの消費金額 (円)")
plt.scatter(x,y)
plt.show()
plt.close()
### ライブラリを一切使わない方法
# ※1 xとyの長さが違う場合、長さ0の場合はエラーとし、返り値Noneを返す。
# ※2 Pythonではwarning(警告)を返す機能などもあるが、授業では扱わないのでNoneを返す関数とした。
def cor_coeff(x,y):
if len(x) != len(y) or len(x)==len(y)==0:
print("Error: x&y must satisfy len(x) = len(y) != 0") # ※1
return None # ※2
n = len(x)
## 平均を計算
xbar = sum(x)/n; ybar = sum(y)/n
##分子(numerator)の和を計算 (初期値を0に)
s_n = 0.0
for i in range(n):
s_n += (x[i]-xbar)*(y[i]-ybar)
##分母(denominator)の計算 (和を先に計算して積を取り、最後にsquare rootをとる)
s_x = 0.0; s_y = 0.0
for i in range(n):
s_x += (x[i]-xbar)**2
s_y += (y[i]-ybar)**2
s_d = (s_x * s_y)**0.5
# 一行で書くなら
#s_d = ( sum([(x[i]-xbar)**2 for i in range(n)]) * sum([(y[i]-ybar)**2 for i in range(n)]) )**0.5
return s_n/s_d # 分子/分母の値を返す
cor_coeff(x,y)
def cor_coeff_np(x,y):
xbar = np.mean(x); ybar=np.mean(y) #np.mean()は整数・実数値が入ったリスト(やnumpy array)の平均を計算
return np.dot(x - xbar,y-ybar) / np.sqrt( np.dot(x-xbar,x-xbar) * np.dot(y-ybar,y-ybar) )
cor_coeff_np(x,y)
print(np.corrcoef(x,y))
print("r(x,y)=", np.corrcoef(x,y)[0,1])
# sample_size: データの数
# std: standard deviation (標準偏差σ)
def create_toy_data(sample_size, std):
x = np.linspace(0, 1, sample_size)
t = np.sin(2*np.pi*x) + np.random.normal(scale=std, size=x.shape)
return x, t
np.random.seed(1234) #私と皆さんで結果が変わらないよう乱数のseedを固定, 詳しくは8章で
x,y = create_toy_data(10,1.e-1)
fig = plt.figure(figsize=(10,4))
ax = fig.add_subplot(111)
ax.set_xlabel("x"); ax.set_ylabel("y")
ax.scatter(x, y, facecolor="none", edgecolor="b", s=50, label="Data")
ax.legend()
plt.show()
plt.close()
## 多項式をplotするためのxの値を準備(グラフをなめらかにするために、0から1までの間の500点を等間隔に取る)
xp = np.linspace(0, 1, 500)
p=3 #多項式の次元を決める. 今は3次式.
coeff = np.polyfit(x, y, p)
yp = np.poly1d( coeff )(xp)
print("係数",coeff)
#お絵かき
fig = plt.figure(figsize=(10,4))
ax = fig.add_subplot(111)
ax.set_xlabel("x"); ax.set_ylabel("y")
ax.scatter(x, y, facecolor="none", edgecolor="b", s=50, label="Data")
ax.plot(xp, yp,label="p=3")
ax.legend()
plt.show()
plt.close()
ps = [0,1,3,6,9]
ys = []
xp = np.linspace(0, 1, 500) ## 多項式をplotするためのxの値を準備
for p in ps:
ys += [np.poly1d(np.polyfit(x, y, p))(xp)]
ytrue = np.sin(2*np.pi*xp)
fig = plt.figure(figsize=(12,5))
ax = fig.add_subplot(111)
ax.set_xlabel("x"); ax.set_ylabel("y")
ax.scatter(x, y, facecolor="none", edgecolor="b", s=80, label="Data")
for i in range(len(ps)):
ax.plot(xp, ys[i],label="p="+str(ps[i]),alpha=0.8)
ax.plot(xp,ytrue,linestyle="dotted", label="True",color="k")
ax.legend(loc="upper right")
plt.show()
plt.close()
def complexity(r):
return np.sqrt(np.dot(r,r))
def my_criteria(comp,err,lam=1.0): #lambda=1.0
return err + lam * np.log10(comp)
for p in ps:
coeff = np.polyfit(x, y, p)
diff = np.poly1d(np.polyfit(x, y, p))(x) - y
chi2 = np.dot(diff,diff)
comp = complexity(coeff)
print("p",p, "モデルの複雑さ(log10)→", np.log10(comp),
"二乗誤差", chi2, "モデル選択基準量", my_criteria(comp,chi2))
y = [ 10.06, 10.03,10.02, 9.95,9.93, 9.92,9.9, 9.86,9.85, 9.84, 9.79, 9.78, 9.77, 9.74,9.72,9.69,9.58 ]
x = [1964, 1968,1968,1968,1983,1988,1991,1991,1994,1996,1999,2002,2005,2007,2008,2008,2009 ]
fig = plt.figure(figsize=(12,3))
ax = fig.add_subplot(111)
ax.set_xlabel("year"); ax.set_ylabel("Mens 100m")
ax.scatter(x,y,marker="o",color="red")
plt.show()
plt.close()
xp = np.arange(2020,2101,1)
fig = plt.figure(figsize=(12,6))
ax = fig.add_subplot(111)
ax.set_xlabel("year"); ax.set_ylabel("Mens 100m")
ax.set_xlim(1960,2100)
ax.set_ylim(0,12)
for p in [3]:
yp = np.poly1d(np.polyfit(x, y, p))(xp)
ax.plot(xp,yp,marker="x",label="p="+str(p))
ax.scatter(x,y,marker="x",color="red")
ax.legend(loc="upper right")
plt.show()
plt.close()
| 0.277767 | 0.982151 |
# Import Libraries
```
import configparser
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import numpy as np
import operator
import warnings
from datetime import datetime
warnings.filterwarnings("ignore", category=DeprecationWarning)
```
# Read Config File
```
config = configparser.ConfigParser()
config.read('config.ini')
input_directory = config['DEFAULT']['Input-Files-Directory']
CODE = config['DEFAULT']['Code']
input_file = config['DEFAULT']['Input_Data']
pca_no = config['DEFAULT']['PCA_Component_No']
kmeans_ini_status = config['DEFAULT']['Kmeans_Init_Status']
kmeans_cluster_no = int(config['DEFAULT']['Kmean_Cluster_No'])
ref_cluster_result_file = config['DEFAULT']['Ref-Cluster-Result-File']
aggre_cols_file = config['DEFAULT']['Aggre_cols_File']
iter_num = int(config['DEFAULT']['no_iteration'])
output_file = config['DEFAULT']['Output-File']
```
# Read Input Files
```
df = pd.read_csv("{}/{}.csv".format(input_directory, input_file), sep=',', encoding='utf-8')
ref_df = pd.read_csv("{}.csv".format(ref_cluster_result_file), sep=',', encoding='utf-8')
aggregate_df = pd.read_csv("{}.txt".format(aggre_cols_file), delimiter = ",", comment='#', header=0)
```
# Apply Principal Component Analysis (PCA)
```
features = df.columns.tolist()
features.remove(CODE)
features.remove('pops')
features.remove('hhs')
features.remove('p15')
features.remove('Median Age')
features.remove('Median Monthly Mortgage')
features.remove('Median Ind Income')
features.remove('Median Weekly Rent')
features.remove('Median Fam Income')
features.remove('Median Hhd Income')
features.remove('Av Household Size')
x = df.loc[:, features].values
# set number of components
num = int(pca_no)
pca = PCA(n_components=num)
pc_columns = []
for i in range(1,num+1):
pc_columns.append('pc{}'.format(i))
principalComponents = pca.fit_transform(x)
pca_df = pd.DataFrame(data = principalComponents, columns = pc_columns)
```
# K-means clustering
```
def get_cluster_name(df, ref_df, cluster_name):
""" rename cluster by refering exist clustered data """
cluster_name_dict = {}
for i in range(len(set(df.cluster))):
selected_df1 = df.loc[df.cluster == i].astype(str) # covert data type as str
max_sa1_matched = 0
matched_cluster = cluster_name[0]
for c in cluster_name:
selected_df2 = ref_df.loc[ref_df.cluster == c].astype(str) # covert data type as str
common_sa1 = list(set(selected_df1[CODE].tolist()).intersection(selected_df2[CODE].tolist()))
if max_sa1_matched < len(common_sa1):
max_sa1_matched = len(common_sa1)
matched_cluster = c
cluster_name_dict[i] = matched_cluster
return cluster_name_dict
def replace_cluster_number_to_name(df, ref_df, cluster_name, i):
""" replace cluster number to cluster name. E.g. 1 -> Country Towns """
cluster_name_dict = get_cluster_name(df, ref_df, cluster_name)
for index, row in df.iterrows():
df['cluster'].iloc[index] = cluster_name_dict[row['cluster']]
df.rename(columns={"cluster": "result_{}".format(i)}, inplace=True)
return df
def running_kmeans(kmeans_cluster_no, kmeans_ini_status, pca_df, iter_num, df, ref_df):
cluster_name = list(set(ref_df.cluster))
result_df = pd.DataFrame()
result_df[CODE] = df[CODE]
start_time = datetime.now()
for i in range(0, iter_num):
kmeans = KMeans(
init=kmeans_ini_status,
n_clusters=kmeans_cluster_no,
)
kmeans.fit(pca_df)
result_df['cluster'] = kmeans.labels_
result_df = replace_cluster_number_to_name(result_df, ref_df, cluster_name, i)
end_time = datetime.now()
if i % 10 == 0:
print("Applyig {} kmeans with {} second proceeding times".format(i, end_time - start_time, 2))
return result_df
def find_top_matched_communities(df):
""" read clustering results and save top matching communities in a new dataframe """
new_df = pd.DataFrame()
for index, row in df.iterrows():
count_dic = {}
for i in range(0, len(df.columns.tolist())-1):
# read 100 times kmean clustering results and save into dictionary
matched_community = row['result_{}'.format(i)]
if matched_community not in count_dic.keys():
count_dic[matched_community] = 1
else:
count_dic[matched_community] += 1
# sort the dictionary by value and save into new DF
matching_result = sorted(count_dic.items(), key=lambda item: item[1], reverse=True)
if len(matching_result) > 1:
new_df = new_df.append({CODE: int(row[CODE]),
'top1_community':matching_result[0][0],
'top2_community':matching_result[1][0],
'top1_community_rate':matching_result[0][1],
'top2_community_rate':matching_result[1][1],
}, ignore_index=True)
else:
new_df = new_df.append({CODE: int(row[CODE]),
'top1_community':matching_result[0][0],
'top2_community':'',
'top1_community_rate':matching_result[0][1],
'top2_community_rate':0,
}, ignore_index=True)
return new_df
clustering_result_df = running_kmeans(kmeans_cluster_no, kmeans_ini_status, pca_df, iter_num, df, ref_df)
updated_clustering_result_df = find_top_matched_communities(clustering_result_df)
result_df = pd.merge(df, updated_clustering_result_df, on=CODE)
```
# Aggregate columns
After we get clustering results, we aggregate some variables(columns) to improve our analysability on clustered census data (Australia Community).
```
def aggregate_columns(aggregate_df, df):
copied_df = df.copy()
row = 0
for columns in aggregate_df['columns_to_aggregate']:
total_n = 0
for col in columns.split(','):
total_n += copied_df[col]
# drop column
copied_df.drop(columns=[col], inplace=True)
copied_df[aggregate_df['aggregated_column'][row]] = total_n
row += 1
return copied_df
aggregated_df = aggregate_columns(aggregate_df, result_df)
```
### Change 'Remote' to 'Remote or Disadvantaged'
```
for index, row in aggregated_df.iterrows():
if row['top1_community'] == 'Remote':
aggregated_df['top1_community'].iloc[index] = 'Remote or Disadvantaged'
elif row['top2_community'] == 'Remote':
aggregated_df['top2_community'].iloc[index] = 'Remote or Disadvantaged'
aggregated_df.to_csv('{}.csv'.format(output_file), sep=',', encoding='utf-8', index=False)
```
|
github_jupyter
|
import configparser
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import numpy as np
import operator
import warnings
from datetime import datetime
warnings.filterwarnings("ignore", category=DeprecationWarning)
config = configparser.ConfigParser()
config.read('config.ini')
input_directory = config['DEFAULT']['Input-Files-Directory']
CODE = config['DEFAULT']['Code']
input_file = config['DEFAULT']['Input_Data']
pca_no = config['DEFAULT']['PCA_Component_No']
kmeans_ini_status = config['DEFAULT']['Kmeans_Init_Status']
kmeans_cluster_no = int(config['DEFAULT']['Kmean_Cluster_No'])
ref_cluster_result_file = config['DEFAULT']['Ref-Cluster-Result-File']
aggre_cols_file = config['DEFAULT']['Aggre_cols_File']
iter_num = int(config['DEFAULT']['no_iteration'])
output_file = config['DEFAULT']['Output-File']
df = pd.read_csv("{}/{}.csv".format(input_directory, input_file), sep=',', encoding='utf-8')
ref_df = pd.read_csv("{}.csv".format(ref_cluster_result_file), sep=',', encoding='utf-8')
aggregate_df = pd.read_csv("{}.txt".format(aggre_cols_file), delimiter = ",", comment='#', header=0)
features = df.columns.tolist()
features.remove(CODE)
features.remove('pops')
features.remove('hhs')
features.remove('p15')
features.remove('Median Age')
features.remove('Median Monthly Mortgage')
features.remove('Median Ind Income')
features.remove('Median Weekly Rent')
features.remove('Median Fam Income')
features.remove('Median Hhd Income')
features.remove('Av Household Size')
x = df.loc[:, features].values
# set number of components
num = int(pca_no)
pca = PCA(n_components=num)
pc_columns = []
for i in range(1,num+1):
pc_columns.append('pc{}'.format(i))
principalComponents = pca.fit_transform(x)
pca_df = pd.DataFrame(data = principalComponents, columns = pc_columns)
def get_cluster_name(df, ref_df, cluster_name):
""" rename cluster by refering exist clustered data """
cluster_name_dict = {}
for i in range(len(set(df.cluster))):
selected_df1 = df.loc[df.cluster == i].astype(str) # covert data type as str
max_sa1_matched = 0
matched_cluster = cluster_name[0]
for c in cluster_name:
selected_df2 = ref_df.loc[ref_df.cluster == c].astype(str) # covert data type as str
common_sa1 = list(set(selected_df1[CODE].tolist()).intersection(selected_df2[CODE].tolist()))
if max_sa1_matched < len(common_sa1):
max_sa1_matched = len(common_sa1)
matched_cluster = c
cluster_name_dict[i] = matched_cluster
return cluster_name_dict
def replace_cluster_number_to_name(df, ref_df, cluster_name, i):
""" replace cluster number to cluster name. E.g. 1 -> Country Towns """
cluster_name_dict = get_cluster_name(df, ref_df, cluster_name)
for index, row in df.iterrows():
df['cluster'].iloc[index] = cluster_name_dict[row['cluster']]
df.rename(columns={"cluster": "result_{}".format(i)}, inplace=True)
return df
def running_kmeans(kmeans_cluster_no, kmeans_ini_status, pca_df, iter_num, df, ref_df):
cluster_name = list(set(ref_df.cluster))
result_df = pd.DataFrame()
result_df[CODE] = df[CODE]
start_time = datetime.now()
for i in range(0, iter_num):
kmeans = KMeans(
init=kmeans_ini_status,
n_clusters=kmeans_cluster_no,
)
kmeans.fit(pca_df)
result_df['cluster'] = kmeans.labels_
result_df = replace_cluster_number_to_name(result_df, ref_df, cluster_name, i)
end_time = datetime.now()
if i % 10 == 0:
print("Applyig {} kmeans with {} second proceeding times".format(i, end_time - start_time, 2))
return result_df
def find_top_matched_communities(df):
""" read clustering results and save top matching communities in a new dataframe """
new_df = pd.DataFrame()
for index, row in df.iterrows():
count_dic = {}
for i in range(0, len(df.columns.tolist())-1):
# read 100 times kmean clustering results and save into dictionary
matched_community = row['result_{}'.format(i)]
if matched_community not in count_dic.keys():
count_dic[matched_community] = 1
else:
count_dic[matched_community] += 1
# sort the dictionary by value and save into new DF
matching_result = sorted(count_dic.items(), key=lambda item: item[1], reverse=True)
if len(matching_result) > 1:
new_df = new_df.append({CODE: int(row[CODE]),
'top1_community':matching_result[0][0],
'top2_community':matching_result[1][0],
'top1_community_rate':matching_result[0][1],
'top2_community_rate':matching_result[1][1],
}, ignore_index=True)
else:
new_df = new_df.append({CODE: int(row[CODE]),
'top1_community':matching_result[0][0],
'top2_community':'',
'top1_community_rate':matching_result[0][1],
'top2_community_rate':0,
}, ignore_index=True)
return new_df
clustering_result_df = running_kmeans(kmeans_cluster_no, kmeans_ini_status, pca_df, iter_num, df, ref_df)
updated_clustering_result_df = find_top_matched_communities(clustering_result_df)
result_df = pd.merge(df, updated_clustering_result_df, on=CODE)
def aggregate_columns(aggregate_df, df):
copied_df = df.copy()
row = 0
for columns in aggregate_df['columns_to_aggregate']:
total_n = 0
for col in columns.split(','):
total_n += copied_df[col]
# drop column
copied_df.drop(columns=[col], inplace=True)
copied_df[aggregate_df['aggregated_column'][row]] = total_n
row += 1
return copied_df
aggregated_df = aggregate_columns(aggregate_df, result_df)
for index, row in aggregated_df.iterrows():
if row['top1_community'] == 'Remote':
aggregated_df['top1_community'].iloc[index] = 'Remote or Disadvantaged'
elif row['top2_community'] == 'Remote':
aggregated_df['top2_community'].iloc[index] = 'Remote or Disadvantaged'
aggregated_df.to_csv('{}.csv'.format(output_file), sep=',', encoding='utf-8', index=False)
| 0.364325 | 0.695991 |
# Implementing Pipeline
Using what you learning about pipelining, rewrite your machine learning code from the last section to use sklearn's Pipeline. For reference, the previous main function implementation is provided in the second to last cell. Refactor this in the last cell.
```
import nltk
nltk.download(['punkt', 'wordnet'])
import re
import numpy as np
import pandas as pd
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
url_regex = 'http[s]?://(?:[a-zA-Z]|[0-9]|[$-_@.&+]|[!*\(\),]|(?:%[0-9a-fA-F][0-9a-fA-F]))+'
def load_data():
df = pd.read_csv('corporate_messaging.csv', encoding='latin-1')
df = df[(df["category:confidence"] == 1) & (df['category'] != 'Exclude')]
X = df.text.values
y = df.category.values
return X, y
def tokenize(text):
detected_urls = re.findall(url_regex, text)
for url in detected_urls:
text = text.replace(url, "urlplaceholder")
tokens = word_tokenize(text)
lemmatizer = WordNetLemmatizer()
clean_tokens = []
for tok in tokens:
clean_tok = lemmatizer.lemmatize(tok).lower().strip()
clean_tokens.append(clean_tok)
return clean_tokens
def display_results(y_test, y_pred):
labels = np.unique(y_pred)
confusion_mat = confusion_matrix(y_test, y_pred, labels=labels)
accuracy = (y_pred == y_test).mean()
print("Labels:", labels)
print("Confusion Matrix:\n", confusion_mat)
print("Accuracy:", accuracy)
def old_main():
X, y = load_data()
X_train, X_test, y_train, y_test = train_test_split(X, y)
vect = CountVectorizer(tokenizer=tokenize)
tfidf = TfidfTransformer()
clf = RandomForestClassifier()
# train classifier
X_train_counts = vect.fit_transform(X_train)
X_train_tfidf = tfidf.fit_transform(X_train_counts)
clf.fit(X_train_tfidf, y_train)
# predict on test data
X_test_counts = vect.transform(X_test)
X_test_tfidf = tfidf.transform(X_test_counts)
y_pred = clf.predict(X_test_tfidf)
# display results
display_results(y_test, y_pred)
```
Rewrite the main function to use sklearn's `Pipeline` here:
```
def main():
X, y = load_data()
X_train, X_test, y_train, y_test = train_test_split(X, y)
# build pipeline
pipeline =
# train classifier
# predict on test data
# display results
display_results(y_test, y_pred)
main()
```
# Solution
```
import nltk
nltk.download(['punkt', 'wordnet'])
import re
import numpy as np
import pandas as pd
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer
from sklearn.pipeline import Pipeline
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
url_regex = 'http[s]?://(?:[a-zA-Z]|[0-9]|[$-_@.&+]|[!*\(\),]|(?:%[0-9a-fA-F][0-9a-fA-F]))+'
def load_data():
df = pd.read_csv('corporate_messaging.csv', encoding='latin-1')
df = df[(df["category:confidence"] == 1) & (df['category'] != 'Exclude')]
X = df.text.values
y = df.category.values
return X, y
def tokenize(text):
detected_urls = re.findall(url_regex, text)
for url in detected_urls:
text = text.replace(url, "urlplaceholder")
tokens = word_tokenize(text)
lemmatizer = WordNetLemmatizer()
clean_tokens = []
for tok in tokens:
clean_tok = lemmatizer.lemmatize(tok).lower().strip()
clean_tokens.append(clean_tok)
return clean_tokens
def display_results(y_test, y_pred):
labels = np.unique(y_pred)
confusion_mat = confusion_matrix(y_test, y_pred, labels=labels)
accuracy = (y_pred == y_test).mean()
print("Labels:", labels)
print("Confusion Matrix:\n", confusion_mat)
print("Accuracy:", accuracy)
def main():
X, y = load_data()
X_train, X_test, y_train, y_test = train_test_split(X, y)
pipeline = Pipeline([
('vect', CountVectorizer(tokenizer=tokenize)),
('tfidf', TfidfTransformer()),
('clf', RandomForestClassifier())
])
# train classifier
pipeline.fit(X_train, y_train)
# predict on test data
y_pred = pipeline.predict(X_test)
# display results
display_results(y_test, y_pred)
main()
```
|
github_jupyter
|
import nltk
nltk.download(['punkt', 'wordnet'])
import re
import numpy as np
import pandas as pd
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
url_regex = 'http[s]?://(?:[a-zA-Z]|[0-9]|[$-_@.&+]|[!*\(\),]|(?:%[0-9a-fA-F][0-9a-fA-F]))+'
def load_data():
df = pd.read_csv('corporate_messaging.csv', encoding='latin-1')
df = df[(df["category:confidence"] == 1) & (df['category'] != 'Exclude')]
X = df.text.values
y = df.category.values
return X, y
def tokenize(text):
detected_urls = re.findall(url_regex, text)
for url in detected_urls:
text = text.replace(url, "urlplaceholder")
tokens = word_tokenize(text)
lemmatizer = WordNetLemmatizer()
clean_tokens = []
for tok in tokens:
clean_tok = lemmatizer.lemmatize(tok).lower().strip()
clean_tokens.append(clean_tok)
return clean_tokens
def display_results(y_test, y_pred):
labels = np.unique(y_pred)
confusion_mat = confusion_matrix(y_test, y_pred, labels=labels)
accuracy = (y_pred == y_test).mean()
print("Labels:", labels)
print("Confusion Matrix:\n", confusion_mat)
print("Accuracy:", accuracy)
def old_main():
X, y = load_data()
X_train, X_test, y_train, y_test = train_test_split(X, y)
vect = CountVectorizer(tokenizer=tokenize)
tfidf = TfidfTransformer()
clf = RandomForestClassifier()
# train classifier
X_train_counts = vect.fit_transform(X_train)
X_train_tfidf = tfidf.fit_transform(X_train_counts)
clf.fit(X_train_tfidf, y_train)
# predict on test data
X_test_counts = vect.transform(X_test)
X_test_tfidf = tfidf.transform(X_test_counts)
y_pred = clf.predict(X_test_tfidf)
# display results
display_results(y_test, y_pred)
def main():
X, y = load_data()
X_train, X_test, y_train, y_test = train_test_split(X, y)
# build pipeline
pipeline =
# train classifier
# predict on test data
# display results
display_results(y_test, y_pred)
main()
import nltk
nltk.download(['punkt', 'wordnet'])
import re
import numpy as np
import pandas as pd
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer
from sklearn.pipeline import Pipeline
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
url_regex = 'http[s]?://(?:[a-zA-Z]|[0-9]|[$-_@.&+]|[!*\(\),]|(?:%[0-9a-fA-F][0-9a-fA-F]))+'
def load_data():
df = pd.read_csv('corporate_messaging.csv', encoding='latin-1')
df = df[(df["category:confidence"] == 1) & (df['category'] != 'Exclude')]
X = df.text.values
y = df.category.values
return X, y
def tokenize(text):
detected_urls = re.findall(url_regex, text)
for url in detected_urls:
text = text.replace(url, "urlplaceholder")
tokens = word_tokenize(text)
lemmatizer = WordNetLemmatizer()
clean_tokens = []
for tok in tokens:
clean_tok = lemmatizer.lemmatize(tok).lower().strip()
clean_tokens.append(clean_tok)
return clean_tokens
def display_results(y_test, y_pred):
labels = np.unique(y_pred)
confusion_mat = confusion_matrix(y_test, y_pred, labels=labels)
accuracy = (y_pred == y_test).mean()
print("Labels:", labels)
print("Confusion Matrix:\n", confusion_mat)
print("Accuracy:", accuracy)
def main():
X, y = load_data()
X_train, X_test, y_train, y_test = train_test_split(X, y)
pipeline = Pipeline([
('vect', CountVectorizer(tokenizer=tokenize)),
('tfidf', TfidfTransformer()),
('clf', RandomForestClassifier())
])
# train classifier
pipeline.fit(X_train, y_train)
# predict on test data
y_pred = pipeline.predict(X_test)
# display results
display_results(y_test, y_pred)
main()
| 0.515376 | 0.816845 |
```
import sys
import os
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import scipy.signal as sig
import datetime as dt
import random as rand
import scipy
from scipy import stats, interp
from IPython import embed
from shutil import copyfile, copy2
from load_intan_rhs_format import read_data
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.preprocessing import LabelEncoder
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.metrics import confusion_matrix
from sklearn import svm
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import StratifiedKFold
def calcmeans(df):
means = pd.DataFrame()
for i in range(0,16):
singlech = df.iloc[:,np.add(i,np.multiply(16,range(0,int(df.shape[1]/16-1))))]
means = pd.concat([means,np.mean(singlech, axis=1)],axis=1)
means.columns = range(0,16)
return means
def detrend(df,base):
means = calcmeans(base)
detrended = pd.DataFrame()
for i in range(0,df.shape[1]):
if i % 100 == 0:
print('detrending seg ' + str(i+1) + ' of ' + str(df.shape[1]))
ch = i % 16
orig = df.iloc[:,i]
mean = means[ch]
new = orig - mean
detrended = pd.concat([detrended,new],axis=1)
return detrended
def bandpower(x, fs, fmin, fmax):
f, Pxx = scipy.signal.periodogram(x, fs=fs)
ind_min = scipy.argmax(f > fmin) - 1
ind_max = scipy.argmax(f > fmax) - 1
return scipy.trapz(Pxx[ind_min: ind_max], f[ind_min: ind_max])
def calcfeats(df):
h1 = np.zeros(df.shape[1])
h4 = np.zeros(df.shape[1])
h8 = np.zeros(df.shape[1])
h13 = np.zeros(df.shape[1])
h25 = np.zeros(df.shape[1])
h50 = np.zeros(df.shape[1])
h70 = np.zeros(df.shape[1])
h130 = np.zeros(df.shape[1])
for i in range(0,df.shape[1]):
h1[i] = bandpower(df.iloc[:,i],df.shape[0],1,4)
h4[i] = bandpower(df.iloc[:,i],df.shape[0],4,8)
h8[i] = bandpower(df.iloc[:,i],df.shape[0],8,13)
h13[i] = bandpower(df.iloc[:,i],df.shape[0],13,25)
h25[i] = bandpower(df.iloc[:,i],df.shape[0],25,50)
h70[i] = bandpower(df.iloc[:,i],df.shape[0],70,110)
h130[i] = bandpower(df.iloc[:,i],df.shape[0],130,170)
d = {'max': np.max(df),
'argmax': df.idxmax(),
'min': np.min(df),
'argmin': df.idxmin(),
'1-4hz': h1,
'4-8hz': h4,
'8-13hz': h8,
'13-25hz': h13,
'25-50hz': h25,
'70-110hz': h70,
'130-170hz': h130
}
return pd.DataFrame(d)
def compmat(df1, df2):
# Welch t-test on every feature for every channel pairwise between df1 and df2
try:
df1.shape[1] == df2.shape[1]
except:
print(str(df1) + ' and ' + str(df2) + ' do not have the same number of features!')
comp = pd.DataFrame(1., index=np.arange(16), columns = df1.columns)
for j in range (0,16):
for i in df1.columns:
pval = stats.ttest_ind(df1[i][j],df2[i][j], equal_var=False)[1]
comp[i][j] = pval
return comp
bins = np.linspace(-200, 5000, 100)
plt.hist(prefeat03['1-4hz'][1],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['1-4hz'][1],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
#plt.xlim(-10000,10000)
# loading in previously computed 1second response traces to each stim for interictal
os.chdir('C:\\Users\\Senan\\SpontStimAnalysis\\Interictal\\RespData')
interictal01 = pd.read_pickle('sKH01interictal1s.pkl')
interictal03 = pd.read_pickle('sKH03interictal1s.pkl')
# loading preictal same
os.chdir('C:\\Users\\Senan\\SpontStimAnalysis\\Preictal\\RespData')
preictal01 = pd.read_pickle('sKH01preictal1s.pkl')
preictal03 = pd.read_pickle('sKH03preictal1s.pkl')
# loading sz times
sztimes01 = pd.read_pickle('sKH01sztimes.pkl')
sztimes03 = pd.read_pickle('sKH03sztimes.pkl')
# detrend compute feats on sKH03
# using the first 100 interictal responses to detrend all
# interdat03 = detrend(interictal03,interictal03.iloc[:,0:1600])
preicdat03 = detrend(preictal03, interictal03.iloc[:,0:1600])
# preicdat03.head()
prefeat03 = calcfeats(preicdat03)
print('next')
interfeat03 = calcfeats(interdat03)
print('done')
# interfeat03.head()
interfeat03.head()
prefeat03.head()
preicdat03.head()
os.chdir('C:\\Users\\Senan\\SpontStimAnalysis\\Interictal\\RespData')
interdat03.to_pickle('interictal03_detrended.pkl')
interfeat03.to_pickle('interfeat03.pkl')
preicdat03.to_pickle('preictal03_detrended.pkl')
prefeat03.to_pickle('prefeat03.pkl')
test = pd.read_pickle('interfeat03.pkl')
test.head()
bins = np.linspace(-2000, 0, 100)
plt.hist(prefeat03['min'][2],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['min'][2],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
#plt.xlim(-10000,10000)
bins = np.linspace(-2000, 0, 100)
plt.hist(prefeat03['min'][15],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['min'][15],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
plt.xlim(-2000,0)
prefeatcut = prefeat03.iloc[16*0:16*800]
bins = np.linspace(-2000, 0, 100)
plt.hist(prefeatcut['min'][2],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['min'][2],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
#plt.xlim(-10000,10000)
bins = np.linspace(-200, 5000, 100)
plt.hist(prefeat03['1-4hz'][1],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['1-4hz'][1],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
bins = np.linspace(-200, 5000, 100)
ch = 0
plt.hist(prefeat03['4-8hz'][ch],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['4-8hz'][ch],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
bins = np.linspace(-200, 5000, 100)
ch = 4
feat = '4-8hz'
plt.hist(prefeat03['4-8hz'][ch],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['4-8hz'][ch],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
plt.title()
bins = np.linspace(-200, 2000, 100)
ch = 15
feat = '130-170hz'
plt.hist(prefeat03[feat][ch],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03[feat][ch],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
plt.title('Evoked HFO (130-170Hz) Power Histogram')
plt.xlabel('Power (dB)')
plt.ylabel('PDF')
for ch in range(0,16):
bins = np.linspace(-200, 6000, 100)
feat = '130-170hz'
plt.figure()
plt.hist(prefeat03[feat][ch],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03[feat][ch],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
plt.title(feat + ' ch' + str(ch))
tf01 = compmat(interfeat03,prefeat03) < 0.01/(16*11)
plt.pcolor(tf01)
plt.yticks(np.arange(0.5, len(tf01.index), 1), tf01.index)
plt.xticks(np.arange(0.5, len(tf01.columns), 1), tf01.columns)
plt.plot(0,0,'y')
plt.plot(0,0,'purple')
plt.legend(('Sig','Nonsig'))
plt.title('Baseline-preictal feature changes by Welch T-test (Subject 1)')
tf02 = ~(compmat(interfeat03,prefeat03) < 0.01/(16*11))
fig = plt.pcolor(tf02)
plt.set_cmap('RdBu')
plt.yticks(np.arange(0.5, len(tf01.index), 1), tf01.index)
plt.xticks(np.arange(0.5, len(tf01.columns), 1), tf01.columns)
plt.plot(0,0,'r')
plt.plot(0,0,'b')
plt.legend(('Sig','Nonsig'))
plt.ylabel('Channels', fontsize = 16)
plt.xlabel('Features', fontsize = 16)
plt.title('Interictal-preictal feature changes \n by Welch T-test (Subject 1)', fontsize = 18)
plt.figure(figsize=(160,160))
axe = fig.axes
ax = axe
for tick in ax.xaxis.get_major_ticks():
tick.label.set_fontsize(14)
tick.label.set_rotation('vertical')
prefeat03.shape[0]/16
interfeat03.shape[0]/16
from __future__ import absolute_import, division, print_function
from matplotlib.font_manager import _rebuild; _rebuild()
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow as tf
#Helper libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import scipy.io as spio
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasClassifier
from keras.utils import np_utils
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.preprocessing import LabelEncoder
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.metrics import confusion_matrix
from sklearn import svm
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import roc_curve, auc
from scipy import interp
# Code below from Emma
n_splits_o = 5
n_splits_i = 4
animal_ID = 1
factor_red = 20
# To reduce the computational expense and the number of features to try in PCA during Hyperparameter optimization
nb_feats_min = 1
nb_feats_max = 11
animal_ID = animal_ID
animal_names = {1: "1", 2: "2"}
# Initialize random number generator for reproducibility.
seed = 7
np.random.seed(seed)
# Load in dataset.
# data = spio.loadmat("features_10s_2019-01-30.mat");
featuresp = prefeat03
labelsp = np.ones(prefeat03.shape[0])
features = featuresp.append(interfeat03)
labels = np.append(labelsp, np.zeros(interfeat03.shape[0]))
# animal_id_features = data['animal_id_features'];
# Flatten animal IDs so we can slice by animal.
# id_features = np.ravel(animal_id_features);
# Indexes animal of interest.
# indexes = np.where(id_features == animal_ID)
# indexes = np.ravel(indexes)
# Get only features corresponding to animal selected.
# animal_features = np.array([features[index, :] for index in indexes])
# labels = labels.transpose()
# animal_labels = np.array([labels[index] for index in indexes]);
print(features.shape)
print(labels.shape)
"""Reducing the size of the vectors for easier computation"""
# factor = factor_red
factor = 2
animal_features = features.values
animal_labels = labels
"""Shuffling the data to train/test on smaller subsets"""
shuffled_animal_features = np.empty(animal_features.shape, dtype=animal_features.dtype)
shuffled_animal_labels = np.empty(animal_labels.shape, dtype=animal_labels.dtype)
permutation = np.random.permutation(len(animal_labels))
for old_index, new_index in enumerate(permutation):
shuffled_animal_features [new_index] = animal_features[old_index]
shuffled_animal_labels[new_index] = animal_labels[old_index]
animal_features = shuffled_animal_features
animal_labels = shuffled_animal_labels
animal_features = animal_features[0:int(len(animal_features)/factor),:]
animal_labels = animal_labels[0:np.int(len(animal_labels)/factor)]
print(animal_labels.shape)
print(animal_features.shape)
"""Split data into training and testing sets"""
# parameters:
n_splits_o = n_splits_o
n_splits_i = n_splits_i
nb_features_tot = animal_features.shape[1]
cv_o = StratifiedKFold(n_splits=n_splits_o)
cv_i = StratifiedKFold(n_splits=n_splits_i)
AUC_i = np.zeros((n_splits_o, n_splits_i, nb_features_tot))
AUC_means = np.zeros((n_splits_o, nb_features_tot))
# Acc_train_i = np.zeros((n_splits_o, n_splits_i))
# Acc_val_i = np.zeros((n_splits_o, n_splits_i))
Best_features = np.zeros(n_splits_o)
Best_features_valAUC = np.zeros(n_splits_o)
AUC_o = np.zeros(n_splits_o)
tprs = []
mean_fpr = np.linspace(0, 1, 100)
"""Outer loop"""
k_out = 0
for train_o, test in cv_o.split(animal_features, animal_labels):
data_train_o = animal_features[train_o]
data_test = animal_features[test]
labels_train_o = animal_labels[train_o]
labels_test = animal_labels[test]
"""Inner Loop"""
k_in = 0
for train_i, val in cv_i.split(data_train_o, labels_train_o):
data_train_i = animal_features[train_i]
data_val = animal_features[val]
labels_train_i = animal_labels[train_i]
labels_val = animal_labels[val]
"""Hyperparameter evaluation: Number of features to keep after PCA"""
for k_feat in range(nb_feats_min, nb_feats_max):
features_kept = k_feat + 1
clf = make_pipeline(StandardScaler(), PCA(n_components=features_kept), svm.SVC(kernel='rbf', gamma='scale', probability=True))
y_score = clf.fit(data_train_i, labels_train_i)
y_predict = clf.predict_proba(data_val)
y_predict_train = clf.predict(data_train_i)
# Acc_val_i[k_out, k_in] = metrics.accuracy_score(labels_val, y_predict)
# Acc_train_i[k_out, k_in] = metrics.accuracy_score(labels_train_i, y_predict_train)
fpr, tpr, thresholds = roc_curve(labels_val, y_predict[:, 1])
AUC_i[k_out, k_in, k_feat] = auc(fpr, tpr)
print('Process ended, outer fold ', k_out, ', inner fold ', k_in)
k_in += 1
AUC_means = np.mean(AUC_i, axis=1)
"""Choice of the best performing Hyperparameters:"""
Best_features[k_out] = int(np.argmax(AUC_means[k_out,:]) + 1)
Best_features_valAUC[k_out] = np.max(AUC_means[k_out,:])
"""Performance on the test set"""
clf = make_pipeline(StandardScaler(), PCA(n_components=int(Best_features[k_out])), svm.SVC(kernel='rbf', gamma='scale', probability=True))
y_score = clf.fit(data_train_o, labels_train_o)
y_predict = clf.predict_proba(data_test)
y_predict_train = clf.predict(data_train_o)
"""ROC curve"""
fpr, tpr, thresholds = roc_curve(labels_test, y_predict[:, 1])
tprs.append(interp(mean_fpr, fpr, tpr))
tprs[-1][0] = 0.0
AUC_o[k_out] = auc(fpr, tpr)
plt.plot(fpr, tpr, lw=1, alpha=0.3,
label='ROC fold %d (AUC = %0.2f for %d PCs)' % (k_out+1, AUC_o[k_out], int(Best_features[k_out])))
print('Process ended, outer fold ', k_out)
k_out += 1
"""mean ROC curve"""
mean_tpr = np.mean(tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(AUC_o)
plt.plot(mean_fpr, mean_tpr, color='b',
label=r'Mean ROC (AUC = %0.2f $\pm$ %0.2f)' % (mean_auc, std_auc),
lw=2, alpha=.8)
std_tpr = np.std(tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
plt.fill_between(mean_fpr, tprs_lower, tprs_upper, color='grey', alpha=.2,
label=r'$\pm$ 1 std. dev.')
plt.plot([0, 1], [0, 1], linestyle='--', lw=2, color='r',
label='Chance', alpha=.8)
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic for subject %s (%d folds CV_out, %d folds CV_in, data randomly reduced by factor %d)' % (animal_names[animal_ID], n_splits_o, n_splits_i, factor_red))
plt.legend(loc="lower right")
plt.savefig('ROC_' + animal_names[animal_ID] + '.png')
plt.show()
# why are data not normalized prior to PCA?
# to try on zscored data and original data without PCA
```
|
github_jupyter
|
import sys
import os
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import scipy.signal as sig
import datetime as dt
import random as rand
import scipy
from scipy import stats, interp
from IPython import embed
from shutil import copyfile, copy2
from load_intan_rhs_format import read_data
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.preprocessing import LabelEncoder
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.metrics import confusion_matrix
from sklearn import svm
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import StratifiedKFold
def calcmeans(df):
means = pd.DataFrame()
for i in range(0,16):
singlech = df.iloc[:,np.add(i,np.multiply(16,range(0,int(df.shape[1]/16-1))))]
means = pd.concat([means,np.mean(singlech, axis=1)],axis=1)
means.columns = range(0,16)
return means
def detrend(df,base):
means = calcmeans(base)
detrended = pd.DataFrame()
for i in range(0,df.shape[1]):
if i % 100 == 0:
print('detrending seg ' + str(i+1) + ' of ' + str(df.shape[1]))
ch = i % 16
orig = df.iloc[:,i]
mean = means[ch]
new = orig - mean
detrended = pd.concat([detrended,new],axis=1)
return detrended
def bandpower(x, fs, fmin, fmax):
f, Pxx = scipy.signal.periodogram(x, fs=fs)
ind_min = scipy.argmax(f > fmin) - 1
ind_max = scipy.argmax(f > fmax) - 1
return scipy.trapz(Pxx[ind_min: ind_max], f[ind_min: ind_max])
def calcfeats(df):
h1 = np.zeros(df.shape[1])
h4 = np.zeros(df.shape[1])
h8 = np.zeros(df.shape[1])
h13 = np.zeros(df.shape[1])
h25 = np.zeros(df.shape[1])
h50 = np.zeros(df.shape[1])
h70 = np.zeros(df.shape[1])
h130 = np.zeros(df.shape[1])
for i in range(0,df.shape[1]):
h1[i] = bandpower(df.iloc[:,i],df.shape[0],1,4)
h4[i] = bandpower(df.iloc[:,i],df.shape[0],4,8)
h8[i] = bandpower(df.iloc[:,i],df.shape[0],8,13)
h13[i] = bandpower(df.iloc[:,i],df.shape[0],13,25)
h25[i] = bandpower(df.iloc[:,i],df.shape[0],25,50)
h70[i] = bandpower(df.iloc[:,i],df.shape[0],70,110)
h130[i] = bandpower(df.iloc[:,i],df.shape[0],130,170)
d = {'max': np.max(df),
'argmax': df.idxmax(),
'min': np.min(df),
'argmin': df.idxmin(),
'1-4hz': h1,
'4-8hz': h4,
'8-13hz': h8,
'13-25hz': h13,
'25-50hz': h25,
'70-110hz': h70,
'130-170hz': h130
}
return pd.DataFrame(d)
def compmat(df1, df2):
# Welch t-test on every feature for every channel pairwise between df1 and df2
try:
df1.shape[1] == df2.shape[1]
except:
print(str(df1) + ' and ' + str(df2) + ' do not have the same number of features!')
comp = pd.DataFrame(1., index=np.arange(16), columns = df1.columns)
for j in range (0,16):
for i in df1.columns:
pval = stats.ttest_ind(df1[i][j],df2[i][j], equal_var=False)[1]
comp[i][j] = pval
return comp
bins = np.linspace(-200, 5000, 100)
plt.hist(prefeat03['1-4hz'][1],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['1-4hz'][1],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
#plt.xlim(-10000,10000)
# loading in previously computed 1second response traces to each stim for interictal
os.chdir('C:\\Users\\Senan\\SpontStimAnalysis\\Interictal\\RespData')
interictal01 = pd.read_pickle('sKH01interictal1s.pkl')
interictal03 = pd.read_pickle('sKH03interictal1s.pkl')
# loading preictal same
os.chdir('C:\\Users\\Senan\\SpontStimAnalysis\\Preictal\\RespData')
preictal01 = pd.read_pickle('sKH01preictal1s.pkl')
preictal03 = pd.read_pickle('sKH03preictal1s.pkl')
# loading sz times
sztimes01 = pd.read_pickle('sKH01sztimes.pkl')
sztimes03 = pd.read_pickle('sKH03sztimes.pkl')
# detrend compute feats on sKH03
# using the first 100 interictal responses to detrend all
# interdat03 = detrend(interictal03,interictal03.iloc[:,0:1600])
preicdat03 = detrend(preictal03, interictal03.iloc[:,0:1600])
# preicdat03.head()
prefeat03 = calcfeats(preicdat03)
print('next')
interfeat03 = calcfeats(interdat03)
print('done')
# interfeat03.head()
interfeat03.head()
prefeat03.head()
preicdat03.head()
os.chdir('C:\\Users\\Senan\\SpontStimAnalysis\\Interictal\\RespData')
interdat03.to_pickle('interictal03_detrended.pkl')
interfeat03.to_pickle('interfeat03.pkl')
preicdat03.to_pickle('preictal03_detrended.pkl')
prefeat03.to_pickle('prefeat03.pkl')
test = pd.read_pickle('interfeat03.pkl')
test.head()
bins = np.linspace(-2000, 0, 100)
plt.hist(prefeat03['min'][2],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['min'][2],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
#plt.xlim(-10000,10000)
bins = np.linspace(-2000, 0, 100)
plt.hist(prefeat03['min'][15],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['min'][15],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
plt.xlim(-2000,0)
prefeatcut = prefeat03.iloc[16*0:16*800]
bins = np.linspace(-2000, 0, 100)
plt.hist(prefeatcut['min'][2],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['min'][2],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
#plt.xlim(-10000,10000)
bins = np.linspace(-200, 5000, 100)
plt.hist(prefeat03['1-4hz'][1],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['1-4hz'][1],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
bins = np.linspace(-200, 5000, 100)
ch = 0
plt.hist(prefeat03['4-8hz'][ch],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['4-8hz'][ch],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
bins = np.linspace(-200, 5000, 100)
ch = 4
feat = '4-8hz'
plt.hist(prefeat03['4-8hz'][ch],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03['4-8hz'][ch],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
plt.title()
bins = np.linspace(-200, 2000, 100)
ch = 15
feat = '130-170hz'
plt.hist(prefeat03[feat][ch],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03[feat][ch],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
plt.title('Evoked HFO (130-170Hz) Power Histogram')
plt.xlabel('Power (dB)')
plt.ylabel('PDF')
for ch in range(0,16):
bins = np.linspace(-200, 6000, 100)
feat = '130-170hz'
plt.figure()
plt.hist(prefeat03[feat][ch],bins,color='red',alpha=0.5,density=True, label = 'Preictal')
plt.hist(interfeat03[feat][ch],bins,color='green',alpha=0.5,density=True, label = 'Interictal')
plt.legend(loc = 'upper right')
plt.title(feat + ' ch' + str(ch))
tf01 = compmat(interfeat03,prefeat03) < 0.01/(16*11)
plt.pcolor(tf01)
plt.yticks(np.arange(0.5, len(tf01.index), 1), tf01.index)
plt.xticks(np.arange(0.5, len(tf01.columns), 1), tf01.columns)
plt.plot(0,0,'y')
plt.plot(0,0,'purple')
plt.legend(('Sig','Nonsig'))
plt.title('Baseline-preictal feature changes by Welch T-test (Subject 1)')
tf02 = ~(compmat(interfeat03,prefeat03) < 0.01/(16*11))
fig = plt.pcolor(tf02)
plt.set_cmap('RdBu')
plt.yticks(np.arange(0.5, len(tf01.index), 1), tf01.index)
plt.xticks(np.arange(0.5, len(tf01.columns), 1), tf01.columns)
plt.plot(0,0,'r')
plt.plot(0,0,'b')
plt.legend(('Sig','Nonsig'))
plt.ylabel('Channels', fontsize = 16)
plt.xlabel('Features', fontsize = 16)
plt.title('Interictal-preictal feature changes \n by Welch T-test (Subject 1)', fontsize = 18)
plt.figure(figsize=(160,160))
axe = fig.axes
ax = axe
for tick in ax.xaxis.get_major_ticks():
tick.label.set_fontsize(14)
tick.label.set_rotation('vertical')
prefeat03.shape[0]/16
interfeat03.shape[0]/16
from __future__ import absolute_import, division, print_function
from matplotlib.font_manager import _rebuild; _rebuild()
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow as tf
#Helper libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import scipy.io as spio
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasClassifier
from keras.utils import np_utils
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.preprocessing import LabelEncoder
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.metrics import confusion_matrix
from sklearn import svm
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import roc_curve, auc
from scipy import interp
# Code below from Emma
n_splits_o = 5
n_splits_i = 4
animal_ID = 1
factor_red = 20
# To reduce the computational expense and the number of features to try in PCA during Hyperparameter optimization
nb_feats_min = 1
nb_feats_max = 11
animal_ID = animal_ID
animal_names = {1: "1", 2: "2"}
# Initialize random number generator for reproducibility.
seed = 7
np.random.seed(seed)
# Load in dataset.
# data = spio.loadmat("features_10s_2019-01-30.mat");
featuresp = prefeat03
labelsp = np.ones(prefeat03.shape[0])
features = featuresp.append(interfeat03)
labels = np.append(labelsp, np.zeros(interfeat03.shape[0]))
# animal_id_features = data['animal_id_features'];
# Flatten animal IDs so we can slice by animal.
# id_features = np.ravel(animal_id_features);
# Indexes animal of interest.
# indexes = np.where(id_features == animal_ID)
# indexes = np.ravel(indexes)
# Get only features corresponding to animal selected.
# animal_features = np.array([features[index, :] for index in indexes])
# labels = labels.transpose()
# animal_labels = np.array([labels[index] for index in indexes]);
print(features.shape)
print(labels.shape)
"""Reducing the size of the vectors for easier computation"""
# factor = factor_red
factor = 2
animal_features = features.values
animal_labels = labels
"""Shuffling the data to train/test on smaller subsets"""
shuffled_animal_features = np.empty(animal_features.shape, dtype=animal_features.dtype)
shuffled_animal_labels = np.empty(animal_labels.shape, dtype=animal_labels.dtype)
permutation = np.random.permutation(len(animal_labels))
for old_index, new_index in enumerate(permutation):
shuffled_animal_features [new_index] = animal_features[old_index]
shuffled_animal_labels[new_index] = animal_labels[old_index]
animal_features = shuffled_animal_features
animal_labels = shuffled_animal_labels
animal_features = animal_features[0:int(len(animal_features)/factor),:]
animal_labels = animal_labels[0:np.int(len(animal_labels)/factor)]
print(animal_labels.shape)
print(animal_features.shape)
"""Split data into training and testing sets"""
# parameters:
n_splits_o = n_splits_o
n_splits_i = n_splits_i
nb_features_tot = animal_features.shape[1]
cv_o = StratifiedKFold(n_splits=n_splits_o)
cv_i = StratifiedKFold(n_splits=n_splits_i)
AUC_i = np.zeros((n_splits_o, n_splits_i, nb_features_tot))
AUC_means = np.zeros((n_splits_o, nb_features_tot))
# Acc_train_i = np.zeros((n_splits_o, n_splits_i))
# Acc_val_i = np.zeros((n_splits_o, n_splits_i))
Best_features = np.zeros(n_splits_o)
Best_features_valAUC = np.zeros(n_splits_o)
AUC_o = np.zeros(n_splits_o)
tprs = []
mean_fpr = np.linspace(0, 1, 100)
"""Outer loop"""
k_out = 0
for train_o, test in cv_o.split(animal_features, animal_labels):
data_train_o = animal_features[train_o]
data_test = animal_features[test]
labels_train_o = animal_labels[train_o]
labels_test = animal_labels[test]
"""Inner Loop"""
k_in = 0
for train_i, val in cv_i.split(data_train_o, labels_train_o):
data_train_i = animal_features[train_i]
data_val = animal_features[val]
labels_train_i = animal_labels[train_i]
labels_val = animal_labels[val]
"""Hyperparameter evaluation: Number of features to keep after PCA"""
for k_feat in range(nb_feats_min, nb_feats_max):
features_kept = k_feat + 1
clf = make_pipeline(StandardScaler(), PCA(n_components=features_kept), svm.SVC(kernel='rbf', gamma='scale', probability=True))
y_score = clf.fit(data_train_i, labels_train_i)
y_predict = clf.predict_proba(data_val)
y_predict_train = clf.predict(data_train_i)
# Acc_val_i[k_out, k_in] = metrics.accuracy_score(labels_val, y_predict)
# Acc_train_i[k_out, k_in] = metrics.accuracy_score(labels_train_i, y_predict_train)
fpr, tpr, thresholds = roc_curve(labels_val, y_predict[:, 1])
AUC_i[k_out, k_in, k_feat] = auc(fpr, tpr)
print('Process ended, outer fold ', k_out, ', inner fold ', k_in)
k_in += 1
AUC_means = np.mean(AUC_i, axis=1)
"""Choice of the best performing Hyperparameters:"""
Best_features[k_out] = int(np.argmax(AUC_means[k_out,:]) + 1)
Best_features_valAUC[k_out] = np.max(AUC_means[k_out,:])
"""Performance on the test set"""
clf = make_pipeline(StandardScaler(), PCA(n_components=int(Best_features[k_out])), svm.SVC(kernel='rbf', gamma='scale', probability=True))
y_score = clf.fit(data_train_o, labels_train_o)
y_predict = clf.predict_proba(data_test)
y_predict_train = clf.predict(data_train_o)
"""ROC curve"""
fpr, tpr, thresholds = roc_curve(labels_test, y_predict[:, 1])
tprs.append(interp(mean_fpr, fpr, tpr))
tprs[-1][0] = 0.0
AUC_o[k_out] = auc(fpr, tpr)
plt.plot(fpr, tpr, lw=1, alpha=0.3,
label='ROC fold %d (AUC = %0.2f for %d PCs)' % (k_out+1, AUC_o[k_out], int(Best_features[k_out])))
print('Process ended, outer fold ', k_out)
k_out += 1
"""mean ROC curve"""
mean_tpr = np.mean(tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(AUC_o)
plt.plot(mean_fpr, mean_tpr, color='b',
label=r'Mean ROC (AUC = %0.2f $\pm$ %0.2f)' % (mean_auc, std_auc),
lw=2, alpha=.8)
std_tpr = np.std(tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
plt.fill_between(mean_fpr, tprs_lower, tprs_upper, color='grey', alpha=.2,
label=r'$\pm$ 1 std. dev.')
plt.plot([0, 1], [0, 1], linestyle='--', lw=2, color='r',
label='Chance', alpha=.8)
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic for subject %s (%d folds CV_out, %d folds CV_in, data randomly reduced by factor %d)' % (animal_names[animal_ID], n_splits_o, n_splits_i, factor_red))
plt.legend(loc="lower right")
plt.savefig('ROC_' + animal_names[animal_ID] + '.png')
plt.show()
# why are data not normalized prior to PCA?
# to try on zscored data and original data without PCA
| 0.323273 | 0.353735 |
<a href="https://colab.research.google.com/github/yskmt2018/quantum2021/blob/main/spot_lecture_assign_problem.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# スポット講義割り当て問題 - Spot Lecture Assign Problem
- This notebook was created and tested on Google Colaboratory. (2021/09)
```
!python -V
!pip install --quiet pyqubo==1.0.13 openjij==0.4.3
import re
import numpy as np
import pandas as pd
import pyqubo as pq
import openjij as oj
from IPython.display import display_html
np.random.seed(0)
```
## 目次
1. 目的
2. 問題設定
3. 定式化
4. Hamiltonian & QUBO
5. (疑似)量子アニーリング
6. 可視化
7. 振り返り・展望
## 1. 目的
- スポット講義における「講師の割り当て」問題について、組合せ最適化問題として定式化し、(疑似)量子アニーリングを用いて解を得る。
## 2. 問題設定
今回は、以下の条件を適用する。
- 講師数、講義数、各講義の人数は、2020年度スポット講義の実績値を利用する。
- 各講師は、第1~第3希望を出す。できるだけ高い希望の講義に選ばれるようにする。
- 各講師は、希望しない講義を2つ出す。希望しない講義に選ばれてはならない。
- 各講師は、2つ以上の講義を受け持ってはならない。また、講師全員が何らかの講義を担当しなくてはならない。
- 各講義の定員を満たさなくてはならない。
2021/09追加:
- 第1~第3希望以外の講義に選ばれる講師は、講師全体の10%以下とする。
```
# 講師数(2020年度実績)
Tn = 38
# 講義数(2020年度実績)
Sn = 9
# 講師のリスト
T = list(range(Tn))
print(T)
# 講義のリスト
S = list(range(Sn))
print(S)
# 各講義の参加人数
Sn_s = np.full(shape=Sn, fill_value=4, dtype=np.int)
# 人数が4名の講義が7個、5名の講義が2個(2020年度実績)
Sn_s[3] = 5
Sn_s[7] = 5
print(Sn_s)
# 各講師の希望する講義をランダム選択: 第1-3希望に3-1点, その他:-1点
C_ts = np.full(shape=(Tn, Sn), fill_value=-1, dtype=np.int)
for t in T:
# 希望する講義を S から 3 個ランダムに選択する。replace=False で重複なし
hopes = np.random.choice(S, size=3, replace=False)
C_ts[t][hopes] = [3, 2, 1]
print(C_ts)
# 各講師の希望しない講義をランダム選択: 対象の講義に1, それ以外:0
NG_ts = np.zeros(shape=(Tn, Sn), dtype=np.int)
for t in T:
# 希望しない講義を C_ts で -1 となっている講義から 2 個ランダムに選択する。replace=False で重複なし
ng = np.random.choice(np.where(C_ts[t] == -1)[0], size=2, replace=False)
NG_ts[t][ng] = [1, 1]
print(NG_ts)
# 各講師の第1~第3希望の講義に0, それ以外:1
E_ts = np.where(C_ts == -1, 1, 0)
print(E_ts)
```
## 3. 定式化
- 「目的関数」と「制約項」を作成する。
- 目的関数が「最大(最小)化する指標」を、制約項が「遵守させる条件」を表現する。
- 制約項は、制約違反がない場合0を返す。0でない場合、ハミルトニアン(後述)のエネルギーが極端に大きく(不安定な状態に)なるため、制約を守るように作用する。
### 目的関数
- 各講師の希望(を元にした点数の総和)の最大化を目指す。
- 各講師の点数が C [ t ][ s ] * x [ t ][ s ] であり、その総和(全員の点数の合計)を算出する。
- 目的関数はコスト関数とも呼ばれ、この関数の出力が小さいほど優れた解である。そのため、最大化問題の際には結果に-1を乗し、優れた解であるほど出力を小さくする必要がある。
$$
maximize \sum_{t \in_{T}, s \in_{S}} (C_{ts} * x_{ts})
$$
```
def objective(x):
H = sum(C_ts[t][s] * x[t][s] for t in T for s in S)
# 最大化のため
return H * (-1)
```
### 制約項 1. 受け持つ講義は1つ
- 各講師の受け持つ講義は1つであることを課す。
- 各講師の受け持つ講義の数が sum( x [ t ][ s ] for s in S ) であり、全ての講師 t∈T について、この数が1でなくてはならない。
$$
\forall_{t \in_{T}}, \sum_{s \in_{S}} x_{ts} = 1
$$
```
def constraint_onlyone(x):
# 制約違反の場合、必ず正の値を返す必要があるため、2乗
return sum(
(sum(x[t][s] for s in S) - 1)**2 for t in T
)
```
### 制約項 2. 定員
- 各講義の定員が満たされることを課す。
- 各講義の参加人数が sum( x [ t ][ s ] for t in T ) であり、全ての講義 s∈S について、この数が各講義の参加人数( Sn [ s ] )と一致しなくてはならない。
$$
\forall_{s \in_{S}}, \sum_{t \in_{T}} x_{ts} = Sn_{s}
$$
```
def constraint_capacity(x):
# 制約違反の場合、必ず正の値を返す必要があるため、2乗
return sum(
(sum(x[t][s] for t in T) - Sn_s[s])**2 for s in S
)
```
### 制約項 3. 希望しない講義に割り当てない
- 各講師を希望しない講義に割り当てないことを課す。
- NG [ t ][ s ] * x [ t ][ s ] は、希望しない講義に割り当てられた場合1となる。この合計が0でなくてはならない。
$$
\sum_{t \in_{T}, s \in_{S}} (NG_{ts} * x_{ts}) = 0
$$
```
def constraint_unwanted(x):
return sum(NG_ts[t][s] * x[t][s] for t in T for s in S)
```
### 制約項 4. 第1~第3希望以外の講義に選ばれる講師は、講師全体の10%以下
- 希望以外の講義に選ばれる講師の数の制限を課す。
- E [ t ][ s ] * x [ t ][ s ] は、希望以外の講義に割り当てられた場合1となる。この合計が講師数の10%以下でなくてはならない。
- y はスラック変数(後述)であり、0 <= y <= Tn/10 を満たす整数である。
$$
\sum_{t \in_{T}, s \in_{S}} (E_{ts} * x_{ts}) = y
\\(0 \leq y \leq Tn/10)
$$
```
def constraint_except(x, y):
p = sum(E_ts[t][s] * x[t][s] for t in T for s in S)
# 制約違反の場合、必ず正の値を返す必要があるため、2乗
return (p - y)**2
```
## 4. Hamiltonian & QUBO
- ライブラリを利用して、Hamiltonian(ハミルトニアン)を構築し、QUBO(キューボ)に変換する。ここでは、【[PyQUBO](https://github.com/recruit-communications/pyqubo)】を利用する。
- 利用できるライブラリとして、他に【[JijModeling](https://jijmodeling-docs.jij-cloud.com/)】がある。
### Hamiltonian
- 定式化した目的関数、制約項を結合し、Hamiltonianと呼ばれる、本問題のエネルギーに対応する物理量を表現する。
- 各制約項には、重み係数としてλ(ラムダ)が掛け合わされる。制約項が0以外の値を返却(制約違反)した場合、係数が高い程、重いペナルティが課される。
$$
H = - \sum_{t \in_{T}, s \in_{S}} (C_{ts} * x_{ts})
\\ + \lambda_0 \sum_{t \in_{T}}(\sum_{s \in_{S}} x_{ts} - 1)^2
+ \lambda_1 \sum_{s \in_{S}}(\sum_{t \in_{T}} x_{ts} - Sn_{s})^2
+ \lambda_2 \sum_{t \in_{T}, s \in_{S}} (NG_{ts} * x_{ts})
+ \lambda_3 (\sum_{t \in_{T}, s \in_{S}} (E_{ts} * x_{ts}) - y)^2
\\(0 \leq y \leq Tn/10)
$$
```
# 講師t∈Tが講義s∈Sを担当するかどうかの目的変数
# 今回は38人9講義で38*9=342変数
x_ts = pq.Array.create(name='x', shape=(Tn, Sn), vartype='BINARY')
# 0以上Tn/10以下の整数値をとるスラック変数
# スラック変数は、不等式制約を等式制約に変換するために用いられる
y = pq.LogEncInteger(label='y', value_range=(0, int(Tn/10)))
# Hamiltonianの構築
H = objective(x_ts)
H += pq.Placeholder(label='lambda_0') * pq.Constraint(
hamiltonian=constraint_onlyone(x_ts), label='lambda_0')
H += pq.Placeholder(label='lambda_1') * pq.Constraint(
hamiltonian=constraint_capacity(x_ts), label='lambda_1')
H += pq.Placeholder(label='lambda_2') * pq.Constraint(
hamiltonian=constraint_unwanted(x_ts), label='lambda_2')
H += pq.Placeholder(label='lambda_3') * pq.Constraint(
hamiltonian=constraint_except(x_ts, y), label='lambda_3')
# 各制約項の重み係数を設定
feed_dict = dict(lambda_0=100, lambda_1=100, lambda_2=100, lambda_3=100)
print(feed_dict)
```
### QUBO (Quadratic Unconstrained Binary Optimization)
- QUBOは、組合せ最適化問題の表現形式であり、(疑似)量子アニーリングで問題を解くことができるようになる。
- HamiltonianからQUBOへの変換は、PyQUBOのAPIを利用する。
```
# QUBOへの変換
model = H.compile()
qubo, _ = model.to_qubo(feed_dict=feed_dict)
```
## 5. (疑似)量子アニーリング
- ライブラリを利用して、(疑似)量子アニーリングを実行する。ここでは、【[OpenJij](https://github.com/OpenJij/OpenJij)】を利用する。
- 利用できるライブラリ・環境として、他に【[D-Wave](https://docs.ocean.dwavesys.com/en/stable/index.html)】がある。
```
# SQA(Simulated Quantum Annealing)実行モジュール
# num_reads: サンプリング回数, num_sweeps: サンプリング時間
sampler = oj.SQASampler(num_reads=100, num_sweeps=1000, trotter=20)
%%time
# (疑似)量子アニーリング実行
sampleset = sampler.sample_qubo(Q=qubo)
# 実行結果をデコード
decoded = model.decode_sampleset(sampleset=sampleset, feed_dict=feed_dict)
# 最良解(最もエネルギーの小さい解)を抽出
best = min(decoded, key=lambda d: d.energy)
# 最良解が全制約を満たしているか確認
assert best.constraints(only_broken=True) == {}
# 最良解のエネルギー
print(best.energy)
```
## 6. 可視化
- 最良解の結果をDataFrameに変換し、表示する。
```
df_x = pd.DataFrame(data=np.zeros(shape=(Tn, Sn), dtype=np.int),
index=T, columns=[chr(s+65) for s in S], dtype=int)
# 正規表現を用いて、最良解のサンプリング結果をDataFrameに格納
for key, value in best.sample.items():
if value == 1 and key[0] is 'x':
t_s = re.match(pattern='x\[(\d+)\]\[(\d+)\]', string=key)
t, s = int(t_s.group(1)), int(t_s.group(2))
df_x.iat[t, s] = value
# 講師 0~37 が講義 A~I の中から1つずつ受け持つ
# Colabで見ると色が付きます。GitHubで見ると色が付きません。
display_html(df_x.style.applymap(lambda x: 'color: red' if x == 1 else 'color: gray')._repr_html_(), raw=True)
```
## 7. 振り返り・展望
- 「スポット講義の講師の割り当て」というオリジナルな問題について、問題設定、定式化、構築、実行、評価という量子アニーリングの一連のタスクを実装することができた。
- 本問題の改良の余地として、講師の年次や所属部署の偏りを考慮した割り当ての仕組みを検討していきたい。
|
github_jupyter
|
!python -V
!pip install --quiet pyqubo==1.0.13 openjij==0.4.3
import re
import numpy as np
import pandas as pd
import pyqubo as pq
import openjij as oj
from IPython.display import display_html
np.random.seed(0)
# 講師数(2020年度実績)
Tn = 38
# 講義数(2020年度実績)
Sn = 9
# 講師のリスト
T = list(range(Tn))
print(T)
# 講義のリスト
S = list(range(Sn))
print(S)
# 各講義の参加人数
Sn_s = np.full(shape=Sn, fill_value=4, dtype=np.int)
# 人数が4名の講義が7個、5名の講義が2個(2020年度実績)
Sn_s[3] = 5
Sn_s[7] = 5
print(Sn_s)
# 各講師の希望する講義をランダム選択: 第1-3希望に3-1点, その他:-1点
C_ts = np.full(shape=(Tn, Sn), fill_value=-1, dtype=np.int)
for t in T:
# 希望する講義を S から 3 個ランダムに選択する。replace=False で重複なし
hopes = np.random.choice(S, size=3, replace=False)
C_ts[t][hopes] = [3, 2, 1]
print(C_ts)
# 各講師の希望しない講義をランダム選択: 対象の講義に1, それ以外:0
NG_ts = np.zeros(shape=(Tn, Sn), dtype=np.int)
for t in T:
# 希望しない講義を C_ts で -1 となっている講義から 2 個ランダムに選択する。replace=False で重複なし
ng = np.random.choice(np.where(C_ts[t] == -1)[0], size=2, replace=False)
NG_ts[t][ng] = [1, 1]
print(NG_ts)
# 各講師の第1~第3希望の講義に0, それ以外:1
E_ts = np.where(C_ts == -1, 1, 0)
print(E_ts)
def objective(x):
H = sum(C_ts[t][s] * x[t][s] for t in T for s in S)
# 最大化のため
return H * (-1)
def constraint_onlyone(x):
# 制約違反の場合、必ず正の値を返す必要があるため、2乗
return sum(
(sum(x[t][s] for s in S) - 1)**2 for t in T
)
def constraint_capacity(x):
# 制約違反の場合、必ず正の値を返す必要があるため、2乗
return sum(
(sum(x[t][s] for t in T) - Sn_s[s])**2 for s in S
)
def constraint_unwanted(x):
return sum(NG_ts[t][s] * x[t][s] for t in T for s in S)
def constraint_except(x, y):
p = sum(E_ts[t][s] * x[t][s] for t in T for s in S)
# 制約違反の場合、必ず正の値を返す必要があるため、2乗
return (p - y)**2
# 講師t∈Tが講義s∈Sを担当するかどうかの目的変数
# 今回は38人9講義で38*9=342変数
x_ts = pq.Array.create(name='x', shape=(Tn, Sn), vartype='BINARY')
# 0以上Tn/10以下の整数値をとるスラック変数
# スラック変数は、不等式制約を等式制約に変換するために用いられる
y = pq.LogEncInteger(label='y', value_range=(0, int(Tn/10)))
# Hamiltonianの構築
H = objective(x_ts)
H += pq.Placeholder(label='lambda_0') * pq.Constraint(
hamiltonian=constraint_onlyone(x_ts), label='lambda_0')
H += pq.Placeholder(label='lambda_1') * pq.Constraint(
hamiltonian=constraint_capacity(x_ts), label='lambda_1')
H += pq.Placeholder(label='lambda_2') * pq.Constraint(
hamiltonian=constraint_unwanted(x_ts), label='lambda_2')
H += pq.Placeholder(label='lambda_3') * pq.Constraint(
hamiltonian=constraint_except(x_ts, y), label='lambda_3')
# 各制約項の重み係数を設定
feed_dict = dict(lambda_0=100, lambda_1=100, lambda_2=100, lambda_3=100)
print(feed_dict)
# QUBOへの変換
model = H.compile()
qubo, _ = model.to_qubo(feed_dict=feed_dict)
# SQA(Simulated Quantum Annealing)実行モジュール
# num_reads: サンプリング回数, num_sweeps: サンプリング時間
sampler = oj.SQASampler(num_reads=100, num_sweeps=1000, trotter=20)
%%time
# (疑似)量子アニーリング実行
sampleset = sampler.sample_qubo(Q=qubo)
# 実行結果をデコード
decoded = model.decode_sampleset(sampleset=sampleset, feed_dict=feed_dict)
# 最良解(最もエネルギーの小さい解)を抽出
best = min(decoded, key=lambda d: d.energy)
# 最良解が全制約を満たしているか確認
assert best.constraints(only_broken=True) == {}
# 最良解のエネルギー
print(best.energy)
df_x = pd.DataFrame(data=np.zeros(shape=(Tn, Sn), dtype=np.int),
index=T, columns=[chr(s+65) for s in S], dtype=int)
# 正規表現を用いて、最良解のサンプリング結果をDataFrameに格納
for key, value in best.sample.items():
if value == 1 and key[0] is 'x':
t_s = re.match(pattern='x\[(\d+)\]\[(\d+)\]', string=key)
t, s = int(t_s.group(1)), int(t_s.group(2))
df_x.iat[t, s] = value
# 講師 0~37 が講義 A~I の中から1つずつ受け持つ
# Colabで見ると色が付きます。GitHubで見ると色が付きません。
display_html(df_x.style.applymap(lambda x: 'color: red' if x == 1 else 'color: gray')._repr_html_(), raw=True)
| 0.264168 | 0.874721 |
```
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
```
# Tabular training
> How to use the tabular application in fastai
To illustrate the tabular application, we will use the example of the [Adult dataset](https://archive.ics.uci.edu/ml/datasets/Adult) where we have to predict if a person is earning more or less than $50k per year using some general data.
```
from fastai.tabular.all import *
```
We can download a sample of this dataset with the usual `untar_data` command:
```
path = untar_data(URLs.ADULT_SAMPLE)
path.ls()
```
Then we can have a look at how the data is structured:
```
df = pd.read_csv(path/'adult.csv')
df.head()
```
Some of the columns are continuous (like age) and we will treat them as float numbers we can feed our model directly. Others are categorical (like workclass or education) and we will convert them to a unique index that we will feed to embedding layers. We can specify our categorical and continuous column names, as well as the name of the dependent variable in `TabularDataLoaders` factory methods:
```
dls = TabularDataLoaders.from_csv(path/'adult.csv', path=path, y_names="salary",
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race'],
cont_names = ['age', 'fnlwgt', 'education-num'],
procs = [Categorify, FillMissing, Normalize])
```
The last part is the list of pre-processors we apply to our data:
- `Categorify` is going to take every categorical variable and make a map from integer to unique categories, then replace the values by the corresponding index.
- `FillMissing` will fill the missing values in the continuous variables by the median of existing values (you can choose a specific value if you prefer)
- `Normalize` will normalize the continuous variables (subtract the mean and divide by the std)
To further expose what's going on below the surface, let's rewrite this utilizing `fastai`'s `TabularPandas` class. We will need to make one adjustment, which is defining how we want to split our data. By default the factory method above used a random 80/20 split, so we will do the same:
```
splits = RandomSplitter(valid_pct=0.2)(range_of(df))
to = TabularPandas(df, procs=[Categorify, FillMissing,Normalize],
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race'],
cont_names = ['age', 'fnlwgt', 'education-num'],
y_names='salary',
splits=splits)
```
Once we build our `TabularPandas` object, our data is completely preprocessed as seen below:
```
to.xs.iloc[:2]
```
Now we can build our `DataLoaders` again:
```
dls = to.dataloaders(bs=64)
```
> Later we will explore why using `TabularPandas` to preprocess will be valuable.
The `show_batch` method works like for every other application:
```
dls.show_batch()
```
We can define a model using the `tabular_learner` method. When we define our model, `fastai` will try to infer the loss function based on our `y_names` earlier.
**Note**: Sometimes with tabular data, your `y`'s may be encoded (such as 0 and 1). In such a case you should explicitly pass `y_block = CategoryBlock` in your constructor so `fastai` won't presume you are doing regression.
```
learn = tabular_learner(dls, metrics=accuracy)
```
And we can train that model with the `fit_one_cycle` method (the `fine_tune` method won't be useful here since we don't have a pretrained model).
```
learn.fit_one_cycle(1)
```
We can then have a look at some predictions:
```
learn.show_results()
```
Or use the predict method on a row:
```
row, clas, probs = learn.predict(df.iloc[0])
row.show()
clas, probs
```
To get prediction on a new dataframe, you can use the `test_dl` method of the `DataLoaders`. That dataframe does not need to have the dependent variable in its column.
```
test_df = df.copy()
test_df.drop(['salary'], axis=1, inplace=True)
dl = learn.dls.test_dl(test_df)
```
Then `Learner.get_preds` will give you the predictions:
```
learn.get_preds(dl=dl)
```
> Note: Since machine learning models can't magically understand categories it was never trained on, the data should reflect this. If there are different missing values in your test data you should address this before training
## `fastai` with Other Libraries
As mentioned earlier, `TabularPandas` is a powerful and easy preprocessing tool for tabular data. Integration with libraries such as Random Forests and XGBoost requires only one extra step, that the `.dataloaders` call did for us. Let's look at our `to` again. Its values are stored in a `DataFrame` like object, where we can extract the `cats`, `conts,` `xs` and `ys` if we want to:
```
to.xs[:3]
```
Now that everything is encoded, you can then send this off to XGBoost or Random Forests by extracting the train and validation sets and their values:
```
X_train, y_train = to.train.xs, to.train.ys.values.ravel()
X_test, y_test = to.valid.xs, to.valid.ys.values.ravel()
```
And now we can directly send this in!
|
github_jupyter
|
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
from fastai.tabular.all import *
path = untar_data(URLs.ADULT_SAMPLE)
path.ls()
df = pd.read_csv(path/'adult.csv')
df.head()
dls = TabularDataLoaders.from_csv(path/'adult.csv', path=path, y_names="salary",
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race'],
cont_names = ['age', 'fnlwgt', 'education-num'],
procs = [Categorify, FillMissing, Normalize])
splits = RandomSplitter(valid_pct=0.2)(range_of(df))
to = TabularPandas(df, procs=[Categorify, FillMissing,Normalize],
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race'],
cont_names = ['age', 'fnlwgt', 'education-num'],
y_names='salary',
splits=splits)
to.xs.iloc[:2]
dls = to.dataloaders(bs=64)
dls.show_batch()
learn = tabular_learner(dls, metrics=accuracy)
learn.fit_one_cycle(1)
learn.show_results()
row, clas, probs = learn.predict(df.iloc[0])
row.show()
clas, probs
test_df = df.copy()
test_df.drop(['salary'], axis=1, inplace=True)
dl = learn.dls.test_dl(test_df)
learn.get_preds(dl=dl)
to.xs[:3]
X_train, y_train = to.train.xs, to.train.ys.values.ravel()
X_test, y_test = to.valid.xs, to.valid.ys.values.ravel()
| 0.339828 | 0.988971 |
# Bernoulli Naive Bayes Classifier with MinMaxScaler
This code template is facilitates to solve the problem of classification problem using Bernoulli Naive Bayes Algorithm using MinMaxScaler technique.
### Required Packages
```
!pip install imblearn
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from imblearn.over_sampling import RandomOverSampler
from sklearn.pipeline import make_pipeline
from sklearn.naive_bayes import BernoulliNB
from sklearn.preprocessing import LabelEncoder,MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,plot_confusion_matrix
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X = df[features]
Y = df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), axis=-1, kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
#### Distribution of Target Variable
```
plt.figure(figsize = (10,6))
se.countplot(Y)
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
```
#### Handling Target Imbalance
The challenge of working with imbalanced datasets is that most machine learning techniques will ignore, and in turn have poor performance on, the minority class, although typically it is performance on the minority class that is most important.
One approach to addressing imbalanced datasets is to oversample the minority class. The simplest approach involves duplicating examples in the minority class.We will perform overspampling using imblearn library.
```
x_train,y_train = RandomOverSampler(random_state=123).fit_resample(x_train, y_train)
```
### Model
<code>Bernoulli Naive Bayes Classifier</code> is used for discrete data and it works on Bernoulli distribution. The main feature of Bernoulli Naive Bayes is that it accepts features only as binary values like true or false, yes or no, success or failure, 0 or 1 and so on. So when the feature values are **<code>binary</code>** we know that we have to use Bernoulli Naive Bayes classifier.
#### Model Tuning Parameters
1. alpha : float, default=1.0
> Additive (Laplace/Lidstone) smoothing parameter (0 for no smoothing).
2. binarize : float or None, default=0.0
> Threshold for binarizing (mapping to booleans) of sample features. If None, input is presumed to already consist of binary vectors.
3. fit_prior : bool, default=True
> Whether to learn class prior probabilities or not. If false, a uniform prior will be used.
4. class_prior : array-like of shape (n_classes,), default=None
> Prior probabilities of the classes. If specified the priors are not adjusted according to the data.
#### Data Scaling
Used sklearn.preprocessing.MinMaxScaler
This estimator scales and translates each feature individually such that it is in the given range on the training set, e.g. between zero and one.
Read more at [scikit-learn.org](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html)
```
# Building pipeline with MinMaxScaler as rescaling and BernoulliNB as the model.
model=make_pipeline(MinMaxScaler(),BernoulliNB())
model.fit(x_train,y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
#### Confusion Matrix
A confusion matrix is utilized to understand the performance of the classification model or algorithm in machine learning for a given test set where results are known.
```
plot_confusion_matrix(model,x_test,y_test,cmap=plt.cm.Blues)
```
#### Classification Report
A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True, how many are False.
* **where**:
- Precision:- Accuracy of positive predictions.
- Recall:- Fraction of positives that were correctly identified.
- f1-score:- percent of positive predictions were correct
- support:- Support is the number of actual occurrences of the class in the specified dataset.
```
print(classification_report(y_test,model.predict(x_test)))
```
#### Creator: Snehaan Bhawal , Github: [Profile](https://github.com/Sbhawal)
|
github_jupyter
|
!pip install imblearn
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from imblearn.over_sampling import RandomOverSampler
from sklearn.pipeline import make_pipeline
from sklearn.naive_bayes import BernoulliNB
from sklearn.preprocessing import LabelEncoder,MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,plot_confusion_matrix
warnings.filterwarnings('ignore')
#filepath
file_path= ""
#x_values
features=[]
#y_value
target=''
df=pd.read_csv(file_path)
df.head()
X = df[features]
Y = df[target]
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), axis=-1, kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
plt.figure(figsize = (10,6))
se.countplot(Y)
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
x_train,y_train = RandomOverSampler(random_state=123).fit_resample(x_train, y_train)
# Building pipeline with MinMaxScaler as rescaling and BernoulliNB as the model.
model=make_pipeline(MinMaxScaler(),BernoulliNB())
model.fit(x_train,y_train)
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
plot_confusion_matrix(model,x_test,y_test,cmap=plt.cm.Blues)
print(classification_report(y_test,model.predict(x_test)))
| 0.307566 | 0.956957 |
## 피마 인디언의 당뇨병 예측 실행
```
import pandas as pd
#df = pd.read_csv('../dataset/pima-indians-diabetes.csv', header=None)
df = pd.read_csv('../dataset/pima-indians-diabetes.csv',
names=["pregnant", "plasma", "pressure", "thickness", "insulin", "BMI", "pedigree", "age", "class"])
print(df.head())
print(df.info())
print(df.describe())
df[['pregnant', 'class']]
pregnant_df = df[['pregnant', 'class']].groupby(['pregnant'], as_index=False).mean().sort_values(by='pregnant', ascending=True)
pregnant_df.head()
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(12,12))
sns.heatmap(df.corr(), linewidths=0.1, vmax=0.5, cmap=plt.cm.gist_heat, linecolor='white', annot=True)
plt.show()
grid = sns.FacetGrid(df, col='class')
grid.map(plt.hist, 'plasma', bins=10)
plt.show()
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.callbacks import ModelCheckpoint
print(tf.__version__)
# seed 값 생성
np.random.seed(3)
tf.random.set_seed(3)
X = df.drop(['class'], axis=1, inplace=False).values
Y = df[['class']].values
def build_model():
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(12, input_shape=(8,), activation='relu'),
tf.keras.layers.Dense(8, activation='relu'),
tf.keras.layers.Dense(1)
])
loss = tf.keras.losses.BinaryCrossentropy(from_logits=True)
optimizer = tf.keras.optimizers.Adam(1e-4)
#optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss=loss,
optimizer=optimizer,
metrics=['accuracy'])
return model
modell = build_model()
# 파일 이름에 에포크 번호를 포함시킵니다(`str.format` 포맷)
checkpoint_path = "training_tf/cp-{epoch:04d}.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# 열 번째 에포크마다 가중치를 저장하기 위한 콜백을 만듭니다
cp_callback = [
tf.keras.callbacks.EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=50, baseline=0.4),
tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_path,
monitor='val_loss',
#mode='min',
verbose=1, # verbosity mode, 0 or 1.
save_best_only=True,
save_weights_only=True,
save_freq='epoch')
]
'''
# 딥러닝 구조를 결정(모델을 설정하고 실행하는 부분)
model = Sequential()
model.add(Dense(30, input_dim=17, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
# 딥러닝 실행
#model.compile(loss='mean_squared_error', optimizer='adam', metrics=['accuracy'])
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
'''
def build_model():
model = tf.keras.models.Sequential([
#tf.keras.layers.Dense(64, activation='relu', input_shape=[len(train_dataset.keys())]),
tf.keras.layers.Dense(30, input_dim=17, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid'),
])
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['accuracy', 'mae', 'mse'])
return model
model = build_model()
'''
checkpoint_path = "training_1/cp.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# 모델의 가중치를 저장하는 콜백 만들기
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
save_weights_only=True,
verbose=1)
'''
# 파일 이름에 에포크 번호를 포함시킵니다(`str.format` 포맷)
checkpoint_path = "training_tf/cp-{epoch:04d}.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# 열 번째 에포크마다 가중치를 저장하기 위한 콜백을 만듭니다
cp_callback = [
# tf.keras.callbacks.EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=50, baseline=0.4),
tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_path,
monitor='val_loss',
# mode='min',
verbose=1, # verbosity mode, 0 or 1.
# save_best_only=True,
save_weights_only=True,
#save_freq='epoch',
period=50)
]
model.summary()
history = model.fit(X, Y,
validation_split=0.2,
#validation_data=(X, Y),
epochs=300,
batch_size=64,
verbose=1, # Verbosity mode. 0 = silent, 1 = progress bar(default), 2 = one line per epoch.
callbacks=cp_callback
)
'''Weight들만 저장하기'''
model.save_weights('./checkpoints_tf/my_checkpoint') # 수동으로 가중치 저장하기
'''모델 전체 저장하기'''
path = "./saved_model_tf"
if not os.path.isdir(path):
os.mkdir(path)
model.save(path) # 전체 모델 저장하기
'''모델 전체 불러오기'''
new_model = tf.keras.models.load_model('./saved_model_tf') # 전체 모델 불러오기
# 모델 구조를 확인합니다
new_model.summary()
# 복원된 모델을 평가합니다
loss, acc, mae, mse= new_model.evaluate(X, Y, verbose=2)
print('복원된 모델의 정확도: {:5.2f}%'.format(100*acc))
print(new_model.predict(X).shape)
'''모델 weight 불러오기'''
checkpoint_path = "training_tf/cp-0300.ckpt"
# checkpoint_path = './checkpoints/my_checkpoint'
model.load_weights(checkpoint_path) #
loss, acc, mae, mse = model.evaluate(X, Y, verbose=2)
print(loss)
print("복원된 모델의 정확도: {:5.2f}%".format(100*acc))
print(model.predict(X).shape)
```
|
github_jupyter
|
import pandas as pd
#df = pd.read_csv('../dataset/pima-indians-diabetes.csv', header=None)
df = pd.read_csv('../dataset/pima-indians-diabetes.csv',
names=["pregnant", "plasma", "pressure", "thickness", "insulin", "BMI", "pedigree", "age", "class"])
print(df.head())
print(df.info())
print(df.describe())
df[['pregnant', 'class']]
pregnant_df = df[['pregnant', 'class']].groupby(['pregnant'], as_index=False).mean().sort_values(by='pregnant', ascending=True)
pregnant_df.head()
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(12,12))
sns.heatmap(df.corr(), linewidths=0.1, vmax=0.5, cmap=plt.cm.gist_heat, linecolor='white', annot=True)
plt.show()
grid = sns.FacetGrid(df, col='class')
grid.map(plt.hist, 'plasma', bins=10)
plt.show()
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.callbacks import ModelCheckpoint
print(tf.__version__)
# seed 값 생성
np.random.seed(3)
tf.random.set_seed(3)
X = df.drop(['class'], axis=1, inplace=False).values
Y = df[['class']].values
def build_model():
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(12, input_shape=(8,), activation='relu'),
tf.keras.layers.Dense(8, activation='relu'),
tf.keras.layers.Dense(1)
])
loss = tf.keras.losses.BinaryCrossentropy(from_logits=True)
optimizer = tf.keras.optimizers.Adam(1e-4)
#optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss=loss,
optimizer=optimizer,
metrics=['accuracy'])
return model
modell = build_model()
# 파일 이름에 에포크 번호를 포함시킵니다(`str.format` 포맷)
checkpoint_path = "training_tf/cp-{epoch:04d}.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# 열 번째 에포크마다 가중치를 저장하기 위한 콜백을 만듭니다
cp_callback = [
tf.keras.callbacks.EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=50, baseline=0.4),
tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_path,
monitor='val_loss',
#mode='min',
verbose=1, # verbosity mode, 0 or 1.
save_best_only=True,
save_weights_only=True,
save_freq='epoch')
]
'''
# 딥러닝 구조를 결정(모델을 설정하고 실행하는 부분)
model = Sequential()
model.add(Dense(30, input_dim=17, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
# 딥러닝 실행
#model.compile(loss='mean_squared_error', optimizer='adam', metrics=['accuracy'])
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
'''
def build_model():
model = tf.keras.models.Sequential([
#tf.keras.layers.Dense(64, activation='relu', input_shape=[len(train_dataset.keys())]),
tf.keras.layers.Dense(30, input_dim=17, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid'),
])
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['accuracy', 'mae', 'mse'])
return model
model = build_model()
'''
checkpoint_path = "training_1/cp.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# 모델의 가중치를 저장하는 콜백 만들기
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
save_weights_only=True,
verbose=1)
'''
# 파일 이름에 에포크 번호를 포함시킵니다(`str.format` 포맷)
checkpoint_path = "training_tf/cp-{epoch:04d}.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# 열 번째 에포크마다 가중치를 저장하기 위한 콜백을 만듭니다
cp_callback = [
# tf.keras.callbacks.EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=50, baseline=0.4),
tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_path,
monitor='val_loss',
# mode='min',
verbose=1, # verbosity mode, 0 or 1.
# save_best_only=True,
save_weights_only=True,
#save_freq='epoch',
period=50)
]
model.summary()
history = model.fit(X, Y,
validation_split=0.2,
#validation_data=(X, Y),
epochs=300,
batch_size=64,
verbose=1, # Verbosity mode. 0 = silent, 1 = progress bar(default), 2 = one line per epoch.
callbacks=cp_callback
)
'''Weight들만 저장하기'''
model.save_weights('./checkpoints_tf/my_checkpoint') # 수동으로 가중치 저장하기
'''모델 전체 저장하기'''
path = "./saved_model_tf"
if not os.path.isdir(path):
os.mkdir(path)
model.save(path) # 전체 모델 저장하기
'''모델 전체 불러오기'''
new_model = tf.keras.models.load_model('./saved_model_tf') # 전체 모델 불러오기
# 모델 구조를 확인합니다
new_model.summary()
# 복원된 모델을 평가합니다
loss, acc, mae, mse= new_model.evaluate(X, Y, verbose=2)
print('복원된 모델의 정확도: {:5.2f}%'.format(100*acc))
print(new_model.predict(X).shape)
'''모델 weight 불러오기'''
checkpoint_path = "training_tf/cp-0300.ckpt"
# checkpoint_path = './checkpoints/my_checkpoint'
model.load_weights(checkpoint_path) #
loss, acc, mae, mse = model.evaluate(X, Y, verbose=2)
print(loss)
print("복원된 모델의 정확도: {:5.2f}%".format(100*acc))
print(model.predict(X).shape)
| 0.472197 | 0.738492 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.