code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
<a href="https://colab.research.google.com/github/roopy7890/AttnGAN/blob/master/code/main.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from __future__ import print_function
from miscc.config import cfg, cfg_from_file
from datasets import TextDataset
from trainer import condGANTrainer as trainer
import os
import sys
import time
import random
import pprint
import datetime
import dateutil.tz
import argparse
import numpy as np
import torch
import torchvision.transforms as transforms
dir_path = (os.path.abspath(os.path.join(os.path.realpath(__file__), './.')))
sys.path.append(dir_path)
def parse_args():
parser = argparse.ArgumentParser(description='Train a AttnGAN network')
parser.add_argument('--cfg', dest='cfg_file',
help='optional config file',
default='cfg/bird_attn2.yml', type=str)
parser.add_argument('--gpu', dest='gpu_id', type=int, default=-1)
parser.add_argument('--data_dir', dest='data_dir', type=str, default='')
parser.add_argument('--manualSeed', type=int, help='manual seed')
args = parser.parse_args()
return args
def gen_example(wordtoix, algo):
'''generate images from example sentences'''
from nltk.tokenize import RegexpTokenizer
filepath = '%s/example_filenames.txt' % (cfg.DATA_DIR)
data_dic = {}
with open(filepath, "r") as f:
filenames = f.read().decode('utf8').split('\n')
for name in filenames:
if len(name) == 0:
continue
filepath = '%s/%s.txt' % (cfg.DATA_DIR, name)
with open(filepath, "r") as f:
print('Load from:', name)
sentences = f.read().decode('utf8').split('\n')
# a list of indices for a sentence
captions = []
cap_lens = []
for sent in sentences:
if len(sent) == 0:
continue
sent = sent.replace("\ufffd\ufffd", " ")
tokenizer = RegexpTokenizer(r'\w+')
tokens = tokenizer.tokenize(sent.lower())
if len(tokens) == 0:
print('sent', sent)
continue
rev = []
for t in tokens:
t = t.encode('ascii', 'ignore').decode('ascii')
if len(t) > 0 and t in wordtoix:
rev.append(wordtoix[t])
captions.append(rev)
cap_lens.append(len(rev))
max_len = np.max(cap_lens)
sorted_indices = np.argsort(cap_lens)[::-1]
cap_lens = np.asarray(cap_lens)
cap_lens = cap_lens[sorted_indices]
cap_array = np.zeros((len(captions), max_len), dtype='int64')
for i in range(len(captions)):
idx = sorted_indices[i]
cap = captions[idx]
c_len = len(cap)
cap_array[i, :c_len] = cap
key = name[(name.rfind('/') + 1):]
data_dic[key] = [cap_array, cap_lens, sorted_indices]
algo.gen_example(data_dic)
if __name__ == "__main__":
args = parse_args()
if args.cfg_file is not None:
cfg_from_file(args.cfg_file)
if args.gpu_id != -1:
cfg.GPU_ID = args.gpu_id
else:
cfg.CUDA = False
if args.data_dir != '':
cfg.DATA_DIR = args.data_dir
print('Using config:')
pprint.pprint(cfg)
if not cfg.TRAIN.FLAG:
args.manualSeed = 100
elif args.manualSeed is None:
args.manualSeed = random.randint(1, 10000)
random.seed(args.manualSeed)
np.random.seed(args.manualSeed)
torch.manual_seed(args.manualSeed)
if cfg.CUDA:
torch.cuda.manual_seed_all(args.manualSeed)
now = datetime.datetime.now(dateutil.tz.tzlocal())
timestamp = now.strftime('%Y_%m_%d_%H_%M_%S')
output_dir = '../output/%s_%s_%s' % \
(cfg.DATASET_NAME, cfg.CONFIG_NAME, timestamp)
split_dir, bshuffle = 'train', True
if not cfg.TRAIN.FLAG:
# bshuffle = False
split_dir = 'test'
# Get data loader
imsize = cfg.TREE.BASE_SIZE * (2 ** (cfg.TREE.BRANCH_NUM - 1))
image_transform = transforms.Compose([
transforms.Scale(int(imsize * 76 / 64)),
transforms.RandomCrop(imsize),
transforms.RandomHorizontalFlip()])
dataset = TextDataset(cfg.DATA_DIR, split_dir,
base_size=cfg.TREE.BASE_SIZE,
transform=image_transform)
assert dataset
dataloader = torch.utils.data.DataLoader(
dataset, batch_size=cfg.TRAIN.BATCH_SIZE,
drop_last=True, shuffle=bshuffle, num_workers=int(cfg.WORKERS))
# Define models and go to train/evaluate
algo = trainer(output_dir, dataloader, dataset.n_words, dataset.ixtoword)
start_t = time.time()
if cfg.TRAIN.FLAG:
algo.train()
else:
'''generate images from pre-extracted embeddings'''
if cfg.B_VALIDATION:
algo.sampling(split_dir) # generate images for the whole valid dataset
else:
gen_example(dataset.wordtoix, algo) # generate images for customized captions
end_t = time.time()
print('Total time for training:', end_t - start_t)
```
|
github_jupyter
|
from __future__ import print_function
from miscc.config import cfg, cfg_from_file
from datasets import TextDataset
from trainer import condGANTrainer as trainer
import os
import sys
import time
import random
import pprint
import datetime
import dateutil.tz
import argparse
import numpy as np
import torch
import torchvision.transforms as transforms
dir_path = (os.path.abspath(os.path.join(os.path.realpath(__file__), './.')))
sys.path.append(dir_path)
def parse_args():
parser = argparse.ArgumentParser(description='Train a AttnGAN network')
parser.add_argument('--cfg', dest='cfg_file',
help='optional config file',
default='cfg/bird_attn2.yml', type=str)
parser.add_argument('--gpu', dest='gpu_id', type=int, default=-1)
parser.add_argument('--data_dir', dest='data_dir', type=str, default='')
parser.add_argument('--manualSeed', type=int, help='manual seed')
args = parser.parse_args()
return args
def gen_example(wordtoix, algo):
'''generate images from example sentences'''
from nltk.tokenize import RegexpTokenizer
filepath = '%s/example_filenames.txt' % (cfg.DATA_DIR)
data_dic = {}
with open(filepath, "r") as f:
filenames = f.read().decode('utf8').split('\n')
for name in filenames:
if len(name) == 0:
continue
filepath = '%s/%s.txt' % (cfg.DATA_DIR, name)
with open(filepath, "r") as f:
print('Load from:', name)
sentences = f.read().decode('utf8').split('\n')
# a list of indices for a sentence
captions = []
cap_lens = []
for sent in sentences:
if len(sent) == 0:
continue
sent = sent.replace("\ufffd\ufffd", " ")
tokenizer = RegexpTokenizer(r'\w+')
tokens = tokenizer.tokenize(sent.lower())
if len(tokens) == 0:
print('sent', sent)
continue
rev = []
for t in tokens:
t = t.encode('ascii', 'ignore').decode('ascii')
if len(t) > 0 and t in wordtoix:
rev.append(wordtoix[t])
captions.append(rev)
cap_lens.append(len(rev))
max_len = np.max(cap_lens)
sorted_indices = np.argsort(cap_lens)[::-1]
cap_lens = np.asarray(cap_lens)
cap_lens = cap_lens[sorted_indices]
cap_array = np.zeros((len(captions), max_len), dtype='int64')
for i in range(len(captions)):
idx = sorted_indices[i]
cap = captions[idx]
c_len = len(cap)
cap_array[i, :c_len] = cap
key = name[(name.rfind('/') + 1):]
data_dic[key] = [cap_array, cap_lens, sorted_indices]
algo.gen_example(data_dic)
if __name__ == "__main__":
args = parse_args()
if args.cfg_file is not None:
cfg_from_file(args.cfg_file)
if args.gpu_id != -1:
cfg.GPU_ID = args.gpu_id
else:
cfg.CUDA = False
if args.data_dir != '':
cfg.DATA_DIR = args.data_dir
print('Using config:')
pprint.pprint(cfg)
if not cfg.TRAIN.FLAG:
args.manualSeed = 100
elif args.manualSeed is None:
args.manualSeed = random.randint(1, 10000)
random.seed(args.manualSeed)
np.random.seed(args.manualSeed)
torch.manual_seed(args.manualSeed)
if cfg.CUDA:
torch.cuda.manual_seed_all(args.manualSeed)
now = datetime.datetime.now(dateutil.tz.tzlocal())
timestamp = now.strftime('%Y_%m_%d_%H_%M_%S')
output_dir = '../output/%s_%s_%s' % \
(cfg.DATASET_NAME, cfg.CONFIG_NAME, timestamp)
split_dir, bshuffle = 'train', True
if not cfg.TRAIN.FLAG:
# bshuffle = False
split_dir = 'test'
# Get data loader
imsize = cfg.TREE.BASE_SIZE * (2 ** (cfg.TREE.BRANCH_NUM - 1))
image_transform = transforms.Compose([
transforms.Scale(int(imsize * 76 / 64)),
transforms.RandomCrop(imsize),
transforms.RandomHorizontalFlip()])
dataset = TextDataset(cfg.DATA_DIR, split_dir,
base_size=cfg.TREE.BASE_SIZE,
transform=image_transform)
assert dataset
dataloader = torch.utils.data.DataLoader(
dataset, batch_size=cfg.TRAIN.BATCH_SIZE,
drop_last=True, shuffle=bshuffle, num_workers=int(cfg.WORKERS))
# Define models and go to train/evaluate
algo = trainer(output_dir, dataloader, dataset.n_words, dataset.ixtoword)
start_t = time.time()
if cfg.TRAIN.FLAG:
algo.train()
else:
'''generate images from pre-extracted embeddings'''
if cfg.B_VALIDATION:
algo.sampling(split_dir) # generate images for the whole valid dataset
else:
gen_example(dataset.wordtoix, algo) # generate images for customized captions
end_t = time.time()
print('Total time for training:', end_t - start_t)
| 0.445771 | 0.610686 |
# The Devito domain specific language: an overview
This notebook presents an overview of the Devito symbolic language, used to express and discretise operators, in particular partial differential equations (PDEs).
For convenience, we import all Devito modules:
```
from devito import *
```
## From equations to code in a few lines of Python
The main objective of this tutorial is to demonstrate how Devito and its [SymPy](http://www.sympy.org/en/index.html)-powered symbolic API can be used to solve partial differential equations using the finite difference method with highly optimized stencils in a few lines of Python. We demonstrate how computational stencils can be derived directly from the equation in an automated fashion and how Devito can be used to generate and execute, at runtime, the desired numerical scheme in the form of optimized C code.
## Defining the physical domain
Before we can begin creating finite-difference (FD) stencils we will need to give Devito a few details regarding the computational domain within which we wish to solve our problem. For this purpose we create a `Grid` object that stores the physical `extent` (the size) of our domain and knows how many points we want to use in each dimension to discretise our data.
<img src="figures/grid.png" style="width: 220px;"/>
```
grid = Grid(shape=(5, 6), extent=(1., 1.))
grid
```
## Functions and data
To express our equation in symbolic form and discretise it using finite differences, Devito provides a set of `Function` types. A `Function` object:
1. Behaves like a `sympy.Function` symbol
2. Manages data associated with the symbol
To get more information on how to create and use a `Function` object, or any type provided by Devito, we can take a look at the documentation.
```
print(Function.__doc__)
```
Ok, let's create a function $f(x, y)$ and look at the data Devito has associated with it. Please note that it is important to use explicit keywords, such as `name` or `grid` when creating `Function` objects.
```
f = Function(name='f', grid=grid)
f
f.data
```
By default, Devito `Function` objects use the spatial dimensions `(x, y)` for 2D grids and `(x, y, z)` for 3D grids. To solve a PDE over several timesteps a time dimension is also required by our symbolic function. For this Devito provides an additional function type, the `TimeFunction`, which incorporates the correct dimension along with some other intricacies needed to create a time stepping scheme.
```
g = TimeFunction(name='g', grid=grid)
g
```
Since the default time order of a `TimeFunction` is `1`, the shape of `f` is `(2, 5, 6)`, i.e. Devito has allocated two buffers to represent `g(t, x, y)` and `g(t + dt, x, y)`:
```
g.shape
```
## Derivatives of symbolic functions
The functions we have created so far all act as `sympy.Function` objects, which means that we can form symbolic derivative expressions from them. Devito provides a set of shorthand expressions (implemented as Python properties) that allow us to generate finite differences in symbolic form. For example, the property `f.dx` denotes $\frac{\partial}{\partial x} f(x, y)$ - only that Devito has already discretised it with a finite difference expression. There are also a set of shorthand expressions for left (backward) and right (forward) derivatives:
| Derivative | Shorthand | Discretised | Stencil |
| ---------- |:---------:|:-----------:|:-------:|
| $\frac{\partial}{\partial x}f(x, y)$ (right) | `f.dxr` | $\frac{f(x+h_x,y)}{h_x} - \frac{f(x,y)}{h_x}$ | <img src="figures/stencil_forward.png" style="width: 180px;"/> |
| $\frac{\partial}{\partial x}f(x, y)$ (left) | `f.dxl` | $\frac{f(x,y)}{h_x} - \frac{f(x-h_x,y)}{h_x}$ | <img src="figures/stencil_backward.png" style="width: 180px;"/> |
A similar set of expressions exist for each spatial dimension defined on our grid, for example `f.dy` and `f.dyl`. Obviously, one can also take derivatives in time of `TimeFunction` objects. For example, to take the first derivative in time of `g` you can simply write:
```
g.dt
```
We may also want to take a look at the stencil Devito will generate based on the chosen discretisation:
```
g.dt.evaluate
```
There also exist convenient shortcuts to express the forward and backward stencil points, `g(t+dt, x, y)` and `g(t-dt, x, y)`.
```
g.forward
g.backward
```
And of course, there's nothing to stop us taking derivatives on these objects:
```
g.forward.dt
g.forward.dy
```
## A linear convection operator
**Note:** The following example is derived from [step 5](http://nbviewer.ipython.org/github/barbagroup/CFDPython/blob/master/lessons/07_Step_5.ipynb) in the excellent tutorial series [CFD Python: 12 steps to Navier-Stokes](http://lorenabarba.com/blog/cfd-python-12-steps-to-navier-stokes/).
In this simple example we will show how to derive a very simple convection operator from a high-level description of the governing equation. We will go through the process of deriving a discretised finite difference formulation of the state update for the field variable $u$, before creating a callable `Operator` object. Luckily, the automation provided by SymPy makes the derivation very nice and easy.
The governing equation we want to implement is the linear convection equation:
$$\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial x} + c\frac{\partial u}{\partial y} = 0.$$
Before we begin, we must define some parameters including the grid, the number of timesteps and the timestep size. We will also initialize our velocity `u` with a smooth field:
```
from examples.cfd import init_smooth, plot_field
nt = 100 # Number of timesteps
dt = 0.2 * 2. / 80 # Timestep size (sigma=0.2)
c = 1 # Value for c
# Then we create a grid and our function
grid = Grid(shape=(81, 81), extent=(2., 2.))
u = TimeFunction(name='u', grid=grid)
# We can now set the initial condition and plot it
init_smooth(field=u.data[0], dx=grid.spacing[0], dy=grid.spacing[1])
init_smooth(field=u.data[1], dx=grid.spacing[0], dy=grid.spacing[1])
plot_field(u.data[0])
```
Next, we wish to discretise our governing equation so that a functional `Operator` can be created from it. We begin by simply writing out the equation as a symbolic expression, while using shorthand expressions for the derivatives provided by the `Function` object. This will create a symbolic object of the dicretised equation.
Using the Devito shorthand notation, we can express the governing equations as:
```
eq = Eq(u.dt + c * u.dxl + c * u.dyl)
eq
```
We now need to rearrange our equation so that the term $u(t+dt, x, y)$ is on the left-hand side, since it represents the next point in time for our state variable $u$. Devito provides a utility called `solve`, built on top of SymPy's `solve`, to rearrange our equation so that it represents a valid state update for $u$. Here, we use `solve` to create a valid stencil for our update to `u(t+dt, x, y)`:
```
stencil = solve(eq, u.forward)
update = Eq(u.forward, stencil)
update
```
The right-hand side of the 'update' equation should be a stencil of the shape
<img src="figures/stencil_convection.png" style="width: 160px;"/>
Once we have created this 'update' expression, we can create a Devito `Operator`. This `Operator` will basically behave like a Python function that we can call to apply the created stencil over our associated data, as long as we provide all necessary unknowns. In this case we need to provide the number of timesteps to compute via the keyword `time` and the timestep size via `dt` (both have been defined above):
```
op = Operator(update, opt='noop')
op(time=nt+1, dt=dt)
plot_field(u.data[0])
```
Note that the real power of Devito is hidden within `Operator`, it will automatically generate and compile the optimized C code. We can look at this code (noting that this is not a requirement of executing it) via:
```
print(op.ccode)
```
## Second derivatives and high-order stencils
In the above example only a combination of first derivatives was present in the governing equation. However, second (or higher) order derivatives are often present in scientific problems of interest, notably any PDE modeling diffusion. To generate second order derivatives we must give the `devito.Function` object another piece of information: the desired discretisation of the stencil(s).
First, lets define a simple second derivative in `x`, for which we need to give $u$ a `space_order` of (at least) `2`. The shorthand for this second derivative is `u.dx2`.
```
u = TimeFunction(name='u', grid=grid, space_order=2)
u.dx2
u.dx2.evaluate
```
We can increase the discretisation arbitrarily if we wish to specify higher order FD stencils:
```
u = TimeFunction(name='u', grid=grid, space_order=4)
u.dx2
u.dx2.evaluate
```
To implement the diffusion or wave equations, we must take the Laplacian $\nabla^2 u$, which is the sum of the second derivatives in all spatial dimensions. For this, Devito also provides a shorthand expression, which means we do not have to hard-code the problem dimension (2D or 3D) in the code. To change the problem dimension we can create another `Grid` object and use this to re-define our `Function`'s:
```
grid_3d = Grid(shape=(5, 6, 7), extent=(1., 1., 1.))
u = TimeFunction(name='u', grid=grid_3d, space_order=2)
u
```
We can re-define our function `u` with a different `space_order` argument to change the discretisation order of the stencil expression created. For example, we can derive an expression of the 12th-order Laplacian $\nabla^2 u$:
```
u = TimeFunction(name='u', grid=grid_3d, space_order=12)
u.laplace
```
The same expression could also have been generated explicitly via:
```
u.dx2 + u.dy2 + u.dz2
```
## Derivatives of composite expressions
Derivatives of any arbitrary expression can easily be generated:
```
u = TimeFunction(name='u', grid=grid, space_order=2)
v = TimeFunction(name='v', grid=grid, space_order=2, time_order=2)
v.dt2 + u.laplace
(v.dt2 + u.laplace).dx2
```
Which can, depending on the chosen discretisation, lead to fairly complex stencils:
```
(v.dt2 + u.laplace).dx2.evaluate
```
|
github_jupyter
|
from devito import *
grid = Grid(shape=(5, 6), extent=(1., 1.))
grid
print(Function.__doc__)
f = Function(name='f', grid=grid)
f
f.data
g = TimeFunction(name='g', grid=grid)
g
g.shape
g.dt
g.dt.evaluate
g.forward
g.backward
g.forward.dt
g.forward.dy
from examples.cfd import init_smooth, plot_field
nt = 100 # Number of timesteps
dt = 0.2 * 2. / 80 # Timestep size (sigma=0.2)
c = 1 # Value for c
# Then we create a grid and our function
grid = Grid(shape=(81, 81), extent=(2., 2.))
u = TimeFunction(name='u', grid=grid)
# We can now set the initial condition and plot it
init_smooth(field=u.data[0], dx=grid.spacing[0], dy=grid.spacing[1])
init_smooth(field=u.data[1], dx=grid.spacing[0], dy=grid.spacing[1])
plot_field(u.data[0])
eq = Eq(u.dt + c * u.dxl + c * u.dyl)
eq
stencil = solve(eq, u.forward)
update = Eq(u.forward, stencil)
update
op = Operator(update, opt='noop')
op(time=nt+1, dt=dt)
plot_field(u.data[0])
print(op.ccode)
u = TimeFunction(name='u', grid=grid, space_order=2)
u.dx2
u.dx2.evaluate
u = TimeFunction(name='u', grid=grid, space_order=4)
u.dx2
u.dx2.evaluate
grid_3d = Grid(shape=(5, 6, 7), extent=(1., 1., 1.))
u = TimeFunction(name='u', grid=grid_3d, space_order=2)
u
u = TimeFunction(name='u', grid=grid_3d, space_order=12)
u.laplace
u.dx2 + u.dy2 + u.dz2
u = TimeFunction(name='u', grid=grid, space_order=2)
v = TimeFunction(name='v', grid=grid, space_order=2, time_order=2)
v.dt2 + u.laplace
(v.dt2 + u.laplace).dx2
(v.dt2 + u.laplace).dx2.evaluate
| 0.687735 | 0.992604 |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', None)
survey_apr_20 = pd.read_csv(r"C:\Rajat Dev\ML_Session\ML-for-Good-Hackathon\Data\ProlificAcademic\April 2020\Data\CRISIS_Adult_April_2020.csv")
survey_may_20 = pd.read_csv(r"C:\Rajat Dev\ML_Session\ML-for-Good-Hackathon\Data\ProlificAcademic\May 2020\Data\CRISIS_Adult_May_2020.csv");
survey_nov_20 = pd.read_csv(r"C:\Rajat Dev\ML_Session\ML-for-Good-Hackathon\Data\ProlificAcademic\November 2020\Data\CRISIS_Adult_November_2020.csv");
survey_apr_21 = pd.read_csv(r"C:\Rajat Dev\ML_Session\ML-for-Good-Hackathon\Data\ProlificAcademic\April 2021\Data\CRISIS_Adult_April_2021.csv")
survey_apr_20.head()
survey_apr_20.drop(["sex_other"], axis=1,inplace=True)
survey_apr_20['essentialworkerhome'] = survey_apr_20['essentialworkerhome'].fillna(0)
survey_apr_20['covidfacility'] = survey_apr_20['covidfacility'].fillna(2)
survey_apr_20['goingtoworkplace'] = survey_apr_20['goingtoworkplace'].fillna(2)
survey_apr_20['workfromhome'] = survey_apr_20['workfromhome'].fillna(2)
survey_apr_20['laidoff'] = survey_apr_20['laidoff'].fillna(2)
survey_apr_20['losejob'] = survey_apr_20['losejob'].fillna(2)
survey_apr_20['mentalhealth'] = survey_apr_20['mentalhealth'].fillna(6)
df = survey_apr_20[["working___1","working___2","working___3","working___4","working___5","working___6","working___7","working___8","occupation","military","location","education","educationmother","educationfather","householdnumber","essentialworkers","essentialworkerhome","covidfacility","householdcomp___1","householdcomp___2","householdcomp___3","householdcomp___4","householdcomp___5","householdcomp___6","householdcomp___7","roomsinhouse","insurance","govassist","physicalhealth","work","goingtoworkplace","workfromhome","laidoff","losejob","mentalhealth"]]
df.mentalhealth.unique()
df["occupation"] = pd.Categorical(df["occupation"]).codes
cols = ["military","location", "education", "educationmother","educationfather","householdnumber",
"essentialworkers", "essentialworkerhome", "covidfacility","insurance","govassist",
"physicalhealth", "work", "goingtoworkplace","workfromhome", "laidoff", "losejob"]
for col in cols:
df = pd.get_dummies(df, columns=[col], drop_first=True, dtype=df[col].dtype)
df = pd.get_dummies(df,)
df.head()
def correlation_plot(df):
corr = abs(df.corr()) # correlation matrix
lower_triangle = np.tril(corr, k = -1) # select only the lower triangle of the correlation matrix
mask = lower_triangle == 0 # to mask the upper triangle in the following heatmap
plt.figure(figsize = (10,10)) # setting the figure size
sns.set_style(style = 'white') # Setting it to white so that we do not see the grid lines
sns.heatmap(lower_triangle, center=0.5, cmap= 'Blues', xticklabels = corr.index,
yticklabels = corr.columns,cbar = False, annot= True, linewidths= 1, mask = mask) # Da Heatmap
plt.show()
i=0
while(i<90):
correlation_plot(df.iloc[:,i:i+15])
i=i+15
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', None)
survey_apr_20 = pd.read_csv(r"C:\Rajat Dev\ML_Session\ML-for-Good-Hackathon\Data\ProlificAcademic\April 2020\Data\CRISIS_Adult_April_2020.csv")
survey_may_20 = pd.read_csv(r"C:\Rajat Dev\ML_Session\ML-for-Good-Hackathon\Data\ProlificAcademic\May 2020\Data\CRISIS_Adult_May_2020.csv");
survey_nov_20 = pd.read_csv(r"C:\Rajat Dev\ML_Session\ML-for-Good-Hackathon\Data\ProlificAcademic\November 2020\Data\CRISIS_Adult_November_2020.csv");
survey_apr_21 = pd.read_csv(r"C:\Rajat Dev\ML_Session\ML-for-Good-Hackathon\Data\ProlificAcademic\April 2021\Data\CRISIS_Adult_April_2021.csv")
survey_apr_20.head()
survey_apr_20.drop(["sex_other"], axis=1,inplace=True)
survey_apr_20['essentialworkerhome'] = survey_apr_20['essentialworkerhome'].fillna(0)
survey_apr_20['covidfacility'] = survey_apr_20['covidfacility'].fillna(2)
survey_apr_20['goingtoworkplace'] = survey_apr_20['goingtoworkplace'].fillna(2)
survey_apr_20['workfromhome'] = survey_apr_20['workfromhome'].fillna(2)
survey_apr_20['laidoff'] = survey_apr_20['laidoff'].fillna(2)
survey_apr_20['losejob'] = survey_apr_20['losejob'].fillna(2)
survey_apr_20['mentalhealth'] = survey_apr_20['mentalhealth'].fillna(6)
df = survey_apr_20[["working___1","working___2","working___3","working___4","working___5","working___6","working___7","working___8","occupation","military","location","education","educationmother","educationfather","householdnumber","essentialworkers","essentialworkerhome","covidfacility","householdcomp___1","householdcomp___2","householdcomp___3","householdcomp___4","householdcomp___5","householdcomp___6","householdcomp___7","roomsinhouse","insurance","govassist","physicalhealth","work","goingtoworkplace","workfromhome","laidoff","losejob","mentalhealth"]]
df.mentalhealth.unique()
df["occupation"] = pd.Categorical(df["occupation"]).codes
cols = ["military","location", "education", "educationmother","educationfather","householdnumber",
"essentialworkers", "essentialworkerhome", "covidfacility","insurance","govassist",
"physicalhealth", "work", "goingtoworkplace","workfromhome", "laidoff", "losejob"]
for col in cols:
df = pd.get_dummies(df, columns=[col], drop_first=True, dtype=df[col].dtype)
df = pd.get_dummies(df,)
df.head()
def correlation_plot(df):
corr = abs(df.corr()) # correlation matrix
lower_triangle = np.tril(corr, k = -1) # select only the lower triangle of the correlation matrix
mask = lower_triangle == 0 # to mask the upper triangle in the following heatmap
plt.figure(figsize = (10,10)) # setting the figure size
sns.set_style(style = 'white') # Setting it to white so that we do not see the grid lines
sns.heatmap(lower_triangle, center=0.5, cmap= 'Blues', xticklabels = corr.index,
yticklabels = corr.columns,cbar = False, annot= True, linewidths= 1, mask = mask) # Da Heatmap
plt.show()
i=0
while(i<90):
correlation_plot(df.iloc[:,i:i+15])
i=i+15
| 0.277767 | 0.336535 |
# Load your own PyTorch BERT model
In the previous [example](https://github.com/deepjavalibrary/djl/blob/master/jupyter/BERTQA.ipynb), you run BERT inference with the model from Model Zoo. You can also load the model on your own pre-trained BERT and use custom classes as the input and output.
In general, the PyTorch BERT model from [HuggingFace](https://github.com/huggingface/transformers) requires these three inputs:
- word indices: The index of each word in a sentence
- word types: The type index of the word.
- attention mask: The mask indicates to the model which tokens should be attended to, and which should not after batching sequence together.
We will dive deep into these details later.
## Preparation
This tutorial requires the installation of Java Kernel. To install the Java Kernel, see the [README](https://github.com/deepjavalibrary/djl/blob/master/jupyter/README.md).
There are dependencies we will use.
```
// %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
%maven ai.djl:api:0.16.0
%maven ai.djl.pytorch:pytorch-engine:0.16.0
%maven ai.djl.pytorch:pytorch-model-zoo:0.16.0
%maven org.slf4j:slf4j-simple:1.7.32
```
### Import java packages
```
import java.io.*;
import java.nio.file.*;
import java.util.*;
import java.util.stream.*;
import ai.djl.*;
import ai.djl.ndarray.*;
import ai.djl.ndarray.types.*;
import ai.djl.inference.*;
import ai.djl.translate.*;
import ai.djl.training.util.*;
import ai.djl.repository.zoo.*;
import ai.djl.modality.nlp.*;
import ai.djl.modality.nlp.qa.*;
import ai.djl.modality.nlp.bert.*;
```
**Reuse the previous input**
```
var question = "When did BBC Japan start broadcasting?";
var resourceDocument = "BBC Japan was a general entertainment Channel.\n" +
"Which operated between December 2004 and April 2006.\n" +
"It ceased operations after its Japanese distributor folded.";
QAInput input = new QAInput(question, resourceDocument);
```
## Dive deep into Translator
Inference in deep learning is the process of predicting the output for a given input based on a pre-defined model.
DJL abstracts away the whole process for ease of use. It can load the model, perform inference on the input, and provide
output. DJL also allows you to provide user-defined inputs. The workflow looks like the following:
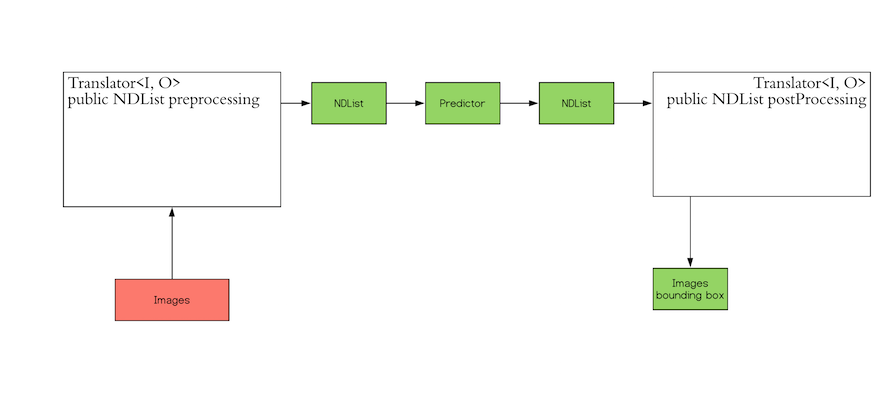
The red block ("Images") in the workflow is the input that DJL expects from you. The green block ("Images
bounding box") is the output that you expect. Because DJL does not know which input to expect and which output format that you prefer, DJL provides the `Translator` interface so you can define your own
input and output.
The `Translator` interface encompasses the two white blocks: Pre-processing and Post-processing. The pre-processing
component converts the user-defined input objects into an NDList, so that the `Predictor` in DJL can understand the
input and make its prediction. Similarly, the post-processing block receives an NDList as the output from the
`Predictor`. The post-processing block allows you to convert the output from the `Predictor` to the desired output
format.
### Pre-processing
Now, you need to convert the sentences into tokens. We provide a powerful tool `BertTokenizer` that you can use to convert questions and answers into tokens, and batchify your sequence together. Once you have properly formatted tokens, you can use `Vocabulary` to map your token to BERT index.
The following code block demonstrates tokenizing the question and answer defined earlier into BERT-formatted tokens.
```
var tokenizer = new BertTokenizer();
List<String> tokenQ = tokenizer.tokenize(question.toLowerCase());
List<String> tokenA = tokenizer.tokenize(resourceDocument.toLowerCase());
System.out.println("Question Token: " + tokenQ);
System.out.println("Answer Token: " + tokenA);
```
`BertTokenizer` can also help you batchify questions and resource documents together by calling `encode()`.
The output contains information that BERT ingests.
- getTokens: It returns a list of strings including the question, resource document and special word to let the model tell which part is the question and which part is the resource document. Because PyTorch BERT was trained with varioue sequence length, you don't pad the tokens.
- getTokenTypes: It returns a list of type indices of the word to indicate the location of the resource document. All Questions will be labelled with 0 and all resource documents will be labelled with 1.
[Question tokens...DocResourceTokens...padding tokens] => [000000...11111....0000]
- getValidLength: It returns the actual length of the question and resource document tokens tokens, which are required by MXNet BERT.
- getAttentionMask: It returns the mask for the model to indicate which part should be paid attention to and which part is the padding. It is required by PyTorch BERT.
[Question tokens...DocResourceTokens...padding tokens] => [111111...11111....0000]
PyTorch BERT was trained with varioue sequence length, so we don't need to pad the tokens.
```
BertToken token = tokenizer.encode(question.toLowerCase(), resourceDocument.toLowerCase());
System.out.println("Encoded tokens: " + token.getTokens());
System.out.println("Encoded token type: " + token.getTokenTypes());
System.out.println("Valid length: " + token.getValidLength());
```
Normally, words and sentences are represented as indices instead of tokens for training.
They typically work like a vector in a n-dimensional space. In this case, you need to map them into indices.
DJL provides `Vocabulary` to take care of you vocabulary mapping.
The bert vocab from Huggingface is of the following format.
```
[PAD]
[unused0]
[unused1]
[unused2]
[unused3]
[unused4]
[unused5]
[unused6]
[unused7]
[unused8]
...
```
We provide the `bert-base-uncased-vocab.txt` from our pre-trained BERT for demonstration.
```
DownloadUtils.download("https://djl-ai.s3.amazonaws.com/mlrepo/model/nlp/question_answer/ai/djl/pytorch/bertqa/0.0.1/bert-base-uncased-vocab.txt.gz", "build/pytorch/bertqa/vocab.txt", new ProgressBar());
var path = Paths.get("build/pytorch/bertqa/vocab.txt");
var vocabulary = DefaultVocabulary.builder()
.optMinFrequency(1)
.addFromTextFile(path)
.optUnknownToken("[UNK]")
.build();
```
You can easily convert the token to the index using `vocabulary.getIndex(token)` and the other way around using `vocabulary.getToken(index)`.
```
long index = vocabulary.getIndex("car");
String token = vocabulary.getToken(2482);
System.out.println("The index of the car is " + index);
System.out.println("The token of the index 2482 is " + token);
```
To properly convert them into `float[]` for `NDArray` creation, here is the helper function:
Now that you have everything you need, you can create an NDList and populate all of the inputs you formatted earlier. You're done with pre-processing!
#### Construct `Translator`
You need to do this processing within an implementation of the `Translator` interface. `Translator` is designed to do pre-processing and post-processing. You must define the input and output objects. It contains the following two override classes:
- `public NDList processInput(TranslatorContext ctx, I)`
- `public String processOutput(TranslatorContext ctx, O)`
Every translator takes in input and returns output in the form of generic objects. In this case, the translator takes input in the form of `QAInput` (I) and returns output as a `String` (O). `QAInput` is just an object that holds questions and answer; We have prepared the Input class for you.
Armed with the needed knowledge, you can write an implementation of the `Translator` interface. `BertTranslator` uses the code snippets explained previously to implement the `processInput`method. For more information, see [`NDManager`](https://javadoc.io/static/ai.djl/api/0.16.0/index.html?ai/djl/ndarray/NDManager.html).
```
manager.create(Number[] data, Shape)
manager.create(Number[] data)
```
```
public class BertTranslator implements Translator<QAInput, String> {
private List<String> tokens;
private Vocabulary vocabulary;
private BertTokenizer tokenizer;
@Override
public void prepare(TranslatorContext ctx) throws IOException {
Path path = Paths.get("build/pytorch/bertqa/vocab.txt");
vocabulary = DefaultVocabulary.builder()
.optMinFrequency(1)
.addFromTextFile(path)
.optUnknownToken("[UNK]")
.build();
tokenizer = new BertTokenizer();
}
@Override
public NDList processInput(TranslatorContext ctx, QAInput input) {
BertToken token =
tokenizer.encode(
input.getQuestion().toLowerCase(),
input.getParagraph().toLowerCase());
// get the encoded tokens that would be used in precessOutput
tokens = token.getTokens();
NDManager manager = ctx.getNDManager();
// map the tokens(String) to indices(long)
long[] indices = tokens.stream().mapToLong(vocabulary::getIndex).toArray();
long[] attentionMask = token.getAttentionMask().stream().mapToLong(i -> i).toArray();
long[] tokenType = token.getTokenTypes().stream().mapToLong(i -> i).toArray();
NDArray indicesArray = manager.create(indices);
NDArray attentionMaskArray =
manager.create(attentionMask);
NDArray tokenTypeArray = manager.create(tokenType);
// The order matters
return new NDList(indicesArray, attentionMaskArray, tokenTypeArray);
}
@Override
public String processOutput(TranslatorContext ctx, NDList list) {
NDArray startLogits = list.get(0);
NDArray endLogits = list.get(1);
int startIdx = (int) startLogits.argMax().getLong();
int endIdx = (int) endLogits.argMax().getLong();
return tokens.subList(startIdx, endIdx + 1).toString();
}
@Override
public Batchifier getBatchifier() {
return Batchifier.STACK;
}
}
```
Congrats! You have created your first Translator! We have pre-filled the `processOutput()` function to process the `NDList` and return it in a desired format. `processInput()` and `processOutput()` offer the flexibility to get the predictions from the model in any format you desire.
With the Translator implemented, you need to bring up the predictor that uses your `Translator` to start making predictions. You can find the usage for `Predictor` in the [Predictor Javadoc](https://javadoc.io/static/ai.djl/api/0.16.0/index.html?ai/djl/inference/Predictor.html). Create a translator and use the `question` and `resourceDocument` provided previously.
```
DownloadUtils.download("https://djl-ai.s3.amazonaws.com/mlrepo/model/nlp/question_answer/ai/djl/pytorch/bertqa/0.0.1/trace_bertqa.pt.gz", "build/pytorch/bertqa/bertqa.pt", new ProgressBar());
BertTranslator translator = new BertTranslator();
Criteria<QAInput, String> criteria = Criteria.builder()
.setTypes(QAInput.class, String.class)
.optModelPath(Paths.get("build/pytorch/bertqa/")) // search in local folder
.optTranslator(translator)
.optProgress(new ProgressBar()).build();
ZooModel model = criteria.loadModel();
String predictResult = null;
QAInput input = new QAInput(question, resourceDocument);
// Create a Predictor and use it to predict the output
try (Predictor<QAInput, String> predictor = model.newPredictor(translator)) {
predictResult = predictor.predict(input);
}
System.out.println(question);
System.out.println(predictResult);
```
Based on the input, the following result will be shown:
```
[december, 2004]
```
That's it!
You can try with more questions and answers. Here are the samples:
**Answer Material**
The Normans (Norman: Nourmands; French: Normands; Latin: Normanni) were the people who in the 10th and 11th centuries gave their name to Normandy, a region in France. They were descended from Norse ("Norman" comes from "Norseman") raiders and pirates from Denmark, Iceland and Norway who, under their leader Rollo, agreed to swear fealty to King Charles III of West Francia. Through generations of assimilation and mixing with the native Frankish and Roman-Gaulish populations, their descendants would gradually merge with the Carolingian-based cultures of West Francia. The distinct cultural and ethnic identity of the Normans emerged initially in the first half of the 10th century, and it continued to evolve over the succeeding centuries.
**Question**
Q: When were the Normans in Normandy?
A: 10th and 11th centuries
Q: In what country is Normandy located?
A: france
For the full source code, see the [DJL repo](https://github.com/deepjavalibrary/djl/blob/master/examples/src/main/java/ai/djl/examples/inference/BertQaInference.java) and translator implementation [MXNet](https://github.com/deepjavalibrary/djl/blob/master/engines/mxnet/mxnet-model-zoo/src/main/java/ai/djl/mxnet/zoo/nlp/qa/MxBertQATranslator.java) [PyTorch](https://github.com/deepjavalibrary/djl/blob/master/engines/pytorch/pytorch-model-zoo/src/main/java/ai/djl/pytorch/zoo/nlp/qa/PtBertQATranslator.java).
|
github_jupyter
|
// %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
%maven ai.djl:api:0.16.0
%maven ai.djl.pytorch:pytorch-engine:0.16.0
%maven ai.djl.pytorch:pytorch-model-zoo:0.16.0
%maven org.slf4j:slf4j-simple:1.7.32
import java.io.*;
import java.nio.file.*;
import java.util.*;
import java.util.stream.*;
import ai.djl.*;
import ai.djl.ndarray.*;
import ai.djl.ndarray.types.*;
import ai.djl.inference.*;
import ai.djl.translate.*;
import ai.djl.training.util.*;
import ai.djl.repository.zoo.*;
import ai.djl.modality.nlp.*;
import ai.djl.modality.nlp.qa.*;
import ai.djl.modality.nlp.bert.*;
var question = "When did BBC Japan start broadcasting?";
var resourceDocument = "BBC Japan was a general entertainment Channel.\n" +
"Which operated between December 2004 and April 2006.\n" +
"It ceased operations after its Japanese distributor folded.";
QAInput input = new QAInput(question, resourceDocument);
var tokenizer = new BertTokenizer();
List<String> tokenQ = tokenizer.tokenize(question.toLowerCase());
List<String> tokenA = tokenizer.tokenize(resourceDocument.toLowerCase());
System.out.println("Question Token: " + tokenQ);
System.out.println("Answer Token: " + tokenA);
BertToken token = tokenizer.encode(question.toLowerCase(), resourceDocument.toLowerCase());
System.out.println("Encoded tokens: " + token.getTokens());
System.out.println("Encoded token type: " + token.getTokenTypes());
System.out.println("Valid length: " + token.getValidLength());
[PAD]
[unused0]
[unused1]
[unused2]
[unused3]
[unused4]
[unused5]
[unused6]
[unused7]
[unused8]
...
DownloadUtils.download("https://djl-ai.s3.amazonaws.com/mlrepo/model/nlp/question_answer/ai/djl/pytorch/bertqa/0.0.1/bert-base-uncased-vocab.txt.gz", "build/pytorch/bertqa/vocab.txt", new ProgressBar());
var path = Paths.get("build/pytorch/bertqa/vocab.txt");
var vocabulary = DefaultVocabulary.builder()
.optMinFrequency(1)
.addFromTextFile(path)
.optUnknownToken("[UNK]")
.build();
long index = vocabulary.getIndex("car");
String token = vocabulary.getToken(2482);
System.out.println("The index of the car is " + index);
System.out.println("The token of the index 2482 is " + token);
manager.create(Number[] data, Shape)
manager.create(Number[] data)
public class BertTranslator implements Translator<QAInput, String> {
private List<String> tokens;
private Vocabulary vocabulary;
private BertTokenizer tokenizer;
@Override
public void prepare(TranslatorContext ctx) throws IOException {
Path path = Paths.get("build/pytorch/bertqa/vocab.txt");
vocabulary = DefaultVocabulary.builder()
.optMinFrequency(1)
.addFromTextFile(path)
.optUnknownToken("[UNK]")
.build();
tokenizer = new BertTokenizer();
}
@Override
public NDList processInput(TranslatorContext ctx, QAInput input) {
BertToken token =
tokenizer.encode(
input.getQuestion().toLowerCase(),
input.getParagraph().toLowerCase());
// get the encoded tokens that would be used in precessOutput
tokens = token.getTokens();
NDManager manager = ctx.getNDManager();
// map the tokens(String) to indices(long)
long[] indices = tokens.stream().mapToLong(vocabulary::getIndex).toArray();
long[] attentionMask = token.getAttentionMask().stream().mapToLong(i -> i).toArray();
long[] tokenType = token.getTokenTypes().stream().mapToLong(i -> i).toArray();
NDArray indicesArray = manager.create(indices);
NDArray attentionMaskArray =
manager.create(attentionMask);
NDArray tokenTypeArray = manager.create(tokenType);
// The order matters
return new NDList(indicesArray, attentionMaskArray, tokenTypeArray);
}
@Override
public String processOutput(TranslatorContext ctx, NDList list) {
NDArray startLogits = list.get(0);
NDArray endLogits = list.get(1);
int startIdx = (int) startLogits.argMax().getLong();
int endIdx = (int) endLogits.argMax().getLong();
return tokens.subList(startIdx, endIdx + 1).toString();
}
@Override
public Batchifier getBatchifier() {
return Batchifier.STACK;
}
}
DownloadUtils.download("https://djl-ai.s3.amazonaws.com/mlrepo/model/nlp/question_answer/ai/djl/pytorch/bertqa/0.0.1/trace_bertqa.pt.gz", "build/pytorch/bertqa/bertqa.pt", new ProgressBar());
BertTranslator translator = new BertTranslator();
Criteria<QAInput, String> criteria = Criteria.builder()
.setTypes(QAInput.class, String.class)
.optModelPath(Paths.get("build/pytorch/bertqa/")) // search in local folder
.optTranslator(translator)
.optProgress(new ProgressBar()).build();
ZooModel model = criteria.loadModel();
String predictResult = null;
QAInput input = new QAInput(question, resourceDocument);
// Create a Predictor and use it to predict the output
try (Predictor<QAInput, String> predictor = model.newPredictor(translator)) {
predictResult = predictor.predict(input);
}
System.out.println(question);
System.out.println(predictResult);
[december, 2004]
| 0.689306 | 0.956513 |
## 9.2 微调
1. **迁移学习(transfer learning)**
- 该数据集上训练的模型可以抽取较通用的图像特征,从而能够帮助识别边缘、纹理、形状和物体组成
- 迁移学习中的一种常用技术: 微调
2. **微调(fine tuning)**
- 在源数据集(如ImageNet数据集)上预训练一个神经网络模型,即源模型
- 创建一个新的神经网络模型,即目标模型
- 复制了源模型上除了输出层外的所有模型设计及其参数
- 假设这些模型参数包含了源数据集上学习到的知识,且这些知识同样适用于目标数据集
- 还假设源模型的输出层跟源数据集的标签紧密相关,因此在目标模型中不予采用
- 为目标模型添加一个输出大小为目标数据集类别个数的输出层,并随机初始化该层的模型参数
- 目标数据集上训练目标模型。我们将从头训练输出层,而其余层的参数都是基于源模型的参数微调得到的

### 9.2.1 热狗识别
1. torchvision的[models](https://pytorch.org/docs/stable/torchvision/models.html)包提供了常用的预训练模型
2. 更多的预训练模型,可以使用使用[pretrained-models](https://github.com/Cadene/pretrained-models.pytorch)仓库
```
%matplotlib inline
import torch
from torch import nn, optim
from torch.utils.data import Dataset, DataLoader
import torchvision
from torchvision.datasets import ImageFolder
from torchvision import transforms
from torchvision import models
import os
import sys
sys.path.append("..")
import d2lzh_pytorch.utils as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
```
#### 9.2.1.1 获取数据集
1. 该数据集含有1400张包含热狗的正类图像,和同样多包含其他食品的负类图像
2. 各类的1000张图像被用于训练,其余则用于测试
```
data_dir = '~/Datasets/'
data_dir = os.path.expanduser(data_dir)
os.listdir(os.path.join(data_dir, "hotdog"))
```
`ImageFolder`实例来分别读取训练数据集和测试数据集中的所有图像文件
```
train_imgs = ImageFolder(os.path.join(data_dir, 'hotdog/train'))
test_imgs = ImageFolder(os.path.join(data_dir, 'hotdog/test'))
# 前八张正类
hotdots = [train_imgs[i][0] for i in range(8)]
# 后八张负类
not_hotdogs = [train_imgs[-i - 1][0] for i in range(8)]
d2l.show_images(hotdots + not_hotdogs, 2, 8, scale=1.5)
```
- 训练
- 先从图像中裁剪出随机大小和随机高宽比的一块随机区域,
- 然后将该区域缩放为高和宽均为224像素的输入
- 测试
- 时,我们将图像的高和宽均缩放为256像素
- 然后从中裁剪出高和宽均为224像素的中心区域作为输入
- 标准化
- 对RGB(红、绿、蓝)三个颜色通道的数值做标准化:每个数值减去该通道所有数值的平均值,再除以该通道所有数值的标准差作为输出
***在使用预训练模型时,一定要和预训练时作同样的预处理***
```
All pre-trained models expect input images normalized in the same way, i.e. mini-batches of 3-channel RGB images of shape (3 x H x W), where H and W are expected to be at least 224. The images have to be loaded in to a range of [0, 1] and then normalized using mean = [0.485, 0.456, 0.406] and std = [0.229, 0.224, 0.225]
```
```
normalize = transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
train_augs = transforms.Compose([
transforms.RandomResizedCrop(size=224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
normalize
])
test_augs = transforms.Compose([
transforms.Resize(size=256),
transforms.CenterCrop(size=224),
transforms.ToTensor(),
normalize
])
```
#### 9.2.1.2 定义和初始化模型
> 不管你是使用的torchvision的models还是pretrained-models.pytorch仓库,默认都会将预训练好的模型参数下载到你的home目录下.cache/torch/checkpoint文件夹。你可以通过修改环境变量`TORCH_MODEL_ZOO`来更改下载目录(windows环境)
> 可直接手动下载,然后放入上面目录中
```
pretrained_net = models.resnet18(pretrained=True)
# 作为一个全连接层,它将ResNet最终的全局平均池化层输出变换成ImageNet数据集上1000类的输出
print(pretrained_net.fc)
# 修改需要的输出类别数
pretrained_net.fc = nn.Linear(512, 2)
print(pretrained_net.fc)
```
1. **此时,pretrained_net的fc层就被随机初始化了,但是其他层依然保存着预训练得到的参数**
2. **由于是在很大的ImageNet数据集上预训练的,所以参数已经足够好,因此一般只需使用较小的学习率来微调这些参数**
3. **而fc中的随机初始化参数一般需要更大的学习率从头训练**
```
# 将fc的学习率设为已经预训练过的部分的10倍
output_params = list(map(id, pretrained_net.fc.parameters()))
feature_params = filter(lambda p: id(p) not in output_params, pretrained_net.parameters())
lr = 0.01
optimizer = optim.SGD([{'params': feature_params},
{'params': pretrained_net.fc.parameters(), 'lr': lr * 10}],
lr=lr, weight_decay=0.001)
```
#### 9.2.1.3 微调模型
```
def train_fine_tuning(net, optimizer, batch_size=8, num_epochs=5):
train_iter = DataLoader(ImageFolder(os.path.join(data_dir, 'hotdog/train'), transform=train_augs),
batch_size, shuffle=True)
test_iter = DataLoader(ImageFolder(os.path.join(data_dir, 'hotdog/test'), transform=test_augs),
batch_size)
loss = torch.nn.CrossEntropyLoss()
d2l.train(train_iter, test_iter, net, loss, optimizer, device, num_epochs)
train_fine_tuning(pretrained_net, optimizer)
```
> 作为对比,我们定义一个相同的模型,但将它的所有模型参数都初始化为随机值。由于整个模型都需要从头训练,我们可以使用较大的学习率
```
scratch_net = models.resnet18(pretrained=False, num_classes=2)
lr = 0.1
optimizer = optim.SGD(scratch_net.parameters(), lr=lr, weight_decay=0.001)
train_fine_tuning(scratch_net, optimizer)
```
|
github_jupyter
|
%matplotlib inline
import torch
from torch import nn, optim
from torch.utils.data import Dataset, DataLoader
import torchvision
from torchvision.datasets import ImageFolder
from torchvision import transforms
from torchvision import models
import os
import sys
sys.path.append("..")
import d2lzh_pytorch.utils as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
data_dir = '~/Datasets/'
data_dir = os.path.expanduser(data_dir)
os.listdir(os.path.join(data_dir, "hotdog"))
train_imgs = ImageFolder(os.path.join(data_dir, 'hotdog/train'))
test_imgs = ImageFolder(os.path.join(data_dir, 'hotdog/test'))
# 前八张正类
hotdots = [train_imgs[i][0] for i in range(8)]
# 后八张负类
not_hotdogs = [train_imgs[-i - 1][0] for i in range(8)]
d2l.show_images(hotdots + not_hotdogs, 2, 8, scale=1.5)
All pre-trained models expect input images normalized in the same way, i.e. mini-batches of 3-channel RGB images of shape (3 x H x W), where H and W are expected to be at least 224. The images have to be loaded in to a range of [0, 1] and then normalized using mean = [0.485, 0.456, 0.406] and std = [0.229, 0.224, 0.225]
normalize = transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
train_augs = transforms.Compose([
transforms.RandomResizedCrop(size=224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
normalize
])
test_augs = transforms.Compose([
transforms.Resize(size=256),
transforms.CenterCrop(size=224),
transforms.ToTensor(),
normalize
])
pretrained_net = models.resnet18(pretrained=True)
# 作为一个全连接层,它将ResNet最终的全局平均池化层输出变换成ImageNet数据集上1000类的输出
print(pretrained_net.fc)
# 修改需要的输出类别数
pretrained_net.fc = nn.Linear(512, 2)
print(pretrained_net.fc)
# 将fc的学习率设为已经预训练过的部分的10倍
output_params = list(map(id, pretrained_net.fc.parameters()))
feature_params = filter(lambda p: id(p) not in output_params, pretrained_net.parameters())
lr = 0.01
optimizer = optim.SGD([{'params': feature_params},
{'params': pretrained_net.fc.parameters(), 'lr': lr * 10}],
lr=lr, weight_decay=0.001)
def train_fine_tuning(net, optimizer, batch_size=8, num_epochs=5):
train_iter = DataLoader(ImageFolder(os.path.join(data_dir, 'hotdog/train'), transform=train_augs),
batch_size, shuffle=True)
test_iter = DataLoader(ImageFolder(os.path.join(data_dir, 'hotdog/test'), transform=test_augs),
batch_size)
loss = torch.nn.CrossEntropyLoss()
d2l.train(train_iter, test_iter, net, loss, optimizer, device, num_epochs)
train_fine_tuning(pretrained_net, optimizer)
scratch_net = models.resnet18(pretrained=False, num_classes=2)
lr = 0.1
optimizer = optim.SGD(scratch_net.parameters(), lr=lr, weight_decay=0.001)
train_fine_tuning(scratch_net, optimizer)
| 0.672869 | 0.937268 |
# 宿題2
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from collections import defaultdict
data = np.loadtxt('data/digit_test0.csv', delimiter=',')
data.shape
data[0]
img = data[0].reshape(16,16)
plt.imshow(img, cmap='gray')
plt.show()
digit = np.array([[1]] * 200)
digit.shape
np.array(data, digit)
np.array([data, [[0]]*200])
test = np.array([1,2,2,3,2,4,5,4])
from collections import Counter
c = Counter(test)
c.most_common(1)[0][0]
```
# kNN
http://blog.amedama.jp/entry/2017/03/18/140238
```
import numpy as np
from collections import Counter
class kNN(object):
def __init__(self, k=1):
self._train_data = None
self._target_data = None
self._k = k
def fit(self, train_data, target_data):
self._train_data = train_data
self._target_data = target_data
def predict(self, x):
distances = np.array([np.linalg.norm(p - x) for p in self._train_data])
nearest_indices = distances.argsort()[:self._k]
nearest_labels = self._target_data[nearest_indices]
c = Counter(nearest_labels)
return c.most_common(1)[0][0]
def load_train_data():
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_feature = np.vstack([train_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
train_label = np.hstack([train_label, temp_label])
return train_feature, train_label
def load_test_data():
for i in range(10):
if i==0:
test_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_label = np.array([i]*test_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_feature = np.vstack([test_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
test_label = np.hstack([test_label, temp_label])
return test_feature, test_label
train_feature, train_label = load_train_data()
train_feature.shape
train_label.shape
train_label[1900]
test_feature, test_label = load_test_data()
test_label.shape
model = kNN()
model.fit(train_feature, train_label)
model._train_data.shape
from sklearn.metrics import accuracy_score
predicted_labels = []
for feature in test_feature:
predicted_label = model.predict(feature)
predicted_labels.append(predicted_label)
accuracy_score(test_label, predicted_labels)
len(predicted_labels)
accuracy_score(test_label, predicted_labels)
def calc_accuracy(train_feature, train_label, test_feature, test_label):
model = kNN()
model.fit(train_feature, train_label)
predicted_labels = []
for feature in test_feature:
predicted_label = model.predict(feature)
predicted_labels.append(predicted_label)
return accuracy_score(test_label, predicted_labels)
calc_accuracy(train_feature, train_label, test_feature, test_label)
```
## 高速化
```
import numpy as np
from collections import Counter
def load_train_data():
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_feature = np.vstack([train_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
train_label = np.hstack([train_label, temp_label])
return train_feature, train_label
def load_test_data():
for i in range(10):
if i==0:
test_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_label = np.array([i]*test_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_feature = np.vstack([test_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
test_label = np.hstack([test_label, temp_label])
return test_feature, test_label
train_feature, train_label = load_train_data()
test_feature, test_label = load_test_data()
import numpy as np
from collections import Counter
class kNN(object):
def __init__(self, k=1):
self._train_data = None
self._target_data = None
self._k = k
def fit(self, train_data, target_data):
self._train_data = train_data
self._target_data = target_data
def predict(self, x):
distances = np.array([np.linalg.norm(p - x) for p in self._train_data])
nearest_indices = distances.argsort()[:self._k]
nearest_labels = self._target_data[nearest_indices]
c = Counter(nearest_labels)
return c.most_common(1)[0][0]
predicted_labels
test_feature.shape
predicted_label
```
## ここまでのまとめ
```
import numpy as np
from collections import Counter
from sklearn.metrics import accuracy_score
class kNN(object):
def __init__(self, k=1):
self._train_data = None
self._target_data = None
self._k = k
def fit(self, train_data, target_data):
self._train_data = train_data
self._target_data = target_data
def predict(self, x):
distances = np.array([np.linalg.norm(p - x) for p in self._train_data])
nearest_indices = distances.argsort()[:self._k]
nearest_labels = self._target_data[nearest_indices]
c = Counter(nearest_labels)
return c.most_common(1)[0][0]
def load_train_data():
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_feature = np.vstack([train_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
train_label = np.hstack([train_label, temp_label])
return train_feature, train_label
def load_test_data():
for i in range(10):
if i==0:
test_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_label = np.array([i]*test_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_feature = np.vstack([test_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
test_label = np.hstack([test_label, temp_label])
return test_feature, test_label
def calc_accuracy(train_feature, train_label, test_feature, test_label, k=1):
model = kNN(k)
model.fit(train_feature, train_label)
predicted_labels = []
for feature in test_feature:
predicted_label = model.predict(feature)
predicted_labels.append(predicted_label)
return accuracy_score(test_label, predicted_labels)
train_feature, train_label = load_train_data()
test_feature, test_label = load_test_data()
calc_accuracy(train_feature, train_label, test_feature, test_label, k=1)
calc_accuracy(train_feature, train_label, test_feature, test_label, k=5)
```
# 交差検証
```
n_split = 5
def load_train_data_cv(n_split):
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
group_feature = np.split(train_feature, n_split)
group_label = np.split(train_label, n_split)
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
temp_group_feature = np.split(temp_feature, n_split)
temp_label = np.array([i]*temp_feature.shape[0])
temp_group_label = np.split(temp_label, n_split)
for m in range(n_split):
group_feature[m] = np.vstack([group_feature[m], temp_group_feature[m]])
group_label[m] = np.hstack([group_label[m], temp_group_label[m]])
return group_feature, group_label
group_feature, group_label = load_train_data_cv(5)
len(group_feature)
group_feature[0].shape
group_label[0].shape
group_label[0][999]
group_feature.pop(2)
temp = np.vstack(group_feature)
temp.shape
```
`pop`はよくなさそう
```
temp = group_feature.copy()
temp.pop(2)
temp1 = np.vstack(temp)
print(temp1.shape)
print(len(group_feature))
def cross_validation(n_split=5, params=[1,2,3,4,5,10,20]):
n_params = len(params)
score_list = np.zeros(n_params)
group_feature, group_label = load_train_data_cv(n_split)
for j in range(n_params):
for i in range(n_split):
temp_group_feature = group_feature.copy()
temp_test_feature = temp_group_feature.pop(i)
temp_train_feature = np.vstack(temp_group_feature)
temp_group_label = group_label.copy()
temp_test_label = temp_group_label.pop(i)
temp_train_label = np.hstack(temp_group_label)
score_list[j] += calc_accuracy(temp_train_feature, temp_train_label, temp_test_feature, temp_test_label, k=params[j])
opt_param = params[np.argmax(score_list)]
print(score_list)
return opt_param
cross_validation(n_split=5, params=[1,3,5])
test = np.array([1,2,3,4,5])
np.split(test, 5)
test = [1,2,3,4]
test.pop(2)
test
test = [4.838, 4.837, 4.825]
for i in test:
print(i/5)
```
# まとめ
```
import numpy as np
from collections import Counter
from sklearn.metrics import accuracy_score
class kNN(object):
def __init__(self, k=1):
self._train_data = None
self._target_data = None
self._k = k
def fit(self, train_data, target_data):
self._train_data = train_data
self._target_data = target_data
def predict(self, x):
distances = np.array([np.linalg.norm(p - x) for p in self._train_data])
nearest_indices = distances.argsort()[:self._k]
nearest_labels = self._target_data[nearest_indices]
c = Counter(nearest_labels)
return c.most_common(1)[0][0]
def load_train_data():
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_feature = np.vstack([train_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
train_label = np.hstack([train_label, temp_label])
return train_feature, train_label
def load_test_data():
for i in range(10):
if i==0:
test_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_label = np.array([i]*test_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_feature = np.vstack([test_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
test_label = np.hstack([test_label, temp_label])
return test_feature, test_label
def calc_accuracy(train_feature, train_label, test_feature, test_label, k=1):
model = kNN(k)
model.fit(train_feature, train_label)
predicted_labels = []
for feature in test_feature:
predicted_label = model.predict(feature)
predicted_labels.append(predicted_label)
return accuracy_score(test_label, predicted_labels)
def load_train_data_cv(n_split=5):
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
group_feature = np.split(train_feature, n_split)
group_label = np.split(train_label, n_split)
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
temp_group_feature = np.split(temp_feature, n_split)
temp_label = np.array([i]*temp_feature.shape[0])
temp_group_label = np.split(temp_label, n_split)
for m in range(n_split):
group_feature[m] = np.vstack([group_feature[m], temp_group_feature[m]])
group_label[m] = np.hstack([group_label[m], temp_group_label[m]])
return group_feature, group_label
def cross_validation(n_split=5, params=[1,2,3,4,5,10,20]):
n_params = len(params)
score_list = np.zeros(n_params)
group_feature, group_label = load_train_data_cv(n_split)
for j in range(n_params):
for i in range(n_split):
temp_group_feature = group_feature.copy()
temp_test_feature = temp_group_feature.pop(i)
temp_train_feature = np.vstack(temp_group_feature)
temp_group_label = group_label.copy()
temp_test_label = temp_group_label.pop(i)
temp_train_label = np.hstack(temp_group_label)
score_list[j] += calc_accuracy(temp_train_feature, temp_train_label, temp_test_feature, temp_test_label, k=params[j])/n_split
opt_param = params[np.argmax(score_list)]
print(score_list)
return opt_param
def main():
k_opt = cross_validation(n_split=5, params=[1,2,3,4,5,10,20])
train_feature, train_label = load_train_data()
test_feature, test_label = load_test_data()
score = calc_accuracy(train_feature, train_label, test_feature, test_label, k=k_opt)
print(score)
main()
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from collections import defaultdict
data = np.loadtxt('data/digit_test0.csv', delimiter=',')
data.shape
data[0]
img = data[0].reshape(16,16)
plt.imshow(img, cmap='gray')
plt.show()
digit = np.array([[1]] * 200)
digit.shape
np.array(data, digit)
np.array([data, [[0]]*200])
test = np.array([1,2,2,3,2,4,5,4])
from collections import Counter
c = Counter(test)
c.most_common(1)[0][0]
import numpy as np
from collections import Counter
class kNN(object):
def __init__(self, k=1):
self._train_data = None
self._target_data = None
self._k = k
def fit(self, train_data, target_data):
self._train_data = train_data
self._target_data = target_data
def predict(self, x):
distances = np.array([np.linalg.norm(p - x) for p in self._train_data])
nearest_indices = distances.argsort()[:self._k]
nearest_labels = self._target_data[nearest_indices]
c = Counter(nearest_labels)
return c.most_common(1)[0][0]
def load_train_data():
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_feature = np.vstack([train_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
train_label = np.hstack([train_label, temp_label])
return train_feature, train_label
def load_test_data():
for i in range(10):
if i==0:
test_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_label = np.array([i]*test_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_feature = np.vstack([test_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
test_label = np.hstack([test_label, temp_label])
return test_feature, test_label
train_feature, train_label = load_train_data()
train_feature.shape
train_label.shape
train_label[1900]
test_feature, test_label = load_test_data()
test_label.shape
model = kNN()
model.fit(train_feature, train_label)
model._train_data.shape
from sklearn.metrics import accuracy_score
predicted_labels = []
for feature in test_feature:
predicted_label = model.predict(feature)
predicted_labels.append(predicted_label)
accuracy_score(test_label, predicted_labels)
len(predicted_labels)
accuracy_score(test_label, predicted_labels)
def calc_accuracy(train_feature, train_label, test_feature, test_label):
model = kNN()
model.fit(train_feature, train_label)
predicted_labels = []
for feature in test_feature:
predicted_label = model.predict(feature)
predicted_labels.append(predicted_label)
return accuracy_score(test_label, predicted_labels)
calc_accuracy(train_feature, train_label, test_feature, test_label)
import numpy as np
from collections import Counter
def load_train_data():
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_feature = np.vstack([train_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
train_label = np.hstack([train_label, temp_label])
return train_feature, train_label
def load_test_data():
for i in range(10):
if i==0:
test_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_label = np.array([i]*test_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_feature = np.vstack([test_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
test_label = np.hstack([test_label, temp_label])
return test_feature, test_label
train_feature, train_label = load_train_data()
test_feature, test_label = load_test_data()
import numpy as np
from collections import Counter
class kNN(object):
def __init__(self, k=1):
self._train_data = None
self._target_data = None
self._k = k
def fit(self, train_data, target_data):
self._train_data = train_data
self._target_data = target_data
def predict(self, x):
distances = np.array([np.linalg.norm(p - x) for p in self._train_data])
nearest_indices = distances.argsort()[:self._k]
nearest_labels = self._target_data[nearest_indices]
c = Counter(nearest_labels)
return c.most_common(1)[0][0]
predicted_labels
test_feature.shape
predicted_label
import numpy as np
from collections import Counter
from sklearn.metrics import accuracy_score
class kNN(object):
def __init__(self, k=1):
self._train_data = None
self._target_data = None
self._k = k
def fit(self, train_data, target_data):
self._train_data = train_data
self._target_data = target_data
def predict(self, x):
distances = np.array([np.linalg.norm(p - x) for p in self._train_data])
nearest_indices = distances.argsort()[:self._k]
nearest_labels = self._target_data[nearest_indices]
c = Counter(nearest_labels)
return c.most_common(1)[0][0]
def load_train_data():
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_feature = np.vstack([train_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
train_label = np.hstack([train_label, temp_label])
return train_feature, train_label
def load_test_data():
for i in range(10):
if i==0:
test_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_label = np.array([i]*test_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_feature = np.vstack([test_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
test_label = np.hstack([test_label, temp_label])
return test_feature, test_label
def calc_accuracy(train_feature, train_label, test_feature, test_label, k=1):
model = kNN(k)
model.fit(train_feature, train_label)
predicted_labels = []
for feature in test_feature:
predicted_label = model.predict(feature)
predicted_labels.append(predicted_label)
return accuracy_score(test_label, predicted_labels)
train_feature, train_label = load_train_data()
test_feature, test_label = load_test_data()
calc_accuracy(train_feature, train_label, test_feature, test_label, k=1)
calc_accuracy(train_feature, train_label, test_feature, test_label, k=5)
n_split = 5
def load_train_data_cv(n_split):
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
group_feature = np.split(train_feature, n_split)
group_label = np.split(train_label, n_split)
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
temp_group_feature = np.split(temp_feature, n_split)
temp_label = np.array([i]*temp_feature.shape[0])
temp_group_label = np.split(temp_label, n_split)
for m in range(n_split):
group_feature[m] = np.vstack([group_feature[m], temp_group_feature[m]])
group_label[m] = np.hstack([group_label[m], temp_group_label[m]])
return group_feature, group_label
group_feature, group_label = load_train_data_cv(5)
len(group_feature)
group_feature[0].shape
group_label[0].shape
group_label[0][999]
group_feature.pop(2)
temp = np.vstack(group_feature)
temp.shape
temp = group_feature.copy()
temp.pop(2)
temp1 = np.vstack(temp)
print(temp1.shape)
print(len(group_feature))
def cross_validation(n_split=5, params=[1,2,3,4,5,10,20]):
n_params = len(params)
score_list = np.zeros(n_params)
group_feature, group_label = load_train_data_cv(n_split)
for j in range(n_params):
for i in range(n_split):
temp_group_feature = group_feature.copy()
temp_test_feature = temp_group_feature.pop(i)
temp_train_feature = np.vstack(temp_group_feature)
temp_group_label = group_label.copy()
temp_test_label = temp_group_label.pop(i)
temp_train_label = np.hstack(temp_group_label)
score_list[j] += calc_accuracy(temp_train_feature, temp_train_label, temp_test_feature, temp_test_label, k=params[j])
opt_param = params[np.argmax(score_list)]
print(score_list)
return opt_param
cross_validation(n_split=5, params=[1,3,5])
test = np.array([1,2,3,4,5])
np.split(test, 5)
test = [1,2,3,4]
test.pop(2)
test
test = [4.838, 4.837, 4.825]
for i in test:
print(i/5)
import numpy as np
from collections import Counter
from sklearn.metrics import accuracy_score
class kNN(object):
def __init__(self, k=1):
self._train_data = None
self._target_data = None
self._k = k
def fit(self, train_data, target_data):
self._train_data = train_data
self._target_data = target_data
def predict(self, x):
distances = np.array([np.linalg.norm(p - x) for p in self._train_data])
nearest_indices = distances.argsort()[:self._k]
nearest_labels = self._target_data[nearest_indices]
c = Counter(nearest_labels)
return c.most_common(1)[0][0]
def load_train_data():
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_feature = np.vstack([train_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
train_label = np.hstack([train_label, temp_label])
return train_feature, train_label
def load_test_data():
for i in range(10):
if i==0:
test_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_label = np.array([i]*test_feature.shape[0])
else:
temp_feature = np.loadtxt('data/digit_test{}.csv'.format(i), delimiter=',')
test_feature = np.vstack([test_feature, temp_feature])
temp_label = np.array([i]*temp_feature.shape[0])
test_label = np.hstack([test_label, temp_label])
return test_feature, test_label
def calc_accuracy(train_feature, train_label, test_feature, test_label, k=1):
model = kNN(k)
model.fit(train_feature, train_label)
predicted_labels = []
for feature in test_feature:
predicted_label = model.predict(feature)
predicted_labels.append(predicted_label)
return accuracy_score(test_label, predicted_labels)
def load_train_data_cv(n_split=5):
for i in range(10):
if i==0:
train_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
train_label = np.array([i]*train_feature.shape[0])
group_feature = np.split(train_feature, n_split)
group_label = np.split(train_label, n_split)
else:
temp_feature = np.loadtxt('data/digit_train{}.csv'.format(i), delimiter=',')
temp_group_feature = np.split(temp_feature, n_split)
temp_label = np.array([i]*temp_feature.shape[0])
temp_group_label = np.split(temp_label, n_split)
for m in range(n_split):
group_feature[m] = np.vstack([group_feature[m], temp_group_feature[m]])
group_label[m] = np.hstack([group_label[m], temp_group_label[m]])
return group_feature, group_label
def cross_validation(n_split=5, params=[1,2,3,4,5,10,20]):
n_params = len(params)
score_list = np.zeros(n_params)
group_feature, group_label = load_train_data_cv(n_split)
for j in range(n_params):
for i in range(n_split):
temp_group_feature = group_feature.copy()
temp_test_feature = temp_group_feature.pop(i)
temp_train_feature = np.vstack(temp_group_feature)
temp_group_label = group_label.copy()
temp_test_label = temp_group_label.pop(i)
temp_train_label = np.hstack(temp_group_label)
score_list[j] += calc_accuracy(temp_train_feature, temp_train_label, temp_test_feature, temp_test_label, k=params[j])/n_split
opt_param = params[np.argmax(score_list)]
print(score_list)
return opt_param
def main():
k_opt = cross_validation(n_split=5, params=[1,2,3,4,5,10,20])
train_feature, train_label = load_train_data()
test_feature, test_label = load_test_data()
score = calc_accuracy(train_feature, train_label, test_feature, test_label, k=k_opt)
print(score)
main()
| 0.385837 | 0.741276 |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
import numdifftools as ndt
from scipy.stats import f
# load flow rate data
flow_data = pd.read_csv('flow_data.csv')
lc_data = pd.read_csv('lc_data.csv')
teaf = 0.00721
teaden = 0.728
cBf = teaf
tQf = np.insert(flow_data['t'].values, 0, 0)
Qf = np.insert(flow_data["Qf"].values / teaden, 0, 0)
tlc = lc_data['t'].values
lc = lc_data['lc_meas'].values
Qf_if = interp1d(tQf, Qf, 'previous', bounds_error = False)
t_i = np.arange(0.0, 850.0)
Qf_i = [Qf_if(t) for t in t_i]
fig, ax = plt.subplots()
ax.scatter(tQf, Qf)
ax.plot(t_i, Qf_i)
def rates(t, y, p):
vR = y[0]
nA = y[1]
nB = y[2]
nC = y[3]
nD = y[4]
Qf_if = p[0]
k1 = p[1]
k2 = p[2]
cBf = 0.00721
dvR = Qf_if
dnA = -k1 * nA * nB / vR
dnB = Qf_if * cBf - nB * (k1 * nA + k2 * nC) / vR
dnC = nB * (k1 * nA - k2 * nC) / vR
dnD = k2 * nC * nB / vR
return [dvR, dnA, dnB, dnC, dnD]
def simprob(p, tQf, Qf):
y0 = [2370.0, p[0], 0.0, 0.0, 0.0]
for (i, t) in enumerate(tQf[:-1]):
#print(i)
tspan = [0.0, tQf[i+1] - tQf[i]]
p_ext = [Qf[i], p[1], p[2]]
sol = solve_ivp(rates, tspan, y0, method = "BDF", args = (p_ext,))
sol.t = sol.t + tQf[i]
y0 = sol.y[:,-1]
if i == 0:
sol_l_t = np.copy(sol.t)
sol_l_y = np.copy(sol.y)
else:
sol_l_t = np.concatenate((sol_l_t, sol.t))
sol_l_y = np.concatenate((sol_l_y, sol.y), axis = 1)
return sol_l_t, sol_l_y
def get_lcpred(sol):
lc_pred = 1 / (1 + 2.0*sol[1,:]/np.maximum(sol[0,:], 1e-6))
return lc_pred
def get_lc_sse(sol_l_t, sol_l_y, lc_data):
tlc = lc_data['t'].values
lc = lc_data['lc_meas'].values
sol_nC_int = interp1d(sol_l_t, sol_l_y[3,:], 'linear', bounds_error = False)
sol_nD_int = interp1d(sol_l_t, sol_l_y[4,:], 'linear', bounds_error = False)
sol_nC = np.array([sol_nC_int(t) for t in tlc])
sol_nD = np.array([sol_nD_int(t) for t in tlc])
sol = np.vstack((sol_nC, sol_nD))
lc_pred = get_lcpred(sol)
lc_ratio = lc_pred/lc
sse = np.sum((lc_ratio - 1.0)**2)
return sse
sol_l_t, sol_l_y = simprob([2.35, 2500.0, 1250.0], tQf, Qf)
fig, ax = plt.subplots()
ax.plot(sol_l_t, sol_l_y[3,:])
ax.plot(sol_l_t, sol_l_y[4,:])
lc_sim = get_lcpred(sol_l_y[3:5,:])
lc_sim
fig, ax = plt.subplots()
ax.scatter(tlc, lc)
ax.plot(sol_l_t, lc_sim)
ax.set_xlim([400.0, 850.0])
ax.set_ylim([0.0, 0.2])
tmp = get_lc_sse(sol_l_t, sol_l_y, lc_data)
tmp
def calc_SSE(pest, data):
sol_l_t, sol_l_y = simprob(pest, data['tQf'], data['Qf'])
SSE = get_lc_sse(sol_l_t, sol_l_y, data['lc_data'])
return SSE
pest_data = {'Qf_if': Qf_if, 'lc_data': lc_data, 'tQf': tQf, 'Qf': Qf}
calc_SSE([2.35, 2500.0, 1250.0], pest_data)
pe_sol = minimize(calc_SSE, [2.35, 1000.0, 1000.0], args = pest_data, method = "L-BFGS-B")
pe_sol
calc_SSE_lam = lambda pest: calc_SSE(pest, pest_data)
Hfn = ndt.Hessian(calc_SSE_lam)
H = Hfn([2.35, 2500.0, 1250.0])
H
np.linalg.inv(H)
nparam = 2
ndata = 35
mse = calc_SSE([2.35, 2500.0, 1250.0], pest_data)/(ndata - nparam)
mse
cov_est = 2 * mse * np.linalg.inv(H)
cov_est
nparam = 2
ndata = 35
alpha = 0.95
mult_factor = nparam * f.ppf(alpha, nparam, ndata - nparam)
mult_factor
conf_delta = np.sqrt(np.diag(cov_est) * mult_factor)
conf_delta
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
import numdifftools as ndt
from scipy.stats import f
# load flow rate data
flow_data = pd.read_csv('flow_data.csv')
lc_data = pd.read_csv('lc_data.csv')
teaf = 0.00721
teaden = 0.728
cBf = teaf
tQf = np.insert(flow_data['t'].values, 0, 0)
Qf = np.insert(flow_data["Qf"].values / teaden, 0, 0)
tlc = lc_data['t'].values
lc = lc_data['lc_meas'].values
Qf_if = interp1d(tQf, Qf, 'previous', bounds_error = False)
t_i = np.arange(0.0, 850.0)
Qf_i = [Qf_if(t) for t in t_i]
fig, ax = plt.subplots()
ax.scatter(tQf, Qf)
ax.plot(t_i, Qf_i)
def rates(t, y, p):
vR = y[0]
nA = y[1]
nB = y[2]
nC = y[3]
nD = y[4]
Qf_if = p[0]
k1 = p[1]
k2 = p[2]
cBf = 0.00721
dvR = Qf_if
dnA = -k1 * nA * nB / vR
dnB = Qf_if * cBf - nB * (k1 * nA + k2 * nC) / vR
dnC = nB * (k1 * nA - k2 * nC) / vR
dnD = k2 * nC * nB / vR
return [dvR, dnA, dnB, dnC, dnD]
def simprob(p, tQf, Qf):
y0 = [2370.0, p[0], 0.0, 0.0, 0.0]
for (i, t) in enumerate(tQf[:-1]):
#print(i)
tspan = [0.0, tQf[i+1] - tQf[i]]
p_ext = [Qf[i], p[1], p[2]]
sol = solve_ivp(rates, tspan, y0, method = "BDF", args = (p_ext,))
sol.t = sol.t + tQf[i]
y0 = sol.y[:,-1]
if i == 0:
sol_l_t = np.copy(sol.t)
sol_l_y = np.copy(sol.y)
else:
sol_l_t = np.concatenate((sol_l_t, sol.t))
sol_l_y = np.concatenate((sol_l_y, sol.y), axis = 1)
return sol_l_t, sol_l_y
def get_lcpred(sol):
lc_pred = 1 / (1 + 2.0*sol[1,:]/np.maximum(sol[0,:], 1e-6))
return lc_pred
def get_lc_sse(sol_l_t, sol_l_y, lc_data):
tlc = lc_data['t'].values
lc = lc_data['lc_meas'].values
sol_nC_int = interp1d(sol_l_t, sol_l_y[3,:], 'linear', bounds_error = False)
sol_nD_int = interp1d(sol_l_t, sol_l_y[4,:], 'linear', bounds_error = False)
sol_nC = np.array([sol_nC_int(t) for t in tlc])
sol_nD = np.array([sol_nD_int(t) for t in tlc])
sol = np.vstack((sol_nC, sol_nD))
lc_pred = get_lcpred(sol)
lc_ratio = lc_pred/lc
sse = np.sum((lc_ratio - 1.0)**2)
return sse
sol_l_t, sol_l_y = simprob([2.35, 2500.0, 1250.0], tQf, Qf)
fig, ax = plt.subplots()
ax.plot(sol_l_t, sol_l_y[3,:])
ax.plot(sol_l_t, sol_l_y[4,:])
lc_sim = get_lcpred(sol_l_y[3:5,:])
lc_sim
fig, ax = plt.subplots()
ax.scatter(tlc, lc)
ax.plot(sol_l_t, lc_sim)
ax.set_xlim([400.0, 850.0])
ax.set_ylim([0.0, 0.2])
tmp = get_lc_sse(sol_l_t, sol_l_y, lc_data)
tmp
def calc_SSE(pest, data):
sol_l_t, sol_l_y = simprob(pest, data['tQf'], data['Qf'])
SSE = get_lc_sse(sol_l_t, sol_l_y, data['lc_data'])
return SSE
pest_data = {'Qf_if': Qf_if, 'lc_data': lc_data, 'tQf': tQf, 'Qf': Qf}
calc_SSE([2.35, 2500.0, 1250.0], pest_data)
pe_sol = minimize(calc_SSE, [2.35, 1000.0, 1000.0], args = pest_data, method = "L-BFGS-B")
pe_sol
calc_SSE_lam = lambda pest: calc_SSE(pest, pest_data)
Hfn = ndt.Hessian(calc_SSE_lam)
H = Hfn([2.35, 2500.0, 1250.0])
H
np.linalg.inv(H)
nparam = 2
ndata = 35
mse = calc_SSE([2.35, 2500.0, 1250.0], pest_data)/(ndata - nparam)
mse
cov_est = 2 * mse * np.linalg.inv(H)
cov_est
nparam = 2
ndata = 35
alpha = 0.95
mult_factor = nparam * f.ppf(alpha, nparam, ndata - nparam)
mult_factor
conf_delta = np.sqrt(np.diag(cov_est) * mult_factor)
conf_delta
| 0.316475 | 0.45647 |
<center>
<img src="../../img/ods_stickers.jpg">
## Открытый курс по машинному обучению
<center>Автор материала: Александровская Вера (@shlur), DS в Lamoda.
# Рисуем интерактивные карты с Folium
В питоне есть множество библиотек, с помощью которых можно рисовать и анализировать пространственную информацию (spatial analysis).
Вот некоторые из них:
* folium
* gmaps
* basemap
* cartopy
* geoplotlib
В этом туториале пойдет речь о библиотеке Folium (https://github.com/python-visualization/folium), которая представляет собой питон-обертку над JS библиотекой Leaflet.
"Manipulate your data in Python, then visualize it in on a Leaflet map via Folium." (c) github
Большим плюсом по сравнению с другими библиотеками является интерактивность. Карты можно зумить, исследовать, кликать на маркеры, создать сложные типы визуализации.
Минусом является производительность. Создание карты с большим количеством точек может составлять минуты.
К сожалению, информация по работе с библиотекой раскидана по разным сайтам и туториалам. В официальной документации информации очень мало, а в русскоязычном интернете вообще ничего нет.
Будем исследовать датасет с пабами Москвы =).
Датасет в виде списка пабов Москвы с их координатами выгружен с http://openstreetmap.ru
## Подготовка данных
```
import json
import folium
import pandas as pd
import requests
with open('../../data/pubs.json') as json_data:
d = json.load(json_data)
columns = ['lat', 'lon', 'name_ru', 'opening_hours', 'website']
index = range(0, len(d["data"]))
pubs = pd.DataFrame(columns = columns, index = index)
for i in range(0, len(d["data"])):
pubs['lat'][i] = d["data"][i]["lat"]
pubs['lon'][i] = d["data"][i]["lon"]
pubs['opening_hours'].iloc[i] = d["data"][i]["opening_hours"]
pubs['website'][i] = d["data"][i]["website"]
pubs['name_ru'][i] = d["data"][i]["name_ru"]
pubs.head(3)
# Для центрирования карт я выбрала центральную точку Москвы
kremlin = [55.750730, 37.617322]
```
## Dot density map
Самый простой вариант анализа - отобразить данные как точки (или маркеры) на карте. В popup (выноску) положим название заведения и часы работы.
Карта инициализируется с помощью синтаксиса `map = folium.Map(location=kremlin, zoom_start=11)`.
Добавляем маркеры `folium.Marker().add_to(map)`.
Различные типы маркеров задаются функциями:
- Marker (использую для визуализации ниже)
- RegularPolygonMarker
- CircleMarker
- PolygonMarker
Возможные атрибуты:
- color
- fill_color
- weight
- radius
- number_of_sides (для RegularPolygonMarker)
Так же в выноску можно передавать график vincent (https://github.com/wrobstory/vincent) с помощью синтаксиса:
`folium.Popup().add_child(folium.Vega())`
`tiles` - источник тайлов карт. Я обычно использую openstreetmaps - они идут по умолчанию.
```
pubs_map = folium.Map(location=kremlin, zoom_start=11)
for i in range(0, len(pubs)):
folium.Marker([pubs['lat'][i], pubs['lon'][i]], popup = str(pubs['name_ru'][i]) + ": "
+ str(pubs['opening_hours'][i])).add_to(pubs_map)
pubs_map
```
Cluster marker - раскраска в зависимости от плотности точек. Близкие точки сливаются в один маркер.
Судя по данным, наибольшая плотность пабов в Москве - на серево-востоке от Кремля, в районе Чистых прудов.
```
from folium import features
pubs_map = folium.Map(location=kremlin, zoom_start=12)
mc = features.MarkerCluster()
for i in range(0, len(pubs)):
mk = features.Marker([pubs['lat'][i], pubs['lon'][i]])
mc.add_child(mk)
pubs_map.add_child(mc)
```
## Heatmap
Построим Heatmap распределения пабов по Москве
```
import random
import numpy as np
from folium import plugins
pubs_map = folium.Map(location=kremlin, zoom_start=10)
data = [[x[0], x[1], 1] for x in np.array(pubs[['lat', 'lon']])]
HeatMap(data, radius = 20).add_to(pubs_map)
pubs_map
```
## Линии
Добавим на карту линии, соединяющую локации. Она создаётся с помощью folium.PolyLine, который принимает координаты соединяемых точек, и настраивается параметрами, схожими с параметрами маркеров.
Здесь мы выбрали и соединили 4 заведения в Сокольниках:
```
sololniki = [55.791981, 37.664456]
pubs_map_sokolniki = folium.Map(location=sololniki, zoom_start=13)
path = []
for i in [100, 101, 102, 103]:
folium.Marker([pubs['lat'][i], pubs['lon'][i]], popup = str(pubs['name_ru'][i]) + ": "
+ str(pubs['opening_hours'][i])).add_to(pubs_map_sokolniki)
path.append([[pubs['lat'][i], pubs['lon'][i]], [pubs['lat'][i+1], pubs['lon'][i+1]]])
folium.PolyLine(path[0:3], color='blue', weight=4, opacity=0.7, popup=str(i)).add_to(pubs_map_sokolniki)
pubs_map_sokolniki
```
## Найдем и отобразим кратчайший путь через пабы Москвы :)
В заключении туториала, приведу пример отображения кратчайшего пути через пабы Москвы. Идея нагло украдена отсюда: http://www.math.uwaterloo.ca/tsp/pubs/
Для нахождения кратчайшего пути использую библиотеку Google or-tools, которая включает в себя алгоритмы решения задач нахождения маршрута. Работа с ней это тема для отдельного туториала, поэтому загружаю найденное решение из внешнего файла.
Пути между заведениями тут уже строятся не отрезками, соединяющими пары пабов, а следуют кратчайшему маршруту из паба в паб, подобранному с помощью http://project-osrm.org
```
import pickle
# инициализируем карту
map = folium.Map(location=kremlin, zoom_start=14)
# грузим файл с данными о маршрутах
file = open('../../data/tutorial_data.pickle', 'rb')
routes = pickle.load(file,encoding='latin1')
file.close()
# Рисуем большой полилайн полного маршрута...
for path in routes['paths']:
folium.PolyLine(path, color='black', weight=3, opacity=0.8).add_to(map)
# ...и маркеры пабов
for point in routes['points']:
folium.Marker(point).add_to(map)
map
```
Have fun =)
|
github_jupyter
|
import json
import folium
import pandas as pd
import requests
with open('../../data/pubs.json') as json_data:
d = json.load(json_data)
columns = ['lat', 'lon', 'name_ru', 'opening_hours', 'website']
index = range(0, len(d["data"]))
pubs = pd.DataFrame(columns = columns, index = index)
for i in range(0, len(d["data"])):
pubs['lat'][i] = d["data"][i]["lat"]
pubs['lon'][i] = d["data"][i]["lon"]
pubs['opening_hours'].iloc[i] = d["data"][i]["opening_hours"]
pubs['website'][i] = d["data"][i]["website"]
pubs['name_ru'][i] = d["data"][i]["name_ru"]
pubs.head(3)
# Для центрирования карт я выбрала центральную точку Москвы
kremlin = [55.750730, 37.617322]
pubs_map = folium.Map(location=kremlin, zoom_start=11)
for i in range(0, len(pubs)):
folium.Marker([pubs['lat'][i], pubs['lon'][i]], popup = str(pubs['name_ru'][i]) + ": "
+ str(pubs['opening_hours'][i])).add_to(pubs_map)
pubs_map
from folium import features
pubs_map = folium.Map(location=kremlin, zoom_start=12)
mc = features.MarkerCluster()
for i in range(0, len(pubs)):
mk = features.Marker([pubs['lat'][i], pubs['lon'][i]])
mc.add_child(mk)
pubs_map.add_child(mc)
import random
import numpy as np
from folium import plugins
pubs_map = folium.Map(location=kremlin, zoom_start=10)
data = [[x[0], x[1], 1] for x in np.array(pubs[['lat', 'lon']])]
HeatMap(data, radius = 20).add_to(pubs_map)
pubs_map
sololniki = [55.791981, 37.664456]
pubs_map_sokolniki = folium.Map(location=sololniki, zoom_start=13)
path = []
for i in [100, 101, 102, 103]:
folium.Marker([pubs['lat'][i], pubs['lon'][i]], popup = str(pubs['name_ru'][i]) + ": "
+ str(pubs['opening_hours'][i])).add_to(pubs_map_sokolniki)
path.append([[pubs['lat'][i], pubs['lon'][i]], [pubs['lat'][i+1], pubs['lon'][i+1]]])
folium.PolyLine(path[0:3], color='blue', weight=4, opacity=0.7, popup=str(i)).add_to(pubs_map_sokolniki)
pubs_map_sokolniki
import pickle
# инициализируем карту
map = folium.Map(location=kremlin, zoom_start=14)
# грузим файл с данными о маршрутах
file = open('../../data/tutorial_data.pickle', 'rb')
routes = pickle.load(file,encoding='latin1')
file.close()
# Рисуем большой полилайн полного маршрута...
for path in routes['paths']:
folium.PolyLine(path, color='black', weight=3, opacity=0.8).add_to(map)
# ...и маркеры пабов
for point in routes['points']:
folium.Marker(point).add_to(map)
map
| 0.14442 | 0.952926 |
```
from __future__ import print_function
import os
import sys
from keras.callbacks import ModelCheckpoint, EarlyStopping, TensorBoard
from keras.datasets import mnist
from keras.layers import Dense, Dropout, Flatten, Input
from keras.layers import Conv2D, MaxPooling2D
from keras.models import Model
from utils import angle_error, RotNetDataGenerator, binarize_images
#sys.path.append(os.path.dirname(os.path.dirname(os.path.abspath(__file__))))
# we don't need the labels indicating the digit value, so we only load the images
(X_train, _), (X_test, _) = mnist.load_data()
model_name = 'rotnet_mnist'
# number of convolutional filters to use
nb_filters = 64
# size of pooling area for max pooling
pool_size = (2, 2)
# convolution kernel size
kernel_size = (3, 3)
# number of classes
nb_classes = 360
nb_train_samples, img_rows, img_cols = X_train.shape
img_channels = 1
input_shape = (img_rows, img_cols, img_channels)
nb_test_samples = X_test.shape[0]
print('Input shape:', input_shape)
print(nb_train_samples, 'train samples')
print(nb_test_samples, 'test samples')
# model definition
input = Input(shape=(img_rows, img_cols, img_channels))
x = Conv2D(nb_filters, kernel_size, activation='relu')(input)
x = Conv2D(nb_filters, kernel_size, activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Dropout(0.25)(x)
x = Flatten()(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.25)(x)
x = Dense(nb_classes, activation='softmax')(x)
model = Model(inputs=input, outputs=x)
model.summary()
# model compilation
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=[angle_error])
# training parameters
batch_size = 128
nb_epoch = 50
output_folder = 'models'
if not os.path.exists(output_folder):
os.makedirs(output_folder)
# callbacks
checkpointer = ModelCheckpoint(
filepath=os.path.join(output_folder, model_name + '.hdf5'),
save_best_only=True
)
early_stopping = EarlyStopping(patience=2)
tensorboard = TensorBoard()
# training loop
model.fit_generator(
RotNetDataGenerator(
X_train,
batch_size=batch_size,
preprocess_func=binarize_images,
shuffle=True
),
steps_per_epoch=nb_train_samples / batch_size,
epochs=nb_epoch,
validation_data=RotNetDataGenerator(
X_test,
batch_size=batch_size,
preprocess_func=binarize_images
),
validation_steps=nb_test_samples / batch_size,
verbose=1,
callbacks=[checkpointer, early_stopping, tensorboard]
)
```
|
github_jupyter
|
from __future__ import print_function
import os
import sys
from keras.callbacks import ModelCheckpoint, EarlyStopping, TensorBoard
from keras.datasets import mnist
from keras.layers import Dense, Dropout, Flatten, Input
from keras.layers import Conv2D, MaxPooling2D
from keras.models import Model
from utils import angle_error, RotNetDataGenerator, binarize_images
#sys.path.append(os.path.dirname(os.path.dirname(os.path.abspath(__file__))))
# we don't need the labels indicating the digit value, so we only load the images
(X_train, _), (X_test, _) = mnist.load_data()
model_name = 'rotnet_mnist'
# number of convolutional filters to use
nb_filters = 64
# size of pooling area for max pooling
pool_size = (2, 2)
# convolution kernel size
kernel_size = (3, 3)
# number of classes
nb_classes = 360
nb_train_samples, img_rows, img_cols = X_train.shape
img_channels = 1
input_shape = (img_rows, img_cols, img_channels)
nb_test_samples = X_test.shape[0]
print('Input shape:', input_shape)
print(nb_train_samples, 'train samples')
print(nb_test_samples, 'test samples')
# model definition
input = Input(shape=(img_rows, img_cols, img_channels))
x = Conv2D(nb_filters, kernel_size, activation='relu')(input)
x = Conv2D(nb_filters, kernel_size, activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Dropout(0.25)(x)
x = Flatten()(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.25)(x)
x = Dense(nb_classes, activation='softmax')(x)
model = Model(inputs=input, outputs=x)
model.summary()
# model compilation
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=[angle_error])
# training parameters
batch_size = 128
nb_epoch = 50
output_folder = 'models'
if not os.path.exists(output_folder):
os.makedirs(output_folder)
# callbacks
checkpointer = ModelCheckpoint(
filepath=os.path.join(output_folder, model_name + '.hdf5'),
save_best_only=True
)
early_stopping = EarlyStopping(patience=2)
tensorboard = TensorBoard()
# training loop
model.fit_generator(
RotNetDataGenerator(
X_train,
batch_size=batch_size,
preprocess_func=binarize_images,
shuffle=True
),
steps_per_epoch=nb_train_samples / batch_size,
epochs=nb_epoch,
validation_data=RotNetDataGenerator(
X_test,
batch_size=batch_size,
preprocess_func=binarize_images
),
validation_steps=nb_test_samples / batch_size,
verbose=1,
callbacks=[checkpointer, early_stopping, tensorboard]
)
| 0.656438 | 0.471527 |
# Kentel Python3 - Grafikoù
## Dispenn an izotopoù radioaktivel
Gant ar fonksionoù ankivil [aléatoires] (pe kentoc'h damankivil [pseudo-aléatoire]) hag ar fed gallout ober kalz a jedadennoù buan tre eo an urzhiataerioù ostilhoù dispar evit ober darvanoù [simulations] luziet.
Klasket e vo darvanañ digresk eksponantel ur c'hementad a rannigoù radioaktivel e kerz an amzer.<br>
Kroget e vo da tresañ grafik fonksion matematikel an digresk eksponantel evit gwelet he stumm ha pleustriñ gant ar grafikoù.<br>
Kendalc'het e vo gant un darvan eeunek ha difetiz a-walc'h (met reiz memes tra).<br>
Echuet e vo gant un darvan tostoc'h d'ar gwirion (ar pezh a fell deomp).
Gouzout a reomp un digresk eksponantel a zo eus ar stumm<br>
$\begin{equation}
N(t) = N_0 \times e^{-\lambda t}
\end{equation}$<br><br>
Gant :<br>
$N_0$ Niver a rannigoù radioaktivel da gentañ (en amzer $t_0$)<br>
$\lambda$ Ar c'honstantenn digresk<br>
$t$ an amzer
## Grafikoù gant ar module `matplotlib`
Tu vefe termeniñ ur fonksion `N(t)` gant Python met `matplotlib` ne oar ket tresañ fonksionoù evel-se. Implijet e vez **listennoù roadennoù niverel** nemetken evit tresañ grafikoù.
```
# Enframmet e vez ar module evit tresañ grafikoù
import matplotlib.pyplot as plt
# Ar ger 'as' a servij d'ober un alias etre matplotlib.pyplot ha plt
# Berroc'h ha kevatal e vo skrivañ 'plt' eget 'matplotlib.pyplot'
# Ur skouer simpl
roadennou = [1, 2.2, 4, 8.9, 6, 5, 3, 1, 1.5, 0.2]
plt.plot(roadennou) # Tresañ ar grafik (e memor an urzhiataer)
plt.show() # Diskouez ar grafik war ar skramm
# Tresomp an digresk eksponantel bremañ
# Kavet e vez ar fonksion eksponantel e-barzh ar module 'math'
from math import exp
kde = 0.1 # Konstantenn digresk eksponantel
n0 = 1000
roadennou = []
# Jedet e vez 100 talvoud da-heul
for t in range(100):
roadennou.append(n0*exp(-kde*t))
plt.plot(roadennou)
plt.show()
```
## Un darvan difetiz
Pep rannig radioaktivel eus ar memes sort en eus ar memes probablentez bezañ dispennet e pad ur c'houlzad bennak.<br>
Ma vez lavaret, da skouer, ez eo 1% ar probablentez evit ur rannig bezañ dispennet e-kerzh ur c'houlzad e dalvez ivez e vo dispennet 1% eus kementad ar rannigoù e-kerzh ar c'houlzad.
```
prob_dispenn = 0.1
n0 = 1000
# Lakaet e vez talvoud n0 el listenn
roadennou = [n0]
for i in range(100):
# Kemeret e vez an talvoud diwezhañ el listenn
# Lemet e vez an niver a rannigoù dispennet e-kerzh ar c'houlzad
# ouzhpennet e vez an talvoud nevez e fin al listenn
roadennou.append(roadennou[i] - roadennou[i]*prob_dispenn)
plt.plot(roadennou)
plt.show()
```
## Un darvan tostoc'h eus ar gwirionnez
Ar skouerioù a-us a heulie formulennoù matematikel anavezet en araok. Ar formulennoù matematikel a zo dedennus evit diskriv ar fenomenoù naturel a-bell, a geidenn hag en un doare parfed met ar fenomenoù naturel ne heuliont ket formulennoù matematikel dre ret pa vezont sellet a-dost. Setup perak ne oant ket darvanoù da vat.<br>
Evit kaout un darvan gwir e vez roet perzhioù ar sistem nemetken hag an diskoulm a vez dianavezet en araok. Pep gwech ma vez peurgaset an darvan e c'heller kavout un diskoulm disheñvel.
```
# Enframmañ ar module evit implij fonksionoù ankivil
import random
# Cheñchit talvoud ar roadennoù-se hervez o c'hoantoù
prob_dispenn = 0.1
rannigou = 1000
# El listenn 'mañ e vo miret ar roadennou net jedet
roadennou = [rannigou]
while rannigou>0:
# Evit pep rannig a chom e vez tennet un niverenn d'ar sort
for i in range(rannigou):
# Ma 'vez tennet un niverenn bihanoc'h eget ar probablentez dibabet
# e vez dispennet ur rannig
if random.random() < prob_dispenn:
rannigou -= 1
# E fin ar roll e vez stoked a niver a rannigoù a chom en omp listennad data
roadennou.append(rannigou)
```
Bremañ ne chom nemet da dresañ an data bet jedet war ur grafik brav gant ar stadamantoù da-heul.
```
# Cheñch ment ar grafik
plt.rcParams["figure.figsize"] = [12, 8]
# Tresañ ar grafik
plt.plot(roadennou)
# Dibab un titl (dirediet)
plt.title("Dispenn an izotopoù radioaktivel")
# Dibab anvioù evit an axoù (dirediet)
plt.xlabel("Red an amzer (koulzadoù)")
plt.ylabel("Niver a rannigoù")
# Diskouez ar grafik
plt.show()
```
|
github_jupyter
|
# Enframmet e vez ar module evit tresañ grafikoù
import matplotlib.pyplot as plt
# Ar ger 'as' a servij d'ober un alias etre matplotlib.pyplot ha plt
# Berroc'h ha kevatal e vo skrivañ 'plt' eget 'matplotlib.pyplot'
# Ur skouer simpl
roadennou = [1, 2.2, 4, 8.9, 6, 5, 3, 1, 1.5, 0.2]
plt.plot(roadennou) # Tresañ ar grafik (e memor an urzhiataer)
plt.show() # Diskouez ar grafik war ar skramm
# Tresomp an digresk eksponantel bremañ
# Kavet e vez ar fonksion eksponantel e-barzh ar module 'math'
from math import exp
kde = 0.1 # Konstantenn digresk eksponantel
n0 = 1000
roadennou = []
# Jedet e vez 100 talvoud da-heul
for t in range(100):
roadennou.append(n0*exp(-kde*t))
plt.plot(roadennou)
plt.show()
prob_dispenn = 0.1
n0 = 1000
# Lakaet e vez talvoud n0 el listenn
roadennou = [n0]
for i in range(100):
# Kemeret e vez an talvoud diwezhañ el listenn
# Lemet e vez an niver a rannigoù dispennet e-kerzh ar c'houlzad
# ouzhpennet e vez an talvoud nevez e fin al listenn
roadennou.append(roadennou[i] - roadennou[i]*prob_dispenn)
plt.plot(roadennou)
plt.show()
# Enframmañ ar module evit implij fonksionoù ankivil
import random
# Cheñchit talvoud ar roadennoù-se hervez o c'hoantoù
prob_dispenn = 0.1
rannigou = 1000
# El listenn 'mañ e vo miret ar roadennou net jedet
roadennou = [rannigou]
while rannigou>0:
# Evit pep rannig a chom e vez tennet un niverenn d'ar sort
for i in range(rannigou):
# Ma 'vez tennet un niverenn bihanoc'h eget ar probablentez dibabet
# e vez dispennet ur rannig
if random.random() < prob_dispenn:
rannigou -= 1
# E fin ar roll e vez stoked a niver a rannigoù a chom en omp listennad data
roadennou.append(rannigou)
# Cheñch ment ar grafik
plt.rcParams["figure.figsize"] = [12, 8]
# Tresañ ar grafik
plt.plot(roadennou)
# Dibab un titl (dirediet)
plt.title("Dispenn an izotopoù radioaktivel")
# Dibab anvioù evit an axoù (dirediet)
plt.xlabel("Red an amzer (koulzadoù)")
plt.ylabel("Niver a rannigoù")
# Diskouez ar grafik
plt.show()
| 0.270095 | 0.812533 |
## Pokemon Data Analysis
### Libraries
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style()
import qgrid
```
### About Data
```
data = pd.read_csv("pokemon_data.csv")
data.head(10)
data.describe()
data[data['Name'] == 'Pikachu']
```
## We will try to find out answers for following questions
* Which are top 20 strongest pokemons?
* Which type of pokemons are best ?
* Top 20 Fastest Pokemons
* Top 10 Aggresive and Defensive Pokemons.
* Find out Correlated parameters
* Generation and Legendary wise analysis
### Data cleaning
```
data.info()
data.isnull().any()
```
we see type 2 has some null values
```
data[data['Type 2'].isnull()]
```
Out of 800 386 have type 2 as Null.
we can't drop them all.
Instead we will set type 2 as type 1
```
data['Type 2'].fillna(data['Type 1'], inplace=True) #fill NaN values in Type2 with corresponding values of Type
data.isnull().any()
```
#### now we dont have any null values in our data
```
data.iloc[4:12] ## confirmation that Nan values of Type 2 are replaced with Type 1
### we don't need the rank column as it is of no use
data.drop('#' ,axis=1 , inplace= True)
data.head()
## we see that in names, Mega Pokemons contained extra and unneeded text.
data[data['Name'].str.contains('Mega')].head(10)
## Remove all the text before "Mega"
# A(?=B) | Lookahead assertion. This matches the expression A only if it is followed by B
data['Name'] = data['Name'].str.replace(".*(?=Mega)", "")
data.head(10)
## let's make name as index
data.set_index('Name' , inplace= True)
data.head()
```
## Lets make some changes in data
```
data['Total_Atk'] = data['Attack'] + data['Sp. Atk']
data['Total_Def'] = data['Defense'] + data['Sp. Def']
data.head()
49 + 65
data['Total'] = data['Total_Atk'] + data['Total_Def']
data.head()
## made list of columns
cols = list(data.columns.values)
cols
# Reorder data for better visualization
data2 = data[cols[0:4] + [cols[5]] + [cols[10]] +
[cols[4]] + [cols[6]] + cols[11:] + cols[7:10]]
data2.head()
data2.describe()
```
### Makes it easy to filter
```
qgrid_widget = qgrid.show_grid(data2 , show_toolbar= True)
qgrid_widget
```
## Visualizations
```
plt.figure(figsize=(10,6)) #manage the size of the plot
sns.heatmap(data2.corr(),annot=True , cmap="magma") #data.corr() makes a correlation matrix and sns.heatmap is used to show the correlations heatmap
plt.show()
```
From the heatmap it can be seen that there is not much correlation between the attributes of the pokemons.
Total is derived from attack and defence so not that special.
The highest informative we can see is the correlation between
* Speed and the Total_Atk = 0.51
* HP and total = 0.48
```
g = sns.PairGrid(data2, vars=['HP', 'Total_Atk', 'Total_Def', 'Total' , 'Speed'])
g.map(plt.scatter )
g.set(xticklabels=[] , yticklabels = [])
g.fig.set_size_inches(12,8)
```
we can see that there is positive correlation between speed and total attack
## Let's see if we can determine how speed is related
```
sns.jointplot(data = data2 ,x="Total_Atk", y="Speed" , kind="reg")
```
This jointplot explains relationship between Total_Attack and Speed..
As speed increases , attack of pokemon increases.
```
sns.jointplot(data = data2 ,y="HP", x="Speed" , kind="reg")
plt.figure(figsize=(15,15))
plt.subplot(221)
plt.title('Speed by Generation' )
sns.boxplot(x = "Generation", y = "Speed",data=data2)
plt.subplot(222)
plt.title('Speed by Legendary' )
sns.boxplot(x = "Legendary", y = "Speed",data=data2)
plt.subplot(223)
plt.title('Speed by Type 1' )
g = sns.boxplot(x = "Type 1", y = "Speed",data=data2)
g.set_xticklabels(labels = data2['Type 1'].unique(),rotation = 90)
plt.axhline(130,color='red',linestyle='dashed')
plt.subplot(224)
plt.title('Speed by Type 2' )
g = sns.boxplot(x = "Type 2", y = "Speed",data=data2)
g.set_xticklabels(labels = data2['Type 2'].unique(),rotation = 90)
plt.show()
data2[data2['Type 2'] == "Flying"].Speed.max() ## crosschecking
data2['Speed'].describe()
```
* There is no significant difference in generations to detect speed.
* From second plots we can say that Legendary pokemons have higher speed than non legendary
* Type 1 desribes alot about speed.
* Almost all Flying pokemons have speed above 100 which is obvious !
* There are some Bug , electric and Psychic Pokemons having speed above 130
* Almost half of type 2 is taken from Type 1 but some of Dragon pokemons have speed above 130
```
data2['Speed'].quantile(.98)
```
### Pokemons having speed above 130 (Superfast)
```
superfast = data2[data2['Speed'] >= 130].sort_values('Speed' , ascending = 0)
superfast[['Type 1' ,'Speed' , 'Legendary'] ]
```
### Fastest Pokemons By Types
```
data2.sort_values(by = 'Speed' , ascending = 0).drop_duplicates(subset=['Type 1'],keep='first')[['Type 1' ,'Speed' , 'Legendary'] ]
```
As we saw positive correlation between speed and Attack tells us that faster pokemons are better at attacking.
We can see that most of them are not legendary , lets find the count.
```
data2['Legendary'].value_counts()
# There are only 65 Legendary pokemons out of 800
superfast['Legendary'].value_counts()
```
Out of 19 superfast pokemons 6 are legendary (almost 33%)
### Let's find out aggressive and defensive pokemons
```
data2['Total_Atk'].describe()
data2['Total_Atk'].quantile(.98)
aggresive = data2[data2['Total_Atk'] >= 285].sort_values('Total_Atk' , ascending = 0)
aggresive[[ 'Type 1' , 'Total_Atk' , 'Legendary']]
aggresive['Type 1'].value_counts()
aggresive['Legendary'].value_counts()
```
### Defensive
```
data2['Total_Def'].describe()
data2['Total_Def'].quantile(.98)
defensive = data2[data2['Total_Def'] >= 265].sort_values('Total_Def' , ascending = 0)
defensive[[ 'Type 1' , 'Total_Def' , 'Legendary']]
defensive['Legendary'].value_counts()
defensive['Type 1'].value_counts()
```
### making an attack defense index where we will get to know that pokemon has higher attack or defense
* positive index value means aggresive
* negative index value means defensive
```
pd.options.mode.chained_assignment = None # default='warn'
data2['AD_index'] = round(1 - data2['Total_Def']/data2['Total_Atk'],3)
data2.head(10)[['Total_Def','Total_Atk', 'AD_index']]
# data2['AD_status'] = ["Aggresive" if data2['AD_index'] > 0 else "Defensive"]
#data2.head(10)[['Total_Def','Total_Atk', 'AD_index' , 'AD_status']]
data2['AD_status'] = np.where(data2['AD_index'] > 0, 'Aggresive', 'Defensive')
data2.loc[data2['AD_index'] == float(0), ('AD_status')] = "Neutral"
data2.head(10)[['Total_Def','Total_Atk', 'AD_index' , 'AD_status']]
data2.tail()
data2['AD_index'].describe()
plt.figure(figsize=(10,8))
x = data2['AD_index']
sns.distplot(x, bins=10)
plt.show()
# This is some kind of histogram graph about AD_index
data2[data2['AD_index'] < -2]
```
shuckle is an outlier having Total def = 460 but Total atk = 10 only
It is defensive but attack is too low
```
plt.figure(figsize=(10,8))
x = data2[data2['AD_index'] > -3]['AD_index'] ## excluding -22
sns.distplot(x, bins=20 )
plt.show()
# This is some kind of histogram graph about AD_index
(data2['AD_status']).value_counts()
data2[data2['Total_Atk'] >= 285].sort_values('Total' , ascending = 0)[[ 'Type 1' ,'Total_Atk', 'Total_Def' ,'Total' ,'AD_index']]
## Descending gives us aggressive pokemons
data2[data2['Total_Def'] >= 265].sort_values('AD_index' , ascending = 1)[[ 'Type 1' ,'Total_Atk', 'Total_Def' ,'Total' ,'AD_index']]
```
#### Obviously we can't decide our strongest pokemon with parameter total becuase strongest pokemon must have attack and defense ,speed , HP high (above 75%) ,
```
data2[[ 'HP' ,'Speed' ,'Total_Atk', 'Total_Def','Total' ]].describe()
qt = 0.75
print(data2['HP'].quantile(qt))
print(data2['Speed'].quantile(qt))
print(data2['Total_Atk'].quantile(qt))
print(data2['Total_Def'].quantile(qt))
strongest = data2[(data2['Total_Def'] >= data2['Total_Def'].quantile(qt)) &
(data2['Total_Atk'] >= data2['Total_Atk'].quantile(qt)) &
(data2['HP'] >= data2['HP'].quantile(qt)) &
(data2['Speed'] >= data2['Speed'].quantile(qt))].sort_values(by = 'Total' , ascending = 0)
strongest.head(10)[[ 'Type 1' ,'HP' ,'Speed' ,'Total_Atk', 'Total_Def' ,'Total' ]]
strongest.shape
strongest
strongest['Type 1'].value_counts()
```
### strongest by types
```
strongest.drop_duplicates(subset=['Type 1'],keep='first')[[ 'Type 1' ,'HP' ,'Speed' ,'Total_Atk', 'Total_Def' ,'Total','AD_status' ]]
qgrid_widget = qgrid.show_grid(data2 , show_toolbar= True)
qgrid_widget
data2['Type 1'].value_counts()
plt.figure(figsize=(8,8))
data2['Type 1'].value_counts().plot.pie( autopct='%1.1f%%', pctdistance=0.8)
plt.show()
#Some kind of Pie Chart
plt.figure(figsize=(8,8))
data2['Generation'].value_counts().plot.pie( autopct='%1.1f%%', pctdistance=0.8)
plt.show()
data2['Generation'].value_counts().sort_index()
strongest['Generation'].value_counts().sort_index()
perp = strongest['Generation'].value_counts().sort_index()/data2['Generation'].value_counts().sort_index()
perp
plt.bar(sorted(strongest['Generation'].unique()) ,perp )
plt.show()
```
Generation 3 4 and 5 have strongest pokemons compared to others
```
data2['Legendary'].value_counts()
strongest['Legendary'].value_counts().sort_index()
contigency= pd.crosstab(data2['Legendary'], strongest['Legendary'])
contigency
import scikit_l
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style()
import qgrid
data = pd.read_csv("pokemon_data.csv")
data.head(10)
data.describe()
data[data['Name'] == 'Pikachu']
data.info()
data.isnull().any()
data[data['Type 2'].isnull()]
data['Type 2'].fillna(data['Type 1'], inplace=True) #fill NaN values in Type2 with corresponding values of Type
data.isnull().any()
data.iloc[4:12] ## confirmation that Nan values of Type 2 are replaced with Type 1
### we don't need the rank column as it is of no use
data.drop('#' ,axis=1 , inplace= True)
data.head()
## we see that in names, Mega Pokemons contained extra and unneeded text.
data[data['Name'].str.contains('Mega')].head(10)
## Remove all the text before "Mega"
# A(?=B) | Lookahead assertion. This matches the expression A only if it is followed by B
data['Name'] = data['Name'].str.replace(".*(?=Mega)", "")
data.head(10)
## let's make name as index
data.set_index('Name' , inplace= True)
data.head()
data['Total_Atk'] = data['Attack'] + data['Sp. Atk']
data['Total_Def'] = data['Defense'] + data['Sp. Def']
data.head()
49 + 65
data['Total'] = data['Total_Atk'] + data['Total_Def']
data.head()
## made list of columns
cols = list(data.columns.values)
cols
# Reorder data for better visualization
data2 = data[cols[0:4] + [cols[5]] + [cols[10]] +
[cols[4]] + [cols[6]] + cols[11:] + cols[7:10]]
data2.head()
data2.describe()
qgrid_widget = qgrid.show_grid(data2 , show_toolbar= True)
qgrid_widget
plt.figure(figsize=(10,6)) #manage the size of the plot
sns.heatmap(data2.corr(),annot=True , cmap="magma") #data.corr() makes a correlation matrix and sns.heatmap is used to show the correlations heatmap
plt.show()
g = sns.PairGrid(data2, vars=['HP', 'Total_Atk', 'Total_Def', 'Total' , 'Speed'])
g.map(plt.scatter )
g.set(xticklabels=[] , yticklabels = [])
g.fig.set_size_inches(12,8)
sns.jointplot(data = data2 ,x="Total_Atk", y="Speed" , kind="reg")
sns.jointplot(data = data2 ,y="HP", x="Speed" , kind="reg")
plt.figure(figsize=(15,15))
plt.subplot(221)
plt.title('Speed by Generation' )
sns.boxplot(x = "Generation", y = "Speed",data=data2)
plt.subplot(222)
plt.title('Speed by Legendary' )
sns.boxplot(x = "Legendary", y = "Speed",data=data2)
plt.subplot(223)
plt.title('Speed by Type 1' )
g = sns.boxplot(x = "Type 1", y = "Speed",data=data2)
g.set_xticklabels(labels = data2['Type 1'].unique(),rotation = 90)
plt.axhline(130,color='red',linestyle='dashed')
plt.subplot(224)
plt.title('Speed by Type 2' )
g = sns.boxplot(x = "Type 2", y = "Speed",data=data2)
g.set_xticklabels(labels = data2['Type 2'].unique(),rotation = 90)
plt.show()
data2[data2['Type 2'] == "Flying"].Speed.max() ## crosschecking
data2['Speed'].describe()
data2['Speed'].quantile(.98)
superfast = data2[data2['Speed'] >= 130].sort_values('Speed' , ascending = 0)
superfast[['Type 1' ,'Speed' , 'Legendary'] ]
data2.sort_values(by = 'Speed' , ascending = 0).drop_duplicates(subset=['Type 1'],keep='first')[['Type 1' ,'Speed' , 'Legendary'] ]
data2['Legendary'].value_counts()
# There are only 65 Legendary pokemons out of 800
superfast['Legendary'].value_counts()
data2['Total_Atk'].describe()
data2['Total_Atk'].quantile(.98)
aggresive = data2[data2['Total_Atk'] >= 285].sort_values('Total_Atk' , ascending = 0)
aggresive[[ 'Type 1' , 'Total_Atk' , 'Legendary']]
aggresive['Type 1'].value_counts()
aggresive['Legendary'].value_counts()
data2['Total_Def'].describe()
data2['Total_Def'].quantile(.98)
defensive = data2[data2['Total_Def'] >= 265].sort_values('Total_Def' , ascending = 0)
defensive[[ 'Type 1' , 'Total_Def' , 'Legendary']]
defensive['Legendary'].value_counts()
defensive['Type 1'].value_counts()
pd.options.mode.chained_assignment = None # default='warn'
data2['AD_index'] = round(1 - data2['Total_Def']/data2['Total_Atk'],3)
data2.head(10)[['Total_Def','Total_Atk', 'AD_index']]
# data2['AD_status'] = ["Aggresive" if data2['AD_index'] > 0 else "Defensive"]
#data2.head(10)[['Total_Def','Total_Atk', 'AD_index' , 'AD_status']]
data2['AD_status'] = np.where(data2['AD_index'] > 0, 'Aggresive', 'Defensive')
data2.loc[data2['AD_index'] == float(0), ('AD_status')] = "Neutral"
data2.head(10)[['Total_Def','Total_Atk', 'AD_index' , 'AD_status']]
data2.tail()
data2['AD_index'].describe()
plt.figure(figsize=(10,8))
x = data2['AD_index']
sns.distplot(x, bins=10)
plt.show()
# This is some kind of histogram graph about AD_index
data2[data2['AD_index'] < -2]
plt.figure(figsize=(10,8))
x = data2[data2['AD_index'] > -3]['AD_index'] ## excluding -22
sns.distplot(x, bins=20 )
plt.show()
# This is some kind of histogram graph about AD_index
(data2['AD_status']).value_counts()
data2[data2['Total_Atk'] >= 285].sort_values('Total' , ascending = 0)[[ 'Type 1' ,'Total_Atk', 'Total_Def' ,'Total' ,'AD_index']]
## Descending gives us aggressive pokemons
data2[data2['Total_Def'] >= 265].sort_values('AD_index' , ascending = 1)[[ 'Type 1' ,'Total_Atk', 'Total_Def' ,'Total' ,'AD_index']]
data2[[ 'HP' ,'Speed' ,'Total_Atk', 'Total_Def','Total' ]].describe()
qt = 0.75
print(data2['HP'].quantile(qt))
print(data2['Speed'].quantile(qt))
print(data2['Total_Atk'].quantile(qt))
print(data2['Total_Def'].quantile(qt))
strongest = data2[(data2['Total_Def'] >= data2['Total_Def'].quantile(qt)) &
(data2['Total_Atk'] >= data2['Total_Atk'].quantile(qt)) &
(data2['HP'] >= data2['HP'].quantile(qt)) &
(data2['Speed'] >= data2['Speed'].quantile(qt))].sort_values(by = 'Total' , ascending = 0)
strongest.head(10)[[ 'Type 1' ,'HP' ,'Speed' ,'Total_Atk', 'Total_Def' ,'Total' ]]
strongest.shape
strongest
strongest['Type 1'].value_counts()
strongest.drop_duplicates(subset=['Type 1'],keep='first')[[ 'Type 1' ,'HP' ,'Speed' ,'Total_Atk', 'Total_Def' ,'Total','AD_status' ]]
qgrid_widget = qgrid.show_grid(data2 , show_toolbar= True)
qgrid_widget
data2['Type 1'].value_counts()
plt.figure(figsize=(8,8))
data2['Type 1'].value_counts().plot.pie( autopct='%1.1f%%', pctdistance=0.8)
plt.show()
#Some kind of Pie Chart
plt.figure(figsize=(8,8))
data2['Generation'].value_counts().plot.pie( autopct='%1.1f%%', pctdistance=0.8)
plt.show()
data2['Generation'].value_counts().sort_index()
strongest['Generation'].value_counts().sort_index()
perp = strongest['Generation'].value_counts().sort_index()/data2['Generation'].value_counts().sort_index()
perp
plt.bar(sorted(strongest['Generation'].unique()) ,perp )
plt.show()
data2['Legendary'].value_counts()
strongest['Legendary'].value_counts().sort_index()
contigency= pd.crosstab(data2['Legendary'], strongest['Legendary'])
contigency
import scikit_l
| 0.279927 | 0.919859 |
# Introducing Pandas
Pandas is a Python library that makes handling tabular data easier. Since we're doing data science - this is something we'll use from time to time!
It's one of three libraries you'll encounter repeatedly in the field of data science:
## Pandas
Introduces "Data Frames" and "Series" that allow you to slice and dice rows and columns of information.
## NumPy
Usually you'll encounter "NumPy arrays", which are multi-dimensional array objects. It is easy to create a Pandas DataFrame from a NumPy array, and Pandas DataFrames can be cast as NumPy arrays. NumPy arrays are mainly important because of...
## Scikit_Learn
The machine learning library we'll use throughout this course is scikit_learn, or sklearn, and it generally takes NumPy arrays as its input.
So, a typical thing to do is to load, clean, and manipulate your input data using Pandas. Then convert your Pandas DataFrame into a NumPy array as it's being passed into some Scikit_Learn function. That conversion can often happen automatically.
Let's start by loading some comma-separated value data using Pandas into a DataFrame:
```
%matplotlib inline
import numpy as np
import pandas as pd
df = pd.read_csv("PastHires.csv")
df.head()
```
head() is a handy way to visualize what you've loaded. You can pass it an integer to see some specific number of rows at the beginning of your DataFrame:
```
df.head(10)
```
You can also view the end of your data with tail():
```
df.tail(4)
```
We often talk about the "shape" of your DataFrame. This is just its dimensions. This particular CSV file has 13 rows with 7 columns per row:
```
df.shape
```
The total size of the data frame is the rows * columns:
```
df.size
```
The len() function gives you the number of rows in a DataFrame:
```
len(df)
```
If your DataFrame has named columns (in our case, extracted automatically from the first row of a .csv file,) you can get an array of them back:
```
df.columns
```
Extracting a single column from your DataFrame looks like this - this gives you back a "Series" in Pandas:
```
df['Hired']
```
You can also extract a given range of rows from a named column, like so:
```
df['Hired'][::2]
```
Or even extract a single value from a specified column / row combination:
```
df['Hired'][4:13:2]
```
To extract more than one column, you pass in an array of column names instead of a single one:
```
df[['Years Experience', 'Hired']]
```
You can also extract specific ranges of rows from more than one column, in the way you'd expect:
```
df[['Years Experience', 'Hired']][0:5:2]
```
Sorting your DataFrame by a specific column looks like this:
```
df.sort_values(['Years Experience'])
```
You can break down the number of unique values in a given column into a Series using value_counts() - this is a good way to understand the distribution of your data:
```
degree_counts = df['Employed?'].value_counts()
degree_counts
#type(degree_counts)
```
Pandas even makes it easy to plot a Series or DataFrame - just call plot():
```
degree_counts.plot(kind='bar')
```
## Exercise
Try extracting rows 5-10 of our DataFrame, preserving only the "Previous Employers" and "Hired" columns. Assign that to a new DataFrame, and create a histogram plotting the distribution of the previous employers in this subset of the data.
|
github_jupyter
|
%matplotlib inline
import numpy as np
import pandas as pd
df = pd.read_csv("PastHires.csv")
df.head()
df.head(10)
df.tail(4)
df.shape
df.size
len(df)
df.columns
df['Hired']
df['Hired'][::2]
df['Hired'][4:13:2]
df[['Years Experience', 'Hired']]
df[['Years Experience', 'Hired']][0:5:2]
df.sort_values(['Years Experience'])
degree_counts = df['Employed?'].value_counts()
degree_counts
#type(degree_counts)
degree_counts.plot(kind='bar')
| 0.218169 | 0.993593 |
# SIT742: Modern Data Science
**(Module 04: Exploratory Data Analysis)**
---
- Materials in this module include resources collected from various open-source online repositories.
- You are free to use, change and distribute this package.
- If you found any issue/bug for this document, please submit an issue at [tulip-lab/sit742](https://github.com/tulip-lab/sit742/issues)
Prepared by **SIT742 Teaching Team**
---
## Session 4C - `Pyplot` (Optional)
Matplotlib has two interfaces. The first is an object-oriented (OO) interface. In this case, we utilize an instance of axes.Axes in order to render visualizations on an instance of figure.Figure. The second is based on MATLAB and uses a state-based interface. This is encapsulated in the pyplot module. See the pyplot tutorials for a more in-depth look at the pyplot interface. The **pyplot** interface is the most common way to interact with the library. In this lesson, we'll cover some of the basics of the **pyplot** interface and see a few examples of it in action.
## Introduction
`matplotlib.pyplot` is a collection of command style functions that make matplotlib work like MATLAB. Each pyplot function makes some change to a figure: e.g., creates a figure, creates a plotting area in a figure, plots some lines in a plotting area, decorates the plot with labels, etc. In `matplotlib.pyplot` various states are preserved across function calls, so that it keeps track of things like the current figure and plotting area, and the plotting functions are directed to the current axes (please note that “axes” here and in most places in the documentation refers to the axes part of a figure and not the strict mathematical term for more than one axis).
## Importing the Interface
Rather than talk at length about the `pyplot` interface, let's just go ahead and jump right in and start playing around with it. The very first thing you'll want to do is set the notebook up for showing matplotlib output inline. The very first line of code below shows how to do this by calling the `%matplotlib` magic function and passing in the term `'inline'`.
```
%matplotlib inline
```
Following that, you'll want to import the `pyplot` module, and if you remember from an earlier lesson, I mentioned that pretty much every module you'll use in matplotlib, and the scientific python stack for that matter, has an agreed upon way to import it. Line two shows the canonical way to import the `pyplot` module.
```
import matplotlib.pyplot as plt
```
Finally, if you're following along on the command line, you'll need to call the `pyplot.ion()` function that you see in the next cell. Don't worry about what it does just yet, we'll learn about that in just a bit, but for now go ahead and call it so you can follow along with the rest of the tutorial.
```
# This does nothing after calling %matplotlib inline,
# but it turns on interactive mode in the command line.
plt.ion()
```
NOTE: The code in the next cell is only needed if you're running the code on a retina-enabled, or for you non-Mac users, a high PPI display.
### Retina Screens
The last thing that I want to cover before we end this lesson is using matplotlib on a retina enabled device. If, like me, you're on a mac that has a retina screen, you may have noticed that the plot above looks a tad bit fuzzy. If you've run into this issue, fear not, IPython provides a function that allows you to specify the output formats that you want to support, and one of those just happens to be the 'retina' format.
To add support for retina output, you'll have to import a function called `set_matplotlib_formats` from the `IPython.display` module. Then call it and pass in the string `'retina'`. Once you've executed the `set_matplotlib_formats` function, you should be able to rerun the example plot that we created above and now see it print out in full retina glory!
```
# Turn on retina mode
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('retina')
```
## Understanding the `pyplot` Interface
Before we go any further, there are a few things that you need to understand about the `pyplot` interface that will make working with matplotlib a lot smoother. First, the `pyplot` interface is a stateful interface, and second, it has two modes: interactive and non-interactive mode.
### A Stateful Interface
Now, what do I mean when I say that `pyplot` provides a "stateful interface"? Well, when you create a visualization there are usually several steps you need to work through to get it just right. For example, you'll need to plot the data itself. Then, you may need to adjust the limits of the axes, and possibly change the labels for the tick marks as well. To make the visualization easier to understand, you may want to add x- and y-axis labels, a title, and maybe even a legend. Doing all of these modifications in one command would be tough enough from a script, but in an interactive interpreter session, like this one, it would be simply too painful to even bother with. Instead, a better way to do this would be to perform each change in a seperate step allowing you to focus on one task at a time. The `pyplot` interface does exactly that through its "stateful interface".
In short, every `pyplot` function you call changes the internal state of the current visualization. So, a call to the `plot()` function, for example, may create several objects in the background, or simply update existing ones that were created by a previous function call. The point is, you don't have to worry about creating instances of classes or modifying them directly, instead you can just focus on the visualization.
Let's give the stateful interface a try now by building up a simple plot. We'll start by plotting a few randomly generated lines, then we'll add a title to our plot to make it a bit easier to understand what it's displaying. We'll do this in two separate steps to show off the stateful nature of the `pyplot` interface.
So, first things first, let's import the numpy library to give us access to some nice functions for generating random data.
```
import numpy as np
```
Now, we can create our plot. First, we'll create a `for` loop, and at each iteration, we'll plot some randomly generated, normally distributed data by calling the `numpy.random.randn` function. After you plot your data, call the `pyplot.title` function to add the title "Normally Distributed Random Samples" to the plot.
```
# Plot 3 randomly generated lines
for i in range(3):
plt.plot(np.random.randn(10))
# Add a title to the plot
plt.title('Normally Distributed Random Samples');
```
The main thing to notice here is that we had four different interactions with the `pyplot` module: 3 calls to the `plot()` function and 1 to the `title()` function, and in each case, the result was that the current visualization was updated with the requested change. The components of that visualization, i.e., the class instances that make up the visualization, are completely invisible to us. Instead, we simply concentrate on the how the visualization should look and ignore everything that goes into making that visualization. This ends up being such an intuitive interface, and it's easy to see why this is the preferred method for interactive data visualization with matplotlib. You essentially lower your cognitive load by concentrating on only one aspect of a visualization at a time and build it up step-by-step.
### Interactive Mode
Now, if you're working from the command line, you may have noticed that the very first call to the `plot` function caused a new figure to pop up in a separate window. The subsequent call to the `title` function actually updated the already existing figure like magic, right in front of your eyes. That's because the call you made earlier to the `ion` function turned on `pyplot's` interactive mode. In interactive mode, every call you make to the `pyplot` module results in a change to the currently displayed figure. Without interactive mode turned on, you would need to call the `pyplot.show` function to display the current figure, but you would lose the ability to interact with that figure once you did. You can give it a try now by first calling the `pyplot.ioff` function to turn off interactive mode.
```
plt.ioff()
```
Incidentally, you can always check if you're currently in interactive mode by calling the `plt.isinteractive()` function. Let's try it out now.
```
plt.isinteractive()
```
Now that we've turned off interactive mode, we can make any number of calls to the `pyplot` interface, and you won't see any output until you call the `pyplot.show` function. Let's give it a try now by plotting a histogram of some randomly generated data.
```
plt.hist(np.random.randn(1000));
```
If you're following along from the command line, you should no longer be seeing a figure pop up when you ran the last line of code. However, for those of you following along in a Jupyter notebook, you may have noticed that a histogram plot appeared as soon as you executed the previous cell. Unfortunately, turning off interactive mode in a notebook is not as easy as just calling the `pyplot.ioff` function. The reason is that our earlier call to the `%matplotlib inline` magic function does a little bit of extra setup for us to get interactive mode working properly in a notebook. So, to turn off interactive mode in this case, we'll need to undo that extra setup. Specifically, an event listener was added to the `'post_execute'` event that will flush the current figure every time we execute the code in a cell. To remove the event listener, we'll first need to grab a reference to the current IPython shell (the one we're currently interacting with), and then we'll remove the `flush_figures` function from the `'post_execute'` event listener for the current shell.
So, let's get started by first getting a reference to the current shell. To do so, you can simply call the `get_ipython()` function.
```
# Get a reference to the current IPython shell
shell = get_ipython()
```
Once you have a reference to the current IPython shell, you can call the `unregister` function on the `events` object and pass in the name of the event, in our case that'll be the `'post_execute'` event, followed by a reference to the event handler that we want to remove from the listener, which will be the `flush_figures` function. To do this, we'll first need to import the `flush_figures` function.
```
# Import the event handler function that we are trying to unregister
from ipykernel.pylab.backend_inline import flush_figures
```
Then, we can remove the `flush_figures` function from the list of callback functions registered with the `post_execute` event listener. To do that, we simply call the `unregister` function and pass in the event name and function reference.
```
# Unregister the event handler for the current shell session
shell.events.unregister('post_execute', flush_figures)
```
Now, we should be able to call the `pyplot.hist` function again without displaying anything.
```
plt.hist(np.random.randn(1000));
```
To show our plot now, we'll need to call the `pyplot.show` function, so let's go ahead and do that now.
```
plt.show()
```
Having that extra step of calling the `show` function may seem a little unecessarily burdensome to you, but I assure you both modes have their uses. Obviously, when working with your data interactively, as we've been doing here, interactive mode is the way to go. However, if you plan on writing a script to process data "offline" and create a handful of visualizations with that data, non-interactive mode is the one to choose. In fact, the default mode for matplotlib is non-interactive as is evidenced by the fact that you have to explicitly turn on interactive mode in both the command line interpreter and a Jupyter notebook (remember the call we made to the `%matplotlib inline` magic function did that for us).
So, in short, when writing a script to create visualizations with matplotlib, leave interactive mode off. However, when interacting directly with your data in a command line, or Jupyter notebook session, having interactive mode on makes the interaction much more pleasant on the whole.
## Conclusion
And, with that said, we've come to the end of this session. To recap, in this lesson, we learned about `pyplot`'s stateful interface, and we played around with both the interactive and non-interactive modes a bit and learned when it's appropriate to use each one. Though this lesson is done, we're not done with the `pyplot` interface just yet. Over the next several lessons we'll explore what the `pyplot` interface has to offer by diving into each of the most commonly used plotting functions in the `pyplot` module.
|
github_jupyter
|
%matplotlib inline
import matplotlib.pyplot as plt
# This does nothing after calling %matplotlib inline,
# but it turns on interactive mode in the command line.
plt.ion()
# Turn on retina mode
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('retina')
import numpy as np
# Plot 3 randomly generated lines
for i in range(3):
plt.plot(np.random.randn(10))
# Add a title to the plot
plt.title('Normally Distributed Random Samples');
plt.ioff()
plt.isinteractive()
plt.hist(np.random.randn(1000));
# Get a reference to the current IPython shell
shell = get_ipython()
# Import the event handler function that we are trying to unregister
from ipykernel.pylab.backend_inline import flush_figures
# Unregister the event handler for the current shell session
shell.events.unregister('post_execute', flush_figures)
plt.hist(np.random.randn(1000));
plt.show()
| 0.594434 | 0.993307 |
```
ls
cat noise1.py
run noise1.py
cat noise1.py
run noise1.py
run noise1.py
run noise1.py
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.random.randn(100)
plt.plot(x)
plt.show()
cat noise1.py
run noise1.py
import numpy as np
np.sqrt(4)
import numpy
numpy.sqrt(5)
import numpy as np
np.sqrt(6)
from numpy import sqrt
sqrt(4)
cat noise2.py
run noise2.py
```
### Lists
```
x = [10, 'foo', False]
type(x)
x
x.append(2.5)
x[0]
x[1]
type(x)
x
x.append(6)
x[1]
x
```
The For Loop
```
animals = ['dog','cat','bird']
for animal in animals:
print("The plural of " + animal + " is " + animal + "s" )
```
### While Loops
```
cat whileLoops.py
run whileLoops.py
```
### Defined Funtions
```
cat definition_functions.py
run definition_functions.py
```
### Conditions
```
cat conditions.py
run conditions.py
cat conditions2.py
run conditions2.py
cat condition3.py
run condition3.py
max(7,2,6,7,6,9)
m = max
m(7,5,6)
```
### List Comprehensions
```
animals = ['dog', 'cat', 'bird']
plurals = [animal + 's' for animal in animals]
plurals
range(0,8)
range(8)
doubles = [2*x for x in range(20)]
doubles
e_values = []
for i in range(n):
e = generator_type()
e_values.append()
def factorial(num):
if num == 1:
return 1
else:
return num * factorial(num - 1)
factorial(8)
```
## Exercise 2
The **binomial random variable** $Y ~ Bin(n,p)$ represents the number of successes in $n$ binary trials, where each trial succeeds with probability $p$
```
from numpy.random import uniform
def binomial_rv(n, p):
count = 0
for i in range(n):
U = uniform()
if U < p:
count += 1 # Or count += 1
return count
binomial_rv(10, 0.5)
import numpy as np
n = 100000
count = 0
for i in range(n):
u,v = np.random.uniform(), np.random.uniform()
d = np.sqrt((u - 0.5)**2 + (v - 0.5)**2)
if d < 0.5:
count += 1
area_estimate = count / n
print(area_estimate * 4)
from numpy.random import uniform
payoff = 0
count = 0
for i in range(10):
U = uniform()
count = count + 1 if U < 0.5 else 0
if count == 3:
payoff =1
print(payoff)
import numpy as np
import matplotlib.pyplot as plt
alpha = 0.9
ts_length = 200
current_x = 0
x_values = []
for i in range(ts_length + 1):
x_values.append(current_x)
current_x = alpha * current_x + np.random.randn()
plt.plot(x_values)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
alphas = [0.0, 0.8, 0.98]
ts_length = 200
for alpha in alphas:
x_values = []
current_x = 0
for i in range(ts_length):
x_values.append(current_x)
current_x = alpha * current_x + np.random.randn()
plt.plot(x_values, label=f'alpha = {alpha}')
x = [np.random.randn() for i in range(100)]
plt.plot(x, label="white noise")
plt.legend()
plt.show()
```
|
github_jupyter
|
ls
cat noise1.py
run noise1.py
cat noise1.py
run noise1.py
run noise1.py
run noise1.py
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.random.randn(100)
plt.plot(x)
plt.show()
cat noise1.py
run noise1.py
import numpy as np
np.sqrt(4)
import numpy
numpy.sqrt(5)
import numpy as np
np.sqrt(6)
from numpy import sqrt
sqrt(4)
cat noise2.py
run noise2.py
x = [10, 'foo', False]
type(x)
x
x.append(2.5)
x[0]
x[1]
type(x)
x
x.append(6)
x[1]
x
animals = ['dog','cat','bird']
for animal in animals:
print("The plural of " + animal + " is " + animal + "s" )
cat whileLoops.py
run whileLoops.py
cat definition_functions.py
run definition_functions.py
cat conditions.py
run conditions.py
cat conditions2.py
run conditions2.py
cat condition3.py
run condition3.py
max(7,2,6,7,6,9)
m = max
m(7,5,6)
animals = ['dog', 'cat', 'bird']
plurals = [animal + 's' for animal in animals]
plurals
range(0,8)
range(8)
doubles = [2*x for x in range(20)]
doubles
e_values = []
for i in range(n):
e = generator_type()
e_values.append()
def factorial(num):
if num == 1:
return 1
else:
return num * factorial(num - 1)
factorial(8)
from numpy.random import uniform
def binomial_rv(n, p):
count = 0
for i in range(n):
U = uniform()
if U < p:
count += 1 # Or count += 1
return count
binomial_rv(10, 0.5)
import numpy as np
n = 100000
count = 0
for i in range(n):
u,v = np.random.uniform(), np.random.uniform()
d = np.sqrt((u - 0.5)**2 + (v - 0.5)**2)
if d < 0.5:
count += 1
area_estimate = count / n
print(area_estimate * 4)
from numpy.random import uniform
payoff = 0
count = 0
for i in range(10):
U = uniform()
count = count + 1 if U < 0.5 else 0
if count == 3:
payoff =1
print(payoff)
import numpy as np
import matplotlib.pyplot as plt
alpha = 0.9
ts_length = 200
current_x = 0
x_values = []
for i in range(ts_length + 1):
x_values.append(current_x)
current_x = alpha * current_x + np.random.randn()
plt.plot(x_values)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
alphas = [0.0, 0.8, 0.98]
ts_length = 200
for alpha in alphas:
x_values = []
current_x = 0
for i in range(ts_length):
x_values.append(current_x)
current_x = alpha * current_x + np.random.randn()
plt.plot(x_values, label=f'alpha = {alpha}')
x = [np.random.randn() for i in range(100)]
plt.plot(x, label="white noise")
plt.legend()
plt.show()
| 0.348423 | 0.968351 |
### Models e Banco de Dados
| [Anterior](4.Estrutura-Diretorios.ipynb)| [Próximo](6.Rotas-e-Paginas.ipynb) |
| :------------- | :----------:|
### 1. Exemplo "Modelo" simulando um twitter

### 2. Flask e SQLAlchemy (ORM)
Site: https://flask-sqlalchemy.palletsprojects.com/en/2.x/
* **Instalação** Saiba mais em [Flask-SQLAlchemy pip install](https://pypi.org/project/Flask-SQLAlchemy/)
> $ pip install -U Flask-SQLAlchemy
**OBS:** Lembre-se de instalá-lo no ambiente virtual (venv) do seu projeto.
### 3. Configurações iniciais do SQLAlchemy
* Imports e Declarações iniciais
```
import os.path
from flask import Flask
from flask_sqlalchemy import SQLAlchemy # (Import principal do SQLAlchemy)
basedir = os.path.abspath(os.path.dirname(__file__))
app = Flask(__name__)
app.config['SQLALCHEMY_DATABASE_URI'] = 'sqlite:///' + os.path.join(basedir, 'posts_twitter.db') # (Banco de Dados SQLite)
db = SQLAlchemy(app) # (Criando uma instância padrão db)
```
* A configuração acima deve ser declarada no arquivo "app/__ init __.py"
* **OBS:** É importante saber que o SQLAlchemy gerencia (abertura e fechamento) as conexões com o banco de dados para mim.
### 4. Trabalhando com Models no SQLAlchemy (arquivo tables.py ou arquivo models.py)
```
# Lembrando que "db = SQLAlchemy()"
from app import db
from flask_sqlalchemy import SQLAlchemy
import datetime
class User(db.Model):
_tablename_ = "users"
id = db.Column(db.Integer, primary_key=True)
username = db.Column(db.String, unique=True)
password = db.Column(db.String(20))
name = db.Column(db.String(300))
email = db.Column(db.String, unique=True, nullable=False)
create_date = db.Column(db.DateTime, default=datetime.datetime.now)
def __init__(self, username, password, name, email):
self.username = username
self.password = password
self.name = name
self.email = email
# Representação (representation) - Define como o User será representado
def __repr__(self):
return '<User %r>' % self.username
```
### 5. Migrações no Bancos de Dados
* Módulo Flask-Migrate: https://flask-migrate.readthedocs.io/en/latest/
> **Instalando:** $ pip install Flask-Migrate
* Módulo Flask-Script: https://flask-script.readthedocs.io/en/latest/
> Fornece suporte para escrever scripts externos no Flask. <br/>
> **Instalando:** $ pip install Flask-Script
* Realizando os **imports** do Flask-Migrate e Flask-Script no arquivo 'app/__ init __.py'
> from flask_migrate import Migrate <br />
> from flask_script import Manager, MigrateCommand <== Não funcionou
* Instanciando o Script e o Migrate
```
...
migrate = Migrate(app, db) # Instancia o Migrate
# O Manager se preocupa com os comandos de inicialização
manager = Manager(app) <== Não funcionou
manager.add_command('db', MigrateCommand) <== Não funcionou
...
```
* Com o Manager instanciado o arquivo "run.py" poderá ser alterado
Alterando a forma de execução da aplicação para adicionar comandos a ela:
> from app import manager <br/><br/>
if __ name __ == "__ main __":
......manager.run()
* Criando o banco de dados e as respectivas tabelas somente quando o app estiver pronto
> if __ name __ == "__ main __": <br/>
......db.init_app(app=app) <br/>
------# Sincroniza banco de dados e aplicação <br/>
............with app.app_context(): <br/>
..................db.create_all() <br/>
......app.run()
* Comandos diversos - após configuração acima
```
$ flask db init # Inicia o arquivo SQLite em ...
.../flask-api/migrations/<arquivos de migração e tabela alembic>
$ flask db migrate -m "Initial migration."
$ flask db upgrade
- Com isso, será criado o arquivo "posts_twitter" na raiz do projeto.
```
### 6. Configurações relacionadas ao Banco de Dados
* Arquivo de Configuração `config.py` na raiz do projeto
> DEBUG = True # Enquanto estiver desenvolvendo - ativa a atualização e compilação automática
> SQLALCHEMY_DATABASE_URI = 'sqlite:///posts_twitter.db' <br/>
> SQLALCHEMY_TRACK_MODIFICATIONS = True
* Importanto o arquivo `config.py` dentro do `app/__ init __.py`
> ```app.config.from_object('config')```
### 7. Gerando senhas criptografadas (Models)
**1. Importe werkzeug.securyty**
```
from werkzeug.security import generate_password_hash
...
```
**2. Configure o arquivo `models.py` para realizar a criptografia (geração de um hash de 66 caracteres) da senha do usuário**
```
...
def __ init __(self, username, email, password):
self.username = username
self.email - email
self.password = _create_password(password)
...
def _create_password(self, password):
return generate_password_hash(password)
```
### 8. Criando relacionamento entre as Tabelas
Para aprender, basta acessar: https://flask-sqlalchemy.palletsprojects.com/en/2.x/quickstart/
|
github_jupyter
|
import os.path
from flask import Flask
from flask_sqlalchemy import SQLAlchemy # (Import principal do SQLAlchemy)
basedir = os.path.abspath(os.path.dirname(__file__))
app = Flask(__name__)
app.config['SQLALCHEMY_DATABASE_URI'] = 'sqlite:///' + os.path.join(basedir, 'posts_twitter.db') # (Banco de Dados SQLite)
db = SQLAlchemy(app) # (Criando uma instância padrão db)
# Lembrando que "db = SQLAlchemy()"
from app import db
from flask_sqlalchemy import SQLAlchemy
import datetime
class User(db.Model):
_tablename_ = "users"
id = db.Column(db.Integer, primary_key=True)
username = db.Column(db.String, unique=True)
password = db.Column(db.String(20))
name = db.Column(db.String(300))
email = db.Column(db.String, unique=True, nullable=False)
create_date = db.Column(db.DateTime, default=datetime.datetime.now)
def __init__(self, username, password, name, email):
self.username = username
self.password = password
self.name = name
self.email = email
# Representação (representation) - Define como o User será representado
def __repr__(self):
return '<User %r>' % self.username
...
migrate = Migrate(app, db) # Instancia o Migrate
# O Manager se preocupa com os comandos de inicialização
manager = Manager(app) <== Não funcionou
manager.add_command('db', MigrateCommand) <== Não funcionou
...
$ flask db init # Inicia o arquivo SQLite em ...
.../flask-api/migrations/<arquivos de migração e tabela alembic>
$ flask db migrate -m "Initial migration."
$ flask db upgrade
- Com isso, será criado o arquivo "posts_twitter" na raiz do projeto.
### 7. Gerando senhas criptografadas (Models)
**1. Importe werkzeug.securyty**
**2. Configure o arquivo `models.py` para realizar a criptografia (geração de um hash de 66 caracteres) da senha do usuário**
| 0.325413 | 0.76908 |
# Diversity Test
This notebook compares categorical index diversity in the ranked recommendations. If you want to see distance comparisons, head out to the next note.
Number of sampled actions: 50
``` ddpg_action = ddpg_action[np.random.randint(0, 5000, 50)].detach().cpu().numpy() <- that 50 ```
K parameter for TopK ranking: 20 (changed in the query function arguments)
Next part contains A LOT of various graphs that are not grouped. If you want GROUPED comparison, go to the bottom section
```
import torch # conda install faiss-gpu cudatoolkit=10.0 -c pytorch # For CUDA10
import numpy as np
from tqdm.auto import tqdm
import pandas as pd
from milvus import MetricType
from sklearn.preprocessing import normalize
import matplotlib.pyplot as plt
%matplotlib inline
from jupyterthemes import jtplot
jtplot.style(theme='grade3')
# == recnn ==
import sys
sys.path.append("../../")
import recnn
from recnn.data.db_con import MilvusConnection
cuda = torch.device('cuda')
tqdm.pandas()
ddpg = recnn.nn.models.Actor(1290, 128, 256).to(cuda)
td3 = recnn.nn.models.Actor(1290, 128, 256).to(cuda)
ddpg.load_state_dict(torch.load('../../models/ddpg_policy.pt'))
td3.load_state_dict(torch.load('../../models/td3_policy.pt'))
frame_size = 10
batch_size = 1
# embeddgings: https://drive.google.com/open?id=1EQ_zXBR3DKpmJR3jBgLvt-xoOvArGMsL
dirs = recnn.data.env.DataPath(
base="../../data/",
embeddings="embeddings/ml20_pca128.pkl",
ratings="ml-20m/ratings.csv",
cache="cache/frame_env.pkl", # cache will generate after you run
use_cache=True
)
env = recnn.data.env.FrameEnv(dirs, frame_size, batch_size)
milvus_l2 = MilvusConnection(env, name="movies_L2", param={'metric_type':MetricType.L2})
milvus_ip = MilvusConnection(env, name="movies_IP", param={'metric_type': MetricType.IP})
test_batch = next(iter(env.test_dataloader))
state, action, reward, next_state, done = recnn.data.get_base_batch(test_batch)
```
# DDPG
```
ddpg_action = ddpg(state)
ddpg_action = ddpg_action[np.random.randint(0, state.size(0), 50)].detach().cpu().numpy()
```
## L2: number the movie was recommended
```
%matplotlib inline
topK = milvus_l2.search(ddpg_action, topk=20)
uniques, counts = np.unique(topK, return_counts=True)
plt.figure(figsize=(16,9))
# p.s. expluding one
ax = plt.subplot()
ax.bar(range(len(counts[counts>1])), sorted(counts[counts>1]))
ax.set_xlabel("id")
ax.set_ylabel("n recommendations")
l2_ddpg = counts
```
## L2: counts of n recommendations
```
ax = pd.Series(counts).value_counts().plot(kind='bar', figsize=(16, 9))
ax.set_xlabel("n movie recommended")
ax.set_ylabel("n counts")
```
## InnerProduct
```
topK = milvus_ip.search(ddpg_action, topk=20)
uniques, counts = np.unique(topK, return_counts=True)
plt.figure(figsize=(16,9))
# p.s. expluding one
ax = plt.subplot()
ax.bar(range(len(counts[counts>1])), sorted(counts[counts>1]))
ax.set_xlabel("id")
ax.set_ylabel("n recommendations")
ip_ddpg = counts
ax = pd.Series(counts).value_counts().plot(kind='bar', figsize=(16, 9))
ax.set_xlabel("n movie recommended")
ax.set_ylabel("n counts")
```
# TD3
```
td3_action = td3(state)
td3_action = td3_action[np.random.randint(0, state.size(0), 50)].detach().cpu().numpy()
```
## L2
```
topK = milvus_l2.search(td3_action, topk=20)
uniques, counts = np.unique(topK, return_counts=True)
plt.figure(figsize=(16,9))
# p.s. expluding one
ax = plt.subplot()
ax.bar(range(len(counts[counts>1])), sorted(counts[counts>1]))
ax.set_xlabel("id")
ax.set_ylabel("n recommendations")
l2_td3 = counts
ax = pd.Series(counts).value_counts().plot(kind='bar', figsize=(16, 9))
ax.set_xlabel("n movie recommended")
ax.set_ylabel("n counts")
```
# InnerProduct
```
topK = milvus_ip.search(td3_action, topk=20)
uniques, counts = np.unique(topK, return_counts=True)
plt.figure(figsize=(16,9))
# p.s. expluding one
ax = plt.subplot()
ax.bar(range(len(counts)), sorted(counts))
ax.set_xlabel("id")
ax.set_ylabel("n recommendations")
ip_td3 = counts
ax = pd.Series(counts).value_counts().plot(kind='bar', figsize=(16, 9))
ax.set_xlabel("n movie recommended")
ax.set_ylabel("n counts")
# Grouped comparison
```
## L2 top 30
```
def plot_comp(ddpg, td3):
barWidth = 0.25
r1 = np.arange(len(ddpg))[:30]
r2 = [x + barWidth for x in r1]
r3 = [x + barWidth for x in r2]
plt.figure(figsize=(16, 9))
plt.bar(r1, ddpg, width=barWidth, edgecolor='white', label='ddpg')
plt.bar(r2, td3, width=barWidth, edgecolor='white', label='td3')
# Add xticks on the middle of the group bars
plt.xlabel('id')
plt.ylabel('n recommended')
# Create legend & Show graphic
plt.legend()
plt.show()
def plot_counts(l2_ddpg, l2_td3):
l2_ddpg_counts, l2_td3_counts = [pd.Series(i).value_counts() for i in [l2_ddpg, l2_td3]]
l2_ddpg_counts, l2_td3_counts = [i[i > 1] for i in [l2_ddpg_counts, l2_td3_counts]]
unique_idx = l2_ddpg_counts.index.unique()| l2_td3_counts.index.unique()
for arr in [l2_ddpg_counts, l2_td3_counts]:
for i in unique_idx:
if i not in arr:
arr[i] = 0
barWidth = 0.25
r1 = np.arange(len(l2_ddpg_counts))
r2 = [x + barWidth for x in r1]
r3 = [x + barWidth for x in r2]
plt.figure(figsize=(16, 9))
plt.bar(r1, l2_ddpg_counts, width=barWidth, edgecolor='white', label='ddpg')
plt.bar(r2, l2_td3_counts, width=barWidth, edgecolor='white', label='td3')
# Add xticks on the middle of the group bars
plt.xlabel('n recommended')
plt.ylabel('counts')
# Create legend & Show graphic
plt.legend()
plt.show()
l2_ddpg_ = np.sort(l2_ddpg)[::-1][:30]
l2_td3_ = np.sort(l2_td3)[::-1][:30]
plot_comp(l2_ddpg_, l2_td3_)
plot_counts(l2_ddpg, l2_td3)
```
## InnerProduct top 30
```
ip_ddpg_ = np.sort(ip_ddpg)[::-1][:30]
ip_td3_ = np.sort(ip_td3)[::-1][:30]
plot_comp(ip_ddpg_, ip_td3_)
```
## InnerProduct top 30-50
```
ip_ddpg_ = np.sort(ip_ddpg)[::-1][30:50]
ip_td3_ = np.sort(ip_td3)[::-1][30:50]
plot_comp(ip_ddpg_, ip_td3_)
plot_counts(ip_ddpg, ip_td3)
```
|
github_jupyter
|
K parameter for TopK ranking: 20 (changed in the query function arguments)
Next part contains A LOT of various graphs that are not grouped. If you want GROUPED comparison, go to the bottom section
# DDPG
## L2: number the movie was recommended
## L2: counts of n recommendations
## InnerProduct
# TD3
## L2
# InnerProduct
## L2 top 30
## InnerProduct top 30
## InnerProduct top 30-50
| 0.458591 | 0.866246 |
# Pandora: a new stereo matching framework
<img src="img/logo-cnes-triangulaire.jpg" width="200" height="200">
*Cournet, M., Sarrazin, E., Dumas, L., Michel, J., Guinet, J., Youssefi, D., Defonte, V., Fardet, Q., 2020. Ground-truth generation and disparity estimation for optical satellite imagery. ISPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences.*
# Introduction and basic usage
#### Imports and external functions
```
import io
from IPython.display import Image, display
import io
import matplotlib.pyplot as plt
import numpy as np
import os
from pathlib import Path
import rasterio
from snippets.utils import *
def plot_image(img, title=None, output_dir=None, cmap="viridis"):
fig = plt.figure()
plt.title(title)
plt.imshow(img, cmap=cmap, vmin=np.min(img), vmax=np.max(img))
plt.colorbar()
if output_dir is not None:
fig.savefig(os.path.join(output_dir,title + '.pdf'))
def plot_state_machine(machine):
stream = io.BytesIO()
try:
pandora_machine.get_graph().draw(stream, prog='dot', format='png')
display(Image(stream.getvalue()))
except:
print("It is not possible to show the graphic of the state machine. To solve it, please install graphviz on your system (apt-get install graphviz if operating in Linux) and install python package with pip install graphviz")
```
# What is Pandora ?
* Pandora is a Toolbox to estimate disparity
* It is inspired by the work of [Scharstein 2002]
* Pandora embeds several state-of-art algorithms
* It is easy to configure and modular
* Will be used in the 3D reconstruction pipeline CARS for CO3D mission
[Scharstein 2002] *A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms*, D. Scharstein and R. Szeliski,
vol. 47, International Journal of Computer Vision}, 2002
<img src="img/logo_diagram.png" width="500">
## Inputs
* Stereo rectified image pair (with associated masks)
* Disparity range to explore
* Configuration file
## Outputs
* Disparity and validity maps in left image geometry
* Disparity and validity maps in righ image geometry (*optional*)
## Pandora's pipeline
Pandora provides the following steps:
* matching cost computation (**mandatory**)
* cost aggregation
* cost optimization
* disparity computation (**mandatory**)
* subpixel disparity refinement
* disparity filtering
* validation
* multiscale processing
<img src="img/schema_complet.png" width="1000">
### Available implementations for each step
| Step | Algorithms implemented |
|:--------------------------|:-----------------------|
| Matching cost computation | Census / SAD / SSD / ZNNC / MC-CNN |
| Cost aggregation | Cross Based Cost Aggregation |
| Cost optimization | SGM |
| Disparity computation | Winner-Take-All |
| Subpixel disparity refinement | Vfit / Quadratic |
| Disparity filtering | Median / Bilateral |
| Validation | Cross checking |
| Multiscale | Fixed zoom pyramid |
# Pandora execution options with state machine
#### Imports of pandora
```
# Load pandora imports
import pandora
from pandora.img_tools import read_img
from pandora.check_json import check_pipeline_section, concat_conf, memory_consumption_estimation
from pandora.state_machine import PandoraMachine
from pandora import import_plugin, check_conf
```
#### (Optional) If Pandora plugins are to be used, import them
Available Pandora Plugins include :
- MC-CNN Matching cost computation
- SGM Optimization
```
# Load plugins
import_plugin()
```
#### Load and visualize input data
Provide image path
```
# Paths to left and right images
img_left_path = "data/Cones_LEFT.tif"
img_right_path = "data/Cones_RIGHT.tif"
# Paths to masks (None if not provided)
left_mask_path = None
right_mask_path = None
```
Provide image configuration
```
image_cfg = {'image': {'no_data_left': np.nan, 'no_data_right': np.nan}}
```
Provide output directory to write results
```
output_dir = os.path.join(os.getcwd(),"output")
# If necessary, create output dir
Path(output_dir).mkdir(exist_ok=True,parents=True)
```
Convert input data to dataset
```
img_left = read_img(img_left_path, no_data=image_cfg['image']['no_data_left'],
mask=left_mask_path)
img_right = read_img(img_right_path, no_data=image_cfg['image']['no_data_right'],
mask=right_mask_path)
```
Visualize input data
```
plot_image(img_left.im, "Left input image", output_dir, cmap="gray")
```
# Option 1 : trigger all the steps of the machine at ones
#### Instantiate the machine
```
pandora_machine = PandoraMachine()
```
#### Define pipeline configuration
```
user_pipeline_cfg = {
'pipeline':{
"right_disp_map": {
"method": "accurate"
},
"matching_cost" : {
"matching_cost_method": "zncc",
"window_size": 5,
"subpix": 4
},
"disparity": {
"disparity_method": "wta",
"invalid_disparity": "NaN"
},
"refinement": {
"refinement_method": "quadratic"
},
"filter": {
"filter_method": "median"
},
"validation": {
"validation_method": "cross_checking"
},
"filter.this_time_after_validation" : {
"filter_method": "median",
"filter_size": 3
}
}
}
```
Disparity interval used
```
disp_min = -60
disp_max = 0
```
#### Check the configuration and sequence of steps
```
checked_cfg = check_pipeline_section(user_pipeline_cfg, pandora_machine)
pipeline_cfg = checked_cfg['pipeline']
print(pipeline_cfg)
```
#### Estimate the memory consumption of the pipeline
```
min_mem_consump, max_mem_consump = memory_consumption_estimation(user_pipeline_cfg, [img_left_path, disp_min, disp_max], pandora_machine)
print("Estimated maximum memory consumption between {:.2f} GiB and {:.2f} GiB".format(min_mem_consump, max_mem_consump))
```
#### Prepare the machine
```
pandora_machine.run_prepare(pipeline_cfg, img_left, img_right, disp_min, disp_max)
```
#### Trigger all the steps of the machine at ones
```
left_disparity, right_disparity = pandora.run(pandora_machine, img_left, img_right, disp_min, disp_max, pipeline_cfg)
```
Visualize output disparity map
```
plot_image(left_disparity.disparity_map, "Left disparity map", output_dir, cmap=pandora_cmap())
```
# Option 2 : trigger the machine step by step
The implementation of Pandora with a state machine makes it possible to set up a more flexible pipeline, which makes it possible to choose via a configuration file the steps as well as the order of the steps that one wishes to follow in Pandora.
Moreover, the state machine allows to run each step of the pipeline independently, giving the possibility to save and visualize the results after each step.
The state machine has three states :
* Begin
* Cost volume
* Disparity map
Being the connections between them the different steps of the pipeline.
<img src="../doc/sources/Images/Machine_state_diagram.png" width="700">
#### Instantiate the machine
```
pandora_machine = PandoraMachine()
```
#### Define pipeline configuration
```
user_pipeline_cfg = {
'pipeline':{
"right_disp_map": {
"method": "accurate"
},
"matching_cost" : {
"matching_cost_method": "zncc",
"window_size": 5,
"subpix": 4
},
"aggregation": {
"aggregation_method": "cbca"
},
"disparity": {
"disparity_method": "wta",
"invalid_disparity": "NaN"
},
"refinement": {
"refinement_method": "quadratic"
},
"filter": {
"filter_method": "median"
},
"validation": {
"validation_method": "cross_checking"
}
}
}
```
Disparity interval used
```
disp_min = -60
disp_max = 0
```
#### Check the pipeline configuration and sequence of steps
```
checked_cfg = check_pipeline_section(user_pipeline_cfg, pandora_machine)
print(checked_cfg)
pipeline_cfg = checked_cfg['pipeline']
```
#### Estimate the memory consumption of the pipeline
```
min_mem_consump, max_mem_consump = memory_consumption_estimation(user_pipeline_cfg, [img_left_path, disp_min, disp_max], pandora_machine)
print("Estimated maximum memory consumption between {:.2f} GiB and {:.2f} GiB".format(min_mem_consump, max_mem_consump))
```
#### Prepare the machine
```
pandora_machine.run_prepare(pipeline_cfg, img_left, img_right, disp_min, disp_max)
```
#### Trigger the machine step by step
```
plot_state_machine(pandora_machine)
```
Run matching cost
```
pandora_machine.run('matching_cost', pipeline_cfg)
plot_state_machine(pandora_machine)
pandora_machine.run('aggregation', pipeline_cfg)
plot_state_machine(pandora_machine)
```
Run disparity
```
pandora_machine.run('disparity', pipeline_cfg)
plot_state_machine(pandora_machine)
```
Run refinement
```
pandora_machine.run('refinement', pipeline_cfg)
plot_state_machine(pandora_machine)
```
Run filter
```
pandora_machine.run('filter', pipeline_cfg)
plot_state_machine(pandora_machine)
```
Run validation
```
pandora_machine.run('validation', pipeline_cfg)
plot_state_machine(pandora_machine)
```
Visualize output disparity map
```
plot_image(pandora_machine.left_disparity.disparity_map, "Left disparity map", output_dir, cmap=pandora_cmap())
```
|
github_jupyter
|
import io
from IPython.display import Image, display
import io
import matplotlib.pyplot as plt
import numpy as np
import os
from pathlib import Path
import rasterio
from snippets.utils import *
def plot_image(img, title=None, output_dir=None, cmap="viridis"):
fig = plt.figure()
plt.title(title)
plt.imshow(img, cmap=cmap, vmin=np.min(img), vmax=np.max(img))
plt.colorbar()
if output_dir is not None:
fig.savefig(os.path.join(output_dir,title + '.pdf'))
def plot_state_machine(machine):
stream = io.BytesIO()
try:
pandora_machine.get_graph().draw(stream, prog='dot', format='png')
display(Image(stream.getvalue()))
except:
print("It is not possible to show the graphic of the state machine. To solve it, please install graphviz on your system (apt-get install graphviz if operating in Linux) and install python package with pip install graphviz")
# Load pandora imports
import pandora
from pandora.img_tools import read_img
from pandora.check_json import check_pipeline_section, concat_conf, memory_consumption_estimation
from pandora.state_machine import PandoraMachine
from pandora import import_plugin, check_conf
# Load plugins
import_plugin()
# Paths to left and right images
img_left_path = "data/Cones_LEFT.tif"
img_right_path = "data/Cones_RIGHT.tif"
# Paths to masks (None if not provided)
left_mask_path = None
right_mask_path = None
image_cfg = {'image': {'no_data_left': np.nan, 'no_data_right': np.nan}}
output_dir = os.path.join(os.getcwd(),"output")
# If necessary, create output dir
Path(output_dir).mkdir(exist_ok=True,parents=True)
img_left = read_img(img_left_path, no_data=image_cfg['image']['no_data_left'],
mask=left_mask_path)
img_right = read_img(img_right_path, no_data=image_cfg['image']['no_data_right'],
mask=right_mask_path)
plot_image(img_left.im, "Left input image", output_dir, cmap="gray")
pandora_machine = PandoraMachine()
user_pipeline_cfg = {
'pipeline':{
"right_disp_map": {
"method": "accurate"
},
"matching_cost" : {
"matching_cost_method": "zncc",
"window_size": 5,
"subpix": 4
},
"disparity": {
"disparity_method": "wta",
"invalid_disparity": "NaN"
},
"refinement": {
"refinement_method": "quadratic"
},
"filter": {
"filter_method": "median"
},
"validation": {
"validation_method": "cross_checking"
},
"filter.this_time_after_validation" : {
"filter_method": "median",
"filter_size": 3
}
}
}
disp_min = -60
disp_max = 0
checked_cfg = check_pipeline_section(user_pipeline_cfg, pandora_machine)
pipeline_cfg = checked_cfg['pipeline']
print(pipeline_cfg)
min_mem_consump, max_mem_consump = memory_consumption_estimation(user_pipeline_cfg, [img_left_path, disp_min, disp_max], pandora_machine)
print("Estimated maximum memory consumption between {:.2f} GiB and {:.2f} GiB".format(min_mem_consump, max_mem_consump))
pandora_machine.run_prepare(pipeline_cfg, img_left, img_right, disp_min, disp_max)
left_disparity, right_disparity = pandora.run(pandora_machine, img_left, img_right, disp_min, disp_max, pipeline_cfg)
plot_image(left_disparity.disparity_map, "Left disparity map", output_dir, cmap=pandora_cmap())
pandora_machine = PandoraMachine()
user_pipeline_cfg = {
'pipeline':{
"right_disp_map": {
"method": "accurate"
},
"matching_cost" : {
"matching_cost_method": "zncc",
"window_size": 5,
"subpix": 4
},
"aggregation": {
"aggregation_method": "cbca"
},
"disparity": {
"disparity_method": "wta",
"invalid_disparity": "NaN"
},
"refinement": {
"refinement_method": "quadratic"
},
"filter": {
"filter_method": "median"
},
"validation": {
"validation_method": "cross_checking"
}
}
}
disp_min = -60
disp_max = 0
checked_cfg = check_pipeline_section(user_pipeline_cfg, pandora_machine)
print(checked_cfg)
pipeline_cfg = checked_cfg['pipeline']
min_mem_consump, max_mem_consump = memory_consumption_estimation(user_pipeline_cfg, [img_left_path, disp_min, disp_max], pandora_machine)
print("Estimated maximum memory consumption between {:.2f} GiB and {:.2f} GiB".format(min_mem_consump, max_mem_consump))
pandora_machine.run_prepare(pipeline_cfg, img_left, img_right, disp_min, disp_max)
plot_state_machine(pandora_machine)
pandora_machine.run('matching_cost', pipeline_cfg)
plot_state_machine(pandora_machine)
pandora_machine.run('aggregation', pipeline_cfg)
plot_state_machine(pandora_machine)
pandora_machine.run('disparity', pipeline_cfg)
plot_state_machine(pandora_machine)
pandora_machine.run('refinement', pipeline_cfg)
plot_state_machine(pandora_machine)
pandora_machine.run('filter', pipeline_cfg)
plot_state_machine(pandora_machine)
pandora_machine.run('validation', pipeline_cfg)
plot_state_machine(pandora_machine)
plot_image(pandora_machine.left_disparity.disparity_map, "Left disparity map", output_dir, cmap=pandora_cmap())
| 0.563738 | 0.938181 |
<a href="https://colab.research.google.com/github/rca32/pythoncs_2019/blob/master/12_pandas_2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 샘플 Data 읽어 드리기
# pandas, numpy matplotlib 설정
```
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
pd.options.display.max_rows = 20
```
# Selecting , filtering
1. **label** 선택하기
2. **position** 선택하기
```
df = pd.read_csv("titanic.csv")
```
### [] -> 우리가 아는 일반적인 파이선의 data선택
DataFrame에서 하나의 컬럼을 선택
```
df['Age']
```
2개의 컬럼을 선택
```
df[['Age', 'Fare']]
```
## 하지만 범위 선택은 row를 선택
```
df[10:15]
```
### `loc` 와 `iloc`을 이용한 좀더 체계적인 data selecting
`[]`을 사용하면 column이나 row를 동시에 선택이 안됨...
* `loc`: selection by label
* `iloc`: selection by position
```
df = df.set_index('Name')
df.loc['Bonnell, Miss. Elizabeth', 'Fare']
df.loc['Bonnell, Miss. Elizabeth':'Andersson, Mr. Anders Johan', :]
```
`iloc` 는 위치로 선택 가능
```
df.iloc[0:2,1:3]
```
선택된 값의 변경도 가능
```
df.loc['Braund, Mr. Owen Harris', 'Survived'] = 100
df
```
### Boolean indexing (filtering)
```
df['Fare'] > 50
df[df['Fare'] > 50]
```
연습하기
남성 승객의 모든 행(row)을 선택하고 승객의 평균 연령을 계산한다.
여성 승객은.
```
df = pd.read_csv("data/titanic.csv")
```
연습하기
타이타닉에 50세 이상의 승객이 몇 명이었는가?
타이타닉에 50세이상70세 이이하 의 승객이 몇 명이었는가?
# group-by
### split-apply-combine
```
df = pd.DataFrame({'key':['A','B','C','A','B','C','A','B','C'],
'data': [0, 5, 10, 5, 10, 15, 10, 15, 20]})
df
```
### aggregating functions
```
df['data'].sum()
for key in ['A', 'B', 'C']:
print(key, df[df['key'] == key]['data'].sum())
```
### Groupby: applying functions per group
<img src="https://github.com/jorisvandenbossche/pandas-tutorial/raw/8308a6eb7d144fff95a6853930e3be4e8ddb2e0f/img/splitApplyCombine.png">
```
df.groupby('key').sum()
df.groupby('key')['data'].sum()
```
### titanic 분석해보기
```
df = pd.read_csv("data/titanic.csv")
df.head()
```
연습하기:
각 성별 평균 구하기
```
df.groupby('Sex')['Age'].mean()
```
연습하기:
모든 승객의 평균 생존율을 계산한다.
```
df['Survived'].mean()
```
연습하기:
25세 이하 승객의 평균 생존율을 계산한다.
연습하기:
남녀 생존률
```
df.groupby('Sex')['Survived'].mean()
```
연습하기:
PClass별 생존율 그리기
```
df.groupby('Pclass')['Survived'].mean().plot(kind='bar')
```
연습하기:
각 나이대별 별 생존율 그리기
```
df['AgeClass'] = pd.cut(df['Age'], bins=np.arange(0,90,10))
df.groupby('AgeClass')['Survived'].mean().plot(kind='bar')
```
# time series
```
no2 = pd.read_csv('20000101_20161231-NO2.csv', sep=';', skiprows=[1], na_values=['n/d'], index_col=0, parse_dates=True)
no2.head()
no2["2010-01-01 09:00": "2010-01-01 12:00"]
no2['2012-01':'2012-03']
no2.index.hour
no2.index.year
```
# resample
```
no2.plot(figsize=(16,8))
```
Daily로 변경
```
no2.head()
no2.resample('M').mean().head(9)
no2.resample('M').max().head(17)
```
https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html#offset-aliases
```
no2.resample('M').mean().plot() # 'A'
no2['2012'].resample('D').mean().plot()
#https://pandas.pydata.org/pandas-docs/stable/reference/groupby.html#computations-descriptive-stats
no2.loc['2009':, 'VERS'].resample('M').agg(['mean']).plot()
no2.resample('A').mean().plot()
no2.mean(axis=1).resample('A').median().plot(color='k', linestyle='--', linewidth=4)
```
# 응용~ 월별 그래프
# 응용~ 시간별
```
no2.groupby(no2.index.weekday).mean().plot()
```
응용~ 시간별
BASCH 지역에 주일과 주말과 차이를 시간대별로 구하세요
```
no2['weekday'] = no2.index.weekday
no2['weekend'] = no2['weekday'].isin([5, 6])
no2.groupby('weekend').mean().plot(kind='bar')
no2.groupby(['weekend',no2.index.hour])['BASCH'].mean().unstack(0).plot()
#https://pandas.pydata.org/pandas-docs/stable/user_guide/reshaping.html
no2['hour'] = no2.index.hour
no2.pivot_table(columns='weekend', index='hour', values='BASCH')
```
#연습
유럽기준이 시간당 평균이 200이 넘는 날이 1년에 18일 이상 되면 안된다.
최악의 경우 80일이 넘을 경우 Euro에서 제재를 가할수 있다.
```
# re-reading the data to have a clean version
no2 = pd.read_csv('20000101_20161231-NO2.csv', sep=';', skiprows=[1], na_values=['n/d'], index_col=0, parse_dates=True)
초과 = no2>200
초과.head()
ax = 초과.groupby(초과.index.year).sum().plot(kind='bar',figsize=(16,6))
ax.axhline(18,color='k',linestyle='--')
ax.axhline(68,color='r',linestyle='--')
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
pd.options.display.max_rows = 20
df = pd.read_csv("titanic.csv")
df['Age']
df[['Age', 'Fare']]
df[10:15]
df = df.set_index('Name')
df.loc['Bonnell, Miss. Elizabeth', 'Fare']
df.loc['Bonnell, Miss. Elizabeth':'Andersson, Mr. Anders Johan', :]
df.iloc[0:2,1:3]
df.loc['Braund, Mr. Owen Harris', 'Survived'] = 100
df
df['Fare'] > 50
df[df['Fare'] > 50]
df = pd.read_csv("data/titanic.csv")
df = pd.DataFrame({'key':['A','B','C','A','B','C','A','B','C'],
'data': [0, 5, 10, 5, 10, 15, 10, 15, 20]})
df
df['data'].sum()
for key in ['A', 'B', 'C']:
print(key, df[df['key'] == key]['data'].sum())
df.groupby('key').sum()
df.groupby('key')['data'].sum()
df = pd.read_csv("data/titanic.csv")
df.head()
df.groupby('Sex')['Age'].mean()
df['Survived'].mean()
df.groupby('Sex')['Survived'].mean()
df.groupby('Pclass')['Survived'].mean().plot(kind='bar')
df['AgeClass'] = pd.cut(df['Age'], bins=np.arange(0,90,10))
df.groupby('AgeClass')['Survived'].mean().plot(kind='bar')
no2 = pd.read_csv('20000101_20161231-NO2.csv', sep=';', skiprows=[1], na_values=['n/d'], index_col=0, parse_dates=True)
no2.head()
no2["2010-01-01 09:00": "2010-01-01 12:00"]
no2['2012-01':'2012-03']
no2.index.hour
no2.index.year
no2.plot(figsize=(16,8))
no2.head()
no2.resample('M').mean().head(9)
no2.resample('M').max().head(17)
no2.resample('M').mean().plot() # 'A'
no2['2012'].resample('D').mean().plot()
#https://pandas.pydata.org/pandas-docs/stable/reference/groupby.html#computations-descriptive-stats
no2.loc['2009':, 'VERS'].resample('M').agg(['mean']).plot()
no2.resample('A').mean().plot()
no2.mean(axis=1).resample('A').median().plot(color='k', linestyle='--', linewidth=4)
no2.groupby(no2.index.weekday).mean().plot()
no2['weekday'] = no2.index.weekday
no2['weekend'] = no2['weekday'].isin([5, 6])
no2.groupby('weekend').mean().plot(kind='bar')
no2.groupby(['weekend',no2.index.hour])['BASCH'].mean().unstack(0).plot()
#https://pandas.pydata.org/pandas-docs/stable/user_guide/reshaping.html
no2['hour'] = no2.index.hour
no2.pivot_table(columns='weekend', index='hour', values='BASCH')
# re-reading the data to have a clean version
no2 = pd.read_csv('20000101_20161231-NO2.csv', sep=';', skiprows=[1], na_values=['n/d'], index_col=0, parse_dates=True)
초과 = no2>200
초과.head()
ax = 초과.groupby(초과.index.year).sum().plot(kind='bar',figsize=(16,6))
ax.axhline(18,color='k',linestyle='--')
ax.axhline(68,color='r',linestyle='--')
| 0.38769 | 0.975507 |
## Import Libraries
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
from scipy.stats import wilcoxon
```
## Read Data
```
folder = "Data/"
file_name = "Results_N9"
y_label = "Lennard-Jones potential"
fontsize = 15
df = pd.read_excel(folder + file_name + ".xlsx", engine='openpyxl',)
```
## Create Boxplot
```
df.drop(columns=["Unnamed: 0"],inplace=True)
df_1 = df[["GA_Binary_rw", "GA_Binary_t", "GA_Real_t", "PSO_gbest", "PSO_lbest"]]
boxplot = df_1.boxplot(grid=False, rot=0, fontsize=fontsize, figsize = (12, 8))
boxplot.set_ylabel(y_label, fontsize = fontsize)
boxplot.set_title(file_name.replace("_", " "), fontsize = fontsize)
plt.savefig("Boxplot_solutions_quality", facecolor='w')
boxplot = df[["GA_Binary_rw_iteration", "GA_Binary_t_iteration", "GA_Real_t_iteration", "PSO_gbest_iteration", "PSO_lbest_iteration"]].boxplot(grid=False, rot=10, fontsize=fontsize, figsize = (12, 8))
boxplot.set_ylabel("Iterations", fontsize = fontsize)
boxplot.set_title(file_name.replace("_", " "), fontsize = fontsize)
plt.savefig("Boxplot_iterations", facecolor='whitesmoke')
df
```
## Statistics
```
statistics = {"Mean":df_1.mean(), "Median":df_1.median(), "St.Dev.":df_1.std(), "Min":df_1.min(), "Max":df_1.max()}
df_statistics = pd.DataFrame(statistics)
df_statistics.to_excel(file_name + "_solutions_quality_Statistics.xlsx")
df_statistics
df_2 = df[["GA_Binary_rw_iteration", "GA_Binary_t_iteration", "GA_Real_t_iteration", "PSO_gbest_iteration", "PSO_lbest_iteration"]]
statistics = {"Mean":df_2.mean(), "Median":df_2.median(), "St.Dev.":df_2.std(), "Min":df_2.min(), "Max":df_2.max()}
df_statistics = pd.DataFrame(statistics)
df_statistics.to_excel(file_name + "_iterations_Statistics.xlsx")
df_statistics
```
## Pvalues for solution quality
```
gab_rw_t = wilcoxon(df_1["GA_Binary_rw"], df_1["GA_Binary_t"])[1]
gab_rw_gar_t = wilcoxon(df_1["GA_Binary_rw"], df_1["GA_Real_t"])[1]
gab_rw_pso_gbest = wilcoxon(df_1["GA_Binary_rw"], df_1["PSO_gbest"])[1]
gab_rw_pso_lbest = wilcoxon(df_1["GA_Binary_rw"], df_1["PSO_lbest"])[1]
gab_t_gar_t = wilcoxon(df_1["GA_Binary_t"], df_1["GA_Real_t"])[1]
gab_t_pso_gbest = wilcoxon(df_1["GA_Binary_t"], df_1["PSO_gbest"])[1]
gab_t_pso_lbest = wilcoxon(df_1["GA_Binary_t"], df_1["PSO_lbest"])[1]
gar_t_pso_gbest = wilcoxon(df_1["GA_Real_t"], df_1["PSO_gbest"])[1]
gar_t_pso_lbest = wilcoxon(df_1["GA_Real_t"], df_1["PSO_lbest"])[1]
pso_gbest_pso_lbest = wilcoxon(df_1["PSO_gbest"], df_1["PSO_lbest"])[1]
pvalues = np.array([[np.nan, gab_rw_t, gab_rw_gar_t, gab_rw_pso_gbest, gab_rw_pso_lbest],
[np.nan, np.nan, gab_t_gar_t, gab_t_pso_gbest, gab_t_pso_lbest],
[np.nan, np.nan, np.nan, gar_t_pso_gbest, gar_t_pso_lbest],
[np.nan, np.nan, np.nan, np.nan, pso_gbest_pso_lbest]])
mux = pd.MultiIndex.from_arrays([["GA_Binary_rw", "GA_Binary_t", "GA_Real_t", "PSO_gbest"]])
pvalues_df = pd.DataFrame(pvalues, index=mux, columns = ["GA_Binary_rw", "GA_Binary_t", "GA_Real_t",
"PSO_gbest", "PSO_lbest"])
pvalues_df.fillna(value="-", inplace=True)
#pvalues_df.to_excel(file_name + "_pvalues_table.xlsx")
pvalues_df.to_excel(file_name + "_solutions_quality_pvalues.xlsx")
pvalues_df
gab_rw_t = wilcoxon(df["GA_Binary_rw_iteration"], df["GA_Binary_t_iteration"])[1]
gab_rw_gar_t = wilcoxon(df["GA_Binary_rw_iteration"], df["GA_Real_t_iteration"])[1]
gab_rw_pso_gbest = wilcoxon(df["GA_Binary_rw_iteration"], df["PSO_gbest_iteration"])[1]
gab_rw_pso_lbest = wilcoxon(df["GA_Binary_rw_iteration"], df["PSO_lbest_iteration"])[1]
gab_t_gar_t = wilcoxon(df["GA_Binary_t_iteration"], df["GA_Real_t_iteration"])[1]
gab_t_pso_gbest = wilcoxon(df["GA_Binary_t_iteration"], df["PSO_gbest_iteration"])[1]
gab_t_pso_lbest = wilcoxon(df["GA_Binary_t_iteration"], df["PSO_lbest_iteration"])[1]
gar_t_pso_gbest = wilcoxon(df["GA_Real_t_iteration"], df["PSO_gbest_iteration"])[1]
gar_t_pso_lbest = wilcoxon(df["GA_Real_t_iteration"], df["PSO_lbest_iteration"])[1]
pso_gbest_pso_lbest = wilcoxon(df["PSO_gbest_iteration"], df["PSO_lbest_iteration"])[1]
pvalues = np.array([[np.nan, gab_rw_t, gab_rw_gar_t, gab_rw_pso_gbest, gab_rw_pso_lbest],
[np.nan, np.nan, gab_t_gar_t, gab_t_pso_gbest, gab_t_pso_lbest],
[np.nan, np.nan, np.nan, gar_t_pso_gbest, gar_t_pso_lbest],
[np.nan, np.nan, np.nan, np.nan, pso_gbest_pso_lbest]])
mux = pd.MultiIndex.from_arrays([["GA_Binary_rw_iteration", "GA_Binary_t_iteration", "GA_Real_t_iteration", "PSO_gbest_iteration"]])
pvalues_df = pd.DataFrame(pvalues, index=mux, columns = ["GA_Binary_rw_iteration", "GA_Binary_t_iteration", "GA_Real_t_iteration",
"PSO_gbest_iteration", "PSO_lbest_iteration"])
pvalues_df.fillna(value="-", inplace=True)
#pvalues_df.to_excel(file_name + "_pvalues_table.xlsx")
pvalues_df.to_excel(file_name + "_iterations_pvalues.xlsx")
pvalues_df
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
from scipy.stats import wilcoxon
folder = "Data/"
file_name = "Results_N9"
y_label = "Lennard-Jones potential"
fontsize = 15
df = pd.read_excel(folder + file_name + ".xlsx", engine='openpyxl',)
df.drop(columns=["Unnamed: 0"],inplace=True)
df_1 = df[["GA_Binary_rw", "GA_Binary_t", "GA_Real_t", "PSO_gbest", "PSO_lbest"]]
boxplot = df_1.boxplot(grid=False, rot=0, fontsize=fontsize, figsize = (12, 8))
boxplot.set_ylabel(y_label, fontsize = fontsize)
boxplot.set_title(file_name.replace("_", " "), fontsize = fontsize)
plt.savefig("Boxplot_solutions_quality", facecolor='w')
boxplot = df[["GA_Binary_rw_iteration", "GA_Binary_t_iteration", "GA_Real_t_iteration", "PSO_gbest_iteration", "PSO_lbest_iteration"]].boxplot(grid=False, rot=10, fontsize=fontsize, figsize = (12, 8))
boxplot.set_ylabel("Iterations", fontsize = fontsize)
boxplot.set_title(file_name.replace("_", " "), fontsize = fontsize)
plt.savefig("Boxplot_iterations", facecolor='whitesmoke')
df
statistics = {"Mean":df_1.mean(), "Median":df_1.median(), "St.Dev.":df_1.std(), "Min":df_1.min(), "Max":df_1.max()}
df_statistics = pd.DataFrame(statistics)
df_statistics.to_excel(file_name + "_solutions_quality_Statistics.xlsx")
df_statistics
df_2 = df[["GA_Binary_rw_iteration", "GA_Binary_t_iteration", "GA_Real_t_iteration", "PSO_gbest_iteration", "PSO_lbest_iteration"]]
statistics = {"Mean":df_2.mean(), "Median":df_2.median(), "St.Dev.":df_2.std(), "Min":df_2.min(), "Max":df_2.max()}
df_statistics = pd.DataFrame(statistics)
df_statistics.to_excel(file_name + "_iterations_Statistics.xlsx")
df_statistics
gab_rw_t = wilcoxon(df_1["GA_Binary_rw"], df_1["GA_Binary_t"])[1]
gab_rw_gar_t = wilcoxon(df_1["GA_Binary_rw"], df_1["GA_Real_t"])[1]
gab_rw_pso_gbest = wilcoxon(df_1["GA_Binary_rw"], df_1["PSO_gbest"])[1]
gab_rw_pso_lbest = wilcoxon(df_1["GA_Binary_rw"], df_1["PSO_lbest"])[1]
gab_t_gar_t = wilcoxon(df_1["GA_Binary_t"], df_1["GA_Real_t"])[1]
gab_t_pso_gbest = wilcoxon(df_1["GA_Binary_t"], df_1["PSO_gbest"])[1]
gab_t_pso_lbest = wilcoxon(df_1["GA_Binary_t"], df_1["PSO_lbest"])[1]
gar_t_pso_gbest = wilcoxon(df_1["GA_Real_t"], df_1["PSO_gbest"])[1]
gar_t_pso_lbest = wilcoxon(df_1["GA_Real_t"], df_1["PSO_lbest"])[1]
pso_gbest_pso_lbest = wilcoxon(df_1["PSO_gbest"], df_1["PSO_lbest"])[1]
pvalues = np.array([[np.nan, gab_rw_t, gab_rw_gar_t, gab_rw_pso_gbest, gab_rw_pso_lbest],
[np.nan, np.nan, gab_t_gar_t, gab_t_pso_gbest, gab_t_pso_lbest],
[np.nan, np.nan, np.nan, gar_t_pso_gbest, gar_t_pso_lbest],
[np.nan, np.nan, np.nan, np.nan, pso_gbest_pso_lbest]])
mux = pd.MultiIndex.from_arrays([["GA_Binary_rw", "GA_Binary_t", "GA_Real_t", "PSO_gbest"]])
pvalues_df = pd.DataFrame(pvalues, index=mux, columns = ["GA_Binary_rw", "GA_Binary_t", "GA_Real_t",
"PSO_gbest", "PSO_lbest"])
pvalues_df.fillna(value="-", inplace=True)
#pvalues_df.to_excel(file_name + "_pvalues_table.xlsx")
pvalues_df.to_excel(file_name + "_solutions_quality_pvalues.xlsx")
pvalues_df
gab_rw_t = wilcoxon(df["GA_Binary_rw_iteration"], df["GA_Binary_t_iteration"])[1]
gab_rw_gar_t = wilcoxon(df["GA_Binary_rw_iteration"], df["GA_Real_t_iteration"])[1]
gab_rw_pso_gbest = wilcoxon(df["GA_Binary_rw_iteration"], df["PSO_gbest_iteration"])[1]
gab_rw_pso_lbest = wilcoxon(df["GA_Binary_rw_iteration"], df["PSO_lbest_iteration"])[1]
gab_t_gar_t = wilcoxon(df["GA_Binary_t_iteration"], df["GA_Real_t_iteration"])[1]
gab_t_pso_gbest = wilcoxon(df["GA_Binary_t_iteration"], df["PSO_gbest_iteration"])[1]
gab_t_pso_lbest = wilcoxon(df["GA_Binary_t_iteration"], df["PSO_lbest_iteration"])[1]
gar_t_pso_gbest = wilcoxon(df["GA_Real_t_iteration"], df["PSO_gbest_iteration"])[1]
gar_t_pso_lbest = wilcoxon(df["GA_Real_t_iteration"], df["PSO_lbest_iteration"])[1]
pso_gbest_pso_lbest = wilcoxon(df["PSO_gbest_iteration"], df["PSO_lbest_iteration"])[1]
pvalues = np.array([[np.nan, gab_rw_t, gab_rw_gar_t, gab_rw_pso_gbest, gab_rw_pso_lbest],
[np.nan, np.nan, gab_t_gar_t, gab_t_pso_gbest, gab_t_pso_lbest],
[np.nan, np.nan, np.nan, gar_t_pso_gbest, gar_t_pso_lbest],
[np.nan, np.nan, np.nan, np.nan, pso_gbest_pso_lbest]])
mux = pd.MultiIndex.from_arrays([["GA_Binary_rw_iteration", "GA_Binary_t_iteration", "GA_Real_t_iteration", "PSO_gbest_iteration"]])
pvalues_df = pd.DataFrame(pvalues, index=mux, columns = ["GA_Binary_rw_iteration", "GA_Binary_t_iteration", "GA_Real_t_iteration",
"PSO_gbest_iteration", "PSO_lbest_iteration"])
pvalues_df.fillna(value="-", inplace=True)
#pvalues_df.to_excel(file_name + "_pvalues_table.xlsx")
pvalues_df.to_excel(file_name + "_iterations_pvalues.xlsx")
pvalues_df
| 0.26827 | 0.784278 |
# Afternoon Session 2
This session will focus on gaining pratical experience writing python through the use of some moderately challenging coding problems from [Project Euler](https://projecteuler.net/about)
But before we get into challenging coding problems, lets review some of the basics from this morning
## addition, mulitplication, powers, modulo
```
a = 3
b = 2
a +b
a*b
a ** b
a % b
```
## loops
```
for i in [1, 2, 3, 4]:
print(i)
```
## indexing
```
l = [1,2,3,4]
l[3]
k = 'afsddsf'
k[0:4]
```
## ranges
```
for i in range(1,6):
print(i)
```
## conditionals
```
k = 3
if k == 2:
print('k is 2')
elif k == 3:
print('k is 3')
```
## Problem 1
If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.
Find the sum of all the multiples of 3 or 5 below 1000. (Answer: 233168)
```
total = 0
for i in range(1000):
if i % 3 == 0:
total += i
elif i % 5 == 0:
total += i
print(total)
```
# Problem 2
Each new term in the Fibonacci sequence is generated by adding the previous two terms. By starting with 1 and 2, the first 10 terms will be:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms. (Answer: 4613732)
```
fib = 1
fib_total = 0
fib_tmp = 0
fib_prev = 0
while True:
if fib > 4 * 10 ** 6:
break
fib_tmp = fib
fib = fib + fib_prev
fib_prev = fib_tmp
if fib % 2 == 0:
fib_total += fib
print(fib_total)
```
# Problem 3
The prime factors of 13195 are 5, 7, 13 and 29.
What is the largest prime factor of the number 600851475143? (Answer: 6857)
```
n = 600851475143
factor = 2
factors = []
while n != 1:
if n % factor == 0:
isprime = True
for i in range(2, factor):
if factor % i == 0:
isprime = False
if isprime == True:
n /= factor
factors.append(factor)
factor = 2
else:
factor += 1
else:
factor += 1
print(max(factors))
```
# Problem 4
A palindromic number reads the same both ways. The largest palindrome made from the product of two 2-digit numbers is 9009 = 91 × 99.
Find the largest palindrome made from the product of two 3-digit numbers. (Answer: 906609)
# Problem 5
2520 is the smallest number that can be divided by each of the numbers from 1 to 10 without any remainder.
What is the smallest positive number that is evenly divisible by all of the numbers from 1 to 20? (Answer: 232792560)
|
github_jupyter
|
a = 3
b = 2
a +b
a*b
a ** b
a % b
for i in [1, 2, 3, 4]:
print(i)
l = [1,2,3,4]
l[3]
k = 'afsddsf'
k[0:4]
for i in range(1,6):
print(i)
k = 3
if k == 2:
print('k is 2')
elif k == 3:
print('k is 3')
total = 0
for i in range(1000):
if i % 3 == 0:
total += i
elif i % 5 == 0:
total += i
print(total)
fib = 1
fib_total = 0
fib_tmp = 0
fib_prev = 0
while True:
if fib > 4 * 10 ** 6:
break
fib_tmp = fib
fib = fib + fib_prev
fib_prev = fib_tmp
if fib % 2 == 0:
fib_total += fib
print(fib_total)
n = 600851475143
factor = 2
factors = []
while n != 1:
if n % factor == 0:
isprime = True
for i in range(2, factor):
if factor % i == 0:
isprime = False
if isprime == True:
n /= factor
factors.append(factor)
factor = 2
else:
factor += 1
else:
factor += 1
print(max(factors))
| 0.081444 | 0.959154 |
## POLICY GRADIENT on CartPole
Policy Gradient algorithms find an optimal behavior strategy optimizing directly the policy.
The policy is a parametrized function respect to $\theta$ $\pi_\theta(a|s)$
The reward function is defined as
$$J(\theta) = \sum_{s}d^\pi(s)\sum_{a}\pi_\theta(a|s)Q^\pi(s,a)$$
In Vanilla Policy Gradient, we estimate the return $R_t$ (REINFORCE algorithm) and update the policy subtracting a baseline value from $R_t$ to reduce the variance.
<img src="https://github.com/stevearonson/Reinforcement-Learning/blob/master/Week4/imgs/Vanilla_policy_gradient.png?raw=1" alt="drawing" width="500"/>
Credit: John Schulman
```
!pip install tensorboardX
import numpy as np
import gym
from tensorboardX import SummaryWriter
import time
from collections import namedtuple
from collections import deque
import datetime
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class PG_nn(nn.Module):
'''
Policy neural net
'''
def __init__(self, input_shape, n_actions):
super(PG_nn, self).__init__()
self.mlp = nn.Sequential(
nn.Linear(input_shape[0], 64),
nn.ReLU(),
nn.Linear(64, n_actions))
def forward(self, x):
return self.mlp(x.float())
def discounted_rewards(memories, gamma):
'''
Compute the discounted reward backward
'''
disc_rew = np.zeros(len(memories))
run_add = 0
for t in reversed(range(len(memories))):
if memories[t].done: run_add = 0
run_add = run_add * gamma + memories[t].reward
disc_rew[t] = run_add
return disc_rew
Memory = namedtuple('Memory', ['obs', 'action', 'new_obs', 'reward', 'done'], verbose=False, rename=False)
GAMMA = 0.99
LEARNING_RATE = 0.002
ENTROPY_BETA = 0.01
ENV_NAME = 'CartPole-v0'
MAX_N_GAMES = 10000
n_games = 0
device = 'cpu'
now = datetime.datetime.now()
date_time = "{}_{}.{}.{}".format(now.day, now.hour, now.minute, now.second)
env = gym.make(ENV_NAME)
obs = env.reset()
# Initialize the writer
writer = SummaryWriter(log_dir='content/runs/A2C'+ENV_NAME+'_'+date_time)
# create the agent neural net
action_n = env.action_space.n
agent_nn = PG_nn(env.observation_space.shape, action_n).to(device)
# Adam optimizer
optimizer = optim.Adam(agent_nn.parameters(), lr=LEARNING_RATE)
experience = []
tot_reward = 0
n_iter = 0
# deque list to keep the baseline
baseline = deque(maxlen=30000)
game_rew = 0
## MAIN BODY
while n_games < MAX_N_GAMES:
n_iter += 1
# execute the agent
act = agent_nn(torch.tensor(obs))
act_soft = F.softmax(act)
# get an action following the policy distribution
action = int(np.random.choice(np.arange(action_n), p=act_soft.detach().numpy(), size=1))
# make a step in the env
new_obs, reward, done, _ = env.step(action)
game_rew += reward
# update the experience list with the last memory
experience.append(Memory(obs=obs, action=action, new_obs=new_obs, reward=reward, done=done))
obs = new_obs
if done:
# Calculate the discounted rewards
disc_rewards = discounted_rewards(experience, GAMMA)
# update the baseline
baseline.extend(disc_rewards)
# subtract the baseline mean from the discounted reward.
disc_rewards -= np.mean(baseline)
# run the agent NN on the obs in the experience list
acts = agent_nn(torch.tensor([e.obs for e in experience]))
# take the log softmax of the action taken previously
game_act_log_softmax_t = F.log_softmax(acts, dim=1)[:,[e.action for e in experience]]
disc_rewards_t = torch.tensor(disc_rewards, dtype=torch.float32).to(device)
# compute the loss entropy
l_entropy = ENTROPY_BETA * torch.mean(torch.sum(F.softmax(acts, dim=1) * F.log_softmax(acts, dim=1), dim=1))
# compute the loss
loss = - torch.mean(disc_rewards_t * game_act_log_softmax_t)
loss = loss + l_entropy
# optimize
optimizer.zero_grad()
loss.backward()
optimizer.step()
# print the stats
writer.add_scalar('loss', loss, n_iter)
writer.add_scalar('reward', game_rew, n_iter)
print(n_games, loss.detach().numpy(), game_rew, np.mean(disc_rewards), np.mean(baseline))
# reset the variables and env
experience = []
game_rew = 0
obs = env.reset()
n_games += 1
writer.close()
```

```
```
|
github_jupyter
|
!pip install tensorboardX
import numpy as np
import gym
from tensorboardX import SummaryWriter
import time
from collections import namedtuple
from collections import deque
import datetime
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class PG_nn(nn.Module):
'''
Policy neural net
'''
def __init__(self, input_shape, n_actions):
super(PG_nn, self).__init__()
self.mlp = nn.Sequential(
nn.Linear(input_shape[0], 64),
nn.ReLU(),
nn.Linear(64, n_actions))
def forward(self, x):
return self.mlp(x.float())
def discounted_rewards(memories, gamma):
'''
Compute the discounted reward backward
'''
disc_rew = np.zeros(len(memories))
run_add = 0
for t in reversed(range(len(memories))):
if memories[t].done: run_add = 0
run_add = run_add * gamma + memories[t].reward
disc_rew[t] = run_add
return disc_rew
Memory = namedtuple('Memory', ['obs', 'action', 'new_obs', 'reward', 'done'], verbose=False, rename=False)
GAMMA = 0.99
LEARNING_RATE = 0.002
ENTROPY_BETA = 0.01
ENV_NAME = 'CartPole-v0'
MAX_N_GAMES = 10000
n_games = 0
device = 'cpu'
now = datetime.datetime.now()
date_time = "{}_{}.{}.{}".format(now.day, now.hour, now.minute, now.second)
env = gym.make(ENV_NAME)
obs = env.reset()
# Initialize the writer
writer = SummaryWriter(log_dir='content/runs/A2C'+ENV_NAME+'_'+date_time)
# create the agent neural net
action_n = env.action_space.n
agent_nn = PG_nn(env.observation_space.shape, action_n).to(device)
# Adam optimizer
optimizer = optim.Adam(agent_nn.parameters(), lr=LEARNING_RATE)
experience = []
tot_reward = 0
n_iter = 0
# deque list to keep the baseline
baseline = deque(maxlen=30000)
game_rew = 0
## MAIN BODY
while n_games < MAX_N_GAMES:
n_iter += 1
# execute the agent
act = agent_nn(torch.tensor(obs))
act_soft = F.softmax(act)
# get an action following the policy distribution
action = int(np.random.choice(np.arange(action_n), p=act_soft.detach().numpy(), size=1))
# make a step in the env
new_obs, reward, done, _ = env.step(action)
game_rew += reward
# update the experience list with the last memory
experience.append(Memory(obs=obs, action=action, new_obs=new_obs, reward=reward, done=done))
obs = new_obs
if done:
# Calculate the discounted rewards
disc_rewards = discounted_rewards(experience, GAMMA)
# update the baseline
baseline.extend(disc_rewards)
# subtract the baseline mean from the discounted reward.
disc_rewards -= np.mean(baseline)
# run the agent NN on the obs in the experience list
acts = agent_nn(torch.tensor([e.obs for e in experience]))
# take the log softmax of the action taken previously
game_act_log_softmax_t = F.log_softmax(acts, dim=1)[:,[e.action for e in experience]]
disc_rewards_t = torch.tensor(disc_rewards, dtype=torch.float32).to(device)
# compute the loss entropy
l_entropy = ENTROPY_BETA * torch.mean(torch.sum(F.softmax(acts, dim=1) * F.log_softmax(acts, dim=1), dim=1))
# compute the loss
loss = - torch.mean(disc_rewards_t * game_act_log_softmax_t)
loss = loss + l_entropy
# optimize
optimizer.zero_grad()
loss.backward()
optimizer.step()
# print the stats
writer.add_scalar('loss', loss, n_iter)
writer.add_scalar('reward', game_rew, n_iter)
print(n_games, loss.detach().numpy(), game_rew, np.mean(disc_rewards), np.mean(baseline))
# reset the variables and env
experience = []
game_rew = 0
obs = env.reset()
n_games += 1
writer.close()
| 0.829354 | 0.894421 |
# Random forest regression example
As an experiment, we'll look at a dataset uniquely well suited to modeling with random forest regression.
```
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt
```
## Generate fake data
```
n = 2000
df = pd.DataFrame({
'a': np.random.normal(size=n),
'b': np.random.normal(size=n),
'c': np.random.normal(size=n),
'd': np.random.uniform(size=n),
'e': np.random.uniform(size=n),
'f': np.random.choice(list('abc'), size=n, replace=True),
'g': np.random.choice(list('efghij'), size=n, replace=True),
})
df = pd.get_dummies(df)
df.head()
```
The target variable is a little bit complicated. One of the categorical variables is used to select which continuous variable comes into play.
```
y = df.a*df.f_a + df.b*df.f_b + df.c*df.f_c + 3*df.d + np.random.normal(scale=1/3, size=n)
```
## Best possible model
To calibrate our expectations, even if we have perfect insight, there's still some noise involved. How well could we do, in the best case?
```
y_pred = df.a*df.f_a + df.b*df.f_b + df.c*df.f_c + 3*df.d
r2_score(y, y_pred)
plt.scatter(y, y_pred)
```
## Model with random forest regression
### Train / test split
```
i = np.random.choice((1,2,3), size=n, replace=True, p=(3/5,1/5,1/5))
i = np.array([1]*int(3/5*n) + [2]*int(1/5*n) + [3]*int(1/5*n))
np.random.shuffle(i)
len(i) == n
df_train = df[i==1]
df_val = df[i==2]
df_test = df[i==3]
y_train = y[i==1]
y_val = y[i==2]
y_test = y[i==3]
len(df_train), len(df_val), len(df_test)
```
### Train model
```
regr = RandomForestRegressor(n_estimators=200, oob_score=True)
regr.fit(df_train, y_train)
print(regr.oob_score_)
```
Cross-validate to select params *max_depth*, *min_samples_leaf*?
### Predict on test set
```
y_pred = regr.predict(df_test)
r2_score(y_test, y_pred)
plt.scatter(y_test, y_pred)
```
## Compare to linear regression
The idea was that random forest could capture the interaction with the categorical variable. If that's true, it should outperform standard linear regression. Let's fit a linear regression to the same data and see how that does.
```
from sklearn.linear_model import LinearRegression
```
### Fit
```
lm = LinearRegression()
lm.fit(df_train, y_train)
```
### Predict
```
y_pred = lm.predict(df_test)
```
### Score and plot
```
r2_score(y_test, y_pred)
plt.scatter(y_test, y_pred)
```
## Easy example
```
n = 2000
df = pd.DataFrame({
'a': np.random.normal(size=n),
'b': np.random.normal(size=n),
'c': np.random.choice(list('xyz'), size=n, replace=True),
})
df = pd.get_dummies(df)
df.head()
y = 0.234*df.a + -0.678*df.b + -0.456*df.c_x + 0.123*df.c_y + 0.811*df.c_z + np.random.normal(scale=1/3, size=n)
i = np.random.choice((1,2,3), size=n, replace=True, p=(3/5,1/5,1/5))
i = np.array([1]*int(3/5*n) + [2]*int(1/5*n) + [3]*int(1/5*n))
np.random.shuffle(i)
len(i) == n
df_train = df[i==1]
df_val = df[i==2]
df_test = df[i==3]
y_train = y[i==1]
y_val = y[i==2]
y_test = y[i==3]
len(df_train), len(df_val), len(df_test)
regr = RandomForestRegressor(n_estimators=10, oob_score=True)
regr.fit(df_train, y_train)
print(regr.oob_score_)
y_pred = regr.predict(df_test)
r2_score(y_test, y_pred)
plt.scatter(y_test, y_pred)
lm = LinearRegression()
lm.fit(df_train, y_train)
y_pred = lm.predict(df_test)
r2_score(y_test, y_pred)
plt.scatter(y_test, y_pred)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt
n = 2000
df = pd.DataFrame({
'a': np.random.normal(size=n),
'b': np.random.normal(size=n),
'c': np.random.normal(size=n),
'd': np.random.uniform(size=n),
'e': np.random.uniform(size=n),
'f': np.random.choice(list('abc'), size=n, replace=True),
'g': np.random.choice(list('efghij'), size=n, replace=True),
})
df = pd.get_dummies(df)
df.head()
y = df.a*df.f_a + df.b*df.f_b + df.c*df.f_c + 3*df.d + np.random.normal(scale=1/3, size=n)
y_pred = df.a*df.f_a + df.b*df.f_b + df.c*df.f_c + 3*df.d
r2_score(y, y_pred)
plt.scatter(y, y_pred)
i = np.random.choice((1,2,3), size=n, replace=True, p=(3/5,1/5,1/5))
i = np.array([1]*int(3/5*n) + [2]*int(1/5*n) + [3]*int(1/5*n))
np.random.shuffle(i)
len(i) == n
df_train = df[i==1]
df_val = df[i==2]
df_test = df[i==3]
y_train = y[i==1]
y_val = y[i==2]
y_test = y[i==3]
len(df_train), len(df_val), len(df_test)
regr = RandomForestRegressor(n_estimators=200, oob_score=True)
regr.fit(df_train, y_train)
print(regr.oob_score_)
y_pred = regr.predict(df_test)
r2_score(y_test, y_pred)
plt.scatter(y_test, y_pred)
from sklearn.linear_model import LinearRegression
lm = LinearRegression()
lm.fit(df_train, y_train)
y_pred = lm.predict(df_test)
r2_score(y_test, y_pred)
plt.scatter(y_test, y_pred)
n = 2000
df = pd.DataFrame({
'a': np.random.normal(size=n),
'b': np.random.normal(size=n),
'c': np.random.choice(list('xyz'), size=n, replace=True),
})
df = pd.get_dummies(df)
df.head()
y = 0.234*df.a + -0.678*df.b + -0.456*df.c_x + 0.123*df.c_y + 0.811*df.c_z + np.random.normal(scale=1/3, size=n)
i = np.random.choice((1,2,3), size=n, replace=True, p=(3/5,1/5,1/5))
i = np.array([1]*int(3/5*n) + [2]*int(1/5*n) + [3]*int(1/5*n))
np.random.shuffle(i)
len(i) == n
df_train = df[i==1]
df_val = df[i==2]
df_test = df[i==3]
y_train = y[i==1]
y_val = y[i==2]
y_test = y[i==3]
len(df_train), len(df_val), len(df_test)
regr = RandomForestRegressor(n_estimators=10, oob_score=True)
regr.fit(df_train, y_train)
print(regr.oob_score_)
y_pred = regr.predict(df_test)
r2_score(y_test, y_pred)
plt.scatter(y_test, y_pred)
lm = LinearRegression()
lm.fit(df_train, y_train)
y_pred = lm.predict(df_test)
r2_score(y_test, y_pred)
plt.scatter(y_test, y_pred)
| 0.2819 | 0.948917 |
```
import csv, json
import pandas as pd
import numpy as np
from scipy.sparse import coo_matrix
df = pd.read_csv('/Users/jilljenn/code/qna/data/factor-analysis-data.csv')
qmatrix = pd.read_csv('/Users/jilljenn/code/qna/data/q-info.csv')
df.head()
students = df['stu_id'].unique()
questions = pd.concat((df['q_txt_id'], qmatrix['q_txt_id'])).unique()
USER_NUM = len(students)
ITEM_NUM = len(questions)
encode_stu = dict(zip(students, range(USER_NUM)))
encode_q = dict(zip(questions, range(ITEM_NUM)))
df['user_id'] = df['stu_id'].map(encode_stu)
df['item_id'] = df['q_txt_id'].map(encode_q)
df.head()
len(questions)
```
# QMatrix
```
qmatrix.head()
skills = qmatrix['qset_id'].unique()
SKILL_NUM = len(skills)
encode_skill = dict(zip(skills, range(SKILL_NUM)))
qmatrix['item_id'] = qmatrix['q_txt_id'].map(encode_q)
qmatrix['skill_id'] = qmatrix['qset_id'].map(encode_skill)
qmatrix.head()
rows = qmatrix['item_id']
cols = qmatrix['skill_id']
sp_qmatrix = coo_matrix(([1] * ITEM_NUM, (rows, cols)), shape=(ITEM_NUM, SKILL_NUM)).tocsr()
from scipy.sparse import save_npz
import os.path
DATA_DIR = '/Users/jilljenn/code/TF-recomm/data/berkeley0/'
save_npz(os.path.join(DATA_DIR, 'qmatrix.npz'), sp_qmatrix)
```
# Number of attempts
```
sp_qmatrix[14].indices[0]
from collections import Counter
acc_wins = Counter()
acc_fails = Counter()
nb_wins = []
nb_fails = []
for user_id, work_id, outcome in np.array(df[['user_id', 'item_id', 'is_correct']]):
skill_id = sp_qmatrix[work_id].indices[0]
nb_wins.append(acc_wins[user_id, skill_id])
nb_fails.append(acc_fails[user_id, skill_id])
if outcome == 1:
acc_wins[user_id, skill_id] += 1
else:
acc_fails[user_id, skill_id] += 1
df['nb_wins'] = nb_wins
df['nb_fails'] = nb_fails
df.head()
len(df)
import numpy as np
nb_users = len(encode_stu) # 2
nb_items = len(encode_q) # 3
nb_skills = len(encode_skill) # 3
count_item_wins = np.zeros((nb_users, nb_items))
count_item_fails = np.zeros((nb_users, nb_items))
count_skill_wins = np.zeros((nb_users, nb_skills))
count_skill_fails = np.zeros((nb_users, nb_skills))
all_skill_wins = []
all_skill_fails = []
all_item_wins = []
all_item_fails = []
for user_id, item_id, outcome in np.array(df[['user_id', 'item_id', 'is_correct']]):
skill_ids = sp_qmatrix[item_id]
item_wins = count_item_wins[user_id, item_id]
item_fails = count_item_fails[user_id, item_id]
all_item_wins.append(item_wins)
all_item_fails.append(item_fails)
skill_wins = skill_ids.multiply(count_skill_wins[user_id])
skill_fails = skill_ids.multiply(count_skill_fails[user_id])
all_skill_wins.append(skill_wins)
all_skill_fails.append(skill_fails)
if outcome == 1:
count_item_wins[user_id, item_id] += 1
count_skill_wins[user_id, skill_ids.indices] += 1
else:
count_item_fails[user_id, item_id] += 1
count_skill_fails[user_id, skill_ids.indices] += 1
df['wins'] = all_item_wins
df['fails'] = all_item_fails
df[['user_id', 'item_id', 'is_correct', 'wins', 'fails']].to_csv('/Users/jilljenn/code/TF-recomm/data/berkeley0/all.csv', index=False, header=False)
from scipy.sparse import vstack
skill_wins = vstack(all_skill_wins).tocsr()
save_npz('/Users/jilljenn/code/TF-recomm/data/berkeley0/skill_wins.npz', skill_wins)
skill_wins.shape
skill_fails = vstack(all_skill_fails).tocsr()
save_npz('/Users/jilljenn/code/TF-recomm/data/berkeley0/skill_fails.npz', skill_fails)
skill_fails.shape
```
# Cross-validation
```
from sklearn.model_selection import train_test_split
train, test = train_test_split(df[['user_id', 'item_id', 'is_correct', 'nb_wins', 'nb_fails']], test_size=0.2)
len(train), len(test)
train.to_csv(os.path.join(DATA_DIR, 'train.csv'), header=False, index=False)
test.to_csv(os.path.join(DATA_DIR, 'val.csv'), header=False, index=False)
test.to_csv(os.path.join(DATA_DIR, 'test.csv'), header=False, index=False)
import yaml
with open(os.path.join(DATA_DIR, 'config.yml'), 'w') as f:
config = {
'USER_NUM': USER_NUM,
'ITEM_NUM': ITEM_NUM,
'NB_CLASSES': 2,
'BATCH_SIZE': 0
}
f.write(yaml.dump(config, default_flow_style=False))
```
|
github_jupyter
|
import csv, json
import pandas as pd
import numpy as np
from scipy.sparse import coo_matrix
df = pd.read_csv('/Users/jilljenn/code/qna/data/factor-analysis-data.csv')
qmatrix = pd.read_csv('/Users/jilljenn/code/qna/data/q-info.csv')
df.head()
students = df['stu_id'].unique()
questions = pd.concat((df['q_txt_id'], qmatrix['q_txt_id'])).unique()
USER_NUM = len(students)
ITEM_NUM = len(questions)
encode_stu = dict(zip(students, range(USER_NUM)))
encode_q = dict(zip(questions, range(ITEM_NUM)))
df['user_id'] = df['stu_id'].map(encode_stu)
df['item_id'] = df['q_txt_id'].map(encode_q)
df.head()
len(questions)
qmatrix.head()
skills = qmatrix['qset_id'].unique()
SKILL_NUM = len(skills)
encode_skill = dict(zip(skills, range(SKILL_NUM)))
qmatrix['item_id'] = qmatrix['q_txt_id'].map(encode_q)
qmatrix['skill_id'] = qmatrix['qset_id'].map(encode_skill)
qmatrix.head()
rows = qmatrix['item_id']
cols = qmatrix['skill_id']
sp_qmatrix = coo_matrix(([1] * ITEM_NUM, (rows, cols)), shape=(ITEM_NUM, SKILL_NUM)).tocsr()
from scipy.sparse import save_npz
import os.path
DATA_DIR = '/Users/jilljenn/code/TF-recomm/data/berkeley0/'
save_npz(os.path.join(DATA_DIR, 'qmatrix.npz'), sp_qmatrix)
sp_qmatrix[14].indices[0]
from collections import Counter
acc_wins = Counter()
acc_fails = Counter()
nb_wins = []
nb_fails = []
for user_id, work_id, outcome in np.array(df[['user_id', 'item_id', 'is_correct']]):
skill_id = sp_qmatrix[work_id].indices[0]
nb_wins.append(acc_wins[user_id, skill_id])
nb_fails.append(acc_fails[user_id, skill_id])
if outcome == 1:
acc_wins[user_id, skill_id] += 1
else:
acc_fails[user_id, skill_id] += 1
df['nb_wins'] = nb_wins
df['nb_fails'] = nb_fails
df.head()
len(df)
import numpy as np
nb_users = len(encode_stu) # 2
nb_items = len(encode_q) # 3
nb_skills = len(encode_skill) # 3
count_item_wins = np.zeros((nb_users, nb_items))
count_item_fails = np.zeros((nb_users, nb_items))
count_skill_wins = np.zeros((nb_users, nb_skills))
count_skill_fails = np.zeros((nb_users, nb_skills))
all_skill_wins = []
all_skill_fails = []
all_item_wins = []
all_item_fails = []
for user_id, item_id, outcome in np.array(df[['user_id', 'item_id', 'is_correct']]):
skill_ids = sp_qmatrix[item_id]
item_wins = count_item_wins[user_id, item_id]
item_fails = count_item_fails[user_id, item_id]
all_item_wins.append(item_wins)
all_item_fails.append(item_fails)
skill_wins = skill_ids.multiply(count_skill_wins[user_id])
skill_fails = skill_ids.multiply(count_skill_fails[user_id])
all_skill_wins.append(skill_wins)
all_skill_fails.append(skill_fails)
if outcome == 1:
count_item_wins[user_id, item_id] += 1
count_skill_wins[user_id, skill_ids.indices] += 1
else:
count_item_fails[user_id, item_id] += 1
count_skill_fails[user_id, skill_ids.indices] += 1
df['wins'] = all_item_wins
df['fails'] = all_item_fails
df[['user_id', 'item_id', 'is_correct', 'wins', 'fails']].to_csv('/Users/jilljenn/code/TF-recomm/data/berkeley0/all.csv', index=False, header=False)
from scipy.sparse import vstack
skill_wins = vstack(all_skill_wins).tocsr()
save_npz('/Users/jilljenn/code/TF-recomm/data/berkeley0/skill_wins.npz', skill_wins)
skill_wins.shape
skill_fails = vstack(all_skill_fails).tocsr()
save_npz('/Users/jilljenn/code/TF-recomm/data/berkeley0/skill_fails.npz', skill_fails)
skill_fails.shape
from sklearn.model_selection import train_test_split
train, test = train_test_split(df[['user_id', 'item_id', 'is_correct', 'nb_wins', 'nb_fails']], test_size=0.2)
len(train), len(test)
train.to_csv(os.path.join(DATA_DIR, 'train.csv'), header=False, index=False)
test.to_csv(os.path.join(DATA_DIR, 'val.csv'), header=False, index=False)
test.to_csv(os.path.join(DATA_DIR, 'test.csv'), header=False, index=False)
import yaml
with open(os.path.join(DATA_DIR, 'config.yml'), 'w') as f:
config = {
'USER_NUM': USER_NUM,
'ITEM_NUM': ITEM_NUM,
'NB_CLASSES': 2,
'BATCH_SIZE': 0
}
f.write(yaml.dump(config, default_flow_style=False))
| 0.158793 | 0.313164 |
# TVM Mortgage
<hr>
<p><i>A mortgage calculator that takes into account the time-value of money (TVM)</i></p>
<p>By Andrew Chap</p>
<hr>
## What do other mortgage calculators lack?
There are other good mortgage calculators out there, but they are limited to calculating monthly payments and the total nominal cost of a mortgage. However, they don't differentiate a payment made now vs a payment made in the future.
## The time-value of money
<p>This calculator takes into account that money today is worth more than future money (assuming a positive interest rate). To be specific, an amount of money today ${v_0}$ has a future value <span style = "color:#080#">$v_t$</span> at future time <span style = "color:#080#">$t$</span> (in years) by compounding at an (annual) interest rate <span style = "color:#080#">$i_\text{tvm}$</span> by the relation
</p>
<p style = "color:#080#">
$$v_t = v_0(1+i_\text{tvm})^t.$$
</p>
<p>
This is equivalent to saying that if you invest <span style = "color:#080#">$v_0$</span> in the market, which has an annual rate of return of <span style = "color:#080#">$i_\text{tvm}$</span>, after <span style = "color:#080#">$t$</span> years you can sell those investments for <span style = "color:#080#">$v_t$</span>.
</p>
<p>This also applies to payments made now vs. payments in the future. If you are scheduled to make a payment of <span style = "color:#080#">$p_t$</span> in <span style = "color:#080#">$t$</span> years from now, the amount <span style = "color:#080#">$p_0$</span> you would need to invest today is
</p>
<p style = "color:#080#">
$$p_0 = p_t(1+i_\text{tvm})^{-t}$$
</p>
<p>
which is simply a rearrangement of Eq. (1). If you need to make a payment of <span style = "color:#080#">$p_t = \$100$</span> in <span style = "color:#080#">$t=5$</span> years, and the stock market has an <span style = "color:#080#">$i_\text{tvm}=6%$</span> annual return, an investment now of <span style = "color:#080#">$p_0 = \$75$</span> will suffice. In other words, with an interest rate of <span style = "color:#080#">$i_\text{tvm}=6%$</span>, <span style = "color:#080#">\$100</span> in <span style = "color:#080#">5</span> years is worth <span style = "color:#080#">\$75</span> now.
## A demonstrative example
<p>"Paying points" is common option offered by mortgage lenders, in which you pay an upfront cost in order to lower your interest rate. Say your mortgage lender offers you the following options on a
<span style="color:#080">
$l = \$100{,}000$</span>,
<span style="color:#080">
$t = 30\,\text{years}$
</span>
loan:</p>
<table>
<tr align="center">
<th> </th>
<th> Upfront fee $$f$$ </th>
<th> Mortgage interest rate $$i_\text{m}$$ </th>
<th> Monthly payment $$p$$ </th>
</tr>
<tr>
<td><i> Option 1 </i></td>
<td> $\$0$ </td>
<td> $4.0\%$ </td>
<td> $\$477.42$ </td>
</tr>
<tr>
<td><i> Option 2 </i></td>
<td> $\$4{,}000$ </td>
<td> $3.5\%$ </td>
<td> $\$449.04$ </td>
</tr>
</table>
<p>where the monthly payment <span style="color:#080">$p$</span> is calculated from the standard payment formula:
</p>
<p style="color:#080">
$$p = l\frac{nc_\text{m}(1+c_\text{m})}{n(1 + c_\text{m})-1}$$
</p><p>
with
</p><p style="color:#080">
$$
\begin{eqnarray}
n & \equiv & 30\,\text{years} \times 12\,\text{payments}/\text{year} = 360\,\text{payments} \\
c_\text{m} & \equiv & \frac{i_\text{m}}{12\,\text{payments}/\text{year}}
\end{eqnarray}
$$
</p><p>
and the total nominal cost is calculated by summing up all the payments plus any upfront costs:
</p><p style="color:#080">$$
\text{Total cost} = f + \sum_{n=0}^{360} p
$$</p>
### The nominal long-term cost of each option
<p>
With <i>Option 1</i> costing \$0 upfront with monthly payments of \$477.42 and <i>Option 2</i> costing \$4,000 upfront with monthly payments of \$449.04 (which would be referred to as paying for two "discount points" on your mortgage rate) it is easy to calculate the total nominal cost of each loan:
</p>
<p style="color:#080"> $$
\begin{eqnarray}
\text{Option 1 total cost} & = & \$0 &+& \$477.42 \times 360 & = & \$171{,}870 \\
\text{Option 2 total cost} & = & \$4{,}000 &+& \$449.04 \times 360 & = & \$165{,}656
\end{eqnarray}
$$ </p>
Visually, we can plot the total amount you would pay for each loan as a function of time:
```
import plotly.offline as py; import plotly.graph_objs as go; import numpy as np
py.init_notebook_mode(connected=True)
r1 = 0.04/12.; r2 = 0.035/12.; time = np.linspace(0,30,361)
option1 = [100000*(r1*(1+r1)**360)/((1+r1)**360 - 1)*x for x in range(0,361)]
option2 = [5000 + 100000*(r2*(1+r2)**360)/((1+r2)**360 - 1)*x for x in range(0,361)]
data = [go.Scatter(x = time, y = option1, name = 'Option 1'),
go.Scatter(x = time, y = option2, name = 'Option 2')]
layout = go.Layout(xaxis = {'title':'time (years)'}, yaxis = {'title':'Total spent ($)'})
fig = go.Figure(data=data,layout=layout); py.iplot(fig)
```
<p>
The intersection point happens at 11 years and 9 months. I've had a lender tell me that this is how long it takes to recover the cost of paying for the discount points, and so if you own the house for longer than this length of time it is worth it to pay for the discount points if you can afford it. If you keep the home for the entire length of the mortgage, you save more than \$6,000! The flaw in this logic, of course, is that money today is worth more than the same quantity of money in the future, which we explore in the next section.
</p>
### Option 3: take option 1 but invest the \$4000 that you would have spent on Option 2
<p>
If you had the \$4,000 on hand to pay down the points, what if you chose option 1, invested that \$4,000, and each month you withdrew \$28.37 from your investment (the difference between the monthly payments of options 1 and 2) to go towards your monthly mortgage payment? In that way you would still be paying \$4,000 upfront, and you would still need to come up with \$449.04/month for you mortgage payments, only instead of choosing option 2, you are choosing option 1 and paying your upfront cost into the stock market.
If the rate of return on your investment is 8% annually (which is equivalent to 0.49% compounded monthly), we can track your investment as follows. In the first month you withdraw \$28.37, then your investment (called $I_\text{month 0})$ appreciates by 0.64%.
</p>
<p style="color:#080">
$$
I_\text{month 1} = \left(\$4{,}000 - \$28.37\right)\times(1 + 0.0064) = \$3997.18
$$
</p>
<p>
This iteration can be repeated through the 360<sup>th</sup> month:
</p>
<p style="color:#080">
$$ \begin{eqnarray}
I_\text{month 2} & = & \left(I_\text{month 1} - \$28.37\right)\times(1 + 0.0049) &=& \$3994.35 \\
I_\text{month 3} & = & \left(I_\text{month 2} - \$28.37\right)\times(1 + 0.0049) &=& \$3991.49 \\
& ... & \\
I_\text{month 359} & = & \left(I_\text{month 358} - \$28.37\right)\times(1 + 0.0049) &=& \$60.25\\
I_\text{month 360} & = & \left(I_\text{month 359} - \$28.37\right)\times(1 + 0.0049) &=& \$32.08
\end{eqnarray} $$
</p>
<p>
In this case, you've saved \$32.08 by choosing your "Option 3" version of Option 1, rather than Option 2. Even better, if you sell your home before the end of the mortgage, you won't be losing out on any of the rate benefit you would have otherwise used the \$4,000 to pay for.
</p>
<p>
In other words, the time-value of money shifts the crossover point on how long you have to stay in the house to "make your money back" to justify paying for points, and in some cases (such as the one above) you never do.
</p>
<p>
In other words, if the market is performing at a rate of return of 8% (which is a reasonable long-term assumption) you are better off not paying for discount points <b> even if you think you will own the home for 30 years or more.</b> Of course, you have to be able to tolerate the risk of investing that \$4,000, since the market fluctuates, and if you really did withdraw money from the market every month, the fees would eliminate any advantage. Rather than being a real-world example, this is a demonstration of how the time value of money should influence mortgage decisions.
</p>
# Generalization
<p>
To visualize the advantage of option 1 over option 2 using the time-value of money, we can discount the future value of money by the interest rate. To do this we define a future value discount <span style="color:#080">$\phi$</span> as a function of the month number <span style="color:#080">$n$</span>:
</p>
<p style="color:#080">
$$ \phi(n) = (1 + c_\text{tvm})^{-n} $$
</p>
<p> where <span style="color:#080">$c_\text{tvm}$</span> is the monthly TVM (market) rate, calculated from the annual TVM rate <span style="color:#080">$i_\text{tvm}$</span> by:
<p style="color:#080">
$$ c_\text{tvm} = (1 + i_\text{tvm})^\frac{1}{12} - 1 $$
</p><p>
which for <span style="color:#080">$i_\text{tvm} = 8\%$</span>, we get <span style="color:#080">$c_\text{tvm} = 0.64\%$</span>
</p><p>
We can then calculate the TVM-corrected total cost by multiplying each monthly payment by <span style="color:#080">$\phi$</span>:
<p style="color:#080">
$$\text{Total cost} = f + p\sum_{n=0}^{360} (1 + c_\text{tvm})^{-n}$$
</p>
<p>
where <span style="color:#080">$f$</span> is the upfront cost of the mortgage and <span style="color:#080">$p$</span> is the monthly payment. Using this equation, we can plot the TVM-corrected cost of each mortgage as follows:
```
import plotly.offline as py; import plotly.graph_objs as go; import numpy as np
py.init_notebook_mode(connected=True)
r1 = 0.04/12.; r2 = 0.035/12.; n=360; t=30; time = np.linspace(0,t,n+1)
i_tvm = 0.08
c_tvm = (1+i_tvm)**(1/12.) - 1
#c_tvm = i_tvm/12.
option1 = [0]*(n+1);
option2 = [0]*(n+1); option2[0] = 4000
for x in range(0,n):
option1[x+1] = option1[x] + 100000*(r1*(1+r1)**n)/((1+r1)**n - 1)*(1+c_tvm)**(-x)
option2[x+1] = option2[x] + 100000*(r2*(1+r2)**n)/((1+r2)**n - 1)*(1+c_tvm)**(-x)
data = [go.Scatter(x = time, y = option1, name = 'Option 1'),
go.Scatter(x = time, y = option2, name = 'Option 2')]
layout = go.Layout(xaxis = {'title':'time (years)'}, yaxis = {'title':'Total spent ($)'})
fig = go.Figure(data=data,layout=layout); py.iplot(fig)
diff = (option2[-1] - option1[-1])
difftvm = diff*(1+c_tvm)**(n)
print(diff)
print(difftvm)
print("c_tvm = {}".format(c_tvm))
```
In the case above, the difference in the total amount paid in option 1 and option 2 is only \$3.19, scaled by the TVM factor. To find this difference in nominal dollars, the difference between the loan in TVM dollars is scaled by <span style="color:#080">$(1 + c_\text{tvm})^{360}$</span> to get \$32.08. It is also interesting (and perhaps not too surprising) to note that even if you had the money on hand to buy a home in cash, as long as rate of return on the market (i.e. the TVM rate) is a bit higher than the mortgage interest rate, it is better to get a mortgage, and leaving otherwise available funds in the market.
|
github_jupyter
|
import plotly.offline as py; import plotly.graph_objs as go; import numpy as np
py.init_notebook_mode(connected=True)
r1 = 0.04/12.; r2 = 0.035/12.; time = np.linspace(0,30,361)
option1 = [100000*(r1*(1+r1)**360)/((1+r1)**360 - 1)*x for x in range(0,361)]
option2 = [5000 + 100000*(r2*(1+r2)**360)/((1+r2)**360 - 1)*x for x in range(0,361)]
data = [go.Scatter(x = time, y = option1, name = 'Option 1'),
go.Scatter(x = time, y = option2, name = 'Option 2')]
layout = go.Layout(xaxis = {'title':'time (years)'}, yaxis = {'title':'Total spent ($)'})
fig = go.Figure(data=data,layout=layout); py.iplot(fig)
import plotly.offline as py; import plotly.graph_objs as go; import numpy as np
py.init_notebook_mode(connected=True)
r1 = 0.04/12.; r2 = 0.035/12.; n=360; t=30; time = np.linspace(0,t,n+1)
i_tvm = 0.08
c_tvm = (1+i_tvm)**(1/12.) - 1
#c_tvm = i_tvm/12.
option1 = [0]*(n+1);
option2 = [0]*(n+1); option2[0] = 4000
for x in range(0,n):
option1[x+1] = option1[x] + 100000*(r1*(1+r1)**n)/((1+r1)**n - 1)*(1+c_tvm)**(-x)
option2[x+1] = option2[x] + 100000*(r2*(1+r2)**n)/((1+r2)**n - 1)*(1+c_tvm)**(-x)
data = [go.Scatter(x = time, y = option1, name = 'Option 1'),
go.Scatter(x = time, y = option2, name = 'Option 2')]
layout = go.Layout(xaxis = {'title':'time (years)'}, yaxis = {'title':'Total spent ($)'})
fig = go.Figure(data=data,layout=layout); py.iplot(fig)
diff = (option2[-1] - option1[-1])
difftvm = diff*(1+c_tvm)**(n)
print(diff)
print(difftvm)
print("c_tvm = {}".format(c_tvm))
| 0.31542 | 0.877582 |
# More Reading Material
* [The Math of Machine Learning](https://gwthomas.github.io/docs/math4ml.pdf)
# Taking Symbolic Derivatives with Python
```
from sympy import *
from IPython.display import display
from sympy.printing.mathml import mathml
from IPython.display import display, Math, Latex
x, y, z = symbols('x y z')
init_printing(use_unicode=True)
def mprint(e):
display(Math(latex(e)))
mprint(x**2)
mprint(diff(2*x**3))
expr = (x**3 + x**2 - x - 1)/(x**2 + 2*x + 1)
display(Math(latex(expr)))
expr = simplify(expr)
print(type(expr))
print(latex(expr))
display(Math(latex(expr)))
from IPython.display import display, Math, Latex
display(Math('\\frac{1_a^x}{2}'))
print(expr.subs(x,5))
eql = Eq(3*x+5,10)
z = solveset(eql,x)
display(Math(latex(z)))
from sympy import *
x, y, z = symbols('x y z')
init_printing(use_unicode=True)
expr = diff(sin(x)/x**2, x)
mprint(expr)
expr_i = integrate(expr,x)
mprint(expr_i)
```
# Keras Customization: Loss and Activation Functions
Your functions must be defined with TensorFlow graph commands. The derivative will be taken automatically. (assuming all components of your function are differentiable)
# TensorFlow for Calculation
```
import tensorflow as tf
tf.multiply(tf.constant(2.0),tf.constant(5.0)).numpy()
import numpy as np
tf.multiply(np.array([2,4]),np.array([2,4]))
tf.multiply(2,4).numpy()
tf.divide(2,4)
tf.pow(2.0,4).numpy()
x = 5.0
y = tf.divide(1.0,tf.add(1,tf.exp(tf.negative(x))))
y
```
# Calculus with TensorFlow
How do we take derivatives?
* [Symbolic differentiation](http://tutorial.math.lamar.edu/pdf/common_derivatives_integrals.pdf)
* [Numerical differentiation](https://en.wikipedia.org/wiki/Finite_difference) (the method of finite differences)
* [Automatic differentiation](https://en.wikipedia.org/wiki/Automatic_differentiation)
Take the derivative of $f(x) = x^2$.
Symbolic derivative $f'(x) = rx^{r-1}$
$f(4) = 4^2 = 16$
$f'(4) = 2 \cdot 4 = 8$
This can be done in TensorFlow:
```
x = tf.constant(4.0)
with tf.GradientTape() as t:
t.watch(x)
z = tf.multiply(x, x)
# Derivative of z with respect to the original input tensor x
dz_dx = t.gradient(z, x)
print(dz_dx)
```
Lets express the [Logistic function](https://en.wikipedia.org/wiki/Logistic_function) in TensorFlow. This is also called the Sigmoid Activation function in neural network literature.
$f(x) = \frac{1}{1 + e^{-x}}$
Written in TensorFlow:
```
x = tf.constant([5.0])
with tf.GradientTape() as t:
t.watch(x)
y = tf.divide(1.0,tf.add(1,tf.exp(tf.negative(x))))
print(y)
dy_dx = t.gradient(y, x)
print(dy_dx)
```
Lets check the regular function.
```
import math
1/(1+math.exp(-5))
```
And lets check the derivative:
$f'(x) = \frac{e^x}{(e^x + 1)^2}$
```
math.exp(-5)/(math.exp(-5)+1)**2
x = tf.ones((2, 2))
y = tf.reduce_sum(x)
z = tf.multiply(y, y)
y.numpy()
```
How to take second (and beyond) derivatives:
```
x = tf.constant(3.0)
with tf.GradientTape() as g:
g.watch(x)
with tf.GradientTape() as gg:
gg.watch(x)
y = x * x
dy_dx = gg.gradient(y, x) # Will compute to 6.0
d2y_dx2 = g.gradient(dy_dx, x) # Will compute to 2.0
```
# Custom Loss (Objective) Function
$ \operatorname{RMSE}=\sqrt{\frac{\sum_{t=1}^T (\hat y_t - y_t)^2}{T}} $
```
def mean_pred(y_true, y_pred):
return tf.sqrt(tf.divide(tf.reduce_sum(tf.pow(tf.subtract(y_true, y_pred),2.0)),tf.cast(tf.size(y_true), tf.float32)))
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
import pandas as pd
import io
import os
import requests
import numpy as np
from sklearn import metrics
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/auto-mpg.csv",
na_values=['NA', '?'])
cars = df['name']
# Handle missing value
df['horsepower'] = df['horsepower'].fillna(df['horsepower'].median())
# Pandas to Numpy
x = df[['cylinders', 'displacement', 'horsepower', 'weight',
'acceleration', 'year', 'origin']].values
y = df['mpg'].values # regression
# Build the neural network
model = Sequential()
model.add(Dense(25, input_dim=x.shape[1], activation='relu')) # Hidden 1
model.add(Dense(10, activation='relu')) # Hidden 2
model.add(Dense(1)) # Output
model.compile(loss=mean_pred, optimizer='adam')
model.fit(x,y,verbose=2,epochs=100)
```
# Custom Activation (Transfer) Functions
```
import tensorflow as tf
def elliot_sym(x):
return tf.divide(x,tf.add(1.0,tf.abs(x)))
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
import pandas as pd
import io
import os
import requests
import numpy as np
from sklearn import metrics
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/auto-mpg.csv",
na_values=['NA', '?'])
cars = df['name']
# Handle missing value
df['horsepower'] = df['horsepower'].fillna(df['horsepower'].median())
# Pandas to Numpy
x = df[['cylinders', 'displacement', 'horsepower', 'weight',
'acceleration', 'year', 'origin']].values
y = df['mpg'].values # regression
# Build the neural network
sgd = tf.keras.optimizers.SGD(lr=1e-10, decay=1e-6, momentum=0.9, nesterov=True)
model = Sequential()
model.add(Dense(25, input_dim=x.shape[1], activation=elliot_sym)) # Hidden 1
model.add(Dense(10, activation=elliot_sym)) # Hidden 2
model.add(Dense(1)) # Output
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x,y,verbose=2,epochs=400)
```
|
github_jupyter
|
from sympy import *
from IPython.display import display
from sympy.printing.mathml import mathml
from IPython.display import display, Math, Latex
x, y, z = symbols('x y z')
init_printing(use_unicode=True)
def mprint(e):
display(Math(latex(e)))
mprint(x**2)
mprint(diff(2*x**3))
expr = (x**3 + x**2 - x - 1)/(x**2 + 2*x + 1)
display(Math(latex(expr)))
expr = simplify(expr)
print(type(expr))
print(latex(expr))
display(Math(latex(expr)))
from IPython.display import display, Math, Latex
display(Math('\\frac{1_a^x}{2}'))
print(expr.subs(x,5))
eql = Eq(3*x+5,10)
z = solveset(eql,x)
display(Math(latex(z)))
from sympy import *
x, y, z = symbols('x y z')
init_printing(use_unicode=True)
expr = diff(sin(x)/x**2, x)
mprint(expr)
expr_i = integrate(expr,x)
mprint(expr_i)
import tensorflow as tf
tf.multiply(tf.constant(2.0),tf.constant(5.0)).numpy()
import numpy as np
tf.multiply(np.array([2,4]),np.array([2,4]))
tf.multiply(2,4).numpy()
tf.divide(2,4)
tf.pow(2.0,4).numpy()
x = 5.0
y = tf.divide(1.0,tf.add(1,tf.exp(tf.negative(x))))
y
x = tf.constant(4.0)
with tf.GradientTape() as t:
t.watch(x)
z = tf.multiply(x, x)
# Derivative of z with respect to the original input tensor x
dz_dx = t.gradient(z, x)
print(dz_dx)
x = tf.constant([5.0])
with tf.GradientTape() as t:
t.watch(x)
y = tf.divide(1.0,tf.add(1,tf.exp(tf.negative(x))))
print(y)
dy_dx = t.gradient(y, x)
print(dy_dx)
import math
1/(1+math.exp(-5))
math.exp(-5)/(math.exp(-5)+1)**2
x = tf.ones((2, 2))
y = tf.reduce_sum(x)
z = tf.multiply(y, y)
y.numpy()
x = tf.constant(3.0)
with tf.GradientTape() as g:
g.watch(x)
with tf.GradientTape() as gg:
gg.watch(x)
y = x * x
dy_dx = gg.gradient(y, x) # Will compute to 6.0
d2y_dx2 = g.gradient(dy_dx, x) # Will compute to 2.0
def mean_pred(y_true, y_pred):
return tf.sqrt(tf.divide(tf.reduce_sum(tf.pow(tf.subtract(y_true, y_pred),2.0)),tf.cast(tf.size(y_true), tf.float32)))
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
import pandas as pd
import io
import os
import requests
import numpy as np
from sklearn import metrics
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/auto-mpg.csv",
na_values=['NA', '?'])
cars = df['name']
# Handle missing value
df['horsepower'] = df['horsepower'].fillna(df['horsepower'].median())
# Pandas to Numpy
x = df[['cylinders', 'displacement', 'horsepower', 'weight',
'acceleration', 'year', 'origin']].values
y = df['mpg'].values # regression
# Build the neural network
model = Sequential()
model.add(Dense(25, input_dim=x.shape[1], activation='relu')) # Hidden 1
model.add(Dense(10, activation='relu')) # Hidden 2
model.add(Dense(1)) # Output
model.compile(loss=mean_pred, optimizer='adam')
model.fit(x,y,verbose=2,epochs=100)
import tensorflow as tf
def elliot_sym(x):
return tf.divide(x,tf.add(1.0,tf.abs(x)))
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
import pandas as pd
import io
import os
import requests
import numpy as np
from sklearn import metrics
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/auto-mpg.csv",
na_values=['NA', '?'])
cars = df['name']
# Handle missing value
df['horsepower'] = df['horsepower'].fillna(df['horsepower'].median())
# Pandas to Numpy
x = df[['cylinders', 'displacement', 'horsepower', 'weight',
'acceleration', 'year', 'origin']].values
y = df['mpg'].values # regression
# Build the neural network
sgd = tf.keras.optimizers.SGD(lr=1e-10, decay=1e-6, momentum=0.9, nesterov=True)
model = Sequential()
model.add(Dense(25, input_dim=x.shape[1], activation=elliot_sym)) # Hidden 1
model.add(Dense(10, activation=elliot_sym)) # Hidden 2
model.add(Dense(1)) # Output
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x,y,verbose=2,epochs=400)
| 0.715921 | 0.972362 |
# Example 3: Wave propagation calculators
Use RVT input motion with:
1. Linear elastic
2. Equivalent linear (e.g., SHAKE)
3. Frequency-dependent equivalent linear
```
import matplotlib.pyplot as plt
import numpy as np
import pysra
%matplotlib inline
# Increased figure sizes
plt.rcParams['figure.dpi'] = 120
```
## Create a point source theory RVT motion
```
motion = pysra.motion.SourceTheoryRvtMotion(7.0, 30, 'wna')
motion.calc_fourier_amps()
```
## Create site profile
Create a simple soil profile with a single soil layer with nonlinear properties defined by the Darendeli nonlinear model.
```
profile = pysra.site.Profile([
pysra.site.Layer(
pysra.site.DarendeliSoilType(
18., plas_index=30, ocr=1, stress_mean=200),
30, 400
),
pysra.site.Layer(
pysra.site.SoilType(
'Rock', 24., None, 0.01
),
0, 1200
),
]).auto_discretize()
```
## Create the site response calculator
```
calcs = [
('LE', pysra.propagation.LinearElasticCalculator()),
('EQL', pysra.propagation.EquivalentLinearCalculator(
strain_ratio=0.65)),
('FDM', pysra.propagation.FrequencyDependentEqlCalculator(
use_smooth_spectrum=False)),
]
```
## Specify the output
```
freqs = np.logspace(-1, 2, num=500)
outputs = pysra.output.OutputCollection([
pysra.output.AccelTransferFunctionOutput(
# Frequency
freqs,
# Location in (denominator),
pysra.output.OutputLocation('outcrop', index=-1),
# Location out (numerator)
pysra.output.OutputLocation('outcrop', index=0),
),
pysra.output.ResponseSpectrumOutput(
# Frequency
freqs,
# Location of the output
pysra.output.OutputLocation('outcrop', index=0),
# Damping
0.05
),
pysra.output.ResponseSpectrumRatioOutput(
# Frequency
freqs,
# Location in (denominator),
pysra.output.OutputLocation('outcrop', index=-1),
# Location out (numerator)
pysra.output.OutputLocation('outcrop', index=0),
# Damping
0.05
),
pysra.output.MaxStrainProfile(),
pysra.output.InitialVelProfile(),
pysra.output.CompatVelProfile()
])
```
## Perform the calculation
Compute the response of the site, and store the state within the calculation object. Use the calculator, to compute the outputs.
```
calcs
len(profile)
properties = {}
for name, calc in calcs:
calc(motion, profile, profile.location('outcrop', index=-1))
outputs(calc, name)
properties[name] = {
key: getattr(profile[0], key)
for key in ['shear_mod_reduc', 'damping']
}
```
## Plot the properties of the EQL and EQL-FDM methods
```
for key in properties['EQL'].keys():
fig, ax = plt.subplots()
ax.axhline(
properties['EQL'][key], label='EQL', color='C0')
ax.plot(
motion.freqs, properties['FDM'][key], label='FDM', color='C1')
ax.set(
ylabel={'damping': 'Damping (dec)',
'shear_mod_reduc': r'$G/G_{max}$'}[key],
xlabel='Frequency (Hz)', xscale='log'
)
ax.legend()
```
## Plot the outputs
Create a few plots of the output.
```
for o in outputs[:-3]:
fig, ax = plt.subplots()
for name, refs, values in o.iter_results():
ax.plot(refs, values, label=name)
ax.set(xlabel=o.xlabel, xscale='log', ylabel=o.ylabel)
ax.legend()
fig.tight_layout();
for o in outputs[-3:]:
fig, ax = plt.subplots()
for name, refs, values in o.iter_results():
if name == 'LE':
# No strain results for LE analyses
continue
ax.plot(values, refs, label=name)
ax.set(xlabel=o.xlabel, xscale='log', ylabel=o.ylabel)
ax.invert_yaxis()
ax.legend()
fig.tight_layout();
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import numpy as np
import pysra
%matplotlib inline
# Increased figure sizes
plt.rcParams['figure.dpi'] = 120
motion = pysra.motion.SourceTheoryRvtMotion(7.0, 30, 'wna')
motion.calc_fourier_amps()
profile = pysra.site.Profile([
pysra.site.Layer(
pysra.site.DarendeliSoilType(
18., plas_index=30, ocr=1, stress_mean=200),
30, 400
),
pysra.site.Layer(
pysra.site.SoilType(
'Rock', 24., None, 0.01
),
0, 1200
),
]).auto_discretize()
calcs = [
('LE', pysra.propagation.LinearElasticCalculator()),
('EQL', pysra.propagation.EquivalentLinearCalculator(
strain_ratio=0.65)),
('FDM', pysra.propagation.FrequencyDependentEqlCalculator(
use_smooth_spectrum=False)),
]
freqs = np.logspace(-1, 2, num=500)
outputs = pysra.output.OutputCollection([
pysra.output.AccelTransferFunctionOutput(
# Frequency
freqs,
# Location in (denominator),
pysra.output.OutputLocation('outcrop', index=-1),
# Location out (numerator)
pysra.output.OutputLocation('outcrop', index=0),
),
pysra.output.ResponseSpectrumOutput(
# Frequency
freqs,
# Location of the output
pysra.output.OutputLocation('outcrop', index=0),
# Damping
0.05
),
pysra.output.ResponseSpectrumRatioOutput(
# Frequency
freqs,
# Location in (denominator),
pysra.output.OutputLocation('outcrop', index=-1),
# Location out (numerator)
pysra.output.OutputLocation('outcrop', index=0),
# Damping
0.05
),
pysra.output.MaxStrainProfile(),
pysra.output.InitialVelProfile(),
pysra.output.CompatVelProfile()
])
calcs
len(profile)
properties = {}
for name, calc in calcs:
calc(motion, profile, profile.location('outcrop', index=-1))
outputs(calc, name)
properties[name] = {
key: getattr(profile[0], key)
for key in ['shear_mod_reduc', 'damping']
}
for key in properties['EQL'].keys():
fig, ax = plt.subplots()
ax.axhline(
properties['EQL'][key], label='EQL', color='C0')
ax.plot(
motion.freqs, properties['FDM'][key], label='FDM', color='C1')
ax.set(
ylabel={'damping': 'Damping (dec)',
'shear_mod_reduc': r'$G/G_{max}$'}[key],
xlabel='Frequency (Hz)', xscale='log'
)
ax.legend()
for o in outputs[:-3]:
fig, ax = plt.subplots()
for name, refs, values in o.iter_results():
ax.plot(refs, values, label=name)
ax.set(xlabel=o.xlabel, xscale='log', ylabel=o.ylabel)
ax.legend()
fig.tight_layout();
for o in outputs[-3:]:
fig, ax = plt.subplots()
for name, refs, values in o.iter_results():
if name == 'LE':
# No strain results for LE analyses
continue
ax.plot(values, refs, label=name)
ax.set(xlabel=o.xlabel, xscale='log', ylabel=o.ylabel)
ax.invert_yaxis()
ax.legend()
fig.tight_layout();
| 0.61555 | 0.973062 |
# 1.Introduction
<font color = green> <strong>MUST READ:</strong></font> This Notebook tutorial will allow you to perform IP Protection using TFLXTLS device.
The CryptoAuthentication device supports different modes of operation with MAC command. The mode used here is “Move the Challenge to TempKey” where the host sends a random seed to the device and the device generates a nonce (number used once) which incorporates it. The generated nonce here is the challenge. The application sends the MAC command to the device to generate response with the challenge and the symmetric key in it. The generated response is sent to the application and the application performs the same operation done on the device side to generate the response. Finally, the application compares the response from the device and its own calculated response to authenticate.
Before running this Notebook,
1. Make sure CryptoAuth Trust Platform is having factory reset program
### Prerequisites:
This step of the tutorial will attempt to load all the necessary modules and their dependencies on your machine. If the modules are already installed you can safely step over the next Tutorial step.
<font color = orange> <strong>Note</strong></font>
1. Installation time for prerequisites depends upon system and network speed.
2. Installing prerequisites for the first time takes more time and watch the kernel status for progress. Following image helps to locate the Kernel status,
<center><img src="../../../assets/notebook/img/kerner_status.png" alt="**Check Kernel Status**" /></center>
3. Installing prerequisites gives the following error and it can be safely ignored. Functionality remains unaffected.
- <font color = orange> azure-cli 2.0.76 has requirement colorama~=0.4.1, but you'll have colorama 0.3.9 which is incompatible.</font>
- <font color = orange> azure-cli 2.0.76 has requirement pytz==2019.1, but you'll have pytz 2019.3 which is incompatible. </font>
```
import sys, os
home_path = os.path.dirname(os.path.dirname(os.path.dirname(os.path.realpath(os.getcwd()))))
module_path = os.path.join(home_path, 'assets', 'python')
if not module_path in sys.path:
sys.path.append(module_path)
from requirements_helper import requirements_installer
obj = requirements_installer(os.path.join(home_path, 'assets', 'requirements.txt'))
from trustplatform import program_flash
programmer = program_flash()
```
### Setup Modules and Hardware
This step loads the required modules and helper functions to perform the resource generation sequence. It also
1. Initializes the interface with TFLXTLS hardware and establishes commmunication with TFLXTLS.
2. Performs device initialization to verify the actual device attached
```
import argparse,time
import warnings
from cryptoauthlib import *
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import hashes
from asn1crypto import pem
from ipywidgets import widgets
from trustplatform import *
SHARED_SECRET_SLOT = 5 #The slot which contains the symmetric key
MAC_MODE = 0x41
warnings.filterwarnings('ignore')
print("Importing modules - Successful")
#TFLXTLS device I2C address 0x6C; #TNGTLS device I2C address 0x6A;
common_helper.connect_to_secure_element('ATECC608A', ATCAKitType.ATCA_KIT_I2C_IFACE, 0x6C)
print("Device initialization - Successful")
```
### Generate MAC from TFLXTLS part
Generate the MAC with ECC608A device.The MAC is generated with the symmetric key in slot, Random number and with device serial number.The MAC generated from the device uses the Random number generator and the generated MAC is unique and will not repeat in future.
<center><img src="img/4.png" alt="**Get your Secure Elements here!**" /></center>
```
seed_in = bytearray(20)
rand_out = bytearray(32)
nonce = bytearray()
device_mac = bytearray(32)
# Generate the nonce in device and return the random number
assert atcab_nonce_rand(seed_in,rand_out) == Status.ATCA_SUCCESS, "Random nonce from device failed"
# Calculate the nonce value on the host side
nonce.extend(rand_out[0:32])
nonce.extend(seed_in[0:20])
nonce.append(0x16)
nonce.append(0)
nonce.append(0)
digest = hashes.Hash(hashes.SHA256(), backend=default_backend())
digest.update(bytes(nonce))
nonce = digest.finalize()
# Calculate the mac in device with its symmetric diversified key in slot
assert atcab_mac(MAC_MODE, SHARED_SECRET_SLOT, 0, device_mac) == Status.ATCA_SUCCESS, "MAC from device failed"
print("MAC Received from device:")
print(common_helper.pretty_print_hex(device_mac, indent=' '))
```
### Verify Expected MAC on Host
Calculate the MAC on the host side.The host with the help of the symmetric key, random nonce and with the TFLXTLS serial number generates the Expected MAC. It then compares the Expected MAC with the MAC sent from TFLXTLS device and executes application after successfull authentication.
<center><img src="img/5.png" alt="**Get your Secure Elements here!**" /></center>
```
def mac_mac_resp_verify(b):
serial_number = bytearray(9)
host_mac = bytearray()
# Symmetric key to be used host mac calculation
Symmetric_key = bytearray()
with open(os.path.join(home_path, 'TrustFLEX', '00_resource_generation', 'slot_5_secret_key.pem'), 'rb') as f:
pem_bytes = f.read()
type_name, headers, Symmetric_key = pem.unarmor(pem_bytes)
Symmetric_key = Symmetric_key[17: len(Symmetric_key)]
#Read the serial number from device
assert atcab_read_serial_number(serial_number) == Status.ATCA_SUCCESS, "Serial number read from device failed"
# Calculate the mac on the host side
host_mac.extend(Symmetric_key[0:32])
host_mac.extend(nonce[0:32])
host_mac.append(8)
host_mac.append(MAC_MODE)
host_mac.append(SHARED_SECRET_SLOT)
host_mac.append(0)
host_mac.extend([0 for i in range(11)])
host_mac.append(serial_number[8])
host_mac.extend(serial_number[4:8])
host_mac.extend(serial_number[0:2])
host_mac.extend(serial_number[2:4])
digest = hashes.Hash(hashes.SHA256(), backend=default_backend())
digest.update(bytes(host_mac))
host_mac = digest.finalize()
#uncomment following line to try wrong mac
#host_mac = bytes(b'00000000000000000000000000000000')
print("MAC calculated on host:")
print(common_helper.pretty_print_hex(host_mac, indent=' '))
if (device_mac == host_mac):
print('\nApplication authenticated successfully!')
mac_verify.button_style = 'success'
else:
mac_verify.button_style = 'danger'
print('\nApplication not authenticated...')
tooltip = 'Click to perform MAC-Response Verify'
mac_verify = widgets.Button(description = 'Verify MAC', tooltip=tooltip)
mac_verify.on_click(mac_mac_resp_verify)
display(mac_verify)
```
|
github_jupyter
|
import sys, os
home_path = os.path.dirname(os.path.dirname(os.path.dirname(os.path.realpath(os.getcwd()))))
module_path = os.path.join(home_path, 'assets', 'python')
if not module_path in sys.path:
sys.path.append(module_path)
from requirements_helper import requirements_installer
obj = requirements_installer(os.path.join(home_path, 'assets', 'requirements.txt'))
from trustplatform import program_flash
programmer = program_flash()
import argparse,time
import warnings
from cryptoauthlib import *
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import hashes
from asn1crypto import pem
from ipywidgets import widgets
from trustplatform import *
SHARED_SECRET_SLOT = 5 #The slot which contains the symmetric key
MAC_MODE = 0x41
warnings.filterwarnings('ignore')
print("Importing modules - Successful")
#TFLXTLS device I2C address 0x6C; #TNGTLS device I2C address 0x6A;
common_helper.connect_to_secure_element('ATECC608A', ATCAKitType.ATCA_KIT_I2C_IFACE, 0x6C)
print("Device initialization - Successful")
seed_in = bytearray(20)
rand_out = bytearray(32)
nonce = bytearray()
device_mac = bytearray(32)
# Generate the nonce in device and return the random number
assert atcab_nonce_rand(seed_in,rand_out) == Status.ATCA_SUCCESS, "Random nonce from device failed"
# Calculate the nonce value on the host side
nonce.extend(rand_out[0:32])
nonce.extend(seed_in[0:20])
nonce.append(0x16)
nonce.append(0)
nonce.append(0)
digest = hashes.Hash(hashes.SHA256(), backend=default_backend())
digest.update(bytes(nonce))
nonce = digest.finalize()
# Calculate the mac in device with its symmetric diversified key in slot
assert atcab_mac(MAC_MODE, SHARED_SECRET_SLOT, 0, device_mac) == Status.ATCA_SUCCESS, "MAC from device failed"
print("MAC Received from device:")
print(common_helper.pretty_print_hex(device_mac, indent=' '))
def mac_mac_resp_verify(b):
serial_number = bytearray(9)
host_mac = bytearray()
# Symmetric key to be used host mac calculation
Symmetric_key = bytearray()
with open(os.path.join(home_path, 'TrustFLEX', '00_resource_generation', 'slot_5_secret_key.pem'), 'rb') as f:
pem_bytes = f.read()
type_name, headers, Symmetric_key = pem.unarmor(pem_bytes)
Symmetric_key = Symmetric_key[17: len(Symmetric_key)]
#Read the serial number from device
assert atcab_read_serial_number(serial_number) == Status.ATCA_SUCCESS, "Serial number read from device failed"
# Calculate the mac on the host side
host_mac.extend(Symmetric_key[0:32])
host_mac.extend(nonce[0:32])
host_mac.append(8)
host_mac.append(MAC_MODE)
host_mac.append(SHARED_SECRET_SLOT)
host_mac.append(0)
host_mac.extend([0 for i in range(11)])
host_mac.append(serial_number[8])
host_mac.extend(serial_number[4:8])
host_mac.extend(serial_number[0:2])
host_mac.extend(serial_number[2:4])
digest = hashes.Hash(hashes.SHA256(), backend=default_backend())
digest.update(bytes(host_mac))
host_mac = digest.finalize()
#uncomment following line to try wrong mac
#host_mac = bytes(b'00000000000000000000000000000000')
print("MAC calculated on host:")
print(common_helper.pretty_print_hex(host_mac, indent=' '))
if (device_mac == host_mac):
print('\nApplication authenticated successfully!')
mac_verify.button_style = 'success'
else:
mac_verify.button_style = 'danger'
print('\nApplication not authenticated...')
tooltip = 'Click to perform MAC-Response Verify'
mac_verify = widgets.Button(description = 'Verify MAC', tooltip=tooltip)
mac_verify.on_click(mac_mac_resp_verify)
display(mac_verify)
| 0.309337 | 0.873539 |
# Preparing a proposal
The Story: Suppose that you are preparing to write a proposal on NGC1365, aiming to investigate the intriguing black hole spin this galaxy with Chandra grating observations (see: https://www.space.com/19980-monster-black-hole-spin-discovery.html )
In writing proposals, there are often the same tasks that are required: including finding and analyzing previous observations of the proposal, and creating figures that include, e.g., multiwavelength images and spectrum for the source.
```
# As a hint, we include the code block for Python modules that you will likely need to import:
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
# For downloading files
from astropy.utils.data import download_file
from astropy.io import fits
import pyvo as vo
## There are a number of relatively unimportant warnings that
## show up, so for now, suppress them:
import warnings
warnings.filterwarnings("ignore", module="astropy.io.votable.*")
warnings.filterwarnings("ignore", module="pyvo.utils.xml.*")
```
### Step 1: Find out what the previously quoted Chandra 2-10 keV flux of the central source is for NGC 1365.
Hint: Do a Registry search for tables served by the HEASARC (where high energy data are archived) to find potential table with this information
```
# This gets all services matching, which should be a list of only one:
tap_services=vo.regsearch(servicetype='table',keywords=['heasarc'])
# This fetches the list of tables that this service serves:
heasarc_tables=tap_services[0].service.tables
```
Hint: The Chansngcat ( https://heasarc.gsfc.nasa.gov/W3Browse/chandra/chansngcat.html ) table is likely the best table. Create a table with ra, dec, exposure time, and flux (and flux errors) from the public.chansngcat catalog for Chandra observations matched within 0.1 degree.
```
for tablename in heasarc_tables.keys():
if "chansng" in tablename:
print("Table {} has columns={}\n".format(
tablename,
sorted([k.name for k in heasarc_tables[tablename].columns ])))
# Get the coordinate for NGC 1365
import astropy.coordinates as coord
pos=coord.SkyCoord.from_name("ngc1365")
# Construct a query that will get the ra, dec, exposure time, flux, and flux errors
# from this catalog in the region around this source:
query="""SELECT ra, dec, exposure, flux, flux_lower, flux_upper FROM public.chansngcat as cat
where contains(point('ICRS',cat.ra,cat.dec),circle('ICRS',{},{},0.1))=1
and cat.exposure > 0 order by cat.exposure""".format(pos.ra.deg, pos.dec.deg)
# Submit the query. (See the CS_Catalog_queries.ipynb for
# information about these two search options.)
results=tap_services[0].service.run_async(query)
#results=tap_services[0].search(query)
# Look at the results
results.to_table()
```
### Step 2: Make Images:
#### Create ultraviolet and X-ray images
Hint: Start by checking what UV image services exist (e.g., GALEX?)
```
## Note that to browse the columns, use the .to_table() method
uv_services=vo.regsearch(servicetype='image',keywords='galex', waveband='uv')
uv_services.to_table()['ivoid','short_name']
```
The keyword search for 'galex' returned a bunch of things that may have mentioned it, but let's just use the ones that have GALEX as their short name:
```
uv_services.to_table()[
np.array(['GALEX' in u.short_name for u in uv_services])
]['ivoid', 'short_name', 'access_url']
```
Though using the result as an Astropy Table makes it easier to look at the contents, to call the service itself, we cannot use the row of that table. You have to use the entry in the service result list itself. So use the table to browse, but select the list of services itself using the properties that have been defined as attributes such as short_name and ivoid:
```
galex_stsci=[s for s in uv_services if 'GALEX' in s.short_name and 'stsci' in s.ivoid][0]
galex_heasarc=[s for s in uv_services if 'GALEX' in s.short_name and 'heasarc' in s.ivoid][0]
```
Hint: Next create a UV image for the source
```
# Do an image search for NGC 1365 in the UV service found above
im_table_stsci=galex_stsci.search(pos=pos,size=0.1)
im_table_stsci.to_table()
# Let's see what HEASARC offers, and this time limit it to FITS
# this option doesn't currently work for STScI's service)
im_table_heasarc=galex_heasarc.search(pos=pos,size=0.1,format='image/fits')
im_table_heasarc.to_table()
## If you only run this once, you can do it in memory in one line:
## This fetches the FITS as an astropy.io.fits object in memory
#dataobj=im_table_heasarc[0].getdataobj()
## But if you might run this notebook repeatedly with limited bandwidth,
## download it once and cache it.
file_name = download_file(im_table_heasarc[0].getdataurl(),cache=True)
dataobj=fits.open(file_name)
print(type(dataobj))
# Get the FITS file (which is index 0 for the NUV image or index=2 for the FUV image)
from pylab import figure, cm
from matplotlib.colors import LogNorm
plt.matshow(dataobj[0].data, origin='lower', cmap=cm.gray_r, norm=LogNorm(vmin=0.005, vmax=0.3))
```
Hint: Repeat steps for X-ray image. (Note: Ideally, we would find an image in the Chandra 'cxc' catalog)
```
x_services=vo.regsearch(servicetype='image',keywords=['chandra'], waveband='x-ray')
print(x_services.to_table()['short_name','ivoid'])
## Do an image search for NGC 1365 in the X-ray CDA service found above
xim_table=x_services[0].search(pos=pos,size=0.2)
## Some of these are FITS and some JPEG. Look at the columns:
print( xim_table.to_table().columns )
first_fits_image_row = [x for x in xim_table if 'image/fits' in x.format][0]
## Create an image from the first FITS file (index=1) by downloading:
## See above for options
#xhdu_list=first_fits_image_row.getdataobj()
file_name = download_file(first_fits_image_row.getdataurl(),cache=True)
xhdu_list=fits.open(file_name)
plt.imshow(xhdu_list[0].data, origin='lower', cmap='cool', norm=LogNorm(vmin=0.1, vmax=500.))
plt.xlim(460, 560)
plt.ylim(460, 560)
```
### Step 3: Make a spectrum:
#### Find what Chandra spectral observations exist already for this source.
Hint: try searching for X-ray spectral data tables using the registry query
```
# Use the TAP protocol to list services that contain X-ray spectral data
xsp_services=vo.regsearch(servicetype='ssa',waveband='x-ray')
xsp_services.to_table()['short_name','ivoid','waveband']
```
Hint 2: Take a look at what data exist for our candidate, NGC 1365.
```
spec_tables=xsp_services[0].search(pos=pos,radius=0.2,verbose=True)
spec_tables.to_table()
```
Hint 3: Download the data to make a spectrum. Note: you might end here and use Xspec to plot and model the spectrum. Or ... you can also try to take a quick look at the spectrum.
```
# Get it and look at it:
#hdu_list=spec_tables[0].getdataobj()
file_name = download_file(spec_tables[0].getdataurl(),cache=True)
hdu_list=fits.open(file_name)
spectra=hdu_list[1].data
print(spectra.columns)
print(len(spectra))
## Or write it to disk
import os
if not os.path.isdir('downloads'):
os.makedirs("downloads")
fname=spec_tables[0].make_dataset_filename()
# Known issue where the suffix is incorrect:
fname=fname.replace('None','fits')
with open('downloads/{}'.format(fname),'wb') as outfile:
outfile.write(spec_tables[0].getdataset().read())
```
Extension: Making a "quick look" spectrum. For our purposes, the 1st order of the HEG grating data would be sufficient.
```
j=1
for i in range(len(spectra)):
matplotlib.rcParams['figure.figsize'] = (8, 3)
if abs(spectra['TG_M'][i]) == 1 and (spectra['TG_PART'][i]) == 1:
ax=plt.subplot(1,2,j)
pha = plt.plot( spectra['CHANNEL'][i],spectra['COUNTS'][i])
ax.set_yscale('log')
if spectra['TG_PART'][i] == 1:
instr='HEG'
ax.set_title("{grating}{order:+d}".format(grating=instr, order=spectra['TG_M'][i]))
plt.tight_layout()
j=j+1
```
This can then be analyzed in your favorite spectral analysis tool, e.g., [pyXspec](https://heasarc.gsfc.nasa.gov/xanadu/xspec/python/html/index.html). (For the winter 2018 AAS workshop, we demonstrated this in a [notebook](https://github.com/NASA-NAVO/aas_workshop_2018/blob/master/heasarc/heasarc_Spectral_Access.ipynb) that you can consult for how to use pyXspec, but the pyXspec documentation will have more information.)
Congratulations! You have completed this notebook exercise.
|
github_jupyter
|
# As a hint, we include the code block for Python modules that you will likely need to import:
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
# For downloading files
from astropy.utils.data import download_file
from astropy.io import fits
import pyvo as vo
## There are a number of relatively unimportant warnings that
## show up, so for now, suppress them:
import warnings
warnings.filterwarnings("ignore", module="astropy.io.votable.*")
warnings.filterwarnings("ignore", module="pyvo.utils.xml.*")
# This gets all services matching, which should be a list of only one:
tap_services=vo.regsearch(servicetype='table',keywords=['heasarc'])
# This fetches the list of tables that this service serves:
heasarc_tables=tap_services[0].service.tables
for tablename in heasarc_tables.keys():
if "chansng" in tablename:
print("Table {} has columns={}\n".format(
tablename,
sorted([k.name for k in heasarc_tables[tablename].columns ])))
# Get the coordinate for NGC 1365
import astropy.coordinates as coord
pos=coord.SkyCoord.from_name("ngc1365")
# Construct a query that will get the ra, dec, exposure time, flux, and flux errors
# from this catalog in the region around this source:
query="""SELECT ra, dec, exposure, flux, flux_lower, flux_upper FROM public.chansngcat as cat
where contains(point('ICRS',cat.ra,cat.dec),circle('ICRS',{},{},0.1))=1
and cat.exposure > 0 order by cat.exposure""".format(pos.ra.deg, pos.dec.deg)
# Submit the query. (See the CS_Catalog_queries.ipynb for
# information about these two search options.)
results=tap_services[0].service.run_async(query)
#results=tap_services[0].search(query)
# Look at the results
results.to_table()
## Note that to browse the columns, use the .to_table() method
uv_services=vo.regsearch(servicetype='image',keywords='galex', waveband='uv')
uv_services.to_table()['ivoid','short_name']
uv_services.to_table()[
np.array(['GALEX' in u.short_name for u in uv_services])
]['ivoid', 'short_name', 'access_url']
galex_stsci=[s for s in uv_services if 'GALEX' in s.short_name and 'stsci' in s.ivoid][0]
galex_heasarc=[s for s in uv_services if 'GALEX' in s.short_name and 'heasarc' in s.ivoid][0]
# Do an image search for NGC 1365 in the UV service found above
im_table_stsci=galex_stsci.search(pos=pos,size=0.1)
im_table_stsci.to_table()
# Let's see what HEASARC offers, and this time limit it to FITS
# this option doesn't currently work for STScI's service)
im_table_heasarc=galex_heasarc.search(pos=pos,size=0.1,format='image/fits')
im_table_heasarc.to_table()
## If you only run this once, you can do it in memory in one line:
## This fetches the FITS as an astropy.io.fits object in memory
#dataobj=im_table_heasarc[0].getdataobj()
## But if you might run this notebook repeatedly with limited bandwidth,
## download it once and cache it.
file_name = download_file(im_table_heasarc[0].getdataurl(),cache=True)
dataobj=fits.open(file_name)
print(type(dataobj))
# Get the FITS file (which is index 0 for the NUV image or index=2 for the FUV image)
from pylab import figure, cm
from matplotlib.colors import LogNorm
plt.matshow(dataobj[0].data, origin='lower', cmap=cm.gray_r, norm=LogNorm(vmin=0.005, vmax=0.3))
x_services=vo.regsearch(servicetype='image',keywords=['chandra'], waveband='x-ray')
print(x_services.to_table()['short_name','ivoid'])
## Do an image search for NGC 1365 in the X-ray CDA service found above
xim_table=x_services[0].search(pos=pos,size=0.2)
## Some of these are FITS and some JPEG. Look at the columns:
print( xim_table.to_table().columns )
first_fits_image_row = [x for x in xim_table if 'image/fits' in x.format][0]
## Create an image from the first FITS file (index=1) by downloading:
## See above for options
#xhdu_list=first_fits_image_row.getdataobj()
file_name = download_file(first_fits_image_row.getdataurl(),cache=True)
xhdu_list=fits.open(file_name)
plt.imshow(xhdu_list[0].data, origin='lower', cmap='cool', norm=LogNorm(vmin=0.1, vmax=500.))
plt.xlim(460, 560)
plt.ylim(460, 560)
# Use the TAP protocol to list services that contain X-ray spectral data
xsp_services=vo.regsearch(servicetype='ssa',waveband='x-ray')
xsp_services.to_table()['short_name','ivoid','waveband']
spec_tables=xsp_services[0].search(pos=pos,radius=0.2,verbose=True)
spec_tables.to_table()
# Get it and look at it:
#hdu_list=spec_tables[0].getdataobj()
file_name = download_file(spec_tables[0].getdataurl(),cache=True)
hdu_list=fits.open(file_name)
spectra=hdu_list[1].data
print(spectra.columns)
print(len(spectra))
## Or write it to disk
import os
if not os.path.isdir('downloads'):
os.makedirs("downloads")
fname=spec_tables[0].make_dataset_filename()
# Known issue where the suffix is incorrect:
fname=fname.replace('None','fits')
with open('downloads/{}'.format(fname),'wb') as outfile:
outfile.write(spec_tables[0].getdataset().read())
j=1
for i in range(len(spectra)):
matplotlib.rcParams['figure.figsize'] = (8, 3)
if abs(spectra['TG_M'][i]) == 1 and (spectra['TG_PART'][i]) == 1:
ax=plt.subplot(1,2,j)
pha = plt.plot( spectra['CHANNEL'][i],spectra['COUNTS'][i])
ax.set_yscale('log')
if spectra['TG_PART'][i] == 1:
instr='HEG'
ax.set_title("{grating}{order:+d}".format(grating=instr, order=spectra['TG_M'][i]))
plt.tight_layout()
j=j+1
| 0.553385 | 0.953708 |
**4장 – 모델 훈련**
_이 노트북은 4장에 있는 모든 샘플 코드와 연습문제 해답을 가지고 있습니다._
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/rickiepark/handson-ml2/blob/master/04_training_linear_models.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩에서 실행하기</a>
</td>
</table>
# 설정
먼저 몇 개의 모듈을 임포트합니다. 맷플롯립 그래프를 인라인으로 출력하도록 만들고 그림을 저장하는 함수를 준비합니다. 또한 파이썬 버전이 3.5 이상인지 확인합니다(파이썬 2.x에서도 동작하지만 곧 지원이 중단되므로 파이썬 3을 사용하는 것이 좋습니다). 사이킷런 버전이 0.20 이상인지도 확인합니다.
```
# 파이썬 ≥3.5 필수
import sys
assert sys.version_info >= (3, 5)
# 사이킷런 ≥0.20 필수
import sklearn
assert sklearn.__version__ >= "0.20"
# 공통 모듈 임포트
import numpy as np
import os
# 노트북 실행 결과를 동일하게 유지하기 위해
np.random.seed(42)
# 깔끔한 그래프 출력을 위해
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# 그림을 저장할 위치
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "training_linear_models"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("그림 저장:", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# 불필요한 경고를 무시합니다 (사이파이 이슈 #5998 참조)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
```
# 정규 방정식을 사용한 선형 회귀
```
import numpy as np
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
save_fig("generated_data_plot")
plt.show()
```
정규 방정식:
$\hat{\boldsymbol{\theta}} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}$
```
X_b = np.c_[np.ones((100, 1)), X] # 모든 샘플에 x0 = 1을 추가합니다.
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best
```
$\hat{y} = \mathbf{X} \boldsymbol{\hat{\theta}}$
```
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new] # 모든 샘플에 x0 = 1을 추가합니다.
y_predict = X_new_b.dot(theta_best)
y_predict
plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")
plt.axis([0, 2, 0, 15])
plt.show()
```
책에 있는 그림은 범례와 축 레이블이 있는 그래프입니다:
```
plt.plot(X_new, y_predict, "r-", linewidth=2, label="Predictions")
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 2, 0, 15])
save_fig("linear_model_predictions_plot")
plt.show()
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_
lin_reg.predict(X_new)
```
`LinearRegression` 클래스는 `scipy.linalg.lstsq()` 함수("least squares"의 약자)를 사용하므로 이 함수를 직접 사용할 수 있습니다:
```
# 싸이파이 lstsq() 함수를 사용하려면 scipy.linalg.lstsq(X_b, y)와 같이 씁니다.
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd
```
이 함수는 $\mathbf{X}^+\mathbf{y}$을 계산합니다. $\mathbf{X}^{+}$는 $\mathbf{X}$의 _유사역행렬_ (pseudoinverse)입니다(Moore–Penrose 유사역행렬입니다). `np.linalg.pinv()`을 사용해서 유사역행렬을 직접 계산할 수 있습니다:
$\boldsymbol{\hat{\theta}} = \mathbf{X}^{-1}\hat{y}$
```
np.linalg.pinv(X_b).dot(y)
```
# 배치 경사 하강법을 사용한 선형 회귀
$
\dfrac{\partial}{\partial \boldsymbol{\theta}} \text{MSE}(\boldsymbol{\theta})
= \dfrac{2}{m} \mathbf{X}^T (\mathbf{X} \boldsymbol{\theta} - \mathbf{y})
$
$
\boldsymbol{\theta}^{(\text{next step})} = \boldsymbol{\theta} - \eta \dfrac{\partial}{\partial \boldsymbol{\theta}} \text{MSE}(\boldsymbol{\theta})
$
```
eta = 0.1 # 학습률
n_iterations = 1000
m = 100
theta = np.random.randn(2,1) # 랜덤 초기화
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
theta
X_new_b.dot(theta)
theta_path_bgd = []
def plot_gradient_descent(theta, eta, theta_path=None):
m = len(X_b)
plt.plot(X, y, "b.")
n_iterations = 1000
for iteration in range(n_iterations):
if iteration < 10:
y_predict = X_new_b.dot(theta)
style = "b-" if iteration > 0 else "r--"
plt.plot(X_new, y_predict, style)
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
if theta_path is not None:
theta_path.append(theta)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 2, 0, 15])
plt.title(r"$\eta = {}$".format(eta), fontsize=16)
np.random.seed(42)
theta = np.random.randn(2,1) # random initialization
plt.figure(figsize=(10,4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.02)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)
save_fig("gradient_descent_plot")
plt.show()
```
# 확률적 경사 하강법
```
theta_path_sgd = []
m = len(X_b)
np.random.seed(42)
n_epochs = 50
t0, t1 = 5, 50 # 학습 스케줄 하이퍼파라미터
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) # 랜덤 초기화
for epoch in range(n_epochs):
for i in range(m):
if epoch == 0 and i < 20: # 책에는 없음
y_predict = X_new_b.dot(theta) # 책에는 없음
style = "b-" if i > 0 else "r--" # 책에는 없음
plt.plot(X_new, y_predict, style) # 책에는 없음
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m + i)
theta = theta - eta * gradients
theta_path_sgd.append(theta) # 책에는 없음
plt.plot(X, y, "b.") # 책에는 없음
plt.xlabel("$x_1$", fontsize=18) # 책에는 없음
plt.ylabel("$y$", rotation=0, fontsize=18) # 책에는 없음
plt.axis([0, 2, 0, 15]) # 책에는 없음
save_fig("sgd_plot") # 책에는 없음
plt.show() # 책에는 없음
theta
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_
```
# 미니배치 경사 하강법
```
theta_path_mgd = []
n_iterations = 50
minibatch_size = 20
np.random.seed(42)
theta = np.random.randn(2,1) # 랜덤 초기화
t0, t1 = 200, 1000
def learning_schedule(t):
return t0 / (t + t1)
t = 0
for epoch in range(n_iterations):
shuffled_indices = np.random.permutation(m)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0, m, minibatch_size):
t += 1
xi = X_b_shuffled[i:i+minibatch_size]
yi = y_shuffled[i:i+minibatch_size]
gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(t)
theta = theta - eta * gradients
theta_path_mgd.append(theta)
theta
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize=(7,4))
plt.plot(theta_path_sgd[:, 0], theta_path_sgd[:, 1], "r-s", linewidth=1, label="Stochastic")
plt.plot(theta_path_mgd[:, 0], theta_path_mgd[:, 1], "g-+", linewidth=2, label="Mini-batch")
plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], "b-o", linewidth=3, label="Batch")
plt.legend(loc="upper left", fontsize=16)
plt.xlabel(r"$\theta_0$", fontsize=20)
plt.ylabel(r"$\theta_1$ ", fontsize=20, rotation=0)
plt.axis([2.5, 4.5, 2.3, 3.9])
save_fig("gradient_descent_paths_plot")
plt.show()
```
# 다항 회귀
```
import numpy as np
import numpy.random as rnd
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig("quadratic_data_plot")
plt.show()
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
X_poly[0]
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])
save_fig("quadratic_predictions_plot")
plt.show()
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
for style, width, degree in (("g-", 1, 300), ("b--", 2, 2), ("r-+", 2, 1)):
polybig_features = PolynomialFeatures(degree=degree, include_bias=False)
std_scaler = StandardScaler()
lin_reg = LinearRegression()
polynomial_regression = Pipeline([
("poly_features", polybig_features),
("std_scaler", std_scaler),
("lin_reg", lin_reg),
])
polynomial_regression.fit(X, y)
y_newbig = polynomial_regression.predict(X_new)
plt.plot(X_new, y_newbig, style, label=str(degree), linewidth=width)
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig("high_degree_polynomials_plot")
plt.show()
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=10)
train_errors, val_errors = [], []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
plt.legend(loc="upper right", fontsize=14) # 책에는 없음
plt.xlabel("Training set size", fontsize=14) # 책에는 없음
plt.ylabel("RMSE", fontsize=14) # 책에는 없음
lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)
plt.axis([0, 80, 0, 3]) # 책에는 없음
save_fig("underfitting_learning_curves_plot") # 책에는 없음
plt.show() # 책에는 없음
from sklearn.pipeline import Pipeline
polynomial_regression = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("lin_reg", LinearRegression()),
])
plot_learning_curves(polynomial_regression, X, y)
plt.axis([0, 80, 0, 3]) # 책에는 없음
save_fig("learning_curves_plot") # 책에는 없음
plt.show() # 책에는 없음
```
# 규제가 있는 모델
```
np.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
X_new = np.linspace(0, 3, 100).reshape(100, 1)
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
ridge_reg = Ridge(alpha=1, solver="sag", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
from sklearn.linear_model import Ridge
def plot_model(model_class, polynomial, alphas, **model_kargs):
for alpha, style in zip(alphas, ("b-", "g--", "r:")):
model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression()
if polynomial:
model = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("std_scaler", StandardScaler()),
("regul_reg", model),
])
model.fit(X, y)
y_new_regul = model.predict(X_new)
lw = 2 if alpha > 0 else 1
plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r"$\alpha = {}$".format(alpha))
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left", fontsize=15)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 3, 0, 4])
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42)
save_fig("ridge_regression_plot")
plt.show()
```
**노트**: 향후 버전이 바뀌더라도 동일한 결과를 만들기 위해 사이킷런 0.21 버전의 기본값인 `max_iter=1000`과 `tol=1e-3`으로 지정합니다.
```
sgd_reg = SGDRegressor(penalty="l2", max_iter=1000, tol=1e-3, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
from sklearn.linear_model import Lasso
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), random_state=42)
save_fig("lasso_regression_plot")
plt.show()
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 2 + X + 0.5 * X**2 + np.random.randn(m, 1)
X_train, X_val, y_train, y_val = train_test_split(X[:50], y[:50].ravel(), test_size=0.5, random_state=10)
```
조기 종료 예제:
```
from sklearn.base import clone
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=90, include_bias=False)),
("std_scaler", StandardScaler())
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train) # 중지된 곳에서 다시 시작합니다
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val, y_val_predict)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)
```
그래프를 그립니다:
```
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
n_epochs = 500
train_errors, val_errors = [], []
for epoch in range(n_epochs):
sgd_reg.fit(X_train_poly_scaled, y_train)
y_train_predict = sgd_reg.predict(X_train_poly_scaled)
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
train_errors.append(mean_squared_error(y_train, y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
best_epoch = np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])
plt.annotate('Best model',
xy=(best_epoch, best_val_rmse),
xytext=(best_epoch, best_val_rmse + 1),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.05),
fontsize=16,
)
best_val_rmse -= 0.03 # just to make the graph look better
plt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], "k:", linewidth=2)
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="Validation set")
plt.plot(np.sqrt(train_errors), "r--", linewidth=2, label="Training set")
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("Epoch", fontsize=14)
plt.ylabel("RMSE", fontsize=14)
save_fig("early_stopping_plot")
plt.show()
best_epoch, best_model
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
t1a, t1b, t2a, t2b = -1, 3, -1.5, 1.5
t1s = np.linspace(t1a, t1b, 500)
t2s = np.linspace(t2a, t2b, 500)
t1, t2 = np.meshgrid(t1s, t2s)
T = np.c_[t1.ravel(), t2.ravel()]
Xr = np.array([[1, 1], [1, -1], [1, 0.5]])
yr = 2 * Xr[:, :1] + 0.5 * Xr[:, 1:]
J = (1/len(Xr) * np.sum((T.dot(Xr.T) - yr.T)**2, axis=1)).reshape(t1.shape)
N1 = np.linalg.norm(T, ord=1, axis=1).reshape(t1.shape)
N2 = np.linalg.norm(T, ord=2, axis=1).reshape(t1.shape)
t_min_idx = np.unravel_index(np.argmin(J), J.shape)
t1_min, t2_min = t1[t_min_idx], t2[t_min_idx]
t_init = np.array([[0.25], [-1]])
def bgd_path(theta, X, y, l1, l2, core = 1, eta = 0.05, n_iterations = 200):
path = [theta]
for iteration in range(n_iterations):
gradients = core * 2/len(X) * X.T.dot(X.dot(theta) - y) + l1 * np.sign(theta) + l2 * theta
theta = theta - eta * gradients
path.append(theta)
return np.array(path)
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(10.1, 8))
for i, N, l1, l2, title in ((0, N1, 2., 0, "Lasso"), (1, N2, 0, 2., "Ridge")):
JR = J + l1 * N1 + l2 * 0.5 * N2**2
tr_min_idx = np.unravel_index(np.argmin(JR), JR.shape)
t1r_min, t2r_min = t1[tr_min_idx], t2[tr_min_idx]
levelsJ=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(J) - np.min(J)) + np.min(J)
levelsJR=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(JR) - np.min(JR)) + np.min(JR)
levelsN=np.linspace(0, np.max(N), 10)
path_J = bgd_path(t_init, Xr, yr, l1=0, l2=0)
path_JR = bgd_path(t_init, Xr, yr, l1, l2)
path_N = bgd_path(np.array([[2.0], [0.5]]), Xr, yr, np.sign(l1)/3, np.sign(l2), core=0)
ax = axes[i, 0]
ax.grid(True)
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
ax.contourf(t1, t2, N / 2., levels=levelsN)
ax.plot(path_N[:, 0], path_N[:, 1], "y--")
ax.plot(0, 0, "ys")
ax.plot(t1_min, t2_min, "ys")
ax.set_title(r"$\ell_{}$ penalty".format(i + 1), fontsize=16)
ax.axis([t1a, t1b, t2a, t2b])
if i == 1:
ax.set_xlabel(r"$\theta_1$", fontsize=16)
ax.set_ylabel(r"$\theta_2$", fontsize=16, rotation=0)
ax = axes[i, 1]
ax.grid(True)
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
ax.contourf(t1, t2, JR, levels=levelsJR, alpha=0.9)
ax.plot(path_JR[:, 0], path_JR[:, 1], "w-o")
ax.plot(path_N[:, 0], path_N[:, 1], "y--")
ax.plot(0, 0, "ys")
ax.plot(t1_min, t2_min, "ys")
ax.plot(t1r_min, t2r_min, "rs")
ax.set_title(title, fontsize=16)
ax.axis([t1a, t1b, t2a, t2b])
if i == 1:
ax.set_xlabel(r"$\theta_1$", fontsize=16)
save_fig("lasso_vs_ridge_plot")
plt.show()
```
# 로지스틱 회귀
```
t = np.linspace(-10, 10, 100)
sig = 1 / (1 + np.exp(-t))
plt.figure(figsize=(9, 3))
plt.plot([-10, 10], [0, 0], "k-")
plt.plot([-10, 10], [0.5, 0.5], "k:")
plt.plot([-10, 10], [1, 1], "k:")
plt.plot([0, 0], [-1.1, 1.1], "k-")
plt.plot(t, sig, "b-", linewidth=2, label=r"$\sigma(t) = \frac{1}{1 + e^{-t}}$")
plt.xlabel("t")
plt.legend(loc="upper left", fontsize=20)
plt.axis([-10, 10, -0.1, 1.1])
save_fig("logistic_function_plot")
plt.show()
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
print(iris.DESCR)
X = iris["data"][:, 3:] # 꽃잎 너비
y = (iris["target"] == 2).astype(np.int) # Iris virginica이면 1 아니면 0
```
**노트**: 향후 버전이 바뀌더라도 동일한 결과를 만들기 위해 사이킷런 0.22 버전의 기본값인 `solver="lbfgs"`로 지정합니다.
```
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver="lbfgs", random_state=42)
log_reg.fit(X, y)
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")
```
책에 실린 그림은 조금 더 예쁘게 꾸몄습니다:
```
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]
plt.figure(figsize=(8, 3))
plt.plot(X[y==0], y[y==0], "bs")
plt.plot(X[y==1], y[y==1], "g^")
plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")
plt.text(decision_boundary+0.02, 0.15, "Decision boundary", fontsize=14, color="k", ha="center")
plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel("Petal width (cm)", fontsize=14)
plt.ylabel("Probability", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 3, -0.02, 1.02])
save_fig("logistic_regression_plot")
plt.show()
decision_boundary
log_reg.predict([[1.7], [1.5]])
from sklearn.linear_model import LogisticRegression
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.int)
log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42)
log_reg.fit(X, y)
x0, x1 = np.meshgrid(
np.linspace(2.9, 7, 500).reshape(-1, 1),
np.linspace(0.8, 2.7, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = log_reg.predict_proba(X_new)
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs")
plt.plot(X[y==1, 0], X[y==1, 1], "g^")
zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)
left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]
plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.5, "Not Iris virginica", fontsize=14, color="b", ha="center")
plt.text(6.5, 2.3, "Iris virginica", fontsize=14, color="g", ha="center")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7])
save_fig("logistic_regression_contour_plot")
plt.show()
X = iris["data"][:, (2, 3)] # 꽃잎 길이, 꽃잎 너비
y = iris["target"]
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)
x0, x1 = np.meshgrid(
np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)
zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])
save_fig("softmax_regression_contour_plot")
plt.show()
softmax_reg.predict([[5, 2]])
softmax_reg.predict_proba([[5, 2]])
```
# 연습문제 해답
## 1. to 11.
부록 A를 참고하세요.
## 12. 조기 종료를 사용한 배치 경사 하강법으로 소프트맥스 회귀 구현하기
(사이킷런을 사용하지 않고)
먼저 데이터를 로드합니다. 앞서 사용했던 Iris 데이터셋을 재사용하겠습니다.
```
X = iris["data"][:, (2, 3)] # 꽃잎 길이, 꽃잎 넓이
y = iris["target"]
```
모든 샘플에 편향을 추가합니다 ($x_0 = 1$):
```
X_with_bias = np.c_[np.ones([len(X), 1]), X]
```
결과를 일정하게 유지하기 위해 랜덤 시드를 지정합니다:
```
np.random.seed(2042)
```
데이터셋을 훈련 세트, 검증 세트, 테스트 세트로 나누는 가장 쉬운 방법은 사이킷런의 `train_test_split()` 함수를 사용하는 것입니다. 하지만 이 연습문제의 목적은 직접 만들어 보면서 알고리즘을 이해하는 것이므로 다음과 같이 수동으로 나누어 보겠습니다:
```
test_ratio = 0.2
validation_ratio = 0.2
total_size = len(X_with_bias)
test_size = int(total_size * test_ratio)
validation_size = int(total_size * validation_ratio)
train_size = total_size - test_size - validation_size
rnd_indices = np.random.permutation(total_size)
X_train = X_with_bias[rnd_indices[:train_size]]
y_train = y[rnd_indices[:train_size]]
X_valid = X_with_bias[rnd_indices[train_size:-test_size]]
y_valid = y[rnd_indices[train_size:-test_size]]
X_test = X_with_bias[rnd_indices[-test_size:]]
y_test = y[rnd_indices[-test_size:]]
```
타깃은 클래스 인덱스(0, 1 그리고 2)이지만 소프트맥스 회귀 모델을 훈련시키기 위해 필요한 것은 타깃 클래스의 확률입니다. 각 샘플에서 확률이 1인 타깃 클래스를 제외한 다른 클래스의 확률은 0입니다(다른 말로하면 주어진 샘플에 대한 클래스 확률이 원-핫 벡터입니다). 클래스 인덱스를 원-핫 벡터로 바꾸는 간단한 함수를 작성하겠습니다:
```
def to_one_hot(y):
n_classes = y.max() + 1
m = len(y)
Y_one_hot = np.zeros((m, n_classes))
Y_one_hot[np.arange(m), y] = 1
return Y_one_hot
```
10개 샘플만 넣어 이 함수를 테스트해 보죠:
```
y_train[:10]
to_one_hot(y_train[:10])
```
잘 되네요, 이제 훈련 세트와 테스트 세트의 타깃 클래스 확률을 담은 행렬을 만들겠습니다:
```
Y_train_one_hot = to_one_hot(y_train)
Y_valid_one_hot = to_one_hot(y_valid)
Y_test_one_hot = to_one_hot(y_test)
```
이제 소프트맥스 함수를 만듭니다. 다음 공식을 참고하세요:
$\sigma\left(\mathbf{s}(\mathbf{x})\right)_k = \dfrac{\exp\left(s_k(\mathbf{x})\right)}{\sum\limits_{j=1}^{K}{\exp\left(s_j(\mathbf{x})\right)}}$
```
def softmax(logits):
exps = np.exp(logits)
exp_sums = np.sum(exps, axis=1, keepdims=True)
return exps / exp_sums
```
훈련을 위한 준비를 거의 마쳤습니다. 입력과 출력의 개수를 정의합니다:
```
n_inputs = X_train.shape[1] # == 3 (특성 2개와 편향)
n_outputs = len(np.unique(y_train)) # == 3 (3개의 붓꽃 클래스)
```
이제 좀 복잡한 훈련 파트입니다! 이론적으로는 간단합니다. 그냥 수학 공식을 파이썬 코드로 바꾸기만 하면 됩니다. 하지만 실제로는 꽤 까다로운 면이 있습니다. 특히, 항이나 인덱스의 순서가 뒤섞이기 쉽습니다. 제대로 작동할 것처럼 코드를 작성했더라도 실제 제대로 계산하지 못합니다. 확실하지 않을 때는 각 항의 크기를 기록하고 이에 상응하는 코드가 같은 크기를 만드는지 확인합니다. 각 항을 독립적으로 평가해서 출력해 보는 것도 좋습니다. 사실 사이킷런에 이미 잘 구현되어 있기 때문에 이렇게 할 필요는 없습니다. 하지만 직접 만들어 보면 어떻게 작동하는지 이해하는데 도움이 됩니다.
구현할 공식은 비용함수입니다:
$J(\mathbf{\Theta}) =
- \dfrac{1}{m}\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{K}{y_k^{(i)}\log\left(\hat{p}_k^{(i)}\right)}$
그리고 그레이디언트 공식입니다:
$\nabla_{\mathbf{\theta}^{(k)}} \, J(\mathbf{\Theta}) = \dfrac{1}{m} \sum\limits_{i=1}^{m}{ \left ( \hat{p}^{(i)}_k - y_k^{(i)} \right ) \mathbf{x}^{(i)}}$
$\hat{p}_k^{(i)} = 0$이면 $\log\left(\hat{p}_k^{(i)}\right)$를 계산할 수 없습니다. `nan` 값을 피하기 위해 $\log\left(\hat{p}_k^{(i)}\right)$에 아주 작은 값 $\epsilon$을 추가하겠습니다.
```
eta = 0.01
n_iterations = 5001
m = len(X_train)
epsilon = 1e-7
Theta = np.random.randn(n_inputs, n_outputs)
for iteration in range(n_iterations):
logits = X_train.dot(Theta)
Y_proba = softmax(logits)
loss = -np.mean(np.sum(Y_train_one_hot * np.log(Y_proba + epsilon), axis=1))
error = Y_proba - Y_train_one_hot
if iteration % 500 == 0:
print(iteration, loss)
gradients = 1/m * X_train.T.dot(error)
Theta = Theta - eta * gradients
```
바로 이겁니다! 소프트맥스 모델을 훈련시켰습니다. 모델 파라미터를 확인해 보겠습니다:
```
Theta
```
검증 세트에 대한 예측과 정확도를 확인해 보겠습니다:
```
logits = X_valid.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
```
와우, 이 모델이 매우 잘 작동하는 것 같습니다. 연습을 위해서 $\ell_2$ 규제를 조금 추가해 보겠습니다. 다음 코드는 위와 거의 동일하지만 손실에 $\ell_2$ 페널티가 추가되었고 그래디언트에도 항이 추가되었습니다(`Theta`의 첫 번째 원소는 편향이므로 규제하지 않습니다). 학습률 `eta`도 증가시켜 보겠습니다.
```
eta = 0.1
n_iterations = 5001
m = len(X_train)
epsilon = 1e-7
alpha = 0.1 # 규제 하이퍼파라미터
Theta = np.random.randn(n_inputs, n_outputs)
for iteration in range(n_iterations):
logits = X_train.dot(Theta)
Y_proba = softmax(logits)
xentropy_loss = -np.mean(np.sum(Y_train_one_hot * np.log(Y_proba + epsilon), axis=1))
l2_loss = 1/2 * np.sum(np.square(Theta[1:]))
loss = xentropy_loss + alpha * l2_loss
error = Y_proba - Y_train_one_hot
if iteration % 500 == 0:
print(iteration, loss)
gradients = 1/m * X_train.T.dot(error) + np.r_[np.zeros([1, n_outputs]), alpha * Theta[1:]]
Theta = Theta - eta * gradients
```
추가된 $\ell_2$ 페널티 때문에 이전보다 손실이 조금 커보이지만 더 잘 작동하는 모델이 되었을까요? 확인해 보죠:
```
logits = X_valid.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
```
와우, 완벽한 정확도네요! 운이 좋은 검증 세트일지 모르지만 잘 된 것은 맞습니다.
이제 조기 종료를 추가해 보죠. 이렇게 하려면 매 반복에서 검증 세트에 대한 손실을 계산해서 오차가 증가하기 시작할 때 멈춰야 합니다.
```
eta = 0.1
n_iterations = 5001
m = len(X_train)
epsilon = 1e-7
alpha = 0.1 # 규제 하이퍼파라미터
best_loss = np.infty
Theta = np.random.randn(n_inputs, n_outputs)
for iteration in range(n_iterations):
logits = X_train.dot(Theta)
Y_proba = softmax(logits)
xentropy_loss = -np.mean(np.sum(Y_train_one_hot * np.log(Y_proba + epsilon), axis=1))
l2_loss = 1/2 * np.sum(np.square(Theta[1:]))
loss = xentropy_loss + alpha * l2_loss
error = Y_proba - Y_train_one_hot
gradients = 1/m * X_train.T.dot(error) + np.r_[np.zeros([1, n_outputs]), alpha * Theta[1:]]
Theta = Theta - eta * gradients
logits = X_valid.dot(Theta)
Y_proba = softmax(logits)
xentropy_loss = -np.mean(np.sum(Y_valid_one_hot * np.log(Y_proba + epsilon), axis=1))
l2_loss = 1/2 * np.sum(np.square(Theta[1:]))
loss = xentropy_loss + alpha * l2_loss
if iteration % 500 == 0:
print(iteration, loss)
if loss < best_loss:
best_loss = loss
else:
print(iteration - 1, best_loss)
print(iteration, loss, "조기 종료!")
break
logits = X_valid.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
```
여전히 완벽하지만 더 빠릅니다.
이제 전체 데이터셋에 대한 모델의 예측을 그래프로 나타내 보겠습니다:
```
x0, x1 = np.meshgrid(
np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
X_new_with_bias = np.c_[np.ones([len(X_new), 1]), X_new]
logits = X_new_with_bias.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
zz1 = Y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 7, 0, 3.5])
plt.show()
```
이제 테스트 세트에 대한 모델의 최종 정확도를 측정해 보겠습니다:
```
logits = X_test.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_test)
accuracy_score
```
완벽했던 최종 모델의 성능이 조금 떨어졌습니다. 이런 차이는 데이터셋이 작기 때문일 것입니다. 훈련 세트와 검증 세트, 테스트 세트를 어떻게 샘플링했는지에 따라 매우 다른 결과를 얻을 수 있습니다. 몇 번 랜덤 시드를 바꾸고 이 코드를 다시 실행해 보면 결과가 달라지는 것을 확인할 수 있습니다.
|
github_jupyter
|
# 파이썬 ≥3.5 필수
import sys
assert sys.version_info >= (3, 5)
# 사이킷런 ≥0.20 필수
import sklearn
assert sklearn.__version__ >= "0.20"
# 공통 모듈 임포트
import numpy as np
import os
# 노트북 실행 결과를 동일하게 유지하기 위해
np.random.seed(42)
# 깔끔한 그래프 출력을 위해
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# 그림을 저장할 위치
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "training_linear_models"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("그림 저장:", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# 불필요한 경고를 무시합니다 (사이파이 이슈 #5998 참조)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
import numpy as np
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
save_fig("generated_data_plot")
plt.show()
X_b = np.c_[np.ones((100, 1)), X] # 모든 샘플에 x0 = 1을 추가합니다.
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new] # 모든 샘플에 x0 = 1을 추가합니다.
y_predict = X_new_b.dot(theta_best)
y_predict
plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")
plt.axis([0, 2, 0, 15])
plt.show()
plt.plot(X_new, y_predict, "r-", linewidth=2, label="Predictions")
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 2, 0, 15])
save_fig("linear_model_predictions_plot")
plt.show()
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_
lin_reg.predict(X_new)
# 싸이파이 lstsq() 함수를 사용하려면 scipy.linalg.lstsq(X_b, y)와 같이 씁니다.
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd
np.linalg.pinv(X_b).dot(y)
eta = 0.1 # 학습률
n_iterations = 1000
m = 100
theta = np.random.randn(2,1) # 랜덤 초기화
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
theta
X_new_b.dot(theta)
theta_path_bgd = []
def plot_gradient_descent(theta, eta, theta_path=None):
m = len(X_b)
plt.plot(X, y, "b.")
n_iterations = 1000
for iteration in range(n_iterations):
if iteration < 10:
y_predict = X_new_b.dot(theta)
style = "b-" if iteration > 0 else "r--"
plt.plot(X_new, y_predict, style)
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
if theta_path is not None:
theta_path.append(theta)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 2, 0, 15])
plt.title(r"$\eta = {}$".format(eta), fontsize=16)
np.random.seed(42)
theta = np.random.randn(2,1) # random initialization
plt.figure(figsize=(10,4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.02)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)
save_fig("gradient_descent_plot")
plt.show()
theta_path_sgd = []
m = len(X_b)
np.random.seed(42)
n_epochs = 50
t0, t1 = 5, 50 # 학습 스케줄 하이퍼파라미터
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) # 랜덤 초기화
for epoch in range(n_epochs):
for i in range(m):
if epoch == 0 and i < 20: # 책에는 없음
y_predict = X_new_b.dot(theta) # 책에는 없음
style = "b-" if i > 0 else "r--" # 책에는 없음
plt.plot(X_new, y_predict, style) # 책에는 없음
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m + i)
theta = theta - eta * gradients
theta_path_sgd.append(theta) # 책에는 없음
plt.plot(X, y, "b.") # 책에는 없음
plt.xlabel("$x_1$", fontsize=18) # 책에는 없음
plt.ylabel("$y$", rotation=0, fontsize=18) # 책에는 없음
plt.axis([0, 2, 0, 15]) # 책에는 없음
save_fig("sgd_plot") # 책에는 없음
plt.show() # 책에는 없음
theta
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_
theta_path_mgd = []
n_iterations = 50
minibatch_size = 20
np.random.seed(42)
theta = np.random.randn(2,1) # 랜덤 초기화
t0, t1 = 200, 1000
def learning_schedule(t):
return t0 / (t + t1)
t = 0
for epoch in range(n_iterations):
shuffled_indices = np.random.permutation(m)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0, m, minibatch_size):
t += 1
xi = X_b_shuffled[i:i+minibatch_size]
yi = y_shuffled[i:i+minibatch_size]
gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(t)
theta = theta - eta * gradients
theta_path_mgd.append(theta)
theta
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize=(7,4))
plt.plot(theta_path_sgd[:, 0], theta_path_sgd[:, 1], "r-s", linewidth=1, label="Stochastic")
plt.plot(theta_path_mgd[:, 0], theta_path_mgd[:, 1], "g-+", linewidth=2, label="Mini-batch")
plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], "b-o", linewidth=3, label="Batch")
plt.legend(loc="upper left", fontsize=16)
plt.xlabel(r"$\theta_0$", fontsize=20)
plt.ylabel(r"$\theta_1$ ", fontsize=20, rotation=0)
plt.axis([2.5, 4.5, 2.3, 3.9])
save_fig("gradient_descent_paths_plot")
plt.show()
import numpy as np
import numpy.random as rnd
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig("quadratic_data_plot")
plt.show()
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
X_poly[0]
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])
save_fig("quadratic_predictions_plot")
plt.show()
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
for style, width, degree in (("g-", 1, 300), ("b--", 2, 2), ("r-+", 2, 1)):
polybig_features = PolynomialFeatures(degree=degree, include_bias=False)
std_scaler = StandardScaler()
lin_reg = LinearRegression()
polynomial_regression = Pipeline([
("poly_features", polybig_features),
("std_scaler", std_scaler),
("lin_reg", lin_reg),
])
polynomial_regression.fit(X, y)
y_newbig = polynomial_regression.predict(X_new)
plt.plot(X_new, y_newbig, style, label=str(degree), linewidth=width)
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig("high_degree_polynomials_plot")
plt.show()
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=10)
train_errors, val_errors = [], []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
plt.legend(loc="upper right", fontsize=14) # 책에는 없음
plt.xlabel("Training set size", fontsize=14) # 책에는 없음
plt.ylabel("RMSE", fontsize=14) # 책에는 없음
lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)
plt.axis([0, 80, 0, 3]) # 책에는 없음
save_fig("underfitting_learning_curves_plot") # 책에는 없음
plt.show() # 책에는 없음
from sklearn.pipeline import Pipeline
polynomial_regression = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("lin_reg", LinearRegression()),
])
plot_learning_curves(polynomial_regression, X, y)
plt.axis([0, 80, 0, 3]) # 책에는 없음
save_fig("learning_curves_plot") # 책에는 없음
plt.show() # 책에는 없음
np.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
X_new = np.linspace(0, 3, 100).reshape(100, 1)
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
ridge_reg = Ridge(alpha=1, solver="sag", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
from sklearn.linear_model import Ridge
def plot_model(model_class, polynomial, alphas, **model_kargs):
for alpha, style in zip(alphas, ("b-", "g--", "r:")):
model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression()
if polynomial:
model = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("std_scaler", StandardScaler()),
("regul_reg", model),
])
model.fit(X, y)
y_new_regul = model.predict(X_new)
lw = 2 if alpha > 0 else 1
plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r"$\alpha = {}$".format(alpha))
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left", fontsize=15)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 3, 0, 4])
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42)
save_fig("ridge_regression_plot")
plt.show()
sgd_reg = SGDRegressor(penalty="l2", max_iter=1000, tol=1e-3, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
from sklearn.linear_model import Lasso
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), random_state=42)
save_fig("lasso_regression_plot")
plt.show()
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 2 + X + 0.5 * X**2 + np.random.randn(m, 1)
X_train, X_val, y_train, y_val = train_test_split(X[:50], y[:50].ravel(), test_size=0.5, random_state=10)
from sklearn.base import clone
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=90, include_bias=False)),
("std_scaler", StandardScaler())
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train) # 중지된 곳에서 다시 시작합니다
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val, y_val_predict)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
n_epochs = 500
train_errors, val_errors = [], []
for epoch in range(n_epochs):
sgd_reg.fit(X_train_poly_scaled, y_train)
y_train_predict = sgd_reg.predict(X_train_poly_scaled)
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
train_errors.append(mean_squared_error(y_train, y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
best_epoch = np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])
plt.annotate('Best model',
xy=(best_epoch, best_val_rmse),
xytext=(best_epoch, best_val_rmse + 1),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.05),
fontsize=16,
)
best_val_rmse -= 0.03 # just to make the graph look better
plt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], "k:", linewidth=2)
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="Validation set")
plt.plot(np.sqrt(train_errors), "r--", linewidth=2, label="Training set")
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("Epoch", fontsize=14)
plt.ylabel("RMSE", fontsize=14)
save_fig("early_stopping_plot")
plt.show()
best_epoch, best_model
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
t1a, t1b, t2a, t2b = -1, 3, -1.5, 1.5
t1s = np.linspace(t1a, t1b, 500)
t2s = np.linspace(t2a, t2b, 500)
t1, t2 = np.meshgrid(t1s, t2s)
T = np.c_[t1.ravel(), t2.ravel()]
Xr = np.array([[1, 1], [1, -1], [1, 0.5]])
yr = 2 * Xr[:, :1] + 0.5 * Xr[:, 1:]
J = (1/len(Xr) * np.sum((T.dot(Xr.T) - yr.T)**2, axis=1)).reshape(t1.shape)
N1 = np.linalg.norm(T, ord=1, axis=1).reshape(t1.shape)
N2 = np.linalg.norm(T, ord=2, axis=1).reshape(t1.shape)
t_min_idx = np.unravel_index(np.argmin(J), J.shape)
t1_min, t2_min = t1[t_min_idx], t2[t_min_idx]
t_init = np.array([[0.25], [-1]])
def bgd_path(theta, X, y, l1, l2, core = 1, eta = 0.05, n_iterations = 200):
path = [theta]
for iteration in range(n_iterations):
gradients = core * 2/len(X) * X.T.dot(X.dot(theta) - y) + l1 * np.sign(theta) + l2 * theta
theta = theta - eta * gradients
path.append(theta)
return np.array(path)
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(10.1, 8))
for i, N, l1, l2, title in ((0, N1, 2., 0, "Lasso"), (1, N2, 0, 2., "Ridge")):
JR = J + l1 * N1 + l2 * 0.5 * N2**2
tr_min_idx = np.unravel_index(np.argmin(JR), JR.shape)
t1r_min, t2r_min = t1[tr_min_idx], t2[tr_min_idx]
levelsJ=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(J) - np.min(J)) + np.min(J)
levelsJR=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(JR) - np.min(JR)) + np.min(JR)
levelsN=np.linspace(0, np.max(N), 10)
path_J = bgd_path(t_init, Xr, yr, l1=0, l2=0)
path_JR = bgd_path(t_init, Xr, yr, l1, l2)
path_N = bgd_path(np.array([[2.0], [0.5]]), Xr, yr, np.sign(l1)/3, np.sign(l2), core=0)
ax = axes[i, 0]
ax.grid(True)
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
ax.contourf(t1, t2, N / 2., levels=levelsN)
ax.plot(path_N[:, 0], path_N[:, 1], "y--")
ax.plot(0, 0, "ys")
ax.plot(t1_min, t2_min, "ys")
ax.set_title(r"$\ell_{}$ penalty".format(i + 1), fontsize=16)
ax.axis([t1a, t1b, t2a, t2b])
if i == 1:
ax.set_xlabel(r"$\theta_1$", fontsize=16)
ax.set_ylabel(r"$\theta_2$", fontsize=16, rotation=0)
ax = axes[i, 1]
ax.grid(True)
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
ax.contourf(t1, t2, JR, levels=levelsJR, alpha=0.9)
ax.plot(path_JR[:, 0], path_JR[:, 1], "w-o")
ax.plot(path_N[:, 0], path_N[:, 1], "y--")
ax.plot(0, 0, "ys")
ax.plot(t1_min, t2_min, "ys")
ax.plot(t1r_min, t2r_min, "rs")
ax.set_title(title, fontsize=16)
ax.axis([t1a, t1b, t2a, t2b])
if i == 1:
ax.set_xlabel(r"$\theta_1$", fontsize=16)
save_fig("lasso_vs_ridge_plot")
plt.show()
t = np.linspace(-10, 10, 100)
sig = 1 / (1 + np.exp(-t))
plt.figure(figsize=(9, 3))
plt.plot([-10, 10], [0, 0], "k-")
plt.plot([-10, 10], [0.5, 0.5], "k:")
plt.plot([-10, 10], [1, 1], "k:")
plt.plot([0, 0], [-1.1, 1.1], "k-")
plt.plot(t, sig, "b-", linewidth=2, label=r"$\sigma(t) = \frac{1}{1 + e^{-t}}$")
plt.xlabel("t")
plt.legend(loc="upper left", fontsize=20)
plt.axis([-10, 10, -0.1, 1.1])
save_fig("logistic_function_plot")
plt.show()
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
print(iris.DESCR)
X = iris["data"][:, 3:] # 꽃잎 너비
y = (iris["target"] == 2).astype(np.int) # Iris virginica이면 1 아니면 0
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver="lbfgs", random_state=42)
log_reg.fit(X, y)
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]
plt.figure(figsize=(8, 3))
plt.plot(X[y==0], y[y==0], "bs")
plt.plot(X[y==1], y[y==1], "g^")
plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")
plt.text(decision_boundary+0.02, 0.15, "Decision boundary", fontsize=14, color="k", ha="center")
plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel("Petal width (cm)", fontsize=14)
plt.ylabel("Probability", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 3, -0.02, 1.02])
save_fig("logistic_regression_plot")
plt.show()
decision_boundary
log_reg.predict([[1.7], [1.5]])
from sklearn.linear_model import LogisticRegression
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.int)
log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42)
log_reg.fit(X, y)
x0, x1 = np.meshgrid(
np.linspace(2.9, 7, 500).reshape(-1, 1),
np.linspace(0.8, 2.7, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = log_reg.predict_proba(X_new)
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs")
plt.plot(X[y==1, 0], X[y==1, 1], "g^")
zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)
left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]
plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.5, "Not Iris virginica", fontsize=14, color="b", ha="center")
plt.text(6.5, 2.3, "Iris virginica", fontsize=14, color="g", ha="center")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7])
save_fig("logistic_regression_contour_plot")
plt.show()
X = iris["data"][:, (2, 3)] # 꽃잎 길이, 꽃잎 너비
y = iris["target"]
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)
x0, x1 = np.meshgrid(
np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)
zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])
save_fig("softmax_regression_contour_plot")
plt.show()
softmax_reg.predict([[5, 2]])
softmax_reg.predict_proba([[5, 2]])
X = iris["data"][:, (2, 3)] # 꽃잎 길이, 꽃잎 넓이
y = iris["target"]
X_with_bias = np.c_[np.ones([len(X), 1]), X]
np.random.seed(2042)
test_ratio = 0.2
validation_ratio = 0.2
total_size = len(X_with_bias)
test_size = int(total_size * test_ratio)
validation_size = int(total_size * validation_ratio)
train_size = total_size - test_size - validation_size
rnd_indices = np.random.permutation(total_size)
X_train = X_with_bias[rnd_indices[:train_size]]
y_train = y[rnd_indices[:train_size]]
X_valid = X_with_bias[rnd_indices[train_size:-test_size]]
y_valid = y[rnd_indices[train_size:-test_size]]
X_test = X_with_bias[rnd_indices[-test_size:]]
y_test = y[rnd_indices[-test_size:]]
def to_one_hot(y):
n_classes = y.max() + 1
m = len(y)
Y_one_hot = np.zeros((m, n_classes))
Y_one_hot[np.arange(m), y] = 1
return Y_one_hot
y_train[:10]
to_one_hot(y_train[:10])
Y_train_one_hot = to_one_hot(y_train)
Y_valid_one_hot = to_one_hot(y_valid)
Y_test_one_hot = to_one_hot(y_test)
def softmax(logits):
exps = np.exp(logits)
exp_sums = np.sum(exps, axis=1, keepdims=True)
return exps / exp_sums
n_inputs = X_train.shape[1] # == 3 (특성 2개와 편향)
n_outputs = len(np.unique(y_train)) # == 3 (3개의 붓꽃 클래스)
eta = 0.01
n_iterations = 5001
m = len(X_train)
epsilon = 1e-7
Theta = np.random.randn(n_inputs, n_outputs)
for iteration in range(n_iterations):
logits = X_train.dot(Theta)
Y_proba = softmax(logits)
loss = -np.mean(np.sum(Y_train_one_hot * np.log(Y_proba + epsilon), axis=1))
error = Y_proba - Y_train_one_hot
if iteration % 500 == 0:
print(iteration, loss)
gradients = 1/m * X_train.T.dot(error)
Theta = Theta - eta * gradients
Theta
logits = X_valid.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
eta = 0.1
n_iterations = 5001
m = len(X_train)
epsilon = 1e-7
alpha = 0.1 # 규제 하이퍼파라미터
Theta = np.random.randn(n_inputs, n_outputs)
for iteration in range(n_iterations):
logits = X_train.dot(Theta)
Y_proba = softmax(logits)
xentropy_loss = -np.mean(np.sum(Y_train_one_hot * np.log(Y_proba + epsilon), axis=1))
l2_loss = 1/2 * np.sum(np.square(Theta[1:]))
loss = xentropy_loss + alpha * l2_loss
error = Y_proba - Y_train_one_hot
if iteration % 500 == 0:
print(iteration, loss)
gradients = 1/m * X_train.T.dot(error) + np.r_[np.zeros([1, n_outputs]), alpha * Theta[1:]]
Theta = Theta - eta * gradients
logits = X_valid.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
eta = 0.1
n_iterations = 5001
m = len(X_train)
epsilon = 1e-7
alpha = 0.1 # 규제 하이퍼파라미터
best_loss = np.infty
Theta = np.random.randn(n_inputs, n_outputs)
for iteration in range(n_iterations):
logits = X_train.dot(Theta)
Y_proba = softmax(logits)
xentropy_loss = -np.mean(np.sum(Y_train_one_hot * np.log(Y_proba + epsilon), axis=1))
l2_loss = 1/2 * np.sum(np.square(Theta[1:]))
loss = xentropy_loss + alpha * l2_loss
error = Y_proba - Y_train_one_hot
gradients = 1/m * X_train.T.dot(error) + np.r_[np.zeros([1, n_outputs]), alpha * Theta[1:]]
Theta = Theta - eta * gradients
logits = X_valid.dot(Theta)
Y_proba = softmax(logits)
xentropy_loss = -np.mean(np.sum(Y_valid_one_hot * np.log(Y_proba + epsilon), axis=1))
l2_loss = 1/2 * np.sum(np.square(Theta[1:]))
loss = xentropy_loss + alpha * l2_loss
if iteration % 500 == 0:
print(iteration, loss)
if loss < best_loss:
best_loss = loss
else:
print(iteration - 1, best_loss)
print(iteration, loss, "조기 종료!")
break
logits = X_valid.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
x0, x1 = np.meshgrid(
np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
X_new_with_bias = np.c_[np.ones([len(X_new), 1]), X_new]
logits = X_new_with_bias.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
zz1 = Y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 7, 0, 3.5])
plt.show()
logits = X_test.dot(Theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_test)
accuracy_score
| 0.373533 | 0.9858 |
<a href="https://www.bigdatauniversity.com"><img src = "https://ibm.box.com/shared/static/ugcqz6ohbvff804xp84y4kqnvvk3bq1g.png" width = 300, align = "center"></a>
<h1 align=center><font size = 5>Data Analysis with Python</font></h1>
# House Sales in King County, USA
This dataset contains house sale prices for King County, which includes Seattle. It includes homes sold between May 2014 and May 2015.
<b>id</b> :a notation for a house
<b> date</b>: Date house was sold
<b>price</b>: Price is prediction target
<b>bedrooms</b>: Number of Bedrooms/House
<b>bathrooms</b>: Number of bathrooms/bedrooms
<b>sqft_living</b>: square footage of the home
<b>sqft_lot</b>: square footage of the lot
<b>floors</b> :Total floors (levels) in house
<b>waterfront</b> :House which has a view to a waterfront
<b>view</b>: Has been viewed
<b>condition</b> :How good the condition is Overall
<b>grade</b>: overall grade given to the housing unit, based on King County grading system
<b>sqft_above</b> :square footage of house apart from basement
<b>sqft_basement</b>: square footage of the basement
<b>yr_built</b> :Built Year
<b>yr_renovated</b> :Year when house was renovated
<b>zipcode</b>:zip code
<b>lat</b>: Latitude coordinate
<b>long</b>: Longitude coordinate
<b>sqft_living15</b> :Living room area in 2015(implies-- some renovations) This might or might not have affected the lotsize area
<b>sqft_lot15</b> :lotSize area in 2015(implies-- some renovations)
You will require the following libraries
```
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler,PolynomialFeatures
%matplotlib inline
```
# 1.0 Importing the Data
Load the csv:
```
file_name='https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DA0101EN/coursera/project/kc_house_data_NaN.csv'
df=pd.read_csv(file_name)
```
we use the method <code>head</code> to display the first 5 columns of the dataframe.
```
df.head()
```
#### Question 1
Display the data types of each column using the attribute dtype, then take a screenshot and submit it, include your code in the image.
```
df.dtypes
```
We use the method describe to obtain a statistical summary of the dataframe.
```
df.describe()
```
# 2.0 Data Wrangling
#### Question 2
Drop the columns <code>"id"</code> and <code>"Unnamed: 0"</code> from axis 1 using the method <code>drop()</code>, then use the method <code>describe()</code> to obtain a statistical summary of the data. Take a screenshot and submit it, make sure the inplace parameter is set to <code>True</code>
```
df.drop(columns=['id', 'Unnamed: 0'], axis=1, inplace=True)
df.describe()
```
we can see we have missing values for the columns <code> bedrooms</code> and <code> bathrooms </code>
```
print("number of NaN values for the column bedrooms :", df['bedrooms'].isnull().sum())
print("number of NaN values for the column bathrooms :", df['bathrooms'].isnull().sum())
```
We can replace the missing values of the column <code>'bedrooms'</code> with the mean of the column <code>'bedrooms' </code> using the method replace. Don't forget to set the <code>inplace</code> parameter top <code>True</code>
```
mean=df['bedrooms'].mean()
df['bedrooms'].replace(np.nan, mean, inplace=True)
```
We also replace the missing values of the column <code>'bathrooms'</code> with the mean of the column <code>'bedrooms' </codse> using the method replace.Don't forget to set the <code> inplace </code> parameter top <code> Ture </code>
```
mean=df['bathrooms'].mean()
df['bathrooms'].replace(np.nan,mean, inplace=True)
print("number of NaN values for the column bedrooms :", df['bedrooms'].isnull().sum())
print("number of NaN values for the column bathrooms :", df['bathrooms'].isnull().sum())
```
# 3.0 Exploratory data analysis
#### Question 3
Use the method value_counts to count the number of houses with unique floor values, use the method .to_frame() to convert it to a dataframe.
```
df_floors = df['floors'].value_counts()
df_floors.to_frame()
```
### Question 4
Use the function <code>boxplot</code> in the seaborn library to determine whether houses with a waterfront view or without a waterfront view have more price outliers .
```
sns.boxplot(x=df['waterfront'], y=df['price'], data=df)
```
### Question 5
Use the function <code> regplot</code> in the seaborn library to determine if the feature <code>sqft_above</code> is negatively or positively correlated with price.
```
sns.regplot(x='sqft_above', y='price', data=df, ci=None)
```
We can use the Pandas method <code>corr()</code> to find the feature other than price that is most correlated with price.
```
df.corr()['price'].sort_values()
```
# Module 4: Model Development
Import libraries
```
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
```
We can Fit a linear regression model using the longitude feature <code> 'long'</code> and caculate the R^2.
```
X = df[['long']]
Y = df['price']
lm = LinearRegression()
lm
lm.fit(X,Y)
lm.score(X, Y)
```
### Question 6
Fit a linear regression model to predict the <code>'price'</code> using the feature 'sqft_living' then calculate the R^2. Take a screenshot of your code and the value of the R^2.
```
X2 = df[['sqft_living']]
lm2 = LinearRegression()
print(lm2)
lm2.fit(X2, Y)
lm2.score(X2, Y)
```
### Question 7
Fit a linear regression model to predict the 'price' using the list of features:
```
features =["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]
```
the calculate the R^2. Take a screenshot of your code
```
X3 = df[features]
lm3 = LinearRegression()
lm3.fit(X3, Y)
lm3.score(X3, Y)
```
#### this will help with Question 8
Create a list of tuples, the first element in the tuple contains the name of the estimator:
<code>'scale'</code>
<code>'polynomial'</code>
<code>'model'</code>
The second element in the tuple contains the model constructor
<code>StandardScaler()</code>
<code>PolynomialFeatures(include_bias=False)</code>
<code>LinearRegression()</code>
```
Input=[('scale',StandardScaler()),('polynomial', PolynomialFeatures(include_bias=False)),('model',LinearRegression())]
```
### Question 8
Use the list to create a pipeline object, predict the 'price', fit the object using the features in the list <code> features </code>, then fit the model and calculate the R^2
```
pipe=Pipeline(Input)
pipe
pipe.fit(X3,Y)
pipe.score(X3,Y)
```
# Module 5: MODEL EVALUATION AND REFINEMENT
import the necessary modules
```
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
print("done")
```
we will split the data into training and testing set
```
features =["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]
X = df[features ]
Y = df['price']
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.15, random_state=1)
print("number of test samples :", x_test.shape[0])
print("number of training samples:",x_train.shape[0])
```
### Question 9
Create and fit a Ridge regression object using the training data, setting the regularization parameter to 0.1 and calculate the R^2 using the test data.
```
from sklearn.linear_model import Ridge
RidgeModel = Ridge(alpha=0.1)
RidgeModel.fit(x_train, y_train)
RidgeModel.score(x_test, y_test)
```
### Question 10
Perform a second order polynomial transform on both the training data and testing data. Create and fit a Ridge regression object using the training data, setting the regularisation parameter to 0.1. Calculate the R^2 utilising the test data provided. Take a screenshot of your code and the R^2.
```
#Perform a second order polynomial transform on both the training data and testing data.
pr = PolynomialFeatures(degree=2)
x_train_pr = pr.fit_transform(x_train)
x_test_pr = pr.fit_transform(x_test)
pr
#Create and fit a Ridge regression object using the training data, setting the regularisation parameter to 0.1.
RidgeModel2 = Ridge(alpha=0.1)
RidgeModel2.fit(x_train_pr, y_train)
#Calculate the R^2 utilising the test data provided.
RidgeModel2.score(x_test_pr, y_test)
```
<p>Once you complete your notebook you will have to share it. Select the icon on the top right a marked in red in the image below, a dialogue box should open, select the option all content excluding sensitive code cells.</p>
<p><img width="600" src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DA0101EN/coursera/project/save_notebook.png" alt="share notebook" style="display: block; margin-left: auto; margin-right: auto;"/></p>
<p></p>
<p>You can then share the notebook via a URL by scrolling down as shown in the following image:</p>
<p style="text-align: center;"><img width="600" src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DA0101EN/coursera/project/url_notebook.png" alt="HTML" style="display: block; margin-left: auto; margin-right: auto;" /></p>
<p> </p>
<h2>About the Authors:</h2>
<a href="https://www.linkedin.com/in/joseph-s-50398b136/">Joseph Santarcangelo</a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
Other contributors: <a href="https://www.linkedin.com/in/michelleccarey/">Michelle Carey</a>, <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a">Mavis Zhou</a>
|
github_jupyter
|
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler,PolynomialFeatures
%matplotlib inline
file_name='https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DA0101EN/coursera/project/kc_house_data_NaN.csv'
df=pd.read_csv(file_name)
df.head()
df.dtypes
df.describe()
df.drop(columns=['id', 'Unnamed: 0'], axis=1, inplace=True)
df.describe()
print("number of NaN values for the column bedrooms :", df['bedrooms'].isnull().sum())
print("number of NaN values for the column bathrooms :", df['bathrooms'].isnull().sum())
mean=df['bedrooms'].mean()
df['bedrooms'].replace(np.nan, mean, inplace=True)
mean=df['bathrooms'].mean()
df['bathrooms'].replace(np.nan,mean, inplace=True)
print("number of NaN values for the column bedrooms :", df['bedrooms'].isnull().sum())
print("number of NaN values for the column bathrooms :", df['bathrooms'].isnull().sum())
df_floors = df['floors'].value_counts()
df_floors.to_frame()
sns.boxplot(x=df['waterfront'], y=df['price'], data=df)
sns.regplot(x='sqft_above', y='price', data=df, ci=None)
df.corr()['price'].sort_values()
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
X = df[['long']]
Y = df['price']
lm = LinearRegression()
lm
lm.fit(X,Y)
lm.score(X, Y)
X2 = df[['sqft_living']]
lm2 = LinearRegression()
print(lm2)
lm2.fit(X2, Y)
lm2.score(X2, Y)
features =["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]
X3 = df[features]
lm3 = LinearRegression()
lm3.fit(X3, Y)
lm3.score(X3, Y)
Input=[('scale',StandardScaler()),('polynomial', PolynomialFeatures(include_bias=False)),('model',LinearRegression())]
pipe=Pipeline(Input)
pipe
pipe.fit(X3,Y)
pipe.score(X3,Y)
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
print("done")
features =["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]
X = df[features ]
Y = df['price']
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.15, random_state=1)
print("number of test samples :", x_test.shape[0])
print("number of training samples:",x_train.shape[0])
from sklearn.linear_model import Ridge
RidgeModel = Ridge(alpha=0.1)
RidgeModel.fit(x_train, y_train)
RidgeModel.score(x_test, y_test)
#Perform a second order polynomial transform on both the training data and testing data.
pr = PolynomialFeatures(degree=2)
x_train_pr = pr.fit_transform(x_train)
x_test_pr = pr.fit_transform(x_test)
pr
#Create and fit a Ridge regression object using the training data, setting the regularisation parameter to 0.1.
RidgeModel2 = Ridge(alpha=0.1)
RidgeModel2.fit(x_train_pr, y_train)
#Calculate the R^2 utilising the test data provided.
RidgeModel2.score(x_test_pr, y_test)
| 0.686475 | 0.989521 |
# Example analysis of a PPG waveform using the vital_sqi package
The following notebook shows an example of PPG waveform processing using the vital_sqi package. The aim of the package is to automate signal quality classification for PPG waveforms. It is achieved by computing various signal quality indices for each signal segment and using them to form a decision.
## The pipeline can be briefly summarized as follows:
1. Load dataset under analysis
2. Preprocess and segment the dataset
3. Compute SQI for each dataset segment
4. Make decision for each segment
## Global Imports
```
import numpy as np
import warnings
import pandas as pd
import matplotlib.pyplot as plt
import vital_sqi
```
### Start by importing the signal via the PPG_reader function
The function expects a .csv or similar data format with named columns. The column names are used to separate between data column, timestamp columns and any additional information columns.
This returns a SignalSQI class that is compatible with other vital_sqi package functions, the main class members of interest are:
* signals: an ndarray of shape (m, n) where m is the number of rows and n is the number of channels of the signal
* sqi_indexes: an ndarray of shape (m, n) where m is the number of signal segments, n is the number of SQIs.
* sampling_rate: sampling rate in hertz (Hz)
```
from vital_sqi.data.signal_io import PPG_reader
#Prepare variables for analysis
sampling_rate = 100 #Hz
hp_filt_params = (1, 1) #(Hz, order)
lp_filt_params = (20, 4) #(Hz, order)
filter_type = 'butter'
trim_amount = 20 #s
segment_length = 10 #s
file_name = "ppg_smartcare.csv"
ppg_data = PPG_reader(os.path.join("../tests/test_data",file_name),
signal_idx=['PLETH'],
timestamp_idx= ['TIMESTAMP_MS'],
info_idx=['SPO2_PCT','PULSE_BPM','PERFUSION_INDEX'],
timestamp_unit='ms', sampling_rate=sampling_rate, start_datetime=None)
#We have loaded a single data column, therefore we only have 1D timeseries
print(ppg_data.signals)
#Plot a random 10s segment of the signal
s = np.arange(0,1000,1)
fig, ax = plt.subplots()
ax.plot(s, ppg_data.signals['PLETH'][4000:5000])
plt.show()
```
### Filter each signal channel by a band pass filter and trim
The filter_preprocess function applies two digital filters in succession. First high-pass filter followed by a low-pass. The touples used as function parameters stand for cutoff frequency and filter order respectively. Finally, a plot in this example shows the filtered signal centered around 0 as expected.
```
import vital_sqi.highlevel_functions.highlevel as sqi_hl
sqis = sqi_hl.compute_SQI(ppg_data.signals, '30s', 7, 6, ppg_data.wave_type, ppg_data.sampling_rate, 1)
print(sqis)
```
### Example peak detection on one segment
Using the Billauer peak detector we can illustrate the output of the peak detector
```
from vital_sqi.common.rpeak_detection import PeakDetector
detector = PeakDetector()
signal_seg = ppg_data.signals['PLETH'][1000:2000]
peak_list, trough_list = detector.ppg_detector(signal_seg, 7)
#Plot results of peak detection
s = np.arange(0,1000,1)
fig, ax = plt.subplots()
ax.plot(s, signal_seg)
if len(peak_list)!=0:
ax.scatter(peak_list,signal_seg[peak_list],color="r",marker="v")
if len(trough_list)!=0:
ax.scatter(trough_list,signal_seg[trough_list],color="b",marker="v")
plt.show()
warnings.filterwarnings("ignore")
#Plot a single period
fig, ax = plt.subplots()
ax.plot(signal_seg[trough_list[0]:trough_list[1]])
plt.show()
```
|
github_jupyter
|
import numpy as np
import warnings
import pandas as pd
import matplotlib.pyplot as plt
import vital_sqi
from vital_sqi.data.signal_io import PPG_reader
#Prepare variables for analysis
sampling_rate = 100 #Hz
hp_filt_params = (1, 1) #(Hz, order)
lp_filt_params = (20, 4) #(Hz, order)
filter_type = 'butter'
trim_amount = 20 #s
segment_length = 10 #s
file_name = "ppg_smartcare.csv"
ppg_data = PPG_reader(os.path.join("../tests/test_data",file_name),
signal_idx=['PLETH'],
timestamp_idx= ['TIMESTAMP_MS'],
info_idx=['SPO2_PCT','PULSE_BPM','PERFUSION_INDEX'],
timestamp_unit='ms', sampling_rate=sampling_rate, start_datetime=None)
#We have loaded a single data column, therefore we only have 1D timeseries
print(ppg_data.signals)
#Plot a random 10s segment of the signal
s = np.arange(0,1000,1)
fig, ax = plt.subplots()
ax.plot(s, ppg_data.signals['PLETH'][4000:5000])
plt.show()
import vital_sqi.highlevel_functions.highlevel as sqi_hl
sqis = sqi_hl.compute_SQI(ppg_data.signals, '30s', 7, 6, ppg_data.wave_type, ppg_data.sampling_rate, 1)
print(sqis)
from vital_sqi.common.rpeak_detection import PeakDetector
detector = PeakDetector()
signal_seg = ppg_data.signals['PLETH'][1000:2000]
peak_list, trough_list = detector.ppg_detector(signal_seg, 7)
#Plot results of peak detection
s = np.arange(0,1000,1)
fig, ax = plt.subplots()
ax.plot(s, signal_seg)
if len(peak_list)!=0:
ax.scatter(peak_list,signal_seg[peak_list],color="r",marker="v")
if len(trough_list)!=0:
ax.scatter(trough_list,signal_seg[trough_list],color="b",marker="v")
plt.show()
warnings.filterwarnings("ignore")
#Plot a single period
fig, ax = plt.subplots()
ax.plot(signal_seg[trough_list[0]:trough_list[1]])
plt.show()
| 0.499756 | 0.981858 |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow as tf
from tensorflow import keras
dataset = pd.read_csv('../input/digit-recognizer/train.csv')
print(dataset.shape)
# Pixel0 ~ Pixel783までの計784カラム, sqrt(784) = 28 * 28 の画像データ
label_counts = dataset['label'].value_counts()
print(f'Label counts:\n {label_counts}')
fig, ax = plt.subplots(4,5)
fig.set_figheight(5)
num_read_img = 20
for image_index in range(0,num_read_img):
pixels = dataset.iloc[image_index,1:].values.reshape(28,28)
draw_axis= ax[int(image_index/5),int(image_index%5)]
draw_axis.imshow(pixels, cmap='gray')
draw_axis.set_title(dataset.iloc[image_index,0])
draw_axis.axes.xaxis.set_visible(False)
draw_axis.axes.yaxis.set_visible(False)
plt.tight_layout()
plt.show()
label = dataset.loc[:,'label']
#label = pd.get_dummies(label, drop_first=False)
images = dataset.iloc[:,1:].values
# https://keras.io/ja/layers/convolutional/
# 入力: 'data_format='channels_first'の場合, (batch_size, channels, rows, cols)の4階テンソル'
# 'data_format='channels_last'の場合, (batch_size, rows, cols, channels)の4階テンソルになります.
# Conv2D層への入力のため、4次元にreshpae。 batsh_sizeはtrain_test_splitで変わるのですべてを意味する"-1"
images = images.reshape(-1,28,28,1)/255
# labelは名義尺度のため、そのままでは数値尺度として扱われてしまう?
# ということでOnehot-encoding
label = pd.get_dummies(label, columns=['label'], drop_first=False)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(images,label, test_size=0.2)
print(X_train.shape)
datagen = keras.preprocessing.image.ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
rotation_range=10, # randomly rotate images in the range (degrees, 0 to 180)
zoom_range = 0.1, # Randomly zoom image
width_shift_range=0.1, # randomly shift images horizontally (fraction of total width)
height_shift_range=0.1, # randomly shift images vertically (fraction of total height)
horizontal_flip=False, # randomly flip images
vertical_flip=False) # randomly flip images
datagen.fit(X_train)
datagen.flow(X_train, batch_size=32, save_to_dir='../output/datagen', save_format='png')
# CNNの初期化。単純なSequentialモデルで作成。
cnn = tf.keras.models.Sequential()
# 畳み込み https://keras.io/ja/layers/convolutional/
# 128x128 RGB画像ではinput_shape=(128, 128, 3)となります.
# 最初のレイヤーだけは、入り口となる入力シェイプが必要
cnn.add(tf.keras.layers.Conv2D(filters=32, kernel_regularizer=keras.regularizers.l2(0.001), kernel_size=(5,5), padding="same", activation="relu", input_shape=[28, 28, 1], data_format='channels_last'))
cnn.add(tf.keras.layers.LeakyReLU())
# tf.keras.layers.BatchNormalization https://www.tensorflow.org/api_docs/python/tf/keras/layers/BatchNormalization
# Batch Normalization:ニューラルネットワークの学習を加速させる汎用的で強力な手法 - DeepAge https://deepage.net/deep_learning/2016/10/26/batch_normalization.html
cnn.add(tf.keras.layers.BatchNormalization())
# Poolingにより、ダウンサンプリング
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2, padding='valid'))
# 画像サイズはPoolingにより14*14に
cnn.add(tf.keras.layers.Dropout(0.25))
# 2層目の中間層を追加
cnn.add(tf.keras.layers.Conv2D(filters=64, kernel_regularizer=keras.regularizers.l2(0.001), kernel_size=(3,3), padding="same", activation="relu"))
cnn.add(tf.keras.layers.LeakyReLU())
cnn.add(tf.keras.layers.BatchNormalization())
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2, padding='valid'))
# 画像サイズはPoolingにより7*7に
cnn.add(tf.keras.layers.Dropout(0.25))
# 3層目の中間層を追加
cnn.add(tf.keras.layers.Conv2D(filters=64, kernel_regularizer=keras.regularizers.l2(0.001), kernel_size=(3,3), padding="same", activation="relu"))
cnn.add(tf.keras.layers.LeakyReLU())
cnn.add(tf.keras.layers.BatchNormalization())
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2, padding='valid'))
# 画像サイズはPoolingにより7*7に
cnn.add(tf.keras.layers.Dropout(0.3))
# Flattening
cnn.add(tf.keras.layers.Flatten())
# 接続
# unitsは レイヤーの出力形状
cnn.add(tf.keras.layers.Dense(units=128, kernel_regularizer=keras.regularizers.l2(0.001), activation='relu'))
cnn.add(tf.keras.layers.Dropout(0.5))
# 出力層
#cnn.add(tf.keras.layers.Dense(units=10, activation='sigmoid'))
cnn.add(tf.keras.layers.Dense(10, activation='softmax'))
optimizer = tf.keras.optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0)
#optimizer = tf.keras.optimizers.Adam(lr=0.005, decay=5e-4)
# Compiling the CNN
# 評価関数の選定 -> https://keras.io/ja/metrics/
# The difference between sparse_categorical_crossentropy and categorical_crossentropy is whether your targets are one-hot encoded.
cnn.compile(optimizer = optimizer, loss = tf.keras.losses.categorical_crossentropy, metrics = ['accuracy'])
checkpoint_name = 'BestModel.hdf5'
checkpoint = tf.keras.callbacks.ModelCheckpoint(checkpoint_name, monitor='val_accuracy', verbose=1, save_best_only=True, mode='auto')
reduce_learning = tf.keras.callbacks.ReduceLROnPlateau(monitor='val_accuracy', patience=3, verbose=1, factor=0.5, min_lr=0.00001)
callback_list = [checkpoint, reduce_learning]
history = cnn.fit(datagen.flow(X_train,y_train, batch_size=1024), validation_data=(X_test, y_test), epochs = 100, batch_size = 1024, callbacks=callback_list)
model = keras.models.load_model('BestModel.hdf5')
test_dataset = pd.read_csv('../input/digit-recognizer/test.csv')
y_pred = model.predict(test_dataset.iloc[:,:].values.reshape(-1,28,28,1)/255)
imageId = np.arange(1,28001)
y_pred_selected = np.argmax(y_pred,axis=1)
print(y_pred_selected)
result_table = pd.DataFrame({ 'ImageId': imageId,
'Label': y_pred_selected })
result_table.to_csv('prediction.csv', index=False)
print(X_train.shape)
dataaa = datagen.fit(X_train)
print(X_train.shape)
dataaa
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow as tf
from tensorflow import keras
dataset = pd.read_csv('../input/digit-recognizer/train.csv')
print(dataset.shape)
# Pixel0 ~ Pixel783までの計784カラム, sqrt(784) = 28 * 28 の画像データ
label_counts = dataset['label'].value_counts()
print(f'Label counts:\n {label_counts}')
fig, ax = plt.subplots(4,5)
fig.set_figheight(5)
num_read_img = 20
for image_index in range(0,num_read_img):
pixels = dataset.iloc[image_index,1:].values.reshape(28,28)
draw_axis= ax[int(image_index/5),int(image_index%5)]
draw_axis.imshow(pixels, cmap='gray')
draw_axis.set_title(dataset.iloc[image_index,0])
draw_axis.axes.xaxis.set_visible(False)
draw_axis.axes.yaxis.set_visible(False)
plt.tight_layout()
plt.show()
label = dataset.loc[:,'label']
#label = pd.get_dummies(label, drop_first=False)
images = dataset.iloc[:,1:].values
# https://keras.io/ja/layers/convolutional/
# 入力: 'data_format='channels_first'の場合, (batch_size, channels, rows, cols)の4階テンソル'
# 'data_format='channels_last'の場合, (batch_size, rows, cols, channels)の4階テンソルになります.
# Conv2D層への入力のため、4次元にreshpae。 batsh_sizeはtrain_test_splitで変わるのですべてを意味する"-1"
images = images.reshape(-1,28,28,1)/255
# labelは名義尺度のため、そのままでは数値尺度として扱われてしまう?
# ということでOnehot-encoding
label = pd.get_dummies(label, columns=['label'], drop_first=False)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(images,label, test_size=0.2)
print(X_train.shape)
datagen = keras.preprocessing.image.ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
rotation_range=10, # randomly rotate images in the range (degrees, 0 to 180)
zoom_range = 0.1, # Randomly zoom image
width_shift_range=0.1, # randomly shift images horizontally (fraction of total width)
height_shift_range=0.1, # randomly shift images vertically (fraction of total height)
horizontal_flip=False, # randomly flip images
vertical_flip=False) # randomly flip images
datagen.fit(X_train)
datagen.flow(X_train, batch_size=32, save_to_dir='../output/datagen', save_format='png')
# CNNの初期化。単純なSequentialモデルで作成。
cnn = tf.keras.models.Sequential()
# 畳み込み https://keras.io/ja/layers/convolutional/
# 128x128 RGB画像ではinput_shape=(128, 128, 3)となります.
# 最初のレイヤーだけは、入り口となる入力シェイプが必要
cnn.add(tf.keras.layers.Conv2D(filters=32, kernel_regularizer=keras.regularizers.l2(0.001), kernel_size=(5,5), padding="same", activation="relu", input_shape=[28, 28, 1], data_format='channels_last'))
cnn.add(tf.keras.layers.LeakyReLU())
# tf.keras.layers.BatchNormalization https://www.tensorflow.org/api_docs/python/tf/keras/layers/BatchNormalization
# Batch Normalization:ニューラルネットワークの学習を加速させる汎用的で強力な手法 - DeepAge https://deepage.net/deep_learning/2016/10/26/batch_normalization.html
cnn.add(tf.keras.layers.BatchNormalization())
# Poolingにより、ダウンサンプリング
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2, padding='valid'))
# 画像サイズはPoolingにより14*14に
cnn.add(tf.keras.layers.Dropout(0.25))
# 2層目の中間層を追加
cnn.add(tf.keras.layers.Conv2D(filters=64, kernel_regularizer=keras.regularizers.l2(0.001), kernel_size=(3,3), padding="same", activation="relu"))
cnn.add(tf.keras.layers.LeakyReLU())
cnn.add(tf.keras.layers.BatchNormalization())
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2, padding='valid'))
# 画像サイズはPoolingにより7*7に
cnn.add(tf.keras.layers.Dropout(0.25))
# 3層目の中間層を追加
cnn.add(tf.keras.layers.Conv2D(filters=64, kernel_regularizer=keras.regularizers.l2(0.001), kernel_size=(3,3), padding="same", activation="relu"))
cnn.add(tf.keras.layers.LeakyReLU())
cnn.add(tf.keras.layers.BatchNormalization())
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2, padding='valid'))
# 画像サイズはPoolingにより7*7に
cnn.add(tf.keras.layers.Dropout(0.3))
# Flattening
cnn.add(tf.keras.layers.Flatten())
# 接続
# unitsは レイヤーの出力形状
cnn.add(tf.keras.layers.Dense(units=128, kernel_regularizer=keras.regularizers.l2(0.001), activation='relu'))
cnn.add(tf.keras.layers.Dropout(0.5))
# 出力層
#cnn.add(tf.keras.layers.Dense(units=10, activation='sigmoid'))
cnn.add(tf.keras.layers.Dense(10, activation='softmax'))
optimizer = tf.keras.optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0)
#optimizer = tf.keras.optimizers.Adam(lr=0.005, decay=5e-4)
# Compiling the CNN
# 評価関数の選定 -> https://keras.io/ja/metrics/
# The difference between sparse_categorical_crossentropy and categorical_crossentropy is whether your targets are one-hot encoded.
cnn.compile(optimizer = optimizer, loss = tf.keras.losses.categorical_crossentropy, metrics = ['accuracy'])
checkpoint_name = 'BestModel.hdf5'
checkpoint = tf.keras.callbacks.ModelCheckpoint(checkpoint_name, monitor='val_accuracy', verbose=1, save_best_only=True, mode='auto')
reduce_learning = tf.keras.callbacks.ReduceLROnPlateau(monitor='val_accuracy', patience=3, verbose=1, factor=0.5, min_lr=0.00001)
callback_list = [checkpoint, reduce_learning]
history = cnn.fit(datagen.flow(X_train,y_train, batch_size=1024), validation_data=(X_test, y_test), epochs = 100, batch_size = 1024, callbacks=callback_list)
model = keras.models.load_model('BestModel.hdf5')
test_dataset = pd.read_csv('../input/digit-recognizer/test.csv')
y_pred = model.predict(test_dataset.iloc[:,:].values.reshape(-1,28,28,1)/255)
imageId = np.arange(1,28001)
y_pred_selected = np.argmax(y_pred,axis=1)
print(y_pred_selected)
result_table = pd.DataFrame({ 'ImageId': imageId,
'Label': y_pred_selected })
result_table.to_csv('prediction.csv', index=False)
print(X_train.shape)
dataaa = datagen.fit(X_train)
print(X_train.shape)
dataaa
| 0.535098 | 0.617369 |
# Math and Data Types
This might be old news to you, as much of things so far has been, but it may be a nice refresher. Let's run through it.
```
print("hi")
```
This is the `print()` function. It prints stuff out to terminal.
```
print("hi", "there")
```
The `print` function takes multiple arguments (also called parameters). These arguments go between the parenthesis `()`. Each argument is separated by a comma. For `print`, a space is put between each argument. You could just type "hi there", but I just wanted to demonstrate how this worked.
```
x = 5
```
This is a variable. We've created a variable called `x`, and we've set its initial value to `5`. This value can change. When referenced, the value of the variable is used. What does that mean?
```
print("x is", x)
```
This means that `5` will take the place of the `x` outside quotations here. When there is text inside either single or double quotation marks, it is treated as text data. We call this a string. Why? Each letter/number/punctuation/etc is called a character. A string is a sequence (or string) of characters put together. If there is text outside of quotations, Python attempts to treat it as code. In this case, it sees `x` outside of quotations, so it looks for either a variable or function called `x`. It finds the variable we defined above, and it substitutes the value of the variable into the print function.
We can also modify variables.
```
x = x + 1
print("added 1 to x:", x)
```
You'll see that x is now `6`. In line 18, we set the new value of `x` to the existing value of `x` plus one. Some people find this remarkably difficult to understand at first. Just remembered that when we're doing assignment (or setting the value of things), whatever is right of the equals sign happens first. In this case, `x + 1` is evaluated to `5 + 1`, which then becomes `6`. Then `x` is set to `6`.
We can also be a liiiiittle lazier
```
x += 1
print("added 1 more to x:", x)
```
This is the same as the previous code bloc, just written differently.
Let's take a step aside for a moment. Notice that `x` was set in the previous code block, but we were able to use it again here. Jupyter Notebook maintains state within a notebook. Remember talking about how each code block is numbered in the order it was ran? Since the state of the notebook is maintained, this ordering helps you understand the current state of the notebook. If we run code blocks in a different order, the values of variables would be set differently. Jupyter Notebook denotes this to reduce potential confusion.
Moving on, you can also subtract
```
x -= 1
print("removed 1 from x:", x)
```
You can multiply
```
x *= 2
print("multiplied x by 2:", x)
```
You can also divide
```
x /= 2
print("divided x by 2:", x)
```
You'll notice that `x` now appears as `6.0` instead of `6`. We'll cover why in a minute
You can also floor divide, which cuts off any non-whole-number amount
```
print("x floor divided by 4:", x // 4)
```
There's also the modulo operator, which will give you the remainder of a division operation
```
print("x modulo 4:", x % 4)
```
Okay, now why did dividing give us `6.0` instead of `6`? This is due to the concept of data types. Python tries to make things such that you don't need to worry about data types, but there really is no escaping it. Initially, `x` is an integer - a whole number. However, the division operation does not produce an integer. It produces a floating point number, or a decimal. Normally, I'd skip what floating point means, but if you're doing number crunching, it's important to know. Let's say we have a number like this: `436,312,683,904,124,673`. Big number. The computer doesn't have unlimited data. It has limited amounts of data it can store, and it wants to be efficient. Representing that number in binary would be quite large. Similar to laboratory sciences, we use approximations. In lab science, we might represent this number as `4.36312 x 10^16`. We cut off the remaining numbers because they're not significant with respect to the size of this number. Computers do similar things. A computer only wants to use so much data to represent numbers, so it will only store the most significant digits and a reference of where the decimal (or point) is located. In this method, the point can float or move around depending on the size of the number. Hence, we call this a floating point number. This is the default way to represent decimals in Python. Since division may not return a whole number, it outputs a floating point in all cases for purposes of consistency. Other mathematical operations return the same data type as whatever was input. The reason for this is that your code likely doesn't expect data to change type terribly often. Division is kind of a special case in this regard.
So how do we get it back to an integer?
```
print("x back as an integer:", int(x))
```
Integer in python is referenced as `int`. There is an `int` function that takes whatever the input is and converts it to an integer, if possible. Similar functions exist for `float` and `str` (string). Play with these and see what you get.
The last thing to cover is comments. Comments are text within your code files that isn't run. This is useful for temporarily disabling code or for adding notes within your code. With Jupyter, you may think that comments may not be necessary, but there are cases where you would want some body of code to be in continuous block, run as an atomic unit, rather than split up into smaller code blocks. To write a comment, just toss a `#` before the code you don't want executed. Everything after the `#` on that line will be ignored by Python.
```
# This does nothing!
```
## Now it's Your Turn
Now that you've got some basics down, try it out yourself. Throughout this, I'll have code blocks for you to run. They'll give you feedback on whether what you've written is correct. Let's dive in.
### Variable Setting and Basic Math
In the below code block, between the noted comments, set variables `m`, `x`, and `b`. Next, calculate a new variable `y` using the [formula for a line](https://www.mathsisfun.com/equation_of_line.html) (I'm trying to avoid writing it here).
```
# SET M, X, AND B HERE
# DONE SETTING M, X, AND B
print('m:', m)
print('x:', x)
print('b:', b)
# SET Y HERE
# DONE SETTING Y
print('y:', y)
```
|
github_jupyter
|
print("hi")
print("hi", "there")
x = 5
print("x is", x)
x = x + 1
print("added 1 to x:", x)
x += 1
print("added 1 more to x:", x)
x -= 1
print("removed 1 from x:", x)
x *= 2
print("multiplied x by 2:", x)
x /= 2
print("divided x by 2:", x)
print("x floor divided by 4:", x // 4)
print("x modulo 4:", x % 4)
print("x back as an integer:", int(x))
# This does nothing!
# SET M, X, AND B HERE
# DONE SETTING M, X, AND B
print('m:', m)
print('x:', x)
print('b:', b)
# SET Y HERE
# DONE SETTING Y
print('y:', y)
| 0.19521 | 0.9851 |
# 99 Scala Exercises (46 to 50)
### 46\. Truth tables for logical expressions.
Define functions and, or, nand, nor, xor, impl, and equ (for logical equivalence) which return true or false according to the result of their respective operations; e.g. and(A, B) is true if and only if both A and B are true.
```
import scalaz.effect.IO._
import scalaz.effect.IO
def and(a: Boolean, b: Boolean): Boolean = a && b
def or(a: Boolean, b: Boolean): Boolean = a || b
def xor(a: Boolean, b: Boolean): Boolean = a ^ b
def nand(a: Boolean, b: Boolean): Boolean = !and(a, b)
def nor(a: Boolean, b: Boolean): Boolean = !or(a, b)
def impl(a: Boolean, b: Boolean): Boolean = !a || b
def equ(a: Boolean, b: Boolean): Boolean = a == b
def not(a: Boolean): Boolean = !a
def table2(f: (Boolean, Boolean) => Boolean): IO[Unit] = for {
_ <- putStrLn("A B result")
_ <- putStrLn(s"True True ${ f(true, true) }")
_ <- putStrLn(s"True False ${ f(true, false) }")
_ <- putStrLn(s"False True ${ f(false, true) }")
_ <- putStrLn(s"False False ${ f(false, false) }")
} yield ()
table2(or).unsafePerformIO
```
### 47\. Truth tables for logical expressions (2).
Continue problem P46 by redefining and, or, etc as operators. (i.e. make them methods of a new class with an implicit conversion from Boolean.) not will have to be left as a object method.
```
implicit class BooleanOps(val a: Boolean) {
def not(): Boolean = !a
def and(b: Boolean): Boolean = a && b
def or(b: Boolean): Boolean = a || b
def xor(b: Boolean): Boolean = a ^ b
def nand(b: Boolean): Boolean = !(a and b)
def nor(b: Boolean): Boolean = !(a or b)
def impl(b: Boolean): Boolean = !a || b
def equ(b: Boolean): Boolean = a == b
}
table2((a: Boolean, b: Boolean) => a and (a or not(b))).unsafePerformIO
```
### 49\. Gray code.
An n-bit Gray code is a sequence of n-bit strings constructed according to certain rules. For example,
n = 1: C(1) = ("0", "1").
n = 2: C(2) = ("00", "01", "11", "10").
n = 3: C(3) = ("000", "001", "011", "010", "110", "111", "101", "100").
Find out the construction rules and write a function to generate Gray codes.
```
// Function wrapper that allow memoization.
case class Memoize[A,B](val f: A => B) extends (A => B) {
val cache = collection.mutable.HashMap[A,B]()
def apply(a: A): B = cache getOrElseUpdate(a, f(a))
}
val gray: Memoize[Int, List[String]] = Memoize { n =>
n match {
case 2 => List("00", "01", "11", "10")
case _ => {
val g = gray(n-1)
g.map("0"+_) ++ g.reverse.map("1"+_)
}
}
}
gray(3)
```
### Huffman code.
First of all, consult a good book on discrete mathematics or algorithms for a detailed description of Huffman codes!
We suppose a set of symbols with their frequencies, given as a list of (S, F) Tuples. E.g. (("a", 45), ("b", 13), ("c", 12), ("d", 16), ("e", 9), ("f", 5)). Our objective is to construct a list of (S, C) Tuples, where C is the Huffman code word for the symbol S.
```
// Simple binary tree.
sealed trait HTree {
def weight(): Int = this match {
case HLeaf(_, f) => f
case HFork(s, _, _) => s
}
def merge(other: HTree): HTree =
HFork(this.weight + other.weight, this, other)
}
final case class HLeaf(s: String, freq: Int) extends HTree
final case class HFork(sum: Int, l: HTree, r: HTree) extends HTree
implicit object HTreeOrdering extends Ordering[HTree] {
def compare(a: HTree, b: HTree): Int = a.weight compare b.weight
}
// Insert element in a sorted list.
def insertBy[A](l: List[A], x: A)(implicit ord: Ordering[A]): List[A] = {
val (first, last) = l partition { ord.lteq(_, x) }
first:::x::last
}
def buildTree(sl: List[(String, Int)]): Option[HTree] = {
val nl = sl.sortBy(_._2) map { case (s, f) => HLeaf(s, f) }
@annotation.tailrec
def inner(accum: List[HTree]): Option[HTree] = accum match {
case x::y::xs => inner(insertBy(xs, x merge y))
case x::Nil => Some(x)
case _ => None
}
inner(nl)
}
def codify(tree: HTree): List[(String, String)] = {
def inner(tree: HTree, prefix: String): List[(String, String)] = tree match {
case HLeaf(s, _) => List((s, prefix))
case HFork(_, l, r) => inner(l, prefix + "0") ++ inner(r, prefix + "1")
}
inner(tree, "")
}
def huffman(sl: List[(String, Int)]): Option[List[(String, String)]] =
buildTree(sl) map(codify(_).sortBy(_._1))
huffman(List(("a", 45), ("b", 13), ("c", 12), ("d", 16), ("e", 9), ("f", 5)))
```
|
github_jupyter
|
import scalaz.effect.IO._
import scalaz.effect.IO
def and(a: Boolean, b: Boolean): Boolean = a && b
def or(a: Boolean, b: Boolean): Boolean = a || b
def xor(a: Boolean, b: Boolean): Boolean = a ^ b
def nand(a: Boolean, b: Boolean): Boolean = !and(a, b)
def nor(a: Boolean, b: Boolean): Boolean = !or(a, b)
def impl(a: Boolean, b: Boolean): Boolean = !a || b
def equ(a: Boolean, b: Boolean): Boolean = a == b
def not(a: Boolean): Boolean = !a
def table2(f: (Boolean, Boolean) => Boolean): IO[Unit] = for {
_ <- putStrLn("A B result")
_ <- putStrLn(s"True True ${ f(true, true) }")
_ <- putStrLn(s"True False ${ f(true, false) }")
_ <- putStrLn(s"False True ${ f(false, true) }")
_ <- putStrLn(s"False False ${ f(false, false) }")
} yield ()
table2(or).unsafePerformIO
implicit class BooleanOps(val a: Boolean) {
def not(): Boolean = !a
def and(b: Boolean): Boolean = a && b
def or(b: Boolean): Boolean = a || b
def xor(b: Boolean): Boolean = a ^ b
def nand(b: Boolean): Boolean = !(a and b)
def nor(b: Boolean): Boolean = !(a or b)
def impl(b: Boolean): Boolean = !a || b
def equ(b: Boolean): Boolean = a == b
}
table2((a: Boolean, b: Boolean) => a and (a or not(b))).unsafePerformIO
// Function wrapper that allow memoization.
case class Memoize[A,B](val f: A => B) extends (A => B) {
val cache = collection.mutable.HashMap[A,B]()
def apply(a: A): B = cache getOrElseUpdate(a, f(a))
}
val gray: Memoize[Int, List[String]] = Memoize { n =>
n match {
case 2 => List("00", "01", "11", "10")
case _ => {
val g = gray(n-1)
g.map("0"+_) ++ g.reverse.map("1"+_)
}
}
}
gray(3)
// Simple binary tree.
sealed trait HTree {
def weight(): Int = this match {
case HLeaf(_, f) => f
case HFork(s, _, _) => s
}
def merge(other: HTree): HTree =
HFork(this.weight + other.weight, this, other)
}
final case class HLeaf(s: String, freq: Int) extends HTree
final case class HFork(sum: Int, l: HTree, r: HTree) extends HTree
implicit object HTreeOrdering extends Ordering[HTree] {
def compare(a: HTree, b: HTree): Int = a.weight compare b.weight
}
// Insert element in a sorted list.
def insertBy[A](l: List[A], x: A)(implicit ord: Ordering[A]): List[A] = {
val (first, last) = l partition { ord.lteq(_, x) }
first:::x::last
}
def buildTree(sl: List[(String, Int)]): Option[HTree] = {
val nl = sl.sortBy(_._2) map { case (s, f) => HLeaf(s, f) }
@annotation.tailrec
def inner(accum: List[HTree]): Option[HTree] = accum match {
case x::y::xs => inner(insertBy(xs, x merge y))
case x::Nil => Some(x)
case _ => None
}
inner(nl)
}
def codify(tree: HTree): List[(String, String)] = {
def inner(tree: HTree, prefix: String): List[(String, String)] = tree match {
case HLeaf(s, _) => List((s, prefix))
case HFork(_, l, r) => inner(l, prefix + "0") ++ inner(r, prefix + "1")
}
inner(tree, "")
}
def huffman(sl: List[(String, Int)]): Option[List[(String, String)]] =
buildTree(sl) map(codify(_).sortBy(_._1))
huffman(List(("a", 45), ("b", 13), ("c", 12), ("d", 16), ("e", 9), ("f", 5)))
| 0.520253 | 0.876211 |
<img style="float: left;padding: 1.3em" src="https://indico.in2p3.fr/event/18313/logo-786578160.png">
# Gravitational Wave Open Data Workshop #3
#### Tutorial 1.2: Introduction to GWpy
This tutorial will briefly describe GWpy, a python package for gravitational astrophysics, and walk-through how you can use this to speed up access to, and processing of, GWOSC data.
[Click this link to view this tutorial in Google Colaboratory](https://colab.research.google.com/github/gw-odw/odw-2019/blob/master/Day_1/Tuto%201.2%20Open%20Data%20access%20with%20GWpy.ipynb)
<div class="alert alert-info">This notebook were generated using python 3.7, but should work on python 2.7, 3.6, or 3.7.</div>
## Installation (execute only if running on a cloud platform or if you haven't done the installation already!)
Note: we use [`pip`](https://docs.python.org/3.6/installing/), but **it is recommended** to use [conda](https://docs.ligo.org/lscsoft/conda/) on your own machine, as explained in the [installation instructions](https://github.com/gw-odw/odw-2019/blob/master/setup.md). This usage might look a little different than normal, simply because we want to do this directly from the notebook.
```
# -- Uncomment following line if running in Google Colab
#! pip install -q 'gwpy==1.0.1'
```
**Important:** With Google Colab, you may need to restart the runtime after running the cell above.
## Initialization
```
import gwpy
print(gwpy.__version__)
```
## A note on object-oriented programming
Before we dive too deeply, its worth a quick aside on object-oriented programming (OOP).
GWpy is heavily object-oriented, meaning almost all of the code you run using GWpy is based around an object of some type, e.g. `TimeSeries`.
Most of the methods (functions) we will use are attached to an object, rather than standing alone, meaning you should have a pretty good idea of what sort of data you are dealing with (without having to read the documentation!).
For a quick overview of object-oriented programming in Python, see [this blog post by Jeff Knupp](https://jeffknupp.com/blog/2014/06/18/improve-your-python-python-classes-and-object-oriented-programming/).
## Handling data in the time domain
#### Finding open data
We have seen already that the `gwosc` module can be used to query for what data are available on GWOSC.
The next thing to do is to actually read some open data. Let's try to get some for GW150914, the first direct detection of an astrophysical gravitational-wave signal from a BBH (binary black hole system).
We can use the [`TimeSeries.fetch_open_data`](https://gwpy.github.io/docs/stable/api/gwpy.timeseries.TimeSeries.html#gwpy.timeseries.TimeSeries.fetch_open_data) method to download data directly from https://www.gw-openscience.org, but we need to know the GPS times.
We can query for the GPS time of an event as follows:
```
from gwosc.datasets import event_gps
gps = event_gps('GW150914')
print(gps)
```
Now we can build a `[start, end)` GPS segment to 10 seconds around this time, using integers for convenience:
```
segment = (int(gps)-5, int(gps)+5)
print(segment)
```
and can now query for the full data.
For this example we choose to retrieve data for the LIGO-Livingston interferometer, using the identifier `'L1'`.
We could have chosen any of
- `'G1`' - GEO600
- `'H1'` - LIGO-Hanford
- `'L1'` - LIGO-Livingston
- `'V1'` - (Advanced) Virgo
In the future, the Japanese observatory KAGRA will come online, with the identifier `'K1'`.
```
from gwpy.timeseries import TimeSeries
ldata = TimeSeries.fetch_open_data('L1', *segment, verbose=True)
print(ldata)
```
##### The `verbose=True` flag lets us see that GWpy has discovered two files that provides the data for the given interval, downloaded them, and loaded the data.
The files are not stored permanently, so next time you do the same call, it will be downloaded again, however, if you know you might repeat the same call many times, you can use `cache=True` to store the file on your computer.
Notes:
* To read data from a local file instead of from the GWOSC server, we can use [`TimeSeries.read`](https://gwpy.github.io/docs/stable/api/gwpy.timeseries.TimeSeries.html#gwpy.timeseries.TimeSeries.read) method.
We have now downloaded real LIGO data for GW150914! These are the actual data used in the analysis that discovered the first binary black hole merger.
To sanity check things, we can easily make a plot, using the [`plot()`](https://gwpy.github.io/docs/stable/timeseries/plot.html) method of the `data` `TimeSeries`.
<div class="alert alert-info">
Since this is the first time we are plotting something in this notebook, we need to make configure `matplotlib` (the plotting library) to work within the notebook properly:
</div>
Matplotlib documentation can be found [`here`](https://matplotlib.org/contents.html).
```
%matplotlib inline
plot = ldata.plot()
```
Notes: There are alternatives ways to access the GWOSC data.
* [`readligo`](https://losc.ligo.org/s/sample_code/readligo.py) is a light-weight Python module that returns the time series into a Numpy array.
* The [PyCBC](http://github.com/ligo-cbc/pycbc) package has the `pycbc.frame.query_and_read_frame` and `pycbc.frame.read_frame` methods. We use [PyCBC](http://github.com/ligo-cbc/pycbc) in Tutorial 2.1, 2.2 and 2.3.
## Handling data in the frequency domain using the Fourier transform
The [Fourier transform](https://en.wikipedia.org/wiki/Fourier_transform) is a widely-used mathematical tool to expose the frequency-domain content of a time-domain signal, meaning we can see which frequencies contian lots of power, and which have less.
We can calculate the Fourier transform of our `TimeSeries` using the [`fft()`](https://gwpy.github.io/docs/stable/api/gwpy.timeseries.TimeSeries.html#gwpy.timeseries.TimeSeries.fft) method:
```
fft = ldata.fft()
print(fft)
```
The result is a [`FrequencySeries`](https://gwpy.github.io/docs/stable/frequencyseries/), with complex amplitude, representing the amplitude and phase of each frequency in our data.
We can use `abs()` to extract the amplitude and plot that:
```
plot = fft.abs().plot(xscale="log", yscale="log")
plot.show(warn=False)
```
This doesn't look correct at all!
The problem is that the FFT works under the assumption that our data are periodic, which means that the edges of our data look like discontinuities when transformed.
We need to apply a window function to our time-domain data before transforming, which we can do using the [`scipy.signal`](https://docs.scipy.org/doc/scipy/reference/signal.html) module:
```
from scipy.signal import get_window
window = get_window('hann', ldata.size)
lwin = ldata * window
```
Let's try our transform again and see what we get
```
fftamp = lwin.fft().abs()
plot = fftamp.plot(xscale="log", yscale="log")
plot.show(warn=False)
```
This looks a little more like what we expect for the amplitude spectral density of a gravitational-wave detector.
## Calculating the power spectral density
In practice, we typically use a large number of FFTs to estimate an averages power spectral density over a long period of data.
We can do this using the [`asd()`](https://gwpy.github.io/docs/stable/api/gwpy.timeseries.TimeSeries.html#gwpy.timeseries.TimeSeries.asd) method, which uses [Welch's method](https://en.wikipedia.org/wiki/Welch%27s_method) to combine FFTs of overlapping, windowed chunks of data.
```
asd = ldata.asd(fftlength=4, method="median")
plot = asd.plot()
plot.show(warn=False)
ax = plot.gca()
ax.set_xlim(10, 1400)
ax.set_ylim(2e-24, 1e-20)
plot
```
The ASD is a standard tool used to study the frequency-domain sensitivity of a gravitational-wave detector.
For the LIGO-Livingston data we loaded, we can see large spikes at certain frequencies, including
- ~300 Hz
- ~500 Hz
- ~1000 Hz
The [O2 spectral lines](https://www.gw-openscience.org/o2speclines/) page on GWOSC describes a number of these spectral features for O2, with some of them being forced upon us, and some being deliberately introduced to help with interferometer control.
Loading more data allows for more FFTs to be averaged during the ASD calculation, meaning random variations get averaged out, and we can see more detail:
```
ldata2 = TimeSeries.fetch_open_data('L1', int(gps)-512, int(gps)+512, cache=True)
lasd2 = ldata2.asd(fftlength=4, method="median")
plot = lasd2.plot()
ax = plot.gca()
ax.set_xlim(10, 1400)
ax.set_ylim(5e-24, 1e-20)
plot.show(warn=False)
```
Now we can see some more features, including sets of lines around ~30 Hz and ~65 Hz, and some more isolate lines through the more sensitive region.
For comparison, we can load the LIGO-Hanford data and plot that as well:
```
# get Hanford data
hdata2 = TimeSeries.fetch_open_data('H1', int(gps)-512, int(gps)+512, cache=True)
hasd2 = hdata2.asd(fftlength=4, method="median")
# and plot using standard colours
ax.plot(hasd2, label='LIGO-Hanford', color='gwpy:ligo-hanford')
# update the Livingston line to use standard colour, and have a label
lline = ax.lines[0]
lline.set_color('gwpy:ligo-livingston') # change colour of Livingston data
lline.set_label('LIGO-Livingston')
ax.set_ylabel(r'Strain noise [$1/\sqrt{\mathrm{Hz}}$]')
ax.legend()
plot
```
Now we can see clearly the relative sensitivity of each LIGO instrument, the common features between both, and those unique to each observatory.
# Challenges:
##### Quiz Question 1:
The peak amplitude in the LIGO-Livingston data occurs at approximately 5 seconds into the plot above and is undetectable above the background noise by the eye. Plot the data for the LIGO-Hanford detector around GW150914. Looking at your new LIGO-Handford plot, can your eye identify a signal peak?
# Quiz Question 2 :
Make an ASD around the time of an O3 event, GW190412 for L1 detector . Compare this with the ASDs around GW150914 for L1 detector. Which data have lower noise - and so are more sensitive - around 100 Hz?
|
github_jupyter
|
# -- Uncomment following line if running in Google Colab
#! pip install -q 'gwpy==1.0.1'
import gwpy
print(gwpy.__version__)
from gwosc.datasets import event_gps
gps = event_gps('GW150914')
print(gps)
segment = (int(gps)-5, int(gps)+5)
print(segment)
from gwpy.timeseries import TimeSeries
ldata = TimeSeries.fetch_open_data('L1', *segment, verbose=True)
print(ldata)
%matplotlib inline
plot = ldata.plot()
fft = ldata.fft()
print(fft)
plot = fft.abs().plot(xscale="log", yscale="log")
plot.show(warn=False)
from scipy.signal import get_window
window = get_window('hann', ldata.size)
lwin = ldata * window
fftamp = lwin.fft().abs()
plot = fftamp.plot(xscale="log", yscale="log")
plot.show(warn=False)
asd = ldata.asd(fftlength=4, method="median")
plot = asd.plot()
plot.show(warn=False)
ax = plot.gca()
ax.set_xlim(10, 1400)
ax.set_ylim(2e-24, 1e-20)
plot
ldata2 = TimeSeries.fetch_open_data('L1', int(gps)-512, int(gps)+512, cache=True)
lasd2 = ldata2.asd(fftlength=4, method="median")
plot = lasd2.plot()
ax = plot.gca()
ax.set_xlim(10, 1400)
ax.set_ylim(5e-24, 1e-20)
plot.show(warn=False)
# get Hanford data
hdata2 = TimeSeries.fetch_open_data('H1', int(gps)-512, int(gps)+512, cache=True)
hasd2 = hdata2.asd(fftlength=4, method="median")
# and plot using standard colours
ax.plot(hasd2, label='LIGO-Hanford', color='gwpy:ligo-hanford')
# update the Livingston line to use standard colour, and have a label
lline = ax.lines[0]
lline.set_color('gwpy:ligo-livingston') # change colour of Livingston data
lline.set_label('LIGO-Livingston')
ax.set_ylabel(r'Strain noise [$1/\sqrt{\mathrm{Hz}}$]')
ax.legend()
plot
| 0.489748 | 0.988301 |
# Simphony circuit simulator
[Simphony](https://simphonyphotonics.readthedocs.io/en/latest/) is a circuit simulator based on [scikit-rf](https://scikit-rf.readthedocs.io/en/latest/)
The main advantage of simphony over [SAX](https://flaport.github.io/sax/) is that simphony works in Windows, Linux and MacOs. While SAX only works on MacOs and Linux.
It also supports the SiEPIC PDK library natively.
## Component models
You can use component models from :
- Sparameters from Lumerical FDTD simulations thanks to the gdsfactory Lumerical plugin
- [SiPANN](https://sipann.readthedocs.io/en/latest/?badge=latest) open source package
```
import numpy as np
import matplotlib.pyplot as plt
import gdsfactory as gf
import gdsfactory.simulation.simphony as gs
import gdsfactory.simulation.simphony.components as gc
c = gf.components.mzi()
n = c.get_netlist()
c
c.plot_netlist()
```
### Straight
Lets start with the Sparameter model of a straight waveguide.
The models are for lossless elements.
```
m = gc.straight()
wavelengths = np.linspace(1500, 1600, 128) * 1e-9
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
m = gc.straight()
wavelengths = np.linspace(1500, 1600, 128) * 1e-9
gs.plot_model(m, phase=True, wavelengths=wavelengths)
```
### Bend
```
m = gc.bend_circular(radius=2) # this bend should have some loss
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
m = gc.mmi1x2() # this model comes from Lumerical FDTD 3D sims
gs.plot_model(m, pin_in="o1")
m = gc.mmi1x2() # this model comes from Lumerical FDTD 3D sims
gs.plot_model(m, pin_in="o1", pins=['o2', 'o3'])
m = gc.mmi1x2()
gs.plot_model(m, pin_in="o1", phase=True)
m.pins
pin = m.pins[0]
```
As you can see the MMI has -20dB reflection and -3dB transmission
```
gs.plot_model(m, pins=('o2', "o3"))
m = gc.mmi2x2() # this model comes from Lumerical FDTD 3D sims
gs.plot_model(m)
gs.plot_model(m, pins=('o3', "o4"))
m = gc.coupler_ring()
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
gc.coupler_ring?
m = gc.coupler_ring(gap=0.3)
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
m = gc.coupler(gap=0.3)
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
m = gc.gc1550te()
gs.plot_model(m, logscale=True, pin_in="port 1")
m = gc.gc1550te()
gs.plot_model(m, logscale=True, pin_in="port 1")
m = gc.gc1550te()
gs.plot_model(m, logscale=False, pin_in="port 1")
```
## Circuit simulations
With Simphony you can also combine components into circuits
### MZI interferometer
```
import matplotlib.pyplot as plt
import gdsfactory.simulation.simphony as gs
import gdsfactory.simulation.simphony.components as gc
import gdsfactory as gf
c = gf.components.mzi(delta_length=10)
c
c.plot_netlist()
circuit = gs.components.mzi(delta_length=10, splitter=gs.components.mmi1x2)
gs.plot_circuit(
circuit,
start=1500e-9,
stop=1600e-9,
logscale=True,
)
circuit = gs.components.mzi(delta_length=100, splitter=gs.components.mmi1x2)
gs.plot_circuit(
circuit,
start=1500e-9,
stop=1600e-9,
logscale=True,
)
```
Lets add grating couplers to the mzi circuit.
```
mzi_layout = gf.components.mzi(delta_length=100)
mzi_with_gc_layout = gf.routing.add_fiber_single(
component=mzi_layout, with_loopback=False
)
mzi_with_gc_layout
c = gc.gc1550te()
gs.plot_model(c, pin_in="port 1")
```
### MZI intereferometer from layout
```
import gdsfactory as gf
import gdsfactory.simulation.simphony as gs
import gdsfactory.simulation.simphony.components as gc
from simphony.libraries import siepic
c = gf.components.mzi(delta_length=10)
c
cm = gs.component_to_circuit(c)
gs.plot_circuit(cm)
c = gf.components.mzi(delta_length=20) # Double the delta length should reduce FSR by half
cm = gs.component_to_circuit(c)
gs.plot_circuit(cm)
```
### Ring resonator
```
c = gf.components.ring_double(radius=5)
c
c = gc.ring_double(radius=5)
gs.plot_circuit(c, pins_out=["o2", "o3", "o4"])
c = gf.components.ring_double(radius=10) # double radius, reduces FSR by half.
c
c = gs.components.ring_double(radius=10)
gs.plot_circuit(c, pins_out=["o2", "o3", "o4"])
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import gdsfactory as gf
import gdsfactory.simulation.simphony as gs
import gdsfactory.simulation.simphony.components as gc
c = gf.components.mzi()
n = c.get_netlist()
c
c.plot_netlist()
m = gc.straight()
wavelengths = np.linspace(1500, 1600, 128) * 1e-9
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
m = gc.straight()
wavelengths = np.linspace(1500, 1600, 128) * 1e-9
gs.plot_model(m, phase=True, wavelengths=wavelengths)
m = gc.bend_circular(radius=2) # this bend should have some loss
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
m = gc.mmi1x2() # this model comes from Lumerical FDTD 3D sims
gs.plot_model(m, pin_in="o1")
m = gc.mmi1x2() # this model comes from Lumerical FDTD 3D sims
gs.plot_model(m, pin_in="o1", pins=['o2', 'o3'])
m = gc.mmi1x2()
gs.plot_model(m, pin_in="o1", phase=True)
m.pins
pin = m.pins[0]
gs.plot_model(m, pins=('o2', "o3"))
m = gc.mmi2x2() # this model comes from Lumerical FDTD 3D sims
gs.plot_model(m)
gs.plot_model(m, pins=('o3', "o4"))
m = gc.coupler_ring()
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
gc.coupler_ring?
m = gc.coupler_ring(gap=0.3)
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
m = gc.coupler(gap=0.3)
gs.plot_model(m, logscale=False, wavelengths=wavelengths)
m = gc.gc1550te()
gs.plot_model(m, logscale=True, pin_in="port 1")
m = gc.gc1550te()
gs.plot_model(m, logscale=True, pin_in="port 1")
m = gc.gc1550te()
gs.plot_model(m, logscale=False, pin_in="port 1")
import matplotlib.pyplot as plt
import gdsfactory.simulation.simphony as gs
import gdsfactory.simulation.simphony.components as gc
import gdsfactory as gf
c = gf.components.mzi(delta_length=10)
c
c.plot_netlist()
circuit = gs.components.mzi(delta_length=10, splitter=gs.components.mmi1x2)
gs.plot_circuit(
circuit,
start=1500e-9,
stop=1600e-9,
logscale=True,
)
circuit = gs.components.mzi(delta_length=100, splitter=gs.components.mmi1x2)
gs.plot_circuit(
circuit,
start=1500e-9,
stop=1600e-9,
logscale=True,
)
mzi_layout = gf.components.mzi(delta_length=100)
mzi_with_gc_layout = gf.routing.add_fiber_single(
component=mzi_layout, with_loopback=False
)
mzi_with_gc_layout
c = gc.gc1550te()
gs.plot_model(c, pin_in="port 1")
import gdsfactory as gf
import gdsfactory.simulation.simphony as gs
import gdsfactory.simulation.simphony.components as gc
from simphony.libraries import siepic
c = gf.components.mzi(delta_length=10)
c
cm = gs.component_to_circuit(c)
gs.plot_circuit(cm)
c = gf.components.mzi(delta_length=20) # Double the delta length should reduce FSR by half
cm = gs.component_to_circuit(c)
gs.plot_circuit(cm)
c = gf.components.ring_double(radius=5)
c
c = gc.ring_double(radius=5)
gs.plot_circuit(c, pins_out=["o2", "o3", "o4"])
c = gf.components.ring_double(radius=10) # double radius, reduces FSR by half.
c
c = gs.components.ring_double(radius=10)
gs.plot_circuit(c, pins_out=["o2", "o3", "o4"])
| 0.441191 | 0.924688 |
```
import random
import pickle
import numpy as np
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
import pygmo as pg
import tengp
import symreg
from experiment_settings import nguyen7_funset, pagie_funset, keijzer_funset, korns12_funset, vlad_funset
TRIALS = 50
OUTPUT_FOLDER = 'results/abc/'
PARALLEL = False
def run_parallel(current_data):
if not PARALLEL:
logs = run_experiment(current_data, cost_function)
else:
name, (x_train, y_train, x_test, y_test), params = current_data
print(name)
bounds = tengp.individual.IndividualBuilder(params).create().bounds[:]
logs = Parallel(n_jobs=num_cores)(delayed(run_experiment_instance)(_, cost_function, x_train, y_train, params, bounds)
for _ in range(TRIALS))
return logs
def run_experiment(data_item, cost_function):
logs = []
name, (x_train, y_train, x_test, y_test), params = data_item
print(name)
bounds = tengp.individual.IndividualBuilder(params).create().bounds[:]
for i in range(TRIALS):
log = run_experiment_instance(i, cost_function, x_train, y_train, params, bounds)
logs.append(log)
return logs
def run_experiment_instance(i, cost_function, x_train, y_train, params, bounds):
print(i, end=',')
prob = pg.problem(cost_function(np.c_[np.ones(len(x_train)), x_train], y_train, params, bounds))
algo = pg.algorithm(pg.bee_colony(gen=2000))
algo.set_verbosity(1)
pop = pg.population(prob, 25)
pop = algo.evolve(pop)
uda = algo.extract(pg.bee_colony)
return [x[2] for x in uda.get_log()]
class cost_function:
def __init__(self, X, Y, params, bounds):
self.params = params
self.bounds = bounds
self.X = X
self.Y = Y
def fitness(self, x):
individual = tengp.individual.NPIndividual(list(x), self.bounds, self.params)
pred = individual.transform(self.X)
try:
return [mean_squared_error(pred, self.Y)]
except ValueError:
return [10000000000]
def get_bounds(self):
return self.bounds
kw_params = {'real_valued': True, 'max_back': 20}
params_nguyen4 = tengp.Parameters(2, 1, 1, 50, nguyen7_funset, **kw_params)
params_nguyen7 = tengp.Parameters(2, 1, 1, 50, nguyen7_funset, **kw_params)
params_nguyen10 = tengp.Parameters(3, 1, 1, 50, nguyen7_funset, **kw_params)
params_pagie1 = tengp.Parameters(3, 1, 1, 50, pagie_funset, **kw_params)
params_keijzer6 = tengp.Parameters(2, 1, 1, 50, keijzer_funset, **kw_params)
params_korns = tengp.Parameters(6, 1, 1, 50, korns12_funset, **kw_params)
params_vlad = tengp.Parameters(6, 1, 1, 50, vlad_funset, **kw_params)
all_params = [params_nguyen7, params_pagie1, params_keijzer6, params_korns, params_vlad]
random.seed(42)
data = [
('nguyen4', symreg.get_benchmark_poly(random, 6), params_nguyen4),
('nguyen7', symreg.get_benchmark_nguyen7(random, None), params_nguyen7),
('nguyen10', symreg.get_benchmark_nguyen10(random, None), params_nguyen10),
('pagie1', symreg.get_benchmark_pagie1(random, None), params_pagie1),
('keijzer6', symreg.get_benchmark_keijzer(random, 6), params_keijzer6),
('korns12', symreg.get_benchmark_korns(random, 12), params_korns),
('vladislasleva4', symreg.get_benchmark_vladislasleva4(random, None), params_vlad)
]
```
# Nguyen 4
```
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[0])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}ng4_log', 'wb'))
```
# Nguyen 7
```
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[1])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}ng7_log', 'wb'))
np.warnings.filterwarnings('ignore')
```
# Pagie
```
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[3])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}pag1_log', 'wb'))
```
# Keijzer 6
```
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[4])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}kei6_log', 'wb'))
```
# Korns 12
```
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[5])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}korns12_log', 'wb'))
```
# Vladislasleva 4
```
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[6])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}vlad4_log', 'wb'))
```
|
github_jupyter
|
import random
import pickle
import numpy as np
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
import pygmo as pg
import tengp
import symreg
from experiment_settings import nguyen7_funset, pagie_funset, keijzer_funset, korns12_funset, vlad_funset
TRIALS = 50
OUTPUT_FOLDER = 'results/abc/'
PARALLEL = False
def run_parallel(current_data):
if not PARALLEL:
logs = run_experiment(current_data, cost_function)
else:
name, (x_train, y_train, x_test, y_test), params = current_data
print(name)
bounds = tengp.individual.IndividualBuilder(params).create().bounds[:]
logs = Parallel(n_jobs=num_cores)(delayed(run_experiment_instance)(_, cost_function, x_train, y_train, params, bounds)
for _ in range(TRIALS))
return logs
def run_experiment(data_item, cost_function):
logs = []
name, (x_train, y_train, x_test, y_test), params = data_item
print(name)
bounds = tengp.individual.IndividualBuilder(params).create().bounds[:]
for i in range(TRIALS):
log = run_experiment_instance(i, cost_function, x_train, y_train, params, bounds)
logs.append(log)
return logs
def run_experiment_instance(i, cost_function, x_train, y_train, params, bounds):
print(i, end=',')
prob = pg.problem(cost_function(np.c_[np.ones(len(x_train)), x_train], y_train, params, bounds))
algo = pg.algorithm(pg.bee_colony(gen=2000))
algo.set_verbosity(1)
pop = pg.population(prob, 25)
pop = algo.evolve(pop)
uda = algo.extract(pg.bee_colony)
return [x[2] for x in uda.get_log()]
class cost_function:
def __init__(self, X, Y, params, bounds):
self.params = params
self.bounds = bounds
self.X = X
self.Y = Y
def fitness(self, x):
individual = tengp.individual.NPIndividual(list(x), self.bounds, self.params)
pred = individual.transform(self.X)
try:
return [mean_squared_error(pred, self.Y)]
except ValueError:
return [10000000000]
def get_bounds(self):
return self.bounds
kw_params = {'real_valued': True, 'max_back': 20}
params_nguyen4 = tengp.Parameters(2, 1, 1, 50, nguyen7_funset, **kw_params)
params_nguyen7 = tengp.Parameters(2, 1, 1, 50, nguyen7_funset, **kw_params)
params_nguyen10 = tengp.Parameters(3, 1, 1, 50, nguyen7_funset, **kw_params)
params_pagie1 = tengp.Parameters(3, 1, 1, 50, pagie_funset, **kw_params)
params_keijzer6 = tengp.Parameters(2, 1, 1, 50, keijzer_funset, **kw_params)
params_korns = tengp.Parameters(6, 1, 1, 50, korns12_funset, **kw_params)
params_vlad = tengp.Parameters(6, 1, 1, 50, vlad_funset, **kw_params)
all_params = [params_nguyen7, params_pagie1, params_keijzer6, params_korns, params_vlad]
random.seed(42)
data = [
('nguyen4', symreg.get_benchmark_poly(random, 6), params_nguyen4),
('nguyen7', symreg.get_benchmark_nguyen7(random, None), params_nguyen7),
('nguyen10', symreg.get_benchmark_nguyen10(random, None), params_nguyen10),
('pagie1', symreg.get_benchmark_pagie1(random, None), params_pagie1),
('keijzer6', symreg.get_benchmark_keijzer(random, 6), params_keijzer6),
('korns12', symreg.get_benchmark_korns(random, 12), params_korns),
('vladislasleva4', symreg.get_benchmark_vladislasleva4(random, None), params_vlad)
]
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[0])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}ng4_log', 'wb'))
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[1])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}ng7_log', 'wb'))
np.warnings.filterwarnings('ignore')
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[3])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}pag1_log', 'wb'))
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[4])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}kei6_log', 'wb'))
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[5])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}korns12_log', 'wb'))
%%time
pg.set_global_rng_seed(seed = 42)
logs = run_parallel(data[6])
pickle.dump(logs, open(f'{OUTPUT_FOLDER}vlad4_log', 'wb'))
| 0.407333 | 0.292918 |
# Text Classification with BERT
BERT and other Transformer encoder architectures have been wildly successful on a variety of tasks in NLP (natural language processing). They compute vector-space representations of natural language that are suitable for use in deep learning models. The BERT family of models uses the Transformer encoder architecture to process each token of input text in the full context of all tokens before and after, hence the name: Bidirectional Encoder Representations from Transformers.
BERT models are usually pre-trained on a large corpus of text, then fine-tuned for specific tasks.
```
## Loading required packages
import os
import shutil
import pandas as pd
import numpy as np
import tensorflow as tf
import tensorflow_hub as hub
import tensorflow_text as text
from official.nlp import optimization # to create AdamW optimizer
import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import classification_report
tf.get_logger().setLevel('ERROR')
# check keras and TF version used
print('TF Version:', tf.__version__)
print('Keras Version:', keras.__version__)
print('Number of available GPUs:', len(tf.config.list_physical_devices('GPU')))
```
## Reading the data
```
# Read the data
df = pd.read_csv('../data/interim/covid_articles_preprocessed.csv')
## Merge Tags
tag_map = {'consumer':'general',
'healthcare':'science',
'automotive':'business',
'environment':'science',
'construction':'business',
'ai':'tech'}
df['tags'] = [(lambda tags: tag_map[tags] if tags in tag_map.keys() else tags)(tags)
for tags in df['topic_area']]
df.tags.value_counts()
X = df.content.values
y = df.tags.values
enc = LabelEncoder()
y = enc.fit_transform(y)
enc_tags_mapping = dict(zip(enc.transform(enc.classes_), enc.classes_))
## Split the data in train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=21)
X_train, X_validation, y_train, y_validation = train_test_split(X_train, y_train, test_size=0.2, random_state=21)
```
## Encoding the raw text
## Build the Model
```
def build_classifier_model(tfhub_handle_preprocess, tfhub_handle_encoder):
text_input = tf.keras.layers.Input(shape=(), dtype=tf.string, name='text')
preprocessing_layer = hub.KerasLayer(tfhub_handle_preprocess, name='preprocessing')
encoder_inputs = preprocessing_layer(text_input)
encoder = hub.KerasLayer(tfhub_handle_encoder, trainable=True, name='BERT_encoder')
outputs = encoder(encoder_inputs)
net = outputs['pooled_output']
net = tf.keras.layers.Dropout(0.1)(net)
net = tf.keras.layers.Dense(5, activation='softmax', name='classifier')(net)
return tf.keras.Model(text_input, net)
```
In this notebook I will use a version of small BERT. Small BERTs have the same general architecture but fewer and/or smaller Transformer blocks, which lets you explore tradeoffs between speed, size and quality.
Text inputs need to be transformed to numeric token ids and arranged in several Tensors before being input to BERT. TensorFlow Hub provides a matching preprocessing model for each of the BERT models, which implements this transformation using TF ops from the `TF.text` library. It is not necessary to run pure Python code outside the TensorFlow model to preprocess text.
```
tfhub_handle_preprocess = 'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3'
tfhub_handle_encoder = 'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-4_H-512_A-8/1'
classifier_model = build_classifier_model(tfhub_handle_preprocess, tfhub_handle_encoder)
```
## Train the model
I just assembelled all pieces required in my BERT model including the preprocessing module, BERT encoder, data, and classifier. The next step is to train the model using the news dataset.
I will use the `tf.keras.losses.SparseCategoricalCrossentropy` for multi-class classification. For For fine-tuning I will use Adam, the same optimizer that BERT was originally trained with.
```
loss = tf.keras.losses.SparseCategoricalCrossentropy(name='sparse_categorical_crossentropy')
metrics = tf.metrics.SparseCategoricalAccuracy('accuracy')
```
For the learning rate (init_lr), I will use the same schedule as BERT pre-training: linear decay of a notional initial learning rate, prefixed with a linear warm-up phase over the first 10% of training steps (num_warmup_steps). In line with the BERT paper, the initial learning rate is smaller for fine-tuning (best of 5e-5, 3e-5, 2e-5).
```
epochs = 10
steps_per_epoch = tf.data.experimental.cardinality(tf.data.Dataset.from_tensor_slices(X_train)).numpy()
num_train_steps = steps_per_epoch * epochs
num_warmup_steps = int(0.1*num_train_steps)
init_lr = 3e-5
optimizer = optimization.create_optimizer(init_lr=init_lr,
num_train_steps=num_train_steps,
num_warmup_steps=num_warmup_steps,
optimizer_type='adamw')
classifier_model.compile(optimizer=optimizer,
loss=loss,
metrics=metrics)
classifier_model.summary()
```
## Run the model
```
print(f'Training model with {tfhub_handle_encoder}')
checkpoint_path = "../models/DL/bert-train/cp.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# Create a callback that saves the model's weights
my_callbacks = [
keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
save_weights_only=True,
verbose=False),
keras.callbacks.EarlyStopping(monitor='val_loss',
patience=1,
restore_best_weights=False),
]
history = classifier_model.fit(X_train, y_train,
epochs=epochs,
verbose=True,
validation_data=(X_validation, y_validation),
callbacks=[my_callbacks])
y_pred_prob = classifier_model.predict(X_test)
y_pred = np.argmax(y_pred_prob, axis=1)
print(classification_report(y_test, y_pred, target_names=list(enc_tags_mapping.values())))
```
The results indicates that Small BERT provide a lower accuracy compared to the custom CNN model I created for this problem. I will save model for future use.
```
classifier_model.save( "../models/DL/bert-model")
```
|
github_jupyter
|
## Loading required packages
import os
import shutil
import pandas as pd
import numpy as np
import tensorflow as tf
import tensorflow_hub as hub
import tensorflow_text as text
from official.nlp import optimization # to create AdamW optimizer
import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import classification_report
tf.get_logger().setLevel('ERROR')
# check keras and TF version used
print('TF Version:', tf.__version__)
print('Keras Version:', keras.__version__)
print('Number of available GPUs:', len(tf.config.list_physical_devices('GPU')))
# Read the data
df = pd.read_csv('../data/interim/covid_articles_preprocessed.csv')
## Merge Tags
tag_map = {'consumer':'general',
'healthcare':'science',
'automotive':'business',
'environment':'science',
'construction':'business',
'ai':'tech'}
df['tags'] = [(lambda tags: tag_map[tags] if tags in tag_map.keys() else tags)(tags)
for tags in df['topic_area']]
df.tags.value_counts()
X = df.content.values
y = df.tags.values
enc = LabelEncoder()
y = enc.fit_transform(y)
enc_tags_mapping = dict(zip(enc.transform(enc.classes_), enc.classes_))
## Split the data in train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=21)
X_train, X_validation, y_train, y_validation = train_test_split(X_train, y_train, test_size=0.2, random_state=21)
def build_classifier_model(tfhub_handle_preprocess, tfhub_handle_encoder):
text_input = tf.keras.layers.Input(shape=(), dtype=tf.string, name='text')
preprocessing_layer = hub.KerasLayer(tfhub_handle_preprocess, name='preprocessing')
encoder_inputs = preprocessing_layer(text_input)
encoder = hub.KerasLayer(tfhub_handle_encoder, trainable=True, name='BERT_encoder')
outputs = encoder(encoder_inputs)
net = outputs['pooled_output']
net = tf.keras.layers.Dropout(0.1)(net)
net = tf.keras.layers.Dense(5, activation='softmax', name='classifier')(net)
return tf.keras.Model(text_input, net)
tfhub_handle_preprocess = 'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3'
tfhub_handle_encoder = 'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-4_H-512_A-8/1'
classifier_model = build_classifier_model(tfhub_handle_preprocess, tfhub_handle_encoder)
loss = tf.keras.losses.SparseCategoricalCrossentropy(name='sparse_categorical_crossentropy')
metrics = tf.metrics.SparseCategoricalAccuracy('accuracy')
epochs = 10
steps_per_epoch = tf.data.experimental.cardinality(tf.data.Dataset.from_tensor_slices(X_train)).numpy()
num_train_steps = steps_per_epoch * epochs
num_warmup_steps = int(0.1*num_train_steps)
init_lr = 3e-5
optimizer = optimization.create_optimizer(init_lr=init_lr,
num_train_steps=num_train_steps,
num_warmup_steps=num_warmup_steps,
optimizer_type='adamw')
classifier_model.compile(optimizer=optimizer,
loss=loss,
metrics=metrics)
classifier_model.summary()
print(f'Training model with {tfhub_handle_encoder}')
checkpoint_path = "../models/DL/bert-train/cp.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# Create a callback that saves the model's weights
my_callbacks = [
keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
save_weights_only=True,
verbose=False),
keras.callbacks.EarlyStopping(monitor='val_loss',
patience=1,
restore_best_weights=False),
]
history = classifier_model.fit(X_train, y_train,
epochs=epochs,
verbose=True,
validation_data=(X_validation, y_validation),
callbacks=[my_callbacks])
y_pred_prob = classifier_model.predict(X_test)
y_pred = np.argmax(y_pred_prob, axis=1)
print(classification_report(y_test, y_pred, target_names=list(enc_tags_mapping.values())))
classifier_model.save( "../models/DL/bert-model")
| 0.771069 | 0.936807 |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sn
import statsmodels.api as sm
raw_data= pd.read_csv('Final_raw_data.csv')
raw_data.head()
raw_data=raw_data.fillna(0)
gender_columns=pd.get_dummies(raw_data, columns=['gender', 'age_group', 'income_group', 'ethnicity', 'urbanicity'], drop_first=True)
gender_columns.head()
data= gender_columns
data=data.drop(['email_acq'], axis=1)
h2od=data
data=data.drop(['Flag'], axis=1)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test= train_test_split(data, raw_data['Flag'], test_size=0.3, random_state=0)
```
# Feature Engineering
```
raw_data.corr()
data.describe()
from sklearn.ensemble import ExtraTreesClassifier
# Building the model
extra_tree_forest = ExtraTreesClassifier(n_estimators = 100,
criterion ='gini')
# Training the model
extra_tree_forest.fit(x_train, y_train)
# Computing the importance of each feature
feature_importance = extra_tree_forest.feature_importances_
# Normalizing the individual importances
feature_importance_normalized = np.std([tree.feature_importances_ for tree in
extra_tree_forest.estimators_],
axis = 0)
x_train.columns
feature_importance_normalized
matrix=[x_train.columns, feature_importance_normalized]
matrix
from matplotlib.pyplot import figure
figure(num=None, figsize=(20, 40), dpi=80, facecolor='w', edgecolor='k')
plt.bar(feature_importance_normalized, x_train.columns)
plt.xlabel('Feature Labels')
plt.ylabel('Feature Importances')
plt.title('Comparison of different Feature Importances')
plt.show()
from mlbox.preprocessing import *
from mlbox.optimisation import *
from mlbox.prediction import *
opt = Optimiser(scoring = 'accuracy', n_folds = 3)
best = opt.optimise(space, df,15)
prd = Predictor()
prd.fit_predict(best, df)
train.to_csv (r'C:\Users\praneeth.p\Documents\Praneeth\NoteBooks\GITHUB\Tredence\LTR analysis\train.csv', index = False, header=True)
test.to_csv (r'C:\Users\praneeth.p\Documents\Praneeth\NoteBooks\GITHUB\Tredence\LTR analysis\test.csv', index = False, header=True)
import h2o
from h2o.estimators.random_forest import H2ORandomForestEstimator
from h2o.automl import H2OAutoML
h2o.init()
train=h2o.import_file("train.csv")
testh=h2o.import_file("test buf.csv")
testh.shape
test
train['Flag']=train['Flag'].asfactor()
x=[train.drop(["Flag"], axis=1)]
aml=H2OAutoML(max_runtime_secs=3600)
aml.train(y="Flag", training_frame=train)
lb = aml.leaderboard
lb.head()
# Get model ids for all models in the AutoML Leaderboard
model_ids = list(aml.leaderboard['model_id'].as_data_frame().iloc[:,0])
# Get the "All Models" Stacked Ensemble model
se = h2o.get_model([mid for mid in model_ids if "StackedEnsemble_AllModels" in mid][0])
# Get the Stacked Ensemble metalearner model
metalearner = h2o.get_model(se.metalearner()['name'])
%matplotlib inline
metalearner.std_coef_plot()
pred=aml.predict(testh)
pred
h2o.get_model(model_id= GBM_3_AutoML_20200314_141047)
aml.confusion_matrix(valid=True)
from sklearn.metrics import classification_report
from sklearn import metrics
print(classification_report(train,pred))
print("Accuracy:",metrics.accuracy_score(train, pred))
metrics.confusion_matrix(train, pred)
x_train.shape
y_train.shape
from numpy import loadtxt
from xgboost import XGBClassifier
# fit model no training data
model = XGBClassifier()
model.fit(x_train, y_train)
# make predictions for test data
y_pred = model.predict(x_test)
predictions = [round(value) for value in y_pred]
# evaluate predictions
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
predictions
from sklearn.metrics import classification_report
from sklearn import metrics
print(classification_report(y_test,predictions))
print("Accuracy:",metrics.accuracy_score(y_test, predictions))
metrics.confusion_matrix(y_test, predictions)
raw_data['Flag']
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test= train_test_split(data, raw_data['Flag'], test_size=0.3, random_state=0)
from sklearn.linear_model import LogisticRegression
logistic= LogisticRegression()
logistic.fit(x_train, y_train)
logistic_prediction= logistic.predict(x_test)
from sklearn.metrics import classification_report
from sklearn import metrics
print(classification_report(y_test,logistic_prediction))
print("Accuracy:",metrics.accuracy_score(y_test, logistic_prediction))
metrics.confusion_matrix(y_test, logistic_prediction)
x_train.shape
y_train.shape
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sn
import statsmodels.api as sm
raw_data= pd.read_csv('Final_raw_data.csv')
raw_data.head()
raw_data=raw_data.fillna(0)
gender_columns=pd.get_dummies(raw_data, columns=['gender', 'age_group', 'income_group', 'ethnicity', 'urbanicity'], drop_first=True)
gender_columns.head()
data= gender_columns
data=data.drop(['email_acq'], axis=1)
h2od=data
data=data.drop(['Flag'], axis=1)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test= train_test_split(data, raw_data['Flag'], test_size=0.3, random_state=0)
raw_data.corr()
data.describe()
from sklearn.ensemble import ExtraTreesClassifier
# Building the model
extra_tree_forest = ExtraTreesClassifier(n_estimators = 100,
criterion ='gini')
# Training the model
extra_tree_forest.fit(x_train, y_train)
# Computing the importance of each feature
feature_importance = extra_tree_forest.feature_importances_
# Normalizing the individual importances
feature_importance_normalized = np.std([tree.feature_importances_ for tree in
extra_tree_forest.estimators_],
axis = 0)
x_train.columns
feature_importance_normalized
matrix=[x_train.columns, feature_importance_normalized]
matrix
from matplotlib.pyplot import figure
figure(num=None, figsize=(20, 40), dpi=80, facecolor='w', edgecolor='k')
plt.bar(feature_importance_normalized, x_train.columns)
plt.xlabel('Feature Labels')
plt.ylabel('Feature Importances')
plt.title('Comparison of different Feature Importances')
plt.show()
from mlbox.preprocessing import *
from mlbox.optimisation import *
from mlbox.prediction import *
opt = Optimiser(scoring = 'accuracy', n_folds = 3)
best = opt.optimise(space, df,15)
prd = Predictor()
prd.fit_predict(best, df)
train.to_csv (r'C:\Users\praneeth.p\Documents\Praneeth\NoteBooks\GITHUB\Tredence\LTR analysis\train.csv', index = False, header=True)
test.to_csv (r'C:\Users\praneeth.p\Documents\Praneeth\NoteBooks\GITHUB\Tredence\LTR analysis\test.csv', index = False, header=True)
import h2o
from h2o.estimators.random_forest import H2ORandomForestEstimator
from h2o.automl import H2OAutoML
h2o.init()
train=h2o.import_file("train.csv")
testh=h2o.import_file("test buf.csv")
testh.shape
test
train['Flag']=train['Flag'].asfactor()
x=[train.drop(["Flag"], axis=1)]
aml=H2OAutoML(max_runtime_secs=3600)
aml.train(y="Flag", training_frame=train)
lb = aml.leaderboard
lb.head()
# Get model ids for all models in the AutoML Leaderboard
model_ids = list(aml.leaderboard['model_id'].as_data_frame().iloc[:,0])
# Get the "All Models" Stacked Ensemble model
se = h2o.get_model([mid for mid in model_ids if "StackedEnsemble_AllModels" in mid][0])
# Get the Stacked Ensemble metalearner model
metalearner = h2o.get_model(se.metalearner()['name'])
%matplotlib inline
metalearner.std_coef_plot()
pred=aml.predict(testh)
pred
h2o.get_model(model_id= GBM_3_AutoML_20200314_141047)
aml.confusion_matrix(valid=True)
from sklearn.metrics import classification_report
from sklearn import metrics
print(classification_report(train,pred))
print("Accuracy:",metrics.accuracy_score(train, pred))
metrics.confusion_matrix(train, pred)
x_train.shape
y_train.shape
from numpy import loadtxt
from xgboost import XGBClassifier
# fit model no training data
model = XGBClassifier()
model.fit(x_train, y_train)
# make predictions for test data
y_pred = model.predict(x_test)
predictions = [round(value) for value in y_pred]
# evaluate predictions
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
predictions
from sklearn.metrics import classification_report
from sklearn import metrics
print(classification_report(y_test,predictions))
print("Accuracy:",metrics.accuracy_score(y_test, predictions))
metrics.confusion_matrix(y_test, predictions)
raw_data['Flag']
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test= train_test_split(data, raw_data['Flag'], test_size=0.3, random_state=0)
from sklearn.linear_model import LogisticRegression
logistic= LogisticRegression()
logistic.fit(x_train, y_train)
logistic_prediction= logistic.predict(x_test)
from sklearn.metrics import classification_report
from sklearn import metrics
print(classification_report(y_test,logistic_prediction))
print("Accuracy:",metrics.accuracy_score(y_test, logistic_prediction))
metrics.confusion_matrix(y_test, logistic_prediction)
x_train.shape
y_train.shape
| 0.512937 | 0.670003 |
```
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
```
# Reflect Tables into SQLAlchemy ORM
```
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func
# create engine to hawaii.sqlite
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
# reflect an existing database into a new model
Base = automap_base()
# reflect the tables
Base.prepare(engine, reflect=True)
# View all of the classes that automap found
Base.classes.keys()
# Save references to each table
Measurement = Base.classes.measurement
Station = Base.classes.station
# Create our session (link) from Python to the DB
session = Session(engine)
```
# Exploratory Precipitation Analysis
```
# Find the most recent date in the data set.
# Design a query to retrieve the last 12 months of precipitation data and plot the results.
# Starting from the most recent data point in the database.
last_date = session.query(func.max(func.strftime("%Y-%m-%d", Measurement.date))).limit(5).all()
last_date[0][0]
# Calculate the date one year from the last date in data set.
precipitation_data = session.query(func.strftime("%Y-%m-%d", Measurement.date), Measurement.prcp).\
filter(func.strftime("%Y-%m-%d", Measurement.date) >= dt.date(2016, 8, 23)).all()
# Perform a query to retrieve the data and precipitation scores
precipitation_df = pd.DataFrame(precipitation_data, columns = ['date', 'precipitation'])
# Save the query results as a Pandas DataFrame and set the index to the date column
precipitation_df.set_index('date', inplace = True)
precipitation_df.head()
# Sort the dataframe by date
precipitation_df = precipitation_df.sort_values(by = 'date')
precipitation_df.head()
# Use Pandas to calcualte the summary statistics for the precipitation data
fig, ax = plt.subplots(figsize = (15, 7))
precipitation_df.plot(ax = ax, x_compat = True)
#Create labels and title
ax.set_xlabel('Date')
ax.set_ylabel('Inches')
ax.set_title("Honolulu, HI Precipitation ('16 - '17)")
# save plot
plt.savefig("Images/precipitation.png")
# display plot
plt.show()
# Use Pandas to calcualte the summary statistics for the precipitation data
precipitation_df.describe()
```
# Exploratory Station Analysis
```
# Design a query to calculate the total number stations in the dataset
station_num = session.query(Station.id).distinct().count()
station_num
# Design a query to find the most active stations (i.e. what stations have the most rows?)
# List the stations and the counts in descending order.
station_rows = session.query(Station.station, func.count(Measurement.id)).select_from(Measurement).\
join(Station, Measurement.station == Station.station).group_by(Station.station).\
order_by(func.count(Measurement.id).desc()).all()
for result in station_rows:
print(f"{result[0]}\tCount: {result[1]}")
# Using the most active station id from the previous query, calculate the lowest, highest, and average temperature.
most_active = 'USC00519281'
most_active_temps = session.query(func.min(Measurement.tobs), func.max(Measurement.tobs), func.avg(Measurement.tobs)).\
filter(Measurement.station == most_active).all()
print(f"Lowest Temperature: {most_active_temps[0][0]} Fahrenheit, Highest Temperature: {most_active_temps[0][1]} Fahrenheit, Average Temperature: {round(most_active_temps[0][2], 2)} Fahrenheit ")
# Using the most active station id
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram
year_temps = session.query(Measurement.date, Measurement.tobs).filter(Measurement.station == most_active).\
filter(func.strftime("%Y-%m-%d", Measurement.date) >= dt.date(2016, 8, 23)).all()
# Save as a data frame
year_temps_df = pd.DataFrame(year_temps, columns = ['date', 'temperature'])
# Set index by date
year_temps_df.set_index('date', inplace = True)
fig, ax = plt.subplots()
year_temps_df.plot.hist(bins = 12, ax = ax)
#set labels
ax.set_xlabel('Temperature (Fahrenheit)')
ax.set_ylabel('Frequency')
ax.set_title("Honolulu, HI Temperatures ('16 - '17)")
#save figure
plt.savefig("Images/temperature_history.png")
#plot
plt.show()
```
# Close session
```
# Close Session
session.close()
```
|
github_jupyter
|
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func
# create engine to hawaii.sqlite
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
# reflect an existing database into a new model
Base = automap_base()
# reflect the tables
Base.prepare(engine, reflect=True)
# View all of the classes that automap found
Base.classes.keys()
# Save references to each table
Measurement = Base.classes.measurement
Station = Base.classes.station
# Create our session (link) from Python to the DB
session = Session(engine)
# Find the most recent date in the data set.
# Design a query to retrieve the last 12 months of precipitation data and plot the results.
# Starting from the most recent data point in the database.
last_date = session.query(func.max(func.strftime("%Y-%m-%d", Measurement.date))).limit(5).all()
last_date[0][0]
# Calculate the date one year from the last date in data set.
precipitation_data = session.query(func.strftime("%Y-%m-%d", Measurement.date), Measurement.prcp).\
filter(func.strftime("%Y-%m-%d", Measurement.date) >= dt.date(2016, 8, 23)).all()
# Perform a query to retrieve the data and precipitation scores
precipitation_df = pd.DataFrame(precipitation_data, columns = ['date', 'precipitation'])
# Save the query results as a Pandas DataFrame and set the index to the date column
precipitation_df.set_index('date', inplace = True)
precipitation_df.head()
# Sort the dataframe by date
precipitation_df = precipitation_df.sort_values(by = 'date')
precipitation_df.head()
# Use Pandas to calcualte the summary statistics for the precipitation data
fig, ax = plt.subplots(figsize = (15, 7))
precipitation_df.plot(ax = ax, x_compat = True)
#Create labels and title
ax.set_xlabel('Date')
ax.set_ylabel('Inches')
ax.set_title("Honolulu, HI Precipitation ('16 - '17)")
# save plot
plt.savefig("Images/precipitation.png")
# display plot
plt.show()
# Use Pandas to calcualte the summary statistics for the precipitation data
precipitation_df.describe()
# Design a query to calculate the total number stations in the dataset
station_num = session.query(Station.id).distinct().count()
station_num
# Design a query to find the most active stations (i.e. what stations have the most rows?)
# List the stations and the counts in descending order.
station_rows = session.query(Station.station, func.count(Measurement.id)).select_from(Measurement).\
join(Station, Measurement.station == Station.station).group_by(Station.station).\
order_by(func.count(Measurement.id).desc()).all()
for result in station_rows:
print(f"{result[0]}\tCount: {result[1]}")
# Using the most active station id from the previous query, calculate the lowest, highest, and average temperature.
most_active = 'USC00519281'
most_active_temps = session.query(func.min(Measurement.tobs), func.max(Measurement.tobs), func.avg(Measurement.tobs)).\
filter(Measurement.station == most_active).all()
print(f"Lowest Temperature: {most_active_temps[0][0]} Fahrenheit, Highest Temperature: {most_active_temps[0][1]} Fahrenheit, Average Temperature: {round(most_active_temps[0][2], 2)} Fahrenheit ")
# Using the most active station id
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram
year_temps = session.query(Measurement.date, Measurement.tobs).filter(Measurement.station == most_active).\
filter(func.strftime("%Y-%m-%d", Measurement.date) >= dt.date(2016, 8, 23)).all()
# Save as a data frame
year_temps_df = pd.DataFrame(year_temps, columns = ['date', 'temperature'])
# Set index by date
year_temps_df.set_index('date', inplace = True)
fig, ax = plt.subplots()
year_temps_df.plot.hist(bins = 12, ax = ax)
#set labels
ax.set_xlabel('Temperature (Fahrenheit)')
ax.set_ylabel('Frequency')
ax.set_title("Honolulu, HI Temperatures ('16 - '17)")
#save figure
plt.savefig("Images/temperature_history.png")
#plot
plt.show()
# Close Session
session.close()
| 0.638835 | 0.908049 |
# Сбор данных по источникам коэффициента CAPE
<h1>Содержание<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Сбор-данных-по-CAPE" data-toc-modified-id="Сбор-данных-по-CAPE-1"><span class="toc-item-num">1 </span>Сбор данных по CAPE</a></span><ul class="toc-item"><li><span><a href="#Данные-с--Barclays" data-toc-modified-id="Данные-с--Barclays-1.1"><span class="toc-item-num">1.1 </span>Данные с Barclays</a></span></li><li><span><a href="#Данные-с--Researchaffiliates" data-toc-modified-id="Данные-с--Researchaffiliates-1.2"><span class="toc-item-num">1.2 </span>Данные с Researchaffiliates</a></span></li><li><span><a href="#Объединение-данных-по-CAPE" data-toc-modified-id="Объединение-данных-по-CAPE-1.3"><span class="toc-item-num">1.3 </span>Объединение данных по CAPE</a></span></li></ul></li><li><span><a href="#Сбор-тикеров-ETF" data-toc-modified-id="Сбор-тикеров-ETF-2"><span class="toc-item-num">2 </span>Сбор тикеров ETF</a></span></li><li><span><a href="#Сбор-данных-по-коэфциенту-P/B" data-toc-modified-id="Сбор-данных-по-коэфциенту-P/B-3"><span class="toc-item-num">3 </span>Сбор данных по коэфциенту P/B</a></span></li><li><span><a href="#Расчет-долей-портфеля" data-toc-modified-id="Расчет-долей-портфеля-4"><span class="toc-item-num">4 </span>Расчет долей портфеля</a></span></li><li><span><a href="#Экспорт-данных-в-google-drive" data-toc-modified-id="Экспорт-данных-в-google-drive-5"><span class="toc-item-num">5 </span>Экспорт данных в google drive</a></span></li></ul></div>
```
# подключение библиотек:
import pandas as pd # работа с таблицами
import numpy as np # работа с таблицами
import datetime # работа с датами
import requests # http запросы
from bs4 import BeautifulSoup
import gspread # работа с google таблицами
from gspread_dataframe import set_with_dataframe
import time
from selenium import webdriver
import math
import matplotlib.pyplot as plt
```
## Сбор данных по CAPE
### Данные с Barclays
```
barclays_url = 'https://indices.barclays/file.app?action=shared&path=shiller/cape.csv' # ссылка на файл с CAPE
barclays_data = pd.read_csv(barclays_url, sep=",") # сохраним файл в датафрейм для последующей обработки
barclays_data # вывод данных
barclays_data_len = len(barclays_data) # посчитаем количество строк
barclays_last_string = barclays_data[barclays_data_len - 1:] # возьмем последнюю строку (актуальные данные)
barclays_last_string
barclays_date = barclays_last_string['Date'].values[0] # сохраним дату крайнего исследования
barclays_result = barclays_last_string.T # транспонируем строку
barclays_result.head() # выведем первые 5 строк из того что получилось
barclays_result.reset_index(inplace=True) # обновим таблицу, чтобы индексами таблицы были целые числа, а не названия стран
barclays_result
barclays_result = barclays_result.drop(barclays_result.index[[0]]) # удалим нулевую строку, которая содержит дату
barclays_result
barclays_column_name = 'Barclays CAPE ' + barclays_date # создаем название для столбца
barclays_result.set_axis (['country', barclays_column_name], axis=1, inplace=True) # заменяем названия столбцов
barclays_result
```
Поменяем UK на United Kingdom
```
barclays_result['country'] = barclays_result['country'].apply(lambda x : x if x != 'UK' else 'United Kingdom')
barclays_result['country'] = barclays_result['country'].apply(lambda x : x if x != 'USA' else 'US Large')
barclays_result['country'] = barclays_result['country'].apply(lambda x : x if x != 'Korea' else 'South Korea')
```
### Данные с Researchaffiliates
```
# функция переводит дату в формат url
def date_to_url_format(date, eu_format=False):
delimeter = '%2F' # разделитель дат в url запросах
if eu_format: # от этого параметра меняется порядок дня и месяца
return date.strftime("%d") + delimeter + date.strftime("%m") + delimeter + date.strftime("%Y")
return date.strftime("%m") + delimeter + date.strftime("%d") + delimeter + date.strftime("%Y")
```
Найдем дату исследования
```
data_date_str = ''
try:
driver = webdriver.Firefox(
executable_path=r'C:\Users\User\AppData\Local\python\geckodriver.exe'
)
driver.get('https://interactive.researchaffiliates.com/asset-allocation#!/?currency=USD&email=undefined&expanded=tertiary&group=core&model=ER&models=ER&scale=LINEAR&terms=REAL&tertiary=shiller-pe-cape-ratio-box&type=Equities')
time.sleep(5)
soup = BeautifulSoup(driver.page_source, "lxml")
date_div = soup.find('div',attrs={'class': 'settings-toolbar__asof'})
# price_book_selector = '#fundPortfolioData > section > div:nth-child(4) > span'
# data = soup.select(price_book_selector)
data_date_str = date_div.text.strip()[-10:]
print(data_date_str)
except Exception as ex:
print(ex)
finally:
driver.close()
driver.quit()
```
Подготовим переменные, которые требуются в запросе к Researchaffiliates
```
one_day = datetime.timedelta(days=1) # сдвиг на один день
today = datetime.date.today() # сегодня
first_day_month = today.replace(day=1) # первый день текущего месяца
#last_month = first_day_month - one_day # последний день предыдущего месяца
researchaffiliates_URL_start = 'https://download.researchaffiliates.com/download/asset-allocation/excel?webAccountId=36b8786b-0fef-491f-a785-4fe24574fd5d¤cy=USD&terms=REAL&model=ER'
date_str = 'Fri, 24 Apr 2021 16:22:54 +0000'
research_date_raw = datetime.datetime.strptime(data_date_str, '%m/%d/%Y')
research_date = '&dataDate=' + date_to_url_format(research_date_raw)
#research_date = '&dataDate=05%2F31%2F2021'
try_run = 0
print('Параметр "дата исследования"', research_date)
researchaffiliates_URL = ''
# ищем правильный URL методом перебора
for try_run in range(0, 95): # диапазон дат - от начала до 95 дней вперед
#run_url = '&runDate=' + date_to_url_format(today - one_day * try_run) # ставим очередную дату в URL
run_url = '&runDate=' + date_to_url_format(research_date_raw + one_day * try_run) # ставим очередную дату в URL
test_URL = researchaffiliates_URL_start + research_date + run_url # собираем URL
resp = requests.get(test_URL) # запрос по URL
if resp.status_code == 200: # Если файл с отчетом нашёлся
researchaffiliates_URL = test_URL # сохраняем URL
break
if researchaffiliates_URL == '':
print('Правильный URL для Researchaffiliates не найден')
researchaffiliates_URL
```
Делаем запрос к Researchaffiliates с подобранными параметрами
```
# скачиваем Excel файл, выбираем страницу Shiller.PE
researchaffiliates_data = pd.read_excel(researchaffiliates_URL, sheet_name='Shiller.PE')
researchaffiliates_data
```
Заготовим переменные, в которые потом положим адреса необходимых колонок и ячеек
```
market_column = '' # сюда потом сохраним название колонки "рынок страны"
index_column = '' # сюда потом сохраним название колонки индекса, который предлагает Research Affiliates
cape_column = '' # сюда потом сохраним название колонки с CAPE
start_string = 0 # сюда потом сохраним номер строки, с которой начинаются данные (заголовки строк не учитываем)
# пройдем в цикле по всем колонкам таблицы
for column in researchaffiliates_data.columns:
market_in_column = len(researchaffiliates_data[researchaffiliates_data[column] =='Market'].index.values)
if market_in_column: # если ячейка в колонке содержит слово Market
market_column = column # значит, это колонка с названием страны
start_string = researchaffiliates_data[researchaffiliates_data[column] =='Market'].index[0] + 1 # со следующей ячейки начинаются данные
index_in_column = len(researchaffiliates_data[researchaffiliates_data[column] =='Index'].index.values)
if index_in_column: # если ячейка в колонке содержит слово Index
index_column = column # значит, это колонка с названием индекса
cape_in_column = len(researchaffiliates_data[researchaffiliates_data[column] =='Current'].index.values)
if cape_in_column: # если ячейка в колонке содержит слово Current
cape_column = column # значит, это колонка с CAPE
researchaffiliates_result = researchaffiliates_data.loc[start_string:, [market_column, index_column, cape_column]] # вырежем из таблицы необходимые данные
researchaffiliates_result
researchaffiliates_result.set_axis(['country', 'RA_Index', 'RA_CAPE'], axis=1, inplace=True) # переименуем названия колонок
researchaffiliates_result.dropna(subset = ['RA_CAPE'], inplace = True) # Удаляем строки, если в них не заполнен CAPE
researchaffiliates_result
researchaffiliates_result['RA_CAPE'] = researchaffiliates_result['RA_CAPE'].astype('float') # преобразуем данные по CAPE из строки в число
researchaffiliates_result = researchaffiliates_result.round(2) # округлим до двух знаков после запятой
```
### Объединение данных по CAPE
Объеденим данные с источников по колонке 'country'. Тип объединения outer - сохранение данных с всех таблиц (если в одной из таблиц нет данных по стране, то получим пустую ячейку).
```
final_data = barclays_result.merge(researchaffiliates_result, on='country', how='outer')
final_data
# final_data.to_excel('result.xlsx') # сохраним полученные данные в файл
# files.download('result.xlsx') # скачаем файл
```
## Сбор тикеров ETF
```
USA_index = final_data.query('country =="US Large"').index[0] # запомним номер USA
final_data.loc[USA_index, 'country'] = 'U.S.' # поменяем название как на сайте ETFdb
final_data
countries = final_data['country'].tolist()
countries
countries_string = '"' + '", "'.join(countries) + '"'
countries_string
```
Соберем все ETF стран, по которым есть информация по CAPE
```
etf_URL = 'https://etfdb.com/api/screener/'
#data = '{"sort_by":"average_volume","sort_direction":"desc","page":1,"asset_class":"equity","regions":["Egypt" , "Nigeria", "jopasrukoi", "Israel"],"active_or_passive":"Passive","structure":["ETF"],"only":["meta","data","count"]}'
data_start = '{"sort_by":"average_volume","per_page":999,"sort_direction":"desc","page":1,"asset_class":"equity","regions":['
data_end = '],"active_or_passive":"Passive","structure":["ETF"],"only":["meta","data","count"]}'
data = data_start + countries_string + data_end
response = requests.post(etf_URL, data= data).json()
```
Разложим данные по спискам
```
etf_tickers = []
etf_names = []
etf_assets = []
for etf in response['data']:
etf_tickers.append(etf['symbol']['text'] )
etf_names.append(etf['name']['text'] )
assets = etf['assets']
assets = assets.replace("$", "")
assets = assets.replace(",", "")
etf_assets.append( assets)
```
Создадим датафрейм с информацией о ETF
```
pd.options.display.max_rows = 250
tickers_data = pd.DataFrame(list(zip(etf_tickers, etf_names, etf_assets)), columns =['ticker', 'name', 'assets($M)'])
tickers_data
tickers_data.info()
```
Уберем из списка ETF отраслевые, с плечом, активные, шорты и т.д.
```
banned_words = ['tech', '2x', '3x', '4x', '5x', 'divid', '5g', 'health', 'energ', 'material', 'pharm', 'utilit', 'short', 'innov']
def ban_etf(name):
for bann_word in banned_words:
if bann_word in name.lower():
return True
return False
tickers_data['banned'] = tickers_data['name'].apply(ban_etf)
```
Посмотрим, например, Израиль - все ли отраслевые ETF забанили
```
tickers_data[tickers_data.name.str.contains("Israel") == True]
```
Оставим только индексные страновые ETF
```
tickers_data = tickers_data.query('banned == False')
tickers_data.info()
tickers_data.dropna(subset =['assets($M)'], inplace = True) # убираем тикеры без данных об активах
len(tickers_data)
#pd.options.display.max_rows = 800
tickers_data.sort_values(by='assets($M)')
```
Убираем текстовые значения 'N/A'
```
tickers_data['assets($M)'] = tickers_data['assets($M)'].apply(lambda x: 0 if x=='N/A' else x)
```
Меняем тип текст на float
```
tickers_data['assets($M)'] = tickers_data['assets($M)'].astype('float')
tickers_data.info()
```
Функция ищет страну в названии ETF
```
def get_country(name):
for country in countries:
if country.lower() in name.lower():
return country
return ''
tickers_data['country'] = tickers_data['name'].apply(get_country)
tickers_data.sort_values(by=[ 'country', 'assets($M)'])
```
Приводим названия тикеров по США к формату 'U.S.'
```
def sp500_to_us(row):
if 'S\u0026P 500' in row['name']:
return 'U.S.'
if 'S&P 500' in row['name']:
return 'U.S.'
return row['country']
tickers_data['country'] = tickers_data.apply(sp500_to_us, axis=1)
tickers_data.sort_values(by='assets($M)', ascending=False)
```
Сделаем выборку ETF с самым большим числом активов по каждой стране
```
high_assets = tickers_data.sort_values(by='assets($M)', ascending=False).groupby('country').first().reset_index()
high_assets = high_assets.drop('banned', 1)
high_assets
```
Если не заполнена страна у ETF VTI
```
if high_assets[high_assets['ticker']=='VTI']['country'].to_string().strip() == '0':
str_num = high_assets[high_assets['ticker']=='VTI'].index
high_assets.loc[str_num,'country'] = 'All country' # заполняем
```
Объединим данные по CAPE и страновым ETF в одну таблицу
```
aggregated_data = final_data.merge(high_assets, on='country', how='outer')
aggregated_data
aggregated_data[barclays_column_name] = aggregated_data[barclays_column_name].astype('float64')
aggregated_data
```
## Сбор данных по коэфциенту P/B
Функция для добычи коэффициента P/B с сайта etf.com
```
def get_price_book_ratio(ticker):
if ticker is None:
return None
url = "https://www.etf.com/"
try:
driver = webdriver.Firefox(
executable_path=r'C:\Users\User\AppData\Local\python\geckodriver.exe'
)
driver.get(url = url + ticker)
time.sleep(5)
soup = BeautifulSoup(driver.page_source, "lxml")
price_book_selector = '#fundPortfolioData > section > div:nth-child(4) > span'
data = soup.select(price_book_selector)
return data[0].text
except Exception as ex:
print('Exception:', ticker, ex)
finally:
driver.close()
driver.quit()
```
Заполним значения P/B для каждой страны
```
aggregated_data['PB'] = aggregated_data['ticker'].apply(get_price_book_ratio)
aggregated_data
```
Переводим строку в число
```
aggregated_data['PB'] = aggregated_data['PB'].astype('float')
```
## Расчет долей портфеля
Функция считает средний коэффициент по двум значениеям CAPE и одному PB
```
def get_aggregated_factor(row):
cape1 = row['RA_CAPE']
cape2 = row[barclays_column_name]
pb = row['PB']
if (cape1 is None) or (cape2 is None) or (pb is None) :
return None
if math.isnan(cape1) or math.isnan(cape2) or math.isnan(pb) :
return None
medium = (cape1 + cape1 + pb*10 ) / 3
return round(medium, 2)
```
Считаем аггрегированый коэффициент
```
aggregated_data['aggregated_factor'] = aggregated_data.apply(get_aggregated_factor, axis=1)
aggregated_data = aggregated_data.sort_values('aggregated_factor').reset_index(drop=True)
aggregated_data
```
Создадим коэффициент, который обратно пропорцианален посчитанному
```
aggregated_data['reverse_factor'] = 1 / aggregated_data['aggregated_factor']
```
Посчитаем коэффициент, который надо делить на коэффициент страны, чтобы по топ 10 недооцененных стран сумма долей была 100%
```
koef = 100 / aggregated_data[:10]['reverse_factor'].sum()
koef
```
Удалим ненужный коэффициент
```
aggregated_data = aggregated_data.drop('reverse_factor', 1)
```
Посчитаем доли в портфеле
```
aggregated_data['portfolio %'] = np.round( koef / aggregated_data['aggregated_factor'], 1)
aggregated_data
```
Всем ETF, которые не вошли в первую десятку по недооцененности, ставим 0% присутствия в портфеле
```
aggregated_data.loc[aggregated_data.index > 9, 'portfolio %'] = 0
aggregated_data
```
Построим диаграмму долей стран в портфеле
```
top_10 = aggregated_data.head(10)
fig1, ax = plt.subplots(figsize=(10,10))
plt.title('Доли индексов в портфеле')
ax.pie(top_10['portfolio %'], labels = top_10['RA_Index'], autopct='%1.f%%' )
plt.show()
```
## Экспорт данных в google drive
Создадим функцию для подготовки данных к отправке в google sheet. Она будет менять float на string с запятой вместо точки
```
def prepare_to_google_sheets(df):
new_df = df.copy()
for col in new_df.columns:
if new_df[col].dtype == 'float64':
new_df[col] = new_df[col].astype('string')
new_df[col] = new_df[col].str.replace('.',',')
return new_df
```
Обновим данные в google drive
```
google_service = gspread.service_account(filename='underestimated-countries-cb59d0c70a49.json')
google_sheet = google_service.open_by_key('1r3pmRTKgIj2HthrY7f6PG63lWesYYIEeN8Q6XvOd_jI')
worksheet = google_sheet.get_worksheet(0) #-> 0 - first sheet, 1 - second sheet etc.
worksheet.clear()
# APPEND DATA TO SHEET
set_with_dataframe(worksheet, prepare_to_google_sheets(aggregated_data)) #-> THIS EXPORTS YOUR DATAFRAME TO THE GOOGLE SHEET
```
|
github_jupyter
|
# подключение библиотек:
import pandas as pd # работа с таблицами
import numpy as np # работа с таблицами
import datetime # работа с датами
import requests # http запросы
from bs4 import BeautifulSoup
import gspread # работа с google таблицами
from gspread_dataframe import set_with_dataframe
import time
from selenium import webdriver
import math
import matplotlib.pyplot as plt
barclays_url = 'https://indices.barclays/file.app?action=shared&path=shiller/cape.csv' # ссылка на файл с CAPE
barclays_data = pd.read_csv(barclays_url, sep=",") # сохраним файл в датафрейм для последующей обработки
barclays_data # вывод данных
barclays_data_len = len(barclays_data) # посчитаем количество строк
barclays_last_string = barclays_data[barclays_data_len - 1:] # возьмем последнюю строку (актуальные данные)
barclays_last_string
barclays_date = barclays_last_string['Date'].values[0] # сохраним дату крайнего исследования
barclays_result = barclays_last_string.T # транспонируем строку
barclays_result.head() # выведем первые 5 строк из того что получилось
barclays_result.reset_index(inplace=True) # обновим таблицу, чтобы индексами таблицы были целые числа, а не названия стран
barclays_result
barclays_result = barclays_result.drop(barclays_result.index[[0]]) # удалим нулевую строку, которая содержит дату
barclays_result
barclays_column_name = 'Barclays CAPE ' + barclays_date # создаем название для столбца
barclays_result.set_axis (['country', barclays_column_name], axis=1, inplace=True) # заменяем названия столбцов
barclays_result
barclays_result['country'] = barclays_result['country'].apply(lambda x : x if x != 'UK' else 'United Kingdom')
barclays_result['country'] = barclays_result['country'].apply(lambda x : x if x != 'USA' else 'US Large')
barclays_result['country'] = barclays_result['country'].apply(lambda x : x if x != 'Korea' else 'South Korea')
# функция переводит дату в формат url
def date_to_url_format(date, eu_format=False):
delimeter = '%2F' # разделитель дат в url запросах
if eu_format: # от этого параметра меняется порядок дня и месяца
return date.strftime("%d") + delimeter + date.strftime("%m") + delimeter + date.strftime("%Y")
return date.strftime("%m") + delimeter + date.strftime("%d") + delimeter + date.strftime("%Y")
data_date_str = ''
try:
driver = webdriver.Firefox(
executable_path=r'C:\Users\User\AppData\Local\python\geckodriver.exe'
)
driver.get('https://interactive.researchaffiliates.com/asset-allocation#!/?currency=USD&email=undefined&expanded=tertiary&group=core&model=ER&models=ER&scale=LINEAR&terms=REAL&tertiary=shiller-pe-cape-ratio-box&type=Equities')
time.sleep(5)
soup = BeautifulSoup(driver.page_source, "lxml")
date_div = soup.find('div',attrs={'class': 'settings-toolbar__asof'})
# price_book_selector = '#fundPortfolioData > section > div:nth-child(4) > span'
# data = soup.select(price_book_selector)
data_date_str = date_div.text.strip()[-10:]
print(data_date_str)
except Exception as ex:
print(ex)
finally:
driver.close()
driver.quit()
one_day = datetime.timedelta(days=1) # сдвиг на один день
today = datetime.date.today() # сегодня
first_day_month = today.replace(day=1) # первый день текущего месяца
#last_month = first_day_month - one_day # последний день предыдущего месяца
researchaffiliates_URL_start = 'https://download.researchaffiliates.com/download/asset-allocation/excel?webAccountId=36b8786b-0fef-491f-a785-4fe24574fd5d¤cy=USD&terms=REAL&model=ER'
date_str = 'Fri, 24 Apr 2021 16:22:54 +0000'
research_date_raw = datetime.datetime.strptime(data_date_str, '%m/%d/%Y')
research_date = '&dataDate=' + date_to_url_format(research_date_raw)
#research_date = '&dataDate=05%2F31%2F2021'
try_run = 0
print('Параметр "дата исследования"', research_date)
researchaffiliates_URL = ''
# ищем правильный URL методом перебора
for try_run in range(0, 95): # диапазон дат - от начала до 95 дней вперед
#run_url = '&runDate=' + date_to_url_format(today - one_day * try_run) # ставим очередную дату в URL
run_url = '&runDate=' + date_to_url_format(research_date_raw + one_day * try_run) # ставим очередную дату в URL
test_URL = researchaffiliates_URL_start + research_date + run_url # собираем URL
resp = requests.get(test_URL) # запрос по URL
if resp.status_code == 200: # Если файл с отчетом нашёлся
researchaffiliates_URL = test_URL # сохраняем URL
break
if researchaffiliates_URL == '':
print('Правильный URL для Researchaffiliates не найден')
researchaffiliates_URL
# скачиваем Excel файл, выбираем страницу Shiller.PE
researchaffiliates_data = pd.read_excel(researchaffiliates_URL, sheet_name='Shiller.PE')
researchaffiliates_data
market_column = '' # сюда потом сохраним название колонки "рынок страны"
index_column = '' # сюда потом сохраним название колонки индекса, который предлагает Research Affiliates
cape_column = '' # сюда потом сохраним название колонки с CAPE
start_string = 0 # сюда потом сохраним номер строки, с которой начинаются данные (заголовки строк не учитываем)
# пройдем в цикле по всем колонкам таблицы
for column in researchaffiliates_data.columns:
market_in_column = len(researchaffiliates_data[researchaffiliates_data[column] =='Market'].index.values)
if market_in_column: # если ячейка в колонке содержит слово Market
market_column = column # значит, это колонка с названием страны
start_string = researchaffiliates_data[researchaffiliates_data[column] =='Market'].index[0] + 1 # со следующей ячейки начинаются данные
index_in_column = len(researchaffiliates_data[researchaffiliates_data[column] =='Index'].index.values)
if index_in_column: # если ячейка в колонке содержит слово Index
index_column = column # значит, это колонка с названием индекса
cape_in_column = len(researchaffiliates_data[researchaffiliates_data[column] =='Current'].index.values)
if cape_in_column: # если ячейка в колонке содержит слово Current
cape_column = column # значит, это колонка с CAPE
researchaffiliates_result = researchaffiliates_data.loc[start_string:, [market_column, index_column, cape_column]] # вырежем из таблицы необходимые данные
researchaffiliates_result
researchaffiliates_result.set_axis(['country', 'RA_Index', 'RA_CAPE'], axis=1, inplace=True) # переименуем названия колонок
researchaffiliates_result.dropna(subset = ['RA_CAPE'], inplace = True) # Удаляем строки, если в них не заполнен CAPE
researchaffiliates_result
researchaffiliates_result['RA_CAPE'] = researchaffiliates_result['RA_CAPE'].astype('float') # преобразуем данные по CAPE из строки в число
researchaffiliates_result = researchaffiliates_result.round(2) # округлим до двух знаков после запятой
final_data = barclays_result.merge(researchaffiliates_result, on='country', how='outer')
final_data
# final_data.to_excel('result.xlsx') # сохраним полученные данные в файл
# files.download('result.xlsx') # скачаем файл
USA_index = final_data.query('country =="US Large"').index[0] # запомним номер USA
final_data.loc[USA_index, 'country'] = 'U.S.' # поменяем название как на сайте ETFdb
final_data
countries = final_data['country'].tolist()
countries
countries_string = '"' + '", "'.join(countries) + '"'
countries_string
etf_URL = 'https://etfdb.com/api/screener/'
#data = '{"sort_by":"average_volume","sort_direction":"desc","page":1,"asset_class":"equity","regions":["Egypt" , "Nigeria", "jopasrukoi", "Israel"],"active_or_passive":"Passive","structure":["ETF"],"only":["meta","data","count"]}'
data_start = '{"sort_by":"average_volume","per_page":999,"sort_direction":"desc","page":1,"asset_class":"equity","regions":['
data_end = '],"active_or_passive":"Passive","structure":["ETF"],"only":["meta","data","count"]}'
data = data_start + countries_string + data_end
response = requests.post(etf_URL, data= data).json()
etf_tickers = []
etf_names = []
etf_assets = []
for etf in response['data']:
etf_tickers.append(etf['symbol']['text'] )
etf_names.append(etf['name']['text'] )
assets = etf['assets']
assets = assets.replace("$", "")
assets = assets.replace(",", "")
etf_assets.append( assets)
pd.options.display.max_rows = 250
tickers_data = pd.DataFrame(list(zip(etf_tickers, etf_names, etf_assets)), columns =['ticker', 'name', 'assets($M)'])
tickers_data
tickers_data.info()
banned_words = ['tech', '2x', '3x', '4x', '5x', 'divid', '5g', 'health', 'energ', 'material', 'pharm', 'utilit', 'short', 'innov']
def ban_etf(name):
for bann_word in banned_words:
if bann_word in name.lower():
return True
return False
tickers_data['banned'] = tickers_data['name'].apply(ban_etf)
tickers_data[tickers_data.name.str.contains("Israel") == True]
tickers_data = tickers_data.query('banned == False')
tickers_data.info()
tickers_data.dropna(subset =['assets($M)'], inplace = True) # убираем тикеры без данных об активах
len(tickers_data)
#pd.options.display.max_rows = 800
tickers_data.sort_values(by='assets($M)')
tickers_data['assets($M)'] = tickers_data['assets($M)'].apply(lambda x: 0 if x=='N/A' else x)
tickers_data['assets($M)'] = tickers_data['assets($M)'].astype('float')
tickers_data.info()
def get_country(name):
for country in countries:
if country.lower() in name.lower():
return country
return ''
tickers_data['country'] = tickers_data['name'].apply(get_country)
tickers_data.sort_values(by=[ 'country', 'assets($M)'])
def sp500_to_us(row):
if 'S\u0026P 500' in row['name']:
return 'U.S.'
if 'S&P 500' in row['name']:
return 'U.S.'
return row['country']
tickers_data['country'] = tickers_data.apply(sp500_to_us, axis=1)
tickers_data.sort_values(by='assets($M)', ascending=False)
high_assets = tickers_data.sort_values(by='assets($M)', ascending=False).groupby('country').first().reset_index()
high_assets = high_assets.drop('banned', 1)
high_assets
if high_assets[high_assets['ticker']=='VTI']['country'].to_string().strip() == '0':
str_num = high_assets[high_assets['ticker']=='VTI'].index
high_assets.loc[str_num,'country'] = 'All country' # заполняем
aggregated_data = final_data.merge(high_assets, on='country', how='outer')
aggregated_data
aggregated_data[barclays_column_name] = aggregated_data[barclays_column_name].astype('float64')
aggregated_data
def get_price_book_ratio(ticker):
if ticker is None:
return None
url = "https://www.etf.com/"
try:
driver = webdriver.Firefox(
executable_path=r'C:\Users\User\AppData\Local\python\geckodriver.exe'
)
driver.get(url = url + ticker)
time.sleep(5)
soup = BeautifulSoup(driver.page_source, "lxml")
price_book_selector = '#fundPortfolioData > section > div:nth-child(4) > span'
data = soup.select(price_book_selector)
return data[0].text
except Exception as ex:
print('Exception:', ticker, ex)
finally:
driver.close()
driver.quit()
aggregated_data['PB'] = aggregated_data['ticker'].apply(get_price_book_ratio)
aggregated_data
aggregated_data['PB'] = aggregated_data['PB'].astype('float')
def get_aggregated_factor(row):
cape1 = row['RA_CAPE']
cape2 = row[barclays_column_name]
pb = row['PB']
if (cape1 is None) or (cape2 is None) or (pb is None) :
return None
if math.isnan(cape1) or math.isnan(cape2) or math.isnan(pb) :
return None
medium = (cape1 + cape1 + pb*10 ) / 3
return round(medium, 2)
aggregated_data['aggregated_factor'] = aggregated_data.apply(get_aggregated_factor, axis=1)
aggregated_data = aggregated_data.sort_values('aggregated_factor').reset_index(drop=True)
aggregated_data
aggregated_data['reverse_factor'] = 1 / aggregated_data['aggregated_factor']
koef = 100 / aggregated_data[:10]['reverse_factor'].sum()
koef
aggregated_data = aggregated_data.drop('reverse_factor', 1)
aggregated_data['portfolio %'] = np.round( koef / aggregated_data['aggregated_factor'], 1)
aggregated_data
aggregated_data.loc[aggregated_data.index > 9, 'portfolio %'] = 0
aggregated_data
top_10 = aggregated_data.head(10)
fig1, ax = plt.subplots(figsize=(10,10))
plt.title('Доли индексов в портфеле')
ax.pie(top_10['portfolio %'], labels = top_10['RA_Index'], autopct='%1.f%%' )
plt.show()
def prepare_to_google_sheets(df):
new_df = df.copy()
for col in new_df.columns:
if new_df[col].dtype == 'float64':
new_df[col] = new_df[col].astype('string')
new_df[col] = new_df[col].str.replace('.',',')
return new_df
google_service = gspread.service_account(filename='underestimated-countries-cb59d0c70a49.json')
google_sheet = google_service.open_by_key('1r3pmRTKgIj2HthrY7f6PG63lWesYYIEeN8Q6XvOd_jI')
worksheet = google_sheet.get_worksheet(0) #-> 0 - first sheet, 1 - second sheet etc.
worksheet.clear()
# APPEND DATA TO SHEET
set_with_dataframe(worksheet, prepare_to_google_sheets(aggregated_data)) #-> THIS EXPORTS YOUR DATAFRAME TO THE GOOGLE SHEET
| 0.171373 | 0.934455 |
---
_You are currently looking at **version 1.1** of this notebook. To download notebooks and datafiles, as well as get help on Jupyter notebooks in the Coursera platform, visit the [Jupyter Notebook FAQ](https://www.coursera.org/learn/python-data-analysis/resources/0dhYG) course resource._
---
```
import pandas as pd
import numpy as np
from scipy.stats import ttest_ind
```
# Assignment 4 - Hypothesis Testing
This assignment requires more individual learning than previous assignments - you are encouraged to check out the [pandas documentation](http://pandas.pydata.org/pandas-docs/stable/) to find functions or methods you might not have used yet, or ask questions on [Stack Overflow](http://stackoverflow.com/) and tag them as pandas and python related. And of course, the discussion forums are open for interaction with your peers and the course staff.
Definitions:
* A _quarter_ is a specific three month period, Q1 is January through March, Q2 is April through June, Q3 is July through September, Q4 is October through December.
* A _recession_ is defined as starting with two consecutive quarters of GDP decline, and ending with two consecutive quarters of GDP growth.
* A _recession bottom_ is the quarter within a recession which had the lowest GDP.
* A _university town_ is a city which has a high percentage of university students compared to the total population of the city.
**Hypothesis**: University towns have their mean housing prices less effected by recessions. Run a t-test to compare the ratio of the mean price of houses in university towns the quarter before the recession starts compared to the recession bottom. (`price_ratio=quarter_before_recession/recession_bottom`)
The following data files are available for this assignment:
* From the [Zillow research data site](http://www.zillow.com/research/data/) there is housing data for the United States. In particular the datafile for [all homes at a city level](http://files.zillowstatic.com/research/public/City/City_Zhvi_AllHomes.csv), ```City_Zhvi_AllHomes.csv```, has median home sale prices at a fine grained level.
* From the Wikipedia page on college towns is a list of [university towns in the United States](https://en.wikipedia.org/wiki/List_of_college_towns#College_towns_in_the_United_States) which has been copy and pasted into the file ```university_towns.txt```.
* From Bureau of Economic Analysis, US Department of Commerce, the [GDP over time](http://www.bea.gov/national/index.htm#gdp) of the United States in current dollars (use the chained value in 2009 dollars), in quarterly intervals, in the file ```gdplev.xls```. For this assignment, only look at GDP data from the first quarter of 2000 onward.
Each function in this assignment below is worth 10%, with the exception of ```run_ttest()```, which is worth 50%.
```
# Use this dictionary to map state names to two letter acronyms
states = {'OH': 'Ohio', 'KY': 'Kentucky', 'AS': 'American Samoa', 'NV': 'Nevada', 'WY': 'Wyoming', 'NA': 'National', 'AL': 'Alabama', 'MD': 'Maryland', 'AK': 'Alaska', 'UT': 'Utah', 'OR': 'Oregon', 'MT': 'Montana', 'IL': 'Illinois', 'TN': 'Tennessee', 'DC': 'District of Columbia', 'VT': 'Vermont', 'ID': 'Idaho', 'AR': 'Arkansas', 'ME': 'Maine', 'WA': 'Washington', 'HI': 'Hawaii', 'WI': 'Wisconsin', 'MI': 'Michigan', 'IN': 'Indiana', 'NJ': 'New Jersey', 'AZ': 'Arizona', 'GU': 'Guam', 'MS': 'Mississippi', 'PR': 'Puerto Rico', 'NC': 'North Carolina', 'TX': 'Texas', 'SD': 'South Dakota', 'MP': 'Northern Mariana Islands', 'IA': 'Iowa', 'MO': 'Missouri', 'CT': 'Connecticut', 'WV': 'West Virginia', 'SC': 'South Carolina', 'LA': 'Louisiana', 'KS': 'Kansas', 'NY': 'New York', 'NE': 'Nebraska', 'OK': 'Oklahoma', 'FL': 'Florida', 'CA': 'California', 'CO': 'Colorado', 'PA': 'Pennsylvania', 'DE': 'Delaware', 'NM': 'New Mexico', 'RI': 'Rhode Island', 'MN': 'Minnesota', 'VI': 'Virgin Islands', 'NH': 'New Hampshire', 'MA': 'Massachusetts', 'GA': 'Georgia', 'ND': 'North Dakota', 'VA': 'Virginia'}
def get_list_of_university_towns():
'''Returns a DataFrame of towns and the states they are in from the
university_towns.txt list. The format of the DataFrame should be:
DataFrame( [ ["Michigan", "Ann Arbor"], ["Michigan", "Yipsilanti"] ],
columns=["State", "RegionName"] )
The following cleaning needs to be done:
1. For "State", removing characters from "[" to the end.
2. For "RegionName", when applicable, removing every character from " (" to the end.
3. Depending on how you read the data, you may need to remove newline character '\n'. '''
#ut = []
file = open('university_towns.txt','r',encoding='utf-8')
ut = file.readlines()
import re
ut = map(lambda x:re.sub(r' \(.*\n','',x),ut)
ut = map(lambda x:re.sub(r'\n','',x),ut)
ut=list(ut)
u_towns = pd.DataFrame(ut,columns = ["RegionName"])
u_towns['State'] = u_towns["RegionName"][u_towns["RegionName"].str.contains('\[edit\]')]
u_towns = u_towns.fillna(method='ffill')
u_towns = u_towns.drop(labels = u_towns.index[u_towns["RegionName"].str.contains('\[edit\]')])
u_towns['State'] = u_towns['State'].str.replace('\[edit\]','')
u_towns = u_towns[["State", "RegionName"]].reset_index().drop('index',axis=1)
return u_towns
get_list_of_university_towns()
def get_recession_start():
'''Returns the year and quarter of the recession start time as a
string value in a format such as 2005q3'''
gdp = pd.read_excel('gdplev.xls',header = None,skiprows = 220,usecols = [4,6],names=['quarter','GDP'])
gdp = gdp.set_index('quarter')
for k in range(gdp.shape[0]-2):
if(((gdp.iloc[k]-gdp.iloc[k+1])>0) & ((gdp.iloc[k+1]-gdp.iloc[k+2])>0)).bool():
start = k
break
return gdp.index[start+1]
get_recession_start()
def get_recession_end():
'''Returns the year and quarter of the recession end time as a
string value in a format such as 2005q3'''
gdp = pd.read_excel('gdplev.xls',header = None,skiprows = 220,usecols = [4,6],names=['quarter','GDP'])
gdp = gdp.set_index('quarter')
for k in range(gdp.shape[0]-2):
if(((gdp.iloc[k]-gdp.iloc[k+1])>0) & ((gdp.iloc[k+1]-gdp.iloc[k+2])>0)).bool():
start = k
break
for i in range(start+1,gdp.shape[0]-2):
if(((gdp.iloc[i]-gdp.iloc[i+1])<0) & ((gdp.iloc[i+1]-gdp.iloc[i+2])<0)).bool():
end = i+2
break
return gdp.index[end]
get_recession_end()
def get_recession_bottom():
'''Returns the year and quarter of the recession bottom time as a
string value in a format such as 2005q3'''
gdp = pd.read_excel('gdplev.xls',header = None,skiprows = 220,usecols = [4,6],names=['quarter','GDP'])
gdp = gdp.set_index('quarter')
for k in range(gdp.shape[0]-2):
if(((gdp.iloc[k]-gdp.iloc[k+1])>0) & ((gdp.iloc[k+1]-gdp.iloc[k+2])>0)).bool():
start = k
break
for i in range(start+1,gdp.shape[0]-2):
if(((gdp.iloc[i]-gdp.iloc[i+1])<0) & ((gdp.iloc[i+1]-gdp.iloc[i+2])<0)).bool():
end = i+2
break
return gdp.iloc[range(start,end)].idxmin()[0]
get_recession_bottom()
def convert_housing_data_to_quarters():
'''Converts the housing data to quarters and returns it as mean
values in a dataframe. This dataframe should be a dataframe with
columns for 2000q1 through 2016q3, and should have a multi-index
in the shape of ["State","RegionName"].
Note: Quarters are defined in the assignment description, they are
not arbitrary three month periods.
The resulting dataframe should have 67 columns, and 10,730 rows.
'''
house = pd.read_csv('City_Zhvi_AllHomes.csv')
#house = house.set_index(["State","RegionName"])
cols = [str(i)+j for i in (range(2000,2017)) for j in ['q1','q2','q3','q4'] if (str(i)+j) != '2016q4' ]
house_data = house[["State","RegionName"]].copy()
i=0
def mean_row(data,house,rows):
start = list(house.columns).index(rows)
data[cols[i]] = house.iloc[:,[start,start+1,start+2]].mean(axis = 1)
return data
for q in pd.period_range(start = '2000-01',end = '2016-06',freq = '3M'):
house_data = mean_row(house_data,house,q.start_time.strftime('%Y-%m'))
i = i+1
house_data[cols[66]] = house[['2016-07','2016-08']].mean(axis = 1)
house_data = house_data.set_index(["State","RegionName"]).rename(index = states)
return house_data
convert_housing_data_to_quarters()
def run_ttest():
'''First creates new data showing the decline or growth of housing prices
between the recession start and the recession bottom. Then runs a ttest
comparing the university town values to the non-university towns values,
return whether the alternative hypothesis (that the two groups are the same)
is true or not as well as the p-value of the confidence.
Return the tuple (different, p, better) where different=True if the t-test is
True at a p<0.01 (we reject the null hypothesis), or different=False if
otherwise (we cannot reject the null hypothesis). The variable p should
be equal to the exact p value returned from scipy.stats.ttest_ind(). The
value for better should be either "university town" or "non-university town"
depending on which has a lower mean price ratio (which is equivilent to a
reduced market loss).'''
ch = convert_housing_data_to_quarters()
u_towns = get_list_of_university_towns()
u_town = pd.DataFrame(u_towns['State'].unique(),columns = ['State'])
u_town['u_t'] = '1'
ch = ch.reset_index().set_index('State')
ch_t = pd.merge(ch, u_town, how = 'left' ,left_index = True,right_on = 'State')
ch_t = ch_t.fillna({'u_t':'0'})
ch_t = ch_t.set_index(["State","RegionName"])
p = ttest_ind(ch_t.groupby('u_t').mean().iloc[0],ch_t.groupby('u_t').mean().iloc[1]).pvalue
return (p<0.01,p, ["university town", "non-university town"][p>0.01])
run_ttest()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
from scipy.stats import ttest_ind
# Use this dictionary to map state names to two letter acronyms
states = {'OH': 'Ohio', 'KY': 'Kentucky', 'AS': 'American Samoa', 'NV': 'Nevada', 'WY': 'Wyoming', 'NA': 'National', 'AL': 'Alabama', 'MD': 'Maryland', 'AK': 'Alaska', 'UT': 'Utah', 'OR': 'Oregon', 'MT': 'Montana', 'IL': 'Illinois', 'TN': 'Tennessee', 'DC': 'District of Columbia', 'VT': 'Vermont', 'ID': 'Idaho', 'AR': 'Arkansas', 'ME': 'Maine', 'WA': 'Washington', 'HI': 'Hawaii', 'WI': 'Wisconsin', 'MI': 'Michigan', 'IN': 'Indiana', 'NJ': 'New Jersey', 'AZ': 'Arizona', 'GU': 'Guam', 'MS': 'Mississippi', 'PR': 'Puerto Rico', 'NC': 'North Carolina', 'TX': 'Texas', 'SD': 'South Dakota', 'MP': 'Northern Mariana Islands', 'IA': 'Iowa', 'MO': 'Missouri', 'CT': 'Connecticut', 'WV': 'West Virginia', 'SC': 'South Carolina', 'LA': 'Louisiana', 'KS': 'Kansas', 'NY': 'New York', 'NE': 'Nebraska', 'OK': 'Oklahoma', 'FL': 'Florida', 'CA': 'California', 'CO': 'Colorado', 'PA': 'Pennsylvania', 'DE': 'Delaware', 'NM': 'New Mexico', 'RI': 'Rhode Island', 'MN': 'Minnesota', 'VI': 'Virgin Islands', 'NH': 'New Hampshire', 'MA': 'Massachusetts', 'GA': 'Georgia', 'ND': 'North Dakota', 'VA': 'Virginia'}
def get_list_of_university_towns():
'''Returns a DataFrame of towns and the states they are in from the
university_towns.txt list. The format of the DataFrame should be:
DataFrame( [ ["Michigan", "Ann Arbor"], ["Michigan", "Yipsilanti"] ],
columns=["State", "RegionName"] )
The following cleaning needs to be done:
1. For "State", removing characters from "[" to the end.
2. For "RegionName", when applicable, removing every character from " (" to the end.
3. Depending on how you read the data, you may need to remove newline character '\n'. '''
#ut = []
file = open('university_towns.txt','r',encoding='utf-8')
ut = file.readlines()
import re
ut = map(lambda x:re.sub(r' \(.*\n','',x),ut)
ut = map(lambda x:re.sub(r'\n','',x),ut)
ut=list(ut)
u_towns = pd.DataFrame(ut,columns = ["RegionName"])
u_towns['State'] = u_towns["RegionName"][u_towns["RegionName"].str.contains('\[edit\]')]
u_towns = u_towns.fillna(method='ffill')
u_towns = u_towns.drop(labels = u_towns.index[u_towns["RegionName"].str.contains('\[edit\]')])
u_towns['State'] = u_towns['State'].str.replace('\[edit\]','')
u_towns = u_towns[["State", "RegionName"]].reset_index().drop('index',axis=1)
return u_towns
get_list_of_university_towns()
def get_recession_start():
'''Returns the year and quarter of the recession start time as a
string value in a format such as 2005q3'''
gdp = pd.read_excel('gdplev.xls',header = None,skiprows = 220,usecols = [4,6],names=['quarter','GDP'])
gdp = gdp.set_index('quarter')
for k in range(gdp.shape[0]-2):
if(((gdp.iloc[k]-gdp.iloc[k+1])>0) & ((gdp.iloc[k+1]-gdp.iloc[k+2])>0)).bool():
start = k
break
return gdp.index[start+1]
get_recession_start()
def get_recession_end():
'''Returns the year and quarter of the recession end time as a
string value in a format such as 2005q3'''
gdp = pd.read_excel('gdplev.xls',header = None,skiprows = 220,usecols = [4,6],names=['quarter','GDP'])
gdp = gdp.set_index('quarter')
for k in range(gdp.shape[0]-2):
if(((gdp.iloc[k]-gdp.iloc[k+1])>0) & ((gdp.iloc[k+1]-gdp.iloc[k+2])>0)).bool():
start = k
break
for i in range(start+1,gdp.shape[0]-2):
if(((gdp.iloc[i]-gdp.iloc[i+1])<0) & ((gdp.iloc[i+1]-gdp.iloc[i+2])<0)).bool():
end = i+2
break
return gdp.index[end]
get_recession_end()
def get_recession_bottom():
'''Returns the year and quarter of the recession bottom time as a
string value in a format such as 2005q3'''
gdp = pd.read_excel('gdplev.xls',header = None,skiprows = 220,usecols = [4,6],names=['quarter','GDP'])
gdp = gdp.set_index('quarter')
for k in range(gdp.shape[0]-2):
if(((gdp.iloc[k]-gdp.iloc[k+1])>0) & ((gdp.iloc[k+1]-gdp.iloc[k+2])>0)).bool():
start = k
break
for i in range(start+1,gdp.shape[0]-2):
if(((gdp.iloc[i]-gdp.iloc[i+1])<0) & ((gdp.iloc[i+1]-gdp.iloc[i+2])<0)).bool():
end = i+2
break
return gdp.iloc[range(start,end)].idxmin()[0]
get_recession_bottom()
def convert_housing_data_to_quarters():
'''Converts the housing data to quarters and returns it as mean
values in a dataframe. This dataframe should be a dataframe with
columns for 2000q1 through 2016q3, and should have a multi-index
in the shape of ["State","RegionName"].
Note: Quarters are defined in the assignment description, they are
not arbitrary three month periods.
The resulting dataframe should have 67 columns, and 10,730 rows.
'''
house = pd.read_csv('City_Zhvi_AllHomes.csv')
#house = house.set_index(["State","RegionName"])
cols = [str(i)+j for i in (range(2000,2017)) for j in ['q1','q2','q3','q4'] if (str(i)+j) != '2016q4' ]
house_data = house[["State","RegionName"]].copy()
i=0
def mean_row(data,house,rows):
start = list(house.columns).index(rows)
data[cols[i]] = house.iloc[:,[start,start+1,start+2]].mean(axis = 1)
return data
for q in pd.period_range(start = '2000-01',end = '2016-06',freq = '3M'):
house_data = mean_row(house_data,house,q.start_time.strftime('%Y-%m'))
i = i+1
house_data[cols[66]] = house[['2016-07','2016-08']].mean(axis = 1)
house_data = house_data.set_index(["State","RegionName"]).rename(index = states)
return house_data
convert_housing_data_to_quarters()
def run_ttest():
'''First creates new data showing the decline or growth of housing prices
between the recession start and the recession bottom. Then runs a ttest
comparing the university town values to the non-university towns values,
return whether the alternative hypothesis (that the two groups are the same)
is true or not as well as the p-value of the confidence.
Return the tuple (different, p, better) where different=True if the t-test is
True at a p<0.01 (we reject the null hypothesis), or different=False if
otherwise (we cannot reject the null hypothesis). The variable p should
be equal to the exact p value returned from scipy.stats.ttest_ind(). The
value for better should be either "university town" or "non-university town"
depending on which has a lower mean price ratio (which is equivilent to a
reduced market loss).'''
ch = convert_housing_data_to_quarters()
u_towns = get_list_of_university_towns()
u_town = pd.DataFrame(u_towns['State'].unique(),columns = ['State'])
u_town['u_t'] = '1'
ch = ch.reset_index().set_index('State')
ch_t = pd.merge(ch, u_town, how = 'left' ,left_index = True,right_on = 'State')
ch_t = ch_t.fillna({'u_t':'0'})
ch_t = ch_t.set_index(["State","RegionName"])
p = ttest_ind(ch_t.groupby('u_t').mean().iloc[0],ch_t.groupby('u_t').mean().iloc[1]).pvalue
return (p<0.01,p, ["university town", "non-university town"][p>0.01])
run_ttest()
| 0.384681 | 0.980729 |
# Defining `ufuncs` using `vectorize`
You have been able to define your own NumPy [`ufuncs`](http://docs.scipy.org/doc/numpy/reference/ufuncs.html) for quite some time, but it's a little involved.
You can read through the [documentation](http://docs.scipy.org/doc/numpy/user/c-info.ufunc-tutorial.html), the example they post there is a ufunc to perform
$$f(a) = \log \left(\frac{a}{1-a}\right)$$
It looks like this:
```c
static void double_logit(char **args, npy_intp *dimensions,
npy_intp* steps, void* data)
{
npy_intp i;
npy_intp n = dimensions[0];
char *in = args[0], *out = args[1];
npy_intp in_step = steps[0], out_step = steps[1];
double tmp;
for (i = 0; i < n; i++) {
/*BEGIN main ufunc computation*/
tmp = *(double *)in;
tmp /= 1-tmp;
*((double *)out) = log(tmp);
/*END main ufunc computation*/
in += in_step;
out += out_step;
}
}
```
And **note**, that's just for a `double`. If you want `floats`, `long doubles`, etc... you have to write all of those, too. And then create a `setup.py` file to install it. And I left out a bunch of boilerplate stuff to set up the import hooks, etc...
# Making your first ufunc
We can use Numba to define ufuncs without all of the pain.
```
%matplotlib inline
import numpy
import math
```
Let's define a function that operates on two inputs
```
def trig(a, b):
return math.sin(a**2) * math.exp(b)
trig(1, 1)
```
Seems reasonable. However, the `math` library only works on scalars. If we try to pass in arrays, we'll get an error.
```
a = numpy.ones((5,5))
b = numpy.ones((5,5))
trig(a, b)
from numba import vectorize
vec_trig = vectorize()(trig)
vec_trig(a, b)
```
And just like that, the scalar function `trig` is now a NumPy `ufunc` called `vec_trig`
Note that this is a "Dynamic UFunc" with no signature given.
How does it compare to just using NumPy? Let's check
```
def numpy_trig(a, b):
return numpy.sin(a**2) * numpy.exp(b)
a = numpy.random.random((1000, 1000))
b = numpy.random.random((1000, 1000))
%timeit vec_trig(a, b)
%timeit numpy_trig(a, b)
```
What happens if we do specify a signature? Is there a speed boost?
```
vec_trig = vectorize('float64(float64, float64)')(trig)
%timeit vec_trig(a, b)
```
No, not really. But(!), if we have a signature, then we can add the target `kwarg`.
```
vec_trig = vectorize('float64(float64, float64)', target='parallel')(trig)
%timeit vec_trig(a, b)
```
Automatic multicore operations!
**Note**: `target='parallel'` is not always the best option. There is overhead in setting up the threading, so if the individual scalar operations that make up a `ufunc` are simple you'll probably get better performance in serial. If the individual operations are more expensive (like trig!) then parallel is (usually) a good option.
### Passing multiple signatures
If you use multiple signatures, they have to be listed in order of most specific -> least specific
```
@vectorize(['int32(int32, int32)',
'int64(int64, int64)',
'float32(float32, float32)',
'float64(float64, float64)'])
def trig(a, b):
return math.sin(a**2) * math.exp(b)
trig(1, 1)
trig(1., 1.)
trig.ntypes
```
## Exercise: Clipping an array
Yes, NumPy has a `clip` ufunc already, but let's pretend it doesn't.
Create a Numba vectorized ufunc that takes a vector `a`, a lower limit `amin` and an upper limit `amax`. It should return the vector `a` with all values clipped to be between $a_{min}$ and $a_{max}$:
```
def truncate(a, amin, amax):
pass # Put your implementation here
vec_truncate_serial = vectorize(['float64(float64, float64, float64)'])(truncate)
vec_truncate_par = vectorize(['float64(float64, float64, float64)'], target='parallel')(truncate)
a = numpy.random.random((5000))
amin = .2
amax = .6
%timeit vec_truncate_serial(a, amin, amax)
%timeit vec_truncate_par(a, amin, amax)
%timeit numpy.clip(a, amin, amax)
a = numpy.random.random((100000))
%timeit vec_truncate_serial(a, amin, amax)
%timeit vec_truncate_par(a, amin, amax)
%timeit numpy.clip(a, amin, amax)
```
## Exercise: Monte Carlo in a Ufunc
A ufunc does not need to be deterministic. Let's suppose your a simulating a tournament with the following rules:
1. The player plays a sequence of games until they complete the tournament.
2. The player has a fixed probability $p$ to win each game.
3. Once the player has won 12 games or lost 3 games overall, they have completed the tournament.
What is the average number of wins per tournament for different values of $p$?
```
from numba import jit
MAX_WINS = 12
MAX_LOSSES = 3
@jit(nopython=True)
def run_tournament(p):
'''Run one randomized tournament and return the number of wins'''
pass # Insert your solution here
# Let's test:
for i in range(3):
print(run_tournament(0.5))
@vectorize
def avg_wins(p, trials):
'''Return the average number of wins for the requested number of trials'''
pass # Insert your solution here
```
Test your implementation:
```
prob = numpy.linspace(0.0, 1.0, 1000)
results = avg_wins(prob, 100)
import matplotlib.pyplot as plt
plt.plot(prob, results)
```
## Performance of `vectorize` vs. regular array-wide operations
```
@vectorize
def discriminant(a, b, c):
return b**2 - 4 * a * c
a = numpy.arange(10000)
b = numpy.arange(10000)
c = numpy.arange(10000)
%timeit discriminant(a, b, c)
%timeit b**2 - 4 * a * c
```
What's going on?
* Each array operation creates a temporary copy
* Each of these arrays are loaded into and out of cache a whole bunch
```
del a, b, c
```
|
github_jupyter
|
static void double_logit(char **args, npy_intp *dimensions,
npy_intp* steps, void* data)
{
npy_intp i;
npy_intp n = dimensions[0];
char *in = args[0], *out = args[1];
npy_intp in_step = steps[0], out_step = steps[1];
double tmp;
for (i = 0; i < n; i++) {
/*BEGIN main ufunc computation*/
tmp = *(double *)in;
tmp /= 1-tmp;
*((double *)out) = log(tmp);
/*END main ufunc computation*/
in += in_step;
out += out_step;
}
}
%matplotlib inline
import numpy
import math
def trig(a, b):
return math.sin(a**2) * math.exp(b)
trig(1, 1)
a = numpy.ones((5,5))
b = numpy.ones((5,5))
trig(a, b)
from numba import vectorize
vec_trig = vectorize()(trig)
vec_trig(a, b)
def numpy_trig(a, b):
return numpy.sin(a**2) * numpy.exp(b)
a = numpy.random.random((1000, 1000))
b = numpy.random.random((1000, 1000))
%timeit vec_trig(a, b)
%timeit numpy_trig(a, b)
vec_trig = vectorize('float64(float64, float64)')(trig)
%timeit vec_trig(a, b)
vec_trig = vectorize('float64(float64, float64)', target='parallel')(trig)
%timeit vec_trig(a, b)
@vectorize(['int32(int32, int32)',
'int64(int64, int64)',
'float32(float32, float32)',
'float64(float64, float64)'])
def trig(a, b):
return math.sin(a**2) * math.exp(b)
trig(1, 1)
trig(1., 1.)
trig.ntypes
def truncate(a, amin, amax):
pass # Put your implementation here
vec_truncate_serial = vectorize(['float64(float64, float64, float64)'])(truncate)
vec_truncate_par = vectorize(['float64(float64, float64, float64)'], target='parallel')(truncate)
a = numpy.random.random((5000))
amin = .2
amax = .6
%timeit vec_truncate_serial(a, amin, amax)
%timeit vec_truncate_par(a, amin, amax)
%timeit numpy.clip(a, amin, amax)
a = numpy.random.random((100000))
%timeit vec_truncate_serial(a, amin, amax)
%timeit vec_truncate_par(a, amin, amax)
%timeit numpy.clip(a, amin, amax)
from numba import jit
MAX_WINS = 12
MAX_LOSSES = 3
@jit(nopython=True)
def run_tournament(p):
'''Run one randomized tournament and return the number of wins'''
pass # Insert your solution here
# Let's test:
for i in range(3):
print(run_tournament(0.5))
@vectorize
def avg_wins(p, trials):
'''Return the average number of wins for the requested number of trials'''
pass # Insert your solution here
prob = numpy.linspace(0.0, 1.0, 1000)
results = avg_wins(prob, 100)
import matplotlib.pyplot as plt
plt.plot(prob, results)
@vectorize
def discriminant(a, b, c):
return b**2 - 4 * a * c
a = numpy.arange(10000)
b = numpy.arange(10000)
c = numpy.arange(10000)
%timeit discriminant(a, b, c)
%timeit b**2 - 4 * a * c
del a, b, c
| 0.485844 | 0.944638 |
## House Price Prediction - Assignment Solution
The solution is divided into the following sections:
- Data understanding and exploration
- Data cleaning
- Data preparation
- Model building and evaluation
### 1. Data Understanding and Exploration
Let's first import the required libraries and have a look at the dataset and understand the size, attribute names etc.
```
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
# Reading the dataset
house = pd.read_csv("train.csv", na_values="NAN")
# Let's take a look at the first few rows
house.head()
print(house.info())
# Summary of the dataset : 1460 rows, 81 columns
sns.distplot(house['SalePrice'])
print("Skewness: %f" % house['SalePrice'].skew())
print("Kurtosis: %f" % house['SalePrice'].kurt())
var = 'GrLivArea'
data = pd.concat([house['SalePrice'], house[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
var = 'TotalBsmtSF'
data = pd.concat([house['SalePrice'], house[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
#box plot overallqual/saleprice
var = 'OverallQual'
data = pd.concat([house['SalePrice'], house[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
var = 'YearBuilt'
data = pd.concat([house['SalePrice'], house[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.xticks(rotation=90);
#correlation matrix
corrmat = house.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);
#saleprice correlation matrix
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(house[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
#scatterplot
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(house[cols], size = 2.5)
plt.show();
```
# Missing data
Important questions when thinking about missing data:
How prevalent is the missing data?
Is missing data random or does it have a pattern?
The answer to these questions is important for practical reasons because missing data can imply a reduction of the sample size. This can prevent us from proceeding with the analysis. Moreover, from a substantive perspective, we need to ensure that the missing data process is not biased and hidding an inconvenient truth.
```
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)
```
## Imputing Null Values
With data this large, it is not surprising that there are a lot of missing values in the cells. In order to effectively train our model we build, we must first deal with the missing values. There are missing values for both numerical and categorical data. We will see how to deal with both.
For numerical imputing, we would typically fill the missing values with a measure like median, mean, or mode. For categorical imputing, I chose to fill the missing values with the most common term that appeared from the entire column. There are other ways to do the imputing though, and I ecnourage you to test out your own creative ways!
### Places Where NaN Means Something
If you look at the data description file provided, you will see that for some categories, NaN actually means something. This means that if a value is NaN, the house might not have that certain attribute, which will affect the price of the house. Therefore, it is better to not drop, but fill in the null cell with a value called "None" which serves as its own category.
```
#you can find these features on the description data file provided
null_has_meaning = ["Alley", "BsmtQual", "BsmtCond", "BsmtExposure", "BsmtFinType1", "BsmtFinType2", "FireplaceQu", "GarageType", "GarageFinish", "GarageQual", "GarageCond", "PoolQC", "Fence", "MiscFeature"]
for i in null_has_meaning:
house[i].fillna("None", inplace=True)
house[i].fillna("None", inplace=True)
```
## Imputing "Real" NaN Values
These are the real NaN values that we have to deal with accordingly because they were not recorded.
```
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy="median")
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(6)
```
LotFrontage has too many Null values and it is a numerical value so it may be better to just drop it.
```
house.drop("LotFrontage", axis=1, inplace=True)
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head()
```
GarageYrBlt, MasVnrArea, and MasVnrType all have a fairly decent amount of missing values. MasVnrType is categorical so we can replace the missing values with "None", as we did before. We can fill the others with median.
```
house["GarageYrBlt"].fillna(house["GarageYrBlt"].median(), inplace=True)
house["MasVnrArea"].fillna(house["MasVnrArea"].median(), inplace=True)
house["MasVnrType"].fillna("None", inplace=True)
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head()
```
Now that only one row has a null entry, we will drop the row.
```
house.dropna(inplace=True)
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head()
print(house.info())
```
### Now we will determine the data type of all features remaining
```
types_train = house.dtypes #type of each feature in data: int, float, object
num_train = types_train[(types_train == 'int64') | (types_train == float)] #numerical values are either type int or float
cat_train = types_train[types_train == object] #categorical values are type object
pd.DataFrame(types_train).reset_index().set_index(0).reset_index()[0].value_counts()
#we should convert num_train to a list to make it easier to work with
numerical_values_train = list(num_train.index)
print(numerical_values_train)
```
These are all the numerical features in our data.
```
categorical_values_train = list(cat_train.index)
print(categorical_values_train)
```
These are all the caregorical features in our data.
# Data Preparation
Ok, now that we have dealt with all the missing values, it looks like it's time for some feature engineering, the second part of our data preprocessing. We need to create feature vectors in order to get the data ready to be fed into our model as training data. This requires us to convert the categorical values into representative numbers.
```
sns.distplot(house["SalePrice"])
sns.distplot(np.log(house["SalePrice"]))
```
It appears that the target, SalePrice, is very skewed and a transformation like a logarithm would make it more normally distributed. Machine Learning models tend to work much better with normally distributed targets, rather than greatly skewed targets. By transforming the prices, we can boost model performance.
```
house["TransformedPrice"] = np.log(house["SalePrice"])
print(categorical_values_train)
for i in categorical_values_train:
feature_set = set(house[i])
for j in feature_set:
feature_list = list(feature_set)
house.loc[house[i] == j, i] = feature_list.index(j)
house.head()
```
Great! It seems like we have changed all the categorical strings into a representative number. We are ready to build our models!
# Model Building
Now that we've preprocessed and explored our data, we have a much better understanding of the type of data that we're dealing with. Now, we can began to build and test different models for regression to predict the Sale Price of each house.
```
X = house.drop(["Id", "SalePrice", "TransformedPrice"], axis=1).values
y = house["TransformedPrice"].values
# split into train and test
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
train_size=0.7,
test_size = 0.3, random_state=100)
# list of alphas to tune
params = {'alpha': [0.0001, 0.001, 0.01, 0.05, 0.1,
0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 2.0, 3.0,
4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 20, 50, 100, 500, 1000 ]}
# Importing the relevant libraries
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV
from sklearn import linear_model
# Applying Lasso
lasso = Lasso()
# cross validation
folds = 5
model_cv = GridSearchCV(estimator = lasso,
param_grid = params,
scoring= 'neg_mean_absolute_error',
cv = folds,
return_train_score=True,
verbose = 1)
model_cv.fit(X_train, y_train)
cv_results = pd.DataFrame(model_cv.cv_results_)
cv_results.head()
# plotting mean test and train scoes with alpha
cv_results['param_alpha'] = cv_results['param_alpha'].astype('float32')
# plotting
plt.plot(cv_results['param_alpha'], cv_results['mean_train_score'])
plt.plot(cv_results['param_alpha'], cv_results['mean_test_score'])
plt.xlabel('alpha')
plt.ylabel('Negative Mean Absolute Error')
plt.title("Negative Mean Absolute Error and alpha")
plt.legend(['train score', 'test score'], loc='upper left')
plt.show()
alpha = 50
lasso = Lasso(alpha=alpha)
lasso.fit(X_train, y_train)
lasso.coef_
# Applying Ridge
ridge = Ridge()
# cross validation
folds = 5
model_cv = GridSearchCV(estimator = ridge,
param_grid = params,
scoring= 'neg_mean_absolute_error',
cv = folds,
return_train_score=True,
verbose = 1)
model_cv.fit(X_train, y_train)
cv_results = pd.DataFrame(model_cv.cv_results_)
cv_results = cv_results[cv_results['param_alpha']<=200]
cv_results.head()
# plotting mean test and train scoes with alpha
cv_results['param_alpha'] = cv_results['param_alpha'].astype('int32')
# plotting
plt.plot(cv_results['param_alpha'], cv_results['mean_train_score'])
plt.plot(cv_results['param_alpha'], cv_results['mean_test_score'])
plt.xlabel('alpha')
plt.ylabel('Negative Mean Absolute Error')
plt.title("Negative Mean Absolute Error and alpha")
plt.legend(['train score', 'test score'], loc='upper left')
plt.show()
alpha = 10
ridge = Ridge(alpha=alpha)
ridge.fit(X_train, y_train)
ridge.coef_
```
|
github_jupyter
|
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
# Reading the dataset
house = pd.read_csv("train.csv", na_values="NAN")
# Let's take a look at the first few rows
house.head()
print(house.info())
# Summary of the dataset : 1460 rows, 81 columns
sns.distplot(house['SalePrice'])
print("Skewness: %f" % house['SalePrice'].skew())
print("Kurtosis: %f" % house['SalePrice'].kurt())
var = 'GrLivArea'
data = pd.concat([house['SalePrice'], house[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
var = 'TotalBsmtSF'
data = pd.concat([house['SalePrice'], house[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
#box plot overallqual/saleprice
var = 'OverallQual'
data = pd.concat([house['SalePrice'], house[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
var = 'YearBuilt'
data = pd.concat([house['SalePrice'], house[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.xticks(rotation=90);
#correlation matrix
corrmat = house.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);
#saleprice correlation matrix
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(house[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
#scatterplot
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(house[cols], size = 2.5)
plt.show();
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)
#you can find these features on the description data file provided
null_has_meaning = ["Alley", "BsmtQual", "BsmtCond", "BsmtExposure", "BsmtFinType1", "BsmtFinType2", "FireplaceQu", "GarageType", "GarageFinish", "GarageQual", "GarageCond", "PoolQC", "Fence", "MiscFeature"]
for i in null_has_meaning:
house[i].fillna("None", inplace=True)
house[i].fillna("None", inplace=True)
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy="median")
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(6)
house.drop("LotFrontage", axis=1, inplace=True)
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head()
house["GarageYrBlt"].fillna(house["GarageYrBlt"].median(), inplace=True)
house["MasVnrArea"].fillna(house["MasVnrArea"].median(), inplace=True)
house["MasVnrType"].fillna("None", inplace=True)
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head()
house.dropna(inplace=True)
#missing data
total = house.isnull().sum().sort_values(ascending=False)
percent = (house.isnull().sum()/house.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head()
print(house.info())
types_train = house.dtypes #type of each feature in data: int, float, object
num_train = types_train[(types_train == 'int64') | (types_train == float)] #numerical values are either type int or float
cat_train = types_train[types_train == object] #categorical values are type object
pd.DataFrame(types_train).reset_index().set_index(0).reset_index()[0].value_counts()
#we should convert num_train to a list to make it easier to work with
numerical_values_train = list(num_train.index)
print(numerical_values_train)
categorical_values_train = list(cat_train.index)
print(categorical_values_train)
sns.distplot(house["SalePrice"])
sns.distplot(np.log(house["SalePrice"]))
house["TransformedPrice"] = np.log(house["SalePrice"])
print(categorical_values_train)
for i in categorical_values_train:
feature_set = set(house[i])
for j in feature_set:
feature_list = list(feature_set)
house.loc[house[i] == j, i] = feature_list.index(j)
house.head()
X = house.drop(["Id", "SalePrice", "TransformedPrice"], axis=1).values
y = house["TransformedPrice"].values
# split into train and test
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
train_size=0.7,
test_size = 0.3, random_state=100)
# list of alphas to tune
params = {'alpha': [0.0001, 0.001, 0.01, 0.05, 0.1,
0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 2.0, 3.0,
4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 20, 50, 100, 500, 1000 ]}
# Importing the relevant libraries
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV
from sklearn import linear_model
# Applying Lasso
lasso = Lasso()
# cross validation
folds = 5
model_cv = GridSearchCV(estimator = lasso,
param_grid = params,
scoring= 'neg_mean_absolute_error',
cv = folds,
return_train_score=True,
verbose = 1)
model_cv.fit(X_train, y_train)
cv_results = pd.DataFrame(model_cv.cv_results_)
cv_results.head()
# plotting mean test and train scoes with alpha
cv_results['param_alpha'] = cv_results['param_alpha'].astype('float32')
# plotting
plt.plot(cv_results['param_alpha'], cv_results['mean_train_score'])
plt.plot(cv_results['param_alpha'], cv_results['mean_test_score'])
plt.xlabel('alpha')
plt.ylabel('Negative Mean Absolute Error')
plt.title("Negative Mean Absolute Error and alpha")
plt.legend(['train score', 'test score'], loc='upper left')
plt.show()
alpha = 50
lasso = Lasso(alpha=alpha)
lasso.fit(X_train, y_train)
lasso.coef_
# Applying Ridge
ridge = Ridge()
# cross validation
folds = 5
model_cv = GridSearchCV(estimator = ridge,
param_grid = params,
scoring= 'neg_mean_absolute_error',
cv = folds,
return_train_score=True,
verbose = 1)
model_cv.fit(X_train, y_train)
cv_results = pd.DataFrame(model_cv.cv_results_)
cv_results = cv_results[cv_results['param_alpha']<=200]
cv_results.head()
# plotting mean test and train scoes with alpha
cv_results['param_alpha'] = cv_results['param_alpha'].astype('int32')
# plotting
plt.plot(cv_results['param_alpha'], cv_results['mean_train_score'])
plt.plot(cv_results['param_alpha'], cv_results['mean_test_score'])
plt.xlabel('alpha')
plt.ylabel('Negative Mean Absolute Error')
plt.title("Negative Mean Absolute Error and alpha")
plt.legend(['train score', 'test score'], loc='upper left')
plt.show()
alpha = 10
ridge = Ridge(alpha=alpha)
ridge.fit(X_train, y_train)
ridge.coef_
| 0.557966 | 0.97367 |
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import torch
import random
device = 'cuda' if torch.cuda.is_available() else 'cpu'
from scipy.ndimage import gaussian_filter
import sys
from tqdm import tqdm
from functools import partial
import acd
from copy import deepcopy
sys.path.append('..')
from transforms_torch import bandpass_filter
plt.style.use('dark_background')
sys.path.append('../../dsets/mnist')
import dset
from model import Net
from util import *
from numpy.fft import *
from torch import nn
from style import *
from captum.attr import (
GradientShap,
DeepLift,
DeepLiftShap,
IntegratedGradients,
LayerConductance,
NeuronConductance,
NoiseTunnel,
)
import pickle as pkl
from torchvision import datasets, transforms
from sklearn.decomposition import NMF
```
# scores in fft space
```
im_torch, im_orig, label = dset.get_im_and_label(251, device=device) # this will download the mnist dataset
model = Net().to(device)
im_torch = im_torch.to(device)
model.load_state_dict(torch.load('../../dsets/mnist/mnist.model', map_location=device))
model = model.eval().to(device)
class Net_with_transform(nn.Module):
def __init__(self, model):
super(Net_with_transform, self).__init__()
self.model = model
def forward(self, x):
'''
Params
------
x: torch.Tensor
(batch_size, H, W, 2), where 2 contains the real then imaginary part
'''
# print('forwarding', x.shape)
x = torch.ifft(x, signal_ndim=2)
# print('post ifft', x.shape)
x = x[..., 0]
if x.ndim < 4:
x = x.unsqueeze(1)
# print('pre-model', x.shape)
x = self.model(x)
return x
model_t = Net_with_transform(model).to(device)
# plt.imshow(im_orig)
# plt.show()
# could just use torch.rfft
im_new = torch.zeros(list(im_orig.shape) + [2]) # add imag dim
im_new[:, :, 0] = torch.Tensor(im_orig)
im_f = torch.fft(im_new, signal_ndim=2)
# im = torch.ifft(im_f, signal_ndim=2)
# print('im_f.shape', im_f.shape, 'im.shape', im.shape)
# im_f = torch.fft
# im_f = fft2(im_orig)
# plt.imshow(fftshift(np.abs(im_f)))
# plt.show()
# this only works with cpu
device_captum = 'cpu'
x = im_f.unsqueeze(0).to(device_captum)
x.requires_grad = True
class_num = 1
baseline = torch.zeros(x.shape).to(device_captum)
ig = IntegratedGradients(model_t.to(device_captum))
attributions_ig, delta_ig = ig.attribute(deepcopy(x), deepcopy(baseline),
target=class_num, return_convergence_delta=True)
attributions_ig = to_freq(attributions_ig)
dl = DeepLift(model_t.to(device_captum))
attributions_dl, delta_dl = dl.attribute(x, baseline,
target=class_num, return_convergence_delta=True)
attributions_dl = to_freq(attributions_dl)
x.requires_grad = False
sweep_dim = 1
tiles = acd.tiling_2d.gen_tiles(im_orig, fill=0, method='cd', sweep_dim=sweep_dim)
scores_cd = np.zeros((tiles.shape[0], 10))
for i in tqdm(range(tiles.shape[0])):
transform = partial(bandpass_filter, mask=tiles[i])
score = acd.cd(im_torch, model, mask=None, model_type='mnist', device='cuda',
transform=transform)[0].flatten().detach().cpu().numpy()
scores_cd[i] = score
'''
im_t = transform(im_torch)
im_t = im_t.cpu().squeeze().numpy()
plt.imshow(im_t)
'''
def signshow(x):
max_abs = np.max(np.abs(x))
plt.imshow(x, cmap=cm, vmin=-max_abs, vmax=max_abs)
plt.colorbar()
R, C, = 2, 3
plt.figure(dpi=150)
plt.subplot(R, C, 1)
plt.imshow(im_orig, cmap='gray')
plt.title('Original image')
plt.axis('off')
plt.subplot(R, C, 2)
plt.imshow(fftshift(mag(im_f)))
plt.title('Original FFT')
plt.axis('off')
plt.subplot(R, C, C + 1)
signshow(attributions_ig)
plt.title('IG')
plt.axis('off')
plt.subplot(R, C, C + 2)
signshow(attributions_dl)
plt.title('DeepLift')
plt.axis('off')
plt.subplot(R, C, C + 3)
signshow(scores_cd[:, class_num].reshape(28, 28))
plt.title('CD')
plt.axis('off')
plt.tight_layout()
plt.show()
```
**scores in the image domain**
```
x.requires_grad = False
sweep_dim = 1
tiles = acd.tiling_2d.gen_tiles(im_orig, fill=0, method='cd', sweep_dim=sweep_dim)
cd_scores_im = acd.get_scores_2d(model, method='cd', ims=tiles, im_torch=im_torch)
```
# cd score without transform
```
class_num = 1
scores = []
band_centers = np.linspace(0.11, 0.89, 120)
for band_center in tqdm(band_centers):
score = acd.cd(im_torch, model, mask=None, model_type='mnist', device='cuda',
transform=partial(bandpass_filter, band_center=band_center))[0].flatten()[class_num].item()
scores.append(score)
# plot
plt.figure(dpi=150)
plt.plot(band_centers, scores, 'o-')
plt.xlabel('frequency band $\pm 0.1$')
plt.ylabel('cd score')
plt.show()
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import torch
import random
device = 'cuda' if torch.cuda.is_available() else 'cpu'
from scipy.ndimage import gaussian_filter
import sys
from tqdm import tqdm
from functools import partial
import acd
from copy import deepcopy
sys.path.append('..')
from transforms_torch import bandpass_filter
plt.style.use('dark_background')
sys.path.append('../../dsets/mnist')
import dset
from model import Net
from util import *
from numpy.fft import *
from torch import nn
from style import *
from captum.attr import (
GradientShap,
DeepLift,
DeepLiftShap,
IntegratedGradients,
LayerConductance,
NeuronConductance,
NoiseTunnel,
)
import pickle as pkl
from torchvision import datasets, transforms
from sklearn.decomposition import NMF
im_torch, im_orig, label = dset.get_im_and_label(251, device=device) # this will download the mnist dataset
model = Net().to(device)
im_torch = im_torch.to(device)
model.load_state_dict(torch.load('../../dsets/mnist/mnist.model', map_location=device))
model = model.eval().to(device)
class Net_with_transform(nn.Module):
def __init__(self, model):
super(Net_with_transform, self).__init__()
self.model = model
def forward(self, x):
'''
Params
------
x: torch.Tensor
(batch_size, H, W, 2), where 2 contains the real then imaginary part
'''
# print('forwarding', x.shape)
x = torch.ifft(x, signal_ndim=2)
# print('post ifft', x.shape)
x = x[..., 0]
if x.ndim < 4:
x = x.unsqueeze(1)
# print('pre-model', x.shape)
x = self.model(x)
return x
model_t = Net_with_transform(model).to(device)
# plt.imshow(im_orig)
# plt.show()
# could just use torch.rfft
im_new = torch.zeros(list(im_orig.shape) + [2]) # add imag dim
im_new[:, :, 0] = torch.Tensor(im_orig)
im_f = torch.fft(im_new, signal_ndim=2)
# im = torch.ifft(im_f, signal_ndim=2)
# print('im_f.shape', im_f.shape, 'im.shape', im.shape)
# im_f = torch.fft
# im_f = fft2(im_orig)
# plt.imshow(fftshift(np.abs(im_f)))
# plt.show()
# this only works with cpu
device_captum = 'cpu'
x = im_f.unsqueeze(0).to(device_captum)
x.requires_grad = True
class_num = 1
baseline = torch.zeros(x.shape).to(device_captum)
ig = IntegratedGradients(model_t.to(device_captum))
attributions_ig, delta_ig = ig.attribute(deepcopy(x), deepcopy(baseline),
target=class_num, return_convergence_delta=True)
attributions_ig = to_freq(attributions_ig)
dl = DeepLift(model_t.to(device_captum))
attributions_dl, delta_dl = dl.attribute(x, baseline,
target=class_num, return_convergence_delta=True)
attributions_dl = to_freq(attributions_dl)
x.requires_grad = False
sweep_dim = 1
tiles = acd.tiling_2d.gen_tiles(im_orig, fill=0, method='cd', sweep_dim=sweep_dim)
scores_cd = np.zeros((tiles.shape[0], 10))
for i in tqdm(range(tiles.shape[0])):
transform = partial(bandpass_filter, mask=tiles[i])
score = acd.cd(im_torch, model, mask=None, model_type='mnist', device='cuda',
transform=transform)[0].flatten().detach().cpu().numpy()
scores_cd[i] = score
'''
im_t = transform(im_torch)
im_t = im_t.cpu().squeeze().numpy()
plt.imshow(im_t)
'''
def signshow(x):
max_abs = np.max(np.abs(x))
plt.imshow(x, cmap=cm, vmin=-max_abs, vmax=max_abs)
plt.colorbar()
R, C, = 2, 3
plt.figure(dpi=150)
plt.subplot(R, C, 1)
plt.imshow(im_orig, cmap='gray')
plt.title('Original image')
plt.axis('off')
plt.subplot(R, C, 2)
plt.imshow(fftshift(mag(im_f)))
plt.title('Original FFT')
plt.axis('off')
plt.subplot(R, C, C + 1)
signshow(attributions_ig)
plt.title('IG')
plt.axis('off')
plt.subplot(R, C, C + 2)
signshow(attributions_dl)
plt.title('DeepLift')
plt.axis('off')
plt.subplot(R, C, C + 3)
signshow(scores_cd[:, class_num].reshape(28, 28))
plt.title('CD')
plt.axis('off')
plt.tight_layout()
plt.show()
x.requires_grad = False
sweep_dim = 1
tiles = acd.tiling_2d.gen_tiles(im_orig, fill=0, method='cd', sweep_dim=sweep_dim)
cd_scores_im = acd.get_scores_2d(model, method='cd', ims=tiles, im_torch=im_torch)
class_num = 1
scores = []
band_centers = np.linspace(0.11, 0.89, 120)
for band_center in tqdm(band_centers):
score = acd.cd(im_torch, model, mask=None, model_type='mnist', device='cuda',
transform=partial(bandpass_filter, band_center=band_center))[0].flatten()[class_num].item()
scores.append(score)
# plot
plt.figure(dpi=150)
plt.plot(band_centers, scores, 'o-')
plt.xlabel('frequency band $\pm 0.1$')
plt.ylabel('cd score')
plt.show()
| 0.630571 | 0.761139 |
### Stationarity is defined using very strict criterion. However, for practical purposes we can assume the series to be stationary if it has constant statistical properties over time, ie. the following:
* constant mean
* constant variance
* an autocovariance that does not depend on time.
```
# Import packages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()
df = pd.read_csv('data/multiTimeline.csv', skiprows=1)
df.head()
df.info()
df.columns = ['month', 'diet', 'gym', 'finance']
df.head()
df.month = pd.to_datetime(df.month)
df.set_index('month', inplace=True)
df.head()
df.plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20)
df[['diet']].plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
```
### There are several ways to think about identifying trends in time series. One popular way is by taking a rolling average, which means that, for each time point, you take the average of the points on either side of it. Note that the number of points is specified by a window size, which you need to choose. What happens then because you take the average is it tends to smooth out noise and seasonality. You'll see an example of that right now.
```
diet = df[['diet']]
diet.rolling(12).mean().plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20)
```
### Note that in the code chunk above you used two sets of squared brackets to extract the 'diet' column as a DataFrame; If you would have used one set, like df['diet'], you would have created a pandas Series.
### Now you have the trend that you're looking for! You have removed most of the seasonality compared to the previous plot.
```
gym = df[['gym']]
gym.rolling(12).mean().plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
```
### You have successfully removed the seasonality and you see an upward trend for "gym"! But how do these two search terms compare?
```
df_rm = pd.concat([diet.rolling(12).mean(), gym.rolling(12).mean()], axis=1)
df_rm.plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
```
### One way to think about the seasonal components to the time series of your data is to remove the trend from a time series, so that you can more easily investigate seasonality. To remove the trend, you can subtract the trend you computed above (rolling mean) from the original signal. This, however, will be dependent on how many data points you averaged over.
### Another way to remove the trend is called "differencing", where you look at the difference between successive data points (called "first-order differencing", because you're only looking at the difference between one data point and the one before it).
```
diet.diff().plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
```
### See that you have removed much of the trend and you can really see the peaks in January every year. Each January, there is a huge spike of 20 or more percent on the highest search item you've seen!
### Note: you can also perform 2nd order differencing, which means that you would be looking at the difference between one data point and the two that precede it, if the trend is not yet entirely removed.
### Transformations such as logarithms can help to stabilize the variance of a time series. Differencing can help stabilize the mean of a time series by removing changes in the level of a time series, and so eliminating trend and seasonality.
### A time series is periodic if it repeats itself at equally spaced intervals, say, every 12 months.
### Another way to think of this is that if the time series has a peak somewhere, then it will have a peak 12 months after that and, if it has a trough somewhere, it will also have a trough 12 months after that.
### Yet another way of thinking about this is that the time series is correlated with itself shifted by 12 months. That means that, if you took the time series and moved it 12 months backwards or forwards, it would map onto itself in some way.
### Considering the correlation of a time series with such a shifted version of itself is captured by the concept of autocorrelation.
```
df.plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
df.corr()
```
### Let's focus on 'diet' and 'gym'; They are negatively correlated. That's very interesting! Remember that you have a seasonal and a trend component. From the correlation coefficient, 'diet' and 'gym' are negatively correlated. However, from looking at the times series, it looks as though their seasonal components would be positively correlated and their trends negatively correlated.
### The actual correlation coefficient is actually capturing both of those.
### What you want to do now is plot the first-order differences of these time series and then compute the correlation of those because that will be the correlation of the seasonal components, approximately. Remember that removing the trend may reveal correlation in seasonality.
```
df.diff().plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
df.diff().corr()
```
### Note that once again, there was a slight negative correlation when you were thinking about the trend and the seasonal component. Now, you can see that with the seasonal component, 'diet' and 'gym' are highly correlated, with a coefficient of 0.76.
### Autocorrelation
### Now you've taken a dive into correlation of variables and correlation of time series, it's time to plot the autocorrelation of the 'diet' series: on the x-axis, you have the lag and on the y-axis, you have how correlated the time series is with itself at that lag.
### So, this means that if the original time series repeats itself every two days, you would expect to see a spike in the autocorrelation function at 2 days.
### Here, you'll look at the plot and what you should expect to see here is a spike in the autocorrelation function at 12 months: the time series is correlated with itself shifted by twelve months.
```
pd.plotting.autocorrelation_plot(diet);
```
### If you included more lags in your axes, you'd see that it is 12 months at which you have this huge peak in correlation. You have another peak at a 24 month interval, where it's also correlated with itself. You have another peak at 36, but as you move further away, there's less and less of a correlation.
### Of course, you have a correlation of itself with itself at a lag of 0.
### The dotted lines in the above plot actually tell you about the statistical significance of the correlation. In this case, you can say that the 'diet' series is genuinely autocorrelated with a lag of twelve months.
### You have identified the seasonality of this 12 month repetition!
|
github_jupyter
|
# Import packages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()
df = pd.read_csv('data/multiTimeline.csv', skiprows=1)
df.head()
df.info()
df.columns = ['month', 'diet', 'gym', 'finance']
df.head()
df.month = pd.to_datetime(df.month)
df.set_index('month', inplace=True)
df.head()
df.plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20)
df[['diet']].plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
diet = df[['diet']]
diet.rolling(12).mean().plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20)
gym = df[['gym']]
gym.rolling(12).mean().plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
df_rm = pd.concat([diet.rolling(12).mean(), gym.rolling(12).mean()], axis=1)
df_rm.plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
diet.diff().plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
df.plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
df.corr()
df.diff().plot(figsize=(20,10), linewidth=5, fontsize=20)
plt.xlabel('Year', fontsize=20);
df.diff().corr()
pd.plotting.autocorrelation_plot(diet);
| 0.428951 | 0.964987 |
___
<a href='https://www.udemy.com/user/joseportilla/'><img src='../Pierian_Data_Logo.png'/></a>
___
<center><em>Content Copyright by Pierian Data</em></center>
# Lists
Earlier when discussing strings we introduced the concept of a *sequence* in Python. Lists can be thought of the most general version of a *sequence* in Python. Unlike strings, they are mutable, meaning the elements inside a list can be changed!
In this section we will learn about:
1.) Creating lists
2.) Indexing and Slicing Lists
3.) Basic List Methods
4.) Nesting Lists
5.) Introduction to List Comprehensions
Lists are constructed with brackets [] and commas separating every element in the list.
Let's go ahead and see how we can construct lists!
```
# Assign a list to an variable named my_list
my_list = [1,2,3]
new_list=[1,2,3,4,5,6,7,8]
new_list
new_list=[5.6, 123, "strings",(1,2,3,4), [123,323,4215]]
new_list
```
We just created a list of integers, but lists can actually hold different object types. For example:
```
my_list = ['A string',23,100.232,'o']
```
Just like strings, the len() function will tell you how many items are in the sequence of the list.
```
len(my_list)
len(new_list)
```
### Indexing and Slicing
Indexing and slicing work just like in strings. Let's make a new list to remind ourselves of how this works:
```
my_list = ['one','two','three',4,5]
# Grab element at index 0
my_list[0]
new_list
new_list[2]
# Grab index 1 and everything past it
my_list[1:]
new_list[1:]
new_list[:1]
new_list[2:4]
# Grab everything UP TO index 3
my_list[:3]
```
We can also use + to concatenate lists, just like we did for strings.
```
my_list + ['new item']
new_list + ["Haider"]
new_list
```
Note: This doesn't actually change the original list!
```
my_list
```
You would have to reassign the list to make the change permanent.
```
# Reassign
my_list = my_list + ['add new item permanently']
my_list
new_list=new_list + ['haider']
new_list
```
We can also use the * for a duplication method similar to strings:
```
# Make the list double
my_list * 2
new_list * 2
# Again doubling not permanent
my_list
new_list
```
## Basic List Methods
If you are familiar with another programming language, you might start to draw parallels between arrays in another language and lists in Python. Lists in Python however, tend to be more flexible than arrays in other languages for a two good reasons: they have no fixed size (meaning we don't have to specify how big a list will be), and they have no fixed type constraint (like we've seen above).
Let's go ahead and explore some more special methods for lists:
```
# Create a new list
list1 = [1,2,3]
list2=[1,"qwer",34.54]
list2.append("this one")
list2
```
Use the **append** method to permanently add an item to the end of a list:
```
# Append
list1.append('append me!')
# Show
list1
```
Use **pop** to "pop off" an item from the list. By default pop takes off the last index, but you can also specify which index to pop off. Let's see an example:
```
# Pop off the 0 indexed item
list1.pop(0)
# Show
list1
# Assign the popped element, remember default popped index is -1
popped_item = list1.pop()
popped_item
# Show remaining list
list1
```
It should also be noted that lists indexing will return an error if there is no element at that index. For example:
```
list1[100]
```
We can use the **sort** method and the **reverse** methods to also effect your lists:
```
new_list = ['a','e','x','b','c']
#Show
new_list
# Use reverse to reverse order (this is permanent!)
new_list.reverse()
new_list
# Use sort to sort the list (in this case alphabetical order, but for numbers it will go ascending)
new_list.sort()
new_list
```
## Nesting Lists
A great feature of of Python data structures is that they support *nesting*. This means we can have data structures within data structures. For example: A list inside a list.
Let's see how this works!
```
# Let's make three lists
lst_1=[1,2,3]
lst_2=[4,5,6]
lst_3=[7,8,9]
# Make a list of lists to form a matrix
matrix = [lst_1,lst_2,lst_3]
# Show
matrix
matrix[1][1]
```
We can again use indexing to grab elements, but now there are two levels for the index. The items in the matrix object, and then the items inside that list!
```
# Grab first item in matrix object
matrix[0]
# Grab first item of the first item in the matrix object
matrix[0][0]
```
# List Comprehensions
Python has an advanced feature called list comprehensions. They allow for quick construction of lists. To fully understand list comprehensions we need to understand for loops. So don't worry if you don't completely understand this section, and feel free to just skip it since we will return to this topic later.
But in case you want to know now, here are a few examples!
```
for x in matrix:
y=x[0]
y
```
# Problem Facing
## Not able to understand list comprehension
```
# Build a list comprehension by deconstructing a for loop within a []
first_col = [row[0] for row in matrix]
first_col
```
We used a list comprehension here to grab the first element of every row in the matrix object. We will cover this in much more detail later on!
For more advanced methods and features of lists in Python, check out the Advanced Lists section later on in this course!
|
github_jupyter
|
# Assign a list to an variable named my_list
my_list = [1,2,3]
new_list=[1,2,3,4,5,6,7,8]
new_list
new_list=[5.6, 123, "strings",(1,2,3,4), [123,323,4215]]
new_list
my_list = ['A string',23,100.232,'o']
len(my_list)
len(new_list)
my_list = ['one','two','three',4,5]
# Grab element at index 0
my_list[0]
new_list
new_list[2]
# Grab index 1 and everything past it
my_list[1:]
new_list[1:]
new_list[:1]
new_list[2:4]
# Grab everything UP TO index 3
my_list[:3]
my_list + ['new item']
new_list + ["Haider"]
new_list
my_list
# Reassign
my_list = my_list + ['add new item permanently']
my_list
new_list=new_list + ['haider']
new_list
# Make the list double
my_list * 2
new_list * 2
# Again doubling not permanent
my_list
new_list
# Create a new list
list1 = [1,2,3]
list2=[1,"qwer",34.54]
list2.append("this one")
list2
# Append
list1.append('append me!')
# Show
list1
# Pop off the 0 indexed item
list1.pop(0)
# Show
list1
# Assign the popped element, remember default popped index is -1
popped_item = list1.pop()
popped_item
# Show remaining list
list1
list1[100]
new_list = ['a','e','x','b','c']
#Show
new_list
# Use reverse to reverse order (this is permanent!)
new_list.reverse()
new_list
# Use sort to sort the list (in this case alphabetical order, but for numbers it will go ascending)
new_list.sort()
new_list
# Let's make three lists
lst_1=[1,2,3]
lst_2=[4,5,6]
lst_3=[7,8,9]
# Make a list of lists to form a matrix
matrix = [lst_1,lst_2,lst_3]
# Show
matrix
matrix[1][1]
# Grab first item in matrix object
matrix[0]
# Grab first item of the first item in the matrix object
matrix[0][0]
for x in matrix:
y=x[0]
y
# Build a list comprehension by deconstructing a for loop within a []
first_col = [row[0] for row in matrix]
first_col
| 0.188697 | 0.941922 |
### toytree quartet functions (in progress)
```
import toytree
import itertools
import numpy as np
```
### get two random trees
```
t0 = toytree.rtree.unittree(10, seed=0)
t1 = toytree.rtree.unittree(10, seed=1)
toytree.mtree([t0, t1]).draw(ts='p', height=200);
```
### Plan for counting quartets (Illustrated below)
We will traverse the tree visiting every node in turn. At each node we will select the edge above it (towards the root) to be the focal 'split'. Each split can represent many possible quartets, where at least one tip can be sampled from each of the four edges leading from the split. In the example below, we are visiting node 12, and the focal split is shown in black. The four edges leaving this split are shown in red, pink, blue, and aqua. To get all quartets from this split we must sample all possible combinations of one sample from each colored set.
```
t0.draw(
ts='p',
node_colors="lightgrey",
edge_widths=3,
edge_colors=t0.get_edge_values_mapped(
{11: 'red', 3: 'pink', 4: 'blue', 18: 'aqua', 12: 'black'},
),
);
```
### Example to sample tips from each quartet edge
```
# focal node
nidx = 12
# get all tips as a set
fullset = set(i for i in t0.get_tip_labels())
# get tips from each child of a given node
down0 = set(t0.idx_dict[nidx].children[0].get_leaf_names())
down1 = set(t0.idx_dict[nidx].children[1].get_leaf_names())
up0 = set(t0.idx_dict[nidx].up.get_leaf_names()) - down0 - down1
up1 = fullset - down0 - down1 - up0
print(down0)
print(down1)
print(up0)
print(up1)
```
### Example to get all quartet sets from sampled tips
```
set(itertools.product(down0, down1, up0, up1))
```
### Combine into a function
```
def get_quartets(ttre):
# store all quartets in this SET
qset = set([])
# get a SET with all tips in the tree
fullset = set(ttre.get_tip_labels())
# get a SET of the descendants from each internal node
for node in ttre.idx_dict.values():
# skip leaf nodes
if not node.is_leaf():
children = set(node.get_leaf_names())
prod = itertools.product(
itertools.combinations(children, 2),
itertools.combinations(fullset - children, 2),
)
quartets = set([tuple(itertools.chain(*i)) for i in prod])
qset = qset.union(quartets)
# order tups in sets
sorted_set = set()
for qs in qset:
if np.argmin(qs) > 1:
tup = tuple(sorted(qs[2:]) + sorted(qs[:2]))
sorted_set.add(tup)
else:
tup = tuple(sorted(qs[:2]) + sorted(qs[2:]))
sorted_set.add(tup)
return sorted_set
get_quartets(t1)
```
### Compare quartet sets
```
q0 = get_quartets(t0)
q1 = get_quartets(t1)
# quartets that are in one tree but not the other
q0.symmetric_difference(q1)
```
### what proportion of quartets are shared or different?
|
github_jupyter
|
import toytree
import itertools
import numpy as np
t0 = toytree.rtree.unittree(10, seed=0)
t1 = toytree.rtree.unittree(10, seed=1)
toytree.mtree([t0, t1]).draw(ts='p', height=200);
t0.draw(
ts='p',
node_colors="lightgrey",
edge_widths=3,
edge_colors=t0.get_edge_values_mapped(
{11: 'red', 3: 'pink', 4: 'blue', 18: 'aqua', 12: 'black'},
),
);
# focal node
nidx = 12
# get all tips as a set
fullset = set(i for i in t0.get_tip_labels())
# get tips from each child of a given node
down0 = set(t0.idx_dict[nidx].children[0].get_leaf_names())
down1 = set(t0.idx_dict[nidx].children[1].get_leaf_names())
up0 = set(t0.idx_dict[nidx].up.get_leaf_names()) - down0 - down1
up1 = fullset - down0 - down1 - up0
print(down0)
print(down1)
print(up0)
print(up1)
set(itertools.product(down0, down1, up0, up1))
def get_quartets(ttre):
# store all quartets in this SET
qset = set([])
# get a SET with all tips in the tree
fullset = set(ttre.get_tip_labels())
# get a SET of the descendants from each internal node
for node in ttre.idx_dict.values():
# skip leaf nodes
if not node.is_leaf():
children = set(node.get_leaf_names())
prod = itertools.product(
itertools.combinations(children, 2),
itertools.combinations(fullset - children, 2),
)
quartets = set([tuple(itertools.chain(*i)) for i in prod])
qset = qset.union(quartets)
# order tups in sets
sorted_set = set()
for qs in qset:
if np.argmin(qs) > 1:
tup = tuple(sorted(qs[2:]) + sorted(qs[:2]))
sorted_set.add(tup)
else:
tup = tuple(sorted(qs[:2]) + sorted(qs[2:]))
sorted_set.add(tup)
return sorted_set
get_quartets(t1)
q0 = get_quartets(t0)
q1 = get_quartets(t1)
# quartets that are in one tree but not the other
q0.symmetric_difference(q1)
| 0.338186 | 0.917967 |
```
%matplotlib inline
```
# Rotated EOF analysis
EOF analysis is often used in climate science to interpret the obtained
eigenvectors (EOFs) as patterns of climatic variability. Given the mathematical
nature of EOF analysis which leads to orthogonal EOFs, this interpretation
is questionable for all but the first EOF. Rotated EOF anaylsis helps to
alleviate the orthogonal constraint of the EOFs by applying an additional
rotation to the (loaded) EOFs by means of a optimization criteria (Varimax,
Promax). Varimax (orthogonal) and Promax (oblique) rotation have the additional
side effect of creating "sparse" solutions, i.e. turning the otherwise dense
EOFs into a more "interpretable" solutions by reducing the number of variables
contributing to an EOF. As such, rotation acts as a kind of regularization of
the EOF solution, with the ``power`` parameter defining its strength (the
higher, the more sparse the EOFs become). In case of small regularization, i.e.
``power=1``, the Promax rotation reduces to a Varimax rotation.
Here we compare the first three modes of EOF analysis (1) without
regularization, (2) with Varimax rotation and (3) with Promax rotation.
Load packages and data:
```
import xarray as xr
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.gridspec import GridSpec
from cartopy.crs import Orthographic, PlateCarree
from xeofs.xarray import EOF, Rotator
sns.set_context('paper')
t2m = xr.tutorial.load_dataset('air_temperature')['air']
```
Perform the actual analysis
```
eofs = []
pcs = []
# (1) Standard EOF without regularization
model = EOF(t2m, dim=['time'], weights='coslat')
model.solve()
eofs.append(model.eofs())
pcs.append(model.pcs())
# (2) Varimax-rotated EOF analysis
model_var = EOF(t2m, dim=['time'], weights='coslat')
model_var.solve()
rot_var = Rotator(model, n_rot=50, power=1)
eofs.append(rot_var.eofs())
pcs.append(rot_var.pcs())
# (3) Promax-rotated EOF analysis
model_pro = EOF(t2m, dim=['time'], weights='coslat')
model_pro.solve()
rot_pro = Rotator(model, n_rot=50, power=2)
eofs.append(rot_pro.eofs())
pcs.append(rot_pro.pcs())
```
Create figure showing the first 6 modes for all 3 cases. While the first mode
is very similar in all three cases the subsequent modes of the standard
solution exhibit dipole and tripole-like patterns. Under Varimax and Promax
rotation, these structures completely disappear suggesting that these patterns
were mere artifacts due to the orthogonality.
```
proj = Orthographic(central_latitude=30, central_longitude=-80)
kwargs = {
'cmap' : 'RdBu', 'transform': PlateCarree(), 'vmin': -.1, 'vmax': +.1,
'add_colorbar': False
}
titles = [
'(1) Covariances', '(2) Covariances + coslat',
'(3) Correlation'
]
fig = plt.figure(figsize=(15, 5))
gs = GridSpec(3, 6)
ax_std = [fig.add_subplot(gs[0, i], projection=proj) for i in range(6)]
ax_var = [fig.add_subplot(gs[1, i], projection=proj) for i in range(6)]
ax_pro = [fig.add_subplot(gs[2, i], projection=proj) for i in range(6)]
for i, (a0, a1, a2) in enumerate(zip(ax_std, ax_var, ax_pro)):
mode = i + 1
a0.coastlines(color='.5')
a1.coastlines(color='.5')
a2.coastlines(color='.5')
eofs[0].sel(mode=mode).plot(ax=a0, **kwargs)
eofs[1].sel(mode=mode).plot(ax=a1, **kwargs)
eofs[2].sel(mode=mode).plot(ax=a2, **kwargs)
title_kwargs = dict(rotation=90, va='center', weight='bold')
ax_std[0].text(-.1, .5, 'Standard', transform=ax_std[0].transAxes, **title_kwargs)
ax_var[0].text(-.1, .5, 'Varimax', transform=ax_var[0].transAxes, **title_kwargs)
ax_pro[0].text(-.1, .5, 'Promax', transform=ax_pro[0].transAxes, **title_kwargs)
plt.tight_layout()
plt.savefig('rotated_eof.jpg', dpi=200)
```
|
github_jupyter
|
%matplotlib inline
import xarray as xr
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.gridspec import GridSpec
from cartopy.crs import Orthographic, PlateCarree
from xeofs.xarray import EOF, Rotator
sns.set_context('paper')
t2m = xr.tutorial.load_dataset('air_temperature')['air']
eofs = []
pcs = []
# (1) Standard EOF without regularization
model = EOF(t2m, dim=['time'], weights='coslat')
model.solve()
eofs.append(model.eofs())
pcs.append(model.pcs())
# (2) Varimax-rotated EOF analysis
model_var = EOF(t2m, dim=['time'], weights='coslat')
model_var.solve()
rot_var = Rotator(model, n_rot=50, power=1)
eofs.append(rot_var.eofs())
pcs.append(rot_var.pcs())
# (3) Promax-rotated EOF analysis
model_pro = EOF(t2m, dim=['time'], weights='coslat')
model_pro.solve()
rot_pro = Rotator(model, n_rot=50, power=2)
eofs.append(rot_pro.eofs())
pcs.append(rot_pro.pcs())
proj = Orthographic(central_latitude=30, central_longitude=-80)
kwargs = {
'cmap' : 'RdBu', 'transform': PlateCarree(), 'vmin': -.1, 'vmax': +.1,
'add_colorbar': False
}
titles = [
'(1) Covariances', '(2) Covariances + coslat',
'(3) Correlation'
]
fig = plt.figure(figsize=(15, 5))
gs = GridSpec(3, 6)
ax_std = [fig.add_subplot(gs[0, i], projection=proj) for i in range(6)]
ax_var = [fig.add_subplot(gs[1, i], projection=proj) for i in range(6)]
ax_pro = [fig.add_subplot(gs[2, i], projection=proj) for i in range(6)]
for i, (a0, a1, a2) in enumerate(zip(ax_std, ax_var, ax_pro)):
mode = i + 1
a0.coastlines(color='.5')
a1.coastlines(color='.5')
a2.coastlines(color='.5')
eofs[0].sel(mode=mode).plot(ax=a0, **kwargs)
eofs[1].sel(mode=mode).plot(ax=a1, **kwargs)
eofs[2].sel(mode=mode).plot(ax=a2, **kwargs)
title_kwargs = dict(rotation=90, va='center', weight='bold')
ax_std[0].text(-.1, .5, 'Standard', transform=ax_std[0].transAxes, **title_kwargs)
ax_var[0].text(-.1, .5, 'Varimax', transform=ax_var[0].transAxes, **title_kwargs)
ax_pro[0].text(-.1, .5, 'Promax', transform=ax_pro[0].transAxes, **title_kwargs)
plt.tight_layout()
plt.savefig('rotated_eof.jpg', dpi=200)
| 0.475118 | 0.957497 |
# Using a Fundamental Vector Class
Copyright (c) 2019 Tor Olav Kristensen, http://subcube.com
https://github.com/t-o-k/scikit-vectors
Use of this source code is governed by a BSD-license that can be found in the LICENSE file.
```
from skvectors import create_class_Fundamental_Vector
# Create a 3-dimensional fundamental vector class
# The first argument is a string with the name of the class
# to be created.
# The number of elements in the iterable given as the second
# argument determines the number of dimensions for the class.
FVC = create_class_Fundamental_Vector('FVC', 'abc')
# Explicit alternative:
# FVC = \
# create_class_Fundamental_Vector(
# name = 'FVC',
# component_names = [ 'a', 'b', 'c' ],
# brackets = [ '<', '>' ],
# sep = ', '
# )
# Number of dimensions for vectors in the class
FVC.dimensions()
# Brackets for vectors in the class
# (Used when printing a vector and when applying str to a vector)
FVC.brackets
# Separator between components for vectors in the class
# (Used when printing a vector and when applying str or repr to a vector)
FVC.sep
# List of component names for vectors in the class
FVC.component_names()
# Initialize a vector
FVC(1, -2, +3)
# Initialize a vector
FVC(a=1, b=-2, c=+3)
# Initialize a vector
l = [ 1, -2, 3 ]
FVC(*l)
# Initialize vector
d = { 'a': 1, 'b': -2, 'c': 3 }
FVC(**d)
# Initialize a vector
FVC.fill(8)
# Number of dimensions of vector
u = FVC(0, 0, 0)
u.dimensions()
# Number of dimensions of vector
u = FVC(0, 0, 0)
len(u)
# List of component names for vector
u = FVC(0, 0, 0)
u.cnames
# Check if something is a vector
u = FVC(-3, 4, 5)
FVC.is_vector(u)
# Check if something is a vector
d = { 'a': -3, 'b': 4, 'c': 5 }
FVC.is_vector(d)
# Print a vector
u = FVC(2, 4, 6)
print(u)
# Applying str to a vector
u = FVC(2, 4, 6)
str(u)
# Applying str to a vector inside a string
u = FVC(-3.3, 4.6, -5.5)
'str applied to a vector: {!s}'.format(u)
# Applying repr to a vector
u = FVC(2, 4, 6)
repr(u)
# NB: This does only work if the sep parameter in the class
# creation above contains a comma, or a comma and space(s)
# Applying repr to a vector
u = FVC(2, 4, 6)
eval(repr(u))
# Applying repr to a vector inside a string
u = FVC(-3.3, 4.6, -5.5)
'repr applied to a vector: {!r}'.format(u)
# Applying format to a vector
u = FVC(2.222222, 4.444444, 6.6666666)
format(u, '.3e')
# Applying format to vectors inside a string
u = FVC(2.222222, 4.444444, 6.6666666)
v = FVC(-3.3, 4.6, -5.5)
'format applied to two vectors: {:.4e} and {:.2e}'.format(u, v)
# Check if vector contains a value
u = FVC(2, 3, 4)
3 in u
# Check if a vector does not contain a value
u = FVC(2, 3, 4)
3.0 not in u
# The component values of a vector
u = FVC(-6, 8, 3)
u.a, u.b, u.c
# Change the component values of a vector
u = FVC(0, 0, 0)
u.a, u.b, u.c = 6, 7, 8
u
# Change a component value of a vector
u = FVC(0, 0, 0)
u.a += 100
u
# Change a component value of a vector
u = FVC(3, -4, 20)
u.c //= 8
u
# The component values / Indexing of vector
u = FVC(7, -8, 9)
u[0], u[1], u[2]
# The component values / Indexing of vector
u = FVC(7, -8, 9)
u[-3], u[-2], u[-1]
# Indexing of a vector
u = FVC(7, -8, 9)
u[0:3], u[:], u[::]
# Change the component values of a vector
u = FVC(0, 0, 0)
u[0], u[1], u[2] = 7, -8, 9
u
# Change the component values of a vector
u = FVC(0, 0, 0)
u[0:3] = 7, -8, 9
u
# Change the component values of a vector
u = FVC(0, 0, 0)
v = FVC(7, -8, 9)
u[:] = v
u
# Change the component values of a vector
u = FVC(0, 0, 0)
u[:] = (cv for cv in [ 7, -8, 9 ])
u
# List of the component values of a vector
u = FVC(7, -8, 9)
u.cvalues, u.component_values(), u[:]
# List of the component values
u = FVC(7, -8, 9)
list(u), [ *u ], [ getattr(u, cn) for cn in u.cnames ]
# Iterate over the components
u = FVC(7, -8, 9)
x, y, z = u
x, y, z
# Iterate over the components
u = FVC(7, -8, 9)
g = (cv for cv in u)
print(*g)
# Iterate over the components
u = FVC(7, -8, 9)
components = iter(u)
next(components), next(components), next(components)
# Check if a vector is equal to another
u = FVC(2.0, 4.0, 6.0)
v = FVC(2, 4, 6)
u == v
# Check if a vector is not equal to another
u = FVC(2, 4, 6)
v = FVC(2.0, 4.0, 6.0)
u != v
# Create a dictionary from the components of a vector and their names
u = FVC(2, 4, 6)
u.as_dict()
# Make shallow copy of vector
u = FVC(2, 4, 6)
v = FVC(*u)
v
# Make shallow copy of vector
u = FVC(2, 4, 6)
v = u.copy()
v
# Create a vector by applying a lambda function to each of its components
u = FVC(-3.3, 4.6, -5.5)
u(lambda s: 10 + s * 1000)
# Create a vector by applying abs to each of its components
u = FVC(-3.3, 4.6, -5.5)
u(abs)
# Create a vector by applying abs to each of its components
u = FVC(-3, 4, -5)
FVC(*map(abs, u))
# Create a vector by applying the int class to each of its components
u = FVC(-3.3, 4.6, -5.5)
u(int)
# Change the components of a vector by applying the int class to each component
u = FVC(-3.3, 4.6, -5.5)
u[:] = map(int, u)
u
# Create a vector method that takes 1 vector as argument
def square(s):
return s**2
FVC.create_vector_method_arg1('square', square)
u = FVC(2, 3, -4)
u.vector_square()
# Create, from a built in function, a vector method that takes 1 vector as argument
FVC.create_vector_method_arg1('abs', lambda s: abs(s))
u = FVC(2, 3, -4)
u.vector_abs()
# Create a vector method that takes 2 vectors as arguments
def add(s, t):
return s + t
FVC.create_vector_method_arg2('add', add)
u = FVC(2, 3, -4)
v = FVC(1, -2, 3)
s = 1000
u.vector_add(v), v.vector_add(s)
# Create a vector method that takes 3 vectors as arguments
def select(r, s, t):
if r < 0:
result = s
else:
result = t
return result
FVC.create_vector_method_arg3('select', select)
u = FVC(-2, 0, 3)
v = FVC(1, 3, 5)
w = FVC(2, 4, 6)
s = 0
t = 100
u.vector_select(v, w), u.vector_select(s, t)
```
|
github_jupyter
|
from skvectors import create_class_Fundamental_Vector
# Create a 3-dimensional fundamental vector class
# The first argument is a string with the name of the class
# to be created.
# The number of elements in the iterable given as the second
# argument determines the number of dimensions for the class.
FVC = create_class_Fundamental_Vector('FVC', 'abc')
# Explicit alternative:
# FVC = \
# create_class_Fundamental_Vector(
# name = 'FVC',
# component_names = [ 'a', 'b', 'c' ],
# brackets = [ '<', '>' ],
# sep = ', '
# )
# Number of dimensions for vectors in the class
FVC.dimensions()
# Brackets for vectors in the class
# (Used when printing a vector and when applying str to a vector)
FVC.brackets
# Separator between components for vectors in the class
# (Used when printing a vector and when applying str or repr to a vector)
FVC.sep
# List of component names for vectors in the class
FVC.component_names()
# Initialize a vector
FVC(1, -2, +3)
# Initialize a vector
FVC(a=1, b=-2, c=+3)
# Initialize a vector
l = [ 1, -2, 3 ]
FVC(*l)
# Initialize vector
d = { 'a': 1, 'b': -2, 'c': 3 }
FVC(**d)
# Initialize a vector
FVC.fill(8)
# Number of dimensions of vector
u = FVC(0, 0, 0)
u.dimensions()
# Number of dimensions of vector
u = FVC(0, 0, 0)
len(u)
# List of component names for vector
u = FVC(0, 0, 0)
u.cnames
# Check if something is a vector
u = FVC(-3, 4, 5)
FVC.is_vector(u)
# Check if something is a vector
d = { 'a': -3, 'b': 4, 'c': 5 }
FVC.is_vector(d)
# Print a vector
u = FVC(2, 4, 6)
print(u)
# Applying str to a vector
u = FVC(2, 4, 6)
str(u)
# Applying str to a vector inside a string
u = FVC(-3.3, 4.6, -5.5)
'str applied to a vector: {!s}'.format(u)
# Applying repr to a vector
u = FVC(2, 4, 6)
repr(u)
# NB: This does only work if the sep parameter in the class
# creation above contains a comma, or a comma and space(s)
# Applying repr to a vector
u = FVC(2, 4, 6)
eval(repr(u))
# Applying repr to a vector inside a string
u = FVC(-3.3, 4.6, -5.5)
'repr applied to a vector: {!r}'.format(u)
# Applying format to a vector
u = FVC(2.222222, 4.444444, 6.6666666)
format(u, '.3e')
# Applying format to vectors inside a string
u = FVC(2.222222, 4.444444, 6.6666666)
v = FVC(-3.3, 4.6, -5.5)
'format applied to two vectors: {:.4e} and {:.2e}'.format(u, v)
# Check if vector contains a value
u = FVC(2, 3, 4)
3 in u
# Check if a vector does not contain a value
u = FVC(2, 3, 4)
3.0 not in u
# The component values of a vector
u = FVC(-6, 8, 3)
u.a, u.b, u.c
# Change the component values of a vector
u = FVC(0, 0, 0)
u.a, u.b, u.c = 6, 7, 8
u
# Change a component value of a vector
u = FVC(0, 0, 0)
u.a += 100
u
# Change a component value of a vector
u = FVC(3, -4, 20)
u.c //= 8
u
# The component values / Indexing of vector
u = FVC(7, -8, 9)
u[0], u[1], u[2]
# The component values / Indexing of vector
u = FVC(7, -8, 9)
u[-3], u[-2], u[-1]
# Indexing of a vector
u = FVC(7, -8, 9)
u[0:3], u[:], u[::]
# Change the component values of a vector
u = FVC(0, 0, 0)
u[0], u[1], u[2] = 7, -8, 9
u
# Change the component values of a vector
u = FVC(0, 0, 0)
u[0:3] = 7, -8, 9
u
# Change the component values of a vector
u = FVC(0, 0, 0)
v = FVC(7, -8, 9)
u[:] = v
u
# Change the component values of a vector
u = FVC(0, 0, 0)
u[:] = (cv for cv in [ 7, -8, 9 ])
u
# List of the component values of a vector
u = FVC(7, -8, 9)
u.cvalues, u.component_values(), u[:]
# List of the component values
u = FVC(7, -8, 9)
list(u), [ *u ], [ getattr(u, cn) for cn in u.cnames ]
# Iterate over the components
u = FVC(7, -8, 9)
x, y, z = u
x, y, z
# Iterate over the components
u = FVC(7, -8, 9)
g = (cv for cv in u)
print(*g)
# Iterate over the components
u = FVC(7, -8, 9)
components = iter(u)
next(components), next(components), next(components)
# Check if a vector is equal to another
u = FVC(2.0, 4.0, 6.0)
v = FVC(2, 4, 6)
u == v
# Check if a vector is not equal to another
u = FVC(2, 4, 6)
v = FVC(2.0, 4.0, 6.0)
u != v
# Create a dictionary from the components of a vector and their names
u = FVC(2, 4, 6)
u.as_dict()
# Make shallow copy of vector
u = FVC(2, 4, 6)
v = FVC(*u)
v
# Make shallow copy of vector
u = FVC(2, 4, 6)
v = u.copy()
v
# Create a vector by applying a lambda function to each of its components
u = FVC(-3.3, 4.6, -5.5)
u(lambda s: 10 + s * 1000)
# Create a vector by applying abs to each of its components
u = FVC(-3.3, 4.6, -5.5)
u(abs)
# Create a vector by applying abs to each of its components
u = FVC(-3, 4, -5)
FVC(*map(abs, u))
# Create a vector by applying the int class to each of its components
u = FVC(-3.3, 4.6, -5.5)
u(int)
# Change the components of a vector by applying the int class to each component
u = FVC(-3.3, 4.6, -5.5)
u[:] = map(int, u)
u
# Create a vector method that takes 1 vector as argument
def square(s):
return s**2
FVC.create_vector_method_arg1('square', square)
u = FVC(2, 3, -4)
u.vector_square()
# Create, from a built in function, a vector method that takes 1 vector as argument
FVC.create_vector_method_arg1('abs', lambda s: abs(s))
u = FVC(2, 3, -4)
u.vector_abs()
# Create a vector method that takes 2 vectors as arguments
def add(s, t):
return s + t
FVC.create_vector_method_arg2('add', add)
u = FVC(2, 3, -4)
v = FVC(1, -2, 3)
s = 1000
u.vector_add(v), v.vector_add(s)
# Create a vector method that takes 3 vectors as arguments
def select(r, s, t):
if r < 0:
result = s
else:
result = t
return result
FVC.create_vector_method_arg3('select', select)
u = FVC(-2, 0, 3)
v = FVC(1, 3, 5)
w = FVC(2, 4, 6)
s = 0
t = 100
u.vector_select(v, w), u.vector_select(s, t)
| 0.857679 | 0.905657 |
# Analyze All-Time Kicks
Every kick from every match is also saved in a separate branch of the database so that we can query analytics for players and their kicks across multiple matches. We call these the "all-time kicks" dataset.
We have stripped the player user names so that the dataset can be analyzed. This notebook summarizes the dataset.
```
import sys
sys.path.append("../")
from haxml.utils import (
is_target_stadium,
is_shot
)
import json
import pandas as pd
ALL_TIME_KICKS = "../data/all_time_kicks.json"
with open(ALL_TIME_KICKS, "r") as file:
all_time_kicks = json.load(file)
df = pd.DataFrame(all_time_kicks.values())
```
## Dataset Summary
```
df.head().T
```
The three stadiums we will spend the most time playing in and analyzing are the two main NAFL (Futsal) maps (1v1, 2v2, 3v3, 4v4) and the Classic HaxBall map. We want to create a model that can be applied across multiple stadiums (as long as the stadium meets our assumptions), but we can focus our analysis and development on these three stadiums.
```
def summarize_df(df):
n_matches = df["match"].nunique()
n_players = df["fromName"].nunique()
print(f"Rows: {df.shape[0]:,} kicks")
print(f"Columns: {df.shape[1]:,} features")
print(f"Matches: {n_matches:,} matches")
print(f"Players: {n_players:,} unique players")
print("All-Time Kicks:")
summarize_df(df)
print()
print("From Target Stadiums:")
df_target = df[df["stadium"].apply(is_target_stadium)]
summarize_df(df_target)
```
### Table 1. Count of kicks, by stadium.
```
gp_stadium = df.groupby("stadium")["kick"].count()
pd.DataFrame(gp_stadium.sort_values(ascending=False)).reset_index()
```
### Table 2. Count of matches, by stadium.
```
gp_matches = df.groupby("stadium")["match"].nunique()
pd.DataFrame(gp_matches.sort_values(ascending=False)).reset_index()
```
### Table 3. Count of unique players who kicked (from), by stadium.
```
gp_players = df.groupby("stadium")["fromName"].nunique()
pd.DataFrame(gp_players.sort_values(ascending=False)).reset_index()
```
### Table 4. Count of kicks, by stadium and by type.
Showing target stadiums only.
```
df_types = df_target.groupby(["stadium", "type"])["kick"].count()
df_types_stadium = df_types.groupby("stadium", group_keys=False)
df_tsv = df_types_stadium.apply(lambda x: x.sort_values(ascending=False))
df_tsk = df_tsv.sort_index(level=0, key=lambda x: gp_stadium[x], ascending=False)
pd.DataFrame(df_tsk)
```
### Table 5. Fraction of kicks that are goals, by stadium.
```
"""
Calculate the fraction of kicks that are goals.
"""
def get_goal_fraction(kick_types):
goals = sum(1 if val == "goal" else 0 for val in kick_types)
return goals / len(kick_types)
gp_goals = df.groupby("stadium")["type"].agg(get_goal_fraction)
gp_goals_sorted = gp_goals.sort_index(key=lambda x: gp_stadium[x], ascending=False)
pd.DataFrame(gp_goals_sorted).reset_index()
```
|
github_jupyter
|
import sys
sys.path.append("../")
from haxml.utils import (
is_target_stadium,
is_shot
)
import json
import pandas as pd
ALL_TIME_KICKS = "../data/all_time_kicks.json"
with open(ALL_TIME_KICKS, "r") as file:
all_time_kicks = json.load(file)
df = pd.DataFrame(all_time_kicks.values())
df.head().T
def summarize_df(df):
n_matches = df["match"].nunique()
n_players = df["fromName"].nunique()
print(f"Rows: {df.shape[0]:,} kicks")
print(f"Columns: {df.shape[1]:,} features")
print(f"Matches: {n_matches:,} matches")
print(f"Players: {n_players:,} unique players")
print("All-Time Kicks:")
summarize_df(df)
print()
print("From Target Stadiums:")
df_target = df[df["stadium"].apply(is_target_stadium)]
summarize_df(df_target)
gp_stadium = df.groupby("stadium")["kick"].count()
pd.DataFrame(gp_stadium.sort_values(ascending=False)).reset_index()
gp_matches = df.groupby("stadium")["match"].nunique()
pd.DataFrame(gp_matches.sort_values(ascending=False)).reset_index()
gp_players = df.groupby("stadium")["fromName"].nunique()
pd.DataFrame(gp_players.sort_values(ascending=False)).reset_index()
df_types = df_target.groupby(["stadium", "type"])["kick"].count()
df_types_stadium = df_types.groupby("stadium", group_keys=False)
df_tsv = df_types_stadium.apply(lambda x: x.sort_values(ascending=False))
df_tsk = df_tsv.sort_index(level=0, key=lambda x: gp_stadium[x], ascending=False)
pd.DataFrame(df_tsk)
"""
Calculate the fraction of kicks that are goals.
"""
def get_goal_fraction(kick_types):
goals = sum(1 if val == "goal" else 0 for val in kick_types)
return goals / len(kick_types)
gp_goals = df.groupby("stadium")["type"].agg(get_goal_fraction)
gp_goals_sorted = gp_goals.sort_index(key=lambda x: gp_stadium[x], ascending=False)
pd.DataFrame(gp_goals_sorted).reset_index()
| 0.351756 | 0.926103 |
# First Method of Simulated Moments (MSM) estimation with estimagic
This tutorial shows how to do a Method of Simulated Moments estimation in estimagic. The Method of Simulated Moments (MSM) is a nonlinear estimation principle that is very useful to fit complicated models to data. The only thing that is needed is a function that simulates model outcomes that you observe in some empirical dataset.
In this tutorial we will use a simple linear regression model. This is the same model which we use in the tutorial on maximum likelihood estimation.
Throughout the tutorial we only talk about MSM estimation, however, the more general case of indirect inference estimation works exactly the same way.
## Steps of MSM estimation
- load (simulate) empirical data
- define a function to calculate estimation moments on the data
- calculate the covariance matrix of the empirical moments (with ``get_moments_cov``)
- define a function to simulate moments from the model
- estimate the model, calculate standard errors, do sensitivity analysis (with ``estimate_msm``)
## Example: Estimating the parameters of a regression model
The model we consider is simple regression model with one variable. The goal is to estimate the slope coefficients and the error variance from a simulated data set.
The estimation mechanics are exactly the same for more complicated models. A model is always defined by a function that can take parameters (here: the mean, variance and lower_cutoff and upper_cutoff) and returns a number of simulated moments (mean, variance, soft_min and soft_max of simulated exam points).
### Model:
$$ y = \beta_0 + \beta_1 x + \epsilon, \text{ where } \epsilon \sim N(0, \sigma^2)$$
We aim to estimate $\beta_0, \beta_1, \sigma^2$.
```
import numpy as np
import pandas as pd
np.random.seed(0)
```
## Simulate data
```
def simulate_data(params, n_draws):
x = np.random.normal(0, 1, size=n_draws)
e = np.random.normal(0, params.loc["sd", "value"], size=n_draws)
y = params.loc["intercept", "value"] + params.loc["slope", "value"] * x + e
return pd.DataFrame({"y": y, "x": x})
true_params = pd.DataFrame(
data=[[2, -np.inf], [-1, -np.inf], [1, 1e-10]],
columns=["value", "lower_bound"],
index=["intercept", "slope", "sd"],
)
data = simulate_data(true_params, n_draws=100)
```
## Calculate Moments
```
def calculate_moments(sample):
moments = {
"y_mean": sample["y"].mean(),
"x_mean": sample["x"].mean(),
"yx_mean": (sample["y"] * sample["x"]).mean(),
"y_sqrd_mean": (sample["y"] ** 2).mean(),
"x_sqrd_mean": (sample["x"] ** 2).mean(),
}
return pd.Series(moments)
empirical_moments = calculate_moments(data)
empirical_moments
```
## Calculate the covariance matrix of empirical moments
The covariance matrix of the empirical moments (``moments_cov``) is needed for three things:
1. to calculate the weighting matrix
2. to calculate standard errors
3. to calculate sensitivity measures
We will calculate ``moments_cov`` via a bootstrap. Depending on your problem there can be other ways to do it.
```
from estimagic import get_moments_cov
moments_cov = get_moments_cov(
data, calculate_moments, bootstrap_kwargs={"n_draws": 5_000, "seed": 0}
)
moments_cov
```
``get_moments_cov`` mainly just calls estimagic's bootstrap function. See our [bootstrap_tutorial](../how_to_guides/inference/how_to_do_bootstrap_inference.ipynb) for background information.
## Define a function to calculate simulated moments
In a real application, this is the step that takes most of the time. However, in our very simple example, all the work is already done by numpy.
```
def simulate_moments(params, n_draws=10_000, seed=0):
np.random.seed(seed)
sim_data = simulate_data(params, n_draws)
sim_moments = calculate_moments(sim_data)
return sim_moments
simulate_moments(true_params)
```
## Estimate the model parameters
Estimating a model consists of the following steps:
- Building a criterion function that measures a distance between simulated and empirical moments
- Minimizing this criterion function
- Calculating the Jacobian of the model
- Calculating standard errors, confidence intervals and p values
- Calculating sensitivity measures
This can all be done in one go with the ``estimate_msm`` function. This function has good default values, so you only need a minimum number of inputs. However, you can configure almost every aspect of the workflow via optional arguments. If you need even more control, you can call the low level functions ``estimate_msm`` is built on directly.
```
from estimagic import estimate_msm
start_params = true_params.assign(value=[100, 100, 100])
res = estimate_msm(
simulate_moments,
empirical_moments,
moments_cov,
start_params,
optimize_options={"algorithm": "scipy_lbfgsb"},
)
res["summary"]
```
## What's in the result?
The result is a dictionary with the following entries:
```
res.keys()
```
- summary: A DataFrame with estimated parameters, standard errors, p_values and confidence intervals. This is ideal for use with our `estimation_table` function.
- cov: A DataFrame with the full covariance matrix of the estimated parameters. You can use this for hypothesis tests.
- optimize_res: A dictionary with the complete output of the numerical optimization (if one was performed)
- numdiff_info: A dictionary with the complete output of the numerical differentiation (if one was performed)
- jacobian: A DataFrame with the jacobian of `simulate_moments` with respect to the free parameters.
- sensitivity: A dictionary of DataFrames with the six sensitivity measures from Honore, Jorgensen and DePaula (2020)
## How to visualize sensitivity measures
For more background on the sensitivity measures and their interpretation, check out the [how to guide](../how_to_guides/miscellaneous/how_to_visualize_and_interpret_sensitivity_measures.ipynb) on sensitivity measures.
Here we are just showing you how to plot them:
```
from estimagic.visualization.lollipop_plot import lollipop_plot
sensitivity_data = res["sensitivity"]["sensitivity_to_bias"].abs().T
fig = lollipop_plot(sensitivity_data)
fig = fig.update_layout(height=500, width=900)
fig.show(renderer="png")
```
|
github_jupyter
|
import numpy as np
import pandas as pd
np.random.seed(0)
def simulate_data(params, n_draws):
x = np.random.normal(0, 1, size=n_draws)
e = np.random.normal(0, params.loc["sd", "value"], size=n_draws)
y = params.loc["intercept", "value"] + params.loc["slope", "value"] * x + e
return pd.DataFrame({"y": y, "x": x})
true_params = pd.DataFrame(
data=[[2, -np.inf], [-1, -np.inf], [1, 1e-10]],
columns=["value", "lower_bound"],
index=["intercept", "slope", "sd"],
)
data = simulate_data(true_params, n_draws=100)
def calculate_moments(sample):
moments = {
"y_mean": sample["y"].mean(),
"x_mean": sample["x"].mean(),
"yx_mean": (sample["y"] * sample["x"]).mean(),
"y_sqrd_mean": (sample["y"] ** 2).mean(),
"x_sqrd_mean": (sample["x"] ** 2).mean(),
}
return pd.Series(moments)
empirical_moments = calculate_moments(data)
empirical_moments
from estimagic import get_moments_cov
moments_cov = get_moments_cov(
data, calculate_moments, bootstrap_kwargs={"n_draws": 5_000, "seed": 0}
)
moments_cov
def simulate_moments(params, n_draws=10_000, seed=0):
np.random.seed(seed)
sim_data = simulate_data(params, n_draws)
sim_moments = calculate_moments(sim_data)
return sim_moments
simulate_moments(true_params)
from estimagic import estimate_msm
start_params = true_params.assign(value=[100, 100, 100])
res = estimate_msm(
simulate_moments,
empirical_moments,
moments_cov,
start_params,
optimize_options={"algorithm": "scipy_lbfgsb"},
)
res["summary"]
res.keys()
from estimagic.visualization.lollipop_plot import lollipop_plot
sensitivity_data = res["sensitivity"]["sensitivity_to_bias"].abs().T
fig = lollipop_plot(sensitivity_data)
fig = fig.update_layout(height=500, width=900)
fig.show(renderer="png")
| 0.563618 | 0.992481 |
# Ajuste de Curvas a Uma Lista de Pontos
## Método dos Mínimos Quadrados
---
## Função Exponencial
Dada um lista de $n$ ponto no plano $\mathbb{R}^2$: $(x_1,y_1), (x_2,y_2), \ldots, (x_n,y_n)$. Um ajuste de uma curva da forma $y(x) = \alpha + \beta e^x$ à lista de pontos pode ser obtida, pelo método dos mínimos quadrados, com:
$$
x = (A^tA)^{-1}(A^tb)
$$
Onde $A = \left[ \begin{matrix} 1 & e^{x_1} \\ 1 & e^{x_2} \\ \vdots & \vdots \\ 1 & e^{x_n} \end{matrix} \right]$, $b = \left[ \begin{matrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{matrix} \right]$.
O vetor $x$, resultado das operações $(A^tA)^{-1}(A^tb)$, tem a forma $x = \left[ \begin{matrix} \alpha \\ \beta \end{matrix} \right]$, onde $\alpha$ e $\beta$ são os coeficientes da função exponencial ajustada:
$$
y(x) = \alpha + \beta e^x
$$
---
### Exemplo 1
Vamos ajustar uma curva exponencial da forma $y(x) = \alpha + \beta e^x$ aos pontos: $(1,1),(3,2),(5,3),(6,5),(7,7)$
No [GeoGebra](https://www.geogebra.org/m/ajynvkuz) marcamos os pontos no plano, para termos uma ideia de como será a curva ajustadas aos mesmos.
```
# Usando Python para plotar os pontos listados
# Importando o pyplot: biblioteca python para plotagem de gráficos
from matplotlib import pyplot as plt
# Eixo x, Eixo y
plt.plot([1,3,5,6,7],[1,2,3,5,7],'o') # O argumento 'o' plota os pontos
plt.axis([0, 8, 0, 8]) # [xmin, xmax, ymin, ymax]
plt.xlabel('x'), plt.ylabel('y') # Rótulos dos eixos x e y
plt.grid() # Exibindo a grade do plano
plt.show()
# Resolvendo a operações x = (A^tA)^(-1)(A^tb)
# Importando a biblioteca para trabalha com matrizes e matemática
import numpy as np
# Criando e exibindo as matrizes necessárias para os cálculos
# Atribuindo uma aproximação de e à variável e
e = 2.71828
A = np.array([[1,e**1], [1,e**3], [1,e**5], [1,e**6], [1,e**7]])
b = np.array([[1],[2],[3],[5],[7]])
A, b
M = A.T # a variável M recebe a tranposta da matriz A
M = M.dot(A) # a variável M recebe o protudo MA
# usamos o método inv do pacote de algebra linear de numpy para inverter M
M = np.linalg.inv(M)
M # Exibindo M
N = A.T # a variável N recebe a transposta de A
N = N.dot(b) # a variável N recebe o produto Nb
N # Exibindo N
# Com as operações realizadas temos
# M = (A^tA)^(-1) e N = A^tb
# A viável x recebe o produto MN
x = M.dot(N)
# Exibindo o vetor x
x
```
Assim nossa função, com alguns arendodamentos, é da forma
$$
y=1.921 + 0.005 ℯ^{x}
$$
Usamos o geogebra para plotar a curva e os pontos.
[GeoGebra](https://www.geogebra.org/m/thuykp7m)
```
# Usando Python para plotar os pontos e a curva ajustada
# Plotando os pontos
plt.plot([1,3,5,6,7],[1,2,3,5,7],'o')
# Preparo para a plotagem da curva
x = np.linspace(0, 8, 1000) # 1000 pontos em [0, 8]
y = 1.921 + 0.005*e**x # Calculo dos valores y para cada x
# Plotando a curva
plt.plot(x,y)
# Configurações do Plano
plt.axis([0, 8, 0, 8])
plt.xlabel('x'), plt.ylabel('y')
plt.grid()
plt.show()
```
---
## Algoritmo para ajuste de uma curva exponencial a uma lista de pontos
```
'''
Método para o ajuste da curva de uma Função Exponencial a uma lista de pontos
Mínimos Quadrados
Observações:
--> Os argumentos da função são duas listas de mesmo tamanho;
--> A primeira lista com as coordenadas x dos pontos que queremos ajustar;
--> E a segunda lista com as coordenadas y dos pontos.
A função retorna um vetor x = [a,b]^T, onde y = a + b*e^x é a função exponencial.
'''
def exponencial_minimos_quadrados(X,Y):
import numpy as np
from numpy.linalg import inv
n = len(X)
if len(X) != len(Y):
return 'Dados de entrada incorretos.'
else:
A = np.zeros((n,2))
v = np.zeros((n,1))
for i in range(len(X)):
v[i] = Y[i]
A[i][0] = 1
A[i][1] = (np.e)**(X[i])
At = np.transpose(A)
M = np.dot(At,A)
N = np.dot(At,v)
Mi = inv(M)
x = np.dot(Mi,N)
return x
# Aplicação do método para a lista de pontos
# (1,1),(3,2),(5,3),(6,5),(7,7)
X = [1,3,5,6,7]
Y = [1,2,3,5,7]
print(exponencial_minimos_quadrados(X,Y))
# Aplicando o método para outra lista de pontos
# (1.5,1), (2.5,1.8), (3,4), (4,7)
X = [1.5,2.5,3,4]
Y = [1,1.8,4,7]
c = exponencial_minimos_quadrados(X,Y) # Vetor coeficientes
print(c)
# Plotando os pontos e a curva ajustada
from matplotlib import pyplot as plt
import numpy as np
# Plotando os pontos
plt.plot(X,Y,'o')
x = np.linspace(0, 8, 1000)
y = c[0] + c[1]*(np.e)**x # Calculo dos valores y para cada x
# Plotando a curva
plt.plot(x,y)
# Configurações do Plano
plt.axis([0, 8, 0, 8])
plt.xlabel('x'), plt.ylabel('y')
plt.grid()
plt.show()
```
|
github_jupyter
|
# Usando Python para plotar os pontos listados
# Importando o pyplot: biblioteca python para plotagem de gráficos
from matplotlib import pyplot as plt
# Eixo x, Eixo y
plt.plot([1,3,5,6,7],[1,2,3,5,7],'o') # O argumento 'o' plota os pontos
plt.axis([0, 8, 0, 8]) # [xmin, xmax, ymin, ymax]
plt.xlabel('x'), plt.ylabel('y') # Rótulos dos eixos x e y
plt.grid() # Exibindo a grade do plano
plt.show()
# Resolvendo a operações x = (A^tA)^(-1)(A^tb)
# Importando a biblioteca para trabalha com matrizes e matemática
import numpy as np
# Criando e exibindo as matrizes necessárias para os cálculos
# Atribuindo uma aproximação de e à variável e
e = 2.71828
A = np.array([[1,e**1], [1,e**3], [1,e**5], [1,e**6], [1,e**7]])
b = np.array([[1],[2],[3],[5],[7]])
A, b
M = A.T # a variável M recebe a tranposta da matriz A
M = M.dot(A) # a variável M recebe o protudo MA
# usamos o método inv do pacote de algebra linear de numpy para inverter M
M = np.linalg.inv(M)
M # Exibindo M
N = A.T # a variável N recebe a transposta de A
N = N.dot(b) # a variável N recebe o produto Nb
N # Exibindo N
# Com as operações realizadas temos
# M = (A^tA)^(-1) e N = A^tb
# A viável x recebe o produto MN
x = M.dot(N)
# Exibindo o vetor x
x
# Usando Python para plotar os pontos e a curva ajustada
# Plotando os pontos
plt.plot([1,3,5,6,7],[1,2,3,5,7],'o')
# Preparo para a plotagem da curva
x = np.linspace(0, 8, 1000) # 1000 pontos em [0, 8]
y = 1.921 + 0.005*e**x # Calculo dos valores y para cada x
# Plotando a curva
plt.plot(x,y)
# Configurações do Plano
plt.axis([0, 8, 0, 8])
plt.xlabel('x'), plt.ylabel('y')
plt.grid()
plt.show()
'''
Método para o ajuste da curva de uma Função Exponencial a uma lista de pontos
Mínimos Quadrados
Observações:
--> Os argumentos da função são duas listas de mesmo tamanho;
--> A primeira lista com as coordenadas x dos pontos que queremos ajustar;
--> E a segunda lista com as coordenadas y dos pontos.
A função retorna um vetor x = [a,b]^T, onde y = a + b*e^x é a função exponencial.
'''
def exponencial_minimos_quadrados(X,Y):
import numpy as np
from numpy.linalg import inv
n = len(X)
if len(X) != len(Y):
return 'Dados de entrada incorretos.'
else:
A = np.zeros((n,2))
v = np.zeros((n,1))
for i in range(len(X)):
v[i] = Y[i]
A[i][0] = 1
A[i][1] = (np.e)**(X[i])
At = np.transpose(A)
M = np.dot(At,A)
N = np.dot(At,v)
Mi = inv(M)
x = np.dot(Mi,N)
return x
# Aplicação do método para a lista de pontos
# (1,1),(3,2),(5,3),(6,5),(7,7)
X = [1,3,5,6,7]
Y = [1,2,3,5,7]
print(exponencial_minimos_quadrados(X,Y))
# Aplicando o método para outra lista de pontos
# (1.5,1), (2.5,1.8), (3,4), (4,7)
X = [1.5,2.5,3,4]
Y = [1,1.8,4,7]
c = exponencial_minimos_quadrados(X,Y) # Vetor coeficientes
print(c)
# Plotando os pontos e a curva ajustada
from matplotlib import pyplot as plt
import numpy as np
# Plotando os pontos
plt.plot(X,Y,'o')
x = np.linspace(0, 8, 1000)
y = c[0] + c[1]*(np.e)**x # Calculo dos valores y para cada x
# Plotando a curva
plt.plot(x,y)
# Configurações do Plano
plt.axis([0, 8, 0, 8])
plt.xlabel('x'), plt.ylabel('y')
plt.grid()
plt.show()
| 0.599368 | 0.984471 |
[Search in Rotated Sorted Array](https://leetcode.com/problems/search-in-rotated-sorted-array/)。**2019作业帮手撕代码题**。在一个不含重复元素的旋转有序数组中查找关键字,找不到返回$-1$。
思路:旋转数组的有序性被破坏掉了,但是仍然保留了一部分的有序性,关键就是找出有序的部分。首先定位到中点```mid```,一个正常的有序数组,其中值应该大于左边界而小于右边界。因为在计算中值时会偏左,考虑到左右边界相邻时的特殊情况,选择将中值与右边界比较。
若中值小于右边界,则中值右边是一个有序子数组,判断关键字是否在右边;若中值大于右边界,则中值左边是一个有序数组,判断关键字是否在左边。
```
def search(nums, target: int) -> int:
if not nums:
return -1
left, right = 0, len(nums)-1
while left < right:
mid = (left+right) >> 1
if nums[mid] == target:
return mid
if nums[mid] < nums[right]: # 右边有序
if nums[mid] <= target <= nums[right]: # 是否在有序的那一边
left = mid+1
else:
right = mid
else: # 左边有序
if nums[left] <= target <= nums[mid]: # 是否在有序的那一边
right = mid
else:
left = mid+1
return left if nums[left] == target else -1
```
[Search in Rotated Sorted Array II](https://leetcode.com/problems/search-in-rotated-sorted-array-ii/)。在一含重复元素的有序旋转数组中判定关键字是否存在。
思路:思路同上题,仍然是在有序的部分中进行查找。但是因为引入了重复元素,所以需要增加一种情况:中值与右边界相等。当中值有右边界相等时,说明遇到了重复元素,最简单的处理办法就是逐元素地缩小边界。这样一来最坏的时间复杂度为$O(n)$。
```
def search(nums, target: int) -> bool:
if not nums:
return False
left, right = 0, len(nums)-1
while left < right:
mid = (left+right) >> 1
if nums[mid] == target:
return True
if nums[mid] < nums[right]:
if nums[mid] <= target <= nums[right]:
left = mid+1
else:
right = mid
elif nums[mid] > nums[right]:
if nums[left] <= target <= nums[mid]:
right = mid
else:
left = mid+1
else: # 新增加的情况
right -= 1
return True if nums[left] == target else False
```
[Find Minimum in Rotated Sorted Array](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/)。在旋转数组中寻找最小值。
思路:在旋转数组中寻找值的思路,就是将中值与右值去比较。
```
def findMin(nums) -> int:
n = len(nums)
if n == 1:
return nums[0]
left, right = 0, n-1
while left < right:
mid = (left+right) >> 1
if nums[mid] <= nums[right]:
right = mid
else:
left = mid+1
return nums[left]
```
[Peak Index in a Mountain Array](https://leetcode.com/problems/peak-index-in-a-mountain-array/)。顶峰搜索,给一长度大于$3$的数组,该数组前一段满足递增,后一段满足递减。求该数组中的最大值。保证顶峰存在。
思路:最简单的线性扫描时间复杂度为$O(n)$,使用二分搜索查找一个同时大于左右邻居的位置。
```
def peakIndexInMountainArray(A) -> int:
n = len(A)
left, right = 1, n-2
while left < right:
mid = (left+right) >> 1
if A[mid-1] < A[mid] > A[mid+1]:
return mid
elif A[mid-1] < A[mid] < A[mid+1]:
left = mid+1
else:
right = mid
return left
```
[Find First and Last Position of Element in Sorted Array](https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/)。给一有序整形数组$nums$,查找一个元素出现的位置范围。
思路:二分查找有一个变种,就是不管找没找到都会返回一个插入位置。另外因为数组是整形,所以可以查找$target-0.5$与$target+0.5$的插入位置。
```
def searchRange(nums, target: int):
def BinSearch(key):
left, right = 0, len(nums)
while left < right:
mid = (left+right) >> 1
if nums[mid] < key:
left = mid+1
else:
right = mid
return left
start = BinSearch(target-0.5)
end = BinSearch(target+0.5)-1 # 末位位置要-1
return [start, end] if start <= end else [-1, -1]
```
[First Bad Version](https://leetcode.com/problems/first-bad-version/)。给一个长度为$n$的正整数数组,其中从某一个数开始后都是坏点,有一个API```isBadVersion(num)```用于检测坏点。找到坏点开始的位置。
思路:二分查找。
```
def firstBadVersion(n: int) -> int:
res = None
left, right = 0, n-1
while left < right:
mid = (left+right) >> 1
if isBadVersion(mid+1):
res = mid+1
right = mid
else:
left = mid+1
return left+1 if isBadVersion(left+1) else res
```
[Find Peak Element](https://leetcode.com/problems/find-peak-element/)。给一数组$nums$,假设数组两边的边界都是负无穷,随便返回一个大于邻居值的位置索引。
思路:只要数组不为空就必定存在一个顶峰。二分搜索,如果中值大于其右边的值,则中值及其左边的部分至少存在一个顶峰;否则在右边至少存在一个顶峰。
```
def findPeakElement(nums) -> int:
n = len(nums)
if n < 2:
return 0
left, right = 0, n-1
while left < right:
mid = (left+right) >> 1
if nums[mid] > nums[mid+1]:
right = mid
else:
left = mid+1
return left
```
[Valid Perfect Square](https://leetcode.com/problems/valid-perfect-square/)。判断一数字是否是一个完全平方数。
思路:在$[0,num]$范围内二分搜索,若$mid^{2}>num$则在左区间搜索,反之在右区间搜索。
```
def isPerfectSquare(num: int) -> bool:
left, right = 0, num
while left < right:
mid = (left+right) >> 1
test = mid*mid
if test == num:
return True
elif test > num:
right = mid
else:
left = mid+1
return left*left == num
```
[Arranging Coins](https://leetcode.com/problems/arranging-coins/)。给$n$个硬币去铺台阶,要求第$1$阶需要$1$个硬币,第$2$阶需要$2$个硬币,……。问这$n$个硬币能铺满多少级台阶。
思路:最简单的线性搜索,但是这种顺序线性搜索问题都能优化成二分搜索。
```
def arrangeCoins(n: int) -> int:
left, right = 0, n
while left < right:
mid = (left+right) >> 1
need = (1+mid)*mid//2
if n >= need:
left = mid+1
else:
right = mid
return left-1 if n > 1 else n
```
[Kth Smallest Element in a Sorted Matrix](https://leetcode.com/problems/kth-smallest-element-in-a-sorted-matrix/)。给一矩阵,该矩阵的每行每列都是升序排列的,求该矩阵中第$k$大的数字。
思路:利用矩阵的有序性质,可以使用二分搜索。定义一个辅助函数```count(x)```用于计算矩阵中小于等于$x$的数字有多少个。若该值小于$k$则说明可以增大$x$,反之需要减小$x$。
```
def kthSmallest(matrix, k: int) -> int:
rows, cols = len(matrix), len(matrix[0])
left, right = matrix[0][0], matrix[-1][-1]
def count(x): # 统计小于等于x的数量
row, col = rows-1, 0
res = 0
while row >= 0 and col < cols:
if matrix[row][col] <= x:
res += row+1
col += 1
else:
row -= 1
return res
while left < right:
mid = (left+right) >> 1
if count(mid) < k:
left = mid+1
else:
right = mid
return left
```
|
github_jupyter
|
def search(nums, target: int) -> int:
if not nums:
return -1
left, right = 0, len(nums)-1
while left < right:
mid = (left+right) >> 1
if nums[mid] == target:
return mid
if nums[mid] < nums[right]: # 右边有序
if nums[mid] <= target <= nums[right]: # 是否在有序的那一边
left = mid+1
else:
right = mid
else: # 左边有序
if nums[left] <= target <= nums[mid]: # 是否在有序的那一边
right = mid
else:
left = mid+1
return left if nums[left] == target else -1
def search(nums, target: int) -> bool:
if not nums:
return False
left, right = 0, len(nums)-1
while left < right:
mid = (left+right) >> 1
if nums[mid] == target:
return True
if nums[mid] < nums[right]:
if nums[mid] <= target <= nums[right]:
left = mid+1
else:
right = mid
elif nums[mid] > nums[right]:
if nums[left] <= target <= nums[mid]:
right = mid
else:
left = mid+1
else: # 新增加的情况
right -= 1
return True if nums[left] == target else False
def findMin(nums) -> int:
n = len(nums)
if n == 1:
return nums[0]
left, right = 0, n-1
while left < right:
mid = (left+right) >> 1
if nums[mid] <= nums[right]:
right = mid
else:
left = mid+1
return nums[left]
def peakIndexInMountainArray(A) -> int:
n = len(A)
left, right = 1, n-2
while left < right:
mid = (left+right) >> 1
if A[mid-1] < A[mid] > A[mid+1]:
return mid
elif A[mid-1] < A[mid] < A[mid+1]:
left = mid+1
else:
right = mid
return left
def searchRange(nums, target: int):
def BinSearch(key):
left, right = 0, len(nums)
while left < right:
mid = (left+right) >> 1
if nums[mid] < key:
left = mid+1
else:
right = mid
return left
start = BinSearch(target-0.5)
end = BinSearch(target+0.5)-1 # 末位位置要-1
return [start, end] if start <= end else [-1, -1]
def firstBadVersion(n: int) -> int:
res = None
left, right = 0, n-1
while left < right:
mid = (left+right) >> 1
if isBadVersion(mid+1):
res = mid+1
right = mid
else:
left = mid+1
return left+1 if isBadVersion(left+1) else res
def findPeakElement(nums) -> int:
n = len(nums)
if n < 2:
return 0
left, right = 0, n-1
while left < right:
mid = (left+right) >> 1
if nums[mid] > nums[mid+1]:
right = mid
else:
left = mid+1
return left
def isPerfectSquare(num: int) -> bool:
left, right = 0, num
while left < right:
mid = (left+right) >> 1
test = mid*mid
if test == num:
return True
elif test > num:
right = mid
else:
left = mid+1
return left*left == num
def arrangeCoins(n: int) -> int:
left, right = 0, n
while left < right:
mid = (left+right) >> 1
need = (1+mid)*mid//2
if n >= need:
left = mid+1
else:
right = mid
return left-1 if n > 1 else n
def kthSmallest(matrix, k: int) -> int:
rows, cols = len(matrix), len(matrix[0])
left, right = matrix[0][0], matrix[-1][-1]
def count(x): # 统计小于等于x的数量
row, col = rows-1, 0
res = 0
while row >= 0 and col < cols:
if matrix[row][col] <= x:
res += row+1
col += 1
else:
row -= 1
return res
while left < right:
mid = (left+right) >> 1
if count(mid) < k:
left = mid+1
else:
right = mid
return left
| 0.438545 | 0.907107 |
```
import tensorflow as tf
tf.config.experimental.list_physical_devices()
tf.test.is_built_with_cuda()
```
# Importing Libraries
```
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import os.path as op
import pickle
import tensorflow as tf
from tensorflow import keras
from keras.models import Model,Sequential,load_model
from keras.layers import Input, Embedding
from keras.layers import Dense, Bidirectional
from keras.layers.recurrent import LSTM
import keras.metrics as metrics
import itertools
from tensorflow.python.keras.utils.data_utils import Sequence
from decimal import Decimal
from keras import backend as K
from keras.layers import Conv1D,MaxPooling1D,Flatten,Dense
```
# Data Fetching
```
A1=np.empty((0,5),dtype='float32')
U1=np.empty((0,7),dtype='float32')
node=['150','149','147','144','142','140','136','61']
mon=['Apr','Mar','Aug','Jun','Jul','Sep','May','Oct']
for j in node:
for i in mon:
inp= pd.read_csv('../../../data_gkv/AT510_Node_'+str(j)+'_'+str(i)+'19_OutputFile.csv',usecols=[1,2,3,15,16])
out= pd.read_csv('../../../data_gkv/AT510_Node_'+str(j)+'_'+str(i)+'19_OutputFile.csv',usecols=[5,6,7,8,17,18,19])
inp=np.array(inp,dtype='float32')
out=np.array(out,dtype='float32')
A1=np.append(A1, inp, axis=0)
U1=np.append(U1, out, axis=0)
print(A1)
print(U1)
```
# Min Max Scaler
```
from sklearn.decomposition import PCA
import warnings
scaler_obj1=PCA(svd_solver='full')
scaler_obj2=PCA(svd_solver='full')
X1=scaler_obj1.fit_transform(A1)
Y1=scaler_obj2.fit_transform(U1)
warnings.filterwarnings(action='ignore', category=UserWarning)
X1=X1[:,np.newaxis,:]
Y1=Y1[:,np.newaxis,:]
def rmse(y_true, y_pred):
return K.sqrt(K.mean(K.square(y_pred - y_true), axis=-1))
def coeff_determination(y_true, y_pred):
SS_res = K.sum(K.square( y_true-y_pred ))
SS_tot = K.sum(K.square( y_true - K.mean(y_true) ) )
return ( 1 - SS_res/(SS_tot + K.epsilon()) )
```
# Model
```
inp=keras.Input(shape=(1,5))
l=keras.layers.Conv1D(16,1,padding="same",activation="tanh",kernel_initializer="glorot_uniform")(inp)
output = keras.layers.Conv1D(7,4,padding="same",activation='sigmoid')(l)
model1=keras.Model(inputs=inp,outputs=output)
model1.compile(optimizer=keras.optimizers.Adam(learning_rate=1e-5), loss='binary_crossentropy',metrics=['accuracy','mse','mae',rmse])
model1.summary()
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X1, Y1, test_size=0.25, random_state=42)
history1 = model1.fit(x_train,y_train,batch_size=256,epochs=50, validation_data=(x_test, y_test),verbose = 2, shuffle= False)
model1.evaluate(x_test,y_test)
```
# Saving Model as File
```
model1.evaluate(x_train,y_train)
df1=pd.DataFrame(history1.history['loss'],columns=["Loss"])
df1=df1.join(pd.DataFrame(history1.history["val_loss"],columns=["Val Loss"]))
df1=df1.join(pd.DataFrame(history1.history["accuracy"],columns=['Accuracy']))
df1=df1.join(pd.DataFrame(history1.history["val_accuracy"],columns=['Val Accuracy']))
df1=df1.join(pd.DataFrame(history1.history["mse"],columns=['MSE']))
df1=df1.join(pd.DataFrame(history1.history["val_mse"],columns=['Val MSE']))
df1=df1.join(pd.DataFrame(history1.history["mae"],columns=['MAE']))
df1=df1.join(pd.DataFrame(history1.history["val_mae"],columns=['Val MAE']))
df1=df1.join(pd.DataFrame(history1.history["rmse"],columns=['RMSE']))
df1=df1.join(pd.DataFrame(history1.history["val_mse"],columns=['Val RMSE']))
df1
df1.to_excel("GRU_tanh_mse.xlsx")
model_json = model1.to_json()
with open("cnn_relu.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model1.save_weights("cnn_relu.h5")
print("Saved model to disk")
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X1, Y1, test_size=0.25, random_state=42)
from keras.models import model_from_json
json_file = open('cnn_relu.json', 'r')
loaded_model_json = json_file.read()
json_file.close()
loaded_model = model_from_json(loaded_model_json)
# load weights into new model
loaded_model.load_weights("cnn_relu.h5")
print("Loaded model from disk")
loaded_model.compile(optimizer=keras.optimizers.Adam(learning_rate=1e-5), loss='mse',metrics=['accuracy','mse','mae',rmse])
loaded_model.evaluate(x_train, y_train, verbose=0)
loaded_model.evaluate(x_test, y_test, verbose=0)
```
# Error Analysis
```
# summarize history for loss
plt.plot(history1.history['loss'])
plt.plot(history1.history['val_loss'])
plt.title('Model Loss',fontweight ='bold',fontsize = 15)
plt.ylabel('Loss',fontweight ='bold',fontsize = 15)
plt.xlabel('Epoch',fontweight ='bold',fontsize = 15)
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
# summarize history for accuracy
plt.plot(history1.history['accuracy'])
plt.plot(history1.history['val_accuracy'])
plt.title('Model accuracy',fontweight ='bold',fontsize = 15)
plt.ylabel('Accuracy',fontweight ='bold',fontsize = 15)
plt.xlabel('Epoch',fontweight ='bold',fontsize = 15)
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X1, Y1, test_size=0.25, random_state=42)
y_test_pred=loaded_model.predict(x_test)
y_test_pred
y_test
y_test=y_test[:,0]
y_test_pred=y_test_pred[:,0]
from numpy import savetxt
savetxt('cnn_y_test_pred.csv', y_test_pred[:1001], delimiter=',')
from numpy import savetxt
savetxt('cnn_y_test.csv', y_test[:1001], delimiter=',')
#completed
```
|
github_jupyter
|
import tensorflow as tf
tf.config.experimental.list_physical_devices()
tf.test.is_built_with_cuda()
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import os.path as op
import pickle
import tensorflow as tf
from tensorflow import keras
from keras.models import Model,Sequential,load_model
from keras.layers import Input, Embedding
from keras.layers import Dense, Bidirectional
from keras.layers.recurrent import LSTM
import keras.metrics as metrics
import itertools
from tensorflow.python.keras.utils.data_utils import Sequence
from decimal import Decimal
from keras import backend as K
from keras.layers import Conv1D,MaxPooling1D,Flatten,Dense
A1=np.empty((0,5),dtype='float32')
U1=np.empty((0,7),dtype='float32')
node=['150','149','147','144','142','140','136','61']
mon=['Apr','Mar','Aug','Jun','Jul','Sep','May','Oct']
for j in node:
for i in mon:
inp= pd.read_csv('../../../data_gkv/AT510_Node_'+str(j)+'_'+str(i)+'19_OutputFile.csv',usecols=[1,2,3,15,16])
out= pd.read_csv('../../../data_gkv/AT510_Node_'+str(j)+'_'+str(i)+'19_OutputFile.csv',usecols=[5,6,7,8,17,18,19])
inp=np.array(inp,dtype='float32')
out=np.array(out,dtype='float32')
A1=np.append(A1, inp, axis=0)
U1=np.append(U1, out, axis=0)
print(A1)
print(U1)
from sklearn.decomposition import PCA
import warnings
scaler_obj1=PCA(svd_solver='full')
scaler_obj2=PCA(svd_solver='full')
X1=scaler_obj1.fit_transform(A1)
Y1=scaler_obj2.fit_transform(U1)
warnings.filterwarnings(action='ignore', category=UserWarning)
X1=X1[:,np.newaxis,:]
Y1=Y1[:,np.newaxis,:]
def rmse(y_true, y_pred):
return K.sqrt(K.mean(K.square(y_pred - y_true), axis=-1))
def coeff_determination(y_true, y_pred):
SS_res = K.sum(K.square( y_true-y_pred ))
SS_tot = K.sum(K.square( y_true - K.mean(y_true) ) )
return ( 1 - SS_res/(SS_tot + K.epsilon()) )
inp=keras.Input(shape=(1,5))
l=keras.layers.Conv1D(16,1,padding="same",activation="tanh",kernel_initializer="glorot_uniform")(inp)
output = keras.layers.Conv1D(7,4,padding="same",activation='sigmoid')(l)
model1=keras.Model(inputs=inp,outputs=output)
model1.compile(optimizer=keras.optimizers.Adam(learning_rate=1e-5), loss='binary_crossentropy',metrics=['accuracy','mse','mae',rmse])
model1.summary()
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X1, Y1, test_size=0.25, random_state=42)
history1 = model1.fit(x_train,y_train,batch_size=256,epochs=50, validation_data=(x_test, y_test),verbose = 2, shuffle= False)
model1.evaluate(x_test,y_test)
model1.evaluate(x_train,y_train)
df1=pd.DataFrame(history1.history['loss'],columns=["Loss"])
df1=df1.join(pd.DataFrame(history1.history["val_loss"],columns=["Val Loss"]))
df1=df1.join(pd.DataFrame(history1.history["accuracy"],columns=['Accuracy']))
df1=df1.join(pd.DataFrame(history1.history["val_accuracy"],columns=['Val Accuracy']))
df1=df1.join(pd.DataFrame(history1.history["mse"],columns=['MSE']))
df1=df1.join(pd.DataFrame(history1.history["val_mse"],columns=['Val MSE']))
df1=df1.join(pd.DataFrame(history1.history["mae"],columns=['MAE']))
df1=df1.join(pd.DataFrame(history1.history["val_mae"],columns=['Val MAE']))
df1=df1.join(pd.DataFrame(history1.history["rmse"],columns=['RMSE']))
df1=df1.join(pd.DataFrame(history1.history["val_mse"],columns=['Val RMSE']))
df1
df1.to_excel("GRU_tanh_mse.xlsx")
model_json = model1.to_json()
with open("cnn_relu.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model1.save_weights("cnn_relu.h5")
print("Saved model to disk")
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X1, Y1, test_size=0.25, random_state=42)
from keras.models import model_from_json
json_file = open('cnn_relu.json', 'r')
loaded_model_json = json_file.read()
json_file.close()
loaded_model = model_from_json(loaded_model_json)
# load weights into new model
loaded_model.load_weights("cnn_relu.h5")
print("Loaded model from disk")
loaded_model.compile(optimizer=keras.optimizers.Adam(learning_rate=1e-5), loss='mse',metrics=['accuracy','mse','mae',rmse])
loaded_model.evaluate(x_train, y_train, verbose=0)
loaded_model.evaluate(x_test, y_test, verbose=0)
# summarize history for loss
plt.plot(history1.history['loss'])
plt.plot(history1.history['val_loss'])
plt.title('Model Loss',fontweight ='bold',fontsize = 15)
plt.ylabel('Loss',fontweight ='bold',fontsize = 15)
plt.xlabel('Epoch',fontweight ='bold',fontsize = 15)
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
# summarize history for accuracy
plt.plot(history1.history['accuracy'])
plt.plot(history1.history['val_accuracy'])
plt.title('Model accuracy',fontweight ='bold',fontsize = 15)
plt.ylabel('Accuracy',fontweight ='bold',fontsize = 15)
plt.xlabel('Epoch',fontweight ='bold',fontsize = 15)
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X1, Y1, test_size=0.25, random_state=42)
y_test_pred=loaded_model.predict(x_test)
y_test_pred
y_test
y_test=y_test[:,0]
y_test_pred=y_test_pred[:,0]
from numpy import savetxt
savetxt('cnn_y_test_pred.csv', y_test_pred[:1001], delimiter=',')
from numpy import savetxt
savetxt('cnn_y_test.csv', y_test[:1001], delimiter=',')
#completed
| 0.668664 | 0.675484 |
```
import pickle
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0)
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
mnist = pickle.Unpickler(open('mnist.pkl', 'rb'), encoding = 'latin1').load()
(train, validation, test) = mnist
(train_images, train_labels) = train
(validation_images, validation_labels) = validation
(test_images, test_labels) = test
image_size = 28
features_size = 784
classes_count = 10
print(train_images.shape)
print(validation_images.shape)
print(test_images.shape)
for i in range(10):
plt.subplot(1, 10, i + 1)
plt.title(str(train_labels[i]))
plt.imshow(train_images[i].reshape((image_size, image_size)))
plt.axis('off')
hidden_neurons = 400
minibatch_size = 200
regularization_factor = 0.05
learning_rate = 0.5
learning_rate_decay = 0.99
# 1 relu layers, 1 output softmax layer
# it's actually stemmed 4 layers network hence strange names of variables
W3 = np.random.uniform(high = 1.0 / hidden_neurons, size = (features_size, hidden_neurons))
b3 = np.zeros(shape = (hidden_neurons,))
W4 = np.random.uniform(high = 1.0 / hidden_neurons, size = (hidden_neurons, classes_count))
b4 = np.zeros(shape = (classes_count,))
learning_history = []
for epoch in range(2000):
choice = np.random.choice(train_images.shape[0], minibatch_size)
X = train_images[choice]
y = train_labels[choice]
# forward pass
H2 = X
H3 = np.maximum(np.dot(H2, W3) + b3, 0)
H4 = np.dot(H3, W4) + b4
scores = H4 - np.max(H4, axis = 1, keepdims = True)
probs = np.exp(scores)
probs /= np.sum(probs, axis = 1, keepdims = True)
labels = np.argmax(probs, axis = 1)
accuracy = np.mean(labels == y)
loss = np.sum(-np.log(probs[range(minibatch_size), y])) / minibatch_size
loss += 0.5 * regularization_factor * (np.sum(W3 * W3) + np.sum(b3 * b3))
loss += 0.5 * regularization_factor * (np.sum(W4 * W4) + np.sum(b4 * b4))
learning_history.append((accuracy, loss))
if epoch % 200 == 0:
print('epoch %d: accuracy = %f, loss = %f' % (epoch, accuracy, loss))
for i in range(10):
plt.subplot(10, 10, epoch / 200 + i * 10 + 1)
plt.imshow(W3[:, i * 20].reshape(image_size, image_size))
plt.axis('off')
# backprop
# layer 4
dL_dH4 = np.array(probs)
dL_dH4[range(minibatch_size), y] -= 1
dL_dH4 /= minibatch_size
dH4_dW4 = np.array(H3)
dL_dW4 = np.dot(dH4_dW4.T, dL_dH4)
dL_dW4 += regularization_factor * W4
dL_db4 = np.sum(dL_dH4, axis = 0)
dL_db4 += regularization_factor * b4
# layer 3
dH3_dW3 = np.array(H2)
dH3_db3 = np.ones(shape = H2.shape[0])
dH4_dH3 = np.array(W4)
dL_dH3 = np.dot(dL_dH4, dH4_dH3.T)
dL_dH3[H3 <= 0] = 0
dL_dW3 = np.dot(dH3_dW3.T, dL_dH3)
dL_dW3 += regularization_factor * W3
dL_db3 = np.dot(dH3_db3.T, dL_dH3)
dL_db3 += regularization_factor * b3
W4 += - learning_rate * dL_dW4
b4 += - learning_rate * dL_db4
W3 += - learning_rate * dL_dW3
b3 += - learning_rate * dL_db3
learning_rate *= learning_rate_decay
plt.subplot(2, 1, 1)
plt.plot([x[0] for x in learning_history])
plt.xlabel('iteration')
plt.ylabel('accuracy')
plt.subplot(2, 1, 2)
plt.plot([x[1] for x in learning_history])
plt.xlabel('iteration')
plt.ylabel('loss')
for i in range(25):
plt.subplot(5, 5, i + 1)
plt.imshow(W3[:, i].reshape(image_size, image_size))
plt.axis('off')
for i in range(25):
plt.subplot(5, 5, i + 1)
plt.imshow(W3[:, i + 25].reshape(image_size, image_size))
plt.axis('off')
```
|
github_jupyter
|
import pickle
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0)
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
mnist = pickle.Unpickler(open('mnist.pkl', 'rb'), encoding = 'latin1').load()
(train, validation, test) = mnist
(train_images, train_labels) = train
(validation_images, validation_labels) = validation
(test_images, test_labels) = test
image_size = 28
features_size = 784
classes_count = 10
print(train_images.shape)
print(validation_images.shape)
print(test_images.shape)
for i in range(10):
plt.subplot(1, 10, i + 1)
plt.title(str(train_labels[i]))
plt.imshow(train_images[i].reshape((image_size, image_size)))
plt.axis('off')
hidden_neurons = 400
minibatch_size = 200
regularization_factor = 0.05
learning_rate = 0.5
learning_rate_decay = 0.99
# 1 relu layers, 1 output softmax layer
# it's actually stemmed 4 layers network hence strange names of variables
W3 = np.random.uniform(high = 1.0 / hidden_neurons, size = (features_size, hidden_neurons))
b3 = np.zeros(shape = (hidden_neurons,))
W4 = np.random.uniform(high = 1.0 / hidden_neurons, size = (hidden_neurons, classes_count))
b4 = np.zeros(shape = (classes_count,))
learning_history = []
for epoch in range(2000):
choice = np.random.choice(train_images.shape[0], minibatch_size)
X = train_images[choice]
y = train_labels[choice]
# forward pass
H2 = X
H3 = np.maximum(np.dot(H2, W3) + b3, 0)
H4 = np.dot(H3, W4) + b4
scores = H4 - np.max(H4, axis = 1, keepdims = True)
probs = np.exp(scores)
probs /= np.sum(probs, axis = 1, keepdims = True)
labels = np.argmax(probs, axis = 1)
accuracy = np.mean(labels == y)
loss = np.sum(-np.log(probs[range(minibatch_size), y])) / minibatch_size
loss += 0.5 * regularization_factor * (np.sum(W3 * W3) + np.sum(b3 * b3))
loss += 0.5 * regularization_factor * (np.sum(W4 * W4) + np.sum(b4 * b4))
learning_history.append((accuracy, loss))
if epoch % 200 == 0:
print('epoch %d: accuracy = %f, loss = %f' % (epoch, accuracy, loss))
for i in range(10):
plt.subplot(10, 10, epoch / 200 + i * 10 + 1)
plt.imshow(W3[:, i * 20].reshape(image_size, image_size))
plt.axis('off')
# backprop
# layer 4
dL_dH4 = np.array(probs)
dL_dH4[range(minibatch_size), y] -= 1
dL_dH4 /= minibatch_size
dH4_dW4 = np.array(H3)
dL_dW4 = np.dot(dH4_dW4.T, dL_dH4)
dL_dW4 += regularization_factor * W4
dL_db4 = np.sum(dL_dH4, axis = 0)
dL_db4 += regularization_factor * b4
# layer 3
dH3_dW3 = np.array(H2)
dH3_db3 = np.ones(shape = H2.shape[0])
dH4_dH3 = np.array(W4)
dL_dH3 = np.dot(dL_dH4, dH4_dH3.T)
dL_dH3[H3 <= 0] = 0
dL_dW3 = np.dot(dH3_dW3.T, dL_dH3)
dL_dW3 += regularization_factor * W3
dL_db3 = np.dot(dH3_db3.T, dL_dH3)
dL_db3 += regularization_factor * b3
W4 += - learning_rate * dL_dW4
b4 += - learning_rate * dL_db4
W3 += - learning_rate * dL_dW3
b3 += - learning_rate * dL_db3
learning_rate *= learning_rate_decay
plt.subplot(2, 1, 1)
plt.plot([x[0] for x in learning_history])
plt.xlabel('iteration')
plt.ylabel('accuracy')
plt.subplot(2, 1, 2)
plt.plot([x[1] for x in learning_history])
plt.xlabel('iteration')
plt.ylabel('loss')
for i in range(25):
plt.subplot(5, 5, i + 1)
plt.imshow(W3[:, i].reshape(image_size, image_size))
plt.axis('off')
for i in range(25):
plt.subplot(5, 5, i + 1)
plt.imshow(W3[:, i + 25].reshape(image_size, image_size))
plt.axis('off')
| 0.551091 | 0.772531 |
```
dataset = sm.datasets.get_rdataset("clouds", package = "HSAUR")
df = dataset.data
df.tail()
```
##### 1.1 선형모형
- 종속변수 rainfall을 다른 변수로 예측하는 선형 모형을 만들고 결정계수로 성능을 구하여라
```
%matplotlib inline
from matplotlib import rc
plt.style.use('seaborn')
rc('font', family='NanumGothic')
plt.rcParams['axes.unicode_minus'] = False
formula_simple = "rainfall ~ " + "seeding + scale(time) + scale(sne) + scale(cloudcover)\
+ scale(prewetness) + echomotion"
model1 = sm.OLS.from_formula(formula_simple, data=df)
result1 = model1.fit()
print(result1.summary())
```
##### 1.3 seeding이 영향을 끼치는지?
- ANOVA분석으로 검정, 유의수준 10%
```
sns.boxplot(x = "seeding", y = "rainfall", data=df)
plt.show()
model = sm.OLS.from_formula("rainfall ~ seeding", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# R-squared 값이 0인가 아닌가를 테스트 하는게 핵심
# F-test
# 답 : ANOVA 분석의 유의확률은 72%이므로 seeding은 영향을 미치지 않는다.
```
##### 1.4 seeding과 다른 변수의 상호작용(interrection) 확인
- 위 단순 모형에 seeding과 다른 변수의 상호작용을 추가하여 변수 중 seeding과의 상호작용이 유의한 변수를 찾아라
```
# seeding - time 상호작용
# 유의함
model = sm.OLS.from_formula("rainfall ~ seeding : scale(time)", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# seeding - sne 상호작용
model = sm.OLS.from_formula("rainfall ~ seeding : scale(sne)", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# seeding - cloudcover 상호작용
# 유의함
model = sm.OLS.from_formula("rainfall ~ seeding : scale(cloudcover)", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# seeding - echomotion 상호작용
model = sm.OLS.from_formula("rainfall ~ seeding : echomotion", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# seeding - prewetness 상호작용
model = sm.OLS.from_formula("rainfall ~ seeding : scale(prewetness)", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# 이렇게 찾아주는게 좋다
formula_interact = "rainfall ~ " + "seeding*(scale(time) + scale(sne) + scale(cloudcover)\
+ scale(prewetness) + echomotion)"
model_interact = sm.OLS.from_formula(formula_interact, data = df)
result_interact = model_interact.fit()
print(result_interact.summary())
# 범수형 자료형과 실수형 자료형의 상호작용
# -> 기울기가 달라짐
# 최종적으로 유의한 것들만 모으기
formula_last = "rainfall ~ scale(time) + seeding:scale(sne)"
model_last = sm.OLS.from_formula(formula_last, data = df)
result_last = model_last.fit()
print(result_last.summary())
# seeding을 안했을 경우 p-value : 0.786
# coef값이 0.2222는 믿을수 없는 값임 -> 0이라고 생각
```
#### 2. 다항회귀
```
dataset = sm.datasets.get_rdataset("Salaries", package = "carData")
df = dataset.data[["yrs.since.phd", "salary"]]
df = df.rename(columns = {"yrs.since.phd": "experience"})
df.tail()
sns.scatterplot(x = "experience", y = "salary", data = df)
plt.show()
model = sm.OLS.from_formula("salary ~ experience", data=df)
result = model.fit()
print(result.summary())
sns.regplot(x = "experience", y = "salary", data = df)
plt.show()
model2 = sm.OLS.from_formula("salary ~ experience + I(experience**2)", data=df)
result2 = model2.fit()
print(result2.summary())
# y값에 log를 취해줌
model2 = sm.OLS.from_formula("np.log(salary) ~ experience + I(experience**2)", data=df)
result2 = model2.fit()
print(result2.summary())
# cross validation을 해서 train data에서 퍼포먼스 늘리는것 x -> test 데이터에서 퍼포먼스를 늘려야함
# 근본적으로는 test 퍼포먼스만 좋아지면 일단은 된거임
# 상대방에게 설득력을 높이기 위해서는 현실에서 왜 이런 현상이 일어났는가를 설명할수 있으면 더 좋다
mtcars = sm.datasets.get_rdataset("mtcars")
df = mtcars.data
df.tail()
print(mtcars.__doc__)
formula0 = "mpg ~ cyl + disp + hp + drat + wt + qsec + vs + am + gear + carb"
model0 = sm.OLS.from_formula(formula0, data = df)
result0 = model0.fit()
print(result0.summary())
# 스캐일링
formula1 = "mpg ~ scale(cyl) + scale(disp) + scale(hp) + scale(drat) + scale(wt) + scale(qsec)\
+ C(vs) + C(am) + C(gear) + C(carb)"
model1 = sm.OLS.from_formula(formula1, data = df)
result1 = model1.fit()
print(result1.summary())
formula2 = "mpg ~ scale(cyl) + scale(disp) + scale(hp) + scale(drat) + scale(wt) + scale(qsec)\
+ C(vs) + C(am) + scale(gear) + scale(carb)"
model2 = sm.OLS.from_formula(formula2, data = df)
result2 = model2.fit()
print(result2.summary())
# wt만 유의함
formula3 = "mpg ~ scale(wt) + C(am):(scale(wt) + scale(qsec))"
model3 = sm.OLS.from_formula(formula3, data = df)
result3 = model3.fit()
print(result3.summary())
```
#### 텍스트 분석
```
# !wget -nc https://raw.githubusercontent.com/e9t/nsmc/master/ratings_train.txt
import codecs
with codecs.open("ratings_train.txt", encoding = 'utf-8') as f:
data = [line.split('\t') for line in f.read().splitlines()]
data = data[ 1:]
docs = list(zip(*data))[1]
docs
```
````
doc : list of str
list of list of str
[["아버지", "가", "방","에"], ....]
````
```
from konlpy.tag import Okt
tagger = Okt()
def tokenize(doc):
tokens = [t for t in tagger.nouns(doc)]
return tokens
tokenize(docs[0])
%%time
sentences = [tokenize(d) for d in docs[:10000]]
words = [word for sentence in sentences for word in sentence]
from nltk import FreqDist
fd = FreqDist(words)
fd.most_common(10)
from wordcloud import WordCloud
font_path = '/usr/share/fonts/truetype/nanum/NanumGothic.ttf'
wc = WordCloud(width=1000, height=600, background_color="white", random_state=0, font_path=font_path)
plt.imshow(wc.generate_from_frequencies(fd))
plt.axis("off")
plt.show()
```
|
github_jupyter
|
dataset = sm.datasets.get_rdataset("clouds", package = "HSAUR")
df = dataset.data
df.tail()
%matplotlib inline
from matplotlib import rc
plt.style.use('seaborn')
rc('font', family='NanumGothic')
plt.rcParams['axes.unicode_minus'] = False
formula_simple = "rainfall ~ " + "seeding + scale(time) + scale(sne) + scale(cloudcover)\
+ scale(prewetness) + echomotion"
model1 = sm.OLS.from_formula(formula_simple, data=df)
result1 = model1.fit()
print(result1.summary())
sns.boxplot(x = "seeding", y = "rainfall", data=df)
plt.show()
model = sm.OLS.from_formula("rainfall ~ seeding", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# R-squared 값이 0인가 아닌가를 테스트 하는게 핵심
# F-test
# 답 : ANOVA 분석의 유의확률은 72%이므로 seeding은 영향을 미치지 않는다.
# seeding - time 상호작용
# 유의함
model = sm.OLS.from_formula("rainfall ~ seeding : scale(time)", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# seeding - sne 상호작용
model = sm.OLS.from_formula("rainfall ~ seeding : scale(sne)", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# seeding - cloudcover 상호작용
# 유의함
model = sm.OLS.from_formula("rainfall ~ seeding : scale(cloudcover)", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# seeding - echomotion 상호작용
model = sm.OLS.from_formula("rainfall ~ seeding : echomotion", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# seeding - prewetness 상호작용
model = sm.OLS.from_formula("rainfall ~ seeding : scale(prewetness)", data=df)
result = model.fit()
sm.stats.anova_lm(result)
# 이렇게 찾아주는게 좋다
formula_interact = "rainfall ~ " + "seeding*(scale(time) + scale(sne) + scale(cloudcover)\
+ scale(prewetness) + echomotion)"
model_interact = sm.OLS.from_formula(formula_interact, data = df)
result_interact = model_interact.fit()
print(result_interact.summary())
# 범수형 자료형과 실수형 자료형의 상호작용
# -> 기울기가 달라짐
# 최종적으로 유의한 것들만 모으기
formula_last = "rainfall ~ scale(time) + seeding:scale(sne)"
model_last = sm.OLS.from_formula(formula_last, data = df)
result_last = model_last.fit()
print(result_last.summary())
# seeding을 안했을 경우 p-value : 0.786
# coef값이 0.2222는 믿을수 없는 값임 -> 0이라고 생각
dataset = sm.datasets.get_rdataset("Salaries", package = "carData")
df = dataset.data[["yrs.since.phd", "salary"]]
df = df.rename(columns = {"yrs.since.phd": "experience"})
df.tail()
sns.scatterplot(x = "experience", y = "salary", data = df)
plt.show()
model = sm.OLS.from_formula("salary ~ experience", data=df)
result = model.fit()
print(result.summary())
sns.regplot(x = "experience", y = "salary", data = df)
plt.show()
model2 = sm.OLS.from_formula("salary ~ experience + I(experience**2)", data=df)
result2 = model2.fit()
print(result2.summary())
# y값에 log를 취해줌
model2 = sm.OLS.from_formula("np.log(salary) ~ experience + I(experience**2)", data=df)
result2 = model2.fit()
print(result2.summary())
# cross validation을 해서 train data에서 퍼포먼스 늘리는것 x -> test 데이터에서 퍼포먼스를 늘려야함
# 근본적으로는 test 퍼포먼스만 좋아지면 일단은 된거임
# 상대방에게 설득력을 높이기 위해서는 현실에서 왜 이런 현상이 일어났는가를 설명할수 있으면 더 좋다
mtcars = sm.datasets.get_rdataset("mtcars")
df = mtcars.data
df.tail()
print(mtcars.__doc__)
formula0 = "mpg ~ cyl + disp + hp + drat + wt + qsec + vs + am + gear + carb"
model0 = sm.OLS.from_formula(formula0, data = df)
result0 = model0.fit()
print(result0.summary())
# 스캐일링
formula1 = "mpg ~ scale(cyl) + scale(disp) + scale(hp) + scale(drat) + scale(wt) + scale(qsec)\
+ C(vs) + C(am) + C(gear) + C(carb)"
model1 = sm.OLS.from_formula(formula1, data = df)
result1 = model1.fit()
print(result1.summary())
formula2 = "mpg ~ scale(cyl) + scale(disp) + scale(hp) + scale(drat) + scale(wt) + scale(qsec)\
+ C(vs) + C(am) + scale(gear) + scale(carb)"
model2 = sm.OLS.from_formula(formula2, data = df)
result2 = model2.fit()
print(result2.summary())
# wt만 유의함
formula3 = "mpg ~ scale(wt) + C(am):(scale(wt) + scale(qsec))"
model3 = sm.OLS.from_formula(formula3, data = df)
result3 = model3.fit()
print(result3.summary())
# !wget -nc https://raw.githubusercontent.com/e9t/nsmc/master/ratings_train.txt
import codecs
with codecs.open("ratings_train.txt", encoding = 'utf-8') as f:
data = [line.split('\t') for line in f.read().splitlines()]
data = data[ 1:]
docs = list(zip(*data))[1]
docs
doc : list of str
list of list of str
[["아버지", "가", "방","에"], ....]
from konlpy.tag import Okt
tagger = Okt()
def tokenize(doc):
tokens = [t for t in tagger.nouns(doc)]
return tokens
tokenize(docs[0])
%%time
sentences = [tokenize(d) for d in docs[:10000]]
words = [word for sentence in sentences for word in sentence]
from nltk import FreqDist
fd = FreqDist(words)
fd.most_common(10)
from wordcloud import WordCloud
font_path = '/usr/share/fonts/truetype/nanum/NanumGothic.ttf'
wc = WordCloud(width=1000, height=600, background_color="white", random_state=0, font_path=font_path)
plt.imshow(wc.generate_from_frequencies(fd))
plt.axis("off")
plt.show()
| 0.399343 | 0.937498 |
# Data Types
When reading in a data set, pandas will try to guess the data type of each column like float, integer, datettime, bool, etc. In Pandas, strings are called "object" dtypes.
However, Pandas does not always get this right. That was the issue with the World Bank projects data. Hence, the dtype was specified as a string:
```
df_projects = pd.read_csv('../data/projects_data.csv', dtype=str)
```
Run the code cells below to read in the indicator and projects data. Then run the following code cell to see the dtypes of the indicator data frame.
```
# Run this code cell
import pandas as pd
# read in the population data and drop the final column
df_indicator = pd.read_csv('../data/population_data.csv', skiprows=4)
df_indicator.drop(['Unnamed: 62'], axis=1, inplace=True)
# read in the projects data set with all columns type string
df_projects = pd.read_csv('../data/projects_data.csv', dtype=str)
df_projects.drop(['Unnamed: 56'], axis=1, inplace=True)
# Run this code cell
df_indicator.dtypes
```
These results look reasonable. Country Name, Country Code, Indicator Name and Indicator Code were all read in as strings. The year columns, which contain the population data, were read in as floats.
# Exercise 1
Since the population indicator data was read in correctly, you can run calculations on the data. In this first exercise, sum the populations of the United States, Canada, and Mexico by year.
```
# TODO: Calculate the population sum by year for Canada,
# the United States, and Mexico.
#
keepcol = ['Country Name']
for i in range(1960, 2018, 1):
keepcol.append(str(i))
df_nafta = df_indicator[(df_indicator['Country Name'] == 'Canada') |
(df_indicator['Country Name'] == 'United States') |
(df_indicator['Country Name'] == 'Mexico')].iloc[:,]
df_nafta.sum(axis=0)[keepcol]
```
# Exercise 2
Now, run the code cell below to look at the dtypes for the projects data set. They should all be "object" types, ie strings, because that's what was specified in the code when reading in the csv file. As a reminder, this was the code:
```
df_projects = pd.read_csv('../data/projects_data.csv', dtype=str)
```
```
# Run this code cell
df_projects.dtypes
```
Many of these columns should be strings, so there's no problem; however, a few columns should be other data types. For example, `boardapprovaldate` should be a datettime and `totalamt` should be an integer. You'll learn about datetime formatting in the next part of the lesson. For this exercise, focus on the 'totalamt' and 'lendprojectcost' columns. Run the code cell below to see what that data looks like
```
# Run this code cell
df_projects[['totalamt', 'lendprojectcost']].head()
# Run this code cell to take the sum of the total amount column
df_projects['totalamt'].sum()
```
What just happened? Pandas treated the totalamts like strings. In Python, adding strings concatenates the strings together.
There are a few ways to remedy this. When using pd.read_csv(), you could specify the column type for every column in the data set. The pd.read_csv() dtype option can accept a dictionary mapping each column name to its data type. You could also specify the `thousands` option with `thousands=','`. This specifies that thousands are separated by a comma in this data set.
However, this data is somewhat messy, contains missing values, and has a lot of columns. It might be faster to read in the entire data set with string types and then convert individual columns as needed. For this next exercise, convert the `totalamt` column from a string to an integer type.
```
# TODO: Convert the totalamt column from a string to a float and save the results back into the totalamt column
# Step 1: Remove the commas from the 'totalamt' column
# HINT: https://pandas.pydata.org/pandas-docs/version/0.22/generated/pandas.Series.str.replace.html
# Step 2: Convert the 'totalamt' column from an object data type (ie string) to an integer data type.
# HINT: https://pandas.pydata.org/pandas-docs/version/0.23/generated/pandas.to_numeric.html
df_projects['totalamt'] = pd.to_numeric(df_projects['totalamt'].str.replace(',',""))
```
# Conclusion
With messy data, you might find it easier to read in everything as a string; however, you'll sometimes have to convert those strings to more appropriate data types. When you output the dtypes of a dataframe, you'll generally see these values in the results:
* float64
* int64
* bool
* datetime64
* timedelta
* object
where timedelta is the difference between two datetimes and object is a string. As you've seen here, you sometimes need to convert data types from one type to another type. Pandas has a few different methods for converting between data types, and here are link to the documentation:
* [astype](https://pandas.pydata.org/pandas-docs/version/0.22/generated/pandas.DataFrame.astype.html#pandas.DataFrame.astype)
* [to_datetime](https://pandas.pydata.org/pandas-docs/version/0.22/generated/pandas.to_datetime.html#pandas.to_datetime)
* [to_numeric](https://pandas.pydata.org/pandas-docs/version/0.22/generated/pandas.to_numeric.html#pandas.to_numeric)
* [to_timedelta](https://pandas.pydata.org/pandas-docs/version/0.22/generated/pandas.to_timedelta.html#pandas.to_timedelta)
|
github_jupyter
|
df_projects = pd.read_csv('../data/projects_data.csv', dtype=str)
# Run this code cell
import pandas as pd
# read in the population data and drop the final column
df_indicator = pd.read_csv('../data/population_data.csv', skiprows=4)
df_indicator.drop(['Unnamed: 62'], axis=1, inplace=True)
# read in the projects data set with all columns type string
df_projects = pd.read_csv('../data/projects_data.csv', dtype=str)
df_projects.drop(['Unnamed: 56'], axis=1, inplace=True)
# Run this code cell
df_indicator.dtypes
# TODO: Calculate the population sum by year for Canada,
# the United States, and Mexico.
#
keepcol = ['Country Name']
for i in range(1960, 2018, 1):
keepcol.append(str(i))
df_nafta = df_indicator[(df_indicator['Country Name'] == 'Canada') |
(df_indicator['Country Name'] == 'United States') |
(df_indicator['Country Name'] == 'Mexico')].iloc[:,]
df_nafta.sum(axis=0)[keepcol]
df_projects = pd.read_csv('../data/projects_data.csv', dtype=str)
# Run this code cell
df_projects.dtypes
# Run this code cell
df_projects[['totalamt', 'lendprojectcost']].head()
# Run this code cell to take the sum of the total amount column
df_projects['totalamt'].sum()
# TODO: Convert the totalamt column from a string to a float and save the results back into the totalamt column
# Step 1: Remove the commas from the 'totalamt' column
# HINT: https://pandas.pydata.org/pandas-docs/version/0.22/generated/pandas.Series.str.replace.html
# Step 2: Convert the 'totalamt' column from an object data type (ie string) to an integer data type.
# HINT: https://pandas.pydata.org/pandas-docs/version/0.23/generated/pandas.to_numeric.html
df_projects['totalamt'] = pd.to_numeric(df_projects['totalamt'].str.replace(',',""))
| 0.166743 | 0.945851 |
<img alt="QuantRocket logo" src="https://www.quantrocket.com/assets/img/notebook-header-logo.png">
© Copyright Quantopian Inc.<br>
© Modifications Copyright QuantRocket LLC<br>
Licensed under the [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/legalcode).
<a href="https://www.quantrocket.com/disclaimer/">Disclaimer</a>
# Linear Regression
By Evgenia "Jenny" Nitishinskaya and Delaney Granizo-Mackenzie with example algorithms by David Edwards
Linear regression is a technique that measures the relationship between two variables. If we have an independent variable $X$, and a dependent outcome variable $Y$, linear regression allows us to determine which linear model $Y = \alpha + \beta X$ best explains the data. As an example, let's consider Apple (AAPL) and Home Depot (HD). We would like to know how AAPL varies as a function of how HD varies, so we will take the daily returns of each and regress them against each other.
Python's `statsmodels` library has a built-in linear fit function. Note that this will give a line of best fit; whether or not the relationship it shows is significant is for you to determine. The output will also have some statistics about the model, such as R-squared and the F value, which may help you quantify how good the fit actually is.
```
# Import libraries
import numpy as np
from statsmodels import regression
import statsmodels.api as sm
import matplotlib.pyplot as plt
import math
```
First we'll define a function that performs linear regression and plots the results.
```
def linreg(X,Y):
# Running the linear regression
X = sm.add_constant(X)
model = regression.linear_model.OLS(Y, X).fit()
a = model.params[0]
b = model.params[1]
X = X[:, 1]
# Return summary of the regression and plot results
X2 = np.linspace(X.min(), X.max(), 100)
Y_hat = X2 * b + a
plt.scatter(X, Y, alpha=0.3) # Plot the raw data
plt.plot(X2, Y_hat, 'r', alpha=0.9); # Add the regression line, colored in red
plt.xlabel('X Value')
plt.ylabel('Y Value')
return model.summary()
```
Now we'll get pricing data on AAPL and MSFT and perform a regression.
```
from quantrocket.master import get_securities
from quantrocket import get_prices
securities = get_securities(symbols=['AAPL', 'HD'], vendors='usstock')
start = '2014-01-01'
end = '2015-01-01'
closes = get_prices('usstock-free-1min', data_frequency='daily', sids=securities.index.tolist(), fields='Close', start_date=start, end_date=end).loc['Close']
sids_to_symbols = securities.Symbol.to_dict()
closes = closes.rename(columns=sids_to_symbols)
# We have to take the percent changes to get to returns
# Get rid of the first (0th) element because it is NAN
aapl_returns = closes['AAPL'].pct_change()[1:]
hd_returns = closes['HD'].pct_change()[1:]
linreg(hd_returns.values, aapl_returns.values)
```
Each point on the above graph represents a day, with the x-coordinate being the return of HD, and the y-coordinate being the return of AAPL. As we can see, the line of best fit tells us that for every 1% increased return we see from the HD, we should see an extra 0.41% from AAPL. This is expressed by the parameter $\beta$, which is 0.4147 as estimated. Of course, for losses we will also see increased losses in AAPL, so we haven't gained anything, we are just more volatile.
## Linear Regression vs. Correlation
* Linear regression gives us a specific linear model, but is limited to cases of linear dependence.
* Correlation is general to linear and non-linear dependencies, but doesn't give us an actual model.
* Both are measures of covariance.
* Linear regression can give us relationship between Y and many independent variables by making X multidimensional.
## Knowing Parameters vs. Estimates
It is very important to keep in mind that all $\alpha$ and $\beta$ parameters estimated by linear regression are just that - estimates. You can never know the underlying true parameters unless you know the physical process producing the data. The parameters you estimate today may not be the same analysis done including tomorrow's data, and the underlying true parameters may be moving. As such it is very important when doing actual analysis to pay attention to the standard error of the parameter estimates. More material on the standard error will be presented in a later lecture. One way to get a sense of how stable your parameter estimates are is to estimate them using a rolling window of data and see how much variance there is in the estimates.
## Example case
Now let's see what happens if we regress two purely random variables.
```
X = np.random.rand(100)
Y = np.random.rand(100)
linreg(X, Y)
```
The above shows a fairly uniform cloud of points. It is important to note that even with 100 samples, the line has a visible slope due to random chance. This is why it is crucial that you use statistical tests and not visualizations to verify your results.
Now let's make Y dependent on X plus some random noise.
```
# Generate ys correlated with xs by adding normally-destributed errors
Y = X + 0.2*np.random.randn(100)
linreg(X,Y)
```
In a situation like the above, the line of best fit does indeed model the dependent variable Y quite well (with a high $R^2$ value).
# Evaluating and reporting results
The regression model relies on several assumptions:
* The independent variable is not random.
* The variance of the error term is constant across observations. This is important for evaluating the goodness of the fit.
* The errors are not autocorrelated. The Durbin-Watson statistic detects this; if it is close to 2, there is no autocorrelation.
* The errors are normally distributed. If this does not hold, we cannot use some of the statistics, such as the F-test.
If we confirm that the necessary assumptions of the regression model are satisfied, we can safely use the statistics reported to analyze the fit. For example, the $R^2$ value tells us the fraction of the total variation of $Y$ that is explained by the model.
When making a prediction based on the model, it's useful to report not only a single value but a confidence interval. The linear regression reports 95% confidence intervals for the regression parameters, and we can visualize what this means using the `seaborn` library, which plots the regression line and highlights the 95% (by default) confidence interval for the regression line:
```
import seaborn
seaborn.regplot(x=hd_returns, y=aapl_returns);
```
## Mathematical Background
This is a very brief overview of linear regression. For more, please see:
https://en.wikipedia.org/wiki/Linear_regression
## Ordinary Least Squares
Regression works by optimizing the placement of the line of best fit (or plane in higher dimensions). It does so by defining how bad the fit is using an objective function. In ordinary least squares regression (OLS), what we use here, the objective function is:
$$\sum_{i=1}^n (Y_i - a - bX_i)^2$$
We use $a$ and $b$ to represent the potential candidates for $\alpha$ and $\beta$. What this objective function means is that for each point on the line of best fit we compare it with the real point and take the square of the difference. This function will decrease as we get better parameter estimates. Regression is a simple case of numerical optimization that has a closed form solution and does not need any optimizer. We just find the results that minimize the objective function.
We will denote the eventual model that results from minimizing our objective function as:
$$ \hat{Y} = \hat{\alpha} + \hat{\beta}X $$
With $\hat{\alpha}$ and $\hat{\beta}$ being the chosen estimates for the parameters that we use for prediction and $\hat{Y}$ being the predicted values of $Y$ given the estimates.
## Standard Error
We can also find the standard error of estimate, which measures the standard deviation of the error term $\epsilon$, by getting the `scale` parameter of the model returned by the regression and taking its square root. The formula for standard error of estimate is
$$ s = \left( \frac{\sum_{i=1}^n \epsilon_i^2}{n-2} \right)^{1/2} $$
If $\hat{\alpha}$ and $\hat{\beta}$ were the true parameters ($\hat{\alpha} = \alpha$ and $\hat{\beta} = \beta$), we could represent the error for a particular predicted value of $Y$ as $s^2$ for all values of $X_i$. We could simply square the difference $(Y - \hat{Y})$ to get the variance because $\hat{Y}$ incorporates no error in the parameter estimates themselves. Because $\hat{\alpha}$ and $\hat{\beta}$ are merely estimates in our construction of the model of $Y$, any predicted values , $\hat{Y}$, will have their own standard error based on the distribution of the $X$ terms that we plug into the model. This forecast error is represented by the following:
$$ s_f^2 = s^2 \left( 1 + \frac{1}{n} + \frac{(X - \mu_X)^2}{(n-1)\sigma_X^2} \right) $$
where $\mu_X$ is the mean of our observations of $X$ and $\sigma_X$ is the standard deviation of $X$. This adjustment to $s^2$ incorporates the uncertainty in our parameter estimates. Then the 95% confidence interval for the prediction is $\hat{Y} \pm t_cs_f$, where $t_c$ is the critical value of the t-statistic for $n$ samples and a desired 95% confidence.
---
**Next Lecture:** [Maximum Likelihood Estimation](Lecture13-Maximum-Likelihood-Estimation.ipynb)
[Back to Introduction](Introduction.ipynb)
---
*This presentation is for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation for any security; nor does it constitute an offer to provide investment advisory or other services by Quantopian, Inc. ("Quantopian") or QuantRocket LLC ("QuantRocket"). Nothing contained herein constitutes investment advice or offers any opinion with respect to the suitability of any security, and any views expressed herein should not be taken as advice to buy, sell, or hold any security or as an endorsement of any security or company. In preparing the information contained herein, neither Quantopian nor QuantRocket has taken into account the investment needs, objectives, and financial circumstances of any particular investor. Any views expressed and data illustrated herein were prepared based upon information believed to be reliable at the time of publication. Neither Quantopian nor QuantRocket makes any guarantees as to their accuracy or completeness. All information is subject to change and may quickly become unreliable for various reasons, including changes in market conditions or economic circumstances.*
|
github_jupyter
|
# Import libraries
import numpy as np
from statsmodels import regression
import statsmodels.api as sm
import matplotlib.pyplot as plt
import math
def linreg(X,Y):
# Running the linear regression
X = sm.add_constant(X)
model = regression.linear_model.OLS(Y, X).fit()
a = model.params[0]
b = model.params[1]
X = X[:, 1]
# Return summary of the regression and plot results
X2 = np.linspace(X.min(), X.max(), 100)
Y_hat = X2 * b + a
plt.scatter(X, Y, alpha=0.3) # Plot the raw data
plt.plot(X2, Y_hat, 'r', alpha=0.9); # Add the regression line, colored in red
plt.xlabel('X Value')
plt.ylabel('Y Value')
return model.summary()
from quantrocket.master import get_securities
from quantrocket import get_prices
securities = get_securities(symbols=['AAPL', 'HD'], vendors='usstock')
start = '2014-01-01'
end = '2015-01-01'
closes = get_prices('usstock-free-1min', data_frequency='daily', sids=securities.index.tolist(), fields='Close', start_date=start, end_date=end).loc['Close']
sids_to_symbols = securities.Symbol.to_dict()
closes = closes.rename(columns=sids_to_symbols)
# We have to take the percent changes to get to returns
# Get rid of the first (0th) element because it is NAN
aapl_returns = closes['AAPL'].pct_change()[1:]
hd_returns = closes['HD'].pct_change()[1:]
linreg(hd_returns.values, aapl_returns.values)
X = np.random.rand(100)
Y = np.random.rand(100)
linreg(X, Y)
# Generate ys correlated with xs by adding normally-destributed errors
Y = X + 0.2*np.random.randn(100)
linreg(X,Y)
import seaborn
seaborn.regplot(x=hd_returns, y=aapl_returns);
| 0.701509 | 0.99193 |
# Amazon SageMaker Debugger - Using built-in rule
[Amazon SageMaker](https://aws.amazon.com/sagemaker/) is managed platform to build, train and host maching learning models. Amazon SageMaker Debugger is a new feature which offers the capability to debug machine learning models during training by identifying and detecting problems with the models in near real-time.
In this notebook you'll be looking at how to use a SageMaker provided built in rule during a TensorFlow training job.
## How does Amazon SageMaker Debugger work?
Amazon SageMaker Debugger lets you go beyond just looking at scalars like losses and accuracies during training and gives you full visibility into all tensors 'flowing through the graph' during training. Furthermore, it helps you monitor your training in near real-time using rules and provides you alerts, once it has detected inconsistency in training flow.
### Concepts
* **Tensors**: These represent the state of the training network at intermediate points during its execution
* **Debug Hook**: Hook is the construct with which Amazon SageMaker Debugger looks into the training process and captures the tensors requested at the desired step intervals
* **Rule**: A logical construct, implemented as Python code, which helps analyze the tensors captured by the hook and report anomalies, if at all
With these concepts in mind, let's understand the overall flow of things that Amazon SageMaker Debugger uses to orchestrate debugging
### Saving tensors during training
The tensors captured by the debug hook are stored in the S3 location specified by you. There are two ways you can configure Amazon SageMaker Debugger to save tensors:
#### With no changes to your training script
If you use one of Amazon SageMaker provided [Deep Learning Containers](https://docs.aws.amazon.com/sagemaker/latest/dg/pre-built-containers-frameworks-deep-learning.html) for 1.15, then you don't need to make any changes to your training script for the tensors to be stored. Amazon SageMaker Debugger will use the configuration you provide through Amazon SageMaker SDK's Tensorflow `Estimator` when creating your job to save the tensors in the fashion you specify. You can review the script we are going to use at [src/mnist_zerocodechange.py](src/mnist_zerocodechange.py). You will note that this is an untouched TensorFlow script which uses the `tf.estimator` interface. Please note that Amazon SageMaker Debugger only supports `tf.keras`, `tf.Estimator` and `tf.MonitoredSession` interfaces. Full description of support is available at [Amazon SageMaker Debugger with TensorFlow ](https://github.com/awslabs/sagemaker-debugger/tree/master/docs/tensorflow.md)
#### Orchestrating your script to store tensors
For other containers, you need to make couple of lines of changes to your training script. The Amazon SageMaker Debugger exposes a library `smdebug` which allows you to capture these tensors and save them for analysis. It's highly customizable and allows to save the specific tensors you want at different frequencies and possibly with other configurations. Refer [DeveloperGuide](https://github.com/awslabs/sagemaker-debugger/tree/master/docs) for details on how to use the Debugger library with your choice of framework in your training script. Here we have an example script orchestrated at [src/mnist_byoc](src/mnist_byoc.py). You also need to ensure that your container has the `smdebug` library installed.
### Analysis of tensors
Once the tensors are saved, Amazon SageMaker Debugger can be configured to run debugging ***Rules*** on them. At a very broad level, a rule is python code used to detect certain conditions during training. Some of the conditions that a data scientist training an algorithm may care about are monitoring for gradients getting too large or too small, detecting overfitting, and so on. Amazon Sagemaker Debugger will come pre-packaged with certain first-party (1P) rules. Users can write their own rules using Amazon Sagemaker Debugger APIs. You can also analyze raw tensor data outside of the Rules construct in say, a Sagemaker notebook, using Amazon Sagemaker Debugger's full set of APIs. This notebook will show you how to use a built in SageMaker Rule with your training job as well as provide a sneak peak into these APIs for interactive exploration. Please refer [Analysis Developer Guide](https://github.com/awslabs/sagemaker-debugger/blob/master/docs/api.md) for more on these APIs.
## Setup
Follow this one time setup to get your notebook up and running to use Amazon SageMaker Debugger. This is only needed because we plan to perform interactive analysis using this library in the notebook.
```
! pip install smdebug
```
With the setup out of the way let's start training our TensorFlow model in SageMaker with the debugger enabled.
## Training TensorFlow models in SageMaker with Amazon SageMaker Debugger
### SageMaker TensorFlow as a framework
We'll train a TensorFlow model in this notebook with Amazon Sagemaker Debugger enabled and monitor the training jobs with Amazon Sagemaker Debugger Rules. This will be done using Amazon SageMaker [TensorFlow 1.15.0](https://docs.aws.amazon.com/sagemaker/latest/dg/pre-built-containers-frameworks-deep-learning.html) Container as a framework.
```
import boto3
import os
import sagemaker
from sagemaker.tensorflow import TensorFlow
```
Let's import the libraries needed for our demo of Amazon SageMaker Debugger.
```
from sagemaker.debugger import Rule, DebuggerHookConfig, TensorBoardOutputConfig, CollectionConfig, rule_configs
```
Now we'll define the configuration for our training to run. We'll using image recognition using MNIST dataset as our training example.
```
# define the entrypoint script
entrypoint_script='src/mnist_zerocodechange.py'
hyperparameters = {
"num_epochs": 3
}
```
### Setting up the Estimator
Now it's time to setup our TensorFlow estimator. We've added new parameters to the estimator to enable your training job for debugging through Amazon SageMaker Debugger. These new parameters are explained below.
* **debugger_hook_config**: This new parameter accepts a local path where you wish your tensors to be written to and also accepts the S3 URI where you wish your tensors to be uploaded to. SageMaker will take care of uploading these tensors transparently during execution.
* **rules**: This new parameter will accept a list of rules you wish to evaluate against the tensors output by this training job. For rules, Amazon SageMaker Debugger supports two types:
* **SageMaker Rules**: These are rules specially curated by the data science and engineering teams in Amazon SageMaker which you can opt to evaluate against your training job.
* **Custom Rules**: You can optionally choose to write your own rule as a Python source file and have it evaluated against your training job. To provide Amazon SageMaker Debugger to evaluate this rule, you would have to provide the S3 location of the rule source and the evaluator image.
#### Using Amazon SageMaker Rules
In this example we'll demonstrate how to use SageMaker rules to be evaluated against your training. You can find the list of SageMaker rules and the configurations best suited for using them [here](https://github.com/awslabs/sagemaker-debugger-rulesconfig).
The rules we'll use are **VanishingGradient** and **LossNotDecreasing**. As the names suggest, the rules will attempt to evaluate if there are vanishing gradients in the tensors captured by the debugging hook during training and also if the loss is not decreasing.
```
rules = [
Rule.sagemaker(rule_configs.vanishing_gradient()),
Rule.sagemaker(rule_configs.loss_not_decreasing())
]
estimator = TensorFlow(
role=sagemaker.get_execution_role(),
base_job_name='smdebugger-demo-mnist-tensorflow',
train_instance_count=1,
train_instance_type='ml.m4.xlarge',
train_volume_size=400,
entry_point=entrypoint_script,
framework_version='1.15',
py_version='py3',
train_max_run=3600,
script_mode=True,
hyperparameters=hyperparameters,
## New parameter
rules = rules
)
```
*Note that Amazon Sagemaker Debugger is only supported for py_version='py3' currently.*
Let's start the training by calling `fit()` on the TensorFlow estimator.
```
estimator.fit(wait=True)
```
## Result
As a result of calling the `fit()` Amazon SageMaker Debugger kicked off two rule evaluation jobs to monitor vanishing gradient and loss decrease, in parallel with the training job. The rule evaluation status(es) will be visible in the training logs at regular intervals. As you can see, in the summary, there was no step in the training which reported vanishing gradients in the tensors. Although, the loss was not found to be decreasing at step 1900.
```
estimator.latest_training_job.rule_job_summary()
```
Let's try and look at the logs of the rule job for loss not decreasing. To do that, we'll use this utlity function to get a link to the rule job logs.
```
def _get_rule_job_name(training_job_name, rule_configuration_name, rule_job_arn):
"""Helper function to get the rule job name with correct casing"""
return "{}-{}-{}".format(
training_job_name[:26], rule_configuration_name[:26], rule_job_arn[-8:]
)
def _get_cw_url_for_rule_job(rule_job_name, region):
return "https://{}.console.aws.amazon.com/cloudwatch/home?region={}#logStream:group=/aws/sagemaker/ProcessingJobs;prefix={};streamFilter=typeLogStreamPrefix".format(region, region, rule_job_name)
def get_rule_jobs_cw_urls(estimator):
region = boto3.Session().region_name
training_job = estimator.latest_training_job
training_job_name = training_job.describe()["TrainingJobName"]
rule_eval_statuses = training_job.describe()["DebugRuleEvaluationStatuses"]
result={}
for status in rule_eval_statuses:
if status.get("RuleEvaluationJobArn", None) is not None:
rule_job_name = _get_rule_job_name(training_job_name, status["RuleConfigurationName"], status["RuleEvaluationJobArn"])
result[status["RuleConfigurationName"]] = _get_cw_url_for_rule_job(rule_job_name, region)
return result
get_rule_jobs_cw_urls(estimator)
```
## Data Analysis - Interactive Exploration
Now that we have trained a job, and looked at automated analysis through rules, let us also look at another aspect of Amazon SageMaker Debugger. It allows us to perform interactive exploration of the tensors saved in real time or after the job. Here we focus on after-the-fact analysis of the above job. We import the `smdebug` library, which defines a concept of Trial that represents a single training run. Note how we fetch the path to debugger artifacts for the above job.
```
from smdebug.trials import create_trial
trial = create_trial(estimator.latest_job_debugger_artifacts_path())
```
We can list all the tensors that were recorded to know what we want to plot. Each one of these names is the name of a tensor, which is auto-assigned by TensorFlow. In some frameworks where such names are not available, we try to create a name based on the layer's name and whether it is weight, bias, gradient, input or output.
```
trial.tensor_names()
```
We can also retrieve tensors by some default collections that `smdebug` creates from your training job. Here we are interested in the losses collection, so we can retrieve the names of tensors in losses collection as follows. Amazon SageMaker Debugger creates default collections such as weights, gradients, biases, losses automatically. You can also create custom collections from your tensors.
```
trial.tensor_names(collection="losses")
import matplotlib.pyplot as plt
import re
# Define a function that, for the given tensor name, walks through all
# the iterations for which we have data and fetches the value.
# Returns the set of steps and the values
def get_data(trial, tname):
tensor = trial.tensor(tname)
steps = tensor.steps()
vals = [tensor.value(s) for s in steps]
return steps, vals
def plot_tensors(trial, collection_name, ylabel=''):
"""
Takes a `trial` and plots all tensors that match the given regex.
"""
plt.figure(
num=1, figsize=(8, 8), dpi=80,
facecolor='w', edgecolor='k')
tensors = trial.tensor_names(collection=collection_name)
for tensor_name in sorted(tensors):
steps, data = get_data(trial, tensor_name)
plt.plot(steps, data, label=tensor_name)
plt.legend(bbox_to_anchor=(1.04,1), loc='upper left')
plt.xlabel('Iteration')
plt.ylabel(ylabel)
plt.show()
plot_tensors(trial, "losses", ylabel="Loss")
```
|
github_jupyter
|
! pip install smdebug
import boto3
import os
import sagemaker
from sagemaker.tensorflow import TensorFlow
from sagemaker.debugger import Rule, DebuggerHookConfig, TensorBoardOutputConfig, CollectionConfig, rule_configs
# define the entrypoint script
entrypoint_script='src/mnist_zerocodechange.py'
hyperparameters = {
"num_epochs": 3
}
rules = [
Rule.sagemaker(rule_configs.vanishing_gradient()),
Rule.sagemaker(rule_configs.loss_not_decreasing())
]
estimator = TensorFlow(
role=sagemaker.get_execution_role(),
base_job_name='smdebugger-demo-mnist-tensorflow',
train_instance_count=1,
train_instance_type='ml.m4.xlarge',
train_volume_size=400,
entry_point=entrypoint_script,
framework_version='1.15',
py_version='py3',
train_max_run=3600,
script_mode=True,
hyperparameters=hyperparameters,
## New parameter
rules = rules
)
estimator.fit(wait=True)
estimator.latest_training_job.rule_job_summary()
def _get_rule_job_name(training_job_name, rule_configuration_name, rule_job_arn):
"""Helper function to get the rule job name with correct casing"""
return "{}-{}-{}".format(
training_job_name[:26], rule_configuration_name[:26], rule_job_arn[-8:]
)
def _get_cw_url_for_rule_job(rule_job_name, region):
return "https://{}.console.aws.amazon.com/cloudwatch/home?region={}#logStream:group=/aws/sagemaker/ProcessingJobs;prefix={};streamFilter=typeLogStreamPrefix".format(region, region, rule_job_name)
def get_rule_jobs_cw_urls(estimator):
region = boto3.Session().region_name
training_job = estimator.latest_training_job
training_job_name = training_job.describe()["TrainingJobName"]
rule_eval_statuses = training_job.describe()["DebugRuleEvaluationStatuses"]
result={}
for status in rule_eval_statuses:
if status.get("RuleEvaluationJobArn", None) is not None:
rule_job_name = _get_rule_job_name(training_job_name, status["RuleConfigurationName"], status["RuleEvaluationJobArn"])
result[status["RuleConfigurationName"]] = _get_cw_url_for_rule_job(rule_job_name, region)
return result
get_rule_jobs_cw_urls(estimator)
from smdebug.trials import create_trial
trial = create_trial(estimator.latest_job_debugger_artifacts_path())
trial.tensor_names()
trial.tensor_names(collection="losses")
import matplotlib.pyplot as plt
import re
# Define a function that, for the given tensor name, walks through all
# the iterations for which we have data and fetches the value.
# Returns the set of steps and the values
def get_data(trial, tname):
tensor = trial.tensor(tname)
steps = tensor.steps()
vals = [tensor.value(s) for s in steps]
return steps, vals
def plot_tensors(trial, collection_name, ylabel=''):
"""
Takes a `trial` and plots all tensors that match the given regex.
"""
plt.figure(
num=1, figsize=(8, 8), dpi=80,
facecolor='w', edgecolor='k')
tensors = trial.tensor_names(collection=collection_name)
for tensor_name in sorted(tensors):
steps, data = get_data(trial, tensor_name)
plt.plot(steps, data, label=tensor_name)
plt.legend(bbox_to_anchor=(1.04,1), loc='upper left')
plt.xlabel('Iteration')
plt.ylabel(ylabel)
plt.show()
plot_tensors(trial, "losses", ylabel="Loss")
| 0.65379 | 0.985014 |
# How to use BaaL with Scikit-Learn models
In this tutorial, you will learn how to use BaaL on a scikit-learn model.
In this case, we will use `RandomForestClassifier`.
This tutorial is based on the tutorial from [Saimadhu Polamuri](https://dataaspirant.com/2017/06/26/random-forest-classifier-python-scikit-learn/).
First, if you have not done it yet, let's install BaaL.
```bash
pip install baal
```
```
%load_ext autoreload
%autoreload 2
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.model_selection import train_test_split
HEADERS = ["CodeNumber", "ClumpThickness", "UniformityCellSize", "UniformityCellShape", "MarginalAdhesion",
"SingleEpithelialCellSize", "BareNuclei", "BlandChromatin", "NormalNucleoli", "Mitoses", "CancerType"]
import pandas as pd
data = 'https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data'
dataset = pd.read_csv(data)
dataset.columns = HEADERS
# Handle missing labels
dataset = dataset[dataset[HEADERS[6]] != '?']
# Split
train_x, test_x, train_y, test_y = train_test_split(dataset[HEADERS[1:-1]], dataset[HEADERS[-1]],
train_size=0.7)
clf = RandomForestClassifier()
clf.fit(train_x, train_y)
# Get metrics
predictions = clf.predict(test_x)
print("Train Accuracy :: ", accuracy_score(train_y, clf.predict(train_x)))
print("Test Accuracy :: ", accuracy_score(test_y, predictions))
print(" Confusion matrix ", confusion_matrix(test_y, predictions))
```
Now that you have a trained model, you can use it to perform uncertainty estimation.
The SKLearn API directly propose `RandomForestClassifier.predict_proba` which would return the mean
response from the RandomForest.
But if you wish to try one of our heuristics in `baal.active.heuristics`, here's how.
```
import numpy as np
from baal.active.heuristics import BALD
print(f"Using {len(clf.estimators_)} estimators")
# Predict independently for all estimators.
x = np.array(list(map(lambda e: e.predict_proba(test_x), clf.estimators_)))
# Roll axis because BaaL expect [n_samples, n_classes, ..., n_estimations]
x = np.rollaxis(x, 0, 3)
print("Uncertainty per sample")
print(BALD().compute_score(x))
print("Ranks")
print(BALD()(x))
```
## Active learning with SkLearn
You can also try Active learning by using `ActiveNumpyArray`.
**NOTE**: Because we focus on images, we have not made experiments on this setup.
```
from baal.active.dataset import ActiveNumpyArray
dataset = ActiveNumpyArray((train_x, train_y))
# We start with a 10 labelled samples.
dataset.label_randomly(10)
heuristic = BALD()
# We will use a RandomForest in this case.
clf = RandomForestClassifier()
def predict(test, clf):
# Predict with all fitted estimators.
x = np.array(list(map(lambda e: e.predict_proba(test[0]), clf.estimators_)))
# Roll axis because BaaL expect [n_samples, n_classes, ..., n_estimations]
x = np.rollaxis(x, 0, 3)
return x
for _ in range(5):
print("Dataset size", len(dataset))
clf.fit(*dataset.dataset)
predictions = clf.predict(test_x)
print("Test Accuracy :: ", accuracy_score(test_y, predictions))
probs = predict(dataset.pool, clf)
to_label = heuristic(probs)
ndata_to_label = 10
if len(to_label) > 0:
dataset.label(to_label[: ndata_to_label])
else:
break
```
|
github_jupyter
|
pip install baal
%load_ext autoreload
%autoreload 2
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.model_selection import train_test_split
HEADERS = ["CodeNumber", "ClumpThickness", "UniformityCellSize", "UniformityCellShape", "MarginalAdhesion",
"SingleEpithelialCellSize", "BareNuclei", "BlandChromatin", "NormalNucleoli", "Mitoses", "CancerType"]
import pandas as pd
data = 'https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data'
dataset = pd.read_csv(data)
dataset.columns = HEADERS
# Handle missing labels
dataset = dataset[dataset[HEADERS[6]] != '?']
# Split
train_x, test_x, train_y, test_y = train_test_split(dataset[HEADERS[1:-1]], dataset[HEADERS[-1]],
train_size=0.7)
clf = RandomForestClassifier()
clf.fit(train_x, train_y)
# Get metrics
predictions = clf.predict(test_x)
print("Train Accuracy :: ", accuracy_score(train_y, clf.predict(train_x)))
print("Test Accuracy :: ", accuracy_score(test_y, predictions))
print(" Confusion matrix ", confusion_matrix(test_y, predictions))
import numpy as np
from baal.active.heuristics import BALD
print(f"Using {len(clf.estimators_)} estimators")
# Predict independently for all estimators.
x = np.array(list(map(lambda e: e.predict_proba(test_x), clf.estimators_)))
# Roll axis because BaaL expect [n_samples, n_classes, ..., n_estimations]
x = np.rollaxis(x, 0, 3)
print("Uncertainty per sample")
print(BALD().compute_score(x))
print("Ranks")
print(BALD()(x))
from baal.active.dataset import ActiveNumpyArray
dataset = ActiveNumpyArray((train_x, train_y))
# We start with a 10 labelled samples.
dataset.label_randomly(10)
heuristic = BALD()
# We will use a RandomForest in this case.
clf = RandomForestClassifier()
def predict(test, clf):
# Predict with all fitted estimators.
x = np.array(list(map(lambda e: e.predict_proba(test[0]), clf.estimators_)))
# Roll axis because BaaL expect [n_samples, n_classes, ..., n_estimations]
x = np.rollaxis(x, 0, 3)
return x
for _ in range(5):
print("Dataset size", len(dataset))
clf.fit(*dataset.dataset)
predictions = clf.predict(test_x)
print("Test Accuracy :: ", accuracy_score(test_y, predictions))
probs = predict(dataset.pool, clf)
to_label = heuristic(probs)
ndata_to_label = 10
if len(to_label) > 0:
dataset.label(to_label[: ndata_to_label])
else:
break
| 0.797517 | 0.959687 |
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
```
## Does nn.Conv2d init work well?
```
#export
from exp.nb_02 import *
def get_data():
path = datasets.download_data(MNIST_URL, ext='.gz')
with gzip.open(path, 'rb') as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding='latin-1')
return map(tensor, (x_train,y_train,x_valid,y_valid))
def normalize(x, m, s):
return (x - m) / s
torch.nn.modules.conv._ConvNd.reset_parameters??
x_train,y_train,x_valid,y_valid = get_data()
train_mean, train_std = x_train.mean(), x_train.std()
x_train = normalize(x_train, train_mean, train_std)
x_valid = normalize(x_valid, train_mean, train_std)
x_train.mean(), x_train.std()
x_valid.mean(), x_valid.std()
x_train = x_train.view(-1, 1, 28, 28)
x_valid = x_valid.view(-1, 1, 28, 28)
x_train.shape, x_valid.shape
n, *_ = x_train.shape
c = y_train.max() + 1
nh = 32
n, c, nh
l1 = nn.Conv2d(1, nh, 5)
x = x_valid[:100]
x.shape
def stats(x):
return x.mean(), x.std()
l1.weight.shape
l1.weight.shape
stats(l1.weight)
stats(l1.bias)
t = l1(x)
stats(t)
init.kaiming_normal_(l1.weight, a=1.)
stats(l1(x))
import torch.nn.functional as F
def f1(x, a=0):
return F.leaky_relu(l1(x), a)
init.kaiming_normal_(l1.weight, a=0)
stats(f1(x))
l1 = nn.Conv2d(1, nh, 5)
stats(f1(x))
l1.weight.shape
# receptive field size
rec_fs = l1.weight[0][0].numel()
rec_fs
nf, ni, *_ = l1.weight.shape
nf, ni
fan_in = ni * rec_fs
fan_out = nf * rec_fs
fan_in, fan_out
def gain(a):
return math.sqrt(2.0 / (1 + a**2))
gain(1),gain(0),gain(0.01),gain(0.1),gain(math.sqrt(5.))
torch.zeros(10000).uniform_(-1,1).std() # standard deviation of uniform distribution
1 / math.sqrt(3)
def kaiming2(x,a, use_fan_out=False):
nf, ni, *_ = x.shape
rec_fs = x[0][0].numel()
fan = nf * rec_fs if use_fan_out else ni * rec_fs
std = gain(a) / math.sqrt(fan)
bound = math.sqrt(3.) * std
x.data.uniform_(-bound,bound)
kaiming2(l1.weight, a=0);
stats(f1(x))
kaiming2(l1.weight, a=math.sqrt(5.))
stats(f1(x))
class Flatten(nn.Module):
def forward(self, x):
return x.view(-1)
m = nn.Sequential(
nn.Conv2d(1, 8, 5, stride=2, padding=2), nn.ReLU(),
nn.Conv2d(8, 16, 3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 32, 3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(32, 1, 3, stride=2, padding=1),
nn.AdaptiveAvgPool2d(1),
Flatten()
)
y = y_valid[:100].float()
t = m(x)
stats(t)
l = mse(t, y)
l.backward()
stats(m[0].weight.grad)
init.kaiming_uniform_??
for l in m:
if isinstance(l, nn.Conv2d):
init.kaiming_uniform_(l.weight)
l.bias.data.zero_()
t = m(x)
stats(t)
l = mse(t,y)
l.backward()
stats(m[0].weight.grad)
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
%matplotlib inline
#export
from exp.nb_02 import *
def get_data():
path = datasets.download_data(MNIST_URL, ext='.gz')
with gzip.open(path, 'rb') as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding='latin-1')
return map(tensor, (x_train,y_train,x_valid,y_valid))
def normalize(x, m, s):
return (x - m) / s
torch.nn.modules.conv._ConvNd.reset_parameters??
x_train,y_train,x_valid,y_valid = get_data()
train_mean, train_std = x_train.mean(), x_train.std()
x_train = normalize(x_train, train_mean, train_std)
x_valid = normalize(x_valid, train_mean, train_std)
x_train.mean(), x_train.std()
x_valid.mean(), x_valid.std()
x_train = x_train.view(-1, 1, 28, 28)
x_valid = x_valid.view(-1, 1, 28, 28)
x_train.shape, x_valid.shape
n, *_ = x_train.shape
c = y_train.max() + 1
nh = 32
n, c, nh
l1 = nn.Conv2d(1, nh, 5)
x = x_valid[:100]
x.shape
def stats(x):
return x.mean(), x.std()
l1.weight.shape
l1.weight.shape
stats(l1.weight)
stats(l1.bias)
t = l1(x)
stats(t)
init.kaiming_normal_(l1.weight, a=1.)
stats(l1(x))
import torch.nn.functional as F
def f1(x, a=0):
return F.leaky_relu(l1(x), a)
init.kaiming_normal_(l1.weight, a=0)
stats(f1(x))
l1 = nn.Conv2d(1, nh, 5)
stats(f1(x))
l1.weight.shape
# receptive field size
rec_fs = l1.weight[0][0].numel()
rec_fs
nf, ni, *_ = l1.weight.shape
nf, ni
fan_in = ni * rec_fs
fan_out = nf * rec_fs
fan_in, fan_out
def gain(a):
return math.sqrt(2.0 / (1 + a**2))
gain(1),gain(0),gain(0.01),gain(0.1),gain(math.sqrt(5.))
torch.zeros(10000).uniform_(-1,1).std() # standard deviation of uniform distribution
1 / math.sqrt(3)
def kaiming2(x,a, use_fan_out=False):
nf, ni, *_ = x.shape
rec_fs = x[0][0].numel()
fan = nf * rec_fs if use_fan_out else ni * rec_fs
std = gain(a) / math.sqrt(fan)
bound = math.sqrt(3.) * std
x.data.uniform_(-bound,bound)
kaiming2(l1.weight, a=0);
stats(f1(x))
kaiming2(l1.weight, a=math.sqrt(5.))
stats(f1(x))
class Flatten(nn.Module):
def forward(self, x):
return x.view(-1)
m = nn.Sequential(
nn.Conv2d(1, 8, 5, stride=2, padding=2), nn.ReLU(),
nn.Conv2d(8, 16, 3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 32, 3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(32, 1, 3, stride=2, padding=1),
nn.AdaptiveAvgPool2d(1),
Flatten()
)
y = y_valid[:100].float()
t = m(x)
stats(t)
l = mse(t, y)
l.backward()
stats(m[0].weight.grad)
init.kaiming_uniform_??
for l in m:
if isinstance(l, nn.Conv2d):
init.kaiming_uniform_(l.weight)
l.bias.data.zero_()
t = m(x)
stats(t)
l = mse(t,y)
l.backward()
stats(m[0].weight.grad)
| 0.813794 | 0.794265 |
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Get-all-types-of-events" data-toc-modified-id="Get-all-types-of-events-1"><span class="toc-item-num">1 </span>Get all types of events</a></span><ul class="toc-item"><li><span><a href="#Family-events" data-toc-modified-id="Family-events-1.1"><span class="toc-item-num">1.1 </span><a href="https://www.meetup.com/find/us--tx--dallas/parents-family" target="_blank">Family events</a></a></span></li><li><span><a href="#Outdoors-&-Adventure-events" data-toc-modified-id="Outdoors-&-Adventure-events-1.2"><span class="toc-item-num">1.2 </span><a href="https://www.meetup.com/find/outdoors-adventure" target="_blank">Outdoors & Adventure events</a></a></span></li><li><span><a href="#Downloader" data-toc-modified-id="Downloader-1.3"><span class="toc-item-num">1.3 </span>Downloader</a></span></li></ul></li></ul></div>
# Get events data from [meetup](https://www.meetup.com/)
## Get all types of events
```
import sys
sys.path.append(r'F:\geostats')
from geostats import Scraping
from get_groupinfo import *
from get_eventsInfo import *
from urllib.error import HTTPError
import time,random,os
opener = Scraping.setProxy()
urllib.request.install_opener(opener)
url = "https://www.meetup.com/"
content = Scraping.parseHtml(url)
Categories = content.xpath('///*[@id="gatsby-focus-wrapper"]//a/div/div//text()')
# Sub_Url_10miles = list(content.xpath('//*[@id="mupMain"]/div[3]/div/section[3]/div[2]/ul/li/div/div/a/@href'))
# Sub_Url = [url_10miles + '?allMeetups=false&radius=50&userFreeform=Dallas%2C+TX&mcId=z75201&mcName=Dallas%2C+TX&sort=default' for url_10miles in Sub_Url_10miles]
# random_lst = list(range(0,len(Sub_Url)))
# random.shuffle(random_lst)
print(Categories)
Sub_Url_raw = list(content.xpath('//*[@id="gatsby-focus-wrapper"]//div[@class="categoryGridList css-1q80wuk"]//a/@href'))
Sub_Url = [x.replace('/find/','https://www.meetup.com/find/us--tx--dallas/') for x in Sub_Url_raw]
Sub_Url
```
### [Family events](https://www.meetup.com/find/us--tx--dallas/parents-family)
```
import requests
url = 'https://api.meetup.com/gql'
data = {"operationName":"categoryEvents","variables":{"topicId":232,"startDateRange":"2020-09-01T14:04:39","lat":32.80,"lon":-96.80,"first":20},"query":"query categoryEvents($lat: Float!, $lon: Float!, $topicId: Int, $startDateRange: DateTime, $endDateRange: DateTime, $first: Int, $after: String) {\n searchEvents: upcomingEvents(search: {lat: $lat, lon: $lon, categoryId: $topicId, startDateRange: $startDateRange, endDateRange: $endDateRange}, input: {first: $first, after: $after}) {\n pageInfo {\n hasNextPage\n endCursor\n __typename\n }\n count\n recommendationSource\n recommendationId\n edges {\n node {\n group {\n name\n urlname\n timezone\n link\n groupPhoto {\n id\n baseUrl\n __typename\n }\n __typename\n }\n description\n fee\n feeCurrency\n id\n title\n dateTime\n eventPhoto {\n id\n baseUrl\n __typename\n }\n venue {\n id\n name\n address1\n address2\n address3\n city\n state\n country\n zip\n phone\n venueType\n __typename\n }\n going {\n totalCount\n edges {\n metadata {\n memberGroupPhoto {\n thumbUrl\n __typename\n }\n __typename\n }\n __typename\n }\n __typename\n }\n link\n isSaved\n __typename\n }\n __typename\n }\n __typename\n }\n}\n"}
headers = {'authority':'api.meetup.com',
'user-agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/65.0.3325.181 Safari/537.36'}
r = requests.post(url,headers = headers,json = data)
events_json = r.json()
events_json['data']['searchEvents']['edges'][0]
len(events_json['data']['searchEvents']['edges'])
import requests
url = 'https://api.meetup.com/gql'
data = {"operationName":"categoryEvents","variables":{"topicId":232,"startDateRange":"2020-05-21T14:04:39","lat":32.84,"lon":-96.7,"first":20},"query":"query categoryEvents($lat: Float!, $lon: Float!, $topicId: Int, $startDateRange: DateTime, $endDateRange: DateTime, $first: Int, $after: String) {\n searchEvents: upcomingEvents(search: {lat: $lat, lon: $lon, categoryId: $topicId, startDateRange: $startDateRange, endDateRange: $endDateRange}, input: {first: $first, after: $after}) {\n pageInfo {\n hasNextPage\n endCursor\n __typename\n }\n count\n recommendationSource\n recommendationId\n edges {\n node {\n group {\n name\n urlname\n timezone\n link\n groupPhoto {\n id\n baseUrl\n __typename\n }\n __typename\n }\n description\n fee\n feeCurrency\n id\n title\n dateTime\n eventPhoto {\n id\n baseUrl\n __typename\n }\n venue {\n id\n name\n address1\n address2\n address3\n city\n state\n country\n zip\n phone\n venueType\n __typename\n }\n going {\n totalCount\n edges {\n metadata {\n memberGroupPhoto {\n thumbUrl\n __typename\n }\n __typename\n }\n __typename\n }\n __typename\n }\n link\n isSaved\n __typename\n }\n __typename\n }\n __typename\n }\n}\n"}
headers = {'authority':'api.meetup.com',
'user-agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/65.0.3325.181 Safari/537.36'}
r = requests.post(url,headers = headers,json = data)
events_json = r.json()
events_json['data']['searchEvents']['edges'][0]
```
### [Outdoors & Adventure events](https://www.meetup.com/find/outdoors-adventure)
```
import requests,json
import pandas as pd
url = 'https://api.meetup.com/gql'
data = {"operationName":"categoryEvents","variables":{"topicId":242,"startDateRange":"2020-09-01T12:54:14","lat":32.84,"lon":-96.7,"first":100},"query":"query categoryEvents($lat: Float!, $lon: Float!, $topicId: Int, $startDateRange: DateTime, $endDateRange: DateTime, $first: Int, $after: String) {\n searchEvents: upcomingEvents(search: {lat: $lat, lon: $lon, categoryId: $topicId, startDateRange: $startDateRange, endDateRange: $endDateRange}, input: {first: $first, after: $after}) {\n pageInfo {\n hasNextPage\n endCursor\n __typename\n }\n count\n recommendationSource\n recommendationId\n edges {\n node {\n group {\n name\n urlname\n timezone\n link\n groupPhoto {\n id\n baseUrl\n __typename\n }\n __typename\n }\n description\n fee\n feeCurrency\n id\n title\n dateTime\n eventPhoto {\n id\n baseUrl\n __typename\n }\n venue {\n id\n name\n address1\n address2\n address3\n city\n state\n country\n zip\n phone\n venueType\n __typename\n }\n going {\n totalCount\n edges {\n metadata {\n memberGroupPhoto {\n thumbUrl\n __typename\n }\n __typename\n }\n __typename\n }\n __typename\n }\n link\n isSaved\n __typename\n }\n __typename\n }\n __typename\n }\n}\n"}
headers = {'authority':'api.meetup.com',
'user-agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/65.0.3325.181 Safari/537.36'}
r = requests.post(url,json = data)
events_json = r.json()
print(len(events_json['data']['searchEvents']['edges']))
# events_json['data']['searchEvents']['edges'][0]
import requests,json
import pandas as pd
url = 'https://api.meetup.com/gql'
data = {"operationName":"categoryEvents","variables":{"topicId":242,"startDateRange":"2020-09-01T12:54:14","lat":32.84,"lon":-96.7,"first":100},"query":"query categoryEvents($lat: Float!, $lon: Float!, $topicId: Int, $startDateRange: DateTime, $endDateRange: DateTime, $first: Int, $after: String) {\n searchEvents: upcomingEvents(search: {lat: $lat, lon: $lon, categoryId: $topicId, startDateRange: $startDateRange, endDateRange: $endDateRange}, input: {first: $first, after: $after}) {\n pageInfo {\n hasNextPage\n endCursor\n __typename\n }\n count\n recommendationSource\n recommendationId\n edges {\n node {\n group {\n name\n urlname\n timezone\n link\n groupPhoto {\n id\n baseUrl\n __typename\n }\n __typename\n }\n description\n fee\n feeCurrency\n id\n title\n dateTime\n eventPhoto {\n id\n baseUrl\n __typename\n }\n venue {\n id\n name\n address1\n address2\n address3\n city\n state\n country\n zip\n phone\n venueType\n __typename\n }\n going {\n totalCount\n edges {\n metadata {\n memberGroupPhoto {\n thumbUrl\n __typename\n }\n __typename\n }\n __typename\n }\n __typename\n }\n link\n isSaved\n __typename\n }\n __typename\n }\n __typename\n }\n}\n"}
headers = {'authority':'api.meetup.com',
'content-type': 'application/json',
'content-length':1706,
'path':'/gql',
'accept-encoding': 'gzip, deflate, br',
'apollographql-client-name': 'build-meetup web',
'referer': 'https://www.meetup.com/find/outdoors-adventure',
'user-agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/65.0.3325.181 Safari/537.36'}
r = requests.post(url,json = data)
events_json = r.json()
print(len(events_json['data']['searchEvents']['edges']))
# events_json['data']['searchEvents']['edges'][0]
```
### Downloader
```
from datetime import datetime,timezone
now = datetime.strftime(datetime.now(timezone.utc), "%Y-%m-%dT%H:%M:%S")
now
events = []
for edge in events_json['data']['searchEvents']['edges']:
event = {}
event['Title'] = edge['node']['title']
event['Date'] = edge['node']['dateTime']
event['Group Name'] = edge['node']['group']['name']
try:
event['Place'] = edge['node']['venue']['name']
except:
event['Place'] = None
try:
event['Zip'] = edge['node']['venue']['zip']
event['address1'] = edge['node']['venue']['address1']
except:
event['Zip'] = None
event['address1'] = None
event['Url'] = edge['node']['link']
events.append(event)
df = pd.DataFrame(events)
df
df.Url[19]
```
|
github_jupyter
|
import sys
sys.path.append(r'F:\geostats')
from geostats import Scraping
from get_groupinfo import *
from get_eventsInfo import *
from urllib.error import HTTPError
import time,random,os
opener = Scraping.setProxy()
urllib.request.install_opener(opener)
url = "https://www.meetup.com/"
content = Scraping.parseHtml(url)
Categories = content.xpath('///*[@id="gatsby-focus-wrapper"]//a/div/div//text()')
# Sub_Url_10miles = list(content.xpath('//*[@id="mupMain"]/div[3]/div/section[3]/div[2]/ul/li/div/div/a/@href'))
# Sub_Url = [url_10miles + '?allMeetups=false&radius=50&userFreeform=Dallas%2C+TX&mcId=z75201&mcName=Dallas%2C+TX&sort=default' for url_10miles in Sub_Url_10miles]
# random_lst = list(range(0,len(Sub_Url)))
# random.shuffle(random_lst)
print(Categories)
Sub_Url_raw = list(content.xpath('//*[@id="gatsby-focus-wrapper"]//div[@class="categoryGridList css-1q80wuk"]//a/@href'))
Sub_Url = [x.replace('/find/','https://www.meetup.com/find/us--tx--dallas/') for x in Sub_Url_raw]
Sub_Url
import requests
url = 'https://api.meetup.com/gql'
data = {"operationName":"categoryEvents","variables":{"topicId":232,"startDateRange":"2020-09-01T14:04:39","lat":32.80,"lon":-96.80,"first":20},"query":"query categoryEvents($lat: Float!, $lon: Float!, $topicId: Int, $startDateRange: DateTime, $endDateRange: DateTime, $first: Int, $after: String) {\n searchEvents: upcomingEvents(search: {lat: $lat, lon: $lon, categoryId: $topicId, startDateRange: $startDateRange, endDateRange: $endDateRange}, input: {first: $first, after: $after}) {\n pageInfo {\n hasNextPage\n endCursor\n __typename\n }\n count\n recommendationSource\n recommendationId\n edges {\n node {\n group {\n name\n urlname\n timezone\n link\n groupPhoto {\n id\n baseUrl\n __typename\n }\n __typename\n }\n description\n fee\n feeCurrency\n id\n title\n dateTime\n eventPhoto {\n id\n baseUrl\n __typename\n }\n venue {\n id\n name\n address1\n address2\n address3\n city\n state\n country\n zip\n phone\n venueType\n __typename\n }\n going {\n totalCount\n edges {\n metadata {\n memberGroupPhoto {\n thumbUrl\n __typename\n }\n __typename\n }\n __typename\n }\n __typename\n }\n link\n isSaved\n __typename\n }\n __typename\n }\n __typename\n }\n}\n"}
headers = {'authority':'api.meetup.com',
'user-agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/65.0.3325.181 Safari/537.36'}
r = requests.post(url,headers = headers,json = data)
events_json = r.json()
events_json['data']['searchEvents']['edges'][0]
len(events_json['data']['searchEvents']['edges'])
import requests
url = 'https://api.meetup.com/gql'
data = {"operationName":"categoryEvents","variables":{"topicId":232,"startDateRange":"2020-05-21T14:04:39","lat":32.84,"lon":-96.7,"first":20},"query":"query categoryEvents($lat: Float!, $lon: Float!, $topicId: Int, $startDateRange: DateTime, $endDateRange: DateTime, $first: Int, $after: String) {\n searchEvents: upcomingEvents(search: {lat: $lat, lon: $lon, categoryId: $topicId, startDateRange: $startDateRange, endDateRange: $endDateRange}, input: {first: $first, after: $after}) {\n pageInfo {\n hasNextPage\n endCursor\n __typename\n }\n count\n recommendationSource\n recommendationId\n edges {\n node {\n group {\n name\n urlname\n timezone\n link\n groupPhoto {\n id\n baseUrl\n __typename\n }\n __typename\n }\n description\n fee\n feeCurrency\n id\n title\n dateTime\n eventPhoto {\n id\n baseUrl\n __typename\n }\n venue {\n id\n name\n address1\n address2\n address3\n city\n state\n country\n zip\n phone\n venueType\n __typename\n }\n going {\n totalCount\n edges {\n metadata {\n memberGroupPhoto {\n thumbUrl\n __typename\n }\n __typename\n }\n __typename\n }\n __typename\n }\n link\n isSaved\n __typename\n }\n __typename\n }\n __typename\n }\n}\n"}
headers = {'authority':'api.meetup.com',
'user-agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/65.0.3325.181 Safari/537.36'}
r = requests.post(url,headers = headers,json = data)
events_json = r.json()
events_json['data']['searchEvents']['edges'][0]
import requests,json
import pandas as pd
url = 'https://api.meetup.com/gql'
data = {"operationName":"categoryEvents","variables":{"topicId":242,"startDateRange":"2020-09-01T12:54:14","lat":32.84,"lon":-96.7,"first":100},"query":"query categoryEvents($lat: Float!, $lon: Float!, $topicId: Int, $startDateRange: DateTime, $endDateRange: DateTime, $first: Int, $after: String) {\n searchEvents: upcomingEvents(search: {lat: $lat, lon: $lon, categoryId: $topicId, startDateRange: $startDateRange, endDateRange: $endDateRange}, input: {first: $first, after: $after}) {\n pageInfo {\n hasNextPage\n endCursor\n __typename\n }\n count\n recommendationSource\n recommendationId\n edges {\n node {\n group {\n name\n urlname\n timezone\n link\n groupPhoto {\n id\n baseUrl\n __typename\n }\n __typename\n }\n description\n fee\n feeCurrency\n id\n title\n dateTime\n eventPhoto {\n id\n baseUrl\n __typename\n }\n venue {\n id\n name\n address1\n address2\n address3\n city\n state\n country\n zip\n phone\n venueType\n __typename\n }\n going {\n totalCount\n edges {\n metadata {\n memberGroupPhoto {\n thumbUrl\n __typename\n }\n __typename\n }\n __typename\n }\n __typename\n }\n link\n isSaved\n __typename\n }\n __typename\n }\n __typename\n }\n}\n"}
headers = {'authority':'api.meetup.com',
'user-agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/65.0.3325.181 Safari/537.36'}
r = requests.post(url,json = data)
events_json = r.json()
print(len(events_json['data']['searchEvents']['edges']))
# events_json['data']['searchEvents']['edges'][0]
import requests,json
import pandas as pd
url = 'https://api.meetup.com/gql'
data = {"operationName":"categoryEvents","variables":{"topicId":242,"startDateRange":"2020-09-01T12:54:14","lat":32.84,"lon":-96.7,"first":100},"query":"query categoryEvents($lat: Float!, $lon: Float!, $topicId: Int, $startDateRange: DateTime, $endDateRange: DateTime, $first: Int, $after: String) {\n searchEvents: upcomingEvents(search: {lat: $lat, lon: $lon, categoryId: $topicId, startDateRange: $startDateRange, endDateRange: $endDateRange}, input: {first: $first, after: $after}) {\n pageInfo {\n hasNextPage\n endCursor\n __typename\n }\n count\n recommendationSource\n recommendationId\n edges {\n node {\n group {\n name\n urlname\n timezone\n link\n groupPhoto {\n id\n baseUrl\n __typename\n }\n __typename\n }\n description\n fee\n feeCurrency\n id\n title\n dateTime\n eventPhoto {\n id\n baseUrl\n __typename\n }\n venue {\n id\n name\n address1\n address2\n address3\n city\n state\n country\n zip\n phone\n venueType\n __typename\n }\n going {\n totalCount\n edges {\n metadata {\n memberGroupPhoto {\n thumbUrl\n __typename\n }\n __typename\n }\n __typename\n }\n __typename\n }\n link\n isSaved\n __typename\n }\n __typename\n }\n __typename\n }\n}\n"}
headers = {'authority':'api.meetup.com',
'content-type': 'application/json',
'content-length':1706,
'path':'/gql',
'accept-encoding': 'gzip, deflate, br',
'apollographql-client-name': 'build-meetup web',
'referer': 'https://www.meetup.com/find/outdoors-adventure',
'user-agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/65.0.3325.181 Safari/537.36'}
r = requests.post(url,json = data)
events_json = r.json()
print(len(events_json['data']['searchEvents']['edges']))
# events_json['data']['searchEvents']['edges'][0]
from datetime import datetime,timezone
now = datetime.strftime(datetime.now(timezone.utc), "%Y-%m-%dT%H:%M:%S")
now
events = []
for edge in events_json['data']['searchEvents']['edges']:
event = {}
event['Title'] = edge['node']['title']
event['Date'] = edge['node']['dateTime']
event['Group Name'] = edge['node']['group']['name']
try:
event['Place'] = edge['node']['venue']['name']
except:
event['Place'] = None
try:
event['Zip'] = edge['node']['venue']['zip']
event['address1'] = edge['node']['venue']['address1']
except:
event['Zip'] = None
event['address1'] = None
event['Url'] = edge['node']['link']
events.append(event)
df = pd.DataFrame(events)
df
df.Url[19]
| 0.263126 | 0.638004 |
```
import sys, os
from joblib import Parallel, delayed
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from hyppo.tools import power
sys.path.append(os.path.realpath('..'))
sns.set(color_codes=True, style='white', context='talk', font_scale=1.5)
PALETTE = sns.color_palette("Set1")
sns.set_palette(PALETTE[1:5] + PALETTE[6:], n_colors=9)
MAX_SAMPLE_SIZE = 100
STEP_SIZE = 5
SAMP_SIZES = range(5, MAX_SAMPLE_SIZE + STEP_SIZE, STEP_SIZE)
POWER_REPS = 5
SIMULATIONS = {
"linear": "Linear",
"exponential": "Exponential",
"cubic": "Cubic",
"joint_normal": "Joint Normal",
"step": "Step",
"quadratic": "Quadratic",
"w_shaped": "W-Shaped",
"spiral": "Spiral",
"uncorrelated_bernoulli": "Bernoulli",
"logarithmic": "Logarithmic",
"fourth_root": "Fourth Root",
"sin_four_pi": "Sine 4\u03C0",
"sin_sixteen_pi": "Sine 16\u03C0",
"square": "Square",
"two_parabolas": "Two Parabolas",
"circle": "Circle",
"ellipse": "Ellipse",
"diamond": "Diamond",
"multiplicative_noise": "Multiplicative",
"multimodal_independence": "Independence"
}
TESTS = [
["MaxMargin", "Dcorr"],
# "KMERF",
# "MGC",
"Dcorr",
# "Hsic",
# "HHG",
# "CCA",
# "RV",
]
def estimate_power(sim, test):
est_power = np.array(
[
np.mean(
[
power(test, sim_type="indep", sim=sim, n=i, p=3, auto=True)
for _ in range(POWER_REPS)
]
)
for i in SAMP_SIZES
]
)
test = test[0] if type(test) is list else test
np.savetxt(
"../max_margin/vs_samplesize/{}_{}.csv".format(sim, test),
est_power,
delimiter=",",
)
return est_power
outputs = Parallel(n_jobs=-1, verbose=100)(
[delayed(estimate_power)(sim, test) for sim in SIMULATIONS.keys() for test in TESTS]
)
def plot_power():
fig, ax = plt.subplots(nrows=4, ncols=5, figsize=(25, 20))
plt.suptitle(
"Multivariate Independence Testing (Increasing Sample Size)",
y=0.93,
va="baseline",
)
for i, row in enumerate(ax):
for j, col in enumerate(row):
count = 5 * i + j
sim = list(SIMULATIONS.keys())[count]
for test in TESTS:
test = test[0] if type(test) is list else test
power = np.genfromtxt(
"../max_margin/vs_samplesize/{}_{}.csv".format(sim, test),
delimiter=",",
)
kwargs = {
"label": test,
"lw": 2,
}
if test in ["MaxMargin"]:
kwargs["color"] = "#e41a1c"
kwargs["lw"] = 4
col.plot(SAMP_SIZES, power, **kwargs)
col.set_xticks([])
if i == 3:
col.set_xticks([SAMP_SIZES[0], SAMP_SIZES[-1]])
col.set_ylim(-0.05, 1.05)
col.set_yticks([])
if j == 0:
col.set_yticks([0, 1])
col.set_title(SIMULATIONS[sim])
fig.text(0.5, 0.07, "Sample Size", ha="center")
fig.text(
0.07,
0.5,
"Absolute Power",
va="center",
rotation="vertical",
)
leg = plt.legend(
bbox_to_anchor=(0.5, 0.07),
bbox_transform=plt.gcf().transFigure,
ncol=len(TESTS),
loc="upper center",
)
leg.get_frame().set_linewidth(0.0)
for legobj in leg.legendHandles:
legobj.set_linewidth(5.0)
plt.subplots_adjust(hspace=0.50)
plt.savefig(
"../max_margin/figs/indep_power_sampsize.pdf", transparent=True, bbox_inches="tight"
)
plot_power()
```
|
github_jupyter
|
import sys, os
from joblib import Parallel, delayed
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from hyppo.tools import power
sys.path.append(os.path.realpath('..'))
sns.set(color_codes=True, style='white', context='talk', font_scale=1.5)
PALETTE = sns.color_palette("Set1")
sns.set_palette(PALETTE[1:5] + PALETTE[6:], n_colors=9)
MAX_SAMPLE_SIZE = 100
STEP_SIZE = 5
SAMP_SIZES = range(5, MAX_SAMPLE_SIZE + STEP_SIZE, STEP_SIZE)
POWER_REPS = 5
SIMULATIONS = {
"linear": "Linear",
"exponential": "Exponential",
"cubic": "Cubic",
"joint_normal": "Joint Normal",
"step": "Step",
"quadratic": "Quadratic",
"w_shaped": "W-Shaped",
"spiral": "Spiral",
"uncorrelated_bernoulli": "Bernoulli",
"logarithmic": "Logarithmic",
"fourth_root": "Fourth Root",
"sin_four_pi": "Sine 4\u03C0",
"sin_sixteen_pi": "Sine 16\u03C0",
"square": "Square",
"two_parabolas": "Two Parabolas",
"circle": "Circle",
"ellipse": "Ellipse",
"diamond": "Diamond",
"multiplicative_noise": "Multiplicative",
"multimodal_independence": "Independence"
}
TESTS = [
["MaxMargin", "Dcorr"],
# "KMERF",
# "MGC",
"Dcorr",
# "Hsic",
# "HHG",
# "CCA",
# "RV",
]
def estimate_power(sim, test):
est_power = np.array(
[
np.mean(
[
power(test, sim_type="indep", sim=sim, n=i, p=3, auto=True)
for _ in range(POWER_REPS)
]
)
for i in SAMP_SIZES
]
)
test = test[0] if type(test) is list else test
np.savetxt(
"../max_margin/vs_samplesize/{}_{}.csv".format(sim, test),
est_power,
delimiter=",",
)
return est_power
outputs = Parallel(n_jobs=-1, verbose=100)(
[delayed(estimate_power)(sim, test) for sim in SIMULATIONS.keys() for test in TESTS]
)
def plot_power():
fig, ax = plt.subplots(nrows=4, ncols=5, figsize=(25, 20))
plt.suptitle(
"Multivariate Independence Testing (Increasing Sample Size)",
y=0.93,
va="baseline",
)
for i, row in enumerate(ax):
for j, col in enumerate(row):
count = 5 * i + j
sim = list(SIMULATIONS.keys())[count]
for test in TESTS:
test = test[0] if type(test) is list else test
power = np.genfromtxt(
"../max_margin/vs_samplesize/{}_{}.csv".format(sim, test),
delimiter=",",
)
kwargs = {
"label": test,
"lw": 2,
}
if test in ["MaxMargin"]:
kwargs["color"] = "#e41a1c"
kwargs["lw"] = 4
col.plot(SAMP_SIZES, power, **kwargs)
col.set_xticks([])
if i == 3:
col.set_xticks([SAMP_SIZES[0], SAMP_SIZES[-1]])
col.set_ylim(-0.05, 1.05)
col.set_yticks([])
if j == 0:
col.set_yticks([0, 1])
col.set_title(SIMULATIONS[sim])
fig.text(0.5, 0.07, "Sample Size", ha="center")
fig.text(
0.07,
0.5,
"Absolute Power",
va="center",
rotation="vertical",
)
leg = plt.legend(
bbox_to_anchor=(0.5, 0.07),
bbox_transform=plt.gcf().transFigure,
ncol=len(TESTS),
loc="upper center",
)
leg.get_frame().set_linewidth(0.0)
for legobj in leg.legendHandles:
legobj.set_linewidth(5.0)
plt.subplots_adjust(hspace=0.50)
plt.savefig(
"../max_margin/figs/indep_power_sampsize.pdf", transparent=True, bbox_inches="tight"
)
plot_power()
| 0.375821 | 0.42483 |
## Get your data ready for training
This module defines the basic [`DataBunch`](/basic_data.html#DataBunch) object that is used inside [`Learner`](/basic_train.html#Learner) to train a model. This is the generic class, that can take any kind of fastai [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) or [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader). You'll find helpful functions in the data module of every application to directly create this [`DataBunch`](/basic_data.html#DataBunch) for you.
```
from fastai.gen_doc.nbdoc import *
from fastai.basics import *
show_doc(DataBunch)
```
It also ensure all the dataloaders are on `device` and apply to them `tfms` as batch are drawn (like normalization). `path` is used internally to store temporary files, `collate_fn` is passed to the pytorch `Dataloader` (replacing the one there) to explain how to collate the samples picked for a batch. By default, it applies data to the object sent (see in [`vision.image`](/vision.image.html#vision.image) or the [data block API](/data_block.html) why this can be important).
`train_dl`, `valid_dl` and optionally `test_dl` will be wrapped in [`DeviceDataLoader`](/basic_data.html#DeviceDataLoader).
### Factory method
```
show_doc(DataBunch.create)
```
`num_workers` is the number of CPUs to use, `tfms`, `device` and `collate_fn` are passed to the init method.
```
jekyll_warn("You can pass regular pytorch Dataset here, but they'll require more attributes than the basic ones to work with the library. See below for more details.")
```
### Visualization
```
show_doc(DataBunch.show_batch)
```
### Grabbing some data
```
show_doc(DataBunch.dl)
show_doc(DataBunch.one_batch)
show_doc(DataBunch.one_item)
show_doc(DataBunch.sanity_check)
```
### Load and save
You can save your [`DataBunch`](/basic_data.html#DataBunch) object for future use with this method.
```
show_doc(DataBunch.save)
show_doc(load_data)
jekyll_important("The arguments you passed when you created your first `DataBunch` aren't saved, so you should pass them here if you don't want the default.")
```
This is to allow you to easily create a new [`DataBunch`](/basic_data.html#DataBunch) with a different bath size for instance. You will also need to reapply any normalization (in vision) you might have done on your original [`DataBunch`](/basic_data.html#DataBunch).
### Empty [`DataBunch`](/basic_data.html#DataBunch) for inference
```
show_doc(DataBunch.export)
show_doc(DataBunch.load_empty, full_name='load_empty')
```
This method should be used to create a [`DataBunch`](/basic_data.html#DataBunch) at inference, see the corresponding [tutorial](/tutorial.inference.html).
```
show_doc(DataBunch.add_test)
```
### Dataloader transforms
```
show_doc(DataBunch.add_tfm)
```
Adds a transform to all dataloaders.
## Using a custom Dataset in fastai
If you want to use your pytorch [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) in fastai, you may need to implement more attributes/methods if you want to use the full functionality of the library. Some functions can easily be used with your pytorch [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) if you just add an attribute, for others, the best would be to create your own [`ItemList`](/data_block.html#ItemList) by following [this tutorial](/tutorial.itemlist.html). Here is a full list of what the library will expect.
### Basics
First of all, you obviously need to implement the methods `__len__` and `__getitem__`, as indicated by the pytorch docs. Then the most needed things would be:
- `c` attribute: it's used in most functions that directly create a [`Learner`](/basic_train.html#Learner) ([`tabular_learner`](/tabular.data.html#tabular_learner), [`text_classifier_learner`](/text.learner.html#text_classifier_learner), [`unet_learner`](/vision.learner.html#unet_learner), [`cnn_learner`](/vision.learner.html#cnn_learner)) and represents the number of outputs of the final layer of your model (also the number of classes if applicable).
- `classes` attribute: it's used by [`ClassificationInterpretation`](/train.html#ClassificationInterpretation) and also in [`collab_learner`](/collab.html#collab_learner) (best to use [`CollabDataBunch.from_df`](/collab.html#CollabDataBunch.from_df) than a pytorch [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset)) and represents the unique tags that appear in your data.
- maybe a `loss_func` attribute: that is going to be used by [`Learner`](/basic_train.html#Learner) as a default loss function, so if you know your custom [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) requires a particular loss, you can put it.
### For a specific application
In text, your dataset will need to have a `vocab` attribute that should be an instance of [`Vocab`](/text.transform.html#Vocab). It's used by [`text_classifier_learner`](/text.learner.html#text_classifier_learner) and [`language_model_learner`](/text.learner.html#language_model_learner) when building the model.
In tabular, your dataset will need to have a `cont_names` attribute (for the names of continuous variables) and a `get_emb_szs` method that returns a list of tuple `(n_classes, emb_sz)` representing, for each categorical variable, the number of different codes (don't forget to add 1 for nan) and the corresponding embedding size. Those two are used with the `c` attribute by [`tabular_learner`](/tabular.data.html#tabular_learner).
### Functions that really won't work
To make those last functions work, you really need to use the [data block API](/data_block.html) and maybe write your own [custom ItemList](/tutorial.itemlist.html).
- [`DataBunch.show_batch`](/basic_data.html#DataBunch.show_batch) (requires `.x.reconstruct`, `.y.reconstruct` and `.x.show_xys`)
- [`Learner.predict`](/basic_train.html#Learner.predict) (requires `x.set_item`, `.y.analyze_pred`, `.y.reconstruct` and maybe `.x.reconstruct`)
- [`Learner.show_results`](/basic_train.html#Learner.show_results) (requires `x.reconstruct`, `y.analyze_pred`, `y.reconstruct` and `x.show_xyzs`)
- `DataBunch.set_item` (requires `x.set_item`)
- [`Learner.backward`](/basic_train.html#Learner.backward) (uses `DataBunch.set_item`)
- [`DataBunch.export`](/basic_data.html#DataBunch.export) (requires `export`)
```
show_doc(DeviceDataLoader)
```
Put the batches of `dl` on `device` after applying an optional list of `tfms`. `collate_fn` will replace the one of `dl`. All dataloaders of a [`DataBunch`](/basic_data.html#DataBunch) are of this type.
### Factory method
```
show_doc(DeviceDataLoader.create)
```
The given `collate_fn` will be used to put the samples together in one batch (by default it grabs their data attribute). `shuffle` means the dataloader will take the samples randomly if that flag is set to `True`, or in the right order otherwise. `tfms` are passed to the init method. All `kwargs` are passed to the pytorch [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader) class initialization.
### Methods
```
show_doc(DeviceDataLoader.add_tfm)
show_doc(DeviceDataLoader.remove_tfm)
show_doc(DeviceDataLoader.new)
show_doc(DeviceDataLoader.proc_batch)
show_doc(DatasetType, doc_string=False)
```
Internal enumerator to name the training, validation and test dataset/dataloader.
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(DeviceDataLoader.collate_fn)
```
## New Methods - Please document or move to the undocumented section
|
github_jupyter
|
from fastai.gen_doc.nbdoc import *
from fastai.basics import *
show_doc(DataBunch)
show_doc(DataBunch.create)
jekyll_warn("You can pass regular pytorch Dataset here, but they'll require more attributes than the basic ones to work with the library. See below for more details.")
show_doc(DataBunch.show_batch)
show_doc(DataBunch.dl)
show_doc(DataBunch.one_batch)
show_doc(DataBunch.one_item)
show_doc(DataBunch.sanity_check)
show_doc(DataBunch.save)
show_doc(load_data)
jekyll_important("The arguments you passed when you created your first `DataBunch` aren't saved, so you should pass them here if you don't want the default.")
show_doc(DataBunch.export)
show_doc(DataBunch.load_empty, full_name='load_empty')
show_doc(DataBunch.add_test)
show_doc(DataBunch.add_tfm)
show_doc(DeviceDataLoader)
show_doc(DeviceDataLoader.create)
show_doc(DeviceDataLoader.add_tfm)
show_doc(DeviceDataLoader.remove_tfm)
show_doc(DeviceDataLoader.new)
show_doc(DeviceDataLoader.proc_batch)
show_doc(DatasetType, doc_string=False)
show_doc(DeviceDataLoader.collate_fn)
| 0.686895 | 0.979235 |
# Builtin Types
## Numeric Types
### Reference
https://docs.python.org/3.6/library/stdtypes.html#typesnumeric
### Int
In Python **int** type represents all positive and negative whole numbers. The range of the integer type is system dependent. For 32-bit systems the min and max values are: -2147483647 to 2147483647 while for 64-bit systems the min and max values are: -9223372036854775808 to 9223372036854775807. Below is some code that will print the min/max integer value on your system.
```
# How to find the maximum integer value for your system?
import sys
print(sys.maxsize)
print(-1 - sys.maxsize)
# Note: Older versions of Python had sys.maxint instead of maxsize
```
#### Working With Integers
Because integers are numbers they support operations you would expect, such as, addition, subtraction, multiplication and division. Each of these operations uses the expected symbol:
* **`+`** : addition
* **`-`** : subtraction
* **`*`** : multiplication
However, integer division is has a special symbol so that the result of the division remains an integer. This is known as integer division and the symbol **`//`**.
**Note: If you use the **`/`** symbol, the quotient will be a floating point number, a number with real and fractional parts.**
```
print(1 + 1)
print(3 - 5)
print(5 * 5)
# The quotient will be an integer
print(6 // 3)
# The quotient will also be an integer
print(3 // 6)
# The quotient will be a floating point number
print(3 / 6)
```
Other useful operators are:
* **`+=`** : add and assign
* **`-=`** : subtract and assign
* **`*=`** : multiply and assign
* **`/=`** : divide and assign
** Note: Python does not support `++` or `--` operators**
See the reference above for defined operators.
#### Conversion
Sometimes you need to convert a string or floating point number into an **`int`**. Python provides the **`int()`** function.
```
# Convert text to an integer
print(int("534234"))
print(int("0x043", 16))
print(int(3.1415))
```
### Float
The **`float`** type in Python is used to hold real and fraction part of a number. For example **`pi`** is a floating point number. Like integers, floating point numbers are also system dependent and that information is made available through the sys module.
```
import sys
print(sys.float_info)
```
#### Working With Float
The **`float`** type supports the same basic math operations as **`int`**.
```
print(1.34 + 2.54)
print(6.455 - 2.1)
print(26.34 * 1.2)
print(2354.3 / 34.2)
# Note: Integer division where either number is a float returns a float, but only the integer portion of the quotient
print(5.0 // 2)
```
#### Conversion
Like **`int`**, we sometime need to convert values into **`float`**. To do that we use the **`float()`** function.
```
print(float('+1.23'))
print(float(' -12345\n'))
print(float('1e-003'))
print(float(10))
```
### Complex
Python supports a **`complex`** type to represent imaginary numbers. The type of each component of a complex number is **`float`**. See the reference for more information.
### Exercises
1. Write a program to compute the Area of a Circle
2. Write a program to parse a string to Float or Integer
3. Write a program to convert the distance (in feet) to inches, yards, and miles
4. Write a program to convert Fahrenheit to Celcius and Celcius to Fahrenheit
```
# 1. Write a program to compute the Area of a Circle
import math
radius = float(input("Enter the raidus of the circle: "))
print("The area is: {}".format(2 * math.pi * radius))
# 2. Write a program to parse a string to Float or Integer
value = input("Enter a number: ")
try:
value = int(value)
print("{} is an integer".format(value))
except ValueError:
try:
value = float(value)
print("{} is a floating point number".format(value))
except ValueError:
print("I don't know what {} is. Try again.".format(value))
# 3. Write a program to convert the distance (in feet) to inches, yards, and miles
value = input("Enter the distance (in feet): ")
try:
value = float(value)
print("Distance {:.1e} (in feet) is {:.1e} inches, {:.1e} yards, and {:.1e} miles.".format(value, value * 12, value / 3, value / 5280))
except ValueError:
print("I don't know what {} is. Try again.".format(value))
# 4. Write a program to convert Fahrenheit to Celcius and Celcius to Fahrenheit
value = input("Temperature Conversion - Enter system (F or C), a space, the temperature (ex. F 32.0):")
sys, temp = value.split()
if sys.lower() == 'f':
print("{} F is {:1f} C".format(temp, (float(temp) - 32) * 5 / 9))
if sys.lower() == 'c':
print("{} C is {:1f} F".format(temp, float(temp) * 9 / 5 + 32))
```
---------------------------------------------------------------------
## Sequence Types
### Reference
https://docs.python.org/3.6/library/stdtypes.html#sequence-types-list-tuple-range
### Text Sequence Type
#### Reference
https://docs.python.org/3.6/library/stdtypes.html#text-sequence-type-str
What is a 'Text Sequence Type'? It is a sequence of text characters, like a sentence or paragraph, referred to in programming as a 'string', as in, a 'string of text characters'. In Python, a text sequence is represented by the **`str`** type. The text of this document would be considered a string. An example of how to create a **`str`** in Python follows:
**Note: Text sequences have similar properties as other Python sequences. I present the text sequence type first because text sequences are easy to understand (we use them all the time when writing, texting, emailing, etc).**
```
print("this is a string of characters or letters")
print('')
print('In Python, strings can be delineated using either double quotes " or single quotes \' (one on each end)')
print("")
print("""Python also supports a triple quote (either \" or ')
which allows for very long strings or
strings that have embedded
formating""")
print('''''')
print('Also, long strings can \
be split \
across multiple lines without \
embedded carriage returns \
by using a \
line continuation character - \
look Ma, no carriabe returns!')
```
#### Working With Strings
##### Methods
Of course, there are lots of things we can do with strings (and sequences in general). Python provides 'methods' that can be called on a **`str`** type to perform some operation or functionality.
```
print("capitalize this".capitalize())
print('upper case this'.upper())
print('LOWER CASE THIS'.lower())
print("""Count the c's characters""".count('c'))
print('''Find the position of the first i in this string'''.find('i'))
print("put {0} here->{0} put {1}, here->{1}, put {2} here->{2}".format(1, 2, 3))
print("split this sentence into a sequence (a list actually) or words separated by spaces".split())
```
##### Indexing
It is often useful to access the elements of a string using an index. Indexing for sequences is zero-based ranging from 0 to N-1, where N is the number elements in the sequence. Indexing notation uses the left/right bracket, **`[]`**. In addition, Python supports the notion of a negative index which is applied starting from the end of the sequence.
```
var = "This is a string"
print(var[0])
print(var[5])
print(var[-1])
print(var[-6])
```
##### Slicing
Another useful operation for sequences is slicing. Slicing is similar to indexing but involves selecting 1 or more elements from a sequence. Slicing notation uses the left/right bracket, **`[]`** and the **`:`**. The values specified for the slice represent the start and stop (non-inclusive) and stride (number of characters taken at a time).
```
var = "This_is_a_string"
print(var[2:5])
print(var[3:9])
print(var[5:])
print(var[:7])
print(var[-1:])
print(var[:-4])
print(var[-len(var):])
print(var[::-1])
```
#### Conversion
String conversion uses the **`str()`** function. The **`str()`** is quite flexible and will default to a representation of the underlying object if no suitable option is available.
```
print(str(1000))
print(str(3.1435))
print(str(lambda : None))
print(str(['this', 'is', 'a', 'list', 'of', 'words']))
```
#### Exercises
1. Write a Python program to calculate the length of a string.
2. Write a Python function that takes a list of words and returns the length of the longest one.
3. Write a Python script that takes input from the user and displays that input back in upper and lower cases.
4. Write a Python function to reverses a string if it's length is a multiple of 4.
5. Write a Python program to count occurrences of a substring in a string.
```
# 1. Write a Python program to calculate the length of a string.
var = "this is a string"
print(len(var))
# 2. Write a Python function that takes a list of words and returns the length of the longest one.
var = "this is a string with a bunch of word in it"
words = var.split()
max_len = 0
for w in words:
if len(w) > max_len:
max_len = len(w)
print("The maximum length is {}".format(max_len))
# Alternate 2
print("The maximum length is {}".format(max([len(w) for w in words])))
# 3. Write a Python script that takes input from the user and displays that input back in upper and lower cases.
var = input("Enter a string: ")
print("Upper: {}, Lower: {}".format(var.upper(), var.lower()))
# 4. Write a Python function to reverse a string if it's length is a multiple of 4.
var1 = "This is a string who's multiple is four!"
var2 = "This is a string that is not!"
for v in var1, var2:
if len(v) % 4 == 0:
print(var1[::-1])
else:
print("Not multiple of 4")
# 5. Write a Python program to count occurrences of a substring in a string.
var = "This is a long string that is quite useful if the issue is that there is not a problem!"
sub_str = 'is'
print(var.count(sub_str))
# Alternate
print(len(var.split('is')) - 1)
```
------------------------------------------------------------------------------------------------------
### List Sequence Type
#### Reference
https://docs.python.org/3.6/library/stdtypes.html#list
A list is a sequence of values where the values can be of the same or different types. A list is defined by writing a series of comma-separated values enclosed by brackets.
#### Working With Lists
l = [1, 2, 3, 4] # List of four integers
l = ['a', 'b', 'c', 'd'] # list of four characters
l = [] # empty list
l = list() # empty list
##### Methods
* append(x)
* clear()
* copy()
* extend(t)
* insert(x)
* pop([i])
* remove(x)
* reverse()
##### Indexing
##### Slicing
#### Conversion
#### Examples
------------------------------------------------------------------------------------------------------
### Tuple Sequence Type
#### Reference
https://docs.python.org/3.6/library/stdtypes.html#tuple
Tuples are immutable sequences, typically used to store collections of heterogeneous data. A tuple is defined by writing a series of comma-separated values encluded by parenthesis.
**Note: As an immutable type, tuple is hashable and therefore can be used as a key in a dictionary and stored in a set.**
#### Methods
##### Indexing
##### Slicing
#### Conversion
#### Examples
------------------------------------------------------------------------------------------------------
### Range Sequence Type
#### Reference
https://docs.python.org/3.6/library/stdtypes.html#tuple
Tuples are immutable sequences, typically used to store collections of heterogeneous data. A tuple is defined by writing a series of comma-separated values encluded by parenthesis.
**Note: As an immutable type, tuple is hashable and therefore can be used as a key in a dictionary and stored in a set.**
https://docs.python.org/3.6/library/stdtypes.html#range
### Range
#### Definition
The range type represents an immutable sequence of numbers and is commonly used for looping a specific number of times in for loops.
#### Nomenclature
#### Operations
##
# Set
#### Definition
A set object is a mutable unordered collection of distinct hashable objects. Common uses include membership testing, removing duplicates from a sequence, and computing mathematical operations such as intersection, union, difference, and symmetric difference.
#### Nomenclature
s = set([1, 2, 3, 4, 5]) # Set of five integers from list
s = set(('a', 'b', 'c', 'd')) # Set of characters from tuple
s = set('asdf') # Set of four characters from string
s = set() # Empty set
#### Operations
* isdisjoint
* issubset or set <= other
* set < other
* issuperset or set >= other
* set > other
* union or set | other | ...
* intersection or set & other & ...
* difference or set - other - ...
* symmetric_difference or set ^ other
* copy
* update or set |= other
* intersection_update or set &= other
* difference_update or set -= other
* symmetric_difference_update or set ^= other
* add(x)
* remove(x)
* discard(x)
* pop()
* clear()
### Bytes
#### Definitions
Bytes objects are immutable sequences of single bytes.
#### Nomenclature
b = b'12345656' # Bytes object of length 8
b = bytes(10) # Zero-filled bytes object of length 10
b = bytes(range(10)) # Bytes object of length 10 filled with values 0 through 9
#### Operations
* hex() - Converts ASCII to hex values
* fromhex(x) - Converts hex string to ASCII bytes
**Note: Contains many ASCII-based (string-type) operations. Care must be taken when using these operations with non-ASCII data.
### ByteArray
Immutable counterpart to Bytes
### Common Sequence Operations
* x in s
* x not in s
* s + t (concatenate)
* s * n or n * s (repeat)
* s[i]
* s[start:stop]
* s[start:stop:step]
* len(s)
* min(s)
* max(s)
* s.index(x)
* s.count(x)
### Exercises
### List
### Tuple
### Set
### Bytes/ByteArray
# Mapping
## Dictionary
### Keys
### Values
### Items
## Exercise
Rock, Paper, Scissors
------------------------------------------------------------------------------------------------------
Now that we have learned some basics of programming, input, processing and output, its time to learn new ways to represent the information that is stored within a program. The mechanisms we use to store information are called data structures. Python has several useful builtin data structures and also allows a programmer to create her own.
**List**
**Note: While a list can hold values of different types, typically, a list contains values of a single type.**
```
[1, 2, 3, 4, 5]
['a', 'b', 'c', 'd', 'e']
[1, 'a', 2, 'b', 3, 'c']
```
Python also provides a **list** function that will create a list from an iterable. An iterable is defined as:
Iterable: An object capable of returning its members one at a time.
Iteration is a fundamental property used by many data structures throughout Python.
```
list('abcde')
list('12345')
list(range(10))
```
**List Operations**
append
index
slice
insert
pop
* Append
l = []
l.append('a')
l.append('b')
l.append('c')
l.append('d')
* Index
l = [1, 2, 3, 4, 5]
l.index[3]
l.index[0]
l.index[-1]
* Slice
l = [1, 2, 3, 4, 5]
l[0:5]
l[:]
l[3:5]
l[-1:-3]
* Push
l = []
l.push('a')
l.push('b')
l.push('c')
* Pop
l = [1, 2, 3, 4, 5]
l.pop(0)
**List Exercises**
1. Write a Python program to sum all the items in a list.
```
l = [1, 2, 3, 4, 5]
sum(l)
```
2. Write a Python program to multiplies all the items in a list.
```
def mul(iterable):
x = 1
for i in iterable:
x*=i
return x
l = [1, 2, 3, 4, 5]
mul(l)
```
3. Write a Python program to get the largest number from a list.
```
l = [1, 2, 3, 4, 5]
max(l)
```
4. Write a Python program to get the smallest number from a list.
```
l = [1, 2, 3, 4, 5]
min(l)
```
5. Write a Python program to count the number of strings where the string length is 2 or more and the first and last character are same from a given list of strings.
```
s = ['this', 'that', 'these', 'those', 'it', 'what', 'wish']
for i in s:
if len(i) >= 2 and i[0] == i[-1]:
print(i)
```
6. Write a Python program to get a list, sorted in increasing order by the last element in each tuple from a given list of non-empty tuples.
```
l = [(1, 2), (3, 2), (2, 3), (5, 3), (7,2)]
sorted(l, key=lambda i: i[1], reverse=True)
```
7. Write a Python program to remove duplicates from a list.
```
l = [1, 2, 3, 4, 1, 5, 6, 5, 7, 6]
list(set(l))
```
8. Write a Python program to check a list is empty or not.
```
def is_empty(l):
return l is None
l = [1, 2, 3, 4, 5]
print(is_empty(l))
l = None
print(is_empty(l))
```
9. Write a Python program to clone or copy a list.
```
l = [1, 2, 3, 4, 5]
print(id(l))
m = l.copy()
print(id(m))
```
10. Write a Python program to find the list of words that are longer than n from a given list of words.
```
l = ['this', 'that', 'these', 'those', 'which', 'what', 'who', 'where']
n = 4
m = [i for i in l if len(i) > n]
print(m)
```
11. Write a Python function that takes two lists and returns True if they have at least one common member.
```
l = [1, 2, 3, 4, 5, 6, 7, 8, 9]
m = [9, 5, 3, 1, 3, 8]
True if True in [
i == j
for i in m
for j in l] else False
```
12. Write a Python program to print a specified list after removing the 0th, 4th and 5th elements.
```
l = [1, 3, 2, 6, 5, 7, 8, 9, 4]
r = [0, 4, 5]
m = [v for i,v in enumerate(l) if i not in r]
print(m)
```
13. Write a Python program to generate a 3*4*6 3D array whose each element is *.
```
def make_3d_array(i, j, k):
return [[[ '*' for _i in range(i)] for _j in range(j)] for _k in range(k)]
make_3d_array(3, 4, 6)
```
14. Write a Python program to print the numbers of a specified list after removing even numbers from it.
```
l = [1, 4, 3, 2, 5, 7 ,4, 5, 8]
[i for i in l if i % 2 == 0]
```
15. Write a Python program to shuffle and print a specified list.
```
import random
l = [1, 2, 3, 4, 5, 6]
random.shuffle(l)
print(l)
```
16. Write a Python program to generate and print a list of first and last 5 elements where the values are square of numbers between 1 and 30 (both included).
```
import random
import math
l = [random.randint(0, 1000) for _ in range(100)]
m = [i for i in l if 1 < math.sqrt(i) < 30]
print(m[:5] + m[-5:])
```
17. Write a Python program to generate and print a list except for the first 5 elements, where the values are square of numbers between 1 and 30 (both included).
```
import random
l = [random.randint(0, 1000) for _ in range(100)]
m = [i for i in l if 1 < i < 30*30]
print(m[5:])
```
18. Write a Python program to generate all permutations of a list in Python.
```
import random
import itertools
n = 3
l = [random.randint(0,n) for i in range(n)]
[i for i in itertools.permutations(l)]
```
19. Write a Python program to get the difference between the two lists.
```
l = [1, 2, 3]
m = [5, 8, 3, 2, 1]
print(list(set(m)-set(l)))
```
20. Write a Python program access the index of a list.
```
l = [1, 2, 3, 4, 5]
for k, v in enumerate(l):
print(k, v)
```
21. Write a Python program to convert a list of characters into a string.
```
l = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h']
''.join(l)
```
22. Write a Python program to find the index of an item in a specified list.
```
l = ['a', 'b', 'c', 'd', 'e', 'f', 'g']
print(l.index('a'))
print(l.index('e'))
```
23. Write a Python program to flatten a shallow list.
```
import itertools
l = [[2,4,3],[1,5,6], [9], [7,9,0]]
m = list(itertools.chain(*l))
print(m)
```
24. Write a Python program to append a list to the second list.
```
l = [1, 2, 3, 4, 5]
m = ['a', 'b', 'c', 'd']
print(m + l)
m.extend(l)
print(m)
```
25. Write a Python program to select an item randomly from a list.
```
import random
l = [1, 2, 3, 4, 5, 6]
l[random.randint(0, len(l))]
```
26. Write a python program to check whether two lists are circularly identical.
```
list1 = [10, 10, 0, 0, 10]
list2 = [10, 10, 10, 0, 0]
list3 = [1, 10, 10, 0, 0]
def rotate(l, n=1):
t = l.pop(0)
l.append(t)
def linearly_circular(l1, l2):
for i in range(len(l1)):
rotate(l1)
if l1 == l2:
return True
return False
linearly_circular(list2, list3)
list1 = [10, 10, 0, 0, 10]
list2 = [10, 10, 10, 0, 0]
list3 = [1, 10, 10, 0, 0]
def linearly_circular(l1, l2):
return ''.join(map(str, l1)) in ''.join(map(str, l2*2))
linearly_circular(list1, list2)
```
27. Write a Python program to find the second smallest number in a list.
```
import random
l = [random.randint(0, 100) for _ in range(100)]
l.sort()
print(l[1])
```
28. Write a Python program to find the second largest number in a list.
```
import random
l = [random.randint(0, 100) for _ in range(100)]
l.sort()
print(l[-2])
```
29. Write a Python program to get unique values from a list.
```
import random
l = [random.randint(0, 100) for _ in range(100)]
print(set(l))
```
30. Write a Python program to get the frequency of the elements in a list.
```
import random
import collections
l = [random.randint(0, 100) for _ in range(100)]
collections.Counter(l)
```
31. Write a Python program to count the number of elements in a list within a specified range.
```
import random
import collections
l = [random.randint(0, 100) for _ in range(100)]
def count_elements_in_range(l, min, max):
return collections.Counter([i for i in l if min < i < max])
count_elements_in_range(l, 40, 60)
```
32. Write a Python program to check whether a list contains a sublist.
```
l = [1, 2, 3, 4, 5]
s = [1, 2, 3]
print(set(s).issubset(set(l)) is not None)
print(set(s) <= set(l))
```
**Dictionary**
http://www.w3resource.com/python-exercises/
|
github_jupyter
|
# How to find the maximum integer value for your system?
import sys
print(sys.maxsize)
print(-1 - sys.maxsize)
# Note: Older versions of Python had sys.maxint instead of maxsize
print(1 + 1)
print(3 - 5)
print(5 * 5)
# The quotient will be an integer
print(6 // 3)
# The quotient will also be an integer
print(3 // 6)
# The quotient will be a floating point number
print(3 / 6)
# Convert text to an integer
print(int("534234"))
print(int("0x043", 16))
print(int(3.1415))
import sys
print(sys.float_info)
print(1.34 + 2.54)
print(6.455 - 2.1)
print(26.34 * 1.2)
print(2354.3 / 34.2)
# Note: Integer division where either number is a float returns a float, but only the integer portion of the quotient
print(5.0 // 2)
print(float('+1.23'))
print(float(' -12345\n'))
print(float('1e-003'))
print(float(10))
# 1. Write a program to compute the Area of a Circle
import math
radius = float(input("Enter the raidus of the circle: "))
print("The area is: {}".format(2 * math.pi * radius))
# 2. Write a program to parse a string to Float or Integer
value = input("Enter a number: ")
try:
value = int(value)
print("{} is an integer".format(value))
except ValueError:
try:
value = float(value)
print("{} is a floating point number".format(value))
except ValueError:
print("I don't know what {} is. Try again.".format(value))
# 3. Write a program to convert the distance (in feet) to inches, yards, and miles
value = input("Enter the distance (in feet): ")
try:
value = float(value)
print("Distance {:.1e} (in feet) is {:.1e} inches, {:.1e} yards, and {:.1e} miles.".format(value, value * 12, value / 3, value / 5280))
except ValueError:
print("I don't know what {} is. Try again.".format(value))
# 4. Write a program to convert Fahrenheit to Celcius and Celcius to Fahrenheit
value = input("Temperature Conversion - Enter system (F or C), a space, the temperature (ex. F 32.0):")
sys, temp = value.split()
if sys.lower() == 'f':
print("{} F is {:1f} C".format(temp, (float(temp) - 32) * 5 / 9))
if sys.lower() == 'c':
print("{} C is {:1f} F".format(temp, float(temp) * 9 / 5 + 32))
print("this is a string of characters or letters")
print('')
print('In Python, strings can be delineated using either double quotes " or single quotes \' (one on each end)')
print("")
print("""Python also supports a triple quote (either \" or ')
which allows for very long strings or
strings that have embedded
formating""")
print('''''')
print('Also, long strings can \
be split \
across multiple lines without \
embedded carriage returns \
by using a \
line continuation character - \
look Ma, no carriabe returns!')
print("capitalize this".capitalize())
print('upper case this'.upper())
print('LOWER CASE THIS'.lower())
print("""Count the c's characters""".count('c'))
print('''Find the position of the first i in this string'''.find('i'))
print("put {0} here->{0} put {1}, here->{1}, put {2} here->{2}".format(1, 2, 3))
print("split this sentence into a sequence (a list actually) or words separated by spaces".split())
var = "This is a string"
print(var[0])
print(var[5])
print(var[-1])
print(var[-6])
var = "This_is_a_string"
print(var[2:5])
print(var[3:9])
print(var[5:])
print(var[:7])
print(var[-1:])
print(var[:-4])
print(var[-len(var):])
print(var[::-1])
print(str(1000))
print(str(3.1435))
print(str(lambda : None))
print(str(['this', 'is', 'a', 'list', 'of', 'words']))
# 1. Write a Python program to calculate the length of a string.
var = "this is a string"
print(len(var))
# 2. Write a Python function that takes a list of words and returns the length of the longest one.
var = "this is a string with a bunch of word in it"
words = var.split()
max_len = 0
for w in words:
if len(w) > max_len:
max_len = len(w)
print("The maximum length is {}".format(max_len))
# Alternate 2
print("The maximum length is {}".format(max([len(w) for w in words])))
# 3. Write a Python script that takes input from the user and displays that input back in upper and lower cases.
var = input("Enter a string: ")
print("Upper: {}, Lower: {}".format(var.upper(), var.lower()))
# 4. Write a Python function to reverse a string if it's length is a multiple of 4.
var1 = "This is a string who's multiple is four!"
var2 = "This is a string that is not!"
for v in var1, var2:
if len(v) % 4 == 0:
print(var1[::-1])
else:
print("Not multiple of 4")
# 5. Write a Python program to count occurrences of a substring in a string.
var = "This is a long string that is quite useful if the issue is that there is not a problem!"
sub_str = 'is'
print(var.count(sub_str))
# Alternate
print(len(var.split('is')) - 1)
[1, 2, 3, 4, 5]
['a', 'b', 'c', 'd', 'e']
[1, 'a', 2, 'b', 3, 'c']
list('abcde')
list('12345')
list(range(10))
l = [1, 2, 3, 4, 5]
sum(l)
def mul(iterable):
x = 1
for i in iterable:
x*=i
return x
l = [1, 2, 3, 4, 5]
mul(l)
l = [1, 2, 3, 4, 5]
max(l)
l = [1, 2, 3, 4, 5]
min(l)
s = ['this', 'that', 'these', 'those', 'it', 'what', 'wish']
for i in s:
if len(i) >= 2 and i[0] == i[-1]:
print(i)
l = [(1, 2), (3, 2), (2, 3), (5, 3), (7,2)]
sorted(l, key=lambda i: i[1], reverse=True)
l = [1, 2, 3, 4, 1, 5, 6, 5, 7, 6]
list(set(l))
def is_empty(l):
return l is None
l = [1, 2, 3, 4, 5]
print(is_empty(l))
l = None
print(is_empty(l))
l = [1, 2, 3, 4, 5]
print(id(l))
m = l.copy()
print(id(m))
l = ['this', 'that', 'these', 'those', 'which', 'what', 'who', 'where']
n = 4
m = [i for i in l if len(i) > n]
print(m)
l = [1, 2, 3, 4, 5, 6, 7, 8, 9]
m = [9, 5, 3, 1, 3, 8]
True if True in [
i == j
for i in m
for j in l] else False
l = [1, 3, 2, 6, 5, 7, 8, 9, 4]
r = [0, 4, 5]
m = [v for i,v in enumerate(l) if i not in r]
print(m)
def make_3d_array(i, j, k):
return [[[ '*' for _i in range(i)] for _j in range(j)] for _k in range(k)]
make_3d_array(3, 4, 6)
l = [1, 4, 3, 2, 5, 7 ,4, 5, 8]
[i for i in l if i % 2 == 0]
import random
l = [1, 2, 3, 4, 5, 6]
random.shuffle(l)
print(l)
import random
import math
l = [random.randint(0, 1000) for _ in range(100)]
m = [i for i in l if 1 < math.sqrt(i) < 30]
print(m[:5] + m[-5:])
import random
l = [random.randint(0, 1000) for _ in range(100)]
m = [i for i in l if 1 < i < 30*30]
print(m[5:])
import random
import itertools
n = 3
l = [random.randint(0,n) for i in range(n)]
[i for i in itertools.permutations(l)]
l = [1, 2, 3]
m = [5, 8, 3, 2, 1]
print(list(set(m)-set(l)))
l = [1, 2, 3, 4, 5]
for k, v in enumerate(l):
print(k, v)
l = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h']
''.join(l)
l = ['a', 'b', 'c', 'd', 'e', 'f', 'g']
print(l.index('a'))
print(l.index('e'))
import itertools
l = [[2,4,3],[1,5,6], [9], [7,9,0]]
m = list(itertools.chain(*l))
print(m)
l = [1, 2, 3, 4, 5]
m = ['a', 'b', 'c', 'd']
print(m + l)
m.extend(l)
print(m)
import random
l = [1, 2, 3, 4, 5, 6]
l[random.randint(0, len(l))]
list1 = [10, 10, 0, 0, 10]
list2 = [10, 10, 10, 0, 0]
list3 = [1, 10, 10, 0, 0]
def rotate(l, n=1):
t = l.pop(0)
l.append(t)
def linearly_circular(l1, l2):
for i in range(len(l1)):
rotate(l1)
if l1 == l2:
return True
return False
linearly_circular(list2, list3)
list1 = [10, 10, 0, 0, 10]
list2 = [10, 10, 10, 0, 0]
list3 = [1, 10, 10, 0, 0]
def linearly_circular(l1, l2):
return ''.join(map(str, l1)) in ''.join(map(str, l2*2))
linearly_circular(list1, list2)
import random
l = [random.randint(0, 100) for _ in range(100)]
l.sort()
print(l[1])
import random
l = [random.randint(0, 100) for _ in range(100)]
l.sort()
print(l[-2])
import random
l = [random.randint(0, 100) for _ in range(100)]
print(set(l))
import random
import collections
l = [random.randint(0, 100) for _ in range(100)]
collections.Counter(l)
import random
import collections
l = [random.randint(0, 100) for _ in range(100)]
def count_elements_in_range(l, min, max):
return collections.Counter([i for i in l if min < i < max])
count_elements_in_range(l, 40, 60)
l = [1, 2, 3, 4, 5]
s = [1, 2, 3]
print(set(s).issubset(set(l)) is not None)
print(set(s) <= set(l))
| 0.368406 | 0.987448 |
```
import numpy as np
# will return set of images of cardinality = num, each image has channels=3, width=3, height = 4
def get_set(num):
set_ = []
for i in xrange(num):
image = []
for j in xrange(3):
channel = []
for k in xrange(3):
col = []
for l in xrange(4):
col.append((i+1) * 1000 + (j+1) * 100 + (k+1) * 10 + (l+1))
channel.append(col)
channel = np.array(channel).transpose()
image.append(channel)
set_.append(image)
set_=np.array(set_)
return set_
set_ = get_set(8)
#mask shows how prepare convolution produce matrix of neighbourhood for one channel
mask = np.array([[00,00,00,00,11,12,00,21,22],
[00,00,00,11,12,13,21,22,23],
[00,00,00,12,13,14,22,23,24],
[00,00,00,13,14,00,23,24,00],
[00,11,12,00,21,22,00,31,32],
[11,12,13,21,22,23,31,32,33],
[12,13,14,22,23,24,32,33,34],
[13,14,00,23,24,00,33,34,00],
[00,21,22,00,31,32,00,00,00],
[21,22,23,31,32,33,00,00,00],
[22,23,24,32,33,34,00,00,00],
[23,24,00,33,34,00,00,00,00]])
#how channel look like
channel = [[11, 21, 31],
[12, 22, 32],
[13, 23, 33],
[14, 24, 34]]
#result mask will count the occurances for each element of channel in prepared convolution matrix
result_mask = []
for row in channel:
result_row = []
for elem in row:
result_row.append(np.sum((mask==elem).astype(np.int32)))
result_mask.append(result_row)
result_mask = np.array(result_mask)
#this block prepare result for backpropogation of prepare convolution same
set_result = []
for image in set_:
image_result = []
for channel in image:
image_result.append(np.multiply(channel, result_mask))
set_result.append(image_result)
set_result = np.array(set_result)
# block will create input matrix of size (3*3*4, num) where 3*3*4 is size of each image and num is number of images
def convert_channel_to_column(channel):
return np.ravel(channel, order='F')
def convert_image_to_column(image):
result = []
for channel in image:
result += convert_channel_to_column(channel).tolist()
return result
def convert_set_to_matrix(set_):
result = []
for image in set_:
result += convert_image_to_column(image)
return np.reshape(np.array(result), [3*3*4, set_.shape[0]], order='F')
output_matrix = convert_set_to_matrix(set_result)
np.savetxt('/home/ahsan/squirrel_latest/squirrel/trunk/src/Test/test-case-data/prepare-conv-same-back-r.txt', output_matrix, fmt='%i', delimiter=' ', header='36 8')
```
|
github_jupyter
|
import numpy as np
# will return set of images of cardinality = num, each image has channels=3, width=3, height = 4
def get_set(num):
set_ = []
for i in xrange(num):
image = []
for j in xrange(3):
channel = []
for k in xrange(3):
col = []
for l in xrange(4):
col.append((i+1) * 1000 + (j+1) * 100 + (k+1) * 10 + (l+1))
channel.append(col)
channel = np.array(channel).transpose()
image.append(channel)
set_.append(image)
set_=np.array(set_)
return set_
set_ = get_set(8)
#mask shows how prepare convolution produce matrix of neighbourhood for one channel
mask = np.array([[00,00,00,00,11,12,00,21,22],
[00,00,00,11,12,13,21,22,23],
[00,00,00,12,13,14,22,23,24],
[00,00,00,13,14,00,23,24,00],
[00,11,12,00,21,22,00,31,32],
[11,12,13,21,22,23,31,32,33],
[12,13,14,22,23,24,32,33,34],
[13,14,00,23,24,00,33,34,00],
[00,21,22,00,31,32,00,00,00],
[21,22,23,31,32,33,00,00,00],
[22,23,24,32,33,34,00,00,00],
[23,24,00,33,34,00,00,00,00]])
#how channel look like
channel = [[11, 21, 31],
[12, 22, 32],
[13, 23, 33],
[14, 24, 34]]
#result mask will count the occurances for each element of channel in prepared convolution matrix
result_mask = []
for row in channel:
result_row = []
for elem in row:
result_row.append(np.sum((mask==elem).astype(np.int32)))
result_mask.append(result_row)
result_mask = np.array(result_mask)
#this block prepare result for backpropogation of prepare convolution same
set_result = []
for image in set_:
image_result = []
for channel in image:
image_result.append(np.multiply(channel, result_mask))
set_result.append(image_result)
set_result = np.array(set_result)
# block will create input matrix of size (3*3*4, num) where 3*3*4 is size of each image and num is number of images
def convert_channel_to_column(channel):
return np.ravel(channel, order='F')
def convert_image_to_column(image):
result = []
for channel in image:
result += convert_channel_to_column(channel).tolist()
return result
def convert_set_to_matrix(set_):
result = []
for image in set_:
result += convert_image_to_column(image)
return np.reshape(np.array(result), [3*3*4, set_.shape[0]], order='F')
output_matrix = convert_set_to_matrix(set_result)
np.savetxt('/home/ahsan/squirrel_latest/squirrel/trunk/src/Test/test-case-data/prepare-conv-same-back-r.txt', output_matrix, fmt='%i', delimiter=' ', header='36 8')
| 0.352648 | 0.593167 |
# 합성곱 신경망의 시각화
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/rickiepark/hg-mldl/blob/master/8-3.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩에서 실행하기</a>
</td>
</table>
## 가중치 시각화
```
from tensorflow import keras
# 코랩에서 실행하는 경우에는 다음 명령을 실행하여 best-cnn-model.h5 파일을 다운로드받아 사용하세요.
!wget https://github.com/rickiepark/hg-mldl/raw/master/best-cnn-model.h5
model = keras.models.load_model('best-cnn-model.h5')
model.layers
conv = model.layers[0]
print(conv.weights[0].shape, conv.weights[1].shape)
conv_weights = conv.weights[0].numpy()
print(conv_weights.mean(), conv_weights.std())
import matplotlib.pyplot as plt
plt.hist(conv_weights.reshape(-1, 1))
plt.xlabel('weight')
plt.ylabel('count')
plt.show()
fig, axs = plt.subplots(2, 16, figsize=(15,2))
for i in range(2):
for j in range(16):
axs[i, j].imshow(conv_weights[:,:,0,i*16 + j], vmin=-0.5, vmax=0.5)
axs[i, j].axis('off')
plt.show()
no_training_model = keras.Sequential()
no_training_model.add(keras.layers.Conv2D(32, kernel_size=3, activation='relu',
padding='same', input_shape=(28,28,1)))
no_training_conv = no_training_model.layers[0]
print(no_training_conv.weights[0].shape)
no_training_weights = no_training_conv.weights[0].numpy()
print(no_training_weights.mean(), no_training_weights.std())
plt.hist(no_training_weights.reshape(-1, 1))
plt.xlabel('weight')
plt.ylabel('count')
plt.show()
fig, axs = plt.subplots(2, 16, figsize=(15,2))
for i in range(2):
for j in range(16):
axs[i, j].imshow(no_training_weights[:,:,0,i*16 + j], vmin=-0.5, vmax=0.5)
axs[i, j].axis('off')
plt.show()
```
## 함수형 API
```
print(model.input)
conv_acti = keras.Model(model.input, model.layers[0].output)
```
## 특성 맵 시각화
```
(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
plt.imshow(train_input[0], cmap='gray_r')
plt.show()
inputs = train_input[0:1].reshape(-1, 28, 28, 1)/255.0
feature_maps = conv_acti.predict(inputs)
print(feature_maps.shape)
fig, axs = plt.subplots(4, 8, figsize=(15,8))
for i in range(4):
for j in range(8):
axs[i, j].imshow(feature_maps[0,:,:,i*8 + j])
axs[i, j].axis('off')
plt.show()
conv2_acti = keras.Model(model.input, model.layers[2].output)
feature_maps = conv2_acti.predict(train_input[0:1].reshape(-1, 28, 28, 1)/255.0)
print(feature_maps.shape)
fig, axs = plt.subplots(8, 8, figsize=(12,12))
for i in range(8):
for j in range(8):
axs[i, j].imshow(feature_maps[0,:,:,i*8 + j])
axs[i, j].axis('off')
plt.show()
```
|
github_jupyter
|
from tensorflow import keras
# 코랩에서 실행하는 경우에는 다음 명령을 실행하여 best-cnn-model.h5 파일을 다운로드받아 사용하세요.
!wget https://github.com/rickiepark/hg-mldl/raw/master/best-cnn-model.h5
model = keras.models.load_model('best-cnn-model.h5')
model.layers
conv = model.layers[0]
print(conv.weights[0].shape, conv.weights[1].shape)
conv_weights = conv.weights[0].numpy()
print(conv_weights.mean(), conv_weights.std())
import matplotlib.pyplot as plt
plt.hist(conv_weights.reshape(-1, 1))
plt.xlabel('weight')
plt.ylabel('count')
plt.show()
fig, axs = plt.subplots(2, 16, figsize=(15,2))
for i in range(2):
for j in range(16):
axs[i, j].imshow(conv_weights[:,:,0,i*16 + j], vmin=-0.5, vmax=0.5)
axs[i, j].axis('off')
plt.show()
no_training_model = keras.Sequential()
no_training_model.add(keras.layers.Conv2D(32, kernel_size=3, activation='relu',
padding='same', input_shape=(28,28,1)))
no_training_conv = no_training_model.layers[0]
print(no_training_conv.weights[0].shape)
no_training_weights = no_training_conv.weights[0].numpy()
print(no_training_weights.mean(), no_training_weights.std())
plt.hist(no_training_weights.reshape(-1, 1))
plt.xlabel('weight')
plt.ylabel('count')
plt.show()
fig, axs = plt.subplots(2, 16, figsize=(15,2))
for i in range(2):
for j in range(16):
axs[i, j].imshow(no_training_weights[:,:,0,i*16 + j], vmin=-0.5, vmax=0.5)
axs[i, j].axis('off')
plt.show()
print(model.input)
conv_acti = keras.Model(model.input, model.layers[0].output)
(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
plt.imshow(train_input[0], cmap='gray_r')
plt.show()
inputs = train_input[0:1].reshape(-1, 28, 28, 1)/255.0
feature_maps = conv_acti.predict(inputs)
print(feature_maps.shape)
fig, axs = plt.subplots(4, 8, figsize=(15,8))
for i in range(4):
for j in range(8):
axs[i, j].imshow(feature_maps[0,:,:,i*8 + j])
axs[i, j].axis('off')
plt.show()
conv2_acti = keras.Model(model.input, model.layers[2].output)
feature_maps = conv2_acti.predict(train_input[0:1].reshape(-1, 28, 28, 1)/255.0)
print(feature_maps.shape)
fig, axs = plt.subplots(8, 8, figsize=(12,12))
for i in range(8):
for j in range(8):
axs[i, j].imshow(feature_maps[0,:,:,i*8 + j])
axs[i, j].axis('off')
plt.show()
| 0.801159 | 0.938463 |
# Lesson 1 Class Exercises: NumPy Part 1
```
import numpy as np
```
## Exercise #1
Write Python code to generate five random numbers from the normal distribution.
Look at the online documentation for [NumPy random number generators](https://docs.scipy.org/doc/numpy-1.15.0/reference/routines.random.html)
```
x = np.random.normal(loc = 1, scale = 2, size =5)
print(x)
```
## Exercise #2
Write Python code to generate six random integers between 10 and 30
Look at the online documentation for [NumPy random number generators](https://docs.scipy.org/doc/numpy-1.15.0/reference/routines.random.html)
```
np.random.randint(low =10, high = 30, size = 6 )
```
## Exercise #3
Write Python code to
+ create a 5x5 array with random values
+ print the array,
+ find and print the minimum and maximum values.
```
arr = np.random.random((5, 5))
print(arr)
print(np.amin(arr))
print(np.amax(arr))
```
## Exercise #4
Write code using NumPy that would create a grid that could be used for the game of life. Follow these criteria
+ the grid must have 30 rows and 80 columns
+ it must be initalized to zeros.
+ print the grid dimensions to prove its size.
+ print the grid to show it is initalized to zeros.
```
arr = np.zeros((30, 80))
print(arr)
np.ndim(arr)
```
## Exercise #5
Read the documentation about [genfromtxt()](https://docs.scipy.org/doc/numpy/reference/generated/numpy.genfromtxt.html) function of NumPy. What does it do? Do you understand what the arguments do?
A file has been provided to you named data2.txt. Be sure to place it in the same folder with this notebook. It contains the following text:
```
Value1,Value2,Value3
0.4839,0.4536,0.3561
0.1292,0.6875,NA
0.1781,0.3049,0.8928
NA,0.5801,0.2038
0.5993,0.4357,0.7410
```
Notice it has missing values. Write some code that
+ uses the `genfromtxt` function to read in this file into a numpy array.
+ prints the resulting array.
```
np.genfromtxt('./data2.txt', dtype = float, delimiter = ",", skip_header = 1, missing_values=["NA"])
```
## Exercise #6
Write some code that
+ Creates an array of 100 rows and 10 columns filled with random values between 0 and 1
+ Print the first 10 rows.
+ Caculate the following statistics about each row and column
+ mean, variance, standard deviation and quartiles of each row.
+ print these values.
## Exercise #7
Write code that
+ Create an array of 100 rows and 10 columns of integer values with the minimum number 0 and the maximum 10,000
+ Print the first 10 rows of the matrix.
+ Calculate values for a histogram with 10 bins.
+ save in one variable the values of each bin
+ save in another variable the value at the left edge of the bin.
|
github_jupyter
|
import numpy as np
x = np.random.normal(loc = 1, scale = 2, size =5)
print(x)
np.random.randint(low =10, high = 30, size = 6 )
arr = np.random.random((5, 5))
print(arr)
print(np.amin(arr))
print(np.amax(arr))
arr = np.zeros((30, 80))
print(arr)
np.ndim(arr)
Value1,Value2,Value3
0.4839,0.4536,0.3561
0.1292,0.6875,NA
0.1781,0.3049,0.8928
NA,0.5801,0.2038
0.5993,0.4357,0.7410
np.genfromtxt('./data2.txt', dtype = float, delimiter = ",", skip_header = 1, missing_values=["NA"])
| 0.094913 | 0.983925 |
## Scikit-Learn Regression
The library `scikit-learn` is a great machine-learning toolkit that provides a large collection of regression methods.
By default, `chaospy` only support traditional least-square regression, but is also designed to work together with the various regression functions provided by `scikit-learn`.
Because `scikit-learn` isn't a required dependency, you might need to install it first with e.g. `pip install scikit-learn`. When that is done, it should be importable:
```
import sklearn
```
As en example to follow, consider the following artificial case:
```
import numpy
import chaospy
samples = numpy.linspace(0, 5, 50)
numpy.random.seed(1000)
noise = chaospy.Normal(0, 0.1).sample(50)
evals = numpy.sin(samples) + noise
from matplotlib import pyplot
pyplot.rc("figure", figsize=[15, 6])
pyplot.scatter(samples, evals)
pyplot.show()
```
### Least squares regression
By default, `chaospy` does not use `sklearn` (and can be used without `sklearn` being installed). Instead it uses `scipy.linalg.lstsq`, which is the ordinary least squares method, the classical regression problem by minimizing the residulals squared.
In practice:
```
q0 = chaospy.variable()
expansion = chaospy.polynomial([1, q0, q0**2, q0**3])
fitted_polynomial = chaospy.fit_regression(
expansion, samples, evals)
pyplot.scatter(samples, evals)
pyplot.plot(samples, fitted_polynomial(samples))
pyplot.show()
fitted_polynomial.round(4)
```
Least squares regression is also supported by `sklearn`. So it is possible to get the same result using the `LinearRegression` model. For example:
```
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=False)
fitted_polynomial = chaospy.fit_regression(
expansion, samples, evals, model=model)
pyplot.scatter(samples, evals)
pyplot.plot(samples, fitted_polynomial(samples))
pyplot.show()
fitted_polynomial.round(4)
```
It is important to note that sklearn often does extra operations that may interfer with the compatability of `chaospy`. Here `fit_intercept=False` ensures that an extra columns isn't added needlessly. An error will be raised if this is forgotton.
### Single Variable Regression Methods
While in most cases least squares regression is sufficient, that is not always the case. For those deviating cases `scikit-learn` provides a set of alternative methods. Even though `chaospy` doesn't differentiate between single dimensional and multi-dimensional responses, `scikit-learn` do.
The methods that support single dimensional responses are:
* `least squares` -- Simple $L_2$ regression without any extra features.
* `elastic net` -- $L_2$ regression with both $L_1$ and $L_2$ regularization terms.
* `lasso` -- $L_2$ regression with an extra $L_1$ regularization term, and a preference for fewer non-zero terms.
* `lasso lars` -- An implementation of `lasso` meant for high dimensional data.
* `lars` -- $L_1$ regression well suited for high dimensional data.
* `orthogonal matching pursuit` -- $L_2$ regression with enforced number of non-zero terms.
* `ridge` -- $L_2$ regression with an $L_2$ regularization term.
* `bayesian ridge` -- Same as `ridge`, but uses Bayesian probability to let data estimate the complexity parameter.
* `auto relevant determination` -- Same as `bayesian ridge`, but also favors fewer non-zero terms.
```
from sklearn import linear_model as lm
kws = {"fit_intercept": False}
univariate_models = {
"least squares": lm.LinearRegression(**kws),
"elastic net": lm.ElasticNet(alpha=0.1, **kws),
"lasso": lm.Lasso(alpha=0.1, **kws),
"lasso lars": lm.LassoLars(alpha=0.1, **kws),
"lars": lm.Lars(**kws),
"orthogonal matching pursuit":
lm.OrthogonalMatchingPursuit(n_nonzero_coefs=3, **kws),
"ridge": lm.Ridge(alpha=0.1, **kws),
"bayesian ridge": lm.BayesianRidge(**kws),
"auto relevant determination": lm.ARDRegression(**kws),
}
```
Again, as the polynomials already addresses the constant term, it is important to remember to include `fit_intercept=False` for each model.
We can then create a fit for each of the univariate models:
```
for label, model in univariate_models.items():
fitted_polynomial = chaospy.fit_regression(
expansion, samples, evals, model=model)
pyplot.plot(samples, fitted_polynomial(samples), label=label)
pyplot.scatter(samples, evals)
pyplot.legend(loc="upper right")
pyplot.show()
```
### Multi-variable Regression Methods
This part of the tutorial uses the same example as the [example introduction](./example_introduction.ipynb).
In other words:
```
from chaospy.example import (
coordinates, exponential_model, distribution,
error_mean, error_variance
)
```
The methods that support multi-label dimensional responses are:
* `least squares` -- Simple $L_2$ regression without any extra features.
* `elastic net` -- $L_2$ regression with both $L_1$ and $L_2$ regularization terms.
* `lasso` -- $L_2$ regression with an extra $L_1$ regularization term, and a preference for fewer non-zero terms.
* `lasso lars` -- An implementation of `lasso` meant for high dimensional data.
* `orthogonal matching pursuit` -- $L_2$ regression with enforced number of non-zero terms.
* `ridge` -- $L_2$ regression with an $L_2$ regularization term.
```
multivariate_models = {
"least squares": lm.LinearRegression(**kws),
"elastic net": lm.MultiTaskElasticNet(alpha=0.2, **kws),
"lasso": lm.MultiTaskLasso(alpha=0.2, **kws),
"lasso lars": lm.LassoLars(alpha=0.2, **kws),
"lars": lm.Lars(n_nonzero_coefs=3, **kws),
"orthogonal matching pursuit": \
lm.OrthogonalMatchingPursuit(n_nonzero_coefs=3, **kws),
"ridge": lm.Ridge(alpha=0.2, **kws),
}
```
To illustrate the difference between the methods, we do the simple error analysis:
```
# NBVAL_CHECK_OUTPUT
import warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
expansion = chaospy.generate_expansion(2, distribution)
samples = distribution.sample(50)
evals = numpy.array([exponential_model(sample)
for sample in samples.T])
for label, model in multivariate_models.items():
fitted_polynomial, coeffs = chaospy.fit_regression(
expansion, samples, evals, model=model, retall=True)
self_evals = fitted_polynomial(*samples)
error_mean_ = error_mean(chaospy.E(
fitted_polynomial, distribution))
error_var_ = error_variance(chaospy.Var(
fitted_polynomial, distribution))
count_non_zero = numpy.sum(numpy.any(coeffs, axis=-1))
print(f"{label:<30} {error_mean_:.5f} " +
f"{error_var_:.5f} {count_non_zero}")
```
It is worth noting that as some of the method removes coefficients, it can function at higher polynomial order than the saturate methods.
|
github_jupyter
|
import sklearn
import numpy
import chaospy
samples = numpy.linspace(0, 5, 50)
numpy.random.seed(1000)
noise = chaospy.Normal(0, 0.1).sample(50)
evals = numpy.sin(samples) + noise
from matplotlib import pyplot
pyplot.rc("figure", figsize=[15, 6])
pyplot.scatter(samples, evals)
pyplot.show()
q0 = chaospy.variable()
expansion = chaospy.polynomial([1, q0, q0**2, q0**3])
fitted_polynomial = chaospy.fit_regression(
expansion, samples, evals)
pyplot.scatter(samples, evals)
pyplot.plot(samples, fitted_polynomial(samples))
pyplot.show()
fitted_polynomial.round(4)
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=False)
fitted_polynomial = chaospy.fit_regression(
expansion, samples, evals, model=model)
pyplot.scatter(samples, evals)
pyplot.plot(samples, fitted_polynomial(samples))
pyplot.show()
fitted_polynomial.round(4)
from sklearn import linear_model as lm
kws = {"fit_intercept": False}
univariate_models = {
"least squares": lm.LinearRegression(**kws),
"elastic net": lm.ElasticNet(alpha=0.1, **kws),
"lasso": lm.Lasso(alpha=0.1, **kws),
"lasso lars": lm.LassoLars(alpha=0.1, **kws),
"lars": lm.Lars(**kws),
"orthogonal matching pursuit":
lm.OrthogonalMatchingPursuit(n_nonzero_coefs=3, **kws),
"ridge": lm.Ridge(alpha=0.1, **kws),
"bayesian ridge": lm.BayesianRidge(**kws),
"auto relevant determination": lm.ARDRegression(**kws),
}
for label, model in univariate_models.items():
fitted_polynomial = chaospy.fit_regression(
expansion, samples, evals, model=model)
pyplot.plot(samples, fitted_polynomial(samples), label=label)
pyplot.scatter(samples, evals)
pyplot.legend(loc="upper right")
pyplot.show()
from chaospy.example import (
coordinates, exponential_model, distribution,
error_mean, error_variance
)
multivariate_models = {
"least squares": lm.LinearRegression(**kws),
"elastic net": lm.MultiTaskElasticNet(alpha=0.2, **kws),
"lasso": lm.MultiTaskLasso(alpha=0.2, **kws),
"lasso lars": lm.LassoLars(alpha=0.2, **kws),
"lars": lm.Lars(n_nonzero_coefs=3, **kws),
"orthogonal matching pursuit": \
lm.OrthogonalMatchingPursuit(n_nonzero_coefs=3, **kws),
"ridge": lm.Ridge(alpha=0.2, **kws),
}
# NBVAL_CHECK_OUTPUT
import warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
expansion = chaospy.generate_expansion(2, distribution)
samples = distribution.sample(50)
evals = numpy.array([exponential_model(sample)
for sample in samples.T])
for label, model in multivariate_models.items():
fitted_polynomial, coeffs = chaospy.fit_regression(
expansion, samples, evals, model=model, retall=True)
self_evals = fitted_polynomial(*samples)
error_mean_ = error_mean(chaospy.E(
fitted_polynomial, distribution))
error_var_ = error_variance(chaospy.Var(
fitted_polynomial, distribution))
count_non_zero = numpy.sum(numpy.any(coeffs, axis=-1))
print(f"{label:<30} {error_mean_:.5f} " +
f"{error_var_:.5f} {count_non_zero}")
| 0.805173 | 0.985286 |
<a href="https://colab.research.google.com/github/tomek-l/deep-learning-with-python-notebooks/blob/master/5.1-introduction-to-convnets.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import keras
keras.__version__
```
# 5.1 - Introduction to convnets
This notebook contains the code sample found in Chapter 5, Section 1 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
----
First, let's take a practical look at a very simple convnet example. We will use our convnet to classify MNIST digits, a task that you've already been
through in Chapter 2, using a densely-connected network (our test accuracy then was 97.8%). Even though our convnet will be very basic, its
accuracy will still blow out of the water that of the densely-connected model from Chapter 2.
The 6 lines of code below show you what a basic convnet looks like. It's a stack of `Conv2D` and `MaxPooling2D` layers. We'll see in a
minute what they do concretely.
Importantly, a convnet takes as input tensors of shape `(image_height, image_width, image_channels)` (not including the batch dimension).
In our case, we will configure our convnet to process inputs of size `(28, 28, 1)`, which is the format of MNIST images. We do this via
passing the argument `input_shape=(28, 28, 1)` to our first layer.
```
from keras import layers
from keras import models
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
```
Let's display the architecture of our convnet so far:
```
model.summary()
```
You can see above that the output of every `Conv2D` and `MaxPooling2D` layer is a 3D tensor of shape `(height, width, channels)`. The width
and height dimensions tend to shrink as we go deeper in the network. The number of channels is controlled by the first argument passed to
the `Conv2D` layers (e.g. 32 or 64).
The next step would be to feed our last output tensor (of shape `(3, 3, 64)`) into a densely-connected classifier network like those you are
already familiar with: a stack of `Dense` layers. These classifiers process vectors, which are 1D, whereas our current output is a 3D tensor.
So first, we will have to flatten our 3D outputs to 1D, and then add a few `Dense` layers on top:
```
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
```
We are going to do 10-way classification, so we use a final layer with 10 outputs and a softmax activation. Now here's what our network
looks like:
```
model.summary()
```
As you can see, our `(3, 3, 64)` outputs were flattened into vectors of shape `(576,)`, before going through two `Dense` layers.
Now, let's train our convnet on the MNIST digits. We will reuse a lot of the code we have already covered in the MNIST example from Chapter
2.
```
from keras.datasets import mnist
from keras.utils import to_categorical
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype('float32') / 255
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5, batch_size=64)
```
Let's evaluate the model on the test data:
```
test_loss, test_acc = model.evaluate(test_images, test_labels)
test_acc
```
While our densely-connected network from Chapter 2 had a test accuracy of 97.8%, our basic convnet has a test accuracy of 99.3%: we
decreased our error rate by 68% (relative). Not bad!
|
github_jupyter
|
import keras
keras.__version__
from keras import layers
from keras import models
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.summary()
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
model.summary()
from keras.datasets import mnist
from keras.utils import to_categorical
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype('float32') / 255
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5, batch_size=64)
test_loss, test_acc = model.evaluate(test_images, test_labels)
test_acc
| 0.838614 | 0.992408 |
Example 7 - Hydrodinamic Bearings
=====
In this example, we use the rotor seen in Example 5.9.6 from 'Dynamics of Rotating Machinery' by MI Friswell, JET Penny, SD Garvey & AW Lees, published by Cambridge University Press, 2010.
Same rotor of Example 3, but the bearings are replaced with hydrodynamic bearings. In order to instantiate them, rather than giving the stiffness and damping data, we will calculate them using their hydrodinamic data, as provided by Example 5.5.1 from the book: The oil-film bearings have a diameter of 100 mm, are 30 mm long, and each supports a static load of 525 N, which represents half of the weight of the rotor. The radial clearance in the bearings is 0.1 mm and the oil film has a viscosity of 0.1 Pa s.
```
from bokeh.io import output_notebook, show
import ross as rs
import numpy as np
output_notebook()
# Classic Instantiation of the rotor
shaft_elements = []
bearing_seal_elements = []
disk_elements = []
Steel = rs.materials. steel
for i in range(6):
shaft_elements.append(rs.ShaftElement(L=0.25, material=Steel, n=i, i_d=0, o_d=0.05))
disk_elements.append(rs.DiskElement.from_geometry(n=2,
material=Steel,
width=0.07,
i_d=0.05,
o_d=0.28
)
)
disk_elements.append(rs.DiskElement.from_geometry(n=4,
material=Steel,
width=0.07,
i_d=0.05,
o_d=0.35
)
)
bearing_seal_elements.append(rs.BearingElement.from_fluid_flow(n=0, nz=30, ntheta=20, nradius=11,
length=0.03, omega=157.1, p_in=0,
p_out=0, radius_rotor=0.0499,
radius_stator=0.05, visc=0.1,
rho=860., load=525))
bearing_seal_elements.append(rs.BearingElement.from_fluid_flow(n=6, nz=30, ntheta=20, nradius=11,
length=0.03, omega=157.1, p_in=0,
p_out=0, radius_rotor=0.0499,
radius_stator=0.05, visc=0.1,
rho=860., load=525))
rotor596c = rs.Rotor(shaft_elements=shaft_elements,
bearing_seal_elements=bearing_seal_elements,
disk_elements=disk_elements, n_eigen=12)
show(rotor596c.plot_rotor())
# From_section class method instantiation
bearing_seal_elements = []
disk_elements = []
shaft_length_data = 3*[0.5]
i_d = 3*[0]
o_d = 3*[0.05]
disk_elements.append(rs.DiskElement.from_geometry(n=1,
material=Steel,
width=0.07,
i_d=0.05,
o_d=0.28
)
)
disk_elements.append(rs.DiskElement.from_geometry(n=2,
material=Steel,
width=0.07,
i_d=0.05,
o_d=0.35
)
)
bearing_seal_elements.append(rs.BearingElement(n=0, kxx=1e6, kyy=1e6, cxx=3e3, cyy=3e3))
bearing_seal_elements.append(rs.BearingElement(n=3, kxx=1e6, kyy=1e6, cxx=3e3, cyy=3e3))
rotor596fs = rs.Rotor.from_section(brg_seal_data=bearing_seal_elements,
disk_data=disk_elements, leng_data=shaft_length_data,
i_ds_data=i_d,o_ds_data=o_d
)
show(rotor596fs.plot_rotor())
# Obtaining results for w = 200 rpm
modal596c = rotor596c.run_modal(200*np.pi/30)
modal596fs = rotor596fs.run_modal(200*np.pi/30)
print('Normal Instantiation =', modal596c.wn/(2*np.pi), '[Hz]')
print('\n')
print('From Section Instantiation =', modal596fs.wn/(2*np.pi), '[Hz]')
# Obtaining results for w=4000RPM
modal596c = rotor596c.run_modal(4000*np.pi/30)
print('Normal Instantiation =', modal596c.wn/(2*np.pi))
show(rotor596c.run_campbell(np.linspace(0, 4000*np.pi/30, 50)).plot())
```
|
github_jupyter
|
from bokeh.io import output_notebook, show
import ross as rs
import numpy as np
output_notebook()
# Classic Instantiation of the rotor
shaft_elements = []
bearing_seal_elements = []
disk_elements = []
Steel = rs.materials. steel
for i in range(6):
shaft_elements.append(rs.ShaftElement(L=0.25, material=Steel, n=i, i_d=0, o_d=0.05))
disk_elements.append(rs.DiskElement.from_geometry(n=2,
material=Steel,
width=0.07,
i_d=0.05,
o_d=0.28
)
)
disk_elements.append(rs.DiskElement.from_geometry(n=4,
material=Steel,
width=0.07,
i_d=0.05,
o_d=0.35
)
)
bearing_seal_elements.append(rs.BearingElement.from_fluid_flow(n=0, nz=30, ntheta=20, nradius=11,
length=0.03, omega=157.1, p_in=0,
p_out=0, radius_rotor=0.0499,
radius_stator=0.05, visc=0.1,
rho=860., load=525))
bearing_seal_elements.append(rs.BearingElement.from_fluid_flow(n=6, nz=30, ntheta=20, nradius=11,
length=0.03, omega=157.1, p_in=0,
p_out=0, radius_rotor=0.0499,
radius_stator=0.05, visc=0.1,
rho=860., load=525))
rotor596c = rs.Rotor(shaft_elements=shaft_elements,
bearing_seal_elements=bearing_seal_elements,
disk_elements=disk_elements, n_eigen=12)
show(rotor596c.plot_rotor())
# From_section class method instantiation
bearing_seal_elements = []
disk_elements = []
shaft_length_data = 3*[0.5]
i_d = 3*[0]
o_d = 3*[0.05]
disk_elements.append(rs.DiskElement.from_geometry(n=1,
material=Steel,
width=0.07,
i_d=0.05,
o_d=0.28
)
)
disk_elements.append(rs.DiskElement.from_geometry(n=2,
material=Steel,
width=0.07,
i_d=0.05,
o_d=0.35
)
)
bearing_seal_elements.append(rs.BearingElement(n=0, kxx=1e6, kyy=1e6, cxx=3e3, cyy=3e3))
bearing_seal_elements.append(rs.BearingElement(n=3, kxx=1e6, kyy=1e6, cxx=3e3, cyy=3e3))
rotor596fs = rs.Rotor.from_section(brg_seal_data=bearing_seal_elements,
disk_data=disk_elements, leng_data=shaft_length_data,
i_ds_data=i_d,o_ds_data=o_d
)
show(rotor596fs.plot_rotor())
# Obtaining results for w = 200 rpm
modal596c = rotor596c.run_modal(200*np.pi/30)
modal596fs = rotor596fs.run_modal(200*np.pi/30)
print('Normal Instantiation =', modal596c.wn/(2*np.pi), '[Hz]')
print('\n')
print('From Section Instantiation =', modal596fs.wn/(2*np.pi), '[Hz]')
# Obtaining results for w=4000RPM
modal596c = rotor596c.run_modal(4000*np.pi/30)
print('Normal Instantiation =', modal596c.wn/(2*np.pi))
show(rotor596c.run_campbell(np.linspace(0, 4000*np.pi/30, 50)).plot())
| 0.449393 | 0.848659 |
# Collaboration and Competition
---
In this notebook, you will learn how to use the Unity ML-Agents environment for the third project of the [Deep Reinforcement Learning Nanodegree](https://www.udacity.com/course/deep-reinforcement-learning-nanodegree--nd893) program.
### 1. Start the Environment
We begin by importing the necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
```
%load_ext autoreload
%autoreload 2
import os
from os import path
import sys
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from functools import partial
import datetime as dt
import time
repo_path = path.dirname(path.dirname(path.abspath("__file__")))
repo_path
sys.path.append(repo_path)
from unityagents import UnityEnvironment
import numpy as np
from collections import deque
from src.ac_agent import AgentDDPG, GaussianProcess, OUNoise
from src.utils import action_scaler_fn
from unity_tennis_utils import train
EXP_NAME = 'ddpg:v01'
EXP_FOLDER = 'ddpg1'
action_scaler = partial(action_scaler_fn, lower=-1., upper=1.)
```
Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/Tennis.app"`
- **Windows** (x86): `"path/to/Tennis_Windows_x86/Tennis.exe"`
- **Windows** (x86_64): `"path/to/Tennis_Windows_x86_64/Tennis.exe"`
- **Linux** (x86): `"path/to/Tennis_Linux/Tennis.x86"`
- **Linux** (x86_64): `"path/to/Tennis_Linux/Tennis.x86_64"`
- **Linux** (x86, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86"`
- **Linux** (x86_64, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86_64"`
For instance, if you are using a Mac, then you downloaded `Tennis.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="Tennis.app")
```
```
env = UnityEnvironment(file_name="Tennis_Windows_x86_64/Tennis.exe")
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
In this environment, two agents control rackets to bounce a ball over a net. If an agent hits the ball over the net, it receives a reward of +0.1. If an agent lets a ball hit the ground or hits the ball out of bounds, it receives a reward of -0.01. Thus, the goal of each agent is to keep the ball in play.
The observation space consists of 8 variables corresponding to the position and velocity of the ball and racket. Two continuous actions are available, corresponding to movement toward (or away from) the net, and jumping.
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents
num_agents = len(env_info.agents)
print('Number of agents:', num_agents)
# size of each action
action_size = brain.vector_action_space_size
print('Size of each action:', action_size)
# examine the state space
states = env_info.vector_observations
state_size = states.shape[1]
print('There are {} agents. Each observes a state with length: {}'.format(states.shape[0], state_size))
print('The state for the first agent looks like:', states[0])
```
### 3. Take Random Actions in the Environment
In the next code cell, you will learn how to use the Python API to control the agents and receive feedback from the environment.
Once this cell is executed, you will watch the agents' performance, if they select actions at random with each time step. A window should pop up that allows you to observe the agents.
Of course, as part of the project, you'll have to change the code so that the agents are able to use their experiences to gradually choose better actions when interacting with the environment!
1. After each episode, we add up the rewards that each agent received (without discounting), to get a score for each agent. This yields 2 (potentially different) scores. We then take the maximum of these 2 scores.
2. This yields a single score for each episode.
3. The environment is considered solved, when the average (over 100 episodes) of those scores is at least +0.5.
When finished, you can close the environment.
### 4. It's Your Turn!
Now it's your turn to train your own agent to solve the environment! When training the environment, set `train_mode=True`, so that the line for resetting the environment looks like the following:
```python
env_info = env.reset(train_mode=True)[brain_name]
```
```
RND_SEED = 123
# Problem
N_EPISODES = 1000
MAX_STEPS = 1000
SOLVED_AT = .5
GAMMA = .99 # Discount factor
# Noise
NOISE_MU = 0
NOISE_SIGMA = 0.1
NOISE_DECAY = 0.9995
NOISE_MIN_WEIGHT = .1
# Agent
ACT_HID_LAYERS = (256, 128)
CRIT_HID_LAYERS = (256, 128)
ACT_ADD_BN = (True)
CRIT_ADD_BN = (True)
GRAD_CLIP = (False, 1.) # (actor, critic)
BATCH_SIZE = 256
LEARNING_RATES = (1e-3, 1e-3) # (actor, critic)
WEIGHT_DECAY = (0, 0) # (actor, critic)
SOFT_UPD_PARAM = 2e-3
UPDATE_EVERY = 1
BUFFER_SIZE = int(1e6)
LEARN_EVERY = 1
LEARN_NUM = 10
g_noise = GaussianProcess(action_size, RND_SEED, mu=NOISE_MU, sigma=NOISE_SIGMA)
ddpg = AgentDDPG(state_size=state_size, action_size=action_size, gamma=GAMMA,
actor_hidden_layers=ACT_HID_LAYERS,
critic_hidden_layers=CRIT_HID_LAYERS,
actor_add_bn=ACT_ADD_BN,
critic_add_bn=CRIT_ADD_BN,
grad_clipping=GRAD_CLIP,
learning_rates=LEARNING_RATES,
weight_decay=WEIGHT_DECAY,
batch_size=BATCH_SIZE,
soft_upd_param=SOFT_UPD_PARAM,
update_every=UPDATE_EVERY,
buffer_size=BUFFER_SIZE,
noise=g_noise,
learn_every=LEARN_EVERY,
learn_num=LEARN_NUM,
seed=RND_SEED)
path_agent = os.path.join('models', EXP_FOLDER)
scores_agent = train(env, brain_name, ddpg, n_episodes=N_EPISODES, max_t=MAX_STEPS, solved=SOLVED_AT,
action_scaler_fn=action_scaler, add_noise=True, noise_decay=NOISE_DECAY, min_noise_weight=NOISE_MIN_WEIGHT,
model_save_path=path_agent)
scores_agent['experiment'] = EXP_NAME
checkpoint_metadata = pd.Series(index=['N_episodes', 'gamma', 'actor_hidden_layers', 'critic_hidden_layers',
'grad_clipping', 'batch_size', 'learning_rates',
'soft_upd_param', 'update_every', 'buffer_size', 'noise', 'learn_every', 'learn_num', 'solved',
'checkpoint_folder'],
data = [len(scores_agent), GAMMA, ACT_HID_LAYERS, CRIT_HID_LAYERS,
GRAD_CLIP, BATCH_SIZE, LEARNING_RATES,SOFT_UPD_PARAM, UPDATE_EVERY, BUFFER_SIZE, 'g-noise', LEARN_EVERY, LEARN_NUM, False, EXP_FOLDER], name=f'experiment:{EXP_NAME}')
checkpoint_metadata
experiment_dt = dt.datetime.strftime(dt.datetime.now(), "%Y%m%d%H%M%S")
checkpoint_metadata.to_json(f'models/experiments/hparams_{experiment_dt}.json')
scores_agent.to_csv(f'models/experiments/scores_{experiment_dt}.csv')
env.close()
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
import os
from os import path
import sys
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from functools import partial
import datetime as dt
import time
repo_path = path.dirname(path.dirname(path.abspath("__file__")))
repo_path
sys.path.append(repo_path)
from unityagents import UnityEnvironment
import numpy as np
from collections import deque
from src.ac_agent import AgentDDPG, GaussianProcess, OUNoise
from src.utils import action_scaler_fn
from unity_tennis_utils import train
EXP_NAME = 'ddpg:v01'
EXP_FOLDER = 'ddpg1'
action_scaler = partial(action_scaler_fn, lower=-1., upper=1.)
env = UnityEnvironment(file_name="Tennis.app")
env = UnityEnvironment(file_name="Tennis_Windows_x86_64/Tennis.exe")
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents
num_agents = len(env_info.agents)
print('Number of agents:', num_agents)
# size of each action
action_size = brain.vector_action_space_size
print('Size of each action:', action_size)
# examine the state space
states = env_info.vector_observations
state_size = states.shape[1]
print('There are {} agents. Each observes a state with length: {}'.format(states.shape[0], state_size))
print('The state for the first agent looks like:', states[0])
env_info = env.reset(train_mode=True)[brain_name]
RND_SEED = 123
# Problem
N_EPISODES = 1000
MAX_STEPS = 1000
SOLVED_AT = .5
GAMMA = .99 # Discount factor
# Noise
NOISE_MU = 0
NOISE_SIGMA = 0.1
NOISE_DECAY = 0.9995
NOISE_MIN_WEIGHT = .1
# Agent
ACT_HID_LAYERS = (256, 128)
CRIT_HID_LAYERS = (256, 128)
ACT_ADD_BN = (True)
CRIT_ADD_BN = (True)
GRAD_CLIP = (False, 1.) # (actor, critic)
BATCH_SIZE = 256
LEARNING_RATES = (1e-3, 1e-3) # (actor, critic)
WEIGHT_DECAY = (0, 0) # (actor, critic)
SOFT_UPD_PARAM = 2e-3
UPDATE_EVERY = 1
BUFFER_SIZE = int(1e6)
LEARN_EVERY = 1
LEARN_NUM = 10
g_noise = GaussianProcess(action_size, RND_SEED, mu=NOISE_MU, sigma=NOISE_SIGMA)
ddpg = AgentDDPG(state_size=state_size, action_size=action_size, gamma=GAMMA,
actor_hidden_layers=ACT_HID_LAYERS,
critic_hidden_layers=CRIT_HID_LAYERS,
actor_add_bn=ACT_ADD_BN,
critic_add_bn=CRIT_ADD_BN,
grad_clipping=GRAD_CLIP,
learning_rates=LEARNING_RATES,
weight_decay=WEIGHT_DECAY,
batch_size=BATCH_SIZE,
soft_upd_param=SOFT_UPD_PARAM,
update_every=UPDATE_EVERY,
buffer_size=BUFFER_SIZE,
noise=g_noise,
learn_every=LEARN_EVERY,
learn_num=LEARN_NUM,
seed=RND_SEED)
path_agent = os.path.join('models', EXP_FOLDER)
scores_agent = train(env, brain_name, ddpg, n_episodes=N_EPISODES, max_t=MAX_STEPS, solved=SOLVED_AT,
action_scaler_fn=action_scaler, add_noise=True, noise_decay=NOISE_DECAY, min_noise_weight=NOISE_MIN_WEIGHT,
model_save_path=path_agent)
scores_agent['experiment'] = EXP_NAME
checkpoint_metadata = pd.Series(index=['N_episodes', 'gamma', 'actor_hidden_layers', 'critic_hidden_layers',
'grad_clipping', 'batch_size', 'learning_rates',
'soft_upd_param', 'update_every', 'buffer_size', 'noise', 'learn_every', 'learn_num', 'solved',
'checkpoint_folder'],
data = [len(scores_agent), GAMMA, ACT_HID_LAYERS, CRIT_HID_LAYERS,
GRAD_CLIP, BATCH_SIZE, LEARNING_RATES,SOFT_UPD_PARAM, UPDATE_EVERY, BUFFER_SIZE, 'g-noise', LEARN_EVERY, LEARN_NUM, False, EXP_FOLDER], name=f'experiment:{EXP_NAME}')
checkpoint_metadata
experiment_dt = dt.datetime.strftime(dt.datetime.now(), "%Y%m%d%H%M%S")
checkpoint_metadata.to_json(f'models/experiments/hparams_{experiment_dt}.json')
scores_agent.to_csv(f'models/experiments/scores_{experiment_dt}.csv')
env.close()
| 0.272315 | 0.954732 |
```
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "2"
%pylab inline
from tqdm import tqdm
import cmasher as cmr
import matplotlib.colors as colors
import jax_cosmo as jc
mesh_shape= [64, 64, 64]
box_size = [25., 25., 25.]
cosmo = jc.Planck15(Omega_c= 0.3 - 0.049, Omega_b=0.049, n_s=0.9624, h=0.6711, sigma8=0.8)
import readgadget
init_cond = '/data/CAMELS/Sims/IllustrisTNG_DM/1P_1_0/ICs/ics'
header = readgadget.header(init_cond)
BoxSize = header.boxsize/1e3 #Mpc/h
Nall = header.nall #Total number of particles
Masses = header.massarr*1e10 #Masses of the particles in Msun/h
Omega_m = header.omega_m #value of Omega_m
Omega_l = header.omega_l #value of Omega_l
h = header.hubble #value of h
redshift = header.redshift #redshift of the snapshot
Hubble = 100.0*np.sqrt(Omega_m*(1.0+redshift)**3+Omega_l)#Value of H(z) in km/s/(Mpc/h)
ptype = [1] #dark matter is particle type 1
ids_i = np.argsort(readgadget.read_block(init_cond, "ID ", ptype)-1) #IDs starting from 0
pos_i = readgadget.read_block(init_cond, "POS ", ptype)[ids_i]/1e3 #positions in Mpc/h
vel_i = readgadget.read_block(init_cond, "VEL ", ptype)[ids_i] #peculiar velocities in km/s
# Reordering data for simple reshaping
pos_i = pos_i.reshape(4,4,4,64,64,64,3).transpose(0,3,1,4,2,5,6).reshape(-1,3)
vel_i = vel_i.reshape(4,4,4,64,64,64,3).transpose(0,3,1,4,2,5,6).reshape(-1,3)
pos_i = (pos_i/BoxSize*64).reshape([256,256,256,3])[::4,::4,::4,:].reshape([-1,3])
vel_i = (vel_i / 100 * (1./(1+redshift)) / BoxSize*64).reshape([256,256,256,3])[::4,::4,::4,:].reshape([-1,3])
a_i = 1./(1+redshift)
scales = []
poss = []
vels = []
# Loading all the intermediate snapshots
for i in tqdm(range(34)):
snapshot='/data/CAMELS/Sims/IllustrisTNG_DM/1P_1_0/snap_%03d.hdf5'%i
header = readgadget.header(snapshot)
redshift = header.redshift #redshift of the snapshot
h = header.hubble #value of h
ptype = [1] #dark matter is particle type 1
ids = np.argsort(readgadget.read_block(snapshot, "ID ", ptype)-1) #IDs starting from 0
pos = readgadget.read_block(snapshot, "POS ", ptype)[ids] / 1e3 #positions in Mpc/h
vel = readgadget.read_block(snapshot, "VEL ", ptype)[ids] #peculiar velocities in km/s
# Reordering data for simple reshaping
pos = pos.reshape(4,4,4,64,64,64,3).transpose(0,3,1,4,2,5,6).reshape(-1,3)
vel = vel.reshape(4,4,4,64,64,64,3).transpose(0,3,1,4,2,5,6).reshape(-1,3)
pos = (pos / BoxSize * 64).reshape([256,256,256,3])[::4,::4,::4,:].reshape([-1,3])
vel = (vel / 100 * (1./(1+redshift)) / BoxSize*64).reshape([256,256,256,3])[::4,::4,::4,:].reshape([-1,3])
scales.append((1./(1+redshift)))
poss.append(pos)
vels.append(vel)
import jax
import jax.numpy as jnp
import jax_cosmo as jc
import haiku as hk
from jax.experimental.ode import odeint
from jaxpm.painting import cic_paint, cic_read, compensate_cic
from jaxpm.pm import linear_field, lpt, make_ode_fn, pm_forces
from jaxpm.kernels import fftk, gradient_kernel, laplace_kernel, longrange_kernel
from jaxpm.nn import NeuralSplineFourierFilter
from jaxpm.utils import power_spectrum
import numpyro
rng_seq = hk.PRNGSequence(1)
# Run the reference simulation without correction at the same steps
resi = odeint(make_ode_fn(mesh_shape), [poss[0], vels[0]], jnp.array(scales), cosmo, rtol=1e-5, atol=1e-5)
# High res simulation
figure(figsize=[10,10])
for i in range(16):
subplot(4,4,i+1)
imshow(cic_paint(jnp.zeros(mesh_shape), poss[::2][i]).sum(axis=0), cmap='gist_stern', vmin=0)
k, pk_ref = power_spectrum(
compensate_cic(cic_paint(jnp.zeros(mesh_shape), poss[-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
k, pk_i = power_spectrum(
compensate_cic(cic_paint(jnp.zeros(mesh_shape), resi[0][-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
model = hk.without_apply_rng(hk.transform(lambda x,a : NeuralSplineFourierFilter(n_knots=16, latent_size=32)(x,a)))
import pickle
params = pickle.load( open( "correction_params/camels_25_64_CV_0_lambda1_01.params", "rb" ) )
def neural_nbody_ode(state, a, cosmo, params):
"""
state is a tuple (position, velocities)
"""
pos, vel = state
kvec = fftk(mesh_shape)
delta = cic_paint(jnp.zeros(mesh_shape), pos)
delta_k = jnp.fft.rfftn(delta)
# Computes gravitational potential
pot_k = delta_k * laplace_kernel(kvec) * longrange_kernel(kvec, r_split=0)
# Apply a correction filter
kk = jnp.sqrt(sum((ki/pi)**2 for ki in kvec))
pot_k = pot_k *(1. + model.apply(params, kk, jnp.atleast_1d(a)))
# Computes gravitational forces
forces = jnp.stack([cic_read(jnp.fft.irfftn(gradient_kernel(kvec, i)*pot_k), pos)
for i in range(3)],axis=-1)
forces = forces * 1.5 * cosmo.Omega_m
# Computes the update of position (drift)
dpos = 1. / (a**3 * jnp.sqrt(jc.background.Esqr(cosmo, a))) * vel
# Computes the update of velocity (kick)
dvel = 1. / (a**2 * jnp.sqrt(jc.background.Esqr(cosmo, a))) * forces
return dpos, dvel
res = odeint(neural_nbody_ode, [poss[0], vels[0]], jnp.array(scales), cosmo, params, rtol=1e-5, atol=1e-5)
k, pk_ref = power_spectrum(
(cic_paint(jnp.zeros(mesh_shape), poss[-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
k, pk_i = power_spectrum(
(cic_paint(jnp.zeros(mesh_shape), resi[0][-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
k, pk_c = power_spectrum(
(cic_paint(jnp.zeros(mesh_shape), res[0][-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
params_pgd = pickle.load( open( "correction_params/camels_25_64_pkloss_PGD_CV_0.params", "rb" ) )
def PGD_kernel(kvec, kl, ks):
kk = sum(ki**2 for ki in kvec)
kl2 = kl**2
ks4 = ks**4
mask = (kk == 0).nonzero()
kk[mask] = 1
v = jnp.exp(-kl2 / kk) * jnp.exp(-kk**2 / ks4)
imask = (~(kk == 0)).astype(int)
v *= imask
return v
def pgd_correction(pos, params):
"""
state is a tuple (position, velocities)
"""
kvec = fftk(mesh_shape)
delta = cic_paint(jnp.zeros(mesh_shape), pos)
alpha, kl, ks = params
delta_k = jnp.fft.rfftn(delta)
PGD_range=PGD_kernel(kvec, kl, ks)
pot_k_pgd=(delta_k * laplace_kernel(kvec))*PGD_range
forces_pgd= jnp.stack([cic_read(jnp.fft.irfftn(gradient_kernel(kvec, i)*pot_k_pgd), pos)
for i in range(3)],axis=-1)
dpos_pgd = forces_pgd*alpha
return dpos_pgd
k, pk_pgd = power_spectrum(
(cic_paint(jnp.zeros(mesh_shape), resi[0][-1]+pgd_correction(resi[0][-1],params_pgd))),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
import cmasher as cmr
import matplotlib.colors as colors
cmap = cmr.eclipse
col = cmr.eclipse(np.linspace(0.,1,4))
col = cmr.eclipse([0.,0,0.55,0.85])
sm = plt.cm.ScalarMappable(cmap=cmap, norm=plt.Normalize(vmin=0., vmax=1))
```
### Loss function with position and power spectrum
```
from matplotlib import gridspec
col = cmr.eclipse([0.,0.13,0.55,0.85])
fig = plt.figure(figsize=(8, 6))
gs = gridspec.GridSpec(2, 1, height_ratios=[3, 1],hspace=0)
ax0 = plt.subplot(gs[0])
ax0.loglog(k, pk_ref,'--', label='CAMELS',color=col[0])
ax0.loglog(k, pk_i,label='PM without correction',color=col[1])
ax0.loglog(k, pk_c, label='PM with NN-correction',color=col[2])
ax0.loglog(k, pk_pgd, label='PM with PGD-correction',color=col[3])
ax0.label_outer()
plt.legend(fontsize='large')
ax0.set_xlabel(r"$k$ [$h \ \mathrm{Mpc}^{-1}$]",fontsize=14)
ax0.set_ylabel(r"$P(k)$", fontsize=14)
ax1 = plt.subplot(gs[1])
ax1.semilogx(k, (pk_i/pk_ref)-1,label='PM without correction',color=col[1])
ax1.semilogx(k, (pk_c/pk_ref)-1,label='PM with NN-correction',color=col[2])
ax1.semilogx(k, (pk_pgd/pk_ref)-1,label='PM with PGD-correction',color=col[3])
ax1.set_ylabel(r"$ (P(k) \ / \ P^{Camels}(k))-1$",fontsize=14)
ax1.set_xlabel(r"$k$ [$h \ \mathrm{Mpc}^{-1}$]",fontsize=14)
ax0.set_title('Different seed',fontsize=15)
ax1.set_ylim(-1.5,1.5)
plt.tight_layout()
plt.grid(True)
plt.savefig('../figures/camels_comparison_residual_diffomega_seed.pdf')
im1=cic_paint(jnp.zeros(mesh_shape), poss[-1]).sum(axis=0)
im2=cic_paint(jnp.zeros(mesh_shape), resi[0][-1]).sum(axis=0)
im3=cic_paint(jnp.zeros(mesh_shape), res[0][-1]).sum(axis=0)
im4=cic_paint(jnp.zeros(mesh_shape), resi[0][-1]+pgd_correction(resi[0][-1],params_pgd)).sum(axis=0)
TI=['CAMELS','PM','PM+NN','PM+PGD']
image_paths=[im1,im2,im3,im4]
cmap = cmr.eclipse
fig, axes = plt.subplots(nrows=1, ncols=4)
for imp, ax, ci in zip(image_paths, axes.ravel(),TI):
norm=colors.LogNorm(vmax=cic_paint(jnp.zeros(mesh_shape), res[0][-1]).sum(axis=0).max(),
vmin=cic_paint(jnp.zeros(mesh_shape), res[0][-1]).sum(axis=0).min())
ax.imshow(imp, cmap=cmap, norm=norm)
ax.set_title(ci)
ax.axis('off')
fig.tight_layout()
#plt.savefig('../figures/all_cluster_1P_1_0.pdf')
```
|
github_jupyter
|
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "2"
%pylab inline
from tqdm import tqdm
import cmasher as cmr
import matplotlib.colors as colors
import jax_cosmo as jc
mesh_shape= [64, 64, 64]
box_size = [25., 25., 25.]
cosmo = jc.Planck15(Omega_c= 0.3 - 0.049, Omega_b=0.049, n_s=0.9624, h=0.6711, sigma8=0.8)
import readgadget
init_cond = '/data/CAMELS/Sims/IllustrisTNG_DM/1P_1_0/ICs/ics'
header = readgadget.header(init_cond)
BoxSize = header.boxsize/1e3 #Mpc/h
Nall = header.nall #Total number of particles
Masses = header.massarr*1e10 #Masses of the particles in Msun/h
Omega_m = header.omega_m #value of Omega_m
Omega_l = header.omega_l #value of Omega_l
h = header.hubble #value of h
redshift = header.redshift #redshift of the snapshot
Hubble = 100.0*np.sqrt(Omega_m*(1.0+redshift)**3+Omega_l)#Value of H(z) in km/s/(Mpc/h)
ptype = [1] #dark matter is particle type 1
ids_i = np.argsort(readgadget.read_block(init_cond, "ID ", ptype)-1) #IDs starting from 0
pos_i = readgadget.read_block(init_cond, "POS ", ptype)[ids_i]/1e3 #positions in Mpc/h
vel_i = readgadget.read_block(init_cond, "VEL ", ptype)[ids_i] #peculiar velocities in km/s
# Reordering data for simple reshaping
pos_i = pos_i.reshape(4,4,4,64,64,64,3).transpose(0,3,1,4,2,5,6).reshape(-1,3)
vel_i = vel_i.reshape(4,4,4,64,64,64,3).transpose(0,3,1,4,2,5,6).reshape(-1,3)
pos_i = (pos_i/BoxSize*64).reshape([256,256,256,3])[::4,::4,::4,:].reshape([-1,3])
vel_i = (vel_i / 100 * (1./(1+redshift)) / BoxSize*64).reshape([256,256,256,3])[::4,::4,::4,:].reshape([-1,3])
a_i = 1./(1+redshift)
scales = []
poss = []
vels = []
# Loading all the intermediate snapshots
for i in tqdm(range(34)):
snapshot='/data/CAMELS/Sims/IllustrisTNG_DM/1P_1_0/snap_%03d.hdf5'%i
header = readgadget.header(snapshot)
redshift = header.redshift #redshift of the snapshot
h = header.hubble #value of h
ptype = [1] #dark matter is particle type 1
ids = np.argsort(readgadget.read_block(snapshot, "ID ", ptype)-1) #IDs starting from 0
pos = readgadget.read_block(snapshot, "POS ", ptype)[ids] / 1e3 #positions in Mpc/h
vel = readgadget.read_block(snapshot, "VEL ", ptype)[ids] #peculiar velocities in km/s
# Reordering data for simple reshaping
pos = pos.reshape(4,4,4,64,64,64,3).transpose(0,3,1,4,2,5,6).reshape(-1,3)
vel = vel.reshape(4,4,4,64,64,64,3).transpose(0,3,1,4,2,5,6).reshape(-1,3)
pos = (pos / BoxSize * 64).reshape([256,256,256,3])[::4,::4,::4,:].reshape([-1,3])
vel = (vel / 100 * (1./(1+redshift)) / BoxSize*64).reshape([256,256,256,3])[::4,::4,::4,:].reshape([-1,3])
scales.append((1./(1+redshift)))
poss.append(pos)
vels.append(vel)
import jax
import jax.numpy as jnp
import jax_cosmo as jc
import haiku as hk
from jax.experimental.ode import odeint
from jaxpm.painting import cic_paint, cic_read, compensate_cic
from jaxpm.pm import linear_field, lpt, make_ode_fn, pm_forces
from jaxpm.kernels import fftk, gradient_kernel, laplace_kernel, longrange_kernel
from jaxpm.nn import NeuralSplineFourierFilter
from jaxpm.utils import power_spectrum
import numpyro
rng_seq = hk.PRNGSequence(1)
# Run the reference simulation without correction at the same steps
resi = odeint(make_ode_fn(mesh_shape), [poss[0], vels[0]], jnp.array(scales), cosmo, rtol=1e-5, atol=1e-5)
# High res simulation
figure(figsize=[10,10])
for i in range(16):
subplot(4,4,i+1)
imshow(cic_paint(jnp.zeros(mesh_shape), poss[::2][i]).sum(axis=0), cmap='gist_stern', vmin=0)
k, pk_ref = power_spectrum(
compensate_cic(cic_paint(jnp.zeros(mesh_shape), poss[-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
k, pk_i = power_spectrum(
compensate_cic(cic_paint(jnp.zeros(mesh_shape), resi[0][-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
model = hk.without_apply_rng(hk.transform(lambda x,a : NeuralSplineFourierFilter(n_knots=16, latent_size=32)(x,a)))
import pickle
params = pickle.load( open( "correction_params/camels_25_64_CV_0_lambda1_01.params", "rb" ) )
def neural_nbody_ode(state, a, cosmo, params):
"""
state is a tuple (position, velocities)
"""
pos, vel = state
kvec = fftk(mesh_shape)
delta = cic_paint(jnp.zeros(mesh_shape), pos)
delta_k = jnp.fft.rfftn(delta)
# Computes gravitational potential
pot_k = delta_k * laplace_kernel(kvec) * longrange_kernel(kvec, r_split=0)
# Apply a correction filter
kk = jnp.sqrt(sum((ki/pi)**2 for ki in kvec))
pot_k = pot_k *(1. + model.apply(params, kk, jnp.atleast_1d(a)))
# Computes gravitational forces
forces = jnp.stack([cic_read(jnp.fft.irfftn(gradient_kernel(kvec, i)*pot_k), pos)
for i in range(3)],axis=-1)
forces = forces * 1.5 * cosmo.Omega_m
# Computes the update of position (drift)
dpos = 1. / (a**3 * jnp.sqrt(jc.background.Esqr(cosmo, a))) * vel
# Computes the update of velocity (kick)
dvel = 1. / (a**2 * jnp.sqrt(jc.background.Esqr(cosmo, a))) * forces
return dpos, dvel
res = odeint(neural_nbody_ode, [poss[0], vels[0]], jnp.array(scales), cosmo, params, rtol=1e-5, atol=1e-5)
k, pk_ref = power_spectrum(
(cic_paint(jnp.zeros(mesh_shape), poss[-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
k, pk_i = power_spectrum(
(cic_paint(jnp.zeros(mesh_shape), resi[0][-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
k, pk_c = power_spectrum(
(cic_paint(jnp.zeros(mesh_shape), res[0][-1])),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
params_pgd = pickle.load( open( "correction_params/camels_25_64_pkloss_PGD_CV_0.params", "rb" ) )
def PGD_kernel(kvec, kl, ks):
kk = sum(ki**2 for ki in kvec)
kl2 = kl**2
ks4 = ks**4
mask = (kk == 0).nonzero()
kk[mask] = 1
v = jnp.exp(-kl2 / kk) * jnp.exp(-kk**2 / ks4)
imask = (~(kk == 0)).astype(int)
v *= imask
return v
def pgd_correction(pos, params):
"""
state is a tuple (position, velocities)
"""
kvec = fftk(mesh_shape)
delta = cic_paint(jnp.zeros(mesh_shape), pos)
alpha, kl, ks = params
delta_k = jnp.fft.rfftn(delta)
PGD_range=PGD_kernel(kvec, kl, ks)
pot_k_pgd=(delta_k * laplace_kernel(kvec))*PGD_range
forces_pgd= jnp.stack([cic_read(jnp.fft.irfftn(gradient_kernel(kvec, i)*pot_k_pgd), pos)
for i in range(3)],axis=-1)
dpos_pgd = forces_pgd*alpha
return dpos_pgd
k, pk_pgd = power_spectrum(
(cic_paint(jnp.zeros(mesh_shape), resi[0][-1]+pgd_correction(resi[0][-1],params_pgd))),
boxsize=np.array([25.] * 3),
kmin=np.pi / 25.,
dk=2 * np.pi / 25.)
import cmasher as cmr
import matplotlib.colors as colors
cmap = cmr.eclipse
col = cmr.eclipse(np.linspace(0.,1,4))
col = cmr.eclipse([0.,0,0.55,0.85])
sm = plt.cm.ScalarMappable(cmap=cmap, norm=plt.Normalize(vmin=0., vmax=1))
from matplotlib import gridspec
col = cmr.eclipse([0.,0.13,0.55,0.85])
fig = plt.figure(figsize=(8, 6))
gs = gridspec.GridSpec(2, 1, height_ratios=[3, 1],hspace=0)
ax0 = plt.subplot(gs[0])
ax0.loglog(k, pk_ref,'--', label='CAMELS',color=col[0])
ax0.loglog(k, pk_i,label='PM without correction',color=col[1])
ax0.loglog(k, pk_c, label='PM with NN-correction',color=col[2])
ax0.loglog(k, pk_pgd, label='PM with PGD-correction',color=col[3])
ax0.label_outer()
plt.legend(fontsize='large')
ax0.set_xlabel(r"$k$ [$h \ \mathrm{Mpc}^{-1}$]",fontsize=14)
ax0.set_ylabel(r"$P(k)$", fontsize=14)
ax1 = plt.subplot(gs[1])
ax1.semilogx(k, (pk_i/pk_ref)-1,label='PM without correction',color=col[1])
ax1.semilogx(k, (pk_c/pk_ref)-1,label='PM with NN-correction',color=col[2])
ax1.semilogx(k, (pk_pgd/pk_ref)-1,label='PM with PGD-correction',color=col[3])
ax1.set_ylabel(r"$ (P(k) \ / \ P^{Camels}(k))-1$",fontsize=14)
ax1.set_xlabel(r"$k$ [$h \ \mathrm{Mpc}^{-1}$]",fontsize=14)
ax0.set_title('Different seed',fontsize=15)
ax1.set_ylim(-1.5,1.5)
plt.tight_layout()
plt.grid(True)
plt.savefig('../figures/camels_comparison_residual_diffomega_seed.pdf')
im1=cic_paint(jnp.zeros(mesh_shape), poss[-1]).sum(axis=0)
im2=cic_paint(jnp.zeros(mesh_shape), resi[0][-1]).sum(axis=0)
im3=cic_paint(jnp.zeros(mesh_shape), res[0][-1]).sum(axis=0)
im4=cic_paint(jnp.zeros(mesh_shape), resi[0][-1]+pgd_correction(resi[0][-1],params_pgd)).sum(axis=0)
TI=['CAMELS','PM','PM+NN','PM+PGD']
image_paths=[im1,im2,im3,im4]
cmap = cmr.eclipse
fig, axes = plt.subplots(nrows=1, ncols=4)
for imp, ax, ci in zip(image_paths, axes.ravel(),TI):
norm=colors.LogNorm(vmax=cic_paint(jnp.zeros(mesh_shape), res[0][-1]).sum(axis=0).max(),
vmin=cic_paint(jnp.zeros(mesh_shape), res[0][-1]).sum(axis=0).min())
ax.imshow(imp, cmap=cmap, norm=norm)
ax.set_title(ci)
ax.axis('off')
fig.tight_layout()
#plt.savefig('../figures/all_cluster_1P_1_0.pdf')
| 0.355999 | 0.265863 |
```
from fastai.nlp import *
from fastai.lm_rnn import *
from fastai import sgdr
from torchtext import vocab, data
import pdb
class CharSeqStatefulLSTM(nn.Module):
def __init__(self, vocab_size, n_fac, bs, nl):
super().__init__()
self.vocab_size,self.nl = vocab_size,nl
self.e = nn.Embedding(vocab_size, n_fac)
self.rnn = nn.LSTM(n_fac, n_hidden, nl, dropout=0.5)
self.l_out = nn.Linear(n_hidden, vocab_size)
self.init_hidden(bs)
def forward(self, cs, **kwargs):
bs = cs[0].size(0)
if self.h[0].size(1) != bs: self.init_hidden(bs)
self.rnn.flatten_parameters()
self.h = (self.h[0].cpu(), self.h[1].cpu())
ecs = self.e(cs)
outp,h = self.rnn(ecs, self.h)
#pdb.set_trace()
#self.h = repackage_var(h)
return F.log_softmax(self.l_out(outp), dim=-1).view(-1, self.vocab_size)
def init_hidden(self, bs):
self.h = (V(torch.zeros(self.nl, bs, n_hidden)),
V(torch.zeros(self.nl, bs, n_hidden)))
class CharSeqStatefulLSTM512(nn.Module):
def __init__(self, vocab_size, n_fac, bs, nl):
super().__init__()
self.vocab_size,self.nl = vocab_size,nl
self.e = nn.Embedding(vocab_size, n_fac)
self.rnn = nn.LSTM(n_fac, n_hidden2, nl, dropout=0.5)
self.l_out = nn.Linear(n_hidden2, vocab_size)
self.init_hidden(bs)
def forward(self, cs, **kwargs):
bs = cs[0].size(0)
if self.h[0].size(1) != bs: self.init_hidden(bs)
self.rnn.flatten_parameters()
self.h = (self.h[0].cpu(), self.h[1].cpu())
ecs = self.e(cs)
outp,h = self.rnn(ecs, self.h)
#pdb.set_trace()
#self.h = repackage_var(h)
return F.log_softmax(self.l_out(outp), dim=-1).view(-1, self.vocab_size)
def init_hidden(self, bs):
self.h = (V(torch.zeros(self.nl, bs, n_hidden2)),
V(torch.zeros(self.nl, bs, n_hidden2)))
PATH='data/proverbs/'
PATH2='data/proverbs2/'
PATH3='data/proverbs3/'
TRN_PATH = 'train/'
VAL_PATH = 'valid/'
TRN = PATH + TRN_PATH
VAL = PATH + VAL_PATH
TRN2 = PATH2 + TRN_PATH
VAL2 = PATH2 + VAL_PATH
TRN3 = PATH3 + TRN_PATH
VAL3 = PATH3 + VAL_PATH
PATH, TRN, VAL
TEXT = data.Field(lower=True, tokenize=list)
bs=64; bptt=8; n_fac=42; n_hidden=128
TEXT
TEXT3 = data.Field(lower=True, tokenize=list)
bs=64; bptt=8; n_fac=42; n_hidden2=512
TEXT3
FILES = dict(train=TRN_PATH, validation=VAL_PATH, test=VAL_PATH)
md = LanguageModelData.from_text_files(PATH, TEXT, **FILES, bs=bs, bptt=bptt, min_freq=3)
md
m = CharSeqStatefulLSTM(md.nt, n_fac, 256, 2)
m.load_state_dict(torch.load(f'{PATH}models/gen_0_dict', map_location=lambda storage, loc: storage))
m = m.cpu()
m.eval()
FILES2 = dict(train=TRN_PATH, validation=VAL_PATH, test=VAL_PATH)
md2 = LanguageModelData.from_text_files(PATH2, TEXT, **FILES, bs=bs, bptt=bptt, min_freq=3)
m2 = CharSeqStatefulLSTM(md2.nt, n_fac, 256, 2)
m2.load_state_dict(torch.load(PATH2 + 'models/gen_1_dict', map_location=lambda storage, loc: storage))
m2.eval()
FILES3 = dict(train=TRN_PATH, validation=VAL_PATH, test=VAL_PATH)
md3 = LanguageModelData.from_text_files(PATH3, TEXT3, **FILES, bs=bs, bptt=bptt, min_freq=3)
m3 = CharSeqStatefulLSTM512(md3.nt, n_fac, 256, 2)
m3.load_state_dict(torch.load(PATH3 + 'models/gen_2_dict', map_location=lambda storage, loc: storage))
m3.eval()
def get_next(inp, gen):
new_TEXT = ''
if gen == 1:
sel_m = m2
new_TEXT = TEXT
elif gen == 2:
sel_m = m3
new_TEXT = TEXT3
else:
sel_m = m
new_TEXT = TEXT
idxs = new_TEXT.numericalize(inp, device=-1)
pid = idxs.transpose(0,1)
pid = pid.cpu()
vpid = VV(pid)
vpid = vpid.cpu()
p = sel_m(vpid)
r = torch.multinomial(p[-1].exp(), 1)
return new_TEXT.vocab.itos[to_np(r)[0]]
def get_next_n(inp, n, gen):
res = inp
for i in range(n):
c = get_next(inp, gen)
res += c
inp = inp[1:]+c
if c == '.': break
return res
get_next_n('People ', 1000, 2)
```
|
github_jupyter
|
from fastai.nlp import *
from fastai.lm_rnn import *
from fastai import sgdr
from torchtext import vocab, data
import pdb
class CharSeqStatefulLSTM(nn.Module):
def __init__(self, vocab_size, n_fac, bs, nl):
super().__init__()
self.vocab_size,self.nl = vocab_size,nl
self.e = nn.Embedding(vocab_size, n_fac)
self.rnn = nn.LSTM(n_fac, n_hidden, nl, dropout=0.5)
self.l_out = nn.Linear(n_hidden, vocab_size)
self.init_hidden(bs)
def forward(self, cs, **kwargs):
bs = cs[0].size(0)
if self.h[0].size(1) != bs: self.init_hidden(bs)
self.rnn.flatten_parameters()
self.h = (self.h[0].cpu(), self.h[1].cpu())
ecs = self.e(cs)
outp,h = self.rnn(ecs, self.h)
#pdb.set_trace()
#self.h = repackage_var(h)
return F.log_softmax(self.l_out(outp), dim=-1).view(-1, self.vocab_size)
def init_hidden(self, bs):
self.h = (V(torch.zeros(self.nl, bs, n_hidden)),
V(torch.zeros(self.nl, bs, n_hidden)))
class CharSeqStatefulLSTM512(nn.Module):
def __init__(self, vocab_size, n_fac, bs, nl):
super().__init__()
self.vocab_size,self.nl = vocab_size,nl
self.e = nn.Embedding(vocab_size, n_fac)
self.rnn = nn.LSTM(n_fac, n_hidden2, nl, dropout=0.5)
self.l_out = nn.Linear(n_hidden2, vocab_size)
self.init_hidden(bs)
def forward(self, cs, **kwargs):
bs = cs[0].size(0)
if self.h[0].size(1) != bs: self.init_hidden(bs)
self.rnn.flatten_parameters()
self.h = (self.h[0].cpu(), self.h[1].cpu())
ecs = self.e(cs)
outp,h = self.rnn(ecs, self.h)
#pdb.set_trace()
#self.h = repackage_var(h)
return F.log_softmax(self.l_out(outp), dim=-1).view(-1, self.vocab_size)
def init_hidden(self, bs):
self.h = (V(torch.zeros(self.nl, bs, n_hidden2)),
V(torch.zeros(self.nl, bs, n_hidden2)))
PATH='data/proverbs/'
PATH2='data/proverbs2/'
PATH3='data/proverbs3/'
TRN_PATH = 'train/'
VAL_PATH = 'valid/'
TRN = PATH + TRN_PATH
VAL = PATH + VAL_PATH
TRN2 = PATH2 + TRN_PATH
VAL2 = PATH2 + VAL_PATH
TRN3 = PATH3 + TRN_PATH
VAL3 = PATH3 + VAL_PATH
PATH, TRN, VAL
TEXT = data.Field(lower=True, tokenize=list)
bs=64; bptt=8; n_fac=42; n_hidden=128
TEXT
TEXT3 = data.Field(lower=True, tokenize=list)
bs=64; bptt=8; n_fac=42; n_hidden2=512
TEXT3
FILES = dict(train=TRN_PATH, validation=VAL_PATH, test=VAL_PATH)
md = LanguageModelData.from_text_files(PATH, TEXT, **FILES, bs=bs, bptt=bptt, min_freq=3)
md
m = CharSeqStatefulLSTM(md.nt, n_fac, 256, 2)
m.load_state_dict(torch.load(f'{PATH}models/gen_0_dict', map_location=lambda storage, loc: storage))
m = m.cpu()
m.eval()
FILES2 = dict(train=TRN_PATH, validation=VAL_PATH, test=VAL_PATH)
md2 = LanguageModelData.from_text_files(PATH2, TEXT, **FILES, bs=bs, bptt=bptt, min_freq=3)
m2 = CharSeqStatefulLSTM(md2.nt, n_fac, 256, 2)
m2.load_state_dict(torch.load(PATH2 + 'models/gen_1_dict', map_location=lambda storage, loc: storage))
m2.eval()
FILES3 = dict(train=TRN_PATH, validation=VAL_PATH, test=VAL_PATH)
md3 = LanguageModelData.from_text_files(PATH3, TEXT3, **FILES, bs=bs, bptt=bptt, min_freq=3)
m3 = CharSeqStatefulLSTM512(md3.nt, n_fac, 256, 2)
m3.load_state_dict(torch.load(PATH3 + 'models/gen_2_dict', map_location=lambda storage, loc: storage))
m3.eval()
def get_next(inp, gen):
new_TEXT = ''
if gen == 1:
sel_m = m2
new_TEXT = TEXT
elif gen == 2:
sel_m = m3
new_TEXT = TEXT3
else:
sel_m = m
new_TEXT = TEXT
idxs = new_TEXT.numericalize(inp, device=-1)
pid = idxs.transpose(0,1)
pid = pid.cpu()
vpid = VV(pid)
vpid = vpid.cpu()
p = sel_m(vpid)
r = torch.multinomial(p[-1].exp(), 1)
return new_TEXT.vocab.itos[to_np(r)[0]]
def get_next_n(inp, n, gen):
res = inp
for i in range(n):
c = get_next(inp, gen)
res += c
inp = inp[1:]+c
if c == '.': break
return res
get_next_n('People ', 1000, 2)
| 0.836154 | 0.182353 |
# Tutorial for dlm regression with DLMMC
**In this notebook I walk through step-by-step how to read in your time-series and regressors, set-up and run the dlm, and process the outputs. If you are familiar with python it shouldn't take more than 15 minutes to read through this notebook (running the code as you go), and by the end I hope you will be geared up and ready to start running dlms on your own time-series data! So without further ado...**
## Import the required packages
```
# Import required modules
import pystan
import matplotlib.pyplot as plt
import numpy as np
import time
import scipy.interpolate as interpolate
import netCDF4
import pickle
import scipy.stats as stats
from utils.utils import *
%matplotlib inline
```
# Import the dlm model
**Note: make sure you have ran `compile_dlm_models.py` before you do this!**
**There are a number of models to choose from: the standard model below `dlm_vanilla_ar1` has a non-linear trend, seasonal cycle with 6- and 12-month components with time-varying amplitude and phase, regressor (proxy) variables and an AR1 process. This is usually a good starting point. For specific model descriptions see `models/model_descriptions.pdf`**
```
# Import the DLM model
dlm_model = pickle.load(open('models/dlm_vanilla_ar1.pkl', 'rb'))
```
# Import your data
**In this example we import the BASIC stratospheric ozone composite [Ball et al 2017](https://www.research-collection.ethz.ch/handle/20.500.11850/202027) and pick out a single time-series to analyse as a demo.**
**You can load in your data however you like, but in the end you must have the following variables loaded into python:**
`d` np.array(N) *the data time-series*<br/>
`s` np.array(N) *std-deviation error-bars on each data point*
**Note: for missing data values, you should set those data NaNs and pass `d` and `s` into the function `prepare_missing_data()` (see below). This function just sets up the missing data values appropriately for the DLM code to understand: this function will just set the missing values to the mean of the rest of the data, but give them enormous error bars (1e20).**
**Note: If you do not have measurement uncertainties available for your data, set `s` to be an array of small numbers (eg, 1e-20). The AR process will estimate the noise level on-the-fly, but note that you will then be assuming homoscedastic (but correlated) noise.**
```
# Import the data
# Import data from a netCDF
data = netCDF4.Dataset('data/BASIC_V1_2017_lotus_seascyc_gcsw2017_fac2.nc')
# Extract time, pressure and latitude variables from the netCDF
T = data['time'][:]
P = data['pressure'][:]
L = data['latitude'][:]
# Which pressure and latitude index do you want to analyze?
pressure = 22
latitude = 8
# Pick out a pressure and latitude panel: this is the "data" time-series from the netCDF
d = data['o3'][:, pressure, latitude]
# Extract the error-bars on the time-series from the netCDF
s = data['o3_sigma'][:, pressure, latitude]
# Sort out missing data if there is any: missing data should be NaNs (see notes above)
d, s = prepare_missing_data(d, s)
# Let's plot the data with uncertainties to check it looks OK
# Plot the selected data and error bars
plt.title('Pressure {:.2f} hPa; Latitude {:+.0f} deg'.format(P[pressure], L[latitude]))
plt.plot(T, d, color = 'red')
plt.fill_between(T, d - s, d + s, color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel(r'$O_3$ [ppm]')
plt.show()
```
## Import the regressors
**Here we import some standard regressors that are provided in the `regressors/` folder, but of course you can import your own regressors here as you please. In this example I import regressor data and interpolate on to the same time-grid as the imported data. For this example we import some standard indicies for: El Nino Southern Oscillation (ENSO), Solar activity (Solar), the Quasi-Biennial Oscillation (QBO; two indicies QBO30 and QBO50) and stratospheric aerosol optical depth (SAOD) for volcanic eruptions.**
**Again you can import the regressors however you like, but the result must be the following variable loaded into python:**
`regressors` np.array(N, nreg) *2d array with each column representing one regressor (evaluated on the same time-grid as your data)*
**Note: Missing values/NaNs in the regressors are not currently supported, please interpolate missing values so that they are all real valued. It is also good practice to normalize your regressors to be zero mean and have a range [-0.5, 0.5], so they are all on the same scale. Having regressors with wildly different scales can cause issues.**
```
# Import the regressors
# ENSO
regressor_data = np.loadtxt('regressors/ENSO_MEI_1950_201802.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
enso = Y(T)
# SOLAR
regressor_data = np.loadtxt('regressors/Flux_F30_monthly_195111_201803_absolute.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
solar = Y(T)
# QBO30
regressor_data = np.loadtxt('regressors/multi_qbo30_1953_2018.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
qbo30 = Y(T)
# QBO50
regressor_data = np.loadtxt('regressors/multi_qbo50_1953_2018.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
qbo50 = Y(T)
# SAOD
regressor_data = np.loadtxt('regressors/sad_1979_2017_10deg_60S_60N.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
saod = Y(T)
# Stack the regressors into big 2d array
regressors = np.column_stack([enso, solar, qbo30, qbo50, saod]) # Stack of all the regressors together in a 2d array
# Plot all the regressors to check they look OK
plt.plot(T, enso)
plt.title('ENSO')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
plt.plot(T, solar)
plt.title('Solar F30')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
plt.plot(T, qbo30)
plt.title('QBO30')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
plt.plot(T, qbo50)
plt.title('QBO50')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
plt.plot(T, saod)
plt.title('SAOD')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
```
## Set the data and initialization to be fed into the dlm
### `input_data`
**First we set the `input_data` - a dictionary of all the data and input parameters than the dlm model requires in order to run. The input data must have the following entries:**
`time_series` np.array(N) *data vector (time-series to be analyzed)*<br/>
`stddev` np.array(N) *standard deviation error bars for the time-series*<br/>
`N` (int) *number of time-steps in the time-series ie., length of your data vector*<br/>
`nreg` (int) *number of regressors*<br/>
`regressors` np.array(N, nreg) *the regressors: 2D array of size (data vector length, number of regressors)*<br/>
`sampling` (float) *sampling rate of the data: specify "daily", "monthly" or "annual" to the function sampling()*<br/>
`S` (float) *variance of the Gaussian prior on the regression coefficients; set to 10 as default*<br/>
`sigma_trend_prior` (float) *standard deviation of the half-Gaussian prior on* `sigma_trend` *that controls how wiggly the trend can be; set to 1e-4 as default*<br/>
`sigma_seas_prior` (float) *standard deviation of the half-Gaussian prior on* `sigma_seas`, *controls how dynamic the seaonal cycle can be; set to 0.01 as default*<br/>
`sigma_AR_prior` (float) *standard deviation of the half_Gaussian prior on the AR1 process's standard deviation; set to 0.5 as default*<br/>
`sigma_reg_prior` np.array(nreg) *standard deviation of the half_Gaussian prior on* `sigma_reg` *parameters, controling how dynamic the regressor amplitudes can be (in time); set to 1e-4 for all as default*
**Note: You should leave out parameters that are not included in your model, eg, if you are running a model without dynamical regressors you can leave out `sigma_reg_prior`, or if you are running a model without regressors you can leave out `regressors`. See Table 1 of `models/model_descriptions.pdf` for details of which parameters are included for which models.**
**Units: Note that the std-deviation hyper-parameters (`sigma_trend`, `sigma_seas`, `sigma_AR` and `sigma_reg`) controlling how dynamic various components of the DLM model are, are defined in units of the range of the input data, ie, / (max(time_series) - min(time_series)). In this sense they define fractional standard-deviations wrt the data. This provides a common ground for defining priors on the dynamics hyper-parameters irrespective of the units of the data.**
### `initial_state`
**Second, we set the `initial_state` - a dictionary of initial guesses for the hyper-parameters for initializing the MCMC sampler. This must have the following entries (with sugegsted default values):**
`sigma_trend` (float) *initial value for* `sigma_trend`; *default to 0.0001*<br/>
`sigma_seas` (float) *initial value for* `sigma_seas`; *default to 0.001*<br/>
`sigma_AR` (float) *initial value for* `sigma_AR`; *default to 0.01*<br/>
`rhoAR1` (float) *initial value for* `rhoAR1`; *default to 0.1*<br/>
`rhoAR2` (float) *initial value for* `rhoAR2`; *default to 0*<br/>
`sigma_reg` np.array(nreg) *initial value for* `sigma_reg`; *default to 1e-4 for all*
**Note: Again, you can leave out parameters that are not included in your model, ie if you are running one of the AR1 models you do not need `rhoAR2`, and if you are running models without dynamical regressors you can leave out `sigma_reg`. See `models/model_descriptions.pdf` (Table 1) for details of which parameters are included for which models.**
```
# Set the data and initialization of parameters that are fed into the DLM
# Input data: this is a dictionary of all of the data/inputs that the DLM model needs (descriptions below)
input_data = {
'time_series':d, # float[N] data vector
'stddev':s, # float[N] std-dev error bars
'N':len(d), # (int) number of time-steps in the time-series
'nreg':len(regressors.T), # (int) number of regressors
'regressors':regressors, # float[N, nreg] the regressors
'sampling':sampling_rate("monthly"), # must be "daily", "monthly", or "annual"
'S':10., # prior variance on the regression coefficients
'sigma_trend_prior':1e-4, # std-dev of the half-Gaussian prior on sigma_trend
'sigma_seas_prior':0.01, # std-dev of the half-Gaussian prior on sigma_seas
'sigma_AR_prior':0.5 # std-dev of the half_Gaussian prior on the AR1 process std-dev
}
# Initialization: Initial guess values for the hyper-parameters
initial_state = {
'sigma_trend':0.0001,
'sigma_seas':0.001,
'sigma_AR':0.01,
'rhoAR1':0.1,
}
```
## OK let's run the DLM!
**Now we're set up we can run the dlm. Below we run an HMC sampler (using `pystan`) together with Kalman filtering (and smoothing) steps to obtain samples from the joint posterior of the dlm model parameters given the input data and uncertainties, ie.,**
$P(nonlinear\;trend,\,seasonal\;cycle,\,AR\;process,\,regressor\;coefficients,\,hyperparameters | data)$
**The input parameters to the function `sampling()` below have the following meanings:**
`data` = *input data dictionary from above*<br/>
`iter` = *total number of MCMC samples to get; should be at least a few thousand*<br/>
`warmup` = *how many evaluations are allowed for the HMC sampler to "warm-up" (these are discarded in the final output)*<br/>
`chains` = *how many parallel chains to run? (see below for running parallel chains)*<br/>
`init` = *list of initial state dictionaries (from above), one per chain*<br/>
`pars` = *which parameters do you actually want to save as output in the results? (see below)*
**The `pars` parameter controls which parameters you want to save in the output results. You can choose any number from the following:**
`sigma_trend` (float) *hyper-parameter controlling how wiggly the trend can be*<br/>
`sigma_seas` (float) *hyper-parameter controlling how dynamic the seasonal cycle can be*<br/>
`sigma_AR` (float) *standard deviation parameter for the AR process*<br/>
`rhoAR1` (float) *first correlation parameter for the AR process*<br/>
`rhoAR2` (float) *second correlation parameter for the AR process*<br/>
`sigma_reg` np.array(nreg) *hyper-parameter controlling how dynamic the regressor amplitudes can be*<br/>
`beta` np.array(nreg, N) *dynamical regression coefficients*<br/>
`trend` np.array(N) *non-inear DLM trend (as function of time)*<br/>
`slope` np.array(N) *slope of the non-linear DLM trend (as function of time)*<br/>
`seasonal` np.array(N) *seasonal cycle with 6- and 12- month components (as function of time)*<br/>
`ar` np.array(N) *fitted AR process (as function of time)*
**Note: you can only inlcude things in `pars` that are actually included in the model you are running. See Table 1 of `models/model_descriptions.pdf` for which parameters are available in each of the models.**
**NOTE: you should limit your output `pars` to things you really want to look at after to keep the output smaller - it will be faster to work with for making plots etc later on, and take up less memory. If you do not set pars it will automatically save everything by default.**
**Running multiple chains in parallel: It is easy to run multiple chains in parallel by simply setting `chains` > 1. If you do this you must also provide a list of initial state dictionaries to `init`, ie., `init` = [initial_state1, initial_state2, ...] (precicely one initial state per chain, and they need not be different although it is good practice to give the chains different starting points)**
**OK let's do it! NB it will take a few minutes to run so be patient**
```
# Ok, let's run it
fit = dlm_model.sampling(data=input_data, iter=3000, warmup=1000, chains=1, init = [initial_state], verbose=True, pars=('sigma_trend', 'sigma_seas', 'sigma_AR', 'rhoAR1', 'trend', 'slope', 'beta', 'seasonal'))
```
## Extract the results
**By this point, the `fit` object contains "n_samples = (iter - warmup) x chains" samples of each of the parameters in "pars" that you chose to output. To access the samples for any individual parameter, just do:**
parameter_samples = fit.extract()['insert parameter name here'] (see examples below)
**For example, if you do `fit.extract()['trend']` it will give an array `np.array(n_samples, N)`, n_samples
samples of the full DLM trend, which has lengh N.**
**All outputs from the fit object will have shape n_samples x dimension of variable (see above).**
**To make life easier for anlysing the results in the rest of the notebook, let's extract all the samples here in one go...**
```
# Extract the various bits from the fit-object.
# Trend
trend = fit.extract()['trend'][:,:]
# Gradient of the DLM trend
slope = fit.extract()['slope'][:,:]
# Seasonal cycle
seasonal_cycle = fit.extract()['seasonal'][:,:]
# Regressor coefficients
regressor_coefficients = fit.extract()['beta'][:,:]
# DLM hyper parameters
sigma_trend = fit.extract()['sigma_trend']
sigma_seas = fit.extract()['sigma_seas']
sigma_AR = fit.extract()['sigma_AR']
rhoAR1 = fit.extract()['rhoAR1']
```
## Finally, let's make some plots of the outputs!
**Obviously we can compute and plot whatever we like now we have the results, but let's make a few example plots of the various parameters we have inferred to showcase the results.**
### Let's start by plotting the recovered dlm trend and corresponding (1$\sigma$) uncertainties:
```
# Plot recovered trend against the data
# Plot the data
plt.plot(T, d, lw = 2, alpha = 0.2)
# Plot the mean trend
plt.plot(T, np.mean(trend, axis = 0), color = 'red', ls = '--')
# Plot a grey band showing the error on the extracted DLM trend
# NOTE: this includes the error on the shape of the trend, but also on the overall offset, so can look deceptively large
plt.fill_between(T, np.mean(trend, axis = 0) - np.std(trend, axis = 0), np.mean(trend, axis = 0) + np.std(trend, axis = 0), color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel(r'$O_3$ [ppm]')
plt.show()
# Same plot but without the data behind (for a closer look at the DLM trend)
plt.plot(T, np.mean(trend, axis = 0), color = 'red', ls = '--')
plt.fill_between(T, np.mean(trend, axis = 0) - np.std(trend, axis = 0), np.mean(trend, axis = 0) + np.std(trend, axis = 0), color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel(r'$O_3$ [ppm]')
plt.show()
```
### We can also plot the recovered slope of the trend as a function of time (negative slope indicates ozone depletion, positive slope indicates recovery):
```
# Plot the slope of the recovered trend
plt.plot(T, np.mean(slope, axis = 0), color = 'red', ls = '--')
plt.fill_between(T, np.mean(slope, axis = 0) - np.std(slope, axis = 0), np.mean(slope, axis = 0) + np.std(slope, axis = 0), color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel(r'd$O_3$/dT [ppm month$^{-1}$]')
plt.show()
```
### Now for the recovered seasonal cycle - note that modulation in the amplitude of the seasonal cycle is allowed in the dlm model (and here is preferred by the data):
```
# Plot the recovered seasonal cycle and uncertainties
plt.plot(T, np.mean(seasonal_cycle, axis = 0))
plt.fill_between(T, np.mean(seasonal_cycle, axis = 0) - np.std(seasonal_cycle, axis = 0), np.mean(seasonal_cycle, axis = 0) + np.std(seasonal_cycle, axis = 0), color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel('seasonal cycle $O_3$ [ppm]')
plt.show()
# Plot posteriors for the regression coefficients
regressor_names = ['ENSO', 'SOLAR', 'QBO30', 'QBO50', 'SAOD']
for i in range(len(regressors.T)):
beta = regressor_coefficients[:,i]
kde = stats.gaussian_kde(beta)
x = np.linspace(min(beta) - np.ptp(beta)*0.1, max(beta) + np.ptp(beta)*0.1, 300)
plt.hist(beta, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title(regressor_names[i])
plt.ylabel('posterior density')
plt.xlabel(r'$\beta_{}$'.format(i))
plt.show()
```
### We can also plot histograms of the dlm hyper-parameter posteriors:
```
# Plot posteriors for the DLM hyper parameters
kde = stats.gaussian_kde(sigma_trend)
x = np.linspace(0, max(sigma_trend)*1.1, 300)
plt.hist(sigma_trend, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title('sigma_trend')
plt.ylabel('posterior density')
plt.xlabel(r'$\sigma_\mathrm{trend}$')
plt.show()
kde = stats.gaussian_kde(sigma_seas)
x = np.linspace(0, max(sigma_seas)*1.1, 300)
plt.hist(sigma_seas, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title('sigma_seas')
plt.ylabel('posterior density')
plt.xlabel(r'$\sigma_\mathrm{seas}$')
plt.show()
kde = stats.gaussian_kde(sigma_AR)
x = np.linspace(min(sigma_AR) - np.ptp(sigma_AR)*0.1, max(sigma_AR) + np.ptp(sigma_AR)*0.1, 300)
plt.hist(sigma_AR, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title('sigma_AR')
plt.ylabel('posterior density')
plt.xlabel(r'$\sigma_\mathrm{AR}$')
plt.show()
kde = stats.gaussian_kde(rhoAR1)
x = np.linspace(min(rhoAR1) - np.ptp(rhoAR1)*0.1, max(rhoAR1) + np.ptp(rhoAR1)*0.1, 300)
plt.hist(rhoAR1, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title('rhoAR1')
plt.ylabel('posterior density')
plt.xlabel(r'$\rho_\mathrm{AR1}$')
plt.show()
```
### Now for some trace plots of the MCMC samples of the hyper-parameters:
### This provides a good visual check of whether the chains have converged - if they look like noise it indicates that the chains are well converged, whilst if you see drifts in these trace plots then you need to go back and run longer chains (ie increase "iter" in the sampling() step above).
```
# Do trace plots of the MCMC chains of the hyper-parameters
plt.plot(sigma_trend)
plt.title('sigma_trend')
plt.xlabel('sample #')
plt.ylabel(r'$\sigma_\mathrm{trend}$')
plt.show()
plt.plot(sigma_seas)
plt.title('sigma_seas')
plt.xlabel('sample #')
plt.ylabel(r'$\sigma_\mathrm{seas}$')
plt.show()
plt.plot(sigma_AR)
plt.title('sigma_AR')
plt.xlabel('sample #')
plt.ylabel(r'$\sigma_\mathrm{AR}$')
plt.show()
plt.plot(rhoAR1)
plt.title('rhoAR1')
plt.xlabel('sample #')
plt.ylabel(r'$\rho_\mathrm{AR1}$')
plt.show()
```
### Finally, we can do things like plot the posterior for the net background change in ozone between two key dates (here, January 1998 and December 2017)
```
# Plot the posterior on the overall change in O3 between two dates eg, jan1998 and dec2017
# Time indices for the two dates
jan1998 = 156 # index of the T array corresponding to Jan 1998
dec2017 = -1 # (end of time series; december 2017)
# Construct MCMC samples for the change in O3 between those two dates by differencing the trend samples at those dates
deltaO3_jan1998_dec2017 = trend[:,dec2017] - trend[:,jan1998]
# Plot the histogram of the posterior samples of DeltaO3 between Jan 1998 and Dec 2017
kde = stats.gaussian_kde(deltaO3_jan1998_dec2017)
x = np.linspace(min(deltaO3_jan1998_dec2017) - np.ptp(deltaO3_jan1998_dec2017)*0.1, max(deltaO3_jan1998_dec2017) + np.ptp(deltaO3_jan1998_dec2017)*0.1, 300)
plt.hist(deltaO3_jan1998_dec2017, bins = 15, alpha = 0.1, density = True)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.xlabel(r'$\Delta O_3$ Jan 1998 to Dec 2017, [ppm]')
plt.ylabel('posterior density')
plt.show()
```
## Congratulations, you made it to the end of the tutorial!
## By now you should get the idea and, I hope, be able to use this notebook as a template for performing dlm regression on your own data. Good luck and happy DLMing!
|
github_jupyter
|
# Import required modules
import pystan
import matplotlib.pyplot as plt
import numpy as np
import time
import scipy.interpolate as interpolate
import netCDF4
import pickle
import scipy.stats as stats
from utils.utils import *
%matplotlib inline
# Import the DLM model
dlm_model = pickle.load(open('models/dlm_vanilla_ar1.pkl', 'rb'))
# Import the data
# Import data from a netCDF
data = netCDF4.Dataset('data/BASIC_V1_2017_lotus_seascyc_gcsw2017_fac2.nc')
# Extract time, pressure and latitude variables from the netCDF
T = data['time'][:]
P = data['pressure'][:]
L = data['latitude'][:]
# Which pressure and latitude index do you want to analyze?
pressure = 22
latitude = 8
# Pick out a pressure and latitude panel: this is the "data" time-series from the netCDF
d = data['o3'][:, pressure, latitude]
# Extract the error-bars on the time-series from the netCDF
s = data['o3_sigma'][:, pressure, latitude]
# Sort out missing data if there is any: missing data should be NaNs (see notes above)
d, s = prepare_missing_data(d, s)
# Let's plot the data with uncertainties to check it looks OK
# Plot the selected data and error bars
plt.title('Pressure {:.2f} hPa; Latitude {:+.0f} deg'.format(P[pressure], L[latitude]))
plt.plot(T, d, color = 'red')
plt.fill_between(T, d - s, d + s, color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel(r'$O_3$ [ppm]')
plt.show()
# Import the regressors
# ENSO
regressor_data = np.loadtxt('regressors/ENSO_MEI_1950_201802.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
enso = Y(T)
# SOLAR
regressor_data = np.loadtxt('regressors/Flux_F30_monthly_195111_201803_absolute.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
solar = Y(T)
# QBO30
regressor_data = np.loadtxt('regressors/multi_qbo30_1953_2018.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
qbo30 = Y(T)
# QBO50
regressor_data = np.loadtxt('regressors/multi_qbo50_1953_2018.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
qbo50 = Y(T)
# SAOD
regressor_data = np.loadtxt('regressors/sad_1979_2017_10deg_60S_60N.txt')
Y = interpolate.InterpolatedUnivariateSpline(regressor_data[:,0], regressor_data[:,1])
saod = Y(T)
# Stack the regressors into big 2d array
regressors = np.column_stack([enso, solar, qbo30, qbo50, saod]) # Stack of all the regressors together in a 2d array
# Plot all the regressors to check they look OK
plt.plot(T, enso)
plt.title('ENSO')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
plt.plot(T, solar)
plt.title('Solar F30')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
plt.plot(T, qbo30)
plt.title('QBO30')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
plt.plot(T, qbo50)
plt.title('QBO50')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
plt.plot(T, saod)
plt.title('SAOD')
plt.xlabel('time, T [Julian date]')
plt.ylabel('[re-scaled units]')
plt.show()
# Set the data and initialization of parameters that are fed into the DLM
# Input data: this is a dictionary of all of the data/inputs that the DLM model needs (descriptions below)
input_data = {
'time_series':d, # float[N] data vector
'stddev':s, # float[N] std-dev error bars
'N':len(d), # (int) number of time-steps in the time-series
'nreg':len(regressors.T), # (int) number of regressors
'regressors':regressors, # float[N, nreg] the regressors
'sampling':sampling_rate("monthly"), # must be "daily", "monthly", or "annual"
'S':10., # prior variance on the regression coefficients
'sigma_trend_prior':1e-4, # std-dev of the half-Gaussian prior on sigma_trend
'sigma_seas_prior':0.01, # std-dev of the half-Gaussian prior on sigma_seas
'sigma_AR_prior':0.5 # std-dev of the half_Gaussian prior on the AR1 process std-dev
}
# Initialization: Initial guess values for the hyper-parameters
initial_state = {
'sigma_trend':0.0001,
'sigma_seas':0.001,
'sigma_AR':0.01,
'rhoAR1':0.1,
}
# Ok, let's run it
fit = dlm_model.sampling(data=input_data, iter=3000, warmup=1000, chains=1, init = [initial_state], verbose=True, pars=('sigma_trend', 'sigma_seas', 'sigma_AR', 'rhoAR1', 'trend', 'slope', 'beta', 'seasonal'))
# Extract the various bits from the fit-object.
# Trend
trend = fit.extract()['trend'][:,:]
# Gradient of the DLM trend
slope = fit.extract()['slope'][:,:]
# Seasonal cycle
seasonal_cycle = fit.extract()['seasonal'][:,:]
# Regressor coefficients
regressor_coefficients = fit.extract()['beta'][:,:]
# DLM hyper parameters
sigma_trend = fit.extract()['sigma_trend']
sigma_seas = fit.extract()['sigma_seas']
sigma_AR = fit.extract()['sigma_AR']
rhoAR1 = fit.extract()['rhoAR1']
# Plot recovered trend against the data
# Plot the data
plt.plot(T, d, lw = 2, alpha = 0.2)
# Plot the mean trend
plt.plot(T, np.mean(trend, axis = 0), color = 'red', ls = '--')
# Plot a grey band showing the error on the extracted DLM trend
# NOTE: this includes the error on the shape of the trend, but also on the overall offset, so can look deceptively large
plt.fill_between(T, np.mean(trend, axis = 0) - np.std(trend, axis = 0), np.mean(trend, axis = 0) + np.std(trend, axis = 0), color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel(r'$O_3$ [ppm]')
plt.show()
# Same plot but without the data behind (for a closer look at the DLM trend)
plt.plot(T, np.mean(trend, axis = 0), color = 'red', ls = '--')
plt.fill_between(T, np.mean(trend, axis = 0) - np.std(trend, axis = 0), np.mean(trend, axis = 0) + np.std(trend, axis = 0), color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel(r'$O_3$ [ppm]')
plt.show()
# Plot the slope of the recovered trend
plt.plot(T, np.mean(slope, axis = 0), color = 'red', ls = '--')
plt.fill_between(T, np.mean(slope, axis = 0) - np.std(slope, axis = 0), np.mean(slope, axis = 0) + np.std(slope, axis = 0), color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel(r'd$O_3$/dT [ppm month$^{-1}$]')
plt.show()
# Plot the recovered seasonal cycle and uncertainties
plt.plot(T, np.mean(seasonal_cycle, axis = 0))
plt.fill_between(T, np.mean(seasonal_cycle, axis = 0) - np.std(seasonal_cycle, axis = 0), np.mean(seasonal_cycle, axis = 0) + np.std(seasonal_cycle, axis = 0), color = 'grey', alpha = 0.5)
plt.xlabel('time, T [Julian date]')
plt.ylabel('seasonal cycle $O_3$ [ppm]')
plt.show()
# Plot posteriors for the regression coefficients
regressor_names = ['ENSO', 'SOLAR', 'QBO30', 'QBO50', 'SAOD']
for i in range(len(regressors.T)):
beta = regressor_coefficients[:,i]
kde = stats.gaussian_kde(beta)
x = np.linspace(min(beta) - np.ptp(beta)*0.1, max(beta) + np.ptp(beta)*0.1, 300)
plt.hist(beta, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title(regressor_names[i])
plt.ylabel('posterior density')
plt.xlabel(r'$\beta_{}$'.format(i))
plt.show()
# Plot posteriors for the DLM hyper parameters
kde = stats.gaussian_kde(sigma_trend)
x = np.linspace(0, max(sigma_trend)*1.1, 300)
plt.hist(sigma_trend, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title('sigma_trend')
plt.ylabel('posterior density')
plt.xlabel(r'$\sigma_\mathrm{trend}$')
plt.show()
kde = stats.gaussian_kde(sigma_seas)
x = np.linspace(0, max(sigma_seas)*1.1, 300)
plt.hist(sigma_seas, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title('sigma_seas')
plt.ylabel('posterior density')
plt.xlabel(r'$\sigma_\mathrm{seas}$')
plt.show()
kde = stats.gaussian_kde(sigma_AR)
x = np.linspace(min(sigma_AR) - np.ptp(sigma_AR)*0.1, max(sigma_AR) + np.ptp(sigma_AR)*0.1, 300)
plt.hist(sigma_AR, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title('sigma_AR')
plt.ylabel('posterior density')
plt.xlabel(r'$\sigma_\mathrm{AR}$')
plt.show()
kde = stats.gaussian_kde(rhoAR1)
x = np.linspace(min(rhoAR1) - np.ptp(rhoAR1)*0.1, max(rhoAR1) + np.ptp(rhoAR1)*0.1, 300)
plt.hist(rhoAR1, bins=20, density=True, alpha = 0.1)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.title('rhoAR1')
plt.ylabel('posterior density')
plt.xlabel(r'$\rho_\mathrm{AR1}$')
plt.show()
# Do trace plots of the MCMC chains of the hyper-parameters
plt.plot(sigma_trend)
plt.title('sigma_trend')
plt.xlabel('sample #')
plt.ylabel(r'$\sigma_\mathrm{trend}$')
plt.show()
plt.plot(sigma_seas)
plt.title('sigma_seas')
plt.xlabel('sample #')
plt.ylabel(r'$\sigma_\mathrm{seas}$')
plt.show()
plt.plot(sigma_AR)
plt.title('sigma_AR')
plt.xlabel('sample #')
plt.ylabel(r'$\sigma_\mathrm{AR}$')
plt.show()
plt.plot(rhoAR1)
plt.title('rhoAR1')
plt.xlabel('sample #')
plt.ylabel(r'$\rho_\mathrm{AR1}$')
plt.show()
# Plot the posterior on the overall change in O3 between two dates eg, jan1998 and dec2017
# Time indices for the two dates
jan1998 = 156 # index of the T array corresponding to Jan 1998
dec2017 = -1 # (end of time series; december 2017)
# Construct MCMC samples for the change in O3 between those two dates by differencing the trend samples at those dates
deltaO3_jan1998_dec2017 = trend[:,dec2017] - trend[:,jan1998]
# Plot the histogram of the posterior samples of DeltaO3 between Jan 1998 and Dec 2017
kde = stats.gaussian_kde(deltaO3_jan1998_dec2017)
x = np.linspace(min(deltaO3_jan1998_dec2017) - np.ptp(deltaO3_jan1998_dec2017)*0.1, max(deltaO3_jan1998_dec2017) + np.ptp(deltaO3_jan1998_dec2017)*0.1, 300)
plt.hist(deltaO3_jan1998_dec2017, bins = 15, alpha = 0.1, density = True)
plt.plot(x, kde(x), lw = 3)
plt.xlim(x[0], x[-1])
plt.xlabel(r'$\Delta O_3$ Jan 1998 to Dec 2017, [ppm]')
plt.ylabel('posterior density')
plt.show()
| 0.755997 | 0.963848 |
# Supervised Learning and K Nearest Neighbors Exercises
## Introduction
We will be using customer churn data from the telecom industry. We will load this data and use K-nearest neighbors to predict customer churn based on account characteristics. The data we will use are in a file called `Orange_Telecom_Churn_Data_OK.csv` found in the [GitHub repository](https://github.com/rosalvoneto/InteligenciaComputacional).
## Question 1
* Begin by importing the data. Examine the columns and data.
```
# Import the data
import pandas as pd
df = pd.read_csv('data/Orange_Telecom_Churn_Data_OK.csv')
df
```
## Question 2
* Notice that the data contains a phone number. Do you think this is good feature to use when building a machine learning model? Why or why not?
We will not be using it, so it can be dropped from the data.
```
# Remove phone_number column
df = df.drop(['phone_number'], axis = 1)
```
## Question 3
* Separate the feature columns (everything except `churned`) from the label (`churned`). This will create two tables.
* Fit a K-nearest neighbors model with a value of `k=3` to this data and predict the outcome on the same data.
```
# Split the data into two dataframes
df_label = df.churned
df_feature = df.drop(['churned'], axis = 1)
print(df_label)
df_feature
# Fit a K-nearest neighbors model with a value of k=3
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
```
## Question 4
Ways to measure error haven't been discussed in class yet, but accuracy is an easy one to understand--it is simply the percent of labels that were correctly predicted (either true or false).
* Write a function to calculate accuracy using the actual and predicted labels.
* Using the function, calculate the accuracy of this K-nearest neighbors model on the data.
```
# Function to calculate accuracy
from sklearn.metrics import accuracy_score
def knn_accuracy(X_data, Y_data):
KNN = KNeighborsClassifier(n_neighbors=3)
KNN = KNN.fit(X_data, Y_data)
Y_predicted = KNN.predict(X_data)
return accuracy_score(Y_data, Y_predicted)
# Using the function
knn_accuracy(df_feature, df_label)
```
## Question 5
* Fit a K-nearest neighbors model using values of `k` (`n_neighbors`) ranging from 1 to 20. Store the accuracy and the value of `k` used from each of these fits in a list or dictionary.
* Plot (or view the table of) the `accuracy` vs `k`. What do you notice happens when `k=1`? Why do you think this is? *Hint:* it's for the same reason discussed above.
```
# K-nearest neighbors model
fits = {
'k': list(range(1, 21)),
'accuracy': [
x for x in [
accuracy_score(df_label,
KNeighborsClassifier(n_neighbors=k).fit(df_feature, df_label).predict(df_feature)
) for k in range(1, 21)
]
]
}
fits
# Plot
import matplotlib.pyplot as plt
plt.xlabel('K')
plt.ylabel('accuracy')
plt.title('KNN Accuracy')
ticks = [ x for x in fits['k'] if x%2 == 1 ]
plt.xticks(ticks, ticks)
plt.bar(fits['k'], fits['accuracy'], width=0.5)
```
|
github_jupyter
|
# Import the data
import pandas as pd
df = pd.read_csv('data/Orange_Telecom_Churn_Data_OK.csv')
df
# Remove phone_number column
df = df.drop(['phone_number'], axis = 1)
# Split the data into two dataframes
df_label = df.churned
df_feature = df.drop(['churned'], axis = 1)
print(df_label)
df_feature
# Fit a K-nearest neighbors model with a value of k=3
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
# Function to calculate accuracy
from sklearn.metrics import accuracy_score
def knn_accuracy(X_data, Y_data):
KNN = KNeighborsClassifier(n_neighbors=3)
KNN = KNN.fit(X_data, Y_data)
Y_predicted = KNN.predict(X_data)
return accuracy_score(Y_data, Y_predicted)
# Using the function
knn_accuracy(df_feature, df_label)
# K-nearest neighbors model
fits = {
'k': list(range(1, 21)),
'accuracy': [
x for x in [
accuracy_score(df_label,
KNeighborsClassifier(n_neighbors=k).fit(df_feature, df_label).predict(df_feature)
) for k in range(1, 21)
]
]
}
fits
# Plot
import matplotlib.pyplot as plt
plt.xlabel('K')
plt.ylabel('accuracy')
plt.title('KNN Accuracy')
ticks = [ x for x in fits['k'] if x%2 == 1 ]
plt.xticks(ticks, ticks)
plt.bar(fits['k'], fits['accuracy'], width=0.5)
| 0.812979 | 0.991546 |
<h3>Linear Regression</h3>
<h4>Packages Used</h4>
<ul>
<li>numpy</li>
<li>matplotlib</li>
</ul>
<h3>Import necessary packages</h3>
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams['figure.figsize'] = [10, 8]
```
<h3>ReadData(data,separator): Helper function to read data</h3>
<h4> Assumes data is of the form X[0], X[1], ..., X[n], Y</h4>
<h5>Where X[i] is a feature and Y is the label</h5>
```
def ReadData(data, separator):
XY = np.genfromtxt(data, delimiter=separator)
m = XY.shape[0]
Y = XY[:, -1].reshape(m, 1)
X = XY[:, 0:-1]
bias = np.zeros((1, 1))
theta = np.zeros((X.shape[1], 1))
return X, Y, m, bias, theta
```
<h3>Normalize(data): Helper function to Normalize data</h3>
```
def Normalize(data):
Mu = np.mean(X, axis=0, keepdims=True)
Sigma = np.std(X, axis=0, keepdims=True)
data = ((data-Mu)/Sigma)
return data, Mu, Sigma
```
<h3>GradDescent_CostCalc(iter1,X,theta,bias,Y,learningratebym,costweight): Function to calculate costs, final theata, biases using Gradient Descent</h3>
```
def GradDescent_CostCalc(iter1, X, theta, bias, Y, learningratebym, costweight):
costs = []
for i in range(iter1):
H = np.dot(X, theta) + bias
diff = H - Y
delta = learningratebym * np.dot(diff.T, X).T
theta = theta - delta
bias = bias - (learningratebym * np.sum(diff,keepdims = True))
J = costweight * sum(np.square(diff))
costs.append(J.item(0))
return costs, bias, theta
```
<h3>CostCalc(X,theta,bias,Y,costweight): Function to calculate cost</h3>
```
def CostCalc(X, theta, bias, Y, costweight):
H = np.dot(X, theta) + bias
diff = H - Y
J = costweight * sum(np.square(diff))
return J
```
<h3>PlotData(Original_X,Normalized_X,Y,trainedtheta,trainedbias,costs,fignumber=1): Helper function to Plot data,predicted target and costs</h3>
```
def PlotData(Original_X, Normalized_X, Y, trainedtheta, trainedbias, costs, fignumber=1):
plt.style.use('ggplot')
fig = plt.figure(fignumber)
ax = fig.add_subplot(111, projection='3d')
ax.scatter(Original_X[:,0], Original_X[:,1], Y[:,0], marker = '*', c='#ef0909')
Y = np.linspace(min(Original_X[:,1]), max(Original_X[:,1]), 5)
X = np.linspace(min(Original_X[:,0]), max(Original_X[:,0]), 100)
X1 = np.array([ (i,j) for i in X for j in Y])
Z = np.dot(Normalize(X1)[0],trainedtheta) + trainedbias
X, Y = np.meshgrid(X, Y, sparse=False, indexing='ij')
ax.scatter(X, Y, Z, marker = '*', c='#493d35')
ax.set_xlabel('Feature 0')
ax.set_ylabel('Feature 1')
ax.set_zlabel('Label')
plt.figure(fignumber+1)
plt.ylabel('Cost')
plt.xlabel('Iteration')
plt.plot(range(iter1),costs, '-')
return
```
<h2>Main Code below</h2>
```
X, Y, m, bias, theta = ReadData('LinRegDS2.txt', ',')
Original_X = X
X, Mu, Sigma = Normalize(X)
learningrate = 0.1
iter1 = 50
learningratebym = learningrate/m
costweight = 1/(2*m)
costs, trainedbias, trainedtheta = GradDescent_CostCalc(iter1, X, theta, bias, Y,
learningratebym, costweight)
PlotData(Original_X, X, Y, trainedtheta, trainedbias, costs)
actual_input = np.array([1650,3]).reshape(1, 2)
normalized_input = (actual_input-Mu)/Sigma
print(f'For population = {actual_input.item(0)},'
f' we predict a profit of {(trainedbias + np.dot(normalized_input, trainedtheta)).item(0)}')
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams['figure.figsize'] = [10, 8]
def ReadData(data, separator):
XY = np.genfromtxt(data, delimiter=separator)
m = XY.shape[0]
Y = XY[:, -1].reshape(m, 1)
X = XY[:, 0:-1]
bias = np.zeros((1, 1))
theta = np.zeros((X.shape[1], 1))
return X, Y, m, bias, theta
def Normalize(data):
Mu = np.mean(X, axis=0, keepdims=True)
Sigma = np.std(X, axis=0, keepdims=True)
data = ((data-Mu)/Sigma)
return data, Mu, Sigma
def GradDescent_CostCalc(iter1, X, theta, bias, Y, learningratebym, costweight):
costs = []
for i in range(iter1):
H = np.dot(X, theta) + bias
diff = H - Y
delta = learningratebym * np.dot(diff.T, X).T
theta = theta - delta
bias = bias - (learningratebym * np.sum(diff,keepdims = True))
J = costweight * sum(np.square(diff))
costs.append(J.item(0))
return costs, bias, theta
def CostCalc(X, theta, bias, Y, costweight):
H = np.dot(X, theta) + bias
diff = H - Y
J = costweight * sum(np.square(diff))
return J
def PlotData(Original_X, Normalized_X, Y, trainedtheta, trainedbias, costs, fignumber=1):
plt.style.use('ggplot')
fig = plt.figure(fignumber)
ax = fig.add_subplot(111, projection='3d')
ax.scatter(Original_X[:,0], Original_X[:,1], Y[:,0], marker = '*', c='#ef0909')
Y = np.linspace(min(Original_X[:,1]), max(Original_X[:,1]), 5)
X = np.linspace(min(Original_X[:,0]), max(Original_X[:,0]), 100)
X1 = np.array([ (i,j) for i in X for j in Y])
Z = np.dot(Normalize(X1)[0],trainedtheta) + trainedbias
X, Y = np.meshgrid(X, Y, sparse=False, indexing='ij')
ax.scatter(X, Y, Z, marker = '*', c='#493d35')
ax.set_xlabel('Feature 0')
ax.set_ylabel('Feature 1')
ax.set_zlabel('Label')
plt.figure(fignumber+1)
plt.ylabel('Cost')
plt.xlabel('Iteration')
plt.plot(range(iter1),costs, '-')
return
X, Y, m, bias, theta = ReadData('LinRegDS2.txt', ',')
Original_X = X
X, Mu, Sigma = Normalize(X)
learningrate = 0.1
iter1 = 50
learningratebym = learningrate/m
costweight = 1/(2*m)
costs, trainedbias, trainedtheta = GradDescent_CostCalc(iter1, X, theta, bias, Y,
learningratebym, costweight)
PlotData(Original_X, X, Y, trainedtheta, trainedbias, costs)
actual_input = np.array([1650,3]).reshape(1, 2)
normalized_input = (actual_input-Mu)/Sigma
print(f'For population = {actual_input.item(0)},'
f' we predict a profit of {(trainedbias + np.dot(normalized_input, trainedtheta)).item(0)}')
| 0.580233 | 0.977088 |
## Project Objective
Par Inc., is a major manufacturer of golf equipment. Management believes that Par’s market share could be increased with the introduction of a cutresistant, longer-lasting golf ball. Therefore, the research group at Par has been investigating a new golf ball coating designed to resist cuts and provide a more durable ball. The tests with the coating have been promising.
One of the researchers voiced concern about the effect of the new coating on driving distances. Par would like the new cut-resistant ball to offer driving distances comparable to those of the current-model golf ball.
To compare the driving distances for the two balls, 40 balls of both the new and current models were subjected to distance tests.
The testing was performed with a mechanical hitting machine so that any difference between the mean distances for the two models could be attributed to a difference in the design.
The results of the tests, with distances measured to the nearest yard, are contained in the data set “Golf”.
Prepare a Managerial Report
1. Formulate and present the rationale for a hypothesis test that par could use to compare the driving distances of the current and new golf balls
2. Analyze the data to provide the hypothesis testing conclusion. What is the p-value for your test? What is your recommendation for Par Inc.?
3. Do you see a need for larger sample sizes and more testing with the golf balls? Discuss.

# Type :- Mean
# Sample :- Two
# Null Hypothesis :-
# Alternate Hypothesis :-
# Tails :-
# Level of significance
# Test Stats
```
import numpy as np
from scipy.stats import ttest_ind, levene, shapiro, iqr
import pandas as pd
import matplotlib.pyplot as plt
xlsfile = pd.ExcelFile('SM4-Golf.xls')
dframe = xlsfile.parse('Data')
a= dframe.Current
b=dframe.New
dframe.describe()
dframe.info()
```
# 1. Test of Normality
#1. histogram
#2. Skew & kurtosis
#3. Probablity plot ( shapiro test )
#4 Chi-sequre goodness of fit
```
# HIstogram
plt.hist(a)
plt.show()
# Skew and kurtosis
import scipy.stats as st
print ('kurtosis is',st.kurtosis(a))
print ('Skew is ',st.skew(a))
# Histogram
plt.hist(b)
plt.show()
print ('kurtosis is',st.kurtosis(b))
print ('Skew is ',st.skew(b))
import statsmodels.api as sm
from matplotlib import pyplot as plt
#data = sm.datasets.longley.load()
#data.exog = sm.add_constant(data.exog)
#mod_fit = sm.OLS(data.endog, data.exog).fit()
#res = mod_fit.resid # residuals
fig = sm.qqplot(a)
plt.show()
# Test of normality
# H0 :- Data is normal
# Ha :- Data is not normal
#1. histogram
#2. Skew & kurtosis
#3. Probablity plot
#4 Chi-sequre goodness of fit
shapiro(a)
shapiro(b)
```
# Test of Homogenity
```
#Bartletts test
# H0: The groups are homogenous in variance
# Ha: The groups are not homogenous in variance
levene(a,b)
```
# Run the Two Sample Test
```
# H0 : m1= m2
# Ha : m1 <> m2
t,p = ttest_ind(a,b)
print(t,p)
import scipy
def sample_power_difftest(d,s,power=0.8,sig=0.05):
z = scipy.stats.norm.isf([sig/2])
zp = -1 * scipy.stats.norm.isf([power])
n = (2*(s**2)) * ((zp+z)**2) / (d**2)
return int(round(n[0]))
mean_current=a.mean()
mean_new=b.mean()
std_current=a.std()
std_new=b.std()
print('Std_current',std_current,'std_new',std_new)
d = mean_current - mean_new
s = np.sqrt(((8.753**2)+(9.897**2))/2)
print(s,d)
n=sample_power_difftest(d,s,power=0.8,sig=0.5)
E_size = d/s
print(E_size)
```
# Power of Test
```
from statsmodels.stats.power import TTestIndPower
# parameters for power analysis
#effect = 0.8
effect = d/s
alpha = 0.05
power = 0.8
# perform power analysis
analysis = TTestIndPower()
result = analysis.solve_power(0.8, power=power, nobs1=None, ratio=1.0, alpha=alpha)
print('Sample Size: %.3f' % result)
print( effect)
import numpy as np
# calculate power curves from multiple power analyses
analysis = TTestIndPower()
analysis.plot_power(dep_var='nobs', nobs=np.arange(5, 100), effect_size=np.array([0.2, 0.5, 0.8]))
```
|
github_jupyter
|
import numpy as np
from scipy.stats import ttest_ind, levene, shapiro, iqr
import pandas as pd
import matplotlib.pyplot as plt
xlsfile = pd.ExcelFile('SM4-Golf.xls')
dframe = xlsfile.parse('Data')
a= dframe.Current
b=dframe.New
dframe.describe()
dframe.info()
# HIstogram
plt.hist(a)
plt.show()
# Skew and kurtosis
import scipy.stats as st
print ('kurtosis is',st.kurtosis(a))
print ('Skew is ',st.skew(a))
# Histogram
plt.hist(b)
plt.show()
print ('kurtosis is',st.kurtosis(b))
print ('Skew is ',st.skew(b))
import statsmodels.api as sm
from matplotlib import pyplot as plt
#data = sm.datasets.longley.load()
#data.exog = sm.add_constant(data.exog)
#mod_fit = sm.OLS(data.endog, data.exog).fit()
#res = mod_fit.resid # residuals
fig = sm.qqplot(a)
plt.show()
# Test of normality
# H0 :- Data is normal
# Ha :- Data is not normal
#1. histogram
#2. Skew & kurtosis
#3. Probablity plot
#4 Chi-sequre goodness of fit
shapiro(a)
shapiro(b)
#Bartletts test
# H0: The groups are homogenous in variance
# Ha: The groups are not homogenous in variance
levene(a,b)
# H0 : m1= m2
# Ha : m1 <> m2
t,p = ttest_ind(a,b)
print(t,p)
import scipy
def sample_power_difftest(d,s,power=0.8,sig=0.05):
z = scipy.stats.norm.isf([sig/2])
zp = -1 * scipy.stats.norm.isf([power])
n = (2*(s**2)) * ((zp+z)**2) / (d**2)
return int(round(n[0]))
mean_current=a.mean()
mean_new=b.mean()
std_current=a.std()
std_new=b.std()
print('Std_current',std_current,'std_new',std_new)
d = mean_current - mean_new
s = np.sqrt(((8.753**2)+(9.897**2))/2)
print(s,d)
n=sample_power_difftest(d,s,power=0.8,sig=0.5)
E_size = d/s
print(E_size)
from statsmodels.stats.power import TTestIndPower
# parameters for power analysis
#effect = 0.8
effect = d/s
alpha = 0.05
power = 0.8
# perform power analysis
analysis = TTestIndPower()
result = analysis.solve_power(0.8, power=power, nobs1=None, ratio=1.0, alpha=alpha)
print('Sample Size: %.3f' % result)
print( effect)
import numpy as np
# calculate power curves from multiple power analyses
analysis = TTestIndPower()
analysis.plot_power(dep_var='nobs', nobs=np.arange(5, 100), effect_size=np.array([0.2, 0.5, 0.8]))
| 0.323701 | 0.97622 |
# In-Class Tutorial for SVM
In this tutorial, we'll learn about SVMs!
SVMs, or **Support Vector Machines**, are advanced supervised machine learning models used for classification and/or regression.
Here, we'll be talking primarily about classification using SVMs.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline
import seaborn as sns
from scipy import stats
from sklearn.datasets.samples_generator import make_blobs, make_circles
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from ipywidgets import interact, fixed
from mpl_toolkits import mplot3d
```
## How do we classify these data?
Let's create some blobs using some internal library methods to test out the functionality of SVM Classifiers!
```
X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
```
## Wait... which decision boundary is right? Why?
How do we know that our decision boundary calculation is fitting to the best possible location?
In other words, **how can we optimize** our decision boundary?
```
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.plot([0.6], [2.1], 'x', color='red', markeredgewidth=2, markersize=10)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);
```
The red X is showing our best fit, but obviously we can write some unstable MatPlotLib code every time we want to run an SVM... *especially* not for larger datasets!
Let's talk about our **minimization-maximization algorithm** (a.k.a. the *seesaw*!).
## An Algorithm that Minimizes Misclassification while Maximizing the Decision Margin!
```
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
```
Our **min-max algorithm** allows us to simulate our *margin*, which is indicative of the optimizer.
In other words, this allows us to see the best fit linear model, since the best fit is where the *distance between the decision boundary and our support vectors* is **maximized** and the *ratio of misclassified to correctly classified data* is **minimized**.
## Let's initialize our Support Vector Machine Classifier.
Enough talk!
Let's dive right into some cool code!
At this point, you should roughly know how to initialize ML models and fit data to them.
SVMs are no different, save some particular parameters.
For now, let's leave that second line of code *commented out*. Trust me on this one.
```
svc_model = SVC()
# svc_model = SVC(kernel="linear", C=1E10)
svc_model.fit(X, y)
```
Wow, those are a **lot** of parameters.
---
Sometimes, I like to imagine a machine learning model as a big family.
The algorithms underlying the machine learning model, like our minimization-maximization algorithm, are the parents and guardians, bringing order, functionality, and stability to our model.
Without them, our model simply wouldn't work.
Then I imagine the parameters of our model, like our *kernel* and *C* arguments commented out above, are the little kids of the family, bringing an element of fun, creativity, and flexibility to our model that, if left unchecked, could result in chaos, destruction, and the end of all things as we know it.
And that's why we call those parameters **hyperparameters**!
---
Let's see how those hyperparameters affect our model, shall we?
## Let's write a function to plot our SVC decision boundary function.
Don't worry about exactly how and why all this is working!
This is some handy dandy little MatPlotLib code to plot our decision boundary function with our simulated margins.
This time, rather than shading in the margin region, we're simply going to denote the margin boundaries with dotted lines.
```
def plot_svc_decision_function(model=svc_model, ax=None, plot_support=True):
"""Plot the decision function for a 2D SVC"""
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
# plot decision boundary and margins
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)
```
## Let's plot our margin and decision boundary. What went wrong?
```
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(model=svc_model);
```
Hmm, that's not quite what we expected.
What could have gone wrong?
If you're wondering why our dotted lines are now surrounding our data clusters without abiding by a linear decision function, you should ask yourself: *how does our SVM know to use a linear boundary function*?
Short answer? **It doesn't**.
Long answer? The `SVC()` class defaults to thinking that the ideal kernel is a *radial basis function*, which approximates a circular boundary function.
We certainly don't want that; we only want a simple line dividing our data clusters.
That's why we have to tell it!
---
Let's go back up to our cell where we *initialize our SVM Classifier* and *fit the model to our data*.
Now, **comment the empty initialized SVC()** out and **uncomment the second SVC() initializing line**.
Run that cell and then run the cell above. See any changes?
;-)
## Let's write a function that plots our margin and SVC decision boundary.
Now that we've played around with initializing and fitting our SVM classifier to our dummy data, let's take a quick aside to see how our data actually affects our classifier.
This is a *critical concept*, since we as data scientists want to understand why we'd use one model over another down to the very data structures entering and exiting our models.
What actually separates SVMs from other models?
Why use it?
Let's find out!
```
def plot_svm(N=10, ax=None):
X, y = make_blobs(n_samples=200, centers=2,
random_state=0, cluster_std=0.60)
X = X[:N]
y = y[:N]
svc_model = SVC(kernel="linear", C=1E10)
svc_model.fit(X, y)
ax = ax or plt.gca()
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
ax.set_xlim(-1, 4)
ax.set_ylim(-1, 6)
plot_svc_decision_function(svc_model, ax)
fig, ax = plt.subplots(1, 3, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, N in zip(ax, [50, 100, 200]):
plot_svm(N, axi)
axi.set_title("N = {0}".format(N))
```
In our example here, we've just plotted three data clusters of similar distributions fitted by SVM Classifiers, but with one critical difference.
Our first plot contains only half as many points as the second plot (or, the second plot contains exactly double the points as the first plot - whatever suits your fancy).
Likewise for the second and third plots.
However, even though we're *doubling* our data each time, we're barely making a dent in our model's fitness. Why?
...
Want to know the answer?
It's because the model doesn't fit the decision boundary to all data points, but rather fits the decision boundary to the support vectors. As you can see, the intersected support vector count doesn't change dramatically across any plot, even though we're dramatically changing the number of data values included.
This is **super important**.
SVMs are so nice because rather than storing every data point in memory to measure against every other data point (I'm looking at you, *k-Nearest Neighbors* algorithms), they only need the relative Euclidean metrics for the support vectors to approximate the decision boundary.
# Do SVCs work for non-linearly distributed data?
Now, we can spend all day using SVMs to draw lines, but let's be honest.
Any one and their mother's rudimentary CS 101 algorithms can probably effectively divide up data based on label.
However, the magic of SVMs lie in another algorithm that runs under the hood: the **kernel function**.
The kernel we specify to our SVM Classifier allows the machine to understand the approximate distribution of data, where to draw support vectors, and how to wrap our data to better achieve an optimal approximation for linear separability.
Let's explore this concept through failure: *let's fit a linear SVM classifier to a non-linear data distribution*.
```
X, y = make_circles(100, factor=0.1, noise=0.1)
clf_svc_bad = SVC(kernel="linear")
clf_svc_bad.fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
plot_svc_decision_function(clf_svc_bad, plot_support=False);
```
Eugh. Pretty abysmal, right?
In fact, try running it a few times. Each time, the data is only very slightly shifted randomly, but with completely different approximations for the linear decision boundary.
Obviously, this is because the data distribution is *non-linear*.
How do we tell that to the SVM?
We do that through the **kernel function** - by instructing the SVM that the data takes a certain distribution that requires transforming the way we *look at the data*.
That's a very important point to make: the kernel function *does not* transform our data.
Rather, it changes the way we look at it through the arithmetic transfiguration of dimensions in order to better calculate a mechanism to linearly separate our data.
Let's check that out by visualizing a unique kernel function for our sample data.
## Let's change our kernel function to see what other dimensional ways there are to separate our classes.
```
rbf = np.exp(-(X ** 2).sum(1))
def plot_3D(elev=30, azim=30, X=X, y=y):
ax = plt.subplot(projection="3d")
ax.scatter3D(X[:, 0], X[:, 1], rbf, c=y, s=50, cmap="autumn")
ax.view_init(elev=elev, azim=azim)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("rbf")
```
Just a lot of weird MatPlotLib - trust me, you don't need to know how or why this works.
Only that it works!
Now that we have our 3-dimensional visualization function, let's see it in action!
```
interact(plot_3D, elev=[0, 30], azip=(-180, 180),
X=fixed(X), y=fixed(y));
```
Pretty cool, right?
Here, we can clearly see that despite the data distribution hasn't changed with regard to our core X features, our added dimension allows us to better see a linear function (to be precise, a *plane*) that can separate our data.
---
In terms of the Support Vector Machine, this exact relationship in converting our data's dimensional frame of reference can be described by a specific kernel function called the **radial basis function**.
## We can use the _Radial Basis Function_ to better model our data.
Let's invoke the *radial basis function* as our kernel function for our Support Vector Machine classifier.
```
clf_svc_good = SVC(kernel="rbf", C=1E6)
clf_svc_good.fit(X, y)
```
Now that we've fit our data to our classifier model, let's visualize how the kernel trick allows us to achieve linear separation via our 3D hyperplane.
## Using the RBF, we can see how the extra dimension impacts the shape of our decision boundary.
Particularly, when we use our MatPlotlib utilities to visualize our decision boundary, we can see how the classifer model's accuracy is now vastly improved due to the shape of our data.
```
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
plot_svc_decision_function(clf_svc_good)
plt.scatter(clf_svc_good.support_vectors_[:, 0], clf_svc_good.support_vectors_[:, 1],
s=300, lw=1, facecolors="none");
```
## What happens when we have data that's not perfectly linearly separable?
We've spent plenty of time with our ideal case, but let's be real - most data we deal with in the real world isn't going to be perfectly linearly separable.
Rather, much of the data is likely to have *overlap*. We call this **linear non-separability**.
Let's throw some dummy data out there to better understand this.
```
X, y = make_blobs(n_samples=100, centers=2,
random_state=4, cluster_std=1.2)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn");
```
We can definitely see that our data isn't as linearly separable as we want!
To be precise, there is no specific linear function in our current frame of reference that can perfectly separate all our data into two groups.
---
When our data isn't ideal, we can use **hyperparameter tuning** to optimize our model to achieve a maximized predictive score for our model across our data.
Let's start with our C-parameter, which is used for *hardening* and *softening* our decision boundary margin.
## Tuning our C-parameter to 'harden' or 'soften' our margins.
Using the power of MatPlotLib, we can manipulate the C-parameter to affect our margin.
To be more precise, the more C-parameter increases, the harsher data points are *penalized* for being contained within the boundaries of the decision margin.
Likewise, the more C-parameter decreases, the easier it is for data points to be contained within the decision margin.
We can see this depicted with the visualizations below!
```
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=1.2)
fig, ax = plt.subplots(1, 3, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, C in zip(ax, [10.0, 0.1, 0.01]):
clf_svc_tuned = SVC(kernel="linear", C=C)
clf_svc_tuned.fit(X, y)
axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
plot_svc_decision_function(clf_svc_tuned, axi)
axi.scatter(clf_svc_tuned.support_vectors_[:, 0],
clf_svc_tuned.support_vectors_[:, 1],
s=300, lw=1, facecolors="none");
axi.set_title("C = {:.2f}".format(C), size=14)
```
As we can see, there's quite a bit to unpack with Support Vector Machine Classifiers.
Including hyperparameter tuning, model fitness, and kernel function initialization, there's a few critical factors to ensuring that our SVM model works optimally.
---
In order to wrap up our understanding of SVMs, let's tackle a coding example of applying an SVM classifier to some data you may be familiar with: **the Iris Dataset**.
# SVM Classification using the Iris Dataset.
---
For our SVM classification for the Iris data, we start by initializing our dataset and target variable vector.
```
data = load_iris()
print(data.DESCR)
```
## Let's play with Parameter Tuning!
- **kernel**: ("linear", "rbf")
<br>Changes the _linear transformation function_ to fit around our data (decision boundary function).<br><br>
- **C**: (0, inf)
<br>Controls trade-off between _smooth decision boundary_ and _minimizing training misclassification_.<br><br>
- **gamma**: (0, inf)
<br>Kernel coefficient; controls _'fitness'_ of model to training data.
We've already played a little with hyperparameter tuning, but now let's take it to the next level.
We can combine our knowledge of Python programming with our newfound skills in machine learning to construct several different models with varying levels of hyperparameterization to identify the optimal model setup.
Let's functionalize that below.
```
def svc_iris_classifier(iris, kernel="linear", C=1.0, gamma="auto"):
X, y = iris.data[:, :2], iris.target
clf_svc_iris = SVC(kernel=kernel, C=C, gamma=gamma)
clf_svc_iris.fit(X, y)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min) / 100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
plt.subplot(1, 1, 1)
Z = clf_svc_iris.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.BuGn_r)
plt.xlabel("Sepal Length")
plt.ylabel("Sepal Width")
plt.xlim(xx.min(), xx.max())
plt.title("SVC (kernel='{}', C={}, gamma={})".format(kernel, C, gamma))
```
The function above may seem a little daunting at the start, but we've actually built the entirety of it before.
In addition to our Iris data, our function `svc_iris_classifier()` takes three keyword arguments: the *kernel function*, the *C-parameter*, and our *gamma* value for model fitness.
The function is capable of generating a contour map overlay using MatPlotLib across our data, clearly visualizing what's happening under the hood of the SVM - the SVM is creating decision boundaries by which it can effectively predict the target label of new data points by simply checking which decision boundary range they fall into.
---
Give it a try!
Try manipulating the values of `kernel`, `C`, and `gamma`.
What happens to our contour map?
```
svc_iris_classifier(data, kernel="rbf", C=1.0, gamma=0.1)
```
This is nice and all, but how can we more accurately calculate the optimal SVC model?
It would certainly help if there were numerical measures to determing the accuracy of a model, right?
Right?
# And now, tying it all together for prediction...
Let's put this all together.
After defining our training and testing Iris data, create your fitted model and run our `.predict()` and `.score()` methods.
```
X, y = data.data[:, :2], data.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
clf_svc_iris = SVC(kernel="linear", C=1.0, gamma="auto")
clf_svc_iris.fit(X_train, y_train)
y_pred = clf_svc_iris.predict(X_test)
clf_svc_iris.score(X_test, y_test)
```
Our `y_pred` is of the same shape of our `y_test`, as expected, and our score is reasonable!
So far, so good.
Let's pull it all together one last time with a custom engineered pipeline.
## How can we ascertain the best model configuration?
```
X, y = data.data[:, :2], data.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
possible_kernels = ["linear", "rbf"]
possible_Cs = [1.0, 10.0, 100.0, 1000.0]
possible_gammas = ["auto", 0.1, 1.0, 10.0, 100.0]
def get_tuned_SVC_score(kernel, C, gamma):
clf = SVC(kernel=kernel, C=C, gamma=gamma)
clf.fit(X_train, y_train)
return clf.score(X_test, y_test)
clf_scores = list()
for kernel in possible_kernels:
for C in possible_Cs:
for gamma in possible_gammas:
clf_scores.append((get_tuned_SVC_score(kernel=kernel, C=C, gamma=gamma), kernel, C, gamma))
rel_max, position = 0, 0
for index, item in enumerate(clf_scores):
if item[0] > rel_max:
rel_max = item[0]
position = index
print("\nBEST SVM CLASSIFIER SCORE WITH DETAILS IS: \n\n - Score: {}\n - Kernel: '{}'\n - C: {}\n - Gamma: {}\n".format(clf_scores[position][0], clf_scores[position][1], clf_scores[position][2], clf_scores[position][3]))
```
Above, we constructed some basic Python code to grab several model scores based on many differently tuned hyperparameters.
This way, we can confidently say our SVM classifier is as optimized as we can tune it to be with what we currently have to work with.
I encourage you to look into other hyperparameters surrounding SVMs and other ways you can optimize machine learning models, including cross-validation and other pipeline-related mechanics.
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline
import seaborn as sns
from scipy import stats
from sklearn.datasets.samples_generator import make_blobs, make_circles
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from ipywidgets import interact, fixed
from mpl_toolkits import mplot3d
X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.plot([0.6], [2.1], 'x', color='red', markeredgewidth=2, markersize=10)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
svc_model = SVC()
# svc_model = SVC(kernel="linear", C=1E10)
svc_model.fit(X, y)
def plot_svc_decision_function(model=svc_model, ax=None, plot_support=True):
"""Plot the decision function for a 2D SVC"""
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
# plot decision boundary and margins
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(model=svc_model);
def plot_svm(N=10, ax=None):
X, y = make_blobs(n_samples=200, centers=2,
random_state=0, cluster_std=0.60)
X = X[:N]
y = y[:N]
svc_model = SVC(kernel="linear", C=1E10)
svc_model.fit(X, y)
ax = ax or plt.gca()
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
ax.set_xlim(-1, 4)
ax.set_ylim(-1, 6)
plot_svc_decision_function(svc_model, ax)
fig, ax = plt.subplots(1, 3, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, N in zip(ax, [50, 100, 200]):
plot_svm(N, axi)
axi.set_title("N = {0}".format(N))
X, y = make_circles(100, factor=0.1, noise=0.1)
clf_svc_bad = SVC(kernel="linear")
clf_svc_bad.fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
plot_svc_decision_function(clf_svc_bad, plot_support=False);
rbf = np.exp(-(X ** 2).sum(1))
def plot_3D(elev=30, azim=30, X=X, y=y):
ax = plt.subplot(projection="3d")
ax.scatter3D(X[:, 0], X[:, 1], rbf, c=y, s=50, cmap="autumn")
ax.view_init(elev=elev, azim=azim)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("rbf")
interact(plot_3D, elev=[0, 30], azip=(-180, 180),
X=fixed(X), y=fixed(y));
clf_svc_good = SVC(kernel="rbf", C=1E6)
clf_svc_good.fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
plot_svc_decision_function(clf_svc_good)
plt.scatter(clf_svc_good.support_vectors_[:, 0], clf_svc_good.support_vectors_[:, 1],
s=300, lw=1, facecolors="none");
X, y = make_blobs(n_samples=100, centers=2,
random_state=4, cluster_std=1.2)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn");
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=1.2)
fig, ax = plt.subplots(1, 3, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, C in zip(ax, [10.0, 0.1, 0.01]):
clf_svc_tuned = SVC(kernel="linear", C=C)
clf_svc_tuned.fit(X, y)
axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
plot_svc_decision_function(clf_svc_tuned, axi)
axi.scatter(clf_svc_tuned.support_vectors_[:, 0],
clf_svc_tuned.support_vectors_[:, 1],
s=300, lw=1, facecolors="none");
axi.set_title("C = {:.2f}".format(C), size=14)
data = load_iris()
print(data.DESCR)
def svc_iris_classifier(iris, kernel="linear", C=1.0, gamma="auto"):
X, y = iris.data[:, :2], iris.target
clf_svc_iris = SVC(kernel=kernel, C=C, gamma=gamma)
clf_svc_iris.fit(X, y)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min) / 100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
plt.subplot(1, 1, 1)
Z = clf_svc_iris.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.BuGn_r)
plt.xlabel("Sepal Length")
plt.ylabel("Sepal Width")
plt.xlim(xx.min(), xx.max())
plt.title("SVC (kernel='{}', C={}, gamma={})".format(kernel, C, gamma))
svc_iris_classifier(data, kernel="rbf", C=1.0, gamma=0.1)
X, y = data.data[:, :2], data.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
clf_svc_iris = SVC(kernel="linear", C=1.0, gamma="auto")
clf_svc_iris.fit(X_train, y_train)
y_pred = clf_svc_iris.predict(X_test)
clf_svc_iris.score(X_test, y_test)
X, y = data.data[:, :2], data.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
possible_kernels = ["linear", "rbf"]
possible_Cs = [1.0, 10.0, 100.0, 1000.0]
possible_gammas = ["auto", 0.1, 1.0, 10.0, 100.0]
def get_tuned_SVC_score(kernel, C, gamma):
clf = SVC(kernel=kernel, C=C, gamma=gamma)
clf.fit(X_train, y_train)
return clf.score(X_test, y_test)
clf_scores = list()
for kernel in possible_kernels:
for C in possible_Cs:
for gamma in possible_gammas:
clf_scores.append((get_tuned_SVC_score(kernel=kernel, C=C, gamma=gamma), kernel, C, gamma))
rel_max, position = 0, 0
for index, item in enumerate(clf_scores):
if item[0] > rel_max:
rel_max = item[0]
position = index
print("\nBEST SVM CLASSIFIER SCORE WITH DETAILS IS: \n\n - Score: {}\n - Kernel: '{}'\n - C: {}\n - Gamma: {}\n".format(clf_scores[position][0], clf_scores[position][1], clf_scores[position][2], clf_scores[position][3]))
| 0.705075 | 0.984109 |
# Introduction
In this notebook, we will explore the use of matrix representations of graphs, and show how their are direct matrix parallels for some of the algorithms that we have investigated.
```
import networkx as nx
from networkx import bipartite
import matplotlib.pyplot as plt
import nxviz as nv
from custom.load_data import load_university_social_network, load_amazon_reviews
from matplotlib import animation
from IPython.display import HTML
import numpy as np
%load_ext autoreload
%autoreload 2
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
```
For this notebook, we will specifically see the connection between matrix operations and pathfinding between nodes.
# Toy Example: Linear Chain
To start, let us use a simple four-node network, in which nodes are joined in a chain. Convince yourself that this is is a linear chain by running the cell below.
```
nodes = list(range(4))
G1 = nx.Graph()
G1.add_nodes_from(nodes)
G1.add_edges_from(zip(nodes, nodes[1:]))
```
## Graph Form
When visualized as circles and lines, the graph looks like this:
```
nx.draw(G1, with_labels=True)
```
## Matrix Form
When represented in matrix form, it looks like the plot below. (Explain row by columns = node by nodes.)
```
nv.MatrixPlot(G1).draw()
```
## Playing with the matrix form
NetworkX provides a `to_numpy_array()` function that will return a numpy array of the graph. That is used behind-the-scenes in `nxviz` to generate the MatrixPlot.
```
A1 = nx.to_numpy_array(G1, nodelist=sorted(G1.nodes()))
A1
```
One neat result is that if we take the adjacency matrix, and matrix-matrix multiply it against itself ("matrix power 2"), we will get back a new matrix that has interesting properties.
```
import numpy as np
# One way of coding this up
np.linalg.matrix_power(A1, 2)
# Another equivalent way, that takes advantage of Python 3.5's matrix multiply operator
A1 @ A1
```
**Firstly**, if we look at the off-diagonals of the new matrix, this corresponds to the number of paths of length 2 that exist between those two nodes.
```
np.diag(A1 @ A1)
```
Here, one path of length 2 exists between node 0 and node 2, and one path of length 2 exists between node 1 and node 3.
**Secondly**, you may notice that the diagonals look like the degree of the nodes. This is a unique property of the 2nd adjacency matrix power: for every node, there are $ d $ degree paths of length two to get back to that same node.
Not convinced? To get from a node and back, that's a path length of 2! :-)
Let's see if the following statment is true: The $ k^{th} $ matrix power of the graph adjacency matrix indicates how many paths of length $ k $ exist between each pair of nodes.
```
np.linalg.matrix_power(A1, 3)
```
Indeed, if we think about it, there is, by definition, no way sequence of graph traversals that will allow us to go back to a node within 3 steps. We will always end up at some neighboring node.
In addition, to get to the neighboring node in 3 steps, there are two ways to go about it:
- node -> neighbor -> node -> neighbor
- node -> neighbor -> neighbor's neighbor -> neighbor
Or for the case of this chain graph:
- 0 -> 1 -> 0 -> 1
- 0 -> 1 -> 2 -> 1
# Toy Example: Directed Linear Chain
Let's see if the same properties hold for a directed graph.
```
nodes
G2 = nx.DiGraph()
G2.add_nodes_from(nodes)
G2.add_edges_from(zip(nodes, nodes[1:]))
nx.draw(G2, with_labels=True)
```
Recall that in a directed graph, the matrix representation is not guaranteed to be symmetric.
```
A2 = nx.to_numpy_array(G2)
A2
```
Let's look at the 2nd matrix power: the number of paths of length 2 between any pair of nodes.
```
np.linalg.matrix_power(A2, 2)
```
We see that there's only one path from node 0 to node 2 of length 2, and one path from node 1 to node 3. If you're not convinced of this, trace it for yourself!
## Exercise
In this directed graph, how many paths are there from node 0 to node 3 of length 3? Compute the 3rd matrix power and verify your answer.
```
np.linalg.matrix_power(A2, 3)
```
# Real Data
Now that we've looked at a toy example, let's play around with a real dataset!
This dataset is a residence hall rating dataset. From the [source website](http://konect.cc/networks/moreno_oz):
> This directed network contains friendship ratings between 217 residents living at a residence hall located on the Australian National University campus. A node represents a person and edges contain ratings of one friend to another.
For the purposes of this exercise, we will treat the edges as if they were unweighted.
```
G = load_university_social_network()
```
## Exercise
Use nxviz's MatrixPlot to draw the graph.
```
nv.MatrixPlot(G).draw()
```
## Exercise
Using what you know from the previous material, find out how many connected component subgraphs there are in the subgraph.
**Hint:** You may need to convert the graph to an undirected one first.
```
list(nx.connected_components(G.to_undirected()))
```
## Exercise
Since there is only one connected component subgraph, pick two nodes in the graph and see how many shortest paths there exist between those two nodes.
**Hint:** You will first need to know what the shortest path length is between those two nodes.
```
nx.shortest_path(G, 30, 100)
A = nx.to_numpy_array(G)
np.linalg.matrix_power(A, 4)[29, 99]
```
# Message Passing
Message passing on graphs is a fascinating topic to explore. It's a neat way to think about a wide variety of problems, including the spread of infectious disease agents, rumours, and more. As it turns out, there's a direct matrix interpretation of the message passing operation.
To illustrate this more clearly, let's go back to the directed chain graph, `G2`.
```
nx.draw(G2, with_labels=True)
```
If we have a message that begins at node 0, and it is only passed to its neighbors, then node 1 is the next one that possess the message. Node 1 then passes it to node 2, and so on, until it reaches node 3.
There are two key ideas to introduce here. Firstly, there is the notion of the **"wavefront"** of message passing: at the first time step, node 0 is the wavefront, and as time progresses, node 1, 2 and 3 progressively become the wavefront.
Secondly, as the message gets passed, the number of nodes that have seen the message progressively increases.
Let's see how this gets implemented in matrix form.
## Matrix Message Passing
To represent the data, we start with a vertical array of messages of shape `(1, 4)`. Let's use the following conventions:
- `1` indicates that a node currently has the message.
- `0` indicates that a node currently does not have the message.
Since the message starts at node 0, let's put a `1` in that cell of the array, and `0`s elsewhere.
```
msg = np.array([1, 0, 0, 0]).reshape(1, 4)
msg
```
In order to simulate one round of message passing, we matrix multiply the message with the adjacency matrix.
```
msg2 = msg @ A2
msg2
```
The interpretation now is that the message is currently at node 1.
To simulate a second round, we take that result and matrix multiply it against the adjacency matrix again.
```
msg3 = msg2 @ A2
msg3
```
The interpretation now is that the message is currently at node 2.
### Exercise
Let's make an animation of this. I have pre-written the animation functions for you; your task is to implement the message passing function `propagate()` to precompute at each time step the message status.
```
# fig, ax = plt.subplots()
def propagate(G, msg, n_frames):
"""
Computes the node values based on propagation.
Intended to be used before or when being passed into the
anim() function (defined below).
:param G: A NetworkX Graph.
:param msg: The initial state of the message.
:returns: A list of 1/0 representing message status at
each node.
"""
# Initialize a list to store message states at each timestep.
msg_states = []
# Set a variable `new_msg` to be the initial message state.
new_msg = msg
# Get the adjacency matrix of the graph G.
A = nx.to_numpy_array(G)
# Perform message passing at each time step
for i in range(n_frames):
msg_states.append(new_msg)
new_msg = new_msg @ A
# Return the message states.
return msg_states
```
The rest of the `matplotlib` animation functions are shown below.
```
def update_func(step, nodes, colors):
"""
The update function for each animation time step.
:param step: Passed in from matplotlib's FuncAnimation. Must
be present in the function signature.
:param nodes: Returned from nx.draw_networkx_edges(). Is an
array of colors.
:param colors: A list of pre-computed colors.
"""
nodes.set_array(colors[step].ravel())
return nodes
def anim(G, initial_state, n_frames=4):
colors = propagate(G, initial_state, n_frames)
fig = plt.figure()
pos = {i:(i, i) for i in range(len(G))}
adj = nx.to_numpy_array(G)
pos = nx.kamada_kawai_layout(G)
nodes = nx.draw_networkx_nodes(G, pos=pos, node_color=colors[0].ravel(), node_size=20)
ax = nx.draw_networkx_edges(G, pos)
return animation.FuncAnimation(fig, update_func, frames=range(n_frames), fargs=(nodes, colors))
# Initialize the message
msg = np.zeros(len(G2))
msg[0] = 1
# Animate the graph with message propagation.
HTML(anim(G2, msg, n_frames=4).to_html5_video())
```
### Exercise
Visualize how a rumour would spread in the university dorm network. You can initialize the message on any node of your choice.
```
msg = np.zeros(len(G))
msg[0] = 1
HTML(anim(G, msg, n_frames=4).to_html5_video())
```
# Bipartite Graph Matrices
The section on message passing above assumed unipartite graphs, or at least graphs for which messages can be meaningfully passed between nodes.
In this section, we will look at bipartite graphs.
Recall from before the definition of a bipartite graph:
- Nodes are separated into two partitions (hence 'bi'-'partite').
- Edges can only occur between nodes of different partitions.
Bipartite graphs have a natural matrix representation, known as the **biadjacency matrix**. Nodes on one partition are the rows, and nodes on the other partition are the columns.
NetworkX's `bipartite` module provides a function for computing the biadjacency matrix of a bipartite graph.
Let's start by looking at a toy bipartite graph, a "customer-product" purchase record graph, with 4 products and 3 customers. The matrix representation might be as follows:
```
import numpy as np
# Rows = customers, columns = products, 1 = customer purchased product, 0 = customer did not purchase product.
cp_mat = np.array([[0, 1, 0, 0],
[1, 0, 1, 0],
[1, 1, 1, 1]])
```
From this "bi-adjacency" matrix, one can compute the projection onto the customers, matrix multiplying the matrix with its transpose.
```
c_mat = cp_mat @ cp_mat.T # c_mat means "customer matrix"
c_mat
```
**Pause here and read carefully!**
What we get is the connectivity matrix of the customers, based on shared purchases. The diagonals are the degree of the customers in the original graph, i.e. the number of purchases they originally made, and the off-diagonals are the connectivity matrix, based on shared products.
To get the products matrix, we make the transposed matrix the left side of the matrix multiplication.
```
p_mat = cp_mat.T @ cp_mat # p_mat means "product matrix"
p_mat
```
You may now try to convince yourself that the diagonals are the number of times a customer purchased that product, and the off-diagonals are the connectivity matrix of the products, weighted by how similar two customers are.
## Exercises
In the following exercises, you will now play with a customer-product graph from Amazon. This dataset was downloaded from [UCSD's Julian McAuley's website](http://jmcauley.ucsd.edu/data/amazon/), and corresponds to the digital music dataset.
This is a bipartite graph. The two partitions are:
- `customers`: The customers that were doing the reviews.
- `products`: The music that was being reviewed.
In the original dataset (see the original JSON in the `datasets/` directory), they are referred to as:
- `customers`: `reviewerID`
- `products`: `asin`
```
G_amzn = load_amazon_reviews()
```
NetworkX provides [`nx.bipartite.matrix.biadjacency_matrix()`](https://networkx.github.io/documentation/stable/reference/algorithms/generated/networkx.algorithms.bipartite.matrix.biadjacency_matrix.html#networkx.algorithms.bipartite.matrix.biadjacency_matrix) function that lets you get the biadjacency matrix of a graph object. This returns a `scipy.sparse` matrix. Sparse matrices are commonly used to represent graphs, especially large ones, as they take up much less memory.
### Exercise
Read the [docs](https://networkx.github.io/documentation/stable/reference/algorithms/generated/networkx.algorithms.bipartite.matrix.biadjacency_matrix.html#networkx.algorithms.bipartite.matrix.biadjacency_matrix) on how to use the `biadjacency_matrix()` function.
You probably would want to first define a function that gets all nodes from a partition.
```
def get_partition_nodes(G, partition):
"""
A function that returns nodes from one partition.
Assumes that the attribute key that stores the partition information
is 'bipartite'.
"""
return [n for n, d in G.nodes(data=True) if d['bipartite'] == partition]
```
### Exercise
Now, use the `get_partition_nodes()` function to get the `row_order` and `column_order` nodes from the Amazon music review graph, then get the biadjacency matrix.
```
customer_nodes = get_partition_nodes(G_amzn, 'customer')
mat = nx.bipartite.biadjacency_matrix(G_amzn, customer_nodes)
```
### Exercise
Let's find out which customers reviewed the most number of music items.
To do so, you can break the problem into a few steps.
First off, compute the customer projection using matrix operations.
```
customer_mat = mat @ mat.T
```
Next, get the diagonals of the customer-customer matrix. Recall here that in `customer_mat`, the diagonals correspond to the degree of the customer nodes in the bipartite matrix.
**Hint:** SciPy sparse matrices provide a `.diagonal()` method that returns the diagonal elements.
```
# Get the diagonal.
degrees = customer_mat.diagonal()
```
Finally, find the index of the customer that has the highest degree.
```
cust_idx = np.argmax(degrees)
cust_idx
```
It should be customer 294 in the `customer_nodes` list.
### Exercise
Verify that this holds when looking at the degrees of each customer in `customer_nodes`.
```
cust_degrees = [G_amzn.degree(n) for n in customer_nodes]
np.argmax(cust_degrees)
```
### Exercise
Let's now also compute which two customers are similar, based on shared reviews. To do so involves the following steps:
1. We construct a sparse matrix consisting of only the diagonals. `scipy.sparse.diags(elements)` will construct a sparse diagonal matrix based on the elements inside `elements`.
1. Subtract the diagonals from the customer matrix projection. This yields the customer-customer similarity matrix, which should only consist of the off-diagonal elements of the customer matrix projection.
1. Finally, get the indices where the weight (shared number of between the customers is highest. (*This code is provided for you.*)
```
import scipy.sparse as sp
# Construct diagonal elements.
customer_diags = sp.diags(degrees)
# Subtract off-diagonals.
off_diagonals = customer_mat - customer_diags
# Compute index of most similar individuals.
np.unravel_index(np.argmax(off_diagonals), customer_mat.shape)
```
# Performance: Object vs. Matrices
Finally, to motivate why you might want to use matrices rather than graph objects to compute some of these statistics, let's time the two ways of getting to the same answer.
## Objects
```
from time import time
start = time()
# Compute the projection
G_cust = nx.bipartite.weighted_projected_graph(G_amzn, customer_nodes)
# Identify the most similar customers
most_similar_customers = sorted(G_cust.edges(data=True), key=lambda x: x[2]['weight'], reverse=True)[0]
end = time()
print(f'{end - start:.3f} seconds')
print(f'Most similar customers: {most_similar_customers}')
```
## Matrices
```
start = time()
# Compute the projection using matrices
mat = nx.bipartite.matrix.biadjacency_matrix(G_amzn, customer_nodes)
cust_mat = mat @ mat.T
# Identify the most similar customers
degrees = customer_mat.diagonal()
customer_diags = sp.diags(degrees)
off_diagonals = customer_mat - customer_diags
c1, c2 = np.unravel_index(np.argmax(off_diagonals), customer_mat.shape)
end = time()
print(f'{end - start:.3f} seconds')
print(f'Most similar customers: {customer_nodes[c1]}, {customer_nodes[c2]}, {cust_mat[c1, c2]}')
```
You may notice that it's much easier to read the "objects" code, but the matrix code way outperforms the object code. This then becomes a great reason to use matrices (even better, sparse matrices)!
|
github_jupyter
|
import networkx as nx
from networkx import bipartite
import matplotlib.pyplot as plt
import nxviz as nv
from custom.load_data import load_university_social_network, load_amazon_reviews
from matplotlib import animation
from IPython.display import HTML
import numpy as np
%load_ext autoreload
%autoreload 2
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
nodes = list(range(4))
G1 = nx.Graph()
G1.add_nodes_from(nodes)
G1.add_edges_from(zip(nodes, nodes[1:]))
nx.draw(G1, with_labels=True)
nv.MatrixPlot(G1).draw()
A1 = nx.to_numpy_array(G1, nodelist=sorted(G1.nodes()))
A1
import numpy as np
# One way of coding this up
np.linalg.matrix_power(A1, 2)
# Another equivalent way, that takes advantage of Python 3.5's matrix multiply operator
A1 @ A1
np.diag(A1 @ A1)
np.linalg.matrix_power(A1, 3)
nodes
G2 = nx.DiGraph()
G2.add_nodes_from(nodes)
G2.add_edges_from(zip(nodes, nodes[1:]))
nx.draw(G2, with_labels=True)
A2 = nx.to_numpy_array(G2)
A2
np.linalg.matrix_power(A2, 2)
np.linalg.matrix_power(A2, 3)
G = load_university_social_network()
nv.MatrixPlot(G).draw()
list(nx.connected_components(G.to_undirected()))
nx.shortest_path(G, 30, 100)
A = nx.to_numpy_array(G)
np.linalg.matrix_power(A, 4)[29, 99]
nx.draw(G2, with_labels=True)
msg = np.array([1, 0, 0, 0]).reshape(1, 4)
msg
msg2 = msg @ A2
msg2
msg3 = msg2 @ A2
msg3
# fig, ax = plt.subplots()
def propagate(G, msg, n_frames):
"""
Computes the node values based on propagation.
Intended to be used before or when being passed into the
anim() function (defined below).
:param G: A NetworkX Graph.
:param msg: The initial state of the message.
:returns: A list of 1/0 representing message status at
each node.
"""
# Initialize a list to store message states at each timestep.
msg_states = []
# Set a variable `new_msg` to be the initial message state.
new_msg = msg
# Get the adjacency matrix of the graph G.
A = nx.to_numpy_array(G)
# Perform message passing at each time step
for i in range(n_frames):
msg_states.append(new_msg)
new_msg = new_msg @ A
# Return the message states.
return msg_states
def update_func(step, nodes, colors):
"""
The update function for each animation time step.
:param step: Passed in from matplotlib's FuncAnimation. Must
be present in the function signature.
:param nodes: Returned from nx.draw_networkx_edges(). Is an
array of colors.
:param colors: A list of pre-computed colors.
"""
nodes.set_array(colors[step].ravel())
return nodes
def anim(G, initial_state, n_frames=4):
colors = propagate(G, initial_state, n_frames)
fig = plt.figure()
pos = {i:(i, i) for i in range(len(G))}
adj = nx.to_numpy_array(G)
pos = nx.kamada_kawai_layout(G)
nodes = nx.draw_networkx_nodes(G, pos=pos, node_color=colors[0].ravel(), node_size=20)
ax = nx.draw_networkx_edges(G, pos)
return animation.FuncAnimation(fig, update_func, frames=range(n_frames), fargs=(nodes, colors))
# Initialize the message
msg = np.zeros(len(G2))
msg[0] = 1
# Animate the graph with message propagation.
HTML(anim(G2, msg, n_frames=4).to_html5_video())
msg = np.zeros(len(G))
msg[0] = 1
HTML(anim(G, msg, n_frames=4).to_html5_video())
import numpy as np
# Rows = customers, columns = products, 1 = customer purchased product, 0 = customer did not purchase product.
cp_mat = np.array([[0, 1, 0, 0],
[1, 0, 1, 0],
[1, 1, 1, 1]])
c_mat = cp_mat @ cp_mat.T # c_mat means "customer matrix"
c_mat
p_mat = cp_mat.T @ cp_mat # p_mat means "product matrix"
p_mat
G_amzn = load_amazon_reviews()
def get_partition_nodes(G, partition):
"""
A function that returns nodes from one partition.
Assumes that the attribute key that stores the partition information
is 'bipartite'.
"""
return [n for n, d in G.nodes(data=True) if d['bipartite'] == partition]
customer_nodes = get_partition_nodes(G_amzn, 'customer')
mat = nx.bipartite.biadjacency_matrix(G_amzn, customer_nodes)
customer_mat = mat @ mat.T
# Get the diagonal.
degrees = customer_mat.diagonal()
cust_idx = np.argmax(degrees)
cust_idx
cust_degrees = [G_amzn.degree(n) for n in customer_nodes]
np.argmax(cust_degrees)
import scipy.sparse as sp
# Construct diagonal elements.
customer_diags = sp.diags(degrees)
# Subtract off-diagonals.
off_diagonals = customer_mat - customer_diags
# Compute index of most similar individuals.
np.unravel_index(np.argmax(off_diagonals), customer_mat.shape)
from time import time
start = time()
# Compute the projection
G_cust = nx.bipartite.weighted_projected_graph(G_amzn, customer_nodes)
# Identify the most similar customers
most_similar_customers = sorted(G_cust.edges(data=True), key=lambda x: x[2]['weight'], reverse=True)[0]
end = time()
print(f'{end - start:.3f} seconds')
print(f'Most similar customers: {most_similar_customers}')
start = time()
# Compute the projection using matrices
mat = nx.bipartite.matrix.biadjacency_matrix(G_amzn, customer_nodes)
cust_mat = mat @ mat.T
# Identify the most similar customers
degrees = customer_mat.diagonal()
customer_diags = sp.diags(degrees)
off_diagonals = customer_mat - customer_diags
c1, c2 = np.unravel_index(np.argmax(off_diagonals), customer_mat.shape)
end = time()
print(f'{end - start:.3f} seconds')
print(f'Most similar customers: {customer_nodes[c1]}, {customer_nodes[c2]}, {cust_mat[c1, c2]}')
| 0.739893 | 0.992583 |
```
data = """
V. Niculescu, D. Bufnea, A. Sterca. Enhancing Java Streams API with PowerList Computation. 2020 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), (to appear).
V. Niculescu, F. Loulergue, D. Bufnea, A. Sterca. Pattern-driven Design of a Multiparadigm Parallel Programming Framework. In Proceedings of the 15th International Conference on Evaluation of Novel Approaches to Software Engineering - Volume 1: ENASE, 50-61, 2020. [DOI]
V. Niculescu. Efficient Decorator Pattern Variants through C++ Policies.In Proceedings of the 15th International Conference on Evaluation of Novel Approaches to Software Engineering - Volume 1: ENASE, 281-288, 2020. [DOI]
V. Niculescu, C. Serban, A. Vescan. Does Cyclic Learning have Positive Impact on Teaching Object-Oriented Programming? , Proceedings of 49th Annual Frontiers in Education Conference, FIE' 2019, Cincinatti Oct. 16-19 2019 [DOI]
V. Niculescu, D. Bufnea, A. Sterca, R. Silimon. Multi-way Divide and Conquer Parallel Programming based on PLists. Proceedings of 2019 International Conference on Software, Telecommunications and Computer Networks (SoftCOM)At: Split, Croatia, Sept 2019.
V. Niculescu, D. Bufnea, A. Sterca. MPI Scaling Up for Powerlist Based Parallel Programs. In Proceedings of the 27th Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP 2019), pp. 199-204, February 13-15, 2019, Pavia, Italy (.pdf) [DOI] .
Virginia Niculescu, Frédéric Loulergue.Transforming powerlist based divide&conquer programs for an improved execution model. 11th High Level Parallel Programming and Applications. HLPP 2018, Orleans, France.
Virginia Niculescu, Darius Bufnea. Experience with Teaching PDC Topics into Babes-Bolyai University's CS Courses. In 23rd International Conference on Parallel and Distributed Computing (EuroPar'2017). Santiago de Compostela, Spain, August 28 – September 1, 2017, Proceedings of workshops. LNCS, pp 240-251.( .pdf) [DOI] .
Virginia Niculescu, Frédéric Loulergue, Darius Bufnea, and Adrian Sterca. A Java Framework for High Level Parallel Programming using Powerlists. In 18th Parallel and Distributed Computing, Applications and Technologies (PDCAT). IEEE, Taipei Taiwan 2017, 17, pp.255-262. [DOI]
Virginia Niculescu.MixDecorator: An Enhanced Version of the Decorator Pattern. In Proceedings 20th European Conference on Pattern Languages of Programs (EuroPLoP'2015) Kloster Irsee, Germany 8-12 July 2015(link) [DOI]
Frédéric Loulergue, Virginia Niculescu, Julien Tesson. Implementing powerlists with Bulk Synchronous Parallel ML. In 16th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC2014), Timisoara, Romania, 22-25 sept. 2014, IEEE Computer Society, 2014, pp 325-332. [DOI]
Frédéric Loulergue, Virginia Niculescu, and Simon Robillard. Powerlists in Coq: Programming and Reasoning. In Proceedings of First International Symposium on Computing and Networking (CANDAR 2013) Matsuyama, Japan, Dec. 4-6, 2013, pages 57-65. IEEE Computer Society, 2013. [DOI]
V. Niculescu, D. Lupsa. A Decorator Based Design for Collections, in Proceedings of KEPT 2013: The Fourth International Conference On Knowledge Engineering, Principles and Techniques (June 2013) Studia Universitatis "Babes-Bolyai", Informatica, Volume LVIII, Number 3 (Sept. 2013). pp. 54-64 (.pdf)
V. Niculescu. Formal Refinement of BSP Programs with Early Cost Evaluation. Proceedings of the 10th International Symposium on Parallel and Distributed Computing (ISPDC), 6-8 July 2011, Cluj-Napoca, IEEE Society Press, pp. 49 - 56, [DOI].
V. Niculescu. Patterns for Decoupling Data Structures Implementations, Post-Proceedings of KEPT 2011, Knowledge Engineering: Principles and Techniques, International Conference, Babes-Bolyai University, Presa Universitara Clujeana, 2011. pag. 271-282. (.pdf)
V. Niculescu, A. Guran. Bounded Parallelism in PowerList and ParList Theories, SYNASC 2009, Proceedings of the 11th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Timisoara, 2009, IEEE Society Press, pp. 237-244 (DOI)
V. Niculescu, A. Guran, Efficient Recursive Parallel Programs for Polynomial Interpolation, Post-Proceedings of KEPT 2009, Knowledge Engineering: Principles and Techniques, International Conference, Babes-Bolyai University, Presa Universitara Clujeana, 2009, pp. 265-274 (ISI - Conference Proceedings Citation Index)(.pdf)
V. Niculescu. Efficient Algorithms for Hermite Interpolation, Proceedings of the International Conference on Numerical Analysis and Approximation Theory, NAAT 2006, July 5-8, 2006, Cluj-Napoca, Eds. O. Agratini and P. Blaga, ISBN 973-686-961-X, 978-973-686-961-7, pp. 311-322.
V. Niculescu. Cost Evaluation from Specifications for BSP Programs, Proceedings 20th IEEE International Parallel & Distributed Processing Symposium (IPDPS 2006), Rhodes Island, 2006, pg. 6. IEEE Computer Society [DOI].
V. Niculescu, G.S. Moldovan. Building an Object Oriented Computational Algebra System Based on Design Patterns. Proceedings of InternationalSymposium on Symbolic and Numeric Algorithms for Scientific Computing SYNASC'05, Timisoara, IEEE Computer Society Press, Romania, Sept . 2005, pp. 101-108.(ISI - Conference Proceedings Citation Index)[DOI]
V. Niculescu, G.S. Moldovan. OOLACA: an object oriented library for abstract and computational algebra, Companion to the 19th annual ACM SIGPLAN conference on Object-oriented programming systems, languages, and applications OOPSLA 2004, Vancouver, BC, CANADA, ACM Press New York, NY, USA, pp. 160-162 [DOI]
V. Niculescu, M. Frentiu. Designing Correct Parallel Programs from Specifications, Proceedings of Eight World Multi-Conference on Systemics, Cybernetics and Informatics, July 18-21, 2004 - Orlando, Florida, 2004, 14, pp.173-178.
V. Niculescu. Formal Derivation Based on Set-Distribution of a Parallel Program for Hermite Interpolation, Proceedings of InternationalSymposium on Symbolic and Numeric Algorithms for Scientific Computing SYNASC'04, Timisoara, Romania, Sept .26 -30 , 2004, pp.250-258.
V. Niculescu.Teaching about Creational Design Patterns, Workshop on Pedagogies and Tools for Learning Object-Oriented Concepts, ECOOP'2003, Germany, July 21-25, 2003(.pdf).
V. Niculescu. A Model for Constructions of Parallel Programs, Proceedings of International Symposium on Symbolic and Numeric Algorithms for Scientific Computing SYNASC'02, Timisoara, Romania, Oct. 9-12 , 2002, pp.215-232.
V. Niculescu. Parallel Programs Development, Proceedings of International Conference on Parallel and Distributed Processing Techniques and Applications (PDPTA’2001), Las Vegas, Nevada, USA, June 25-28, 2001, CSREA Press, pp. 94-100.
V. Niculescu. Using Set-Distribution in Construction of a Parallel Program for Hermite Interpolation, Proceedings of the Fifth Joint Conference on Mathematics and Computer Science, Debrecen, Hungary, June, 2004, pp. 75.
V. Niculescu. Parallel Algorithms for Lagrange Interpolation, Proceedings of abstracts of the Fourth Joint Conference on Mathematics and Computer Science, Felix, Oradea, România, June 5-10, 2001, pp. 78.
V. Niculescu. Linear Data Structures for Specification of Parallel Numerical Algorithms, Proceedings of abstracts of the Third Joint Conference on Mathematics and Computer Science, Visegrad, Hungary, June 6-12, 1999, pp. 58.
Published in journals:
V. Niculescu, A. Sterca, D. Bufnea. PList-based Divide and Conquer parallel programming. Journal of Communications Software and Systems, 2020. (DOI) :
V. Niculescu On the Impact of High Performance Computing in Big Data Analytics for Medicine, Applied Medical Informatics. 30Mar.2020;42(1):9-8. (link)
V. Niculescu, F. Loulergue.Transforming powerlist-based divide-and-conquer programs for an improved execution model. The Journal of Supercomputing. 2020 vol. 76, 5016-5037. (doi)
D. Lupsa, V. Niculescu, R.Lupsa. Collections as Combinations of Features. Acta Universitatis Apulensis ISSN: 1582-5329 No. 42 (2015), pp. 67-78 doi: 10.17114/j.aua.2015.42.05 (.pdf).
V. Niculescu. A Design Patterns Perspective on Data Structures. Acta Universitatis Apulensis ISSN: 1582-5329 No. 34 (2013) , pp.335-355 (.pdf).
V. Niculescu. Performance and Reliability in the Development of a Decorator Based Collections Framework, Studia Universitatis "Babes-Bolyai",Informatica, Volume LVIII, Number 4 (Dec. 2013), pp. 87-101 (.pdf).
V. Niculescu.PARES - A Model for Parallel Recursive Programs, Romanian Journal of Information Science and Technology (ROMJIST), Ed.Academiei Romane, Volume 14(2011), No. 2, pp. 159–182, 2011 (.pdf).
V. Niculescu, D. Lupsa, R. Lupsa. Issues in Collections Framework Design. Studia Universitatis "Babes-Bolyai", Informatica,Volume LVII, Number 4 (Dec. 2012), pp.30-38 (.pdf)
V. Niculescu.Building Granularity in Highly Abstract Parallel Computation Models. Studia Universitatis "Babes-Bolyai", Informatica,Vol. LVII, No.3 (Sept. 2012), pp. 3-12(.pdf).
V. Niculescu. Storage Independence in Data Structures Implementation. Studia Universitatis "Babes-Bolyai", Informatica, Special Issue, Vol. LVI(3), pp. 21-26, 2011.(.pdf)
V. Niculescu. On Using Generics for Implementing Algebraic Structures. Studia Universitatis "Babes-Bolyai", Informatica, Vol. LVI(3), pp.17-32, 2011(.pdf).
V. Niculescu, A. Guran. Efficient Recursive Parallel Programs for Polynomial Interpolation, Studia Universitatis "Babes-Bolyai", Informatica, Special Issue, Vol. LIV , 2009, pp. 227-230 (.pdf).
V. Niculescu. Cost-efficient parallel programs based on set-distributions for polynomial interpolation, Journal of Parallel and Distributed Computing, Elsevier, Volume 67, Issue 8 (August 2007), pp. 935-946 (DOI ).
V. Niculescu. Introducing Data-Distributions into PowerList Theory, Studia Universitatis "Babes-Bolyai", Informatica, Special Issue, LIV(1), 2007, Cluj-Napoca, pp. 261-268 (.pdf).
V. Niculescu. Data-Distributions in PowerList Theory. Lecture Notes in Computer Science Vol. 4711: Theoretical Aspects of Computing, Proceedings of ICTAC 2007, Springer-Verlag, 2007: 396-409 [DOI].
V. Niculescu. A Software Development Methodology for BSP Model, Romanian Journal of Information Science and Technology (ROMJIST), Ed.Academiei Romane, Volume 9, No. 3, 2006, pp. 185-200 .
V. Niculescu. A Uniform Analysis of Lists Based on a General Non-recursive Definition, Studia Universitatis "Babes-Bolyai", Informatica, Vol. LI, No. 1 pp. 91-98 (2006) (.pdf).
V. Niculescu. A Refinement Calculus Based on Domain Decomposition of Parallel Programs, Romanian Journal of Information Science and Technology (ROMJIST), Ed. Academiei Romane, Vol. 8, nr 2,2005, pp. 87-98.
V. Niculescu, G. S. Moldovan. Integrating Conversions into a Computational Algebraic System, Studia Universitatis "Babes-Bolyai", Informatica,Vol XLXII, No. 2, 2005, pp.41-48.
V. Niculescu. On Data Distribution in the Construction of Parallel Programs, The Journal of Supercomputing, Kluwer Academic Publishers, 29(1): 5-25, July 2004(pdf).
V. Niculescu. Unbounded and Bounded Parallelism in BMF. Case Study: Rank Sorting, Studia Universitatis "Babes-Bolyai", Informatica, Vol XLIX, No. 1, 2004, pp. 91-98 (.pdf).
V. Niculescu. A Design Proposal for an Object Oriented Algebraic Library , Studia Universitatis "Babes-Bolyai", Informatica, Vol XLVIII, No. 1, 2003, pp. 89-100 (.pdf).
V. Niculescu. Parallel Algorithms for Fast Fourier Transformation using PowerList, ParList and PList Theories, Lecture Notes in Computer Science: Proceedings of International Conference EuroPar’2002, Paderborn, Germany, August 2002, Springer-Verlag, pp. 400-404 [DOI].
V. Niculescu. Multidimensional Data Structures for Parallel Programs Description, PU.M.A. (Pure Mathematics and Applications), Vol. 11, No. 2, 2000, pp. 351-360
V. Niculescu.Some Nondeterministic Parallel Programs, Studia Universitatis, "Babes-Bolyai", Informatica, Vol. XLV, No. 2, 2000, pp. 51-59.
V. Niculescu. Parallel Programs Description with PowerList, ParList and PList, Studia Universitatis "Babes-Bolyai", Informatica, vol XLIV, No. 1, 1999, pp. 41-50.
V. Niculescu. Data Distributions for Parallel Programs, Studia Universitatis, "Babes-Bolyai", Informatica, vol XLIII, No. 2, 1998, pp. 64-72.
Published in proceedings_of_national_conferences:
Virginia Niculescu,.Comparing C# and Java Extension Methods in the Context of Implementing MixDecorator, Book of abstracts of KEPT 2015, EDITORS: Militon FRENT¸ IU Horia F. POP Simona MOTOGNA.
V. Niculescu. On Granularity in Parallel Computing Models with High Degree of Abstractness. Proceedings of the Symposium "Zilele AcademiceClujene" (ISSN 2066-5768), 2012, pp. 3-8.
V. Niculescu. D. Lupsa, R. Lupsa, Exploring the space between theory and practice in collections frameworks design. Proceedings of the Symposium "Zilele Academice Clujene" ISSN 2066-5768), 2012, pp. 9-14.
V. Niculescu. A Formal Refinement Method for Divide&Conquer Parallel Programs, Proceedings of the Symposium "Zilele Academice Clujene", 2008, pp. 3-10.
V. Niculescu. Priority Queues Implementation Based on Design Patterns , Proceedings of the Symposium "Zilele Academice Clujene", 2006, pp. 27-32.
V. Niculescu. Designing a Divide&Conquer Parallel Algorithm for Lagrange Interpolation Using Power, Par, and P Theories, Proceedings of the Symposium "Zilele Academice Clujene", 2004, pp. 39-46.
V. Niculescu. On Choosing Between Templates and Polymorphic Types. Case-study: Representation of Algebraic Structures, Proceedings of the Symposium "Colocviul Academic Clujean de Informatica", 2003, pp. 71-78 ()
Published in Special_Issues
V. Niculescu. Boolean Matrices Multiplication, Seminar of Numerical and Statistic Calculus, Preprint no.1, 1999, pp. 89-96.
V. Niculescu. A Design Method for Parallel Programs. Applications, Seminar on Numerical and Statistic Calculus, Preprint no.1, 1996, pp. 61-77.
Books
V. Niculescu, G. Czibula.Fundamental Data Structures and Algorithms. An Object-Oriented Perspective. Casa Cărţii de Stiinţă, 2011(230 pg.)(in Romanian).
V. Niculescu. Parallel Computation. Design and Formal Development of Parallel Programs. Cluj-Napoca University Press, 2005 (301 pg.) ISBN 973-610-393-5(in Romanian)draft.
I. Lazăr, M. Frenţiu, V. Niculescu. Object Oriented Programming in Java, Univ. “Petru-Maior” Târgu-Mureş Press, 1999 (283 pg.), ISBN 973-99054-8-X (in Romanian).
V. Niculescu [and many other authors]. Algorithmic Problems, Computer Libris AGORA, 1998 (216 pg.), ISBN 973-97515-2-0 (in Romanian).
Translations
Introduction to Algorithms, T.H. Cormen, C.E. Leiserson, R.R Rivest
[many other authors],Introducere în algoritmi, Computer Libris AGORA, 2000 (880 pg.), ISBN 973-97534-3-4,
Conferences
International Conferences
ENASE 2020. 15th International Conference on Evaluation of Novel Approaches to Software Engineering. May 5-6, 2020, Praga/Online,
PDP 2019. 27th Euromicro International Conference on Parallel, Distributed and Network-Based Processing. February 13-15, 2019, Pavia, Italy
HLPP 2018, 11th High Level Parallel Programming and Applications. July 12-13, 2018 Orleans, France.
EuroPar 2017, 23th International Euro-Par Conference on Parallel Processing, Santiano de Compostela, Spain, August 2017.
EuroPLoP 2015, 20th European Conference on Pattern Languages of Programs, Kloster Irsee, Germany 8-12 July 2015
GECON 2015, Economics of Grids, Clouds, Systems, and Services, Cluj-Napoca, 15-17 sept 2015.
SYNASC 2014 -16th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Timisoara, Romania, 22-25 sept.2014
ELSEDIMA 2014, Environmental Legislation,Safety Engineering and Disaster Management
HLPP 2013, International Symposium on High-level Parallel Programming and Applications. Paris, 1-2 July 2013
KEPT 2013, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 4-6, 2013.
FraDeCoP-(2) 2012 -- Second Workshop on Frameworks for the Development of Correct (parallel) Programs, LIFO, Univ. of Orleans, November 26, 2012:
On Granularity in Data-Parallel Programs Development, International Conference
ISPDC 2011, The 10th International Symposium on Parallel and Distributed Computing, 6-8 July 2011, Cluj-Napoca
KEPT 2011, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 2-4, 2011.
KEPT 2009, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 2-4, 2009.
SYNASC 2009, International Symposium on Symbolic and Numeric Algorithms for Scientific Computing , Timisoara, Romania, Sept. 2009.
ICTAC 2007,4th International Colloquium, Macau, China, September 26-28, 2007.
KEPT 2007, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 6-8, 2007.
NAAT 2006, International conference of Numerical Analysis and Approximation Theory, Cluj-Napoca, Romania, July 5-8, 2006.
SYNASC 2005 International Symposium on Symbolic and Numeric Algorithms for Scientific Computing , Timisoara, Romania, Sept. 2005.
SYNASC 2004 International Symposium on Symbolic and Numeric Algorithms for Scientific Computing , Timisoara, Romania, Sept. 2004.
SYNASC 2002 International Symposium on Symbolic and Numeric Algorithms for Scientific Computing , Timisoara, Romania, Sept. 2002.
OOPSLA 2004, 19th annual ACM SIGPLAN conference on Object-oriented programming systems, languages, and applications, Vancouver, BC, CANADA, 2004.
ECOOP 2003 - 17th European Conference on Object-Oriented Programming, Darmstadt, Germany, July 21-25, 2003.
Euro-Par 2002, 8th International Euro-Par Conference on Parallel Processing, Paderborn, Germany, August 2002.
PDPTA 2001 - International Conference on Parallel and Distributed Processing Techniques and Applications, Las Vegas, Nevada, USA, June 25-28, 2001
ECOOP 2001 - 15th European Conference on Object-Oriented Programming Budapest, Hungary, June 18-22, 2001.
Fifth Joint Conference on Mathematics and Computer Science, organized by “Babeş-Bolyai” University Cluj-Napoca, and “Eötvös Loránd” University,Debrecen, Hungary, June, 2004,
Fourth Joint Conference on Mathematics and Computer Science, Felix, Oradea, România, organized by “Babeş-Bolyai” University Cluj-Napoca, and “Eötvös Loránd” University, Budapest, June 5-10, 2001.
Third Joint Conference on Mathematics and Computer Science, Visegrad, Hungary, organized by “Babeş-Bolyai” University Cluj-Napoca, and “Eötvös Loránd” University Budapest, June 6-12, 1999.
Romanian Conferences
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2018.
KEPT 2015, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 6-8, 2015.
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2014.
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2012.
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2008.
Conferinţă Naţională Didactica Matematicii, Cluj-Napoca, May, 2008
Behavioral, Creational and structural Design Patterns Used in Data Structures Implementation http://www.cs.ubbcluj.ro/~vniculescu/didactic/SD_DID/
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2006.
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2004.
Colocviul Academic Clujean de Informatica, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2003.
Sesiunea de comunicări ştiinţifice a Facultăţii de Matematică şi Informatică, UBB, Octomber , 2001.
Sesiunea de comunicări ştiinţifice a Facultăţii de Matematică şi Informatică, UBB, April, 2000.
Colocviul Naţional Studenţesc de Informatică “Grigore Moisil”, Iaşi April 1994.An Interactive Environment for Solving Geometrical Problems
Workshop of e-infrastructure services for society, organizat in cadrul HOST Project, Universitatea de Vest Timisoara, 29.07.2014
Local Conferences
It Today for a Cloud-Ready Tomorrow, Cluj-Napoca:17-18 oct. 2012, Brinel Conference
What is High Performance Computing, Cluj-Napoca:30-31 mai. 2012, Brinel Conference
High Performance Computing, Cluj-Napoca:30-31 mai. 2013, IBM Workshop
"""
papers = []
for line in data.split('\n'):
# print(line)
if line == "":
continue
else:
print(line)
if len(line.split(' ')) <= 3:
continue
authors = [k for k in line.split('.') if len(k.split(' ')) < 3]
# print("authors: ", authors)
sl = line.split(',')
sl = [(len(k), k) for k in sl ]
sl.sort(reverse=True)
title, affiliations = sl[0][1], sl[1][1]
papers.append((title, affiliations, authors))
print("title: ", affiliations.lstrip())
print("---")
for paper in papers:
print(paper[0])
import mariadb
import json
with open('../credentials.json', 'r') as crd_json_fd:
json_text = crd_json_fd.read()
json_obj = json.loads(json_text)
credentials = json_obj["Credentials"]
username = credentials["username"]
password = credentials["password"]
table_name = "publications_cache"
db_name = "ubbcluj"
mariadb_connection = mariadb.connect(user=username, password=password, database=db_name)
mariadb_cursor = mariadb_connection.cursor()
for paper in papers:
title = ""
pub_date = ""
affiliations = ""
try:
pub_date = paper[2].lstrip()
pub_date = str(pub_date) + "-01-01"
if len(pub_date) != 10:
pub_date = ""
except:
pass
try:
title = paper[0].lstrip()
except:
pass
try:
authors = paper[2].lstrip()
except:
pass
try:
affiliations = paper[1].lstrip()
except AttributeError:
pass
insert_string = "INSERT INTO {0} SET ".format(table_name)
insert_string += "Title=\'{0}\', ".format(title.split('\'')[0])
insert_string += "ProfessorId=\'{0}\', ".format(14)
if pub_date != "":
insert_string += "PublicationDate=\'{0}\', ".format(str(pub_date))
insert_string += "Authors=\'{0}\', ".format("")
insert_string += "Affiliations=\'{0}\' ".format(affiliations)
print("title:", insert_string)
try:
mariadb_cursor.execute(insert_string)
except mariadb.ProgrammingError as pe:
print("Error")
raise pe
except mariadb.IntegrityError:
continue
```
|
github_jupyter
|
data = """
V. Niculescu, D. Bufnea, A. Sterca. Enhancing Java Streams API with PowerList Computation. 2020 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), (to appear).
V. Niculescu, F. Loulergue, D. Bufnea, A. Sterca. Pattern-driven Design of a Multiparadigm Parallel Programming Framework. In Proceedings of the 15th International Conference on Evaluation of Novel Approaches to Software Engineering - Volume 1: ENASE, 50-61, 2020. [DOI]
V. Niculescu. Efficient Decorator Pattern Variants through C++ Policies.In Proceedings of the 15th International Conference on Evaluation of Novel Approaches to Software Engineering - Volume 1: ENASE, 281-288, 2020. [DOI]
V. Niculescu, C. Serban, A. Vescan. Does Cyclic Learning have Positive Impact on Teaching Object-Oriented Programming? , Proceedings of 49th Annual Frontiers in Education Conference, FIE' 2019, Cincinatti Oct. 16-19 2019 [DOI]
V. Niculescu, D. Bufnea, A. Sterca, R. Silimon. Multi-way Divide and Conquer Parallel Programming based on PLists. Proceedings of 2019 International Conference on Software, Telecommunications and Computer Networks (SoftCOM)At: Split, Croatia, Sept 2019.
V. Niculescu, D. Bufnea, A. Sterca. MPI Scaling Up for Powerlist Based Parallel Programs. In Proceedings of the 27th Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP 2019), pp. 199-204, February 13-15, 2019, Pavia, Italy (.pdf) [DOI] .
Virginia Niculescu, Frédéric Loulergue.Transforming powerlist based divide&conquer programs for an improved execution model. 11th High Level Parallel Programming and Applications. HLPP 2018, Orleans, France.
Virginia Niculescu, Darius Bufnea. Experience with Teaching PDC Topics into Babes-Bolyai University's CS Courses. In 23rd International Conference on Parallel and Distributed Computing (EuroPar'2017). Santiago de Compostela, Spain, August 28 – September 1, 2017, Proceedings of workshops. LNCS, pp 240-251.( .pdf) [DOI] .
Virginia Niculescu, Frédéric Loulergue, Darius Bufnea, and Adrian Sterca. A Java Framework for High Level Parallel Programming using Powerlists. In 18th Parallel and Distributed Computing, Applications and Technologies (PDCAT). IEEE, Taipei Taiwan 2017, 17, pp.255-262. [DOI]
Virginia Niculescu.MixDecorator: An Enhanced Version of the Decorator Pattern. In Proceedings 20th European Conference on Pattern Languages of Programs (EuroPLoP'2015) Kloster Irsee, Germany 8-12 July 2015(link) [DOI]
Frédéric Loulergue, Virginia Niculescu, Julien Tesson. Implementing powerlists with Bulk Synchronous Parallel ML. In 16th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC2014), Timisoara, Romania, 22-25 sept. 2014, IEEE Computer Society, 2014, pp 325-332. [DOI]
Frédéric Loulergue, Virginia Niculescu, and Simon Robillard. Powerlists in Coq: Programming and Reasoning. In Proceedings of First International Symposium on Computing and Networking (CANDAR 2013) Matsuyama, Japan, Dec. 4-6, 2013, pages 57-65. IEEE Computer Society, 2013. [DOI]
V. Niculescu, D. Lupsa. A Decorator Based Design for Collections, in Proceedings of KEPT 2013: The Fourth International Conference On Knowledge Engineering, Principles and Techniques (June 2013) Studia Universitatis "Babes-Bolyai", Informatica, Volume LVIII, Number 3 (Sept. 2013). pp. 54-64 (.pdf)
V. Niculescu. Formal Refinement of BSP Programs with Early Cost Evaluation. Proceedings of the 10th International Symposium on Parallel and Distributed Computing (ISPDC), 6-8 July 2011, Cluj-Napoca, IEEE Society Press, pp. 49 - 56, [DOI].
V. Niculescu. Patterns for Decoupling Data Structures Implementations, Post-Proceedings of KEPT 2011, Knowledge Engineering: Principles and Techniques, International Conference, Babes-Bolyai University, Presa Universitara Clujeana, 2011. pag. 271-282. (.pdf)
V. Niculescu, A. Guran. Bounded Parallelism in PowerList and ParList Theories, SYNASC 2009, Proceedings of the 11th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Timisoara, 2009, IEEE Society Press, pp. 237-244 (DOI)
V. Niculescu, A. Guran, Efficient Recursive Parallel Programs for Polynomial Interpolation, Post-Proceedings of KEPT 2009, Knowledge Engineering: Principles and Techniques, International Conference, Babes-Bolyai University, Presa Universitara Clujeana, 2009, pp. 265-274 (ISI - Conference Proceedings Citation Index)(.pdf)
V. Niculescu. Efficient Algorithms for Hermite Interpolation, Proceedings of the International Conference on Numerical Analysis and Approximation Theory, NAAT 2006, July 5-8, 2006, Cluj-Napoca, Eds. O. Agratini and P. Blaga, ISBN 973-686-961-X, 978-973-686-961-7, pp. 311-322.
V. Niculescu. Cost Evaluation from Specifications for BSP Programs, Proceedings 20th IEEE International Parallel & Distributed Processing Symposium (IPDPS 2006), Rhodes Island, 2006, pg. 6. IEEE Computer Society [DOI].
V. Niculescu, G.S. Moldovan. Building an Object Oriented Computational Algebra System Based on Design Patterns. Proceedings of InternationalSymposium on Symbolic and Numeric Algorithms for Scientific Computing SYNASC'05, Timisoara, IEEE Computer Society Press, Romania, Sept . 2005, pp. 101-108.(ISI - Conference Proceedings Citation Index)[DOI]
V. Niculescu, G.S. Moldovan. OOLACA: an object oriented library for abstract and computational algebra, Companion to the 19th annual ACM SIGPLAN conference on Object-oriented programming systems, languages, and applications OOPSLA 2004, Vancouver, BC, CANADA, ACM Press New York, NY, USA, pp. 160-162 [DOI]
V. Niculescu, M. Frentiu. Designing Correct Parallel Programs from Specifications, Proceedings of Eight World Multi-Conference on Systemics, Cybernetics and Informatics, July 18-21, 2004 - Orlando, Florida, 2004, 14, pp.173-178.
V. Niculescu. Formal Derivation Based on Set-Distribution of a Parallel Program for Hermite Interpolation, Proceedings of InternationalSymposium on Symbolic and Numeric Algorithms for Scientific Computing SYNASC'04, Timisoara, Romania, Sept .26 -30 , 2004, pp.250-258.
V. Niculescu.Teaching about Creational Design Patterns, Workshop on Pedagogies and Tools for Learning Object-Oriented Concepts, ECOOP'2003, Germany, July 21-25, 2003(.pdf).
V. Niculescu. A Model for Constructions of Parallel Programs, Proceedings of International Symposium on Symbolic and Numeric Algorithms for Scientific Computing SYNASC'02, Timisoara, Romania, Oct. 9-12 , 2002, pp.215-232.
V. Niculescu. Parallel Programs Development, Proceedings of International Conference on Parallel and Distributed Processing Techniques and Applications (PDPTA’2001), Las Vegas, Nevada, USA, June 25-28, 2001, CSREA Press, pp. 94-100.
V. Niculescu. Using Set-Distribution in Construction of a Parallel Program for Hermite Interpolation, Proceedings of the Fifth Joint Conference on Mathematics and Computer Science, Debrecen, Hungary, June, 2004, pp. 75.
V. Niculescu. Parallel Algorithms for Lagrange Interpolation, Proceedings of abstracts of the Fourth Joint Conference on Mathematics and Computer Science, Felix, Oradea, România, June 5-10, 2001, pp. 78.
V. Niculescu. Linear Data Structures for Specification of Parallel Numerical Algorithms, Proceedings of abstracts of the Third Joint Conference on Mathematics and Computer Science, Visegrad, Hungary, June 6-12, 1999, pp. 58.
Published in journals:
V. Niculescu, A. Sterca, D. Bufnea. PList-based Divide and Conquer parallel programming. Journal of Communications Software and Systems, 2020. (DOI) :
V. Niculescu On the Impact of High Performance Computing in Big Data Analytics for Medicine, Applied Medical Informatics. 30Mar.2020;42(1):9-8. (link)
V. Niculescu, F. Loulergue.Transforming powerlist-based divide-and-conquer programs for an improved execution model. The Journal of Supercomputing. 2020 vol. 76, 5016-5037. (doi)
D. Lupsa, V. Niculescu, R.Lupsa. Collections as Combinations of Features. Acta Universitatis Apulensis ISSN: 1582-5329 No. 42 (2015), pp. 67-78 doi: 10.17114/j.aua.2015.42.05 (.pdf).
V. Niculescu. A Design Patterns Perspective on Data Structures. Acta Universitatis Apulensis ISSN: 1582-5329 No. 34 (2013) , pp.335-355 (.pdf).
V. Niculescu. Performance and Reliability in the Development of a Decorator Based Collections Framework, Studia Universitatis "Babes-Bolyai",Informatica, Volume LVIII, Number 4 (Dec. 2013), pp. 87-101 (.pdf).
V. Niculescu.PARES - A Model for Parallel Recursive Programs, Romanian Journal of Information Science and Technology (ROMJIST), Ed.Academiei Romane, Volume 14(2011), No. 2, pp. 159–182, 2011 (.pdf).
V. Niculescu, D. Lupsa, R. Lupsa. Issues in Collections Framework Design. Studia Universitatis "Babes-Bolyai", Informatica,Volume LVII, Number 4 (Dec. 2012), pp.30-38 (.pdf)
V. Niculescu.Building Granularity in Highly Abstract Parallel Computation Models. Studia Universitatis "Babes-Bolyai", Informatica,Vol. LVII, No.3 (Sept. 2012), pp. 3-12(.pdf).
V. Niculescu. Storage Independence in Data Structures Implementation. Studia Universitatis "Babes-Bolyai", Informatica, Special Issue, Vol. LVI(3), pp. 21-26, 2011.(.pdf)
V. Niculescu. On Using Generics for Implementing Algebraic Structures. Studia Universitatis "Babes-Bolyai", Informatica, Vol. LVI(3), pp.17-32, 2011(.pdf).
V. Niculescu, A. Guran. Efficient Recursive Parallel Programs for Polynomial Interpolation, Studia Universitatis "Babes-Bolyai", Informatica, Special Issue, Vol. LIV , 2009, pp. 227-230 (.pdf).
V. Niculescu. Cost-efficient parallel programs based on set-distributions for polynomial interpolation, Journal of Parallel and Distributed Computing, Elsevier, Volume 67, Issue 8 (August 2007), pp. 935-946 (DOI ).
V. Niculescu. Introducing Data-Distributions into PowerList Theory, Studia Universitatis "Babes-Bolyai", Informatica, Special Issue, LIV(1), 2007, Cluj-Napoca, pp. 261-268 (.pdf).
V. Niculescu. Data-Distributions in PowerList Theory. Lecture Notes in Computer Science Vol. 4711: Theoretical Aspects of Computing, Proceedings of ICTAC 2007, Springer-Verlag, 2007: 396-409 [DOI].
V. Niculescu. A Software Development Methodology for BSP Model, Romanian Journal of Information Science and Technology (ROMJIST), Ed.Academiei Romane, Volume 9, No. 3, 2006, pp. 185-200 .
V. Niculescu. A Uniform Analysis of Lists Based on a General Non-recursive Definition, Studia Universitatis "Babes-Bolyai", Informatica, Vol. LI, No. 1 pp. 91-98 (2006) (.pdf).
V. Niculescu. A Refinement Calculus Based on Domain Decomposition of Parallel Programs, Romanian Journal of Information Science and Technology (ROMJIST), Ed. Academiei Romane, Vol. 8, nr 2,2005, pp. 87-98.
V. Niculescu, G. S. Moldovan. Integrating Conversions into a Computational Algebraic System, Studia Universitatis "Babes-Bolyai", Informatica,Vol XLXII, No. 2, 2005, pp.41-48.
V. Niculescu. On Data Distribution in the Construction of Parallel Programs, The Journal of Supercomputing, Kluwer Academic Publishers, 29(1): 5-25, July 2004(pdf).
V. Niculescu. Unbounded and Bounded Parallelism in BMF. Case Study: Rank Sorting, Studia Universitatis "Babes-Bolyai", Informatica, Vol XLIX, No. 1, 2004, pp. 91-98 (.pdf).
V. Niculescu. A Design Proposal for an Object Oriented Algebraic Library , Studia Universitatis "Babes-Bolyai", Informatica, Vol XLVIII, No. 1, 2003, pp. 89-100 (.pdf).
V. Niculescu. Parallel Algorithms for Fast Fourier Transformation using PowerList, ParList and PList Theories, Lecture Notes in Computer Science: Proceedings of International Conference EuroPar’2002, Paderborn, Germany, August 2002, Springer-Verlag, pp. 400-404 [DOI].
V. Niculescu. Multidimensional Data Structures for Parallel Programs Description, PU.M.A. (Pure Mathematics and Applications), Vol. 11, No. 2, 2000, pp. 351-360
V. Niculescu.Some Nondeterministic Parallel Programs, Studia Universitatis, "Babes-Bolyai", Informatica, Vol. XLV, No. 2, 2000, pp. 51-59.
V. Niculescu. Parallel Programs Description with PowerList, ParList and PList, Studia Universitatis "Babes-Bolyai", Informatica, vol XLIV, No. 1, 1999, pp. 41-50.
V. Niculescu. Data Distributions for Parallel Programs, Studia Universitatis, "Babes-Bolyai", Informatica, vol XLIII, No. 2, 1998, pp. 64-72.
Published in proceedings_of_national_conferences:
Virginia Niculescu,.Comparing C# and Java Extension Methods in the Context of Implementing MixDecorator, Book of abstracts of KEPT 2015, EDITORS: Militon FRENT¸ IU Horia F. POP Simona MOTOGNA.
V. Niculescu. On Granularity in Parallel Computing Models with High Degree of Abstractness. Proceedings of the Symposium "Zilele AcademiceClujene" (ISSN 2066-5768), 2012, pp. 3-8.
V. Niculescu. D. Lupsa, R. Lupsa, Exploring the space between theory and practice in collections frameworks design. Proceedings of the Symposium "Zilele Academice Clujene" ISSN 2066-5768), 2012, pp. 9-14.
V. Niculescu. A Formal Refinement Method for Divide&Conquer Parallel Programs, Proceedings of the Symposium "Zilele Academice Clujene", 2008, pp. 3-10.
V. Niculescu. Priority Queues Implementation Based on Design Patterns , Proceedings of the Symposium "Zilele Academice Clujene", 2006, pp. 27-32.
V. Niculescu. Designing a Divide&Conquer Parallel Algorithm for Lagrange Interpolation Using Power, Par, and P Theories, Proceedings of the Symposium "Zilele Academice Clujene", 2004, pp. 39-46.
V. Niculescu. On Choosing Between Templates and Polymorphic Types. Case-study: Representation of Algebraic Structures, Proceedings of the Symposium "Colocviul Academic Clujean de Informatica", 2003, pp. 71-78 ()
Published in Special_Issues
V. Niculescu. Boolean Matrices Multiplication, Seminar of Numerical and Statistic Calculus, Preprint no.1, 1999, pp. 89-96.
V. Niculescu. A Design Method for Parallel Programs. Applications, Seminar on Numerical and Statistic Calculus, Preprint no.1, 1996, pp. 61-77.
Books
V. Niculescu, G. Czibula.Fundamental Data Structures and Algorithms. An Object-Oriented Perspective. Casa Cărţii de Stiinţă, 2011(230 pg.)(in Romanian).
V. Niculescu. Parallel Computation. Design and Formal Development of Parallel Programs. Cluj-Napoca University Press, 2005 (301 pg.) ISBN 973-610-393-5(in Romanian)draft.
I. Lazăr, M. Frenţiu, V. Niculescu. Object Oriented Programming in Java, Univ. “Petru-Maior” Târgu-Mureş Press, 1999 (283 pg.), ISBN 973-99054-8-X (in Romanian).
V. Niculescu [and many other authors]. Algorithmic Problems, Computer Libris AGORA, 1998 (216 pg.), ISBN 973-97515-2-0 (in Romanian).
Translations
Introduction to Algorithms, T.H. Cormen, C.E. Leiserson, R.R Rivest
[many other authors],Introducere în algoritmi, Computer Libris AGORA, 2000 (880 pg.), ISBN 973-97534-3-4,
Conferences
International Conferences
ENASE 2020. 15th International Conference on Evaluation of Novel Approaches to Software Engineering. May 5-6, 2020, Praga/Online,
PDP 2019. 27th Euromicro International Conference on Parallel, Distributed and Network-Based Processing. February 13-15, 2019, Pavia, Italy
HLPP 2018, 11th High Level Parallel Programming and Applications. July 12-13, 2018 Orleans, France.
EuroPar 2017, 23th International Euro-Par Conference on Parallel Processing, Santiano de Compostela, Spain, August 2017.
EuroPLoP 2015, 20th European Conference on Pattern Languages of Programs, Kloster Irsee, Germany 8-12 July 2015
GECON 2015, Economics of Grids, Clouds, Systems, and Services, Cluj-Napoca, 15-17 sept 2015.
SYNASC 2014 -16th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Timisoara, Romania, 22-25 sept.2014
ELSEDIMA 2014, Environmental Legislation,Safety Engineering and Disaster Management
HLPP 2013, International Symposium on High-level Parallel Programming and Applications. Paris, 1-2 July 2013
KEPT 2013, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 4-6, 2013.
FraDeCoP-(2) 2012 -- Second Workshop on Frameworks for the Development of Correct (parallel) Programs, LIFO, Univ. of Orleans, November 26, 2012:
On Granularity in Data-Parallel Programs Development, International Conference
ISPDC 2011, The 10th International Symposium on Parallel and Distributed Computing, 6-8 July 2011, Cluj-Napoca
KEPT 2011, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 2-4, 2011.
KEPT 2009, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 2-4, 2009.
SYNASC 2009, International Symposium on Symbolic and Numeric Algorithms for Scientific Computing , Timisoara, Romania, Sept. 2009.
ICTAC 2007,4th International Colloquium, Macau, China, September 26-28, 2007.
KEPT 2007, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 6-8, 2007.
NAAT 2006, International conference of Numerical Analysis and Approximation Theory, Cluj-Napoca, Romania, July 5-8, 2006.
SYNASC 2005 International Symposium on Symbolic and Numeric Algorithms for Scientific Computing , Timisoara, Romania, Sept. 2005.
SYNASC 2004 International Symposium on Symbolic and Numeric Algorithms for Scientific Computing , Timisoara, Romania, Sept. 2004.
SYNASC 2002 International Symposium on Symbolic and Numeric Algorithms for Scientific Computing , Timisoara, Romania, Sept. 2002.
OOPSLA 2004, 19th annual ACM SIGPLAN conference on Object-oriented programming systems, languages, and applications, Vancouver, BC, CANADA, 2004.
ECOOP 2003 - 17th European Conference on Object-Oriented Programming, Darmstadt, Germany, July 21-25, 2003.
Euro-Par 2002, 8th International Euro-Par Conference on Parallel Processing, Paderborn, Germany, August 2002.
PDPTA 2001 - International Conference on Parallel and Distributed Processing Techniques and Applications, Las Vegas, Nevada, USA, June 25-28, 2001
ECOOP 2001 - 15th European Conference on Object-Oriented Programming Budapest, Hungary, June 18-22, 2001.
Fifth Joint Conference on Mathematics and Computer Science, organized by “Babeş-Bolyai” University Cluj-Napoca, and “Eötvös Loránd” University,Debrecen, Hungary, June, 2004,
Fourth Joint Conference on Mathematics and Computer Science, Felix, Oradea, România, organized by “Babeş-Bolyai” University Cluj-Napoca, and “Eötvös Loránd” University, Budapest, June 5-10, 2001.
Third Joint Conference on Mathematics and Computer Science, Visegrad, Hungary, organized by “Babeş-Bolyai” University Cluj-Napoca, and “Eötvös Loránd” University Budapest, June 6-12, 1999.
Romanian Conferences
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2018.
KEPT 2015, Knowledge Engineering: Principles and Techniques, Cluj-Napoca, Romania, June 6-8, 2015.
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2014.
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2012.
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2008.
Conferinţă Naţională Didactica Matematicii, Cluj-Napoca, May, 2008
Behavioral, Creational and structural Design Patterns Used in Data Structures Implementation http://www.cs.ubbcluj.ro/~vniculescu/didactic/SD_DID/
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2006.
Zilele Academice Clujene, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2004.
Colocviul Academic Clujean de Informatica, Universitatea Babes-Bolyai, Cluj-Napoca, June, 2003.
Sesiunea de comunicări ştiinţifice a Facultăţii de Matematică şi Informatică, UBB, Octomber , 2001.
Sesiunea de comunicări ştiinţifice a Facultăţii de Matematică şi Informatică, UBB, April, 2000.
Colocviul Naţional Studenţesc de Informatică “Grigore Moisil”, Iaşi April 1994.An Interactive Environment for Solving Geometrical Problems
Workshop of e-infrastructure services for society, organizat in cadrul HOST Project, Universitatea de Vest Timisoara, 29.07.2014
Local Conferences
It Today for a Cloud-Ready Tomorrow, Cluj-Napoca:17-18 oct. 2012, Brinel Conference
What is High Performance Computing, Cluj-Napoca:30-31 mai. 2012, Brinel Conference
High Performance Computing, Cluj-Napoca:30-31 mai. 2013, IBM Workshop
"""
papers = []
for line in data.split('\n'):
# print(line)
if line == "":
continue
else:
print(line)
if len(line.split(' ')) <= 3:
continue
authors = [k for k in line.split('.') if len(k.split(' ')) < 3]
# print("authors: ", authors)
sl = line.split(',')
sl = [(len(k), k) for k in sl ]
sl.sort(reverse=True)
title, affiliations = sl[0][1], sl[1][1]
papers.append((title, affiliations, authors))
print("title: ", affiliations.lstrip())
print("---")
for paper in papers:
print(paper[0])
import mariadb
import json
with open('../credentials.json', 'r') as crd_json_fd:
json_text = crd_json_fd.read()
json_obj = json.loads(json_text)
credentials = json_obj["Credentials"]
username = credentials["username"]
password = credentials["password"]
table_name = "publications_cache"
db_name = "ubbcluj"
mariadb_connection = mariadb.connect(user=username, password=password, database=db_name)
mariadb_cursor = mariadb_connection.cursor()
for paper in papers:
title = ""
pub_date = ""
affiliations = ""
try:
pub_date = paper[2].lstrip()
pub_date = str(pub_date) + "-01-01"
if len(pub_date) != 10:
pub_date = ""
except:
pass
try:
title = paper[0].lstrip()
except:
pass
try:
authors = paper[2].lstrip()
except:
pass
try:
affiliations = paper[1].lstrip()
except AttributeError:
pass
insert_string = "INSERT INTO {0} SET ".format(table_name)
insert_string += "Title=\'{0}\', ".format(title.split('\'')[0])
insert_string += "ProfessorId=\'{0}\', ".format(14)
if pub_date != "":
insert_string += "PublicationDate=\'{0}\', ".format(str(pub_date))
insert_string += "Authors=\'{0}\', ".format("")
insert_string += "Affiliations=\'{0}\' ".format(affiliations)
print("title:", insert_string)
try:
mariadb_cursor.execute(insert_string)
except mariadb.ProgrammingError as pe:
print("Error")
raise pe
except mariadb.IntegrityError:
continue
| 0.780662 | 0.824144 |
**Important note:** You should always work on a duplicate of the course notebook. On the page you used to open this, tick the box next to the name of the notebook and click duplicate to easily create a new version of this notebook.
You will get errors each time you try to update your course repository if you don't do this, and your changes will end up being erased by the original course version.
# Welcome to Jupyter Notebooks!
If you want to learn how to use this tool you've come to the right place. This article will teach you all you need to know to use Jupyter Notebooks effectively. You only need to go through Section 1 to learn the basics and you can go into Section 2 if you want to further increase your productivity.
You might be reading this tutorial in a web page (maybe Github or the course's webpage). We strongly suggest to read this tutorial in a (yes, you guessed it) Jupyter Notebook. This way you will be able to actually *try* the different commands we will introduce here.
## Section 1: Need to Know
### Introduction
Let's build up from the basics, what is a Jupyter Notebook? Well, you are reading one. It is a document made of cells. You can write like I am writing now (markdown cells) or you can perform calculations in Python (code cells) and run them like this:
```
1+1
```
Cool huh? This combination of prose and code makes Jupyter Notebook ideal for experimentation: we can see the rationale for each experiment, the code and the results in one comprehensive document. In fast.ai, each lesson is documented in a notebook and you can later use that notebook to experiment yourself.
Other renowned institutions in academy and industry use Jupyter Notebook: Google, Microsoft, IBM, Bloomberg, Berkeley and NASA among others. Even Nobel-winning economists [use Jupyter Notebooks](https://paulromer.net/jupyter-mathematica-and-the-future-of-the-research-paper/) for their experiments and some suggest that Jupyter Notebooks will be the [new format for research papers](https://www.theatlantic.com/science/archive/2018/04/the-scientific-paper-is-obsolete/556676/).
### Writing
A type of cell in which you can write like this is called _Markdown_. [_Markdown_](https://en.wikipedia.org/wiki/Markdown) is a very popular markup language. To specify that a cell is _Markdown_ you need to click in the drop-down menu in the toolbar and select _Markdown_.
Click on the the '+' button on the left and select _Markdown_ from the toolbar.
Now you can type your first _Markdown_ cell. Write 'My first markdown cell' and press run.

You should see something like this:
My first markdown cell
Now try making your first _Code_ cell: follow the same steps as before but don't change the cell type (when you add a cell its default type is _Code_). Type something like 3/2. You should see '1.5' as output.
```
3/2
```
### Modes
If you made a mistake in your *Markdown* cell and you have already ran it, you will notice that you cannot edit it just by clicking on it. This is because you are in **Command Mode**. Jupyter Notebooks have two distinct modes:
1. **Edit Mode**: Allows you to edit a cell's content.
2. **Command Mode**: Allows you to edit the notebook as a whole and use keyboard shortcuts but not edit a cell's content.
You can toggle between these two by either pressing <kbd>ESC</kbd> and <kbd>Enter</kbd> or clicking outside a cell or inside it (you need to double click if its a Markdown cell). You can always know which mode you're on since the current cell has a green border if in **Edit Mode** and a blue border in **Command Mode**. Try it!
### Other Important Considerations
1. Your notebook is autosaved every 120 seconds. If you want to manually save it you can just press the save button on the upper left corner or press <kbd>s</kbd> in **Command Mode**.

2. To know if your kernel is computing or not you can check the dot in your upper right corner. If the dot is full, it means that the kernel is working. If not, it is idle. You can place the mouse on it and see the state of the kernel be displayed.

3. There are a couple of shortcuts you must know about which we use **all** the time (always in **Command Mode**). These are:
<kbd>Shift</kbd>+<kbd>Enter</kbd>: Runs the code or markdown on a cell
<kbd>Up Arrow</kbd>+<kbd>Down Arrow</kbd>: Toggle across cells
<kbd>b</kbd>: Create new cell
<kbd>0</kbd>+<kbd>0</kbd>: Reset Kernel
You can find more shortcuts in the Shortcuts section below.
4. You may need to use a terminal in a Jupyter Notebook environment (for example to git pull on a repository). That is very easy to do, just press 'New' in your Home directory and 'Terminal'. Don't know how to use the Terminal? We made a tutorial for that as well. You can find it [here](https://course.fast.ai/terminal_tutorial.html).

That's it. This is all you need to know to use Jupyter Notebooks. That said, we have more tips and tricks below ↓↓↓
## Section 2: Going deeper
### Markdown formatting
#### Italics, Bold, Strikethrough, Inline, Blockquotes and Links
The five most important concepts to format your code appropriately when using markdown are:
1. *Italics*: Surround your text with '\_' or '\*'
2. **Bold**: Surround your text with '\__' or '\**'
3. `inline`: Surround your text with '\`'
4. > blockquote: Place '\>' before your text.
5. [Links](https://course.fast.ai/): Surround the text you want to link with '\[\]' and place the link adjacent to the text, surrounded with '()'
#### Headings
Notice that including a hashtag before the text in a markdown cell makes the text a heading. The number of hashtags you include will determine the priority of the header ('#' is level one, '##' is level two, '###' is level three and '####' is level four). We will add three new cells with the '+' button on the left to see how every level of heading looks.
Double click on some headings and find out what level they are!
#### Lists
There are three types of lists in markdown.
Ordered list:
1. Step 1
2. Step 1B
3. Step 3
Unordered list
* learning rate
* cycle length
* weight decay
Task list
- [x] Learn Jupyter Notebooks
- [x] Writing
- [x] Modes
- [x] Other Considerations
- [ ] Change the world
Double click on each to see how they are built!
### Code Capabilities
**Code** cells are different than **Markdown** cells in that they have an output cell. This means that we can _keep_ the results of our code within the notebook and share them. Let's say we want to show a graph that explains the result of an experiment. We can just run the necessary cells and save the notebook. The output will be there when we open it again! Try it out by running the next four cells.
```
# Import necessary libraries
from fastai.vision import *
import matplotlib.pyplot as plt
from PIL import Image
a = 1
b = a + 1
c = b + a + 1
d = c + b + a + 1
a, b, c ,d
plt.plot([a,b,c,d])
plt.show()
```
We can also print images while experimenting. I am watching you.
```
Image.open('images/notebook_tutorial/cat_example.jpg')
```
### Running the app locally
You may be running Jupyter Notebook from an interactive coding environment like Gradient, Sagemaker or Salamander. You can also run a Jupyter Notebook server from your local computer. What's more, if you have installed Anaconda you don't even need to install Jupyter (if not, just `pip install jupyter`).
You just need to run `jupyter notebook` in your terminal. Remember to run it from a folder that contains all the folders/files you will want to access. You will be able to open, view and edit files located within the directory in which you run this command but not files in parent directories.
If a browser tab does not open automatically once you run the command, you should CTRL+CLICK the link starting with 'https://localhost:' and this will open a new tab in your default browser.
### Creating a notebook
Click on 'New' in the upper right corner and 'Python 3' in the drop-down list (we are going to use a [Python kernel](https://github.com/ipython/ipython) for all our experiments).

Note: You will sometimes hear people talking about the Notebook 'kernel'. The 'kernel' is just the Python engine that performs the computations for you.
### Shortcuts and tricks
#### Command Mode Shortcuts
There are a couple of useful keyboard shortcuts in `Command Mode` that you can leverage to make Jupyter Notebook faster to use. Remember that to switch back and forth between `Command Mode` and `Edit Mode` with <kbd>Esc</kbd> and <kbd>Enter</kbd>.
<kbd>m</kbd>: Convert cell to Markdown
<kbd>y</kbd>: Convert cell to Code
<kbd>D</kbd>+<kbd>D</kbd>: Delete the cell(if it's not the only cell) or delete the content of the cell and reset cell to Code(if only one cell left)
<kbd>o</kbd>: Toggle between hide or show output
<kbd>Shift</kbd>+<kbd>Arrow up/Arrow down</kbd>: Selects multiple cells. Once you have selected them you can operate on them like a batch (run, copy, paste etc).
<kbd>Shift</kbd>+<kbd>M</kbd>: Merge selected cells.
<kbd>Shift</kbd>+<kbd>Tab</kbd>: [press these two buttons at the same time, once] Tells you which parameters to pass on a function
<kbd>Shift</kbd>+<kbd>Tab</kbd>: [press these two buttons at the same time, three times] Gives additional information on the method
#### Cell Tricks
```
from fastai import*
from fastai.vision import *
```
There are also some tricks that you can code into a cell.
`?function-name`: Shows the definition and docstring for that function
```
?ImageDataBunch
```
`??function-name`: Shows the source code for that function
```
??ImageDataBunch
```
`doc(function-name)`: Shows the definition, docstring **and links to the documentation** of the function
(only works with fastai library imported)
```
doc(ImageDataBunch)
```
#### Line Magics
Line magics are functions that you can run on cells and take as an argument the rest of the line from where they are called. You call them by placing a '%' sign before the command. The most useful ones are:
`%matplotlib inline`: This command ensures that all matplotlib plots will be plotted in the output cell within the notebook and will be kept in the notebook when saved.
`%reload_ext autoreload`, `%autoreload 2`: Reload all modules before executing a new line. If a module is edited, it is not necessary to rerun the import commands, the modules will be reloaded automatically.
These three commands are always called together at the beginning of every notebook.
```
%matplotlib inline
%reload_ext autoreload
%autoreload 2
```
`%timeit`: Runs a line a ten thousand times and displays the average time it took to run it.
```
%timeit [i+1 for i in range(1000)]
```
`%debug`: Allows to inspect a function which is showing an error using the [Python debugger](https://docs.python.org/3/library/pdb.html).
```
for i in range(1000):
a = i+1
b = 'string'
c = b+1
%debug
```
|
github_jupyter
|
1+1
3/2
# Import necessary libraries
from fastai.vision import *
import matplotlib.pyplot as plt
from PIL import Image
a = 1
b = a + 1
c = b + a + 1
d = c + b + a + 1
a, b, c ,d
plt.plot([a,b,c,d])
plt.show()
Image.open('images/notebook_tutorial/cat_example.jpg')
from fastai import*
from fastai.vision import *
?ImageDataBunch
??ImageDataBunch
doc(ImageDataBunch)
%matplotlib inline
%reload_ext autoreload
%autoreload 2
%timeit [i+1 for i in range(1000)]
for i in range(1000):
a = i+1
b = 'string'
c = b+1
%debug
| 0.243642 | 0.974508 |
<a href="https://colab.research.google.com/github/pravina5/Pravina-Bhalerao-Grip-TSF/blob/main/Grip_task1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Name : Pravina Bhalerao
The Spark Foundation
Data Science and Business Analytics Task#1
Predict the Percentage of a Student based on no of hrs of study using Simple Linear Regression with 2 variables.
Question : What will be the predicted score if the student studies for 9.25 hrs/day
# **1.Importing Libraries**
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import cm
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import pandas as pd
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
```
# **2. Importing Dataset**
The dataset has two features :No of hours a student studies and the scores obtained.
```
# Reading data from link
data = pd.read_csv("http://bit.ly/w-data")
# displays the first 10 rows of the dataset
data.head(10)
```
# **3.Understanding Data**
```
# Shape of our dataset
data.shape
''' Info our dataset. Use to see if there are any null values. If yes the we need to manipulate the data by deleting rows
if there are enough example or replace with mean/median/mode '''
data.info()
# as all the values are NON-Null there is no need to perform any manipulation
# Describe our dataset. It is used to check if there is any sudden jump
data.describe()
```
# **4.Let's visualize the dataset and see the relation between the data**
```
sns.set(color_codes=True)
x= data["Hours"]
y= data["Scores"]
sns.scatterplot(x=x,y=y, data = data,palette = 'dark',size= 7)
plt.show()
# Visualizing the data using heatmap. It is visible from this Hours and Scores are correlated to each other.
sns.heatmap(data.corr(), cmap="YlGnBu", annot = True)
plt.show()
```
# **5. Performing Linear Regression**
Equation of simple linear regression
y = c + mX
In our case:
Scores = c + m * Hours
The m values are known as model coefficients or model parameters.
# **5.a Create X and y**
```
X = data['Hours'] #Independant variable
y= data['Scores'] #Target variable
```
# **5.b Create Train and Test Set**
We need to split our variables into **training and testing sets**. Using the **training set**, we’ll **build the model** and perform the model on the testing set. We’ll divide the training and testing sets into a **8:2 ratio**, respectively as this is the most common ratio.
```
# Splitting the varaibles as training and testing
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size = 0.8,
test_size = 0.2, random_state = 100)
# Training set after spilting
X_train #hours
print(X_train.shape)
print(X_test.shape)
y_train #Scores
# Shape of the train set without adding column
X_train.shape #(20,)
# Adding additional column to the train and test data
X_train = X_train.values.reshape(-1,1)
X_test = X_test.values.reshape(-1,1)
print(X_train.shape)
print(X_test.shape)
```
# **5.c Now, let’s fit the line to the plot importing the LinearRegression library from the sklearn.linear_model.**
```
from sklearn.linear_model import LinearRegression
# Creating an object of Linear Regression
lm = LinearRegression()
# Fit the model using .fit() method
lm.fit(X_train, y_train)
# Intercept value
print("Intercept :",lm.intercept_)
# Slope value
print('Slope :',lm.coef_)
```
**Equation of Line:**
y=9.84X+1.99
Scores = 9.84*Hours+1.99
```
# Plotting the regression line
line = lm.coef_*X+lm.intercept_
# Plotting for the test data
plt.scatter(X, y)
plt.plot(X, line);
plt.xlabel('No of Hours')
plt.ylabel('Scores')
plt.show()
lm.score(X_train,y_train) #shows accuracy of the model
```
# Evaluating Regression Model Using R² value
```
# Making Predictions of y_value
y_train_pred = lm.predict(X_train)
y_test_pred = lm.predict(X_test)
# Comparing the r2 value of both train and test data
print("R² value of train set data:",r2_score(y_train,y_train_pred))
print("R² value of train set data:",r2_score(y_test,y_test_pred))
```
# **The R² value on test data is within 5% of the R² value on training data. We can apply the model to the unseen test set in the future.**
# Evaluating Regression Model using Mean Absolute Error
```
from sklearn import metrics
print('Mean Absolute Error:',
metrics.mean_absolute_error(y_test, y_pred))
print('No of hours (Test data)')
print(X_test) # Testing data - In Hours
y_pred = lm.predict(X_test) # Predicting the scores
# Comparing Actual vs Predicted
df = pd.DataFrame({'Actual': y_test, 'Predicted': y_pred})
df
```
# **Making Own Prediction:**
```
hours =9.25
own_pred =lm.predict(np.array([[9.25]]))
print("No of Hours = {}".format(hours))
print("Predicted Score = {}".format(own_pred[0]))
```
# **The predicted score if the student studies for 9.25 hrs/day is 92.96**
**References:**
https://towardsdatascience.com/simple-linear-regression-model-using-python-machine-learning-eab7924d18b4
https://drive.google.com/file/d/1koGHPElsHuXo9HPL4BQkZWRMJkOEHiv4/view?usp=sharing
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import cm
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import pandas as pd
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
# Reading data from link
data = pd.read_csv("http://bit.ly/w-data")
# displays the first 10 rows of the dataset
data.head(10)
# Shape of our dataset
data.shape
''' Info our dataset. Use to see if there are any null values. If yes the we need to manipulate the data by deleting rows
if there are enough example or replace with mean/median/mode '''
data.info()
# as all the values are NON-Null there is no need to perform any manipulation
# Describe our dataset. It is used to check if there is any sudden jump
data.describe()
sns.set(color_codes=True)
x= data["Hours"]
y= data["Scores"]
sns.scatterplot(x=x,y=y, data = data,palette = 'dark',size= 7)
plt.show()
# Visualizing the data using heatmap. It is visible from this Hours and Scores are correlated to each other.
sns.heatmap(data.corr(), cmap="YlGnBu", annot = True)
plt.show()
X = data['Hours'] #Independant variable
y= data['Scores'] #Target variable
# Splitting the varaibles as training and testing
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size = 0.8,
test_size = 0.2, random_state = 100)
# Training set after spilting
X_train #hours
print(X_train.shape)
print(X_test.shape)
y_train #Scores
# Shape of the train set without adding column
X_train.shape #(20,)
# Adding additional column to the train and test data
X_train = X_train.values.reshape(-1,1)
X_test = X_test.values.reshape(-1,1)
print(X_train.shape)
print(X_test.shape)
from sklearn.linear_model import LinearRegression
# Creating an object of Linear Regression
lm = LinearRegression()
# Fit the model using .fit() method
lm.fit(X_train, y_train)
# Intercept value
print("Intercept :",lm.intercept_)
# Slope value
print('Slope :',lm.coef_)
# Plotting the regression line
line = lm.coef_*X+lm.intercept_
# Plotting for the test data
plt.scatter(X, y)
plt.plot(X, line);
plt.xlabel('No of Hours')
plt.ylabel('Scores')
plt.show()
lm.score(X_train,y_train) #shows accuracy of the model
# Making Predictions of y_value
y_train_pred = lm.predict(X_train)
y_test_pred = lm.predict(X_test)
# Comparing the r2 value of both train and test data
print("R² value of train set data:",r2_score(y_train,y_train_pred))
print("R² value of train set data:",r2_score(y_test,y_test_pred))
from sklearn import metrics
print('Mean Absolute Error:',
metrics.mean_absolute_error(y_test, y_pred))
print('No of hours (Test data)')
print(X_test) # Testing data - In Hours
y_pred = lm.predict(X_test) # Predicting the scores
# Comparing Actual vs Predicted
df = pd.DataFrame({'Actual': y_test, 'Predicted': y_pred})
df
hours =9.25
own_pred =lm.predict(np.array([[9.25]]))
print("No of Hours = {}".format(hours))
print("Predicted Score = {}".format(own_pred[0]))
| 0.775605 | 0.985482 |
### 基于贝叶斯决策理论的分类方法
朴素贝叶斯的优缺点:
- 优点:在数据较少的情况下仍然有效,可以处理多类别问题。
- 缺点:对于输入数据的准备方式较为敏感。
- 适用数据类型:标称型数据。
```
%run create2Normal.py
```
对于上图,我们用p1(x,y)来表示数据点(x,y)属于类别1(红色圆点)的概率,用p2(x,y)来表示数据点(x,y)属于类别2(蓝色三角)的概率。
对于一个新的数据点(x,y),可以用下面的规则来判断它的类别:
- 如果p1(x,y) > p2(x,y),那么类别为1
- 如果p2(x,y) > p1(x,y),那么类别为2
即我们会选择高概率对应的类别。这就是**贝叶斯决策理论的核心思想** ,即**选择具有最高概率的决策** 。
### 条件概率
一种有效计算条件概率的方法称为贝叶斯准则。贝叶斯准则告诉我们如何交换条件概率中的条件和结果,即如果已知P(x|c),要求P(c|x),则可以用如下的条件概率计算公式:
$$p(c|x) = \frac{p(x|c) \cdot p(c)}{p(x)}$$
### 使用条件概率来分类
使用贝叶斯准则在进行类似第一节中的比较时,需要计算和比较$p(c_{1}|x,y)$和$p(c_{2}|x,y)$。应用贝叶斯准则可以得到:
$$p(c_{i}|x,\mathbf y) = \frac{p(x,\mathbf y| c_{i}) \cdot p(c_{i})}{p(x,\mathbf y)}$$
使用这些定义可以定义贝叶斯分类准则为:
- 如果$P(c_{1}|x,y) > P(c_{2}|x,y)$,那么属于类别$c_{1}$。
- 如果$P(c_{1}|x,y) < P(c_{2}|x,y)$,那么属于类别$c_{2}$。
### 使用朴素贝叶斯进行文档分类
朴素贝叶斯的一般过程
(1)收集数据:可以使用任何方法。本章使用RSS源。
(2)准备数据:需要数值型或者布尔型数据。
(3)分析数据:有大量特征时,绘制特征作用不大,此时使用直方图效果最好。
(4)训练算法:计算不同的独立特征的条件概率。
(5)测试算法:计算错误率。
(6)使用算法:一个常见的朴素贝叶斯应用是文档分类。可以在任意的分类场景中使用朴素贝叶斯分类器,不一定非要是文本。
根据统计学知识,如果每个特征需要N个样本,对于10个特征就要有$N^{10}$个样本,对于包含1000个特征(1000个单词作为特征)的词汇表则需要$N^{1000}$个样本。**如果特征之间相互独立,就可以把样本数从$N^{1000}$压缩到$1000 \times N$** 。
这里的独立是统计意义上的独立,即**一个特征或者单词出现的可能性与它和其他单词相邻没有关系** 。
朴素贝叶斯分类器的另一个假设是**每个特征同等重要** 。朴素贝叶斯分类器通常有两种实现方式:一种基于贝努利模型实现,另一种基于多项式模型实现。这里采用前一种实现方式。该实现方式中并**不考虑词在文档中出现的次数**,只考虑出不出现,因此在这个意义上相当于假设词是等权重的。后面**考虑词在文档中出现次数**的模型是**多项式模型**。
### 使用Python进行文本分类
```
import bayes
listOPosts, listClasses = bayes.loadDataSet()
myVocabList = bayes.createVocabList(listOPosts)
print myVocabList
print bayes.setOfWords2Vec(myVocabList, listOPosts[0])
print bayes.setOfWords2Vec(myVocabList, listOPosts[3])
```
重写贝叶斯准则,将x,y替换为$\mathbf w$,$\mathbf w$表示一个向量。
$$p(c_{i}|\mathbf w) = \frac{p(\mathbf w|c_{i}) \cdot p(c_{i})}{p(\mathbf w)}$$
我们可以先通过类别i(侮辱性语言或者非侮辱性语言)中文档数除以总文档数来计算概率$p(c_{i})$。接下来计算$p(\mathbf w | c_{i})$,这里会用到朴素贝叶斯假设。如果将$\mathbf w$展开为一个个独立特征,则可以将上述概率写成$p(w_{0}, w_{1},w_{2}, \cdot \cdot \cdot , w_{n}|c_{i})$。这里假设所有词都相互独立,该假设也称为**条件独立性假设** ,它意味着可以使用$p(w_{0}|c_{i})p(w_{1}|c_{i})p(w_{2}|c_{i})\cdot \cdot \cdot p(w_{N}|c_{i})$来计算上述概率。
函数伪代码如下:
计算每个类别中的文档数目
对每篇训练文档:
对每个类别:
如果词条出现在文档中->增加该词条的计数值
增加所有词条的计数值
对每个类别:
对每个词条:
将该词条的数目除以总词条数目得到条件概率
返回每个类别的条件概率
```
import numpy as np
reload(bayes)
listOPosts, listClasses = bayes.loadDataSet()
myVocabList = bayes.createVocabList(listOPosts)
trainMat = []
for postinDoc in listOPosts:
trainMat.append(bayes.setOfWords2Vec(myVocabList, postinDoc))
p0V, p1V, pAb = bayes.trainNB0_Old(trainMat, listClasses)
pAb
p0V
p1V
```
在编写trainNB0函数的朴素贝叶斯算法时,需要计算$p(w_{0}|1)p(w_{1}|1)p(w_{2}|1)$。如果一个概率为0,则最后乘积也为0。为了降低这种影响,可以将所有词的出现数初始化为1,并将分母初始化为2。
另一个问题是下溢出,由于太多很小的数相乘造成。一般解决办法是取对数,将乘法变为加法,从而避免下溢出的错误。
```
reload(bayes)
bayes.testingNB()
```
目前我们将每个词出现与否作为一个特征,这可以被描述为**词集模型(set-of-words model)** 。如果一个词在文档中出现不止一次,这可能意味着包含该词是否出现在文档中所不能表达的某种信息,这种方法称为**词袋模型(bag-of-words model)** 。
词袋模型中每个单词可以出现多次,而词集中,每个单词只能出现一次。
### 使用朴素贝叶斯过滤垃圾邮件
使用朴素贝叶斯对电子邮件进行分类
(1)收集数据:提供文本文件。
(2)准备数据:将文本文件解析成词条向量。
(3)分析数据:检查词条确保解析的正确性。
(4)训练算法:使用我们之前建立的trainNB0()函数。
(5)测试算法:使用classifyNB(),并且构建一个新的测试函数来计算文档集的错误率。
(6)使用算法:构建一个完整的程序对一组文档进行分类,将错分的文档输出到屏幕上。
```
mySent = 'This book is the best book on Python or M.L. I have ever laid eyes upon.'
mySent.split()
import re
regEx = re.compile('\\W*')
listOfTokens = regEx.split(mySent)
listOfTokens
[tok for tok in listOfTokens if len(tok) > 0]
[tok.lower() for tok in listOfTokens if len(tok) > 0]
emailText = open('email/ham/6.txt', 'r').read()
listOfTokens = regEx.split(emailText)
```
在spamTest函数中的随机构造训练集的部分,随机选择数据的一部分作为训练集,剩余部分作为测试集的过程称为**留存交叉验证(hold-out cross validation)** 。假定现在只完成了一次迭代,那么为了更精确地估计分类器的错误率,就应该进行多次迭代后求出平均错误。
```
reload(bayes)
bayes.spamTest()
bayes.spamTest()
```
|
github_jupyter
|
%run create2Normal.py
import bayes
listOPosts, listClasses = bayes.loadDataSet()
myVocabList = bayes.createVocabList(listOPosts)
print myVocabList
print bayes.setOfWords2Vec(myVocabList, listOPosts[0])
print bayes.setOfWords2Vec(myVocabList, listOPosts[3])
import numpy as np
reload(bayes)
listOPosts, listClasses = bayes.loadDataSet()
myVocabList = bayes.createVocabList(listOPosts)
trainMat = []
for postinDoc in listOPosts:
trainMat.append(bayes.setOfWords2Vec(myVocabList, postinDoc))
p0V, p1V, pAb = bayes.trainNB0_Old(trainMat, listClasses)
pAb
p0V
p1V
reload(bayes)
bayes.testingNB()
mySent = 'This book is the best book on Python or M.L. I have ever laid eyes upon.'
mySent.split()
import re
regEx = re.compile('\\W*')
listOfTokens = regEx.split(mySent)
listOfTokens
[tok for tok in listOfTokens if len(tok) > 0]
[tok.lower() for tok in listOfTokens if len(tok) > 0]
emailText = open('email/ham/6.txt', 'r').read()
listOfTokens = regEx.split(emailText)
reload(bayes)
bayes.spamTest()
bayes.spamTest()
| 0.127273 | 0.877161 |
## Live Disparity Map ##
<b>Description:</b> After you use the disparity map tuner to find the best values for the resulting image, then run this code to see a live view of your disparity map.
<hr>
#### Cell Block 1 ####
<b>Description:</b> This cell block just imports all the necessary libraries and loads up the necessary variables
```
import cv2
import numpy as np
import traitlets
from IPython.display import display, HTML, clear_output
import ipywidgets.widgets as widgets
from jetcam.utils import bgr8_to_jpeg
from jetcam.usb_camera import USBCamera
from matplotlib import pyplot as plt
from matplotlib.widgets import Slider, Button
from stereovision.calibration import StereoCalibrator
from stereovision.calibration import StereoCalibration
import os
camWidth=640
camHeight=480
cameraR = USBCamera(width=camWidth, height=camHeight, capture_device=0)
cameraL = USBCamera(width=camWidth, height=camHeight, capture_device=1)
imageR = cameraR.read()
imageL = cameraL.read()
cameraR.running = True
cameraL.running = True
image_widgetR = widgets.Image(format='jpeg')
image_widgetR.value = bgr8_to_jpeg(imageR)
image_widgetL = widgets.Image(format='jpeg')
image_widgetL.value = bgr8_to_jpeg(imageL)
button_layout = widgets.Layout(width='128px', height='64px')
button = widgets.Button(description="Take Picture", button_style='success', layout=button_layout)
camera_linkR = traitlets.dlink((cameraR, 'value'), (image_widgetR, 'value'), transform=bgr8_to_jpeg)
camera_linkL = traitlets.dlink((cameraL, 'value'), (image_widgetL, 'value'), transform=bgr8_to_jpeg)
print('done')
```
#### Cell Block 2 ####
<b>Description:</b> Here we import the calibration data
```
# Implementing calibration data
print('Read calibration data...')
calibration = StereoCalibration(input_folder='calib_result')
print('done')
```
#### Cell Block 3 ####
<b>Description:</b> Finally, run a live view of the disparity map from a live feed of the stereo cameras.
```
import time
SWS=5
PFS=5
PFC=29
MDS=-81
NOD=128
TTH=100
UR=6
SR=12
SPWS=120
dm_colors_autotune = True
disp_max = -100000
disp_min = 10000
def stereo_depth_map(rectified_pair):
global disp_max, disp_min
c, r = rectified_pair[0].shape
disparity = np.zeros((c, r), np.uint8)
sbm = cv2.StereoBM_create(numDisparities=16, blockSize=15)
sbm.setPreFilterType(1)
sbm.setPreFilterSize(PFS)
sbm.setPreFilterCap(PFC)
sbm.setMinDisparity(MDS)
sbm.setNumDisparities(NOD)
sbm.setTextureThreshold(TTH)
sbm.setUniquenessRatio(UR)
sbm.setSpeckleRange(SR)
sbm.setSpeckleWindowSize(SPWS)
dmLeft = rectified_pair[0]
dmRight = rectified_pair[1]
disparity = sbm.compute(dmLeft, dmRight)
local_max = disparity.max()
local_min = disparity.min()
if (dm_colors_autotune):
disp_max = max(local_max,disp_max)
disp_min = min(local_min,disp_min)
local_max = disp_max
local_min = disp_min
disparity_grayscale = (disparity-local_min)*(65535.0/(local_max-local_min))
disparity_fixtype = cv2.convertScaleAbs(disparity_grayscale, alpha=(255.0/65535.0))
disparity_color = cv2.applyColorMap(disparity_fixtype, cv2.COLORMAP_JET)
return disparity_color
frameWidgetL = widgets.Image(format='jpeg', width=camWidth, height=camHeight)
frameWidgetR = widgets.Image(format='jpeg', width=camWidth, height=camHeight)
cameraBool = True
display(widgets.HBox([image_widgetR, image_widgetL]))
display(frameWidgetL)
output2 = widgets.Output()
display(output2)
while cameraBool:
with output2:
cameraL_frame = cameraL.value
cameraR_frame = cameraR.value
newFrameL = cv2.cvtColor(cameraL_frame, cv2.COLOR_BGR2GRAY)
newFrameR = cv2.cvtColor(cameraR_frame, cv2.COLOR_BGR2GRAY)
rectified_pair = calibration.rectify((newFrameL, newFrameR))
disparity = stereo_depth_map(rectified_pair)
frameWidgetL.value = bgr8_to_jpeg(disparity)
time.sleep(0.001)
```
|
github_jupyter
|
import cv2
import numpy as np
import traitlets
from IPython.display import display, HTML, clear_output
import ipywidgets.widgets as widgets
from jetcam.utils import bgr8_to_jpeg
from jetcam.usb_camera import USBCamera
from matplotlib import pyplot as plt
from matplotlib.widgets import Slider, Button
from stereovision.calibration import StereoCalibrator
from stereovision.calibration import StereoCalibration
import os
camWidth=640
camHeight=480
cameraR = USBCamera(width=camWidth, height=camHeight, capture_device=0)
cameraL = USBCamera(width=camWidth, height=camHeight, capture_device=1)
imageR = cameraR.read()
imageL = cameraL.read()
cameraR.running = True
cameraL.running = True
image_widgetR = widgets.Image(format='jpeg')
image_widgetR.value = bgr8_to_jpeg(imageR)
image_widgetL = widgets.Image(format='jpeg')
image_widgetL.value = bgr8_to_jpeg(imageL)
button_layout = widgets.Layout(width='128px', height='64px')
button = widgets.Button(description="Take Picture", button_style='success', layout=button_layout)
camera_linkR = traitlets.dlink((cameraR, 'value'), (image_widgetR, 'value'), transform=bgr8_to_jpeg)
camera_linkL = traitlets.dlink((cameraL, 'value'), (image_widgetL, 'value'), transform=bgr8_to_jpeg)
print('done')
# Implementing calibration data
print('Read calibration data...')
calibration = StereoCalibration(input_folder='calib_result')
print('done')
import time
SWS=5
PFS=5
PFC=29
MDS=-81
NOD=128
TTH=100
UR=6
SR=12
SPWS=120
dm_colors_autotune = True
disp_max = -100000
disp_min = 10000
def stereo_depth_map(rectified_pair):
global disp_max, disp_min
c, r = rectified_pair[0].shape
disparity = np.zeros((c, r), np.uint8)
sbm = cv2.StereoBM_create(numDisparities=16, blockSize=15)
sbm.setPreFilterType(1)
sbm.setPreFilterSize(PFS)
sbm.setPreFilterCap(PFC)
sbm.setMinDisparity(MDS)
sbm.setNumDisparities(NOD)
sbm.setTextureThreshold(TTH)
sbm.setUniquenessRatio(UR)
sbm.setSpeckleRange(SR)
sbm.setSpeckleWindowSize(SPWS)
dmLeft = rectified_pair[0]
dmRight = rectified_pair[1]
disparity = sbm.compute(dmLeft, dmRight)
local_max = disparity.max()
local_min = disparity.min()
if (dm_colors_autotune):
disp_max = max(local_max,disp_max)
disp_min = min(local_min,disp_min)
local_max = disp_max
local_min = disp_min
disparity_grayscale = (disparity-local_min)*(65535.0/(local_max-local_min))
disparity_fixtype = cv2.convertScaleAbs(disparity_grayscale, alpha=(255.0/65535.0))
disparity_color = cv2.applyColorMap(disparity_fixtype, cv2.COLORMAP_JET)
return disparity_color
frameWidgetL = widgets.Image(format='jpeg', width=camWidth, height=camHeight)
frameWidgetR = widgets.Image(format='jpeg', width=camWidth, height=camHeight)
cameraBool = True
display(widgets.HBox([image_widgetR, image_widgetL]))
display(frameWidgetL)
output2 = widgets.Output()
display(output2)
while cameraBool:
with output2:
cameraL_frame = cameraL.value
cameraR_frame = cameraR.value
newFrameL = cv2.cvtColor(cameraL_frame, cv2.COLOR_BGR2GRAY)
newFrameR = cv2.cvtColor(cameraR_frame, cv2.COLOR_BGR2GRAY)
rectified_pair = calibration.rectify((newFrameL, newFrameR))
disparity = stereo_depth_map(rectified_pair)
frameWidgetL.value = bgr8_to_jpeg(disparity)
time.sleep(0.001)
| 0.383526 | 0.721559 |
# Assignment 1
The goal of this assignment is to supply you with machine learning models and algorithms. In this notebook, we will cover linear and nonlinear models, the concept of loss functions and some optimization techniques. All mathematical operations should be implemented in **NumPy** only.
## Table of contents
* [1. Logistic Regression](#1.-Logistic-Regression)
* [1.1 Linear Mapping](#1.1-Linear-Mapping)
* [1.2 Sigmoid](#1.2-Sigmoid)
* [1.3 Negative Log Likelihood](#1.3-Negative-Log-Likelihood)
* [1.4 Model](#1.4-Model)
* [1.5 Simple Experiment](#1.5-Simple-Experiment)
* [2. Decision Tree](#2.-Decision-Tree)
* [2.1 Gini Index & Data Split](#2.1-Gini-Index-&-Data-Split)
* [2.2 Terminal Node](#2.2-Terminal-Node)
* [2.3 Build the Decision Tree](#2.3-Build-the-Decision-Tree)
* [3. Experiments](#3.-Experiments)
* [3.1 Decision Tree for Heart Disease Prediction](#3.1-Decision-Tree-for-Heart-Disease-Prediction)
* [3.2 Logistic Regression for Heart Disease Prediction](#3.2-Logistic-Regression-for-Heart-Disease-Prediction)
### Note
Some of the concepts below have not (yet) been discussed during the lecture. These will be discussed further during the next lectures.
### Before you begin
To check whether the code you've written is correct, we'll use **automark**. For this, we created for each of you an account with the username being your student number.
```
import automark as am
# fill in you student number as your username
username = '12743674'
# to check your progress, you can run this function
am.get_progress(username)
```
So far all your tests are 'not attempted'. At the end of this notebook you'll need to have completed all test. The output of `am.get_progress(username)` should at least match the example below. However, we encourage you to take a shot at the 'not attempted' tests!
```
---------------------------------------------
| Your name / student number |
| your_email@your_domain.whatever |
---------------------------------------------
| linear_forward | not attempted |
| linear_grad_W | not attempted |
| linear_grad_b | not attempted |
| nll_forward | not attempted |
| nll_grad_input | not attempted |
| sigmoid_forward | not attempted |
| sigmoid_grad_input | not attempted |
| tree_data_split_left | not attempted |
| tree_data_split_right | not attempted |
| tree_gini_index | not attempted |
| tree_to_terminal | not attempted |
---------------------------------------------
```
```
from __future__ import print_function, absolute_import, division # You don't need to know what this is.
import numpy as np # this imports numpy, which is used for vector- and matrix calculations
```
This notebook makes use of **classes** and their **instances** that we have already implemented for you. It allows us to write less code and make it more readable. If you are interested in it, here are some useful links:
* The official [documentation](https://docs.python.org/3/tutorial/classes.html)
* Video by *sentdex*: [Object Oriented Programming Introduction](https://www.youtube.com/watch?v=ekA6hvk-8H8)
* Antipatterns in OOP: [Stop Writing Classes](https://www.youtube.com/watch?v=o9pEzgHorH0)
# 1. Logistic Regression
We start with a very simple algorithm called **Logistic Regression**. It is a generalized linear model for 2-class classification.
It can be generalized to the case of many classes and to non-linear cases as well. However, here we consider only the simplest case.
Let us consider a data with 2 classes. Class 0 and class 1. For a given test sample, logistic regression returns a value from $[0, 1]$ which is interpreted as a probability of belonging to class 1. The set of points for which the prediction is $0.5$ is called a *decision boundary*. It is a line on a plane or a hyper-plane in a space.

Logistic regression has two trainable parameters: a weight $W$ and a bias $b$. For a vector of features $X$, the prediction of logistic regression is given by
$$
f(X) = \frac{1}{1 + \exp(-[XW + b])} = \sigma(h(X))
$$
where $\sigma(z) = \frac{1}{1 + \exp(-z)}$ and $h(X)=XW + b$.
Parameters $W$ and $b$ are fitted by maximizing the log-likelihood (or minimizing the negative log-likelihood) of the model on the training data. For a training subset $\{X_j, Y_j\}_{j=1}^N$ the normalized negative log likelihood (NLL) is given by
$$
\mathcal{L} = -\frac{1}{N}\sum_j \log\Big[ f(X_j)^{Y_j} \cdot (1-f(X_j))^{1-Y_j}\Big]
= -\frac{1}{N}\sum_j \Big[ Y_j\log f(X_j) + (1-Y_j)\log(1-f(X_j))\Big]
$$
There are different ways of fitting this model. In this assignment we consider Logistic Regression as a one-layer neural network. We use the following algorithm for the **forward** pass:
1. Linear mapping: $h=XW + b$
2. Sigmoid activation function: $f=\sigma(h)$
3. Calculation of NLL: $\mathcal{L} = -\frac{1}{N}\sum_j \Big[ Y_j\log f_j + (1-Y_j)\log(1-f_j)\Big]$
In order to fit $W$ and $b$ we perform Gradient Descent ([GD](https://en.wikipedia.org/wiki/Gradient_descent)). We choose a small learning rate $\gamma$ and after each computation of forward pass, we update the parameters
$$W_{\text{new}} = W_{\text{old}} - \gamma \frac{\partial \mathcal{L}}{\partial W}$$
$$b_{\text{new}} = b_{\text{old}} - \gamma \frac{\partial \mathcal{L}}{\partial b}$$
We use Backpropagation method ([BP](https://en.wikipedia.org/wiki/Backpropagation)) to calculate the partial derivatives of the loss function with respect to the parameters of the model.
$$
\frac{\partial\mathcal{L}}{\partial W} =
\frac{\partial\mathcal{L}}{\partial h} \frac{\partial h}{\partial W} =
\frac{\partial\mathcal{L}}{\partial f} \frac{\partial f}{\partial h} \frac{\partial h}{\partial W}
$$
$$
\frac{\partial\mathcal{L}}{\partial b} =
\frac{\partial\mathcal{L}}{\partial h} \frac{\partial h}{\partial b} =
\frac{\partial\mathcal{L}}{\partial f} \frac{\partial f}{\partial h} \frac{\partial h}{\partial b}
$$
## 1.1 Linear Mapping
First of all, you need to implement the forward pass of a linear mapping:
$$
h(X) = XW +b
$$
**Note**: here we use `n_out` as the dimensionality of the output. For logisitc regression `n_out = 1`. However, we will work with cases of `n_out > 1` in next assignments. You will **pass** the current assignment even if your implementation works only in case `n_out = 1`. If your implementation works for the cases of `n_out > 1` then you will not have to modify your method next week. All **numpy** operations are generic. It is recommended to use numpy when is it possible.
```
def linear_forward(x_input, W, b):
"""Perform the mapping of the input
# Arguments
x_input: input of the linear function - np.array of size `(n_objects, n_in)`
W: np.array of size `(n_in, n_out)`
b: np.array of size `(n_out,)`
# Output
the output of the linear function
np.array of size `(n_objects, n_out)`
"""
# output = x_input * np.transpose(W) + b
output = np.dot(x_input, W) + b
return output
```
Let's check your first function. We set the matrices $X, W, b$:
$$
X = \begin{bmatrix}
1 & -1 \\
-1 & 0 \\
1 & 1 \\
\end{bmatrix} \quad
W = \begin{bmatrix}
4 \\
2 \\
\end{bmatrix} \quad
b = \begin{bmatrix}
3 \\
\end{bmatrix}
$$
And then compute
$$
XW = \begin{bmatrix}
1 & -1 \\
-1 & 0 \\
1 & 1 \\
\end{bmatrix}
\begin{bmatrix}
4 \\
2 \\
\end{bmatrix} =
\begin{bmatrix}
2 \\
-4 \\
6 \\
\end{bmatrix} \\
XW + b =
\begin{bmatrix}
5 \\
-1 \\
9 \\
\end{bmatrix}
$$
```
X_test = np.array([[1, -1],
[-1, 0],
[1, 1]])
W_test = np.array([[4],
[2]])
b_test = np.array([3])
h_test = linear_forward(X_test, W_test, b_test)
print(h_test)
am.test_student_function(username, linear_forward, ['x_input', 'W', 'b'])
```
Now you need to implement the calculation of the partial derivative of the loss function with respect to the parameters of the model. As this expressions are used for the updates of the parameters, we refer to them as gradients.
$$
\frac{\partial \mathcal{L}}{\partial W} =
\frac{\partial \mathcal{L}}{\partial h}
\frac{\partial h}{\partial W} \\
\frac{\partial \mathcal{L}}{\partial b} =
\frac{\partial \mathcal{L}}{\partial h}
\frac{\partial h}{\partial b} \\
$$
```
def linear_grad_W(x_input, grad_output, W, b):
"""Calculate the partial derivative of
the loss with respect to W parameter of the function
dL / dW = (dL / dh) * (dh / dW)
# Arguments
x_input: input of a dense layer - np.array of size `(n_objects, n_in)`
grad_output: partial derivative of the loss functions with
respect to the ouput of the dense layer (dL / dh)
np.array of size `(n_objects, n_out)`
W: np.array of size `(n_in, n_out)`
b: np.array of size `(n_out,)`
# Output
the partial derivative of the loss
with respect to W parameter of the function
np.array of size `(n_in, n_out)`
"""
# grad_W = np.gradient(np.dot(x_input, W) + b, W)
# grad_W = grad_output * np.gradient(linear_forward(x_input, W, b), W)
grad_W = np.dot(np.transpose(x_input), grad_output)
return grad_W
am.test_student_function(username, linear_grad_W, ['x_input', 'grad_output', 'W', 'b'])
def linear_grad_b(x_input, grad_output, W, b):
"""Calculate the partial derivative of
the loss with respect to b parameter of the function
dL / db = (dL / dh) * (dh / db)
# Arguments
x_input: input of a dense layer - np.array of size `(n_objects, n_in)`
grad_output: partial derivative of the loss functions with
respect to the ouput of the linear function (dL / dh)
np.array of size `(n_objects, n_out)`
W: np.array of size `(n_in, n_out)`
b: np.array of size `(n_out,)`
# Output
the partial derivative of the loss
with respect to b parameter of the linear function
np.array of size `(n_out,)`
"""
# grad_b = np.dot(np.transpose(1), grad_output)
# grad_b = 1* grad_output
grad_b = np.dot(np.transpose(np.ones(grad_output.shape)), grad_output)
return grad_b
am.test_student_function(username, linear_grad_b, ['x_input', 'grad_output', 'W', 'b'])
am.get_progress(username)
```
## 1.2 Sigmoid
$$
f = \sigma(h) = \frac{1}{1 + e^{-h}}
$$
Sigmoid function is applied element-wise. It does not change the dimensionality of the tensor and its implementation is shape-agnostic in general.
```
def sigmoid_forward(x_input):
"""sigmoid nonlinearity
# Arguments
x_input: np.array of size `(n_objects, n_in)`
# Output
the output of relu layer
np.array of size `(n_objects, n_in)`
"""
output = 1 / (1 + np.exp(- x_input))
return output
am.test_student_function(username, sigmoid_forward, ['x_input'])
```
Now you need to implement the calculation of the partial derivative of the loss function with respect to the input of sigmoid.
$$
\frac{\partial \mathcal{L}}{\partial h} =
\frac{\partial \mathcal{L}}{\partial f}
\frac{\partial f}{\partial h}
$$
Tensor $\frac{\partial \mathcal{L}}{\partial f}$ comes from the loss function. Let's calculate $\frac{\partial f}{\partial h}$
$$
\frac{\partial f}{\partial h} =
\frac{\partial \sigma(h)}{\partial h} =
\frac{\partial}{\partial h} \Big(\frac{1}{1 + e^{-h}}\Big)
= \frac{e^{-h}}{(1 + e^{-h})^2}
= \frac{1}{1 + e^{-h}} \frac{e^{-h}}{1 + e^{-h}}
= f(h) (1 - f(h))
$$
Therefore, in order to calculate the gradient of the loss with respect to the input of sigmoid function you need
to
1. calculate $f(h) (1 - f(h))$
2. multiply it element-wise by $\frac{\partial \mathcal{L}}{\partial f}$
```
def sigmoid_grad_input(x_input, grad_output):
"""sigmoid nonlinearity gradient.
Calculate the partial derivative of the loss
with respect to the input of the layer
# Arguments
x_input: np.array of size `(n_objects, n_in)`
grad_output: np.array of size `(n_objects, n_in)`
dL / df
# Output
the partial derivative of the loss
with respect to the input of the function
np.array of size `(n_objects, n_in)`
dL / dh
"""
# grad_input = np.dot(np.transpose((1/(1+np.exp(- x_input)))*(np.exp(- x_input)/(1+np.exp(- x_input))), grad_output))
grad_input = (1/(1+np.exp(- x_input))*(np.exp(- x_input)/(1+np.exp(- x_input)))) * grad_output
return grad_input
am.test_student_function(username, sigmoid_grad_input, ['x_input', 'grad_output'])
```
## 1.3 Negative Log Likelihood
$$
\mathcal{L}
= -\frac{1}{N}\sum_j \Big[ Y_j\log \dot{Y}_j + (1-Y_j)\log(1-\dot{Y}_j)\Big]
$$
Here $N$ is the number of objects. $Y_j$ is the real label of an object and $\dot{Y}_j$ is the predicted one.
```
def nll_forward(target_pred, target_true):
"""Compute the value of NLL
for a given prediction and the ground truth
# Arguments
target_pred: predictions - np.array of size `(n_objects, 1)`
target_true: ground truth - np.array of size `(n_objects, 1)`
# Output
the value of NLL for a given prediction and the ground truth
scalar
"""
output = -(1/len(target_pred))*np.sum(target_true*np.log(target_pred)+(1-target_true)*np.log(1-target_pred))
return output
am.test_student_function(username, nll_forward, ['target_pred', 'target_true'])
```
Now you need to calculate the partial derivative of NLL with with respect to its input.
$$
\frac{\partial \mathcal{L}}{\partial \dot{Y}}
=
\begin{pmatrix}
\frac{\partial \mathcal{L}}{\partial \dot{Y}_0} \\
\frac{\partial \mathcal{L}}{\partial \dot{Y}_1} \\
\vdots \\
\frac{\partial \mathcal{L}}{\partial \dot{Y}_N}
\end{pmatrix}
$$
Let's do it step-by-step
\begin{equation}
\begin{split}
\frac{\partial \mathcal{L}}{\partial \dot{Y}_0}
&= \frac{\partial}{\partial \dot{Y}_0} \Big(-\frac{1}{N}\sum_j \Big[ Y_j\log \dot{Y}_j + (1-Y_j)\log(1-\dot{Y}_j)\Big]\Big) \\
&= -\frac{1}{N} \frac{\partial}{\partial \dot{Y}_0} \Big(Y_0\log \dot{Y}_0 + (1-Y_0)\log(1-\dot{Y}_0)\Big) \\
&= -\frac{1}{N} \Big(\frac{Y_0}{\dot{Y}_0} - \frac{1-Y_0}{1-\dot{Y}_0}\Big)
= \frac{1}{N} \frac{\dot{Y}_0 - Y_0}{\dot{Y}_0 (1 - \dot{Y}_0)}
\end{split}
\end{equation}
And for the other components it can be done in exactly the same way. So the result is the vector where each component is given by
$$\frac{1}{N} \frac{\dot{Y}_j - Y_j}{\dot{Y}_j (1 - \dot{Y}_j)}$$
Or if we assume all multiplications and divisions to be done element-wise the output can be calculated as
$$
\frac{\partial \mathcal{L}}{\partial \dot{Y}} = \frac{1}{N} \frac{\dot{Y} - Y}{\dot{Y} (1 - \dot{Y})}
$$
```
def nll_grad_input(target_pred, target_true):
"""Compute the partial derivative of NLL
with respect to its input
# Arguments
target_pred: predictions - np.array of size `(n_objects, 1)`
target_true: ground truth - np.array of size `(n_objects, 1)`
# Output
the partial derivative
of NLL with respect to its input
np.array of size `(n_objects, 1)`
"""
grad_input = (1/len(target_pred))*((target_pred-target_true)/(target_pred*(1-target_pred)))
return grad_input
am.test_student_function(username, nll_grad_input, ['target_pred', 'target_true'])
am.get_progress(username)
```
## 1.4 Model
Here we provide a model for your. It consist of the function which you have implmeneted above
```
class LogsticRegressionGD(object):
def __init__(self, n_in, lr=0.05):
super().__init__()
self.lr = lr
self.b = np.zeros(1, )
self.W = np.random.randn(n_in, 1)
def forward(self, x):
self.h = linear_forward(x, self.W, self.b)
y = sigmoid_forward(self.h)
return y
def update_params(self, x, nll_grad):
# compute gradients
grad_h = sigmoid_grad_input(self.h, nll_grad)
grad_W = linear_grad_W(x, grad_h, self.W, self.b)
grad_b = linear_grad_b(x, grad_h, self.W, self.b)
# update params
self.W = self.W - self.lr * grad_W
self.b = self.b - self.lr * grad_b
```
## 1.5 Simple Experiment
```
import matplotlib.pyplot as plt
%matplotlib inline
# Generate some data
def generate_2_circles(N=100):
phi = np.linspace(0.0, np.pi * 2, 100)
X1 = 1.1 * np.array([np.sin(phi), np.cos(phi)])
X2 = 3.0 * np.array([np.sin(phi), np.cos(phi)])
Y = np.concatenate([np.ones(N), np.zeros(N)]).reshape((-1, 1))
X = np.hstack([X1,X2]).T
return X, Y
def generate_2_gaussians(N=100):
phi = np.linspace(0.0, np.pi * 2, 100)
X1 = np.random.normal(loc=[1, 2], scale=[2.5, 0.9], size=(N, 2))
X1 = X1.dot(np.array([[0.7, -0.7], [0.7, 0.7]]))
X2 = np.random.normal(loc=[-2, 0], scale=[1, 1.5], size=(N, 2))
X2 = X2.dot(np.array([[0.7, 0.7], [-0.7, 0.7]]))
Y = np.concatenate([np.ones(N), np.zeros(N)]).reshape((-1, 1))
X = np.vstack([X1,X2])
return X, Y
def split(X, Y, train_ratio=0.7):
size = len(X)
train_size = int(size * train_ratio)
indices = np.arange(size)
np.random.shuffle(indices)
train_indices = indices[:train_size]
test_indices = indices[train_size:]
return X[train_indices], Y[train_indices], X[test_indices], Y[test_indices]
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
X, Y = generate_2_circles()
ax1.scatter(X[:,0], X[:,1], c=Y.ravel(), edgecolors= 'none')
ax1.set_aspect('equal')
X, Y = generate_2_gaussians()
ax2.scatter(X[:,0], X[:,1], c=Y.ravel(), edgecolors= 'none')
ax2.set_aspect('equal')
X_train, Y_train, X_test, Y_test = split(*generate_2_gaussians(), 0.7)
# let's train our model
model = LogsticRegressionGD(2, 0.05)
for step in range(30):
Y_pred = model.forward(X_train)
loss_value = nll_forward(Y_pred, Y_train)
accuracy = ((Y_pred > 0.5) == Y_train).mean()
print('Step: {} \t Loss: {:.3f} \t Acc: {:.1f}%'.format(step, loss_value, accuracy * 100))
loss_grad = nll_grad_input(Y_pred, Y_train)
model.update_params(X_train, loss_grad)
print('\n\nTesting...')
Y_test_pred = model.forward(X_test)
test_accuracy = ((Y_test_pred > 0.5) == Y_test).mean()
print('Acc: {:.1f}%'.format(test_accuracy * 100))
def plot_model_prediction(prediction_func, X, Y, hard=True):
u_min = X[:, 0].min()-1
u_max = X[:, 0].max()+1
v_min = X[:, 1].min()-1
v_max = X[:, 1].max()+1
U, V = np.meshgrid(np.linspace(u_min, u_max, 100), np.linspace(v_min, v_max, 100))
UV = np.stack([U.ravel(), V.ravel()]).T
c = prediction_func(UV).ravel()
if hard:
c = c > 0.5
plt.scatter(UV[:,0], UV[:,1], c=c, edgecolors= 'none', alpha=0.15)
plt.scatter(X[:,0], X[:,1], c=Y.ravel(), edgecolors= 'black')
plt.xlim(left=u_min, right=u_max)
plt.ylim(bottom=v_min, top=v_max)
plt.axes().set_aspect('equal')
plt.show()
plot_model_prediction(lambda x: model.forward(x), X_train, Y_train, False)
plot_model_prediction(lambda x: model.forward(x), X_train, Y_train, True)
# Now run the same experiment on 2 circles
# run the same code with 2 training sets (?)
# split the data 50-50 (?) and run it again
```
# 2. Decision Tree
The next model we look at is called **Decision Tree**. This type of model is non-parametric, meaning in contrast to **Logistic Regression** we do not have any parameters here that need to be trained.
Let us consider a simple binary decision tree for deciding on the two classes of "creditable" and "Not creditable".

Each node, except the leafs, asks a question about the the client in question. A decision is made by going from the root node to a leaf node, while considering the clients situation. The situation of the client, in this case, is fully described by the features:
1. Checking account balance
2. Duration of requested credit
3. Payment status of previous loan
4. Length of current employment
In order to build a decision tree we need training data. To carry on the previous example: we need a number of clients for which we know the properties 1.-4. and their creditability.
The process of building a decision tree starts with the root node and involves the following steps:
1. Choose a splitting criteria and add it to the current node.
2. Split the dataset at the current node into those that fullfil the criteria and those that do not.
3. Add a child node for each data split.
4. For each child node decide on either A. or B.:
1. Repeat from 1. step
2. Make it a leaf node: The predicted class label is decided by the majority vote over the training data in the current split.
## 2.1 Gini Index & Data Split
Deciding on how to split your training data at each node is dominated by the following two criterias:
1. Does the rule help me make a final decision?
2. Is the rule general enough such that it applies not only to my training data, but also to new unseen examples?
When considering our previous example, splitting the clients by their handedness would not help us deciding on their creditability. Knowning if a rule will generalize is usually a hard call to make, but in practice we rely on [Occam's razor](https://en.wikipedia.org/wiki/Occam%27s_razor) principle. Thus the less rules we use, the better we believe it to generalize to previously unseen examples.
One way to measure the quality of a rule is by the [**Gini Index**](https://en.wikipedia.org/wiki/Gini_coefficient).
Since we only consider binary classification, it is calculated by:
$$
Gini = \sum_{n\in\{L,R\}}\frac{|S_n|}{|S|}\left( 1 - \sum_{c \in C} p_{S_n}(c)^2\right)\\
p_{S_n}(c) = \frac{|\{\mathbf{x}_{i}\in \mathbf{X}|y_{i} = c, i \in S_n\}|}{|S_n|}, n \in \{L, R\}
$$
with $|C|=2$ being your set of class labels and $S_L$ and $S_R$ the two splits determined by the splitting criteria.
The lower the gini score, the better the split. In the extreme case, where all class labels are the same in each split respectively, the gini index takes the value of $0$.
```
def tree_gini_index(Y_left, Y_right, classes):
"""Compute the Gini Index.
# Arguments
Y_left: class labels of the data left set
np.array of size `(n_objects, 1)`
Y_right: class labels of the data right set
np.array of size `(n_objects, 1)`
classes: list of all class values
# Output
gini: scalar `float`
"""
gini = 0.0
pL0 = (Y_left[Y_left==classes[0]].size)/len(Y_left)
pL1 = (Y_left[Y_left==classes[1]].size)/len(Y_left)
pR0 = (Y_right[Y_right==classes[0]].size)/len(Y_right)
pR1 = (Y_right[Y_right==classes[1]].size)/len(Y_right)
# pL0 = (len(Y_left==classes[0]))/len(Y_left)
# pL1 = (len(Y_left==classes[1]))/len(Y_left)
# pR0 = (len(Y_right==classes[0]))/len(Y_right)
# pR1 = (len(Y_right==classes[1]))/len(Y_right)
left = ((len(Y_left))/(len(Y_left)+len(Y_right)))*(1-(pL0**2 + pL1**2))
right = ((len(Y_right))/(len(Y_right)+len(Y_left)))*(1-(pR0**2 + pR1**2))
gini = left + right
return gini
am.test_student_function(username, tree_gini_index, ['Y_left', 'Y_right', 'classes'])
```
At each node in the tree, the data is split according to a split criterion and each split is passed onto the left/right child respectively.
Implement the following function to return all rows in `X` and `Y` such that the left child gets all examples that are less than the split value and vice versa.
```
def tree_split_data_left(X, Y, feature_index, split_value):
"""Split the data `X` and `Y`, at the feature indexed by `feature_index`.
If the value is less than `split_value` then return it as part of the left group.
# Arguments
X: np.array of size `(n_objects, n_in)`
Y: np.array of size `(n_objects, 1)`
feature_index: index of the feature to split at
split_value: value to split between
# Output
(XY_left): np.array of size `(n_objects_left, n_in + 1)`
"""
X_left, Y_left = None, None
index = np.where(X[:,feature_index] < split_value)
X_left = X[index]
Y_left = Y[index]
XY_left = np.concatenate([X_left, Y_left], axis=-1)
return XY_left
def tree_split_data_right(X, Y, feature_index, split_value):
"""Split the data `X` and `Y`, at the feature indexed by `feature_index`.
If the value is greater or equal than `split_value` then return it as part of the right group.
# Arguments
X: np.array of size `(n_objects, n_in)`
Y: np.array of size `(n_objects, 1)`
feature_index: index of the feature to split at
split_value: value to split between
# Output
(XY_left): np.array of size `(n_objects_left, n_in + 1)`
"""
X_right, Y_right = None, None
index = np.where(X[:,feature_index] >= split_value)
X_right = X[index]
Y_right = Y[index]
XY_right = np.concatenate([X_right, Y_right], axis=-1)
return XY_right
am.test_student_function(username, tree_split_data_left, ['X', 'Y', 'feature_index', 'split_value'])
am.test_student_function(username, tree_split_data_right, ['X', 'Y', 'feature_index', 'split_value'])
am.get_progress(username)
```
Now to find the split rule with the lowest gini score, we brute-force search over all features and values to split by.
```
def tree_best_split(X, Y):
class_values = list(set(Y.flatten().tolist()))
r_index, r_value, r_score = float("inf"), float("inf"), float("inf")
r_XY_left, r_XY_right = (X,Y), (X,Y)
for feature_index in range(X.shape[1]):
for row in X:
XY_left = tree_split_data_left(X, Y, feature_index, row[feature_index])
XY_right = tree_split_data_right(X, Y, feature_index, row[feature_index])
XY_left, XY_right = (XY_left[:,:-1], XY_left[:,-1:]), (XY_right[:,:-1], XY_right[:,-1:])
gini = tree_gini_index(XY_left[1], XY_right[1], class_values)
if gini < r_score:
r_index, r_value, r_score = feature_index, row[feature_index], gini
r_XY_left, r_XY_right = XY_left, XY_right
return {'index':r_index, 'value':r_value, 'XY_left': r_XY_left, 'XY_right':r_XY_right}
```
## 2.2 Terminal Node
The leaf nodes predict the label of an unseen example, by taking a majority vote over all training class labels in that node.
```
def tree_to_terminal(Y):
"""The most frequent class label, out of the data points belonging to the leaf node,
is selected as the predicted class.
# Arguments
Y: np.array of size `(n_objects)`
# Output
label: most frequent label of `Y.dtype`
"""
label = None
label = np.argmax(np.bincount(Y.flatten().astype(int)))
return label
am.test_student_function(username, tree_to_terminal, ['Y'])
am.get_progress(username)
```
## 2.3 Build the Decision Tree
Now we recursively build the decision tree, by greedily splitting the data at each node according to the gini index.
To prevent the model from overfitting, we transform a node into a terminal/leaf node, if:
1. a maximum depth is reached.
2. the node does not reach a minimum number of training samples.
```
def tree_recursive_split(X, Y, node, max_depth, min_size, depth):
XY_left, XY_right = node['XY_left'], node['XY_right']
del(node['XY_left'])
del(node['XY_right'])
# check for a no split
if XY_left[0].size <= 0 or XY_right[0].size <= 0:
node['left_child'] = node['right_child'] = tree_to_terminal(np.concatenate((XY_left[1], XY_right[1])))
return
# check for max depth
if depth >= max_depth:
node['left_child'], node['right_child'] = tree_to_terminal(XY_left[1]), tree_to_terminal(XY_right[1])
return
# process left child
if XY_left[0].shape[0] <= min_size:
node['left_child'] = tree_to_terminal(XY_left[1])
else:
node['left_child'] = tree_best_split(*XY_left)
tree_recursive_split(X, Y, node['left_child'], max_depth, min_size, depth+1)
# process right child
if XY_right[0].shape[0] <= min_size:
node['right_child'] = tree_to_terminal(XY_right[1])
else:
node['right_child'] = tree_best_split(*XY_right)
tree_recursive_split(X, Y, node['right_child'], max_depth, min_size, depth+1)
def build_tree(X, Y, max_depth, min_size):
root = tree_best_split(X, Y)
tree_recursive_split(X, Y, root, max_depth, min_size, 1)
return root
```
By printing the split criteria or the predicted class at each node, we can visualise the decising making process.
Both the tree and a a prediction can be implemented recursively, by going from the root to a leaf node.
```
def print_tree(node, depth=0):
if isinstance(node, dict):
print('%s[X%d < %.3f]' % ((depth*' ', (node['index']+1), node['value'])))
print_tree(node['left_child'], depth+1)
print_tree(node['right_child'], depth+1)
else:
print('%s[%s]' % ((depth*' ', node)))
def tree_predict_single(x, node):
if isinstance(node, dict):
if x[node['index']] < node['value']:
return tree_predict_single(x, node['left_child'])
else:
return tree_predict_single(x, node['right_child'])
return node
def tree_predict_multi(X, node):
Y = np.array([tree_predict_single(row, node) for row in X])
return Y[:, None] # size: (n_object,) -> (n_object, 1)
```
Let's test our decision tree model on some toy data.
```
X_train, Y_train, X_test, Y_test = split(*generate_2_circles(), 0.7)
tree = build_tree(X_train, Y_train, 4, 1)
Y_pred = tree_predict_multi(X_test, tree)
test_accuracy = (Y_pred == Y_test).mean()
print('Test Acc: {:.1f}%'.format(test_accuracy * 100))
```
We print the decision tree in [pre-order](https://en.wikipedia.org/wiki/Tree_traversal#Pre-order_(NLR)).
```
print_tree(tree)
plot_model_prediction(lambda x: tree_predict_multi(x, tree), X_test, Y_test)
```
# 3. Experiments
The [Cleveland Heart Disease](https://archive.ics.uci.edu/ml/datasets/Heart+Disease) dataset aims at predicting the presence of heart disease based on other available medical information of the patient.
Although the whole database contains 76 attributes, we focus on the following 14:
1. Age: age in years
2. Sex:
* 0 = female
* 1 = male
3. Chest pain type:
* 1 = typical angina
* 2 = atypical angina
* 3 = non-anginal pain
* 4 = asymptomatic
4. Trestbps: resting blood pressure in mm Hg on admission to the hospital
5. Chol: serum cholestoral in mg/dl
6. Fasting blood sugar: > 120 mg/dl
* 0 = false
* 1 = true
7. Resting electrocardiographic results:
* 0 = normal
* 1 = having ST-T wave abnormality (T wave inversions and/or ST elevation or depression of > 0.05 mV)
* 2 = showing probable or definite left ventricular hypertrophy by Estes' criteria
8. Thalach: maximum heart rate achieved
9. Exercise induced angina:
* 0 = no
* 1 = yes
10. Oldpeak: ST depression induced by exercise relative to rest
11. Slope: the slope of the peak exercise ST segment
* 1 = upsloping
* 2 = flat
* 3 = downsloping
12. Ca: number of major vessels (0-3) colored by flourosopy
13. Thal:
* 3 = normal
* 6 = fixed defect
* 7 = reversable defect
14. Target: diagnosis of heart disease (angiographic disease status)
* 0 = < 50% diameter narrowing
* 1 = > 50% diameter narrowing
The 14. attribute is the target variable that we would like to predict based on the rest.
We have prepared some helper functions to download and pre-process the data in `heart_disease_data.py`
```
import heart_disease_data
X, Y = heart_disease_data.download_and_preprocess()
X_train, Y_train, X_test, Y_test = split(X, Y, 0.7)
```
Let's have a look at some examples
```
print(X_train[0:2])
print(Y_train[0:2])
# TODO feel free to explore more examples and see if you can predict the presence of a heart disease
```
## 3.1 Decision Tree for Heart Disease Prediction
Let's build a decision tree model on the training data and see how well it performs
```
# TODO: you are free to make use of code that we provide in previous cells
# TODO: play around with different hyper parameters and see how these impact your performance
tree = build_tree(X_train, Y_train, 5, 4)
Y_pred = tree_predict_multi(X_test, tree)
test_accuracy = (Y_pred == Y_test).mean()
print('Test Acc: {:.1f}%'.format(test_accuracy * 100))
```
How did changing the hyper parameters affect the test performance? Usually hyper parameters are tuned using a hold-out [validation set](https://en.wikipedia.org/wiki/Training,_validation,_and_test_sets#Validation_dataset) instead of the test set.
## 3.2 Logistic Regression for Heart Disease Prediction
Instead of manually going through the data to find possible correlations, let's try training a logistic regression model on the data.
```
# TODO: you are free to make use of code that we provide in previous cells
# TODO: play around with different hyper parameters and see how these impact your performance
```
How well did your model perform? Was it actually better then guessing? Let's look at the empirical mean of the target.
```
Y_train.mean()
```
So what is the problem? Let's have a look at the learned parameters of our model.
```
print(model.W, model.b)
```
If you trained sufficiently many steps you'll probably see how some weights are much larger than others. Have a look at what range the parameters were initialized and how much change we allow per step (learning rate). Compare this to the scale of the input features. Here an important concept arises, when we want to train on real world data:
[Feature Scaling](https://en.wikipedia.org/wiki/Feature_scaling).
Let's try applying it on our data and see how it affects our performance.
```
# TODO: Rescale the input features and train again
```
Notice that we did not need any rescaling for the decision tree. Can you think of why?
|
github_jupyter
|
import automark as am
# fill in you student number as your username
username = '12743674'
# to check your progress, you can run this function
am.get_progress(username)
---------------------------------------------
| Your name / student number |
| your_email@your_domain.whatever |
---------------------------------------------
| linear_forward | not attempted |
| linear_grad_W | not attempted |
| linear_grad_b | not attempted |
| nll_forward | not attempted |
| nll_grad_input | not attempted |
| sigmoid_forward | not attempted |
| sigmoid_grad_input | not attempted |
| tree_data_split_left | not attempted |
| tree_data_split_right | not attempted |
| tree_gini_index | not attempted |
| tree_to_terminal | not attempted |
---------------------------------------------
from __future__ import print_function, absolute_import, division # You don't need to know what this is.
import numpy as np # this imports numpy, which is used for vector- and matrix calculations
def linear_forward(x_input, W, b):
"""Perform the mapping of the input
# Arguments
x_input: input of the linear function - np.array of size `(n_objects, n_in)`
W: np.array of size `(n_in, n_out)`
b: np.array of size `(n_out,)`
# Output
the output of the linear function
np.array of size `(n_objects, n_out)`
"""
# output = x_input * np.transpose(W) + b
output = np.dot(x_input, W) + b
return output
X_test = np.array([[1, -1],
[-1, 0],
[1, 1]])
W_test = np.array([[4],
[2]])
b_test = np.array([3])
h_test = linear_forward(X_test, W_test, b_test)
print(h_test)
am.test_student_function(username, linear_forward, ['x_input', 'W', 'b'])
def linear_grad_W(x_input, grad_output, W, b):
"""Calculate the partial derivative of
the loss with respect to W parameter of the function
dL / dW = (dL / dh) * (dh / dW)
# Arguments
x_input: input of a dense layer - np.array of size `(n_objects, n_in)`
grad_output: partial derivative of the loss functions with
respect to the ouput of the dense layer (dL / dh)
np.array of size `(n_objects, n_out)`
W: np.array of size `(n_in, n_out)`
b: np.array of size `(n_out,)`
# Output
the partial derivative of the loss
with respect to W parameter of the function
np.array of size `(n_in, n_out)`
"""
# grad_W = np.gradient(np.dot(x_input, W) + b, W)
# grad_W = grad_output * np.gradient(linear_forward(x_input, W, b), W)
grad_W = np.dot(np.transpose(x_input), grad_output)
return grad_W
am.test_student_function(username, linear_grad_W, ['x_input', 'grad_output', 'W', 'b'])
def linear_grad_b(x_input, grad_output, W, b):
"""Calculate the partial derivative of
the loss with respect to b parameter of the function
dL / db = (dL / dh) * (dh / db)
# Arguments
x_input: input of a dense layer - np.array of size `(n_objects, n_in)`
grad_output: partial derivative of the loss functions with
respect to the ouput of the linear function (dL / dh)
np.array of size `(n_objects, n_out)`
W: np.array of size `(n_in, n_out)`
b: np.array of size `(n_out,)`
# Output
the partial derivative of the loss
with respect to b parameter of the linear function
np.array of size `(n_out,)`
"""
# grad_b = np.dot(np.transpose(1), grad_output)
# grad_b = 1* grad_output
grad_b = np.dot(np.transpose(np.ones(grad_output.shape)), grad_output)
return grad_b
am.test_student_function(username, linear_grad_b, ['x_input', 'grad_output', 'W', 'b'])
am.get_progress(username)
def sigmoid_forward(x_input):
"""sigmoid nonlinearity
# Arguments
x_input: np.array of size `(n_objects, n_in)`
# Output
the output of relu layer
np.array of size `(n_objects, n_in)`
"""
output = 1 / (1 + np.exp(- x_input))
return output
am.test_student_function(username, sigmoid_forward, ['x_input'])
def sigmoid_grad_input(x_input, grad_output):
"""sigmoid nonlinearity gradient.
Calculate the partial derivative of the loss
with respect to the input of the layer
# Arguments
x_input: np.array of size `(n_objects, n_in)`
grad_output: np.array of size `(n_objects, n_in)`
dL / df
# Output
the partial derivative of the loss
with respect to the input of the function
np.array of size `(n_objects, n_in)`
dL / dh
"""
# grad_input = np.dot(np.transpose((1/(1+np.exp(- x_input)))*(np.exp(- x_input)/(1+np.exp(- x_input))), grad_output))
grad_input = (1/(1+np.exp(- x_input))*(np.exp(- x_input)/(1+np.exp(- x_input)))) * grad_output
return grad_input
am.test_student_function(username, sigmoid_grad_input, ['x_input', 'grad_output'])
def nll_forward(target_pred, target_true):
"""Compute the value of NLL
for a given prediction and the ground truth
# Arguments
target_pred: predictions - np.array of size `(n_objects, 1)`
target_true: ground truth - np.array of size `(n_objects, 1)`
# Output
the value of NLL for a given prediction and the ground truth
scalar
"""
output = -(1/len(target_pred))*np.sum(target_true*np.log(target_pred)+(1-target_true)*np.log(1-target_pred))
return output
am.test_student_function(username, nll_forward, ['target_pred', 'target_true'])
def nll_grad_input(target_pred, target_true):
"""Compute the partial derivative of NLL
with respect to its input
# Arguments
target_pred: predictions - np.array of size `(n_objects, 1)`
target_true: ground truth - np.array of size `(n_objects, 1)`
# Output
the partial derivative
of NLL with respect to its input
np.array of size `(n_objects, 1)`
"""
grad_input = (1/len(target_pred))*((target_pred-target_true)/(target_pred*(1-target_pred)))
return grad_input
am.test_student_function(username, nll_grad_input, ['target_pred', 'target_true'])
am.get_progress(username)
class LogsticRegressionGD(object):
def __init__(self, n_in, lr=0.05):
super().__init__()
self.lr = lr
self.b = np.zeros(1, )
self.W = np.random.randn(n_in, 1)
def forward(self, x):
self.h = linear_forward(x, self.W, self.b)
y = sigmoid_forward(self.h)
return y
def update_params(self, x, nll_grad):
# compute gradients
grad_h = sigmoid_grad_input(self.h, nll_grad)
grad_W = linear_grad_W(x, grad_h, self.W, self.b)
grad_b = linear_grad_b(x, grad_h, self.W, self.b)
# update params
self.W = self.W - self.lr * grad_W
self.b = self.b - self.lr * grad_b
import matplotlib.pyplot as plt
%matplotlib inline
# Generate some data
def generate_2_circles(N=100):
phi = np.linspace(0.0, np.pi * 2, 100)
X1 = 1.1 * np.array([np.sin(phi), np.cos(phi)])
X2 = 3.0 * np.array([np.sin(phi), np.cos(phi)])
Y = np.concatenate([np.ones(N), np.zeros(N)]).reshape((-1, 1))
X = np.hstack([X1,X2]).T
return X, Y
def generate_2_gaussians(N=100):
phi = np.linspace(0.0, np.pi * 2, 100)
X1 = np.random.normal(loc=[1, 2], scale=[2.5, 0.9], size=(N, 2))
X1 = X1.dot(np.array([[0.7, -0.7], [0.7, 0.7]]))
X2 = np.random.normal(loc=[-2, 0], scale=[1, 1.5], size=(N, 2))
X2 = X2.dot(np.array([[0.7, 0.7], [-0.7, 0.7]]))
Y = np.concatenate([np.ones(N), np.zeros(N)]).reshape((-1, 1))
X = np.vstack([X1,X2])
return X, Y
def split(X, Y, train_ratio=0.7):
size = len(X)
train_size = int(size * train_ratio)
indices = np.arange(size)
np.random.shuffle(indices)
train_indices = indices[:train_size]
test_indices = indices[train_size:]
return X[train_indices], Y[train_indices], X[test_indices], Y[test_indices]
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
X, Y = generate_2_circles()
ax1.scatter(X[:,0], X[:,1], c=Y.ravel(), edgecolors= 'none')
ax1.set_aspect('equal')
X, Y = generate_2_gaussians()
ax2.scatter(X[:,0], X[:,1], c=Y.ravel(), edgecolors= 'none')
ax2.set_aspect('equal')
X_train, Y_train, X_test, Y_test = split(*generate_2_gaussians(), 0.7)
# let's train our model
model = LogsticRegressionGD(2, 0.05)
for step in range(30):
Y_pred = model.forward(X_train)
loss_value = nll_forward(Y_pred, Y_train)
accuracy = ((Y_pred > 0.5) == Y_train).mean()
print('Step: {} \t Loss: {:.3f} \t Acc: {:.1f}%'.format(step, loss_value, accuracy * 100))
loss_grad = nll_grad_input(Y_pred, Y_train)
model.update_params(X_train, loss_grad)
print('\n\nTesting...')
Y_test_pred = model.forward(X_test)
test_accuracy = ((Y_test_pred > 0.5) == Y_test).mean()
print('Acc: {:.1f}%'.format(test_accuracy * 100))
def plot_model_prediction(prediction_func, X, Y, hard=True):
u_min = X[:, 0].min()-1
u_max = X[:, 0].max()+1
v_min = X[:, 1].min()-1
v_max = X[:, 1].max()+1
U, V = np.meshgrid(np.linspace(u_min, u_max, 100), np.linspace(v_min, v_max, 100))
UV = np.stack([U.ravel(), V.ravel()]).T
c = prediction_func(UV).ravel()
if hard:
c = c > 0.5
plt.scatter(UV[:,0], UV[:,1], c=c, edgecolors= 'none', alpha=0.15)
plt.scatter(X[:,0], X[:,1], c=Y.ravel(), edgecolors= 'black')
plt.xlim(left=u_min, right=u_max)
plt.ylim(bottom=v_min, top=v_max)
plt.axes().set_aspect('equal')
plt.show()
plot_model_prediction(lambda x: model.forward(x), X_train, Y_train, False)
plot_model_prediction(lambda x: model.forward(x), X_train, Y_train, True)
# Now run the same experiment on 2 circles
# run the same code with 2 training sets (?)
# split the data 50-50 (?) and run it again
def tree_gini_index(Y_left, Y_right, classes):
"""Compute the Gini Index.
# Arguments
Y_left: class labels of the data left set
np.array of size `(n_objects, 1)`
Y_right: class labels of the data right set
np.array of size `(n_objects, 1)`
classes: list of all class values
# Output
gini: scalar `float`
"""
gini = 0.0
pL0 = (Y_left[Y_left==classes[0]].size)/len(Y_left)
pL1 = (Y_left[Y_left==classes[1]].size)/len(Y_left)
pR0 = (Y_right[Y_right==classes[0]].size)/len(Y_right)
pR1 = (Y_right[Y_right==classes[1]].size)/len(Y_right)
# pL0 = (len(Y_left==classes[0]))/len(Y_left)
# pL1 = (len(Y_left==classes[1]))/len(Y_left)
# pR0 = (len(Y_right==classes[0]))/len(Y_right)
# pR1 = (len(Y_right==classes[1]))/len(Y_right)
left = ((len(Y_left))/(len(Y_left)+len(Y_right)))*(1-(pL0**2 + pL1**2))
right = ((len(Y_right))/(len(Y_right)+len(Y_left)))*(1-(pR0**2 + pR1**2))
gini = left + right
return gini
am.test_student_function(username, tree_gini_index, ['Y_left', 'Y_right', 'classes'])
def tree_split_data_left(X, Y, feature_index, split_value):
"""Split the data `X` and `Y`, at the feature indexed by `feature_index`.
If the value is less than `split_value` then return it as part of the left group.
# Arguments
X: np.array of size `(n_objects, n_in)`
Y: np.array of size `(n_objects, 1)`
feature_index: index of the feature to split at
split_value: value to split between
# Output
(XY_left): np.array of size `(n_objects_left, n_in + 1)`
"""
X_left, Y_left = None, None
index = np.where(X[:,feature_index] < split_value)
X_left = X[index]
Y_left = Y[index]
XY_left = np.concatenate([X_left, Y_left], axis=-1)
return XY_left
def tree_split_data_right(X, Y, feature_index, split_value):
"""Split the data `X` and `Y`, at the feature indexed by `feature_index`.
If the value is greater or equal than `split_value` then return it as part of the right group.
# Arguments
X: np.array of size `(n_objects, n_in)`
Y: np.array of size `(n_objects, 1)`
feature_index: index of the feature to split at
split_value: value to split between
# Output
(XY_left): np.array of size `(n_objects_left, n_in + 1)`
"""
X_right, Y_right = None, None
index = np.where(X[:,feature_index] >= split_value)
X_right = X[index]
Y_right = Y[index]
XY_right = np.concatenate([X_right, Y_right], axis=-1)
return XY_right
am.test_student_function(username, tree_split_data_left, ['X', 'Y', 'feature_index', 'split_value'])
am.test_student_function(username, tree_split_data_right, ['X', 'Y', 'feature_index', 'split_value'])
am.get_progress(username)
def tree_best_split(X, Y):
class_values = list(set(Y.flatten().tolist()))
r_index, r_value, r_score = float("inf"), float("inf"), float("inf")
r_XY_left, r_XY_right = (X,Y), (X,Y)
for feature_index in range(X.shape[1]):
for row in X:
XY_left = tree_split_data_left(X, Y, feature_index, row[feature_index])
XY_right = tree_split_data_right(X, Y, feature_index, row[feature_index])
XY_left, XY_right = (XY_left[:,:-1], XY_left[:,-1:]), (XY_right[:,:-1], XY_right[:,-1:])
gini = tree_gini_index(XY_left[1], XY_right[1], class_values)
if gini < r_score:
r_index, r_value, r_score = feature_index, row[feature_index], gini
r_XY_left, r_XY_right = XY_left, XY_right
return {'index':r_index, 'value':r_value, 'XY_left': r_XY_left, 'XY_right':r_XY_right}
def tree_to_terminal(Y):
"""The most frequent class label, out of the data points belonging to the leaf node,
is selected as the predicted class.
# Arguments
Y: np.array of size `(n_objects)`
# Output
label: most frequent label of `Y.dtype`
"""
label = None
label = np.argmax(np.bincount(Y.flatten().astype(int)))
return label
am.test_student_function(username, tree_to_terminal, ['Y'])
am.get_progress(username)
def tree_recursive_split(X, Y, node, max_depth, min_size, depth):
XY_left, XY_right = node['XY_left'], node['XY_right']
del(node['XY_left'])
del(node['XY_right'])
# check for a no split
if XY_left[0].size <= 0 or XY_right[0].size <= 0:
node['left_child'] = node['right_child'] = tree_to_terminal(np.concatenate((XY_left[1], XY_right[1])))
return
# check for max depth
if depth >= max_depth:
node['left_child'], node['right_child'] = tree_to_terminal(XY_left[1]), tree_to_terminal(XY_right[1])
return
# process left child
if XY_left[0].shape[0] <= min_size:
node['left_child'] = tree_to_terminal(XY_left[1])
else:
node['left_child'] = tree_best_split(*XY_left)
tree_recursive_split(X, Y, node['left_child'], max_depth, min_size, depth+1)
# process right child
if XY_right[0].shape[0] <= min_size:
node['right_child'] = tree_to_terminal(XY_right[1])
else:
node['right_child'] = tree_best_split(*XY_right)
tree_recursive_split(X, Y, node['right_child'], max_depth, min_size, depth+1)
def build_tree(X, Y, max_depth, min_size):
root = tree_best_split(X, Y)
tree_recursive_split(X, Y, root, max_depth, min_size, 1)
return root
def print_tree(node, depth=0):
if isinstance(node, dict):
print('%s[X%d < %.3f]' % ((depth*' ', (node['index']+1), node['value'])))
print_tree(node['left_child'], depth+1)
print_tree(node['right_child'], depth+1)
else:
print('%s[%s]' % ((depth*' ', node)))
def tree_predict_single(x, node):
if isinstance(node, dict):
if x[node['index']] < node['value']:
return tree_predict_single(x, node['left_child'])
else:
return tree_predict_single(x, node['right_child'])
return node
def tree_predict_multi(X, node):
Y = np.array([tree_predict_single(row, node) for row in X])
return Y[:, None] # size: (n_object,) -> (n_object, 1)
X_train, Y_train, X_test, Y_test = split(*generate_2_circles(), 0.7)
tree = build_tree(X_train, Y_train, 4, 1)
Y_pred = tree_predict_multi(X_test, tree)
test_accuracy = (Y_pred == Y_test).mean()
print('Test Acc: {:.1f}%'.format(test_accuracy * 100))
print_tree(tree)
plot_model_prediction(lambda x: tree_predict_multi(x, tree), X_test, Y_test)
import heart_disease_data
X, Y = heart_disease_data.download_and_preprocess()
X_train, Y_train, X_test, Y_test = split(X, Y, 0.7)
print(X_train[0:2])
print(Y_train[0:2])
# TODO feel free to explore more examples and see if you can predict the presence of a heart disease
# TODO: you are free to make use of code that we provide in previous cells
# TODO: play around with different hyper parameters and see how these impact your performance
tree = build_tree(X_train, Y_train, 5, 4)
Y_pred = tree_predict_multi(X_test, tree)
test_accuracy = (Y_pred == Y_test).mean()
print('Test Acc: {:.1f}%'.format(test_accuracy * 100))
# TODO: you are free to make use of code that we provide in previous cells
# TODO: play around with different hyper parameters and see how these impact your performance
Y_train.mean()
print(model.W, model.b)
# TODO: Rescale the input features and train again
| 0.663233 | 0.988992 |
# Rule-Based System (RBS) Optimiser Example
The RBS Optimiser is used to optimise which rules are leveraged to generate decisions as part of an RBS Pipeline.
An RBS Pipeline allows a user to configure a logical flow for decisioning events. Each stage in the pipeline consists of a set of rules which are linked to a decision. The decision that is applied to each event is dictated by the rule(s) that trigger first.
For example, in the case of approving and rejecting transactions for a e-commerce transaction use case, you might have 3 approve rules and 3 reject rules. These rules could be used in an RBS Pipeline to approve and reject transactions like so:
1. If any approve rules trigger, approve the transaction.
2. If no approve rules trigger, but any reject rules trigger, reject the transaction.
3. If no rules trigger, approve any remaining transactions.
This example shows how we can create and optimise this RBS Pipeline.
## Requirements
To run, you'll need the following:
* A set of rules that you want to use in the RBS (in this example, we'll generate these).
* A labelled, processed dataset (nulls imputed, categorical features encoded).
----
## Import packages
```
from iguanas.rule_generation import RuleGeneratorDT
from iguanas.rbs import RBSPipeline, RBSOptimiser
from iguanas.metrics.classification import FScore
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay, classification_report
```
## Read in data
Let's read in some labelled, processed dummy data:
```
X_train = pd.read_csv(
'dummy_data/X_train.csv',
index_col='eid'
)
y_train = pd.read_csv(
'dummy_data/y_train.csv',
index_col='eid'
).squeeze()
X_test = pd.read_csv(
'dummy_data/X_test.csv',
index_col='eid'
)
y_test = pd.read_csv(
'dummy_data/y_test.csv',
index_col='eid'
).squeeze()
```
----
## Generate rules
Let's first generate some rules (both for approving and rejecting transactions) that we'll use later in our RBS Pipeline.
**Note:** in this dataset, positive cases in the target column refers to a fraudulent transaction, so we'll need to flip `y` when generating approve rules.
### Reject rules
```
fs = FScore(beta=1)
params = {
'n_total_conditions': 4,
'metric': fs.fit,
'tree_ensemble': RandomForestClassifier(n_estimators=5, random_state=0, bootstrap=False),
'precision_threshold': 0,
'num_cores': 1,
'target_feat_corr_types': 'Infer',
'verbose': 0,
'rule_name_prefix': 'RejectRule'
}
rg_reject = RuleGeneratorDT(**params)
X_rules_reject = rg_reject.fit(
X=X_train,
y=y_train,
sample_weight=None
)
```
### Approve rules
```
params = {
'n_total_conditions': 4,
'metric': fs.fit,
'tree_ensemble': RandomForestClassifier(n_estimators=2, random_state=0, bootstrap=False),
'precision_threshold': 0,
'num_cores': 1,
'target_feat_corr_types': 'Infer',
'verbose': 0,
'rule_name_prefix': 'ApproveRule'
}
rg_approve = RuleGeneratorDT(**params)
X_rules_approve = rg_approve.fit(
X=X_train,
y=(1-y_train), # We flip y here so non-fraudulent transactions become the target
sample_weight=None
)
```
Now let's combine the binary columns of the approve and reject rules into one dataframe:
```
X_rules = pd.concat([X_rules_reject, X_rules_approve], axis=1)
X_rules.head()
X_rules_reject.shape[1], X_rules_approve.shape[1]
```
## Setting up the RBS Pipeline
Now, let's set up our RBS Pipeline using the rules we've generated. To reiterate our approach:
1. If any approve rules trigger, approve the transaction.
2. If no approve rules trigger, but any reject rules trigger, reject the transaction.
3. If no rules trigger, approve any remaining transactions.
To set up the pipeline using the logic above, we first need to create the `config` parameter. This is just a list which outlines the stages of the pipeline. Each stage should be defined using a tuple of two elements:
1. The first element should be an integer which corresponds to the decision made at that stage (either `0` or `1`)
2. The second element should be a list that dictates which rules should trigger for that decision to be made.
In our example, the `config` will be:
```
config = [
(0, X_rules_approve.columns.tolist()),
(1, X_rules_reject.columns.tolist()),
]
```
Here, the first stage is configured via the tuple in the first element of the list. This says to apply a decision of `0` (i.e. approve) to transactions where the approve rules have triggered. The second stage is configured via the tuple in the second element of the list. This says to apply a decision of `1` (i.e. reject) to transactions where the reject rules have triggered (**and no approve rules have triggered**).
We also need to specify the final decision to be made if no rules are triggered - this is set via the `final_decision` parameter. In our case this should be `0`, as we want to approve any remaining transactions:
```
final_decision = 0
```
With these parameters configured, we can now create our RBS Pipeline by instantiating the `RBSPipeline` class:
```
rbsp = RBSPipeline(
config=config,
final_decision=final_decision
)
```
We can then apply the pipeline to the dataset using the `predict` method:
```
y_pred_init = rbsp.predict(
X_rules=X_rules
)
```
### Outputs
The `predict` method returns the prediction of the pipeline by applying the pipeline to the given dataset.
We can use Sklearn's *classification_report* and *confusion_matrix* functions to generate some performance metrics for the pipeline:
```
print(
classification_report(
y_true=y_train,
y_pred=y_pred_init,
digits=4
)
)
cm = ConfusionMatrixDisplay(
confusion_matrix(
y_true=y_train,
y_pred=y_pred_init
)
)
cm.plot()
```
## Optimising the RBS Pipeline
Now that we have our basic RBS Pipeline set up, we can optimise it using the RBS Optimiser. Here, we just pass the instatiated pipeline class to the `pipeline` parameter in the `RBSOptimiser` class:
```
rbso = RBSOptimiser(
pipeline=rbsp,
metric=fs.fit,
n_iter=60,
verbose=1
)
```
Then we run the `fit_predict` method to optimise the pipeline using the given dataset, then apply it to the dataset:
```
y_pred_opt = rbso.fit_predict(
X_rules=X_rules,
y=y_train
)
```
### Outputs
The `fit_predict` method optimises the pipeline and returns the prediction of the optimised pipeline by applying it to the given dataset. See the `Attributes` section in the class docstring for a description of each attribute generated:
```
rbso.config
```
We can use Sklearn's *classification_report* and *confusion_matrix* functions to generate some performance metrics for the pipeline:
```
print(
classification_report(
y_true=y_train,
y_pred=y_pred_opt,
digits=4
)
)
cm = ConfusionMatrixDisplay(
confusion_matrix(
y_true=y_train,
y_pred=y_pred_opt
)
)
cm.plot()
```
By comparing these performance metrics to those of the original pipeline, we can see that the RBS Optimiser has indeed improved the performance of the original RBS Pipeline:
```
print(f'Original RBS Pipeline F1 score: {fs.fit(y_pred_init, y_train)}')
print(f'Optimised RBS Pipeline F1 score: {fs.fit(y_pred_opt, y_train)}')
```
----
## Optimising the RBS Pipeline (without a `config`)
In the previous example, we instantiated a pipeline with a `config` before optimising.
However, if we don't know what structure the `config` should have, or don't have any requirements for its structure, we can use the RBS Optimiser to generate a new `config` from scratch, which will optimise the overall performance of the RBS Pipeline.
To do this, we follow a similar process as before - **the only difference being that we instantiate the RBS Pipeline with an empty dictionary for the** `config` **parameter**:
```
rbsp = RBSPipeline(
config=[], # Empty config
final_decision=final_decision
)
```
We feed this pipeline into the RBS Optimiser as before, but this time provide an extra parameter - `rule_types` - which is just a dictionary showing which decision (`0` or `1`) should be linked to each set of rules:
```
rbso = RBSOptimiser(
pipeline=rbsp,
metric=fs.fit,
n_iter=15,
pos_pred_rules=X_rules_reject.columns.tolist(),
neg_pred_rules=X_rules_approve.columns.tolist(),
verbose=1
)
```
Then we run the `fit_predict` method to optimise the pipeline using the given dataset, then apply it to the dataset:
```
y_pred_opt = rbso.fit_predict(
X_rules=X_rules,
y=y_train
)
```
### Outputs
The `fit_predict` method optimises the pipeline and returns the prediction of the optimised pipeline by applying it to the given dataset. See the `Attributes` section in the class docstring for a description of each attribute generated:
```
rbso.config
```
We can use Sklearn's *classification_report* and *confusion_matrix* functions to generate some performance metrics for the pipeline:
```
print(
classification_report(
y_true=y_train,
y_pred=y_pred_opt,
digits=4
)
)
cm = ConfusionMatrixDisplay(
confusion_matrix(
y_true=y_train,
y_pred=y_pred_opt
)
)
cm.plot()
```
---
|
github_jupyter
|
from iguanas.rule_generation import RuleGeneratorDT
from iguanas.rbs import RBSPipeline, RBSOptimiser
from iguanas.metrics.classification import FScore
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay, classification_report
X_train = pd.read_csv(
'dummy_data/X_train.csv',
index_col='eid'
)
y_train = pd.read_csv(
'dummy_data/y_train.csv',
index_col='eid'
).squeeze()
X_test = pd.read_csv(
'dummy_data/X_test.csv',
index_col='eid'
)
y_test = pd.read_csv(
'dummy_data/y_test.csv',
index_col='eid'
).squeeze()
fs = FScore(beta=1)
params = {
'n_total_conditions': 4,
'metric': fs.fit,
'tree_ensemble': RandomForestClassifier(n_estimators=5, random_state=0, bootstrap=False),
'precision_threshold': 0,
'num_cores': 1,
'target_feat_corr_types': 'Infer',
'verbose': 0,
'rule_name_prefix': 'RejectRule'
}
rg_reject = RuleGeneratorDT(**params)
X_rules_reject = rg_reject.fit(
X=X_train,
y=y_train,
sample_weight=None
)
params = {
'n_total_conditions': 4,
'metric': fs.fit,
'tree_ensemble': RandomForestClassifier(n_estimators=2, random_state=0, bootstrap=False),
'precision_threshold': 0,
'num_cores': 1,
'target_feat_corr_types': 'Infer',
'verbose': 0,
'rule_name_prefix': 'ApproveRule'
}
rg_approve = RuleGeneratorDT(**params)
X_rules_approve = rg_approve.fit(
X=X_train,
y=(1-y_train), # We flip y here so non-fraudulent transactions become the target
sample_weight=None
)
X_rules = pd.concat([X_rules_reject, X_rules_approve], axis=1)
X_rules.head()
X_rules_reject.shape[1], X_rules_approve.shape[1]
config = [
(0, X_rules_approve.columns.tolist()),
(1, X_rules_reject.columns.tolist()),
]
final_decision = 0
rbsp = RBSPipeline(
config=config,
final_decision=final_decision
)
y_pred_init = rbsp.predict(
X_rules=X_rules
)
print(
classification_report(
y_true=y_train,
y_pred=y_pred_init,
digits=4
)
)
cm = ConfusionMatrixDisplay(
confusion_matrix(
y_true=y_train,
y_pred=y_pred_init
)
)
cm.plot()
rbso = RBSOptimiser(
pipeline=rbsp,
metric=fs.fit,
n_iter=60,
verbose=1
)
y_pred_opt = rbso.fit_predict(
X_rules=X_rules,
y=y_train
)
rbso.config
print(
classification_report(
y_true=y_train,
y_pred=y_pred_opt,
digits=4
)
)
cm = ConfusionMatrixDisplay(
confusion_matrix(
y_true=y_train,
y_pred=y_pred_opt
)
)
cm.plot()
print(f'Original RBS Pipeline F1 score: {fs.fit(y_pred_init, y_train)}')
print(f'Optimised RBS Pipeline F1 score: {fs.fit(y_pred_opt, y_train)}')
rbsp = RBSPipeline(
config=[], # Empty config
final_decision=final_decision
)
rbso = RBSOptimiser(
pipeline=rbsp,
metric=fs.fit,
n_iter=15,
pos_pred_rules=X_rules_reject.columns.tolist(),
neg_pred_rules=X_rules_approve.columns.tolist(),
verbose=1
)
y_pred_opt = rbso.fit_predict(
X_rules=X_rules,
y=y_train
)
rbso.config
print(
classification_report(
y_true=y_train,
y_pred=y_pred_opt,
digits=4
)
)
cm = ConfusionMatrixDisplay(
confusion_matrix(
y_true=y_train,
y_pred=y_pred_opt
)
)
cm.plot()
| 0.532182 | 0.955277 |
# Assignment Chaper 01 (Think Stats 2, Allen B. Downey)
Self-study on statistics using pyhton
Github: **@rafaelmm82**
```
from __future__ import print_function, division
import nsfg
import numpy as np
```
## Examples from Chapter 1
Read NSFG data into a Pandas DataFrame.
```
preg = nsfg.ReadFemPreg()
preg.head()
```
Print the column names.
```
preg.columns
```
Select a single column name.
```
preg.columns[1]
```
Select a column and check what type it is.
```
pregordr = preg['pregordr']
type(pregordr)
```
Print a column.
```
pregordr
```
Select a single element from a column.
```
pregordr[0]
```
Select a slice from a column.
```
pregordr[2:5]
```
Select a column using dot notation.
```
pregordr = preg.pregordr
```
Count the number of times each value occurs.
```
preg.outcome.value_counts().sort_index()
```
Check the values of another variable.
```
preg.birthwgt_lb.value_counts().sort_index()
```
Make a dictionary that maps from each respondent's `caseid` to a list of indices into the pregnancy `DataFrame`. Use it to select the pregnancy outcomes for a single respondent.
```
caseid = 10229
preg_map = nsfg.MakePregMap(preg)
indices = preg_map[caseid]
preg.outcome[indices].values
```
## Exercises
Select the `birthord` column, print the value counts, and compare to results published in the [codebook](http://www.icpsr.umich.edu/nsfg6/Controller?displayPage=labelDetails&fileCode=PREG§ion=A&subSec=8016&srtLabel=611933)
```
# Solution goes here
preg.birthord.value_counts().sort_index()
```
We can also use `isnull` to count the number of nans.
```
preg.birthord.isnull().sum()
```
Select the `prglngth` column, print the value counts, and compare to results published in the [codebook](http://www.icpsr.umich.edu/nsfg6/Controller?displayPage=labelDetails&fileCode=PREG§ion=A&subSec=8016&srtLabel=611931)
```
# Solution goes here
prglngth = preg.prglngth.value_counts().sort_index()
print(np.sum(prglngth[0:14]))
print(np.sum(prglngth[14:27]))
print(np.sum(prglngth[27:51]))
print(np.sum(prglngth))
```
To compute the mean of a column, you can invoke the `mean` method on a Series. For example, here is the mean birthweight in pounds:
```
preg.totalwgt_lb.mean()
```
Create a new column named <tt>totalwgt_kg</tt> that contains birth weight in kilograms. Compute its mean. Remember that when you create a new column, you have to use dictionary syntax, not dot notation.
```
# Solution goes here
preg['totalwgt_kg'] = preg.totalwgt_lb * 0.453592
print(preg.totalwgt_kg.mean())
preg.head()
```
`nsfg.py` also provides `ReadFemResp`, which reads the female respondents file and returns a `DataFrame`:
```
resp = nsfg.ReadFemResp()
```
`DataFrame` provides a method `head` that displays the first five rows:
```
resp.head()
```
Select the `age_r` column from `resp` and print the value counts. How old are the youngest and oldest respondents?
```
# Solution goes here
resp_age = resp.age_r.value_counts().sort_index()
print('Youngest (years): ',resp_age.index[0])
print('Oldest (years): ',resp_age.index[-1])
```
We can use the `caseid` to match up rows from `resp` and `preg`. For example, we can select the row from `resp` for `caseid` 2298 like this:
```
resp[resp.caseid==2298]
```
And we can get the corresponding rows from `preg` like this:
```
preg[preg.caseid==2298]
```
How old is the respondent with `caseid` 1?
```
# Solution goes here
resp[resp.caseid==1].age_r
```
What are the pregnancy lengths for the respondent with `caseid` 2298?
```
# Solution goes here
preg[preg.caseid==2298].prglngth
```
What was the birthweight of the first baby born to the respondent with `caseid` 5012?
```
# Solution goes here
print(preg[preg.caseid==5012].birthwgt_lb)
```
|
github_jupyter
|
from __future__ import print_function, division
import nsfg
import numpy as np
preg = nsfg.ReadFemPreg()
preg.head()
preg.columns
preg.columns[1]
pregordr = preg['pregordr']
type(pregordr)
pregordr
pregordr[0]
pregordr[2:5]
pregordr = preg.pregordr
preg.outcome.value_counts().sort_index()
preg.birthwgt_lb.value_counts().sort_index()
caseid = 10229
preg_map = nsfg.MakePregMap(preg)
indices = preg_map[caseid]
preg.outcome[indices].values
# Solution goes here
preg.birthord.value_counts().sort_index()
preg.birthord.isnull().sum()
# Solution goes here
prglngth = preg.prglngth.value_counts().sort_index()
print(np.sum(prglngth[0:14]))
print(np.sum(prglngth[14:27]))
print(np.sum(prglngth[27:51]))
print(np.sum(prglngth))
preg.totalwgt_lb.mean()
# Solution goes here
preg['totalwgt_kg'] = preg.totalwgt_lb * 0.453592
print(preg.totalwgt_kg.mean())
preg.head()
resp = nsfg.ReadFemResp()
resp.head()
# Solution goes here
resp_age = resp.age_r.value_counts().sort_index()
print('Youngest (years): ',resp_age.index[0])
print('Oldest (years): ',resp_age.index[-1])
resp[resp.caseid==2298]
preg[preg.caseid==2298]
# Solution goes here
resp[resp.caseid==1].age_r
# Solution goes here
preg[preg.caseid==2298].prglngth
# Solution goes here
print(preg[preg.caseid==5012].birthwgt_lb)
| 0.336331 | 0.977862 |
# NumPy - Multidimensional Arrays
The numpy module is an extremely powerful package for dealing with numerical calculations. At its core it provides a way for users to create and manipulate N-dimensional arrays. It also provides a number of mathematical functions (e.g. exponential and trigonometric functions) and solvers (e.g. FFTW).
More importantly, these arrays behave much like arrays in C, C++, and Fortran:
* Arrays have a fixed size at creation (no dynamic growth)
* Homogeneous datatypes (e.g. all floats). Means known, fixed memory size for array
* Contiguous in memory (improved performance)
These features allow for better performance, while still maintaining the flexibility and ease of use of Python.
To get started, we'll import the NumPy module:
```
import numpy as np
```
## Creating NumPy Arrays
You can initialise NumPy arrays in a variety of ways:
* Python lists and tuples
* NumPy functions (`arange`, `zeros`, etc.)
* Input data from files
### Lists/tuples
```
# vector example
x = np.array([1,2,3,4])
x
A = np.array([[1, 2], [3, 4]])
A
```
We can inspect the type of the arrays:
```
type(x), type(A)
```
If we want to know more about the dimensions of our arrays, we can use the `size` and `shape` functions:
```
x.shape
A.shape
A.size
```
Note that these functions are acutally called as `ndarray.size` and `ndarray.shape`. They are functions available to ndarray objects via the NumPy module. Equivalently, you can call the same functions directly from the NumPy module:
```
np.shape(A)
```
These arrays look very much like Python lists...so why not just use a list for computation? Python is great with lists, why do we need a new datatype?
Performance.
As mentioned in the slides, Python lists are dynamically typed, have an inefficient memory layout (at least for numerical computations), and don't support common array operations like dot products.
NumPy arrays only support certain datatypes:
```
A[0,0] = "Brian"
A.dtype
```
Supported datatypes include `int`, `float`, `complex`, `bool`, Python objects, and more. We can even set bit size for these:
```
B = np.array([[1,3],[2,4]], dtype=complex)
B
```
#### A note on memory layout
We've mentioned that NumPy stores arrays in contiguous memory. But what does that mean, and how does it apply to multi-dimensional arrays? Simply, a multidimensional array is actually "stretched out" and stored in memory as a long, 1D array. There are a few ways we can "stretch" our arrays, and they're known as ***row major*** and ***column major*** order:
<img src="../img/rowcolumnarrays.jpg" style="height:350px">
Why does this matter?
Imagine we traverse this 2D array in a for loop, and assume it's stored in row major form, where `n` is the number of rows and `m` is the number of columns. What happens if we access the code like this?
`for j in 0:m
for i in 0:n
A[i][j] += x[i]`
The problem is we'll be jumping around in memory, destroying our performance. Modern compilers try to pull in contiguous blocks of data from RAM, and put them in cache (smaller, but faster, regions of memory closer to the CPU). This staging process provides a LOT of performance, and choosing the wrong storage format (or using the wrong indices) will destroy your performance.
By default, NumPy stores arrays in row major order:
```
A = np.random.rand(3,3)
A.flags
```
The hint here is ***C_CONTIGUOUS***. Traditionally, C/C++ store data in row major form, and Fortran stores it in column major form. The convention carries over still today, and so Python denotes row major as `C` and column major as `F`
Python actually allows you to change the order (if you want):
```
A = np.random.rand(3,3)
A = np.asfortranarray(A)
A.flags
```
### Functions
Generally we don't manually set up the elements of an array; instead we can use built-in functions to generate arrays.
#### arange
```
# start, stop, step size
x = np.arange(0, 5, 1)
x
x = np.arange(-1, 1, 0.2)
x
```
#### mgrid
Similar to `meshgrid` in MATLAB, it generates 2 arrays where the values correspond to the indices.
```
x, y = np.mgrid[0:4, 0:4]
x
y
```
#### rand
NumPy also allows you to generate random numbers:
```
# Generates uniform range of numbers in [0,1]
A = np.random.rand(3,3)
A
```
#### zeros and ones
```
x = np.zeros(3)
x
x = np.ones((5,5))
x
```
### I/O
We can read in CSV data into a NumPy array as well. We'll use some example temperature data along with the `genfromtxt` function:
```
!head ../example_data/temp_data.dat
import numpy as np
data = np.genfromtxt('../demos/data/temp_data.dat')
data.shape
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(14,4))
ax.plot(data[:,0]+data[:,1]/12.0+data[:,2]/365, data[:,5])
ax.axis('tight')
ax.set_title('Temperatures in Stockholm')
ax.set_xlabel('Year')
ax.set_ylabel('Temperature (C)')
```
We can also write out CSV files from NumPy arrays:
```
A = np.random.rand(5,5)
A
np.savetxt("../demos/data/rand_mat.csv",A)
!head ../demos/data/rand_mat.csv
# Let's specify a file format
np.savetxt("../demos/data/rand_mat.csv", A, fmt='%.3f')
!cat ../demos/data/rand_mat.csv
```
## Manipulating arrays: indexing
Indexing arrays in NumPy is done via square brackets:
```
A[1,1]
A[1][1]
```
With multi-dimensional arrays, if you omit an index it will show the whole row:
```
A[1]
```
Assigning values works the same:
```
A[0,0] = 0.5
A
```
We can also use `:` to access all elements in a row or column (array slicing):
```
A[1,:]
A[:,1]
A[0,:] = 1
A
# Slice out several columns of A
cols = A[:,[0,2]]
cols
```
***Note:*** These slices aren't copies...they just point to the original array
```
# A before we modify it
A
# Pull out row 3 from A
test_row = A[3,:]
test_row
# Zero out the row
test_row[:] = 0
test_row
# Print A
A
```
If we want an explicit copy, we can use the `copy` function:
```
test_row = A[2,:]
copyrow = test_row.copy()
copyrow
```
## Linear algebra
NumPy allows for us for to do common operations like matrix-vector multiplication, scalar multiplications, dot products, etc. These operations are so important to computation that entire libraries have been developed and optimized just to handle things like `a*x+y` or `A*B=C` (e.g. BLAS, LAPACK, MKL, etc.). NumPy is able to provide performant versions of these operations via something called ***ufuncs*** (universal functions). Ufuncs provide a convenient interface to ***vectorized*** routines in compiled libraries.
<img src="../img/vectorize.jpg" style="height:350px">
```
def compute_square(vals):
sq_vals = np.zeros(len(vals))
for i in range(len(vals)):
sq_vals[i] = vals[i] * vals[i]
return sq_vals
compute_square(np.random.randint(1, 10, size=5))
big_array = np.random.randint(1, 100, size=1000000)
%timeit compute_square(big_array)
```
Imagine you have a 2D grid of points, ~3000 points in each direction....if you have to compute a square for each value (which is not an uncommon operation) you'll be waiting several seconds to do this. Now imagine you have to this several thousand (or million) times in a simulation. As we've mentioned earlier, the delay is not the multiplication operation itself, but rather all of the type checking and dynamic lookups the Python interpreter has to do.
Now let's try a ufunc:
```
%timeit np.square(big_array)
```
Massive difference.
### Element-wise Operations
```
x = np.arange(10)
x
# Scalar addition
x+1
# Exponentiation
2**x
# Division
a = np.random.randint(1,100,size=10000)
b = np.random.randint(1,100,size=10000)
%timeit c = a / b
```
Note that each of these operations is simply a wrapper around a specific NumPy function:
| Operation | NumPy Function | Action |
| --- | --- | --- |
| `+` | `np.add` | Addition (e.g., 1 + 1 = 2) |
|`-`|`np.subtract`|Subtraction (e.g., 3 - 2 = 1)|
|`-`|`np.negative`|Unary negation (e.g., -2)|
|`*`|`np.multiply`|Multiplication (e.g., 2 * 3 = 6)|
|`/`|`np.divide`|Division (e.g., 3 / 2 = 1.5)|
|`//`|`np.floor_divide`|Floor division (e.g., 3 // 2 = 1)|
|`**`|`np.power`|Exponentiation (e.g., 2 ** 3 = 8)|
|`%`|`np.mod`|Modulus/remainder (e.g., 9 % 4 = 1)|
### Dot product
Be careful if you're trying to do things like dot products. Remember, the above functions are **element-wise** operations:
```
a.shape
b.shape
a * b
```
Normally, we'd expect a scalar value (remember, a dot product between vectors produces a scalar value). We can do this with the `dot` function:
```
np.dot(a, b)
# Example with matrices
A = np.random.randint(1,10,size=(5,5))
B = np.random.randint(1,10,size=(5,5))
# Matrix-vector product
x = np.random.rand(5)
np.dot(A,x)
np.dot(A,B)
```
We can also cast these arrays as matrices, using the `matrix` function. This lets us use the arithmetic operators for **matrix algebra**:
```
# Cast a new matrix
M = np.matrix(A)
# Create a column vector
# Note: T is the transpose operator
v = np.matrix(x).T
M * v
```
### Matrix Computations
NumPy's `linalg` module provides a range of common operations for computing things like inverses, norms, eigenvalues, decompositions, and even basic linear solvers.
#### Inverse
```
np.linalg.inv(A)
# Equivalent matrix function
C = np.matrix(A)
C.I
```
Just to check:
```
I_mat = C.I * C
np.set_printoptions(precision=1)
print(I_mat)
```
#### Determinants
```
np.linalg.det(C)
```
#### Eigenvalues
```
w,v = np.linalg.eig(A)
w
v
```
Returns an object with 2 arrays: the first array are the eigenvalues, and the second array is composed of the eigenvectors (normalised).
Note that the `ith` column of v (`v[:,i]`) corresponds to the `ith` eigenvalue of w (`w[i]`)
#### Norms
NumPy provides a lot of different norms to choose from:
```
# 2-norm for vectors
np.linalg.norm(x)
# 2-norm for matrices (aka Frobenius)
np.linalg.norm(A)
# Infinity norm for vectors
np.linalg.norm(x,np.inf)
# Negative infinity norm for matrices
np.linalg.norm(A, -np.inf)
```
#### Max and Min
```
A.min()
A
x.max()
```
## Reshaping Arrays
NumPy has methods for quickly and efficiently manipulating arrays that don't involve making a copy of the data (which would greatly impact performance)
```
A
n, m = A.shape
# Flatten the matrix into an n*m 1D array
B = A.reshape((1,n*m))
B
```
Let's alter the array:
```
B[0,0:10] = 0
B
A
```
Original values in A were changed...B is simply a pointer to A
There are situations where you want to reshape and make a copy. In that case, you can use the `flatten` function:
```
B = A.flatten()
B[0,0:10] = -1
B[0:10] = -1
B
A
```
## Final Thoughts
NumPy's power comes from being able to couple Python's convenience with the speed of compiled libraries. It should be your starting point for (just about) any HPC Python development work.
* Vectorise, vectorise, vectorise!
* You probably don't need to write a new function or solver (someone likely has, and done it better already)
* Give thought to your data structures...they affect performance
|
github_jupyter
|
import numpy as np
# vector example
x = np.array([1,2,3,4])
x
A = np.array([[1, 2], [3, 4]])
A
type(x), type(A)
x.shape
A.shape
A.size
np.shape(A)
A[0,0] = "Brian"
A.dtype
B = np.array([[1,3],[2,4]], dtype=complex)
B
A = np.random.rand(3,3)
A.flags
A = np.random.rand(3,3)
A = np.asfortranarray(A)
A.flags
# start, stop, step size
x = np.arange(0, 5, 1)
x
x = np.arange(-1, 1, 0.2)
x
x, y = np.mgrid[0:4, 0:4]
x
y
# Generates uniform range of numbers in [0,1]
A = np.random.rand(3,3)
A
x = np.zeros(3)
x
x = np.ones((5,5))
x
!head ../example_data/temp_data.dat
import numpy as np
data = np.genfromtxt('../demos/data/temp_data.dat')
data.shape
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(14,4))
ax.plot(data[:,0]+data[:,1]/12.0+data[:,2]/365, data[:,5])
ax.axis('tight')
ax.set_title('Temperatures in Stockholm')
ax.set_xlabel('Year')
ax.set_ylabel('Temperature (C)')
A = np.random.rand(5,5)
A
np.savetxt("../demos/data/rand_mat.csv",A)
!head ../demos/data/rand_mat.csv
# Let's specify a file format
np.savetxt("../demos/data/rand_mat.csv", A, fmt='%.3f')
!cat ../demos/data/rand_mat.csv
A[1,1]
A[1][1]
A[1]
A[0,0] = 0.5
A
A[1,:]
A[:,1]
A[0,:] = 1
A
# Slice out several columns of A
cols = A[:,[0,2]]
cols
# A before we modify it
A
# Pull out row 3 from A
test_row = A[3,:]
test_row
# Zero out the row
test_row[:] = 0
test_row
# Print A
A
test_row = A[2,:]
copyrow = test_row.copy()
copyrow
def compute_square(vals):
sq_vals = np.zeros(len(vals))
for i in range(len(vals)):
sq_vals[i] = vals[i] * vals[i]
return sq_vals
compute_square(np.random.randint(1, 10, size=5))
big_array = np.random.randint(1, 100, size=1000000)
%timeit compute_square(big_array)
%timeit np.square(big_array)
x = np.arange(10)
x
# Scalar addition
x+1
# Exponentiation
2**x
# Division
a = np.random.randint(1,100,size=10000)
b = np.random.randint(1,100,size=10000)
%timeit c = a / b
a.shape
b.shape
a * b
np.dot(a, b)
# Example with matrices
A = np.random.randint(1,10,size=(5,5))
B = np.random.randint(1,10,size=(5,5))
# Matrix-vector product
x = np.random.rand(5)
np.dot(A,x)
np.dot(A,B)
# Cast a new matrix
M = np.matrix(A)
# Create a column vector
# Note: T is the transpose operator
v = np.matrix(x).T
M * v
np.linalg.inv(A)
# Equivalent matrix function
C = np.matrix(A)
C.I
I_mat = C.I * C
np.set_printoptions(precision=1)
print(I_mat)
np.linalg.det(C)
w,v = np.linalg.eig(A)
w
v
# 2-norm for vectors
np.linalg.norm(x)
# 2-norm for matrices (aka Frobenius)
np.linalg.norm(A)
# Infinity norm for vectors
np.linalg.norm(x,np.inf)
# Negative infinity norm for matrices
np.linalg.norm(A, -np.inf)
A.min()
A
x.max()
A
n, m = A.shape
# Flatten the matrix into an n*m 1D array
B = A.reshape((1,n*m))
B
B[0,0:10] = 0
B
A
B = A.flatten()
B[0,0:10] = -1
B[0:10] = -1
B
A
| 0.542863 | 0.989622 |
# Numerical integration: introduction
This notebook is based on Chapters 7 and 10 of
<a id="thebook"></a>
> Süli, Endre and Mayers, David F. _An introduction to numerical analysis_. Cambridge University Press, Cambridge, 2003.
<https://doi.org/10.1017/CBO9780511801181> (ebook in [Helka](https://helka.helsinki.fi/permalink/358UOH_INST/1h3k2rg/alma9926836783506253))
We know how to evaluate some simple integrals of elementary functions by pen and paper but, in general, symbolic evaluation of integrals is a complicated problem, see for example the Wikipedia article of on the [Risch algorithm](https://en.wikipedia.org/wiki/Risch_algorithm). Here we consider numerical evaluation of integrals, a much simpler problem.
```
import sympy as sp
from sympy.abc import x
from IPython.display import Math
def display_risch(f):
int_tex = r'\int ' + sp.latex(f) + ' dx'
F = sp.integrate(f, x, risch=True)
if not isinstance(F, sp.integrals.Integral):
# The integral is elementary and we display the antiderivative
display(Math(int_tex + '=' + sp.latex(F)))
elif isinstance(F, sp.integrals.risch.NonElementaryIntegral):
# The integral is proven to be nonelementary by the algorithm,
# meaning the integral cannot be represented using a combination of
# exponentials, logarithms, trig functions, powers, rational functions,
# algebraic functions, and function composition
display(Math(int_tex + r'\,\text{ is not an elementary function}'))
else:
# The version implemented in SymPy only supports a small subset of
# the full Risch algorithm, no conclusion can be drawn from this case
display(Math(int_tex + r'\,\text{ can not be handled by the algorithm}'))
# Example from pp. 82-84 (Examples 2 and 3) of
# Grozin, A. Introduction to Mathematica for Physicists. Springer, 2014.
# shows that a small change in the integrand makes it impossible to express
# an integral by using elementary functions
display_risch(sp.log(x)/x)
display_risch(sp.log(x)/(x + 1))
# Example in the Wikipedia article on the Risch algorithm
display_risch(x / sp.sqrt(x**4 + 10*x**2 - 96*x - 72))
```
# Newton-Cotes formulae
The _Newton-Cotes formula_ of order $n = 1, 2, \dots$ is obtained by letting $p \in \mathbb P_n$ be the Lagrange interpolation polynomial of a function $f$ at $a = x_0 < x_1 < \dots < x_n = b$ on an interval $[a,b]$, and approximating
$$
\int_a^b f(x) dx \approx \int_a^b p(x) dx.
$$
Recall that
$$
p(x) = \sum_{k=0}^n f(x_k) L_k(x),
$$
where $L_k \in \mathbb P_n$ are the polynomials satisfying $L_k(x_i) = \delta_{ki}$.
Hence
$$
\int_a^b p(x) dx = \sum_{k=0}^n w_k f(x_k), \qquad w_k = \int_a^b L_k(x) dx.
$$
```
import numpy as np
import scipy.interpolate as interp
def nc_weights_demo(a, b, n):
'''Compute the quadrature weights for Newton-Cotes formula of order n on [a, b]'''
N = n+1
xs = np.linspace(a, b, N) # uniform grid
ws = np.zeros(N)
for k in range(N):
ys = np.zeros(N)
ys[k] = 1
l = interp.lagrange(xs, ys) # L_k
L = np.polyint(l)
ws[k] = L(b) - L(a)
return ws, xs
def integrate(ws, xs, f):
'''Integrate f using the quadrature weights ws and points xs'''
return np.sum(ws * f(xs))
a, b = 0, 1
def test_integrate(ws, xs, expr):
# Convert a symbolic expression with x as a free variable to a function
f = sp.lambdify(x, expr)
n = len(ws)-1
display(Math(r'\text{' +
f'Integrate gives {integrate(ws, xs, f):.2f} '
r' for }\int' + f'_{a}^{b}' + sp.latex(expr) +
f' dx = {sp.integrate(expr, (x, a, b))}'))
n = 1
ws_demo, xs = nc_weights_demo(a, b, n)
test_integrate(ws_demo, xs, 1)
test_integrate(ws_demo, xs, x)
test_integrate(ws_demo, xs, x**2)
n = 2
ws_demo, xs = nc_weights_demo(a, b, n)
fs = [x**n for n in range(5)]
for f in fs:
test_integrate(ws_demo, xs, f)
from scipy import integrate as integ
ws_scipy, _ = integ.newton_cotes(n, equal=1)
ws_scipy *= (b-a)/n
print('Using SciPy')
test_integrate(ws_scipy, xs, fs[-1])
```
## Theorem: error in Newton-Cotes
>
> Let $n=1,2,\dots$ and $f \in C^{n+1}(a,b)$. Let $w_i, x_i$, $i=0,\dots,n$, be the quadrature weights and points in the Newton-Cotes formula of order $n$ on $[a,b]$. Then
>
>\begin{align*}
&\left|\int_a^b f(x) dx - \sum_{k=0}^n w_k f(x_k) \right|
\\&\quad\le
\frac{\|f^{(n+1)}\|_\infty}{(n+1)!} \int_a^b |x-x_0|\dots|x-x_n| dx.
\end{align*}
For a proof, see Theorem 7.1 in [the book](#thebook). The Newton-Cotes formula of order $n$ is exact (that is, it gives the exactly correct integral) for polynomials of degree $n$. When $n$ is even and the grid is uniform, it is exact also for polynomials of degree $n+1$, leading to a better estimate than that in the theorem. For the sharp estimate in the case $n=2$, see Theorem 7.2 in [the book](#thebook).
```
def nc_weights_sym(n):
'''Compute symbolically the weights for Newton-Cotes formula of order n'''
from sympy.abc import a, b, x
ws = []
h = (b - a)/n
xs = [sp.simplify(a + k*h) for k in range(n+1)]
for k in range(len(xs)):
L = 1
for i in range(len(xs)):
if i != k:
L *= (x - xs[i]) / (xs[k] -xs[i])
ws.append(sp.simplify(sp.integrate(L, (x, a, b))))
return ws, xs
def nc_formula(n):
'''Compute symbolic expression for Newton-Cotes formula of order n'''
w, x = nc_weights_sym(n)
f = sp.Function('f')
nc_form = 0
for k in range(len(w)):
nc_form += w[k] * f(x[k])
return sp.simplify(nc_form)
print('Trapezium rule')
display(Math(sp.latex(nc_formula(1))))
print("Simpson's rule")
display(Math(sp.latex(nc_formula(2))))
```
Recall that the Lagrange interpolation polynomial of
$$
f(x) = \frac{1}{1+x^2}
$$
gives a poor approximation of $f$ on $[-5, 5]$ due to the Runge phenomenon.
Thus the Newton-Cotes formulae are expected to work poorly for
$$
\int_{-5}^5 f(x) dx.
$$
```
def f(x):
return 1 / (1 + x**2)
ns = range(2, 13, 2)
N = np.size(ns)
data = np.zeros(N)
for k in range(N):
ws, xs = nc_weights_demo(-5, 5, ns[k])
data[k] = integrate(ws, xs, f)
import pandas as pd
df = pd.DataFrame(data)
df.columns = ['$I_n$']
df.index = ns
df.index.name = 'n'
df.style.format('{:.5f}')
```
# Composite formulae
Analogously to splines, we will use a division to small subintervals.
Let $a = x_0 < x_1 < \dots < x_n = b$ be equally spaced
and write $h = (b-a)/n$ for the spacing. For $f \in C(a,b)$ there holds
$$
\int_a^b f(x) dx = \sum_{i=1}^n \int_{x_{i-1}}^{x_i} f(x) dx.
$$
We approximate using the trapezium rule
$$
\int_{x_{i-1}}^{x_i} f(x) dx \approx \frac{x_i - x_{i-1}}{2}(f(x_{i-1}) + f(x_i))
=
\frac h 2 (f(x_{i-1}) + f(x_i)),
$$
and obtain the _composite trapezium rule_
$$
\int_a^b f(x) dx
\approx
h \left( \frac12 f(x_0) + f(x_1) + \dots + f(x_{n-1}) + \frac12 f(x_n) \right).
$$
## Theorem: error in composite trapezium rule
> Let $f \in C^2(a,b)$ and write $I_h f$ for the composite trapezium rule applied to $f$ with the spacing $h>0$. Then there is $C>0$, independent of $f$ and $h$, such that
>
>$$
\left|\int_a^b f dx - I_h f \right| \le C \|(h\partial)^2 f\|_\infty.
$$
_Proof_. By the error in Newton-Cotes theorem,
\begin{align*}
\left| \int_a^b f(x) dx - I_h f \right|
\le
\sum_{i=1}^n \left|\int_{x_{i-1}}^{x_i} f(x) dx - \frac h 2 (f(x_{i-1}) + f(x_i)) \right|
\le n \|f''\|_\infty h^3.
\end{align*}
The claim follows from $h = (a-b)/n$.
$\blacksquare$
# Gaussian quadrature
The Gaussian quadrature is an approximation of the form
\begin{align*}
\int_a^b f(x) dx = \sum_{k=0}^n w_k f(x_k)
\end{align*}
where the quarature points $x_k \in [a,b]$ and weights $w_k$ are chosen so that the formula is exact for polynomials up to degree $2n + 1$.
In order to construct the points and weights we need to study Hermite interpolation that reads
> Let $x_i, y_i, z_i \in \mathbb R$, $i=0,\dots,n$, and suppose that $x_i \ne x_j$ for $i \ne j$.
>
> Find $p \in \mathbb P_{2n +1}$ such that $p(x_i) = y_i$ and $p'(x_i) = z_i$ for all $i=0,\dots,n$.
## Theorem: Hermite interpolation
> Let $n \ge 0$ be an integer let $x_i \in \mathbb R$, $i=0,\dots,n$, be distinct.
> Then for any $y_i, z_i \in \mathbb R$, $i=0,\dots,n$, there is a unique $p \in \mathbb P_{2n+1}$
> such that $p(x_i) = y_i$ and $p'(x_i) = z_i$ for all $i=0,\dots,n$.
For a proof, see Theorem 6.3 in [the book](#thebook).
## Theorem: error in Hermite interpolation
> Let $x_0, \dots x_n \in [a,b]$ be distinct, let $f \in C^{2n+2}(a,b)$, and
> let $p \in \mathbb P_{2n+1}$ be the Hermite interpolation polynomial of $f$, that is,
>
>\begin{align*}
p(x_i) = f(x_i), \quad p'(x_i) = f'(x_i), \qquad i=0,\dots,n.
\end{align*}
>
> Then for all $x \in [a,b]$ there is $\xi \in (a,b)$ such that
>
>\begin{align*}
f(x) - p(x) = \frac{f^{(2n+2)}(\xi)}{(2n+2)!} \prod_{i=0}^n (x-x_i)^2.
\end{align*}
For a proof, see Theorem 6.4 in [the book](#thebook).
Let $f \in C^{2n+2}(a,b)$, let
\begin{align*}
p(x) = \sum_{k=0}^n f(x_k) H_k(x) + \sum_{k=0}^n f'(x_k) K_k(x)
\end{align*}
be its Hermite interpolation polynomial, and consider the approximation
\begin{align*}
\int_a^b f(x) dx \approx \int_a^b p(x) dx = \sum_{k=0}^n w_k f(x_k) + \sum_{k=0}^n \tilde w_k f'(x_k),
\end{align*}
where
\begin{align*}
w_k = \int_a^b H_k(x) dx, \quad \tilde w_k = \int_a^b K_k(x) dx.
\end{align*}
The idea of the Gaussian quadrature is to choose the points $x_k$ so that $\tilde w_k = 0$ for all $k=0,\dots,n.$
Using
\begin{align*}
K_k(x) = L_k^2(x) (x - x_k), \quad L_k(x) = \prod_{i=0, i \ne k}^n \frac{x-x_i}{x_k-x_i}, \qquad k=0,\dots,n,
\end{align*}
we have
\begin{align*}
\tilde w_k = \int_a^b K_k(x) dx = c_n \int_a^b L_k(x) \pi(x) dx,
\end{align*}
where
\begin{align*}
\pi(x) = \prod_{i=0}^n (x-x_i),\quad c_n = \prod_{i=0, i \ne k}^n \frac{1}{x_k-x_i}.
\end{align*}
(In the case $n=0$, the formula holds with $c_n = 1$.) We see that $\tilde w_k = 0$ if $\pi \in \mathbb P_{n+1}$ is orthogonal to all polynomials in $\mathbb P_{n}$ in the sense of $L^2(a,b)$.
In the case that $a=-1$ and $b=1$, the [Legendre polynomials](https://en.wikipedia.org/wiki/Legendre_polynomials) $P_n \in \mathbb P_n$, $n=0,1,\dots$, are orthogonal with respect to the inner product $L^2(a,b)$. The points $x_i$, $i=0,\dots,n$ are chosen as the roots of $P_{n+1}$.
```
from numpy.polynomial import legendre as leg
from matplotlib import pyplot as plt
xs_plot = np.linspace(-1,1)
for n in range(1, 4):
cs = np.zeros(n + 2)
cs[-1] = 1
plt.plot(xs_plot, leg.legval(xs_plot, cs), label=f'$P_{n+1}$')
roots = leg.legroots(cs)
plt.scatter(roots, np.zeros(len(roots)))
plt.legend();
```
The case of arbitrary $a < b$ can be reduced to the case $a = -1$ and $b = 1$ by the change of variable
\begin{align*}
y = \frac{b - a} 2 x + \frac{a + b}2.
\end{align*}
Note that $x=-1$ corresponds to $y = a$ and $x = 1$ to $y = b$. Hence
\begin{align*}
\int_a^b f(y) dy
&= \frac{b - a} 2 \int_{-1}^1 f(\frac{b - a} 2 x + \frac{a + b}2) dx
\\&\approx \sum_{k=0}^n \frac{b - a} 2 w_k f(\frac{b - a} 2 x_k + \frac{a + b}2),
\end{align*}
where $w_k$ and $x_k$ are the quadrature weights and points on $[-1,1]$.
```
def change_of_interval(x, a, b):
return (b - a)/2 * x + (a + b)/2
a, b = 0, 1
n = 1
xs, ws = leg.leggauss(n + 1)
xs = change_of_interval(xs, a, b)
ws *= (b - a) / 2
fs = [x**n for n in range(5)]
for f in fs:
test_integrate(ws, xs, f)
```
## Theorem: error in Gaussian quadrature
> Let $n=1,2,\dots$ and $f \in C^{2n+2}(a,b)$.
> Let $w_i, x_i$, $i=0,\dots,n$, be the quadrature weights and points in the Gaussian quadrature of order $n$ on $[a,b]$. Then
>
>\begin{align*}
&\left|\int_a^b f(x) dx - \sum_{k=0}^n w_k f(x_k) \right|
\\&\quad\le
\frac{\|f^{(2n+2)}\|_\infty}{(2n+2)!} \int_a^b (x-x_0)^2\dots(x-x_n)^2 dx.
\end{align*}
# On the integration sub-package of SciPy
The composite formulae are well-suited for approximation of integrals when the integrand is known only at some points $x_i$, $i=0,\dots,n$. The composite trapezium rule is implemented by [trapezoid](https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.trapezoid.html) and its second order analogue, the composite Simpson's rule, by [simpson](https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.simpson.html#scipy.integrate.simpson).
For highly regular grids $x_i$, $i=0,\dots,n$, there are methods that outperform the composite rules. If the samples are equally-spaced and the number of samples is $2^k + 1$ for some integer $k=1,2,\dots$, then Romberg integration [romb](https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.romb.html#scipy.integrate.romb) can be used to obtain high-precision estimates of the integral using the available samples. This method is described in Section 7.7 of [the book](#thebook).
If the integrand can be evaluated at any point on the region of integration, then [quad](https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.quad.html) can be used. This calls the Fortran library [QUADPACK](https://en.wikipedia.org/wiki/QUADPACK). The main focus of this library is on automatic integration in which the algorithm attempts to perform an integration with an error no larger than that requested. The library uses an [adaptive quadrature](https://en.wikipedia.org/wiki/Adaptive_quadrature) that divides the region of integration into adaptively refined subintervals. Generally, adaptive algorithms are just as efficient as composite rules for smooth integrands, but they may work for non-smooth integrands for which traditional algorithms may fail.
For more details on integration with SciPy see the [tutorial](https://docs.scipy.org/doc/scipy/tutorial/integrate.html).
```
import scipy.integrate as integ
def f(x):
return np.log(x)/(x+1)
a, b = 1, 2
xs = np.linspace(a, b)
ys = f(xs)
print(f'trapezoid gives {integ.trapezoid(ys, xs)}')
print(f'simpson gives {integ.simpson(ys, xs)}')
xs, dx = np.linspace(a, b, 33, retstep=True)
ys = f(xs)
print(f'romb gives {integ.romb(ys, dx)}')
# quad returns also an estimate of the absolute error in the result
print(f'quad gives {integ.quad(f, a, b)}')
def f(x):
return 1/np.sqrt(x)
a, b = np.finfo(float).eps, 1
xs = np.linspace(a, b)
ys = f(xs)
print(f'trapezoid gives {integ.trapezoid(ys, xs)}')
print(f'simpson gives {integ.simpson(ys, xs)}')
xs, dx = np.linspace(a, b, 33, retstep=True)
ys = f(xs)
print(f'romb gives {integ.romb(ys, dx)}')
print(f'quad gives {integ.quad(f, a, b)}')
print(f'correct value 2 (up to machine precision)')
```
|
github_jupyter
|
import sympy as sp
from sympy.abc import x
from IPython.display import Math
def display_risch(f):
int_tex = r'\int ' + sp.latex(f) + ' dx'
F = sp.integrate(f, x, risch=True)
if not isinstance(F, sp.integrals.Integral):
# The integral is elementary and we display the antiderivative
display(Math(int_tex + '=' + sp.latex(F)))
elif isinstance(F, sp.integrals.risch.NonElementaryIntegral):
# The integral is proven to be nonelementary by the algorithm,
# meaning the integral cannot be represented using a combination of
# exponentials, logarithms, trig functions, powers, rational functions,
# algebraic functions, and function composition
display(Math(int_tex + r'\,\text{ is not an elementary function}'))
else:
# The version implemented in SymPy only supports a small subset of
# the full Risch algorithm, no conclusion can be drawn from this case
display(Math(int_tex + r'\,\text{ can not be handled by the algorithm}'))
# Example from pp. 82-84 (Examples 2 and 3) of
# Grozin, A. Introduction to Mathematica for Physicists. Springer, 2014.
# shows that a small change in the integrand makes it impossible to express
# an integral by using elementary functions
display_risch(sp.log(x)/x)
display_risch(sp.log(x)/(x + 1))
# Example in the Wikipedia article on the Risch algorithm
display_risch(x / sp.sqrt(x**4 + 10*x**2 - 96*x - 72))
import numpy as np
import scipy.interpolate as interp
def nc_weights_demo(a, b, n):
'''Compute the quadrature weights for Newton-Cotes formula of order n on [a, b]'''
N = n+1
xs = np.linspace(a, b, N) # uniform grid
ws = np.zeros(N)
for k in range(N):
ys = np.zeros(N)
ys[k] = 1
l = interp.lagrange(xs, ys) # L_k
L = np.polyint(l)
ws[k] = L(b) - L(a)
return ws, xs
def integrate(ws, xs, f):
'''Integrate f using the quadrature weights ws and points xs'''
return np.sum(ws * f(xs))
a, b = 0, 1
def test_integrate(ws, xs, expr):
# Convert a symbolic expression with x as a free variable to a function
f = sp.lambdify(x, expr)
n = len(ws)-1
display(Math(r'\text{' +
f'Integrate gives {integrate(ws, xs, f):.2f} '
r' for }\int' + f'_{a}^{b}' + sp.latex(expr) +
f' dx = {sp.integrate(expr, (x, a, b))}'))
n = 1
ws_demo, xs = nc_weights_demo(a, b, n)
test_integrate(ws_demo, xs, 1)
test_integrate(ws_demo, xs, x)
test_integrate(ws_demo, xs, x**2)
n = 2
ws_demo, xs = nc_weights_demo(a, b, n)
fs = [x**n for n in range(5)]
for f in fs:
test_integrate(ws_demo, xs, f)
from scipy import integrate as integ
ws_scipy, _ = integ.newton_cotes(n, equal=1)
ws_scipy *= (b-a)/n
print('Using SciPy')
test_integrate(ws_scipy, xs, fs[-1])
def nc_weights_sym(n):
'''Compute symbolically the weights for Newton-Cotes formula of order n'''
from sympy.abc import a, b, x
ws = []
h = (b - a)/n
xs = [sp.simplify(a + k*h) for k in range(n+1)]
for k in range(len(xs)):
L = 1
for i in range(len(xs)):
if i != k:
L *= (x - xs[i]) / (xs[k] -xs[i])
ws.append(sp.simplify(sp.integrate(L, (x, a, b))))
return ws, xs
def nc_formula(n):
'''Compute symbolic expression for Newton-Cotes formula of order n'''
w, x = nc_weights_sym(n)
f = sp.Function('f')
nc_form = 0
for k in range(len(w)):
nc_form += w[k] * f(x[k])
return sp.simplify(nc_form)
print('Trapezium rule')
display(Math(sp.latex(nc_formula(1))))
print("Simpson's rule")
display(Math(sp.latex(nc_formula(2))))
def f(x):
return 1 / (1 + x**2)
ns = range(2, 13, 2)
N = np.size(ns)
data = np.zeros(N)
for k in range(N):
ws, xs = nc_weights_demo(-5, 5, ns[k])
data[k] = integrate(ws, xs, f)
import pandas as pd
df = pd.DataFrame(data)
df.columns = ['$I_n$']
df.index = ns
df.index.name = 'n'
df.style.format('{:.5f}')
from numpy.polynomial import legendre as leg
from matplotlib import pyplot as plt
xs_plot = np.linspace(-1,1)
for n in range(1, 4):
cs = np.zeros(n + 2)
cs[-1] = 1
plt.plot(xs_plot, leg.legval(xs_plot, cs), label=f'$P_{n+1}$')
roots = leg.legroots(cs)
plt.scatter(roots, np.zeros(len(roots)))
plt.legend();
def change_of_interval(x, a, b):
return (b - a)/2 * x + (a + b)/2
a, b = 0, 1
n = 1
xs, ws = leg.leggauss(n + 1)
xs = change_of_interval(xs, a, b)
ws *= (b - a) / 2
fs = [x**n for n in range(5)]
for f in fs:
test_integrate(ws, xs, f)
import scipy.integrate as integ
def f(x):
return np.log(x)/(x+1)
a, b = 1, 2
xs = np.linspace(a, b)
ys = f(xs)
print(f'trapezoid gives {integ.trapezoid(ys, xs)}')
print(f'simpson gives {integ.simpson(ys, xs)}')
xs, dx = np.linspace(a, b, 33, retstep=True)
ys = f(xs)
print(f'romb gives {integ.romb(ys, dx)}')
# quad returns also an estimate of the absolute error in the result
print(f'quad gives {integ.quad(f, a, b)}')
def f(x):
return 1/np.sqrt(x)
a, b = np.finfo(float).eps, 1
xs = np.linspace(a, b)
ys = f(xs)
print(f'trapezoid gives {integ.trapezoid(ys, xs)}')
print(f'simpson gives {integ.simpson(ys, xs)}')
xs, dx = np.linspace(a, b, 33, retstep=True)
ys = f(xs)
print(f'romb gives {integ.romb(ys, dx)}')
print(f'quad gives {integ.quad(f, a, b)}')
print(f'correct value 2 (up to machine precision)')
| 0.66628 | 0.9598 |
<img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# Johns Hopkins - Covid19 Active Cases
<a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/Johns%20Hopkins/Johns_Hopkins_Covid19_Active_Cases.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
**Tags:** #johnshopkins #opendata #analytics #plotly
**Author:** [Jeremy Ravenel](https://www.linkedin.com/in/ACoAAAJHE7sB5OxuKHuzguZ9L6lfDHqw--cdnJg/)
## Input
### Import libraries
```
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
import matplotlib.pyplot as plt
```
### Variables
```
# URLs of the raw csv dataset
urls = [
'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv',
'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv',
'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv'
]
confirmed_df, deaths_df, recovered_df = tuple(pd.read_csv(url) for url in urls)
```
## Model
Mostly adopted from this [COVID19 Data Processing Tutorial](https://towardsdatascience.com/covid-19-data-processing-58aaa3663f6)
Clean the dataset to show the cases by country
Steps:
1. Convert from Wide to Long Dataframe (Convert all datetimes to a single column)
2. Merge/Join the Confirmed, Deaths and Recovered tables into a single table
3. Converting Date from string to datetime
4. Replacing missing values/NaNs
5. Coronavirus cases reported from 3 cruise ships should be treated differently and adjustments need to be made for Canada (deciding to drop Canada due to missing recovery data)
6. Get Active Cases = Confirmed - Deaths - Recovered
```
#Wide to Long DataFrame conversion
dates = confirmed_df.columns[4:]
confirmed_df_long = confirmed_df.melt(
id_vars=['Province/State', 'Country/Region', 'Lat', 'Long'],
value_vars=dates,
var_name='Date',
value_name='Confirmed'
)
deaths_df_long = deaths_df.melt(
id_vars=['Province/State', 'Country/Region', 'Lat', 'Long'],
value_vars=dates,
var_name='Date',
value_name='Deaths'
)
recovered_df_long = recovered_df.melt(
id_vars=['Province/State', 'Country/Region', 'Lat', 'Long'],
value_vars=dates,
var_name='Date',
value_name='Recovered'
)
# Adjust for Canada
recovered_df_long = recovered_df_long[(recovered_df_long['Country/Region']!='Canada')]
# Join into one single dataframe/table
# Merging confirmed_df_long and deaths_df_long
full_table = confirmed_df_long.merge(
right=deaths_df_long,
how='left',
on=['Province/State', 'Country/Region', 'Date', 'Lat', 'Long']
)
# Merging full_table and recovered_df_long
full_table = full_table.merge(
right=recovered_df_long,
how='left',
on=['Province/State', 'Country/Region', 'Date', 'Lat', 'Long']
)
# Convert date strings to actual dates
full_table['Date'] = pd.to_datetime(full_table['Date'])
# Handle some missing values / NaNs
full_table['Recovered'] = full_table['Recovered'].fillna(0).astype('int64')
full_table.isna().sum()
# full_table.dtypes
# Adjust for Canada and 3 cruise ships
ship_rows = full_table['Province/State'].str.contains('Grand Princess') | full_table['Province/State'].str.contains('Diamond Princess') | full_table['Country/Region'].str.contains('Diamond Princess') | full_table['Country/Region'].str.contains('MS Zaandam')
full_ship = full_table[ship_rows]
full_table = full_table[~(ship_rows)]
# Add one more entry for each day to get the entire world's counts/totals
world_dict = {"Country/Region": "World", "Confirmed": pd.Series(full_table.groupby(['Date'])['Confirmed'].sum()), "Deaths": pd.Series(full_table.groupby(['Date'])['Deaths'].sum()),"Recovered": pd.Series(full_table.groupby(['Date'])['Recovered'].sum())}
world_df = pd.DataFrame.from_dict(world_dict).reset_index()
print(world_df.columns)
full_table = pd.concat([full_table, world_df], ignore_index=True)
# Active Cases = Confirmed - Deaths - Recovered
full_table['Active'] = full_table['Confirmed'] - full_table['Deaths'] - full_table['Recovered']
full_grouped = full_table.groupby(['Date', 'Country/Region'])['Confirmed', 'Deaths', 'Recovered', 'Active'].sum().reset_index()
len(full_grouped["Country/Region"].unique())
```
### Interactive Dropdown Visualization for Active Cases by Country
First, need to go back from long to wide for a format suited to the visualization using `df.pivot()`
Mostly adopted from this [Interactive Dropdown Tutorial](https://towardsdatascience.com/how-to-create-an-interactive-dropdown-in-jupyter-322277f58a68)
```
# Go back from long to wide for viz purposes
df = full_grouped
df.rename(columns={"Country/Region": "Country"}, inplace=True)
df_confirmed = df[["Date", "Country", "Confirmed"]]
df_deaths = df[["Date", "Country", "Deaths"]]
df_active = df[["Date", "Country", "Active"]]
df_recovered = df[["Date", "Country", "Recovered"]]
df_confirmed = df_confirmed.pivot(index="Date", columns="Country", values="Confirmed")
df_deaths = df_deaths.pivot(index="Date", columns="Country", values="Deaths")
df_recovered = df_recovered.pivot(index="Date", columns="Country", values="Recovered")
df_active = df_active.pivot(index="Date", columns="Country", values="Active")
def create_layout_button(df, column):
first, latest = df.index.values[0], df.index.values[-1]
return dict(label = column,
method = 'update',
args = [{'visible': df.columns.isin([column]),
'title': column,
'xaxis.range': [first, latest],
'showlegend': True
}])
def multi_plot(df, title, addAll = True):
first, latest = df.index.values[0], df.index.values[-1]
fig = go.Figure()
for column in df.columns.to_list():
fig.add_trace(
go.Scatter(
x = df.index,
y = df[column],
name = column
)
)
button_all = dict(label = 'All',
method = 'update',
args = [{'visible': df.columns.isin(df.columns),
'title': 'All',
'xaxis.range': [first, latest],
'showlegend':True}])
# Need "World" to be the default choice if "All" is not shown
button_world = create_layout_button(df, "World")
fig.update_layout(
updatemenus=[{
"active": 0,
"buttons": ([button_all] * addAll) + [button_world] + [create_layout_button(df, column) for column in df.columns if column != "World"],
"showactive": True
}
],
yaxis_type="log"
)
# Update remaining layout properties
fig.update_layout(
title_text=title,
# annotations=[dict(
# text="Country:",
# x=0, y=0
# )]
)
fig.show()
# test_df_active = df_active.swapaxes("index", "columns")
test_df_active = df_active
latest = test_df_active.index.values[-1]
print(latest)
test_df_active = test_df_active.T.sort_values(by=latest, ascending=False).head(11).T
test_df_active
```
## Output
### Logarithmic COVID-19 time series
```
multi_plot(test_df_active, title="Logarithmic COVID-19 time series Active Cases by Country (Top 10)")
multi_plot(df_active, title="Logarithmic COVID-19 time series Active Cases by Country", addAll=False)
```
### World Health Indicator (WHI)
Using a scale of **0 - 10** and rescaling the number of Active Cases / Confirmed Cases on the entire World's Data
(where 0 is the worst and 10 is the best)
<!-- \begin{equation*}
WHI = 10 - 10 \times \frac{\text{Current Monthly average} - Min(\text{Monthly average})}{Max(\text{Monthly average}) - Min(\text{Monthly average})}
\end{equation*}
-->
\begin{equation*}
WHI = 10 - 10 \times \frac{Current - Min}{Max - Min}
\end{equation*}
(Using **Linear Scaling** for now, will discuss and develop a better scaling mechanism if required)
```
# Uncomment to get a 30 day Moving Average Statistics and a health indicator based on that
# df_active["MonthlyAverage"] = df_active["World"].rolling('30D').mean().astype('int64')
# curr_30d = df_active.loc[latest, "MonthlyAverage"]
# max_30d = df_active["MonthlyAverage"].max()
# min_30d = df_active["MonthlyAverage"].min()
# WHI_30d = 10 - 10 * ((curr_30d - min_30d) / (max_30d - min_30d))
#print(f"World Health Indicator (30 day Moving Average): {round(WHI_30d, 2)}")
WHI = 10 - 10 * ((df_active.loc[latest, "World"] - df_active["World"].min()) / (df_active["World"].max() - df_active["World"].min()))
print(f"World Health Indicator (Raw values): {round(WHI, 2)}")
WHI_data = pd.DataFrame.from_dict({"DATE_PROCESSED": pd.to_datetime("today").date(), "INDICATOR": "COVID-19 Active Cases", "VALUE": [round(WHI, 2)]})
WHI_data
```
|
github_jupyter
|
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
import matplotlib.pyplot as plt
# URLs of the raw csv dataset
urls = [
'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv',
'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv',
'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv'
]
confirmed_df, deaths_df, recovered_df = tuple(pd.read_csv(url) for url in urls)
#Wide to Long DataFrame conversion
dates = confirmed_df.columns[4:]
confirmed_df_long = confirmed_df.melt(
id_vars=['Province/State', 'Country/Region', 'Lat', 'Long'],
value_vars=dates,
var_name='Date',
value_name='Confirmed'
)
deaths_df_long = deaths_df.melt(
id_vars=['Province/State', 'Country/Region', 'Lat', 'Long'],
value_vars=dates,
var_name='Date',
value_name='Deaths'
)
recovered_df_long = recovered_df.melt(
id_vars=['Province/State', 'Country/Region', 'Lat', 'Long'],
value_vars=dates,
var_name='Date',
value_name='Recovered'
)
# Adjust for Canada
recovered_df_long = recovered_df_long[(recovered_df_long['Country/Region']!='Canada')]
# Join into one single dataframe/table
# Merging confirmed_df_long and deaths_df_long
full_table = confirmed_df_long.merge(
right=deaths_df_long,
how='left',
on=['Province/State', 'Country/Region', 'Date', 'Lat', 'Long']
)
# Merging full_table and recovered_df_long
full_table = full_table.merge(
right=recovered_df_long,
how='left',
on=['Province/State', 'Country/Region', 'Date', 'Lat', 'Long']
)
# Convert date strings to actual dates
full_table['Date'] = pd.to_datetime(full_table['Date'])
# Handle some missing values / NaNs
full_table['Recovered'] = full_table['Recovered'].fillna(0).astype('int64')
full_table.isna().sum()
# full_table.dtypes
# Adjust for Canada and 3 cruise ships
ship_rows = full_table['Province/State'].str.contains('Grand Princess') | full_table['Province/State'].str.contains('Diamond Princess') | full_table['Country/Region'].str.contains('Diamond Princess') | full_table['Country/Region'].str.contains('MS Zaandam')
full_ship = full_table[ship_rows]
full_table = full_table[~(ship_rows)]
# Add one more entry for each day to get the entire world's counts/totals
world_dict = {"Country/Region": "World", "Confirmed": pd.Series(full_table.groupby(['Date'])['Confirmed'].sum()), "Deaths": pd.Series(full_table.groupby(['Date'])['Deaths'].sum()),"Recovered": pd.Series(full_table.groupby(['Date'])['Recovered'].sum())}
world_df = pd.DataFrame.from_dict(world_dict).reset_index()
print(world_df.columns)
full_table = pd.concat([full_table, world_df], ignore_index=True)
# Active Cases = Confirmed - Deaths - Recovered
full_table['Active'] = full_table['Confirmed'] - full_table['Deaths'] - full_table['Recovered']
full_grouped = full_table.groupby(['Date', 'Country/Region'])['Confirmed', 'Deaths', 'Recovered', 'Active'].sum().reset_index()
len(full_grouped["Country/Region"].unique())
# Go back from long to wide for viz purposes
df = full_grouped
df.rename(columns={"Country/Region": "Country"}, inplace=True)
df_confirmed = df[["Date", "Country", "Confirmed"]]
df_deaths = df[["Date", "Country", "Deaths"]]
df_active = df[["Date", "Country", "Active"]]
df_recovered = df[["Date", "Country", "Recovered"]]
df_confirmed = df_confirmed.pivot(index="Date", columns="Country", values="Confirmed")
df_deaths = df_deaths.pivot(index="Date", columns="Country", values="Deaths")
df_recovered = df_recovered.pivot(index="Date", columns="Country", values="Recovered")
df_active = df_active.pivot(index="Date", columns="Country", values="Active")
def create_layout_button(df, column):
first, latest = df.index.values[0], df.index.values[-1]
return dict(label = column,
method = 'update',
args = [{'visible': df.columns.isin([column]),
'title': column,
'xaxis.range': [first, latest],
'showlegend': True
}])
def multi_plot(df, title, addAll = True):
first, latest = df.index.values[0], df.index.values[-1]
fig = go.Figure()
for column in df.columns.to_list():
fig.add_trace(
go.Scatter(
x = df.index,
y = df[column],
name = column
)
)
button_all = dict(label = 'All',
method = 'update',
args = [{'visible': df.columns.isin(df.columns),
'title': 'All',
'xaxis.range': [first, latest],
'showlegend':True}])
# Need "World" to be the default choice if "All" is not shown
button_world = create_layout_button(df, "World")
fig.update_layout(
updatemenus=[{
"active": 0,
"buttons": ([button_all] * addAll) + [button_world] + [create_layout_button(df, column) for column in df.columns if column != "World"],
"showactive": True
}
],
yaxis_type="log"
)
# Update remaining layout properties
fig.update_layout(
title_text=title,
# annotations=[dict(
# text="Country:",
# x=0, y=0
# )]
)
fig.show()
# test_df_active = df_active.swapaxes("index", "columns")
test_df_active = df_active
latest = test_df_active.index.values[-1]
print(latest)
test_df_active = test_df_active.T.sort_values(by=latest, ascending=False).head(11).T
test_df_active
multi_plot(test_df_active, title="Logarithmic COVID-19 time series Active Cases by Country (Top 10)")
multi_plot(df_active, title="Logarithmic COVID-19 time series Active Cases by Country", addAll=False)
# Uncomment to get a 30 day Moving Average Statistics and a health indicator based on that
# df_active["MonthlyAverage"] = df_active["World"].rolling('30D').mean().astype('int64')
# curr_30d = df_active.loc[latest, "MonthlyAverage"]
# max_30d = df_active["MonthlyAverage"].max()
# min_30d = df_active["MonthlyAverage"].min()
# WHI_30d = 10 - 10 * ((curr_30d - min_30d) / (max_30d - min_30d))
#print(f"World Health Indicator (30 day Moving Average): {round(WHI_30d, 2)}")
WHI = 10 - 10 * ((df_active.loc[latest, "World"] - df_active["World"].min()) / (df_active["World"].max() - df_active["World"].min()))
print(f"World Health Indicator (Raw values): {round(WHI, 2)}")
WHI_data = pd.DataFrame.from_dict({"DATE_PROCESSED": pd.to_datetime("today").date(), "INDICATOR": "COVID-19 Active Cases", "VALUE": [round(WHI, 2)]})
WHI_data
| 0.46393 | 0.881309 |
# An optimization problem in the Brazilian flight data
## 1. Introduction
The Brazilian flight data shared by their Civil Aviation Authority (ANAC) brings some airline marketing metrics, and also variables that enables one to recalculate these metrics. While testing for the consistency of these values, I have arrived at a model optimization problem: what is the average weight for passengers that airlines use for their flight plans? Are they the same for Brazilian and foreign airlines?
Let's check it out.
The data used in this notebook may be found at:
- https://www.gov.br/anac/pt-br/assuntos/dados-e-estatisticas/dados-estatisticos/arquivos/resumo_anual_2019.csv
- https://www.gov.br/anac/pt-br/assuntos/dados-e-estatisticas/dados-estatisticos/arquivos/resumo_anual_2020.csv
- https://www.gov.br/anac/pt-br/assuntos/dados-e-estatisticas/dados-estatisticos/arquivos/resumo_anual_2021.csv
## 2. Importing the libraries and data clean-up
NOTE: this section #2 is exactly the same found in the EDA article below:
# LINK FOR ARTICLE
If you have already read it, you can skip this section.
First of all, let's import the libraries we are going to use:
```
import os
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import unidecode
```
I am using the Seaborn library instead of matplotlib. I am also using the unidecode library to convert the column names to a more friendly format.
Now the files are loaded and merged into a single dataframe.
```
folder = r'C:\Users\thiag\data\ANAC-transport'
dffiles = ['resumo_anual_2019.csv',
'resumo_anual_2020.csv',
'resumo_anual_2021.csv']
df = pd.concat([pd.read_csv(os.path.join(folder, x),
sep=';', encoding=('ISO-8859-1'))
for x in dffiles])
```
Let's look at the data.
```
print(df.head())
```
The following can be observed about the column names:
- They are written in Portuguese and contain accentuation;
- They are all in upper case letters;
- They contain spaces and parenthesis.
To facilitate readability we will modify the column names by:
- Replacing the spaces with underlines "_";
- Removing the parenthesis;
- Making all letters lowercase; and
- Removing the accents.
This convention is called snake_case and, even though not standard, it is frequently used. For more information, refer to: https://en.wikipedia.org/wiki/Snake_case
```
print("Column names before changes:\n")
print(df.columns)
df.columns = [unidecode.unidecode(z.lower())
.replace(' ','_')
.replace('(','')
.replace(')','')
for z in df.columns]
df.to_csv('3years.csv', sep=';', index=False)
print("Column names after changes:\n")
print(df.columns)
```
This looks better.
Let's add some new columns to this dataframe, to support our analysis:
- Since we are looking for a cronologic observation, it is insteresting to concatenate the calendar months and years into a single variable called 'data' (Portuguese for date. I am keeping Portuguese names for consistency). Let's also add a column named 'quarto' (Portuguese for quarter) to concatenate variables around the months of the year 3-by-3.
- We can also infer the routes from the origin and destination airport variables (respectivelly called aeroporto_de_origem_sigla and aeroporto_de_destino_sigla). A variable named 'rota' (Portuguese for route) will be created to store the 'origin->destination' string. Another variable with the names of the airports (instead of the codes) will be created (and alled 'rota_nome') for readability (not everyone knows all airport codes).
- Dividing RPK for ASK we get the load factor, which is a very important metric for airlines economics. This variable will also be created.
```
df['data'] = [str(x['ano']) + '-' + "{:02}".format(x['mes'])
for index, x in df.iterrows()]
df['rota'] = [str(x['aeroporto_de_origem_sigla']) + '->' +
str(x['aeroporto_de_destino_sigla'])
for index, x in df.iterrows()]
df['rota_nome'] = [str(x['aeroporto_de_origem_nome']) + '->' +
str(x['aeroporto_de_destino_nome'])
for index, x in df.iterrows()]
df['load_factor'] = df['rpk']/df['ask']
def quarter(x):
year = x['ano']
mes = x['mes']
if mes in [1, 2, 3]:
quarter = str(year) + '-Q1'
elif mes in [4, 5, 6]:
quarter = str(year) + '-Q2'
elif mes in [7, 8, 9]:
quarter = str(year) + '-Q3'
elif mes in [10, 11, 12]:
quarter = str(year) + '-Q4'
return quarter
df['quarter'] = df.apply(quarter, axis=1)
```
## 3. Airline metrics for efficiency and capacity
Since there is no data dictionary, it is now a good time to talk about some interesting variables:
- RPK meaning "Revenue Passenger Kilometers" is an air transport industry metric that aggregates the number of paying passengers and the quantity of kilometers traveled by them. It is calculated by multiplying the number of paying passengers by the distance traveled in kilometers.
- ASK meaning "Available Seat Kilometers" is similar to the RPK but instead of using the paying passengers, the passenger capacity (number of seats available in the aircraft) is multiplied by the traveled distance.
- RTK (for "Revenue tonne kilometres") measures the revenue cargo load in tonnes multiplied by the distance flown in kilometers.
- ATK (for "Available tonne kilometres") measures the aircraft capacity of cargo load in tonnes multiplied by the distance flown in kilometers.
The dataframe presents not only the value of these parameters but also the variables that compose their formula. Therefore, let's make a consistency check, verifying it is possible to reproduce their values through the variables.
The formulas of the variables are:
$ RPK = \frac{\sum{PayingPassengers} \ \times \ distance}{\sum{flights}} $
$ ASK = \frac{\sum{Seats} \ \times \ distance}{\sum{flights}} $
$ RTK = \frac{(AvgWeight \ \times \ \sum{PayingPassengers \ + \ BaggageWeight \ + \ CargoWeight \ + \ MailWeight) } \ \times \ distance}{1000 \ \times \ \sum{flights}} $
$ ASK = \frac{\sum{Payload} \ \times \ distance}{1000 \ \times \ \sum{flights}} $
The only variable not given in our data set is the AvgWeight variable. How about we calculate the AvgWeight that gives the best difference between the given RTK and the calculated RTK?
This is an optimization problem that we will define below:
$$\min_{AvgWeight} RTK_{given} - \frac{(AvgWeight \ \times \ \sum{PayingPassengers \ + \ BaggageWeight \ + \ CargoWeight \ + \ MailWeight) } \ \times \ distance}{1000 \ \times \ \sum{flights}} $$
Let's define the optimization function (with some margin of error) and use the library Scipy to optimize this problem.
```
def matching(k):
dummy = []
for index, x in df.iterrows():
if x['decolagens'] == 0:
dummy.append(abs(x['rtk']) < 1000)
else:
dummy.append(abs(x['rtk'] - (k*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg'])*x['distancia_voada_km']/
(1000*x['decolagens'])) < 1000)
return 1/sum(dummy)
from scipy import optimize
res = optimize.minimize_scalar(matching, bounds=(70,150), method='bounded',
options={'maxiter':100})
print(res)
```
Great, so we have the value 75. Let's apply it and calculate the consistency of this vari
```
dummy = []
for index, x in df.iterrows():
if x['decolagens'] == 0:
dummy.append(abs(x['rtk']) < 1000)
else:
dummy.append(abs(x['rtk'] - (75*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg'] )*
x['distancia_voada_km']/(1000*x['decolagens'])) < 1000)
print('The number of rtk values that correspond to rtk calculation is: {:.2f}%'.format(100*sum(dummy)/len(dummy)))
df['rtk_calc']=(75*df['passageiros_pagos']+df['carga_paga_kg']+df['correio_kg']+df['bagagem_kg']
)*df['distancia_voada_km']/(1000*df['decolagens'])
```
We can see that the consistency is a little over 50%.
One clear disadvantage of the calculated RTK is that the same average weight (75 kg) was used for all passengers of all airlines. This assumption implies that Brazilian and foreign companies use (or have to use) the same value for passenger weight to do their flight planning, which may not be true.
Let's observe if being a Brazilian airline or foreign airline has an effect in the relationship between reported RTK and calculated RTK:
```
sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['empresa_nacionalidade'])
```
We can see clearly that the line y=x has many Brazilian airlines into it, but not foreign. Also, there is a second line below the y=x line, suggesting a different tendency for some foreign airlines.
Let's improve the optimization problem by considering this fact. The optimization function defined above will be split in two: one to optimize the weight for Brazilian airlines and the other one for foreign airlines.
```
def matching_br(k):
dummy = []
for index, x in df[df['empresa_nacionalidade']=='BRASILEIRA'].iterrows():
if x['decolagens'] == 0:
dummy.append(abs(x['rtk']) < 1000)
else:
dummy.append(abs(x['rtk'] - (k*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg'])*x['distancia_voada_km']/
(1000*x['decolagens'])) < 1000)
return 1/sum(dummy)
def matching_frgn(k):
dummy = []
for index, x in df[df['empresa_nacionalidade']=='ESTRANGEIRA'].iterrows():
if x['decolagens'] == 0:
dummy.append(abs(x['rtk']) < 1000)
else:
dummy.append(abs(x['rtk'] - (k*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg'])*x['distancia_voada_km']/
(1000*x['decolagens'])) < 1000)
return 1/sum(dummy)
res_br = optimize.minimize_scalar(matching_br, bounds=(70,150), method='bounded',
options={'maxiter':100})
print(res_br)
res_frgn = optimize.minimize_scalar(matching_frgn, bounds=(70,150), method='bounded',
options={'maxiter':100})
print(res_frgn)
```
By optimizing the error between RKT and calculated RTK for Brazilian airlines and foreign airlines separately, we arrive at the following values:
- Brazilian airlines have 75kg as the best average value for passenger weight;
- Foreign airlines have 90kg as the best average value for passenger weight.
With this knowledge, let's calculate again the RTK:
```
dummy = []
rtk_calc = []
for index, x in df.iterrows():
if x['empresa_nacionalidade'] == 'BRASILEIRA':
avgw = 75
elif x['empresa_nacionalidade'] == 'ESTRANGEIRA':
avgw = 90
if x['decolagens'] == 0:
rtk = float('NaN')
dummy.append(abs(x['rtk']) < 1000)
else:
rtk = (avgw*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg']
)*x['distancia_voada_km']/(1000*x['decolagens'])
dummy.append(abs(x['rtk'] - rtk) < 1000)
rtk_calc.append(rtk)
print('The number of rtk values that correspond to rtk calculation is: {:.2f}%'.format(100*sum(dummy)/len(dummy)))
df['rtk_calc'] = rtk_calc
del dummy, rtk_calc, rtk
```
We see now that the match of RTK values passed from 56.28% to 58.90%. Let's also reprint the previous graphic with the corrected calculated RTK.
```
sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['empresa_nacionalidade'])
```
We can see that the second tendency line is gone, since we have took into consideration its behaviour in our model.
It would be very interesting to find other behaviors to use in this optimization problem. Other variables, however, are not clearly related to clusters in the model to account for their use.
Out of curiosity, let's check a few examples.
```
ax = sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['decolagens'])
ax = sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['assentos'])
ax = sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['payload'])
```
As Data Scientists, we should verify we have questioned all our assumptions and made all the cross-checkings before accepting a model as the best outcome possible.
When problems similar to this are presented, the Scipy is an excellent tool, being able to solve even more complex problems.
Don't forget to check the article in which the other data of this data set is explored, and we verify the airports most affected by travel restrictions in 2020. The link is:
# LINK TO THE OTHER ARTICLE
See you there!
|
github_jupyter
|
import os
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import unidecode
folder = r'C:\Users\thiag\data\ANAC-transport'
dffiles = ['resumo_anual_2019.csv',
'resumo_anual_2020.csv',
'resumo_anual_2021.csv']
df = pd.concat([pd.read_csv(os.path.join(folder, x),
sep=';', encoding=('ISO-8859-1'))
for x in dffiles])
print(df.head())
print("Column names before changes:\n")
print(df.columns)
df.columns = [unidecode.unidecode(z.lower())
.replace(' ','_')
.replace('(','')
.replace(')','')
for z in df.columns]
df.to_csv('3years.csv', sep=';', index=False)
print("Column names after changes:\n")
print(df.columns)
df['data'] = [str(x['ano']) + '-' + "{:02}".format(x['mes'])
for index, x in df.iterrows()]
df['rota'] = [str(x['aeroporto_de_origem_sigla']) + '->' +
str(x['aeroporto_de_destino_sigla'])
for index, x in df.iterrows()]
df['rota_nome'] = [str(x['aeroporto_de_origem_nome']) + '->' +
str(x['aeroporto_de_destino_nome'])
for index, x in df.iterrows()]
df['load_factor'] = df['rpk']/df['ask']
def quarter(x):
year = x['ano']
mes = x['mes']
if mes in [1, 2, 3]:
quarter = str(year) + '-Q1'
elif mes in [4, 5, 6]:
quarter = str(year) + '-Q2'
elif mes in [7, 8, 9]:
quarter = str(year) + '-Q3'
elif mes in [10, 11, 12]:
quarter = str(year) + '-Q4'
return quarter
df['quarter'] = df.apply(quarter, axis=1)
def matching(k):
dummy = []
for index, x in df.iterrows():
if x['decolagens'] == 0:
dummy.append(abs(x['rtk']) < 1000)
else:
dummy.append(abs(x['rtk'] - (k*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg'])*x['distancia_voada_km']/
(1000*x['decolagens'])) < 1000)
return 1/sum(dummy)
from scipy import optimize
res = optimize.minimize_scalar(matching, bounds=(70,150), method='bounded',
options={'maxiter':100})
print(res)
dummy = []
for index, x in df.iterrows():
if x['decolagens'] == 0:
dummy.append(abs(x['rtk']) < 1000)
else:
dummy.append(abs(x['rtk'] - (75*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg'] )*
x['distancia_voada_km']/(1000*x['decolagens'])) < 1000)
print('The number of rtk values that correspond to rtk calculation is: {:.2f}%'.format(100*sum(dummy)/len(dummy)))
df['rtk_calc']=(75*df['passageiros_pagos']+df['carga_paga_kg']+df['correio_kg']+df['bagagem_kg']
)*df['distancia_voada_km']/(1000*df['decolagens'])
sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['empresa_nacionalidade'])
def matching_br(k):
dummy = []
for index, x in df[df['empresa_nacionalidade']=='BRASILEIRA'].iterrows():
if x['decolagens'] == 0:
dummy.append(abs(x['rtk']) < 1000)
else:
dummy.append(abs(x['rtk'] - (k*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg'])*x['distancia_voada_km']/
(1000*x['decolagens'])) < 1000)
return 1/sum(dummy)
def matching_frgn(k):
dummy = []
for index, x in df[df['empresa_nacionalidade']=='ESTRANGEIRA'].iterrows():
if x['decolagens'] == 0:
dummy.append(abs(x['rtk']) < 1000)
else:
dummy.append(abs(x['rtk'] - (k*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg'])*x['distancia_voada_km']/
(1000*x['decolagens'])) < 1000)
return 1/sum(dummy)
res_br = optimize.minimize_scalar(matching_br, bounds=(70,150), method='bounded',
options={'maxiter':100})
print(res_br)
res_frgn = optimize.minimize_scalar(matching_frgn, bounds=(70,150), method='bounded',
options={'maxiter':100})
print(res_frgn)
dummy = []
rtk_calc = []
for index, x in df.iterrows():
if x['empresa_nacionalidade'] == 'BRASILEIRA':
avgw = 75
elif x['empresa_nacionalidade'] == 'ESTRANGEIRA':
avgw = 90
if x['decolagens'] == 0:
rtk = float('NaN')
dummy.append(abs(x['rtk']) < 1000)
else:
rtk = (avgw*x['passageiros_pagos']+x['carga_paga_kg']+x['correio_kg']+x['bagagem_kg']
)*x['distancia_voada_km']/(1000*x['decolagens'])
dummy.append(abs(x['rtk'] - rtk) < 1000)
rtk_calc.append(rtk)
print('The number of rtk values that correspond to rtk calculation is: {:.2f}%'.format(100*sum(dummy)/len(dummy)))
df['rtk_calc'] = rtk_calc
del dummy, rtk_calc, rtk
sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['empresa_nacionalidade'])
ax = sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['decolagens'])
ax = sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['assentos'])
ax = sns.scatterplot(x=df['rtk'],y=df['rtk_calc'],hue=df['payload'])
| 0.20466 | 0.944434 |
```
import pandas as pd
import numpy as np
import scipy.io
import imageio
from tqdm import tqdm
df = pd.read_csv("data/parsed_training.csv")
df.head()
df.info()
df.raw_name.describe()
class_images = df.groupby(["raw_name", "file_name"]).size().groupby(level=0).size()
class_images[class_images >= 100].sort_values(ascending=False)
df.raw_name.nunique(), df.class_name.nunique()
classes = df.groupby("class_name").size()
classes[classes > 100].shape
fname = pd.DataFrame(df.file_name.str.split("/").values.tolist())
df["image_id"] = fname[7].combine_first(fname[6]).combine_first(fname[5]).str.extract("(\d+)")
def get_scene(row):
scene = "/".join([row[5] or "", row[6] or "", row[7] or ""])
return scene[:scene.find("ADE")].rstrip("/") or row[4]
scenes = fname.apply(get_scene, axis=1)
df["scene"] = scenes.values
df.sort_values(["image_id", "instance_number"])
mat = scipy.io.loadmat('data/ADE20K_2016_07_26/index_ade20k.mat')
classes = []
for x in mat["index"][0][0][6][0]:
classes.append(x[0])
mask = imageio.imread(
"data/ADE20K_2016_07_26/images/training/a/airport_terminal/ADE_train_00000001_seg.png"
).astype(np.uint16)
uniq, counts = np.unique((mask[:, :, 0] // 10) * 256 + mask[:, :, 1], return_counts=True)
labeled = uniq[uniq != 0] - 1 # matlab index starts from 1, it took me 4 hours to fix this LMAO
sorted(np.array(classes)[labeled])
dict(zip(np.array(classes)[labeled], counts[uniq!=0]/(mask.shape[0]*mask.shape[1])))
with_pix_ratio = []
for img in tqdm(range(1, df.image_id.astype(int).max()+1)):
curr_img_id = str(img).zfill(8)
subset = df[df.image_id == curr_img_id]
for level in subset.part_level.unique():
if level == 0:
filename = subset.file_name.values[0].replace("_atr.txt", "_seg.png")
else:
filename = subset.file_name.values[0].replace("_atr.txt", f"_parts_{level}.png")
mask = imageio.imread(filename).astype(np.uint16)
_, instances = np.unique(mask[:, :, 2], return_inverse=True)
uniq, counts = np.unique(instances, return_counts=True)
newdf = pd.DataFrame()
newdf["instance_number"] = uniq
newdf["pixel_ratio"] = counts / (mask.shape[0]*mask.shape[1])
newdf["part_level"] = level
newdf["image_id"] = curr_img_id
with_pix_ratio.append(newdf)
newdf = pd.concat(with_pix_ratio)
newdf.head()
joined = df.merge(newdf, how="left", on=["instance_number", "part_level", "image_id"])
joined.to_csv("data/clean_parsed_training.csv", index=False)
joined.groupby("scene", as_index=False).image_id.nunique().to_csv("data/scenes.csv", index=False)
grouped = joined.groupby("class_name", as_index=False).agg({"pixel_ratio": ["min", "mean", "max"], "instance_number": "count", "image_id": "nunique"})
def images_1pct(row):
return row[row.pixel_ratio > 0.01].image_id.nunique()
images_1pct.__name__ = "images_1pct"
images_1pct_df = joined.groupby("class_name", as_index=False).apply(images_1pct)
images_1pct_df.columns = ["class_name", "images_1pct"]
grouped.columns = ["_".join(c).strip("_") for c in grouped.columns]
grouped.merge(images_1pct_df, on=["class_name"]).to_csv("data/object_stats.csv", index=False)
scenes = ["living_room", "bedroom", "kitchen", "bathroom"]
indoor = joined[joined.scene.isin(scenes) & (joined.part_level <= 1)]
indoor_g = indoor.groupby("class_name", as_index=False).agg({"pixel_ratio": ["min", "mean", "max"], "instance_number": "count", "image_id": "nunique"})
indoor_g.head()
images_1pct_indoor = indoor.groupby("class_name", as_index=False).apply(images_1pct)
images_1pct_indoor.columns = ["class_name", "images_1pct"]
indoor_g.columns = ["_".join(c).strip("_") for c in indoor_g.columns]
indoor_g.merge(images_1pct_indoor, on=["class_name"]).to_csv("data/house_indoor_object_stats.csv", index=False)
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import scipy.io
import imageio
from tqdm import tqdm
df = pd.read_csv("data/parsed_training.csv")
df.head()
df.info()
df.raw_name.describe()
class_images = df.groupby(["raw_name", "file_name"]).size().groupby(level=0).size()
class_images[class_images >= 100].sort_values(ascending=False)
df.raw_name.nunique(), df.class_name.nunique()
classes = df.groupby("class_name").size()
classes[classes > 100].shape
fname = pd.DataFrame(df.file_name.str.split("/").values.tolist())
df["image_id"] = fname[7].combine_first(fname[6]).combine_first(fname[5]).str.extract("(\d+)")
def get_scene(row):
scene = "/".join([row[5] or "", row[6] or "", row[7] or ""])
return scene[:scene.find("ADE")].rstrip("/") or row[4]
scenes = fname.apply(get_scene, axis=1)
df["scene"] = scenes.values
df.sort_values(["image_id", "instance_number"])
mat = scipy.io.loadmat('data/ADE20K_2016_07_26/index_ade20k.mat')
classes = []
for x in mat["index"][0][0][6][0]:
classes.append(x[0])
mask = imageio.imread(
"data/ADE20K_2016_07_26/images/training/a/airport_terminal/ADE_train_00000001_seg.png"
).astype(np.uint16)
uniq, counts = np.unique((mask[:, :, 0] // 10) * 256 + mask[:, :, 1], return_counts=True)
labeled = uniq[uniq != 0] - 1 # matlab index starts from 1, it took me 4 hours to fix this LMAO
sorted(np.array(classes)[labeled])
dict(zip(np.array(classes)[labeled], counts[uniq!=0]/(mask.shape[0]*mask.shape[1])))
with_pix_ratio = []
for img in tqdm(range(1, df.image_id.astype(int).max()+1)):
curr_img_id = str(img).zfill(8)
subset = df[df.image_id == curr_img_id]
for level in subset.part_level.unique():
if level == 0:
filename = subset.file_name.values[0].replace("_atr.txt", "_seg.png")
else:
filename = subset.file_name.values[0].replace("_atr.txt", f"_parts_{level}.png")
mask = imageio.imread(filename).astype(np.uint16)
_, instances = np.unique(mask[:, :, 2], return_inverse=True)
uniq, counts = np.unique(instances, return_counts=True)
newdf = pd.DataFrame()
newdf["instance_number"] = uniq
newdf["pixel_ratio"] = counts / (mask.shape[0]*mask.shape[1])
newdf["part_level"] = level
newdf["image_id"] = curr_img_id
with_pix_ratio.append(newdf)
newdf = pd.concat(with_pix_ratio)
newdf.head()
joined = df.merge(newdf, how="left", on=["instance_number", "part_level", "image_id"])
joined.to_csv("data/clean_parsed_training.csv", index=False)
joined.groupby("scene", as_index=False).image_id.nunique().to_csv("data/scenes.csv", index=False)
grouped = joined.groupby("class_name", as_index=False).agg({"pixel_ratio": ["min", "mean", "max"], "instance_number": "count", "image_id": "nunique"})
def images_1pct(row):
return row[row.pixel_ratio > 0.01].image_id.nunique()
images_1pct.__name__ = "images_1pct"
images_1pct_df = joined.groupby("class_name", as_index=False).apply(images_1pct)
images_1pct_df.columns = ["class_name", "images_1pct"]
grouped.columns = ["_".join(c).strip("_") for c in grouped.columns]
grouped.merge(images_1pct_df, on=["class_name"]).to_csv("data/object_stats.csv", index=False)
scenes = ["living_room", "bedroom", "kitchen", "bathroom"]
indoor = joined[joined.scene.isin(scenes) & (joined.part_level <= 1)]
indoor_g = indoor.groupby("class_name", as_index=False).agg({"pixel_ratio": ["min", "mean", "max"], "instance_number": "count", "image_id": "nunique"})
indoor_g.head()
images_1pct_indoor = indoor.groupby("class_name", as_index=False).apply(images_1pct)
images_1pct_indoor.columns = ["class_name", "images_1pct"]
indoor_g.columns = ["_".join(c).strip("_") for c in indoor_g.columns]
indoor_g.merge(images_1pct_indoor, on=["class_name"]).to_csv("data/house_indoor_object_stats.csv", index=False)
| 0.246261 | 0.334331 |
<table width="100%"> <tr>
<td style="background-color:#ffffff;">
<a href="http://qworld.lu.lv" target="_blank"><img src="../images/qworld.jpg" width="35%" align="left"> </a></td>
<td style="background-color:#ffffff;vertical-align:bottom;text-align:right;">
prepared by Abuzer Yakaryilmaz (<a href="http://qworld.lu.lv/index.php/qlatvia/" target="_blank">QLatvia</a>)
</td>
</tr></table>
<table width="100%"><tr><td style="color:#bbbbbb;background-color:#ffffff;font-size:11px;font-style:italic;text-align:right;">This cell contains some macros. If there is a problem with displaying mathematical formulas, please run this cell to load these macros. </td></tr></table>
$ \newcommand{\bra}[1]{\langle #1|} $
$ \newcommand{\ket}[1]{|#1\rangle} $
$ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
$ \newcommand{\dot}[2]{ #1 \cdot #2} $
$ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
$ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
$ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
$ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
$ \newcommand{\mypar}[1]{\left( #1 \right)} $
$ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
$ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
$ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
$ \newcommand{\onehalf}{\frac{1}{2}} $
$ \newcommand{\donehalf}{\dfrac{1}{2}} $
$ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
$ \newcommand{\vzero}{\myvector{1\\0}} $
$ \newcommand{\vone}{\myvector{0\\1}} $
$ \newcommand{\vhadamardzero}{\myvector{ \sqrttwo \\ \sqrttwo } } $
$ \newcommand{\vhadamardone}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
$ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
$ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
$ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
$ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
$ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
$ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
<h2> <font color="blue"> Solutions for </font> Vectors: One Dimensional List </h2>
<a id="task1"></a>
<h3> Task 1 </h3>
Create two 7-dimensional vectors $u$ and $ v $ as two different lists in Python having entries randomly picked between $-10$ and $10$.
Print their entries.
<h3>Solution</h3>
```
from random import randrange
dimension = 7
# create u and v as empty lists
u = []
v = []
for i in range(dimension):
u.append(randrange(-10,11)) # add a randomly picked number to the list u
v.append(randrange(-10,11)) # add a randomly picked number to the list v
# print both lists
print("u is",u)
print("v is",v)
```
<a id="task2"></a>
<h3> Task 2 </h3>
By using the same vectors, find the vector $ (3 u-2 v) $ and print its entries. Here $ 3u $ and $ 2v $ means $u$ and $v$ are multiplied by $3$ and $2$, respectively.
<h3>Solution</h3>
```
# please execute the cell for Task 1 to define u and v
# create a result list
# the first method
result=[]
# fill it with zeros
for i in range(dimension):
result.append(0)
print("by using the first method, the result vector is initialized to",result)
# the second method
# alternative and shorter solution for creating a list with zeros
result = [0] * 7
print("by using the second method, the result vector is initialized to",result)
# calculate 3u-2v
for i in range(dimension):
result[i] = 3 * u[i] - 2 * v[i]
# print all lists
print("u is",u)
print("v is",v)
print("3u-2v is",result)
```
<a id="task3"></a>
<h3> Task 3 </h3>
Let $ u = \myrvector{1 \\ -2 \\ -4 \\ 2} $ be a four dimensional vector.
Verify that $ \norm{4 u} = 4 \cdot \norm{u} $ in Python.
Remark that $ 4u $ is another vector obtained from $ u $ by multiplying it with 4.
<h3>Solution</h3>
```
u = [1,-2,-4,2]
fouru=[4,-8,-16,8]
len_u = 0
len_fouru = 0
for i in range(len(u)):
len_u = len_u + u[i]**2 # adding square of each value
len_fouru = len_fouru + fouru[i]**2 # adding square of each value
len_u = len_u ** 0.5 # taking square root of the summation
len_fouru = len_fouru ** 0.5 # taking square root of the summation
# print the lengths
print("length of u is",len_u)
print("4 * length of u is",4 * len_u)
print("length of 4u is",len_fouru)
```
<a id="task4"></a>
<h3> Task 4 </h3>
Let $ u = \myrvector{1 \\ -2 \\ -4 \\ 2} $ be a four dimensional vector.
Randomly pick a number $r$ from $ \left\{ \dfrac{1}{10}, \dfrac{2}{10}, \cdots, \dfrac{9}{10} \right\} $.
Find the vector $(-r)\cdot u$ and then its length.
<h3>Solution</h3>
```
from random import randrange
u = [1,-2,-4,2]
print("u is",u)
r = randrange(9) # r is a number in {0,...,8}
r = r + 1 # r is a number in {1,...,9}
r = r/10 # r is a number in {1/10,...,9/10}
print()
print("r is",r)
newu=[]
for i in range(len(u)):
newu.append(-1*r*u[i])
print()
print("-ru is",newu)
print()
length = 0
for i in range(len(newu)):
length = length + newu[i]**2 # adding square of each number
print(newu[i],"->[square]->",newu[i]**2)
print()
print("the summation of squares is",length)
length = length**0.5 # taking square root
print("the length of",newu,"is",length)
```
Remark that:
The length of $ u $ is 5.
The length of $ (-r)u $ will be $ 5r $.
|
github_jupyter
|
from random import randrange
dimension = 7
# create u and v as empty lists
u = []
v = []
for i in range(dimension):
u.append(randrange(-10,11)) # add a randomly picked number to the list u
v.append(randrange(-10,11)) # add a randomly picked number to the list v
# print both lists
print("u is",u)
print("v is",v)
# please execute the cell for Task 1 to define u and v
# create a result list
# the first method
result=[]
# fill it with zeros
for i in range(dimension):
result.append(0)
print("by using the first method, the result vector is initialized to",result)
# the second method
# alternative and shorter solution for creating a list with zeros
result = [0] * 7
print("by using the second method, the result vector is initialized to",result)
# calculate 3u-2v
for i in range(dimension):
result[i] = 3 * u[i] - 2 * v[i]
# print all lists
print("u is",u)
print("v is",v)
print("3u-2v is",result)
u = [1,-2,-4,2]
fouru=[4,-8,-16,8]
len_u = 0
len_fouru = 0
for i in range(len(u)):
len_u = len_u + u[i]**2 # adding square of each value
len_fouru = len_fouru + fouru[i]**2 # adding square of each value
len_u = len_u ** 0.5 # taking square root of the summation
len_fouru = len_fouru ** 0.5 # taking square root of the summation
# print the lengths
print("length of u is",len_u)
print("4 * length of u is",4 * len_u)
print("length of 4u is",len_fouru)
from random import randrange
u = [1,-2,-4,2]
print("u is",u)
r = randrange(9) # r is a number in {0,...,8}
r = r + 1 # r is a number in {1,...,9}
r = r/10 # r is a number in {1/10,...,9/10}
print()
print("r is",r)
newu=[]
for i in range(len(u)):
newu.append(-1*r*u[i])
print()
print("-ru is",newu)
print()
length = 0
for i in range(len(newu)):
length = length + newu[i]**2 # adding square of each number
print(newu[i],"->[square]->",newu[i]**2)
print()
print("the summation of squares is",length)
length = length**0.5 # taking square root
print("the length of",newu,"is",length)
| 0.123736 | 0.991946 |
<a href="https://colab.research.google.com/github/lionelsamrat10/machine-learning-a-to-z/blob/main/Model%20Selection/K%20Fold%20Cross%20Validation/k_fold_cross_validation_samrat.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# k-Fold Cross Validation (For Classification Problems)
## Importing the libraries
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
```
## Importing the dataset
```
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
```
## Splitting the dataset into the Training set and Test set
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
```
## Feature Scaling
```
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
```
## Training the Kernel SVM model on the Training set
```
from sklearn.svm import SVC
classifier = SVC(kernel = 'rbf', random_state = 0)
classifier.fit(X_train, y_train)
```
## Making the Confusion Matrix
```
from sklearn.metrics import confusion_matrix, accuracy_score
y_pred = classifier.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)
```
## Applying k-Fold Cross Validation
```
from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(estimator = classifier, X = X_train, y = y_train, cv = 10) # cv defines the number of iterations we need
print("Accuracy: {:.2f} %".format(accuracies.mean()*100))
print("Standard Deviation: {:.2f} %".format(accuracies.std()*100))
```
## Visualising the Training set results
```
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
```
## Visualising the Test set results
```
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
from sklearn.svm import SVC
classifier = SVC(kernel = 'rbf', random_state = 0)
classifier.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix, accuracy_score
y_pred = classifier.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)
from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(estimator = classifier, X = X_train, y = y_train, cv = 10) # cv defines the number of iterations we need
print("Accuracy: {:.2f} %".format(accuracies.mean()*100))
print("Standard Deviation: {:.2f} %".format(accuracies.std()*100))
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
| 0.665628 | 0.986992 |
```
# Dependencies and Setup
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# Hide warning messages in notebook
import warnings
warnings.filterwarnings('ignore')
# File to Load (Remember to Change These)
mouse_drug_data_to_load = "data/mouse_drug_data.csv"
clinical_trial_data_to_load = "data/clinicaltrial_data.csv"
# Read the Mouse and Drug Data and the Clinical Trial Data
mouse_drug = pd.read_csv(mouse_drug_data_to_load)
clinical_trial = pd.read_csv(clinical_trial_data_to_load)
# Combine the data into a single dataset
trial = pd.merge(clinical_trial, mouse_drug, on="Mouse ID", how="left")
# Display the data table for preview
trial.head()
```
## Tumor Response to Treatment
```
# Store the Mean Tumor Volume Data Grouped by Drug and Timepoint
volume_mean=trial.groupby(['Drug','Timepoint'])['Tumor Volume (mm3)'].mean()
volume_mean.head()
# Convert to DataFrame
volume_mean=pd.DataFrame(volume_mean)
# Preview DataFrame
volume_mean.head()
# Store the Standard Error of Tumor Volumes Grouped by Drug and Timepoint
volume_sem=trial.groupby(['Drug','Timepoint'])['Tumor Volume (mm3)'].sem()
volume_sem.head()
# Convert to DataFrame
volume_sem=pd.DataFrame(volume_sem)
# Preview DataFrame
volume_sem.head()
pd.DataFrame()
# Minor Data Munging to Re-Format the Data Frames
pivot_mean = pd.pivot_table(volume_mean, values='Tumor Volume (mm3)', index=['Timepoint'], columns=['Drug'])
# Preview that Reformatting worked
pivot_mean.head()
# Generate the Plot (with Error Bars)
scatter=pivot_mean[['Capomulin','Infubinol','Ketapril','Placebo']]
scatter.head()
yerror=volume_sem
Capomulin, =plt.plot(scatter['Capomulin'], marker ='o', color='red', label="Capomulin", linestyle='dashed', linewidth=0.5, markersize=5)
Infubinol, =plt.plot(scatter['Infubinol'], marker ='^', color='blue', label="Infubinol", linestyle='dashed', linewidth=0.5, markersize=5)
Ketapril, =plt.plot(scatter['Ketapril'], marker ='s', color='green', label="Ketapril", linestyle='dashed', linewidth=0.5, markersize=5)
Placebo, =plt.plot(scatter['Placebo'], marker ='d', color='black', label="Placebo", linestyle='dashed', linewidth=0.5, markersize=5)
plt.grid(which='major',axis='y', color='gray', linestyle='-', linewidth=.5)
plt.title("Tumor Response to Treatment")
plt.xlabel("Time (Days)")
plt.ylabel("Tumor Volume (mm3)")
plt.legend(handles=[Capomulin, Infubinol,Ketapril,Placebo ], loc="best")
# Save the Figure
plt.savefig("TumorResponse.png")
# Show the Figure
plt.show();
# DO NOT FORGET TO ADD THE ERROR BARS
```
## Metastatic Response to Treatment
```
# Store the Mean Met. Site Data Grouped by Drug and Timepoint
sites_mean=trial.groupby(['Drug','Timepoint'])['Metastatic Sites'].mean()
sites_mean.head()
# Convert to DataFrame
sites_mean=pd.DataFrame(sites_mean)
# Preview DataFrame
sites_mean.head()
# Store the Standard Error associated with Met. Sites Grouped by Drug and Timepoint
sites_sem=trial.groupby(['Drug','Timepoint'])['Metastatic Sites'].sem()
sites_sem.head()
# Convert to DataFrame
sites_sem=pd.DataFrame(sites_sem)
# Preview DataFrame
sites_sem.head()
# Minor Data Munging to Re-Format the Data Frames
pivot_meta = pd.pivot_table(sites_mean, values='Metastatic Sites', index=['Timepoint'], columns=['Drug'])
# Preview that Reformatting worked
pivot_meta.head()
# Generate the Plot (with Error Bars)
scatter=pivot_meta[['Capomulin','Infubinol','Ketapril','Placebo']]
scatter.head()
Capomulin, =plt.plot(scatter['Capomulin'], marker ='o', color='red', label="Capomulin", linestyle='dashed', linewidth=0.5, markersize=5)
Infubinol, =plt.plot(scatter['Infubinol'], marker ='^', color='blue', label="Infubinol", linestyle='dashed', linewidth=0.5, markersize=5)
Ketapril, =plt.plot(scatter['Ketapril'], marker ='s', color='green', label="Ketapril", linestyle='dashed', linewidth=0.5, markersize=5)
Placebo, =plt.plot(scatter['Placebo'], marker ='d', color='black', label="Placebo", linestyle='dashed', linewidth=0.5, markersize=5)
plt.grid(which='major',axis='y', color='gray', linestyle='-', linewidth=.5)
plt.title("Metastatic Spread During Treatment")
plt.xlabel("Treatment Duration (Days)")
plt.ylabel("Met. Sites")
plt.legend(handles=[Capomulin, Infubinol,Ketapril,Placebo ], loc="best")
# Save the Figure
plt.savefig("MetastaticSpread.png")
# Show the Figure
plt.show();
# DO NOT FORGET TO ADD THE ERROR BARS
```
## Survival Rates
```
trial.head()
# Store the Count of Mice Grouped by Drug and Timepoint (W can pass any metric)
mouse_count=trial.groupby(['Drug','Timepoint'])['Mouse ID'].count()
mouse_count.head()
# Convert to DataFrame
mouse_count=pd.DataFrame(mouse_count)
# Preview DataFrame
mouse_count.head()
# Minor Data Munging to Re-Format the Data Frames
pivot_mouse = pd.pivot_table(mouse_count, values='Mouse ID', index=['Timepoint'], columns=['Drug'])
# Preview that Reformatting worked
pivot_mouse.head()
# Generate the Plot (Accounting for percentages)
scatter=pivot_mouse[['Capomulin','Infubinol','Ketapril','Placebo']]
scatter.head()
Capomulin, =plt.plot(scatter['Capomulin'], marker ='o', color='red', label="Capomulin", linestyle='dashed', linewidth=0.5, markersize=5)
Infubinol, =plt.plot(scatter['Infubinol'], marker ='^', color='blue', label="Infubinol", linestyle='dashed', linewidth=0.5, markersize=5)
Ketapril, =plt.plot(scatter['Ketapril'], marker ='s', color='green', label="Ketapril", linestyle='dashed', linewidth=0.5, markersize=5)
Placebo, =plt.plot(scatter['Placebo'], marker ='d', color='black', label="Placebo", linestyle='dashed', linewidth=0.5, markersize=5)
plt.grid(which='major',axis='both', color='gray', linestyle='-', linewidth=.5)
plt.title("Survival During Treatment")
plt.xlabel("Time (Days)")
plt.ylabel("Survival Rate (%)")
plt.legend(handles=[Capomulin, Infubinol,Ketapril,Placebo ], loc="best")
# Save the Figure
plt.savefig("Survival.png")
# Show the Figure
plt.show();
#MAKE SURE TO CHANGE THE Y-AXIS TO 100
```

## Summary Bar Graph
```
# Calculate the percent changes for each drug
per_change = trial.pivot_table(index='Drug', columns='Timepoint', values='Tumor Volume (mm3)')
per_change['% Change']=(per_change[45]-per_change[0])/per_change[0]*100
# Display the data to confirm
per_change2=per_change[['% Change']]
per_change2.iloc[0:]
Drugs=['Capomulin', 'Infubinol','Ketapril','Placebo']
per_change3=per_change2[per_change2.index.isin(Drugs)]
per_change3
x_axis = np.arange(len(per_change3))
yticks=np.arange(-20, 80, step=20)
y= per_change3['% Change']
mask1 = y < 0
mask2 = y >= 0
# plt.bar(x_axis[mask1], y[mask1], color = 'red')
# plt.bar(x[mask2], y[mask2], color = 'blue')
# plt.bar
plt.bar(x_axis[mask1], y[mask1], color='red', align="edge")
plt.bar(x_axis[mask2], y[mask2], color='green', align="edge")
tick_locations = [value for value in x_axis]
plt.xticks(tick_locations, per_change3.index)
plt.yticks(yticks)
plt.title("Tumor Change Over 45 Day Treatment")
plt.ylabel("% Tumor Volume Change")
plt.grid(which='major',axis='both')
# Save the Figure
plt.savefig("barchart.png")
# Show the Figure
plt.show();
# DON'T FORGET TO ADD THE PERCENTAGES ON THE BAR CHART
# Store all Relevant Percent Changes into a Tuple
# Splice the data between passing and failing drugs
# Orient widths. Add labels, tick marks, etc.
# Use functions to label the percentages of changes
# Call functions to implement the function calls
# Save the Figure
# Show the Figure
fig.show()
```

|
github_jupyter
|
# Dependencies and Setup
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# Hide warning messages in notebook
import warnings
warnings.filterwarnings('ignore')
# File to Load (Remember to Change These)
mouse_drug_data_to_load = "data/mouse_drug_data.csv"
clinical_trial_data_to_load = "data/clinicaltrial_data.csv"
# Read the Mouse and Drug Data and the Clinical Trial Data
mouse_drug = pd.read_csv(mouse_drug_data_to_load)
clinical_trial = pd.read_csv(clinical_trial_data_to_load)
# Combine the data into a single dataset
trial = pd.merge(clinical_trial, mouse_drug, on="Mouse ID", how="left")
# Display the data table for preview
trial.head()
# Store the Mean Tumor Volume Data Grouped by Drug and Timepoint
volume_mean=trial.groupby(['Drug','Timepoint'])['Tumor Volume (mm3)'].mean()
volume_mean.head()
# Convert to DataFrame
volume_mean=pd.DataFrame(volume_mean)
# Preview DataFrame
volume_mean.head()
# Store the Standard Error of Tumor Volumes Grouped by Drug and Timepoint
volume_sem=trial.groupby(['Drug','Timepoint'])['Tumor Volume (mm3)'].sem()
volume_sem.head()
# Convert to DataFrame
volume_sem=pd.DataFrame(volume_sem)
# Preview DataFrame
volume_sem.head()
pd.DataFrame()
# Minor Data Munging to Re-Format the Data Frames
pivot_mean = pd.pivot_table(volume_mean, values='Tumor Volume (mm3)', index=['Timepoint'], columns=['Drug'])
# Preview that Reformatting worked
pivot_mean.head()
# Generate the Plot (with Error Bars)
scatter=pivot_mean[['Capomulin','Infubinol','Ketapril','Placebo']]
scatter.head()
yerror=volume_sem
Capomulin, =plt.plot(scatter['Capomulin'], marker ='o', color='red', label="Capomulin", linestyle='dashed', linewidth=0.5, markersize=5)
Infubinol, =plt.plot(scatter['Infubinol'], marker ='^', color='blue', label="Infubinol", linestyle='dashed', linewidth=0.5, markersize=5)
Ketapril, =plt.plot(scatter['Ketapril'], marker ='s', color='green', label="Ketapril", linestyle='dashed', linewidth=0.5, markersize=5)
Placebo, =plt.plot(scatter['Placebo'], marker ='d', color='black', label="Placebo", linestyle='dashed', linewidth=0.5, markersize=5)
plt.grid(which='major',axis='y', color='gray', linestyle='-', linewidth=.5)
plt.title("Tumor Response to Treatment")
plt.xlabel("Time (Days)")
plt.ylabel("Tumor Volume (mm3)")
plt.legend(handles=[Capomulin, Infubinol,Ketapril,Placebo ], loc="best")
# Save the Figure
plt.savefig("TumorResponse.png")
# Show the Figure
plt.show();
# DO NOT FORGET TO ADD THE ERROR BARS
# Store the Mean Met. Site Data Grouped by Drug and Timepoint
sites_mean=trial.groupby(['Drug','Timepoint'])['Metastatic Sites'].mean()
sites_mean.head()
# Convert to DataFrame
sites_mean=pd.DataFrame(sites_mean)
# Preview DataFrame
sites_mean.head()
# Store the Standard Error associated with Met. Sites Grouped by Drug and Timepoint
sites_sem=trial.groupby(['Drug','Timepoint'])['Metastatic Sites'].sem()
sites_sem.head()
# Convert to DataFrame
sites_sem=pd.DataFrame(sites_sem)
# Preview DataFrame
sites_sem.head()
# Minor Data Munging to Re-Format the Data Frames
pivot_meta = pd.pivot_table(sites_mean, values='Metastatic Sites', index=['Timepoint'], columns=['Drug'])
# Preview that Reformatting worked
pivot_meta.head()
# Generate the Plot (with Error Bars)
scatter=pivot_meta[['Capomulin','Infubinol','Ketapril','Placebo']]
scatter.head()
Capomulin, =plt.plot(scatter['Capomulin'], marker ='o', color='red', label="Capomulin", linestyle='dashed', linewidth=0.5, markersize=5)
Infubinol, =plt.plot(scatter['Infubinol'], marker ='^', color='blue', label="Infubinol", linestyle='dashed', linewidth=0.5, markersize=5)
Ketapril, =plt.plot(scatter['Ketapril'], marker ='s', color='green', label="Ketapril", linestyle='dashed', linewidth=0.5, markersize=5)
Placebo, =plt.plot(scatter['Placebo'], marker ='d', color='black', label="Placebo", linestyle='dashed', linewidth=0.5, markersize=5)
plt.grid(which='major',axis='y', color='gray', linestyle='-', linewidth=.5)
plt.title("Metastatic Spread During Treatment")
plt.xlabel("Treatment Duration (Days)")
plt.ylabel("Met. Sites")
plt.legend(handles=[Capomulin, Infubinol,Ketapril,Placebo ], loc="best")
# Save the Figure
plt.savefig("MetastaticSpread.png")
# Show the Figure
plt.show();
# DO NOT FORGET TO ADD THE ERROR BARS
trial.head()
# Store the Count of Mice Grouped by Drug and Timepoint (W can pass any metric)
mouse_count=trial.groupby(['Drug','Timepoint'])['Mouse ID'].count()
mouse_count.head()
# Convert to DataFrame
mouse_count=pd.DataFrame(mouse_count)
# Preview DataFrame
mouse_count.head()
# Minor Data Munging to Re-Format the Data Frames
pivot_mouse = pd.pivot_table(mouse_count, values='Mouse ID', index=['Timepoint'], columns=['Drug'])
# Preview that Reformatting worked
pivot_mouse.head()
# Generate the Plot (Accounting for percentages)
scatter=pivot_mouse[['Capomulin','Infubinol','Ketapril','Placebo']]
scatter.head()
Capomulin, =plt.plot(scatter['Capomulin'], marker ='o', color='red', label="Capomulin", linestyle='dashed', linewidth=0.5, markersize=5)
Infubinol, =plt.plot(scatter['Infubinol'], marker ='^', color='blue', label="Infubinol", linestyle='dashed', linewidth=0.5, markersize=5)
Ketapril, =plt.plot(scatter['Ketapril'], marker ='s', color='green', label="Ketapril", linestyle='dashed', linewidth=0.5, markersize=5)
Placebo, =plt.plot(scatter['Placebo'], marker ='d', color='black', label="Placebo", linestyle='dashed', linewidth=0.5, markersize=5)
plt.grid(which='major',axis='both', color='gray', linestyle='-', linewidth=.5)
plt.title("Survival During Treatment")
plt.xlabel("Time (Days)")
plt.ylabel("Survival Rate (%)")
plt.legend(handles=[Capomulin, Infubinol,Ketapril,Placebo ], loc="best")
# Save the Figure
plt.savefig("Survival.png")
# Show the Figure
plt.show();
#MAKE SURE TO CHANGE THE Y-AXIS TO 100
# Calculate the percent changes for each drug
per_change = trial.pivot_table(index='Drug', columns='Timepoint', values='Tumor Volume (mm3)')
per_change['% Change']=(per_change[45]-per_change[0])/per_change[0]*100
# Display the data to confirm
per_change2=per_change[['% Change']]
per_change2.iloc[0:]
Drugs=['Capomulin', 'Infubinol','Ketapril','Placebo']
per_change3=per_change2[per_change2.index.isin(Drugs)]
per_change3
x_axis = np.arange(len(per_change3))
yticks=np.arange(-20, 80, step=20)
y= per_change3['% Change']
mask1 = y < 0
mask2 = y >= 0
# plt.bar(x_axis[mask1], y[mask1], color = 'red')
# plt.bar(x[mask2], y[mask2], color = 'blue')
# plt.bar
plt.bar(x_axis[mask1], y[mask1], color='red', align="edge")
plt.bar(x_axis[mask2], y[mask2], color='green', align="edge")
tick_locations = [value for value in x_axis]
plt.xticks(tick_locations, per_change3.index)
plt.yticks(yticks)
plt.title("Tumor Change Over 45 Day Treatment")
plt.ylabel("% Tumor Volume Change")
plt.grid(which='major',axis='both')
# Save the Figure
plt.savefig("barchart.png")
# Show the Figure
plt.show();
# DON'T FORGET TO ADD THE PERCENTAGES ON THE BAR CHART
# Store all Relevant Percent Changes into a Tuple
# Splice the data between passing and failing drugs
# Orient widths. Add labels, tick marks, etc.
# Use functions to label the percentages of changes
# Call functions to implement the function calls
# Save the Figure
# Show the Figure
fig.show()
| 0.681621 | 0.900179 |
# Ethereum ECDSA signature playground
## Prepare
To interact with Ethereum network, you need Ethereum node up and running.
You can run both notebook and ganache-cli node emulator by `./start.sh` script.
Or you can run ganache-cli Ethereum emulator in separate terminal
`npx ganache-cli -m "dawn finish orchard pluck festival genuine absorb van bike mirror kiss loop"`
(12 words are the seed passphrase to keep addresses and keys constant)
## Connect to Web3
Now connect to Ethereum provider via web3 RPC
```
from web3 import Web3
w3 = Web3(Web3.HTTPProvider('http://127.0.0.1:8545'))
w3.eth.defaultAccount = w3.eth.accounts[0]
```
Check if web3 up and running
```
w3.eth.getBlock('latest')
```
## Solidity version
Solc compiler has to be installed on your machine. Check solidity version (should match pragma statement in your contract)
```
import subprocess, re, json
solc = subprocess.Popen(['solc', '--version'], stdout=subprocess.PIPE, stdin=subprocess.PIPE)
solc_output = solc.communicate()
m = re.search(r"Version: ([\w\.\+]+)", str(solc_output[0]))
m.group(1)
```
## Solidity verification contract
The contract which uses ECRECOVER solidity function to recover address from hash of the data and its signature.
```
contract_source_code = b"""
pragma solidity ^0.5.7;
contract Auth {
function verify(address p, bytes32 hash, uint8 v, bytes32 r, bytes32 s) pure public returns(bool) {
return ecrecover(hash, v, r, s) == p;
}
}
"""
```
Actually compile and generate ABI
```
solc = subprocess.Popen(['solc', '--combined-json', 'bin,abi', '-'], stdout=subprocess.PIPE, stdin=subprocess.PIPE)
solc_output = solc.communicate(contract_source_code)
```
See the contract bytecode
```
bytecode = json.loads(solc_output[0])['contracts']['<stdin>:Auth']['bin']
bytecode
```
See the contract ABI interfaces
```
abi = json.loads(solc_output[0])['contracts']['<stdin>:Auth']['abi']
abi
```
## Deploy
Instantiate contract fabric and deploy the contract on the net
```
AuthContract = w3.eth.contract(abi=abi, bytecode=bytecode)
tx_hash = AuthContract.constructor().transact()
tx_hash
```
Get Tx receipt (see contractAddress)
```
tx_receipt = w3.eth.waitForTransactionReceipt(tx_hash)
tx_receipt
```
Initialize contract instance at given address
```
auth_contract = w3.eth.contract(
address=tx_receipt.contractAddress,
abi=abi,
)
auth_contract
```
## Interact
Call the contract methods (ToDo)
```
auth_contract.functions.verify(
'0x7E5F4552091A69125d5DfCb7b8C2659029395Bdf',
bytes(0),
1,
bytes(b'\xff'*32),
bytes(b'\xff'*32)).call()
```
|
github_jupyter
|
from web3 import Web3
w3 = Web3(Web3.HTTPProvider('http://127.0.0.1:8545'))
w3.eth.defaultAccount = w3.eth.accounts[0]
w3.eth.getBlock('latest')
import subprocess, re, json
solc = subprocess.Popen(['solc', '--version'], stdout=subprocess.PIPE, stdin=subprocess.PIPE)
solc_output = solc.communicate()
m = re.search(r"Version: ([\w\.\+]+)", str(solc_output[0]))
m.group(1)
contract_source_code = b"""
pragma solidity ^0.5.7;
contract Auth {
function verify(address p, bytes32 hash, uint8 v, bytes32 r, bytes32 s) pure public returns(bool) {
return ecrecover(hash, v, r, s) == p;
}
}
"""
solc = subprocess.Popen(['solc', '--combined-json', 'bin,abi', '-'], stdout=subprocess.PIPE, stdin=subprocess.PIPE)
solc_output = solc.communicate(contract_source_code)
bytecode = json.loads(solc_output[0])['contracts']['<stdin>:Auth']['bin']
bytecode
abi = json.loads(solc_output[0])['contracts']['<stdin>:Auth']['abi']
abi
AuthContract = w3.eth.contract(abi=abi, bytecode=bytecode)
tx_hash = AuthContract.constructor().transact()
tx_hash
tx_receipt = w3.eth.waitForTransactionReceipt(tx_hash)
tx_receipt
auth_contract = w3.eth.contract(
address=tx_receipt.contractAddress,
abi=abi,
)
auth_contract
auth_contract.functions.verify(
'0x7E5F4552091A69125d5DfCb7b8C2659029395Bdf',
bytes(0),
1,
bytes(b'\xff'*32),
bytes(b'\xff'*32)).call()
| 0.499023 | 0.74382 |
<a href="https://colab.research.google.com/github/shmilyface/DS-Unit-2-Tree-Ensembles/blob/master/Copy_of_DS_Sprint_Challenge_7_Classification_1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
_Lambda School Data Science, Unit 2_
# Sprint Challenge: Predict Steph Curry's shots 🏀
For your Sprint Challenge, you'll use a dataset with all Steph Curry's NBA field goal attempts. (Regular season and playoff games, from October 28, 2009, through June 5, 2019.)
You'll use information about the shot and the game to predict whether the shot was made. This is hard to predict! Try for an accuracy score in the high 50's or low 60's. The dataset was collected with the [nba_api](https://github.com/swar/nba_api) Python library.
```
import pandas as pd
url = 'https://drive.google.com/uc?export=download&id=1fL7KPyxgGYfQDsuJoBWHIWwCAf-HTFpX'
df = pd.read_csv(url, parse_dates=['game_date']).set_index('game_date')
assert df.shape == (13958, 19)
df.head()
```
This Sprint Challenge has two parts. To demonstrate mastery on each part, do all the required, numbered instructions. To earn a score of "3" for the part, also do the stretch goals.
## Part 1. Prepare to model
### Required
1. **Do train/validate/test split.** Use the 2009-10 season through 2016-17 season to train, the 2017-18 season to validate, and the 2018-19 season to test. NBA seasons begin in October and end in June. You'll know you've split the data correctly when your train set has 11081 observations, your validation set has 1168 observations, and your test set has 1709 observations.
2. **Begin with baselines for classification.** Your target to predict is `shot_made_flag`. What is the baseline accuracy for the validation set, if you guessed the majority class for every prediction?
3. **Use Ordinal Encoding _or_ One-Hot Encoding,** for the categorical features you select.
4. **Train a Random Forest _or_ Logistic Regression** with the features you select.
### Stretch goals
Engineer at least 4 of these 5 features:
- **Homecourt Advantage**: Is the home team (`htm`) the Golden State Warriors (`GSW`) ?
- **Opponent**: Who is the other team playing the Golden State Warriors?
- **Seconds remaining in the period**: Combine minutes remaining with seconds remaining, to get the total number of seconds remaining in the period.
- **Seconds remaining in the game**: Combine period, and seconds remaining in the period, to get the total number of seconds remaining in the game. A basketball game has 4 periods, each 12 minutes long.
- **Made previous shot**: Was Steph Curry's previous shot successful?
## Part 2. Evaluate models
### Required
1. Get your model's **validation accuracy.** (Multiple times if you try multiple iterations.)
2. Get your model's **test accuracy.** (One time, at the end.)
3. Get and plot your Random Forest's **feature importances** _or_ your Logistic Regression's **coefficients.**
4. Imagine this is the confusion matrix for a binary classification model. **Calculate accuracy, precision, and recall for this confusion matrix:**
<table>
<tr>
<td colspan="2" rowspan="2"></td>
<td colspan="2">Predicted</td>
</tr>
<tr>
<td>Negative</td>
<td>Positive</td>
</tr>
<tr>
<td rowspan="2">Actual</td>
<td>Negative</td>
<td style="border: solid">85</td>
<td style="border: solid">58</td>
</tr>
<tr>
<td>Positive</td>
<td style="border: solid">8</td>
<td style="border: solid"> 36</td>
</tr>
</table>
### Stretch goals
- Calculate F1 score for the provided, imaginary confusion matrix.
- Plot a real confusion matrix for your basketball model, with row and column labels.
- Print the classification report for your model.
```
#Part 1
#train/validate
#one hot encoding
#train model
#split data at June 2017 for test
#split data at 2009 - June 2017 for train
#validate is to June 2018
#test would be to June 2019
#installs
!pip install category_encoders
!pip install pandas_profiling
#imports
%matplotlib inline
import category_encoders as ce
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import RobustScaler
from sklearn.metrics import accuracy_score
#train, val, test
train = df.loc['2009-07-01' : '2017-6-30']
val = df.loc['2017-07-07' : '2018-6-30']
test = df.loc['2018-6-30' : '2019-6-5']
train.shape, val.shape, test.shape
#determine majority class
y_val = val['shot_made_flag']
y_val.value_counts(normalize=True)
#majority class for every prediction
majority = y_val.mode()[0]
y_pred = [majority]*len(y_val)
y_pred[:5]
#validation baseline using majority as prediction
accuracy_score(y_val, y_pred)
#Part 1: One Hot Encoding
encoder = ce.OneHotEncoder(use_cat_names=True)
encoded = encoder.fit_transform(train[['action_type', 'shot_type']])
encoded[:5]
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import make_pipeline
from sklearn.impute import SimpleImputer
pipeline = make_pipeline(
ce.OneHotEncoder (use_cat_names=True),
SimpleImputer(strategy='median'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
#target
target = 'shot_made_flag'
#features
features = ['action_type', 'shot_type']
x_train = train[features]
y_train = train[target]
x_test = test[features]
y_test = test[target]
x_val = val[features]
y_val = val[target]
#fit on train, score on val, predict on test
pipeline.fit(x_train, y_train)
#Validation Accuracy Score
print('Validation Accuracy', pipeline.score(x_val, y_val))
print('Test Accuracy', pipeline.score(x_test, y_test))
#feature importance
feature_names = pipeline.named_steps['onehotencoder'].transform(x_val).columns
importances = pipeline.named_steps['randomforestclassifier'].feature_importances_
fi_ser = pd.Series(importances, feature_names)
n = 20
plt.figure(figsize=(10,n/2))
plt.title(f'Top {n} Features')
fi_ser.sort_values()[-n:].plot.barh();
```
4. Imagine this is the confusion matrix for a binary classification model. **Calculate accuracy, precision, and recall for this confusion matrix:**
<table>
<tr>
<td colspan="2" rowspan="2"></td>
<td colspan="2">Predicted</td>
</tr>
<tr>
<td>Negative</td>
<td>Positive</td>
</tr>
<tr>
<td rowspan="2">Actual</td>
<td>Negative</td>
<td style="border: solid">85</td>
<td style="border: solid">58</td>
</tr>
<tr>
<td>Positive</td>
<td style="border: solid">8</td>
<td style="border: solid"> 36</td>
</tr>
</table>
```
#confusion matrix
x = 85 + 36
y = 85 + 58 + 8 + 36
accuracy = x / y
precision = 36 / (36 + 58)
recall = 36 / (36 + 8)
print('Total Correct:', x)
print('Total Predictions:', y)
print('Accuracy: ', accuracy)
print('Precision: ', precision)
print('Recall: ', recall)
```
|
github_jupyter
|
import pandas as pd
url = 'https://drive.google.com/uc?export=download&id=1fL7KPyxgGYfQDsuJoBWHIWwCAf-HTFpX'
df = pd.read_csv(url, parse_dates=['game_date']).set_index('game_date')
assert df.shape == (13958, 19)
df.head()
#Part 1
#train/validate
#one hot encoding
#train model
#split data at June 2017 for test
#split data at 2009 - June 2017 for train
#validate is to June 2018
#test would be to June 2019
#installs
!pip install category_encoders
!pip install pandas_profiling
#imports
%matplotlib inline
import category_encoders as ce
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import RobustScaler
from sklearn.metrics import accuracy_score
#train, val, test
train = df.loc['2009-07-01' : '2017-6-30']
val = df.loc['2017-07-07' : '2018-6-30']
test = df.loc['2018-6-30' : '2019-6-5']
train.shape, val.shape, test.shape
#determine majority class
y_val = val['shot_made_flag']
y_val.value_counts(normalize=True)
#majority class for every prediction
majority = y_val.mode()[0]
y_pred = [majority]*len(y_val)
y_pred[:5]
#validation baseline using majority as prediction
accuracy_score(y_val, y_pred)
#Part 1: One Hot Encoding
encoder = ce.OneHotEncoder(use_cat_names=True)
encoded = encoder.fit_transform(train[['action_type', 'shot_type']])
encoded[:5]
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import make_pipeline
from sklearn.impute import SimpleImputer
pipeline = make_pipeline(
ce.OneHotEncoder (use_cat_names=True),
SimpleImputer(strategy='median'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
#target
target = 'shot_made_flag'
#features
features = ['action_type', 'shot_type']
x_train = train[features]
y_train = train[target]
x_test = test[features]
y_test = test[target]
x_val = val[features]
y_val = val[target]
#fit on train, score on val, predict on test
pipeline.fit(x_train, y_train)
#Validation Accuracy Score
print('Validation Accuracy', pipeline.score(x_val, y_val))
print('Test Accuracy', pipeline.score(x_test, y_test))
#feature importance
feature_names = pipeline.named_steps['onehotencoder'].transform(x_val).columns
importances = pipeline.named_steps['randomforestclassifier'].feature_importances_
fi_ser = pd.Series(importances, feature_names)
n = 20
plt.figure(figsize=(10,n/2))
plt.title(f'Top {n} Features')
fi_ser.sort_values()[-n:].plot.barh();
#confusion matrix
x = 85 + 36
y = 85 + 58 + 8 + 36
accuracy = x / y
precision = 36 / (36 + 58)
recall = 36 / (36 + 8)
print('Total Correct:', x)
print('Total Predictions:', y)
print('Accuracy: ', accuracy)
print('Precision: ', precision)
print('Recall: ', recall)
| 0.501221 | 0.977197 |
# Projecting terrestrial biodiversity using PREDICTS and LUH2
This notebook shows how to use rasterset to project a PREDICTS model using the LUH2 land-use data.
You can set three parameters below:
- scenario: can be either historical (850CE - 2015CE) or one of he LUH2 scenarios available (all in lowercase, e.g. ssp1_rcp2.6_image).
- year: year for which to generate the projection. For the historical scenario the year must be between 850-2015. For the SSP scenarios the year must be between 2015-2100.
- what: the name of the variable to evaluate. Many abundance models evaluate a variable called *LogAbund*. If you want to project abundance than what should be *LogAbund*. But you can use any of the intermediate variables as well. For example setting what to *hpd* will generate a projection of human population density.
### Imports (non-local)
```
import click
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import numpy.ma as ma
import rasterio
from rasterio.plot import show, show_hist
```
### Local imports
```
from projections.rasterset import RasterSet, Raster
from projections.simpleexpr import SimpleExpr
import projections.r2py.modelr as modelr
import projections.predicts as predicts
import projections.utils as utils
```
### Parameters
```
scenario = 'historical'
year = 2000
what = 'LogAbund'
```
### Models
This notebook uses Sam's LUH2 abundance models. Thus we need to load a forested and a non-forested model, project using both and then combine the projection.
```
modf = modelr.load('ab-fst-1.rds')
intercept_f = modf.intercept
predicts.predictify(modf)
modn = modelr.load('ab-nfst-1.rds')
intercept_n = modn.intercept
predicts.predictify(modn)
```
### Rastersets
Use the PREDICTS python module to generate the appropriate *rastersets*. Each rasterset is like a DataFrame or hash (dict in python). The columns are variables and hold a function that describes how to compute the data.
Generating a rasterset is a two-step process. First generate a hash (dict in python) and then pass the dict to the constructor.
Each model will be evaluated only where the forested mask is set (or not set). Load the mask from the LUH2 statis data set.
Note that we need to explicitly assign the R model we loaded in the previous cell to the corresponding variable of the rasterset.
```
fstnf = rasterio.open(utils.luh2_static('fstnf'))
rastersf = predicts.rasterset('luh2', scenario, year, 'f')
rsf = RasterSet(rastersf, mask=fstnf, maskval=0.0)
rastersn = predicts.rasterset('luh2', scenario, year, 'n')
rsn = RasterSet(rastersn, mask=fstnf, maskval=1.0)
vname = modf.output
assert modf.output == modn.output
rsf[vname] = modf
rsn[vname] = modn
```
### Eval
Now evaluate each model in turn and then combine the data. Because we are guaranteed that the data is non-overlaping (no cell should have valid data in both projections) we can simply add them together (with masked values filled in as 0). The overall mask is the logical **AND** of the two invalid masks.
```
datan, meta = rsn.eval(what, quiet=True)
dataf, _ = rsf.eval(what, quiet=True)
data_vals = dataf.filled(0) + datan.filled(0)
data = data_vals.view(ma.MaskedArray)
data.mask = np.logical_and(dataf.mask, datan.mask)
```
### Rendering
Use matplotlib (via rasterio.plot) to render the generated data. This will display the data in-line in the notebook.
```
show(data, cmap='viridis')
```
|
github_jupyter
|
import click
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import numpy.ma as ma
import rasterio
from rasterio.plot import show, show_hist
from projections.rasterset import RasterSet, Raster
from projections.simpleexpr import SimpleExpr
import projections.r2py.modelr as modelr
import projections.predicts as predicts
import projections.utils as utils
scenario = 'historical'
year = 2000
what = 'LogAbund'
modf = modelr.load('ab-fst-1.rds')
intercept_f = modf.intercept
predicts.predictify(modf)
modn = modelr.load('ab-nfst-1.rds')
intercept_n = modn.intercept
predicts.predictify(modn)
fstnf = rasterio.open(utils.luh2_static('fstnf'))
rastersf = predicts.rasterset('luh2', scenario, year, 'f')
rsf = RasterSet(rastersf, mask=fstnf, maskval=0.0)
rastersn = predicts.rasterset('luh2', scenario, year, 'n')
rsn = RasterSet(rastersn, mask=fstnf, maskval=1.0)
vname = modf.output
assert modf.output == modn.output
rsf[vname] = modf
rsn[vname] = modn
datan, meta = rsn.eval(what, quiet=True)
dataf, _ = rsf.eval(what, quiet=True)
data_vals = dataf.filled(0) + datan.filled(0)
data = data_vals.view(ma.MaskedArray)
data.mask = np.logical_and(dataf.mask, datan.mask)
show(data, cmap='viridis')
| 0.442637 | 0.992169 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.