prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Precipitation exercises
***
## <font color=steelblue>Exercise 3 - Double-mass curve</font>
<font color=steelblue>Perform a double-mass curve analysis with the data in sheet *Exercise_003* from file *RainfallData.xlsx*.</font>
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
sns.set_context('notebook')
from scipy.optimize import curve_fit
```
### Import data
```
# Importar los datos
data3 = pd.read_excel('../data/RainfallData.xlsx', sheet_name='Exercise_003',
skiprows=0, index_col=0)
# name of the gages
gages = data3.columns
# calculate the mean across stations
data3['AVG'] = data3.mean(axis=1)
data3.head()
```
### Double-mass curves
We are going to plot simultaneously the double-mass curve for all the stations, so we can start identifying stations that may have problems.
To plot several plots in the same figure, we will use the function `subplots` in `Matplotlib`.
```
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(12, 8), sharex=True, sharey=True)
for (gage, ax) in zip(gages, axes.flatten()):
# line of slope 1
ax.plot((0, 800), (0, 800), ':k', label='1:1 line')
# double-mass curve
ax.plot(data3.AVG.cumsum(), data3[gage].cumsum(), '.-', label='data')
ax.set_title('gage ' + gage)
ax.legend()
axes[1, 2].axis('off');
```
From the plot we are certain that the series in gage C is correct, but there might be problems in the rest of the gages.
### Identify errors
The double-mass curve must represent a linear regression with no intercept. We will create a function representing this linear regression which we will use in the following steps.
```
def linear_reg(x, m):
"""Linear regression with no intecept
y = m * x
Input:
------
x: float. Independet value
m: float. Slope of the linear regression
Output:
-------
y: float. Regressed value"""
y = m * x
return y
```
#### Gage A
To identify errors, we will have to fit the linear regression with no intercept to both the series before and after a specific year; if the diference in the fitted slope for those two series exceed an error threshold, we identify that year as a break point in the double-mass curve. We will iterate this process for each year and set a error threshold (or tolerance) to find all the possible break points in the series.
```
# define the gage
gage = 'A'
# define the error threshold
error = .2
for year in data3.index[3:-3]:
# fit the regression from 1978 onwards
m1 = curve_fit(linear_reg, data3.loc[:year, 'AVG'].cumsum(), data3.loc[:year, gage].cumsum())[0][0]
# fit the regression from 1978 onwards
m2 = curve_fit(linear_reg, data3.loc[year:, 'AVG'].cumsum(), data3.loc[year:, gage].cumsum())[0][0]
## correction factor
#factor = m1 / m2
#if (factor < 1 - error) | (factor > 1. + error):
if abs(m1 - m2) > error:
print('{0} m1 = {1:.3f} m2 = {2:.3f} factor = {3:.3f}'.format(year, m1, m2, factor))
```
There are no errors in the series of gage A.
#### All gages
Simply changing the name of the gage in the previous section we can repeat the process. Let's create a function and the run it in a a loop.
```
def identify_errors(dataGage, dataAVG, error=.1):
"""Identify possible break points in the double-mass curve
Parameters:
-----------
dataGage: series. Annual series for the gage to be checked
dataAVG: series. Annual series of the mean across gages in a region
error: float. Error threshold
Output:
-------
It will print the years with a difference in slopes higher than 'error', alon with the values of the slopes.
"""
for year in dataGage.index[3:-3]:
# fit the regression from 1978 onwards
m1 = curve_fit(linear_reg, dataAVG.loc[:year].cumsum(), dataGage.loc[:year].cumsum())[0][0]
# fit the regression from 1978 onwards
m2 = curve_fit(linear_reg, dataAVG.loc[year:].cumsum(), dataGage.loc[year:].cumsum())[0][0]
## correction factor
#factor = m1 / m2
#if (factor < 1 - error) | (factor > 1. + error):
if abs(m1 - m2) > error:
print('{0} m1 = {1:.3f} m2 = {2:.3f}'.format(year, m1, m2))
for gage in gages:
print('Gage ', gage)
identify_errors(data3['AVG'], data3[gage], error=.1)
print()
```
We have identified errors in gages B, D and E. This was an automatic search to discard correct stations. Now, we have to analyse one by one these three stations that might have errors.
### Correct errors
#### Gage B
##### Analyse the series
We have identified anomalies in the years between 1929 and 1939. It will probably mean that there are two break points in the double mass curve. Let's look at the double mass curve and the specific points representing those two years.
```
# set gage and year corresponding to the break in the line
gage = 'B'
breaks = [1929, 1939]
# visualize
plt.figure(figsize=(5, 5))
plt.axis('equal')
plt.plot((0, 800), (0, 800), '--k')
plt.plot(data3.AVG.cumsum(), data3[gage].cumsum(), '.-', label='original')
plt.plot(data3.AVG.cumsum().loc[breaks], data3[gage].cumsum().loc[breaks], '.', label='breaks')
plt.legend();
```
At a glance, we can identify three periods. There is period at the beginning of the series with a higher than usual slope; this period seem so extend until 1930 (not 1929 as we had identified). There is aperiod at the end of the series with a lower than usual slope; this period seems to start in 1938 (not 1939 as we had identified).
We will reset the break points and calculate the slope of the regression to check it.
```
# reset the break points
breaks = [1930, 1938]
# fit the regression untill the first break
m1 = curve_fit(linear_reg, data3.loc[:breaks[0], 'AVG'].cumsum(), data3.loc[:breaks[0], gage].cumsum())[0][0]
# fit the regression from the first to the second break
m2 = curve_fit(linear_reg, data3.loc[breaks[0]:breaks[1], 'AVG'].cumsum(), data3.loc[breaks[0]:breaks[1], gage].cumsum())[0][0]
# fit the regression from t
m3 = curve_fit(linear_reg, data3.loc[breaks[1]:, 'AVG'].cumsum(), data3.loc[breaks[1]:, gage].cumsum())[0][0]
print('m1 = {0:.3f} m2 = {1:.3f} m3 = {2:.3f}'.format(m1, m2, m3))
```
As expected, there are three different slopes in the series. We will assume that the correct data is that from 1930 to 1937, because it is longest period of the three and its slope is closer to 1. Therefore, we have to calculate the correction factors for two periods: before 1930 and after 1937; with these factors we can correct the series.
##### Correct the series
```
# correction factors
factor12 = m2 / m1
factor23 = m2 / m3
factor12, factor23
# copy of the original series
data3['B_'] = data3[gage].copy()
# correct period before the first break
data3.loc[:breaks[0], 'B_'] *= factor12
# correct period after the second break
data3.loc[breaks[1]:, 'B_'] *= factor23
plt.figure(figsize=(5, 5))
plt.axis('equal')
plt.plot((0, 800), (0, 800), '--k')
plt.plot(data3.AVG.cumsum(), data3[gage].cumsum(), '.-', label='original')
plt.plot(data3.AVG.cumsum(), data3['B_'].cumsum(), '.-', label='corrected')
plt.legend();
```
Now we can check again for errors in the correceted series.
```
# chech again for errors
identify_errors(data3.B_, data3.AVG)
```
There aren't any more errors, so we've done correcting data from gage B.
#### Gage D
##### Analyse the series
We found a break point in year 1930.
```
# set gage and year corresponding to the break in the line
gage = 'D'
breaks = [1930]
# visualize
plt.figure(figsize=(5, 5))
plt.axis('equal')
plt.plot((0, 800), (0, 800), '--k')
plt.plot(data3.AVG.cumsum(), data3[gage].cumsum(), '.-', label='original')
plt.plot(data3.AVG.cumsum().loc[breaks], data3[gage].cumsum().loc[breaks], '.', label='breaks')
plt.legend();
# fit the regression untill the break
m1 = curve_fit(linear_reg, data3.loc[:breaks[0], 'AVG'].cumsum(), data3.loc[:breaks[0], gage].cumsum())[0][0]
# fit the regression after the break
m2 = curve_fit(linear_reg, data3.loc[breaks[0]:, 'AVG'].cumsum(), data3.loc[breaks[0]:, gage].cumsum())[0][0]
print('m1 = {0:.3f} m2 = {1:.3f}'.format(m1, m2))
```
This case is simpler than the previous and we easily spot the breal point in 1930. THe period before 1930 has a slope closer to 1, so we will assume that this is the correct part of the series.
##### Correct the series
```
# correction factor
factor = m1 / m2
factor
# copy of the original series
data3[gage + '_'] = data3[gage].copy()
# correct period after the break
data3.loc[breaks[0]:, gage + '_'] *= factor
plt.figure(figsize=(5, 5))
plt.axis('equal')
plt.plot((0, 800), (0, 800), '--k')
plt.plot(data3.AVG.cumsum(), data3[gage].cumsum(), '.-', label='original')
plt.plot(data3.AVG.cumsum(), data3[gage + '_'].cumsum(), '.-', label='corrected')
plt.legend();
# chech again for errors
identify_errors(data3[gage + '_'], data3.AVG, error=.1)
```
We identify two more possible break point in the corrected series. Both might indicate that the last section of the series has a higher slope that the initial. Let's correct the series from 1935 on, and this may solve the second break point in 1937.
```
gage = 'D_'
breaks = [1935]
# fit the regression untill the break
m1 = curve_fit(linear_reg, data3.loc[:breaks[0], 'AVG'].cumsum(), data3.loc[:breaks[0], gage].cumsum())[0][0]
# fit the regression after the break
m2 = curve_fit(linear_reg, data3.loc[breaks[0]:, 'AVG'].cumsum(), data3.loc[breaks[0]:, gage].cumsum())[0][0]
print('m1 = {0:.3f} m2 = {1:.3f}'.format(m1, m2))
# correction factor
factor = m1 / m2
factor
# copy of the original series
data3[gage + '_'] = data3[gage].copy()
# correct period after the break
data3.loc[breaks[0]:, gage + '_'] *= factor
plt.figure(figsize=(5, 5))
plt.axis('equal')
plt.plot((0, 800), (0, 800), '--k')
plt.plot(data3.AVG.cumsum(), data3[gage].cumsum(), '.-', label='original')
plt.plot(data3.AVG.cumsum(), data3[gage + '_'].cumsum(), '.-', label='corrected')
plt.legend();
# chech again for errors
identify_errors(data3[gage + '_'], data3.AVG, error=.1)
```
#### Gage E
##### Analyse the series
The series in gage E has a similar behaviour to series B. There is an anomaly in the series between 1929 and 1938, indicating that there might be two break points in the double-mass curve.
```
# set gage and year corresponding to the break in the line
gage = 'E'
breaks = [1929, 1938]
# visualize
plt.figure(figsize=(5, 5))
plt.axis('equal')
plt.plot((0, 800), (0, 800), '--k')
plt.plot(data3.AVG.cumsum(), data3[gage].cumsum(), '.-', label='original')
plt.plot(data3.AVG.cumsum().loc[breaks], data3[gage].cumsum().loc[breaks], '.', label='1929')
plt.legend();
# fit the regression untill the first break
m1 = curve_fit(linear_reg, data3.loc[:breaks[0], 'AVG'].cumsum(), data3.loc[:breaks[0], gage].cumsum())[0][0]
# fit the regression from the first to the second break
m2 = curve_fit(linear_reg, data3.loc[breaks[0]:breaks[1], 'AVG'].cumsum(), data3.loc[breaks[0]:breaks[1], gage].cumsum())[0][0]
# fit the regression from the second break on
m3 = curve_fit(linear_reg, data3.loc[breaks[1]:, 'AVG'].cumsum(), data3.loc[breaks[1]:, gage].cumsum())[0][0]
print('m1 = {0:.3f} m2 = {1:.3f} m3 = {2:.3f}'.format(m1, m2, m3))
```
There seems to be only one break in the line between the first and the second period. The slopes in the second and third periods are that close that, most probably, there isn't a change from 1938 on. Apart from that, the break in the line seems to be stronger in 1930 than in 1929, so we will change the breaks to only include 1930. We will assume that the period to be corrected is that before 1930.
```
breaks = [1930]
# fit the regression untill the first break
m1 = curve_fit(linear_reg, data3.loc[:breaks[0], 'AVG'].cumsum(), data3.loc[:breaks[0], gage].cumsum())[0][0]
# fit the regression from the first break
m2 = curve_fit(linear_reg, data3.loc[breaks[0]:, 'AVG'].cumsum(), data3.loc[breaks[0]:, gage].cumsum())[0][0]
m1, m2
```
##### Correct the series
```
# correction factor
factor = m2 / m1
factor
# copy of the original series
data3['E_'] = data3[gage].copy()
# correct period before the first break
data3.loc[:breaks[0], 'E_'] *= factor
plt.figure(figsize=(5, 5))
plt.axis('equal')
plt.plot((0, 800), (0, 800), '--k')
plt.plot(data3.AVG.cumsum(), data3[gage].cumsum(), '.-', label='original')
plt.plot(data3.AVG.cumsum(), data3[gage + '_'].cumsum(), '.-', label='corrected')
plt.legend();
# chech again for errors
identify_errors(data3[gage + '_'], data3.AVG)
```
We don't identify any more errors, so the assumption that the slopes of the second and third period were close enough was correct.
#### Redraw the double-mass plot
```
# recalculate the average
gages = ['A', 'B_', 'C', 'D__', 'E_']
data3['AVG_'] = data3[gages].mean(axis=1)
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(12, 8), sharex=True, sharey=True)
for (gage, ax) in zip(gages, axes.flatten()):
ax.plot((0, 800), (0, 800), ':k')
# double-mass curve
ax.plot(data3.AVG_.cumsum(), data3[gage].cumsum(), '.-', label='corrected')
ax.set_title('gage ' + gage)
axes[1, 2].axis('off');
# save figure
plt.savefig('../output/Ex3_double-mass curve.png', dpi=300)
# export corrected series
data3_ = data3.loc[:, gages]
data3_.columns = ['A', 'B', 'C', 'D', 'E']
data3_.to_csv('../output/Ex3_corrected series.csv', float_format='%.2f')
```
| true |
code
| 0.597021 | null | null | null | null |
|
Originaly taken from https://www.easy-tensorflow.com and adapted for the purpose of the course
# Imports
```
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
```
# Load the MNIST dataset
## Data dimenstion
```
from tensorflow.examples.tutorials.mnist import input_data
img_h = img_w = 28 # MNIST images are 28x28
img_size_flat = img_h * img_w # 28x28=784, the total number of pixels
n_classes = 10 # Number of classes, one class per digit
n_channels = 1
```
## Helper functions to load the MNIST data
```
def load_data(mode='train'):
"""
Function to (download and) load the MNIST data
:param mode: train or test
:return: images and the corresponding labels
"""
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
if mode == 'train':
x_train, y_train, x_valid, y_valid = mnist.train.images, mnist.train.labels, \
mnist.validation.images, mnist.validation.labels
x_train, _ = reformat(x_train, y_train)
x_valid, _ = reformat(x_valid, y_valid)
return x_train, y_train, x_valid, y_valid
elif mode == 'test':
x_test, y_test = mnist.test.images, mnist.test.labels
x_test, _ = reformat(x_test, y_test)
return x_test, y_test
def reformat(x, y):
"""
Reformats the data to the format acceptable for convolutional layers
:param x: input array
:param y: corresponding labels
:return: reshaped input and labels
"""
img_size, num_ch, num_class = int(np.sqrt(x.shape[-1])), 1, len(np.unique(np.argmax(y, 1)))
dataset = x.reshape((-1, img_size, img_size, num_ch)).astype(np.float32)
labels = (np.arange(num_class) == y[:, None]).astype(np.float32)
return dataset, labels
def randomize(x, y):
""" Randomizes the order of data samples and their corresponding labels"""
permutation = np.random.permutation(y.shape[0])
shuffled_x = x[permutation, :, :, :]
shuffled_y = y[permutation]
return shuffled_x, shuffled_y
def get_next_batch(x, y, start, end):
x_batch = x[start:end]
y_batch = y[start:end]
return x_batch, y_batch
```
## Load the data and display the sizes
Now we can use the defined helper function in "train" mode which loads the train and validation images and their corresponding labels. We'll also display their sizes:
```
x_train, y_train, x_valid, y_valid = load_data(mode='train')
print("Size of:")
print("- Training-set:\t\t{}".format(len(y_train)))
print("- Validation-set:\t{}".format(len(y_valid)))
```
# Hyperparameters
```
logs_path = "./logs" # path to the folder that we want to save the logs for Tensorboard
lr = 0.001 # The optimization initial learning rate
epochs = 10 # Total number of training epochs
batch_size = 100 # Training batch size
display_freq = 100 # Frequency of displaying the training results
```
# Network configuration
```
# 1st Convolutional Layer
filter_size1 = 5 # Convolution filters are 5 x 5 pixels.
num_filters1 = 16 # There are 16 of these filters.
stride1 = 1 # The stride of the sliding window
# 2nd Convolutional Layer
filter_size2 = 5 # Convolution filters are 5 x 5 pixels.
num_filters2 = 32 # There are 32 of these filters.
stride2 = 1 # The stride of the sliding window
# Fully-connected layer.
h1 = 128 # Number of neurons in fully-connected layer.
```
# Create network helper functions
## Helper functions for creating new variables
```
# weight and bais wrappers
def weight_variable(shape):
"""
Create a weight variable with appropriate initialization
:param name: weight name
:param shape: weight shape
:return: initialized weight variable
"""
initer = tf.truncated_normal_initializer(stddev=0.01)
return tf.get_variable('W',
dtype=tf.float32,
shape=shape,
initializer=initer)
def bias_variable(shape):
"""
Create a bias variable with appropriate initialization
:param name: bias variable name
:param shape: bias variable shape
:return: initialized bias variable
"""
initial = tf.constant(0., shape=shape, dtype=tf.float32)
return tf.get_variable('b',
dtype=tf.float32,
initializer=initial)
```
## Helper-function for creating a new Convolutional Layer
```
def conv_layer(x, filter_size, num_filters, stride, name):
"""
Create a 2D convolution layer
:param x: input from previous layer
:param filter_size: size of each filter
:param num_filters: number of filters (or output feature maps)
:param stride: filter stride
:param name: layer name
:return: The output array
"""
with tf.variable_scope(name):
num_in_channel = x.get_shape().as_list()[-1]
shape = [filter_size, filter_size, num_in_channel, num_filters]
W = weight_variable(shape=shape)
tf.summary.histogram('weight', W)
b = bias_variable(shape=[num_filters])
tf.summary.histogram('bias', b)
layer = tf.nn.conv2d(x, W,
strides=[1, stride, stride, 1],
padding="SAME")
layer += b
return tf.nn.relu(layer)
```
## Helper-function for creating a new Max-pooling Layer
```
def max_pool(x, ksize, stride, name):
"""
Create a max pooling layer
:param x: input to max-pooling layer
:param ksize: size of the max-pooling filter
:param stride: stride of the max-pooling filter
:param name: layer name
:return: The output array
"""
return tf.nn.max_pool(x,
ksize=[1, ksize, ksize, 1],
strides=[1, stride, stride, 1],
padding="SAME",
name=name)
```
# Helper-function for flattening a layer
```
def flatten_layer(layer):
"""
Flattens the output of the convolutional layer to be fed into fully-connected layer
:param layer: input array
:return: flattened array
"""
with tf.variable_scope('Flatten_layer'):
layer_shape = layer.get_shape()
num_features = layer_shape[1:4].num_elements()
layer_flat = tf.reshape(layer, [-1, num_features])
return layer_flat
```
## Helper-function for creating a new fully-connected Layer
```
def fc_layer(x, num_units, name, use_relu=True):
"""
Create a fully-connected layer
:param x: input from previous layer
:param num_units: number of hidden units in the fully-connected layer
:param name: layer name
:param use_relu: boolean to add ReLU non-linearity (or not)
:return: The output array
"""
with tf.variable_scope(name):
in_dim = x.get_shape()[1]
W = weight_variable(shape=[in_dim, num_units])
tf.summary.histogram('weight', W)
b = bias_variable(shape=[num_units])
tf.summary.histogram('bias', b)
layer = tf.matmul(x, W)
layer += b
if use_relu:
layer = tf.nn.relu(layer)
return layer
```
# Network graph
## Placeholders for the inputs (x) and corresponding labels (y)
```
with tf.name_scope('Input'):
x = tf.placeholder(tf.float32, shape=[None, img_h, img_w, n_channels], name='X')
y = tf.placeholder(tf.float32, shape=[None, n_classes], name='Y')
```
## Create the network layers
```
conv1 = conv_layer(x, filter_size1, num_filters1, stride1, name='conv1')
pool1 = max_pool(conv1, ksize=2, stride=2, name='pool1')
conv2 = conv_layer(pool1, filter_size2, num_filters2, stride2, name='conv2')
pool2 = max_pool(conv2, ksize=2, stride=2, name='pool2')
layer_flat = flatten_layer(pool2)
fc1 = fc_layer(layer_flat, h1, 'FC1', use_relu=True)
output_logits = fc_layer(fc1, n_classes, 'OUT', use_relu=False)
```
## Define the loss function, optimizer, accuracy, and predicted class
```
with tf.variable_scope('Train'):
with tf.variable_scope('Loss'):
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=output_logits), name='loss')
tf.summary.scalar('loss', loss)
with tf.variable_scope('Optimizer'):
optimizer = tf.train.AdamOptimizer(learning_rate=lr, name='Adam-op').minimize(loss)
with tf.variable_scope('Accuracy'):
correct_prediction = tf.equal(tf.argmax(output_logits, 1), tf.argmax(y, 1), name='correct_pred')
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32), name='accuracy')
tf.summary.scalar('accuracy', accuracy)
with tf.variable_scope('Prediction'):
cls_prediction = tf.argmax(output_logits, axis=1, name='predictions')
```
## Initialize all variables and merge the summaries
```
# Initialize the variables
init = tf.global_variables_initializer()
# Merge all summaries
merged = tf.summary.merge_all()
```
# Train
```
sess = tf.InteractiveSession()
sess.run(init)
global_step = 0
summary_writer = tf.summary.FileWriter(logs_path, sess.graph)
# Number of training iterations in each epoch
num_tr_iter = int(len(y_train) / batch_size)
for epoch in range(epochs):
print('Training epoch: {}'.format(epoch + 1))
x_train, y_train = randomize(x_train, y_train)
for iteration in range(num_tr_iter):
global_step += 1
start = iteration * batch_size
end = (iteration + 1) * batch_size
x_batch, y_batch = get_next_batch(x_train, y_train, start, end)
# Run optimization op (backprop)
feed_dict_batch = {x: x_batch, y: y_batch}
sess.run(optimizer, feed_dict=feed_dict_batch)
if iteration % display_freq == 0:
# Calculate and display the batch loss and accuracy
loss_batch, acc_batch, summary_tr = sess.run([loss, accuracy, merged],
feed_dict=feed_dict_batch)
summary_writer.add_summary(summary_tr, global_step)
print("iter {0:3d}:\t Loss={1:.2f},\tTraining Accuracy={2:.01%}".
format(iteration, loss_batch, acc_batch))
# Run validation after every epoch
feed_dict_valid = {x: x_valid, y: y_valid}
loss_valid, acc_valid = sess.run([loss, accuracy], feed_dict=feed_dict_valid)
print('---------------------------------------------------------')
print("Epoch: {0}, validation loss: {1:.2f}, validation accuracy: {2:.01%}".
format(epoch + 1, loss_valid, acc_valid))
print('---------------------------------------------------------')
```
# Test
```
def plot_images(images, cls_true, cls_pred=None, title=None):
"""
Create figure with 3x3 sub-plots.
:param images: array of images to be plotted, (9, img_h*img_w)
:param cls_true: corresponding true labels (9,)
:param cls_pred: corresponding true labels (9,)
"""
fig, axes = plt.subplots(3, 3, figsize=(9, 9))
fig.subplots_adjust(hspace=0.3, wspace=0.3)
for i, ax in enumerate(axes.flat):
# Plot image.
ax.imshow(np.squeeze(images[i]), cmap='binary')
# Show true and predicted classes.
if cls_pred is None:
ax_title = "True: {0}".format(cls_true[i])
else:
ax_title = "True: {0}, Pred: {1}".format(cls_true[i], cls_pred[i])
ax.set_title(ax_title)
# Remove ticks from the plot.
ax.set_xticks([])
ax.set_yticks([])
if title:
plt.suptitle(title, size=20)
plt.show(block=False)
def plot_example_errors(images, cls_true, cls_pred, title=None):
"""
Function for plotting examples of images that have been mis-classified
:param images: array of all images, (#imgs, img_h*img_w)
:param cls_true: corresponding true labels, (#imgs,)
:param cls_pred: corresponding predicted labels, (#imgs,)
"""
# Negate the boolean array.
incorrect = np.logical_not(np.equal(cls_pred, cls_true))
# Get the images from the test-set that have been
# incorrectly classified.
incorrect_images = images[incorrect]
# Get the true and predicted classes for those images.
cls_pred = cls_pred[incorrect]
cls_true = cls_true[incorrect]
# Plot the first 9 images.
plot_images(images=incorrect_images[0:9],
cls_true=cls_true[0:9],
cls_pred=cls_pred[0:9],
title=title)
# Test the network when training is done
x_test, y_test = load_data(mode='test')
feed_dict_test = {x: x_test, y: y_test}
loss_test, acc_test = sess.run([loss, accuracy], feed_dict=feed_dict_test)
print('---------------------------------------------------------')
print("Test loss: {0:.2f}, test accuracy: {1:.01%}".format(loss_test, acc_test))
print('---------------------------------------------------------')
# Plot some of the correct and misclassified examples
cls_pred = sess.run(cls_prediction, feed_dict=feed_dict_test)
cls_true = np.argmax(y_test, axis=1)
plot_images(x_test, cls_true, cls_pred, title='Correct Examples')
plot_example_errors(x_test, cls_true, cls_pred, title='Misclassified Examples')
plt.show()
# close the session after you are done with testing
sess.close()
```
At this step our coding is done. We can inspect more in our network using the Tensorboard open your terminal and move inside the notebookz folder in my case *C:\Dev\UpdateConference2019\notebooks*
and type:
```
tensorboard --logdir=logs --host localhost
```
| true |
code
| 0.858985 | null | null | null | null |
|
# Calculating the Bilingual Evaluation Understudy (BLEU) score: Ungraded Lab
In this ungraded lab, we will implement a popular metric for evaluating the quality of machine-translated text: the BLEU score proposed by Kishore Papineni, et al. In their 2002 paper ["BLEU: a Method for Automatic Evaluation of Machine Translation"](https://www.aclweb.org/anthology/P02-1040.pdf), the BLEU score works by comparing "candidate" text to one or more "reference" translations. The result is better the closer the score is to 1. Let's see how to get this value in the following sections.
# Part 1: BLEU Score
## 1.1 Importing the Libraries
We will first start by importing the Python libraries we will use in the first part of this lab. For learning, we will implement our own version of the BLEU Score using Numpy. To verify that our implementation is correct, we will compare our results with those generated by the [SacreBLEU library](https://github.com/mjpost/sacrebleu). This package provides hassle-free computation of shareable, comparable, and reproducible BLEU scores. It also knows all the standard test sets and handles downloading, processing, and tokenization.
```
%%capture
!pip3 install sacrebleu
%%capture
!wget https://raw.githubusercontent.com/martin-fabbri/colab-notebooks/master/deeplearning.ai/nlp/datasets/wmt19_can.txt
!wget https://raw.githubusercontent.com/martin-fabbri/colab-notebooks/master/deeplearning.ai/nlp/datasets/wmt19_ref.txt
!wget https://raw.githubusercontent.com/martin-fabbri/colab-notebooks/master/deeplearning.ai/nlp/datasets/wmt19_src.txt
import math
from collections import Counter
import matplotlib.pyplot as plt
import nltk
import numpy as np
import sacrebleu
from nltk.util import ngrams
nltk.download("punkt")
!pip list | grep "nltk\|sacrebleu"
```
## 1.2 Defining the BLEU Score
You have seen the formula for calculating the BLEU score in this week's lectures. More formally, we can express the BLEU score as:
$$BLEU = BP\Bigl(\prod_{i=1}^{4}precision_i\Bigr)^{(1/4)}$$
with the Brevity Penalty and precision defined as:
$$BP = min\Bigl(1, e^{(1-({ref}/{cand}))}\Bigr)$$
$$precision_i = \frac {\sum_{snt \in{cand}}\sum_{i\in{snt}}min\Bigl(m^{i}_{cand}, m^{i}_{ref}\Bigr)}{w^{i}_{t}}$$
where:
* $m^{i}_{cand}$, is the count of i-gram in candidate matching the reference translation.
* $m^{i}_{ref}$, is the count of i-gram in the reference translation.
* $w^{i}_{t}$, is the total number of i-grams in candidate translation.
## 1.3 Explaining the BLEU score
### Brevity Penalty (example):
```
ref_length = np.ones(100)
can_length = np.linspace(1.5, 0.5, 100)
x = ref_length / can_length
y = 1 - x
y = np.exp(y)
y = np.minimum(np.ones(y.shape), y)
# Code for in order to make the plot
fig, ax = plt.subplots(1)
lines = ax.plot(x, y)
ax.set(
xlabel="Ratio of the length of the reference to the candidate text",
ylabel="Brevity Penalty",
)
plt.show()
```
The brevity penalty penalizes generated translations that are too short compared to the closest reference length with an exponential decay. The brevity penalty compensates for the fact that the BLEU score has no recall term.
### N-Gram Precision (example):
```
data = {"1-gram": 0.8, "2-gram": 0.7, "3-gram": 0.6, "4-gram": 0.5}
names = list(data.keys())
values = list(data.values())
fig, ax = plt.subplots(1)
bars = ax.bar(names, values)
ax.set(ylabel="N-gram precision")
plt.show()
```
The n-gram precision counts how many unigrams, bigrams, trigrams, and four-grams (i=1,...,4) match their n-gram counterpart in the reference translations. This term acts as a precision metric. Unigrams account for adequacy while longer n-grams account for fluency of the translation. To avoid overcounting, the n-gram counts are clipped to the maximal n-gram count occurring in the reference ($m_{n}^{ref}$). Typically precision shows exponential decay with the with the degree of the n-gram.
### N-gram BLEU score (example):
```
data = {"1-gram": 0.8, "2-gram": 0.77, "3-gram": 0.74, "4-gram": 0.71}
names = list(data.keys())
values = list(data.values())
fig, ax = plt.subplots(1)
bars = ax.bar(names, values)
ax.set(ylabel="Modified N-gram precision")
plt.show()
```
When the n-gram precision is multiplied by the BP, then the exponential decay of n-grams is almost fully compensated. The BLEU score corresponds to a geometric average of this modified n-gram precision.
## 1.4 Example Calculations of the BLEU score
In this example we will have a reference translation and 2 candidates translations. We will tokenize all sentences using the NLTK package introduced in Course 2 of this NLP specialization.
```
reference = "The NASA Opportunity rover is battling a massive dust storm on planet Mars."
candidate_1 = "The Opportunity rover is combating a big sandstorm on planet Mars."
candidate_2 = "A NASA rover is fighting a massive storm on planet Mars."
tokenized_ref = nltk.word_tokenize(reference.lower())
tokenized_cand_1 = nltk.word_tokenize(candidate_1.lower())
tokenized_cand_2 = nltk.word_tokenize(candidate_2.lower())
print(f"{reference} -> {tokenized_ref}")
print("\n")
print(f"{candidate_1} -> {tokenized_cand_1}")
print("\n")
print(f"{candidate_2} -> {tokenized_cand_2}")
```
### STEP 1: Computing the Brevity Penalty
```
def brevity_penalty(candidate, reference):
ref_length = len(reference)
can_length = len(candidate)
# Brevity Penalty
if ref_length < can_length: # if reference length is less than candidate length
BP = 1 # set BP = 1
else:
penalty = 1 - (ref_length / can_length) # else set BP=exp(1-(ref_length/can_length))
BP = np.exp(penalty)
return BP
```
### STEP 2: Computing the Precision
```
def clipped_precision(candidate, reference):
"""
Clipped precision function given a original and a machine translated sentences
"""
clipped_precision_score = []
for i in range(1, 5):
ref_n_gram = Counter(ngrams(reference,i))
cand_n_gram = Counter(ngrams(candidate,i))
c = sum(cand_n_gram.values())
for j in cand_n_gram: # for every n-gram up to 4 in candidate text
if j in ref_n_gram: # check if it is in the reference n-gram
if cand_n_gram[j] > ref_n_gram[j]: # if the count of the candidate n-gram is bigger
# than the corresponding count in the reference n-gram,
cand_n_gram[j] = ref_n_gram[j] # then set the count of the candidate n-gram to be equal
# to the reference n-gram
else:
cand_n_gram[j] = 0 # else set the candidate n-gram equal to zero
clipped_precision_score.append(sum(cand_n_gram.values())/c)
weights =[0.25]*4
s = (w_i * math.log(p_i) for w_i, p_i in zip(weights, clipped_precision_score))
s = math.exp(math.fsum(s))
return s
```
### STEP 3: Computing the BLEU score
```
def bleu_score(candidate, reference):
BP = brevity_penalty(candidate, reference)
precision = clipped_precision(candidate, reference)
return BP * precision
```
### STEP 4: Testing with our Example Reference and Candidates Sentences
```
print(
"Results reference versus candidate 1 our own code BLEU: ",
round(bleu_score(tokenized_cand_1, tokenized_ref) * 100, 1),
)
print(
"Results reference versus candidate 2 our own code BLEU: ",
round(bleu_score(tokenized_cand_2, tokenized_ref) * 100, 1),
)
```
### STEP 5: Comparing the Results from our Code with the SacreBLEU Library
```
print(
"Results reference versus candidate 1 sacrebleu library BLEU: ",
round(sacrebleu.corpus_bleu(candidate_1, reference).score, 1),
)
print(
"Results reference versus candidate 2 sacrebleu library BLEU: ",
round(sacrebleu.corpus_bleu(candidate_2, reference).score, 1),
)
```
# Part 2: BLEU computation on a corpus
## Loading Data Sets for Evaluation Using the BLEU Score
In this section, we will show a simple pipeline for evaluating machine translated text. Due to storage and speed constraints, we will not be using our own model in this lab (you'll get to do that in the assignment!). Instead, we will be using [Google Translate](https://translate.google.com) to generate English to German translations and we will evaluate it against a known evaluation set. There are three files we will need:
1. A source text in English. In this lab, we will use the first 1671 words of the [wmt19](http://statmt.org/wmt19/translation-task.html) evaluation dataset downloaded via SacreBLEU. We just grabbed a subset because of limitations in the number of words that can be translated using Google Translate.
2. A reference translation to German of the corresponding first 1671 words from the original English text. This is also provided by SacreBLEU.
3. A candidate machine translation to German from the same 1671 words. This is generated by feeding the source text to a machine translation model. As mentioned above, we will use Google Translate to generate the translations in this file.
With that, we can now compare the reference an candidate translation to get the BLEU Score.
```
# Loading the raw data
wmt19_src = open("wmt19_src.txt", "rU")
wmt19_src_1 = wmt19_src.read()
wmt19_src.close()
wmt19_ref = open("wmt19_ref.txt", "rU")
wmt19_ref_1 = wmt19_ref.read()
wmt19_ref.close()
wmt19_can = open("wmt19_can.txt", "rU")
wmt19_can_1 = wmt19_can.read()
wmt19_can.close()
tokenized_corpus_src = nltk.word_tokenize(wmt19_src_1.lower())
tokenized_corpus_ref = nltk.word_tokenize(wmt19_ref_1.lower())
tokenized_corpus_cand = nltk.word_tokenize(wmt19_can_1.lower())
print("English source text:")
print("\n")
print(f"{wmt19_src_1[0:170]} -> {tokenized_corpus_src[0:30]}")
print("\n")
print("German reference translation:")
print("\n")
print(f"{wmt19_ref_1[0:219]} -> {tokenized_corpus_ref[0:35]}")
print("\n")
print("German machine translation:")
print("\n")
print(f"{wmt19_can_1[0:199]} -> {tokenized_corpus_cand[0:29]}")
print(
"Results reference versus candidate 1 our own BLEU implementation: ",
round(bleu_score(tokenized_corpus_cand, tokenized_corpus_ref) * 100, 1),
)
print(
"Results reference versus candidate 1 sacrebleu library BLEU: ",
round(sacrebleu.corpus_bleu(wmt19_can_1, wmt19_ref_1).score, 1),
)
```
**BLEU Score Interpretation on a Corpus**
|Score | Interpretation |
|:---------:|:-------------------------------------------------------------:|
| < 10 | Almost useless |
| 10 - 19 | Hard to get the gist |
| 20 - 29 | The gist is clear, but has significant grammatical errors |
| 30 - 40 | Understandable to good translations |
| 40 - 50 | High quality translations |
| 50 - 60 | Very high quality, adequate, and fluent translations |
| > 60 | Quality often better than human |
From the table above (taken [here](https://cloud.google.com/translate/automl/docs/evaluate)), we can see the translation is high quality (*if you see "Hard to get the gist", please open your workspace, delete `wmt19_can.txt` and get the latest version via the Lab Help button*). Moreover, the results of our coded BLEU score are almost identical to those of the SacreBLEU package.
| true |
code
| 0.562056 | null | null | null | null |
|
Avani Gupta <br>
Roll: 2019121004
# Excercise - Multi-class classification of MNIST using Perceptron
In binary perceptron, where $\mathbf{y} \in \{-1, +1\}$, we used to update our weights only for wrongly classified examples.
The multi-class perceptron is regarded as a generalization of binary perceptron. Learning through iteration is the same as the perceptron. Weighted inputs are passed through a multiclass signum activation function. If the predicted output label is the same as true label then weights are not updated. However, when predicted output label $\neq$ true label, then the wrongly classified input example is added to the weights of the correct label and subtracted from the weights of the incorrect label. Effectively, this amounts to ’rewarding’ the correct weight vector, ’punishing’ the misleading, incorrect weight
vector, and leaving alone an other weight vectors.
```
from sklearn import datasets
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import random
import numpy as np
import seaborn as sns; sns.set();
import pandas as pd
import math
import gif
import warnings
warnings.filterwarnings('ignore')
# Setting the seed to ensure reproducibility of experiments
np.random.seed(11)
# One-hot encoding of target label, Y
def one_hot(a):
b = -1 * np.ones((a.size, a.max()+1))
b[np.arange(a.size), a] = 1
return b
# Loading digits datasets
digits = datasets.load_digits()
# One-hot encoding of target label, Y
Y = digits.target
Y = one_hot(Y)
# Adding column of ones to absorb bias b of the hyperplane into X
X = digits.data
bias_ones = np.ones((len(X), 1))
X = np.hstack((X, bias_ones))
# Train-val-test data
X_train_val, X_test, Y_train_val, Y_test = train_test_split(X, Y, shuffle=True, test_size = 0.2)
X_train, X_val, Y_train, Y_val = train_test_split(X_train_val, Y_train_val, test_size = 0.12517)
print("Training dataset: ", X_train.shape)
print("Validation dataset: ", X_val.shape)
print("Test dataset: ", X_test.shape)
sns.reset_orig();
plt.gray()
plt.matshow(digits.images[10])
plt.show();
```
#### Write your code below
tut notebook functions
```
# Defining signum activation function
def signum(vec_w_x):
""" signum activation for perceptron
Parameters
------------
vec_w_x: ndarray
Weighted inputs
"""
vec_w_x[vec_w_x >= 0] = 1
vec_w_x[vec_w_x < 0] = -1
return vec_w_x
# multi-class signum
def multi_class_signum(vec_w_x):
""" Multiclass signum activation.
Parameters
------------
vec_w_x: ndarray
Weighted inputs
"""
flag = np.all(vec_w_x == 0)
if flag:
return vec_w_x
else:
num_examples, num_outputs = np.shape(vec_w_x)
range_examples = np.array(range(0, num_examples))
zero_idxs = np.argwhere(np.all(vec_w_x == 0, axis=1))
non_zero_examples = np.delete(range_examples, zero_idxs[:, 0])
signum_vec_w_x = vec_w_x[non_zero_examples]
maxvals = np.amax(signum_vec_w_x, axis=1)
for i in range(num_examples):
idx = np.argwhere(signum_vec_w_x == maxvals[i])[0]
signum_vec_w_x[idx[0], idx[1]] = 1
non_maxvals_idxs = np.argwhere(signum_vec_w_x != 1)
signum_vec_w_x[non_maxvals_idxs[:, 0], non_maxvals_idxs[:, 1]] = -1
vec_w_x[non_zero_examples] = signum_vec_w_x
return vec_w_x
# Evaluation for train, val, and test set.
def get_accuracy(y_predicted, Y_input_set, num_datapoints):
miscls_points = np.argwhere(np.any(y_predicted != Y_input_set, axis=1))
miscls_points = np.unique(miscls_points)
accuracy = (1-len(miscls_points)/num_datapoints)*100
return accuracy
def get_prediction(X_input_set, Y_input_set, weights, get_acc=True, model_type='perceptron', predict='no'):
if len(Y_input_set) != 0:
num_datapoints, num_categories = np.shape(Y_input_set)
vec_w_transpose_x = np.dot(X_input_set, weights)
if num_categories > 1: # Multi-class
if model_type == 'perceptron':
y_pred_out = multi_class_signum(vec_w_transpose_x)
elif model_type == 'logreg':
y_pred_out = softmax(X_input_set, vec_w_transpose_x, predict=predict)
else: # Binary class
if model_type == 'perceptron' or model_type == 'LinearDA':
y_pred_out = signum(vec_w_transpose_x)
elif model_type == 'logreg':
y_pred_out = sigmoid(vec_w_transpose_x, predict=predict)
# Both prediction and evaluation
if get_acc:
cls_acc = get_accuracy(y_pred_out, Y_input_set, num_datapoints)
return cls_acc
# Only prediction
return y_pred_out
# Perceptron training algorithm
def train(X_train, Y_train, weights, learning_rate=1, total_epochs=100):
"""Training method for Perceptron.
Parameters
-----------
X_train: ndarray (num_examples(rows) vs num_features(columns))
Input dataset which perceptron will use to learn optimal weights
Y_train: ndarray (num_examples(rows) vs class_labels(columns))
Class labels for input data
weights: ndarray (num_features vs n_output)
Weights used to train the network and predict on test set
learning_rate: int
Learning rate use to learn and update weights
total_epochs: int
Max number of epochs to train the perceptron model
"""
n_samples, _ = np.shape(X_train)
history_weights = []
epoch = 1
# Number of missclassified points we would like to see in the train set.
# While training, its value will change every epoch. If m==0, our training
# error will be zero.
m = 1
# If the most recent weights gave 0 misclassifications, break the loop.
# Else continue until total_epochs is completed.
while m != 0 and epoch <= total_epochs:
m = 0
# Compute weighted inputs and predict class labels on training set.
weights_transpose_x = np.dot(X_train, weights)
weights_transpose_x = signum(weights_transpose_x)
y_train_out = np.multiply(Y_train, weights_transpose_x)
epoch += 1
# Collecting misclassified indexes and count them
y_miscls_idxs = np.argwhere(y_train_out <= 0)[:, 0]
y_miscls_idxs = np.unique(y_miscls_idxs)
m = len(y_miscls_idxs)
# Calculate gradients and update weights
dweights = np.dot((X_train[y_miscls_idxs]).T, Y_train[y_miscls_idxs])
weights += (learning_rate/n_samples) * dweights
weights = np.round(weights, decimals=4)
# Append weights to visualize decision boundary later
history_weights.append(weights)
if m == 0 and epoch <= total_epochs:
print("Training has stabilized with all points classified: ", epoch)
else:
print(f'Training completed at {epoch-1} epochs. {m} misclassified points remain.')
return history_weights
```
My code
```
weights_arr = np.zeros((X_train.shape[1], Y_train.shape[1]))
for i in range(Y_train.shape[1]):
weights = np.zeros((X_train.shape[1], 1))
weights_arr[:, i:i+1] = train(X_train, Y_train[:, i].reshape((-1,1)), weights, 1, 10000)[-1].copy()
def accuracy(X, Y, W):
pred = X @ W
Class_value = np.max(pred, axis=1, keepdims=True)
pred = (pred == Class_value )
class1 = np.where(Y == 1, True, False)
match = pred[class1]
acc = np.mean(match) * 100
return acc
train_acc = accuracy(X_train, Y_train, weights_arr)
print("Train accuracy: ",train_acc)
val_acc = accuracy(X_val, Y_val, weights_arr)
print("Validation accuracy: ", val_acc)
test_acc = accuracy(X_test, Y_test, weights_arr)
print("Test accuracy: ", test_acc)
```
| true |
code
| 0.782761 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/bs3537/dengueAI/blob/master/V5_San_Juan_XGB_all_environmental_features.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#https://www.drivendata.org/competitions/44/dengai-predicting-disease-spread/page/80/
#Your goal is to predict the total_cases label for each (city, year, weekofyear) in the test set.
#Performance metric = mean absolute error
```
##LIST OF FEATURES:
You are provided the following set of information on a (year, weekofyear) timescale:
(Where appropriate, units are provided as a _unit suffix on the feature name.)
###City and date indicators
1. city – City abbreviations: sj for San Juan and iq for Iquitos
2. week_start_date – Date given in yyyy-mm-dd format
###NOAA's GHCN daily climate data weather station measurements
1. station_max_temp_c – Maximum temperature
2. station_min_temp_c – Minimum temperature
3. station_avg_temp_c – Average temperature
4. station_precip_mm – Total precipitation
5. station_diur_temp_rng_c – Diurnal temperature range
###PERSIANN satellite precipitation measurements (0.25x0.25 degree scale)
6. precipitation_amt_mm – Total precipitation
###NOAA's NCEP Climate Forecast System Reanalysis measurements (0.5x0.5 degree scale)
7. reanalysis_sat_precip_amt_mm – Total precipitation
8. reanalysis_dew_point_temp_k – Mean dew point temperature
9. reanalysis_air_temp_k – Mean air temperature
10. reanalysis_relative_humidity_percent – Mean relative humidity
11. reanalysis_specific_humidity_g_per_kg – Mean specific humidity
12. reanalysis_precip_amt_kg_per_m2 – Total precipitation
13. reanalysis_max_air_temp_k – Maximum air temperature
14. reanalysis_min_air_temp_k – Minimum air temperature
15. reanalysis_avg_temp_k – Average air temperature
16. reanalysis_tdtr_k – Diurnal temperature range
###Satellite vegetation - Normalized difference vegetation index (NDVI) - NOAA's CDR Normalized Difference Vegetation Index (0.5x0.5 degree scale) measurements
17. ndvi_se – Pixel southeast of city centroid
18. ndvi_sw – Pixel southwest of city centroid
19. ndvi_ne – Pixel northeast of city centroid
20. ndvi_nw – Pixel northwest of city centroid
####TARGET VARIABLE = total_cases label for each (city, year, weekofyear)
```
import sys
#Load train features and labels datasets
train_features = pd.read_csv('https://s3.amazonaws.com/drivendata/data/44/public/dengue_features_train.csv')
train_features.head()
train_features.shape
train_labels = pd.read_csv('https://s3.amazonaws.com/drivendata/data/44/public/dengue_labels_train.csv')
train_labels.head()
train_labels.shape
#Merge train features and labels datasets
train = pd.merge(train_features, train_labels)
train.head()
train.shape
#city, year and week of year columns are duplicate in train_features and train_labels datasets so the total_cases column is added to the features dataset
train.dtypes
#Data rows for San Juan
train.city.value_counts()
#San Juan has 936 rows which we can isolate and analyze separately
train = train[train['city'].str.match('sj')]
train.head(5)
train.shape
#Thus, we have isolated the train dataset with only city data for San Juan
#Distribution of the target
import seaborn as sns
sns.distplot(train['total_cases'])
#The target distribution is skewed
#Find outliers
train['total_cases'].describe()
#Remove outliers
train = train[(train['total_cases'] >= np.percentile(train['total_cases'], 0.5)) &
(train['total_cases'] <= np.percentile(train['total_cases'], 99.5))]
train.shape
sns.distplot(train['total_cases'])
#Do train, val split
from sklearn.model_selection import train_test_split
train, val = train_test_split(train, train_size=0.80, test_size=0.20,
random_state=42)
train.shape, val.shape
#Load test features dataset (for the competition)
test = pd.read_csv('https://s3.amazonaws.com/drivendata/data/44/public/dengue_features_test.csv')
#Pandas Profiling
```
#####Baseline statistics (mean and MAE) for the target variable total_cases in train dataset and baseline validation MAE
```
train['total_cases']. describe()
#Baseline mean and mean absolute error
guess = train['total_cases'].mean()
print(f'At the baseline, the mean total number of dengue cases in a year is: {guess:.2f}')
#If we had just guessed that the total number of dengue cases was 31.58 for a city in a particular year, we would be off by how much?
from sklearn.metrics import mean_absolute_error
# Arrange y target vectors
target = 'total_cases'
y_train = train[target]
y_val = val[target]
# Get mean baseline
print('Mean Baseline (using 0 features)')
guess = y_train.mean()
# Train Error
y_pred = [guess] * len(y_train)
mae = mean_absolute_error(y_train, y_pred)
print(f'Train mean absolute error: {mae:.2f} dengue cases per year')
# Test Error
y_pred = [guess] * len(y_val)
mae = mean_absolute_error(y_val, y_pred)
print(f'Validation mean absolute error: {mae:.2f} dengue cases per year')
#we need to convert week_start_date to numeric form uisng pd.to_dateime function
#wrangle function
def wrangle(X):
X = X.copy()
# Convert week_start_date to numeric form
X['week_start_date'] = pd.to_datetime(X['week_start_date'], infer_datetime_format=True)
# Extract components from date_recorded, then drop the original column
X['year_recorded'] = X['week_start_date'].dt.year
X['month_recorded'] = X['week_start_date'].dt.month
#X['day_recorded'] = X['week_start_date'].dt.day
X = X.drop(columns='week_start_date')
X = X.drop(columns='year')
X = X.drop(columns='station_precip_mm')
#I engineered few features which represent standing water, high risk feature for mosquitos
#1. X['standing water feature 1'] = X['station_precip_mm'] / X['station_max_temp_c']
#Standing water features
X['total satellite vegetation index of city'] = X['ndvi_se'] + X['ndvi_sw'] + X['ndvi_ne'] + X['ndvi_nw']
#Standing water features
#Standing water feature 1 = 'NOAA GCN precipitation amount in kg per m2 reanalyzed' * (total vegetation, sum of all 4 parts of the city)
X['standing water feature 1'] = X['reanalysis_precip_amt_kg_per_m2'] * X['total satellite vegetation index of city']
#Standing water feature 2: 'NOAA GCN precipitation amount in kg per m2 reanalyzed'} * 'NOAA GCN mean relative humidity in pct reanalyzed'}
X['standing water feature 2'] = X['reanalysis_precip_amt_kg_per_m2'] * X['reanalysis_relative_humidity_percent']
#Standing water feature 3: 'NOAA GCN precipitation amount in kg per m2 reanalyzed'} * 'NOAA GCN mean relative humidity in pct reanalyzed'} * (total vegetation)
X['standing water feature 3'] = X['reanalysis_precip_amt_kg_per_m2'] * X['reanalysis_relative_humidity_percent'] * X['total satellite vegetation index of city']
#Standing water feature 4: 'NOAA GCN precipitation amount in kg per m2 reanalyzed'} / 'NOAA GCN max air temp reanalyzed'
X['standing water feature 4'] = X['reanalysis_precip_amt_kg_per_m2'] / X['reanalysis_max_air_temp_k']
#Standing water feature 5: ['NOAA GCN precipitation amount in kg per m2 reanalyzed'} * 'NOAA GCN mean relative humidity in pct reanalyzed'} * (total vegetation)]/['NOAA GCN max air temp reanalyzed']
X['standing water feature 5'] = X['reanalysis_precip_amt_kg_per_m2'] * X['reanalysis_relative_humidity_percent'] * X['total satellite vegetation index of city'] / X['reanalysis_max_air_temp_k']
#Rename columns
X.rename(columns= {'reanalysis_air_temp_k':'Mean air temperature in K'}, inplace=True)
X.rename(columns= {'reanalysis_min_air_temp_k':'Minimum air temperature in K'}, inplace=True)
X.rename(columns= {'weekofyear':'Week of Year'}, inplace=True)
X.rename(columns= {'station_diur_temp_rng_c':'Diurnal temperature range in C'}, inplace=True)
X.rename(columns= {'reanalysis_precip_amt_kg_per_m2':'Total precipitation kg/m2'}, inplace=True)
X.rename(columns= {'reanalysis_tdtr_k':'Diurnal temperature range in K'}, inplace=True)
X.rename(columns= {'reanalysis_max_air_temp_k':'Maximum air temperature in K'}, inplace=True)
X.rename(columns= {'year_recorded':'Year recorded'}, inplace=True)
X.rename(columns= {'reanalysis_relative_humidity_percent':'Mean relative humidity'}, inplace=True)
X.rename(columns= {'month_recorded':'Month recorded'}, inplace=True)
X.rename(columns= {'reanalysis_dew_point_temp_k':'Mean dew point temp in K'}, inplace=True)
X.rename(columns= {'precipitation_amt_mm':'Total precipitation in mm'}, inplace=True)
X.rename(columns= {'station_min_temp_c':'Minimum temp in C'}, inplace=True)
X.rename(columns= {'ndvi_se':'Southeast vegetation index'}, inplace=True)
X.rename(columns= {'ndvi_ne':'Northeast vegetation index'}, inplace=True)
X.rename(columns= {'ndvi_nw':'Northwest vegetation index'}, inplace=True)
X.rename(columns= {'ndvi_sw':'Southwest vegetation index'}, inplace=True)
X.rename(columns= {'reanalysis_avg_temp_k':'Average air temperature in K'}, inplace=True)
X.rename(columns= {'reanalysis_sat_precip_amt_mm':'Total precipitation in mm (2)'}, inplace=True)
X.rename(columns= {'reanalysis_specific_humidity_g_per_kg':'Mean specific humidity'}, inplace=True)
X.rename(columns= {'station_avg_temp_c':'Average temp in C'}, inplace=True)
X.rename(columns= {'station_max_temp_c':'Maximum temp in C'}, inplace=True)
X.rename(columns= {'total_cases':'Total dengue cases in the week'}, inplace=True)
#Drop columns
X = X.drop(columns='Year recorded')
X = X.drop(columns='Week of Year')
X = X.drop(columns='Month recorded')
X = X.drop(columns='Total precipitation in mm (2)')
X = X.drop(columns='Average temp in C')
X = X.drop(columns='Maximum temp in C')
X = X.drop(columns='Minimum temp in C')
X = X.drop(columns='Diurnal temperature range in C')
X = X.drop(columns='Average air temperature in K')
X = X.drop(columns='city')
# return the wrangled dataframe
return X
train = wrangle(train)
val = wrangle(val)
test = wrangle(test)
train.head().T
#Before we build the model to train on train dataset, log transform target variable due to skew
import numpy as np
target_log = np.log1p(train['Total dengue cases in the week'])
sns.distplot(target_log)
plt.title('Log-transformed target');
target_log_series = pd.Series(target_log)
train = train.assign(log_total_cases = target_log_series)
#drop total_cases target column while training the model
train = train.drop(columns='Total dengue cases in the week')
#Do the same log transformation with validation dataset
target_log_val = np.log1p(val['Total dengue cases in the week'])
target_log_val_series = pd.Series(target_log_val)
val = val.assign(log_total_cases = target_log_val_series)
val = val.drop(columns='Total dengue cases in the week')
#Fitting XGBoost Regresser model
#Define target and features
# The status_group column is the target
target = 'log_total_cases'
# Get a dataframe with all train columns except the target
train_features = train.drop(columns=[target])
# Get a list of the numeric features
numeric_features = train_features.select_dtypes(include='number').columns.tolist()
# Combine the lists
features = numeric_features
# Arrange data into X features matrix and y target vector
X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]
pip install category_encoders
from sklearn.pipeline import make_pipeline
import category_encoders as ce
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder
import xgboost as xgb
from xgboost import XGBRegressor
from sklearn import model_selection, preprocessing
processor = make_pipeline(
SimpleImputer(strategy='mean')
)
X_train_processed = processor.fit_transform(X_train)
X_val_processed = processor.transform(X_val)
model = XGBRegressor(n_estimators=200, objective='reg:squarederror', n_jobs=-1)
eval_set = [(X_train_processed, y_train),
(X_val_processed, y_val)]
model.fit(X_train_processed, y_train, eval_set=eval_set, eval_metric='mae',
early_stopping_rounds=10)
results = model.evals_result()
train_error = results['validation_0']['mae']
val_error = results['validation_1']['mae']
iterations = range(1, len(train_error) + 1)
plt.figure(figsize=(10,7))
plt.plot(iterations, train_error, label='Train')
plt.plot(iterations, val_error, label='Validation')
plt.title('XGBoost Validation Curve')
plt.ylabel('Mean Absolute Error (log transformed)')
plt.xlabel('Model Complexity (n_estimators)')
plt.legend();
#predict on X_val
y_pred = model.predict(X_val_processed)
print('XGBoost Validation Mean Absolute Error, log transformed)', mean_absolute_error(y_val, y_pred))
#Transform y_pred back to original units from log transformed
y_pred_original = np.expm1(y_pred)
y_val_original = np.expm1(y_val)
print('XGBoost Validation Mean Absolute Error (non-log transformed)', mean_absolute_error(y_val_original, y_pred_original))
```
| true |
code
| 0.588357 | null | null | null | null |
|
# Neural networks with PyTorch
Deep learning networks tend to be massive with dozens or hundreds of layers, that's where the term "deep" comes from. You can build one of these deep networks using only weight matrices as we did in the previous notebook, but in general it's very cumbersome and difficult to implement. PyTorch has a nice module `nn` that provides a nice way to efficiently build large neural networks.
```
# Import necessary packages
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import numpy as np
import torch
import helper
import matplotlib.pyplot as plt
```
Now we're going to build a larger network that can solve a (formerly) difficult problem, identifying text in an image. Here we'll use the MNIST dataset which consists of greyscale handwritten digits. Each image is 28x28 pixels, you can see a sample below
<img src='assets/mnist.png'>
Our goal is to build a neural network that can take one of these images and predict the digit in the image.
First up, we need to get our dataset. This is provided through the `torchvision` package. The code below will download the MNIST dataset, then create training and test datasets for us. Don't worry too much about the details here, you'll learn more about this later.
```
### Run this cell
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),
])
# Download and load the training data
trainset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
```
We have the training data loaded into `trainloader` and we make that an iterator with `iter(trainloader)`. Later, we'll use this to loop through the dataset for training, like
```python
for image, label in trainloader:
## do things with images and labels
```
You'll notice I created the `trainloader` with a batch size of 64, and `shuffle=True`. The batch size is the number of images we get in one iteration from the data loader and pass through our network, often called a *batch*. And `shuffle=True` tells it to shuffle the dataset every time we start going through the data loader again. But here I'm just grabbing the first batch so we can check out the data. We can see below that `images` is just a tensor with size `(64, 1, 28, 28)`. So, 64 images per batch, 1 color channel, and 28x28 images.
```
dataiter = iter(trainloader)
images, labels = dataiter.next()
print(type(images))
print(images.shape)
print(labels.shape)
```
This is what one of the images looks like.
```
plt.imshow(images[1].numpy().squeeze(), cmap='Greys_r');
```
First, let's try to build a simple network for this dataset using weight matrices and matrix multiplications. Then, we'll see how to do it using PyTorch's `nn` module which provides a much more convenient and powerful method for defining network architectures.
The networks you've seen so far are called *fully-connected* or *dense* networks. Each unit in one layer is connected to each unit in the next layer. In fully-connected networks, the input to each layer must be a one-dimensional vector (which can be stacked into a 2D tensor as a batch of multiple examples). However, our images are 28x28 2D tensors, so we need to convert them into 1D vectors. Thinking about sizes, we need to convert the batch of images with shape `(64, 1, 28, 28)` to a have a shape of `(64, 784)`, 784 is 28 times 28. This is typically called *flattening*, we flattened the 2D images into 1D vectors.
Previously you built a network with one output unit. Here we need 10 output units, one for each digit. We want our network to predict the digit shown in an image, so what we'll do is calculate probabilities that the image is of any one digit or class. This ends up being a discrete probability distribution over the classes (digits) that tells us the most likely class for the image. That means we need 10 output units for the 10 classes (digits). We'll see how to convert the network output into a probability distribution next.
> **Exercise:** Flatten the batch of images `images`. Then build a multi-layer network with 784 input units, 256 hidden units, and 10 output units using random tensors for the weights and biases. For now, use a sigmoid activation for the hidden layer. Leave the output layer without an activation, we'll add one that gives us a probability distribution next.
```
## Solution
def activation(x):
return 1/(1+torch.exp(-x))
# Flatten the input images
inputs = images.view(images.shape[0], -1)
# Create parameters
w1 = torch.randn(784, 256)
b1 = torch.randn(256)
w2 = torch.randn(256, 10)
b2 = torch.randn(10)
h = activation(torch.mm(inputs, w1) + b1)
out = torch.mm(h, w2) + b2
```
Now we have 10 outputs for our network. We want to pass in an image to our network and get out a probability distribution over the classes that tells us the likely class(es) the image belongs to. Something that looks like this:
<img src='assets/image_distribution.png' width=500px>
Here we see that the probability for each class is roughly the same. This is representing an untrained network, it hasn't seen any data yet so it just returns a uniform distribution with equal probabilities for each class.
To calculate this probability distribution, we often use the [**softmax** function](https://en.wikipedia.org/wiki/Softmax_function). Mathematically this looks like
$$
\Large \sigma(x_i) = \cfrac{e^{x_i}}{\sum_k^K{e^{x_k}}}
$$
What this does is squish each input $x_i$ between 0 and 1 and normalizes the values to give you a proper probability distribution where the probabilites sum up to one.
> **Exercise:** Implement a function `softmax` that performs the softmax calculation and returns probability distributions for each example in the batch. Note that you'll need to pay attention to the shapes when doing this. If you have a tensor `a` with shape `(64, 10)` and a tensor `b` with shape `(64,)`, doing `a/b` will give you an error because PyTorch will try to do the division across the columns (called broadcasting) but you'll get a size mismatch. The way to think about this is for each of the 64 examples, you only want to divide by one value, the sum in the denominator. So you need `b` to have a shape of `(64, 1)`. This way PyTorch will divide the 10 values in each row of `a` by the one value in each row of `b`. Pay attention to how you take the sum as well. You'll need to define the `dim` keyword in `torch.sum`. Setting `dim=0` takes the sum across the rows while `dim=1` takes the sum across the columns.
```
## Solution
def softmax(x):
return torch.exp(x)/torch.sum(torch.exp(x), dim=1).view(-1, 1)
probabilities = softmax(out)
# Does it have the right shape? Should be (64, 10)
print(probabilities.shape)
# Does it sum to 1?
print(probabilities.sum(dim=1))
```
## Building networks with PyTorch
PyTorch provides a module `nn` that makes building networks much simpler. Here I'll show you how to build the same one as above with 784 inputs, 256 hidden units, 10 output units and a softmax output.
```
from torch import nn
class Network(nn.Module):
def __init__(self):
super().__init__()
# Inputs to hidden layer linear transformation
self.hidden = nn.Linear(784, 256)
# Output layer, 10 units - one for each digit
self.output = nn.Linear(256, 10)
# Define sigmoid activation and softmax output
self.sigmoid = nn.Sigmoid()
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
# Pass the input tensor through each of our operations
x = self.hidden(x)
x = self.sigmoid(x)
x = self.output(x)
x = self.softmax(x)
return x
```
Let's go through this bit by bit.
```python
class Network(nn.Module):
```
Here we're inheriting from `nn.Module`. Combined with `super().__init__()` this creates a class that tracks the architecture and provides a lot of useful methods and attributes. It is mandatory to inherit from `nn.Module` when you're creating a class for your network. The name of the class itself can be anything.
```python
self.hidden = nn.Linear(784, 256)
```
This line creates a module for a linear transformation, $x\mathbf{W} + b$, with 784 inputs and 256 outputs and assigns it to `self.hidden`. The module automatically creates the weight and bias tensors which we'll use in the `forward` method. You can access the weight and bias tensors once the network (`net`) is created with `net.hidden.weight` and `net.hidden.bias`.
```python
self.output = nn.Linear(256, 10)
```
Similarly, this creates another linear transformation with 256 inputs and 10 outputs.
```python
self.sigmoid = nn.Sigmoid()
self.softmax = nn.Softmax(dim=1)
```
Here I defined operations for the sigmoid activation and softmax output. Setting `dim=1` in `nn.Softmax(dim=1)` calculates softmax across the columns.
```python
def forward(self, x):
```
PyTorch networks created with `nn.Module` must have a `forward` method defined. It takes in a tensor `x` and passes it through the operations you defined in the `__init__` method.
```python
x = self.hidden(x)
x = self.sigmoid(x)
x = self.output(x)
x = self.softmax(x)
```
Here the input tensor `x` is passed through each operation a reassigned to `x`. We can see that the input tensor goes through the hidden layer, then a sigmoid function, then the output layer, and finally the softmax function. It doesn't matter what you name the variables here, as long as the inputs and outputs of the operations match the network architecture you want to build. The order in which you define things in the `__init__` method doesn't matter, but you'll need to sequence the operations correctly in the `forward` method.
Now we can create a `Network` object.
```
# Create the network and look at it's text representation
model = Network()
model
```
You can define the network somewhat more concisely and clearly using the `torch.nn.functional` module. This is the most common way you'll see networks defined as many operations are simple element-wise functions. We normally import this module as `F`, `import torch.nn.functional as F`.
```
import torch.nn.functional as F
class Network(nn.Module):
def __init__(self):
super().__init__()
# Inputs to hidden layer linear transformation
self.hidden = nn.Linear(784, 256)
# Output layer, 10 units - one for each digit
self.output = nn.Linear(256, 10)
def forward(self, x):
# Hidden layer with sigmoid activation
x = F.sigmoid(self.hidden(x))
# Output layer with softmax activation
x = F.softmax(self.output(x), dim=1)
return x
```
### Activation functions
So far we've only been looking at the softmax activation, but in general any function can be used as an activation function. The only requirement is that for a network to approximate a non-linear function, the activation functions must be non-linear. Here are a few more examples of common activation functions: Tanh (hyperbolic tangent), and ReLU (rectified linear unit).
<img src="assets/activation.png" width=700px>
In practice, the ReLU function is used almost exclusively as the activation function for hidden layers.
### Your Turn to Build a Network
<img src="assets/mlp_mnist.png" width=600px>
> **Exercise:** Create a network with 784 input units, a hidden layer with 128 units and a ReLU activation, then a hidden layer with 64 units and a ReLU activation, and finally an output layer with a softmax activation as shown above. You can use a ReLU activation with the `nn.ReLU` module or `F.relu` function.
It's good practice to name your layers by their type of network, for instance 'fc' to represent a fully-connected layer. As you code your solution, use `fc1`, `fc2`, and `fc3` as your layer names.
```
## Solution
class Network(nn.Module):
def __init__(self):
super().__init__()
# Defining the layers, 128, 64, 10 units each
self.fc1 = nn.Linear(784, 128)
self.fc2 = nn.Linear(128, 64)
# Output layer, 10 units - one for each digit
self.fc3 = nn.Linear(64, 10)
def forward(self, x):
''' Forward pass through the network, returns the output logits '''
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = F.relu(x)
x = self.fc3(x)
x = F.softmax(x, dim=1)
return x
model = Network()
model
```
### Initializing weights and biases
The weights and such are automatically initialized for you, but it's possible to customize how they are initialized. The weights and biases are tensors attached to the layer you defined, you can get them with `model.fc1.weight` for instance.
```
print(model.fc1.weight)
print(model.fc1.bias)
```
For custom initialization, we want to modify these tensors in place. These are actually autograd *Variables*, so we need to get back the actual tensors with `model.fc1.weight.data`. Once we have the tensors, we can fill them with zeros (for biases) or random normal values.
```
# Set biases to all zeros
model.fc1.bias.data.fill_(0)
# sample from random normal with standard dev = 0.01
model.fc1.weight.data.normal_(std=0.01)
```
### Forward pass
Now that we have a network, let's see what happens when we pass in an image.
```
# Grab some data
dataiter = iter(trainloader)
images, labels = dataiter.next()
# Resize images into a 1D vector, new shape is (batch size, color channels, image pixels)
images.resize_(64, 1, 784)
# or images.resize_(images.shape[0], 1, 784) to automatically get batch size
# Forward pass through the network
img_idx = 0
ps = model.forward(images[img_idx,:])
img = images[img_idx]
helper.view_classify(img.view(1, 28, 28), ps)
```
As you can see above, our network has basically no idea what this digit is. It's because we haven't trained it yet, all the weights are random!
### Using `nn.Sequential`
PyTorch provides a convenient way to build networks like this where a tensor is passed sequentially through operations, `nn.Sequential` ([documentation](https://pytorch.org/docs/master/nn.html#torch.nn.Sequential)). Using this to build the equivalent network:
```
# Hyperparameters for our network
input_size = 784
hidden_sizes = [128, 64]
output_size = 10
# Build a feed-forward network
model = nn.Sequential(nn.Linear(input_size, hidden_sizes[0]),
nn.ReLU(),
nn.Linear(hidden_sizes[0], hidden_sizes[1]),
nn.ReLU(),
nn.Linear(hidden_sizes[1], output_size),
nn.Softmax(dim=1))
print(model)
# Forward pass through the network and display output
images, labels = next(iter(trainloader))
images.resize_(images.shape[0], 1, 784)
ps = model.forward(images[0,:])
helper.view_classify(images[0].view(1, 28, 28), ps)
```
The operations are availble by passing in the appropriate index. For example, if you want to get first Linear operation and look at the weights, you'd use `model[0]`.
```
print(model[0])
model[0].weight
```
You can also pass in an `OrderedDict` to name the individual layers and operations, instead of using incremental integers. Note that dictionary keys must be unique, so _each operation must have a different name_.
```
from collections import OrderedDict
model = nn.Sequential(OrderedDict([
('fc1', nn.Linear(input_size, hidden_sizes[0])),
('relu1', nn.ReLU()),
('fc2', nn.Linear(hidden_sizes[0], hidden_sizes[1])),
('relu2', nn.ReLU()),
('output', nn.Linear(hidden_sizes[1], output_size)),
('softmax', nn.Softmax(dim=1))]))
model
```
Now you can access layers either by integer or the name
```
print(model[0])
print(model.fc1)
```
In the next notebook, we'll see how we can train a neural network to accuractly predict the numbers appearing in the MNIST images.
| true |
code
| 0.830405 | null | null | null | null |
|
# Learning MNIST & Fashion
In this exercise you will design a classifier for the very simple but very popular [MNIST dataset](http://yann.lecun.com/exdb/mnist/), a classic of dataset in computer vision and one of the first real world problems solved by neural networks.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import SGD, Adam, RMSprop
from keras.utils import to_categorical
```
Keras provides access to a few simple datasets for convenience in the `keras.datasets` module. Here we will load MNIST, a standard benchmark dataset for image classification. This will download the dataset if you have run this code before.
```
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train.shape
```
MNIST is a simple dataset of grayscale hand-written digits 28x28 pixels big. So there are 10 classes in the dataset corresponding to the digits 0-9. We can get a sense for what this dataset is like (always a good idea) by looking at some random samples for the training data:
```
plt.imshow(X_train[np.random.randint(len(X_train))], cmap='gray')
```
We need to do a little preprocessing of the dataset. Firstly, we will flatten the 28x28 images to a 784 dimensional vector. This is because our first model below does not care about the spatial dimensions, only the pixel values. The images are represented by numpy arrays of integers between 0 and 255. Since this is a fixed range, we should scale the values down to be from 0 to 1. This normalization simplifies things is usually a good idea, especially since weights are usually initialized randomly near zero.
Read the code below and make sure you understand what we are doing to the data.
```
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
y_train_cat = to_categorical(y_train, 10)
y_test_cat = to_categorical(y_test, 10)
```
## Exercise 1 - design a fully conncted network for MNIST
Build a fully connected network. It is up to you what the structure of the model will be, but keep in mind that this problem is much higher dimensional than previous problems we have worked on. This is your first chance to design a model on real data! See if you can get 90% accuracy or better.
Here are some of the things you will need to decide about your model:
* number of layers
* activation function
* number of dimensions in each layer
* batch size
* number of epochs
* learning rate
Suggestions:
* You can pass the argument `verbose=2` to the `model.fit` method to quiet the output a bit, which will speed up the training as well.
* You already divided the training and test data, but since you will be trying a series of experiments and changing your model, it is good practice to set aside a **validation** dataset for you to use to track your model improvements. You should only use the test data after you believe you have a good model to evaluate the final performance. Keras can create a validation set for you if you pass the `validation_split=0.1` argument to `model.fit` to tell Keras to hold out 10% of the training data to use as validation.
* You can use the `plot_loss` if you find it useful in setting your learning rate etc. during your experiments.
* You can refer to previous notebooks and the [documentation](http://keras.io/models/sequential/).
If you want to talk over design decisions, feel free to ask.
```
def plot_loss(hist):
loss = hist.history['loss']
plt.plot(range(len(loss)), loss)
plt.title('loss')
plt.xlabel('epochs')
# Final test evaluation
score = model.evaluate(X_test, y_test_cat, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
```
## Exercise 2: Fashion Mnist
Repeat the classification exercise using the Fashion Mnist dataset from Zalando Research:
https://github.com/zalandoresearch/fashion-mnist
This dataset has the same specs as MNIST but it's designed to be more indicative of a real image classification problem. It contains 10 classes of clothing items:
Label Description
0 T-shirt/top
1 Trouser
2 Pullover
3 Dress
4 Coat
5 Sandal
6 Shirt
7 Sneaker
8 Bag
9 Ankle boot
Do you get to similar performance?
| true |
code
| 0.720805 | null | null | null | null |
|
# NNCP Splitter
[](https://colab.research.google.com/github/byronknoll/tensorflow-compress/blob/master/nncp-splitter.ipynb)
Made by Byron Knoll. GitHub repository: https://github.com/byronknoll/tensorflow-compress
### Description
This notebook can be used to split files that have been preprocessed by NNCP. This is for compression using [tensorflow-compress](https://colab.research.google.com/github/byronknoll/tensorflow-compress/blob/master/tensorflow-compress.ipynb). The primary use-case is to get around Colab's session time limit by processing large files in smaller parts.
This file splitting does not use the naive method of dividing the file into consecutive parts. Instead, it takes into account the batch size used in tensorflow-compress so that the same sequence of symbols will be used for compressing the split parts as for the original file.
### Instructions
1. In tensorflow-compress, using "preprocess_only" mode, choose "nncp" preprocessor and download the result.
2. Upload the preprocessed file (named "preprocessed.dat") to this notebook, and download the split parts.
3. In tensorflow-compress, compress each split part sequentially, enabling the checkpoint option. Choose "nncp-done" as the preprocessor.
4. In tensorflow-compress, decompress each split part sequentially, enabling the checkpoint option. Choose "nncp-done" as the preprocessor.
5. Upload the decompressed parts to this notebook to reproduce the original file. The files should be named: part.0, part.1, ..., part.N. Also upload the original NNCP dictionary file (named "dictionary.words").
## Parameters
```
batch_size = 96 #@param {type:"integer"}
#@markdown >_Set this to the same value that will be used in tensorflow-compress._
mode = 'split' #@param ["split", "join"]
num_parts = 4 #@param {type:"integer"}
#@markdown >_This is the number of parts the file should be split to._
http_path = '' #@param {type:"string"}
#@markdown >_The file from this URL will be downloaded. It is recommended to use Google Drive URLs to get fast transfer speed. Use this format for Google Drive files: https://drive.google.com/uc?id= and paste the file ID at the end of the URL. You can find the file ID from the "Get Link" URL in Google Drive. You can enter multiple URLs here, space separated._
local_upload = False #@param {type:"boolean"}
#@markdown >_If enabled, you will be prompted in the "Setup Files" section to select files to upload from your local computer. You can upload multiple files. Note: the upload speed can be quite slow (use "http_path" for better transfer speeds)._
download_option = "no_download" #@param ["no_download", "local", "google_drive"]
#@markdown >_If this is set to "local", the output files will be downloaded to your computer. If set to "google_drive", they will be copied to your Google Drive account (which is significantly faster than downloading locally)._
```
## Setup
```
#@title Imports
from google.colab import files
from google.colab import drive
import math
#@title Mount Google Drive
if download_option == "google_drive":
drive.mount('/content/gdrive')
#@title Setup Files
!mkdir -p "data"
if local_upload:
%cd data
files.upload()
%cd ..
if http_path:
%cd data
paths = http_path.split()
for path in paths:
!gdown $path
%cd ..
if mode == "join":
!gdown --id 1EzVPbRkBIIbgOzvEMeM0YpibDi2R4SHD
!tar -xf nncp-2019-11-16.tar.gz
%cd nncp-2019-11-16/
!make preprocess
%cd ..
```
## Run
```
#@title Split/Join
if mode == "split":
input_path = "data/preprocessed.dat"
orig = open(input_path, 'rb').read()
int_list = []
for i in range(0, len(orig), 2):
int_list.append(orig[i] * 256 + orig[i+1])
file_len = len(int_list)
split = math.ceil(file_len / batch_size)
part_split = math.ceil(file_len / (num_parts * batch_size))
pos = 0
for i in range(num_parts):
output = []
for j in range(batch_size):
for k in range(part_split):
if pos + k >= split:
break
index = pos + (j*split) + k
if index >= file_len:
break
output.append(int_list[index])
pos += part_split
with open(("data/part." + str(i)), "wb") as out:
for j in range(len(output)):
out.write(bytes(((output[j] // 256),)))
out.write(bytes(((output[j] % 256),)))
if mode == "join":
file_len = 0
for i in range(num_parts):
part = open("data/part." + str(i), 'rb').read()
file_len += len(part) / 2
split = math.ceil(file_len / batch_size)
part_split = math.ceil(file_len / (num_parts * batch_size))
int_list = [0] * math.floor(file_len)
pos = 0
for i in range(num_parts):
part = open("data/part." + str(i), 'rb').read()
part_list = []
for j in range(0, len(part), 2):
part_list.append(part[j] * 256 + part[j+1])
index2 = 0
for j in range(batch_size):
for k in range(part_split):
if pos + k >= split:
break
index = pos + (j*split) + k
if index >= file_len:
break
int_list[index] = part_list[index2]
index2 += 1
pos += part_split
with open("data/output.dat", "wb") as out:
for i in range(len(int_list)):
out.write(bytes(((int_list[i] // 256),)))
out.write(bytes(((int_list[i] % 256),)))
!./nncp-2019-11-16/preprocess d data/dictionary.words ./data/output.dat ./data/final.dat
#@title File Sizes
!ls -l data
#@title MD5
!md5sum data/*
#@title Download Result
def download(path):
"""Downloads the file at the specified path."""
if download_option == 'local':
files.download(path)
elif download_option == 'google_drive':
!cp -f $path /content/gdrive/My\ Drive
if mode == "split":
for i in range(num_parts):
download("data/part." + str(i))
if mode == "join":
download("data/final.dat")
```
| true |
code
| 0.487124 | null | null | null | null |
|
# Point-based and Parallel Processing Water Observations from Space (WOfS) Product in Africa <img align="right" src="../Supplementary_data/DE_Africa_Logo_Stacked_RGB_small.jpg">
* **Products used:**
[ga_ls8c_wofs_2](https://explorer.digitalearth.africa/ga_ls8c_wofs_2)
## Description
The [Water Observations from Space (WOfS)](https://www.ga.gov.au/scientific-topics/community-safety/flood/wofs/about-wofs) is a derived product from Landsat 8 satellite observations as part of provisional Landsat 8 Collection 2 surface reflectance and shows surface water detected in Africa.
Individual water classified images are called Water Observation Feature Layers (WOFLs), and are created in a 1-to-1 relationship with the input satellite data.
Hence there is one WOFL for each satellite dataset processed for the occurrence of water.
The data in a WOFL is stored as a bit field. This is a binary number, where each digit of the number is independantly set or not based on the presence (1) or absence (0) of a particular attribute (water, cloud, cloud shadow etc). In this way, the single decimal value associated to each pixel can provide information on a variety of features of that pixel.
For more information on the structure of WOFLs and how to interact with them, see [Water Observations from Space](../Datasets/Water_Observations_from_Space.ipynb) and [Applying WOfS bitmasking](../Frequently_used_code/Applying_WOfS_bitmasking.ipynb) notebooks.
This notebook explains how you can query WOfS product for each collected validation points in Africa based on point-based sampling approach.
The notebook demonstrates how to:
1. Load validation points for each partner institutions following cleaning stage described in
2. Query WOFL data for validation points and capture available WOfS defined class using point-based sampling and multiprocessing functionality
3. Extract a LUT for each point that contains both information for validation points and WOfS class as well number of clear observation in each month
***
## Getting started
To run this analysis, run all the cells in the notebook, starting with the "Load packages" cell.
### Load packages
Import Python packages that are used for the analysis.
```
%matplotlib inline
import datacube
from datacube.utils import masking, geometry
import sys
import os
import rasterio
import xarray
import glob
import numpy as np
import pandas as pd
import seaborn as sn
import geopandas as gpd
import matplotlib.pyplot as plt
import multiprocessing as mp
import scipy, scipy.ndimage
import warnings
warnings.filterwarnings("ignore") #this will suppress the warnings for multiple UTM zones in your AOI
sys.path.append("../Scripts")
from geopandas import GeoSeries, GeoDataFrame
from shapely.geometry import Point
from sklearn.metrics import confusion_matrix, accuracy_score
from sklearn.metrics import plot_confusion_matrix, f1_score
from deafrica_plotting import map_shapefile,display_map, rgb
from deafrica_spatialtools import xr_rasterize
from deafrica_datahandling import wofs_fuser, mostcommon_crs,load_ard,deepcopy
from deafrica_dask import create_local_dask_cluster
from tqdm import tqdm
```
### Analysis parameters
To analyse validation points collected by each partner institution, we need to obtain WOfS surface water observation data that corresponds with the labelled input data locations.
- Path2csv: the path to CEO validation points labelled by each partner institutions in Africa
- ValPoints: CEO validation points labelled by each partner institutions in Africa in ESRI shapefile format
- Path: Direct path to the ESRI shapefile in case that the shapefile in available
- input_data: geopandas datafram for CEO validation points labelled by each partner institutions in Africa
*** Note: Run the following three cells in case that you dont have a ESRI shapefile for validation points.
```
path2csv = '../Data/Processed/AGRYHMET/AGRYHMET_ValidationPoints.csv'
df = pd.read_csv(path2csv,delimiter=",")
geometries = [Point(xy) for xy in zip(df.LON, df.LAT)]
crs = {'init': 'epsg:4326'}
ValPoints = GeoDataFrame(df, crs=crs, geometry=geometries)
ValPoints.to_file(filename='../Data/Processed/AGRYHMET/AGRYHMET_ValidationPoints.shp')
```
*** Note: In case that you have ESRI shapefile for validation points, please continute from this point onward.
```
path = '../Data/Processed/AGRYHMET/AGRYHMET_ValidationPoints.shp'
#reading the table and converting CRS to metric
input_data = gpd.read_file(path).to_crs('epsg:6933')
input_data.columns
input_data= input_data.drop(['Unnamed_ 0'], axis=1)
#Checking the size of the input data
input_data.shape
```
### Sample WOfS at the ground truth coordinates
To load WOFL data, we can first create a re-usable query as below that will define two particular items, `group_by` solar day, ensuring that the data between scenes is combined correctly. The second parameter is `resampling` method that is set to be nearest. This query will later be updated in the script for other parameters to conduct WOfS query. the time period we are interested in, as well as other important parameters that are used to correctly load the data.
We can convert the WOFL bit field into a binary array containing True and False values. This allows us to use the WOFL data as a mask that can be applied to other datasets. The `make_mask` function allows us to create a mask using the flag labels (e.g. "wet" or "dry") rather than the binary numbers we used above. For more details on how to do masking on WOfS, see the [Applying_WOfS_bit_masking](../Frequently_used_code/Applying_WOfS_bitmasking.ipynb) notebook in Africa sandbox.
```
#generate query object
query ={'group_by':'solar_day',
'resampling':'nearest'}
```
Defining a function to query WOfS database according to the first five days before and after of each calendar month
```
def get_wofs_for_point(index, row, input_data, query, results_wet, results_clear):
dc = datacube.Datacube(app='WOfS_accuracy')
#get the month value for each index
month = input_data.loc[index]['MONTH']
#get the value for time including year, month, start date and end date
timeYM = '2018-'+f'{month:02d}'
start_date = np.datetime64(timeYM) - np.timedelta64(5,'D')
end_date = np.datetime64(timeYM) + np.timedelta64(5,'D')
time = (str(start_date),str(end_date))
plot_id = input_data.loc[index]['PLOT_ID']
#having the original query as it is
dc_query = deepcopy(query)
geom = geometry.Geometry(input_data.geometry.values[index].__geo_interface__, geometry.CRS('EPSG:6933'))
q = {"geopolygon":geom}
t = {"time":time}
#updating the query
dc_query.update(t)
dc_query.update(q)
#loading landsat-8 WOfs product and set the values for x and y (point-based) and also (window-based)
wofls = dc.load(product ="ga_ls8c_wofs_2",
y = (input_data.geometry.y[index], input_data.geometry.y[index]),
x =(input_data.geometry.x[index], input_data.geometry.x[index]),
#y = (input_data.geometry.y[index] - 30.5, input_data.geometry.y[index] + 30.5), # setting x and y coordinates based on 3*3 pixel window-based query
#x =(input_data.geometry.x[index] - 30.5, input_data.geometry.x[index] + 30.5),
crs = 'EPSG:6933',
time=time,
output_crs = 'EPSG:6933',
resolution=(-30,30))
#exclude the records that wofl return as empty for water
if not 'water' in wofls:
pass
else:
#Define a mask for wet and clear pixels
wet_nocloud = {"water_observed":True, "cloud_shadow":False, "cloud":False,"nodata":False}
#Define a mask for dry and clear pixels
dry_nocloud = {"water_observed":False, "cloud_shadow":False, "cloud":False, "nodata":False}
wofl_wetnocloud = masking.make_mask(wofls, **wet_nocloud).astype(int)
wofl_drynocloud = masking.make_mask(wofls, **dry_nocloud).astype(int)
clear = (wofl_wetnocloud | wofl_drynocloud).water.all(dim=['x','y']).values
#record the total number of clear observations for each point in each month and use it to filter out month with no valid data
n_clear = clear.sum()
#condition to identify whether WOfS seen water in specific month for a particular location
if n_clear > 0:
wet = wofl_wetnocloud.isel(time=clear).water.max().values
else:
wet = 0
#updating results for both wet and clear observations
results_wet.update({str(int(plot_id))+"_"+str(month) : int(wet)})
results_clear.update({str(int(plot_id))+"_"+str(month) : int(n_clear)})
return time
```
Define a function for parallel processing
```
def _parallel_fun(input_data, query, ncpus):
manager = mp.Manager()
results_wet = manager.dict()
results_clear = manager.dict()
# progress bar
pbar = tqdm(total=len(input_data))
def update(*a):
pbar.update()
with mp.Pool(ncpus) as pool:
for index, row in input_data.iterrows():
pool.apply_async(get_wofs_for_point,
[index,
row,
input_data,
query,
results_wet,
results_clear], callback=update)
pool.close()
pool.join()
pbar.close()
return results_wet, results_clear
```
Test the for loop
```
results_wet_test = dict()
results_clear_test = dict()
for index, row in input_data[0:14].iterrows():
time = get_wofs_for_point(index, row, input_data, query, results_wet_test, results_clear_test)
print(time)
```
Point-based query and parallel processing on WOfS
```
wet, clear = _parallel_fun(input_data, query, ncpus=15)
#extracting the final table with both CEO labels and WOfS class Wet and clear observations
wetdf = pd.DataFrame.from_dict(wet, orient = 'index')
cleardf = pd.DataFrame.from_dict(clear,orient='index')
df2 = wetdf.merge(cleardf, left_index=True, right_index=True)
df2 = df2.rename(columns={'0_x':'CLASS_WET','0_y':'CLEAR_OBS'})
#split the index (which is plotid + month) into seperate columns
for index, row in df2.iterrows():
df2.at[index,'PLOT_ID'] = index.split('_')[0] +'.0'
df2.at[index,'MONTH'] = index.split('_')[1]
#reset the index
df2 = df2.reset_index(drop=True)
#convert plot id and month to str to help with matching
input_data['PLOT_ID'] = input_data.PLOT_ID.astype(str)
input_data['MONTH']= input_data.MONTH.astype(str)
# merge both dataframe at locations where plotid and month match
final_df = pd.merge(input_data, df2, on=['PLOT_ID','MONTH'], how='outer')
#Defining the shape of final table
final_df.shape
#Counting the number of rows in the final table with NaN values in class_wet and clear observation (Optional)
#This part is to test the parallel processig function returns identicial results each time that it runs
countA = final_df["CLASS_WET"].isna().sum()
countB = final_df["CLEAR_OBS"].isna().sum()
countA, countB
final_df.to_csv(('../../Results/WOfS_Assessment/Point_Based/Institutions/AGRYHMET_PointBased_5D.csv'))
print(datacube.__version__)
```
***
## Additional information
**License:** The code in this notebook is licensed under the [Apache License, Version 2.0](https://www.apache.org/licenses/LICENSE-2.0).
Digital Earth Africa data is licensed under the [Creative Commons by Attribution 4.0](https://creativecommons.org/licenses/by/4.0/) license.
**Contact:** If you need assistance, please post a question on the [Open Data Cube Slack channel](http://slack.opendatacube.org/) or on the [GIS Stack Exchange](https://gis.stackexchange.com/questions/ask?tags=open-data-cube) using the `open-data-cube` tag (you can view previously asked questions [here](https://gis.stackexchange.com/questions/tagged/open-data-cube)).
If you would like to report an issue with this notebook, you can file one on [Github](https://github.com/digitalearthafrica/deafrica-sandbox-notebooks).
**Last modified:** September 2020
**Compatible datacube version:**
## Tags
Browse all available tags on the DE Africa User Guide's [Tags Index](https://) (placeholder as this does not exist yet)
| true |
code
| 0.305076 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Adminixtrator/gpt-2/blob/master/GPT_2_With_SQuAD.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Calling file from Repository
```
!git clone https://github.com/adminixtrator/gpt-2.git
%cd gpt-2
%ls
```
# Using the gpt-2 model 345M
```
#Download the gpt-2 model 345M..
!python3 download_model.py 345M
#Encoding..
!export PYTHONIOENCODING=UTF-8
```
# Now to Implementing gpt-2
```
#Changing directory..
import os
os.chdir('src')
!pip install regex #For OpenAI GPT
#Importing the necessary libraries..
import json
import numpy as np
import tensorflow as tf
import model, sample, encoder
#Function to use the interaction model..
def interact_model(model_name, seed, nsamples, batch_size, length, temperature, top_k, models_dir):
models_dir = os.path.expanduser(os.path.expandvars(models_dir))
if batch_size is None:
batch_size = 1
assert nsamples % batch_size == 0
enc = encoder.get_encoder(model_name, models_dir)
hparams = model.default_hparams()
with open(os.path.join(models_dir, model_name, 'hparams.json')) as f:
hparams.override_from_dict(json.load(f))
if length is None:
length = hparams.n_ctx // 2
elif length > hparams.n_ctx:
raise ValueError("Can't get samples longer than window size: %s" % hparams.n_ctx)
with tf.Session(graph=tf.Graph()) as sess:
context = tf.placeholder(tf.int32, [batch_size, None])
np.random.seed(seed)
tf.set_random_seed(seed)
output = sample.sample_sequence(hparams=hparams, length=length, context=context, batch_size=batch_size, temperature=temperature, top_k=top_k)
saver = tf.train.Saver(save_relative_paths=True)
ckpt = tf.train.latest_checkpoint(os.path.join(models_dir, model_name))
saver.restore(sess, ckpt)
while True:
raw_text = input("\nModel prompt >>> ")
if raw_text == 'ADMIN_NIXTRATOR':
raw_text = False
break
while not raw_text:
print('\nPrompt should not be empty!')
raw_text = input("\nModel prompt >>> ")
context_tokens = enc.encode(raw_text)
generated = 0
for _ in range(nsamples // batch_size):
out = sess.run(output, feed_dict={
context: [context_tokens for _ in range(batch_size)]
})[:, len(context_tokens):]
for i in range(batch_size):
generated += 1
text = enc.decode(out[i])
print("=" * 40 + " SAMPLE " + str(generated) + " " + "=" * 40)
print(text)
print("=" * 80)
```
# **Code Explanation**
## **model_name**:
This indicates which model we are using. In our case, we are using the GPT-2 model with 345 million parameters or weights
## **seed**:
Integer seed for random number generators, fix seed to reproduce results
## **nsamples**:
This represents the number of sample texts generated in our output
## **batch_size**:
This only affects speed/memory. This must also divide nsamples
*Note: To generate more than one sample, you need to change the values of both nsamples and batch_size and also have to keep them equal.*
## **length**:
It represents the number of tokens in the generated text. If the length is None, then the number of tokens is decided by model hyperparameters
## **temperature**:
This controls randomness in Boltzmann distribution. Lower temperature results in less random completions. As the temperature approaches zero, the model will become deterministic and repetitive. Higher temperature results in more random completions
## **top_k**:
This parameter controls diversity. If the value of top_k is set to 1, this means that only 1 word is considered for each step (token). If top_k is set to 40, that means 40 words are considered at each step. 0 (default) is a special setting meaning no restrictions. top_k = 40 generally is a good value
## **models_dir**:
It represents the path to parent folder containing model subfolders (contains the <model_name> folder)
# Results
```
#Using the arguements above..
interact_model('345M', None, 1, 1, 20, 1, 0, '/content/gpt-2/models')
```
# Fine-tuning on SQuAD for question-answering
```
#Checking Directory..
os.chdir('/content/gpt-2/SQuAD/')
%ls
#Importing the neccessary libraries..
import numpy as np, pandas as pd
import json
import ast
from textblob import TextBlob
import nltk
import torch
import pickle
from scipy import spatial
import warnings
warnings.filterwarnings('ignore')
import spacy
from nltk import Tree
en_nlp = spacy.load('en')
from nltk.stem.lancaster import LancasterStemmer
st = LancasterStemmer()
from sklearn.feature_extraction.text import TfidfVectorizer, TfidfTransformer
#Train set
train = pd.read_json("data/train-v2.0.json")
#Familiarizing with the dataset..
train.shape
```
## Loading Embedding dictionary
```
def get_target(x):
idx = -1
for i in range(len(x["sentences"])):
if x["text"] in x["sentences"][i]: idx = i
return idx
train.data
train.dropna(inplace=True)
train.shape
```
## Data Processing
```
def process_data(train):
print("step 1")
train['sentences'] = train['context'].apply(lambda x: [item.raw for item in TextBlob(x).sentences])
print("step 2")
train["target"] = train.apply(get_target, axis = 1)
print("step 3")
train['sent_emb'] = train['sentences'].apply(lambda x: [dict_emb[item][0] if item in\
dict_emb else np.zeros(4096) for item in x])
print("step 4")
train['quest_emb'] = train['question'].apply(lambda x: dict_emb[x] if x in dict_emb else np.zeros(4096) )
return train
train = process_data(train)
def cosine_sim(x):
li = []
for item in x["sent_emb"]:
li.append(spatial.distance.cosine(item,x["quest_emb"][0]))
return li
def pred_idx(distances):
return np.argmin(distances)
#Function to make predictions..
def predictions(train):
train["cosine_sim"] = train.apply(cosine_sim, axis = 1)
train["diff"] = (train["quest_emb"] - train["sent_emb"])**2
train["euclidean_dis"] = train["diff"].apply(lambda x: list(np.sum(x, axis = 1)))
del train["diff"]
print("cosine start")
train["pred_idx_cos"] = train["cosine_sim"].apply(lambda x: pred_idx(x))
train["pred_idx_euc"] = train["euclidean_dis"].apply(lambda x: pred_idx(x))
return train
#Making predictions..
predicted = predictions(train)
```
## Accuracy
```
#Function to check accuracy..
def accuracy(target, predicted):
acc = (target==predicted).sum()/len(target)
return acc
print(accuracy(predicted["target"], predicted["pred_idx_euc"])) #Accuracy for euclidean Distance
print(accuracy(predicted["target"], predicted["pred_idx_cos"])) #Accuracy for Cosine Similarity
```
## Combed Accuracy
```
label = []
for i in range(predicted.shape[0]):
if predicted.iloc[i,10] == predicted.iloc[i,11]:
label.append(predicted.iloc[i,10])
else:
label.append((predicted.iloc[i,10],predicted.iloc[i,10]))
ct = 0
for i in range(75206):
item = predicted["target"][i]
try:
if label[i] == predicted["target"][i]: ct +=1
except:
if item in label[i]: ct +=1
ct/75206 #Accuracy..
```
| true |
code
| 0.49707 | null | null | null | null |
|
## Churn Prediction using Logisitic Regression
## Data Dictionary
There are multiple variables in the dataset which can be cleanly divided in 3 categories:
### Demographic information about customers
<b>customer_id</b> - Customer id
<b>vintage</b> - Vintage of the customer with the bank in number of days
<b>age</b> - Age of customer
<b>gender</b> - Gender of customer
<b>dependents</b> - Number of dependents
<b>occupation</b> - Occupation of the customer
<b>city</b> - City of customer (anonymised)
### Customer Bank Relationship
<b>customer_nw_category</b> - Net worth of customer (3:Low 2:Medium 1:High)
<b>branch_code</b> - Branch Code for customer account
<b>days_since_last_transaction</b> - No of Days Since Last Credit in Last 1 year
### Transactional Information
<b>current_balance</b> - Balance as of today
<b>previous_month_end_balance</b> - End of Month Balance of previous month
<b>average_monthly_balance_prevQ</b> - Average monthly balances (AMB) in Previous Quarter
<b>average_monthly_balance_prevQ2</b> - Average monthly balances (AMB) in previous to previous quarter
<b>current_month_credit</b> - Total Credit Amount current month
<b>previous_month_credit</b> - Total Credit Amount previous month
<b>current_month_debit</b> - Total Debit Amount current month
<b>previous_month_debit</b> - Total Debit Amount previous month
<b>current_month_balance</b> - Average Balance of current month
<b>previous_month_balance</b> - Average Balance of previous month
<b>churn</b> - Average balance of customer falls below minimum balance in the next quarter (1/0)
## Churn Prediction
* Load Data & Packages for model building & preprocessing
* Preprocessing & Missing value imputation
* Select features on the basis of EDA Conclusions & build baseline model
* Decide Evaluation Metric on the basis of business problem
* Build model using all features & compare with baseline
### Loading Packages
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold, StratifiedKFold, train_test_split
from sklearn.metrics import roc_auc_score, accuracy_score, confusion_matrix, roc_curve, precision_score, recall_score, precision_recall_curve
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
warnings.simplefilter(action='ignore', category=UserWarning)
```
### Loading Data
```
df = pd.read_csv('churn_prediction.csv')
```
### Missing Values
Before we go on to build the model, we must look for missing values within the dataset as treating the missing values is a necessary step before we fit a model on the dataset.
```
pd.isnull(df).sum()
```
The result of this function shows that there are quite a few missing values in columns gender, dependents, city, days since last transaction and Percentage change in credits. Let us go through each of them 1 by 1 to find the appropriate missing value imputation strategy for each of them.
#### Gender
L
et us look at the categories within gender column
```
df['gender'].value_counts()
```
So there is a good mix of males and females and arguably missing values cannot be filled with any one of them. We could create a seperate category by assigning the value -1 for all missing values in this column.
Before that, first we will convert the gender into 0/1 and then replace missing values with -1
```
#Convert Gender
dict_gender = {'Male': 1, 'Female':0}
df.replace({'gender': dict_gender}, inplace = True)
df['gender'] = df['gender'].fillna(-1)
```
#### Dependents, occupation and city with mode
Next we will have a quick look at the dependents & occupations column and impute with mode as this is sort of an ordinal variable
```
df['dependents'].value_counts()
df['occupation'].value_counts()
df['dependents'] = df['dependents'].fillna(0)
df['occupation'] = df['occupation'].fillna('self_employed')
```
Similarly City can also be imputed with most common category 1020
```
df['city'] = df['city'].fillna(1020)
```
#### Days since Last Transaction
A fair assumption can be made on this column as this is number of days since last transaction in 1 year, we can substitute missing values with a value greater than 1 year say 999
```
df['days_since_last_transaction'] = df['days_since_last_transaction'].fillna(999)
```
### Preprocessing
Now, before applying linear model such as logistic regression, we need to scale the data and keep all features as numeric strictly.
### Dummies with Multiple Categories
```
# Convert occupation to one hot encoded features
df = pd.concat([df,pd.get_dummies(df['occupation'],prefix = str('occupation'),prefix_sep='_')],axis = 1)
```
### Scaling Numerical Features for Logistic Regression
Now, we remember that there are a lot of outliers in the dataset especially when it comes to previous and current balance features. Also, the distributions are skewed for these features. We will take 2 steps to deal with that here:
* Log Transformation
* Standard Scaler
Standard scaling is anyways a necessity when it comes to linear models and we have done that here after doing log transformation on all balance features.
```
num_cols = ['customer_nw_category', 'current_balance',
'previous_month_end_balance', 'average_monthly_balance_prevQ2', 'average_monthly_balance_prevQ',
'current_month_credit','previous_month_credit', 'current_month_debit',
'previous_month_debit','current_month_balance', 'previous_month_balance']
for i in num_cols:
df[i] = np.log(df[i] + 17000)
std = StandardScaler()
scaled = std.fit_transform(df[num_cols])
scaled = pd.DataFrame(scaled,columns=num_cols)
df_df_og = df.copy()
df = df.drop(columns = num_cols,axis = 1)
df = df.merge(scaled,left_index=True,right_index=True,how = "left")
y_all = df.churn
df = df.drop(['churn','customer_id','occupation'],axis = 1)
```
## Model Building and Evaluation Metrics
Since this is a binary classification problem, we could use the following 2 popular metrics:
1. Recall
2. Area under the Receiver operating characteristic curve
Now, we are looking at the recall value here because a customer falsely marked as churn would not be as bad as a customer who was not detected as a churning customer and appropriate measures were not taken by the bank to stop him/her from churning
The ROC AUC is the area under the curve when plotting the (normalized) true positive rate (x-axis) and the false positive rate (y-axis).
Our main metric here would be Recall values, while AUC ROC Score would take care of how well predicted probabilites are able to differentiate between the 2 classes.
### Conclusions from EDA
* For debit values, we see that there is a significant difference in the distribution for churn and non churn and it might be turn out to be an important feature
* For all the balance features the lower values have much higher proportion of churning customers
* For most frequent vintage values, the churning customers are slightly higher, while for higher values of vintage, we have mostly non churning customers which is in sync with the age variable
* We see significant difference for different occupations and certainly would be interesting to use as a feature for prediction of churn.
Now, we will first split our dataset into test and train and using the above conclusions select columns and build a baseline logistic regression model to check the ROC-AUC Score & the confusion matrix
### Baseline Columns
```
baseline_cols = ['current_month_debit', 'previous_month_debit','current_balance','previous_month_end_balance','vintage'
,'occupation_retired', 'occupation_salaried','occupation_self_employed', 'occupation_student']
df_baseline = df[baseline_cols]
```
### Train Test Split to create a validation set
```
# Splitting the data into Train and Validation set
xtrain, xtest, ytrain, ytest = train_test_split(df_baseline,y_all,test_size=1/3, random_state=11, stratify = y_all)
model = LogisticRegression()
model.fit(xtrain,ytrain)
pred = model.predict_proba(xtest)[:,1]
```
### AUC ROC Curve & Confusion Matrix
Now, let us quickly look at the AUC-ROC curve for our logistic regression model and also the confusion matrix to see where the logistic regression model is failing here.
```
from sklearn.metrics import roc_curve
fpr, tpr, _ = roc_curve(ytest,pred)
auc = roc_auc_score(ytest, pred)
plt.figure(figsize=(12,8))
plt.plot(fpr,tpr,label="Validation AUC-ROC="+str(auc))
x = np.linspace(0, 1, 1000)
plt.plot(x, x, linestyle='-')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc=4)
plt.show()
# Confusion Matrix
pred_val = model.predict(xtest)
label_preds = pred_val
cm = confusion_matrix(ytest,label_preds)
def plot_confusion_matrix(cm, normalized=True, cmap='bone'):
plt.figure(figsize=[7, 6])
norm_cm = cm
if normalized:
norm_cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
sns.heatmap(norm_cm, annot=cm, fmt='g', xticklabels=['Predicted: No','Predicted: Yes'], yticklabels=['Actual: No','Actual: Yes'], cmap=cmap)
plot_confusion_matrix(cm, ['No', 'Yes'])
# Recall Score
recall_score(ytest,pred_val)
```
### Cross validation
Cross Validation is one of the most important concepts in any type of data modelling. It simply says, try to leave a sample on which you do not train the model and test the model on this sample before finalizing the model.
We divide the entire population into k equal samples. Now we train models on k-1 samples and validate on 1 sample. Then, at the second iteration we train the model with a different sample held as validation.
In k iterations, we have basically built model on each sample and held each of them as validation. This is a way to reduce the selection bias and reduce the variance in prediction power.
Since it builds several models on different subsets of the dataset, we can be more sure of our model performance if we use CV for testing our models.
```
def cv_score(ml_model, rstate = 12, thres = 0.5, cols = df.columns):
i = 1
cv_scores = []
df1 = df.copy()
df1 = df[cols]
# 5 Fold cross validation stratified on the basis of target
kf = StratifiedKFold(n_splits=5,random_state=rstate,shuffle=True)
for df_index,test_index in kf.split(df1,y_all):
print('\n{} of kfold {}'.format(i,kf.n_splits))
xtr,xvl = df1.loc[df_index],df1.loc[test_index]
ytr,yvl = y_all.loc[df_index],y_all.loc[test_index]
# Define model for fitting on the training set for each fold
model = ml_model
model.fit(xtr, ytr)
pred_probs = model.predict_proba(xvl)
pp = []
# Use threshold to define the classes based on probability values
for j in pred_probs[:,1]:
if j>thres:
pp.append(1)
else:
pp.append(0)
# Calculate scores for each fold and print
pred_val = pp
roc_score = roc_auc_score(yvl,pred_probs[:,1])
recall = recall_score(yvl,pred_val)
precision = precision_score(yvl,pred_val)
sufix = ""
msg = ""
msg += "ROC AUC Score: {}, Recall Score: {:.4f}, Precision Score: {:.4f} ".format(roc_score, recall,precision)
print("{}".format(msg))
# Save scores
cv_scores.append(roc_score)
i+=1
return cv_scores
baseline_scores = cv_score(LogisticRegression(), cols = baseline_cols)
```
Now let us try using all columns available to check if we get significant improvement.
```
all_feat_scores = cv_score(LogisticRegression())
```
There is some improvement in both ROC AUC Scores and Precision/Recall Scores.
```
from sklearn.ensemble import RandomForestClassifier
rf_all_features = cv_score(RandomForestClassifier(n_estimators=100, max_depth=8))
```
## Comparison of Different model fold wise
Let us visualise the cross validation scores for each fold for the following 3 models and observe differences:
* Baseline Model
* Model based on all features
* Model based on top 10 features obtained from RFE
```
results_df = pd.DataFrame({'baseline':baseline_scores, 'all_feats': all_feat_scores, 'random_forest': rf_all_features})
results_df.plot(y=["baseline", "all_feats", "random_forest"], kind="bar")
```
Here, we can see that the random forest model is giving the best result for each fold and students are encouraged to try and fine tune the model to get the best results.
| true |
code
| 0.499634 | null | null | null | null |
|
# Sample notebook showcasing R on Jupyter
An overview of some plotting controls available in R for visualizing networks and visualizing tree models.
To execute a cell, select it and then use **[Shift] + [Enter]**.
```
# Default plot size is 7 inches x 7 inches; change to 7 x 3
options(repr.plot.height=3)
library(rpart) # CART tree models
library(rpart.plot) # Pretty plotting
library(vcd) # Spline plotting
titanic <- as.data.frame(Titanic)
head(titanic, n=5)
summary(titanic)
```
## Data visualization
Before making the tree models, try some visualization.
```
Survival.by.Sex <- xtabs(Freq~Sex+Survived, data=titanic)
Survival.by.Class <- xtabs(Freq~Class+Survived, data=titanic)
Survival.by.Age <- xtabs(Freq~Age+Survived, data=titanic)
oldpar <- par(mfrow=c(1,3))
options(repr.plot.width=7)
spineplot(Survival.by.Sex, col=c(rgb(0, 0, 0.5), rgb(0.3, 0.3, 1)))
spineplot(Survival.by.Class, col=c(rgb(0, 0, 0.5), rgb(0.3, 0.3, 1)))
spineplot(Survival.by.Age, col=c(rgb(0, 0, 0.5), rgb(0.3, 0.3, 1)))
par(oldpar)
cart.control <- rpart.control(minbucket=1, cp=0, maxdepth=5)
model.cart = rpart(
Survived ~ . ,
data=titanic[ , -5],
weights=titanic$Freq,
method="class",
#xval=10,
control=cart.control
)
print(model.cart)
printcp(model.cart)
# The standard Tree plot
plot(model.cart, margin=0.01)
text(model.cart, use.n=TRUE, cex=.8)
options(repr.plot.height=5)
# Better visualization using rpart.plot
prp(x=model.cart,
fallen.leaves=TRUE, branch=.5, faclen=0, trace=1,
extra=1, under=TRUE,
branch.lty=3,
split.box.col="whitesmoke", split.border.col="darkgray", split.round=0.4)
# Confusion Matrix given a cutoff
threshold = 0.8
cm <- table(titanic$Survived,
predict(model.cart, titanic[,-5], type="prob")[,2] > threshold)
print(cm)
```
# For fun, let's make a Caffeine molecule
This notebook also demonstrates importing an extra library, `igraph`.
The Docker container sets this up, without the student needing to import anything
(grep for igraph).
We'll use an adjacency matrix to describe the network topology of Caffeine, and create the graph
using `graph.adjacency(<the-adjacency-matrix>)` to demonstrate some standard selection and
plotting functions using R's `igraph` library. The chemical formula below demonstrates use of inline LaTeX math markup, and the image inline image placement.
$$C_8H_{10}N_4O_2$$
<img src="https://upload.wikimedia.org/wikipedia/commons/thumb/a/a1/Koffein_-_Caffeine.svg/220px-Koffein_-_Caffeine.svg.png" alt="Caffeine molecule"></img>
[mybinder]: http://mybinder.org
```
library(igraph)
caffeine.adjacency <- as.matrix(read.table("caffeine.txt", sep=" "))
caffeine <- graph.adjacency(caffeine.adjacency, mode='undirected')
V(caffeine)$name <- strsplit('CHHHNCOCNCHHHCHNCNCHHHCO', '')[[1]]
V(caffeine)$color <- rgb(1, 1, 1)
V(caffeine)[name == 'C']$color <- rgb(0, 0, 0, 0.7)
V(caffeine)[name == 'O']$color <- rgb(1, 0, 0, 0.7)
V(caffeine)[name == 'N']$color <- rgb(0, 0, 1, 0.7)
plot(caffeine)
options(repr.plot.height=5, repr.plot.width=5)
```
| true |
code
| 0.667256 | null | null | null | null |
|
```
%matplotlib inline
```
# Classifier comparison
A comparison of a several classifiers in scikit-learn on synthetic datasets.
The point of this example is to illustrate the nature of decision boundaries
of different classifiers.
This should be taken with a grain of salt, as the intuition conveyed by
these examples does not necessarily carry over to real datasets.
Particularly in high-dimensional spaces, data can more easily be separated
linearly and the simplicity of classifiers such as naive Bayes and linear SVMs
might lead to better generalization than is achieved by other classifiers.
The plots show training points in solid colors and testing points
semi-transparent. The lower right shows the classification accuracy on the test
set.
```
print(__doc__)
# Code source: Gaël Varoquaux
# Andreas Müller
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons, make_circles, make_classification
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
h = .02 # step size in the mesh
names = ["Nearest Neighbors", "Linear SVM", "RBF SVM", "Gaussian Process",
"Decision Tree", "Random Forest", "Neural Net", "AdaBoost",
"Naive Bayes", "QDA"]
classifiers = [
KNeighborsClassifier(3),
SVC(kernel="linear", C=0.025),
SVC(gamma=2, C=1),
GaussianProcessClassifier(1.0 * RBF(1.0)),
DecisionTreeClassifier(max_depth=5),
RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1),
MLPClassifier(alpha=1, max_iter=1000),
AdaBoostClassifier(),
GaussianNB(),
QuadraticDiscriminantAnalysis()]
X, y = make_classification(n_features=2, n_redundant=0, n_informative=2,
random_state=1, n_clusters_per_class=1)
rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
linearly_separable = (X, y)
datasets = [make_moons(noise=0.3, random_state=0),
make_circles(noise=0.2, factor=0.5, random_state=1),
linearly_separable
]
figure = plt.figure(figsize=(27, 9))
i = 1
# iterate over datasets
for ds_cnt, ds in enumerate(datasets):
# preprocess dataset, split into training and test part
X, y = ds
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=.4, random_state=42)
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# just plot the dataset first
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
if ds_cnt == 0:
ax.set_title("Input data")
# Plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright,
edgecolors='k')
# Plot the testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6,
edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
i += 1
# iterate over classifiers
for name, clf in zip(names, classifiers):
ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
if hasattr(clf, "decision_function"):
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
else:
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
# Put the result into a color plot
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=cm, alpha=.8)
# Plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright,
edgecolors='k')
# Plot the testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright,
edgecolors='k', alpha=0.6)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
if ds_cnt == 0:
ax.set_title(name)
ax.text(xx.max() - .3, yy.min() + .3, ('%.2f' % score).lstrip('0'),
size=15, horizontalalignment='right')
i += 1
plt.tight_layout()
plt.show()
```
| true |
code
| 0.690976 | null | null | null | null |
|
# Introduction to obspy
The obspy package is very useful to download seismic data and to do some signal processing on them. Most signal processing methods are based on the signal processing method in the Python package scipy.
First we import useful packages.
```
import obspy
import obspy.clients.earthworm.client as earthworm
import obspy.clients.fdsn.client as fdsn
from obspy import read
from obspy import read_inventory
from obspy import UTCDateTime
from obspy.core.stream import Stream
from obspy.signal.cross_correlation import correlate
import matplotlib.pyplot as plt
import numpy as np
import os
import urllib.request
%matplotlib inline
```
We are going to download data from an array of seismic stations.
```
network = 'XU'
arrayName = 'BS'
staNames = ['BS01', 'BS02', 'BS03', 'BS04', 'BS05', 'BS06', 'BS11', 'BS20', 'BS21', 'BS22', 'BS23', 'BS24', 'BS25', \
'BS26', 'BS27']
chaNames = ['SHE', 'SHN', 'SHZ']
staCodes = 'BS01,BS02,BS03,BS04,BS05,BS06,BS11,BS20,BS21,BS22,BS23,BS24,BS25,BS26,BS27'
chans = 'SHE,SHN,SHZ'
```
We also need to define the time period for which we want to download data.
```
myYear = 2010
myMonth = 8
myDay = 17
myHour = 6
TDUR = 2 * 3600.0
Tstart = UTCDateTime(year=myYear, month=myMonth, day=myDay, hour=myHour)
Tend = Tstart + TDUR
```
We start by defining the client for downloading the data
```
fdsn_client = fdsn.Client('IRIS')
```
Download the seismic data for all the stations in the array.
```
Dtmp = fdsn_client.get_waveforms(network=network, station=staCodes, location='--', channel=chans, starttime=Tstart, \
endtime=Tend, attach_response=True)
```
Some stations did not record the entire two hours. We delete these and keep only stations with a complte two hour recording.
```
ntmp = []
for ksta in range(0, len(Dtmp)):
ntmp.append(len(Dtmp[ksta]))
ntmp = max(set(ntmp), key=ntmp.count)
D = Dtmp.select(npts=ntmp)
```
This is a function for plotting after each operation on the data.
```
def plot_2hour(D, channel, offset, title):
""" Plot seismograms
D = Stream
channel = 'E', 'N', or 'Z'
offset = Offset between two stations
title = Title of the figure
"""
fig, ax = plt.subplots(figsize=(15, 10))
Dplot = D.select(component=channel)
t = (1.0 / Dplot[0].stats.sampling_rate) * np.arange(0, Dplot[0].stats.npts)
for ksta in range(0, len(Dplot)):
plt.plot(t, ksta * offset + Dplot[ksta].data, 'k')
plt.xlim(np.min(t), np.max(t))
plt.ylim(- offset, len(Dplot) * offset)
plt.title(title, fontsize=24)
plt.xlabel('Time (s)', fontsize=24)
ax.set_yticklabels([])
ax.tick_params(labelsize=20)
plot_2hour(D, 'E', 1200.0, 'Downloaded data')
```
We start by detrending the data.
```
D
D.detrend(type='linear')
plot_2hour(D, 'E', 1200.0, 'Detrended data')
```
We then taper the data.
```
D.taper(type='hann', max_percentage=None, max_length=5.0)
plot_2hour(D, 'E', 1200.0, 'Tapered data')
```
And we remove the instrment response.
```
D.remove_response(output='VEL', pre_filt=(0.2, 0.5, 10.0, 15.0), water_level=80.0)
plot_2hour(D, 'E', 1.0e-6, 'Deconvolving the instrument response')
```
Then we filter the data.
```
D.filter('bandpass', freqmin=2.0, freqmax=8.0, zerophase=True)
plot_2hour(D, 'E', 1.0e-6, 'Filtered data')
```
And we resample the data.
```
D.interpolate(100.0, method='lanczos', a=10)
D.decimate(5, no_filter=True)
plot_2hour(D, 'E', 1.0e-6, 'Resampled data')
```
We can also compute the envelope of the signal.
```
for index in range(0, len(D)):
D[index].data = obspy.signal.filter.envelope(D[index].data)
plot_2hour(D, 'E', 1.0e-6, 'Envelope')
```
You can also download the instrument response separately:
```
network = 'XQ'
station = 'ME12'
channels = 'BHE,BHN,BHZ'
location = '01'
```
This is to download the instrument response.
```
fdsn_client = fdsn.Client('IRIS')
inventory = fdsn_client.get_stations(network=network, station=station, level='response')
inventory.write('response/' + network + '_' + station + '.xml', format='STATIONXML')
```
We then read the data and start precessing the signal as we did above.
```
fdsn_client = fdsn.Client('IRIS')
Tstart = UTCDateTime(year=2008, month=4, day=1, hour=4, minute=49)
Tend = UTCDateTime(year=2008, month=4, day=1, hour=4, minute=50)
D = fdsn_client.get_waveforms(network=network, station=station, location=location, channel=channels, starttime=Tstart, endtime=Tend, attach_response=False)
D.detrend(type='linear')
D.taper(type='hann', max_percentage=None, max_length=5.0)
```
But we now use the xml file that contains the instrment response to remove it from the signal.
```
filename = 'response/' + network + '_' + station + '.xml'
inventory = read_inventory(filename, format='STATIONXML')
D.attach_response(inventory)
D.remove_response(output='VEL', pre_filt=(0.2, 0.5, 10.0, 15.0), water_level=80.0)
```
We resume signal processing.
```
D.filter('bandpass', freqmin=2.0, freqmax=8.0, zerophase=True)
D.interpolate(100.0, method='lanczos', a=10)
D.decimate(5, no_filter=True)
```
And we plot.
```
t = (1.0 / D[0].stats.sampling_rate) * np.arange(0, D[0].stats.npts)
plt.plot(t, D[0].data, 'k')
plt.xlim(np.min(t), np.max(t))
plt.title('Single waveform', fontsize=18)
plt.xlabel('Time (s)', fontsize=18)
```
Not all seismic data are stored on IRIS. This is an example of how to download data from the Northern California Earthquake Data Center (NCEDC).
```
network = 'BK'
station = 'WDC'
channels = 'BHE,BHN,BHZ'
location = '--'
```
This is to download the instrument response.
```
url = 'http://service.ncedc.org/fdsnws/station/1/query?net=' + network + '&sta=' + station + '&level=response&format=xml&includeavailability=true'
s = urllib.request.urlopen(url)
contents = s.read()
file = open('response/' + network + '_' + station + '.xml', 'wb')
file.write(contents)
file.close()
```
And this is to download the data.
```
Tstart = UTCDateTime(year=2007, month=2, day=12, hour=1, minute=11, second=54)
Tend = UTCDateTime(year=2007, month=2, day=12, hour=1, minute=12, second=54)
request = 'waveform_' + station + '.request'
file = open(request, 'w')
message = '{} {} {} {} '.format(network, station, location, channels) + \
'{:04d}-{:02d}-{:02d}T{:02d}:{:02d}:{:02d} '.format( \
Tstart.year, Tstart.month, Tstart.day, Tstart.hour, Tstart.minute, Tstart.second) + \
'{:04d}-{:02d}-{:02d}T{:02d}:{:02d}:{:02d}\n'.format( \
Tend.year, Tend.month, Tend.day, Tend.hour, Tend.minute, Tend.second)
file.write(message)
file.close()
miniseed = 'station_' + station + '.miniseed'
request = 'curl -s --data-binary @waveform_' + station + '.request -o ' + miniseed + ' http://service.ncedc.org/fdsnws/dataselect/1/query'
os.system(request)
D = read(miniseed)
D.detrend(type='linear')
D.taper(type='hann', max_percentage=None, max_length=5.0)
filename = 'response/' + network + '_' + station + '.xml'
inventory = read_inventory(filename, format='STATIONXML')
D.attach_response(inventory)
D.remove_response(output='VEL', pre_filt=(0.2, 0.5, 10.0, 15.0), water_level=80.0)
D.filter('bandpass', freqmin=2.0, freqmax=8.0, zerophase=True)
D.interpolate(100.0, method='lanczos', a=10)
D.decimate(5, no_filter=True)
t = (1.0 / D[0].stats.sampling_rate) * np.arange(0, D[0].stats.npts)
plt.plot(t, D[0].data, 'k')
plt.xlim(np.min(t), np.max(t))
plt.title('Single waveform', fontsize=18)
plt.xlabel('Time (s)', fontsize=18)
```
| true |
code
| 0.508544 | null | null | null | null |
|
```
! nvidia-smi
```
# Install
ติดตั้ง Library Transformers จาก HuggingFace
```
! pip install transformers -q
! pip install fastai2 -q
```
# Import
เราจะ Import
```
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
```
# Download Pre-trained Model
ดาวน์โหลด Weight ของโมเดล ที่เทรนไว้เรียบร้อยแล้ว ชื่อ GPT2
```
pretrained_weights = 'gpt2'
tokenizer = GPT2TokenizerFast.from_pretrained(pretrained_weights)
model = GPT2LMHeadModel.from_pretrained(pretrained_weights)
```
ใช้ Tokenizer ตัดตำ โดย Tokenizer ของ HuggingFace นี้ encode จะ Tokenize แปลงเป็น ตัวเลข Numericalize ในขั้นตอนเดียว
```
ids = tokenizer.encode("A lab at Florida Atlantic University is simulating a human cough")
ids
```
หรือ เราสามารถแยกเป็น 2 Step ได้
```
# toks = tokenizer.tokenize("A lab at Florida Atlantic University is simulating a human cough")
# toks, tokenizer.convert_tokens_to_ids(toks)
```
decode กลับเป็นข้อความต้นฉบับ
```
tokenizer.decode(ids)
```
# Generate text
```
import torch
t = torch.LongTensor(ids)[None]
preds = model.generate(t)
preds.shape
preds[0]
tokenizer.decode(preds[0].numpy())
```
# Fastai
```
from fastai2.text.all import *
path = untar_data(URLs.WIKITEXT_TINY)
path.ls()
df_train = pd.read_csv(path/"train.csv", header=None)
df_valid = pd.read_csv(path/"test.csv", header=None)
df_train.head()
all_texts = np.concatenate([df_train[0].values, df_valid[0].values])
len(all_texts)
```
# Creating TransformersTokenizer Transform
เราจะนำ Tokenizer ของ Transformer มาสร้าง Transform ใน fastai ด้วยการกำหนด encodes, decodes และ setups
```
class TransformersTokenizer(Transform):
def __init__(self, tokenizer): self.tokenizer = tokenizer
def encodes(self, x):
toks = self.tokenizer.tokenize(x)
return tensor(self.tokenizer.convert_tokens_to_ids(toks))
def decodes(self, x):
return TitledStr(self.tokenizer.decode(x.cpu().numpy()))
```
ใน encodes เราจะไม่ได้ใช้ tokenizer.encode เนื่องจากภายในนั้น มีการ preprocessing นอกจาก tokenize และ numericalize ที่เรายังไม่ต้องการในขณะนี้ และ decodes จะ return TitledStr แทนที่ string เฉย ๆ จะได้รองรับ show method
```
# list(range_of(df_train))
# list(range(len(df_train), len(all_texts)))
```
เราจะเอา Transform ที่สร้างด้านบน ไปใส่ TfmdLists โดย split ตามลำดับที่ concat ไว้ และ กำหนด dl_type DataLoader Type เป็น LMDataLoader สำหรับใช้ในงาน Lanugage Model
```
splits = [list(range_of(df_train)), list(range(len(df_train), len(all_texts)))]
tls = TfmdLists(all_texts, TransformersTokenizer(tokenizer), splits=splits, dl_type=LMDataLoader)
# tls
```
ดูข้อมูล Record แรก ของ Training Set
```
tls.train[0].shape, tls.train[0]
```
ดูเป็นข้อมูล ที่ decode แล้ว
```
# show_at(tls.train, 0)
```
ดูข้อมูล Record แรก ของ Validation Set
```
tls.valid[0].shape, tls.valid[0]
```
ดูเป็นข้อมูล ที่ decode แล้ว
```
# show_at(tls.valid, 0)
```
# DataLoaders
สร้าง DataLoaders เพื่อส่งให้กับ Model ด้วย Batch Size ขนาด 64 และ Sequence Length 1024 ตามที่ GPT2 ใช้
```
bs, sl = 4, 1024
dls = tls.dataloaders(bs=bs, seq_len=sl)
dls
dls.show_batch(max_n=5)
```
จะได้ DataLoader สำหรับ Lanugage Model ที่มี input และ label เหลื่อมกันอยู่ 1 Token สำหรับให้โมเดล Predict คำต่อไปของประโยค
# Preprocessing ไว้ก่อนให้หมด
อีกวิธีนึงคือ เราสามารถ Preprocessing ข้อมูลทั้งหมดไว้ก่อนได้เลย
```
# def tokenize(text):
# toks = tokenizer.tokenize(text)
# return tensor(tokenizer.convert_tokens_to_ids(toks))
# tokenized = [tokenize(t) for t in progress_bar(all_texts)]
# len(tokenized), tokenized[0]
```
เราจะประกาศ TransformersTokenizer ใหม่ ให้ใน encodes ไม่ต้องทำอะไร (แต่ถ้าไม่เป็น Tensor มาก็ให้ tokenize ใหม่)
```
# class TransformersTokenizer(Transform):
# def __init__(self, tokenizer): self.tokenizer = tokenizer
# def encodes(self, x):
# return x if isinstance(x, Tensor) else tokenize(x)
# def decodes(self, x):
# return TitledStr(self.tokenizer.decode(x.cpu().numpy()))
```
แล้วจึงสร้าง TfmdLists โดยส่ง tokenized (ข้อมูลทั้งหมดที่ถูก tokenize เรียบร้อยแล้ว) เข้าไป
```
# tls = TfmdLists(tokenized, TransformersTokenizer(tokenizer), splits=splits, dl_type=LMDataLoader)
# dls = tls.dataloaders(bs=bs, seq_len=sl)
# dls.show_batch(max_n=5)
```
# Fine-tune Model
เนื่องจากโมเดลของ HuggingFace นั่น return output เป็น Tuple ที่ประกอบด้วย Prediction และ Activation เพิ่มเติมอื่น ๆ สำหรับใช้ในงานอื่น ๆ แต่ในเคสนี้เรายังไม่ต้องการ ทำให้เราต้องสร้าง after_pred Callback มาคั่นเพื่อเปลี่ยนให้ return แต่ Prediction เพื่อส่งไปให้กับ Loss Function ทำงานได้ตามปกติเหมือนเดิม
```
class DropOutput(Callback):
def after_pred(self): self.learn.pred = self.pred[0]
```
ใน callback เราสามารถอ้างถึง Prediction ของโมเดล ได้ด้วย self.pred ได้เลย แต่จะเป็นการ Read-only ถ้าต้องการ Write ต้องอ้างเต็ม ๆ ด้วย self.learn.pred
ตอนนี้เราสามารถสร้าง learner เพื่อเทรนโมเดลได้แล้ว
```
learn = None
torch.cuda.empty_cache()
Perplexity??
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), cbs=[DropOutput], metrics=Perplexity()).to_fp16()
learn
```
ดูประสิทธิภาพของโมเดล ก่อนที่จะ Fine-tuned ตัวเลขแรกคือ Validation Loss ตัวที่สอง คือ Metrics ในที่นี้คือ Perplexity
```
learn.validate()
```
ได้ Perplexity 25.6 คือไม่เลวเลยทีเดียว
# Training
ก่อนเริ่มต้นเทรน เราจะเรียก lr_find หา Learning Rate กันก่อน
```
learn.lr_find()
```
แล้วเทรนไปแค่ 1 Epoch
```
learn.fit_one_cycle(1, 3e-5)
```
เราเทรนไปแค่ 1 Epoch โดยไม่ได้ปรับอะไรเลย โมเดลไม่ได้ประสิทธิภาพดีขึ้นสักเท่าไร เพราะมันดีมากอยู่แล้ว ต่อมาเราจะมาลองใช้โมเดล generate ข้อความดู ดังรูปแบบตัวอย่างใน Validation Set
```
df_valid.head(1)
prompt = "\n = Modern economy = \n \n The modern economy is driven by data, and that trend is being accelerated by"
prompt_ids = tokenizer.encode(prompt)
# prompt_ids
inp = torch.LongTensor(prompt_ids)[None].cuda()
inp.shape
preds = learn.model.generate(inp, max_length=50, num_beams=5, temperature=1.6)
preds.shape
preds[0]
tokenizer.decode(preds[0].cpu().numpy())
```
# Credit
* https://dev.fast.ai/tutorial.transformers
* https://github.com/huggingface/transformers
```
```
| true |
code
| 0.63375 | null | null | null | null |
|
**Course Announcements**
Due Friday (11:59 PM):
- D8
- Q8
- A4
- weekly project survey (*optional*)
# Geospatial Analysis
- Analysis:
- Exploratory Spatial Data Analysis
- K-Nearest Neighbors
- Tools:
- `shapely` - create and manipulate shape objects
- `geopandas` - shapely + dataframe + visualization
Today's notes are adapted from the [Scipy 2018 Tutorial - Introduction to Geospatial Data Analysis with Python](https://github.com/geopandas/scipy2018-geospatial-data).
To get all notes and examples from this workshop, do the following:
```
git clone https://github.com/geopandas/scipy2018-geospatial-data # get materials
conda env create -f environment.yml # download packages
python check_environment.py # check environment
```
Additional resource for mapping data with `geopandas`: http://darribas.org/gds15/content/labs/lab_03.html
```
# uncomment below if not yet installed
# !pip install --user geopandas
# !pip install --user descartes
%matplotlib inline
import pandas as pd
import geopandas as gpd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (17, 5)
plt.rcParams.update({'font.size': 16})
from mpl_toolkits.axes_grid1 import make_axes_locatable
import seaborn as sns
import shapely.geometry as shp
import sklearn.neighbors as skn
import sklearn.metrics as skm
import warnings
warnings.filterwarnings('ignore')
pd.options.display.max_rows = 10
#improve resolution
#comment this line if erroring on your machine/screen
%config InlineBackend.figure_format ='retina'
```
# `geopandas` basics
Examples here are from `geopandas` documentation: http://geopandas.org/mapping.html
## The Data
```
world = gpd.read_file(gpd.datasets.get_path('naturalearth_lowres'))
cities = gpd.read_file(gpd.datasets.get_path('naturalearth_cities'))
world
cities
```
## Population Estimates
```
# Plot population estimates with an accurate legend
fig, ax = plt.subplots(1, 1, figsize=(17, 7))
divider = make_axes_locatable(ax)
world.plot(column='pop_est', ax=ax, legend=True);
# Plot population estimates with a different color scale
fig, ax = plt.subplots(1, 1, figsize=(17, 7))
divider = make_axes_locatable(ax)
world.plot(column='pop_est', ax=ax, cmap='GnBu', legend=True);
```
## GDP per capita
```
# Plot by GDP per capita
# specify data
world = world[(world.pop_est>0) & (world.name!="Antarctica")]
world['gdp_per_cap'] = world.gdp_md_est / world.pop_est
# plot choropleth
fig, ax = plt.subplots(1, 1, figsize=(17, 7))
divider = make_axes_locatable(ax)
world.plot(column='gdp_per_cap', ax = ax, figsize=(17, 6), cmap='GnBu', legend = True);
world[world['gdp_per_cap'] > 0.08]
# combining maps
base = world.plot(column='pop_est', cmap='GnBu')
cities.plot(ax=base, marker='o', color='red', markersize=5);
```
## Geospatial Analysis
- Data
- EDA (Visualization)
- Analysis
### District data: Berlin
```
# berlin districts
df = gpd.read_file('https://raw.githubusercontent.com/geopandas/scipy2018-geospatial-data/master/data/berlin-districts.geojson')
df.shape
df.head()
```
### Exploratory Spatial Data Analysis
```
sns.distplot(df['median_price']);
```
We get an idea of what the median price for listings in this area of Berlin is, but we don't know how this information is spatially related.
```
df.plot(column='median_price', figsize=(18, 12), cmap='GnBu', legend=True);
```
Unless you happen to know something about this area of Germany, interpreting what's going on in this choropleth is likely a little tricky, but we can see there is some variation in median prices across this region.
### Spatial Autocorrelation
Note that if prices were distributed randomly, there would be no clustering of similar values.
To visualize the existence of global spatial autocorrelation, let's take it to the extreme. Let's look at the 68 districts with the highest Airbnb prices and those with the lowest prices.
```
# get data to dichotomize
y = df['median_price']
yb = y > y.median()
labels = ["0 Low", "1 High"]
yb = [labels[i] for i in 1*yb]
df['yb'] = yb
# take a look
fig = plt.figure(figsize=(12,10))
ax = plt.gca()
df.plot(column='yb', cmap='binary',
edgecolor='grey', legend=True, ax=ax);
```
### Airbnb Listings: Berlin
- kernel regressions
- "borrow strength" from nearby observations
A reminder that in geospatial data, there *two simultaneous senses of what is near:*
- things that similar in attribute (classical kernel regression)
- things that are similar in spatial position (spatial kernel regression)
### Question
What features would you consider including in a model to predict an Airbnb's nightly price?
First, though, let's try to predict the log of an **Airbnb's nightly price** based on a few factors:
- `accommodates`: the number of people the airbnb can accommodate
- `review_scores_rating`: the aggregate rating of the listing
- `bedrooms`: the number of bedrooms the airbnb has
- `bathrooms`: the number of bathrooms the airbnb has
- `beds`: the number of beds the airbnb offers
### Airbnb Listings: The Data
```
listings = pd.read_csv('https://raw.githubusercontent.com/geopandas/scipy2018-geospatial-data/master/data/berlin-listings.csv.gz')
listings['geometry'] = listings[['longitude', 'latitude']].apply(shp.Point, axis=1)
listings = gpd.GeoDataFrame(listings)
listings.crs = {'init':'epsg:4269'} # coordinate reference system
listings = listings.to_crs(epsg=3857)
listings.shape
listings.head()
```
### Airbnb Listings: Outcome Variable
```
fig, ax = plt.subplots(1, 1, figsize=(11, 7))
divider = make_axes_locatable(ax)
listings.sort_values('price').plot('price', cmap='plasma',
figsize=(10, 18), ax=ax, legend=True);
# distribution of price
sns.distplot(listings['price']);
listings['price_log'] = np.log(listings['price'])
fig, ax = plt.subplots(1, 1, figsize=(11, 7))
divider = make_axes_locatable(ax)
listings.sort_values('price_log').plot('price_log', cmap='plasma',
figsize=(10, 18), ax=ax, legend=True);
# distribution of log price
sns.distplot(listings['price_log'], bins=10);
```
### The Models
```
# get data for attributes model
model_data = listings[['accommodates', 'review_scores_rating',
'bedrooms', 'bathrooms', 'beds',
'price', 'geometry']].dropna()
# specify predictors (X) and outcome (y)
Xnames = ['accommodates', 'review_scores_rating',
'bedrooms', 'bathrooms', 'beds' ]
X = model_data[Xnames].values
X = X.astype(float)
y = np.log(model_data[['price']].values)
```
We'll need the spatial coordinates for each listing...
```
# get spatial coordinates
coordinates = np.vstack(model_data.geometry.apply(lambda p: np.hstack(p.xy)).values)
```
`scikit-learn`'s neighbor regressions are contained in the sklearn.neighbors module, and there are two main types:
- **KNeighborsRegressor** - uses a k-nearest neighborhood of observations around each focal site
- **RadiusNeighborsRegressor** - considers all observations within a fixed radius around each focal site.
Further, these methods can use inverse distance weighting to rank the relative importance of sites around each focal; in this way, near things are given more weight than far things, even when there's a lot of near things.
#### Training & Test
```
# specify training and test set
shuffle = np.random.permutation(len(y))
num = int(0.8*len(shuffle))
train, test = shuffle[:num],shuffle[num:]
```
#### Three Models
So, let's fit three models:
- `spatial`: using inverse distance weighting on the nearest 100 neighbors geographical space
- `attribute`: using inverse distance weighting on the nearest 100 neighbors in attribute space
- `both`: using inverse distance weighting in both geographical and attribute space.
```
# spatial
KNNR = skn.KNeighborsRegressor(weights='distance', n_neighbors=100)
spatial = KNNR.fit(coordinates[train,:],
y[train,:])
# attribute
KNNR = skn.KNeighborsRegressor(weights='distance', n_neighbors=100)
attribute = KNNR.fit(X[train,:],
y[train,])
# both
KNNR = skn.KNeighborsRegressor(weights='distance', n_neighbors=100)
both = KNNR.fit(np.hstack((coordinates,X))[train,:],
y[train,:])
```
### Performance
To score them, I'm going to look at the scatterplot and get their % explained variance:
#### Training Data
```
# generate predictions in the training set
sp_ypred_train = spatial.predict(coordinates[train,:]) # spatial
att_ypred_train = attribute.predict(X[train,:]) # attribute
both_ypred_train = both.predict(np.hstack((X,coordinates))[train,:]) # combo
# variance explained in training data
(skm.explained_variance_score(y[train,], sp_ypred_train),
skm.explained_variance_score(y[train,], att_ypred_train),
skm.explained_variance_score(y[train,], both_ypred_train))
# take a look at predictions
plt.plot(y[train,], sp_ypred_train, '.')
plt.xlabel('reported')
plt.ylabel('predicted');
```
#### Test Data
```
# generate predictions in the test set
sp_ypred = spatial.predict(coordinates[test,:])
att_ypred = attribute.predict(X[test,:])
both_ypred = both.predict(np.hstack((X,coordinates))[test,:])
(skm.explained_variance_score(y[test,], sp_ypred),
skm.explained_variance_score(y[test,], att_ypred),
skm.explained_variance_score(y[test,], both_ypred))
# take a look at predictions
plt.plot(y[test,], both_ypred, '.')
plt.xlabel('reported')
plt.ylabel('predicted');
```
### Model Improvement
None of these models is performing particularly well...
Cosiderations for improvement:
- features included in attribute model
- model tuning (i.e. number of nearest neighbors)
- model selected
- etc...
One method that can exploit the fact that local data may be more informative in predicting $y$ at site $i$ than distant data is **Geographically Weighted Regression**, a type of Generalized Additive Spatial Model. Kind of like a Kernel Regression, GWR conducts a bunch of regressions at each training site only considering data near that site. This means it works like the kernel regressions above, but uses *both* the coordinates *and* the data in $X$ to predict $y$ at each site. It optimizes its sense of "local" depending on some information criteria or fit score.
You can find this in the `gwr` package, and significant development is ongoing on this at `https://github.com/pysal/gwr`.
| true |
code
| 0.691107 | null | null | null | null |
|
## Coding Exercise #0703
### 1. Softmax regression (multi-class logistic regression):
```
# import tensorflow as tf
import tensorflow.compat.v1 as tf
import numpy as np
import pandas as pd
from sklearn.preprocessing import scale
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
tf.disable_v2_behavior()
```
#### 1.1. Read in the data:
```
# We will use Iris data.
# 4 explanatory variables.
# 3 classes for the response variable.
data_raw = load_iris()
data_raw.keys()
# Print out the description.
# print(data_raw['DESCR'])
X = data_raw['data']
y = data_raw['target']
# Check the shape.
print(X.shape)
print(y.shape)
```
#### 1.2. Data pre-processing:
```
# One-Hot-Encoding.
y = np.array(pd.get_dummies(y, drop_first=False)) # drop_frist = False for one-hot-encoding.
y.shape
# Scaling
X = scale(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=3)
n_train_size = y_train.shape[0]
```
#### 1.3. Do the necessary definitions:
```
batch_size = 100 # Size of each (mini) batch.
n_epochs = 30000 # Number of epochs.
learn_rate = 0.05
W = tf.Variable(tf.ones([4,3])) # Initial value of the weights = 1.
b = tf.Variable(tf.ones([3])) # Initial value of the bias = 1.
X_ph = tf.placeholder(tf.float32, shape=(None, 4)) # Number of rows not specified. Number of columns = numbmer of X variables = 4.
y_ph = tf.placeholder(tf.float32, shape=(None,3)) # Number of rows not specified. Number of columns = number of classes of the y variable = 3.
# Model.
# Not strictly necessary to apply the softmax activation. => in the end we will apply argmax() function to predict the label!
# y_model = tf.nn.softmax(tf.matmul(X_ph, W) + b)
# The following will work just fine.
y_model = tf.matmul(X_ph, W) + b
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels=y_ph, logits=y_model)) # Loss = cross entropy.
optimizer = tf.train.GradientDescentOptimizer(learning_rate = learn_rate)
train = optimizer.minimize(loss) # Define training.
init = tf.global_variables_initializer() # Define Variable initialization.
```
#### 1.4. Training and Testing:
```
with tf.Session() as sess:
# Variables initialization.
sess.run(init)
# Training.
for i in range(n_epochs):
idx_rnd = np.random.choice(range(n_train_size),batch_size,replace=False) # Random sampling w/o replacement for the batch indices.
batch_X, batch_y = [X_train[idx_rnd,:], y_train[idx_rnd,:]] # Get a batch.
my_feed = {X_ph:batch_X, y_ph:batch_y} # Prepare the feed data as a dictionary.
sess.run(train, feed_dict = my_feed)
if (i + 1) % 2000 == 0: print("Step : {}".format(i + 1)) # Print the step number at every multiple of 2000.
# Testing.
correct_predictions = tf.equal(tf.argmax(y_ph, axis=1), tf.argmax(y_model, axis=1)) # In argmax(), axis=1 means horizontal direction.
accuracy = tf.reduce_mean(tf.cast(correct_predictions, tf.float32)) # Recast the Boolean as float32 first. Then calculate the mean.
accuracy_value = sess.run(accuracy, feed_dict={X_ph:X_test, y_ph:y_test}) # Actually run the test with the test data.
```
Print the testing result.
```
print("Accuracy = {:5.3f}".format(accuracy_value))
```
| true |
code
| 0.689711 | null | null | null | null |
|
<img src="qiskit-heading.gif" width="500 px" align="center">
# _*Qiskit Aqua: Experimenting with Traveling Salesman problem with variational quantum eigensolver*_
This notebook is based on an official notebook by Qiskit team, available at https://github.com/qiskit/qiskit-tutorial under the [Apache License 2.0](https://github.com/Qiskit/qiskit-tutorial/blob/master/LICENSE) license.
The original notebook was developed by Antonio Mezzacapo<sup>[1]</sup>, Jay Gambetta<sup>[1]</sup>, Kristan Temme<sup>[1]</sup>, Ramis Movassagh<sup>[1]</sup>, Albert Frisch<sup>[1]</sup>, Takashi Imamichi<sup>[1]</sup>, Giacomo Nannicni<sup>[1]</sup>, Richard Chen<sup>[1]</sup>, Marco Pistoia<sup>[1]</sup>, Stephen Wood<sup>[1]</sup>(<sup>[1]</sup>IBMQ)
Your **TASK** is to execute every step of this notebook while learning to use qiskit-aqua and also how to leverage general problem modeling into know problems that qiskit-aqua can solve, namely the [Travelling salesman problem](https://en.wikipedia.org/wiki/Travelling_salesman_problem).
## Introduction
Many problems in quantitative fields such as finance and engineering are optimization problems. Optimization problems lay at the core of complex decision-making and definition of strategies.
Optimization (or combinatorial optimization) means searching for an optimal solution in a finite or countably infinite set of potential solutions. Optimality is defined with respect to some criterion function, which is to be minimized or maximized. This is typically called cost function or objective function.
**Typical optimization problems**
Minimization: cost, distance, length of a traversal, weight, processing time, material, energy consumption, number of objects
Maximization: profit, value, output, return, yield, utility, efficiency, capacity, number of objects
We consider here max-cut problem of practical interest in many fields, and show how they can mapped on quantum computers.
### Weighted Max-Cut
Max-Cut is an NP-complete problem, with applications in clustering, network science, and statistical physics. To grasp how practical applications are mapped into given Max-Cut instances, consider a system of many people that can interact and influence each other. Individuals can be represented by vertices of a graph, and their interactions seen as pairwise connections between vertices of the graph, or edges. With this representation in mind, it is easy to model typical marketing problems. For example, suppose that it is assumed that individuals will influence each other's buying decisions, and knowledge is given about how strong they will influence each other. The influence can be modeled by weights assigned on each edge of the graph. It is possible then to predict the outcome of a marketing strategy in which products are offered for free to some individuals, and then ask which is the optimal subset of individuals that should get the free products, in order to maximize revenues.
The formal definition of this problem is the following:
Consider an $n$-node undirected graph *G = (V, E)* where *|V| = n* with edge weights $w_{ij}>0$, $w_{ij}=w_{ji}$, for $(i, j)\in E$. A cut is defined as a partition of the original set V into two subsets. The cost function to be optimized is in this case the sum of weights of edges connecting points in the two different subsets, *crossing* the cut. By assigning $x_i=0$ or $x_i=1$ to each node $i$, one tries to maximize the global profit function (here and in the following summations run over indices 0,1,...n-1)
$$\tilde{C}(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j).$$
In our simple marketing model, $w_{ij}$ represents the probability that the person $j$ will buy a product after $i$ gets a free one. Note that the weights $w_{ij}$ can in principle be greater than $1$, corresponding to the case where the individual $j$ will buy more than one product. Maximizing the total buying probability corresponds to maximizing the total future revenues. In the case where the profit probability will be greater than the cost of the initial free samples, the strategy is a convenient one. An extension to this model has the nodes themselves carry weights, which can be regarded, in our marketing model, as the likelihood that a person granted with a free sample of the product will buy it again in the future. With this additional information in our model, the objective function to maximize becomes
$$C(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j)+\sum_i w_i x_i. $$
In order to find a solution to this problem on a quantum computer, one needs first to map it to an Ising Hamiltonian. This can be done with the assignment $x_i\rightarrow (1-Z_i)/2$, where $Z_i$ is the Pauli Z operator that has eigenvalues $\pm 1$. Doing this we find that
$$C(\textbf{Z}) = \sum_{i,j} \frac{w_{ij}}{4} (1-Z_i)(1+Z_j) + \sum_i \frac{w_i}{2} (1-Z_i) = -\frac{1}{2}\left( \sum_{i<j} w_{ij} Z_i Z_j +\sum_i w_i Z_i\right)+\mathrm{const},$$
where const = $\sum_{i<j}w_{ij}/2+\sum_i w_i/2 $. In other terms, the weighted Max-Cut problem is equivalent to minimizing the Ising Hamiltonian
$$ H = \sum_i w_i Z_i + \sum_{i<j} w_{ij} Z_iZ_j.$$
Aqua can generate the Ising Hamiltonian for the first profit function $\tilde{C}$.
### Approximate Universal Quantum Computing for Optimization Problems
There has been a considerable amount of interest in recent times about the use of quantum computers to find a solution to combinatorial problems. It is important to say that, given the classical nature of combinatorial problems, exponential speedup in using quantum computers compared to the best classical algorithms is not guaranteed. However, due to the nature and importance of the target problems, it is worth investigating heuristic approaches on a quantum computer that could indeed speed up some problem instances. Here we demonstrate an approach that is based on the Quantum Approximate Optimization Algorithm by Farhi, Goldstone, and Gutman (2014). We frame the algorithm in the context of *approximate quantum computing*, given its heuristic nature.
The Algorithm works as follows:
1. Choose the $w_i$ and $w_{ij}$ in the target Ising problem. In principle, even higher powers of Z are allowed.
2. Choose the depth of the quantum circuit $m$. Note that the depth can be modified adaptively.
3. Choose a set of controls $\theta$ and make a trial function $|\psi(\boldsymbol\theta)\rangle$, built using a quantum circuit made of C-Phase gates and single-qubit Y rotations, parameterized by the components of $\boldsymbol\theta$.
4. Evaluate $C(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)~|H|~\psi(\boldsymbol\theta)\rangle = \sum_i w_i \langle\psi(\boldsymbol\theta)~|Z_i|~\psi(\boldsymbol\theta)\rangle+ \sum_{i<j} w_{ij} \langle\psi(\boldsymbol\theta)~|Z_iZ_j|~\psi(\boldsymbol\theta)\rangle$ by sampling the outcome of the circuit in the Z-basis and adding the expectation values of the individual Ising terms together. In general, different control points around $\boldsymbol\theta$ have to be estimated, depending on the classical optimizer chosen.
5. Use a classical optimizer to choose a new set of controls.
6. Continue until $C(\boldsymbol\theta)$ reaches a minimum, close enough to the solution $\boldsymbol\theta^*$.
7. Use the last $\boldsymbol\theta$ to generate a final set of samples from the distribution $|\langle z_i~|\psi(\boldsymbol\theta)\rangle|^2\;\forall i$ to obtain the answer.
It is our belief the difficulty of finding good heuristic algorithms will come down to the choice of an appropriate trial wavefunction. For example, one could consider a trial function whose entanglement best aligns with the target problem, or simply make the amount of entanglement a variable. In this tutorial, we will consider a simple trial function of the form
$$|\psi(\theta)\rangle = [U_\mathrm{single}(\boldsymbol\theta) U_\mathrm{entangler}]^m |+\rangle$$
where $U_\mathrm{entangler}$ is a collection of C-Phase gates (fully entangling gates), and $U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})$, where $n$ is the number of qubits and $m$ is the depth of the quantum circuit. The motivation for this choice is that for these classical problems this choice allows us to search over the space of quantum states that have only real coefficients, still exploiting the entanglement to potentially converge faster to the solution.
One advantage of using this sampling method compared to adiabatic approaches is that the target Ising Hamiltonian does not have to be implemented directly on hardware, allowing this algorithm not to be limited to the connectivity of the device. Furthermore, higher-order terms in the cost function, such as $Z_iZ_jZ_k$, can also be sampled efficiently, whereas in adiabatic or annealing approaches they are generally impractical to deal with.
References:
- A. Lucas, Frontiers in Physics 2, 5 (2014)
- E. Farhi, J. Goldstone, S. Gutmann e-print arXiv 1411.4028 (2014)
- D. Wecker, M. B. Hastings, M. Troyer Phys. Rev. A 94, 022309 (2016)
- E. Farhi, J. Goldstone, S. Gutmann, H. Neven e-print arXiv 1703.06199 (2017)
```
# useful additional packages
import matplotlib.pyplot as plt
import matplotlib.axes as axes
%matplotlib inline
import numpy as np
import networkx as nx
from qiskit.tools.visualization import plot_histogram
from qiskit.aqua import Operator, run_algorithm, get_algorithm_instance
from qiskit.aqua.input import get_input_instance
from qiskit.aqua.translators.ising import max_cut, tsp
# setup aqua logging
import logging
from qiskit.aqua._logging import set_logging_config, build_logging_config
# set_logging_config(build_logging_config(logging.DEBUG)) # choose INFO, DEBUG to see the log
# ignoring deprecation errors on matplotlib
import warnings
import matplotlib.cbook
warnings.filterwarnings("ignore",category=matplotlib.cbook.mplDeprecation)
```
### [Optional] Setup token to run the experiment on a real device
If you would like to run the experiement on a real device, you need to setup your account first.
Note: If you do not store your token yet, use `IBMQ.save_accounts()` to store it first.
```
from qiskit import IBMQ
IBMQ.load_accounts()
```
## Traveling Salesman Problem
In addition to being a notorious NP-complete problem that has drawn the attention of computer scientists and mathematicians for over two centuries, the Traveling Salesman Problem (TSP) has important bearings on finance and marketing, as its name suggests. Colloquially speaking, the traveling salesman is a person that goes from city to city to sell merchandise. The objective in this case is to find the shortest path that would enable the salesman to visit all the cities and return to its hometown, i.e. the city where he started traveling. By doing this, the salesman gets to maximize potential sales in the least amount of time.
The problem derives its importance from its "hardness" and ubiquitous equivalence to other relevant combinatorial optimization problems that arise in practice.
The mathematical formulation with some early analysis was proposed by W.R. Hamilton in the early 19th century. Mathematically the problem is, as in the case of Max-Cut, best abstracted in terms of graphs. The TSP on the nodes of a graph asks for the shortest *Hamiltonian cycle* that can be taken through each of the nodes. A Hamilton cycle is a closed path that uses every vertex of a graph once. The general solution is unknown and an algorithm that finds it efficiently (e.g., in polynomial time) is not expected to exist.
Find the shortest Hamiltonian cycle in a graph $G=(V,E)$ with $n=|V|$ nodes and distances, $w_{ij}$ (distance from vertex $i$ to vertex $j$). A Hamiltonian cycle is described by $N^2$ variables $x_{i,p}$, where $i$ represents the node and $p$ represents its order in a prospective cycle. The decision variable takes the value 1 if the solution occurs at node $i$ at time order $p$. We require that every node can only appear once in the cycle, and for each time a node has to occur. This amounts to the two constraints (here and in the following, whenever not specified, the summands run over 0,1,...N-1)
$$\sum_{i} x_{i,p} = 1 ~~\forall p$$
$$\sum_{p} x_{i,p} = 1 ~~\forall i.$$
For nodes in our prospective ordering, if $x_{i,p}$ and $x_{j,p+1}$ are both 1, then there should be an energy penalty if $(i,j) \notin E$ (not connected in the graph). The form of this penalty is
$$\sum_{i,j\notin E}\sum_{p} x_{i,p}x_{j,p+1}>0,$$
where it is assumed the boundary condition of the Hamiltonian cycle $(p=N)\equiv (p=0)$. However, here it will be assumed a fully connected graph and not include this term. The distance that needs to be minimized is
$$C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}.$$
Putting this all together in a single objective function to be minimized, we get the following:
$$C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}+ A\sum_p\left(1- \sum_i x_{i,p}\right)^2+A\sum_i\left(1- \sum_p x_{i,p}\right)^2,$$
where $A$ is a free parameter. One needs to ensure that $A$ is large enough so that these constraints are respected. One way to do this is to choose $A$ such that $A > \mathrm{max}(w_{ij})$.
Once again, it is easy to map the problem in this form to a quantum computer, and the solution will be found by minimizing a Ising Hamiltonian.
```
# Generating a graph of 3 nodes
n = 3
num_qubits = n ** 2
ins = tsp.random_tsp(n)
G = nx.Graph()
G.add_nodes_from(np.arange(0, n, 1))
colors = ['r' for node in G.nodes()]
pos = {k: v for k, v in enumerate(ins.coord)}
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G, node_color=colors, node_size=600, alpha=.8, ax=default_axes, pos=pos)
print('distance\n', ins.w)
```
### Brute force approach
```
from itertools import permutations
def brute_force_tsp(w, N):
a=list(permutations(range(1,N)))
last_best_distance = 1e10
for i in a:
distance = 0
pre_j = 0
for j in i:
distance = distance + w[j,pre_j]
pre_j = j
distance = distance + w[pre_j,0]
order = (0,) + i
if distance < last_best_distance:
best_order = order
last_best_distance = distance
print('order = ' + str(order) + ' Distance = ' + str(distance))
return last_best_distance, best_order
best_distance, best_order = brute_force_tsp(ins.w, ins.dim)
print('Best order from brute force = ' + str(best_order) + ' with total distance = ' + str(best_distance))
def draw_tsp_solution(G, order, colors, pos):
G2 = G.copy()
n = len(order)
for i in range(n):
j = (i + 1) % n
G2.add_edge(order[i], order[j])
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G2, node_color=colors, node_size=600, alpha=.8, ax=default_axes, pos=pos)
draw_tsp_solution(G, best_order, colors, pos)
```
### Mapping to the Ising problem
```
qubitOp, offset = tsp.get_tsp_qubitops(ins)
algo_input = get_input_instance('EnergyInput')
algo_input.qubit_op = qubitOp
```
### Checking that the full Hamiltonian gives the right cost
```
#Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
algorithm_cfg = {
'name': 'ExactEigensolver',
}
params = {
'problem': {'name': 'ising'},
'algorithm': algorithm_cfg
}
result = run_algorithm(params,algo_input)
print('energy:', result['energy'])
#print('tsp objective:', result['energy'] + offset)
x = tsp.sample_most_likely(result['eigvecs'][0])
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos)
```
### Running it on quantum computer
We run the optimization routine using a feedback loop with a quantum computer that uses trial functions built with Y single-qubit rotations, $U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})$, and entangler steps $U_\mathrm{entangler}$.
```
algorithm_cfg = {
'name': 'VQE',
'operator_mode': 'matrix'
}
optimizer_cfg = {
'name': 'SPSA',
'max_trials': 300
}
var_form_cfg = {
'name': 'RY',
'depth': 5,
'entanglement': 'linear'
}
params = {
'problem': {'name': 'ising', 'random_seed': 10598},
'algorithm': algorithm_cfg,
'optimizer': optimizer_cfg,
'variational_form': var_form_cfg,
'backend': {'name': 'statevector_simulator'}
}
result = run_algorithm(params,algo_input)
print('energy:', result['energy'])
print('time:', result['eval_time'])
#print('tsp objective:', result['energy'] + offset)
x = tsp.sample_most_likely(result['eigvecs'][0])
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos)
# run quantum algorithm with shots
params['algorithm']['operator_mode'] = 'grouped_paulis'
params['backend']['name'] = 'qasm_simulator'
params['backend']['shots'] = 1024
result = run_algorithm(params,algo_input)
print('energy:', result['energy'])
print('time:', result['eval_time'])
#print('tsp objective:', result['energy'] + offset)
x = tsp.sample_most_likely(result['eigvecs'][0])
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
plot_histogram(result['eigvecs'][0])
draw_tsp_solution(G, z, colors, pos)
```
| true |
code
| 0.472379 | null | null | null | null |
|
```
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
#export
from fastai.basics import *
from fastai.text.core import *
from fastai.text.data import *
from fastai.text.models.core import *
from fastai.text.models.awdlstm import *
from fastai.callback.rnn import *
from fastai.callback.progress import *
#hide
from nbdev.showdoc import *
#default_exp text.learner
```
# Learner for the text application
> All the functions necessary to build `Learner` suitable for transfer learning in NLP
The most important functions of this module are `language_model_learner` and `text_classifier_learner`. They will help you define a `Learner` using a pretrained model. See the [text tutorial](http://docs.fast.ai/tutorial.text) for exmaples of use.
## Loading a pretrained model
In text, to load a pretrained model, we need to adapt the embeddings of the vocabulary used for the pre-training to the vocabulary of our current corpus.
```
#export
def match_embeds(old_wgts, old_vocab, new_vocab):
"Convert the embedding in `old_wgts` to go from `old_vocab` to `new_vocab`."
bias, wgts = old_wgts.get('1.decoder.bias', None), old_wgts['0.encoder.weight']
wgts_m = wgts.mean(0)
new_wgts = wgts.new_zeros((len(new_vocab),wgts.size(1)))
if bias is not None:
bias_m = bias.mean(0)
new_bias = bias.new_zeros((len(new_vocab),))
old_o2i = old_vocab.o2i if hasattr(old_vocab, 'o2i') else {w:i for i,w in enumerate(old_vocab)}
for i,w in enumerate(new_vocab):
idx = old_o2i.get(w, -1)
new_wgts[i] = wgts[idx] if idx>=0 else wgts_m
if bias is not None: new_bias[i] = bias[idx] if idx>=0 else bias_m
old_wgts['0.encoder.weight'] = new_wgts
if '0.encoder_dp.emb.weight' in old_wgts: old_wgts['0.encoder_dp.emb.weight'] = new_wgts.clone()
old_wgts['1.decoder.weight'] = new_wgts.clone()
if bias is not None: old_wgts['1.decoder.bias'] = new_bias
return old_wgts
```
For words in `new_vocab` that don't have a corresponding match in `old_vocab`, we use the mean of all pretrained embeddings.
```
wgts = {'0.encoder.weight': torch.randn(5,3)}
new_wgts = match_embeds(wgts.copy(), ['a', 'b', 'c'], ['a', 'c', 'd', 'b'])
old,new = wgts['0.encoder.weight'],new_wgts['0.encoder.weight']
test_eq(new[0], old[0])
test_eq(new[1], old[2])
test_eq(new[2], old.mean(0))
test_eq(new[3], old[1])
#hide
#With bias
wgts = {'0.encoder.weight': torch.randn(5,3), '1.decoder.bias': torch.randn(5)}
new_wgts = match_embeds(wgts.copy(), ['a', 'b', 'c'], ['a', 'c', 'd', 'b'])
old_w,new_w = wgts['0.encoder.weight'],new_wgts['0.encoder.weight']
old_b,new_b = wgts['1.decoder.bias'], new_wgts['1.decoder.bias']
test_eq(new_w[0], old_w[0])
test_eq(new_w[1], old_w[2])
test_eq(new_w[2], old_w.mean(0))
test_eq(new_w[3], old_w[1])
test_eq(new_b[0], old_b[0])
test_eq(new_b[1], old_b[2])
test_eq(new_b[2], old_b.mean(0))
test_eq(new_b[3], old_b[1])
#export
def _get_text_vocab(dls):
vocab = dls.vocab
if isinstance(vocab, L): vocab = vocab[0]
return vocab
#export
def load_ignore_keys(model, wgts):
"Load `wgts` in `model` ignoring the names of the keys, just taking parameters in order"
sd = model.state_dict()
for k1,k2 in zip(sd.keys(), wgts.keys()): sd[k1].data = wgts[k2].data.clone()
return model.load_state_dict(sd)
#export
def _rm_module(n):
t = n.split('.')
for i in range(len(t)-1, -1, -1):
if t[i] == 'module':
t.pop(i)
break
return '.'.join(t)
#export
#For previous versions compatibility, remove for release
def clean_raw_keys(wgts):
keys = list(wgts.keys())
for k in keys:
t = k.split('.module')
if f'{_rm_module(k)}_raw' in keys: del wgts[k]
return wgts
#export
#For previous versions compatibility, remove for release
def load_model_text(file, model, opt, with_opt=None, device=None, strict=True):
"Load `model` from `file` along with `opt` (if available, and if `with_opt`)"
distrib_barrier()
if isinstance(device, int): device = torch.device('cuda', device)
elif device is None: device = 'cpu'
state = torch.load(file, map_location=device)
hasopt = set(state)=={'model', 'opt'}
model_state = state['model'] if hasopt else state
get_model(model).load_state_dict(clean_raw_keys(model_state), strict=strict)
if hasopt and ifnone(with_opt,True):
try: opt.load_state_dict(state['opt'])
except:
if with_opt: warn("Could not load the optimizer state.")
elif with_opt: warn("Saved filed doesn't contain an optimizer state.")
#export
@log_args(but_as=Learner.__init__)
@delegates(Learner.__init__)
class TextLearner(Learner):
"Basic class for a `Learner` in NLP."
def __init__(self, dls, model, alpha=2., beta=1., moms=(0.8,0.7,0.8), **kwargs):
super().__init__(dls, model, moms=moms, **kwargs)
self.add_cbs([ModelResetter(), RNNRegularizer(alpha=alpha, beta=beta)])
def save_encoder(self, file):
"Save the encoder to `file` in the model directory"
if rank_distrib(): return # don't save if child proc
encoder = get_model(self.model)[0]
if hasattr(encoder, 'module'): encoder = encoder.module
torch.save(encoder.state_dict(), join_path_file(file, self.path/self.model_dir, ext='.pth'))
def load_encoder(self, file, device=None):
"Load the encoder `file` from the model directory, optionally ensuring it's on `device`"
encoder = get_model(self.model)[0]
if device is None: device = self.dls.device
if hasattr(encoder, 'module'): encoder = encoder.module
distrib_barrier()
wgts = torch.load(join_path_file(file,self.path/self.model_dir, ext='.pth'), map_location=device)
encoder.load_state_dict(clean_raw_keys(wgts))
self.freeze()
return self
def load_pretrained(self, wgts_fname, vocab_fname, model=None):
"Load a pretrained model and adapt it to the data vocabulary."
old_vocab = load_pickle(vocab_fname)
new_vocab = _get_text_vocab(self.dls)
distrib_barrier()
wgts = torch.load(wgts_fname, map_location = lambda storage,loc: storage)
if 'model' in wgts: wgts = wgts['model'] #Just in case the pretrained model was saved with an optimizer
wgts = match_embeds(wgts, old_vocab, new_vocab)
load_ignore_keys(self.model if model is None else model, clean_raw_keys(wgts))
self.freeze()
return self
#For previous versions compatibility. Remove at release
@delegates(load_model_text)
def load(self, file, with_opt=None, device=None, **kwargs):
if device is None: device = self.dls.device
if self.opt is None: self.create_opt()
file = join_path_file(file, self.path/self.model_dir, ext='.pth')
load_model_text(file, self.model, self.opt, device=device, **kwargs)
return self
```
Adds a `ModelResetter` and an `RNNRegularizer` with `alpha` and `beta` to the callbacks, the rest is the same as `Learner` init.
This `Learner` adds functionality to the base class:
```
show_doc(TextLearner.load_pretrained)
```
`wgts_fname` should point to the weights of the pretrained model and `vocab_fname` to the vocabulary used to pretrain it.
```
show_doc(TextLearner.save_encoder)
```
The model directory is `Learner.path/Learner.model_dir`.
```
show_doc(TextLearner.load_encoder)
```
## Language modeling predictions
For language modeling, the predict method is quite different form the other applications, which is why it needs its own subclass.
```
#export
def decode_spec_tokens(tokens):
"Decode the special tokens in `tokens`"
new_toks,rule,arg = [],None,None
for t in tokens:
if t in [TK_MAJ, TK_UP, TK_REP, TK_WREP]: rule = t
elif rule is None: new_toks.append(t)
elif rule == TK_MAJ:
new_toks.append(t[:1].upper() + t[1:].lower())
rule = None
elif rule == TK_UP:
new_toks.append(t.upper())
rule = None
elif arg is None:
try: arg = int(t)
except: rule = None
else:
if rule == TK_REP: new_toks.append(t * arg)
else: new_toks += [t] * arg
return new_toks
test_eq(decode_spec_tokens(['xxmaj', 'text']), ['Text'])
test_eq(decode_spec_tokens(['xxup', 'text']), ['TEXT'])
test_eq(decode_spec_tokens(['xxrep', '3', 'a']), ['aaa'])
test_eq(decode_spec_tokens(['xxwrep', '3', 'word']), ['word', 'word', 'word'])
#export
@log_args(but_as=TextLearner.__init__)
class LMLearner(TextLearner):
"Add functionality to `TextLearner` when dealing with a language model"
def predict(self, text, n_words=1, no_unk=True, temperature=1., min_p=None, no_bar=False,
decoder=decode_spec_tokens, only_last_word=False):
"Return `text` and the `n_words` that come after"
self.model.reset()
idxs = idxs_all = self.dls.test_dl([text]).items[0].to(self.dls.device)
if no_unk: unk_idx = self.dls.vocab.index(UNK)
for _ in (range(n_words) if no_bar else progress_bar(range(n_words), leave=False)):
with self.no_bar(): preds,_ = self.get_preds(dl=[(idxs[None],)])
res = preds[0][-1]
if no_unk: res[unk_idx] = 0.
if min_p is not None:
if (res >= min_p).float().sum() == 0:
warn(f"There is no item with probability >= {min_p}, try a lower value.")
else: res[res < min_p] = 0.
if temperature != 1.: res.pow_(1 / temperature)
idx = torch.multinomial(res, 1).item()
idxs = idxs_all = torch.cat([idxs_all, idxs.new([idx])])
if only_last_word: idxs = idxs[-1][None]
num = self.dls.train_ds.numericalize
tokens = [num.vocab[i] for i in idxs_all if num.vocab[i] not in [BOS, PAD]]
sep = self.dls.train_ds.tokenizer.sep
return sep.join(decoder(tokens))
@delegates(Learner.get_preds)
def get_preds(self, concat_dim=1, **kwargs): return super().get_preds(concat_dim=1, **kwargs)
show_doc(LMLearner, title_level=3)
show_doc(LMLearner.predict)
```
The words are picked randomly among the predictions, depending on the probability of each index. `no_unk` means we never pick the `UNK` token, `temperature` is applied to the predictions, if `min_p` is passed, we don't consider the indices with a probability lower than it. Set `no_bar` to `True` if you don't want any progress bar, and you can pass a long a custom `decoder` to process the predicted tokens.
## `Learner` convenience functions
```
#export
from fastai.text.models.core import _model_meta
#export
def _get_text_vocab(dls):
vocab = dls.vocab
if isinstance(vocab, L): vocab = vocab[0]
return vocab
#export
@log_args(to_return=True, but_as=Learner.__init__)
@delegates(Learner.__init__)
def language_model_learner(dls, arch, config=None, drop_mult=1., backwards=False, pretrained=True, pretrained_fnames=None, **kwargs):
"Create a `Learner` with a language model from `dls` and `arch`."
vocab = _get_text_vocab(dls)
model = get_language_model(arch, len(vocab), config=config, drop_mult=drop_mult)
meta = _model_meta[arch]
learn = LMLearner(dls, model, loss_func=CrossEntropyLossFlat(), splitter=meta['split_lm'], **kwargs)
url = 'url_bwd' if backwards else 'url'
if pretrained or pretrained_fnames:
if pretrained_fnames is not None:
fnames = [learn.path/learn.model_dir/f'{fn}.{ext}' for fn,ext in zip(pretrained_fnames, ['pth', 'pkl'])]
else:
if url not in meta:
warn("There are no pretrained weights for that architecture yet!")
return learn
model_path = untar_data(meta[url] , c_key='model')
try: fnames = [list(model_path.glob(f'*.{ext}'))[0] for ext in ['pth', 'pkl']]
except IndexError: print(f'The model in {model_path} is incomplete, download again'); raise
learn = learn.load_pretrained(*fnames)
return learn
```
You can use the `config` to customize the architecture used (change the values from `awd_lstm_lm_config` for this), `pretrained` will use fastai's pretrained model for this `arch` (if available) or you can pass specific `pretrained_fnames` containing your own pretrained model and the corresponding vocabulary. All other arguments are passed to `Learner`.
```
path = untar_data(URLs.IMDB_SAMPLE)
df = pd.read_csv(path/'texts.csv')
dls = TextDataLoaders.from_df(df, path=path, text_col='text', is_lm=True, valid_col='is_valid')
learn = language_model_learner(dls, AWD_LSTM)
```
You can then use the `.predict` method to generate new text.
```
learn.predict('This movie is about', n_words=20)
```
By default the entire sentence is feed again to the model after each predicted word, this little trick shows an improvement on the quality of the generated text. If you want to feed only the last word, specify argument `only_last_word`.
```
learn.predict('This movie is about', n_words=20, only_last_word=True)
#export
@log_args(to_return=True, but_as=Learner.__init__)
@delegates(Learner.__init__)
def text_classifier_learner(dls, arch, seq_len=72, config=None, backwards=False, pretrained=True, drop_mult=0.5, n_out=None,
lin_ftrs=None, ps=None, max_len=72*20, y_range=None, **kwargs):
"Create a `Learner` with a text classifier from `dls` and `arch`."
vocab = _get_text_vocab(dls)
if n_out is None: n_out = get_c(dls)
assert n_out, "`n_out` is not defined, and could not be inferred from data, set `dls.c` or pass `n_out`"
model = get_text_classifier(arch, len(vocab), n_out, seq_len=seq_len, config=config, y_range=y_range,
drop_mult=drop_mult, lin_ftrs=lin_ftrs, ps=ps, max_len=max_len)
meta = _model_meta[arch]
learn = TextLearner(dls, model, splitter=meta['split_clas'], **kwargs)
url = 'url_bwd' if backwards else 'url'
if pretrained:
if url not in meta:
warn("There are no pretrained weights for that architecture yet!")
return learn
model_path = untar_data(meta[url], c_key='model')
try: fnames = [list(model_path.glob(f'*.{ext}'))[0] for ext in ['pth', 'pkl']]
except IndexError: print(f'The model in {model_path} is incomplete, download again'); raise
learn = learn.load_pretrained(*fnames, model=learn.model[0])
learn.freeze()
return learn
```
You can use the `config` to customize the architecture used (change the values from `awd_lstm_clas_config` for this), `pretrained` will use fastai's pretrained model for this `arch` (if available). `drop_mult` is a global multiplier applied to control all dropouts. `n_out` is usually inferred from the `dls` but you may pass it.
The model uses a `SentenceEncoder`, which means the texts are passed `seq_len` tokens at a time, and will only compute the gradients on the last `max_len` steps. `lin_ftrs` and `ps` are passed to `get_text_classifier`.
All other arguments are passed to `Learner`.
```
path = untar_data(URLs.IMDB_SAMPLE)
df = pd.read_csv(path/'texts.csv')
dls = TextDataLoaders.from_df(df, path=path, text_col='text', label_col='label', valid_col='is_valid')
learn = text_classifier_learner(dls, AWD_LSTM)
```
## Show methods -
```
#export
@typedispatch
def show_results(x: LMTensorText, y, samples, outs, ctxs=None, max_n=10, **kwargs):
if ctxs is None: ctxs = get_empty_df(min(len(samples), max_n))
for i,l in enumerate(['input', 'target']):
ctxs = [b.show(ctx=c, label=l, **kwargs) for b,c,_ in zip(samples.itemgot(i),ctxs,range(max_n))]
ctxs = [b.show(ctx=c, label='pred', **kwargs) for b,c,_ in zip(outs.itemgot(0),ctxs,range(max_n))]
display_df(pd.DataFrame(ctxs))
return ctxs
#export
@typedispatch
def show_results(x: TensorText, y, samples, outs, ctxs=None, max_n=10, trunc_at=150, **kwargs):
if ctxs is None: ctxs = get_empty_df(min(len(samples), max_n))
samples = L((s[0].truncate(trunc_at),*s[1:]) for s in samples)
ctxs = show_results[object](x, y, samples, outs, ctxs=ctxs, max_n=max_n, **kwargs)
display_df(pd.DataFrame(ctxs))
return ctxs
#export
@typedispatch
def plot_top_losses(x: TensorText, y:TensorCategory, samples, outs, raws, losses, trunc_at=150, **kwargs):
rows = get_empty_df(len(samples))
samples = L((s[0].truncate(trunc_at),*s[1:]) for s in samples)
for i,l in enumerate(['input', 'target']):
rows = [b.show(ctx=c, label=l, **kwargs) for b,c in zip(samples.itemgot(i),rows)]
outs = L(o + (TitledFloat(r.max().item()), TitledFloat(l.item())) for o,r,l in zip(outs, raws, losses))
for i,l in enumerate(['predicted', 'probability', 'loss']):
rows = [b.show(ctx=c, label=l, **kwargs) for b,c in zip(outs.itemgot(i),rows)]
display_df(pd.DataFrame(rows))
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| true |
code
| 0.741738 | null | null | null | null |
|
<img align="right" src="images/tf.png" width="128"/>
<img align="right" src="images/etcbc.png" width="128"/>
<img align="right" src="images/syrnt.png" width="128"/>
<img align="right" src="images/peshitta.png" width="128"/>
# Use lectionaries in the Peshitta (OT and NT)
This notebook shows just one way to use the Syriac Lectionary data by Geert Jan Veldman
together with the Peshitta texts, OT and NT.
It has been used in the Syriac Bootcamp at the ETCBC, VU Amsterdam, on 2019-01-18.
## Provenance
The lectionary data can be downloaded from the
[DANS archive](https://dans.knaw.nl/en/front-page?set_language=en)
through this DOI:
[10.17026/dans-26t-hhv7](https://doi.org/10.17026/dans-26t-hhv7).
The Peshitta (OT) and (NT) text sources in text-fabric format are on GitHub:
* OT: [etcbc/peshitta](https://github.com/ETCBC/peshitta)
* NT: [etcbc/syrnt](https://github.com/ETCBC/syrnt)
The program that generated the text-fabric features linking the lectionaries with the text is in
a Jupyter notebook:
* [makeLectio](https://nbviewer.jupyter.org/github/etcbc/linksyr/blob/master/programs/lectionaries/makeLectio.ipynb)
## Run it yourself!
Make sure you have installed
* Python (3.6.3 or higher)
* Jupyter
```pip3 install jupyter```
* Text-Fabric
```pip3 install text-fabric```
If you have already installed text-fabric before, make sure to do
```pip3 install --upgrade text-fabric```
because Text-Fabric is in active development every now and then.
```
%load_ext autoreload
%autoreload 2
import os
import re
from tf.app import use
```
# Context
We will be working with two TF data sources,
* the `peshitta`, (OT Peshitta) which name we store in variable `P`
* the `syrnt`, (NT Peshitta) which name we store in variable `S`
They both contain Syriac text and transcriptions, but the SyrNT has linguistic annotations and lexemes, while the
Peshitta (OT) lacks them.
```
P = 'peshitta'
S = 'syrnt'
A = {P: None, S: None}
```
# Text-Fabric browser
Let's first look at the data in your own browser.
What you need to do is to open a command prompt.
If you do not know what that is: on Windows it is the program `cmd.exe`, on the Mac it is the app called `Terminal`,
and on Linux you know what it is.
You can use it from any directory.
If one of the commands below do not work, you have installed things differently than I assume here, or the installation was not succesful.
For more information, consult
[Install](https://annotation.github.io/text-fabric/tf/about/install.html) and/or
[FAQ](https://annotation.github.io/text-fabric/tf/about/faq.html)
Start the TF browser as follows:
### Old Testament
```
text-fabric peshitta -c --mod=etcbc/linksyr/data/tf/lectio/peshitta
```
### New Testament
Open a new command prompt and say there:
```
text-fabric syrnt -c --mod=etcbc/linksyr/data/tf/lectio/syrnt
```
### Example queries
In both cases, issue a query such as
```
verse taksa link
```
or a more refined one:
```
verse taksa link
word word_etcbc=LLJ>
```
You will see all verses that are associated with a lectionary that has a `taksa` and a `link` value.
After playing around with the browsing interface on both testaments, return to this notebook.
We are going to load both texts here in our program:
```
for volume in A:
A[volume] = use(volume+':clone', mod=f'etcbc/linksyr/data/tf/lectio/{volume}')
```
Above you can see that we have loaded the `peshitta` and `syrnt` data sources but also additional data from
* **etcbc/linksyr/data/tf/lectio/peshitta**
* **etcbc/linksyr/data/tf/lectio/syrnt**
From both additional sources we have loaded several features: `lectio`, `mark1`, `mark2`, `siglum`, `taksa`, `taksaTr`.
Every lectionary has a number. A lectionary is linked to several verses.
Here is what kind of information the features contain:
feature | description
--- | ---
**lectio** | comma separated list of numbers of lectionaries associated with this verse
**mark1** | comma separated list of words which mark the precise location of where the lectionaries start
**taksa** | newline separated list of liturgical events associated with the lectionaries (in Syriac)
**taksaTr** | same as **taksa**, but now in English
**siglum** | newline separated list of document references that mention specify the lectionary
**link** | newline separated list of links to the *sigla*
**mark2** | same as **mark2**, but the word is in a different language
When you work with TF, you usually have handy variables called `F`, `L`, `T` ready with which you access all data in the text.
Since we use two TF resources in this program, we make a double set of these variables, and instead of just `F`, we'll say
`F[P]` for accessing the Peshitta (OT) and `F[S]` for accessing the SyrNT. Same pattern for `L` and `T`.
For the meaning of these variables, consult
* [F Features](https://annotation.github.io/text-fabric/tf/core/nodefeature.html)
* [L Locality](https://annotation.github.io/text-fabric/tf/core/locality.html)
* [T Text](https://annotation.github.io/text-fabric/tf/core/text.html)
```
Fs = {}
F = {}
T = {}
L = {}
for volume in A:
thisApi = A[volume].api
F[volume] = thisApi.F
Fs[volume] = thisApi.Fs
T[volume] = thisApi.T
L[volume] = thisApi.L
extraFeatures = '''
lectio
mark1 mark2
'''.strip().split()
```
# Liturgicalness
We measure the *liturgicalness* of a word by counting the number of lectionaries it is involved in.
As a first step, we collect for each words the set of lectionaries it is involved in.
In the Peshitta OT we use the word form, since we do not have lemmas.
The word form is in the feature `word`.
In the SyrNT we use the word lemma, which is in the feature `lexeme`.
We collect the information in the dictionary `liturgical`, which maps each word form unto the set of lectionaries it is involved in.
```
# this function can do the collection in either Testament
def getLiturgical(volume):
wordRep = 'word' if volume == P else 'lexeme'
mapping = {}
# we traverse all verse nodes
for verseNode in F[volume].otype.s('verse'):
# we retrieve the value of feature 'lectio' for that verse node
lectioStr = F[volume].lectio.v(verseNode)
if lectioStr:
# we split the lectio string into a set of individual lectio numbers
lectios = lectioStr.split(',')
# we descend into the words of the verse
for wordNode in L[volume].d(verseNode, otype='word'):
# we use either the feature 'word' or 'lexeme', depending on the volume
word = Fs[volume](wordRep).v(wordNode)
# if this is the first time we encounter the word,
# we add it to the mapping and give it a start value: the empty set
if word not in mapping:
mapping[word] = set()
# in any case, we add the new found lectio numbers to the existing set for this word
mapping[word] |= set(lectios)
# we report how many words we have collected
print(f'Found {len(mapping)} words in {volume}')
# we return the mapping as result
return mapping
```
Before we call the function above for Peshitta and SyrNT, we make a place where the results can land:
```
liturgical = {}
for volume in A:
liturgical[volume] = getLiturgical(volume)
```
Remember that we count word occurrences in the Peshitta, and lemmas in the SyrNT, so we get much smaller numbers for the NT.
Let's show some mapping members for each volume:
```
for volume in liturgical:
print(f'IN {volume}:')
for (word, lectios) in list(liturgical[volume].items())[0:10]:
print(f'\t{word}')
print(f'\t\t{",".join(sorted(lectios)[0:5])} ...')
```
We are not done yet, because we are not interested in the actual lectionaries, but in their number.
So we make a new mapping `liturgicalNess`, which maps each word to the number of lectionaries it is associated with.
```
liturgicalNess = {}
for volume in liturgical:
for word in liturgical[volume]:
nLectio = len(liturgical[volume][word])
liturgicalNess.setdefault(volume, {})[word] = nLectio
```
Lets print the top twenty of each volume
```
for volume in liturgicalNess:
print(f'IN {volume}:')
for (word, lNess) in sorted(
liturgicalNess[volume].items(),
key=lambda x: (-x[1], x[0]),
)[0:20]:
print(f'\t{lNess:>5} {word}')
```
# Frequency lists
Here is how to get a frequency list of a volume.
We can produce the frequency of any feature, but let us do it here for words in the Peshitta (OT) and
lexemes in the SyrNY.
There is a hidden snag: in the SyrNT we do not have only word nodes, but also lexeme nodes.
When we count frequencies, we have to take care to count word nodes only.
The function [freqList](https://annotation.github.io/text-fabric/tf/core/nodefeature.html#tf.core.nodefeature.NodeFeature.freqList)
can do that.
Lets use it and produce the top twenty list of frequent words in both sources, and also the number of hapaxes.
```
# first we define a function to generate the table per volume
def showFreqList(volume):
print(f'IN {volume}:')
wordRep = 'word' if volume == P else 'lexeme'
freqs = Fs[volume](wordRep).freqList(nodeTypes={'word'})
# now the members of freqs are pairs (word, freqency)
# we print the top frequent words
for (word, freq) in freqs[0:10]:
print(f'\t{freq:>5} x {word}')
# we collect all hapaxes: the items with frequency 1
hapaxes = [word for (word, freq) in freqs if freq == 1]
print(f'{len(hapaxes)} hapaxes')
for hapax in hapaxes[100:105]:
print(f'\t{hapax}')
# then we execute it on both volumes
for volume in A:
showFreqList(volume)
```
# Queries
First a simple query with all verses with a lectionary (with taksa and link)
```
query = '''
verse taksa link
'''
```
We run them in both the Old and the New Testament
```
results = {}
for volume in A:
results[volume] = A[volume].search(query)
```
Let's show some results from the New Testament:
```
A[S].show(results[S], start=1, end=1)
```
Let's show some results from the New Testament:
```
A[P].show(results[P], start=1, end=1)
```
# Word study: CJN>
We want to study a word, in both volumes.
First we show a verse where the word occurs: James 3:18.
It is in the New Testament.
The
[`T.nodeFromSection()`](https://annotation.github.io/text-fabric/tf/core/text.html#tf.core.text.Text.nodeFromSection)
function can find the node (bar code) for a verse specified by a passage reference.
```
# we have to pass the section reference as a triple:
section = ('James', 3, 18)
# we retrieve the verse node
verseNode = T[S].nodeFromSection(('James', 3, 18))
# in case you're curious: here is the node, but it should not be meaningful to you,
# only to the program
print(verseNode)
```
Finally we show the corresponding verse by means of the function
[pretty()](https://annotation.github.io/text-fabric/tf/advanced/display.html#tf.advanced.display.pretty)
```
A[S].pretty(verseNode)
```
Now we use a query to find this word in the New Testament
```
queryS = '''
word lexeme_etcbc=CJN>
'''
resultsS = A[S].search(queryS)
```
We show them all:
```
A[S].show(resultsS)
```
For the OT, we do not have the lexeme value, so we try looking for word forms that *match* `CJN>` rather than those that are exactly equal to it.
Note that we have replaced '=' by '~' in the query below
```
queryP = '''
word word_etcbc~CJN>
'''
resultsP = A[P].search(queryP)
# We show only 20 results
A[P].show(resultsP, end=20)
```
Here ends the bootcamp session.
Interested? Send [me](mailto:dirk.roorda@dans.knaw.nl) a note.
| true |
code
| 0.69928 | null | null | null | null |
|
<a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Creative Commons License" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/88x31.png" /></a><br /><span xmlns:dct="http://purl.org/dc/terms/" property="dct:title"><b>A Magic Square Solver</b></span> by <a xmlns:cc="http://creativecommons.org/ns#" href="http://mate.unipv.it/gualandi" property="cc:attributionName" rel="cc:attributionURL">Stefano Gualandi</a> is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License</a>.<br />Based on a work at <a xmlns:dct="http://purl.org/dc/terms/" href="https://github.com/mathcoding/opt4ds" rel="dct:source">https://github.com/mathcoding/opt4ds</a>.
**NOTE:** Run the following script whenever running this script on a Google Colab.
```
import shutil
import sys
import os.path
if not shutil.which("pyomo"):
!pip install -q pyomo
assert(shutil.which("pyomo"))
if not (shutil.which("glpk") or os.path.isfile("glpk")):
if "google.colab" in sys.modules:
!apt-get install -y -qq glpk-utils
else:
try:
!conda install -c conda-forge glpk
except:
pass
```
# Magic Square Solver
In this notebook, we propose an ILP model to the [Magic Square](https://en.wikipedia.org/wiki/Magic_square) puzzle.
The puzzle asks to place into a grid of size $n \times n$ the digits from $1$ to $n^2$, in such a way that the sum of the digits in each row, the sum of digits in each column, and the sum of the digits on the two main diagonals, is equal to the same number.
## ILP Model
The model we propose is as follows.
**Decision Variables:** We use two type of variables:
* The variable $x_{ijk} \in \{0,1\}$ is equal to 1 if the cell in position $(i,j)$ contains the digit $k$, and it is equal to 0 otherwise. For easy of exposition, we use the set $I,J:=\{1,\dots,n\}$ and $K := \{1,\dots,n^2\}$.
* The variable $z\in\mathbb{Z}_+$ represents the magic number.
**Objective function:** Since the problem is a feasibility problem, we can set the objective function equal to a constant value. Otherwise, we can add the sum of every variable (this way we avoid also a warning from the solver).
**Constraints:** We introduce the following linear constraints, which encode the puzzle rules:
1. Every digit, we can be placed into a single position:
$$
\sum_{i \in I}\sum_{j \in J} x_{ijk} = 1, \;\; \forall k \in K
$$
2. In every position, we can place a single digit:
$$
\sum_{k \in K} x_{ijk} = 1, \;\; \forall i \in I, \; \forall j \in J
$$
3. The sum of the digits in each row must be equal to $z$:
$$
\sum_{j \in J}\sum_{k \in K} k x_{ijk} = z, \;\; \forall i \in I
$$
3. The sum of the digits in each column must be equal to $z$:
$$
\sum_{i \in I}\sum_{k \in K} k x_{ijk} = z, \;\; \forall j \in J
$$
4. The sum of the digits over the two main diagonals is equal to $z$:
$$
\sum_{i \in I} \sum_{k \in K} x_{iik} = z,
$$
$$
\sum_{i \in I} \sum_{k \in K} x_{i(n-i+1)k} = z,
$$
We show next how to implement this model in Pyomo.
## Pyomo implementation
As a first step we import the Pyomo libraries.
```
from pyomo.environ import ConcreteModel, Var, Objective, Constraint, SolverFactory
from pyomo.environ import Binary, RangeSet, ConstraintList, PositiveIntegers
```
We create an instance of the class *ConcreteModel*, and we start to add the *RangeSet* and *Var* corresponding to the index sets and the variables of our model. We set also the objective function.
```
# Create concrete model
model = ConcreteModel()
n = 4
# Set of indices
model.I = RangeSet(1, n)
model.J = RangeSet(1, n)
model.K = RangeSet(1, n*n)
# Variables
model.z = Var(within=PositiveIntegers)
model.x = Var(model.I, model.J, model.K, within=Binary)
# Objective Function
model.obj = Objective(expr = model.z)
```
Then, we encode all the constraints of our model using the Pyomo syntax.
```
def Unique(model, k):
return sum(model.x[i,j,k] for j in model.J for i in model.I) == 1
model.unique = Constraint(model.K, rule = Unique)
def CellUnique(model, i, j):
return sum(model.x[i,j,k] for k in model.K) == 1
model.cellUnique = Constraint(model.I, model.J, rule = CellUnique)
def Row(model, i):
return sum(k*model.x[i,j,k] for j in model.J for k in model.K) == model.z
model.row = Constraint(model.I, rule = Row)
def Col(model, j):
return sum(k*model.x[i,j,k] for i in model.I for k in model.K) == model.z
model.column = Constraint(model.J, rule = Col)
model.diag1 = Constraint(
expr = sum(k*model.x[i,i,k] for i in model.I for k in model.K) == model.z)
model.diag2 = Constraint(
expr = sum(k*model.x[i,n-i+1,k] for i in model.I for k in model.K) == model.z)
```
Finally, we solve the model for a given $n$ and we check the solution status.
```
# Solve the model
sol = SolverFactory('glpk').solve(model)
# CHECK SOLUTION STATUS
# Get a JSON representation of the solution
sol_json = sol.json_repn()
# Check solution status
if sol_json['Solver'][0]['Status'] != 'ok':
print("Problem unsolved")
if sol_json['Solver'][0]['Termination condition'] != 'optimal':
print("Problem unsolved")
```
If the problem is solved and a feasible solution is available, we write the solution into a colorful **magic square**.
```
def PlotMagicSquare(x, n):
# Report solution value
import matplotlib.pyplot as plt
import numpy as np
import itertools
sol = np.zeros((n,n), dtype=int)
for i, j, k in x:
if x[i,j,k]() > 0.5:
sol[i-1,j-1] = k
cmap = plt.get_cmap('Blues')
plt.figure(figsize=(6,6))
plt.imshow(sol, interpolation='nearest', cmap=cmap)
plt.title("Magic Square, Size: {}".format(n))
plt.axis('off')
for i, j in itertools.product(range(n), range(n)):
plt.text(j, i, "{:d}".format(sol[i, j]),
fontsize=24, ha='center', va='center')
plt.tight_layout()
plt.show()
PlotMagicSquare(model.x, n)
```
| true |
code
| 0.428801 | null | null | null | null |
|
```
%matplotlib inline
from fastai.vision.all import *
from fastai.vision.gan import *
```
## LSun bedroom data
For this lesson, we'll be using the bedrooms from the [LSUN dataset](http://lsun.cs.princeton.edu/2017/). The full dataset is a bit too large so we'll use a sample from [kaggle](https://www.kaggle.com/jhoward/lsun_bedroom).
```
path = untar_data(URLs.LSUN_BEDROOMS)
```
We then grab all the images in the folder with the data block API. We don't create a validation set here for reasons we'll explain later. It consists of random noise of size 100 by default (can be changed if you replace `generate_noise` by `partial(generate_noise, size=...)`) as inputs and the images of bedrooms as targets.
```
dblock = DataBlock(blocks = (TransformBlock, ImageBlock),
get_x = generate_noise,
get_items = get_image_files,
splitter = IndexSplitter([]))
def get_dls(bs, size):
dblock = DataBlock(blocks = (TransformBlock, ImageBlock),
get_x = generate_noise,
get_items = get_image_files,
splitter = IndexSplitter([]),
item_tfms=Resize(size, method=ResizeMethod.Crop),
batch_tfms = Normalize.from_stats(torch.tensor([0.5,0.5,0.5]), torch.tensor([0.5,0.5,0.5])))
return dblock.dataloaders(path, path=path, bs=bs)
```
We'll begin with a small size since GANs take a lot of time to train.
```
dls = get_dls(128, 64)
dls.show_batch(max_n=16)
```
## Models
GAN stands for [Generative Adversarial Nets](https://arxiv.org/pdf/1406.2661.pdf) and were invented by Ian Goodfellow. The concept is that we will train two models at the same time: a generator and a critic. The generator will try to make new images similar to the ones in our dataset, and the critic will try to classify real images from the ones the generator does. The generator returns images, the critic a single number (usually 0. for fake images and 1. for real ones).
We train them against each other in the sense that at each step (more or less), we:
1. Freeze the generator and train the critic for one step by:
- getting one batch of true images (let's call that `real`)
- generating one batch of fake images (let's call that `fake`)
- have the critic evaluate each batch and compute a loss function from that; the important part is that it rewards positively the detection of real images and penalizes the fake ones
- update the weights of the critic with the gradients of this loss
2. Freeze the critic and train the generator for one step by:
- generating one batch of fake images
- evaluate the critic on it
- return a loss that rewards posisitivly the critic thinking those are real images; the important part is that it rewards positively the detection of real images and penalizes the fake ones
- update the weights of the generator with the gradients of this loss
Here, we'll use the [Wassertein GAN](https://arxiv.org/pdf/1701.07875.pdf).
We create a generator and a critic that we pass to `gan_learner`. The noise_size is the size of the random vector from which our generator creates images.
```
generator = basic_generator(64, n_channels=3, n_extra_layers=1)
critic = basic_critic (64, n_channels=3, n_extra_layers=1, act_cls=partial(nn.LeakyReLU, negative_slope=0.2))
learn = GANLearner.wgan(dls, generator, critic, opt_func = partial(Adam, mom=0.))
learn.recorder.train_metrics=True
learn.recorder.valid_metrics=False
learn.fit(30, 2e-4, wd=0)
#learn.gan_trainer.switch(gen_mode=True)
learn.show_results(max_n=16, figsize=(8,8), ds_idx=0)
```
| true |
code
| 0.694665 | null | null | null | null |
|
## The Basic Idea of Machine-learning
Imagine a monkey drawing on a canvas (say, of `128 * 128` pixels). What's the probability that it draw a human-face? Almost none, isn't it. This implies that
* the manifold of human-face involved in $\mathbb{R}^{128 \times 128}$ has relatively much smaller dimensions.
* Even, the manifold is spares.
To see this, imagine you modify the background of a painting with a human-face in the foreground, the points in $\mathbb{R}^{128 \times 128}$ before and after the modification are generally far from each other.
Thus, the task of machine-learning is to find out the low-dimensional spares manifold, mapping the manifold to a lower dimensional compact space, and mapping the element there back to generate real-world object, like painting.
We call the real-world object "observable", and the low-dimensional spares manifold "latent" space.
This serves both to data-compression and data-abstraction. In fact, these are two aspects of one thing: the probability distribution of data (which we will talk in the next topic).
## Auto-encoder
### Conceptions
This basic idea naturally forces to "auto-encoder", which has two parts:
1. Encoder: mapping the observable to latent.
2. Decoder: mapping the latent to observable.
Let $X$ the space of observable, and $Z$ the latent. Let $f: X \mapsto Z$ denotes the encoder, and $g: Z \mapsto X$ the decoder. Then, for $\forall x \in X$, we would expect
\begin{equation}
g \circ f(x) \approx x.
\end{equation}
To numerically characterize this approximation, let $d_{\text{obs}}$ some pre-defined distance in the space of observable, we can define loss
\begin{equation}
\mathcal{L}_{\text{recon}} = \frac{1}{|D|} \sum_{x \in D} d_{\text{obs}} \left(x, g \circ f (x) \right).
\end{equation}
We call this "reconstruction" loss, since $g \circ f (x)$ is a reconstruction of $x$.
For ensuring the compactness of the latent, an additional regularizer is added to the reconstruction loss, by some pre-defined distance in the latant space $d_{\text{lat}}$. Thus, the total loss is
\begin{equation}
\mathcal{L} = \frac{1}{|D|} \sum_{x \in D} d_{\text{obs}} \left(x, g \circ f (x) \right)
+ d_{\text{lat}} \left( f(x), 0 \right).
\end{equation}
The task is thus to find the functions $f$ and $g$ that minimize the total loss. This utilizes the universality property of neural network.
### Reference:
1. [Wikipedia](https://en.wikipedia.org/wiki/Autoencoder).
## Implementation
```
%matplotlib inline
from IPython.display import display
import matplotlib.pyplot as plt
from tqdm import tqdm
from PIL import Image
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
data_path = '../../dat/MNIST/'
mnist = input_data.read_data_sets(
data_path, one_hot=True,
source_url='http://yann.lecun.com/exdb/mnist/')
def get_encoder(latent_dim, hidden_layers):
def encoder(observable, name='encoder', reuse=None):
with tf.variable_scope(name, reuse=reuse):
hidden = observable
for hidden_layer in hidden_layers:
hidden = tf.layers.dense(hidden, hidden_layer,
activation=tf.nn.relu)
latent = tf.layers.dense(hidden, latent_dim, activation=None)
return latent
return encoder
def get_decoder(observable_dim, hidden_layers):
def decoder(latent, name='decoder', reuse=None):
with tf.variable_scope(name, reuse=reuse):
hidden = latent
for hidden_layer in hidden_layers:
hidden = tf.layers.dense(hidden, hidden_layer,
activation=tf.nn.relu)
reconstructed = tf.layers.dense(hidden, observable_dim,
activation=tf.nn.sigmoid)
return reconstructed
return decoder
def get_loss(observable, encoder, decoder, regularizer=None, reuse=None):
if regularizer is None:
regularizer = lambda latent: 0.0
with tf.name_scope('loss'):
# shape: [batch_size, latent_dim]
latent = encoder(observable, reuse=reuse)
# shape: [batch_size, observable_dim]
reconstructed = decoder(latent, reuse=reuse)
# shape: [batch_size]
squared_errors = tf.reduce_sum(
(reconstructed - observable) ** 2,
axis=1)
mean_square_error = tf.reduce_mean(squared_errors)
return mean_square_error + regularizer(latent)
latent_dim = 64
encoder = get_encoder(latent_dim=latent_dim,
hidden_layers=[512, 256, 128])
decoder = get_decoder(observable_dim=28*28,
hidden_layers=[128, 256, 512])
observable = tf.placeholder(shape=[None, 28*28],
dtype='float32',
name='observable')
latent_samples = tf.placeholder(shape=[None, latent_dim],
dtype='float32',
name='latent_samples')
generated = decoder(latent_samples, reuse=tf.AUTO_REUSE)
def regularizer(latent, name='regularizer'):
with tf.name_scope(name):
distances = tf.reduce_sum(latent ** 2, axis=1)
return tf.reduce_mean(distances)
loss = get_loss(observable, encoder, decoder,
regularizer=regularizer,
reuse=tf.AUTO_REUSE)
optimizer = tf.train.AdamOptimizer(epsilon=1e-3)
train_op = optimizer.minimize(loss)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
loss_vals = []
for i in tqdm(range(100000)):
X, y = mnist.train.next_batch(batch_size=128)
_, loss_val = sess.run([train_op, loss], {observable: X})
if np.isnan(loss_Xy_val):
raise ValueError('Loss has been NaN.')
loss_vals.append(loss_val)
print('Final loss:', np.mean(loss_vals[-100:]))
plt.plot(loss_vals)
plt.xlabel('steps')
plt.ylabel('loss')
plt.show()
def get_image(array):
"""
Args:
array: Numpy array with shape `[28*28]`.
Returns:
An image.
"""
array = 255 * array
array = array.reshape([28, 28])
array = array.astype(np.uint8)
return Image.fromarray(array)
latent_sample_vals = np.random.normal(size=[128, latent_dim])
generated_vals = sess.run(generated, {latent_samples: latent_sample_vals})
# Display the results
n_display = 5
for i in range(n_display):
print('Gnerated:')
display(get_image(generated_vals[i]))
print()
```
| true |
code
| 0.742147 | null | null | null | null |
|
# Monodepth Estimation with OpenVINO
This tutorial demonstrates Monocular Depth Estimation with MidasNet in OpenVINO. Model information: https://docs.openvinotoolkit.org/latest/omz_models_model_midasnet.html

### What is Monodepth?
Monocular Depth Estimation is the task of estimating scene depth using a single image. It has many potential applications in robotics, 3D reconstruction, medical imaging and autonomous systems. For this demo, we use a neural network model called [MiDaS](https://github.com/intel-isl/MiDaS) which was developed by the [Embodied AI Foundation](https://www.embodiedaifoundation.org/). Check out the research paper below to learn more.
R. Ranftl, K. Lasinger, D. Hafner, K. Schindler and V. Koltun, ["Towards Robust Monocular Depth Estimation: Mixing Datasets for Zero-shot Cross-dataset Transfer,"](https://ieeexplore.ieee.org/document/9178977) in IEEE Transactions on Pattern Analysis and Machine Intelligence, doi: 10.1109/TPAMI.2020.3019967.
## Preparation
### Imports
```
import sys
import time
from pathlib import Path
import cv2
import matplotlib.cm
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import (
HTML,
FileLink,
Pretty,
ProgressBar,
Video,
clear_output,
display,
)
from openvino.inference_engine import IECore
sys.path.append("../utils")
from notebook_utils import load_image
```
### Settings
```
DEVICE = "CPU"
MODEL_FILE = "model/MiDaS_small.xml"
model_xml_path = Path(MODEL_FILE)
```
## Functions
```
def normalize_minmax(data):
"""Normalizes the values in `data` between 0 and 1"""
return (data - data.min()) / (data.max() - data.min())
def convert_result_to_image(result, colormap="viridis"):
"""
Convert network result of floating point numbers to an RGB image with
integer values from 0-255 by applying a colormap.
`result` is expected to be a single network result in 1,H,W shape
`colormap` is a matplotlib colormap.
See https://matplotlib.org/stable/tutorials/colors/colormaps.html
"""
cmap = matplotlib.cm.get_cmap(colormap)
result = result.squeeze(0)
result = normalize_minmax(result)
result = cmap(result)[:, :, :3] * 255
result = result.astype(np.uint8)
return result
def to_rgb(image_data) -> np.ndarray:
"""
Convert image_data from BGR to RGB
"""
return cv2.cvtColor(image_data, cv2.COLOR_BGR2RGB)
```
## Load the Model
Load the model in Inference Engine with `ie.read_network` and load it to the specified device with `ie.load_network`. Get input and output keys and the expected input shape for the model.
```
ie = IECore()
net = ie.read_network(model=model_xml_path, weights=model_xml_path.with_suffix(".bin"))
exec_net = ie.load_network(network=net, device_name=DEVICE)
input_key = list(exec_net.input_info)[0]
output_key = list(exec_net.outputs.keys())[0]
network_input_shape = exec_net.input_info[input_key].tensor_desc.dims
network_image_height, network_image_width = network_input_shape[2:]
```
## Monodepth on Image
### Load, resize and reshape input image
The input image is read with OpenCV, resized to network input size, and reshaped to (N,C,H,W) (N=number of images, C=number of channels, H=height, W=width).
```
IMAGE_FILE = "data/coco_bike.jpg"
image = load_image(path=IMAGE_FILE)
# resize to input shape for network
resized_image = cv2.resize(src=image, dsize=(network_image_height, network_image_width))
# reshape image to network input shape NCHW
input_image = np.expand_dims(np.transpose(resized_image, (2, 0, 1)), 0)
```
### Do inference on image
Do the inference, convert the result to an image, and resize it to the original image shape
```
result = exec_net.infer(inputs={input_key: input_image})[output_key]
# convert network result of disparity map to an image that shows
# distance as colors
result_image = convert_result_to_image(result=result)
# resize back to original image shape. cv2.resize expects shape
# in (width, height), [::-1] reverses the (height, width) shape to match this
result_image = cv2.resize(result_image, image.shape[:2][::-1])
```
### Display monodepth image
```
fig, ax = plt.subplots(1, 2, figsize=(20, 15))
ax[0].imshow(to_rgb(image))
ax[1].imshow(result_image);
```
## Monodepth on Video
By default, only the first 100 frames are processed, in order to quickly check that everything works. Change NUM_FRAMES in the cell below to modify this. Set NUM_FRAMES to 0 to process the whole video.
### Video Settings
```
# Video source: https://www.youtube.com/watch?v=fu1xcQdJRws (Public Domain)
VIDEO_FILE = "data/Coco Walking in Berkeley.mp4"
# Number of seconds of input video to process. Set to 0 to process
# the full video.
NUM_SECONDS = 4
# Set ADVANCE_FRAMES to 1 to process every frame from the input video
# Set ADVANCE_FRAMES to 2 to process every second frame. This reduces
# the time it takes to process the video
ADVANCE_FRAMES = 2
# Set SCALE_OUTPUT to reduce the size of the result video
# If SCALE_OUTPUT is 0.5, the width and height of the result video
# will be half the width and height of the input video
SCALE_OUTPUT = 0.5
# The format to use for video encoding. vp09 is slow,
# but it works on most systems.
# Try the THEO encoding if you have FFMPEG installed.
# FOURCC = cv2.VideoWriter_fourcc(*"THEO")
FOURCC = cv2.VideoWriter_fourcc(*"vp09")
# Create Path objects for the input video and the resulting video
output_directory = Path("output")
output_directory.mkdir(exist_ok=True)
result_video_path = output_directory / f"{Path(VIDEO_FILE).stem}_monodepth.mp4"
```
### Load Video
Load video from `VIDEO_FILE`, set in the *Video Settings* cell above. Open the video to read the frame width and height and fps, and compute values for these properties for the monodepth video.
```
cap = cv2.VideoCapture(str(VIDEO_FILE))
ret, image = cap.read()
if not ret:
raise ValueError(f"The video at {VIDEO_FILE} cannot be read.")
input_fps = cap.get(cv2.CAP_PROP_FPS)
input_video_frame_height, input_video_frame_width = image.shape[:2]
target_fps = input_fps / ADVANCE_FRAMES
target_frame_height = int(input_video_frame_height * SCALE_OUTPUT)
target_frame_width = int(input_video_frame_width * SCALE_OUTPUT)
cap.release()
print(
f"The input video has a frame width of {input_video_frame_width}, "
f"frame height of {input_video_frame_height} and runs at {input_fps:.2f} fps"
)
print(
"The monodepth video will be scaled with a factor "
f"{SCALE_OUTPUT}, have width {target_frame_width}, "
f" height {target_frame_height}, and run at {target_fps:.2f} fps"
)
```
### Do Inference on a Video and Create Monodepth Video
```
# Initialize variables
input_video_frame_nr = 0
start_time = time.perf_counter()
total_inference_duration = 0
# Open input video
cap = cv2.VideoCapture(str(VIDEO_FILE))
# Create result video
out_video = cv2.VideoWriter(
str(result_video_path),
FOURCC,
target_fps,
(target_frame_width * 2, target_frame_height),
)
num_frames = int(NUM_SECONDS * input_fps)
total_frames = cap.get(cv2.CAP_PROP_FRAME_COUNT) if num_frames == 0 else num_frames
progress_bar = ProgressBar(total=total_frames)
progress_bar.display()
try:
while cap.isOpened():
ret, image = cap.read()
if not ret:
cap.release()
break
if input_video_frame_nr >= total_frames:
break
# Only process every second frame
# Prepare frame for inference
# resize to input shape for network
resized_image = cv2.resize(src=image, dsize=(network_image_height, network_image_width))
# reshape image to network input shape NCHW
input_image = np.expand_dims(np.transpose(resized_image, (2, 0, 1)), 0)
# Do inference
inference_start_time = time.perf_counter()
result = exec_net.infer(inputs={input_key: input_image})[output_key]
inference_stop_time = time.perf_counter()
inference_duration = inference_stop_time - inference_start_time
total_inference_duration += inference_duration
if input_video_frame_nr % (10 * ADVANCE_FRAMES) == 0:
clear_output(wait=True)
progress_bar.display()
# input_video_frame_nr // ADVANCE_FRAMES gives the number of
# frames that have been processed by the network
display(
Pretty(
f"Processed frame {input_video_frame_nr // ADVANCE_FRAMES}"
f"/{total_frames // ADVANCE_FRAMES}. "
f"Inference time: {inference_duration:.2f} seconds "
f"({1/inference_duration:.2f} FPS)"
)
)
# Transform network result to RGB image
result_frame = to_rgb(convert_result_to_image(result))
# Resize image and result to target frame shape
result_frame = cv2.resize(result_frame, (target_frame_width, target_frame_height))
image = cv2.resize(image, (target_frame_width, target_frame_height))
# Put image and result side by side
stacked_frame = np.hstack((image, result_frame))
# Save frame to video
out_video.write(stacked_frame)
input_video_frame_nr = input_video_frame_nr + ADVANCE_FRAMES
cap.set(1, input_video_frame_nr)
progress_bar.progress = input_video_frame_nr
progress_bar.update()
except KeyboardInterrupt:
print("Processing interrupted.")
finally:
clear_output()
processed_frames = num_frames // ADVANCE_FRAMES
out_video.release()
cap.release()
end_time = time.perf_counter()
duration = end_time - start_time
print(
f"Processed {processed_frames} frames in {duration:.2f} seconds. "
f"Total FPS (including video processing): {processed_frames/duration:.2f}."
f"Inference FPS: {processed_frames/total_inference_duration:.2f} "
)
print(f"Monodepth Video saved to '{str(result_video_path)}'.")
```
### Display Monodepth Video
```
video = Video(result_video_path, width=800, embed=True)
if not result_video_path.exists():
plt.imshow(stacked_frame)
raise ValueError("OpenCV was unable to write the video file. Showing one video frame.")
else:
print(f"Showing monodepth video saved at\n{result_video_path.resolve()}")
print(
"If you cannot see the video in your browser, please click on the "
"following link to download the video "
)
video_link = FileLink(result_video_path)
video_link.html_link_str = "<a href='%s' download>%s</a>"
display(HTML(video_link._repr_html_()))
display(video)
```
| true |
code
| 0.572842 | null | null | null | null |
|
# Lambda School Data Science - Logistic Regression
Logistic regression is the baseline for classification models, as well as a handy way to predict probabilities (since those too live in the unit interval). While relatively simple, it is also the foundation for more sophisticated classification techniques such as neural networks (many of which can effectively be thought of as networks of logistic models).
## Lecture - Where Linear goes Wrong
### Return of the Titanic 🚢
You've likely already explored the rich dataset that is the Titanic - let's use regression and try to predict survival with it. The data is [available from Kaggle](https://www.kaggle.com/c/titanic/data), so we'll also play a bit with [the Kaggle API](https://github.com/Kaggle/kaggle-api).
### Get data, option 1: Kaggle API
#### Sign up for Kaggle and get an API token
1. [Sign up for a Kaggle account](https://www.kaggle.com/), if you don’t already have one.
2. [Follow these instructions](https://github.com/Kaggle/kaggle-api#api-credentials) to create a Kaggle “API Token” and download your `kaggle.json` file. If you are using Anaconda, put the file in the directory specified in the instructions.
_This will enable you to download data directly from Kaggle. If you run into problems, don’t worry — I’ll give you an easy alternative way to download today’s data, so you can still follow along with the lecture hands-on. And then we’ll help you through the Kaggle process after the lecture._
#### Put `kaggle.json` in the correct location
- ***If you're using Anaconda,*** put the file in the directory specified in the [instructions](https://github.com/Kaggle/kaggle-api#api-credentials).
- ***If you're using Google Colab,*** upload the file to your Google Drive, and run this cell:
```
from google.colab import drive
drive.mount('/content/drive')
%env KAGGLE_CONFIG_DIR=/content/drive/My Drive/
```
#### Install the Kaggle API package and use it to get the data
You also have to join the Titanic competition to have access to the data
```
!pip install kaggle
!kaggle competitions download -c titanic
```
### Get data, option 2: Download from the competition page
1. [Sign up for a Kaggle account](https://www.kaggle.com/), if you don’t already have one.
2. [Go to the Titanic competition page](https://www.kaggle.com/c/titanic) to download the [data](https://www.kaggle.com/c/titanic/data).
### Get data, option 3: Use Seaborn
```
import seaborn as sns
train = sns.load_dataset('titanic')
```
But Seaborn's version of the Titanic dataset is not identical to Kaggle's version, as we'll see during this lesson!
### Read data
```
import pandas as pd
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
train.shape, test.shape
```
Notice that `train.csv` has one more column than `test.csv` : The target, `Survived`.
Kaggle provides test labels, but not test targets. Instead, you submit your test predictions to Kaggle to get your test scores. Why? This is model validaton best practice, makes competitons fair, and helps us learn about over- and under-fitting.
```
train.sample(n=5)
test.sample(n=5)
```
Do some data exploration.
About 62% of passengers did not survive.
```
target = 'Survived'
train[target].value_counts(normalize=True)
```
Describe the numeric columns
```
train.describe(include='number')
```
Describe the non-numeric columns
```
train.describe(exclude='number')
```
### How would we try to do this with linear regression?
We choose a few numeric features, split the data into X and y, [impute missing values](https://scikit-learn.org/stable/modules/impute.html), and fit a Linear Regression model on the train set.
```
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LinearRegression
features = ['Pclass', 'Age', 'Fare']
target = 'Survived'
X_train = train[features]
y_train = train[target]
X_test = test[features]
imputer = SimpleImputer()
X_train_imputed = imputer.fit_transform(X_train)
X_test_imputed = imputer.transform(X_test)
lin_reg = LinearRegression()
lin_reg.fit(X_train_imputed, y_train)
```
Let's consider a test case. What does our Linear Regression predict for a 1st class, 5 year-old, with a fare of 500?
119% probability of survival.
```
import numpy as np
test_case = np.array([[1, 5, 500]]) # Rich 5-year old in first class
lin_reg.predict(test_case)
```
Based on the Linear Regression's intercept and coefficients, it will predict probabilities greater than 100%, or less than 0%, given high enough / low enough values for the features.
```
print('Intercept', lin_reg.intercept_)
coefficients = pd.Series(lin_reg.coef_, X_train.columns)
print(coefficients.to_string())
```
### How would we do this with Logistic Regression?
The scikit-learn API is consistent, so the code is similar.
We instantiate our model (here with `LogisticRegression()` instead of `LinearRegression()`)
We use the same method to fit the model on the training data: `.fit(X_train_imputed, y_train)`
We use the same method to make a predict for our test case: `.predict(test_case)` — But this returns different results. Regressors return continuous values, but classifiers return discrete predictions of the class label. In this binary classification problem, our discrete class labels are `0` (did not survive) or `1` (did survive).
Classifiers also have a `.predict_proba` method, which returns predicted probabilities for each class. The probabilities sum to 1.
We predict ~3% probability that our test case did not surive, and 97% probability that our test case did survive. This result is what we want and expect for our test case: to predict survival, with high probability, but less than 100%.
```
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver='lbfgs')
log_reg.fit(X_train_imputed, y_train)
print('Prediction for rich 5 year old:', log_reg.predict(test_case))
print('Predicted probabilities for rich 5 year old:', log_reg.predict_proba(test_case))
```
Logistic Regression calculates predicted probablities between the range of 0 and 1. By default, scikit-learn makes a discrete prediction by returning whichever class had the highest predicted probability for that observation.
In the case of binary classification, this is equivalent to using a threshold of 0.5. However, we could choose a different threshold, for different trade-offs between false positives versus false negatives.
```
threshold = 0.5
probabilities = log_reg.predict_proba(X_test_imputed)[:,1]
manual_predictions = (probabilities > threshold).astype(int)
direct_predictions = log_reg.predict(X_test_imputed)
all(manual_predictions == direct_predictions)
```
### How accurate is the Logistic Regression?
Scikit-learn estimators provide a convenient method, `.score`. It uses the X features to generate predictions. Then it compares the predictions to the y ground truth labels. Then it returns the score.
For regressors, `.score` returns R^2.
For classifiers, `.score` returns Accuracy.
Our Logistic Regression model has 70% training accuracy. (This is higher than the 62% accuracy we would get with a baseline that predicts every passenger does not survive.)
```
score = log_reg.score(X_train_imputed, y_train)
print('Train Accuracy Score', score)
```
Accuracy is just the number of correct predictions divided by the total number of predictions.
For example, we can look at our first five predictions:
```
y_pred = log_reg.predict(X_train_imputed)
y_pred[:5]
```
And compare to the ground truth labels for these first five observations:
```
y_train[:5].values
```
We have four correct predictions, divided by five total predictions, for 80% accuracy.
```
correct_predictions = 4
total_predictions = 5
accuracy = correct_predictions / total_predictions
print(accuracy)
```
scikit-learn's `accuracy_score` function works the same way and returns the same result.
```
from sklearn.metrics import accuracy_score
accuracy_score(y_train[:5], y_pred[:5])
```
We don't want to just score our model on the training data.
We cannot calculate a test accuracy score ourselves in this notebook, because Kaggle does not provide test labels.
We could split the train data into train and validation sets. However, we don't have many observations. (Fewer than 1,000.)
As another alternative, we can use cross-validation:
```
from sklearn.model_selection import cross_val_score
scores = cross_val_score(log_reg, X_train_imputed, y_train, cv=10)
print('Cross-Validation Accuracy Scores', scores)
```
We can see a range of scores:
```
scores = pd.Series(scores)
scores.min(), scores.mean(), scores.max()
```
To learn more about Cross-Validation, see these links:
- https://scikit-learn.org/stable/modules/cross_validation.html
- https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html
- https://github.com/LambdaSchool/DS-Unit-2-Sprint-3-Classification-Validation/blob/master/module2-baselines-validation/model-validation-preread.md#what-is-cross-validation
### What's the equation for Logistic Regression?
https://en.wikipedia.org/wiki/Logistic_function
https://en.wikipedia.org/wiki/Logistic_regression#Probability_of_passing_an_exam_versus_hours_of_study
```
print('Intercept', log_reg.intercept_[0])
coefficients = pd.Series(log_reg.coef_[0], X_train.columns)
print(coefficients.to_string())
# The logistic sigmoid "squishing" function,
# implemented to work with numpy arrays
def sigmoid(x):
return 1 / (1 + np.e**(-x))
sigmoid(np.dot(log_reg.coef_, test_case.T) + log_reg.intercept_)
```
Or we can write the code with the `@` operator instead of numpy's dot product function
```
sigmoid(log_reg.coef_ @ test_case.T + log_reg.intercept_)
```
Either way, we get the same result as our scikit-learn Logistic Regression
```
log_reg.predict_proba(test_case)
```
## Feature Engineering
Get the [Category Encoder](http://contrib.scikit-learn.org/categorical-encoding/) library
If you're running on Google Colab:
```
!pip install category_encoders
```
If you're running locally with Anaconda:
```
!conda install -c conda-forge category_encoders
```
#### Notice that Seaborn's version of the Titanic dataset has more features than Kaggle's version
```
import seaborn as sns
sns_titanic = sns.load_dataset('titanic')
print(sns_titanic.shape)
sns_titanic.head()
```
#### We can make the `adult_male` and `alone` features, and we can extract features from `Name`
```
def make_features(X):
X = X.copy()
X['adult_male'] = (X['Sex'] == 'male') & (X['Age'] >= 16)
X['alone'] = (X['SibSp'] == 0) & (X['Parch'] == 0)
X['last_name'] = X['Name'].str.split(',').str[0]
X['title'] = X['Name'].str.split(',').str[1].str.split('.').str[0]
return X
train = make_features(train)
test = make_features(test)
train.head()
train['adult_male'].value_counts()
train['alone'].value_counts()
train['title'].value_counts()
train.describe(include='number')
train.describe(exclude='number')
```
### Category Encoders!
http://contrib.scikit-learn.org/categorical-encoding/onehot.html
End-to-end example
```
import category_encoders as ce
pd.set_option('display.max_columns', 1000)
features = ['Pclass', 'Age', 'Fare', 'Sex', 'Embarked', 'adult_male', 'alone', 'title']
target = 'Survived'
X_train = train[features]
X_test = test[features]
y_train = train[target]
y_test = train[target]
encoder = ce.OneHotEncoder(use_cat_names=True)
imputer = SimpleImputer()
log_reg = LogisticRegression(solver='lbfgs', max_iter=1000)
X_train_encoded = encoder.fit_transform(X_train)
X_test_encoded = encoder.transform(X_test)
X_train_imputed = imputer.fit_transform(X_train_encoded)
X_test_imputed = imputer.transform(X_test_encoded)
scores = cross_val_score(log_reg, X_train_imputed, y_train, cv=10)
print('Cross-Validation Accuracy Scores', scores)
```
Here's what the one-hot encoded data looks like
```
X_train_encoded.sample(n=5)
```
The cross-validation accuracy scores improve with the additional features
```
%matplotlib inline
import matplotlib.pyplot as plt
log_reg.fit(X_train_imputed, y_train)
coefficients = pd.Series(log_reg.coef_[0], X_train_encoded.columns)
plt.figure(figsize=(10,10))
coefficients.sort_values().plot.barh(color='grey');
```
### Scaler
https://scikit-learn.org/stable/modules/preprocessing.html#scaling-features-to-a-range
End-to-end example
```
from sklearn.preprocessing import MinMaxScaler
encoder = ce.OneHotEncoder(use_cat_names=True)
imputer = SimpleImputer()
scaler = MinMaxScaler()
log_reg = LogisticRegression(solver='lbfgs', max_iter=1000)
X_train_encoded = encoder.fit_transform(X_train)
X_test_encoded = encoder.transform(X_test)
X_train_imputed = imputer.fit_transform(X_train_encoded)
X_test_imputed = imputer.transform(X_test_encoded)
X_train_scaled = scaler.fit_transform(X_train_imputed)
X_test_scaled = scaler.transform(X_test_imputed)
scores = cross_val_score(log_reg, X_train_scaled, y_train, cv=10)
print('Cross-Validation Accuracy Scores', scores)
```
Now all the features have a min of 0 and a max of 1
```
pd.DataFrame(X_train_scaled).describe()
```
The model coefficients change with scaling
```
log_reg.fit(X_train_scaled, y_train)
coefficients = pd.Series(log_reg.coef_[0], X_train_encoded.columns)
plt.figure(figsize=(10,10))
coefficients.sort_values().plot.barh(color='grey');
```
### Pipeline
https://scikit-learn.org/stable/modules/compose.html#pipeline
```
from sklearn.pipeline import make_pipeline
pipe = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
MinMaxScaler(),
LogisticRegression(solver='lbfgs', max_iter=1000)
)
scores = cross_val_score(pipe, X_train, y_train, cv=10)
print('Cross-Validation Accuracy Scores', scores)
pipe.fit(X_train, y_train)
y_pred = pipe.predict(X_test)
submission = test[['PassengerId']].copy()
submission['Survived'] = y_pred
submission.to_csv('kaggle-submission-001.csv', index=False)
```
## Assignment: real-world classification
We're going to check out a larger dataset - the [FMA Free Music Archive data](https://github.com/mdeff/fma). It has a selection of CSVs with metadata and calculated audio features that you can load and try to use to classify genre of tracks. To get you started:
### Get and unzip the data
#### Google Colab
```
!wget https://os.unil.cloud.switch.ch/fma/fma_metadata.zip
!unzip fma_metadata.zip
```
#### Windows
- Download the [zip file](https://os.unil.cloud.switch.ch/fma/fma_metadata.zip)
- You may need to use [7zip](https://www.7-zip.org/download.html) to unzip it
#### Mac
- Download the [zip file](https://os.unil.cloud.switch.ch/fma/fma_metadata.zip)
- You may need to use [p7zip](https://superuser.com/a/626731) to unzip it
### Look at first 4 lines of raw `tracks.csv` file
```
!head -n 4 fma_metadata/tracks.csv
```
### Read with pandas
https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_csv.html
```
tracks = pd.read_csv('fma_metadata/tracks.csv', header=[0,1], index_col=0)
tracks.head()
```
### More data prep
Get value counts of the target. (The syntax is different because the header has two levels, it's a "MultiIndex.")
The target has multiple classes, and many missing values.
```
tracks['track']['genre_top'].value_counts(normalize=True, dropna=False)
```
We can't do supervised learning where targets are missing. (In other words, we can't do supervised learning without supervision.)
So, only keep observations where the target is not null.
```
target_not_null = tracks['track']['genre_top'].notnull()
tracks = tracks[target_not_null]
```
Load `features.csv`: "common features extracted from the audio with [librosa](https://librosa.github.io/librosa/)"
It has 3 levels of columns!
```
features = pd.read_csv('fma_metadata/features.csv', header=[0,1,2], index_col=0)
features.head()
```
I want to [drop a level](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.MultiIndex.droplevel.html) here from the audio features dataframe, so it has the same number of levels (2) as the tracks metadata dataframe, so that I can better merge the two together.
```
features.columns = features.columns.droplevel(level=2)
features.head()
```
Merge the metadata with the audio features, on track id (the index for both dataframes).
```
df = pd.merge(tracks, features, left_index=True, right_index=True)
```
And drop a level of columns again, because dealing with MultiIndex is hard
```
df.columns = df.columns.droplevel()
```
This is now a pretty big dataset. Almost 500,000 rows, over 500 columns, and over 200 megabytes in RAM.
```
print(df.shape)
df.info()
```
### Fit Logistic Regression!
```
from sklearn.model_selection import train_test_split
y = df['genre_top']
X = df.select_dtypes('number').drop(columns=['longitude', 'latitude'])
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.50, test_size=0.50,
random_state=42, stratify=y)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
model = LogisticRegression(solver='lbfgs', multi_class='auto')
model.fit(X_train, y_train)
```
Accuracy is 37%, which sounds bad, BUT ...
```
model.score(X_test, y_test)
```
... remember we have 16 classes, and the majority class (Rock) occurs 29% of the time, so the model isn't worse than random guessing for this problem
```
y.value_counts(normalize=True)
```
This dataset is bigger than many you've worked with so far, and while it should fit in Colab, it can take awhile to run. That's part of the challenge!
Your tasks:
- Clean up the variable names in the dataframe
- Use logistic regression to fit a model predicting (primary/top) genre
- Inspect, iterate, and improve your model
- Answer the following questions (written, ~paragraph each):
- What are the best predictors of genre?
- What information isn't very useful for predicting genre?
- What surprised you the most about your results?
*Important caveats*:
- This is going to be difficult data to work with - don't let the perfect be the enemy of the good!
- Be creative in cleaning it up - if the best way you know how to do it is download it locally and edit as a spreadsheet, that's OK!
- If the data size becomes problematic, consider sampling/subsetting, or [downcasting numeric datatypes](https://www.dataquest.io/blog/pandas-big-data/).
- You do not need perfect or complete results - just something plausible that runs, and that supports the reasoning in your written answers
If you find that fitting a model to classify *all* genres isn't very good, it's totally OK to limit to the most frequent genres, or perhaps trying to combine or cluster genres as a preprocessing step. Even then, there will be limits to how good a model can be with just this metadata - if you really want to train an effective genre classifier, you'll have to involve the other data (see stretch goals).
This is real data - there is no "one correct answer", so you can take this in a variety of directions. Just make sure to support your findings, and feel free to share them as well! This is meant to be practice for dealing with other "messy" data, a common task in data science.
## Resources and stretch goals
- Check out the other .csv files from the FMA dataset, and see if you can join them or otherwise fit interesting models with them
- [Logistic regression from scratch in numpy](https://blog.goodaudience.com/logistic-regression-from-scratch-in-numpy-5841c09e425f) - if you want to dig in a bit more to both the code and math (also takes a gradient descent approach, introducing the logistic loss function)
- Create a visualization to show predictions of your model - ideally show a confidence interval based on error!
- Check out and compare classification models from scikit-learn, such as [SVM](https://scikit-learn.org/stable/modules/svm.html#classification), [decision trees](https://scikit-learn.org/stable/modules/tree.html#classification), and [naive Bayes](https://scikit-learn.org/stable/modules/naive_bayes.html). The underlying math will vary significantly, but the API (how you write the code) and interpretation will actually be fairly similar.
- Sign up for [Kaggle](https://kaggle.com), and find a competition to try logistic regression with
- (Not logistic regression related) If you enjoyed the assignment, you may want to read up on [music informatics](https://en.wikipedia.org/wiki/Music_informatics), which is how those audio features were actually calculated. The FMA includes the actual raw audio, so (while this is more of a longterm project than a stretch goal, and won't fit in Colab) if you'd like you can check those out and see what sort of deeper analysis you can do.
| true |
code
| 0.521654 | null | null | null | null |
|
<h2> Import Libraries</h2>
```
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
```
## Load the Data
The boston house-price dataset is one of datasets scikit-learn comes with that do not require the downloading of any file from some external website. The code below loads the boston dataset.
```
data = load_boston()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['target'] = data.target
df.head()
```
<h2> Remove Missing or Impute Values</h2>
If you want to build models with your data, null values are (almost) never allowed. It is important to always see how many samples have missing values and for which columns.
```
# Look at the shape of the dataframe
df.shape
# There are no missing values in the dataset
df.isnull().sum()
```
<h2> Arrange Data into Features Matrix and Target Vector </h2>
What we are predicing is the continuous column "target" which is the median value of owner-occupied homes in $1000’s.
```
X = df.loc[:, ['RM', 'LSTAT', 'PTRATIO']]
y = df.loc[:, 'target']
```
## Splitting Data into Training and Test Sets
```
# Original random state is 2
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2)
```
## Train Test Split Visualization
A relatively new feature of pandas is conditional formatting. https://pandas.pydata.org/pandas-docs/stable/user_guide/style.html
```
X_train = pd.DataFrame(X_train, columns=['RM', 'LSTAT', 'PTRATIO'])
X_test = pd.DataFrame(X_test, columns=['RM', 'LSTAT', 'PTRATIO'])
X_train['split'] = 'train'
X_test['split'] = 'test'
X_train
X_train['target'] = y_train
X_test['target'] = y_test
fullDF = pd.concat([X_train, X_test], axis = 0, ignore_index=False)
fullDF.head(10)
len(fullDF.index)
len(np.unique(fullDF.index))
fullDFsplit = fullDF.copy()
fullDF = fullDF.drop(columns = ['split'])
def highlight_color(s, fullDFsplit):
'''
highlight the the entire dataframe cyan.
'''
colorDF = s.copy()
colorDF.loc[fullDFsplit['split'] == 'train', ['RM', 'LSTAT', 'PTRATIO']] = 'background-color: #40E0D0'
colorDF.loc[fullDFsplit['split'] == 'test', ['RM', 'LSTAT', 'PTRATIO']] = 'background-color: #00FFFF'
# #9370DB
# FF D7 00
colorDF.loc[fullDFsplit['split'] == 'train', ['target']] = 'background-color: #FFD700'
# EE82EE
# BD B7 6B
colorDF.loc[fullDFsplit['split'] == 'test', ['target']] = 'background-color: #FFFF00'
return(colorDF)
temp = fullDF.sort_index().loc[0:9,:].style.apply(lambda x: highlight_color(x,pd.DataFrame(fullDFsplit['split'])), axis = None)
temp.set_properties(**{'border-color': 'black',
'border': '1px solid black'})
```
<h3>Train test split key</h3>
```
# Train test split key
temp = pd.DataFrame(data = [['X_train','X_test','y_train','y_test']]).T
temp
def highlight_mini(s):
'''
highlight the the entire dataframe cyan.
'''
colorDF = s.copy()
# colorDF.loc[0, [0]] = 'background-color: #40E0D0'
# train features
colorDF.loc[0, [0]] = 'background-color: #40E0D0'
# test features
colorDF.loc[1, [0]] = 'background-color: #00FFFF'
# train target
colorDF.loc[2, [0]] = 'background-color: #FFD700'
# test target
colorDF.loc[3, [0]] = 'background-color: #FFFF00'
return(colorDF)
temp2 = temp.sort_index().style.apply(lambda x: highlight_mini(x), axis = None)
temp2.set_properties(**{'border-color': 'black',
'border': '1px solid black',
})
```
After that I was lazy and used powerpoint to make that graph.
| true |
code
| 0.463991 | null | null | null | null |
|
# Assignment 5: Exploring Hashing
In this exercise, we will begin to explore the concept of hashing and how it related to various object containers with respect to computational complexity. We will begin with the base code for as described in Chapter 5 of Grokking Algorithms (Bhargava 2016).
## Deliverables:
We will again generate random data for this assignment.
1) Create a list of 100,000 names (randomly pick 10 characters e.g. abcdefghij, any order is fine, just make sure there are no duplicates names) and store those names in an unsorted list.
2) Now store the above names in a set
3) Make a separate copy of the list and sort it using any sorting algorithm that you have learned so far and justify why are you using it. Capture the time it takes to sort the list.
4) Pick the names from the unsorted array that are at 10,000th, 30,000th, 50,000th, 70,000th, 90,000th, and 100,000th positions, and store them in a temporary array somewhere for later use.
5) Search for these six names in each of the collections. Use linear search for the unsorted list, binary search for the sorted list, and use the set.remove() (or the in keyword) builtin for the set. Capture the time it takes using all three algorithms.
6) Create a table and plot comparing times of linear search, binary search and set lookup for the six names using Python (matplotlib or Seaborn) or JavaScript (D3) visualization tools to illustrate algorithm performance.
### Prepare an executive summary of your results, referring to the table and figures you have generated. Explain how your results relate to big O notation. Describe your results in language that management can understand. This summary should be included as text paragraphs in the Jupyter notebook. Explain how the algorithm works and why it is a useful to data engineers.
# A. Setup: Library imports, Function construction and Array generation
```
import numpy as np
import pandas as pd
import seaborn as sns
import time
import random
import string
RANDOM_SEED = 8 #sets random seed
def random_string(str_length, num_strings):
str_list = [] #instantiates an empty list to hold the strings
for i in range(0,num_strings): #loop to generate the specified number of strings
str_list.append(''.join(random.choice(string.ascii_lowercase) for m in range(str_length))) #generates a string of the defined character length
return str_list #returns the string list
def MergeSort(arr):
if len(arr) > 1:
mid = len(arr)//2 # gets middle
Left = arr[:mid] #splits elements left of middle
Right = arr[mid:] #splits elements right of middle
MergeSort(Left) #recursive call on left
MergeSort(Right) #recursive call on right
#set all indicies to 0
i=0
k=0
j=0
#below checks the values for if elements are sorted, if unsorted: swap. Merge to the original list
while i < len(Left) and j < len(Right):
if Left[i] < Right[j]:
arr[k] = Left[i] #makes k index of arr left[i] if it's less than Right[j]
i += 1 #increments i (the left index)
else:
arr[k] = Right[j] #if right value is lss than left, makes arr[k] the value of right and increments the right index
j += 1 #increments j
k += 1 #increments the arr index
while i < len(Left): #checks to see if reamaining elements in left (less than mid), if so adds to arr at k index and increments i and k
arr[k] = Left[i]
i += 1 #increments i
k += 1 #increments k
while j < len(Right): #checks to see if remaining elements in right (greater than mid), if so adds to arr at k index and increments j and k.
arr[k] = Right[j]
j += 1 #increments j
k += 1 #increments k
return arr
def Container(arr, fun):
objects = [] #instantiates an empty list to collect the returns
times = [] #instantiates an empty list to collect times for each computation
start= time.perf_counter() #collects the start time
obj = fun(arr) # applies the function to the arr object
end = time.perf_counter() # collects end time
duration = (end-start)* 1E3 #converts to milliseconds
objects.append(obj)# adds the returns of the functions to the objects list
times.append(duration) # adds the duration for computation to list
return objects, duration
#function SimpleSearch uses a value counter "low" which increments after a non successful evalution of equivalence for the item within a given array. It returns the milliseconds elapsed and a register of all the incremental guesses.
def SimpleSearch(array, item):
i = 0
guess = array[i]
start = time.perf_counter() # gets fractional seconds
while item != guess:
i += 1
guess = array[i] #increments low
end = time.perf_counter() # gets fractional seconds
duration = end - start # calcualates difference in fractional seconds
MilliElapsed = duration*1E3
# returns a tuple which contains search time in milliseconds and register of the guesses
return MilliElapsed
#function BinarySearch determines the range of the array and guwsses the midpoint of the range. A loop continues to to perform iterative range evaluations so long as the low value is equal or less than the high value of the array. When the gues converges to the item of interest, a tuple is returned with the time elapsed in milliseconds and the register of guesses.
# binary search for the sorted list
def BinarySearch(array, item):
i = 0
length = len(array)-1
low = array[i] #finds lowest value in array
high = array[length] #finds highest value in array
register = [] # creates empty register of increments; for debug purposes
start = time.perf_counter() # gets fractional seconds
while i <= length:
mid= (i + length)/2 # calculates midpoint of the range
guess = int(mid)
register.append(array[guess]) # appends increments to register; for debug purposes
if array[guess] == item:
end = time.perf_counter() #datetime.utcnow()
duration = end - start
MilliElapsed = duration*1E3
#print('the string is found for:', n)
#returns a tuple which contains search time in milliseconds and register of the guesses
return MilliElapsed #, register
elif array[guess] > item: ##### loop for if guess is higher than the item
high = array[guess] #resets high to the item at the guess index
low = array[i] #resets low to the item at the i index (typically index 0)
length = guess#resets length to guess
#print('The guess went too high!', n, i, array[guess])
elif array[guess] < item: ######loop for if guess is lower the the item
low = array[guess] #reset low to the index of guess
length = len(array)-1 #get the length of the array to pass to high
high = array[length] #reset high to be the end of the list
i = guess+1 #make sure we increment i so that it can become the end of the list, otherwise you are going to have a bad time!
#print('The guess went too low!',n, i, high, length, low)
str100000 = random_string(str_length=10, num_strings=100000) #generates random strings
str100000_copy = str100000[:] #creates a copy of the random strings
start = time.perf_counter()
MergeSort(str100000)
end = time.perf_counter()
duration = end - start
MS_time = duration*1E3
positions = [9999, 29999, 49999, 69999, 89999, 99999] #positions of the names (needles)
needles = [str100000_copy[i] for i in positions] #collects the needles from the haystack
str100000_container =Container(str100000, MergeSort) #uses mergesort to sort the strings.
temp =str100000_container[0]
str100000_sorted =temp[0]
set_str100000 = set(str100000_copy)
print('the needles are:' , needles)
print('the length of the set is:' ,len(set_str100000))
print('the length of the unsorted copy is:' , len(str100000_copy))
print('the length of the sorted list (mergesort) is:', len(str100000_sorted))
```
# B. Sorting
Search for these six names in each of the collections. Use linear search for the unsorted list, binary search for the sorted list, and use the set.remove() (or the in keyword) builtin for the set. Capture the time it takes using all three algorithms.
### B1. Linear Search of the unsorted list
```
#linear search for the unsorted list
Linear_times = []
for n in needles:
temp_time = SimpleSearch(str100000_copy, n)
Linear_times.append(temp_time)
print('The time reqired for each element in the unsorted array using linear search is:', Linear_times)
```
### B2. Binary Search of the sorted list
```
Binary_times = []
for n in needles:
temp_time = BinarySearch(str100000, n)
Binary_times.append(temp_time)
print('The time reqired for each element in the unsorted array using Binary search is:', Binary_times)
```
### B3. Set Removal for the Set
```
set_needles = set(needles)
set_times = {}
for needle in set_needles:
start = time.perf_counter()
set_str100000.intersection(needle)
end = time.perf_counter()
duration = end - start
MilliElapsed = duration*1E3
set_times[needle] = MilliElapsed
set_times
```
# C. Summary
## Figure 1: Search times in milliseconds for Strings within an array of 100000 elements (each string 10 random lowercase alpha characters)
```
Strings = {
'String': [needles[0], needles[1],needles[2], needles[3],needles[4], needles[5]],
'PostionInSortedArray': [10000, 30000, 50000, 70000, 90000, 100000],
'LinearSearch(Unsorted)': [Linear_times[0], Linear_times[1], Linear_times[2], Linear_times[3], Linear_times[4], Linear_times[5]],
'BinarySearch(Sorted)': [Binary_times[0], Binary_times[1], Binary_times[2], Binary_times[3], Binary_times[4], Binary_times[5]],
'SetIntersection(Unsorted)': [set_times.get(needles[0]), set_times.get(needles[1]), set_times.get(needles[2]), set_times.get(needles[3]), set_times.get(needles[4]), set_times.get(needles[5])]
}
string_df = pd.DataFrame.from_dict(Strings)
string_df['Binary+Sort'] = string_df['BinarySearch(Sorted)']+MS_time
string_df
```
## Table 1: Times for each algorithm given the length of the starting list
```
long_df = string_df.melt(id_vars=['String', 'PostionInSortedArray'],
value_vars=['LinearSearch(Unsorted)', 'BinarySearch(Sorted)', 'SetIntersection(Unsorted)'],var_name='Algo', value_name='Time(ms)')
```
## Figure 1: Sorth Algorithm Time Complexity
```
sns.barplot(data = long_df, x='PostionInSortedArray', hue='Algo', y='Time(ms)')
plot = sns.barplot(data = long_df, x='PostionInSortedArray', hue='Algo', y='Time(ms)')
plot.set_yscale('log')
```
## Figure 2: Merge and Quick Sort time complexity
# Discussion
Three sorting algorithms were tested for their time complexity in sorting lists of varying sizes of string elements. Each string element in the list was randomly populated with 50 alphabetic lower case characters. The number of elements within the list was varied. Five lists containing 200, 400, 600, 800, and 1000 strings were sorted via BubbleSort, MergeSort, and QuickSort. The times (given in milliseconds) required to perform the sort are collected and displayed in Table 1. By far, the most inefficient sorting algorithm demonstrated here is the bubble sort whose complexity is shown graphically (figure 1) to grow at n\*n or O(n^2) rate. This makes sense for bubble sort as it compares n elements amongst n elements.
Alternatively, the other two methodologies utilize a divide and conquer strategy. The list of strings when using QuickSort are divided into two arrays (greater and less) which contain values which are greater or less than a pivot value. In MergeSort a similar strategy is achieved by dividing the list into two arrays (left and right) which are left and right respectivly from the center element of the list. In both of these arrays recursion is used as the QuickSort and MergeSort functions are called on the subarrays. The result of this divide and conquer strategy is a complexity of n*logn or O(n*logn) in big O notation. A direct comparision of the times required for sorting the lists with these two methodologies are shown in Figure 2.
In rare instances QuickSort may also dramatically underperform as the pivot element is always selected as the first item of the array (or subarray). If an array contained a list which was sorted largest to smallest already, this method could also have very high complexity as you would not divide the list recursively for an array of n size (this would also be n\*n complexity O(n^2)). It is interesting the QuickSort seems to perform slightly better than MergeSort, but both are quite efficient. Because of the splitting methodology employed by the MergeSort, there lacks a risk of any deviation from the O(n*logn) complexity. The begining array and subarrays are always split in half size-wise. It's therefore recommended that the MergeSort method be used as the time complexity will always be constant.
# ------------------------ END ------------------------
```
# binary search for the sorted list
def BinarySearch(array, item):
i = 0
length = len(array)-1
low = array[i] #finds lowest value in array
high = array[length] #finds highest value in array
register = [] # creates empty register of increments; for debug purposes
start = time.perf_counter() # gets fractional seconds
while i <= length:
mid= (i + length)/2 # calculates midpoint of the range
guess = int(mid)
register.append(array[guess]) # appends increments to register; for debug purposes
if array[guess] == item:
end = time.perf_counter() #datetime.utcnow()
duration = end - start
MilliElapsed = duration*1E3
#print('the string is found for:', n)
#returns a tuple which contains search time in milliseconds and register of the guesses
return MilliElapsed #, register
elif array[guess] > item:
high = array[guess]
low = array[i]
length = guess
#print('The guess went too high!', n, i, array[guess])
elif array[guess] < item:
low = array[guess]
length = len(array)-1
high = array[length]
i = guess+1
#print('The guess went too low!',n, i, high, length, low)
else:
print('item not found!')
```
| true |
code
| 0.287893 | null | null | null | null |
|
# Demo: RAIL Evaluation
The purpose of this notebook is to demonstrate the application of the metrics scripts to be used on the photo-z PDF catalogs produced by the PZ working group. The first implementation of the _evaluation_ module is based on the refactoring of the code used in [Schmidt et al. 2020](https://arxiv.org/pdf/2001.03621.pdf), available on Github repository [PZDC1paper](https://github.com/LSSTDESC/PZDC1paper).
To run this notebook, you must install qp and have the notebook in the same directory as `utils.py` (available in RAIL's examples directrory). You must also install some run-of-the-mill Python packages: numpy, scipy, matplotlib, and seaborn.
### Contents
* [Data](#data)
- [Photo-z Results](#fzboost)
* [CDF-based metrics](#metrics)
- [PIT](#pit)
- [QQ plot](#qq)
* [Summary statistics of CDF-based metrics](#summary_stats)
- [KS](#ks)
- [CvM](#cvm)
- [AD](#ad)
- [KLD](#kld)
* [CDE loss](#cde_loss)
* [Summary](#summary)
```
from rail.evaluation.metrics.pit import *
from rail.evaluation.metrics.cdeloss import *
from utils import read_pz_output, plot_pit_qq, ks_plot
from main import Summary
import qp
import os
%matplotlib inline
%reload_ext autoreload
%autoreload 2
```
<a class="anchor" id="data"></a>
# Data
To compute the photo-z metrics of a given test sample, it is necessary to read the output of a photo-z code containing galaxies' photo-z PDFs. Let's use the toy data available in `tests/data/` (**test_dc2_training_9816.hdf5** and **test_dc2_validation_9816.hdf5**) and the configuration file available in `examples/configs/FZBoost.yaml` to generate a small sample of photo-z PDFs using the **FZBoost** algorithm available on RAIL's _estimation_ module.
<a class="anchor" id="fzboost"></a>
### Photo-z Results
#### Run FZBoost
Go to dir `<your_path>/RAIL/examples/estimation/` and run the command:
`python main.py configs/FZBoost.yaml`
The photo-z output files (inputs for this notebook) will be writen at:
`<your_path>/RAIL/examples/estimation/results/FZBoost/test_FZBoost.hdf5`.
Let's use the ancillary function **read_pz_output** to facilitate the reading of all necessary data.
```
my_path = '/Users/sam/WORK/software/TMPRAIL/RAIL' # replace this with your local path to RAIL's parent dir
pdfs_file = os.path.join(my_path, "examples/estimation/results/FZBoost/test_FZBoost.hdf5")
ztrue_file = os.path.join(my_path, "tests/data/test_dc2_validation_9816.hdf5")
pdfs, zgrid, ztrue, photoz_mode = read_pz_output(pdfs_file, ztrue_file) # all numpy arrays
```
The inputs for the metrics shown above are the array of true (or spectroscopic) redshifts, and an ensemble of photo-z PDFs (a `qp.Ensemble` object).
```
fzdata = qp.Ensemble(qp.interp, data=dict(xvals=zgrid, yvals=pdfs))
```
***
<a class="anchor" id="metrics"></a>
# Metrics
<a class="anchor" id="pit"></a>
## PIT
The Probability Integral Transform (PIT), is the Cumulative Distribution Function (CDF) of the photo-z PDF
$$ \mathrm{CDF}(f, q)\ =\ \int_{-\infty}^{q}\ f(z)\ dz $$
evaluated at the galaxy's true redshift for every galaxy $i$ in the catalog.
$$ \mathrm{PIT}(p_{i}(z);\ z_{i})\ =\ \int_{-\infty}^{z^{true}_{i}}\ p_{i}(z)\ dz $$
```
pitobj = PIT(fzdata, ztrue)
quant_ens, metamets = pitobj.evaluate()
```
The _evaluate_ method PIT class returns two objects, a quantile distribution based on the full set of PIT values (a frozen distribution object), and a dictionary of meta metrics associated to PIT (to be detailed below).
```
quant_ens
metamets
```
PIT values
```
pit_vals = np.array(pitobj._pit_samps)
pit_vals
```
### PIT outlier rate
The PIT outlier rate is a global metric defined as the fraction of galaxies in the sample with extreme PIT values. The lower and upper limits for considering a PIT as outlier are optional parameters set at the Metrics instantiation (default values are: PIT $<10^{-4}$ or PIT $>0.9999$).
```
pit_out_rate = PITOutRate(pit_vals, quant_ens).evaluate()
print(f"PIT outlier rate of this sample: {pit_out_rate:.6f}")
```
<a class="anchor" id="qq"></a>
## PIT-QQ plot
The histogram of PIT values is a useful tool for a qualitative assessment of PDFs quality. It shows whether the PDFs are:
* biased (tilted PIT histogram)
* under-dispersed (excess counts close to the boudaries 0 and 1)
* over-dispersed (lack of counts close the boudaries 0 and 1)
* well-calibrated (flat histogram)
Following the standards in DC1 paper, the PIT histogram is accompanied by the quantile-quantile (QQ), which can be used to compare qualitatively the PIT distribution obtained with the PDFs agaist the ideal case (uniform distribution). The closer the QQ plot is to the diagonal, the better is the PDFs calibration.
```
plot_pit_qq(pdfs, zgrid, ztrue, title="PIT-QQ - toy data", code="FZBoost",
pit_out_rate=pit_out_rate, savefig=False)
```
The black horizontal line represents the ideal case where the PIT histogram would behave as a uniform distribution U(0,1).
***
<a class="anchor" id="summary_stats"></a>
# Summary statistics of CDF-based metrics
To evaluate globally the quality of PDFs estimates, `rail.evaluation` provides a set of metrics to compare the empirical distributions of PIT values with the reference uniform distribution, U(0,1).
<a class="anchor" id="ks"></a>
### Kolmogorov-Smirnov
Let's start with the traditional Kolmogorov-Smirnov (KS) statistic test, which is the maximum difference between the empirical and the expected cumulative distributions of PIT values:
$$
\mathrm{KS} \equiv \max_{PIT} \Big( \left| \ \mathrm{CDF} \small[ \hat{f}, z \small] - \mathrm{CDF} \small[ \tilde{f}, z \small] \ \right| \Big)
$$
Where $\hat{f}$ is the PIT distribution and $\tilde{f}$ is U(0,1). Therefore, the smaller value of KS the closer the PIT distribution is to be uniform. The `evaluate` method of the PITKS class returns a named tuple with the statistic and p-value.
```
ksobj = PITKS(pit_vals, quant_ens)
ks_stat_and_pval = ksobj.evaluate()
ks_stat_and_pval
```
Visual interpretation of the KS statistic:
```
ks_plot(pitobj)
print(f"KS metric of this sample: {ks_stat_and_pval.statistic:.4f}")
```
<a class="anchor" id="cvm"></a>
### Cramer-von Mises
Similarly, let's calculate the Cramer-von Mises (CvM) test, a variant of the KS statistic defined as the mean-square difference between the CDFs of an empirical PDF and the true PDFs:
$$ \mathrm{CvM}^2 \equiv \int_{-\infty}^{\infty} \Big( \mathrm{CDF} \small[ \hat{f}, z \small] \ - \ \mathrm{CDF} \small[ \tilde{f}, z \small] \Big)^{2} \mathrm{dCDF}(\tilde{f}, z) $$
on the distribution of PIT values, which should be uniform if the PDFs are perfect.
```
cvmobj = PITCvM(pit_vals, quant_ens)
cvm_stat_and_pval = cvmobj.evaluate()
print(f"CvM metric of this sample: {cvm_stat_and_pval.statistic:.4f}")
```
<a class="anchor" id="ad"></a>
### Anderson-Darling
Another variation of the KS statistic is the Anderson-Darling (AD) test, a weighted mean-squared difference featuring enhanced sensitivity to discrepancies in the tails of the distribution.
$$ \mathrm{AD}^2 \equiv N_{tot} \int_{-\infty}^{\infty} \frac{\big( \mathrm{CDF} \small[ \hat{f}, z \small] \ - \ \mathrm{CDF} \small[ \tilde{f}, z \small] \big)^{2}}{\mathrm{CDF} \small[ \tilde{f}, z \small] \big( 1 \ - \ \mathrm{CDF} \small[ \tilde{f}, z \small] \big)}\mathrm{dCDF}(\tilde{f}, z) $$
```
adobj = PITAD(pit_vals, quant_ens)
ad_stat_crit_sig = adobj.evaluate()
ad_stat_crit_sig
ad_stat_crit_sig
print(f"AD metric of this sample: {ad_stat_crit_sig.statistic:.4f}")
```
It is possible to remove catastrophic outliers before calculating the integral for the sake of preserving numerical instability. For instance, Schmidt et al. computed the Anderson-Darling statistic within the interval (0.01, 0.99).
```
ad_stat_crit_sig_cut = adobj.evaluate(pit_min=0.01, pit_max=0.99)
print(f"AD metric of this sample: {ad_stat_crit_sig.statistic:.4f}")
print(f"AD metric for 0.01 < PIT < 0.99: {ad_stat_crit_sig_cut.statistic:.4f}")
```
<a class="anchor" id="cde_loss"></a>
# CDE Loss
In the absence of true photo-z posteriors, the metric used to evaluate individual PDFs is the **Conditional Density Estimate (CDE) Loss**, a metric analogue to the root-mean-squared-error:
$$ L(f, \hat{f}) \equiv \int \int {\big(f(z | x) - \hat{f}(z | x) \big)}^{2} dzdP(x), $$
where $f(z | x)$ is the true photo-z PDF and $\hat{f}(z | x)$ is the estimated PDF in terms of the photometry $x$. Since $f(z | x)$ is unknown, we estimate the **CDE Loss** as described in [Izbicki & Lee, 2017 (arXiv:1704.08095)](https://arxiv.org/abs/1704.08095). :
$$ \mathrm{CDE} = \mathbb{E}\big( \int{{\hat{f}(z | X)}^2 dz} \big) - 2{\mathbb{E}}_{X, Z}\big(\hat{f}(Z, X) \big) + K_{f}, $$
where the first term is the expectation value of photo-z posterior with respect to the marginal distribution of the covariates X, and the second term is the expectation value with respect to the joint distribution of observables X and the space Z of all possible redshifts (in practice, the centroids of the PDF bins), and the third term is a constant depending on the true conditional densities $f(z | x)$.
```
cdelossobj = CDELoss(fzdata, zgrid, ztrue)
cde_stat_and_pval = cdelossobj.evaluate()
cde_stat_and_pval
print(f"CDE loss of this sample: {cde_stat_and_pval.statistic:.2f}")
```
<a class="anchor" id="summary"></a>
# Summary
```
summary = Summary(pdfs, zgrid, ztrue)
summary.markdown_metrics_table(pitobj=pitobj) # pitobj as optional input to speed-up metrics evaluation
summary.markdown_metrics_table(pitobj=pitobj, show_dc1="FlexZBoost")
```
| true |
code
| 0.693421 | null | null | null | null |
|
# Model Selection/Evaluation with Yellowbrick
Oftentimes with a new dataset, the choice of the best machine learning algorithm is not always obvious at the outset. Thanks to the scikit-learn API, we can easily approach the problem of model selection using model *evaluation*. As we'll see in these examples, Yellowbrick is helpful for facilitating the process.
## Evaluating Classifiers
Classification models attempt to predict a target in a discrete space, that is assign an instance of dependent variables one or more categories. Classification score visualizers display the differences between classes as well as a number of classifier-specific visual evaluations.
### ROCAUC
A `ROCAUC` (Receiver Operating Characteristic/Area Under the Curve) plot allows the user to visualize the tradeoff between the classifier’s sensitivity and specificity.
The Receiver Operating Characteristic (ROC) is a measure of a classifier’s predictive quality that compares and visualizes the tradeoff between the model’s sensitivity and specificity. When plotted, a ROC curve displays the true positive rate on the Y axis and the false positive rate on the X axis on both a global average and per-class basis. The ideal point is therefore the top-left corner of the plot: false positives are zero and true positives are one.
This leads to another metric, area under the curve (AUC), which is a computation of the relationship between false positives and true positives. The higher the AUC, the better the model generally is. However, it is also important to inspect the “steepness” of the curve, as this describes the maximization of the true positive rate while minimizing the false positive rate.
```
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from yellowbrick.classifier import ROCAUC
from yellowbrick.datasets import load_occupancy
# Load the classification data set
X, y = load_occupancy()
# Specify the classes of the target
classes = ["unoccupied", "occupied"]
# Create the train and test data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# Instantiate the visualizer with the classification model
visualizer = ROCAUC(LogisticRegression(
multi_class="auto", solver="liblinear"
), classes=classes, size=(1080, 720)
)
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Draw the data
```
Yellowbrick’s `ROCAUC` Visualizer also allows for plotting **multiclass** classification curves. ROC curves are typically used in binary classification, and in fact the Scikit-Learn `roc_curve` metric is only able to perform metrics for binary classifiers. Yellowbrick addresses this by binarizing the output (per-class) or to use one-vs-rest (micro score) or one-vs-all (macro score) strategies of classification.
```
from sklearn.linear_model import RidgeClassifier
from sklearn.preprocessing import OrdinalEncoder, LabelEncoder
from yellowbrick.datasets import load_game
# Load multi-class classification dataset
X, y = load_game()
classes = ['win', 'loss', 'draw']
# Encode the non-numeric columns
X = OrdinalEncoder().fit_transform(X)
y = LabelEncoder().fit_transform(y)
# Create the train and test data
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2
)
visualizer = ROCAUC(
RidgeClassifier(), classes=classes, size=(1080, 720)
)
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Draw the data
```
### ClassificationReport Heatmap
The classification report visualizer displays the precision, recall, F1, and support scores for the model. In order to support easier interpretation and problem detection, the report integrates numerical scores with a color-coded heatmap. All heatmaps are in the range `(0.0, 1.0)` to facilitate easy comparison of classification models across different classification reports.
```
from sklearn.naive_bayes import GaussianNB
from yellowbrick.classifier import ClassificationReport
# Load the classification data set
X, y = load_occupancy()
classes = ["unoccupied", "occupied"]
# Create the train and test data
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2
)
# Instantiate the classification model and visualizer
bayes = GaussianNB()
visualizer = ClassificationReport(
bayes, classes=classes, support=True, size=(1080, 720)
)
visualizer.fit(X_train, y_train) # Fit the visualizer and the model
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Draw the data
```
The classification report shows a representation of the main classification metrics on a per-class basis. This gives a deeper intuition of the classifier behavior over global accuracy which can mask functional weaknesses in one class of a multiclass problem. Visual classification reports are used to compare classification models to select models that are “redder”, e.g. have stronger classification metrics or that are more balanced.
The metrics are defined in terms of true and false positives, and true and false negatives. Positive and negative in this case are generic names for the classes of a binary classification problem. In the example above, we would consider true and false occupied and true and false unoccupied. Therefore a true positive is when the actual class is positive as is the estimated class. A false positive is when the actual class is negative but the estimated class is positive. Using this terminology the meterics are defined as follows:
**precision**
Precision is the ability of a classiifer not to label an instance positive that is actually negative. For each class it is defined as as the ratio of true positives to the sum of true and false positives. Said another way, “for all instances classified positive, what percent was correct?”
**recall**
Recall is the ability of a classifier to find all positive instances. For each class it is defined as the ratio of true positives to the sum of true positives and false negatives. Said another way, “for all instances that were actually positive, what percent was classified correctly?”
**f1 score**
The F1 score is a weighted harmonic mean of precision and recall such that the best score is 1.0 and the worst is 0.0. Generally speaking, F1 scores are lower than accuracy measures as they embed precision and recall into their computation. As a rule of thumb, the weighted average of F1 should be used to compare classifier models, not global accuracy.
**support**
Support is the number of actual occurrences of the class in the specified dataset. Imbalanced support in the training data may indicate structural weaknesses in the reported scores of the classifier and could indicate the need for stratified sampling or rebalancing. Support doesn’t change between models but instead diagnoses the evaluation process.
### ClassPredictionError
The Yellowbrick `ClassPredictionError` plot is a twist on other and sometimes more familiar classification model diagnostic tools like the Confusion Matrix and Classification Report. Like the Classification Report, this plot shows the support (number of training samples) for each class in the fitted classification model as a stacked bar chart. Each bar is segmented to show the proportion of predictions (including false negatives and false positives, like a Confusion Matrix) for each class. You can use a `ClassPredictionError` to visualize which classes your classifier is having a particularly difficult time with, and more importantly, what incorrect answers it is giving on a per-class basis. This can often enable you to better understand strengths and weaknesses of different models and particular challenges unique to your dataset.
The class prediction error chart provides a way to quickly understand how good your classifier is at predicting the right classes.
```
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from yellowbrick.classifier import ClassPredictionError
from yellowbrick.datasets import load_credit
X, y = load_credit()
classes = ['account in default', 'current with bills']
# Perform 80/20 training/test split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.20, random_state=42
)
# Instantiate the classification model and visualizer
visualizer = ClassPredictionError(
RandomForestClassifier(n_estimators=10),
classes=classes, size=(1080, 720)
)
# Fit the training data to the visualizer
visualizer.fit(X_train, y_train)
# Evaluate the model on the test data
visualizer.score(X_test, y_test)
# Draw visualization
visualizer.show()
```
## Evaluating Regressors
Regression models attempt to predict a target in a continuous space. Regressor score visualizers display the instances in model space to better understand how the model is making predictions.
### PredictionError
A prediction error plot shows the actual targets from the dataset against the predicted values generated by our model. This allows us to see how much variance is in the model. Data scientists can diagnose regression models using this plot by comparing against the 45 degree line, where the prediction exactly matches the model.
```
from sklearn.linear_model import Lasso
from yellowbrick.regressor import PredictionError
from yellowbrick.datasets import load_concrete
# Load regression dataset
X, y = load_concrete()
# Create the train and test data
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# Instantiate the linear model and visualizer
model = Lasso()
visualizer = PredictionError(model, size=(1080, 720))
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Draw the data
```
### Residuals Plot
Residuals, in the context of regression models, are the difference between the observed value of the target variable (y) and the predicted value (ŷ), i.e. the error of the prediction. The residuals plot shows the difference between residuals on the vertical axis and the dependent variable on the horizontal axis, allowing you to detect regions within the target that may be susceptible to more or less error.
```
from sklearn.linear_model import Ridge
from yellowbrick.regressor import ResidualsPlot
# Instantiate the linear model and visualizer
model = Ridge()
visualizer = ResidualsPlot(model, size=(1080, 720))
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Draw the data
```
### Try them all
```
from sklearn.svm import SVR
from sklearn.neural_network import MLPRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import BayesianRidge, LinearRegression
regressors = {
"support vector machine": SVR(),
"multilayer perceptron": MLPRegressor(),
"nearest neighbors": KNeighborsRegressor(),
"bayesian ridge": BayesianRidge(),
"linear regression": LinearRegression(),
}
for _, regressor in regressors.items():
visualizer = ResidualsPlot(regressor)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show()
```
## Diagnostics
Target visualizers specialize in visually describing the dependent variable for supervised modeling, often referred to as y or the target.
### Class Balance Report
One of the biggest challenges for classification models is an imbalance of classes in the training data. Severe class imbalances may be masked by relatively good F1 and accuracy scores – the classifier is simply guessing the majority class and not making any evaluation on the underrepresented class.
There are several techniques for dealing with class imbalance such as stratified sampling, down sampling the majority class, weighting, etc. But before these actions can be taken, it is important to understand what the class balance is in the training data. The `ClassBalance` visualizer supports this by creating a bar chart of the support for each class, that is the frequency of the classes’ representation in the dataset.
```
from yellowbrick.target import ClassBalance
# Load multi-class classification dataset
X, y = load_game()
# Instantiate the visualizer
visualizer = ClassBalance(
labels=["draw", "loss", "win"], size=(1080, 720)
)
visualizer.fit(y)
visualizer.show()
```
Yellowbrick visualizers are intended to steer the model selection process. Generally, model selection is a search problem defined as follows: given N instances described by numeric properties and (optionally) a target for estimation, find a model described by a triple composed of features, an algorithm and hyperparameters that best fits the data. For most purposes the “best” triple refers to the triple that receives the best cross-validated score for the model type.
The yellowbrick.model_selection package provides visualizers for inspecting the performance of cross validation and hyper parameter tuning. Many visualizers wrap functionality found in `sklearn.model_selection` and others build upon it for performing multi-model comparisons.
### Cross Validation
Generally we determine whether a given model is optimal by looking at it’s F1, precision, recall, and accuracy (for classification), or it’s coefficient of determination (R2) and error (for regression). However, real world data is often distributed somewhat unevenly, meaning that the fitted model is likely to perform better on some sections of the data than on others. Yellowbrick’s `CVScores` visualizer enables us to visually explore these variations in performance using different cross validation strategies.
Cross-validation starts by shuffling the data (to prevent any unintentional ordering errors) and splitting it into `k` folds. Then `k` models are fit on $\frac{k-1} {k}$ of the data (called the training split) and evaluated on $\frac {1} {k}$ of the data (called the test split). The results from each evaluation are averaged together for a final score, then the final model is fit on the entire dataset for operationalization.
In Yellowbrick, the `CVScores` visualizer displays cross-validated scores as a bar chart (one bar for each fold) with the average score across all folds plotted as a horizontal dotted line.
```
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import StratifiedKFold
from yellowbrick.model_selection import CVScores
# Load the classification data set
X, y = load_occupancy()
# Create a cross-validation strategy
cv = StratifiedKFold(n_splits=12, random_state=42)
# Instantiate the classification model and visualizer
model = MultinomialNB()
visualizer = CVScores(
model, cv=cv, scoring='f1_weighted', size=(1080, 720)
)
visualizer.fit(X, y)
visualizer.show()
```
Visit the Yellowbrick docs for more about visualizers for [classification](http://www.scikit-yb.org/en/latest/api/classifier/index.html), [regression](http://www.scikit-yb.org/en/latest/api/regressor/index.html) and [model selection](http://www.scikit-yb.org/en/latest/api/model_selection/index.html)!
| true |
code
| 0.858185 | null | null | null | null |
|
```
from cmp import *
import pdir
%matplotlib qt
# Control variables
plot_lattice_unfinished_1 = True
plot_lattice_unfinished_2 = True
plot_lattice_demo = True
plot_lattice_planes = True
plot_scattering_none = True
plot_scattering_systemic = True
plot_band_structure_none = True
plot_band_structure_strong = True
plot_nearly_free_band = True
```
### Lattice with unfinished unit cells
```
if plot_lattice_unfinished_1:
a1, a2, a3 = np.eye(3)
basis = np.array([[0, 0, 0],
[0.5, 0.5, 0.5]])
colors = ['xkcd:cement', 'b']
sizes = [2, 2]
grid_type = "latticevectors"
type_ = "primitive"
n_min = np.array([0, 0, 0])
n_max = np.array([1, 1, 1])
(atomic_positions, lattice_coefficients, atomic_colors, atomic_sizes,
lattice_position) = lattices.generator(a1, a2, a3, basis, colors, sizes,
n_min, n_max)
# Create the figure
fig = plt.figure(figsize=(2,2))
ax = fig.gca(projection="3d")
# Plot atoms
ax.scatter(atomic_positions[:, 0], atomic_positions[:, 1],
atomic_positions[:, 2], c=atomic_colors, s=atomic_sizes)
# Get the relevant gridlines:
g_col = 'k'
g_w = 0.5
pruned_lines = lattices.grid_lines(a1, a2, a3, atomic_positions,
lattice_position, grid_type)
for line in pruned_lines:
ax.plot(line[0], line[1], line[2], color=g_col, linewidth=g_w)
ax.set_aspect('equal')
ax.set_proj_type('ortho')
ax.grid(False)
ax.axis('off')
# make the panes transparent (the plot box)
ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.view_init(15, -60)
fig.subplots_adjust(left=-0.15, right=1.15, top=1.15, bottom=-0.15)
fig.savefig('thesis/figures/lattice_unfinished_1.pdf')
```
### Lattice with unfinished unit cells 2
```
if plot_lattice_unfinished_2:
a1, a2, a3 = np.array([[0.5, 0.5, 0],
[0.5, 0, 0.5],
[0, 0.5, 0.5]])
basis = np.array([0, 0, 0])
colors = ['xkcd:cement']
sizes = [1]
grid_type = "latticevectors"
type_ = "primitive"
n_min = np.array([0, 0, 0])
n_max = np.array([2, 2, 2])
(atomic_positions, lattice_coefficients, atomic_colors, atomic_sizes,
lattice_position) = lattices.generator(a1, a2, a3, basis, colors, sizes,
n_min, n_max)
# Create the figure
fig = plt.figure(figsize=(2,2))
ax = fig.gca(projection="3d")
# Plot atoms
ax.scatter(atomic_positions[:, 0], atomic_positions[:, 1],
atomic_positions[:, 2], c=atomic_colors, s=atomic_sizes)
# Get the relevant gridlines:
g_col = 'k'
g_w = 0.3
pruned_lines = []
r_min, r_max = 0, 2
for nx in range(n_min[0], n_max[0] + 1):
for ny in range(n_min[1], n_max[1] + 1):
pruned_lines.append([np.array([nx, nx]),
np.array([ny, ny]),
np.array([r_min, r_max])])
for nz in range(n_min[2], n_max[2] + 1):
pruned_lines.append([np.array([nx, nx]),
np.array([r_min, r_max]),
np.array([nz, nz])])
for ny in range(n_min[1], n_max[1] + 1):
for nz in range(n_min[2], n_max[2] + 1):
pruned_lines.append([np.array([r_min, r_max]),
np.array([ny, ny]),
np.array([nz, nz])])
for line in pruned_lines:
ax.plot(line[0], line[1], line[2], color=g_col, linewidth=g_w)
ax.set_aspect('equal')
ax.set_proj_type('ortho')
ax.grid(False)
ax.axis('off')
# make the panes transparent (the plot box)
ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.view_init(15, -100)
fig.subplots_adjust(left=-0.2, right=1.2, top=1.2, bottom=-0.2)
fig.savefig('thesis/figures/lattice_unfinished_2.pdf')
```
### Demo of proper lattice
```
if plot_lattice_demo:
fig, ax = Lattice(lattice_name="conventional bcc", sizes=1,
colors=['xkcd:cement', 'b'], returns=True)
margin = 0.2
fig.set_size_inches(2,2)
fig.subplots_adjust(left=-margin, right=1+margin, top=1+margin, bottom=-margin)
ax.view_init(10, -80)
fig.savefig('thesis/figures/lattice_demo_1.pdf')
fig, ax = Lattice(lattice_name="hexagonal", sizes=1,
returns=True)
margin = 0.2
fig.set_size_inches(2,2)
fig.subplots_adjust(left=-margin, right=1+margin, top=1+margin, bottom=-margin)
ax.view_init(18, -84)
fig.savefig('thesis/figures/lattice_demo_2.pdf')
```
### Family of lattice planes
```
if plot_lattice_planes:
fig, ax = Reciprocal(lattice_name="bcc", indices=(0,0,1), max_=(0,0,4), returns=True)
ax.view_init(10, -80)
margin = 0.2
fig.set_size_inches(2,2)
fig.subplots_adjust(left=-margin, right=1+margin, top=1+margin, bottom=-margin)
fig.savefig('thesis/figures/lattice_planes_1.pdf')
```
### Scattering!
```
if plot_scattering_none:
fig, ax, ax2 = Scattering(basis=np.array([[0, 0, 0],
[0.5, 0.5, 0],
[0.5, 0, 0.5],
[0, 0.5, 0.5]]),
form_factor=np.array([1, 0.5, 0.5, 0.5]),
highlight=[1,1,2],
returns=True)
ax.view_init(5, -50)
fig.savefig('thesis/figures/scattering_no_systemic.pdf')
if plot_scattering_systemic:
fig, ax, ax2 = Scattering(basis=np.array([[0, 0, 0],
[0.5, 0.5, 0],
[0.5, 0, 0.5],
[0, 0.5, 0.5]]),
form_factor=np.array([1, 1, 1, 1]),
colors=['xkcd:cement'] * 4,
returns=True)
ax.view_init(5, -55)
fig.savefig('thesis/figures/scattering_systemic.pdf')
```
### Band structures
```
if plot_band_structure_none:
fig, ax, ax2 = Band_structure(edges=True, returns=True)
ax.view_init(33, -48)
fig.savefig('thesis/figures/band_structure_none.pdf')
if plot_band_structure_strong:
fig, ax, ax2 = Band_structure(edges=True, V0=1, returns=True)
ax.view_init(33, -48)
fig.savefig('thesis/figures/band_structure_strong.pdf')
import itertools
def calc_1D_band_structure(V0=0, n_k=101, G_range=list(range(-3,4)),
potential=band_structure.VG_dirac, extra=0.1):
kx = np.linspace(-1 / 2 - extra, 1 / 2 + extra, n_k)
ky = np.linspace(-1 / 2 - extra, 1 / 2 + extra, n_k)
num_Gs = (len(G_range))**2
# First we create the relevant matrix for some k:
b1 = np.array([1, 0])
b2 = np.array([0, 1])
ms = np.array(list(itertools.product(G_range, G_range)))
recip = np.array([b1, b2])
Gs = ms @ recip
E = np.zeros((num_Gs, n_k))
VG_mat = band_structure.potential_matrix(range_=G_range, potential=potential, V0=V0)
kxs, kys = np.meshgrid(kx, ky)
for i in range(n_k):
k = np.array([kx[i], 0])
Diag = np.diag(lattices.mag(k - Gs)**2) / 2
Full = Diag + VG_mat
Eigs = np.linalg.eigvalsh(Full)
E[:, i] = Eigs
band_to_return = E[0]
return kx, band_to_return
if plot_nearly_free_band:
n_k = 201
G = 3
extra = 0.05
o1 = calc_1D_band_structure(V0=0,
n_k=n_k,
G_range=list(range(-G,G+1)),
extra=0)
k_free, E_free = o1
o2 = calc_1D_band_structure(V0=0.05,
n_k=n_k,
G_range=list(range(-G,G+1)),
extra=extra)
k_small, E_small = o2
E_small = E_small - np.amin(E_small)
fig = plt.figure()
ax = fig.gca()
fig.set_size_inches([2,2])
ax.set_xlabel('$k$')
ax.set_xticks([-np.pi, 0, np.pi])
ax.set_xticklabels(['$-\pi/a$', '0', '$\pi/a$'])
ax.set_yticks([])
ax.set_ylabel('$E$')
ax.plot(k_free * 2 * np.pi, E_free, '--')
ax.plot(k_small * 2 * np.pi, E_small)
fig.tight_layout()
fig.savefig('thesis/figures/nearly_free.pdf')
```
| true |
code
| 0.690611 | null | null | null | null |
|
# DCASE-2021 Audio-Video
Author: Maximo Cobos
```
# Import necessary standard packages
import tensorflow as tf
import numpy as np
import pandas as pd
from pathlib import Path
import matplotlib.pyplot as plt
#import tensorflow_addons as tfa
tf.version.VERSION
```
## Input Data
Specify path to folder containing the video dataset and the output path for the tfrecords:
```
# TFRecords folder
main_dir = '.\\tfrecords_gamma'
root_path = Path(main_dir)
# Train Fold
train_fold_path = '.\\dataset\\evaluation_setup\\fold1_train.csv'
traindf = pd.read_csv(train_fold_path, sep='\t', lineterminator='\r')
trainlist = traindf[traindf.columns[1]].tolist()
trainfiles = [Path(f).with_suffix('.tfrecords').name for f in trainlist]
#trainfiles = trainfiles[0:int(0.33*len(trainfiles))]
# Validation Fold
val_fold_path = '.\\dataset\\evaluation_setup\\fold1_test.csv'
valdf = pd.read_csv(val_fold_path, sep='\t', lineterminator='\r')
vallist = valdf[valdf.columns[1]].tolist()
valfiles = [Path(f).with_suffix('.tfrecords').name for f in vallist]
#valfiles = valfiles[0:int(0.33*len(valfiles))]
len(trainfiles), len(valfiles)
```
Get class weights:
```
def get_label(filepath):
'''Receives a path to a video and returns its label
'''
scn_dict = {'airport': 0, 'shopping_mall': 1, 'metro_station': 2,
'street_pedestrian': 3, 'public_square': 4, 'street_traffic': 5,
'tram': 6, 'bus': 7, 'metro': 8, 'park': 9}
fileid = Path(filepath).name
scn_id = fileid.split('-')[0]
label = scn_dict[scn_id]
return label
# Get labels
train_labels = [get_label(f) for f in trainfiles]
val_labels = [get_label(f) for f in valfiles]
trainfiles = [main_dir + '\\' + str(label) + '\\' + f for f,label in zip(trainfiles,train_labels)]
valfiles = [main_dir + '\\' + str(label) + '\\' + f for f,label in zip(valfiles,val_labels)]
N_val = len(valfiles)
# Get number of examples per class
num_class_ex = []
for i in range(10):
num_class_ex.append(train_labels.count(i))
# Get class weights
N_train = len(train_labels)
num_classes = 10
class_weights = []
for i in range(num_classes):
weight = ( 1 / num_class_ex[i]) * N_train / num_classes
class_weights.append(weight)
keylst = np.arange(0,len(class_weights))
class_weights = {keylst[i]: class_weights[i] for i in range(0, len(class_weights))}
print("Class weights: ", class_weights)
```
### Parsing function
```
def parse_sequence(sequence_example, avmode = 'audiovideo'):
"""this function is the sequence parser for the created TFRecords file"""
sequence_features = {'VideoFrames': tf.io.FixedLenSequenceFeature([], dtype=tf.string),
'Labels': tf.io.FixedLenSequenceFeature([], dtype=tf.int64)}
context_features = {'AudioFrames': tf.io.FixedLenFeature((96000,), dtype=tf.float32),
'length': tf.io.FixedLenFeature([], dtype=tf.int64)}
context, sequence = tf.io.parse_single_sequence_example(
sequence_example, context_features=context_features, sequence_features=sequence_features)
# get features context
seq_length = tf.cast(context['length'], dtype = tf.int32)
# decode video and audio
video = tf.io.decode_raw(sequence['VideoFrames'], tf.uint8)
video = tf.reshape(video, shape=(seq_length, 224, 224, 3))
audio = tf.cast(context['AudioFrames'], tf.float32)
audio = tf.reshape(audio, shape=(64, 500, 3))
label = tf.cast(sequence['Labels'], dtype = tf.int32)
video = tf.cast(video, tf.float32)
if avmode == 'audio':
return audio, label
elif avmode == 'video':
return video, label
elif avmode == 'audiovideo':
return video, audio, label
```
Check parsing function:
```
# Check parsing function
filesds = tf.data.Dataset.from_tensor_slices(trainfiles)
dataset = tf.data.TFRecordDataset(filesds)
dataset = dataset.map(lambda tf_file: parse_sequence(tf_file,'audiovideo'), num_parallel_calls=4)
datait = iter(dataset)
example = datait.get_next()
print(example[0].shape, example[1].shape, example[2].shape)
plt.imshow(example[0][0,::].numpy().astype(np.uint8))
plt.show()
plt.imshow(example[1][:,:,0]);
```
## Augmentation
Mix-Up
```
def sample_beta_distribution(size, concentration_0=0.2, concentration_1=0.2):
gamma_1_sample = tf.random.gamma(shape=[size], alpha=concentration_1)
gamma_2_sample = tf.random.gamma(shape=[size], alpha=concentration_0)
return gamma_1_sample / (gamma_1_sample + gamma_2_sample)
def mix_up(ds_one, ds_two, alpha=0.2):
# Unpack two datasets
images_one, labels_one = ds_one
images_two, labels_two = ds_two
batch_size = tf.shape(images_one)[0]
# Sample lambda and reshape it to do the mixup
l = sample_beta_distribution(batch_size, alpha, alpha)
x_l = tf.reshape(l, (batch_size, 1, 1, 1))
y_l = tf.reshape(l, (batch_size, 1))
# Perform mixup on both images and labels by combining a pair of images/labels
# (one from each dataset) into one image/label
images = images_one * x_l + images_two * (1 - x_l)
labels = labels_one * y_l + labels_two * (1 - y_l)
return (images, labels)
def mix_up_audiovideo(ds_one, ds_two, alpha=0.2):
# Unpack two datasets
imagesaudio_one, labels_one = ds_one
imagesaudio_two, labels_two = ds_two
images_one = imagesaudio_one[0]
audios_one = imagesaudio_one[1]
batch_size = tf.shape(images_one)[0]
images_two = imagesaudio_two[0]
audios_two = imagesaudio_two[1]
# Sample lambda and reshape it to do the mixup
l = sample_beta_distribution(batch_size, alpha, alpha)
x_laudio = tf.reshape(l, (batch_size, 1, 1, 1))
x_lvideo = tf.reshape(l, (batch_size, 1, 1, 1, 1))
y_l = tf.reshape(l, (batch_size, 1))
# Perform mixup on both images and labels by combining a pair of images/labels
# (one from each dataset) into one image/label
images = images_one * x_lvideo + images_two * (1 - x_lvideo)
audios = audios_one * x_laudio + audios_two * (1 - x_laudio)
labels = labels_one * y_l + labels_two * (1 - y_l)
images = tf.cast(images, tf.uint8)
return (images, audios), labels
```
## Pipeline
### Audiovisual Modality
Useful functions for the pipeline
```
def normalize_sp(sp):
sp = sp - tf.math.reduce_min(sp)
sp = sp / tf.math.reduce_max(sp)
sp = 2*(sp-0.5)
return sp
def reshape_batch(data, labels):
data_video = tf.reshape(data[0], shape=(-1,5,224,224,3))
data_audio = tf.reshape(data[1], shape=(-1,64,50,3))
data_labels = tf.reshape(labels, shape=(-1,10))
return (data_video, data_audio), data_labels
def random_cut_gammavideo(video, audio, cut_length, audio_fs = 44100, audio_hop = 882, video_fps = 5):
video_length = tf.shape(video)[0]
audio_length = tf.shape(audio)[1]
# Generate random index for initial frame
min_v = 0
cut_length_frames = tf.cast(tf.math.round(cut_length*video_fps), dtype=tf.dtypes.int32)
max_v = video_length - cut_length_frames
rnum = tf.random.uniform([1], minval=min_v, maxval=max_v, dtype=tf.dtypes.int32)
# Cut video
video = video[rnum[0]:rnum[0]+cut_length_frames,...]
# Cut audio accordingly
ini_frame = tf.math.round(tf.cast(rnum[0], dtype=tf.dtypes.float32)*(1/video_fps)*audio_fs*(1/audio_hop))
end_frame = tf.math.round(ini_frame + cut_length*audio_fs/audio_hop)
ini_frame = tf.cast(ini_frame, dtype=tf.dtypes.int32)
end_frame = tf.cast(end_frame, dtype=tf.dtypes.int32)
audio = audio[:,ini_frame:end_frame,:]
return video, audio
def process_ds_audiovideo(video, audio, label, mode):
# Cut randomly to 1 second
if mode == 'train':
video, audio = random_cut_gammavideo(video, audio, 1.0)
audio = normalize_sp(audio)
label = label[0]
label = tf.one_hot(label,10)
if mode == 'val':
video = tf.reshape(video, shape=(10,5,224,224,3))
audio = tf.transpose(audio,(1,0,2))
audio = tf.reshape(audio, shape=(10,50,64,3))
audio =tf.map_fn(fn=lambda t: normalize_sp(t) , elems=audio)
audio = tf.transpose(audio,(0,2,1,3))
label = label[0:10]
label = tf.one_hot(label,10)
return (video, audio), label
train_batch_size = 16
do_mixup = False
if do_mixup == True:
train_ds_one = tf.data.Dataset.from_tensor_slices(trainfiles)
train_ds_one = train_ds_one.shuffle(N_train)
train_ds_one = train_ds_one.repeat()
train_ds_one = tf.data.TFRecordDataset(train_ds_one)
train_ds_one = train_ds_one.map(lambda tf_file: parse_sequence(tf_file,'audiovideo'), num_parallel_calls=4)
train_ds_one = train_ds_one.map(lambda video, audio, label: process_ds_audiovideo(video, audio, label, 'train'), num_parallel_calls=4)
train_ds_one = train_ds_one.batch(train_batch_size)
train_ds_two = tf.data.Dataset.from_tensor_slices(trainfiles)
train_ds_two = train_ds_two.shuffle(N_train)
train_ds_two = train_ds_two.repeat()
train_ds_two = tf.data.TFRecordDataset(train_ds_two)
train_ds_two = train_ds_two.map(lambda tf_file: parse_sequence(tf_file,'audiovideo'), num_parallel_calls=4)
train_ds_two = train_ds_two.map(lambda video, audio, label: process_ds_audiovideo(video, audio, label, 'train'), num_parallel_calls=4)
train_ds_two = train_ds_two.batch(train_batch_size)
trainds = tf.data.Dataset.zip((train_ds_one, train_ds_two))
trainds = trainds.map(
lambda ds_one, ds_two: mix_up_audiovideo(ds_one, ds_two, alpha=0.3), num_parallel_calls=4
)
else:
trainds = tf.data.Dataset.from_tensor_slices(trainfiles)
trainds = trainds.shuffle(N_train)
trainds = trainds.repeat()
trainds = tf.data.TFRecordDataset(trainds)
trainds = trainds.map(lambda tf_file: parse_sequence(tf_file,'audiovideo'), num_parallel_calls=4)
trainds = trainds.map(lambda video, audio, label: process_ds_audiovideo(video, audio, label, 'train'), num_parallel_calls=4)
trainds = trainds.batch(train_batch_size)
val_batch_size = 16
valds = tf.data.Dataset.from_tensor_slices(valfiles)
valds = tf.data.TFRecordDataset(valds)
valds = valds.map(lambda tf_file: parse_sequence(tf_file,'audiovideo'), num_parallel_calls=4)
valds = valds.map(lambda video, audio, label: process_ds_audiovideo(video, audio, label, 'val'), num_parallel_calls=4)
#valds = valds.batch(val_batch_size)
#valds = valds.map(lambda data, labels: reshape_batch(data, labels), num_parallel_calls=4)
datait = iter(trainds)
example = datait.get_next()
print(example[0][0].shape, example[0][1].shape)
plt.imshow(example[0][0][0,0,:,:,:].numpy().astype(np.uint8))
plt.show()
plt.imshow(example[0][1][0,:,:,0]);
plt.show()
datait = iter(valds)
example = datait.get_next()
print(example[0][0].shape, example[0][1].shape, example[1].shape)
plt.imshow(example[0][0][0,0,:,:,:].numpy().astype(np.uint8))
plt.show()
plt.imshow(example[0][1][0,:,:,0]);
plt.colorbar()
plt.show()
```
## Audio Network
```
from tensorflow.keras.layers import (Conv2D, Dense, Permute, GlobalAveragePooling2D, GlobalMaxPooling2D,
Reshape, BatchNormalization, ELU, Lambda, Input, MaxPooling2D, Activation,
Dropout, add, multiply)
import tensorflow.keras.backend as k
from tensorflow.keras.models import Model
import tensorflow as tf
from tensorflow.keras.regularizers import l2
regularization = l2(0.0001)
def construct_asc_network_csse(include_classification=True, nclasses=10, **parameters):
"""
Args:
include_classification (bool): include classification layer
**parameters (dict): setting use to construct the network presented in
(https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9118879)
"""
nfilters = parameters['nfilters']
pooling = parameters['pooling']
dropout = parameters['dropout']
top_flatten = parameters['top_flatten']
ratio = parameters['ratio']
pre_act = parameters['pre_act']
spectrogram_dim = parameters['spectrogram_dim']
verbose = parameters['verbose']
inp = Input(shape=spectrogram_dim)
for i in range(0, len(nfilters)):
if i == 0:
x = conv_standard_post(inp, nfilters[i], ratio, pre_act=pre_act)
else:
x = conv_standard_post(x, nfilters[i], ratio, pre_act=pre_act)
x = MaxPooling2D(pool_size=pooling[i])(x)
x = Dropout(rate=dropout[i])(x)
# Javier network
if top_flatten == 'avg':
x = GlobalAveragePooling2D()(x)
elif top_flatten == 'max':
x = GlobalMaxPooling2D()(x)
if include_classification:
x = Dense(units=nclasses, activation='softmax', name='SP_Pred')(x)
model = Model(inputs=inp, outputs=x)
if verbose:
print(model.summary())
return model
def conv_standard_post(inp, nfilters, ratio, pre_act=False):
"""
Block presented in (https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9118879)
Args:
inp (tensor): input to the block
nfilters (int): number of filters of a specific block
ratio (int): ratio used in the channel excitation
pre_act (bool): presented in this work, use a pre-activation residual block
Returns:
"""
x1 = inp
if pre_act:
x = BatchNormalization()(inp)
x = ELU()(x)
x = Conv2D(nfilters, 3, padding='same')(x)
x = BatchNormalization()(x)
x = Conv2D(nfilters, 3, padding='same')(x)
else:
x = Conv2D(nfilters, 3, padding='same')(inp)
x = BatchNormalization()(x)
x = ELU()(x)
x = Conv2D(nfilters, 3, padding='same')(x)
x = BatchNormalization()(x)
# shortcut
x1 = Conv2D(nfilters, 1, padding='same')(x1)
x1 = BatchNormalization()(x1)
x = module_addition(x, x1)
x = ELU()(x)
x = channel_spatial_squeeze_excite(x, ratio=ratio)
x = module_addition(x, x1)
return x
def channel_spatial_squeeze_excite(input_tensor, ratio=16):
""" Create a spatial squeeze-excite block
Args:
input_tensor: input Keras tensor
ratio: number of output filters
Returns: a Keras tensor
References
- [Squeeze and Excitation Networks](https://arxiv.org/abs/1709.01507)
- [Concurrent Spatial and Channel Squeeze & Excitation in Fully Convolutional Networks]
(https://arxiv.org/abs/1803.02579)
"""
cse = squeeze_excite_block(input_tensor, ratio)
sse = spatial_squeeze_excite_block(input_tensor)
x = add([cse, sse])
return x
def squeeze_excite_block(input_tensor, ratio=16):
""" Create a channel-wise squeeze-excite block
Args:
input_tensor: input Keras tensor
ratio: number of output filters
Returns: a Keras tensor
References
- [Squeeze and Excitation Networks](https://arxiv.org/abs/1709.01507)
"""
init = input_tensor
channel_axis = 1 if k.image_data_format() == "channels_first" else -1
filters = _tensor_shape(init)[channel_axis]
se_shape = (1, 1, filters)
se = GlobalAveragePooling2D()(init)
se = Reshape(se_shape)(se)
se = Dense(filters // ratio, activation='relu', kernel_initializer='he_normal', use_bias=False)(se)
se = Dense(filters, activation='sigmoid', kernel_initializer='he_normal', use_bias=False)(se)
if k.image_data_format() == 'channels_first':
se = Permute((3, 1, 2))(se)
x = multiply([init, se])
return x
def spatial_squeeze_excite_block(input_tensor):
""" Create a spatial squeeze-excite block
Args:
input_tensor (): input Keras tensor
Returns: a Keras tensor
References
- [Concurrent Spatial and Channel Squeeze & Excitation in Fully Convolutional Networks]
(https://arxiv.org/abs/1803.02579)
"""
se = Conv2D(1, (1, 1), activation='sigmoid', use_bias=False,
kernel_initializer='he_normal')(input_tensor)
x = multiply([input_tensor, se])
return x
def module_addition(inp1, inp2):
"""
Module of addition of two tensors with same H and W, but can have different channels
If number of channels of the second tensor is the half of the other, this dimension is repeated
Args:
inp1 (tensor): one branch of the addition module
inp2 (tensor): other branch of the addition module
Returns:
"""
if k.int_shape(inp1)[3] != k.int_shape(inp2)[3]:
x = add(
[inp1, Lambda(lambda y: k.repeat_elements(y, rep=int(k.int_shape(inp1)[3] // k.int_shape(inp2)[3]),
axis=3))(inp2)])
else:
x = add([inp1, inp2])
return x
def _tensor_shape(tensor):
"""
Obtain shape in order to use channel excitation
Args:
tensor (tensor): input tensor
Returns:
"""
return tensor.get_shape()
audio_network_settings = {
'nfilters': (32, 64, 128),
#'pooling': [(2, 1), (2, 1), (2, 1)],
'pooling': [(1, 2), (1, 2), (1, 1)],
'dropout': [0.0, 0.0, 0.0],
'top_flatten': 'avg',
'ratio': 2,
'pre_act': False,
'spectrogram_dim': (64, 50, 3),
'verbose': True
}
audio_model = construct_asc_network_csse(include_classification=True, **audio_network_settings)
# Load weights
pretrained_audio_path = 'BEST_AUDIO_MODEL'
audio_model.load_weights(pretrained_audio_path)
```
## Video Network
```
from tensorflow.keras.layers import TimeDistributed, GRU, Activation, GlobalAveragePooling1D, Bidirectional
regularization = l2(0.001)
num_classes = 10
input_shape = (5,224,224,3)
input_vid = Input(shape = input_shape)
# Block 1
x = TimeDistributed(Conv2D(filters=64, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block1_conv1')(input_vid)
x = TimeDistributed(Conv2D(filters=64, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block1_conv2')(x)
x = TimeDistributed(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)), name="block1_pool")(x)
# Block 2
x = TimeDistributed(Conv2D(filters=128, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block2_conv1')(x)
x = TimeDistributed(Conv2D(filters=128, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block2_conv2')(x)
x = TimeDistributed(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)), name="block2_pool")(x)
# Block 3
x = TimeDistributed(Conv2D(filters=256, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block3_conv1')(x)
x = TimeDistributed(Conv2D(filters=256, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block3_conv2')(x)
x = TimeDistributed(Conv2D(filters=256, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block3_conv3')(x)
x = TimeDistributed(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)), name="block3_pool")(x)
# Block 4
x = TimeDistributed(Conv2D(filters=512, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block4_conv1')(x)
x = TimeDistributed(Conv2D(filters=512, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block4_conv2')(x)
x = TimeDistributed(Conv2D(filters=512, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block4_conv3')(x)
x = TimeDistributed(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)), name="block4_pool")(x)
# Block 5
x = TimeDistributed(Conv2D(filters=512, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block5_conv1')(x)
x = TimeDistributed(Conv2D(filters=512, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block5_conv2')(x)
x = TimeDistributed(Conv2D(filters=512, kernel_size=3, strides=(1, 1), padding='same',
kernel_regularizer=l2(0.0002),
activation='relu'), name='block5_conv3')(x)
x = TimeDistributed(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)), name="block5_pool")(x)
x = TimeDistributed(GlobalMaxPooling2D(), name='TD_C_GlobAvPooling2D')(x)
# Recurrent Block
fw = GRU(32, return_sequences=True, stateful=False, recurrent_dropout = 0.0, name='VID_RNN_fw')
bw = GRU(32, return_sequences=True, stateful=False, recurrent_dropout = 0.0, go_backwards=True, name='VID_RNN_bw')
x = Bidirectional(fw, backward_layer=bw, name='VID_RNN_bidir')(x)
x = Dropout(0.5, name='VID_C2_Dropout')(x) #0.35
x = Dense(num_classes, kernel_regularizer = regularization, name ='VID_C2_Dense')(x)
x = Activation('softmax', name = 'VID_C2_Act_softmax_1')(x)
x = GlobalAveragePooling1D(name='VID_Pred')(x)
video_model = Model(inputs=input_vid, outputs=x)
video_model.summary()
# load weights
pretrained_video_path = 'BEST_VIDEO_MODEL'
video_model.load_weights(pretrained_video_path)
```
## Join Sub-Networks (RNN)
```
audio_sub_input = audio_model.input
audioout = audio_model.layers[-1].output
x = audio_model.layers[-3].output
x = tf.keras.layers.Permute((2,1,3))(x)
x = tf.keras.layers.TimeDistributed(tf.keras.layers.GlobalAveragePooling1D())(x)
audio_sub_output = tf.keras.layers.AveragePooling1D(3,2)(x)
audio_subnetwork = Model(inputs=audio_sub_input, outputs=audioout)
# Freeze all layers
for layer in audio_subnetwork.layers:
print('Setting layer {} non-trainable'.format(layer.name))
layer.trainable = False
audio_subnetwork.summary()
video_sub_input = video_model.input
videoout = video_model.layers[-1].output
video_sub_output = video_model.layers[-6].output
video_subnetwork = Model(inputs=video_sub_input, outputs=videoout)
# Freeze all layers
for layer in video_subnetwork.layers:
print('Setting layer {} non-trainable'.format(layer.name))
layer.trainable = False
video_subnetwork.summary()
from tensorflow.keras.layers import concatenate
x = concatenate([audio_sub_output, video_sub_output])
fw = tf.keras.layers.GRU(64,return_sequences=True, stateful=False, dropout = 0.0, name='RNN_fw')
bw = tf.keras.layers.GRU(64,return_sequences=True, stateful=False, dropout = 0.0, go_backwards= True, name='RNN_bw')
x = tf.keras.layers.Bidirectional(fw, backward_layer=bw, name='RNN_bidir')(x)
x = tf.keras.layers.GlobalAveragePooling1D()(x)
x = Dense(num_classes, activation='softmax')(x)
x = concatenate([x, audioout, videoout])
x = Dense(num_classes, name ='MULTI_C2_Dense2')(x)
x = Activation('softmax', name='MULTI_Pred')(x)
multi_model = Model(inputs=[video_sub_input, audio_sub_input], outputs=x)
multi_model.summary()
```
## Compile and train
```
# learning_rate = 0.001
# weight_decay = 0.0001
# opt = tfa.optimizers.AdamW(learning_rate=learning_rate, weight_decay=weight_decay)
learning_rate = 0.0001
opt = tf.keras.optimizers.Adam(learning_rate = learning_rate)
multi_model.compile(
loss = {'MULTI_Pred': 'categorical_crossentropy'},
optimizer=opt,
metrics = {'MULTI_Pred': 'accuracy'},
)
from tensorflow.keras.callbacks import CSVLogger, ModelCheckpoint, EarlyStopping, ReduceLROnPlateau
import os
callbacks = []
ckpt_dir = 'PATH_TO_STORE\checkpoints_multi'
model_name = 'multi_final'
callbacks.append(
ModelCheckpoint(
filepath=os.path.join(ckpt_dir, '%s-{epoch:02d}-{val_accuracy:.2f}.hdf5' % model_name),
monitor="val_accuracy",
mode="max",
save_best_only=True,
save_weights_only=True,
verbose=True,
)
)
callbacks.append(
EarlyStopping(
monitor="val_loss",
patience=80,
)
)
callbacks.append(
ReduceLROnPlateau(
monitor="val_loss",
factor=0.5,
patience=15,
verbose=True,
)
)
callbacks.append(
CSVLogger(
filename = os.path.join(ckpt_dir, '%s.csv' % model_name),
append = False,
)
)
# Train model
history = multi_model.fit(
trainds,
epochs=200,
steps_per_epoch= int(N_train/train_batch_size), # Set according to number of examples and training batch size
validation_data = valds,
#validation_steps = int(N_val/val_batch_size),
validation_steps = int(N_val),
callbacks=callbacks, # Include list of callbacks
#class_weight = class_weights,
)
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
# summarize history for accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.subplot(1,2,2)
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
```
### Final Fine-Tuning
```
multi_model.load_weights('BEST_AUDIOVISUAL_MODEL')
# Un-Freeze all layers
for layer in multi_model.layers:
print('Setting layer {} trainable'.format(layer.name))
layer.trainable = True
multi_model.summary()
learning_rate = 0.000001
opt = tf.keras.optimizers.Adam(learning_rate = learning_rate)
multi_model.compile(
loss = {'MULTI_Pred': 'categorical_crossentropy'},
optimizer=opt,
metrics = {'MULTI_Pred': 'accuracy'},
)
from tensorflow.keras.callbacks import CSVLogger, ModelCheckpoint, EarlyStopping, ReduceLROnPlateau
import os
callbacks = []
ckpt_dir = 'PATH_TO_STORE\checkpoints_multi'
model_name = 'multi_finalun_2'
callbacks.append(
ModelCheckpoint(
filepath=os.path.join(ckpt_dir, '%s-{epoch:02d}-{val_accuracy:.2f}.hdf5' % model_name),
monitor="val_accuracy",
mode="max",
save_best_only=True,
save_weights_only=True,
verbose=True,
)
)
callbacks.append(
EarlyStopping(
monitor="val_loss",
patience=80,
)
)
callbacks.append(
ReduceLROnPlateau(
monitor="val_loss",
factor=0.5,
patience=15,
verbose=True,
)
)
callbacks.append(
CSVLogger(
filename = os.path.join(ckpt_dir, '%s.csv' % model_name),
append = False,
)
)
# Train model
history = multi_model.fit(
trainds,
epochs=200,
steps_per_epoch= int(N_train/train_batch_size), # Set according to number of examples and training batch size
validation_data = valds,
#validation_steps = int(N_val/val_batch_size),
validation_steps = int(N_val),
callbacks=callbacks, # Include list of callbacks
#class_weight = class_weights,
)
```
## Evaluate Model
```
def process_ds_eval(video, audio, label):
video = tf.reshape(video, shape=(10,5,224,224,3))
audio = tf.transpose(audio,(1,0,2))
audio = tf.reshape(audio, shape=(10,50,64,3))
audio =tf.map_fn(fn=lambda t: normalize_sp(t) , elems=audio)
audio = tf.transpose(audio,(0,2,1,3))
label = label[0:10]
label = tf.one_hot(label,10)
return (video, audio), label
evalds = tf.data.Dataset.from_tensor_slices(valfiles)
evalds = tf.data.TFRecordDataset(evalds)
evalds = evalds.map(lambda tf_file: parse_sequence(tf_file,'audiovideo'), num_parallel_calls=4)
evalds = evalds.map(lambda video, audio, label: process_ds_eval(video, audio, label), num_parallel_calls=4)
# it = iter(evalds)
# ex = it.get_next()
# ex[0][0].shape
multi_model.load_weights('FINAL_BEST_AUDIOVISUAL')
multi_model.evaluate(evalds)
```
| true |
code
| 0.496948 | null | null | null | null |
|

# Callysto’s Weekly Data Visualization
## Weekly Title
### Recommended grade level: 5-12
### Instructions
#### “Run” the cells to see the graphs
Click “Cell” and select “Run All”.<br> This will import the data and run all the code, so you can see this week's data visualization. Scroll to the top after you’ve run the cells.<br>

**You don’t need to do any coding to view the visualizations**.
The plots generated in this notebook are interactive. You can hover over and click on elements to see more information.
Email contact@callysto.ca if you experience issues.
### About this Notebook
Callysto's Weekly Data Visualization is a learning resource that aims to develop data literacy skills. We provide Grades 5-12 teachers and students with a data visualization, like a graph, to interpret. This companion resource walks learners through how the data visualization is created and interpreted by a data scientist.
The steps of the data analysis process are listed below and applied to each weekly topic.
1. Question - What are we trying to answer?
2. Gather - Find the data source(s) you will need.
3. Organize - Arrange the data, so that you can easily explore it.
4. Explore - Examine the data to look for evidence to answer the question. This includes creating visualizations.
5. Interpret - Describe what's happening in the data visualization.
6. Communicate - Explain how the evidence answers the question.
## Question
How much time do Canadians spend playing video games and how does this change with demographics? We will use official Statistics Canada data to examine this question.
### Goal
Our goal is to create a series of histograms to observe how much time Canadians spend gaming.
## Gather
The code below will import the Python programming libraries we need to gather and organize the data to answer our question.
```
import plotly.express as px #used to create interactive plots
```
The code below creates lists data from [this 2010 StatsCan table](https://www150.statcan.gc.ca/n1/pub/89-647-x/2011001/tbl/tbl31-eng.htm). The same study was done more recently in 2015. However, the more recent time use survey did not ask about video games.
Our lists are as follows:
| List Name | List Purpose |
|------------------------|------------------------------------------------------------------------------------------|
| categories | holds names for the age catagories for our bar chart |
| leisure_time | holds number of minutes in "leisure" activities for the average person on an average day |
| videogame_time_all | holds number of minutes spent gaming for the average person on an average day |
| videogame_time_players | holds number of minutes spent gaming for the average gamer on an average day |
```
## import data
categories = ["15 to 24", "25 to 34", "35 to 44", "45 to 54", "55 to 64", "65 to 74", "75 and over"]
leisure_time = [5*60+57, 4*60+53, 4*60+6, 4*60+44, 5*60+55, 7*60+19, 7*60+34]
videogame_time_all = [27, 10, 4, 4, 6, 6, 4]
videogame_time_players = [2*60+44, 2*60+34, 109, 127, 118, 133, 2*60+32]
```
## Organize
Since our data is just 4 simple lists there is no need to organize it further.
## Explore-1
The code below will be used to help us look for evidence to answer our question. This can involve looking at data in table format, applying math and statistics, and creating different types of visualizations to represent our data.
```
fig1 = px.bar(x=videogame_time_all, y=categories,
title="Average Number of Minutes Spent Playing Video Games Per Day",
labels={'y':'Age of Canadians - Years', 'x':'Minutes Gaming on Average Day'})
fig1.show()
```
## Interpret-1
Our first figure shows 15-24 year olds spending a lot more time than their older counterparts playing computer games but with a small bump for Canadians in early retirement age (55-64 and 65-75).
## Explore-2
```
fig2 = px.bar(x=videogame_time_players, y=categories,
title="Average Number of Minutes Spent Playing Video Games Per Day",
labels={'y':'Age of Canadians Who Play Computer Games - Years', 'x':'Minutes Gaming on Average Day'})
fig2.show()
```
## Interpret-2
There is a subtle difference between the last set of data, the data for the first figure, and this figure's data. The first calculated averages using all respondents to the census survey. This second figure just includes those who do actually play some computer games. Essentially, this second plot ignores any respondents who game zero hours on the average day.
We see a very different plot for this second figure. This figure is decidedly U-shaped. Those Canadians outside of working age seem to game the most.
## Explore-3
```
fig3 = px.bar(x=leisure_time, y=categories,
title="Average Number of Minutes Spent on Leisure Activities Per Week",
labels={'y':'Age of Canadians - Years', 'x':'Minutes of Leisure Activities Per Day'})
fig3.show()
```
## Interpret-3
This third plot isn't directly about gaming, but provides some context for the first few figures. It's showing how much free time each age group has that is spent on leisure including gaming. It seems to closely match the second figure.
## Communicate
Below we will reflect on the new information that is presented from the data. When we look at the evidence, think about what you perceive about the information. Is this perception based on what the evidence shows? If others were to view it, what perceptions might they have? These writing prompts can help you reflect.
- Why do you think the second and third charts are so alike?
- What does it mean that when you look at the population of Canadians, the average 15-24 year old spends much more time gaming than the 75 and over, but they're almost the same when you only look at people who game at least some?
- If we had current data, how do you think these plots would look?
[](https://github.com/callysto/curriculum-notebooks/blob/master/LICENSE.md)
| true |
code
| 0.60644 | null | null | null | null |
|
# Udacity - Machine Learning Engineer Nanodegree
## Capstone Project
### Title: Development of a LSTM Network to Predict Students’ Answers on Exam Questions
### Implementation of DKT:
#### Part 1: Define constants
```
dataset = "data/ASSISTments_skill_builder_data.csv" # Dataset path
best_model_file = "saved_models/ASSISTments.best.model.weights.hdf5" # File to save the model.
train_log = "logs/dktmodel.train.log" # File to save the training log.
eval_log = "logs/dktmodel.eval.log" # File to save the testing log.
optimizer = "adagrad" # Optimizer to use
lstm_units = 250 # Number of LSTM units
batch_size = 20 # Batch size
epochs = 100 # Number of epochs to train
dropout_rate = 0.6 # Dropout rate
verbose = 1 # Verbose = {0,1,2}
testing_rate = 0.2 # Portion of data to be used for testing
validation_rate = 0.2 # Portion of training data to be used for validation
```
#### Part 2: Pre-processing
```
from Utils import *
dataset, num_skills = read_file(dataset)
X_train, X_val, X_test, y_train, y_val, y_test = split_dataset(dataset, validation_rate, testing_rate)
print("======== Data Summary ========")
print("Data size: %d" % len(dataset))
print("Training data size: %d" % len(X_train))
print("Validation data size: %d" % len(X_val))
print("Testing data size: %d" % len(X_test))
print("Number of skills: %d" % num_skills)
print("==============================")
```
#### Part 3: Building the model
```
from StudentModel import DKTModel, DataGenerator
# Create generators for training/testing/validation
train_gen = DataGenerator(X_train[0:10], y_train[0:10], num_skills, batch_size)
val_gen = DataGenerator(X_val[0:10], y_val[0:10], num_skills, batch_size)
test_gen = DataGenerator(X_test[0:10], y_test[0:10], num_skills, batch_size)
# Create model
student_model = DKTModel(num_skills=train_gen.num_skills,
num_features=train_gen.feature_dim,
optimizer=optimizer,
hidden_units=lstm_units,
batch_size=batch_size,
dropout_rate=dropout_rate)
```
#### Part 4: Train the Model
```
history = student_model.fit(train_gen,
epochs=epochs,
val_gen=val_gen,
verbose=verbose,
filepath_bestmodel=best_model_file,
filepath_log=train_log)
```
#### Part 5: Load the Model with the Best Validation Loss
```
student_model.load_weights(best_model_file)
```
#### Part 6: Test the Model
```
result = student_model.evaluate(test_gen, metrics=['auc','acc','pre'], verbose=verbose, filepath_log=eval_log)
```
| true |
code
| 0.618809 | null | null | null | null |
|
# Prepare data
```
from __future__ import print_function, division
import os
import torch
import pandas as pd
from skimage import io, transform
import numpy as np
import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms, utils
# Ignore warnings
import warnings
warnings.filterwarnings("ignore")
plt.ion() # interactive mode
landmarks_frame = pd.read_csv('data-faces/faces/face_landmarks.csv')
n = 65
img_name = landmarks_frame.iloc[n, 0]
landmarks = landmarks_frame.iloc[n, 1:]
landmarks = np.asarray(landmarks)
landmarks = landmarks.astype('float').reshape(-1, 2)
print('Image name: {}'.format(img_name))
print('Landmarks shape: {}'.format(landmarks.shape))
print('First 4 Landmarks: {}'.format(landmarks[:4]))
def show_landmarks(image, landmarks):
"""Show image with landmarks"""
plt.imshow(image)
plt.scatter(landmarks[:, 0], landmarks[:, 1], s=10, marker='.', c='r')
plt.pause(0.001) # pause a bit so that plots are updated
plt.figure()
show_landmarks(io.imread(os.path.join('data-faces/faces/', img_name)),
landmarks)
plt.show()
```
# Dataset class
torch.utils.data.Dataset is an abstract class representing a dataset. Your custom dataset should inherit Dataset and override the following methods:
* __len__ so that len(dataset) returns the size of the dataset.
* __getitem__ to support the indexing such that dataset[i] can be used to get iith sample.
Let’s create a dataset class for our face landmarks dataset. We will read the csv in __init__ but leave the reading of images to __getitem__. This is memory efficient because all the images are not stored in the memory at once but read as required.
Sample of our dataset will be a dict {'image': image, 'landmarks': landmarks}. Our dataset will take an optional argument transform so that any required processing can be applied on the sample. We will see the usefulness of transform in the next section.
```
class FaceLandmarksDataset(Dataset):
"""Face Landmarks dataset."""
def __init__(self, csv_file, root_dir, transform=None):
"""
Args:
csv_file (string): Path to the csv file with annotations.
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.landmarks_frame = pd.read_csv(csv_file)
self.root_dir = root_dir
self.transform = transform
def __len__(self):
return len(self.landmarks_frame)
def __getitem__(self, idx):
if torch.is_tensor(idx):
idx = idx.tolist()
img_name = os.path.join(self.root_dir,
self.landmarks_frame.iloc[idx, 0])
image = io.imread(img_name)
landmarks = self.landmarks_frame.iloc[idx, 1:]
landmarks = np.array([landmarks])
landmarks = landmarks.astype('float').reshape(-1, 2)
sample = {'image': image, 'landmarks': landmarks}
if self.transform:
sample = self.transform(sample)
return sample
```
Let’s instantiate this class and iterate through the data samples. We will print the sizes of first 4 samples and show their landmarks.
```
face_dataset = FaceLandmarksDataset(csv_file='data-faces/faces/face_landmarks.csv',
root_dir='data-faces/faces/')
fig = plt.figure()
for i in range(len(face_dataset)):
sample = face_dataset[i]
print(i, sample['image'].shape, sample['landmarks'].shape)
ax = plt.subplot(1, 4, i + 1)
plt.tight_layout()
ax.set_title('Sample #{}'.format(i))
ax.axis('off')
show_landmarks(**sample)
if i == 3:
plt.show()
break
```
# Transforms
One issue we can see from the above is that the samples are not of the same size. Most neural networks expect the images of a fixed size. Therefore, we will need to write some preprocessing code. Let’s create three transforms:
* Rescale: to scale the image
* RandomCrop: to crop from image randomly. This is data augmentation.
* ToTensor: to convert the numpy images to torch images (we need to swap axes).
We will write them as callable classes instead of simple functions so that parameters of the transform need not be passed everytime it’s called. For this, we just need to implement __call__ method and if required, __init__ method. We can then use a transform like this:
```
tsfm = Transform(params)
transformed_sample = tsfm(sample)
```
```
class Rescale(object):
"""Rescale the image in a sample to a given size.
Args:
output_size (tuple or int): Desired output size. If tuple, output is
matched to output_size. If int, smaller of image edges is matched
to output_size keeping aspect ratio the same.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
self.output_size = output_size
def __call__(self, sample):
image, landmarks = sample['image'], sample['landmarks']
h, w = image.shape[:2]
if isinstance(self.output_size, int):
if h > w:
new_h, new_w = self.output_size * h / w, self.output_size
else:
new_h, new_w = self.output_size, self.output_size * w / h
else:
new_h, new_w = self.output_size
new_h, new_w = int(new_h), int(new_w)
img = transform.resize(image, (new_h, new_w))
# h and w are swapped for landmarks because for images,
# x and y axes are axis 1 and 0 respectively
landmarks = landmarks * [new_w / w, new_h / h]
return {'image': img, 'landmarks': landmarks}
class RandomCrop(object):
"""Crop randomly the image in a sample.
Args:
output_size (tuple or int): Desired output size. If int, square crop
is made.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
if isinstance(output_size, int):
self.output_size = (output_size, output_size)
else:
assert len(output_size) == 2
self.output_size = output_size
def __call__(self, sample):
image, landmarks = sample['image'], sample['landmarks']
h, w = image.shape[:2]
new_h, new_w = self.output_size
top = np.random.randint(0, h - new_h)
left = np.random.randint(0, w - new_w)
image = image[top: top + new_h,
left: left + new_w]
landmarks = landmarks - [left, top]
return {'image': image, 'landmarks': landmarks}
class ToTensor(object):
"""Convert ndarrays in sample to Tensors."""
def __call__(self, sample):
image, landmarks = sample['image'], sample['landmarks']
# swap color axis because
# numpy image: H x W x C
# torch image: C x H x W
image = image.transpose((2, 0, 1))
return {'image': torch.from_numpy(image),
'landmarks': torch.from_numpy(landmarks)}
```
# Compose transforms
Now, we apply the transforms on a sample.
Let’s say we want to rescale the shorter side of the image to 256 and then randomly crop a square of size 224 from it. i.e, we want to compose Rescale and RandomCrop transforms. torchvision.transforms.Compose is a simple callable class which allows us to do this.
```
scale = Rescale(256)
crop = RandomCrop(128)
composed = transforms.Compose([Rescale(256),
RandomCrop(224)])
# Apply each of the above transforms on sample.
fig = plt.figure()
sample = face_dataset[65]
for i, tsfrm in enumerate([scale, crop, composed]):
transformed_sample = tsfrm(sample)
ax = plt.subplot(1, 3, i + 1)
plt.tight_layout()
ax.set_title(type(tsfrm).__name__)
show_landmarks(**transformed_sample)
plt.show()
```
# Iterating through the dataset
Let’s put this all together to create a dataset with composed transforms. To summarize, every time this dataset is sampled:
* An image is read from the file on the fly
* Transforms are applied on the read image
* Since one of the transforms is random, data is augmented on sampling
We can iterate over the created dataset with a for i in range loop as before.
```
transformed_dataset = FaceLandmarksDataset(csv_file='data-faces/faces/face_landmarks.csv',
root_dir='data-faces/faces/',
transform=transforms.Compose([
Rescale(256),
RandomCrop(224),
ToTensor()
]))
for i in range(len(transformed_dataset)):
sample = transformed_dataset[i]
print(i, sample['image'].size(), sample['landmarks'].size())
if i == 3:
break
```
However, we are losing a lot of features by using a simple for loop to iterate over the data. In particular, we are missing out on:
* Batching the data
* Shuffling the data
* Load the data in parallel using multiprocessing workers.
torch.utils.data.DataLoader is an iterator which provides all these features. Parameters used below should be clear. One parameter of interest is collate_fn. You can specify how exactly the samples need to be batched using collate_fn. However, default collate should work fine for most use cases.
```
dataloader = DataLoader(transformed_dataset, batch_size=4,
shuffle=True, num_workers=0)
# Helper function to show a batch
def show_landmarks_batch(sample_batched):
"""Show image with landmarks for a batch of samples."""
images_batch, landmarks_batch = \
sample_batched['image'], sample_batched['landmarks']
batch_size = len(images_batch)
im_size = images_batch.size(2)
grid_border_size = 2
grid = utils.make_grid(images_batch)
plt.imshow(grid.numpy().transpose((1, 2, 0)))
for i in range(batch_size):
plt.scatter(landmarks_batch[i, :, 0].numpy() + i * im_size + (i + 1) * grid_border_size,
landmarks_batch[i, :, 1].numpy() + grid_border_size,
s=10, marker='.', c='r')
plt.title('Batch from dataloader')
for i_batch, sample_batched in enumerate(dataloader):
print(i_batch, sample_batched['image'].size(),
sample_batched['landmarks'].size())
# observe 4th batch and stop.
if i_batch == 3:
plt.figure()
show_landmarks_batch(sample_batched)
plt.axis('off')
plt.ioff()
plt.show()
break
```
# Afterword: torchvision
In this tutorial, we have seen how to write and use datasets, transforms and dataloader. torchvision package provides some common datasets and transforms. You might not even have to write custom classes. One of the more generic datasets available in torchvision is ImageFolder. It assumes that images are organized in the following way:
```
root/ants/xxx.png
root/ants/xxy.jpeg
root/ants/xxz.png
.
.
.
root/bees/123.jpg
root/bees/nsdf3.png
root/bees/asd932_.png
```
where ‘ants’, ‘bees’ etc. are class labels. Similarly generic transforms which operate on PIL.Image like RandomHorizontalFlip, Scale, are also available. You can use these to write a dataloader like this:
```
import torch
from torchvision import transforms, datasets
data_transform = transforms.Compose([
transforms.RandomSizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
])
hymenoptera_dataset = datasets.ImageFolder(root='hymenoptera_data/train',
transform=data_transform)
dataset_loader = torch.utils.data.DataLoader(hymenoptera_dataset,
batch_size=4, shuffle=True,
num_workers=4)
```
| true |
code
| 0.819569 | null | null | null | null |
|
# Convolutional Neural Networks with TensorFlow
"Deep Learning" is a general term that usually refers to the use of neural networks with multiple layers that synthesize the way the human brain learns and makes decisions. A convolutional neural network is a kind of neural network that extracts *features* from matrices of numeric values (often images) by convolving multiple filters over the matrix values to apply weights and identify patterns, such as edges, corners, and so on in an image. The numeric representations of these patterns are then passed to a fully-connected neural network layer to map the features to specific classes.
There are several commonly used frameworks for creating CNNs. In this notebook, we'll build a simple example CNN using TensorFlow.
## Install and import libraries
First, let's install and import the TensorFlow libraries we'll need.
```
!pip install --upgrade tensorflow
import tensorflow
from tensorflow import keras
print('TensorFlow version:',tensorflow.__version__)
print('Keras version:',keras.__version__)
```
## Explore the data
In this exercise, you'll train a CNN-based classification model that can classify images of geometric shapes. Let's take a look at the classes of shape the model needs to identify.
```
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import os
%matplotlib inline
# The images are in the data/shapes folder
data_folder = 'data/shapes'
# Get the class names
classes = os.listdir(data_folder)
classes.sort()
print(len(classes), 'classes:')
print(classes)
# Show the first image in each folder
fig = plt.figure(figsize=(8, 12))
i = 0
for sub_dir in os.listdir(data_folder):
i+=1
img_file = os.listdir(os.path.join(data_folder,sub_dir))[0]
img_path = os.path.join(data_folder, sub_dir, img_file)
img = mpimg.imread(img_path)
a=fig.add_subplot(1, len(classes),i)
a.axis('off')
imgplot = plt.imshow(img)
a.set_title(img_file)
plt.show()
```
## Prepare the data
Before we can train the model, we need to prepare the data. We'll divide the feature values by 255 to normalize them as floating point values between 0 and 1, and we'll split the data so that we can use 70% of it to train the model, and hold back 30% to validate it. When loading the data, the data generator will assing "hot-encoded" numeric labels to indicate which class each image belongs to based on the subfolders in which the data is stored. In this case, there are three subfolders - *circle*, *square*, and *triangle*, so the labels will consist of three *0* or *1* values indicating which of these classes is associated with the image - for example the label [0 1 0] indicates that the image belongs to the second class (*square*).
```
from tensorflow.keras.preprocessing.image import ImageDataGenerator
img_size = (128, 128)
batch_size = 30
print("Getting Data...")
datagen = ImageDataGenerator(rescale=1./255, # normalize pixel values
validation_split=0.3) # hold back 30% of the images for validation
print("Preparing training dataset...")
train_generator = datagen.flow_from_directory(
data_folder,
target_size=img_size,
batch_size=batch_size,
class_mode='categorical',
subset='training') # set as training data
print("Preparing validation dataset...")
validation_generator = datagen.flow_from_directory(
data_folder,
target_size=img_size,
batch_size=batch_size,
class_mode='categorical',
subset='validation') # set as validation data
classnames = list(train_generator.class_indices.keys())
print('Data generators ready')
```
## Define the CNN
Now we're ready to create our model. This involves defining the layers for our CNN, and compiling them for multi-class classification.
```
# Define a CNN classifier network
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Dropout, Flatten, Dense
# Define the model as a sequence of layers
model = Sequential()
# The input layer accepts an image and applies a convolution that uses 32 6x6 filters and a rectified linear unit activation function
model.add(Conv2D(32, (6, 6), input_shape=train_generator.image_shape, activation='relu'))
# Next we'll add a max pooling layer with a 2x2 patch
model.add(MaxPooling2D(pool_size=(2,2)))
# We can add as many layers as we think necessary - here we'll add another convolution and max pooling layer
model.add(Conv2D(32, (6, 6), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
# And another set
model.add(Conv2D(32, (6, 6), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
# A dropout layer randomly drops some nodes to reduce inter-dependencies (which can cause over-fitting)
model.add(Dropout(0.2))
# Flatten the feature maps
model.add(Flatten())
# Generate a fully-cpnnected output layer with a predicted probability for each class
# (softmax ensures all probabilities sum to 1)
model.add(Dense(train_generator.num_classes, activation='softmax'))
# With the layers defined, we can now compile the model for categorical (multi-class) classification
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
print(model.summary())
```
## Train the model
With the layers of the CNN defined, we're ready to train the model using our image data. In the example below, we use 5 iterations (*epochs*) to train the model in 30-image batches, holding back 30% of the data for validation. After each epoch, the loss function measures the error (*loss*) in the model and adjusts the weights (which were randomly generated for the first iteration) to try to improve accuracy.
> **Note**: We're only using 5 epochs to minimze the training time for this simple example. A real-world CNN is usually trained over more epochs than this. CNN model training is processor-intensive, involving a lot of matrix and vector-based operations; so it's recommended to perform this on a system that can leverage GPUs, which are optimized for these kinds of calculation. This will take a while to complete on a CPU-based system - status will be displayed as the training progresses.
```
# Train the model over 5 epochs using 30-image batches and using the validation holdout dataset for validation
num_epochs = 5
history = model.fit(
train_generator,
steps_per_epoch = train_generator.samples // batch_size,
validation_data = validation_generator,
validation_steps = validation_generator.samples // batch_size,
epochs = num_epochs)
```
## View the loss history
We tracked average training and validation loss history for each epoch. We can plot these to verify that loss reduced as the model was trained, and to detect *overfitting* (which is indicated by a continued drop in training loss after validation loss has levelled out or started to increase).
```
%matplotlib inline
from matplotlib import pyplot as plt
epoch_nums = range(1,num_epochs+1)
training_loss = history.history["loss"]
validation_loss = history.history["val_loss"]
plt.plot(epoch_nums, training_loss)
plt.plot(epoch_nums, validation_loss)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['training', 'validation'], loc='upper right')
plt.show()
```
## Evaluate model performance
We can see the final accuracy based on the test data, but typically we'll want to explore performance metrics in a little more depth. Let's plot a confusion matrix to see how well the model is predicting each class.
```
# Tensorflow doesn't have a built-in confusion matrix metric, so we'll use SciKit-Learn
import numpy as np
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
%matplotlib inline
print("Generating predictions from validation data...")
# Get the image and label arrays for the first batch of validation data
x_test = validation_generator[0][0]
y_test = validation_generator[0][1]
# Use the model to predict the class
class_probabilities = model.predict(x_test)
# The model returns a probability value for each class
# The one with the highest probability is the predicted class
predictions = np.argmax(class_probabilities, axis=1)
# The actual labels are hot encoded (e.g. [0 1 0], so get the one with the value 1
true_labels = np.argmax(y_test, axis=1)
# Plot the confusion matrix
cm = confusion_matrix(true_labels, predictions)
plt.imshow(cm, interpolation="nearest", cmap=plt.cm.Blues)
plt.colorbar()
tick_marks = np.arange(len(classnames))
plt.xticks(tick_marks, classnames, rotation=85)
plt.yticks(tick_marks, classnames)
plt.xlabel("Predicted Shape")
plt.ylabel("Actual Shape")
plt.show()
```
## Save the Trained model
Now that you've trained a working model, you can save it (including the trained weights) for use later.
```
# Save the trained model
modelFileName = 'models/shape_classifier.h5'
model.save(modelFileName)
del model # deletes the existing model variable
print('model saved as', modelFileName)
```
## Use the trained model
When you have a new image, you can use the saved model to predict its class.
```
from tensorflow.keras import models
import numpy as np
from random import randint
import os
%matplotlib inline
# Function to predict the class of an image
def predict_image(classifier, image):
from tensorflow import convert_to_tensor
# The model expects a batch of images as input, so we'll create an array of 1 image
imgfeatures = img.reshape(1, img.shape[0], img.shape[1], img.shape[2])
# We need to format the input to match the training data
# The generator loaded the values as floating point numbers
# and normalized the pixel values, so...
imgfeatures = imgfeatures.astype('float32')
imgfeatures /= 255
# Use the model to predict the image class
class_probabilities = classifier.predict(imgfeatures)
# Find the class predictions with the highest predicted probability
index = int(np.argmax(class_probabilities, axis=1)[0])
return index
# Function to create a random image (of a square, circle, or triangle)
def create_image (size, shape):
from random import randint
import numpy as np
from PIL import Image, ImageDraw
xy1 = randint(10,40)
xy2 = randint(60,100)
col = (randint(0,200), randint(0,200), randint(0,200))
img = Image.new("RGB", size, (255, 255, 255))
draw = ImageDraw.Draw(img)
if shape == 'circle':
draw.ellipse([(xy1,xy1), (xy2,xy2)], fill=col)
elif shape == 'triangle':
draw.polygon([(xy1,xy1), (xy2,xy2), (xy2,xy1)], fill=col)
else: # square
draw.rectangle([(xy1,xy1), (xy2,xy2)], fill=col)
del draw
return np.array(img)
# Create a random test image
classnames = os.listdir(os.path.join('data', 'shapes'))
classnames.sort()
img = create_image ((128,128), classnames[randint(0, len(classnames)-1)])
plt.axis('off')
plt.imshow(img)
# Use the classifier to predict the class
model = models.load_model(modelFileName) # loads the saved model
class_idx = predict_image(model, img)
print (classnames[class_idx])
```
## Further Reading
To learn more about training convolutional neural networks with TensorFlow, see the [TensorFlow documentation](https://www.tensorflow.org/overview).
## Challenge: Safari Image Classification
Hopefully this notebook has shown you the main steps in training and evaluating a CNN. Why not put what you've learned into practice with our Safari image classification challenge in the [/challenges/05 - Safari CNN Challenge.ipynb](./challenges/05%20-%20Safari%20CNN%20Challenge.ipynb) notebook?
> **Note**: The time to complete this optional challenge is not included in the estimated time for this exercise - you can spend as little or as much time on it as you like!
| true |
code
| 0.641984 | null | null | null | null |
|
# Regex
In this lesson, we'll learn about a useful tool in the NLP toolkit: regex.
Let's consider two motivating examples:
#### 1. The phone number problem
Suppose we are given some data that includes phone numbers:
123-456-7890
123 456 7890
101 Howard
Some of the phone numbers have different formats (hyphens, no hyphens). Also, there are some errors in the data-- 101 Howard isn't a phon number! How can we find all the phone numbers?
#### 2. Creating our own tokens
In the previous lessons, we used sklearn or fastai to tokenize our text. What if we want to do it ourselves?
## The phone number problem
Suppose we are given some data that includes phone numbers:
123-456-7890
123 456 7890
(123)456-7890
101 Howard
Some of the phone numbers have different formats (hyphens, no hyphens, parentheses). Also, there are some errors in the data-- 101 Howard isn't a phone number! How can we find all the phone numbers?
We will attempt this without regex, but will see that this quickly leads to lot of if/else branching statements and isn't a veyr promising approach:
### Attempt 1 (without regex)
```
phone1 = "123-456-7890"
phone2 = "123 456 7890"
not_phone1 = "101 Howard"
string.digits
def check_phone(inp):
valid_chars = string.digits + ' -()'
for char in inp:
if char not in valid_chars:
return False
return True
assert(check_phone(phone1))
assert(check_phone(phone2))
assert(not check_phone(not_phone1))
```
### Attempt 2 (without regex)
```
not_phone2 = "1234"
assert(not check_phone(not_phone2))
def check_phone(inp):
nums = string.digits
valid_chars = nums + ' -()'
num_counter = 0
for char in inp:
if char not in valid_chars:
return False
if char in nums:
num_counter += 1
if num_counter==10:
return True
else:
return False
assert(check_phone(phone1))
assert(check_phone(phone2))
assert(not check_phone(not_phone1))
assert(not check_phone(not_phone2))
```
### Attempt 3 (without regex)
But we also need to extract the digits!
Also, what about:
34!NA5098gn#213ee2
```
not_phone3 = "34 50 98 21 32"
assert(not check_phone(not_phone3))
not_phone4 = "(34)(50)()()982132"
assert(not check_phone(not_phone3))
```
This is getting increasingly unwieldy. We need a different approach.
## Introducing regex
Useful regex resources:
- https://regexr.com/
- http://callumacrae.github.io/regex-tuesday/
- https://regexone.com/
**Best practice: Be as specific as possible.**
Parts of the following section were adapted from Brian Spiering, who taught the MSDS [NLP elective last summer](https://github.com/brianspiering/nlp-course).
### What is regex?
Regular expressions is a pattern matching language.
Instead of writing `0 1 2 3 4 5 6 7 8 9`, you can write `[0-9]` or `\d`
It is Domain Specific Language (DSL). Powerful (but limited language).
**What other DSLs do you already know?**
- SQL
- Markdown
- TensorFlow
### Matching Phone Numbers (The "Hello, world!" of Regex)
`[0-9][0-9][0-9]-[0-9][0-9][0-9]-[0-9][0-9][0-9][0-9]` matches US telephone number.
Refactored: `\d\d\d-\d\d\d-\d\d\d\d`
A **metacharacter** is one or more special characters that have a unique meaning and are NOT used as literals in the search expression. For example "\d" means any digit.
**Metacharacters are the special sauce of regex.**
Quantifiers
-----
Allow you to specify how many times the preceding expression should match.
`{}` is an extact qualifer
Refactored: `\d{3}-\d{3}-\d{4}`
Unexact quantifiers
-----
1. `?` question mark - zero or one
2. `*` star - zero or more
3. `+` plus sign - one or more |
### Regex can look really weird, since it's so concise
The best (only?) way to learn it is through practice. Otherwise, you feel like you're just reading lists of rules.
Let's take 15 minutes to begin working through the lessons on [regexone](https://regexone.com/).
**Reminder: Be as specific as possible!**
### Pros & Cons of Regex
**What are the advantages of regex?**
1. Concise and powerful pattern matching DSL
2. Supported by many computer languages, including SQL
**What are the disadvantages of regex?**
1. Brittle
2. Hard to write, can get complex to be correct
3. Hard to read
## Revisiting tokenization
In the previous lessons, we used a tokenizer. Now, let's learn how we could do this ourselves, and get a better understanding of tokenization.
What if we needed to create our own tokens?
```
import re
re_punc = re.compile("([\"\''().,;:/_?!—\-])") # add spaces around punctuation
re_apos = re.compile(r"n ' t ") # n't
re_bpos = re.compile(r" ' s ") # 's
re_mult_space = re.compile(r" *") # replace multiple spaces with just one
def simple_toks(sent):
sent = re_punc.sub(r" \1 ", sent)
sent = re_apos.sub(r" n't ", sent)
sent = re_bpos.sub(r" 's ", sent)
sent = re_mult_space.sub(' ', sent)
return sent.lower().split()
text = "I don't know who Kara's new friend is-- is it 'Mr. Toad'?"
' '.join(simple_toks(text))
text2 = re_punc.sub(r" \1 ", text); text2
text3 = re_apos.sub(r" n't ", text2); text3
text4 = re_bpos.sub(r" 's ", text3); text4
re_mult_space.sub(' ', text4)
sentences = ['All this happened, more or less.',
'The war parts, anyway, are pretty much true.',
"One guy I knew really was shot for taking a teapot that wasn't his.",
'Another guy I knew really did threaten to have his personal enemies killed by hired gunmen after the war.',
'And so on.',
"I've changed all their names."]
tokens = list(map(simple_toks, sentences))
tokens
```
Once we have our tokens, we need to convert them to integer ids. We will also need to know our vocabulary, and have a way to convert between words and ids.
```
import collections
PAD = 0; SOS = 1
def toks2ids(sentences):
voc_cnt = collections.Counter(t for sent in sentences for t in sent)
vocab = sorted(voc_cnt, key=voc_cnt.get, reverse=True)
vocab.insert(PAD, "<PAD>")
vocab.insert(SOS, "<SOS>")
w2id = {w:i for i,w in enumerate(vocab)}
ids = [[w2id[t] for t in sent] for sent in sentences]
return ids, vocab, w2id, voc_cnt
ids, vocab, w2id, voc_cnt = toks2ids(tokens)
ids
vocab
```
Q: what could be another name of the `vocab` variable above?
```
w2id
```
What are the uses of RegEx?
---
1. Find / Search
1. Find & Replace
2. Cleaning
Don't forgot about Python's `str` methods
-----
`str.<tab>`
str.find()
```
str.find?
```
Regex vs. String methods
-----
1. String methods are easier to understand.
1. String methods express the intent more clearly.
-----
1. Regex handle much broader use cases.
1. Regex can be language independent.
1. Regex can be faster at scale.
## What about unicode?
```
message = "😒🎦 🤢🍕"
re_frown = re.compile(r"😒|🤢")
re_frown.sub(r"😊", message)
```
## Regex Errors:
__False positives__ (Type I): Matching strings that we should __not__ have
matched
__False negatives__ (Type II): __Not__ matching strings that we should have matched
Reducing the error rate for a task often involves two antagonistic efforts:
1. Minimizing false positives
2. Minimizing false negatives
**Important to have tests for both!**
In a perfect world, you would be able to minimize both but in reality you often have to trade one for the other.
Useful Tools:
----
- [Regex cheatsheet](http://www.cheatography.com/davechild/cheat-sheets/regular-expressions/)
- [regexr.com](http://regexr.com/) Realtime regex engine
- [pyregex.com](https://pythex.org/) Realtime Python regex engine
Summary
----
1. We use regex as a metalanguage to find string patterns in blocks of text
1. `r""` are your IRL friends for Python regex
1. We are just doing binary classification so use the same performance metrics
1. You'll make a lot of mistakes in regex 😩.
- False Positive: Thinking you are right but you are wrong
- False Negative: Missing something
<center><img src="images/face_tat.png" width="700"/></center>
<br>
<br>
---
<center><img src="https://imgs.xkcd.com/comics/perl_problems.png" width="700"/></center>
<center><img src="https://imgs.xkcd.com/comics/regex_golf.png" width="700"/></center>
Regex Terms
----
- __target string__: This term describes the string that we will be searching, that is, the string in which we want to find our match or search pattern.
- __search expression__: The pattern we use to find what we want. Most commonly called the regular expression.
- __literal__: A literal is any character we use in a search or matching expression, for example, to find 'ind' in 'windows' the 'ind' is a literal string - each character plays a part in the search, it is literally the string we want to find.
- __metacharacter__: A metacharacter is one or more special characters that have a unique meaning and are NOT used as literals in the search expression. For example "." means any character.
Metacharacters are the special sauce of regex.
- __escape sequence__: An escape sequence is a way of indicating that we want to use a metacharacters as a literal.
In a regular expression an escape sequence involves placing the metacharacter \ (backslash) in front of the metacharacter that we want to use as a literal.
`'\.'` means find literal period character (not match any character)
Regex Workflow
---
1. Create pattern in Plain English
2. Map to regex language
3. Make sure results are correct:
- All Positives: Captures all examples of pattern
- No Negatives: Everything captured is from the pattern
4. Don't over-engineer your regex.
- Your goal is to Get Stuff Done, not write the best regex in the world
- Filtering before and after are okay.
| true |
code
| 0.211295 | null | null | null | null |
|
# Naive Bayes Models
In this lab you will work with **naive Bayes models**. Naive Bayes models are a surprisingly useful and effective simplification of the general Bayesian models. Naive Bayes models make the naive assumption of statistical independence of the features. In many cases, naive Bayes module are surprisingly effective despite violating the assumption of independence.
In simple terms, naive Bayes models use empirical distributions of the features to compute probabilities of the labels. The naive Bayes models can use most any family of distributions for the features. It is important to select the correct distribution family for the data you are working with. Common cases are:
- **Gaussian;** for continuous or numerical features.
- **Bernoulli;** for features with binary values.
- **Multinomial;** for features with more than two categories.
These is one pit fall, the model fails if a zero probability is encountered. This situation occurs when there is a 'hole' in the sample space where there are no samples. A simple smoothing procedure can deal with this problem. The smoothing hyperparameter, usually called alpha, is one of the few required for naive Bayes models.
Some properties of naive Bayes models are:
- Computational complexity is linear in number of parameter/features, making naive Bayes models highly scalable. There are out or core approaches suitable for massive datasets.
- Requires minimal data to produce models that generalizes well. If there are only a few cases per category to train a model a naive Bayes model can be a good choice.
- Have a simple and inherent regularization.
Naive Bayes models are used in many situations including:
- Document classification
- SPAM detection
- Image classification
As a first step, execute the code in the cell below to load the required packages to run the rest of this notebook.
```
from sklearn import preprocessing
from sklearn.naive_bayes import GaussianNB, BernoulliNB
#from statsmodels.api import datasets
from sklearn import datasets ## Get dataset from sklearn
import sklearn.model_selection as ms
import sklearn.metrics as sklm
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import numpy.random as nr
%matplotlib inline
```
To get a feel for these data, you will now load and plot them. The code in the cell below does the following:
1. Loads the iris data as a Pandas data frame.
2. Adds column names to the data frame.
3. Displays all 4 possible scatter plot views of the data.
Execute this code and examine the results.
```
def plot_iris(iris):
'''Function to plot iris data by type'''
setosa = iris[iris['Species'] == 'setosa']
versicolor = iris[iris['Species'] == 'versicolor']
virginica = iris[iris['Species'] == 'virginica']
fig, ax = plt.subplots(2, 2, figsize=(12,12))
x_ax = ['Sepal_Length', 'Sepal_Width']
y_ax = ['Petal_Length', 'Petal_Width']
for i in range(2):
for j in range(2):
ax[i,j].scatter(setosa[x_ax[i]], setosa[y_ax[j]], marker = 'x')
ax[i,j].scatter(versicolor[x_ax[i]], versicolor[y_ax[j]], marker = 'o')
ax[i,j].scatter(virginica[x_ax[i]], virginica[y_ax[j]], marker = '+')
ax[i,j].set_xlabel(x_ax[i])
ax[i,j].set_ylabel(y_ax[j])
## Import the dataset from sklearn.datasets
iris = datasets.load_iris()
## Create a data frame from the dictionary
species = [iris.target_names[x] for x in iris.target]
iris = pd.DataFrame(iris['data'], columns = ['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width'])
iris['Species'] = species
## Plot views of the iris data
plot_iris(iris)
```
You can see that Setosa (blue) is well separated from the other two categories. The Versicolor (orange) and the Virginica (green) show considerable overlap. The question is how well our classifier will separate these categories.
Scikit Learn classifiers require numerically coded numpy arrays for the features and as a label. The code in the cell below does the following processing:
1. Creates a numpy array of the features.
2. Numerically codes the label using a dictionary lookup, and converts it to a numpy array.
Execute this code.
```
Features = np.array(iris[['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width']])
levels = {'setosa':0, 'versicolor':1, 'virginica':2}
Labels = np.array([levels[x] for x in iris['Species']])
```
Next, execute the code in the cell below to split the dataset into test and training set. Notice that unusually, 100 of the 150 cases are being used as the test dataset.
```
## Randomly sample cases to create independent training and test data
nr.seed(1115)
indx = range(Features.shape[0])
indx = ms.train_test_split(indx, test_size = 100)
X_train = Features[indx[0],:]
y_train = np.ravel(Labels[indx[0]])
X_test = Features[indx[1],:]
y_test = np.ravel(Labels[indx[1]])
```
As is always the case with machine learning, numeric features must be scaled. The code in the cell below performs the following processing:
1. A Zscore scale object is defined using the `StandarScaler` function from the scikit-learn preprocessing package.
2. The scaler is fit to the training features. Subsequently, this scaler is used to apply the same scaling to the test data and in production.
3. The training features are scaled using the `transform` method.
Execute this code.
```
scale = preprocessing.StandardScaler()
scale.fit(X_train)
X_train = scale.transform(X_train)
```
Now you will define and fit a Gaussian naive Bayes model. A Gaussian model is appropriate here since all of the features are numeric.
The code in the cell below defines a Gaussian naive Bayes model object using the `GaussianNB` function from the scikit-learn naive_bayes package, and then fits the model. Execute this code.
```
NB_mod = GaussianNB()
NB_mod.fit(X_train, y_train)
```
Notice that the Gaussian naive Bayes model object has only one hyperparameter.
Next, the code in the cell below performs the following processing to score the test data subset:
1. The test features are scaled using the scaler computed for the training features.
2. The `predict` method is used to compute the scores from the scaled features.
Execute this code.
```
X_test = scale.transform(X_test)
scores = NB_mod.predict(X_test)
```
It is time to evaluate the model results. Keep in mind that the problem has been made deliberately difficult, by having more test cases than training cases.
The iris data has three species categories. Therefore it is necessary to use evaluation code for a three category problem. The function in the cell below extends code from previous labs to deal with a three category problem.
Execute this code, examine the results, and answer **Question 1** on the course page.
```
def print_metrics_3(labels, scores):
conf = sklm.confusion_matrix(labels, scores)
print(' Confusion matrix')
print(' Score Setosa Score Versicolor Score Virginica')
print('Actual Setosa %6d' % conf[0,0] + ' %5d' % conf[0,1] + ' %5d' % conf[0,2])
print('Actual Versicolor %6d' % conf[1,0] + ' %5d' % conf[1,1] + ' %5d' % conf[1,2])
print('Actual Vriginica %6d' % conf[2,0] + ' %5d' % conf[2,1] + ' %5d' % conf[2,2])
## Now compute and display the accuracy and metrics
print('')
print('Accuracy %0.2f' % sklm.accuracy_score(labels, scores))
metrics = sklm.precision_recall_fscore_support(labels, scores)
print(' ')
print(' Setosa Versicolor Virginica')
print('Num case %0.2f' % metrics[3][0] + ' %0.2f' % metrics[3][1] + ' %0.2f' % metrics[3][2])
print('Precision %0.2f' % metrics[0][0] + ' %0.2f' % metrics[0][1] + ' %0.2f' % metrics[0][2])
print('Recall %0.2f' % metrics[1][0] + ' %0.2f' % metrics[1][1] + ' %0.2f' % metrics[1][2])
print('F1 %0.2f' % metrics[2][0] + ' %0.2f' % metrics[2][1] + ' %0.2f' % metrics[2][2])
print_metrics_3(y_test, scores)
```
Examine these results. Notice the following:
1. The confusion matrix has dimension 3X3. You can see that most cases are correctly classified.
2. The overall accuracy is 0.91. Since the classes are roughly balanced, this metric indicates relatively good performance of the classifier, particularly since it was only trained on 50 cases. As was mentioned previously, naive Bayes models require only small amounts of training data.
3. The precision, recall and F1 for each of the classes is relatively good. Versicolor has the worst metrics since it has the largest number of misclassified cases.
To get a better feel for what the classifier is doing, the code in the cell below displays a set of plots showing correctly (as '+') and incorrectly (as 'o') cases, with the species color-coded. Execute this code and examine the results.
```
def plot_iris_score(iris, y_test, scores):
'''Function to plot iris data by type'''
## Find correctly and incorrectly classified cases
true = np.equal(scores, y_test).astype(int)
## Create data frame from the test data
iris = pd.DataFrame(iris)
levels = {0:'setosa', 1:'versicolor', 2:'virginica'}
iris['Species'] = [levels[x] for x in y_test]
iris.columns = ['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width', 'Species']
## Set up for the plot
fig, ax = plt.subplots(2, 2, figsize=(12,12))
markers = ['o', '+']
x_ax = ['Sepal_Length', 'Sepal_Width']
y_ax = ['Petal_Length', 'Petal_Width']
for t in range(2): # loop over correct and incorect classifications
setosa = iris[(iris['Species'] == 'setosa') & (true == t)]
versicolor = iris[(iris['Species'] == 'versicolor') & (true == t)]
virginica = iris[(iris['Species'] == 'virginica') & (true == t)]
# loop over all the dimensions
for i in range(2):
for j in range(2):
ax[i,j].scatter(setosa[x_ax[i]], setosa[y_ax[j]], marker = markers[t], color = 'blue')
ax[i,j].scatter(versicolor[x_ax[i]], versicolor[y_ax[j]], marker = markers[t], color = 'orange')
ax[i,j].scatter(virginica[x_ax[i]], virginica[y_ax[j]], marker = markers[t], color = 'green')
ax[i,j].set_xlabel(x_ax[i])
ax[i,j].set_ylabel(y_ax[j])
plot_iris_score(X_test, y_test, scores)
```
Examine these plots. You can see how the classifier has divided the feature space between the classes. Notice that most of the errors occur in the overlap region between Virginica and Versicolor. This behavior is to be expected.
## Summary
In this lab you have accomplished the following:
1. Used a Gaussian naive model to classify the cases of the iris data. The overall model performance was reasonable.
| true |
code
| 0.717544 | null | null | null | null |
|
# Comparison between the magnetic field produced by a oblate ellipsoid and a sphere
### Import the required modules and functions
```
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import BoundaryNorm
from matplotlib.ticker import MaxNLocator
from fatiando import gridder, utils
from fatiando.gravmag import sphere
from fatiando.mesher import Sphere
import oblate_ellipsoid
from mesher import OblateEllipsoid
# Set some plot parameters
from matplotlib import rcParams
rcParams['figure.dpi'] = 300.
rcParams['font.size'] = 6
rcParams['xtick.labelsize'] = 'medium'
rcParams['ytick.labelsize'] = 'medium'
rcParams['axes.labelsize'] = 'large'
rcParams['legend.fontsize'] = 'medium'
rcParams['savefig.dpi'] = 300.
```
### Set some parameters for modelling
```
# The local-geomagnetic field
F, inc, dec = 60000, 50, 20
# Create a regular grid at z = 0 m
shape = (50, 50)
area = [-5000, 5000, -4000, 6000]
xp, yp, zp = gridder.regular(area, shape, z=0)
```
### Oblate ellipsoid versus sphere
This test compares the total-field anomalies produced by an onlate ellipsoid with that produced by a sphere. The ellipsoid has semi-axes $a$ and $b$ equal to `499.9 m` and `500.1 m`, respectively, and the sphere has a radius equal to `500 m`. Both bodies are centered at the point `(0, 0, 1000)` and have the same magnetization.
##### Triaxial ellipsoid
```
ellipsoid = OblateEllipsoid(0, 0, 1000, 499.9, 500.1, 40, -60, 180,
{'principal susceptibilities': [0.01, 0.01, 0.01],
'susceptibility angles': [-40, 90, 7],
'remanent magnetization': [0.7, -7, 10]})
magnetization = oblate_ellipsoid.magnetization(ellipsoid, F, inc, dec, demag=True)
magnetization
```
##### Sphere
```
spherical_body = Sphere(ellipsoid.x, ellipsoid.y, ellipsoid.z,
0.5*(ellipsoid.large_axis + ellipsoid.small_axis),
{'magnetization': magnetization})
spherical_body.props['magnetization']
```
##### Total-field anomalies
```
# total-field anomaly produced by the ellipsoid (in nT)
tf_t = oblate_ellipsoid.tf(xp, yp, zp, [ellipsoid],
F, inc, dec)
# total-field anomaly produced by the sphere (in nT)
tf_s = sphere.tf(xp, yp, zp, [spherical_body], inc, dec)
# residuals
tf_r = tf_t - tf_s
plt.figure(figsize=(3.15, 7))
plt.axis('scaled')
ranges = np.max(np.abs([np.min(tf_t), np.max(tf_t),
np.min(tf_s), np.max(tf_s)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('RdBu_r')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)
plt.subplot(3,1,1)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
tf_t.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
cbar = plt.colorbar()
plt.annotate(s='(a)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
plt.subplot(3,1,2)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
tf_s.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
plt.colorbar()
plt.annotate(s='(b)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
ranges = np.max(np.abs([np.min(tf_r), np.max(tf_r)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('RdBu_r')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)
plt.subplot(3,1,3)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
tf_r.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlabel('y (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
plt.colorbar()
plt.annotate(s='(c)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
plt.tight_layout()
plt.show()
```
##### Field components
```
# field components produced by the ellipsoid (in nT)
bx_t = oblate_ellipsoid.bx(xp, yp, zp, [ellipsoid],
F, inc, dec)
by_t = oblate_ellipsoid.by(xp, yp, zp, [ellipsoid],
F, inc, dec)
bz_t = oblate_ellipsoid.bz(xp, yp, zp, [ellipsoid],
F, inc, dec)
bt = [bx_t, by_t, bz_t]
# field components produced by the sphere (in nT)
bx_s = sphere.bx(xp, yp, zp, [spherical_body])
by_s = sphere.by(xp, yp, zp, [spherical_body])
bz_s = sphere.bz(xp, yp, zp, [spherical_body])
bs = [bx_s, by_s, bz_s]
# residuals
bx_r = bx_t - bx_s
by_r = by_t - by_s
bz_r = bz_t - bz_s
br = [bx_r, by_r, bz_r]
plt.figure(figsize=(3.15, 7))
plt.axis('scaled')
ranges = np.max(np.abs([np.min(bx_t), np.max(bx_t),
np.min(bx_s), np.max(bx_s)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('RdBu_r')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)
plt.subplot(3,1,1)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
bx_t.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
cbar = plt.colorbar()
plt.annotate(s='(a)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
plt.subplot(3,1,2)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
bx_s.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
plt.colorbar()
plt.annotate(s='(b)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
ranges = np.max(np.abs([np.min(bx_r), np.max(bx_r)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('RdBu_r')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)
plt.subplot(3,1,3)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
bx_r.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlabel('y (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
plt.colorbar()
plt.annotate(s='(c)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
plt.tight_layout()
plt.show()
plt.figure(figsize=(3.15, 7))
plt.axis('scaled')
ranges = np.max(np.abs([np.min(by_t), np.max(by_t),
np.min(by_s), np.max(by_s)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('RdBu_r')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)
plt.subplot(3,1,1)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
by_t.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
cbar = plt.colorbar()
plt.annotate(s='(a)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
plt.subplot(3,1,2)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
by_s.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
plt.colorbar()
plt.annotate(s='(b)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
ranges = np.max(np.abs([np.min(by_r), np.max(by_r)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('RdBu_r')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)
plt.subplot(3,1,3)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
by_r.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlabel('y (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
plt.colorbar()
plt.annotate(s='(c)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
plt.tight_layout()
plt.show()
plt.figure(figsize=(3.15, 7))
plt.axis('scaled')
ranges = np.max(np.abs([np.min(bz_t), np.max(bz_t),
np.min(bz_s), np.max(bz_s)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('RdBu_r')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)
plt.subplot(3,1,1)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
bz_t.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
cbar = plt.colorbar()
plt.annotate(s='(a)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
plt.subplot(3,1,2)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
bz_s.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
plt.colorbar()
plt.annotate(s='(b)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
ranges = np.max(np.abs([np.min(bz_r), np.max(bz_r)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('RdBu_r')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)
plt.subplot(3,1,3)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
bz_r.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlabel('y (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
plt.colorbar()
plt.annotate(s='(c)', xy=(0.88,0.92),
xycoords = 'axes fraction', color='k',
fontsize = 10)
plt.tight_layout()
plt.show()
```
| true |
code
| 0.667906 | null | null | null | null |
|
# Recommendation Engine
## Building a Movie Recommendation Engine using MovieLens dataset
We will be using a MovieLens dataset. This dataset contains 100004 ratings across 9125 movies for 671 users. All selected users had at least rated 20 movies.
We are going to build a recommendation engine which will suggest movies for a user which he hasn't watched yet based on the movies which he has already rated. We will be using k-nearest neighbour algorithm which we will implement from scratch.
```
import pandas as pd
```
Movie file contains information like movie id, title, genre of movies and ratings file contains data like user id, movie id, rating and timestamp in which each line after header row represents one rating of one movie by one user.
```
movie_file = "data\movie_dataset\movies.csv"
movie_data = pd.read_csv(movie_file, usecols = [0, 1])
movie_data.head()
ratings_file = "data\\movie_dataset\\ratings.csv"
ratings_info = pd.read_csv(ratings_file, usecols = [0, 1, 2])
ratings_info.head()
movie_info = pd.merge(movie_data, ratings_info, left_on = 'movieId', right_on = 'movieId')
movie_info.head()
movie_info.loc[0:10, ['userId']]
movie_info[movie_info.title == "Toy Story (1995)"].head()
movie_info = pd.DataFrame.sort_values(movie_info, ['userId', 'movieId'], ascending = [0, 1])
movie_info.head()
```
Let us see the number of users and number of movies in our dataset
```
num_users = max(movie_info.userId)
num_movies = max(movie_info.movieId)
print(num_users)
print(num_movies)
```
how many movies were rated by each user and the number of users rated each movie
```
movie_per_user = movie_info.userId.value_counts()
movie_per_user.head()
users_per_movie = movie_info.title.value_counts()
users_per_movie.head()
```
Function to find top N favourite movies of a user
```
def fav_movies(current_user, N):
# get rows corresponding to current user and then sort by rating in descending order
# pick top N rows of the dataframe
fav_movies = pd.DataFrame.sort_values(movie_info[movie_info.userId == current_user],
['rating'], ascending = [0]) [:N]
# return list of titles
return list(fav_movies.title)
print(fav_movies(5, 3))
```
Lets build recommendation engine now
- We will use a neighbour based collaborative filtering model.
- The idea is to use k-nearest neighbour algorithm to find neighbours of a user
- We will use their ratings to predict ratings of a movie not already rated by a current user.
We will represent movies watched by a user in a vector - the vector will have values for all the movies in our dataset.
If a user hasn't rated a movie, it would be represented as NaN.
```
user_movie_rating_matrix = pd.pivot_table(movie_info, values = 'rating', index=['userId'], columns=['movieId'])
user_movie_rating_matrix.head()
```
Now, we will find the similarity between 2 users by using correlation
```
from scipy.spatial.distance import correlation
import numpy as np
def similarity(user1, user2):
# normalizing user1 rating i.e mean rating of user1 for any movie
# nanmean will return mean of an array after ignore NaN values
user1 = np.array(user1) - np.nanmean(user1)
user2 = np.array(user2) - np.nanmean(user2)
# finding the similarity between 2 users
# finding subset of movies rated by both the users
common_movie_ids = [i for i in range(len(user1)) if user1[i] > 0 and user2[i] > 0]
if(len(common_movie_ids) == 0):
return 0
else:
user1 = np.array([user1[i] for i in common_movie_ids])
user2 = np.array([user2[i] for i in common_movie_ids])
return correlation(user1, user2)
```
We will now use the similarity function to find the nearest neighbour of a current user
```
# nearest_neighbour_ratings function will find the k nearest neighbours of the current user and
# then use their ratings to predict the current users ratings for other unrated movies
def nearest_neighbour_ratings(current_user, K):
# Creating an empty matrix whose row index is userId and the value
# will be the similarity of that user to the current user
similarity_matrix = pd.DataFrame(index = user_movie_rating_matrix.index,
columns = ['similarity'])
for i in user_movie_rating_matrix.index:
# finding the similarity between user i and the current user and add it to the similarity matrix
similarity_matrix.loc[i] = similarity(user_movie_rating_matrix.loc[current_user],
user_movie_rating_matrix.loc[i])
# Sorting the similarity matrix in descending order
similarity_matrix = pd.DataFrame.sort_values(similarity_matrix,
['similarity'], ascending= [0])
# now we will pick the top k nearest neighbou
nearest_neighbours = similarity_matrix[:K]
neighbour_movie_ratings = user_movie_rating_matrix.loc[nearest_neighbours.index]
# This is empty dataframe placeholder for predicting the rating of current user using neighbour movie ratings
predicted_movie_rating = pd.DataFrame(index = user_movie_rating_matrix.columns, columns = ['rating'])
# Iterating all movies for a current user
for i in user_movie_rating_matrix.columns:
# by default, make predicted rating as the average rating of the current user
predicted_rating = np.nanmean(user_movie_rating_matrix.loc[current_user])
for j in neighbour_movie_ratings.index:
# if user j has rated the ith movie
if(user_movie_rating_matrix.loc[j,i] > 0):
predicted_rating += ((user_movie_rating_matrix.loc[j,i] -np.nanmean(user_movie_rating_matrix.loc[j])) *
nearest_neighbours.loc[j, 'similarity']) / nearest_neighbours['similarity'].sum()
predicted_movie_rating.loc[i, 'rating'] = predicted_rating
return predicted_movie_rating
```
Predicting top N recommendations for a current user
```
def top_n_recommendations(current_user, N):
predicted_movie_rating = nearest_neighbour_ratings(current_user, 10)
movies_already_watched = list(user_movie_rating_matrix.loc[current_user]
.loc[user_movie_rating_matrix.loc[current_user] > 0].index)
predicted_movie_rating = predicted_movie_rating.drop(movies_already_watched)
top_n_recommendations = pd.DataFrame.sort_values(predicted_movie_rating, ['rating'], ascending=[0])[:N]
top_n_recommendation_titles = movie_data.loc[movie_data.movieId.isin(top_n_recommendations.index)]
return list(top_n_recommendation_titles.title)
```
finding out the recommendations for a user
```
current_user = 140
print("User's favorite movies are : ", fav_movies(current_user, 5),
"\nUser's top recommendations are: ", top_n_recommendations(current_user, 3))
```
## Conclusion
We have built a movie recommendation engine using k-nearest neighbour algorithm implemented from scratch.
| true |
code
| 0.409752 | null | null | null | null |
|
**Chapter 1 – The Machine Learning landscape**
_This is the code used to generate some of the figures in chapter 1._
# Setup
First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "fundamentals"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
```
# Code example 1-1
This function just merges the OECD's life satisfaction data and the IMF's GDP per capita data. It's a bit too long and boring and it's not specific to Machine Learning, which is why I left it out of the book.
```
def prepare_country_stats(oecd_bli, gdp_per_capita):
oecd_bli = oecd_bli[oecd_bli["INEQUALITY"]=="TOT"]
oecd_bli = oecd_bli.pivot(index="Country", columns="Indicator", values="Value")
gdp_per_capita.rename(columns={"2015": "GDP per capita"}, inplace=True)
gdp_per_capita.set_index("Country", inplace=True)
full_country_stats = pd.merge(left=oecd_bli, right=gdp_per_capita,
left_index=True, right_index=True)
full_country_stats.sort_values(by="GDP per capita", inplace=True)
remove_indices = [0, 1, 6, 8, 33, 34, 35]
keep_indices = list(set(range(36)) - set(remove_indices))
return full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[keep_indices]
```
The code in the book expects the data files to be located in the current directory. I just tweaked it here to fetch the files in datasets/lifesat.
```
import os
datapath = os.path.join("datasets", "lifesat", "")
# Code example
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn.linear_model
# Load the data
oecd_bli = pd.read_csv(datapath + "oecd_bli_2015.csv", thousands=',')
gdp_per_capita = pd.read_csv(datapath + "gdp_per_capita.csv",thousands=',',delimiter='\t',
encoding='latin1', na_values="n/a")
# Prepare the data
country_stats = prepare_country_stats(oecd_bli, gdp_per_capita)
X = np.c_[country_stats["GDP per capita"]]
y = np.c_[country_stats["Life satisfaction"]]
# Visualize the data
country_stats.plot(kind='scatter', x="GDP per capita", y='Life satisfaction')
plt.show()
# Select a linear model
model = sklearn.linear_model.LinearRegression()
# Train the model
model.fit(X, y)
# Make a prediction for Cyprus
X_new = [[22587]] # Cyprus' GDP per capita
print(model.predict(X_new)) # outputs [[ 5.96242338]]
```
# Note: you can ignore the rest of this notebook, it just generates many of the figures in chapter 1.
机器学习项目成功的关键之一是用好特征工程进行训练
1. 特征选择:所有存在的特征中选取最有用的特征来进行训练
2. 特征提取:组合存在的特征,生成一个更有用的特征(如前面所看到的可以使用降维算法)
3. 手机新数据创建新特征
# Load and prepare Life satisfaction data
If you want, you can get fresh data from the OECD's website.
Download the CSV from http://stats.oecd.org/index.aspx?DataSetCode=BLI
and save it to `datasets/lifesat/`.
```
oecd_bli = pd.read_csv(datapath + "oecd_bli_2015.csv", thousands=',')
oecd_bli = oecd_bli[oecd_bli["INEQUALITY"]=="TOT"]
oecd_bli = oecd_bli.pivot(index="Country", columns="Indicator", values="Value")
oecd_bli.head(2)
oecd_bli["Life satisfaction"].head()
```
# Load and prepare GDP per capita data
Just like above, you can update the GDP per capita data if you want. Just download data from http://goo.gl/j1MSKe (=> imf.org) and save it to `datasets/lifesat/`.
```
gdp_per_capita = pd.read_csv(datapath+"gdp_per_capita.csv", thousands=',', delimiter='\t',
encoding='latin1', na_values="n/a")
gdp_per_capita.rename(columns={"2015": "GDP per capita"}, inplace=True)
gdp_per_capita.set_index("Country", inplace=True)
gdp_per_capita.head(2)
full_country_stats = pd.merge(left=oecd_bli, right=gdp_per_capita, left_index=True, right_index=True)
full_country_stats.sort_values(by="GDP per capita", inplace=True)
full_country_stats
full_country_stats[["GDP per capita", 'Life satisfaction']].loc["United States"]
remove_indices = [0, 1, 6, 8, 33, 34, 35]
keep_indices = list(set(range(36)) - set(remove_indices))
sample_data = full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[keep_indices]
missing_data = full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[remove_indices]
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3))
plt.axis([0, 60000, 0, 10])
position_text = {
"Hungary": (5000, 1),
"Korea": (18000, 1.7),
"France": (29000, 2.4),
"Australia": (40000, 3.0),
"United States": (52000, 3.8),
}
for country, pos_text in position_text.items():
pos_data_x, pos_data_y = sample_data.loc[country]
country = "U.S." if country == "United States" else country
plt.annotate(country, xy=(pos_data_x, pos_data_y), xytext=pos_text,
arrowprops=dict(facecolor='black', width=0.5, shrink=0.1, headwidth=5))
plt.plot(pos_data_x, pos_data_y, "ro")
save_fig('money_happy_scatterplot')
plt.show()
sample_data.to_csv(os.path.join("datasets", "lifesat", "lifesat.csv"))
sample_data.loc[list(position_text.keys())]
import numpy as np
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3))
plt.axis([0, 60000, 0, 10])
X=np.linspace(0, 60000, 1000)
plt.plot(X, 2*X/100000, "r")
plt.text(40000, 2.7, r"$\theta_0 = 0$", fontsize=14, color="r")
plt.text(40000, 1.8, r"$\theta_1 = 2 \times 10^{-5}$", fontsize=14, color="r")
plt.plot(X, 8 - 5*X/100000, "g")
plt.text(5000, 9.1, r"$\theta_0 = 8$", fontsize=14, color="g")
plt.text(5000, 8.2, r"$\theta_1 = -5 \times 10^{-5}$", fontsize=14, color="g")
plt.plot(X, 4 + 5*X/100000, "b")
plt.text(5000, 3.5, r"$\theta_0 = 4$", fontsize=14, color="b")
plt.text(5000, 2.6, r"$\theta_1 = 5 \times 10^{-5}$", fontsize=14, color="b")
save_fig('tweaking_model_params_plot')
plt.show()
from sklearn import linear_model
lin1 = linear_model.LinearRegression()
Xsample = np.c_[sample_data["GDP per capita"]]
ysample = np.c_[sample_data["Life satisfaction"]]
lin1.fit(Xsample, ysample)
t0, t1 = lin1.intercept_[0], lin1.coef_[0][0]
t0, t1
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3))
plt.axis([0, 60000, 0, 10])
X=np.linspace(0, 60000, 1000)
plt.plot(X, t0 + t1*X, "b")
plt.text(5000, 3.1, r"$\theta_0 = 4.85$", fontsize=14, color="b")
plt.text(5000, 2.2, r"$\theta_1 = 4.91 \times 10^{-5}$", fontsize=14, color="b")
save_fig('best_fit_model_plot')
plt.show()
cyprus_gdp_per_capita = gdp_per_capita.loc["Cyprus"]["GDP per capita"]
print(cyprus_gdp_per_capita)
cyprus_predicted_life_satisfaction = lin1.predict([[cyprus_gdp_per_capita]])[0][0]
cyprus_predicted_life_satisfaction
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3), s=1)
X=np.linspace(0, 60000, 1000)
plt.plot(X, t0 + t1*X, "b")
plt.axis([0, 60000, 0, 10])
plt.text(5000, 7.5, r"$\theta_0 = 4.85$", fontsize=14, color="b")
plt.text(5000, 6.6, r"$\theta_1 = 4.91 \times 10^{-5}$", fontsize=14, color="b")
plt.plot([cyprus_gdp_per_capita, cyprus_gdp_per_capita], [0, cyprus_predicted_life_satisfaction], "r--")
plt.text(25000, 5.0, r"Prediction = 5.96", fontsize=14, color="b")
plt.plot(cyprus_gdp_per_capita, cyprus_predicted_life_satisfaction, "ro")
save_fig('cyprus_prediction_plot')
plt.show()
sample_data[7:10]
(5.1+5.7+6.5)/3
backup = oecd_bli, gdp_per_capita
def prepare_country_stats(oecd_bli, gdp_per_capita):
oecd_bli = oecd_bli[oecd_bli["INEQUALITY"]=="TOT"]
oecd_bli = oecd_bli.pivot(index="Country", columns="Indicator", values="Value")
gdp_per_capita.rename(columns={"2015": "GDP per capita"}, inplace=True)
gdp_per_capita.set_index("Country", inplace=True)
full_country_stats = pd.merge(left=oecd_bli, right=gdp_per_capita,
left_index=True, right_index=True)
full_country_stats.sort_values(by="GDP per capita", inplace=True)
remove_indices = [0, 1, 6, 8, 33, 34, 35]
keep_indices = list(set(range(36)) - set(remove_indices))
return full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[keep_indices]
# Code example
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn
# Load the data
oecd_bli = pd.read_csv(datapath + "oecd_bli_2015.csv", thousands=',')
gdp_per_capita = pd.read_csv(datapath + "gdp_per_capita.csv",thousands=',',delimiter='\t',
encoding='latin1', na_values="n/a")
# Prepare the data
country_stats = prepare_country_stats(oecd_bli, gdp_per_capita)
X = np.c_[country_stats["GDP per capita"]]
y = np.c_[country_stats["Life satisfaction"]]
# Visualize the data
country_stats.plot(kind='scatter', x="GDP per capita", y='Life satisfaction')
plt.show()
# Select a linear model
model = sklearn.linear_model.LinearRegression()
# Train the model
model.fit(X, y)
# Make a prediction for Cyprus
X_new = [[22587]] # Cyprus' GDP per capita
print(model.predict(X_new)) # outputs [[ 5.96242338]]
oecd_bli, gdp_per_capita = backup
missing_data
position_text2 = {
"Brazil": (1000, 9.0),
"Mexico": (11000, 9.0),
"Chile": (25000, 9.0),
"Czech Republic": (35000, 9.0),
"Norway": (60000, 3),
"Switzerland": (72000, 3.0),
"Luxembourg": (90000, 3.0),
}
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(8,3))
plt.axis([0, 110000, 0, 10])
for country, pos_text in position_text2.items():
pos_data_x, pos_data_y = missing_data.loc[country]
plt.annotate(country, xy=(pos_data_x, pos_data_y), xytext=pos_text,
arrowprops=dict(facecolor='black', width=0.5, shrink=0.1, headwidth=5))
plt.plot(pos_data_x, pos_data_y, "rs")
X=np.linspace(0, 110000, 1000)
plt.plot(X, t0 + t1*X, "b:")
lin_reg_full = linear_model.LinearRegression()
Xfull = np.c_[full_country_stats["GDP per capita"]]
yfull = np.c_[full_country_stats["Life satisfaction"]]
lin_reg_full.fit(Xfull, yfull)
t0full, t1full = lin_reg_full.intercept_[0], lin_reg_full.coef_[0][0]
X = np.linspace(0, 110000, 1000)
plt.plot(X, t0full + t1full * X, "k")
save_fig('representative_training_data_scatterplot')
plt.show()
full_country_stats.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(8,3))
plt.axis([0, 110000, 0, 10])
from sklearn import preprocessing
from sklearn import pipeline
poly = preprocessing.PolynomialFeatures(degree=60, include_bias=False)
scaler = preprocessing.StandardScaler()
lin_reg2 = linear_model.LinearRegression()
pipeline_reg = pipeline.Pipeline([('poly', poly), ('scal', scaler), ('lin', lin_reg2)])
pipeline_reg.fit(Xfull, yfull)
curve = pipeline_reg.predict(X[:, np.newaxis])
plt.plot(X, curve)
save_fig('overfitting_model_plot')
plt.show()
full_country_stats.loc[[c for c in full_country_stats.index if "W" in c.upper()]]["Life satisfaction"]
gdp_per_capita.loc[[c for c in gdp_per_capita.index if "W" in c.upper()]].head()
plt.figure(figsize=(8,3))
plt.xlabel("GDP per capita")
plt.ylabel('Life satisfaction')
plt.plot(list(sample_data["GDP per capita"]), list(sample_data["Life satisfaction"]), "bo")
plt.plot(list(missing_data["GDP per capita"]), list(missing_data["Life satisfaction"]), "rs")
X = np.linspace(0, 110000, 1000)
plt.plot(X, t0full + t1full * X, "r--", label="Linear model on all data")
plt.plot(X, t0 + t1*X, "b:", label="Linear model on partial data")
ridge = linear_model.Ridge(alpha=10**9.5)
Xsample = np.c_[sample_data["GDP per capita"]]
ysample = np.c_[sample_data["Life satisfaction"]]
ridge.fit(Xsample, ysample)
t0ridge, t1ridge = ridge.intercept_[0], ridge.coef_[0][0]
plt.plot(X, t0ridge + t1ridge * X, "b", label="Regularized linear model on partial data")
plt.legend(loc="lower right")
plt.axis([0, 110000, 0, 10])
save_fig('ridge_model_plot')
plt.show()
backup = oecd_bli, gdp_per_capita
def prepare_country_stats(oecd_bli, gdp_per_capita):
return sample_data
# Replace this linear model:
import sklearn.linear_model
model = sklearn.linear_model.LinearRegression()
# with this k-neighbors regression model:
import sklearn.neighbors
model = sklearn.neighbors.KNeighborsRegressor(n_neighbors=3)
X = np.c_[country_stats["GDP per capita"]]
y = np.c_[country_stats["Life satisfaction"]]
# Train the model
model.fit(X, y)
# Make a prediction for Cyprus
X_new = np.array([[22587.0]]) # Cyprus' GDP per capita
print(model.predict(X_new)) # outputs [[ 5.76666667]]
```
| true |
code
| 0.643217 | null | null | null | null |
|
# 03. DQN example with CartPole
## Colab 용 package 설치 코드
```
!pip install gym
!pip install JSAnimation
```
### package import
```
# The typical imports
from IPython.display import clear_output
import gym
import numpy as np
import matplotlib.pyplot as plt
import random
%matplotlib inline
import tensorflow as tf
np.random.seed(777)
tf.set_random_seed(777)
random.seed(777)
print("tensorflow version: ", tf.__version__)
print("gym version: ", gym.__version__)
```
### 게임 화면을 보여주기 위한 함수
```
# Imports specifically so we can render outputs in Jupyter.
from JSAnimation.IPython_display import display_animation
from matplotlib import animation
from IPython.display import display
def display_frames_as_gif(frames):
"""
Displays a list of frames as a gif, with controls
"""
#plt.figure(figsize=(frames[0].shape[1] / 72.0, frames[0].shape[0] / 72.0), dpi = 72)
patch = plt.imshow(frames[0])
plt.axis('off')
def animate(i):
patch.set_data(frames[i])
anim = animation.FuncAnimation(plt.gcf(), animate, frames = len(frames), interval=50)
display(display_animation(anim, default_mode='loop'))
```
### 그래프를 그리기 위한 함수
```
def plot(frame_idx, episode, rewards, losses):
clear_output(True)
plt.figure(figsize=(20,5))
plt.subplot(131)
plt.title('episode %s. reward: %s' % (episode, np.mean(rewards[-10:])))
plt.plot(rewards)
plt.subplot(132)
plt.title('loss')
plt.plot(losses)
plt.show()
```
<script src='https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.4/MathJax.js?config=TeX-MML-AM_CHTML' async></script>
## CartPole
CartPole is game that ballance pole on the car.
this game's observation is $x$, $x\prime$, $\theta$, $\theta\prime$
$x$ : 카트의 위치
$\theta$ : 막대의 각도
$x\prime$ : 카트의 속도
$\theta\prime$ : 막대의 각속도
Action is **Left** or **Right**
모든 step 마다 보상을 1 받으며, 아래 3가지 경우에 episode가 끝난다.
1. 카트가 바깥으로 나갈 때
2. 기둥이 너무 많이 기울었을 때
3. 200 step 지났을 때
<img src="./img/cartpole.gif" width="60%" align="left">
```
# CartPole 환경
env_id = "CartPole-v0"
env = gym.make(env_id)
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
print("Observation size : ", state_size)
print("Action size : ", action_size)
```
## DQN Agent
### Replay Buffer
```
state = env.reset()
action = env.action_space.sample()
next_state, reward, done, _ = env.step(action)
print("state_size:", np.shape(state))
print("next_state_size:", np.shape(next_state))
# deque buffer 생성
buffer = []
# buffer에 transition((state, action, reward, next_state, done))을 append
transition =
# buffer에 append
print(np.shape(buffer))
print(buffer)
# buffer에서 batch size만큼 sampling
for i in range(5):
buffer.append(transition)
# {} 빈칸을 채우세요.
idxs = np.random.choice({}, size={}, replace=False)
state, action, reward, next_state, done = [], [], [], [], []
for i in {}:
s, a, r, n_s, d = buffer[{}]
state.append(np.array({}, copy=False))
action.append(np.array({}, copy=False))
reward.append(np.array({}, copy=False))
next_state.append(np.array({}, copy=False))
done.append(np.array({}, copy=False))
state = np.array({})
action = np.array({})
reward = np.array({})
next_state = np.array({})
done = np.array({})
print(np.shape(state))
print(next_state)
print(action)
print(reward)
print(done)
```
### Replay Buffer class
```
# Unifrom Replay Buffer
class ReplayBuffer(object):
def __init__(self, capacity):
self.buffer =
self.capacity =
self.idx = 0
# buffer 길이 체크
def __len__(self):
# buffer에 sample 추가
def add(self, state, action, reward, next_state, done):
transition = (state, action, reward, next_state, done)
if len(self.buffer) == self.capacity:
# buffer가 꽉차면 0번째부터 다시 채운다
else:
# buffer append
# buffer에서 batch_size만큼 뽑기
def sample(self, batch_size):
# sample code 작성
return state, action, reward, next_state, done
# buffer 검증
b = ReplayBuffer(5)
print(len(b))
s, a, r, n_s, d = transition
for _ in range(5):
b.add(s, a, r, n_s, d)
print("sample", b.sample(2))
# add 검증
a = np.array([3,3])
d = True
for _ in range(5):
b.add(s, a, r, n_s, d)
print(len(b))
print("new sample", b.sample(2))
```
### DQN Agent Class
<img src="./img/hyperparameters.png" width="100%" align="left">
Q Learning에서 Q함수의 업데이트식은 다음과 같다.
$$Q(S,A) \gets Q(S,A) + \alpha [r + \gamma max_{a\prime}Q(S \prime, a \prime) - Q(S,A)]$$
DQN에서는 업데이트식에서 TD error 부분을 Loss로 보고 학습한다.
$$ Loss = E [(y - Q(S,A))^{2}]$$
```
layer = tf.contrib.layers
class DQNAgent:
def __init__(self, sess, state_size, action_size):
self.sess = sess
self.state_size = state_size
self.action_size = action_size
# hyper parameter
self.batch_size = 32
self.gamma = 0.99
self.learning_rate = 0.00025
# epsilon
self.s_epsilon = 1.0
self.e_epsilon = 0.01
self.n_epsilon_decay = 1000
self.epsilon = self.s_epsilon
# place holder
self.input_policy = tf.placeholder(tf.float32, shape=(None, self.state_size))
self.input_target = tf.placeholder(tf.float32, shape=(None, self.state_size))
self.actions = tf.placeholder(tf.int32, shape=None)
self.targets = tf.placeholder(tf.float32, shape=None)
# network
self.policy_q = self._build_network(self.input_policy, net_name="policy_net")
self.target_q = self._build_network(self.input_target, net_name="target_net")
self.sess.run(tf.global_variables_initializer())
self.update_target_network()
# replay buffer
# 직접 작성해보세요.
self.buffer =
# optimizer
self.loss_op, self.train_op = self._build_op()
def _build_network(self, inputs, name):
"""
tf.contrib.layers.fully_connected()를 이용해
hidden layer가 하나인 신경망을 구성합니다.
입력 : 상태 (state_size)
출력 : q-value (action_size)
hidden layer size : 128
activation function : Relu
"""
# 빈칸 {} 을 지우고 채워주세요.
# 참고) layer.fully_connected(입력, 출력 사이즈, activation function)
# 참고2) relu -> tf.nn.relu
with tf.variable_scope(net_name):
fc1 = layer.{}(
inputs={},
num_outputs={},
activation_fn={},
)
fc2 = layer.{}(
inputs={},
num_outputs={},
activation_fn=tf.nn.relu,
)
q_value = layer.{}(
inputs={},
num_outputs={},
activation_fn=None,
)
return q_value
def _build_op(self):
"""신경망 학습을 위한 Loss function과 Optimaizer를 정의합니다."""
# 직접 작성해보세요.
# 참고) # 이전 실습에서 현재 action에 대한 Q_value 구하는 연산
# curr_action = tf.one_hot(input_action, action_size)
# curr_q_value = tf.reduce_sum(tf.multiply(q_value, curr_action))
action_one_hot =
predict_q =
# 참고) 이전 실습에서 Loss 함수 구성
# loss_op = tf.square(target - curr_q_value)
# opt = tf.train.GradientDescentOptimizer(learning_rate=0.1)
# train_op = opt.minimize(loss_op)
loss_op = tf.reduce_mean(tf.square(self.targets - predict_q))
train_op = tf.train.RMSPropOptimizer(
learning_rate=self.learning_rate,
decay=0.95,
momentum=0.95,
epsilon=0.01
).minimize(loss_op)
return loss_op, train_op
def update_model(self):
"""
replay buffer에서 batch size만큼 가져온 후
학습 네트워크를 학습합니다.
loss function은 위의 수식 참고
"""
# replay buffer로부터 transition을 가져옴
# 직접 작성해보세요.
# 참고) 위에 작성한 replay buffer class, replay_buffer.sample()
states, actions, rewards, next_states, dones = self.buffer.sample(self.batch_size)
# target 계산
# 아래 eval코드는 sess.run과 같은 동작을 함.
target_q = self.target_q.eval({self.input_target: next_states}, self.sess)
target_q = # max
targets = # target 계산
# loss 계산 및 학습
loss, _ = self.sess.run(
[{}, {}],
feed_dict={self.{}: {}, # state
self.{}: {}, # action
self.{}: {}}) # target
return loss
def update_target_network(self):
"""
학습 네트웍의 변수의 값들을 타겟 네트웍으로 복사해서 타겟 네트웍의 값들을 최신으로 업데이트합니다.
"""
copy_op = []
main_q_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='policy_net')
target_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='target_net')
for main_q_var, target_var in zip(main_q_vars, target_vars):
copy_op.append(target_var.assign(main_q_var.value()))
self.sess.run(copy_op)
def select_action(self, state):
"""epsilon-greedy로 action을 선택합니다."""
# epsilon greedy policy
if self.epsilon > np.random.random():
# random action
selected_action = np.random.randint(self.action_size)
else:
# policy action 구현
# 매 step마다 epsilon을 줄여나갑니다.
if self.epsilon >= self.e_epsilon:
self.epsilon -= (self.s_epsilon - self.e_epsilon) / self.n_epsilon_decay
return selected_action
```
### DQN agent train
```
# Session 열기
tf.reset_default_graph()
sess = tf.Session()
# DQN Agent 객체 생성
agent = DQNAgent(sess, state_size, action_size)
# 변수 초기화
sess.run(tf.global_variables_initializer())
```
### DQN 학습
```
EPISODE = 30
replay_initial = 50
target_update = 10
total_step = 1
all_episode_reward = []
losses = []
for e in range(EPISODE):
print("EPISODE: {}".format(e+1))
observation = env.reset()
done = False
step = 1
episode_reward = 0
frames = []
while not done:
# 직접 작성해보세요.
# action 선택
action =
# 선택한 action으로 env.step()
next_observation, reward, done, _ = env.step(action)
step += 1
total_step += 1
episode_reward += reward
# trajectory(S, A, R, S', done)를 Replay buffer에 저장
# replay buffer에 저장하는 코드 작성
{}
observation = next_observation
# 만약에 episode가 끝났으면 reward 저장
if done:
all_episode_reward.append(episode_reward)
# replay buffer가 일정 이상 채워지면 학습 시작
if len(agent.buffer) > replay_initial:
# 신경망 업데이트 코드 작성
loss =
losses.append(loss)
# 일정 step마다 target Q 업데이트
if total_step > replay_initial and total_step % target_update == 0:
# policy network를 target network에 복사해주는 코드 작성
# 그래프 그리기
if total_step % 100 == 0:
plot(step, e, all_episode_reward, losses)
print(total_step)
env.close()
```
### 학습된 DQN 테스트
```
EPISODE = 1
all_episode_reward = []
losses = []
for e in range(EPISODE):
print("EPISODE: {}".format(e+1))
observation = env.reset()
done = False
step = 1
episode_reward = 0
frames = []
agent.epsilon = 0
while not done:
action = int(agent.select_action(observation))
next_observation, reward, done, _ = env.step(action)
step += 1
total_step += 1
episode_reward += reward
observation = next_observation
if done:
all_episode_reward.append(episode_reward)
# 게임화면 보여주기
if e % 1 == 0:
frames.append(env.render(mode = 'rgb_array'))
env.close()
print("step", step)
print("reward", episode_reward)
if len(frames) > 0:
display_frames_as_gif(frames)
```
| true |
code
| 0.657016 | null | null | null | null |
|
# Using SageMaker Neo to Compile a Tensorflow U-Net Model
[SageMaker Neo](https://aws.amazon.com/sagemaker/neo/) makes it easy to compile pre-trained TensorFlow models and build an inference optimized container without the need for any custom model serving or inference code.
<img src="https://paperswithcode.com/media/methods/Screen_Shot_2020-07-07_at_9.08.00_PM_rpNArED.png" align="center" style="padding: 8px;width:500px;">
[U-Net](https://paperswithcode.com/method/u-net) is an architecture for semantic segmentation. It's a popular model for biological images including Ultrasound, Microscopy, CT, MRI and more.
In this example, we will show how deploy a pre-trained U-Net model to a SageMaker Endpoint with Neo compilation using the [SageMaker Python SDK](https://github.com/aws/sagemaker-python-sdk), and then use the models to perform inference requests. We also provide a performance comparison so you can see the benefits of model compilation.
## Setup
First, we need to ensure we have SageMaker Python SDK 1.x and Tensorflow 1.15.x. Then, import necessary Python packages.
```
!pip install -U --quiet --upgrade "sagemaker"
!pip install -U --quiet "tensorflow==1.15.3"
import tarfile
import numpy as np
import sagemaker
import time
from sagemaker.utils import name_from_base
```
Next, we'll get the IAM execution role and a few other SageMaker specific variables from our notebook environment, so that SageMaker can access resources in your AWS account later in the example.
```
from sagemaker import get_execution_role
from sagemaker.session import Session
role = get_execution_role()
sess = Session()
region = sess.boto_region_name
bucket = sess.default_bucket()
```
SageMaker [Neo supports Tensorflow 1.15.x](https://docs.amazonaws.cn/en_us/sagemaker/latest/dg/neo-supported-cloud.html). Check your version of Tensorflow to prevent downstream framework errors.
```
import tensorflow as tf
print(tf.__version__) # This notebook runs on TensorFlow 1.15.x or earlier
```
## Download U-Net Model
The SageMaker Neo TensorFlow Serving Container works with any model stored in TensorFlow's [SavedModel format](https://www.tensorflow.org/guide/saved_model). This could be the output of your own training job or a model trained elsewhere. For this example, we will use a pre-trained version of the U-Net model based on this [repo](https://github.com/kamalkraj/DATA-SCIENCE-BOWL-2018).
```
model_name = 'unet_medical'
export_path = 'export'
model_archive_name = 'unet-medical.tar.gz'
model_archive_url = 'https://sagemaker-neo-artifacts.s3.us-east-2.amazonaws.com/{}'.format(model_archive_name)
!wget {model_archive_url}
```
The pre-trained model and its artifacts are saved in a compressed tar file (.tar.gz) so unzip first with:
```
!tar -xvzf unet-medical.tar.gz
```
After downloading the model, we can inspect it using TensorFlow's ``saved_model_cli`` command. In the command output, you should see
```
MetaGraphDef with tag-set: 'serve' contains the following SignatureDefs:
signature_def['serving_default']:
...
```
The command output should also show details of the model inputs and outputs.
```
import os
model_path = os.path.join(export_path, 'Servo/1')
!saved_model_cli show --all --dir {model_path}
```
Next we need to create a model archive file containing the exported model.
## Upload the model archive file to S3
We now have a suitable model archive ready in our notebook. We need to upload it to S3 before we can create a SageMaker Model that. We'll use the SageMaker Python SDK to handle the upload.
```
model_data = Session().upload_data(path=model_archive_name, key_prefix='model')
print('model uploaded to: {}'.format(model_data))
```
## Create a SageMaker Model and Endpoint
Now that the model archive is in S3, we can create an unoptimized Model and deploy it to an
Endpoint.
```
from sagemaker.tensorflow.serving import Model
instance_type = 'ml.c4.xlarge'
framework = "TENSORFLOW"
framework_version = "1.15.3"
sm_model = Model(model_data=model_data, framework_version=framework_version,role=role)
uncompiled_predictor = sm_model.deploy(initial_instance_count=1, instance_type=instance_type)
```
## Make predictions using the endpoint
The endpoint is now up and running, and ready to handle inference requests. The `deploy` call above returned a `predictor` object. The `predict` method of this object handles sending requests to the endpoint. It also automatically handles JSON serialization of our input arguments, and JSON deserialization of the prediction results.
We'll use this sample image:
<img src="https://sagemaker-neo-artifacts.s3.us-east-2.amazonaws.com/cell-4.png" align="left" style="padding: 8px;">
```
sample_img_fname = 'cell-4.png'
sample_img_url = 'https://sagemaker-neo-artifacts.s3.us-east-2.amazonaws.com/{}'.format(sample_img_fname)
!wget {sample_img_url}
# read the image file into a tensor (numpy array)
import cv2
image = cv2.imread(sample_img_fname)
original_shape = image.shape
import matplotlib.pyplot as plt
plt.imshow(image, cmap='gray', interpolation='none')
plt.show()
image = np.resize(image, (256, 256, 3))
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image = np.asarray(image)
image = np.expand_dims(image, axis=0)
start_time = time.time()
# get a prediction from the endpoint
# the image input is automatically converted to a JSON request.
# the JSON response from the endpoint is returned as a python dict
result = uncompiled_predictor.predict(image)
print("Prediction took %.2f seconds" % (time.time() - start_time))
# show the predicted segmentation image
cutoff = 0.4
segmentation_img = np.squeeze(np.asarray(result['predictions'])) > cutoff
segmentation_img = segmentation_img.astype(np.uint8)
segmentation_img = np.resize(segmentation_img, (original_shape[0], original_shape[1]))
plt.imshow(segmentation_img, "gray")
plt.show()
```
## Uncompiled Predictor Performance
```
shape_input = np.random.rand(1, 256, 256, 3)
uncompiled_results = []
for _ in range(100):
start = time.time()
uncompiled_predictor.predict(image)
uncompiled_results.append((time.time() - start) * 1000)
print("\nPredictions for un-compiled model: \n")
print('\nP95: ' + str(np.percentile(uncompiled_results, 95)) + ' ms\n')
print('P90: ' + str(np.percentile(uncompiled_results, 90)) + ' ms\n')
print('P50: ' + str(np.percentile(uncompiled_results, 50)) + ' ms\n')
print('Average: ' + str(np.average(uncompiled_results)) + ' ms\n')
```
## Compile model using SageMaker Neo
```
# Replace the value of data_shape below and
# specify the name & shape of the expected inputs for your trained model in JSON
# Note that -1 is replaced with 1 for the batch size placeholder
data_shape = {'inputs':[1, 224, 224, 3]}
instance_family = 'ml_c4'
compilation_job_name = name_from_base('medical-tf-Neo')
# output path for compiled model artifact
compiled_model_path = 's3://{}/{}/output'.format(bucket, compilation_job_name)
optimized_estimator = sm_model.compile(target_instance_family=instance_family,
input_shape=data_shape,
job_name=compilation_job_name,
role=role,
framework=framework.lower(),
framework_version=framework_version,
output_path=compiled_model_path
)
```
## Create Optimized Endpoint
```
optimized_predictor = optimized_estimator.deploy(initial_instance_count = 1, instance_type = instance_type)
start_time = time.time()
# get a prediction from the endpoint
# the image input is automatically converted to a JSON request.
# the JSON response from the endpoint is returned as a python dict
result = optimized_predictor.predict(image)
print("Prediction took %.2f seconds" % (time.time() - start_time))
```
## Compiled Predictor Performance
```
compiled_results = []
test_input = {"instances": np.asarray(shape_input).tolist()}
#Warmup inference.
optimized_predictor.predict(image)
# Inferencing 100 times.
for _ in range(100):
start = time.time()
optimized_predictor.predict(image)
compiled_results.append((time.time() - start) * 1000)
print("\nPredictions for compiled model: \n")
print('\nP95: ' + str(np.percentile(compiled_results, 95)) + ' ms\n')
print('P90: ' + str(np.percentile(compiled_results, 90)) + ' ms\n')
print('P50: ' + str(np.percentile(compiled_results, 50)) + ' ms\n')
print('Average: ' + str(np.average(compiled_results)) + ' ms\n')
```
## Performance Comparison
Here we compare inference speed up provided by SageMaker Neo. P90 is 90th percentile latency. We add this because it represents the tail of the latency distribution (worst case). More information on latency percentiles [here](https://blog.bramp.net/post/2018/01/16/measuring-percentile-latency/).
```
p90 = np.percentile(uncompiled_results, 90) / np.percentile(compiled_results, 90)
p50 = np.percentile(uncompiled_results, 50) / np.percentile(compiled_results, 50)
avg = np.average(uncompiled_results) / np.average(compiled_results)
print("P90 Speedup: %.2f" % p90)
print("P50 Speedup: %.2f" % p50)
print("Average Speedup: %.2f" % avg)
```
## Additional Information
## Cleaning up
To avoid incurring charges to your AWS account for the resources used in this tutorial, you need to delete the SageMaker Endpoint.
```
uncompiled_predictor.delete_endpoint()
optimized_predictor.delete_endpoint()
```
| true |
code
| 0.566498 | null | null | null | null |
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/JavaScripts/Image/Polynomial.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/JavaScripts/Image/Polynomial.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/JavaScripts/Image/Polynomial.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# Applies a non-linear contrast enhancement to a MODIS image using
# function -0.2 + 2.4x - 1.2x^2.
# Load a MODIS image and apply the scaling factor.
img = ee.Image('MODIS/006/MOD09GA/2012_03_09') \
.select(['sur_refl_b01', 'sur_refl_b04', 'sur_refl_b03']) \
.multiply(0.0001)
# Apply the polynomial enhancement.
adj = img.polynomial([-0.2, 2.4, -1.2])
Map.setCenter(-107.24304, 35.78663, 8)
Map.addLayer(img, {'min': 0, 'max': 1}, 'original')
Map.addLayer(adj, {'min': 0, 'max': 1}, 'adjusted')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
| true |
code
| 0.607547 | null | null | null | null |
|
# Instructions
Implement a PyTorch dataset for keypoint detection.
Read about custom datasets here:
* https://jdhao.github.io/2017/10/23/pytorch-load-data-and-make-batch/
Image augmentation is an important part of deep learning pipelines. It artificially increases your training sample by generating transformed versions of images.
<img src="static/imgaug.jpg" alt="Drawing" style="width: 600px;"/>
You can read about it here:
* https://blog.keras.io/building-powerful-image-classification-models-using-very-little-data.html
* https://github.com/aleju/imgaug
You should implement the following augmentations:
* randomly fliping left and right
* randomly fliping up and down
* randomly translating by up to 4 pixels
* randomly rotating the image by 180 degrees
* randomly scaling the image from 1.0 to 1.5
Apart from reading images and augmenting, the loader is also cropping the input image by using outputs of the localizer network (bounding box coordinates).
# Your Solution
Your solution function should be called solution. In this case we leave it for consistency but you don't need to do anything with it.
CONFIG is a dictionary with all parameters that you want to pass to your solution function.
```
def solution():
return DatasetAligner
class DatasetAligner(Dataset):
def __init__(self, X, y, crop_coordinates, img_dirpath, augmentation, target_size, bins_nr):
super().__init__()
self.X = X.reset_index(drop=True)
self.y = y.reset_index(drop=True)
self.crop_coordinates = crop_coordinates
self.img_dirpath = img_dirpath
self.target_size = target_size
self.bins_nr = bins_nr
self.augmentation = augmentation
def load_image(self, img_name):
"""
Read image from disk to numpy array
"""
return img_array
def __len__(self):
"""
Determine the length of the dataset
"""
return length
def __getitem__(self, index):
"""
This method should take the image filepath at X[index] and targets at y[index] and
preprocess them. Use your aligner_preprocessing function.
Xi_tensor: is a torch.FloatTensor for image
yi_tensors: is a torch.LongTensor for targets it's shape should be 1 x k where k is the number of outputs
"""
return Xi_tensor, yi_tensors
def aligner_preprocessing(img, target, crop_coordinates, augmentation, *, org_size, target_size, bins_nr):
"""
Run augmentations and transformations on image and target
"""
processed_image, processed_target = crop_image_and_adjust_target(img, target, crop_coordinates)
if augmentation:
"""
Run augmentations on Image (and target if needed)
"""
"""
Transform coordinates to bin numbers as explained below and normalize the image
"""
processed_target = bin_quantizer(processed_target, (height, width), bins_nr)
processed_image = normalize_img(processed_image)
return processed_image, processed_target
def crop_image_and_adjust_target(img, target, crop_coordinates):
"""
crop image by using localization network predictions.
Remember to adjust the keypoint positions to the cropped image
"""
return cropped_image, adjusted_target
def bin_quantizer(coordinates, shape, bins_nr):
"""
Quantize the height and width and transform coordinates to bin numbers
"""
return binned_coordinates
def normalize_img(img):
mean = [0.28201905, 0.37246801, 0.42341868]
std = [0.13609867, 0.12380088, 0.13325344]
"""
Normalize Image
"""
return normalized_img
```
| true |
code
| 0.814883 | null | null | null | null |
|
<table width="100%"> <tr>
<td style="background-color:#ffffff;">
<a href="https://qsoftware.lu.lv/index.php/qworld/" target="_blank"><img src="../images/qworld.jpg" width="35%" align="left"> </a></td>
<td style="background-color:#ffffff;vertical-align:bottom;text-align:right;">
prepared by Abuzer Yakaryilmaz (<a href="http://qworld.lu.lv/index.php/qlatvia/" target="_blank">QLatvia</a>)
</td>
</tr></table>
<table width="100%"><tr><td style="color:#bbbbbb;background-color:#ffffff;font-size:11px;font-style:italic;text-align:right;">This cell contains some macros. If there is a problem with displaying mathematical formulas, please run this cell to load these macros. </td></tr></table>
$ \newcommand{\bra}[1]{\langle #1|} $
$ \newcommand{\ket}[1]{|#1\rangle} $
$ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
$ \newcommand{\dot}[2]{ #1 \cdot #2} $
$ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
$ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
$ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
$ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
$ \newcommand{\mypar}[1]{\left( #1 \right)} $
$ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
$ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
$ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
$ \newcommand{\onehalf}{\frac{1}{2}} $
$ \newcommand{\donehalf}{\dfrac{1}{2}} $
$ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
$ \newcommand{\vzero}{\myvector{1\\0}} $
$ \newcommand{\vone}{\myvector{0\\1}} $
$ \newcommand{\vhadamardzero}{\myvector{ \sqrttwo \\ \sqrttwo } } $
$ \newcommand{\vhadamardone}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
$ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
$ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
$ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
$ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
$ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
$ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
<h2> <font color="blue"> Solutions for </font>Coin Flip: A Probabilistic Bit</h2>
<a id="task1"></a>
<h3> Task 1: Simulating FairCoin in Python</h3>
Flip a fair coin 100 times. Calculate the total number of heads and tails, and then check the ratio of the number of heads and the number of tails.
Do the same experiment 1000 times.
Do the same experiment 10,000 times.
Do the same experiment 100,000 times.
Do your results get close to the ideal case (the numbers of heads and tails are equal)?
<h3>Solution</h3>
```
from random import randrange
for experiment in [100,1000,10000,100000]:
heads = tails = 0
for i in range(experiment):
if randrange(2) == 0: heads = heads + 1
else: tails = tails + 1
print("experiment:",experiment)
print("heads =",heads," tails = ",tails)
print("the ratio of #heads/#tails is",(round(heads/tails,4)))
print() # empty line
```
<a id="task2"></a>
<h3> Task 2: Simulating BiasedCoin in Python</h3>
Flip the following biased coin 100 times. Calcuate the total numbers of heads and tails, and then check the ratio of the number of heads and the number of tails.
$
BiasedCoin = \begin{array}{c|cc} & \mathbf{Head} & \mathbf{Tail} \\ \hline \mathbf{Head} & 0.6 & 0.6 \\ \mathbf{Tail} & 0.4 & 0.4 \end{array}
$
Do the same experiment 1000 times.
Do the same experiment 10,000 times.
Do the same experiment 100,000 times.
Do your results get close to the ideal case $ \mypar{ \dfrac{ \mbox{# of heads} }{ \mbox{# of tails} } = \dfrac{0.6}{0.4} = 1.50000000 } $?
<h3>Solution</h3>
```
from random import randrange
# let's pick a random number between {0,1,...,99}
# it is expected to be less than 60 with probability 0.6
# and greater than or equal to 60 with probability 0.4
for experiment in [100,1000,10000,100000]:
heads = tails = 0
for i in range(experiment):
if randrange(100) <60: heads = heads + 1 # with probability 0.6
else: tails = tails + 1 # with probability 0.4
print("experiment:",experiment)
print("heads =",heads," tails = ",tails)
print("the ratio of #heads/#tails is",(round(heads/tails,4)))
print() # empty line
```
<a id="task3"></a>
<h3> Task 3</h3>
Write a function to implement the described biased coin,
The inputs are integers $ N >0 $ and $ 0 \leq B < N $.
The output is either "Heads" or "Tails".
<h3>Solution</h3>
```
def biased_coin(N,B):
from random import randrange
random_number = randrange(N)
if random_number < B:
return "Heads"
else:
return "Tails"
```
<a id="task4"></a>
<h3> Task 4</h3>
We use the biased coin described in Task 3.
(You may use the function given in the solution.)
We pick $ N $ as 101.
Our task is to determine the value of $ B $ experimentially without checking its value directly.
Flip the (same) biased coin 500 times, collect the statistics, and then guess the bias.
Compare your guess with the actual bias by calculating the error (the absolute value of the difference).
<h3>Solution</h3>
```
def biased_coin(N,B):
from random import randrange
random_number = randrange(N)
if random_number < B:
return "Heads"
else:
return "Tails"
from random import randrange
N = 101
B = randrange(100)
total_tosses = 500
the_number_of_heads = 0
for i in range(total_tosses):
if biased_coin(N,B) == "Heads":
the_number_of_heads = the_number_of_heads + 1
my_guess = the_number_of_heads/total_tosses
real_bias = B/N
error = abs(my_guess-real_bias)/real_bias*100
print("my guess is",my_guess)
print("real bias is",real_bias)
print("error (%) is",error)
```
| true |
code
| 0.246692 | null | null | null | null |
|
# Introduction to Deep Learning with PyTorch
In this notebook, you'll get introduced to [PyTorch](http://pytorch.org/), a framework for building and training neural networks. PyTorch in a lot of ways behaves like the arrays you love from Numpy. These Numpy arrays, after all, are just tensors. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with Python and the Numpy/Scipy stack compared to TensorFlow and other frameworks.
## Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
<img src="assets/simple_neuron.png" width=400px>
Mathematically this looks like:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
With vectors this is the dot/inner product of two vectors:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## Tensors
It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
<img src="assets/tensor_examples.svg" width=600px>
With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
```
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 5 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
```
Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
`features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
`weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice benefits though such as GPU acceleration which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
> **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
```
## Calculate the output of this network using the weights and bias tensors
def metwork_op(features,weights,bias):
return activation(torch.sum(torch.mm(features,weights)))
```
You can do the multiplication and sum in the same operation using a matrix multiplication. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
```python
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second column. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
**Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), and [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view).
* `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
* `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
* `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
> **Exercise**: Calculate the output of our little network using matrix multiplication.
```
## Calculate the output of this network using matrix multiplication
print(features.shape)
c=features.reshape(5,1)
print(c)
print(weights.shape)
print(metwork_op(c,weights,bias))
```
### Stack them up!
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
<img src='assets/multilayer_diagram_weights.png' width=450px>
The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on the right) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
```
> **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
```
## Your solution here
print(features.shape)
print(W1.shape)
print(W2.shape)
print(B1.shape)
c=activation(torch.add(torch.mm(features,W1),B1))
d=activation(torch.add(torch.mm(c,W2),B2))
print(c)
print(d)
```
If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
The number of hidden units a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
## Numpy to Torch and back
Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
```
import numpy as np
a = np.random.rand(4,3)
a
b = torch.from_numpy(a)
b
b.numpy()
```
The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
```
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
```
| true |
code
| 0.628863 | null | null | null | null |
|
```
#from preprocess import *
#standard module
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# import sklearn
from sklearn import linear_model
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import PolynomialFeatures
from sklearn import neighbors
from sklearn.metrics import f1_score
from sklearn.metrics import precision_score
from sklearn.metrics import accuracy_score
from scipy.spatial.distance import squareform
from scipy.stats import rankdata
from matplotlib.backends.backend_pdf import PdfPages
from sklearn.neural_network import MLPRegressor
sns.set_context("paper", font_scale=1.5, rc={"lines.linewidth": 2.5})
import sys
sys.path.append("../../tools/")
from preprocess import *
```
## Simple machine learning model
```
#load data
alldata_15G=np.loadtxt('../../mddata/15grid_shuffled.dat')
alldata = alldata_15G
```
Linear Regression
```
def linear_models_with_regularizations(X_train, X_test, y_train, y_test, alpha_ridge, alpha_lasso):
"""
Parameters
--------------
X_train, X_test: numpy matrix
y_train, y_test: numpy array
ridge: boolean
set ridge = True for including Ridge regression
Return: float
r2_score
"""
logTrans = False
if logTrans is True:
y_test = np.log(y_test)
y_train = np.log(y_train)
regr = linear_model.LinearRegression()
regr.fit(X_train, y_train)
y_pred_regr = regr.predict(X_test)
#accuracy_score(Y_test, Y_pred)
# The coefficients
#print('Coefficients: \n', regr.coef_)
print("Mean squared error Linear Regression: %.2f" % mean_squared_error(y_test, y_pred_regr))
# Explained variance score: 1 is perfect prediction
#ac1 = r2_score(y_test, y_pred)
print("RMSE: %lf" %np.sqrt(np.sum(np.square(y_test-y_pred_regr))/len(y_test)))
print('r2_score: %.2f' % r2_score(y_test, y_pred_regr))
ysorted= np.sort(y_test)
xx = np.linspace(ysorted[0], ysorted[-1], len(ysorted))
plt.plot(xx, xx, 'r')
plt.plot(y_pred_regr, y_test, 'bo', alpha=0.5)
plt.xlabel('Predicted yield stress') #change the name here stress/strain
plt.ylabel('True yield stress')
plt.title('OLS with polynomial degree=2')
#plt.ylim(0, 1.2)
#plt.xlim(0, 1.2)
#plt.show()
#yy = y_test.reshape((len(y_test), 1))
plt.show()
ridge = linear_model.Ridge(alpha=alpha_ridge)
ridge.fit(X_train, y_train)
y_pred_ridge=ridge.predict(X_test)
#accuracy_score(Y_test, Y_pred)
# The coefficients
#print('Coefficients: \n', clf.coef_)
print("Mean squared error Ridge Regression: %.2f" % mean_squared_error(y_test, y_pred_ridge))
# Explained variance score: 1 is perfect prediction
print("RMSE: %lf" %np.sqrt(np.sum(np.square(y_test-y_pred_ridge))/len(y_test)))
print('r2_score: %.2f' % r2_score(y_test, y_pred_ridge))
#ac_ridge = r2_score(y_test, y_pred)
#plt.plot(y_pred, y_test, 'bo', alpha=0.5)
#plt.xlabel('y_test (fracture strain)')
#plt.ylabel('y_pred (fracture strain)')
#plt.title('Ridge Regression')
lasso = linear_model.Lasso(alpha=alpha_lasso)
lasso.fit(X_train, y_train)
y_pred_lasso=lasso.predict(X_test)
#accuracy_score(Y_test, Y_pred)
# The coefficients
#print('Coefficients: \n', clf.coef_)
print("Mean squared error LASSO: %.2f" % mean_squared_error(y_test, y_pred_lasso))
# Explained variance score: 1 is perfect prediction
print("RMSE: %lf" %np.sqrt(np.sum(np.square(y_test-y_pred_lasso))/len(y_test)))
print('r2_score: %.2f' % r2_score(y_test, y_pred_lasso))
#ac_lasso = r2_score(y_test, y_pred)
#plt.plot(y_test, y_pred, 'o')
#plt.xlabel('y_test (fracture strain)')
#plt.ylabel('y_pred (fracture strain)')
#plt.title('LASSO Regression')
#plt.show()
return y_pred_regr, y_pred_ridge, y_pred_lasso, regr.coef_, ridge.coef_, lasso.coef_
```
## Training
You can choose how many features to train
```
#split data into training and test set
sns.set_context("paper", font_scale=1.5, rc={"lines.linewidth": .5})
#np.random.shuffle(alldata)
x, y=create_matrix(alldata, False, 2, 0.3, 15)
x = (x-.5)*2
X_train, X_valid, X_test, y_train, y_valid, y_test = split_data(x, y, 0.8, 0.2)
#choose polynomial degrees
poly = PolynomialFeatures(2, interaction_only=True, include_bias=True)
#poly = PolynomialFeatures(2)
X_train2 = poly.fit_transform(X_train)
print("Number of features: %d" %len(X_train2[0]))
X_test2 = poly.fit_transform(X_test)
#linear_models(X_train2, X_test2, y_train, y_test, ridge=True)
#y_train = (y_train-0.45937603178269587)/0.22056868516982353
#y_test = (y_test-0.45937603178269587)/0.22056868516982353
alpha=0.1
y_pred_regr, y_pred_ridge, y_pred_lasso, coef_regr, coef_ridge, coef_lasso = linear_models_with_regularizations(X_train2, X_test2, y_train, y_test, 10, 0.1)
#split data into training and test set
sns.set_context("paper", font_scale=1.5, rc={"lines.linewidth": .5})
#np.random.shuffle(alldata)
x, y=create_matrix(alldata, False, 0, 0.3, 15)
x = (x-.5)*2
X_train, X_valid, X_test, y_train, y_valid, y_test = split_data(x, y, 0.8, 0.2)
#choose polynomial degrees
poly = PolynomialFeatures(3, interaction_only=True, include_bias=True)
#poly = PolynomialFeatures(2)
X_train2 = poly.fit_transform(X_train)
print("Number of features: %d" %len(X_train2[0]))
X_test2 = poly.fit_transform(X_test)
#linear_models(X_train2, X_test2, y_train, y_test, ridge=True)
#y_train = (y_train-0.45937603178269587)/0.22056868516982353
#y_test = (y_test-0.45937603178269587)/0.22056868516982353
alpha=0.1
y_pred_regr, y_pred_ridge, y_pred_lasso, coef_regr, coef_ridge, coef_lasso = linear_models_with_regularizations(X_train2, X_test2, y_train, y_test, 10, 0.1)
def NN_regressor(alldata, hl, obj, transform):
nn_regr = MLPRegressor(solver='lbfgs', alpha=1e-2, hidden_layer_sizes=hl, activation='relu', random_state=1)
#sorted_data = alldata[alldata[:,15].argsort()] #index 18 prob bad design, small -> goode design
np.random.shuffle(alldata)
#0nly fit top 20%
#sorted_data = sorted_data[int(0.8*len(sorted_data)):]
#np.random.shuffle(sorted_data)
#cutoff = sorted_data[int(len(alldata)/2), 17]
#x, y=create_matrix(sorted_data, True, 2, 30, NCcell_x*NCcell_y)
x, y=create_matrix(alldata, False, obj, 0.375, 15)
X_train, X_valid, X_test, y_train, y_valid, y_test = split_data(x, y, 0.8, 0.2)
#poly = PolynomialFeatures(1, interaction_only=True, include_bias=False)
#poly = PolynomialFeatures(interaction_only=True)
#X_train2 = X_train
#poly.fit_transform(X_train)
#x2 = poly.fit_transform(x)
#print("Number of features: %d" %len(X_train2[0]))
#X_test2 = poly.fit_transform(X_test)
if (transform is True):
poly = PolynomialFeatures(2, interaction_only=True, include_bias=False)
#poly = PolynomialFeatures(interaction_only=True)
X_train2 = poly.fit_transform(X_train)
#x2 = poly.fit_transform(x)
#print("Number of features: %d" %len(X_train2[0]))
X_test2 = poly.fit_transform(X_test)
else:
X_train2 = X_train
X_test2 = X_test
nn_regr.fit(X_train2, y_train)
y_pred_nn= nn_regr.predict(X_test2)
ysorted= np.sort(y_test)
xx = np.linspace(ysorted[0], ysorted[-1], len(ysorted))
plt.plot(xx, xx, 'r')
plt.plot(y_pred_nn, y_test, 'bo', alpha=0.5)
plt.xlabel('Predicted yield stress')
plt.ylabel('True yield strain')
plt.title('Neural Network')
print("Mean squared error: %lf" % mean_squared_error(y_test, y_pred_nn))
print("RMSE: %lf" %np.sqrt(np.sum(np.square(y_test-y_pred_nn))/len(y_test)))
# Explained variance score: 1 is perfect prediction
print('r2_score: %.2f' % r2_score(y_test, y_pred_nn))
return hl[0], np.sqrt(np.sum(np.square(y_test-y_pred_nn))/len(y_test)), r2_score(y_test, y_pred_nn), y_test, y_pred_nn
hl, rmse, ac, y_test, y_pred=NN_regressor(alldata, (1024, ), 0, False)
```
| true |
code
| 0.693161 | null | null | null | null |
|
# Clustering Sprint Challenge
Objectives:
* Describe two clustering algorithms
* Create k clusters with the k-Means algorithm
* Compare/contrast the performance of the two algorithms on two datasets
### 1. Describe two different clustering algorithms
There are many clustering algorithms with profoundly different implementations. Their objective is the same - to identify groups in unlabeled data.
Fill out the below python objects.
```
# Clustering algorithm 1:
algorithm_one_name = "K Means"
algorithm_one_description = "K centroids are initialized, randomly or through sampling \
\nThen loop through the following 2 steps: \
\n1. Each point is assigned to the nearest centroid \
\n2. New centroids are calculated by taking the means of the assigned points \
\nClusters found minimize within-cluster sum of squares, or 'inertia' \
\nWorks best when clusters are convex and isotropic\n"
# Clustering algorithm 2:
algorithm_two_name = "Spectral Clustering"
algorithm_two_description = "An affinity matrix is first computed \
\nIt contains some sort of pairwise distance/similarity measure \
\nThe matrix is then factored through eigendecomposition \
\nThe eigenvectors corresponding to the lowest nonzero eigenvalues are then selected \
\nTogether, they make up a lower dimensional feature space \
\nThe data is projected onto the lower dimension, and K Means is performed \
\nOther standard clustering algorithms are also acceptable \
\nUseful when clusters are non-convex"
print(algorithm_one_name)
print(algorithm_one_description)
print(algorithm_two_name)
print(algorithm_two_description)
```
### 2. Create k clusters with k-Means algorithm
```
# Import libraries
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans, SpectralClustering
# Dataset
set1 = pd.read_csv('https://www.dropbox.com/s/zakq7e0r8n1tob9/clustering_set1.csv?raw=1', index_col=0)
set1.head()
plt.scatter(set1['x'], set1['y']);
```
There appear to be 2 clusters.
```
# Create kmeans object
model = KMeans(n_clusters=2)
# Fit kmeans object to data
model.fit(set1.as_matrix())
# Print location of clusters learned by kmeans object
centroids = model.cluster_centers_
print('Cluster Centroids:\n' + str(centroids))
plt.scatter(set1['x'], set1['y'])
plt.plot(centroids[:,0], centroids[:,1], 'ro');
```
### 3. Compare/contrast the performance of your two algorithms with two datasets
```
# Second dataset
set2 = pd.read_csv('https://www.dropbox.com/s/zakq7e0r8n1tob9/clustering_set2.csv?raw=1', index_col=0)
set2.head()
plt.scatter(set2['x'], set2['y']);
```
The data seems to be the same as in part 1.
The clusters are mostly convex, meaning that given two points in the cluster, the points on the line connecting them are likely to also be in the cluster. They are also isotropic (the same in any direction), since they cover about 8 units of distance in both the x and y directions, and appear circular.
Because of this, I expect K means to perform well. Spectral clustering should also perform well, but wont be too useful, especially given that the clusters are linearly separable in the first place. In fact, because it discards information during the projection onto a lower dimension, it may even perform worse.
```
n_clusters=2
model1 = KMeans(n_clusters)
model2 = SpectralClustering(n_clusters)
model1.fit(set2.as_matrix())
model2.fit(set2.as_matrix())
plt.scatter(set2['x'], set2['y'], c=model1.labels_, cmap='coolwarm')
plt.title('K Means Clustering');
plt.scatter(set2['x'], set2['y'], c=model2.labels_, cmap='coolwarm')
plt.title('Spectral Clustering');
```
Interestingly, Spectral Clustering labeled some of the outlying points as part of the wrong cluster. This may have something to do with the information lost when projecting onto a lower dimension. Aside from this, both algorithms performed similarly, as expected.
| true |
code
| 0.664622 | null | null | null | null |
|
#EOSC 582 Assignment V (SSMI)
```
__author__ = 'Yingkai (Kyle) Sha'
__email__ = 'yingkai@eos.ubc.ca'
import h5py
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap
% matplotlib inline
import warnings
warnings.filterwarnings('ignore')
```
Function for histogram.
```
def hist_SSMI(CWV_unfixed, CWV_both, CWV_19, CWL_unfixed, CWL_both, CWL_19):
CWV_unfixed = CWV_unfixed.flatten(); CWV_both = CWV_both.flatten(); CWV_19 = CWV_19.flatten()
CWL_unfixed = CWL_unfixed.flatten(); CWL_both = CWL_both.flatten(); CWL_19 = CWL_19.flatten()
binCWV = np.arange(0, 70+1, 1); binCWL = np.arange(0, 0.7+0.01, 0.01)
fig = plt.figure(figsize=(16, 4))
ax1=plt.subplot2grid((1, 2), (0, 0), colspan=1, rowspan=1)
ax2=plt.subplot2grid((1, 2), (0, 1), colspan=1, rowspan=1)
ax1.hist(CWV_unfixed[~np.isnan(CWV_unfixed)], binCWV, color='y', linewidth=2.5, histtype='step', label='unfixed');
ax1.hist(CWV_both[~np.isnan(CWV_both)], binCWV, color='b', linewidth=2.5, histtype='step', label='fixed: both 19, 37 GHz');
ax1.hist(CWV_19[~np.isnan(CWV_19)], binCWV, color='r', linewidth=2.5, histtype='step', label='fixed: 19 GHz only');
ax1.legend(); ax1.grid(); ax1.set_xlabel('CWV', fontsize=12)
ax1.set_title('(a) unfixed v.s. fixed CWV Histogram', fontsize=12, fontweight='bold')
ax2.hist(CWL_unfixed[~np.isnan(CWL_unfixed)], binCWL, color='y', linewidth=2.5, histtype='step', label='unfixed');
ax2.hist(CWL_both[~np.isnan(CWL_both)], binCWL, color='b', linewidth=2.5, histtype='step', label='fixed: both 19, 37 GHz');
ax2.hist(CWL_19[~np.isnan(CWL_19)], binCWL, color='r', linewidth=2.5, histtype='step', label='fixed: 19 GHz only');
ax2.legend(); ax2.grid(); ax2.set_xlabel('CWL', fontsize=12)
ax2.set_title('(b) unfixed v.s. fixed CWL Histogram', fontsize=12, fontweight='bold')
```
Function for maps
```
def single_map(ax):
proj = Basemap(projection='moll', lon_0=180, resolution='c', ax=ax)
proj.drawcoastlines()
proj.drawmeridians(np.arange(0, 360, 60));
proj.drawparallels(np.arange(-90, 90, 30));
return proj
def SSMI_map(lon, lat, CWV_unfixed, CWV_both, CWV_19, CWL_unfixed, CWL_both, CWL_19):
levCWV = np.arange(0, 80+5, 5); levCWL = np.arange(0, 0.7+0.07, 0.07)
fig = plt.figure(figsize=(12, 8))
ax1=plt.subplot2grid((3, 2), (0, 0), colspan=1, rowspan=1); ax2=plt.subplot2grid((3, 2), (1, 0), colspan=1, rowspan=1)
ax3=plt.subplot2grid((3, 2), (2, 0), colspan=1, rowspan=1); ax4=plt.subplot2grid((3, 2), (0, 1), colspan=1, rowspan=1)
ax5=plt.subplot2grid((3, 2), (1, 1), colspan=1, rowspan=1); ax6=plt.subplot2grid((3, 2), (2, 1), colspan=1, rowspan=1)
proj=single_map(ax1); x, y = proj(lon, lat)
CS = proj.contourf(x, y, CWV_unfixed, levCWV, cmap=plt.cm.RdYlGn, extend='max')
ax1.set_title('(a.1) CWV unfixed (Jan 1990)', fontsize=12, fontweight='bold', y = 1.025)
proj=single_map(ax2); x, y = proj(lon, lat)
CS = proj.contourf(x, y, CWV_both, levCWV, cmap=plt.cm.RdYlGn, extend='max')
ax2.set_title('(a.2) CWV fixed: both (Jan 1990)', fontsize=12, fontweight='bold', y = 1.025)
proj=single_map(ax3); x, y = proj(lon, lat)
CS = proj.contourf(x, y, CWV_19, levCWV, cmap=plt.cm.RdYlGn, extend='max')
ax3.set_title('(a.3) CWV fixed: 19 GHz only (Jan 1990)', fontsize=12, fontweight='bold', y = 1.025)
cax = fig.add_axes([0.175, 0.05, 0.25, 0.02])
CBar = fig.colorbar(CS, cax=cax, orientation='horizontal')
CBar.ax.tick_params(axis='x', length=12.5)
CBar.set_label('CWV $\mathrm{kg/m^2}$', fontsize=12)
proj=single_map(ax4); x, y = proj(lon, lat)
CS = proj.contourf(x, y, CWL_unfixed, levCWL, cmap=plt.cm.gist_ncar_r, extend='max')
ax4.set_title('(b.1) CWL unfixed (Jan 1990)', fontsize=12, fontweight='bold', y = 1.025)
proj=single_map(ax5); x, y = proj(lon, lat)
CS = proj.contourf(x, y, CWL_both, levCWL, cmap=plt.cm.gist_ncar_r, extend='max')
ax5.set_title('(b.2) CWL fixed: both (Jan 1990)', fontsize=12, fontweight='bold', y = 1.025)
proj=single_map(ax6); x, y = proj(lon, lat)
CS = proj.contourf(x, y, CWL_19, levCWL, cmap=plt.cm.gist_ncar_r, extend='max')
ax6.set_title('(b.3) CWL fixed: 19 GHz only (Jan 1990)', fontsize=12, fontweight='bold', y = 1.025)
cax = fig.add_axes([0.6, 0.05, 0.25, 0.02])
CBar = fig.colorbar(CS, cax=cax, orientation='horizontal')
CBar.ax.tick_params(axis='x', length=12.5)
CBar.set_label('CWL', fontsize=12)
```
# Retrieval functions
SSMI.py including functions calculates emissivity and absorption coefficient at at 19 and 37 GHz SSMI channel.
Code are Python version of <a href='http://www.aos.wisc.edu/~tristan/aos740.php'>**UW-Madison AOS-704**</a> 's FORTRAN77 code.
```
import site
site.addsitedir('_libs')
from SSMI import *
```
Approximation of windspeed and main retrieval function in Greenwald et al., 1993.
```
# windspeed
def wind_speed(sst, t19v, t22v, t37h, t37v):
"""
input: sst (K), t19v (K), t22v (K), t37h (K)
output: windspeed (m/s)
"""
speed=1.0969*(t19v)-0.4555e0*(t22v)- 1.76*(t37v)+0.786*(t37h)+ 147.9
return speed
# retrival, based on EOSC 582 Website
def SSMI_retrieval(SST, theta, T19H, T19V, T22V, T37H, T37V, iter_num=5, correction='both'):
'''
Using 4 SSMI channel brightness temperature retrive total precipitable water and liquid water path
=========================================================================
CMV, CWL = SSMI_retrieval(SST, theta, T19H, T19V, T22V, T37H, T37V, iter_num=5)
-------------------------------------------------------------------------
Input:
SST: Sea Surface Temperature (K)
theta: Incidence angle
T#H: Brightness temperature in #GHz band with horizontal polarization
T#V: Brightness temperature in #GHz band with vertical polarization
iter_num: = 0 means no correction, > 0 applies correction to CWV > 25kg/m^2
Output:
CWV: Total precipitable water
CWL: Liquid water path
==========================================================================
Author:
Yingkai (Kyle) Sha
yingkai@eos.ubc.ca
'''
M, N = np.shape(SST)
# Parameters
mu = np.cos(theta*np.pi/180.) # Incidence angle
GAMMA = -5.8E-3 # Lapse rate: -5.8 K/km = -5.8E-3 K/m
Hw = 2.2E3 # Water vapor scaling height: 2.2km
# Correction for cold bias
# (Greenwald et al., 1993)
T37H= T37H + 3.58
T37V= T37V + 3.58
# delta T
dT19 = T19H - T19V
dT37 = T37H - T37V
# Frequency bands (GHz)
freq = [19, 22, 37, 85]
# Allocate memorise
emissv = np.empty([len(freq), M, N])
emissh = np.empty([len(freq), M, N])
KL19 = np.empty([M, N])
KL37 = np.empty([M, N])
KV19 = np.empty([M, N])
KV37 = np.empty([M, N])
TOX19 = np.empty([M, N])
TOX37 = np.empty([M, N])
# Emperical windspeed
windspeed = wind_speed(SST, T19V, T22V, T37H-3.58, T37V-3.58)
# Calculate emission, absorbtion coef.
for m in range(M):
for n in range(N):
for i in range(len(freq)):
emissv[i, m, n], emissh[i, m, n] = emiss(i+1, windspeed[m, n], SST[m, n], theta)
KL19[m, n], KL37[m, n], KV19[m, n], KV37[m, n], TOX19[m, n], TOX37[m, n] = coef(SST[m, n])
# Retrieve function
R37V=(1.0 - emissv[2, :, :])
R19V=(1.0 - emissv[0, :, :])
R37H=(1.0 - emissh[2, :, :])
R19H=(1.0 - emissh[0, :, :])
# Iteration correction of F19, F37 for CWV > 25kg/m^2
# Greenwald et al., 1993) equation (4)
CWV = np.zeros(SST.shape)
#CWL = np.zeros(SST.shape)
T019 = SST
T037 = SST
for iteration in range(iter_num):
hit = CWV > 25
# transmission
Tau19V = np.exp(-1*KV19*CWV/mu)
Tau37V = np.exp(-1*KV37*CWV/mu)
f19 = np.exp(50*KV19/mu)
f37 = np.exp(50*KV37/mu)
if iteration > 0:
# in the first timestep, T019, T037 = SST
T019[hit] = SST[hit] + GAMMA*Hw*(1-f19[hit]*Tau19V[hit]**2)*TOX19[hit]
if correction == 'both':
T037[hit] = SST[hit] + GAMMA*Hw*(1-f37[hit]*Tau37V[hit]**2)*TOX37[hit]
#T037[hit] = SST[hit]
# Correction
F19 = (T19H - T019)/(T19V - T019)
F37 = (T37H - T037)/(T37V - T037)
R1 = -1*mu/2.*np.log(dT19/(SST*R19V*(1-F19)*TOX19**2.))
R2 = -1*mu/2.*np.log(dT37/(SST*R37V*(1-F37)*TOX37**2.))
# Linear algebra
M = KV19*KL37 - KL19*KV37
CWV = (R1*KL37 - R2*KL19)/M
#print('iteration step = {}'.format(iteration))
# get CWL
CWL = (R2*KV19 - R1*KV37)/M
return CWV, CWL
theta = 53.1
# boardcasting because my retrival function supports 2D array
SST = 271.75*np.ones([1, 1])
T19H = 113.57*np.ones([1, 1])
T19V = 183.24*np.ones([1, 1])
T22V = 194.80*np.ones([1, 1])
T37H = 148.13*np.ones([1, 1])
T37V = 208.11*np.ones([1, 1])
SSMI_retrieval(SST, theta, T19H, T19V, T22V, T37H, T37V, iter_num=4, correction='both')
```
# Full Retrival
## Jan
```
TB_obj = h5py.File('_data/bright_temps.h5', 'r')
lat = TB_obj['lat'][:]
lon = TB_obj['lon'][:]
SST = TB_obj['jan/sst'][:]
T19H = TB_obj['jan/t19h'][:]
T19V = TB_obj['jan/t19v'][:]
T22V = TB_obj['jan/t22v'][:]
T37H = TB_obj['jan/t37h'][:]
T37V = TB_obj['jan/t37v'][:]
TB_obj.close()
theta = 53.1
CWV1_unfixed, CWL1_unfixed = SSMI_retrieval(SST, theta, T19H, T19V, T22V, T37H, T37V, iter_num=1)
CWV1_both, CWL1_both = SSMI_retrieval(SST, theta, T19H, T19V, T22V, T37H, T37V, iter_num=5, correction='both')
CWV1_19, CWL1_19 = SSMI_retrieval(SST, theta, T19H, T19V, T22V, T37H, T37V, iter_num=5, correction='19')
hist_SSMI(CWV1_unfixed, CWV1_both, CWV1_19, CWL1_unfixed, CWL1_both, CWL1_19)
SSMI_map(lon, lat, CWV1_unfixed, CWV1_both, CWV1_19, CWL1_unfixed, CWL1_both, CWL1_19)
```
## Jul
```
TB_obj = h5py.File('_data/bright_temps.h5', 'r')
SST = TB_obj['july/sst'][:]
T19H = TB_obj['july/t19h'][:]
T19V = TB_obj['july/t19v'][:]
T22V = TB_obj['july/t22v'][:]
T37H = TB_obj['july/t37h'][:]
T37V = TB_obj['july/t37v'][:]
TB_obj.close()
CWV7_unfixed, CWL7_unfixed = SSMI_retrieval(SST, theta, T19H, T19V, T22V, T37H, T37V, iter_num=1)
CWV7_both, CWL7_both = SSMI_retrieval(SST, theta, T19H, T19V, T22V, T37H, T37V, iter_num=5, correction='both')
CWV7_19, CWL7_19 = SSMI_retrieval(SST, theta, T19H, T19V, T22V, T37H, T37V, iter_num=5, correction='19')
hist_SSMI(CWV7_unfixed, CWV7_both, CWV7_19, CWL7_unfixed, CWL7_both, CWL7_19)
SSMI_map(lon, lat, CWV7_unfixed, CWV7_both, CWV7_19, CWL7_unfixed, CWL7_both, CWL7_19)
```
## Zonal mean results
```
CWV1z_19 = np.nanmean(CWV1_19, 1); CWL1z_19 = np.nanmean(CWL1_19, 1)
CWV7z_19 = np.nanmean(CWV7_19, 1); CWL7z_19 = np.nanmean(CWL7_19, 1)
CWV1z_both = np.nanmean(CWV1_both, 1); CWL1z_both = np.nanmean(CWL1_both, 1)
CWV7z_both = np.nanmean(CWV7_both, 1); CWL7z_both = np.nanmean(CWL7_both, 1)
CWV1z_unfixed = np.nanmean(CWV1_unfixed, 1); CWL1z_unfixed = np.nanmean(CWL1_unfixed, 1)
CWV7z_unfixed = np.nanmean(CWV7_unfixed, 1); CWL7z_unfixed = np.nanmean(CWL7_unfixed, 1)
fig = plt.figure(figsize=(14, 12))
ax1=plt.subplot2grid((2, 2), (0, 0), colspan=1, rowspan=1)
ax2=plt.subplot2grid((2, 2), (0, 1), colspan=1, rowspan=1)
ax3=plt.subplot2grid((2, 2), (1, 0), colspan=1, rowspan=1)
ax4=plt.subplot2grid((2, 2), (1, 1), colspan=1, rowspan=1)
ax1.plot(lat[:, 0], CWV1z_unfixed, color=[0, 0.2, 0.4], linewidth=3.5, label='Jan unfixed');
ax1.plot(lat[:, 0], CWV1z_both, color=[0, 0.5, 0.7], linewidth=3.5, label='Jan fixed: both');
ax1.plot(lat[:, 0], CWV1z_19, color=[0, 0.8, 1], linewidth=3.5, label='Jan fixed: 19 GHz only');
ax1.grid(); ax1.legend(loc=4); ax1.set_xlim(-90, 90);
ax1.set_title('(a) Zonal mean CWV | Jan', fontsize=12, fontweight='bold')
ax2.plot(lat[:, 0], CWV7z_unfixed, color=[0.4, 0.2, 0], linewidth=3.5, label='Jul unfixed');
ax2.plot(lat[:, 0], CWV7z_both, color=[0.7, 0.5, 0], linewidth=3.5, label='Jul fixed: both');
ax2.plot(lat[:, 0], CWV7z_19, color=[1, 0.8, 0], linewidth=3.5, label='Jul fixed: 19 GHz only');
ax2.grid(); ax2.legend(loc=4); ax2.set_xlim(-90, 90);
ax2.set_title('(b) Zonal mean CWV | Jul', fontsize=12, fontweight='bold')
ax3.plot(lat[:, 0], CWL1z_unfixed, color=[0, 0.2, 0.4], linewidth=3.5, label='Jan unfixed');
ax3.plot(lat[:, 0], CWL1z_both, color=[0, 0.5, 0.7], linewidth=3.5, label='Jan fixed: both');
ax3.plot(lat[:, 0], CWL1z_19, color=[0, 0.8, 1], linewidth=3.5, label='Jan fixed: 19 GHz only');
ax3.grid(); ax3.legend(loc=4); ax3.set_xlim(-90, 90);
ax3.set_title('(c) Zonal mean CWL | Jan', fontsize=12, fontweight='bold')
ax4.plot(lat[:, 0], CWL7z_unfixed, color=[0.4, 0.2, 0], linewidth=3.5, label='Jul unfixed');
ax4.plot(lat[:, 0], CWL7z_both, color=[0.7, 0.5, 0], linewidth=3.5, label='Jul fixed: both');
ax4.plot(lat[:, 0], CWL7z_19, color=[1, 0.8, 0], linewidth=3.5, label='Jul fixed: 19 GHz only');
ax4.grid(); ax4.legend(loc=4); ax4.set_xlim(-90, 90);
ax4.set_title('(d) Zonal mean CWL | Jul', fontsize=12, fontweight='bold')
```
| true |
code
| 0.505249 | null | null | null | null |
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
def r2(x, y):
return stats.pearsonr(x, y)[0] ** 2
%matplotlib inline
```
# Preparing Data
```
test_counts = {'yes': 256, 'no': 252, 'up': 272, 'down': 253, 'left': 267, 'right': 259, 'on': 246, 'off': 262, 'stop': 249, 'go': 251}
param_counts = {
'cnn_one_fstride4': {
'params': 220000,
'multiplies': 1430000
},
'cnn_one_fstride8': {
'params': 337000,
'multiplies': 1430000
},
'cnn_tpool2': {
'params': 1090000,
'multiplies': 103000000
},
'cnn_tpool3': {
'params': 823000,
'multiplies': 73700000
},
'cnn_trad_fpool3': {
'params': 1370000,
'multiplies': 125000000
},
'google-speech-dataset-compact': {
'params': 964000,
'multiplies': 5760000
},
'google-speech-dataset-full': {
'params': 1380000,
'multiplies': 98800000
}
}
def get_observations(fname):
observations = {'model': [], 'keyword': [], 'accuracy': [], 'time': [], 'total_energy': [], 'peak_power': [], 'params': [], 'multiplies': []}
with open(fname, 'r') as f:
for _ in range(7):
for i in range(10):
line = f.readline().rstrip()
parts = line.split(' ')
model, keyword, accuracy, time, total_energy, peak_power = parts
model = model.rstrip('\.onnx')
accuracy, time, total_energy, peak_power = list(map(float, [accuracy, time, total_energy, peak_power]))
accuracy *= 100
total_energy = 1000 * (total_energy - 1.9*time)
time *= 1000
peak_power -= 1.9
observations['model'].append(model)
observations['keyword'].append(keyword)
observations['accuracy'].append(accuracy)
observations['time'].append(time / test_counts[keyword])
observations['total_energy'].append(total_energy / test_counts[keyword])
observations['peak_power'].append(peak_power)
observations['params'].append(param_counts[model]['params'])
observations['multiplies'].append(param_counts[model]['multiplies'])
for i in range(6):
line = f.readline()
return observations
df = pd.DataFrame(get_observations('experiment_output_e2e.txt'))
df.head()
df_pre = pd.DataFrame(get_observations('experiment_output_preprocessing.txt'))
df_pre.head()
```
# Analysis
```
df_grouped = df.groupby('model')
df_grouped_means = df_grouped['accuracy', 'total_energy', 'peak_power', 'time', 'params', 'multiplies'].mean()
df_grouped_means.round(2)
df_pre_grouped = df_pre.groupby('model')
df_pre_grouped_means = df_pre_grouped['accuracy', 'total_energy', 'peak_power', 'time', 'params', 'multiplies'].mean()
df_pre_grouped_means
df_pre_grouped_means['time'].mean()
df_pre_grouped_means['total_energy'].mean()
df_pre_grouped_means['peak_power'].mean()
df_inf_only = df_grouped_means - df_pre_grouped_means
df_inf_only['peak_power'] = df_grouped_means['peak_power']
df_inf_only['params'] = df_grouped_means['params']
df_inf_only['multiplies'] = df_grouped_means['multiplies']
df_inf_only.round(2)
dims = (14, 6)
fig, ax = plt.subplots(figsize=dims)
g = sns.factorplot(x="accuracy", y="total_energy", hue="model", data=df, ax=ax)
g.set(xlim=(0, None), ylim=(0, None))
for ind, label in enumerate(ax.get_xticklabels()):
if ind % 10 == 0: # every 10th label is kept
label.set_visible(True)
else:
label.set_visible(False)
```
# Visualizations
## Energy vs. Multiplies
```
df_inf_aggregated = df_inf_only.reset_index()
ax = sns.regplot(x=df['params'], y=df['total_energy'])
ax = sns.regplot(x=df['multiplies'], y=df['total_energy'])
df.to_csv('observations.csv', index=False)
df_inf_aggregated.to_csv('observations_agg.csv', index=False)
```
| true |
code
| 0.499939 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/daemon-Lee/simplex_method_for_linear_program/blob/master/project/simplex_method/Simplex_method.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Copyright 2020 Duy L.Dinh. { display-mode: "form" }
#@markdown CS1302 HE130655.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Project MAO302
This is final project of MAO302 Course make by FPT University
## Part 1: simplex method for linear program (LP)
```
import numpy as np
np.random.seed(2020)
```
### Generate input matrices of a standard linear program in matrix from
```
def gen_problem(n_var, n_contrain):
contrain = np.random.randint(low=-7, high=19, size=(n_var,n_contrain))
bacis = np.eye(n_contrain)
# A will contain the coefficients of the constraints
A = np.vstack((contrain,bacis)).T
# b will contain the amount of resources
b = np.random.randint(low=-7, high=19, size=(n_contrain,))
# c will contain coefficients of objective function Z
cz = np.random.randint(low=-7, high=19, size=(n_var,))
cb = np.zeros((n_contrain,))
c = np.concatenate([cz,cb])
return A, b, c
```
### Write a code to solve the generated LP using to phase simplex method in matrix form
```
#@title THE SIMPLEX METHOD IN MATRIX NOTATION
class Simplex_method:
#@markdown First input A, b, c, where:
#@markdown - **A** will contain the coefficients of the constraints
#@markdown - **b** will contain the amount of resources
#@markdown - **c** will contain coefficients of objective function Z
def __init__(self, A, b, c):
self.A = A
self.c = c
self.B = 0
self.n = 0
#@markdown Generate *B* and *N*
#@markdown - **B** will contain the Basic set
#@markdown - **n** will contain the nonbasic set
n_contrain = len(self.A)
n_var = len(self.c) - n_contrain
self.B = np.arange(n_var, n_var + n_contrain)[np.newaxis].T
self.n = np.arange(0, n_var)[np.newaxis].T
#@markdown - The initial values of the basic variables: xb = b
self.xb = np.transpose([b])
#@markdown - The initial values of the nonbasic dual variables: zn = -cn
self.zn = -self.c[self.n]
self.status = 'Optimal'
self.objective = 0
def solve(self, verbor=False):
self.count = 0
for i in self.n:
if True not in (self.A[:, i] > 0) and self.c[i] > 0:
print("Unbounded")
self.status = 'Unbounded'
sol = np.zeros(len(self.c))
sol[self.B] = self.xb
return {
'status': self.status,
"iter": self.count,
"objective": self.objective,
"sol": sol
}
#@markdown Find solution for problem
#@markdown - Check for Optimality. If xb ≥ 0 and zn ≥ 0, stop. The current
#@markdown solution is optimal.
if False not in (self.xb >= 0) and False not in (self.zn <= 0):
print("Optimal — the problem was trivial")
sol = np.zeros(len(self.c))
sol[self.B] = self.xb
return {
'status': self.status,
"iter": self.count,
"objective": self.objective,
"sol": sol
}
#@markdown - Since xb ≥ 0, the initial solution is **Primal feasible**, and hence
#@markdown we can apply the simplex method without needing any Phase I procedure.
elif False not in (self.xb >= 0) and False in (self.zn <= 0):
print("primal feasible")
print("run primal simplex method")
result = self.primal_simplex(verbor=verbor)
#@markdown - Since xb ≥ 0, the initial solution is **Dual feasible**
elif False in (self.xb >= 0) and False not in (self.zn <= 0):
print("run dual simplex method")
result = self.solve_two_phase(verbor=verbor)
#@markdown - Where both xb and cn have components of the wrong sign.
#@markdown In this case, we must employ a **two-phase procedure**.
else:
print("dual feasible")
print("Start convert negative components")
# self.zn = np.maximum(self.zn, -self.zn)
# self.zn = np.maximum(self.zn, 0)
print("run two phase simplex method")
result = self.solve_two_phase(verbor=verbor)
return result
def solve_two_phase(self, verbor=False):
#@markdown - In Phase I apply the dual simplex method to find an optimal solution
#@markdown of this modified problem Phase I is most likely not optimal, but it
#@markdown is feasible, and therefore the primal simplex method can be used to
#@markdown find the optimal solution to the original problem.
print("Phase one")
result = self.dual_simplex(verbor=verbor)
if result['status'] == 'Infeasible':
return result
print("Phase two")
result = self.primal_simplex(verbor=verbor)
return result
def primal_simplex(self, verbor=False):
objective = -np.inf
count = 0
Bi = self.A[:, self.B].reshape((-1, len(self.B)))
N = self.A[:, self.n].reshape((-1, len(self.n)))
if verbor:
A_hat = np.concatenate([self.B.T, self.xb.T, N.T, Bi.T]).T
print("Objective\n", np.concatenate([self.zn, self.xb]).T)
print("Dictionary\n", A_hat)
while(np.min(self.zn) < 0):
j = np.argmin(self.zn)
ej = np.zeros((1, len(self.zn))).T
ej[j] = 1
delta_xb = np.linalg.inv(Bi).dot(N).dot(ej)
t = np.max(delta_xb/self.xb)**-1
if t < 0 or t == np.inf:
self.status = 'Unbounded'
sol = np.zeros(len(self.c))
sol[self.B] = self.xb
return {
'status': self.status,
"iter": self.count,
"objective": self.objective,
"sol": sol
}
i = np.argmax(delta_xb/self.xb)
ei = np.zeros((1, len(self.xb))).T
ei[i] = 1
delta_zn = -(np.linalg.inv(Bi).dot(N)).T.dot(ei)
s = self.zn[j]/delta_zn[j]
self.xb = self.xb - t*delta_xb
self.zn = self.zn - s*delta_zn
self.xb[i] = t
self.zn[j] = s
# pivot swap
pivot = self.B[i].copy()
self.B[i] = self.n[j].copy()
self.n[j] = pivot
Bi = self.A[:, self.B].reshape((-1, len(self.B)))
N = self.A[:, self.n].reshape((-1, len(self.n)))
count += 1
self.count += 1
self.objective = self.xb.T.dot(self.c[self.B]).reshape(-1)[0]
if verbor:
A_hat = np.concatenate([self.B.T, self.xb.T, N.T, Bi.T]).T
print("iter:", count)
print("Dictionary\n", A_hat)
print("objective:", self.objective)
if self.objective > objective:
objective = self.objective
else:
self.status = 'Infeasible'
sol = np.zeros(len(self.c))
sol[self.B] = self.xb
return {
'status': self.status,
"iter": self.count,
"objective": self.objective,
"sol": sol
}
sol = np.zeros(len(self.c))
sol[self.B] = self.xb
return {
'status': self.status,
"iter": self.count,
"optimal": self.objective,
"sol": sol
}
def dual_simplex(self, verbor=False):
objective = np.inf
count = 0
Bi = self.A[:, self.B].reshape((-1, len(self.B)))
N = self.A[:, self.n].reshape((-1, len(self.n)))
if verbor:
A_hat = np.concatenate([self.B.T, self.xb.T, N.T, Bi.T]).T
print("Objective\n", np.concatenate([self.zn, self.xb]).T)
print("Dictionary\n", A_hat)
while(np.min(self.xb) < 0):
i = np.argmin(self.xb)
ei = np.zeros((1, len(self.xb))).T
ei[i] = 1
delta_zn = -(np.linalg.inv(Bi).dot(N)).T.dot(ei)
s = np.max(delta_zn/self.zn)**-1
j = np.argmax(delta_zn/self.zn)
ej = np.zeros((1, len(self.zn))).T
ej[j] = 1
delta_xb = np.linalg.inv(Bi).dot(N).dot(ej)
t = self.xb[i]/delta_xb[i]
self.xb = self.xb - t*delta_xb
self.zn = self.zn - s*delta_zn
self.xb[i] = t
self.zn[j] = s
# pivot
pivot = self.B[i].copy()
self.B[i] = self.n[j].copy()
self.n[j] = pivot
Bi = self.A[:, self.B].reshape((-1, len(self.B)))
N = self.A[:, self.n].reshape((-1, len(self.n)))
A_hat = np.concatenate([self.B.T, self.xb.T, N.T, Bi.T]).T
count += 1
self.count += 1
self.objective = self.xb.T.dot(self.c[self.B]).reshape(-1)[0]
if verbor:
A_hat = np.concatenate([self.B.T, self.xb.T, N.T, Bi.T]).T
print("iter:", count)
print("Dictionary\n", A_hat)
print("objective:", self.objective)
if self.objective < objective:
objective = self.objective
else:
self.status = 'Infeasible'
sol = np.zeros(len(self.c))
sol[self.B] = self.xb
return {
'status': self.status,
"iter": self.count,
"objective": self.objective,
"sol": sol
}
sol = np.zeros(len(self.c))
sol[self.B] = self.xb
return {
'status': self.status,
"iter": self.count,
"objective": self.objective,
"sol": sol
}
print("Exercise 2.3")
# A will contain the coefficients of the constraints
A = np.array([[-1, -1, -1, 1, 0],
[2, -1, 1, 0, 1]])
# b will contain the amount of resources
b = np.array([-2, 1])
# c will contain coefficients of objective function Z
c = np.array([2, -6, 0, 0, 0])
simplex = Simplex_method(A, b, c)
print(simplex.solve(verbor=True))
```
### Solve the genarated LP by a pulp and cplex tool
#### pulp lib
Install pulp
```
!pip install pulp
print("Exercise 2.3")
# A will contain the coefficients of the constraints
A = np.array([[-1, -1, -1, 1, 0],
[2, -1, 1, 0, 1]])
# b will contain the amount of resources
b = np.array([-2, 1])
# c will contain coefficients of objective function Z
c = np.array([2, -6, 0, 0, 0])
import pulp as p
# Generate B and N
n_contrain = len(A)
n_var = len(c) - n_contrain
B = np.arange(n_var, n_var + n_contrain)[np.newaxis].T
n = np.arange(0, n_var)[np.newaxis].T
# Create a LP Minimization problem
Lp_prob = p.LpProblem('Problem', p.LpMaximize)
# Create problem Variables
x = [p.LpVariable("x"+str(i), lowBound = 0) for i in range(1,n_var+1)]
# Objective Function
objective = 0
for i in range(n_var):
objective += c[i]*x[i]
Lp_prob += objective
# Constraints:
for i in range(n_contrain):
contrain = 0
for j in range(n_var):
contrain += A[i,j]*x[j] <= b[i]/n_var
Lp_prob += contrain
# Display the problem
print(Lp_prob)
status = Lp_prob.solve() # Solver
print(p.LpStatus[status]) # The solution status
# Printing the final solution
print(p.value(x[0]), p.value(x[1]), p.value(x[2]), p.value(Lp_prob.objective))
import pulp as p
def pulp_lib(A, b, c, verbor=False):
# Generate B and N
n_contrain = len(A)
n_var = len(c) - n_contrain
B = np.arange(n_var, n_var + n_contrain)[np.newaxis].T
n = np.arange(0, n_var)[np.newaxis].T
# Create a LP Minimization problem
Lp_prob = p.LpProblem('Problem', p.LpMaximize)
# Create problem Variables
x = [p.LpVariable("x"+str(i), lowBound = 0) for i in range(1,n_var+1)]
# Objective Function
objective = 0
for i in range(n_var):
objective += c[i]*x[i]
Lp_prob += objective
# Constraints:
for i in range(n_contrain):
contrain = 0
for j in range(n_var):
contrain += A[i,j]*x[j] <= b[i]/n_var
Lp_prob += contrain
status = Lp_prob.solve() # Solver
if verbor:
print(p.LpStatus[status]) # The solution status
# Printing the final solution
print(p.value(Lp_prob.objective))
return {
'status': p.LpStatus[status],
'objective': p.value(Lp_prob.objective)
}
```
#### cplex
```
!pip install cplex
import cplex
def cplex_lib(A, b, c):
# Input all the data and parameters here
num_constraints = len(A)
num_decision_var = len(c) - num_constraints
n = np.arange(0, num_decision_var)[np.newaxis].T
A = A[:,n.T].reshape(num_constraints, num_decision_var).tolist()
b = b.tolist()
c = c[n].T.reshape(len(n)).tolist()
# constraint_type = ["L", "L", "L"] # Less, Greater, Equal
constraint_type = ["L"]*num_constraints
# ============================================================
# Establish the Linear Programming Model
myProblem = cplex.Cplex()
# Add the decision variables and set their lower bound and upper bound (if necessary)
myProblem.variables.add(names= ["x"+str(i) for i in range(num_decision_var)])
for i in range(num_decision_var):
myProblem.variables.set_lower_bounds(i, 0.0)
# Add constraints
for i in range(num_constraints):
myProblem.linear_constraints.add(
lin_expr= [cplex.SparsePair(ind= [j for j in range(num_decision_var)], val= A[i])],
rhs= [b[i]],
names = ["c"+str(i)],
senses = [constraint_type[i]]
)
# Add objective function and set its sense
for i in range(num_decision_var):
myProblem.objective.set_linear([(i, c[i])])
myProblem.objective.set_sense(myProblem.objective.sense.maximize)
# Solve the model and print the answer
myProblem.solve()
return{
'objective': myProblem.solution.get_objective_value(),
'status': myProblem.solution.get_status_string(),
'sol': myProblem.solution.get_values()
}
print("Exercise 2.3")
# A will contain the coefficients of the constraints
A = np.array([[-1, -1, -1, 1, 0],
[2, -1, 1, 0, 1]])
# b will contain the amount of resources
b = np.array([-2, 1])
# c will contain coefficients of objective function Z
c = np.array([2, -6, 0, 0, 0])
cplex_lib(A, b, c)
```
### Repeat (1)-(3) one hundred timnes and compare the mean and standard deviation of running time of your code with those of the chosen tool.
```
n_sample = 100
np.random.seed(2020)
A_list = []
b_list = []
c_list = []
for i in range(n_sample):
n_var = np.random.randint(low=2, high=7)
n_contrain = np.random.randint(low=2, high=7)
A, b, c = gen_problem(n_var, n_contrain)
A_list.append(A)
b_list.append(b)
c_list.append(c)
from time import time
running_time_pulp = []
output_pulp = []
for i in range(n_sample):
start = time()
output_pulp.append(pulp_lib(A, b, c, verbor=False))
end = time() - start
running_time_pulp.append(end)
running_time_cplex = []
output_cplex = []
for i in range(n_sample):
start = time()
output_cplex.append(pulp_lib(A, b, c, verbor=False))
end = time() - start
running_time_cplex.append(end)
running_time_simplex_method = []
output_simplex_method= []
for i in range(n_sample):
start = time()
simplex = Simplex_method(A, b, c)
output_simplex_method.append(simplex.solve(verbor=False))
end = time() - start
running_time_simplex_method.append(end)
#@title Compare pulp and Simplex method
# Simplex method
mean_Simplex_method = np.mean(running_time_simplex_method)
std_Simplex_method = np.std(running_time_simplex_method)
# pulp
mean_pulp = np.mean(running_time_pulp)
std_pulp = np.std(running_time_pulp)
# cplex
mean_cplex = np.mean(running_time_cplex)
std_cplex = np.std(running_time_cplex)
print("mean running time of pulp - simplex_method (s):", mean_pulp - mean_Simplex_method)
print("standard deviation running time of pulp - simplex_method (s):", std_pulp - std_Simplex_method)
import seaborn as sns; sns.set()
import matplotlib.pyplot as plt
mean = np.array([mean_Simplex_method, mean_pulp, mean_cplex])[np.newaxis]
ax = sns.heatmap(mean, annot=True)
plt.title("Compare mean")
ax.set_xticklabels(['code','pulp','cplex'])
std = np.array([std_Simplex_method, std_pulp, std_cplex])[np.newaxis]
ax = sns.heatmap(std, annot=True)
plt.title("Compare standard deviation")
ax.set_xticklabels(['code','pulp','cplex'])
```
| true |
code
| 0.78316 | null | null | null | null |
|
# CrowdTruth for Multiple Choice Tasks: Relation Extraction
In this tutorial, we will apply CrowdTruth metrics to a **multiple choice** crowdsourcing task for **Relation Extraction** from sentences. The workers were asked to read a sentence with 2 highlighted terms, then pick from a multiple choice list what are the relations expressed between the 2 terms in the sentence. The task was executed on [FigureEight](https://www.figure-eight.com/). For more crowdsourcing annotation task examples, click [here](https://raw.githubusercontent.com/CrowdTruth-core/tutorial/getting_started.md).
To replicate this experiment, the code used to design and implement this crowdsourcing annotation template is available here: [template](https://raw.githubusercontent.com/CrowdTruth/CrowdTruth-core/master/tutorial/templates/Relex-Multiple-Choice/template.html), [css](https://raw.githubusercontent.com/CrowdTruth/CrowdTruth-core/master/tutorial/templates/Relex-Multiple-Choice/template.css), [javascript](https://raw.githubusercontent.com/CrowdTruth/CrowdTruth-core/master/tutorial/templates/Relex-Multiple-Choice/template.js).
This is a screenshot of the task as it appeared to workers:

A sample dataset for this task is available in [this file](https://raw.githubusercontent.com/CrowdTruth/CrowdTruth-core/master/tutorial/data/relex-multiple-choice.csv), containing raw output from the crowd on FigureEight. Download the file and place it in a folder named `data` that has the same root as this notebook. Now you can check your data:
```
import pandas as pd
test_data = pd.read_csv("../data/relex-multiple-choice.csv")
test_data.head()
```
## Declaring a pre-processing configuration
The pre-processing configuration defines how to interpret the raw crowdsourcing input. To do this, we need to define a configuration class. First, we import the default CrowdTruth configuration class:
```
import crowdtruth
from crowdtruth.configuration import DefaultConfig
```
Our test class inherits the default configuration `DefaultConfig`, while also declaring some additional attributes that are specific to the Relation Extraction task:
* **`inputColumns`:** list of input columns from the .csv file with the input data
* **`outputColumns`:** list of output columns from the .csv file with the answers from the workers
* **`annotation_separator`:** string that separates between the crowd annotations in `outputColumns`
* **`open_ended_task`:** boolean variable defining whether the task is open-ended (i.e. the possible crowd annotations are not known beforehand, like in the case of free text input); in the task that we are processing, workers pick the answers from a pre-defined list, therefore the task is not open ended, and this variable is set to `False`
* **`annotation_vector`:** list of possible crowd answers, mandatory to declare when `open_ended_task` is `False`; for our task, this is the list of relations
* **`processJudgments`:** method that defines processing of the raw crowd data; for this task, we process the crowd answers to correspond to the values in `annotation_vector`
The complete configuration class is declared below:
```
class TestConfig(DefaultConfig):
inputColumns = ["sent_id", "term1", "b1", "e1", "term2", "b2", "e2", "sentence"]
outputColumns = ["relations"]
annotation_separator = "\n"
# processing of a closed task
open_ended_task = False
annotation_vector = [
"title", "founded_org", "place_of_birth", "children", "cause_of_death",
"top_member_employee_of_org", "employee_or_member_of", "spouse",
"alternate_names", "subsidiaries", "place_of_death", "schools_attended",
"place_of_headquarters", "charges", "origin", "places_of_residence",
"none"]
def processJudgments(self, judgments):
# pre-process output to match the values in annotation_vector
for col in self.outputColumns:
# transform to lowercase
judgments[col] = judgments[col].apply(lambda x: str(x).lower())
return judgments
```
## Pre-processing the input data
After declaring the configuration of our input file, we are ready to pre-process the crowd data:
```
data, config = crowdtruth.load(
file = "../data/relex-multiple-choice.csv",
config = TestConfig()
)
data['judgments'].head()
```
## Computing the CrowdTruth metrics
The pre-processed data can then be used to calculate the CrowdTruth metrics:
```
results = crowdtruth.run(data, config)
```
`results` is a dict object that contains the quality metrics for sentences, relations and crowd workers.
The **sentence metrics** are stored in `results["units"]`:
```
results["units"].head()
```
The `uqs` column in `results["units"]` contains the **sentence quality scores**, capturing the overall workers agreement over each sentence. Here we plot its histogram:
```
import matplotlib.pyplot as plt
%matplotlib inline
plt.hist(results["units"]["uqs"])
plt.xlabel("Sentence Quality Score")
plt.ylabel("Sentences")
```
The `unit_annotation_score` column in `results["units"]` contains the **sentence-relation scores**, capturing the likelihood that a relation is expressed in a sentence. For each sentence, we store a dictionary mapping each relation to its sentence-relation score.
```
results["units"]["unit_annotation_score"].head()
```
The **worker metrics** are stored in `results["workers"]`:
```
results["workers"].head()
```
The `wqs` columns in `results["workers"]` contains the **worker quality scores**, capturing the overall agreement between one worker and all the other workers.
```
plt.hist(results["workers"]["wqs"])
plt.xlabel("Worker Quality Score")
plt.ylabel("Workers")
```
The **relation metrics** are stored in `results["annotations"]`. The `aqs` column contains the **relation quality scores**, capturing the overall worker agreement over one relation.
```
results["annotations"]
```
| true |
code
| 0.414988 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Chapter-1---Exploring-Tick,-Volume,-DV-Bars" data-toc-modified-id="Chapter-1---Exploring-Tick,-Volume,-DV-Bars-1" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">1 </span>Chapter 1 - Exploring Tick, Volume, DV Bars</a></span><ul class="toc-item"><li><span><a href="#Introduction" data-toc-modified-id="Introduction-1.1" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">1.1 </span>Introduction</a></span></li><li><span><a href="#Read-and-Clean-Data" data-toc-modified-id="Read-and-Clean-Data-1.2" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">1.2 </span>Read and Clean Data</a></span></li><li><span><a href="#Remove-Obvious-Price-Errors-in-Tick-Data" data-toc-modified-id="Remove-Obvious-Price-Errors-in-Tick-Data-1.3" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">1.3 </span>Remove Obvious Price Errors in Tick Data</a></span></li></ul></li><li><span><a href="#Tick-Bars" data-toc-modified-id="Tick-Bars-2" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">2 </span>Tick Bars</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Bonus-Exercise:-Make-OHLC-Bars-from-Custom-Bars" data-toc-modified-id="Bonus-Exercise:-Make-OHLC-Bars-from-Custom-Bars-2.0.1" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">2.0.1 </span>Bonus Exercise: Make OHLC Bars from Custom Bars</a></span></li></ul></li></ul></li><li><span><a href="#Volume-Bars" data-toc-modified-id="Volume-Bars-3" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">3 </span>Volume Bars</a></span></li><li><span><a href="#Dollar-Value-Bars" data-toc-modified-id="Dollar-Value-Bars-4" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">4 </span>Dollar Value Bars</a></span></li><li><span><a href="#Analyzing-the-Bars" data-toc-modified-id="Analyzing-the-Bars-5" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">5 </span>Analyzing the Bars</a></span><ul class="toc-item"><li><span><a href="#Count-Quantity-of-Bars-By-Each-Bar-Type-(Weekly)" data-toc-modified-id="Count-Quantity-of-Bars-By-Each-Bar-Type-(Weekly)-5.1" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">5.1 </span>Count Quantity of Bars By Each Bar Type (Weekly)</a></span></li><li><span><a href="#Which-Bar-Type-Has-Most-Stable-Counts?" data-toc-modified-id="Which-Bar-Type-Has-Most-Stable-Counts?-5.2" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">5.2 </span>Which Bar Type Has Most Stable Counts?</a></span></li><li><span><a href="#Which-Bar-Type-Has-the-Lowest-Serial-Correlation?" data-toc-modified-id="Which-Bar-Type-Has-the-Lowest-Serial-Correlation?-5.3" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">5.3 </span>Which Bar Type Has the Lowest Serial Correlation?</a></span></li><li><span><a href="#Partition-Bar-Series-into-Monthly,-Compute-Variance-of-Returns,-and-Variance-of-Variance" data-toc-modified-id="Partition-Bar-Series-into-Monthly,-Compute-Variance-of-Returns,-and-Variance-of-Variance-5.4" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">5.4 </span>Partition Bar Series into Monthly, Compute Variance of Returns, and Variance of Variance</a></span></li><li><span><a href="#Compute-Jarque-Bera-Test,-Which-Has-Lowest-Test-Statistic?" data-toc-modified-id="Compute-Jarque-Bera-Test,-Which-Has-Lowest-Test-Statistic?-5.5" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">5.5 </span>Compute Jarque-Bera Test, Which Has Lowest Test Statistic?</a></span></li><li><span><a href="#Compute-Shapiro-Wilk-Test" data-toc-modified-id="Compute-Shapiro-Wilk-Test-5.6" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">5.6 </span>Compute Shapiro-Wilk Test</a></span></li></ul></li><li><span><a href="#Compare-Serial-Correlation-between-Dollar-and-Dollar-Imbalance-Bars" data-toc-modified-id="Compare-Serial-Correlation-between-Dollar-and-Dollar-Imbalance-Bars-6" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">6 </span>Compare Serial Correlation between Dollar and Dollar Imbalance Bars</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Update-[05.04.18]" data-toc-modified-id="Update-[05.04.18]-6.0.1" data-vivaldi-spatnav-clickable="1"><span class="toc-item-num">6.0.1 </span>Update [05.04.18]</a></span></li></ul></li></ul></li></ul></div>
Advances in Machine Learning
# Chapter 1 - Exploring Tick, Volume, DV Bars
```
%load_ext watermark
%watermark
%load_ext autoreload
%autoreload 2
# import standard libs
from IPython.display import display
from IPython.core.debugger import set_trace as bp
from pathlib import PurePath, Path
import sys
import time
from collections import OrderedDict as od
import re
import os
import json
os.environ['THEANO_FLAGS'] = 'device=cpu,floatX=float32'
# import python scientific stack
import pandas as pd
import pandas_datareader.data as web
pd.set_option('display.max_rows', 100)
from dask import dataframe as dd
from dask.diagnostics import ProgressBar
pbar = ProgressBar()
pbar.register()
import numpy as np
import scipy.stats as stats
import statsmodels.api as sm
from numba import jit
import math
import pymc3 as pm
from theano import shared, theano as tt
# import visual tools
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
%matplotlib inline
import seaborn as sns
plt.style.use('seaborn-talk')
plt.style.use('bmh')
#plt.rcParams['font.family'] = 'DejaVu Sans Mono'
#plt.rcParams['font.size'] = 9.5
plt.rcParams['font.weight'] = 'medium'
#plt.rcParams['figure.figsize'] = 10,7
blue, green, red, purple, gold, teal = sns.color_palette('colorblind', 6)
# import util libs
import pyarrow as pa
import pyarrow.parquet as pq
from tqdm import tqdm, tqdm_notebook
import warnings
warnings.filterwarnings("ignore")
import missingno as msno
from src.utils.utils import *
from src.features.bars import get_imbalance
import src.features.bars as brs
import src.features.snippets as snp
RANDOM_STATE = 777
print()
%watermark -p pandas,pandas_datareader,dask,numpy,pymc3,theano,sklearn,statsmodels,scipy,matplotlib,seaborn,pyarrow,fastparquet
```
## Introduction
This notebook explores the idea of sampling prices as a function of something other than fixed time intervals. For example using the number of ticks, volume or dollar volume traded as the sampling interval. The rest of this notebook works through some of the exercises found in chapters 1 and 2 of the book.
This notebook makes use of the following script found here: `./src/features/bars.py`
## Read and Clean Data
The data set used in this example is too large to be hosted on github. It is a sample of equity tick data, symbol `IVE`, provided by [kibot.com (caution: download link)](http://api.kibot.com/?action=history&symbol=IVE&interval=tickbidask&bp=1&user=guest). Download this data to the `./data/raw/` directory in your local repo.
```
def read_kibot_ticks(fp):
# read tick data from http://www.kibot.com/support.aspx#data_format
cols = list(map(str.lower,['Date','Time','Price','Bid','Ask','Size']))
df = (pd.read_csv(fp, header=None)
.rename(columns=dict(zip(range(len(cols)),cols)))
.assign(dates=lambda df: (pd.to_datetime(df['date']+df['time'],
format='%m/%d/%Y%H:%M:%S')))
.assign(v=lambda df: df['size']) # volume
.assign(dv=lambda df: df['price']*df['size']) # dollar volume
.drop(['date','time'],axis=1)
.set_index('dates')
.drop_duplicates())
return df
infp = PurePath(data_dir/'raw'/'IVE_tickbidask.txt')
df = read_kibot_ticks(infp)
cprint(df)
```
Save initial processed data as parquet in the `./data/interim/` folder and reload.
```
outfp = PurePath(data_dir/'interim'/'IVE_tickbidask.parq')
df.to_parquet(outfp)
infp=PurePath(data_dir/'interim'/'IVE_tickbidask.parq')
df = pd.read_parquet(infp)
cprint(df)
msno.matrix(df)
```
## Remove Obvious Price Errors in Tick Data
```
sns.boxplot(df.price)
@jit(nopython=True)
def mad_outlier(y, thresh=3.):
'''
compute outliers based on mad
# args
y: assumed to be array with shape (N,1)
thresh: float()
# returns
array index of outliers
'''
median = np.median(y)
diff = np.sum((y - median)**2, axis=-1)
diff = np.sqrt(diff)
med_abs_deviation = np.median(diff)
modified_z_score = 0.6745 * diff / med_abs_deviation
return modified_z_score > thresh
mad = mad_outlier(df.price.values.reshape(-1,1))
df.loc[mad]
sns.boxplot(df.loc[~mad].price)
```
Drop outliers from dataset and save cleaned data in the `./data/processed/` folder.
```
df = df.loc[~mad]
cprint(df)
outfp = PurePath(data_dir/'processed'/'clean_IVE_fut_prices.parq')
df.to_parquet(outfp)
infp=PurePath(data_dir/'processed'/'clean_IVE_fut_prices.parq')
df = pd.read_parquet(infp)
cprint(df)
```
# Tick Bars
```
def tick_bars(df, price_column, m):
'''
compute tick bars
# args
df: pd.DataFrame()
column: name for price data
m: int(), threshold value for ticks
# returns
idx: list of indices
'''
t = df[price_column]
ts = 0
idx = []
for i, x in enumerate(tqdm(t)):
ts += 1
if ts >= m:
idx.append(i)
ts = 0
continue
return idx
def tick_bar_df(df, price_column, m):
idx = tick_bars(df, price_column, m)
return df.iloc[idx].drop_duplicates()
```
There are many ways to choose `M`, or the threshold value for sampling prices. One way is based on ratios of total dollar value/volume traded vs number of ticks. The rest of the notebook uses an arbitrary but sensible `M` value. I leave it as an exercise for the reader to see how the results change based on different values of `M`.
```
n_ticks = df.shape[0]
volume_ratio = (df.v.sum()/n_ticks).round()
dollar_ratio = (df.dv.sum()/n_ticks).round()
print(f'num ticks: {n_ticks:,}')
print(f'volume ratio: {volume_ratio}')
print(f'dollar ratio: {dollar_ratio}')
tick_M = 100 # arbitrary
print(f'tick threshold: {tick_M:,}')
tidx = tick_bars(df, 'price', tick_M)
tidx[:10]
df.iloc[tidx].shape, df.shape
```
Dataset is large so select smaller example for quick exploration
```
tick_df = tick_bar_df(df, 'price', tick_M)
tick_df.shape
def select_sample_data(ref, sub, price_col, date):
'''
select a sample of data based on date, assumes datetimeindex
# args
ref: pd.DataFrame containing all ticks
sub: subordinated pd.DataFrame of prices
price_col: str(), price column
date: str(), date to select
# returns
xdf: ref pd.Series
xtdf: subordinated pd.Series
'''
xdf = ref[price_col].loc[date]
xtdf = sub[price_col].loc[date]
return xdf, xtdf
## try different dates to see how the quantity of tick bars changes
xDate ='2009-10-01' #'2017-10-4'
xdf, xtdf = select_sample_data(df, tick_df, 'price', xDate)
xdf.shape, xtdf.shape
def plot_sample_data(ref, sub, bar_type, *args, **kwds):
f,axes=plt.subplots(3,sharex=True, sharey=True, figsize=(10,7))
ref.plot(*args, **kwds, ax=axes[0], label='price')
sub.plot(*args, **kwds, ax=axes[0], marker='X', ls='', label=bar_type)
axes[0].legend();
ref.plot(*args, **kwds, ax=axes[1], label='price', marker='o')
sub.plot(*args, **kwds, ax=axes[2], ls='', marker='X',
color='r', label=bar_type)
for ax in axes[1:]: ax.legend()
plt.tight_layout()
return
plot_sample_data(xdf, xtdf, 'tick bar', alpha=0.5, markersize=7)
```
### Bonus Exercise: Make OHLC Bars from Custom Bars
Extract `tick_df.price` and `df.price` into two pandas series.
```
sub = tick_df.price
ref = df.price
```
The function below creates the OHLC dataframe by:
1. Iterating over the subordinated series' index extracting idx and idx+1 period
2. Selecting the same date period from the reference series
3. Extracting the max, min prices from the reference series.
4. Combining the o,h,l,c and start and end timestamps into a row
5. Returning the aggregated rows as a pandas dataframe.
```
def get_ohlc(ref, sub):
'''
fn: get ohlc from custom bars
# args
ref : reference pandas series with all prices
sub : custom tick pandas series
# returns
tick_df : dataframe with ohlc values
'''
ohlc = []
for i in tqdm(range(sub.index.shape[0]-1)):
start,end = sub.index[i], sub.index[i+1]
tmp_ref = ref.loc[start:end]
max_px, min_px = tmp_ref.max(), tmp_ref.min()
o,h,l,c = sub.iloc[i], max_px, min_px, sub.iloc[i+1]
ohlc.append((end,start,o,h,l,c))
cols = ['end','start','open','high','low','close']
return (pd.DataFrame(ohlc,columns=cols))
## uncomment below to run (takes about 5-6 mins on my machine)
#tick_bars_ohlc = get_ohlc(ref, sub)
#cprint(tick_bars_ohlc)
#outfp = PurePath(data_dir/'processed'/'tick_bars_ohlc.parq')
#tick_bars_ohlc.to_parquet(outfp)
```
# Volume Bars
```
def volume_bars(df, volume_column, m):
'''
compute volume bars
# args
df: pd.DataFrame()
volume_column: name for volume data
m: int(), threshold value for volume
# returns
idx: list of indices
'''
t = df[volume_column]
ts = 0
idx = []
for i, x in enumerate(tqdm(t)):
ts += x
if ts >= m:
idx.append(i)
ts = 0
continue
return idx
def volume_bar_df(df, volume_column, m):
idx = volume_bars(df, volume_column, m)
return df.iloc[idx].drop_duplicates()
volume_M = 10_000 # arbitrary
print(f'volume threshold: {volume_M:,}')
v_bar_df = volume_bar_df(df, 'v', 'price', volume_M)
cprint(v_bar_df)
xDate = '2009-10-1'
xdf, xtdf = select_sample_data(df, v_bar_df, 'price', xDate)
print(f'xdf shape: {xdf.shape}, xtdf shape: {xtdf.shape}')
plot_sample_data(xdf, xtdf, 'volume bar', alpha=0.5, markersize=7)
```
# Dollar Value Bars
```
def dollar_bars(df, dv_column, m):
'''
compute dollar bars
# args
df: pd.DataFrame()
dv_column: name for dollar volume data
m: int(), threshold value for dollars
# returns
idx: list of indices
'''
t = df[column]
ts = 0
idx = []
for i, x in enumerate(tqdm(t)):
ts += x
if ts >= m:
idx.append(i)
ts = 0
continue
return idx
def dollar_bar_df(df, dv_column, m):
idx = dollar_bars(df, dv_column, m)
return df.iloc[idx].drop_duplicates()
dollar_M = 1_000_000 # arbitrary
print(f'dollar threshold: {dollar_M:,}')
dv_bar_df = dollar_bar_df(df, 'dv', 'price', dollar_M)
cprint(dv_bar_df)
xDate = '2009-10-1'
xdf, xtdf = select_sample_data(df, dv_bar_df, 'price', xDate)
print(f'xdf shape: {xdf.shape}, xtdf shape: {xtdf.shape}')
plot_sample_data(xdf, xtdf, 'dollar bar', alpha=0.5, markersize=7)
```
# Analyzing the Bars
## Count Quantity of Bars By Each Bar Type (Weekly)
```
def count_bars(df, price_col='price'):
return df.groupby(pd.TimeGrouper('1W'))[price_col].count()
def scale(s):
return (s-s.min())/(s.max()-s.min())
# count series
# scale to compare 'apples to apples'
tc = scale(count_bars(tick_df))
vc = scale(count_bars(v_bar_df))
dc = scale(count_bars(dv_bar_df))
dfc = scale(count_bars(df))
# plot time series of count
f,ax=plt.subplots(figsize=(10,7))
tc.plot(ax=ax, ls='-', label='tick count')
vc.plot(ax=ax, ls='--', label='volume count')
dc.plot(ax=ax, ls='-.', label='dollar count')
ax.set_title('scaled bar counts')
ax.legend()
```
## Which Bar Type Has Most Stable Counts?
```
print(f'tc std: {tc.std():.2%}, vc std: {vc.std():.2%}, dc std: {dc.std():.2%}')
bar_types = ['tick','volume','dollar','df']
bar_std = [tc.std(),vc.std(),dc.std(),dfc.std()]
counts = (pd.Series(bar_std,index=bar_types))
counts.sort_values()
```
## Which Bar Type Has the Lowest Serial Correlation?
```
def returns(s):
arr = np.diff(np.log(s))
return (pd.Series(arr, index=s.index[1:]))
tr = returns(tick_df.price)
vr = returns(v_bar_df.price)
dr = returns(dv_bar_df.price)
df_ret = returns(df.price)
bar_returns = [tr, vr, dr, df_ret]
def get_test_stats(bar_types,bar_returns,test_func,*args,**kwds):
dct = {bar:(int(bar_ret.shape[0]), test_func(bar_ret,*args,**kwds))
for bar,bar_ret in zip(bar_types,bar_returns)}
df = (pd.DataFrame.from_dict(dct)
.rename(index={0:'sample_size',1:f'{test_func.__name__}_stat'})
.T)
return df
autocorrs = get_test_stats(bar_types,bar_returns,pd.Series.autocorr)
display(autocorrs.sort_values('autocorr_stat'),
autocorrs.abs().sort_values('autocorr_stat'))
def plot_autocorr(bar_types,bar_returns):
f,axes=plt.subplots(len(bar_types),figsize=(10,7))
for i, (bar, typ) in enumerate(zip(bar_returns, bar_types)):
sm.graphics.tsa.plot_acf(bar, lags=120, ax=axes[i],
alpha=0.05, unbiased=True, fft=True,
zero=False,
title=f'{typ} AutoCorr')
plt.tight_layout()
def plot_hist(bar_types,bar_rets):
f,axes=plt.subplots(len(bar_types),figsize=(10,6))
for i, (bar, typ) in enumerate(zip(bar_returns, bar_types)):
g = sns.distplot(bar, ax=axes[i], kde=False, label=typ)
g.set(yscale='log')
axes[i].legend()
plt.tight_layout()
plot_autocorr(bar_types,bar_returns)
plot_hist(bar_types,bar_returns)
```
## Partition Bar Series into Monthly, Compute Variance of Returns, and Variance of Variance
```
def partition_monthly(s):
return s.resample('1M').var()
tr_rs = partition_monthly(tr)
vr_rs = partition_monthly(vr)
dr_rs = partition_monthly(dr)
df_ret_rs = partition_monthly(df_ret)
monthly_vars = [tr_rs, vr_rs, dr_rs, df_ret_rs]
get_test_stats(bar_types,monthly_vars,np.var).sort_values('var_stat')
```
## Compute Jarque-Bera Test, Which Has Lowest Test Statistic?
```
def jb(x,test=True):
np.random.seed(12345678)
if test: return stats.jarque_bera(x)[0]
return stats.jarque_bera(x)[1]
get_test_stats(bar_types,bar_returns,jb).sort_values('jb_stat')
```
## Compute Shapiro-Wilk Test
Shapiro-Wilk test statistic > larger is better.
```
def shapiro(x,test=True):
np.random.seed(12345678)
if test: return stats.shapiro(x)[0]
return stats.shapiro(x)[1]
(get_test_stats(bar_types,bar_returns,shapiro)
.sort_values('shapiro_stat')[::-1])
```
# Compare Serial Correlation between Dollar and Dollar Imbalance Bars
### Update [05.04.18]
Earlier version was missing some additional code. Before we can compare we must compute the Dollar Imbalance Bar. This is my initial implementation of this concept but is experimental and may need some adjustments.
1. Compute the sequence ${bt}_{t=1,...,T}$.
2. Compute the imbalance at time $T$ defined as $\theta_T = \sum_{t=1}^{T}b_tv_t$.
3. Compute the expected value of $T$ as ewma of previous $T$ values.
4. Compute the expected value of $\theta_T$ as ewma of $b_tv_t$ values.
5. for each index:
- compute $\lvert\theta_t\rvert >= E_0[T] * \lvert2v^+-E_0[v_t]\rvert$
- if the condition is met capture the quantity of ticks
- reset tick count
- continue
```
tidx = get_imbalance(df.price.values)*df.dv.iloc[1:]
cprint(tidx)
wndo = tidx.shape[0]//1000
print(f'window size: {wndo:,.2f}')
## Expected value of bs approximated by ewm
E_bs = tidx.ewm(wndo).mean() # expected `bs`
## what is E_T???
## in this implementation E_T is ewm of index values
E_T = pd.Series(range(tidx.shape[0]), index=tidx.index).ewm(wndo).mean()
df0 =(pd.DataFrame().assign(bs=tidx)
.assign(E_T=E_T).assign(E_bs=E_bs)
.assign(absMul=lambda df: df.E_T*np.abs(df.E_bs))
.assign(absTheta=tidx.cumsum().abs()))
cprint(df0)
df0[['E_T','E_bs']].plot(subplots=True, figsize=(10,6));
display(df0.describe()/1000)
(df0.loc['2010-06',['absMul','absTheta']]
.reset_index(drop=True)
.plot(figsize=(10,5)))
def test_t_abs(absTheta,t,E_bs):
"""
Bool function to test inequality
*row is assumed to come from df.itertuples()
-absTheta: float(), row.absTheta
-t: pd.Timestamp()
-E_bs: float(), row.E_bs
"""
return (absTheta >= t*E_bs)
def agg_imbalance_bars(df):
"""
Implements the accumulation logic
"""
start = df.index[0]
bars = []
for row in df.itertuples():
t_abs = row.absTheta
rowIdx = row.Index
E_bs = row.E_bs
t = df.loc[start:rowIdx].shape[0]
if t<1: t=1 # if t lt 1 set equal to 1
if test_t_abs(t_abs,t,E_bs):
bars.append((start,rowIdx,t))
start = rowIdx
return bars
bars = agg_imbalance_bars(df0)
test_imb_bars = (pd.DataFrame(bars,columns=['start','stop','Ts'])
.drop_duplicates())
cprint(test_imb_bars)
test_imb_bars.Ts.describe().round()
test_imb_bars.set_index('stop')['Ts'].plot()
dvImbBars = df.price.loc[test_imb_bars.stop].drop_duplicates()
cprint(dvImbBars)
dvBar = dv_bar_df.price
cprint(dvBar)
dr = returns(dv_bar_df.price)
drImb = returns(dvImbBars)
bar_types = ['dvBar','dvImb']
bar_rets = [dr, drImb]
get_test_stats(bar_types,bar_rets,pd.Series.autocorr)
plot_autocorr(bar_types,bar_returns)
plot_hist(bar_types,bar_returns)
jbs = get_test_stats(bar_types,bar_returns,jb).sort_values('jb_stat')
shaps = (get_test_stats(bar_types,bar_returns,shapiro)
.sort_values('shapiro_stat')[::-1])
display(jbs,shaps)
```
| true |
code
| 0.538619 | null | null | null | null |
|
# Feature Engineering
Author : [Alexandre Gramfort](http://alexandre.gramfort.net)
with some code snippets from [Olivier Grisel](http://ogrisel.com/) (leaf encoder)
It is the most creative aspect of Data Science!
We will use here the Titanic dataset.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
df = sns.load_dataset("titanic")
df.head()
```
Let's look at the dtypes of the different columns. You will observe that it contains columns that
are explicitly marked as `category`.
```
df.info()
```
This allows you to do things like:
```
from sklearn.compose import make_column_selector
make_column_selector(dtype_include='category')(df)
```
in order to get quickly the names of the columns to treat as categorical.
As you can see the data contains both quantitative and categorical variables. These categorical have some predictive power:
```
sns.catplot(data=df, x='pclass', y='survived', hue='sex', kind='bar')
```
The question is how to feed these non-quantitative features to a supervised learning model?
## Categorical features
- Nearly always need some treatment
- High cardinality can create very sparse data
- Difficult to impute missing
### One-Hot encoding
**Idea:** Each category is coded as a 0 or 1 in a dedicated column.
- It is the most basic method. It is used with most linear algorithms
- Drop first column to avoid collinearity
- It uses sparse format which is memory-friendly
- Most current implementations don’t gracefully treat missing, unseen variables
Example with the `embarked` column. We have here 3 categories:
```
df['embarked'].value_counts()
df1 = df[['embarked']]
df1.head(10)
```
Let's use a [scikit-learn OneHotEncoder](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html)
```
from sklearn.preprocessing import OneHotEncoder
ohe = OneHotEncoder()
ohe.fit_transform(df1.head(10)).toarray()
```
To know which column corresponds to what you can look at:
```
ohe.categories_
```
Basically the first column will be a 1 if category was 'C', etc.
Now if we have missing values:
```
ohe = OneHotEncoder()
ohe.fit_transform(df1).toarray()
```
We have now 4 columns, one corresponding to NaNs:
```
ohe.categories_
```
As the columns are linearly dependant after one-hot encoding you can drop one column with:
```
OneHotEncoder(drop='first').fit_transform(df1.head(10)).toarray()
```
This avoids colinearity, which for example leads to slower optimization solvers.
# Ordinal encoding
**Idea:** Each category is coded with a different integer. The order being arbitrary.
- Give every categorical variable a unique numerical ID
- Useful for non-linear tree-based algorithms (forests, gradient-boosting)
- Does not increase dimensionality
```
from sklearn.preprocessing import OrdinalEncoder
oe = OrdinalEncoder()
oe.fit_transform(df1.head(10))
oe.categories_
```
This means that 'C' will be coded as 0, 'Q' as a 1 and 'S' as a 2.
## Count encoding
**Idea:** Replace categorical variables with their count in the train set
- Useful for both linear and non-linear algorithms
- Can be sensitive to outliers
- May add log-transform, works well with counts
- Replace unseen variables with `1`
- May give collisions: same encoding, different variables
You'll need to install the `category_encoders` package with:
pip install category_encoders
```
import category_encoders as ce
ce.__version__
df1.head(10)
ce.CountEncoder().fit_transform(df1.head(10)).values
```
'S' is replaced by 7 as it appears 7 times in the fitted data, etc.
## Label / Ordinal count encoding
**Idea:** Rank categorical variables by count and use this rank as encoding value. It is an ordinal encoding where the value is taking from the frequence of each category.
- Useful for both linear and non-linear algorithms
- Not sensitive to outliers
- Won’t give same encoding to different variables
- Best of both worlds
As it is not available in any package we will implement this ourselves:
```
from sklearn.preprocessing import OrdinalEncoder
class CountOrdinalEncoder(OrdinalEncoder):
"""Encode categorical features as an integer array
usint count information.
"""
def __init__(self, categories='auto', dtype=np.float64):
self.categories = categories
self.dtype = dtype
def fit(self, X, y=None):
"""Fit the OrdinalEncoder to X.
Parameters
----------
X : array-like, shape [n_samples, n_features]
The data to determine the categories of each feature.
Returns
-------
self
"""
self.handle_unknown = 'use_encoded_value'
self.unknown_value = np.nan
super().fit(X)
X_list, _, _ = self._check_X(X)
# now we'll reorder by counts
for k, cat in enumerate(self.categories_):
counts = []
for c in cat:
counts.append(np.sum(X_list[k] == c))
order = np.argsort(counts)
self.categories_[k] = cat[order]
return self
coe = CountOrdinalEncoder()
coe.fit_transform(pd.DataFrame(df1.head(10)))
```
'S' is replace by 2 as it's the most frequent, then 'C' is 1 and 'Q' is 0.
This encoding is robust to collision which can happen with the CountEncoder when certain categories happen the same number of times. Example:
```
coe.fit_transform(pd.DataFrame(['es', 'fr', 'fr', 'en', 'en', 'es']))
```
vs.
```
ce.CountEncoder().fit_transform(pd.DataFrame(['es', 'fr', 'fr', 'en', 'en', 'es']))
```
# Hash encoding
**Idea:** Does “OneHot-encoding” with arrays of a fixed length.
- Avoids extremely sparse data
- May introduce collisions
- Can repeat with different hash functions and bag result for small bump in accuracy
- Collisions usually degrade results, but may improve it.
- Gracefully deals with new variables (eg: new user-agents)
```
df1.head(10)
ce.hashing.HashingEncoder(n_components=4).fit_transform(df1.head(10).values)
```
## Target encoding
Encode categorical variables by their ratio of target (binary classification or regression)
Formula reads:
$$
TE(X) = \alpha(n(X)) E[ y | x=X ] + (1 - \alpha(n(X))) E[y]
$$
where $n(X)$ is the count of category $X$ and $\alpha$ is a monotonically increasing function bounded between 0 and 1.[1].
- Add smoothing to avoid setting variable encodings to 0.
```
[1] Micci-Barreca, 2001: A preprocessing scheme for
high-cardinality categorical attributes in classification
and prediction problems.
```
You will need the [dirty cat](https://pypi.org/project/dirty-cat/) package. You can install it with:
pip install dirty_cat
```
import dirty_cat as dc # install with: pip install dirty_cat
X = np.array(['A', 'B', 'C', 'A', 'B', 'B'])[:, np.newaxis]
y = np.array([1 , 1 , 1 , 0 , 0 , 1])
dc.TargetEncoder(clf_type='binary-clf').fit_transform(X, y)
# If \alpha was 1 you would get: [0.5, 0.66, 1, 0.5, 0.66, 0.66]
```
## NaN encoding
It is quite frequent in real life that the fact one variable is missing
has some predictive power. For example in the Titanic dataset the 'deck'
parameter is very often missing and it is missing often for passengers who
did not have a proper cabin and there who were most likely to die.
To inform your supervised model you can explicit encode the missingness
with a dedicated column.
You can do this with a [SimpleImputer](https://scikit-learn.org/stable/modules/generated/sklearn.impute.SimpleImputer.html)
```
from sklearn.impute import SimpleImputer
X = np.array([0, 1., np.nan, 2., 0.])[:, None]
SimpleImputer(strategy='median', add_indicator=True).fit_transform(X)
```
or [MissingIndicator](https://scikit-learn.org/stable/modules/generated/sklearn.impute.MissingIndicator.html)
```
from sklearn.impute import MissingIndicator
X = np.array([0, 1., np.nan, 2., 0.])[:, None]
MissingIndicator().fit_transform(X)
```
## Polynomial encoding
**Idea:** Encode interactions between categorical variables
- Linear algorithms without interactions can not solve the XOR problem
- A polynomial kernel *can* solve XOR
```
X = np.array([[0, 1], [1, 1], [1, 0], [0, 0]])
X
from sklearn.preprocessing import PolynomialFeatures
PolynomialFeatures(include_bias=False, interaction_only=True).fit_transform(X)
```
## To go beyond
You can also use some form of embedding eg using a Neural Network to create dense embeddings from categorical variables.
- Map categorical variables in a function approximation problem into Euclidean spaces
- Faster model training.
- Less memory overhead.
- Can give better accuracy than 1-hot encoded.
- See for example https://arxiv.org/abs/1604.06737
# Binning
See https://scikit-learn.org/stable/auto_examples/preprocessing/plot_discretization_classification.html
[KBinsDiscretizer](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.KBinsDiscretizer.html) allows you to estimate non-linear model in the original feature space while only using a linear logistic regression.
See this [example in regression](https://scikit-learn.org/stable/auto_examples/preprocessing/plot_discretization.html).
What it does:
```
from sklearn.preprocessing import KBinsDiscretizer
rng = np.random.RandomState(42)
X = rng.randn(10, 2)
X
KBinsDiscretizer(n_bins=2).fit_transform(X).toarray()
```
# Scaling
Scale to numerical variables into a certain range
- Standard (Z) Scaling
- MinMax Scaling
- Root scaling
- Log scaling
```
from sklearn.preprocessing import StandardScaler, MinMaxScaler
rng = np.random.RandomState(42)
X = 10 + rng.randn(10, 1)
X
StandardScaler().fit_transform(X)
MinMaxScaler().fit_transform(X)
from sklearn.preprocessing import FunctionTransformer
X = np.arange(1, 10)[:, np.newaxis]
FunctionTransformer(func=np.log).fit_transform(X)
```
# Leaf coding
The following is an implementation of a trick found in:
Practical Lessons from Predicting Clicks on Ads at Facebook
Junfeng Pan, He Xinran, Ou Jin, Tianbing XU, Bo Liu, Tao Xu, Yanxin Shi, Antoine Atallah, Ralf Herbrich, Stuart Bowers, Joaquin Quiñonero Candela
International Workshop on Data Mining for Online Advertising (ADKDD)
https://research.fb.com/wp-content/uploads/2016/11/practical-lessons-from-predicting-clicks-on-ads-at-facebook.pdf
```
from sklearn.base import BaseEstimator, TransformerMixin, clone
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.preprocessing import LabelBinarizer
from scipy.sparse import hstack
class TreeTransform(BaseEstimator, TransformerMixin):
"""One-hot encode samples with an ensemble of trees
This transformer first fits an ensemble of trees (e.g. gradient
boosted trees or a random forest) on the training set.
Then each leaf of each tree in the ensembles is assigned a fixed
arbitrary feature index in a new feature space. If you have 100
trees in the ensemble and 2**3 leafs per tree, the new feature
space has 100 * 2**3 == 800 dimensions.
Each sample of the training set go through the decisions of each tree
of the ensemble and ends up in one leaf per tree. The sample if encoded
by setting features with those leafs to 1 and letting the other feature
values to 0.
The resulting transformer learn a supervised, sparse, high-dimensional
categorical embedding of the data.
This transformer is typically meant to be pipelined with a linear model
such as logistic regression, linear support vector machines or
elastic net regression.
"""
def __init__(self, estimator):
self.estimator = estimator
def fit(self, X, y):
self.fit_transform(X, y)
return self
def fit_transform(self, X, y):
self.estimator_ = clone(self.estimator)
self.estimator_.fit(X, y)
self.binarizers_ = []
sparse_applications = []
estimators = np.asarray(self.estimator_.estimators_).ravel()
for t in estimators:
lb = LabelBinarizer(sparse_output=True)
X_leafs = t.tree_.apply(X.astype(np.float32))
sparse_applications.append(lb.fit_transform(X_leafs))
self.binarizers_.append(lb)
return hstack(sparse_applications)
def transform(self, X, y=None):
sparse_applications = []
estimators = np.asarray(self.estimator_.estimators_).ravel()
for t, lb in zip(estimators, self.binarizers_):
X_leafs = t.tree_.apply(X.astype(np.float32))
sparse_applications.append(lb.transform(X_leafs))
return hstack(sparse_applications)
boosted_trees = GradientBoostingClassifier(
max_leaf_nodes=5, learning_rate=0.1,
n_estimators=10, random_state=0,
)
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
TreeTransform(boosted_trees).fit_transform(X, y)
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
Limiting yourself to LogisticRegression propose features to predict survival.
</li>
</ul>
</div>
```
from sklearn.linear_model import LogisticRegression
from sklearn.compose import make_column_transformer
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import cross_val_score
y = df.survived.values
X = df.drop(['survived', 'alive'], axis=1)
X.head()
lr = LogisticRegression(solver='lbfgs')
ct = make_column_transformer(
(make_pipeline(SimpleImputer(), StandardScaler()), ['age', 'pclass', 'fare'])
)
clf = make_pipeline(ct, lr)
np.mean(cross_val_score(clf, X, y, cv=10))
```
### Now do better !
| true |
code
| 0.701688 | null | null | null | null |
|
# Using AWS Lambda and PyWren for Landsat 8 Time Series
This notebook is a simple demonstration of drilling a timeseries of [NDVI](https://en.wikipedia.org/wiki/Normalized_difference_vegetation_index) values from the [Landsat 8 satellite images held on AWS](https://landsatonaws.com/). You can view these [time series of satellite images interactively](https://search.remotepixel.ca/#7.43/41.788/-88.447) as well, if you would like to see what they look like.
The code relies on the l8_ndvi_point function from the [remotepixel-api](https://github.com/RemotePixel/remotepixel-api) to compute an NDVI value for a given set of coordinates. It's recommended that you install this yourself, but currently a version of the API is accepting requests at the URL in the code below, and we will use this API (which is an AWS Lambda function) for the sake of this demo. It works by sending a request to an endpoint with a sceneID and a location like this:
[https://w5xm4e5886.execute-api.us-west-2.amazonaws.com/production/l8_ndvi_point?coords=-87.596890,41.7856533&scene=LC08_L1TP_023031_20191007_20191018_01_T1](https://w5xm4e5886.execute-api.us-west-2.amazonaws.com/production/l8_ndvi_point?coords=-87.596890,41.7856533&scene=LC08_L1TP_023031_20191007_20191018_01_T1)
This will return:
`{"ndvi": 0.21664535999298096, "date": "2019-10-07", "cloud": 0.07}`
If you haven't already, please [install/configure PyWren](http://pywren.io/pages/gettingstarted.html) in order to run this notebook. We will be using [PyWren](https://github.com/pywren/pywren) to call the Remote Pixel API in parallel on satellite images that were taken over the past seven years, calculating a single NDVI value for each image. The satellite images themselves are held in a public S3 bucket. Thus, we are taking advantage of two levels of serverless parallelism (see workflow below): one for the API calls and one for the calculations themselves.
Once we have the results back as a list of dictionaries, drawn from a timeseries of more than 100 images, we can simply plot the resulting timeseries or do further analysis. BUT, the points may well be cloud or cloud shadow contaminated. We haven’t done any cloud masking to the imagery, but we do have the scene metadata on the probable amount of cloud across the entire scene. We use this to weight a [smoothing spline](https://docs.scipy.org/doc/scipy-0.19.1/reference/generated/scipy.interpolate.UnivariateSpline.html), such that an observation with no reported cloud over the scene has full weight, and an observation with a reported 100% of the scene with cloud has zero weight.
<img src="pywren_workflow.png" width="800">
Original Code Credit: Peter Scarth (Joint Remote Sensing Research Program)
```
import requests, json, numpy, datetime
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
import pywren
# Function to return a Landsat 8 scene list given a Longitude,Latitude string
# This uses the amazing developmentseed Satellite API
# https://github.com/sat-utils/sat-api
def getSceneList(lonLat):
scenes=[]
url = "https://api.developmentseed.org/satellites/landsat"
params = dict(
contains=lonLat,
satellite_name="landsat-8",
limit="1000")
# Call the API to grab the scene metadata
sceneMetaData = json.loads(requests.get(url=url, params=params).content)
# Parse the metadata
for record in sceneMetaData["results"]:
scene = str(record['aws_index'].split('/')[-2])
if scene[-2:] == '01':
scene = scene[:-2] + '00'
if scene[-2:] == '02':
scene = scene[:-2] + '00'
if scene[-2:] == '03':
scene = scene[:-2] + '02'
scenes.append(scene)
return scenes
# Function to call a AWS Lambda function to drill a single pixel and compute the NDVI
def getNDVI(scene):
url = "https://w5xm4e5886.execute-api.us-west-2.amazonaws.com/production/l8_ndvi_point"
params = dict(
coords=lonLat,
scene=scene)
# Call the API and return the JSON results
resp = requests.get(url=url, params=params)
return json.loads(resp.text)
```
Let's compute the NDVI time series for the home of the MACSS program, [1155 E. 60th Street, Chicago, IL](https://www.google.com/maps/place/41%C2%B047'08.4%22N+87%C2%B035'48.8%22W).
```
%%time
# 1155 E. 60th Street, Chicago, IL (Home of MACSS Program)
lonLat = '-87.596890,41.7856533'
# Call the api to retrieve the scenes available under the point of interest
scenes = getSceneList(lonLat)
# Set up a pywren executor and map the NDVI retrieval across all the available scenes
pwex = pywren.default_executor()
timeSeries = pywren.get_all_results(pwex.map(getNDVI, scenes))
# Extract the data trom the list of results
timeStamps = [datetime.datetime.strptime(obs['date'],'%Y-%m-%d') for obs in timeSeries if 'date' in obs]
ndviSeries = [obs['ndvi'] for obs in timeSeries if 'ndvi' in obs]
cloudSeries = [obs['cloud']/100 for obs in timeSeries if 'cloud' in obs]
# Create a time variable as the x axis to fit the observations
# First we convert to seconds
timeSecs = numpy.array([(obsTime-datetime.datetime(1970,1,1)).total_seconds() for obsTime in timeStamps])
# And then normalise from 0 to 1 to avoid any numerical issues in the fitting
fitTime = ((timeSecs-numpy.min(timeSecs))/(numpy.max(timeSecs)-numpy.min(timeSecs)))
# Smooth the data by fitting a spline weighted by cloud amount
smoothedNDVI=UnivariateSpline(
fitTime[numpy.argsort(fitTime)],
numpy.array(ndviSeries)[numpy.argsort(fitTime)],
w=(1.0-numpy.array(cloudSeries)[numpy.argsort(fitTime)])**2.0,
k=2,
s=0.1)(fitTime)
# Setup the figure and plot the data, fit and cloud amount
fig = plt.figure(figsize=(16,10))
plt.plot(timeStamps,ndviSeries, 'gx',label='Raw NDVI Data')
plt.plot(timeStamps,ndviSeries, 'g:', linewidth=1)
plt.plot(timeStamps,cloudSeries, 'b.', linewidth=1,label='Scene Cloud Percent')
plt.plot(timeStamps,smoothedNDVI, 'r--', linewidth=3,label='Cloudfree Weighted Spline')
plt.xlabel('Date', fontsize=16)
plt.ylabel('NDVI', fontsize=16)
plt.title('AWS Lambda Landsat 8 NDVI Drill', fontsize=20)
plt.grid(True)
plt.ylim([-.1,1.0])
plt.legend(fontsize=14)
plt.show()
#plt.savefig('lambdaNDVI.png', bbox_inches='tight')
```
| true |
code
| 0.59131 | null | null | null | null |
|
# PyTorch
```
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
seed = 1
lr = 0.001
momentum = 0.5
batch_size = 64
test_batch_size = 64
epochs = 5
no_cuda = False
log_interval = 100
```
## Model
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 20, 5, 1)
self.conv2 = nn.Conv2d(20, 50, 5, 1)
self.fc1 = nn.Linear(4*4*50, 500)
self.fc2 = nn.Linear(500, 10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2, 2)
x = x.view(-1, 4*4*50)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return F.log_softmax(x, dim=1)
```
## Preprocess
```
train_dir = '../../Fast Campus/dataset/mnist_png/training/'
test_dir = '../../Fast Campus/dataset/mnist_png/testing/'
```
grayscale은 안 되는 이유
https://github.com/pytorch/vision/blob/master/torchvision/datasets/folder.py#L157
```
torch.manual_seed(seed)
use_cuda = not no_cuda and torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
train_dataset = datasets.ImageFolder(root=train_dir,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
]))
test_dataset = datasets.ImageFolder(root=test_dir,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
]))
train_loader = torch.utils.data.DataLoader(train_dataset,
batch_size=2,
shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset,
batch_size=2
)
```
## Optimization
```
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=lr, momentum=momentum)
```
## Training
```
for epoch in range(1, epochs + 1):
# Train Mode
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad() # backpropagation 계산하기 전에 0으로 기울기 계산
output = model(data)
loss = F.nll_loss(output, target) # https://pytorch.org/docs/stable/nn.html#nll-loss
loss.backward() # 계산한 기울기를
optimizer.step()
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
# Test mode
model.eval() # batch norm이나 dropout 등을 train mode 변환
test_loss = 0
correct = 0
with torch.no_grad(): # autograd engine, 즉 backpropagatin이나 gradient 계산 등을 꺼서 memory usage를 줄이고 속도를 높임
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item() # pred와 target과 같은지 확인
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
```
| true |
code
| 0.865423 | null | null | null | null |
|
# Multiple Time Series, Pre-trained Models and Covariates
This notebook serves as a tutorial for:
* Training a single model on multiple time series
* Using a pre-trained model to obtain forecasts for any time series unseen during training
* Training and using a model using covariates
First, some necessary imports:
```
# fix python path if working locally
from utils import fix_pythonpath_if_working_locally
fix_pythonpath_if_working_locally()
import pandas as pd
import numpy as np
import torch
import matplotlib.pyplot as plt
from darts import TimeSeries
from darts.utils.timeseries_generation import (
gaussian_timeseries,
linear_timeseries,
sine_timeseries,
)
from darts.models import (
RNNModel,
TCNModel,
TransformerModel,
NBEATSModel,
BlockRNNModel,
)
from darts.metrics import mape, smape
from darts.dataprocessing.transformers import Scaler
from darts.utils.timeseries_generation import datetime_attribute_timeseries
from darts.datasets import AirPassengersDataset, MonthlyMilkDataset
# for reproducibility
torch.manual_seed(1)
np.random.seed(1)
```
### Read Data
Let's start by reading two time series - one containing the monthly number of air passengers, and another containing the monthly milk production per cow. These time series have not much to do with each other, except that they both have a monthly frequency with a marked yearly periodicity and upward trend, and (completely coincidentaly) they contain values of a comparable order of magnitude.
```
series_air = AirPassengersDataset().load()
series_milk = MonthlyMilkDataset().load()
series_air.plot(label="Number of air passengers")
series_milk.plot(label="Pounds of milk produced per cow")
plt.legend()
```
### Preprocessing
Usually neural networks tend to work better on normalised/standardised data. Here we'll use the `Scaler` class to normalise both of our time series between 0 and 1:
```
scaler_air, scaler_milk = Scaler(), Scaler()
series_air_scaled = scaler_air.fit_transform(series_air)
series_milk_scaled = scaler_milk.fit_transform(series_milk)
series_air_scaled.plot(label="air")
series_milk_scaled.plot(label="milk")
plt.legend()
```
### Train / Validation split
Let's keep the last 36 months of both series as validation:
```
train_air, val_air = series_air_scaled[:-36], series_air_scaled[-36:]
train_milk, val_milk = series_milk_scaled[:-36], series_milk_scaled[-36:]
```
## Global Forecasting Models
Darts contains many forecasting models, but not all of them can be trained on several time series. The models that support training on multiple series are called *global* models. At the time of writing, there are 5 global models:
* BlockRNNModel
* RNNModel
* Temporal Convolutional Networks (TCNs)
* N-Beats
* Transformer model
In the following, we will distinguish two sorts of time series:
* The **target time series** is the time series we are interested to forecast (given its history)
* A **covariate time series** is a time series which may help in the forecasting of the target series, but that we are not interested in forecasting. It's sometimes also called *external data*.
We further differentiate covariates series, depending on whether they can be known in advance or not:
* **Past Covariates** denote time series whose past values are known at prediction time. These are usually things that have to be measured or observed.
* **Future Covariates** denote time series whose future values are already known at prediction time for the span of the forecast horizon. These can for instance represent known future holidays, or weather forecasts.
Some models use only past covariates, others use only future covariates, and some models might use both. We will dive deeper in this topic in some other notebook, but for now it is enough to know this:
* `BlockRNNModel`, `TCNModel`, `NBEATSModel` and `TransformerModel` all use `past_covariates`.
* `RNNModel` uses `future_covariates`.
All of the global models listed above support training on multiple series. In addition, they also all support *multivariate series*. This means that they can seamlessly be used with time series of more than one dimension; the target series can contain one (as is often the case) or several dimensions. A time series with several dimensions is really just a regular time series where the values at each time stamps are vectors instead of scalars.
As an example, the 4 models supporting `past_covariates` follow a "block" architecture. They contain a neural network that takes chunks of time series in input, and outputs chunks of (predicted) future time series values. The input dimensionality is the number of dimensions (components) of the target series, plus the number of components of all the covariates - stacked together. The output dimensionality is simply the number of dimensions of the target series:

The `RNNModel` works differently, in a recurrent fashion (which is also why they support future covariates).
The good news is that as a user, we don't have to worry too much about the different model types and input/output dimensionalities. The dimensionalities are automatically inferred for us by the model based on the training data, and the support for past or future covariates is simply handled by the `past_covariates` or `future_covariates` arguments.
We'll still have to specify two important parameters when building our models:
* `input_chunk_length`: this is the length of the lookback window of the model; so each output will be computed by the model by reading the previous `input_chunk_length` points.
* `output_chunk_length`: this is the length of the outputs (forecasts) produced by the internal model. However, the `predict()` method of the "outer" Darts model (e.g., the one of `NBEATSModel`, `TCNModel`, etc) can be called for a longer time horizon. In these cases, if `predict()` is called for a horizon longer than `output_chunk_length`, the internal model will simply be called repeatedly, feeding on its own previous outputs in an auto-regressive fashion. If `past_covariates` are used it requires these covariates to be known for long enough in advance.
### Example with One Series
Let's look at a first example. We'll build an N-BEATS model that has a lookback window of 24 points (`input_chunk_length=24`) and predicts the next 12 points (`output_chunk_length=12`). We chose these values so it'll make our model produce successive predictions for one year at a time, looking at the past two years.
```
model_air = NBEATSModel(
input_chunk_length=24, output_chunk_length=12, n_epochs=200, random_state=0
)
```
This model can be used like any other Darts forecasting model, beeing fit on a single time series:
```
model_air.fit(train_air, verbose=True)
```
And like any other Darts forecasting models, we can then get a forecast by calling `predict()`. Note that below, we are calling `predict()` with a horizon of 36, which is longer than the model internal `output_chunk_length` of 12. That's not a problem here - as explained above, in such a case the internal model will simply be called auto-regressively on its own outputs. In this case, it will be called three times so that the three 12-points outputs make up the final 36-points forecast - but all of this is done transparently behind the scenes.
```
pred = model_air.predict(n=36)
series_air_scaled.plot(label="actual")
pred.plot(label="forecast")
plt.legend()
print("MAPE = {:.2f}%".format(mape(series_air_scaled, pred)))
```
### Training Process (behind the scenes)
So what happened when we called `model_air.fit()` above?
In order to train the internal neural network, Darts first makes a dataset of inputs/outputs examples from the provided time series (in this case: `series_air_scaled`). There are several ways this can be done and Darts contains a few different dataset implementations in the `darts.utils.data` package.
By default, `NBEATSModel` will instantiate a `darts.utils.data.PastCovariatesSequentialDataset`, which simply builds all the consecutive pairs of input/output sub-sequences (of lengths `input_chunk_length` and `output_chunk_length`) existing in the series).
For an example series of length 14, with `input_chunk_length=4` and `output_chunk_length=2`, it looks as follows:

For such a dataset, a series of length `N` would result in a "training set" of `N - input_chunk_length - output_chunk_length + 1` samples. In the toy example above, we have `N=14`, `input_chunk_length=4` and `output_chunk_length=2`, so the number of samples used for training would be K = 9. In this context, a training *epoch* consists in complete pass (possibly consisting of several mini-batches) over all the samples.
Note that different models are susceptible to use different datasets by default. For instance, `darts.utils.data.HorizonBasedDataset` is inspired by the [N-BEATS paper](https://arxiv.org/abs/1905.10437) and produces samples that are "close" to the end of the series, possibly even ignoring the beginning of the series.
If you have the need to control the way training samples are produced from `TimeSeries` instances, you can implement your own training dataset by inheriting the abstract `darts.utils.data.TrainingDataset` class. Darts datasets are inheriting from torch `Dataset`, which means it's easy to implement lazy versions that do not load all data in memory at once. Once you have your own instance of a dataset, you can directly call the `fit_from_dataset()` method, which is supported by all global forecasting models.
## Training a Model on Multiple Time Series
All this machinery can be seamlessly used with multiple time series. Here's how a sequential dataset with `input_chunk_length=4` and `output_chunk_length=2` looks for two series of lengths N and M:

Note a few things here:
* The different series do not need to have the same length, or even to share the same time stamps.
* In fact, they don't even need to have the same frequency.
* The total number of samples in the training dataset will be the union of all the training samples contained in each series; so a training epoch will now span all samples from all series.
### Training on Both Air Traffic and Milk Series
Let's look at another example where we fit another model instance on our two time series (air passengers and milk production). Since using two series of (roughly) the same length (roughly) doubles the training dataset size, we will use half of the number of epochs:
```
model_air_milk = NBEATSModel(
input_chunk_length=24, output_chunk_length=12, n_epochs=100, random_state=0
)
```
Then, fitting the model on two (or more) series is as simple as giving a list of series (instead of a single series) in argument to the `fit()` function:
```
model_air_milk.fit([train_air, train_milk], verbose=True)
```
### Producing Forecasts After the End of a Series
Now, importantly, when computing the forecasts we have to specify which time series we want to forecast the future for.
We didn't have this constraint earlier. When fitting models on one series only, the model remembers this series internally, and if `predict()` is called without the `series` argument, it returns a forecast for the (unique) training series. This does not work anymore as soon as a model is fit on more than one series - in this case the `series` argument of `predict()` becomes mandatory.
So, let's say we want to predict future of air traffic. In this case we specify `series=train_air` to the `predict()` function in order to say we want to get a forecast for what comes after `train_air`:
```
pred = model_air_milk.predict(n=36, series=train_air)
series_air_scaled.plot(label="actual")
pred.plot(label="forecast")
plt.legend()
print("MAPE = {:.2f}%".format(mape(series_air_scaled, pred)))
```
## Wait... does this mean that milk consumption helps to predict air traffic??
Well, in this particular instance with this model, it seems to be the case (at least in terms of MAPE error). This is not so weird if you think about it, though. Air traffic is heavily characterized by the yearly seasonality and upward trend. The milk series exhibits these two traits as well, and in this case it's probably helping the model to capture them.
Note that this points towards the possibility of *pre-training* forecasting models; training models once and for all and later using them to forecast series that are not in the train set.
With our toy model we can really forecast the future values of any other series, even series never seen during training. For the sake of example, let's say we want to forecast the future of some arbitrary sine wave series:
```
any_series = sine_timeseries(length=50, freq="M")
pred = model_air_milk.predict(n=36, series=any_series)
any_series.plot(label='"any series, really"')
pred.plot(label="forecast")
plt.legend()
```
This forecast isn't good (the sine doesn't even have a yearly seasonality), but you get the idea.
Similar to what is supported by the `fit()` function, we can also give a list of series in argument to the `predict()` function, in which case it will return a list of forecast series. For example, we can get the forecasts for both the air traffic and the milk series in one go as follows:
```
pred_list = model_air_milk.predict(n=36, series=[train_air, train_milk])
for series, label in zip(pred_list, ["air passengers", "milk production"]):
series.plot(label=f"forecast {label}")
plt.legend()
```
The two series returned correspond to the forecasts after then end of `train_air` and `train_milk`, respectively.
## Covariates Series
Until now, we have only been playing with models that only use the history of the *target* series to predict its future. However, as explained above, the global Darts models also support the use of *covariates* time series. These are time series of "external data", which we are not necessarily interested in predicting, but which we would still like to feed as input of our models because they can contain valuable information.
#### Building Covariates
Let's see a simple example with our air and milk series, where we'll try to use the year and month-of-the-year as covariates:
```
# build year and month series:
air_year = datetime_attribute_timeseries(series_air_scaled, attribute="year")
air_month = datetime_attribute_timeseries(series_air_scaled, attribute="month")
milk_year = datetime_attribute_timeseries(series_milk_scaled, attribute="year")
milk_month = datetime_attribute_timeseries(series_milk_scaled, attribute="month")
# stack year and month to obtain series of 2 dimensions (year and month):
air_covariates = air_year.stack(air_month)
milk_covariates = milk_year.stack(milk_month)
# scale them between 0 and 1:
scaler_dt_air = Scaler()
air_covariates = scaler_dt_air.fit_transform(air_covariates)
scaler_dt_milk = Scaler()
milk_covariates = scaler_dt_milk.fit_transform(milk_covariates)
# split in train/validation sets:
air_train_covariates, air_val_covariates = air_covariates[:-36], air_covariates[-36:]
milk_train_covariates, milk_val_covariates = (
milk_covariates[:-36],
milk_covariates[-36:],
)
# plot the covariates:
plt.figure()
air_covariates.plot()
plt.title("Air traffic covariates (year and month)")
plt.figure()
milk_covariates.plot()
plt.title("Milk production covariates (year and month)")
```
Good, so for each target series (air and milk), we have built a covariates series having the same time axis and containing the year and the month.
Note that here the covariates series are **multivariate time series**: they contain two dimensions - one dimension for the year and one for the month.
### Training with Covariates
Let's revisit our example again, this time with covariates. We will build a `BlockRNNModel` here:
```
model_cov = BlockRNNModel(
model="LSTM",
input_chunk_length=24,
output_chunk_length=12,
n_epochs=300,
random_state=0,
)
```
Now, to train the model with covariates, it is as simple as providing the covariates (in form of a list matching the target series) as `future_covariates` argument to the `fit()` function. The argument is named `future_covariates` to remind us that the model can use future values of these covariates in order to make a prediction.
```
model_cov.fit(
series=[train_air, train_milk],
past_covariates=[air_train_covariates, milk_train_covariates],
verbose=True,
)
```
### Forecasting with Covariates
similarly, getting a forecast is now only a matter of specifying the `future_covariates` argument to the `predict()` function.
```
pred_cov = model_cov.predict(n=36, series=train_air, past_covariates=air_covariates)
series_air_scaled.plot(label="actual")
pred_cov.plot(label="forecast")
plt.legend()
```
Note that here we called `predict()` with a forecast horizon `n` that is larger than the `output_chunk_length` we trained our model with. We were able to do this because even though `BlockRNNModel` uses past covariates, in this case these covariates are also known into the future, so Darts is able to compute the forecasts auto-regressively for `n` time steps in the future.
### Backtesting with Covariates
We can also backtest the model using covariates. Say for instance we are interested in evaluating the running accuracy with a horizon of 12 months, starting at 75% of the air series:
```
backtest_cov = model_cov.historical_forecasts(
series_air_scaled,
past_covariates=air_covariates,
start=0.6,
forecast_horizon=12,
stride=1,
retrain=False,
verbose=True,
)
series_air_scaled.plot(label="actual")
backtest_cov.plot(label="forecast")
plt.legend()
print("MAPE (using covariates) = {:.2f}%".format(mape(series_air_scaled, backtest_cov)))
```
### A few more words on past covariates, future covariates and other conditioning
At the moment Darts supports covariates that are themselves time series. These covariates are used as model inputs, but are never themselves subject to prediction. The covariates do not necessarily have to be aligned with the target series (e.g. they do not need to start at the same time). Darts will use the actual time values of the `TimeSeries` time axes in order to jointly slice the targets and covariates correctly, both for training and inference. Of course the covariates still need to have a sufficient span, otherwise Darts will complain.
As explained above, `TCNModel`, `NBEATSModel`, `BlockRNNModel`, `TransformerModel` use past covariates (they will complain if you try using `future_covariates`). If these past covariates happen to also be known into the future, then these models are also able to produce forecasts for `n > output_chunk_length` (as shown above for `BlockRNNModel`) in an auto-regressive way.
By contrast, `RNNModel` uses future covariates (it will complain if you try specifying `past_covariates`). This means that prediction with this model requires the covariates (at least) `n` time steps into the future after prediction time.
Past and future covariates (as well as the way they are consummed by the different models) an important but non-trivial topic, and we plan to dedicate a future notebook (or article) to explain this further.
At the time of writing, Darts does not support covariates that are not time series - such as for instance class label informations or other conditioning variables. One trivial (although likely suboptimal) way to go around this is to build time series filled with constant values encoding the class labels. Supporting more general types of conditioning is a future feature on the Darts development roadmap.
| true |
code
| 0.690859 | null | null | null | null |
|
```
import pandas as pd
import geoplot
import geopandas
import matplotlib.pyplot as plt
%matplotlib inline
from shapely.geometry import Polygon
import warnings
warnings.filterwarnings(action="ignore")
#Check geopandas version
geopandas.__version__
#Set figure size and font size
plt.rcParams["figure.figsize"]=(12,10)
plt.rcParams["font.size"]=12
```
# Getting the canvas ready
```
world = geopandas.read_file(geopandas.datasets.get_path('naturalearth_lowres'))
world.plot()
fig=geoplot.polyplot(world,projection=geoplot.crs.Orthographic())
plt.show()
europe=world[world.continent=="Europe"]
europe.plot()
europe=europe[(europe.name!="Russia") & (europe.name!="Iceland")]
europe.plot()
```
## Clip French Guinea off of map of Europe
```
# Create a custom polygon
polygon = Polygon([(-25,35), (40,35), (40,75),(-25,75)])
poly_gdf = geopandas.GeoDataFrame([1], geometry=[polygon], crs=world.crs)
fig,ax=plt.subplots()
ax=europe.plot(ax=ax)
poly_gdf.plot(edgecolor="red",ax=ax, alpha=0.1)
plt.show()
#Clip polygon from the map of Europe
europe=geopandas.clip(europe, polygon) #Input and feature to be clipped
europe.plot()
```
## Data Preparation
Source: https://ourworldindata.org/grapher/carbon-intensity-electricity
```
df=pd.read_csv("carbon-intensity-electricity.csv")
df
df["Entity"].unique()
len(df["Entity"].unique())
europe.name.unique()
len(europe.name.unique())
list(europe.name.unique())
```
### Check if countries in df are present in europe geodataframe or not
```
#Initialize an empty list for countries which are present in df, but not in europe
unmatched=[]
for country in list(df["Entity"].unique()):
if country in (list(europe.name.unique())):
pass
else:
unmatched.append(country)
unmatched
df["Year"].dtypes
#Retain values for 2010, 2015 and 2020 only
df=df[(df.Year==2000)|(df.Year==2005)|(df.Year==2010) | (df.Year==2015) | (df.Year==2020)]
#Drop Code column
df.drop("Code",axis=1, inplace=True)
#Remove unmatched items from df
df=df[(df.Entity!="Cyprus") & (df.Entity!="EU-27") & (df.Entity!="EU27+1") & (df.Entity!="Malta")]
#Make pivot
df=pd.pivot_table(df, index="Entity",columns="Year")
df
df.columns=["2000","2005","2010","2015","2020"]
df=df.reset_index()
df.rename({"Entity":"name"},axis=1,inplace=True)
df
selected_countries=europe[europe.name.isin(list(df.name))]
selected_countries
selected_countries=selected_countries.merge(df,on="name",how="left")
selected_countries
#Range of Variable you see as map color. Here I select the minimum and maximum of all the years selected.
vmin=selected_countries[["2000","2005","2010","2015","2020"]].min().min()
vmax=selected_countries[["2000","2005","2010","2015","2020"]].max().max()
fig,axs=plt.subplots(2,3) #3 columns and 1 row
fig.suptitle("Emissions Intensity from electricity generation in Europe 2000-2020", fontweight="bold",fontsize=15)
#Adjust space betweeen rows
plt.subplots_adjust(bottom=0.2, top=0.9, hspace=0.25)
axs[0,0]=europe.plot(color="whitesmoke",edgecolor="black",ax=axs[0,0])
selected_countries.plot("2000",cmap="Reds",edgecolor="black",ax=axs[0,0], vmin=vmin, vmax=vmax)
axs[0,0].set_title("2000")
axs[0,0].xaxis.set_visible(False)
axs[0,1]=europe.plot(color="whitesmoke",edgecolor="black",ax=axs[0,1])
selected_countries.plot("2005",cmap="Reds",edgecolor="black",ax=axs[0,1], vmin=vmin, vmax=vmax)
axs[0,1].set_title("2005")
axs[0,1].xaxis.set_visible(False)
axs[0,1].yaxis.set_visible(False)
axs[0,2]=europe.plot(color="whitesmoke",edgecolor="black",ax=axs[0,2])
selected_countries.plot("2010",cmap="Reds",edgecolor="black",ax=axs[0,2], vmin=vmin, vmax=vmax)
axs[0,2].set_title("2010")
axs[0,2].xaxis.set_visible(False)
axs[0,2].yaxis.set_visible(False)
axs[1,0]=europe.plot(color="whitesmoke",edgecolor="black",ax=axs[1,0])
selected_countries.plot("2015",cmap="Reds",edgecolor="black",ax=axs[1,0], vmin=vmin, vmax=vmax)
axs[1,0].set_title("2015")
axs[1,1]=europe.plot(color="whitesmoke",edgecolor="black",ax=axs[1,1])
selected_countries.plot("2020",cmap="Reds",edgecolor="black",ax=axs[1,1], vmin=vmin, vmax=vmax)
axs[1,1].set_title("2020")
axs[1,1].yaxis.set_visible(False)
axs[1,2]=europe.plot(color="whitesmoke",edgecolor="black",ax=axs[1,2])
axs[1,2].set_title("Future?")
axs[1,2].yaxis.set_visible(False)
# add colorbar
cax = fig.add_axes([0.92, 0.2, 0.03, 0.7]) #[left, bottom, width, height]
sm = plt.cm.ScalarMappable(cmap='Reds', norm=plt.Normalize(vmin=vmin, vmax=vmax))
# fake up the array of the scalar mappable. Urgh...
sm._A = []
lgd=fig.colorbar(sm, cax=cax).set_label("gCO$_2$e/kWh", rotation=0,y=1.05, labelpad=-35)
plt.savefig("Emissions Intensity over the past two decades.jpeg",
dpi=300)
plt.show()
pd.set_option("display.max_columns",None)
df
df
df.set_index("name",inplace=True)
df=df.T
df[["Estonia","Poland","Sweden","United Kingdom","Germany","France"]].plot(marker="o",linestyle="dashed",figsize=(8,6))
plt.title("Carbon Intensity of Electricity Generation Of Selective Countries")
plt.xlabel("Years"); plt.ylabel("gCO$_2$/kWh")
lgd=plt.legend(bbox_to_anchor=(1,1))
plt.savefig("Selective Countries Carbon Intensity",
dpi=300,
bbox_extra_artists=(lgd,),
bbox_inches="tight")
plt.show()
selected_countries.head()
#Getting the lan and lat here from geometry data
selected_countries['coordinates']=selected_countries['geometry'].apply(lambda x: x.representative_point().coords[:][0])
selected_countries.head()
```
## Analysing carbon intensity in 2020
```
fig, ax=plt.subplots()
ax=europe.plot(color="whitesmoke",
edgecolor='black',
ax=ax)
selected_countries.plot("2020",
ax=ax,
cmap="Reds",
legend=True)
#Add names of county here
for idx, row in selected_countries.iterrows():
plt.annotate(s=row["name"], xy=row['coordinates'],
horizontalalignment='center', color='black',fontsize=10, fontweight='light')
plt.title("Carbon Intensity of Electricity Generation in Europe in 2020 (gCO$_2$/kWh)")
plt.savefig("2020 figure", dpi=300)
#cax = fig.add_axes([0.92, 0.2, 0.03, 0.7])
#sm=plt.cm.ScalarMappable(cmap='Reds',
# norm=plt.Normalize(vmin=selected_countries["2020"].min(), vmax=selected_countries["2020"].max()))
#lgd=fig.colorbar(sm,cax=cax).set_label("gCO$_2$e/kWh", rotation=0,y=1.05, labelpad=-35)
```
| true |
code
| 0.627637 | null | null | null | null |
|
### SVM (Support Vector Machine)
In this notebook we are going to implement the Support Vector Machine algorithim from scratch using python and numpy.
### Definition
Support Vector Machine (SVM) is a relatively simple Supervised Machine Learning Algorithm used for classification and/or regression. It is more preferred for classification but is sometimes very useful for regression as well. Basically, SVM finds a hyper-plane that creates a boundary between the types of data. In 2-dimensional space, this hyper-plane is nothing but a line.
In SVM, we plot each data item in the dataset in an N-dimensional space, where N is the number of features/attributes in the data. Next, find the optimal hyperplane to separate the data. So by this, you must have understood that inherently, SVM can only perform binary classification (i.e., choose between two classes). However, there are various techniques to use for multi-class problems.
### Imports for implementation.
```
import numpy as np
```
### The SVM class
In the following code cell we are going then to create an SVM algorithm using numpy.
```
class SVM:
"""
The init function takes the following parameters:
* lr - leaning rate defalt is .001
* lambda_param - default is .01
* n_inters - number of iterations default is 10000
"""
def __init__(self, lr=0.001, lambda_param=.01, n_iters=1000):
self.lr= lr
self.lambda_param = lambda_param
self.n_iters = n_iters
self.w = None
self.b = None
def fit(self, X, y):
n_samples, n_features = X.shape
y_ = np.where(y<=0, -1, 1)
self.b = 0
self.w = np.zeros(n_features)
for _ in range(self.n_iters):
for i, x_i in enumerate(X):
condition = y_[i] * (np.dot(x_i, self.w) - self.b) >= 1
if condition:
self.w -= self.lr * (2 * self.lambda_param * self.w)
else:
self.w -= self.lr * (
2 * self.lambda_param * self.w - np.dot(x_i, y_[i])
)
self.b -= self.lr * y_[i]
def predict(self, X):
approx = np.dot(X, self.w) - self.b
return np.sign(approx)
def evaluate(self, y_true, y_pred):
return f"Acc: {np.equal(y_true, y_pred).sum()/len(y_true) * 100}%"
```
### Fit, Predict and evaluate
In the following code cells we are going to create a dummy dataset from `sklearn` and call the fit, predict and evaluate function from the SVM classifier
```
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
X, y = datasets.make_blobs(
n_samples=150, n_features=2, centers=2, cluster_std=1.05,
random_state=42
)
y = np.where(y == 0, -1, 1)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=.2
)
```
### Intance of a classifier
```
clf = SVM()
clf.fit(X_train, y_train)
predictions = clf.predict(X_test)
predictions[:10]
clf.evaluate(predictions, y_test)
```
### Ref
1. [geeks for geeks](https://www.geeksforgeeks.org/introduction-to-support-vector-machines-svm/)
2. [python engineer](https://github.com/python-engineer/MLfromscratch/blob/master/mlfromscratch/svm.py)
```
```
| true |
code
| 0.579757 | null | null | null | null |
|
# Exploration of the UC Berkeley Milling Data Set
> In this notebook we introduce a metal machining data set. We’ll explore the data set and see how it is structured. Data exploration is an important first step in any new data science problem. (notebook originally featured at [tvhahn.com](https://www.tvhahn.com/), official GitHub repo: https://github.com/tvhahn/ml-tool-wear)
Let’s pretend that you're at a manufacturing company engaged in metal machining. You're an engineer working at this company, and the CEO has tasked you to develop a system to detect tool wear. Where to start?
UC Berkeley created a milling data set in 2008, which you can download from the [NASA Prognostics Center of Excellence web page](https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/). We’ll use this data set to try out some ideas. In this notebook we’ll briefly cover what milling is before exploring and visualizing the data set.
## Setup Notebook
The notebook can be run with google colab. Alternatively, clone the repo and run on your local machine. You'll need python 3.6+ with the following packages in your local environment:
* Numpy
* SciPy
* Pandas
* Matplotlib
* Seaborn
First, we will load all the neccessary packages.
```
import numpy as np
import scipy.io as sio # for reading matlab files
import pathlib
from pathlib import Path
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import os
import zipfile
%matplotlib inline
```
Set the appropriate working folders.
```
# move into the root directory of 'Manufacturing-Data-Science-with-Python'
os.chdir('../')
root_dir = Path.cwd() # set the root directory as a Pathlib path
folder_raw_data = root_dir / 'Data Sets/milling_uc_berkeley/raw/' # raw data folder that holds the .zip .mat files for milling data
folder_processed_data = root_dir / 'Data Sets/milling_uc_berkeley/processed/' # processed data folder
working_folder = root_dir / 'Metal Machining' # working folder
```
We now need to prepare the notebook by downloading the milling data file and other important files. This needs to be done if you are running in google colab. If the repository has been cloned from github, then there is no need.
```
# if the the raw data folder does not exist, then you are likely
# in a google colab environment. In that case, we will create the
# raw data and processed data folders and download the appropriate
# files
if folder_raw_data.exists() == False:
pathlib.Path(folder_raw_data).mkdir(parents=True, exist_ok=True)
os.chdir(folder_raw_data)
!wget 'https://github.com/tvhahn/Manufacturing-Data-Science-with-Python/raw/master/Data%20Sets/milling_uc_berkeley/raw/mill.zip'
if folder_processed_data.exists() == False:
pathlib.Path(folder_processed_data).mkdir(parents=True, exist_ok=True)
os.chdir(folder_processed_data)
!wget 'https://raw.githubusercontent.com/tvhahn/Manufacturing-Data-Science-with-Python/master/Data%20Sets/milling_uc_berkeley/processed/labels_with_tool_class.csv'
# if working folder does not exist, then create it
pathlib.Path(working_folder).mkdir(parents=True, exist_ok=True)
if (working_folder / 'data_prep.py').exists() == False:
os.chdir(working_folder)
# download important python files into the 'Metal Machining' directory
!wget 'https://raw.githubusercontent.com/tvhahn/Manufacturing-Data-Science-with-Python/master/Metal%20Machining/data_prep.py'
# extract mill.mat from the zip file
with zipfile.ZipFile(folder_raw_data / 'mill.zip', 'r') as zip_ref:
zip_ref.extractall(folder_raw_data)
os.chdir(working_folder)
```
# What is milling?
In milling, a rotary cutter removes material as it moves along a work piece. Most often, milling is performed on metal – it's metal machining – and that’s what is happening at the company you’re at.
The picture below demonstrates a face milling procedure. The cutter is progressed forward while rotating. As the cutter rotates, the tool inserts “bite” into the metal and remove it.
<br>
<div style="text-align: center; ">
<figure>
<img src="images/face_milling.svg" alt="milling tool cutting into metal" style="background:none; border:none; box-shadow:none; text-align:center" width="400px"/>
<div style="text-align: center; ">
<br>
<figcaption style="color:grey; font-size:smaller"> A milling tool has serveral tool inserts on it. As the tool rotates, and is pushed forward, the inserts cut into the metal. (Image modified from <a href="https://commons.wikimedia.org/wiki/File:Fraisage_surfacage.svg#/media/File:Fraisage_surfacage.svg">Wikipedia</a>)</figcaption>
</div>
</figure>
</div>
Over time, the tool inserts wear. Specifically, the flank of the tool wears, as shown below. In the UC Berkeley milling data set the flank wear (VB) is measured as the tool wears.
<div style="text-align: center; ">
<figure>
<img src="images/flank_wear.svg" alt="flank wear on tool insert" style="background:none; border:none; box-shadow:none; text-align:center" width="500px"/>
<!-- <div style="text-align: left; "> -->
<figcaption style="color:grey; font-size:smaller">Flank wear on a tool insert (perspective and front view). <i>VB</i> is the measure of flank wear. (Image from author)</figcaption>
<!-- </div> -->
</figure>
</div>
# Data Exploration
Data exploration is the first important step when tackling any new data science problem. Where to begin? The first step is understanding how the data is structured. How is the data stored? In a database? In an array? Where is the meta-data (things like labels and time-stamps)?
## Data Structure
The UC Berkeley milling data set is contained in a structured MATLAB array. We can load the .mat file using the scipy.io module and the loadmat function.
```
os.chdir(working_folder) # make sure you're in the right folder
# load the data from the matlab file
m = sio.loadmat(folder_raw_data / 'mill.mat',struct_as_record=True)
```
The data is stored as a dictionary. Let's look to see what it is made of.
```
# show some of the info from the matlab file
print('Keys in the matlab dict file: \n', m.keys(), '\n')
```
Only the 'mill' part of the dictionary contains useful information. We'll put that in a new numpy array called 'data.
```
# check to see what m['mill'] is
print(type(m['mill']))
# store the 'mill' data in a seperate np array
data = m['mill']
```
We now want to see what the 'data' array is made up of.
```
# store the field names in the data np array in a tuple, l
l = data.dtype.names
print('List of the field names:\n',l)
```
## Meta-Data
The documentation with the UC Berkeley milling data set contains additional information, and highlights information about the meta-data. The data set is made of 16 cases of milling tools performing cuts in metal. Six cutting parameters were used in the creation of the data:
* the metal type (either cast iron or steel, labelled as 1 or 2 in the data set, respectively)
* the depth of cut (either 0.75 mm or 1.5 mm)
* the feed rate (either 0.25 mm/rev or 0.5 mm/rev)
Each of the 16 cases is a combination of the cutting parameters (for example, case one has a depth of cut of 1.5 mm, a feed rate of 0.5 mm/rev, and is performed on cast iron).
The cases are made up of individual cuts from when the tool is new to degraded or worn. There are 167 cuts (called 'runs' in the documentation) amongst all 16 cases. Many of the cuts are accompanied by a measure of flank wear (VB). We'll use this later to label the cuts as eigther healthy, degraded, or worn.
Finally, six signals were collected during each cut: acoustic emission (AE) signals from the spindle and table; vibration from the spindle and table; and AC/DC current from the spindle motor. The signals were collected at 250 Hz and each cut has 9000 sampling points, for a total signal length of 36 seconds.
We will extract the meta-data from the numpy array and store it as a pandas dataframe -- we'll call this dataframe `df_labels` since it contains the label information we'll be interested in. This is how we create the dataframe.
```
# store the field names in the data np array in a tuple, l
l = data.dtype.names
# create empty dataframe for the labels
df_labels = pd.DataFrame()
# get the labels from the original .mat file and put in dataframe
for i in range(7):
# list for storing the label data for each field
x = []
# iterate through each of the unique cuts
for j in range(167):
x.append(data[0,j][i][0][0])
x = np.array(x)
df_labels[str(i)] = x
# add column names to the dataframe
df_labels.columns = l[0:7]
# create a column with the unique cut number
df_labels['cut_no'] = [i for i in range(167)]
df_labels.head()
```
## Data Visualization
Visuallizing a new data set is a great way to get an understanding of what is going on, and detect any strange things going on. I also love data visualization, so we'll create a beautiful graphic using Seaborn and Matplotlib.
There are only 167 cuts in this data set, which isn't a huge amount. Thus, we can visually inspect each cut to find abnormalities. Fortunately, I've already done that for you.... Below is a highlight.
First, we'll look at a fairly "normal" cut -- cut number 167.
```
# look at cut number 167 (index 166)
cut_no = 166
fig, ax = plt.subplots()
ax.plot(data[0,cut_no]['smcAC'], label='smcAC')
ax.plot(data[0,cut_no]['smcDC'], label='smcDC')
ax.plot(data[0,cut_no]['vib_table'], label='vib_table')
ax.plot(data[0,cut_no]['vib_spindle'], label='vib_spindle')
ax.plot(data[0,cut_no]['AE_table'], label='AE_table')
ax.plot(data[0,cut_no]['AE_spindle'], label='AE_spindle')
plt.legend()
```
However, if you look at all the cuts, you'll find that cuts 18 and 95 (index 17 and 94) are off -- they will need to be discarded when we start building our anomaly detection model.
```
# plot cut no. 18 (index 17). Only plot current signals for simplicity.
cut_no = 17
fig, ax = plt.subplots()
ax.plot(data[0,cut_no]['smcAC'], label='smcAC')
ax.plot(data[0,cut_no]['smcDC'], label='smcDC')
plt.legend()
# plot cut no. 95 (index 94). Only plot current signals for simplicity.
cut_no = 94
fig, ax = plt.subplots()
ax.plot(data[0,cut_no]['smcAC'], label='smcAC')
ax.plot(data[0,cut_no]['smcDC'], label='smcDC')
plt.legend()
```
Cut 106 is also weird...
```
cut_no = 105
fig, ax = plt.subplots()
ax.plot(data[0,cut_no]['smcAC'], label='smcAC')
ax.plot(data[0,cut_no]['smcDC'], label='smcDC')
plt.legend()
```
Finally, we'll create a beautiful plot that nicely visualizes each of the six signals together.
```
def plot_cut(cut_signal, signals_trend, cut_no):
# define colour palette and seaborn style
pal = sns.cubehelix_palette(6, rot=-0.25, light=0.7)
sns.set(style="white", context="notebook")
fig, axes = plt.subplots(
6, 1, dpi=150, figsize=(5, 6), sharex=True, constrained_layout=True,
)
# the "revised" signal names so it looks good on the chart
signal_names_revised = [
"AE Spindle",
"AE Table",
"Vibe Spindle",
"Vibe Table",
"DC Current",
"AC Current",
]
# go through each of the signals
for i in range(6):
# plot the signal
# note, we take the length of the signal (9000 data point)
# and divide it by the frequency (250 Hz) to get the x-axis
# into seconds
axes[i].plot(np.arange(0,9000)/250.0,
cut_signal[signals_trend[i]],
color=pal[i],
linewidth=0.5,
alpha=1)
axis_label = signal_names_revised[i]
axes[i].set_ylabel(
axis_label, fontsize=7,
)
# if it's not the last signal on the plot
# we don't want to show the subplot outlines
if i != 5:
axes[i].spines["top"].set_visible(False)
axes[i].spines["right"].set_visible(False)
axes[i].spines["left"].set_visible(False)
axes[i].spines["bottom"].set_visible(False)
axes[i].set_yticks([]) # also remove the y-ticks, cause ugly
# for the last signal we will show the x-axis labels
# which are the length (in seconds) of the signal
else:
axes[i].spines["top"].set_visible(False)
axes[i].spines["right"].set_visible(False)
axes[i].spines["left"].set_visible(False)
axes[i].spines["bottom"].set_visible(False)
axes[i].set_yticks([])
axes[i].tick_params(axis="x", labelsize=7)
axes[i].set_xlabel('Seconds', size=5)
signals_trend = list(l[7:]) # there are 6 types of signals, smcAC to AE_spindle
signals_trend = signals_trend[::-1] # reverse the signal order so that it is matching other charts
# we'll plot signal 146 (index 145)
cut_signal = data[0, 145]
plot_cut(cut_signal, signals_trend, "cut_146")
# plt.savefig('cut_signals.png',format='png') # save the figure
plt.show()
```
| true |
code
| 0.527317 | null | null | null | null |
|
# Alternative methods for chemical equilibrium
The methods previously examined for determining the equilibrium composition rely on knowing the chemical reaction(s) occurring, and can involve highly nonlinear equations.
Fortunately, we have methods that do not require knowing what reaction(s) are occurring.
We will compare two such solution methods:
1. {ref}`gibbs-minimization`
2. {ref}`lagrange-method`
This modules introduces these methods using the same example as {doc}`equilibrium-constant`: consider a mixture with 1 kilomole of carbon monoxide (CO) that reacts with 0.5 kmol of oxygen (O$_2$) to form a mixture of CO, CO$_2$, and O$_2$, with the equilibrium conditions of 2500 K and (a) 1 atm (b) 10 atm. Find the equilibrium composition in terms of the mole fraction. Assume the mixture behaves as an ideal gas.
```
import numpy as np
import cantera as ct
from scipy.optimize import root, minimize
from pint import UnitRegistry
ureg = UnitRegistry()
Q_ = ureg.Quantity
# for convenience:
def to_si(quant):
'''Converts a Pint Quantity to magnitude at base SI units.
'''
return quant.to_base_units().magnitude
```
(gibbs-minimization)=
## Direct minimization of Gibbs free energy
One method to finding the equilibrium composition is to directly minimize the Gibbs free energy of the mixture.
The total Gibbs free energy of the mixture is
$$
G = \sum_{i=1}^C n_i \mu_i \;,
$$
where $C$ is the number of components (i.e., chemical species), $n_i$ is the number of moles of component $i$, and $\mu_i$ is the chemical potential of component $i$.
For an ideal gas in a mixture, the chemical potential can be calculated using
$$
\mu_i = \mu_i^{\circ} + R_{\text{univ}} T \ln \left( \frac{y_i P}{P^{\circ}} \right) \;,
$$
where $R_{\text{univ}}$ is the universal gas constant, $P$ is the mixture pressure,
$P^{\circ}$ is the (standard-state) reference pressure (usually 1 atm or 100 kPa),
and $\mu_i^{\circ}$ is the chemical potential of pure substance $i$ at temperature $T$ and reference pressure $P^{\circ}$, which is the same as the standard-state molar specific Gibbs free energy $\overline{g}_i^{\circ}$:
$$
\mu_i^{\circ} = \overline{g}_i^{\circ} = \overline{h}_i^{\circ} - T \overline{s}_i^{\circ} \;.
$$
This method works by treating this as an optimization problem, where the objective is to minimize $G$, which is a function of the composition $n_i$.
**Constraints:** However, this problem is constrained because the amount of each element must be balanced:
$$
E_j = E_{0, j}
$$
where $E_j = \sum_{i=1}^C n_i e_{i,j}$ is the number of moles of each element $j$ ($E$ is the total number of elements), $E_{0, j} = \sum_{i=1}^C n_{0,i} e_{i,j}$ is the initial number of moles of each element, $n_{0,i}$ is the initial number of moles of each component $i$, and $e_{i,j}$ is the number of moles of element $j$ in component $i$ (defined by the chemical formula).
In addition, the number of moles of each component must remain non-negative:
$$
n_i \geq 0
$$
This is thus a **constrained optimization** problem—we can solve these for simpler problems, but they can become computationally expensive for a larger number of unknowns. For now, we can use the [`SLSQP`](https://docs.scipy.org/doc/scipy/reference/optimize.minimize-slsqp.html) optimization method provided by the SciPy [`minimize`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html) function.
The formal statement of our problem is:
$$
\min_{n_0, n_1, n_2} \left( n_0 \mu_0 (n_0, n_1, n_2) + n_1 \mu_1 (n_0, n_1, n_2) + n_2 \mu_2 (n_0, n_1, n_2) \right) \\
\text{subject to:} \quad \sum_{i} n_i e_{i,0} - \sum_{i} n_{0,i} e_{i,0} = 0\\
\phantom{subject to:} \quad \sum_{i} n_i e_{i,1} - \sum_{i} n_{1,i} e_{i,0} = 0\\
\phantom{subject to:} \quad n_0 \geq 0 \\
\phantom{subject to:} \quad n_1 \geq 0 \\
\phantom{subject to:} \quad n_2 \geq 0
$$
We will need to define three functions:
1. Evaluate the Gibbs free energy of the mixture,
2. Evaluate the equality constraints on elemental balances
3. Evaluate the inequality constraints on numbers of moles
First, let's input the known information:
```
# Known information
components = ['CO', 'O2', 'CO2']
moles_initial = np.array([1.0, 0.5, 0.0])
temperature = Q_(2500, 'K')
pressures = [1, 10] * Q_('atm')
# elemental composition of species
elemental_comp = np.array([
[1, 0, 1], # carbon
[1, 2, 2], # oxygen
])
# initial molar amounts of each element
initial_elements = np.dot(elemental_comp, moles_initial)
def calc_total_gibbs(moles, temperature, pressure, components, gas):
'''Evaluate Gibbs free energy of mixture, based on component numbers of moles.
'''
moles = Q_(moles, 'kmol')
mole_fractions = moles / np.sum(moles)
# get standard-state Gibbs free energy of each component
gibbs = np.zeros(len(components))
for idx, comp in enumerate(components):
gas.TPX = (
to_si(temperature), to_si(Q_(1, 'atm')),
f'{comp}:1.0'
)
gibbs[idx] = gas.gibbs_mole
gibbs *= Q_('J/kmol')
gas_constant = Q_(ct.gas_constant, 'J/(kmol*K)')
chemical_potentials = (
gibbs + gas_constant * temperature * np.log(
mole_fractions * pressure / Q_(1.0, 'atm')
)
)
# scale this result down
return to_si(np.sum(moles * chemical_potentials)) / 1e6
# We need to define functions for the constraints:
def inequality_cons(x):
'''Inequality constraint: all numbers of moles must be ≥ 0.
'''
return x
def equality_cons(x):
'''Equality constraint: Number of moles of each element remain constant.
'''
return np.dot(elemental_comp, x) - initial_elements
```
```{margin} Potential issues
Notice that this function evaluating Gibbs free energy of the mixture scales the result down by $10^6$.
I found this was necessary for the solver to converge. However, this means that the function does not return the Gibbs free energy in units of J, but instead MJ.
```
```
# Solve for first pressure
pressure = pressures[0]
gas = ct.Solution('gri30.cti')
x0 = np.array([0.5, 0.5, 0.5])
sol = minimize(
calc_total_gibbs, x0, method='SLSQP',
args=(temperature, pressure, components, gas),
constraints=[
{'type': 'eq','fun': equality_cons},
{'type': 'ineq','fun': inequality_cons}
],
options={'maxiter': 1000}
)
moles = sol.x
mole_fractions = moles / np.sum(moles)
print('Successful convergence: ', sol.success)
# check constraints
print('All moles non-negative: ', all(moles > 0))
print('All elements balanced: ', all(equality_cons(moles) == 0))
print()
print(f'Mole fractions at {pressure: .1f}:')
for idx, comp in enumerate(components):
print(f'{comp}: {mole_fractions[idx]: .3f}')
# Now try next pressure
pressure = pressures[1]
gas = ct.Solution('gri30.cti')
x0 = np.array([0.5, 0.5, 0.5])
sol = minimize(
calc_total_gibbs, x0, method='SLSQP',
args=(temperature, pressure, components, gas),
constraints=[
{'type': 'eq','fun': equality_cons},
{'type': 'ineq','fun': inequality_cons}
],
options={'maxiter': 1000}
)
moles = sol.x
mole_fractions = moles / np.sum(moles)
print('Successful convergence: ', sol.success)
# check constraints
print('All moles non-negative: ', all(moles > 0))
print('All elements balanced: ', all(equality_cons(moles) == 0))
print()
print(f'Mole fractions at {pressure: .1f}:')
for idx, comp in enumerate(components):
print(f'{comp}: {mole_fractions[idx]: .3f}')
```
These results match the values we found previously—whew! 😅
(lagrange-method)=
## Lagrange's method of undetermined multipliers
This method converts the problem into a system of algebraic equations, where the number of equations equal the number of unknowns. It does this by introducing a set of unknown multipliers, $\lambda_j$, with one for each element in the system.
Then, the system of equations we need to solve includes the element balances and equations involving the multipliers:
$$
\sum_{i=1}^C n_i e_{i,j} - \sum_{i=1}^C n_{0,i} e_{i,j} = 0 \quad \text{for } j=1, \ldots, E \;, \\
\mu_i + \sum_{j=1}^E \lambda_j e_{i,j} = 0 \quad \text{for } i=1, \ldots, C \;, \\
$$
where the unknowns are the numbers of moles for each compound $n_i$ where $i = 1, \ldots, C$ and the multipliers for each element $\lambda_j$ where $j = 1, \ldots, E$.
In this system, $e_{i,j}$ is the number of moles of element $j$ in component $i$, $n_{0,i}$ is the initial number of moles of component $i$, $\mu_i$ is the chemical potential of component $i$, $E$ is the number of elements, and $C$ is the number of components (chemical species).
The chemical potentials can be calculated for each component of an ideal gas:
$$
\mu_i = \mu_i^{\circ} + R_{\text{univ}} T \ln \left( \frac{y_i P}{P^{\circ}} \right) \;,
$$
where $R_{\text{univ}}$ is the universal gas constant, $P$ is the mixture pressure,
$P^{\circ}$ is the (standard-state) reference pressure (usually 1 atm or 100 kPa),
and $\mu_i^{\circ}$ is the chemical potential of pure substance $i$ at temperature $T$ and reference pressure $P^{\circ}$, which is the same as the standard-state molar specific Gibbs free energy $\overline{g}_i^{\circ}$:
$$
\mu_i^{\circ} = \overline{g}_i^{\circ} = \overline{h}_i^{\circ} - T \overline{s}_i^{\circ} \;.
$$
We can evaluate $\overline{g}_i^{\circ} (T)$ using a Cantera `Solution` object and specifying the temperature, pressure (using the 1 atm reference), and composition of each component as a pure substance.
```
# Known information
components = ['CO', 'O2', 'CO2']
moles_initial = np.array([1.0, 0.5, 0.0])
# Elemental makeup of components
elemental_comp = np.array([
[1, 0, 1], # carbon
[1, 2, 2], # oxygen
])
temperature = Q_(2500, 'K')
pressures = [1, 10] * Q_('atm')
def lagrange_system(x, temperature, pressure, components,
gas, elemental_comp, moles_initial):
'''System of equations for Lagrange multiplier approach.
'''
moles = np.array([x[0], x[1], x[2]])
multipliers = np.array([x[3], x[4]])
mole_fractions = moles / np.sum(moles)
# get standard-state Gibbs free energy of each component
gibbs = np.zeros(len(components))
for idx, comp in enumerate(components):
gas.TPX = (
to_si(temperature), to_si(Q_(1, 'atm')),
f'{comp}:1.0'
)
gibbs[idx] = gas.gibbs_mole
gibbs *= Q_('J/kmol')
gas_constant = Q_(ct.gas_constant, 'J/(kmol*K)')
chemical_potentials = (
gibbs + gas_constant * temperature * np.log(
mole_fractions * pressure / Q_(1.0, 'atm')
)
)
# initial molar amounts of each element
initial_moles_elements = np.dot(elemental_comp, moles_initial)
moles_elements = np.dot(elemental_comp, moles)
# We can take advantage of element-wise operations with these arrays,
# and concisely evaluate all the equations
element_equations = moles_elements - initial_moles_elements
multiplier_equations = to_si(
chemical_potentials +
np.dot(multipliers, elemental_comp) * Q_('J/kmol')
)
# Return the set of equations joined together
return np.concatenate((element_equations, multiplier_equations))
```
After setting up the function to evaluate the system of equations, we can solve for the equilibrium composition at the first pressure using the [`root`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.root.html) function, with the `lm` (Levenberg-Marquardt) method.
We do need to specify some initial guess values for each of the unknowns; while guess values for the numbers of moles of each component may be straightforward (e.g., typically around one), the Lagrange multipliers are more abstract and may take some trial and error.
```
# Solve at first pressure
pressure = pressures[0]
gas = ct.Solution('gri30.cti')
# initial guesses
x0 = [1.0, 1.0, 1.0, 1e6, 1e6]
sol = root(
lagrange_system, x0, method='lm',
args=(temperature, pressure, components, gas, elemental_comp, moles_initial)
)
print('Root-finding algorithm success: ', sol.success)
print(f'Function evaluation (should be small): {sol.fun}')
print('Number of function evaluations: ', sol.nfev)
print()
moles = sol.x[0:3]
mole_fractions = moles / np.sum(moles)
print(f'Mole fractions at {pressure: .1f}:')
for idx, comp in enumerate(components):
print(f'{comp}: {mole_fractions[idx]: .3f}')
pressure = pressures[1]
gas = ct.Solution('gri30.cti')
x0 = [1.0, 1.0, 1.0, 1e6, 1e6]
sol = root(
lagrange_system, x0, method='lm',
args=(temperature, pressure, components, gas, elemental_comp, moles_initial)
)
print('Root-finding algorithm success: ', sol.success)
print(f'Function evaluation (should be near zero): {sol.fun}')
print('Number of function evaluations: ', sol.nfev)
print()
moles = sol.x[0:3]
mole_fractions = moles / np.sum(moles)
print(f'Mole fractions at {pressure: .1f}:')
for idx, comp in enumerate(components):
print(f'{comp}: {mole_fractions[idx]: .3f}')
```
As expected, this approach also produces the same equilibrium composition! 🎉
| true |
code
| 0.657043 | null | null | null | null |
|
```
#export
from fastai2.test import *
from fastai2.basics import *
from fastai2.callback.progress import *
from fastai2.text.data import TensorText
from nbdev.showdoc import *
#default_exp callback.wandb
```
# Wandb
> Integration with [wandb](https://www.wandb.com/)
First thing first, you need to install wandb with
```
pip install wandb
```
Create a free account then run
```
wandb login
```
in your terminal. Follow the link to get an API token that you will need to paste, then you're all set!
```
#export
import wandb
#export
class WandbCallback(Callback):
"Saves model topology, losses & metrics"
toward_end = True
# Record if watch has been called previously (even in another instance)
_wandb_watch_called = False
def __init__(self, log="gradients", log_preds=True, valid_dl=None, n_preds=36, seed=12345):
# W&B log step (number of training updates)
self._wandb_step = 0
self._wandb_epoch = 0
# Check if wandb.init has been called
if wandb.run is None:
raise ValueError('You must call wandb.init() before WandbCallback()')
store_attr(self, 'log,log_preds,valid_dl,n_preds,seed')
def begin_fit(self):
"Call watch method to log model topology, gradients & weights"
self.run = not hasattr(self.learn, 'lr_finder') and not hasattr(self, "gather_preds")
if not self.run: return
if not WandbCallback._wandb_watch_called:
WandbCallback._wandb_watch_called = True
# Logs model topology and optionally gradients and weights
wandb.watch(self.learn.model, log=self.log)
if hasattr(self, 'save_model'): self.save_model.add_save = Path(wandb.run.dir)/'bestmodel.pth'
if self.log_preds and not self.valid_dl:
#Initializes the batch watched
wandbRandom = random.Random(self.seed) # For repeatability
self.n_preds = min(self.n_preds, len(self.dbunch.valid_ds))
idxs = wandbRandom.sample(range(len(self.dbunch.valid_ds)), self.n_preds)
items = [self.dbunch.valid_ds.items[i] for i in idxs]
test_tls = [tl._new(items, split_idx=1) for tl in self.dbunch.valid_ds.tls]
self.valid_dl = self.dbunch.valid_dl.new(DataSource(tls=test_tls), bs=self.n_preds)
def after_batch(self):
"Log hyper-parameters and training loss"
if self.training:
self._wandb_step += 1
self._wandb_epoch += 1/self.n_iter
hypers = {f'{k}_{i}':v for i,h in enumerate(self.opt.hypers) for k,v in h.items()}
wandb.log({'epoch': self._wandb_epoch,'train_loss': self.smooth_loss, **hypers}, step=self._wandb_step)
def after_epoch(self):
"Log validation loss and custom metrics & log prediction samples"
# Correct any epoch rounding error and overwrite value
self._wandb_epoch = round(self._wandb_epoch)
wandb.log({'epoch': self._wandb_epoch}, step=self._wandb_step)
# Log sample predictions
if self.log_preds:
b = self.valid_dl.one_batch()
self.learn.one_batch(0, b)
preds = getattr(self.loss_func, 'activation', noop)(self.pred)
out = getattr(self.loss_func, 'decodes', noop)(preds)
x,y,its,outs = self.valid_dl.show_results(b, out, show=False, max_n=self.n_preds)
wandb.log({"Prediction Samples": wandb_process(x, y, its, outs)}, step=self._wandb_step)
wandb.log({n:s for n,s in zip(self.recorder.metric_names, self.recorder.log) if n not in ['train_loss', 'epoch', 'time']}, step=self._wandb_step)
def after_fit(self):
self.run = True
wandb.log({}) #To trigger one last synch
```
Optionally logs weights and or gradients depending on `log` (can be "gradients", "parameters", "all" or None), sample predictions if ` log_preds=True` that will come from `valid_dl` or a random sample pf the validation set (determined by `seed`). `n_preds` are logged in this case.
If used in combination with `SaveModelCallback`, the best model is saved as well.
## Example of use:
Once your have defined your `Learner`, before you call to `fit` or `fit_one_cycle`, you need to initialize wandb:
```
import wandb
wandb.init(project=PROJECT_NAME, entity=USER_NAME)
```
(replace `PROJECT_NAME` and `USER_NAME`). Then you add the callback in your call to fit, potentially with `SaveModelCallback` if you want to save the best model:
```
from fastai2.callback.wandb import *
# To log only during one training phase
learn.fit(..., cbs=WandbCallback())
# To log continuously for all training phases
learn = learner(..., cbs=WandbCallback())
```
```
#export
@typedispatch
def wandb_process(x:TensorImage, y, samples, outs):
"Process `sample` and `out` depending on the type of `x/y`"
res = []
for s,o in zip(samples, outs):
img = s[0].permute(1,2,0)
res.append(wandb.Image(img, caption='Input data', grouping=3))
for t, capt in ((o[0], "Prediction"), (s[1], "Ground Truth")):
# Resize plot to image resolution (from https://stackoverflow.com/a/13714915)
my_dpi = 100
fig = plt.figure(frameon=False, dpi=my_dpi)
h, w = img.shape[:2]
fig.set_size_inches(w / my_dpi, h / my_dpi)
ax = plt.Axes(fig, [0., 0., 1., 1.])
ax.set_axis_off()
fig.add_axes(ax)
# Superimpose label or prediction to input image
ax = img.show(ctx=ax)
ax = t.show(ctx=ax)
res.append(wandb.Image(fig, caption=capt))
plt.close(fig)
return res
#export
@typedispatch
def wandb_process(x:TensorImage, y:(TensorCategory,TensorMultiCategory), samples, outs):
return [wandb.Image(s[0].permute(1,2,0), caption=f'Ground Truth: {s[1]}\nPrediction: {o[0]}')
for s,o in zip(samples,outs)]
#export
@typedispatch
def wandb_process(x:TensorText, y:(TensorCategory,TensorMultiCategory), samples, outs):
data = [[s[0], s[1], o[0]] for s,o in zip(samples,outs)]
return wandb.Table(data=data, columns=["Text", "Target", "Prediction"])
#export
_all_ = ['wandb_process']
```
## Export -
```
#hide
from nbdev.export import *
notebook2script()
```
| true |
code
| 0.589421 | null | null | null | null |
|
```
import casadi as cs
from urdf2casadi import urdfparser as u2c
import urdf2casadi.geometry.dual_quaternion as dual_quaternion_geometry
import os # For current directory
dual_quaternion_to_transformation_matrix = dual_quaternion_geometry.to_numpy_transformation_matrix
# urdf2casadi uses cs.SX, which can be hard to read as these are sparse matrices.
# This short function just makes it so that the result will be a numpy matrix
# Use for
def cs2np(asd):
return cs.Function("temp",[],[asd])()["o0"].toarray()
# NOTE: casadi imports numpy as np, so cs.np is numpy
```
# Importing UR5 urdf
```
urdf_path = "../urdf/ur5_mod.urdf"
root_link = "base_link"
end_link = "tool0"
robot_parser = u2c.URDFparser()
robot_parser.from_file(urdf_path)
fk_dict = robot_parser.get_forward_kinematics(root_link, end_link)
print(fk_dict.keys())
```
`fk_dict` is a python dictionary with some of the things we can extract from the URDF. In this example we will show the forward kinematics for the UR5 as a transformation matrix, as a dual quaternion, and a way of calculating the jacobians for the forward kinematics.
## Joint information
```
# CasADi SX symbol giving the joint symbols:
q = fk_dict["q"]
# Upper limits of the joint values
q_upper = fk_dict["upper"]
# Lower limits of the joint values
q_lower = fk_dict["lower"]
# Joint names
joint_names = fk_dict["joint_names"]
print("Number of joints:", q.size()[0])
print("Upper limits:", q_upper)
print("Lower limits:", q_lower)
print("Joint names:", joint_names)
```
## Forward kinematics
```
# CasADi SX function for transformation matrix of the forward kinematics:
T_fk = fk_dict["T_fk"]
# CasADi SX function for dual_quaternion of the forward kinematics:
Q_fk = fk_dict["dual_quaternion_fk"]
```
So what's the position when all joint values are zero?
```
T0 = T_fk([0., 0., 0., 0., 0., 0.])
p0 = T0[:3, 3]
R0 = T0[:3, :3]
print("Transformation matrix:\n",cs2np(T0))
print("Position:\n", "x:",p0[0]," y:", p0[1], " z:", p0[2])
print("Distance from origin:\n", cs.np.linalg.norm(p0), "m")
```
And how about as a dual quaternion?
```
Q0 = Q_fk([0., 0., 0., 0., 0., 0.])
TofQ0 = dual_quaternion_to_transformation_matrix(Q0)
print("Dual quaternion:\n", cs2np(Q0))
print("Dual quaternion as transformation matrix:\n", cs2np(TofQ0))
if cs.np.linalg.norm(cs2np(TofQ0) - cs2np(T0)) < 1e-12:
print("||TofQ0 - T0||< 1e-12, so they are equal")
```
## Jacobians
As we're dealing with symbols, we formulate the symbolic expression for the jacobian, and then we create the functions for them.
```
# Create symbols
fk_position_jacobian_sym = cs.jacobian(T_fk(q)[:3,3], q)
fk_rotation_jacobian_sym = cs.jacobian(T_fk(q)[:3,:3], q)
fk_dual_quaternion_jacobian_sym = cs.jacobian(Q_fk(q), q)
# Create functions
fk_position_jacobian = cs.Function("jac_fk_pos", [q], [fk_position_jacobian_sym], ["q"], ["jac_fk_pos"])
fk_rotation_jacobian = cs.Function("jac_fk_rot", [q], [fk_rotation_jacobian_sym], ["q"], ["jac_fk_rot"])
fk_dual_quaternion_jacobian = cs.Function("jac_fk_Q", [q], [fk_dual_quaternion_jacobian_sym], ["q"], ["jac_fk_Q"])
```
Now let's test them out!
```
joint_vals = [0., 0., 0., 0., 0., 0.,]
pos_jac = fk_position_jacobian(joint_vals)
print("Positional jacobian at ", joint_vals, "is:\n", cs2np(pos_jac))
```
What does this tell us? Let's look at each of the x, y, and z directions separately.
```
print("Comparative measure of how readily each direction is controlled:")
print("Norm of jac in x direction:", cs.np.linalg.norm(cs2np(pos_jac[0,:])))
print("Norm of jac in y direction:", cs.np.linalg.norm(cs2np(pos_jac[1,:])))
print("Norm of jac in z direction:", cs.np.linalg.norm(cs2np(pos_jac[2,:])))
print("\nComparative measure of how readily each joint affects positions:")
for i in range(len(joint_names)):
print(joint_names[i]+":",cs.np.linalg.norm(cs2np(pos_jac[:,i])))
```
So the Z direction is most affected by any of the joint values (but the last), motion in the T direction can only be done by the shoulder pan joint (`q[0]`) because all the motors are standing perpendicular to the y direction. Oh, and the last joint seems to do nothing, well, that's because it's the infinite rotational joint at the end of the UR robot that is just used for rotating the end-effector frame. So basically it doesn't change the position.
What are these comparative measures we're talking about? Essentially it amounts to asking, if we take the same tiny step on each of the joints, which one is the most affected, or if wish to move, which direction is most affect by a tiny step or set of tiny steps?
The following are not as tidy and easily read, but given for completion
```
joint_vals = [0., 0., 0., 0., 0., 0.,]
rot_jac = fk_rotation_jacobian(joint_vals)
print(cs2np(rot_jac))
joint_vals = [0., 0., 0., 0., 0., 0.,]
Q_jac = fk_dual_quaternion_jacobian(joint_vals)
print(cs2np(Q_jac))
print(cs2np(Q_jac)[:4,0])
print("Comparative measure of joint effect on rotation")
for i in range(len(joint_names)):
print(joint_names[i]+":",cs.np.linalg.norm(cs2np(Q_jac)[:4,i])) # First four elements = rotation quaternion
```
Basically taking a tiny step on any of the joints is equally capable at causing rotation regardless of which of the joints we choose to move.
| true |
code
| 0.457985 | null | null | null | null |
|
# Rational Expectations Agricultural Market Model
**Randall Romero Aguilar, PhD**
This demo is based on the original Matlab demo accompanying the <a href="https://mitpress.mit.edu/books/applied-computational-economics-and-finance">Computational Economics and Finance</a> 2001 textbook by Mario Miranda and Paul Fackler.
Original (Matlab) CompEcon file: **demintro01.m**
Running this file requires the Python version of CompEcon. This can be installed with pip by running
!pip install compecon --upgrade
<i>Last updated: 2021-Oct-01</i>
<hr>
```
import numpy as np
import matplotlib.pyplot as plt
from compecon import demo, qnwlogn, discmoments
%matplotlib inline
plt.style.use('seaborn')
```
Generate yield distribution
```
sigma2 = 0.2 ** 2
y, w = qnwlogn(25, -0.5 * sigma2, sigma2)
```
Compute rational expectations equilibrium using function iteration, iterating on acreage planted
```
A = lambda aa, pp: 0.5 + 0.5 * np.dot(w, np.maximum(1.5 - 0.5 * aa * y, pp))
ptarg = 1
a = 1
for it in range(50):
aold = a
a = A(a, ptarg)
print('{:3d} {:8.4f} {:8.1e}'.format(it, a, np.linalg.norm(a - aold)))
if np.linalg.norm(a - aold) < 1.e-8:
break
```
Intermediate outputs
```
q = a * y # quantity produced in each state
p = 1.5 - 0.5 * a * y # market price in each state
f = np.maximum(p, ptarg) # farm price in each state
r = f * q # farm revenue in each state
g = (f - p) * q #government expenditures
xavg, xstd = discmoments(w, np.vstack((p, f, r, g)))
varnames = ['Market Price', 'Farm Price', 'Farm Revenue', 'Government Expenditures']
```
Print results
```
print('\n{:24s} {:8s} {:8s}'.format('Variable', 'Expect', 'Std Dev'))
for varname, av, sd in zip(varnames, xavg, xstd):
print(f'{varname:24s} {av:8.4f} {sd:8.4f}')
```
Generate fixed-point mapping
```
aeq = a
a = np.linspace(0, 2, 100)
g = np.array([A(k, ptarg) for k in a])
```
### Graph rational expectations equilibrium
```
fig1 = plt.figure(figsize=[6, 6])
ax = fig1.add_subplot(111, title='Rational expectations equilibrium', aspect=1,
xlabel='Acreage Planted', xticks=[0, aeq, 2], xticklabels=['0', '$a^{*}$', '2'],
ylabel='Rational Acreage Planted', yticks=[0, aeq, 2],yticklabels=['0', '$a^{*}$', '2'])
ax.plot(a, g, 'b', linewidth=4)
ax.plot(a, a, ':', color='grey', linewidth=2)
ax.plot([0, aeq, aeq], [aeq, aeq, 0], 'r--', linewidth=3)
ax.plot([aeq], [aeq], 'ro', markersize=12)
ax.text(0.05, 0, '45${}^o$', color='grey')
ax.text(1.85, aeq - 0.15,'$g(a)$', color='blue')
fig1.show()
```
### Compute rational expectations equilibrium as a function of the target price
```
nplot = 50
ptarg = np.linspace(0, 2, nplot)
a = 1
Ep, Ef, Er, Eg, Sp, Sf, Sr, Sg = (np.empty(nplot) for k in range(8))
for ip in range(nplot):
for it in range(50):
aold = a
a = A(a, ptarg[ip])
if np.linalg.norm((a - aold) < 1.e-10):
break
q = a * y # quantity produced
p = 1.5 - 0.5 * a * y # market price
f = np.maximum(p, ptarg[ip]) # farm price
r = f * q # farm revenue
g = (f - p) * q # government expenditures
xavg, xstd = discmoments(w, np.vstack((p, f, r, g)))
Ep[ip], Ef[ip], Er[ip], Eg[ip] = tuple(xavg)
Sp[ip], Sf[ip], Sr[ip], Sg[ip] = tuple(xstd)
zeroline = lambda y: plt.axhline(y[0], linestyle=':', color='gray')
```
### Graph expected prices vs target price
```
fig2 = plt.figure(figsize=[8, 6])
ax1 = fig2.add_subplot(121, title='Expected price',
xlabel='Target price', xticks=[0, 1, 2],
ylabel='Expectation', yticks=[0.5, 1, 1.5, 2], ylim=[0.5, 2.0])
zeroline(Ep)
ax1.plot(ptarg, Ep, linewidth=4, label='Market Price')
ax1.plot(ptarg, Ef, linewidth=4, label='Farm Price')
ax1.legend(loc='upper left')
# Graph expected prices vs target price
ax2 = fig2.add_subplot(122, title='Price variabilities',
xlabel='Target price', xticks=[0, 1, 2],
ylabel='Standard deviation', yticks=[0, 0.1, 0.2]) #plt.ylim(0.5, 2.0)
zeroline(Sf)
ax2.plot(ptarg, Sp, linewidth=4, label='Market Price')
ax2.plot(ptarg, Sf, linewidth=4, label='Farm Price')
ax2.legend(loc='upper left')
fig2.show()
# Graph expected farm revenue vs target price
fig3 = plt.figure(figsize=[12, 6])
ax1 = fig3.add_subplot(131, title='Expected revenue',
xlabel='Target price', xticks=[0, 1, 2],
ylabel='Expectation', yticks=[1, 2, 3], ylim=[0.8, 3.0])
zeroline(Er)
ax1.plot(ptarg, Er, linewidth=4)
# Graph standard deviation of farm revenue vs target price
ax2 = fig3.add_subplot(132, title='Farm Revenue Variability',
xlabel='Target price', xticks=[0, 1, 2],
ylabel='Standard deviation', yticks=[0, 0.2, 0.4])
zeroline(Sr)
ax2.plot(ptarg, Sr, linewidth=4)
# Graph expected government expenditures vs target price
ax3 = fig3.add_subplot(133, title='Expected Government Expenditures',
xlabel='Target price', xticks=[0, 1, 2],
ylabel='Expectation', yticks=[0, 1, 2], ylim=[-0.05, 2.0])
zeroline(Eg)
ax3.plot(ptarg, Eg, linewidth=4)
plt.show()
#fig1.savefig('demintro02--01.png')
#fig2.savefig('demintro02--02.png')
#fig3.savefig('demintro02--03.png')
```
| true |
code
| 0.607809 | null | null | null | null |
|
# Anatomy of an MD simulation script File
Different simulation packages often use different languages and have different syntax. For example, HOOMD-Blue uses a Python based interface, LAMMPS uses its own custom scripting language, and GROMACS relies upon an input file to define parameters and methods. However, despite these differences they all generally require the same information to be passed to the code
### Basic components of most script/input files
#### system/code initialization
>box size, particle types, particle initial positions
#### interaction definition
>how do the different species interact with each other
#### integrator setup
>what algorithm will we use to advance particles in time, time step of integration, thermodynamic state point (i.e., T or P).
#### runtime parameters
>total simulation time, which quantities to output and how frequently
## Basic HOOMD-Blue script file
As an example of defining each of these various components, consider setting a very simple simulation consisting of spheres that interact via the Lennard-Jones potential. This exercise is based on the following tutorial created by HOOMD developer Josh Anderson:
http://nbviewer.jupyter.org/github/joaander/hoomd-examples/blob/master/Tutorial%20-%20MD%20-%20Lennard%20Jones.ipynb
### Initialization
HOOMD-Blue uses a Python interface, so we must first import the relevant library and functions.
```
import hoomd
import hoomd.md
```
Next we must specify the 'execution context' to tell the code whether to run on the GPU and CPU. Note, by default HOOMD-Blue will run on the GPU if a compatible one is available, unless otherwise specified via the command line options or by passing an argument to the context initializer.
```
hoomd.context.initialize("")
```
Note, one can pass arguments to the intialize function (see [the documentation](https://hoomd-blue.readthedocs.io/en/stable/module-hoomd-context.html), to e.g., specify it to run on the CPU with a set number of threads,
```context.initialize("--mode=cpu --nthreads=64")```
Particle positions next need to be specified. HOOMD includes a few helper functions, primarily for the purposes of benchmarking, that allow simple systems to be defined. Note, in most cases, you will specify particle positions in a separate file (using the [GSD](http://gsd.readthedocs.io/en/stable/) format) and import this into hoomd (see [the documentation](https://hoomd-blue.readthedocs.io/en/stable/module-hoomd-init.html). Here we will create an 'n' by 'n' by 'n' lattice of particles, with 'n'=5.
```
hoomd.init.create_lattice(unitcell=hoomd.lattice.sc(a=2.0), n=5)
```
Note, by default, these particles will be labeled as type "A".
### Interaction Definition
Next we will define how particles interact. In this case, we will consider all interactions to be of type Lennard-Jones. In HOOMD, when defining a pair potential, we must also pass a neighborlist. Note, HOOMD-Blue supports several different types of neighborlists that will be discussed in detail later. Here, we will specify a 'cell'-based neighborlist (```nl```) and define the Lennard-Jones pair potential (```lj```), with a cutoff of 2.5.
```
nl = hoomd.md.nlist.cell()
lj = hoomd.md.pair.lj(r_cut=2.5, nlist=nl)
```
Next we need to specify the pair coefficients, i.e., epsilon and sigma for the LJ interaction, for each pair of particle types in the system. Since we only have a single type in our system ('A'), we need only define a single pair. Note, if you fail to define the interactions, a useful error message will be provided when you try to run the simulation:
```
**ERROR**: Type pair ('A', 'A') not found in pair coeff
**ERROR**: Not all pair coefficients are set
```
```
lj.pair_coeff.set('A', 'A', epsilon=1.0, sigma=1.0)
```
### Integrator Setup
To actually move particles through time, we will specify the timestep of integration (i.e., our time resolution for the numerical integration):
```
hoomd.md.integrate.mode_standard(dt=0.005)
```
Next we specify the integration scheme and which particles it will apply to. Note, in most codes, users do not explicitly specify the underlying algorithm for numerical integration (e.g., Velocity-Verlet), as this is implicitly defined when selecting the larger integration scheme (i.e., selecting a thermostatting scheme).
Below, we create a [group](https://hoomd-blue.readthedocs.io/en/stable/module-hoomd-group.html) named "all" (that includes all particles) and use the [Langevin](https://hoomd-blue.readthedocs.io/en/stable/module-md-integrate.html?highlight=langevin) method:
```
all = hoomd.group.all();
hoomd.md.integrate.langevin(group=all, kT=0.2, seed=42);
```
### Runtime parameters
It is not typically useful to run a simulation without logging the thermodynamic quantities and structure. Here we define a log file using the [analyze function](https://hoomd-blue.readthedocs.io/en/stable/module-hoomd-analyze.html) to output specific thermodynamic quantities and the frequency for outputting them:
```
hoomd.analyze.log(filename="log-output.log",
quantities=['potential_energy', 'temperature'],
period=100,
overwrite=True)
```
Similarly, we define the name and frequency for outputting a trajectory using the [dump function](https://hoomd-blue.readthedocs.io/en/stable/module-hoomd-dump.html). Note that DCD trajectories can also be written, however, GSD files contain the necessary information to restart a simulation.
```
hoomd.dump.gsd("trajectory.gsd", period=2e3, group=all, overwrite=True)
```
Finally, we must specify the time period to run. Note, in HOOMD the system will begin running as soon as the run time is defined. A HOOMD script can have multiple calls to ```run```, as will be discussed later.
```
hoomd.run(1e4)
```
### Full script
```
import hoomd
import hoomd.md
hoomd.context.initialize("");
hoomd.init.create_lattice(unitcell=hoomd.lattice.sc(a=2.0), n=5)
nl = hoomd.md.nlist.cell();
lj = hoomd.md.pair.lj(r_cut=2.5, nlist=nl);
lj.pair_coeff.set('A', 'A', epsilon=1.0, sigma=1.0);
hoomd.md.integrate.mode_standard(dt=0.005)
all = hoomd.group.all();
hoomd.md.integrate.langevin(group=all, kT=0.2, seed=42);
hoomd.analyze.log(filename="log-output.log",
quantities=['potential_energy', 'temperature'],
period=100,
overwrite=True)
hoomd.dump.gsd("trajectory.gsd", period=2e3, group=all, overwrite=True)
hoomd.run(1e4)
```
### Examining the log
The log file generated by hoomd can be easily plotted in matplotlib by using the ```genfromtxt``` function to read in the data. Similar to matlab, individual columns can be separated using the syntax ```data[:,column_num]```where column_num would vary between 0 and 2 in this case as each line in the data file is formatted as: ```time potential_energy temperature```. The plot below could easily be changed to output the temperature as a function of time by changing ```data[:,1]``` to ```data[:,2]```
```
%%bash
###output the first 10 lines of the datafile
cat log-output.log | head -n 10
import numpy
from matplotlib import pyplot
%matplotlib inline
data = numpy.genfromtxt(fname='log-output.log', skip_header=True);
pyplot.figure(figsize=(4,2.2), dpi=140);
pyplot.plot(data[:,0], data[:,1]);
pyplot.xlabel('time step');
pyplot.ylabel('potential_energy');
```
| true |
code
| 0.733422 | null | null | null | null |
|
### Custom data generator for loading video data for action recognition
```
import pandas as pd
import cv2
import numpy as np
from sklearn.utils import shuffle
import os
from collections import deque
import copy
import matplotlib
import matplotlib.pyplot as plt
from keras.utils import np_utils
from config import Config
%matplotlib inline
```
#### A helper function for loading the samples in the format of
[[[frame1_filename,frame2_filename,…],label1], [[frame1_filename,frame2_filename,…],label2],……….]
```
# reading the video files from the csv file
def file_generator(data_path,data_files,temporal_stride=1,temporal_length=16):
'''
data_files - list of csv files to be read.
'''
for f in data_files: # read all the csv files (one csv file corresponds to one vdieo) in data_files one by one
tmp_df = pd.read_csv(os.path.join(data_path,f))
label_list = list(tmp_df['Label']) # Load all the labels in the label_list
total_images = len(label_list)
if total_images>=temporal_length: # only if the number of frames in the video is greater tha temporal length, use that video
num_samples = int((total_images-temporal_length)/temporal_stride)+1
print ('num of samples from vid seq-{}: {}'.format(f,num_samples))
img_list = list(tmp_df['FileName'])
else: # if the number of frames are less than temporal length , discard it
print ('num of frames is less than temporal length; hence discarding this file-{}'.format(f))
continue
start_frame = 0
samples = deque() # initliaze a queue to store the frames
samp_count=0 # a counter to count the number of smaple. one smaple has as many frames as defined by temporal length
for img in img_list:
samples.append(img)
if len(samples)==temporal_length: #if the queue has as many frames as temporal length, return it as one sample
samples_c=copy.deepcopy(samples) # copy the queue as in the next stage frames would be popped
samp_count+=1
for t in range(temporal_stride): # pop out as many frames as described by the stride from the left to accomodate new frames
samples.popleft()
yield samples_c,label_list[0] # return a sample(consisting of as many frames as defined by temporal length)
# and its corsponding label
```
#### A load function for loading the samples in the format of
[[[frame1_filename,frame2_filename,…],label1], [[frame1_filename,frame2_filename,…],label2],……….]
```
# Load the samples and their corresponding label for each video
def load_samples(data_cat='train',temporal_stride=1,temporal_length=16):
data_path = os.path.join('data_files',data_cat)
data_files = os.listdir(data_path)
# define a generator to read the samples
file_gen = file_generator(data_path,data_files,temporal_stride,temporal_length)
iterator = True
data_list = []
while iterator:
try:
x,y = next(file_gen)
x=list(x)
data_list.append([x,y])
except Exception as e:
print ('the exception: ',e)
iterator = False
print ('end of data generator')
return data_list
```
#### load the train data
```
train_data = load_samples(data_cat='train',temporal_stride=4,temporal_length=16)
print ('Total number of train samples:',len(train_data))
train_data[0]
train_data[5000:5002]
```
#### Load the test data
```
test_data = load_samples(data_cat='test',temporal_stride=4)
len(test_data)
```
#### Shuffle the dataset
```
def shuffle_data(samples):
data = shuffle(samples,random_state=2)
return data
def preprocess_image(img):
img = cv2.resize(img,(224,224))
img = img/255
return img
def data_generator(data,batch_size=10,temporal_padding='same',shuffle=True):
"""
Yields the next training batch.
data is an array [[img1_filename,img2_filename...,img16_filename],label1], [image2_filename,label2],...].
"""
num_samples = len(data)
if shuffle:
data = shuffle_data(data)
while True:
for offset in range(0, num_samples, batch_size):
print ('startring index: ', offset)
# Get the samples you'll use in this batch
batch_samples = data[offset:offset+batch_size]
# Initialise X_train and y_train arrays for this batch
X_train = []
y_train = []
# For each example
for batch_sample in batch_samples: # Loop over every batch
# Load image (X)
x = batch_sample[0]
y = batch_sample[1]
temp_data_list = []
for img in x:
try:
img = cv2.imread(img)
#apply any kind of preprocessing here
#img = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
img = preprocess_image(img)
temp_data_list.append(img)
except Exception as e:
print (e)
print ('error reading file: ',img)
# Read label (y)
#label = label_names[y]
# Add example to arrays
X_train.append(temp_data_list)
y_train.append(y)
# Make sure they're numpy arrays (as opposed to lists)
X_train = np.array(X_train)
#X_train = np.rollaxis(X_train,1,4)
y_train = np.array(y_train)
# convert to one hot encoding for training keras model
y_train = np_utils.to_categorical(y_train, 3)
# yield the next training batch
yield X_train, y_train
```
#### create a generator object with training data
```
train_generator = data_generator(train_data,batch_size=4,shuffle=True)
x,y = next(train_generator)
print ('x shape: ',x.shape)
print ('y shape: ',y.shape)
y
```
#### Let's visualize the first sample
```
x_0=x[2]
y_0=y[2]
print('x_0 shape: ',x_0.shape)
print('y_0 shape: ',y_0.shape)
Config.labels_to_class
activity = Config.labels_to_class[np.argmax(y_0)]
activity
```
#### Plot the first sample
```
num_of_images=16
fig=plt.figure(figsize=(8,8))
plt.title("one sample with {} frames ; activity:{}".format(num_of_images,activity))
subplot_num = int(np.ceil(np.sqrt(num_of_images)))
for i in range(int(num_of_images)):
ax = fig.add_subplot(subplot_num, subplot_num, i+1)
#ax.imshow(output_image[0,:,:,i],interpolation='nearest' ) #to see the first filter
ax.imshow(x_0[i,:,:,::-1])
plt.xticks([])
plt.yticks([])
plt.tight_layout()
plt.show()
```
| true |
code
| 0.506836 | null | null | null | null |
|
<a href ="https://colab.research.google.com/github/GEM-benchmark/NL-Augmenter/blob/main/notebooks/Write_a_sample_transformation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
https://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
# NL-Augmenter Colab example
* Play with an existing **transformation**
* Write your own **transformation**
* Play with an existing **filter**
* Write your own **filter**
Total running time: ~10 min
## Install NL-Augmenter from GitHub
```
!git clone https://www.github.com/GEM-benchmark/NL-Augmenter
cd NL-Augmenter
!pip install -r requirements.txt --quiet
```
## Load modules
```
from transformations.butter_fingers_perturbation.transformation import ButterFingersPerturbation
from transformations.change_person_named_entities.transformation import ChangePersonNamedEntities
from transformations.replace_numerical_values.transformation import ReplaceNumericalValues
from interfaces.SentenceOperation import SentenceOperation
from interfaces.QuestionAnswerOperation import QuestionAnswerOperation
from evaluation.evaluation_engine import evaluate, execute_model
from tasks.TaskTypes import TaskType
```
## Play with some existing transformations
```
t1 = ButterFingersPerturbation(max_outputs=3)
t1.generate("Jason wants to move back to India by the end of next year.")
t2 = ChangePersonNamedEntities(max_outputs=2)
t2.generate("Jason wants to move back to India by the end of next year.")
t3 = ReplaceNumericalValues(max_outputs=1)
t3.generate("Jason's 3 sisters want to move back to India")
```
## Define a simple transformation
Let's define a very basic transformation which just uppercases the sentence.
This transformation could be used for many [tasks](https://github.com/GEM-benchmark/NL-Augmenter/blob/add_filters_for_contrast_sets/tasks/TaskTypes.py) including text classification and generation. So, we need to populate the `tasks` variable to `[TaskType.TEXT_CLASSIFICATION, TaskType.TEXT_TO_TEXT_GENERATION]`. That's it!
```
class MySimpleTransformation(SentenceOperation):
tasks = [TaskType.TEXT_CLASSIFICATION, TaskType.TEXT_TO_TEXT_GENERATION]
languages = ["en"]
def generate(self, sentence):
return [sentence.upper()]
my_transformation = MySimpleTransformation()
my_transformation.generate("John was n't the person I had n't imagined.")
```
Obviously this can barely be called a transformation. What could this really achieve? Duh.
So, let's quickly compare the performance of a trained text classifier on a common test set, and a test set with MySimpleTransformation applied (or also called as a pertubed set) with this one line of code. And you need to hold your breadth for around 5 minutes!
```
execute_model(MySimpleTransformation, "TEXT_CLASSIFICATION", percentage_of_examples=1)
```
### 🕺 Voila! The accuracy on the perturbed set has fallen by 6% with this simple transformation!
So what happened internally? --> `execute_model` depending on the transformation type [SentenceOperation](https://github.com/GEM-benchmark/NL-Augmenter/blob/main/interfaces/SentenceOperation.py)) and the task you provided (TEXT_CLASSIFICATION) evaluated a pre-trained model of HuggingFace. In this case, a sentiment analysis model [aychang/roberta-base-imdb](https://huggingface.co/aychang/roberta-base-imdb) was chosen and evaluated on 1% of the [IMDB dataset](https://huggingface.co/datasets/imdb) with and without the transformation to check if the sentiment is predicted correctly.
If you want to evaluate this on your own model and dataset, you can pass the parameters as shown below in the `execute_model` method. Note that we obviously can't support each and every model type and dataset type and hence some models and datasets might require refactoring in the `evaluation_engine` class from your side and we are happy to help. 😊
```
# Here are the different parameters which are used as defaults!
# execute_model(MySimpleTransformation, "TEXT_CLASSIFICATION", "en", model_name = "aychang/roberta-base-imdb", dataset="imdb", percentage_of_examples=1)
```
## A Model Based Transformation
We don't want to restrict ourselves with just string level changes! We want to do more, don't we? So, let's use a pre-trained paraphrase generator to transform question answering examples. There is an exisiting interface [QuestionAnswerOperation](https://github.com/GEM-benchmark/NL-Augmenter/blob/main/interfaces/QuestionAnswerOperation.py) which takes as input the context, the question and the answer as inputs. Let's use that to augment our training data for question answering!
```
import torch
from transformers import T5ForConditionalGeneration, AutoTokenizer
class MySecondTransformation(QuestionAnswerOperation):
tasks = [TaskType.QUESTION_ANSWERING, TaskType.QUESTION_GENERATION]
languages = ["en"]
def __init__(self, max_outputs=5):
super().__init__()
model_name="prithivida/parrot_paraphraser_on_T5"
self.tokenizer = AutoTokenizer.from_pretrained(model_name)
self.model = T5ForConditionalGeneration.from_pretrained(model_name)
self.max_outputs = max_outputs
def generate(self, context, question, answers): # Note that the choice of inputs for 'generate' is consistent with those in QuestionAnswerOperation
# Let's call the HF model to generate a paraphrase for the question
paraphrase_input = question
batch = self.tokenizer([paraphrase_input],truncation=True,padding='longest',max_length=60, return_tensors="pt")
translated = self.model.generate(**batch,max_length=60,num_beams=10, num_return_sequences=self.max_outputs, temperature=1.5)
paraphrased_questions = self.tokenizer.batch_decode(translated, skip_special_tokens=True)
# context = "Apply your own logic here"
# answers = "And here too :)"
# return the list of new question-answering examples
return [(context, paraphrase, answers) for paraphrase in paraphrased_questions]
t4 = MySecondTransformation()
t4.generate(context="Mumbai, Bengaluru, New Delhi are among the many famous places in India.",
question="What are the famous places we should not miss in India?",
answers=["Mumbai", "Bengaluru", "Delhi", "New Delhi"])
```
Voila! Seems like you have created a new training example now for question-answering and question-generation! 🎉 🎊 🎉
#Now you are all ready to contribute a transformation to [NL-Augmenter 🦎 → 🐍](https://github.com/GEM-benchmark/NL-Augmenter)!
## What is this deal with filters?
So, just the way transformations can transform examples of text, filters can identify whether an example follows some pattern of text! The only difference is that while transformations return another example of the same input format, filters return True or False!
sentence --> SentenceOperation.**generate**(sentence) --> List of perturbed sentence
sentence --> SentenceOperation.**filter**(sentence) --> TRUE/FALSE
#So, let's play with some existing filters!
```
from filters.keywords import TextContainsKeywordsFilter
from filters.length import TextLengthFilter, SentenceAndTargetLengthFilter
```
The `TextLengthFilter` accepts an input sentence if the length of the input sentence is within the initialised range. Let's initialise this filter to accept all sentences with length greater than 10 tokens!
```
f1 = TextLengthFilter(">", 10)
f1.filter("This sentence is long enough to pass while you think of implementing your own filter!")
f1.filter("This one's too short!")
```
Let's say you have a lot of paraphrasing data and you intend to train a paraphrase generator to convert longer sentences to shorter ones! Check how the `SentenceAndTargetLengthFilter` can be used for this!
```
f2 = SentenceAndTargetLengthFilter([">", "<"], [10,8])
f2.filter("That show is going to take place in front of immensely massive crowds.",
"Large crowds would attend the show.")
f2.filter("The film was nominated for the Academy Award for Best Art Direction.",
"The movie was a nominee for the Academy Award for Best Art Direction.")
```
Okay, now that you've said to yourself that these filters are too basic, let's try to make a simple and interesting one!
Let's define a filter which selects question-answer pairs which share a low lexical overlap between the question and the context!
```
import spacy
class LowLexicalOverlapFilter(QuestionAnswerOperation):
tasks = [TaskType.QUESTION_ANSWERING, TaskType.QUESTION_GENERATION]
languages = ["en"]
def __init__(self, threshold=3):
super().__init__()
self.nlp = spacy.load("en_core_web_sm")
self.threshold = threshold
def filter(self, context, question, answers):
# Note that the only difference between a filter and a transformation is this method!
# The inputs remain the same!
question_tokenized = self.nlp(question, disable=["parser", "tagger", "ner"])
context_tokenized = self.nlp(context, disable=["parser", "tagger", "ner"])
q_tokens = set([t.text for t in question_tokenized])
c_tokens = set([t.text for t in context_tokenized])
low_lexical_overlap = len(q_tokens.intersection(c_tokens)) > self.threshold
return low_lexical_overlap
f3 = LowLexicalOverlapFilter()
f3.filter("New York, is the most populous city in the United States.",
"Which is the most populous city of the United States?",
["New York"])
f3.filter("New York, is the most populous city in the United States.",
"Which city has the largest population in the US?",
["New York"])
```
That's it! So you have created a new filter which can separate the hard examples from the easy one! 🎉 🎊 🎉
#Now go ahead and contribute a nice filter to [NL-Augmenter 🦎 → 🐍](https://github.com/GEM-benchmark/NL-Augmenter)!
| true |
code
| 0.716789 | null | null | null | null |
|
# Load Image
### This code loads train & valid/test images and converts it to data frame
```
import cv2
import numpy as np
import pandas as pd
from keras.preprocessing.image import img_to_array
from sklearn.model_selection import train_test_split
from keras.utils import to_categorical
from keras.preprocessing.image import ImageDataGenerator
from PIL import Image
import matplotlib.pyplot as plt
def LoadImage(dirPath, trainFldr, validFldr, TrainCSVName, ValidCSVName):
# Train Path
TrainPath= dirPath + '\\' + trainFldr
TrainCSVPath= dirPath + '\\' + TrainCSVName
TrainCSV= pd.read_csv(TrainCSVPath, sep= ',', names= ["Label", "Image Path"])
# TainLabel All Raws & Label
#####################################SAMPLE ONLY 1000
#TrainLabel= TrainCSV.iloc[:,0]
TrainLabel= TrainCSV.iloc[:,0]
TrainLabel= np.array(TrainLabel)
# Valid/Test Path
ValidPath= dirPath + '\\' + validFldr
ValidCSVPath= dirPath + '\\' + ValidCSVName
ValidCSV= pd.read_csv(ValidCSVPath, sep= ',', names= ["Label", "Image Path"])
# ValidLabel All Raws & Label
#####################################SAMPLE ONLY 1000
#ValidLabel= ValidCSV.iloc[:,0]
ValidLabel= ValidCSV.iloc[:,0]
ValidLabel= np.array(ValidLabel)
# Initialize train & valid/test images and labels
print('\n [INFO] laoding images...')
data=[]
#label=[]
# Load images, pre-process & store it
i=0
# i from 0 to length of TainLabel -1
#####################################SAMPLE ONLY 1000
#for i in range(len(TrainLabel)):
for i in range(len(TrainLabel)):
j=format(i, '0>5')
imagePath= str(TrainPath + "\\" + "TrIm-" + j + ".png")
image= cv2.imread(imagePath)
image=cv2.resize(image, (150, 150))
imageArr=img_to_array(image)
#image= Image.open(imagePath).convert("L")
#image= image.resize( (150, 150), 0)
#imageArr= np.asarray(image)
data.append(imageArr)
# scale the raw pixel intensities to the range [0, 1]
print('\n [INFO] scale the raw pixel...')
data = np.array(data, dtype="float") / 255.0
return data, TrainLabel;
# Load Image
Path= 'C:\\Users\\Moris\\MURA Code\\Shoulder'
TrnFldr= 'Train'
VldFldr= 'Valid'
TrnNm= 'Code-train_labeled_studies.csv'
VldNm= 'Code-valid_labeled_studies.csv'
dt, TrnLabel= LoadImage(Path, TrnFldr, VldFldr, TrnNm, VldNm)
# partition the data into training and testing splits using 75% of
# the data for training and the remaining 25% for testing
print('\n [INFO] partition the data...')
(trainX, testX, trainY, testY) = train_test_split(dt,TrnLabel, test_size=0.25, random_state=42)
# convert the labels from integers to vectors
trainY = to_categorical(trainY, num_classes=2)
testY = to_categorical(testY, num_classes=2)
# construct the image generator for data augmentation
#aug = ImageDataGenerator(rotation_range=30, width_shift_range=0.1,
# height_shift_range=0.1, shear_range=0.2, zoom_range=0.2,
# horizontal_flip=True, fill_mode="nearest")
```
# Building Keras Model
```
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.optimizers import Adam
from keras.layers.normalization import BatchNormalization
from keras.utils import np_utils
from keras.layers import Conv2D, MaxPooling2D, ZeroPadding2D, GlobalAveragePooling2D
from keras.layers.advanced_activations import LeakyReLU
from keras.preprocessing.image import ImageDataGenerator
input_shape= (150, 150, 3)
batch_size= 32
epochs= 5
classes = np.unique(trainY)
nClasses = len(classes)
model = Sequential()
#model.add(Conv2D(32, (3, 3), input_shape=input_shape))
model.add(Conv2D(32, (3, 3), padding='same', activation='relu', input_shape=input_shape))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(32, (3, 3), padding='same', activation='relu'))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(64, (3, 3), padding='same', activation='relu'))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(64))
model.add(Activation('relu'))
model.add(Dropout(0.5))
#model.add(Dense(1))
#model.add(Activation('sigmoid'))
model.add(Dense(nClasses, activation='softmax'))
#model.compile(loss='binary_crossentropy',
# optimizer='rmsprop',
# metrics=['accuracy'])
model.compile(loss='categorical_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
# this is the augmentation configuration we will use for training
train_datagen = ImageDataGenerator(
rescale=1. / 255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
# this is the augmentation configuration we will use for testing:
# only rescaling
test_datagen = ImageDataGenerator(rescale=1. / 255)
train_generator = train_datagen.flow(trainX, trainY, batch_size=16)
test_generator = test_datagen.flow(testX, testY, batch_size=16)
model.fit_generator(
train_generator, steps_per_epoch= len(trainX) / batch_size,
epochs=epochs,
validation_data= test_generator,
validation_steps= len(testX) / batch_size)
model.save_weights('first_try.h5')
```
# References:
### 1-Image Classification with Keras and Deep Learning
##### LeNet is a small Convolutional Neural Network
https://www.pyimagesearch.com/2017/12/11/image-classification-with-keras-and-deep-learning/
### 2-Grayscale to RGB Conversion
##### 33% of Red, 33% of Green, 33% of Blue
##### New grayscale image = ( (0.3 * R) + (0.59 * G) + (0.11 * B) )
https://www.tutorialspoint.com/dip/grayscale_to_rgb_conversion.htm
### 3-Image Module
https://pillow.readthedocs.io/en/3.1.x/reference/Image.html
### 4-Applying Convolutional Neural Network on the MNIST dataset
https://yashk2810.github.io/Applying-Convolutional-Neural-Network-on-the-MNIST-dataset/
### 5-classifier_from_little_data_script_1.py
https://gist.github.com/fchollet/0830affa1f7f19fd47b06d4cf89ed44d
### 6-How do I load train and test data from the local drive for a deep learning Keras model?
https://www.quora.com/How-do-I-load-train-and-test-data-from-the-local-drive-for-a-deep-learning-Keras-model
### 7-Image Preprocessing ImageDataGenerator class
https://keras.io/preprocessing/image/
### 8-Returning Multiple Values in Python
https://www.geeksforgeeks.org/g-fact-41-multiple-return-values-in-python/
### 9-Starter's Guide to building a CNN with keras (TF), openCV and google drive for image storage
https://github.com/chibuk/simple-cnn-keras-colaboratory/blob/master/Starter_s%20Guide%20to%20Convolutional%20Neural%20Networks%2C%20Part%201_%20Keras%20(TF)%20%2B%20OpenCV.ipynb
### 10-Create your first Image Recognition Classifier using CNN, Keras and Tensorflow backend
https://medium.com/nybles/create-your-first-image-recognition-classifier-using-cnn-keras-and-tensorflow-backend-6eaab98d14dd
### 11-Building powerful image classification models using very little data
https://blog.keras.io/building-powerful-image-classification-models-using-very-little-data.html
# Helping & Testing Code
```
from keras.preprocessing.image import img_to_array
import cv2
import matplotlib.pyplot as plt
xx= 'C:\\Users\\Moris\\MURA Code\\Shoulder\\Train\\TrIm-00011.png'
xx2= cv2.imread(xx)
xx2=cv2.resize(xx2, (120, 120))
xx2Arr=img_to_array(xx2)
#data.append(xx2)
#cv2.imshow('color_image',xx2)
imgplot = plt.imshow(xx2)
if(len(xx2.shape)<3):
print('gray')
elif len(xx2.shape)==3:
print('Color(RGB)')
else:
print('others')
#xx3= cv2.imread(xx, cv2.IMREAD_GRAYSCALE)
xx3= cv2.imread(xx, 0)
#xx3 = xx3[:,:,0]
imgplot = plt.imshow(xx3)
print(xx3)
from PIL import Image
def is_grey_scale(img_path):
im = Image.open(img_path).convert('RGB')
w,h = im.size
for i in range(w):
for j in range(h):
r,g,b = im.getpixel((i,j))
if r != g != b: return False
return True
asd1= is_grey_scale("C:\\Users\\Moris\\MURA Code\\Shoulder\\Train\\TrIm-00011.png")
print(asd1)
xx4=cv2.resize(xx2, (120, 120))
xx4=img_to_array(xx4)
yy1=xx4[:, : , 0]
print(xx4.shape)
#print(xx4)
print(yy1)
print(yy1.shape)
yy2=yy1
for k1 in range(120):
for k2 in range(120):
d1= yy1[k1, k2]
yy2[k1, k2]= 0.3*d1 + 0.59*d1 + 0.11*d1
#imgplot = plt.imshow(yy1)
imgplot = plt.imshow(yy2)
xx4= xx4.ravel()
print(xx4)
mz1= Image.open(xx).convert("L")
mz2= np.asarray(mz1)
plt.imshow(mz2, cmap='gray')
plt.show()
print(mz2.shape)
plt.imshow(mz2)
mz3=mz1.resize( (120, 120), 0)
plt.imshow(mz3)
mz4= np.asarray(mz3)
print(mz4.shape)
testY
```
| true |
code
| 0.551815 | null | null | null | null |
|
# Name Classifier
http://pytorch.org/tutorials/intermediate/char_rnn_classification_tutorial.html
```
import glob
import unicodedata
import string
def findFiles(path): return glob.glob(path)
print(findFiles('data/names/*.txt'))
all_letters = string.ascii_letters + " .,;'"
n_letters = len(all_letters)
# Turn a Unicode string to plain ASCII, thanks to http://stackoverflow.com/a/518232/2809427
def unicodeToAscii(s):
return ''.join(
c for c in unicodedata.normalize('NFD', s)
if unicodedata.category(c) != 'Mn'
and c in all_letters
)
print(unicodeToAscii('Ślusàrski'))
# Build the category_lines dictionary, a list of names per language
category_lines = {}
all_categories = []
# Read a file and split into lines
def readLines(filename):
lines = open(filename, encoding='utf-8').read().strip().split('\n')
return [unicodeToAscii(line) for line in lines]
for filename in findFiles('data/names/*.txt'):
category = filename.split('/')[-1].split('.')[0]
all_categories.append(category)
lines = readLines(filename)
category_lines[category] = lines
n_categories = len(all_categories)
print(n_categories)
import torch
# Find letter index from all_letters, e.g. "a" = 0
def letterToIndex(letter):
return all_letters.find(letter)
# Just for demonstration, turn a letter into a <1 x n_letters> Tensor
def letterToTensor(letter):
tensor = torch.zeros(1, n_letters)
tensor[0][letterToIndex(letter)] = 1
return tensor
# Turn a line into a <line_length x 1 x n_letters>,
# or an array of one-hot letter vectors
def lineToTensor(line):
tensor = torch.zeros(len(line), 1, n_letters)
for li, letter in enumerate(line):
tensor[li][0][letterToIndex(letter)] = 1
return tensor
print(letterToTensor('J'))
print(lineToTensor('Jones').size())
import torch.nn as nn
from torch.autograd import Variable
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(RNN, self).__init__()
self.hidden_size = hidden_size
self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
self.i2o = nn.Linear(input_size + hidden_size, output_size)
self.softmax = nn.LogSoftmax(dim=1)
def forward(self, input, hidden):
combined = torch.cat((input, hidden), 1)
hidden = self.i2h(combined)
output = self.i2o(combined)
output = self.softmax(output)
return output, hidden
def initHidden(self):
return Variable(torch.zeros(1, self.hidden_size))
n_hidden = 128
rnn = RNN(n_letters, n_hidden, n_categories)
input = Variable(lineToTensor('Albert'))
hidden = Variable(torch.zeros(1, n_hidden))
output, next_hidden = rnn(input[0], hidden)
print(output)
def categoryFromOutput(output):
top_n, top_i = output.data.topk(1) # Tensor out of Variable with .data
category_i = top_i[0][0]
return all_categories[category_i], category_i
print(categoryFromOutput(output))
import random
def randomChoice(l):
return l[random.randint(0, len(l) - 1)]
def randomTrainingExample():
category = randomChoice(all_categories)
line = randomChoice(category_lines[category])
category_tensor = Variable(torch.LongTensor([all_categories.index(category)]))
line_tensor = Variable(lineToTensor(line))
return category, line, category_tensor, line_tensor
for i in range(10):
category, line, category_tensor, line_tensor = randomTrainingExample()
print('category =', category, '/ line =', line)
```
## Training
```
criterion = nn.NLLLoss()
learning_rate = 0.005 # If you set this too high, it might explode. If too low, it might not learn
def train(category_tensor, line_tensor):
hidden = rnn.initHidden()
rnn.zero_grad()
for i in range(line_tensor.size()[0]):
output, hidden = rnn(line_tensor[i], hidden)
loss = criterion(output, category_tensor)
loss.backward()
# Add parameters' gradients to their values, multiplied by learning rate
for p in rnn.parameters():
p.data.add_(-learning_rate, p.grad.data)
return output, loss.data[0]
import time
import math
n_iters = 100000
print_every = 5000
plot_every = 1000
# Keep track of losses for plotting
current_loss = 0
all_losses = []
def timeSince(since):
now = time.time()
s = now - since
m = math.floor(s / 60)
s -= m * 60
return '%dm %ds' % (m, s)
start = time.time()
for iter in range(1, n_iters + 1):
category, line, category_tensor, line_tensor = randomTrainingExample()
output, loss = train(category_tensor, line_tensor)
current_loss += loss
# Print iter number, loss, name and guess
if iter % print_every == 0:
guess, guess_i = categoryFromOutput(output)
correct = '✓' if guess == category else '✗ (%s)' % category
print('%d %d%% (%s) %.4f %s / %s %s' % (iter, iter / n_iters * 100, timeSince(start), loss, line, guess, correct))
# Add current loss avg to list of losses
if iter % plot_every == 0:
all_losses.append(current_loss / plot_every)
current_loss = 0
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
plt.figure()
plt.plot(all_losses)
plt.show()
```
## Evaluating the Results
```
# Keep track of correct guesses in a confusion matrix
confusion = torch.zeros(n_categories, n_categories)
n_confusion = 10000
# Just return an output given a line
def evaluate(line_tensor):
hidden = rnn.initHidden()
for i in range(line_tensor.size()[0]):
output, hidden = rnn(line_tensor[i], hidden)
return output
# Go through a bunch of examples and record which are correctly guessed
for i in range(n_confusion):
category, line, category_tensor, line_tensor = randomTrainingExample()
output = evaluate(line_tensor)
guess, guess_i = categoryFromOutput(output)
category_i = all_categories.index(category)
confusion[category_i][guess_i] += 1
# Normalize by dividing every row by its sum
for i in range(n_categories):
confusion[i] = confusion[i] / confusion[i].sum()
# Set up plot
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(confusion.numpy())
fig.colorbar(cax)
# Set up axes
ax.set_xticklabels([''] + all_categories, rotation=90)
ax.set_yticklabels([''] + all_categories)
# Force label at every tick
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
# sphinx_gallery_thumbnail_number = 2
plt.show()
```
| true |
code
| 0.567517 | null | null | null | null |
|
# Tensorflowing (small stream)
```
%matplotlib inline
import tensorflow as tf
from skimage import data
from matplotlib import pyplot as plt
import numpy as np
# create a tf Tensor that holds 100 values evenly spaced from -3 to 3
x = tf.linspace(-3.0, 3.0, 100)
print(x)
# create a graph (holds the theory of the computation)
g = tf.get_default_graph()
[op.name for op in g.get_operations()]
sess = tf.Session()
computed_x = sess.run(x)
print(computed_x)
sess.close()
```
# Vermessung der Welt
```
mean = 0
sigma = 1.0
# I do not understand this formula, it is just copied... :/
z = (tf.exp(tf.neg(tf.pow(x - mean, 2.0) /
(2.0 * tf.pow(sigma, 2.0)))) *
(1.0 / (sigma * tf.sqrt(2.0 * 3.1415))))
sess = tf.Session()
graph = sess.run(z)
plt.plot(graph)
# what exactly is this? the shape dimensions of the gaussian curve
ksize = z.get_shape().as_list()[0]
ksize
# essentially it seems we're just multiplying two gaussians, but don't ask me what's going on
z_2d = tf.matmul(tf.reshape(z, [ksize, 1]), tf.reshape(z, [1, ksize]))
# run the session with the new operations (graph?) fed to it
graph_2d = sess.run(z_2d)
# display the 2D gaussian as an image
plt.imshow(graph_2d)
```
# Creating a Collection
## at first, a detour
http://sipi.usc.edu/database/database.php/n/database.php?volume=misc
```
dir(data)
# or do the tab trick
# get a list of all the actual imgs available as attributes
img_list = [i for i in dir(data) if not i.startswith("_")]
non_imgs = ['use_plugin', 'deprecated', 'binary_blobs', 'data_dir', 'imread', 'load', 'lena']
for ni in non_imgs:
img_list.remove(ni)
img_list
# a horrible way of getting (not quite) what I wanted :D
# haha, oh well...
for i in img_list:
img = eval("data." + i + "().astype(np.float32)")
plt.imshow(img, cmap="gray")
```
okay, that's the end of the detour. :) haha, I just did things one shouldn't do. back to normality.
## now the real thing
```
img = data.moon().astype(np.float32)
plt.imshow(img, cmap="gray")
img.shape
# seems we need a 4D tensor for fun times, so let's do it
img_4d = tf.reshape(img, [1, img.shape[0], img.shape[1], 1])
img_4d.get_shape()
# reshaping the kernel works somewhat differently: [Kh, Kw, C, NK]
kernel_height, kernel_width = ksize, ksize
channels, num_kernels = 1, 1
z_4d = tf.reshape(z_2d, [kernel_height, kernel_width, channels, num_kernels])
print(z_4d.get_shape().as_list())
# now we're doing some convolution stuff
convolved = tf.nn.conv2d(img_4d, z_4d, strides=[1, 1, 1, 1], padding="SAME")
res_4d = sess.run(convolved)
print(res_4d.shape)
# matplotlib can't visualize 4d images, so we need to convert it back to original height and width
plt.imshow(np.squeeze(res_4d), cmap="gray")
```
^ it seems that I surprised the moon! : o
| true |
code
| 0.635477 | null | null | null | null |
|
# Configuring Sonnet's BatchNorm Module
This colab walks you through Sonnet's BatchNorm module's different modes of operation.
The module's behaviour is determined by three main parameters: One constructor argument (```update_ops_collection```) and two arguments that are passed to the graph builder (```is_training``` and ```test_local_stats```).
```python
bn = BatchNorm(update_ops_collection)
bn(inputs, is_training, test_local_stats)
```
The following diagram visualizes how different parameter settings lead to different modes of operation. Bold arrows mark the current default values of the arguments.
```
#@title Decision tree
%%svg
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg
xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink" width="971px" height="384px" version="1.1" content="<mxfile userAgent="Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/58.0.3029.110 Safari/537.36" version="6.7.3" editor="www.draw.io"><diagram name="Page-1">7Vptc5s4EP41fLQHkMHxx9pNrh96mZtJb3r3ySODDLoKxAnhl/76roR4C7bHl5CEXOuZTORHy2q1++yuZNtCq+Twm8BZ/DsPCbNcOzxY6KPlwstz4Z9CjiUyd+wSiAQNS8hpgAf6nRiwEitoSPKOoOScSZp1wYCnKQlkB8NC8H1XbMtZd9UMR6QHPASY9dGvNJRxid64foN/IjSKq5Udf1HObHDwLRK8SM16lou2+lVOJ7jSZTaaxzjk+xaEbi20EpzLcpQcVoQp31ZuK5+7OzNb2y1IKq95wDNmyGO1dW08UdO2hZaxTBgMHRiSA5V/KXjqmXd/m5l/iJRHE0RcSA4QFzLmEU8x+8x5VmkIwclmpUbgtkGXQSF2em0lnkvBv9X+R4CUxio1Z7droJwXIjBShosSi4gYKVS7GihMeEKkOIKIIAxLuutqx4ZLUS3X+BMGxqWn3TsvVewwK4zSLwJGj30uyUF2nS1ITr/jjRZQccg4TaU2xFta3kdAMKNRCkAAWycCgB0RkgKFP5iJhIahdirDG8KWNTFXnHGh162oiZZbnso7nFCm8nUFvqOg0rXvyd5MVmEzPlFrkcOpVDQ2NwxvB8c77XajaGJPnTlC5WPHjvKrA2OU/6Hc1RLh220OsX8cudqGq4Lp9+L2Hwn9gqk1WGbMXikzbnqZcYdZ/t5S41nZ4F/MBkgGuwrQKOjv9iJmuT5TwckExM2P1JDmaykwTWkaVbOgtyXQzyHGoKurYOxjKslDhjU793Cw6Mb9rK97JD/rUxfZnepSRWXf9HjHNljc6u+e/XzCO05/66MpH0O1WtQvKI59OiSDVxSnT9AHKTQR31VNGa7dOpezAfqt20mHyZjKjYNGnC+DZcfitZJj1kuOe57+VO3WOXPor/uta89nnXwY0+ETXdN9KyiAC3mFFVmIJVnzLF8HnDHwEuVpqze3ZUfYsmezbst25id69uKlevZ8xDWo27OfXpVmJ3r2mYva8GVp0aP1T3cNKEl28VaMZotOEoypT9efZI0/R55+rj2VI2eub4PnSKXj14dIbcJdujePKDv6x64r27YkuVwzDqFY5xJD1N5Nx57M37Bj9/tJ5aGCPfYZox0n+f8WvPT8QU5MYnwACUa2spmtlNxzkYAQVCDX5oXMCkWdItfXTVvHzVLfBsgg1osAE3NIrHYY1fIDGvSnPufBdMJ3pRUYwogjkiv3pKroYW3Mlos9FqGOaX7ZIADbbntEqqZuO69CLM/vEgvZfWLV3yC1ieUPcRS0fzEL7hAlf1QrjM9xDas6ZGcMmBBW1MPwl+JEA80tZGqpWl5auKlW+xKTY60l5Wrz5ECCQuqHVbNPsG5R7Dht7XlzgrtjJzSyb55G6PpDymcx2hsFo3PJhQ5tj0vTl6P0PVcWdHldMi4QBMDw8trjopHnvWFZ9EdBorcoi/8rDk1c+/WaK7xtfuFQHqqbn5Gg2x8=</diagram></mxfile>" style="background-color: rgb(255, 255, 255);">
<defs/>
<g transform="translate(0.5,0.5)">
<path d="M 480 50 Q 480 100 607.5 100 Q 735 100 735 139.9" fill="none" stroke="#000000" stroke-width="1" stroke-miterlimit="10" pointer-events="none"/>
<path d="M 735 146.65 L 730.5 137.65 L 735 139.9 L 739.5 137.65 Z" fill="#000000" stroke="#000000" stroke-width="1" stroke-miterlimit="10" pointer-events="none"/>
<g transform="translate(562.5,93.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="29" height="12" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: "Courier New"; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; white-space: nowrap; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;background-color:#ffffff;">True
</div>
</div>
</foreignObject>
<text x="15" y="12" fill="#000000" text-anchor="middle" font-size="12px" font-family="Courier New">True</text>
</switch>
</g>
<path d="M 480 50 Q 480 100 352.5 100 Q 225 100 225 143.63" fill="none" stroke="#000000" stroke-miterlimit="10" pointer-events="none"/>
<path d="M 225 148.88 L 221.5 141.88 L 225 143.63 L 228.5 141.88 Z" fill="#000000" stroke="#000000" stroke-miterlimit="10" pointer-events="none"/>
<g transform="translate(316.5,94.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="36" height="12" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: "Courier New"; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; white-space: nowrap; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;background-color:#ffffff;">False
</div>
</div>
</foreignObject>
<text x="18" y="12" fill="#000000" text-anchor="middle" font-size="12px" font-family="Courier New">False</text>
</switch>
</g>
<ellipse cx="480" cy="25" rx="50" ry="25" fill="#ffffff" stroke="#000000" pointer-events="none"/>
<g transform="translate(439.5,6.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="80" height="36" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: Helvetica; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; width: 80px; white-space: nowrap; word-wrap: normal; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;">
<pre>is_training</pre>
</div>
</div>
</foreignObject>
<text x="40" y="24" fill="#000000" text-anchor="middle" font-size="12px" font-family="Helvetica"><pre>is_training</pre></text>
</switch>
</g>
<path d="M 735 200 Q 735 240 674 240 Q 613 240 613 269.9" fill="none" stroke="#000000" stroke-width="3" stroke-miterlimit="10" pointer-events="none"/>
<path d="M 613 276.65 L 608.5 267.65 L 613 269.9 L 617.5 267.65 Z" fill="#000000" stroke="#000000" stroke-width="3" stroke-miterlimit="10" pointer-events="none"/>
<g transform="translate(672.5,232.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="43" height="12" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: "Courier New"; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; white-space: nowrap; font-weight: bold; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;background-color:#ffffff;">String
</div>
</div>
</foreignObject>
<text x="22" y="12" fill="#000000" text-anchor="middle" font-size="12px" font-family="Courier New" font-weight="bold">String</text>
</switch>
</g>
<path d="M 735 200 Q 735 240 800 240 Q 865 240 865 273.63" fill="none" stroke="#000000" stroke-miterlimit="10" pointer-events="none"/>
<path d="M 865 278.88 L 861.5 271.88 L 865 273.63 L 868.5 271.88 Z" fill="#000000" stroke="#000000" stroke-miterlimit="10" pointer-events="none"/>
<g transform="translate(807.5,233.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="29" height="12" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: "Courier New"; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; white-space: nowrap; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;background-color:#ffffff;">None
</div>
</div>
</foreignObject>
<text x="15" y="12" fill="#000000" text-anchor="middle" font-size="12px" font-family="Courier New">None</text>
</switch>
</g>
<ellipse cx="735" cy="175" rx="95" ry="25" fill="#ffffff" stroke="#000000" pointer-events="none"/>
<g transform="translate(658.5,156.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="152" height="36" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: Helvetica; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; width: 152px; white-space: nowrap; word-wrap: normal; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;">
<pre>update_ops_collection</pre>
</div>
</div>
</foreignObject>
<text x="76" y="24" fill="#000000" text-anchor="middle" font-size="12px" font-family="Helvetica"><pre><code>update_ops_collection</code></pre></text>
</switch>
</g>
<path d="M 225 200 Q 225 240 292.5 240 Q 360 240 360 273.63" fill="none" stroke="#000000" stroke-miterlimit="10" pointer-events="none"/>
<path d="M 360 278.88 L 356.5 271.88 L 360 273.63 L 363.5 271.88 Z" fill="#000000" stroke="#000000" stroke-miterlimit="10" pointer-events="none"/>
<g transform="translate(260.5,232.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="36" height="12" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: "Courier New"; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; white-space: nowrap; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;background-color:#ffffff;">False
</div>
</div>
</foreignObject>
<text x="18" y="12" fill="#000000" text-anchor="middle" font-size="12px" font-family="Courier New">False</text>
</switch>
</g>
<path d="M 225 200 Q 225 240 165 240 Q 105 240 105 269.9" fill="none" stroke="#000000" stroke-width="3" stroke-miterlimit="10" pointer-events="none"/>
<path d="M 105 276.65 L 100.5 267.65 L 105 269.9 L 109.5 267.65 Z" fill="#000000" stroke="#000000" stroke-width="3" stroke-miterlimit="10" pointer-events="none"/>
<g transform="translate(140.5,234.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="29" height="12" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: "Courier New"; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; white-space: nowrap; font-weight: bold; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;background-color:#ffffff;">True
</div>
</div>
</foreignObject>
<text x="15" y="12" fill="#000000" text-anchor="middle" font-size="12px" font-family="Courier New" font-weight="bold">True</text>
</switch>
</g>
<ellipse cx="225" cy="175" rx="95" ry="25" fill="#ffffff" stroke="#000000" pointer-events="none"/>
<g transform="translate(166.5,156.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="116" height="36" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: Helvetica; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; width: 116px; white-space: nowrap; word-wrap: normal; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;">
<pre>test_local_stats</pre>
</div>
</div>
</foreignObject>
<text x="58" y="24" fill="#000000" text-anchor="middle" font-size="12px" font-family="Helvetica"><pre><code>test_local_stats</code></pre></text>
</switch>
</g>
<rect x="760" y="280" width="210" height="60" rx="9" ry="9" fill="#ffffff" stroke="#000000" pointer-events="none"/>
<g transform="translate(761.5,270.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="206" height="78" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: Helvetica; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; width: 206px; white-space: normal; word-wrap: normal; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;">
<ul>
<li style="text-align: left">Normalize output using local batch statistics</li>
<li style="text-align: left">Update moving averages in each forward pass</li>
</ul>
</div>
</div>
</foreignObject>
<text x="103" y="45" fill="#000000" text-anchor="middle" font-size="12px" font-family="Helvetica">[Not supported by viewer]</text>
</switch>
</g>
<rect x="508" y="280" width="210" height="100" rx="15" ry="15" fill="#ffffff" stroke="#000000" pointer-events="none"/>
<g transform="translate(509.5,276.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="206" height="106" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: Helvetica; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; width: 206px; white-space: normal; word-wrap: normal; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;">
<ul>
<li style="text-align: left">Normalize output using local batch statistics</li>
<li style="text-align: left">Update ops for the moving averages are placed in a named collection.
<b>They are not executed automatically.</b>
</li>
</ul>
</div>
</div>
</foreignObject>
<text x="103" y="59" fill="#000000" text-anchor="middle" font-size="12px" font-family="Helvetica">[Not supported by viewer]</text>
</switch>
</g>
<rect x="255" y="280" width="210" height="60" rx="9" ry="9" fill="#ffffff" stroke="#000000" pointer-events="none"/>
<g transform="translate(256.5,277.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="206" height="64" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: Helvetica; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; width: 206px; white-space: normal; word-wrap: normal; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;">
<ul>
<li style="text-align: left">Normalize output using stored moving averages.</li>
<li style="text-align: left">No update ops are created.</li>
</ul>
</div>
</div>
</foreignObject>
<text x="103" y="38" fill="#000000" text-anchor="middle" font-size="12px" font-family="Helvetica">[Not supported by viewer]</text>
</switch>
</g>
<rect x="0" y="280" width="210" height="60" rx="9" ry="9" fill="#ffffff" stroke="#000000" pointer-events="none"/>
<g transform="translate(1.5,277.5)">
<switch>
<foreignObject style="overflow:visible;" pointer-events="all" width="206" height="64" requiredFeatures="http://www.w3.org/TR/SVG11/feature#Extensibility">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display: inline-block; font-size: 12px; font-family: Helvetica; color: rgb(0, 0, 0); line-height: 1.2; vertical-align: top; width: 206px; white-space: normal; word-wrap: normal; text-align: center;">
<div
xmlns="http://www.w3.org/1999/xhtml" style="display:inline-block;text-align:inherit;text-decoration:inherit;">
<ul>
<li style="text-align: left">Normalize output using local batch statistics</li>
<li style="text-align: left">No update ops are created.</li>
</ul>
</div>
</div>
</foreignObject>
<text x="103" y="38" fill="#000000" text-anchor="middle" font-size="12px" font-family="Helvetica">[Not supported by viewer]</text>
</switch>
</g>
</g>
</svg>
#@title Setup
import numpy as np
import tensorflow as tf
import sonnet as snt
import matplotlib.pyplot as plt
from matplotlib import patches
%matplotlib inline
def run_and_visualize(inputs, outputs, bn_module):
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
inputs_collection = []
outputs_collection = []
for i in range(1000):
current_inputs, current_outputs = sess.run([inputs, outputs])
inputs_collection.append(current_inputs)
outputs_collection.append(current_outputs)
bn_mean, bn_var = sess.run([bn_module._moving_mean,
bn_module._moving_variance])
inputs_collection = np.concatenate(inputs_collection, axis=0)
outputs_collection = np.concatenate(outputs_collection, axis=0)
print("Number of update ops in collection: {}".format(
len(tf.get_collection(tf.GraphKeys.UPDATE_OPS))))
print("Input mean: {}".format(np.mean(inputs_collection, axis=0)))
print("Input variance: {}".format(np.var(inputs_collection, axis=0)))
print("Moving mean: {}".format(bn_mean))
print("Moving variance: {}".format(bn_var))
plt.figure()
# Plot the learned Gaussian distribution.
ellipse = patches.Ellipse(xy=bn_mean[0], width=bn_var[0, 0],
height=bn_var[0, 1], angle=0, edgecolor='g',
fc='None', zorder=1000, linestyle='solid',
linewidth=2)
# Plot the input distribution.
input_ax = plt.scatter(inputs_collection[:, 0], inputs_collection[:, 1],
c='r', alpha=0.1, zorder=1)
# Plot the output distribution.
output_ax = plt.scatter(outputs_collection[:, 0], outputs_collection[:, 1],
c='b', alpha=0.1, zorder=1)
ax = plt.gca()
ellipse_ax = ax.add_patch(ellipse)
plt.legend((input_ax, output_ax, ellipse_ax),
("Inputs", "Outputs", "Aggregated statistics"),
loc="lower right")
plt.axis("equal")
def get_inputs():
return tf.concat([
tf.random_normal((10, 1), 10, 1),
tf.random_normal((10, 1), 10, 2)],
axis=1)
```
# Examples
## Default mode
```
tf.reset_default_graph()
inputs = get_inputs()
bn = snt.BatchNorm()
outputs = bn(inputs, is_training=True)
run_and_visualize(inputs, outputs, bn)
```
**Results**
1. The outputs have been normalized. This is indicated by the blue isotropic Gaussian distribution.
1. Update ops have been created and placed in a collection.
1. No moving statistics have been collected. The green circle shows the learned Gaussian distribution. It is initialized to have mean 0 and standard deviation 1. Because the update ops were created but not executed, these statistics have not been updated.
1. The "boxy" shape of the normalized data points comes from the rather small batch size of 10. Because the batch statistics are only computed over 10 data points, they are very noisy.
## Collecting statistics during training
### First option: Update statistics automatically on every forward pass
```
tf.reset_default_graph()
inputs = get_inputs()
bn = snt.BatchNorm(update_ops_collection=None)
outputs = bn(inputs, is_training=True)
run_and_visualize(inputs, outputs, bn)
```
**Results**
1. The outputs have been normalized as we can tell from the blue isotropic Gaussian distribution.
1. Update ops have been created and executed. We can see that the moving statistics no longer have their default values (i.e. the green ellipsis has changed). The aggregated statistics don't represent the input distribution yet because we only ran 1000 forward passes.
### Second option: Explicitly add update ops as control dependencies
```
tf.reset_default_graph()
inputs = get_inputs()
bn = snt.BatchNorm(update_ops_collection=None)
outputs = bn(inputs, is_training=True)
# Add the update ops as control dependencies
# This can usually be done when defining the gradient descent
# ops
update_ops = tf.group(*tf.get_collection(tf.GraphKeys.UPDATE_OPS))
with tf.control_dependencies([update_ops]):
outputs = tf.identity(outputs)
run_and_visualize(inputs, outputs, bn)
```
**Results**
The actual results are identical to the previous run. However, this time, the update ops have not been executed automatically whenever we did a forward pass. We have to explicitly make the updates a dependency of our output by using ```tf.control_dependencies```. Usually, we would add the dependencies to our learning ops.
# Using statistics at test time
## Default mode
```
tf.reset_default_graph()
inputs = get_inputs()
bn = snt.BatchNorm()
outputs = bn(inputs, is_training=False)
run_and_visualize(inputs, outputs, bn)
```
**Results**
1. No update ops have been created and the moving statistics still have their initial values (mean 0, standard deviation 1).
2. The inputs have been normalized using the batch statistics as we can tell from the blue isotropic Gaussian distribution.
This means: In the default testing mode, the inputs are normalized using the batch statistics and the aggregated statistics are ignored.
## Using moving averages at test time
```
def hacky_np_initializer(array):
"""Allows us to initialize a tf variable with a numpy array."""
def _init(shape, dtype, partition_info):
return tf.constant(np.asarray(array, dtype='float32'))
return _init
tf.reset_default_graph()
inputs = get_inputs()
# We initialize the moving mean and variance to non-standard values
# so we can see the effect of this setting
bn = snt.BatchNorm(initializers={
"moving_mean": hacky_np_initializer([[10, 10]]),
"moving_variance": hacky_np_initializer([[1, 4]])
})
outputs = bn(inputs, is_training=False, test_local_stats=False)
run_and_visualize(inputs, outputs, bn)
```
**Results**
We have now manually initialized the moving statistics to the moments of the input distribution. We can see that the inputs have been normalized according to our stored statistics.
| true |
code
| 0.299614 | null | null | null | null |
|
In this tutorial, you will learn what a **categorical variable** is, along with three approaches for handling this type of data.
# Introduction
A **categorical variable** takes only a limited number of values.
- Consider a survey that asks how often you eat breakfast and provides four options: "Never", "Rarely", "Most days", or "Every day". In this case, the data is categorical, because responses fall into a fixed set of categories.
- If people responded to a survey about which what brand of car they owned, the responses would fall into categories like "Honda", "Toyota", and "Ford". In this case, the data is also categorical.
You will get an error if you try to plug these variables into most machine learning models in Python without preprocessing them first. In this tutorial, we'll compare three approaches that you can use to prepare your categorical data.
# Three Approaches
### 1) Drop Categorical Variables
The easiest approach to dealing with categorical variables is to simply remove them from the dataset. This approach will only work well if the columns did not contain useful information.
### 2) Ordinal Encoding
**Ordinal encoding** assigns each unique value to a different integer.

This approach assumes an ordering of the categories: "Never" (0) < "Rarely" (1) < "Most days" (2) < "Every day" (3).
This assumption makes sense in this example, because there is an indisputable ranking to the categories. Not all categorical variables have a clear ordering in the values, but we refer to those that do as **ordinal variables**. For tree-based models (like decision trees and random forests), you can expect ordinal encoding to work well with ordinal variables.
### 3) One-Hot Encoding
**One-hot encoding** creates new columns indicating the presence (or absence) of each possible value in the original data. To understand this, we'll work through an example.

In the original dataset, "Color" is a categorical variable with three categories: "Red", "Yellow", and "Green". The corresponding one-hot encoding contains one column for each possible value, and one row for each row in the original dataset. Wherever the original value was "Red", we put a 1 in the "Red" column; if the original value was "Yellow", we put a 1 in the "Yellow" column, and so on.
In contrast to ordinal encoding, one-hot encoding *does not* assume an ordering of the categories. Thus, you can expect this approach to work particularly well if there is no clear ordering in the categorical data (e.g., "Red" is neither _more_ nor _less_ than "Yellow"). We refer to categorical variables without an intrinsic ranking as **nominal variables**.
One-hot encoding generally does not perform well if the categorical variable takes on a large number of values (i.e., you generally won't use it for variables taking more than 15 different values).
# Example
As in the previous tutorial, we will work with the [Melbourne Housing dataset](https://www.kaggle.com/dansbecker/melbourne-housing-snapshot/home).
We won't focus on the data loading step. Instead, you can imagine you are at a point where you already have the training and validation data in `X_train`, `X_valid`, `y_train`, and `y_valid`.
```
import pandas as pd
from sklearn.model_selection import train_test_split
# Read the data
data = pd.read_csv('../input/melbourne-housing-snapshot/melb_data.csv')
# Separate target from predictors
y = data.Price
X = data.drop(['Price'], axis=1)
# Divide data into training and validation subsets
X_train_full, X_valid_full, y_train, y_valid = train_test_split(X, y, train_size=0.8, test_size=0.2,
random_state=0)
# Drop columns with missing values (simplest approach)
cols_with_missing = [col for col in X_train_full.columns if X_train_full[col].isnull().any()]
X_train_full.drop(cols_with_missing, axis=1, inplace=True)
X_valid_full.drop(cols_with_missing, axis=1, inplace=True)
# "Cardinality" means the number of unique values in a column
# Select categorical columns with relatively low cardinality (convenient but arbitrary)
low_cardinality_cols = [cname for cname in X_train_full.columns if X_train_full[cname].nunique() < 10 and
X_train_full[cname].dtype == "object"]
# Select numerical columns
numerical_cols = [cname for cname in X_train_full.columns if X_train_full[cname].dtype in ['int64', 'float64']]
# Keep selected columns only
my_cols = low_cardinality_cols + numerical_cols
X_train = X_train_full[my_cols].copy()
X_valid = X_valid_full[my_cols].copy()
```
We take a peek at the training data with the `head()` method below.
```
X_train.head()
```
Next, we obtain a list of all of the categorical variables in the training data.
We do this by checking the data type (or **dtype**) of each column. The `object` dtype indicates a column has text (there are other things it could theoretically be, but that's unimportant for our purposes). For this dataset, the columns with text indicate categorical variables.
```
# Get list of categorical variables
s = (X_train.dtypes == 'object')
object_cols = list(s[s].index)
print("Categorical variables:")
print(object_cols)
```
### Define Function to Measure Quality of Each Approach
We define a function `score_dataset()` to compare the three different approaches to dealing with categorical variables. This function reports the [mean absolute error](https://en.wikipedia.org/wiki/Mean_absolute_error) (MAE) from a random forest model. In general, we want the MAE to be as low as possible!
```
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
# Function for comparing different approaches
def score_dataset(X_train, X_valid, y_train, y_valid):
model = RandomForestRegressor(n_estimators=100, random_state=0)
model.fit(X_train, y_train)
preds = model.predict(X_valid)
return mean_absolute_error(y_valid, preds)
```
### Score from Approach 1 (Drop Categorical Variables)
We drop the `object` columns with the [`select_dtypes()`](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.select_dtypes.html) method.
```
drop_X_train = X_train.select_dtypes(exclude=['object'])
drop_X_valid = X_valid.select_dtypes(exclude=['object'])
print("MAE from Approach 1 (Drop categorical variables):")
print(score_dataset(drop_X_train, drop_X_valid, y_train, y_valid))
```
### Score from Approach 2 (Ordinal Encoding)
Scikit-learn has a [`OrdinalEncoder`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OrdinalEncoder.html) class that can be used to get ordinal encodings. We loop over the categorical variables and apply the ordinal encoder separately to each column.
```
from sklearn.preprocessing import OrdinalEncoder
# Make copy to avoid changing original data
label_X_train = X_train.copy()
label_X_valid = X_valid.copy()
# Apply ordinal encoder to each column with categorical data
ordinal_encoder = OrdinalEncoder()
label_X_train[object_cols] = ordinal_encoder.fit_transform(X_train[object_cols])
label_X_valid[object_cols] = ordinal_encoder.transform(X_valid[object_cols])
print("MAE from Approach 2 (Ordinal Encoding):")
print(score_dataset(label_X_train, label_X_valid, y_train, y_valid))
```
In the code cell above, for each column, we randomly assign each unique value to a different integer. This is a common approach that is simpler than providing custom labels; however, we can expect an additional boost in performance if we provide better-informed labels for all ordinal variables.
### Score from Approach 3 (One-Hot Encoding)
We use the [`OneHotEncoder`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html) class from scikit-learn to get one-hot encodings. There are a number of parameters that can be used to customize its behavior.
- We set `handle_unknown='ignore'` to avoid errors when the validation data contains classes that aren't represented in the training data, and
- setting `sparse=False` ensures that the encoded columns are returned as a numpy array (instead of a sparse matrix).
To use the encoder, we supply only the categorical columns that we want to be one-hot encoded. For instance, to encode the training data, we supply `X_train[object_cols]`. (`object_cols` in the code cell below is a list of the column names with categorical data, and so `X_train[object_cols]` contains all of the categorical data in the training set.)
```
from sklearn.preprocessing import OneHotEncoder
# Apply one-hot encoder to each column with categorical data
OH_encoder = OneHotEncoder(handle_unknown='ignore', sparse=False)
OH_cols_train = pd.DataFrame(OH_encoder.fit_transform(X_train[object_cols]))
OH_cols_valid = pd.DataFrame(OH_encoder.transform(X_valid[object_cols]))
# One-hot encoding removed index; put it back
OH_cols_train.index = X_train.index
OH_cols_valid.index = X_valid.index
# Remove categorical columns (will replace with one-hot encoding)
num_X_train = X_train.drop(object_cols, axis=1)
num_X_valid = X_valid.drop(object_cols, axis=1)
# Add one-hot encoded columns to numerical features
OH_X_train = pd.concat([num_X_train, OH_cols_train], axis=1)
OH_X_valid = pd.concat([num_X_valid, OH_cols_valid], axis=1)
print("MAE from Approach 3 (One-Hot Encoding):")
print(score_dataset(OH_X_train, OH_X_valid, y_train, y_valid))
```
# Which approach is best?
In this case, dropping the categorical columns (**Approach 1**) performed worst, since it had the highest MAE score. As for the other two approaches, since the returned MAE scores are so close in value, there doesn't appear to be any meaningful benefit to one over the other.
In general, one-hot encoding (**Approach 3**) will typically perform best, and dropping the categorical columns (**Approach 1**) typically performs worst, but it varies on a case-by-case basis.
# Conclusion
The world is filled with categorical data. You will be a much more effective data scientist if you know how to use this common data type!
# Your Turn
Put your new skills to work in the **[next exercise](https://www.kaggle.com/kernels/fork/3370279)**!
---
*Have questions or comments? Visit the [course discussion forum](https://www.kaggle.com/learn/intermediate-machine-learning/discussion) to chat with other learners.*
| true |
code
| 0.556038 | null | null | null | null |
|
# NVE
## Phase Space, Liuville's Theorem and Ergoicity ideas
Conservative systems are govenred by Hamilton's equation of motion. That is changes in position and momenta stay on the surface: $H(p,q)=E$
$$\dot{q} = \frac{\partial H}{\partial p}$$
$$\dot{p} = -\frac{\partial H}{\partial q}$$
To see how ensemble N body mechanical conervative system evoleves we are introducing probability distribution of classical trajecotires in phase space
$$\rho(p,q,t)dq dp $$
### Continuity equation and Liuville's theorem
$$\frac{\partial \rho(p,q,t)}{\partial t} = -\nabla J = - \nabla(\rho \vec{v})$$
Where flux $J= \rho \vec{v}$ is defined in terms of the velcotiy of points in phase space $v = (\dot{q},\dot{p})$. Combinging the continuity expression combined with Hamilton's equation of motion:
$$\dot{p_i} = -\partial_{q_i} H \,\,\,\,\ \dot{q_i} = \partial_{p_i} H$$
$$\frac{\partial \rho(p,q,t)}{\partial t} + \sum_i \Big [ \frac{\partial \rho}{\partial q_i}\dot{q_i}+\frac{\partial \rho}{\partial p_i} \dot{p_i} \Big] + \rho \sum_i \Big [ \frac{\partial \dot{q_i}}{\partial q_i}+ \frac{\partial \dot{p_i}}{\partial p_i} \Big]=0$$
Where the last term is zero one we plug Hamilton's equation. We thus arrive at a crucial conclusion that the space volume is preserved during conservative dynamics
$$\frac{\partial \rho(p,q,t)}{\partial t} + \sum_i \Big [ \frac{\partial \rho}{\partial q_i}\dot{q_i}+\frac{\partial \rho}{\partial p_i} \dot{p_i} \Big]=\frac{d \rho}{ dt} = 0$$
Furthermore we see that the time dependence of phase space probability density vanishes if it is a function of hamiltonian $\rho = f(H)$
$$\frac{\partial \rho}{\partial t} = \sum_i \Big [ \frac{\partial \rho}{\partial q_i}\cdot{q_i}+\frac{\partial \rho}{\partial p_i}\cdot{p_i} \Big] = -\{H,\rho \}$$
### Liuville theorem illustrated
According to Liuvile's theorem small phase space area element under time evolution gets deform but preserves the volume. For example, assume the initial distribution is a rectangle in phase space (x , v)
$${x 0 − d x ≤ x ≤ x 0 + d x}$$
$$ {v 0 − d v ≤ v ≤ v 0 + d v } $$
As time progresses this rectangle will deform, but its area will not change (assuming $d x$ and $d v$ are sufficiently small which ensure energy conservation)
```
import matplotlib.pyplot as plt
import numpy as np
import scipy as sci
from matplotlib.patches import Polygon # for making rectangles from four points
a = 1.0 # acceleration
x0, v0 = 0., 0. # center of initial phase space element
dx, dv = 0.1, 0.1 # (half of) width of initial phase space element
p0 = np.array(((x0-dx,v0-dv),(x0-dx,v0+dv),(x0+dx,v0+dv),(x0+dx,v0-dv))) # initial phase space element
def propagate(p0, t):
"""Propagates a phase space patch p0 for time t."""
x0, v0 = p0.T
x = x0 + v0*t + 0.5*a*t**2
v = v0 + a*t
return np.column_stack((x,v))
fig, ax = plt.subplots(figsize=(9,3))
for t in np.arange(4):
p = propagate(p0,t)
x, y = np.mean(p,axis=0)
ax.add_patch(Polygon(p))
ax.text(x, y-0.3, f"t={t}")
ax.set_xlabel("Position x", fontsize=15)
ax.set_ylabel("Velocity v", fontsize=15)
ax.set_xlim(-0.5,5.5)
ax.set_ylim(-0.5,3.5)
```
### Hamiltonian, conservative dynamics in phase space
```
# range of x and y grid
xmax = 5
ymax = 5
# make a grid of x and y values, Y = dot X
X, Y = np.meshgrid(np.arange(-xmax,xmax,.1), np.arange(-ymax,ymax,.1) )
H = 0.5*Y*Y +0.5*X*X #here is the Hamiltonian
#cs = plt.contour(X,Y,H,20,cmap='inferno')
#plt.clabel(cs,inline=1,fontsize=10)
plt.xlabel('q')
plt.ylabel('dq/dt')
plt.axis([-1.1*xmax, 1.1*xmax, -1.1*ymax, 1.1*ymax])
# Hamilton's equations define a vector field U,V
U = Y
V = - X
Q = plt.streamplot(X,Y, U, V,density=1)
# range of x and y grid
xmax = np.pi*2.0
ymax = 2
# make a grid of x and y values, Y = dot X
X, Y = np.meshgrid(np.arange(-xmax,xmax,.1),np.arange(-ymax,ymax,.1) )
epsilon=0.3
H = 0.5*Y*Y - epsilon*np.cos(X) #here is the Hamiltonian
# Hamilton's equations define a vector field U,V
U = Y
V = -epsilon*np.sin(X)
#cs =plt.contour(X,Y,H,10,cmap='inferno')
#plt.clabel(cs,inline=1,fontsize=10)
plt.xlabel('x')
plt.ylabel('dx/dt')
plt.axis([-xmax, xmax, -ymax, ymax])
Q = plt.streamplot(X,Y, U, V,density=1) # plot the vector field
```
| true |
code
| 0.681912 | null | null | null | null |
|
## Pipelines
Pipeline can be used to chain multiple estimators into one. This is useful as there is often a fixed sequence of steps in processing the data, for example feature selection, normalization and classification. Pipeline serves two purposes here:
* Convenience: You only have to call fit and predict once on your data to fit a whole sequence of estimators.
* Joint parameter selection: You can grid search over parameters of all estimators in the pipeline at once.
All estimators in a pipeline, except the last one, must be transformers (i.e. must have a transform method). The last estimator may be any type (transformer, classifier, etc.).
```
from sklearn.pipeline import Pipeline
Pipeline?
from sklearn.svm import SVC
from sklearn.decomposition import PCA
estimators = [('reduce_dim', PCA(n_components=2)), ('clf', SVC())]
pipe = Pipeline(estimators)
pipe
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
# Notice no need to PCA the Xs in the score!
pipe.fit(X, y).score(X, y)
```
The utility function make_pipeline is a shorthand for constructing pipelines; it takes a variable number of estimators and returns a pipeline, filling in the names automatically:
```
from sklearn.pipeline import make_pipeline
from sklearn.naive_bayes import MultinomialNB
from sklearn.preprocessing import Binarizer
make_pipeline(Binarizer(), MultinomialNB())
pipe.steps[0]
pipe.named_steps['reduce_dim']
pipe.set_params(clf__C=10)
from sklearn.model_selection import GridSearchCV
params = dict(reduce_dim__n_components=[2, 5, 10],
clf__C=[0.1, 10, 100])
grid_search = GridSearchCV(pipe, param_grid=params)
from sklearn.linear_model import LogisticRegression
params = dict(reduce_dim=[None, PCA(5), PCA(10)],
clf=[SVC(), LogisticRegression()],
clf__C=[0.1, 10, 100])
grid_search = GridSearchCV(pipe, param_grid=params)
```
## Feature Union
FeatureUnion combines several transformer objects into a new transformer that combines their output. A FeatureUnion takes a list of transformer objects. During fitting, each of these is fit to the data independently. For transforming data, the transformers are applied in parallel, and the sample vectors they output are concatenated end-to-end into larger vectors.
FeatureUnion serves the same purposes as Pipeline - convenience and joint parameter estimation and validation.
FeatureUnion and Pipeline can be combined to create complex models.
(A FeatureUnion has no way of checking whether two transformers might produce identical features. It only produces a union when the feature sets are disjoint, and making sure they are the caller’s responsibility.)
```
from sklearn.pipeline import FeatureUnion
from sklearn.decomposition import PCA
from sklearn.decomposition import KernelPCA
estimators = [('linear_pca', PCA()), ('kernel_pca', KernelPCA())]
combined = FeatureUnion(estimators)
combined
combined.fit_transform(X).shape
combined.set_params(kernel_pca=None)
combined.fit_transform(X).shape
```
| true |
code
| 0.813173 | null | null | null | null |
|
# Multi-model metadata generation
> experiment in combining text and tabular models to generate web archive metadata
- toc: true
- badges: false
- comments: true
- categories: [metadata, multi-model]
- search_exclude: false
# Learning from multiple input types
Deep learning models usually take one type of input (image, text etc.) to predict output labels (category, entities etc). This usually makes sense if the data you are using to make predictions contains a lot of information. i.e. a chunk of text from a movie review or an image.
Recently I have been playing around with a Website Classification Dataset from the UK web archive. The dataset is derived from a manually curated web archive which contains a primary and secondary category for each web page. The UK web archive has made a [dataset](https://data.webarchive.org.uk/opendata/ukwa.ds.1/classification/) available based on this archive which contains the manually classified subject categories alongside the page URL and the page title.
As part of playing around with this dataset I was keen to see if a multi-input model would work well. In this case exploring a model that takes both text and tabular data as input. A preview of the data:
```
#hide_input
import pandas as pd
tsv ='https://gist.githubusercontent.com/davanstrien/5e22b725046eddc2f1ee06b108f27e48/raw/71426e6b92c7fa98140a95728a5ea55171b948cd/classification.tsv'
df = pd.read_csv(tsv, error_bad_lines=False, index_col=0)
df.head()
```
Based on this data the UK web archive are interested:
>"in understanding whether high-level metadata like this can be used to train an appropriate automatic classification system so that we might use this manually generated dataset to partially automate the categorisation of our larger archives."
This is going to be fairly tricky but offers a nice excuse to try to use models with multiple inputs to predict our categories.
## Looking at the data
Taking a closer look at the data:
```
#hide_input
tsv = 'https://gist.githubusercontent.com/davanstrien/5e22b725046eddc2f1ee06b108f27e48/raw/71426e6b92c7fa98140a95728a5ea55171b948cd/classification.tsv'
df = pd.read_csv(tsv, error_bad_lines=False,)
```
### Unique primary categories
```
len(df['Primary Category'].unique())
```
### Unique secondary categories
```
len(df['Secondary Category'].unique())
```
Predicting a 104 different labels is going to be pretty difficult so I've only used 'Primary Category' as the the ```y``` target. What is the distribution of these categories like?
```
#hide_input
df['Primary Category'].value_counts()
```
😬 We also have a fairly skewed datasets. I could drop some of rows which don't occur often but since the main objective here is to see if we can use a multi-input model we'll leave the data as it is for now.
# Multi-input model
The rest of the notebook will describe some experiments with using [fastai](https://docs.fast.ai/) to create a model which takes tabular and text data as an input. The aim here wasn't for me to create the best model but get my head around how to combine models. I heavily relied on some existing [notebooks](https://nbviewer.jupyter.org/gist/joshfp/b62b76eae95e6863cb511997b5a63118/5.full-deep-learning.ipynb), kaggle [writeup](https://www.kaggle.com/c/petfinder-adoption-prediction/discussion/89491) and forum posts on the [fastai forums](forums.fast.ai/).
## Tabular model
In the dataset above we start of with two columns of data which can be used as inputs for the model. The title is fairly obviously something which we can treat like other text inputs. The URL is a little less obvious. It could be treated as a text input but an alternative is to treat a URL as parts which each contain some information which could be useful for our model.
```
#hide_input
print(df.URL.sample(10).to_list()[3])
print(df.URL.sample(10).to_list()[4])
print(df.URL.sample(10).to_list()[3])
```
Each part of the URL could be split into smaller parts
```
#hide_input
print(df.URL.sample(10).to_list()[3].split('.'))
```
Whether a url has '.org' or '.uk' or '.com' could be meaningful for predicting our categories (it might also not be meaningful). It also offers us a way of taking the URLs and composing it into a format which looks more tabular.
```
#hide_input
csv ='https://gist.githubusercontent.com/davanstrien/5e22b725046eddc2f1ee06b108f27e48/raw/4c2a27772bf4d959bf3e58cfa8de9e0b9be69ca7/03_classification_valid_train.csv'
df = pd.read_csv(csv, index_col=0)
df[['scheme','url1','url3','url4','url5']].sample(5)
```
So far I've only done this very crudely. I suspect tidying up this part of the data will help improve things. At this point though we have something which is a little more tabular looking we can pass to ```fastai.tabular``` learner. Now we have some 'categories' rather than unique urls.
```
print(len(df.url3.unique()))
print(len(df.url4.unique()))
```
## How does this tabular model do?
Once some preprocessing of the url has been done we train a model using the tabular learner. I didn't do much to try to optimize this model. Tracking best ```f2``` score we end up with:
```Better model found at epoch 36 with f_beta value: 0.17531482875347137``` and an accuracy of ```0.334121```
## How well does a text model do?
Next I tried training using the title field in a NLP model. I tried a few things here.
### SentencePiece tokenization
By default fastai uses SpaCy to do tokenization with a few additional special tokens added by fastai. I wanted to see if using [sentencePiece](https://github.com/google/sentencepiece) would work better for processing title fields. SentencePiece allows for various sub-word tokeinzation. This can be useful for agglutinative languages but could also be useful when you have a lot of out of vocabulary words in your corpus. I wanted to see if this also was useful for processing titles since these may contain domain specific terms. I only tried using SentencePiece with 'unigram' tokenization. The best score I got for this was:
```Better model found at epoch 1 with f_beta value: 0.21195338666439056.```
### Default SpaCy tokenization
I compared the above to using the default fastai tokenizer which uses SpaCy. In this case the default approach worked better. This is probably because we didn't have a large pre-trained model using the SentencePiece tokenization to use as a starting point. The best score I got for this model was:
```Better model found at epoch 27 with f_beta value: 0.33327043056488037.```
### Using the URL as text input
I wanted to do a quick comparison to the tabular model and use the URL as a text input instead. In this case I used SentencePiece with byte-pair-encoding (BPE). The best score in this case was:
```Better model found at epoch 3 with f_beta value: 0.2568161189556122.```
This might end up being a better approach compared to the tabular approach described above.
# Combining inputs
Neither of these models is doing super well but my main question was whether combining the two would improve things at all. There are different approaches to combining these models. I followed existing examples and removed some layers from the text and tabular models which are then combined in a concat model. I won't cover all the steps here but all the notebooks can be found in this [GitHub repo](https://github.com/davanstrien/Website-Classification).
```
#hide
from fastai.tabular import *
from pathlib import Path
import pandas as pd
from fastai import *
from fastai.tabular import *
from fastai.callbacks import *
from fastai.text import *
from fastai.metrics import accuracy, MultiLabelFbeta
```
One of the things we need to do to create a model with multiple input is create a new Pytorch dataset which combines our text and tabular ```x``` inputs with our target. This is pretty straightforward:
```
#collapse_show
class ConcatDataset(Dataset):
def __init__(self, x1, x2, y):
self.x1,self.x2,self.y = x1,x2,y
def __len__(self):
return len(self.y)
def __getitem__(self, i):
return (self.x1[i], self.x2[i]), self.y[i]
```
One of the other pieces was creating a ```ConcatModel```
```
#collapse_show
class ConcatModel(nn.Module):
def __init__(self, model_tab, model_nlp, layers, drops):
super().__init__()
self.model_tab = model_tab
self.model_nlp = model_nlp
lst_layers = []
activs = [nn.ReLU(inplace=True),] * (len(layers)-2) + [None]
for n_in,n_out,p,actn in zip(layers[:-1], layers[1:], drops, activs):
lst_layers += bn_drop_lin(n_in, n_out, p=p, actn=actn) # https://docs.fast.ai/layers.html#bn_drop_lin
self.layers = nn.Sequential(*lst_layers)
def forward(self, *x):
x_tab = self.model_tab(*x[0])
x_nlp = self.model_nlp(x[1])[0]
x = torch.cat([x_tab, x_nlp], dim=1)
return self.layers(x)
```
```lst_layer``` is dependent on the layers from the tabular and nlp models. This layer is manually defined at the moment, so if changes are made to the number of layers in the tab model this needs to be manually changed.
```bn_drop_lin``` is a fastai helper function that returns a a sequence of batch normalization, dropout and a linear layer which is the final layer of the model.
## How does this combined model do? 🤷♂️
The best result I got was``` f_beta value: 0.39341238141059875``` with an accuracy of ```0.595348```. A summary of the scores for each models:
| Model | F2 score |
|-------|--------|
|SentencePiece text | 0.211 |
| Spacy text | 0.333|
| Tabular | 0.175 |
|Concat| **0.393** |
This provides some improvement on the tabular or nlp models on their own. I found the combined model was fairly tricky to train and suspect that there could be some improvements in how the model is set up that might improve it's performance. I am keen to try a similar approach with a dataset where there is more abundant information available to train with.
# tl;dr
It wasn't possible to get a very good f2 score on this website classification dataset. As the UK web archive say:
> We expect that a appropriate classifier might require more information about each site in order to produce reliable results, and are looking at augmenting this dataset with further information in the future. Options include:
For each site, make the titles of every page on that site available.
For each site, extract a set of keywords that summarise the site, via the full-text index.
I suspect that having a either of these additional components would help improve the performance of the classifier.
| true |
code
| 0.44342 | null | null | null | null |
|
# Supervised Contrastive Learning
**Author:** [Khalid Salama](https://www.linkedin.com/in/khalid-salama-24403144/)<br>
**Date created:** 2020/11/30<br>
**Last modified:** 2020/11/30<br>
**Description:** Using supervised contrastive learning for image classification.
```
import tensorflow as tf
import tensorflow_addons as tfa
import numpy as np
import keras
from keras import layers
```
## Prepare the data
```
num_classes = 10
input_shape = (32, 32, 3)
# Load the train and test data splits
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar10.load_data()
# Display shapes of train and test datasets
print(f"x_train shape: {x_train.shape} - y_train shape: {y_train.shape}")
print(f"x_test shape: {x_test.shape} - y_test shape: {y_test.shape}")
```
## Using image data augmentation
```
data_augmentation = keras.Sequential(
[
layers.experimental.preprocessing.Normalization(),
layers.experimental.preprocessing.RandomFlip("horizontal"),
layers.experimental.preprocessing.RandomRotation(0.02),
layers.experimental.preprocessing.RandomWidth(0.2),
layers.experimental.preprocessing.RandomHeight(0.2),
]
)
# Setting the state of the normalization layer.
data_augmentation.layers[0].adapt(x_train)
```
## Build the encoder model
The encoder model takes the image as input and turns it into a 2048-dimensional
feature vector.
```
def create_encoder():
resnet = keras.applications.ResNet50V2(
include_top=False, weights=None, input_shape=input_shape, pooling="avg"
)
inputs = keras.Input(shape=input_shape)
augmented = data_augmentation(inputs)
outputs = resnet(augmented)
model = keras.Model(inputs=inputs, outputs=outputs, name="cifar10-encoder")
return model
encoder = create_encoder()
encoder.summary()
learning_rate = 0.001
batch_size = 265
hidden_units = 512
projection_units = 128
num_epochs = 50
dropout_rate = 0.5
temperature = 0.05
```
## Build the classification model
The classification model adds a fully-connected layer on top of the encoder,
plus a softmax layer with the target classes.
```
def create_classifier(encoder, trainable=True):
for layer in encoder.layers:
layer.trainable = trainable
inputs = keras.Input(shape=input_shape)
features = encoder(inputs)
features = layers.Dropout(dropout_rate)(features)
features = layers.Dense(hidden_units, activation="relu")(features)
features = layers.Dropout(dropout_rate)(features)
outputs = layers.Dense(num_classes, activation="softmax")(features)
model = keras.Model(inputs=inputs, outputs=outputs, name="cifar10-classifier")
model.compile(
optimizer=keras.optimizers.Adam(learning_rate),
loss=keras.losses.SparseCategoricalCrossentropy(),
metrics=[keras.metrics.SparseCategoricalAccuracy()],
)
return model
```
## Experiment 1: Train the baseline classification model
In this experiment, a baseline classifier is trained as usual, i.e., the
encoder and the classifier parts are trained together as a single model
to minimize the crossentropy loss.
```
encoder = create_encoder()
classifier = create_classifier(encoder)
classifier.summary()
history = classifier.fit(x=x_train, y=y_train, batch_size=batch_size, epochs=num_epochs)
accuracy = classifier.evaluate(x_test, y_test)[1]
print(f"Test accuracy: {round(accuracy * 100, 2)}%")
```
We get to ~78.4% test accuracy.
## Experiment 2: Use supervised contrastive learning
In this experiment, the model is trained in two phases. In the first phase,
the encoder is pretrained to optimize the supervised contrastive loss,
described in [Prannay Khosla et al.](https://arxiv.org/abs/2004.11362).
In the second phase, the classifier is trained using the trained encoder with
its weights freezed; only the weights of fully-connected layers with the
softmax are optimized.
### 1. Supervised contrastive learning loss function
```
class SupervisedContrastiveLoss(keras.losses.Loss):
def __init__(self, temperature=1, name=None):
super(SupervisedContrastiveLoss, self).__init__(name=name)
self.temperature = temperature
def __call__(self, labels, feature_vectors, sample_weight=None):
# Normalize feature vectors
feature_vectors_normalized = tf.math.l2_normalize(feature_vectors, axis=1)
# Compute logits
logits = tf.divide(
tf.matmul(
feature_vectors_normalized, tf.transpose(feature_vectors_normalized)
),
temperature,
)
return tfa.losses.npairs_loss(tf.squeeze(labels), logits)
def add_projection_head(encoder):
inputs = keras.Input(shape=input_shape)
features = encoder(inputs)
outputs = layers.Dense(projection_units, activation="relu")(features)
model = keras.Model(
inputs=inputs, outputs=outputs, name="cifar-encoder_with_projection-head"
)
return model
```
### 2. Pretrain the encoder
```
encoder = create_encoder()
encoder_with_projection_head = add_projection_head(encoder)
encoder_with_projection_head.compile(
optimizer=keras.optimizers.Adam(learning_rate),
loss=SupervisedContrastiveLoss(temperature),
)
encoder_with_projection_head.summary()
history = encoder_with_projection_head.fit(
x=x_train, y=y_train, batch_size=batch_size, epochs=num_epochs
)
```
### 3. Train the classifier with the frozen encoder
```
classifier = create_classifier(encoder, trainable=False)
history = classifier.fit(x=x_train, y=y_train, batch_size=batch_size, epochs=num_epochs)
accuracy = classifier.evaluate(x_test, y_test)[1]
print(f"Test accuracy: {round(accuracy * 100, 2)}%")
```
We get to ~82.6% test accuracy.
## Conclusion
As shown in the experiments, using the supervised contrastive learning technique
outperformed the conventional technique in terms of the test accuracy. Note that
the same training budget (i.e., number of epochs) was given to each technique.
Supervised contrastive learning pays off when the encoder involves a complex
architecture, like ResNet, and multi-class problems with many labels.
In addition, large batch sizes and multi-layer projection heads
improve its effectiveness. See the [Supervised Contrastive Learning](https://arxiv.org/abs/2004.11362)
paper for more details.
| true |
code
| 0.842976 | null | null | null | null |
|
```
# PCA
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values
dataset.head()
# X is created by extracting the Age and Estimated Salary fields from the dataset
X[0:3]
# Y is the purchased field
y[0:3]
# Dataset split into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = 1)
# Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# Applying Kernel PCA
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(n_components = 2, kernel = 'rbf')
X_train = kpca.fit_transform(X_train)
X_test = kpca.transform(X_test)
# Fitting Logistic Regression to the Training set
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)
# Predicting the Test set results
y_pred = classifier.predict(X_test)
# Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
# Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Logistic Regression (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
```
| true |
code
| 0.722197 | null | null | null | null |
|
# CT-LTI: Multi-sample Training and Eval
In this notebook we train over different graphs and initial-target state pairs.
We change parametrization slightly from the single sample, using Xavier normal instead of Kaiming initialization and higher decelaration rate for training. Preliminary results on few runs indicated the above choices would lead to faster convergence on BA and Tree graphs. Still, extensive hyper-parameter optimization would be preferable in the future, especially to optimize performance further.
Please make sure that the required data folder is available at the paths used by the script.
You may generate the required data by running the python script
```nodec_experiments/ct_lti/gen_parameters.py```.
This notebook takes around 15 hours per graph on RTX TITAN GPU, so plesae be patient when you generate new results.
## Imports
```
# %load_ext autoreload
# %autoreload 2
import os
os.sys.path.append('../../../')
import torch
from torchdiffeq import odeint
import numpy as np
import pandas as pd
import networkx as nx
from tqdm.cli import tqdm
from nnc.controllers.baselines.ct_lti.dynamics import ContinuousTimeInvariantDynamics
from nnc.controllers.baselines.ct_lti.optimal_controllers import ControllabiltyGrammianController
from nnc.helpers.torch_utils.graphs import adjacency_tensor, drivers_to_tensor
from nnc.helpers.graph_helper import load_graph
from nnc.helpers.torch_utils.evaluators import FixedInteractionEvaluator
from nnc.helpers.torch_utils.losses import FinalStepMSE
from nnc.helpers.torch_utils.trainers import NODECTrainer
from nnc.controllers.neural_network.nnc_controllers import NNCDynamics
from nnc.helpers.torch_utils.nn_architectures.fully_connected import StackedDenseTimeControl
from plotly import graph_objects as go
from plotly.subplots import make_subplots
```
## Load graph and dynamics parameters
```
experiment_data_folder = '../../../../data/parameters/ct_lti/'
graph='tree' # please use one of the following: lattice, ba, tree
device = 'cuda:0'
results_data_folder = '../../../../results/ct_lti/multi_sample/'+graph + '/'
os.makedirs(results_data_folder, exist_ok=True)
# load graph data
graph_folder = experiment_data_folder+graph+'/'
adj_matrix = torch.load(graph_folder+'adjacency.pt').to(dtype=torch.float, device=device)
n_nodes = adj_matrix.shape[0]
drivers = torch.load(graph_folder + 'drivers.pt')
n_drivers = len(drivers)
pos = pd.read_csv(graph_folder + 'pos.csv').set_index('index').values
driver_matrix = drivers_to_tensor(n_nodes, drivers).to(device)
# select dynamics type and initial-target states
dyn = ContinuousTimeInvariantDynamics(adj_matrix, driver_matrix)
target_states = torch.load(graph_folder+'target_states.pt').to(device)
initial_states = torch.load(experiment_data_folder+'init_states.pt').to(device)
# total time for control
total_time=0.5
```
## Train and evaluate all baselines
```
# For all sample indices
for i in tqdm(range(initial_states.shape[0])):
current_sample_id = i
# load current sample
x0 = initial_states[current_sample_id].unsqueeze(0)
xstar = target_states[current_sample_id].unsqueeze(0)
# calculate optimal control
oc = ControllabiltyGrammianController(
adj_matrix,
driver_matrix,
total_time,
x0,
xstar,
simpson_evals=100,
progress_bar=tqdm,
use_inverse=False,
)
# OC evaluations for different interaciton intervals.
loss_fn = FinalStepMSE(xstar, total_time=total_time)
all_n_interactions = [50, 500, 5000]
for n_interactions in all_n_interactions:
oc_evaluator = FixedInteractionEvaluator(
'oc_sample'+str(current_sample_id)+'_ninter_' + str(n_interactions),
log_dir=results_data_folder,
n_interactions=n_interactions,
loss_fn=loss_fn,
ode_solver=None,
ode_solver_kwargs={'method' : 'dopri5'},
preserve_intermediate_states=False,
preserve_intermediate_controls=True,
preserve_intermediate_times=False,
preserve_intermediate_energies=False,
preserve_intermediate_losses=False,
preserve_params=False,
)
oc_res = oc_evaluator.evaluate(dyn, oc, x0, total_time, epoch=0)
oc_evaluator.write_to_file(oc_res)
# neural network controller
# prepare neural network.
torch.manual_seed(1)
nn = StackedDenseTimeControl(n_nodes,
n_drivers,
n_hidden=0,#1,
hidden_size=15,#*n_nodes,
activation=torch.nn.functional.elu,
use_bias=True
).to(x0.device)
nndyn = NNCDynamics(dyn, nn).to(x0.device)
nn_trainer = NODECTrainer(
nndyn,
x0,
xstar,
total_time,
obj_function=None,
optimizer_class = torch.optim.LBFGS,
optimizer_params=dict(lr=1.2,
#momentum =0.5
max_iter=1,
max_eval=1,
history_size=100
),
ode_solver_kwargs=dict(method='dopri5'),
logger=None,
closure=None,
use_adjoint=False,
)
# here we initialize with Xavier which seemed to help NODEC converge faster for tree/ba graphs
for name, param in nn.named_parameters():
if len(param.shape) > 1:
torch.nn.init.xavier_normal_(param)
# here we use higher decelaration rate, which seemed to help NODEC converge faster for tree/ba graphs
# train for 100 epochs
nndyn = nn_trainer.train_best(epochs=100,
lr_acceleration_rate=0,
lr_deceleration_rate=0.99,
loss_variance_tolerance=10,
verbose=True
)
# Evaluate after 100 epochs of training for 50 interactions.
nn_logger_50 = FixedInteractionEvaluator('nn_sample_'+str(current_sample_id)+'_train_50',
log_dir=results_data_folder,
n_interactions=50,
loss_fn=loss_fn,
ode_solver=None,
ode_solver_kwargs={'method' : 'dopri5'},
preserve_intermediate_states=False,
preserve_intermediate_controls=False,
preserve_intermediate_times=False,
preserve_intermediate_energies=False,
preserve_intermediate_losses=False,
preserve_params=True,
)
nn_res = nn_logger_50.evaluate(dyn, nndyn.nnc, x0, total_time, epoch=100)
nn_logger_50.write_to_file(nn_res)
# keep training for 2400 epochs
nndyn = nn_trainer.train_best(epochs=2400,
lr_acceleration_rate=0,
lr_deceleration_rate=0.99,
loss_variance_tolerance=10,
verbose=True)
# evaluate for 500 interactions
nn_logger_500 = FixedInteractionEvaluator(
'nn_sample_'+str(current_sample_id)+'_train_500',
log_dir=results_data_folder,
n_interactions=500,
loss_fn=loss_fn,
ode_solver=None,
ode_solver_kwargs={'method' : 'dopri5'},
preserve_intermediate_states=False,
preserve_intermediate_controls=False,
preserve_intermediate_times=False,
preserve_intermediate_energies=False,
preserve_intermediate_losses=False,
preserve_params=False,
)
nn_res = nn_logger_500.evaluate(dyn, nndyn.nnc, x0, total_time, epoch=2500)
nn_logger_500.write_to_file(nn_res)
# evaluate for 5000 interactions
nn_logger_5000= FixedInteractionEvaluator(
'nn_sample_'+str(current_sample_id)+'_train_5000',
log_dir=results_data_folder,
n_interactions=5000,
loss_fn=loss_fn,
ode_solver=None,
ode_solver_kwargs={'method' : 'dopri5'},
preserve_intermediate_states=False,
preserve_intermediate_controls=False,
preserve_intermediate_times=False,
preserve_intermediate_energies=False,
preserve_intermediate_losses=False,
preserve_params=True,
)
nn_res = nn_logger_5000.evaluate(dyn, nndyn.nnc, x0, total_time, epoch=2500)
nn_logger_5000.write_to_file(nn_res)
```
| true |
code
| 0.620392 | null | null | null | null |
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
# https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.plotting.register_matplotlib_converters.html
# Register converters for handling timestamp values in plots
```
<h2>Kaggle Bike Sharing Demand Dataset</h2>
<h4>To download dataset, sign-in and download from this link: https://www.kaggle.com/c/bike-sharing-demand/data</h4>
<br>
Input Features:<br>
['season', 'holiday', 'workingday', 'weather', 'temp', 'atemp', 'humidity', 'windspeed', 'year', 'month', 'day', 'dayofweek','hour']<br>
Target:<br>
['count']<br>
Objective:
You are provided hourly rental data spanning two years.
For this competition, the training set is comprised of the first 19 days of each month, while the test set is the 20th to the end of the month.
You must predict the total count of bikes rented during each hour covered by the test set, using only information available prior to the rental period
Reference: https://www.kaggle.com/c/bike-sharing-demand/data
```
columns = ['count', 'season', 'holiday', 'workingday', 'weather', 'temp',
'atemp', 'humidity', 'windspeed', 'year', 'month', 'day', 'dayofweek','hour']
df = pd.read_csv('train.csv', parse_dates=['datetime'],index_col=0)
df_test = pd.read_csv('test.csv', parse_dates=['datetime'],index_col=0)
df.head()
# We need to convert datetime to numeric for training.
# Let's extract key features into separate numeric columns
def add_features(df):
df['year'] = df.index.year
df['month'] = df.index.month
df['day'] = df.index.day
df['dayofweek'] = df.index.dayofweek
df['hour'] = df.index.hour
# Add New Features
add_features(df)
add_features(df_test)
df.head()
# Need to predict the missing data
plt.title('Rental Count - Gaps')
df['2011-01':'2011-02']['count'].plot()
plt.show()
# Rentals change hourly!
plt.plot(df['2011-01-01']['count'])
plt.xticks(fontsize=14, rotation=45)
plt.xlabel('Date')
plt.ylabel('Rental Count')
plt.title('Hourly Rentals for Jan 01, 2011')
plt.show()
# Seasonal
plt.plot(df['2011-01']['count'])
plt.xticks(fontsize=14, rotation=45)
plt.xlabel('Date')
plt.ylabel('Rental Count')
plt.title('Jan 2011 Rentals (1 month)')
plt.show()
group_hour = df.groupby(['hour'])
average_by_hour = group_hour['count'].mean()
plt.plot(average_by_hour.index,average_by_hour)
plt.xlabel('Hour')
plt.ylabel('Rental Count')
plt.xticks(np.arange(24))
plt.grid(True)
plt.title('Average Hourly Rental Count')
# Year to year trend
plt.plot(df['2011']['count'],label='2011')
plt.plot(df['2012']['count'],label='2012')
plt.xticks(fontsize=14, rotation=45)
plt.xlabel('Date')
plt.ylabel('Rental Count')
plt.title('2011 and 2012 Rentals (Year to Year)')
plt.legend()
plt.show()
group_year_month = df.groupby(['year','month'])
average_year_month = group_year_month['count'].mean()
average_year_month
for year in average_year_month.index.levels[0]:
plt.plot(average_year_month[year].index,average_year_month[year],label=year)
plt.legend()
plt.xlabel('Month')
plt.ylabel('Count')
plt.grid(True)
plt.title('Average Monthly Rental Count for 2011, 2012')
plt.show()
group_year_hour = df.groupby(['year','hour'])
average_year_hour = group_year_hour['count'].mean()
for year in average_year_hour.index.levels[0]:
#print (year)
#print(average_year_month[year])
plt.plot(average_year_hour[year].index,average_year_hour[year],label=year)
plt.legend()
plt.xlabel('Hour')
plt.ylabel('Count')
plt.xticks(np.arange(24))
plt.grid(True)
plt.title('Average Hourly Rental Count - 2011, 2012')
group_workingday_hour = df.groupby(['workingday','hour'])
average_workingday_hour = group_workingday_hour['count'].mean()
for workingday in average_workingday_hour.index.levels[0]:
#print (year)
#print(average_year_month[year])
plt.plot(average_workingday_hour[workingday].index,average_workingday_hour[workingday],
label=workingday)
plt.legend()
plt.xlabel('Hour')
plt.ylabel('Count')
plt.xticks(np.arange(24))
plt.grid(True)
plt.title('Average Hourly Rental Count by Working Day')
plt.show()
# Let's look at correlation beween features and target
df.corr()['count']
# Any relation between temperature and rental count?
plt.scatter(x=df.temp,y=df["count"])
plt.grid(True)
plt.xlabel('Temperature')
plt.ylabel('Count')
plt.title('Temperature vs Count')
plt.show()
# Any relation between humidity and rental count?
plt.scatter(x=df.humidity,y=df["count"],label='Humidity')
plt.grid(True)
plt.xlabel('Humidity')
plt.ylabel('Count')
plt.title('Humidity vs Count')
plt.show()
# Save all data
df.to_csv('bike_all.csv',index=True,index_label='datetime',columns=columns)
```
## Training and Validation Set
### Target Variable as first column followed by input features
### Training, Validation files do not have a column header
```
# Training = 70% of the data
# Validation = 30% of the data
# Randomize the datset
np.random.seed(5)
l = list(df.index)
np.random.shuffle(l)
df = df.loc[l]
rows = df.shape[0]
train = int(.7 * rows)
test = rows-train
rows, train, test
columns
# Write Training Set
df.iloc[:train].to_csv('bike_train.csv'
,index=False,header=False
,columns=columns)
# Write Validation Set
df.iloc[train:].to_csv('bike_validation.csv'
,index=False,header=False
,columns=columns)
# Test Data has only input features
df_test.to_csv('bike_test.csv',index=True,index_label='datetime')
print(','.join(columns))
# Write Column List
with open('bike_train_column_list.txt','w') as f:
f.write(','.join(columns))
```
| true |
code
| 0.527925 | null | null | null | null |
|
# Unsplash Image Search
Using this notebook you can search for images from the [Unsplash Dataset](https://unsplash.com/data) using natural language queries. The search is powered by OpenAI's [CLIP](https://github.com/openai/CLIP) neural network.
This notebook uses the precomputed feature vectors for almost 2 million images from the full version of the [Unsplash Dataset](https://unsplash.com/data). If you want to compute the features yourself, see [here](https://github.com/haltakov/natural-language-image-search#on-your-machine).
This project was created by [Vladimir Haltakov](https://twitter.com/haltakov) and the full code is open-sourced on [GitHub](https://github.com/haltakov/natural-language-image-search).
## Setup Environment
In this section we will setup the environment.
First we need to install CLIP and then upgrade the version of torch to 1.7.1 with CUDA support (by default CLIP installs torch 1.7.1 without CUDA). Google Colab currently has torch 1.7.0 which doesn't work well with CLIP.
```
!pip install git+https://github.com/openai/CLIP.git
!pip install torch==1.7.1+cu101 torchvision==0.8.2+cu101 -f https://download.pytorch.org/whl/torch_stable.html
```
We can now load the pretrained public CLIP model.
```
import clip
import torch
# Load the open CLIP model
device = "cuda" if torch.cuda.is_available() else "cpu"
model, preprocess = clip.load("ViT-B/32", device=device)
```
## Download the Precomputed Data
In this section the precomputed feature vectors for all photos are downloaded.
In order to compare the photos from the Unsplash dataset to a text query, we need to compute the feature vector of each photo using CLIP. This is a time consuming task, so you can use the feature vectors that I precomputed and uploaded to Google Drive (with the permission from Unsplash). If you want to compute the features yourself, see [here](https://github.com/haltakov/natural-language-image-search#on-your-machine).
We need to download two files:
* `photo_ids.csv` - a list of the photo IDs for all images in the dataset. The photo ID can be used to get the actual photo from Unsplash.
* `features.npy` - a matrix containing the precomputed 512 element feature vector for each photo in the dataset.
The files are available on [Google Drive](https://drive.google.com/drive/folders/1WQmedVCDIQKA2R33dkS1f980YsJXRZ-q?usp=sharing).
```
from pathlib import Path
# Create a folder for the precomputed features
!mkdir unsplash-dataset
# Download the photo IDs and the feature vectors
!gdown --id 1FdmDEzBQCf3OxqY9SbU-jLfH_yZ6UPSj -O unsplash-dataset/photo_ids.csv
!gdown --id 1L7ulhn4VeN-2aOM-fYmljza_TQok-j9F -O unsplash-dataset/features.npy
# Download from alternative source, if the download doesn't work for some reason (for example download quota limit exceeded)
if not Path('unsplash-dataset/photo_ids.csv').exists():
!wget https://transfer.army/api/download/TuWWFTe2spg/EDm6KBjc -O unsplash-dataset/photo_ids.csv
if not Path('unsplash-dataset/features.npy').exists():
!wget https://transfer.army/api/download/LGXAaiNnMLA/AamL9PpU -O unsplash-dataset/features.npy
```
After the files are downloaded we need to load them using `pandas` and `numpy`.
```
import pandas as pd
import numpy as np
# Load the photo IDs
photo_ids = pd.read_csv("unsplash-dataset/photo_ids.csv")
photo_ids = list(photo_ids['photo_id'])
# Load the features vectors
photo_features = np.load("unsplash-dataset/features.npy")
# Convert features to Tensors: Float32 on CPU and Float16 on GPU
if device == "cpu":
photo_features = torch.from_numpy(photo_features).float().to(device)
else:
photo_features = torch.from_numpy(photo_features).to(device)
# Print some statistics
print(f"Photos loaded: {len(photo_ids)}")
```
## Define Functions
Some important functions for processing the data are defined here.
The `encode_search_query` function takes a text description and encodes it into a feature vector using the CLIP model.
```
def encode_search_query(search_query):
with torch.no_grad():
# Encode and normalize the search query using CLIP
text_encoded = model.encode_text(clip.tokenize(search_query).to(device))
text_encoded /= text_encoded.norm(dim=-1, keepdim=True)
# Retrieve the feature vector
return text_encoded
```
The `find_best_matches` function compares the text feature vector to the feature vectors of all images and finds the best matches. The function returns the IDs of the best matching photos.
```
def find_best_matches(text_features, photo_features, photo_ids, results_count=3):
# Compute the similarity between the search query and each photo using the Cosine similarity
similarities = (photo_features @ text_features.T).squeeze(1)
# Sort the photos by their similarity score
best_photo_idx = (-similarities).argsort()
# Return the photo IDs of the best matches
return [photo_ids[i] for i in best_photo_idx[:results_count]]
```
The `display_photo` function displays a photo from Unsplash given its ID.
This function needs to call the Unsplash API to get the URL of the photo and some metadata about the photographer. Since I'm [not allowed](https://help.unsplash.com/en/articles/2511245-unsplash-api-guidelines) to share my Unsplash API access key publicly, I created a small proxy that queries the Unsplash API and returns the data (see the code [here](https://github.com/haltakov/natural-language-image-search/tree/main/unsplash-proxy)). In this way you can play around without creating a developer account at Unsplash, while keeping my key private. I hope I don't hit the API rate limit.
If you already have an Unsplash developer account, you can uncomment the relevant code and plugin your own access key.
```
from IPython.display import Image
from IPython.core.display import HTML
from urllib.request import urlopen
import json
def display_photo(photo_id):
# Proxy for the Unsplash API so that I don't expose my access key
unsplash_api_url = f"https://haltakov.net/unsplash-proxy/{photo_id}"
# Alternatively, you can use your own Unsplash developer account with this code
# unsplash_api_url = f"https://api.unsplash.com/photos/{photo_id}?client_id=YOUR_UNSPLASH_ACCESS_KEY"
# Fetch the photo metadata from the Unsplash API
photo_data = json.loads(urlopen(unsplash_api_url).read().decode("utf-8"))
# Get the URL of the photo resized to have a width of 480px
photo_image_url = photo_data["urls"]["raw"] + "&w=320"
# Display the photo
display(Image(url=photo_image_url))
# Display the attribution text
display(HTML(f'Photo by <a target="_blank" href="https://unsplash.com/@{photo_data["user"]["username"]}?utm_source=NaturalLanguageImageSearch&utm_medium=referral">{photo_data["user"]["name"]}</a> on <a target="_blank" href="https://unsplash.com/?utm_source=NaturalLanguageImageSearch&utm_medium=referral">Unsplash</a>'))
print()
```
Putting it all together in one function.
```
def search_unslash(search_query, photo_features, photo_ids, results_count=3):
# Encode the search query
text_features = encode_search_query(search_query)
# Find the best matches
best_photo_ids = find_best_matches(text_features, photo_features, photo_ids, results_count)
# Display the best photos
for photo_id in best_photo_ids:
display_photo(photo_id)
```
## Search Unsplash
Now we are ready to search the dataset using natural language. Check out the examples below and feel free to try out your own queries.
> ⚠️ WARNING ⚠️
> Since many people are currently using the notebook, it seems that the Unsplash API limit is hit from time to time (even with caching in the proxy). I applied for production status which will solve the problem. In the meantime, you can just try when a new hour starts. Alternatively, you can use your own Unsplash API key.
### "Two dogs playing in the snow"
```
search_query = "Two dogs playing in the snow"
search_unslash(search_query, photo_features, photo_ids, 3)
```
### "The word love written on the wall"
```
search_query = "The word love written on the wall"
search_unslash(search_query, photo_features, photo_ids, 3)
```
### "The feeling when your program finally works"
```
search_query = "The feeling when your program finally works"
search_unslash(search_query, photo_features, photo_ids, 3)
```
### "The Syndey Opera House and the Harbour Bridge at night"
```
search_query = "The Syndey Opera House and the Harbour Bridge at night"
search_unslash(search_query, photo_features, photo_ids, 3)
```
| true |
code
| 0.619874 | null | null | null | null |
|
## GANs
```
%matplotlib inline
from fastai.gen_doc.nbdoc import *
from fastai.vision import *
from fastai.vision.gan import *
```
GAN stands for [Generative Adversarial Nets](https://arxiv.org/pdf/1406.2661.pdf) and were invented by Ian Goodfellow. The concept is that we will train two models at the same time: a generator and a critic. The generator will try to make new images similar to the ones in our dataset, and the critic's job will try to classify real images from the fake ones the generator does. The generator returns images, the discriminator a feature map (it can be a single number depending on the input size). Usually the discriminator will be trained to return 0. everywhere for fake images and 1. everywhere for real ones.
This module contains all the necessary function to create a GAN.
We train them against each other in the sense that at each step (more or less), we:
1. Freeze the generator and train the discriminator for one step by:
- getting one batch of true images (let's call that `real`)
- generating one batch of fake images (let's call that `fake`)
- have the discriminator evaluate each batch and compute a loss function from that; the important part is that it rewards positively the detection of real images and penalizes the fake ones
- update the weights of the discriminator with the gradients of this loss
2. Freeze the discriminator and train the generator for one step by:
- generating one batch of fake images
- evaluate the discriminator on it
- return a loss that rewards posisitivly the discriminator thinking those are real images; the important part is that it rewards positively the detection of real images and penalizes the fake ones
- update the weights of the generator with the gradients of this loss
```
show_doc(GANLearner)
```
This is the general constructor to create a GAN, you might want to use one of the factory methods that are easier to use. Create a GAN from [`data`](/vision.data.html#vision.data), a `generator` and a `critic`. The [`data`](/vision.data.html#vision.data) should have the inputs the `generator` will expect and the images wanted as targets.
`gen_loss_func` is the loss function that will be applied to the `generator`. It takes three argument `fake_pred`, `target`, `output` and should return a rank 0 tensor. `output` is the result of the `generator` applied to the input (the xs of the batch), `target` is the ys of the batch and `fake_pred` is the result of the `discriminator` being given `output`. `output`and `target` can be used to add a specific loss to the GAN loss (pixel loss, feature loss) and for a good training of the gan, the loss should encourage `fake_pred` to be as close to 1 as possible (the `generator` is trained to fool the `critic`).
`crit_loss_func` is the loss function that will be applied to the `critic`. It takes two arguments `real_pred` and `fake_pred`. `real_pred` is the result of the `critic` on the target images (the ys of the batch) and `fake_pred` is the result of the `critic` applied on a batch of fake, generated byt the `generator` from the xs of the batch.
`switcher` is a [`Callback`](/callback.html#Callback) that should tell the GAN when to switch from critic to generator and vice versa. By default it does 5 iterations of the critic for 1 iteration of the generator. The model begins the training with the `generator` if `gen_first=True`. If `switch_eval=True`, the model that isn't trained is switched on eval mode (left in training mode otherwise, which means some statistics like the running mean in batchnorm layers are updated, or the dropouts are applied).
`clip` should be set to a certain value if one wants to clip the weights (see the [Wassertein GAN](https://arxiv.org/pdf/1701.07875.pdf) for instance).
If `show_img=True`, one image generated by the GAN is shown at the end of each epoch.
### Factory methods
```
show_doc(GANLearner.from_learners)
```
Directly creates a [`GANLearner`](/vision.gan.html#GANLearner) from two [`Learner`](/basic_train.html#Learner): one for the `generator` and one for the `critic`. The `switcher` and all `kwargs` will be passed to the initialization of [`GANLearner`](/vision.gan.html#GANLearner) along with the following loss functions:
- `loss_func_crit` is the mean of `learn_crit.loss_func` applied to `real_pred` and a target of ones with `learn_crit.loss_func` applied to `fake_pred` and a target of zeros
- `loss_func_gen` is the mean of `learn_crit.loss_func` applied to `fake_pred` and a target of ones (to full the discriminator) with `learn_gen.loss_func` applied to `output` and `target`. The weights of each of those contributions can be passed in `weights_gen` (default is 1. and 1.)
```
show_doc(GANLearner.wgan)
```
The Wasserstein GAN is detailed in [this article]. `switcher` and the `kwargs` will be passed to the [`GANLearner`](/vision.gan.html#GANLearner) init, `clip`is the weight clipping.
## Switchers
In any GAN training, you will need to tell the [`Learner`](/basic_train.html#Learner) when to switch from generator to critic and vice versa. The two following [`Callback`](/callback.html#Callback) are examples to help you with that.
As usual, don't call the `on_something` methods directly, the fastai library will do it for you during training.
```
show_doc(FixedGANSwitcher, title_level=3)
show_doc(FixedGANSwitcher.on_train_begin)
show_doc(FixedGANSwitcher.on_batch_end)
show_doc(AdaptiveGANSwitcher, title_level=3)
show_doc(AdaptiveGANSwitcher.on_batch_end)
```
## Discriminative LR
If you want to train your critic at a different learning rate than the generator, this will let you do it automatically (even if you have a learning rate schedule).
```
show_doc(GANDiscriminativeLR, title_level=3)
show_doc(GANDiscriminativeLR.on_batch_begin)
show_doc(GANDiscriminativeLR.on_step_end)
```
## Specific models
```
show_doc(basic_critic)
```
This model contains a first 4 by 4 convolutional layer of stride 2 from `n_channels` to `n_features` followed by `n_extra_layers` 3 by 3 convolutional layer of stride 1. Then we put as many 4 by 4 convolutional layer of stride 2 with a number of features multiplied by 2 at each stage so that the `in_size` becomes 1. `kwargs` can be used to customize the convolutional layers and are passed to [`conv_layer`](/layers.html#conv_layer).
```
show_doc(basic_generator)
```
This model contains a first 4 by 4 transposed convolutional layer of stride 1 from `noise_size` to the last numbers of features of the corresponding critic. Then we put as many 4 by 4 transposed convolutional layer of stride 2 with a number of features divided by 2 at each stage so that the image ends up being of height and widht `in_size//2`. At the end, we add`n_extra_layers` 3 by 3 convolutional layer of stride 1. The last layer is a transpose convolution of size 4 by 4 and stride 2 followed by `tanh`. `kwargs` can be used to customize the convolutional layers and are passed to [`conv_layer`](/layers.html#conv_layer).
```
show_doc(gan_critic)
show_doc(GANTrainer)
```
[`LearnerCallback`](/basic_train.html#LearnerCallback) that will be responsible to handle the two different optimizers (one for the generator and one for the critic), and do all the work behind the scenes so that the generator (or the critic) are in training mode with parameters requirement gradients each time we switch.
`switch_eval=True` means that the [`GANTrainer`](/vision.gan.html#GANTrainer) will put the model that isn't training into eval mode (if it's `False` its running statistics like in batchnorm layers will be updated and dropout will be applied). `clip` is the clipping applied to the weights (if not `None`). `beta` is the coefficient for the moving averages as the [`GANTrainer`](/vision.gan.html#GANTrainer)tracks separately the generator loss and the critic loss. `gen_first=True` means the training begins with the generator (with the critic if it's `False`). If `show_img=True` we show a generated image at the end of each epoch.
```
show_doc(GANTrainer.switch)
```
If `gen_mode` is left as `None`, just put the model in the other mode (critic if it was in generator mode and vice versa).
```
show_doc(GANTrainer.on_train_begin)
show_doc(GANTrainer.on_epoch_begin)
show_doc(GANTrainer.on_batch_begin)
show_doc(GANTrainer.on_backward_begin)
show_doc(GANTrainer.on_epoch_end)
show_doc(GANTrainer.on_train_end)
```
## Specific modules
```
show_doc(GANModule, title_level=3)
```
If `gen_mode` is left as `None`, just put the model in the other mode (critic if it was in generator mode and vice versa).
```
show_doc(GANModule.switch)
show_doc(GANLoss, title_level=3)
show_doc(AdaptiveLoss, title_level=3)
show_doc(accuracy_thresh_expand)
```
## Data Block API
```
show_doc(NoisyItem, title_level=3)
show_doc(GANItemList, title_level=3)
```
Inputs will be [`NoisyItem`](/vision.gan.html#NoisyItem) of `noise_sz` while the default class for target is [`ImageList`](/vision.data.html#ImageList).
```
show_doc(GANItemList.show_xys)
show_doc(GANItemList.show_xyzs)
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(GANLoss.critic)
show_doc(GANModule.forward)
show_doc(GANLoss.generator)
show_doc(NoisyItem.apply_tfms)
show_doc(AdaptiveLoss.forward)
show_doc(GANItemList.get)
show_doc(GANItemList.reconstruct)
show_doc(AdaptiveLoss.forward)
```
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.71802 | null | null | null | null |
|
<a id=top></a>
# Pea3 smFISH Analysis
## Table of Contents
----
1. [Preparations](#prep)
2. [QC: Spot Detection](#QC_spots)
3. [QC: Cell Shape](#QC_shape)
4. [Data Visualization](#viz)
5. [Predicting Expression from Shape: Testing](#atlas_test)
6. [Predicting Expression from Shape: Running](#atlas_run)
7. [Predicting Expression from Shape: Visualization](#atlas_viz)
<a id=prep></a>
## 1. Preparations
[back to top](#top)
----
```
### Import modules
# External, general
from __future__ import division
import os, sys, pickle
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# External, specific
import ipywidgets as widgets
import scipy.stats as stats
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from skimage import io
from sklearn import model_selection, metrics, multioutput
import sklearn.svm as svm
# Internal
import katachi.utilities.loading as ld
### Load general data
# Prep loader
loader = ld.DataLoaderIDR()
loader.find_imports(r"data/experimentB/extracted_measurements/", recurse=True, verbose=True)
# Import shape spaces
fspace_TFOR, prim_IDs, fspace_idx = loader.load_dataset("shape_TFOR_raw_measured.tsv")
fspace_CFOR, _, _ = loader.load_dataset("shape_CFOR_raw_measured.tsv", IDs=prim_IDs)
print "Imported TFOR shape space of shape:", fspace_TFOR.shape
print "Imported CFOR shape space of shape:", fspace_CFOR.shape
# Standardization and PCA
fspace_TFOR_z = StandardScaler().fit_transform(fspace_TFOR)
pca_TFOR = PCA()
fspace_TFOR_pca = pca_TFOR.fit_transform(fspace_TFOR_z)
fspace_CFOR_z = StandardScaler().fit_transform(fspace_CFOR)
pca_CFOR = PCA()
fspace_CFOR_pca = pca_CFOR.fit_transform(fspace_CFOR_z)
# Import TFOR centroid locations
centroids = loader.load_dataset("_other_measurements.tsv", IDs=prim_IDs)[0][:,3:6][:,::-1]
print "Imported TFOR centroids of shape:", centroids.shape
# Import & standardize engineered features
covar_df, _, _ = loader.load_dataset("_other_measurements.tsv", IDs=prim_IDs, force_df=True)
del covar_df['Centroids RAW X']; del covar_df['Centroids RAW Y']; del covar_df['Centroids RAW Z']
covar_names = list(covar_df.columns)
covar_df_z = (covar_df - covar_df.mean()) / covar_df.std()
print "Imported engineered features of shape:", covar_df.shape
### Load smFISH data
# Counts
rna_counts, _, _ = loader.load_dataset("pea3smFISH_RNAcounts_measured.tsv", IDs=prim_IDs)
print "Imported RNA counts data of shape:", rna_counts.shape
# Spots
rna_spots, _, _= loader.load_dataset("pea3smFISH_RNAspot_coordinates.tsv", IDs=prim_IDs, force_dict=True)
print "Imported RNA spot coordinates for", len(rna_spots), "samples, the first having shape", rna_spots[prim_IDs[0]].shape
### Outlier removal
# Remove samples with `mean(rna_counts) <= mean_count_thresh` as a simple and helpful quality threshold
mean_count_thresh = 2
count_means = [np.mean(rna_counts[fspace_idx==prim_idx]) for prim_idx in range(len(prim_IDs))]
rna_exclude_prim_mask = np.array(count_means) > mean_count_thresh
rna_exclude_cell_mask = rna_exclude_prim_mask[fspace_idx]
# Report
print "Excluding", np.sum(~rna_exclude_prim_mask), "prims /", np.sum(~rna_exclude_cell_mask), "cells,",
print "resulting in", np.sum(rna_exclude_prim_mask), "prims /", np.sum(rna_exclude_cell_mask), "cells",
print "left for analysis."
```
<a id=QC_spots></a>
## 2. QC: Spot Detection
[back to top](#top)
----
```
### Boxplot of mean counts & per-cell counts
# Note:
# - Durdu et al. found a mean of ~11 spots/cell in their manually analyzed data.
# This plot is designed to fit their way of reporting the results.
# - This is recapitulated quite well here, except for a couple of outliers with
# unrealistically low expression.
# - However, note that the cell-level distribution is very non-normal, so the mean
# is not a very good summary characteristic.
# Get count means
count_means = np.array([np.mean(rna_counts[fspace_idx==prim_idx])
for prim_idx in range(len(prim_IDs))])
# Fig prep
fig, ax = plt.subplots(1, 2, figsize=(3.5, 4.5))
# Make boxplots
bp_m = ax[0].boxplot(count_means, widths=0.5, patch_artist=True)
bp_a = ax[1].boxplot(rna_counts, widths=0.5, patch_artist=True, showfliers=False)
# Boxplot styling function (making it similar to Sevi's paper)
def style_boxplot(bp):
for patch in bp['boxes']:
patch.set(edgecolor='black', linewidth=1.2,)
for whisker in bp['whiskers']:
whisker.set(color='black', linestyle='-')
for cap in bp['caps']:
cap.set(linewidth=1.2)
for median in bp['medians']:
median.set(color='black', linewidth=1.2)
# Style the boxplots
style_boxplot(bp_m)
style_boxplot(bp_a)
# Add scatter
ax[0].scatter(np.random.normal(1.0, 0.06, len(count_means)), count_means,
zorder=10, s=20, alpha=0.7, c='midnightblue', edgecolor='')
ax[0].set_ylim([-2, 47])
ax[1].scatter(np.random.normal(1.0, 0.06, len(rna_counts)), rna_counts,
zorder=10, s=2, alpha=0.1, c='midnightblue', edgecolor='')
ax[1].set_ylim([-2, 100])
# Remove ticks
ax[0].yaxis.set_ticks_position('left')
ax[0].xaxis.set_ticks_position('bottom')
ax[1].yaxis.set_ticks_position('left')
ax[1].xaxis.set_ticks_position('bottom')
# Axis labels
from matplotlib import rcParams
rcParams['mathtext.default'] = 'regular'
ax[0].set_ylabel(r'$\it{pea3}$ transcripts per cell (mean)', fontsize=12, labelpad=5)
ax[0].set_xticklabels(['WT 880'], rotation=90, fontsize=12)
ax[1].set_ylabel(r'$\it{pea3}$ transcripts per cell (all)', fontsize=12, labelpad=0)
ax[1].set_xticklabels(['WT 880'], rotation=90, fontsize=12)
plt.tight_layout()
# Show
plt.show()
### Histograms of RNA counts for each sample
# Prep
n_plot_cols = 7
n_plot_rows = int(np.ceil(len(prim_IDs) / n_plot_cols))
fig, ax = plt.subplots(n_plot_rows, n_plot_cols, figsize=(1.5*n_plot_cols, 1.5*n_plot_rows),
sharex=True, sharey=True)
ax = ax.flatten()
[ax[i].axis('off') for i in range(len(prim_IDs), n_plot_cols*n_plot_rows)]
# For each sample...
for axx, prim_idx, prim_ID, is_outlier in zip(ax, range(len(prim_IDs)), prim_IDs, ~rna_exclude_prim_mask):
# Generate the histogram
axx.hist(rna_counts[fspace_idx==prim_idx],
bins=40, range=(rna_counts.min(), rna_counts.max()),
histtype='stepfilled', color='darkblue' if not is_outlier else 'darkred', alpha=0.5)
axx.set_title(prim_ID, fontsize=9)
# Set common axis labels
fig.text(0.5, -0.01, 'RNA Counts', ha='center', va='center')
fig.text(-0.01, 0.50, 'Histogram\nof Cells', ha='center', va='center', rotation='vertical')
# Done
plt.tight_layout()
plt.show()
### Histogram of counts over all cells
# Prep
plt.figure(figsize=(5, 3))
# Make hist
plt.hist(rna_counts, bins=100, histtype='stepfilled', color='b', alpha=0.5)
# Label
plt.xlabel('RNA Count')
plt.ylabel('Histogram of Cells')
# Done
plt.show()
```
<a id=QC_shape></a>
## 3. QC: Cell Shape (Fixation Effects)
[back to top](#top)
----
```
### Load live imaging reference data
# Prep loader
ref_loader = ld.DataLoaderIDR()
ref_loader.find_imports(r"data/experimentA/extracted_measurements/", recurse=True, verbose=True)
# Use only the 24 samples that were single-color imaged
ref_IDs = ['056F63395C', '08B96BE794', '0B51F8B46C', '1C43D83E9A', '2902E38204', '4DC24FC301',
'6F18162F4C', '8C633380D2', 'B95A4F6D95', 'CB87D7CBC9', '0E48AB134C', '3612A6CEF5',
'8713481504', '8C83D4387F', 'AB98466077', 'C95F528559', 'E013272A99', 'E6E56C3F42',
'22DF2AE1A0', '2B23352582', '673A65D087', '8CA33561B5', 'EC77708A51', 'FC90367714']
# Import shape spaces
ref_TFOR, _, ref_idx = ref_loader.load_dataset("shape_TFOR_raw_measured.tsv", IDs=ref_IDs)
ref_CFOR, _, _ = ref_loader.load_dataset("shape_CFOR_raw_measured.tsv", IDs=ref_IDs)
print "Imported TFOR shape space of shape:", ref_TFOR.shape
print "Imported CFOR shape space of shape:", ref_CFOR.shape
# Standardization and apply PCA (fitted above)
ref_TFOR_z = StandardScaler().fit_transform(ref_TFOR)
ref_TFOR_pca = pca_TFOR.transform(ref_TFOR_z)
ref_CFOR_z = StandardScaler().fit_transform(ref_CFOR)
ref_CFOR_pca = pca_CFOR.transform(ref_CFOR_z)
# Import & standardize engineered features
ref_covar_df, _, _ = ref_loader.load_dataset("_other_measurements.tsv", IDs=ref_IDs, force_df=True)
del ref_covar_df['Centroids RAW X']; del ref_covar_df['Centroids RAW Y']; del ref_covar_df['Centroids RAW Z']
ref_covar_names = list(ref_covar_df.columns)
ref_covar_df_z = (ref_covar_df - ref_covar_df.mean()) / ref_covar_df.std()
print "Imported engineered features of shape:", ref_covar_df.shape
### Compare to reference shape spaces: overlay
# Set interactions
@widgets.interact(PCx=(1, fspace_TFOR_pca.shape[1], 1),
PCy=(1, fspace_TFOR_pca.shape[1], 1))
# Show
def show_PCs(PCx=1, PCy=2):
# Prep
fig, ax = plt.subplots(1, 2, figsize=(12,5))
# Plot TFOR
ax[0].scatter(ref_TFOR_pca[:,PCx-1], ref_TFOR_pca[:,PCy-1],
c='b', cmap=plt.cm.plasma, edgecolor='',
s=20, alpha=0.25, label='reference')
ax[0].scatter(fspace_TFOR_pca[:,PCx-1], fspace_TFOR_pca[:,PCy-1],
c='r', cmap=plt.cm.plasma, edgecolor='',
s=20, alpha=0.25, label='fixed')
# Plot CFOR
ax[1].scatter(ref_CFOR_pca[:,PCx-1], ref_CFOR_pca[:,PCy-1],
c='b', cmap=plt.cm.plasma, edgecolor='',
s=20, alpha=0.25, label='reference')
ax[1].scatter(fspace_CFOR_pca[:,PCx-1], fspace_CFOR_pca[:,PCy-1],
c='r', cmap=plt.cm.plasma, edgecolor='',
s=20, alpha=0.25, label='fixed')
# Cosmetics
ax[0].legend(fontsize=8, frameon=False)
ax[0].set_xlabel("PC "+str(PCx))
ax[1].set_xlabel("PC "+str(PCx))
ax[0].set_ylabel("PC "+str(PCy))
ax[1].set_ylabel("PC "+str(PCy))
ax[0].set_title("TFOR")
ax[1].set_title("CFOR")
# Done
plt.tight_layout()
plt.show()
### Compare to reference cell extents
# Prep for plots
fig, ax = plt.subplots(1, 3, figsize=(6.5,3), sharey=True)
# Create plots
for i, lbl in enumerate(['Z', 'Y', 'X']):
# Violinplot
vio = ax[i].violinplot([ref_covar_df[lbl+' Axis Length'],
covar_df[lbl+' Axis Length']],
widths=0.60, showextrema=False)
# Violinplot cosmetics
vio['bodies'][0].set_facecolors('lightskyblue')
vio['bodies'][1].set_facecolors('tomato')
ax[i].set_xlim(0.3, 2.7)
ax[i].set_xticks([1.0, 2.0])
ax[i].set_xticklabels(["Reference", "Fixed"])
ax[i].set_ylabel(lbl)
# Jitter
for j,y in enumerate([ref_covar_df[lbl+' Axis Length'], covar_df[lbl+' Axis Length']]):
x = np.random.normal(j+1, 0.08, size=len(y))
ax[i].plot(x, y, '.', color=['blue', 'red'][j], alpha=[0.1, 0.1][j], ms=2)
# Done
plt.tight_layout()
plt.show()
### Compare to reference cell sphericity
# Violinplot
plt.figure(figsize=(2,3))
vio = plt.violinplot([ref_covar_df['Sphericity'], covar_df['Sphericity']],
widths=0.60, showextrema=False)
# Violinplot cosmetics
vio['bodies'][0].set_facecolors('lightskyblue')
vio['bodies'][1].set_facecolors('tomato')
plt.xlim(0.3, 2.7)
plt.xticks([1.0, 2.0])
plt.gca().set_xticklabels(["Reference", "Fixed"])
plt.ylabel("Cell Sphericity")
# Jitter
for i,y in enumerate([ref_covar_df['Sphericity'], covar_df['Sphericity']]):
x = np.random.normal(i+1, 0.08, size=len(y))
plt.plot(x, y, '.', color=['blue', 'red'][i], alpha=[0.1, 0.1][i], ms=2)
# Done
plt.show()
### Compare to reference cell volume
# Violinplot
plt.figure(figsize=(2,3))
vio = plt.violinplot([ref_covar_df['Volume'], covar_df['Volume']], widths=0.60, showextrema=False)
# Violinplot cosmetics
vio['bodies'][0].set_facecolors('lightskyblue')
vio['bodies'][1].set_facecolors('tomato')
plt.xlim(0.3, 2.7)
plt.xticks([1.0, 2.0])
plt.gca().set_xticklabels(["Reference", "Fixed"])
plt.ylabel("Cell Volume")
# Jitter
for i,y in enumerate([ref_covar_df['Volume'], covar_df['Volume']]):
x = np.random.normal(i+1, 0.08, size=len(y))
plt.plot(x, y, '.', color=['blue', 'red'][i], alpha=[0.1, 0.1][i], ms=2)
# Done
plt.show()
### For publication: compare to diverse set of shape references
# Prep for plots
fig, ax = plt.subplots(1, 3, figsize=(8, 3.5))
# Violinplot
vio_data = [[ref_TFOR_pca[:,0], fspace_TFOR_pca[:,0]], # TFOR PC 1
[ref_CFOR_pca[:,0], fspace_CFOR_pca[:,0]], # CFOR PC 1
[ref_covar_df['Z Axis Length'], covar_df['Z Axis Length']]] # Cell Height
# Create plots
for i, lbl in enumerate(['TFOR-PC1 (D-V orient.)',
'CFOR-PC1 (sphericity)',
r'Cell height $\it{[\mu m]}$']):
# Violinplot
vio = ax[i].violinplot(vio_data[i], widths=0.70, showextrema=False)
# Violinplot cosmetics
vio['bodies'][0].set_facecolors('w')
vio['bodies'][1].set_facecolors('w')
ax[i].set_xlim(0.3, 2.7)
ylims = ax[i].get_ylim()
ax[i].set_ylim(ylims[0]-(ylims[1]-ylims[0])*0.05, ylims[1]+(ylims[1]-ylims[0])*0.2)
ax[i].set_xticks([1.0, 2.0])
ax[i].set_xticklabels(["Live", "Fixed"], fontsize=14)
ax[i].set_ylabel(lbl, fontsize=14, labelpad=0)
ax[i].set_yticklabels([int(n) for n in ax[i].get_yticks()], fontsize=14)
# Jitter
for j,y in enumerate(vio_data[i]):
x = np.random.normal(j+1, 0.08, size=len(y))
ax[i].plot(x, y, '.', color=['blue', 'midnightblue'][j], alpha=[0.1, 0.1][j], ms=2)
# Print stats
print 'pMWU('+lbl+'):', stats.mannwhitneyu(*vio_data[i], alternative='two-sided')[1]
# Cosmetics
plt.tight_layout()
# Done
plt.show()
```
<a id=viz></a>
## 4. Data Visualization
[back to top](#top)
----
```
### Overlay of counts on shape spaces
# Set interactions
@widgets.interact(PCx=(1, fspace_TFOR_pca.shape[1], 1),
PCy=(1, fspace_TFOR_pca.shape[1], 1),
vmax_factor=(0.0, 1.0, 0.1))
# Show
def show_PCs(PCx=1, PCy=2, vmax_factor=0.5):
# Prep
fig, ax = plt.subplots(1, 2, figsize=(12,5))
# Plot TFOR
ax[0].scatter(fspace_TFOR_pca[:,PCx-1], fspace_TFOR_pca[:,PCy-1],
c=rna_counts, cmap=plt.cm.plasma,
vmax=vmax_factor*np.max(rna_counts),
s=20, edgecolor='', alpha=0.5)
# Plot CFOR
ax[1].scatter(fspace_CFOR_pca[:,PCx-1], fspace_CFOR_pca[:,PCy-1],
c=rna_counts, cmap=plt.cm.plasma,
vmax=vmax_factor*np.max(rna_counts),
s=20, edgecolor='', alpha=0.5)
# Cosmetics
ax[0].set_xlabel("PC "+str(PCx))
ax[1].set_xlabel("PC "+str(PCx))
ax[0].set_ylabel("PC "+str(PCy))
ax[1].set_ylabel("PC "+str(PCy))
ax[0].set_title("TFOR")
ax[1].set_title("CFOR")
# Done
plt.tight_layout()
plt.show()
### Tissue consensus map
# Note: This suffers a little because some prims are so weirdly angled in the images
# that the TFOR transform didn't get them quite right.
# Settings
xlim = (-130, 8)
ylim = ( -19, 19)
# Exclude weirdly TFOR-ed prims (those with centroids of `x > 0`) for cleaner visualization
centroid_exclude_prim_mask = np.array([np.max(centroids[fspace_idx==prim_idx,-1])
for prim_idx in range(len(prim_IDs))]) < 5
centroid_exclude_cell_mask = centroid_exclude_prim_mask[fspace_idx]
plot_exclude_cell_mask = rna_exclude_cell_mask & centroid_exclude_cell_mask
# Get plot values & remove outliers
plot_values = rna_counts[plot_exclude_cell_mask]
# Tools for smoothing on scatter
from katachi.utilities.pcl_helpers import pcl_gaussian_smooth
from scipy.spatial.distance import pdist, squareform
# Cut off at prim contour outline
kernel_prim = stats.gaussian_kde(centroids[plot_exclude_cell_mask,1:].T)
f_prim = kernel_prim(centroids[plot_exclude_cell_mask,1:].T)
f_prim_mask = f_prim > f_prim.min() + (f_prim.max()-f_prim.min())*0.1
plot_values = plot_values[f_prim_mask]
plot_centroids = centroids[plot_exclude_cell_mask][f_prim_mask]
# Smoothen?
pdists = squareform(pdist(plot_centroids[:,1:]))
plot_values = pcl_gaussian_smooth(pdists, plot_values[:,np.newaxis], sg_percentile=0.5)[:,0]
# Initialize figure
fig, ax = plt.subplots(1, figsize=(8, 2.8))
# Contourf plot
cfset = ax.tricontourf(plot_centroids[:,2], plot_centroids[:,1], plot_values, 20,
cmap='plasma', vmax=20) # Note: vmax manually set for consistency across plots!
# Illustrative centroids from a single prim
plt.scatter(centroids[fspace_idx==prim_IDs.index(prim_IDs[12]), 2],
centroids[fspace_idx==prim_IDs.index(prim_IDs[12]), 1],
c='', alpha=0.5)
# Cosmetics
ax.set_xlabel('TFOR x', fontsize=16)
ax.set_ylabel('TFOR y', fontsize=16)
plt.tick_params(axis='both', which='major', labelsize=13)
plt.xlim(xlim); plt.ylim(ylim)
ax.invert_yaxis() # To match images
# Colorbar
cbar = plt.colorbar(cfset, ax=ax, pad=0.01)
cbar.set_label('RNA Counts', rotation=270, labelpad=15, fontsize=16)
cbar.ax.tick_params(labelsize=13)
# Finalize
plt.tight_layout()
# Done
plt.show()
```
<a id=atlas_test></a>
## 5. Predicting Expression from Shape: Testing
[back to top](#top)
----
```
### Settings, scoring & metrics
# General
use_PCs = 10
num_CVs = 5
test_size = 0.3
# Shuffle split for CV
cv_sets = model_selection.ShuffleSplit(n_splits=num_CVs, test_size=test_size, random_state=42)
# Prepare CV scorers
scoring = {'explained_variance' : metrics.make_scorer(metrics.explained_variance_score),
'mean_squared_error' : metrics.make_scorer(metrics.mean_squared_error),
'r2_score' : metrics.make_scorer(metrics.r2_score)}
### Various prep of feature/target spaces
# Prepare counts by adding 2nd dim
rna_counts_rdy = np.expand_dims(rna_counts, -1)
# Prepare location data by z-scoring
centroids_z = StandardScaler().fit_transform(centroids)
### Remove prims/cells that were excluded as outliers
# Prepare fspaces & counts by removing excluded prims and subselecting PCs
rna_counts_rdy = rna_counts_rdy[rna_exclude_cell_mask]
fspace_TFOR_pca_rdy = fspace_TFOR_pca[rna_exclude_cell_mask, :use_PCs]
fspace_CFOR_pca_rdy = fspace_CFOR_pca[rna_exclude_cell_mask, :use_PCs]
centroids_z_rdy = centroids_z[rna_exclude_cell_mask]
### Simple score reporting function
def report_score(scores, score_key):
print "%s: %.3f +/- %.3f" % (score_key, np.mean(scores[score_key]), np.std(scores[score_key]))
```
#### Predicting expression from TFOR
```
### Prepare single train-test split for visualization
# Split
out = model_selection.train_test_split(fspace_TFOR_pca_rdy, rna_counts_rdy,
test_size=test_size, random_state=42)
X_train, X_test, y_train, y_test = out
# Report
print "Final source fspace (full, train, test):", fspace_TFOR_pca_rdy.shape, X_train.shape, X_test.shape
print "Final target fspace (full, train, test):", rna_counts_rdy.shape, y_train.shape, y_test.shape
# Hyperparameter screening for SVR
# Param grid
gd = 1.0 / X_test.shape[1]
param_grid = [{'C': [0.01, 0.1, 1.0, 10.0, 100.0],
'epsilon': [0.01, 0.1, 0.5, 1.0],
'gamma': [gd*10.0, gd, gd*0.1, gd*0.01]}]
# Prep regressor
svr = svm.SVR(kernel='rbf')
# Run grid search
clf = model_selection.GridSearchCV(svr, param_grid,
cv=cv_sets, scoring=scoring['explained_variance'],
n_jobs=6, verbose=2)
clf.fit(fspace_TFOR_pca_rdy, rna_counts_rdy.ravel())
# Report
print "Best estimator:", clf.best_estimator_
print "Best score:", clf.best_score_
# Use best estimator for cross validation
svr = clf.best_estimator_
scores = model_selection.cross_validate(svr, fspace_TFOR_pca_rdy, rna_counts_rdy,
scoring=scoring, cv=cv_sets,
return_train_score=True, n_jobs=num_CVs)
# Report CV scores
print('\nCV scores:')
report_score(scores, 'train_explained_variance')
report_score(scores, 'train_r2_score')
report_score(scores, 'train_mean_squared_error')
report_score(scores, 'test_explained_variance')
report_score(scores, 'test_r2_score')
report_score(scores, 'test_mean_squared_error')
### Regression Plot
# Single prediction
svr.fit(X_train, y_train.ravel())
y_train_pred = svr.predict(X_train)
y_test_pred = svr.predict(X_test)
# Prep plot
fig, ax = plt.subplots(1, 2, figsize=(6,3), sharey=True)
# Create plot
ax[0].scatter(y_train, y_train_pred, color='cyan', edgecolor='darkcyan', alpha=0.5)
ax[1].scatter(y_test, y_test_pred, color='cyan', edgecolor='darkcyan', alpha=0.5)
# Reference line
max_count = rna_counts_rdy.max()
ax[0].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
ax[1].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
# Axis adjustments
ax[0].set_xlim([0, max_count])
ax[0].set_ylim([0, max_count])
ax[1].set_xlim([0, max_count])
ax[1].set_ylim([0, max_count])
# Labeling
ax[0].set_title('Training Data (TFOR)')
ax[0].set_xlabel('Ground Truth')
ax[0].set_ylabel('Predicted')
ax[1].set_title('Test Data (TFOR)')
ax[1].set_xlabel('Ground Truth')
# Done
plt.tight_layout()
plt.show()
```
#### Predicting expression from CFOR
```
### Prepare single train-test split for parametrization/visualization
# Split
out = model_selection.train_test_split(fspace_CFOR_pca_rdy, rna_counts_rdy,
test_size=test_size, random_state=42)
X_train, X_test, y_train, y_test = out
# Report
print "Final source fspace (full, train, test):", fspace_CFOR_pca_rdy.shape, X_train.shape, X_test.shape
print "Final target fspace (full, train, test):", rna_counts_rdy.shape, y_train.shape, y_test.shape
# Hyperparam screening for SVR
# Param grid
gd = 1.0 / X_test.shape[1]
param_grid = [{'C': [0.01, 0.1, 1.0, 10.0, 100.0],
'epsilon': [0.01, 0.1, 0.5, 1.0],
'gamma': [gd*10.0, gd, gd*0.1, gd*0.01]}]
# Prep regressor
svr = svm.SVR(kernel='rbf')
# Run grid search
clf = model_selection.GridSearchCV(svr, param_grid,
cv=cv_sets, scoring=scoring['explained_variance'],
n_jobs=6, verbose=2)
clf.fit(fspace_CFOR_pca_rdy, rna_counts_rdy.ravel())
# Report
print "Best estimator:", clf.best_estimator_
print "Best score:", clf.best_score_
# Use best estimator for cross validation
svr = clf.best_estimator_
scores = model_selection.cross_validate(svr, fspace_CFOR_pca_rdy, rna_counts_rdy,
scoring=scoring, cv=cv_sets,
return_train_score=True, n_jobs=num_CVs)
# Report CV scores
print('\nCV scores:')
report_score(scores, 'train_explained_variance')
report_score(scores, 'train_r2_score')
report_score(scores, 'train_mean_squared_error')
report_score(scores, 'test_explained_variance')
report_score(scores, 'test_r2_score')
report_score(scores, 'test_mean_squared_error')
### Regression Plot
# Single prediction
svr.fit(X_train, y_train.ravel())
y_train_pred = svr.predict(X_train)
y_test_pred = svr.predict(X_test)
# Prep plot
fig, ax = plt.subplots(1, 2, figsize=(6,3), sharey=True)
# Create plot
ax[0].scatter(y_train, y_train_pred, color='cyan', edgecolor='darkcyan', alpha=0.5)
ax[1].scatter(y_test, y_test_pred, color='cyan', edgecolor='darkcyan', alpha=0.5)
# Reference line
max_count = rna_counts_rdy.max()
ax[0].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
ax[1].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
# Axis adjustments
ax[0].set_xlim([0, max_count])
ax[0].set_ylim([0, max_count])
ax[1].set_xlim([0, max_count])
ax[1].set_ylim([0, max_count])
# Labeling
ax[0].set_title('Training Data (CFOR)')
ax[0].set_xlabel('Ground Truth')
ax[0].set_ylabel('Predicted')
ax[1].set_title('Test Data (CFOR)')
ax[1].set_xlabel('Ground Truth')
# Done
plt.tight_layout()
plt.show()
```
#### Predicting expression from position
```
### Prepare single train-test split for parametrization/visualization
# Split
out = model_selection.train_test_split(centroids_z_rdy, rna_counts_rdy,
test_size=test_size, random_state=42)
X_train, X_test, y_train, y_test = out
# Report
print "Final source fspace (full, train, test):", centroids_z_rdy.shape, X_train.shape, X_test.shape
print "Final target fspace (full, train, test):", rna_counts_rdy.shape, y_train.shape, y_test.shape
# Hyperparam screening for SVR
# Param grid
gd = 1.0 / X_test.shape[1]
param_grid = [{'C': [0.01, 0.1, 1.0, 10.0, 100.0],
'epsilon': [0.01, 0.1, 0.5, 1.0],
'gamma': [gd*10.0, gd, gd*0.1, gd*0.01]}]
# Prep regressor
svr = svm.SVR(kernel='rbf')
# Run grid search
clf = model_selection.GridSearchCV(svr, param_grid,
cv=cv_sets, scoring=scoring['explained_variance'],
n_jobs=6, verbose=2)
clf.fit(centroids_z_rdy, rna_counts_rdy.ravel())
# Report
print "Best estimator:", clf.best_estimator_
print "Best score:", clf.best_score_
# Use best estimator for cross validation
svr = clf.best_estimator_
scores = model_selection.cross_validate(svr, centroids_z_rdy, rna_counts_rdy,
scoring=scoring, cv=cv_sets,
return_train_score=True, n_jobs=num_CVs)
# Report CV scores
print('\nCV scores:')
report_score(scores, 'train_explained_variance')
report_score(scores, 'train_r2_score')
report_score(scores, 'train_mean_squared_error')
report_score(scores, 'test_explained_variance')
report_score(scores, 'test_r2_score')
report_score(scores, 'test_mean_squared_error')
### Regression Plot
# Single prediction
svr.fit(X_train, y_train.ravel())
y_train_pred = svr.predict(X_train)
y_test_pred = svr.predict(X_test)
# Prep plot
fig, ax = plt.subplots(1, 2, figsize=(6,3), sharey=True)
# Create plot
ax[0].scatter(y_train, y_train_pred, color='cyan', edgecolor='darkcyan', alpha=0.5)
ax[1].scatter(y_test, y_test_pred, color='cyan', edgecolor='darkcyan', alpha=0.5)
# Reference line
max_count = rna_counts_rdy.max()
ax[0].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
ax[1].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
# Axis adjustments
ax[0].set_xlim([0, max_count])
ax[0].set_ylim([0, max_count])
ax[1].set_xlim([0, max_count])
ax[1].set_ylim([0, max_count])
# Labeling
ax[0].set_title('Training Data (Location)')
ax[0].set_xlabel('Ground Truth')
ax[0].set_ylabel('Predicted')
ax[1].set_title('Test Data (Location)')
ax[1].set_xlabel('Ground Truth')
# Done
plt.tight_layout()
plt.show()
```
#### Predicting expression from TFOR+CFOR+position
```
### Prep combined data data
# Combine
fspace_combined = np.concatenate([fspace_TFOR_pca_rdy, fspace_CFOR_pca_rdy, centroids_z_rdy], axis=1)
### Prepare single train-test split for parametrization/visualization
# Split
out = model_selection.train_test_split(fspace_combined, rna_counts_rdy,
test_size=test_size, random_state=42)
X_train, X_test, y_train, y_test = out
# Report
print "Final source fspace (full, train, test):", fspace_combined.shape, X_train.shape, X_test.shape
print "Final target fspace (full, train, test):", rna_counts_rdy.shape, y_train.shape, y_test.shape
# Hyperparam screening for SVR
# Param grid
gd = 1.0 / X_test.shape[1]
param_grid = [{'C': [0.01, 0.1, 1.0, 10.0, 100.0],
'epsilon': [0.01, 0.1, 0.5, 1.0],
'gamma': [gd*10.0, gd, gd*0.1, gd*0.01]}]
# Prep regressor
svr = svm.SVR(kernel='rbf')
# Run grid search
clf = model_selection.GridSearchCV(svr, param_grid,
cv=cv_sets, scoring=scoring['explained_variance'],
n_jobs=6, verbose=2)
clf.fit(fspace_combined, rna_counts_rdy.ravel())
# Report
print "Best estimator:", clf.best_estimator_
print "Best score:", clf.best_score_
# Use best estimator for cross validation
svr = clf.best_estimator_
scores = model_selection.cross_validate(svr, fspace_combined, rna_counts_rdy,
scoring=scoring, cv=cv_sets,
return_train_score=True, n_jobs=num_CVs)
# Report CV scores
print('\nCV scores:')
report_score(scores, 'train_explained_variance')
report_score(scores, 'train_r2_score')
report_score(scores, 'train_mean_squared_error')
report_score(scores, 'test_explained_variance')
report_score(scores, 'test_r2_score')
report_score(scores, 'test_mean_squared_error')
### Regression Plot
# Single prediction
svr.fit(X_train, y_train.ravel())
y_train_pred = svr.predict(X_train)
y_test_pred = svr.predict(X_test)
# Prep plot
fig, ax = plt.subplots(1, 2, figsize=(6,3), sharey=True)
# Create plot
ax[0].scatter(y_train, y_train_pred, color='cyan', edgecolor='darkcyan', alpha=0.5)
ax[1].scatter(y_test, y_test_pred, color='cyan', edgecolor='darkcyan', alpha=0.5)
# Reference line
max_count = rna_counts_rdy.max()
ax[0].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
ax[1].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
# Axis adjustments
ax[0].set_xlim([0, max_count])
ax[0].set_ylim([0, max_count])
ax[1].set_xlim([0, max_count])
ax[1].set_ylim([0, max_count])
# Labeling
ax[0].set_title('Training Data (COMBINED)')
ax[0].set_xlabel('Ground Truth')
ax[0].set_ylabel('Predicted')
ax[1].set_title('Test Data (COMBINED)')
ax[1].set_xlabel('Ground Truth')
# Done
plt.tight_layout()
plt.show()
# Pretty regression plot for publication
# Single prediction
svr.fit(X_train, y_train.ravel())
y_train_pred = svr.predict(X_train)
y_test_pred = svr.predict(X_test)
# Prep plot
fig, ax = plt.subplots(1, 2, figsize=(6, 3.2), sharey=True)
# Create plot
ax[0].scatter(y_train, y_train_pred,
color='midnightblue', edgecolor='', alpha=0.3, s=5)
ax[1].scatter(y_test, y_test_pred,
color='midnightblue', edgecolor='', alpha=0.3, s=5)
# Reference line
max_count = rna_counts_rdy.max()
ax[0].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
ax[1].plot([0,max_count], [0,max_count], '-', c='0.75', zorder=0)
# Crop off and add cropped points back as arrows
crop = 60
if np.any(y_train_pred>crop) or np.any(y_test_pred>crop):
raise ValueError('Some predicted values are higher than `crop`!')
ax[0].scatter([crop-0.5 for i in range(np.sum(y_train[:,0]>60))], y_train_pred[y_train[:,0]>60],
color='midnightblue', edgecolor='', alpha=0.5, s=10, marker='>')
ax[1].scatter([crop-0.5 for i in range(np.sum(y_test[:,0]>60))], y_test_pred[y_test[:,0]>60],
color='midnightblue', edgecolor='', alpha=0.5, s=10, marker='>')
# Axis adjustments
ax[0].set_xlim([0, crop])
ax[0].set_ylim([0, crop])
ax[1].set_xlim([0, crop])
ax[1].set_ylim([0, crop])
# Axis cosmetics
ax[0].yaxis.set_ticks_position('left')
ax[0].xaxis.set_ticks_position('bottom')
ax[1].yaxis.set_ticks_position('left')
ax[1].xaxis.set_ticks_position('bottom')
# Labeling & other cosmetics
ax[0].set_title('Training Data')
ax[0].set_xlabel('$\it{pea3}$ counts (ground truth)')
ax[0].set_ylabel('$\it{pea3}$ counts (predicted)')
ax[1].set_title('Test Data')
ax[1].set_xlabel('$\it{pea3}$ counts (ground truth)')
plt.tight_layout()
# Done
plt.show()
```
<a id=atlas_run></a>
## 6. Predicting Expression from Shape: Running
[back to top](#top)
----
```
### Load and prepare full live-imaged shape space
# Prep loader
expA_loader = ld.DataLoaderIDR()
expA_loader.find_imports(r"data/experimentA/extracted_measurements/", recurse=True, verbose=True)
# Import shape spaces
expA_TFOR_pca, expA_IDs, expA_idx = expA_loader.load_dataset("shape_TFOR_pca_measured.tsv")
expA_CFOR_pca, _, _ = expA_loader.load_dataset("shape_CFOR_pca_measured.tsv", IDs=expA_IDs)
print "Imported TFOR shape space of shape:", expA_TFOR_pca.shape
print "Imported CFOR shape space of shape:", expA_CFOR_pca.shape
# Import TFOR centroid locations
expA_centroids = expA_loader.load_dataset("_other_measurements.tsv", IDs=expA_IDs)[0][:,3:6][:,::-1]
print "Imported TFOR centroids of shape:", expA_centroids.shape
expA_centroids_z = StandardScaler().fit_transform(expA_centroids)
# Combine
expA_combined = np.concatenate([expA_TFOR_pca[:,:use_PCs], expA_CFOR_pca[:,:use_PCs], expA_centroids_z], axis=1)
# Report
print expA_TFOR_pca.shape, expA_CFOR_pca.shape, expA_centroids_z.shape, expA_combined.shape
### Run best possible smFISH count prediction for entire atlas
# Prepare the best regressor
svr = svm.SVR(kernel='rbf', C=10.0, epsilon=0.01, gamma = 1.0 / X_test.shape[1] * 0.1)
# Train based on entire smFISH dataset
svr.fit(fspace_combined, rna_counts_rdy.ravel())
# Predict for entire atlas
expA_counts = svr.predict(expA_combined)
# Set the occasional negative count to zero
expA_counts[expA_counts < 0.0] = 0.0
```
<a id=atlas_viz></a>
## 7. Predicting Expression from Shape: Visualization
[back to top](#top)
----
```
### QC: Compare predicted atlas counts to measured counts
# Note:
# This looks quite good. The prediction obviously doesn't capture the long
# tail of the real measurements, which also pulls the overall average down
# a bit. This was to be expected and may not even be wrong.
# Get count means
count_means = np.array([np.mean(rna_counts[fspace_idx==prim_idx])
for prim_idx in range(len(prim_IDs))])
expA_means = np.array([np.mean(expA_counts[expA_idx==prim_idx])
for prim_idx in range(len(expA_IDs))])
# Fig prep
fig, ax = plt.subplots(1, 2, figsize=(6, 4.5), sharey=True)
# Make boxplots
bp_m = ax[0].boxplot([count_means, expA_means], widths=0.65, patch_artist=True, showfliers=False)
bp_a = ax[1].boxplot([rna_counts, expA_counts], widths=0.65, patch_artist=True, showfliers=False)
# Boxplot styling function (making it similar to Sevi's paper)
def style_boxplot(bp):
for patch in bp['boxes']:
patch.set(edgecolor='black', linewidth=1.2,)
for whisker in bp['whiskers']:
whisker.set(color='black', linestyle='-')
for cap in bp['caps']:
cap.set(linewidth=1.2)
for median in bp['medians']:
median.set(color='black', linewidth=1.2)
# Style the boxplots
style_boxplot(bp_m)
style_boxplot(bp_a)
# Add scatter
ax[0].scatter(np.random.normal(1.0, 0.06, len(count_means)), count_means,
zorder=10, s=20, alpha=0.7, c='midnightblue', edgecolor='')
ax[0].scatter(np.random.normal(2.0, 0.08, len(expA_means)), expA_means,
zorder=10, s=20, alpha=0.3, c='purple', edgecolor='')
ax[1].scatter(np.random.normal(1.0, 0.06, len(rna_counts)), rna_counts,
zorder=10, s=2, alpha=0.2, c='midnightblue', edgecolor='')
ax[1].scatter(np.random.normal(2.0, 0.10, len(expA_counts)), expA_counts,
zorder=10, s=2, alpha=0.05, c='purple', edgecolor='')
# Add arrows for outliers
crop = 50
ax[1].scatter(np.random.normal(1.0, 0.06, np.sum(rna_counts>crop)),
[crop-0.5 for i in range(np.sum(rna_counts>crop))],
color='midnightblue', edgecolor='', alpha=0.2, s=10, marker='^')
if np.any(expA_counts > crop): raise ValueError()
# Set axis limits
ax[0].set_ylim([-2, crop])
# Remove axis ticks
ax[0].yaxis.set_ticks_position('left')
ax[0].xaxis.set_ticks_position('bottom')
ax[1].yaxis.set_ticks_position('left')
ax[1].xaxis.set_ticks_position('bottom')
# Axis labels
from matplotlib import rcParams
rcParams['mathtext.default'] = 'regular'
ax[0].set_ylabel(r'$\it{pea3}$ transcripts per cell', fontsize=16, labelpad=5)
ax[0].set_title('sample means', fontsize=16)
ax[1].set_title('all cells', fontsize=16)
ax[0].set_xticklabels(['smFISH', 'atlas'], fontsize=14)
ax[1].set_xticklabels(['smFISH', 'atlas'], fontsize=14)
ax[0].tick_params(axis='y', which='major', labelsize=14)
plt.tight_layout()
# Print stats
print 'pMWU(means):', stats.mannwhitneyu(count_means, expA_means, alternative='two-sided')[1]
print 'pMWU(all):', stats.mannwhitneyu(rna_counts, expA_counts, alternative='two-sided')[1]
# Show
plt.show()
### Atlas tissue consensus map
# Settings
xlim = (-130, 8)
ylim = ( -19, 19)
# Get plot values & remove outliers
plot_values = expA_counts
# Tools for smoothing on scatter
from katachi.utilities.pcl_helpers import pcl_gaussian_smooth
from scipy.spatial.distance import pdist, squareform
# Cut off at prim contour outline
kernel_prim = stats.gaussian_kde(expA_centroids[:,1:].T)
f_prim = kernel_prim(expA_centroids[:,1:].T)
f_prim_mask = f_prim > f_prim.min() + (f_prim.max()-f_prim.min())*0.1
plot_values = plot_values[f_prim_mask]
plot_centroids = expA_centroids[f_prim_mask]
# Smoothen?
pdists = squareform(pdist(plot_centroids[:,1:]))
plot_values = pcl_gaussian_smooth(pdists, plot_values[:,np.newaxis], sg_percentile=0.5)[:,0]
# Initialize figure
fig, ax = plt.subplots(1, figsize=(8, 2.8))
# Contourf plot
cfset = ax.tricontourf(plot_centroids[:,2], plot_centroids[:,1], plot_values, 20,
cmap='plasma', vmax=20) # NOTE: vmax set to be consistent with measured plot!
# Illustrative centroids from a single prim
plt.scatter(expA_centroids[expA_idx==expA_IDs.index(expA_IDs[0]), 2],
expA_centroids[expA_idx==expA_IDs.index(expA_IDs[0]), 1],
c='', alpha=0.5)
# Cosmetics
ax.set_xlabel('TFOR x', fontsize=16)
ax.set_ylabel('TFOR y', fontsize=16)
plt.tick_params(axis='both', which='major', labelsize=13)
plt.xlim(xlim); plt.ylim(ylim)
ax.invert_yaxis() # To match images
# Colorbar
cbar = plt.colorbar(cfset, ax=ax, pad=0.01)
cbar.set_label('RNA Counts', rotation=270, labelpad=15, fontsize=16)
cbar.ax.tick_params(labelsize=13)
# Finalize
plt.tight_layout()
plt.show()
```
----
[back to top](#top)
| true |
code
| 0.779259 | null | null | null | null |
|
# Heart disease classification
## USING SUPPORT VECTOR MACHINE (SVM)
### IMPORTING THE LIBRARIES
```
#importing the libraries.....
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
### IMPORTING THE DATASET
```
#Reading the dataset
ds=pd.read_csv('heart.csv')
print(ds)
ds.head()
ds.describe()
#splitting the dataset into independent and dependent variables
X = ds.iloc[:,:-1].values
y = ds.iloc[:,-1].values
print(X)
print(y)
```
### FEATURE SCALING
```
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X = sc.fit_transform(X)
print(X)
```
### SPLITTING THE DATASET INTO TRAINING SET AND TEST SET
```
from sklearn.model_selection import train_test_split
X_train,X_test ,y_train, y_test = train_test_split(X, y, test_size=0.25,random_state=5)
```
### CREATING THE MODEL
```
from sklearn.svm import SVC
classifier = SVC(kernel = 'linear' , random_state = 1)
clf = classifier.fit(X_train , y_train)
y_pred=classifier.predict(X_test)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
#confusion matrix is used to check how many datapoints are predicted exactly
from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test,y_pred)
print(cm)
print(round(accuracy_score(y_test,y_pred) , 2))
```
### CONFUSION MATRIX
```
from sklearn.metrics import plot_confusion_matrix
a = plot_confusion_matrix(clf , X_test , y_test)
plt.show()
```
## Using K-Nearest Neighbor Classifier (K-NN)
### IMPORTING DATASET
```
X = ds.iloc[:,:-1].values
y = ds.iloc[:,13].values
```
### Splitting data
```
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.25, random_state= 0)
```
### Normalize the data
```
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)
```
### Accuracy based on K values
```
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classifier = KNeighborsClassifier(n_neighbors = 9, metric = 'minkowski', p = 2)
classifier = classifier.fit(X_train,y_train)
#prediction
y_pred = classifier.predict(X_test)
#check accuracy
accuracy = metrics.accuracy_score(y_test, y_pred)
print('Accuracy: {:.2f}'.format(accuracy))
```
### Confusion Matrix
```
#confusion matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
import seaborn as sns
sns.heatmap(cm,annot=True,cmap="YlOrRd")
plt.show()
```
## Using SVM WITH PCA
### Extracting x and y
```
X=ds.iloc[:,:-1].values
y=ds.iloc[:,-1].values
```
### STANDARDIZING 'X'
```
from sklearn.preprocessing import StandardScaler
sc=StandardScaler()
X=sc.fit_transform(X)
print(X)
```
### Splitting the dataset into train and test data
```
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=4)
```
### Applying the PCA
```
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
X_train=pca.fit_transform(X_train)
X_test=pca.transform(X_test)
explained_variance=pca.explained_variance_ratio_
print(explained_variance)
```
### Training the svm model on training set
```
from sklearn.svm import SVC
classifier=SVC(kernel='linear',random_state=0)
classifier.fit(X_train,y_train)
```
### Predicting the Test Resuts
```
from sklearn import metrics
y_pred=classifier.predict(X_test)
print(y_pred)
```
### Calculating the Accuracy
```
accuracy=metrics.accuracy_score(y_test,y_pred)
print('Accuracy: {:.2f}'.format(accuracy))
```
### Creating the Confusion Matrix
```
from sklearn.metrics import confusion_matrix
cm=confusion_matrix(y_test,y_pred)
print(cm)
```
### Plotting the Confusion Matrix
```
import seaborn as sns
sns.heatmap(cm,annot=True,cmap="YlOrRd")
plt.show()
```
## Using KNN with PCA
### Extracting x and y
```
X=ds.iloc[:,:-1].values
y=ds.iloc[:,13].values
```
### STANDARDIZING 'X'
```
from sklearn.preprocessing import StandardScaler
sc= StandardScaler()
X=sc.fit_transform(X)
```
## SPLITTING THE DATASET INTO TRAIN AND TEST DATA
```
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.15,random_state=0)
```
### APPLYING 'PCA'
```
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
X_train=pca.fit_transform(X_train)
X_test=pca.transform(X_test)
explained_variance=pca.explained_variance_ratio_
print(explained_variance)
```
### TRAINING THE K-NN MODEL ON TRAINING SET
```
from sklearn.neighbors import KNeighborsClassifier
clas=KNeighborsClassifier(n_neighbors =6,metric='minkowski',p=2)
clas.fit(X_train,y_train)
```
### PREDICTING THE TEST RESULTS
```
y_pred=clas.predict(X_test)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
```
### CONFUSION MATRIX AND ACCURACY
```
from sklearn.metrics import confusion_matrix,accuracy_score
cm = confusion_matrix(y_test,y_pred)
print(cm)
accuracy_score(y_test,y_pred)
```
### PLOT OF CONFUSION MATRIX
```
import seaborn as sns
sns.heatmap(cm,annot=True,cmap="YlOrRd")
plt.show()
```
## BAR PLOT FOR COUNT OF PEOPLE DISEASED AND NOT DISEASED
```
import seaborn as sns
sns.countplot(x = 'target' , data = ds)
plt.show()
```
## SCATTER PLOT BETWEEN AGE AND MAX. HEART RATE
```
plt.scatter(x=ds.age[ds.target==1], y=ds.thalach[(ds.target==1)], c="yellow")
plt.scatter(x=ds.age[ds.target==0], y=ds.thalach[(ds.target==0)], c = 'red')
plt.legend(["Disease", "No Disease"])
plt.xlabel("Age")
plt.ylabel("Maximum Heart Rate")
plt.show()
```
## COUNT OF MALE AND FEMALE
```
pd.crosstab(ds.sex,ds.target).plot(kind="bar",figsize=(10,5),color=['#1CA53B','#EE0000'])
plt.title('Heart Disease Frequency for Sex')
plt.xlabel('Sex (0 = Female,1 = Male)')
plt.xticks(rotation=0 )
plt.legend(["No Disease", " Disease "])
plt.ylabel("Frequency")
plt.show()
```
| true |
code
| 0.665356 | null | null | null | null |
|
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="figures/PDSH-cover-small.png">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
<!--NAVIGATION-->
< [In-Depth: Decision Trees and Random Forests](05.08-Random-Forests.ipynb) | [Contents](Index.ipynb) | [In-Depth: Manifold Learning](05.10-Manifold-Learning.ipynb) >
<a href="https://colab.research.google.com/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.09-Principal-Component-Analysis.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open and Execute in Google Colaboratory"></a>
# In Depth: Principal Component Analysis
Up until now, we have been looking in depth at supervised learning estimators: those estimators that predict labels based on labeled training data.
Here we begin looking at several unsupervised estimators, which can highlight interesting aspects of the data without reference to any known labels.
In this section, we explore what is perhaps one of the most broadly used of unsupervised algorithms, principal component analysis (PCA).
PCA is fundamentally a dimensionality reduction algorithm, but it can also be useful as a tool for visualization, for noise filtering, for feature extraction and engineering, and much more.
After a brief conceptual discussion of the PCA algorithm, we will see a couple examples of these further applications.
We begin with the standard imports:
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
```
## Introducing Principal Component Analysis
Principal component analysis is a fast and flexible unsupervised method for dimensionality reduction in data, which we saw briefly in [Introducing Scikit-Learn](05.02-Introducing-Scikit-Learn.ipynb).
Its behavior is easiest to visualize by looking at a two-dimensional dataset.
Consider the following 200 points:
```
rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal');
```
By eye, it is clear that there is a nearly linear relationship between the x and y variables.
This is reminiscent of the linear regression data we explored in [In Depth: Linear Regression](05.06-Linear-Regression.ipynb), but the problem setting here is slightly different: rather than attempting to *predict* the y values from the x values, the unsupervised learning problem attempts to learn about the *relationship* between the x and y values.
In principal component analysis, this relationship is quantified by finding a list of the *principal axes* in the data, and using those axes to describe the dataset.
Using Scikit-Learn's ``PCA`` estimator, we can compute this as follows:
```
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
```
The fit learns some quantities from the data, most importantly the "components" and "explained variance":
```
print(pca.components_)
print(pca.explained_variance_)
```
To see what these numbers mean, let's visualize them as vectors over the input data, using the "components" to define the direction of the vector, and the "explained variance" to define the squared-length of the vector:
```
def draw_vector(v0, v1, ax=None):
ax = ax or plt.gca()
arrowprops=dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
ax.annotate('', v1, v0, arrowprops=arrowprops)
# plot data
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal');
```
These vectors represent the *principal axes* of the data, and the length of the vector is an indication of how "important" that axis is in describing the distribution of the data—more precisely, it is a measure of the variance of the data when projected onto that axis.
The projection of each data point onto the principal axes are the "principal components" of the data.
If we plot these principal components beside the original data, we see the plots shown here:

[figure source in Appendix](06.00-Figure-Code.ipynb#Principal-Components-Rotation)
This transformation from data axes to principal axes is an *affine transformation*, which basically means it is composed of a translation, rotation, and uniform scaling.
While this algorithm to find principal components may seem like just a mathematical curiosity, it turns out to have very far-reaching applications in the world of machine learning and data exploration.
### PCA as dimensionality reduction
Using PCA for dimensionality reduction involves zeroing out one or more of the smallest principal components, resulting in a lower-dimensional projection of the data that preserves the maximal data variance.
Here is an example of using PCA as a dimensionality reduction transform:
```
pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
print("original shape: ", X.shape)
print("transformed shape:", X_pca.shape)
```
The transformed data has been reduced to a single dimension.
To understand the effect of this dimensionality reduction, we can perform the inverse transform of this reduced data and plot it along with the original data:
```
X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis('equal');
```
The light points are the original data, while the dark points are the projected version.
This makes clear what a PCA dimensionality reduction means: the information along the least important principal axis or axes is removed, leaving only the component(s) of the data with the highest variance.
The fraction of variance that is cut out (proportional to the spread of points about the line formed in this figure) is roughly a measure of how much "information" is discarded in this reduction of dimensionality.
This reduced-dimension dataset is in some senses "good enough" to encode the most important relationships between the points: despite reducing the dimension of the data by 50%, the overall relationship between the data points are mostly preserved.
### PCA for visualization: Hand-written digits
The usefulness of the dimensionality reduction may not be entirely apparent in only two dimensions, but becomes much more clear when looking at high-dimensional data.
To see this, let's take a quick look at the application of PCA to the digits data we saw in [In-Depth: Decision Trees and Random Forests](05.08-Random-Forests.ipynb).
We start by loading the data:
```
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
```
Recall that the data consists of 8×8 pixel images, meaning that they are 64-dimensional.
To gain some intuition into the relationships between these points, we can use PCA to project them to a more manageable number of dimensions, say two:
```
pca = PCA(2) # project from 64 to 2 dimensions
projected = pca.fit_transform(digits.data)
print(digits.data.shape)
print(projected.shape)
digits.target
i=int(np.random.random()*1797)
plt.imshow(digits.data[i].reshape(8,8),cmap='Blues')
digits.target[i]
digits.data[i].reshape(8,8)
```
We can now plot the first two principal components of each point to learn about the data:
```
plt.scatter(projected[:, 0], projected[:, 1],
c=digits.target, edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('Spectral', 10))
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar();
```
Recall what these components mean: the full data is a 64-dimensional point cloud, and these points are the projection of each data point along the directions with the largest variance.
Essentially, we have found the optimal stretch and rotation in 64-dimensional space that allows us to see the layout of the digits in two dimensions, and have done this in an unsupervised manner—that is, without reference to the labels.
### What do the components mean?
We can go a bit further here, and begin to ask what the reduced dimensions *mean*.
This meaning can be understood in terms of combinations of basis vectors.
For example, each image in the training set is defined by a collection of 64 pixel values, which we will call the vector $x$:
$$
x = [x_1, x_2, x_3 \cdots x_{64}]
$$
One way we can think about this is in terms of a pixel basis.
That is, to construct the image, we multiply each element of the vector by the pixel it describes, and then add the results together to build the image:
$$
{\rm image}(x) = x_1 \cdot{\rm (pixel~1)} + x_2 \cdot{\rm (pixel~2)} + x_3 \cdot{\rm (pixel~3)} \cdots x_{64} \cdot{\rm (pixel~64)}
$$
One way we might imagine reducing the dimension of this data is to zero out all but a few of these basis vectors.
For example, if we use only the first eight pixels, we get an eight-dimensional projection of the data, but it is not very reflective of the whole image: we've thrown out nearly 90% of the pixels!

[figure source in Appendix](06.00-Figure-Code.ipynb#Digits-Pixel-Components)
The upper row of panels shows the individual pixels, and the lower row shows the cumulative contribution of these pixels to the construction of the image.
Using only eight of the pixel-basis components, we can only construct a small portion of the 64-pixel image.
Were we to continue this sequence and use all 64 pixels, we would recover the original image.
But the pixel-wise representation is not the only choice of basis. We can also use other basis functions, which each contain some pre-defined contribution from each pixel, and write something like
$$
image(x) = {\rm mean} + x_1 \cdot{\rm (basis~1)} + x_2 \cdot{\rm (basis~2)} + x_3 \cdot{\rm (basis~3)} \cdots
$$
PCA can be thought of as a process of choosing optimal basis functions, such that adding together just the first few of them is enough to suitably reconstruct the bulk of the elements in the dataset.
The principal components, which act as the low-dimensional representation of our data, are simply the coefficients that multiply each of the elements in this series.
This figure shows a similar depiction of reconstructing this digit using the mean plus the first eight PCA basis functions:

[figure source in Appendix](06.00-Figure-Code.ipynb#Digits-PCA-Components)
Unlike the pixel basis, the PCA basis allows us to recover the salient features of the input image with just a mean plus eight components!
The amount of each pixel in each component is the corollary of the orientation of the vector in our two-dimensional example.
This is the sense in which PCA provides a low-dimensional representation of the data: it discovers a set of basis functions that are more efficient than the native pixel-basis of the input data.
### Choosing the number of components
A vital part of using PCA in practice is the ability to estimate how many components are needed to describe the data.
This can be determined by looking at the cumulative *explained variance ratio* as a function of the number of components:
```
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
```
This curve quantifies how much of the total, 64-dimensional variance is contained within the first $N$ components.
For example, we see that with the digits the first 10 components contain approximately 75% of the variance, while you need around 50 components to describe close to 100% of the variance.
Here we see that our two-dimensional projection loses a lot of information (as measured by the explained variance) and that we'd need about 20 components to retain 90% of the variance. Looking at this plot for a high-dimensional dataset can help you understand the level of redundancy present in multiple observations.
## PCA as Noise Filtering
PCA can also be used as a filtering approach for noisy data.
The idea is this: any components with variance much larger than the effect of the noise should be relatively unaffected by the noise.
So if you reconstruct the data using just the largest subset of principal components, you should be preferentially keeping the signal and throwing out the noise.
Let's see how this looks with the digits data.
First we will plot several of the input noise-free data:
```
def plot_digits(data):
fig, axes = plt.subplots(4, 10, figsize=(10, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
plot_digits(digits.data)
```
Now lets add some random noise to create a noisy dataset, and re-plot it:
```
np.random.seed(42)
noisy = np.random.normal(digits.data, 4)
plot_digits(noisy)
```
It's clear by eye that the images are noisy, and contain spurious pixels.
Let's train a PCA on the noisy data, requesting that the projection preserve 50% of the variance:
```
pca = PCA(0.50).fit(noisy)
pca.n_components_
```
Here 50% of the variance amounts to 12 principal components.
Now we compute these components, and then use the inverse of the transform to reconstruct the filtered digits:
```
components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)
```
This signal preserving/noise filtering property makes PCA a very useful feature selection routine—for example, rather than training a classifier on very high-dimensional data, you might instead train the classifier on the lower-dimensional representation, which will automatically serve to filter out random noise in the inputs.
## Example: Eigenfaces
Earlier we explored an example of using a PCA projection as a feature selector for facial recognition with a support vector machine (see [In-Depth: Support Vector Machines](05.07-Support-Vector-Machines.ipynb)).
Here we will take a look back and explore a bit more of what went into that.
Recall that we were using the Labeled Faces in the Wild dataset made available through Scikit-Learn:
```
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=60)
print(faces.target_names)
print(faces.images.shape)
```
Let's take a look at the principal axes that span this dataset.
Because this is a large dataset, we will use ``RandomizedPCA``—it contains a randomized method to approximate the first $N$ principal components much more quickly than the standard ``PCA`` estimator, and thus is very useful for high-dimensional data (here, a dimensionality of nearly 3,000).
We will take a look at the first 150 components:
```
# from sklearn.decomposition import RandomizedPCA
from sklearn.decomposition import PCA as RandomizedPCA
pca = RandomizedPCA(150)
pca.fit(faces.data)
```
In this case, it can be interesting to visualize the images associated with the first several principal components (these components are technically known as "eigenvectors,"
so these types of images are often called "eigenfaces").
As you can see in this figure, they are as creepy as they sound:
```
fig, axes = plt.subplots(3, 8, figsize=(9, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(pca.components_[i].reshape(62, 47), cmap='bone')
```
The results are very interesting, and give us insight into how the images vary: for example, the first few eigenfaces (from the top left) seem to be associated with the angle of lighting on the face, and later principal vectors seem to be picking out certain features, such as eyes, noses, and lips.
Let's take a look at the cumulative variance of these components to see how much of the data information the projection is preserving:
```
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
```
We see that these 150 components account for just over 90% of the variance.
That would lead us to believe that using these 150 components, we would recover most of the essential characteristics of the data.
To make this more concrete, we can compare the input images with the images reconstructed from these 150 components:
```
# Compute the components and projected faces
pca = RandomizedPCA(150).fit(faces.data)
components = pca.transform(faces.data)
projected = pca.inverse_transform(components)
# Plot the results
fig, ax = plt.subplots(2, 10, figsize=(10, 2.5),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i in range(10):
ax[0, i].imshow(faces.data[i].reshape(62, 47), cmap='binary_r')
ax[1, i].imshow(projected[i].reshape(62, 47), cmap='binary_r')
ax[0, 0].set_ylabel('full-dim\ninput')
ax[1, 0].set_ylabel('150-dim\nreconstruction');
```
The top row here shows the input images, while the bottom row shows the reconstruction of the images from just 150 of the ~3,000 initial features.
This visualization makes clear why the PCA feature selection used in [In-Depth: Support Vector Machines](05.07-Support-Vector-Machines.ipynb) was so successful: although it reduces the dimensionality of the data by nearly a factor of 20, the projected images contain enough information that we might, by eye, recognize the individuals in the image.
What this means is that our classification algorithm needs to be trained on 150-dimensional data rather than 3,000-dimensional data, which depending on the particular algorithm we choose, can lead to a much more efficient classification.
## Principal Component Analysis Summary
In this section we have discussed the use of principal component analysis for dimensionality reduction, for visualization of high-dimensional data, for noise filtering, and for feature selection within high-dimensional data.
Because of the versatility and interpretability of PCA, it has been shown to be effective in a wide variety of contexts and disciplines.
Given any high-dimensional dataset, I tend to start with PCA in order to visualize the relationship between points (as we did with the digits), to understand the main variance in the data (as we did with the eigenfaces), and to understand the intrinsic dimensionality (by plotting the explained variance ratio).
Certainly PCA is not useful for every high-dimensional dataset, but it offers a straightforward and efficient path to gaining insight into high-dimensional data.
PCA's main weakness is that it tends to be highly affected by outliers in the data.
For this reason, many robust variants of PCA have been developed, many of which act to iteratively discard data points that are poorly described by the initial components.
Scikit-Learn contains a couple interesting variants on PCA, including ``RandomizedPCA`` and ``SparsePCA``, both also in the ``sklearn.decomposition`` submodule.
``RandomizedPCA``, which we saw earlier, uses a non-deterministic method to quickly approximate the first few principal components in very high-dimensional data, while ``SparsePCA`` introduces a regularization term (see [In Depth: Linear Regression](05.06-Linear-Regression.ipynb)) that serves to enforce sparsity of the components.
In the following sections, we will look at other unsupervised learning methods that build on some of the ideas of PCA.
<!--NAVIGATION-->
< [In-Depth: Decision Trees and Random Forests](05.08-Random-Forests.ipynb) | [Contents](Index.ipynb) | [In-Depth: Manifold Learning](05.10-Manifold-Learning.ipynb) >
<a href="https://colab.research.google.com/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.09-Principal-Component-Analysis.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open and Execute in Google Colaboratory"></a>
| true |
code
| 0.690716 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Saurabh-Bagchi/Traffic-Sign-Classification.keras/blob/master/Questions_Project_1_Computer_Vision_JPMC_v3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>

Proprietary content. © Great Learning. All Rights Reserved. Unauthorized use or distribution prohibited.
# German Traffic Sign Recognition
Multi-class, single-image classification
### Dataset
The German Traffic Sign Benchmark is a multi-class, single-image classification challenge held at the International Joint Conference on Neural Networks (IJCNN) 2011. They cordially invite researchers from relevant fields to participate: The competition is designed to allow for participation without special domain knowledge. Their benchmark has the following properties:
- Single-image, multi-class classification problem
- More than 40 classes
- More than 50,000 images in total
- Large, lifelike database
#### Notes
- If the model is taking too much time to get trained then you can reduce the number of classes. There are around 43 classes in the dataset, model should be trained on a minimum of 15 classes.
### Initialize ImageDataGenerator (7 Marks)
- Rescale the images
- Specify value for validation_split & get 75% data in training and 25% data in training
### Import the necessary libraries
```
import itertools
import os
import matplotlib.pylab as plt
import numpy as np
import tensorflow as tf
import tensorflow_hub as hub
print("TF version:", tf.__version__)
print("Hub version:", hub.__version__)
print("GPU is", "available" if tf.config.list_physical_devices('GPU') else "NOT AVAILABLE")
# set the matplotlib backend so figures can be saved in the background
import matplotlib
matplotlib.use("Agg")
# import the necessary packages
#from pyimagesearch.resnet import ResNet
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.utils import to_categorical
from imutils import paths
import matplotlib.pyplot as plt
import argparse
import cv2
import os
import time
import pandas as pd
from PIL import Image
from tensorflow import keras
from sklearn.metrics import accuracy_score
np.random.seed(42)
tf.random.set_seed(42)
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation, Flatten
from keras.layers.convolutional import Conv2D
from keras.layers.pooling import MaxPooling2D
from keras.optimizers import SGD
from keras import backend as K
K.set_image_data_format('channels_last')
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from sklearn.model_selection import train_test_split
train_datagen = ImageDataGenerator(rescale = 1./255,
shear_range = 0.2,
zoom_range = 0.2,
horizontal_flip = True,
validation_split=0.25)
test_datagen = ImageDataGenerator(rescale=1./255)
#test_size = 0.25
random_state = 42
#x_train, x_validation, y_train, y_validation = train_test_split(x_train, y_train, test_size=0.2, random_state=42)
from google.colab import drive
drive.mount('/content/drive/')
project_path = '/content/drive/MyDrive/German Traffic/'
images_zip_path = project_path + "Data - German Traffic Sign Recognition-20210113T122622Z-001.zip"
from zipfile import ZipFile
with ZipFile(images_zip_path, 'r') as z:
z.extractall()
```
### Get training data from ImageDataGenerator (5 Marks)
- Give directory path
- Give target size
- Give batch_size
- Specify classes, if you wish to use less number of classes you need to give class names in a list (Atleast 15 classes should be there)
- Specify class_mode
- Specify color_mode
- Specify subset
You can get details here
https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/image/ImageDataGenerator
```
img_rows = 32
img_cols = 32
train_data_dir_path = '/content/Data - German Traffic Sign Recognition/Train'
test_data_dir_path = '/content/Data - German Traffic Sign Recognition'
training_set = train_datagen.flow_from_directory(train_data_dir_path,
target_size = (img_rows, img_cols),
batch_size = 1,
classes = ['0','1','2','3','4','5',
'6','7','8','9','10','11','12','13','14','15',
'16','17','18','19','20','21','22','23','24','25',
'26','27','28','29','30','31','32','33','34','35','36','37',
'38','39','40','41','42'],
class_mode='categorical',
color_mode='rgb',
subset='training')
def generate_data_from_set(gen=training_set, image_target_size = 32, batch_size = 1,
channels = 3, class_mode = 'sparse' ):
'''fetch all out test data from directory'''
total_images = gen.n
steps = total_images//batch_size
#iterations to cover all data, so if batch is 5, it will take total_images/5 iteration
x , y = [] , []
for i in range(steps):
a , b = gen.next()
x.extend(a)
y.extend(b)
return np.array(x), np.array(y)
x_train, y_train = generate_data_from_set()
x_train.shape
```
### Get validation data from ImageDataGenerator (5 Marks)
- Give directory path
- Give target size
- Give batch_size
- Specify classes, if you wish to use less number of classes you need to give class names in a list (Atleast 15 classes should be there)
- Specify class_mode
- Specify color_mode
- Specify subset
You can get details here
https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/image/ImageDataGenerator
```
validation_set = train_datagen.flow_from_directory(train_data_dir_path,
target_size = (img_rows, img_cols),
batch_size = 1,
classes = ['0','1','2','3','4','5',
'6','7','8','9','10','11','12','13','14','15',
'16','17','18','19','20','21','22','23','24','25',
'26','27','28','29','30','31','32','33','34','35','36','37',
'38','39','40','41','42'],
class_mode='categorical',
color_mode='rgb',
subset='validation')
import contextlib
import os
#os.mkdir("frivolous_directory")
#with contextlib.suppress(UnidentifiedImageError):
x_val, y_val = generate_data_from_set(gen=validation_set)
testing_set = test_datagen.flow_from_directory(test_data_dir_path,
target_size = (img_rows, img_cols),
batch_size = 1,
classes = ['Meta'],
class_mode='categorical',
color_mode='rgb')
x_test, y_test = generate_data_from_set(gen=testing_set)
```
### Exploratory data analysis to understand German Traffic Signal Images
#### Let us check the total number of training and meta images, we have 39,209 training images and 43 reference images
```
import glob
train_image_names = glob.glob('/content/Data - German Traffic Sign Recognition/Train/*/*.png')
test_image_names = glob.glob('/content/Data - German Traffic Sign Recognition/Meta/*.png')
print("Total number of training images: ", len(train_image_names))
print("Total number of test images: ", len(test_image_names))
# make train_image_names as serie object
train_image_names = pd.Series(train_image_names)
test_image_names = pd.Series(test_image_names)
```
#### Create a dataframe of training image name and class labels so that it is easier to see distribution and identify class imbalance and also plot a sample of them
```
# train_df: a dataframe with 2 field: Filename, ClassId
train_df = pd.DataFrame()
# generate Filename field
train_df['Filename'] = train_image_names.map(lambda img_name: img_name.split("/")[-1])
# generate ClassId field
train_df['ClassId'] = train_image_names.map(lambda img_name: int(img_name.split("/")[-2]))
train_df.head()
#test_image_names
```
#### Replicate the same dataframe for the reference images available in Meta folder
```
# train_df: a dataframe with 2 field: Filename, ClassId
test_df = pd.DataFrame()
# generate Filename field
test_df['Filename'] = test_image_names.map(lambda img_name: img_name.split("/")[-1])
# generate ClassId field
test_df['ClassId'] = test_image_names.map(lambda img_name: int(img_name.split(".")[0].split("/")[-1]))
test_df.head()
```
#### Plot sample images for the training dataset, we see that images are severely blurred, some are bright while others are dull, which might impact classification, the class labels are shown as image titles
```
plot_df = train_df.sample(9).reset_index()
plt.figure(figsize=(10, 10))
for i in range(9):
img_name = plot_df.loc[i, 'Filename']
label_str = "%d"%(plot_df.loc[i, 'ClassId'])
plt.subplot(3,3,i+1)
plt.imshow(plt.imread(os.path.join('/content/Data - German Traffic Sign Recognition/Train/',label_str, img_name)))
plt.title(label_str)
plt.xticks([])
plt.yticks([])
```
#### Plotting the reference images in meta data folder, we see that these are proper images
```
plot_df = test_df.sample(9).reset_index()
plt.figure(figsize=(10, 10))
for i in range(9):
img_name = plot_df.loc[i, 'Filename']
label_str = "%d"%(plot_df.loc[i, 'ClassId'])
plt.subplot(3,3,i+1)
plt.imshow(plt.imread(os.path.join('/content/Data - German Traffic Sign Recognition/Meta/',img_name)))
plt.title(label_str)
plt.xticks([])
plt.yticks([])
```
#### We see that there is class imbalance in the training data some classes are overrepresented while some are underrepresented, so accuracy would be good if we are able to predict better in the majority class like label 38 vs label 37
```
class_id_distribution = train_df['ClassId'].value_counts()
class_id_distribution.head(10)
plt.figure(figsize=(13,5))
plt.xticks(np.arange(43))
plt.bar(class_id_distribution.index, class_id_distribution.values);
```
#### For Meta folder (reference images) we have one image for each class label
```
class_id_distribution = test_df['ClassId'].value_counts()
class_id_distribution.head(10)
plt.figure(figsize=(13,5))
plt.xticks(np.arange(43))
plt.bar(class_id_distribution.index, class_id_distribution.values);
```
### Define model (10 Marks)
- Initialize a Sequential Model
- Add Convolution, Maxpool, Dropout, Flatten & Dense layers according to your model architecture
```
# define model
from tensorflow.keras import optimizers
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Conv2D
from tensorflow.keras import layers
nb_epoch = 30
rows, cols = 32, 32
n_channels = 3
batch_size = 128
n_classes = 43
n_filter = 30
n_pool = 2
n_conv = 3
from keras import backend as K
#K.set_image_dim_ordering('th')
K.set_image_data_format('channels_last')
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation, Flatten
from keras.layers.convolutional import Conv2D
from keras.layers.pooling import MaxPooling2D
from keras.optimizers import SGD
from keras import backend as K
K.set_image_data_format('channels_last')
model_conv = Sequential()
## If You preprocessed with gray scaling and local histogram equivalization then input_shape = (32,32,1) else (32,32,3)
model_conv.add(Conv2D(32, kernel_size=(3, 3),activation='relu', input_shape=(32, 32, 3)))
model_conv.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model_conv.add(MaxPooling2D(pool_size=(2, 2),padding='Valid'))
#model.add(BatchNormalization())
model_conv.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model_conv.add(MaxPooling2D(pool_size=(2, 2),padding='Valid'))
#model.add(BatchNormalization())
model_conv.add(Dropout(0.25))
model_conv.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model_conv.add(MaxPooling2D(pool_size=(2, 2),padding='Valid'))
#model.add(BatchNormalization())
model_conv.add(Dropout(0.5))
model_conv.add(Flatten())
model_conv.add(Dense(128, activation='relu'))
model_conv.add(Dropout(0.5))
model_conv.add(Dense(n_classes, activation='softmax'))
```
### Compile the model (5 Marks)
- Specify optimizer, loss & metrics
```
# build the model
#model = cnn_model()
model_conv.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
```
### Get model summary (3 Marks)
```
model_conv.summary()
```
### Fit the model (5 Marks)
- Specify epochs
- Specify batch_size
- Give validation_data
- Validation accuracy should be more than 90%
```
from keras.callbacks import ModelCheckpoint, EarlyStopping
filepath="/content/Data - German Traffic Sign Recognition/German_Traffic_ConvNetworkModel.hdf5"
early = EarlyStopping(monitor='val_accuracy', min_delta=0, patience=2, verbose=1, mode='auto')
checkpoint_conv = ModelCheckpoint(filepath, monitor='val_accuracy',
verbose=1, save_best_only=True)
callbacks_list_conv = [checkpoint_conv,early]
training_set.n
history = model_conv.fit(x_train, y_train, batch_size=128, epochs=100, verbose=1,
callbacks=callbacks_list_conv,validation_data=(x_val, y_val))
```
### Draw plots (5 Marks)
- Plot training accuracy and validation accuracy with respect to epochs
- Plot training loss and validation loss with respect to epochs
```
import keras
from matplotlib import pyplot as plt
#history = model1.fit(train_x, train_y,validation_split = 0.1, epochs=50, batch_size=4)
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='upper left')
plt.show()
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='upper left')
plt.show()
```
## Future work (ungraded)
- Try to apply transfer learning and see if you can improve the performance.
- Using transfer learning with VGG-16 to see if performance can be improved
- Using imagenet weights and including input shape compatible with current problem
```
from keras.applications.vgg16 import VGG16
from keras.models import Model
vggmodel = VGG16(weights='imagenet', include_top=False, input_shape=(32,32,3))
vggmodel.summary()
```
#### The first 19 layers are not trainable, we are using the weights as such
```
for layers in (vggmodel.layers)[:19]:
#print(layers)
layers.trainable = False
```
#### We are specifying are own outut layer as well with the number of classes and softmax activation function
```
vggmodel.summary(line_length=150)
flatten = Flatten()
new_layer2 = Dense(n_classes, activation='softmax', name='my_dense_2')
inp2 = vggmodel.input
out2 = new_layer2(flatten(vggmodel.output))
model_final = Model(inp2, out2)
model_final.summary(line_length=150)
```
#### Compiling the model and specifying optimizer and metrics as before
```
model_final.compile(loss = "categorical_crossentropy",
optimizer = optimizers.SGD(lr=0.0001, momentum=0.9), metrics=["accuracy"])
model_final.summary()
from keras.callbacks import ModelCheckpoint, EarlyStopping
checkpoint = ModelCheckpoint("vgg16_1.h5", monitor='val_accuracy',
verbose=1, save_best_only=True, save_weights_only=False, mode='auto', period=1)
early = EarlyStopping(monitor='val_accuracy', min_delta=0, patience=40, verbose=1, mode='auto')
history2 = model_final.fit(x_train, y_train, batch_size=128, epochs=100, verbose=1,
callbacks=[checkpoint,early],validation_data=(x_val, y_val))
model_final.save_weights("vgg16_1.h5")
import keras
from matplotlib import pyplot as plt
#history = model1.fit(train_x, train_y,validation_split = 0.1, epochs=50, batch_size=4)
plt.plot(history2.history['accuracy'])
plt.plot(history2.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='upper left')
plt.show()
# summarize history for loss
plt.plot(history2.history['loss'])
plt.plot(history2.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='upper left')
plt.show()
```
### Transfer learning using VGG-16 is not very helpful as we were able to get validation accuracy of 31.0% while in our trained model using own network we were able to achieve validation accuracy of 92.9%
```
%%shell
jupyter nbconvert --to html /content/Questions_Project_1_Computer_Vision_JPMC_v3.ipynb
```
| true |
code
| 0.491517 | null | null | null | null |
|
```
# Import Libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random
from random import gauss
import math
pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)
import warnings
warnings.filterwarnings('ignore')
# CONSTANT Variables
NUM_SOURCE = 6
X1 = 21
X2 = 21
V = 441
N = 240
```
### Question 1.1
```
def over_N(tc, N):
""" Check whether numpy array tc is over length of the temporal source
tc : numpy array of temporal source, TC
N : integer of the length of each temporal source
Return : True or False
"""
if len(tc) >= N:
return True
else:
return False
def standardise(tc):
""" Standardise TC
tc : numpy array
Return : numpy array of standardised TC
"""
tc = tc - np.mean(tc)
tc = tc / np.std(tc)
return tc
def construct(AV, IV, duration):
""" Construct matrix TC of size 240 x 6 consisting of six temporal sources using three vectors
AV : onset arrival vector
IV : increment vector
duration : duration of ones
Return : numpy array of matrix TC.
"""
# Initialise value
iv_count = IV
tc = np.array([])
# onset arrival vector. Fills zeroes to tc
tc = np.zeros(AV)
while len(tc) < N:
# build up duration of ones
for i in range(duration):
if over_N(tc, N) == True:
break
# Add ones into TC.
tc = np.append(tc, 1)
# incremeting the vector
while (len(tc) < iv_count) & (len(tc) < N):
tc = np.append(tc, 0)
iv_count += IV
# build up onsets arrival vector
for i in range(AV):
if over_N(tc, N) == True:
break
tc = np.append(tc, 0)
# Standardise TC
tc = standardise(tc)
return tc
# Construct matrix TC
tc1 = construct(0, 30, 15)
tc2 = construct(20, 45, 20)
tc3 = construct(0, 60, 25)
tc4 = construct(0, 40, 15)
tc5 = construct(0, 40, 20)
tc6 = construct(0, 40, 25)
TC = [tc1, tc2, tc3, tc4, tc5, tc6]
# Plot each source TCs
count = 0
for tc in TC:
count += 1
plt.plot(tc)
plt.title("TC " + str(count))
plt.xlabel("N")
plt.xticks([0, 20, 40, 60, 120, 240])
plt.savefig('plots/TC_'+str(count)) #save plots
plt.show()
```
### Question 1.2¶
```
tc_df = pd.DataFrame(TC)
tc_df = tc_df.T
# Build up a correlation matrix between 6 variables
ax = sns.heatmap(tc_df.corr())
plt.title("Correlation Matrix between 6 variables");
plt.savefig('plots/CM_TC')
```
### Question 1.3
```
def slice_one(hori_start, hori_finish, verti_start, verti_finish):
""" Construct an array tmpSM of size (21 x 21) consisting of ones and zeros, by
placing ones at these pixels along "vertical, horizontl" directoon of the slice
hori_start : integer of the starting point of placing one in horizontal direction
hori_finish : integer of the finishing point of placing one in horizontal direction
verti_start : integer of the starting point of placing one in vertical direction
verti_finish : integer of the finishing point of placing one in vertical direction
Return : an array tmpSM of size 21x21
"""
tmp_sm = np.zeros(V).reshape((X1,X2))
for row in range(hori_start-1, hori_finish):
for col in range(verti_start-1, verti_finish):
# Place one
tmp_sm[row][col] = 1.0
return tmp_sm
# Construct array tmpSM of 6 different sources
tmp1 = slice_one(2, 6, 2, 6)
tmp2 = slice_one(2, 6, 15, 19)
tmp3 = slice_one(8, 13, 2, 6)
tmp4 = slice_one(8, 13, 15, 19)
tmp5 = slice_one(15, 19, 2, 6)
tmp6 = slice_one(15, 19, 15, 19)
# Construct an array tmpSM of size 6 x (21 x 21)
tmpSM = np.array([tmp1, tmp2, tmp3, tmp4, tmp5, tmp6])
count = 0
for tmp in tmpSM:
tmp_df = pd.DataFrame(tmp)
count += 1
ax = sns.heatmap(tmp_df)
plt.title("SM " + str(count))
plt.savefig('plots/SM_'+str(count))
plt.show()
# Reshape SM to size 6 X 441
SM = tmpSM.reshape((NUM_SOURCE, V))
sm_df = pd.DataFrame(SM)
sm_df = sm_df.T
# Build up a correlation matrix between 6 vectored SMs
sns.heatmap(sm_df.corr())
plt.title("Correlation Matrix between 6 vectored SMs")
plt.savefig('plots/CM_SM');
```
### Question 1.4
```
def contruct_gaussian_noise(mean, variance, length):
""" Construct white Gaussian noise
mean : mean of the gaussian noise, integer
variance : variance of the gaussian noise, integer
length : length of the gaussian noise, integer
Return : a numpy array of gaussian noise
"""
noise = np.array([gauss(mean, math.sqrt(variance)) for i in range(length * NUM_SOURCE)])
return noise
temp_noise = contruct_gaussian_noise(0.0, 0.25, N)
temp_noise = temp_noise.reshape((N,NUM_SOURCE))
spatial_noise = contruct_gaussian_noise(0.0, 0.015, V)
spatial_noise = spatial_noise.reshape((NUM_SOURCE,V))
# Correlation matrix between spatial noise
snoise_df = pd.DataFrame(spatial_noise)
snoise_df = snoise_df.T
sns.heatmap(snoise_df.corr())
plt.title("Correlation matrix between spatial noise");
plt.savefig('plots/CM_SpatialNoise');
# Correlation matrix between temporal noise
tnoise_df = pd.DataFrame(temp_noise)
sns.heatmap(tnoise_df.corr())
plt.title("Correlation matrix between temporal noise");
plt.savefig('plots/CM_TemporalNoise');
# Histogram of spatial noise
sns.histplot(data=snoise_df)
plt.title("Histogram of spatial noise");
plt.savefig('plots/Histogram_SpatialNoise');
# Histogram of temporal noise
sns.histplot(data=tnoise_df)
plt.title("Histogram of temporal noise");
plt.savefig('plots/Histogram_TemporalNoise');
# Build up product TtTs
TtTs = np.dot(temp_noise, spatial_noise)
ttts_df = pd.DataFrame(TtTs)
# Correlation of product TtTs of a subset of TtTs
mini_ttts = ttts_df[[0, 1, 2, 3, 4, 5, 6, 7, 8]]
sns.heatmap(mini_ttts.corr())
plt.title("Correlation of product TtTs");
plt.savefig('plots/CM_TtTs');
```
### Question 1.5
```
TC = np.transpose(TC)
# Build up standardised X
X = np.dot((TC + temp_noise), (SM + spatial_noise))
X_df = pd.DataFrame(X)
# Randomly select 100 time-series from X
randomly_selected = random.sample(list(range(0,V)), 100)
sample = X_df[randomly_selected]
# Plot 100 randomly selected time series from X
sns.lineplot(data = sample)
plt.title("Line plot of 100 randomly selected time series from X");
plt.xlabel("N")
plt.savefig('plots/Lineplot_randomX');
# Get variance of X acriss 441 variables
var = np.var(X_df)
# Plot variance of 441 variables
sns.scatterplot(data = var)
plt.title("Variance of 441 variables");
plt.savefig('plots/Variance_X');
# Standardise X
X = standardise(X)
```
### Question 2.1
```
def solve_lsr(TC, X):
"""
Solve a Least Square Regression (LSR) model given :
TC : a numpy matrix of 240 x 6
X : a numpy matrix of 240 x 441
Returns: 4 numpy arrays which are processed in the LSR model
"""
DTD = np.dot(np.transpose(TC), TC)
DTD_inv = np.linalg.inv(DTD)
DTX = np.dot(np.transpose(TC), X)
A_lsr = np.dot(DTD_inv, DTX)
D_lsr = np.dot(X, np.transpose(A_lsr))
return DTD, DTD_inv, DTX, A_lsr, D_lsr
# Solve LSR
DTD, DTD_inv, DTX, A_lsr, D_lsr = solve_lsr(TC, X)
# Reshape Retrieval of SM, A to size 21 x 21
Alsr = []
for row in A_lsr:
Alsr.append(row.reshape((X1, X2)))
# Plot the retrieval SM and TC which are A and D of LSR
dlsr_df = pd.DataFrame(D_lsr)
for col in range(0, NUM_SOURCE):
fig, axes = plt.subplots(1, 2, figsize=(10,3))
sns.heatmap(data = Alsr[col], ax = axes[0])
sns.lineplot(data=dlsr_df[col], ax = axes[1])
plt.title("Source " + str(col+1))
plt.tight_layout()
plt.savefig("plots/LSR_source"+str(col+1))
plt.show()
# Plot scatter plots required
sns.scatterplot(dlsr_df[2], X_df[9*X1 + 2])
plt.xlabel("3rd column of Dlsr")
plt.ylabel("30th column of standardized X")
plt.title("Scatter plot of 3rd column of Dlsr vs 30th column of standarized X")
plt.savefig("plots/scatterplot_3rdDlsr_vs_X")
plt.show()
sns.scatterplot(dlsr_df[3], X_df[9*X1 + 2])
plt.xlabel("4th column of Dlsr")
plt.ylabel("30th column of standardized X")
plt.title("Scatter plot of 4th column of Dlsr vs 30th column of standarized X")
plt.savefig("plots/scatterplot_4thDlsr_vs_X")
plt.show()
```
### Question 2.2
```
def solve_RR(lambda_value, DTD, DTX):
"""
Solve Ridge Regression (RR) Model given :
lambda_value : the regularization term in RR, integer
DTD : Product of Transpose of D and D, numpy array
DTX : Product of Transpose of D and standardised X,numpy array
Return :
A_rr : Retrieval of SM, numpy array
D_rr : Retrieval of TC, numpy array
"""
lamda_hat = lambda_value * V
I = np.identity(6)
Z = DTD + np.dot(lamda_hat, I)
Z_inv = np.linalg.inv(Z)
A_rr = np.dot(Z_inv, DTX)
D_rr = np.dot(X, np.transpose(A_rr))
return A_rr, D_rr
# Solve RR with lambda value = 0.5
A_rr, D_rr = solve_RR(0.5, DTD, DTX)
# Construct a Perason correlation of TC and D of LSR and RR
from scipy.stats import pearsonr
ctlsr = []
ctrr = []
for i in range(NUM_SOURCE):
corr, _ = pearsonr(TC[i], D_lsr[i])
ctlsr.append(corr)
corr2, _ = pearsonr(TC[i], D_rr[i])
ctrr.append(corr2)
print("Sum of CtRR greater than Sum of CtLSR: ", sum(ctrr) > sum(ctlsr))
print("Sum of CtRR: " + str(sum(ctrr)))
print("Sum of CtLSR: " + str(sum(ctlsr)))
# Solve RR with lambda value = 1000
Arr_alt, Drr_alt = solve_RR(1000, DTD, DTX)
Arr_alt_df = pd.DataFrame(Arr_alt)
Arr_alt_df = Arr_alt_df.T
alsr_df = pd.DataFrame(A_lsr)
alsr_df = alsr_df.T
# Plot First vector of Alsr vs First vector of Arr
sns.scatterplot(Arr_alt_df[0], alsr_df[0])
plt.xlabel("First vector of Arr")
plt.ylabel("First vector of Alsr")
plt.title("First vector of Alsr vs First vector of Arr")
plt.savefig("plots/arr_vs_alsr")
Arr_df = pd.DataFrame(np.transpose(A_rr))
# Plot Arr when lambda is 0.5 vs 1000
sns.lineplot(data=Arr_df[0], label='Arr when lamda=0.5')
sns.lineplot(data=Arr_alt_df[0], label='Arr when lamda=1000')
plt.title("Arr when lambda is 0.5 vs 1000")
plt.savefig("plots/arr_lambda")
Alsr_df = pd.DataFrame(A_lsr)
Drr_df = pd.DataFrame(D_rr)
tc_df = pd.DataFrame(TC)
X_df.to_csv("datafile/X.csv")
sm_df.to_csv("datafile/SM.csv")
tc_df.to_csv("datafile/TC.csv")
Arr_df.to_csv("datafile/Arr.csv")
Drr_df.to_csv("datafile/Drr.csv")
def contruct_X(i):
"""
Construct X and output the data into a csv file with corresponding i
in the filename
"""
temp_noise = contruct_gaussian_noise(0.0, 0.25, N)
temp_noise = temp_noise.reshape((N,NUM_SOURCE))
spatial_noise = contruct_gaussian_noise(0.0, 0.015, V)
spatial_noise = spatial_noise.reshape((NUM_SOURCE,V))
X = np.dot((TC + temp_noise), (SM + spatial_noise))
X_df = pd.DataFrame(X)
X_df.to_csv("datafile/X" + str(i) + ".csv")
return
for i in range(10):
contruct_X(i+1)
```
### Next : Q2.3-R.ipynb¶
| true |
code
| 0.700972 | null | null | null | null |
|
# Out-of-core Learning - Large Scale Text Classification for Sentiment Analysis
## Scalability Issues
The `sklearn.feature_extraction.text.CountVectorizer` and `sklearn.feature_extraction.text.TfidfVectorizer` classes suffer from a number of scalability issues that all stem from the internal usage of the `vocabulary_` attribute (a Python dictionary) used to map the unicode string feature names to the integer feature indices.
The main scalability issues are:
- **Memory usage of the text vectorizer**: all the string representations of the features are loaded in memory
- **Parallelization problems for text feature extraction**: the `vocabulary_` would be a shared state: complex synchronization and overhead
- **Impossibility to do online or out-of-core / streaming learning**: the `vocabulary_` needs to be learned from the data: its size cannot be known before making one pass over the full dataset
To better understand the issue let's have a look at how the `vocabulary_` attribute work. At `fit` time the tokens of the corpus are uniquely indentified by a integer index and this mapping stored in the vocabulary:
```
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(min_df=1)
vectorizer.fit([
"The cat sat on the mat.",
])
vectorizer.vocabulary_
```
The vocabulary is used at `transform` time to build the occurrence matrix:
```
X = vectorizer.transform([
"The cat sat on the mat.",
"This cat is a nice cat.",
]).toarray()
print(len(vectorizer.vocabulary_))
print(vectorizer.get_feature_names())
print(X)
```
Let's refit with a slightly larger corpus:
```
vectorizer = CountVectorizer(min_df=1)
vectorizer.fit([
"The cat sat on the mat.",
"The quick brown fox jumps over the lazy dog.",
])
vectorizer.vocabulary_
```
The `vocabulary_` is the (logarithmically) growing with the size of the training corpus. Note that we could not have built the vocabularies in parallel on the 2 text documents as they share some words hence would require some kind of shared datastructure or synchronization barrier which is complicated to setup, especially if we want to distribute the processing on a cluster.
With this new vocabulary, the dimensionality of the output space is now larger:
```
X = vectorizer.transform([
"The cat sat on the mat.",
"This cat is a nice cat.",
]).toarray()
print(len(vectorizer.vocabulary_))
print(vectorizer.get_feature_names())
print(X)
```
## The IMDb movie dataset
To illustrate the scalability issues of the vocabulary-based vectorizers, let's load a more realistic dataset for a classical text classification task: sentiment analysis on text documents. The goal is to tell apart negative from positive movie reviews from the [Internet Movie Database](http://www.imdb.com) (IMDb).
In the following sections, with a [large subset](http://ai.stanford.edu/~amaas/data/sentiment/) of movie reviews from the IMDb that has been collected by Maas et al.
- A. L. Maas, R. E. Daly, P. T. Pham, D. Huang, A. Y. Ng, and C. Potts. Learning Word Vectors for Sentiment Analysis. In the proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, pages 142–150, Portland, Oregon, USA, June 2011. Association for Computational Linguistics.
This dataset contains 50,000 movie reviews, which were split into 25,000 training samples and 25,000 test samples. The reviews are labeled as either negative (neg) or positive (pos). Moreover, *positive* means that a movie received >6 stars on IMDb; negative means that a movie received <5 stars, respectively.
Assuming that the `../fetch_data.py` script was run successfully the following files should be available:
```
import os
train_path = os.path.join('datasets', 'IMDb', 'aclImdb', 'train')
test_path = os.path.join('datasets', 'IMDb', 'aclImdb', 'test')
```
Now, let's load them into our active session via scikit-learn's `load_files` function
```
from sklearn.datasets import load_files
train = load_files(container_path=(train_path),
categories=['pos', 'neg'])
test = load_files(container_path=(test_path),
categories=['pos', 'neg'])
```
<div class="alert alert-warning">
<b>NOTE</b>:
<ul>
<li>
Since the movie datasets consists of 50,000 individual text files, executing the code snippet above may take ~20 sec or longer.
</li>
</ul>
</div>
The `load_files` function loaded the datasets into `sklearn.datasets.base.Bunch` objects, which are Python dictionaries:
```
train.keys()
```
In particular, we are only interested in the `data` and `target` arrays.
```
import numpy as np
for label, data in zip(('TRAINING', 'TEST'), (train, test)):
print('\n\n%s' % label)
print('Number of documents:', len(data['data']))
print('\n1st document:\n', data['data'][0])
print('\n1st label:', data['target'][0])
print('\nClass names:', data['target_names'])
print('Class count:',
np.unique(data['target']), ' -> ',
np.bincount(data['target']))
```
As we can see above the `'target'` array consists of integers `0` and `1`, where `0` stands for negative and `1` stands for positive.
## The Hashing Trick
Remember the bag of word representation using a vocabulary based vectorizer:
<img src="figures/bag_of_words.svg" width="100%">
To workaround the limitations of the vocabulary-based vectorizers, one can use the hashing trick. Instead of building and storing an explicit mapping from the feature names to the feature indices in a Python dict, we can just use a hash function and a modulus operation:
<img src="figures/hashing_vectorizer.svg" width="100%">
More info and reference for the original papers on the Hashing Trick in the [following site](http://www.hunch.net/~jl/projects/hash_reps/index.html) as well as a description specific to language [here](http://blog.someben.com/2013/01/hashing-lang/).
```
from sklearn.utils.murmurhash import murmurhash3_bytes_u32
# encode for python 3 compatibility
for word in "the cat sat on the mat".encode("utf-8").split():
print("{0} => {1}".format(
word, murmurhash3_bytes_u32(word, 0) % 2 ** 20))
```
This mapping is completely stateless and the dimensionality of the output space is explicitly fixed in advance (here we use a modulo `2 ** 20` which means roughly 1M dimensions). The makes it possible to workaround the limitations of the vocabulary based vectorizer both for parallelizability and online / out-of-core learning.
The `HashingVectorizer` class is an alternative to the `CountVectorizer` (or `TfidfVectorizer` class with `use_idf=False`) that internally uses the murmurhash hash function:
```
from sklearn.feature_extraction.text import HashingVectorizer
h_vectorizer = HashingVectorizer(encoding='latin-1')
h_vectorizer
```
It shares the same "preprocessor", "tokenizer" and "analyzer" infrastructure:
```
analyzer = h_vectorizer.build_analyzer()
analyzer('This is a test sentence.')
```
We can vectorize our datasets into a scipy sparse matrix exactly as we would have done with the `CountVectorizer` or `TfidfVectorizer`, except that we can directly call the `transform` method: there is no need to `fit` as `HashingVectorizer` is a stateless transformer:
```
docs_train, y_train = train['data'], train['target']
docs_valid, y_valid = test['data'][:12500], test['target'][:12500]
docs_test, y_test = test['data'][12500:], test['target'][12500:]
```
The dimension of the output is fixed ahead of time to `n_features=2 ** 20` by default (nearly 1M features) to minimize the rate of collision on most classification problem while having reasonably sized linear models (1M weights in the `coef_` attribute):
```
h_vectorizer.transform(docs_train)
```
Now, let's compare the computational efficiency of the `HashingVectorizer` to the `CountVectorizer`:
```
h_vec = HashingVectorizer(encoding='latin-1')
%timeit -n 1 -r 3 h_vec.fit(docs_train, y_train)
count_vec = CountVectorizer(encoding='latin-1')
%timeit -n 1 -r 3 count_vec.fit(docs_train, y_train)
```
As we can see, the HashingVectorizer is much faster than the Countvectorizer in this case.
Finally, let us train a LogisticRegression classifier on the IMDb training subset:
```
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
h_pipeline = Pipeline([
('vec', HashingVectorizer(encoding='latin-1')),
('clf', LogisticRegression(random_state=1)),
])
h_pipeline.fit(docs_train, y_train)
print('Train accuracy', h_pipeline.score(docs_train, y_train))
print('Validation accuracy', h_pipeline.score(docs_valid, y_valid))
import gc
del count_vec
del h_pipeline
gc.collect()
```
# Out-of-Core learning
Out-of-Core learning is the task of training a machine learning model on a dataset that does not fit into memory or RAM. This requires the following conditions:
- a **feature extraction** layer with **fixed output dimensionality**
- knowing the list of all classes in advance (in this case we only have positive and negative reviews)
- a machine learning **algorithm that supports incremental learning** (the `partial_fit` method in scikit-learn).
In the following sections, we will set up a simple batch-training function to train an `SGDClassifier` iteratively.
But first, let us load the file names into a Python list:
```
train_path = os.path.join('datasets', 'IMDb', 'aclImdb', 'train')
train_pos = os.path.join(train_path, 'pos')
train_neg = os.path.join(train_path, 'neg')
fnames = [os.path.join(train_pos, f) for f in os.listdir(train_pos)] +\
[os.path.join(train_neg, f) for f in os.listdir(train_neg)]
fnames[:3]
```
Next, let us create the target label array:
```
y_train = np.zeros((len(fnames), ), dtype=int)
y_train[:12500] = 1
np.bincount(y_train)
```
Now, we implement the `batch_train function` as follows:
```
from sklearn.base import clone
def batch_train(clf, fnames, labels, iterations=25, batchsize=1000, random_seed=1):
vec = HashingVectorizer(encoding='latin-1')
idx = np.arange(labels.shape[0])
c_clf = clone(clf)
rng = np.random.RandomState(seed=random_seed)
for i in range(iterations):
rnd_idx = rng.choice(idx, size=batchsize)
documents = []
for i in rnd_idx:
with open(fnames[i], 'r', encoding='latin-1') as f:
documents.append(f.read())
X_batch = vec.transform(documents)
batch_labels = labels[rnd_idx]
c_clf.partial_fit(X=X_batch,
y=batch_labels,
classes=[0, 1])
return c_clf
```
Note that we are not using `LogisticRegression` as in the previous section, but we will use a `SGDClassifier` with a logistic cost function instead. SGD stands for `stochastic gradient descent`, an optimization alrogithm that optimizes the weight coefficients iteratively sample by sample, which allows us to feed the data to the classifier chunk by chuck.
And we train the `SGDClassifier`; using the default settings of the `batch_train` function, it will train the classifier on 25*1000=25000 documents. (Depending on your machine, this may take >2 min)
```
from sklearn.linear_model import SGDClassifier
sgd = SGDClassifier(loss='log', random_state=1, max_iter=1000)
sgd = batch_train(clf=sgd,
fnames=fnames,
labels=y_train)
```
Eventually, let us evaluate its performance:
```
vec = HashingVectorizer(encoding='latin-1')
sgd.score(vec.transform(docs_test), y_test)
```
### Limitations of the Hashing Vectorizer
Using the Hashing Vectorizer makes it possible to implement streaming and parallel text classification but can also introduce some issues:
- The collisions can introduce too much noise in the data and degrade prediction quality,
- The `HashingVectorizer` does not provide "Inverse Document Frequency" reweighting (lack of a `use_idf=True` option).
- There is no easy way to inverse the mapping and find the feature names from the feature index.
The collision issues can be controlled by increasing the `n_features` parameters.
The IDF weighting might be reintroduced by appending a `TfidfTransformer` instance on the output of the vectorizer. However computing the `idf_` statistic used for the feature reweighting will require to do at least one additional pass over the training set before being able to start training the classifier: this breaks the online learning scheme.
The lack of inverse mapping (the `get_feature_names()` method of `TfidfVectorizer`) is even harder to workaround. That would require extending the `HashingVectorizer` class to add a "trace" mode to record the mapping of the most important features to provide statistical debugging information.
In the mean time to debug feature extraction issues, it is recommended to use `TfidfVectorizer(use_idf=False)` on a small-ish subset of the dataset to simulate a `HashingVectorizer()` instance that have the `get_feature_names()` method and no collision issues.
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
In our implementation of the batch_train function above, we randomly draw *k* training samples as a batch in each iteration, which can be considered as a random subsampling ***with*** replacement. Can you modify the `batch_train` function so that it iterates over the documents ***without*** replacement, i.e., that it uses each document ***exactly once*** per iteration?
</li>
</ul>
</div>
```
# %load solutions/23_batchtrain.py
```
| true |
code
| 0.506591 | null | null | null | null |
|
# Numpy Basics
NumPy provides an N-dimensional array type, the ndarray, which describes a collection of “items” of the *same* type.
The items can be indexed using for example N integers.
All ndarrays are homogeneous: every item takes up the same size block of memory, and all blocks are interpreted in exactly the same way.
An item extracted from an array, e.g., by indexing, is represented by a Python object whose type is one of the array scalar types built in NumPy.
<p align="center">
<img src="https://numpy.org/doc/stable/_images/threefundamental.png">
</p>
## NumPy Array Attributes
```
import numpy as np
np.random.seed(0)
def array_info(array: np.ndarray) -> None:
print(f"ndim: {array.ndim}")
print(f"shape: {array.shape}")
print(f"size: {array.size}")
print(f"dtype: {array.dtype}")
print(f"values:\n{array}\n")
```
## Array Indexing and Slicing
Array indexing refers to any use of the square brackets ([]) to index array values. There are many options to indexing, which give numpy indexing great power.
Most of the following examples show the use of indexing when referencing data in an array. The examples work just as well when assigning to an array.
Note that slices of arrays do not copy the internal array data but only produce new views of the original data.

```
x = np.array([[1, 2], [3, 4], [5, 6]])
array_info(x)
print(x[:3])
print(x[1:])
print(x[1:2])
print(x[::-1])
print(x[0, :])
print(x[0])
print(x[:, 0])
mean = [0, 0]
cov = [[1, 2],
[2, 5]]
x = np.random.multivariate_normal(mean=mean, cov=cov, size=10)
print(x)
print(x.shape)
rand_idxs = np.random.randint(low=0, high=x.shape[0], size=3)
print(rand_idxs)
x_subsample = x[rand_idxs, :]
print(x_subsample)
x_subsample = x[rand_idxs]
print(x_subsample)
```
## Subarrays are views
```
print(x)
x_sub_array = x[:2, :2]
array_info(x_sub_array)
x_sub_array[0, 0] = -1
array_info(x_sub_array)
array_info(x)
```
## Creating copies of arrays
```
x_copy = x[:2, :2].copy()
array_info(x_copy)
x_copy[0, 0] = 42
array_info(x_copy)
array_info(x)
```
## Reshaping of Arrays
```
a = np.arange(start=1, stop=10)
array_info(a)
grid = np.reshape(a, newshape=(3, 3))
array_info(grid)
x = np.array([1, 2, 3])
array_info(x)
x = np.reshape(x, newshape=(1, 3))
array_info(x)
array_info(x)
x = x[np.newaxis, :]
array_info(x)
array_info(x)
x = x.reshape((3, 1))
array_info(x)
array_info(x)
x = x.ravel()
array_info(x)
x = x.reshape((3, 1))
array_info(x)
x = x.flatten()
array_info(x)
```
### “Automatic” Reshaping
```
a = np.arange(30)
array_info(a)
b = a.reshape((2, -1, 3))
array_info(b)
```
## Changing the Dtype
| Numpy type | C type | Description |
|-|-|-|
| numpy.int8 | int8_t | Byte (-128 to 127) |
| numpy.int16 | int16_t | Integer (-32768 to 32767) |
| numpy.int32 | int32_t | Integer (-2147483648 to 2147483647) |
| numpy.int64 | int64_t | Integer (-9223372036854775808 to 9223372036854775807) |
| numpy.uint8 | uint8_t | Unsigned integer (0 to 255) |
| numpy.uint16 | uint16_t | Unsigned integer (0 to 65535) |
| numpy.uint32 | uint32_t | Unsigned integer (0 to 4294967295) |
| numpy.uint64 | uint64_t | Unsigned integer (0 to 18446744073709551615) |
| numpy.intp | intptr_t | Integer used for indexing, typically the same as ssize_t |
| numpy.uintp | uintptr_t | Integer large enough to hold a pointer |
| numpy.float32 | float | |
| numpy.float64 | double | Note that this matches the precision of the builtin python float. |
| numpy.complex64 | float complex | Complex number, represented by two 32-bit floats. |
| numpy.complex128 | double complex | Note that this matches the precision of the builtin python complex. |
```
x = np.float32([-1.0, 2.0, 3.0])
array_info(x)
x = np.array([-1.0, 2.0, 3.0], dtype=np.float32)
y = x.astype(np.int8)
array_info(y)
z = np.uint16(x)
array_info(z)
```
## Concatenation of arrays
```
x = np.array([1, 2, 3])
y = np.array([3, 2, 1])
result = np.concatenate([x, y])
array_info(result)
grid = np.array([[1, 2, 3],
[4, 5, 6]])
array_info(grid)
result = np.concatenate([grid, grid])
array_info(result)
result = np.concatenate([grid, grid], axis=0)
array_info(result)
result = np.concatenate([grid, grid], axis=1)
array_info(result)
x = np.array([1, 2, 3])
grid = np.array([[4, 5, 6],
[7, 8, 9]])
result = np.vstack([x, grid])
array_info(result)
y = np.array([[-1], [-1]])
result = np.hstack([grid, y])
array_info(result)
```
| true |
code
| 0.272436 | null | null | null | null |
|
```
!pip install qucumber
import numpy as np
import torch
import matplotlib.pyplot as plt
from qucumber.nn_states import ComplexWaveFunction
from qucumber.callbacks import MetricEvaluator
import qucumber.utils.unitaries as unitaries
import qucumber.utils.cplx as cplx
import qucumber.utils.training_statistics as ts
import qucumber.utils.data as data
import qucumber
# set random seed on cpu but not gpu, since we won't use gpu for this tutorial
qucumber.set_random_seed(1234, cpu=True, gpu=False)
```
The main difference between the previous tasks and the additional data provided is that in the first cases we tried to reconstruct the energy of the system from which we measured, while in the latter the reconstruction is of the original state from which the measurements were made.
In the following code we made a 4 qubit LiH state reconstruction by another method using the qucumber library and following the example with 2 qubits at the following link:
https://github.com/PIQuIL/QuCumber/blob/master/examples/Tutorial2_TrainComplexWaveFunction/tutorial_qubits.ipynb
# Reconstruction of a LiH
## The wavefunction to be reconstructed
The four qubits wavefunction below (coefficients stored in `LiH - psi.txt`) will be reconstructed.
$$\vert\psi \rangle = \alpha1 \vert0000\rangle + \beta1 \vert 0001\rangle + \gamma1 \vert0010\rangle + \delta1 \vert0011\rangle $$
+
$$\alpha2 \vert0100\rangle + \beta2 \vert 0101\rangle + \gamma2 \vert0110\rangle + \delta2 \vert0111\rangle$$
+
$$\alpha3 \vert1000\rangle + \beta3 \vert 1001\rangle + \gamma3 \vert1010\rangle + \delta3 \vert1011\rangle$$
+
$$\alpha4 \vert1100\rangle + \beta4 \vert 1101\rangle + \gamma4 \vert1110\rangle + \delta4 \vert1111\rangle$$
where
$$
\alpha 1 = 4.9639 e-03
\beta 1 = -1.8227 e-16
\gamma 1 = 5.7627 e-02
\delta 1 = -1.1165 e-01
$$
;
$$
\alpha 2 = 3.2638 e-02
\beta 2 = 2.4447 e-16
\gamma 2 = -3.5453 e-02
\delta 2 = 5.7627 e-02
$$
;
$$
\alpha 3 = -8.1068 e-17
\beta 3 = 2.1391 e-16
\gamma 3 = -4.5975 e-16
\delta 3 = 7.6073 e-16
$$
;
$$
\alpha 4 = 9.8866 e-01
\beta 4 = 4.2995 e-16
\gamma 4 = 3.2638 e-02
\delta 4 = 4.9639 e-03
$$
The example dataset, `LiH - train_samples.txt`, comprises of 500 $\sigma$ measurements made in various bases (X, Y and Z). A corresponding file containing the bases for each data point in `LiH - train_samples.txt`, `LiH - train_bases.txt.txt`, is also required. As per convention, spins are represented in binary notation with zero and one denoting spin-down and spin-up, respectively.
## Using qucumber to reconstruct the wavefunction
The Python class `ComplexWaveFunction` contains generic properties of a RBM meant to reconstruct a complex wavefunction, the most notable one being the gradient function required for stochastic gradient descent.
To instantiate a `ComplexWaveFunction` object, one needs to specify the number of visible and hidden units in the RBM. The number of visible units, `num_visible`, is given by the size of the physical system, i.e. the number of spins or qubits (2 in this case), while the number of hidden units, `num_hidden`, can be varied to change the expressiveness of the neural network.
**Note:** The optimal `num_hidden` : `num_visible` ratio will depend on the system. For the two-qubit wavefunction described above, good results can be achieved when this ratio is 1.
On top of needing the number of visible and hidden units, a `ComplexWaveFunction` object requires the user to input a dictionary containing the unitary operators (2x2) that will be used to rotate the qubits in and out of the computational basis, Z, during the training process. The `unitaries` utility will take care of creating this dictionary.
The `MetricEvaluator` class and `training_statistics` utility are built-in amenities that will allow the user to evaluate the training in real time.
Lastly, the `cplx` utility allows QuCumber to be able to handle complex numbers as they are not currently supported by PyTorch.
### Training
To evaluate the training in real time, the fidelity between the true wavefunction of the system and the wavefunction that QuCumber reconstructs, $\vert\langle\psi\vert\psi_{RBM}\rangle\vert^2$, will be calculated along with the Kullback-Leibler (KL) divergence (the RBM's cost function). First, the training data and the true wavefunction of this system need to be loaded using the `data` utility.
```
train_path = "LiH - train_samples.txt"
train_bases_path = "LiH - train_bases.txt"
psi_path = "LiH - psi.txt"
bases_path = "LiH - qubit_bases.txt"
train_samples, true_psi, train_bases, bases = data.load_data(
train_path, psi_path, train_bases_path, bases_path
)
train_samples = train_samples[0:10000,:]
train_bases = train_bases[0:10000,:]
unitary_dict = unitaries.create_dict()
nv = train_samples.shape[-1]
nh = nv
nn_state = ComplexWaveFunction(
num_visible=nv, num_hidden=nh, unitary_dict=unitary_dict, gpu=True
)
epochs = 500
pbs = 100 # pos_batch_size
nbs = pbs # neg_batch_size
lr = 0.01
k = 10
def alpha1(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
alpha_ = cplx.norm(
torch.tensor([rbm_psi[0][0], rbm_psi[1][0]], device=nn_state.device)
/ normalization
)
return alpha_
def beta1(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
beta_ = cplx.norm(
torch.tensor([rbm_psi[0][1], rbm_psi[1][1]], device=nn_state.device)
/ normalization
)
return beta_
def gamma1(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
gamma_ = cplx.norm(
torch.tensor([rbm_psi[0][2], rbm_psi[1][2]], device=nn_state.device)
/ normalization
)
return gamma_
def delta1(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
delta_ = cplx.norm(
torch.tensor([rbm_psi[0][3], rbm_psi[1][3]], device=nn_state.device)
/ normalization
)
return delta_
def alpha2(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
alpha_ = cplx.norm(
torch.tensor([rbm_psi[0][4], rbm_psi[1][4]], device=nn_state.device)
/ normalization
)
return alpha_
def beta2(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
beta_ = cplx.norm(
torch.tensor([rbm_psi[0][5], rbm_psi[1][5]], device=nn_state.device)
/ normalization
)
return beta_
def gamma2(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
gamma_ = cplx.norm(
torch.tensor([rbm_psi[0][6], rbm_psi[1][6]], device=nn_state.device)
/ normalization
)
return gamma_
def delta2(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
delta_ = cplx.norm(
torch.tensor([rbm_psi[0][7], rbm_psi[1][7]], device=nn_state.device)
/ normalization
)
return delta_
def alpha3(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
alpha_ = cplx.norm(
torch.tensor([rbm_psi[0][8], rbm_psi[1][8]], device=nn_state.device)
/ normalization
)
return alpha_
def beta3(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
beta_ = cplx.norm(
torch.tensor([rbm_psi[0][9], rbm_psi[1][9]], device=nn_state.device)
/ normalization
)
return beta_
def gamma3(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
gamma_ = cplx.norm(
torch.tensor([rbm_psi[0][10], rbm_psi[1][10]], device=nn_state.device)
/ normalization
)
return gamma_
def delta3(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
delta_ = cplx.norm(
torch.tensor([rbm_psi[0][11], rbm_psi[1][11]], device=nn_state.device)
/ normalization
)
return delta_
def alpha4(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
alpha_ = cplx.norm(
torch.tensor([rbm_psi[0][12], rbm_psi[1][12]], device=nn_state.device)
/ normalization
)
return alpha_
def beta4(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
beta_ = cplx.norm(
torch.tensor([rbm_psi[0][13], rbm_psi[1][13]], device=nn_state.device)
/ normalization
)
return beta_
def gamma4(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
gamma_ = cplx.norm(
torch.tensor([rbm_psi[0][14], rbm_psi[1][14]], device=nn_state.device)
/ normalization
)
return gamma_
def delta4(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.normalization(space).sqrt_()
delta_ = cplx.norm(
torch.tensor([rbm_psi[0][15], rbm_psi[1][15]], device=nn_state.device)
/ normalization
)
return delta_
period = 25
space = nn_state.generate_hilbert_space()
callbacks = [
MetricEvaluator(
period,
{
"Fidelity": ts.fidelity,
"KL": ts.KL,
#"normα1": alpha1,
# "normβ1": beta1,
# "normγ1": gamma1,
"normδ1": delta1,
#"normα2": alpha2,
# "normβ2": beta2,
# "normγ2": gamma2,
# "normδ2": delta2,
#"normα3": alpha3,
# "normβ3": beta3,
# "normγ3": gamma3,
# "normδ3": delta3,
#"normα4": alpha4,
# "normβ4": beta4,
# "normγ4": gamma4,
# "normδ4": delta4,
},
target=true_psi,
bases=bases,
verbose=True,
space=space,
)
]
nn_state.fit(
train_samples,
epochs=epochs,
pos_batch_size=pbs,
neg_batch_size=nbs,
lr=lr,
k=k,
input_bases=train_bases,
callbacks=callbacks,
time=True,
)
fidelities = callbacks[0].Fidelity
KLs = callbacks[0]["KL"]
coeffs = callbacks[0]["normδ1"]
epoch = np.arange(period, epochs + 1, period)
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(14, 3))
ax = axs[0]
ax.plot(epoch, fidelities, color="C0", markeredgecolor="black")
ax.set_ylabel(r"Fidelity")
ax.set_xlabel(r"Epoch")
ax.set_ylim([0.8,1])
ax = axs[1]
ax.plot(epoch, KLs, color="C1", markeredgecolor="black")
ax.set_ylabel(r"KL Divergence")
ax.set_xlabel(r"Epoch")
ax.set_ylim([0,0.2])
ax = axs[2]
ax.plot(epoch, coeffs, color="C2", markeredgecolor="black")
ax.set_ylabel(r"$\vert\delta 1\vert$")
ax.set_xlabel(r"Epoch")
#ax.set_ylim([0.01,0.03])
plt.tight_layout()
plt.show()
```
| true |
code
| 0.820919 | null | null | null | null |
|
# Solutions: Corollary 0.0.4 in $\mathbb R^2$
*These are **solutions** to the worksheet on corollary 0.0.4. Please **DO NOT LOOK AT IT** if you haven't given the worksheet a fair amount of thought.*
In this worksheet we will run through the proof of Corollary 0.0.4 from Vershynin. We will "pythonize" the proof step-by-step in the case of a polytope in $\mathbb R^2$ and visualize it. Please fill in the code wherever indicated. Here is the corollary (slightly generalized) for reference:
**Corollary 0.0.4 (Generalized)**: Let $P$ be a polytope in $\mathbb R^n$ with $N$ vertices. Then $P$ can be covered by at most $N^{\lceil (\text{diam}(T)/\epsilon)^2 \rceil}$ Euclidean balls of radii $\epsilon > 0$.
```
# Some useful imports:
import numpy as np
import matplotlib.pyplot as plt
import itertools as it
import math
```
## The Proof of Corollary 0.0.4 in $\mathbb R^2$
Fix $\epsilon > 0$ and a polytope $P$ in $\mathbb R^n$ (in our case $n = 2$). Denote by $T$ the set of vertices of $P$.
```
# Set epsilon to your favorite positive number
epsilon = 1.0
# Represent a polytope P in R2 by listing its points clockwise
# Represent the points as numpy arrays of length 2
P = [np.array([0,0]),
np.array([0,1]),
np.array([1,1]),
np.array([1.5,.5]),
np.array([1,0])]
# Set N to the number of vertices of P (don't hard-code it in if you want to be able to change P easily later)
N = len(P)
```
Let us define the centers of the balls as follows. \
Let $k := \lceil (\text{diam}(T)/\epsilon)^2 \rceil$. Recall that the $\text{diam}(T) = \sup_{x, y \in T} \lvert x - y \rvert$.
```
# Compute diam(T)
diamT = 0
for i in range(N):
for j in range(i+1, N):
d_xixj = np.sqrt(np.sum((P[i] - P[j])**2))
diamT = d_xixj if (d_xixj > diamT) else diamT
# Compute k
k = math.ceil((diamT/epsilon)**2)
```
Consider the set
\begin{equation}
\mathcal N := \left\{ \frac{1}{k} \sum_{j=1}^k x_j : x_j \text{ are vertices of } P \right\}
\end{equation}
```
# Construct \mathcal N
calN = []
# This gives an iterator over all combinations
# of k elements of P with replacement.
combinations = it.combinations_with_replacement(P, k)
# Compute the vector average and append it to calN
for comb in combinations:
vec_sum = np.array([0,0])
for vec in comb:
vec_sum = vec_sum + vec
calN.append(vec_sum / k)
```
We claim that the family of $\epsilon$-balls centered at $\mathcal N$ satisfy the conclusion of the corollary. To check this, note that the polytope $P$ is the convex hull of the set of its vertices. Thus we apply Theorem 0.0.2 to any point $x \in P = \text{conv}(T)$ and deduce that $x$ is within distance $\text{diam(T)} / \sqrt k \leq \epsilon$ from some point in $\mathcal N$. This shows that the $\epsilon$-balls centered at $\mathcal N$ indeed cover $P$.
```
# We visualize the covering here
# Feel free to play around with the visualization!
scale = 10
figure, axes = plt.subplots(figsize=(scale, scale))
axes.axis('equal')
axes.set_xlim([-1, 1.5])
axes.set_ylim([-1,1.5])
plt.fill([p[0] for p in P], [p[1] for p in P], 'y', fill = True)
plt.plot([p[0] for p in calN], [p[1] for p in calN], 'or')
for p in calN:
axes.add_artist(plt.Circle((p[0], p[1]), epsilon, fill = False))
```
We can bound the cardinality of $\mathcal N$ by noting that there are $N^k$ ways to choose $k$ out of $N$ vertices with repetition. Thus $|\mathcal N| \leq N^k = N^{\lceil (\text{diam}(T)/\epsilon)^2 \rceil}$. In fact we can be more clever by noticing that the order in which we choose the elements does not matter (this is addressed in exercise 0.0.6).
## Further Questions
At least in $\mathbb R^2$, Corollary 0.0.4 is rather wasteful. How can we come up with a more efficient covering of a polytope?
Is there a way to cleverly construct a subset of $\mathcal N$ that gets the job done?
Copyright (c) 2020 TRIPODS/GradStemForAll 2020 Team
| true |
code
| 0.626781 | null | null | null | null |
|
# Pypi & Pip
PyPi is short form for Python Package Index (PyPI). PyPI helps you find and install open source software developed and shared by the Python community. All the python packages are distributed to python community through pypi.org . These packages are called as Distributed or intallable packages. To install any distributed or installable package we use command called Pip.
```
pip install <package-name>
pip install requests
```
you can also specify which version of python package to install in the command.
```
pip install <package-name>==<version>
pip install requests==2.1.0
```
# How does pip install work?
Every package/distribution that is being installed will have a setup.py. When you call pip install <package-name> that is nothing but python setup.py build and python setup.py install
What happens in this flow, with python setup.py build, it will download all the code of package to build folder installing any dependant packages, after that it will build a binary wheel specifically for your machine out of the source. Then it needs to determine which library directory to install the package in—the system's, the user's, or a virtualenv's? This is controlled by sys.prefix, which in turn is controlled by pip's executable path and the PYTHONPATH and PYTHONHOME environment variables. Finally, it moves the wheel files into the appropriate library directory, and compiles the python source files into bytecode for faster execution.
```
# sample setup.py
import os
from setuptools import setup, find_packages
setup(
name='<package_name>',
version='0.3.1',
packages=find_packages(exclude=['tests', 'tests.*']),
include_package_data=True,
description='A brief description of your package',
long_description=README,
url='<your package github repo url>',
author='<author name>',
author_email='<Author email>',
classifiers=[
'Environment :: Web Environment',
'Intended Audience :: Developers',
'Operating System :: OS Independent',
'License :: OSI Approved :: MIT License',
'Programming Language :: Python',
'Programming Language :: Python :: 2.7',
'Programming Language :: Python :: 3',
'Programming Language :: Python :: 3.2',
'Programming Language :: Python :: 3.3',
],
install_requires=[
<list of any other packages that needs to be installed.>
],
)
```
# Virtualenv
A Virtual Environment is an isolated working copy of Python which allows you to work on a specific project without worry of affecting other projects. It enables multiple side-by-side installations of Python, one for each project. Following are the commands to install virtualenv.
On macOS and Linux:
```
python3 -m pip install --user virtualenv
```
On Windows:
```
py -m pip install --user virtualenv
```
We create vitrualenv using the following commands
On macOS and Linux:
```
python3 -m venv env
```
On Windows:
```
py -m venv env
```
Before you can start installing or using packages in your virtual environment you’ll need to activate it. To activate the environment use the following commands
On macOS and Linux:
```
source env/bin/activate
```
On Windows:
```
.\env\Scripts\activate
```
Following are some important commands when we use virtualenv
> pip freeze
shows packages YOU installed via pip in that environment
> pip freeze > requirements.txt
used to write the installed packages into the file.
> pip install -r requrements.txt
Used to install all the packages inside requirements
# Create your own package
We will see how to publish a simple helloworld as a pypi package. I'm creating a simple package with hellow as a folder and to make it a package I'm adding __init__.py to it.
Inside that folder I'm creating a simple file called greeting and inside my greeting file, I'm adding a simple function called hello_world that prints hello_world
```
helloworld/
├── hellow
├── __init__.py
└── greeting.py
1 directory, 2 files
# in greeting.py
def hello_world():
print ("hello world")
```
As discussed earlier we need setup.py file to make a python package into a distributed package. So I'm creating a setup.py file parallet to hellow folder. In my setup.py I'll add corresponding information required for that package.
```
├── hellow
│ ├── __init__.py
│ └── greeting.py
└── setup.py
1 directory, 3 files
# in setup.py
import os
from setuptools import setup, find_packages
setup(
name='chaitu_210_hw_greeting',
version='1.0',
packages=['hellow'],
include_package_data=True,
description='A brief description of your package',
long_description='',
url='https://www.test.com/',
author='chaitanya',
author_email='chaitu210@gmail.com',
classifiers=[
'Environment :: Web Environment',
'Intended Audience :: Developers',
'Operating System :: OS Independent',
'License :: OSI Approved :: MIT License',
'Programming Language :: Python',
'Programming Language :: Python :: 2.7',
'Programming Language :: Python :: 3',
'Programming Language :: Python :: 3.2',
'Programming Language :: Python :: 3.3',
],
install_requires=[
],
)
```
Before make our python package as a distributed package, we will create an account in pypi.org, you can create an using the following link
https://pypi.org/account/register/
Now to upload our package we run the following commands
```
> python setup.py bdist_wheel sdist
> pip install twine
> twine upload dist/*
```
On running the last command it will ask for your pypi username and password. On successful upload we are now ready to use the package in any other project or any python developer can install the package using
pip install chaitu_210_hw_greeting
There are more options that we can research while create a package for Eg: Manifest.in, docs, README.md etc.
Manifest.in : Used for adding the non python files like htmls
Docs: If your package has more documentation you will use this.
README.md: This is used to give detailed description/usage about your package.
| true |
code
| 0.366561 | null | null | null | null |
|
<h1> Structured data prediction using Cloud ML Engine </h1>
This notebook illustrates:
<ol>
<li> Exploring a BigQuery dataset using Datalab
<li> Creating datasets for Machine Learning using Dataflow
<li> Creating a model using the high-level Estimator API
<li> Training on Cloud ML Engine
<li> Deploying model
<li> Predicting with model
</ol>
Before starting the lab, upgrade packages that are required for this notebook.
```
%%bash
pip install --upgrade tensorflow==1.4
pip install --ignore-installed --upgrade pytz==2018.4
pip uninstall -y google-cloud-dataflow
pip install --upgrade apache-beam[gcp]==2.6
```
**Now you have to restart the kernel by clicking the "Reset Session" in the menu bar** to reflect the newly installed modules.
After restarting the kernel, you can resume the code execution from the next cell.
```
# change these to try this notebook out
BUCKET = 'cloud-training-demos-ml'
PROJECT = 'cloud-training-demos'
REGION = 'us-central1'
import os
os.environ['BUCKET'] = BUCKET
os.environ['PROJECT'] = PROJECT
os.environ['REGION'] = REGION
%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
%%bash
if ! gsutil ls | grep -q gs://${BUCKET}/; then
gsutil mb -l ${REGION} gs://${BUCKET}
fi
```
<h1>Part 1: Data Analysis and Preparation</h1>
<h2> Exploring data </h2>
The data is natality data (record of births in the US). My goal is to predict the baby's weight given a number of factors about the pregnancy and the baby's mother. Later, we will want to split the data into training and eval datasets. The hash of the year-month will be used for that.
```
query="""
SELECT
weight_pounds,
is_male,
mother_age,
plurality,
gestation_weeks,
FARM_FINGERPRINT(CONCAT(CAST(YEAR AS STRING), CAST(month AS STRING))) AS hashmonth
FROM
publicdata.samples.natality
WHERE year > 2000
"""
import google.datalab.bigquery as bq
df = bq.Query(query + " LIMIT 100").execute().result().to_dataframe()
df.head()
```
Let's write a query to find the unique values for each of the columns and the count of those values.
```
def get_distinct_values(column_name):
sql = """
SELECT
{0},
COUNT(1) AS num_babies,
AVG(weight_pounds) AS avg_wt
FROM
publicdata.samples.natality
WHERE
year > 2000
GROUP BY
{0}
""".format(column_name)
return bq.Query(sql).execute().result().to_dataframe()
df = get_distinct_values('is_male')
df.plot(x='is_male', y='num_babies', kind='bar');
df.plot(x='is_male', y='avg_wt', kind='bar');
df = get_distinct_values('mother_age')
df = df.sort_values('mother_age')
df.plot(x='mother_age', y='num_babies');
df.plot(x='mother_age', y='avg_wt');
df = get_distinct_values('plurality')
df = df.sort_values('plurality')
df.plot(x='plurality', y='num_babies', logy=True, kind='bar');
df.plot(x='plurality', y='avg_wt', kind='bar');
df = get_distinct_values('gestation_weeks')
df = df.sort_values('gestation_weeks')
df.plot(x='gestation_weeks', y='num_babies', logy=True, kind='bar', color='royalblue');
df.plot(x='gestation_weeks', y='avg_wt', kind='bar', color='royalblue');
```
All these factors seem to play a part in the baby's weight. Male babies are heavier on average than female babies. Teenaged and older moms tend to have lower-weight babies. Twins, triplets, etc. are lower weight than single births. Preemies weigh in lower as do babies born to single moms. In addition, it is important to check whether you have enough data (number of babies) for each input value. Otherwise, the model prediction against input values that doesn't have enough data may not be reliable.
<p>
In the rest of this notebook, we will use machine learning to combine all of these factors to come up with a prediction of a baby's weight.
<h2> Creating a ML dataset using Dataflow </h2>
<p>
I'm going to use Cloud Dataflow to read in the BigQuery data, do some preprocessing, and write it out as CSV files.
Instead of using Beam/Dataflow, I had three other options:
<ol>
<li> Use Cloud Dataprep to visually author a Dataflow pipeline. Cloud Dataprep also allows me to explore the data, so we could have avoided much of the handcoding of Python/Seaborn calls above as well!
<li> Read from BigQuery directly using TensorFlow.
<li> Use the BigQuery console (http://bigquery.cloud.google.com) to run a Query and save the result as a CSV file. For larger datasets, you may have to select the option to "allow large results" and save the result into a CSV file on Google Cloud Storage.
</ol>
<p>
However, in this case, I want to do some preprocessing. I want to modify the data such that we can simulate what is known if no ultrasound has been performed. If I didn't need preprocessing, I could have used the web console. Also, I prefer to script it out rather than run queries on the user interface. Therefore, I am using Cloud Dataflow for the preprocessing.
```
import apache_beam as beam
import datetime
def to_csv(rowdict):
# pull columns from BQ and create a line
import hashlib
import copy
CSV_COLUMNS = 'weight_pounds,is_male,mother_age,plurality,gestation_weeks'.split(',')
# create synthetic data where we assume that no ultrasound has been performed
# and so we don't know sex of the baby. Let's assume that we can tell the difference
# between single and multiple, but that the errors rates in determining exact number
# is difficult in the absence of an ultrasound.
no_ultrasound = copy.deepcopy(rowdict)
w_ultrasound = copy.deepcopy(rowdict)
no_ultrasound['is_male'] = 'Unknown'
if rowdict['plurality'] > 1:
no_ultrasound['plurality'] = 'Multiple(2+)'
else:
no_ultrasound['plurality'] = 'Single(1)'
# Change the plurality column to strings
w_ultrasound['plurality'] = ['Single(1)', 'Twins(2)', 'Triplets(3)', 'Quadruplets(4)', 'Quintuplets(5)'][rowdict['plurality']-1]
# Write out two rows for each input row, one with ultrasound and one without
for result in [no_ultrasound, w_ultrasound]:
data = ','.join([str(result[k]) if k in result else 'None' for k in CSV_COLUMNS])
key = hashlib.sha224(data).hexdigest() # hash the columns to form a key
yield str('{},{}'.format(data, key))
def preprocess(in_test_mode):
job_name = 'preprocess-babyweight-features' + '-' + datetime.datetime.now().strftime('%y%m%d-%H%M%S')
if in_test_mode:
OUTPUT_DIR = './preproc'
else:
OUTPUT_DIR = 'gs://{0}/babyweight/preproc/'.format(BUCKET)
options = {
'staging_location': os.path.join(OUTPUT_DIR, 'tmp', 'staging'),
'temp_location': os.path.join(OUTPUT_DIR, 'tmp'),
'job_name': job_name,
'project': PROJECT,
'teardown_policy': 'TEARDOWN_ALWAYS',
'max_num_workers': 3, # CHANGE THIS IF YOU HAVE MORE QUOTA
'no_save_main_session': True
}
opts = beam.pipeline.PipelineOptions(flags=[], **options)
if in_test_mode:
RUNNER = 'DirectRunner'
else:
RUNNER = 'DataflowRunner'
p = beam.Pipeline(RUNNER, options=opts)
query = """
SELECT
weight_pounds,
is_male,
mother_age,
plurality,
gestation_weeks,
FARM_FINGERPRINT(CONCAT(CAST(YEAR AS STRING), CAST(month AS STRING))) AS hashmonth
FROM
publicdata.samples.natality
WHERE year > 2000
AND weight_pounds > 0
AND mother_age > 0
AND plurality > 0
AND gestation_weeks > 0
AND month > 0
"""
if in_test_mode:
query = query + ' LIMIT 100'
for step in ['train', 'eval']:
if step == 'train':
selquery = 'SELECT * FROM ({}) WHERE ABS(MOD(hashmonth, 4)) < 3'.format(query)
else:
selquery = 'SELECT * FROM ({}) WHERE ABS(MOD(hashmonth, 4)) = 3'.format(query)
(p
| '{}_read'.format(step) >> beam.io.Read(beam.io.BigQuerySource(query=selquery, use_standard_sql=True))
| '{}_csv'.format(step) >> beam.FlatMap(to_csv)
| '{}_out'.format(step) >> beam.io.Write(beam.io.WriteToText(os.path.join(OUTPUT_DIR, '{}.csv'.format(step))))
)
job = p.run()
preprocess(in_test_mode=False)
```
You may get a warning about access scopes. It's safe to ignore this.
Note that after you launch this, the actual processing is happening on the Cloud. Go to the GCP web console to the Dataflow section and monitor the running job. You'll see a job that's running. If you click it, you should get a screen like this. It took about <b>55 minutes</b> for me.
<img src="dataflow.png" width="500"/>
Once the job has completed, run the cell below to check the location of the are processed files.
```
%bash
gsutil ls gs://${BUCKET}/babyweight/preproc/*-00000*
```
<h1>Part 2: Developing a Machine Learning Model using TensorFlow and Cloud ML Engine</h1>
<h2> Creating a TensorFlow model using the Estimator API </h2>
<p>
First, write an input_fn to read the data.
```
import shutil
import numpy as np
import tensorflow as tf
```
We may get a few warnings when we run this. Don't worry about them.
```
CSV_COLUMNS = 'weight_pounds,is_male,mother_age,plurality,gestation_weeks,key'.split(',')
LABEL_COLUMN = 'weight_pounds'
KEY_COLUMN = 'key'
DEFAULTS = [[0.0], ['null'], [0.0], ['null'], [0.0], ['nokey']]
TRAIN_STEPS = 1000
def read_dataset(prefix, pattern, batch_size=512):
# use prefix to create filename
filename = 'gs://{}/babyweight/preproc/{}*{}*'.format(BUCKET, prefix, pattern)
if prefix == 'train':
mode = tf.estimator.ModeKeys.TRAIN
num_epochs = None # indefinitely
else:
mode = tf.estimator.ModeKeys.EVAL
num_epochs = 1 # end-of-input after this
# the actual input function passed to TensorFlow
def _input_fn():
# could be a path to one file or a file pattern.
input_file_names = tf.train.match_filenames_once(filename)
filename_queue = tf.train.string_input_producer(
input_file_names, shuffle=True, num_epochs=num_epochs)
# read CSV
reader = tf.TextLineReader()
_, value = reader.read_up_to(filename_queue, num_records=batch_size)
if mode == tf.estimator.ModeKeys.TRAIN:
value = tf.train.shuffle_batch([value], batch_size, capacity=10*batch_size,
min_after_dequeue=batch_size, enqueue_many=True,
allow_smaller_final_batch=False)
value_column = tf.expand_dims(value, -1)
columns = tf.decode_csv(value_column, record_defaults=DEFAULTS)
features = dict(zip(CSV_COLUMNS, columns))
features.pop(KEY_COLUMN)
label = features.pop(LABEL_COLUMN)
return features, label
return _input_fn
```
Next, define the feature columns.
```
def get_wide_deep():
# define column types
is_male,mother_age,plurality,gestation_weeks = \
[\
tf.feature_column.categorical_column_with_vocabulary_list('is_male',
['True', 'False', 'Unknown']),
tf.feature_column.numeric_column('mother_age'),
tf.feature_column.categorical_column_with_vocabulary_list('plurality',
['Single(1)', 'Twins(2)', 'Triplets(3)',
'Quadruplets(4)', 'Quintuplets(5)','Multiple(2+)']),
tf.feature_column.numeric_column('gestation_weeks')
]
# discretize
age_buckets = tf.feature_column.bucketized_column(mother_age,
boundaries=np.arange(15,45,1).tolist())
gestation_buckets = tf.feature_column.bucketized_column(gestation_weeks,
boundaries=np.arange(17,47,1).tolist())
# sparse columns are wide
wide = [is_male,
plurality,
age_buckets,
gestation_buckets]
# feature cross all the wide columns and embed into a lower dimension
crossed = tf.feature_column.crossed_column(wide, hash_bucket_size=20000)
embed = tf.feature_column.embedding_column(crossed, 3)
# continuous columns are deep
deep = [mother_age,
gestation_weeks,
embed]
return wide, deep
```
To predict with the TensorFlow model, we also need a serving input function. We will want all the inputs from our user.
```
def serving_input_fn():
feature_placeholders = {
'is_male': tf.placeholder(tf.string, [None]),
'mother_age': tf.placeholder(tf.float32, [None]),
'plurality': tf.placeholder(tf.string, [None]),
'gestation_weeks': tf.placeholder(tf.float32, [None])
}
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
```
Finally, train!
```
from tensorflow.contrib.learn.python.learn.utils import saved_model_export_utils
from tensorflow.contrib.learn.python.learn import learn_runner
PATTERN = "00000-of-" # process only one of the shards, for testing purposes
def train_and_evaluate(output_dir):
wide, deep = get_wide_deep()
estimator = tf.estimator.DNNLinearCombinedRegressor(
model_dir=output_dir,
linear_feature_columns=wide,
dnn_feature_columns=deep,
dnn_hidden_units=[64, 32])
train_spec=tf.estimator.TrainSpec(
input_fn=read_dataset('train', PATTERN),
max_steps=TRAIN_STEPS)
exporter = tf.estimator.FinalExporter('exporter',serving_input_fn)
eval_spec=tf.estimator.EvalSpec(
input_fn=read_dataset('eval', PATTERN),
steps=None,
exporters=exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
shutil.rmtree('babyweight_trained', ignore_errors=True) # start fresh each time
train_and_evaluate('babyweight_trained')
```
Now that we have the TensorFlow code working on a subset of the data (in the code above, I was reading only the 00000-of-x file), we can package the TensorFlow code up as a Python module and train it on Cloud ML Engine.
<p>
<h2> Training on Cloud ML Engine </h2>
<p>
Training on Cloud ML Engine requires:
<ol>
<li> Making the code a Python package
<li> Using gcloud to submit the training code to Cloud ML Engine
</ol>
<p>
The code in model.py is the same as in the above cells. I just moved it to a file so that I could package it up as a module.
(explore the <a href="babyweight/trainer">directory structure</a>).
```
%bash
grep "^def" babyweight/trainer/model.py
```
After moving the code to a package, make sure it works standalone. (Note the --pattern and --train_steps lines so that I am not trying to boil the ocean on my laptop). Even then, this takes about <b>a minute</b> in which you won't see any output ...
```
%bash
echo "bucket=${BUCKET}"
rm -rf babyweight_trained
export PYTHONPATH=${PYTHONPATH}:${PWD}/babyweight
python -m trainer.task \
--bucket=${BUCKET} \
--output_dir=babyweight_trained \
--job-dir=./tmp \
--pattern="00000-of-" --train_steps=1000
```
Once the code works in standalone mode, you can run it on Cloud ML Engine. Because this is on the entire dataset, it will take a while. The training run took about <b> 30 min </b> for me. You can monitor the job from the GCP console in the Cloud Machine Learning Engine section.
```
%bash
OUTDIR=gs://${BUCKET}/babyweight/trained_model
JOBNAME=babyweight_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
#gsutil -m rm -rf $OUTDIR
gcloud ml-engine jobs submit training $JOBNAME \
--region=$REGION \
--module-name=trainer.task \
--package-path=$(pwd)/babyweight/trainer \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=STANDARD_1 \
--runtime-version 1.4 \
-- \
--bucket=${BUCKET} \
--output_dir=${OUTDIR} \
--train_steps=100000
```
Training finished with a RMSE of about 1 lb. Obviously, this is our first model. We could probably add in some features and do some hyper-parameter tuning to get to a lower RMSE. I'll leave that to you. If you create a better model, I'd love to hear about it -- please do write a short blog post about what you did, and tweet it at me -- @lak_gcp.
```
from google.datalab.ml import TensorBoard
TensorBoard().start('gs://{}/babyweight/trained_model'.format(BUCKET))
for pid in TensorBoard.list()['pid']:
TensorBoard().stop(pid)
print('Stopped TensorBoard with pid {}'.format(pid))
```
<table width="70%">
<tr><td><img src="weights.png"/></td><td><img src="rmse.png" /></tr>
</table>
<h2> Deploying the trained model </h2>
<p>
Deploying the trained model to act as a REST web service is a simple gcloud call.
```
%bash
gsutil ls gs://${BUCKET}/babyweight/trained_model/export/exporter
%bash
MODEL_NAME="babyweight"
MODEL_VERSION="soln"
MODEL_LOCATION=$(gsutil ls gs://${BUCKET}/babyweight/trained_model/export/exporter/ | tail -1)
echo "Deleting and deploying $MODEL_NAME $MODEL_VERSION from $MODEL_LOCATION ... this will take a few minutes"
#gcloud ml-engine versions delete ${MODEL_VERSION} --model ${MODEL_NAME}
#gcloud ml-engine models delete ${MODEL_NAME}
gcloud ml-engine models create ${MODEL_NAME} --regions $REGION
gcloud ml-engine versions create ${MODEL_VERSION} --model ${MODEL_NAME} --origin ${MODEL_LOCATION} --runtime-version 1.4
```
Once this has been created, it will display 'done'.
<h2> Using the model to predict </h2>
<p>
Send a JSON request to the endpoint of the service to make it predict a baby's weight ... I am going to try out how well the model would have predicted the weights of our two kids and a couple of variations while we are at it ...
```
from googleapiclient import discovery
from oauth2client.client import GoogleCredentials
import json
credentials = GoogleCredentials.get_application_default()
api = discovery.build('ml', 'v1', credentials=credentials)
request_data = {'instances':
[
{
'is_male': 'True',
'mother_age': 26.0,
'plurality': 'Single(1)',
'gestation_weeks': 39
},
{
'is_male': 'False',
'mother_age': 29.0,
'plurality': 'Single(1)',
'gestation_weeks': 38
},
{
'is_male': 'True',
'mother_age': 26.0,
'plurality': 'Triplets(3)',
'gestation_weeks': 39
},
{
'is_male': 'Unknown',
'mother_age': 29.0,
'plurality': 'Multiple(2+)',
'gestation_weeks': 38
},
]
}
parent = 'projects/%s/models/%s/versions/%s' % (PROJECT, 'babyweight', 'soln')
response = api.projects().predict(body=request_data, name=parent).execute()
print(json.dumps(response, sort_keys = True, indent = 4))
```
When I ran this, the four predictions for each of the requests in `request_data` above are 7.6, 7.2, 6.5, and 6.2 pounds. Yours may be different.
Copyright 2018 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.41478 | null | null | null | null |
|
# Logistic Regression
Implementation of logistic regression for binary class.
### Imports
```
import torch
import numpy as np
import matplotlib.pyplot as plt
from io import BytesIO
%matplotlib inline
```
### Dataset
```
data_source = np.lib.DataSource()
data = data_source.open('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data')
x = np.genfromtxt(BytesIO(data.read().encode()), delimiter=',', usecols=range(2), max_rows=100)
y = np.zeros(100)
y[50:] = 1
np.random.seed(1)
idx = np.arange(y.shape[0])
np.random.shuffle(idx)
X_test, y_test = x[idx[:25]], y[idx[:25]]
X_train, y_train = x[idx[25:]], y[idx[25:]]
mu, std = np.mean(X_train, axis=0), np.std(X_train, axis=0)
X_train, X_test = (X_train - mu) / std, (X_test - mu) / std
plt.scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], label='class 0', marker='o')
plt.scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], label='class 1', marker='s')
plt.xlabel('feature 1')
plt.ylabel('feature 2')
plt.legend()
plt.show()
```
### Model
```
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
class LogisticRegression(torch.nn.Module):
def __init__(self, num_features):
super(LogisticRegression, self).__init__()
self.linear = torch.nn.Linear(num_features, 1)
# change random weigths to zero
self.linear.weight.detach().zero_()
self.linear.bias.detach().zero_()
def forward(self, x):
netinputs = self.linear(x)
output = torch.sigmoid(netinputs)
return output
```
### Train
```
model = LogisticRegression(num_features=2).to(device)
cost_fn = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
X_train_tensor = torch.tensor(X_train, dtype=torch.float32, device=device)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32, device=device).view(-1, 1)
def custom_where(cond, x_1, x_2):
return (cond * x_1) + ((1-cond) * x_2)
def comp_accuracy(label_var, pred_probas):
pred_labels = custom_where((pred_probas > 0.5).float(), 1, 0).view(-1)
acc = torch.sum(pred_labels == label_var.view(-1)).float() / label_var.size(0)
return acc
for epoch in range(10):
# Compute outputs
out = model(X_train_tensor)
# Compute gradients
loss = cost_fn(out, y_train_tensor)
optimizer.zero_grad()
loss.backward()
# Update weights
optimizer.step()
pred_probas = model(X_train_tensor)
acc = comp_accuracy(y_train_tensor, pred_probas)
print('Epoch: %03d' % (epoch + 1), end="")
print('Train Accuracy: %.3f' % acc, end="")
print('Cost: %.3f' % cost_fn(pred_probas, y_train_tensor))
print('\nModel parameters:')
print(' Weights: %s' % model.linear.weight)
print(' Bias: %s' % model.linear.bias)
```
### Test
```
X_test_tensor = torch.tensor(X_test, dtype=torch.float32, device=device)
y_test_tensor = torch.tensor(y_test, dtype=torch.float32, device=device)
pred_probas = model(X_test_tensor)
test_acc = comp_accuracy(y_test_tensor, pred_probas)
print('Test set accuracy: %.2f%%' % (test_acc*100))
```
| true |
code
| 0.773462 | null | null | null | null |
|
```
# Jovian Commit Essentials
# Please retain and execute this cell without modifying the contents for `jovian.commit` to work
!pip install jovian --upgrade -q
import jovian
jovian.set_project('05b-cifar10-resnet')
jovian.set_colab_id('1JkC4y1mnrW0E0JPrhY-6aWug3uGExuRf')
```
# Classifying CIFAR10 images using ResNets, Regularization and Data Augmentation in PyTorch
_A.K.A. Training an image classifier from scratch to over 90% accuracy in less than 5 minutes on a single GPU_
### Part 6 of "Deep Learning with Pytorch: Zero to GANs"
This tutorial series is a hands-on beginner-friendly introduction to deep learning using [PyTorch](https://pytorch.org), an open-source neural networks library. These tutorials take a practical and coding-focused approach. The best way to learn the material is to execute the code and experiment with it yourself. Check out the full series here:
1. [PyTorch Basics: Tensors & Gradients](https://jovian.ai/aakashns/01-pytorch-basics)
2. [Gradient Descent & Linear Regression](https://jovian.ai/aakashns/02-linear-regression)
3. [Working with Images & Logistic Regression](https://jovian.ai/aakashns/03-logistic-regression)
4. [Training Deep Neural Networks on a GPU](https://jovian.ai/aakashns/04-feedforward-nn)
5. [Image Classification using Convolutional Neural Networks](https://jovian.ai/aakashns/05-cifar10-cnn)
6. [Data Augmentation, Regularization and ResNets](https://jovian.ai/aakashns/05b-cifar10-resnet)
7. [Generating Images using Generative Adversarial Networks](https://jovian.ai/aakashns/06b-anime-dcgan/)
In this tutorial, we'll use the following techniques to train a state-of-the-art model in less than 5 minutes to achieve over 90% accuracy in classifying images from the CIFAR10 dataset:
- Data normalization
- Data augmentation
- Residual connections
- Batch normalization
- Learning rate scheduling
- Weight Decay
- Gradient clipping
- Adam optimizer
### How to run the code
This tutorial is an executable [Jupyter notebook](https://jupyter.org) hosted on [Jovian](https://www.jovian.ai). You can _run_ this tutorial and experiment with the code examples in a couple of ways: *using free online resources* (recommended) or *on your computer*.
#### Option 1: Running using free online resources (1-click, recommended)
The easiest way to start executing the code is to click the **Run** button at the top of this page and select **Run on Colab**. [Google Colab](https://colab.research.google.com) is a free online platform for running Jupyter notebooks using Google's cloud infrastructure. You can also select "Run on Binder" or "Run on Kaggle" if you face issues running the notebook on Google Colab.
#### Option 2: Running on your computer locally
To run the code on your computer locally, you'll need to set up [Python](https://www.python.org), download the notebook and install the required libraries. We recommend using the [Conda](https://docs.conda.io/projects/conda/en/latest/user-guide/install/) distribution of Python. Click the **Run** button at the top of this page, select the **Run Locally** option, and follow the instructions.
### Using a GPU for faster training
You can use a [Graphics Processing Unit](https://en.wikipedia.org/wiki/Graphics_processing_unit) (GPU) to train your models faster if your execution platform is connected to a GPU manufactured by NVIDIA. Follow these instructions to use a GPU on the platform of your choice:
* _Google Colab_: Use the menu option "Runtime > Change Runtime Type" and select "GPU" from the "Hardware Accelerator" dropdown.
* _Kaggle_: In the "Settings" section of the sidebar, select "GPU" from the "Accelerator" dropdown. Use the button on the top-right to open the sidebar.
* _Binder_: Notebooks running on Binder cannot use a GPU, as the machines powering Binder aren't connected to any GPUs.
* _Linux_: If your laptop/desktop has an NVIDIA GPU (graphics card), make sure you have installed the [NVIDIA CUDA drivers](https://docs.nvidia.com/cuda/cuda-installation-guide-linux/index.html).
* _Windows_: If your laptop/desktop has an NVIDIA GPU (graphics card), make sure you have installed the [NVIDIA CUDA drivers](https://docs.nvidia.com/cuda/cuda-installation-guide-microsoft-windows/index.html).
* _macOS_: macOS is not compatible with NVIDIA GPUs
If you do not have access to a GPU or aren't sure what it is, don't worry, you can execute all the code in this tutorial just fine without a GPU.
Let's begin by installing and importing the required libraries.
```
# Uncomment and run the appropriate command for your operating system, if required
# No installation is reqiured on Google Colab / Kaggle notebooks
# Linux / Binder / Windows (No GPU)
# !pip install numpy matplotlib torch==1.7.0+cpu torchvision==0.8.1+cpu torchaudio==0.7.0 -f https://download.pytorch.org/whl/torch_stable.html
# Linux / Windows (GPU)
# pip install torch==1.7.1+cu110 torchvision==0.8.2+cu110 torchaudio==0.7.2 -f https://download.pytorch.org/whl/torch_stable.html
# MacOS (NO GPU)
# !pip install numpy matplotlib torch torchvision torchaudio
import os
import torch
import torchvision
import tarfile
import torch.nn as nn
import numpy as np
import torch.nn.functional as F
from torchvision.datasets.utils import download_url
from torchvision.datasets import ImageFolder
from torch.utils.data import DataLoader
import torchvision.transforms as tt
from torch.utils.data import random_split
from torchvision.utils import make_grid
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
matplotlib.rcParams['figure.facecolor'] = '#ffffff'
project_name='05b-cifar10-resnet'
```
## Preparing the CIFAR10 Dataset
This notebook is an extension to the tutorial [Image Classification using CNNs in PyTorch](https://jovian.ai/aakashns/05-cifar10-cnn), where we trained a deep convolutional neural network to classify images from the CIFAR10 dataset with around 75% accuracy. Here are some images from the dataset:

Let's begin by downloading the dataset and creating PyTorch datasets to load the data, just as we did in the previous tutorial.
```
from torchvision.datasets.utils import download_url
# Dowload the dataset
dataset_url = "https://s3.amazonaws.com/fast-ai-imageclas/cifar10.tgz"
download_url(dataset_url, '.')
# Extract from archive
with tarfile.open('./cifar10.tgz', 'r:gz') as tar:
tar.extractall(path='./data')
# Look into the data directory
data_dir = './data/cifar10'
print(os.listdir(data_dir))
classes = os.listdir(data_dir + "/train")
print(classes)
```
We can create training and validation datasets using the `ImageFolder` class from `torchvision`. In addition to the `ToTensor` transform, we'll also apply some other transforms to the images. There are a few important changes we'll make while creating PyTorch datasets for training and validation:
1. **Use test set for validation**: Instead of setting aside a fraction (e.g. 10%) of the data from the training set for validation, we'll simply use the test set as our validation set. This just gives a little more data to train with. In general, once you have picked the best model architecture & hypeparameters using a fixed validation set, it is a good idea to retrain the same model on the entire dataset just to give it a small final boost in performance.
2. **Channel-wise data normalization**: We will normalize the image tensors by subtracting the mean and dividing by the standard deviation across each channel. As a result, the mean of the data across each channel is 0, and standard deviation is 1. Normalizing the data prevents the values from any one channel from disproportionately affecting the losses and gradients while training, simply by having a higher or wider range of values that others.
<img src="https://i.imgur.com/LYxXBVg.png" width="360">
3. **Randomized data augmentations**: We will apply randomly chosen transformations while loading images from the training dataset. Specifically, we will pad each image by 4 pixels, and then take a random crop of size 32 x 32 pixels, and then flip the image horizontally with a 50% probability. Since the transformation will be applied randomly and dynamically each time a particular image is loaded, the model sees slightly different images in each epoch of training, which allows it generalize better.

```
# Data transforms (normalization & data augmentation)
stats = ((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010))
train_tfms = tt.Compose([tt.RandomCrop(32, padding=4, padding_mode='reflect'),
tt.RandomHorizontalFlip(),
# tt.RandomRotate
# tt.RandomResizedCrop(256, scale=(0.5,0.9), ratio=(1, 1)),
# tt.ColorJitter(brightness=0.1, contrast=0.1, saturation=0.1, hue=0.1),
tt.ToTensor(),
tt.Normalize(*stats,inplace=True)])
valid_tfms = tt.Compose([tt.ToTensor(), tt.Normalize(*stats)])
# PyTorch datasets
train_ds = ImageFolder(data_dir+'/train', train_tfms)
valid_ds = ImageFolder(data_dir+'/test', valid_tfms)
```
Next, we can create data loaders for retrieving images in batches. We'll use a relatively large batch size of 500 to utlize a larger portion of the GPU RAM. You can try reducing the batch size & restarting the kernel if you face an "out of memory" error.
```
batch_size = 400
# PyTorch data loaders
train_dl = DataLoader(train_ds, batch_size, shuffle=True, num_workers=3, pin_memory=True)
valid_dl = DataLoader(valid_ds, batch_size*2, num_workers=3, pin_memory=True)
```
Let's take a look at some sample images from the training dataloader. To display the images, we'll need to _denormalize_ the pixels values to bring them back into the range `(0,1)`.
```
def denormalize(images, means, stds):
means = torch.tensor(means).reshape(1, 3, 1, 1)
stds = torch.tensor(stds).reshape(1, 3, 1, 1)
return images * stds + means
def show_batch(dl):
for images, labels in dl:
fig, ax = plt.subplots(figsize=(12, 12))
ax.set_xticks([]); ax.set_yticks([])
denorm_images = denormalize(images, *stats)
ax.imshow(make_grid(denorm_images[:64], nrow=8).permute(1, 2, 0).clamp(0,1))
break
show_batch(train_dl)
```
The colors seem out of place because of the normalization. Note that normalization is also applied during inference. If you look closely, you can see the cropping and reflection padding in some of the images. Horizontal flip is a bit difficult to detect from visual inspection.
## Using a GPU
To seamlessly use a GPU, if one is available, we define a couple of helper functions (`get_default_device` & `to_device`) and a helper class `DeviceDataLoader` to move our model & data to the GPU as required. These are described in more detail in a [previous tutorial](https://jovian.ml/aakashns/04-feedforward-nn#C21).
```
def get_default_device():
"""Pick GPU if available, else CPU"""
if torch.cuda.is_available():
return torch.device('cuda')
else:
return torch.device('cpu')
def to_device(data, device):
"""Move tensor(s) to chosen device"""
if isinstance(data, (list,tuple)):
return [to_device(x, device) for x in data]
return data.to(device, non_blocking=True)
class DeviceDataLoader():
"""Wrap a dataloader to move data to a device"""
def __init__(self, dl, device):
self.dl = dl
self.device = device
def __iter__(self):
"""Yield a batch of data after moving it to device"""
for b in self.dl:
yield to_device(b, self.device)
def __len__(self):
"""Number of batches"""
return len(self.dl)
```
Based on where you're running this notebook, your default device could be a CPU (`torch.device('cpu')`) or a GPU (`torch.device('cuda')`)
```
device = get_default_device()
device
```
We can now wrap our training and validation data loaders using `DeviceDataLoader` for automatically transferring batches of data to the GPU (if available).
```
train_dl = DeviceDataLoader(train_dl, device)
valid_dl = DeviceDataLoader(valid_dl, device)
```
## Model with Residual Blocks and Batch Normalization
One of the key changes to our CNN model this time is the addition of the resudial block, which adds the original input back to the output feature map obtained by passing the input through one or more convolutional layers.
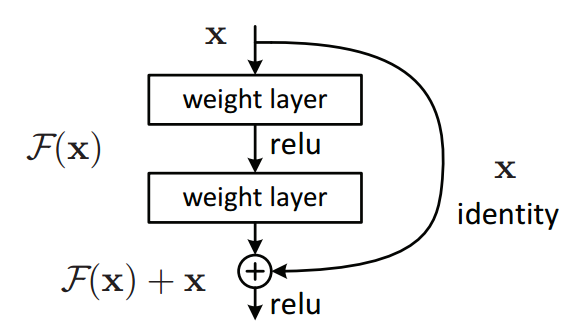
Here is a very simple Residual block:
```
class SimpleResidualBlock(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(in_channels=3, out_channels=3, kernel_size=3, stride=1, padding=1)
self.relu1 = nn.ReLU()
self.conv2 = nn.Conv2d(in_channels=3, out_channels=3, kernel_size=3, stride=1, padding=1)
self.relu2 = nn.ReLU()
def forward(self, x):
out = self.conv1(x)
out = self.relu1(out)
out = self.conv2(out)
return self.relu2(out) + x # ReLU can be applied before or after adding the input
simple_resnet = to_device(SimpleResidualBlock(), device)
for images, labels in train_dl:
out = simple_resnet(images)
print(out.shape)
break
del simple_resnet, images, labels
torch.cuda.empty_cache()
```
This seeming small change produces a drastic improvement in the performance of the model. Also, after each convolutional layer, we'll add a batch normalization layer, which normalizes the outputs of the previous layer.
Go through the following blog posts to learn more:
* Why and how residual blocks work: https://towardsdatascience.com/residual-blocks-building-blocks-of-resnet-fd90ca15d6ec
* Batch normalization and dropout explained: https://towardsdatascience.com/batch-normalization-and-dropout-in-neural-networks-explained-with-pytorch-47d7a8459bcd
We will use the ResNet9 architecture, as described in [this blog series](https://www.myrtle.ai/2018/09/24/how_to_train_your_resnet/) :

```
def accuracy(outputs, labels):
_, preds = torch.max(outputs, dim=1)
return torch.tensor(torch.sum(preds == labels).item() / len(preds))
class ImageClassificationBase(nn.Module):
def training_step(self, batch):
images, labels = batch
out = self(images) # Generate predictions
loss = F.cross_entropy(out, labels) # Calculate loss
return loss
def validation_step(self, batch):
images, labels = batch
out = self(images) # Generate predictions
loss = F.cross_entropy(out, labels) # Calculate loss
acc = accuracy(out, labels) # Calculate accuracy
return {'val_loss': loss.detach(), 'val_acc': acc}
def validation_epoch_end(self, outputs):
batch_losses = [x['val_loss'] for x in outputs]
epoch_loss = torch.stack(batch_losses).mean() # Combine losses
batch_accs = [x['val_acc'] for x in outputs]
epoch_acc = torch.stack(batch_accs).mean() # Combine accuracies
return {'val_loss': epoch_loss.item(), 'val_acc': epoch_acc.item()}
def epoch_end(self, epoch, result):
print("Epoch [{}], last_lr: {:.5f}, train_loss: {:.4f}, val_loss: {:.4f}, val_acc: {:.4f}".format(
epoch, result['lrs'][-1], result['train_loss'], result['val_loss'], result['val_acc']))
def conv_block(in_channels, out_channels, pool=False):
layers = [nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=True)]
if pool: layers.append(nn.MaxPool2d(2))
return nn.Sequential(*layers)
class ResNet9(ImageClassificationBase):
def __init__(self, in_channels, num_classes):
super().__init__()
# 3 x 32 x 32 with batch size 400
self.conv1 = conv_block(in_channels, 64) # 64 x 32 x 32
self.conv2 = conv_block(64, 128, pool=True) # 128 x 16 x 16, feature map is reduced to 16 x 16 because pool is set to true
self.res1 = nn.Sequential(conv_block(128, 128),
conv_block(128, 128)) # 128 x 16 x 16
self.conv3 = conv_block(128, 256, pool=True) # 256 x 8 x 8
self.conv4 = conv_block(256, 512, pool=True) # 512 x 4 x 4
self.res2 = nn.Sequential(conv_block(512, 512),
conv_block(512, 512)) # 512 x 4 x 4
self.classifier = nn.Sequential(nn.MaxPool2d(4), # 512 x 1 x 1
nn.Flatten(), # 512
nn.Dropout(0.2), # 512. Dropout makes the model learn by analyzing relationships not by specific values
nn.Linear(512, num_classes)) # 10
def forward(self, xb):
out = self.conv1(xb)
out = self.conv2(out)
out = self.res1(out) + out
out = self.conv3(out)
out = self.conv4(out)
out = self.res2(out) + out
out = self.classifier(out)
return out
model = to_device(ResNet9(3, 10), device)
model
```
## Training the model
Before we train the model, we're going to make a bunch of small but important improvements to our `fit` function:
* **Learning rate scheduling**: Instead of using a fixed learning rate, we will use a learning rate scheduler, which will change the learning rate after every batch of training. There are many strategies for varying the learning rate during training, and the one we'll use is called the **"One Cycle Learning Rate Policy"**, which involves starting with a low learning rate, gradually increasing it batch-by-batch to a high learning rate for about 30% of epochs, then gradually decreasing it to a very low value for the remaining epochs. Learn more: https://sgugger.github.io/the-1cycle-policy.html
* **Weight decay**: We also use weight decay, which is yet another regularization technique which prevents the weights from becoming too large by adding an additional term to the loss function.Learn more: https://towardsdatascience.com/this-thing-called-weight-decay-a7cd4bcfccab
* **Gradient clipping**: Apart from the layer weights and outputs, it also helpful to limit the values of gradients to a small range to prevent undesirable changes in parameters due to large gradient values. This simple yet effective technique is called gradient clipping. Learn more: https://towardsdatascience.com/what-is-gradient-clipping-b8e815cdfb48
Let's define a `fit_one_cycle` function to incorporate these changes. We'll also record the learning rate used for each batch.
```
@torch.no_grad()
def evaluate(model, val_loader):
model.eval()
outputs = [model.validation_step(batch) for batch in val_loader]
return model.validation_epoch_end(outputs)
def get_lr(optimizer):
for param_group in optimizer.param_groups:
return param_group['lr']
def fit_one_cycle(epochs, max_lr, model, train_loader, val_loader,
weight_decay=0, grad_clip=None, opt_func=torch.optim.SGD):
torch.cuda.empty_cache()
history = []
# Set up cutom optimizer with weight decay
optimizer = opt_func(model.parameters(), max_lr, weight_decay=weight_decay)
# Set up one-cycle learning rate scheduler
sched = torch.optim.lr_scheduler.OneCycleLR(optimizer, max_lr, epochs=epochs,
steps_per_epoch=len(train_loader))
for epoch in range(epochs):
# Training Phase
model.train()
train_losses = []
lrs = []
for batch in train_loader:
loss = model.training_step(batch)
train_losses.append(loss)
loss.backward()
# Gradient clipping
if grad_clip:
nn.utils.clip_grad_value_(model.parameters(), grad_clip)
optimizer.step()
optimizer.zero_grad()
# Record & update learning rate
lrs.append(get_lr(optimizer))
sched.step()
# Validation phase
result = evaluate(model, val_loader)
result['train_loss'] = torch.stack(train_losses).mean().item()
result['lrs'] = lrs
model.epoch_end(epoch, result)
history.append(result)
return history
history = [evaluate(model, valid_dl)]
history
```
We're now ready to train our model. Instead of SGD (stochastic gradient descent), we'll use the Adam optimizer which uses techniques like momentum and adaptive learning rates for faster training. You can learn more about optimizers here: https://ruder.io/optimizing-gradient-descent/index.html
```
epochs = 8
max_lr = 0.01
grad_clip = 0.1
weight_decay = 1e-4
opt_func = torch.optim.Adam
%%time
history += fit_one_cycle(epochs, max_lr, model, train_dl, valid_dl,
grad_clip=grad_clip,
weight_decay=weight_decay,
opt_func=opt_func)
train_time='4:24'
```
Our model trained to over **90% accuracy in under 5 minutes**! Try playing around with the data augmentations, network architecture & hyperparameters to achive the following results:
1. 94% accuracy in under 10 minutes (easy)
2. 90% accuracy in under 2.5 minutes (intermediate)
3. 94% accuracy in under 5 minutes (hard)
Let's plot the valdation set accuracies to study how the model improves over time.
```
def plot_accuracies(history):
accuracies = [x['val_acc'] for x in history]
plt.plot(accuracies, '-x')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.title('Accuracy vs. No. of epochs');
plot_accuracies(history)
```
We can also plot the training and validation losses to study the trend.
```
def plot_losses(history):
train_losses = [x.get('train_loss') for x in history]
val_losses = [x['val_loss'] for x in history]
plt.plot(train_losses, '-bx')
plt.plot(val_losses, '-rx')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['Training', 'Validation'])
plt.title('Loss vs. No. of epochs');
plot_losses(history)
```
It's clear from the trend that our model isn't overfitting to the training data just yet. Try removing batch normalization, data augmentation and residual layers one by one to study their effect on overfitting.
Finally, let's visualize how the learning rate changed over time, batch-by-batch over all the epochs.
```
def plot_lrs(history):
lrs = np.concatenate([x.get('lrs', []) for x in history])
plt.plot(lrs)
plt.xlabel('Batch no.')
plt.ylabel('Learning rate')
plt.title('Learning Rate vs. Batch no.');
plot_lrs(history)
```
As expected, the learning rate starts at a low value, and gradually increases for 30% of the iterations to a maximum value of `0.01`, and then gradually decreases to a very small value.
## Testing with individual images
While we have been tracking the overall accuracy of a model so far, it's also a good idea to look at model's results on some sample images. Let's test out our model with some images from the predefined test dataset of 10000 images.
```
def predict_image(img, model):
# Convert to a batch of 1
xb = to_device(img.unsqueeze(0), device)
# Get predictions from model
yb = model(xb)
# Pick index with highest probability
_, preds = torch.max(yb, dim=1)
# Retrieve the class label
return train_ds.classes[preds[0].item()]
img, label = valid_ds[0]
plt.imshow(img.permute(1, 2, 0).clamp(0, 1))
print('Label:', train_ds.classes[label], ', Predicted:', predict_image(img, model))
img, label = valid_ds[1002]
plt.imshow(img.permute(1, 2, 0))
print('Label:', valid_ds.classes[label], ', Predicted:', predict_image(img, model))
img, label = valid_ds[6153]
plt.imshow(img.permute(1, 2, 0))
print('Label:', train_ds.classes[label], ', Predicted:', predict_image(img, model))
```
Identifying where our model performs poorly can help us improve the model, by collecting more training data, increasing/decreasing the complexity of the model, and changing the hypeparameters.
## Save and Commit
Let's save the weights of the model, record the hyperparameters, and commit our experiment to Jovian. As you try different ideas, make sure to record every experiment so you can look back and analyze the results.
```
torch.save(model.state_dict(), 'cifar10-resnet9.pth')
!pip install jovian --upgrade --quiet
import jovian
jovian.reset()
jovian.log_hyperparams(arch='resnet9',
epochs=epochs,
lr=max_lr,
scheduler='one-cycle',
weight_decay=weight_decay,
grad_clip=grad_clip,
opt=opt_func.__name__)
jovian.log_metrics(val_loss=history[-1]['val_loss'],
val_acc=history[-1]['val_acc'],
train_loss=history[-1]['train_loss'],
time=train_time)
jovian.commit(project=project_name, environment=None, outputs=['cifar10-resnet9.pth'])
```
## Summary and Further Reading
You are now ready to train state-of-the-art deep learning models from scratch. Try working on a project on your own by following these guidelines: https://jovian.ai/learn/deep-learning-with-pytorch-zero-to-gans/assignment/course-project
Here's a summary of the different techniques used in this tutorial to improve our model performance and reduce the training time:
* **Data normalization**: We normalized the image tensors by subtracting the mean and dividing by the standard deviation of pixels across each channel. Normalizing the data prevents the pixel values from any one channel from disproportionately affecting the losses and gradients. [Learn more](https://medium.com/@ml_kid/what-is-transform-and-transform-normalize-lesson-4-neural-networks-in-pytorch-ca97842336bd)
* **Data augmentation**: We applied random transformations while loading images from the training dataset. Specifically, we will pad each image by 4 pixels, and then take a random crop of size 32 x 32 pixels, and then flip the image horizontally with a 50% probability. [Learn more](https://www.analyticsvidhya.com/blog/2019/12/image-augmentation-deep-learning-pytorch/)
* **Residual connections**: One of the key changes to our CNN model was the addition of the resudial block, which adds the original input back to the output feature map obtained by passing the input through one or more convolutional layers. We used the ResNet9 architecture [Learn more](https://towardsdatascience.com/residual-blocks-building-blocks-of-resnet-fd90ca15d6ec).
* **Batch normalization**: After each convolutional layer, we added a batch normalization layer, which normalizes the outputs of the previous layer. This is somewhat similar to data normalization, except it's applied to the outputs of a layer, and the mean and standard deviation are learned parameters. [Learn more](https://towardsdatascience.com/batch-normalization-and-dropout-in-neural-networks-explained-with-pytorch-47d7a8459bcd)
* **Learning rate scheduling**: Instead of using a fixed learning rate, we will use a learning rate scheduler, which will change the learning rate after every batch of training. There are [many strategies](https://pytorch.org/docs/stable/optim.html#how-to-adjust-learning-rate) for varying the learning rate during training, and we used the "One Cycle Learning Rate Policy". [Learn more](https://sgugger.github.io/the-1cycle-policy.html)
* **Weight Decay**: We added weight decay to the optimizer, yet another regularization technique which prevents the weights from becoming too large by adding an additional term to the loss function. [Learn more](https://towardsdatascience.com/this-thing-called-weight-decay-a7cd4bcfccab)
* **Gradient clipping**: We also added gradient clippint, which helps limit the values of gradients to a small range to prevent undesirable changes in model parameters due to large gradient values during training. [Learn more.](https://towardsdatascience.com/what-is-gradient-clipping-b8e815cdfb48#63e0)
* **Adam optimizer**: Instead of SGD (stochastic gradient descent), we used the Adam optimizer which uses techniques like momentum and adaptive learning rates for faster training. There are many other optimizers to choose froma and experiment with. [Learn more.](https://ruder.io/optimizing-gradient-descent/index.html)
As an exercise, you should try applying each technique independently and see how much each one affects the performance and training time. As you try different experiments, you will start to cultivate the intuition for picking the right architectures, data augmentation & regularization techniques.
You are now ready to move on to the next tutorial in this series: [Generating Images using Generative Adversarial Networks](https://jovian.ai/aakashns/06b-anime-dcgan/)
| true |
code
| 0.726511 | null | null | null | null |
|
# Make a plot with both redshift and universe age axes using astropy.cosmology
## Authors
Neil Crighton, Stephanie T. Douglas
## Learning Goals
* Plot relationships using `matplotlib`
* Add a second axis to a `matplotlib` plot
* Relate distance, redshift, and age for two different types of cosmology using `astropy.cosmology`
## Keywords
units, physics, cosmology, matplotlib
## Summary
Each redshift corresponds to an age of the universe, so if you're plotting some quantity against redshift, it's often useful show the universe age too. The relationship between the two changes depending the type of cosmology you assume, which is where `astropy.cosmology` comes in. In this tutorial we'll show how to use the tools in `astropy.cosmology` to make a plot like this:
```
# Set up matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
from IPython.display import Image
Image(filename="ang_dist.png", width=500)
```
We start with a cosmology object. We will make a flat cosmology (which means that the curvature density $\Omega_k=0$) with a hubble parameter of $70$ km/s/Mpc and matter density $\Omega_M=0.3$ at redshift 0. The `FlatLambdaCDM` cosmology then automatically infers that the dark energy density $\Omega_\Lambda$ must $=0.7$, because $\Omega_M + \Omega_\Lambda + \Omega_k = 1$.
```
from astropy.cosmology import FlatLambdaCDM
import astropy.units as u
# In this case we just need to define the matter density
# and hubble parameter at z=0.
# Note the default units for the hubble parameter H0 are km/s/Mpc.
# We will pass in a `Quantity` object with the units specified.
cosmo = FlatLambdaCDM(H0=70*u.km/u.s/u.Mpc, Om0=0.3)
```
Note that we could instead use one of the built-in cosmologies, like `WMAP9` or `Planck13`, in which case we would just redefine the `cosmo` variable.
Now we need an example quantity to plot versus redshift. Let's use the angular diameter distance, which is the physical transverse distance (the size of a galaxy, say) corresponding to a fixed angular separation on the sky. To calculate the angular diameter distance for a range of redshifts:
```
import numpy as np
zvals = np.arange(0, 6, 0.1)
dist = cosmo.angular_diameter_distance(zvals)
```
Note that we passed an array of redshifts to `cosmo.angular_diameter_distance` and it produced a corresponding array of distance values, one for each redshift. Let's plot them:
```
fig = plt.figure(figsize=(6,4))
ax = fig.add_subplot(111)
ax.plot(zvals, dist)
```
To check the units of the angular diameter distance, take a look at the unit attribute:
```
dist.unit
```
Now let's put some age labels on the top axis. We're going to pick a series of round age values where we want to place axis ticks. You may need to tweak these depending on your redshift range to get nice, evenly spaced ticks.
```
ages = np.array([13, 10, 8, 6, 5, 4, 3, 2, 1.5, 1.2, 1])*u.Gyr
```
To link the redshift and age axes, we have to find the redshift corresponding to each age. The function `z_at_value` does this for us.
```
from astropy.cosmology import z_at_value
ageticks = [z_at_value(cosmo.age, age) for age in ages]
```
Now we make the second axes, and set the tick positions using these values.
```
fig = plt.figure(figsize=(6,4))
ax = fig.add_subplot(111)
ax.plot(zvals, dist)
ax2 = ax.twiny()
ax2.set_xticks(ageticks)
```
We have ticks on the top axis at the correct ages, but they're labelled with the redshift, not the age. We can fix this by setting the tick labels by hand.
```
fig = plt.figure(figsize=(6,4))
ax = fig.add_subplot(111)
ax.plot(zvals, dist)
ax2 = ax.twiny()
ax2.set_xticks(ageticks)
ax2.set_xticklabels(['{:g}'.format(age) for age in ages.value])
```
We need to make sure the top and bottom axes have the same redshift limits. They may not line up properly in the above plot, for example, depending on your setup (the age of the universe should be ~13 Gyr at z=0).
```
fig = plt.figure(figsize=(6,4))
ax = fig.add_subplot(111)
ax.plot(zvals, dist)
ax2 = ax.twiny()
ax2.set_xticks(ageticks)
ax2.set_xticklabels(['{:g}'.format(age) for age in ages.value])
zmin, zmax = 0.0, 5.9
ax.set_xlim(zmin, zmax)
ax2.set_xlim(zmin, zmax)
```
We're almost done. We just need to label all the axes, and add some minor ticks. Let's also tweak the y axis limits to avoid putting labels right near the top of the plot.
```
fig = plt.figure(figsize=(6,4))
ax = fig.add_subplot(111)
ax.plot(zvals, dist)
ax2 = ax.twiny()
ax2.set_xticks(ageticks)
ax2.set_xticklabels(['{:g}'.format(age) for age in ages.value])
zmin, zmax = 0, 5.9
ax.set_xlim(zmin, zmax)
ax2.set_xlim(zmin, zmax)
ax2.set_xlabel('Time since Big Bang (Gyr)')
ax.set_xlabel('Redshift')
ax.set_ylabel('Angular diameter distance (Mpc)')
ax.set_ylim(0, 1890)
ax.minorticks_on()
```
Now for comparison, let's add the angular diameter distance for a different cosmology, from the Planck 2013 results. And then finally, we save the figure to a png file.
```
from astropy.cosmology import Planck13
dist2 = Planck13.angular_diameter_distance(zvals)
fig = plt.figure(figsize=(6,4))
ax = fig.add_subplot(111)
ax.plot(zvals, dist2, label='Planck 2013')
ax.plot(zvals, dist, label=
'$h=0.7,\ \Omega_M=0.3,\ \Omega_\Lambda=0.7$')
ax.legend(frameon=0, loc='lower right')
ax2 = ax.twiny()
ax2.set_xticks(ageticks)
ax2.set_xticklabels(['{:g}'.format(age) for age in ages.value])
zmin, zmax = 0.0, 5.9
ax.set_xlim(zmin, zmax)
ax2.set_xlim(zmin, zmax)
ax2.set_xlabel('Time since Big Bang (Gyr)')
ax.set_xlabel('Redshift')
ax.set_ylabel('Angular diameter distance (Mpc)')
ax.minorticks_on()
ax.set_ylim(0, 1890)
fig.savefig('ang_dist.png', dpi=200, bbox_inches='tight')
```
`bbox_inches='tight'` automatically trims any whitespace from around the plot edges.
And we're done!
## Exercise
Well, almost done. Notice that we calculated the times on the upper axis using the original cosmology, not the new cosmology based on the Planck 2013 results. So strictly speaking, this axis applies only to the original cosmology, although the difference between the two is small. As an exercise, you can try plot two different upper axes, slightly offset from each other, to show the times corresponding to each cosmology. Take a look at the first answer to [this question on Stack Overflow](http://stackoverflow.com/questions/7733693/matplotlib-overlay-plots-with-different-scales) for some hints on how to go about this.
| true |
code
| 0.683697 | null | null | null | null |
|
# Travelling Salesman Problem with subtour elimination
This example shows how to solve a TSP by eliminating subtours using:
1. amplpy (defining the subtour elimination constraint in AMPL and instantiating it appropriately)
2. ampls (adding cuts directly from the solver callback)
### Options
```
SOLVER = "xpress"
SOLVER_OPTIONS = ['outlev=1']
USE_CALLBAKCS = True
PLOTSUBTOURS = True
TSP_FILE = "../tsp/a280.tsp"
import sys
sys.path.append('D:/Development/ampl/solvers-private/build/vs64/bin')
```
### Imports
```
# Import utilities
from amplpy import AMPL, DataFrame # pip install amplpy
if SOLVER == "gurobi":
import amplpy_gurobi as ampls # pip install ampls-gurobi
elif SOLVER == "cplex":
import amplpy_cplex as ampls # pip install ampls-
elif SOLVER == "xpress":
import amplpy_xpress as ampls # pip install ampls-gurobi
import tsplib95 as tsp # pip install tsplib95
import matplotlib.pyplot as plt # pip install matplotlib
import matplotlib.colors as colors
from time import time
plt.rcParams['figure.dpi'] = 200
```
### Register jupyter magics for AMPL
```
from amplpy import register_magics
register_magics('_ampl_cells') # Store %%ampl cells in the list _ampl_cells
```
### Define TSP model in AMPL
```
%%ampl
set NODES ordered;
param hpos {NODES};
param vpos {NODES};
set PAIRS := {i in NODES, j in NODES: ord(i) < ord(j)};
param distance {(i,j) in PAIRS}
:= sqrt((hpos[j]-hpos[i])**2 + (vpos[j]-vpos[i])**2);
var X {PAIRS} binary;
minimize Tour_Length: sum {(i,j) in PAIRS} distance[i,j] * X[i,j];
subject to Visit_All {i in NODES}:
sum {(i, j) in PAIRS} X[i,j] + sum {(j, i) in PAIRS} X[j,i] = 2;
```
Function to load TSP data files and return a dictionary of (nodeid : coordinate)
```
def getDictFromTspFile(tspFile):
p = tsp.load(tspFile)
if not p.is_depictable:
print("Problem is not depictable!")
# Amendments as we need the nodes lexographically ordered
nnodes = len(list(p.get_nodes()))
i = 0
while nnodes>1:
nnodes = nnodes/10
i+=1
formatString = f"{{:0{i}d}}"
nodes = {formatString.format(value) : p.node_coords[index+1] for index, value in enumerate(p.get_nodes())}
return nodes
```
Create AMPL object with amplpy and load model and data
```
# Get the model from the cell above
tsp_model = _ampl_cells[0]
# Load model in AMPL
ampl = AMPL()
ampl.eval(tsp_model)
ampl.option["solver"] = SOLVER
ampl.option[SOLVER + "_options"] = ' '.join(SOLVER_OPTIONS)
# Set problem data from tsp file
nodes = getDictFromTspFile(TSP_FILE)
# Pass them to AMPL using a dataframe
df = DataFrame(index=[('NODES')], columns=['hpos', 'vpos'])
df.setValues(nodes)
ampl.setData(df, "NODES")
# Set some globals that never change during the execution of the problem
NODES = set(nodes.keys())
CPOINTS = {node : complex(coordinate[0], coordinate[1]) for (node, coordinate) in nodes.items()}
```
Define some helpers functions to plot the tours
```
def plotTours(tours: list, points_coordinate: dict):
# Plot all the tours in the list each with a different color
colors = ['b', 'g', 'c', 'm', 'y', 'k']
for i, tour in enumerate(tours):
tourCoordinates = [points_coordinate[point.strip("'")] for point in tour]
color = colors[i % len(colors)]
plot_all(tourCoordinates, color = color)
plt.show()
def plot_all(tour, alpha=1, color=None):
# Plot the tour as blue lines between blue circles
plotline(list(tour) + [tour[0]], alpha=alpha, color=color)
plotline([tour[0]], 's', alpha=alpha, color=color)
def plotline(points, style='o-', alpha=1, color=None):
"Plot a list of points (complex numbers) in the 2-D plane."
X, Y = XY(points)
if color:
plt.plot(X, Y, style, alpha=alpha, color=color)
else:
plt.plot(X, Y, style, alpha=alpha)
def XY(points):
"Given a list of points, return two lists: X coordinates, and Y coordinates."
return [p.real for p in points], [p.imag for p in points]
```
Define some helper functions to help with the graphs (e.g. get the subtour given a set of arcs)
```
# Graphs helper routines
def trasverse(node, arcs: set, allnodes: set, subtour = None) -> list:
# Trasverses all the arcs in the set arcs, starting from node
# and returns the tour
if not subtour:
subtour = list()
# Find arcs involving the current node
myarcs = [(i,j) for (i,j) in arcs if node == i or node == j]
if len(myarcs) == 0:
return
# Append the current node to the current subtour
subtour.append(node)
# Use the first arc found
myarc = myarcs[0]
# Find destination (or origin) node
destination = next(i for i in myarc if i != node)
# Remove from arcs and nodes to visit
arcs.remove(myarc)
if node in allnodes:
allnodes.remove(node)
trasverse(destination, arcs, allnodes, subtour)
return subtour
def findSubTours(arcs: set, allnodes: set):
"""Find all the subtours defined by a set of arcs and
return them as a list of list
"""
subtours = list()
allnodes = allnodes.copy()
while len(allnodes) > 0:
l = trasverse(next(iter(allnodes)), arcs, allnodes)
subtours.append(l)
return subtours
```
AMPLPY implementation of sub-tours elimination
```
def amplSubTourElimination(ampl: AMPL):
# Add the constraint and the needed parameters
subToursAMPL = """param nSubtours >= 0 integer, default 0;
set SUB {1..nSubtours} within NODES;
subject to Subtour_Elimination {k in 1..nSubtours}:
sum {i in SUB[k], j in NODES diff SUB[k]}
if (i, j) in PAIRS then X[i, j] else X[j, i] >= 2;"""
ampl.eval(subToursAMPL)
nSubtoursParam = ampl.getParameter("nSubtours")
SubtoursSet = ampl.getSet("SUB")
allsubtours = list()
while True: # Repeat until the solution contains only one tour
ampl.solve()
# Get solution
ARCS = ampl.getData("{(i,j) in PAIRS : X[i,j] > 0} X[i,j];")
ARCS = set([(i, j) for (i, j, k)in ARCS.toList()])
subtours = findSubTours(ARCS, NODES)
# If we have only one tour, the solution is valid
if len(subtours) <= 1:
break
print(f"Found {len(subtours)} subtours, plotting them and adding cuts")
if PLOTSUBTOURS:
plotTours(subtours, CPOINTS)
# Else add the current tours to the list of subtours
allsubtours.extend(subtours)
# And add those to the constraints by assigning the values to
# the parameter and the set
nSubtoursParam.set(len(allsubtours))
for (i, tour) in enumerate(allsubtours):
SubtoursSet[i+1].setValues(tour)
```
ampls callbacks implementation of subtours elimination
```
# Callback class that actually add the cuts if subtours are found in a solution
class MyCallback(ampls.GenericCallback):
def __init__(self):
# Constructor, simply sets the iteration number to 0
super().__init__()
self.iteration = 0
def run(self):
try:
# For each solution
if self.getAMPLWhere() == ampls.Where.MIPSOL:
self.iteration += 1
print(f"/nIteration {self.iteration}: Finding subtours")
sol = self.getSolutionVector()
arcs = [xvars[i] for i, value in enumerate(sol) if value > 0]
subTours = findSubTours(set(arcs), set(vertices))
if len(subTours) ==1:
print("No subtours detected. Not adding any cut")
return 0
print(f"Adding {len(subTours)} cuts")
if PLOTSUBTOURS:
plotTours(subTours, CPOINTS)
for subTour in subTours:
st1 = set(subTour)
nst1 = set(vertices) - st1
externalArcs = [(i, j) if i < j else (j, i) for i in st1 for j in nst1]
varsExternalArcs = [xinverse[i, j] for (i, j) in externalArcs]
coeffs = [1 for i in range(len(varsExternalArcs))]
if PLOTSUBTOURS:
print("Adding cut for subtour:", st1)
self.addLazyIndices(varsExternalArcs, coeffs, ampls.CutDirection.GE, 2)
if len(subTours) == 2:
return 0
print("Continue solving")
return 0
except Exception as e:
print('Error:', e)
return 1
# Global variables to store entities needed by the callbacks
# that never change
xvars = None
xinverse = None
vertices = None
def solverSubTourElimination(ampl: AMPL, solver, solver_options):
global xvars, xinverse, vertices
# Export the model using ampls
model = ampl.exportModel(solver, solver_options)
model.enableLazyConstraints()
# Get the global maps between solver vars and AMPL entities
varMap = model.getVarMapFiltered("X")
#print("varMap:", varMap)
inverse = model.getVarMapInverse()
xvars = {index: ampls.var2tuple(var)[1:] for var, index in varMap.items()}
xinverse = {ampls.var2tuple(var)[1:]: index for index, var in inverse.items()}
vertices = list(sorted(set([x[0] for x in xvars.values()] + [x[1] for x in xvars.values()])))
# Assign the callback
callback = MyCallback()
model.setCallback(callback)
print("Start optimization")
# Start the optimization
model.optimize()
# Import the solution back to AMPL
ampl.importSolution(model)
```
Script running the optimization
```
t0 = time()
if not USE_CALLBAKCS:
amplSubTourElimination(ampl)
else:
solverSubTourElimination(ampl, SOLVER, SOLVER_OPTIONS)
```
Get the solution, print it and display it
```
# Get the solution into ARCS
ARCS = ampl.getData("{(i,j) in PAIRS : X[i,j] > 0} X[i,j];")
ARCS = set([(i,j) for (i,j,k) in ARCS.toList()])
# Display it
tours = findSubTours(ARCS, NODES)
for st in tours:
print(st)
plotTours(tours, CPOINTS)
ampl.getValue('Tour_Length')
time()-t0
```
| true |
code
| 0.354503 | null | null | null | null |
|
```
print("Bismillahir Rahmanir Rahim")
```
## Imports and Paths
```
from IPython.display import display, HTML
from lime.lime_tabular import LimeTabularExplainer
from pprint import pprint
from scipy.spatial.distance import pdist, squareform
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score, confusion_matrix
from sklearn.utils.multiclass import unique_labels
from sklearn import metrics
from sklearn.metrics import classification_report
from sklearn.metrics.pairwise import cosine_similarity
from scipy import spatial
%matplotlib inline
import glob
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import numpy as np
import pandas as pd
import pathlib
import sklearn
import seaborn as sns
import statsmodels
import eli5
import lime
import shap
shap.initjs()
```
# 1. Predictive Models
## Load and preprocess data
Train/test split = 0.80/0.20
```
# Set the seed experimentations and interpretations.
np.random.seed(111)
project_path = pathlib.Path.cwd().parent.parent.parent
modelling_result_path = str(project_path) + '/datasets/modelling-results/'
plots_path = str(project_path) + '/plots/'
# print(project_path)
from sklearn.datasets import load_iris
iris = load_iris()
train, test, labels_train, labels_test = train_test_split(iris.data, iris.target, train_size=0.80)
x_testset = test
feature_names = iris.feature_names
target_names = iris.target_names
total_targets = len(target_names) # total number of unique target names
unique_targets = np.unique(iris.target) # LIME only takes integer
targets_labels = dict(zip(unique_targets, target_names))
print("Feature names", feature_names)
print("Target names", target_names)
print("Number of uniques label or target names", unique_targets)
print("Target labels as unique target (key) with target names (value)", targets_labels)
print("Training record", train[0:1])
print("Label for training record", labels_train[0:1])
```
## Train and evaluate models.
Train Random Forest model so these can be used as black box models when evaluating explanations methods.
### Fit Random Forest
```
rf = RandomForestClassifier(n_estimators=500, class_weight='balanced_subsample')
rf.fit(train, labels_train)
```
### Predict using random forest model
```
labels_pred_rf = rf.predict(test)
score_rf = metrics.accuracy_score(labels_test, labels_pred_rf)
print("\nRandom Forest accuracy score.", score_rf)
predict_proba_rf = rf.predict_proba(test[:5])
print("\nRandom Forest predict probabilities\n\n", predict_proba_rf)
predict_rf = rf.predict(test[:5])
print("\nRandom Forest predictions", predict_rf)
```
### Classification report of random forest
```
report_rf = classification_report(labels_test, labels_pred_rf, target_names=target_names)
print("Random Forestclassification report.")
print(report_rf)
```
### Classification report of random forest displayed as dataframe
```
report_rf = classification_report(labels_test, labels_pred_rf, target_names=target_names, output_dict=True)
report_rf = pd.DataFrame(report_rf).transpose().round(2)
report_rf = report_rf.iloc[:total_targets,:-1]
display(report_rf)
```
### Average F1-score of random forest model
```
avg_f1_rf = report_rf['f1-score'].mean()
print("Random Forest average f1-score", avg_f1_rf)
```
### Confusion matrix of random forest model
```
matrix_rf = confusion_matrix(labels_test, labels_pred_rf)
matrix_rf = pd.DataFrame(matrix_rf, columns=target_names).transpose()
matrix_rf.columns = target_names
display(matrix_rf)
```
### Combine confusion matrix and classification report of random forest model
```
matrix_report_rf = pd.concat([matrix_rf, report_rf], axis=1)
display(matrix_report_rf)
```
### Saving confusion matrix and classification report of random forest model into csv
It is because CSV can be used to draw table in LaTex easily.
```
filename = 'iris_matrix_report_rf.csv'
matrix_report_rf.to_csv(modelling_result_path + filename, index=True)
```
### Extract target names for prediction of random forest model
```
labels_names_pred_rf = []
for label in labels_pred_rf:
labels_names_pred_rf.append(targets_labels[label])
print("Random Forest predicted targets and their names.\n")
print(labels_pred_rf)
print(labels_names_pred_rf)
```
# 2. Explanation Models
## a. Interpreting models using LIME
### LIME util functions
```
def lime_explanations(index, x_testset, explainer, model, unique_targets, class_predictions):
instance = x_testset[index]
exp = explainer.explain_instance(instance,
model.predict_proba,
labels=unique_targets,
top_labels=None,
num_features=len(x_testset[index]),
num_samples=6000)
# Array class_predictions contains predicted class labels
exp_vector_predicted_class = exp.as_map()[class_predictions[index]]
return (exp_vector_predicted_class, exp.score), exp
def explanation_to_dataframe(index, x_testset, explainer, model, unique_targets, class_predictions, dataframe):
feature_imp_tuple, exp = lime_explanations(index,
x_testset,
explainer,
model,
unique_targets,
class_predictions)
exp_val = tuple(sorted(feature_imp_tuple[0]))
data = dict((x, y) for x, y in exp_val)
list_val = list(data.values())
list_val.append(feature_imp_tuple[1])
dataframe.loc[index] = list_val
return dataframe, exp
""" Define LIME Explainer
"""
explainer_lime = LimeTabularExplainer(train,
mode = 'classification',
training_labels = labels_train,
feature_names=feature_names,
verbose=False,
class_names=target_names,
feature_selection='auto',
discretize_continuous=True)
from tqdm import tqdm
col_names = list(feature_names)
col_names.append('lime_score')
```
### Interpret random forest model for all test instances using LIME
```
explanations_lime_rf = pd.DataFrame(columns=col_names)
for index in tqdm(range(0,len(test))):
explanations_lime_rf, exp = explanation_to_dataframe(index,
test,
explainer_lime,
rf, # random forest model
unique_targets,
labels_pred_rf, # random forest predictions
explanations_lime_rf)
print("LIME explanations on random forest.")
display(explanations_lime_rf.head())
display(explanations_lime_rf.iloc[:,:-1].head(1))
```
## b. Interpreting models using SHAP
### SHAP util functions
```
def shapvalue_to_dataframe(test, labels_pred, shap_values, feature_names):
exp_shap_array = []
for test_index in range(0, len(test)):
label_pred = labels_pred[test_index]
exp_shap_array.append(shap_values[label_pred][test_index])
df_exp_shap = pd.DataFrame(exp_shap_array)
df_exp_shap.columns = feature_names
return df_exp_shap
```
### Interpret random forest model for all test instances using SHAP
```
shap_values_rf = shap.TreeExplainer(rf).shap_values(test)
shap.summary_plot(shap_values_rf, test, feature_names=feature_names)
```
### Extracting SHAP values as explanations
**_shap_values_** returns 3D array in a form of (num_classes, num_test_instance, num_features) e.g. for iris dataset the 3D array shape would be (3, 30, 4)
### Extract explanations (SHAP values) of random forest predictions.
```
explanations_shap_rf = shapvalue_to_dataframe(test,
labels_pred_rf,
shap_values_rf,
feature_names)
display(explanations_shap_rf.head())
display(explanations_shap_rf.iloc[:,:].head(1))
```
# 3. Local lipschitz estimation as a stability measure
### Local lipschitz estimation util functions
```
def norm(Xs, x0, norm=2):
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.norm.html
norm = np.linalg.norm(x0 - Xs, norm) # /np.linalg.norm(b[0] - b, 2)
return norm
def neighborhood_with_euclidean(x_points, anchor_index, radius):
# http://mathonline.wikidot.com/open-and-closed-balls-in-euclidean-space
x_i = x_points[anchor_index]
x_js = x_points.tolist()
dist = (x_i - x_js)**2
dist = np.sum(dist, axis=1)
dist = np.sqrt(dist)
neighborhood_indices = []
for index in range(0, len(dist)):
if dist[index] < radius:
neighborhood_indices.append(index)
return neighborhood_indices
def neighborhood_with_KDTree(x_points, anchor_index, radius):
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.KDTree.query_ball_point.html
tree = spatial.KDTree(x_points)
neighborhood_indices = tree.query_ball_point(x_points[anchor_index],
radius * np.sqrt(len(x_points[anchor_index])))
return neighborhood_indices
```
### Local Lipschitz of explanation methods
```
def lipschitz_formula(nearby_points, nearby_points_exp, anchorX, anchorX_exp):
anchorX_norm2 = np.apply_along_axis(norm, 1, nearby_points, anchorX)
anchorX_exp_norm2 = np.apply_along_axis(norm, 1, nearby_points_exp, anchorX_exp)
anchorX_avg_norm2 = anchorX_exp_norm2/anchorX_norm2
anchorX_LC_argmax = np.argmax(anchorX_avg_norm2)
return anchorX_avg_norm2, anchorX_LC_argmax
def lipschitz_estimate(anchorX, x_points, explanations_x_points, anchor_index, neighborhood_indices):
# extract anchor point explanations
anchorX_exp = explanations_x_points[anchor_index]
# extract anchor point neighborhood's explanations
nearby_points = x_points[neighborhood_indices]
nearby_points_exp = explanations_x_points[neighborhood_indices]
# find local lipschitz estimate (lc)
anchorX_avg_norm2, anchorX_LC_argmax = lipschitz_formula(nearby_points,
nearby_points_exp,
anchorX,
anchorX_exp)
return anchorX_avg_norm2, anchorX_LC_argmax
def find_lipschitz_estimates(x_points, x_points_lime_exp, x_points_shap_exp, radii):
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.apply_along_axis.html
# https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.argmax.html
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.KDTree.query_ball_point.html
instances = []
anchor_x_index = []
lc_coefficient_lime = []
x_deviation_index_lime = []
x_deviation_index_shap = []
lc_coefficient_shap = []
radiuses = []
neighborhood_size = []
for radius in radii:
for anchor_index in range(0, len(x_points)):
# define neighorbood of around anchor point using radius and KDTree
# neighborhood_indices = neighborhood_with_KDTree(x_points, anchor_index, radius)
# define neighorbood of around anchor point using radius and Euclidean Distance
neighborhood_indices = neighborhood_with_euclidean(x_points, anchor_index, radius)
# remove anchor index to remove anchor point and append neighborhood_size
neighborhood_indices.remove(anchor_index)
neighborhood_size.append(len(neighborhood_indices))
# append radius (it is useful column when apply filtering based on radius)
radiuses.append(radius)
# extract anchor point and its original index
anchorX = x_points[anchor_index]
instances.append(anchorX)
anchor_x_index.append(anchor_index)
if len(neighborhood_indices) != 0:
# find local lipschitz estimate (lc) LIME
anchorX_avg_norm2, anchorX_LC_argmax = lipschitz_estimate(anchorX,
x_points,
x_points_lime_exp,
anchor_index,
neighborhood_indices)
lc_coefficient_lime.append(anchorX_avg_norm2[anchorX_LC_argmax])
# find deviation point from anchor point LIME explanations
deviation_point_index = neighborhood_indices[anchorX_LC_argmax]
x_deviation_index_lime.append(deviation_point_index)
# find local lipschitz estimate (lc) SHAP
anchorX_avg_norm2, anchorX_LC_argmax = lipschitz_estimate(anchorX,
x_points,
x_points_shap_exp,
anchor_index,
neighborhood_indices)
lc_coefficient_shap.append(anchorX_avg_norm2[anchorX_LC_argmax])
# find deviation point from anchor point LIME explanations
deviation_point_index = neighborhood_indices[anchorX_LC_argmax]
x_deviation_index_shap.append(deviation_point_index)
else:
lc_coefficient_lime.append(-1)
x_deviation_index_lime.append('NaN')
lc_coefficient_shap.append(-1)
x_deviation_index_shap.append('NaN')
# columns_lipschitz will be reused so to avoid confusion naming convention should remain similar
columns_lipschitz = ['instance', 'anchor_x_index', 'lc_coefficient_lime', 'x_deviation_index_lime',
'lc_coefficient_shap', 'x_deviation_index_shap', 'radiuses', 'neighborhood_size']
zippedList = list(zip(instances, anchor_x_index, lc_coefficient_lime, x_deviation_index_lime,
lc_coefficient_shap, x_deviation_index_shap, radiuses, neighborhood_size))
return zippedList, columns_lipschitz
```
### Set instances, explanations and epsilon choices
```
X = pd.DataFrame(test)
display(X.head().values)
x_points = X.copy().values
radii = [1.00]
# radii = [0.75, 1.00, 1.25]
```
### Lipschitz estimations
Predictive model: random forest
Explanation methods: LIME, SHAP
```
print("LIME generated explanations")
X_lime_exp = explanations_lime_rf.iloc[:,:-1].copy()
display(X_lime_exp.head())
print("SHAP generated explanations")
X_shap_exp = explanations_shap_rf.iloc[:,:].copy()
display(X_shap_exp.head())
x_points_lime_exp = X_lime_exp.copy().values
x_points_shap_exp = X_shap_exp.copy().values
zippedList, columns_lipschitz = find_lipschitz_estimates(x_points,
x_points_lime_exp,
x_points_shap_exp,
radii)
rf_lipschitz = pd.DataFrame(zippedList, columns=columns_lipschitz)
display(rf_lipschitz)
```
# 4. Results
## a. Selecting anchor point or point of interest to demonstrate results
Here the selection is made based on max 'lc_coefficient_lime' just to take an example point.
### Anchor point
```
highest_deviation_example = rf_lipschitz.loc[rf_lipschitz['lc_coefficient_lime'].idxmax()]
display(highest_deviation_example)
print("Anchor Point")
anchor_point_index = highest_deviation_example["anchor_x_index"]
anchor_point = highest_deviation_example['instance']
print(anchor_point)
```
### Deviation point with respect to LIME explanation
```
print("\nDeviation Point with respect to LIME explanation")
deviation_point_lime_index = highest_deviation_example["x_deviation_index_lime"]
deviation_point_lime = rf_lipschitz['instance'][deviation_point_lime_index]
print(deviation_point_lime)
```
### Deviation point with respect to SHAP explanation
```
print("\nDeviation Point with respect to SHAP explanation")
deviation_point_shap_index = highest_deviation_example["x_deviation_index_shap"]
deviation_point_shap = rf_lipschitz['instance'][deviation_point_shap_index]
print(deviation_point_shap)
```
### Anchor point and deviation point LIME explanation
```
print("Anchor Point LIME explanation")
anchor_point_lime_exp = x_points_lime_exp[anchor_point_index]
anchor_point_lime_exp = [ round(elem, 3) for elem in anchor_point_lime_exp ]
print(anchor_point_lime_exp)
print("\nDeviation Point LIME explanation")
deviation_point_lime_exp = x_points_lime_exp[deviation_point_lime_index]
deviation_point_lime_exp = [ round(elem, 3) for elem in deviation_point_lime_exp ]
print(deviation_point_lime_exp)
```
### Anchor point and deviation point SHAP explanation
```
print("Anchor Point SHAP explanation")
anchor_point_shap_exp = x_points_shap_exp[anchor_point_index]
anchor_point_shap_exp = [ round(elem, 3) for elem in anchor_point_shap_exp ]
print(anchor_point_shap_exp)
print("\nDeviation Point SHAP explanation")
deviation_point_shap_exp = x_points_shap_exp[deviation_point_shap_index]
deviation_point_shap_exp = [ round(elem, 3) for elem in deviation_point_shap_exp ]
print(deviation_point_shap_exp)
```
## b. Preparing results for box plots
Predictive model: random forest
Epsilon: 1.00
Explanation methods: LIME, SHAP
Evaluation: Lipschitz estimations as stability
```
epsilon1 = rf_lipschitz.loc[rf_lipschitz['neighborhood_size'] > 0]
epsilon1 = epsilon1[epsilon1['radiuses'] == 1.00]
display(epsilon1.head())
epsilon1_lc_lime_aggre = np.mean(epsilon1['lc_coefficient_lime'])
epsilon1_lc_shap_aggre = np.mean(epsilon1['lc_coefficient_shap'])
print("\nLIME, epsilon 1.00, Aggregated L(x) = ", epsilon1_lc_lime_aggre)
print("SHAP, epsilon 1.00, Aggregated L(x) = ", epsilon1_lc_shap_aggre)
lc_lime_df = epsilon1.loc[:, ['lc_coefficient_lime']]
lc_lime_df.rename(columns={'lc_coefficient_lime': 'Lipschitz Estimates'}, inplace=True)
lc_lime_df['method'] = 'LIME'
lc_lime_df['Dataset'] = 'Iris'
lc_shap_df = epsilon1.loc[:, ['lc_coefficient_shap']]
lc_shap_df.rename(columns={'lc_coefficient_shap': 'Lipschitz Estimates'}, inplace=True)
lc_shap_df['method'] = 'SHAP'
lc_shap_df['Dataset'] = 'Iris'
```
# 5. Visualize Results
### Highest deviation example and corresponding LIME and SHAP examples
```
print(feature_names)
print('\nAnchor Point in worst deviation case')
print(anchor_point)
print(anchor_point_lime_exp)
print(anchor_point_shap_exp)
print('\nDeviation Point in worst deviation case')
print(deviation_point)
print(deviation_point_lime_exp)
print(deviation_point_shap_exp)
```
## Final plot to explain deviation as unstability in explanations
```
# Some example data to display
x = np.linspace(0, 2 * np.pi, 400)
y = np.sin(x ** 2)
fig, axs = plt.subplots(2, 4)
fig.set_size_inches(28.5, 14.5)
# position axs[0, 0]
axs[0, 0].set_title('Feature Value')
colors = [["#3DE8F7","w"],[ "#3DE8F7","w"], [ "#3DE8F7","w"], [ "#3DE8F7","w"]]
anchor_point_dict = dict(zip(feature_names, anchor_point))
anchor_point_df = pd.DataFrame.from_dict(anchor_point_dict, orient='index').reset_index()
table = axs[0, 0].table(
cellText = anchor_point_df.values,
loc = 'center',
cellColours = colors,
colWidths=[0.3] * 2)
table.set_fontsize(12)
table.scale(1.5,6)
cellDict = table.get_celld()
cellDict[(0,1)].set_width(0.15)
cellDict[(1,1)].set_width(0.15)
cellDict[(2,1)].set_width(0.15)
cellDict[(3,1)].set_width(0.15)
axs[0, 0].axis('off')
axs[0, 0].axis('tight')
# position axs[0, 1]
axs[0, 1].set_title('Explanation')
x = feature_names[::-1]
y = np.array(anchor_point_shap_exp[::-1]) # anchor_point_shap_exp
# print(x, y)
width = 0.75 # the width of the bars
ind = np.arange(len(y)) # the x locations for the groups
above_threshold = np.maximum(y - threshold, 0)
below_threshold = np.minimum(y, threshold)
axs[0, 1].barh(x, below_threshold, width, color="#FF4D4D") # below threshold value
axs[0, 1].barh(x, above_threshold, width, color="#3DE8F7", left=below_threshold) # above threshold value
axs[0, 1].set_yticks(ind+width/2)
# position axs[0, 2]
axs[0, 2].set_title('Feature Value')
colors = [["#3DE8F7","w"],[ "#3DE8F7","w"], [ "#3DE8F7","w"], [ "#3DE8F7","w"]]
anchor_point_dict = dict(zip(feature_names, anchor_point))
anchor_point_df = pd.DataFrame.from_dict(anchor_point_dict, orient='index').reset_index()
table = axs[0, 2].table(
cellText = anchor_point_df.values,
loc = 'center',
cellColours = colors,
colWidths=[0.3] * 2)
table.set_fontsize(12)
table.scale(1.5,6)
cellDict = table.get_celld()
cellDict[(0,1)].set_width(0.15)
cellDict[(1,1)].set_width(0.15)
cellDict[(2,1)].set_width(0.15)
cellDict[(3,1)].set_width(0.15)
axs[0, 2].axis('off')
axs[0, 2].axis('tight')
# position axs[0, 3]
axs[0, 3].set_title('Explanation')
x = feature_names[::-1]
y = np.array(anchor_point_lime_exp[::-1]) # # anchor_point_lime_exp
# print(x, y)
width = 0.75 # the width of the bars
ind = np.arange(len(y)) # the x locations for the groups
above_threshold = np.maximum(y - threshold, 0)
below_threshold = np.minimum(y, threshold)
# ax.barh(ind, y, width, color="#3DE8F7")
axs[0, 3].barh(x, below_threshold, width, color="#FF4D4D") # below threshold value
axs[0, 3].barh(x, above_threshold, width, color="#3DE8F7", left=below_threshold) # above threshold value
axs[0, 3].set_yticks(ind+width/2)
# position axs[1, 0]
axs[1, 0].set_title('Feature Value')
colors = [["#FF4D4D","w"],[ "#3DE8F7","w"], [ "#3DE8F7","w"], [ "#3DE8F7","w"]]
deviation_point_dict = dict(zip(feature_names, deviation_point_shap)) # deviation_point_shap
deviation_point_df = pd.DataFrame.from_dict(deviation_point_dict, orient='index').reset_index()
table = axs[1, 0].table(
cellText = deviation_point_df.values,
loc = 'center',
cellColours = colors,
colWidths=[0.3] * 2)
table.set_fontsize(12)
table.scale(1.5,6)
cellDict = table.get_celld()
cellDict[(0,1)].set_width(0.15)
cellDict[(1,1)].set_width(0.15)
cellDict[(2,1)].set_width(0.15)
cellDict[(3,1)].set_width(0.15)
axs[1, 0].axis('off')
axs[1, 0].axis('tight')
# position axs[1, 1]
axs[1, 1].set_title('Explanation')
x = feature_names[::-1]
y = np.array(deviation_point_shap_exp[::-1]) # deviation_point_shap_exp
# print(x, y)
width = 0.75 # the width of the bars
ind = np.arange(len(y)) # the x locations for the groups
above_threshold = np.maximum(y - threshold, 0)
below_threshold = np.minimum(y, threshold)
# ax.barh(ind, y, width, color="#3DE8F7")
axs[1, 1].barh(x, below_threshold, width, color="#FF4D4D") # below threshold value
axs[1, 1].barh(x, above_threshold, width, color="#3DE8F7", left=below_threshold) # above threshold value
axs[1, 1].set_yticks(ind+width/2)
# position axs[1, 2]
axs[1, 2].set_title('Feature Value')
colors = [["#3DE8F7","w"],[ "#3DE8F7","w"], [ "#FF4D4D","w"], [ "#FF4D4D","w"]]
deviation_point_dict = dict(zip(feature_names, deviation_point_lime)) # deviation_point_lime
deviation_point_df = pd.DataFrame.from_dict(deviation_point_dict, orient='index').reset_index()
table = axs[1, 2].table(
cellText = deviation_point_df.values,
loc = 'center',
cellColours = colors,
colWidths=[0.3] * 2)
table.set_fontsize(12)
table.scale(1.5,6)
cellDict = table.get_celld()
cellDict[(0,1)].set_width(0.15)
cellDict[(1,1)].set_width(0.15)
cellDict[(2,1)].set_width(0.15)
cellDict[(3,1)].set_width(0.15)
axs[1, 2].axis('off')
axs[1, 2].axis('tight')
# position axs[1, 3]
axs[1, 3].set_title('Explanation')
x = feature_names[::-1]
y = np.array(deviation_point_lime_exp[::-1]) # deviation_point_lime_exp
# print(x,y)
width = 0.75 # the width of the bars
ind = np.arange(len(y)) # the x locations for the groups
above_threshold = np.maximum(y - threshold, 0)
below_threshold = np.minimum(y, threshold)
# ax.barh(ind, y, width, color="#3DE8F7")
axs[1, 3].barh(x, below_threshold, width, color="#FF4D4D") # below threshold value
axs[1, 3].barh(x, above_threshold, width, color="#3DE8F7", left=below_threshold) # above threshold value
axs[1, 3].set_yticks(ind+width/2)
# for ax in axs.flat:
# ax.set(xlabel='x-label', ylabel='y-label')
# # Hide x labels and tick labels for top plots and y ticks for right plots.
# for ax in axs.flat:
# ax.label_outer()
# fig.suptitle('(a) SHAP (L=0.2)', fontsize=16)
fig.text(0.3, 0.04, '(a) SHAP (L=0.20)', ha='center', fontsize=20, fontstyle='italic')
fig.text(0.7, 0.04, '(a) LIME (L=2.80)', ha='center', fontsize=20, fontstyle='italic')
fig.savefig(plots_path + 'experiments_figure1.png')
```
### 1. Visualize anchor point and corresponding LIME explanation
```
''' anchor point
'''
anchor_point_dict = dict(zip(feature_names, anchor_point))
# print(anchor_point_dict)
anchor_point_columns = ['Feature', 'Value']
colors = [["#3DE8F7","w"],[ "#3DE8F7","w"], [ "#3DE8F7","w"], [ "#3DE8F7","w"]]
anchor_point_df = pd.DataFrame.from_dict(anchor_point_dict, orient='index').reset_index()
fig, ax = plt.subplots()
table = ax.table(cellText = anchor_point_df.values,
# colLabels = anchor_point_df.columns,
loc = 'center',
cellColours = colors,
colWidths=[0.3] * 2)
table.set_fontsize(10)
table.scale(1,4)
cellDict = table.get_celld()
cellDict[(0,1)].set_width(0.15)
cellDict[(1,1)].set_width(0.15)
cellDict[(2,1)].set_width(0.15)
cellDict[(3,1)].set_width(0.15)
ax.axis('off')
ax.axis('tight')
fig.patch.set_visible(False)
fig.tight_layout()
plt.title('Feature Value')
''' corresponding LIME explanation
'''
x = feature_names[::-1]
print(x)
y = np.array(anchor_point_lime_exp[::-1]) # anchor_x_maximise_lc_exp_lime
print(y)
fig, ax = plt.subplots()
width = 0.75 # the width of the bars
ind = np.arange(len(y)) # the x locations for the groups
# split it up
above_threshold = np.maximum(y - threshold, 0)
below_threshold = np.minimum(y, threshold)
# ax.barh(ind, y, width, color="#3DE8F7")
ax.barh(x, below_threshold, width, color="#FF4D4D") # below threshold value
ax.barh(x, above_threshold, width, color="#3DE8F7", left=below_threshold) # above threshold value
ax.set_yticks(ind+width/2)
```
### 2. Visualize anchor point and corresponding SHAP explanation
```
''' anchor point
'''
anchor_point_dict = dict(zip(feature_names, anchor_point))
colors = [["#3DE8F7","w"],[ "#3DE8F7","w"], [ "#3DE8F7","w"], [ "#3DE8F7","w"]]
anchor_point_df = pd.DataFrame.from_dict(anchor_point_dict, orient='index').reset_index()
fig, ax = plt.subplots()
table = ax.table(cellText = anchor_point_df.values,
# colLabels = anchor_point_df.columns,
loc = 'center',
cellColours = colors,
colWidths=[0.3] * 2)
table.set_fontsize(10)
table.scale(1,4)
cellDict = table.get_celld()
cellDict[(0,1)].set_width(0.15)
cellDict[(1,1)].set_width(0.15)
cellDict[(2,1)].set_width(0.15)
cellDict[(3,1)].set_width(0.15)
ax.axis('off')
ax.axis('tight')
fig.patch.set_visible(False)
fig.tight_layout()
plt.title('Feature Value')
''' corresponding LIME explanation
'''
x = feature_names[::-1]
print(x)
y = np.array(anchor_point_shap_exp[::-1]) # anchor_x_maximise_lc_exp_lime
print(y)
fig, ax = plt.subplots()
width = 0.75 # the width of the bars
ind = np.arange(len(y)) # the x locations for the groups
# split it up
above_threshold = np.maximum(y - threshold, 0)
below_threshold = np.minimum(y, threshold)
# ax.barh(ind, y, width, color="#3DE8F7")
ax.barh(x, below_threshold, width, color="#FF4D4D") # below threshold value
ax.barh(x, above_threshold, width, color="#3DE8F7", left=below_threshold) # above threshold value
ax.set_yticks(ind+width/2)
plt.title('Explanation')
```
### 3. Visualize deviation point and corresponding LIME explanation
```
''' anchor point
'''
deviation_point_dict = dict(zip(feature_names, deviation_point))
# print(anchor_point_dict)
deviation_point_columns = ['Feature', 'Value']
colors = [["#3DE8F7","w"],[ "#3DE8F7","w"], [ "#FF4D4D","w"], [ "#FF4D4D","w"]]
deviation_point_df = pd.DataFrame.from_dict(deviation_point_dict, orient='index').reset_index()
# deviation_point_df.rename(columns={'index': 'Feature', 0: 'Value' }, inplace=True)
fig, ax = plt.subplots()
table = ax.table(cellText = deviation_point_df.values,
# colLabels = deviation_point_df.columns,
loc = 'center',
cellColours = colors,
colWidths=[0.3] * 2)
table.set_fontsize(10)
table.scale(1,4)
cellDict = table.get_celld()
cellDict[(0,1)].set_width(0.15)
cellDict[(1,1)].set_width(0.15)
cellDict[(2,1)].set_width(0.15)
cellDict[(3,1)].set_width(0.15)
ax.axis('off')
ax.axis('tight')
fig.patch.set_visible(False)
fig.tight_layout()
plt.title('Feature Value')
''' corresponding LIME explanation
'''
x = feature_names[::-1]
print(x)
y = np.array(deviation_point_lime_exp[::-1]) # anchor_x_maximise_lc_exp_lime
print(y)
fig, ax = plt.subplots()
width = 0.75 # the width of the bars
ind = np.arange(len(y)) # the x locations for the groups
# split it up
above_threshold = np.maximum(y - threshold, 0)
below_threshold = np.minimum(y, threshold)
# ax.barh(ind, y, width, color="#3DE8F7")
ax.barh(x, below_threshold, width, color="#FF4D4D") # below threshold value
ax.barh(x, above_threshold, width, color="#3DE8F7", left=below_threshold) # above threshold value
ax.set_yticks(ind+width/2)
plt.title('Explanation')
# for key, cell in cellDict.items():
# print (str(key[0])+", "+ str(key[1])+"\t"+str(cell.get_text()))
```
### 4. Visualize deviation point and corresponding SHAP explanation
```
''' anchor point
'''
deviation_point_dict = dict(zip(feature_names, deviation_point))
# print(anchor_point_dict)
deviation_point_columns = ['Feature', 'Value']
colors = [["#3DE8F7","w"],[ "#3DE8F7","w"], [ "#3DE8F7","w"], [ "#3DE8F7","w"]]
deviation_point_df = pd.DataFrame.from_dict(deviation_point_dict, orient='index').reset_index()
# deviation_point_df.rename(columns={'index': 'Feature', 0: 'Value' }, inplace=True)
fig, ax = plt.subplots()
table = ax.table(cellText = deviation_point_df.values,
# colLabels = deviation_point_df.columns,
loc = 'center',
cellColours = colors,
colWidths=[0.3] * 2)
table.set_fontsize(10)
table.scale(1,4)
cellDict = table.get_celld()
cellDict[(0,1)].set_width(0.15)
cellDict[(1,1)].set_width(0.15)
cellDict[(2,1)].set_width(0.15)
cellDict[(3,1)].set_width(0.15)
ax.axis('off')
ax.axis('tight')
fig.patch.set_visible(False)
fig.tight_layout()
plt.title('Feature Value')
''' corresponding LIME explanation
'''
x = feature_names[::-1]
print(x)
y = np.array(deviation_point_shap_exp[::-1]) # anchor_x_maximise_lc_exp_lime
print(y)
fig, ax = plt.subplots()
width = 0.75 # the width of the bars
ind = np.arange(len(y)) # the x locations for the groups
# split it up
above_threshold = np.maximum(y - threshold, 0)
below_threshold = np.minimum(y, threshold)
# ax.barh(ind, y, width, color="#3DE8F7")
ax.barh(x, below_threshold, width, color="#FF4D4D") # below threshold value
ax.barh(x, above_threshold, width, color="#3DE8F7", left=below_threshold) # above threshold value
ax.set_yticks(ind+width/2)
plt.title('Explanation')
```
### Visualize lipschitz estimations for all test instances
```
df = lc_lime_df.append(lc_shap_df)
ax = sns.boxplot(x='method', y="Lipschitz Estimates", data=df)
ax = sns.boxplot(x="Dataset", y="Lipschitz Estimates",
hue="method",
data=df)
sns.despine(offset=10, trim=True)
```
### LIME visualizations by single points
```
explainer_lime = LimeTabularExplainer(train,
mode = 'classification',
training_labels = labels_train,
feature_names=feature_names,
verbose=False,
class_names=target_names,
feature_selection='auto',
discretize_continuous=True)
x_instance = test[anchor_index]
LR_exp_lime = explainer_lime.explain_instance(x_instance,
LR_iris.predict_proba,
labels=np.unique(iris.target),
top_labels=None,
num_features=len(x_instance),
num_samples=6000)
LR_exp_lime.show_in_notebook()
x_instance = test[similar_point_index]
LR_exp_lime = explainer_lime.explain_instance(x_instance,
LR_iris.predict_proba,
labels=np.unique(iris.target),
top_labels=None,
num_features=len(x_instance),
num_samples=6000)
LR_exp_lime.show_in_notebook()
i = np.random.randint(0, test.shape[0])
i = 0
LR_exp_lime_map = LR_exp_lime.as_map()
# pprint(LR_exp_lime_map)
print('Predicted class for i:', labels_pred_lr[i])
LR_exp_lime_list = LR_exp_lime.as_list(label=labels_pred_lr[i])
# pprint(LR_exp_lime_list)
```
## Conclusions
```
lr_lime_iris = [2.657, 3.393, 1.495]
rf_lime_iris = [3.010, 3.783, 1.767]
lr_shap_iris = [2.716, 3.512, 1.463]
rf_shap_iris = [1.969, 3.546, 2.136]
find_min_vector = np.array([lr_lime_iris, rf_lime_iris, lr_shap_iris, rf_shap_iris])
np.amin(find_min_vector, axis=0)
from sklearn.linear_model import Ridge
import numpy as np
n_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)
clf = Ridge(alpha=1.0)
clf.fit(X, y)
```
### Debuging Space
```
""" Use euclidean distance to define neighborhood points
"""
display(X.head())
points = X.values
epsilon = 0.75 * np.sqrt(len(points[0]))
dist = (points[0] - points[1:])**2
dist = np.sum(dist, axis=1)
dist = np.sqrt(dist)
print(dist)
neighborhood_indices = []
for index in range(0, len(dist)):
if dist[index] < epsilon:
neighborhood_indices.append(index)
print(neighborhood_indices)
```
| true |
code
| 0.484685 | null | null | null | null |
|
# 1. Multi-layer Perceptron
### Train and evaluate a simple MLP on the Reuters newswire topic classification task.
This is a collection of documents that appeared on Reuters newswire in 1987. The documents were assembled and indexed with categories.
Dataset of 11,228 newswires from Reuters, labeled over 46 topics. As with the IMDB dataset, each wire is encoded as a sequence of word indexes (same conventions).
Each wire is encoded as a sequence of word indexes (integers). For convenience, words are indexed by overall frequency in the dataset, so that for instance the integer "3" encodes the 3rd most frequent word in the data. This allows for quick filtering operations such as: "only consider the top 10,000 most common words, but eliminate the top 20 most common words".
As a convention, "0" does not stand for a specific word, but instead is used to encode any unknown word.
Source: https://archive.ics.uci.edu/ml/datasets/Reuters-21578+Text+Categorization+Collection
```
# Reuters data
from __future__ import print_function
import numpy as np
np.random.seed(1337) # for reproducibility
#Import keras
from keras.datasets import reuters
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.utils import np_utils
from keras.preprocessing.text import Tokenizer
max_words = 1000
batch_size = 32
nb_epoch = 5
import os
path_to_data = os.path.abspath(os.path.join('..', 'data', 'reuters.pkl'))
print('Loading data...')
(X_train, y_train), (X_test, y_test) = reuters.load_data(path_to_data, nb_words=max_words, test_split=0.2)
print(len(X_train), 'train sequences')
print(len(X_test), 'test sequences')
nb_classes = np.max(y_train)+1
print(nb_classes, 'classes')
print('Vectorizing sequence data...')
tokenizer = Tokenizer(nb_words=max_words)
X_train = tokenizer.sequences_to_matrix(X_train, mode='binary')
X_test = tokenizer.sequences_to_matrix(X_test, mode='binary')
print('X_train shape:', X_train.shape)
print('X_test shape:', X_test.shape)
print('Convert class vector to binary class matrix (for use with categorical_crossentropy)')
Y_train = np_utils.to_categorical(y_train, nb_classes)
Y_test = np_utils.to_categorical(y_test, nb_classes)
print('Y_train shape:', Y_train.shape)
print('Y_test shape:', Y_test.shape)
print('Building model...')
model = Sequential()
model.add(Dense(512, input_shape=(max_words,)))
model.add(Activation('relu'))
model.add(Dense(nb_classes))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy',
optimizer='sgd',
metrics=['accuracy'])
history = model.fit(X_train, Y_train,
nb_epoch=nb_epoch, batch_size=batch_size,
verbose=1, validation_split=0.1)
score = model.evaluate(X_test, Y_test,
batch_size=batch_size, verbose=1)
print('Test score:', score[0])
print('Test accuracy:', score[1])
```
### Exercise
1. Add more dense layers: Try with one more dense layer. Then with two dense layers. Evaluate accuracy
2. Add dropout using the following code and evaluate accuracy:
`model.add(Dropout(0.5))`
| true |
code
| 0.674908 | null | null | null | null |
|
# Distributed
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Distributed" data-toc-modified-id="Distributed-1"><span class="toc-item-num">1 </span>Distributed</a></span><ul class="toc-item"><li><span><a href="#Distributed-Cluster" data-toc-modified-id="Distributed-Cluster-1.1"><span class="toc-item-num">1.1 </span>Distributed Cluster</a></span></li><li><span><a href="#Create-and-Connect-to-Dask-Distributed-Cluster" data-toc-modified-id="Create-and-Connect-to-Dask-Distributed-Cluster-1.2"><span class="toc-item-num">1.2 </span>Create and Connect to Dask Distributed Cluster</a></span></li><li><span><a href="#Perfom-computation-on-a-dask-array" data-toc-modified-id="Perfom-computation-on-a-dask-array-1.3"><span class="toc-item-num">1.3 </span>Perfom computation on a dask array</a></span></li><li><span><a href="#Going-Further" data-toc-modified-id="Going-Further-1.4"><span class="toc-item-num">1.4 </span>Going Further</a></span></li></ul></li></ul></div>
## Distributed Cluster
As we have seen so far, Dask allows you to simply construct graphs of tasks with dependencies, as well as have graphs created automatically for you using functional, Numpy syntax on data collections. None of this would be very useful, if there weren't also a way to execute these graphs, in a parallel and memory-aware way. So far we have been calling `thing.compute()` or `dask.compute(thing)` without worrying what this entails. Now we will discuss the options available for that execution, and in particular, the distributed scheduler, which comes with additional functionality.
## Create and Connect to Dask Distributed Cluster
Let's begin by importing `Client` and `LocalCluster` objects/classes
```
from dask.distributed import Client, LocalCluster
# Setup a local cluster.
# By default this sets up 1 worker per core
cluster = LocalCluster()
cluster
```
☝️ Don't forget to click the link above to view the scheduler dashboard! (you may wish to have both the notebook and dashboard side-by-side)
```
client = Client(cluster) # Connect to a Dask cluster in order to submit computation
client
```
## Perfom computation on a dask array
```
import dask.array as da
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
bigshape = (500, 2400, 3600)
chunk_shape = (10, 1200, 1800)
big_ones = da.ones(bigshape, chunks=chunk_shape)
big_ones
big_calc = (big_ones * big_ones[::-1, ::-1]).mean()
big_calc
%time big_calc.compute()
```
**Create a histogram**
```
random_values = da.random.normal(size=(1e8,), chunks=(20e6,))
hist, bins = da.histogram(random_values, bins=10, range=[-5, 5])
random_values
hist
hist.visualize()
%%time
x = 0.5 * (bins[1:] + bins[:-1])
width = np.diff(bins)
plt.bar(x, hist, width);
```
## Going Further
- [Dask Tutorial on Distributed](https://github.com/dask/dask-tutorial/blob/master/05_distributed.ipynb)
- [Dask Tutorial on Advanced Distributed](https://github.com/dask/dask-tutorial/blob/master/06_distributed_advanced.ipynb)
<div class="alert alert-block alert-success">
<p>Previous: <a href="02_dask_arrays.ipynb">Dask Arrays</a></p>
<p>Next: <a href="04_dask_and_xarray.ipynb">Dask + Xarray</a></p>
</div>
| true |
code
| 0.632673 | null | null | null | null |
|
# DAG Creation and Submission
Launch this tutorial in a Jupyter Notebook on Binder:
[](https://mybinder.org/v2/gh/htcondor/htcondor-python-bindings-tutorials/master?urlpath=lab/tree/DAG-Creation-And-Submission.ipynb)
In this tutorial, we will learn how to use `htcondor.dags` to create and submit an HTCondor DAGMan workflow.
Our goal will be to create an image of the Mandelbrot set.
This is a perfect problem for high-throughput computing because each point in the image can be calculated completely independently of any other point, so we are free to divide the image creation up into patches, each created by a single HTCondor job.
DAGMan will enter the picture to coordinate stitching the image patches we create back into a single image.
## Making a Mandelbrot set image locally
We'll use `goatbrot` (https://github.com/beejjorgensen/goatbrot) to make the image.
`goatbrot` can be run from the command line, and takes a series of options to specify which part of the Mandelbrot set to draw, as well as the properties of the image itself.
`goatbrot` options:
- `-i 1000` The number of iterations.
- `-c 0,0` The center point of the image region.
- `-w 3` The width of the image region.
- `-s 1000,1000` The pixel dimensions of the image.
- `-o test.ppm` The name of the output file to generate.
We can run a shell command from Jupyter by prefixing it with a `!`:
```
! ./goatbrot -i 10 -c 0,0 -w 3 -s 500,500 -o test.ppm
! convert test.ppm test.png
```
Let's take a look at the test image. It won't be very good, because we didn't run for very many iterations.
We'll use HTCondor to produce a better image!
```
from IPython.display import Image
Image('test.png')
```
## What is the workflow?
We can parallelize this calculation by drawing rectangular sub-regions of the full region ("tiles") we want and stitching them together into a single image using `montage`.
Let's draw this out as a graph, showing how data (image patches) will flow through the system.
(Don't worry about this code, unless you want to know how to make dot diagrams in Python!)
```
from graphviz import Digraph
import itertools
num_tiles_per_side = 2
dot = Digraph()
dot.node('montage')
for x, y in itertools.product(range(num_tiles_per_side), repeat = 2):
n = f'tile_{x}-{y}'
dot.node(n)
dot.edge(n, 'montage')
dot
```
Since we can chop the image up however we'd like, we have as many tiles per side as we'd like (try changing `num_tiles_per_side` above).
The "shape" of the DAG is the same: there is a "layer" of `goatbrot` jobs that calculate tiles, which all feed into `montage`.
Now that we know the structure of the problem, we can start describing it to HTCondor.
## Describing `goatbrot` as an HTCondor job
We describe a job using a `Submit` object.
It corresponds to the submit *file* used by the command line tools.
It mostly behaves like a standard Python dictionary, where the keys and values correspond to submit descriptors.
```
import htcondor
tile_description = htcondor.Submit(
executable = 'goatbrot', # the program we want to run
arguments = '-i 10000 -c $(x),$(y) -w $(w) -s 500,500 -o tile_$(tile_x)-$(tile_y).ppm', # the arguments to pass to the executable
log = 'mandelbrot.log', # the HTCondor job event log
output = 'goatbrot.out.$(tile_x)_$(tile_y)', # stdout from the job goes here
error = 'goatbrot.err.$(tile_x)_$(tile_y)', # stderr from the job goes here
request_cpus = '1', # resource requests; we don't need much per job for this problem
request_memory = '128MB',
request_disk = '1GB',
)
print(tile_description)
```
Notice the heavy use of macros like `$(x)` to specify the tile.
Those aren't built-in submit macros; instead, we will plan on passing their values in through **vars**.
Vars will let us customize each individual job in the tile layer by filling in those macros individually.
Each job will recieve a dictionary of macro values; our next goal is to make a list of those dictionaries.
We will do this using a function that takes the number of tiles per side as an argument.
As mentioned above, the **structure** of the DAG is the same no matter how "wide" the tile layer is.
This is why we define a function to produce the tile vars instead of just calculating them once: we can vary the width of the DAG by passing different arguments to `make_tile_vars`.
More customizations could be applied to make different images (for example, you could make it possible to set the center point of the image).
```
def make_tile_vars(num_tiles_per_side, width = 3):
width_per_tile = width / num_tiles_per_side
centers = [
width_per_tile * (n + 0.5 - (num_tiles_per_side / 2))
for n in range(num_tiles_per_side)
]
vars = []
for (tile_y, y), (tile_x, x) in itertools.product(enumerate(centers), repeat = 2):
var = dict(
w = width_per_tile,
x = x,
y = -y, # image coordinates vs. Cartesian coordinates
tile_x = str(tile_x).rjust(5, '0'),
tile_y = str(tile_y).rjust(5, '0'),
)
vars.append(var)
return vars
tile_vars = make_tile_vars(2)
for var in tile_vars:
print(var)
```
If we want to increase the number of tiles per side, we just pass in a larger number.
Because the `tile_description` is **parameterized** in terms of these variables, it will work the same way no matter what we pass in as `vars`.
```
tile_vars = make_tile_vars(4)
for var in tile_vars:
print(var)
```
## Describing montage as an HTCondor job
Now we can write the `montage` job description.
The problem is that the arguments and input files depend on how many tiles we have, which we don't know ahead-of-time.
We'll take the brute-force approach of just writing a function that takes the tile `vars` we made in the previous section and using them to build the `montage` job description.
Not that some of the work of building up the submit description is done in Python.
This is a major advantage of communicating with HTCondor via Python: you can do the hard work in Python instead of in submit language!
One area for possible improvement here is to remove the duplication of the format of the input file names, which is repeated here from when it was first used in the `goatbrot` submit object. When building a larger, more complicated workflow, it is important to reduce duplication of information to make it easier to modify the workflow in the future.
```
def make_montage_description(tile_vars):
num_tiles_per_side = int(len(tile_vars) ** .5)
input_files = [f'tile_{d["tile_x"]}-{d["tile_y"]}.ppm' for d in tile_vars]
return htcondor.Submit(
executable = '/usr/bin/montage',
arguments = f'{" ".join(input_files)} -mode Concatenate -tile {num_tiles_per_side}x{num_tiles_per_side} mandelbrot.png',
transfer_input_files = ', '.join(input_files),
log = 'mandelbrot.log',
output = 'montage.out',
error = 'montage.err',
request_cpus = '1',
request_memory = '128MB',
request_disk = '1GB',
)
montage_description = make_montage_description(make_tile_vars(2))
print(montage_description)
```
## Describing the DAG using `htcondor.dags`
Now that we have the job descriptions, all we have to do is use `htcondor.dags` to tell DAGMan about the dependencies between them.
`htcondor.dags` is a subpackage of the HTCondor Python bindings that lets you write DAG descriptions using a higher-level language than raw DAG description file syntax.
Incidentally, it also lets you use Python to drive the creation process, increasing your flexibility.
**Important Concept:** the code from `dag = dags.DAG()` onwards only defines the **topology** (or **structure**) of the DAG.
The `tile` layer can be flexibly grown or shrunk by adjusting the `tile_vars` without changing the topology, and this can be clearly expressed in the code.
The `tile_vars` are driving the creation of the DAG. Try changing `num_tiles_per_side` to some other value!
```
from htcondor import dags
num_tiles_per_side = 2
# create the tile vars early, since we need to pass them to multiple places later
tile_vars = make_tile_vars(num_tiles_per_side)
dag = dags.DAG()
# create the tile layer, passing in the submit description for a tile job and the tile vars
tile_layer = dag.layer(
name = 'tile',
submit_description = tile_description,
vars = tile_vars,
)
# create the montage "layer" (it only has one job in it, so no need for vars)
# note that the submit description is created "on the fly"!
montage_layer = tile_layer.child_layer(
name = 'montage',
submit_description = make_montage_description(tile_vars),
)
```
We can get a textual description of the DAG structure by calling the `describe` method:
```
print(dag.describe())
```
## Write the DAG to disk
We still need to write the DAG to disk to get DAGMan to work with it.
We also need to move some files around so that the jobs know where to find them.
```
from pathlib import Path
import shutil
dag_dir = (Path.cwd() / 'mandelbrot-dag').absolute()
# blow away any old files
shutil.rmtree(dag_dir, ignore_errors = True)
# make the magic happen!
dag_file = dags.write_dag(dag, dag_dir)
# the submit files are expecting goatbrot to be next to them, so copy it into the dag directory
shutil.copy2('goatbrot', dag_dir)
print(f'DAG directory: {dag_dir}')
print(f'DAG description file: {dag_file}')
```
## Submit the DAG via the Python bindings
Now that we have written out the DAG description file, we can submit it for execution using the standard Python bindings submit mechanism.
The `Submit` class has a static method which can read a DAG description and generate a corresponding `Submit` object:
```
dag_submit = htcondor.Submit.from_dag(str(dag_file), {'force': 1})
print(dag_submit)
```
Now we can enter the DAG directory and submit the DAGMan job, which will execute the graph:
```
import os
os.chdir(dag_dir)
schedd = htcondor.Schedd()
with schedd.transaction() as txn:
cluster_id = dag_submit.queue(txn)
print(f"DAGMan job cluster is {cluster_id}")
os.chdir('..')
```
Let's wait for the DAGMan job to complete by reading it's event log:
```
dag_job_log = f"{dag_file}.dagman.log"
print(f"DAG job log file is {dag_job_log}")
# read events from the log, waiting forever for the next event
dagman_job_events = htcondor.JobEventLog(str(dag_job_log)).events(None)
# this event stream only contains the events for the DAGMan job itself, not the jobs it submits
for event in dagman_job_events:
print(event)
# stop waiting when we see the terminate event
if event.type is htcondor.JobEventType.JOB_TERMINATED and event.cluster == cluster_id:
break
```
Let's look at the final image!
```
Image(dag_dir / "mandelbrot.png")
```
| true |
code
| 0.243103 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.