prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Distributed Federated Learning using PySyft
```
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import syft as sy
hook = sy.TorchHook(torch)
bob = sy.VirtualWorker(hook, id='bob')
alice = sy.VirtualWorker(hook, id='alice')
jane = sy.VirtualWorker(hook, id='jane')
federated_train_loader = sy.FederatedDataLoader(
datasets.MNIST('data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
]))
.federate((bob, alice, jane)),
batch_size=32, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=32, shuffle=True)
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 64)
self.fc3 = nn.Linear(64, 10)
def forward(self, x):
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return F.log_softmax(x, dim=1)
def train(model, federated_train_loader, optimizer, epochs):
model.train()
for epoch in range(epochs):
for batch_idx, (data, targets) in enumerate(federated_train_loader):
model.send(data.location)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, targets)
loss.backward()
optimizer.step()
model.get()
if batch_idx % 2 == 0:
loss = loss.get()
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * 32, len(federated_train_loader) * 32,
100. * batch_idx / len(federated_train_loader), loss.item()))
def test(model, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
model = Classifier()
optimizer = optim.SGD(model.parameters(), lr=0.005)
train(model, federated_train_loader, optimizer, 3)
test(model, test_loader)
```
| true |
code
| 0.881971 | null | null | null | null |
|
```
import pandas as pd
import numpy as np
import scipy.stats
from scipy.integrate import quad
from scipy.optimize import minimize
from scipy.special import expit, logit
from scipy.stats import norm
```
# Dataset
```
df = pd.read_csv("bank-note/bank-note/train.csv", header=None)
d = df.to_numpy()
X = d[:,:-1]
Y = d[:,-1]
X.shape, Y.shape
df = pd.read_csv("bank-note/bank-note/test.csv", header=None)
d = df.to_numpy()
Xtest = d[:,:-1]
Ytest = d[:,-1]
Xtest.shape, Ytest.shape
```
# Part 1
```
def initialise_w(initialise):
if(initialise == 'random'):
w = np.random.randn(d,1)
print("w is initialised from N[0,1]")
elif(initialise == 'zeros'):
w = np.zeros((d,1))
print("w is initialised as a zero vector")
else:
print("Method unknown")
return w
def compute_mu(X, w):
mu = expit(np.dot(X,w))
mu = mu.reshape(X.shape[0],1)
return mu
def first_derivative(w):
mu = compute_mu(X, w)
epsilon = 1e-12
grad = np.matmul(np.transpose(X), (mu-Y)) + w.reshape(d,1)
grad = grad.squeeze()
return(grad)
def second_deivative(w,X,y):
mu = compute_mu(X, w)
R = np.eye(n)
for i in range(n):
R[i,i] = mu[i,0] * (1-mu[i,0])
return(np.dot(np.dot(np.transpose(X),R),X) + np.eye(d))
def test(w, X, y):
n,d = X.shape
mu = compute_mu(X, w)
yhat = np.zeros((n,1)).astype(np.float64)
yhat[mu>0.5]=1
correct = np.sum(yhat==y)
return(correct,n)
def train(initialise):
np.random.seed(0)
w = initialise_w(initialise)
for j in range(100):
grad1 = first_derivative(w.squeeze()).reshape(d,1)
H = second_deivative(w, X, Y)
delta_w = np.dot(np.linalg.inv(H),grad1)
w = w - delta_w
diff = np.linalg.norm(delta_w)
correct,n = test(w, Xtest, Ytest)
print("Iteration : {} \t Accuracy : {}%".format(j,correct/n*100))
if(diff < 1e-5):
print("tolerance reached at the iteration : ",j)
break
print("Training done...")
print("Model weights : ", np.transpose(w))
n,d = X.shape
n1,d1 = Xtest.shape
Y = Y.reshape(n,1)
Ytest = Ytest.reshape(n1,1)
train('random')
```
# Part 2
```
# LBFGS
def compute_mu(X, w):
phi=np.dot(X,w)
mu = norm.cdf(phi)
mu = mu.reshape(X.shape[0],1)
return mu
def first_derivative(w):
mu = compute_mu(X, w)
epsilon = 1e-12
phi=np.dot(X,w)
grad_mu = X*(scipy.stats.norm.pdf(phi,0,1).reshape(-1,1))
return(np.sum((- Y*(1/(mu)) + (1-Y)*(1/(1+epsilon-mu)))*grad_mu,0) + w).squeeze()
def second_deivative(w,X,y):
mu = compute_mu(X, w)
R = np.eye(n)
phi=np.dot(X,w)
for i in range(n):
t1 = (y[i] - mu[i,0])/(mu[i,0] * (1-mu[i,0]))
t2 = scipy.stats.norm.pdf(phi[i,0],0,1)
t3 = (1-y[i])/np.power(1-mu[i,0],2) + y[i]/np.power(mu[i,0],2)
R[i,i] = t1*t2*np.dot(X[i],w) + t3*t2*t2
return(np.dot(np.dot(np.transpose(X),R),X) + np.eye(d))
def neg_log_posterior(w):
w=w.reshape(-1,1)
epsilon = 1e-12
mu = compute_mu(X, w)
prob_1 = Y*np.log(mu+epsilon)
prob_0 = (1-Y)*np.log(1-mu+epsilon)
log_like = np.sum(prob_1) + np.sum(prob_0)
w_norm = np.power(np.linalg.norm(w),2)
neg_log_pos = -log_like+w_norm/2
print("neg_log_posterior = {:.4f} \tlog_like = {:.4f} \tw_norm = {:.4f}".format(neg_log_pos, log_like, w_norm))
return(neg_log_pos)
def test(w, X, y):
n,d = X.shape
mu = compute_mu(X, w)
#print(mu.shape, n, d)
yhat = np.zeros((n,1)).astype(np.float64)
yhat[mu>0.5]=1
correct = np.sum(yhat==y)
return(correct,n)
res = minimize(neg_log_posterior, initialise_w('random'), method='BFGS', jac=first_derivative,
tol= 1e-5, options={'maxiter': 100})
correct,n = test(res.x, Xtest, Ytest)
print("\n_____________Model trained______________\n")
print("\nModel weights : ", res.x)
print("\n_____________Test Accuracy______________\n")
print("Accuracy : {}% ".format(correct/n*100))
```
# Part 3
```
def compute_mu(X, w):
phi=np.dot(X,w)
mu = norm.cdf(phi)
mu = mu.reshape(X.shape[0],1)
return mu
def first_derivative(w):
mu = compute_mu(X, w)
epsilon = 1e-12
phi=np.dot(X,w)
grad_mu = X*(scipy.stats.norm.pdf(phi,0,1).reshape(-1,1))
return(np.sum((- Y*(1/(mu)) + (1-Y)*(1/(1+epsilon-mu)))*grad_mu,0) + w).squeeze()
def second_deivative(w,X,y):
mu = compute_mu(X, w)
R = np.eye(n)
phi=np.dot(X,w)
for i in range(n):
t1 = (y[i] - mu[i,0])/(mu[i,0] * (1-mu[i,0]))
t2 = scipy.stats.norm.pdf(phi[i,0],0,1)
t3 = (1-y[i])/np.power(1-mu[i,0],2) + y[i]/np.power(mu[i,0],2)
R[i,i] = t1*t2*np.dot(X[i],w) + t3*t2*t2
return(np.dot(np.dot(np.transpose(X),R),X) + np.eye(d))
def neg_log_posterior(w):
w=w.reshape(-1,1)
epsilon = 1e-12
mu = compute_mu(X, w)
prob_1 = Y*np.log(mu+epsilon)
prob_0 = (1-Y)*np.log(1-mu+epsilon)
log_like = np.sum(prob_1) + np.sum(prob_0)
w_norm = np.power(np.linalg.norm(w),2)
neg_log_pos = -log_like+w_norm/2
print("neg_log_posterior = {:.4f} \tlog_like = {:.4f} \tw_norm = {:.4f}".format(neg_log_pos, log_like, w_norm))
return(neg_log_pos)
def test(w, X, y):
n,d = X.shape
mu = compute_mu(X, w)
#print(mu.shape, n, d)
yhat = np.zeros((n,1)).astype(np.float64)
yhat[mu>0.5]=1
correct = np.sum(yhat==y)
return(correct,n)
def train(initialise):
np.random.seed(0)
w = initialise_w(initialise)
for j in range(100):
grad1 = first_derivative(w.squeeze()).reshape(d,1)
H = second_deivative(w, X, Y)
delta_w = np.dot(np.linalg.inv(H),grad1)
w = w - delta_w
diff = np.linalg.norm(delta_w)
correct,n = test(w, Xtest, Ytest)
print("Iteration : {} \t Accuracy : {}%".format(j,correct/n*100))
if(diff < 1e-5):
print("tolerance reached at the iteration : ",j)
break
print("Training done...")
print("Model weights : ", np.transpose(w))
n,d = X.shape
n1,d1 = Xtest.shape
Y = Y.reshape(n,1)
Ytest = Ytest.reshape(n1,1)
train('zeros')
```
| true |
code
| 0.467453 | null | null | null | null |
|
### Clinical BCI Challenge-WCCI2020
- [website link](https://sites.google.com/view/bci-comp-wcci/?fbclid=IwAR37WLQ_xNd5qsZvktZCT8XJerHhmVb_bU5HDu69CnO85DE3iF0fs57vQ6M)
- [Dataset Link](https://github.com/5anirban9/Clinical-Brain-Computer-Interfaces-Challenge-WCCI-2020-Glasgow)
```
import mne
from scipy.io import loadmat
import scipy
import sklearn
import numpy as np
import pandas as pd
import glob
from mne.decoding import CSP
import os
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import LinearSVC, SVC
from sklearn.model_selection import train_test_split, cross_val_score, GridSearchCV, StratifiedShuffleSplit
from sklearn.preprocessing import StandardScaler
from sklearn.compose import make_column_transformer, make_column_selector
from sklearn.pipeline import make_pipeline
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as lda
import warnings
warnings.filterwarnings('ignore') # to ignore warnings
verbose = False # to universally just change it to true/false for different output display
mne.set_log_level(verbose=verbose) # to suppress large info outputs
# using kappa as evaluation metric
kappa = sklearn.metrics.make_scorer(sklearn.metrics.cohen_kappa_score) # kappa scorer
acc = sklearn.metrics.make_scorer(sklearn.metrics.accuracy_score) # accuracy scorer
scorer = kappa # just assign another scorer to replace kappa scorer
n_jobs = None # for multicore parallel processing, set it to 1 if cause memory issues, for full utilization set to -1
```
## Data Loading and Conversion to MNE Datatypes
[Mike Cohen Tutorials link for EEG Preprocessing](https://www.youtube.com/watch?v=uWB5tjhataY&list=PLn0OLiymPak2gDD-VDA90w9_iGDgOOb2o)
```
current_folder = globals()['_dh'][0] # a hack to get path of current folder in which juptyter file is located
data_path = os.path.join(current_folder, 'Data')
all_files = glob.glob(data_path + '/*.mat')
training_files = glob.glob(data_path + '/*T.mat')
evaluation_files = glob.glob(data_path + '/*E.mat')
len(all_files), len(training_files), len(evaluation_files) # if these return zero,then no file is loaded
def get_mne_epochs(filepath, verbose=verbose, t_start=2, fs=512, mode='train'):
'''
This function reads the EEG data from .mat file and convert it to MNE-Python Compatible epochs
data structure. It takes data from [0, 8] sec range and return it by setting t = 0 at cue onset
i.e. 3 seconds and dropping first two seconds so the output data is in [-1.0, 5.0] sec range. The
Details can be found in the preprocessing section of the attached document
'''
mat_data = loadmat(filepath) # read .mat file
eeg_data= mat_data['RawEEGData']
idx_start = fs*t_start
eeg_data = eeg_data[:, :, idx_start:]
event_id = {'left-hand': 1, 'right-hand': 2}
channel_names = ['F3', 'FC3', 'C3', 'CP3', 'P3', 'FCz', 'CPz', 'F4', 'FC4', 'C4', 'CP4', 'P4']
info = mne.create_info(ch_names=channel_names, sfreq=fs, ch_types='eeg')
epochs = mne.EpochsArray(eeg_data, info, verbose=verbose, tmin=t_start-3.0)
epochs.set_montage('standard_1020')
epochs.filter(1., None)
epochs.apply_baseline(baseline=(-.250, 0)) # linear baseline correction
if mode == 'train': # this in only applicable for training data
epochs.event_id = event_id
epochs.events[:,2] = mat_data['Labels'].ravel()
return epochs
def get_labels(filepath):
mat_data = loadmat(filepath) # read .mat file
return mat_data['Labels'].ravel()
epochs, labels = get_mne_epochs(training_files[0], verbose=verbose), get_labels(training_files[0])
data = epochs.get_data()
print('Shape of EEG Data: ', data.shape, '\t Shape of Labels: ', labels.shape)
```
### Training Data
```
# loading original data
epochs_list_train = []
for i in training_files:
epochs_list_train.append(get_mne_epochs(i, verbose=verbose))
```
### Evaluation Data
first 8 for single subject and last 2 are for cross subject
```
epochs_list_eval = []
for i in evaluation_files:
epochs_list_eval.append(get_mne_epochs(i, mode='test', verbose=verbose))
```
### Bandpass filtering of data
```
for epochs in epochs_list_train:
epochs.filter(7.0, 32.0)
for epochs in epochs_list_eval:
epochs.filter(7.0, 32.0)
```
## Lets try doing some classification
```
cv = StratifiedShuffleSplit(n_splits=5, random_state=0)
epochs = epochs_list_train[3]
psds, freqs = mne.time_frequency.psd_multitaper(epochs, tmin=0.5, tmax=4.5, fmin=8, fmax=30 ,n_jobs=1)
psds = 10 * np.log10(psds) # to convert powers to DB
labels = epochs.events[:,-1]
x_trainVal, x_test, y_trainVal, y_test = train_test_split(psds, labels.ravel(), shuffle=True, stratify=labels, random_state=0) to avoid confusing names and reusing x_trainVal
print('train set: features: ', x_trainVal.shape, 'labels: ', y_trainVal.shape)
print('Test set: features: ', x_test.shape, 'labels: ', y_test.shape)
y_train = y_trainVal
# using all channels
trials, channels, eeg = x_trainVal.shape
x_train = x_trainVal.reshape(trials, channels*eeg)
print('*'*10, 'Classification Scores Comparison with default Parameters' ,'*'*10)
print('#'*15, 'Using All Channels', '#'*15)
print('KNN : ', np.mean(cross_val_score(make_pipeline(StandardScaler(),KNeighborsClassifier()), x_train, y_train, cv=cv, scoring=scorer)))
print('Log-Regression: ', np.mean(cross_val_score(make_pipeline(StandardScaler(),LogisticRegression(max_iter=1000)), x_train, y_train, cv=cv, scoring=scorer)))
print('Linear SVM : ', np.mean(cross_val_score(make_pipeline(StandardScaler(),LinearSVC(random_state=0)), x_train, y_train, cv=cv, scoring=scorer)))
print('kernal SVM : ', np.mean(cross_val_score(make_pipeline(StandardScaler(), SVC(gamma='scale')), x_train, y_train, cv=cv, scoring=scorer)))
print('LDA : ', np.mean(cross_val_score(make_pipeline(StandardScaler(), lda()), x_train, y_train, cv=cv, scoring=scorer)))
```
## Grid Search
with [0.5, 4.5] seconds time interval and [8, 30] Hz freqs
```
cv = StratifiedShuffleSplit(10, random_state=0)
# for linear svm
param_grid_linear_svm = { 'linearsvc__C' : np.logspace(-4, 2, 15)}
# lda, auto shrinkage performs pretty well mostly
shrinkage = list(np.arange(0.1,1.01,0.1))
shrinkage.append('auto')
param_grid_lda = {'lineardiscriminantanalysis__shrinkage': shrinkage}
grids_linear_svm_list = [GridSearchCV(make_pipeline(StandardScaler(), LinearSVC(random_state=0)),
param_grid=param_grid_linear_svm, cv=cv, n_jobs=n_jobs, scoring=scorer)
for _ in range(len(training_files))]
grids_lda_list = [GridSearchCV(make_pipeline(StandardScaler(), lda(solver='eigen')),
param_grid=param_grid_lda, cv=cv, n_jobs=n_jobs, scoring=scorer)
for _ in range(len(training_files))]
def training_function(subject_index=0):
# this time training function trains on whole training set
print('-'*25, 'Training for Subject:', subject_index+1, '-'*25)
epochs = epochs_list_train[subject_index]
psds, freqs = mne.time_frequency.psd_multitaper(epochs, tmin=0.5, tmax=4.5, fmin=8, fmax=30 ,n_jobs=1)
psds = 10 * np.log10(psds)
psds = psds.reshape(psds.shape[0], -1)
labels = epochs.events[:,-1]
grids_linear_svm_list[subject_index].fit(psds, labels)
print('LinearSVM: Maximum Cross Validation Score = ', round(grids_linear_svm_list[subject_index].best_score_,3))
grids_lda_list[subject_index].fit(psds, labels)
print('LDA : Maximum Cross Validation Score = ', round(grids_lda_list[subject_index].best_score_,3))
print()
def evaluation_function(subject_index=0):
# prints the prediction counts for each class
epochs = epochs_list_eval[subject_index]
psds, freqs = mne.time_frequency.psd_multitaper(epochs, tmin=0.5, tmax=4.5, fmin=8, fmax=30 ,n_jobs=1)
psds = 10 * np.log10(psds)
psds = psds.reshape(psds.shape[0], -1)
preds_linear_svm = grids_linear_svm_list[subject_index].predict(psds)
preds_lda = grids_lda_list[subject_index].predict(psds)
print('-'*25, 'Predictions Counts Subject:', subject_index+1, '-'*25)
print('Linear SVM: Class 1 =', sum(preds_linear_svm==1), 'Class 2 =', sum(preds_linear_svm==2))
print('LDA : Class 1 =', sum(preds_lda==1), 'Class 2 =', sum(preds_lda==2))
print()
```
### It's Training Time
```
for subject in range(len(training_files)):
training_function(subject)
for subject in range(len(training_files)):
evaluation_function(subject)
```
### Results
svm always better except the last subject so only last entry for lda and all others for svm in excel file
| true |
code
| 0.557243 | null | null | null | null |
|
Lambda School Data Science
*Unit 4, Sprint 2, Module 4*
---
# Neural Network Frameworks (Prepare)
## Learning Objectives
* <a href="#p1">Part 1</a>: Implemenent Regularization Strategies
* <a href="#p2">Part 2</a>: Deploy a Keras Model
* <a href="#p3">Part 3</a>: Write a Custom Callback Function (Optional)
Today's class will also focus heavily on Callback objects. We will use a variety of callbacks to monitor and manipulate our models based on data that our model produces at the end of an epoch.
> A callback is an object that can perform actions at various stages of training (e.g. at the start or end of an epoch, before or after a single batch, etc). -- [Keras Documentation](https://keras.io/api/callbacks/)
# Regularization Strategies (Learn)
## Overview
Neural Networks are highly parameterized models and can be easily overfit to the training data. The most salient way to combat this problem is with regularization strategies.

There are four common ways of regularization in neural networks which we cover briefly. Here's a quick summary of how to apply them:
1. Always use EarlyStopping. This strategy will prevent your weights from being updated well past the point of their peak usefulness.
2. Use EarlyStopping, L1/L2 regularization and Dropout
3. Use EarlyStopping, Weight Constraint and Dropout
Weight Decay and Weigh Constraint accomplish similar purposes - preventing over fitting the parameters by regularizing the values. The mechanics are just slightly different. That's why you would not necessary want to apply them together.
## Follow Along
### Early Stopping
```
%load_ext tensorboard
from tensorflow.keras.datasets import fashion_mnist
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
import matplotlib.pyplot as plt
plt.title(y_train[2])
plt.imshow(X_train[2]);
X_train, X_test = X_train / 255., X_test / 255.
from tensorflow.keras.callbacks import EarlyStopping, TensorBoard
from tensorflow.keras.layers import Flatten, Dense
from tensorflow.keras.layers import ReLU
import tensorflow as tf
import os
logdir = os.path.join("logs", "EarlyStopping-Loss")
tensorboard_callback = tf.keras.callbacks.TensorBoard(logdir, histogram_freq=1)
stop = EarlyStopping(monitor='val_loss', min_delta=0.001, patience=3)
model = tf.keras.Sequential([
Flatten(input_shape=(28,28)),
Dense(128),
ReLU(negative_slope=.01),
Dense(128),
ReLU(negative_slope=.01),
Dense(128),
ReLU(negative_slope=.01),
Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer='nadam', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=99,
validation_data=(X_test,y_test),
callbacks=[tensorboard_callback, stop])
%tensorboard --logdir logs
```
### L1/L2 regularization
```python
Dense(64, input_dim=64, kernel_regularizer=regularizers.l2(0.01))
Dense(64, input_dim=64, kernel_regularizer=regularizers.l1(0.01))
```
Note:
The terms "L2 regularization" and "weight decay" are often used interchagebly, but they only mean the same thing for vanilla SGD optimization.
They mean different things for all other optimizers based on SGD (Adam, AdamW, RSMProp, etc).
See:
- https://www.fast.ai/2018/07/02/adam-weight-decay/
- https://arxiv.org/pdf/1711.05101.pdf
- https://bbabenko.github.io/weight-decay/
```
from tensorflow.keras import regularizers
```
### Weight Constraint
```python
tf.keras.constraints.MaxNorm(
max_value=2, axis=0
)
```
```
from tensorflow.keras.constraints import MaxNorm
```
### Dropout
```
from tensorflow.keras.layers import Dropout
%tensorboard --logdir logs
```
## Challenge
You will apply regularization strategies inside your neural network today, as you try to avoid overfitting it.
---
# Deploy (Learn)
## Overview
You've built a dope image classification model, but it's just sitting your Jupyter Notebook. What now? Well you deploy to some down stream application. TensorFlow supports three ways of deploying it's models:
- In-Browswer with TensorFlow.js
- API with TensorFlow Serving (TFX) or another Framework
- On-Device with TensorFlow Lite
You are already familiar with deploying a model as an API from Unit 3, so we will focus on deploying a model in browser. Both methods rely on the same core idea: save your weights and architecture information, load those parameters into application, and perform inference.
## Follow Along
### Train Your Model
### Save / Export Your Model
### Move Weights to Web Application
Not all models are small enough to work well in-browser. Many neural networks are deploy as micro-service APIs. Micro-service APIs are the architecture you studied during Unit 3.
## Challenge
You will be expected to be able to export your model weights and architecutre on the assignment.
# Custom Callbacks (Learn)
## Overview
Custom callbacks all you to access data at any point during the training: on batch end, on epoch end, on epoch start, on batch start. Our use case today is a simple one. Let's stop training once we reach a benchmark accuracy.
## Follow Along
## Challenge
Experiment with improving our custom callback function.
| true |
code
| 0.714952 | null | null | null | null |
|
# Video Super Resolution with OpenVINO
Super Resolution is the process of enhancing the quality of an image by increasing the pixel count using deep learning. This notebook applies Single Image Super Resolution (SISR) to frames in a 360p (480×360) video in 360p resolution. We use a model called [single-image-super-resolution-1032](https://docs.openvino.ai/latest/omz_models_model_single_image_super_resolution_1032.html) which is available from the Open Model Zoo. It is based on the research paper cited below.
Y. Liu et al., ["An Attention-Based Approach for Single Image Super Resolution,"](https://arxiv.org/abs/1807.06779) 2018 24th International Conference on Pattern Recognition (ICPR), 2018, pp. 2777-2784, doi: 10.1109/ICPR.2018.8545760.
**NOTE:** The Single Image Super Resolution (SISR) model used in this demo is not optimized for video. Results may vary depending on the video.
## Preparation
### Imports
```
import time
import urllib
from pathlib import Path
import cv2
import numpy as np
from IPython.display import HTML, FileLink, Pretty, ProgressBar, Video, clear_output, display
from openvino.inference_engine import IECore
from pytube import YouTube
```
### Settings
```
# Device to use for inference. For example, "CPU", or "GPU"
DEVICE = "CPU"
# 1032: 4x superresolution, 1033: 3x superresolution
MODEL_FILE = "model/single-image-super-resolution-1032.xml"
model_name = Path(MODEL_FILE).name
model_xml_path = Path(MODEL_FILE).with_suffix(".xml")
```
### Functions
```
def write_text_on_image(image: np.ndarray, text: str) -> np.ndarray:
"""
Write the specified text in the top left corner of the image
as white text with a black border.
:param image: image as numpy array with HWC shape, RGB or BGR
:param text: text to write
:return: image with written text, as numpy array
"""
font = cv2.FONT_HERSHEY_PLAIN
org = (20, 20)
font_scale = 4
font_color = (255, 255, 255)
line_type = 1
font_thickness = 2
text_color_bg = (0, 0, 0)
x, y = org
image = cv2.UMat(image)
(text_w, text_h), _ = cv2.getTextSize(
text=text, fontFace=font, fontScale=font_scale, thickness=font_thickness
)
result_im = cv2.rectangle(
img=image, pt1=org, pt2=(x + text_w, y + text_h), color=text_color_bg, thickness=-1
)
textim = cv2.putText(
img=result_im,
text=text,
org=(x, y + text_h + font_scale - 1),
fontFace=font,
fontScale=font_scale,
color=font_color,
thickness=font_thickness,
lineType=line_type,
)
return textim.get()
def load_image(path: str) -> np.ndarray:
"""
Loads an image from `path` and returns it as BGR numpy array.
:param path: path to an image filename or url
:return: image as numpy array, with BGR channel order
"""
if path.startswith("http"):
# Set User-Agent to Mozilla because some websites block requests
# with User-Agent Python
request = urllib.request.Request(url=path, headers={"User-Agent": "Mozilla/5.0"})
response = urllib.request.urlopen(url=request)
array = np.asarray(bytearray(response.read()), dtype="uint8")
image = cv2.imdecode(buf=array, flags=-1) # Loads the image as BGR
else:
image = cv2.imread(filename=path)
return image
def convert_result_to_image(result) -> np.ndarray:
"""
Convert network result of floating point numbers to image with integer
values from 0-255. Values outside this range are clipped to 0 and 255.
:param result: a single superresolution network result in N,C,H,W shape
"""
result = result.squeeze(0).transpose(1, 2, 0)
result *= 255
result[result < 0] = 0
result[result > 255] = 255
result = result.astype(np.uint8)
return result
```
## Load the Superresolution Model
Load the model in Inference Engine with `ie.read_network` and load it to the specified device with `ie.load_network`
```
ie = IECore()
net = ie.read_network(model=model_xml_path)
exec_net = ie.load_network(network=net, device_name=DEVICE)
```
Get information about network inputs and outputs. The Super Resolution model expects two inputs: 1) the input image, 2) a bicubic interpolation of the input image to the target size 1920x1080. It returns the super resolution version of the image in 1920x1800.
```
# Network inputs and outputs are dictionaries. Get the keys for the
# dictionaries.
original_image_key = list(exec_net.input_info)[0]
bicubic_image_key = list(exec_net.input_info)[1]
output_key = list(exec_net.outputs.keys())[0]
# Get the expected input and target shape. `.dims[2:]` returns the height
# and width. OpenCV's resize function expects the shape as (width, height),
# so we reverse the shape with `[::-1]` and convert it to a tuple
input_height, input_width = tuple(exec_net.input_info[original_image_key].tensor_desc.dims[2:])
target_height, target_width = tuple(exec_net.input_info[bicubic_image_key].tensor_desc.dims[2:])
upsample_factor = int(target_height / input_height)
print(f"The network expects inputs with a width of {input_width}, " f"height of {input_height}")
print(f"The network returns images with a width of {target_width}, " f"height of {target_height}")
print(
f"The image sides are upsampled by a factor {upsample_factor}. "
f"The new image is {upsample_factor**2} times as large as the "
"original image"
)
```
## Superresolution on Video
Download a YouTube\* video with PyTube and enhance the video quality with superresolution.
By default only the first 100 frames of the video are processed. Change NUM_FRAMES in the cell below to modify this.
**Note:**
- The resulting video does not contain audio.
- The input video should be a landscape video and have an input resolution of 360p (640x360) for the 1032 model, or 480p (720x480) for the 1033 model.
### Settings
```
VIDEO_DIR = "data"
OUTPUT_DIR = "output"
Path(OUTPUT_DIR).mkdir(exist_ok=True)
# Maximum number of frames to read from the input video. Set to 0 to read all frames.
NUM_FRAMES = 100
# The format for saving the result videos. vp09 is slow, but widely available.
# If you have FFMPEG installed, you can change FOURCC to `*"THEO"` to improve video writing speed.
FOURCC = cv2.VideoWriter_fourcc(*"vp09")
```
### Download and Prepare Video
```
# Use pytube to download a video. It downloads to the videos subdirectory.
# You can also place a local video there and comment out the following lines
VIDEO_URL = "https://www.youtube.com/watch?v=V8yS3WIkOrA"
yt = YouTube(VIDEO_URL)
# Use `yt.streams` to see all available streams. See the PyTube documentation
# https://python-pytube.readthedocs.io/en/latest/api.html for advanced
# filtering options
try:
Path(VIDEO_DIR).mkdir(exist_ok=True)
stream = yt.streams.filter(resolution="360p").first()
filename = Path(stream.default_filename.encode("ascii", "ignore").decode("ascii")).stem
stream.download(output_path=OUTPUT_DIR, filename=filename)
print(f"Video {filename} downloaded to {OUTPUT_DIR}")
# Create Path objects for the input video and the resulting videos
video_path = Path(stream.get_file_path(filename, OUTPUT_DIR))
except Exception:
# If PyTube fails, use a local video stored in the VIDEO_DIR directory
video_path = Path(rf"{VIDEO_DIR}/CEO Pat Gelsinger on Leading Intel.mp4")
# Path names for the result videos
superres_video_path = Path(f"{OUTPUT_DIR}/{video_path.stem}_superres.mp4")
bicubic_video_path = Path(f"{OUTPUT_DIR}/{video_path.stem}_bicubic.mp4")
comparison_video_path = Path(f"{OUTPUT_DIR}/{video_path.stem}_superres_comparison.mp4")
# Open the video and get the dimensions and the FPS
cap = cv2.VideoCapture(filename=str(video_path))
ret, image = cap.read()
if not ret:
raise ValueError(f"The video at '{video_path}' cannot be read.")
fps = cap.get(cv2.CAP_PROP_FPS)
frame_count = cap.get(cv2.CAP_PROP_FRAME_COUNT)
if NUM_FRAMES == 0:
total_frames = frame_count
else:
total_frames = min(frame_count, NUM_FRAMES)
original_frame_height, original_frame_width = image.shape[:2]
cap.release()
print(
f"The input video has a frame width of {original_frame_width}, "
f"frame height of {original_frame_height} and runs at {fps:.2f} fps"
)
```
Create superresolution video, bicubic video and comparison video. The superresolution video contains the enhanced video, upsampled with superresolution, the bicubic video is the input video upsampled with bicubic interpolation, the combination video sets the bicubic video and the superresolution side by side.
```
superres_video = cv2.VideoWriter(
filename=str(superres_video_path),
fourcc=FOURCC,
fps=fps,
frameSize=(target_width, target_height),
)
bicubic_video = cv2.VideoWriter(
filename=str(bicubic_video_path),
fourcc=FOURCC,
fps=fps,
frameSize=(target_width, target_height),
)
comparison_video = cv2.VideoWriter(
filename=str(comparison_video_path),
fourcc=FOURCC,
fps=fps,
frameSize=(target_width * 2, target_height),
)
```
### Do Inference
Read video frames and enhance them with superresolution. Save the superresolution video, the bicubic video and the comparison video to file.
The code in this cell reads the video frame by frame. Each frame is resized and reshaped to network input shape and upsampled with bicubic interpolation to target shape. Both the original and the bicubic image are propagated through the network. The network result is a numpy array with floating point values, with a shape of (1,3,1920,1080). This array is converted to an 8-bit image with shape (1080,1920,3) and written to `superres_video`. The bicubic image is written to `bicubic_video` for comparison. Lastly, the bicubic and result frames are combined side by side and written to `comparison_video`. A progress bar shows the progress of the process. Inference time is measured, as well as total time to process each frame, which includes inference time as well as the time it takes to process and write the video.
```
start_time = time.perf_counter()
frame_nr = 0
total_inference_duration = 0
progress_bar = ProgressBar(total=total_frames)
progress_bar.display()
cap = cv2.VideoCapture(filename=str(video_path))
try:
while cap.isOpened():
ret, image = cap.read()
if not ret:
cap.release()
break
if frame_nr >= total_frames:
break
# Resize the input image to network shape and convert from (H,W,C) to
# (N,C,H,W)
resized_image = cv2.resize(src=image, dsize=(input_width, input_height))
input_image_original = np.expand_dims(resized_image.transpose(2, 0, 1), axis=0)
# Resize and reshape the image to the target shape with bicubic
# interpolation
bicubic_image = cv2.resize(
src=image, dsize=(target_width, target_height), interpolation=cv2.INTER_CUBIC
)
input_image_bicubic = np.expand_dims(bicubic_image.transpose(2, 0, 1), axis=0)
# Do inference
inference_start_time = time.perf_counter()
result = exec_net.infer(
inputs={
original_image_key: input_image_original,
bicubic_image_key: input_image_bicubic,
}
)[output_key]
inference_stop_time = time.perf_counter()
inference_duration = inference_stop_time - inference_start_time
total_inference_duration += inference_duration
# Transform inference result into an image
result_frame = convert_result_to_image(result=result)
# Write resulting image and bicubic image to video
superres_video.write(image=result_frame)
bicubic_video.write(image=bicubic_image)
stacked_frame = np.hstack((bicubic_image, result_frame))
comparison_video.write(image=stacked_frame)
frame_nr = frame_nr + 1
# Update progress bar and status message
progress_bar.progress = frame_nr
progress_bar.update()
if frame_nr % 10 == 0 or frame_nr == total_frames:
clear_output(wait=True)
progress_bar.display()
display(
Pretty(
f"Processed frame {frame_nr}. Inference time: "
f"{inference_duration:.2f} seconds "
f"({1/inference_duration:.2f} FPS)"
)
)
except KeyboardInterrupt:
print("Processing interrupted.")
finally:
superres_video.release()
bicubic_video.release()
comparison_video.release()
end_time = time.perf_counter()
duration = end_time - start_time
print(f"Video's saved to {comparison_video_path.parent} directory.")
print(
f"Processed {frame_nr} frames in {duration:.2f} seconds. Total FPS "
f"(including video processing): {frame_nr/duration:.2f}. "
f"Inference FPS: {frame_nr/total_inference_duration:.2f}."
)
```
### Show Side-by-Side Video of Bicubic and Superresolution Version
```
if not comparison_video_path.exists():
raise ValueError("The comparison video does not exist.")
else:
video_link = FileLink(comparison_video_path)
video_link.html_link_str = "<a href='%s' download>%s</a>"
display(
HTML(
f"Showing side by side comparison. If you cannot see the video in "
"your browser, please click on the following link to download "
f"the video<br>{video_link._repr_html_()}"
)
)
display(Video(comparison_video_path, width=800, embed=True))
```
| true |
code
| 0.709114 | null | null | null | null |
|
# Notebook contents:
This notebook contains a lecture. The code for generating plots are found at the of the notebook. Links below.
- [presentation](#Session-1b:)
- [code for plots](#Code-for-plots)
# Session 2:
## Effective ML
*Andreas Bjerre-Nielsen*
## Vaaaamos
```
import warnings
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
```
## Agenda
1. [model bias and variance](#Model-bias-and-variance)
1. [model building](#Model-building)
1. model selection
- [basic validation](#Model-selection)
- [cross validation](#Cross-validation)
- [tools for selection](#Tools-for-model-selection)
# Review
## Two agendas (1)
What are the objectives of empirical research?
1. *causation*: what is the effect of a particular variable on an outcome?
2. *prediction*: find some function that provides a good prediction of $y$ as a function of $x$
## Two agendas (2)
How might we express the agendas in a model?
$$ y = \alpha + \beta x + \varepsilon $$
- *causation*: interested in $\hat{\beta}$
- *prediction*: interested in $\hat{y}$
## Model fitting (1)
*How does over- and underfitting look like for regression?*
```
f_bias_var['regression'][2]
```
## Model fitting (2)
*What does underfitting and overfitting look like for classification?*
```
f_bias_var['classification'][2]
```
## What tools have seen?
- Supervised learning (having a target variable)
- Classification problems: Perceptron, Adaline, Logistic regression
- Regression problems: Linear regression
- We learned about optimization: gradient descent
- How can we say whether a model generalizes:
- We split data randomly into training and testing data.
## Fitting a polynomial (1)
Polyonomial: $f(x) = 2+8*x^4$
Try models of increasing order polynomials.
- Split data into train and test (50/50)
- For polynomial order 0 to 9:
- Iteration n: $y = \sum_{k=0}^{n}(\beta_k\cdot x^k)+\varepsilon$. (Taylor expansion)
- Estimate order n model on training data
- Evaluate with on test data with $\log RMSE$ ($= \log \sqrt{SSE/n}$)
## Fitting a polynomial (2)
We generate samples of data from true model (fourth order polynomial).
```
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
def true_fct(X):
return 2+X**4
n_samples = 25
np.random.seed(0)
X_train = np.random.normal(size=(n_samples,1))
y_train = true_fct(X_train).reshape(-1) + np.random.randn(n_samples)
X_test = np.random.normal(size=(n_samples,1))
y_test = true_fct(X_test).reshape(-1) + np.random.randn(n_samples)
```
## Fitting a polynomial (3)
We estimate the polynomials and store MSE for train and test:
```
from sklearn.metrics import mean_squared_error as mse
test_mse = []
train_mse = []
parameters = []
max_degree = 15
degrees = range(max_degree+1)
for p in degrees:
X_train_p = PolynomialFeatures(degree=p).fit_transform(X_train)
X_test_p = PolynomialFeatures(degree=p).fit_transform(X_test)
reg = LinearRegression().fit(X_train_p, y_train)
train_mse += [mse(reg.predict(X_train_p),y_train)]
test_mse += [mse(reg.predict(X_test_p),y_test)]
parameters.append(reg.coef_)
```
## Fitting a polynomial (4)
*So what happens to the model performance in- and out-of-sample?*
```
degree_index = pd.Index(degrees,name='Polynomial degree ~ model complexity')
ax = pd.DataFrame({'Train set':train_mse, 'Test set':test_mse})\
.set_index(degree_index).plot(figsize=(14,5), logy=True)
ax.set_ylabel('Mean squared error')
```
## Fitting a polynomial (5)
*Quiz: Why does it go wrong on the test data?*
- more spurious parameters
- (we include variables beyond those in true model, i.e. $x^4$ and the bias term)
- the coefficient size increases (next slide)
## Fitting a polynomial (6)
*What do you mean coefficient size increase?*
```
order_idx = pd.Index(range(len(degrees)),name='Polynomial order')
ax = pd.DataFrame(parameters,index=order_idx)\
.abs().mean(1).plot(figsize=(14,5),logy=True)
ax.set_ylabel('Mean parameter size')
```
## Fitting a polynomial (7)
*How else could we visualize this problem?*
```
f_bias_var['regression'][2]
```
# The curse of overfitting and regularization
## Looking for a remedy
*How might we solve the overfitting problem?*
- too many number of variables (spurious relations)
- excessive magnitude of the coefficient size of variables
Could we incorporate these two issues in our optimization problem?
## Regularization (1)
*Why do we regularize?*
- To mitigate overfitting > better model predictions
*How do we regularize?*
- We make models which are less complex:
- reducing the **number** of coefficient;
- reducing the **size** of the coefficients.
## Regularization (2)
*What does regularization look like?*
We add a penalty term our optimization procedure:
$$ \text{arg min}_\beta \, \underset{\text{MSE=SSE/n}}{\underbrace{E[(y_0 - \hat{f}(x_0))^2]}} + \underset{\text{penalty}}{\underbrace{\lambda \cdot R(\beta)}}$$
Introduction of penalties implies that increased model complexity has to be met with high increases precision of estimates.
## Regularization (3)
*What are some used penalty functions?*
The two most common penalty functions are L1 and L2 regularization.
- L1 regularization (***Lasso***): $R(\beta)=\sum_{j=1}^{p}|\beta_j|$
- Makes coefficients sparse, i.e. selects variables by removing some (if $\lambda$ is high)
- L2 regularization (***Ridge***): $R(\beta)=\sum_{j=1}^{p}\beta_j^2$
- Reduce coefficient size
- Fast due to analytical solution
*To note:* The *Elastic Net* uses a combination of L1 and L2 regularization.
## Regularization (4)
*How the Lasso (L1 reg.) deviates from OLS*
<center><img src='http://rasbt.github.io/mlxtend/user_guide/general_concepts/regularization-linear_files/l1.png' alt="Drawing" style="width: 800px;"/></center>
## Regularization (5)
*How the Ridge regression (L2 reg.) deviates from OLS*
<center><img src='http://rasbt.github.io/mlxtend/user_guide/general_concepts/regularization-linear_files/l2.png' alt="Drawing" style="width: 550px;"/></center>
## Regularization (6)
*How might we describe the $\lambda$ of Lasso and Ridge?*
These are hyperparameters that we can optimize over.
## Regularization (7)
*Is there a generalization of of Lasso and Ridge?*
Yes, the elastic net allows both types of regularization. Thererfore, it has two hyperparameters.
# Implementation details
## Underfitting remedies
*Is it possible to solve the underfitting problem?*
Yes, there are in general two ways.
- Using polynomial interactions of all features.
- This is known as Taylor expansion
- Note: we need to use regularization too curb impact of overfitting!
- Using non-linear models who can capture all patterns.
- These are called universal approximators
- Return to an overview of these in Session 14.
## Underfitting remedies (2)
*Some of the models we see here, e.g. Perceptrons, seem too simple - are they ever useful?*
- No, not for serious machine learning.
- But for exposition (your learning), yes.
- However, the perceptron and related models are building blocks for building neural networks.
## The devils in the details (1)
*So we just run regularization?*
We need to rescale our features:
- convert to zero mean:
- standardize to unit std:
Compute in Python:
- option 1: `StandardScaler` in `sklearn` (RECOMMENDED)
- option 2: `(X - np.mean(X)) / np.std(X)`
## The devils in the details (2)
*So we just scale our test and train?*
# NO
Fit to the distribution in the **training data first**, then rescale train and test! See more [here](https://stats.stackexchange.com/questions/174823/how-to-apply-standardization-normalization-to-train-and-testset-if-prediction-i).
## The devils in the details (3)
*So we just rescale before using polynomial features?*
# NO
Otherwise the interacted varaibles are not gaussian distributed.
## The devils in the details (4)
*Does sklearn's `PolynomialFeatures` work for more than variable?*
# Model bias and variance
## Bias and variance (1)
*How do we describe the modelling error?*
From [Wikipedia](https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff) 2019:
- model **bias**: _an error from erroneous assumptions in the learning algorithm_
- high bias can cause an algorithm to miss the relevant relations between features and target outputs (**underfitting**)
- model **variance**: _an error from sensitivity to small fluctuations in the training set_
- high variance can cause an algorithm to model the random noise in the training data, rather than the intended outputs (**overfitting**).
## Bias and variance (2)
*So what is overfitting?*
Overfitting is: low bias / high variance
- traning our model captures all patterns but we also find some irrelevant
- reacts too much to training sample errors
- some errors are just noise, and thus we find too many spurious relations
- examples of causes:
- too much polynomial expansion of variables (`PolynomialFeatures`)
- non-linear/logistic without properly tuned hyperparameters:
- Decision Trees, Support Vector Machines or Neural Networks
## Bias and variance (3)
*So what is underfitting?*
Underfitting is: high bias / low variance
- oversimplification of models, cannot approximate all patterns found
- examples of causes:
- linear and logistic regression (without polynomial expansion)
## Bias and variance (4)
*Not so fast.. OLS is unbiased, right?*
Yes, OLS is unbiased. But...?
- But .. only by assumption..
- Requires we know the true form of the model.
- However, we never know do..
*What happens if we introduce regularization?*
- Then model is no longer unbiased.
- (if we assume the model is true)
# Model building
## Model pipelines (1)
*Is there a smart way to build ML models?*
Yes, we build a pipeline (input (tidy) -> target)
- Preprocessing data
- Standard: adding polynomials, imputation, rescaling
- Unsupervised learning
- Supervised learning
## Model pipelines (2)
*How does the pipeline look? Is there data leakage?*
<center><img src='https://github.com/rasbt/python-machine-learning-book-2nd-edition/raw/master/code/ch06/images/06_01.png' alt="Drawing" style="width: 700px;"/></center>
## Model pipelines (3)
*What are the advantages of using a pipeline?*
- Ensures good practice - we only fit on training data.
- No leakage of data from train to test!
- Much less code!
## Applying a model pipeline (1)
*What would this look like in Python?*
```
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
pipe_preproc = make_pipeline(PolynomialFeatures(),
StandardScaler())
print(pipe_preproc.steps[0])
print(pipe_preproc.steps[1])
```
## Applying a model pipeline (2)
*Does this remind you of something?*
# YES!
### Method chaining from Pandas
## Applying a model pipeline (3)
*Let's some load Boston house price data*
```
from sklearn.datasets import load_boston
boston = load_boston()
# print(boston['DESCR'])
# print('\n'.join(load_boston()['DESCR'].split('\n')[12:26]))
X = boston.data # features
y = boston.target # target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
```
## Applying a model pipeline (4)
*And how do I apply the pipe on the data?*
```
pipe_preproc = make_pipeline(PolynomialFeatures(),
StandardScaler()) # apply preproc - fit on train
X_train_prep = pipe_preproc.fit_transform(X_train) # transform training data
X_test_prep = pipe_preproc.transform(X_test) # transform test data
```
## Applying a model pipeline (5)
*What would it like look if we did use the pipe..?*
The more steps we have, the more code we save.
```
poly_trans = PolynomialFeatures()
scaler = StandardScaler()
# we call both transformations twice on both test and train
X_train_poly = poly_trans.fit_transform(X_train)
X_test_poly = poly_trans.transform(X_test)
X_train_prep_alt = scaler.fit_transform(X_train_poly)
X_test_prep_alt = scaler.transform(X_test_poly)
```
# Model selection
## Measuring the problem
*Does machine learning work out of the box?*
- In some cases ML works quite well out of the box.
- Often ML requires making careful choices.
- Note that automated machine learning packages and services exist.
- E.g. AutoML - this a hot research topic
*Which choices are to be made?*
- We need to pick model building hyperparameters.
- E.g elastic net hyperparameters: $\lambda$ for L1 and L2 regularization
- i.e. $\lambda$ for Lasso, Ridge and Elastic Net
## Model validation (1)
*How do we measure our model's performance for different hyperparameters?*
- Remember we cannot use the test set.
*Could we somehow mimick what we do with test data?*
- Yes, we can split the remaining non-test data into training and validation data:
- we train model for various hyperparameters on training data;
- pick the hyperparameters which performs best on validation data.
## Model validation (2)
*The non-test data is split into training and validation*
<center><img src='https://github.com/rasbt/python-machine-learning-book-2nd-edition/raw/master/code/ch06/images/06_02.png' alt="Drawing" style="width: 500px;"/></center>
## Model validation (3)
*What would this look like in Python?*
```
# splitting into development (2/3) and test data (1/3)
X_dev, X_test, y_dev, y_test = train_test_split(X, y, test_size=1/3, random_state=1)
# splitting development into train (1/3) and validation (1/3)
X_train, X_val, y_train, y_val = train_test_split(X_dev, y_dev, test_size=1/2, random_state=1)
```
## Model validation (4)
Let's train a linear regression model
```
from sklearn.linear_model import Lasso, LinearRegression
pipe_lr = make_pipeline(PolynomialFeatures(include_bias=True),
StandardScaler(),
LinearRegression())
pipe_lr.fit(X_dev, y_dev)
```
## Model validation (5)
Let's find the Lasso model which performs best in the validation set
```
from sklearn.metrics import mean_squared_error as mse
perform = []
lambdas = np.logspace(-4, 4, 33)
for lambda_ in lambdas:
pipe_lasso = make_pipeline(PolynomialFeatures(include_bias=True),
StandardScaler(),
Lasso(alpha=lambda_, random_state=1))
pipe_lasso.fit(X_train, y_train)
y_pred = pipe_lasso.predict(X_val)
perform.append(mse(y_pred, y_val))
hyperparam_perform = pd.Series(perform,index=lambdas)
optimal = hyperparam_perform.nsmallest(1)
print('Optimal lambda:', optimal.index[0])
print('Validation MSE: %.3f' % optimal.values[0])
```
## Model validation (6)
Let's compare the performance of the Lasso vs. Linear Regression
```
# insert optimal lambda into new model
pipe_lasso = make_pipeline(PolynomialFeatures(include_bias=False),
StandardScaler(),
Lasso(alpha=optimal.index[0]))
# fit new model on all of the development (non-test) data
pipe_lasso.fit(X_dev, y_dev)
# compare model performance on test data
print('Lasso', round(mse(pipe_lasso.predict(X_test),y_test), 1))
print('LinReg', round(mse(pipe_lr.predict(X_test),y_test), 1))
```
## Smarter validation
*Is this approach the smartest way for deciding on choice of hyperparameters?*
# NO
Our model choice depends a lot on which sample we pick. Could we use more of the data?
# Cross validation
## The holdout method
*How do we got the more out of the data?*
We reuse the data in the development set repeatedly
- We test on all the data
- Rotate which parts of data is used for test and train.
## Leave-one-out CV
*How do we got the most of the data?*
The most robust approach
- Each single observation in the training data we use the remaining data to train.
- Makes number of models equal to the number of observations
- Very computing intensive - does not scale!
LOOCV
## K fold method (1)
*How do balance computing time vs. overfitting?*
We split the sample into $K$ even sized test bins.
- For each test bin $k$ we use the remaining data for training.
Advantages:
- We use all our data for testing.
- Training is done with 100-(100/K) pct. of the data, i.e. 90 pct. for K=10.
## K fold method (2)
In K-fold cross validation we average the errors.
<center><img src='https://github.com/rasbt/python-machine-learning-book-2nd-edition/raw/master/code/ch06/images/06_03.png' alt="Drawing" style="width: 900px;"/></center>
## K fold method (3)
*How to do K-fold cross validation to select our model?*
We compute MSE for every lambda and every fold (nested for loop)
## K fold method (3)
Code for implementation
```
from sklearn.model_selection import KFold
kfolds = KFold(n_splits=10)
folds = list(kfolds.split(X_dev, y_dev))
# outer loop: lambdas
mseCV = []
for lambda_ in lambdas:
# inner loop: folds
mseCV_ = []
for train_idx, val_idx in folds:
# train model and compute MSE on test fold
pipe_lassoCV = make_pipeline(PolynomialFeatures(degree=2, include_bias=True),
StandardScaler(),
Lasso(alpha=lambda_, random_state=1))
X_train, y_train = X_dev[train_idx], y_dev[train_idx]
X_val, y_val = X_dev[val_idx], y_dev[val_idx]
pipe_lassoCV.fit(X_train, y_train)
mseCV_.append(mse(pipe_lassoCV.predict(X_val), y_val))
# store result
mseCV.append(mseCV_)
# convert to DataFrame
lambdaCV = pd.DataFrame(mseCV, index=lambdas)
```
# K fold method (4)
Training the model with optimal hyperparameters and compare MSE
```
# choose optimal hyperparameters
optimal_lambda = lambdaCV.mean(axis=1).nsmallest(1)
# retrain/re-estimate model using optimal hyperparameters
pipe_lassoCV = make_pipeline(PolynomialFeatures(include_bias=False),
StandardScaler(),
Lasso(alpha=optimal_lambda.index[0], random_state=1))
pipe_lassoCV.fit(X_dev,y_dev)
# compare performance
models = {'Lasso': pipe_lasso, 'Lasso CV': pipe_lassoCV, 'LinReg': pipe_lr}
for name, model in models.items():
score = mse(model.predict(X_test),y_test)
print(name, round(score, 1))
```
## K fold method (5)
*What else could we use cross-validation for?*
- Getting more evaluations of our model performance.
- We can cross validate at two levels:
- Outer: we make multiple splits of test and train/dev.
- Inner: within each train/dev. dataset we make cross validation to choose hyperparameters
# Tools for model selection
## Learning curves (1)
*What does a model that balances over- and underfitting look like?*
<center><img src='https://github.com/rasbt/python-machine-learning-book-2nd-edition/raw/master/code/ch06/images/06_04.png' alt="Drawing" style="width: 700px;"/></center>
## Learning curves (2)
*Is it easy to make learning curves in Python?*
```
from sklearn.model_selection import learning_curve
train_sizes, train_scores, test_scores = \
learning_curve(estimator=pipe_lassoCV,
X=X_dev,
y=y_dev,
train_sizes=np.arange(0.2, 1.05, .05),
scoring='neg_mean_squared_error',
cv=3)
mse_ = pd.DataFrame({'Train':-train_scores.mean(axis=1),
'Test':-test_scores.mean(axis=1)})\
.set_index(pd.Index(train_sizes,name='sample size'))
print(mse_.head(5))
```
## Learning curves (3)
```
f_learn, ax = plt.subplots(figsize=(10,4))
ax.plot(train_sizes,-test_scores.mean(1), alpha=0.25, linewidth=2, label ='Test', color='blue')
ax.plot(train_sizes,-train_scores.mean(1),alpha=0.25, linewidth=2, label='Train', color='orange')
ax.set_title('Mean performance')
ax.set_ylabel('Mean squared error')
ax.set_yscale('log')
ax.legend()
```
## Learning curves (4)
```
f_learn, ax = plt.subplots(figsize=(10,4))
plot_info = [(train_scores, 'Train','orange'), (test_scores, 'Test','blue')]
for scores, label, color in plot_info:
ax.fill_between(train_sizes, -scores.min(1), -scores.max(1),
alpha=0.25, label =label, color=color)
ax.set_title('Range of performance (min, max)')
ax.set_ylabel('Mean squared error')
ax.set_yscale('log')
ax.legend()
```
## Validation curves (1)
*Can we plot the optimal hyperparameters?*
```
from sklearn.model_selection import validation_curve
train_scores, test_scores = \
validation_curve(estimator=pipe_lasso,
X=X_dev,
y=y_dev,
param_name='lasso__alpha',
param_range=lambdas,
scoring='neg_mean_squared_error',
cv=3)
mse_score = pd.DataFrame({'Train':-train_scores.mean(axis=1),
'Validation':-test_scores.mean(axis=1),
'lambda':lambdas})\
.set_index('lambda')
print(mse_score.Validation.nsmallest(1))
```
## Validation curves (2)
```
f,ax = plt.subplots(figsize=(10,6))
mse_score.plot(logx=True, logy=True, ax=ax)
ax.axvline(mse_score.Validation.idxmin(), color='black',linestyle='--')
```
## Grid search (1)
*How do we search for two or more optimal parameters? (e.g. elastic net)*
- Goal: find the optimal parameter combination: $$\lambda_1^*,\lambda_2^*=\arg\min_{\lambda_1,\lambda_2}MSE^{CV}(X_{train},y_{train})$$
- Option 1: We can loop over the joint grid of parameters.
- One level for each parameter.
- Caveats: a lot of code / SLOW
- Option 2: sklearn has `GridSearchCV` has a tool which tests all parameter combinations.
## Grid search (2)
*How does this look in Python?*
```
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import ElasticNet
pipe_el = make_pipeline(PolynomialFeatures(include_bias=False),
StandardScaler(),
ElasticNet())
gs = GridSearchCV(estimator=pipe_el,
param_grid={'elasticnet__alpha':np.logspace(-4,4,10)*2,
'elasticnet__l1_ratio':np.linspace(0,1,10)},
scoring='neg_mean_squared_error',
n_jobs=4,
cv=10)
models['ElasicNetCV'] = gs.fit(X_dev, y_dev)
```
- Notation: double underscore between estimator and hyperparameter, e.g. 'est__hyperparam'
- Scoring: negative MSE as we're maximizing the score ~ minimize MSE.
## Grid search (3)
*What does the grid search yield?*
```
for name, model in models.items():
score = mse(model.predict(X_test),y_test)
print(name, round(score, 2))
print()
print('CV params:', gs.best_params_)
```
## Grid search (4)
*What if we have 10,000 parameter combinations?*
- Option 1: you buy a cluster on Amazon, learn how to parallelize across computers.
- Option 2: you drop some of the parameter values
- Option 3: `RandomizedSearchCV` searches a subset of the combinations.
## Miscellanous
*How do we get the coefficient from the models?*
```
lasso_model = pipe_lassoCV.steps[2][1] # extract model from pipe
lasso_model.coef_[0:13] # extract coeffiecients from model
```
# The end
[Return to agenda](#Agenda)
# Code for plots
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import seaborn as sns
plt.style.use('ggplot')
%matplotlib inline
SMALL_SIZE = 16
MEDIUM_SIZE = 18
BIGGER_SIZE = 20
plt.rc('font', size=SMALL_SIZE) # controls default text sizes
plt.rc('axes', titlesize=SMALL_SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=MEDIUM_SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SMALL_SIZE) # legend fontsize
plt.rc('figure', titlesize=BIGGER_SIZE) # fontsize of the figure title
plt.rcParams['figure.figsize'] = 10, 4 # set default size of plots
```
### Plots of ML types
```
%run ../base/ML_plots.ipynb
```
| true |
code
| 0.58516 | null | null | null | null |
|
In [The Mean as Predictor](mean_meaning), we found that the mean had some good
properties as a single best predictor for a whole distribution.
* The mean gives a total prediction error of zero. Put otherwise, on average,
your prediction error is zero.
* The mean gives the lowest squared error. Put otherwise, the mean gives the
lowest average squared difference from the observed value.
Now we can consider what predictor we should use when predicting one set of values, from a different set of values.
We load our usual libraries.
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Make plots look a little bit more fancy
plt.style.use('fivethirtyeight')
# Print to 4 decimal places, show tiny values as 0
np.set_printoptions(precision=4, suppress=True)
import pandas as pd
```
We start with some [data on chronic kidney
disease]({{ site.baseurl }}/data/chronic_kidney_disease).
Download the data to your computer via this link: [ckd_clean.csv]({{
site.baseurl }}/data/ckd_clean.csv).
This is a data table with one row per patient and one column per test on that
patient. Many of columns are values from blood tests. Most of the patients
have chronic kidney disease.
To make things a bit easier this dataset is a version from which we have already dropped all missing values. See the dataset page linked above for more detail.
```
# Run this cell
ckd = pd.read_csv('ckd_clean.csv')
ckd.head()
```
We are interested in two columns from this data frame, "Packed Cell Volume" and "Hemoglobin".
[Packed Cell Volume](https://en.wikipedia.org/wiki/Hematocrit) (PCV) is a
measurement of the percentage of blood volume taken up by red blood cells. It
is a measurement of anemia, and anemia is a common consequence of chronic
kidney disease.
```
# Get the packed cell volume values as a Series.
pcv_series = ckd['Packed Cell Volume']
# Show the distribution.
pcv_series.hist()
```
"Hemoglobin" (HGB) is the concentration of the
[hemoglobin](https://en.wikipedia.org/wiki/Hemoglobin) molecule in blood, in
grams per deciliter. Hemoglobin is the iron-containing protein in red blood
cells that carries oxygen to the tissues.
```
# Get the hemoglobin concentration values as a Series.
hgb_series = ckd['Hemoglobin']
# Show the distribution.
hgb_series.hist()
```
We convert these Series into arrays, to make them simpler to work with. We do
this with the Numpy `array` function, that makes arrays from many other types
of object.
```
pcv = np.array(pcv_series)
hgb = np.array(hgb_series)
```
## Looking for straight lines
The [Wikipedia page for PCV](https://en.wikipedia.org/wiki/Hematocrit) says (at
the time of writing):
> An estimated hematocrit as a percentage may be derived by tripling the
> hemoglobin concentration in g/dL and dropping the units.
> [source](https://www.doctorslounge.com/hematology/labs/hematocrit.htm).
This rule-of-thumb suggests that the values for PCV will be roughly three times
the values for HGB.
Therefore, if we plot the HGB values on the x-axis of a plot, and the PCV
values on the y-axis, we should see something that is roughly compatible with a
straight line going through 0, 0, and with a slope of about 3.
Here is the plot. This time, for fun, we add a label to the X and Y axes with
`xlabel` and `ylabel`.
```
# Plot HGB on the x axis, PCV on the y axis
plt.plot(hgb, pcv, 'o')
plt.xlabel('Hemoglobin concentration')
plt.ylabel('Packed cell volume')
```
The `'o'` argument to the plot function above is a "plot marker". It tells
Matplotlib to plot the points as points, rather than joining them with lines.
The markers for the points will be filled circles, with `'o'`, but we can also
ask for other symbols such as plus marks (with `'+'`) and crosses (with `'x'`).
The line does look a bit like it has a slope of about 3. But - is that true?
Is the *best* slope 3? What slope would we find, if we looked for the *best*
slope? What could *best* mean, for *best slope*?
## Adjusting axes
We would like to see what this graph looks like in relation to the origin -
x=0, y=0. In order to this, we can add a `plt.axis` function call, like this:
```
# Plot HGB on the x axis, PCV on the y axis
plt.plot(hgb, pcv, 'o')
plt.xlabel('Hemoglobin concentration')
plt.ylabel('Packed cell volume')
# Set the x axis to go from 0 to 18, y axis from 0 to 55.
plt.axis([0, 18, 0, 55])
```
It does look plausible that this line goes through the origin, and that makes
sense. All hemoglobin is in red blood cells; we might expect the volume of red
blood cells to be zero when the hemoglobin concentration is zero.
## Putting points on plots
Before we go on, we will need some machinery to plot arbitrary points on plots.
In fact this works in exactly the same way as the points you have already seen
on plots. We use the `plot` function, with a suitable plot marker. The x
coordinates of the points go in the first argument, and the y coordinates go in
the second.
To plot a single point, pass a single x and y coordinate value:
```
plt.plot(hgb, pcv, 'o')
# A red point at x=5, y=40
plt.plot(5, 40, 'o', color='red')
```
To plot more than one point, pass multiple x and y coordinate values:
```
plt.plot(hgb, pcv, 'o')
# Two red points, one at [5, 40], the other at [10, 50]
plt.plot([5, 10], [40, 50], 'o', color='red')
```
## The mean as applied to plots
We want a straight line that fits these points.
The straight line should do the best job it can in *predicting* the PCV values from the HGB values.
We found that the mean was a good predictor for a distribution of values. We
could try and find a line or something similar that went through the mean of
the PCV values, at any given HGB value.
Let's split the HGB values up into bins centered on 7.5, 8.5, and so on. Then
we take the mean of all the PCV values corresponding to HGB values between 7
and 8, 8 and 9, and so on.
```
# The centers for our HGB bins
hgb_bin_centers = np.arange(7.5, 17.5)
hgb_bin_centers
# The number of bins
n_bins = len(hgb_bin_centers)
n_bins
```
Show the center of the bins on the x axis of the plot.
```
plt.plot(hgb, pcv, 'o')
plt.plot(hgb_bin_centers, np.zeros(n_bins), 'o', color='red')
```
Take the mean of the PCV values for each bin.
```
pcv_means = np.zeros(n_bins)
for i in np.arange(n_bins):
mid = hgb_bin_centers[i]
# Boolean identifing indices withing the HGB bin
fr_within_bin = (hgb >= mid - 0.5) & (hgb < mid + 0.5)
# Take the mean of the corresponding PCV values
pcv_means[i] = np.mean(pcv[fr_within_bin])
pcv_means
```
These means should be good predictors for PCV values, given an HGB value. We
check the bin of the HGB value and take the corresponding PCV mean as the
prediction.
Here is a plot of the means of PCV for every bin:
```
plt.plot(hgb, pcv, 'o')
plt.plot(hgb_bin_centers, pcv_means, 'o', color='red')
```
## Finding a predicting line
The means per bin give some prediction of the PCV values from the HGB. Can we
do better? Can we find a line that predicts the PCV data from the HGB data?
Remember, any line can be fully described by an *intercept* $c$ and a *slope*
$s$. A line predicts the $y$ values from the $x$ values, using the slope $s$
and the intercept $c$:
$$
y = c + x * s
$$
The *intercept* is the value of the line when x is equal to 0. It is therefore
where the line crosses the y axis.
In our case, let us assume the intercept is 0. We will assume PCV of 0 if
there is no hemoglobin.
Now we want to find a good *slope*. The *slope* is the amount that the y
values increase for a one unit increase in the x values. In our case, it is
the increase in the PCV for a 1 gram / deciliter increase in the HGB.
Let's guess the slope is 3, as Wikipedia told us it should be:
```
slope = 3
```
Remember our line prediction for y (PCV) is:
$$
y = c + x * s
$$
where x is the HGB. In our case we assume the intercept is 0, so:
```
pcv_predicted = hgb * slope
```
Plot the predictions in red on the original data in blue.
```
plt.plot(hgb, pcv, 'o')
plt.plot(hgb, pcv_predicted, 'o', color='red')
```
The red are the predictions, the blue are the original data. At each PCV value
we have a prediction, and therefore, an error in our prediction; the difference
between the predicted value and the actual values.
```
error = pcv - pcv_predicted
error[:10]
```
In this plot, for each point, we draw a thin dotted line between the prediction
of PCV for each point, and its actual value.
```
plt.plot(hgb, pcv, 'o')
plt.plot(hgb, pcv_predicted, 'o', color='red')
# Draw a line between predicted and actual
for i in np.arange(len(hgb)):
x = hgb[i]
y_0 = pcv_predicted[i]
y_1 = pcv[i]
plt.plot([x, x], [y_0, y_1], ':', color='black', linewidth=1)
```
## What is a good line?
We have guessed a slope, and so defined a line. We calculated the errors from
our guessed line.
How would we decide whether our slope was a good one? Put otherwise, how would
we decide when we have a good line?
A good line should have small prediction errors. That is, the line should give
a good prediction of the points. That is, the line should result in small
*errors*.
We would like a slope that gives us the smallest error.
## One metric for the line
[The Mean as Predictor](mean_meaning) section showed that the mean is the value
with the smallest squared distance from the other values in the distribution.
The mean is the predictor value that minimizes the sum of squared distances
from the other values.
We can use the same metric for our line. Instead of using a single vector as a
predictor, now we are using the values on the line as predictors. We want the
HGB slope, in our case, that gives the best predictors of the PCV values.
Specifically, we want the slope that gives the smallest sum of squares
difference between the line prediction and the actual values.
We have already calculated the prediction and error for our slope of 3, but
let's do it again, and then calculate the *sum of squares* of the error:
```
slope = 3
pcv_predicted = hgb * slope
error = pcv - pcv_predicted
# The sum of squared error
np.sum(error ** 2)
```
We are about to do this calculation many times, for many different slopes. We
need a *function*.
In the function below, we are using [function world](../07/functions)
to get the values of `hgb` and `pcv` defined here at the top level,
outside *function world*. The function can see these values, from
function world.
```
def sos_error(slope):
predicted = hgb * slope # 'hgb' comes from the top level
error = pcv - predicted # 'pcv' comes from the top level
return np.sum(error ** 2)
```
First check we get the same answer as the calculation above:
```
sos_error(3)
```
Does 3.5 give a higher or lower sum of squared error?
```
sos_error(3.5)
```
Now we can use the same strategy as we used in the [mean meaning](mean_meaning)
page, to try lots of slopes, and find the one that gives the smallest sum of
squared error.
```
# Slopes to try
some_slopes = np.arange(2, 4, 0.01)
n_slopes = len(some_slopes)
# Try all these slopes, calculate and record sum of squared error
sos_errors = np.zeros(n_slopes)
for i in np.arange(n_slopes):
slope = some_slopes[i]
sos_errors[i] = sos_error(slope)
# Show the first 10 values
sos_errors[:10]
```
We plot the slopes we have tried, on the x axis, against the sum of squared
error, on the y-axis.
```
plt.plot(some_slopes, sos_errors)
plt.xlabel('Candidate slopes')
plt.ylabel('Sum of squared error')
```
The minimum of the sum of squared error is:
```
np.min(sos_errors)
```
We want to find the slope that corresponds to this minimum. We can use
[argmin](where_and_argmin).
```
# Index of minumum value
i_of_min = np.argmin(sos_errors)
i_of_min
```
This is the index position of the minimum. We will therefore get the minimum
(again) if we index into the original array with the index we just found:
```
# Check we do in fact get the minimum at this index
sos_errors[i_of_min]
```
Now we can get and show the slope value that corresponds the minimum sum of
squared error:
```
best_slope = some_slopes[i_of_min]
best_slope
```
Plot the data, predictions and errors for the line that minimizes the sum of
squared error:
```
best_predicted = hgb * best_slope
plt.plot(hgb, pcv, 'o')
plt.plot(hgb, best_predicted, 'o', color='red')
for i in np.arange(len(hgb)):
x = hgb[i]
y_0 = best_predicted[i]
y_1 = pcv[i]
plt.plot([x, x], [y_0, y_1], ':', color='black', linewidth=1)
plt.title('The best-fit line using least-squared error')
```
The algorithm we have used so far, is rather slow and clunky, because we had to
make an array with lots of slopes to try, and then go through each one to find
the slope that minimizes the squared error.
In fact, we will soon see, we can use some tricks to get Python to do all this
work for us, much more quickly.
Finding techniques for doing this automatically is a whole mathematical field,
called [optimization](https://en.wikipedia.org/wiki/Mathematical_optimization).
For now, let's leap to using these techniques on our problem, of finding the
best slope:
```
from scipy.optimize import minimize
# 3 below is the slope value to start the search.
res = minimize(sos_error, 3)
res
```
The slope is in the `x` attribute of the return value:
```
res.x
```
## The magic of maths
We found the best (sum of squares) slope by trying lots of slopes, above, and then, rather more efficiently, by using `minimize` to do that job for us.
You don't need to understand the argument below, to follow this class, but in
this case we can work out the best slope with some [fairly simple calculus and
algebra](../extra/slope_deviations). It turns out like this:
```
maths_slope = np.sum(hgb * pcv) / np.sum(hgb ** 2)
maths_slope
```
See the page linked above for why this formula works for any set of x and y
values, where the intercept is zero.
But - we won't be using these mathematical short cuts in this course, we will
be using `minimize` and friends to find the best slope by trial and error.
| true |
code
| 0.451024 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Ravio1i/ki-lab/blob/master/0_Simple_NN.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Simple Neural Network with PyTorch. Original source can be found [here](https://pytorch.org/tutorials/beginner/pytorch_with_examples.html).
```
import torch
import torch.nn.functional as F
from torch import optim
import torchvision
import matplotlib.pyplot as plt
from time import time
print(torch.__version__)
print(torchvision.__version__)
```
# Network
TwoLayerNet with configurable activation function
```
class TwoLayerNet(torch.nn.Module):
def __init__(self, input_size: int, hidden_size: int, output_size: int, activation_function: F.log_softmax):
"""
In the constructor we instantiate two nn.Linear modules and assign them as member variables.
"""
super(TwoLayerNet, self).__init__()
self.linear1 = torch.nn.Linear(input_size, hidden_size)
self.linear2 = torch.nn.Linear(hidden_size, output_size)
self.activation_function = F.log_softmax
def forward(self, x):
"""
In the forward function we accept a Tensor of input data and we must return
a Tensor of output data. We can use Modules defined in the constructor as
well as arbitrary operators on Tensors.
"""
# Relu von pytorch
h_relu = F.relu(self.linear1(x))
#h_relu = self.linear1(x).clamp(min=0)
y_pred = self.linear2(h_relu)
return self.activation_function(y_pred)
```
# DATA LOADER
Using QMNIST, because MNIST is not reachable
```
#!wget www.di.ens.fr/~lelarge/MNIST.tar.gz
#!tar -zxvf MNIST.tar.gz
batch_size_train = 64
batch_size_test = 1000
train_loader = torch.utils.data.DataLoader(
torchvision.datasets.QMNIST('/files/', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size_train, shuffle=True
)
test_loader = torch.utils.data.DataLoader(
torchvision.datasets.QMNIST('/files/', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_test, shuffle=True
)
```
# Preprocessing
Showing the data size and sample data
```
examples = enumerate(test_loader)
batch_idx, (example_data, example_targets) = next(examples)
print(example_data.shape)
fig = plt.figure()
for i in range(6):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(example_data[i][0], cmap='gray', interpolation='none')
plt.title("Ground Truth: {}".format(example_targets[i]))
plt.xticks([])
plt.yticks([])
fig
# get data and labels from train_loader
x, y = next(iter(train_loader))
print(x.shape)
# Flatten tensor
print(x.view(x.shape[0], -1).shape)
#print(x.flatten().shape)
```
# Train
Method to train the model with configurable parameters
```
def train(model, epoch: int, loss_function: torch.nn.functional, optimizer: torch.optim, device: torch.device, log_interval: int = 100):
"""Forward pass: Compute predicted y by passing x to the model
"""
global train_losses, train_counter
for batch_idx, (x, y) in enumerate(train_loader):
x, y = x.to(device), y.to(device)
x = x.view(x.shape[0], -1)
optimizer.zero_grad()
y_pred = model(x)
# Compute and print loss
loss = loss_function(y_pred, y)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(x), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
train_losses.append(loss.item())
train_counter.append(
(batch_idx*64) + ((epoch-1)*len(train_loader.dataset)))
```
# Test
Method to test model with data from test loader
```
def test(model, device):
global test_losses
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for x, y in test_loader:
x, y = x.to(device), y.to(device)
x = x.view(x.shape[0], -1)
y_hat = model(x)
test_loss += F.nll_loss(y_hat, y, reduction='sum').item()
pred = y_hat.data.max(1, keepdim=True)[1]
correct += pred.eq(y.data.view_as(pred)).sum()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
```
## PLOT
Plots the Loss of Train and Test
```
def plot():
global train_losses, train_counter, test_losses, test_counter
fig = plt.figure()
print(train_counter)
print(train_losses)
plt.plot(train_counter, train_losses, color='blue')
print(test_counter)
print(test_losses)
plt.scatter(test_counter, test_losses, color='red')
plt.legend(['Train Loss', 'Test Loss'], loc='upper right')
plt.xlabel('number of training examples seen')
plt.ylabel('negative log likelihood loss')
fig
```
# Execute
Rerunnable Execution of training and test
```
def run(device_name: str, input_size: int, hidden_size: int, output_size: int, n_epochs: int = 50, activation_function: F = F.log_softmax, loss_function: F = F.nll_loss):
# INITIATE VARIABLE
global train_losses, train_counter, test_losses, test_counter
train_losses = []
train_counter = []
test_losses = []
test_counter = [0, n_epochs*len(train_loader.dataset)] #[i*len(train_loader.dataset) for i in range(n_epochs + 1)]
device = torch.device(device_name)
out = """
DEVICE: {}
EPOCHS: {}
INPUT_SIZE: {}
HIDDEN_SIZE: {}
OUTPUT_SIZE: {}
ACTIVATION_FUNCTION: {}
LOSS_FUNCTION: {}
""".format(device_name, n_epochs, input_size, hidden_size, output_size, activation_function, loss_function)
print(out)
# Construct our model by instantiating the class defined above
model = TwoLayerNet(input_size, hidden_size, output_size, activation_function)
model.to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1e-4)
# TRAIN
test(model, device)
time_start = time()
for epoch in range(1, n_epochs + 1):
train(model, epoch, loss_function, optimizer, device)
print("Training Time (in minutes) =",(time()-time_start)/60)
test(model, device)
plot()
train_losses = []
train_counter = []
test_losses = []
test_counter = []
```
## CPU
```
run(
device_name="cpu",
input_size=784,
hidden_size=100,
output_size=10,
n_epochs=50,
)
```
## GPU (CUDA)
```
run(
device_name="cuda",
input_size=784,
hidden_size=100,
output_size=10,
n_epochs=50,
)
```
## Hidden Layers
```
run(
device_name="cuda",
input_size=784,
hidden_size=200,
output_size=10
)
run(
device_name="cuda",
input_size=784,
hidden_size=784,
output_size=10
)
```
## Softmax
```
run(
device_name="cuda",
input_size=784,
hidden_size=100,
output_size=10,
activation_function=F.softmax,
loss_function=torch.nn.CrossEntropyLoss()
)
```
| true |
code
| 0.789923 | null | null | null | null |
|
# GPU-Accelerated Numerical Computing with MatX
## Tutorial List
1. [Introduction](01_introduction.ipynb)
2. [Operators](02_operators.ipynb)
3. Executors (this tutorial)
4. [Radar Pipeline Example](04_radar_pipeline.ipynb)
## Executors
MatX executors are a generic name given to functions that execute work on the device. Operators and generators were introduced in the last tutorial as a way to generate a CUDA kernel from an expression, but they do not execute any work on the device. The `run` took an operator as input and executed it on the device. Many other types of executors exist in MatX where more complex functions can be executed alongside operators. Some executors are wrappers around existing CUDA libraries, while others are custom executors inside of MatX. This distinction is hidden from developers so that the implementation of an executor can change over time without modifying the client code. Some executors can take an operator as input, while others can only take tensors as input. These restrictions are noted in the MatX documentation, and may be relaxed or removed in future versions.
Besides `run`, other executors typically allow non-element-wise kernels to execute using highly-optimized library backends. Some examples of this would be a matrix multiply (GEMM), reduction, FFT, sorting, and linear solvers. Besides the type of inputs allowed, executors may also have restrictions on the rank and/or size of a tensor. For example, performing a GEMM requires that the tensors are at least rank 2 (i.e. be a matrix), and the last dimension of the first tensor must match the second-to-last dimension of the second tensor (`MxK * KxN`). Most executors support batching, and anything above the nominal rank will result in batching dimensions. In a 1D FFT this would mean that any dimension above 1 is treated as another 1D batched FFT, and a 2D FFT would batch any dimensions above 2.
Some executors use CUDA libraries to implement their functionality, and those libraries require either a handle or a plan to operated. MatX hides this complexity by creating and caching the plan on the first call, and using the same plan on future calls where possible. More advanced users may use the handle interface directly to avoid the caching. Only the caching interface will be covered in this tutorial since it's the recommended approach, but the non-cached version can be found in the documentation.
### Matrix Multiply
The `matmul` executor performs the matrix-matrix multiply of $$C = {\alpha}A * B + {\beta}C$$ where `A` is of dimensions `MxK`, `B` is `KxN`, and `C` is `MxN`. We first populate the `A` and `B` matrices with random values before the multiply as we did in the example above, then the GEMM is performed. Since the random number generator allocates memory sufficient to randomize the entire tensor, we create a random number generator large enough to generate values for both A or B. This allows us to create a single random number generator, but pull different random values for A and B by simply calling `run` twice. As mentioned above, any rank above 2 is consiered a batching dimension.
We use rectangular matrices for `A` and `B`, while `C` will be a square matrix due to the outer dimensions of `A` and `B` matching.
```c++
randomGenerator_t<float> randData(C.TotalSize(), 0);
auto randTensor1 = randData.GetTensorView<2>({8, 4}, NORMAL);
auto randTensor2 = randData.GetTensorView<2>({4, 8}, NORMAL);
(A = randTensor1).run();
(B = randTensor2).run();
matmul(C, A, B);
```
Open the file [exercises/example3_gemm.cu](exercises/example3_gemm.cu) and edit the contents where you see TODO markers.
```
!./exercises/compile_and_run.sh example3_gemm
```
Expected output:
```sh
A:
000000: -0.9247 -0.4253 -2.6438 0.1452
000001: -0.1209 -0.5797 -0.6229 -0.3284
000002: -1.0745 -0.3631 -1.6711 2.2655
000003: 0.3117 -0.1842 1.2866 1.1820
000004: -0.1271 1.2169 1.4353 1.0605
000005: -0.4941 -1.4244 -0.7244 -1.2973
000006: 0.0697 -0.0074 1.8969 0.6878
000007: -0.0779 -0.8373 1.3506 -0.2879
B:
000000: 0.9911 1.0676 -0.6272 0.3202 -0.3110 -0.3441 -1.1709 -0.5371
000001: 1.3390 -0.2401 1.2149 -0.2052 1.2999 0.2181 -1.2135 -1.3723
000002: -0.4635 -0.4089 -0.0032 0.2967 -0.3587 -1.0455 -0.0450 -0.0985
000003: 1.7608 0.9107 0.0288 -1.1128 0.0929 -0.1502 -0.9854 0.7889
C:
000000: -0.0050 0.3283 0.0760 -1.1547 0.6966 2.9677 1.5747 1.4554
000001: -1.1856 -0.0342 -0.6359 0.2609 -0.5231 0.6156 1.1966 0.6628
000002: 3.2124 1.6864 0.3035 -3.2863 0.6721 1.6973 -0.4584 3.0275
000003: 1.5472 0.9272 -0.3894 -0.7960 -0.6881 -1.6701 -1.3640 0.8911
000004: 2.7056 -0.0490 1.5840 -1.0446 1.2051 -1.3507 -2.4374 -0.9065
000005: -4.3456 -1.0707 -1.4556 1.3628 -1.5586 0.8115 3.6179 1.2680
000006: 0.3910 -0.0732 -0.0391 -0.1788 -0.6479 -2.1121 -0.8357 0.3284
000007: -2.3314 -0.6966 -0.9810 0.8679 -1.5754 -1.5246 1.3302 0.8306
```
### FFT
MatX provides an interface to do both 1D Fast Fourier Transforms (FFTs) and 2D FFTs. Any tensor above rank 1 will be batched in a 1D FFT, and any tensor above rank 2 will be batched in a 2D FFT. FFTs may either be done in-place or out-of-place by using the same or different variables for the output and inputs. Since the tensors are strongly-typed, the type of FFT (C2C, R2C, etc) is inferred by the tensor type at compile time. Similarly, the input and output size of the executor is deduced by the type of transform, and the input/output tensors must match those sizes. There's one exception to this rule, and it's when the input FFT is to be zero-padded at the end. In this case, the input tensor can be shorter than the output tensor, and the input will be zero-padded to the length of the output tensor. This is a common tactic used in signal and image processing for both speed and FFT resolution.
In this example, we execute a 1D batched FFT on a 2D tensor populated with random complex floating point data. Since the FFT executor is performed in-place, the input and output types of the tensors are the same, and the type of the FFT is inferred as a complex-to-complex (`C2C`). The FFT length is specified by the inner dimension of the tensor, or 4 in this example, and the outer dimension is the number of batches, or 2. After the FFT completes, we perform on IFFT on the same tensor using the `ifft` interface. Ignoring floating point inaccuracies, the result of `ifft(fft(A))` should be the same as `A`, and this is shown by printing the tensors at each step. To perform a batched FFT on columns instead of rows, the tensor can be transposed by calling the `Permute` function used in the first tutorial. When the library detects a permuted tensor is being used, it can use technique to speed the FFT up over the naive method of converting the data in memory.
```c++
C.Print();
fft(C, C);
C.Print();
ifft(C, C);
C.Print();
```
Open the file [exercises/example3_1dfft.cu](exercises/example3_1dfft.cu) and edit the contents where you see TODO markers.
```
!./exercises/compile_and_run.sh example3_1dfft
```
Expected output:
```sh
Initial C tensor:
000000: -0.9247+0.9911j -0.4253+1.0676j -2.6438-0.6272j 0.1452+0.3202j
000001: -0.1209-0.3110j -0.5797-0.3441j -0.6229-1.1709j -0.3284-0.5371j
After FFT:
000000: -3.8487+1.7517j 2.4666+2.1889j -3.2883-1.0238j 0.9718+1.0478j
000001: -1.6518-2.3630j 0.6950+1.1112j 0.1644-0.6007j 0.3090+0.6085j
After IFFT and normalization:
000000: -0.9247+0.9911j -0.4253+1.0676j -2.6438-0.6272j 0.1452+0.3202j
000001: -0.1209-0.3110j -0.5797-0.3441j -0.6229-1.1709j -0.3284-0.5371j
```
Next, we take the same 2D tensor and perform a 2D FFT on it. Since the rank is 2, it will not be batched as in the previous example.
```c++
C.Print();
fft2(C, C);
C.Print();
ifft2(C, C);
C.Print();
```
As before, the results after the IFFT closely match the original `C` tensor, but with floating point error.
Open the file [exercises/example3_2dfft.cu](exercises/example3_2dfft.cu) and edit the contents where you see TODO markers.
```
!./exercises/compile_and_run.sh example3_2dfft
```
Expected output:
```sh
Intial C tensor:
000000: -0.9247+0.9911j -0.4253+1.0676j -2.6438-0.6272j 0.1452+0.3202j
000001: -0.1209-0.3110j -0.5797-0.3441j -0.6229-1.1709j -0.3284-0.5371j
After FFT:
000000: -2.0506+1.4036j -0.0405-0.0434j -2.6438-0.6272j 0.1452+0.3202j
000001: -2.0051+2.7593j -0.4662-0.5353j -0.6229-1.1709j -0.3284-0.5371j
After IFFT and normalization:
000000: -1.8493+1.9823j -0.8507+2.1352j -0.6610-0.1568j 0.0363+0.0800j
000001: -0.2417-0.6220j -1.1595-0.6882j -0.1557-0.2927j -0.0821-0.1343j
```
### Reductions
A reduction operation takes multiple values and aggregates those into a smaller number of values. Most reductions take a large number of values and reduces them to a single value. Reductions are one of the most common operations perfomed on the GPU, which means they've been heavily researched and optimized for highly-parallel processors. Modern NVIDIA GPUs have special instructions for performing reductions to give even larger speedups over naive implementations. All of these details are hidden from the user and MatX automatically chooses the optimized path based on the hardware capabilities.
MatX provides a set of optimized primitives to perform reductions on tensors for many common types. Reductions are supported across individual dimensions or on entire tensors, depending on the size of the output tensor. Currently supported reduction functions are `sum`, `min`, `max`,` mean`, `any`, and `all`. Note that the max and min reductions use the name `rmin` and `rmax` to avoid name collision with the element-wise `min` and `max` operators.
#### Full Reduction
In this example we reduce an entire tensor to a single value by applying the reduction across all dimensions of the tensor. We apply the same random initialization from previous examples on a 2D tensor `A`. Note that the output tensor must be zeroed for a `sum` reduction since that value is continually added to during the reduction. Not initializing the output tensor will give undefined results since the variables are used as accumulators throughout the reduction. With the tensor initialized, we perform both a `max` and `sum` reduction across all dimensions of the tensor:
```c++
rmax(MD0, A);
sum(AD0, A);
```
Open the file [exercises/example3_full_reduce.cu](exercises/example3_full_reduce.cu) and edit the contents where you see TODO markers.
```
!./exercises/compile_and_run.sh example3_full_reduce
```
Expected output:
```sh
A:
000000: -0.9247 -0.4253 -2.6438 0.1452 -0.1209
000001: -0.5797 -0.6229 -0.3284 -1.0745 -0.3631
000002: -1.6711 2.2655 0.3117 -0.1842 1.2866
000003: 1.1820 -0.1271 1.2169 1.4353 1.0605
Max: 2.265505
Sum: -0.162026
```
#### Dimensional Reductions
Reductions can also be performed across certain dimensions instead of the whole tensor. Dimensional reductions are useful in situations where each row contains data for a different user, for example, and we wish to sum up each user's data. By setting the output tensor view to a 1D tensor, independent reductions can be performed across the input tensor where each output element corresponds to a single row reduction from the input. Using the same tensor `A` from the previous example, we only change the output tensor type to be a 1D tensor instead of a scalar:
```c++
rmax(MD1, A);
sum(AD1, A);
```
Printing the new reduction tensors shows the reduced values across each row of the input tensor `A`.
Open the file [exercises/example3_partial_reduce.cu](exercises/example3_partial_reduce.cu) and edit the contents where you see TODO markers.
```
!./exercises/compile_and_run.sh example3_partial_reduce
```
Expected output:
```sh
A:
000000: -0.9247 -0.4253 -2.6438 0.1452 -0.1209
000001: -0.5797 -0.6229 -0.3284 -1.0745 -0.3631
000002: -1.6711 2.2655 0.3117 -0.1842 1.2866
000003: 1.1820 -0.1271 1.2169 1.4353 1.0605
Max:
000000: 0.1452
000001: -0.3284
000002: 2.2655
000003: 1.4353
Sum:
000000: -3.9695
000001: -2.9686
000002: 2.0086
000003: 4.7676
```
### Convolution
MatX supports both 1D and 2D direct convolution using the `conv1d` and `conv2d` functions. FFT-based convolution can also be performed as a combination of existing primitives as a potentially faster alternative to direct convolution for large tensors. Both forms of direct convolution take in an extra mode which specifies how much of the output is saved, where `MATX_C_MODE_FULL` saves the entire filter ramp-up and down, `MATX_C_MODE_SAME` makes the input and output tensors the same size, and `MATX_C_MODE_VALID` only keeps valid samples (when the entire filter was part of the convolution). Convolution can be used to perform a rolling average of an input by making all filter values 1/N, where N is the length of the filter. In this example, we use a filter of length 3 to create a running average of the last 3 elements:
```c++
conv1d(Co, C, filt, MATX_C_MODE_FULL, 0);
```
```
!./exercises/compile_and_run.sh example3_conv1d
```
Expected output:
```sh
Initial C tensor:
000000: -0.9247
000001: -0.4253
000002: -2.6438
000003: 0.1452
000004: -0.1209
000005: -0.5797
000006: -0.6229
000007: -0.3284
000008: -1.0745
000009: -0.3631
000010: -1.6711
000011: 2.2655
000012: 0.3117
000013: -0.1842
000014: 1.2866
000015: 1.1820
After conv1d:
000000: -0.3082
000001: -0.4500
000002: -1.3313
000003: -0.9747
000004: -0.8732
000005: -0.1851
000006: -0.4411
000007: -0.5103
000008: -0.6753
000009: -0.5887
000010: -1.0362
000011: 0.0771
000012: 0.3020
000013: 0.7977
000014: 0.4714
000015: 0.7615
000016: 0.8229
000017: 0.3940
```
Similar to a 1D convolution, a 2D convolution does the same computation over two dimensions. A tensor of at least rank 2 is needed for a 2D convolution. Below we use a filter of all ones using the `ones` operator to demonstrate the filter can also be an operator and not an existing tensor view. The result is the sum of the four values around each cell on the input:
```c++
conv2d(Co, C, filt, MATX_C_MODE_FULL, 0);
```
```
!./exercises/compile_and_run.sh example3_conv2d
```
Last, we mentioned above that convolution can also be done in the frequency domain using FFTs. This is the preferred method for larger tensors since FFTs are much faster than direct convolutions in large sizes, and because FFT libraries are highly-optimized. FFT convolution uses more memory than direct if the inputs are not to be destroyed since it requires running an FFT on both the input signal and filter before filtering. If not done in-place, this typically requires `2N + L - 1` new elements in memory, where N is the signal length and L is the filter length. A full FFT convolution example can be found in `fft_conv.cu` in the MatX examples, but the main convolution code is shown below:
```c++
// Perform the FFT in-place on both signal and filter
fft(sig_freq, sig_freq);
fft(filt_freq, filt_freq);
// Perform the pointwise multiply. Overwrite signal buffer with result
(sig_freq = sig_freq * filt_freq).run();
// IFFT in-place
ifft(sig_freq, sig_freq);
```
Since the expected output size of the full filtering operation is signal_len + filter_len - 1, both the filter and signal time domain inputs are shorter than the output. This would normally require a separate stage of allocating buffers of the appropriate size, zeroing them out, copying the time domain data to the buffers, and performing the FFT. However, MatX has an API to do all of this automatically in the library using asynchronous allocations. This makes the call have a noticeable performance hit on the first call, but subsequent calls will be close to the time without allocation. To recognize that automatic padding is wanted, MatX uses the output tensor size compared to the input tensor size to determine whether to pad the input with zeros. In this case the output signal (sig_time and filt_time) are shorter than the output tensors (sig_freq and filt_freq), so it will automatically zero-pad the input.
Using the convolution property $ h*x \leftrightarrow H \cdot X$ we simply multiply the signals element-wise after the FFT, then do an IFFT to go back to the time domain.
Next, we do the same operation in the time domain using the `conv1d` function:
```c++
conv1d(time_out, sig_time, filt_time, matxConvCorrMode_t::MATX_C_MODE_FULL, 0);
```
To match the FFT results we do a full convolution to get all the samples from the filter ramp up and ramp down. However, if we wanted either valid or same mode we could slice the FFT convolution output at the appropriate places to give the same answer. Edit the file [exercises/example3_fft_conv.cu](exercises/example3_fft_conv.cu) and add the missing code where you see TODOs. After running the verification code at the bottom will check for accuracy.
Expected output:
```sh
Verification successful
```
```
!./exercises/compile_and_run.sh example3_fft_conv
```
This concludes the third tutorial on MatX. In this tutorial you learned what executors are, and how they can be applied on tensor views. In the next example you will walk through an entire radar signal processing pipeline using all the primites learned up to this point.
[Start Next Tutorial](04_radar_pipeline.ipynb)
| true |
code
| 0.633127 | null | null | null | null |
|
## 0.使用opencv展示图像
```
import cv2
def cv2_display(image_ndarray):
windowName = 'display'
cv2.imshow(windowName, image_ndarray)
# 按Esc键或者q键可以退出循环
pressKey = cv2.waitKey(0)
if 27 == pressKey or ord('q') == pressKey:
cv2.destroyAllWindows()
```
## 1.加载2张图片文件为图像数据
```
image_ndarray_1 = cv2.imread('../resources/1.jpg')
image_ndarray_2 = cv2.imread('../resources/2.jpg')
```
### 1.1 展示原始图像数据
```
# 按Esc键或者q键可以退出cv2显示窗口
cv2_display(image_ndarray_1)
cv2_display(image_ndarray_2)
```
## 2.图像处理
```
def get_processedImage(image_ndarray):
# 对拍摄图像进行图像处理,先转灰度图,再进行高斯滤波。
image_ndarray_1 = cv2.cvtColor(image_ndarray, cv2.COLOR_BGR2GRAY)
# 用高斯滤波对图像处理,避免亮度、震动等参数微小变化影响效果
filter_size = 7
image_ndarray_2 = cv2.GaussianBlur(image_ndarray_1, (filter_size, filter_size), 0)
return image_ndarray_2
image_ndarray_1_2 = get_processedImage(image_ndarray_1)
image_ndarray_2_2 = get_processedImage(image_ndarray_2)
```
### 2.1 展示处理后的图像数据
```
cv2_display(image_ndarray_1_2)
cv2_display(image_ndarray_2_2)
```
## 3.图像相减
```
absdiff_ndarray = cv2.absdiff(image_ndarray_1_2, image_ndarray_2_2)
```
### 3.1 展示相减后的图像数据
```
cv2_display(absdiff_ndarray)
```
### 4. 图像二值化
```
result_1 = cv2.threshold(absdiff_ndarray, 25, 255, cv2.THRESH_BINARY)
type(result_1)
len(result_1)
type(result_1[0])
result_1[0]
type(result_1[1])
result_1[1].shape
cv2_display(result_1[1])
threshhold_ndarray = result_1[1]
```
### 4.1 显示二值化后的图像
```
cv2_display(threshhold_ndarray)
```
## 5. 获取轮廓列表,并做响应操作
```
contour_list = cv2.findContours(threshhold_ndarray, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)[0]
import datetime
image_ndarray_3 = image_ndarray_2.copy()
for contour in contour_list:
# 对于较小矩形区域,选择忽略
if cv2.contourArea(contour) < 2000:
continue
else:
x1, y1, w, h = cv2.boundingRect(contour)
x2, y2 = x1 + w, y1 + h
leftTop_coordinate = x1, y1
rightBottom_coordinate = x2, y2
bgr_color = (0, 0, 255)
thickness = 2
cv2.rectangle(image_ndarray_3, leftTop_coordinate, rightBottom_coordinate, bgr_color, thickness)
text = "Find motion object! x=%d, y=%d" %(x1, y1)
print(text)
cv2.putText(image_ndarray_3, text, (10, 50), cv2.FONT_HERSHEY_SIMPLEX, 1, bgr_color, thickness)
time_string = datetime.datetime.now().strftime("%A %d %B %Y %I:%M:%S%p")
_ = cv2.putText(image_ndarray_3, time_string, (10, 100), cv2.FONT_HERSHEY_SIMPLEX, 1, bgr_color, thickness)
```
### 5.1 根据轮廓绘制方框后,显示图像
```
cv2_display(image_ndarray_3)
```
| true |
code
| 0.230054 | null | null | null | null |
|
```
import os
os.environ.get('GDS_ENV_VERSION')
```
# Generate illustrations of tessellation
This notebook contains one function `pipeline`, which for a given point (lat, lon) generates a sequence of seven images illustrating the process of creation of morphologicla tessellation within 250m buffer. The function is used to generate animations and figures in the blogpost.
```
import geopandas as gpd
import momepy as mm
import osmnx as ox
import pygeos
import numpy as np
from scipy.spatial import Voronoi
import pandas as pd
from mapclassify import greedy
import contextily as ctx
import matplotlib.pyplot as plt
from palettable.wesanderson import FantasticFox2_5
from shapely.geometry import Point
def pipeline(lat, lon, path, prefix, dist=250, figsize=(12, 12)):
point = (lat, lon)
gdf = ox.geometries.geometries_from_point(point, dist=dist, tags={'building':True})
gdf_projected = ox.projection.project_gdf(gdf)
bounds = gdf_projected.total_bounds
limit = Point(np.mean([bounds[0], bounds[2]]), np.mean([bounds[1], bounds[3]])).buffer(250)
blg = gpd.clip(gdf_projected, limit).explode()
bounds = limit.bounds
# figure 1 - aerial
fig, ax = plt.subplots(figsize=figsize)
ax.axis([bounds[0], bounds[2], bounds[1], bounds[3]])
gpd.GeoSeries([limit.buffer(150).difference(limit)]).plot(ax=ax, color='white')
ctx.add_basemap(ax, crs=blg.crs, source=ctx.providers.Esri.WorldImagery)
ax.set_axis_off()
plt.savefig(path + prefix + "01.png", bbox_inches='tight')
plt.close()
print("Figure 1 saved to " + path + prefix + "01.png")
# figure 2 - overlay
fig, ax = plt.subplots(figsize=figsize)
ax.axis([bounds[0], bounds[2], bounds[1], bounds[3]])
gpd.GeoSeries([limit.buffer(150).difference(limit)]).plot(ax=ax, color='white')
ctx.add_basemap(ax, crs=blg.crs, source=ctx.providers.Esri.WorldImagery)
blg.plot(ax=ax, color='#0ea48f', edgecolor='k', alpha=.6)
ax.set_axis_off()
plt.savefig(path + prefix + "02.png", bbox_inches='tight')
plt.close()
print("Figure 2 saved to " + path + prefix + "02.png")
# figure 3 - footprints
fig, ax = plt.subplots(figsize=figsize)
ax.axis([bounds[0], bounds[2], bounds[1], bounds[3]])
blg.plot(ax=ax, color='#0ea48f', edgecolor='k').set_axis_off()
plt.savefig(path + prefix + "03.png", bbox_inches='tight')
plt.close()
print("Figure 3 saved to " + path + prefix + "03.png")
shrinked = blg.buffer(-2)
shrinked = shrinked[~shrinked.is_empty]
# figure 4 - shrinked
fig, ax = plt.subplots(figsize=figsize)
ax.axis([bounds[0], bounds[2], bounds[1], bounds[3]])
blg.plot(ax=ax, facecolor='none', linewidth=.5, edgecolor='k')
shrinked.plot(ax=ax, color='#0ea48f')
ax.set_axis_off()
plt.savefig(path + prefix + "04.png", bbox_inches='tight')
plt.close()
print("Figure 4 saved to " + path + prefix + "04.png")
distance = 4
points = np.empty((0, 2))
ids = []
lines = shrinked.boundary.values.data
lengths = shrinked.length
for ix, line, length in zip(shrinked.index, lines, lengths):
if length > distance:
pts = pygeos.line_interpolate_point(
line,
np.linspace(0.1, length - 0.1, num=int((length - 0.1) // distance)),
) # .1 offset to keep a gap between two segments
if len(pts) > 0:
points = np.append(points, pygeos.get_coordinates(pts), axis=0)
ids += [ix] * len(pts)
# figure 5 - points
fig, ax = plt.subplots(figsize=figsize)
ax.axis([bounds[0], bounds[2], bounds[1], bounds[3]])
blg.plot(ax=ax, facecolor='none', linewidth=.5, edgecolor='k')
gpd.GeoSeries(pygeos.points(points)).plot(ax=ax, markersize=1, color='#0ea48f')
ax.set_axis_off()
plt.savefig(path + prefix + "05.png", bbox_inches='tight')
plt.close()
print("Figure 5 saved to " + path + prefix + "05.png")
# add hull to resolve issues with infinity
# this is just a correction step ensuring the algorithm will work correctly
stop = points.shape[0]
series = gpd.GeoSeries(limit)
hull = series.geometry[[0]].buffer(500)
line = hull.boundary.values.data[0]
length = hull.length[0]
pts = pygeos.line_interpolate_point(
line,
np.linspace(0.1, length - 0.1, num=int((length - 0.1) // distance)),
) # .1 offset to keep a gap between two segments
points = np.append(points, pygeos.get_coordinates(pts), axis=0)
ids += [-1] * len(pts)
voronoi_diagram = Voronoi(np.array(points))
vertices = pd.Series(voronoi_diagram.regions).take(voronoi_diagram.point_region)
polygons = []
for region in vertices:
if -1 not in region:
polygons.append(pygeos.polygons(voronoi_diagram.vertices[region]))
else:
polygons.append(None)
regions_gdf = gpd.GeoDataFrame(
{'unique_id': ids}, geometry=polygons
).dropna()
regions_gdf = regions_gdf.loc[
regions_gdf['unique_id'] != -1
] # delete hull-based cells
voronoi_tessellation = gpd.clip(regions_gdf, limit)
# figure 6 - voronoi
fig, ax = plt.subplots(figsize=figsize)
ax.axis([bounds[0], bounds[2], bounds[1], bounds[3]])
gpd.GeoSeries(pygeos.points(points[:stop])).plot(ax=ax, markersize=1, zorder=3, color='#0ea48f')
voronoi_tessellation.plot(ax=ax, facecolor='none', linewidth=.2, edgecolor='gray')
ax.set_axis_off()
plt.savefig(path + prefix + "06.png", bbox_inches='tight')
plt.close()
print("Figure 6 saved to " + path + prefix + "06.png")
# figure 7 - tessellation
fig, ax = plt.subplots(figsize=figsize)
ax.axis([bounds[0], bounds[2], bounds[1], bounds[3]])
blg = blg[blg.geom_type == 'Polygon']
blg = blg.reset_index(drop=True)
blg['uid'] = range(len(blg))
tessellation = mm.Tessellation(blg, 'uid', limit, verbose=False).tessellation
tessellation.plot(greedy(tessellation, strategy='smallest_last'), ax=ax, categorical=True, edgecolor='w', alpha=.6, cmap=FantasticFox2_5.mpl_colormap)
ax.set_axis_off()
plt.savefig(path + prefix + "07.png", bbox_inches='tight')
plt.close()
print("Figure 7 saved to " + path + prefix + "07.png")
pipeline(33.9488360, -118.2372975, path='./', prefix='la_', figsize=(15, 15))
pipeline(41.3907594, 2.1573404, path='./', prefix='bcn_', figsize=(15, 15))
pipeline(38.995888, -77.135073, path='./', prefix='atl_', figsize=(15, 15))
pipeline(44.4942640, 11.3473233, path='./', prefix='bol_', figsize=(15, 15))
pipeline(-15.8038355, -47.8918796, path='./', prefix='bra_', figsize=(15, 15))
```
| true |
code
| 0.47792 | null | null | null | null |
|
<img src="ine_400x141.jpg" width="200" height="200" align="right"/>
## <left>DERFE-Dirección de Estadística</left>
# <center>A crash course on Data Science with Python</center>
## <center>Motivation</center>
### <center>Part I: Data Science</center>

### <center>Part II: Become an expert in Data Science</center>

### <center>Part III: What language to choose? Python vs R</center>
<img src="Data science wars Python vs R.jpg" width="1000" height="1000" align="center"/>
### Homework:
- Python's history
https://en.wikipedia.org/wiki/History_of_Python
- Basics of Python
https://www.learnpython.org/
https://realpython.com/jupyter-notebook-introduction/
- Choosing R or Python for Data Analysis? An Infographic
https://www.datacamp.com/community/tutorials/r-or-python-for-data-analysis#gs.nrBsDZQ
- Why become a data scientist?
https://365datascience.com/defining-data-science/
- Comparisons between languages
https://www.codingame.com/blog/best-programming-language-learn-2019/
https://towardsdatascience.com/data-science-101-is-python-better-than-r-b8f258f57b0f
https://www.tiobe.com/tiobe-index/
http://pypl.github.io/PYPL.html
https://redmonk.com/sogrady/2018/03/07/language-rankings-1-18/
https://octoverse.github.com/projects#languages
- Visualizations in Python
https://towardsdatascience.com/5-quick-and-easy-data-visualizations-in-python-with-code-a2284bae952f
## <center>Introduction to Data Science with Python</center>
### <center>Part I: Learning path</center>
<img src="final-1.jpg" width="1000" height="1000" align="center"/>
### Homework:
#### Installation of Python/Anaconda/Jupyter notebook
https://www.anaconda.com/
https://www.freecodecamp.org/news/how-to-get-started-with-python-for-deep-learning-and-data-science-3bed07f91a08/
https://www.w3schools.com/python/default.asp
#### Python basic syntax
https://jupyter.org/index.html
#### Books
- How to Think Like a Computer Scientist: Learning with Python 3 Documentation
- Data Science Essentials in Python
- Introduction to Machine Learning with Python
- Think Python
- Data Science from Scratch
Check the following link: https://inemexico-my.sharepoint.com/:f:/g/personal/miguel_alvarez_ine_mx/EkVbN-eSMI5FpX1NDprCReMBJHPCbxzOCppSUtP79dCsKg?e=JVp4FE
### <center>Part II: Jupyter notebooks</center>
### Launching the Jupyter Notebook
To run the Jupyter Notebook, open an OS terminal, go to ~/minibook/ (or into the directory where you've downloaded the book's notebooks), and type jupyter notebook. This will start the Jupyter server and open a new window in your browser (if that's not the case, go to the following URL: http://localhost:8888).
The Notebook is most convenient when you start a complex analysis project that will involve a substantial amount of interactive experimentation with your code. Other common use-cases include keeping track of your interactive session (like a lab notebook), or writing technical documents that involve code, equations, and figures.
In the rest of this section, we will focus on the Notebook interface.
### The Notebook dashboard
The dashboard contains several tabs:
- Files shows all files and notebooks in the current directory.
- Running shows all kernels currently running on your computer.
- Clusters lets you launch kernels for parallel computing (covered in Chapter 5, High-Performance Computing).
- A notebook is an interactive document containing code, text, and other elements. A notebook is saved in a file with the .ipynb extension. This file is a plain text file storing a JSON data structure.
A kernel is a process running an interactive session. When using IPython, this kernel is a Python process. There are kernels in many languages other than Python.
In Jupyter, notebooks and kernels are strongly separated. A notebook is a file, whereas a kernel is a process. The kernel receives snippets of code from the Notebook interface, executes them, and sends the outputs and possible errors back to the Notebook interface. Thus, in general, the kernel has no notion of Notebook. A notebook is persistent (it's a file), whereas a kernel may be closed at the end of an interactive session and it is therefore not persistent. When a notebook is re-opened, it needs to be re-executed.
In general, no more than one Notebook interface can be connected to a given kernel. However, several IPython console can be connected to a given kernel.
### The Notebook user interface
To create a new notebook, click on the New button, and select Notebook (Python 3). A new browser tab opens and shows the Notebook interface:
```
from IPython.display import Image
Image(filename='nbui-2.png')
```
Here are the main components of the interface, from top to bottom:
The notebook name, that you can change by clicking on it. This is also the name of the .ipynb file.
The menu bar gives you access to several actions pertaining to either the notebook or the kernel.
To the right of the menu bar is the Kernel name. You can change the kernel language of your notebook from the Kernel menu. We will see in Chapter 6, Customizing IPython how to manage different kernel languages.
The toolbar contains icons for common actions. In particular, the dropdown menu showing Code lets you change the type of a cell.
Below is the main component of the UI: the actual Notebook. It consists of a linear list of cells. We will detail below the structure of a cell.
### Structure of a notebook cell
There are two main types of cells: Markdown cells and code cells.
A Markdown cell contains rich text. In addition to classic formatting options like bold or italics, we can add links, images, HTML elements, LaTeX mathematical equations, and more. We will cover Markdown in more detail in the Ten Jupyter/IPython essentials section of this chapter.
A code cell contains code to be executed by the kernel. The programming language corresponds to the kernel's language. We will only use Python in this book, but you can use many other languages.
You can change the type of a cell by first clicking on a cell to select it, and then choosing the cell's type in the toolbar's dropdown menu showing Markdown or Code.
#### Markdown cells
Here is a screenshot of a Markdown cell:
```
Image(filename='markdown-both.png')
```
The top panel shows the cell in edit mode, while the bottom one shows it in render mode. The edit mode lets you edit the text, while the render mode lets you display the rendered cell. We will explain the differences between these modes in greater detail below.
#### Code cells
Here is a screenshot of a complex code cell:

This code cell contains several parts:
- The prompt number shows the cell's number. This number increases everytime you run the cell. Since you can run cells of a notebook out of order, nothing guarantees that code numbers are linearly increasing in a given notebook.
- The input area contains a multiline text editor that lets you write one or several lines of code with syntax highlighting.
- The widget area may contain graphical controls; here, it displays a slider.
- The output area can contain multiple outputs, here:
- Standard output (text in black)
- Error output (text with a red background)
- Rich output (an HTML table and an image here)
### Running Code
First and foremost, the Jupyter Notebook is an interactive environment for writing and running code. The notebook is capable of running code in a wide range of languages. However, each notebook is associated with a single kernel. This notebook is associated with the IPython kernel, therefore runs Python code.
Code cells allow you to enter and run code
Run a code cell using Shift-Enter or pressing the button in the toolbar above:
```
print("Hello world!")
a = 10
a
```
There are two other keyboard shortcuts for running code:
- Alt-Enter runs the current cell and inserts a new one below.
- Ctrl-Enter run the current cell and enters command mode.
### Cell menu
The "Cell" menu has a number of menu items for running code in different ways. These includes:
Run and Select Below
Run and Insert Below
Run All
Run All Above
Run All Below
```
from IPython.display import HTML, YouTubeVideo
HTML('''
<table style="border: 2px solid black;">
''' +
''.join(['<tr>' +
''.join([f'<td>{row},{col}</td>'
for col in range(5)]) +
'</tr>' for row in range(5)]) +
'''
</table>
''')
YouTubeVideo('VQBZ2MqWBZI')
```
### <center>Part III: Python Basics</center>
### Variables
Let's use Python as a calculator. Here, 2 * 2 is an expression statement. This operation is performed, the result is returned, and IPython displays it in the notebook cell's output.
TIP (Division): In Python 3, 3 / 2 returns 1.5 (floating-point division), whereas it returns 1 in Python 2 (integer division). This can be source of errors when porting Python 2 code to Python 3. It is recommended to always use the explicit 3.0 / 2.0 for floating-point division (by using floating-point numbers) and 3 // 2 for integer division. Both syntaxes work in Python 2 and Python 3. See http://python3porting.com/differences.html#integer-division for more details.
```
2 * 2
3 // 2
3/2
```
Other built-in mathematical operators include +, -, ** for the exponentiation, and others. You will find more details at https://docs.python.org/3/reference/expressions.html#the-power-operator.
Variables form a fundamental concept of any programming language. A variable has a name and a value. Here is how to create a new variable in Python:
```
a = 2
```
And here is how to use an existing variable:
```
a * 3
```
Several variables can be defined at once (this is called unpacking):
```
a, b = 2, 6
```
There are different types of variables. Here, we have used a number (more precisely, an integer). Other important types include floating-point numbers to represent real numbers, strings to represent text, and booleans to represent True/False values. Here are a few examples:
```
somefloat = 3.1415 # The "dot" character represents the radix point.
sometext = 'pi is about' # Use single or double quotes for strings.
print(sometext, somefloat) # This displays several variables concatenated.
```
Note how we used the # character to write comments. Whereas Python discards the comments completely, adding comments in the code is important when the code is to be read by other humans (including yourself in the future).
### String escaping
String escaping refers to the ability to insert special characters in a string. For example, how can you insert ' and ", given that these characters are used to delimit a string in Python code? The backslash \ is the go-to escape character in Python (and in many other languages too). Here are a few examples:
```
print("Hello \"world\"")
print("A list:\n* item 1\n* item 2")
print("C:\\path\\on\\windows")
print(r"C:\path\on\windows")
```
The special character \n is the new line (or line feed) character. To insert a backslash, you need to escape it, which explains why it needs to be doubled as \\.
You can also disable escaping by using raw literals with a r prefix before the string, like in the last example above. In this case, backslashes are considered as normal characters.
This is convenient when writing Windows paths, since Windows uses backslash separators instead of forward slashes like on Unix systems. A very common error on Windows is forgetting to escape backslashes in paths: writing "C:\path" may lead to subtle errors.
You will find the list of special characters in Python at https://docs.python.org/3.4/reference/lexical_analysis.html#string-and-bytes-literals
### Lists
A list contains a sequence of items. You can concisely instruct Python to perform repeated actions on the elements of a list. Let's first create a list of numbers:
```
items = [1, 3, 0, 4, 1]
```
Note the syntax we used to create the list: square brackets [], and commas , to separate the items.
The built-in function len() returns the number of elements in a list:
```
len(items)
```
Python comes with a set of built-in functions, including print(), len(), max(), functional routines like filter() and map(), and container-related routines like all(), any(), range() and sorted(). You will find the full list of built-in functions at https://docs.python.org/3.4/library/functions.html.
Now, let's compute the sum of all elements in the list. Python provides a built-in function for this:
```
sum(items)
```
We can also access individual elements in the list, using the following syntax:
```
items[0]
items[-1]
```
Note that indexing starts at 0 in Python: the first element of the list is indexed by 0, the second by 1, and so on. Also, -1 refers to the last element, -2, to the penultimate element, and so on.
The same syntax can be used to alter elements in the list:
```
items[1] = 9
items
```
We can access sublists with the following syntax:
Here, 1:3 represents a slice going from element 1 included (this is the second element of the list) to element 3 excluded. Thus, we get a sublist with the second and third element of the original list. The first-included/last-excluded asymmetry leads to an intuitive treatment of overlaps between consecutive slices. Also, note that a sublist refers to a dynamic view of the original list, not a copy; changing elements in the sublist automatically changes them in the original list.
```
items[1:3]
```
Python provides several other types of containers:
Tuples are immutable and contain a fixed number of elements:
```
my_tuple = (1, 2, 3)
my_tuple[1]
```
Dictionaries contain key-value pairs. They are extremely useful and common:
```
my_dict = {'a': 1, 'b': 2, 'c': 3}
print('a:', my_dict['a'])
print(my_dict.keys())
```
There is no notion of order in a dictionary. However, the native collections module provides an OrderedDict structure that keeps the insertion order (see https://docs.python.org/3.4/library/collections.html).
Sets, like mathematical sets, contain distinct elements:
```
my_set = set([1, 2, 3, 2, 1])
my_set
```
A Python object is mutable if its value can change after it has been created. Otherwise, it is immutable. For example, a string is immutable; to change it, a new string needs to be created. A list, a dictionary, or a set is mutable; elements can be added or removed. By contrast, a tuple is immutable, and it is not possible to change the elements it contains without recreating the tuple. See https://docs.python.org/3.4/reference/datamodel.html for more details.
### Loops
We can run through all elements of a list using a for loop:
```
for item in items:
print(item)
```
There are several things to note here:
- The for item in items syntax means that a temporary variable named item is created at every iteration. This variable contains the value of every item in the list, one at a time.
- Note the colon : at the end of the for statement. Forgetting it will lead to a syntax error!
- The statement print(item) will be executed for all items in the list.
- Note the four spaces before print: this is called the indentation. You will find more details about indentation in the next subsection.
Python supports a concise syntax to perform a given operation on all elements of a list:
```
squares = [item * item for item in items]
squares
```
This is called a list comprehension. A new list is created here; it contains the squares of all numbers in the list. This concise syntax leads to highly readable and Pythonic code.
### Indentation
Indentation refers to the spaces that may appear at the beginning of some lines of code. This is a particular aspect of Python's syntax.
In most programming languages, indentation is optional and is generally used to make the code visually clearer. But in Python, indentation also has a syntactic meaning. Particular indentation rules need to be followed for Python code to be correct.
In general, there are two ways to indent some text: by inserting a tab character (also referred as \t), or by inserting a number of spaces (typically, four). It is recommended to use spaces instead of tab characters. Your text editor should be configured such that the Tabular key on the keyboard inserts four spaces instead of a tab character.
In the Notebook, indentation is automatically configured properly; so you shouldn't worry about this issue. The question only arises if you use another text editor for your Python code.
Finally, what is the meaning of indentation? In Python, indentation delimits coherent blocks of code, for example, the contents of a loop, a conditional branch, a function, and other objects. Where other languages such as C or JavaScript use curly braces to delimit such blocks, Python uses indentation.
### Conditional branches
Sometimes, you need to perform different operations on your data depending on some condition. For example, let's display all even numbers in our list:
```
for item in items:
if item % 2 == 0:
print(item)
```
Again, here are several things to note:
- An if statement is followed by a boolean expression.
- If a and b are two integers, the modulo operand a % b returns the remainder from the division of a by b. Here, item % 2 is 0 for even numbers, and 1 for odd numbers.
- The equality is represented by a double equal sign == to avoid confusion with the assignment operator = that we use when we create variables.
- Like with the for loop, the if statement ends with a colon :.
- The part of the code that is executed when the condition is satisfied follows the if statement. It is indented. Indentation is cumulative: since this if is inside a for loop, there are eight spaces before the print(item) statement.
Python supports a concise syntax to select all elements in a list that satisfy certain properties. Here is how to create a sublist with only even numbers:
```
even = [item for item in items if item % 2 == 0]
even
```
This is also a form of list comprehension.
### Functions
Code is typically organized into functions. A function encapsulates part of your code. Functions allow you to reuse bits of functionality without copy-pasting the code. Here is a function that tells whether an integer number is even or not:
```
def is_even(number):
"""Return whether an integer is even or not."""
return number % 2 == 0
```
There are several things to note here:
- A function is defined with the def keyword.
- After def comes the function name. A general convention in Python is to only use lowercase characters, and separate words with an underscore _. A function name generally starts with a verb.
- The function name is followed by parentheses, with one or several variable names called the arguments. These are the inputs of the function. There is a single argument here, named number.
- No type is specified for the argument. This is because Python is dynamically typed; you could pass a variable of any type. This function would work fine with floating point numbers, for example (the modulo operation works with floating point numbers in addition to integers).
- The body of the function is indented (and note the colon : at the end of the def statement).
- There is a docstring wrapped by triple quotes """. This is a particular form of comment that explains what the function does. It is not mandatory, but it is strongly recommended to write docstrings for the functions exposed to the user.
- The return keyword in the body of the function specifies the output of the function. Here, the output is a Boolean, obtained from the expression number % 2 == 0. It is possible to return several values; just use a comma to separate them (in this case, a tuple of Booleans would be returned).
Once a function is defined, it can be called like this:
```
is_even(3)
is_even(4)
```
Here, 3 and 4 are successively passed as arguments to the function.
### Positional and keyword arguments
A Python function can accept an arbitrary number of arguments, called positional arguments. It can also accept optional named arguments, called keyword arguments. Here is an example:
```
def remainder(number, divisor=2):
return number % divisor
```
The second argument of this function, divisor, is optional. If it is not provided by the caller, it will default to the number 2, as show here:
```
remainder(5)
```
There are two equivalent ways of specifying a keyword argument when calling a function:
```
remainder(5, 3)
remainder(5, divisor=3)
```
In the first case, 3 is understood as the second argument, divisor. In the second case, the name of the argument is given explicitly by the caller. This second syntax is clearer and less error-prone than the first one.
Functions can also accept arbitrary sets of positional and keyword arguments, using the following syntax:
```
def f(*args, **kwargs):
print("Positional arguments:", args)
print("Keyword arguments:", kwargs)
f(1, 2, c=3, d=4)
```
Inside the function, args is a tuple containing positional arguments, and kwargs is a dictionary containing keyword arguments.
### Passage by assignment
When passing a parameter to a Python function, a reference to the object is actually passed (passage by assignment):
- If the passed object is mutable, it can be modified by the function.
- If the passed object is immutable, it cannot be modified by the function.
Here is an example:
```
my_list = [1, 2]
def add(some_list, value):
some_list.append(value)
add(my_list, 3)
my_list
```
The function add() modifies an object defined outside it (in this case, the object my_list); we say this function has side-effects. A function with no side-effects is called a pure function: it doesn't modify anything in the outer context, and it deterministically returns the same result for any given set of inputs. Pure functions are to be preferred over functions with side-effects.
Knowing this can help you spot out subtle bugs. There are further related concepts that are useful to know, including function scopes, naming, binding, and more. Here are a couple of links:
- Passage by reference at https://docs.python.org/3/faq/programming.html#how-do-i-write-a-function-with-output-parameters-call-by-reference
- Naming, binding, and scope at https://docs.python.org/3.4/reference/executionmodel.html
### Errors
Let's discuss about errors in Python. As you learn, you will inevitably come across errors and exceptions. The Python interpreter will most of the time tell you what the problem is, and where it occurred. It is important to understand the vocabulary used by Python so that you can more quickly find and correct your errors.
Let's see an example:
```
def divide(a, b):
return a / b
divide(1, 0)
```
Here, we defined a divide() function, and called it to divide 1 by 0. Dividing a number by 0 is an error in Python. Here, a ZeroDivisionError exception was raised. An exception is a particular type of error that can be raised at any point in a program. It is propagated from the innards of the code up to the command that launched the code. It can be caught and processed at any point. You will find more details about exceptions at https://docs.python.org/3/tutorial/errors.html, and common exception types at https://docs.python.org/3/library/exceptions.html#bltin-exceptions.
The error message you see contains the stack trace and the exception's type and message. The stack trace shows all functions calls between the raised exception and the script calling point.
The top frame, indicated by the first arrow ---->, shows the entry point of the code execution. Here, it is divide(1, 0) which was called directly in the Notebook. The error occurred while this function was called.
The next and last frame is indicated by the second arrow. It corresponds to line 2 in our function divide(a, b). It is the last frame in the stack trace: this means that the error occurred there.
### Object-oriented programming
Object-oriented programming (or OOP) is a relatively advanced topic. Although we won't use it much in this book, it is useful to know the basics. Also, mastering OOP is often essential when you start to have a large code base.
In Python, everything is an object. A number, a string, a function is an object. An object is an instance of a type (also known as class). An object has attributes and methods, as specified by its type. An attribute is a variable bound to an object, giving some information about it. A method is a function that applies to the object.
For example, the object 'hello' is an instance of the built-in str type (string). The type() function returns the type of an object, as shown here:
```
type('hello')
```
There are native types, like str or int (integer), and custom types, also called classes, that can be created by the user.
In IPython, you can discover the attributes and methods of any object with the dot syntax and tab completion. For example, typing 'hello'.u and pressing Tab automatically shows us the existence of the upper() method:
```
'hello'.upper()
```
Here, upper() is a method available to all str objects; it returns an uppercase copy of a string.
A useful string method is format(). This simple and convenient templating system lets you generate strings dynamically:
```
'Hello {0:s}!'.format('Python')
```
The {0:s} syntax means "replace this with the first argument of format() which should be a string". The variable type after the colon is especially useful for numbers, where you can specify how to display the number (for example, .3f to display three decimals). The 0 makes it possible to replace a given value several times in a given string. You can also use a name instead of a position, for example 'Hello {name}!'.format(name='Python').
Some methods are prefixed with an underscore _; they are private and are generally not meant to be used directly. IPython's tab completion won't show you these private attributes and methods unless you explicitly type _ before pressing Tab.
In practice, the most important thing to remember is that appending a dot . to any Python object and pressing Tab in IPython will show you a lot of functionality pertaining to that object.
### Functional programming
Python is a multi-paradigm language; it notably supports imperative, object-oriented, and functional programming models. Python functions are objects and can be handled like other objects. In particular, they can be passed as arguments to other functions (also called higher-order functions). This the essence of functional programming.
Decorators provide a convenient syntax construct to define higher-order functions. Here is an example using the is_even() function from the previous Functions section:
```
def show_output(func):
def wrapped(*args, **kwargs):
output = func(*args, **kwargs)
print("The result is:", output)
return wrapped
```
The show_output() function transforms an arbitrary function func() to a new function, named wrapped(), that displays the result of the function:
```
f = show_output(is_even)
f(3)
```
Equivalently, this higher-order function can also be used with a decorator:
```
@show_output
def square(x):
return x * x
square(3)
```
You can find more information about Python decorators at https://en.wikipedia.org/wiki/Python_syntax_and_semantics#Decorators and at http://thecodeship.com/patterns/guide-to-python-function-decorators/.
### Going beyond the basics
You now know the fundamentals of Python, the bare minimum that you will need in this book. As you can imagine, there is much more to say about Python.
There are a few further basic concepts that are often useful and that we cannot cover here, unfortunately. You are highly encouraged to have a look at them in the references given at the end of this section:
- range and enumerate
- pass, break, and, continue, to be used in loops
- working with files
- creating and importing modules
- the Python standard library provides a wide range of functionality (OS, network, file systems, compression, mathematics, and more)
Here are some slightly more advanced concepts that you might find useful if you want to strengthen your Python skills:
- regular expressions for advanced string processing
- lambda functions for defining small anonymous functions
- generators for controlling custom loops
- exceptions for handling errors
- with statements for safely handling contexts
- advanced object-oriented programming
- metaprogramming for modifying Python code dynamically
- the pickle module for persisting Python objects on disk and exchanging them across a network
Finally, here are a few references:
- Getting started with Python: https://www.python.org/about/gettingstarted/
- A Python tutorial: https://docs.python.org/3/tutorial/index.html
- The Python Standard Library: https://docs.python.org/3/library/index.html
- Interactive tutorial: http://www.learnpython.org/
- Codecademy Python course: http://www.codecademy.com/tracks/python
- Language reference (expert level): https://docs.python.org/3/reference/index.html
- Python Cookbook, by David Beazley and Brian K. Jones, O'Reilly Media (advanced level, highly recommended if you want to become a Python expert).
# <center>Examples with Python (under construction ...)</center>
## Exploring a dataset in the Notebook
### Provenance of the data
### Downloading and loading a dataset
```
import zipfile
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#with zipfile.ZipFile("nyc_taxi.zip","r") as zip_ref:
# zip_ref.extractall("C:/Users/miguel.alvarez/Desktop/chapter1")
data_filename = 'nyc_data.csv'
fare_filename = 'nyc_fare.csv'
data = pd.read_csv(data_filename, parse_dates=['pickup_datetime',
'dropoff_datetime'])
fare = pd.read_csv(fare_filename, parse_dates=['pickup_datetime'])
data.head(3)
```
### Making plots with matplotlib
```
data.columns
p_lng = data.pickup_longitude
p_lat = data.pickup_latitude
d_lng = data.dropoff_longitude
d_lat = data.dropoff_latitude
p_lng
def lat_lng_to_pixels(lat, lng):
lat_rad = lat * np.pi / 180.0
lat_rad = np.log(np.tan((lat_rad + np.pi / 2.0) / 2.0))
x = 100 * (lng + 180.0) / 360.0
y = 100 * (lat_rad - np.pi) / (2.0 * np.pi)
return (x, y)
px, py = lat_lng_to_pixels(p_lat, p_lng)
px
plt.scatter(px, py)
plt.figure(figsize=(8, 6))
plt.scatter(px, py, s=.1, alpha=.03)
plt.axis('equal')
plt.xlim(29.40, 29.55)
plt.ylim(-37.63, -37.54)
plt.axis('off')
```
### Descriptive statistics with pandas and seaborn
```
px.count(), px.min(), px.max()
px.mean(), px.median(), px.std()
#!conda install seaborn -q -y
import seaborn as sns
sns.__version__
data.trip_distance.hist(bins=np.linspace(0., 10., 100))
```
### References
- https://www.analyticsvidhya.com/blog/2016/01/complete-tutorial-learn-data-science-python-scratch-2/
| true |
code
| 0.405449 | null | null | null | null |
|
# Averaging over a region
Although this may not sound like _real_ regridding, averaging a gridded field
over a region is supported by `ESMF`. This works because the `conservative`
regridding method preserves the areal average of the input field. That is, _the
value at each output grid cell is the average input value over the output grid
area_. Instead of mapping the input field unto rectangular outputs cells, it's
mapped unto an irregular mesh defined by an outer polygon. In other words,
applying the regridding weights computes the exact areal-average of the input
grid over each polygon.
This process relies on converting `shapely.Polygon` and `shapely.MultiPolygon`
objects into `ESMF.Mesh` objects. However, ESMF meshes do not support all
features that come with shapely's (Multi)Polyons. Indeed, mesh elements do not
support interior holes, or multiple non-touching parts, as do `shapely` objects.
The `xesmf.SpatialAverager` class works around these issues by computing
independent weights for interior holes and multi-part geometries, before
combining the weights.
Transforming polygons into a `ESMF.Mesh` is a slow process. Users looking for
faster (but approximate) methods may want to explore
[regionmask](https://regionmask.readthedocs.io/) or
[clisops](https://clisops.readthedocs.io).
The following example shows just how simple it is to compute the average over
different countries. The notebook used `geopandas`, a simple and efficient
container for geometries, and `descartes` for plotting maps. Make sure both
packages are installed, as they are not `xesmf` dependencies.
```
%matplotlib inline
import matplotlib.pyplot as plt
import geopandas as gpd
import pandas as pd
from shapely.geometry import Polygon, MultiPolygon
import numpy as np
import xarray as xr
import xesmf as xe
import warnings
warnings.filterwarnings("ignore")
xr.set_options(display_style='text')
```
## Simple example
In this example we'll create a synthetic global field, then compute its average
over six countries.
### Download country outlines
```
# Load some polygons from the internet
regs = gpd.read_file(
"https://cdn.jsdelivr.net/npm/world-atlas@2/countries-10m.json"
)
# Select a few countries for the sake of the example
regs = regs.iloc[[5, 9, 37, 67, 98, 155]]
# Simplify the geometries to a 0.02 deg tolerance, which is 1/100 of our grid.
# The simpler the polygons, the faster the averaging, but we lose some precision.
regs["geometry"] = regs.simplify(tolerance=0.02, preserve_topology=True)
regs
# Create synthetic global data
ds = xe.util.grid_global(2, 2)
ds = ds.assign(field=xe.data.wave_smooth(ds.lon, ds.lat))
ds
# Display the global field and countries' outline.
fig, ax = plt.subplots()
ds.field.plot(ax=ax, x="lon", y="lat")
regs.plot(ax=ax, edgecolor="k", facecolor="none")
```
### Compute the field average over each country
`xesmf.SpatialAverager` is a class designed to average an `xarray.DataArray`
over a list of polygons. It behaves similarly to `xesmf.Regridder`, but has
options to deal specifically with polygon outputs. It uses the `conservative`
regridding, and can store and reuse weights.
```
savg = xe.SpatialAverager(ds, regs.geometry, geom_dim_name="country")
savg
```
When called, the `SpatialAverager` instance returns a `DataArray` of averages
over the `geom` dimension, here countries. `lon` and `lat` coordinates are the
centroids each polygon.
```
out = savg(ds.field)
out = out.assign_coords(country=xr.DataArray(regs["name"], dims=("country",)))
out
```
As the order of the polygons is conserved in the output, we can easily include
the results back into our `geopandas` dataframe.
```
regs["field_avg"] = out.values
regs
fig, ax = plt.subplots(figsize=(12, 5))
ds.field.plot(ax=ax, x="lon", y="lat", cmap="Greys_r")
handles = regs.plot(
column="field_avg", ax=ax, edgecolor="k", vmin=1, vmax=3, cmap="viridis"
)
```
### Extract the weight mask from the averager
The weights are stored in a sparse matrix structure in
`SpatialAverager.weights`. The sparse matrix can be converted to a full
DataArray, but note that this will increase memory usage proportional to the
number of polygons.
```
# Convert sparse matrix to numpy array, it has size : (n_in, n_out)
# So reshape to the same shape as ds + polygons
w = xr.DataArray(
savg.weights.toarray().reshape(regs.geometry.size, *ds.lon.shape),
dims=("country", *ds.lon.dims),
coords=dict(country=out.country, **ds.lon.coords),
)
plt.subplots_adjust(top=0.9)
facets = w.plot(col="country", col_wrap=2, aspect=2, vmin=0, vmax=0.05)
facets.cbar.set_label("Averaging weights")
```
This also allows to quickly check that the weights are indeed normalized, that
the sum of each mask is 1.
```
w.sum(dim=["y", "x"]).values
```
| true |
code
| 0.642517 | null | null | null | null |
|
# MMS in pyRFU
Louis RICHARD (louis.richard@irfu.se)
## Getting Started
To get up and running with Python, virtual environments and pyRFU, see: \
https://pyrfu.readthedocs.io/en/latest/getting_started.html#installation
Python 3.8 or later is required; we recommend installing Anaconda to get everything up and running.
### Virtual environments
It's best to setup and use virtual environments when using Python - these allow you to avoid common dependency problems when you install multiple packages\
`python -m venv pyspedas-tutorial`\
Then, to run the virtual environment, on Mac and Linux :\
`source pyspedas-tutorial/bin/activate`\
To exit the current virtual environment, type `deactivate`
### Install pyRFU
`pip install pyrfu`
### Upgrade pyRFU
`pip install pyrfu--upgrade`
### Local data directory
We use environment variables to set the local data directories:\
data_path (root data directory for all missions in pyRFU) e.g., if you set data_path="/Volumes/mms", your data will be stored in /Volumes/mms
The load routines supported include:
- Fluxgate Magnetometer (FGM)
- Search-coil Magnetometer (SCM)
- Electric field Double Probe (EDP)
- Fast Plasma Investigation (FPI)
- Hot Plasma Composition Analyzer (HPCA)
- Energetic Ion Spectrometer (EIS)
- Fly's Eye Energetic Particle Sensor (FEEPS)
- Ephemeris and Coordinates (MEC)
## Import MMS routines
```
from pyrfu import mms
```
## Define time interval
```
tint = ["2019-09-14T07:54:00.000", "2019-09-14T08:11:00.000"]
```
## Load data
Keywords to access data can be found in the help of mms.get_data
```
help(mms.get_data)
```
### Load magnetic field from (FGM)
```
b_xyz = mms.get_data("b_gse_fgm_srvy_l2", tint, 1)
```
### Load ions and electrons bulk velocity, number density and DEF (FPI)
```
n_i, n_e = [mms.get_data(f"n{s}_fpi_fast_l2", tint, 1) for s in ["i", "e"]]
# n_i, n_e = [mms.get_data("n{}_fpi_fast_l2".format(s), tint, 1) for s in ["i", "e"]]
v_xyz_i, v_xyz_e = [mms.get_data(f"v{s}_gse_fpi_fast_l2", tint, 1) for s in ["i", "e"]]
def_omni_i, def_omni_e = [mms.get_data(f"def{s}_fpi_fast_l2", tint, 1) for s in ["i", "e"]]
```
### Load electric field (EDP)
```
e_xyz = mms.get_data("e_gse_edp_fast_l2", tint, 1)
```
## Plot overview
```
import matplotlib.pyplot as plt
from pyrfu.plot import plot_line, plot_spectr
%matplotlib notebook
legend_options = dict(frameon=True, loc="upper right")
fig, axs = plt.subplots(7, sharex="all", figsize=(8, 11))
fig.subplots_adjust(bottom=.05, top=.95, left=.11, right=.89, hspace=0)
# magnetic field
plot_line(axs[0], b_xyz)
axs[0].legend(["$B_x$", "$B_y$", "$B_z$"], ncol=3, **legend_options)
axs[0].set_ylabel("$B$ [nT]")
# electric field
plot_line(axs[1], e_xyz)
axs[1].legend(["$E_x$", "$E_y$", "$E_z$"], ncol=3, **legend_options)
axs[1].set_ylabel("$E$ [mV.m$^{-1}$]")
# number density
plot_line(axs[2], n_i, "tab:red")
plot_line(axs[2], n_e, "tab:blue")
axs[2].legend(["$Ions$", "$Electrons$"], ncol=2, **legend_options)
axs[2].set_ylabel("$n$ [cm$^{-3}$]")
# Ion bulk velocity
plot_line(axs[3], v_xyz_i)
axs[3].legend(["$V_{i,x}$", "$V_{i,y}$", "$V_{i,z}$"], ncol=3, **legend_options)
axs[3].set_ylabel("$V_i$ [km.s$^{-1}$]")
# Ion DEF
axs[4], caxs4 = plot_spectr(axs[4], def_omni_i, yscale="log", cscale="log", cmap="Spectral_r")
axs[4].set_ylabel("$E_i$ [eV]")
caxs4.set_ylabel("DEF" + "\n" + "[kev/(cm$^2$ s sr keV)]")
# Electron bulk velocity
plot_line(axs[5], v_xyz_e)
axs[5].legend(["$V_{e,x}$", "$V_{e,y}$", "$V_{e,z}$"], ncol=3, **legend_options)
axs[5].set_ylabel("$V_e$ [km.s$^{-1}$]")
# Electron DEF
axs[6], caxs6 = plot_spectr(axs[6], def_omni_e, yscale="log", cscale="log", cmap="Spectral_r")
axs[6].set_ylabel("$E_e$ [eV]")
caxs6.set_ylabel("DEF" + "\n" + "[kev/(cm$^2$ s sr keV)]")
```
## Load data for all spacecraft
### Spacecaft position (MEC)
```
r_mms = [mms.get_data("R_gse", tint, i) for i in range(1, 5)]
```
### Magnetic field (FGM)
```
b_mms = [mms.get_data("b_gse_fgm_srvy_l2", tint, i) for i in range(1, 5)]
```
### Plot
```
f, axs = plt.subplots(3, sharex="all", figsize=(6.5, 5))
f.subplots_adjust(hspace=0)
labels = ["MMS{:d}".format(i + 1) for i in range(4)]
legend_options = dict(ncol=4, frameon=True, loc="upper right")
for ax, j, c in zip(axs, [0, 1, 2], ["x", "y", "z"]):
for i, b in enumerate(b_mms):
plot_line(ax, b[:, j])
ax.legend(labels, **legend_options)
ax.set_ylabel("$B_{}$ [nT]".format(c))
```
| true |
code
| 0.633297 | null | null | null | null |
|
# Setup
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from mlwpy_video_extras import (regression_errors,
regression_residuals)
import collections as co
import itertools as it
from sklearn import (datasets,
dummy,
linear_model,
metrics,
model_selection as skms,
neighbors,
pipeline,
preprocessing as skpre)
import warnings
warnings.filterwarnings("ignore")
np.random.seed(42)
```
# Baseline Regressors
```
diabetes = datasets.load_diabetes()
tts = skms.train_test_split(diabetes.data, diabetes.target,
test_size=.25, random_state=42)
(diabetes_train_ftrs, diabetes_test_ftrs,
diabetes_train_tgt, diabetes_test_tgt) = tts
baseline = dummy.DummyRegressor(strategy='mean')
baseline = dummy.DummyRegressor(strategy='median')
strategies = ['constant', 'quantile', 'mean', 'median', ]
baseline_args = [{"strategy":s} for s in strategies]
# additional args for constant and quantile
baseline_args[0]['constant'] = 50.0
baseline_args[1]['quantile'] = 0.75
# helper to unpack arguments for each DummyRegresor and
# do a fit-predict-eval sequence
def do_one_diabetes(**args):
baseline = dummy.DummyRegressor(**args)
baseline.fit(diabetes_train_ftrs, diabetes_train_tgt)
base_preds = baseline.predict(diabetes_test_ftrs)
return metrics.mean_squared_error(base_preds, diabetes_test_tgt)
# gather all results via a list comprehension
mses = [do_one_diabetes(**bla) for bla in baseline_args]
display(pd.DataFrame({'mse':mses,
'rmse':np.sqrt(mses)},
index=strategies))
```
# Regression Metrics
##### Custom Metrics and RMSE
```
# we could define mean_squared_error as:
# sse = np.sum((actual - predicted)**2) [sum-of-squared errors]
# mse = sse / len(actual)
def rms_error(actual, predicted):
' root-mean-squared-error function '
# lesser values are better (a<b ... a is better)
mse = metrics.mean_squared_error(actual, predicted)
return np.sqrt(mse)
def neg_rmse_score(actual, predicted):
' rmse based score function '
# greater values are better (a<b ... b better)
return -rms_error(actual, predicted)
# routines like cross_val_score need a "scorer"
def neg_rmse_scorer(model, ftrs, tgt_actual):
' rmse scorer suitable for scoring arg '
tgt_pred = model.predict(ftrs)
return neg_rmse_score(tgt_actual, tgt_pred)
knn = neighbors.KNeighborsRegressor(n_neighbors=3)
skms.cross_val_score(knn, diabetes.data, diabetes.target,
scoring=neg_rmse_scorer)
metrics.SCORERS['neg_mean_squared_error']
knn = neighbors.KNeighborsRegressor(n_neighbors=3)
nrmse = skms.cross_val_score(knn, diabetes.data, diabetes.target,
scoring='neg_root_mean_squared_error')
nrmse
# the primary regression metrics available
[k for k in metrics.SCORERS.keys() if k.endswith('error')]
```
### Understanding the Default Regression Metric $R^2$
```
lr = linear_model.LinearRegression()
# help(lr.score) #for full output
print(lr.score.__doc__.splitlines()[0])
```
$$R^2 = 1 - \frac{{SSE}_{our\ predictions}}{{SSE}_{mean\ as\ prediction}}$$
```
# where does the mean come from!?!
# calculate the mean on the training set and evaluate on the test set
# calculate the mean on the **test** set and evaluate on the test set
errors_mean_train_on_train = np.mean(diabetes_train_tgt) - diabetes_train_tgt
errors_mean_train_on_test = np.mean(diabetes_train_tgt) - diabetes_test_tgt
errors_mean_test_on_test = np.mean(diabetes_test_tgt) - diabetes_test_tgt
# calculate sum-of-squared-errors two ways:
via_manual = (errors_mean_train_on_train**2).sum()
via_npdot = np.dot(errors_mean_train_on_train,
errors_mean_train_on_train)
np.allclose(via_manual, via_npdot)
def sse(errors):
return np.sum(errors**2) # you'll np.dot()
sse_mean_train_on_train = sse(errors_mean_train_on_train)
sse_mean_train_on_test = sse(errors_mean_train_on_test)
sse_mean_test_on_test = sse(errors_mean_test_on_test)
print("mean train on train:", sse_mean_train_on_train)
print("mean train on test:", sse_mean_train_on_test)
print("mean test on test: ", sse_mean_test_on_test)
# now, imagine we have a simple linear regression model:
lr = linear_model.LinearRegression()
lr_preds = (lr.fit(diabetes_train_ftrs, diabetes_train_tgt)
.predict(diabetes_test_ftrs))
lr_r2 = metrics.r2_score(diabetes_test_tgt, lr_preds)
lr_r2
# compare
# the sse of linear_regression trained on train, evaluated on test
sse_lr = sse(lr_preds-diabetes_test_tgt)
# the sse of baseline-mean trained on *test*, evaluated on test
sse_mean_test_on_test = sse(errors_mean_test_on_test)
1 - (sse_lr/sse_mean_test_on_test)
# we can demonstrate that with builtins:
base_model = dummy.DummyRegressor(strategy='mean')
base_model.fit(diabetes_test_ftrs, diabetes_test_tgt) # WARNING! this is the weird step!
base_model_test_preds = base_model.predict(diabetes_test_ftrs)
# you might notice we use MSE instead of SSE:
# it's ok, because we'll do it in two places and a factor of (1/n) will simply cancel out
base_model_mse = metrics.mean_squared_error(diabetes_test_tgt,
base_model_test_preds)
print(base_model_mse)
models = {'knn': neighbors.KNeighborsRegressor(n_neighbors=3),
'lr' : linear_model.LinearRegression()}
results = co.defaultdict(dict)
for name in models:
m = models[name]
preds = (m.fit(diabetes_train_ftrs, diabetes_train_tgt)
.predict(diabetes_test_ftrs))
results[name]['r2'] = metrics.r2_score(diabetes_test_tgt, preds)
results[name]['mse'] = metrics.mean_squared_error(diabetes_test_tgt, preds)
df = pd.DataFrame(results).T
df['r2 via mse'] = 1 - (df['mse'] / base_model_mse)
display(df)
```
# Errors and Residuals
```
ape_df = pd.DataFrame({'predicted' : [4, 2, 9],
'actual' : [3, 5, 7]})
ape_df['error'] = ape_df['predicted'] - ape_df['actual']
ape_df.index.name = 'example'
display(ape_df)
regression_errors((6,3), ape_df.predicted, ape_df.actual)
lr = linear_model.LinearRegression()
preds = (lr.fit(diabetes_train_ftrs, diabetes_train_tgt)
.predict(diabetes_test_ftrs))
regression_errors((8,4), preds, diabetes_test_tgt, errors=[-20])
ape_df = pd.DataFrame({'predicted' : [4, 2, 9],
'actual' : [3, 5, 7]})
ape_df['error'] = ape_df['predicted'] - ape_df['actual']
ape_df['resid'] = ape_df['actual'] - ape_df['predicted']
ape_df.index.name = 'example'
display(ape_df)
fig, (ax1, ax2) = plt.subplots(1,2,figsize=(8,4))
ax1.plot(ape_df.predicted, ape_df.actual, 'r.', # pred v actual
[0,10], [0,10], 'b-') # perfect line
ax1.set_xlabel('Predicted')
ax1.set_ylabel('Actual')
regression_residuals(ax2, ape_df.predicted, ape_df.actual,
'all', right=True)
lr = linear_model.LinearRegression()
knn = neighbors.KNeighborsRegressor()
models = [lr, knn]
fig, axes = plt.subplots(1, 2, figsize=(10,5),
sharex=True, sharey=True)
fig.tight_layout()
for model, ax, on_right in zip(models, axes, [False, True]):
preds = (model.fit(diabetes_train_ftrs, diabetes_train_tgt)
.predict(diabetes_test_ftrs))
regression_residuals(ax, preds, diabetes_test_tgt, [-20], on_right)
axes[0].set_title('Linear Regression Residuals')
axes[1].set_title('kNN-Regressor Rediduals');
print(diabetes_test_tgt[-20])
```
# A Quick Pipeline and Standardization for Linear Regression
```
# 1-D standardization
# place evenly spaced values in a dataframe
xs = np.linspace(-5, 10, 20)
df = pd.DataFrame(xs, columns=['x'])
# center ( - mean) and scale (/ std)
df['std-ized'] = (df.x - df.x.mean()) / df.x.std()
# show original and new data; compute statistics
fig, ax = plt.subplots(1,1,figsize=(3,3))
sns.stripplot(data=df)
display(df.describe().loc[['mean', 'std']])
# 2 1-D standardizations
xs = np.linspace(-5, 10, 20)
ys = 3*xs + 2 + np.random.uniform(20, 40, 20)
print("First Row Values")
df = pd.DataFrame({'x':xs, 'y':ys})
display(df.head())
print("Standardized")
df_std_ized = (df - df.mean()) / df.std()
display(df_std_ized.describe().loc[['mean', 'std']])
fig, ax = plt.subplots(2,2, figsize=(5,5))
ax[0,0].plot(df.x, df.y, '.')
ax[0,1].plot(df_std_ized.x, df_std_ized.y, '.')
ax[0,0].set_ylabel('"Natural" Scale')
ax[1,0].plot(df.x, df.y, '.')
ax[1,1].plot(df_std_ized.x, df_std_ized.y, '.')
ax[1,0].axis([-10, 50, -10, 50])
ax[1,1].axis([-10, 50, -10, 50])
ax[1,0].set_ylabel('Fixed/Shared Scale')
ax[1,0].set_xlabel('Original Data')
ax[1,1].set_xlabel('Standardized Data');
train_xs, test_xs = skms.train_test_split(xs.reshape(-1,1), test_size=.5)
scaler = skpre.StandardScaler()
scaler.fit(train_xs).transform(test_xs)
(train_xs, test_xs,
train_ys, test_ys)= skms.train_test_split(xs.reshape(-1,1),
ys.reshape(-1,1),
test_size=.5)
scaler = skpre.StandardScaler()
lr = linear_model.LinearRegression()
std_lr_pipe = pipeline.make_pipeline(scaler, lr)
std_lr_pipe.fit(train_xs, train_ys).predict(test_xs)
```
# Case Study: A Regression Comparison
```
boston = datasets.load_boston()
boston_df = pd.DataFrame(boston.data, columns=boston.feature_names)
boston_df['tgt'] = boston.target
boston_df.head()
boston_ftrs = boston.data
boston_tgt = boston.target
models = {'base' : dummy.DummyRegressor(strategy='mean'),
'lr' : linear_model.LinearRegression(),
'knn_3' : neighbors.KNeighborsRegressor(n_neighbors=3),
'knn_10': neighbors.KNeighborsRegressor(n_neighbors=10)}
# join these into standarization pipelines
make_p = pipeline.make_pipeline
scaler = skpre.StandardScaler()
pipes = {m:make_p(scaler, models[m]) for m in models}
scorers = {'neg. mae' :metrics.SCORERS['neg_median_absolute_error'],
'neg. rmse':metrics.SCORERS['neg_root_mean_squared_error']}
fig, axes = plt.subplots(2, 1, figsize=(6,4))
fig.tight_layout()
for name in pipes:
p = pipes[name]
cv_results = skms.cross_validate(p, boston_ftrs, boston_tgt,
scoring = scorers, cv=10)
for ax, msr in zip(axes, scorers):
msr_results = cv_results["test_" + msr]
my_lbl = "{:12s} {:.3f} {:.2f}".format(name,
msr_results.mean(),
msr_results.std())
ax.plot(msr_results, 'o--', label=my_lbl)
ax.set_title(msr)
ax.legend()
fig,ax = plt.subplots(1,1,figsize=(6,3))
baseline_mse = skms.cross_val_score(models['base'],
boston_ftrs, boston_tgt,
scoring = scorers['neg. rmse'], cv=10)
for name in pipes:
p = pipes[name]
cv_results = skms.cross_val_score(p, boston_ftrs, boston_tgt,
scoring = scorers['neg. rmse'], cv=10)
my_lbl = "{:12s} {:.3f} {:.2f}".format(name,
cv_results.mean(),
cv_results.std())
ax.plot(cv_results / baseline_mse, 'o--', label=my_lbl)
ax.set_title("RMSE(model) / RMSE(baseline)\n$<1$ is better than baseline")
ax.legend();
# this time, just metrics (not scorers)
msrs = {'mad' : metrics.mean_absolute_error,
'rmse' : rms_error}
results = {}
for name in pipes:
p = pipes[name]
cv_preds = skms.cross_val_predict(p, boston_ftrs, boston_tgt,
cv=10)
for ax, msr in zip(axes, msrs):
msr_results = msrs[msr](boston_tgt, cv_preds)
results.setdefault(msr, []).append(msr_results)
df = pd.DataFrame(results, index=pipes.keys())
df
fig, axes = plt.subplots(1, 4, figsize=(10,5),
sharex=True, sharey=True)
fig.tight_layout()
for name, ax in zip(pipes, axes):
p = pipes[name]
preds = skms.cross_val_predict(p, boston_ftrs, boston_tgt,
cv=10)
regression_residuals(ax, preds, boston_tgt)
ax.set_title(name + " residuals")
pd.DataFrame(boston_tgt).describe().T
```
| true |
code
| 0.562056 | null | null | null | null |
|
# Trees
```
import numpy as np
import matplotlib.pyplot as plt
% matplotlib inline
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print(cancer.DESCR)
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=0)
```
# tree visualization
```
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=2)
tree.fit(X_train, y_train)
# import from local file, not in sklearn yet
from tree_plotting import plot_tree
plt.figure(dpi=200)
plot_tree(tree, feature_names=cancer.feature_names, filled=True)
```
# Parameter Tuning
```
tree = DecisionTreeClassifier().fit(X_train, y_train)
plt.figure(figsize=(15, 5))
plot_tree(tree, feature_names=cancer.feature_names, filled=True)
tree = DecisionTreeClassifier(max_depth=3).fit(X_train, y_train)
plt.figure(figsize=(15, 5))
plot_tree(tree, feature_names=cancer.feature_names)
tree = DecisionTreeClassifier(max_leaf_nodes=8).fit(X_train, y_train)
plot_tree(tree, feature_names=cancer.feature_names, filled=True)
tree = DecisionTreeClassifier(min_samples_split=50).fit(X_train, y_train)
plot_tree(tree, feature_names=cancer.feature_names, filled=True)
tree = DecisionTreeClassifier(min_impurity_decrease=.01).fit(X_train, y_train)
plot_tree(tree, feature_names=cancer.feature_names, filled=True)
from sklearn.model_selection import GridSearchCV
param_grid = {'max_depth':range(1, 7)}
grid = GridSearchCV(DecisionTreeClassifier(random_state=0), param_grid=param_grid, cv=10)
grid.fit(X_train, y_train)
from sklearn.model_selection import GridSearchCV, StratifiedShuffleSplit
param_grid = {'max_depth':range(1, 7)}
grid = GridSearchCV(DecisionTreeClassifier(random_state=0), param_grid=param_grid,
cv=StratifiedShuffleSplit(100), return_train_score=True)
grid.fit(X_train, y_train)
scores = pd.DataFrame(grid.cv_results_)
scores.plot(x='param_max_depth', y=['mean_train_score', 'mean_test_score'], ax=plt.gca())
plt.legend(loc=(1, 0))
from sklearn.model_selection import GridSearchCV
param_grid = {'max_leaf_nodes': range(2, 20)}
grid = GridSearchCV(DecisionTreeClassifier(random_state=0), param_grid=param_grid,
cv=StratifiedShuffleSplit(100, random_state=1),
return_train_score=True)
grid.fit(X_train, y_train)
scores = pd.DataFrame(grid.cv_results_)
scores.plot(x='param_max_leaf_nodes', y=['mean_train_score', 'mean_test_score'], ax=plt.gca())
plt.legend(loc=(1, 0))
scores = pd.DataFrame(grid.cv_results_)
scores.plot(x='param_max_leaf_nodes', y='mean_train_score', yerr='std_train_score', ax=plt.gca())
scores.plot(x='param_max_leaf_nodes', y='mean_test_score', yerr='std_test_score', ax=plt.gca())
grid.best_params_
plot_tree(grid.best_estimator_, feature_names=cancer.feature_names, filled=True)
pd.Series(grid.best_estimator_.feature_importances_,
index=cancer.feature_names).plot(kind="barh")
```
# Exercise
Apply a decision tree to the "adult" dataset and visualize it.
Tune parameters with grid-search; try at least max_leaf_nodes and max_depth, but separately.
Visualize the resulting tree and it's feature importances.
| true |
code
| 0.657291 | null | null | null | null |
|
# PyTorch Model + Transformer Example
This notebook demonstrates how to deploy a PyTorch model and a custom transformer. It uses cifar10 model model that accepts a tensor input. The transformer has preprocessing step that allows the user to send a raw image data and convert it to a tensor input.
## Requirements
- Authenticated to gcloud (```gcloud auth application-default login```)
```
!pip install --upgrade -r requirements.txt > /dev/null
import warnings
warnings.filterwarnings('ignore')
```
## 1. Initialize Merlin
### 1.1 Set Merlin Server
```
import merlin
MERLIN_URL = "<MERLIN_HOST>/api/merlin"
merlin.set_url(MERLIN_URL)
```
### 1.2 Set Active Project
`project` represent a project in real life. You may have multiple model within a project.
`merlin.set_project(<project-name>)` will set the active project into the name matched by argument. You can only set it to an existing project. If you would like to create a new project, please do so from the MLP UI.
```
PROJECT_NAME = "sample"
merlin.set_project(PROJECT_NAME)
```
### 1.3 Set Active Model
`model` represents an abstract ML model. Conceptually, `model` in Merlin is similar to a class in programming language. To instantiate a `model` you'll have to create a `model_version`.
Each `model` has a type, currently model type supported by Merlin are: sklearn, xgboost, tensorflow, pytorch, and user defined model (i.e. pyfunc model).
`model_version` represents a snapshot of particular `model` iteration. You'll be able to attach information such as metrics and tag to a given `model_version` as well as deploy it as a model service.
`merlin.set_model(<model_name>, <model_type>)` will set the active model to the name given by parameter, if the model with given name is not found, a new model will be created.
```
from merlin.model import ModelType
MODEL_NAME = "transformer-pytorch"
merlin.set_model(MODEL_NAME, ModelType.PYTORCH)
```
## 2. Train Model
### 2.1 Prepare Training Data
```
import torch
import torchvision
import torchvision.transforms as transforms
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
shuffle=True, num_workers=2)
```
### 2.2 Create PyTorch Model
```
import torch.nn as nn
import torch.nn.functional as F
class PyTorchModel(nn.Module):
def __init__(self):
super(PyTorchModel, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
```
### 2.3 Train Model
```
import torch.optim as optim
net = PyTorchModel()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs; data is a list of [inputs, labels]
inputs, labels = data
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
```
### 2.4 Check Prediction
```
dataiter = iter(trainloader)
inputs, labels = dataiter.next()
predict_out = net(inputs[0:1])
predict_out
```
## 3. Deploy Model and Transformer
### 3.1 Serialize Model
```
import os
model_dir = "pytorch-model"
model_path = os.path.join(model_dir, "model.pt")
torch.save(net.state_dict(), model_path)
```
### 3.2 Save PyTorchModel Class
We also need to save the PyTorchModel class and upload it to Merlin alongside the serialized model. The next cell will write the PyTorchModel we defined above to `pytorch-model/model.py` file.
```
%%file pytorch-model/model.py
import torch.nn as nn
import torch.nn.functional as F
class PyTorchModel(nn.Module):
def __init__(self):
super(PyTorchModel, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
```
### 3.3 Create Model Version and Upload
`merlin.new_model_version()` is a convenient method to create a model version and start its development process. It is equal to following codes:
```
v = model.new_model_version()
v.start()
v.log_pytorch_model(model_dir=model_dir)
v.finish()
```
```
# Create new version of the model
with merlin.new_model_version() as v:
# Upload the serialized model to Merlin
merlin.log_pytorch_model(model_dir=model_dir)
```
### 3.4 Deploy Model and Transformer
To deploy a model and its transformer, you must pass a `transformer` object to `deploy()` function. Each of deployed model version will have its own generated url.
```
from merlin.resource_request import ResourceRequest
from merlin.transformer import Transformer
# Create a transformer object and its resources requests
resource_request = ResourceRequest(min_replica=1, max_replica=1,
cpu_request="100m", memory_request="200Mi")
transformer = Transformer("gcr.io/kubeflow-ci/kfserving/image-transformer:latest",
resource_request=resource_request)
endpoint = merlin.deploy(v, transformer=transformer)
```
### 3.5 Send Test Request
```
import json
import requests
with open(os.path.join("input-raw-image.json"), "r") as f:
req = json.load(f)
resp = requests.post(endpoint.url, json=req)
resp.text
```
## 4. Clean Up
## 4.1 Delete Deployment
```
merlin.undeploy(v)
```
| true |
code
| 0.767946 | null | null | null | null |
|
```
import panel as pn
import numpy as np
import holoviews as hv
pn.extension()
```
For a large variety of use cases we do not need complete control over the exact layout of each individual component on the page, as could be achieved with a [custom template](../../user_guide/Templates.ipynb), we just want to achieve a more polished look and feel. For these cases Panel ships with a number of default templates, which are defined by declaring three main content areas on the page, which can be populated as desired:
* **`header`**: The header area of the HTML page
* **`sidebar`**: A collapsible sidebar
* **`main`**: The main area of the application
* **`modal`**: A modal area which can be opened and closed from Python
These three areas behave very similarly to other Panel layout components and have list-like semantics. This means we can easily append new components into these areas. Unlike other layout components however, the contents of the areas is fixed once rendered. If you need a dynamic layout you should therefore insert a regular Panel layout component (e.g. a `Column` or `Row`) and modify it in place once added to one of the content areas.
Templates can allow for us to quickly and easily create web apps for displaying our data. Panel comes with a default Template, and includes multiple Templates that extend the default which add some customization for a better display.
#### Parameters:
In addition to the four different areas we can populate, the `FastListTemplate` also provide additional parameters:
* **`busy_indicator`** (BooleanIndicator): Visual indicator of application busy state.
* **`header_background`** (str): Optional header background color override.
* **`header_color`** (str): Optional header text color override.
* **`favicon`** (str): URI of favicon to add to the document head (if local file, favicon is base64 encoded as URI).
* **`logo`** (str): URI of logo to add to the header (if local file, logo is base64 encoded as URI).
* **`theme`** (Theme): A Theme class (available in `panel.template`. One of `DefaultTheme` or `DarkTheme`).
- For convenience you can provide "default" or "dark" string to the constructor.
- If you add `?theme=default` or `?theme=dark` in the url this will set the theme unless explicitly declared
* **`site`** (str): The name of the site. Will be shown in the header and link to the root (/) of the site. Default is '', i.e. not shown.
* **`title`** (str): A title to show in the header. Also added to the document head meta settings and as the browser tab title.
* **`main_max_width`** (str): The maximum width of the main area. For example '800px' or '80%'. If the string is '' (default) no max width is set.
* **`sidebar_footer`** (str): Can be used to insert additional HTML. For example a menu, some additional info, links etc.
* **`enable_theme_toggle`** (boolean): If `True` a switch to toggle the Theme is shown. Default is `True`.
* **`config`** (TemplateConfig): Contains configuration options similar to `pn.config` but applied to the current Template only. (Currently only `css_files` is supported)
________
In this case we are using the `FastListTemplate`, built using the [Fast.design](https://www.fast.design/) framework. Here is an example of how you can set up a display using this template:
```
template = pn.template.FastListTemplate(title='FastListTemplate')
pn.config.sizing_mode = 'stretch_width'
xs = np.linspace(0, np.pi)
freq = pn.widgets.FloatSlider(name="Frequency", start=0, end=10, value=2)
phase = pn.widgets.FloatSlider(name="Phase", start=0, end=np.pi)
@pn.depends(freq=freq, phase=phase)
def sine(freq, phase):
return hv.Curve((xs, np.sin(xs*freq+phase))).opts(
responsive=True, min_height=400, title="Sine")
@pn.depends(freq=freq, phase=phase)
def cosine(freq, phase):
return hv.Curve((xs, np.cos(xs*freq+phase))).opts(
responsive=True, min_height=400, title="Cosine")
template.sidebar.append(pn.pane.Markdown("## Settings"))
template.sidebar.append(freq)
template.sidebar.append(phase)
template.main.append(hv.DynamicMap(sine),)
template.main.append(hv.DynamicMap(cosine))
template.servable();
```
<h3><b>FastListTemplate with DefaultTheme</b></h3>
<img src="../../assets/FastListTemplate.png" style="margin-left: auto; margin-right: auto; display: block;"></img>
</br>
<h3><b>FastListTemplate with DarkTheme</b></h3>
<img src="../../assets/FastListTemplateDark.png" style="margin-left: auto; margin-right: auto; display: block;"></img>
The app can be displayed within the notebook by using `.servable()`, or rendered in another tab by replacing it with `.show()`.
Themes can be added using the optional keyword argument `theme`. This template comes with a `DarkTheme` and a `DefaultTheme`, which can be set via `FastlistTemplate(theme=DarkTheme)`. If no theme is set, then `DefaultTheme` will be applied.
It should be noted **this template currently does not render correctly in a notebook**, and for the best performance the should ideally be deployed to a server.
| true |
code
| 0.458894 | null | null | null | null |
|
# Image Captioning with RNNs
In this exercise you will implement a vanilla recurrent neural networks and use them it to train a model that can generate novel captions for images.
```
# As usual, a bit of setup
from __future__ import print_function
import time, os, json
import numpy as np
import matplotlib.pyplot as plt
from cs231n.gradient_check import eval_numerical_gradient, eval_numerical_gradient_array
from cs231n.rnn_layers import *
from cs231n.captioning_solver import CaptioningSolver
from cs231n.classifiers.rnn import CaptioningRNN
from cs231n.coco_utils import load_coco_data, sample_coco_minibatch, decode_captions
from cs231n.image_utils import image_from_url
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# for auto-reloading external modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
def rel_error(x, y):
""" returns relative error """
return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))
```
## Install h5py
The COCO dataset we will be using is stored in HDF5 format. To load HDF5 files, we will need to install the `h5py` Python package. From the command line, run: <br/>
`pip install h5py` <br/>
If you receive a permissions error, you may need to run the command as root: <br/>
```sudo pip install h5py```
You can also run commands directly from the Jupyter notebook by prefixing the command with the "!" character:
```
!pip3 install h5py
```
# Microsoft COCO
For this exercise we will use the 2014 release of the [Microsoft COCO dataset](http://mscoco.org/) which has become the standard testbed for image captioning. The dataset consists of 80,000 training images and 40,000 validation images, each annotated with 5 captions written by workers on Amazon Mechanical Turk.
You should have already downloaded the data by changing to the `cs231n/datasets` directory and running the script `get_assignment3_data.sh`. If you haven't yet done so, run that script now. Warning: the COCO data download is ~1GB.
We have preprocessed the data and extracted features for you already. For all images we have extracted features from the fc7 layer of the VGG-16 network pretrained on ImageNet; these features are stored in the files `train2014_vgg16_fc7.h5` and `val2014_vgg16_fc7.h5` respectively. To cut down on processing time and memory requirements, we have reduced the dimensionality of the features from 4096 to 512; these features can be found in the files `train2014_vgg16_fc7_pca.h5` and `val2014_vgg16_fc7_pca.h5`.
The raw images take up a lot of space (nearly 20GB) so we have not included them in the download. However all images are taken from Flickr, and URLs of the training and validation images are stored in the files `train2014_urls.txt` and `val2014_urls.txt` respectively. This allows you to download images on the fly for visualization. Since images are downloaded on-the-fly, **you must be connected to the internet to view images**.
Dealing with strings is inefficient, so we will work with an encoded version of the captions. Each word is assigned an integer ID, allowing us to represent a caption by a sequence of integers. The mapping between integer IDs and words is in the file `coco2014_vocab.json`, and you can use the function `decode_captions` from the file `cs231n/coco_utils.py` to convert numpy arrays of integer IDs back into strings.
There are a couple special tokens that we add to the vocabulary. We prepend a special `<START>` token and append an `<END>` token to the beginning and end of each caption respectively. Rare words are replaced with a special `<UNK>` token (for "unknown"). In addition, since we want to train with minibatches containing captions of different lengths, we pad short captions with a special `<NULL>` token after the `<END>` token and don't compute loss or gradient for `<NULL>` tokens. Since they are a bit of a pain, we have taken care of all implementation details around special tokens for you.
You can load all of the MS-COCO data (captions, features, URLs, and vocabulary) using the `load_coco_data` function from the file `cs231n/coco_utils.py`. Run the following cell to do so:
```
# Load COCO data from disk; this returns a dictionary
# We'll work with dimensionality-reduced features for this notebook, but feel
# free to experiment with the original features by changing the flag below.
data = load_coco_data(pca_features=True)
# Print out all the keys and values from the data dictionary
for k, v in data.items():
if type(v) == np.ndarray:
print(k, type(v), v.shape, v.dtype)
else:
print(k, type(v), len(v))
```
## Look at the data
It is always a good idea to look at examples from the dataset before working with it.
You can use the `sample_coco_minibatch` function from the file `cs231n/coco_utils.py` to sample minibatches of data from the data structure returned from `load_coco_data`. Run the following to sample a small minibatch of training data and show the images and their captions. Running it multiple times and looking at the results helps you to get a sense of the dataset.
Note that we decode the captions using the `decode_captions` function and that we download the images on-the-fly using their Flickr URL, so **you must be connected to the internet to view images**.
```
# Sample a minibatch and show the images and captions
batch_size = 3
captions, features, urls = sample_coco_minibatch(data, batch_size=batch_size)
for i, (caption, url) in enumerate(zip(captions, urls)):
plt.imshow(image_from_url(url))
plt.axis('off')
caption_str = decode_captions(caption, data['idx_to_word'])
plt.title(caption_str)
plt.show()
```
# Recurrent Neural Networks
As discussed in lecture, we will use recurrent neural network (RNN) language models for image captioning. The file `cs231n/rnn_layers.py` contains implementations of different layer types that are needed for recurrent neural networks, and the file `cs231n/classifiers/rnn.py` uses these layers to implement an image captioning model.
We will first implement different types of RNN layers in `cs231n/rnn_layers.py`.
# Vanilla RNN: step forward
Open the file `cs231n/rnn_layers.py`. This file implements the forward and backward passes for different types of layers that are commonly used in recurrent neural networks.
First implement the function `rnn_step_forward` which implements the forward pass for a single timestep of a vanilla recurrent neural network. After doing so run the following to check your implementation. You should see errors less than 1e-8.
```
N, D, H = 3, 10, 4
x = np.linspace(-0.4, 0.7, num=N*D).reshape(N, D)
prev_h = np.linspace(-0.2, 0.5, num=N*H).reshape(N, H)
Wx = np.linspace(-0.1, 0.9, num=D*H).reshape(D, H)
Wh = np.linspace(-0.3, 0.7, num=H*H).reshape(H, H)
b = np.linspace(-0.2, 0.4, num=H)
next_h, _ = rnn_step_forward(x, prev_h, Wx, Wh, b)
expected_next_h = np.asarray([
[-0.58172089, -0.50182032, -0.41232771, -0.31410098],
[ 0.66854692, 0.79562378, 0.87755553, 0.92795967],
[ 0.97934501, 0.99144213, 0.99646691, 0.99854353]])
print('next_h error: ', rel_error(expected_next_h, next_h))
```
# Vanilla RNN: step backward
In the file `cs231n/rnn_layers.py` implement the `rnn_step_backward` function. After doing so run the following to numerically gradient check your implementation. You should see errors less than `1e-8`.
```
from cs231n.rnn_layers import rnn_step_forward, rnn_step_backward
np.random.seed(231)
N, D, H = 4, 5, 6
x = np.random.randn(N, D)
h = np.random.randn(N, H)
Wx = np.random.randn(D, H)
Wh = np.random.randn(H, H)
b = np.random.randn(H)
out, cache = rnn_step_forward(x, h, Wx, Wh, b)
dnext_h = np.random.randn(*out.shape)
fx = lambda x: rnn_step_forward(x, h, Wx, Wh, b)[0]
fh = lambda prev_h: rnn_step_forward(x, h, Wx, Wh, b)[0]
fWx = lambda Wx: rnn_step_forward(x, h, Wx, Wh, b)[0]
fWh = lambda Wh: rnn_step_forward(x, h, Wx, Wh, b)[0]
fb = lambda b: rnn_step_forward(x, h, Wx, Wh, b)[0]
dx_num = eval_numerical_gradient_array(fx, x, dnext_h)
dprev_h_num = eval_numerical_gradient_array(fh, h, dnext_h)
dWx_num = eval_numerical_gradient_array(fWx, Wx, dnext_h)
dWh_num = eval_numerical_gradient_array(fWh, Wh, dnext_h)
db_num = eval_numerical_gradient_array(fb, b, dnext_h)
dx, dprev_h, dWx, dWh, db = rnn_step_backward(dnext_h, cache)
print('dx error: ', rel_error(dx_num, dx))
print('dprev_h error: ', rel_error(dprev_h_num, dprev_h))
print('dWx error: ', rel_error(dWx_num, dWx))
print('dWh error: ', rel_error(dWh_num, dWh))
print('db error: ', rel_error(db_num, db))
```
# Vanilla RNN: forward
Now that you have implemented the forward and backward passes for a single timestep of a vanilla RNN, you will combine these pieces to implement a RNN that process an entire sequence of data.
In the file `cs231n/rnn_layers.py`, implement the function `rnn_forward`. This should be implemented using the `rnn_step_forward` function that you defined above. After doing so run the following to check your implementation. You should see errors less than `1e-7`.
```
N, T, D, H = 2, 3, 4, 5
x = np.linspace(-0.1, 0.3, num=N*T*D).reshape(N, T, D)
h0 = np.linspace(-0.3, 0.1, num=N*H).reshape(N, H)
Wx = np.linspace(-0.2, 0.4, num=D*H).reshape(D, H)
Wh = np.linspace(-0.4, 0.1, num=H*H).reshape(H, H)
b = np.linspace(-0.7, 0.1, num=H)
h, _ = rnn_forward(x, h0, Wx, Wh, b)
expected_h = np.asarray([
[
[-0.42070749, -0.27279261, -0.11074945, 0.05740409, 0.22236251],
[-0.39525808, -0.22554661, -0.0409454, 0.14649412, 0.32397316],
[-0.42305111, -0.24223728, -0.04287027, 0.15997045, 0.35014525],
],
[
[-0.55857474, -0.39065825, -0.19198182, 0.02378408, 0.23735671],
[-0.27150199, -0.07088804, 0.13562939, 0.33099728, 0.50158768],
[-0.51014825, -0.30524429, -0.06755202, 0.17806392, 0.40333043]]])
print('h error: ', rel_error(expected_h, h))
```
# Vanilla RNN: backward
In the file `cs231n/rnn_layers.py`, implement the backward pass for a vanilla RNN in the function `rnn_backward`. This should run back-propagation over the entire sequence, calling into the `rnn_step_backward` function that you defined above. You should see errors less than 5e-7.
```
np.random.seed(231)
N, D, T, H = 2, 3, 10, 5
x = np.random.randn(N, T, D)
h0 = np.random.randn(N, H)
Wx = np.random.randn(D, H)
Wh = np.random.randn(H, H)
b = np.random.randn(H)
out, cache = rnn_forward(x, h0, Wx, Wh, b)
dout = np.random.randn(*out.shape)
dx, dh0, dWx, dWh, db = rnn_backward(dout, cache)
fx = lambda x: rnn_forward(x, h0, Wx, Wh, b)[0]
fh0 = lambda h0: rnn_forward(x, h0, Wx, Wh, b)[0]
fWx = lambda Wx: rnn_forward(x, h0, Wx, Wh, b)[0]
fWh = lambda Wh: rnn_forward(x, h0, Wx, Wh, b)[0]
fb = lambda b: rnn_forward(x, h0, Wx, Wh, b)[0]
dx_num = eval_numerical_gradient_array(fx, x, dout)
dh0_num = eval_numerical_gradient_array(fh0, h0, dout)
dWx_num = eval_numerical_gradient_array(fWx, Wx, dout)
dWh_num = eval_numerical_gradient_array(fWh, Wh, dout)
db_num = eval_numerical_gradient_array(fb, b, dout)
print('dx error: ', rel_error(dx_num, dx))
print('dh0 error: ', rel_error(dh0_num, dh0))
print('dWx error: ', rel_error(dWx_num, dWx))
print('dWh error: ', rel_error(dWh_num, dWh))
print('db error: ', rel_error(db_num, db))
```
# Word embedding: forward
In deep learning systems, we commonly represent words using vectors. Each word of the vocabulary will be associated with a vector, and these vectors will be learned jointly with the rest of the system.
In the file `cs231n/rnn_layers.py`, implement the function `word_embedding_forward` to convert words (represented by integers) into vectors. Run the following to check your implementation. You should see error around `1e-8`.
```
N, T, V, D = 2, 4, 5, 3
x = np.asarray([[0, 3, 1, 2], [2, 1, 0, 3]])
W = np.linspace(0, 1, num=V*D).reshape(V, D)
out, _ = word_embedding_forward(x, W)
expected_out = np.asarray([
[[ 0., 0.07142857, 0.14285714],
[ 0.64285714, 0.71428571, 0.78571429],
[ 0.21428571, 0.28571429, 0.35714286],
[ 0.42857143, 0.5, 0.57142857]],
[[ 0.42857143, 0.5, 0.57142857],
[ 0.21428571, 0.28571429, 0.35714286],
[ 0., 0.07142857, 0.14285714],
[ 0.64285714, 0.71428571, 0.78571429]]])
print('out error: ', rel_error(expected_out, out))
```
# Word embedding: backward
Implement the backward pass for the word embedding function in the function `word_embedding_backward`. After doing so run the following to numerically gradient check your implementation. You should see errors less than `1e-11`.
```
np.random.seed(231)
N, T, V, D = 50, 3, 5, 6
x = np.random.randint(V, size=(N, T))
W = np.random.randn(V, D)
out, cache = word_embedding_forward(x, W)
dout = np.random.randn(*out.shape)
dW = word_embedding_backward(dout, cache)
f = lambda W: word_embedding_forward(x, W)[0]
dW_num = eval_numerical_gradient_array(f, W, dout)
print('dW error: ', rel_error(dW, dW_num))
```
# Temporal Affine layer
At every timestep we use an affine function to transform the RNN hidden vector at that timestep into scores for each word in the vocabulary. Because this is very similar to the affine layer that you implemented in assignment 2, we have provided this function for you in the `temporal_affine_forward` and `temporal_affine_backward` functions in the file `cs231n/rnn_layers.py`. Run the following to perform numeric gradient checking on the implementation. You should see errors less than 1e-9.
```
np.random.seed(231)
# Gradient check for temporal affine layer
N, T, D, M = 2, 3, 4, 5
x = np.random.randn(N, T, D)
w = np.random.randn(D, M)
b = np.random.randn(M)
out, cache = temporal_affine_forward(x, w, b)
dout = np.random.randn(*out.shape)
fx = lambda x: temporal_affine_forward(x, w, b)[0]
fw = lambda w: temporal_affine_forward(x, w, b)[0]
fb = lambda b: temporal_affine_forward(x, w, b)[0]
dx_num = eval_numerical_gradient_array(fx, x, dout)
dw_num = eval_numerical_gradient_array(fw, w, dout)
db_num = eval_numerical_gradient_array(fb, b, dout)
dx, dw, db = temporal_affine_backward(dout, cache)
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))
```
# Temporal Softmax loss
In an RNN language model, at every timestep we produce a score for each word in the vocabulary. We know the ground-truth word at each timestep, so we use a softmax loss function to compute loss and gradient at each timestep. We sum the losses over time and average them over the minibatch.
However there is one wrinkle: since we operate over minibatches and different captions may have different lengths, we append `<NULL>` tokens to the end of each caption so they all have the same length. We don't want these `<NULL>` tokens to count toward the loss or gradient, so in addition to scores and ground-truth labels our loss function also accepts a `mask` array that tells it which elements of the scores count towards the loss.
Since this is very similar to the softmax loss function you implemented in assignment 1, we have implemented this loss function for you; look at the `temporal_softmax_loss` function in the file `cs231n/rnn_layers.py`.
Run the following cell to sanity check the loss and perform numeric gradient checking on the function. You should see an error for dx less than 1e-7.
```
# Sanity check for temporal softmax loss
from cs231n.rnn_layers import temporal_softmax_loss
N, T, V = 100, 1, 10
def check_loss(N, T, V, p):
x = 0.001 * np.random.randn(N, T, V)
y = np.random.randint(V, size=(N, T))
mask = np.random.rand(N, T) <= p
print(temporal_softmax_loss(x, y, mask)[0])
check_loss(100, 1, 10, 1.0) # Should be about 2.3
check_loss(100, 10, 10, 1.0) # Should be about 23
check_loss(5000, 10, 10, 0.1) # Should be about 2.3
# Gradient check for temporal softmax loss
N, T, V = 7, 8, 9
x = np.random.randn(N, T, V)
y = np.random.randint(V, size=(N, T))
mask = (np.random.rand(N, T) > 0.5)
loss, dx = temporal_softmax_loss(x, y, mask, verbose=False)
dx_num = eval_numerical_gradient(lambda x: temporal_softmax_loss(x, y, mask)[0], x, verbose=False)
print('dx error: ', rel_error(dx, dx_num))
```
# RNN for image captioning
Now that you have implemented the necessary layers, you can combine them to build an image captioning model. Open the file `cs231n/classifiers/rnn.py` and look at the `CaptioningRNN` class.
Implement the forward and backward pass of the model in the `loss` function. For now you only need to implement the case where `cell_type='rnn'` for vanialla RNNs; you will implement the LSTM case later. After doing so, run the following to check your forward pass using a small test case; you should see error less than `1e-10`.
```
N, D, W, H = 10, 20, 30, 40
word_to_idx = {'<NULL>': 0, 'cat': 2, 'dog': 3}
V = len(word_to_idx)
T = 13
model = CaptioningRNN(word_to_idx,
input_dim=D,
wordvec_dim=W,
hidden_dim=H,
cell_type='rnn',
dtype=np.float64)
# Set all model parameters to fixed values
for k, v in model.params.items():
model.params[k] = np.linspace(-1.4, 1.3, num=v.size).reshape(*v.shape)
features = np.linspace(-1.5, 0.3, num=(N * D)).reshape(N, D)
captions = (np.arange(N * T) % V).reshape(N, T)
loss, grads = model.loss(features, captions)
expected_loss = 9.83235591003
print('loss: ', loss)
print('expected loss: ', expected_loss)
print('difference: ', abs(loss - expected_loss))
```
Run the following cell to perform numeric gradient checking on the `CaptioningRNN` class; you should errors around `5e-6` or less.
```
np.random.seed(231)
batch_size = 2
timesteps = 3
input_dim = 4
wordvec_dim = 5
hidden_dim = 6
word_to_idx = {'<NULL>': 0, 'cat': 2, 'dog': 3}
vocab_size = len(word_to_idx)
captions = np.random.randint(vocab_size, size=(batch_size, timesteps))
features = np.random.randn(batch_size, input_dim)
model = CaptioningRNN(word_to_idx,
input_dim=input_dim,
wordvec_dim=wordvec_dim,
hidden_dim=hidden_dim,
cell_type='rnn',
dtype=np.float64,
)
loss, grads = model.loss(features, captions)
for param_name in sorted(grads):
f = lambda _: model.loss(features, captions)[0]
param_grad_num = eval_numerical_gradient(f, model.params[param_name], verbose=False, h=1e-6)
e = rel_error(param_grad_num, grads[param_name])
print('%s relative error: %e' % (param_name, e))
```
# Overfit small data
Similar to the `Solver` class that we used to train image classification models on the previous assignment, on this assignment we use a `CaptioningSolver` class to train image captioning models. Open the file `cs231n/captioning_solver.py` and read through the `CaptioningSolver` class; it should look very familiar.
Once you have familiarized yourself with the API, run the following to make sure your model overfit a small sample of 100 training examples. You should see losses of less than 0.1.
```
np.random.seed(231)
small_data = load_coco_data(max_train=50)
small_rnn_model = CaptioningRNN(
cell_type='rnn',
word_to_idx=data['word_to_idx'],
input_dim=data['train_features'].shape[1],
hidden_dim=512,
wordvec_dim=256,
)
small_rnn_solver = CaptioningSolver(small_rnn_model, small_data,
update_rule='adam',
num_epochs=50,
batch_size=25,
optim_config={
'learning_rate': 5e-3,
},
lr_decay=0.95,
verbose=True, print_every=10,
)
small_rnn_solver.train()
# Plot the training losses
plt.plot(small_rnn_solver.loss_history)
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Training loss history')
plt.show()
```
# Test-time sampling
Unlike classification models, image captioning models behave very differently at training time and at test time. At training time, we have access to the ground-truth caption, so we feed ground-truth words as input to the RNN at each timestep. At test time, we sample from the distribution over the vocabulary at each timestep, and feed the sample as input to the RNN at the next timestep.
In the file `cs231n/classifiers/rnn.py`, implement the `sample` method for test-time sampling. After doing so, run the following to sample from your overfitted model on both training and validation data. The samples on training data should be very good; the samples on validation data probably won't make sense.
```
for split in ['train', 'val']:
minibatch = sample_coco_minibatch(small_data, split=split, batch_size=2)
gt_captions, features, urls = minibatch
gt_captions = decode_captions(gt_captions, data['idx_to_word'])
sample_captions = small_rnn_model.sample(features)
sample_captions = decode_captions(sample_captions, data['idx_to_word'])
for gt_caption, sample_caption, url in zip(gt_captions, sample_captions, urls):
plt.imshow(image_from_url(url))
plt.title('%s\n%s\nGT:%s' % (split, sample_caption, gt_caption))
plt.axis('off')
plt.show()
```
| true |
code
| 0.807157 | null | null | null | null |
|
# Predicting Titanic Survivers
Like Titanic, this is my maiden voyage, when it comes to Kaggle contest that is!. I've completed the Data Science track on Data Camp, but I'm a relative newbie when it comes to machine learning. I'm going to attempt to work my way through the Titanic: Machine Learning contest. My aim is to submission and initial entry as quickly as possible to get a base line score and then attempt to improve on on it by first looking at missing data, then engineering key features before establishing a secondary base line and trying to improve the model itself. I'd like to be able to achieve a score of .80
Please feel free to post comments or make suggestions as to what i may be doing wrong or could maybe do better and consider upvoting if you find the notebook useful!
Because this notebook has built up over time I have commented out some of the lines that output files so that when i want to output and test a slight change to the code, i don't output files for bit of the notebook that haven't been changed and that i am not especially intereted in. If you are forking this code you can simple remove the hash and output the file. I have also experimented with different models, so the current model in any stage is not necessarily the most efficent (its just the one that i tried last).
# Import the Libraries and Data
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import os
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
from sklearn.cross_validation import KFold
from sklearn.ensemble import (AdaBoostClassifier,BaggingClassifier,ExtraTreesClassifier,GradientBoostingClassifier,RandomForestClassifier,VotingClassifier)
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.linear_model import LogisticRegression, Perceptron, SGDClassifier, LogisticRegression, PassiveAggressiveClassifier,RidgeClassifierCV
from sklearn.metrics import accuracy_score,auc,classification_report,confusion_matrix,mean_squared_error, precision_score, recall_score,roc_curve
from sklearn.model_selection import cross_val_score,cross_val_predict,cross_validate,train_test_split,GridSearchCV,KFold,learning_curve,RandomizedSearchCV,StratifiedKFold
from sklearn.multiclass import OneVsRestClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC, LinearSVC
from sklearn.tree import DecisionTreeClassifier
from sklearn import ensemble, linear_model,neighbors, svm, tree
from scipy.stats import randint
from xgboost import XGBClassifier
#ignore warnings
import warnings
warnings.filterwarnings('ignore')
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
print(os.listdir("../input"))
# Any results you write to the current directory are saved as output.
df_train=pd.read_csv('../input/train.csv',sep=',')
df_test=pd.read_csv('../input/test.csv',sep=',')
df_data = df_train.append(df_test) # The entire data: train + test.
PassengerId = df_test['PassengerId']
Submission=pd.DataFrame()
Submission['PassengerId'] = df_test['PassengerId']
```
# Stage 1 : Explore the Data and create a basic model on raw data
# Explore the data Statistically
### Number of rows and columns
```
# How big are the training and test datasets
print(df_train.shape)
print("----------------------------")
print(df_test.shape)
```
### Column Names
```
# What are the column names
df_train.columns
```
### Data Types
```
# What type of data object are in each column and how many missing values are there
df_data.info()
```
### Missing Data
How much Data is missing from the training and test datasets, how important is that data and how much data cleaning might be required.
```
#check for any other unusable values
print(pd.isnull(df_data).sum())
```
## Observations on missing data.
There are 144 missing ages in the training data and 86 mssing ages in the test data. Age is an important feature so it is worth spending time to address this properly.
There are 468 missing Cabin entries in the training data and 326 in the test data, at this stage I'm not sure how important this feature is so I'm going to revisit this when I know more about the feature.
There are 2 missing embarked data points in the train data and 1 missing fare in the test data, at this stage this does not represent a problem.
## Statistical Overview of the data
```
# Get a statistical overview of the training data
df_train.describe()
# Get a statistical overview of the data
df_test.describe()
```
Note: The mean and Std of each of the columns in the 2 datasets are reasonable close together, so its safe to assume that any relationships we discover in the training data should work similarly in the test data.
```
# Take a look at some sample data
df_train.head(5)
df_train.tail(5)
```
# Explore Data Graphically
## Survival by Age, Class and Gender
```
grid = sns.FacetGrid(df_train, col = "Pclass", row = "Sex", hue = "Survived", palette = 'seismic')
grid = grid.map(plt.scatter, "PassengerId", "Age")
grid.add_legend()
grid
```
## Survival by Age, Port of Embarkation and Gender
```
grid = sns.FacetGrid(df_train, col = "Embarked", row = "Sex", hue = "Survived", palette = 'seismic')
grid = grid.map(plt.scatter, "PassengerId", "Age")
grid.add_legend()
grid
```
This embarkation visualization indicates that a large proportion of passengers embarked at port 'S', with lesser numbers at 'C' and 'Q' it also shows that regardless of embarkation port more women survived than men. It doesn't seem to show any corelation between passenger ID and Embarkation port. Interestingly Embarkation port Q seems to indicate that only 1 man survived while all women with passenger ID below 500 seem to survive while those above didn't this may be chance but it does look odd compared to 'S' and 'C'.
## Survival by Age, Number of Siblings and Gender
```
grid = sns.FacetGrid(df_train, col = "SibSp", row = "Sex", hue = "Survived", palette = 'seismic')
grid = grid.map(plt.scatter, "PassengerId", "Age")
grid.add_legend()
grid
```
## Survival by Age, Number of parch and Gender
```
grid = sns.FacetGrid(df_train, col = "Parch", row = "Sex", hue = "Survived", palette = 'seismic')
grid = grid.map(plt.scatter, "PassengerId", "Age")
grid.add_legend()
grid
```
# Pairplots
To get a very basic idea of the relationships between the different features we can use pairplots from seaborn.
```
g = sns.pairplot(df_train[[u'Survived', u'Pclass', u'Sex', u'Age', u'Parch', u'Fare', u'Embarked']], hue='Survived', palette = 'seismic',size=4,diag_kind = 'kde',diag_kws=dict(shade=True),plot_kws=dict(s=50) )
g.set(xticklabels=[])
```
# Create simple model
Create a baseline score by using old the standard numeric data on on a very basic model, this will be used to see how much any changes we make to the data or model improve performance.
```
NUMERIC_COLUMNS=['Pclass','Age','SibSp','Parch','Fare']
# create test and training data
test = df_test[NUMERIC_COLUMNS].fillna(-1000)
data_to_train = df_train[NUMERIC_COLUMNS].fillna(-1000)
y=df_train['Survived']
X_train, X_test, y_train, y_test = train_test_split(data_to_train, y, test_size=0.3,random_state=21, stratify=y)
clf = SVC()
clf.fit(X_train, y_train)
# Print the accuracy
print("Accuracy: {}".format(clf.score(X_test, y_test)))
```
# Create initial predictions¶
```
Submission['Survived']=clf.predict(test)
print(Submission.head())
print('predictions generated')
```
# Make first Submission
```
# write data frame to csv file
#Submission.set_index('PassengerId', inplace=True)
#Submission.to_csv('myfirstsubmission.csv',sep=',')
print('file created')
```
The result of this first submission was a score of 0.57894. This constitutes performing just above random, if i'd simply flipped a coin fair coin for each passenger i could have achieved this kind of score. So there is plenty of room for improvement.
# Stage 2 : Clean Data & Engineer features to improve results
## Cleaning the data : Filling in the blanks
There are a number of missing values, including fare, embarked, age and cabin. I started off simply using the average value for fare, embarked and age. However after doing some visual data analysis it became obvious that I could use other factors like title to make better estimates on age by simply using the average for people with the same title, the same applied to embarked where average based on fare would give a better estimate and fare based on embarked.
Cabin has so much missing data that it is likely that estimating cabin may add a level of noise to the data that would not be helpful.
## Feature conversion
Some models work better with with categorical data other numberical data, while some work best with binaryl data. In some cases this is as simple as changing male and female to numeric data like 0 or 1. We can replace categorical data like embarkation port 's' to values numeric value 1 or title Master to value 3 Values like age that range from 1 to 80 can be scaled so they a represented by a value between 0 and 1. Scaling values means that features are not given a disproportionate importance simply because they are larger, another option for values like Age or Fare are to split them into a more manageable bands which can then be represented as categories so. Alternately we could put each categorical value into a column of its own, marking each columns with a 0 if they don't apply or a 1 if they do. After doing some initial data eploration i decided it was easiest to convert data into bands and columns, so that I could then compare the models with different options and decide which was best for each before making final predictions.
## Feature Engineering
Here I attempted to manipulate existing data in order to try and create new features that i could use in my model, for example family size can be caluculated with the combination of siblings and parents, and title can be extracted from name.
## Estimate missing Fare Data based on Embarkation
While there is relatively little missing Fare data, the range of possible values is large, so rather than using simply the media of all fares, we can look at the passenger class or embarkation port in order to use a more appropriate average. We'll start by looking at boxplots for the fares to ensure we are making soon assumptions before we go onto estimating the missing values.
```
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True,figsize=(12,6))
sns.boxplot(data = df_data, x = "Pclass", y = "Fare",ax=ax1);
plt.figure(1)
sns.boxplot(data = df_data, x = "Embarked", y = "Fare",ax=ax2);
plt.show()
# Fill the na values in Fare based on embarked data
embarked = ['S', 'C', 'Q']
for port in embarked:
fare_to_impute = df_data.groupby('Embarked')['Fare'].median()[embarked.index(port)]
df_data.loc[(df_data['Fare'].isnull()) & (df_data['Embarked'] == port), 'Fare'] = fare_to_impute
# Fare in df_train and df_test:
df_train["Fare"] = df_data['Fare'][:891]
df_test["Fare"] = df_data['Fare'][891:]
print('Missing Fares Estimated')
```
## FareBand feature
```
#fill in missing Fare value in training set based on mean fare for that Pclass
for x in range(len(df_train["Fare"])):
if pd.isnull(df_train["Fare"][x]):
pclass = df_train["Pclass"][x] #Pclass = 3
df_train["Fare"][x] = round(df_train[df_train["Pclass"] == pclass]["Fare"].mean(), 8)
#fill in missing Fare value in test set based on mean fare for that Pclass
for x in range(len(df_test["Fare"])):
if pd.isnull(df_test["Fare"][x]):
pclass = df_test["Pclass"][x] #Pclass = 3
df_test["Fare"][x] = round(df_test[df_test["Pclass"] == pclass]["Fare"].mean(), 8)
#map Fare values into groups of numerical values
df_data["FareBand"] = pd.qcut(df_data['Fare'], 8, labels = [1, 2, 3, 4,5,6,7,8]).astype('int')
df_train["FareBand"] = pd.qcut(df_train['Fare'], 8, labels = [1, 2, 3, 4,5,6,7,8]).astype('int')
df_test["FareBand"] = pd.qcut(df_test['Fare'], 8, labels = [1, 2, 3, 4,5,6,7,8]).astype('int')
df_train[["FareBand", "Survived"]].groupby(["FareBand"], as_index=False).mean()
print('FareBand feature created')
```
*** Note:*** There are several ways that machine learning can evaluate data, you can use discrete data like fare, or you can make that data categorical by grouping it into bands as i have done here or your can take those categories and turn each category into a column. Different models work, differently depending on how you give them the data. I'm going to create all 3 different structures for some features like fare and age and see how they compare. You shoud not over emphasis a feature by using multiple structures of the same data in a model, we'll therefore filter the differnet stuctures before we evaluate the models.
## Embarked Feature
```
#map each Embarked value to a numerical value
embarked_mapping = {"S": 1, "C": 2, "Q": 3}
df_data["Embarked"] = df_data["Embarked"].map(embarked_mapping)
# split Embanked into df_train and df_test:
df_train["Embarked"] = df_data["Embarked"][:891]
df_test["Embarked"] = df_data["Embarked"][891:]
print('Embarked feature created')
df_data[['Embarked', 'Survived']].groupby(['Embarked'], as_index=False).mean()
```
## Estimate missing Embarkation Data
```
# Fill the na values in Embanked based on fareband data
fareband = [1,2,3,4]
for fare in fareband:
embark_to_impute = df_data.groupby('FareBand')['Embarked'].median()[fare]
df_data.loc[(df_data['Embarked'].isnull()) & (df_data['FareBand'] == fare), 'Embarked'] = embark_to_impute
# Fare in df_train and df_test:
df_train["Embarked"] = df_data['Embarked'][:891]
df_test["Embarked"] = df_data['Embarked'][891:]
print('Missing Embarkation Estimated')
```
We will come back to fill in the missing age data a little later. Initially i created an estimate based on the mean age and standard deviation, using random numbers to evenly distribute age estimates, which worked, but actually there is a better way using title. As we have not yet extracted the title data yet, we will wait to estimate ages until we have.
## Gender Feature
```
# convert categories to Columns
dummies=pd.get_dummies(df_train[['Sex']], prefix_sep='_') #Gender
df_train = pd.concat([df_train, dummies], axis=1)
testdummies=pd.get_dummies(df_test[['Sex']], prefix_sep='_') #Gender
df_test = pd.concat([df_test, testdummies], axis=1)
print('Gender Feature added ')
#map each Gendre value to a numerical value
gender_mapping = {"female": 0, "male": 1}
df_data["Sex"] = df_data['Sex'].map(gender_mapping)
df_data["Sex"]=df_data["Sex"].astype('int')
# Family_Survival in TRAIN_DF and TEST_DF:
df_train["Sex"] = df_data["Sex"][:891]
df_test["Sex"] = df_data["Sex"][891:]
print('Gender Category created')
```
## Name Length
```
df_data['NameLen'] = df_data['Name'].apply(lambda x: len(x))
print('Name Length calculated')
# split to test and training
df_train["NameLen"] = df_data["NameLen"][:891]
df_test["NameLen"] = df_data["NameLen"][891:]
df_train["NameBand"] = pd.cut(df_train["NameLen"], bins=5, labels = [1,2,3,4,5])
df_test["NameBand"] = pd.cut(df_test["NameLen"], bins=5, labels = [1,2,3,4,5])
# convert AgeGroup categories to Columns
dummies=pd.get_dummies(df_train[["NameBand"]].astype('category'), prefix_sep='_') #Embarked
df_train = pd.concat([df_train, dummies], axis=1)
dummies=pd.get_dummies(df_test[["NameBand"]].astype('category'), prefix_sep='_') #Embarked
df_test = pd.concat([df_test, dummies], axis=1)
print("Name Length categories created")
pd.qcut(df_train['NameLen'],5).value_counts()
```
## Title Feature
```
#Get titles
df_data["Title"] = df_data.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
#Unify common titles.
df_data["Title"] = df_data["Title"].replace('Mlle', 'Miss')
df_data["Title"] = df_data["Title"].replace('Master', 'Master')
df_data["Title"] = df_data["Title"].replace(['Mme', 'Dona', 'Ms'], 'Mrs')
df_data["Title"] = df_data["Title"].replace(['Jonkheer','Don'],'Mr')
df_data["Title"] = df_data["Title"].replace(['Capt','Major', 'Col','Rev','Dr'], 'Millitary')
df_data["Title"] = df_data["Title"].replace(['Lady', 'Countess','Sir'], 'Honor')
# Age in df_train and df_test:
df_train["Title"] = df_data['Title'][:891]
df_test["Title"] = df_data['Title'][891:]
# convert Title categories to Columns
titledummies=pd.get_dummies(df_train[['Title']], prefix_sep='_') #Title
df_train = pd.concat([df_train, titledummies], axis=1)
ttitledummies=pd.get_dummies(df_test[['Title']], prefix_sep='_') #Title
df_test = pd.concat([df_test, ttitledummies], axis=1)
print('Title categories added')
```
## Title Cetegory
```
# Mapping titles
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Millitary": 5, "Honor": 6}
df_data["TitleCat"] = df_data['Title'].map(title_mapping)
df_data["TitleCat"] = df_data["TitleCat"].astype(int)
df_train["TitleCat"] = df_data["TitleCat"][:891]
df_test["TitleCat"] = df_data["TitleCat"][891:]
print('Title Category created')
```
## Fill age based on title
The Visualisations of age by title suggests that if we create our age estimate by looking at the passengers title and using the average age for that title it may produce a more accurate estimate.
```
titles = ['Master', 'Miss', 'Mr', 'Mrs', 'Millitary','Honor']
for title in titles:
age_to_impute = df_data.groupby('Title')['Age'].median()[title]
df_data.loc[(df_data['Age'].isnull()) & (df_data['Title'] == title), 'Age'] = age_to_impute
# Age in df_train and df_test:
df_train["Age"] = df_data['Age'][:891]
df_test["Age"] = df_data['Age'][891:]
print('Missing Ages Estimated')
```
## Create AgeBands
```
# sort Age into band categories
bins = [0,12,24,45,60,np.inf]
labels = ['Child', 'Young Adult', 'Adult','Older Adult','Senior']
df_train["AgeBand"] = pd.cut(df_train["Age"], bins, labels = labels)
df_test["AgeBand"] = pd.cut(df_test["Age"], bins, labels = labels)
print('Age Feature created')
# convert AgeGroup categories to Columns
dummies=pd.get_dummies(df_train[["AgeBand"]], prefix_sep='_') #Embarked
df_train = pd.concat([df_train, dummies], axis=1)
dummies=pd.get_dummies(df_test[["AgeBand"]], prefix_sep='_') #Embarked
df_test = pd.concat([df_test, dummies], axis=1)
print('AgeBand feature created')
```
## Visualize Age Data
```
# Visualise Age Data
fig, (axis1,axis2) = plt.subplots(1,2,figsize=(15,4))
axis1.set_title('Training Age values - Titanic')
axis2.set_title('Test Age values - Titanic')
# plot original Age values
df_train['Age'].dropna().astype(int).hist(bins=70, ax=axis1)
#df_test['Age'].dropna().astype(int).hist(bins=70, ax=axis1)
# plot new Age Values
#df_train['Age'].hist(bins=70, ax=axis2)
df_test['Age'].hist(bins=70, ax=axis2)
# peaks for survived/not survived passengers by their age
facet = sns.FacetGrid(df_train, hue="Survived",palette = 'seismic',aspect=4)
facet.map(sns.kdeplot,'Age',shade= True)
facet.set(xlim=(0, df_train['Age'].max()))
facet.add_legend()
sns.boxplot(data = df_train, x = "Title", y = "Age");
```
## Lone Travellers Feature
```
df_train["Alone"] = np.where(df_train['SibSp'] + df_train['Parch'] + 1 == 1, 1,0) # People travelling alone
df_test["Alone"] = np.where(df_test['SibSp'] + df_test['Parch'] + 1 == 1, 1,0) # People travelling alone
print('Lone traveller feature created')
```
## Mother
We know that a higher proportion of women survived than die, but of the women that did not survive a large number of these women were women with families that stayed together, we can add a feature to identify women with children.
```
df_data['Mother'] = (df_data['Title'] == 'Mrs') & (df_data['Parch'] > 0)
df_data['Mother'] = df_data['Mother'].astype(int)
df_train["Mother"] = df_data["Mother"][:891]
df_test["Mother"] = df_data["Mother"][891:]
print('Mother Category created')
```
## Family Size Feature
We know that many families stayed together and that the bigger the less likely that family would be to find a lifeboat together.
```
df_train["Family Size"] = (df_train['SibSp'] + df_train['Parch'] + 1)
df_test["Family Size"] = df_test['SibSp'] + df_test['Parch'] + 1
print('Family size feature created')
```
## Family Survival
This is based on code taken from from https://www.kaggle.com/shunjiangxu/blood-is-thicker-than-water-friendship-forever
```
# get last name
df_data["Last_Name"] = df_data['Name'].apply(lambda x: str.split(x, ",")[0])
# Set survival value
DEFAULT_SURVIVAL_VALUE = 0.5
df_data["Family_Survival"] = DEFAULT_SURVIVAL_VALUE
# Find Family groups by Fare
for grp, grp_df in df_data[['Survived','Name', 'Last_Name', 'Fare', 'Ticket', 'PassengerId',
'SibSp', 'Parch', 'Age', 'Cabin']].groupby(['Last_Name', 'Fare']):
if (len(grp_df) != 1):
# A Family group is found.
for ind, row in grp_df.iterrows():
smax = grp_df.drop(ind)['Survived'].max()
smin = grp_df.drop(ind)['Survived'].min()
passID = row['PassengerId']
if (smax == 1.0):
df_data.loc[df_data['PassengerId'] == passID, 'Family_Survival'] = 1
elif (smin==0.0):
df_data.loc[df_data['PassengerId'] == passID, 'Family_Survival'] = 0
print("Number of passengers with family survival information:",
df_data.loc[df_data['Family_Survival']!=0.5].shape[0])
# Find Family groups by Ticket
for _, grp_df in df_data.groupby('Ticket'):
if (len(grp_df) != 1):
for ind, row in grp_df.iterrows():
if (row['Family_Survival'] == 0) | (row['Family_Survival']== 0.5):
smax = grp_df.drop(ind)['Survived'].max()
smin = grp_df.drop(ind)['Survived'].min()
passID = row['PassengerId']
if (smax == 1.0):
df_data.loc[df_data['PassengerId'] == passID, 'Family_Survival'] = 1
elif (smin==0.0):
df_data.loc[df_data['PassengerId'] == passID, 'Family_Survival'] = 0
print("Number of passenger with family/group survival information: "
+str(df_data[df_data['Family_Survival']!=0.5].shape[0]))
# Family_Survival in df_train and df_test:
df_train["Family_Survival"] = df_data['Family_Survival'][:891]
df_test["Family_Survival"] = df_data['Family_Survival'][891:]
```
## Cabin feature
```
# check if cabin inf exists
df_data["HadCabin"] = (df_data["Cabin"].notnull().astype('int'))
# split Embanked into df_train and df_test:
df_train["HadCabin"] = df_data["HadCabin"][:891]
df_test["HadCabin"] = df_data["HadCabin"][891:]
print('Cabin feature created')
```
## Deck feature
```
# Extract Deck
df_data["Deck"] = df_data.Cabin.str.extract('([A-Za-z])', expand=False)
df_data["Deck"] = df_data["Deck"].fillna("N")
# Map Deck
deck_mapping = {"N":0,"A": 1, "B": 2, "C": 3, "D": 4, "E": 5}
df_data['Deck'] = df_data['Deck'].map(deck_mapping)
#Split to training and test
df_train["Deck"] = df_data["Deck"][:891]
df_test["Deck"] = df_data["Deck"][891:]
print('Deck feature created')
#Map and Create Deck feature for training
df_data["Deck"] = df_data.Cabin.str.extract('([A-Za-z])', expand=False)
deck_mapping = {"0":0,"A": 1, "B": 2, "C": 3, "D": 4, "E": 5}
df_data['Deck'] = df_data['Deck'].map(deck_mapping)
df_data["Deck"] = df_data["Deck"].fillna("0")
df_data["Deck"]=df_data["Deck"].astype('int')
df_train["Deck"] = df_data['Deck'][:891]
df_test["Deck"] = df_data['Deck'][891:]
print('Deck feature created')
# convert categories to Columns
dummies=pd.get_dummies(df_train[['Deck']].astype('category'), prefix_sep='_') #Gender
df_train = pd.concat([df_train, dummies], axis=1)
dummies=pd.get_dummies(df_test[['Deck']].astype('category'), prefix_sep='_') #Gender
df_test = pd.concat([df_test,dummies], axis=1)
print('Deck Categories created')
```
## Ticket feature
```
## Treat Ticket by extracting the ticket prefix. When there is no prefix it returns X.
Ticket = []
for i in list(df_data.Ticket):
if not i.isdigit() :
Ticket.append(i.replace(".","").replace("/","").strip().split(' ')[0]) #Take prefix
else:
Ticket.append("X")
df_data["Ticket"] = Ticket
df_data["Ticket"].head()
df_train["Ticket"] = df_data["Ticket"][:891]
df_test["Ticket"] = df_data["Ticket"][891:]
print('Ticket feature created')
```
## Ticket Type Feature
```
# ticket prefix
df_data['TicketRef'] = df_data['Ticket'].apply(lambda x: str(x)[0])
df_data['TicketRef'].value_counts()
#df_data["ticketBand"] = pd.qcut(df_data['ticket_ref'], 5, labels = [1, 2, 3, 4,5]).astype('int')
# split to test and training
df_train["TicketRef"] = df_data["TicketRef"][:891]
df_test["TicketRef"] = df_data["TicketRef"][891:]
# convert AgeGroup categories to Columns
dummies=pd.get_dummies(df_train[["TicketRef"]].astype('category'), prefix_sep='_') #Embarked
df_train = pd.concat([df_train, dummies], axis=1)
dummies=pd.get_dummies(df_test[["TicketRef"]].astype('category'), prefix_sep='_') #Embarked
df_test = pd.concat([df_test, dummies], axis=1)
print("TicketBand categories created")
```
## Passenger Class Feature
```
# convert AgeGroup categories to Columns
dummies=pd.get_dummies(df_train[["Pclass"]].astype('category'), prefix_sep='_') #Embarked
df_train = pd.concat([df_train, dummies], axis=1)
dummies=pd.get_dummies(df_test[["Pclass"]].astype('category'), prefix_sep='_') #Embarked
df_test = pd.concat([df_test, dummies], axis=1)
print("pclass categories created")
```
## Free Passage
I noticed that the minimum fare is 0.00 and that the ticket type for some of those is 'LINE' . All of those people with a zero ticket cost seem to be male with no siblings so its possible that these people are in some way associated with 'crew' positions. The majority of the people with a ticket price of 0.00 seemed not to survive, so i'm making free a feature to see whether that makes a difference to the model.
```
# create free feature based on fare = 0
df_data["Free"] = np.where(df_data['Fare'] ==0, 1,0)
df_data["Free"] = df_data['Free'].astype(int)
df_train["Free"] = df_data["Free"][:891]
df_test["Free"] = df_data["Free"][891:]
print('Free Category created')
```
## FareBand
```
Pclass = [1,2,3]
for aclass in Pclass:
fare_to_impute = df_data.groupby('Pclass')['Fare'].median()[aclass]
df_data.loc[(df_data['Fare'].isnull()) & (df_data['Pclass'] == aclass), 'Fare'] = fare_to_impute
df_train["Fare"] = df_data["Fare"][:891]
df_test["Fare"] = df_data["Fare"][891:]
#map Fare values into groups of numerical values
df_train["FareBand"] = pd.qcut(df_train['Fare'], 4, labels = [1, 2, 3, 4]).astype('category')
df_test["FareBand"] = pd.qcut(df_test['Fare'], 4, labels = [1, 2, 3, 4]).astype('category')
# convert FareBand categories to Columns
dummies=pd.get_dummies(df_train[["FareBand"]], prefix_sep='_') #Embarked
df_train = pd.concat([df_train, dummies], axis=1)
dummies=pd.get_dummies(df_test[["FareBand"]], prefix_sep='_') #Embarked
df_test = pd.concat([df_test, dummies], axis=1)
print("Fareband categories created")
```
## Embarked categories
```
# convert Embarked categories to Columns
dummies=pd.get_dummies(df_train[["Embarked"]].astype('category'), prefix_sep='_') #Embarked
df_train = pd.concat([df_train, dummies], axis=1)
dummies=pd.get_dummies(df_test[["Embarked"]].astype('category'), prefix_sep='_') #Embarked
df_test = pd.concat([df_test, dummies], axis=1)
print("Embarked feature created")
```
# Exploring the Engineered data
## Missing Data
```
#check for any other unusable values
print(len(df_test.columns))
print(pd.isnull(df_test).sum())
```
## Statistical Overview
```
df_train.describe()
```
# Visualizing age data
We could estimate all of the ages based on the mean and standard deviation of the data set, however as age is obviously an important feature in pridicting survival and we need to look at the other features and see if we can work out a way to make a more accurate estimate of age for any given passenger. First lets look at the different age distributions of passengers by title.
```
# Groupby title
df_train[['Title', 'Survived']].groupby(['Title'], as_index=False).mean()
# plot age distribution by title
facet = sns.FacetGrid(data = df_train, hue = "Title", legend_out=True, size = 5)
facet = facet.map(sns.kdeplot, "Age")
facet.add_legend();
```
The age distribution looks slightly suspect and possibly merits further investigation, for example while master generally refers to male's under 16 there a number that are over 40, this might be explained if master is also a title in nautical terms like 'Master Seaman'. You might also expect a quite Normal distribution of ages for any given title, but in many cases this doesn't seem to be the case, this is most likely caused by out estimated numbers skewing the data, one way to avoid this would be to use a random number based on the standard deviation in the estimate for each to get a more natural dataset. We could also use age bands rather than age in the model.
### Survival by FareBand and Gender
```
grid = sns.FacetGrid(df_train, col = "FareBand", row = "Sex", hue = "Survived", palette = 'seismic')
grid = grid.map(plt.scatter, "PassengerId", "Age")
grid.add_legend()
grid
```
### Survival by Deck and Gender
```
grid = sns.FacetGrid(df_train, col = "Deck", row = "Sex", hue = "Survived", palette = 'seismic')
grid = grid.map(plt.scatter, "PassengerId", "Age")
grid.add_legend()
grid
```
### Survival by Family Size and Gender
```
grid = sns.FacetGrid(df_train, col = "Family Size", row = "Sex", hue = "Survived", palette = 'seismic')
grid = grid.map(plt.scatter, "PassengerId", "Age")
grid.add_legend()
grid
```
### Survival by Passenger Class and Family Size
```
fig, (axis1,axis2) = plt.subplots(1,2,figsize=(15,4))
axis1.set_title('Training Age values - Titanic')
axis2.set_title('Test Age values - Titanic')
x1=df_train[df_train["Survived"]==0]
x2=df_train[df_train["Survived"]==1]
# Set up the matplotlib figure
plt.figure(1)
sns.jointplot(x="Family Size", y="Pclass", data=x1, kind="kde", color='b');
plt.figure(2)
sns.jointplot(x="Family Size", y="Pclass", data=x2, kind="kde", color='r');
plt.show()
```
### Fare Jointplot
```
sns.jointplot(data=x1, x='PassengerId', y='Age', kind='scatter',color='b')
plt.figure(4)
sns.jointplot(data=x2, x='PassengerId', y='Age', kind='scatter',color='r')
# sns.plt.show()
```
# Re-train the model on new features
```
df_train.columns
df_train.head()
```
## Select Columns of Interest
```
# Create list of interesting columns
SIMPLE_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Sex_female','Sex_male','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked'] #84
INTERESTING_COLUMNS=['Survived','Pclass','Age','SibSp','Parch','Title','Alone','Mother','Family Size','Family_Survival','Embarked','FareBand','TicketRef']
CATEGORY_COLUMNS=['Family Size','Family_Survival','Alone','Mother','Sex_female','Sex_male','AgeBand_Child',
'AgeBand_Young Adult', 'AgeBand_Adult', 'AgeBand_Older Adult',
'AgeBand_Senior','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','NameBand_1',
'NameBand_2', 'NameBand_3', 'NameBand_4', 'NameBand_5','Embarked','TicketRef_A', 'TicketRef_C', 'TicketRef_F', 'TicketRef_L',
'TicketRef_P', 'TicketRef_S', 'TicketRef_W', 'TicketRef_X','Pclass_1', 'Pclass_2', 'Pclass_3','HadCabin','Free','FareBand_1', 'FareBand_2', 'FareBand_3', 'FareBand_4']
```
# Re-evaluate the on new features
```
# create test and training data
test = df_test[CATEGORY_COLUMNS].fillna(-1000)
data_to_train = df_train[CATEGORY_COLUMNS].fillna(-1000)
X_train, X_test, y_train, y_test = train_test_split(data_to_train, df_train['Survived'], test_size=0.3,random_state=21, stratify=df_train['Survived'])
RandomForest = RandomForestClassifier(random_state = 0)
RandomForest.fit(X_train, y_train)
print('Evaluation complete')
# Print the accuracy# Print
print("Accuracy: {}".format(RandomForest.score(X_test, y_test)))
```
## Feature Correlation
```
#map feature correlation
f,ax = plt.subplots(figsize=(12, 12))
sns.heatmap(df_train[INTERESTING_COLUMNS].corr(),annot=True, linewidths=.5, fmt= '.1f',ax=ax)
```
## Feature Importance (for random forest)
```
RandomForest_checker = RandomForestClassifier()
RandomForest_checker.fit(X_train, y_train)
importances_df = pd.DataFrame(RandomForest_checker.feature_importances_, columns=['Feature_Importance'],
index=X_train.columns)
importances_df.sort_values(by=['Feature_Importance'], ascending=False, inplace=True)
print(importances_df)
```
# Re-forcast predictions based on new features
```
Submission['Survived']=RandomForest.predict(test)
print(Submission.head())
print('Submission created')
```
# Make revised submission
```
# write data frame to csv file
# Submission.set_index('PassengerId', inplace=True)
Submission.to_csv('randomforestcat01.csv',sep=',')
print('file created')
```
The second revised submission scored 0.75598 which was an improvement of the original revision which scored 0.64593, this used was is an improvement on the original score of 0.57894. This advanced the submission to 9117 place on the leaderboard, from the starting point of 10599th place! Obviousy a step in the right direction but still needing work.
# Stage 3 : Test Different Models and parameters
## Split data into test and training
```
REVISED_NUMERIC_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked'] #84
SIMPLE_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Sex_female','Sex_male','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked'] #84
INTERESTING_COLUMNS=['Survived','Pclass','Age','SibSp','Parch','Title','Alone','Mother','Family Size','Family_Survival','Embarked','FareBand','TicketRef']
CATEGORY_COLUMNS=['Pclass','SibSp','Parch','Family Size','Family_Survival','Alone','Mother','Sex_female','Sex_male','AgeBand_Child',
'AgeBand_Young Adult', 'AgeBand_Adult', 'AgeBand_Older Adult',
'AgeBand_Senior','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','NameBand_1',
'NameBand_2', 'NameBand_3', 'NameBand_4', 'NameBand_5','Embarked','TicketRef_A', 'TicketRef_C', 'TicketRef_F', 'TicketRef_L',
'TicketRef_P', 'TicketRef_S', 'TicketRef_W', 'TicketRef_X','HadCabin','Free']
CATEGORY_COLUMNS=['Pclass','SibSp','Parch','Family Size','Family_Survival','Alone','Mother','Sex_female','Sex_male','AgeBand_Child',
'AgeBand_Young Adult', 'AgeBand_Adult', 'AgeBand_Older Adult',
'AgeBand_Senior','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','NameBand_1',
'NameBand_2', 'NameBand_3', 'NameBand_4', 'NameBand_5','Embarked','TicketRef_A', 'TicketRef_C', 'TicketRef_F', 'TicketRef_L',
'TicketRef_P', 'TicketRef_S', 'TicketRef_W', 'TicketRef_X','HadCabin','Free']
#print(df_test.columns)
# create test and training data
data_to_train = df_train[CATEGORY_COLUMNS].fillna(-1000)
prediction = df_train["Survived"]
test = df_test[CATEGORY_COLUMNS].fillna(-1000)
X_train, X_val, y_train, y_val = train_test_split(data_to_train, prediction, test_size = 0.3,random_state=21, stratify=y)
print('Data split')
```
## AdaBoost
```
adaboost=AdaBoostClassifier()
adaboost.fit(X_train, y_train)
y_pred = adaboost.predict(X_val)
acc_adaboost = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_adaboost)
```
## Bagging
```
bagging=BaggingClassifier()
bagging.fit(X_train, y_train)
y_pred = bagging.predict(X_val)
acc_bagging = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_bagging)
```
## Decision Tree
```
#Decision Tree
decisiontree = DecisionTreeClassifier()
decisiontree.fit(X_train, y_train)
y_pred = decisiontree.predict(X_val)
acc_decisiontree = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_decisiontree)
```
## Extra Trees
```
# ExtraTreesClassifier
et = ExtraTreesClassifier()
et.fit(X_train, y_train)
y_pred = et.predict(X_val)
acc_et = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_et)
```
## Gaussian Naive Bayes
```
# Gaussian Naive Bayes
gaussian = GaussianNB()
gaussian.fit(X_train, y_train)
y_pred = gaussian.predict(X_val)
acc_gaussian = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_gaussian)
```
## Gradient Boosting
```
# Gradient Boosting Classifier
gbk = GradientBoostingClassifier()
gbk.fit(X_train, y_train)
y_pred = gbk.predict(X_val)
acc_gbk = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_gbk)
```
## K Nearest Neighbors
```
# KNN or k-Nearest Neighbors
knn = KNeighborsClassifier()
knn.fit(X_train, y_train)
y_pred = knn.predict(X_val)
acc_knn = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_knn)
```
## Linear Discriminant Analysis
```
linear_da=LinearDiscriminantAnalysis()
linear_da.fit(X_train, y_train)
y_pred = linear_da.predict(X_val)
acc_linear_da = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_linear_da)
```
## LinearSVC
```
# Linear SVC
linear_svc = LinearSVC()
linear_svc.fit(X_train, y_train)
y_pred = linear_svc.predict(X_val)
acc_linear_svc = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_linear_svc)
```
## Logistic Regression
```
# Logistic Regression
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_val)
acc_logreg = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_logreg)
```
## MLP
```
MLP = MLPClassifier()
MLP.fit(X_train, y_train)
y_pred = MLP.predict(X_val)
acc_MLP= round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_MLP)
```
## Passive Aggressive
```
passiveaggressive = PassiveAggressiveClassifier()
passiveaggressive.fit(X_train, y_train)
y_pred = passiveaggressive.predict(X_val)
acc_passiveaggressive = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_passiveaggressive)
```
## Perceptron
```
# Perceptron
perceptron = Perceptron()
perceptron.fit(X_train, y_train)
y_pred = perceptron.predict(X_val)
acc_perceptron = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_perceptron)
```
## Random Forest
```
# Random Forest
randomforest = RandomForestClassifier(random_state = 0)
randomforest.fit(X_train, y_train)
y_pred = randomforest.predict(X_val)
acc_randomforest = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_randomforest)
```
## Ridge Classifier
```
ridge = RidgeClassifierCV()
ridge.fit(X_train, y_train)
y_pred = ridge.predict(X_val)
acc_ridge = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_ridge)
```
## Stochastic Gradient Descent
```
# Stochastic Gradient Descent
sgd = SGDClassifier()
sgd.fit(X_train, y_train)
y_pred = sgd.predict(X_val)
acc_sgd = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_sgd)
```
## Support Vector Machines
Has more flexibility in the choice of penalties and loss functions and should scale better to large numbers of samples.
1. This class supports both dense and sparse input and the multiclass support is handled according to a one-vs-the-rest scheme.
```
# instanciate model
clf = SVC()
# fit model
clf.fit(X_train, y_train)
# predict results
y_pred = clf.predict(X_val)
# check accuracy
acc_clf = round(accuracy_score(y_pred, y_val) * 100, 2)
#print accuracy
print(acc_clf)
```
## xgboost
```
# xgboost
xgb = XGBClassifier(n_estimators=10)
xgb.fit(X_train, y_train)
y_pred = xgb.predict(X_val)
acc_xgb = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_xgb)
```
## Comparing the results
```
models = pd.DataFrame({
'Model': ['Support Vector Machines', 'KNN', 'Logistic Regression', 'Ridge Classifier',
'Random Forest', 'Naive Bayes', 'Linear SVC', 'MLP','AdaBoost','Linear discriminant','Passive Aggressive',
'Decision Tree', 'Gradient Boosting Classifier','Extra Trees','Stochastic Gradient Descent','Perceptron','xgboost'],
'Score': [acc_clf, acc_knn, acc_logreg,acc_ridge,acc_randomforest, acc_gaussian,acc_linear_svc, acc_MLP,acc_adaboost,acc_linear_da,acc_passiveaggressive,acc_decisiontree,acc_gbk,acc_et,acc_sgd,acc_perceptron,acc_xgb]})
models.sort_values(by='Score', ascending=False)
```
# Reforcast predictions based on best performing model
```
Submission['Survived']=ridge.predict(test)
print(Submission.head(5))
print('Prediction complete')
```
# Make model submission
```
# write data frame to csv file
Submission.set_index('PassengerId', inplace=True)
Submission.to_csv('ridgesubmission02.csv',sep=',')
print('File created')
```
# Stage 4 : Hyper Tuning the Models
```
REVISED_NUMERIC_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked'] #84
SIMPLE_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Sex_female','Sex_male','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked'] #84
INTERESTING_COLUMNS=['Survived','Pclass','Age','SibSp','Parch','Title','Alone','Mother','Family Size','Family_Survival','Embarked','FareBand','TicketRef']
CATEGORY_COLUMNS=['Pclass','SibSp','Parch','Family Size','Family_Survival','Alone','Mother','Sex_female','Sex_male','AgeBand_Child',
'AgeBand_Young Adult', 'AgeBand_Adult', 'AgeBand_Older Adult',
'AgeBand_Senior','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','NameBand_1',
'NameBand_2', 'NameBand_3', 'NameBand_4', 'NameBand_5','Embarked','TicketRef_A', 'TicketRef_C', 'TicketRef_F', 'TicketRef_L',
'TicketRef_P', 'TicketRef_S', 'TicketRef_W', 'TicketRef_X','HadCabin','Free']
#print(df_test.columns)
# create test and training data
data_to_train = df_train[CATEGORY_COLUMNS].fillna(-1000)
prediction = df_train["Survived"]
test = df_test[CATEGORY_COLUMNS].fillna(-1000)
X_train, X_val, y_train, y_val = train_test_split(data_to_train, prediction, test_size = 0.3,random_state=21, stratify=prediction)
print('Data split')
```
## Linear Regression SVC
```
# Support Vector Classifier parameters
param_grid = {'C':np.arange(1, 7),
'degree':np.arange(1, 7),
'max_iter':np.arange(0, 12),
'kernel':['rbf','linear'],
'shrinking':[0,1]}
clf = SVC()
svc_cv=GridSearchCV(clf, param_grid, cv=10)
svc_cv.fit(X_train, y_train)
print("Tuned SVC Parameters: {}".format(svc_cv.best_params_))
print("Best score is {}".format(svc_cv.best_score_))
acc_svc_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_svc_cv)
```
## Logistic Regression
```
# Logistic Regression
from sklearn.linear_model import LogisticRegression
# create parameter grid as a dictionary where the keys are the hyperparameter names and the values are lists of values that we want to try.
param_grid = {"solver": ['newton-cg','lbfgs','liblinear','sag','saga'],'C': [0.01, 0.1, 1, 10, 100]}
# instanciate classifier
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
logreg_cv = GridSearchCV(logreg, param_grid, cv=30)
logreg_cv.fit(X_train, y_train)
y_pred = logreg_cv.predict(X_val)
print("Tuned Logistic Regression Parameters: {}".format(logreg_cv.best_params_))
print("Best score is {}".format(logreg_cv.best_score_))
acc_logreg_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_logreg_cv)
```
## KNN
```
# KNN or k-Nearest Neighbors with GridSearch
# create parameter grid as a dictionary where the keys are the hyperparameter names and the values are lists of values that we want to try.
param_grid = {"n_neighbors": np.arange(1, 50),
"leaf_size": np.arange(20, 40),
"algorithm": ["ball_tree","kd_tree","brute"]
}
# instanciate classifier
knn = KNeighborsClassifier()
knn.fit(X_train, y_train)
knn_cv = GridSearchCV(knn, param_grid, cv=10)
knn_cv.fit(X_train, y_train)
y_pred = knn_cv.predict(X_val)
print("Tuned knn Parameters: {}".format(knn_cv.best_params_))
print("Best score is {}".format(knn_cv.best_score_))
acc_knn_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_knn_cv)
```
## DecisionTree with RandomizedSearch
```
# DecisionTree with RandomizedSearch
# Setup the parameters and distributions to sample from: param_dist
param_dist = {"random_state" : np.arange(0, 10),
"max_depth": np.arange(1, 10),
"max_features": np.arange(1, 10),
"min_samples_leaf": np.arange(1, 10),
"criterion": ["gini","entropy"]}
# Instantiate a Decision Tree classifier: tree
tree = DecisionTreeClassifier()
# Instantiate the RandomizedSearchCV object: tree_cv
tree_cv = RandomizedSearchCV(tree, param_dist, cv=30)
# Fit it to the data
tree_cv.fit(X_train,y_train)
y_pred = tree_cv.predict(X_val)
# Print the tuned parameters and score
print("Tuned Decision Tree Parameters: {}".format(tree_cv.best_params_))
print("Best score is {}".format(tree_cv.best_score_))
acc_tree_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_tree_cv)
```
## Random Forest
```
# Random Forest
# Setup the parameters and distributions to sample from: param_dist
param_dist = {"random_state" : np.arange(0, 10),
"n_estimators" : np.arange(1, 20),
"max_depth": np.arange(1, 10),
"max_features": np.arange(1, 10),
"min_samples_leaf": np.arange(1, 10),
"criterion": ["gini","entropy"]}
# Instantiate a Decision Tree classifier: tree
randomforest = RandomForestClassifier()
# Instantiate the RandomizedSearchCV object: tree_cv
randomforest_cv = RandomizedSearchCV(randomforest, param_dist, cv=30)
# Fit it to the data
randomforest_cv.fit(X_train,y_train)
y_pred = randomforest_cv.predict(X_val)
# Print the tuned parameters and score
print("Tuned Decision Tree Parameters: {}".format(randomforest_cv.best_params_))
print("Best score is {}".format(randomforest_cv.best_score_))
acc_randomforest_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_randomforest_cv)
```
## Gradient Boosting
```
# Gradient Boosting Classifier
# Setup the parameters and distributions to sample from: param_dist
param_dist = {'max_depth':np.arange(1, 7),
'min_samples_leaf': np.arange(1, 6),
"max_features": np.arange(1, 10),
}
# Instantiate Classifier
gbk = GradientBoostingClassifier()
# Instantiate the RandomizedSearchCV object: tree_cv
gbk_cv = RandomizedSearchCV(gbk, param_dist, cv=30)
gbk_cv.fit(X_train, y_train)
y_pred = gbk_cv.predict(X_val)
print("Tuned Gradient Boost Parameters: {}".format(gbk_cv.best_params_))
print("Best score is {}".format(gbk_cv.best_score_))
acc_gbk_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_gbk_cv)
```
## xgboost
```
# xgboost
# Setup the parameters and distributions to sample from: param_dist
param_dist = {'learning_rate': [.01, .03, .05, .1, .25], #default: .3
'max_depth': np.arange(1, 10), #default 2
'n_estimators': [10, 50, 100, 300],
'booster':['gbtree','gblinear','dart']
#'seed': 5
}
# Instantiate Classifier
xgb = XGBClassifier()
# Instantiate the RandomizedSearchCV object: tree_cv
xgb_cv = RandomizedSearchCV(xgb, param_dist, cv=20)
# Fit model
xgb_cv.fit(X_train, y_train)
# Make prediction
y_pred = xgb_cv.predict(X_val)
# Print results
print("xgBoost Parameters: {}".format(xgb_cv.best_params_))
print("Best score is {}".format(xgb_cv.best_score_))
acc_xgb_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print(acc_xgb_cv)
```
## Comparing the results of the cross validated tuned models (best result)
```
optmodels = pd.DataFrame({
'optModel': ['SVC','KNN','Decision Tree','Gradient Boost','Logistic Regression','xgboost'],
'optScore': [svc_cv.best_score_,knn_cv.best_score_,tree_cv.best_score_,gbk_cv.best_score_,logreg_cv.best_score_,xgb_cv.best_score_]})
optmodels.sort_values(by='optScore', ascending=False)
```
## Comparing the results of the tuned models (accuracy)
```
optmodels = pd.DataFrame({
'optModel': ['Linear Regression','KNearestNieghbours','Decision Tree','Gradient Boost','Logistic Regression','xgboost'],
'optScore': [acc_svc_cv,acc_knn_cv,acc_tree_cv,acc_gbk_cv,acc_logreg_cv,acc_xgb_cv]})
optmodels.sort_values(by='optScore', ascending=False)
```
## Plotting Learning Curves
```
# define function to plot test and training curves
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
n_jobs=-1, train_sizes=np.linspace(.1, 1.0, 5)):
"""Generate a simple plot of the test and training learning curve"""
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.legend(loc="best")
return plt
# Cross validate model with Kfold stratified cross val
kfold = StratifiedKFold(n_splits=10)
# Plot chart for each model
g = plot_learning_curve(svc_cv.best_estimator_,"linear regression learning curves",X_train,y_train,cv=kfold)
g = plot_learning_curve(logreg_cv.best_estimator_,"logistic regression learning curves",X_train,y_train,cv=kfold)
g = plot_learning_curve(knn_cv.best_estimator_,"knn learning curves",X_train,y_train,cv=kfold)
g = plot_learning_curve(tree_cv.best_estimator_,"decision tree learning curves",X_train,y_train,cv=kfold)
g = plot_learning_curve(randomforest_cv.best_estimator_,"random forest learning curves",X_train,y_train,cv=kfold)
g = plot_learning_curve(gbk_cv.best_estimator_,"gradient boosting learning curves",X_train,y_train,cv=kfold)
g = plot_learning_curve(xgb_cv.best_estimator_,"xg boost learning curves",X_train,y_train,cv=kfold)
```
# Optimising the Model
Adding parameters to the basic models generally improved the performance on the training data. These gain on the training data did not always translate to the same increase in performance on the test data, due to over fitting.
# Predictions based on tuned model
```
# Select columns
X_train = df_train[CATEGORY_COLUMNS].fillna(-1000)
y_train = df_train["Survived"]
X_test = df_test[CATEGORY_COLUMNS].fillna(-1000)
from sklearn.tree import DecisionTreeClassifier
test = df_test[REVISED_NUMERIC_COLUMNS].fillna(-1000)
# select classifier
#tree = DecisionTreeClassifier(random_state=0,max_depth=5,max_features=7,min_samples_leaf=2,criterion="entropy") #85,87
#tree = DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=4,max_features=7, max_leaf_nodes=None, min_impurity_decrease=0.0,min_impurity_split=None, min_samples_leaf=9,min_samples_split=2, min_weight_fraction_leaf=0.0,presort=False, random_state=8, splitter='best')
#tree = DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=4,max_features=7, max_leaf_nodes=None, min_impurity_decrease=0.0,min_impurity_split=None, min_samples_leaf=9,min_samples_split=2, min_weight_fraction_leaf=0.0,presort=False, random_state=9, splitter='best')
#knn = KNeighborsClassifier(algorithm='kd_tree',leaf_size=20,n_neighbors=5)
#logreg = LogisticRegression(solver='newton-cg')
#xgboost=XGBClassifier(n_estimators= 300, max_depth= 10, learning_rate= 0.01)
#gbk=GradientBoostingClassifier(min_samples_leaf=1,max_features=4,max_depth=5)
#logreg=LogisticRegression(solver='newton-cg',C= 10)
#gboost=GradientBoostingClassifier(random_state= 7,n_estimators=17,min_samples_leaf= 4, max_features=9,max_depth=5, criterion='gini')
randomf=RandomForestClassifier(random_state= 7,n_estimators=17,min_samples_leaf= 4, max_features=9,max_depth=5, criterion='gini')
# train model
randomf.fit(data_to_train, prediction)
# make predictions
Submission['Survived']=randomf.predict(X_test)
#Submission.set_index('PassengerId', inplace=True)
Submission.to_csv('randomforestcats01.csv',sep=',')
print(Submission.head(5))
print('File created')
```
# Stage 5 : Hyper tuning with confusion matrix
I used a grid search cross validation in the previous stages to estimate the best results, we can use a confusion matrix to find out how well this model works by penalizing incorrect predictions.
```
# knn Hyper Tunning with confusion Matrix
REVISED_NUMERIC_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked'] #84
SIMPLE_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Sex_female','Sex_male','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked'] #84
INTERESTING_COLUMNS=['Survived','Pclass','Age','SibSp','Parch','Title','Alone','Mother','Family Size','Family_Survival','Embarked','FareBand','TicketRef']
CATEGORY_COLUMNS=['Pclass','SibSp','Parch','Family Size','Family_Survival','Alone','Mother','Sex_female','Sex_male','AgeBand_Child',
'AgeBand_Young Adult', 'AgeBand_Adult', 'AgeBand_Older Adult',
'AgeBand_Senior','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','NameBand_1',
'NameBand_2', 'NameBand_3', 'NameBand_4', 'NameBand_5','Embarked','TicketRef_A', 'TicketRef_C', 'TicketRef_F', 'TicketRef_L',
'TicketRef_P', 'TicketRef_S', 'TicketRef_W', 'TicketRef_X','HadCabin','Free']
# create test and training data
data_to_train = df_train[CATEGORY_COLUMNS].fillna(-1000)
X_test2= df_test[CATEGORY_COLUMNS].fillna(-1000)
prediction = df_train["Survived"]
X_train, X_test, y_train, y_test = train_test_split(data_to_train, prediction, test_size = 0.3,random_state=21, stratify=prediction)
print('Data Split')
hyperparams = {'algorithm': ['auto'], 'weights': ['uniform', 'distance'] ,'leaf_size': list(range(1,50,5)),
'n_neighbors':[6,7,8,9,10,11,12,14,16,18,20,22]}
gd=GridSearchCV(estimator = KNeighborsClassifier(), param_grid = hyperparams, verbose=True, cv=10, scoring = "roc_auc")
gd.fit(X_train, y_train)
gd.best_estimator_.fit(X_train,y_train)
y_pred=gd.best_estimator_.predict(X_test)
Submission['Survived']=gd.best_estimator_.predict(X_test2)
# Print the results
print('Best Score')
print(gd.best_score_)
print('Best Estimator')
print(gd.best_estimator_)
acc_gd_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print('Accuracy')
print(acc_gd_cv)
# Generate the confusion matrix and classification report
print('Confusion Matrrix')
print(confusion_matrix(y_test, y_pred))
print('Classification_report')
print(classification_report(y_test, y_pred))
#Submission.set_index('PassengerId', inplace=True)
print('Sample Prediction')
print(Submission.head(10))
#Submission.to_csv('knngridsearch03.csv',sep=',')
print('KNN prediction created')
# Decision Tree Hyper Tunning with confusion Matrix
REVISED_NUMERIC_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked'] #84
SIMPLE_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Sex_female','Sex_male','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked'] #84
INTERESTING_COLUMNS=['Survived','Pclass','Age','SibSp','Parch','Title','Alone','Mother','Family Size','Family_Survival','Embarked','FareBand','TicketRef']
CATEGORY_COLUMNS=['Pclass','SibSp','Parch','Family Size','Family_Survival','Alone','Mother','Sex_female','Sex_male','AgeBand_Child',
'AgeBand_Young Adult', 'AgeBand_Adult', 'AgeBand_Older Adult',
'AgeBand_Senior','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','NameBand_1',
'NameBand_2', 'NameBand_3', 'NameBand_4', 'NameBand_5','Embarked','TicketRef_A', 'TicketRef_C', 'TicketRef_F', 'TicketRef_L',
'TicketRef_P', 'TicketRef_S', 'TicketRef_W', 'TicketRef_X','HadCabin','Free']
# create test and training data
data_to_train = df_train[CATEGORY_COLUMNS].fillna(-1000)
X_test2= df_test[CATEGORY_COLUMNS].fillna(-1000)
prediction = df_train["Survived"]
X_train, X_test, y_train, y_test = train_test_split(data_to_train, prediction, test_size = 0.3,random_state=21, stratify=prediction)
print('Data Split')
hyperparams = {"random_state" : np.arange(0, 10),
"max_depth": np.arange(1, 10),
"max_features": np.arange(1, 10),
"min_samples_leaf": np.arange(1, 10),
"criterion": ["gini","entropy"]}
gd=GridSearchCV(estimator = DecisionTreeClassifier(), param_grid = hyperparams, verbose=True, cv=10, scoring = "roc_auc")
gd.fit(X_train, y_train)
gd.best_estimator_.fit(X_train,y_train)
y_pred=gd.best_estimator_.predict(X_test)
Submission['Survived']=gd.best_estimator_.predict(X_test2)
# Print the results
print('Best Score')
print(gd.best_score_)
print('Best Estimator')
print(gd.best_estimator_)
acc_gd_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print('Accuracy')
print(acc_gd_cv)
# Generate the confusion matrix and classification report
print('Confusion Matrrix')
print(confusion_matrix(y_test, y_pred))
print('Classification_report')
print(classification_report(y_test, y_pred))
#Submission.set_index('PassengerId', inplace=True)
# print head
print(Submission.head(10))
Submission.to_csv('Treegridsearch03.csv',sep=',')
print('Decision Tree prediction created')
# Decision Logistic Regression Hyper Tunning with confusion Matrix
REVISED_NUMERIC_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked']
SIMPLE_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Sex_female','Sex_male','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked']
INTERESTING_COLUMNS=['Survived','Pclass','Age','SibSp','Parch','Title','Alone','Mother','Family Size','Family_Survival','Embarked','FareBand','TicketRef']
CATEGORY_COLUMNS=['Pclass','SibSp','Parch','Family Size','Family_Survival','Alone','Mother','Sex_female','Sex_male','AgeBand_Child',
'AgeBand_Young Adult', 'AgeBand_Adult', 'AgeBand_Older Adult',
'AgeBand_Senior','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','NameBand_1',
'NameBand_2', 'NameBand_3', 'NameBand_4', 'NameBand_5','Embarked','TicketRef_A', 'TicketRef_C', 'TicketRef_F', 'TicketRef_L',
'TicketRef_P', 'TicketRef_S', 'TicketRef_W', 'TicketRef_X','HadCabin','Free']
# create test and training data
data_to_train = df_train[CATEGORY_COLUMNS].fillna(-1000)
X_test2= df_test[CATEGORY_COLUMNS].fillna(-1000)
prediction = df_train["Survived"]
X_train, X_test, y_train, y_test = train_test_split(data_to_train, prediction, test_size = 0.3,random_state=21, stratify=prediction)
print('Data Split')
hyperparams = {'solver':["newton-cg", "lbfgs", "liblinear", "sag", "saga"],
'C': [0.01, 0.1, 1, 10, 100]}
gd=GridSearchCV(estimator = LogisticRegression(), param_grid = hyperparams, verbose=True, cv=10, scoring = "roc_auc")
gd.fit(X_train, y_train)
gd.best_estimator_.fit(X_train,y_train)
y_pred=gd.best_estimator_.predict(X_test)
Submission['Survived']=gd.best_estimator_.predict(X_test2)
# Print the results
print('Best Score')
print(gd.best_score_)
print('Best Estimator')
print(gd.best_estimator_)
acc_gd_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print('Accuracy')
print(acc_gd_cv)
# Generate the confusion matrix and classification report
print('Confusion Matrrix')
print(confusion_matrix(y_test, y_pred))
print('Classification_report')
print(classification_report(y_test, y_pred))
#Submission.set_index('PassengerId', inplace=True)
# print head
print(Submission.head(10))
Submission.to_csv('Logregwithconfusion01.csv',sep=',')
print('Logistic Regression prediction created')
df_train.columns
# Decision Logistic Regression Hyper Tunning with confusion Matrix
# create test and training data
X_train = df_train[CATEGORY_COLUMNS].fillna(-1000)
y_train = df_train["Survived"]
X_test = df_test[CATEGORY_COLUMNS].fillna(-1000)
randomf=RandomForestClassifier(criterion='gini', n_estimators=700, min_samples_split=10,min_samples_leaf=1,max_features='auto',oob_score=True,random_state=1,n_jobs=-1)
randomf.fit(X_train, y_train)
Submission['Survived']=randomf.predict(X_test)
# Print the results
acc_gd_cv = round(accuracy_score(y_pred, y_val) * 100, 2)
print('Accuracy')
print(acc_gd_cv)
#Submission.set_index('PassengerId', inplace=True)
# print head
print(Submission.head(10))
Submission.to_csv('finalrandomforest01.csv',sep=',')
print('Random Forest prediction created')
```
## Plot Area under ROC
```
# List of Machine Learning Algorithm (MLA)
MLA = [
#Ensemble Methods
ensemble.ExtraTreesClassifier(),
ensemble.GradientBoostingClassifier(),
ensemble.RandomForestClassifier(),
#GLM
linear_model.LogisticRegressionCV(),
#Nearest Neighbor
neighbors.KNeighborsClassifier(),
#SVM
svm.SVC(probability=True),
#Trees
#tree.DecisionTreeClassifier(),
#tree.ExtraTreeClassifier(),
]
index = 1
for alg in MLA:
predicted = alg.fit(X_train, y_train).predict(X_test)
fp, tp, th = roc_curve(y_test, predicted)
roc_auc_mla = auc(fp, tp)
MLA_name = alg.__class__.__name__
plt.plot(fp, tp, lw=2, alpha=0.3, label='ROC %s (AUC = %0.2f)' % (MLA_name, roc_auc_mla))
index+=1
plt.title('ROC Curve comparison')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.plot([0,1],[0,1],'r--')
plt.xlim([0,1])
plt.ylim([0,1])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
```
# Stage 6 : Basic Ensemble Modelling
In the last couple of stages I tried a few different models with differnet parameters to try and find the one that produced the best results. Another approach would be to use an Ensemble model, that generates results from a selection of the best performing models and then feeds the results into a another model in a second layer.
```
REVISED_NUMERIC_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked']
SIMPLE_COLUMNS=['Pclass','Age','SibSp','Parch','Family_Survival','Alone','Sex_female','Sex_male','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','Embarked']
INTERESTING_COLUMNS=['Survived','Pclass','Age','SibSp','Parch','Title','Alone','Mother','Family Size','Family_Survival','Embarked','FareBand','TicketRef']
CATEGORY_COLUMNS=['Pclass','SibSp','Parch','Family Size','Family_Survival','Alone','Mother','Sex_female','Sex_male','AgeBand_Child',
'AgeBand_Young Adult', 'AgeBand_Adult', 'AgeBand_Older Adult',
'AgeBand_Senior','Title_Master', 'Title_Miss','Title_Mr', 'Title_Mrs', 'Title_Millitary','NameBand_1',
'NameBand_2', 'NameBand_3', 'NameBand_4', 'NameBand_5','Embarked','TicketRef_A', 'TicketRef_C', 'TicketRef_F', 'TicketRef_L',
'TicketRef_P', 'TicketRef_S', 'TicketRef_W', 'TicketRef_X','HadCabin','Free']
# create test and training data
data_to_train = df_train[REVISED_NUMERIC_COLUMNS].fillna(-1000)
data_to_test = df_test[REVISED_NUMERIC_COLUMNS].fillna(-1000)
prediction = df_train["Survived"]
X_train, X_val, y_train, y_val = train_test_split(data_to_train, prediction, test_size = 0.3,random_state=21, stratify=prediction)
print('Data Split')
```
## Train first layer
```
#logreg = LogisticRegression()
logreg = LogisticRegression(C=10, solver='newton-cg')
logreg.fit(X_train, y_train)
y_pred_train_logreg = cross_val_predict(logreg,X_val, y_val)
y_pred_test_logreg = logreg.predict(X_test)
print('logreg first layer predicted')
#tree = DecisionTreeClassifier()
tree = DecisionTreeClassifier(random_state=8,min_samples_leaf=6, max_features= 7, max_depth= 4, criterion='gini', splitter='best')
tree.fit(X_train, y_train)
y_pred_train_tree = cross_val_predict(tree,X_val,y_val)
y_pred_test_tree = tree.predict(X_test)
print('decision tree first layer predicted')
# randomforest = RandomForestClassifier()
randomforest = RandomForestClassifier(random_state=8, n_estimators=15, min_samples_leaf= 4, max_features= 6, max_depth=4,criterion='gini')
randomforest.fit(X_train, y_train)
y_pred_train_randomforest = cross_val_predict(randomforest, X_val, y_val)
y_pred_test_randomforest = randomforest.predict(X_test)
print('random forest first layer predicted')
#gbk
gbk = GradientBoostingClassifier(min_samples_leaf=3, max_features= 3, max_depth= 3)
gbk.fit(X_train, y_train)
y_pred_train_gbk = cross_val_predict(gbk, X_val, y_val)
y_pred_test_gbk = gbk.predict(X_test)
print('gbk first layer predicted')
#knn
knn = KNeighborsClassifier(algorithm='auto', leaf_size=36, metric='minkowski',metric_params=None, n_jobs=1, n_neighbors=12, p=2,weights='uniform')
knn.fit(X_train, y_train)
y_pred_train_knn = cross_val_predict(knn, X_val, y_val)
y_pred_test_knn = gbk.predict(X_test)
print('knn first layer predicted')
#clf = SVC()
clf = SVC(C=3, degree=1, kernel='linear', max_iter=1, shrinking=0)
clf.fit(X_train, y_train)
y_pred_train_clf = cross_val_predict(clf, X_val, y_val)
y_pred_test_clf = clf.predict(X_test)
print('clf first layer predicted')
```
## VotingClassifier Ensemble
```
from sklearn.ensemble import VotingClassifier
votingC = VotingClassifier(estimators=[('logreg', logreg_cv.best_estimator_), ('gbk', gbk_cv.best_estimator_),
('tree', tree_cv.best_estimator_), ('randomforest',randomforest_cv.best_estimator_),('knn',knn_cv.best_estimator_) ], voting='soft', n_jobs=4)
votingC = votingC.fit(X_train, y_train)
# write data frame to csv file
Submission['Survived'] = votingC.predict(X_test)
# Submission.set_index('PassengerId', inplace=True)
Submission.to_csv('Votingclassifier02.csv',sep=',')
print('Voting Classifier Ensemble File created')
print(Submission.head())
```
# Stage 7 : Hyper Tuned Ensemble Modelling
```
# Create Ensemble Model baseline (tuned model!)
second_layer_train = pd.DataFrame( {'Logistic Regression': y_pred_train_logreg.ravel(),
'Gradient Boosting': y_pred_train_gbk.ravel(),
'Decision Tree': y_pred_train_tree.ravel(),
'Random Forest': y_pred_train_randomforest.ravel()
} )
X_train_second = np.concatenate(( y_pred_train_logreg.reshape(-1, 1), y_pred_train_gbk.reshape(-1, 1),
y_pred_train_tree.reshape(-1, 1), y_pred_train_randomforest.reshape(-1, 1)),
axis=1)
X_test_second = np.concatenate(( y_pred_test_logreg.reshape(-1, 1), y_pred_test_gbk.reshape(-1, 1),
y_pred_test_tree.reshape(-1, 1), y_pred_test_randomforest.reshape(-1, 1)),
axis=1)
#xgb = XGBClassifier(n_estimators= 800,max_depth= 4,min_child_weight= 2,gamma=0.9,subsample=0.8,colsample_bytree=0.8,objective= 'binary:logistic',nthread= -1,scale_pos_weight=1).fit(X_train_second, y_val)
tree = DecisionTreeClassifier(random_state=8,min_samples_leaf=6, max_depth= 4, criterion='gini').fit(X_train_second,y_val)
Submission['Survived'] = tree.predict(X_test_second)
print(Submission.head())
print('Tuned Ensemble model prediction complete')
# write data frame to csv file
#Submission.set_index('PassengerId', inplace=True)
Submission.to_csv('tunedensemblesubmission04.csv',sep=',')
print('tuned Ensemble File created')
```
# Summary
In this project we have explored the Titanic Data Set, we have identified missing data and filled then as best we could, we have converted categorical data to columns of numeric features that we can use in machine learning and we have engineered new features based on the data we had. We improved our score from base line of 0.57894 to a score of 0.78.
Going from a score of 0.57 to 0.77 was the relatively easy part, taking it from 7.8 to 0.8 is a whole different ball game. Its really temping to overwork the data trying to find new features that might improve the score but in really what you gain in new features you loose in the noise you've introduce, its also tempting to keep tweak the parameters of your model to get the best possible score on the test data, but gain what you gain in performance on the training data you loose in overfitting. A better approach is to stick to the features that have the strongest relationships and ensure that any data that you are estimating or engineering is as accurate as you can possibly make it. Using cross validation to hyper tune the model while minimising any over fitting of the data.
When I initially created the project I kept the test and training data completely separate but am I am rapidly coming to the conclusion that combining the two datasets, is possibly a better approach for estimating missing data based on averages across the entire dataset.
I looked at a range of different models and compared the accuracy of each model on the training data before deciding which model to use for the third submission. I then hyper tuned a hanful of the best performing to ensure that I submitted the best performing hyper tuned model.
Having hypertuned a single model the next step in my process was to attempt combining several models in an ensemble. I managed to achieve a result of .803 which was OK but not as good as the best hypertuned models that i'd produced.
I havn't come any where near winning this contest yet, but I survived my first Kaggle contest and got a score of over .8 which has my goal. The main thing is that I had fun and learnt a lot along the way by trying different techniques and looking at what other people were doing.
I've also created a kernal that uses the same data with deep learning, you can find this at https://www.kaggle.com/davidcoxon/deeply-titanic
# Credit where credits due
This competition is predominantly a training exercise and as such I have tried to looks at different approaches and try different techniques to see hw they work. I have looked at some of the existing entries and adopted some of the tequiques that i have found interesting. So firstly a huge thanks to everyone that look the time to document their code and explain step by step what they did and why.
To naming names, some of the notebooks that i found most useful and think deserve special mensions are:
### Aldemuro M.A.Haris
https://www.kaggle.com/aldemuro/comparing-ml-algorithms-train-accuracy-90
Interesting model comparison and ROC graphs
### Anisotropic
https://www.kaggle.com/arthurtok/introduction-to-ensembling-stacking-in-python/notebook
Introduction to Ensembling/Stacking in Python is a very useful project on many levels, in I particular I liked how elegantly this code was written.
### Bisaria
https://www.kaggle.com/bisaria/titanic-lasso-ridge-implementation/code
While this notebook is based on R and I am working in Python, I found some of the visualizations interesting, specifically the port of embarkation and number of siblings and the mosaic. I also liked the idea of the lone traveller feature and the allocation of the cabin data, based on family.
### CalebCastleberry
https://www.kaggle.com/ccastleberry/titanic-cabin-features
This notebook explains the importance of the deck feature and proves you can score 70% on the deck feature alone.
### Henrique Mello
https://www.kaggle.com/hrmello/introduction-to-data-exploration-using-seaborn/notebook
This has some great visualisations of the data and helped me understand the importance of using title in predicting ages when filling in the missing data.
### Konstantin
https://www.kaggle.com/konstantinmasich/titanic-0-82-0-83
### LD Freeman
https://www.kaggle.com/ldfreeman3/a-data-science-framework-to-achieve-99-accuracy
This not only achieves a fantastic score but is a great tutorial on data science techniques
### Nadin Tamer
https://www.kaggle.com/nadintamer/titanic-survival-predictions-beginner/notebook
I found this another really useful kernel. It is very much a step by step approach, with a particularly good section on different types of model and how they perform for this project.
### Omar El Gabry
https://www.kaggle.com/omarelgabry/a-journey-through-titanic?scriptVersionId=447802/notebook
This kernal has an interesting section on estimating the missing ages and calculating pearson co-efficients for the features.
### Oscar Takeshita
https://www.kaggle.com/pliptor/divide-and-conquer-0-82296/code
This kernal was very useful in trying to get over the 0.8 ceiling, its based on R rather than python so i haven't used any of the code, but it helped me focus on the key fearures and to see the benefits of uing the combined training and test dataset for statistics and calculations rather keeping the two at arms length.
### Sina
https://www.kaggle.com/sinakhorami/titanic-best-working-classifier?scriptVersionId=566580
A lot of high scoring kernals reference this notebook, especially the feature engineering discussed in it.
### S.Xu
https://www.kaggle.com/shunjiangxu/blood-is-thicker-than-water-friendship-forever
This kernal is based on an original kernal by Sina, and it uses the last name and ticket details to find families and firends it then looks at the survival of the group as a whole.
### Yassine Ghouzam
https://www.kaggle.com/yassineghouzam/titanic-top-4-with-ensemble-modeling
This kernal has an interesting section on learning curves.
| true |
code
| 0.571408 | null | null | null | null |
|
```
%load_ext watermark
%watermark -d -u -a 'Andreas Mueller, Kyle Kastner, Sebastian Raschka' -v -p numpy,scipy,matplotlib,scikit-learn
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
```
# SciPy 2016 Scikit-learn Tutorial
# Supervised Learning Part 2 -- Regression Analysis
In regression we are trying to predict a continuous output variable -- in contrast to the nominal variables we were predicting in the previous classification examples.
Let's start with a simple toy example with one feature dimension (explanatory variable) and one target variable. We will create a dataset out of a sinus curve with some noise:
```
x = np.linspace(-3, 3, 100)
print(x)
rng = np.random.RandomState(42)
y = np.sin(4 * x) + x + rng.uniform(size=len(x))
plt.plot(x, y, 'o');
```
Linear Regression
=================
The first model that we will introduce is the so-called simple linear regression. Here, we want to fit a line to the data, which
One of the simplest models again is a linear one, that simply tries to predict the data as lying on a line. One way to find such a line is `LinearRegression` (also known as [*Ordinary Least Squares (OLS)*](https://en.wikipedia.org/wiki/Ordinary_least_squares) regression).
The interface for LinearRegression is exactly the same as for the classifiers before, only that ``y`` now contains float values, instead of classes.
As we remember, the scikit-learn API requires us to provide the target variable (`y`) as a 1-dimensional array; scikit-learn's API expects the samples (`X`) in form a 2-dimensional array -- even though it may only consist of 1 feature. Thus, let us convert the 1-dimensional `x` NumPy array into an `X` array with 2 axes:
```
print('Before: ', x.shape)
X = x[:, np.newaxis]
print('After: ', X.shape)
```
Again, we start by splitting our dataset into a training (75%) and a test set (25%):
```
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
```
Next, we use the learning algorithm implemented in `LinearRegression` to **fit a regression model to the training data**:
```
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)
```
After fitting to the training data, we paramerterized a linear regression model with the following values.
```
print('Weight coefficients: ', regressor.coef_)
print('y-axis intercept: ', regressor.intercept_)
```
Since our regression model is a linear one, the relationship between the target variable (y) and the feature variable (x) is defined as
$$y = weight \times x + \text{intercept}$$.
Plugging in the min and max values into thos equation, we can plot the regression fit to our training data:
```
min_pt = X.min() * regressor.coef_[0] + regressor.intercept_
max_pt = X.max() * regressor.coef_[0] + regressor.intercept_
plt.plot([X.min(), X.max()], [min_pt, max_pt])
plt.plot(X_train, y_train, 'o');
```
Similar to the estimators for classification in the previous notebook, we use the `predict` method to predict the target variable. And we expect these predicted values to fall onto the line that we plotted previously:
```
y_pred_train = regressor.predict(X_train)
plt.plot(X_train, y_train, 'o', label="data")
plt.plot(X_train, y_pred_train, 'o', label="prediction")
plt.plot([X.min(), X.max()], [min_pt, max_pt], label='fit')
plt.legend(loc='best')
```
As we can see in the plot above, the line is able to capture the general slope of the data, but not many details.
Next, let's try the test set:
```
y_pred_test = regressor.predict(X_test)
plt.plot(X_test, y_test, 'o', label="data")
plt.plot(X_test, y_pred_test, 'o', label="prediction")
plt.plot([X.min(), X.max()], [min_pt, max_pt], label='fit')
plt.legend(loc='best');
```
Again, scikit-learn provides an easy way to evaluate the prediction quantitatively using the ``score`` method. For regression tasks, this is the R<sup>2</sup> score. Another popular way would be the Mean Squared Error (MSE). As its name implies, the MSE is simply the average squared difference over the predicted and actual target values
$$MSE = \frac{1}{n} \sum^{n}_{i=1} (\text{predicted}_i - \text{true}_i)^2$$
```
regressor.score(X_test, y_test)
```
KNeighborsRegression
=======================
As for classification, we can also use a neighbor based method for regression. We can simply take the output of the nearest point, or we could average several nearest points. This method is less popular for regression than for classification, but still a good baseline.
```
from sklearn.neighbors import KNeighborsRegressor
kneighbor_regression = KNeighborsRegressor(n_neighbors=1)
kneighbor_regression.fit(X_train, y_train)
```
Again, let us look at the behavior on training and test set:
```
y_pred_train = kneighbor_regression.predict(X_train)
plt.plot(X_train, y_train, 'o', label="data", markersize=10)
plt.plot(X_train, y_pred_train, 's', label="prediction", markersize=4)
plt.legend(loc='best');
```
On the training set, we do a perfect job: each point is its own nearest neighbor!
```
y_pred_test = kneighbor_regression.predict(X_test)
plt.plot(X_test, y_test, 'o', label="data", markersize=8)
plt.plot(X_test, y_pred_test, 's', label="prediction", markersize=4)
plt.legend(loc='best');
```
On the test set, we also do a better job of capturing the variation, but our estimates look much messier than before.
Let us look at the R<sup>2</sup> score:
```
kneighbor_regression.score(X_test, y_test)
```
Much better than before! Here, the linear model was not a good fit for our problem; it was lacking in complexity and thus under-fit our data.
Exercise
=========
Compare the KNeighborsRegressor and LinearRegression on the boston housing dataset. You can load the dataset using ``sklearn.datasets.load_boston``. You can learn about the dataset by reading the ``DESCR`` attribute.
```
# %load solutions/06A_knn_vs_linreg.py
```
| true |
code
| 0.620966 | null | null | null | null |
|
# MNIST With SET
This is an example of training an SET network on the MNIST dataset using synapses, pytorch, and torchvision.
```
#Import torch libraries and get SETLayer from synapses
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from synapses import SETLayer
#Some extras for visualizations
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import clear_output
print("done")
```
## SET Layer
The SET layer is a pytorch module that works with a similar API to a standard fully connected layer; to initialize, specify input and output dimensions.<br><br>
NOTE: one condition mentioned in the paper is that epsilon (a hyperparameter controlling layer sparsity) be much less than the input dimension and much less than the output dimension. The default value of epsilon is 11. Keep dimensions much bigger than epsilon! (epsilon can be passed in as an init argument to the layer).
```
#initialize the layer
sprs = SETLayer(128, 256)
#We can see the layer transforms inputs as we expect
inp = torch.randn((2, 128))
print('Input batch shape: ', tuple(inp.shape))
out = sprs(inp)
print('Output batch shape: ', tuple(out.shape))
```
In terms of behavior, the SETLayer transforms an input vector into the output space as would a fcl.
## Initial Connection Distribution
The intialized layer has randomly assigned connections between input nodes and output nodes; each connection is associated with a weight, drawn from a normal distribution.
```
#Inspect init weight distribution
plt.hist(np.array(sprs.weight.data), bins=40)
plt.title('Weights distribution on initialization')
plt.xlabel('Weight Value')
plt.ylabel('Number of weights')
plt.show()
vec = sprs.connections[:, 0]
vec = np.array(vec)
values, counts = np.unique(vec, return_counts=True)
plt.title('Connections to inputs')
plt.bar(values, counts)
plt.xlabel('Input vector index')
plt.ylabel('Number of connections')
plt.show()
print("done")
```
The weights are sampled from a normal distribution, as is done with a standard fcl. The connections to the inputs are uniformly distributed.<br><br>
## Killing Connections
When connections are reassigned in SET, some proportion (defined by hyperparameter zeta) of the weights closest to zero are removed. We can set these to zero using the zero_connections method on the layer. (This method leaves the connections unchanged.)
```
sprs.zero_connections()
#Inspect init weight distribution
plt.hist(np.array(sprs.weight.data), bins=40)
plt.title('Weights distribution after zeroing connections')
plt.xlabel('Weight Value')
plt.ylabel('Number of weights')
plt.show()
print("done")
```
## Evolving Connections
The evolve_connections() method will reassign these weights to new connections between input and output nodes. By default, these weights are initialized by sampling from the same distribution as the init function. Optionally, these weights can be set at zero (with init=False argument).
```
sprs.evolve_connections()
plt.hist(np.array(sprs.weight.data), bins=40)
plt.title('Weights distribution after evolving connections')
plt.show()
plt.title('Connections to inputs')
plt.bar(values, counts)
plt.xlabel('Input vector index')
plt.ylabel('Number of connections')
plt.show()
print("done")
```
We can see these weight values have been re-distributed; the new connections conform to the same uniform distribution as before. (We see in the SET paper, and here later on, that the adaptive algorithm learns to allocate these connections to more important input values.)
## A Simple SET Model
The following is a simple sparsely-connected model using SETLayers with default hyperparameters.
```
class SparseNet(nn.Module):
def __init__(self):
super(SparseNet, self).__init__()
self.set_layers = []
self.set1 = SETLayer(784, 512)
self.set_layers.append(self.set1)
#self.set2 = SETLayer(512, 512)
#self.set_layers.append(self.set2)
self.set2 = SETLayer(512, 128)
self.set_layers.append(self.set2)
#Use a dense layer for output because of low output dimensionality
self.fc1 = nn.Linear(128, 10)
def zero_connections(self):
"""Sets connections to zero for inferences."""
for layer in self.set_layers:
layer.zero_connections()
def evolve_connections(self):
"""Evolves connections."""
for layer in self.set_layers:
layer.evolve_connections()
def forward(self, x):
x = x.reshape(-1, 784)
x = F.relu(self.set1(x))
x = F.relu(self.set2(x))
#x = F.relu(self.set3(x))
x = self.fc1(x)
return F.log_softmax(x, dim=1)
def count_params(model):
prms = 0
for parameter in model.parameters():
n_params = 1
for prm in parameter.shape:
n_params *= prm
prms += n_params
return prms
device = "cpu"
sparse_net = SparseNet().to(device)
print('number of params: ', count_params(sparse_net))
```
Consider a fully-connected model with the same architecture: It would contain more than 20 times the number of parameters!<br>
## Training on MNIST
This code was adapted directly from the [pytorch mnist tutorial](https://github.com/pytorch/examples/blob/master/mnist/main.py).
```
class History(object):
"""Tracks and plots training history"""
def __init__(self):
self.train_loss = []
self.val_loss = []
self.train_acc = []
self.val_acc = []
def plot(self):
clear_output()
plt.plot(self.train_loss, label='train loss')
plt.plot(self.train_acc, label='train acc')
plt.plot(self.val_loss, label='val loss')
plt.plot(self.val_acc, label='val acc')
plt.legend()
plt.show()
def train(log_interval, model, device, train_loader, optimizer, epoch, history):
model.train()
correct = 0
loss_ = []
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
loss = F.nll_loss(output, target)
loss.backward()
loss_.append(loss.item())
optimizer.step()
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
history.train_loss.append(np.array(loss_).mean())
history.train_acc.append(correct/len(train_loader.dataset))
return history
def test(model, device, test_loader, history):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
acc = correct / len(test_loader.dataset)
test_loss /= len(test_loader.dataset)
print('Test set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)'.format(
test_loss, correct, len(test_loader.dataset), 100. * acc))
history.val_loss.append(test_loss)
history.val_acc.append(acc)
return history
print("done")
torch.manual_seed(0)
#Optimizer settings
lr = .01
momentum = .5
epochs = 50
batch_size=128
log_interval = 64
test_batch_size=128
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=test_batch_size, shuffle=True)
print("done")
```
## Dealing with Optimizer Buffers
Synapses recycles parameters. When connections are broken and reassigned, its parameter gets set to zero.<br><br>
This system is designed to be computationally efficient, but it comes with a nasty side-effect. Often, we use optimizers with some sort of buffer; the simplest example is momentum in SGD. When we reset a parameter, the information about the overwritten parameter in the optimizer buffer is not useful. We need to overwrite specific values in the buffer also. To do this in pytorch, we need to pass the optimizer to each SETLayer to let synapses do this for us. <br><br>
<b>Notice: I'm still working out the best way to initialize adaptive optimizers (current version makes a naive attempt to pick good values); SGD with momentum works fine</b>
```
optimizer = optim.SGD(sparse_net.parameters(), lr=lr, momentum=momentum, weight_decay=1e-3)
for layer in sparse_net.set_layers:
#here we tell our set layers about
layer.optimizer = optimizer
#This guy will keep track of optimization metrics.
set_history = History()
print("done")
def show_MNIST_connections(model):
vec = model.set1.connections[:, 0]
vec = np.array(vec)
_, counts = np.unique(vec, return_counts=True)
t = counts.reshape(28, 28)
sns.heatmap(t, cmap='viridis', xticklabels=[], yticklabels=[], square=True);
plt.title('Connections per input pixel');
plt.show();
v = [t[13-i:15+i,13-i:15+i].mean() for i in range(14)]
plt.plot(v)
plt.show()
print("done")
import time
epochs = 1000
for epoch in range(1, epochs + 1):
#In the paper, evolutions occur on each epoch
if epoch != 1:
set_history.plot()
show_MNIST_connections(sparse_net)
if epoch != 1:
print('Train set: Average loss: {:.4f}, Accuracy: {:.2f}%'.format(
set_history.train_loss[epoch-2], 100. * set_history.train_acc[epoch-2]))
print('Test set: Average loss: {:.4f}, Accuracy: {:.2f}%'.format(
set_history.val_loss[epoch-2], 100. * set_history.val_acc[epoch-2]))
sparse_net.evolve_connections()
show_MNIST_connections(sparse_net)
set_history = train(log_interval, sparse_net, device, train_loader, optimizer, epoch, set_history)
#And smallest connections are removed during inference.
sparse_net.zero_connections()
set_history = test(sparse_net, device, test_loader, set_history)
time.sleep(10)
```
| true |
code
| 0.786172 | null | null | null | null |
|
# Get your data ready for training
This module defines the basic [`DataBunch`](/basic_data.html#DataBunch) object that is used inside [`Learner`](/basic_train.html#Learner) to train a model. This is the generic class, that can take any kind of fastai [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) or [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader). You'll find helpful functions in the data module of every application to directly create this [`DataBunch`](/basic_data.html#DataBunch) for you.
```
from fastai.gen_doc.nbdoc import *
from fastai import *
show_doc(DataBunch)
```
It also ensure all the dataloaders are on `device` and apply to them `tfms` as batch are drawn (like normalization). `path` is used internally to store temporary files, `collate_fn` is passed to the pytorch `Dataloader` (replacing the one there) to explain how to collate the samples picked for a batch. By default, it applies data to the object sent (see in [`vision.image`](/vision.image.html#vision.image) or the [data block API](/data_block.html) why this can be important).
`train_dl`, `valid_dl` and optionally `test_dl` will be wrapped in [`DeviceDataLoader`](/basic_data.html#DeviceDataLoader).
### Factory method
```
show_doc(DataBunch.create)
```
`num_workers` is the number of CPUs to use, `tfms`, `device` and `collate_fn` are passed to the init method.
### Visualization
```
show_doc(DataBunch.show_batch)
```
### Grabbing some data
```
show_doc(DataBunch.dl)
show_doc(DataBunch.one_batch)
show_doc(DataBunch.one_item)
```
### Empty [`DataBunch`](/basic_data.html#DataBunch) for inference
```
show_doc(DataBunch.export)
show_doc(DataBunch.load_empty, full_name='load_empty')
```
This method should be used to create a [`DataBunch`](/basic_data.html#DataBunch) at inference, see the corresponding [tutorial](/tutorial.inference.html).
### Dataloader transforms
```
show_doc(DataBunch.add_tfm)
```
Adds a transform to all dataloaders.
```
show_doc(DeviceDataLoader)
```
Put the batches of `dl` on `device` after applying an optional list of `tfms`. `collate_fn` will replace the one of `dl`. All dataloaders of a [`DataBunch`](/basic_data.html#DataBunch) are of this type.
### Factory method
```
show_doc(DeviceDataLoader.create)
```
The given `collate_fn` will be used to put the samples together in one batch (by default it grabs their data attribute). `shuffle` means the dataloader will take the samples randomly if that flag is set to `True`, or in the right order otherwise. `tfms` are passed to the init method. All `kwargs` are passed to the pytorch [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader) class initialization.
### Methods
```
show_doc(DeviceDataLoader.add_tfm)
show_doc(DeviceDataLoader.remove_tfm)
show_doc(DeviceDataLoader.new)
show_doc(DatasetType, doc_string=False)
```
Internal enumerator to name the training, validation and test dataset/dataloader.
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(DeviceDataLoader.proc_batch)
show_doc(DeviceDataLoader.collate_fn)
```
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.770335 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/graviraja/100-Days-of-NLP/blob/applications%2Fclustering/applications/clustering/20newsgroup/Improved%20Topic%20Identification%20in%20News%20using%20LDA.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### Installations
```
!pip install pyldavis -q
import nltk
nltk.download('stopwords')
```
### Imports
```
import re
import spacy
import numpy as np
import pandas as pd
from nltk.corpus import stopwords
from sklearn.decomposition import LatentDirichletAllocation
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import GridSearchCV
import gensim
import gensim.corpora as corpora
from gensim.utils import simple_preprocess
from gensim.models import CoherenceModel
import scipy.sparse
from pprint import pprint
import pyLDAvis
import pyLDAvis.gensim
import pyLDAvis.sklearn
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import seaborn as sns
from wordcloud import WordCloud, STOPWORDS
import warnings
warnings.filterwarnings("ignore",category=DeprecationWarning)
np.random.seed(42)
stop_words = stopwords.words('english')
stop_words.extend(['from', 'subject', 're', 'edu', 'use'])
nlp = spacy.load('en', disable=['parser', 'ner'])
```
### 20 Newsgroup Dataset
```
df = pd.read_json('https://raw.githubusercontent.com/selva86/datasets/master/newsgroups.json')
df.head()
df.target_names.unique()
len(df)
plt.figure(figsize=(20, 5))
sns.countplot(df.target_names.values)
data = df.content.values
```
### Tokenization
```
def sentence_to_tokens(sent):
# remove emails
sent = re.sub(r'\S*@\S*\s?', '', sent)
# remove newline chars
sent = re.sub(r'\s+', ' ', sent)
# remove single quotes
sent = re.sub(r"\'", "", sent)
# converts to lower case tokens and removes tokens that are
# too small & too long. Also remove accent characters & punct
tokens = simple_preprocess(str(sent), deacc=True)
return tokens
%%time
tokenized_data = [sentence_to_tokens(doc) for doc in data]
tokenized_data[0]
```
### Pre-processing
```
%%time
# create bigrams from the tokenized data
bigram = gensim.models.Phrases(tokenized_data, threshold=50)
# make a bigram model
bigram_mod = gensim.models.phrases.Phraser(bigram)
def process_words(texts, allowed_postags=["NOUN", "ADJ", "VERB", "ADV"]):
# remove stopwords
stop_free = [[word for word in doc if word not in stop_words] for doc in texts]
# bigrams
bigram_data = [bigram_mod[doc] for doc in stop_free]
texts_out = []
for sent in bigram_data:
doc = nlp(" ".join(sent))
texts_out.append([token.lemma_ for token in doc if token.pos_ in allowed_postags])
# remove stopwords
texts_out = [[word for word in simple_preprocess(str(doc)) if word not in stop_words] for doc in texts_out]
# join words into sentence in-order to make it useful to tfidf processing
texts_out = [" ".join(words) for words in texts_out]
return texts_out
%%time
processed_data = process_words(tokenized_data)
processed_data[0]
```
### Tfidf
```
tfidf = TfidfVectorizer(analyzer='word', min_df=10, stop_words='english', lowercase=True, token_pattern='[a-zA-Z0-9]{3,}')
data_vectorized = tfidf.fit_transform(processed_data)
```
### LDA Model
```
%%time
lda_model = LatentDirichletAllocation(
n_components=20,
max_iter=10,
n_jobs=-1,
random_state=42
)
lda_output = lda_model.fit_transform(data_vectorized)
# higher the better
print(f"Log Likelihood: {lda_model.score(data_vectorized)}")
# lower the better
print(f"preplexity: {lda_model.perplexity(data_vectorized)}")
```
### Grid Search
```
search_params = {
"n_components": [10, 15, 20, 25],
"learning_decay": [.5, .7, .9]
}
%%time
lda = LatentDirichletAllocation()
model = GridSearchCV(lda, param_grid=search_params)
model.fit(data_vectorized)
```
### Best LDA Model
```
best_lda_model = model.best_estimator_
print(f"Best Log likelihood Score: {model.best_score_}")
print(f"Best Perplexity: {best_lda_model.perplexity(data_vectorized)}")
model.best_params_
```
### Visualization of Topics
```
# Visualize the topics
pyLDAvis.enable_notebook()
vis = pyLDAvis.sklearn.prepare(best_lda_model, data_vectorized, tfidf, mds='tsne')
vis
```
### Topic's keyword distribution
```
topicnames = ["Topic" + str(i) for i in range(best_lda_model.n_components)]
# topic keyword matrix
df_topic_keywords = pd.DataFrame(best_lda_model.components_)
# columns are the words
df_topic_keywords.columns = tfidf.get_feature_names()
# rows are the topics
df_topic_keywords.index = topicnames
df_topic_keywords.head()
```
### Top 15 keywords in each topic
```
def top_words(vectorizer=tfidf, lda_model=lda_model, n_words=15):
keywords = np.array(vectorizer.get_feature_names())
topic_keywords = []
for topic_weights in lda_model.components_:
top_keyword_locs = (-topic_weights).argsort()[:n_words]
topic_keywords.append(keywords.take(top_keyword_locs))
return topic_keywords
topic_keywords = top_words(vectorizer=tfidf, lda_model=best_lda_model, n_words=15)
# Topic - Keywords Dataframe
df_topic_top_keywords = pd.DataFrame(topic_keywords)
df_topic_top_keywords.columns = ['Word '+str(i) for i in range(df_topic_top_keywords.shape[1])]
df_topic_top_keywords.index = ['Topic '+str(i) for i in range(df_topic_top_keywords.shape[0])]
df_topic_top_keywords
```
### Predicting topic of a sentence
```
best_lda_model
def predict_topic(text):
tokens = [sentence_to_tokens(text)]
processed_tokens = process_words(tokens)
tfidf_tokens = tfidf.transform(processed_tokens)
topic_scores = best_lda_model.transform(tfidf_tokens)
topic = np.argmax(topic_scores)
topic_score = topic_scores[0][topic]
topic_keywords = df_topic_top_keywords.iloc[topic, :].values.tolist()
return topic, topic_score, topic_keywords
# Predict the topic
mytext = "I believe in christianity and like the bible"
topic, prob_scores, words = predict_topic(text = mytext)
print(topic)
print(prob_scores)
print(words)
```
| true |
code
| 0.532243 | null | null | null | null |
|
# 2-Semi-Random-Independent-Set
```
import os, sys
module_path = os.path.abspath(os.path.join('../..'))
if module_path not in sys.path:
sys.path.append(module_path)
import time
import numpy as np
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt
import cvxgraphalgs as cvxgr
GRAPH_COLOR = 'green'
HIGHLIGHT_COLOR = 'red'
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
```
## 2.1 Visualization & Analysis Tools
```
def visualize_highlight(graph, special):
colors = []
for vertex in graph.nodes:
color = HIGHLIGHT_COLOR if vertex in special else GRAPH_COLOR
colors.append(color)
%matplotlib inline
nx.draw(graph, node_color=colors)
plt.show()
def average_performance(graph_generator, algorithm, evaluate, trials=50):
times, outputs = [], []
for _ in range(trials):
graph = graph_generator()
start = time.clock()
result = algorithm(graph)
end = time.clock()
elapsed = end - start
times.append(elapsed)
outputs.append(evaluate(result))
return {
'trials': trials,
'time': np.mean(times),
'output': np.mean(outputs)
}
```
## 2.2 Examples on Small Planted Sets
```
GRAPH_SIZE = 20
PLANTED_SIZE = 7
PROB = 0.5
graph, independent = cvxgr.generators.bernoulli_planted_independent(
GRAPH_SIZE, PLANTED_SIZE, PROB)
visualize_highlight(graph, independent)
print('Planted Size:', len(independent))
```
### 2.2.1 Greedy Algorithm
```
result = cvxgr.algorithms.greedy_independent_set(graph)
visualize_highlight(graph, result)
print('Recovered Size (Greedy):', len(result))
```
### 2.2.2 Crude SDP Algorithm
```
result = cvxgr.algorithms.crude_sdp_independent_set(graph)
visualize_highlight(graph, result)
print('Recovered Size (C-SDP):', len(result))
```
## 2.3 Performance Testing
```
GRAPH_SIZES = [5, 10, 25, 50, 100]
PLANTED_SIZES = [int(size / 3) for size in GRAPH_SIZES]
PROB = 0.5
TRIALS = 50
greedy_outputs = []
csdp_outputs = []
spectral_outputs = []
for graph_size, planted_size in zip(GRAPH_SIZES, PLANTED_SIZES):
graph_generator = lambda: cvxgr.generators.bernoulli_planted_independent(
graph_size, planted_size, PROB)[0]
greedy_output = average_performance(
graph_generator,
cvxgr.algorithms.greedy_independent_set,
len,
trials=TRIALS)
greedy_outputs.append(greedy_output)
csdp_output = average_performance(
graph_generator,
cvxgr.algorithms.crude_sdp_independent_set,
len,
trials=TRIALS)
csdp_outputs.append(csdp_output)
spectral_output = average_performance(
graph_generator,
cvxgr.algorithms.planted_spectral_algorithm,
len,
trials=TRIALS)
spectral_outputs.append(spectral_output)
PLOTTING_OPTIONS = {
'title': 'Independent Set Size vs Graph Size',
'legend': [
'Greedy Algorithm Output Size',
'C-SDP Algorithm Output Size',
'Spectral Algorithm Output Size',
'Planted Set Size'
]
}
plt.plot(GRAPH_SIZES, [result['output'] for result in greedy_outputs])
plt.plot(GRAPH_SIZES, [result['output'] for result in csdp_outputs])
plt.plot(GRAPH_SIZES, [result['output'] for result in spectral_outputs])
plt.plot(GRAPH_SIZES, PLANTED_SIZES)
plt.title(PLOTTING_OPTIONS['title'])
plt.legend(PLOTTING_OPTIONS['legend'])
plt.show()
rows = []
for pos in range(len(GRAPH_SIZES)):
rows.append([
GRAPH_SIZES[pos],
greedy_outputs[pos]['output'],
csdp_outputs[pos]['output'],
spectral_outputs[pos]['output'],
PLANTED_SIZES[pos]
])
table = pd.DataFrame(rows)
table.columns = [
'Graph Size',
'Greedy Output Size',
'C-SDP Output Size',
'Spectral Output Size',
'Planted Size']
table
```
| true |
code
| 0.474753 | null | null | null | null |
|
### Trains a simple convnet on the MNIST dataset.
Gets to 99.25% test accuracy after 12 epochs
(there is still a lot of margin for parameter tuning).
16 seconds per epoch on a GRID K520 GPU.
Adapted from [Keras examples directory](https://github.com/fchollet/keras/tree/master/examples).
```
from __future__ import print_function
import numpy as np
np.random.seed(1337) # for reproducibility
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Convolution2D, MaxPooling2D
from keras.utils import np_utils
from keras import backend as K
batch_size = 128
nb_classes = 10
nb_epoch = 12
# input image dimensions
img_rows, img_cols = 28, 28
# number of convolutional filters to use
nb_filters = 32
# size of pooling area for max pooling
pool_size = (2, 2)
# convolution kernel size
kernel_size = (3, 3)
# the data, shuffled and split between train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
if K.image_dim_ordering() == 'th':
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print('X_train shape:', X_train.shape)
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
Y_train = np_utils.to_categorical(y_train, nb_classes)
Y_test = np_utils.to_categorical(y_test, nb_classes)
model = Sequential()
model.add(Convolution2D(nb_filters, kernel_size[0], kernel_size[1],
border_mode='valid',
input_shape=input_shape))
model.add(Activation('relu'))
model.add(Convolution2D(nb_filters, kernel_size[0], kernel_size[1]))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=pool_size))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(nb_classes))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy',
optimizer='adadelta',
metrics=['accuracy'])
model.fit(X_train, Y_train, batch_size=batch_size, nb_epoch=nb_epoch,
verbose=1, validation_data=(X_test, Y_test))
score = model.evaluate(X_test, Y_test, verbose=0)
print('Test score:', score[0])
print('Test accuracy:', score[1])
```
| true |
code
| 0.780035 | null | null | null | null |
|
# Maximizing the ELBO
> In this post, we will cover the complete implementation of Variational AutoEncoder, which can optimize the ELBO objective function. This is the summary of lecture "Probabilistic Deep Learning with Tensorflow 2" from Imperial College London.
- toc: true
- badges: true
- comments: true
- author: Chanseok Kang
- categories: [Python, Coursera, Tensorflow_probability, ICL]
- image: images/fashion_mnist_generated.png
## Packages
```
import tensorflow as tf
import tensorflow_probability as tfp
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from IPython.display import HTML, Image
tfd = tfp.distributions
tfpl = tfp.layers
tfb = tfp.bijectors
plt.rcParams['figure.figsize'] = (10, 6)
plt.rcParams["animation.html"] = "jshtml"
plt.rcParams['animation.embed_limit'] = 2**128
print("Tensorflow Version: ", tf.__version__)
print("Tensorflow Probability Version: ", tfp.__version__)
```
## Overview
### Prior Distribution
$ \text{latent variable } z \sim N(0, I) = p(z) \\
p(x \vert z) = \text{decoder}(z) \\
x \sim p(x \vert z) $
### Approximating True Posterior distribution
$ \text{encoder }(x) = q(z \vert x) \simeq p(z \vert x) \\
\begin{aligned} \log p(x) & \ge \mathbb{E}_{z \sim q(z \vert x)}[-\log q(z \vert x) + \log p(x \vert z)] \quad \leftarrow \text{maximizing this lower bound} \\
&= - \mathrm{KL} (q(z \vert x) \vert \vert p(z)) + \mathbb{E}_{z \sim q(z \vert x)}[\log p(x \vert z)] \quad \leftarrow \text{Evidence Lower Bound (ELBO)} \end{aligned}$
### Sample Encoder Architecture
```python
latent_size = 2
event_shape = (28, 28, 1)
encoder = Sequential([
Conv2D(8, (5, 5), strides=2, activation='tanh', input_shape=event_shape),
Conv2D(8, (5, 5), strides=2, activatoin='tanh'),
Flatten(),
Dense(64, activation='tanh'),
Dense(2 * latent_size),
tfpl.DistributionLambda(lambda t: tfd.MultivariateNormalDiag(
loc=t[..., :latent_size], scale_diag=tf.math.exp(t[..., latent_size:]))),
], name='encoder')
encoder(X_train[:16])
```
### Sample Decoder Architecture
Almose reverse order of Encoder.
```python
decoder = Sequential([
Dense(64, activation='tanh', input_shape=(latent_size, )),
Dense(128, activation='tanh'),
Reshape((4, 4, 8)), # In order to put it in the form required by Conv2D layer
Conv2DTranspose(8, (5, 5), strides=2, output_padding=1, activation='tanh'),
Conv2DTranspose(8, (5, 5), strides=2, output_padding=1, activation='tanh'),
Conv2D(1, (3, 3), padding='SAME'),
Flatten(),
tfpl.IndependentBernoulli(event_shape)
], name='decoder')
decoder(tf.random.normal([16, latent_size])
```
### Prior Distribution for zero-mean gaussian with identity covariance matrix
```python
prior = tfd.MultivariateNormalDiag(loc=tf.zeros(latent_size))
```
### ELBO objective function
One way to implement ELBO function is to use Analytical computation of KL divergence.
```python
def loss_fn(X_true, approx_posterior, X_pred, prior_dist):
"""
X_true: batch of data examples
approx_posterior: the output of encoder
X_pred: output of decoder
prior_dist: Prior distribution
"""
return tf.reduce_mean(tfd.kl_divergence(approx_posterior, prior_dist) - X_pred.log_prob(X_true))
```
The other way is using Monte Carlo Sampling instead of analyticall with the KL Divergence.
```python
def loss_fn(X_true, approx_posterior, X_pred, prior_dist):
reconstruction_loss = -X_pred.log_prob(X_true)
approx_posterior_sample = approx_posterior.sample()
kl_approx = (approx_posterior.log_prob(approx_posterior_sample) - prior_dist.log_prob(approx_posterior_sample))
return tf.reduce_mean(kl_approx + reconstruction_loss)
```
### Calculating Gradient of Loss function
```python
@tf.function
def get_loss_and_grads(x):
with tf.GradientTape() as tape:
approx_posterior = encoder(x)
approx_posterior_sample = approx_posterior.sample()
X_pred = decoder(approx_posterior_sample)
current_loss = loss_fn(x, approx_posterior, X_pred, prior)
grads = tape.gradient(current_loss, encoder.trainable_variables + decoder.trainable_variables)
return current_loss, grads
```
### Training Loop
```python
optimizer = tf.keras.optimizers.Adam()
for epoch in range(num_epochs):
for train_batch in train_data:
loss, grads = get_loss_and_grads(train_batch)
optimizer.apply_gradients(zip(grads, encoder.trainable_variables + decoder.trainable_variables))
```
### Test
```python
z = prior.sample(1) # (1, 2)
x = decoder(z).sample() # (1, 28, 28, 1)
X_encoded = encoder(X_sample)
def vae(inputs):
approx_posterior = encoder(inputs)
decoded = decoder(approx_posterior.sample())
return decoded.sample()
reconstruction = vae(X_sample)
```
## Tutorial
Review of terminology:
- $p(z)$ = prior
- $q(z|x)$ = encoding distribution
- $p(x|z)$ = decoding distribution
$$
\begin{aligned}
\log p(x) &\geq \mathrm{E}_{Z \sim q(z | x)}\big[−\log q(Z | x) + \log p(x, Z)\big]\\
&= - \mathrm{KL}\big[ \ q(z | x) \ || \ p(z) \ \big] + \mathrm{E}_{Z \sim q(z | x)}\big[\log p(x | Z)\big]
\end{aligned}
$$
```
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Dense, Flatten, Reshape
# Import Fashion MNIST, make it a Tensorflow Dataset
(X_train, _), (X_test, _) = tf.keras.datasets.fashion_mnist.load_data()
X_train = X_train.astype('float32') / 255.
X_test = X_test.astype('float32') / 255.
example_X = X_test[:16]
batch_size = 64
X_train = tf.data.Dataset.from_tensor_slices(X_train).batch(batch_size)
# Define the encoding distribution, q(z | x)
latent_size = 2
event_shape = (28, 28)
encoder = Sequential([
Flatten(input_shape=event_shape),
Dense(256, activation='relu'),
Dense(128, activation='relu'),
Dense(64, activation='relu'),
Dense(32, activation='relu'),
Dense(2 * latent_size),
tfpl.DistributionLambda(
lambda t: tfd.MultivariateNormalDiag(
loc=t[..., :latent_size],
scale_diag=tf.math.exp(t[..., latent_size:])
)
)
])
# Pass an example image through the network - should return a batch of MultivariateNormalDiag
encoder(example_X)
# Define the decoding distribution, p(x | z)
decoder = Sequential([
Dense(32, activation='relu'),
Dense(64, activation='relu'),
Dense(128, activation='relu'),
Dense(256, activation='relu'),
Dense(tfpl.IndependentBernoulli.params_size(event_shape)),
tfpl.IndependentBernoulli(event_shape)
])
# Pass a batch of examples to the decoder
decoder(tf.random.normal([16, latent_size]))
# Define the prior, p(z) - a standard bivariate Gaussian
prior = tfd.MultivariateNormalDiag(loc=tf.zeros(latent_size))
```
The loss function we need to estimate is
$$
-\mathrm{ELBO} = \mathrm{KL}[ \ q(z|x) \ || \ p(z) \ ] - \mathrm{E}_{Z \sim q(z|x)}[\log p(x|Z)]\\
$$
where $x = (x_1, x_2, \ldots, x_n)$ refers to all observations, $z = (z_1, z_2, \ldots, z_n)$ refers to corresponding latent variables.
Assumed independence of examples implies that we can write this as
$$
\sum_j \mathrm{KL}[ \ q(z_j|x_j) \ || \ p(z_j) \ ] - \mathrm{E}_{Z_j \sim q(z_j|x_j)}[\log p(x_j|Z_j)]
$$
```
# Specify the loss function, an estimate of the -ELBO
def loss(x, encoding_dist, sampled_decoding_dist, prior):
return tf.reduce_sum(
tfd.kl_divergence(encoding_dist, prior) - sampled_decoding_dist.log_prob(x)
)
# Define a function that returns the loss and its gradients
@tf.function
def get_loss_and_grads(x):
with tf.GradientTape() as tape:
encoding_dist = encoder(x)
sampled_z = encoding_dist.sample()
sampled_decoding_dist = decoder(sampled_z)
current_loss = loss(x, encoding_dist, sampled_decoding_dist, prior)
grads = tape.gradient(current_loss, encoder.trainable_variables + decoder.trainable_variables)
return current_loss, grads
# Compile and train the model
num_epochs = 10
optimizer = tf.keras.optimizers.Adam()
for i in range(num_epochs):
for train_batch in X_train:
current_loss, grads = get_loss_and_grads(train_batch)
optimizer.apply_gradients(zip(grads, encoder.trainable_variables + decoder.trainable_variables))
print('-ELBO after epoch {}: {:.0f}'.format(i + 1, current_loss.numpy()))
# Connect encoder and decoder, compute a reconstruction
def vae(inputs):
approx_posterior = encoder(inputs)
decoding_dist = decoder(approx_posterior.sample())
return decoding_dist.sample()
example_reconstruction = vae(example_X).numpy().squeeze()
# Plot examples against reconstructions
f, axs = plt.subplots(2, 6, figsize=(16, 5))
for j in range(6):
axs[0, j].imshow(example_X[j, :, :].squeeze(), cmap='binary')
axs[1, j].imshow(example_reconstruction[j, :, :], cmap='binary')
axs[0, j].axis('off')
axs[1, j].axis('off')
```
Since the model has lack of reconstruction from grayscale image, So using mean for reconstruction gets more satisfied results.
```
# Connect encoder and decoder, compute a reconstruction with mean
def vae_mean(inputs):
approx_posterior = encoder(inputs)
decoding_dist = decoder(approx_posterior.sample())
return decoding_dist.mean()
example_reconstruction = vae_mean(example_X).numpy().squeeze()
# Plot examples against reconstructions
f, axs = plt.subplots(2, 6, figsize=(16, 5))
for j in range(6):
axs[0, j].imshow(example_X[j, :, :].squeeze(), cmap='binary')
axs[1, j].imshow(example_reconstruction[j, :, :], cmap='binary')
axs[0, j].axis('off')
axs[1, j].axis('off')
# Generate an example - sample a z value, then sample a reconstruction from p(x|z)
z = prior.sample(6)
generated_x = decoder(z).sample()
# Display generated_x
f, axs = plt.subplots(1, 6, figsize=(16, 5))
for j in range(6):
axs[j].imshow(generated_x[j, :, :].numpy().squeeze(), cmap='binary')
axs[j].axis('off')
# Generate an example - sample a z value, then sample a reconstruction from p(x|z)
z = prior.sample(6)
generated_x = decoder(z).mean()
# Display generated_x
f, axs = plt.subplots(1, 6, figsize=(16, 5))
for j in range(6):
axs[j].imshow(generated_x[j, :, :].numpy().squeeze(), cmap='binary')
axs[j].axis('off')
```
What if we use Monte Carlo Sampling for kl divergence?
```
encoder = Sequential([
Flatten(input_shape=event_shape),
Dense(256, activation='relu'),
Dense(128, activation='relu'),
Dense(64, activation='relu'),
Dense(32, activation='relu'),
Dense(2 * latent_size),
tfpl.DistributionLambda(
lambda t: tfd.MultivariateNormalDiag(
loc=t[..., :latent_size],
scale_diag=tf.math.exp(t[..., latent_size:])
)
)
])
decoder = Sequential([
Dense(32, activation='relu'),
Dense(64, activation='relu'),
Dense(128, activation='relu'),
Dense(256, activation='relu'),
Dense(tfpl.IndependentBernoulli.params_size(event_shape)),
tfpl.IndependentBernoulli(event_shape)
])
# Define the prior, p(z) - a standard bivariate Gaussian
prior = tfd.MultivariateNormalDiag(loc=tf.zeros(latent_size))
def loss(x, encoding_dist, sampled_decoding_dist, prior, sampled_z):
reconstruction_loss = -sampled_decoding_dist.log_prob(x)
kl_approx = (encoding_dist.log_prob(sampled_z) - prior.log_prob(sampled_z))
return tf.reduce_sum(kl_approx + reconstruction_loss)
@tf.function
def get_loss_and_grads(x):
with tf.GradientTape() as tape:
encoding_dist = encoder(x)
sampled_z = encoding_dist.sample()
sampled_decoding_dist = decoder(sampled_z)
current_loss = loss(x, encoding_dist, sampled_decoding_dist, prior, sampled_z)
grads = tape.gradient(current_loss, encoder.trainable_variables + decoder.trainable_variables)
return current_loss, grads
# Compile and train the model
num_epochs = 10
optimizer = tf.keras.optimizers.Adam()
for i in range(num_epochs):
for train_batch in X_train:
current_loss, grads = get_loss_and_grads(train_batch)
optimizer.apply_gradients(zip(grads, encoder.trainable_variables + decoder.trainable_variables))
print('-ELBO after epoch {}: {:.0f}'.format(i + 1, current_loss.numpy()))
# Connect encoder and decoder, compute a reconstruction with mean
def vae_mean(inputs):
approx_posterior = encoder(inputs)
decoding_dist = decoder(approx_posterior.sample())
return decoding_dist.mean()
example_reconstruction = vae_mean(example_X).numpy().squeeze()
# Plot examples against reconstructions
f, axs = plt.subplots(2, 6, figsize=(16, 5))
for j in range(6):
axs[0, j].imshow(example_X[j, :, :].squeeze(), cmap='binary')
axs[1, j].imshow(example_reconstruction[j, :, :], cmap='binary')
axs[0, j].axis('off')
axs[1, j].axis('off')
# Generate an example - sample a z value, then sample a reconstruction from p(x|z)
z = prior.sample(6)
generated_x = decoder(z).mean()
# Display generated_x
f, axs = plt.subplots(1, 6, figsize=(16, 5))
for j in range(6):
axs[j].imshow(generated_x[j, :, :].numpy().squeeze(), cmap='binary')
axs[j].axis('off')
```
| true |
code
| 0.78574 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import arviz as az
from statsmodels.tsa import stattools
import statsmodels.api as sm
import pymc3 as pm
import pymc
import sys
sys.path.insert(0, '..')
from utils.plot_lib import set_default
set_default(figsize=(6, 4))
```
### Bayesian EM for Mixture of two gaussians
Implementation of the markup chain Monte Carlo algorithm for
fitting a location mixture of two univariate Gaussian distributions.
```
### Example of an EM algorithm for fitting a location mixture of 2 Gaussian components
### The algorithm is tested using simulated data
from scipy.stats import norm
## Clear the environment and load required libraries
np.random.seed(1)
## Generate data from a mixture with 2 components
KK = 2 # Number of componentes
w_true = [0.6, 0.4] # True weights associated with the components
mu_true = [0, 5] # True mean for the first and secondcomponent
sigma_true = [1, 1] # True standard deviation of all components
n = 120 # Number of observations to be generated
### Step 1 ### Sample component indicators
cc_true = np.random.choice([0, 1], n, p = w_true) # C_i sample
x = []
### Step 2 ### Sample from normal distribution
for i in range(n):
x.append(norm.rvs(loc = mu_true[cc_true[i]], scale = sigma_true[cc_true[i]], size = 1)[0])
x = np.array(x)
print('The first five samples of C_i are: {}'.format(cc_true[:5]))
print('The first five samples of the mixture are: {}'.format(x[:5]))
### Plotting the true distributions
# Plot f(x) along with the observations just sampled
# Values to sample
xx_true = np.linspace(-8, 11.0, num = 200)
yy_true = w_true[0] * norm.pdf(loc = mu_true[0], scale = sigma_true[0], x = xx_true) + w_true[1] * norm.pdf(loc = mu_true[1], scale = sigma_true[1], x = xx_true)
# Plotting the mixture models
fig, ax = plt.subplots(1, 1)
sns.lineplot(xx_true, yy_true)
sns.scatterplot(np.array(x), np.zeros(len(x)), hue = cc_true)
plt.xlabel('xx')
plt.ylabel('Density')
plt.legend(['Density', 'Points sampled 1'])
plt.show()
# Density estimation of X
fig, ax = plt.subplots(1, 1)
sns.histplot(x, stat= 'density', bins = 18)
sns.kdeplot(x, bw_adjust = 1.0, label = 'Density estimate $x$')
plt.title('Histogram of $x$')
plt.show()
```
### Initial guess of data
```
## Initialize the parameters
w = 0.5 # Assign equal weight to each component to start with
mu = norm.rvs(loc = np.mean(x), scale = np.std(x), size = KK, random_state = 1) # Random cluster centers randomly spread over the support of the data
sigma = np.std(x) # Initial standard deviation
print('The initial guess for mu are: {}'.format(mu))
print('The initial guess for sigma are: {}'.format(sigma))
# Values to sample
xx = np.linspace(-8, 11.0, num = 200)
yy = w * norm.pdf(loc = mu[0], scale = sigma, x = xx) + w * norm.pdf(loc = mu[1], scale = sigma, x = xx)
# Plot the initial guess for the density
fig, ax = plt.subplots(1, 1)
sns.lineplot(xx, yy)
sns.scatterplot(np.array(x), np.zeros(len(x)), hue = cc_true)
plt.xlabel('xx')
plt.ylabel('Density')
plt.legend(['Density guess'])
plt.show()
```
### Initializing priors
```
## The actual MCMC algorithm starts here
# Priors
aa = np.ones(KK) # Uniform prior on w
eta = 0 # Mean 0 for the prior on mu_k
tau = 5 # Standard deviation 5 on the prior for mu_l
dd = 2 # Inverse gamma prior for sigma_2, parameter d
qq = 1 # Inverse gamma prior for sigma_2, parameter q
from scipy.stats import beta
from scipy.stats import invgamma
from scipy.stats import beta
# Number of iterations of the sampler
rrr = 6000 # Number of iterations
burn = 1000 # Burning period
# Storing the samples
cc_out = np.zeros((rrr, n)) # Store indicators
w_out = np.zeros(rrr) # Sample of the weights
mu_out = np.zeros((rrr, KK)) # Sample of mus
sigma_out = np.zeros(rrr) # Sample of sigmas
logpost = np.zeros(rrr) # Used to monitor convergence
for s in range(rrr):
# Sample the indicators
cc = np.zeros(n)
for i in range(n):
v = np.zeros(KK)
v[0] = np.log(w) + norm.logpdf(loc = mu[0], scale = sigma, x = x[i]) # Compute the log of the weights
v[1] = np.log(1 - w) + norm.logpdf(loc = mu[1], scale = sigma, x = x[i]) # Compute the log of the weights
v = np.exp(v - max(v)) / np.sum(np.exp(v - max(v))) # Go from logs to actual weights in a numerically stable manner
cc[i] = np.random.choice([0, 1], 1, p = v) # C_i sample
# Sample the weights
w = beta.rvs(a = aa[0] + np.sum(cc == 0), b = aa[1] + np.sum(cc == 1), size = 1)
# Sample the means
for k in range(KK):
nk = np.sum(cc == k)
xsumk = np.sum(x[cc == k])
tau2_hat = 1 / (nk / sigma**2 + 1 / tau**2)
mu_hat = tau2_hat * (xsumk / sigma**2 + eta / tau**2)
mu[k] = norm.rvs(loc = mu_hat, scale = np.sqrt(tau2_hat), size = 1)
# Sample the variances
dd_star = dd + n / 2
mu_temp = [mu[int(c_i)] for c_i in cc] # Create vector of mus
qq_star = qq + np.sum((x - mu_temp)**2) / 2
sigma = np.sqrt(invgamma.rvs(a = dd_star, scale = qq_star, size = 1))
# Store samples
cc_out[s, :] = cc
w_out[s] = w
mu_out[s, :] = mu
sigma_out[s] = sigma
for i in range(n):
# Computing logposterior likelihood term
if cc[i] == 0:
logpost[s] = logpost[s] + np.log(w) + norm.logpdf(loc = mu[0], scale = sigma, x = x[i])
else:
logpost[s] = logpost[s] + np.log(1 - w) + norm.logpdf(loc = mu[1], scale = sigma, x = x[i])
# W term
logpost[s] = logpost[s] + beta.logpdf(a = aa[0], b = aa[1], x = w)
# Mu term
for k in range(KK):
logpost[s] = logpost[s] + norm.logpdf(loc = eta, scale = tau, x = mu[k])
# Sigma term
logpost[s] = logpost[s] + invgamma.logpdf(a = dd, scale = 1 / qq, x = sigma**2)
if s / 500 == np.floor(s / 500):
print('Current iteration is: {}'.format(s))
## Plot the logposterior distribution for various samples
fig, ax = plt.subplots(1, 1)
ax.plot(np.arange(len(logpost)), logpost, 'r-', lw=1, alpha=0.6, label='Trace plot') # Trace plot of data
ax.legend(loc='best', frameon=False)
# plot density estimate of the posterior
plt.title('Trace plot of Logposterior')
plt.show()
print('The final Mu_hat values are: {}'.format(mu))
print('The true mu values are: {}\n'.format(mu_true))
print('The final sigma_hat values are: {}'.format(sigma))
print('The true sigma values are: {}\n'.format(sigma_true))
print('The final w_hat values are: {}'.format(w))
print('The true w values are: {}\n'.format(w_true))
print('The final c_hat values are: {}'.format(cc[:10]))
print('The true c values are: {}\n'.format(cc_true[:10]))
# Values to sample
xx = np.linspace(-8, 11.0, num = 200)
density_posterior = np.zeros((rrr-burn, len(xx)))
for s in range(rrr-burn):
density_posterior[s, :] = density_posterior[s, :] + \
w_out[s + burn] * norm.pdf(loc = mu_out[s + burn, 0], scale = sigma_out[s + burn], x = xx) + \
(1 - w_out[s + burn]) * norm.pdf(loc = mu_out[s + burn, 1], scale = sigma_out[s + burn], x = xx)
density_posterior_m = np.mean(density_posterior, axis = 0)
density_posterior_lq = np.quantile(density_posterior, 0.025, axis = 0)
density_posterior_uq = np.quantile(density_posterior, 0.975, axis = 0)
## Plot the final result distribution for various samples
fig, ax = plt.subplots(1, 1)
# Mean value
ax.plot(xx, density_posterior_m, lw=2, alpha=0.6, label='Mean value') # Trace plot of data
# Plotting original data
for k in range(KK):
ax.scatter(np.array(x[cc_true == k]), np.zeros((x[cc_true == k].shape[0])), label = 'Component {}'.format(k + 1))
# Plotting uncertainty
plt.fill_between(xx, density_posterior_uq, density_posterior_lq, alpha=0.2,
label='Uncertainty Interval')
ax.legend(loc='best', frameon=False)
# plot density estimate of the posterior
plt.title('Trace plot of Logposterior')
plt.show()
```
| true |
code
| 0.602997 | null | null | null | null |
|
# Topic Modeling: Financial News
This notebook contains an example of LDA applied to financial news articles.
## Imports & Settings
```
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
from collections import Counter
from pathlib import Path
import logging
import numpy as np
import pandas as pd
# Visualization
import matplotlib.pyplot as plt
import seaborn as sns
# spacy for language processing
import spacy
# sklearn for feature extraction
from sklearn.feature_extraction.text import TfidfVectorizer
# gensim for topic models
from gensim.models import LdaModel
from gensim.corpora import Dictionary
from gensim.matutils import Sparse2Corpus
# topic model viz
import pyLDAvis
from pyLDAvis.gensim import prepare
sns.set_style('white')
pyLDAvis.enable_notebook()
stop_words = set(pd.read_csv('http://ir.dcs.gla.ac.uk/resources/linguistic_utils/stop_words',
header=None,
squeeze=True).tolist())
```
## Helper Viz Functions
```
def show_word_list(model, corpus, top=10, save=False):
top_topics = model.top_topics(corpus=corpus, coherence='u_mass', topn=20)
words, probs = [], []
for top_topic, _ in top_topics:
words.append([t[1] for t in top_topic[:top]])
probs.append([t[0] for t in top_topic[:top]])
fig, ax = plt.subplots(figsize=(model.num_topics*1.2, 5))
sns.heatmap(pd.DataFrame(probs).T,
annot=pd.DataFrame(words).T,
fmt='',
ax=ax,
cmap='Blues',
cbar=False)
fig.tight_layout()
if save:
fig.savefig(f'fin_news_wordlist_{top}', dpi=300)
def show_coherence(model, corpus, tokens, top=10, cutoff=0.01):
top_topics = model.top_topics(corpus=corpus, coherence='u_mass', topn=20)
word_lists = pd.DataFrame(model.get_topics().T, index=tokens)
order = []
for w, word_list in word_lists.items():
target = set(word_list.nlargest(top).index)
for t, (top_topic, _) in enumerate(top_topics):
if target == set([t[1] for t in top_topic[:top]]):
order.append(t)
fig, axes = plt.subplots(ncols=2, figsize=(15,5))
title = f'# Words with Probability > {cutoff:.2%}'
(word_lists.loc[:, order]>cutoff).sum().reset_index(drop=True).plot.bar(title=title, ax=axes[1]);
umass = model.top_topics(corpus=corpus, coherence='u_mass', topn=20)
pd.Series([c[1] for c in umass]).plot.bar(title='Topic Coherence', ax=axes[0])
fig.tight_layout()
fig.savefig(f'fin_news_coherence_{top}', dpi=300);
def show_top_docs(model, corpus, docs):
doc_topics = model.get_document_topics(corpus)
df = pd.concat([pd.DataFrame(doc_topic,
columns=['topicid', 'weight']).assign(doc=i)
for i, doc_topic in enumerate(doc_topics)])
for topicid, data in df.groupby('topicid'):
print(topicid, docs[int(data.sort_values('weight', ascending=False).iloc[0].doc)])
print(pd.DataFrame(lda.show_topic(topicid=topicid)))
```
## Load Financial News
The data is avaialble from [Kaggle](https://www.kaggle.com/jeet2016/us-financial-news-articles).
Download and unzip into data directory in repository root folder, then rename the enclosing folder to `us-financial-news` and the subfolders so you get the following directory structure:
```
data
|-us-financial-news
|-2018_01
|-2018_02
|-2018_03
|-2018_04
|-2018_05
```
```
data_path = Path('..', 'data', 'us-financial-news')
```
We limit the article selection to the following sections in the dataset:
```
section_titles = ['Press Releases - CNBC',
'Reuters: Company News',
'Reuters: World News',
'Reuters: Business News',
'Reuters: Financial Services and Real Estate',
'Top News and Analysis (pro)',
'Reuters: Top News',
'The Wall Street Journal & Breaking News, Business, Financial and Economic News, World News and Video',
'Business & Financial News, U.S & International Breaking News | Reuters',
'Reuters: Money News',
'Reuters: Technology News']
def read_articles():
articles = []
counter = Counter()
for f in data_path.glob('*/**/*.json'):
article = json.load(f.open())
if article['thread']['section_title'] in set(section_titles):
text = article['text'].lower().split()
counter.update(text)
articles.append(' '.join([t for t in text if t not in stop_words]))
return articles, counter
articles, counter = read_articles()
print(f'Done loading {len(articles):,.0f} articles')
most_common = (pd.DataFrame(counter.most_common(), columns=['token', 'count'])
.pipe(lambda x: x[~x.token.str.lower().isin(stop_words)]))
most_common.head(10)
```
## Preprocessing with SpaCy
```
results_path = Path('results', 'financial_news')
if not results_path.exists():
results_path.mkdir(parents=True)
def clean_doc(d):
doc = []
for t in d:
if not any([t.is_stop, t.is_digit, not t.is_alpha, t.is_punct, t.is_space, t.lemma_ == '-PRON-']):
doc.append(t.lemma_)
return ' '.join(doc)
nlp = spacy.load('en')
nlp.max_length = 6000000
nlp.disable_pipes('ner')
nlp.pipe_names
def preprocess(articles):
iter_articles = (article for article in articles)
clean_articles = []
for i, doc in enumerate(nlp.pipe(iter_articles,
batch_size=100,
n_threads=8), 1):
if i % 1000 == 0:
print(f'{i / len(articles):.2%}', end=' ', flush=True)
clean_articles.append(clean_doc(doc))
return clean_articles
clean_articles = preprocess(articles)
clean_path = results_path / 'clean_text'
clean_path.write_text('\n'.join(clean_articles))
```
## Vectorize data
```
docs = clean_path.read_text().split('\n')
len(docs)
```
### Explore cleaned data
```
article_length, token_count = [], Counter()
for i, doc in enumerate(docs, 1):
if i % 1e6 == 0:
print(i, end=' ', flush=True)
d = doc.lower().split()
article_length.append(len(d))
token_count.update(d)
fig, axes = plt.subplots(ncols=2, figsize=(15, 5))
(pd.DataFrame(token_count.most_common(), columns=['token', 'count'])
.pipe(lambda x: x[~x.token.str.lower().isin(stop_words)])
.set_index('token')
.squeeze()
.iloc[:25]
.sort_values()
.plot
.barh(ax=axes[0], title='Most frequent tokens'))
sns.boxenplot(x=pd.Series(article_length), ax=axes[1])
axes[1].set_xscale('log')
axes[1].set_xlabel('Word Count (log scale)')
axes[1].set_title('Article Length Distribution')
sns.despine()
fig.tight_layout()
fig.savefig(results_path / 'fn_explore', dpi=300);
pd.Series(article_length).describe(percentiles=np.arange(.1, 1.0, .1))
docs = [x.lower() for x in docs]
docs[3]
```
### Set vocab parameters
```
min_df = .005
max_df = .1
ngram_range = (1, 1)
binary = False
vectorizer = TfidfVectorizer(stop_words='english',
min_df=min_df,
max_df=max_df,
ngram_range=ngram_range,
binary=binary)
dtm = vectorizer.fit_transform(docs)
tokens = vectorizer.get_feature_names()
dtm.shape
corpus = Sparse2Corpus(dtm, documents_columns=False)
id2word = pd.Series(tokens).to_dict()
dictionary = Dictionary.from_corpus(corpus, id2word)
```
## Train & Evaluate LDA Model
```
logging.basicConfig(filename='gensim.log',
format="%(asctime)s:%(levelname)s:%(message)s",
level=logging.DEBUG)
logging.root.level = logging.DEBUG
```
### Train models with 5-25 topics
```
num_topics = [5, 10, 15, 20]
for topics in num_topics:
print(topics)
lda_model = LdaModel(corpus=corpus,
id2word=id2word,
num_topics=topics,
chunksize=len(docs),
update_every=1,
alpha='auto', # a-priori belief for the each topics' probability
eta='auto', # a-priori belief on word probability
decay=0.5, # percentage of previous lambda value forgotten
offset=1.0,
eval_every=1,
passes=10,
iterations=50,
gamma_threshold=0.001,
minimum_probability=0.01, # filter topics with lower probability
minimum_phi_value=0.01, # lower bound on term probabilities
random_state=42)
lda_model.save((results_path / f'model_{topics}').as_posix())
```
### Evaluate results
We show results for one model using a vocabulary of 3,800 tokens based on min_df=0.1% and max_df=25% with a single pass to avoid length training time for 20 topics. We can use pyldavis topic_info attribute to compute relevance values for lambda=0.6 that produces the following word list
```
def eval_lda_model(ntopics, model, corpus=corpus, tokens=tokens):
show_word_list(model=model, corpus=corpus, top=ntopics, save=True)
show_coherence(model=model, corpus=corpus, tokens=tokens, top=ntopics)
vis = prepare(model, corpus, dictionary, mds='tsne')
pyLDAvis.save_html(vis, f'lda_{ntopics}.html')
return 2 ** (-model.log_perplexity(corpus))
lda_models = {}
perplexity ={}
for ntopics in num_topics:
print(ntopics)
lda_models[ntopics] = LdaModel.load((results_path / f'model_{ntopics}').as_posix())
perplexity[ntopics] = eval_lda_model(ntopics=ntopics, model=lda_models[ntopics])
```
### Perplexity
```
pd.Series(perplexity).plot.bar()
sns.despine();
```
### PyLDAVis for 15 Topics
```
vis = prepare(lda_models[15], corpus, dictionary, mds='tsne')
pyLDAvis.display(vis)
```
## LDAMultiCore Timing
```
df = pd.read_csv(results_path / 'lda_multicore_test_results.csv')
df.head()
df[df.num_topics==10].set_index('workers')[['duration', 'test_perplexity']].plot.bar(subplots=True, layout=(1,2), figsize=(14,5), legend=False)
sns.despine()
plt.tight_layout();
```
| true |
code
| 0.388995 | null | null | null | null |
|
# Comic Book Cancellations Part I: Web Scraping
While some Marvel comic books run for decades, most series go through cycles. For example, [Charles Soule's *She-Hulk* (2014)](https://www.cbr.com/charles-soule-investigates-she-hulks-blue-file/) was a colorful and quirky crime serial that got cancelled on its 12th issue. However, that was not the end of the titular character. A year after that series cancellation, she reappeared as the lead in [Mario Tamaki's *Hulk* (2016)](https://www.cbr.com/hulk-1-gives-marvel-an-unstable-dangerous-jennifer-walters/) but the tone of the book was completely different. The new titles was introspective and focused on her pain and depression following the murder of her cousin. While these legacy characters may eventually continue after a cancellation, the tone, style, and genre of their stories often change with the new creative team.
So what causes so many of my favorite stories to get cancelled seemingly ahead of their time? Some books end at the author's request because the story has reached its conclusion. When *Young Avengers* (2013) was cancelled, the author Kieron Gillen [stated](http://kierongillen.tumblr.com/post/66995678192/young-avengers-the-end-of-the-season), "When the time came around and Marvel asked if we wanted to do more issues, [the artist] Jamie and I decided we’d actually made our statement, and should leave the stage." However, most Marvel comics are written as serials without the intention of bringing the story to a final conclusion. Instead, as Marvel Executive Editor Tom Brevoort [stated](https://twitter.com/TomBrevoort/status/945861802813984768) in 2017 amidst a string of cancellations, "We go through this cycle every year where weaker-selling titles get pruned".
So are books that get cancelled actually weaker selling? And if so, what criteria determines cancellation? Of [that](https://www.dailydot.com/parsec/marvel-comics-sales-slump-diversity/) [string](https://www.cbr.com/marvel-cancels-generation-x-gwenpool-more/) [of](https://www.cbr.com/marvel-comics-cancels-iceman-luke-cage/) [cancellations](https://www.cbr.com/marvel-comics-cancels-she-hulk/) in early 2017, all of the series had female, queer, or colored leads. This naturally poses the question whether the cancellations are the result of low sales for books with new characters introduced through Marvel's diversity initatives or whether Marvel was caving to [retailers](https://www.cbr.com/marvel-sales-diversity/) who felt like "people didn't want any more diversity".
To answer these questions, I'll use machine learning in order to develop a cancellation criteria based on comic book sales data. This first part will focus on web scrapping publically available comic book sales data and storing it in a SQLite database. The [second part](./2 Comic Book Cancellations - Machine Learning.ipynb) will parse through that data and implement machine learning algorithms to determine why titles got cancellation. While these first two parts show step-by-step how my analysis was done, the [third part](./3 Comic Book Cancellations - Conclusion.ipynb) will summarize the entire process and draw conclusions from my findings.
# 1 Web Scrapping
## Imports
```
import sqlite3
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np
from bs4 import BeautifulSoup
import requests
import re
from scipy.optimize import curve_fit
%matplotlib inline
```
## Web Scrapping
American comic books (like Marvel or DC) generally come out with new issues every month that are sold through comic book stores, however, an increasing minority of comics are sold digitally through sites like [Comixology](https://www.comixology.com/). About twice a year, these individual issues are also collected into trade paperbacks where they are sold by local comic book stores and through most booksellers.
The main comic book store distributor is [Diamond Comic Distributors](https://www.diamondcomics.com/Home/1/1/3/103), and their monthly sales information is freely available from [Comichron](http://www.comichron.com/monthlycomicssales.html) for every month since 1998. This data provides a [good estimate](http://www.comicsbeat.com/a-quick-word-about-sales-estimates-before-we-run-the-distribution-charts/) of single issue sales where the actual sales are ~10% larger, but gives no information about digital comic sales and is less accurate for collected editions of which a sizable number are sold through bookstores. Actual collected edition sales are ~25% more than Diamond's numbers.
The majority of Diamond's sales are through [individual issues](https://www.cnbc.com/2016/06/05/comic-books-buck-trend-as-print-and-digital-sales-flourish.html). As such, while calculating the cancellation criteria, I'll only look into individual issue sales.
In order to scrape the data from the website, I'll be using the Python [Beautiful Soup](https://www.crummy.com/software/BeautifulSoup) package. It will then be saved into a [SQLite](https://sqlite.org/index.html) database. This whole processh can take several minutes to finish so the final database has been made available found [here](./sales.db).
```
# download_comic_sales return a DataFrame contains comic sales from Comichron for the given month and year
def download_comic_sales(month, year):
url = "http://www.comichron.com/monthlycomicssales/{1}/{1}-{0:02}.html".format(month, year)
page = requests.get(url)
soup = BeautifulSoup(page.content, 'html.parser')
table = soup.find('table', id = "Top300Comics")
data = []
rows = table.find_all('tr')
for row in rows:
cols = row.find_all(['td', 'th'])
cols = [ele.text.strip() for ele in cols]
data.append([ele for ele in cols])
comics_table = pd.DataFrame(data[1:], columns=data[0])
comics_table.drop(columns = "On sale", inplace = True, errors = 'ignore')
comics_table.rename(columns={comics_table.columns[0]: "UnitRank", comics_table.columns[1]: "DollarRank"}, inplace=True)
comics_table.drop('UnitRank', 1, inplace=True)
comics_table.drop('DollarRank', 1, inplace=True)
comics_table.rename(columns={'Comic-book Title' : 'Title', 'Est. units' : 'Units'}, inplace=True)
comics_table['Issue'] = comics_table['Issue'].map(lambda x: re.findall('\d+\.?\d*', x)[0] if len(re.findall('\d+\.?\d*', x)) >= 1 else '')
comics_table['Issue'] = pd.to_numeric(comics_table['Issue'], errors='coerce')
comics_table["Title"] = comics_table["Title"].replace("†", "", regex=True)
comics_table["Price"] = comics_table["Price"].replace("\$", "", regex=True).astype(float)
comics_table['Units'] = comics_table['Units'].replace(',', '', regex=True).astype(int)
comics_table['Gross'] = comics_table['Units']*comics_table['Price']
comics_table['Date'] = pd.to_datetime('{}{:02}'.format(year, month), format='%Y%m', errors='ignore')
comics_table = comics_table.dropna(axis='rows')
return(comics_table)
# Loop through every month since 1998 adding data to SQLite database
db = sqlite3.connect('sales.db')
for year in range(1998, 2018):
for month in range(1, 13):
df = download_comic_sales(month, year)
df.to_sql("sales", db, if_exists="append")
for year in range(2018, 2019):
for month in range(1, 6):
df = download_comic_sales(month, year)
df.to_sql("sales", db, if_exists="append")
db.close()
```
# 2 Data Cleaning
I'm specifically going to focus on Marvel comics, however, I need to keep multiple runs of a comic separate even if they have the same title. Marvel commonly starts the numbering of new series with a \#1 issue to indicate to readers that the title has a new creative team and direction. However, many titles later revert back to their legacy numbering system. So long as there is not a new \#1 issue, I'm going to consider it the same series. Each run can be distinguished from each other by its title and starting year. This may ignore some edge cases such as ongoing titles that change the name of the comic in the middle of a run (such as Mario Tamaki's *Hulk* (2016) changing its name to *She-Hulk*) or the possiblity of a new title starting with legacy numbering rather than a \#1.
There are also a variety of other minor details involved in cleaning up the data for analysis. Altogether, the following changes were made:
- Only keep Marvel comics
- Distinguish between multiple runs of the comic with separate \#1 issues
- Aggregate sales and reorders for unique comics (same Title, Starting Year, Issue #)
- Remove .1 issues which are special jumping on points separate from main continuity
- Remove obvious marketing gimmick issues
- Rename some titles so that they're consistent.
- New features added for largest issue number and whether title is current title
```
db = sqlite3.connect('sales.db')
# Load web scrapped data from SQL database for Marvel comics
df = pd.read_sql_query('''
SELECT Title, Issue, Price, Units, Gross, Date
FROM sales
WHERE Publisher = "Marvel"
''', db, parse_dates=['Date'])
db.close()
# Rename titles for consistency and remove extraneous issue
df = df[(df.Issue % 1 == 0) & (df.Issue != 0) & (df.Issue < 900)]
df.loc[df.Title == 'Us Avengers', 'Title'] = "U.S. Avengers"
df.loc[df.Title == 'US Avengers', 'Title'] = "U.S. Avengers"
df.loc[df.Title == 'U.S.Avengers', 'Title'] = "U.S. Avengers"
df.loc[df.Title == 'Avengers Ai', 'Title'] = "Avengers AI"
df.loc[df.Title == 'All New Guardians of Galaxy', 'Title'] = "All New Guardians of the Galaxy"
df.loc[df.Title == 'Marvel Universe Ult Spider-Man Web Warriors', 'Title'] = "Marvel Universe Ultimate Spider-Man Web Warriors"
df.loc[df.Title == 'Kanan The Last Padawan', 'Title'] = "Kanan"
df.loc[df.Title == 'Kanan Last Padawan', 'Title'] = "Kanan"
df.loc[df.Title == 'Star Wars Kanan', 'Title'] = "Kanan"
# Develop table with each series information (Title, StartYear, StartDate)
series_df = df[df['Issue'] == 1].groupby(['Date', 'Title']).agg({'Title':'first', 'Date': 'first'})
series_df['StartYear'] = series_df['Date'].map(lambda x: x.year)
series_df.reset_index(drop=True, inplace=True)
series_df.sort_values(by=['Title', 'Date'], inplace=True)
series_df.reset_index(drop=True, inplace=True)
series_df2 = pd.DataFrame()
series_df2 = series_df2.append(series_df.iloc[0])
for i in range(series_df.shape[0]-1):
if (series_df.Title[i+1] != series_df.Title[i]) or (series_df.Date[i+1] - series_df.Date[i] > pd.Timedelta(3, unit='M')):
series_df2 = series_df2.append(series_df.iloc[i+1])
series_df = series_df2
# Use series table to determine StartYear for each entry in database
df['StartYear'] = pd.Series()
for i in range(df.shape[0]):
title = df.iloc[i].Title
date = df.iloc[i].Date
s = series_df[(series_df.Title == title) & (series_df.Date <= date)].sort_values(by='Date', ascending=False)
if s.shape[0] > 0:
df.loc[df.index[i], 'StartYear'] = s.iloc[0].StartYear
# Remove titles that don't have #1 issues in the data set or other missing data
df = df.dropna(axis='rows')
# Save cleaned up Marvel salse information as separate table in database
db = sqlite3.connect('sales.db')
df.to_sql("marvel_clean", db, if_exists="replace")
db.close()
# Sum sales issue for each unique issue (unique Title, StartYear, Issue #)
df = df.groupby(['Title', 'Issue', 'StartYear']).agg({'Title' : 'first', 'StartYear' : 'first', 'Issue': 'first', 'Date' : 'min', 'Price' : 'first', 'Units' : 'sum', 'Gross' : 'sum' })
df.reset_index(drop=True, inplace=True)
# Add new features for the title's maximum issue and whether it is a current title
df2 = pd.pivot_table(df, values='Issue', index=['Title', 'StartYear'], aggfunc=np.max).rename(columns={'Issue':'MaxIssue'})
df = pd.merge(left=df, right=df2, on=['Title', 'StartYear'], sort=False).sort_values(by='Units', ascending=False)
max_date = df['Date'].max()
df2 = pd.pivot_table(df, values='Date', index=['Title', 'StartYear'], aggfunc=lambda x: max(x) == max_date).rename(columns={'Date':'CurrentTitle'})
df = pd.merge(left=df, right=df2, on=['Title', 'StartYear'], sort=False).sort_values(by='Units', ascending=False)
```
We can see what our data looks like by peeking into the first few rows of the table.
```
df.head(3)
series_df[series_df.Title.str.contains('Moon Girl')]
```
## Preliminary Analysis - Cancellation Issue
The titles need to be classified as to whether they have been cancelled or not. Naively, any books that end have been cancelled whereas current ongoing titles have not been cancelled, but that isn't always the case.
*Amazing Spider-Man* is the long-running, core Spider-Man book and one of Marvel's best selling, flagship titles. Yet, since 1998 it has started over with new \#1 issues multiple times.
```
series_df.loc[series_df.Title == 'Amazing Spider-Man', ['StartYear', 'Title']]
```
In this case, *Amazing Spider-Man* was not cancelled so much as the numbering system was reverted to indicate a new creative direction and typically a mix-up in the creative team as well. For long-running serial titles, it's standard that every several years that the creative team will change.
Meanwhile, many titles never reach beyond their first issue. In which case, they would have been "cancelled" before receiving any sales feedback. These titles are often intended to be one-shots either as a side story or even as a Free Comic Book Day (FCBD) offering.
```
df[df.MaxIssue == 1].head(3)
```
So long-running and extremely short-running titles may not actually have been cancelled.
So let's look at what issue is often the last issue before cancellation.
```
pd.pivot_table(df, values=['Title'], index='MaxIssue', aggfunc={'Title':lambda x: len(x.unique())}).iloc[0:16].plot(
kind='bar', y='Title', figsize=(8,6), legend=False)
plt.ylabel('Counts')
plt.xlabel('Max Issue')
plt.show()
```
Based on length, Marvel comics appear to fall into several categories: (1) one-shots, (2) events and mini-series that run less than 6 issues, (3) ongoing titles that are immediately cancelled around 12 issues, and (4) ongoing titles that continue past 12 issues.
I have no way of determining how each series ended without manually going through each title and looking into them which would be a time-consuming process. However, it appears that the 12th month mark is a common dropping point for comics. For now, I'm going to overly restrict my data and try to determine what allows a book to survive past this first drop point by comparing titles that got cancelled on their 12th issue with those that lasted longer.
# 3 Cancelled Classification
Titles that prematurely finished with 12 issues will be labeled as "Cancelled" whereas books that last longer than that will be labelled as "Kept". I'm then going to aggregate my data by run (title and starting year), keeping features for the unit sales and gross profits for the first 12 months as well as the book's maximum issue and whether it's a current title.
```
# Removed 'Avengers Vs. X-Men' because it is an event comic that lasted 12 issues and was not cancelled per se
df.drop(df.index[df.Title == 'Avengers Vs X-Men'], inplace=True)
# Select cancelled titles that start with an issue #1 and finish with their 12th issue. Group by title and create features for units and gross sales for first 12 months.
dfUnits = df.loc[(df.Issue == 1) & (df.MaxIssue == 12), ['Title', 'StartYear']].reset_index(drop=True)
for i in range(1,13):
dfUnits = pd.merge(left=dfUnits, right=df.loc[(df.Issue == i) & (df.MaxIssue == 12), ['Title', 'StartYear', 'Units']].rename(columns={'Units': 'Units' + str(i)}), on=['Title', 'StartYear'])
dfUnits = dfUnits.dropna(axis='rows')
dfGross = df.loc[(df.Issue == 1) & (df.MaxIssue == 12), ['Title', 'StartYear']].groupby(['Title', 'StartYear']).first().reset_index()
for i in range(1,13):
dfGross = pd.merge(left=dfGross, right=df.loc[(df.Issue == i) & (df.MaxIssue == 12), ['Title', 'StartYear', 'Gross']].rename(columns={'Gross': 'Gross' + str(i)}), on=['Title', 'StartYear'])
dfGross = dfGross.dropna(axis='rows')
df1 = pd.merge(left=dfUnits, right=dfGross, on=['Title', 'StartYear'])
df2 = df[['Title', 'StartYear', 'MaxIssue', 'CurrentTitle']]
df2 = df2.groupby(['Title', 'StartYear']).agg({'MaxIssue':'first',
'CurrentTitle':'first'}).reset_index()
dfCancelled = pd.merge(left=df1, right=df2, on=['Title', 'StartYear'])
dfCancelled['Kept'] = 0
# Select kept titles that start with an issue #1 and then continue past their 12th issue. Group by title and create features for units and gross sales for first 12 months.
dfUnits = df.loc[(df.MaxIssue > 12) & (df.Issue == 1), ['Title', 'StartYear']].reset_index(drop=True)
for i in range(1,13):
dfUnits = pd.merge(left=dfUnits, right=df.loc[(df.Issue == i) & (df.MaxIssue > 12), ['Title', 'StartYear', 'Units']].rename(columns={'Units': 'Units' + str(i)}), on=['Title', 'StartYear'])
dfUnits = dfUnits.dropna(axis='rows')
dfGross = df.loc[(df.MaxIssue > 12) & (df.Issue == 1 | (df.Issue == 12)), ['Title', 'StartYear']].groupby(['Title', 'StartYear']).first().reset_index()
for i in range(1,13):
dfGross = pd.merge(left=dfGross, right=df.loc[(df.Issue == i) & (df.MaxIssue > 12), ['Title', 'StartYear', 'Gross']].rename(columns={'Gross': 'Gross' + str(i)}), on=['Title', 'StartYear'])
dfGross = dfGross.dropna(axis='rows')
df1 = pd.merge(left=dfUnits, right=dfGross, on=['Title', 'StartYear'])
df2 = df.loc[(df['Issue'] <= 12),['Title', 'StartYear', 'MaxIssue', 'CurrentTitle']]
df2 = df2.groupby(['Title', 'StartYear']).agg({'MaxIssue':'first',
'CurrentTitle':'first'}).reset_index()
dfKept = pd.merge(left=df1, right=df2, on=['Title', 'StartYear'])
dfKept['Kept'] = 1
# Combine both Cancelled and Kept titles
df = pd.concat([dfCancelled, dfKept], ignore_index=True, sort=False)
```
Peering into the first few rows shows that we now have sales information (units and gross) for the first 12 months of sales of new titles.
```
df.head(3)
```
# 4 Feature Engineering - Exponential Fitting
Monthly unit sales and gross profit uncannily follow an exponential decay over the course of the first several months. People try new titles for the first several issues to decide whether they like the book. Then within the first few months, they decide whether to drop the book or continue to follow it. After that point, sales tend stay relatively consistent.
In addition to my monthly unit sales, I'm going to engineer some new features based on the exponential fit parameters. These features allow for the entire trend of the sales information with time to be captured in just a few variables.
#### Exponential Models:
$Units(x) = (UI-UF) exp(-(x-1)(UT)) + UF$
$UI$ = Initial Unit Sales <br />
$UT$ = Exponential Time Decay Constant <br />
$UF$ = Asymptotic Final Unit Sales
$Gross(x) = (GI-GF) exp(-(x-1)(GT)) + GF$
$GI$ = Initial Gross Sales <br />
$GT$ = Exponential Time Decay Constant <br />
$GF$ = Asymptotic Final Gross Sales
The exponential fit doesn't describe all the titles. For example, some of them have a linear change in sales without a first issue spike which would most likely happen if the series gets a new \#1 without a real change in direction or creative team. However, for most titles the exponential fit describes the trend of the sales curve without the variance of the montly sales numbers.
```
r = 10 # Number of issues starting from beginning to include in fit
x = np.arange(r)
def exponenial_func(x, I, T, F):
return (I-F)*np.exp(-x/T)+F
UI_list = np.array([])
UT_list = np.array([])
UF_list = np.array([])
for i in range(df.shape[0]):
y = df.iloc[i, 2:2+r].astype(float).values
popt, pcov = curve_fit(exponenial_func, x, y, p0=(100000, 1, 20000))
UI_list = np.append(UI_list, popt[0])
UT_list = np.append(UT_list, popt[1])
UF_list = np.append(UF_list, popt[2])
# List titles that don't fit
if pcov[0,0] == float('Inf'):
print('Trouble Fitting Units for', df.iloc[i]['Title'])
GI_list = np.array([])
GT_list = np.array([])
GF_list = np.array([])
for i in range(df.shape[0]):
y = df.iloc[i, 14:14+r].astype(float).values
popt, pcov = curve_fit(exponenial_func, x, y, p0=(60000, 0.5, 20000))
GI_list = np.append(GI_list, popt[0])
GT_list = np.append(GT_list, popt[1])
GF_list = np.append(GF_list, popt[2])
# List titles that don't fit
if pcov[0,0] == float('Inf'):
print('Trouble fitting Gross for', df.iloc[i]['Title'])
df['UI'] = UI_list
df['UT'] = UT_list
df['UF'] = UF_list
df['GI'] = GI_list
df['GT'] = GT_list
df['GF'] = GF_list
```
## Checking Fits
We confirm how well the fit works by comparing it with the actual sales for a title.
```
title = 'She-Hulk'
start_year = 2014
df2 = df[(df.Title == title) & (df.StartYear == start_year)]
# Monthly Sales Values
x = np.arange(12)
y = df2.iloc[0,2:2+12].astype(float).values
#Exponential Fit Values
def exponenial_func(x, I, T, F):
return (I-F)*np.exp(-x/T)+F
xx = np.linspace(0, 12, 1000)
yy = exponenial_func(xx, df2.UI[0], df2.UT[0], df2.UF[0])
# Plot
ymin = min(y); ymax = max(y)
plt.plot(x,y,'o', xx, yy)
plt.title('Exponential Fit of Units: {} ({})'.format(title, start_year))
plt.xlim([-0.2,11.2])
plt.ylim([0.9*ymin, 1.1*ymax])
plt.ylabel('Units Sold')
plt.xlabel('Months')
plt.show()
```
# 5 Save Databse
```
df = df.reset_index(drop=True)
db = sqlite3.connect('sales.db')
df.to_sql("marvel_sales", db, if_exists="replace")
db.close()
```
In this first part, we've scrapped comic book sales data, cleaned up some of irregularities in issue numbers and title names, aggregated the data into unique runs by the title's name and starting year, classified titles based on whether they were "kept" or "cancelled" after 12 months, and engineered new features based on the regression fit of the sales data to an exponential decay curve.
Now that we have the data, it is ready to be processed by machine learning algorithms in order to determine the cancellation criteria. The step-by-step procedures to do that are demonstrated in [part 2](./2 Comic Book Cancellations - Machine Learning.ipynb). [Part 3](./3 Comic Book Cancellations - Conclusion.ipynb) will then summarize all these steps and present the final conclusion.
| true |
code
| 0.31778 | null | null | null | null |
|

---
## 30. Integración Numérica
Eduard Larrañaga (ealarranaga@unal.edu.co)
---
### Resumen
En este cuaderno se presentan algunas técnicas de integración numérica.
---
Una de las tareas más comunes en astrofísica es evaluar integrales como
\begin{equation}
I = \int_a^b f(x) dx ,
\end{equation}
y, en muchos casos, estas no pueden realizarse en forma analítica. El integrando en estas expresiones puede darse como una función analítica $f(x)$ o como un conjunto discreto de valores $f(x_i)$. Acontinuación describiremos algunas técnicas para realizar estas integrales numéricamente en ambos casos.
---
## Interpolación por intervalos y cuadraturas
Cualquier método de integración que utilice una suma con pesos es denominado **regla de cuadraturas**. Suponga que conocemos (o podemos evaluar) el integrando $f(x)$ en un conjunto finito de *nodos*, $\{x_j\}$ con $j=0,\cdots,n-1$ en el intervalo $[a,b]$ y tal que $x_0 = a$ y $x_{n-1} = b$. Con esto se obtendrá un conjunto de $n$ nodos o equivalentemente $N=n-1$ intervalos. Una aproximación discreta de la integral de esta función está dada por la **regla del rectángulo**,
\begin{equation}
I = \int_a^b f(x) dx \approx \Delta x \sum_{i=0}^{N} f(x_i),
\end{equation}
donde el ancho de los intervalos es $\Delta x = \frac{b-a}{N}$. A partir de la definición de una integral, es claro que esta aproximación converge al valor real de la integral cuando $N\rightarrow \infty$, i.e. cuando $\Delta x \rightarrow 0$.
A pesar de que la regla del rectangulo puede dar una buena aproximación de la integral, puede ser mejorada al utilizar una función interpolada en cada intervalo. Los métodos en los que se utiliza la interpolación de polinomios se denominan, en general, **cuadraturas de Newton-Cotes**.
---
### Regla de punto medio
La modificación más simple a la regla del rectángulo descrita arriba es utilizar el valor central de la función $f(x)$ en cada intervalo en lugar del valor en uno de los nodos. de Esta forma, si es posible evaluar el integrando en el punto medio de cada intervalo, el valor aproximado de la integral estará dado por
\begin{equation}
I = \int_{a}^{b} f(x) dx = \sum _{i=0}^{N} (x_{i+1} - x_i) f(\bar{x}_i ),
\end{equation}
donde $\bar{x}_i = \frac{x_i + x_{i+1}}{2}$ es el punto medio en el intervalo $[x_i, x_{i+1}]$.
Con el fin de estimar el error asociado con este método, se utiliza una expansión en serie de Taylor del integrando en el intervalo $[x_i, x_{i+1}]$ alrededor del punto medio $\bar{x}_i$,
\begin{equation}
f(x) = f(\bar{x}_i) + f'(\bar{x}_i)(x-\bar{x}_i) + \frac{f''(\bar{x}_i)}{2}(x-\bar{x}_i)^2 + \frac{f'''(\bar{x}_i)}{6}(x-\bar{x}_i)^3 + ...
\end{equation}
Integrando esta expresión desde $x_i$ hasta $x_{i+1}$, y notando que los terminos de orden impar se anulan, se obtiene
\begin{equation}
\int_{x_i}^{x_{i+1}} f(x)dx = f(\bar{x}_i)(x_{i+1}-x_i) + \frac{f''(\bar{x}_i)}{24}(x_{i+1}-x_i)^3 + ...
\end{equation}
Esta expansión muestra que el error asociado con la aproximación en cada intervalo es de orden $\varepsilon_i = (x_{i+1}-x_i)^3$. Ya que la integral total se obtiene como una suma de $N$ integrales similares (una por cada subintervalo), el error total es será de orden $\varepsilon = N \varepsilon_i $.
Cuando los nodos están igualmente espaciados, podemos escribir el tamaño de estos intervalos como $\Delta x = \frac{b - a}{N}$ y por ello, el error asociado con cada intervalo es $\varepsilon_i =\frac{(b - a)^3}{n^3} = \Delta x^3$, mientras que el error total de la cuadratúra será de orden $\varepsilon = N \varepsilon_i = \frac{(b - a)^3}{N^2} = N\Delta x^3$.
#### Ejemplo. Integración numérica
Leeremos los datos de la función desde un archivo .txt y estimaremos numéricamente el valor de la integral de esta función utilizando la regla del punto medio. Debido a que la función esdada en forma de puntos discretos (y no en forma analítica), no es posible evaluar el valor de la función en los puntos medios por lo que utilizaremos inicialmente el valor en el primer punto de cada uno de los intervalos para calcular las sumas parciales.
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Reading the data
data = np.loadtxt('data_points1.txt', comments='#', delimiter=',')
x = data[:,0]
f = data[:,1]
n = len(x) # Number of nodes
N = n-1 # Number of intervals
plt.figure(figsize=(7,5))
# Numerical integration loop
Integral = 0.
for i in range(N):
dx = x[i+1] - x[i]
Integral = Integral + dx*f[i]
plt.vlines([x[i], x[i+1]], 0, [f[i], f[i]], color='red')
plt.plot([x[i], x[i+1]], [f[i], f[i]],color='red')
plt.fill_between([x[i], x[i+1]], [f[i], f[i]],color='red', alpha=0.3)
plt.scatter(x, f, color='black')
plt.hlines(0, x.min(), x.max())
plt.title('Integración por la regla del rectángulo')
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.show()
print(f'El resultado de la integración numérica de la función discreta')
print(f'entre x = {x[0]:.1f} y x = {x[N]:.1f} es I = {Integral:.5e}')
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Reading the data
data = np.loadtxt('data_points2.txt', comments='#', delimiter=',')
x = data[:,0]
f = data[:,1]
n = len(x) # Number of nodes
N = n-1 # Number of intervals
plt.figure(figsize=(7,5))
# Numerical integration loop
Integral = 0.
for i in range(N):
dx = x[i+1] - x[i]
Integral = Integral + dx*f[i]
plt.vlines([x[i], x[i+1]], 0, [f[i], f[i]], color='red')
plt.plot([x[i], x[i+1]], [f[i], f[i]],color='red')
plt.fill_between([x[i], x[i+1]], [f[i], f[i]],color='red', alpha=0.3)
plt.scatter(x, f, color='black')
plt.hlines(0, x.min(), x.max())
plt.title('Integración por la regla del rectángulo')
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.show()
print(f'El resultado de la integración numérica de la función discreta')
print(f'entre x = {x[0]:.1f} y x = {x[N]:.1f} es I = {Integral:.5e}')
```
---
### Regla del Trapezoide
La siguiente generalización de la regla del rectángulo corresponde a aproximar la función $f(x)$ con un polinomio lineal en cada uno de los intervalos. Esto se conoce como la **regla del trapezoide** y la correspondiente cuadratura estará dada por
\begin{equation}
I = \int_{a}^{b} f(x) dx = \sum _{i=0}^{N} \frac{1}{2} (x_{i+1} - x_i) \left[ f(x_{i+1}) + f(x_i) \right] .
\end{equation}
Contrario a lo que sucede en la regla del punto medio, este método no necesita la evaluación del integrando en el punto medio sino en los dos nodos de cada intervalo.
#### Ejemplo. Integración con la regla del trapezoide.
De nuevo se leerán los datos de la función a partir de un archivo .txt file y se integrará numéricamente utilizando la regla del trapezoide.
```
import numpy as np
import matplotlib.pyplot as plt
# Reading the data
data = np.loadtxt('data_points1.txt', comments='#', delimiter=',')
x = data[:,0]
f = data[:,1]
n = len(x) # Number of nodes
N = n-1 # Number of intervals
plt.figure(figsize=(7,5))
# Numerical integration loop
Integral = 0.
for i in range(N):
dx = x[i+1] - x[i]
f_mean = (f[i] + f[i+1])/2
Integral = Integral + dx*f_mean
plt.vlines([x[i], x[i+1]], 0, [f[i], f[i+1]], color='red')
plt.plot([x[i], x[i+1]], [f[i], f[i+1]],color='red')
plt.fill_between([x[i], x[i+1]], [f[i], f[i+1]],color='red', alpha=0.3)
plt.scatter(x, f, color='black')
plt.hlines(0, x.min(), x.max())
plt.title('Integración con la regla del trapezoide')
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.show()
print(f'El resultado de la integración numérica de la función discreta')
print(f'entre x = {x[0]:.1f} y x = {x[N]:.1f} es I = {Integral:.5e}')
import numpy as np
import matplotlib.pyplot as plt
# Reading the data
data = np.loadtxt('data_points2.txt', comments='#', delimiter=',')
x = data[:,0]
f = data[:,1]
n = len(x) # Number of nodes
N = n-1 # Number of intervals
plt.figure(figsize=(7,5))
# Numerical integration loop
Integral = 0.
for i in range(N):
dx = x[i+1] - x[i]
f_mean = (f[i] + f[i+1])/2
Integral = Integral + dx*f_mean
plt.vlines([x[i], x[i+1]], 0, [f[i], f[i+1]], color='red')
plt.plot([x[i], x[i+1]], [f[i], f[i+1]],color='red')
plt.fill_between([x[i], x[i+1]], [f[i], f[i+1]],color='red', alpha=0.3)
plt.scatter(x, f, color='black')
plt.hlines(0, x.min(), x.max())
plt.title('Integración con la regla del trapezoide')
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.show()
print(f'El resultado de la integración numérica de la función discreta')
print(f'entre x = {x[0]:.1f} y x = {x[N]:.1f} es I = {Integral:.5e}')
```
---
## Regla de Simpson
La regla de Simpson es un método en el que la integral $f(x)$ se estima aproximando el integrando por un polinomi de segundo orden en cada intervalo.
Si se conocen tres valores de la función; $f_1 =f(x_1)$, $f_2 =f(x_2)$ y $f_3 =f(x_3)$; en los puntos $x_1 < x_2 < x_3$, se puede ajustar un polinomio de segundo orden de la forma
l
\begin{equation}
p_2 (x) = A (x-x_1)^2 + B (x-x_1) + C .
\end{equation}
Al integrar este polinomio en el intervalo $[x_1 , x_3]$, se obtiene
\begin{equation}
\int_{x_1}^{x^3} p_2 (x) dx = \frac{x_3 - x_1}{6} \left( f_1 + 4f_2 + f_3 \right) + \mathcal{O} \left( (x_3 - x_1)^4 \right)
\end{equation}
---
### Regla de Simpson con nodos igualmente espaciados
Si se tienen $n$ nodos igualmente espaciados en el intervalo de integración, o equivalentemente $N=n-1$ intervalos con un ancho constante $\Delta x$, la integral total mediante la regla de Simpson se escribe en la forma
\begin{equation}
I = \int_a^b f(x) dx \approx \frac{\Delta x}{3} \sum_{i=0}^{\frac{N-1}{2}} \left[ f(x_{2i}) + 4f(x_{2i+1}) + f(x_{2i+2}) \right] + \mathcal{O} \left(f''' \Delta x^4 \right)
\end{equation}
El error numérico en cada intervalo es de orden $\Delta x^4$ y por lo tanto, la integral total tendrá un error de orden $N \Delta x^4 = \frac{(a-b)^4}{N^3}$.
#### Ejemplo. Integración con la regla de Simpson
```
import numpy as np
import matplotlib.pyplot as plt
def quadraticInterpolation(x1, x2, x3, f1, f2, f3, x):
p2 = (((x-x2)*(x-x3))/((x1-x2)*(x1-x3)))*f1 + (((x-x1)*(x-x3))/((x2-x1)*(x2-x3)))*f2 +\
(((x-x1)*(x-x2))/((x3-x1)*(x3-x2)))*f3
return p2
# Reading the data
data = np.loadtxt('data_points1.txt', comments='#', delimiter=',')
x = data[:,0]
f = data[:,1]
n = len(x) # Number of nodes
N = n-1 # Number of intervals
plt.figure(figsize=(7,5))
# Numerical integration loop
Integral = 0.
for i in range(int((N-1)/2)):
dx = x[2*i+1] -x[2*i]
Integral = Integral + dx*(f[2*i] + 4*f[2*i+1] + f[2*i+2])/3
x_interval = np.linspace(x[2*i],x[2*i+2],6)
y_interval = quadraticInterpolation(x[2*i], x[2*i+1], x[2*i+2], f[2*i], f[2*i+1], f[2*i+2], x_interval)
plt.plot(x_interval, y_interval,'r')
plt.fill_between(x_interval, y_interval, color='red', alpha=0.3)
plt.scatter(x, f, color='black')
plt.hlines(0, x.min(), x.max())
plt.title('Integración con la regla de Simpson')
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.show()
print(f'El resultado de la integración numérica de la función discreta')
print(f'entre x = {x[0]:.1f} y x = {x[N]:.1f} es I = {Integral:.5e}')
import numpy as np
import matplotlib.pyplot as plt
def quadraticInterpolation(x1, x2, x3, f1, f2, f3, x):
p2 = (((x-x2)*(x-x3))/((x1-x2)*(x1-x3)))*f1 + (((x-x1)*(x-x3))/((x2-x1)*(x2-x3)))*f2 +\
(((x-x1)*(x-x2))/((x3-x1)*(x3-x2)))*f3
return p2
# Reading the data
data = np.loadtxt('data_points2.txt', comments='#', delimiter=',')
x = data[:,0]
f = data[:,1]
n = len(x) # Number of nodes
N = n-1 # Number of intervals
plt.figure(figsize=(7,5))
# Numerical integration loop
Integral = 0.
for i in range(int((N-1)/2)):
dx = x[2*i+1] - x[2*i]
Integral = Integral + dx*(f[2*i] + 4*f[2*i+1] + f[2*i+2])/3
x_interval = np.linspace(x[2*i],x[2*i+2],6)
y_interval = quadraticInterpolation(x[2*i], x[2*i+1], x[2*i+2], f[2*i], f[2*i+1], f[2*i+2], x_interval)
plt.plot(x_interval, y_interval,'r')
plt.fill_between(x_interval, y_interval, color='red', alpha=0.3)
plt.scatter(x, f, color='black')
plt.hlines(0, x.min(), x.max())
plt.title('Integración con la regla de Simpson')
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.show()
print(f'El resultado de la integración numérica de la función discreta')
print(f'entre x = {x[0]:.1f} y x = {x[N]:.1f} es I = {Integral:.5e}')
```
---
### Regla de Simpson para nodos no-equidistantes
Cuando los nodos de la malla de discretización de $f(x)$ no están igualmente espaciados, la regla de Simpson debe modificarse en la forma
\begin{equation}
I = \int_a^b f(x) dx \approx \sum_{i=0}^{\frac{N-1}{2}} \left[ \alpha f(x_{2i}) + \beta f(x_{2i+1}) +\gamma f(x_{2i+2}) \right]
\end{equation}
donde
\begin{align}
\alpha = &\frac{-h_{2i+1}^2 + h_{2i+1} h_{2i} + 2 h_{2i}^2}{6 h_{2i}} \\
\beta = &\frac{ (h_{2i+1} + h_{2i})^3 }{6 h_{2i+1} h_{2i}} \\
\gamma =& \frac{2 h_{2i+1}^2 + h_{2i+1} h_{2i} - h_{2i}^2}{6 h_{2i+1}}
\end{align}
y $h_j = x_{j+1} - x_j$.
---
## Factor de (Auto-)Convergencia para la Regla de Simpson
Para comprobar la precisión del Método de Integración de Simpson, calculamos el factor de auto-convergencia al integrar la función $\sin x$ en el intervalo $0\leq x \leq 2\pi$.
```
import numpy as np
import matplotlib.pyplot as plt
def intsin(n):
x = np.linspace(0, 2*np.pi, n)
f = np.sin(x)
dx = x[1] - x[0]
N = n-1 # Number of intervals
# Numerical integration loop
Integral = 0.
for i in range(int((N-1)/2)):
Integral = Integral + dx*(f[2*i] + 4*f[2*i+1] + f[2*i+2])/3
return Integral
n=1000
y = intsin(n)
print(f'El resultado de la integración numérica con n = {n:.0f} es I = {y:.5f}')
y_1 = intsin(100)
y_2 = intsin(1000)
y_3 = intsin(10000)
C_self = np.abs(y_3 - y_2)/np.abs(y_2 - y_1)
print(f'el factor de convergencia es C = {C_self:.2f}')
print(f'que corresponde a una precision de h^{-np.log10(C_self):.1f}')
```
Recuerde que en la regla de Simpson, el orden de precisión llega hasta
\begin{equation}
\mathcal{O} \left( f''' \Delta x^4\right) \sim \Delta x^2
\end{equation}
debido a que $f''' \sim \Delta x^{-2}$
| true |
code
| 0.438665 | null | null | null | null |
|
# Experiment 02: Study performance stability over time
Study how well models trained on images from early dates perform at test time on images from later dates. This is meant to investigate how stable model performance is over time, as news rooms' image publishing pipelines (possibly) evolve.
For each source, sort the images chronologically by the news article date, then split the images into a training subset (with images from early dates), and a test set (with images from later dates.)
Then train models using the images from early dates, and then test the models on images from late dates.
Only include QM features since they greatly outperformed CL features. Only Study Naive Bayes model here, so the focus is on the effect of time, not the effect of the model (and since NB was a top performing model.)
```
%matplotlib widget
%load_ext autoreload
%autoreload 2
import os
import sys
import subprocess
import random
import pickle
import numpy as np
import pandas as pd
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
# from tqdm.autonotebook import tqdm
from tqdm.notebook import tqdm
import uncertainties
from image_compression_attribution.common.code.models import quant_matrices, compr_levels
from image_compression_attribution.common.code.summarize_quant_matrices import summarize_compression_features
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
pd.set_option('display.width', 500)
pd.set_option('display.max_colwidth', 500)
from sklearn.metrics import make_scorer, roc_curve
from scipy.optimize import brentq
from scipy.interpolate import interp1d
#WARNING: this method does not seem to work well when there are large gaps
#in the ROC curve. Hence, only use this if you have interpolated between
#ROC curve data points to fill in the roc curve on a grid with small intervals.
#https://github.com/scikit-learn/scikit-learn/issues/15247#issuecomment-542138349
def calculate_eer(fpr, tpr):
'''
Returns the equal error rate for a binary classifier output.
'''
eer = brentq(lambda x : 1. - x - interp1d(fpr, tpr)(x), 0., 1.)
return eer
#---------------------------------------------------------------
#Code to combine mean value and uncertainty estimate into
#one formatted string, like 3.14 +/- .02 becomes "3.14(2)"
import string
class ShorthandFormatter(string.Formatter):
"""https://pythonhosted.org/uncertainties/user_guide.html"""
def format_field(self, value, format_spec):
if isinstance(value, uncertainties.UFloat):
return value.format(format_spec+'S') # Shorthand option added
# Special formatting for other types can be added here (floats, etc.)
else:
# Usual formatting:
return super(ShorthandFormatter, self).format_field(
value, format_spec)
def uncertainty_format_arrays(mean_vals, uncertainty_vals):
frmtr_uncertainty = ShorthandFormatter()
vals_formatted = []
for mean, uncert in zip(mean_vals, uncertainty_vals):
number = uncertainties.ufloat(mean, uncert)
str_formatted = frmtr_uncertainty.format("{0:.1u}", number)
vals_formatted.append(str_formatted)
return vals_formatted
RND_SEED=1234
np.random.seed(RND_SEED)
SUMMARY_FILE = "/app/dataset/data.csv"
RESULTS_FOLDER = "results/exp_02"
os.makedirs(RESULTS_FOLDER, exist_ok=True)
df = pd.read_csv(SUMMARY_FILE)
#We'll work with timestamps, so need to convert to a datetime for ease of use
df['timestamp'] = pd.to_datetime(df['timestamp'], utc=True)
#Drop non-image files, e.g. html files returned
#due to download errors
df, df_dropped = df[ df['mime'].str.startswith('image') ].reset_index(drop=True), \
df[ ~df['mime'].str.startswith('image') ].reset_index(drop=True)
sources = sorted(list(df['source'].unique()))
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, auc
from sklearn.ensemble import IsolationForest
#Guide to LabelEncoder:
#https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.LabelEncoder.html
#create numerical class labels for quantization categorical names (suitable for
#use as ML training feature vector)
le_qs = preprocessing.LabelEncoder()
le_qs.fit(df['q_name'])
df['q_name_class'] = le_qs.transform(df['q_name'])
sources = sorted(list(df['source'].unique()))
le_sources = preprocessing.LabelEncoder()
le_sources.fit(sources)
df['source_class'] = le_sources.transform(df['source'])
df
df.groupby('source')['timestamp'].min()
df.groupby('source')['timestamp'].max()
timespan = df.groupby('source')['timestamp'].max() - df.groupby('source')['timestamp'].min()
timespan_list = timespan.tolist()
timespan_list2 = [(x.days + x.seconds/86400.0)/365.2425 for x in timespan_list]
timespan_years = pd.Series(timespan_list2, index=sources)
print("mean timespan = {:.1f} years".format(timespan_years.mean()))
with open(os.path.join(RESULTS_FOLDER,"timespan_years_mean.txt"),"w") as file1:
file1.write("{:.1f}".format(timespan_years.mean()))
print("min timespan = {:.2f} years".format(timespan_years.min()))
with open(os.path.join(RESULTS_FOLDER,"timespan_years_min.txt"),"w") as file1:
file1.write("{:.2f}".format(timespan_years.min()))
print("max timespan = {:.1f} years".format(timespan_years.max()))
with open(os.path.join(RESULTS_FOLDER,"timespan_years_max.txt"),"w") as file1:
file1.write("{:.1f}".format(timespan_years.max()))
timespan_years
```
## Comment:
We see that for most sources we have images across large time spans, which is desireable for these experiments; the average time span is over 10 years, and the timespans range from 0.89 years to 21.4 years
## Method:
Note: date ranges of different sources may not overlap. So instead of picking 1 cutoff date to be shared for all sources, we will instead have a separate cutoff date for each source, to split each source into two parts. Put another way, sort articles from each source by date, and within a source, split the articles into two parts: before and after the date cutoff.
1. All articles (from each source) from before the cutoff date form the train set -- the first 60% of articles.
1. Then form the test set:
1. Select all articles from a source after the cutoff date -- last 40% of articles.
1. Randomly sample an equal number of articles from the remaining sources, also after each's cutoff date.
1. Combine them to form the test set.
1. Since the composition of the test set varies, repeat this 5x to quantify uncertainty.
First do some precomputation: For each source, sort the articles by date, then split articles from each source into an early portion and later portion. Early portions can be used for training, later portions can be used for testing.
```
PERCENT_TEST = 0.40
df_articles = df[['articleHash', 'timestamp', 'source', 'source_class']].drop_duplicates()
articles_predate = {}
articles_postdate = {}
for source in sources:
#get all articles from the source, sorted by date
df_articles_from_source = df_articles[df_articles['source']==source].sort_values(by="timestamp")
num_test_articles_from_source = int(PERCENT_TEST*len(df_articles_from_source))
num_train_articles_from_source = len(df_articles_from_source) - num_test_articles_from_source
df_art_from_source_predate = df_articles_from_source.iloc[0:num_train_articles_from_source,:]
df_art_from_source_postdate = df_articles_from_source.iloc[num_train_articles_from_source:,:]
articles_predate[source] = df_art_from_source_predate
articles_postdate[source] = df_art_from_source_postdate
#Prepare Train and Test Split.
all_q_name_vals = sorted(df['q_name'].unique())
#Sample from articles (so we can keep images from articles grouped together)
df_articles = df[['articleHash', 'timestamp', 'source', 'source_class']].drop_duplicates()
NUM_TRIALS = 5
results_per_trial_qm = {}
for trial in tqdm(range(NUM_TRIALS)):
numsamples_balanced_testset=[]
AUCs_qm = []
results_qm={}
for source in sources:
remaining_sources = [s for s in sources if s != source]
#-----------------------------------
#Form train/test data split. Train set first:
#All articles (from every source) from before their cutoff date form the train set
df_train_articles = None
for src in sources:
if df_train_articles is None:
df_train_articles = articles_predate[src]
else:
df_train_articles = pd.concat([df_train_articles, articles_predate[src] ])
#----------------------
#Test set:
#All articles from a source after its cutoff date contributes to test set:
df_articles_test_from_source = articles_postdate[source]
num_test_articles_from_source = len(df_articles_test_from_source)
#-------
#collect all articles not from remaining sources from after their cutoff dates
df_articles_postdate_not_from_source = None
for src in remaining_sources:
if df_articles_postdate_not_from_source is None:
df_articles_postdate_not_from_source = articles_postdate[src]
else:
df_articles_postdate_not_from_source = pd.concat([df_articles_postdate_not_from_source, articles_postdate[src] ])
#Randomly sample an equal number of articles from the remaining sources, after their cutoff dates.
num_test_articles_not_from_source = num_test_articles_from_source
df_articles_test_not_from_source = df_articles_postdate_not_from_source.sample(num_test_articles_not_from_source)
#------
#combine to build the test set
df_test_articles = pd.concat([df_articles_test_from_source, df_articles_test_not_from_source])
#----------------------
#Get all images articles in train/test splits:
df_train = df[ df['articleHash'].isin(df_train_articles['articleHash']) ].reset_index()
df_test = df[ df['articleHash'].isin(df_test_articles['articleHash']) ].reset_index()
#Set ground truth label: 1 if image misattributed, else 0
df_test['is_misattributed'] = np.array(df_test['source']!=source, dtype=int)
#-----------------------------------
#Fit models
#quantization matrices
qm_model = quant_matrices.attribution_quant_matrices()
qm_model.fit(df_train[['source', 'q_name']], compr_category_names=all_q_name_vals)
#-----------------------------------
#prediction on test set
claimed_source_list = [source]*len(df_test)
LLRs_isfake_qm, probs_fromsource_qm, probs_notfromsource_qm, \
unrecognized_sources_qm = qm_model.predict(df_test['q_name'], claimed_source_list)
df_test['LLR_qm'] = LLRs_isfake_qm
#Determine if prediction is wrong
misclassified_qm = (df_test['is_misattributed'] - .5) * LLRs_isfake_qm < 0
df_test['misclassified_qm'] = misclassified_qm
#-----------------------------------
#Use hypothesis test score to compute ROC curve for this source:
numsamples_balanced_testset.append(len(df_test))
fpr, tpr, thresholds = roc_curve(df_test['is_misattributed'], df_test['LLR_qm'], pos_label=1)
roc_auc = auc(fpr, tpr)
AUCs_qm.append(roc_auc)
results_qm[source] = {'source': source, 'fpr': fpr, 'tpr':tpr,
'auc':roc_auc, 'numsamples':len(df_test),
'scores_isfake': df_test['LLR_qm'],
'label_isfake': df_test['is_misattributed'],
'df_test':df_test}
results_per_trial_qm[trial] = results_qm
```
## Summarize results
```
FPR_THRESHOLD = 0.005 # compute TPR @ this FPR = 0.5%
AUCs_mean_cl = []
AUCs_std_cl = []
tpr_at_fpr_mean_cl = []
AUCs_mean_qm = []
AUCs_std_qm = []
tpr_at_fpr_mean_qm = []
#quantization matrices qm
for source in sources:
AUCs_per_trial = []
tpr_per_trial = []
fpr_per_trial = []
tprs_at_fpr_threshold = []
for trial in range(NUM_TRIALS):
AUCs_per_trial.append(results_per_trial_qm[trial][source]['auc'])
fpr = results_per_trial_qm[trial][source]['fpr']
tpr = results_per_trial_qm[trial][source]['tpr']
fpr_per_trial.append(fpr)
tpr_per_trial.append(tpr)
tprs_at_fpr_threshold.append( np.interp(FPR_THRESHOLD, fpr, tpr) )
AUCs_mean_qm.append(np.mean(AUCs_per_trial))
AUCs_std_qm.append(np.std(AUCs_per_trial))
tpr_at_fpr_mean_qm.append(np.mean(tprs_at_fpr_threshold))
df_summary = pd.DataFrame({'source':sources, 'test_size':numsamples_balanced_testset,
'AUC_mean_qm':AUCs_mean_qm, 'AUC_std_qm':AUCs_std_qm,
'tpr_at_fpr_mean_qm':tpr_at_fpr_mean_qm,
} )
df_summary['AUC_formatted_qm'] = uncertainty_format_arrays(df_summary['AUC_mean_qm'], df_summary['AUC_std_qm'])
df_summary
```
# Plot multiple ROC curves on one graph with uncertainty bands
```
EERs_mean_qm = []
#------------
#New-EER
EERs_all_qm = []
EERs_std_qm = []
#------------
plt.figure(figsize=(6,5))
plt.plot([0, 1], [0, 1], color="black", linestyle="--")
plt.plot(np.linspace(0,1,100), 1-np.linspace(0,1,100), color="red", linestyle="--")
interp_fpr = np.linspace(0, 1, 1000)
for source in sources[0:15]:
#New-EER
EERs_per_src_qm = []
interp_tprs = []
#interpolate between fpr,tpr datapoints to compute tpr at regular fpr intervals
for trial in range(NUM_TRIALS):
fpr = results_per_trial_qm[trial][source]['fpr']
tpr = results_per_trial_qm[trial][source]['tpr']
interp_tpr = np.interp(interp_fpr, fpr, tpr)
interp_tpr[0] = 0.0
interp_tprs.append(interp_tpr)
#------------
#New-EER
EERs_per_src_qm.append(calculate_eer(interp_fpr, interp_tpr)) #get EERs across all trials for this source
EERs_std_qm.append( np.std(EERs_per_src_qm) ) #gives a std of EER for each source, across all 5 trials
EERs_all_qm.append(EERs_per_src_qm) #all data: first index gives src, second index gives trial
#------------
mean_tpr = np.mean(interp_tprs, axis=0)
mean_tpr[-1] = 1.0
EERs_mean_qm.append(calculate_eer(interp_fpr, mean_tpr))
std_tpr = np.std(interp_tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
plt.plot(interp_fpr, mean_tpr, linestyle="-", label=source)
plt.fill_between(interp_fpr, tprs_lower, tprs_upper, color='grey', alpha=.2)
auc_mean = float(df_summary.loc[df_summary['source']==source, 'AUC_mean_qm'])
auc_std = float(df_summary.loc[ df_summary['source']==source, 'AUC_std_qm'])
tpr_at_fpr_mean = float(df_summary.loc[ df_summary['source']==source, 'tpr_at_fpr_mean_qm'])
numsamples = int(df_summary.loc[ df_summary['source']==source, 'test_size'])
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.legend()
plt.title("Verification: Time shift (part 1)")
plt.tight_layout()
plt.show()
#uncomment to save:
plt.savefig(os.path.join(RESULTS_FOLDER,"roc_curves_all_curves1.pdf"), bbox_inches='tight')
plt.figure(figsize=(6,5))
plt.plot([0, 1], [0, 1], color="black", linestyle="--")
plt.plot(np.linspace(0,1,100), 1-np.linspace(0,1,100), color="red", linestyle="--")
interp_fpr = np.linspace(0, 1, 1000)
for source in sources[15:]:
#New-EER
EERs_per_src_qm = []
interp_tprs = []
#interpolate between fpr,tpr datapoints to compute tpr at regular fpr intervals
for trial in range(NUM_TRIALS):
fpr = results_per_trial_qm[trial][source]['fpr']
tpr = results_per_trial_qm[trial][source]['tpr']
interp_tpr = np.interp(interp_fpr, fpr, tpr)
interp_tpr[0] = 0.0
interp_tprs.append(interp_tpr)
#------------
#New-EER
EERs_per_src_qm.append(calculate_eer(interp_fpr, interp_tpr)) #get EERs across all trials for this source
EERs_std_qm.append( np.std(EERs_per_src_qm) ) #gives a std of EER for each source, across all 5 trials
EERs_all_qm.append(EERs_per_src_qm) #all data: first index gives src, second index gives trial
#------------
mean_tpr = np.mean(interp_tprs, axis=0)
mean_tpr[-1] = 1.0
EERs_mean_qm.append(calculate_eer(interp_fpr, mean_tpr))
std_tpr = np.std(interp_tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
plt.plot(interp_fpr, mean_tpr, linestyle="-", label=source)
plt.fill_between(interp_fpr, tprs_lower, tprs_upper, color='grey', alpha=.2)
auc_mean = float(df_summary.loc[df_summary['source']==source, 'AUC_mean_qm'])
auc_std = float(df_summary.loc[ df_summary['source']==source, 'AUC_std_qm'])
tpr_at_fpr_mean = float(df_summary.loc[ df_summary['source']==source, 'tpr_at_fpr_mean_qm'])
numsamples = int(df_summary.loc[ df_summary['source']==source, 'test_size'])
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.legend()
plt.title("Verification: Time shift (part 2)")
plt.tight_layout()
plt.show()
#uncomment to save:
plt.savefig(os.path.join(RESULTS_FOLDER,"roc_curves_all_curves2.pdf"), bbox_inches='tight')
df_summary['EER_mean_qm'] = EERs_mean_qm
#New-EER
df_summary['EER_std_qm'] = EERs_std_qm
df_latex = df_summary[['source', 'test_size', 'AUC_formatted_qm', 'tpr_at_fpr_mean_qm', 'EER_mean_qm']]
df_latex.columns=['source', 'test size', 'AUC', 'tpr@fpr', 'EER']
df_latex
# 3 sig figs use '%.3g'; 3 digits use '%.3f'
latex_table = df_latex.to_latex(index=False, float_format='%.3g')
with open(os.path.join(RESULTS_FOLDER,"table1.tex"),"w") as file1:
file1.write(latex_table)
df_metricplot = df_summary.sort_values(by='AUC_mean_qm', ascending=False).reset_index(drop=True)
sources_metricplot = list(df_metricplot['source'])
AUCs_metricplot = list(df_metricplot['AUC_mean_qm'])
# plt.figure(figsize=(6,3.5))
plt.figure(figsize=(6,2.6))
x_vals = [i for i,_ in enumerate(sources_metricplot)]
# plt.plot(x_vals, df_metricplot['EER_mean_qm'], linestyle='--', marker='.', label="EER", color="tab:blue")
plt.errorbar(x_vals, df_metricplot['EER_mean_qm'], yerr=df_metricplot['EER_std_qm'], fmt=".", linestyle="--",
label="EER", color="tab:blue", mfc="tab:blue", mec='tab:blue', ecolor="tab:blue", capsize=2)
plt.errorbar(x_vals, AUCs_metricplot, yerr=df_metricplot['AUC_std_qm'], fmt=".", linestyle="--",
label="AUC", color="tab:orange", mfc="tab:orange", mec='tab:orange', ecolor="tab:orange", capsize=2)
plt.xticks(x_vals, sources_metricplot, rotation=90)
handles, labels = plt.gca().get_legend_handles_labels()
handles = [handles[1], handles[0]]
labels = [labels[1], labels[0]]
plt.legend(handles, labels, loc="center left")
plt.title("Verification metrics: Time generalization")
# plt.tight_layout()
plt.yticks(np.arange(0.0, 1.2, 0.2))
plt.show()
#uncomment to save:
plt.savefig(os.path.join(RESULTS_FOLDER,"verification_metrics_plot.pdf"), bbox_inches='tight')
df_summary[['source', 'AUC_mean_qm']]
```
### Save results used to make the figure, so I can add the curves to plots made in exp 01 code (to combine figs from experiments 1 and 2)
```
df_metricplot.to_csv(os.path.join(RESULTS_FOLDER,"exp_02_metrics_plot_data.csv"), index=False)
```
| true |
code
| 0.609292 | null | null | null | null |
|
# RNN and LSTM Assignment
<img src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/3c/Chimpanzee_seated_at_typewriter.jpg/603px-Chimpanzee_seated_at_typewriter.jpg" width=400px>
It is said that [infinite monkeys typing for an infinite amount of time](https://en.wikipedia.org/wiki/Infinite_monkey_theorem) will eventually type, among other things, the complete works of Wiliam Shakespeare. Let's see if we can get there a bit faster, with the power of Recurrent Neural Networks and LSTM.
This text file contains the complete works of Shakespeare: https://www.gutenberg.org/files/100/100-0.txt
Use it as training data for an RNN - you can keep it simple and train character level, and that is suggested as an initial approach.
Then, use that trained RNN to generate Shakespearean-ish text. Your goal - a function that can take, as an argument, the size of text (e.g. number of characters or lines) to generate, and returns generated text of that size.
Note - Shakespeare wrote an awful lot. It's OK, especially initially, to sample/use smaller data and parameters, so you can have a tighter feedback loop when you're trying to get things running. Then, once you've got a proof of concept - start pushing it more!
## Stretch goals:
- Refine the training and generation of text to be able to ask for different genres/styles of Shakespearean text (e.g. plays versus sonnets)
- Train a classification model that takes text and returns which work of Shakespeare it is most likely to be from
- Make it more performant! Many possible routes here - lean on Keras, optimize the code, and/or use more resources (AWS, etc.)
- Revisit the news example from class, and improve it - use categories or tags to refine the model/generation, or train a news classifier
- Run on bigger, better data
```
import numpy as np
class RNN_NLP_Generator(object):
"""RNN with one hidden layer"""
def __init__(self):
pass
def forward_prop(self, inputs, targets, h_prev):
xs, hs, ys, ps = {}, {}, {}, {}
hs[-1] = np.copy(h_prev)
loss = 0
for t in range(len(inputs)): # t is a "time step" and is used as a dict key
xs[t] = np.zeros((self.num_chars,1))
xs[t][inputs[t]] = 1
hs[t] = np.tanh(np.dot(self.W_xh, xs[t]) + np.dot(self.W_hh, hs[t-1]) + self.b_h)
ys[t] = np.dot(self.W_hy, hs[t]) + self.b_y # unnormalized log probabilities for next chars
ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars.
# Softmax
loss += -np.log(ps[t][targets[t],0]) # softmax (cross-entropy loss). Efficient and simple code
return loss, ps, hs, xs
def backward_prop(self, ps, inputs, hs, xs, targets):
# make all zero matrices
dWxh, dWhh, dWhy, dbh, dby, dhnext = \
[np.zeros_like(_) for _ in [self.W_xh, self.W_hh, self.W_hy,
self.b_h, self.b_y, hs[0]]]
# reversed
for t in reversed(range(len(inputs))):
dy = np.copy(ps[t]) # shape (num_chars,1). "dy" means "dloss/dy"
dy[targets[t]] -= 1 # backprop into y. After taking the soft max in the input vector, subtract 1 from the value of the element corresponding to the correct label.
dWhy += np.dot(dy, hs[t].T)
dby += dy
dh = np.dot(self.W_hy.T, dy) + dhnext # backprop into h.
dhraw = (1 - hs[t] * hs[t]) * dh # backprop through tanh nonlinearity #tanh'(x) = 1-tanh^2(x)
dbh += dhraw
dWxh += np.dot(dhraw, xs[t].T)
dWhh += np.dot(dhraw, hs[t-1].T)
dhnext = np.dot(self.W_hh.T, dhraw)
for dparam in [dWxh, dWhh, dWhy, dbh, dby]:
np.clip(dparam, -5, 5, out=dparam) # clip to mitigate exploding gradients
return dWxh, dWhh, dWhy, dbh, dby
def train(self, article_text, hidden_size=500, n_iterations=1000, sequence_length=40, learning_rate=1e-1):
self.article_text = article_text
self.hidden_size = hidden_size
chars = list(set(article_text))
self.num_chars = len(chars)
self.char_to_int = {c: i for i, c in enumerate(chars)}
self.int_to_char = {i: c for i, c in enumerate(chars)}
# original text encoded as integers, what we pass into our model
self.integer_encoded = [self.char_to_int[i] for i in article_text]
# Weights
self.W_xh = np.random.randn(hidden_size, self.num_chars) * 0.01
self.W_hh = np.random.randn(hidden_size, hidden_size) * 0.01
self.W_hy = np.random.randn(self.num_chars, hidden_size) * 0.01
# biases
self.b_h = np.zeros((hidden_size, 1))
self.b_y = np.zeros((self.num_chars, 1))
# previous state
self.h_prev = np.zeros((hidden_size, 1)) # h_(t-1)
batch_size = round((len(article_text) / sequence_length) + 0.5) # math.ceil
data_pointer = 0
# memory variables for Adagrad
mWxh, mWhh, mWhy, mbh, mby = \
[np.zeros_like(_) for _ in [self.W_xh, self.W_hh, self.W_hy,
self.b_h, self.b_y]]
for i in range(n_iterations):
h_prev = np.zeros((hidden_size, 1)) # reset RNN memory
data_pointer = 0 # go from start of data
for b in range(batch_size):
inputs = [self.char_to_int[ch]
for ch in self.article_text[data_pointer:data_pointer+sequence_length]]
targets = [self.char_to_int[ch]
for ch in self.article_text[data_pointer+1:data_pointer+sequence_length+1]] # t+1
if (data_pointer+sequence_length+1 >= len(self.article_text) and b == batch_size-1): # processing of the last part of the input data.
targets.append(self.char_to_int[" "]) # When the data doesn't fit, add space(" ") to the back.
loss, ps, hs, xs = self.forward_prop(inputs, targets, h_prev)
dWxh, dWhh, dWhy, dbh, dby = self.backward_prop(ps, inputs, hs, xs, targets)
# perform parameter update with Adagrad
for param, dparam, mem in zip([self.W_xh, self.W_hh, self.W_hy,
self.b_h, self.b_y],
[dWxh, dWhh, dWhy, dbh, dby],
[mWxh, mWhh, mWhy, mbh, mby]):
mem += dparam * dparam # elementwise
param += -learning_rate * dparam / np.sqrt(mem + 1e-8) # adagrad update
data_pointer += sequence_length # move data pointer
if i % 100 == 0:
print ('iter %d, loss: %f' % (i, loss)) # print progress
def predict(self, test_char, length):
x = np.zeros((self.num_chars, 1))
x[self.char_to_int[test_char]] = 1
ixes = []
h = np.zeros((self.hidden_size, 1))
for t in range(length):
h = np.tanh(np.dot(self.W_xh, x) + np.dot(self.W_hh, h) + self.b_h)
y = np.dot(self.W_hy, h) + self.b_y
p = np.exp(y) / np.sum(np.exp(y))
ix = np.random.choice(range(self.num_chars), p=p.ravel()) # ravel -> rank0
# "ix" is a list of indexes selected according to the soft max probability.
x = np.zeros((self.num_chars, 1)) # init
x[ix] = 1
ixes.append(ix) # list
txt = test_char + ''.join(self.int_to_char[i] for i in ixes)
return txt
import requests
url = 'https://www.gutenberg.org/files/100/100-0.txt'
r = requests.get(url)
# subsample
start_i = 2965 # index of first text, THE SONNETS
length = 4000
article_text = r.text[start_i:start_i+length]
article_text = ' '.join(article_text.split())
model = RNN_NLP_Generator()
model.train(article_text)
model.predict(test_char='T', length=100)
```
| true |
code
| 0.673272 | null | null | null | null |
|
Deep Learning
=============
Assignment 3
------------
Previously in `2_fullyconnected.ipynb`, you trained a logistic regression and a neural network model.
The goal of this assignment is to explore regularization techniques.
```
# These are all the modules we'll be using later. Make sure you can import them
# before proceeding further.
from __future__ import print_function
import numpy as np
import tensorflow as tf
from six.moves import cPickle as pickle
```
First reload the data we generated in _notmist.ipynb_.
```
pickle_file = 'notMNIST.pickle'
with open(pickle_file, 'rb') as f:
save = pickle.load(f)
train_dataset = save['train_dataset']
train_labels = save['train_labels']
valid_dataset = save['valid_dataset']
valid_labels = save['valid_labels']
test_dataset = save['test_dataset']
test_labels = save['test_labels']
del save # hint to help gc free up memory
print('Training set', train_dataset.shape, train_labels.shape)
print('Validation set', valid_dataset.shape, valid_labels.shape)
print('Test set', test_dataset.shape, test_labels.shape)
```
Reformat into a shape that's more adapted to the models we're going to train:
- data as a flat matrix,
- labels as float 1-hot encodings.
```
image_size = 28
num_labels = 10
def reformat(dataset, labels):
dataset = dataset.reshape((-1, image_size * image_size)).astype(np.float32)
# Map 1 to [0.0, 1.0, 0.0 ...], 2 to [0.0, 0.0, 1.0 ...]
labels = (np.arange(num_labels) == labels[:,None]).astype(np.float32)
return dataset, labels
train_dataset, train_labels = reformat(train_dataset, train_labels)
valid_dataset, valid_labels = reformat(valid_dataset, valid_labels)
test_dataset, test_labels = reformat(test_dataset, test_labels)
print('Training set', train_dataset.shape, train_labels.shape)
print('Validation set', valid_dataset.shape, valid_labels.shape)
print('Test set', test_dataset.shape, test_labels.shape)
def accuracy(predictions, labels):
return (100.0 * np.sum(np.argmax(predictions, 1) == np.argmax(labels, 1))
/ predictions.shape[0])
```
---
Problem 1
---------
Introduce and tune L2 regularization for both logistic and neural network models. Remember that L2 amounts to adding a penalty on the norm of the weights to the loss. In TensorFlow, you can compute the L2 loss for a tensor `t` using `nn.l2_loss(t)`. The right amount of regularization should improve your validation / test accuracy.
---
First multinomial logistic regression
```
batch_size = 128
graph = tf.Graph()
with graph.as_default():
# Input data. For the training data, we use a placeholder that will be fed
# at run time with a training minibatch.
tf_train_dataset = tf.placeholder(tf.float32,
shape=(batch_size, image_size * image_size))
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels))
tf_valid_dataset = tf.constant(valid_dataset)
tf_test_dataset = tf.constant(test_dataset)
regularization_factor = tf.placeholder(tf.float32)
# Variables.
weights = tf.Variable(
tf.truncated_normal([image_size * image_size, num_labels]))
biases = tf.Variable(tf.zeros([num_labels]))
# Training computation.
logits = tf.matmul(tf_train_dataset, weights) + biases
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels)) + regularization_factor * tf.nn.l2_loss(weights)
# Optimizer.
optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
# Predictions for the training, validation, and test data.
train_prediction = tf.nn.softmax(logits)
valid_prediction = tf.nn.softmax(
tf.matmul(tf_valid_dataset, weights) + biases)
test_prediction = tf.nn.softmax(tf.matmul(tf_test_dataset, weights) + biases)
```
Lets'run it:
```
num_steps = 3001
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized")
for step in range(num_steps):
# Pick an offset within the training data, which has been randomized.
# Note: we could use better randomization across epochs.
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
# Generate a minibatch.
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
# Prepare a dictionary telling the session where to feed the minibatch.
# The key of the dictionary is the placeholder node of the graph to be fed,
# and the value is the numpy array to feed to it.
feed_dict = {tf_train_dataset : batch_data, tf_train_labels : batch_labels, regularization_factor: 1e-3}
_, l, predictions = session.run(
[optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 500 == 0):
print("Minibatch loss at step %d: %f" % (step, l))
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(
valid_prediction.eval(), valid_labels))
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
```
1-layer neural network model
```
batch_size = 128
num_hidden_nodes = 1024
graph = tf.Graph()
with graph.as_default():
# Input batches as placeholder.
tf_train_dataset = tf.placeholder(tf.float32, shape=(batch_size, image_size * image_size)) # 128, 784
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels)) # 128, 10
tf_valid_dataset = tf.constant(valid_dataset) # 10000, 784
tf_test_dataset = tf.constant(test_dataset) # 10000, 784
regularization_factor = tf.placeholder(tf.float32)
# Input variables
W_1 = tf.Variable(tf.truncated_normal([image_size * image_size, num_hidden_nodes])) # 784, 1024
b_1 = tf.Variable(tf.zeros([num_hidden_nodes])) # 1024
# first layer
h_1 = tf.nn.relu(tf.matmul(tf_train_dataset, W_1) + b_1)
# Training computation
W_2 = tf.Variable(tf.truncated_normal([num_hidden_nodes, num_labels])) # 1024, 10
b_2 = tf.Variable(tf.zeros([num_labels])) # 10
logits = tf.matmul(h_1, W_2) + b_2
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels)) + regularization_factor * (tf.nn.l2_loss(W_1) + tf.nn.l2_loss(W_2))
# optimizer
optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
# Predictions
train_prediction = tf.nn.softmax(logits)
valid_fw_pass_1 = tf.nn.relu(tf.matmul(tf_valid_dataset, W_1) + b_1) # First layer forward pass for validation
valid_prediction = tf.nn.softmax(tf.matmul(valid_fw_pass_1, W_2) + b_2) # Softmax for validation
test_fw_pass_1 = tf.nn.relu(tf.matmul(tf_test_dataset, W_1) + b_1)
test_prediction = tf.nn.softmax(tf.matmul(test_fw_pass_1, W_2) + b_2)
```
let's run it:
```
num_steps = 3001
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized")
for step in range(num_steps):
# Minibatches
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
feed_dict = {tf_train_dataset: batch_data, tf_train_labels: batch_labels, regularization_factor: 1e-3}
_, l, predictions = session.run([optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 500 == 0):
print("Minibatch loss at step %d: %f" % (step, l))
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(valid_prediction.eval(), valid_labels))
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
```
Let's try to tune regularization factor
```
num_steps = 3001
regularization = [pow(10, i) for i in np.arange(-4,-1,0.3)]
test_accuracies = []
for beta in regularization:
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized for regularization: %.4f" % beta)
for step in range(num_steps):
# Minibatches
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
feed_dict = {tf_train_dataset: batch_data, tf_train_labels: batch_labels, regularization_factor: beta}
_, l, predictions = session.run([optimizer, loss, train_prediction], feed_dict=feed_dict)
test_accuracies.append(accuracy(test_prediction.eval(), test_labels))
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(regularization,test_accuracies)
plt.xscale('log', linthreshx=0.001)
plt.ylabel('Test accuracy')
plt.xlabel('Regularization factor')
plt.grid(True)
plt.show()
```
---
Problem 2
---------
Let's demonstrate an extreme case of overfitting. Restrict your training data to just a few batches. What happens?
---
```
batch_size = 128
num_hidden_nodes = 1024
graph = tf.Graph()
with graph.as_default():
# Input batches as placeholder.
tf_train_dataset = tf.placeholder(tf.float32, shape=(batch_size, image_size * image_size)) # 128, 784
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels)) # 128, 10
tf_valid_dataset = tf.constant(valid_dataset) # 10000, 784
tf_test_dataset = tf.constant(test_dataset) # 10000, 784
regularization_factor = tf.placeholder(tf.float32)
# Input variables
W_1 = tf.Variable(tf.truncated_normal([image_size * image_size, num_hidden_nodes])) # 784, 1024
b_1 = tf.Variable(tf.zeros([num_hidden_nodes])) # 1024
# first layer
h_1 = tf.nn.relu(tf.matmul(tf_train_dataset, W_1) + b_1)
# Training computation
W_2 = tf.Variable(tf.truncated_normal([num_hidden_nodes, num_labels])) # 1024, 10
b_2 = tf.Variable(tf.zeros([num_labels])) # 10
logits = tf.matmul(h_1, W_2) + b_2
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels)) + regularization_factor * (tf.nn.l2_loss(W_1) + tf.nn.l2_loss(W_2))
# optimizer
optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
# Predictions
train_prediction = tf.nn.softmax(logits)
valid_fw_pass_1 = tf.nn.relu(tf.matmul(tf_valid_dataset, W_1) + b_1) # First layer forward pass for validation
valid_prediction = tf.nn.softmax(tf.matmul(valid_fw_pass_1, W_2) + b_2) # Softmax for validation
test_fw_pass_1 = tf.nn.relu(tf.matmul(tf_test_dataset, W_1) + b_1)
test_prediction = tf.nn.softmax(tf.matmul(test_fw_pass_1, W_2) + b_2)
```
Let's run the 1-layer neural network
```
num_steps = 100
num_batches = 5
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized")
for step in range(num_steps):
# Minibatches
#offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
offset = step % num_batches
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
feed_dict = {tf_train_dataset: batch_data, tf_train_labels: batch_labels, regularization_factor: 1e-3}
_, l, predictions = session.run([optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 5 == 0):
print("Minibatch loss at step %d: %f" % (step, l))
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(valid_prediction.eval(), valid_labels))
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
```
Model overfits to data. Our regularization doesn't prevent it since there are too much parameters.
---
Problem 3
---------
Introduce Dropout on the hidden layer of the neural network. Remember: Dropout should only be introduced during training, not evaluation, otherwise your evaluation results would be stochastic as well. TensorFlow provides `nn.dropout()` for that, but you have to make sure it's only inserted during training.
What happens to our extreme overfitting case?
---
```
batch_size = 128
num_hidden_nodes = 1024
graph = tf.Graph()
with graph.as_default():
# Input batches as placeholder.
tf_train_dataset = tf.placeholder(tf.float32, shape=(batch_size, image_size * image_size)) # 128, 784
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels)) # 128, 10
tf_valid_dataset = tf.constant(valid_dataset) # 10000, 784
tf_test_dataset = tf.constant(test_dataset) # 10000, 784
regularization_factor = tf.placeholder(tf.float32)
# Input variables
W_1 = tf.Variable(tf.truncated_normal([image_size * image_size, num_hidden_nodes])) # 784, 1024
b_1 = tf.Variable(tf.zeros([num_hidden_nodes])) # 1024
# first layer
h_1 = tf.nn.relu(tf.matmul(tf_train_dataset, W_1) + b_1)
# Dropout
drops = tf.nn.dropout(h_1, 0.5)
# Training computation
W_2 = tf.Variable(tf.truncated_normal([num_hidden_nodes, num_labels])) # 1024, 10
b_2 = tf.Variable(tf.zeros([num_labels])) # 10
logits = tf.matmul(drops, W_2) + b_2
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels)) + regularization_factor * (tf.nn.l2_loss(W_1) + tf.nn.l2_loss(W_2))
# optimizer
optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
# Predictions
train_prediction = tf.nn.softmax(logits)
valid_fw_pass_1 = tf.nn.relu(tf.matmul(tf_valid_dataset, W_1) + b_1) # First layer forward pass for validation
valid_prediction = tf.nn.softmax(tf.matmul(valid_fw_pass_1, W_2) + b_2) # Softmax for validation
test_fw_pass_1 = tf.nn.relu(tf.matmul(tf_test_dataset, W_1) + b_1)
test_prediction = tf.nn.softmax(tf.matmul(test_fw_pass_1, W_2) + b_2)
```
Let's run it with dropout
```
num_steps = 100
num_batches = 5
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized")
for step in range(num_steps):
# Minibatches
#offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
offset = step % num_batches
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
feed_dict = {tf_train_dataset: batch_data, tf_train_labels: batch_labels, regularization_factor: 1e-3}
_, l, predictions = session.run([optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 5 == 0):
print("Minibatch loss at step %d: %f" % (step, l))
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(valid_prediction.eval(), valid_labels))
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
```
Even though training accuracy reached 100%, it improved both validation and test accuracy.
---
Problem 4
---------
Try to get the best performance you can using a multi-layer model! The best reported test accuracy using a deep network is [97.1%](http://yaroslavvb.blogspot.com/2011/09/notmnist-dataset.html?showComment=1391023266211#c8758720086795711595).
One avenue you can explore is to add multiple layers.
Another one is to use learning rate decay:
global_step = tf.Variable(0) # count the number of steps taken.
learning_rate = tf.train.exponential_decay(0.5, global_step, ...)
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
---
First let's try 1-layer-neural network with dropout and learning rate decay
```
batch_size = 128
num_hidden_nodes = 1024
graph = tf.Graph()
with graph.as_default():
# Input batches as placeholder.
tf_train_dataset = tf.placeholder(tf.float32, shape=(batch_size, image_size * image_size)) # 128, 784
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels)) # 128, 10
tf_valid_dataset = tf.constant(valid_dataset) # 10000, 784
tf_test_dataset = tf.constant(test_dataset) # 10000, 784
regularization_factor = tf.placeholder(tf.float32)
global_step = tf.Variable(0) # count the number of steps taken.
# Input variables
W_1 = tf.Variable(tf.truncated_normal([image_size * image_size, num_hidden_nodes])) # 784, 1024
b_1 = tf.Variable(tf.zeros([num_hidden_nodes])) # 1024
# first layer
h_1 = tf.nn.relu(tf.matmul(tf_train_dataset, W_1) + b_1)
# Dropout
drops = tf.nn.dropout(h_1, 0.5)
# Training computation
W_2 = tf.Variable(tf.truncated_normal([num_hidden_nodes, num_labels])) # 1024, 10
b_2 = tf.Variable(tf.zeros([num_labels])) # 10
logits = tf.matmul(drops, W_2) + b_2
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels)) + regularization_factor * (tf.nn.l2_loss(W_1) + tf.nn.l2_loss(W_2))
# optimizer
learning_rate = tf.train.exponential_decay(0.5, global_step, 1000, 0.65, staircase=True)
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
# Predictions
train_prediction = tf.nn.softmax(logits)
valid_fw_pass_1 = tf.nn.relu(tf.matmul(tf_valid_dataset, W_1) + b_1) # First layer forward pass for validation
valid_prediction = tf.nn.softmax(tf.matmul(valid_fw_pass_1, W_2) + b_2) # Softmax for validation
test_fw_pass_1 = tf.nn.relu(tf.matmul(tf_test_dataset, W_1) + b_1)
test_prediction = tf.nn.softmax(tf.matmul(test_fw_pass_1, W_2) + b_2)
```
Let's run it:
```
num_steps = 8001
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized")
for step in range(num_steps):
# Minibatches
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
feed_dict = {tf_train_dataset: batch_data, tf_train_labels: batch_labels, regularization_factor: 1e-3}
_, l, predictions = session.run([optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 500 == 0):
print("Minibatch loss at step %d: %f" % (step, l))
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(valid_prediction.eval(), valid_labels))
if (step % 1000 == 0):
print("Learning rate: %f" % learning_rate.eval())
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
```
Now, let's train 2-layer neural network with dropout and learning rate decay
```
batch_size = 128
num_hidden_nodes = 1024
graph = tf.Graph()
with graph.as_default():
# Input batches as placeholder.
tf_train_dataset = tf.placeholder(tf.float32, shape=(batch_size, image_size * image_size)) # 128, 784
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels)) # 128, 10
tf_valid_dataset = tf.constant(valid_dataset) # 10000, 784
tf_test_dataset = tf.constant(test_dataset) # 10000, 784
regularization_factor = tf.placeholder(tf.float32)
global_step = tf.Variable(0) # count the number of steps taken.
# Input variables
W_1 = tf.Variable(tf.truncated_normal([image_size * image_size, num_hidden_nodes])) # 784, 1024
b_1 = tf.Variable(tf.zeros([num_hidden_nodes])) # 1024
# first layer
h_1 = tf.nn.relu(tf.matmul(tf_train_dataset, W_1) + b_1)
# first dropout
drops_1 = tf.nn.dropout(h_1, 0.5)
# Second layer variables
W_2 = tf.Variable(tf.truncated_normal([num_hidden_nodes, num_hidden_nodes])) # 1024, 1024
b_2 = tf.Variable(tf.zeros([num_hidden_nodes])) # 1024
# Second layer
h_2 = tf.nn.relu(tf.matmul(h_1, W_2) + b_2)
# Second dropout
drops_2 = tf.nn.dropout(h_2, 0.5)
# Training computation
W_3 = tf.Variable(tf.truncated_normal([num_hidden_nodes, num_labels])) # 1024, 10
b_3 = tf.Variable(tf.zeros([num_labels])) # 10
logits = tf.matmul(h_2, W_3) + b_3
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels)) + regularization_factor * (tf.nn.l2_loss(W_1) + tf.nn.l2_loss(W_2) + tf.nn.l2_loss(W_3))
# optimizer
learning_rate = tf.train.exponential_decay(0.5, global_step, 1000, 0.65, staircase=True)
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
# Predictions
train_prediction = tf.nn.softmax(logits)
valid_fw_pass_1 = tf.nn.relu(tf.matmul(tf_valid_dataset, W_1) + b_1) # First layer forward pass for validation
valid_fw_pass_2 = tf.nn.relu(tf.matmul(valid_fw_pass_1, W_2) + b_2) # First layer forward pass for validation
valid_prediction = tf.nn.softmax(tf.matmul(valid_fw_pass_2, W_3) + b_3) # Softmax for validation
test_fw_pass_1 = tf.nn.relu(tf.matmul(tf_test_dataset, W_1) + b_1)
test_fw_pass_2 = tf.nn.relu(tf.matmul(test_fw_pass_1, W_2) + b_2)
test_prediction = tf.nn.softmax(tf.matmul(test_fw_pass_2, W_3) + b_3)
```
Let's run it
```
num_steps = 4
w_init = []
w_trained = []
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized")
w_init.append(W_1.eval().flatten())
w_init.append(W_2.eval().flatten())
w_init.append(W_3.eval().flatten())
for step in range(num_steps):
# Minibatches
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
feed_dict = {tf_train_dataset: batch_data, tf_train_labels: batch_labels, regularization_factor: 1e-3}
_, l, predictions = session.run([optimizer, loss, train_prediction], feed_dict=feed_dict)
print("Minibatch loss at step %d: %f" % (step, l))
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(valid_prediction.eval(), valid_labels))
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
w_trained.append(W_1.eval().flatten())
w_trained.append(W_2.eval().flatten())
w_trained.append(W_3.eval().flatten())
fig, axes = plt.subplots(2, 3, figsize=(10, 4))
axes = axes.ravel()
for idx, ax in enumerate(axes):
if idx <= 2:
ax.hist(w_init[idx], bins=100)
ax.set_title("Initialized Weights-%s" % str(idx+1))
else:
ax.hist(w_trained[idx-3], bins=100)
ax.set_title("Learned Weights-%s" % str(idx-2))
ax.set_xlabel("Values")
ax.set_ylabel("Frequency")
fig.tight_layout()
```
Our weights initialization is not good enough. The problem is that the distribution of the outputs from a randomly initialized neuron has a variance that grows with the number of inputs.
A more recent paper on this topic, Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification by He et al., derives an initialization specifically for ReLU neurons, reaching the conclusion that the variance of neurons in the network should be 2.0/n. This gives the initialization w = np.random.randn(n) * sqrt(2.0/n), and is the current recommendation for use in practice in the specific case of neural networks with ReLU neurons.
Let's change it:
```
batch_size = 128
num_hidden_nodes = 1024
graph = tf.Graph()
with graph.as_default():
# Input batches as placeholder.
tf_train_dataset = tf.placeholder(tf.float32, shape=(batch_size, image_size * image_size)) # 128, 784
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels)) # 128, 10
tf_valid_dataset = tf.constant(valid_dataset) # 10000, 784
tf_test_dataset = tf.constant(test_dataset) # 10000, 784
regularization_factor = tf.placeholder(tf.float32)
global_step = tf.Variable(0) # count the number of steps taken.
# Input variables
W_1 = tf.Variable(tf.truncated_normal([image_size * image_size, num_hidden_nodes], stddev=np.sqrt(2.0 / (image_size * image_size)))) # 784, 1024
b_1 = tf.Variable(tf.zeros([num_hidden_nodes])) # 1024
# first layer
h_1 = tf.nn.relu(tf.matmul(tf_train_dataset, W_1) + b_1)
# first dropout
drops_1 = tf.nn.dropout(h_1, 0.5)
# Second layer variables
W_2 = tf.Variable(tf.truncated_normal([num_hidden_nodes, num_hidden_nodes], stddev=np.sqrt(2.0 / num_hidden_nodes))) # 1024, 1024
b_2 = tf.Variable(tf.zeros([num_hidden_nodes])) # 1024
# Second layer
h_2 = tf.nn.relu(tf.matmul(h_1, W_2) + b_2)
# Second dropout
drops_2 = tf.nn.dropout(h_2, 0.5)
# Training computation
W_3 = tf.Variable(tf.truncated_normal([num_hidden_nodes, num_labels], stddev=np.sqrt(2.0 / num_hidden_nodes))) # 1024, 10
b_3 = tf.Variable(tf.zeros([num_labels])) # 10
logits = tf.matmul(h_2, W_3) + b_3
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels)) + regularization_factor * (tf.nn.l2_loss(W_1) + tf.nn.l2_loss(W_2) + tf.nn.l2_loss(W_3))
# optimizer
learning_rate = tf.train.exponential_decay(0.5, global_step, 1000, 0.65, staircase=True)
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
# Predictions
train_prediction = tf.nn.softmax(logits)
valid_fw_pass_1 = tf.nn.relu(tf.matmul(tf_valid_dataset, W_1) + b_1) # First layer forward pass for validation
valid_fw_pass_2 = tf.nn.relu(tf.matmul(valid_fw_pass_1, W_2) + b_2) # First layer forward pass for validation
valid_prediction = tf.nn.softmax(tf.matmul(valid_fw_pass_2, W_3) + b_3) # Softmax for validation
test_fw_pass_1 = tf.nn.relu(tf.matmul(tf_test_dataset, W_1) + b_1)
test_fw_pass_2 = tf.nn.relu(tf.matmul(test_fw_pass_1, W_2) + b_2)
test_prediction = tf.nn.softmax(tf.matmul(test_fw_pass_2, W_3) + b_3)
```
Let's run it:
```
num_steps = 8001
w_init = []
w_trained = []
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized")
w_init.append(W_1.eval().flatten())
w_init.append(W_2.eval().flatten())
w_init.append(W_3.eval().flatten())
for step in range(num_steps):
# Minibatches
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
feed_dict = {tf_train_dataset: batch_data, tf_train_labels: batch_labels, regularization_factor: 1e-3}
_, l, predictions = session.run([optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 500 == 0):
print("Minibatch loss at step %d: %f" % (step, l))
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(valid_prediction.eval(), valid_labels))
if (step % 1000 == 0):
print("Learning rate: %f" % learning_rate.eval())
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
w_trained.append(W_1.eval().flatten())
w_trained.append(W_2.eval().flatten())
w_trained.append(W_3.eval().flatten())
fig, axes = plt.subplots(2, 3, figsize=(10, 4))
axes = axes.ravel()
for idx, ax in enumerate(axes):
if idx <= 2:
ax.hist(w_init[idx], bins=100)
ax.set_title("Initialized Weights-%s" % str(idx+1))
else:
ax.hist(w_trained[idx-3], bins=100)
ax.set_title("Learned Weights-%s" % str(idx-2))
ax.set_xlabel("Values")
ax.set_ylabel("Frequency")
fig.tight_layout()
```
Perfect!
| true |
code
| 0.704859 | null | null | null | null |
|
# Maps
## 1. Introduction
Maps are a way to present information on a (roughly) spherical earth on a flat plane, like a page or a screen. Here are two examples of common map projections. The projection is only accurate in the region where the plane touches the sphere, and is less accurate as the distance between the plane and the sphere increases.
#### Mercator

#### Lambert conformal conic

You can read more about map projections from [_Map Projections – a Working Manual_](http://pubs.usgs.gov/pp/1395/report.pdf), the source of the images above, or, more entertainingly, from [XKCD](https://xkcd.com/977/).
We'll use `cartopy` to plot on maps. Check out the [gallery](http://scitools.org.uk/cartopy/docs/latest/gallery.html) for inspiration.
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import cartopy
import cartopy.crs as ccrs # commonly used shorthand
import cartopy.feature as cfeature
```
Here we have the most basic projection: plate carrée, which is an [equirectangular projection](https://en.wikipedia.org/wiki/Equirectangular_projection), and is essentially equivalent to just plotting the longitude and latitude values without a projection. I will refer to longitude and latitude as "geographic coordinates".
We can make an axes that is plotted in geographic coordinates (or, indeed, any projection we choose) by using the `projection` keyword argument to `fig.add_subplot()`. Here we also plot the coastline and add gridlines.
```
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(1, 1, 1, projection=ccrs.PlateCarree())
ax.coastlines(resolution='110m') # coastline resolution options are '110m', '50m', '10m'
ax.gridlines()
```
`cartopy` provides a number of projections. [Available projections](http://scitools.org.uk/cartopy/docs/latest/crs/projections.html) are:
PlateCarree
AlbersEqualArea
AzimuthalEquidistant
LambertConformal
LambertCylindrical
Mercator
Miller
Mollweide
Orthographic
Robinson
Sinusoidal
Stereographic
TransverseMercator
UTM
InterruptedGoodeHomolosine
RotatedPole
OSGB
EuroPP
Geostationary
Gnomonic
LambertAzimuthalEqualArea
NorthPolarStereo
OSNI
SouthPolarStereo
Lambert Conformal Conic is a useful projection in numerical modeling because it preserves right angles. Here we use the projection without any keyword specifications, but with the coastline plotted so that we have something to look at.
The projection that we choose in the `axes` line with `projection=` is the projection that the plot is in. Data from any projection can be plotted on this map, but we will have to tell it which projection it is in.
```
plt.figure()
ax = plt.axes(projection=ccrs.LambertConformal()) ## The map is in the Lambert Conformal projection
ax.coastlines(resolution='110m')
ax.gridlines()
```
Let's make a map of the Gulf of Mexico using the `LambertConformal` projection. Projections take in different keywords to specify properties. For this projection, we can specify the central longitude and latitude, which control the center of the projection. Our selection in the example is not far off from the default, so it looks similar to the previous plot.
```
# the central_longitude and central_latitude parameters tell the projection where to be centered for the calculation
# The map is in Lambert Conformal
ax = plt.axes(projection=ccrs.LambertConformal(central_longitude=-85.0, central_latitude=25.0))
gl = ax.gridlines(linewidth=0.2, color='gray', alpha=0.5, linestyle='-')
# we control what we actually see in the plot with this:
# We can set the extent using latitude and longitude, but then we need to tell it the projection, which is
# PlateCarree since that is equivalent
# We are choosing the bounds of the map using geographic coordinates,
# then identifying as being in PlateCarree
ax.set_extent([-100, -70, 15, 35], ccrs.PlateCarree())
# add geographic information
ax.add_feature(cartopy.feature.LAND)
ax.add_feature(cartopy.feature.OCEAN)
ax.coastlines(resolution='110m') # looks better with resolution='10m'
ax.add_feature(cartopy.feature.BORDERS, linestyle='-', lw=.5)
ax.add_feature(cartopy.feature.RIVERS)
```
> Don't forget to center your projections around your area of interest to be as accurate as possible for your purposes.
The map is plotted in a projected coordinate system, with units in meters, but the package deals with the projection behind the scenes. We can see this by looking at the limits of the two axes, which don't look like longitude/latitude at all:
```
ax.get_xlim(), ax.get_ylim()
```
This same call to a plot set up with the `PlateCarree` projection, which is in geographic coordinates (lon/lat) does give limits in longitude and latitude, because in that case we told the plot to be in those coordinates, but in this case we said to use a `LambertConformal`.
We can use whatever type of coordinates we want, including latitude and longitude, as long as we tell `cartopy` which type we are using.
As you saw above, we set the limits of the plot not with xlim and ylim, but with `extent` and the appropriate projection object.
---
### _Exercise_
> Create a map of the Gulf of Mexico using a different projection. How does it compare to the map above?
---
This is pretty good, but there are some limitations in this package currently. One is that we can't add labels to the lat/lon lines for the Lambert Conformal Conic projection. We can do this using Mercator, though:
```
plt.figure(figsize=(10, 6))
# the central_longitude parameter tells the projection where to be centered for this axes
ax = plt.axes(projection=ccrs.Mercator(central_longitude=-85.0))
gl = ax.gridlines(linewidth=0.2, color='gray', alpha=0.5, linestyle='-', draw_labels=True)
# we control what we actually see in the plot with this:
# We can set the extent using latitude and longitude, but then we need to tell it the projection, which is
# PlateCarree since that is equivalent
ax.set_extent([-100, -70, 15, 35], ccrs.PlateCarree())
# add geographic information
ax.add_feature(cartopy.feature.LAND)
ax.add_feature(cartopy.feature.OCEAN)
ax.coastlines(resolution='110m') # looks better with resolution='10m'
ax.add_feature(cartopy.feature.BORDERS, linestyle='-', lw=.1)
ax.add_feature(cartopy.feature.RIVERS)
# Now we can add on lat/lon labels:
# more info: http://scitools.org.uk/cartopy/docs/v0.13/matplotlib/gridliner.html
from cartopy.mpl.gridliner import LONGITUDE_FORMATTER, LATITUDE_FORMATTER
import matplotlib.ticker as mticker
# the following two make the labels look like lat/lon format
gl.xformatter = LONGITUDE_FORMATTER
gl.yformatter = LATITUDE_FORMATTER
gl.xlocator = mticker.FixedLocator([-105, -95, -85, -75, -65]) # control where the ticks are
gl.xlabel_style = {'size': 15, 'color': 'gray'} # control how the tick labels look
gl.ylabel_style = {'color': 'red', 'weight': 'bold'}
gl.xlabels_top = False # turn off labels where you don't want them
gl.ylabels_right = False
```
When we want to add something to the plot, we just need to tell it what projection the information is given in using the `transform` keyword argument.
If the information is in latitude/longitude – typical for the way people tend to think about information (instead of projected locations) – then we give the Plate Carree projection with the `transform` keyword argument to the plot call:
> `transform=ccrs.PlateCarree()`
For example, to plot some points with a particular projection, you can type:
> `plt.plot(xpts, ypts, transform=ccrs.projection_that_xpts_and_ypts_are_given_in`)
A nice thing about the `cartopy` package is that you can plot directly data from any projection — you just tell it the projection through the `transform` keyword argument when you add to the plot.
---
### _Exercise_
> The latitude and longitude of College Station are given below. Plot the location of College Station on the map above with a red dot.
lat_cll = 30.0 + 36.0/60.0 + 5.0/3600.0
lon_cll = -(96.0 + 18.0/60.0 + 52.0/3600.0)
_What happens if you put in the wrong projection or no projection?_
---
---
### _Exercise_
> Data from any projection can be added to a map, the data must just be input with its projection using the `transform` keyword.
> The x, y location of Austin, TX, is given below in the Mercator projection. Plot the location of Austin in Mercator coordinates on the map above with a blue 'x'.
x, y = -10880707.173023093, 3516376.324225941
---
## Point conversion
While `cartopy` removes the need to convert points on your own between projections (instead doing it behind the scenes), you can always convert between projections if you want using the following. Or, if you want to transform more than one point, use `projection.transform_points(projection, x, y)`.
```
projection = ccrs.Mercator()
x, y = projection.transform_point(-93.0-45.0/60.0, 27.0+55.0/60.0, ccrs.PlateCarree())
print(x, y)
```
---
### _Exercise_
> Convert the Mercator coordinates given for Austin to latitude and longitude and confirm that they are correct.
---
## Other features you can add
The code we used earlier, like:
ax.add_feature(cartopy.feature.LAND)
was a convenience function wrapping more complex and capable code options. Here we explore a little more the capabilities. Note that this requires downloading data which you will see a warning about the first time you run the code.
We can set up the ability to plot with high resolution land data:
```
# this is another way to do `ax.add_feature(cartopy.feature.LAND)` but to have more control over it
# 50m: moderate resolution data
# set up for plotting land
land_50m = cfeature.NaturalEarthFeature('physical', 'land', '50m',
edgecolor='face', facecolor=cfeature.COLORS['land'])
# set up for plotting water at higher resolution
ocean_50m = cfeature.NaturalEarthFeature('physical', 'ocean', '50m',
edgecolor='face', facecolor=cfeature.COLORS['water'])
```
There are also some built-in colors, but you can use any matplotlib color available to color the land or water.
```
sorted(cfeature.COLORS.keys())
```
Using higher resolution can be pretty significantly different.
Here we will prepare the higher resolution land and ocean information for the highest resolution available, then use it in the plot.
```
land_10m = cfeature.NaturalEarthFeature('physical', 'land', '10m',
edgecolor='face',
facecolor=cfeature.COLORS['land'])
ocean_10m = cfeature.NaturalEarthFeature('physical', 'ocean', '10m',
edgecolor='face',
facecolor=cfeature.COLORS['water'])
projection=ccrs.LambertConformal(central_longitude=-95.0, central_latitude=29.0)
# Galveston Bay
fig = plt.figure(figsize=(15, 15))
# lower resolution
ax1 = fig.add_subplot(1,2,1, projection=projection)
ax1.set_extent([-96, -94, 28.5, 30], ccrs.PlateCarree())
ax1.add_feature(cartopy.feature.LAND)
ax1.add_feature(cartopy.feature.OCEAN)
# now higher resolution
ax2 = fig.add_subplot(1,2,2, projection=projection)
ax2.set_extent([-96, -94, 28.5, 30], ccrs.PlateCarree())
ax2.add_feature(ocean_10m)
ax2.add_feature(land_10m)
```
Here is a list (with reference names in some cases appended) of the [many features](http://www.naturalearthdata.com/features/) that are available through Natural Earth:
*(10, 50, 110 for high, medium, low resolution)*
**Physical Vector Data Themes:**
(`physical`)
* Coastline (10, 50, 110): `coastline`
* Land (10, 50, 110): `land`
* Ocean (10, 50, 110): `ocean`
* Minor Islands (10): `minor_islands`, `minor_islands_coastline`
* Reefs (10): `reefs`
* Physical region features (10): `geography_regions_polys`, `geography_regions_points`, `geography_regions_elevation_points`, `geography_marine_polys`
* Rivers and Lake Centerlines (10, 50, 110): `rivers_lake_centerlines`
* Lakes (10, 50, 110): `lakes`
* Glaciated areas (10, 50, 110): `glaciated_areas`
* Antarctic ice shelves (10, 50): `antarctic_ice_shelves_polys`, `antarctic_ice_shelves_lines`
* Bathymetry (10): `bathymetry_all` or choose which depth(s)
* Geographic lines (10, 50): `geographic_lines`
* Graticules (10, 50, 110): (grid lines) `graticules_all` or choose degree interval
**Raster Data Themes:**
(`raster`: land coloring)
* Cross Blended Hypsometric Tints (10, 50)
* Natural Earth 1 (10, 50)
* Natural Earth 2 (10, 50)
* Ocean Bottom (10, 50)
* Bathymetry (50)
* Shaded Relief (10, 50)
* Gray Earth (10, 50)
* Manual Shaded Relief (10, 50)
**Cultural Vector Data Themes:**
(`cultural`)
* Countries (10, 50, 110): `admin_0_countries`, `admin_0_countries_lakes`, `admin_0_boundary_lines`
* Disputed areas and breakaway regions (10, 50)
* First order admin (provinces, departments, states, etc.) (10, 50): e.g. `admin_1_states_provinces_lines`
* Populated places (10, 50, 110)
* Urban polygons (10, 50)
* Parks and protected areas (10): `parks_and_protected_lands`
* Pacific nation groupings (10, 50, 110)
* Water boundary indicators (10)
Here is an example showing state boundaries:
```
projection=ccrs.PlateCarree()
fig = plt.figure()
ax = fig.add_subplot(111, projection=projection)
ax.set_extent([-125, -70, 24, 50], ccrs.PlateCarree())
ax.add_feature(cartopy.feature.LAND)
ax.add_feature(cartopy.feature.OCEAN)
states = cfeature.NaturalEarthFeature(category='cultural', scale='50m', facecolor='none',
name='admin_1_states_provinces_shp')
ax.add_feature(states, edgecolor='gray')
```
| true |
code
| 0.726829 | null | null | null | null |
|
# Extra Trees Classifier
This Code template is for the Classification tasks using simple ExtraTreesClassifier based on the Extremely randomized trees algorithm.
### Required Packages
```
import numpy as np
import pandas as pd
import seaborn as se
import warnings
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,plot_confusion_matrix
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X = df[features]
Y = df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), axis=-1, kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
#### Distribution Of Target Variable
```
plt.figure(figsize = (10,6))
se.countplot(Y)
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state = 123)
```
### Model
ExtraTreesClassifier is an ensemble learning method fundamentally based on decision trees. ExtraTreesClassifier, like RandomForest, randomizes certain decisions and subsets of data to minimize over-learning from the data and overfitting.
#### Model Tuning Parameters
1.n_estimators:int, default=100
>The number of trees in the forest.
2.criterion:{“gini”, “entropy”}, default="gini"
>The function to measure the quality of a split. Supported criteria are “gini” for the Gini impurity and “entropy” for the information gain.
3.max_depth:int, default=None
>The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min_samples_split samples.
4.max_features:{“auto”, “sqrt”, “log2”}, int or float, default=”auto”
>The number of features to consider when looking for the best split:
```
model=ExtraTreesClassifier(n_jobs = -1,random_state = 123)
model.fit(X_train,y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted
```
print("Accuracy score {:.2f} %\n".format(model.score(X_test,y_test)*100))
```
#### Confusion Matrix
A confusion matrix is utilized to understand the performance of the classification model or algorithm in machine learning for a given test set where results are known.
```
plot_confusion_matrix(model,X_test,y_test,cmap=plt.cm.Blues)
```
#### Classification Report
A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True, how many are False.
* **where**:
- Precision:- Accuracy of positive predictions.
- Recall:- Fraction of positives that were correctly identified.
- f1-score:- percent of positive predictions were correct
- support:- Support is the number of actual occurrences of the class in the specified dataset.
```
print(classification_report(y_test,model.predict(X_test)))
```
#### Feature Importances.
The Feature importance refers to techniques that assign a score to features based on how useful they are for making the prediction.
```
plt.figure(figsize=(8,6))
n_features = len(X.columns)
plt.barh(range(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), X.columns)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
```
#### Creator: Thilakraj Devadiga , Github: [Profile](https://github.com/Thilakraj1998)
| true |
code
| 0.263718 | null | null | null | null |
|
```
%load_ext autoreload
%autoreload 2
# For comparison
import csr2d.core2
```
# 3D CSR Potentials
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
%matplotlib notebook
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
#sigma_z = 40e-6
#sigma_x = 134e-6
#rho = 1538.
#gamma = 58708.
sigma_z = 10e-6
sigma_x = 10e-6
rho = 1.
gamma = 500.
beta = np.sqrt(1 - 1 / gamma ** 2)
beta2 = 1-1/gamma**2
```
# alpha
For convenience we will use the notatation
$\xi \rightarrow z$
$\chi \rightarrow x$
$\zeta \rightarrow y$
Then
$z = \alpha - \frac{\beta}{2}\sqrt{x^2+y^2+4(1+x)\sin^2\alpha}$
```
from csr3d.core import alpha_exact, alpha, old_alpha, alpha_where_z_equals_zero, psi_s
xmax = 40e-6 #1/gamma**2
xmin = -xmax
xptp = xmax-xmin
ymax = 40e-6 #1/gamma**2
ymin = -ymax
yptp = ymax-ymin
zmax = 40e-6 #1/gamma**2
zmin = -zmax
zptp = zmax-zmin
fac = 2
nx = int(32*fac)
ny = int(16*fac)
nz = int(64*fac)
dx = xptp/(nx-1)
dy = yptp/(ny-1)
dz = zptp/(nz-1)
xvec = np.linspace(xmin, xmax, nx)
yvec = np.linspace(ymin, ymax, ny)
zvec = np.linspace(zmin, zmax, nz)
X, Y, Z = np.meshgrid( xvec, yvec, zvec, indexing='ij')
xmax, ymax, zmax
```
# alpha
```
%%timeit
old_alpha(X, Y, Z, gamma)
%%timeit
alpha(X, Y, Z, gamma)
# This will be slow
A0 = alpha_exact(X, Y, Z, gamma)
plt.imshow(A0[:,1,:])
A1 = alpha(X, Y, Z, gamma)
plt.imshow(A1[:,1,:])
err = (A1-A0)/A0
np.abs(err).max()
plt.imshow(err[:,0,:])
fig, ax = plt.subplots()
ax2 = ax.twinx()
for y0 in yvec:
a0 = alpha_exact(xvec, y0, 0, gamma)
a1 = alpha_where_z_equals_zero(xvec, y0, gamma)
err = (a1-a0)/a0
ax.plot(xvec, a0)
ax.plot(xvec, a1, linestyle='--')
ax2.plot(xvec, abs(err)*1e6)
ax.set_title('alpha exact vs quadratic at z=0')
ax.set_xlabel('x')
ax.set_ylabel('alpha')
ax2.set_ylabel('relative error (10^-6)')
```
# psi_s
```
from csr3d.core import psi_s
%%timeit
# This is parallel
psi_s(X, Y, Z, gamma)
psi_s(0,0,0, gamma)
plt.plot(zvec, psi_s(0, 0, zvec, gamma))
plt.plot(xvec, psi_s(xvec, 0, 0, gamma))
plt.plot(yvec, psi_s(0, yvec+1e-6, 0, gamma))
# Compare with CSR2D
def csr2d_psi_s(*a, **k):
return csr2d.core2.psi_s(*a, **k) + csr2d.core2.psi_s_SC(*a, **k)/gamma**2
# x line
fig, ax = plt.subplots()
ax.plot(xvec, psi_s(xvec,0,0,gamma), label='CSR3D', marker='x')
#ax.plot(xvec, csr2d.core2.psi_s(0, xvec, beta), marker='.', label='CSR2D')
ax.plot(xvec,csr2d_psi_s(0, xvec, beta), marker='.', label='CSR2D')
ax.set_title('x line at y=0, z=0')
ax.set_ylabel('psi_s')
ax.set_xlabel('x')
ax.legend()
# y line
fig, ax = plt.subplots()
ax.plot(yvec, psi_s(0,yvec,0,gamma))
ax.set_title('y line at x=0, z=0')
ax.set_ylabel('psi_s')
ax.set_xlabel('y')
#ax.legend()
# z line
fig, ax = plt.subplots()
ax.plot(zvec, psi_s(0,0,zvec,gamma), marker='x', label='CSR2D')
ax.plot(zvec, csr2d.core2.psi_s(zvec, 0,beta), marker='.', label='CSR2D')
ax.set_title('z line at x=0, y=0')
ax.set_ylabel('psi_s')
ax.set_xlabel('z')
ax.legend()
```
# psi_s mesh
```
from csr3d.wake import green_mesh
%%time
G = green_mesh((nx, ny, nz), (dx, dy, dz), rho=rho, gamma=gamma, component='s')
%%time
Gs = green_mesh((nx, ny, nz), (dx, dy, dz/100), rho=rho, gamma=gamma, component='s')
fig, ax = plt.subplots(figsize=(12,8))
ax.imshow(Gs[:,ny//2,:], origin='lower', aspect='equal')
ax.set_title(r'$\psi_s$')
```
# psi_x
```
from csr3d.wake import green_mesh
from csr3d.core import psi_x, psi_x0
# Compare with CSR2D at y=0
import csr2d.core2
%%timeit
psi_x(X, Y, Z, gamma)
%%timeit
# This is parallelized
psi_x0(X, Y, Z, gamma, dx, dy, dz)
# Compare with CSR2D
def csr2d_psi_x(*a, **k):
return csr2d.core2.psi_x(*a, **k) + csr2d.core2.psi_x_SC(*a, **k)/gamma**2
# x line
fig, ax = plt.subplots()
ax.plot(xvec, psi_x(xvec,0,0,gamma), label='CSR3D', marker='x')
ax.plot(xvec, csr2d_psi_x(0, xvec,beta), marker='.', label='CSR2D')
ax.set_title('x line at y=0, z=0')
ax.set_ylabel('psi_x')
ax.set_xlabel('x')
ax.legend()
# y line
fig, ax = plt.subplots()
ax.plot(yvec, psi_x(0,yvec,0,gamma))
ax.set_title('y line at x=0, z=0')
ax.set_ylabel('psi_x')
ax.set_xlabel('y')
#ax.legend()
# z line
fig, ax = plt.subplots()
ax.plot(zvec, psi_x0(0,0,zvec,gamma,1e-6, 1e-6, 1e-6), marker='x', label='CSR2D')
ax.plot(zvec, csr2d.core2.psi_x0(zvec, 0,beta, 1e-6), marker='.', label='CSR2D')
ax.set_title('z line at x=0, y=0')
ax.set_ylabel('psi_x')
ax.set_xlabel('z')
ax.legend()
%%time
Gx = green_mesh((nx, ny, nz), (dx, dy, dz), rho=rho, gamma=gamma, component='x')
#X2, Y2, Z2 = tuple(meshes)
fig, ax = plt.subplots(figsize=(12,8))
ax.imshow(Gx[:,ny-1,:], origin='lower', aspect='equal')
ax.set_title(r'$\psi_x$ at y=0')
ax.set_xlabel('z index')
ax.set_ylabel('x index')
fig, ax = plt.subplots(figsize=(12,8))
ax.imshow(Gx[nx-1,:,:], origin='lower', aspect='equal')
ax.set_title(r'$\psi_x$ at x=0')
ax.set_xlabel('z index')
ax.set_ylabel('y index')
plt.plot(Gx[nx-1,:,nz])
plt.plot(Gx[nx-1-1,:,nz])
plt.plot(Gx[nx-1+1,:,nz])
M = Gx[:,:,nz].T
fig, ax = plt.subplots(figsize=(12,8))
ax.imshow(M, origin='lower', aspect='equal')
ax.set_title(r'$\psi_x$ at z=0')
ax.set_xlabel('x index')
ax.set_ylabel('y index')
```
# psi_y
```
from csr3d.core import psi_y, psi_y0
%%timeit
R2 = psi_y(X, Y, Z, gamma)
%%timeit
R2 = psi_y0(X, Y, Z, gamma, dx, dy, dz)
%%time
Gy = green_mesh((nx, ny, nz), (dx/10, dy/10, dz/100), rho=rho, gamma=gamma, component='y')
#X2, Y2, Z2 = tuple(meshes)
fig, ax = plt.subplots(figsize=(12,8))
ax.imshow(Gy[:,ny-1 +1,:], origin='lower', aspect='equal')
ax.set_title(r'$\psi_y$ at y=+')
ax.set_xlabel('z index')
ax.set_ylabel('x index')
fig, ax = plt.subplots(figsize=(12,8))
ax.imshow(Gy[nx-1,:,:], origin='lower', aspect='equal')
ax.set_title(r'$\psi_y$ at x=0')
ax.set_xlabel('z index')
ax.set_ylabel('y index')
M = Gy[:,:,nz].T
fig, ax = plt.subplots(figsize=(12,8))
ax.imshow(M, origin='lower', aspect='equal')
ax.set_title(r'$\psi_y$ at z=+')
ax.set_xlabel('x index')
ax.set_ylabel('y index')
# x line
fig, ax = plt.subplots()
ax.plot(xvec, psi_y(xvec,0,0,gamma), label='CSR3D', marker='x')
ax.set_title('x line at y=0, z=0')
ax.set_ylabel('psi_y')
ax.set_xlabel('x')
# y line
fig, ax = plt.subplots()
ax.plot(yvec, psi_y(0,yvec,0,gamma))
ax.set_title('y line at x=0, z=0')
ax.set_ylabel('psi_y')
ax.set_xlabel('y')
# z line
fig, ax = plt.subplots()
ax.plot(zvec, psi_y0(0,0,zvec,gamma,1e-6, 1e-6, 1e-6), marker='x', label='CSR2D')
ax.set_title('z line at x=0, y=0')
ax.set_ylabel('psi_y')
ax.set_xlabel('z')
```
| true |
code
| 0.671228 | null | null | null | null |
|
## NSE-TATAGLOBAL DATASETS
## Stock Market Prediction And Forecasting Using Stacked LSTM
# LGMVIP Task-2|| Data Science
### To build the stock price prediction model, we will use the NSE TATA GLOBAL dataset. This is a dataset of Tata Beverages from Tata Global Beverages Limited, National Stock Exchange of India: Tata Global Dataset
## Import Libraries
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import io
import requests
import datetime
```
## Import Datasets
```
url="https://raw.githubusercontent.com/mwitiderrick/stockprice/master/NSE-TATAGLOBAL.csv"
df=pd.read_csv(url)
df.head()
df1=df.reset_index()['Open']
df1
plt.plot(df1)
```
## LSTM are sensitive to the scale of the data. so we apply MinMax scaler
```
from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler(feature_range=(0,1))
df1=scaler.fit_transform(np.array(df1).reshape(-1,1))
print(df1)
```
## splitting dataset into train and test split
```
train_size=int(len(df1)*0.75)
test_size=len(df1)-train_size
train_data,test_data=df1[0:train_size,:],df1[train_size:len(df1),:1]
train_size,test_size
train_data,test_data
```
## convert an array of values into a dataset matrix
```
def create_dataset(dataset, time_step=1):
train_X, train_Y = [], []
for i in range(len(dataset)-time_step-1):
a = dataset[i:(i+time_step), 0] ###i=0, 0,1,2,3-----99 100
train_X.append(a)
train_Y.append(dataset[i + time_step, 0])
return numpy.array(train_X), numpy.array(train_Y)
```
### reshape into X=t,t+1,t+2,t+3 and Y=t+4
```
import numpy
time_step = 100
X_train, y_train = create_dataset(train_data, time_step)
X_test, ytest = create_dataset(test_data, time_step)
print(X_train.shape), print(y_train.shape)
```
## reshape input to be [samples, time steps, features] which is required for LSTM
```
X_train =X_train.reshape(X_train.shape[0],X_train.shape[1] , 1)
X_test = X_test.reshape(X_test.shape[0],X_test.shape[1] , 1)
```
## Create the Stacked LSTM model
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import LSTM
model=Sequential()
model.add(LSTM(50,return_sequences=True,input_shape=(100,1)))
model.add(LSTM(50,return_sequences=True))
model.add(LSTM(50))
model.add(Dense(1))
model.compile(loss='mean_squared_error',optimizer='adam')
model.summary()
model.fit(X_train,y_train,validation_data=(X_test,ytest),epochs=100,batch_size=64,verbose=1)
import tensorflow as tf
tf.__version__
```
## Lets Do the prediction and check performance metrics
```
train_predict=model.predict(X_train)
test_predict=model.predict(X_test)
train_predict=scaler.inverse_transform(train_predict)
test_predict=scaler.inverse_transform(test_predict)
```
## Calculate RMSE performance metrics
```
import math
from sklearn.metrics import mean_squared_error
math.sqrt(mean_squared_error(y_train,train_predict))
```
### Test Data RMSE
```
math.sqrt(mean_squared_error(ytest,test_predict))
```
### shift train predictions for plotting
```
look_back=100
trainPredictPlot = numpy.empty_like(df1)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(train_predict)+look_back, :] = train_predict
```
### shift test predictions for plotting
```
testPredictPlot = numpy.empty_like(df1)
testPredictPlot[:, :] = numpy.nan
testPredictPlot[len(train_predict)+(look_back*2)+1:len(df1)-1, :] = test_predict
```
### plot baseline and predictions
```
plt.plot(scaler.inverse_transform(df1),color='blue')
plt.show()
plt.plot(trainPredictPlot,color='red')
plt.show()
plt.plot(testPredictPlot,color='green')
plt.show()
plt.plot(trainPredictPlot,color='red')
plt.plot(testPredictPlot,color='green')
plt.show()
plt.plot(scaler.inverse_transform(df1),color='blue')
plt.plot(trainPredictPlot,color='red')
plt.plot(testPredictPlot,color='green')
plt.show()
len(test_data)
x_input=test_data[341:].reshape(1,-1)
x_input.shape
model.save("saved_model.h5")
```
| true |
code
| 0.596962 | null | null | null | null |
|
# Neural Networks - Part 2
2016-09-16, Josh Montague
## The Plan
- Quick review of [Part 1](https://github.com/DrSkippy/Data-Science-45min-Intros/tree/master/neural-networks-101)
- The library stack (Keras, Theano, Numpy, oh my!)
- Examples!
- Classification (Iris)
- Classification (MNIST)
- Regression (housing)
## Review
Back in [Part 1, we looked at some history, motivation, and a simple (if only *mostly*-working 😐) implementation of a neural network](https://github.com/DrSkippy/Data-Science-45min-Intros/tree/master/neural-networks-101).
<img src="img/NN-2.jpeg">
Recall the short version of how this worked:
- there is an array of input "nodes" (one per feature)
- the input nodes are "fully-connected" to an arbitrary number of nodes in the next, "hidden layer"
- the value of each of the hidden nodes is computed by taking the inner product of the previous layer with the weights matrix, and then passing that linear combination through an "activation function," $f(\omega^T x)$. We introduced the sigmoid as one possible activation (shown above)
- when there are many nodes in the hidden layer(s), the weights form a matrix; the weight connecting nodes $i$ and $j$ (in sequential layers) is matrix element $w_{ij}$
- "forward propagation" through the network is repeating this for each layer in the network until you get to your predicted output layer
- "backpropagation" is the process of updating the weight matrix elements $\omega_{ij}$ by distributing the prediction error backward through the network according to the prediction error and a chosen loss function
- forward and backward propagation are repeated a bunch of times until some convergence criteria is achieved
Remember that at least one of the reasons why this is an interesting set of techniques to explore is that they a very different way to think of features in a model. We don't have to specify all of the explicit model features in a data matrix e.g. a column for $x$, a column for $x^2$, and $x*y, x*y^2$, and so on. We're defining a structure that allows for stacking of arbitrary, non-linear combinations of the predefined set of data matrix features; this can lead to a more expressive set of features. On the other hand, it also means many more degrees of freedom, which increases computational complexity and decreases interpretability.
Moving beyond our ``for`` loop in Part 1, we can look at some more reasonable approaches to using neural networks in practice! In particular, we'll look at [Keras](https://keras.io/), one of the active and growing libraries for building, training, and using neural networks in Python.
I think it'll be helpful to understand the stack of libraries and their roles, so hang tight while we run through that, first...
## Keras
Keras is a modular library with a ``scikit-learn``-inspired API. It lets you write readable Python code to define the structure of a neural network model, as well as (optionally) detailed configuration of *how* the model should evaluate.
From the [docs](https://keras.io/):
> Keras is a minimalist, highly modular neural networks library, written in Python and capable of running on top of either TensorFlow or Theano. It was developed with a focus on enabling fast experimentation. Being able to go from idea to result with the least possible delay is key to doing good research.
>
> Use Keras if you need a deep learning library that:
>
> - allows for easy and fast prototyping (through total modularity, minimalism, and extensibility).
> - supports both convolutional networks and recurrent networks, as well as combinations of the two.
> - supports arbitrary connectivity schemes (including multi-input and multi-output training).
> - runs seamlessly on CPU and GPU.
There are many libraries for creating neural networks in Python. A quick google search includes:
- Keras
- TensorFlow
- PyBrain
- Blocks
- Lasagne
- Caffe
- nolearn
- PyML
- ... and I'm sure there are more
I read the docs for a few, read some reddit and StackOverflow discussions, and asked some practioners that I know for their opinions. My takeaway: **if you're working in Python, familiar with ``scikit-learn``, and want a good on-ramp to neural networks, Keras is a good choice.**
For more discussion about the library and it's motivations, check out [the recent Quora Q&A](https://www.quora.com/session/Fran%C3%A7ois-Chollet/1) in which the lead developer gave some great insight into the design and plans for the library.
Most of this session will involve writing code with Keras. But Keras doesn't actually do the computation; it uses another library for that (in fact, more than one). For the symbolic computation portion, Keras currently supports [Theano](http://www.deeplearning.net/software/theano/) (the default) and [TensorFlow](https://www.tensorflow.org/). We'll use Theano for this notebook.
## Theano
From [the docs](http://deeplearning.net/software/theano/introduction.html#introduction):
> Theano is a Python library that lets you to define, optimize, and evaluate mathematical expressions, especially ones with multi-dimensional arrays (``numpy.ndarray``). Using Theano it is possible to attain speeds rivaling hand-crafted C implementations for problems involving large amounts of data.
Essentially, by using symbolic mathematical expressions, all sorts of compiler and computational optimizations (including automatic differentiation and dynamically-generated C code!), Theano can make math happen very fast (either using the Python interpreter and ``numpy``, or going right around it to CPU/GPU instructions). An interesting feature of Theano is that executing the same code with a GPU is achieved by simply setting a shell environment variable!
One way to think about how these pieces relate to one another is (loosely):
```
scikit-learn:numpy :: keras:theano(+numpy)
```
Put another way, here's my attempt at a visual version:
<img src="img/nn-stack.png">
# Ok, enough talk, let's build something
```
from IPython.display import Image
Image(data="img/mr-t.jpg")
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
seed = 1234; np.random.seed(seed)
import seaborn as sns
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LogisticRegression
%matplotlib inline
```
## Foreword: "`random`"
Many of the numerical computations that we do in Python involve sampling from distributions. We often want these to be truly random, but computers can only provide so-called "pseudo-random" numbers ([wiki](https://en.wikipedia.org/wiki/Pseudorandom_number_generator), [Python docs](https://docs.python.org/3/library/random.html)).
In many of our modeling use-cases (particularly those which are *ad hoc*), having fluctuations in some pseudo-random values is fine. However, when there are variations in, say, the initial conditions for an algorithm, it can lead to variation in the outcome which is not indicative or representative of any true variance in the underlying data. Examples include choosing the starting centroids in a k-means clustering task, or *choosing the weights of a neural network synapse matrix*.
When you want results to be reproducible (which is generally a good thing!), you have to "seed" the random number generator (RNG). In this way, when you send your code to someone else's computer, or if you run your code 10,000 times, you'll always have the same initial conditions (for parameters that are randomly generated), and you should always get the same results.
In a typical Python script that runs all in one session, the line above (`seed = 1234; np.random.seed(seed)`) can be included once, at the top\*. In an IPython notebook, however, it seems that you need to set the seed in each cell where the random parameter initialization may occur (i.e. in any cell that includes the declaration of a NN model). I'm not 100% positive about this, but this is what I gathered from my experimentation. This is the origin of the assorted calls to `np.random.seed()` you'll see below!
# 1: Classification (Iris)
To get a sense for how Keras works, we'll start with a simple example: the golden oldie, the iris data set. That way we can focus our attention on the code, not the details of the data.
Furthermore, to illustrate the parallels with `scikit-learn`, let's run through *that* demo first. Since the Keras API is ``sklearn``-like (and this team has lots of ``sklearn`` experience), hopefully that will provide some helpful conceptual hooks.
## ``sklearn``
```
# import data (from seaborn, bc it gives you a df with labels)
iris = sns.load_dataset("iris")
iris.tail()
# inspect
sns.pairplot(iris, hue='species')
# get train/test split (no preprocessing)
X = iris[['sepal_length', 'sepal_width', 'petal_length', 'petal_width']].values
y = iris['species'].values
# take a 75/25 split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, random_state=seed)
# verify array sizes
#[x.shape for x in [X_train, X_test, y_train, y_test]]
# fit default LR model
model = LogisticRegression()
model.fit(X_train, y_train)
# score on test (should be ~80-90%)
print("Accuracy = {:.2f}".format(model.score(X_test, y_test)))
```
Not bad for less than ten lines of code!
In practice, we should be a bit more careful and consider some additional work:
- preprocess the data (scaling, normalizing)
- use cross validation techniques to build an uncertainty or confidence (e.g. k-fold cv)
- gridsearch the model parameters
- ... etc. ...
But for now, we're just trying to show the comparison between the libraries, and this will do.
Now, let's write the same kind of classification system in Keras!
## ``keras``
**Warning!** *If you have a dataset the size of the iris data (tiny!), you probably shouldn't use a neural network in practice; instead, consider a model that is more interpretable. We're using #tinydata here because it's simple and common.*
### (One-hot) encode the labels
We can start the same train- and test-split data arrays. But, we have to make a modification to the output data (labels). ``scikit-learn`` estimators transparently convert categorical labels e.g. strings like "virginica" and "setosa" into numerical values (or arrays). But we have to do that step manually for the Keras models.
We want the model output to be a 3x1 array, where the value at each index represents the probability of that category (0, 1, or 2). The format of this training data, where the truth is 1 and all the other possible values are 0 is also known as a **one-hot encoding.**
There are a few ways to do this:
- ``pandas.get_dummies()`` (we'll use this one)
- ``scikit-learn``'s ``LabelEncoder()``
- Keras' ``np_utils.to_categorical()``
- ... or roll your own
Here's an example of how ``pd.get_dummies()`` works:
```
# create a sample array with a few of each species from the original df
species_sample = iris.groupby(by='species').head(3)['species']
species_sample
# get a one-hot-encoded frame from the pandas method
pd.get_dummies(species_sample, prefix='ohe')
```
Now, instead of a single string label as our output (prediction), we have a 3x1 array, where each array item represents one of the possible species, and the non-zero binary value gives us the information we need.
``scikit-learn`` was effectively doing this same procedure for us before, but hiding all of the steps that map the labels to the prediction arrays.
Back to our original data: we can one-hot encode the y arrays that we got from our train-test split earlier, and can re-use the same X arrays.
```
# encode the full y arrays
ohe_y_train = pd.get_dummies(y_train).values
ohe_y_test = pd.get_dummies(y_test).values
```
### Define, compile the model
Time to make our neural network model!
Keras has an object-oriented syntax that starts with a ``model``, then adds ``layers`` and ``activations``.
The ``Sequential`` model is the main one we care about - it assumes that you'll tell it a series of layers (and activations) that define the network. Subsequently, we add layers and activations, and then compile the model before we can train it.
There is art and science to choosing how many hidden layers and nodes within those layers. We're not going to dive into that in this session (mostly because I don't yet know the answers!), so maintain your skepticism, but just sit with it for now.
```
# create a new model
model = Sequential()
# add layers
# - the first hidden layer must specify the dimensions of the input layer (4x1, here)
# - this adds a 10-node, fully-connected layer following the input layer
model.add(Dense(10, input_dim=4))
# add an activation to the hidden layer
model.add(Activation('sigmoid'))
```
For now, we'll stick to a 3-layer network: input, hidden, and output.
The final, output layer needs to have three nodes since we have labels that are 3x1 arrays. So, our layers and sizes are: input (4 nodes), hidden (10 nodes), and output (3 nodes).
At this point, I only have a small amount of guidance for choosing activation layers. See the notes at the end of the notebook for a longer discussion. Importantly, when we want our output values to be between 0 and 1, and to represent probabilities of our classes (summing to 1), we choosing the **softmax** activation function.
```
# add the output layer, and a softmax activation
model.add(Dense(3))
model.add(Activation('softmax'))
```
Finally, we compile the model. This is where we can specify the optimizer, and loss function.
Since we're using multi-class classification, we'll use the ``categorical_crossentropy`` loss function. This is [the advice that I was able to find](https://keras.io/getting-started/sequential-model-guide/#compilation) most often, but I need to learn more about decision criteria for both optimizers, and loss functions. They can have a big effect on your model accuracy.
```
model.compile(optimizer='sgd', loss='categorical_crossentropy', metrics=["accuracy"])
```
Finally, we ``fit()`` the compiled model using the original training data, including the one-hot-encoded labels.
The ``batch_size`` is how many observations are propagated forward before updating the weights (backpropagation). Typically, this number will be much bigger (the default value is 32), but we have a very tiny data set, so we artificially force this network to update weights with each observation (see the **Warning** above).
```
# keras uses the same .fit() convention
model.fit(X_train, ohe_y_train, batch_size=1, nb_epoch=20, verbose=1)
```
We can ``evaluate()`` our accuracy by using that method on the test data; this is equivalent to ``sklearn``'s ``score()``.
```
loss, metrics = model.evaluate(X_test, ohe_y_test, verbose=0)
# score on test (should also be ~80-90%)
print("Accuracy = {:.2f}".format(metrics))
```
Not bad!
There are also ``sklearn``-like methods that return class assignment and their probabilities.
```
classes = model.predict_classes(X_test, verbose=0)
probs = model.predict_proba(X_test, verbose=0)
print('(class) [ probabilities ]')
print('-'*40)
for x in zip(classes, probs):
print('({}) {}'.format(x[0],x[1]))
```
### Now, more compact...
We walked through that in pieces, but here we can collect all of those steps together to see just how few lines of code it required (though remember that we did have the one additional step of creating one-hot-encoded labels).
```
np.random.seed(seed)
# instantiate the model
model = Sequential()
# hidden layer
model.add(Dense(10, input_shape=(4,)))
model.add(Activation('sigmoid'))
# output layer
model.add(Dense(3))
model.add(Activation('softmax'))
# set optimizer, loss fnc, and fit parameters
model.compile(optimizer='sgd', loss='categorical_crossentropy', metrics=["accuracy"])
model.fit(X_train, ohe_y_train, batch_size=1, nb_epoch=20, verbose=0)
# score on test set
loss, metrics = model.evaluate(X_test, ohe_y_test, verbose=0)
print("Accuracy = {:.2f}".format(metrics))
```
Or - even more succinctly - we can build the same model but collapse the structure definition because of Keras' flexible API...
```
np.random.seed(seed)
# move the activations into the *layer* definition
model = Sequential([
Dense(10, input_dim=4, activation='sigmoid'),
Dense(3, activation='softmax'),
])
model.compile(optimizer='sgd', loss='categorical_crossentropy', metrics=["accuracy"])
model.fit(X_train, ohe_y_train, batch_size=1, nb_epoch=20, verbose=0)
loss, metrics = model.evaluate(X_test, ohe_y_test, verbose=0)
print("Accuracy = {:.2f}".format(metrics))
```
Cool! It seems to work pretty well.
### Peeking inside the model
At this point, what *is* the ``model`` we created? In addition to it's network structure (layers with sizes and activation functions), we also have the weight matrices.
```
for layer in model.layers:
print('name: {}'.format(layer.name))
print('dims (in, out): ({}, {})'.format(layer.input_shape, layer.output_shape))
print('activation: {}'.format(layer.activation))
# nb: I believe the second weight array is the bias term
print('weight matrix: {}'.format(layer.get_weights()))
print()
```
### Saving the model
If you're looking to save off a trained network model, these are most of the pieces that you'd need to save to disk. [Keras uses HDF5](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) (sort of "named, organized arrays") to serialize trained models with a ``model.save()`` (and corresponding ``.load()``) method.
If you're looking to save the *definition* of a model, but without all of the weights, you can write it out in simple JSON or YAML representation e.g. ``model.to_json()``.
# 2: Classification (MNIST)
Let's do one more familiar classification problem - last year's 4C dataset: the MNIST image labeling task.
This time we will:
- have more data (good!)
- do a tiny bit of data normalization (smart!)
- build a bigger network (more expressive!)
```
from keras.datasets import mnist
# the data, shuffled and split between tran and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
print("X_train original shape", X_train.shape)
print("y_train original shape", y_train.shape)
print("y_test original shape", y_test.shape)
```
Remember that the MNIST data is an array of 28-pixel by 28-pixel "images" (brightness values), 60k in the training set, 10k in the test set.
```
plt.figure(figsize=(8,4))
for i in range(3):
plt.subplot(1,3,i+1)
plt.imshow(X_train[i], cmap='gray', interpolation='none')
plt.title("Label: {}".format(y_train[i]))
```
### Preprocessing and normalization
If you recall from the last 4C event, the first step we mostly used in preprocessing this data is to unroll the 2D arrays into a single vector.
Then, as with many other optimizations, we'll see better results (with faster convergence) if we standardize the data into a smaller range. This can be done in a number of ways, like `sklearn`'s `StandardScaler` (zero-mean, unit variance), or `Normalize` (scale to unit-norm). For now, we'll just rescale to the range 0-1.
Then, we also need to one-hot encode our labels again.
```
# unroll 2D pixel data into 1D vector
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
# convert from original range (0-255) to 0-1
X_train = X_train / X_train.max()
X_test = X_test / X_test.max()
# OHE the y arrays
ohe_y_train = pd.get_dummies(y_train).values
ohe_y_test = pd.get_dummies(y_test).values
```
Now we'll built another `Sequential` model.
This time, we'll use the more commonly-used `relu` ("rectified linear unit") activation function.
```
np.random.seed(seed)
model = Sequential([
Dense(512, input_dim=784, activation='relu'),
Dense(512, activation='relu'),
Dense(10, activation='softmax')
])
```
The shape of this network is now: 784 (input nodes) => 512 (hidden nodes) => 512 (hidden nodes) => 10 (output nodes). That's about $784*512*512*10 \approx 2x10^9$ weights!
```
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, ohe_y_train, batch_size=128, nb_epoch=5, verbose=1)
loss, metrics = model.evaluate(X_test, ohe_y_test, verbose=1)
print()
#print('Test loss:', loss)
print('Test accuracy:', metrics)
```
If you recall the 2015 4C leaderboard, a score of 98% would have put you in the top 10% of submissions!
Speaking only for myself, the entries that I submitted in that range took **much** more time and effort than those last few notebook cells!
# 3: Regression (Housing)
Finally, let's do an example of modeling a continuous variable - a regresssion task. We'll use another of the canned datasets: the Boston housing price data.
This data comprises a few hundred observations of neighborhoods, each of thirteen related features. The target is the median price of the homes in that area (in thousands of dollars). So, this means that the output variable is a continuous, real (and positive) number.
You can uncomment the `print(...'DESCR')` cell for a longer description.
```
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error
from sklearn.preprocessing import MinMaxScaler, StandardScaler
# load + inspect data
boston = load_boston()
X = boston.data
y = boston.target
labels = boston.feature_names
b_df = pd.DataFrame(X, columns=labels)
b_df.head()
# built-in information about the dataset and features
#print(boston.get("DESCR"))
```
Since the feature values span many orders of magnitude, we should standardize them for optimization efficiency. Then we can split the data into our train/test split.
It's worth noting that we could also experiemnt with standardizing the output variable, as well. For now, we won't.
```
# standardize the feature data (all features now 0-1)
scaler = MinMaxScaler(feature_range=(0, 1))
X = scaler.fit_transform(X)
# train/test split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, random_state=seed)
# build model
np.random.seed(seed)
model = Sequential([
# use a single hidden layer, also with 13 nodes
Dense(13, input_dim=13, activation='relu'),
Dense(1)
])
# compile + fit model
model.compile(loss='mean_squared_error', optimizer='rmsprop', metrics=['accuracy'])
model.fit(X_train, y_train, batch_size=5, nb_epoch=100, verbose=0)
# evaluate on test data
loss, metrics = model.evaluate(X_test, y_test, verbose=1)
#print('Test loss:', loss)
#print('Test accuracy:', metrics)
print('MSE:', metrics)
y_pred = model.predict(X_test)
print('R^2 score:', r2_score(y_test, y_pred))
plt.figure(figsize=(8,8))
# compare the predictions to test
plt.plot(y_test, y_pred, 'o', alpha=0.75, label='model predictions')
# draw a diagonal
xy = np.linspace(min(y_test), max(y_test))
plt.plot(xy, xy, '--', label='truth = pred')
plt.title('3-layer NN')
plt.xlabel('truth ($k)')
plt.ylabel('prediction ($k)')
plt.legend(loc='best')
```
Cool!
It looks like our model struggles a bit with high-valued observations. Something worth digging into if we were to work on optimizing this model for this task.
# BUT
Just to remind you that this is a toy problem that probably *shouldn't* be solved with a neural network, let's look at the corresponding linear regression model.
We use the same data....
```
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print('R^2:', r2_score(y_test, y_pred))
```
And get similar $R^2$ values with a much more interpretable model. We can compare the prediction errors to the same chart from before...
```
plt.figure(figsize=(8,8))
# compare the predictions to test
plt.plot(y_test, y_pred, 'o', alpha=0.75, label='model predictions')
# draw the diagonal
xy = np.linspace(min(y_test), max(y_test))
plt.plot(xy, xy, '--', label='truth = pred')
plt.title('Linear Regression')
plt.xlabel('truth ($k)')
plt.ylabel('prediction ($k)')
plt.legend(loc='best')
```
And - **the reason why a linear model should often be preferred** - we can just look straight at the feature coefficients and read off how they relate to the predictions
```
plt.figure(figsize=(8,8))
# where to position the bars/ticks
locs = range(len(model.coef_))
plt.barh(locs, model.coef_, align='center')
plt.yticks(locs, b_df.columns);
plt.title('linear regression coefficients')
plt.xlabel('value')
plt.ylabel('coefficient')
```
# Wrap Up
Hopefully between [Part 1](https://github.com/DrSkippy/Data-Science-45min-Intros/tree/master/neural-networks-101), and now this - Part 2 - you've gained a bit deeper understanding for how neural networks work, and how to use Keras to build and train them.
At this point, the only thing we haven't *really* illustrated is how to use them at the #bigdata scale (or with unconventional data types) where they have proven particularly valuable. Perhaps there will be a Part 3...
## What next?
If you want to follow up (or go deeper) on the concepts that we covered, here are some links
- [What optimizer should I use?](http://sebastianruder.com/optimizing-gradient-descent/index.html#visualizationofalgorithms)
- [What loss function should I use?](https://keras.io/getting-started/sequential-model-guide/#compilation)
- unfortunately, these are examples and not a rigorous discussion
- [Keras FAQ](https://keras.io/getting-started/faq/)
- [Keras' collection of pre-made examples](https://github.com/fchollet/keras/tree/master/examples)
- [`sklearn` Keras wrappers](https://keras.io/scikit-learn-api/)
- allow you to mix in things from `sklearn` like `Pipeline`, `GridSearch`, etc.
- [Telling Theano to use a GPU](http://deeplearning.net/software/theano/tutorial/using_gpu.html)
## Acknowledgements
In addition to the links already given, most of this notebook was cobbled together based on other examples I found online, including:
- [many MLM posts](http://machinelearningmastery.com/blog/)
- [Fastforward Labs' `keras-hello-world`](https://github.com/fastforwardlabs/keras-hello-world)
- [wxs' `keras-mnist-tutorial`](https://github.com/wxs/keras-mnist-tutorial)
- and probably others...
| true |
code
| 0.755283 | null | null | null | null |
|
# Chapter 10: RNN(Recurrent Neural Network) Application in IMDB Reviews and Sarcasm Reviews Dataset
```
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import tensorflow_datasets as tfds
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
def plotGraph(history):
loss,acc,val_loss,val_acc = history.history.values()
epochs = range(1,len(loss)+1)
# Plot graph
plt.plot(epochs,acc,'r-^',label = 'Training Accuracy')
plt.plot(epochs,val_acc,'b-*', label = 'Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend()
plt.figure()
plt.plot(epochs,loss,'r-^',label='Training Loss')
plt.plot(epochs,val_loss,'b-*',label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.figure()
def trainModel(model, num_epochs):
model.compile(loss ='binary_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
model.summary()
plotGraph(model.fit(training_padded, training_label, epochs=num_epochs, validation_data=(testing_padded, testing_label)))
```
## Section 10.1: IMDB Dataset (Chapte 9.1)
### Model Constructions:
#### Input Layer (Fixed):
* Embedding
---
#### Optional Layers:
1. GlobalMaxPooling1D()
2. LSTM(32)
3. Bidirection(LSTM(64))
4. Bidirection(LSTM(64)) + Bidirection(LSTM(32))
5. Conv1D(128, 5, activation='relu') + GlobalMaxPooling1D()
6. GRU(32, dropout=0.2, recurrent_dropout=0.2)
7. GRU(32, dropout=0.1, recurrent_dropout=0.5)+GRU(32, dropout=0.1, recurrent_dropout=0.5, activation='relu')
---
#### Output Layers (Fixed):
- One relu Dense(4)
- One Sigmod Dense(1)
```
imdb, info = tfds.load('imdb_reviews', with_info = True, as_supervised = True)
training_sentences, training_label = [], []
testing_sentences, testing_label = [], []
for data, label in imdb['train']:
training_sentences.append(str(data.numpy()))
training_label.append(label.numpy())
for data, label in imdb['test']:
testing_sentences.append(str(data.numpy()))
testing_label.append(label)
training_sentences, training_label = np.array(training_sentences), np.array(training_label)
testing_sentences, testing_label = np.array(testing_sentences), np.array(testing_label)
numWords = 10000
maxLen = 200
embedding_dim = 16
tokenizer = Tokenizer(num_words = numWords, oov_token = '<OOV>')
tokenizer.fit_on_texts(training_sentences)
training_sequence = tokenizer.texts_to_sequences(training_sentences)
training_padded = pad_sequences(training_sequence, maxlen= maxLen, padding = 'post', truncating = 'post')
testing_sequence = tokenizer.texts_to_sequences(testing_sentences)
testing_padded = pad_sequences(testing_sequence, maxlen = maxLen)
# GlobalMaxPooling1D()
model = tf.keras.Sequential([
tf.keras.layers.Embedding(numWords, embedding_dim, input_length = maxLen),
tf.keras.layers.GlobalAveragePooling1D(),
tf.keras.layers.Dense(4, activation = 'relu'),
tf.keras.layers.Dense(1, activation = 'sigmoid'),
])
trainModel(model, 10)
# LSTM(32)
model = tf.keras.Sequential([
tf.keras.layers.Embedding(numWords, embedding_dim, input_length = maxLen),
tf.keras.layers.LSTM(16),
tf.keras.layers.Dense(4, activation = 'relu'),
tf.keras.layers.Dense(1, activation = 'sigmoid'),
])
trainModel(model, 10)
# Bidirectional(LSTM(32))
model = tf.keras.Sequential([
tf.keras.layers.Embedding(numWords, embedding_dim, input_length = maxLen),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32)),
tf.keras.layers.Dense(6, activation = 'relu'),
tf.keras.layers.Dense(1, activation = 'sigmoid'),
])
trainModel(model, 10)
# Bidirectional(LSTM(64)) + Bidirectional(LSTM(32))
model = tf.keras.Sequential([
tf.keras.layers.Embedding(numWords, embedding_dim, input_length = maxLen),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32, return_sequences = True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(16)),
tf.keras.layers.Dense(4, activation = 'relu'),
tf.keras.layers.Dense(1, activation = 'sigmoid'),
])
trainModel(model, 10)
# Conv1D(128, 5, activation='relu') + GlobalMaxPooling1D()
model = tf.keras.Sequential([
tf.keras.layers.Embedding(numWords, embedding_dim, input_length = maxLen),
tf.keras.layers.Conv1D(128, 5, activation='relu'),
tf.keras.layers.GlobalMaxPooling1D(),
tf.keras.layers.Dense(4, activation = 'relu'),
tf.keras.layers.Dense(1, activation = 'sigmoid'),
])
trainModel(model, 10)
# GRU(32)
embedding_dim = 32
model = tf.keras.Sequential([
tf.keras.layers.Embedding(numWords, embedding_dim, input_length = maxLen),
tf.keras.layers.GRU(32),
tf.keras.layers.Dense(4, activation = 'relu'),
tf.keras.layers.Dense(1, activation = 'sigmoid'),
])
trainModel(model, 10)
# Bidirectional(GRU(32))
model = tf.keras.Sequential([
tf.keras.layers.Embedding(numWords, embedding_dim, input_length = maxLen),
tf.keras.layers.Bidirectional(tf.keras.layers.GRU(32)),
tf.keras.layers.Dense(12, activation = 'relu'),
tf.keras.layers.Dense(1, activation = 'sigmoid'),
])
trainModel(model, 5)
```
| true |
code
| 0.774498 | null | null | null | null |
|
```
%load_ext autoreload
%autoreload 2
import datetime
import os, sys
import numpy as np
import matplotlib.pyplot as plt
import casadi as cas
##### For viewing the videos in Jupyter Notebook
import io
import base64
from IPython.display import HTML
# from ..</src> import car_plotting
# from .import src.car_plotting
PROJECT_PATH = '/home/nbuckman/Dropbox (MIT)/DRL/2020_01_cooperative_mpc/mpc-multiple-vehicles/'
sys.path.append(PROJECT_PATH)
import src.MPC_Casadi as mpc
import src.car_plotting as cplot
%matplotlib inline
```
# Vehicle Dynamics $\frac{d}{dt} \vec{x} = f(\vec{x}, \vec{u})$
def gen_x_next(x_k, u_k, dt):
k1 = f(x_k, u_k)
k2 = f(x_k+dt/2*k1, u_k)
k3 = f(x_k+dt/2*k2, u_k)
k4 = f(x_k+dt*k3, u_k)
x_next = x_k + dt/6*(k1+2*k2+2*k3+k4)
return x_next
# F = cas.Function('F',[x,u,t],[ode],)
# States
$\vec{x}$ = $[x, y, \phi, \delta, V, s]^T$
$\vec{u}$ = $[\delta^u, v^u]^T$
# Discrete (integrated) dynamics $\vec{x}_{t+1} = F(\vec{x}_{t}, \vec{u}_{t})$
```
T = 10 #numbr of time horizons
dt = 0.1
N = int(T/dt) #Number of control intervals
```
intg_options = {}
intg_options['tf'] = dt # from dt
intg_options['simplify'] = True
intg_options['number_of_finite_elements'] = 6 #from 4
dae = {} #What's a DAE?
dae['x'] = x
dae['p'] = u
dae['ode'] = f(x,u)
intg = cas.integrator('intg','rk', dae, intg_options)
res = intg(x0=x,p=u)
x_next = res['xf']
F = cas.Function('F',[x,u],[x_next],['x','u'],['x_next'])
# Problem Definition
### Parameterization of Desired Trajectory ($\vec{x}_d = f_d(s)$)
```
s = cas.MX.sym('s')
xd = s
yd = 0
phid = 0
des_traj = cas.vertcat(xd, yd, phid)
fd = cas.Function('fd',[s],[des_traj],['s'],['des_traj'])
#Globally true information
min_dist = 2 * (2 * .5**2)**.5
# initial_speed = 6.7
initial_speed = 20 * 0.447 # m/s
# Initial Conditions
x0 = np.array([2*min_dist, 1.2*min_dist, 0, 0, initial_speed, 0]).T
x0_2 = np.array([2*min_dist, 0, .0, 0, initial_speed, 0]).T
x0_amb = np.array([0, 0.0, 0, 0, 1.1 * initial_speed , 0]).T
LANE_WIDTH = min_dist
xd2 = s
yd2 = LANE_WIDTH
phid = 0
des_traj2 = cas.vertcat(xd2, yd2, phid)
fd2 = cas.Function('fd',[s],[des_traj2],['s'],['des_traj2'])
```
## Warm Start
### Solve it centrally just to warm start the solution
```
x1_MPC = mpc.MPC(dt)
x2_MPC = mpc.MPC(dt)
x1_MPC.k_s = -1.0
x2_MPC.k_s = -1.0
amb_MPC = mpc.MPC(dt)
amb_MPC.theta_iamb = 0.0
amb_MPC.k_u_v = 0.10
# amb_MPC.k_u_change = 1.0
amb_MPC.k_s = -1.0
amb_MPC.max_v = 40 * 0.447 # m/s
amb_MPC.max_X_dev = 5.0
x2_MPC.fd = fd
amb_MPC.fd = fd
x1_MPC.fd = fd2
x1_MPC.min_y = -1.1 * LANE_WIDTH
x2_MPC.min_y = -1.1 * LANE_WIDTH
amb_MPC.min_y = -1.1 * LANE_WIDTH
speeding_amb_u = np.zeros((2,N))
speeding_amb_u[1,:10] = np.ones((1,10)) * amb_MPC.max_v_u
u0 = np.zeros((2,N))
u0[0,:10] = np.ones((1,10)) * 0
u0[1,:10] = np.ones((1,10)) * x1_MPC.max_v_u
u1 = np.zeros((2,N))
u1[0,:10] = np.ones((1,10)) * 0
u1[1,:10] = np.ones((1,10)) * x2_MPC.max_v_u
opt = mpc.OptimizationMPC(x1_MPC, x2_MPC,amb_MPC)
opt.generate_optimization(N, min_dist, fd, T, x0, x0_2, x0_amb, 2)
# x_warm, x1_warm, xamb_warm = opt.warm_start(u0, u1, speeding_amb_u, x0, x0_2, x0_amb)
x1, u1, x1_des, x2, u2, x2_des, xamb, uamb, xamb_des = opt.get_solution()
optional_suffix = "_newsclassescentral"
subdir_name = datetime.datetime.now().strftime("%Y%m%d-%H%M%S") + optional_suffix
folder = "results/" + subdir_name + "/"
os.makedirs(folder)
os.makedirs(folder+"imgs/")
print(folder)
cplot.plot_cars(x1, x2, xamb, folder,x1_des, x2_des, xamb_des)
CIRCLES = False
if CIRCLES:
vid_fname = folder + subdir_name + 'circle.mp4'
else:
vid_fname = folder + subdir_name + 'car.mp4'
if os.path.exists(vid_fname):
os.remove(vid_fname)
cmd = 'ffmpeg -r 16 -f image2 -i {}imgs/%03d.png -vcodec libx264 -crf 25 -pix_fmt yuv420p {}'.format(folder, vid_fname)
os.system(cmd)
print('Saving video to: {}'.format(vid_fname))
video = io.open(vid_fname, 'r+b').read()
encoded = base64.b64encode(video)
HTML(data='''<video alt="test" controls>
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>'''.format(encoded.decode('ascii')))
plt.plot(range(x1.shape[1]), x1[4,:])
plt.plot(x1[4,:],c='blue')
plt.plot(xamb[4,:],c='red')
plt.ylabel('Speed [m/s]')
plt.show()
```
## IBR
```
br1 = mpc.IterativeBestResponseMPC(x1_MPC, x2_MPC, amb_MPC)
br1.generate_optimization(N, dt, min_dist, fd, T, x0, x0_2, x0_amb, 2)
x1r1, u1r1, x1_desr1 = br1.get_solution(x2, u2, x2_des, xamb, uamb, xamb_des)
cplot.plot_cars(x1r1, x2, xamb, folder)
CIRCLES = False
if CIRCLES:
vid_fname = folder + subdir_name + 'circle1.mp4'
else:
vid_fname = folder + subdir_name + 'car1.mp4'
if os.path.exists(vid_fname):
os.remove(vid_fname)
cmd = 'ffmpeg -r 16 -f image2 -i {}imgs/%03d.png -vcodec libx264 -crf 25 -pix_fmt yuv420p {}'.format(folder, vid_fname)
os.system(cmd)
print('Saving video to: {}'.format(vid_fname))
video = io.open(vid_fname, 'r+b').read()
encoded = base64.b64encode(video)
HTML(data='''<video alt="test" controls>
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>'''.format(encoded.decode('ascii')))
br2 = mpc.IterativeBestResponseMPC(x2_MPC, x1_MPC, amb_MPC)
br2.generate_optimization(N, dt, min_dist, fd, T, x0_2, x0, x0_amb, 2)
x2r2, u2r2, x2_desr2 = br2.get_solution(x1r1, u1r1, x1_desr1, xamb, uamb, xamb_des)
cplot.plot_cars(x1r1, x2r2, xamb, folder)
CIRCLES = False
if CIRCLES:
vid_fname = folder + subdir_name + 'circle2.mp4'
else:
vid_fname = folder + subdir_name + 'car2.mp4'
if os.path.exists(vid_fname):
os.remove(vid_fname)
cmd = 'ffmpeg -r 16 -f image2 -i {}imgs/%03d.png -vcodec libx264 -crf 25 -pix_fmt yuv420p {}'.format(folder, vid_fname)
os.system(cmd)
print('Saving video to: {}'.format(vid_fname))
car1_v_cost = car1_s_cost
car2_v_cost = car2_s_cost
amb_v_cost = amb_s_cost
car1_sub_costs = [car1_u_delta_cost, car1_u_v_cost, k_lat1*car1_lat_cost, k_lon1*car1_lon_cost, k_phi1*car1_phi_cost, k_phid1*phid1_cost, q_v*car1_v_cost]
car1_sub_costs_labels = ['udel1', 'uv1', 'elat1', 'lon1', 'ephi1', 'v1']
plt.bar(range(len(car1_sub_costs)), [sol.value(c) for c in car1_sub_costs])
plt.xticks(range(len(car1_sub_costs)), car1_sub_costs_labels,rotation=45)
plt.title('Car 1')
plt.xlabel("Subcost")
plt.ylabel("Cost Value")
plt.show()
car2_sub_costs = [car2_u_delta_cost, car2_u_v_cost, 10*car2_lat_cost, 10*car2_lon_cost, k_phi2*car2_phi_cost, k_phid2*phid2_cost, q_v*car2_v_cost]
car2_sub_costs_labels = ['udel2', 'uv2', 'elat2', 'lon2', 'ephi2', 'v2']
plt.bar(range(len(car2_sub_costs)), [sol.value(c) for c in car2_sub_costs])
plt.xticks(range(len(car2_sub_costs)), car2_sub_costs_labels,rotation=45)
plt.title('Car 2')
plt.xlabel("Subcost")
plt.ylabel("Cost Value")
plt.show()
amb_sub_costs = [amb_u_delta_cost, amb_u_v_cost, 10*amb_lat_cost, 10*amb_lon_cost,k_phiamb*amb_phi_cost, k_phidamb*phidamb_cost, q_v*amb_v_cost]
amb_sub_costs_labels = ['udelA', 'uvA', 'elatA', 'lonA', 'ephiA', 'vA']
plt.bar(range(len(amb_sub_costs)), [sol.value(c) for c in amb_sub_costs])
plt.xticks(range(len(amb_sub_costs)), amb_sub_costs_labels,rotation=45)
plt.title('Amb')
plt.xlabel("Subcost")
plt.ylabel("Cost Value")
plt.show()
all_costs = [0.1*c for c in car1_sub_costs] + [0.1 for c in car2_sub_costs] + [10*c for c in amb_sub_costs]
all_labels = car1_sub_costs_labels + car2_sub_costs_labels + amb_sub_costs_labels
plt.bar(range(len(all_costs)), [sol.value(c) for c in all_costs])
plt.xticks(range(len(all_labels)), all_labels,rotation=90)
plt.title('All Cars')
plt.xlabel("Subcost")
plt.ylabel("Cost Value")
for BR_iteration in range(20):
opti2.set_value(x_opt2, sol.value(x_opt))
opti2.set_value(u_opt2, sol.value(u_opt))
opti2.set_value(xamb_opt2, sol.value(xamb_opt))
opti2.set_value(uamb_opt2, sol.value(uamb_opt))
opti2.set_initial(x2_opt2, sol.value(x2_opt))
opti2.set_initial(u2_opt2, sol.value(u2_opt))
sol2 = opti2.solve()
opti3.set_value(x_opt3, sol2.value(x_opt2))
opti3.set_value(u_opt3, sol2.value(u_opt2))
opti3.set_value(x2_opt3, sol2.value(x2_opt2))
opti3.set_value(u2_opt3, sol2.value(uamb_opt2))
opti3.set_initial(xamb_opt3, sol2.value(xamb_opt2))
opti3.set_initial(uamb_opt3, sol2.value(uamb_opt2))
sol3 = opti3.solve()
opti.set_value(x2_opt, sol3.value(x2_opt3))
opti.set_value(xamb_opt, sol3.value(xamb_opt3))
opti.set_value(u2_opt, sol3.value(u2_opt3))
opti.set_value(uamb_opt, sol3.value(uamb_opt3))
opti.set_initial(x_opt, sol3.value(x_opt3))
opti.set_initial(u_opt, sol3.value(u_opt3))
sol = opti.solve()
x_warm = sol.value(x_opt)
u_warm = sol.value(u_opt)
x2_warm = sol.value(x2_opt)
u2_warm = sol.value(u2_opt)
xamb_warm = sol.value(xamb_opt)
uamb_warm = sol.value(uamb_opt)
# x_des = sol/
for k in range(N+1):
fig, ax = ego_car.get_frame(x_warm[:,k])
fig, ax = ego_car.get_frame(x2_warm[:,k], ax)
fig, ax = ego_car.get_frame(xamb_warm[:,k], ax, amb=True)
# ax.plot(x_des[0,:], x_des[1,:], '--')
# ax.plot(x2_des[0,:], x2_des[1,:], '--')
ax = plt.gca()
window_width = 24
window_height = window_width
xmin, xmax = -1, -1+window_width
ymin, ymax = -int(window_height/4.0), int(window_height/4.0)
ax.set_ylim((ymin, ymax))
ax.set_xlim((xmin, xmax))
fig.savefig(folder + 'imgs/' '{:03d}.png'.format(k))
plt.close(fig)
vid_fname = folder + '%02d'%BR_iteration + 'car.mp4'
if os.path.exists(vid_fname):
os.remove(vid_fname)
cmd = 'ffmpeg -r 16 -f image2 -i {}imgs/%03d.png -vcodec libx264 -crf 25 -pix_fmt yuv420p {}'.format(folder, vid_fname)
os.system(cmd)
print('Saving video to: {}'.format(vid_fname))
for BR_iteration in range(20):
vid_fname = folder + '%02d'%BR_iteration + 'car.mp4'
print('Saving video to: {}'.format(vid_fname))
```
## Best Response V2
```
x1 = sol3.value(x_opt3)
x2 = sol3.value(x2_opt3)
xamb = sol3.value(xamb_opt3)
x_des = sol3.value(xamb_desired_3)
for k in range(N+1):
fig, ax = ego_car.get_frame(x1[:,k])
fig, ax = ego_car.get_frame(x2[:,k], ax)
fig, ax = ego_car.get_frame(xamb[:,k], ax, amb=True)
ax.plot(x_des[0,:], x_des[1,:], '--')
# ax.plot(x2_des[0,:], x2_des[1,:], '--')
ax = plt.gca()
window_width = 24
window_height = window_width
xmin, xmax = -1, -1+window_width
ymin, ymax = -int(window_height/4.0), int(window_height/4.0)
ax.set_ylim((ymin, ymax))
ax.set_xlim((xmin, xmax))
fig.savefig(folder + 'imgs/' '{:03d}.png'.format(k))
plt.close(fig)
vid_fname = folder + 'caramb.mp4'
if os.path.exists(vid_fname):
os.remove(vid_fname)
cmd = 'ffmpeg -r 16 -f image2 -i {}imgs/%03d.png -vcodec libx264 -crf 25 -pix_fmt yuv420p {}'.format(folder, vid_fname)
os.system(cmd)
print('Saving video to: {}'.format(vid_fname))
car1_sub_costs = [car1_u_delta_cost, car1_u_v_cost, 10*car1_lat_cost, 10*car1_lon_cost, car1_phi_cost, phid1_cost, q_v*car1_v_cost]
car1_sub_costs_labels = ['udel1', 'uv1', 'elat1', 'lon1', 'ephi1', 'v1']
plt.bar(range(len(car1_sub_costs)), [sol.value(c) for c in car1_sub_costs])
plt.xticks(range(len(car1_sub_costs)), car1_sub_costs_labels,rotation=45)
plt.title('Car 1')
plt.xlabel("Subcost")
plt.ylabel("Cost Value")
plt.show()
car2_sub_costs = [car2_u_delta_cost, car2_u_v_cost, 10*car2_lat_cost, 10*car2_lon_cost, car2_phi_cost, phid2_cost, q_v*car2_v_cost]
car2_sub_costs_labels = ['udel2', 'uv2', 'elat2', 'lon2', 'ephi2', 'v2']
plt.bar(range(len(car2_sub_costs)), [sol.value(c) for c in car2_sub_costs])
plt.xticks(range(len(car2_sub_costs)), car2_sub_costs_labels,rotation=45)
plt.title('Car 2')
plt.xlabel("Subcost")
plt.ylabel("Cost Value")
plt.show()
amb_sub_costs = [amb_u_delta_cost, amb_u_v_cost, 10*amb_lat_cost, 10*amb_lon_cost, amb_phi_cost, phidamb_cost, q_v*amb_v_cost]
amb_sub_costs_labels = ['udelA', 'uvA', 'elatA', 'lonA', 'ephiA', 'vA']
plt.bar(range(len(amb_sub_costs)), [sol.value(c) for c in amb_sub_costs])
plt.xticks(range(len(amb_sub_costs)), amb_sub_costs_labels,rotation=45)
plt.title('Amb')
plt.xlabel("Subcost")
plt.ylabel("Cost Value")
plt.show()
all_costs = [0.1*c for c in car1_sub_costs] + [0.1 for c in car2_sub_costs] + [10*c for c in amb_sub_costs]
all_labels = car1_sub_costs_labels + car2_sub_costs_labels + amb_sub_costs_labels
plt.bar(range(len(all_costs)), [sol.value(c) for c in all_costs])
plt.xticks(range(len(all_labels)), all_labels,rotation=90)
plt.title('All Cars')
plt.xlabel("Subcost")
plt.ylabel("Cost Value")
sol.value(x_opt)[3:5, 10:20]
dt
plt.plot(opti.debug.value(x_opt)[4,:],'o',c='b')
plt.plot(opti.debug.value(x2_opt)[4,:],'o',c='g')
plt.plot(opti.debug.value(xamb_opt)[4,:],'o',c='r')
plt.ylabel("Velocity")
plt.show()
plt.plot(opti.debug.value(u_opt)[1,:],'o',c='b')
plt.plot(opti.debug.value(u2_opt)[1,:],'o',c='g')
plt.plot(opti.debug.value(uamb_opt)[1,:],'o',c='r')
plt.ylabel("Acceleration $\delta V_u$")
plt.show()
plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(x_opt[0:2,k] - x2_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'o',c='b')
plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(x_opt[0:2,k] - x2_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'x',c='g')
plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(x_opt[0:2,k] - xamb_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'o',c='b')
plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(x_opt[0:2,k] - xamb_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'x',c='r')
plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(xamb_opt[0:2,k] - x2_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'o',c='g')
plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(xamb_opt[0:2,k] - x2_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'x',c='r')
plt.hlines(min_dist,0,50)
plt.ylabel('Intervehicle Distance')
plt.ylim([-.1, 2*min_dist])
plt.plot([opti.debug.value(slack1) for k in range(opti.debug.value(x_opt).shape[1])],'.',c='b')
plt.plot([opti.debug.value(slack2) for k in range(opti.debug.value(x_opt).shape[1])],'.',c='r')
plt.plot([opti.debug.value(slack3) for k in range(opti.debug.value(x_opt).shape[1])],'.',c='g')
# plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(x_opt[0:2,k] - x2_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'o',c='b')
# plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(x_opt[0:2,k] - x2_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'x',c='g')
# plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(x_opt[0:2,k] - xamb_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'o',c='b')
# plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(x_opt[0:2,k] - xamb_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'x',c='r')
# plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(xamb_opt[0:2,k] - x2_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'o',c='g')
# plt.plot([np.sqrt(opti.debug.value(cas.sumsqr(xamb_opt[0:2,k] - x2_opt[0:2,k]))) for k in range(opti.debug.value(x_opt).shape[1])],'x',c='r')
plt.ylabel('slack')
# plt.ylim([.7,.71])
if not PLOT_LIVE:
for k in range(N+1):
fig, ax = ego_car.get_frame(x_mpc[:,k])
fig, ax = ego_car.get_frame(x2_mpc[:,k], ax)
fig, ax = ego_car.get_frame(xamb_mpc[:,k], ax, amb=True)
ax.plot(x_des[0,:], x_des[1,:], '--')
ax.plot(x2_des[0,:], x2_des[1,:], '--')
ax = plt.gca()
window_width = 24
window_height = window_width
xmin, xmax = -1, -1+window_width
ymin, ymax = -int(window_height/4.0), int(window_height/4.0)
ax.set_ylim((ymin, ymax))
ax.set_xlim((xmin, xmax))
fig.savefig(folder + 'imgs/' '{:03d}.png'.format(k))
plt.close(fig)
```
| true |
code
| 0.213705 | null | null | null | null |
|
###### Content provided under a Creative Commons Attribution license, CC-BY 4.0; code under BSD 3-Clause license. (c)2014 Lorena A. Barba, Olivier Mesnard. Thanks: NSF for support via CAREER award #1149784.
# Lift on a cylinder
Remember when we computed uniform flow past a [doublet](03_Lesson03_doublet.ipynb)? The stream-line pattern produced flow around a cylinder. When studying the pressure coefficient, we realized that the drag on the cylinder was exactly zero, leading to the _D'Alembert paradox_.
_What about lift?_ Is it possible for a perfectly circular cylinder to experience lift?
What if the cylinder is rotating? Have you heard about the Magnus effect?
You might be surprised to learn that all we need to do is add a [vortex](04_Lesson04_vortex.ipynb) in the center of the cylinder. Let's see how that looks.
First, we recall the equations for the flow of a doublet. In Cartesian coordinates, a doublet located at the origin has a stream function and velocity components given by
$$\psi\left(x,y\right) = -\frac{\kappa}{2\pi}\frac{y}{x^2+y^2}$$
$$u\left(x,y\right) = \frac{\partial\psi}{\partial y} = -\frac{\kappa}{2\pi}\frac{x^2-y^2}{\left(x^2+y^2\right)^2}$$
$$v\left(x,y\right) = -\frac{\partial\psi}{\partial x} = -\frac{\kappa}{2\pi}\frac{2xy}{\left(x^2+y^2\right)^2}$$
## Let's start computing!
We'll place a doublet of strength $\kappa=1$ at the origin, and add a free stream $U_\infty=1$ (yes, we really like the number one). We can re-use the code we have written before; this is always a good thing.
```
import math
import numpy
from matplotlib import pyplot
# embed the figures into the notebook
%matplotlib inline
N = 50 # Number of points in each direction
x_start, x_end = -2.0, 2.0 # x-direction boundaries
y_start, y_end = -1.0, 1.0 # y-direction boundaries
x = numpy.linspace(x_start, x_end, N) # computes a 1D-array for x
y = numpy.linspace(y_start, y_end, N) # computes a 1D-array for y
X, Y = numpy.meshgrid(x, y) # generates a mesh grid
kappa = 1.0 # strength of the doublet
x_doublet, y_doublet = 0.0, 0.0 # location of the doublet
u_inf = 1.0 # freestream speed
```
Here are our function definitions for the doublet:
```
def get_velocity_doublet(strength, xd, yd, X, Y):
"""
Returns the velocity field generated by a doublet.
Parameters
----------
strength: float
Strength of the doublet.
xd: float
x-coordinate of the doublet.
yd: float
y-coordinate of the doublet.
X: 2D Numpy array of floats
x-coordinate of the mesh points.
Y: 2D Numpy array of floats
y-coordinate of the mesh points.
Returns
-------
u: 2D Numpy array of floats
x-component of the velocity vector field.
v: 2D Numpy array of floats
y-component of the velocity vector field.
"""
u = (-strength / (2 * math.pi) *
((X - xd)**2 - (Y - yd)**2) /
((X - xd)**2 + (Y - yd)**2)**2)
v = (-strength / (2 * math.pi) *
2 * (X - xd) * (Y - yd) /
((X - xd)**2 + (Y - yd)**2)**2)
return u, v
def get_stream_function_doublet(strength, xd, yd, X, Y):
"""
Returns the stream-function generated by a doublet.
Parameters
----------
strength: float
Strength of the doublet.
xd: float
x-coordinate of the doublet.
yd: float
y-coordinate of the doublet.
X: 2D Numpy array of floats
x-coordinate of the mesh points.
Y: 2D Numpy array of floats
y-coordinate of the mesh points.
Returns
-------
psi: 2D Numpy array of floats
The stream-function.
"""
psi = -strength / (2 * math.pi) * (Y - yd) / ((X - xd)**2 + (Y - yd)**2)
return psi
```
And now we compute everything to get the flow around a cylinder, by adding a free stream to the doublet:
```
# compute the velocity field on the mesh grid
u_doublet, v_doublet = get_velocity_doublet(kappa, x_doublet, y_doublet, X, Y)
# compute the stream-function on the mesh grid
psi_doublet = get_stream_function_doublet(kappa, x_doublet, y_doublet, X, Y)
# freestream velocity components
u_freestream = u_inf * numpy.ones((N, N), dtype=float)
v_freestream = numpy.zeros((N, N), dtype=float)
# stream-function of the freestream flow
psi_freestream = u_inf * Y
# superposition of the doublet on the freestream flow
u = u_freestream + u_doublet
v = v_freestream + v_doublet
psi = psi_freestream + psi_doublet
```
We are ready to do a nice visualization.
```
# plot the streamlines
width = 10
height = (y_end - y_start) / (x_end - x_start) * width
pyplot.figure(figsize=(width, height))
pyplot.xlabel('x', fontsize=16)
pyplot.ylabel('y', fontsize=16)
pyplot.xlim(x_start, x_end)
pyplot.ylim(y_start, y_end)
pyplot.streamplot(X, Y, u, v, density=2, linewidth=1, arrowsize=1, arrowstyle='->')
pyplot.scatter(x_doublet, y_doublet, color='#CD2305', s=80, marker='o')
# calculate the cylinder radius and add the cylinder to the figure
R = math.sqrt(kappa / (2 * math.pi * u_inf))
circle = pyplot.Circle((0, 0), radius=R, color='#CD2305', alpha=0.5)
pyplot.gca().add_patch(circle)
# calculate the stagnation points and add them to the figure
x_stagn1, y_stagn1 = +math.sqrt(kappa / (2 * math.pi * u_inf)), 0.0
x_stagn2, y_stagn2 = -math.sqrt(kappa / (2 * math.pi * u_inf)), 0.0
pyplot.scatter([x_stagn1, x_stagn2], [y_stagn1, y_stagn2],
color='g', s=80, marker='o');
```
Nice! We have cylinder flow.
Now, let's add a vortex located at the origin with a positive strength $\Gamma$. In Cartesian coordinates, the stream function and velocity components are given by:
$$\psi\left(x,y\right) = \frac{\Gamma}{4\pi}\ln\left(x^2+y^2\right)$$
$$u\left(x,y\right) = \frac{\Gamma}{2\pi}\frac{y}{x^2+y^2} \qquad v\left(x,y\right) = -\frac{\Gamma}{2\pi}\frac{x}{x^2+y^2}$$
Based on these equations, we define the functions `get_velocity_vortex()` and `get_stream_function_vortex()` to do ... well, what's obvious by the function names (you should always try to come up with obvious function names). Play around with the value of $\ \Gamma$ and recalculate the flow. See what happens.
```
gamma = 4.0 # strength of the vortex
x_vortex, y_vortex = 0.0, 0.0 # location of the vortex
def get_velocity_vortex(strength, xv, yv, X, Y):
"""
Returns the velocity field generated by a vortex.
Parameters
----------
strength: float
Strength of the vortex.
xv: float
x-coordinate of the vortex.
yv: float
y-coordinate of the vortex.
X: 2D Numpy array of floats
x-coordinate of the mesh points.
Y: 2D Numpy array of floats
y-coordinate of the mesh points.
Returns
-------
u: 2D Numpy array of floats
x-component of the velocity vector field.
v: 2D Numpy array of floats
y-component of the velocity vector field.
"""
u = +strength / (2 * math.pi) * (Y - yv) / ((X - xv)**2 + (Y - yv)**2)
v = -strength / (2 * math.pi) * (X - xv) / ((X - xv)**2 + (Y - yv)**2)
return u, v
def get_stream_function_vortex(strength, xv, yv, X, Y):
"""
Returns the stream-function generated by a vortex.
Parameters
----------
strength: float
Strength of the vortex.
xv: float
x-coordinate of the vortex.
yv: float
y-coordinate of the vortex.
X: 2D Numpy array of floats
x-coordinate of the mesh points.
Y: 2D Numpy array of floats
y-coordinate of the mesh points.
Returns
-------
psi: 2D Numpy array of floats
The stream-function.
"""
psi = strength / (4 * math.pi) * numpy.log((X - xv)**2 + (Y - yv)**2)
return psi
# compute the velocity field on the mesh grid
u_vortex, v_vortex = get_velocity_vortex(gamma, x_vortex, y_vortex, X, Y)
# compute the stream-function on the mesh grid
psi_vortex = get_stream_function_vortex(gamma, x_vortex, y_vortex, X, Y)
```
Now that we have all the necessary ingredients (uniform flow, doublet and vortex), we apply the principle of superposition, and then we make a nice plot.
```
# superposition of the doublet and the vortex on the freestream flow
u = u_freestream + u_doublet + u_vortex
v = v_freestream + v_doublet + v_vortex
psi = psi_freestream + psi_doublet + psi_vortex
# calculate the cylinder radius
R = math.sqrt(kappa / (2 * math.pi * u_inf))
# calculate the stagnation points
x_stagn1, y_stagn1 = (+math.sqrt(R**2 - (gamma / (4 * math.pi * u_inf))**2),
-gamma / (4 * math.pi * u_inf))
x_stagn2, y_stagn2 = (-math.sqrt(R**2 - (gamma / (4 * math.pi * u_inf))**2),
-gamma / (4 * math.pi * u_inf))
# plot the streamlines
width = 10
height = (y_end - y_start) / (x_end - x_start) * width
pyplot.figure(figsize=(width, height))
pyplot.xlabel('x', fontsize=16)
pyplot.ylabel('y', fontsize=16)
pyplot.xlim(x_start, x_end)
pyplot.ylim(y_start, y_end)
pyplot.streamplot(X, Y, u, v,
density=2, linewidth=1, arrowsize=1.5, arrowstyle='->')
circle = pyplot.Circle((0.0, 0.0), radius=R, color='#CD2305', alpha=0.5)
pyplot.gca().add_patch(circle)
pyplot.scatter(x_vortex, y_vortex, color='#CD2305', s=80, marker='o')
pyplot.scatter([x_stagn1, x_stagn2], [y_stagn1, y_stagn2],
color='g', s=80, marker='o');
```
##### Challenge task
The challenge task in the [doublet notebook](03_Lesson03_doublet.ipynb) was to calculate the radius of the cylinder created by the doublet in a uniform flow. You should have gotten
$$R = \sqrt{\frac{\kappa}{2\pi U_\infty}}$$
The new challenge is to find where the stagnation points are located on the surface of the cylinder, when there's a vortex. (You just need an expression for the angles.)
What hapens if $\ \frac{\Gamma}{4\pi U_\infty R} >1$?
Go back and experiment with a value of $\Gamma$ that causes this.
---
## Pressure coefficient
Let's get the pressure coefficient on the surface of the cylinder and compare with the case with no vortex.
The velocity components in polar coordinates for the combined freestream + doublet + vortex are given by
$$u_r\left(r,\theta\right) = U_\infty \cos\theta \left(1-\frac{R^2}{r^2}\right)$$
$$u_\theta\left(r,\theta\right) = -U_\infty \sin\theta \left(1+\frac{R^2}{r^2}\right) - \frac{\Gamma}{2\pi r}$$
where $R$ is the cylinder radius.
We see that the radial component vanishes on the surface of the cylinder whereas the tangential velocity is given by
$$u_\theta\left(R,\theta\right) = -2U_\infty \sin\theta - \frac{\Gamma}{2\pi R} .$$
As a note, when there is no vortex, the tangential velocity on the cylinder becomes
$$u_\theta\left(R,\theta\right) = -2U_\infty \sin\theta .$$
From the doublet notebook, we know that the pressure coefficient is defined by
$$C_p = 1-\frac{U^2}{U_\infty^2}$$
where $U^2 = u^2+v^2 = u_r^2+u_\theta^2$.
Let's plot it!
```
# calculate the surface tangential velocity on the cylinder
theta = numpy.linspace(0.0, 2 * math.pi, 100)
u_theta = -2 * u_inf * numpy.sin(theta) - gamma / (2 * math.pi * R)
# compute the surface pressure coefficient
cp = 1.0 - (u_theta / u_inf)**2
# if there was no vortex
u_theta_no_vortex = -2 * u_inf * numpy.sin(theta)
cp_no_vortex = 1.0 - (u_theta_no_vortex / u_inf)**2
# plot the surface pressure coefficient
size = 6
pyplot.figure(figsize=(size, size))
pyplot.grid(True)
pyplot.xlabel(r'$\theta$', fontsize=18)
pyplot.ylabel('$C_p$', fontsize=18)
pyplot.xlim(theta.min(), theta.max())
pyplot.plot(theta, cp,
label='with vortex', color='#CD2305', linewidth=2, linestyle='-')
pyplot.plot(theta, cp_no_vortex,
label='without vortex', color='g', linewidth=2, linestyle='-')
pyplot.legend(loc='best', prop={'size':16});
```
## Lift and Drag
The lift is the component of force perpendicular to $U_\infty$, while the drag is the component parallel to $U_\infty$. How could we get them with the information we have above?
Well, the force on the cylinder is a product of the pressure acting on its surface (there is no viscosity here: it's ideal flow). If you draw a free body diagram, you should see that:
$$D = -\int_0^{2\pi} p \ \cos\theta \ R \ d\theta$$
$$L = -\int_0^{2\pi} p \ \sin\theta \ R \ d\theta$$
##### Challenge Task
Using Bernoulli's equation, replace $p$ in the equations above to obtain the lift and drag.
What does this mean?
## The Magnus effect
The force experienced by a rotating cylinder (or sphere, or any object) is known as the _Magnus effect_.
Believe it or not, someone actually tried to build an airplane with this concept: spinning cylinders as "wings." According to an article on [PilotFriend](http://www.pilotfriend.com/photo_albums/potty/2.htm), a plane called the 921-V was built in 1930 and flew "at least once" before crashing.
```
from IPython.display import Image
Image(url='http://upload.wikimedia.org/wikipedia/commons/7/78/Flettner_Rotor_Aircraft.jpg')
```
And nowadays, a handful of hobbyists build RC "rotorwings" taking advantage of the Magnus effect to collect views on YouTube ...
```
from IPython.display import YouTubeVideo
YouTubeVideo('POHre1P_E1k')
```
---
```
from IPython.core.display import HTML
def css_styling(filepath):
styles = open(filepath, 'r').read()
return HTML(styles)
css_styling('../styles/custom.css')
```
| true |
code
| 0.803 | null | null | null | null |
|
# 1. Inference on Synthetic data
Author: [Marc Lelarge](https://www.di.ens.fr/~lelarge/)
Date: 04/05
In this notebook, we test our approach on synthetic data.
The problem can be described as follows: we are given a familly of ODEs $y'=h_\theta(y,t)$, where the function $h$ is parametrized by the parameter $\theta$ and a trajectory $z$, the problem is to find the best value of $\theta$ such that $z'\approx h_{\theta}(z,t)$. In order to find the value of $\theta$, we follow an optimization approach using backpropagation through an ODE solver based on the tool developed in [Neural Ordinary Differential Equations](https://arxiv.org/abs/1806.07366). Namely, for a distance function $D$ on $\mathbb{R}^d$, we define $L = D(y_\theta -z)$ where $y_\theta$ is the solution of the ODE $y'=h_{\theta}(y,t)$ and we minimize the loss $L$ with respect to $\theta$ with SGD.
Here, to test this approach, we choose a parameter $\theta$ and integrate the ODE to get the trajectory $z$. We show that based on $z$, we are able to retrieve the parameter $\theta$.
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
torch.manual_seed(0);
```
## a. the IHD Model
We propose a simple version of the SIR Model at the start of the epidemics. In this case, all the population is susceptible.
The standard SIR model is given by the equations:
\begin{eqnarray}
\dot{S}(t) &=& -\beta S(t) I(t)\\
\dot{I}(t) &=& \beta S(t) I(t) - \gamma I(t) -\nu I(t)\\
\dot{R}(t) &=& \gamma I(t)\\
\dot{D}(t) &=& \nu I(t)
\end{eqnarray}
where $S(t)$, $I(t)$, $R(t)$ and $D(t)$ are, respectively, the fractions of susceptible, infectious, recovered and deceased individuals at time $t$. $\beta$ is the contagion rate, $\gamma$ is the recovery rate and $\nu$ is the death rate.
In the early stage of the epidemics, we make the approximation $S(t) \approx 1$ so that the second equation simplifies to $\dot{I}(t) = \beta I(t) - \gamma I(t) -\nu I(t)$.
We make two other modifications:
- the contagion rate will depend on time $\beta(t)$
- we add a sub-category of the population $H(t)$, the numbers of individuals in hospital at time $t$. We assume that all deceased individuals are first in a hospital.
We obtain the IHD model given by the equations:
\begin{eqnarray}
\dot{I}(t) &=& \beta(t) I(t) -\gamma I(t)-\nu I(t)\\
\dot{R}(t) &=& \gamma I(t)\\
\dot{H}(t) &=& \nu I(t) - \gamma H(t) - \lambda H(t)\\
\dot{D}(t) &=& \lambda H(t)
\end{eqnarray}
note that the recovered individuals can be ignored to compute $I(t),H(t)$ and $D(t)$.
In practice, we will prametrize the function $\beta(t)$ as follows:
$$\beta(t) = \beta_1 +\delta \sigma(t-\tau),$$
where $\sigma(.)$ is the sigmoid function.
The motivation for using this specific function is to understand the impact of the lock-down on the epidemics. We expect the contagious rate to decrease under lock-down so that $\tau$ should be interpreted as the time when social distancing is implemented resulting in a drop in the contagious rate.
```
from model_epidemio import ihd_fit
size = 101
t = torch.linspace(0., size-1, size)
true_init = torch.tensor([[0.01,0., 0.]])
name_parms = ['beta', 'delta','gamma','nu','lambda']
parms = torch.tensor([0.1,-0.04,0.05,0.015,0.02])
time = torch.tensor([30.])
ihd_synt = ihd_fit.IHD_model(parms,time)
```
$\beta_1=0.1, \delta = -0.04, \gamma = 0.05, \nu = 0.015, \lambda = 0.02$
$\tau = 30$
$I(0)=0.01, H(0)=0, D(0)=0$
```
y_synt = ihd_fit.predic_ode(ihd_synt, true_init,t)
plt.plot(t,y_synt[:,0], 'b', label= 'Infected')
plt.plot(t,y_synt[:,1], 'g', label= 'Hospital')
plt.plot(t,y_synt[:,2], 'r', label= 'Deceased')
plt.ylabel('fraction pop')
plt.xlabel('time')
plt.legend();
```
Integration of the ODE: Infected = Blue, Hospital = green, Deaths = red
These trajectories are obtained by integrating the IHD model. To a 'non-specialist', these curves seem plausible: we observe the typical exponential growth at the start of the epidemics and when the R0 goes below one (around time 30), the number of Infected starts to decrease, as well as the number of individuals in hospital.
## b. Inference problem
Now given the trajectory depicted above, we try to recover the parameters of the model.
```
parms_fit = torch.tensor([0.15,-0.05,0.05,0.05,0.05])
time_fit = torch.tensor([50.])
ihd_time = ihd_fit.IHD_fit_time(parms_fit,time_fit)
optimizer_time = optim.RMSprop([{'params': [ihd_time.b1, ihd_time.b2, ihd_time.g, ihd_time.nu, ihd_time.l]},
{'params': ihd_time.time, 'lr' : 1.}], lr=1e-3)
criterion = nn.MSELoss()
best_loss, best_parms = ihd_fit.trainig(ihd_time, init=true_init, t=t, optimizer=optimizer_time,
criterion=criterion,niters=600,data=y_synt)
ihd_inf = ihd_fit.get_best_model(best_parms)
y_inf = ihd_fit.predic_ode(ihd_inf, true_init,t)
plt.plot(y_inf[:,0], 'b', label='Est. I')
plt.plot(y_synt[:,0], 'b--', label='I')
plt.plot(y_inf[:,1], 'g', label='Est. H')
plt.plot(y_synt[:,1], 'g--', label='H')
plt.plot(y_inf[:,2], 'r', label='Est. D')
plt.plot(y_synt[:,2], 'r--', label='D')
plt.ylabel('fraction pop')
plt.xlabel('time')
plt.legend();
```
Infected = Blue, Hospital = green, Deaths = red; dashed = true, plain = estimated.
We see that we have a good fit of the trajectories. Below, we look at the estimation of the parameters directly.
```
for i,p in enumerate(best_parms):
try:
print(name_parms[i],',true: ', parms[i].item(), ',evaluated: ', p.data.item())
except:
print('time',',true: ', time.item(), ',evaluated: ', p.data.item())
```
We see that the switching time is well estimated. The contagious and recovery rates $\gamma$ are overestimated.
## c. Inference problem with missing data
In practice, we will not have access to the whole trajectory.
### c.1 missing hospital numbers
As an example, we consider here the case where the number of individuals in the hospital is not given. Hence, we have only access to the curves $I(t)$ and $D(t)$ but not $H(t)$.
This case fits nicely to our framework and we only need to modify the loss function in the optimization problem.
```
parms_fit = torch.tensor([0.15,-0.05,0.05,0.05,0.05])
time_fit = torch.tensor([50.])
ihd_time = ihd_fit.IHD_fit_time(parms_fit,time_fit)
optimizer_time = optim.RMSprop([{'params': [ihd_time.b1, ihd_time.b2, ihd_time.g, ihd_time.nu, ihd_time.l]},
{'params': ihd_time.time, 'lr' : 1.}], lr=1e-3)
criterion = nn.MSELoss()
best_loss_partial, best_parms_partial = ihd_fit.trainig(ihd_time, init=true_init, t=t, optimizer=optimizer_time,
criterion=criterion,niters=600,data=(y_synt[:,0],y_synt[:,2]),all_data=False)
ihd_inf = ihd_fit.get_best_model(best_parms_partial)
y_inf = ihd_fit.predic_ode(ihd_inf, true_init,t)
plt.plot(y_inf[:,0], 'b', label='Est. I')
plt.plot(y_synt[:,0], 'b--', label='I')
plt.plot(y_inf[:,1], 'g', label='Est. H')
plt.plot(y_synt[:,1], 'g--', label='H')
plt.plot(y_inf[:,2], 'r', label='Est. D')
plt.plot(y_synt[:,2], 'r--', label='D')
plt.ylabel('fraction pop')
plt.xlabel('time')
plt.legend();
```
We see that the number of individuals in hospital cannot be estimated although the number of infected and deceased individuals match very well.
```
for i,p in enumerate(best_parms_partial):
try:
print(name_parms[i], ',true: ', parms[i].item(), ',evaluated: ', p.data.item())
except:
print('time', ',true: ', time.item(), ',evaluated: ', p.data.item())
```
### c.2 missing infected
We now consider a case where the number of infected $I(t)$ is not available (for example, because the population is not tested). We only have acces to the number of individuals in hospital $H(t)$ and deceased individuals $D(t)$.
```
parms_fit = torch.tensor([0.15,-0.05,0.05,0.05,0.05])
time_fit = torch.tensor([50.])
ihd_time = ihd_fit.IHD_fit_time(parms_fit,time_fit)
optimizer_time = optim.RMSprop([{'params': [ihd_time.b1, ihd_time.b2, ihd_time.g, ihd_time.nu, ihd_time.l]},
{'params': ihd_time.time, 'lr' : 1.}], lr=1e-3)
criterion = nn.MSELoss()
best_loss_hosp, best_parms_hosp = ihd_fit.trainig_hosp(ihd_time, init=true_init, t=t, optimizer=optimizer_time,
criterion=criterion,niters=500,data=(y_synt[:,1],y_synt[:,2]))
optimizer_time = optim.RMSprop([{'params': [ihd_time.b1, ihd_time.b2, ihd_time.g, ihd_time.nu, ihd_time.l]},
{'params': ihd_time.time, 'lr' : 1.}], lr=1e-4)
criterion = nn.MSELoss()
best_loss_hosp, best_parms_hosp = ihd_fit.trainig_hosp(ihd_time, init=true_init, t=t, optimizer=optimizer_time,
criterion=criterion,niters=500,data=(y_synt[:,1],y_synt[:,2]))
optimizer_time = optim.RMSprop([{'params': [ihd_time.b1, ihd_time.b2, ihd_time.g, ihd_time.nu, ihd_time.l]},
{'params': ihd_time.time, 'lr' : 1.}], lr=1e-4)
criterion = nn.MSELoss()
best_loss_hosp, best_parms_hosp = ihd_fit.trainig_hosp(ihd_time, init=true_init, t=t, optimizer=optimizer_time,
criterion=criterion,niters=500,data=(y_synt[:,1],y_synt[:,2]))
ihd_inf = ihd_fit.get_best_model(best_parms_hosp)
y_inf = ihd_fit.predic_ode(ihd_inf, true_init,t)
plt.plot(y_inf[:,0], 'b', label='Est. I')
plt.plot(y_synt[:,0], 'b--', label='I')
plt.plot(y_inf[:,1], 'g', label='Est. H')
plt.plot(y_synt[:,1], 'g--', label='H')
plt.plot(y_inf[:,2], 'r', label='Est. D')
plt.plot(y_synt[:,2], 'r--', label='D')
plt.ylabel('fraction pop')
plt.xlabel('time')
plt.legend();
```
We see that we obtain much better results here. Although we do not observe the curve of infected individuals, we are able to get a rough estimate of it.
```
for i,p in enumerate(best_parms_hosp):
try:
print(name_parms[i], ',true: ', parms[i].item(), ',evaluated: ', p.data.item())
except:
print('time', ',true: ', time.item(), ',evaluated: ', p.data.item())
```
| true |
code
| 0.658006 | null | null | null | null |
|
# 04 - Full Waveform Inversion with Devito and Dask
## Introduction
In this tutorial, we will build on the [previous](https://github.com/devitocodes/devito/blob/master/examples/seismic/tutorials/03_fwi.ipynb) FWI tutorial and implement parallel versions of both forward modeling and FWI objective functions. Furthermore, we will show how our parallel FWI function can be passed to black-box third party optimization libraries, such as SciPy's [optimize](https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html) package, to access sophisticated optimization algorithms without having to implement them from scratch!
To implement parallel versions of forward modeling and FWI, we will use [Dask](https://dask.pydata.org/en/latest/#dask), a Python library for distributed computing based on parallel data structures and task-based programming. As computing multiple seismic shot records or gradients for subsequent source locations is an embarassingly parallel process, we will use Dask to dynamically distribute our workload to a pool of available workers and afterwards collect the results.
The first part of this tutorial closely follows [tutorial 3](https://github.com/devitocodes/devito/blob/master/examples/seismic/tutorials/03_fwi.ipynb) and consists of reading the velocity model and setting up the acquisition geometry. Subsequently, we will implement serial versions of forward modeling and FWI objective functions and then show how we can use Dask to implement parallel versions of these functions. Finally, we will show how to write a wrapper that lets us pass our objective function to scipy's optimize package and how to run a small 2D FWI example using a limited-memory Quasi-Newton method.
## GPU Aware Dask
The default method to start a Dask Cluster is LocalCluster(...). This method enables CPU worker threads, but it shares one GPU for all workers. To enable Dask to use multi-GPU, or a GPU per Dask worker, the method to start a Dask Cluster needs to be changed to LocalCUDACluster. This Dask modification is pulled from the Rapids.ai open source project.
Reference: https://github.com/rapidsai/dask-cuda
```
USE_GPU_AWARE_DASK = False
```
## Set up velocity models
As before, we start by reading the true (i.e. unknown) velocity model, as well as the starting model for FWI. For our example, we once again use the 2D Camembert model with a transmission acquisition set up, which involves having sources on one side of the model and receivers on the other side.
In reality, we obvisouly cannot know what the true velocity is, but here we use the true model to generate our own data (inverse crime alert!) and to compare it to our FWI result.
```
from examples.seismic import demo_model
# Set up velocity model
shape = (101, 101) # Number of grid points (nx, nz).
spacing = (10., 10.) # Grid spacing in m. The domain size is now 1km by 1km.
origin = (0, 0) # Need origin to define relative source and receiver locations.
nbl = 40
# True model
model1 = demo_model('circle-isotropic', vp_circle=3.0, vp_background=2.5,
origin=origin, shape=shape, spacing=spacing, nbl=nbl)
# Initial model
model0 = demo_model('circle-isotropic', vp_circle=2.5, vp_background=2.5,
origin=origin, shape=shape, spacing=spacing, nbl=nbl, grid = model1.grid)
```
## Acquisition geometry
For the acquisition geometry, we use the same setup as in tutorial 3 and position 5 source position on one side of the model, and an array of 101 receivers on the other side. Note that now our source coordinate array (`src_coordinates`) is a 5 x 2 array, containing the shot locations of all 5 source experiments. After defining the source/receiver coordinates, we set up individual geometry objects for both the observed data (using `model`) and the predicted data (using `model0`).
```
from examples.seismic import AcquisitionGeometry
import numpy as np
# Set up acquisiton geometry
t0 = 0.
tn = 1000.
f0 = 0.010
# Set up source geometry, but define 5 sources instead of just one.
nsources = 5
src_coordinates = np.empty((nsources, 2))
src_coordinates[:, 1] = np.linspace(0, model1.domain_size[0], num=nsources)
src_coordinates[:, 0] = 20. # Source depth is 20m
# Initialize receivers for synthetic and imaging data
nreceivers = 101
rec_coordinates = np.empty((nreceivers, 2))
rec_coordinates[:, 1] = np.linspace(spacing[0], model1.domain_size[0] - spacing[0], num=nreceivers)
rec_coordinates[:, 0] = 980. # Receiver depth
# Set up geometry objects for observed and predicted data
geometry1 = AcquisitionGeometry(model1, rec_coordinates, src_coordinates, t0, tn, f0=f0, src_type='Ricker')
geometry0 = AcquisitionGeometry(model0, rec_coordinates, src_coordinates, t0, tn, f0=f0, src_type='Ricker')
```
## Forward modeling
Before diving into FWI, we will start with forward modeling and show how we can use Dask to implement a parallel wrapper around a serial modeling function to compute seismic shot records for multiple source locations in parallel.
First, we implement a forward modeling function for a single shot, which takes a geometry data structure as the only mandatory input argument. This function assumes that the geometry structure only contains a *single* source location. To solve the wave equation for the current shot location and model as specified in `geometry`, we use the `AcousticSolver` from previous tutorials, which is an abstract layer built on top of (generic) Devito objects. `AcousticSolver` contains Devito implementations of forward and adjoint wave equations, as well as Jacobians as specified in tutorials 1 and 2, so we don't have to re-implement these PDEs here.
```
from examples.seismic.acoustic import AcousticWaveSolver
# Serial modeling function
def forward_modeling_single_shot(model, geometry, save=False, dt=4.0):
solver = AcousticWaveSolver(model, geometry, space_order=4)
d_obs, u0 = solver.forward(vp=model.vp, save=save)[0:2]
return d_obs.resample(dt), u0
```
With our modeling function for a single shot record in place, we now implement our parallel version of our modeling function, which consists of a loop over all source locations. As the `geometry` object in `forward_modeling_single_shot` expects only a single source location, we set up a new geometry structure for the i-th source location to pass to our modeling function. However, rather than simpling calling the modeling function for single shots, we tell Dask to create a *task* for each source location and to distribute them to the available parallel workers. Dask returns a remote reference to the result on each worker called `future`. The `wait` statement tells our function to wait for all tasks to finish their computations, after which we collect the modeled shot records from the workers.
```
# Parallel modeling function
def forward_modeling_multi_shots(model, geometry, save=False, dt=4.0):
futures = []
for i in range(geometry.nsrc):
# Geometry for current shot
geometry_i = AcquisitionGeometry(model, geometry.rec_positions, geometry.src_positions[i,:],
geometry.t0, geometry.tn, f0=geometry.f0, src_type=geometry.src_type)
# Call serial modeling function for each index
futures.append(client.submit(forward_modeling_single_shot, model, geometry_i, save=save, dt=dt))
# Wait for all workers to finish and collect shots
wait(futures)
shots = []
for i in range(geometry.nsrc):
shots.append(futures[i].result()[0])
return shots
```
We can use this parallel modeling function to generate our own observed data set, which we will subsequently use for our FWI example. In reality, we would instead read our observed data from a SEG-Y file. To compute the data in parallel, we launch a pool of workers on our local machine and then call the parallel modeling function:
```
from distributed import Client, wait
# Start Dask cluster
if USE_GPU_AWARE_DASK:
from dask_cuda import LocalCUDACluster
cluster = LocalCUDACluster(threads_per_worker=1, death_timeout=600)
else:
from distributed import LocalCluster
cluster = LocalCluster(n_workers=nsources, death_timeout=600)
client = Client(cluster)
# Compute observed data in parallel (inverse crime). In real life we would read the SEG-Y data here.
d_obs = forward_modeling_multi_shots(model1, geometry1, save=False)
```
The variable `d_obs` is a list of the 5 shots records and we can plot one of the shot records as follows:
```
from examples.seismic import plot_shotrecord
# Plot shot no. 3 of 5
plot_shotrecord(d_obs[2].data, model1, t0, tn)
```
## Parallel Full-Waveform Inversion
Now that we know how to use Dask to implement a parallel loop around a (serial) modeling function for a single shot, we can apply the same concept to an FWI objective function, which computes the FWI function value and gradient for a given geometry and observed shot record. This function follows largely the structure in tutorial 3 and involves computing the predicted data and backpropagating the residual to compute the gradient. As we do not want to update the velocity in the area of the absorbing boundaries, we only return the gradient on the (original) physical grid.
```
from devito import Function
from examples.seismic import Receiver
# Serial FWI objective function
def fwi_objective_single_shot(model, geometry, d_obs):
# Devito objects for gradient and data residual
grad = Function(name="grad", grid=model.grid)
residual = Receiver(name='rec', grid=model.grid,
time_range=geometry.time_axis,
coordinates=geometry.rec_positions)
solver = AcousticWaveSolver(model, geometry, space_order=4)
# Predicted data and residual
d_pred, u0 = solver.forward(vp=model.vp, save=True)[0:2]
residual.data[:] = d_pred.data[:] - d_obs.resample(geometry.dt).data[:][0:d_pred.data.shape[0], :]
# Function value and gradient
fval = .5*np.linalg.norm(residual.data.flatten())**2
solver.gradient(rec=residual, u=u0, vp=model.vp, grad=grad)
# Convert to numpy array and remove absorbing boundaries
grad_crop = np.array(grad.data[:])[model.nbl:-model.nbl, model.nbl:-model.nbl]
return fval, grad_crop
```
As for the serial modeling function, we can call `fwi_objective_single_shot` with a geometry structure containing a single source location and a single observed shot record. Since we are interested in evaluating this function for multiple sources in parallel, we follow the strategy from our forward modeling example and implement a parallel loop over all shots, in which we create a task for each shot location. As before, we use Dask to create one task per shot location and evaluate the single-shot FWI objective function for each source. We wait for all computations to finish via `wait(futures)` and then we sum the function values and gradients from all workers.
```
# Parallel FWI objective function
def fwi_objective_multi_shots(model, geometry, d_obs):
futures = []
for i in range(geometry.nsrc):
# Geometry for current shot
geometry_i = AcquisitionGeometry(model, geometry.rec_positions, geometry.src_positions[i,:],
geometry.t0, geometry.tn, f0=geometry.f0, src_type=geometry.src_type)
# Call serial FWI objective function for each shot location
futures.append(client.submit(fwi_objective_single_shot, model, geometry_i, d_obs[i]))
# Wait for all workers to finish and collect function values and gradients
wait(futures)
fval = 0.0
grad = np.zeros(model.shape)
for i in range(geometry.nsrc):
fval += futures[i].result()[0]
grad += futures[i].result()[1]
return fval, grad
```
We can compute a single gradient of the FWI objective function for all shots by passing the geometry structure with the initial model to the objective function, as well as the observed data we generated earlier.
```
# Compute FWI gradient for 5 shots
f, g = fwi_objective_multi_shots(model0, geometry0, d_obs)
```
The physical units of the gradient are $s^2/km^2$, which means our gradient is an update of the squared slowness, rather than of the velocity.
```
from examples.seismic import plot_image
# Plot g
plot_image(g.reshape(model1.shape), vmin=-6e3, vmax=6e3, cmap="cividis")
```
## FWI with SciPy's L-BFGS
With our parallel FWI objective function in place, we can in principle implement a wide range of gradient-based optimization algorithms for FWI, such as (stochastic) gradient descent or the nonlinear conjugate gradient method. However, many optimization algorithms, especially second order methods or algorithms for constrained optimization, are far from trivial to implement correctly from scratch. Luckily, many optimization libraries exist that we can adapt for our purposes.
Here, we demonstrate how we can interface the scipy *optimize* package to run FWI with a limited-memory Quasi-Newton method. The scipy optimize package was not specifically designed for FWI, but this does not matter, as the library accepts any Python function that can be evaluated for a current model iterate `x` and returns the function value and gradient:
```
f, g = objective_function(x, args)
```
where `f` is function value and `g` is a one-dimensional numpy array of type `float64`. Our parallel FWI function does not take the current model as an input argument, but instead expects a geometry structure and the observed data. Therefore, we have to write a little wrapper function called `loss`, which provides the input argument structure that is expected by `scipy.optimize`. The function takes the current model iteratve `x` (in squared slowness) as the first input argument and overwrites the current velocity in `geometry` with `x`. The gradient that is returned to `scipy.optimize` is converted to a numpy array of the required type (`float64`).
```
# Wrapper for scipy optimizer: x is current model in squared slowness [s^2/km^2]
def loss(x, model, geometry, d_obs):
# Convert x to velocity
v_curr = 1.0/np.sqrt(x.reshape(model.shape))
# Overwrite current velocity in geometry (don't update boundary region)
model.update('vp', v_curr.reshape(model.shape))
# Evaluate objective function
fval, grad = fwi_objective_multi_shots(model, geometry, d_obs)
return fval, grad.flatten().astype(np.float64) # scipy expects double precision vector
```
The `scipy.optimize` function also takes an optional callback function as an input argument, which can be used to keep track of the model error as a function of the iteration number. The callback function takes the current model iterate `xk` as the only input argument and computes the $\ell_2$-misfit with the true model `m`:
```
# Callback to track model error
model_error = []
def fwi_callback(xk):
vp = model1.vp.data[model1.nbl:-model1.nbl, model1.nbl:-model1.nbl]
m = 1.0 / (vp.reshape(-1).astype(np.float64))**2
model_error.append(np.linalg.norm((xk - m)/m))
```
The final preparation step before we can run our example, is the definition of box constraints for the velocity. At each iteration, the optimizer will project the current model iterate onto a feasible set of velocites as defined by the lower and upper bounds `vmin` and `vmax`. Box contraints allow us to prevent velocities from taking negative values or values that are too small or large for the stability criteria of our modeling stepping scheme. We define the box constraints for the velocity in $km/s$ and then convert them to squared slownesses. Furthermore, we define our initial guess `m0`:
```
# Box contraints
vmin = 1.4 # do not allow velocities slower than water
vmax = 4.0
bounds = [(1.0/vmax**2, 1.0/vmin**2) for _ in range(np.prod(model0.shape))] # in [s^2/km^2]
# Initial guess
v0 = model0.vp.data[model0.nbl:-model0.nbl, model0.nbl:-model0.nbl]
m0 = 1.0 / (v0.reshape(-1).astype(np.float64))**2
```
Finally, we run our 2D FWI example by calling the `optimize.minimize` function. The first input argument is the function to be minimized, which is our `loss` function. The second input argument is the starting value, which in our case is our initial model in squared slowness. The third input argument (`args`) are the arguments that are passed to the loss function other than `x`. For this example we use the L-BFGS algorithm, a limited-memory Quasi-Newton algorithm which builds up an approximation of the (inverse) hessian as we iterate. As our `loss` function returns the analytically computed gradient (as opposed to a numerically approximated gradient), we set the argument `jac=True`. Furthermore, we pass our callback function, box constraints and the maximum number of iterations (in this case 5) to the optimizer.
```
from scipy import optimize
# FWI with L-BFGS
ftol = 0.1
maxiter = 5
result = optimize.minimize(loss, m0, args=(model0, geometry0, d_obs), method='L-BFGS-B', jac=True,
callback=fwi_callback, bounds=bounds, options={'ftol':ftol, 'maxiter':maxiter, 'disp':True})
# Check termination criteria
assert np.isclose(result['fun'], ftol) or result['nit'] == maxiter
```
After either the maximum iteration number is reached or we find the minimum of the objective function within some tolerance level `ftol`, the optimizer returns a dictionary with the results and some additional information. We convert the result back to the velocity in $km/s$ and compare it to the true model:
```
# Plot FWI result
vp = 1.0/np.sqrt(result['x'].reshape(model1.shape))
plot_image(model1.vp.data[model1.nbl:-model1.nbl, model1.nbl:-model1.nbl], vmin=2.4, vmax=2.8, cmap="cividis")
plot_image(vp, vmin=2.4, vmax=2.8, cmap="cividis")
```
Looking at the model error as a function of the iteration number, we find that the error decays monotonically, as we would expect.
```
import matplotlib.pyplot as plt
# Plot model error
plt.plot(range(1, maxiter+1), model_error); plt.xlabel('Iteration number'); plt.ylabel('L2-model error')
plt.show()
```
## Next steps
In our current example, the master process keeps all shot records in memory and distributes the data to the workers in the parallel pool. This works perfectly fine for 2D and even small 3D examples, but quickly becomes infeasible for large-scale data sets. Therefore, an extension of our current code should include the following steps if we want to scale things up in the future:
- Write shot records directly to disk on each worker and return a file pointer back to the master process.
- Avoid sending the velocity model to the workers and read the model directly onto each worker.
- Include optimal checkpointing or domain-decomposition to address the memory bottleneck in the gradient computations.
For scaling Devito to industry-scale problems and being able to work on data sets in the range of multiple terabytes, it is furthermore necessary to have a fast SEG-Y reader that is able to scan through large data volumes and efficiently access blocks of data such as single shot records. Furthermore, we need the SEG-Y reader to be able to interact with Devito and automatically set up `geometry` objects from the SEG-Y headers. For this purpose, please check out the [Julia Devito Inversion framework (JUDI)](https://github.com/slimgroup/JUDI.jl), an extension built on top of Devito in the Julia programming language. JUDI consists on an abstract linear algebra framework and an interface to a fast and parallel SEG-Y reader called [SEGYIO.jl](https://github.com/slimgroup/SegyIO.jl), making it possible to:
- Scan large-scale data sets and create look-up tables from which shot records can be directly accessed through their byte locations (no need to loop over traces or read full files).
- Use look-up tables to automatically set up Devito objects with source and receiver coordinates.
- Work with out-of-core data containers that only read the data into memory when it is used for computations.
You can find a full FWI example of the 3D Overthrust model using a 1.1 TB large data set on [JUDI's Github page](https://github.com/slimgroup/JUDI.jl/blob/master/examples/software_paper/examples/fwi_3D_overthrust_spg.jl).
| true |
code
| 0.676326 | null | null | null | null |
|
# ART decision tree classifier attack
This notebook shows how to compute adversarial examples on decision trees (as described in by Papernot et al. in https://arxiv.org/abs/1605.07277). Due to the structure of the decision tree, an adversarial example can be computed without any explicit gradients, only by traversing the learned tree structure.
Consider the following simple decision tree for four dimensional data, where we go to the left if a condition is true:
F1<3
F2<5 F2>2
F4>3 C1 F3<1 C3*
C1 C2 C3 C1
Given sample [4,4,1,1], the tree outputs C3 (as indicated by the star). To misclassify the sample, we walk one node up and explore the subtree on the left. We find the leaf outputting C1 and change the two features, obtaining [4,1.9,0.9,1]. In this implementation, we change only the features with wrong values, and specify the offset in advance.
## Applying the attack
```
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_digits
from matplotlib import pyplot as plt
import numpy as np
from art.attacks.evasion import DecisionTreeAttack
from art.estimators.classification import SklearnClassifier
digits = load_digits()
X = digits.data
y = digits.target
clf = DecisionTreeClassifier()
clf.fit(X,y)
clf_art = SklearnClassifier(clf)
print(clf.predict(X[:14]))
plt.imshow(X[0].reshape(8,8))
plt.colorbar()
```
We now craft adversarial examples and plot their classification. The difference is really small, and often only one or two features are changed.
```
attack = DecisionTreeAttack(clf_art)
adv = attack.generate(X[:14])
print(clf.predict(adv))
plt.imshow(adv[0].reshape(8,8))
# plt.imshow((X[0]-adv[0]).reshape(8,8)) ##use this to plot the difference
```
The change is possibly larger if we specify which class the sample should be (mis-)classified as. To do this, we just specify a label for each attack point.
```
adv = attack.generate(X[:14],np.array([6,6,7,7,8,8,9,9,1,1,2,2,3,3]))
print(clf.predict(adv))
plt.imshow(adv[0].reshape(8,8))
```
Finally, the attack has an offset parameter which specifies how close the new value of the feature is compared to the learned threshold of the tree. The default value is very small (0.001), however the value can be set larger when desired. Setting it to a very large value might however yield adversarial examples outside the range or normal features!
```
attack = DecisionTreeAttack(clf_art,offset=20.0)
adv = attack.generate(X[:14])
print(clf.predict(adv))
plt.imshow(adv[0].reshape(8,8))
plt.colorbar()
```
| true |
code
| 0.691497 | null | null | null | null |
|
<!-- </style><figure align = "left" style="page-break-inside: avoid;"><figcaption style="font-weight: bold; font-size:16pt; font-family:inherit;" align="center"></figcaption><br> -->
<img src= "images/APEX.png">
## Introduction: What's APEX?
APEX is a portfolio trade scheduler that optimizes execution with the latest intraday risk and market impact models from Goldman Sachs’ Quantitative Execution Services (QES) team.
## Modeling Pillars
<img src= "images/three_pillars.png">
## Constraints and Features
<img src= "images/apex_constraints_and_features.png">
## The APEX Trade Lifecycle
<img src= "images/how_apex_works.png">
### First, let's load a sample portfolio:
#### Import Libs and Utils:
```
from qes_utils import persistXls, plotCost, plotVar, plotBuySellNet, plotGrossRemaining, plotMultiStrategyPortfolioLevelAnalytics
from gs_quant.api.gs.assets import GsAssetApi
from gs_quant.session import GsSession, Environment
from gs_quant.common import Position
from gs_quant.target.risk import OptimizationRequest, OptimizationType
from gs_quant.api.gs.risk import GsRiskApi
import matplotlib.pyplot as plt
import pandas as pd
import datetime
import numpy as np
import copy
import datetime
from matplotlib import cm
```
#### Establish GS_Quant Connection:
- Fill in client_id and client_secret\
- Set up Marquee API: https://marquee.gs.com/s/developer/docs/getting-started
- Once you create the application, click on the Application page and scroll down to the ‘Scope’ section. Request the “read_product_date”& “run_analytics” scope for your application.
```
print('INFO: Setting up Marquee Connection')
client_id =
client_secret =
GsSession.use(Environment.PROD, client_id=client_id, client_secret=client_secret, scopes=['read_product_data', 'run_analytics'])
```
#### Set up the portfolio:
```
print('INFO: Setting up portfolio to schedule using APEX...')
portfolio_input = pd.read_csv('trade_list_world.csv').rename(columns={'Symbol': 'sedol', 'Shares': 'qty'})
portfolio_input.dtypes
```
#### Convert Identifier (SEDOL) to marqueeids:
SEDOL access needs to be requested on Marquee with the following steps:
- Go to https://marquee.gs.com/s/developer/datasets/SEDOL
- Select an application to request access for
- Request will be auto approved
```
assets = GsAssetApi.get_many_assets(sedol=list(portfolio_input['sedol']), fields=['sedol', 'rank'], listed=[True], type='Single Stock')
identifier_to_marqueeid_map = pd.DataFrame([{'sedol': list(filter(lambda x: x.type=='SED', i.identifiers))[0].value, 'ID': i.id, 'rank': i.rank} for i in assets])\
.sort_values(['sedol', 'rank'], ascending=False).groupby('sedol').head(1)[['sedol','ID']].rename(columns={'ID': 'marqueeid'})
print(f'found {len(identifier_to_marqueeid_map)} sedols to mrquee ids map...')
```
#### Identify assets with missing marquee ids and drop them from the portfolio
```
portfolio_input = portfolio_input.merge(indentifier_to_marqueeid_map, how='left', on=identifier_type)
missing_marqueeids = portfolio_input[portfolio_input['marqueeid'].isnull()]
if len(missing_marqueeids):
print(f'WARNING: the following bbids are missing marqueeids:\n{missing_marqueeids}\ndropping from the optimization...')
else:
print('INFO: all the assets has been succesfuly converted to marquee id')
portfolio_input = portfolio_input.dropna()
portfolio_input.head()
```
### At this point, we have a portfolio we can optimize using APEX.
Our portfolio is now ready for optimization with APEX.
### We'll run two variations:
##### 1. single optimization analysis - optimize the basket using defined parameters and investigate the cost-risk trade-off.
##### 2. trade scenario analysis - run multiple optimizations upon different risk aversion (urgency) parameters and compare the cost-risk trade-off among optimized execution strategies
### 1. APEX Optimization: run my trade list in the APEX optimizer and explore the various analytics:
#### in this section, we'll explore how to set optimization parameters and how to display multiple optimal trajectory analytics to develop further intuition for the decisions made by APEX
we'll run an APEX-IS (Arrival) risk-cost minimization optimal trade allocation, in the following form:
\begin{equation*}
Min \displaystyle \Bigg( \lambda \sum_{t=1}^T (\mbox{Risk of Residual Holdings}) + (1-\lambda) \sum_{t=1}^T (\mbox{Market Impact of Trades}) \Bigg)
\end{equation*}
\begin{equation*}s.t.\end{equation*}
\begin{equation*}Ax <= b\end{equation*}
where:
\begin{equation*}(\mbox{Risk of Residual Holdings})\end{equation*}
- Incorporates the intraday and overnight expected risk, utilizing our high frequency intraday QES covariances. in other words, "every $ I decided to trade later, is running at the Risk of missing the arrival price"
\begin{equation*}(\mbox{Market Impact of Trades})\end{equation*}
- Denote the expected market impact per asset, as a function of the physical interaction with the order book. in other words, "every $ that I will trade now, will incur some expected market impact, based on the intraday predicted evolution of spread\volume\volatility\participation rate, and other intraday calibrated parameters"
\begin{equation*}\lambda\end{equation*}
- Risk Aversion parameter
\begin{equation*}Ax <= b\end{equation*}
- set of linear constraints (see features available at the top of the notebook)
#### Set up the optimization constraints
| Optimisation Parameters | Description | Value Chosen |
| :- | :- | -: |
| Start Time \ End Time | APEX allowed "Day1" trade horizon, in GMT* | 11pm previous day to 11pm |
| Urgency | APEX Urgency, from VERY_LOW to VERY_HIGH | Medium |
| Target Benchmark | Currently supports 'IS', 'CLOSE' | IS |
| Imbalance | (Optional) setting dollar imbalance for the trade duration; "the net residual must be within +-5% of the residual gross to trade, throughout the entire trade duration" | 0.05 (5%) |
| Participation rate | Setting volume cap for trading | 0.075 (7.5%) |
- Note that APEX allowed start end times range from 23:00 previous day to 23:00 of the query day.
For example, if today is the 9th of October, APEX global optimization can run from start time of 23:00 on T-1 to 23:00 on T.
- Please also note that APEX will automatically optimize up to 5 business days, providing an optimized intraday solution with granularity of 30\60 minutes.
- For a full set of parameters, please refer to the constraints & features image at the top, review the APEX api guide or contact [gs-qes-quant@gs.com](mailto:gs-qes-quant@gs.com)
```
## set optimization configuration
print('INFO: Constructing Optimization Request...')
date_today = datetime.datetime.now().strftime('%Y-%m-%d')
date_yesterday = (datetime.datetime.now() - datetime.timedelta(days=1)).strftime('%Y-%m-%d')
apex_optimization_config = {
'executionStartTime': date_yesterday + 'T23:00:00.000Z', #execution start time
'executionEndTime': date_today +'T21:15:00.000Z', # execution end time (for day 1, can run multiday if not complete on day 1)
'waitForResults': False,
'parameters': {'urgency': 'MEDIUM', #VERY_LOW, LOW, HIGH, VERY_HIGH...
'targetBenchmark': 'IS', #CLOSE
'imbalance': 0.05, #Optional --> setting $ imbalance for the trade duration to never exceed +-20% of residual gross to trade
'participationRate': 0.075 #setting volume cap of 10%
},
}
```
#### Send Optimization + Analytics request to Marquee
```
def sendApexRequestAndGetAnalytics(portfolio_input, apex_optimization_config):
positions = [Position(asset_id=row.marqueeid, quantity=row.qty) for _, row in portfolio_input.iterrows()]
print('setting up the optimization request....')
request = OptimizationRequest(positions=positions,
execution_start_time=apex_optimization_config['executionStartTime'],
execution_end_time=apex_optimization_config['executionEndTime'],
parameters=apex_optimization_config['parameters'],
**{'type': OptimizationType.APEX})
print('Sending the request to the marquee service...')
opt = GsRiskApi.create_pretrade_execution_optimization(request)
analytics_results = GsRiskApi.get_pretrade_execution_optimization(opt.get('optimizationId'))
print ('COMPLETE!')
return analytics_results
results_dict = sendApexRequestAndGetAnalytics(portfolio_input, apex_optimization_config)
print('INFO: High Level Cost estimation and % expected Completion:')
pd.DataFrame(results_dict['analytics']['portfolioAnalyticsDaily']).set_index('tradeDayNumber')
print('missing assets:')
pd.DataFrame(results_dict['analytics']['assetsExcluded'])
```
#### Actual Optimization Parameters Used in APEX
- Although a set of optimization parameters was specified above, APEX might conclude that the parameters joined feasible space does not exist (infeasible set).
- APEX can then choose to soften/drop/relax the constraints in a hierarchical fashion.
```
constraints_hierarchy = pd.DataFrame(results_dict['analytics']['constraintsConsultations'])['constraints']
pd.concat([pd.DataFrame(constraints_hierarchy.values[i]).assign(iteration=i) for i in constraints_hierarchy.index]).set_index(['iteration', 'name'])['status'].unstack().T
```
#### What kind of Analytics provided by APEX ?
##### APEX provide a vast set of numbers that helps understanding unravel the decision made by the optimizer:
```
results_dict['analytics'].keys()
```
#### Visualise Your Optimisation Results
```
analytics_result_analytics = results_dict['analytics']
intraday = pd.DataFrame(analytics_result_analytics['portfolioAnalyticsIntraday'])
intraday_to_plot = intraday.assign(time = lambda x: pd.to_datetime(x['time'])).set_index('time')
```
#### Four examples of visualizing your intraday analysis throughout trade date
- Gross Remaining
- Buy/Sell/Net
- Cost Contribution
- Risk Contribution
```
intraday_to_plot.head(5).append(intraday_to_plot.tail(5))
plotGrossRemaining(intraday_to_plot)
plotBuySellNet(intraday_to_plot)
plotCost(intraday_to_plot)
plotVar(intraday_to_plot)
```
###### Sources: Goldman Sachs, Bloomberg, Reuters, Axioma
##### The creativity around various analytics are endless, here are couple of examples, derived from the various analytics dataframes we use for our APEX clients:
<img src= "images/apex_analytics_examples.png">
###### Sources: Goldman Sachs, Bloomberg, Reuters, Axioma
##### save all results to excel for further exploration:
```
xls_path = persistXls(xls_report=results_dict['analytics'],
path='',
filename='apex_optimization_detailed_analytics',
indentifier_marqueeid_map=portfolio_input[
[identifier_type, 'marqueeid']])
print('saving all analytics frames to {0}...'.format(xls_path))
```
<img src= "images/apex_excel_example.png">
### 2. APEX Optimization - Trade Scenario Analysis: run my trade list in the APEX optimizer across multiple risk aversions\urgency parameters to assess ideal parameters set.
#### Define a function for running multiple optimizations, keeping all constrains intact and change urgency only:
```
def optimisationMulti(portfolio_input, apex_optimization_config, urgency_list = ['VERY_LOW', 'LOW', 'MEDIUM', 'HIGH', 'VERY_HIGH']):
results_dict_multi = {}
apex_optimization_config_temp = copy.deepcopy(apex_optimization_config)
for u in urgency_list:
apex_optimization_config_temp['parameters']['urgency'] = u
apex_optimization_config_temp['parameters']['imbalance'] = .3
apex_optimization_config_temp['parameters']['participationRate'] = .5
print('INFO Running urgency={0} optimization....'.format(u))
results_dict_multi[u] = sendApexRequestAndGetAnalytics(portfolio_input, apex_optimization_config_temp)
print('INFO: High Level Cost estimation and % expected Completion:\n{0}'\
.format(pd.DataFrame(results_dict_multi[u]['analytics']['portfolioAnalyticsDaily'])))
return results_dict_multi
```
##### Run Optimization Across Urgencies
```
urgency_list = ['VERY_LOW', 'LOW', 'MEDIUM', 'HIGH', 'VERY_HIGH']
results_dict_multi = optimisationMulti(portfolio_input = portfolio_input,\
apex_optimization_config = apex_optimization_config,\
urgency_list=urgency_list)
```
#### Compare Results from Different Urgencies on Day 1:
```
ordering = ['grey', 'sky_blue', 'black', 'cyan', 'light_blue', 'dark_green']
urgency_list = ['VERY_LOW', 'LOW', 'MEDIUM', 'HIGH', 'VERY_HIGH']
ptAnalyticsDaily_list = []
for u in urgency_list:
ptAnalyticsDaily_list.append(pd.DataFrame(results_dict_multi[u]['analytics']['portfolioAnalyticsDaily']).iloc[[0]].assign(urgency=u) )
pd.concat(ptAnalyticsDaily_list).set_index('urgency')
```
#### Visualise Optimization Results
- Plotting 'Trade_cum_sum, Total Cost, Total Risk' against time for the chosen urgencies
- Trade_cum_sum: Cumulative sum of the intraday trades
```
metrics_list = ['tradePercentageCumulativeSum', 'totalRiskBps', 'totalCost', 'advAveragePercentage']
title = ['Intraday Trade', 'Risk', 'Cost', 'Participation Rate']
ylabel = ['Trade Cum Sum %', 'Risk(bps) ', 'Cost(bps)', 'Prate(%)']
plotMultiStrategyPortfolioLevelAnalytics(results_dict_multi, metrics_list, title, ylabel)
```
###### Sources: Goldman Sachs, Bloomberg, Reuters, Axioma
#### Plot the optimal Efficient Frontier - the expected Market Impact vs. Residual Risk Trade-off:
```
initial_gross = pd.DataFrame(results_dict_multi['VERY_LOW']['analytics']['portfolioAnalyticsIntraday'])['gross'].iloc[0]
risk_cost_tradeoff = pd.concat( [\
pd.DataFrame(results_dict_multi[urgency]['analytics']['portfolioAnalyticsDaily'])\
[['estimatedCostBps', 'meanExpectedCostVersusBenchmark']]\
.assign(totalRiskBps = lambda x: x['estimatedCostBps'] - x['meanExpectedCostVersusBenchmark'])\
.iloc[0].rename(urgency).to_frame()
for urgency in ['VERY_LOW', 'LOW', 'MEDIUM']], axis=1).T
cmap = cm.get_cmap('Set1')
ax = risk_cost_tradeoff.plot.scatter(x='totalRiskBps', y='meanExpectedCostVersusBenchmark',\
title='The Example Basket Efficient Frontier',\
colormap=cmap, c=range(len(risk_cost_tradeoff)), s=100)
for k, v in risk_cost_tradeoff[['totalRiskBps', 'meanExpectedCostVersusBenchmark']].iterrows():
ax.annotate(k, v,
xytext=(10,-5), textcoords='offset points',
family='sans-serif', fontsize=10, color='darkslategrey')
ax.plot(risk_cost_tradeoff['totalRiskBps'].values, risk_cost_tradeoff['meanExpectedCostVersusBenchmark'].values,
color='grey', alpha=.5)
```
###### Sources: Goldman Sachs, Bloomberg, Reuters, Axioma
# And That's IT! Find below an holistic view of our APEX platform in visual from:
<img src= "images/apex_box.png">
##### Disclaimers:
###### Indicative Terms/Pricing Levels: This material may contain indicative terms only, including but not limited to pricing levels. There is no representation that any transaction can or could have been effected at such terms or prices. Proposed terms and conditions are for discussion purposes only. Finalized terms and conditions are subject to further discussion and negotiation.
###### www.goldmansachs.com/disclaimer/sales-and-trading-invest-rec-disclosures.html If you are not accessing this material via Marquee ContentStream, a list of the author's investment recommendations disseminated during the preceding 12 months and the proportion of the author's recommendations that are 'buy', 'hold', 'sell' or other over the previous 12 months is available by logging into Marquee ContentStream using the link below. Alternatively, if you do not have access to Marquee ContentStream, please contact your usual GS representative who will be able to provide this information to you.
###### Please refer to https://marquee.gs.com/studio/ for price information of corporate equity securities.
###### Notice to Australian Investors: When this document is disseminated in Australia by Goldman Sachs & Co. LLC ("GSCO"), Goldman Sachs International ("GSI"), Goldman Sachs Bank Europe SE ("GSBE"), Goldman Sachs (Asia) L.L.C. ("GSALLC"), or Goldman Sachs (Singapore) Pte ("GSSP") (collectively the "GS entities"), this document, and any access to it, is intended only for a person that has first satisfied the GS entities that:
###### • the person is a Sophisticated or Professional Investor for the purposes of section 708 of the Corporations Act of Australia; and
###### • the person is a wholesale client for the purpose of section 761G of the Corporations Act of Australia.
###### To the extent that the GS entities are providing a financial service in Australia, the GS entities are each exempt from the requirement to hold an Australian financial services licence for the financial services they provide in Australia. Each of the GS entities are regulated by a foreign regulator under foreign laws which differ from Australian laws, specifically:
###### • GSCO is regulated by the US Securities and Exchange Commission under US laws;
###### • GSI is authorised by the Prudential Regulation Authority and regulated by the Financial Conduct Authority and the Prudential Regulation Authority, under UK laws;
###### • GSBE is subject to direct prudential supervision by the European Central Bank and in other respects is supervised by the German Federal Financial Supervisory Authority (Bundesanstalt für Finanzdienstleistungsaufischt, BaFin) and Deutsche Bundesbank;
###### • GSALLC is regulated by the Hong Kong Securities and Futures Commission under Hong Kong laws; and
###### • GSSP is regulated by the Monetary Authority of Singapore under Singapore laws.
###### Notice to Brazilian Investors
###### Marquee is not meant for the general public in Brazil. The services or products provided by or through Marquee, at any time, may not be offered or sold to the general public in Brazil. You have received a password granting access to Marquee exclusively due to your existing relationship with a GS business located in Brazil. The selection and engagement with any of the offered services or products through Marquee, at any time, will be carried out directly by you. Before acting to implement any chosen service or products, provided by or through Marquee you should consider, at your sole discretion, whether it is suitable for your particular circumstances and, if necessary, seek professional advice. Any steps necessary in order to implement the chosen service or product, including but not limited to remittance of funds, shall be carried out at your discretion. Accordingly, such services and products have not been and will not be publicly issued, placed, distributed, offered or negotiated in the Brazilian capital markets and, as a result, they have not been and will not be registered with the Brazilian Securities and Exchange Commission (Comissão de Valores Mobiliários), nor have they been submitted to the foregoing agency for approval. Documents relating to such services or products, as well as the information contained therein, may not be supplied to the general public in Brazil, as the offering of such services or products is not a public offering in Brazil, nor used in connection with any offer for subscription or sale of securities to the general public in Brazil.
###### The offer of any securities mentioned in this message may not be made to the general public in Brazil. Accordingly, any such securities have not been nor will they be registered with the Brazilian Securities and Exchange Commission (Comissão de Valores Mobiliários) nor has any offer been submitted to the foregoing agency for approval. Documents relating to the offer, as well as the information contained therein, may not be supplied to the public in Brazil, as the offer is not a public offering of securities in Brazil. These terms will apply on every access to Marquee.
###### Ouvidoria Goldman Sachs Brasil: 0800 727 5764 e/ou ouvidoriagoldmansachs@gs.com
###### Horário de funcionamento: segunda-feira à sexta-feira (exceto feriados), das 9hs às 18hs.
###### Ombudsman Goldman Sachs Brazil: 0800 727 5764 and / or ouvidoriagoldmansachs@gs.com
###### Available Weekdays (except holidays), from 9 am to 6 pm.
###### Note to Investors in Israel: GS is not licensed to provide investment advice or investment management services under Israeli law.
###### Notice to Investors in Japan
###### Marquee is made available in Japan by Goldman Sachs Japan Co., Ltd.
###### 本書は情報の提供を目的としております。また、売却・購入が違法となるような法域での有価証券その他の売却若しくは購入を勧めるものでもありません。ゴールドマン・サックスは本書内の取引又はストラクチャーの勧誘を行うものではございません。これらの取引又はストラクチャーは、社内及び法規制等の承認等次第で実際にはご提供できない場合がございます。
###### <適格機関投資家限定 転売制限>
###### ゴールドマン・サックス証券株式会社が適格機関投資家のみを相手方として取得申込みの勧誘(取得勧誘)又は売付けの申込み若しくは買付けの申込みの勧誘(売付け勧誘等)を行う本有価証券には、適格機関投資家に譲渡する場合以外の譲渡が禁止される旨の制限が付されています。本有価証券は金融商品取引法第4条に基づく財務局に対する届出が行われておりません。なお、本告知はお客様によるご同意のもとに、電磁的に交付させていただいております。
###### <適格機関投資家用資料>
###### 本資料は、適格機関投資家のお客さまのみを対象に作成されたものです。本資料における金融商品は適格機関投資家のお客さまのみがお取引可能であり、適格機関投資家以外のお客さまからのご注文等はお受けできませんので、ご注意ください。 商号等/ゴールドマン・サックス証券株式会社 金融商品取引業者 関東財務局長(金商)第69号
###### 加入協会/ 日本証券業協会、一般社団法人金融先物取引業協会、一般社団法人第二種金融商品取引業協会
###### 本書又はその添付資料に信用格付が記載されている場合、日本格付研究所(JCR)及び格付投資情報センター(R&I)による格付は、登録信用格付業者による格付(登録格付)です。その他の格付は登録格付である旨の記載がない場合は、無登録格付です。無登録格付を投資判断に利用する前に、「無登録格付に関する説明書」(http://www.goldmansachs.com/disclaimer/ratings.html)を十分にお読みください。
###### If any credit ratings are contained in this material or any attachments, those that have been issued by Japan Credit Rating Agency, Ltd. (JCR) or Rating and Investment Information, Inc. (R&I) are credit ratings that have been issued by a credit rating agency registered in Japan (registered credit ratings). Other credit ratings are unregistered unless denoted as being registered. Before using unregistered credit ratings to make investment decisions, please carefully read "Explanation Regarding Unregistered Credit Ratings" (http://www.goldmansachs.com/disclaimer/ratings.html).
###### Notice to Mexican Investors: Information contained herein is not meant for the general public in Mexico. The services or products provided by or through Goldman Sachs Mexico, Casa de Bolsa, S.A. de C.V. (GS Mexico) may not be offered or sold to the general public in Mexico. You have received information herein exclusively due to your existing relationship with a GS Mexico or any other Goldman Sachs business. The selection and engagement with any of the offered services or products through GS Mexico will be carried out directly by you at your own risk. Before acting to implement any chosen service or product provided by or through GS Mexico you should consider, at your sole discretion, whether it is suitable for your particular circumstances and, if necessary, seek professional advice. Information contained herein related to GS Mexico services or products, as well as any other information, shall not be considered as a product coming from research, nor it contains any recommendation to invest, not to invest, hold or sell any security and may not be supplied to the general public in Mexico.
###### Notice to New Zealand Investors: When this document is disseminated in New Zealand by Goldman Sachs & Co. LLC ("GSCO") , Goldman Sachs International ("GSI"), Goldman Sachs Bank Europe SE ("GSBE"), Goldman Sachs (Asia) L.L.C. ("GSALLC") or Goldman Sachs (Singapore) Pte ("GSSP") (collectively the "GS entities"), this document, and any access to it, is intended only for a person that has first satisfied; the GS entities that the person is someone:
###### (i) who is an investment business within the meaning of clause 37 of Schedule 1 of the Financial Markets Conduct Act 2013 (New Zealand) (the "FMC Act");
###### (ii) who meets the investment activity criteria specified in clause 38 of Schedule 1 of the FMC Act;
###### (iii) who is large within the meaning of clause 39 of Schedule 1 of the FMC Act; or
###### (iv) is a government agency within the meaning of clause 40 of Schedule 1 of the FMC Act.
###### No offer to acquire the interests is being made to you in this document. Any offer will only be made in circumstances where disclosure is not required under the Financial Markets Conducts Act 2013 or the Financial Markets Conduct Regulations 2014.
###### Notice to Swiss Investors: This is marketing material for financial instruments or services. The information contained in this material is for general informational purposes only and does not constitute an offer, solicitation, invitation or recommendation to buy or sell any financial instruments or to provide any investment advice or service of any kind.
###### THE INFORMATION CONTAINED IN THIS DOCUMENT DOES NOT CONSITUTE, AND IS NOT INTENDED TO CONSTITUTE, A PUBLIC OFFER OF SECURITIES IN THE UNITED ARAB EMIRATES IN ACCORDANCE WITH THE COMMERCIAL COMPANIES LAW (FEDERAL LAW NO. 2 OF 2015), ESCA BOARD OF DIRECTORS' DECISION NO. (9/R.M.) OF 2016, ESCA CHAIRMAN DECISION NO 3/R.M. OF 2017 CONCERNING PROMOTING AND INTRODUCING REGULATIONS OR OTHERWISE UNDER THE LAWS OF THE UNITED ARAB EMIRATES. ACCORDINGLY, THE INTERESTS IN THE SECURITIES MAY NOT BE OFFERED TO THE PUBLIC IN THE UAE (INCLUDING THE DUBAI INTERNATIONAL FINANCIAL CENTRE AND THE ABU DHABI GLOBAL MARKET). THIS DOCUMENT HAS NOT BEEN APPROVED BY, OR FILED WITH THE CENTRAL BANK OF THE UNITED ARAB EMIRATES, THE SECURITIES AND COMMODITIES AUTHORITY, THE DUBAI FINANCIAL SERVICES AUTHORITY, THE FINANCIAL SERVICES REGULATORY AUTHORITY OR ANY OTHER RELEVANT LICENSING AUTHORITIES IN THE UNITED ARAB EMIRATES. IF YOU DO NOT UNDERSTAND THE CONTENTS OF THIS DOCUMENT, YOU SHOULD CONSULT WITH A FINANCIAL ADVISOR. THIS DOCUMENT IS PROVIDED TO THE RECIPIENT ONLY AND SHOULD NOT BE PROVIDED TO OR RELIED ON BY ANY OTHER PERSON.
| true |
code
| 0.352007 | null | null | null | null |
|
**Chapter 1 – The Machine Learning landscape**
_This is the code used to generate some of the figures in chapter 1._
# Setup
First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "fundamentals"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", module="scipy", message="^internal gelsd")
```
# Code example 1-1
This function just merges the OECD's life satisfaction data and the IMF's GDP per capita data. It's a bit too long and boring and it's not specific to Machine Learning, which is why I left it out of the book.
```
def prepare_country_stats(oecd_bli, gdp_per_capita):
oecd_bli = oecd_bli[oecd_bli["INEQUALITY"]=="TOT"]
oecd_bli = oecd_bli.pivot(index="Country", columns="Indicator", values="Value")
gdp_per_capita.rename(columns={"2015": "GDP per capita"}, inplace=True)
gdp_per_capita.set_index("Country", inplace=True)
full_country_stats = pd.merge(left=oecd_bli, right=gdp_per_capita,
left_index=True, right_index=True)
full_country_stats.sort_values(by="GDP per capita", inplace=True)
remove_indices = [0, 1, 6, 8, 33, 34, 35]
keep_indices = list(set(range(36)) - set(remove_indices))
return full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[keep_indices]
```
The code in the book expects the data files to be located in the current directory. I just tweaked it here to fetch the files in datasets/lifesat.
```
import os
datapath = os.path.join("datasets", "lifesat", "")
# Code example
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn.linear_model
# Load the data
oecd_bli = pd.read_csv(datapath + "oecd_bli_2015.csv", thousands=',')
gdp_per_capita = pd.read_csv(datapath + "gdp_per_capita.csv",thousands=',',delimiter='\t',
encoding='latin1', na_values="n/a")
# Prepare the data
country_stats = prepare_country_stats(oecd_bli, gdp_per_capita)
X = np.c_[country_stats["GDP per capita"]]
y = np.c_[country_stats["Life satisfaction"]]
# Visualize the data
country_stats.plot(kind='scatter', x="GDP per capita", y='Life satisfaction')
plt.show()
# Select a linear model
model = sklearn.linear_model.LinearRegression()
# Train the model
model.fit(X, y)
# Make a prediction for Cyprus
X_new = [[22587]] # Cyprus' GDP per capita
print(model.predict(X_new)) # outputs [[ 5.96242338]]
```
# Note: you can ignore the rest of this notebook, it just generates many of the figures in chapter 1.
# Load and prepare Life satisfaction data
If you want, you can get fresh data from the OECD's website.
Download the CSV from http://stats.oecd.org/index.aspx?DataSetCode=BLI
and save it to `datasets/lifesat/`.
```
oecd_bli = pd.read_csv(datapath + "oecd_bli_2015.csv", thousands=',')
oecd_bli = oecd_bli[oecd_bli["INEQUALITY"]=="TOT"]
oecd_bli = oecd_bli.pivot(index="Country", columns="Indicator", values="Value")
oecd_bli.head(2)
oecd_bli["Life satisfaction"].head()
```
# Load and prepare GDP per capita data
Just like above, you can update the GDP per capita data if you want. Just download data from http://goo.gl/j1MSKe (=> imf.org) and save it to `datasets/lifesat/`.
```
gdp_per_capita = pd.read_csv(datapath+"gdp_per_capita.csv", thousands=',', delimiter='\t',
encoding='latin1', na_values="n/a")
gdp_per_capita.rename(columns={"2015": "GDP per capita"}, inplace=True)
gdp_per_capita.set_index("Country", inplace=True)
gdp_per_capita.head(2)
full_country_stats = pd.merge(left=oecd_bli, right=gdp_per_capita, left_index=True, right_index=True)
full_country_stats.sort_values(by="GDP per capita", inplace=True)
full_country_stats
full_country_stats[["GDP per capita", 'Life satisfaction']].loc["United States"]
remove_indices = [0, 1, 6, 8, 33, 34, 35]
keep_indices = list(set(range(36)) - set(remove_indices))
sample_data = full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[keep_indices]
missing_data = full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[remove_indices]
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3))
plt.axis([0, 60000, 0, 10])
position_text = {
"Hungary": (5000, 1),
"Korea": (18000, 1.7),
"France": (29000, 2.4),
"Australia": (40000, 3.0),
"United States": (52000, 3.8),
}
for country, pos_text in position_text.items():
pos_data_x, pos_data_y = sample_data.loc[country]
country = "U.S." if country == "United States" else country
plt.annotate(country, xy=(pos_data_x, pos_data_y), xytext=pos_text,
arrowprops=dict(facecolor='black', width=0.5, shrink=0.1, headwidth=5))
plt.plot(pos_data_x, pos_data_y, "ro")
save_fig('money_happy_scatterplot')
plt.show()
sample_data.to_csv(os.path.join("datasets", "lifesat", "lifesat.csv"))
sample_data.loc[list(position_text.keys())]
import numpy as np
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3))
plt.axis([0, 60000, 0, 10])
X=np.linspace(0, 60000, 1000)
plt.plot(X, 2*X/100000, "r")
plt.text(40000, 2.7, r"$\theta_0 = 0$", fontsize=14, color="r")
plt.text(40000, 1.8, r"$\theta_1 = 2 \times 10^{-5}$", fontsize=14, color="r")
plt.plot(X, 8 - 5*X/100000, "g")
plt.text(5000, 9.1, r"$\theta_0 = 8$", fontsize=14, color="g")
plt.text(5000, 8.2, r"$\theta_1 = -5 \times 10^{-5}$", fontsize=14, color="g")
plt.plot(X, 4 + 5*X/100000, "b")
plt.text(5000, 3.5, r"$\theta_0 = 4$", fontsize=14, color="b")
plt.text(5000, 2.6, r"$\theta_1 = 5 \times 10^{-5}$", fontsize=14, color="b")
save_fig('tweaking_model_params_plot')
plt.show()
from sklearn import linear_model
lin1 = linear_model.LinearRegression()
Xsample = np.c_[sample_data["GDP per capita"]]
ysample = np.c_[sample_data["Life satisfaction"]]
lin1.fit(Xsample, ysample)
t0, t1 = lin1.intercept_[0], lin1.coef_[0][0]
t0, t1
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3))
plt.axis([0, 60000, 0, 10])
X=np.linspace(0, 60000, 1000)
plt.plot(X, t0 + t1*X, "b")
plt.text(5000, 3.1, r"$\theta_0 = 4.85$", fontsize=14, color="b")
plt.text(5000, 2.2, r"$\theta_1 = 4.91 \times 10^{-5}$", fontsize=14, color="b")
save_fig('best_fit_model_plot')
plt.show()
cyprus_gdp_per_capita = gdp_per_capita.loc["Cyprus"]["GDP per capita"]
print(cyprus_gdp_per_capita)
cyprus_predicted_life_satisfaction = lin1.predict(cyprus_gdp_per_capita)[0][0]
cyprus_predicted_life_satisfaction
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3), s=1)
X=np.linspace(0, 60000, 1000)
plt.plot(X, t0 + t1*X, "b")
plt.axis([0, 60000, 0, 10])
plt.text(5000, 7.5, r"$\theta_0 = 4.85$", fontsize=14, color="b")
plt.text(5000, 6.6, r"$\theta_1 = 4.91 \times 10^{-5}$", fontsize=14, color="b")
plt.plot([cyprus_gdp_per_capita, cyprus_gdp_per_capita], [0, cyprus_predicted_life_satisfaction], "r--")
plt.text(25000, 5.0, r"Prediction = 5.96", fontsize=14, color="b")
plt.plot(cyprus_gdp_per_capita, cyprus_predicted_life_satisfaction, "ro")
save_fig('cyprus_prediction_plot')
plt.show()
sample_data[7:10]
(5.1+5.7+6.5)/3
backup = oecd_bli, gdp_per_capita
def prepare_country_stats(oecd_bli, gdp_per_capita):
oecd_bli = oecd_bli[oecd_bli["INEQUALITY"]=="TOT"]
oecd_bli = oecd_bli.pivot(index="Country", columns="Indicator", values="Value")
gdp_per_capita.rename(columns={"2015": "GDP per capita"}, inplace=True)
gdp_per_capita.set_index("Country", inplace=True)
full_country_stats = pd.merge(left=oecd_bli, right=gdp_per_capita,
left_index=True, right_index=True)
full_country_stats.sort_values(by="GDP per capita", inplace=True)
remove_indices = [0, 1, 6, 8, 33, 34, 35]
keep_indices = list(set(range(36)) - set(remove_indices))
return full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[keep_indices]
# Code example
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn
# Load the data
oecd_bli = pd.read_csv(datapath + "oecd_bli_2015.csv", thousands=',')
gdp_per_capita = pd.read_csv(datapath + "gdp_per_capita.csv",thousands=',',delimiter='\t',
encoding='latin1', na_values="n/a")
# Prepare the data
country_stats = prepare_country_stats(oecd_bli, gdp_per_capita)
X = np.c_[country_stats["GDP per capita"]]
y = np.c_[country_stats["Life satisfaction"]]
# Visualize the data
country_stats.plot(kind='scatter', x="GDP per capita", y='Life satisfaction')
plt.show()
# Select a linear model
model = sklearn.linear_model.LinearRegression()
# Train the model
model.fit(X, y)
# Make a prediction for Cyprus
X_new = [[22587]] # Cyprus' GDP per capita
print(model.predict(X_new)) # outputs [[ 5.96242338]]
oecd_bli, gdp_per_capita = backup
missing_data
position_text2 = {
"Brazil": (1000, 9.0),
"Mexico": (11000, 9.0),
"Chile": (25000, 9.0),
"Czech Republic": (35000, 9.0),
"Norway": (60000, 3),
"Switzerland": (72000, 3.0),
"Luxembourg": (90000, 3.0),
}
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(8,3))
plt.axis([0, 110000, 0, 10])
for country, pos_text in position_text2.items():
pos_data_x, pos_data_y = missing_data.loc[country]
plt.annotate(country, xy=(pos_data_x, pos_data_y), xytext=pos_text,
arrowprops=dict(facecolor='black', width=0.5, shrink=0.1, headwidth=5))
plt.plot(pos_data_x, pos_data_y, "rs")
X=np.linspace(0, 110000, 1000)
plt.plot(X, t0 + t1*X, "b:")
lin_reg_full = linear_model.LinearRegression()
Xfull = np.c_[full_country_stats["GDP per capita"]]
yfull = np.c_[full_country_stats["Life satisfaction"]]
lin_reg_full.fit(Xfull, yfull)
t0full, t1full = lin_reg_full.intercept_[0], lin_reg_full.coef_[0][0]
X = np.linspace(0, 110000, 1000)
plt.plot(X, t0full + t1full * X, "k")
save_fig('representative_training_data_scatterplot')
plt.show()
full_country_stats.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(8,3))
plt.axis([0, 110000, 0, 10])
from sklearn import preprocessing
from sklearn import pipeline
poly = preprocessing.PolynomialFeatures(degree=60, include_bias=False)
scaler = preprocessing.StandardScaler()
lin_reg2 = linear_model.LinearRegression()
pipeline_reg = pipeline.Pipeline([('poly', poly), ('scal', scaler), ('lin', lin_reg2)])
pipeline_reg.fit(Xfull, yfull)
curve = pipeline_reg.predict(X[:, np.newaxis])
plt.plot(X, curve)
save_fig('overfitting_model_plot')
plt.show()
full_country_stats.loc[[c for c in full_country_stats.index if "W" in c.upper()]]["Life satisfaction"]
gdp_per_capita.loc[[c for c in gdp_per_capita.index if "W" in c.upper()]].head()
plt.figure(figsize=(8,3))
plt.xlabel("GDP per capita")
plt.ylabel('Life satisfaction')
plt.plot(list(sample_data["GDP per capita"]), list(sample_data["Life satisfaction"]), "bo")
plt.plot(list(missing_data["GDP per capita"]), list(missing_data["Life satisfaction"]), "rs")
X = np.linspace(0, 110000, 1000)
plt.plot(X, t0full + t1full * X, "r--", label="Linear model on all data")
plt.plot(X, t0 + t1*X, "b:", label="Linear model on partial data")
ridge = linear_model.Ridge(alpha=10**9.5)
Xsample = np.c_[sample_data["GDP per capita"]]
ysample = np.c_[sample_data["Life satisfaction"]]
ridge.fit(Xsample, ysample)
t0ridge, t1ridge = ridge.intercept_[0], ridge.coef_[0][0]
plt.plot(X, t0ridge + t1ridge * X, "b", label="Regularized linear model on partial data")
plt.legend(loc="lower right")
plt.axis([0, 110000, 0, 10])
save_fig('ridge_model_plot')
plt.show()
backup = oecd_bli, gdp_per_capita
def prepare_country_stats(oecd_bli, gdp_per_capita):
return sample_data
# Replace this linear model:
model = sklearn.linear_model.LinearRegression()
# with this k-neighbors regression model:
model = sklearn.neighbors.KNeighborsRegressor(n_neighbors=3)
X = np.c_[country_stats["GDP per capita"]]
y = np.c_[country_stats["Life satisfaction"]]
# Train the model
model.fit(X, y)
# Make a prediction for Cyprus
X_new = np.array([[22587.0]]) # Cyprus' GDP per capita
print(model.predict(X_new)) # outputs [[ 5.76666667]]
```
| true |
code
| 0.62949 | null | null | null | null |
|
# Gaussian Processes
## Introduction
[Gaussian Processes](https://en.wikipedia.org/wiki/Gaussian_process) have been used in supervised, unsupervised, and even reinforcement learning problems and are described by an elegant mathematical theory (for an overview of the subject see [1, 4]). They are also very attractive conceptually, since they offer an intuitive way to define priors over functions. And finally, since Gaussian Processes are formulated in a Bayesian setting, they come equipped with a powerful notion of uncertainty.
Happily, Pyro offers some support for Gaussian Processes in the `pyro.contrib.gp` module. The goal of this tutorial is to give a brief introduction to Gaussian Processes (GPs) in the context of this module. We will mostly be focusing on how to use the GP interface in Pyro and refer the reader to the references for more details about GPs in general.
The model we're interested in is defined by
$$f \sim \mathcal{GP}\left(0, \mathbf{K}_f(x, x')\right)$$
and
$$y = f(x) + \epsilon,\quad \epsilon \sim \mathcal{N}\left(0, \beta^{-1}\mathbf{I}\right).$$
Here $x, x' \in\mathbf{X}$ are points in the input space and $y\in\mathbf{Y}$ is a point in the output space. $f$ is a draw from the GP prior specified by the kernel $\mathbf{K}_f$ and represents a function from $\mathbf{X}$ to $\mathbf{Y}$. Finally, $\epsilon$ represents Gaussian observation noise.
We will use the [radial basis function kernel](https://en.wikipedia.org/wiki/Radial_basis_function_kernel) (RBF kernel) as the kernel of our GP:
$$ k(x,x') = \sigma^2 \exp\left(-\frac{\|x-x'\|^2}{2l^2}\right).$$
Here $\sigma^2$ and $l$ are parameters that specify the kernel; specifically, $\sigma^2$ is a variance or amplitude squared and $l$ is a lengthscale. We'll get some intuition for these parameters below.
## Imports
First, we import necessary modules.
```
import os
import matplotlib.pyplot as plt
import torch
import pyro
import pyro.contrib.gp as gp
import pyro.distributions as dist
smoke_test = ('CI' in os.environ) # ignore; used to check code integrity in the Pyro repo
assert pyro.__version__.startswith('1.3.1')
pyro.enable_validation(True) # can help with debugging
pyro.set_rng_seed(0)
```
Throughout the tutorial we'll want to visualize GPs. So we define a helper function for plotting:
```
# note that this helper function does three different things:
# (i) plots the observed data;
# (ii) plots the predictions from the learned GP after conditioning on data;
# (iii) plots samples from the GP prior (with no conditioning on observed data)
def plot(plot_observed_data=False, plot_predictions=False, n_prior_samples=0,
model=None, kernel=None, n_test=500):
plt.figure(figsize=(12, 6))
if plot_observed_data:
plt.plot(X.numpy(), y.numpy(), 'kx')
if plot_predictions:
Xtest = torch.linspace(-0.5, 5.5, n_test) # test inputs
# compute predictive mean and variance
with torch.no_grad():
if type(model) == gp.models.VariationalSparseGP:
mean, cov = model(Xtest, full_cov=True)
else:
mean, cov = model(Xtest, full_cov=True, noiseless=False)
sd = cov.diag().sqrt() # standard deviation at each input point x
plt.plot(Xtest.numpy(), mean.numpy(), 'r', lw=2) # plot the mean
plt.fill_between(Xtest.numpy(), # plot the two-sigma uncertainty about the mean
(mean - 2.0 * sd).numpy(),
(mean + 2.0 * sd).numpy(),
color='C0', alpha=0.3)
if n_prior_samples > 0: # plot samples from the GP prior
Xtest = torch.linspace(-0.5, 5.5, n_test) # test inputs
noise = (model.noise if type(model) != gp.models.VariationalSparseGP
else model.likelihood.variance)
cov = kernel.forward(Xtest) + noise.expand(n_test).diag()
samples = dist.MultivariateNormal(torch.zeros(n_test), covariance_matrix=cov)\
.sample(sample_shape=(n_prior_samples,))
plt.plot(Xtest.numpy(), samples.numpy().T, lw=2, alpha=0.4)
plt.xlim(-0.5, 5.5)
```
## Data
The data consist of $20$ points sampled from
$$ y = 0.5\sin(3x) + \epsilon, \quad \epsilon \sim \mathcal{N}(0, 0.2).$$
with $x$ sampled uniformly from the interval $[0, 5]$.
```
N = 20
X = dist.Uniform(0.0, 5.0).sample(sample_shape=(N,))
y = 0.5 * torch.sin(3*X) + dist.Normal(0.0, 0.2).sample(sample_shape=(N,))
plot(plot_observed_data=True) # let's plot the observed data
```
## Define model
First we define a RBF kernel, specifying the values of the two hyperparameters `variance` and `lengthscale`. Then we construct a `GPRegression` object. Here we feed in another hyperparameter, `noise`, that corresponds to $\epsilon$ above.
```
kernel = gp.kernels.RBF(input_dim=1, variance=torch.tensor(5.),
lengthscale=torch.tensor(10.))
gpr = gp.models.GPRegression(X, y, kernel, noise=torch.tensor(1.))
```
Let's see what samples from this GP function prior look like. Note that this is _before_ we've conditioned on the data. The shape these functions take—their smoothness, their vertical scale, etc.—is controlled by the GP kernel.
```
plot(model=gpr, kernel=kernel, n_prior_samples=2)
```
For example, if we make `variance` and `noise` smaller we will see function samples with smaller vertical amplitude:
```
kernel2 = gp.kernels.RBF(input_dim=1, variance=torch.tensor(0.1),
lengthscale=torch.tensor(10.))
gpr2 = gp.models.GPRegression(X, y, kernel2, noise=torch.tensor(0.1))
plot(model=gpr2, kernel=kernel2, n_prior_samples=2)
```
## Inference
In the above we set the kernel hyperparameters by hand. If we want to learn the hyperparameters from the data, we need to do inference. In the simplest (conjugate) case we do gradient ascent on the log marginal likelihood. In `pyro.contrib.gp`, we can use any [PyTorch optimizer](https://pytorch.org/docs/stable/optim.html) to optimize parameters of a model. In addition, we need a loss function which takes inputs are the pair model and guide and returns an ELBO loss (see [SVI Part I](svi_part_i.ipynb) tutorial).
```
optimizer = torch.optim.Adam(gpr.parameters(), lr=0.005)
loss_fn = pyro.infer.Trace_ELBO().differentiable_loss
losses = []
num_steps = 2500 if not smoke_test else 2
for i in range(num_steps):
optimizer.zero_grad()
loss = loss_fn(gpr.model, gpr.guide)
loss.backward()
optimizer.step()
losses.append(loss.item())
# let's plot the loss curve after 2500 steps of training
plt.plot(losses);
```
Let's see if we're learned anything reasonable:
```
plot(model=gpr, plot_observed_data=True, plot_predictions=True)
```
Here the thick red curve is the mean prediction and the blue band represents the 2-sigma uncertainty around the mean. It seems we learned reasonable kernel hyperparameters, as both the mean and uncertainty give a reasonable fit to the data. (Note that learning could have easily gone wrong if we e.g. chose too large of a learning rate or chose bad initital hyperparameters.)
Note that the kernel is only well-defined if `variance` and `lengthscale` are positive. Under the hood Pyro is using PyTorch constraints (see [docs](http://pytorch.org/docs/master/distributions.html#module-torch.distributions.constraints)) to ensure that hyperparameters are constrained to the appropriate domains. Let's see the constrained values we've learned.
```
gpr.kernel.variance.item()
gpr.kernel.lengthscale.item()
gpr.noise.item()
```
The period of the sinusoid that generated the data is $T = 2\pi/3 \approx 2.09$ so learning a lengthscale that's approximiately equal to a quarter period makes sense.
### Fit the model using MAP
We need to define priors for the hyperparameters.
```
# Define the same model as before.
pyro.clear_param_store()
kernel = gp.kernels.RBF(input_dim=1, variance=torch.tensor(5.),
lengthscale=torch.tensor(10.))
gpr = gp.models.GPRegression(X, y, kernel, noise=torch.tensor(1.))
# note that our priors have support on the positive reals
gpr.kernel.lengthscale = pyro.nn.PyroSample(dist.LogNormal(0.0, 1.0))
gpr.kernel.variance = pyro.nn.PyroSample(dist.LogNormal(0.0, 1.0))
optimizer = torch.optim.Adam(gpr.parameters(), lr=0.005)
loss_fn = pyro.infer.Trace_ELBO().differentiable_loss
losses = []
num_steps = 2500 if not smoke_test else 2
for i in range(num_steps):
optimizer.zero_grad()
loss = loss_fn(gpr.model, gpr.guide)
loss.backward()
optimizer.step()
losses.append(loss.item())
plt.plot(losses);
plot(model=gpr, plot_observed_data=True, plot_predictions=True)
```
Let's inspect the hyperparameters we've learned:
```
# tell gpr that we want to get samples from guides
gpr.set_mode('guide')
print('variance = {}'.format(gpr.kernel.variance))
print('lengthscale = {}'.format(gpr.kernel.lengthscale))
print('noise = {}'.format(gpr.noise))
```
Note that the MAP values are different from the MLE values due to the prior.
## Sparse GPs
For large datasets computing the log marginal likelihood is costly due to the expensive matrix operations involved (e.g. see Section 2.2 of [1]). A variety of so-called 'sparse' variational methods have been developed to make GPs viable for larger datasets. This is a big area of research and we won't be going into all the details. Instead we quickly show how we can use `SparseGPRegression` in `pyro.contrib.gp` to make use of these methods.
First, we generate more data.
```
N = 1000
X = dist.Uniform(0.0, 5.0).sample(sample_shape=(N,))
y = 0.5 * torch.sin(3*X) + dist.Normal(0.0, 0.2).sample(sample_shape=(N,))
plot(plot_observed_data=True)
```
Using the sparse GP is very similar to using the basic GP used above. We just need to add an extra parameter $X_u$ (the inducing points).
```
# initialize the inducing inputs
Xu = torch.arange(20.) / 4.0
# initialize the kernel and model
pyro.clear_param_store()
kernel = gp.kernels.RBF(input_dim=1)
# we increase the jitter for better numerical stability
sgpr = gp.models.SparseGPRegression(X, y, kernel, Xu=Xu, jitter=1.0e-5)
# the way we setup inference is similar to above
optimizer = torch.optim.Adam(sgpr.parameters(), lr=0.005)
loss_fn = pyro.infer.Trace_ELBO().differentiable_loss
losses = []
num_steps = 2500 if not smoke_test else 2
for i in range(num_steps):
optimizer.zero_grad()
loss = loss_fn(sgpr.model, sgpr.guide)
loss.backward()
optimizer.step()
losses.append(loss.item())
plt.plot(losses);
# let's look at the inducing points we've learned
print("inducing points:\n{}".format(sgpr.Xu.data.numpy()))
# and plot the predictions from the sparse GP
plot(model=sgpr, plot_observed_data=True, plot_predictions=True)
```
We can see that the model learns a reasonable fit to the data. There are three different sparse approximations that are currently implemented in Pyro:
- "DTC" (Deterministic Training Conditional)
- "FITC" (Fully Independent Training Conditional)
- "VFE" (Variational Free Energy)
By default, `SparseGPRegression` will use "VFE" as the inference method. We can use other methods by passing a different `approx` flag to `SparseGPRegression`.
## More Sparse GPs
Both `GPRegression` and `SparseGPRegression` above are limited to Gaussian likelihoods. We can use other likelihoods with GPs—for example, we can use the Bernoulli likelihood for classification problems—but the inference problem becomes more difficult. In this section, we show how to use the `VariationalSparseGP` module, which can handle non-Gaussian likelihoods. So we can compare to what we've done above, we're still going to use a Gaussian likelihood. The point is that the inference that's being done under the hood can support other likelihoods.
```
# initialize the inducing inputs
Xu = torch.arange(10.) / 2.0
# initialize the kernel, likelihood, and model
pyro.clear_param_store()
kernel = gp.kernels.RBF(input_dim=1)
likelihood = gp.likelihoods.Gaussian()
# turn on "whiten" flag for more stable optimization
vsgp = gp.models.VariationalSparseGP(X, y, kernel, Xu=Xu, likelihood=likelihood, whiten=True)
# instead of defining our own training loop, we will
# use the built-in support provided by the GP module
num_steps = 1500 if not smoke_test else 2
losses = gp.util.train(vsgp, num_steps=num_steps)
plt.plot(losses);
plot(model=vsgp, plot_observed_data=True, plot_predictions=True)
```
That's all there is to it. For more details on the `pyro.contrib.gp` module see the [docs](http://docs.pyro.ai/en/dev/contrib/gp.html). And for example code that uses a GP for classification see [here](https://github.com/pyro-ppl/pyro/blob/dev/examples/contrib/gp/sv-dkl.py).
## Reference
[1] `Deep Gaussian processes and variational propagation of uncertainty`,<br />
Andreas Damianou
[2] `A unifying framework for sparse Gaussian process approximation using power expectation propagation`,<br />
Thang D. Bui, Josiah Yan, and Richard E. Turner
[3] `Scalable variational Gaussian process classification`,<br />
James Hensman, Alexander G. de G. Matthews, and Zoubin Ghahramani
[4] `Gaussian Processes for Machine Learning`,<br />
Carl E. Rasmussen, and Christopher K. I. Williams
[5] `A Unifying View of Sparse Approximate Gaussian Process Regression`,<br />
Joaquin Quinonero-Candela, and Carl E. Rasmussen
| true |
code
| 0.640327 | null | null | null | null |
|
## Universidade Federal do Rio Grande do Sul (UFRGS)
Programa de Pós-Graduação em Engenharia Civil (PPGEC)
# PEC00025: Introduction to Vibration Theory
### Class 14 - Vibration of beams
[1. The vibrating beam equation](#section_1)
[2. Free vibration solution](#section_2)
[3. Vibration modes and frequencies](#section_3)
[4. Solution by approximation](#section_4)
[5. Assignment](#section_5)
---
_Prof. Marcelo M. Rocha, Dr.techn._ [(ORCID)](https://orcid.org/0000-0001-5640-1020)
_Porto Alegre, RS, Brazil_
```
# Importing Python modules required for this notebook
# (this cell must be executed with "shift+enter" before any other Python cell)
import numpy as np
import matplotlib.pyplot as plt
```
## 1. The vibrating beam equation <a name="section_1"></a>
The static analysis of a beam under Bernoulli's hypothesis (plane sections remain plane after beam
deformation) leads to the well known differential equations:
\begin{align*}
\frac{dQ}{dx} &= -q(x) \\
\frac{dM}{dx} &= Q(x) \\
EI \psi^\prime &= M(x)
\end{align*}
where $q(x)$ is the distributed transversal loading, $Q(x)$ is the shear, $M(x)$ is the bending
moment, $\psi(x)$ is the section rotation, and $EI$ is the flexural stiffness (regarded
hereinafter as constant along the beam length).
<img src="images/dynamic_beam.png" alt="Dynamic beam equilibrium" width="360px"/>
Disregarding shear strains, $\gamma(x) = 0$, implies that the section rotation is approximated as:
$$ \psi \approx -w^\prime(x) $$
what implies that:
\begin{align*}
EI w^{\prime\prime} &\approx -M(x) \\
EI w^{\prime\prime\prime\prime} &\approx q(x)
\end{align*}
where $w(x)$ is the beam transversal displacement, also called _elastic line_. The solution of this
last differential equation is straighforward once the load $q(x)$ and the boundary conditions (two
for each beam extremity) are specified.
We shall now include the inertial forces in these equations, as well as regard now the section mean shear strain,
$$ \gamma(x) = \psi(x) + w^\prime(x) = \frac{Q(x)}{GA_{\rm s}}$$
as relevant, where $GA_{\rm s}$ is the shear stiffness (also regarded hereinafter as constant along
the beam length). Although $\gamma(x)$ is indeed negligible for actual slender beams,
the following analysis may also be applied to other slender structures, like
tall buildings, trusses, etc., for which we may define _equivalent stiffnesses_,
$\left(EI\right)_{\rm eq}$ and $\left(GA_{\rm s}\right)_{\rm eq}$.
The dynamic equilibrium equations now become:
\begin{align*}
Q^\prime &= -q + \mu \ddot{ w} \\
M^\prime &= Q - i_\mu \ddot{\psi}
\end{align*}
where $\mu$ is the beam mass per unit length and $i_\mu$ is the cross section rotational inertia
per unit length. Derivating the equation for $\gamma$ and replacing the solution
$EI \psi^{\prime} = M(x)$ gives the elastic line equation accounting for shear strains:
$$ w^{\prime\prime} = -\frac{M}{EI} + \frac{Q^\prime}{GA_{\rm s}} $$
Now we replace the shear (with inertial loads):
$$ w^{\prime\prime} = -\frac{M}{EI} + \frac{-q + \mu \ddot{ w}}{GA_{\rm s}} $$
and derivate the whole equation replacing for $M^\prime$:
$$ w^{\prime\prime\prime} = \frac{i_\mu \ddot{\psi} - Q}{EI} + \frac{\mu \ddot{w}^\prime - q^\prime}{GA_{\rm s}} $$
The angular acceleration, $\ddot{\psi}$, may be safely disregarded, for the rotations are usually very small.
Derivating the equation a last time and replacing for $Q^\prime$ finally gives:
$$ EI w^{\prime\prime\prime\prime} = q - \mu \ddot{ w} +
\frac{EI}{GA_{\rm s}} \, \left(\mu \ddot{ w}^{\prime\prime} - q^{\prime\prime} \right) $$
which is the dynamic elastic line equation for a constant section beam under forced vibration due to
dynamic load $q(x,t)$, with shear deformation accounted for (although plane section hypothesis still kept along).
The last term may be disregarded whenever the shear stiffness is much larger that the bending stiffness.
## 2. Free vibration solution <a name="section_2"></a>
In this section, we take the vibrating beam equation derived above, disregard the shear deformation and look for
free vibration solution, which implies that $q(x, t) = 0$. The beam equation becomes simply:
$$ EI w^{\prime\prime\prime\prime} = - \mu \ddot{w} $$
To solve this equation we separate the time and space independent variables through the hypothesis:
$$ w(x,t) = \varphi(x)\, \sin \omega t $$
which is pretty much alike we have previously done for multiple degrees of freedom systems.
The free vibration equilibrium equation then become:
$$ \varphi^{\prime\prime\prime\prime} - p^4 \varphi = 0 $$
where we have defined:
$$ p^4 = \left(\frac{\mu}{EI}\right) \omega^2 $$
It can be shown that, in the general case, the space dependent function $\varphi(x)$ has the form:
$$ \varphi(x) = C_1 \left(\cos px + \cosh px \right) +
C_2 \left(\cos px - \cosh px \right) +
C_3 \left(\sin px + \sinh px \right) +
C_4 \left(\sin px - \sinh px \right) $$
The corresponding space derivatives will be required to apply the boundary conditions:
\begin{align*}
\varphi^\prime(x) = p^1&\left[C_1 \left(-\sin px + \sinh px \right) +
C_2 \left(-\sin px - \sinh px \right) +
C_3 \left( \cos px + \cosh px \right) +
C_4 \left( \cos px - \cosh px \right)\right] \\
\varphi^{\prime\prime}(x) = p^2&\left[C_1 \left(-\cos px + \cosh px \right) +
C_2 \left(-\cos px - \cosh px \right) +
C_3 \left(-\sin px + \sinh px \right) +
C_4 \left(-\sin px - \sinh px \right)\right] \\
\varphi^{\prime\prime\prime}(x) = p^3&\left[C_1 \left( \sin px + \sinh px \right) +
C_2 \left( \sin px - \sinh px \right) +
C_3 \left(-\cos px + \cosh px \right) +
C_4 \left(-\cos px - \cosh px \right)\right] \\
\varphi^{\prime\prime\prime\prime}(x) = p^4&\left[C_1 \left( \cos px + \cosh px \right) +
C_2 \left( \cos px - \cosh px \right) +
C_3 \left( \sin px + \sinh px \right) +
C_4 \left( \sin px - \sinh px \right)\right]
\end{align*}
The last equation above proves that the assumed general solution is correct.
Now, to have a particular solution for the vibrating beam the kinematic boundary conditions must be applied.
Let us assume a cantilever beam, fixed at the left end ($x = 0$) and free at the right end ($x = L$).
<img src="images/cantilever_beam.png" alt="Cantilever beam" width="360px"/>
The corresponding boundary conditions are:
\begin{align*}
\varphi(0) &= 0 \\
\varphi^ \prime(0) &= 0 \\
\varphi^{\prime\prime}(L) &= 0 \\
\varphi^{\prime\prime\prime}(L) &= 0
\end{align*}
The two last conditions implies that bending moment and shear force are zero at the right end, respectively.
Applying these conditions at the corresponding derivatives:
\begin{align*}
\varphi(0) &= C_1 \left( 1 + 1 \right) +
C_2 \left( 1 - 1 \right) +
C_3 \left( 0 + 0 \right) +
C_4 \left( 0 - 0 \right) = 0\\
\varphi^\prime(0) &= p \left[C_1 \left(-0 + 0 \right) +
C_2 \left(-0 - 0 \right) +
C_3 \left( 1 + 1 \right) +
C_4 \left( 1 - 1 \right)\right] = 0
\end{align*}
which implies that $C_1 = 0$ and $C_3 = 0$. The other two conditions become:
\begin{align*}
\varphi^{\prime\prime}(L) &= p^2 \left[C_2 \left(-\cos pL - \cosh pL \right) +
C_4 \left(-\sin pL - \sinh pL \right)\right] = 0\\
\varphi^{\prime\prime\prime}(L) &= p^3 \left[C_2 \left( \sin pL - \sinh pL \right) +
C_4 \left(-\cos pL - \cosh pL \right)\right] = 0
\end{align*}
These two equations can be put into matrix form as:
$$ \left[ \begin{array}{cc}
\left(-\cos pL - \cosh pL \right) & \left(-\sin pL - \sinh pL \right) \\
\left( \sin pL - \sinh pL \right) & \left(-\cos pL - \cosh pL \right)
\end{array} \right]
\left[ \begin{array}{c}
C_2 \\
C_4
\end{array} \right] =
\left[ \begin{array}{c}
0 \\
0
\end{array} \right] $$
In order to obtain a non trivial (non zero) solution for the unknown coefficients $C_2$ and $C_4$,
the determinant of the coefficients matrix must be zero. This condition yields a nonlinear equation
to be solved for $pL$. We can use the HP Prime for this purpose, as shown in the figure below.
<table>
<tr>
<td><img src="images/det_cantilever_1.jpg" alt="HP Prime determinant" width="320px"/></td>
<td><img src="images/det_cantilever_2.jpg" alt="HP Prime cantilever" width="320px"/></td>
</tr>
</table>
There will be infinite solutions $\alpha_k = \left( pL \right)_k$, $k = 1, 2, \dots, \infty$,
each one associated to a vibration frequency and a modal shape,
$\left[ \omega_k, \varphi_k(x) \right]$. The natural vibration frequencies are obtained
by recalling the definition of $p$, what finally gives:
$$ \omega_k = \left( \frac{\alpha_k}{L} \right) ^2 \sqrt{\frac{EI}{\mu}}$$
For instance, the fundamental vibration frequency, $f_{\rm n}$, is given by:
$$ f_{\rm n} \approx \frac{1}{2\pi} \left( \frac{1.8751}{L} \right) ^2 \sqrt{\frac{EI}{\mu}}$$
which is a very useful formula for estimating the fundamental frequency of slender piles and towers
with constant cross section.
```
x = np.linspace(0, 10, 1000)
```
## 3. Vibration modes and frequencies <a name="section_3"></a>
The table below was taken from a _Sonderausdruck_ (special edition) of the german _Betonkalender_
(concrete almanac), 1988. It summarizes the solutions for some other support conditions of slender beams.
If more accuracy is desiredfor the $\alpha_k$ constants, one can solve the so-called
_characteristic equation_ with the help of a calculator like the HP Prime, ou HP 50G.
<img src="images/beams.png" alt="Beam solutions" width="640px"/>
The characteristic equations are the determinants of respective coefficients matrix,
which can also be solved with the ``fsolve()`` method from ``scipy``, as shown below.
```
def char_eq(x):
x = x[0]
A = np.array([[-np.cos(x)-np.cosh(x), -np.sin(x)-np.sinh(x)],
[ np.sin(x)-np.sinh(x), -np.cos(x)-np.cosh(x)]])
return np.linalg.det(A) # from coefficientes matrix
# return np.cos(x)*np.cosh(x) + 1 # from characteristic equation
#-----------------------------------------------------------------------
from scipy.optimize import fsolve
ak = fsolve(char_eq, 2)
print('Cantilever beam frequency parameter: {0}'.format(ak[0]))
```
Observe that the result is exactly the same (within the required precision) as previously obtained with the
HP Prime. One can use directly the characteristic equation, or one can program the determinant calculation
using ``np.linalg.det()`` in the user function ``char_eq`` above.
## 4. Solution by approximation <a name="section_4"></a>
The solutions for the beam vibration frequencies presented above may also be calculated by means of
Rayleigh quotient, as long as an educated guess for the $\varphi(x)$ function is assumed.
As an example, let us take a simply supporte beam, for which we assume:
$$ \varphi(x) = 4x \left( \frac{L - x}{L^2} \right) $$
with $\varphi(L/2) = 1$, which obviously _is not_ the correct modal shape.
<img src="images/simply_supported.png" alt="simply supported beam" width="400px"/>
We also assume that the beam is subjected to a constant distributed load, $q$ corresponding
to its self weight. The maximum displacement at the beam center is known to be:
$$ w_{\rm max} = \frac{5 q L^4}{384EI}$$
In the following we shall estimate both the fundamental vibration frequency and the
maximum displacement with the assumed modal shape. The reference kinetic energy is given by:
$$ T_{\rm ref} = \frac{1}{2} \int_0^L {\mu \varphi ^2(x) \, dx} $$
while for the elastic potential energy we need the curvature function, $\varphi^{\prime\prime}(x)$:
$$ V = \frac{1}{2} \int_0^L {EI \left[ \varphi^{\prime\prime}(x) \right] ^2 \, dx}
= \frac{1}{2} \int_0^L {q w(x) \, dx}$$
On the other hand, the modal properties are evaluated with a continuous version of the same formula
presented on [Class 11](https://nbviewer.jupyter.org/github/mmaiarocha/PEC00025/blob/master/Class_11_FreeVibrationMDOF.ipynb?flushcache=true). In particular, the modal mass and the modal load are:
\begin{align*}
\vec\phi_k^{\intercal}{\mathbf M} \vec\phi_k &\implies M_k = \int_0^L{\mu \, \varphi^2(x) \, dx} \\
\vec\phi_k^{\intercal} \vec{F} &\implies F_k = \int_0^L{ q \, \varphi(x) \, dx}
\end{align*}
The static modal response can be calculated as:
$$ u_k = F_k/K_k$$
where $K_k = \omega_k^2 M_k$.
Let us apply this approach to the beam example above.
For the assume modal shape we have the curvature:
$$ \varphi^{\prime\prime}(x) = -\frac{8}{L^2}$$
Hence:
\begin{align*}
T_{\rm ref} &= \frac{1}{2} \int_0^L {\mu \left[ \frac{4x(L - x)}{L^2} \right]^2 \, dx} = \frac{ 4}{15 }\mu L \\
V &= \frac{1}{2} \int_0^L { EI \left[ -\frac{8} {L^2} \right]^2 \, dx} = \frac{32}{L^3} EI
\end{align*}
The Rayleigh quotient results:
$$ \omega_k^2 = \frac{V}{T_{\rm ref}} = \frac{32EI}{L^3} \frac{15}{4\mu L}
= \frac{ 120}{L^4} \left( \frac{EI}{\mu} \right)$$
which gives a fundamental frequency comparing to the exact solution as:
$$ \omega_k \approx \left( \frac{3.31}{L} \right)^2 \sqrt{\frac{EI}{\mu}}
\approx \left( \frac{ \pi}{L} \right)^2 \sqrt{\frac{EI}{\mu}} $$
with an error of approximatelly 11%. The modal shape approximation may also be used to estimate
the displacement at beam center, for which we calculate the modal mass and the modal load as:
\begin{align*}
M_k &= \int_0^L{\mu \, \left[ \frac{4x(L - x)}{L^2} \right]^2 \, dx} = \frac{8}{15}\mu L\\
F_k &= \int_0^L{ q \, \left[ \frac{4x(L - x)}{L^2} \right] \, dx} = \frac{2}{ 3} q L
\end{align*}
The modal stiffness is then:
$$ K_k = \frac{ 120}{L^4} \left( \frac{EI}{\mu} \right) \cdot \frac{8}{15}\mu L = \frac{64EI}{L^3}$$
and the modal displacement is:
$$ u_k = \frac{2}{3} qL \cdot \frac{L^3}{64EI} = \frac{4 q L^4}{384EI} \approx \frac{5 q L^4}{384EI} $$
The modal displacement is already the displacement at the beam center, for $\varphi(L/2) = 1$.
The implied error is hence 20%, not bad for an arbitrary elastic line shape.
The following scripts show how to numerically accomplish these calculations.
```
L = 1 # bar length (m)
EI = 2.6 # bending stiffness (Nm2)
mu = 0.260 # mass per unity length (kg/m)
q = mu*9.81 # distributed load is self weight (N/m)
# Proposed modal shape for first mode (second order polynomial)
x = np.linspace(0, L, 200)
qk = 4*x*(L - x)/L/L # guessed modal shape
q0 = np.sin(np.pi*x/L) # exact modal shape!!!
plt.figure(1, figsize=(8,2))
plt.plot(x, qk, 'b', x, q0, 'r')
plt.xlim( 0.0, L ); plt.xlabel('x');
plt.ylim(-0.5, 1.5); plt.ylabel('phi(x)');
plt.title('Proposed modal shape')
plt.grid(True)
```
The same calculation could be carried out with the correct modal frequency, with much more accurate results:
```
wk = ((np.pi/L)**2)*np.sqrt(EI/mu) # exact fundamental frequency
fk = wk/(2*np.pi)
Mk = np.sum(mu*qk*qk) # modal mass from guessed modal shape
Kk = wk*wk*Mk # improved modal stiffness
print('Available fundamental vibration frequency: {0:5.2f} Hz'.format(fk))
print('Modal mass (integrated over bar length): {0:5.1f} kg'.format(Mk))
print('Modal stiffness (from mass and frequency): {0:5.0f} N/m'.format(Kk))
Fk = np.sum(q*qk) # modal force
uk = Fk/Kk # modal displacement
wp = np.max(uk*qk) # approximated elastic line
w0 = (5*q*L**4)/(384*EI) # exact elastic line
print('Maximum displacement approximation: {0:6.2f}mm'.format(1000*wp))
print('Theoretical maximum displacement: {0:6.2f}mm'.format(1000*w0))
w = uk*qk
V = np.sum( q*w )/2 # potential energy calculated with external work
Tref = np.sum(mu*w*w)/2
wk = np.sqrt(V/Tref)
fk = wk/(2*np.pi)
print('Fundamental frequency from Rayleigh quotient: {0:5.2f} Hz'.format(fk))
```
## 5. Assignments <a name="section_5"></a>
1. Aplicar um carregamento no modelo individual discreto que produza uma deformada semelhante à primeira forma modal, e recalcular a frequência fundamental pelo quociente de Rayleigh.
2. Mantendo uma massa média por unidade de comprimento, determinar um EI (rigidez de flexão equivalente) que resulte em frequência fundamental próxima à correta ao se representar a estrutura como uma barra contínua equivalente.
Trabalho T8 <br>
Prazo: 08/06/2020.
| true |
code
| 0.600598 | null | null | null | null |
|
Everything is a network. [Assortativity](http://arxiv.org/pdf/cond-mat/0205405v1.pdf) is an interesting property of networks. It is the tendency of nodes in a network to be attached to other nodes that are similar in some way. In social networks, this is sometimes called "homophily."
One kind of assortativity that is particularly descriptive of network topology is *degree assortativity*. This is what it sounds like: the *assortativity* (tendency of nodes to attach to other nodes that are similar) of *degree* (the number of edges a node has).
A suggestive observation by [Newman (2002)](http://arxiv.org/pdf/cond-mat/0205405v1.pdf) is that *social* networks such as academic coauthorship networks and film collaborations tend to have positive degree assortativity, while *technical* and *biological* networks tend to have negative degree assortativity. Another way of saying this is that they are *disassortatively mixed*. This has implications for the ways we model these networks forming as well as the robustness of these networks to the removal of nodes.
Looking at open source software collaboration as a *sociotechnical* system, we can ask whether and to what extent the networks of activity are assortatively mixed. Are these networks more like social networks or technical networks? Or are they something in between?
### Email reply networks
One kind of network that we can extract from open source project data are networks of email replies from public mailing lists. [Mailing lists and discussion forums](http://producingoss.com/en/message-forums.html) are often the first point of contact for new community members and can be the site of non-technical social processes that are necessary for the maintenance of the community. Of all the communications media used in coordinating the cooperative work of open source development, mailing lists are the most "social".
We are going to look at the mailing lists associated with a number of open source and on-line collaborative projects. We will construct for each list a network for which nodes are email senders (identified by their email address) and edges are the number of times a sender has replied directly to another participant on the list. Keep in mind that these are public discussions and that in a sense every reply is sent to everybody.
```
from bigbang.archive import Archive
urls = [#"analytics",
"conferences",
"design",
"education",
"gendergap",
"historic",
"hot",
"ietf-privacy",
"ipython-dev",
"ipython-user",
"languages",
"maps-l",
"numpy-discussion",
"playground",
"potlatch-dev",
"python-committers",
"python-dev",
"scipy-dev",
"scipy-user",
"social-media",
"spambayes",
#"wikien-l",
"wikimedia-l"]
archives= [(url,Archive(url,archive_dir="../archives")) for url in urls]
archives = dict(archives)
```
The above code reads in preprocessed email archive data. These mailing lists are from a variety of different sources:
|List name | Project | Description |
|---|---|---|
|analytics| Wikimedia | |
|conferences| Python | |
|design| Wikimedia | |
|education| Wikimedia | |
|gendergap| Wikimedia | |
|historic| OpenStreetMap | |
|hot| OpenStreetMap | Humanitarian OpenStreetMap Team |
|ietf-privacy| IETF | |
|ipython-dev| IPython | Developer's list |
|ipython-user| IPython | User's list |
|languages| Wikimedia | |
|maps-l| Wikimedia | |
|numpy-discussion| Numpy | |
|playground| Python | |
|potlatch-dev| OpenStreetMap | |
|python-committers| Python | |
|python-dev| Python | |
|scipy-dev| SciPy | Developer's list|
|scipy-user| SciPy | User's list |
|social-media| Wikimedia | |
|spambayes| Python | |
|wikien-l| Wikimedia | English language Wikipedia |
|wikimedia-l| Wikimedia | |
```
import bigbang.graph as graph
igs = dict([(k,graph.messages_to_interaction_graph(v.data)) for (k,v) in list(archives.items())])
igs
```
Now we have processed the mailing lists into interaction graphs based on replies. This is what those graphs look like:
```
import networkx as nx
def draw_interaction_graph(ig):
pos = nx.graphviz_layout(ig,prog='neato')
node_size = [data['sent'] * 4 for name,data in ig.nodes(data=True)]
nx.draw(ig,
pos,
node_size = node_size,
node_color = 'b',
alpha = 0.4,
font_size=18,
font_weight='bold'
)
# edge width is proportional to replies sent
edgewidth=[d['weight'] for (u,v,d) in ig.edges(data=True)]
#overlay edges with width based on weight
nx.draw_networkx_edges(ig,pos,alpha=0.5,width=edgewidth,edge_color='r')
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(550,figsize=(12.5, 7.5))
for ln,ig in list(igs.items()):
print(ln)
try:
plt.subplot(550 + i)
#print nx.degree_assortativity_coefficient(ig)
draw_interaction_graph(ig)
except:
print('plotting failure')
plt.show()
```
Well, that didn't work out so well...
I guess I should just go on to compute the assortativity directly.
This is every mailing list, with the total number of nodes and its degree assortativity computed.
```
for ln,ig in list(igs.items()):
print(ln, len(ig.nodes()), nx.degree_assortativity_coefficient(ig,weight='weight'))
```
Maybe it will be helpful to compare these values to those in the Newman, 2002 paper:
<img src="assortativity-values.png">
On the whole, with a few exceptions, these reply networks wind up looking much more like technical or biological networks than the social networks of coauthorship and collaboration. Why is this the case?
One explanation is that the mechanism at work in creating these kinds of "interaction" networks over time is very different from the mechanism for creating collaboration or coauthorship networks. These networks are derived from real communications over time in projects actively geared towards encouraging new members and getting the most out of collaborations. Perhaps these kinds of assortativity numbers are typical in projects with leaders who have inclusivity as a priority.
Another possible explanation is that these interaction networks are mirroring the structures of the technical systems that these communities are built around. There is a theory of [institutional isomorphism](http://www.jstor.org/discover/10.2307/2095101?sid=21105865961831&uid=2&uid=70&uid=2129&uid=3739560&uid=3739256&uid=4) that can be tested in this case, where social and technical institutions are paired.
### Directions for future work
Look at each project domain (IPython, Wikimedia, OSM, etc.) separately but include multiple lists from each and look at assortativity within list as well as across list. This would get at how the cyberinfrastructure topology affects the social topology of the communities that use it.
Use a more systematic sampling of email lists to get a typology of those lists with high and low assortativity. Figure out qualitatively what the differences in structure might mean (can always go in and *read the emails*).
Build a generative graph model that with high probability creates networks with this kind of structure (apparently the existing models don't do thise well.) Test its fit across many interaction graphs, declare victory for science of modeling on-line collaboration.
### References
http://producingoss.com/en/message-forums.html
http://arxiv.org/abs/cond-mat/0205405
http://arxiv.org/pdf/cond-mat/0205405v1.pdf
http://arxiv.org/abs/cond-mat/0209450
http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2005302
http://www.jstor.org/discover/10.2307/2095101?sid=21105865961831&uid=2&uid=70&uid=2129&uid=3739560&uid=3739256&uid=4
| true |
code
| 0.373047 | null | null | null | null |
|
# bioimageio.core usage examples
```
import os
import hashlib
import bioimageio.core
import imageio
# we use napari for visualising images, you can install it via `pip install napari` or`conda install napari`
import napari
import numpy as np
import xarray as xr
from bioimageio.core.prediction_pipeline import create_prediction_pipeline
# helper function for showing multiple images in napari
def show_images(*images, names=None):
v = napari.Viewer()
for i, im in enumerate(images):
name = None if names is None else names[i]
if isinstance(im, str):
im = imageio.imread(im)
v.add_image(im, name=name)
```
## Loading a model
We will use a model that predicts foreground and boundaries in images of nuclei from the [kaggle nucles segmentation challenge](https://www.kaggle.com/c/data-science-bowl-2018).
Find the model on bioimage.io here: https://bioimage.io/#/?id=10.5072%2Fzenodo.881940
First, we will use `bioimageio.core.load_resource_description` to load the model and inspec the obtained model resource.
```
# the model can be loaded using different representations:
# the doi of the zenodo entry corresponding to the model
rdf_doi = "10.5281/zenodo.6287342"
# the url of the yaml file containing the model resource description
rdf_url = "https://zenodo.org/record/6287342/files/rdf.yaml"
# filepath to the downloaded model (either zipped package or yaml)
# to download it from the website:
# - go to https://bioimage.io/#/?id=10.5281%2Fzenodo.5764892%2F5764893
# - click the download icon
# - select "ilastik" weight format
rdf_path = "/home/pape/Downloads/nuclei-segmentation-boundarymodel_pytorch_state_dict.zip"
# load model from link to rdf.yaml
model_resource = bioimageio.core.load_resource_description(rdf_url)
# load model from doi
model_resource = bioimageio.core.load_resource_description(rdf_doi)
# load model from path to the zipped model files
model_resource = bioimageio.core.load_resource_description(rdf_path)
# the "model_resource" instance returned by load_resource_description
# contains the information stored in the resource description (see https://github.com/bioimage-io/spec-bioimage-io/blob/gh-pages/model_spec_latest.md)
# we can e.g. check what weight formats are available in the model (pytorch_state_dict for the model used here)
print("Available weight formats for this model:", model_resource.weights.keys())
# or where the (downloaded) weight files are stored
print("Pytorch state dict weights are stored at:", model_resource.weights["pytorch_state_dict"].source)
print()
# or what inputs the model expects
print("The model requires as inputs:")
for inp in model_resource.inputs:
print("Input with axes:", inp.axes, "and shape", inp.shape)
print()
# and what the model outputs are
print("The model returns the following outputs:")
for out in model_resource.outputs:
print("Output with axes:", out.axes, "and shape", out.shape)
# the function 'test_model' from 'bioimageio.core.resource_tests' can be used to fully test the model,
# including running prediction for the test input(s) and checking that they agree with the test output(s)
# before using a model, it is recommended to check that it properly works with this function
# 'test_model' returns a dict with 'status'='passed'/'failed' and more detailed information
from bioimageio.core.resource_tests import test_model
test_result = test_model(model_resource)
if test_result["status"] == "failed":
print("model test:", test_result["name"])
print("The model test failed with:", test_result["error"])
print("with the traceback:")
print("".join(test_result["traceback"]))
else:
test_result["status"] == "passed"
print("The model passed all tests")
```
## Prediction with the model
`bioimageio.core` implements functionality to run predictions with a model in bioimage.io format.
This includes functions to run prediction with numpy arrays (more precisely xarray DataArrays) and convenience functions to run predictions for inputs stored on disc.
```
# load the example image for this model, which is stored in numpy file format
input_image = np.load(model_resource.test_inputs[0])
# define a function to run prediction on a numpy input
# "devices" can be used to run prediction on a gpu instead of the cpu
# "weight_format" to specify which weight format to use in case the model contains different weight formats
def predict_numpy(model, input_, devices=None, weight_format=None):
# the prediction pipeline combines preprocessing, prediction and postprocessing.
# it should always be used for prediction with a bioimageio model
pred_pipeline = create_prediction_pipeline(
bioimageio_model=model, devices=devices, weight_format=weight_format
)
# the prediction pipeline expects inputs as xarray.DataArrays.
# these are similar to numpy arrays, but allow for named dimensions (the dims keyword argument)
# in bioimage.io the dims have to agree with the input axes required by the model
axes = tuple(model.inputs[0].axes)
input_tensor = xr.DataArray(input_, dims=axes)
# the prediction pipeline call expects the same number of inputs as the number of inputs required by the model
# in the case here, the model just expects a single input. in the case of multiple inputs use
# prediction = pred_pipeline(input1, input2, ...)
# or, if you have the inputs in a list or tuple
# prediction = pred_pipeline(*inputs)
# the call returns a list of output tensors, corresponding to the output tensors of the model
# (in this case, we just have a single output)
prediction = pred_pipeline(input_tensor)[0]
return prediction
# run prediction for the test input and show the result
prediction = predict_numpy(model_resource, input_image)
show_images(input_image, prediction, names=["image", "prediction"])
# the utility function `predict_image` can be used to run prediction with an image stored on disc
from bioimageio.core.prediction import predict_image
# the filepath where the output should be stored, supports most common image formats as well as npy fileformat
outputs = ["prediction.tif"]
predict_image(
model_resource, model_resource.test_inputs, outputs
)
# the output tensor contains 2 channels, which is not supported by normal tif.
# thus, these 2 channels are stored as 2 separate images
fg_pred = imageio.imread("prediction-c0.tif")
bd_pred = imageio.imread("prediction-c1.tif")
show_images(input_image, fg_pred, bd_pred,
names=["image", "foreground-prediction", "boundary-prediction"])
# the utility function `predict_images` can be use to run prediction for a batch of images stored on disc
# note: this only works for models which have a single input and output!
from bioimageio.core.prediction import predict_images
# here, we use a subset of the dsb challenge data for prediction from the stardist (https://github.com/stardist/stardist)
# you can obtain it from: https://github.com/stardist/stardist/releases/download/0.1.0/dsb2018.zip
# select all images in the "test" subfolder
from glob import glob
folder = "/home/pape/Downloads/dsb2018(1)/dsb2018/test"
inputs = glob(os.path.join(folder, "images", "*.tif"))
# create an output folder and specify the output path for each image
output_folder = os.path.join(folder, "predictions")
os.makedirs(output_folder, exist_ok=True)
outputs = [os.path.join(output_folder, os.path.split(inp)[1]) for inp in inputs]
print(len(inputs), "images for prediction were found")
# the model at hand can only predict images which have a xy-size that is
# a multiple of 16. To run with arbitrary size images, we pass the `padding`
# argument to `predict_images` and specify that the input is padded to the next bigger
# size that is divisible by 16 (mode: dynamic)
# as an alternative `"mode": "fixed"` will pad to a fixed shape, e.g.
# `{"x": 512, "y": 512, "mode": "fixed"}` will always pad to a size of 512x512
# the padding is cropped again after the prediction
padding = {"x": 16, "y": 16, "mode": "dynamic"}
predict_images(
model_resource, inputs, outputs, padding=padding, verbose=True
)
# check the first input/output
show_images(inputs[0], outputs[0].replace(".tif", "-c0.tif"), outputs[0].replace(".tif", "-c1.tif"))
# instead of padding, we can also use tiling.
# here, we specify a tile size of 224 and a halo (= extension of tile on both sides)
# size of 16, which results in an effective tile shale of 256 = 224 + 2*16
tiling = {
"tile": {"x": 224, "y": 224},
"halo": {"x": 16, "y": 16},
}
predict_images(
model_resource, inputs, outputs, tiling=tiling, verbose=True
)
# check the first input/output
show_images(inputs[0], outputs[0].replace(".tif", "-c0.tif"), outputs[0].replace(".tif", "-c1.tif"))
```
## Create a biomiage.io model package
`bioimageio.core` also implements functionality to create a model package compatible with the [bioimageio model spec](https://github.com/bioimage-io/spec-bioimage-io/blob/gh-pages/model_spec_latest.md) ready to be shared via
the [bioimage.io model zoo](https://bioimage.io/#/).
Here, we will use this functionality to create two models, one that adds thresholding as post-processing to the outputs and another one that also adds weights in torchscript format.
```
# get the python file defining the architecture.
# this is only required for models with pytorch_state_dict weights
def get_architecture_source(rdf):
# here, we need the raw resource, which contains the information from the resource description
# before evaluation, e.g. the file and name of the python file with the model architecture
raw_resource = bioimageio.core.load_raw_resource_description(rdf)
# the python file defining the architecture for the pytorch weihgts
model_source = raw_resource.weights["pytorch_state_dict"].architecture
# download the source file if necessary
source_file = bioimageio.core.resource_io.utils.resolve_source(
model_source.source_file
)
# if the source file path does not exist, try combining it with the root path of the model
if not os.path.exists(source_file):
source_file = os.path.join(raw_resource.root_path, os.path.split(source_file)[1])
assert os.path.exists(source_file), source_file
class_name = model_source.callable_name
return f"{source_file}:{class_name}"
# first new model: add thresholding of outputs as post-processing
# the convenience function `build_model` creates a biomageio model spec compatible package (=zipped folder)
from bioimageio.core.build_spec import build_model
# create a subfolder to store the files for the new model
model_root = "./new_model"
os.makedirs(model_root, exist_ok=True)
# create the expected output tensor (= outputs thresholded at 0.5)
threshold = 0.5
new_output = prediction > threshold
new_output_path = f"{model_root}/new_test_output.npy"
np.save(new_output_path, new_output)
# add thresholding as post-processing procedure to our model
preprocessing = [[{"name": prep.name, "kwargs": prep.kwargs} for prep in inp.preprocessing] for inp in model_resource.inputs]
postprocessing = [[{"name": "binarize", "kwargs": {"threshold": threshold}}]]
# get the model architecture
# note that this is only necessary for pytorch state dict models
model_source = get_architecture_source(rdf_doi)
# we use the `parent` field to indicate that the new model is created based on
# the nucleus segmentation model we have obtained from bioimage.io
# this field is optional and only needs to be given for models that are created based on other models from bioimage.io
# the parent is specified via it's doi and the hash of its rdf file
model_root_folder = os.path.split(model_resource.weights["pytorch_state_dict"].source)[0]
rdf_file = os.path.join(model_root_folder, "rdf.yaml")
with open(rdf_file, "rb") as f:
rdf_hash = hashlib.sha256(f.read()).hexdigest()
parent = {"uri": rdf_doi, "sha256": rdf_hash}
# the name of the new model and where to save the zipped model package
name = "new-model1"
zip_path = os.path.join(model_root, f"{name}.zip")
# `build_model` needs some additional information about the model, like citation information
# all this additional information is passed as plain python types and will be converted into the bioimageio representation internally
# for more informantion, check out the function signature
# https://github.com/bioimage-io/core-bioimage-io-python/blob/main/bioimageio/core/build_spec/build_model.py#L252
cite = [{"text": cite_entry.text, "url": cite_entry.url} for cite_entry in model_resource.cite]
# the training data used for the model can also be specified by linking to a dataset available on bioimage.io
training_data = {"id": "ilastik/stradist_dsb_training_data"}
# the axes descriptions for the inputs / outputs
input_axes = ["bcyx"]
output_axes = ["bcyx"]
# the pytorch_state_dict weight file
weight_file = model_resource.weights["pytorch_state_dict"].source
# the path to save the new model with torchscript weights
zip_path = f"{model_root}/new_model2.zip"
# build the model! it will be saved to 'zip_path'
new_model_raw = build_model(
weight_uri=weight_file,
test_inputs=model_resource.test_inputs,
test_outputs=[new_output_path],
input_axes=input_axes,
output_axes=output_axes,
output_path=zip_path,
name=name,
description="nucleus segmentation model with thresholding",
authors=[{"name": "Jane Doe"}],
license="CC-BY-4.0",
documentation=model_resource.documentation,
covers=[str(cover) for cover in model_resource.covers],
tags=["nucleus-segmentation"],
cite=cite,
parent=parent,
architecture=model_source,
model_kwargs=model_resource.weights["pytorch_state_dict"].kwargs,
preprocessing=preprocessing,
postprocessing=postprocessing,
training_data=training_data,
)
# load the new model from the zipped package, run prediction and check the result
new_model = bioimageio.core.load_resource_description(zip_path)
prediction = predict_numpy(new_model, input_image)
show_images(input_image, prediction, names=["input", "binarized-prediction"])
```
## Add different weight format and package model with new weights
```
# `convert_weigths_to_pytorch_script` creates torchscript weigths based on the weights loaded from pytorch_state_dict
from bioimageio.core.weight_converter.torch import convert_weights_to_torchscript
# `add_weights` adds new weights to the model specification
from bioimageio.core.build_spec import add_weights
# the path to save the newly created torchscript weights
weight_path = os.path.join(model_root, "weights.torchscript")
convert_weights_to_torchscript(new_model, weight_path)
# the path to save the new model with torchscript weights
zip_path = f"{model_root}/new_model2.zip"
new_model2_raw = add_weights(new_model_raw, weight_path, weight_type="torchscript", output_path=zip_path)
# load the new model from the zipped package, run prediction and check the result
new_model = bioimageio.core.load_resource_description(zip_path)
prediction = predict_numpy(new_model, input_image, weight_format="torchscript")
show_images(input_image, prediction, names=["input", "binarized-prediction"])
# models in the biomageio.core format can also directly be exported as zipped packages
# using `bioimageio.core.export_resource_package`
bioimageio.core.export_resource_package(new_model2_raw, output_path="another_model.zip")
```
| true |
code
| 0.612715 | null | null | null | null |
|
# Getting started with Perceptual Adversarial Robustness
This notebook contains examples of how to load a pretrained model, measure LPIPS distance, and construct perceptual and non-perceptual attacks.
If you are running this notebook in Google Colab, it is recommended to use a GPU. You can enable GPU acceleration by going to **Runtime** > **Change runtime type** and selecting **GPU** from the dropdown.
First, make sure you have installed the `perceptual_advex` package, either from GitHub or PyPI:
```
try:
import perceptual_advex
except ImportError:
!pip install perceptual-advex
```
## Loading a pretrained model
First, let's load the CIFAR-10 dataset along with a pretrained model. The following code will download a model checkpoint and load it, but you can change the `checkpoint_name` parameter to load a different checkpoint. The checkpoint we're downloading here is trained against $L_2$ adversarial attacks with bound $\epsilon = 1$.
```
import subprocess
import os
if not os.path.exists('data/checkpoints/cifar_pgd_l2_1.pt'):
!mkdir -p data/checkpoints
!curl -o data/checkpoints/cifar_pgd_l2_1.pt https://perceptual-advex.s3.us-east-2.amazonaws.com/cifar_pgd_l2_1_cpu.pt
from perceptual_advex.utilities import get_dataset_model
dataset, model = get_dataset_model(
dataset='cifar',
arch='resnet50',
checkpoint_fname='data/checkpoints/cifar_pgd_l2_1.pt',
)
```
If you want to experiment with ImageNet-100 instead, just change the above to
dataset, model = get_dataset_model(
dataset='imagenet100',
# Change this to where ImageNet is downloaded.
dataset_path='/path/to/imagenet',
arch='resnet50',
# Change this to a pretrained checkpoint path.
checkpoint_fname='/path/to/checkpoint',
)
## Viewing images in the dataset
Now that we have a dataset and model loaded, we can view some images in the dataset.
```
import torchvision
import numpy as np
import matplotlib.pyplot as plt
# We'll use this helper function to show images in the Jupyter notebook.
%matplotlib inline
def show(img):
if len(img.size()) == 4:
img = torchvision.utils.make_grid(img, nrow=10, padding=0)
npimg = img.detach().cpu().numpy()
plt.figure(figsize=(18,16), dpi=80, facecolor='w', edgecolor='k')
plt.imshow(np.transpose(npimg, (1,2,0)), interpolation='nearest')
import torch
# Create a validation set loader.
batch_size = 10
_, val_loader = dataset.make_loaders(1, batch_size, only_val=True)
# Get a batch from the validation set.
inputs, labels = next(iter(val_loader))
# If we have a GPU, let's convert everything to CUDA so it's quicker.
if torch.cuda.is_available():
inputs = inputs.cuda()
labels = labels.cuda()
model.cuda()
# Show the batch!
show(inputs)
```
We can also test the accuracy of the model on this set of inputs by comparing the model output to the ground-truth labels.
```
pred_labels = model(inputs).argmax(1)
print('Natural accuracy is', (labels == pred_labels).float().mean().item())
```
If the natural accuracy is very low on this batch of images, you might want to load a new set by re-running the two cells above.
## Generating perceptual adversarial examples
Next, let's generate some perceptual adversarial examples using Lagrange perceptual attack (LPA) with AlexNet bound $\epsilon = 0.5$. Other perceptual attacks (PPGD and Fast-LPA) are also found in the `perceptual_advex.perceptual_attacks` module, and they mostly share the same options.
```
from perceptual_advex.perceptual_attacks import LagrangePerceptualAttack
attack = LagrangePerceptualAttack(
model,
num_iterations=10,
# The LPIPS distance bound on the adversarial examples.
bound=0.5,
# The model to use for calculate LPIPS; here we use AlexNet.
# You can also use 'self' to perform a self-bounded attack.
lpips_model='alexnet_cifar',
)
adv_inputs = attack(inputs, labels)
# Show the adversarial examples.
show(adv_inputs)
# Show the magnified difference between the adversarial examples and unperturbed inputs.
show((adv_inputs - inputs) * 5 + 0.5)
```
Note that while the perturbations are sometimes large, the adversarial examples are still recognizable as the original image and do not appear too different perceptually.
We can calculate the accuracy of the classifier on the adversarial examples:
```
adv_pred_labels = model(adv_inputs).argmax(1)
print('Adversarial accuracy is', (labels == adv_pred_labels).float().mean().item())
```
Even though this network has been trained to be robust to $L_2$ perturbations, there are still imperceptible perturbations found using LPA that fool it almost every time!
## Calculating LPIPS distance
Next, let's calculate the LPIPS distance between the adversarial examples we generated and the original inputs:
```
from perceptual_advex.distances import LPIPSDistance
from perceptual_advex.perceptual_attacks import get_lpips_model
# LPIPS is based on the activations of a classifier, so we need to first
# load the classifier we'll use.
lpips_model = get_lpips_model('alexnet_cifar')
if torch.cuda.is_available():
lpips_model.cuda()
# Now we can define a distance based on the model we loaded.
# We could also do LPIPSDistance(model) for self-bounded LPIPS.
lpips_distance = LPIPSDistance(lpips_model)
# Finally, let's calculate the distance between the inputs and adversarial examples.
print(lpips_distance(inputs, adv_inputs))
```
Note that all the distances are within the bound of 0.5! At this bound, the adversarial perturbations should all have a similar level of perceptibility to the human eye.
Other distance measures between images are also defined in the `perceptual_advex.distances` package, including $L_\infty$, $L_2$, and SSIM.
## Generating non-perceptual adversarial examples
The `perceptual_advex` package also includes code to perform attacks based on other, narrower threat models like $L_\infty$ or $L_2$ distance and spatial transformations. The non-perceptual attacks are all in the `perceptual_advex.attacks` module. First, let's try an $L_2$ attack:
```
from perceptual_advex.attacks import L2Attack
attack = L2Attack(
model,
'cifar',
# The bound is divided by 255, so this is equivalent to eps=1.
bound=255,
)
l2_adv_inputs = attack(inputs, labels)
show(l2_adv_inputs)
show((l2_adv_inputs - inputs) * 5 + 0.5)
l2_adv_pred_labels = model(l2_adv_inputs).argmax(1)
print('L2 adversarial accuracy is', (labels == l2_adv_pred_labels).float().mean().item())
```
Here's an example of a spatial attack (StAdv):
```
from perceptual_advex.attacks import StAdvAttack
attack = StAdvAttack(
model,
bound=0.02,
)
spatial_adv_inputs = attack(inputs, labels)
show(spatial_adv_inputs)
show((spatial_adv_inputs - inputs) * 5 + 0.5)
spatial_adv_pred_labels = model(spatial_adv_inputs).argmax(1)
print('Spatial adversarial accuracy is', (labels == spatial_adv_pred_labels).float().mean().item())
```
## Conclusion
That's pretty much it for how to use the package! As a final note, here is an overview of what each module contains:
* `perceptual_advex.attacks`: non-perceptual attacks (e.g. $L_2$, $L_\infty$, spatial, recoloring, JPEG, etc.)
* `perceptual_advex.datasets`: datasets (e.g. ImageNet-100, CIFAR-10, etc.)
* `perceptual_advex.distances`: distance measures between images (e.g. LPIPS, SSIM, $L_2$)
* `perceptual_advex.evaluation`: functions used for evaluating a trained model against attacks
* `perceptual_advex.models`: classifier architectures (e.g. ResNet, AlexNet, etc.)
* `perceptual_advex.perceptual_attacks`: perceptual attacks (e.g. LPA, PPGD, Fast-LPA)
* `perceptual_advex.trades_wrn`: classifier architecture used by the TRADES defense (Zhang et al.)
* `perceptual_advex.utilites`: various utilites, including `get_dataset_model` function to load a dataset and model
| true |
code
| 0.646628 | null | null | null | null |
|
# Self study 1
In this self study you should work on the code examples below together with the associated questions. The notebook illustrates a basic neural network implementation, where we implement most of the relevant functions from scratch. Except the calculation of gradients, for which we rely on the functionality provided by PyTorch.
The code illustrates the key concepts involved in the learning neural network. Go carefully through the code before starting to answer the questions at the end.
First we import the modules used in this selfstudy
```
import torch
from torchvision import datasets, transforms
from matplotlib import pyplot
import matplotlib.pyplot as plt
import numpy as np
```
Through torch load the MNIST data set, which we will use in this self study. The MNIST database consists of grey scale images of handwritten digits. Each image is of size $28\times 28$; see figure below for an illustration. The data set is divided into a training set consisting of $60000$ images and a test set with $10000$ images; in both
data sets the images are labeled with the correct digits. If interested, you can find more information about the MNIST data set at http://yann.lecun.com/exdb/mnist/, including accuracy results for various machine learning methods.

Using the data loader provided by torch we have an easy way of loading in data in batches (here of size 64). We can also make various other transformation of the data, such as normalization.
```
batch_size = 64
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
```
Each batch is a list of two elements. The first element encodes the digit and has dimensions [64,1,28,28] (the figures are greyscale with no rbg channel, hence the '1'), and the second element contains the class/label information.
```
batch = iter(train_loader).next()
print(f"Batch dimension (digit): {batch[0].shape}")
print(f"Batch dimension (target): {batch[1].shape}")
digit_batch = batch[0]
img = digit_batch[0,:]
pyplot.imshow(img.reshape((28, 28)), cmap="gray")
print(f"Target: {batch[1][0]} with shape {batch[1][0].shape}")
```
With PyTorch we can specify that the tensors require gradients. This will make PyTorch record all operations performed on the tensors, so that we can afterwards calculate the gradients automatically using back propagation. See also the code example from the last lecture.
For the first part of this self study we will specify a neural network, which will encode a softmax function. For this we need a (randomly initialized) weight matrix and a bias, and for both of them we need their gradients wrt. our error function (yet to be defined) in order to perform learning. Note that to facilitate matrix multiplication we will flatten our image from $28\times 28$ to $784$.
```
weights = torch.randn(784, 10) / np.sqrt(784)
weights.requires_grad_()
bias = torch.zeros(10, requires_grad=True)
```
Out model specification
```
def softmax(x):
return x.exp() / x.exp().sum(-1).unsqueeze(-1)
def model(xb):
return softmax(xb @ weights + bias)
```
Let's test our model (with our randomly initialized weights)
```
# We flatten the digit representation so that it is consistent with the weight matrix
xb = digit_batch.flatten(start_dim=1)
print(f"Batch shape: {xb.shape}")
preds = model(xb)
print(f"Prediction on first image {preds[0]}")
print(f"Corresponding classification: {preds[0].argmax()}")
```
Next we define our loss function, in this case the log-loss (or negative log-likelihood):
```
def nll(input, target):
return (-input[range(target.shape[0]), target].log()).mean()
loss_func = nll
# Make a test calculation
yb = batch[1]
print(loss_func(preds,yb))
```
In the end, we are interested in the accuracy of our model
```
def accuracy(out, yb):
preds = torch.argmax(out, dim=1)
return (preds == yb).float().mean()
print(f"Accuracy of model on batch (with random weights): {accuracy(preds, yb)}")
```
Now we are ready to combine it all and perform learning
```
epochs = 4 # how many epochs to train for
lr = 0.01 # learning rate
train_losses = []
for epoch in range(epochs):
for batch_idx, (xb, yb) in enumerate(train_loader):
xb = xb.squeeze().flatten(start_dim=1)
pred = model(xb)
loss = loss_func(pred, yb)
loss.backward()
with torch.no_grad():
weights -= weights.grad * lr
bias -= bias.grad * lr
weights.grad.zero_()
bias.grad.zero_()
if batch_idx % 50 == 0:
with torch.no_grad():
train_loss = np.mean([loss_func(model(txb.squeeze().flatten(start_dim=1)), tyb).item() for txb, tyb in train_loader])
print(f"Epoch: {epoch}, B-idx: {batch_idx}, Training loss: {train_loss}")
train_losses.append(train_loss)
```
Plot the evolution of the training loss
```
plt.plot(range(len(train_losses)), train_losses)
```
__Exercise:__
1. Experiment with different variations of the gradient descent implementation; try varying the learning rate and the batch size. Assuming that you have a fixed time budget (say 2 minutes for learning), what can we then say about the effect of changing the parameters?
2. Implement momentum in the learning algorithm. How does it affect the results?
3. Try with different initialization schemes for the parameters (e.g. allowing for larger values). How does it affect the behavior of the algorithm?
4. Analyze the behavior of the algorithm on the test set and implement a method for evaluating the accuracy over the entire training/test set (for inspiration, see Line 21 above).
| true |
code
| 0.770983 | null | null | null | null |
|
# Random Forest
The aim of this part of the workshop is to give you initial experience in using *random forests*, which is a popular ensemble method that was presented earlier in the lectures. A particular emphasis is given to the *out-of-bag* error (sometimes called out-of-sample error) that can be used to select random forest model complexity.
As a first step, setup the ipython notebook environment to include numpy, scipy, matplotlib etc.
```
%pylab inline
import numpy as np
import matplotlib.pyplot as plt
```
In this tutorial, we are going to use synthetic data. You can also repeat steps of this worksheet with Cats dataset from the previous worksheet.
We are going to generate data using a function defined below. This function produces S-shaped dataset which is mostly separable, but not necessarily linearly separable. We can control the degree of separability. The resulting dataset is going to be two-dimensional (so that we can plot it) with a binary label. That is, the dataset is a $N\times2$ array of instances coupled with an $N\times1$ of labels. The classes are encoded as $-1$ and $1$.
Since the dataset is a tuple of two arrays, we are going to use a special data structure called *named tuple* from a Python module called *collections*.
```
import collections
def generate_s_shaped_data(gap=3):
x = np.random.randn(80, 2)
x[10:20] += np.array([3, 4])
x[20:30] += np.array([0, 8])
x[30:40] += np.array([3, 12])
x[40:50] += np.array([gap, 0])
x[50:60] += np.array([3 + gap, 4])
x[60:70] += np.array([gap, 8])
x[70:80] += np.array([3 + gap, 12])
t = np.hstack([-np.ones(40), np.ones(40)])
d = collections.namedtuple('Dataset', ['x', 't'])
d.x = x
d.t = t
return d
```
We start with generating training data. A random forest is a non-linear model, so it's fine to generate data that is not linearly separable.
```
d = generate_s_shaped_data(2)
x = d.x
t = d.t
plt.plot(x[t==-1,0], x[t==-1,1], "o")
plt.plot(x[t==1,0], x[t==1,1], "o")
```
Next, we need to import modules that implement random forests. The current implementation yields a lot of annoying deprecation warnings that we don't need to care about in this tutorial. Therefore, we suppress the warnings.
```
from sklearn.ensemble import RandomForestClassifier
import warnings
warnings.filterwarnings('ignore')
```
Key parameters for training a random forest are the number of trees (*n_estimators*) and the number of features used in each iteration (*max_features*). First, we are going to train a random forest with only a few trees. Moreover, in this exercise, we are working with a simple 2D data, and there is not much room with features subset selection, so we are going to use both features. Note that *max_features=None* instructs the function to use all features.
```
model = RandomForestClassifier(n_estimators=5, max_features=None)
model.fit(x, t)
```
We now generate test data using the same setup as for the training data. In essense, this mimics the holdout validation approach where the dataset is randomly split in halves for training and testing. The test dataset should look similar, but not identical to the training data.
```
d = generate_s_shaped_data(2)
x_heldout = d.x
t_heldout = d.t
plt.plot(x_heldout[t_heldout==-1,0], x_heldout[t_heldout==-1,1], "o")
plt.plot(x_heldout[t_heldout==1,0], x_heldout[t_heldout==1,1], "o")
```
Let's see what the trained forest predicts for the test data. We will use an auxiliary variable $r$ as an indicator whether the prediction was correct. We will plot correcly classified points in blue and orange for both classes and misclassified points in black. Recall that this is the same test data as above, but instead of color-code labels, we show whether a point was misclassified or not.
```
y = model.predict(x_heldout)
r = y+t_heldout
plt.plot(x_heldout[r==-2,0], x_heldout[r==-2,1], "o")
plt.plot(x_heldout[r==2,0], x_heldout[r==2,1], "o")
plt.plot(x_heldout[r==0,0], x_heldout[r==0,1], "ok")
print('Proportion misclassified:')
print(1 - np.sum(y == t_heldout) / float(t_heldout.shape[0]))
```
It looks like there are quite a few mistakes. Perhaps, this is because we are using too few trees. What do you expect to happen if we increase the number of trees? Try different values to see if you can achieve a perfect classification.
One way of choosing the number of trees would be to measure the error on the test set (heldout set) for different number of trees. However, recall from the lectures that out-of-bag (aka out-of-sample) error can be used to estimate the test error. The *error* here means the proportion of misclassified cases. We are going to use the out-of-bag error for choosing the number of trees. Note the *oob_score* parameter that instruct the function to remember the out-of-bag errors in each training iteration.
```
list_num_trees = [1, 2, 4, 8, 16, 32, 64]
num_cases = len(list_num_trees)
oob_error = np.zeros(num_cases)
test_error = np.zeros(num_cases)
for i in range(num_cases):
model= RandomForestClassifier(n_estimators=list_num_trees[i], max_features=None, oob_score=True)
model.fit(x, t)
oob_error[i] = 1 - model.oob_score_
y = model.predict(x_heldout)
test_error[i] = 1 - np.sum(y == t_heldout) / float(t_heldout.shape[0])
plot(list_num_trees, oob_error, 'b')
plot(list_num_trees, test_error, 'g')
```
We can see that increasing the number of trees helps, but performance eventually stabilizes. Note that we only use training data for computing the out-of-bag error. Implement the heldout validation approach and compare the two errors as a function of number of trees.
| true |
code
| 0.275617 | null | null | null | null |
|
# 삼성전자 첨기연 시각 심화
- **Instructor**: Jongwoo Lim / Jiun Bae
- **Email**: [jlim@hanyang.ac.kr](mailto:jlim@hanyang.ac.kr) / [jiun.maydev@gmail.com](mailto:jiun.maydev@gmail.com)
```
from pathlib import Path
import yaml
import numpy as np
import pandas as pd
import torch
from models.mdnet import MDNet, BCELoss, Precision
from models.extractor import SampleGenerator, RegionDataset
```
## Dataset
Download OTB-50, 100 dataset from [CVLab](http://cvlab.hanyang.ac.kr/tracker_benchmark/datasets.html).
```
class Dataset:
def __init__(self, root: str, options):
self.sequences, self.images, self.ground_truths = map(list, zip(*[(
str(seq.stem),
list(map(str, sorted(seq.glob('img/*.jpg')))),
pd.read_csv(str(seq.joinpath('groundtruth_rect.txt')), header=None, sep=r'\,|\t|\ ', engine='python').values,
) for seq in filter(lambda p: p.is_dir(), Path(root).iterdir())]))
# assertion
for i, _ in enumerate(self.sequences):
if len(self.images[i]) != np.size(self.ground_truths[i], 0):
self.images[i] = self.images[i][:self.ground_truths[i].shape[0]]
self.regions = [RegionDataset(i, g, options) for i, g in zip(self.images, self.ground_truths)]
def __len__(self):
return len(self.sequences)
def __getitem__(self, idx):
return self.regions[idx]
def __iter__(self):
yield from self.regions
```
## Prepare Environments
Download pre-trained imagenet-vgg weights from [link](http://www.vlfeat.org/matconvnet/models/imagenet-vgg-m.mat)
```
wget "http://www.vlfeat.org/matconvnet/models/imagenet-vgg-m.mat"
```
```
opts = yaml.safe_load(open('options.yaml','r'))
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
dataset = Dataset('/home/jiun/workspace/deeplearning_practice/datasets', opts)
model = MDNet(opts['init_model_path'], len(dataset)).to(device)
model.set_learnable_params(opts['ft_layers'])
criterion = BCELoss()
evaluator = Precision()
optimizer = model.optimizer(opts['lr'], opts['lr_mult'])
```
## Train model
```
for b in range(opts['n_cycles']):
model.train()
prec = np.zeros(len(dataset))
permute = np.random.permutation(len(dataset))
for i, j in enumerate(permute):
pos, neg = dataset[j].next()
pos_loss = model(pos.to(device), j)
neg_loss = model(neg.to(device), j)
loss = criterion(pos_loss, neg_loss)
model.zero_grad()
loss.backward()
if 'grad_clip' in opts:
torch.nn.utils.clip_grad_norm_(model.parameters(), opts['grad_clip'])
optimizer.step()
prec[j] = evaluator(pos_loss, neg_loss)
if not i % 10:
print(f'Iter {i:2d} (Domain {j:2d}), Loss {loss.item():.3f}, Precision {prec[j]:.3f}')
print(f'Batch {b:2d}: Mean Precision: {prec.mean():.3f}')
torch.save({
'shared_layers': model.cpu().layers.state_dict()
}, opts['model_path'])
model = model.to(device)
```
## Inference
```
from PIL import Image
import cv2
import matplotlib.pyplot as plt
import torch.optim as optim
from utils import Options, overlap_ratio
from models.extractor import RegionExtractor
from models.regressor import BBRegressor
def forward_samples(model, image, samples, opts, out_layer='conv3'):
model.eval()
extractor = RegionExtractor(image, samples, opts.img_size, opts.padding, opts.batch_test)
for i, regions in enumerate(extractor):
if opts.use_gpu:
regions = regions.cuda()
with torch.no_grad():
feat = model(regions, out_layer=out_layer)
feats = torch.cat((feats, feat.detach().clone()), 0) if i else feat.detach().clone()
return feats
def train(model, criterion, optimizer,
pos_feats, neg_feats, maxiter, opts,
in_layer='fc4'):
model.train()
batch_pos = opts.batch_pos
batch_neg = opts.batch_neg
batch_test = opts.batch_test
batch_neg_cand = max(opts.batch_neg_cand, batch_neg)
pos_idx = np.random.permutation(pos_feats.size(0))
neg_idx = np.random.permutation(neg_feats.size(0))
while len(pos_idx) < batch_pos * maxiter:
pos_idx = np.concatenate([pos_idx, np.random.permutation(pos_feats.size(0))])
while len(neg_idx) < batch_neg_cand * maxiter:
neg_idx = np.concatenate([neg_idx, np.random.permutation(neg_feats.size(0))])
pos_pointer = 0
neg_pointer = 0
for _ in range(maxiter):
# select pos idx
pos_next = pos_pointer + batch_pos
pos_cur_idx = pos_idx[pos_pointer:pos_next]
pos_cur_idx = pos_feats.new(pos_cur_idx).long()
pos_pointer = pos_next
# select neg idx
neg_next = neg_pointer + batch_neg_cand
neg_cur_idx = neg_idx[neg_pointer:neg_next]
neg_cur_idx = neg_feats.new(neg_cur_idx).long()
neg_pointer = neg_next
# create batch
batch_pos_feats = pos_feats[pos_cur_idx]
batch_neg_feats = neg_feats[neg_cur_idx]
# hard negative mining
if batch_neg_cand > batch_neg:
model.eval()
for start in range(0, batch_neg_cand, batch_test):
end = min(start + batch_test, batch_neg_cand)
with torch.no_grad():
score = model(batch_neg_feats[start:end], in_layer=in_layer)
if start == 0:
neg_cand_score = score.detach()[:, 1].clone()
else:
neg_cand_score = torch.cat((neg_cand_score, score.detach()[:, 1].clone()), 0)
_, top_idx = neg_cand_score.topk(batch_neg)
batch_neg_feats = batch_neg_feats[top_idx]
model.train()
# forward
pos_score = model(batch_pos_feats, in_layer=in_layer)
neg_score = model(batch_neg_feats, in_layer=in_layer)
# optimize
loss = criterion(pos_score, neg_score)
model.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), opts.grad_clip)
optimizer.step()
def main(images, init_bbox, ground_truths, opts):
device = ('cuda' if opts.use_gpu else 'cpu')
model = MDNet(opts.model_path).to(device)
criterion = BCELoss()
# Set learnable parameters
for k, p in model.params.items():
p.requires_grad = any([k.startswith(l) for l in opts.ft_layers])
# Set optimizer states
def set_optimizer(lr_base, lr_mult, momentum=0.9, w_decay=0.0005):
param_list = []
for k, p in filter(lambda kp: kp[1].requires_grad, model.params.items()):
lr = lr_base
for l, m in lr_mult.items():
if k.startswith(l):
lr = lr_base * m
param_list.append({'params': [p], 'lr': lr})
return optim.SGD(param_list, lr=lr, momentum=momentum, weight_decay=w_decay)
init_optimizer = set_optimizer(opts.lr_init, opts.lr_mult)
update_optimizer = set_optimizer(opts.lr_update, opts.lr_mult)
# Load first image
image = Image.open(images[0]).convert('RGB')
# Draw pos/neg samples
pos_examples = SampleGenerator('gaussian', image.size, opts.trans_pos, opts.scale_pos)(
init_bbox, opts.n_pos_init, opts.overlap_pos_init)
neg_examples = np.concatenate([
SampleGenerator('uniform', image.size, opts.trans_neg_init, opts.scale_neg_init)(
init_bbox, int(opts.n_neg_init * 0.5), opts.overlap_neg_init),
SampleGenerator('whole', image.size)(
init_bbox, int(opts.n_neg_init * 0.5), opts.overlap_neg_init)])
neg_examples = np.random.permutation(neg_examples)
# Extract pos/neg features
pos_feats = forward_samples(model, image, pos_examples, opts)
neg_feats = forward_samples(model, image, neg_examples, opts)
# Initial training
train(model, criterion, init_optimizer, pos_feats, neg_feats, opts.maxiter_init, opts)
del init_optimizer, neg_feats
torch.cuda.empty_cache()
# Train bbox regressor
bbreg_examples = SampleGenerator('uniform', image.size, opts.trans_bbreg, opts.scale_bbreg, opts.aspect_bbreg)\
(init_bbox, opts.n_bbreg, opts.overlap_bbreg)
bbreg_feats = forward_samples(model, image, bbreg_examples, opts)
bbreg = BBRegressor(image.size)
bbreg.train(bbreg_feats, bbreg_examples, init_bbox)
del bbreg_feats
torch.cuda.empty_cache()
# Init sample generators for update
sample_generator = SampleGenerator('gaussian', image.size, opts.trans, opts.scale)
pos_generator = SampleGenerator('gaussian', image.size, opts.trans_pos, opts.scale_pos)
neg_generator = SampleGenerator('uniform', image.size, opts.trans_neg, opts.scale_neg)
# Init pos/neg features for update
neg_examples = neg_generator(init_bbox, opts.n_neg_update, opts.overlap_neg_init)
neg_feats = forward_samples(model, image, neg_examples, opts)
pos_feats_all = [pos_feats]
neg_feats_all = [neg_feats]
# Main loop
for i, image in enumerate(images[1:], 1):
image = Image.open(image).convert('RGB')
# Estimate target bbox
samples = sample_generator(init_bbox, opts.n_samples)
sample_scores = forward_samples(model, image, samples, opts, out_layer='fc6')
top_scores, top_idx = sample_scores[:, 1].topk(5)
top_idx = top_idx.cpu()
target_score = top_scores.mean()
init_bbox = samples[top_idx]
if top_idx.shape[0] > 1:
init_bbox = init_bbox.mean(axis=0)
success = target_score > 0
# Expand search area at failure
sample_generator.trans = opts.trans if success else min(sample_generator.trans * 1.1, opts.trans_limit)
# Bbox regression
if success:
bbreg_samples = samples[top_idx]
if top_idx.shape[0] == 1:
bbreg_samples = bbreg_samples[None, :]
bbreg_feats = forward_samples(model, image, bbreg_samples, opts)
bbreg_samples = bbreg.predict(bbreg_feats, bbreg_samples)
bbreg_bbox = bbreg_samples.mean(axis=0)
else:
bbreg_bbox = init_bbox
yield init_bbox, bbreg_bbox, overlap_ratio(ground_truths[i], bbreg_bbox)[0], target_score
# Data collect
if success:
pos_examples = pos_generator(init_bbox, opts.n_pos_update, opts.overlap_pos_update)
pos_feats = forward_samples(model, image, pos_examples, opts)
pos_feats_all.append(pos_feats)
if len(pos_feats_all) > opts.n_frames_long:
del pos_feats_all[0]
neg_examples = neg_generator(init_bbox, opts.n_neg_update, opts.overlap_neg_update)
neg_feats = forward_samples(model, image, neg_examples, opts)
neg_feats_all.append(neg_feats)
if len(neg_feats_all) > opts.n_frames_short:
del neg_feats_all[0]
# Short term update
if not success:
nframes = min(opts.n_frames_short, len(pos_feats_all))
pos_data = torch.cat(pos_feats_all[-nframes:], 0)
neg_data = torch.cat(neg_feats_all, 0)
train(model, criterion, update_optimizer, pos_data, neg_data, opts.maxiter_update, opts)
# Long term update
elif i % opts.long_interval == 0:
pos_data = torch.cat(pos_feats_all, 0)
neg_data = torch.cat(neg_feats_all, 0)
train(model, criterion, update_optimizer, pos_data, neg_data, opts.maxiter_update, opts)
torch.cuda.empty_cache()
```
### (Optional)
Refresh image output in IPython
```
from IPython.display import clear_output
%matplotlib inline
```
## Showcase
```
options = Options()
dataset = Path('./datasets/DragonBaby')
images = list(sorted(dataset.joinpath('img').glob('*.jpg')))
ground_truths = pd.read_csv(str(dataset.joinpath('groundtruth_rect.txt')), header=None).values
iou, success = 0, 0
# Run tracker
for i, (result, (x, y, w, h), overlap, score) in \
enumerate(main(images, ground_truths[0], ground_truths, options), 1):
clear_output(wait=True)
image = np.asarray(Image.open(images[i]).convert('RGB'))
gx, gy, gw, gh = ground_truths[i]
cv2.rectangle(image, (int(gx), int(gy)), (int(gx+gw), int(gy+gh)), (0, 255, 0), 2)
cv2.rectangle(image, (int(x), int(y)), (int(x+w), int(y+h)), (255, 0, 0), 2)
iou += overlap
success += overlap > .5
plt.imshow(image)
plt.pause(.1)
plt.title(f'#{i}/{len(images)-1}, Overlap {overlap:.3f}, Score {score:.3f}')
plt.draw()
iou /= len(images) - 1
print(f'Mean IOU: {iou:.3f}, Success: {success} / {len(images)-1}')
```
| true |
code
| 0.703371 | null | null | null | null |
|
# MNIST using RNN
## 시작하기
* 사용할 라이브러리를 import 합니다.
* 본 예제는 tensorflow를 사용합니다.
* 데이터셋은 tensorflow에서 제공하는 mnist 데이터셋을 사용합니다.
```
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
import os
import time
tf.reset_default_graph()
%matplotlib inline
```
## 데이터셋 불러오기
* 사용할 데이터셋을 불러온다.
* images: 0부터 9까지 필기체로 작성된 흑백영상 (1채널).
* label: one_hot 형태로 설정한다.
- 0 = [1 0 0 0 0 0 0 0 0 0]
- 1 = [0 1 0 0 0 0 0 0 0 0]
```
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
print("Number of train data is %d" % (mnist.train.num_examples))
print("Number of test data is %d" % (mnist.test.num_examples))
```
## 데이터셋 확인하기
학습 데이터의 이미지와 레이블을 확인한다.
```
nsample = 3
rand_idx = np.random.randint(mnist.train.images.shape[0], size=nsample)
for i in rand_idx:
curr_img = np.reshape(mnist.train.images[i, :], (28,28))
curr_lbl = np.argmax(mnist.train.labels[i, :])
plt.matshow(curr_img, cmap=plt.get_cmap('gray'))
plt.title(""+str(i)+"th training image "
+ "(label: " + str(curr_lbl) + ")")
plt.show()
```
## 이미지 분류를 위한 RNN 구성
28x28 이미지를 RNN 입력을 위해 아래와 같이 구성한다.
* input_vec_size: 하나의 이미지 (28x28) 중 한 행씩 RNN의 입력으로 사용한다.
* time_step_size: 하나의 이미지 (28x28)를 모두 입력하려면 28개의 행이 필요하다. 따라서 time_step은 28.
* lstm_size: rnn_cell에 포함된 hidden unit의 수
```
# configuration
# O * W + b -> 10 labels for each image, O[? 28], W[28 10], B[10]
# ^ (O: output 28 vec from 28 vec input)
# |
# +-+ +-+ +--+
# |1|->|2|-> ... |28| time_step_size = 28
# +-+ +-+ +--+
# ^ ^ ... ^
# | | |
# img1:[28] [28] ... [28]
# img2:[28] [28] ... [28]
# img3:[28] [28] ... [28]
# ...
# img128 or img256 (batch_size or test_size 256)
# each input size = input_vec_size=lstm_size=28
input_vec_size = lstm_size = 28
time_step_size = 28
batch_size = 128
test_size = 256
```
## RNN 모델 정의
```
def init_weights(shape):
return tf.Variable(tf.random_normal(shape, stddev=0.01))
def model(X, W, B, lstm_size):
# X, input shape: (batch_size, time_step_size, input_vec_size)
XT = tf.transpose(X, [1, 0, 2]) # permute time_step_size and batch_size
# XT shape: (time_step_size, batch_size, input_vec_size)
XR = tf.reshape(XT, [-1, lstm_size]) # each row has input for each lstm cell (lstm_size=input_vec_size)
# XR shape: (time_step_size * batch_size, input_vec_size)
X_split = tf.split(0, time_step_size, XR) # split them to time_step_size (28 arrays)
# Each array shape: (batch_size, input_vec_size)
# Make lstm with lstm_size (each input vector size)
lstm = tf.nn.rnn_cell.BasicLSTMCell(lstm_size, forget_bias=1.0, state_is_tuple=True)
# Get lstm cell output, time_step_size (28) arrays with lstm_size output: (batch_size, lstm_size)
outputs, _states = tf.nn.rnn(lstm, X_split, dtype=tf.float32)
# Linear activation
# Get the last output
return tf.matmul(outputs[-1], W) + B, lstm.state_size # State size to initialize the stat
```
## 데이터 변환
* training과 test 데이터를 1d에서 2d형태로 reshape한다.
* 입력과 출력에 해당하는 placeholder 선언
```
trX, trY, teX, teY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels
trX = trX.reshape(-1, 28, 28)
teX = teX.reshape(-1, 28, 28)
X = tf.placeholder("float", [None, 28, 28])
Y = tf.placeholder("float", [None, 10])
```
## 모델 선언
* Hidden unit과 output unit크기만큼 모델 생성
* 모델 생성
```
# get lstm_size and output 10 labels
W = init_weights([lstm_size, 10])
B = init_weights([10])
py_x, state_size = model(X, W, B, lstm_size)
```
## loss 함수 선언 및 최적화
```
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(py_x, Y))
train_op = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cost)
predict_op = tf.argmax(py_x, 1)
```
## 세션 생성 및 학습 정확도 측정
```
# Launch the graph in a session
with tf.Session() as sess:
# you need to initialize all variables
tf.initialize_all_variables().run()
for i in range(100):
for start, end in zip(range(0, len(trX), batch_size), range(batch_size, len(trX)+1, batch_size)):
sess.run(train_op, feed_dict={X: trX[start:end], Y: trY[start:end]})
test_indices = np.arange(len(teX)) # Get A Test Batch
np.random.shuffle(test_indices)
test_indices = test_indices[0:test_size]
print(i, np.mean(np.argmax(teY[test_indices], axis=1) ==
sess.run(predict_op, feed_dict={X: teX[test_indices],
Y: teY[test_indices]})))
```
| true |
code
| 0.541591 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/pyGuru123/Data-Analysis-and-Visualization/blob/main/Tracking%20Bird%20Migration/bird_migration.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
One fascinating area of research uses GPS to track movements of animals. It is now possible to manufacture a small GPS device that is solar charged, so you don’t need to change batteries and use it to track flight patterns of birds.
# GPS Tracking Gulls
The data for this case study comes from the LifeWatch INBO project. Since 1999, the Research Institute for Nature and Forest (INBO) studies the postnuptial migration, and mate and site fidelity of large gulls, using observer sightings of colour-ringed individuals. In the framework of the Flemish contributions to the LifeWatch infrastructure, a high-tech sensor network was installed (start June 2013) to better monitor the habitat use and migration patterns of large birds, such as the European Herring Gull (Larus argentatus Pontoppidan). Several data sets have been released as part of this project. We will use a small data set that consists of migration data for three gulls named Eric, Nico, and Sanne

Method steps
1. Researcher captures bird, takes biometrics, attaches GPS tracker, and
releases bird.
2. Researcher sets a measurement scheme, which can be updated anytime.
GPS tracker records data.
3. GPS tracker automatically receives new measurement settings and transmits recorded data when a connection can be established with the base station at the colony.
4. Recorded data are automatically harvested, post-processed, and stored in a central PostgreSQL database at UvA-BiTS.
5. Tracking data specific to LifeWatch Flanders are exported, cleaned, and enhanced monthly with a bird tracking ETL.
6. LifeWatch INBO team periodically (re)publishes data as a Darwin Core Archive, registered with GBIF.
7. Data stream stops when bird no longer returns to colony or if GPS tracker no longer functions (typical tracker lifespan: 2-3 years)
# Aim and requirements
**Aim** : Track the movement of three gulls namely – Eric, Nico & Sanne
**Dataset** : [official_datasets](https://inbo.carto.com/u/lifewatch/datasets) ; used dataset – [csv](https://d37djvu3ytnwxt.cloudfront.net/assets/courseware/v1/c72498a54a4513c2eb4ec005adc0010c/asset-v1:HarvardX+PH526x+3T2016+type@asset+block/bird_tracking.csv)
**Dependencies** : Requests, Matplotlib, Pandas, Numpy, Cartopy, Shapely
The csv file contains eight columns and includes variables like latitude, longitude, altitude, and time stamps. In this case study, we will first load the data, visualize some simple flight trajectories, track flight speed, learn about daytime and much, much more.
The case study is divied into six parts:
1. Visualizing longitude and latitude data of the gulls.
2. Visualize the variation of the speed of the gulls.
3. Visualize the time required by the gulls to cover equal distances over the journey.
4. Visualize the daily mean speed of the gulls.
5. Visualize the daily average altitude gulls fly at.
6. Cartographic view of the journey of the gulls.
Importing required libraries
```
import requests
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
Installing Cartopy in colab
```
!apt-get install libproj-dev proj-data proj-bin
!apt-get install libgeos-dev
!pip install cython
!pip install cartopy
```
Installing shapely in colab
```
!pip uninstall shapely
!pip install shapely --no-binary shapely
```
# Downloading and reading dataset
Downloading dataset
```
url = 'https://d37djvu3ytnwxt.cloudfront.net/assets/courseware/v1/c72498a54a4513c2eb4ec005adc0010c/asset-v1:HarvardX+PH526x+3T2016+type@asset+block/bird_tracking.csv'
response = requests.get(url)
data = response.content
with open('bird_tracking.csv', 'wb') as file:
file.write(data)
```
Reading csv data
```
df = pd.read_csv('bird_tracking.csv')
df.info
```
printing dataframe
```
df
```
Getting bird names
```
bird_names = pd.unique(df.bird_name)
print(bird_names)
```
Number of row entries of each bird
```
for bird_name in bird_names:
print(bird_name, len(df.bird_name[df.bird_name == bird_name]))
```
# Visualizing longitude and latitude data of the gulls
Visulization of location for bird Eric
```
plt.figure(figsize=(8,6))
ix = df.bird_name == 'Eric'
x, y = df.longitude[ix], df.latitude[ix]
plt.figure(figsize = (7,7))
plt.plot(x,y, 'b.')
plt.title('location of bird Eric')
plt.show()
```
Visulization of all three birds as subplots
```
plt.style.use('fivethirtyeight')
colors = ['blue', 'orange', 'green']
fig, subplot = plt.subplots(1, 3, figsize=(15,6))
for index, bird_name in enumerate(bird_names):
ix = df.bird_name == bird_name
x, y = df.longitude[ix], df.latitude[ix]
subplot[index].plot(x,y, colors[index] )
subplot[index].title.set_text(bird_name)
plt.show()
```
Visualization of all three birds in 1 plot
```
plt.style.use('default')
plt.figure(figsize = (7,7))
for bird_name in bird_names:
ix = df.bird_name == bird_name
x, y = df.longitude[ix], df.latitude[ix]
plt.plot(x,y , '.', label=bird_name)
plt.xlabel("Longitude")
plt.ylabel("Latitude")
plt.legend(loc="lower right")
plt.show()
```
# Visualize the variation of the speed of the gulls
We are going to visualize 2D speed vs Frequency for the gull named “Sanne”
```
ix = df.bird_name == 'Sanne'
speed = df.speed_2d[ix]
plt.figure(figsize = (8,4))
ind = np.isnan(speed)
plt.hist(speed[~ind], bins = np.linspace(0,30,20))
plt.title('2D Speed vs Frequency for Sanne')
plt.xlabel(" 2D speed (m/s) ")
plt.ylabel(" Frequency ")
plt.show()
```
Speed vs Frequency distri of each bird
```
plt.figure(figsize = (8,4))
for bird_name in bird_names:
ix = df.bird_name == bird_name
speed = df.speed_2d[ix]
ind = np.isnan(speed)
plt.hist(speed[~ind], bins = np.linspace(0,30,30), label=bird_name ,stacked=True)
plt.title('2D Speed vs Frequency for Each bird')
plt.xlabel(" 2D speed (m/s) ")
plt.ylabel(" Frequency ")
plt.legend()
plt.show()
```
# Visualize the time required by the gulls to cover equal distances over the journey
```
print(len(df))
df
```
Extracting date-time column and converting to readble form
```
import datetime
timestamps = []
for i in range(len(df)):
dt = datetime.datetime.strptime(df.date_time.iloc[i][:-3], "%Y-%m-%d %H:%M:%S")
timestamps.append(dt)
```
Adding above extracted list as a new column in dataframe
```
df['timestamps'] = pd.Series(timestamps, index = df.index)
df
```
Extracting time rows for Eric
```
times = df.timestamps[df.bird_name == 'Eric']
print(times[:3])
elapsed_time = [time-times[0] for time in times]
print(elapsed_time[:3])
elapsed_time[-1]
plt.plot(np.array(elapsed_time)/datetime.timedelta(days=1))
plt.xlabel(" Observation ")
plt.ylabel(" Elapsed time (days) ")
plt.show()
plt.style.use('seaborn')
colors = ['blue', 'orange', 'green']
rows_index = [0, 19795, 40916]
fig, subplot = plt.subplots(1, 3, figsize=(14,7), sharex=True, sharey=True)
for index, bird_name in enumerate(bird_names):
times = df.timestamps[df.bird_name == bird_name]
elapsed_time = [time- times[rows_index[index]] for time in times]
subplot[index].plot(np.array(elapsed_time)/datetime.timedelta(days=1))
subplot[index].title.set_text(bird_name)
fig.text(0.5, 0.04, 'Observation', ha='center')
fig.text(0.04, 0.5, ' Elapsed time (days) ', va='center', rotation='vertical')
plt.show()
```
# Visualize the daily mean speed of the gulls
```
df
```
Daily mean speed of Eric
```
data = df[df.bird_name == "Eric"]
times = data.timestamps
elapsed_time = [(time - times[0]) for time in times]
elapsed_days = np.array(elapsed_time)/datetime.timedelta(days=1)
elapsed_days
next_day = 1
inds = []
daily_mean_speed = []
for (i,t) in enumerate(elapsed_days):
if t < next_day:
inds.append(i)
else:
daily_mean_speed.append(np.mean(data.speed_2d[inds]))
next_day += 1
inds = []
plt.style.use('default')
plt.figure(figsize = (8,6))
plt.plot(daily_mean_speed, "rs-")
plt.xlabel(" Day ")
plt.ylabel(" Mean Speed (m/s) ");
plt.show()
```
# Visualize the daily average altitude gulls fly at
```
df
def get_daily_mean_altitude(dataframe, index):
times = data.timestamps
elapsed_time = [(time - times[index]) for time in times]
elapsed_days = np.array(elapsed_time)/datetime.timedelta(days=1)
elapsed_days
next_day = 1
inds = []
daily_mean_altitude = []
for (i,t) in enumerate(elapsed_days):
if t <= next_day:
inds.append(i)
else:
daily_mean_altitude.append(np.mean(data.altitude[inds]))
next_day += 1
inds = []
return daily_mean_altitude
data = df[df.bird_name == "Eric"]
daily_mean_altitude = get_daily_mean_altitude(data, 0)
daily_mean_altitude = pd.Series(daily_mean_altitude)
overall_mean = daily_mean_altitude.mean()
days = [i for i in range(len(daily_mean_altitude))]
overall_average = [overall_mean for i in range(len(daily_mean_altitude))]
plt.style.use('default')
plt.figure(figsize = (8,6))
plt.plot(daily_mean_altitude, "gs-")
plt.plot(overall_average, color='red')
plt.title('Average altitude at which Eric flies')
plt.xlabel(" Day ")
plt.ylabel(" Mean Altitude (m) ");
plt.show()
```
# Cartographic view of the journey of the gulls
```
import cartopy.crs as ccrs
import cartopy.feature as cfeature
proj = ccrs.Mercator()
colors = ['red', 'blue', 'green']
plt.style.use('ggplot')
plt.figure(figsize=(10,10))
ax = plt.axes(projection=proj)
ax.set_extent((-25.0, 20.0, 52.0, 10.0))
ax.add_feature(cfeature.LAND)
ax.add_feature(cfeature.OCEAN)
ax.add_feature(cfeature.COASTLINE)
ax.add_feature(cfeature.BORDERS, linestyle=':')
for index, name in enumerate(bird_names):
ix = df['bird_name'] == name
x,y = df.longitude[ix], df.latitude[ix]
ax.plot(x,y,'.', transform=ccrs.Geodetic(), label=name, color=colors[index])
plt.legend(loc="upper left")
plt.show()
```
That's it
| true |
code
| 0.308008 | null | null | null | null |
|
## Topological Data Analysis - Part 5 - Persistent Homology
This is Part 5 in a series on topological data analysis.
See <a href="TDApart1.html">Part 1</a> | <a href="TDApart2.html">Part 2</a> | <a href="TDApart3.html">Part 3</a> | <a href="TDApart4.html">Part 4</a>
<a href="https://github.com/outlace/OpenTDA/PersistentHomology.py">Download this notebook</a> | <a href="https://github.com/outlace/outlace.github.io/ipython-notebooks/TDA/TDApart5.ipynb">Download the code</a>
In this part we finally utilize all we've learned to compute the persitent homology groups and draw persistence diagrams to summarize the information graphically.
Let's summarize what we know so far.
We know...
1. how to generate a simplicial complex from point-cloud data using an arbitrary $\epsilon$ distance parameter
2. how to calculate homology groups of a simplicial complex
3. how to compute Betti numbers of a simplicial complex
The jump from what we know to persistent homology is small conceptually. We just need to calculate Betti numbers for a set of simplicial complexes generated by continuously varying $\epsilon: 0 \rightarrow \infty$. Then we can see which topological features persist significantly longer than others, and declare those to be signal not noise.
>Note: I'm ignoring an objective definition of "significantly longer" since that is really a statistical question that is outside the scope of this exposition. For all the examples we consider here, it will be obvious which features persist significantly longer just by visual inspection.
Unfortunately, while the coneptual jump is small, the technical jump is more formidable. Especially because we also want to be able to ask which data points in my original data set lie on some particular topological feature.
Let's revisit the code we used to sample points (with some intentional randomness added) from a circle and build a simplicial complex.
```
import numpy as np
import matplotlib.pyplot as plt
n = 30 #number of points to generate
#generate space of parameter
theta = np.linspace(0, 2.0*np.pi, n)
a, b, r = 0.0, 0.0, 5.0
x = a + r*np.cos(theta)
y = b + r*np.sin(theta)
#code to plot the circle for visualization
plt.plot(x, y)
plt.show()
x2 = np.random.uniform(-0.75,0.75,n) + x #add some "jitteriness" to the points
y2 = np.random.uniform(-0.75,0.75,n) + y
fig, ax = plt.subplots()
ax.scatter(x2,y2)
plt.show()
newData = np.array(list(zip(x2,y2)))
import SimplicialComplex
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=3.0) #Notice the epsilon parameter is 3.0
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)
```
As you can see, setting $\epsilon = 3.0$ produces a nice looking simplicial complex that captures the single 1-dimensional "hole" in the original data.
However, let's play around with $\epsilon$ to see how it changes our complex.
```
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=2.0)
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)
```
We decreased $\epsilon$ to $2.0$ and now we have a "break" in our circle. If we calculate the homology and Betti numbers of this complex, we will no longer have a 1-dimensional cycle present. We will only see a single connected component.
Let's decrease it a little bit more to 1.9
```
newData = np.array(list(zip(x2,y2)))
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=1.9)
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)
```
Now we have three connected components and no cycles/holes in the complex. Ok, let's go the other direction and increase $\epsilon$ to 4.0
```
newData = np.array(list(zip(x2,y2)))
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=4.0)
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)
```
Unlike going down by 1, by increasing $\epsilon$ to 4.0, we haven't changed anything about our homology groups. We still have a single connected component and a single 1-dimensional cycle.
Let's make an even bigger jump and set $\epsilon = 7.0$, an increase of 3.
```
graph = SimplicialComplex.buildGraph(raw_data=newData, epsilon=7.0)
ripsComplex = SimplicialComplex.rips(graph=graph, k=3)
SimplicialComplex.drawComplex(origData=newData, ripsComplex=ripsComplex)
```
Alas, even though we've gone up by 4 units from our original nice value of 3.0, we still get a complex with the same topological features: a single connected component and a 1-dimensional cycle.
This is the primary insight of __persistence__ in persistent homology. These features are persistent over a wide range of $\epsilon$ scale parameters and thus are likely to be true features of the underlying data rather than noise.
We can diagram our findings with two major styles: a barcode or a persistence diagram (not shown).
Here's what our barcode might look like for the above example:
<img src="images/TDAimages/barcode_example.png" width="500px" />
>NOTE: I've prepared this barcode "by band," i.e. it is not the precise computed barcode. I've highlighted the "true" topological features amongst the noise. $H_0, H_1, H_2$ refer to the respective homology groups and Betti numbers.
Importantly, it is possible that two different true topological features may exist at different scales and thus can only be captured with a persistent homology, they will be missed in a simplicial complex with a single fixed scale. For example, if we have data that presents a large circle next to a small circle, it is possible at a small $\epsilon$ value only the small circle will be connected, giving rise to a single 1-dimensionl hole, then at a larger $\epsilon$ the big circle will be connected and the small circle will get "filled in." So at no single $\epsilon$ value will both circles be revealed.
#### Filtrations
It turns out there is a relatively straightforward way to extend our previous work on calculating Betti numbers with boundary matrices to the setting of persistent homology where we're dealing with collections of ever expanding complexes.
We define a _filtration complex_ as the sequence of simplicial complexes generated by continuously increasing the scale parameter $\epsilon$.
But rather than building multiple simplicial complexes at various $\epsilon$ parameters and then combining them into a sequence, we can just build a single simplicial complex over our data using a large (maximal) $\epsilon$ value. But we will keep track of the distance between all points of pairs (we already do this with the algorithm we wrote) so we know at what $\epsilon$ scale each pair of points form an edge. Thus "hidden" in any simplicial complex at some $\epsilon$ value is a filtration (sequence of nested complexes) up to that value of $\epsilon$.
Here's a really simple example:
<img src="images/TDAimages/simplicialComplex9a.png" />
So if we take the maximum scale, $\epsilon = 4$, our simplicial complex is:
$$ S = \text{ { {0}, {1}, {2}, {0,1}, {2,0}, {1,2}, {0,1,2} } } $$
But if we keep track of the pair-wise distances between points (i.e. the length/weight of all the edges), then we already have the information necessary for a filtration.
Here are the weights (lengths) of each edge (1-simplex) in this simplicial complex (the vertical bars indicate weight/length):
$$ |{0,1}| = 1.4 \\
|{2,0}| = 2.2 \\
|{1,2}| = 3
$$
And this is how we would use that information to build a filtration:
$$
S_0 \subseteq S_1 \subseteq S_2 \\
S_0 = \text{ { {0}, {1}, {2} } } \\
S_1 = \text{ { {0}, {1}, {2}, {0,1} } } \\
S_2 = \text{ { {0}, {1}, {2}, {0,1}, {2,0}, {1,2}, {0,1,2} } } \\
$$
Basically each simplex in a subcomplex of the filtration will appear when its longest edge appears. So the 2-simplex {0,1,2} appears only once the edge {1,2} appears since that edge is the longest and doesn't show up until $\epsilon \geq 2.2$
For it to be a filtration that we can use in our (future) algorithm, it needs to have a __total order__. A total order is an ordering of the simplices in our filtration such that there is a valid "less than" relationship between any two simplices (i.e. no two simplices are equal in "value"). The most famous example of a set with a total order would be the natural numbers {0,1,2,3,4...} since no two numbers are equal, we can always say one number is greater than or less than another.
How do we determine the "value" (henceforth: filter value) of a simplex in a filtration (and thus determine the ordering of the filtration)? Well I already said part of it. The filter value of a simplex is partly determined by the length of its maximum edge. But sometimes two distinct simplices have maximum edges of the same length, so we have to define a heirarchy of rules for determining the value (the ordering) of our simplices.
For any two simplices, $\sigma_1, \sigma_2$...
1. 0-simplices must be less than 1-simplices must be less than 2-simplices, etc. This implies that any face of a simplex (i.e. $f \subset \sigma$) is automatically less than (comes before in the ordering) of the simplex. I.e. if $dim(\sigma_1) < dim(\sigma_2) \implies \sigma_1 < \sigma_2$ (dim = dimension, the symbol $\implies$ means "implies").
<br /><br />
2. If $\sigma_1, \sigma_2$ are of an equal dimension (and hence one is not the face of the other), then the value of each simplex is determined by its longest (highest weight) 1-simplex (edge). In our example above, $\{0,1\} \lt \{2,0\} \lt \{1,2\}$ due to the weights of each of those. To compare higher-dimensional simplices, you still just compare them by the value of their greatest edge. I.e. if $dim(\sigma_1) = dim(\sigma_2)$ then $max\_edge(\sigma_1) < max\_edge(\sigma_2) \implies \sigma_1 < \sigma_2$
<br /><br />
3. If $\sigma_1,\sigma_2$ are of an equal dimension AND their longest edges are of equal value (i.e. their maximum weight edges enter the filtration at the same $\epsilon$ value), then $max\_vertex(\sigma_1) < max\_vertex(\sigma_2) \implies \sigma_1 < \sigma_2$. What is a maximum node? Well we just have to place an arbitrary ordering over the vertices even though they all appear at the same time.
>Just as an aside, we just discussed a _total order_. The corollary to that idea is a _partial order_ where we have "less than" relationships defined between some but not all elements, and some elements may be equal to others.
Remember from part 3 how we setup the boundary matrices by setting the columns to represent the n-simplices in the n-chain group and the rows to represent the (n-1)-simplices in the (n-1)-chain group? Well we can extend this procedure to calculate Betti numbers across an entire filtration complex in the following way.
Let's use the filtration from above:
$$
S_0 \subseteq S_1 \subseteq S_2 \\
S_0 = \text{ [ {0}, {1}, {2} } ] \\
S_1 = \text{ [ {0}, {1}, {2}, {0,1} ] } \\
S_2 = S = \text{ [ {0}, {1}, {2}, {0,1}, {2,0}, {1,2}, {0,1,2} ] } \\
$$
Notice I already have the simplices in each subcomplex of the filtration in order (I've imposed a total order on the set of simplices) indicated by the square brackets rather than curly braces (although I may abuse this notation).
So we'll build a boundary matrix for the full filtration in the same way we built individual boundary matrices for each homology group before. We'll make a square matrix where the columns (label: $j$) and rows (label: $i$) are the simplices in the filtration in their proper (total) order.
Then, as before, we set each cell $[i,j] = 1$ if $\sigma_i$ is a face of $\sigma_j$ ($\sigma$ meaning simplex). All other cells are $0$.
Here's what it looks like in our very small filtration from above:
$$
\partial_{filtration} =
\begin{array}{c|lcr}
\partial & \{0\} & \{1\} & \{2\} & \{0,1\} & \{2,0\} & \{1,2\} & \{0,1,2\} \\
\hline
\{0\} & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\
\{1\} & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\
\{2\} & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\
\{0,1\} & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
\{2,0\} & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
\{1,2\} & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
\{0,1,2\} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{array}
$$
As before, we will apply an algorithm to change the form of this matrix. However, unlike before, we are now going to convert this boundary matrix into Smith normal form, we are going to change it into something else called column-echelon form. This conversion process is called a __matrix reduction__, implying we're kind of reducing it into a simpler form.
##### Matrix reduction
Now here's where I have to apologize for a mistake I made in our last post, because I never explained _why_ we had to convert our boundary matrix into Smith normal form, I just told you _how_ to do it.
So here's the deal, our boundary matrices from before gave us a linear map from a n-chain group down to the (n-1)-chain group. We could just multiply the boundary matrix by any element in the n-chain and the result would be the corresponding (mapped) element in the (n-1)-chain. When we reduced the matrix to Smith normal form, we altered the boundary matrix such that we can no longer just multiply by it to map elements in that way. What we did was actually apply another linear map over our boundary matrix, the result being the Smith normal form.
More formally, the Smith normal form $R$ of a matrix $A$ is the matrix product: $R = SAT$ where $S,T$ are other matrices. Hence we have a composition of linear maps that forms $R$, and we can in principle decompose $R$ into the individual linear maps (matrices) that compose it.
So the algorithm for reducing to Smith normal form is essentially finding two other matrices $S,T$ such that $SAT$ produces a matrix with 1s along the diagonal (at least partially).
But why do we do that? Well remember that a matrix being a linear map means it maps one vector space to another. If we have a matrix $M: V_1 \rightarrow V_2$, then it is mapping the basis vectors in $V_1$ to basis vectors in $V_2$. So when we reduce a matrix, we're essentially redefining the basis vectors in each vector space. It just so happens that Smith normal form finds the bases that form cycles and boundaries. There are many different types of reduced matrix forms that have useful interpretations and properties. I'm not going to get into anymore of the mathematics about it here, I just wanted to give a little more explanation to this voo doo matrix reduction we're doing.
When we reduce a filtration boundary matrix into column-echelon form via an algorithm, it tells us the information about when certain topological features at each dimension are formed or "die" (by being subsumed into a larger feature) at various stages in the filtration (i.e. at increasing values of $\epsilon$, via our total order implied on the filtration). Hence, once we reduce the boundary matrix, all we need to do is read off the information as intervals when features are born and die, and then we can graph those intervals as a barcode plot.
The column-echelon form $C$ is likewise a composition of linear maps such that $C = VB$ where $V$ is some matrix that makes the composition work, and $B$ is a filtration boundary matrix. We will actually keep a copy of $V$ once we're done reducing $B$ because $V$ records the information necessary to dermine which data points lie on interesting topological features.
The general algorithm for reducing a matrix to column-echelon form is a type of <a src="https://en.wikipedia.org/wiki/Gaussian_elimination">Gaussian elemination</a>:
```python
for j = 1 to n
while there exists i < j with low(i) = low(j)
add column i to column j
end while
end for
```
The function `low` accepts a column `j` and returns the row index with the lowest $1$. For example, if we have a column of a matrix:
$ j = \begin{pmatrix} 1 \\ 0 \\1 \\1 \\ 0 \\0 \\0 \end{pmatrix} $<br />
Then `low(j) = 3` (with indexing starting from 0) since the lowest $1$ in the column is in the fourth row (which is index 3).
So basically the algorithm scans each column in the matrix from left to right, so if we're currently at column `j`, the algorithm looks for all the columns `i` before `j` such that `low(i) == low(j)`, and if it finds such a column `i`, it will add that column to `j`. And we keep a log of everytime we add a column to another in the form of another matrix. If a column is all zeros, then `low(j) = -1` (meaning undefined).
Let's try out the algorithm by hand on our boundary matrix from above. I've removed the column/row labels to be more concise:
$$
\partial_{filtration} =
\begin{Bmatrix}
0 & 0 & 0 & 1 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{Bmatrix}
$$
So remember, columns are some index `j` and rows are some index `i`. We scan from left to right. The first 3 columns are all zeros so `low(j)` is undefined and we don't do anything. And when we get to column 4 (index `j=3`), since all the prior columns were zero, then there's also nothing to do. When we get to column 5 (index `j=4`), then `low(4) = 2` and `low(3) = 1` so since `low(4) != low(3)` we don't do anything and just move on. It isn't until we get to column 6 (index `j=5`) that there is a column `i < j` (in this case column `4 < 5`) such that `low(4) = low(5)`. So we add column 5 to column 6. Since these are binary (using the field $\mathbb Z_2$) columns, $1+1=0$. The result of adding column 5 to 6 is shown below:
$$
\partial_{filtration} =
\begin{Bmatrix}
0 & 0 & 0 & 1 & 1 & 1 & 0 \\
0 & 0 & 0 & 1 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{Bmatrix}
$$
Now we continue on to the end, and the last column's lowest 1 is in a unique row so we don't do anything. Now we start again from the beginning on the left. We get to column 6 (index `j=5`) and we find that column 4 has the same lowest 1, `low(3) = low(5)`, so we add column 4 to 6. The result is shown below:
$$
\partial_{filtration} =
\begin{Bmatrix}
0 & 0 & 0 & 1 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{Bmatrix}
$$
Look, we now have a new column of all zeros! What does this mean? Well it means that column is a new topological feature. It either represent a connected component or some n-dimensional cycle. In this case it represents a 1-dimensional cycle, the cycle formed from the three 1-simplices.
Notice now that the matrix is fully reduced to column-echelon form since all the lowest $1$s are in unique rows, so our algorithm halts in satisfaction. Now that the boundary matrix is reduced, it is no longer the case that each column and row represents a single simplex in the filtration. Since we've been adding columns together, each column may represent multiple simplices in the filtration. In this case, we only added columns together two times and both we're adding to column 6 (index `j = 5`), so column 6 represents the simplices from columns 4 and 5 (which happen to be {0,1} and {2,0}). So column 6 is the group of simplices: $\text{ {0,1}, {2,0}, {1,2} }$, and if you refer back to the graphical depiction of the simplex, those 1-simplices form a 1-dimensional cycle (albeit immediately killed off by the 2-simplex {0,1,2}).
It is important to keep track of what the algorithm does so we can find out what each column represents when the algorithm is done. We do this by setting up another matrix that I call the _memory matrix_. It starts off just being the identity matrix with the same dimensions as the boundary matrix.
$$
M_{memory} =
\begin{Bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
\end{Bmatrix}
$$
But everytime we add a column `i` to column `j` in our reducing algorithm, we record the change in the memory matrix by putting a `1` in the cell `[i,j]`. So in our case, we recorded the events of adding columns 4 and 5 to column 6. Hence in our memory matrix, we will put a 1 in the cells `[3,5]` and `[4,5]` (using indices). This is shown below:
$$
M_{memory} =
\begin{Bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
\end{Bmatrix}
$$
Once the algorithm is done running, we can always refer to this memory matrix to remember what the algorithm actually did and figure out what the columns in the reduced boundary matrix represent.
Let's refer back to our _reduced_ (column-echelon form) boundary matrix of the filtration:
$$
\partial_{reduced} =
\begin{Bmatrix}
0 & 0 & 0 & 1 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{Bmatrix}
$$
To record the intervals of birth and death of topological features, we simply scan each column from left to right. If column `j` has all zeros (i.e. `low(j) = -1`) then we record this as the birth of a new feature (being whatever column `j` represents, maybe a single simplex, maybe a group of simplices).
Otherwise, if a column is not all zeros but has some 1s in it, then we say that the column with index equal to `low(j)` dies at `j`, and hence is the end point of the interval for that feature.
So in our case, all three vertices (the first three columns) are new features that are born (their columns are all zeros, `low(j) = -1`) so we record 3 new intervals with starting points being their column indices. Since we're scanning sequentially from left to right, we don't yet know if or when these features will die, so we'll just tentatively set the end point as `-1` to indicate the end or infinity. Here are the first three intervals:
```python
#Remember the start and end points are column indices
[0,-1], [1,-1], [2,-1]
```
Then we keep scanning left to right and hit column 4 (index `j=3`) and we calculate `low(3) = 1`. So this means the feature that was born in column `j=1` (column 2) just died at `j=3`. Now we can go back and update the tentative end point for that interval, our update intervals being:
```python
#updating intervals...
[0,-1], [1,3], [2,-1]
```
So we just continue this process until the last column and we get all our intervals:
```python
#The final set of intervals
[0,-1], [1,3], [2,4], [5,6]
```
The first three features are 0-simplices and since they are dimension 0, they represent the connected components of the filtration. The 4th feature is the 1-dimensional cycle since its interval indices refer to a group of 1-simplices.
Believe it or not, we've just done persistent homology. That's all there is to it. Once we have the intervals, all we need to do is graph them as a barcode. We should convert the start/end points in these intervals to values of $\epsilon$ by referring back to our set of weights on the edges and assigning an $\epsilon$ value (the value of $\epsilon$ the results in the formation of a particular simplex in the filtration) to each simplex. Here's the barcode:
<img src="images/TDAimages/barcode_example2.png" width="300px" />
>I drew a dot in the $H_1$ group to indicate that the 1-dimensional cycle is born and immediately dies at the same point (since as soon as it forms the 2-simplex subsumes it). Most real barcodes do not produce those dots. We don't care about such ephemeral features.
Notice how we have a bar in the $H_0$ group that is significantly longer than the other two. This suggests our data has only 1 connected component. Groups $H_1, H_2$ don't really have any bars so our data doesn't have any true holes/cycles. Of course with a more realistic data set we would expect to find some cycles.
#### Let's write some code
Alright, so we've basically covered the conceptual framework for computing persistent homology. Let's actually write some code to compute persistent homology on (somewhat) realistic data. I'm not going to spend too much effort explaining all the code and how it works since I'm more concerned with explaining in more abstract terms so you can go write your own algorithms. I've tried to add inline comments that should help. Also keep in mind that since this is educational, these algorithms and data structures will _not_ be very efficient, but will be simple. I hope to write a follow up post at some point that demonstrates how we can make efficient versions of these algorithms and data structures.
Let's start by constructing a simple simplicial complex using the code we wrote in part 4.
```
data = np.array([[1,4],[1,1],[6,1],[6,4]])
#for example... this is with a small epsilon, to illustrate the presence of a 1-dimensional cycle
graph = SimplicialComplex.buildGraph(raw_data=data, epsilon=5.1)
ripsComplex = SimplicialComplex.rips(nodes=graph[0], edges=graph[1], k=3)
SimplicialComplex.drawComplex(origData=data, ripsComplex=ripsComplex, axes=[0,7,0,5])
```
So our simplicial complex is just a box. It obviously has 1 connected component and a 1-dimensional cycle. If we keep increasing $\epsilon$ then the box will "fill in" and we'll get a maximal simplex with all four points forming a 3-dimensional simplex (tetrahedron).
>Note, I have modified the `SimplicialComplex` library a bit (mostly cosmetic/stylistic changes) since <a href="http://outlace.com/Topological+Data+Analysis+Tutorial+-+Part+4/">part 4</a>. Refer to the <a href="https://github.com/outlace/outlace.github.io">GitHub project</a> for changes.
Next we're going to modify the functions from the original `SimplicialComplex` library from part 4 so that it works well with a filtration complex rather than ordinary simplicial complexes.
So I'm just going to drop a block of code on you know and describe what each function does. The `buildGraph` function is the same as before. But we have a several new functions: `ripsFiltration`, `getFilterValue`, `compare` and `sortComplex`.
The `ripsFiltration` function accepts the graph object from `buildGraph` and maximal dimension `k` (e.g. up to what dimensional simpices we will bother calculating) and returns a simplicial complex object sorted by filter values. The filter values are determined as described above. We have a `sortComplex` function that takes a complex and filter values and returns the sorted complex.
So the only difference between our previous simplicial complex function and the `ripsFiltration` function is that the latter also generates filter values for each simplex in the complex and imposes a total order on the simplices in the filtration.
```
import itertools
import functools
def euclidianDist(a,b): #this is the default metric we use but you can use whatever distance function you want
return np.linalg.norm(a - b) #euclidian distance metric
#Build neighorbood graph
def buildGraph(raw_data, epsilon = 3.1, metric=euclidianDist): #raw_data is a numpy array
nodes = [x for x in range(raw_data.shape[0])] #initialize node set, reference indices from original data array
edges = [] #initialize empty edge array
weights = [] #initialize weight array, stores the weight (which in this case is the distance) for each edge
for i in range(raw_data.shape[0]): #iterate through each data point
for j in range(raw_data.shape[0]-i): #inner loop to calculate pairwise point distances
a = raw_data[i]
b = raw_data[j+i] #each simplex is a set (no order), hence [0,1] = [1,0]; so only store one
if (i != j+i):
dist = metric(a,b)
if dist <= epsilon:
edges.append({i,j+i}) #add edge if distance between points is < epsilon
weights.append(dist)
return nodes,edges,weights
def lower_nbrs(nodeSet, edgeSet, node): #lowest neighbors based on arbitrary ordering of simplices
return {x for x in nodeSet if {x,node} in edgeSet and node > x}
def ripsFiltration(graph, k): #k is the maximal dimension we want to compute (minimum is 1, edges)
nodes, edges, weights = graph
VRcomplex = [{n} for n in nodes]
filter_values = [0 for j in VRcomplex] #vertices have filter value of 0
for i in range(len(edges)): #add 1-simplices (edges) and associated filter values
VRcomplex.append(edges[i])
filter_values.append(weights[i])
if k > 1:
for i in range(k):
for simplex in [x for x in VRcomplex if len(x)==i+2]: #skip 0-simplices and 1-simplices
#for each u in simplex
nbrs = set.intersection(*[lower_nbrs(nodes, edges, z) for z in simplex])
for nbr in nbrs:
newSimplex = set.union(simplex,{nbr})
VRcomplex.append(newSimplex)
filter_values.append(getFilterValue(newSimplex, VRcomplex, filter_values))
return sortComplex(VRcomplex, filter_values) #sort simplices according to filter values
def getFilterValue(simplex, edges, weights): #filter value is the maximum weight of an edge in the simplex
oneSimplices = list(itertools.combinations(simplex, 2)) #get set of 1-simplices in the simplex
max_weight = 0
for oneSimplex in oneSimplices:
filter_value = weights[edges.index(set(oneSimplex))]
if filter_value > max_weight: max_weight = filter_value
return max_weight
def compare(item1, item2):
#comparison function that will provide the basis for our total order on the simpices
#each item represents a simplex, bundled as a list [simplex, filter value] e.g. [{0,1}, 4]
if len(item1[0]) == len(item2[0]):
if item1[1] == item2[1]: #if both items have same filter value
if sum(item1[0]) > sum(item2[0]):
return 1
else:
return -1
else:
if item1[1] > item2[1]:
return 1
else:
return -1
else:
if len(item1[0]) > len(item2[0]):
return 1
else:
return -1
def sortComplex(filterComplex, filterValues): #need simplices in filtration have a total order
#sort simplices in filtration by filter values
pairedList = zip(filterComplex, filterValues)
#since I'm using Python 3.5+, no longer supports custom compare, need conversion helper function..its ok
sortedComplex = sorted(pairedList, key=functools.cmp_to_key(compare))
sortedComplex = [list(t) for t in zip(*sortedComplex)]
#then sort >= 1 simplices in each chain group by the arbitrary total order on the vertices
orderValues = [x for x in range(len(filterComplex))]
return sortedComplex
graph2 = buildGraph(raw_data=data, epsilon=7) #epsilon = 9 will build a "maximal complex"
ripsComplex2 = ripsFiltration(graph2, k=3)
SimplicialComplex.drawComplex(origData=data, ripsComplex=ripsComplex2[0], axes=[0,7,0,5])
ripsComplex2
#return the n-simplices and weights in a complex
def nSimplices(n, filterComplex):
nchain = []
nfilters = []
for i in range(len(filterComplex[0])):
simplex = filterComplex[0][i]
if len(simplex) == (n+1):
nchain.append(simplex)
nfilters.append(filterComplex[1][i])
if (nchain == []): nchain = [0]
return nchain, nfilters
#check if simplex is a face of another simplex
def checkFace(face, simplex):
if simplex == 0:
return 1
elif (set(face) < set(simplex) and ( len(face) == (len(simplex)-1) )): #if face is a (n-1) subset of simplex
return 1
else:
return 0
#build boundary matrix for dimension n ---> (n-1) = p
def filterBoundaryMatrix(filterComplex):
bmatrix = np.zeros((len(filterComplex[0]),len(filterComplex[0])), dtype='>i8')
#bmatrix[0,:] = 0 #add "zero-th" dimension as first row/column, makes algorithm easier later on
#bmatrix[:,0] = 0
i = 0
for colSimplex in filterComplex[0]:
j = 0
for rowSimplex in filterComplex[0]:
bmatrix[j,i] = checkFace(rowSimplex, colSimplex)
j += 1
i += 1
return bmatrix
bm = filterBoundaryMatrix(ripsComplex2)
bm #Here is the (non-reduced) boundary matrix
```
The following functions are for reducing the boundary matrix as described above (when we did it by hand).
```
#returns row index of lowest "1" in a column i in the boundary matrix
def low(i, matrix):
col = matrix[:,i]
col_len = len(col)
for i in range( (col_len-1) , -1, -1): #loop through column from bottom until you find the first 1
if col[i] == 1: return i
return -1 #if no lowest 1 (e.g. column of all zeros), return -1 to be 'undefined'
#checks if the boundary matrix is fully reduced
def isReduced(matrix):
for j in range(matrix.shape[1]): #iterate through columns
for i in range(j): #iterate through columns before column j
low_j = low(j, matrix)
low_i = low(i, matrix)
if (low_j == low_i and low_j != -1):
return i,j #return column i to add to column j
return [0,0]
#the main function to iteratively reduce the boundary matrix
def reduceBoundaryMatrix(matrix):
#this refers to column index in the boundary matrix
reduced_matrix = matrix.copy()
matrix_shape = reduced_matrix.shape
memory = np.identity(matrix_shape[1], dtype='>i8') #this matrix will store the column additions we make
r = isReduced(reduced_matrix)
while (r != [0,0]):
i = r[0]
j = r[1]
col_j = reduced_matrix[:,j]
col_i = reduced_matrix[:,i]
#print("Mod: add col %s to %s \n" % (i+1,j+1)) #Uncomment to see what mods are made
reduced_matrix[:,j] = np.bitwise_xor(col_i,col_j) #add column i to j
memory[i,j] = 1
r = isReduced(reduced_matrix)
return reduced_matrix, memory
z = reduceBoundaryMatrix(bm)
z
```
So the `reduceBoundaryMatrix` function returns two matrices, the reduced boundary matrix and a _memory_ matrix that records all the actions of the reduction algorithm. This is necessary so we can look up what each column in the boundary matrix actually refers to. Once it's reduced each column in the boundary matrix is not necessarily a single simplex but possibly a group of simplices such as some n-dimensional cycle.
The following functions use the reduced matrix to read the intervals for all the features that are born and die throughout the filtration
```
def readIntervals(reduced_matrix, filterValues): #reduced_matrix includes the reduced boundary matrix AND the memory matrix
#store intervals as a list of 2-element lists, e.g. [2,4] = start at "time" point 2, end at "time" point 4
#note the "time" points are actually just the simplex index number for now. we will convert to epsilon value later
intervals = []
#loop through each column j
#if low(j) = -1 (undefined, all zeros) then j signifies the birth of a new feature j
#if low(j) = i (defined), then j signifies the death of feature i
for j in range(reduced_matrix[0].shape[1]): #for each column (its a square matrix so doesn't matter...)
low_j = low(j, reduced_matrix[0])
if low_j == -1:
interval_start = [j, -1]
intervals.append(interval_start) # -1 is a temporary placeholder until we update with death time
#if no death time, then -1 signifies feature has no end (start -> infinity)
#-1 turns out to be very useful because in python if we access the list x[-1] then that will return the
#last element in that list. in effect if we leave the end point of an interval to be -1
# then we're saying the feature lasts until the very end
else: #death of feature
feature = intervals.index([low_j, -1]) #find the feature [start,end] so we can update the end point
intervals[feature][1] = j #j is the death point
#if the interval start point and end point are the same, then this feature begins and dies instantly
#so it is a useless interval and we dont want to waste memory keeping it
epsilon_start = filterValues[intervals[feature][0]]
epsilon_end = filterValues[j]
if epsilon_start == epsilon_end: intervals.remove(intervals[feature])
return intervals
def readPersistence(intervals, filterComplex):
#this converts intervals into epsilon format and figures out which homology group each interval belongs to
persistence = []
for interval in intervals:
start = interval[0]
end = interval[1]
homology_group = (len(filterComplex[0][start]) - 1) #filterComplex is a list of lists [complex, filter values]
epsilon_start = filterComplex[1][start]
epsilon_end = filterComplex[1][end]
persistence.append([homology_group, [epsilon_start, epsilon_end]])
return persistence
intervals = readIntervals(z, ripsComplex2[1])
intervals
```
So those are all the intervals for the features that arise and die. The `readPersistence` function will just convert the start/end points from being indices in the boundary matrix to their corresponding $\epsilon$ value. It will also figure out to which homology group (i.e. which Betti number dimension) each interval belongs.
```
persist1 = readPersistence(intervals, ripsComplex2)
persist1
```
This function will just graph the persistence barcode for individual dimensions.
```
import matplotlib.pyplot as plt
def graph_barcode(persistence, homology_group = 0):
#this function just produces the barcode graph for each homology group
xstart = [s[1][0] for s in persistence if s[0] == homology_group]
xstop = [s[1][1] for s in persistence if s[0] == homology_group]
y = [0.1 * x + 0.1 for x in range(len(xstart))]
plt.hlines(y, xstart, xstop, color='b', lw=4)
#Setup the plot
ax = plt.gca()
plt.ylim(0,max(y)+0.1)
ax.yaxis.set_major_formatter(plt.NullFormatter())
plt.xlabel('epsilon')
plt.ylabel("Betti dim %s" % (homology_group,))
plt.show()
graph_barcode(persist1, 0)
graph_barcode(persist1, 1)
```
Schweeeeet! Persistent homology, at last!
So we've graphed the barcode diagrams for the first two Betti numbers. The first barcode is a little underwhelming since what we want to see is some bars that are significantly longer than others, indicating a true feature. In this case, the Betti 0 barcode has a longest bar which represents the single connected componenent that is formed with the box, but it's not _that_ much longer then the next longest bar. That's mostly an artifact of the example being so simple. If I had added in a few more points then we would see a more significant longest bar.
The Betti 1 barcode is in a lot better shape. We clearly just have a single long bar indicating the 1-dimensional cycle that exists up until the box "fills in" at $\epsilon = 5.8$.
An important feature of persistent homology is being able to find the data points that lie on some interesting topological feature. If all persistent homology could do was give us barcodes and tell us how many connected components and cycles then that would be useful but wanting.
What we really want to be able to do is say, "hey look, the barcode shows there's a statistically significant 1-dimensional cycle, I wonder which data points form that cycle?"
To test out this procedure, let's modify our simple "box" simplicial complex a bit and add another edge (giving us another connected component).
```
data_b = np.array([[1,4],[1,1],[6,1],[6,4],[12,3.5],[12,1.5]])
graph2b = buildGraph(raw_data=data_b, epsilon=8) #epsilon is set to a high value to create a maximal complex
rips2b = ripsFiltration(graph2b, k=3)
SimplicialComplex.drawComplex(origData=data_b, ripsComplex=rips2b[0], axes=[0,14,0,6])
```
The depiction shows the maximal complex since we set $\epsilon$ to be a high value. But I tried to design the data so the "true" features are a box (which is a 1-dim cycle) and an edge off to the right, for a total of two "true" connected components.
Alright, let's run persistent homology on this data.
```
bm2b = filterBoundaryMatrix(rips2b)
rbm2b = reduceBoundaryMatrix(bm2b)
intervals2b = readIntervals(rbm2b, rips2b[1])
persist2b = readPersistence(intervals2b, rips2b)
graph_barcode(persist2b, 0)
graph_barcode(persist2b, 1)
```
We can see the two connected components (the two longest bars) in `Betti dim 0` and we see two bars in `Betti dim 1`, but one is clearly almost twice as long as the other. The shorter bar is from when the edge on the right forms a cycle with the two left-most vertices on the left-sided box.
So at this point we're thinking we have one significant 1-dim cycle, but (pretending we can't just plot our data) we don't know which points form this cycle so that we can further analyze that subset of the data if we wish.
In order to figure that out, we just need to use the _memory_ matrix that our reduction algorithm also returns to us. First we find the interval we want from the `intervals2b` list, in this case it is the first element, then we get the start point (since that indicates the birth of the feature). The start point is an index value in the boundary array, so we'll just find that column in the memory array and look for the 1s in that column. The rows with 1s in that column are the other simplices in the group (including the column itself).
```
persist2b
```
First, look at the intervals in homology group 1, then we want the interval that spans the epsilon range from 5.0 to 5.83. That's index 6 in the persistence list, and is likewise index 6 in the intervals list. The intervals list, rather than epsilon start and end, has index values so we can lookup the simplices in the memory matrix.
```
cycle1 = intervals2b[6]
cycle1
#So birth index is 10
column10 = rbm2b[1][:,10]
column10
```
So this is the column in the memory matrix with index=10. So we automatically know that whatever simplex is in index 10 is part of the cycle as well as the rows with 1s in this column.
```
ptsOnCycle = [i for i in range(len(column10)) if column10[i] == 1]
ptsOnCycle
#so the simplices with indices 7,8,9,10 lie on our 1-dimensional cycle, let's find what those simplices are
rips2b[0][7:11] #range [start:stop], but stop is non-inclusive, so put 11 instead of 10
```
Exactly! Now this is the list of 1-simplices that form the 1-dimensional cycle we saw in our barcode. It should be trivial to go from this list to the raw data points so I won't bore you with those details here.
Alright. Let's try this with a little bit more realistic data. We'll use data sampled from a circle like we did in the beginning of this section. For this example, I've set the parameter `k=2` in the `ripsFiltration` function so it will only generate simplices up to 2-simplices. This is just to reduce the memory needed. If you have a fast computer with a lot of memory, you're welcome to set `k` to 3 or so, but I wouldn't make it much greater than that. Usually we're mostly interested in connected components and 1 or 2 dimensional cycles. The utility of topological features in dimensions higher than that seems to be a diminishing return and the price in memory and algorithm running time is generally not worth it.
>__NOTE__: The following may take awhile to run, perhaps several minutes. This is because the code written in these tutorials is optimized for clarity and ease, NOT for efficiency or speed. There are a lot of performance optimizations that can and should be made if we wanted to make this anywhere close to a production ready TDA library. I plan to write a follow up post at some point about the most reasonable algorithm and data structure optimizations that we can make because I hope to develop a reasonable efficient open source TDA library in Python in the future and would appreciate any help I can get.
```
n = 30 #number of points to generate
#generate space of parameter
theta = np.linspace(0, 2.0*np.pi, n)
a, b, r = 0.0, 0.0, 5.0
x = a + r*np.cos(theta)
y = b + r*np.sin(theta)
#code to plot the circle for visualization
plt.plot(x, y)
plt.show()
xc = np.random.uniform(-0.25,0.25,n) + x #add some "jitteriness" to the points (but less than before, reduces memory)
yc = np.random.uniform(-0.25,0.25,n) + y
fig, ax = plt.subplots()
ax.scatter(xc,yc)
plt.show()
circleData = np.array(list(zip(xc,yc)))
graph4 = buildGraph(raw_data=circleData, epsilon=3.0)
rips4 = ripsFiltration(graph4, k=2)
SimplicialComplex.drawComplex(origData=circleData, ripsComplex=rips4[0], axes=[-6,6,-6,6])
```
Clearly, persistent homology should tell us we have 1 connected component and a single 1-dimensional cycle.
```
len(rips4[0])
#On my laptop, a rips filtration with more than about 250 simplices will take >10 mins to compute persistent homology
#anything < ~220 only takes a few minutes or less
%%time
bm4 = filterBoundaryMatrix(rips4)
rbm4 = reduceBoundaryMatrix(bm4)
intervals4 = readIntervals(rbm4, rips4[1])
persist4 = readPersistence(intervals4, rips4)
graph_barcode(persist4, 0)
graph_barcode(persist4, 1)
```
We can clearly see that there is a _significantly_ longer bar than the others in the `Betti dim 0` barcode, indicating we have only one significant connected component. This fits clearly with the circular data we plotted.
The `Betti dim 1` barcode is even easier as it only shows a single bar, so we of course have a significant feature here being a 1-dimensional cycle.
Okay well, as usual, let's make things a little bit tougher to test our algorithms.
We're going to sample points from a shape called a __lemniscate__, more commonly known as a figure-of-eight, since it looks like the number 8 sideways. As you can tell, it should have 1 connected component and two 1-dimensional cycles.
```
n = 50
t = np.linspace(0, 2*np.pi, num=n)
#equations for lemniscate
x = np.cos(t) / (np.sin(t)**2 + 1)
y = np.cos(t) * np.sin(t) / (np.sin(t)**2 + 1)
plt.plot(x, y)
plt.show()
x2 = np.random.uniform(-0.03, 0.03, n) + x #add some "jitteriness" to the points
y2 = np.random.uniform(-0.03, 0.03, n) + y
fig, ax = plt.subplots()
ax.scatter(x2,y2)
plt.show()
figure8Data = np.array(list(zip(x2,y2)))
graph5 = buildGraph(raw_data=figure8Data, epsilon=0.2)
rips5 = ripsFiltration(graph5, k=2)
SimplicialComplex.drawComplex(origData=figure8Data, ripsComplex=rips5[0], axes=[-1.5,1.5,-1, 1])
%%time
bm5 = filterBoundaryMatrix(rips5)
rbm5 = reduceBoundaryMatrix(bm5)
intervals5 = readIntervals(rbm5, rips5[1])
persist5 = readPersistence(intervals5, rips5)
```
Yeah... that took 17 minutes. Good thing I still had enough CPU/RAM to watch YouTube.
```
graph_barcode(persist5, 0)
graph_barcode(persist5, 1)
```
:-) Just as we expected. `Betti dim 0` shows one significantly longer bar than the others and `Betti dim 1` shows us two long bars, our two 1-dim cycles.
Let's add in another component. In this example, I've just added in a small circle in the data. So we should have two connected components and 3 1-dim cycles.
```
theta = np.linspace(0, 2.0*np.pi, 10)
a, b, r = 1.6, 0.5, 0.2
x3 = a + r*np.cos(theta)
y3 = b + r*np.sin(theta)
x4 = np.append(x, x3)
y4 = np.append(y, y3)
fig, ax = plt.subplots()
ax.scatter(x4,y4)
plt.show()
figure8Data2 = np.array(list(zip(x4,y4)))
# I didn't add "jitteriness" this time since that increases the complexity of the subsequent simplicial complex,
# which makes the memory and computation requirements much greater
graph6 = buildGraph(raw_data=figure8Data2, epsilon=0.19)
rips6 = ripsFiltration(graph6, k=2)
SimplicialComplex.drawComplex(origData=figure8Data2, ripsComplex=rips6[0], axes=[-1.5,2.5,-1, 1])
len(rips6[0]) #reasonable size
%%time
bm6 = filterBoundaryMatrix(rips6)
rbm6 = reduceBoundaryMatrix(bm6)
intervals6 = readIntervals(rbm6, rips6[0])
persist6 = readPersistence(intervals6, rips6)
graph_barcode(persist6, 0)
graph_barcode(persist6, 1)
```
Excellent. I think by now I don't need to tell you how to interpret the barcodes.
### The End... What's next?
Well that's it folks. Part 5 is the end of this sub-series on persistent homology. You now should have all the knowledge necessary to understand and use existing persistent homology software tools, or even build your own if you want.
Next, we will turn our attention to the other major tool in topological data analysis, __mapper__. Mapper is an algorithm that allows us to create visualizable graphs from arbitrarily high-dimensional data. In this way, we are able to see global and local topological features. It is very useful for exploratory data analysis and hypothesis generation. Fortunately, the concepts and math behind it are a lot easier than persistent homology.
#### References (Websites):
1. http://dyinglovegrape.com/math/topology_data_1.php
2. http://www.math.uiuc.edu/~r-ash/Algebra/Chapter4.pdf
3. https://en.wikipedia.org/wiki/Group_(mathematics)
4. https://jeremykun.com/2013/04/03/homology-theory-a-primer/
5. http://suess.sdf-eu.org/website/lang/de/algtop/notes4.pdf
6. http://www.mit.edu/~evanchen/napkin.html
7. https://triangleinequality.wordpress.com/2014/01/23/computing-homology
#### References (Academic Publications):
1. Adams, H., Atanasov, A., & Carlsson, G. (2011). Nudged Elastic Band in Topological Data Analysis. arXiv Preprint, 1112.1993v(December 2011). Retrieved from http://arxiv.org/abs/1112.1993
2. Artamonov, O. (2010). Topological Methods for the Representation and Analysis of Exploration Data in Oil Industry by Oleg Artamonov.
3. Basher, M. (2012). On the Folding of Finite Topological Space. International Mathematical Forum, 7(15), 745–752. Retrieved from http://www.m-hikari.com/imf/imf-2012/13-16-2012/basherIMF13-16-2012.pdf
4. Bauer, U., Kerber, M., & Reininghaus, J. (2013). Distributed computation of persistent homology. arXiv Preprint arXiv:1310.0710, 31–38. http://doi.org/10.1137/1.9781611973198.4
5. Bauer, U., Kerber, M., & Reininghaus, J. (2013). Clear and Compress: Computing Persistent Homology in Chunks. arXiv Preprint arXiv:1303.0477, 1–12. http://doi.org/10.1007/978-3-319-04099-8__7
6. Berry, T., & Sauer, T. (2016). Consistent Manifold Representation for Topological Data Analysis. Retrieved from http://arxiv.org/abs/1606.02353
7. Biasotti, S., Giorgi, D., Spagnuolo, M., & Falcidieno, B. (2008). Reeb graphs for shape analysis and applications. Theoretical Computer Science, 392(1–3), 5–22. http://doi.org/10.1016/j.tcs.2007.10.018
8. Boissonnat, J.-D., & Maria, C. (2014). The Simplex Tree: An Efficient Data Structure for General Simplicial Complexes. Algorithmica, 70(3), 406–427. http://doi.org/10.1007/s00453-014-9887-3
9. Cazals, F., Roth, A., Robert, C., & Christian, M. (2013). Towards Morse Theory for Point Cloud Data, (July). Retrieved from http://hal.archives-ouvertes.fr/hal-00848753/
10. Chazal, F., & Michel, B. (2016). Persistent homology in TDA.
11. Cheng, J. (n.d.). Lecture 16 : Computation of Reeb Graphs Topics in Computational Topology : An Algorithmic View Computation of Reeb Graphs, 1, 1–5.
12. Day, M. (2012). Notes on Cayley Graphs for Math 5123 Cayley graphs, 1–6.
13. Dey, T. K., Fan, F., & Wang, Y. (2013). Graph Induced Complex: A Data Sparsifier for Homology Inference.
14. Doktorova, M. (2012). CONSTRUCTING SIMPLICIAL COMPLEXES OVER by, (June).
15. Edelsbrunner, H. (2006). IV.1 Homology. Computational Topology, 81–87. Retrieved from http://www.cs.duke.edu/courses/fall06/cps296.1/
16. Edelsbrunner, H. (2006). VI.1 Persistent Homology. Computational Topology, 128–134. Retrieved from http://www.cs.duke.edu/courses/fall06/cps296.1/
17. Edelsbrunner, H., Letscher, D., & Zomorodian, A. (n.d.). a d “ d A ( gpirqtsuGv I ” dfe h d5e x V W x ( A x Aji x } ~ k g G “ f g I ktg § y V k g G ” f g I ¨ " f g ¡ k g § VXW.
18. Edelsbrunner, H., Letscher, D., & Zomorodian, A. (2002). Topological persistence and simplification. Discrete and Computational Geometry, 28(4), 511–533. http://doi.org/10.1007/s00454-002-2885-2
19. Edelsbrunner, H., & Morozov, D. (2012). Persistent homology: theory and practice. 6th European Congress of Mathematics, 123–142. http://doi.org/10.4171/120-1/3
20. Erickson, J. (1908). Homology. Computational Topology, 1–11.
21. Evan Chen. (2016). An Infinitely Large Napkin.
22. Figure, S., & Figure, S. (n.d.). Chapter 4 : Persistent Homology Topics in Computational Topology : An Algorithmic View Persistent homology, 1–8.
23. Grigor’yan, A., Muranov, Y. V., & Yau, S. T. (2014). Graphs associated with simplicial complexes. Homology, Homotopy and Applications, 16(1), 295–311. http://doi.org/10.4310/HHA.2014.v16.n1.a16
24. Kaczynski, T., Mischaikow, K., & Mrozek, M. (2003). Computing homology. Homology, Homotopy and Applications, 5(2), 233–256. http://doi.org/10.4310/HHA.2003.v5.n2.a8
25. Kerber, M. (2016). Persistent Homology – State of the art and challenges 1 Motivation for multi-scale topology. Internat. Math. Nachrichten Nr, 231(231), 15–33.
26. Khoury, M. (n.d.). Lecture 6 : Introduction to Simplicial Homology Topics in Computational Topology : An Algorithmic View, 1–6.
27. Kraft, R. (2016). Illustrations of Data Analysis Using the Mapper Algorithm and Persistent Homology.
28. Lakshmivarahan, S., & Sivakumar, L. (2016). Cayley Graphs, (1), 1–9.
29. Lewis, R. (n.d.). Parallel Computation of Persistent Homology using the Blowup Complex, 323–331. http://doi.org/10.1145/2755573.2755587
30. Liu, X., Xie, Z., & Yi, D. (2012). A fast algorithm for constructing topological structure in large data. Homology, Homotopy and Applications, 14(1), 221–238. http://doi.org/10.4310/HHA.2012.v14.n1.a11
31. Medina, P. S., & Doerge, R. W. (2016). Statistical Methods in Topological Data Analysis for Complex, High-Dimensional Data. Retrieved from http://arxiv.org/abs/1607.05150
32. Morozov, D. (n.d.). A Practical Guide to Persistent Homology A Practical Guide to Persistent Homology.
33. Murty, N. A., Natarajan, V., & Vadhiyar, S. (2013). Efficient homology computations on multicore and manycore systems. 20th Annual International Conference on High Performance Computing, HiPC 2013. http://doi.org/10.1109/HiPC.2013.6799139
34. Naik, V. (2006). Group theory : a first journey, 1–21.
35. Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., & Harrington, H. A. (2015). A roadmap for the computation of persistent homology. Preprint ArXiv, (June), 17. Retrieved from http://arxiv.org/abs/1506.08903
36. Pearson, P. T. (2013). Visualizing Clusters in Artificial Neural Networks Using Morse Theory. Advances in Artificial Neural Systems, 2013, 1–8. http://doi.org/10.1155/2013/486363
37. Reininghaus, J. (2012). Computational Discrete Morse Theory.
38. Reininghaus, J., Huber, S., Bauer, U., Tu, M., & Kwitt, R. (2015). A Stable Multi-Scale Kernel for Topological Machine Learning, 1–8. Retrieved from papers3://publication/uuid/CA230E5C-90AC-4352-80D2-2F556E8B47D3
39. Rykaczewski, K., Wiśniewski, P., & Stencel, K. (n.d.). An Algorithmic Way to Generate Simplexes for Topological Data Analysis.
40. Semester, A. (2017). § 4 . Simplicial Complexes and Simplicial Homology, 1–13.
41. Siles, V. (n.d.). Computing Persistent Homology within Coq / SSReflect, 243847(243847).
42. Singh, G. (2007). Algorithms for Topological Analysis of Data, (November).
43. Tylianakis, J. (2009). Course Notes. Methodology, (2002), 1–124.
44. Wagner, H., & Dłotko, P. (2014). Towards topological analysis of high-dimensional feature spaces. Computer Vision and Image Understanding, 121, 21–26. http://doi.org/10.1016/j.cviu.2014.01.005
45. Xiaoyin Ge, Issam I. Safa, Mikhail Belkin, & Yusu Wang. (2011). Data Skeletonization via Reeb Graphs. Neural Information Processing Systems 2011, 837–845. Retrieved from https://papers.nips.cc/paper/4375-data-skeletonization-via-reeb-graphs.pdf
46. Zomorodian, A. (2010). Fast construction of the Vietoris-Rips complex. Computers and Graphics (Pergamon), 34(3), 263–271. http://doi.org/10.1016/j.cag.2010.03.007
47. Zomorodian, A. (2009). Computational Topology Notes. Advances in Discrete and Computational Geometry, 2, 109–143. Retrieved from http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.50.7483
48. Zomorodian, A. J. (2001). Computing and Comprehending Topology: Persistence and Hierarchical Morse Complexes, 199. Retrieved from http://www.cs.dartmouth.edu/~afra/papers.html
49. Zomorodian, A., & Carlsson, G. (2005). Computing persistent homology. Discrete and Computational Geometry, 33(2), 249–274. http://doi.org/10.1007/s00454-004-1146-y
50. Groups and their Representations Karen E. Smith. (n.d.).
51. Symmetry and Group Theory 1. (2016), 1–18. http://doi.org/10.1016/B978-0-444-53786-7.00026-5
| true |
code
| 0.55103 | null | null | null | null |
|
#Waymo Open Dataset Tutorial
- Website: https://waymo.com/open
- GitHub: https://github.com/waymo-research/waymo-open-dataset
This tutorial demonstrates how to use the Waymo Open Dataset with two frames of data. Visit the [Waymo Open Dataset Website](https://waymo.com/open) to download the full dataset.
To use, open this notebook in [Colab](https://colab.research.google.com).
Uncheck the box "Reset all runtimes before running" if you run this colab directly from the remote kernel. Alternatively, you can make a copy before trying to run it by following "File > Save copy in Drive ...".
## Install waymo_open_dataset package
```
!rm -rf waymo-od > /dev/null
!git clone https://github.com/waymo-research/waymo-open-dataset.git waymo-od
!cd waymo-od && git branch -a
!cd waymo-od && git checkout remotes/origin/master
!pip3 install --upgrade pip
!pip3 install waymo-open-dataset-tf-2-1-0==1.2.0
import os
import tensorflow.compat.v1 as tf
import math
import numpy as np
import itertools
tf.enable_eager_execution()
from waymo_open_dataset.utils import range_image_utils
from waymo_open_dataset.utils import transform_utils
from waymo_open_dataset.utils import frame_utils
from waymo_open_dataset import dataset_pb2 as open_dataset
```
## Read one frame
Each file in the dataset is a sequence of frames ordered by frame start timestamps. We have extracted two frames from the dataset to demonstrate the dataset format.
```
FILENAME = '/content/waymo-od/tutorial/frames'
dataset = tf.data.TFRecordDataset(FILENAME, compression_type='')
for data in dataset:
frame = open_dataset.Frame()
frame.ParseFromString(bytearray(data.numpy()))
break
(range_images, camera_projections,
_, range_image_top_pose) = frame_utils.parse_range_image_and_camera_projection(
frame)
```
###Examine frame context
Refer to [dataset.proto](https://github.com/waymo-research/waymo-open-dataset/blob/master/waymo_open_dataset/dataset.proto) for the data format. The context contains shared information among all frames in the scene.
```
print(frame.context)
```
## Visualize Camera Images and Camera Labels
```
import matplotlib.pyplot as plt
import matplotlib.patches as patches
def show_camera_image(camera_image, camera_labels, layout, cmap=None):
"""Show a camera image and the given camera labels."""
ax = plt.subplot(*layout)
# Draw the camera labels.
for camera_labels in frame.camera_labels:
# Ignore camera labels that do not correspond to this camera.
if camera_labels.name != camera_image.name:
continue
# Iterate over the individual labels.
for label in camera_labels.labels:
# Draw the object bounding box.
ax.add_patch(patches.Rectangle(
xy=(label.box.center_x - 0.5 * label.box.length,
label.box.center_y - 0.5 * label.box.width),
width=label.box.length,
height=label.box.width,
linewidth=1,
edgecolor='red',
facecolor='none'))
# Show the camera image.
plt.imshow(tf.image.decode_jpeg(camera_image.image), cmap=cmap)
plt.title(open_dataset.CameraName.Name.Name(camera_image.name))
plt.grid(False)
plt.axis('off')
plt.figure(figsize=(25, 20))
for index, image in enumerate(frame.images):
show_camera_image(image, frame.camera_labels, [3, 3, index+1])
```
##Visualize Range Images
```
plt.figure(figsize=(64, 20))
def plot_range_image_helper(data, name, layout, vmin = 0, vmax=1, cmap='gray'):
"""Plots range image.
Args:
data: range image data
name: the image title
layout: plt layout
vmin: minimum value of the passed data
vmax: maximum value of the passed data
cmap: color map
"""
plt.subplot(*layout)
plt.imshow(data, cmap=cmap, vmin=vmin, vmax=vmax)
plt.title(name)
plt.grid(False)
plt.axis('off')
def get_range_image(laser_name, return_index):
"""Returns range image given a laser name and its return index."""
return range_images[laser_name][return_index]
def show_range_image(range_image, layout_index_start = 1):
"""Shows range image.
Args:
range_image: the range image data from a given lidar of type MatrixFloat.
layout_index_start: layout offset
"""
range_image_tensor = tf.convert_to_tensor(range_image.data)
range_image_tensor = tf.reshape(range_image_tensor, range_image.shape.dims)
lidar_image_mask = tf.greater_equal(range_image_tensor, 0)
range_image_tensor = tf.where(lidar_image_mask, range_image_tensor,
tf.ones_like(range_image_tensor) * 1e10)
range_image_range = range_image_tensor[...,0]
range_image_intensity = range_image_tensor[...,1]
range_image_elongation = range_image_tensor[...,2]
plot_range_image_helper(range_image_range.numpy(), 'range',
[8, 1, layout_index_start], vmax=75, cmap='gray')
plot_range_image_helper(range_image_intensity.numpy(), 'intensity',
[8, 1, layout_index_start + 1], vmax=1.5, cmap='gray')
plot_range_image_helper(range_image_elongation.numpy(), 'elongation',
[8, 1, layout_index_start + 2], vmax=1.5, cmap='gray')
frame.lasers.sort(key=lambda laser: laser.name)
show_range_image(get_range_image(open_dataset.LaserName.TOP, 0), 1)
show_range_image(get_range_image(open_dataset.LaserName.TOP, 1), 4)
```
##Point Cloud Conversion and Visualization
```
points, cp_points = frame_utils.convert_range_image_to_point_cloud(
frame,
range_images,
camera_projections,
range_image_top_pose)
points_ri2, cp_points_ri2 = frame_utils.convert_range_image_to_point_cloud(
frame,
range_images,
camera_projections,
range_image_top_pose,
ri_index=1)
# 3d points in vehicle frame.
points_all = np.concatenate(points, axis=0)
points_all_ri2 = np.concatenate(points_ri2, axis=0)
# camera projection corresponding to each point.
cp_points_all = np.concatenate(cp_points, axis=0)
cp_points_all_ri2 = np.concatenate(cp_points_ri2, axis=0)
```
###Examine number of points in each lidar sensor.
First return.
```
print(points_all.shape)
print(cp_points_all.shape)
print(points_all[0:2])
for i in range(5):
print(points[i].shape)
print(cp_points[i].shape)
```
Second return.
```
print(points_all_ri2.shape)
print(cp_points_all_ri2.shape)
print(points_all_ri2[0:2])
for i in range(5):
print(points_ri2[i].shape)
print(cp_points_ri2[i].shape)
```
###Show point cloud
3D point clouds are rendered using an internal tool, which is unfortunately not publicly available yet. Here is an example of what they look like.
```
from IPython.display import Image, display
display(Image('/content/waymo-od/tutorial/3d_point_cloud.png'))
```
##Visualize Camera Projection
```
images = sorted(frame.images, key=lambda i:i.name)
cp_points_all_concat = np.concatenate([cp_points_all, points_all], axis=-1)
cp_points_all_concat_tensor = tf.constant(cp_points_all_concat)
# The distance between lidar points and vehicle frame origin.
points_all_tensor = tf.norm(points_all, axis=-1, keepdims=True)
cp_points_all_tensor = tf.constant(cp_points_all, dtype=tf.int32)
mask = tf.equal(cp_points_all_tensor[..., 0], images[0].name)
cp_points_all_tensor = tf.cast(tf.gather_nd(
cp_points_all_tensor, tf.where(mask)), dtype=tf.float32)
points_all_tensor = tf.gather_nd(points_all_tensor, tf.where(mask))
projected_points_all_from_raw_data = tf.concat(
[cp_points_all_tensor[..., 1:3], points_all_tensor], axis=-1).numpy()
def rgba(r):
"""Generates a color based on range.
Args:
r: the range value of a given point.
Returns:
The color for a given range
"""
c = plt.get_cmap('jet')((r % 20.0) / 20.0)
c = list(c)
c[-1] = 0.5 # alpha
return c
def plot_image(camera_image):
"""Plot a cmaera image."""
plt.figure(figsize=(20, 12))
plt.imshow(tf.image.decode_jpeg(camera_image.image))
plt.grid("off")
def plot_points_on_image(projected_points, camera_image, rgba_func,
point_size=5.0):
"""Plots points on a camera image.
Args:
projected_points: [N, 3] numpy array. The inner dims are
[camera_x, camera_y, range].
camera_image: jpeg encoded camera image.
rgba_func: a function that generates a color from a range value.
point_size: the point size.
"""
plot_image(camera_image)
xs = []
ys = []
colors = []
for point in projected_points:
xs.append(point[0]) # width, col
ys.append(point[1]) # height, row
colors.append(rgba_func(point[2]))
plt.scatter(xs, ys, c=colors, s=point_size, edgecolors="none")
plot_points_on_image(projected_points_all_from_raw_data,
images[0], rgba, point_size=5.0)
```
## Install from source code
The remaining part of this colab covers details of installing the repo form source code which provides a richer API.
### Install dependencies
```
!sudo apt install build-essential
!sudo apt-get install --assume-yes pkg-config zip g++ zlib1g-dev unzip python3 python3-pip
!wget https://github.com/bazelbuild/bazel/releases/download/0.28.0/bazel-0.28.0-installer-linux-x86_64.sh
!sudo bash ./bazel-0.28.0-installer-linux-x86_64.sh
```
###Build and test (this can take 10 mins)
Configure .bazelrc. This works with/without Tensorflow. This colab machine has Tensorflow installed.
```
!cd waymo-od && ./configure.sh && cat .bazelrc && bazel clean
!cd waymo-od && bazel build ... --show_progress_rate_limit=10.0
```
### Metrics computation
The core metrics computation library is written in C++, so it can be extended to other programming languages. It can compute detection metrics (mAP) and tracking metrics (MOTA). See more information about the metrics on the [website](https://waymo.com/open/next/).
We provide command line tools and TensorFlow ops to call the detection metrics library to compute detection metrics. We will provide a similar wrapper for tracking metrics library in the future. You are welcome to contribute your wrappers.
#### Command line detection metrics computation
The command takes a pair of files for prediction and ground truth. Read the comment in waymo_open_dataset/metrics/tools/compute_detection_metrics_main.cc for details of the data format.
```
!cd waymo-od && bazel-bin/waymo_open_dataset/metrics/tools/compute_detection_metrics_main waymo_open_dataset/metrics/tools/fake_predictions.bin waymo_open_dataset/metrics/tools/fake_ground_truths.bin
```
#### TensorFlow custom op
A TensorFlow op is defined at metrics/ops/metrics_ops.cc. We provide a python wrapper of the op at metrics/ops/py_metrics_ops.py, and a tf.metrics-like implementation of the op at metrics/python/detection_metrics.py. This library requires TensorFlow to be installed.
Install TensorFlow and NumPy.
```
!pip3 install numpy tensorflow
```
Reconfigure .bazelrc such that you can compile the TensorFlow ops
```
!cd waymo-od && ./configure.sh && cat .bazelrc
```
Run the op and tf.metrics wrapper unit tests which can be referenced as example usage of the libraries.
```
!cd waymo-od && bazel test waymo_open_dataset/metrics/ops/... && bazel test waymo_open_dataset/metrics/python/...
```
Run all tests in the repo.
```
!cd waymo-od && bazel test ...
```
### Build local PIP package
```
!cd waymo-od && export PYTHON_VERSION=3 && ./pip_pkg_scripts/build.sh
```
You can install the locally compiled package or access any c++ binary compiled from this.
| true |
code
| 0.693992 | null | null | null | null |
|
## Export Data Script "Blanket Script"
This script searches for ArcGIS Online feature layers and exports them as a geodatabase on ArcGIS Online. This script is based on a system-wide backup script and utilizes a keyword search function to archive data.
To start running the script, you can click Run at the top to run the selected cell. Running a header cell (like this) will just move on to the next cell. A number will appear next to the cell when it has been successfully ran. You can also run them all by clicking "Cell" in the menu bar at the top and then click "Run All". You can run one cell several times if you are tinkering with the code, as long as you make sure to run the first cell below to log yourself into AGOL before you begin (and you run any other cells that create data used in the cell you are tinkering).
```
from arcgis.gis import GIS
import datetime as dt
gis = GIS('home')
```
Starting the script, the cell below will gather the ArcGIS Online layers you want to back up. See look at the comments for specifics. This script will find any feature layer with the keyword you identify in the first open line of this cell.
For example, if you use "Bolder Wildfire" as your keyword, this script will return everything with "Bolder" OR "Wildfire" in the title. After you run the script, you will get an output message of the layers to be backed up. Make sure you check what the script finds BEFORE setting a task to automatically run this script. This script will only export feature layers. It will find feature layer views, but they will not be exported.
Comments start with "#"
```
# What folder is this data going to? Put the folder name between the "". I suggest not using spaces in the folder names. You do not have to create a whole new folder to run the script.
# Leaving this blank will make the data backup to the root folder in your ArcGIS Online.
agol_folder = ""
# How many items do you want to search for and backup at one time? This is the max number of layers that will be backed up each time the script is ran.
# Without this, the default is 10. You can change this number to be whatever you want
num_items = 10
```
This cell looks for items in AGOL. Put your desired keyword between the "" in the first line. Whatever you put here has to also be in the items' title, otherwise the code won't know to look for them.
```
keyword = "<INCIDENT NAME>"
query_string = "type:Feature Service, title:{}, owner:{}".format(keyword, username)
items = gis.content.search(query=query_string, max_items=num_items, sort_field='modifed', sort_order='desc')
print(str(len(items)) + " items will be backed up to " + agol_folder + " Folder. See the list below:")
items
```
This section is what does the magic. By default, you do not have to change anything here. However, if you want to change the name of the output file, this would be done in line 10 next to "result". Do not worry if several lines say "An error occurred downloading". This just means that that file is not a feature layer and isn't going to download. If everything gives you this error, check your code and make sure you are grabbing feature layers.
```
def download_as_fgdb(item_list):
for item in item_list:
try:
if 'View Service' in item.typeKeywords:
print(item.title + " is view, not downloading")
else:
print("Downloading " + item.title)
# This line figures out today's date in Year-Month-Day format, then puts the date at the end of the export data name
version=time.strftime('%Y%m%d %H:%M')
result = item.export(version + " UTC " + item.title, "File Geodatabase")
print("Successfully downloaded " + item.title)
result.move(folder= agol_folder)
except Exception as e:
print("An error occurred downloading " + item.title)
print(e)
print("The function has completed")
download_as_fgdb(items)
```
| true |
code
| 0.222869 | null | null | null | null |
|
# Regression Week 4: Ridge Regression (gradient descent)
In this notebook, you will implement ridge regression via gradient descent. You will:
* Convert an SFrame into a Numpy array
* Write a Numpy function to compute the derivative of the regression weights with respect to a single feature
* Write gradient descent function to compute the regression weights given an initial weight vector, step size, tolerance, and L2 penalty
# Fire up graphlab create
Make sure you have the latest version of GraphLab Create (>= 1.7)
```
import graphlab
```
# Load in house sales data
Dataset is from house sales in King County, the region where the city of Seattle, WA is located.
```
sales = graphlab.SFrame('kc_house_data.gl/')
```
If we want to do any "feature engineering" like creating new features or adjusting existing ones we should do this directly using the SFrames as seen in the first notebook of Week 2. For this notebook, however, we will work with the existing features.
# Import useful functions from previous notebook
As in Week 2, we convert the SFrame into a 2D Numpy array. Copy and paste `get_numpy_data()` from the second notebook of Week 2.
```
import numpy as np # note this allows us to refer to numpy as np instead
def get_numpy_data(data_sframe, features, output):
data_sframe['constant'] = 1 # this is how you add a constant column to an SFrame
# add the column 'constant' to the front of the features list so that we can extract it along with the others:
features = ['constant'] + features # this is how you combine two lists
# select the columns of data_SFrame given by the features list into the SFrame features_sframe
# (now including constant):
features_sframe = data_sframe[features]
# the following line will convert the features_SFrame into a numpy matrix:
feature_matrix = features_sframe.to_numpy()
# assign the column of data_sframe associated with the output to the SArray output_sarray
output_sarray = data_sframe[output]
# the following will convert the SArray into a numpy array by first converting it to a list
output_array = output_sarray.to_numpy()
return(feature_matrix, output_array)
```
Also, copy and paste the `predict_output()` function to compute the predictions for an entire matrix of features given the matrix and the weights:
```
def predict_output(feature_matrix, weights):
# assume feature_matrix is a numpy matrix containing the features as columns and weights is a corresponding numpy array
# create the predictions vector by using np.dot()
predictions = np.dot(feature_matrix, weights)
return(predictions)
```
# Computing the Derivative
We are now going to move to computing the derivative of the regression cost function. Recall that the cost function is the sum over the data points of the squared difference between an observed output and a predicted output, plus the L2 penalty term.
```
Cost(w)
= SUM[ (prediction - output)^2 ]
+ l2_penalty*(w[0]^2 + w[1]^2 + ... + w[k]^2).
```
Since the derivative of a sum is the sum of the derivatives, we can take the derivative of the first part (the RSS) as we did in the notebook for the unregularized case in Week 2 and add the derivative of the regularization part. As we saw, the derivative of the RSS with respect to `w[i]` can be written as:
```
2*SUM[ error*[feature_i] ].
```
The derivative of the regularization term with respect to `w[i]` is:
```
2*l2_penalty*w[i].
```
Summing both, we get
```
2*SUM[ error*[feature_i] ] + 2*l2_penalty*w[i].
```
That is, the derivative for the weight for feature i is the sum (over data points) of 2 times the product of the error and the feature itself, plus `2*l2_penalty*w[i]`.
**We will not regularize the constant.** Thus, in the case of the constant, the derivative is just twice the sum of the errors (without the `2*l2_penalty*w[0]` term).
Recall that twice the sum of the product of two vectors is just twice the dot product of the two vectors. Therefore the derivative for the weight for feature_i is just two times the dot product between the values of feature_i and the current errors, plus `2*l2_penalty*w[i]`.
With this in mind complete the following derivative function which computes the derivative of the weight given the value of the feature (over all data points) and the errors (over all data points). To decide when to we are dealing with the constant (so we don't regularize it) we added the extra parameter to the call `feature_is_constant` which you should set to `True` when computing the derivative of the constant and `False` otherwise.
```
def feature_derivative_ridge(errors, feature, weight, l2_penalty, feature_is_constant):
# If feature_is_constant is True, derivative is twice the dot product of errors and feature
if feature_is_constant == True:
derivative = 2 * np.dot(errors, feature)
else :
derivative = 2 * np.dot(errors, feature) + 2*l2_penalty*weight
# Otherwise, derivative is twice the dot product plus 2*l2_penalty*weight
return derivative
```
To test your feature derivartive run the following:
```
(example_features, example_output) = get_numpy_data(sales, ['sqft_living'], 'price')
my_weights = np.array([1., 10.])
test_predictions = predict_output(example_features, my_weights)
errors = test_predictions - example_output # prediction errors
# next two lines should print the same values
print feature_derivative_ridge(errors, example_features[:,1], my_weights[1], 1, False)
print np.sum(errors*example_features[:,1])*2+20.
print ''
# next two lines should print the same values
print feature_derivative_ridge(errors, example_features[:,0], my_weights[0], 1, True)
print np.sum(errors)*2.
```
# Gradient Descent
Now we will write a function that performs a gradient descent. The basic premise is simple. Given a starting point we update the current weights by moving in the negative gradient direction. Recall that the gradient is the direction of *increase* and therefore the negative gradient is the direction of *decrease* and we're trying to *minimize* a cost function.
The amount by which we move in the negative gradient *direction* is called the 'step size'. We stop when we are 'sufficiently close' to the optimum. Unlike in Week 2, this time we will set a **maximum number of iterations** and take gradient steps until we reach this maximum number. If no maximum number is supplied, the maximum should be set 100 by default. (Use default parameter values in Python.)
With this in mind, complete the following gradient descent function below using your derivative function above. For each step in the gradient descent, we update the weight for each feature before computing our stopping criteria.
```
def ridge_regression_gradient_descent(feature_matrix, output, initial_weights, step_size, l2_penalty, max_iterations=100):
print 'Starting gradient descent with l2_penalty = ' + str(l2_penalty)
weights = np.array(initial_weights) # make sure it's a numpy array
iteration = 0 # iteration counter
print_frequency = 1 # for adjusting frequency of debugging output
while iteration < max_iterations :
iteration += 1 # increment iteration counter
### === code section for adjusting frequency of debugging output. ===
if iteration == 10:
print_frequency = 10
if iteration == 100:
print_frequency = 100
if iteration%print_frequency==0:
print('Iteration = ' + str(iteration))
### === end code section ===
# compute the predictions based on feature_matrix and weights using your predict_output() function
predictions = predict_output(feature_matrix, weights)
# compute the errors as predictions - output
errors = predictions - output
# from time to time, print the value of the cost function
if iteration%print_frequency==0:
print 'Cost function = ', str(np.dot(errors,errors) + l2_penalty*(np.dot(weights,weights) - weights[0]**2))
for i in xrange(len(weights)): # loop over each weight
# Recall that feature_matrix[:,i] is the feature column associated with weights[i]
# compute the derivative for weight[i].
#(Remember: when i=0, you are computing the derivative of the constant!)
if () :
feature_derivative_ridge(errors, feature_matrix[:,i], weights[i], l2_penalty, True)
else :
feature_derivative_ridge(errors, feature_matrix[:,i], weights[i], l2_penalty, False)
# subtract the step size times the derivative from the current weight
print 'Done with gradient descent at iteration ', iteration
print 'Learned weights = ', str(weights)
return weights
```
# Visualizing effect of L2 penalty
The L2 penalty gets its name because it causes weights to have small L2 norms than otherwise. Let's see how large weights get penalized. Let us consider a simple model with 1 feature:
```
simple_features = ['sqft_living']
my_output = 'price'
```
Let us split the dataset into training set and test set. Make sure to use `seed=0`:
```
train_data,test_data = sales.random_split(.8,seed=0)
```
In this part, we will only use `'sqft_living'` to predict `'price'`. Use the `get_numpy_data` function to get a Numpy versions of your data with only this feature, for both the `train_data` and the `test_data`.
```
(simple_feature_matrix, output) = get_numpy_data(train_data, simple_features, my_output)
(simple_test_feature_matrix, test_output) = get_numpy_data(test_data, simple_features, my_output)
```
Let's set the parameters for our optimization:
```
initial_weights = np.array([0., 0.])
step_size = 1e-12
max_iterations=1000
```
First, let's consider no regularization. Set the `l2_penalty` to `0.0` and run your ridge regression algorithm to learn the weights of your model. Call your weights:
`simple_weights_0_penalty`
we'll use them later.
```
simple_weights_0_penalty = ridge_regression_gradient_descent(simple_feature_matrix, output, initial_weights, step_size, 0.0, max_iterations=100)
```
Next, let's consider high regularization. Set the `l2_penalty` to `1e11` and run your ridge regression algorithm to learn the weights of your model. Call your weights:
`simple_weights_high_penalty`
we'll use them later.
```
simple_weights_high_penalty = ridge_regression_gradient_descent(simple_feature_matrix, output, initial_weights, step_size, 1e11, max_iterations=100)
```
This code will plot the two learned models. (The blue line is for the model with no regularization and the red line is for the one with high regularization.)
```
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(simple_feature_matrix,output,'k.',
simple_feature_matrix,predict_output(simple_feature_matrix, simple_weights_0_penalty),'b-',
simple_feature_matrix,predict_output(simple_feature_matrix, simple_weights_high_penalty),'r-')
```
Compute the RSS on the TEST data for the following three sets of weights:
1. The initial weights (all zeros)
2. The weights learned with no regularization
3. The weights learned with high regularization
Which weights perform best?
```
test_predicted_output = predict_output(simple_test_feature_matrix, initial_weights)
rss = ((test_output - test_predicted_output )**2).sum()
print rss
test_predicted_output = predict_output(simple_test_feature_matrix, simple_weights_0_penalty)
rss = ((test_output - test_predicted_output )**2).sum()
print rss
test_predicted_output = predict_output(simple_test_feature_matrix, simple_weights_high_penalty)
rss = ((test_output - test_predicted_output )**2).sum()
print rss
```
***QUIZ QUESTIONS***
1. What is the value of the coefficient for `sqft_living` that you learned with no regularization, rounded to 1 decimal place? What about the one with high regularization?
2. Comparing the lines you fit with the with no regularization versus high regularization, which one is steeper?
3. What are the RSS on the test data for each of the set of weights above (initial, no regularization, high regularization)?
# Running a multiple regression with L2 penalty
Let us now consider a model with 2 features: `['sqft_living', 'sqft_living15']`.
First, create Numpy versions of your training and test data with these two features.
```
model_features = ['sqft_living', 'sqft_living15'] # sqft_living15 is the average squarefeet for the nearest 15 neighbors.
my_output = 'price'
(feature_matrix, output) = get_numpy_data(train_data, model_features, my_output)
(test_feature_matrix, test_output) = get_numpy_data(test_data, model_features, my_output)
```
We need to re-inialize the weights, since we have one extra parameter. Let us also set the step size and maximum number of iterations.
```
initial_weights = np.array([0.0,0.0,0.0])
step_size = 1e-12
max_iterations = 1000
```
First, let's consider no regularization. Set the `l2_penalty` to `0.0` and run your ridge regression algorithm to learn the weights of your model. Call your weights:
`multiple_weights_0_penalty`
```
multiple_weights_0_penalty = ridge_regression_gradient_descent(feature_matrix, output, initial_weights, step_size, 0.0, max_iterations=100)
```
Next, let's consider high regularization. Set the `l2_penalty` to `1e11` and run your ridge regression algorithm to learn the weights of your model. Call your weights:
`multiple_weights_high_penalty`
```
multiple_weights_high_penalty = ridge_regression_gradient_descent(feature_matrix, output, initial_weights, step_size, 1e11, max_iterations=100)
```
Compute the RSS on the TEST data for the following three sets of weights:
1. The initial weights (all zeros)
2. The weights learned with no regularization
3. The weights learned with high regularization
Which weights perform best?
```
test_predicted_output = predict_output(test_feature_matrix, initial_weights)
rss = ((test_output - test_predicted_output )**2).sum()
print rss
test_predicted_output = predict_output(test_feature_matrix, multiple_weights_0_penalty)
rss = ((test_output - test_predicted_output )**2).sum()
print rss
test_predicted_output = predict_output(test_feature_matrix, multiple_weights_high_penalty)
rss = ((test_output - test_predicted_output )**2).sum()
print rss
```
Predict the house price for the 1st house in the test set using the no regularization and high regularization models. (Remember that python starts indexing from 0.) How far is the prediction from the actual price? Which weights perform best for the 1st house?
***QUIZ QUESTIONS***
1. What is the value of the coefficient for `sqft_living` that you learned with no regularization, rounded to 1 decimal place? What about the one with high regularization?
2. What are the RSS on the test data for each of the set of weights above (initial, no regularization, high regularization)?
3. We make prediction for the first house in the test set using two sets of weights (no regularization vs high regularization). Which weights make better prediction <u>for that particular house</u>?
| true |
code
| 0.519095 | null | null | null | null |
|
# Bayesian Optimization with Random Forests (SMAC)
## Optimizing a CNN with Scikit-Optimize
In this notebook, we will use **Bayesian Optimization** to select the best **hyperparameters** for a CNN that recognizes digits in images, using the MNIST dataset and the open source Python package [Scikit-Optimize](https://scikit-optimize.github.io/stable/index.html).
We will use Random Forests as the surrogate function to approximate f(x)
The MNIST dataset is availale in [Kaggle](https://www.kaggle.com/c/digit-recognizer/data).
## Download dataset
- Navigate to the [MNIST website in Kaggle](https://www.kaggle.com/c/digit-recognizer/data)
- Download the train.csv file
- Unzip and copy the train.csv file to where you see the SAVE_DATASETS-HERE.txt file
- Rename to mnist.csv
**Remember that you need to be logged in to be able to download the dataset**
## Notebook content
- Data Preparation
- Set up a simple CNN
- Set up the hyperparameter search shape
- Set up the objective function
- Perform Bayesian Optimization
- Evaluate Model Performance
```
# For reproducible results.
# See:
# https://keras.io/getting_started/faq/#how-can-i-obtain-reproducible-results-using-keras-during-development
import os
os.environ['PYTHONHASHSEED'] = '0'
import numpy as np
import tensorflow as tf
import random as python_random
# The below is necessary for starting Numpy generated random numbers
# in a well-defined initial state.
np.random.seed(123)
# The below is necessary for starting core Python generated random numbers
# in a well-defined state.
python_random.seed(123)
# The below set_seed() will make random number generation
# in the TensorFlow backend have a well-defined initial state.
# For further details, see:
# https://www.tensorflow.org/api_docs/python/tf/random/set_seed
tf.random.set_seed(1234)
import itertools
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from keras.utils.np_utils import to_categorical
from keras.models import Sequential, load_model
from keras.layers import Dense, Flatten, Conv2D, MaxPool2D
from keras.optimizers import Adam
from keras.callbacks import ReduceLROnPlateau
from skopt import forest_minimize, gbrt_minimize
from skopt.space import Real, Categorical, Integer
from skopt.plots import plot_convergence
from skopt.plots import plot_objective, plot_evaluations
from skopt.utils import use_named_args
```
# Data Preparation
The dataset contains information about images, each image is a hand-written digit. The aim is to have the computer predict which digit was written by the person, automatically, by "looking" at the image.
Each image is 28 pixels in height and 28 pixels in width (28 x 28), making a total of 784 pixels. Each pixel value is an integer between 0 and 255, indicating the darkness in a gray-scale of that pixel.
The data is stored in a dataframe where each each pixel is a column (so it is flattened and not in the 28 x 28 format).
The data set the has 785 columns. The first column, called "label", is the digit that was drawn by the user. The rest of the columns contain the pixel-values of the associated image.
```
# Load the data
data = pd.read_csv("../mnist.csv")
# first column is the target, the rest of the columns
# are the pixels of the image
# each row is 1 image
data.head()
# split dataset into a train and test set
X_train, X_test, y_train, y_test = train_test_split(
data.drop(['label'], axis=1), # the images
data['label'], # the target
test_size = 0.1,
random_state=0)
X_train.shape, X_test.shape
# number of images for each digit
g = sns.countplot(x=y_train)
plt.xlabel('Digits')
plt.ylabel('Number of images')
```
There are roughly the same amount of images for each of the 10 digits.
## Image re-scaling
We re-scale data for the CNN, between 0 and 1.
```
# Re-scale the data
# 255 is the maximum value a pixel can take
X_train = X_train / 255
X_test = X_test / 255
```
## Reshape
The images were stored in a pandas dataframe as 1-D vectors of 784 values. For a CNN with Keras, we need tensors with the following dimensions: width x height x channel.
Thus, we reshape all data to 28 x 2 8 x 1, 3-D matrices.
The 3rd dimension corresponds to the channel. RGB images have 3 channels. MNIST images are in gray-scale, thus they have only one channel in the 3rd dimension.
```
# Reshape image in 3 dimensions:
# height: 28px X width: 28px X channel: 1
X_train = X_train.values.reshape(-1,28,28,1)
X_test = X_test.values.reshape(-1,28,28,1)
```
## Target encoding
```
# the target is 1 variable with the 9 different digits
# as values
y_train.unique()
# For Keras, we need to create 10 dummy variables,
# one for each digit
# Encode labels to one hot vectors (ex : digit 2 -> [0,0,1,0,0,0,0,0,0,0])
y_train = to_categorical(y_train, num_classes = 10)
y_test = to_categorical(y_test, num_classes = 10)
# the new target
y_train
```
Let's print some example images.
```
# Some image examples
g = plt.imshow(X_train[0][:,:,0])
# Some image examples
g = plt.imshow(X_train[10][:,:,0])
```
# Define the CNN
We will create a CNN, with 2 Convolutional layers followed by Pooling, and varying number of fully-connected Dense We will create a CNN, with 2 Convolutional layers followed by Pooling, and varying number of fully-connected Dense layers. Each Convlutional layer, can itself have more than 1 conv layer.
```
# function to create the CNN
def create_cnn(
# the hyperparam to optimize are passed
# as arguments
learning_rate,
num_conv_layers,
num_dense_layers,
num_dense_nodes,
activation,
):
"""
Hyper-parameters:
learning_rate: Learning-rate for the optimizer.
convolutional layers: Number of conv layers.
num_dense_layers: Number of dense layers.
num_dense_nodes: Number of nodes in each dense layer.
activation: Activation function for all layers.
"""
# Start construction of a Keras Sequential model.
model = Sequential()
# First convolutional layer.
# There are many hyper-parameters in this layer
# For this demo, we will optimize the activation function and
# the number of convolutional layers that it can take.
# We add the different number of conv layers in the following loop:
for i in range(num_conv_layers):
model.add(Conv2D(kernel_size=5, strides=1, filters=16, padding='same',
activation=activation))
model.add(MaxPool2D(pool_size=2, strides=2))
# Second convolutional layer.
# Same hyperparameters to optimize as previous layer.
for i in range(num_conv_layers):
model.add(Conv2D(kernel_size=5, strides=1, filters=36, padding='same',
activation=activation))
model.add(MaxPool2D(pool_size=2, strides=2))
# Flatten the 4-rank output of the convolutional layers
# to 2-rank that can be input to a fully-connected Dense layer.
model.add(Flatten())
# Add fully-connected Dense layers.
# The number of layers is a hyper-parameter we want to optimize.
# We add the different number of layers in the following loop:
for i in range(num_dense_layers):
# Add the dense fully-connected layer to the model.
# This has two hyper-parameters we want to optimize:
# The number of nodes (neurons) and the activation function.
model.add(Dense(num_dense_nodes,
activation=activation,
))
# Last fully-connected dense layer with softmax-activation
# for use in classification.
model.add(Dense(10, activation='softmax'))
# Use the Adam method for training the network.
# We want to find the best learning-rate for the Adam method.
optimizer = Adam(lr=learning_rate)
# In Keras we need to compile the model so it can be trained.
model.compile(optimizer=optimizer,
loss='categorical_crossentropy',
metrics=['accuracy'])
return model
```
# Define the Hyperparameter Space
Scikit-optimize provides an utility function to create the range of values to examine for each hyperparameters. More details in [skopt.Space](https://scikit-optimize.github.io/stable/modules/generated/skopt.Space.html)
We want to find the following hyper-parameters:
- The learning rate of the optimizer.
- The number of convolutional layers.
- The number of fully-connected Dense layers.
- The number of nodes (neurons) for each of the dense layers.
- Whether to use 'sigmoid' or 'relu' activation in all the layers.
```
dim_learning_rate = Real(
low=1e-6, high=1e-2, prior='log-uniform', name='learning_rate',
)
dim_num_conv_layers = Integer(low=1, high=3, name='num_conv_layers')
dim_num_dense_layers = Integer(low=1, high=5, name='num_dense_layers')
dim_num_dense_nodes = Integer(low=5, high=512, name='num_dense_nodes')
dim_activation = Categorical(
categories=['relu', 'sigmoid'], name='activation',
)
# the hyperparameter space grid
param_grid = [dim_learning_rate,
dim_num_conv_layers,
dim_num_dense_layers,
dim_num_dense_nodes,
dim_activation]
```
# Define the Objective Function
```
# we will save the model with this name
path_best_model = 'cnn_model.h5'
# starting point for the optimization
best_accuracy = 0
@use_named_args(param_grid)
def objective(
learning_rate,
num_conv_layers,
num_dense_layers,
num_dense_nodes,
activation,
):
"""
Hyper-parameters:
learning_rate: Learning-rate for the optimizer.
convolutional layers: Number of conv layers.
num_dense_layers: Number of dense layers.
num_dense_nodes: Number of nodes in each dense layer.
activation: Activation function for all layers.
"""
# Print the hyper-parameters.
print('learning rate: {0:.1e}'.format(learning_rate))
print('num_conv_layers:', num_conv_layers)
print('num_dense_layers:', num_dense_layers)
print('num_dense_nodes:', num_dense_nodes)
print('activation:', activation)
print()
# Create the neural network with the hyper-parameters.
# We call the function we created previously.
model = create_cnn(learning_rate=learning_rate,
num_conv_layers=num_conv_layers,
num_dense_layers=num_dense_layers,
num_dense_nodes=num_dense_nodes,
activation=activation)
# Set a learning rate annealer
# this reduces the learning rate if learning does not improve
# for a certain number of epochs
learning_rate_reduction = ReduceLROnPlateau(monitor='val_accuracy',
patience=2,
verbose=1,
factor=0.5,
min_lr=0.00001)
# train the model
# we use 3 epochs to be able to run the notebook in a "reasonable"
# time. If we increase the epochs, we will have better performance
# this could be another parameter to optimize in fact.
history = model.fit(x=X_train,
y=y_train,
epochs=3,
batch_size=128,
validation_split=0.1,
callbacks=learning_rate_reduction)
# Get the classification accuracy on the validation-set
# after the last training-epoch.
accuracy = history.history['val_accuracy'][-1]
# Print the classification accuracy.
print()
print("Accuracy: {0:.2%}".format(accuracy))
print()
# Save the model if it improves on the best-found performance.
# We use the global keyword so we update the variable outside
# of this function.
global best_accuracy
# If the classification accuracy of the saved model is improved ...
if accuracy > best_accuracy:
# Save the new model to harddisk.
# Training CNNs is costly, so we want to avoid having to re-train
# the network with the best found parameters. We save it instead
# as we search for the best hyperparam space.
model.save(path_best_model)
# Update the classification accuracy.
best_accuracy = accuracy
# Delete the Keras model with these hyper-parameters from memory.
del model
# Remember that Scikit-optimize always minimizes the objective
# function, so we need to negate the accuracy (because we want
# the maximum accuracy)
return -accuracy
```
## Test run
```
# Before we run the hyper-parameter optimization,
# let's first check that the everything is working
# by passing some default hyper-parameters.
default_parameters = [1e-5, 1, 1, 16, 'relu']
objective(x=default_parameters)
```
We obtained a mediocre accuracy, but all our code is working. So let's get started with the Optimization now!!
## Bayesian Optimization with Random Forests
- [forest_minimize](https://scikit-optimize.github.io/stable/modules/generated/skopt.forest_minimize.html#skopt.forest_minimize)
- [gbrt_minimize](https://scikit-optimize.github.io/stable/modules/generated/skopt.gbrt_minimize.html#skopt.gbrt_minimize)
```
# we approximate f(x) using Random Forests, we could
# also approximate it with gradient boosting machines
# using gbrt_minimize instead.
fm_ = forest_minimize(
objective, # the objective function to minimize
param_grid, # the hyperparameter space
x0=default_parameters, # the initial parameters to test
acq_func='EI', # the acquisition function
n_calls=30, # the number of subsequent evaluations of f(x)
random_state=0,
)
```
# Analyze results
```
# function value at the minimum.
# note that it is the negative of the accuracy
"Best score=%.4f" % fm_.fun
fm_.x
fm_.space
print("""Best parameters:
=========================
- learning rate=%.6f
- num_conv_laayers=%d
- num_dense_layers=%d
- num_nodes=%d
- activation = %s""" %(
fm_.x[0],
fm_.x[1],
fm_.x[2],
fm_.x[3],
fm_.x[4],
))
```
## Convergence
```
plot_convergence(fm_)
```
## Partially dependency plots
[plot_objective](https://scikit-optimize.github.io/stable/modules/generated/skopt.plots.plot_objective.html#skopt.plots.plot_objective)
```
dim_names = ['learning_rate', 'num_conv_layers', 'num_dense_layers', 'num_dense_nodes', 'activation']
plot_objective(result=fm_, plot_dims=dim_names)
plt.show()
```
## Evaluation order
[plot_evaluations](https://scikit-optimize.github.io/stable/modules/generated/skopt.plots.plot_evaluations.html)
```
plot_evaluations(result=fm_, plot_dims=dim_names)
plt.show()
```
# Evaluate the model
```
# load best model
model = load_model(path_best_model)
# make predictions in test set
result = model.evaluate(x=X_test,
y=y_test)
# print evaluation metrics
for name, value in zip(model.metrics_names, result):
print(name, value)
```
## Confusion matrix
```
# Predict the values from the validation dataset
y_pred = model.predict(X_test)
# Convert predictions classes to one hot vectors
y_pred_classes = np.argmax(y_pred, axis = 1)
# Convert validation observations to one hot vectors
y_true = np.argmax(y_test, axis = 1)
# compute the confusion matrix
cm = confusion_matrix(y_true, y_pred_classes)
cm
# let's make it more colourful
classes = 10
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion matrix')
plt.colorbar()
tick_marks = np.arange(classes)
plt.xticks(tick_marks, range(classes), rotation=45)
plt.yticks(tick_marks, range(classes))
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > 100 else "black",
)
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
```
Here we can see that our CNN performs very well on all digits.
# References
This notebook was based on these resources:
- [TensorFlow Tutorial #19](https://github.com/Hvass-Labs/TensorFlow-Tutorials/blob/master/19_Hyper-Parameters.ipynb)
- [Introduction to CNN Keras - 0.997 (top 6%)](https://www.kaggle.com/yassineghouzam/introduction-to-cnn-keras-0-997-top-6)
- [Keras](https://keras.io/)
# Exploring the Scikit-Optimize minimizer
```
fm_
# the accuracy
fm_.func_vals
# the hyperparameter combinations
fm_.x_iters
# all together in one dataframe, so we can investigate further
tmp = pd.concat([
pd.DataFrame(fm_.x_iters),
pd.Series(fm_.func_vals),
], axis=1)
tmp.columns = dim_names + ['accuracy']
tmp.head()
tmp.sort_values(by='accuracy', ascending=True, inplace=True)
tmp.head(10)
```
| true |
code
| 0.804137 | null | null | null | null |
|
# Leverage
Make sure to watch the video and slides for this lecture for the full explanation!
$ Leverage Ratio = \frac{Debt + Capital Base}{Capital Base}$
## Leverage from Algorithm
Make sure to watch the video for this! Basically run this and grab your own backtestid as shown in the video. More info:
The get_backtest function provides programmatic access to the results of backtests run on the Quantopian platform. It takes a single parameter, the ID of a backtest for which results are desired.
You can find the ID of a backtest in the URL of its full results page, which will be of the form:
https://www.quantopian.com/algorithms/<algorithm_id>/<backtest_id>.
You are only entitled to view the backtests that either:
* 1) you have created
* 2) you are a collaborator on
```
def initialize(context):
context.amzn = sid(16841)
context.ibm = sid(3766)
schedule_function(rebalance,date_rules.every_day(),time_rules.market_open())
schedule_function(record_vars,date_rules.every_day(),time_rules.market_close())
def rebalance(context,data):
order_target_percent(context.amzn,0.5)
order_target_percent(context.ibm,-0.5)
def record_vars(context,data):
record(amzn_close=data.current(context.amzn,'close'))
record(ibm_close=data.current(context.ibm,'close'))
record(Leverage = context.account.leverage)
record(Exposure = context.account.net_leverage)
```
## Backtest Info
```
bt = get_backtest('5986b969dbab994fa4264696')
bt.algo_id
bt.recorded_vars
bt.recorded_vars['Leverage'].plot()
bt.recorded_vars['Exposure'].plot()
```
## High Leverage Example
You can actually specify to borrow on margin (NOT RECOMMENDED)
```
def initialize(context):
context.amzn = sid(16841)
context.ibm = sid(3766)
schedule_function(rebalance,date_rules.every_day(),time_rules.market_open())
schedule_function(record_vars,date_rules.every_day(),time_rules.market_close())
def rebalance(context,data):
order_target_percent(context.ibm,-2.0)
order_target_percent(context.amzn,2.0)
def record_vars(context,data):
record(amzn_close=data.current(context.amzn,'close'))
record(ibm_close=data.current(context.ibm,'close'))
record(Leverage = context.account.leverage)
record(Exposure = context.account.net_leverage)
bt = get_backtest('5986bd68ceda5554428a005b')
bt.recorded_vars['Leverage'].plot()
```
## Set Hard Limit on Leverage
http://www.zipline.io/appendix.html?highlight=leverage#zipline.api.set_max_leverage
```
def initialize(context):
context.amzn = sid(16841)
context.ibm = sid(3766)
set_max_leverage(1.03)
schedule_function(rebalance,date_rules.every_day(),time_rules.market_open())
schedule_function(record_vars,date_rules.every_day(),time_rules.market_close())
def rebalance(context,data):
order_target_percent(context.ibm,-0.5)
order_target_percent(context.amzn,0.5)
def record_vars(context,data):
record(amzn_close=data.current(context.amzn,'close'))
record(ibm_close=data.current(context.ibm,'close'))
record(Leverage = context.account.leverage)
record(Exposure = context.account.net_leverage)
```
| true |
code
| 0.381594 | null | null | null | null |
|
[[source]](../api/alibi.confidence.model_linearity.rst)
# Measuring the linearity of machine learning models
## Overview
Machine learning models include in general linear and non-linear operations: neural networks may include several layers consisting of linear algebra operations followed by non-linear activation functions, while models based on decision trees are by nature highly non-linear. The linearity measure function and class provide an operational definition for the amount of non-linearity of a map acting on vector spaces. Roughly speaking, the amount of non-linearity of the map is defined based on how much the output of the map applied to a linear superposition of input vectors differs from the linear superposition of the map's outputs for each individual vector. In the context of supervised learning, this definition is immediately applicable to machine learning models, which are fundamentally maps from a input vector space (the feature space) to an output vector space that may represent probabilities (for classification models) or actual values of quantities of interest (for regression models).
Given an input vector space $V$, an output vector space $W$ and a map $M: V \rightarrow W$,
the amount of non-linearity of the map $M$ in a region $\beta$ of the input space $V$ and relative to some coefficients $\alpha(v)$ is defined as
$$
L_{\beta, \alpha}^{(M)} = \left\| \int_{\beta} \alpha(v) M(v) dv -
M\left(\int_{\beta}\alpha(v)vdv \right) \right\|,
$$
where $v \in V$ and $\|\cdot\|$ denotes the norm of a vector.
If we consider a finite number of vectors $N$, the amount of non-linearity can be defined as
$$
L_{\beta, \alpha}^{(M)} = \left\| \sum_{i} \alpha_{i} M(v_i) -
M\left(\sum_i \alpha_i v_i \right) \right\|,
$$
where, with an abuse of notation, $\beta$ is no longer a continuous region in
the input space but a collection of input vectors $\{v_i\}$ and $\alpha$ is no longer a function but a collection of real coefficients $\{\alpha_i \}$ with $i \in \{1, ..., N\}$. Note that the second expression may be interpreted as an approximation of the integral quantity defined in the first expression, where the vectors $\{v_i\}$ are sampled uniformly in the region $\beta$.
## Application to machine learning models
In supervised learning, a model can be considered as a function $M$ mapping vectors from the input space (feature vectors) to vectors in the output space. The output space may represents probabilities in the case of a classification model or values of the target quantities in the case of a regression model. The definition of the linearity measure given above can be applied to the case of a regression model (either a single target regression or a multi target regression) in a straightforward way.
In case of a classifier, let us denote by $z$ the logits vector of the model such that the probabilities of the model $M$ are given by $\text{softmax}(z).$ Since the activation function of the last layer is usually highly non-linear, it is convenient to apply the definition of linearity given above to the logits vector $z.$
In the "white box" scenario, in which we have access to the internal architecture of the model, the vector $z$ is accessible and the amount of non-linearity can be calculated immediately. On the other hand, if the only accessible quantities are the output probabilities (the "black box" scenario), we need to invert the last layer's activation function in order to retrieve $z.$ In other words, that means defining a new map $M^\prime = f^{-1} \circ M(v)$ where $f$ is the activation function at the last layer and considering $L_{\beta, \alpha}^{(M^\prime)}$ as a measure of the non-linearity of the model. The activation function of the last layer is usually a sigmoid function for binary classification tasks or a softmax function for multi-class classification.
The inversion of the sigmoid function does not present any particular challenge, and the map $M^\prime$ can be written as
$$
M^\prime = -\log \circ \left(\frac{1-M(v)}{M(v)}\right).
$$
On the other hand, the softmax probabilities $p$ are defined in terms of the vector $z$ as $p_j = e^{z_j}/\sum_j{e^{z_j}},$ where $z_j$ are the components of $z$. The inverse of the softmax function is thus defined up to a constant $C$ which does not depend on $j$ but might depend on the input vector $v.$ The inverse map $M^\prime = \text{softmax}^{-1} \circ M(v)$ is then given by:
$$
M^\prime = \log \circ M(v) + C(v),
$$
where $C(v)$ is an arbitrary constant depending in general on the input vector $v.$
Since in the black box scenario it is not possible to assess the value of $C$, henceforth we will ignore it and define the amount of non-linearity of a machine learning model whose output is a probability distribution as
$$
L_{\beta, \alpha}^{(\log \circ M)} = \left\| \sum_{i}^N \alpha_{i} \log \circ M(v_i) -
\log \circ M\left(\sum_i^N \alpha_i v_i \right)\right\|.
$$
It must be noted that the quantity above may in general be different from the "actual" amount of non-linearity of the model, i.e. the quantity calculated by accessing the activation vectors $z$ directly.
## Implementation
### Sampling
The module implements two different methods for the sampling of vectors in a neighbourhood of the instance of interest $v.$
* The first sampling method ```grid``` consists of defining the region $\beta$ as a discrete lattice of a given size around the instance of interest, with the size defined in terms of the L1 distance in the lattice; the vectors are then sampled from the lattice according to a uniform distribution. The density and the size of the lattice are controlled by the resolution parameter ```res``` and the size parameter ```epsilon```. This method is highly efficient and scalable from a computational point of view.
* The second sampling method ```knn``` consists of sampling from the same probability distribution the instance $v$ was drawn from; this method is implemented by simply selecting the $K$ nearest neighbours to $v$ from a training set, when this is available. The ```knn``` method imposes the constraint that the neighbourhood of $v$ must include only vectors from the training set, and as a consequence it will exclude out-of-distribution instances from the computation of linearity.
### Pairwise vs global linearity
The module implements two different methods to associate a value of the linearity measure to $v.$
* The first method consists of measuring the ```global``` linearity in a region around $v.$ This means that we sample $N$ vectors $\{v_i\}$ from a region $\beta$ of the input space around $v$ and apply
\begin{equation}
L_{\beta, \alpha}^{(M)} = \left\| \sum_{i=1}^N \alpha_{i} M(v_i) -
M\left(\sum_{i=1}^N \alpha_i v_i \right) \right\|,
\end{equation}
* The second method consists of measuring the ```pairwise``` linearity between the instance of interest and other vectors close to it, averaging over all such pairs. In other words, we sample $N$ vectors $\{v_i\}$ from $\beta$ as in the global method, but in this case we calculate the amount of non-linearity $L_{(v,v_i),\alpha}$ for every pair of vectors $(v, v_i)$ and average over all the pairs. Given two coefficients $\{\alpha_0, \alpha_1\}$ such that $\alpha_0 + \alpha_1 = 1,$ we can define the pairwise linearity measure relative to the instance of interest $v$ as
\begin{equation}\label{pairwiselin}
L^{(M)} = \frac{1}{N} \sum_{i=0}^N \left\|\alpha_0 M(v) + \alpha_1 M(v_i) - M(\alpha_0 v + \alpha_1 v_i)\right\|.
\end{equation}
The two methods are slightly different from a conceptual point of view: the global linearity measure combines all $N$ vectors sampled in $\beta$ in a single superposition, and can be conceptually regarded as a direct approximation of the integral quantity. Thus, the quantity is strongly linked to the model behavior in the whole region $\beta.$ On the other hand, the pairwise linearity measure is an averaged quantity over pairs of superimposed vectors, with the instance of interest $v$ included in each pair. For that reason, it is conceptually more tied to the instance $v$ itself rather than the region $\beta$ around it.
## Usage
### LinearityMeasure class
Given a ```model``` class with a ```predict``` method that return probabilities distribution in case of a classifier or numeric values in case of a regressor, the linearity measure $L$ around an instance of interest $X$ can be calculated using the class ```LinearityMeasure``` as follows:
```python
from alibi.confidence.model_linearity import LinearityMeasure
predict_fn = lambda x: model.predict(x)
lm = LinearityMeasure(method='grid',
epsilon=0.04,
nb_samples=10,
res=100,
alphas=None,
model_type='classifier',
agg='pairwise',
verbose=False)
lm.fit(X_train)
L = lm.score(predict_fn, X)
```
Where `x_train` is the dataset the model was trained on. The ```feature_range``` is inferred form `x_train` in the ```fit``` step.
### linearity_measure function
Given a ```model``` class with a ```predict``` method that return probabilities distribution in case of a classifier or numeric values in case of a regressor, the linearity measure $L$ around an instance of interest $X$ can also be calculated using the ```linearity_measure``` function as follows:
```python
from alibi.confidence.model_linearity import linearity_measure, _infer_feature_range
predict_fn = lambda x: model.predict(x)
feature_range = _infer_feature_range(X_train)
L = linearity_measure(predict_fn,
X,
feature_range=feature_range
method='grid',
X_train=None,
epsilon=0.04,
nb_samples=10,
res=100,
alphas=None,
agg='global',
model_type='classifier')
```
Note that in this case the ```feature_range``` must be explicitly passed to the function and it is inferred beforehand.
## Examples
[Iris dataset](../examples/linearity_measure_iris.nblink)
[Fashion MNIST dataset](../examples/linearity_measure_fashion_mnist.nblink)
| true |
code
| 0.935199 | null | null | null | null |
|
# 12 - Introduction to Deep Learning
by [Alejandro Correa Bahnsen](albahnsen.com/)
version 0.1, May 2016
## Part of the class [Machine Learning for Security Informatics](https://github.com/albahnsen/ML_SecurityInformatics)
This notebook is licensed under a [Creative Commons Attribution-ShareAlike 3.0 Unported License](http://creativecommons.org/licenses/by-sa/3.0/deed.en_US)
Based on the slides and presentation by [Alec Radford](https://www.youtube.com/watch?v=S75EdAcXHKk) [github](https://github.com/Newmu/Theano-Tutorials/)
For this class you must install theno
```pip instal theano```
# Motivation
How do we program a computer to recognize a picture of a
handwritten digit as a 0-9?

### What if we have 60,000 of these images and their label?
```
import numpy as np
from load import mnist
X_train, X_test, y_train2, y_test2 = mnist(onehot=True)
y_train = np.argmax(y_train2, axis=1)
y_test = np.argmax(y_test2, axis=1)
X_train[1].reshape((28, 28)).round(2)[:, 4:9].tolist()
from pylab import imshow, show, cm
import matplotlib.pylab as plt
%matplotlib inline
def view_image(image, label="", predicted='', size=4):
"""View a single image."""
plt.figure(figsize = (size, size))
plt.imshow(image.reshape((28, 28)), cmap=cm.gray, )
plt.tick_params(axis='x',which='both', bottom='off',top='off', labelbottom='off')
plt.tick_params(axis='y',which='both', left='off',top='off', labelleft='off')
show()
if predicted == '':
print("Label: %s" % label)
else:
print('Label: ', str(label), 'Predicted: ', str(predicted))
view_image(X_train[1], y_train[1])
view_image(X_train[40000], y_train[40000])
```
# Naive model
For each image, find the “most similar” image and guess
that as the label
```
def similarity(image, images):
similarities = []
image = image.reshape((28, 28))
images = images.reshape((-1, 28, 28))
for i in range(images.shape[0]):
distance = np.sqrt(np.sum(image - images[i]) ** 2)
sim = 1 / distance
similarities.append(sim)
return similarities
np.random.seed(52)
small_train = np.random.choice(X_train.shape[0], 100)
view_image(X_test[0])
similarities = similarity(X_test[0], X_train[small_train])
view_image(X_train[small_train[np.argmax(similarities)]])
```
Lets try an other example
```
view_image(X_test[200])
similarities = similarity(X_test[200], X_train[small_train])
view_image(X_train[small_train[np.argmax(similarities)]])
```
# Logistic Regression
Logistic regression is a probabilistic, linear classifier. It is parametrized
by a weight matrix $W$ and a bias vector $b$ Classification is
done by projecting data points onto a set of hyperplanes, the distance to
which is used to determine a class membership probability.
Mathematically, this can be written as:
$$
P(Y=i\vert x, W,b) = softmax_i(W x + b)
$$
$$
P(Y=i|x, W,b) = \frac {e^{W_i x + b_i}} {\sum_j e^{W_j x + b_j}}
$$
The output of the model or prediction is then done by taking the argmax of
the vector whose i'th element is $P(Y=i|x)$.
$$
y_{pred} = argmax_i P(Y=i|x,W,b)
$$

```
import theano
from theano import tensor as T
import numpy as np
import datetime as dt
theano.config.floatX = 'float32'
```
```
Theano is a Python library that lets you to define, optimize, and evaluate mathematical expressions, especially ones with multi-dimensional arrays (numpy.ndarray). Using Theano it is possible to attain speeds rivaling hand-crafted C implementations for problems involving large amounts of data. It can also surpass C on a CPU by many orders of magnitude by taking advantage of recent GPUs.
Theano combines aspects of a computer algebra system (CAS) with aspects of an optimizing compiler. It can also generate customized C code for many mathematical operations. This combination of CAS with optimizing compilation is particularly useful for tasks in which complicated mathematical expressions are evaluated repeatedly and evaluation speed is critical. For situations where many different expressions are each evaluated once Theano can minimize the amount of compilation/analysis overhead, but still provide symbolic features such as automatic differentiation.
```
```
def floatX(X):
# return np.asarray(X, dtype='float32')
return np.asarray(X, dtype=theano.config.floatX)
def init_weights(shape):
return theano.shared(floatX(np.random.randn(*shape) * 0.01))
def model(X, w):
return T.nnet.softmax(T.dot(X, w))
X = T.fmatrix()
Y = T.fmatrix()
w = init_weights((784, 10))
w.get_value()
```
initialize model
```
py_x = model(X, w)
y_pred = T.argmax(py_x, axis=1)
cost = T.mean(T.nnet.categorical_crossentropy(py_x, Y))
gradient = T.grad(cost=cost, wrt=w)
update = [[w, w - gradient * 0.05]]
train = theano.function(inputs=[X, Y], outputs=cost, updates=update, allow_input_downcast=True)
predict = theano.function(inputs=[X], outputs=y_pred, allow_input_downcast=True)
```
One iteration
```
for start, end in zip(range(0, X_train.shape[0], 128), range(128, X_train.shape[0], 128)):
cost = train(X_train[start:end], y_train2[start:end])
errors = [(np.mean(y_train != predict(X_train)),
np.mean(y_test != predict(X_test)))]
errors
```
Now for 100 epochs
```
t0 = dt.datetime.now()
for i in range(100):
for start, end in zip(range(0, X_train.shape[0], 128),
range(128, X_train.shape[0], 128)):
cost = train(X_train[start:end], y_train2[start:end])
errors.append((np.mean(y_train != predict(X_train)),
np.mean(y_test != predict(X_test))))
print(i, errors[-1])
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
res = np.array(errors)
plt.plot(np.arange(res.shape[0]), res[:, 0], label='train error')
plt.plot(np.arange(res.shape[0]), res[:, 1], label='test error')
plt.legend()
```
### Checking the results
```
y_pred = predict(X_test)
np.random.seed(2)
small_test = np.random.choice(X_test.shape[0], 10)
for i in small_test:
view_image(X_test[i], label=y_test[i], predicted=y_pred[i], size=1)
```
# Simple Neural Net
Add a hidden layer with a sigmoid activation function

```
def sgd(cost, params, lr=0.05):
grads = T.grad(cost=cost, wrt=params)
updates = []
for p, g in zip(params, grads):
updates.append([p, p - g * lr])
return updates
def model(X, w_h, w_o):
h = T.nnet.sigmoid(T.dot(X, w_h))
pyx = T.nnet.softmax(T.dot(h, w_o))
return pyx
w_h = init_weights((784, 625))
w_o = init_weights((625, 10))
py_x = model(X, w_h, w_o)
y_x = T.argmax(py_x, axis=1)
cost = T.mean(T.nnet.categorical_crossentropy(py_x, Y))
params = [w_h, w_o]
updates = sgd(cost, params)
train = theano.function(inputs=[X, Y], outputs=cost, updates=updates, allow_input_downcast=True)
predict = theano.function(inputs=[X], outputs=y_x, allow_input_downcast=True)
t0 = dt.datetime.now()
errors = []
for i in range(100):
for start, end in zip(range(0, X_train.shape[0], 128),
range(128, X_train.shape[0], 128)):
cost = train(X_train[start:end], y_train2[start:end])
errors.append((np.mean(y_train != predict(X_train)),
np.mean(y_test != predict(X_test))))
print(i, errors[-1])
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
res = np.array(errors)
plt.plot(np.arange(res.shape[0]), res[:, 0], label='train error')
plt.plot(np.arange(res.shape[0]), res[:, 1], label='test error')
plt.legend()
```
# Complex Neural Net
Two hidden layers with dropout

```
from theano.sandbox.rng_mrg import MRG_RandomStreams as RandomStreams
srng = RandomStreams()
def rectify(X):
return T.maximum(X, 0.)
```
### Understanding rectifier units

```
def RMSprop(cost, params, lr=0.001, rho=0.9, epsilon=1e-6):
grads = T.grad(cost=cost, wrt=params)
updates = []
for p, g in zip(params, grads):
acc = theano.shared(p.get_value() * 0.)
acc_new = rho * acc + (1 - rho) * g ** 2
gradient_scaling = T.sqrt(acc_new + epsilon)
g = g / gradient_scaling
updates.append((acc, acc_new))
updates.append((p, p - lr * g))
return updates
```
### RMSprop
RMSprop is an unpublished, adaptive learning rate method proposed by Geoff Hinton in
[Lecture 6e of his Coursera Class](http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf)
RMSprop and Adadelta have both been developed independently around the same time stemming from the need to resolve Adagrad's radically diminishing learning rates. RMSprop in fact is identical to the first update vector of Adadelta that we derived above:
$$ E[g^2]_t = 0.9 E[g^2]_{t-1} + 0.1 g^2_t. $$
$$\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}.$$
RMSprop as well divides the learning rate by an exponentially decaying average of squared gradients. Hinton suggests $\gamma$ to be set to 0.9, while a good default value for the learning rate $\eta$ is 0.001.
```
def dropout(X, p=0.):
if p > 0:
retain_prob = 1 - p
X *= srng.binomial(X.shape, p=retain_prob, dtype=theano.config.floatX)
X /= retain_prob
return X
def model(X, w_h, w_h2, w_o, p_drop_input, p_drop_hidden):
X = dropout(X, p_drop_input)
h = rectify(T.dot(X, w_h))
h = dropout(h, p_drop_hidden)
h2 = rectify(T.dot(h, w_h2))
h2 = dropout(h2, p_drop_hidden)
py_x = softmax(T.dot(h2, w_o))
return h, h2, py_x
def softmax(X):
e_x = T.exp(X - X.max(axis=1).dimshuffle(0, 'x'))
return e_x / e_x.sum(axis=1).dimshuffle(0, 'x')
w_h = init_weights((784, 625))
w_h2 = init_weights((625, 625))
w_o = init_weights((625, 10))
noise_h, noise_h2, noise_py_x = model(X, w_h, w_h2, w_o, 0.2, 0.5)
h, h2, py_x = model(X, w_h, w_h2, w_o, 0., 0.)
y_x = T.argmax(py_x, axis=1)
cost = T.mean(T.nnet.categorical_crossentropy(noise_py_x, Y))
params = [w_h, w_h2, w_o]
updates = RMSprop(cost, params, lr=0.001)
train = theano.function(inputs=[X, Y], outputs=cost, updates=updates, allow_input_downcast=True)
predict = theano.function(inputs=[X], outputs=y_x, allow_input_downcast=True)
t0 = dt.datetime.now()
errors = []
for i in range(100):
for start, end in zip(range(0, X_train.shape[0], 128),
range(128, X_train.shape[0], 128)):
cost = train(X_train[start:end], y_train2[start:end])
errors.append((np.mean(y_train != predict(X_train)),
np.mean(y_test != predict(X_test))))
print(i, errors[-1])
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
res = np.array(errors)
plt.plot(np.arange(res.shape[0]), res[:, 0], label='train error')
plt.plot(np.arange(res.shape[0]), res[:, 1], label='test error')
plt.legend()
```
# Convolutional Neural Network
In machine learning, a convolutional neural network (CNN, or ConvNet) is a type of feed-forward artificial neural network in which the connectivity pattern between its neurons is inspired by the organization of the animal visual cortex, whose individual neurons are arranged in such a way that they respond to overlapping regions tiling the visual field. Convolutional networks were inspired by biological processes and are variations of multilayer perceptrons designed to use minimal amounts of preprocessing. (Wikipedia)

### Motivation
Convolutional Neural Networks (CNN) are biologically-inspired variants of MLPs.
From Hubel and Wiesel's early work on the cat's visual cortex, we
know the visual cortex contains a complex arrangement of cells. These cells are
sensitive to small sub-regions of the visual field, called a *receptive
field*. The sub-regions are tiled to cover the entire visual field. These
cells act as local filters over the input space and are well-suited to exploit
the strong spatially local correlation present in natural images.
Additionally, two basic cell types have been identified: Simple cells respond
maximally to specific edge-like patterns within their receptive field. Complex
cells have larger receptive fields and are locally invariant to the exact
position of the pattern.
The animal visual cortex being the most powerful visual processing system in
existence, it seems natural to emulate its behavior. Hence, many
neurally-inspired models can be found in the literature.
### Sparse Connectivity
CNNs exploit spatially-local correlation by enforcing a local connectivity
pattern between neurons of adjacent layers. In other words, the inputs of
hidden units in layer **m** are from a subset of units in layer **m-1**, units
that have spatially contiguous receptive fields. We can illustrate this
graphically as follows:

Imagine that layer **m-1** is the input retina. In the above figure, units in
layer **m** have receptive fields of width 3 in the input retina and are thus
only connected to 3 adjacent neurons in the retina layer. Units in layer
**m+1** have a similar connectivity with the layer below. We say that their
receptive field with respect to the layer below is also 3, but their receptive
field with respect to the input is larger (5). Each unit is unresponsive to
variations outside of its receptive field with respect to the retina. The
architecture thus ensures that the learnt "filters" produce the strongest
response to a spatially local input pattern.
However, as shown above, stacking many such layers leads to (non-linear)
"filters" that become increasingly "global" (i.e. responsive to a larger region
of pixel space). For example, the unit in hidden layer **m+1** can encode a
non-linear feature of width 5 (in terms of pixel space).
### Shared Weights
In addition, in CNNs, each filter $h_i$ is replicated across the entire
visual field. These replicated units share the same parameterization (weight
vector and bias) and form a *feature map*.

In the above figure, we show 3 hidden units belonging to the same feature map.
Weights of the same color are shared---constrained to be identical. Gradient
descent can still be used to learn such shared parameters, with only a small
change to the original algorithm. The gradient of a shared weight is simply the
sum of the gradients of the parameters being shared.
Replicating units in this way allows for features to be detected *regardless
of their position in the visual field.* Additionally, weight sharing increases
learning efficiency by greatly reducing the number of free parameters being
learnt. The constraints on the model enable CNNs to achieve better
generalization on vision problems.
### Details and Notation
A feature map is obtained by repeated application of a function across
sub-regions of the entire image, in other words, by *convolution* of the
input image with a linear filter, adding a bias term and then applying a
non-linear function. If we denote the k-th feature map at a given layer as
$h^k$, whose filters are determined by the weights $W^k$ and bias
$b_k$, then the feature map $h^k$ is obtained as follows (for
$tanh$ non-linearities):
$$
h^k_{ij} = \tanh ( (W^k * x)_{ij} + b_k ).
$$
Note
* Recall the following definition of convolution for a 1D signal.
$$ o[n] = f[n]*g[n] = \sum_{u=-\infty}^{\infty} f[u] g[n-u] = \sum_{u=-\infty}^{\infty} f[n-u] g[u]`.
$$
* This can be extended to 2D as follows:
$$o[m,n] = f[m,n]*g[m,n] = \sum_{u=-\infty}^{\infty} \sum_{v=-\infty}^{\infty} f[u,v] g[m-u,n-v]`.
$$
To form a richer representation of the data, each hidden layer is composed of
*multiple* feature maps, $\{h^{(k)}, k=0..K\}$. The weights $W$ of
a hidden layer can be represented in a 4D tensor containing elements for every
combination of destination feature map, source feature map, source vertical
position, and source horizontal position. The biases $b$ can be
represented as a vector containing one element for every destination feature
map. We illustrate this graphically as follows:
**Figure 1**: example of a convolutional layer

The figure shows two layers of a CNN. **Layer m-1** contains four feature maps.
**Hidden layer m** contains two feature maps ($h^0$ and $h^1$).
Pixels (neuron outputs) in $h^0$ and $h^1$ (outlined as blue and
red squares) are computed from pixels of layer (m-1) which fall within their
2x2 receptive field in the layer below (shown as colored rectangles). Notice
how the receptive field spans all four input feature maps. The weights
$W^0$ and $W^1$ of $h^0$ and $h^1$ are thus 3D weight
tensors. The leading dimension indexes the input feature maps, while the other
two refer to the pixel coordinates.
Putting it all together, $W^{kl}_{ij}$ denotes the weight connecting
each pixel of the k-th feature map at layer m, with the pixel at coordinates
(i,j) of the l-th feature map of layer (m-1).
### The Convolution Operator
ConvOp is the main workhorse for implementing a convolutional layer in Theano.
ConvOp is used by ``theano.tensor.signal.conv2d``, which takes two symbolic inputs:
* a 4D tensor corresponding to a mini-batch of input images. The shape of the
tensor is as follows: [mini-batch size, number of input feature maps, image
height, image width].
* a 4D tensor corresponding to the weight matrix $W$. The shape of the
tensor is: [number of feature maps at layer m, number of feature maps at
layer m-1, filter height, filter width]
### MaxPooling
Another important concept of CNNs is *max-pooling,* which is a form of
non-linear down-sampling. Max-pooling partitions the input image into
a set of non-overlapping rectangles and, for each such sub-region, outputs the
maximum value.
Max-pooling is useful in vision for two reasons:
* By eliminating non-maximal values, it reduces computation for upper layers.
* It provides a form of translation invariance. Imagine
cascading a max-pooling layer with a convolutional layer. There are 8
directions in which one can translate the input image by a single pixel.
If max-pooling is done over a 2x2 region, 3 out of these 8 possible
configurations will produce exactly the same output at the convolutional
layer. For max-pooling over a 3x3 window, this jumps to 5/8.
Since it provides additional robustness to position, max-pooling is a
"smart" way of reducing the dimensionality of intermediate representations.
Max-pooling is done in Theano by way of
``theano.tensor.signal.downsample.max_pool_2d``. This function takes as input
an N dimensional tensor (where N >= 2) and a downscaling factor and performs
max-pooling over the 2 trailing dimensions of the tensor.
### The Full Model: CovNet
Sparse, convolutional layers and max-pooling are at the heart of the LeNet
family of models. While the exact details of the model will vary greatly,
the figure below shows a graphical depiction of a LeNet model.

The lower-layers are composed to alternating convolution and max-pooling
layers. The upper-layers however are fully-connected and correspond to a
traditional MLP (hidden layer + logistic regression). The input to the
first fully-connected layer is the set of all features maps at the layer
below.
From an implementation point of view, this means lower-layers operate on 4D
tensors. These are then flattened to a 2D matrix of rasterized feature maps,
to be compatible with our previous MLP implementation.
```
# from theano.tensor.nnet.conv import conv2d
from theano.tensor.nnet import conv2d
from theano.tensor.signal.downsample import max_pool_2d
```
Modify dropout function
```
def model(X, w, w2, w3, w4, w_o, p_drop_conv, p_drop_hidden):
l1a = rectify(conv2d(X, w, border_mode='full'))
l1 = max_pool_2d(l1a, (2, 2))
l1 = dropout(l1, p_drop_conv)
l2a = rectify(conv2d(l1, w2))
l2 = max_pool_2d(l2a, (2, 2))
l2 = dropout(l2, p_drop_conv)
l3a = rectify(conv2d(l2, w3))
l3b = max_pool_2d(l3a, (2, 2))
# convert from 4tensor to normal matrix
l3 = T.flatten(l3b, outdim=2)
l3 = dropout(l3, p_drop_conv)
l4 = rectify(T.dot(l3, w4))
l4 = dropout(l4, p_drop_hidden)
pyx = softmax(T.dot(l4, w_o))
return l1, l2, l3, l4, pyx
```
reshape into conv 4tensor (b, c, 0, 1) format
```
X_train2 = X_train.reshape(-1, 1, 28, 28)
X_test2 = X_test.reshape(-1, 1, 28, 28)
# now 4tensor for conv instead of matrix
X = T.ftensor4()
Y = T.fmatrix()
w = init_weights((32, 1, 3, 3))
w2 = init_weights((64, 32, 3, 3))
w3 = init_weights((128, 64, 3, 3))
w4 = init_weights((128 * 3 * 3, 625))
w_o = init_weights((625, 10))
noise_l1, noise_l2, noise_l3, noise_l4, noise_py_x = model(X, w, w2, w3, w4, w_o, 0.2, 0.5)
l1, l2, l3, l4, py_x = model(X, w, w2, w3, w4, w_o, 0., 0.)
y_x = T.argmax(py_x, axis=1)
cost = T.mean(T.nnet.categorical_crossentropy(noise_py_x, Y))
params = [w, w2, w3, w4, w_o]
updates = RMSprop(cost, params, lr=0.001)
train = theano.function(inputs=[X, Y], outputs=cost, updates=updates, allow_input_downcast=True)
predict = theano.function(inputs=[X], outputs=y_x, allow_input_downcast=True)
t0 = dt.datetime.now()
errors = []
for i in range(100):
t1 = dt.datetime.now()
for start, end in zip(range(0, X_train.shape[0], 128),
range(128, X_train.shape[0], 128)):
cost = train(X_train2[start:end], y_train2[start:end])
errors.append((np.mean(y_train != predict(X_train2)),
np.mean(y_test != predict(X_test2))))
print(i, errors[-1])
print('Current iter time: ', (dt.datetime.now()-t1).seconds / 60.)
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
res = np.array(errors)
plt.plot(np.arange(res.shape[0]), res[:, 0], label='train error')
plt.plot(np.arange(res.shape[0]), res[:, 1], label='test error')
plt.legend()
```
# Even more complex networks
## GoogLeNet

[examples](http://www.csc.kth.se/~roelof/deepdream/bvlc_googlenet.html)
| true |
code
| 0.843831 | null | null | null | null |
|
# License
***
Copyright (C) 2017 J. Patrick Hall, jphall@gwu.edu
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
***
# **Basic** Gradient Descent for Multiple Linear Regression
```
# imports
import pandas as pd # import pandas for easy data manipulation using data frames
import numpy as np # import numpy for numeric calculations on matrices
import time # for timers
# import h2o to check calculations
import h2o
from h2o.estimators.glm import H2OGeneralizedLinearEstimator
```
#### Assign global constants
```
# data-related constants
IN_FILE_PATH = '../data/loan_clean.csv'
Y = 'STD_IMP_REP_loan_amnt'
DROPS = ['id', 'GRP_REP_home_ownership', 'GRP_addr_state', 'GRP_home_ownership',
'GRP_purpose', 'GRP_verification_status', '_WARN_']
# model-related constants
LEARN_RATE = 0.005 # how much each gradient descent step impacts parameters
CONV = 1e-10 # desired precision in parameters
MAX_ITERS = 10000 # maximum number of gradient descent steps to allow
```
### Import clean data and convert to numpy matrices
```
# import data using Pandas
raw = pd.read_csv(IN_FILE_PATH)
# select target column
y = raw[Y].as_matrix()
print(y)
# create input matrix
# add an additional column of 1's for intercept
# by overlaying inputs onto matrix of 1's
numeric = raw.drop(DROPS + [Y], axis=1).as_matrix()
N, p = numeric.shape
X = np.ones(shape=(N, p + 1))
X[:,1:] = numeric
print(X)
```
### Basic Gradient Descent Routines
#### Define squared loss function
* For linear regression, we minimize the squared distance between the regression plane and points in the conditional distribution of **y** given **X**.
* It is convenient to use a scaled mean squared error (MSE) formula:
```
def squared_loss(n, x, y, betas):
""" Squared loss function for multiple linear regression.
:param n: Number of rows in x.
:param x: Matrix of numeric inputs.
:param y: Vector of known target values.
:param beta: Vector or current model parameters.
:return: Scalar MSE value.
"""
yhat = x.dot(betas)
return ((1 / (2 * n)) * (y - yhat)**2).sum()
```
#### Define gradient of loss function
* The derivative of the loss function w.r.t the model parameters is used to update model parameters at each gradient descent step.
* The gradient of our MSE loss function is trivial:
```
def grad(n, y, yhat):
""" Analytical gradient of scaled MSE loss function.
:param n: Number of rows in X.
:param y: Vector of known target values.
:param yhat: Vector of predicted target values.
:return: Vector of gradient values.
"""
return ((1 / n)*(yhat - y))
```
#### Define function for executing gradient descent minimization
For each gradient descent step:
* Predictions are made using the current model parameters.
* The gradient is calculated for each model pararmeter.
* The gradient is used in combination with the learning rate to update each parameter.
```
def grad_descent(X, y, learn_rate, max_iters, sgd_mini_batch_n=0):
""" Routine for executing simple gradient descent with stochastic gradient descent option.
:param X: Matrix of numeric data.
:param y: Vector of known target values.
:param learn_rate: Learning rate.
:param max_iters: Maximum number of gradient descent steps to perform.
:param sgd_mini_batch_n: Minibatch size for sgd optimization.
If > 0 minibatch stochastic gradient descent is performed.
"""
tic = time.time() # start timer
n_betas = X.shape[1] # number of model parameters including bias
betas = np.zeros(shape=n_betas) # parameters start with value of 0
n = y.shape[0] # number of rows in X
# Pandas dataframe for iteration history
iteration_frame = pd.DataFrame(columns=['Iteration', 'Loss'])
print('Iteration history:')
# loop for gradient descent steps
for i in range(max_iters):
# stochastic gradient descent
if sgd_mini_batch_n > 0:
samp_idx = np.random.randint(n, size=sgd_mini_batch_n)
X_samp = X[samp_idx, :]
y_samp = y[samp_idx]
n_samp = X_samp.shape[0]
yhat_samp = X_samp.dot(betas) # model predictions for iteration
# loop for column-wise parameter updates
for j in range(n_betas):
# select column
# calculate column-wise gradient
# update corresponding parameter based on negative gradient
# calculate loss
xj_samp = X_samp[:, j]
xj_grad_samp = grad(n_samp, y_samp, yhat_samp) * xj_samp
betas[j] = betas[j] - learn_rate * xj_grad_samp.sum()
iter_loss = squared_loss(n_samp, X_samp, y_samp, betas)
# standard gradient descent
else:
yhat = X.dot(betas) # model predictions for iteration
# loop for column-wise parameter updates
for j in range(n_betas):
xj = X[:, j]
xj_grad = grad(n, y, yhat) * xj
betas[j] = betas[j] - learn_rate * xj_grad.sum()
iter_loss = squared_loss(n, X, y, betas)
# update loss history
iteration_frame = iteration_frame.append({'Iteration': i,
'Loss': iter_loss},
ignore_index=True)
# progress indicator
if i % 1000 == 0:
print('iter=%d loss=%.6f' % (i, iter_loss))
# convergence check
if i > 0:
if np.abs(iteration_frame.iat[i-1, 1] - iteration_frame.iat[i, 1]) < CONV:
break
# output
%matplotlib inline
iteration_frame.plot.line(title='Iteration Plot', x='Iteration', y='Loss')
print()
print('Model parameters at iteration ' + str(i) + ':')
print(betas)
print()
print('Model trained in %.2f s.' % (time.time()-tic))
```
#### Execute gradient descent
```
grad_descent(X, y, LEARN_RATE, MAX_ITERS)
```
#### Execute stochastic gradient descent
```
grad_descent(X, y, LEARN_RATE, MAX_ITERS, sgd_mini_batch_n=1000)
```
### Use h2o to check model parameters
```
# start h2o
h2o.init()
DROPS = ['id', 'GRP_REP_home_ownership', 'GRP_addr_state', 'GRP_home_ownership',
'GRP_purpose', 'GRP_verification_status', '_WARN_']
# numeric columns
train = h2o.import_file(IN_FILE_PATH)
train = train.drop(DROPS)
X = train.col_names
# initialize non-penalized GLM model
loan_glm = H2OGeneralizedLinearEstimator(family='gaussian', # uses squared error
solver='IRLSM', # necessary for non-penalized GLM
standardize=False, # data is already standardized
compute_p_values=True, # necessary for non-penalized GLM
lambda_=0) # necessary for non-penalized GLM
# train
loan_glm.train(train.col_names, Y, training_frame=train)
# print trained model info
print()
print('Model parameters:')
for name, val in loan_glm.coef().items():
print(name, val)
print()
# shutdown h2o
h2o.cluster().shutdown()
```
| true |
code
| 0.59972 | null | null | null | null |
|
# Song Gathering
**JC Nacpil 2021/09/06**
In this notebook, we will build a database of Kpop songs with audio features using the Spotify Web API and Spotipy package. The output files will be used for `KpopSongRecommender`.
## Set-up
### Importing libraries
```
# Library for accessing Spotify API
import spotipy
import spotipy.util as util
from spotipy.oauth2 import SpotifyClientCredentials
from spotipy.oauth2 import SpotifyOAuth
# Scientific and vector computation for python
import numpy as np
# Data manipulation and analysis
import pandas as pd
# Library for this notebook providing utilitiy functions
from utils import repeatAPICall
# Progress bar
from tqdm import tqdm
# Cosine similarity calculation
from sklearn.metrics.pairwise import cosine_similarity
# Deep copy of python data structures
from copy import deepcopy
# Plotting library
import matplotlib.pyplot as plt
```
### Setting up Spotify API
The following are the Spotiy API credentials `CLIENT_ID` and `CLIENT_SECRET` for our application. This allows us to access data from Spotify through the <a href='https://developer.spotify.com/documentation/web-api/'>Web API</a>. It is recommended to register your own application and manage these credentials at <a href = "https://developer.spotify.com/dashboard/">My Dashboard</a>.
```
CLIENT_ID = "dc7ef763416f49aca20c740e46bd1f79"
CLIENT_SECRET = "056f146106544a828574e8e903286fb7"
token = SpotifyClientCredentials(client_id=CLIENT_ID, client_secret=CLIENT_SECRET)
cache_token = token.get_access_token(as_dict = False)
sp = spotipy.Spotify(cache_token)
```
### Utility functions
For this notebook, we will use `repeatAPICall`, which is a function that repeatedly makes API calls until a successful request is reached.
```
def repeatAPICall(func, args, max_retry = 5):
"""
Repeatedly calls spotipy func until a successful API request is made.
Parameters:
func : func
Spotipy client function for making api calls
args: dict
Arguments to pass to func; Key: parameter, Value: parameter value
Check Spotipy API of specified func for details
max_retry: int
Maximum iterations before prompting user to retry or skip
Returns:
result: dict
Result of a successful API call, or none
success: bool
True if API call is successful, False otherwise
"""
success = False
res = None
i = 0
while i < max_retry:
try:
res = func(**args)
success = True
return res, success
except:
print("Error in API call; retrying")
i += 1
pass
if i >= max_retry:
reset_loop = input("Max retry limit reached. Retry {} more time/s?".format(max_retry)).upper()
reset_loop = True if reset_loop == 'Y' else False
# Reset the index of the loop if user chooses to reset
i = 0 if reset_loop else max_retry
return res, success
```
## Step 1: Getting playlists of a given category
In this step, we will gather playlists that are categorized as k-pop. We can use this as a starting point to gather an initial list of kpop artists.
This cell gets the list of playlist categories (with ID) available in Spotify. Let's set the country code to PH so we can get PH-specific results.
```
all_categories = sp.categories(limit = 50, country = 'PH')
categories = all_categories['categories']['items']
for cat in categories:
print("Category: {} | ID : {}".format(cat['name'],cat['id']))
```
This indicates that K-pop categories has `id = kpop`!
Note for the future implementation: OPM has `id = opm`
This next cell gathers the playlists for the `kpop` category and saves it to a DataFrame.
```
kpop_playlists_result = sp.category_playlists('kpop', country='PH', limit = 50)
kpop_playlists = kpop_playlists_result['playlists']['items']
while kpop_playlists_result['playlists']['next']:
kpop_playlists_result = sp.next(kpop_playlists_result['playlists'])
kpop_playlists.extend(kpop_playlists_result['playlists']['items'])
playlists = [playlist['name'] for playlist in kpop_playlists]
playlist_uris = [playlist['uri'] for playlist in kpop_playlists]
playlist_df = pd.DataFrame(zip(playlists,playlist_uris),columns = ["playlist", "playlist_uri"]).drop_duplicates().reset_index(drop=True)
# Save the playlist list to .csv file
filename = 'Data/playlists.csv'
playlist_df.to_csv(filename, index=False)
```
## Step 2: Collecting artists from playlists
In this step, we will use the list of playlists and gather all the artists that appear in them. Since we're using k-pop playlists, we assume that most of the artists we get from this step are k-pop.
**Note:** Usually there will be some non-kpop artists appearing in this list, such as Dua Lipa or Ed Sheeran. These are usually artists that appear on k-pop collabs (ex. Dua Lipa and BLACKPINK - Kiss and Make Up)
```
# Load the existing playlist data
playlist_dir = 'Data/playlists.csv'
playlist_df = pd.read_csv(playlist_dir)
# Loop through playlists to build a list of artists
# Get the list of unique identifiers for each playlist
playlists = playlist_df.playlist.values
playlist_uris = playlist_df.playlist_uri.values
# Create dataframe to store artist data
artist_cols = ['artist','artist_uri']
artist_df = pd.DataFrame(columns = artist_cols)
for playlist,uri in zip(playlists, playlist_uris):
print("Current playlist: {}".format(playlist))
playlist_result, success = repeatAPICall(sp.playlist_tracks,{'playlist_id':uri})
if not success:
print("Error in playlist {}".format(playlist))
continue
# Remove value in playlist_result['items'] when track is listed as None object
playlist_result['items'] = [track for track in playlist_result['items'] if track['track'] is not None]
# Skip the playlist if there are any errors
try:
artist_uris = [track['track']['artists'][0]['uri'] for track in playlist_result['items']]
artists = [track['track']['artists'][0]['name'] for track in playlist_result['items']]
except:
print("Error in playlist {}".format(playlist))
temp_df = pd.DataFrame(zip(artists,artist_uris),columns = artist_cols)
artist_df = pd.concat([artist_df.reset_index(drop=True), temp_df.reset_index(drop=True)]).drop_duplicates()
# Reset the index of our resulting dataframe
artist_df = artist_df.drop_duplicates().reset_index(drop=True)
artist_df
```
At this point, we now have 900~ artists in our database! We save our current output as `artists.csv`. In the next succeeding cells, we will extend the list by getting related acts for every artist in our current list.
```
# Save the existing artist data
artists_dir = 'Data/artists.csv'
artist_df.to_csv(artists_dir, index = False)
```
## Step 3: Extending artist data by gathering related artists
In this step, we will extended our current list of artists by adding related artists to our current list. This will run for a set number of iterations, so after getting the initial list of related artists, we can get then gather even more artists from this new batch.
There are two important steps to improve runtime and avoid repeating processes. First, we label each artist with `temp_processed` (bool), which indicates whether we have already processed that artist's related artists. We set this initally to `False` and update it to `True` when an iteration has finished.
Second, we only filter out artists of certain genres that we are interested in. `sp.artist_related_artists()` returns 20 related artists for a given artist, which can blow up our list exponentially and add artists that we don't want. For example, `BLACKPINK` and `BTS` are related to `Dua Lipa` and `Halsey`, respectively, as they feature together on collabs. However, if we keep these two results and get additional related artists based on them, we are likely to get more pop artists (~20) unrelated to the genre we are looking for. `genre_filter` is a list of substrings that we use to match to an artist's own genre list to decide whether to keep that artist in our list.
```
# Load the existing artist data to extend
# For testing: randomly sample rows
artists_dir = 'Data/artists.csv'
artist_extended_df = pd.read_csv(artists_dir)
artist_extended_df
```
In the next cell, the code will go through each artist and get a list of related artists.
```
# Add a 'processed' column to artist_df indicating if its already been processed by this loop
artist_extended_df['temp_processed'] = False
# Filter for genres
# We use 'k-pop' and 'k-rap' as the genre substrings
# We can also add 'korean' to match korean artists that are not considered k-pop (ex. OSTs)
genre_filter = ['k-pop', 'k-rap']
# genre_filter = ['k-','korean']
# Keep track of iteration progress (see sense check section below)
artist_count = [len(artist_extended_df.artist_uri.values)]
iter_count = [0]
removed_count = [0]
# Set maximum iterations
max_iter = 15
for i in range(max_iter):
print("Current iter: {}".format(i+1))
rel_artists = []
rel_artist_uris = []
# Create temporary df to score artists to be processed
temp_df = artist_extended_df.copy()
temp_df = temp_df[temp_df.temp_processed == False]
# If temp df is empty, end the loop
if temp_df.empty:
print("No more artists to be processed! Breaking loop.")
break
artists = temp_df.artist.values
artist_uris = temp_df.artist_uri.values
print("Iter: {} | Artists count: {} | To be processed : {}".format(i+1, len(artist_extended_df.artist_uri.values), len(artist_uris) ))
# Track number of artists removed per iteration
total_removed = 0
# Loop through artists
for artist,uri in zip(artists,artist_uris):
# Get related artists for the current artist
rel_artists_result, success = repeatAPICall(sp.artist_related_artists,{'artist_id':uri})
if not success:
print("Skipping to next artist.")
continue
# Remove artists whose genres do not contain the substrings in genre_filter
old_count = len(rel_artists_result['artists'])
rel_artists_result['artists'] = [rel_artist for rel_artist in rel_artists_result['artists'] if any(genre in ''.join(rel_artist['genres']) for genre in genre_filter)]
new_count = len(rel_artists_result['artists'])
# Track number of removed artists
removed = old_count - new_count
total_removed += removed
rel_artists.extend([artist['name'] for artist in rel_artists_result['artists']])
rel_artist_uris.extend([artist['uri'] for artist in rel_artists_result['artists']])
# Create dataframe of related artists that were gathered
rel_artist_df = pd.DataFrame(zip(rel_artists,rel_artist_uris),columns = ["artist", "artist_uri"]).drop_duplicates()
rel_artist_df['temp_processed'] = False
# At this step, all the entries in artist_df has been processed and labelled accordingly
artist_extended_df['temp_processed'] = True
# Combine artist_extended_df and rel_artist_df
# Drop duplicates and keep first value
# This ensures that we keep the firtst duplicate songs
# between artist and rel_artist_df (with different temp_processed values)
artist_extended_df = pd.concat([artist_extended_df.reset_index(drop=True), rel_artist_df.reset_index(drop=True)]).drop_duplicates(subset = ['artist', 'artist_uri'], keep = 'first')
# Add metrics to array
iter_count.append(i+1)
artist_count.append(len(artist_extended_df.artist_uri.values))
removed_count.append(total_removed)
print("Done! Final count: {}".format(artist_count[-1]))
```
Here's our final list of artists!
```
artist_extended_df
```
### Sense Check
This cell plots the total number of artists gathered (blue) and related artists removed (orange) as function of the number of iterations. We see that the blue line generally plateaus, indicating that we reached a reasonable upper limit of possible artists gathered. We also see that the number of artists removed is large for `i = 1` at around (8000~). This means that the first iteration removes a large number of non-kpop artists. Without removing these artists per iteration, the loop will not converge to a finite list of artists.
```
plt.plot(iter_count,artist_count, label = "Artists in list")
plt.plot(iter_count[1:], removed_count[1:], label = "Removed in processing (not in genre filter)")
plt.xlabel("Number of iterations")
plt.ylabel("Artist count")
plt.legend()
plt.tight_layout()
# Save the existing artist data
# We drop the temp_processed column before writing to csv
artists_extended_dir = 'Data/artists_extended.csv'
artist_extended_df.drop('temp_processed', axis = 1).to_csv(artists_extended_dir, index = False)
```
## Step 4: Loading top tracks per artist
From our list of k-pop artists, we then get their top 10 tracks. This gives us a reasonable number of songs for our Kpop Song Recommender!
```
# Load the existing artist data
artists_dir = 'Data/artists.csv'
artists_dir = 'Data/artists_extended.csv' # Uncomment this if you want to use the extended artists dataset
artist_df = pd.read_csv(artists_dir)
artists = artist_df.artist.values
artist_uris = artist_df.artist_uri.values
# Loop through artist to build a list of tracks from their top 10 songs
# Create dataframe to store artist data
artist_cols = ['artist', 'artist_uri']
track_cols = ['track','track_uri','popularity']
track_df = pd.DataFrame(columns = artist_cols + track_cols)
for artist,uri in tqdm(zip(artists, artist_uris), total = len(artist_uris)):
# print("Current artist: {}".format(artist))
top10_result, success = repeatAPICall(sp.artist_top_tracks,{'artist_id':uri,'country':'PH'})
if not success:
print("Skipping to next artist.")
continue
# Remove value in playlist_result['items'] when track is listed as None object
#top10_result['tracks'] = [track for track in top10_result['tracks'] if track is not None]
# Skip the playlist if there are any errors
try:
track_uris = [track['uri'] for track in top10_result['tracks']]
tracks = [track['name'] for track in top10_result['tracks']]
popularity = [track['popularity'] for track in top10_result['tracks']]
except:
print("Error in playlist {}".format(playlist))
temp_df = pd.DataFrame(zip(tracks,track_uris, popularity),columns = track_cols)
# Set the artist and artist columns
temp_df['artist'] = artist
temp_df['artist_uri'] = uri
track_df = pd.concat([track_df.reset_index(drop=True), temp_df.reset_index(drop=True)]).drop_duplicates()
```
Note: if a track has multiple artists, and those artists have this track, it will show up multiple times. In the cell below, we see that the number of rows is more than the number of unique track_uri.
We will keep these duplicates for now, but keep this in mind when post-processing the data.
```
print("Number of track_df rows: {}\nNumber of unique track_uri: {}".format(len(track_df), track_df['track_uri'].nunique()))
# Save all tracks to file
tracks_dir = 'Data/tracks_top10.csv'
track_df.to_csv(tracks_dir, index = False)
```
## Step 5: Getting audio features per track
In this last step, we will generate the audio features for each track in our database using Spotify's Audio Features functionality. These include a song's danceability, tempo, energy key, time_signature, liveness, etc. In the main notebook, this will be used to as a basis to recommend kpop songs that are similar to a user's top tracks in terms of these features.
```
# Load the track data
tracks_dir = 'Data/tracks_top10.csv'
track_df = pd.read_csv(tracks_dir)
tracks = track_df.track.values
track_uris = track_df.track_uri.values
track_df
```
In this next cell, we will go through each track and generate its audio features (saved as a dataframe). Each track is identified by its unique `track_uri`.
`sp.audio_feautures()` takes a list of track_ids (maximum of 100). We will loop through the list of track uri in batches of 100 to minimize the amount of API requests.
```
batch_size = 100
# This list of columns is taken directly from the keys of a feature dictionary
features_cols = ['danceability',
'energy',
'key',
'loudness',
'mode',
'speechiness',
'acousticness',
'instrumentalness',
'liveness',
'valence',
'tempo',
'type',
'id',
'uri',
'track_href',
'analysis_url',
'duration_ms',
'time_signature']
features_df = pd.DataFrame(columns = features_cols)
for i in tqdm(range(0, len(track_uris), batch_size)):
# Select the current batch
track_uris_batch = track_uris[i:i+batch_size]
features_result, success = repeatAPICall(sp.audio_features,{'tracks':track_uris_batch})
if not success:
print("Skipping to next batch.")
continue
# Deepcopy the list of dictionaries to be modified
# This is necessary for this particular structure
features_dicts = deepcopy(features_result)
# Drop None in features_dict
# This will mean that some of our songs will not have features
if any(d is None for d in features_dicts):
print("Batch: {} to {} | Some songs do not have features; dropping from list.".format(i+1, i+1+batch_size))
print("Count: {}".format(len(features_dicts)))
features_dicts = [d for d in features_dicts if d is not None]
print("New count: {}".format(len(features_dicts)))
temp_df = pd.DataFrame.from_records(features_dicts)
features_df = pd.concat([features_df.reset_index(drop=True), temp_df.reset_index(drop=True)])
temp_df_count = len(temp_df.index)
if temp_df_count != batch_size:
print("Batch: {} to {} | Dataframe rows count: {}".format(i+1, i+1+batch_size, temp_df_count))
# Reset index and rename 'uri' to 'track_uri'
# Drop duplicates based on track_uri
features_df = features_df.rename(columns={'uri':'track_uri'}).drop_duplicates(subset=['track_uri'])
features_df
```
Finally, we left join the features to the `track_df` using `track_uri`
```
# Merge features to track_df by track_uri
# Note: some rows will not have features. We keep them for now to retain the track info
track_features_df = track_df.merge(features_df, on='track_uri', how='left').reset_index(drop = True)
track_features_df
# Save tracks with features to file
# Save all tracks to file
tracks_features_dir = 'Data/tracks_top10_features.csv'
track_features_df.to_csv(tracks_features_dir, index = False)
```
## Done!
After running this notebook, you should now have the following updated files in your Data Folder:
1. playlists.csv
2. artists.csv
3. artists_extended.csv
4. tracks_top10.csv
5. tracks_top10_features.csv
The following code cells will try to load all albums by an artist. This will be more computatinally expensive than the previous segment where we only got an artist's top 10 tracks.
```
# Load the existing artist data
artists_dir = 'Data/artists.csv'
artists_dir = 'Data/artists_extended.csv' # Uncomment this if you want to use the extended artists dataset
artist_df = pd.read_csv(artists_dir)
artists = artist_df.artist.values
artist_uris = artist_df.artist_uri.values
# Loop through artist to build a list of albums
# Create dataframe to store artist data
artist_cols = ['artist', 'artist_uri']
album_cols = ['album','album_uri','release_date','release_date_precision','total_tracks']
album_df = pd.DataFrame(columns = artist_cols + album_cols)
for artist,uri in tqdm(zip(artists, artist_uris), total = len(artist_uris)):
func_params = {
'artist_id':uri,
'country':'PH',
'album_type':['album','single','compilation']
}
albums_result, success = repeatAPICall(sp.artist_albums, func_params)
if not success:
print("Skipping to next artist.")
continue
albums_list = albums_result['items']
while albums_result['next']:
# print("Going to next 50 albums.")
albums_result, success = repeatAPICall(sp.next,{'result':albums_result})
if not success:
print("Skipping to next artist.")
continue
albums_list.extend(albums_result['items'])
# Skip the artist if there are any errors
try:
album_uris = [album['uri'] for album in albums_list]
albums = [album['name'] for album in albums_list]
release_dates = [album['release_date'] for album in albums_list]
release_date_precisions = [album['release_date_precision'] for album in albums_list]
totals = [album['total_tracks'] for album in albums_list]
except:
print("Error in artist {}".format(artist))
temp_df = pd.DataFrame(zip(albums,album_uris, release_dates, release_date_precisions, totals),columns = album_cols)
# Set the artist and artist columns
temp_df['artist'] = artist
temp_df['artist_uri'] = uri
album_df = pd.concat([album_df.reset_index(drop=True), temp_df.reset_index(drop=True)]).drop_duplicates()
album_df = album_df.reset_index(drop = True)
album_df
album_df.sample(50)
```
| true |
code
| 0.318035 | null | null | null | null |
|
```
import numpy as np
import json
from keras.models import Model
from keras.layers import Input
from keras.layers.convolutional import Conv2D
from keras.layers.pooling import MaxPooling2D, AveragePooling2D
from keras.layers.normalization import BatchNormalization
from keras import backend as K
def format_decimal(arr, places=8):
return [round(x * 10**places) / 10**places for x in arr]
```
### pipeline 6
```
data_in_shape = (24, 24, 2)
conv_0 = Conv2D(5, 3, 3, activation='relu', border_mode='valid', subsample=(2, 2), dim_ordering='tf', bias=True)
bn_0 = BatchNormalization(mode=0, axis=-1, epsilon=1e-3)
conv_1 = Conv2D(4, 3, 3, activation='relu', border_mode='same', subsample=(1, 1), dim_ordering='tf', bias=True)
bn_1 = BatchNormalization(mode=0, axis=-1, epsilon=1e-3)
conv_2 = Conv2D(3, 3, 3, activation='relu', border_mode='same', subsample=(1, 1), dim_ordering='tf', bias=True)
bn_2 = BatchNormalization(mode=0, axis=-1, epsilon=1e-3)
pool_0 = MaxPooling2D(pool_size=(2, 2), strides=None, border_mode='valid', dim_ordering='tf')
conv_3 = Conv2D(4, 3, 3, activation='linear', border_mode='valid', subsample=(1, 1), dim_ordering='tf', bias=True)
bn_3 = BatchNormalization(mode=0, axis=-1, epsilon=1e-3)
conv_4 = Conv2D(2, 3, 3, activation='relu', border_mode='same', subsample=(1, 1), dim_ordering='tf', bias=True)
bn_4 = BatchNormalization(mode=0, axis=-1, epsilon=1e-3)
pool_1 = MaxPooling2D(pool_size=(2, 2), strides=None, border_mode='valid', dim_ordering='tf')
input_layer = Input(shape=data_in_shape)
x = conv_0(input_layer)
x = bn_0(x)
x = conv_1(x)
x = bn_1(x)
x = conv_2(x)
x = bn_2(x)
x = pool_0(x)
x = conv_3(x)
x = bn_3(x)
x = conv_4(x)
x = bn_4(x)
output_layer = pool_1(x)
model = Model(input=input_layer, output=output_layer)
np.random.seed(7000)
data_in = 2 * np.random.random(data_in_shape) - 1
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(7000 + i)
if i % 6 == 5:
# std should be positive
weights.append(0.5 * np.random.random(w.shape))
else:
weights.append(np.random.random(w.shape) - 0.5)
model.set_weights(weights)
result = model.predict(np.array([data_in]))
print({
'input': {'data': format_decimal(data_in.ravel().tolist()), 'shape': list(data_in_shape)},
'weights': [{'data': format_decimal(weights[i].ravel().tolist()), 'shape': list(weights[i].shape)} for i in range(len(weights))],
'expected': {'data': format_decimal(result[0].ravel().tolist()), 'shape': list(result[0].shape)}
})
```
| true |
code
| 0.565299 | null | null | null | null |
|
# SHAP
[SHAP](https://github.com/slundberg/shap)'s goal is to explain machine learning output using a game theoretic approach. A primary use of SHAP is to understand how variables and values influence predictions visually and quantitatively. The API of SHAP is built along the `explainers`. These explainers are appropriate only for certain types or classes of algorithms. For example, you should use the `TreeExplainer` for tree-based models. Below, we take a look at three of these explainers.
Note that SHAP is a part of the movement to promote `explanable artificial intelligence (AI)`. There are other APIs available that do similar things to SHAP.
- [LIME](https://github.com/marcotcr/lime)
- [Alibi](https://docs.seldon.io/projects/alibi/en/stable/index.html)
- [ELI5](https://eli5.readthedocs.io/)
A great book on explanable AI or interpretable machine learning is [available online](https://christophm.github.io/interpretable-ml-book/).
## Linear explainer
The `LinearExplainer` is used to understand the outputs of linear predictors (e.g. linear regression). We will generate some data and use the `LinearRegression` model to learn the parameters from the data.
```
%matplotlib inline
import numpy as np
import pandas as pd
from patsy import dmatrices
from numpy.random import normal
import matplotlib.pyplot as plt
np.random.seed(37)
n = 100
x_0 = normal(10, 1, n)
x_1 = normal(5, 2.5, n)
x_2 = normal(20, 1, n)
y = 3.2 + (2.7 * x_0) - (4.8 * x_1) + (1.3 * x_2) + normal(0, 1, n)
df = pd.DataFrame(np.hstack([
x_0.reshape(-1, 1),
x_1.reshape(-1, 1),
x_2.reshape(-1, 1),
y.reshape(-1, 1)]), columns=['x0', 'x1', 'x2', 'y'])
y, X = dmatrices('y ~ x0 + x1 + x2 - 1', df, return_type='dataframe')
print(f'X shape = {X.shape}, y shape {y.shape}')
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
```
Before you can use SHAP, you must initialize the `JavaScript`.
```
import shap
shap.initjs()
```
Here, we create the `LinearExplainer`. We have to pass in the dataset `X`.
```
explainer = shap.LinearExplainer(model, X)
shap_values = explainer.shap_values(X)
```
A force plot can be used to explain each individual data point's prediction. Below, we look at the force plots of the first, second and third observations (indexed 0, 1, 2).
- First observation prediction explanation: the values of x1 and x2 are pushing the prediction value downard.
- Second observation prediction explanation: the x0 value is pushing the prediction value higher, while x1 and x2 are pushing the value lower.
- Third observation prediction explanation: the x0 and x1 values are pushing the prediction value lower and the x2 value is slightly nudging the value lower.
```
shap.force_plot(explainer.expected_value, shap_values[0,:], X.iloc[0,:])
shap.force_plot(explainer.expected_value, shap_values[1,:], X.iloc[1,:])
shap.force_plot(explainer.expected_value, shap_values[2,:], X.iloc[2,:])
```
The force plot can also be used to visualize explanation over all observations.
```
shap.force_plot(explainer.expected_value, shap_values, X)
```
The summary plot is a way to understand variable importance.
```
shap.summary_plot(shap_values, X)
```
Just for comparison, the visualization of the variables' importance coincide with the coefficients of the linear regression model.
```
s = pd.Series(model.coef_[0], index=X.columns)
s
```
## Tree explainer
The `TreeExplainer` is appropriate for algorithms using trees. Here, we generate data for a classification problem and use `RandomForestClassifier` as the model that we want to explain.
```
from scipy.stats import binom
def make_classification(n=100):
X = np.hstack([
np.array([1 for _ in range(n)]).reshape(n, 1),
normal(0.0, 1.0, n).reshape(n, 1),
normal(0.0, 1.0, n).reshape(n, 1)
])
z = np.dot(X, np.array([1.0, 2.0, 3.0])) + normal(0.0, 1.0, n)
p = 1.0 / (1.0 + np.exp(-z))
y = binom.rvs(1, p)
df = pd.DataFrame(np.hstack([X, y.reshape(-1, 1)]), columns=['intercept', 'x0', 'x1', 'y'])
return df
df = make_classification()
y, X = dmatrices('y ~ x0 + x1 - 1', df, return_type='dataframe')
print(f'X shape = {X.shape}, y shape {y.shape}')
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(n_estimators=100, random_state=37)
model.fit(X, y.values.reshape(1, -1)[0])
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X)
shap_interaction_values = explainer.shap_interaction_values(X)
```
Here are the forced plots for three observations.
```
shap.force_plot(explainer.expected_value[1], shap_values[1][0,:], X.iloc[0,:])
shap.force_plot(explainer.expected_value[1], shap_values[1][1,:], X.iloc[1,:])
shap.force_plot(explainer.expected_value[1], shap_values[1][95,:], X.iloc[95,:])
```
Here is the force plot for all observations.
```
shap.force_plot(explainer.expected_value[1], shap_values[1], X)
```
Below is the summary plot.
```
shap.summary_plot(shap_values[1], X)
```
Below are [dependence plots](https://christophm.github.io/interpretable-ml-book/pdp.html).
```
shap.dependence_plot('x0', shap_values[1], X)
shap.dependence_plot('x1', shap_values[1], X)
shap.dependence_plot(('x0', 'x0'), shap_interaction_values[1], X)
shap.dependence_plot(('x0', 'x1'), shap_interaction_values[1], X)
shap.dependence_plot(('x1', 'x1'), shap_interaction_values[1], X)
```
Lastly, the summary plot.
```
shap.summary_plot(shap_interaction_values[1], X)
```
## Kernel explainer
The `KernelExplainer` is the general purpose explainer. Here, we use it to explain the `LogisticRegression` model. Notice the `link` parameter, which can be `identity` or `logit`. This argument specifies the model link to connect the feature importance values to the model output.
```
from sklearn.linear_model import LogisticRegression
df = make_classification(n=10000)
X = df[['x0', 'x1']]
y = df.y
model = LogisticRegression(fit_intercept=True, solver='saga', random_state=37)
model.fit(X, y.values.reshape(1, -1)[0])
df = make_classification()
X = df[['x0', 'x1']]
y = df.y
```
Observe that we pass in the proababilistic prediction function to the `KernelExplainer`.
```
explainer = shap.KernelExplainer(model.predict_proba, link='logit', data=X)
shap_values = explainer.shap_values(X)
```
Again, example force plots on a few observations.
```
shap.force_plot(explainer.expected_value[1], shap_values[1][0,:], X.iloc[0,:], link='logit')
shap.force_plot(explainer.expected_value[1], shap_values[1][1,:], X.iloc[1,:], link='logit')
shap.force_plot(explainer.expected_value[1], shap_values[1][99,:], X.iloc[99,:], link='logit')
```
The force plot over all observations.
```
shap.force_plot(explainer.expected_value[1], shap_values[1], X, link='logit')
```
Lastly, the summary plot.
```
shap.summary_plot(shap_values[1], X)
```
| true |
code
| 0.564699 | null | null | null | null |
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_parent" href="https://github.com/giswqs/geemap/tree/master/tutorials/Image/02_image_visualization.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_parent" href="https://nbviewer.jupyter.org/github/giswqs/geemap/blob/master/tutorials/Image/02_image_visualization.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_parent" href="https://colab.research.google.com/github/giswqs/geemap/blob/master/tutorials/Image/02_image_visualization.ipynb"><img width=26px src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
# Image Visualization
This notebook was adapted from the [Earth Engine JavaScript API Documentation](https://developers.google.com/earth-engine/image_visualization).
The [Get Started](https://developers.google.com/earth-engine/getstarted#adding-data-to-the-map) page illustrates how to visualize an image using `Map.addLayer()`. If you add a layer to the map without any additional parameters, by default the Code Editor assigns the first three bands to red, green and blue, respectively. The default stretch is based on the type of data in the band (e.g. floats are stretched in `[0,1]`, 16-bit data are stretched to the full range of possible values), which may or may not be suitable. To achieve desirable visualization effects, you can provide visualization parameters to `Map.addLayer()`.

## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Add layers to map
```
Map = emap.Map()
# Load an image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20140318')
# Center the map and display the image.
Map.setCenter(-122.1899, 37.5010, 10) # San Francisco Bay
Map.addLayer(image, {}, 'default color composite')
Map.addLayerControl()
Map
```
## RGB composites
The following illustrates the use of parameters to style a Landsat 8 image as a false-color composite:
```
# Create a default map
Map = emap.Map()
# Load an image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20140318')
# Define the visualization parameters.
vizParams = {
'bands': ['B5', 'B4', 'B3'],
'min': 0,
'max': 0.5,
'gamma': [0.95, 1.1, 1]
}
# Center the map and display the image.
Map.setCenter(-122.1899, 37.5010, 10) # San Francisco Bay
Map.addLayer(image, vizParams, 'false color composite')
# Display the map
Map.addLayerControl()
Map
```
## Color palettes
To display a single band of an image in color, set the `parameter` with a color ramp represented by a list of CSS-style color strings. (See this [reference](http://en.wikipedia.org/wiki/Web_colors) for more information). The following example illustrates how to use colors from cyan (`00FFFF`) to blue (`0000FF`) to render a [Normalized Difference Water Index (NDWI)](http://www.tandfonline.com/doi/abs/10.1080/01431169608948714) image.
In this example, note that the `min` and `max` parameters indicate the range of pixel values to which the palette should be applied. Intermediate values are linearly stretched. Also note that the `opt_show` parameter is set to `False`. This results in the visibility of the layer being off when it is added to the map. It can always be turned on again using the Layer Manager in the upper right corner of the map. The result should look something like below.
```
# Create a default map
Map = emap.Map()
#Load an image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20140318')
#Create an NDWI image, define visualization parameters and display.
ndwi = image.normalizedDifference(['B3', 'B5'])
ndwiViz = {'min': 0.5, 'max': 1, 'palette': ['00FFFF', '0000FF']}
Map.setCenter(-122.1899, 37.5010, 10) # San Francisco Bay
Map.addLayer(ndwi, ndwiViz, 'NDWI', True)
# Display the map
Map.addLayerControl()
Map
```
## Masking
You can use `image.updateMask()` to set the opacity of individual pixels based on where pixels in a mask image are non-zero. Pixels equal to zero in the mask are excluded from computations and the opacity is set to 0 for display. The following example uses an NDWI threshold (see the [Relational Operations section](https://developers.google.com/earth-engine/image_relational.html) for information on thresholds) to update the mask on the NDWI layer created previously:
```
# Create a default map
Map = emap.Map()
#Load an image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20140318')
#Create an NDWI image, define visualization parameters and display.
ndwi = image.normalizedDifference(['B3', 'B5'])
ndwiViz = {'min': 0.5, 'max': 1, 'palette': ['00FFFF', '0000FF']}
Map.setCenter(-122.1899, 37.5010, 10) # San Francisco Bay
Map.addLayer(ndwi, ndwiViz, 'NDWI', False)
# Mask the non-watery parts of the image, where NDWI < 0.4.
ndwiMasked = ndwi.updateMask(ndwi.gte(0.4))
Map.addLayer(ndwiMasked, ndwiViz, 'NDWI masked')
# Display the map
Map.addLayerControl()
Map
```
## Visualization images
Use the `image.visualize()` method to convert an image into an 8-bit RGB image for display or export. For example, to convert the false-color composite and NDWI to 3-band display images, use:
```
# Create a default map
Map = emap.Map()
#Load an image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20140318')
#Create an NDWI image, define visualization parameters and display.
ndwi = image.normalizedDifference(['B3', 'B5'])
ndwiViz = {'min': 0.5, 'max': 1, 'palette': ['00FFFF', '0000FF']}
Map.setCenter(-122.1899, 37.5010, 10) # San Francisco Bay
Map.addLayer(ndwi, ndwiViz, 'NDWI', False)
# Mask the non-watery parts of the image, where NDWI < 0.4.
ndwiMasked = ndwi.updateMask(ndwi.gte(0.4));
Map.addLayer(ndwiMasked, ndwiViz, 'NDWI masked', False)
# Create visualization layers.
imageRGB = image.visualize(**{'bands': ['B5', 'B4', 'B3'], 'max': 0.5})
ndwiRGB = ndwiMasked.visualize(**{
'min': 0.5,
'max': 1,
'palette': ['00FFFF', '0000FF']
})
Map.addLayer(imageRGB, {}, 'imageRGB')
Map.addLayer(ndwiRGB, {}, 'ndwiRGB')
# Display the map
Map.addLayerControl()
Map
```
## Mosaicking
You can use masking and `imageCollection.mosaic()` (see the [Mosaicking section](https://developers.google.com/earth-engine/ic_composite_mosaic.html) for information on mosaicking) to achieve various cartographic effects. The `mosaic()` method renders layers in the output image according to their order in the input collection. The following example uses `mosaic()` to combine the masked NDWI and the false color composite and obtain a new visualization.
In this example, observe that a list of the two visualization images is provided to the ImageCollection constructor. The order of the list determines the order in which the images are rendered on the map. The result should look something like below.
```
# Create a default map
Map = emap.Map()
#Load an image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20140318')
#Create an NDWI image, define visualization parameters and display.
ndwi = image.normalizedDifference(['B3', 'B5'])
ndwiViz = {'min': 0.5, 'max': 1, 'palette': ['00FFFF', '0000FF']}
Map.setCenter(-122.1899, 37.5010, 10) # San Francisco Bay
Map.addLayer(ndwi, ndwiViz, 'NDWI', False)
# Mask the non-watery parts of the image, where NDWI < 0.4.
ndwiMasked = ndwi.updateMask(ndwi.gte(0.4));
Map.addLayer(ndwiMasked, ndwiViz, 'NDWI masked', False)
# Create visualization layers.
imageRGB = image.visualize(**{'bands': ['B5', 'B4', 'B3'], 'max': 0.5})
ndwiRGB = ndwiMasked.visualize(**{
'min': 0.5,
'max': 1,
'palette': ['00FFFF', '0000FF']
})
Map.addLayer(imageRGB, {}, 'imageRGB', False)
Map.addLayer(ndwiRGB, {}, 'ndwiRGB', False)
# Mosaic the visualization layers and display (or export).
mosaic = ee.ImageCollection([imageRGB, ndwiRGB]).mosaic()
Map.addLayer(mosaic, {}, 'mosaic');
# Display the map
Map.addLayerControl()
Map
```
## Clipping
The `image.clip()` method is useful for achieving cartographic effects. The following example clips the mosaic shown above to an arbitrary buffer zone around the city of San Francisco.
Note that the coordinates are provided to the `Geometry` constructor and the buffer length is specified as 20,000 meters. Learn more about geometries on the [Geometries page](https://developers.google.com/earth-engine/geometries). The result, shown with the map in the background, should look something like below.
```
# Create a default map
Map = emap.Map()
#Load an image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20140318')
#Create an NDWI image, define visualization parameters and display.
ndwi = image.normalizedDifference(['B3', 'B5'])
ndwiViz = {'min': 0.5, 'max': 1, 'palette': ['00FFFF', '0000FF']}
Map.setCenter(-122.4344, 37.7599, 10) # San Francisco Bay
Map.addLayer(ndwi, ndwiViz, 'NDWI', False)
# Mask the non-watery parts of the image, where NDWI < 0.4.
ndwiMasked = ndwi.updateMask(ndwi.gte(0.4));
Map.addLayer(ndwiMasked, ndwiViz, 'NDWI masked', False)
# Create visualization layers.
imageRGB = image.visualize(**{'bands': ['B5', 'B4', 'B3'], 'max': 0.5})
ndwiRGB = ndwiMasked.visualize(**{
'min': 0.5,
'max': 1,
'palette': ['00FFFF', '0000FF']
})
Map.addLayer(imageRGB, {}, 'imageRGB', False)
Map.addLayer(ndwiRGB, {}, 'ndwiRGB', False)
# Mosaic the visualization layers and display (or export).
mosaic = ee.ImageCollection([imageRGB, ndwiRGB]).mosaic()
Map.addLayer(mosaic, {}, 'mosaic', False);
# Create a circle by drawing a 20000 meter buffer around a point.
roi = ee.Geometry.Point([-122.4481, 37.7599]).buffer(20000)
clipped = mosaic.clip(roi)
# Display a clipped version of the mosaic.
Map.addLayer(clipped, {}, 'Clipped image')
# Display the map
Map.addLayerControl()
Map
```
## Rendering categorical maps
Palettes are also useful for rendering discrete valued maps, for example a land cover map. In the case of multiple classes, use the palette to supply a different color for each class. (The `image.remap()` method may be useful in this context, to convert arbitrary labels to consecutive integers). The following example uses a palette to render land cover categories:
```
# Create a default map
Map = emap.Map()
#Load 2012 MODIS land cover and select the IGBP classification.
cover = ee.Image('MODIS/051/MCD12Q1/2012_01_01') \
.select('Land_Cover_Type_1')
#Define a palette for the 18 distinct land cover classes.
igbpPalette = [
'aec3d4', #water
'152106', '225129', '369b47', '30eb5b', '387242', #forest
'6a2325', 'c3aa69', 'b76031', 'd9903d', '91af40', #shrub, grass
'111149', #wetlands
'cdb33b', #croplands
'cc0013', #urban
'33280d', #crop mosaic
'd7cdcc', #snow and ice
'f7e084', #barren
'6f6f6f' #tundra
]
#Specify the min and max labels and the color palette matching the labels.
Map.setCenter(-99.229, 40.413, 5)
Map.addLayer(cover, {'min': 0, 'max': 17, 'palette': igbpPalette}, 'IGBP classification')
Map.addLayerControl()
Map
```
## Thumbnail images
Use the `ee.Image.getThumbURL()` method to generate a PNG or JPEG thumbnail image for an `ee.Image` object. Printing the outcome of an expression ending with a call to `getThumbURL()` results in a URL being printed to the console. Visiting the URL sets Earth Engine servers to work on generating the requested thumbnail on-the-fly. The image is displayed in the browser when processing completes. It can be downloaded by selecting appropriate options from the image’s right-click context menu.
The `getThumbURL()` method shares parameters with `Map.addLayer()`, described in the [visualization parameters table](https://developers.google.com/earth-engine/image_visualization#mapVisParamTable) above. Additionally, it takes optional `dimension`, `region`, and `crs` arguments that control the spatial extent, size, and display projection of the thumbnail.

A single-band image will default to grayscale unless a `palette` argument is supplied. A multi-band image will default to RGB visualization of the first three bands, unless a `bands` argument is supplied. If only two bands are provided, the first band will map to red, the second to blue, and the green channel will be zero filled.
The following are a series of examples demonstrating various combinations of `getThumbURL()` parameter arguments. Visit the URLs printed to the console when you run this script to view the thumbnails.
```
# Fetch a digital elevation model.
image = ee.Image('CGIAR/SRTM90_V4')
# Request a default thumbnail of the DEM with defined linear stretch.
# Set masked pixels (ocean) to 1000 so they map as gray.
thumbnail1 = image.unmask(1000).getThumbURL({
'min': 0,
'max': 3000,
'dimensions': 500
})
print('Default extent and size:', thumbnail1)
# Specify region by GeoJSON, define palette, set size of the larger aspect dimension.
thumbnail2 = image.getThumbURL({
'min': 0,
'max': 3000,
'palette': ['00A600','63C600','E6E600','E9BD3A','ECB176','EFC2B3','F2F2F2'],
'dimensions': 500,
'region': ee.Geometry.Rectangle([-84.6, -55.9, -32.9, 15.7]),
})
print('GeoJSON region, palette, and max dimension:', thumbnail2)
```
| true |
code
| 0.606091 | null | null | null | null |
|
# Exploring OpenEEW data
## Import openeew package
```
from openeew.data.aws import AwsDataClient
from openeew.data.df import get_df_from_records
```
## Import other packages
```
import folium
from datetime import datetime
import plotnine as pn
import pandas as pd
from geopy.distance import distance
# Allow nested asyncio event loop
# See https://github.com/erdewit/nest_asyncio
import nest_asyncio
nest_asyncio.apply()
```
## Get past earthquake date and location
```
# Check SSN website:
# http://www2.ssn.unam.mx:8080/sismos-fuertes/
eq = {
'latitude': 16.218,
'longitude': -98.0135,
'date_utc': '2018-02-16 23:39:39'
}
```
## View epicenter on map
```
m = folium.Map(
location=[eq['latitude'], eq['longitude']],
zoom_start=7
)
folium.Circle(
radius=10000,
location=[eq['latitude'], eq['longitude']],
color='crimson',
fill='crimson',
).add_to(m)
m
```
## Initialize OpenEEW data client
```
data_client = AwsDataClient('mx')
```
## Get devices as of earthquake date
```
devices = data_client.get_devices_as_of_date(eq['date_utc'])
devices
for d in devices:
folium.Marker(
[d['latitude'], d['longitude']],
popup = folium.Popup(
d['device_id'],
sticky=True
)
).add_to(m)
m
```
## Get records for date range
```
# For generality we could calculate
# these dates based on the eq date
start_date_utc = '2018-02-16 23:39:00'
end_date_utc = '2018-02-16 23:43:00'
records_df = get_df_from_records(
data_client.get_filtered_records(
start_date_utc,
end_date_utc
)
)
# Get UTC date from Unix time sample_t for plotting
records_df['sample_dt'] = \
records_df['sample_t'].apply(lambda x: datetime.utcfromtimestamp(x))
# Select required columns
records_df = records_df[
[
'device_id',
'x',
'y',
'z',
'sample_dt'
]
]
records_df.head()
```
## Plot records for single device
```
def plot_seismograms(device_id):
# Get earthquake date as datetime.datetime object
eq_dt = AwsDataClient._get_dt_from_str(eq['date_utc'])
plots = []
for axis in ['x', 'y', 'z']:
plots.append(
pn.ggplot(
records_df[records_df['device_id'] == device_id],
pn.aes('sample_dt', axis)
) + \
pn.geom_line(color='blue') + \
pn.scales.scale_x_datetime(
date_breaks='1 minute',
date_labels='%H:%M:%S'
) + \
pn.geoms.geom_vline(
xintercept=eq_dt,
color='crimson'
) + \
pn.labels.ggtitle('device {}, axis {}'.format(device_id, axis))
)
for p in plots:
print(p)
plot_seismograms('006')
plot_seismograms('000')
```
## Compare max accelerations
```
# For each device, get max acceleration of horizontal axes
# Store these values as pandas Series
pgas = pd.Series(name='pga')
pgas.index.name = 'device_id'
for device_id in records_df.device_id.unique():
# Get horizontal axes from device metadata
horizontal_axes = [
d['horizontal_axes'] for d in devices
if d['device_id'] == device_id
][0]
# Get max accel as sqrt of sum of squares of horizontal axes
pgas[device_id] = \
(records_df[records_df['device_id'] == device_id][horizontal_axes] ** 2) \
.sum(axis=1) \
.pow(0.5) \
.max()
pgas = pgas.sort_values(ascending=False)
pgas
```
## Compare relationship between distance and max acceleration
```
# Use a pandas DataFrame for convenience
devices_df = pd.DataFrame(devices)
devices_df = devices_df[
[
'device_id',
'latitude',
'longitude'
]
]
# Use the geopy.distance.distance function
# to get distance from devices to epicenter
devices_df['dist_from_eq'] = devices_df.apply(
lambda r: round(
distance(
(r['latitude'], r['longitude']),
(eq['latitude'], eq['longitude'])
).km, 3),
axis=1
)
devices_df = devices_df.merge(pgas, left_on='device_id', right_index=True)
devices_df.sort_values('dist_from_eq')
# Plot using linear scale
pn.ggplot(
devices_df,
pn.aes('dist_from_eq', 'pga')
) + \
pn.geom_point(color='blue') + \
pn.labels.ggtitle('PGA vs distance from epicenter')
```
| true |
code
| 0.605449 | null | null | null | null |
|
# _*Max-Cut and Traveling Salesman Problem*_
## Introduction
Many problems in quantitative fields such as finance and engineering are optimization problems. Optimization problems lie at the core of complex decision-making and definition of strategies.
Optimization (or combinatorial optimization) means searching for an optimal solution in a finite or countably infinite set of potential solutions. Optimality is defined with respect to some criterion function, which is to be minimized or maximized. This is typically called cost function or objective function.
**Typical optimization problems**
Minimization: cost, distance, length of a traversal, weight, processing time, material, energy consumption, number of objects
Maximization: profit, value, output, return, yield, utility, efficiency, capacity, number of objects
We consider here max-cut problems of practical interest in many fields, and show how they can be mapped on quantum computers manually and how Qiskit's optimization module supports this.
### Weighted Max-Cut
Max-Cut is an NP-complete problem, with applications in clustering, network science, and statistical physics. To grasp how practical applications are mapped into given Max-Cut instances, consider a system of many people that can interact and influence each other. Individuals can be represented by vertices of a graph, and their interactions seen as pairwise connections between vertices of the graph, or edges. With this representation in mind, it is easy to model typical marketing problems. For example, suppose that it is assumed that individuals will influence each other's buying decisions, and knowledge is given about how strong they will influence each other. The influence can be modeled by weights assigned on each edge of the graph. It is possible then to predict the outcome of a marketing strategy in which products are offered for free to some individuals, and then ask which is the optimal subset of individuals that should get the free products, in order to maximize revenues.
The formal definition of this problem is the following:
Consider an $n$-node undirected graph *G = (V, E)* where *|V| = n* with edge weights $w_{ij}>0$, $w_{ij}=w_{ji}$, for $(i, j)\in E$. A cut is defined as a partition of the original set V into two subsets. The cost function to be optimized is in this case the sum of weights of edges connecting points in the two different subsets, *crossing* the cut. By assigning $x_i=0$ or $x_i=1$ to each node $i$, one tries to maximize the global profit function (here and in the following summations run over indices 0,1,...n-1)
$$\tilde{C}(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j).$$
In our simple marketing model, $w_{ij}$ represents the probability that the person $j$ will buy a product after $i$ gets a free one. Note that the weights $w_{ij}$ can in principle be greater than $1$ (or even negative), corresponding to the case where the individual $j$ will buy more than one product. Maximizing the total buying probability corresponds to maximizing the total future revenues. In the case where the profit probability will be greater than the cost of the initial free samples, the strategy is a convenient one. An extension to this model has the nodes themselves carry weights, which can be regarded, in our marketing model, as the likelihood that a person granted with a free sample of the product will buy it again in the future. With this additional information in our model, the objective function to maximize becomes
$$C(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j)+\sum_i w_i x_i. $$
In order to find a solution to this problem on a quantum computer, one needs first to map it to an Ising Hamiltonian. This can be done with the assignment $x_i\rightarrow (1-Z_i)/2$, where $Z_i$ is the Pauli Z operator that has eigenvalues $\pm 1$. Doing this we find that
$$C(\textbf{Z}) = \sum_{i,j} \frac{w_{ij}}{4} (1-Z_i)(1+Z_j) + \sum_i \frac{w_i}{2} (1-Z_i) = -\frac{1}{2}\left( \sum_{i<j} w_{ij} Z_i Z_j +\sum_i w_i Z_i\right)+\mathrm{const},$$
where $\mathrm{const} = \sum_{i<j}w_{ij}/2+\sum_i w_i/2 $. In other terms, the weighted Max-Cut problem is equivalent to minimizing the Ising Hamiltonian
$$ H = \sum_i w_i Z_i + \sum_{i<j} w_{ij} Z_iZ_j.$$
Qiskit's optimization module can generate the Ising Hamiltonian for the first profit function $\tilde{C}$.
To this extent, function $\tilde{C}$ can be modeled as a `QuadraticProgram`, which provides the `to_ising()` method.
### Approximate Universal Quantum Computing for Optimization Problems
There has been a considerable amount of interest in recent times about the use of quantum computers to find a solution to combinatorial optimization problems. It is important to say that, given the classical nature of combinatorial problems, exponential speedup in using quantum computers compared to the best classical algorithms is not guaranteed. However, due to the nature and importance of the target problems, it is worth investigating heuristic approaches on a quantum computer that could indeed speed up some problem instances. Here we demonstrate an approach that is based on the *Quantum Approximate Optimization Algorithm* (QAOA) by Farhi, Goldstone, and Gutman (2014). We frame the algorithm in the context of *approximate quantum computing*, given its heuristic nature.
The algorithm works as follows:
1. Choose the $w_i$ and $w_{ij}$ in the target Ising problem. In principle, even higher powers of Z are allowed.
1. Choose the depth of the quantum circuit $m$. Note that the depth can be modified adaptively.
1. Choose a set of controls $\theta$ and make a trial function $|\psi(\boldsymbol\theta)\rangle$, built using a quantum circuit made of C-Phase gates and single-qubit Y rotations, parameterized by the components of $\boldsymbol\theta$.
1. Evaluate
$$C(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)~|H|~\psi(\boldsymbol\theta)\rangle = \sum_i w_i \langle\psi(\boldsymbol\theta)~|Z_i|~\psi(\boldsymbol\theta)\rangle+ \sum_{i<j} w_{ij} \langle\psi(\boldsymbol\theta)~|Z_iZ_j|~\psi(\boldsymbol\theta)\rangle$$
by sampling the outcome of the circuit in the Z-basis and adding the expectation values of the individual Ising terms together. In general, different control points around $\boldsymbol\theta$ have to be estimated, depending on the classical optimizer chosen.
1. Use a classical optimizer to choose a new set of controls.
1. Continue until $C(\boldsymbol\theta)$ reaches a minimum, close enough to the solution $\boldsymbol\theta^*$.
1. Use the last $\boldsymbol\theta$ to generate a final set of samples from the distribution $|\langle z_i~|\psi(\boldsymbol\theta)\rangle|^2\;\forall i$ to obtain the answer.
It is our belief the difficulty of finding good heuristic algorithms will come down to the choice of an appropriate trial wavefunction. For example, one could consider a trial function whose entanglement best aligns with the target problem, or simply make the amount of entanglement a variable. In this tutorial, we will consider a simple trial function of the form
$$|\psi(\theta)\rangle = [U_\mathrm{single}(\boldsymbol\theta) U_\mathrm{entangler}]^m |+\rangle$$
where $U_\mathrm{entangler}$ is a collection of C-Phase gates (fully entangling gates), and $U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})$, where $n$ is the number of qubits and $m$ is the depth of the quantum circuit. The motivation for this choice is that for these classical problems this choice allows us to search over the space of quantum states that have only real coefficients, still exploiting the entanglement to potentially converge faster to the solution.
One advantage of using this sampling method compared to adiabatic approaches is that the target Ising Hamiltonian does not have to be implemented directly on hardware, allowing this algorithm not to be limited to the connectivity of the device. Furthermore, higher-order terms in the cost function, such as $Z_iZ_jZ_k$, can also be sampled efficiently, whereas in adiabatic or annealing approaches they are generally impractical to deal with.
References:
- A. Lucas, Frontiers in Physics 2, 5 (2014)
- E. Farhi, J. Goldstone, S. Gutmann e-print arXiv 1411.4028 (2014)
- D. Wecker, M. B. Hastings, M. Troyer Phys. Rev. A 94, 022309 (2016)
- E. Farhi, J. Goldstone, S. Gutmann, H. Neven e-print arXiv 1703.06199 (2017)
```
# useful additional packages
import matplotlib.pyplot as plt
import matplotlib.axes as axes
%matplotlib inline
import numpy as np
import networkx as nx
from qiskit import Aer
from qiskit.tools.visualization import plot_histogram
from qiskit.circuit.library import TwoLocal
from qiskit.optimization.applications.ising import max_cut, tsp
from qiskit.aqua.algorithms import VQE, NumPyMinimumEigensolver
from qiskit.aqua.components.optimizers import SPSA
from qiskit.aqua import aqua_globals
from qiskit.aqua import QuantumInstance
from qiskit.optimization.applications.ising.common import sample_most_likely
from qiskit.optimization.algorithms import MinimumEigenOptimizer
from qiskit.optimization.problems import QuadraticProgram
# setup aqua logging
import logging
from qiskit.aqua import set_qiskit_aqua_logging
# set_qiskit_aqua_logging(logging.DEBUG) # choose INFO, DEBUG to see the log
```
## Max-Cut problem
```
# Generating a graph of 4 nodes
n=4 # Number of nodes in graph
G=nx.Graph()
G.add_nodes_from(np.arange(0,n,1))
elist=[(0,1,1.0),(0,2,1.0),(0,3,1.0),(1,2,1.0),(2,3,1.0)]
# tuple is (i,j,weight) where (i,j) is the edge
G.add_weighted_edges_from(elist)
colors = ['r' for node in G.nodes()]
pos = nx.spring_layout(G)
def draw_graph(G, colors, pos):
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G, node_color=colors, node_size=600, alpha=.8, ax=default_axes, pos=pos)
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos=pos, edge_labels=edge_labels)
draw_graph(G, colors, pos)
# Computing the weight matrix from the random graph
w = np.zeros([n,n])
for i in range(n):
for j in range(n):
temp = G.get_edge_data(i,j,default=0)
if temp != 0:
w[i,j] = temp['weight']
print(w)
```
### Brute force approach
Try all possible $2^n$ combinations. For $n = 4$, as in this example, one deals with only 16 combinations, but for n = 1000, one has 1.071509e+30 combinations, which is impractical to deal with by using a brute force approach.
```
best_cost_brute = 0
for b in range(2**n):
x = [int(t) for t in reversed(list(bin(b)[2:].zfill(n)))]
cost = 0
for i in range(n):
for j in range(n):
cost = cost + w[i,j]*x[i]*(1-x[j])
if best_cost_brute < cost:
best_cost_brute = cost
xbest_brute = x
print('case = ' + str(x)+ ' cost = ' + str(cost))
colors = ['r' if xbest_brute[i] == 0 else 'c' for i in range(n)]
draw_graph(G, colors, pos)
print('\nBest solution = ' + str(xbest_brute) + ' cost = ' + str(best_cost_brute))
```
### Mapping to the Ising problem
Qiskit provides functionality to directly generate the Ising Hamiltonian as well as create the corresponding `QuadraticProgram`.
```
qubitOp, offset = max_cut.get_operator(w)
print('Offset:', offset)
print('Ising Hamiltonian:')
print(qubitOp.print_details())
# mapping Ising Hamiltonian to Quadratic Program
qp = QuadraticProgram()
qp.from_ising(qubitOp, offset)
qp.to_docplex().prettyprint()
# solving Quadratic Program using exact classical eigensolver
exact = MinimumEigenOptimizer(NumPyMinimumEigensolver())
result = exact.solve(qp)
print(result)
```
Since the problem was cast to a minimization problem, the solution of $-4$ corresponds to the optimum.
### Checking that the full Hamiltonian gives the right cost
```
#Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
ee = NumPyMinimumEigensolver(qubitOp)
result = ee.run()
x = sample_most_likely(result.eigenstate)
print('energy:', result.eigenvalue.real)
print('max-cut objective:', result.eigenvalue.real + offset)
print('solution:', max_cut.get_graph_solution(x))
print('solution objective:', max_cut.max_cut_value(x, w))
colors = ['r' if max_cut.get_graph_solution(x)[i] == 0 else 'c' for i in range(n)]
draw_graph(G, colors, pos)
```
### Running it on quantum computer
We run the optimization routine using a feedback loop with a quantum computer that uses trial functions built with Y single-qubit rotations, $U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})$, and entangler steps $U_\mathrm{entangler}$.
```
aqua_globals.random_seed = np.random.default_rng(123)
seed = 10598
backend = Aer.get_backend('statevector_simulator')
quantum_instance = QuantumInstance(backend, seed_simulator=seed, seed_transpiler=seed)
# construct VQE
spsa = SPSA(maxiter=300)
ry = TwoLocal(qubitOp.num_qubits, 'ry', 'cz', reps=5, entanglement='linear')
vqe = VQE(qubitOp, ry, spsa, quantum_instance=quantum_instance)
# run VQE
result = vqe.run(quantum_instance)
# print results
x = sample_most_likely(result.eigenstate)
print('energy:', result.eigenvalue.real)
print('time:', result.optimizer_time)
print('max-cut objective:', result.eigenvalue.real + offset)
print('solution:', max_cut.get_graph_solution(x))
print('solution objective:', max_cut.max_cut_value(x, w))
# plot results
colors = ['r' if max_cut.get_graph_solution(x)[i] == 0 else 'c' for i in range(n)]
draw_graph(G, colors, pos)
# create minimum eigen optimizer based on VQE
vqe_optimizer = MinimumEigenOptimizer(vqe)
# solve quadratic program
result = vqe_optimizer.solve(qp)
print(result)
colors = ['r' if result.x[i] == 0 else 'c' for i in range(n)]
draw_graph(G, colors, pos)
```
## Traveling Salesman Problem
In addition to being a notorious NP-complete problem that has drawn the attention of computer scientists and mathematicians for over two centuries, the Traveling Salesman Problem (TSP) has important bearings on finance and marketing, as its name suggests. Colloquially speaking, the traveling salesman is a person that goes from city to city to sell merchandise. The objective in this case is to find the shortest path that would enable the salesman to visit all the cities and return to its hometown, i.e. the city where he started traveling. By doing this, the salesman gets to maximize potential sales in the least amount of time.
The problem derives its importance from its "hardness" and ubiquitous equivalence to other relevant combinatorial optimization problems that arise in practice.
The mathematical formulation with some early analysis was proposed by W.R. Hamilton in the early 19th century. Mathematically the problem is, as in the case of Max-Cut, best abstracted in terms of graphs. The TSP on the nodes of a graph asks for the shortest *Hamiltonian cycle* that can be taken through each of the nodes. A Hamilton cycle is a closed path that uses every vertex of a graph once. The general solution is unknown and an algorithm that finds it efficiently (e.g., in polynomial time) is not expected to exist.
Find the shortest Hamiltonian cycle in a graph $G=(V,E)$ with $n=|V|$ nodes and distances, $w_{ij}$ (distance from vertex $i$ to vertex $j$). A Hamiltonian cycle is described by $N^2$ variables $x_{i,p}$, where $i$ represents the node and $p$ represents its order in a prospective cycle. The decision variable takes the value 1 if the solution occurs at node $i$ at time order $p$. We require that every node can only appear once in the cycle, and for each time a node has to occur. This amounts to the two constraints (here and in the following, whenever not specified, the summands run over 0,1,...N-1)
$$\sum_{i} x_{i,p} = 1 ~~\forall p$$
$$\sum_{p} x_{i,p} = 1 ~~\forall i.$$
For nodes in our prospective ordering, if $x_{i,p}$ and $x_{j,p+1}$ are both 1, then there should be an energy penalty if $(i,j) \notin E$ (not connected in the graph). The form of this penalty is
$$\sum_{i,j\notin E}\sum_{p} x_{i,p}x_{j,p+1}>0,$$
where it is assumed the boundary condition of the Hamiltonian cycles $(p=N)\equiv (p=0)$. However, here it will be assumed a fully connected graph and not include this term. The distance that needs to be minimized is
$$C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}.$$
Putting this all together in a single objective function to be minimized, we get the following:
$$C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}+ A\sum_p\left(1- \sum_i x_{i,p}\right)^2+A\sum_i\left(1- \sum_p x_{i,p}\right)^2,$$
where $A$ is a free parameter. One needs to ensure that $A$ is large enough so that these constraints are respected. One way to do this is to choose $A$ such that $A > \mathrm{max}(w_{ij})$.
Once again, it is easy to map the problem in this form to a quantum computer, and the solution will be found by minimizing a Ising Hamiltonian.
```
# Generating a graph of 3 nodes
n = 3
num_qubits = n ** 2
ins = tsp.random_tsp(n, seed=123)
print('distance\n', ins.w)
# Draw the graph
G = nx.Graph()
G.add_nodes_from(np.arange(0, ins.dim, 1))
colors = ['r' for node in G.nodes()]
for i in range(0, ins.dim):
for j in range(i+1, ins.dim):
G.add_edge(i, j, weight=ins.w[i,j])
pos = {k: v for k, v in enumerate(ins.coord)}
draw_graph(G, colors, pos)
```
### Brute force approach
```
from itertools import permutations
def brute_force_tsp(w, N):
a=list(permutations(range(1,N)))
last_best_distance = 1e10
for i in a:
distance = 0
pre_j = 0
for j in i:
distance = distance + w[j,pre_j]
pre_j = j
distance = distance + w[pre_j,0]
order = (0,) + i
if distance < last_best_distance:
best_order = order
last_best_distance = distance
print('order = ' + str(order) + ' Distance = ' + str(distance))
return last_best_distance, best_order
best_distance, best_order = brute_force_tsp(ins.w, ins.dim)
print('Best order from brute force = ' + str(best_order) + ' with total distance = ' + str(best_distance))
def draw_tsp_solution(G, order, colors, pos):
G2 = nx.DiGraph()
G2.add_nodes_from(G)
n = len(order)
for i in range(n):
j = (i + 1) % n
G2.add_edge(order[i], order[j], weight=G[order[i]][order[j]]['weight'])
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G2, node_color=colors, edge_color='b', node_size=600, alpha=.8, ax=default_axes, pos=pos)
edge_labels = nx.get_edge_attributes(G2, 'weight')
nx.draw_networkx_edge_labels(G2, pos, font_color='b', edge_labels=edge_labels)
draw_tsp_solution(G, best_order, colors, pos)
```
### Mapping to the Ising problem
```
qubitOp, offset = tsp.get_operator(ins)
print('Offset:', offset)
print('Ising Hamiltonian:')
print(qubitOp.print_details())
qp = QuadraticProgram()
qp.from_ising(qubitOp, offset, linear=True)
qp.to_docplex().prettyprint()
result = exact.solve(qp)
print(result)
```
### Checking that the full Hamiltonian gives the right cost
```
#Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
ee = NumPyMinimumEigensolver(qubitOp)
result = ee.run()
print('energy:', result.eigenvalue.real)
print('tsp objective:', result.eigenvalue.real + offset)
x = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos)
```
### Running it on quantum computer
We run the optimization routine using a feedback loop with a quantum computer that uses trial functions built with Y single-qubit rotations, $U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})$, and entangler steps $U_\mathrm{entangler}$.
```
aqua_globals.random_seed = np.random.default_rng(123)
seed = 10598
backend = Aer.get_backend('statevector_simulator')
quantum_instance = QuantumInstance(backend, seed_simulator=seed, seed_transpiler=seed)
spsa = SPSA(maxiter=300)
ry = TwoLocal(qubitOp.num_qubits, 'ry', 'cz', reps=5, entanglement='linear')
vqe = VQE(qubitOp, ry, spsa, quantum_instance=quantum_instance)
result = vqe.run(quantum_instance)
print('energy:', result.eigenvalue.real)
print('time:', result.optimizer_time)
x = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos)
aqua_globals.random_seed = np.random.default_rng(123)
seed = 10598
backend = Aer.get_backend('statevector_simulator')
quantum_instance = QuantumInstance(backend, seed_simulator=seed, seed_transpiler=seed)
# create minimum eigen optimizer based on VQE
vqe_optimizer = MinimumEigenOptimizer(vqe)
# solve quadratic program
result = vqe_optimizer.solve(qp)
print(result)
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos)
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
```
| true |
code
| 0.452717 | null | null | null | null |
|
# Midterm Exam 02
- This is a closed book exam
- You should only ever have a SINGLE browser tab open
- The exam lasts 75 minutes, and Sakai will not accept late submissions
- You may use the following:
- TAB completion
- SHIFT-TAB completion for function arguments
- help(func), `?func`, `func?` to get help on `func`
- To create a new cell, use `ESC-A` or `ESC-B`
Note that there are 5 questions, each worth 25 points. The maximum grade you can have is 100.
**Honor Code: By taking this exam, you agree to abide by the Duke Honor Code.**
----
**1**. (25 points)
The Collatz sequence is defined by the following rules for finding the next number
```
if the current number is even, divide by 2
if the current number is odd, multiply by 3 and add 1
if the current number is 1, stop
```
- Find the starting number and length of the longest Collatz sequence for starting integers in `range(1, 10001)` (15 points)
- Make a scatter plot of the sequence length against starting number for starting integers in `range(1, 10001)`. Use a size of 1 (s=1) in the argument to scatter function. (10 points)
Note: The Collatz sequence is only for positive integers. For example, if the starting number is 3, the collatz sequence is `[3, 10, 5, 16, 8, 4, 2, 1]`.
```
```
**2**. (25 points)
The Newton-Rephson algorithm finds zeros of a function using the update
$$
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
$$
- Use the Newton-Raphson algorithm to find all solutions to $x^3 = 1$. Use $2, -2+3i, -2-3i$ as the starting conditions. You can use a brute force function that always terminates after 100 iterations. (15 points)
- Find the solutions by finding the companion matrix and performing an eigendecomposition. (10 points)
Note: Python uses $j$ for the imaginary part, not $i$
```
```
**3**. (25 points)
You are given the following data
```python
A = np.array([[1, 8, 0, 7],
[0, 2, 9, 4],
[2, 8, 8, 3],
[4, 8, 6, 1],
[2, 1, 9, 6],
[0, 7, 0, 1],
[4, 0, 2, 4],
[1, 4, 9, 5],
[6, 2, 6, 6],
[9, 9, 6, 3]], dtype='float')
b = np.array([[2],
[5],
[0],
[0],
[6],
[7],
[2],
[6],
[7],
[9]], dtype='float')
```
- Using SVD directly (not via `lstsq`), find the least squares solution to $Ax = b$ (10 points)
- Use SVE to find the best rank 3 approximation of A (10 points)
- Calculate the approximation error in terms of the Frobenius norm (5 points)
```
```
**4**. (25 points)
We observe some data points $(x_i, y_i)$, and believe that an appropriate model for the data is that
$$
f(x) = b_0 + b_1 x + b_2 x^2
$$
with some added noise.
- Find optimal values of the parameters $\beta = (b_0, b_1, b_2)$ that minimize $\Vert y - f(x) \Vert^2$ using gradient descent and starting with an initial value of $\beta_0 = \begin{bmatrix}1 & 1 &1 \end{bmatrix}$. Use a learning rate of 0.0001 and 10,000 iterations (20 points)
- Plot the fitted quadratic together with the data points (5 points)
Remember to use column vectors for $x$ and $y$.
Data
```
x = np.array([[0],
[1],
[2],
[3],
[4],
[5],
[6],
[7],
[8],
[9]])
y = np.array([[ 4.70612107],
[ 4.63393704],
[ 6.49770138],
[ 12.11243273],
[ 20.51575619],
[ 34.23493694],
[ 53.1814074 ],
[ 74.20612958],
[101.24176654],
[131.85009012]])
```
```
```
**5**. (25 points)
Recall that the page rank of a node is given by the equation

and at steady state, we have the page rank vector $R$

where $d$ is the damping factor, $N$ is the number of nodes, $1$ is a vector of ones, and

where $L(p_j)$ is the number of outgoing links from node $p_j$.
Consider the graph

If $d = 0.9$ find the page rank of each node
- By solving a linear system (15 points)
- By eigendecomposition (10 points)
Note: The Markov matrix constructed as instructed does not follow the usual convention. Here the columns of our Markov matrix are probability vectors, and the page rank is considered to be a column vector of the steady state probabilities.
```
```
| true |
code
| 0.752725 | null | null | null | null |
|
# Introduction to XGBoost-Spark Cross Validation with GPU
The goal of this notebook is to show you how to levarage GPU to accelerate XGBoost spark cross validatoin for hyperparameter tuning. The best model for the given hyperparameters will be returned.
Here takes the application 'Taxi' as an example.
A few libraries are required for this notebook:
1. NumPy
2. cudf jar
2. xgboost4j jar
3. xgboost4j-spark jar
#### Import the Required Libraries
```
from ml.dmlc.xgboost4j.scala.spark import XGBoostRegressionModel, XGBoostRegressor
from ml.dmlc.xgboost4j.scala.spark.rapids import CrossValidator
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.ml.tuning import ParamGridBuilder
from pyspark.sql import SparkSession
from pyspark.sql.types import FloatType, IntegerType, StructField, StructType
from time import time
import os
```
As shown above, here `CrossValidator` is imported from package `ml.dmlc.xgboost4j.scala.spark.rapids`, not the spark's `tuning.CrossValidator`.
#### Create a Spark Session
```
spark = SparkSession.builder.appName("taxi-cv-gpu-python").getOrCreate()
```
#### Specify the Data Schema and Load the Data
```
label = 'fare_amount'
schema = StructType([
StructField('vendor_id', FloatType()),
StructField('passenger_count', FloatType()),
StructField('trip_distance', FloatType()),
StructField('pickup_longitude', FloatType()),
StructField('pickup_latitude', FloatType()),
StructField('rate_code', FloatType()),
StructField('store_and_fwd', FloatType()),
StructField('dropoff_longitude', FloatType()),
StructField('dropoff_latitude', FloatType()),
StructField(label, FloatType()),
StructField('hour', FloatType()),
StructField('year', IntegerType()),
StructField('month', IntegerType()),
StructField('day', FloatType()),
StructField('day_of_week', FloatType()),
StructField('is_weekend', FloatType()),
])
features = [ x.name for x in schema if x.name != label ]
# You need to update them to your real paths!
dataRoot = os.getenv("DATA_ROOT", "/data")
train_data = spark.read.parquet(dataRoot + '/taxi/parquet/train')
trans_data = spark.read.parquet(dataRoot + '/taxi/parquet/eval')
```
#### Build a XGBoost-Spark CrossValidator
```
# First build a regressor of GPU version using *setFeaturesCols* to set feature columns
params = {
'eta': 0.05,
'maxDepth': 8,
'subsample': 0.8,
'gamma': 1.0,
'numRound': 100,
'numWorkers': 1,
'treeMethod': 'gpu_hist',
}
regressor = XGBoostRegressor(**params).setLabelCol(label).setFeaturesCols(features)
# Then build the evaluator and the hyperparameters
evaluator = (RegressionEvaluator()
.setLabelCol(label))
param_grid = (ParamGridBuilder()
.addGrid(regressor.maxDepth, [3, 6])
.addGrid(regressor.numRound, [100, 200])
.build())
# Finally the corss validator
cross_validator = (CrossValidator()
.setEstimator(regressor)
.setEvaluator(evaluator)
.setEstimatorParamMaps(param_grid)
.setNumFolds(3))
```
#### Start Cross Validation by Fitting Data to CrossValidator
```
def with_benchmark(phrase, action):
start = time()
result = action()
end = time()
print('{} takes {} seconds'.format(phrase, round(end - start, 2)))
return result
model = with_benchmark('Cross-Validation', lambda: cross_validator.fit(train_data)).bestModel
```
#### Transform On the Best Model
```
def transform():
result = model.transform(trans_data).cache()
result.foreachPartition(lambda _: None)
return result
result = with_benchmark('Transforming', transform)
result.select(label, 'prediction').show(5)
```
#### Evaluation
```
accuracy = with_benchmark(
'Evaluation',
lambda: RegressionEvaluator().setLabelCol(label).evaluate(result))
print('RMSE is ' + str(accuracy))
spark.stop()
```
| true |
code
| 0.640861 | null | null | null | null |
|
# Convolutional Neural Networks
(c) Deniz Yuret, 2018
* Objectives: See the effect of sparse and shared weights implemented by convolutional networks.
* Prerequisites: MLP models (04.mlp.ipynb), KnetArray, param, param0, dropout, relu, nll
* Knet: conv4, pool, mat (explained)
* Knet: dir, gpu, minibatch, KnetArray (used by mnist.jl)
* Knet: SGD, train!, Train, load, save (used by trainresults)
```
using Pkg
for p in ("Knet","Plots","ProgressMeter")
haskey(Pkg.installed(),p) || Pkg.add(p)
end
```
## Introduction to convolution
```
# Convolution operator in Knet
using Knet: conv4
@doc conv4
# Convolution in 1-D
@show w = reshape([1.0,2.0,3.0], (3,1,1,1))
@show x = reshape([1.0:7.0...], (7,1,1,1))
@show y = conv4(w, x); # size Y = X - W + 1 = 5 by default
# Padding
@show y2 = conv4(w, x, padding=(1,0)); # size Y = X + 2P - W + 1 = 7 with padding=1
# To preserve input size (Y=X) for a given W, what padding P should we use?
# Stride
@show y3 = conv4(w, x; padding=(1,0), stride=3); # size Y = 1 + floor((X+2P-W)/S)
# Mode
@show y4 = conv4(w, x, mode=0); # Default mode (convolution) inverts w
@show y5 = conv4(w, x, mode=1); # mode=1 (cross-correlation) does not invert w
# Convolution in more dimensions
x = reshape([1.0:9.0...], (3,3,1,1))
w = reshape([1.0:4.0...], (2,2,1,1))
y = conv4(w, x)
# Convolution with multiple channels, filters, and instances
# size X = [X1,X2,...,Xd,Cx,N] where d is the number of dimensions, Cx is channels, N is instances
x = reshape([1.0:18.0...], (3,3,2,1))
# size W = [W1,W2,...,Wd,Cx,Cy] where d is the number of dimensions, Cx is input channels, Cy is output channels
w = reshape([1.0:24.0...], (2,2,2,3));
# size Y = [Y1,Y2,...,Yd,Cy,N] where Yi = 1 + floor((Xi+2Pi-Wi)/Si), Cy is channels, N is instances
y = conv4(w,x)
```
See http://cs231n.github.io/assets/conv-demo/index.html for an animated example.
## Introduction to Pooling
```
# Pooling operator in Knet
using Knet: pool
@doc pool
# 1-D pooling example
@show x = reshape([1.0:6.0...], (6,1,1,1))
@show pool(x);
# Window size
@show pool(x; window=3); # size Y = floor(X/W)
# Padding
@show pool(x; padding=(1,0)); # size Y = floor((X+2P)/W)
# Stride
@show x = reshape([1.0:10.0...], (10,1,1,1));
@show pool(x; stride=4); # size Y = 1 + floor((X+2P-W)/S)
# Mode (using KnetArray here; not all modes are implemented on the CPU)
using Knet: KnetArray
x = KnetArray(reshape([1.0:6.0...], (6,1,1,1)))
@show x
@show pool(x; padding=(1,0), mode=0) # max pooling
@show pool(x; padding=(1,0), mode=1) # avg pooling
@show pool(x; padding=(1,0), mode=2); # avg pooling excluding padded values (is not implemented on CPU)
# More dimensions
x = reshape([1.0:16.0...], (4,4,1,1))
pool(x)
# Multiple channels and instances
x = reshape([1.0:32.0...], (4,4,2,1))
# each channel and each instance is pooled separately
pool(x) # size Y = (Y1,...,Yd,Cx,N) where Yi are spatial dims, Cx and N are identical to input X
```
## Experiment setup
```
# Load data (see 02.mnist.ipynb)
using Knet: Knet, KnetArray, gpu, minibatch
include(Knet.dir("data","mnist.jl")) # Load data
dtrn,dtst = mnistdata(); # dtrn and dtst = [ (x1,y1), (x2,y2), ... ] where xi,yi are minibatches of 100
(x,y) = first(dtst)
summary.((x,y))
# For running experiments
using Knet: SGD, train!, nll, zeroone
import ProgressMeter
function trainresults(file,model; o...)
if (print("Train from scratch? ");readline()[1]=='y')
results = Float64[]; updates = 0; prog = ProgressMeter.Progress(60000)
function callback(J)
if updates % 600 == 0
push!(results, nll(model,dtrn), nll(model,dtst), zeroone(model,dtrn), zeroone(model,dtst))
ProgressMeter.update!(prog, updates)
end
return (updates += 1) <= 60000
end
train!(model, dtrn; callback=callback, optimizer=SGD(lr=0.1), o...)
Knet.save(file,"results",reshape(results, (4,:)))
end
isfile(file) || download("http://people.csail.mit.edu/deniz/models/tutorial/$file",file)
results = Knet.load(file,"results")
println(minimum(results,dims=2))
return results
end
```
## A convolutional neural network model for MNIST
```
# Redefine Linear layer (See 03.lin.ipynb):
using Knet: param, param0
struct Linear; w; b; end
(f::Linear)(x) = (f.w * mat(x) .+ f.b)
mat(x)=reshape(x,:,size(x)[end]) # Reshapes 4-D tensor to 2-D matrix so we can use matmul
Linear(inputsize::Int,outputsize::Int) = Linear(param(outputsize,inputsize),param0(outputsize))
# Define a convolutional layer:
struct Conv; w; b; end
(f::Conv)(x) = pool(conv4(f.w,x) .+ f.b)
Conv(w1,w2,cx,cy) = Conv(param(w1,w2,cx,cy), param0(1,1,cy,1))
# Define a convolutional neural network:
struct CNN; layers; end
# Weight initialization for a multi-layer convolutional neural network
# h[i] is an integer for a fully connected layer, a triple of integers for convolution filters and tensor inputs
# use CNN(x,h1,h2,...,hn,y) for a n hidden layer model
function CNN(h...)
w = Any[]
x = h[1]
for i=2:length(h)
if isa(h[i],Tuple)
(x1,x2,cx) = x
(w1,w2,cy) = h[i]
push!(w, Conv(w1,w2,cx,cy))
x = ((x1-w1+1)÷2,(x2-w2+1)÷2,cy) # assuming conv4 with p=0, s=1 and pool with p=0,w=s=2
elseif isa(h[i],Integer)
push!(w, Linear(prod(x),h[i]))
x = h[i]
else
error("Unknown layer type: $(h[i])")
end
end
CNN(w)
end;
using Knet: dropout, relu
function (m::CNN)(x; pdrop=0)
for (i,layer) in enumerate(m.layers)
p = (i <= length(pdrop) ? pdrop[i] : pdrop[end])
x = dropout(x, p)
x = layer(x)
x = (layer == m.layers[end] ? x : relu.(x))
end
return x
end
lenet = CNN((28,28,1), (5,5,20), (5,5,50), 500, 10)
summary.(l.w for l in lenet.layers)
using Knet: nll
(x,y) = first(dtst)
nll(lenet,x,y)
```
## CNN vs MLP
```
using Plots; default(fmt=:png,ls=:auto)
ENV["COLUMNS"] = 92
@time cnn = trainresults("cnn.jld2", lenet; pdrop=(0,0,.3)); # 406s [8.83583e-5, 0.017289, 0.0, 0.0048]
mlp = Knet.load("mlp.jld2","results");
# Comparison to MLP shows faster convergence, better generalization
plot([mlp[1,:], mlp[2,:], cnn[1,:], cnn[2,:]],ylim=(0.0,0.1),
labels=[:trnMLP :tstMLP :trnCNN :tstCNN],xlabel="Epochs",ylabel="Loss")
plot([mlp[3,:], mlp[4,:], cnn[3,:], cnn[4,:]],ylim=(0.0,0.03),
labels=[:trnMLP :tstMLP :trnCNN :tstCNN],xlabel="Epochs",ylabel="Error")
```
## Convolution vs Matrix Multiplication
```
# Convolution and matrix multiplication can be implemented in terms of each other.
# Convolutional networks have no additional representational power, only statistical efficiency.
# Our original 1-D example
@show w = reshape([1.0,2.0,3.0], (3,1,1,1))
@show x = reshape([1.0:7.0...], (7,1,1,1))
@show y = conv4(w, x); # size Y = X - W + 1 = 5 by default
# Convolution as matrix multiplication (1)
# Turn w into a (Y,X) sparse matrix
w2 = Float64[3 2 1 0 0 0 0; 0 3 2 1 0 0 0; 0 0 3 2 1 0 0; 0 0 0 3 2 1 0; 0 0 0 0 3 2 1]
@show y2 = w2 * mat(x);
# Convolution as matrix multiplication (2)
# Turn x into a (W,Y) dense matrix (aka the im2col operation)
# This is used to speed up convolution with known efficient matmul algorithms
x3 = Float64[1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7]
@show w3 = [3.0 2.0 1.0]
@show y3 = w3 * x3;
# Matrix multiplication as convolution
# This could be used to make a fully connected network accept variable sized inputs.
w = reshape([1.0:6.0...], (2,3))
x = reshape([1.0:3.0...], (3,1))
y = w * x
# Consider w with size (Y,X)
# Treat each of the Y rows of w as a convolution filter
w2 = copy(reshape(Array(w)', (3,1,1,2)))
# Reshape x for convolution
x2 = reshape(x, (3,1,1,1))
# Use conv4 for matrix multiplication
y2 = conv4(w2, x2; mode=1)
# So there is no difference between the class of functions representable with an MLP vs CNN.
# Sparse connections and weight sharing give CNNs more generalization power with images.
# Number of parameters in MLP256: (256x784)+256+(10x256)+10 = 203530
# Number of parameters in LeNet: (5*5*1*20)+20+(5*5*20*50)+50+(500*800)+500+(10*500)+10 = 431080
```
| true |
code
| 0.640804 | null | null | null | null |
|
<font color=gray>Oracle Cloud Infrastructure Data Science Demo Notebook
Copyright (c) 2021 Oracle, Inc.<br>
Licensed under the Universal Permissive License v 1.0 as shown at https://oss.oracle.com/licenses/upl.
</font>
# Validation of the CNN Model
```
%load_ext autoreload
%autoreload 2
import keras
from keras.models import Sequential, load_model
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
from keras.utils import plot_model
from matplotlib import pyplot as plt
import numpy as np
import json
import urllib
from zipfile import ZipFile
import skimage as ski
import os
import pandas as pd
import glob
from numpy import random as random
import urllib
import tensorflow as tf
from sklearn.metrics import confusion_matrix
from skimage import transform
from seaborn import heatmap
from utilities import display_xray_image, evaluate_model_performance
path_to_train_dataset = f"./data/chest_xray/train/"
path_to_test_dataset = f"./data/chest_xray/test/"
model_artifact_path = f"./model_artifact"
model_file = f"xray_predictor4-march21.hdf5"
model_path = os.path.join(model_artifact_path, model_file)
# Pulling some statistics about the test dataset:
pneumonia_test_list = glob.glob(path_to_test_dataset+'PNEUMONIA/*')
normal_test_list = glob.glob(path_to_test_dataset+'NORMAL/*')
test_list = pneumonia_test_list + normal_test_list
print("Test sample size = {}, Pneumonia = {}, Normal = {}".format(len(test_list),
len(pneumonia_test_list),
len(normal_test_list)))
# Building out the dataframe that will contain all the metadata about the x-ray images
test_df = pd.DataFrame(data={"path":test_list})
test_df["observed_class"] = test_df["path"].apply(lambda x: 0 if "/NORMAL/" in x else 1 )
test_df["extension"] = test_df["path"].apply(lambda x: os.path.splitext(x)[1])
print(test_df.shape)
test_df.head()
display_xray_image(test_df['path'].iloc[0])
```
## Image Transformations
```
# Defining those image transformations:
def image_transformations(image_path, dims=(200, 300)):
"""
"""
# Resize the original image. Consistent with training dataset:
image = transform.resize(ski.io.imread(image_path), output_shape=dims)
# Take the first channel only:
image = image[:,:,0] if len(image.shape)>2 else image
return image
# Applying transformations to images and observed labels:
test_df['resized_image'] = test_df['path'].apply(lambda x: image_transformations(x))
# encoding the class as a numpy array:
test_df['y'] = test_df['observed_class'].apply(lambda x: np.array([0, 1])
if x==1 else np.array([1, 0]))
Xtest = test_df['resized_image'].values
Ytest = test_df['y'].values
Xtest = np.asarray([i.reshape(200,300,1) for i in Xtest])
Ytest = np.asarray([i.reshape(2) for i in Ytest])
print("Xtest shape: {}, Ytest shape: {}".format(Xtest.shape, Ytest.shape))
display_xray_image(test_df.iloc[0]['resized_image'])
```
# Evaluating the CNN model
```
model = keras.models.load_model(model_path)
evaluate_model_performance(model_path, Xtest, Ytest, test_df['observed_class'].values,
labels=["normal", "pneumonia"])
```
| true |
code
| 0.627124 | null | null | null | null |
|
# The inverted pendulum model of the human standing
Marcos Duarte
Despite the enormous complexity of the human body, part of the mechanical behavior of the human body during the standing still posture, namely the displacements of the center of gravity ($COG$) and center of pressure ($COP$) in the anterior-posterior direction, can be elegantly portraied by a physical-mathematical model of an inverted pendulum with rigid segments articulated by joints.
Using such a model, it's possible to estimate the COG vertical projection (COGv) from the COP displacement. The Python function `cogve.py` (code at the end of this text) performs this estimation. The function signature is:
```python
cogv = cogve(COP, freq, mass, height, show=False, ax=None)
```
Let's now derive the inverted pendulum model of the human standing posture implemented in this function.
## Derivation of the inverted pendulum model
In the most simple version of the model, the human body in the sagittal plane is reduced to a two-link body with a single inverted pendulum articulated by only one joint (representing the feet, with the rest of the body articulated by the ankle joint). Let's deduce the equations for such inverted pendulum model as the representation at the sagital plane of the human standing still posture. The inverted pendulum model and the correspondent free-body diagrams (FBDs) are shown in Figure 1.
<div><figure><img src="./../images/invpendulum.png" width=400 alt="onelink"/><figcaption><b>Figure 1.</b> <i>Model of a two-link inverted pendulum and the external forces acting on it for the representation at the sagital plane of the human standing still posture and the corresponding free-body diagrams. $COG$: body center of gravity; $COG_v$: $COG$ vertical projection (at the horizontal plane) in relation to the ankle joint; $COP$: body center of pressure in relation to the ankle joint; $GRF$: ground reaction force (typically measured by a force plate); $\alpha$: angle of the body in relation to the vertical direction; $m$: mass of the body minus feet; $g$: acceleration of gravity; $F_a$ and $T_a$: resultant force and torque at the ankle joint; $h$: height of the $COG$ in relation to the ankle joint; $m_f$ and $h_f$: mass and height of the feet.</i></figcaption></figure></div>
The equations of motion for each FBD of the feet and rest-of-body segments at the sagittal plane ($xy$ plane) can be expressed in the form of the Newton-Euler equations.
<br>
<div style="background-color:#FBFBEF;border:1px solid black;padding:10px;">
<b>The Newton-Euler equations</b>
<br />
The <a href="http://en.wikipedia.org/wiki/Newton%E2%80%93Euler_equations">Newton-Euler equations</a> are a formalism to describe the combined translational and rotational dynamics of a rigid body.
For a two-dimensional (at the $xy$ plane) movement, their general form are given by:
<br />
$$ \sum \mathbf{F} = m \mathbf{\ddot{r}}_{cm} $$
$$ \sum \mathbf{T}_z = I_{cm} \mathbf{\ddot{\alpha}}_z $$
Where the movement is considered around the center of mass ($cm$) of the body, $\mathbf{F}$ and $\mathbf{T}$ are, respectively, the forces and torques acting on the body, $\mathbf{\ddot{r}}$ and $\mathbf{\ddot{\alpha}}$ are, respectively, the linear and angular accelerations, and $I$ is the body moment of inertia around the $z$ axis passing through the body center of mass.
It can be convenient to describe the rotation of the body around other point than the center of mass. In such cases, we express the moment of inertia around a reference point $o$ instead of around the body center of mass and we will have an additional term to the equation for the torque:
<br />
$$ \sum \mathbf{T}_{z,O} = I_{o} \mathbf{\ddot{\alpha}}_z + \mathbf{r}_{cm,o}\times m \mathbf{\ddot{r}}_o $$
Where $\mathbf{r}_{cm,o}$ is the position vector of the center of mass in relation to the reference point $o$ and $\mathbf{\ddot{r}}_o$ is the linear acceleration of this reference point.
<a href="http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/FreeBodyDiagram.ipynb">See this notebook about free-body diagram</a>.
</div>
For the case of an inverted pendulum representing at the sagittal plane the body at the standing still posture, let's solve the Newton-Euler equations considering the rotation around the ankle joint (because it will simplify the problem) and let's adopt the simplifications that the feet don't move (including the ankle, so $\mathbf{\ddot{r}}_o=0$ in the Newton-Euler equation) and their mass are neglegible in relation to the mass of the rest of the body.
For the feet, we have:
$$ \begin{array}{l l}
-F_{ax} + GRF_x = 0 \\
\\
-F_{ay} + GRF_y = 0 \\
\\
-T_a + COP \cdot GRF_y + h_f \cdot GRF_x = 0
\end{array} $$
And for the rest of the body:
$$ \begin{array}{l l}
F_{ax} = m\ddot{x}_{cm} \\
\\
F_{ay} - mg = m\ddot{y}_{cm} \\
\\
T_a - COG_v \cdot mg = I_a \ddot{\alpha}
\end{array} $$
Where $I_a$ is the moment of inertia of the whole body around the ankle joint.
During the standing still posture, the $GRF$ horizontal component is typically much smaller than the $GRF$ vertical component and the torque of the former can be neglected. In addition, the magnitude of the $GRF$ vertical component is approximately constant and equal to the body weight.
Considering these approximations, the ankle joint torque using the equation for the feet is given by:
$$ T_a \approx COP \cdot mg $$
If now we substitute the ankle joint torque term in the equation for the torques calculated for the rest-of-body segment, we have:
$$ COP - COG_v \approx \frac{I_a}{mg} \ddot{\alpha} $$
That is, the angular acceleration of the body is proportional to the difference between $COP$ and $COG_v$ displacements (with respect to the ankle joint position).
We can continue with the deduction and now substitute the angular displacement by a term proportional to $COG_v$ if we use the following trignometric relation (see figure above): $sin \alpha=COG_v/h$. But, during the standing still posture $\alpha$ is typicall very small and we can approximate $ sin\alpha \approx \alpha $ and $\alpha \approx COG_v/h$. However, bear in mind that $\alpha$ is defined as counterclockwise positive while $COG_v$ is positive when pointing to the right direction. This means that in fact $\alpha \approx -COG_v/h$. As $h$ is constant, the second derivative of $\alpha$ with respect to time is simply the second derivative of $COG_v$ divided by $h$.
Finally, the last equation can be expressed in the following form:
$$ COG_v - COP \approx \frac{I_a}{mgh} \ddot{COG}_v $$
Or simply:
$$ COG_v - COP \approx k \, \ddot{COG}_v $$
Where $k = I_a/(mgh)$.
If the human body is represented as a rigid bar, its moment of inertia will be approximately equal to $1.33mh^2$, so $k \approx 1.33h/g$.
In turn, from the Newton-Euler equations, the horizontal acceleration of $COG$ is equal to the horizontal component of $GRF$ divided by the body mass and the equation above can be expressed as:
$$ COG_v - COP \approx \frac{k}{m} GRF_x $$
## Implications of the inverted pendulum model
These two last equations express a very simple relation between body segment parameters, $COG_v$, $COP$, body acceleration, and horizontal force.
Solely based on these equations it is possible to predict some interesting relations among the variables in these equations, which have been experimentally observed:
- $COG_v-COP$ is positively correlated with the horizontal ground reaction force in the anterior-posterior direction (Winter et al. 1998; Morasso and Schieppati 1999; Zatsiorsky and Duarte 2000);
- $COG_v$ behaves as a low-pass filtered version of the $COP$ signal and this fact has been used in a method to derive $COG_v$ from the $COP$ signal (Winter 1995; Caron et al. 1997; Morasso and Schieppati 1999). This method produces similar results as other methods (Lafond et al. 2004);
- For a continuously regulated inverted pendulum (like the standing still posture), the common frequencies of $COG_v$ and $COP$ signals are in phase (Morasso and Schieppati 1999);
- When the horizontal force is zero, $COG_v$ and $COP$ coincide and this fact has been used as a method to derive $COG_v$ from the $COP$ displacement and the horizontal $GRF$ (King and Zatsiorsky 1997; Zatsiorsky and Duarte 2000).
Note that the four predictions made above are based entirely on the mechanical derivation of the inverted pendulum model. Nothing has been said about what type of neural control is being used for the regulation of the standing posture. This means that the statements above are consequence of the mechanical nature of the modeled phenomenon.
Obviously, the most straightforward prediction of the single inverted pendulum model concerning the **kinematics of the segments** of the human body would be that we should observe merely the motion at the ankle joint and nothing in the other joints. This prediction has not been observed (see for example, Pinter et al. 2008 and Gunther et al. 2009). During standing still, we seem to use all our joints and this is task dependent.
However, one important point to consider is that even if the inverted pendulum fails as a suitable model of the **kinematics of the segments**, the inverted pendulum succeds as a model of the **kinematics of global body variables**, such as $COG_v$ and $COP$, and their relation to kinetic variables, the external forces acting on the body.
Certainly everyone agrees that the inverted pendulum model is insufficient to capture all the essential characteristics of the posture during standing. Nevertheless, the greatest power of the single inverted pendulum model is its simplicity, and it is somewhat surprising to note how much this simple model can capture the of the investigated phenomenon.
## Estimation of COGv from the COP signal
Based on the inverted pendulum model, it's possible to estimate the $COG_v$ displacement from the $COP$ displacement after some mathematical manipulation we show next.
Back to the relation between $COG_v$ and $COP$ displacements, it has the form:
$$ y(t) - x(t) = k\,\ddot{y}(t) $$
Where $y(t)$ stands for the $COG_v$ signal and $x(t)$ for the $COP$ signal, which are functions of time, and $k = I_a/(mgh)$.
The equation above is a linear ordinary differential equation of second order. This equation is solvable in the time domain, but if we transform it to the frequency domain using the Fourier transform, we will find a simpler relation between $COG_v$ and $COP$.
<br>
<div style="background-color:#FBFBEF;border:1px solid black;padding:10px;">
<b>The Fourier transform</b>
The <a href="http://en.wikipedia.org/wiki/Fourier_transform">Fourier transform</a> is a mathematical operation to transform a signal which is function of time, $g(t)$, into a signal which is function of frequency, $G(f)$, and it is defined by:
<br />
$$ \mathcal{F}[g(t)] = G(f) = \int_{-\infty}^{\infty} g(t) e^{-i2\pi ft} dt $$
Its inverse operation is:
<br />
$$ \mathcal{F}^{-1}[G(f)] = g(t) = \int_{-\infty}^{\infty} G(f) e^{i2\pi ft} df $$
The function $G(f)$ is the representation in the frequency domain of the time-domain signal, $g(t)$, and vice-versa. The functions $g(t)$ and $G(f)$ are referred to as a Fourier integral pair, or Fourier transform pair, or simply the Fourier pair.
<a href="http://www.thefouriertransform.com/transform/fourier.php">See here for an introduction to Fourier transform</a> and <a href="http://www.thefouriertransform.com/applications/differentialequations.php">see here for the use of Fourier transform to solve differential equations</a>.
</div>
<br>
Let's apply the Fourier transform to the differential equation with $COG_v$ and $COP$:
$$ Y(j\omega) - X(j\omega) = -k\,\omega^2Y(j\omega) $$
Where we defined $y(t) \Leftrightarrow Y(j\omega)$ and $x(t) \Leftrightarrow X(j\omega)$ as the Fourier pairs, $j$ is the imaginary unit, and $\omega$ is the angular frequency, $2\pi f$.
The reason why we use the Fourier transform is because we started with a second order differential equation and ended with the simple algebraic equation above. Rearranging the equation above:
$$ \frac{Y(j\omega)}{X(j\omega)} = \frac{\omega_0^2}{\omega_0^2 + \omega^2} $$
Where $ \omega_0 = 1/\sqrt{k}$.
If we imagine a system where the $COP$ is the input and the $COG_v$ the output, the right side of the equation above is known as the <a href="http://en.wikipedia.org/wiki/Transfer_function">transfer function</a> of such system, the ratio between the output and the input.
Analysing the transfer function given in the equation above, we see that it is of the type of a low-pass filter (and $\omega_0$ is the cutoff frequency); because of that, we can say that the $COGv$ signal is a low-pass filtered version of the $COP$ signal.
We can implement such low-pass filter in order to determine the $COG_v$ using the $COP$ signal. For that, we simply have to estimate the Fourier transform of the $COP$ signal, multiply by the transfer function (the right side of the equation above), and calculate the inverse Fourier transform of this result. The Python function `cogve.py` (code at the end of this text) estimates the $COG_v$ using the $COP$ data based on this algorithm. Let's test this function, first we have to import the necessary Python libraries and configure the emvironment:
```
# Import the necessary libraries
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import sys
sys.path.insert(1, r'./../functions')
from cogve import cogve
```
Let's use stabilographic data found in the internet:
```
import pandas as pd # use Pandas to read data from a website
fileUrl = 'http://www.udel.edu/biology/rosewc/kaap686/reserve/cop/copdata.txt'
COP = pd.read_table(fileUrl, skipinitialspace=True, sep=None, engine='python')
COP = COP.values / 10 # mm to cm
freq = 100
print('COP shape: ', COP.shape)
fig, ax = plt.subplots(1, 1, figsize=(8, 5))
cogv = cogve(COP[:, 0], freq=100, mass=70, height=175, ax=ax, show=True) # guess mass, height
```
## References
- Caron O, Faure B, et al. (1997) [Estimating the centre of gravity of the body on the basis of the centre of pressure in standing posture](http://www.ncbi.nlm.nih.gov/pubmed/9456386). J. Biomech. 30, 1169-1171.
- Lafond D, Duarte M, et al. (2004) [Comparison of three methods to estimate the center of mass during balance assessment](http://ebm.ufabc.edu.br/publications/md/JB03.pdf). J. Biomech. 37, 1421-1426.
- King D, Zatsiorsky VM (1997) [Extracting gravity line displacement from stabilographic recordings](http://www.sciencedirect.com/science/article/pii/S0966636296011010). Gait & Posture 6, 27-38.
- Morasso PG, Spada G, et al. (1999) [Computing the COM from the COP in postural sway movements](http://www.sciencedirect.com/science/article/pii/S0167945799000391). Human Movement Science 18, 759-767.
- Winter DA (1995) [A.B.C. (Anatomy, Biomechanics and Control) of Balance during Standing and Walking](https://books.google.com.br/books?id=0lSqQgAACAAJ&). Waterloo, Waterloo Biomechanics.
- Winter DA, Patla AE, et al. (1998) [Stiffness control of balance in quiet standing](http://www.ncbi.nlm.nih.gov/pubmed/9744933). J. Neurophysiol. 80, 1211-1221.
- Zatsiorsky VM, Duarte M (2000) [Rambling and trembling in quiet standing](http://ebm.ufabc.edu.br/publications/md/MC00.pdf). Motor Control 4, 185-200.
## Function cogve.py
```
# %load ./../functions/cogve.py
"""COGv estimation using COP data based on the inverted pendulum model."""
from __future__ import division, print_function
import numpy as np
__author__ = 'Marcos Duarte, https://github.com/demotu/BMC'
__version__ = "1.0.2"
__license__ = "MIT"
def cogve(COP, freq, mass, height, show=False, ax=None):
"""COGv estimation using COP data based on the inverted pendulum model.
This function estimates the center of gravity vertical projection (COGv)
displacement from the center of pressure (COP) displacement at the
anterior-posterior direction during quiet upright standing. COP and COGv
displacements are measurements useful to quantify the postural sway of a
person while standing.
The COGv displacement is estimated by low-pass filtering the COP
displacement in the frequency domain according to the person's moment
of rotational inertia as a single inverted pendulum [1]_.
Parameters
----------
COP : 1D array_like
center of pressure data [cm]
freq : float
sampling frequency of the COP data
mass : float
body mass of the subject [kg]
height : float
height of the subject [cm]
show : bool, optional (default = False)
True (1) plots data and results in a matplotlib figure
False (0) to not plot
ax : matplotlib.axes.Axes instance, optional (default = None)
Returns
-------
COGv : 1D array
center of gravity vertical projection data [cm]
References
----------
.. [1] http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/IP_Model.ipynb
Examples
--------
>>> from cogve import cogve
>>> y = np.cumsum(np.random.randn(3000))/50
>>> cogv = cogve(y, freq=100, mass=70, height=170, show=True)
"""
from scipy.signal._arraytools import odd_ext
import scipy.fftpack
COP = np.asarray(COP)
height = height / 100 # cm to m
g = 9.8 # gravity acceleration in m/s2
# height of the COG w.r.t. ankle (McGinnis, 2005; Winter, 2005)
hcog = 0.56 * height - 0.039 * height
# body moment of inertia around the ankle
# (Breniere, 1996), (0.0572 for the ml direction)
I = mass * 0.0533 * height ** 2 + mass * hcog ** 2
# Newton-Euler equation of motion for the inverted pendulum
# COGv'' = w02*(COGv - COP)
# where w02 is the squared pendulum natural frequency
w02 = mass * g * hcog / I
# add (pad) data and remove mean to avoid problems at the extremities
COP = odd_ext(COP, n=freq)
COPm = np.mean(COP)
COP = COP - COPm
# COGv is estimated by filtering the COP data in the frequency domain
# using the transfer function for the inverted pendulum equation of motion
N = COP.size
COPfft = scipy.fftpack.fft(COP, n=N) / N # COP fft
w = 2 * np.pi * scipy.fftpack.fftfreq(n=N, d=1 / freq) # angular frequency
# transfer function
TF = w02 / (w02 + w ** 2)
COGv = np.real(scipy.fftpack.ifft(TF * COPfft) * N)
COGv = COGv[0: N]
# get back the mean and pad off data
COP, COGv = COP + COPm, COGv + COPm
COP, COGv = COP[freq: -freq], COGv[freq: -freq]
if show:
_plot(COP, COGv, freq, ax)
return COGv
def _plot(COP, COGv, freq, ax):
"""Plot results of the cogve function, see its help."""
try:
import matplotlib.pyplot as plt
except ImportError:
print('matplotlib is not available.')
else:
time = np.linspace(0, COP.size / freq, COP.size)
if ax is None:
_, ax = plt.subplots(1, 1)
ax.plot(time, COP, color=[0, 0, 1, .8], lw=2, label='COP')
ax.plot(time, COGv, color=[1, 0, 0, .8], lw=2, label='COGv')
ax.legend(fontsize=14, loc='best', framealpha=.5, numpoints=1)
ax.set_xlabel('Time [s]', fontsize=14)
ax.set_ylabel('Amplitude [cm]', fontsize=14)
ax.set_title('COGv estimation using the COP data', fontsize=16)
ax.set_xlim(time[0], time[-1])
plt.grid()
plt.show()
```
| true |
code
| 0.804502 | null | null | null | null |
|
# Warm-up
1. Review this code for 1 minute, then:
1. Identify how an "Electric-type" Pokemon object would get access to its base statistics
1. Attempt to write a method for `Electric` that will check its `HP` after every action
<img src='../assets/inherit_warmup.png' width=500 align='left' />
---
# Learning Objectives
1. Students will be able to visually identify `class` inheritance
1. Students will be able to write basic `class`es that inherit from others
1. Students will be able to use basic decorators to create `dataclasses`
---
# Object-Oriented Programming Seminar: Expanding Classes
The last major lesson in OOP is class inheritance. Class inheritance is the act of one object "gaining" all of the functionality of another object. [GeeksforGeeks](https://www.geeksforgeeks.org/inheritance-in-python/) states that the main purposes of class inheritance are:
> 1. Represents real-world relationships well
> 1. Provides reusability of code
> 1. It is transitive in nature
## The Big Idea
Any object in Python worth anything should exercise the use of inheritance because it allows for **extensibility**, **reusability**, and _clarity_. Just like a single function should do a single job, a single `class` should do a specific thing. However, we have already expanded the work of a single function before by using nested functions (a function that calls another function). Likewise, we can expand a `class` by "nesting" it with other `class`es.
<img src='../assets/nourdine-diouane-4YJkvZGDcyU-unsplash.jpg' width=700/>
---
# Last Class
For a quick reminder of where we left off last class
```
import class_demo as demo
%psource demo.Pileup
```
---
# Class Inheritance
Class inheritance is when one object takes/gives attributes and methods to another object upon its instantiation.
<img src='../assets/pokegeny.jpg' />
[Shelomi et al. 2012. A Phylogeny and Evolutionary History of the Pokémon. Annals of Improbable Research](../assets/Phylogeny-Pokemon.pdf)
## Salient Functions
```
def generate_random_integers(total, n):
"""Generates a list of n integers that sum up to a given number
Adapted from http://sunny.today/generate-random-integers-with-fixed-sum/
Args:
total (int): the total all the integers are to sum up to
n (int): the number of integers
Returns:
(list): a list if integers that sum approximately to total
"""
μ = total / n
var = int(0.25 * μ)
min_v = μ - var
max_v = μ + var
vals = [min_v] * n
diff = total - min_v * n
while diff > 0:
a = random.randint(0, n - 1)
if vals[a] >= max_v:
continue
vals[a] += 1
diff -= 1
return [int(val) for val in vals]
```
---
# Let's play with the data
```
import pandas as pd
# Read in the pokemon csv
pokedex = pd.read_csv('../datasets/pokemon.csv')
# Show just Pichu's data
pokedex[pokedex.Name == 'Pichu']
```
What is Pichu's type?
## Exploring class inheritance by doing something productive: making Pokemon©
```
# Base class of Pokemon
class Pokemon:
def __init__(self, level = 1, name = None, given_name = None):
self.level = level
self.given_name = given_name
pokedex = pd.read_csv('../datasets/pokemon.csv')
self.name = name.title() if name else None
if name is None:
self.base_hp, \
self.base_attack, \
self.base_defense, \
self.base_sAttack, \
self.base_sDefense, \
self.base_speed = generate_random_integers(random.randint(125, 400), 6)
elif pokedex.Name.str.contains(self.name).any():
self.base_hp, \
self.base_attack, \
self.base_defense, \
self.base_sAttack, \
self.base_sDefense, \
self.base_speed = pokedex.loc[pokedex.Name == self.name, [
'HP',
'Attack',
'Defense',
'Sp. Atk',
'Sp. Def',
'Speed'
]].values[0]
else:
raise ValueError('unregistered Pokemon')
self.current_hp = self.base_hp
self.exp = 0
def __str__(self):
return f'Pokemon(level = {self.level}, name = {self.given_name if self.given_name else self.name if self.name else "MISSINGNO"})'
def __repr__(self):
return f'Pokemon(level = {self.level}, name = {self.name}, given_name = {self.given_name})'
def stats(self):
return pd.Series([self.base_hp, self.base_attack, self.base_defense, self.base_sAttack, self.base_sDefense, self.base_speed],
index = ['HP', 'Attack', 'Defense', 'Sp. Atk', 'Sp. Def', 'Speed'])
magikarp = Pokemon(name='Magikarp')
print(magikarp)
print(repr(magikarp))
magikarp.stats()
class Electric(Pokemon):
def __init__(self, level = 1, name = None, given_name = None):
Pokemon.__init__(self, level, name, given_name)
self.type = 'Electric'
self.weak_def = ('Ground')
self.half_def = ('Electric', 'Flying')
self.strong_att = ('Flying', 'Water')
self.half_att = ('Dragon', 'Electric', 'Grass')
self.no_att = ('Ground')
self.immune = ('Paralyze')
def __repr__(self):
return super().__repr__().replace('Pokemon', 'Electric')
def __str__(self):
return super().__str__().replace('Pokemon', 'Electric')
pichu = Electric(name='Pichu')
pichu.immune
```
---
# Workshop
In groups of 3-4 people:
* Identify the different "types" of Pokemon (not including Electric)
* Choose one "type" (cannot be Electric)
* Write your own "type" subclass
---
```
class Pichu(Electric):
def __init__(self, level = 1, name = 'Pichu', given_name = None):
Electric.__init__(self, level, name, given_name)
self.name = name.title()
def __repr__(self):
return super().__repr__().replace('Electric', 'Pichu')
def __str__(self):
return super().__str__().replace('Electric', 'Pichu')
def thunder_shock(self):
ability_type = 'Electric'
self.thunder_shock_pp = 30
power = 40
accuracy = 1
effect = ('Paralyze', .1)
return (ability_type, effect, accuracy * power * self.base_sAttack)
def charm(self):
ability_type = 'Fairy'
self.charm_pp = 20
power = None
accuracy = None
effect = ('Decrease_Attack', 1)
return (ability_type, effect, None)
def tail_whip(self):
if self.level >= 5:
ability_type = None
self.tail_whip_pp = 30
power = 1
accuracy = 1
effect = None
return (ability_type, effect, accuracy * power * self.base_attack)
else:
raise IndexError('Move not available yet')
def sweet_kiss(self):
if self.leve >= 10:
ability_type = 'Fairy'
self.sweet_kiss_pp = 10
power = None
accuracy = None
effect = ('Confusion', .75)
return (ability_type, effect, None)
else:
raise IndexError('Move not available yet')
def nasty_plot(self):
if self.level >= 13:
ability_type = 'Dark'
self.nasty_plot_pp = 20
power = None
accuracy = None
effect = ('Decrease_sAttack', 1)
return (ability_type, effect, None)
else:
raise IndexError('Move not available yet')
def thunder_wave(self):
if self.level >= 18:
ability_type = 'Electric'
self.thunder_wave_pp = 20
power = 40
accuracy = 0.9
effect = ('Paralyze', 1)
return(ability_type, effect, accuracy * power * self.base_sAttack)
else:
raise IndexError('Move not available yet')
```
| true |
code
| 0.665818 | null | null | null | null |
|
# CBOE VXN Index
In this notebook, we'll take a look at the CBOE VXN Index dataset, available on the [Quantopian Store](https://www.quantopian.com/store). This dataset spans 02 Feb 2001 through the current day. This data has a daily frequency. CBOE VXN measures market expectations of near-term volatility conveyed by NASDAQ-100 Index option prices
## Notebook Contents
There are two ways to access the data and you'll find both of them listed below. Just click on the section you'd like to read through.
- <a href='#interactive'><strong>Interactive overview</strong></a>: This is only available on Research and uses blaze to give you access to large amounts of data. Recommended for exploration and plotting.
- <a href='#pipeline'><strong>Pipeline overview</strong></a>: Data is made available through pipeline which is available on both the Research & Backtesting environment. Recommended for custom factor development and moving back & forth between research/backtesting.
### Limits
One key caveat: we limit the number of results returned from any given expression to 10,000 to protect against runaway memory usage. To be clear, you have access to all the data server side. We are limiting the size of the responses back from Blaze.
With preamble in place, let's get started:
<a id='interactive'></a>
#Interactive Overview
### Accessing the data with Blaze and Interactive on Research
Partner datasets are available on Quantopian Research through an API service known as [Blaze](http://blaze.pydata.org). Blaze provides the Quantopian user with a convenient interface to access very large datasets, in an interactive, generic manner.
Blaze provides an important function for accessing these datasets. Some of these sets are many millions of records. Bringing that data directly into Quantopian Research directly just is not viable. So Blaze allows us to provide a simple querying interface and shift the burden over to the server side.
It is common to use Blaze to reduce your dataset in size, convert it over to Pandas and then to use Pandas for further computation, manipulation and visualization.
Helpful links:
* [Query building for Blaze](http://blaze.readthedocs.io/en/latest/queries.html)
* [Pandas-to-Blaze dictionary](http://blaze.readthedocs.io/en/latest/rosetta-pandas.html)
* [SQL-to-Blaze dictionary](http://blaze.readthedocs.io/en/latest/rosetta-sql.html).
Once you've limited the size of your Blaze object, you can convert it to a Pandas DataFrames using:
> `from odo import odo`
> `odo(expr, pandas.DataFrame)`
###To see how this data can be used in your algorithm, search for the `Pipeline Overview` section of this notebook or head straight to <a href='#pipeline'>Pipeline Overview</a>
```
# For use in Quantopian Research, exploring interactively
from quantopian.interactive.data.quandl import cboe_vxn as dataset
# import data operations
from odo import odo
# import other libraries we will use
import pandas as pd
# Let's use blaze to understand the data a bit using Blaze dshape()
dataset.dshape
# And how many rows are there?
# N.B. we're using a Blaze function to do this, not len()
dataset.count()
# Let's see what the data looks like. We'll grab the first three rows.
dataset[:3]
```
Let's go over the columns:
- **open**: open price for VXN
- **high**: daily high for VXN
- **low**: daily low for VXN
- **close**: close price for VXN
- **asof_date**: the timeframe to which this data applies
- **timestamp**: this is our timestamp on when we registered the data.
We've done much of the data processing for you. Fields like `timestamp` are standardized across all our Store Datasets, so the datasets are easy to combine.
We can select columns and rows with ease. Below, we'll do a simple plot.
```
# Plotting this DataFrame
df = odo(dataset, pd.DataFrame)
df.head(5)
# So we can plot it, we'll set the index as the `asof_date`
df['asof_date'] = pd.to_datetime(df['asof_date'])
df = df.set_index(['asof_date'])
df.head(5)
import matplotlib.pyplot as plt
df['open_'].plot(label=str(dataset))
plt.ylabel(str(dataset))
plt.legend()
plt.title("Graphing %s since %s" % (str(dataset), min(df.index)))
```
<a id='pipeline'></a>
#Pipeline Overview
### Accessing the data in your algorithms & research
The only method for accessing partner data within algorithms running on Quantopian is via the pipeline API. Different data sets work differently but in the case of this data, you can add this data to your pipeline as follows:
Import the data set here
> `from quantopian.pipeline.data.quandl import cboe_vxn`
Then in intialize() you could do something simple like adding the raw value of one of the fields to your pipeline:
> `pipe.add(cboe_vxn.open_.latest, 'open')`
Pipeline usage is very similar between the backtester and Research so let's go over how to import this data through pipeline and view its outputs.
```
# Import necessary Pipeline modules
from quantopian.pipeline import Pipeline
from quantopian.research import run_pipeline
from quantopian.pipeline.factors import AverageDollarVolume
# Import the datasets available
from quantopian.pipeline.data.quandl import cboe_vxn
```
Now that we've imported the data, let's take a look at which fields are available for each dataset.
You'll find the dataset, the available fields, and the datatypes for each of those fields.
```
print "Here are the list of available fields per dataset:"
print "---------------------------------------------------\n"
def _print_fields(dataset):
print "Dataset: %s\n" % dataset.__name__
print "Fields:"
for field in list(dataset.columns):
print "%s - %s" % (field.name, field.dtype)
print "\n"
_print_fields(cboe_vxn)
print "---------------------------------------------------\n"
```
Now that we know what fields we have access to, let's see what this data looks like when we run it through Pipeline.
This is constructed the same way as you would in the backtester. For more information on using Pipeline in Research view this thread:
https://www.quantopian.com/posts/pipeline-in-research-build-test-and-visualize-your-factors-and-filters
```
pipe = Pipeline()
pipe.add(cboe_vxn.open_.latest, 'open_vxn')
# Setting some basic liquidity strings (just for good habit)
dollar_volume = AverageDollarVolume(window_length=20)
top_1000_most_liquid = dollar_volume.rank(ascending=False) < 1000
pipe.set_screen(top_1000_most_liquid & cboe_vxn.open_.latest.notnan())
# The show_graph() method of pipeline objects produces a graph to show how it is being calculated.
pipe.show_graph(format='png')
# run_pipeline will show the output of your pipeline
pipe_output = run_pipeline(pipe, start_date='2013-11-01', end_date='2013-11-25')
pipe_output
```
Here, you'll notice that each security is mapped to the corresponding value, so you could grab any security to get what you need.
Taking what we've seen from above, let's see how we'd move that into the backtester.
```
# This section is only importable in the backtester
from quantopian.algorithm import attach_pipeline, pipeline_output
# General pipeline imports
from quantopian.pipeline import Pipeline
from quantopian.pipeline.factors import AverageDollarVolume
# For use in your algorithms via the pipeline API
from quantopian.pipeline.data.quandl import cboe_vxn
def make_pipeline():
# Create our pipeline
pipe = Pipeline()
# Screen out penny stocks and low liquidity securities.
dollar_volume = AverageDollarVolume(window_length=20)
is_liquid = dollar_volume.rank(ascending=False) < 1000
# Create the mask that we will use for our percentile methods.
base_universe = (is_liquid)
# Add the datasets available
pipe.add(cboe_vxn.open_.latest, 'vxn_open')
# Set our pipeline screens
pipe.set_screen(is_liquid)
return pipe
def initialize(context):
attach_pipeline(make_pipeline(), "pipeline")
def before_trading_start(context, data):
results = pipeline_output('pipeline')
```
Now you can take that and begin to use it as a building block for your algorithms, for more examples on how to do that you can visit our <a href='https://www.quantopian.com/posts/pipeline-factor-library-for-data'>data pipeline factor library</a>
| true |
code
| 0.696423 | null | null | null | null |
|
# 206 Optimizers
View more, visit my tutorial page: https://morvanzhou.github.io/tutorials/
My Youtube Channel: https://www.youtube.com/user/MorvanZhou
Dependencies:
* torch: 0.1.11
* matplotlib
```
import torch
import torch.utils.data as Data
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt
%matplotlib inline
torch.manual_seed(1) # reproducible
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
```
### Generate some fake data
```
# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))
# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()
```
### Put dataset into torch dataset
```
torch_dataset = Data.TensorDataset(data_tensor=x, target_tensor=y)
loader = Data.DataLoader(
dataset=torch_dataset,
batch_size=BATCH_SIZE,
shuffle=True, num_workers=2,)
```
### Default network
```
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(1, 20) # hidden layer
self.predict = torch.nn.Linear(20, 1) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
```
### Different nets
```
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
```
### Different optimizers
```
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []] # record loss
# training
for epoch in range(EPOCH):
print('Epoch: ', epoch)
for step, (batch_x, batch_y) in enumerate(loader): # for each training step
b_x = Variable(batch_x)
b_y = Variable(batch_y)
for net, opt, l_his in zip(nets, optimizers, losses_his):
output = net(b_x) # get output for every net
loss = loss_func(output, b_y) # compute loss for every net
opt.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
opt.step() # apply gradients
l_his.append(loss.data[0]) # loss recoder
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):
plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()
```
| true |
code
| 0.838614 | null | null | null | null |
|
#### Training Sample: train.csv with undersampling
#### Evaluation Sample: validation_under.csv
#### Method: OOB
#### Output: Best hyperparameters; Pr-curve; ROC AUC
# Training Part
```
from imblearn.over_sampling import RandomOverSampler
from imblearn.under_sampling import RandomUnderSampler
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import auc,f1_score,make_scorer,classification_report, matthews_corrcoef, accuracy_score, average_precision_score, roc_auc_score, roc_curve, precision_recall_curve
import matplotlib.pyplot as plt
```
#### Input data is read and named as the following
```
transactions = pd.read_csv('../Data/train.csv')
X_train = transactions.drop(labels='Class', axis=1)
y_train = transactions.loc[:,'Class']
rus = RandomUnderSampler(sampling_strategy=0.8)
X_res, Y_res = rus.fit_resample(X_train, y_train)
```
#### Tuning parameters
```
test = 1
rf = RandomForestClassifier(n_jobs=-1, random_state=1)
if test== 0:
n_estimators = [75,150,800,1000,1200]
min_samples_split = [2, 5]
min_samples_leaf = [1, 5]
else:
n_estimators = [800]
min_samples_split = [2]
min_samples_leaf = [1]
param_grid_rf = {'n_estimators': n_estimators,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf,
'oob_score': [True]
}
grid_rf = GridSearchCV(estimator=rf, param_grid=param_grid_rf,cv = 5,
n_jobs=-1, pre_dispatch='2*n_jobs', verbose=1, return_train_score=False)
grid_rf.fit(X_res, Y_res)
```
#### The best score and the estimator
```
grid_rf.best_score_
grid_rf.best_params_
y_pre = grid_rf.predict(X_res)
print('Classification Report for training')
print(classification_report(y_pre, Y_res))
```
# Evaluation Part
```
evaluation = pd.read_csv('../Data/validation_under.csv')
X_eval = evaluation.drop(labels='Class', axis=1)
y_eval = evaluation.loc[:,'Class']
def Random_Forest_eval(estimator, X_test, y_test):
y_pred = estimator.predict(X_test)
print('Classification Report')
print(classification_report(y_test, y_pred))
y_score = estimator.predict_proba(X_test)[:,1]
print('AUPRC', average_precision_score(y_test, y_score))
print('AUROC', roc_auc_score(y_test, y_score))
Random_Forest_eval(grid_rf, X_eval, y_eval)
```
### Receiver Operating Characteristic Curve
```
def Draw_ROC(Y_prob, Y_observed, model_name = 'Model'):
ns_probs = [0 for _ in range(len(Y_observed))]
# calculate scores
ns_auc = roc_auc_score(Y_observed, ns_probs)
lr_auc = roc_auc_score(Y_observed, Y_prob)
# summarize scores
print('Chance: ROC AUC=%.3f' % (ns_auc))
print('%s: ROC AUC=%.3f' % (model_name, lr_auc))
# calculate roc curves
ns_fpr, ns_tpr, _ = roc_curve(Y_observed, ns_probs, pos_label=1)
lr_fpr, lr_tpr, _ = roc_curve(Y_observed, Y_prob, pos_label=1)
# plot the roc curve for the model
plt.plot(ns_fpr, ns_tpr, linestyle='--', label='Chance')
plt.plot(lr_fpr, lr_tpr, marker='.', label=model_name)
# axis labels
plt.title('Receiver operating characteristic curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
# show the legend
plt.legend()
# show the plot
plt.show()
y_score = grid_rf.predict_proba(X_eval)[:,1]
Draw_ROC(y_score, y_eval,'Random Forest')
```
### Precision Recall Curve
```
def Draw_PR(Y_prob, Y_predicted, Y_observed, model_name = 'Model'):
# predict class values
lr_precision, lr_recall, _ = precision_recall_curve(Y_observed, Y_prob, pos_label=1)
lr_f1, lr_auc = f1_score(Y_observed, Y_predicted), auc(lr_recall, lr_precision)
# summarize scores
print('Random Forest: f1=%.3f auc=%.3f' % (lr_f1, lr_auc))
# plot the precision-recall curves
no_skill = len(Y_observed[Y_observed==1]) / len(Y_observed)
plt.plot([0, 1], [no_skill, no_skill], linestyle='--', label='Chance')
plt.plot(lr_recall, lr_precision, marker='.', label=model_name)
# axis labels
plt.title('2-class Precision-Recall curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
# show the legend
plt.legend()
# show the plot
plt.show()
Y_predicted = grid_rf.predict(X_eval)
Draw_PR(y_score, Y_predicted, y_eval,'Random Forest')
```
| true |
code
| 0.708528 | null | null | null | null |
|
# 05 - Data Preparation and Advanced Model Evaluation
by [Alejandro Correa Bahnsen](http://www.albahnsen.com/) & [Iván Torroledo](http://www.ivantorroledo.com/)
version 1.3, June 2018
## Part of the class [Applied Deep Learning](https://github.com/albahnsen/AppliedDeepLearningClass)
This notebook is licensed under a [Creative Commons Attribution-ShareAlike 3.0 Unported License](http://creativecommons.org/licenses/by-sa/3.0/deed.en_US). Special thanks goes to [Kevin Markham](https://github.com/justmarkham)
# Handling missing values
scikit-learn models expect that all values are **numeric** and **hold meaning**. Thus, missing values are not allowed by scikit-learn.
```
import pandas as pd
import zipfile
with zipfile.ZipFile('../datasets/titanic.csv.zip', 'r') as z:
f = z.open('titanic.csv')
titanic = pd.read_csv(f, sep=',', index_col=0)
titanic.head()
# check for missing values
titanic.isnull().sum()
```
One possible strategy is to **drop missing values**:
```
# drop rows with any missing values
titanic.dropna().shape
# drop rows where Age is missing
titanic[titanic.Age.notnull()].shape
```
Sometimes a better strategy is to **impute missing values**:
```
# mean Age
titanic.Age.mean()
# median Age
titanic.Age.median()
titanic.loc[titanic.Age.isnull()]
```
# most frequent Age
titanic.Age.mode()
```
# fill missing values for Age with the median age
titanic.Age.fillna(titanic.Age.median(), inplace=True)
```
Another strategy would be to build a **KNN model** just to impute missing values. How would we do that?
If values are missing from a categorical feature, we could treat the missing values as **another category**. Why might that make sense?
How do we **choose** between all of these strategies?
# Handling categorical features
How do we include a categorical feature in our model?
- **Ordered categories:** transform them to sensible numeric values (example: small=1, medium=2, large=3)
- **Unordered categories:** use dummy encoding (0/1)
```
titanic.head(10)
# encode Sex_Female feature
titanic['Sex_Female'] = titanic.Sex.map({'male':0, 'female':1})
# create a DataFrame of dummy variables for Embarked
embarked_dummies = pd.get_dummies(titanic.Embarked, prefix='Embarked')
embarked_dummies.drop(embarked_dummies.columns[0], axis=1, inplace=True)
# concatenate the original DataFrame and the dummy DataFrame
titanic = pd.concat([titanic, embarked_dummies], axis=1)
titanic.head(1)
```
- How do we **interpret** the encoding for Embarked?
- Why didn't we just encode Embarked using a **single feature** (C=0, Q=1, S=2)?
- Does it matter which category we choose to define as the **baseline**?
- Why do we only need **two dummy variables** for Embarked?
```
# define X and y
feature_cols = ['Pclass', 'Parch', 'Age', 'Sex_Female', 'Embarked_Q', 'Embarked_S']
X = titanic[feature_cols]
y = titanic.Survived
# train/test split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
# train a logistic regression model
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(C=1e9)
logreg.fit(X_train, y_train)
# make predictions for testing set
y_pred_class = logreg.predict(X_test)
# calculate testing accuracy
from sklearn import metrics
print(metrics.accuracy_score(y_test, y_pred_class))
```
# ROC curves and AUC
```
# predict probability of survival
y_pred_prob = logreg.predict_proba(X_test)[:, 1]
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (8, 6)
plt.rcParams['font.size'] = 14
# plot ROC curve
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pred_prob)
plt.plot(fpr, tpr)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('True Positive Rate (Sensitivity)')
# calculate AUC
print(metrics.roc_auc_score(y_test, y_pred_prob))
```
Besides allowing you to calculate AUC, seeing the ROC curve can help you to choose a threshold that **balances sensitivity and specificity** in a way that makes sense for the particular context.
```
# histogram of predicted probabilities grouped by actual response value
df = pd.DataFrame({'probability':y_pred_prob, 'actual':y_test})
df.hist(column='probability', by='actual', sharex=True, sharey=True)
# ROC curve using y_pred_class - WRONG!
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pred_class)
plt.plot(fpr, tpr)
# AUC using y_pred_class - WRONG!
print(metrics.roc_auc_score(y_test, y_pred_class))
```
If you use **y_pred_class**, it will interpret the zeros and ones as predicted probabilities of 0% and 100%.
# Cross-validation
## Review of model evaluation procedures
**Motivation:** Need a way to choose between machine learning models
- Goal is to estimate likely performance of a model on **out-of-sample data**
**Initial idea:** Train and test on the same data
- But, maximizing **training accuracy** rewards overly complex models which **overfit** the training data
**Alternative idea:** Train/test split
- Split the dataset into two pieces, so that the model can be trained and tested on **different data**
- **Testing accuracy** is a better estimate than training accuracy of out-of-sample performance
- But, it provides a **high variance** estimate since changing which observations happen to be in the testing set can significantly change testing accuracy
```
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics
# define X and y
feature_cols = ['Pclass', 'Parch', 'Age', 'Sex_Female', 'Embarked_Q', 'Embarked_S']
X = titanic[feature_cols]
y = titanic.Survived
# train/test split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
# train a logistic regression model
logreg = LogisticRegression(C=1e9)
logreg.fit(X_train, y_train)
# make predictions for testing set
y_pred_class = logreg.predict(X_test)
# calculate testing accuracy
print(metrics.accuracy_score(y_test, y_pred_class))
# train/test split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2)
# train a logistic regression model
logreg = LogisticRegression(C=1e9)
logreg.fit(X_train, y_train)
# make predictions for testing set
y_pred_class = logreg.predict(X_test)
# calculate testing accuracy
print(metrics.accuracy_score(y_test, y_pred_class))
res=[]
for i in range(100):
# train/test split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=3*i)
# train a logistic regression model
logreg = LogisticRegression(C=1e9)
logreg.fit(X_train, y_train)
# make predictions for testing set
y_pred_class = logreg.predict(X_test)
# calculate testing accuracy
res.append(metrics.accuracy_score(y_test, y_pred_class))
pd.Series(res).plot()
```
train test spliting create bias due to the intrinsic randomness in the sets selection
# K-fold cross-validation
1. Split the dataset into K **equal** partitions (or "folds").
2. Use fold 1 as the **testing set** and the union of the other folds as the **training set**.
3. Calculate **testing accuracy**.
4. Repeat steps 2 and 3 K times, using a **different fold** as the testing set each time.
5. Use the **average testing accuracy** as the estimate of out-of-sample accuracy.
Diagram of **5-fold cross-validation:**
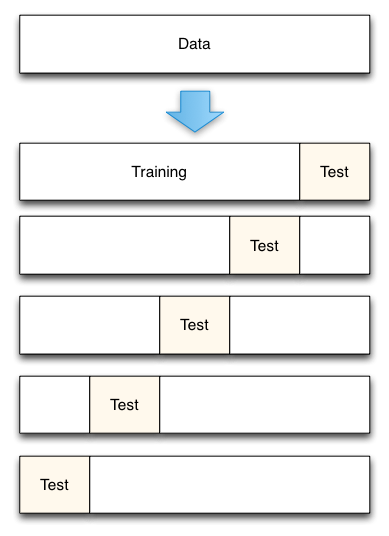
```
# simulate splitting a dataset of 25 observations into 5 folds
from sklearn.cross_validation import KFold
kf = KFold(25, n_folds=5, shuffle=False)
# print the contents of each training and testing set
print('{} {:^61} {}'.format('Iteration', 'Training set observations', 'Testing set observations'))
for iteration, data in enumerate(kf, start=1):
print('{:^9} {} {:^25}'.format(str(iteration), str(data[0]), str(data[1])))
```
- Dataset contains **25 observations** (numbered 0 through 24)
- 5-fold cross-validation, thus it runs for **5 iterations**
- For each iteration, every observation is either in the training set or the testing set, **but not both**
- Every observation is in the testing set **exactly once**
```
# Create k-folds
kf = KFold(X.shape[0], n_folds=10, random_state=0)
results = []
for train_index, test_index in kf:
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y.iloc[train_index], y.iloc[test_index]
# train a logistic regression model
logreg = LogisticRegression(C=1e9)
logreg.fit(X_train, y_train)
# make predictions for testing set
y_pred_class = logreg.predict(X_test)
# calculate testing accuracy
results.append(metrics.accuracy_score(y_test, y_pred_class))
pd.Series(results).describe()
from sklearn.cross_validation import cross_val_score
logreg = LogisticRegression(C=1e9)
results = cross_val_score(logreg, X, y, cv=10, scoring='accuracy')
pd.Series(results).describe()
```
## Comparing cross-validation to train/test split
Advantages of **cross-validation:**
- More accurate estimate of out-of-sample accuracy
- More "efficient" use of data (every observation is used for both training and testing)
Advantages of **train/test split:**
- Runs K times faster than K-fold cross-validation
- Simpler to examine the detailed results of the testing process
## Cross-validation recommendations
1. K can be any number, but **K=10** is generally recommended
2. For classification problems, **stratified sampling** is recommended for creating the folds
- Each response class should be represented with equal proportions in each of the K folds
- scikit-learn's `cross_val_score` function does this by default
## Improvements to cross-validation
**Repeated cross-validation**
- Repeat cross-validation multiple times (with **different random splits** of the data) and average the results
- More reliable estimate of out-of-sample performance by **reducing the variance** associated with a single trial of cross-validation
**Creating a hold-out set**
- "Hold out" a portion of the data **before** beginning the model building process
- Locate the best model using cross-validation on the remaining data, and test it **using the hold-out set**
- More reliable estimate of out-of-sample performance since hold-out set is **truly out-of-sample**
**Feature engineering and selection within cross-validation iterations**
- Normally, feature engineering and selection occurs **before** cross-validation
- Instead, perform all feature engineering and selection **within each cross-validation iteration**
- More reliable estimate of out-of-sample performance since it **better mimics** the application of the model to out-of-sample data
# Overfitting, Underfitting and Model Selection
Now that we've gone over the basics of validation, and cross-validation, it's time to go into even more depth regarding model selection.
The issues associated with validation and
cross-validation are some of the most important
aspects of the practice of machine learning. Selecting the optimal model
for your data is vital, and is a piece of the problem that is not often
appreciated by machine learning practitioners.
Of core importance is the following question:
**If our estimator is underperforming, how should we move forward?**
- Use simpler or more complicated model?
- Add more features to each observed data point?
- Add more training samples?
The answer is often counter-intuitive. In particular, **Sometimes using a
more complicated model will give _worse_ results.** Also, **Sometimes adding
training data will not improve your results.** The ability to determine
what steps will improve your model is what separates the successful machine
learning practitioners from the unsuccessful.
### Illustration of the Bias-Variance Tradeoff
For this section, we'll work with a simple 1D regression problem. This will help us to
easily visualize the data and the model, and the results generalize easily to higher-dimensional
datasets. We'll explore a simple **linear regression** problem.
This can be accomplished within scikit-learn with the `sklearn.linear_model` module.
We'll create a simple nonlinear function that we'd like to fit
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def test_func(x, err=0.5):
y = 10 - 1. / (x + 0.1)
if err > 0:
y = np.random.normal(y, err)
return y
```
Now let's create a realization of this dataset:
```
def make_data(N=40, error=1.0, random_seed=1):
# randomly sample the data
np.random.seed(1)
X = np.random.random(N)[:, np.newaxis]
y = test_func(X.ravel(), error)
return X, y
X, y = make_data(40, error=1)
plt.scatter(X.ravel(), y);
```
Now say we want to perform a regression on this data. Let's use the built-in linear regression function to compute a fit:
```
X_test = np.linspace(-0.1, 1.1, 500)[:, None]
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
model = LinearRegression()
model.fit(X, y)
y_test = model.predict(X_test)
plt.scatter(X.ravel(), y)
plt.plot(X_test.ravel(), y_test,c='r')
plt.title("mean squared error: {0:.3g}".format(mean_squared_error(model.predict(X), y)));
```
We have fit a straight line to the data, but clearly this model is not a good choice. We say that this model is **biased**, or that it **under-fits** the data.
Let's try to improve this by creating a more complicated model. We can do this by adding degrees of freedom, and computing a polynomial regression over the inputs. Scikit-learn makes this easy with the ``PolynomialFeatures`` preprocessor, which can be pipelined with a linear regression.
Let's make a convenience routine to do this:
```
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
```
Now we'll use this to fit a quadratic curve to the data.
```
X_poly = PolynomialFeatures(degree=2).fit_transform(X)
X_test_poly = PolynomialFeatures(degree=2).fit_transform(X_test)
model = LinearRegression()
model.fit(X_poly, y)
y_test = model.predict(X_test_poly)
plt.scatter(X.ravel(), y)
plt.plot(X_test.ravel(), y_test,c='r')
plt.title("mean squared error: {0:.3g}".format(mean_squared_error(model.predict(X_poly), y)));
```
This reduces the mean squared error, and makes a much better fit. What happens if we use an even higher-degree polynomial?
```
X_poly = PolynomialFeatures(degree=30).fit_transform(X)
X_test_poly = PolynomialFeatures(degree=30).fit_transform(X_test)
model = LinearRegression()
model.fit(X_poly, y)
y_test = model.predict(X_test_poly)
plt.scatter(X.ravel(), y)
plt.plot(X_test.ravel(), y_test,c='r')
plt.title("mean squared error: {0:.3g}".format(mean_squared_error(model.predict(X_poly), y)))
plt.ylim(-4, 14);
```
When we increase the degree to this extent, it's clear that the resulting fit is no longer reflecting the true underlying distribution, but is more sensitive to the noise in the training data. For this reason, we call it a **high-variance model**, and we say that it **over-fits** the data.
### Detecting Over-fitting with Validation Curves
Clearly, computing the error on the training data is not enough (we saw this previously). As above, we can use **cross-validation** to get a better handle on how the model fit is working.
Let's do this here, again using the ``validation_curve`` utility. To make things more clear, we'll use a slightly larger dataset:
```
X, y = make_data(120, error=1.0)
plt.scatter(X, y);
from sklearn.model_selection import validation_curve
def rms_error(model, X, y):
y_pred = model.predict(X)
return np.sqrt(np.mean((y - y_pred) ** 2))
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree=2, **kwargs):
return make_pipeline(PolynomialFeatures(degree),
LinearRegression(**kwargs))
degree = np.arange(0, 18)
val_train, val_test = validation_curve(PolynomialRegression(), X, y,
'polynomialfeatures__degree', degree, cv=7,
scoring=rms_error)
```
Now let's plot the validation curves:
```
def plot_with_err(x, data, **kwargs):
mu, std = data.mean(1), data.std(1)
lines = plt.plot(x, mu, '-', **kwargs)
plt.fill_between(x, mu - std, mu + std, edgecolor='none',
facecolor=lines[0].get_color(), alpha=0.2)
plot_with_err(degree, val_train, label='training scores')
plot_with_err(degree, val_test, label='validation scores')
plt.xlabel('degree'); plt.ylabel('rms error')
plt.legend();
```
Notice the trend here, which is common for this type of plot.
1. For a small model complexity, the training error and validation error are very similar. This indicates that the model is **under-fitting** the data: it doesn't have enough complexity to represent the data. Another way of putting it is that this is a **high-bias** model.
2. As the model complexity grows, the training and validation scores diverge. This indicates that the model is **over-fitting** the data: it has so much flexibility, that it fits the noise rather than the underlying trend. Another way of putting it is that this is a **high-variance** model.
3. Note that the training score (nearly) always improves with model complexity. This is because a more complicated model can fit the noise better, so the model improves. The validation data generally has a sweet spot, which here is around 5 terms.
Here's our best-fit model according to the cross-validation:
```
model = PolynomialRegression(4).fit(X, y)
plt.scatter(X, y)
plt.plot(X_test, model.predict(X_test),c='r');
```
### Detecting Data Sufficiency with Learning Curves
As you might guess, the exact turning-point of the tradeoff between bias and variance is highly dependent on the number of training points used. Here we'll illustrate the use of *learning curves*, which display this property.
The idea is to plot the mean-squared-error for the training and test set as a function of *Number of Training Points*
```
from sklearn.learning_curve import learning_curve
def plot_learning_curve(degree=3):
train_sizes = np.linspace(0.05, 1, 20)
N_train, val_train, val_test = learning_curve(PolynomialRegression(degree),
X, y, train_sizes, cv=5,
scoring=rms_error)
plot_with_err(N_train, val_train, label='training scores')
plot_with_err(N_train, val_test, label='validation scores')
plt.xlabel('Training Set Size'); plt.ylabel('rms error')
plt.ylim(0, 3)
plt.xlim(5, 80)
plt.legend()
```
Let's see what the learning curves look like for a linear model:
```
plot_learning_curve(1)
```
This shows a typical learning curve: for very few training points, there is a large separation between the training and test error, which indicates **over-fitting**. Given the same model, for a large number of training points, the training and testing errors converge, which indicates potential **under-fitting**.
As you add more data points, the training error will never increase, and the testing error will never decrease (why do you think this is?)
It is easy to see that, in this plot, if you'd like to reduce the MSE down to the nominal value of 1.0 (which is the magnitude of the scatter we put in when constructing the data), then adding more samples will *never* get you there. For $d=1$, the two curves have converged and cannot move lower. What about for a larger value of $d$?
```
plot_learning_curve(3)
```
Here we see that by adding more model complexity, we've managed to lower the level of convergence to an rms error of 1.0!
What if we get even more complex?
```
plot_learning_curve(10)
```
For an even more complex model, we still converge, but the convergence only happens for *large* amounts of training data.
So we see the following:
- you can **cause the lines to converge** by adding more points or by simplifying the model.
- you can **bring the convergence error down** only by increasing the complexity of the model.
Thus these curves can give you hints about how you might improve a sub-optimal model. If the curves are already close together, you need more model complexity. If the curves are far apart, you might also improve the model by adding more data.
To make this more concrete, imagine some telescope data in which the results are not robust enough. You must think about whether to spend your valuable telescope time observing *more objects* to get a larger training set, or *more attributes of each object* in order to improve the model. The answer to this question has real consequences, and can be addressed using these metrics.
# Recall, Precision and F1-Score
Intuitively, [precision](http://en.wikipedia.org/wiki/Precision_and_recall#Precision) is the ability
of the classifier not to label as positive a sample that is negative, and
[recall](http://en.wikipedia.org/wiki/Precision_and_recall#Recall) is the
ability of the classifier to find all the positive samples.
The [F-measure](http://en.wikipedia.org/wiki/F1_score>)
($F_\beta$ and $F_1$ measures) can be interpreted as a weighted
harmonic mean of the precision and recall. A
$F_\beta$ measure reaches its best value at 1 and its worst score at 0.
With $\beta = 1$, $F_\beta$ and
$F_1$ are equivalent, and the recall and the precision are equally important.
```
import pandas as pd
import zipfile
with zipfile.ZipFile('../datasets/titanic.csv.zip', 'r') as z:
f = z.open('titanic.csv')
titanic = pd.read_csv(f, sep=',', index_col=0)
titanic.head()
# fill missing values for Age with the median age
titanic.Age.fillna(titanic.Age.median(), inplace=True)
# define X and y
feature_cols = ['Pclass', 'Parch', 'Age']
X = titanic[feature_cols]
y = titanic.Survived
# train/test split
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
# train a logistic regression model
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(C=1e9)
logreg.fit(X_train, y_train)
# make predictions for testing set
y_pred_class = logreg.predict(X_test)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_pred_class)
from sklearn.metrics import precision_score, recall_score, f1_score
print('precision_score ', precision_score(y_test, y_pred_class))
print('recall_score ', recall_score(y_test, y_pred_class))
```
### F1Score
The traditional F-measure or balanced F-score (F1 score) is the harmonic mean of precision and recall:
$$F_1 = 2 \cdot \frac{\mathrm{precision} \cdot \mathrm{recall}}{\mathrm{precision} + \mathrm{recall}}.$$
```
print('f1_score ', f1_score(y_test, y_pred_class))
```
## Summary
We've gone over several useful tools for model validation
- The **Training Score** shows how well a model fits the data it was trained on. This is not a good indication of model effectiveness
- The **Validation Score** shows how well a model fits hold-out data. The most effective method is some form of cross-validation, where multiple hold-out sets are used.
- **Validation Curves** are a plot of validation score and training score as a function of **model complexity**:
+ when the two curves are close, it indicates *underfitting*
+ when the two curves are separated, it indicates *overfitting*
+ the "sweet spot" is in the middle
- **Learning Curves** are a plot of the validation score and training score as a function of **Number of training samples**
+ when the curves are close, it indicates *underfitting*, and adding more data will not generally improve the estimator.
+ when the curves are far apart, it indicates *overfitting*, and adding more data may increase the effectiveness of the model.
These tools are powerful means of evaluating your model on your data.
| true |
code
| 0.613787 | null | null | null | null |
|
This notebook shows you how to visualize the changes in ozone and particulate matter from different runs of CCTM. Note that you must first run the `combine` program distributed with CMAQ for the files here to exist. The need for postprocessing of CCTM outputs is explained in [this section](https://github.com/USEPA/CMAQ/blob/main/DOCS/Users_Guide/CMAQ_UG_ch08_analysis_tools.md#82-aggregating-and-transforming-model-species) of the CMAQ User's Guide.
```
import numpy as np
import pandas as pd
import xarray as xr
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import cartopy.feature as cfeature
import cartopy.io.shapereader as shpreader
from matplotlib import cm
from matplotlib import ticker
from matplotlib import colors
from cmaqpy.runcmaq import CMAQModel
from cmaqpy import plots
import monet as m
import monetio as mio
import optwrf.plots as owplt
import wrf as wrfpy
def convert_tz_xr(df, input_tz='UTC', output_tz='US/Eastern'):
tidx_in = df.time.to_index().tz_localize(tz=input_tz)
df.coords['time'] = tidx_in.tz_convert(output_tz).tz_localize(None)
return df
# Specify the start/end times
start_datetime = 'August 06, 2016' # first day that you want run
end_datetime = 'August 14, 2016' # last day you want run
# Define the coordinate name (must match that in GRIDDESC)
coord_name = 'LAM_40N97W'
# Create a CMAQModel object
base_sim = CMAQModel(start_datetime, end_datetime, '2016Base_4OTC2', coord_name, '4OTC2', setup_yaml='dirpaths_2016Base_4OTC2.yml', verbose=True)
ren_sim = CMAQModel(start_datetime, end_datetime, '2016_4OTC2', coord_name, '4OTC2', setup_yaml='dirpaths_2016_4OTC2.yml', verbose=True)
conc_base = f'{base_sim.POST}/COMBINE_ACONC_{base_sim.cctm_runid}_201608.nc'
conc_ren = f'{ren_sim.POST}/COMBINE_ACONC_{ren_sim.cctm_runid}_201608.nc'
c_base = mio.cmaq.open_dataset(fname=conc_base)
c_ren = mio.cmaq.open_dataset(fname=conc_ren)
c_base = convert_tz_xr(c_base)
c_ren = convert_tz_xr(c_ren)
def get_proj(ds):
"""
Extracts the CMAQ projection information from the proj4_srs attribute.
:param ds:
:return:
"""
proj_params = ds.proj4_srs
proj_params = proj_params.replace(' ', '')
proj_params = proj_params.split('+')
proj = proj_params[1].split('=')[1]
truelat1 = float(proj_params[2].split('=')[1])
truelat2 = float(proj_params[3].split('=')[1])
central_latitude = float(proj_params[4].split('=')[1])
central_longitude = float(proj_params[5].split('=')[1])
if proj == 'lcc':
cartopy_crs = ccrs.LambertConformal(central_longitude=central_longitude,
central_latitude=central_latitude,
standard_parallels=[truelat1, truelat2])
return cartopy_crs
else:
raise ValueError('Your projection is not the expected Lambert Conformal.')
def get_domain_boundary(ds, cartopy_crs):
"""
Finds the boundary of the WRF domain.
:param ds:
:param cartopy_crs:
:return:
"""
# Rename the lat-lon corrdinates to get wrf-python to recognize them
variables = {'latitude': 'XLAT',
'longitude': 'XLONG'}
try:
ds = xr.Dataset.rename(ds, variables)
except ValueError:
print(f'Variables {variables} cannot be renamed, '
f'those on the left are not in this dataset.')
# I need to manually convert the boundaries of the WRF domain into Plate Carree to set the limits.
# Get the raw map bounds using a wrf-python utility
raw_bounds = wrfpy.util.geo_bounds(ds)
# Get the projected bounds telling cartopy that the input coordinates are lat/lon (Plate Carree)
projected_bounds = cartopy_crs.transform_points(ccrs.PlateCarree(),
np.array([raw_bounds.bottom_left.lon, raw_bounds.top_right.lon]),
np.array([raw_bounds.bottom_left.lat, raw_bounds.top_right.lat]))
return projected_bounds
def conc_map(plot_var, cmap=cm.get_cmap('bwr'), ax=None, cartopy_crs=None, proj_bounds=None,
vmin=-1, vmax=1, cbar_ticks=[], cbar_label='Concentration'):
"""
Creates a filled colormap across the full domain in the native (Lambert
Conformal) map projection.
"""
if ax is None:
# Create a figure
fig = plt.figure(figsize=(8, 8))
# Set the GeoAxes to the projection used by WRF
ax = fig.add_subplot(1, 1, 1, projection=cartopy_crs)
# Normalize the values, so that the colorbar plots correctly
norm = colors.Normalize(vmin=vmin, vmax=vmax)
# Create the pcolormesh
cn = ax.pcolormesh(wrfpy.to_np(plot_var.longitude), wrfpy.to_np(plot_var.latitude), wrfpy.to_np(plot_var),
transform=ccrs.PlateCarree(),
cmap=cmap,
norm=norm,
)
if proj_bounds is not None:
# Format the projected bounds so they can be used in the xlim and ylim attributes
proj_xbounds = [proj_bounds[0, 0], proj_bounds[1, 0]]
proj_ybounds = [proj_bounds[0, 1], proj_bounds[1, 1]]
# Finally, set the x and y limits
ax.set_xlim(proj_xbounds)
ax.set_ylim(proj_ybounds)
# Download and add the states, coastlines, and lakes
shapename = 'admin_1_states_provinces_lakes'
states_shp = shpreader.natural_earth(resolution='10m',
category='cultural',
name=shapename)
# Add features to the maps
ax.add_geometries(
shpreader.Reader(states_shp).geometries(),
ccrs.PlateCarree(),
facecolor='none',
linewidth=.5,
edgecolor="black"
)
# Add features to the maps
# ax.add_feature(cfeature.LAKES)
# ax.add_feature(cfeature.OCEAN)
# Add color bars
cbar = plt.colorbar(cn,
ax=ax,
ticks=cbar_ticks,
label=cbar_label,
pad=0.05
)
pm25_mean_diff = (c_ren.PM25_TOT - c_base.PM25_TOT).mean(dim='time').squeeze()
pm25_pct_diff = (c_ren.PM25_TOT - c_base.PM25_TOT) / c_base.PM25_TOT
pm25_mean_pct_diff = pm25_pct_diff.mean(dim='time').squeeze()
cartopy_crs = get_proj(c_ren)
proj_bounds = get_domain_boundary(c_ren, cartopy_crs)
conc_map(pm25_mean_diff, cmap=cm.get_cmap('bwr'), ax=None, cartopy_crs=cartopy_crs, proj_bounds=proj_bounds,
vmin=-0.01, vmax=0.01, cbar_ticks=[-0.01, -0.005, 0, 0.005, 0.01], cbar_label='PM$_{2.5}$ Difference ($\mu g/m^{3}$)')
# If you just want to do a quick map visualization
c_base.PM25_TOT.sel(time='2016-08-07 23').monet.quick_map(robust=True)
pm25_mean = c_ren.PM25_TOT.mean(dim='time')
pm25_mean_diff = (c_ren.PM25_TOT - c_base.PM25_TOT).mean(dim='time')
# pm25_pct_diff = (c1.PM25_TOT - c.PM25_TOT) / c.PM25_TOT
# pm25_mean_pct_diff = pm25_pct_diff.mean(dim='time')
plots.conc_compare(pm25_mean, pm25_mean_diff, extent = [-83, -70, 37, 46],
vmin1=0, vmax1=10, vmin2=-1, vmax2=1, cmap1=cm.get_cmap('YlOrBr'), cmap2=cm.get_cmap('bwr'),
cbar_label1='PM$_{2.5}$ ($\mu g/m^{3}$)', cbar_label2='PM$_{2.5}$ Difference ($\mu g/m^{3}$)',
figsize=(7,3.5), savefig=True, figpath1='../cmaqpy/data/plots/PM2.5.png',
figpath2='../cmaqpy/data/plots/PM2.5_diff.png')
o3_mean = c_ren.O3.mean(dim='time')
o3_mean_diff = (c_ren.O3 - c_base.O3).mean(dim='time')
# o3_pct_diff = (c1.O3 - c.O3) / c.O3
# o3_mean_pct_diff = o3_pct_diff.mean(dim='time')
plots.conc_compare(o3_mean, o3_mean_diff, extent = [-83, -70, 37, 46],
vmin1=15, vmax1=45, vmin2=-1, vmax2=1, cmap1=cm.get_cmap('cividis'), cmap2=cm.get_cmap('bwr'),
cbar_label1='O$_{3}$ ($ppbV$)', cbar_label2='O$_{3}$ Difference ($ppbV$)',
figsize=(7,3.5), savefig=True, figpath1='../cmaqpy/data/plots/O3.png',
figpath2='../cmaqpy/data/plots/O3_diff.png')
```
| true |
code
| 0.648327 | null | null | null | null |
|
# Numpy and Pandas Performance Comparison
[Goutham Balaraman](http://gouthamanbalaraman.com)
Pandas and Numpy are two packages that are core to a lot of data analysis. In this post I will compare the performance of numpy and pandas.
tl;dr:
- `numpy` consumes less memory compared to `pandas`
- `numpy` generally performs better than `pandas` for 50K rows or less
- `pandas` generally performs better than `numpy` for 500K rows or more
- for 50K to 500K rows, it is a toss up between `pandas` and `numpy` depending on the kind of operation
```
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use("seaborn-pastel")
%matplotlib inline
import seaborn.apionly as sns
import numpy as np
from timeit import timeit
import sys
iris = sns.load_dataset('iris')
data = pd.concat([iris]*100000)
data_rec = data.to_records()
print (len(data), len(data_rec))
```
Here I have loaded the `iris` dataset and replicated it so as to have 15MM rows of data. The space requirement for 15MM rows of data in a `pandas dataframe` is more than twice that of a `numpy recarray`.
```
MB = 1024*1024
print("Pandas %d MB " % (sys.getsizeof(data)/MB))
print("Numpy %d MB " % (sys.getsizeof(data_rec)/MB))
```
A snippet of the data shown below.
```
data.head()
# <!-- collapse=True -->
def perf(inp, statement, grid=None):
length = len(inp)
gap = int(length/5)
#grid = np.array([int(x) for x in np.logspace(np.log10(gap), np.log10(length+1) , 5)])
if grid is None:
grid = np.array([10000, 100000, 1000000, 5000000, 10000000])
num = 100
time = []
data = {'pd': pd, 'np': np}
for i in grid:
if isinstance(inp, pd.DataFrame):
sel = inp.iloc[:i]
data['data'] = sel
else:
sel = inp[:i]
data['data_rec'] = sel
t = timeit(stmt=statement, globals=data, number=num)
time.append(t/num)
return grid, np.array(time)
def bench(pd_inp, pd_stmt, np_inp, np_stmt, title="", grid=None):
g,v1 = perf(pd_inp, pd_stmt, grid)
g,v2 = perf(np_inp, np_stmt, grid)
fig, ax = plt.subplots()
ax.loglog()
ax.plot(g, v1, label="pandas",marker="o", lw=2)
ax.plot(g, v2, label="numpy", marker="v", lw=2)
ax.set_xticks(g)
plt.legend(loc=2)
plt.xlabel("Number of Records")
plt.ylabel("Time (s)")
plt.grid(True)
plt.xlim(min(g)/2,max(g)*2)
plt.title(title)
```
In this post, performance metrics for a few different categories are compared between `numpy` and `pandas`:
- operations on a column of data, such as mean or applying a vectorised function
- operations on a filtered column of data
- vector operations on a column or filtered column
## Operations on a Column
Here some performance metrics with operations on one column of data. The operations involved in here include fetching a view, and a reduction operation such as `mean`, vectorised `log` or a string based `unique` operation. All these are `O(n)` calculations. The mean calculation is orders of magnitude faster in `numpy` compared to `pandas` for array sizes of 100K or less. For sizes larger than 100K `pandas` maintains a lead over `numpy`.
```
bench(data, "data.loc[:, 'sepal_length'].mean()",
data_rec, "np.mean(data_rec.sepal_length)",
title="Mean on Unfiltered Column")
```
Below, the vectorized `log` operation is faster in `numpy` for sizes less than 100K but pandas costs about the same for sizes larger than 100K.
```
bench(data, "np.log(data.loc[:, 'sepal_length'])",
data_rec, "np.log(data_rec.sepal_length)",
title="Vectorised log on Unfiltered Column")
```
The one differentiating aspect about the test below is that the column `species` is of string type. The operation demonstrated is a `unique` calculation. We observe that the `unique` calculation is roughly an order of magnitude faster in pandas for sizes larger than 1K rows.
```
bench(data, "data.loc[:,'species'].unique()",
data_rec, "np.unique(data_rec.species)",
grid=np.array([100, 1000, 10000, 100000, 1000000]),
title="Unique on Unfiltered String Column")
```
## Operations on a Filtered Column
Below we perform the same tests as above, except that the column is not a full view, but is instead a filtered view. The filters are simple filters with an arithmetic bool comparison for the first two and a string comparison for the third below.
Below, `mean` is calculated for a filtered column `sepal_length`. Here performance of `pandas` is better for row sizes larger than 10K. In the `mean` on unfiltered column shown above, `pandas` performed better for 1MM or more. Just having selection operations has shifted performance chart in favor of `pandas` for even smaller number of records.
```
bench(data, "data.loc[(data.sepal_width>3) & \
(data.petal_length<1.5), 'sepal_length'].mean()",
data_rec, "np.mean(data_rec[(data_rec.sepal_width>3) & \
(data_rec.petal_length<1.5)].sepal_length)",
grid=np.array([1000, 10000, 100000, 1000000]),
title="Mean on Filtered Column")
```
For vectorised `log` operation on a unfiltered column shown above, `numpy` performed better than `pandas` for number of records less than 100K while the performance was comparable for the two for sizes larger than 100K. But the moment you introduce a filter on a column, `pandas` starts to show an edge over `numpy` for number of records larger than 10K.
```
bench(data, "np.log(data.loc[(data.sepal_width>3) & \
(data.petal_length<1.5), 'sepal_length'])",
data_rec, "np.log(data_rec[(data_rec.sepal_width>3) & \
(data_rec.petal_length<1.5)].sepal_length)",
grid=np.array([1000, 10000, 100000, 1000000]),
title="Vectorised log on Filtered Column")
```
Here is another example of a `mean` reduction on a column but with a string filter. We see a similar behavior where `numpy` performs significantly better at small sizes and `pandas` takes a gentle lead for larger number of records.
```
bench(data, "data[data.species=='setosa'].sepal_length.mean()",
data_rec, "np.mean(data_rec[data_rec.species=='setosa'].sepal_length)",
grid=np.array([1000, 10000, 100000, 1000000]),
title="Mean on (String) Filtered Column")
```
## Vectorized Operation on a Column
In this last section, we do vectorised arithmetic using multiple columns. This involves creating a view and vectorised math on these views. Even when there is no filter, `pandas` has a slight edge over `numpy` for large number of records. For smaller than 100K records, `numpy` performs significantly better.
```
bench(data, "data.petal_length * data.sepal_length + \
data.petal_width * data.sepal_width",
data_rec, "data_rec.petal_length*data_rec.sepal_length + \
data_rec.petal_width * data_rec.sepal_width",
title="Vectorised Math on Unfiltered Columns")
```
In the following figure, the filter involves vectorised arithmetic operation, and `mean` reduction is computed on the filtered column. The presence of a filter makes `pandas` significantly faster for sizes larger than 100K, while `numpy` maitains a lead for smaller than 10K number of records.
```
bench(data, "data.loc[data.sepal_width * data.petal_length > \
data.sepal_length, 'sepal_length'].mean()",
data_rec, "np.mean(data_rec[data_rec.sepal_width * data_rec.petal_length \
> data_rec.sepal_length].sepal_length)",
title="Vectorised Math in Filtering Columns",
grid=np.array([100, 1000, 10000, 100000, 1000000]))
```
## Conclusion
`Pandas` is often used in an interactive environment such as through Jupyter notebooks. In such a case, any performance loss from `pandas` will be in significant. But if you have smaller `pandas` dataframes (<50K number of records) in a production environment, then it is worth considering `numpy` recarrays.
- `numpy` consumes (roughtly 1/3) less memory compared to `pandas`
- `numpy` generally performs better than `pandas` for 50K rows or less
- `pandas` generally performs better than `numpy` for 500K rows or more
- for 50K to 500K rows, it is a toss up between `pandas` and `numpy` depending on the kind of operation
| true |
code
| 0.441793 | null | null | null | null |
|
Conditional Generative Adversarial Network
----------------------------------------
A Generative Adversarial Network (GAN) is a type of generative model. It consists of two parts called the "generator" and the "discriminator". The generator takes random values as input and transforms them into an output that (hopefully) resembles the training data. The discriminator takes a set of samples as input and tries to distinguish the real training samples from the ones created by the generator. Both of them are trained together. The discriminator tries to get better and better at telling real from false data, while the generator tries to get better and better at fooling the discriminator.
A Conditional GAN (CGAN) allows additional inputs to the generator and discriminator that their output is conditioned on. For example, this might be a class label, and the GAN tries to learn how the data distribution varies between classes.
For this example, we will create a data distribution consisting of a set of ellipses in 2D, each with a random position, shape, and orientation. Each class corresponds to a different ellipse. Let's randomly generate the ellipses.
```
import deepchem as dc
import numpy as np
import tensorflow as tf
n_classes = 4
class_centers = np.random.uniform(-4, 4, (n_classes, 2))
class_transforms = []
for i in range(n_classes):
xscale = np.random.uniform(0.5, 2)
yscale = np.random.uniform(0.5, 2)
angle = np.random.uniform(0, np.pi)
m = [[xscale*np.cos(angle), -yscale*np.sin(angle)],
[xscale*np.sin(angle), yscale*np.cos(angle)]]
class_transforms.append(m)
class_transforms = np.array(class_transforms)
```
This function generates random data from the distribution. For each point it chooses a random class, then a random position in that class' ellipse.
```
def generate_data(n_points):
classes = np.random.randint(n_classes, size=n_points)
r = np.random.random(n_points)
angle = 2*np.pi*np.random.random(n_points)
points = (r*np.array([np.cos(angle), np.sin(angle)])).T
points = np.einsum('ijk,ik->ij', class_transforms[classes], points)
points += class_centers[classes]
return classes, points
```
Let's plot a bunch of random points drawn from this distribution to see what it looks like. Points are colored based on their class label.
```
%matplotlib inline
import matplotlib.pyplot as plot
classes, points = generate_data(1000)
plot.scatter(x=points[:,0], y=points[:,1], c=classes)
```
Now let's create the model for our CGAN.
```
import deepchem.models.tensorgraph.layers as layers
model = dc.models.TensorGraph(learning_rate=1e-4, use_queue=False)
# Inputs to the model
random_in = layers.Feature(shape=(None, 10)) # Random input to the generator
generator_classes = layers.Feature(shape=(None, n_classes)) # The classes of the generated samples
real_data_points = layers.Feature(shape=(None, 2)) # The training samples
real_data_classes = layers.Feature(shape=(None, n_classes)) # The classes of the training samples
is_real = layers.Weights(shape=(None, 1)) # Flags to distinguish real from generated samples
# The generator
gen_in = layers.Concat([random_in, generator_classes])
gen_dense1 = layers.Dense(30, in_layers=gen_in, activation_fn=tf.nn.relu)
gen_dense2 = layers.Dense(30, in_layers=gen_dense1, activation_fn=tf.nn.relu)
generator_points = layers.Dense(2, in_layers=gen_dense2)
model.add_output(generator_points)
# The discriminator
all_points = layers.Concat([generator_points, real_data_points], axis=0)
all_classes = layers.Concat([generator_classes, real_data_classes], axis=0)
discrim_in = layers.Concat([all_points, all_classes])
discrim_dense1 = layers.Dense(30, in_layers=discrim_in, activation_fn=tf.nn.relu)
discrim_dense2 = layers.Dense(30, in_layers=discrim_dense1, activation_fn=tf.nn.relu)
discrim_prob = layers.Dense(1, in_layers=discrim_dense2, activation_fn=tf.sigmoid)
```
We'll use different loss functions for training the generator and discriminator. The discriminator outputs its predictions in the form of a probability that each sample is a real sample (that is, that it came from the training set rather than the generator). Its loss consists of two terms. The first term tries to maximize the output probability for real data, and the second term tries to minimize the output probability for generated samples. The loss function for the generator is just a single term: it tries to maximize the discriminator's output probability for generated samples.
For each one, we create a "submodel" specifying a set of layers that will be optimized based on a loss function.
```
# Discriminator
discrim_real_data_loss = -layers.Log(discrim_prob+1e-10) * is_real
discrim_gen_data_loss = -layers.Log(1-discrim_prob+1e-10) * (1-is_real)
discrim_loss = layers.ReduceMean(discrim_real_data_loss + discrim_gen_data_loss)
discrim_submodel = model.create_submodel(layers=[discrim_dense1, discrim_dense2, discrim_prob], loss=discrim_loss)
# Generator
gen_loss = -layers.ReduceMean(layers.Log(discrim_prob+1e-10) * (1-is_real))
gen_submodel = model.create_submodel(layers=[gen_dense1, gen_dense2, generator_points], loss=gen_loss)
```
Now to fit the model. Here are some important points to notice about the code.
- We use `fit_generator()` to train only a single batch at a time, and we alternate between the discriminator and the generator. That way. both parts of the model improve together.
- We only train the generator half as often as the discriminator. On this particular model, that gives much better results. You will often need to adjust `(# of discriminator steps)/(# of generator steps)` to get good results on a given problem.
- We disable checkpointing by specifying `checkpoint_interval=0`. Since each call to `fit_generator()` includes only a single batch, it would otherwise save a checkpoint to disk after every batch, which would be very slow. If this were a real project and not just an example, we would want to occasionally call `model.save_checkpoint()` to write checkpoints at a reasonable interval.
```
batch_size = model.batch_size
discrim_error = []
gen_error = []
for step in range(20000):
classes, points = generate_data(batch_size)
class_flags = dc.metrics.to_one_hot(classes, n_classes)
feed_dict={random_in: np.random.random((batch_size, 10)),
generator_classes: class_flags,
real_data_points: points,
real_data_classes: class_flags,
is_real: np.concatenate([np.zeros((batch_size,1)), np.ones((batch_size,1))])}
discrim_error.append(model.fit_generator([feed_dict],
submodel=discrim_submodel,
checkpoint_interval=0))
if step%2 == 0:
gen_error.append(model.fit_generator([feed_dict],
submodel=gen_submodel,
checkpoint_interval=0))
if step%1000 == 999:
print(step, np.mean(discrim_error), np.mean(gen_error))
discrim_error = []
gen_error = []
```
Have the trained model generate some data, and see how well it matches the training distribution we plotted before.
```
classes, points = generate_data(1000)
feed_dict = {random_in: np.random.random((1000, 10)),
generator_classes: dc.metrics.to_one_hot(classes, n_classes)}
gen_points = model.predict_on_generator([feed_dict])
plot.scatter(x=gen_points[:,0], y=gen_points[:,1], c=classes)
```
| true |
code
| 0.539165 | null | null | null | null |
|
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Smoothing
```
#format the book
%matplotlib inline
from __future__ import division, print_function
from book_format import load_style
load_style()
```
## Introduction
The performance of the Kalman filter is not optimal when you consider future data. For example, suppose we are tracking an aircraft, and the latest measurement deviates far from the current track, like so (I'll only consider 1 dimension for simplicity):
```
import matplotlib.pyplot as plt
data = [10.1, 10.2, 9.8, 10.1, 10.2, 10.3,
10.1, 9.9, 10.2, 10.0, 9.9, 11.4]
plt.plot(data)
plt.xlabel('time')
plt.ylabel('position');
```
After a period of near steady state, we have a very large change. Assume the change is past the limit of the aircraft's flight envelope. Nonetheless the Kalman filter incorporates that new measurement into the filter based on the current Kalman gain. It cannot reject the noise because the measurement could reflect the initiation of a turn. Granted it is unlikely that we are turning so abruptly, but it is impossible to say whether
* The aircraft started a turn awhile ago, but the previous measurements were noisy and didn't show the change.
* The aircraft is turning, and this measurement is very noisy
* The measurement is very noisy and the aircraft has not turned
* The aircraft is turning in the opposite direction, and the measurement is extremely noisy
Now, suppose the following measurements are:
11.3 12.1 13.3 13.9 14.5 15.2
```
data2 = [11.3, 12.1, 13.3, 13.9, 14.5, 15.2]
plt.plot(data + data2);
```
Given these future measurements we can infer that yes, the aircraft initiated a turn.
On the other hand, suppose these are the following measurements.
```
data3 = [9.8, 10.2, 9.9, 10.1, 10.0, 10.3, 9.9, 10.1]
plt.plot(data + data3);
```
In this case we are led to conclude that the aircraft did not turn and that the outlying measurement was merely very noisy.
## An Overview of How Smoothers Work
The Kalman filter is a *recursive* filter with the Markov property - it's estimate at step `k` is based only on the estimate from step `k-1` and the measurement at step `k`. But this means that the estimate from step `k-1` is based on step `k-2`, and so on back to the first epoch. Hence, the estimate at step `k` depends on all of the previous measurements, though to varying degrees. `k-1` has the most influence, `k-2` has the next most, and so on.
Smoothing filters incorporate future measurements into the estimate for step `k`. The measurement from `k+1` will have the most effect, `k+2` will have less effect, `k+3` less yet, and so on.
This topic is called *smoothing*, but I think that is a misleading name. I could smooth the data above by passing it through a low pass filter. The result would be smooth, but not necessarily accurate because a low pass filter will remove real variations just as much as it removes noise. In contrast, Kalman smoothers are *optimal* - they incorporate all available information to make the best estimate that is mathematically achievable.
## Types of Smoothers
There are three classes of Kalman smoothers that produce better tracking in these situations.
* Fixed-Interval Smoothing
This is a batch processing based filter. This filter waits for all of the data to be collected before making any estimates. For example, you may be a scientist collecting data for an experiment, and don't need to know the result until the experiment is complete. A fixed-interval smoother will collect all the data, then estimate the state at each measurement using all available previous and future measurements. If it is possible for you to run your Kalman filter in batch mode it is always recommended to use one of these filters a it will provide much better results than the recursive forms of the filter from the previous chapters.
* Fixed-Lag Smoothing
Fixed-lag smoothers introduce latency into the output. Suppose we choose a lag of 4 steps. The filter will ingest the first 3 measurements but not output a filtered result. Then, when the 4th measurement comes in the filter will produce the output for measurement 1, taking measurements 1 through 4 into account. When the 5th measurement comes in, the filter will produce the result for measurement 2, taking measurements 2 through 5 into account. This is useful when you need recent data but can afford a bit of lag. For example, perhaps you are using machine vision to monitor a manufacturing process. If you can afford a few seconds delay in the estimate a fixed-lag smoother will allow you to produce very accurate and smooth results.
* Fixed-Point Smoothing
A fixed-point filter operates as a normal Kalman filter, but also produces an estimate for the state at some fixed time $j$. Before the time $k$ reaches $j$ the filter operates as a normal filter. Once $k>j$ the filter estimates $x_k$ and then also updates its estimate for $x_j$ using all of the measurements between $j\dots k$. This can be useful to estimate initial paramters for a system, or for producing the best estimate for an event that happened at a specific time. For example, you may have a robot that took a photograph at time $j$. You can use a fixed-point smoother to get the best possible pose information for the camera at time $j$ as the robot continues moving.
## Choice of Filters
The choice of these filters depends on your needs and how much memory and processing time you can spare. Fixed-point smoothing requires storage of all measurements, and is very costly to compute because the output is for every time step is recomputed for every measurement. On the other hand, the filter does produce a decent output for the current measurement, so this filter can be used for real time applications.
Fixed-lag smoothing only requires you to store a window of data, and processing requirements are modest because only that window is processed for each new measurement. The drawback is that the filter's output always lags the input, and the smoothing is not as pronounced as is possible with fixed-interval smoothing.
Fixed-interval smoothing produces the most smoothed output at the cost of having to be batch processed. Most algorithms use some sort of forwards/backwards algorithm that is only twice as slow as a recursive Kalman filter.
## Fixed-Interval Smoothing
There are many fixed-lag smoothers available in the literature. I have chosen to implement the smoother invented by Rauch, Tung, and Striebel because of its ease of implementation and efficiency of computation. It is also the smoother I have seen used most often in real applications. This smoother is commonly known as an RTS smoother.
Derivation of the RTS smoother runs to several pages of densely packed math. I'm not going to inflict it on you. Instead I will briefly present the algorithm, equations, and then move directly to implementation and demonstration of the smoother.
The RTS smoother works by first running the Kalman filter in a batch mode, computing the filter output for each step. Given the filter output for each measurement along with the covariance matrix corresponding to each output the RTS runs over the data backwards, incorporating its knowledge of the future into the past measurements. When it reaches the first measurement it is done, and the filtered output incorporates all of the information in a maximally optimal form.
The equations for the RTS smoother are very straightforward and easy to implement. This derivation is for the linear Kalman filter. Similar derivations exist for the EKF and UKF. These steps are performed on the output of the batch processing, going backwards from the most recent in time back to the first estimate. Each iteration incorporates the knowledge of the future into the state estimate. Since the state estimate already incorporates all of the past measurements the result will be that each estimate will contain knowledge of all measurements in the past and future. Here is it very important to distinguish between past, present, and future so I have used subscripts to denote whether the data is from the future or not.
Predict Step
$$\begin{aligned}
\mathbf{P} &= \mathbf{FP}_k\mathbf{F}^\mathsf{T} + \mathbf{Q }
\end{aligned}$$
Update Step
$$\begin{aligned}
\mathbf{K}_k &= \mathbf{P}_k\mathbf{F} \hspace{2 mm}\mathbf{P}^{-1} \\
\mathbf{x}_k &= \mathbf{x}_k + \mathbf{K}_k(\mathbf{x}_{x+1} - \mathbf{FX}_k) \\
\mathbf{P}_k &= \mathbf{P}_k + \mathbf{K}_k(\mathbf{P}_{K+1} - \mathbf{P})\mathbf{K}_k^\mathsf{T}
\end{aligned}$$
As always, the hardest part of the implementation is correctly accounting for the subscripts. A basic implementation without comments or error checking would be:
```python
def rts_smoother(Xs, Ps, F, Q):
n, dim_x, _ = Xs.shape
# smoother gain
K = zeros((n,dim_x, dim_x))
x, P = Xs.copy(), Ps.copy()
for k in range(n-2,-1,-1):
P_pred = dot(F, P[k]).dot(F.T) + Q
K[k] = dot(P[k], F.T).dot(inv(P_pred))
x[k] += dot(K[k], x[k+1] - dot(F, x[k]))
P[k] += dot(K[k], P[k+1] - P_pred).dot(K[k].T)
return (x, P, K)
```
This implementation mirrors the implementation provided in FilterPy. It assumes that the Kalman filter is being run externally in batch mode, and the results of the state and covariances are passed in via the `Xs` and `Ps` variable.
Here is an example.
```
import numpy as np
from numpy import random
from numpy.random import randn
import matplotlib.pyplot as plt
from filterpy.kalman import KalmanFilter
import code.book_plots as bp
def plot_rts(noise, Q=0.001, show_velocity=False):
random.seed(123)
fk = KalmanFilter(dim_x=2, dim_z=1)
fk.x = np.array([0., 1.]) # state (x and dx)
fk.F = np.array([[1., 1.],
[0., 1.]]) # state transition matrix
fk.H = np.array([[1., 0.]]) # Measurement function
fk.P = 10. # covariance matrix
fk.R = noise # state uncertainty
fk.Q = Q # process uncertainty
# create noisy data
zs = np.asarray([t + randn()*noise for t in range (40)])
# filter data with Kalman filter, than run smoother on it
mu, cov, _, _ = fk.batch_filter(zs)
M,P,C = fk.rts_smoother(mu, cov)
# plot data
if show_velocity:
index = 1
print('gu')
else:
index = 0
if not show_velocity:
bp.plot_measurements(zs, lw=1)
plt.plot(M[:, index], c='b', label='RTS')
plt.plot(mu[:, index], c='g', ls='--', label='KF output')
if not show_velocity:
N = len(zs)
plt.plot([0, N], [0, N], 'k', lw=2, label='track')
plt.legend(loc=4)
plt.show()
plot_rts(7.)
```
I've injected a lot of noise into the signal to allow you to visually distinguish the RTS output from the ideal output. In the graph above we can see that the Kalman filter, drawn as the green dotted line, is reasonably smooth compared to the input, but it still wanders from from the ideal line when several measurements in a row are biased towards one side of the line. In contrast, the RTS output is both extremely smooth and very close to the ideal output.
With a perhaps more reasonable amount of noise we can see that the RTS output nearly lies on the ideal output. The Kalman filter output, while much better, still varies by a far greater amount.
```
plot_rts(noise=1.)
```
However, we must understand that this smoothing is predicated on the system model. We have told the filter that that what we are tracking follows a constant velocity model with very low process error. When the filter *looks ahead* it sees that the future behavior closely matches a constant velocity so it is able to reject most of the noise in the signal. Suppose instead our system has a lot of process noise. For example, if we are tracking a light aircraft in gusty winds its velocity will change often, and the filter will be less able to distinguish between noise and erratic movement due to the wind. We can see this in the next graph.
```
plot_rts(noise=7., Q=.1)
```
This underscores the fact that these filters are not *smoothing* the data in colloquial sense of the term. The filter is making an optimal estimate based on previous measurements, future measurements, and what you tell it about the behavior of the system and the noise in the system and measurements.
Let's wrap this up by looking at the velocity estimates of Kalman filter vs the RTS smoother.
```
plot_rts(7.,show_velocity=True)
```
The improvement in the velocity, which is an hidden variable, is even more dramatic.
## Fixed-Lag Smoothing
The RTS smoother presented above should always be your choice of algorithm if you can run in batch mode because it incorporates all available data into each estimate. Not all problems allow you to do that, but you may still be interested in receiving smoothed values for previous estimates. The number line below illustrates this concept.
```
from book_format import figsize
from code.smoothing_internal import *
with figsize(y=2):
show_fixed_lag_numberline()
```
At step $k$ we can estimate $x_k$ using the normal Kalman filter equations. However, we can make a better estimate for $x_{k-1}$ by using the measurement received for $x_k$. Likewise, we can make a better estimate for $x_{k-2}$ by using the measurements recevied for $x_{k-1}$ and $x_{k}$. We can extend this computation back for an arbitrary $N$ steps.
Derivation for this math is beyond the scope of this book; Dan Simon's *Optimal State Estimation* [2] has a very good exposition if you are interested. The essense of the idea is that instead of having a state vector $\mathbf{x}$ we make an augmented state containing
$$\mathbf{x} = \begin{bmatrix}\mathbf{x}_k \\ \mathbf{x}_{k-1} \\ \vdots\\ \mathbf{x}_{k-N+1}\end{bmatrix}$$
This yields a very large covariance matrix that contains the covariance between states at different steps. FilterPy's class `FixedLagSmoother` takes care of all of this computation for you, including creation of the augmented matrices. All you need to do is compose it as if you are using the `KalmanFilter` class and then call `smooth()`, which implements the predict and update steps of the algorithm.
Each call of `smooth` computes the estimate for the current measurement, but it also goes back and adjusts the previous `N-1` points as well. The smoothed values are contained in the list `FixedLagSmoother.xSmooth`. If you use `FixedLagSmoother.x` you will get the most recent estimate, but it is not smoothed and is no different from a standard Kalman filter output.
```
from filterpy.kalman import FixedLagSmoother, KalmanFilter
import numpy.random as random
fls = FixedLagSmoother(dim_x=2, dim_z=1, N=8)
fls.x = np.array([0., .5])
fls.F = np.array([[1.,1.],
[0.,1.]])
fls.H = np.array([[1.,0.]])
fls.P *= 200
fls.R *= 5.
fls.Q *= 0.001
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.x = np.array([0., .5])
kf.F = np.array([[1.,1.],
[0.,1.]])
kf.H = np.array([[1.,0.]])
kf.P *= 200
kf.R *= 5.
kf.Q *= 0.001
N = 4 # size of lag
nom = np.array([t/2. for t in range (0, 40)])
zs = np.array([t + random.randn()*5.1 for t in nom])
for z in zs:
fls.smooth(z)
kf_x, _, _, _ = kf.batch_filter(zs)
x_smooth = np.array(fls.xSmooth)[:, 0]
fls_res = abs(x_smooth - nom)
kf_res = abs(kf_x[:, 0] - nom)
plt.plot(zs,'o', alpha=0.5, marker='o', label='zs')
plt.plot(x_smooth, label='FLS')
plt.plot(kf_x[:, 0], label='KF', ls='--')
plt.legend(loc=4)
print('standard deviation fixed-lag:', np.mean(fls_res))
print('standard deviation kalman:', np.mean(kf_res))
```
Here I have set `N=8` which means that we will incorporate 8 future measurements into our estimates. This provides us with a very smooth estimate once the filter converges, at the cost of roughly 8x the amount of computation of the standard Kalman filter. Feel free to experiment with larger and smaller values of `N`. I chose 8 somewhat at random, not due to any theoretical concerns.
## References
[1] H. Rauch, F. Tung, and C. Striebel. "Maximum likelihood estimates of linear dynamic systems," *AIAA Journal*, **3**(8), pp. 1445-1450 (August 1965).
[2] Dan Simon. "Optimal State Estimation," John Wiley & Sons, 2006.
http://arc.aiaa.org/doi/abs/10.2514/3.3166
| true |
code
| 0.675872 | null | null | null | null |
|
```
import os
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['mathtext.fontset'] = 'stix'
```
# Calculate $\kappa$ sampled from the first training
In the first training, we let 200 independent LSTMs predict 200 trajectories of 200$ns$. Since we are using LSTM as a generative model, we can also train just one LSTM and use it to generate 200 predictions, starting from either the same initial condition or different initial conditions.
Data location: `./Output/`
```
output_dir='./Output'
kappa_list=[]
for i in range(200):
pred_dir=os.path.join(output_dir, '{}/prediction.npy'.format(i))
prediction=np.load(pred_dir)
N0=len(np.where(prediction<=15)[0])
N1=len(np.where(prediction>=16)[0])
kappa=N0/N1
kappa_list.append(kappa)
kappa_arr=np.array(kappa_list)
```
Plot distribution of $\kappa$
```
# Plot distribution
hist = np.histogram( kappa_arr, bins=50 )
prob = hist[0].T
mids = 0.5*(hist[1][1:]+hist[1][:-1])
fig, ax = plt.subplots(figsize=(5,4))
ax.set_title('Distribution', size=20)
ax.plot(mids, prob)
ax.tick_params(axis='both', which='both', direction='in', labelsize=14)
ax.set_xlabel('$\kappa$', size=16)
ax.set_ylabel('Counts', size=16)
ax.set_yscale('log')
plt.show()
```
# Determine $\Delta\lambda$
Following the reference, we want to solve the following equation for $\Delta\lambda$
\begin{align}
\bar{s}^{(j)}_2&=\sum_{\Gamma}P^{(2)}_{\Gamma}s^{(j)}_{\Gamma} \nonumber \\
&=\frac{\sum_{k\in\Omega} s^{(j)}_k e^{-\Delta\lambda_j s^{(j)}_k} }{\sum_{k\in\Omega} e^{-\Delta\lambda_j s^{(j)}_k}} \\
&=f(\Delta\lambda)
\label{eq:lambda_solver}
\end{align}
To determine the $\Delta\lambda$ value, we can calculate the above equation and plot it versus $\Delta\lambda$, and find $\Delta\lambda=\Delta\lambda_{\ast}$ which gives
\begin{align}
\bar{s}^{(j)}_2=f(\Delta\lambda_{\ast})=s^{\rm target}
\end{align}
### $s=\kappa$
```
def f(lm):
return np.sum(kappa_arr*np.exp(-lm*kappa_arr))/np.sum(np.exp(-lm*kappa_arr))
lm_arr = np.linspace(0,5)
f_arr = [f(lm_i) for lm_i in lm_arr]
fig, ax=plt.subplots(figsize=(5,3))
ax.plot(lm_arr, f_arr, label='$\kappa_f$')
ax.plot(lm_arr, [1]*len(lm_arr), '--', label='$\kappa^{\mathrm{target}}$')
ax.tick_params(axis='both', which='both', direction='in', labelsize=14)
ax.set_xlabel('$\lambda$', size=16)
ax.set_ylabel('$f(\lambda)$', size=16)
ax.legend(fontsize=16)
plt.show()
lm=0.317
print( 'f({:.3f}) = {:.3f}'.format(lm, f(lm)) )
```
Let's see if select 10 predictions to build the subset is enough.
```
lm_ast=0.317 # Delta_lambda we used for bias sampling
p=np.exp(-lm_ast*(kappa_arr))
p/=np.sum(p)
subset_mean_arr = []
for i in range(200):
idx = np.random.choice(len(kappa_arr), 10, p=p)
selected = kappa_arr[idx]
mean=np.mean(selected)
subset_mean_arr.append(mean)
fig, ax = plt.subplots(figsize=(6,5), nrows=1, ncols=1)
ax.plot(subset_mean_arr)
ax.plot(np.arange(len(subset_mean_arr)), [1.0]*len(subset_mean_arr), label="constraint $\kappa$")
ax.tick_params(axis='both', which='both', direction='in', labelsize=16)
ax.set_xlabel('indices', size=16)
ax.set_ylabel('$\langle\kappa\\rangle$', size=16)
ax.set_ylim(0.0,3.0)
plt.show()
```
So we will constrain our $\kappa$ to 1 with standard error 0.081. Even though we believe from the above test the subset size=10 is sufficient, there is still some variance in mean constraint. Therefore, we will also constrain the standard deviation of $\kappa$ in the subset.
```
lm_ast=0.317
p=np.exp(-lm_ast*(kappa_arr))
p/=np.sum(p)
mean=np.inf
stdv=np.inf
while abs(mean-1)>0.01 or abs(stdv-0.09)>0.01:
idx = np.random.choice(len(kappa_arr), 10, p=p)
selected = kappa_arr[idx]
mean=np.mean(selected)
stdv=np.std(selected)/np.sqrt(len(selected))
print( 'mean of selected sample = {:.3f}'.format(np.mean(selected)) )
print( 'Standard error stderr[selected sample] = {:.3f}'.format(np.std(selected)/np.sqrt(len(selected))) )
```
Concatenate the subset to a single trajectory, this concatenated trajectory is then used later to re-train a new LSTM.
# Concatenate subset as a new training set
```
conc=[]
output_dir='./Output'
for i in idx:
pred_dir=os.path.join(output_dir, '{}/prediction.npy'.format(i))
prediction=np.load(pred_dir)
N0=len(np.where(prediction<=15)[0])
N1=len(np.where(prediction>=16)[0])
kappa=N0/N1
print(kappa)
conc.extend(prediction)
conc = np.array(conc)
N0=len(np.where(conc<=15)[0])
N1=len(np.where(conc>=16)[0])
kappa_conc = N0/N1
print('kappa_conc:{:.3f}'.format(kappa_conc))
```
| true |
code
| 0.352341 | null | null | null | null |
|
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import IPython
import matplotlib.pyplot as plt
import numpy as np
import soundfile as sf
import time
from tqdm import tqdm
import tensorflow as tf
from nara_wpe.tf_wpe import wpe
from nara_wpe.tf_wpe import online_wpe_step, get_power_online
from nara_wpe.utils import stft, istft, get_stft_center_frequencies
from nara_wpe import project_root
stft_options = dict(
size=512,
shift=128,
window_length=None,
fading=True,
pad=True,
symmetric_window=False
)
```
# Example with real audio recordings
The iterations are dropped in contrast to the offline version. To use past observations the correlation matrix and the correlation vector are calculated recursively with a decaying window. $\alpha$ is the decay factor.
### Setup
```
channels = 8
sampling_rate = 16000
delay = 3
alpha=0.99
taps = 10
frequency_bins = stft_options['size'] // 2 + 1
```
### Audio data
```
file_template = 'AMI_WSJ20-Array1-{}_T10c0201.wav'
signal_list = [
sf.read(str(project_root / 'data' / file_template.format(d + 1)))[0]
for d in range(channels)
]
y = np.stack(signal_list, axis=0)
IPython.display.Audio(y[0], rate=sampling_rate)
```
### Online buffer
For simplicity the STFT is performed before providing the frames.
Shape: (frames, frequency bins, channels)
frames: K+delay+1
```
Y = stft(y, **stft_options).transpose(1, 2, 0)
T, _, _ = Y.shape
def aquire_framebuffer():
buffer = list(Y[:taps+delay, :, :])
for t in range(taps+delay+1, T):
buffer.append(Y[t, :, :])
yield np.array(buffer)
buffer.pop(0)
```
### Non-iterative frame online approach
A frame online example requires, that certain state variables are kept from frame to frame. That is the inverse correlation matrix $\text{R}_{t, f}^{-1}$ which is stored in Q and initialized with an identity matrix, as well as filter coefficient matrix that is stored in G and initialized with zeros.
Again for simplicity the ISTFT is applied in Numpy afterwards.
```
Z_list = []
Q = np.stack([np.identity(channels * taps) for a in range(frequency_bins)])
G = np.zeros((frequency_bins, channels * taps, channels))
with tf.Session() as session:
Y_tf = tf.placeholder(tf.complex128, shape=(taps + delay + 1, frequency_bins, channels))
Q_tf = tf.placeholder(tf.complex128, shape=(frequency_bins, channels * taps, channels * taps))
G_tf = tf.placeholder(tf.complex128, shape=(frequency_bins, channels * taps, channels))
results = online_wpe_step(Y_tf, get_power_online(tf.transpose(Y_tf, (1, 0, 2))), Q_tf, G_tf, alpha=alpha, taps=taps, delay=delay)
for Y_step in tqdm(aquire_framebuffer()):
feed_dict = {Y_tf: Y_step, Q_tf: Q, G_tf: G}
Z, Q, G = session.run(results, feed_dict)
Z_list.append(Z)
Z_stacked = np.stack(Z_list)
z = istft(np.asarray(Z_stacked).transpose(2, 0, 1), size=stft_options['size'], shift=stft_options['shift'])
IPython.display.Audio(z[0], rate=sampling_rate)
```
# Power spectrum
Before and after applying WPE.
```
fig, [ax1, ax2] = plt.subplots(1, 2, figsize=(20, 8))
im1 = ax1.imshow(20 * np.log10(np.abs(Y[200:400, :, 0])).T, origin='lower')
ax1.set_xlabel('')
_ = ax1.set_title('reverberated')
im2 = ax2.imshow(20 * np.log10(np.abs(Z_stacked[200:400, :, 0])).T, origin='lower')
_ = ax2.set_title('dereverberated')
cb = fig.colorbar(im1)
```
| true |
code
| 0.572065 | null | null | null | null |
|
# Prerequisites
Install Theano and Lasagne using the following commands:
```bash
pip install -r https://raw.githubusercontent.com/Lasagne/Lasagne/master/requirements.txt
pip install https://github.com/Lasagne/Lasagne/archive/master.zip
```
Working in a virtual environment is recommended.
# Data preparation
Current code allows to generate geodesic patches from a collection of shapes represented as triangular meshes.
To get started with the pre-processing:
```
git clone https://github.com/jonathanmasci/ShapeNet_data_preparation_toolbox.git
```
The usual processing pipeline is show in ```run_forrest_run.m```.
We will soon update this preparation stage, so perhaps better to start with our pre-computed dataset, and stay tuned! :-)
## Prepared data
All it is required to train on the FAUST_registration dataset for this demo is available for download at
https://www.dropbox.com/s/aamd98nynkvbcop/EG16_tutorial.tar.bz2?dl=0
# ICNN Toolbox
```bash
git clone https://github.com/jonathanmasci/EG16_tutorial.git
```

```
import sys
import os
import numpy as np
import scipy.io
import time
import theano
import theano.tensor as T
import theano.sparse as Tsp
import lasagne as L
import lasagne.layers as LL
import lasagne.objectives as LO
from lasagne.layers.normalization import batch_norm
sys.path.append('..')
from icnn import aniso_utils_lasagne, dataset, snapshotter
```
## Data loading
```
base_path = '/home/shubham/Desktop/IndependentStudy/EG16_tutorial/dataset/FAUST_registrations/data/diam=200/'
# train_txt, test_txt, descs_path, patches_path, geods_path, labels_path, ...
# desc_field='desc', patch_field='M', geod_field='geods', label_field='labels', epoch_size=100
ds = dataset.ClassificationDatasetPatchesMinimal(
'FAUST_registrations_train.txt', 'FAUST_registrations_test.txt',
os.path.join(base_path, 'descs', 'shot'),
os.path.join(base_path, 'patch_aniso', 'alpha=100_nangles=016_ntvals=005_tmin=6.000_tmax=24.000_thresh=99.900_norm=L1'),
None,
os.path.join(base_path, 'labels'),
epoch_size=50)
# inp = LL.InputLayer(shape=(None, 544))
# print(inp.input_var)
# patch_op = LL.InputLayer(input_var=Tsp.csc_fmatrix('patch_op'), shape=(None, None))
# print(patch_op.shape)
# print(patch_op.input_var)
# icnn = LL.DenseLayer(inp, 16)
# print(icnn.output_shape)
# print(icnn.output_shape)
# desc_net = theano.dot(patch_op, icnn)
```
## Network definition
```
nin = 544
nclasses = 6890
l2_weight = 1e-5
def get_model(inp, patch_op):
icnn = LL.DenseLayer(inp, 16)
icnn = batch_norm(aniso_utils_lasagne.ACNNLayer([icnn, patch_op], 16, nscale=5, nangl=16))
icnn = batch_norm(aniso_utils_lasagne.ACNNLayer([icnn, patch_op], 32, nscale=5, nangl=16))
icnn = batch_norm(aniso_utils_lasagne.ACNNLayer([icnn, patch_op], 64, nscale=5, nangl=16))
ffn = batch_norm(LL.DenseLayer(icnn, 512))
ffn = LL.DenseLayer(icnn, nclasses, nonlinearity=aniso_utils_lasagne.log_softmax)
return ffn
inp = LL.InputLayer(shape=(None, nin))
patch_op = LL.InputLayer(input_var=Tsp.csc_fmatrix('patch_op'), shape=(None, None))
ffn = get_model(inp, patch_op)
# L.layers.get_output -> theano variable representing network
output = LL.get_output(ffn)
pred = LL.get_output(ffn, deterministic=True) # in case we use dropout
# target theano variable indicatind the index a vertex should be mapped to wrt the latent space
target = T.ivector('idxs')
# to work with logit predictions, better behaved numerically
cla = aniso_utils_lasagne.categorical_crossentropy_logdomain(output, target, nclasses).mean()
acc = LO.categorical_accuracy(pred, target).mean()
# a bit of regularization is commonly used
regL2 = L.regularization.regularize_network_params(ffn, L.regularization.l2)
cost = cla + l2_weight * regL2
```
## Define the update rule, how to train
```
params = LL.get_all_params(ffn, trainable=True)
grads = T.grad(cost, params)
# computes the L2 norm of the gradient to better inspect training
grads_norm = T.nlinalg.norm(T.concatenate([g.flatten() for g in grads]), 2)
# Adam turned out to be a very good choice for correspondence
updates = L.updates.adam(grads, params, learning_rate=0.001)
```
## Compile
```
funcs = dict()
funcs['train'] = theano.function([inp.input_var, patch_op.input_var, target],
[cost, cla, l2_weight * regL2, grads_norm, acc], updates=updates,
on_unused_input='warn')
funcs['acc_loss'] = theano.function([inp.input_var, patch_op.input_var, target],
[acc, cost], on_unused_input='warn')
funcs['predict'] = theano.function([inp.input_var, patch_op.input_var],
[pred], on_unused_input='warn')
```
# Training (a bit simplified)
```
n_epochs = 50
eval_freq = 1
start_time = time.time()
best_trn = 1e5
best_tst = 1e5
kvs = snapshotter.Snapshotter('demo_training.snap')
for it_count in xrange(n_epochs):
tic = time.time()
b_l, b_c, b_s, b_r, b_g, b_a = [], [], [], [], [], []
for x_ in ds.train_iter():
tmp = funcs['train'](*x_)
# do some book keeping (store stuff for training curves etc)
b_l.append(tmp[0])
b_c.append(tmp[1])
b_r.append(tmp[2])
b_g.append(tmp[3])
b_a.append(tmp[4])
epoch_cost = np.asarray([np.mean(b_l), np.mean(b_c), np.mean(b_r), np.mean(b_g), np.mean(b_a)])
print(('[Epoch %03i][trn] cost %9.6f (cla %6.4f, reg %6.4f), |grad| = %.06f, acc = %7.5f %% (%.2fsec)') %
(it_count, epoch_cost[0], epoch_cost[1], epoch_cost[2], epoch_cost[3], epoch_cost[4] * 100,
time.time() - tic))
if np.isnan(epoch_cost[0]):
print("NaN in the loss function...let's stop here")
break
if (it_count % eval_freq) == 0:
v_c, v_a = [], []
for x_ in ds.test_iter():
tmp = funcs['acc_loss'](*x_)
v_a.append(tmp[0])
v_c.append(tmp[1])
test_cost = [np.mean(v_c), np.mean(v_a)]
print((' [tst] cost %9.6f, acc = %7.5f %%') % (test_cost[0], test_cost[1] * 100))
if epoch_cost[0] < best_trn:
kvs.store('best_train_params', [it_count, LL.get_all_param_values(ffn)])
best_trn = epoch_cost[0]
if test_cost[0] < best_tst:
kvs.store('best_test_params', [it_count, LL.get_all_param_values(ffn)])
best_tst = test_cost[0]
print("...done training %f" % (time.time() - start_time))
```
# Test phase
Now that the model is train it is enough to take the fwd function and apply it to new data.
```
rewrite = True
out_path = '/tmp/EG16_tutorial/dumps/'
print "Saving output to: %s" % out_path
if not os.path.isdir(out_path) or rewrite==True:
try:
os.makedirs(out_path)
except:
pass
a = []
for i,d in enumerate(ds.test_iter()):
fname = os.path.join(out_path, "%s" % ds.test_fnames[i])
print fname,
tmp = funcs['predict'](d[0], d[1])[0]
a.append(np.mean(np.argmax(tmp, axis=1).flatten() == d[2].flatten()))
scipy.io.savemat(fname, {'desc': tmp})
print ", Acc: %7.5f %%" % (a[-1] * 100.0)
print "\nAverage accuracy across all shapes: %7.5f %%" % (np.mean(a) * 100.0)
else:
print "Model predictions already produced."
```
# Results

| true |
code
| 0.57344 | null | null | null | null |
|
# Project - Seminar Computer Vision by Deep Learning (CS4245) 2020/2021
Group Number: 20
Student 1: Stan Zwinkels
Student 2: Ted de Vries Lentsch
Date: June 14, 2021
## Instruction
For correct functioning of this notebook, the dataset [morado_5may](https://www.kaggle.com/teddevrieslentsch/morado-5may) must be in the same directory as this notebook.
## Import necessary libraries
```
# standard libraries
import glob
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
import shutil
import time
# widgets
from IPython.display import display, clear_output
import ipywidgets
```
## Relabel
Make folder with for the annotations with the new labels.
```
root_path = 'morado_5may'
relabel_path = '{}/annotations_relabel'.format(root_path)
if os.path.isdir(relabel_path):
shutil.rmtree(relabel_path)
time.sleep(0.1)
os.makedirs(relabel_path)
else:
os.makedirs(relabel_path)
```
Below is the `ReLabelDataset` class for relabeling.
```
class ReLabelDataset(object):
def __init__(self, root):
self.root = root # directory to dataset
self.imgs = list(sorted(os.listdir('{}/images'.format(root)))) # load images
self.annots = list(sorted(os.listdir('{}/annotations'.format(root)))) # load annotations
self.classes = ['background', 'raw', 'ripe'] # classes
self.idx = 0 # image/annotation index
self.idx_last = -1 # last image/annotation index
self.row_number = -1 # number of the current row
self.start = True # initialize process
self.img = None # image
self.annot = None # annotation
self.done = False # whether all images have been labeled
def plot_patch(self):
with out:
annot = self.annot.loc[self.row_number,0:4].to_numpy()
img = self.img[int(annot[1]):(int(annot[3])+1),int(annot[0]):(int(annot[2])+1),:]
clear_output(True)
if not self.done:
plt.figure(figsize=(5, 5))
plt.imshow(img, zorder=-10)
plt.title('Old label: {}'.format(self.annot.loc[self.row_number, 4]))
plt.show()
else:
plt.figure()
plt.show()
def manage_ids(self):
if self.row_number==len(self.annot)-1:
self.save_annot()
self.row_number = 0
self.idx_last = self.idx
self.idx += 1
if self.idx==len(self.imgs):
self.done = True
else:
self.idx_last = self.idx
self.row_number += 1
def get_data(self):
if self.idx!=self.idx_last:
img_path = '{}/images/{}'.format(self.root, self.imgs[self.idx])
annot_path = '{}/annotations/{}'.format(self.root, self.annots[self.idx])
self.img = np.rot90(plt.imread(img_path), -1)
self.annot = pd.read_csv(annot_path, sep=',', header=None)
def save_annot(self):
annot_re_path = '{}/annotations_relabel/{}'.format(self.root, self.annots[self.idx])
self.annot.sort_values(by=[4], inplace=True)
self.annot.reset_index(drop=True, inplace=True)
self.annot.to_csv(annot_re_path, index=0, header=0)
print('The file {} has been relabeled!'.format(self.annots[self.idx]))
def button_click_action(self, label):
if not self.done:
self.get_data()
if not self.start:
self.annot.at[self.row_number,4] = label
self.start = False
self.manage_ids()
self.plot_patch()
def left_button_click(self, click):
self.button_click_action('raw')
def right_button_click(self, click):
self.button_click_action('ripe')
```
Below is the tool for relabeling. The process is started by clicking on one of the two buttons. The first annotation is then plotted. You can then indicate for each image to which class it belongs. If all the annotations for one image have been made, a new .csv file is saved in the `annotations_relabel` directory that was created above.
```
%matplotlib inline
relabeler = ReLabelDataset(root_path)
# create buttons for the 2 classes
button_left = ipywidgets.Button(description='Raw')
button_right = ipywidgets.Button(description='Ripe')
# assign functions to the press of the buttons
button_left.on_click(relabeler.left_button_click)
button_right.on_click(relabeler.right_button_click)
# output window for the plot
out = ipywidgets.Output()
# widget
ipywidgets.VBox([ipywidgets.HBox([button_left, button_right]), out])
```
| true |
code
| 0.394376 | null | null | null | null |
|
# Plot Entropy of Gaussian
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.integrate import quadrature
def exact_entropy(s):
return np.log(s*np.sqrt(2*np.pi*np.e))
sigmas = [0.4,0.8,1.2,2.0,3.5]
x_pts = np.linspace(-5,5,1000)
fig, axs = plt.subplots(1,2,figsize=(12,3))
axs[0].set_title("Entropy of Various Gaussian pdfs", fontsize=16)
for s in sigmas:
h = exact_entropy(s)
axs[0].plot(x_pts, norm.pdf(x_pts,loc=0,scale=s), label="$H={:0.2f}$".format(h), lw=3)
axs[0].legend(prop={'size': 14})
axs[1].set_title("Gaussian Entropy as a Function of $\sigma$", fontsize=16)
axs[1].plot(np.linspace(0.1,5,1000), exact_entropy(np.linspace(0.1,5,1000)), lw=3)
axs[1].set_ylabel("Differential Entropy", fontsize=14)
axs[1].set_xlabel("standard deviation $\sigma$", fontsize=14)
```
# Plot Entropy Element as Function of Information
```
x_pts = np.linspace(1e-9,1,1000)
fig, axs = plt.subplots(1,3,figsize=(9,2.5))
#axs[0].set_title("Information", fontsize=16)
for b in [1.2,1.3,1.6,2]:
I = -np.log(x_pts)/np.log(b)
axs[0].plot(x_pts, I, label=f"$b={b}$", lw=3)
axs[1].plot(x_pts, x_pts*I, lw=3)
axs[2].plot(I, x_pts*I, label=f"$b={b}$", lw=3)
axs[0].legend(prop={'size': 12})
axs[0].set_ylabel("Information", fontsize=14)
axs[0].set_xlabel("Probability", fontsize=14)
axs[0].legend(prop={'size': 12})
axs[0].set_ylim(-1,30)
axs[1].plot([np.e**(-1)]*2,[0,-(1/np.e)*(np.log(np.e**(-1))/np.log(1.2))],ls='dashed',c='k',label="$p^*$")
axs[1].set_ylabel("Entropy Element", fontsize=14)
axs[1].set_xlabel("Probability", fontsize=14)
axs[1].legend(prop={'size': 12})
axs[2].set_ylabel("Entropy Element", fontsize=14)
axs[2].set_xlabel("Information", fontsize=14)
#axs[2].legend(prop={'size': 11})
axs[2].set_xlim(-1,30)
plt.tight_layout()
```
# Compare Entropy of Gaussian to Entropy of GMM
```
class GMM(): # gaussian mixture model
def __init__(self, pis, params, normed=False):
self.params = np.array(params) # [[mu1, sig1], [mu2, sig2],...]
self.components = self.params.shape[0]
self.pis = np.array(pis)
self.max_val = 1
self.normed = normed
if self.normed:
vals = self.__call__(np.linspace(0,1,10000))
self.max_val = vals.max()
def __call__(self, x):
pis = self.pis
p = self.params
sz = self.components
vals = np.array([pis[i]*norm.pdf(x,*(p[i])) for i in range(sz)]).sum(axis=0)
if self.normed:
vals /= self.max_val
return vals
def sample(self, n_samples=1):
mode_id = np.random.choice(self.components, size=n_samples, replace=True, p=self.pis)
return np.array([norm.rvs(*(self.params[i])) for i in mode_id])
def entropy(p,domain):
def f_i(x):
p_i = p(x)
return -p_i*np.log(p_i)
quad_rslt, quad_err = quadrature(f_i, domain[0], domain[1], tol=1e-8, maxiter=1000)
return (quad_rslt, quad_err)
gmm_var = 0.5
num_modes = 2
gmm = GMM([1/num_modes]*num_modes, [[loc,gmm_var] for loc in np.linspace(-3,3,num_modes)])
g_var = 1.0
p = lambda x: norm.pdf(x,loc=0,scale=g_var)
x_pts = np.linspace(-6,6,1000)
domain = [-6,6]
plt.plot(x_pts, gmm(x_pts), label="$H={:0.5f}$".format(entropy(gmm,domain)[0]))
plt.plot(x_pts, p(x_pts), label="$H={:0.5f}$".format(exact_entropy(g_var)))
plt.title("Comparison of Differential Entropies", fontsize=14)
plt.legend()
5285.57-3215.80
```
| true |
code
| 0.694562 | null | null | null | null |
|
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
```
### Helper Functions
```
import tensorflow as tf
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
```
### Model
```
#with tf.device("/cpu:0"):
# reshape
x = tf.placeholder('float', shape=[None, 784])
x_image = tf.reshape(x, [-1, 28, 28, 1])
# conv
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
z_conv1 = conv2d(x_image, W_conv1) + b_conv1
# relu -> pool
h_conv1 = tf.nn.relu(z_conv1)
h_pool1 = max_pool_2x2(h_conv1)
# conv
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
z_conv2 = conv2d(h_pool1, W_conv2) + b_conv2
# relu -> pool
h_conv2 = tf.nn.relu(z_conv2)
h_pool2 = max_pool_2x2(h_conv2)
# reshape -> fc
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
z_fc1 = tf.matmul(h_pool2_flat, W_fc1) + b_fc1
# relu
h_fc1 = tf.nn.relu(z_fc1)
# dropout
keep_prob = tf.placeholder('float')
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# softmax weights
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
scores = tf.matmul(h_fc1_drop, W_fc2) + b_fc2
# softmax + cross-entropy
probs = tf.nn.softmax(scores)
y = tf.placeholder('float', shape=[None, 10])
cross_entropy = -tf.reduce_sum(y*tf.log(probs))
# evaluation
correct_predictions = tf.equal(tf.argmax(probs, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_predictions, 'float'))
```
### Train
```
sess = tf.InteractiveSession()
#with tf.device("/cpu:0"):
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
init = tf.initialize_all_variables()
sess.run(init)
def train(iters=2000):
for i in range(iters):
batch_xs, batch_ys = mnist.train.next_batch(50)
if not i % 100:
train_accuracy = accuracy.eval(feed_dict={x: batch_xs, y: batch_ys, keep_prob: 1.0})
print 'step {}: training accuracy = {}'.format(i, train_accuracy)
yield train_accuracy
train_step.run(feed_dict={x: batch_xs, y: batch_ys, keep_prob: 0.5})
train_accuracies = list(train())
```
### Evaluate on Test Set
```
accuracy.eval(feed_dict={x: mnist.test.images, y: mnist.test.labels, keep_prob: 1.0})
```
| true |
code
| 0.830216 | null | null | null | null |
|
```
from IPython.display import Image
```
# CNTK 204: Sequence to Sequence Networks with Text Data
## Introduction and Background
This hands-on tutorial will take you through both the basics of sequence-to-sequence networks, and how to implement them in the Microsoft Cognitive Toolkit. In particular, we will implement a sequence-to-sequence model with attention to perform grapheme to phoneme translation. We will start with some basic theory and then explain the data in more detail, and how you can download it.
Andrej Karpathy has a [nice visualization](http://karpathy.github.io/2015/05/21/rnn-effectiveness/) of five common paradigms of neural network architectures:
```
# Figure 1
Image(url="http://cntk.ai/jup/paradigms.jpg", width=750)
```
In this tutorial, we are going to be talking about the fourth paradigm: many-to-many where the length of the output does not necessarily equal the length of the input, also known as sequence-to-sequence networks. The input is a sequence with a dynamic length, and the output is also a sequence with some dynamic length. It is the logical extension of the many-to-one paradigm in that previously we were predicting some category (which could easily be one of `V` words where `V` is an entire vocabulary) and now we want to predict a whole sequence of those categories.
The applications of sequence-to-sequence networks are nearly limitless. It is a natural fit for machine translation (e.g. English input sequences, French output sequences); automatic text summarization (e.g. full document input sequence, summary output sequence); word to pronunciation models (e.g. character [grapheme] input sequence, pronunciation [phoneme] output sequence); and even parse tree generation (e.g. regular text input, flat parse tree output).
## Basic theory
A sequence-to-sequence model consists of two main pieces: (1) an encoder; and (2) a decoder. Both the encoder and the decoder are recurrent neural network (RNN) layers that can be implemented using a vanilla RNN, an LSTM, or GRU Blocks (here we will use LSTM). In the basic sequence-to-sequence model, the encoder processes the input sequence into a fixed representation that is fed into the decoder as a context. The decoder then uses some mechanism (discussed below) to decode the processed information into an output sequence. The decoder is a language model that is augmented with some "strong context" by the encoder, and so each symbol that it generates is fed back into the decoder for additional context (like a traditional LM). For an English to German translation task, the most basic setup might look something like this:
```
# Figure 2
Image(url="http://cntk.ai/jup/s2s.png", width=700)
```
The basic sequence-to-sequence network passes the information from the encoder to the decoder by initializing the decoder RNN with the final hidden state of the encoder as its initial hidden state. The input is then a "sequence start" tag (`<s>` in the diagram above) which primes the decoder to start generating an output sequence. Then, whatever word (or note or image, etc.) it generates at that step is fed in as the input for the next step. The decoder keeps generating outputs until it hits the special "end sequence" tag (`</s>` above).
A more complex and powerful version of the basic sequence-to-sequence network uses an attention model. While the above setup works well, it can start to break down when the input sequences get long. At each step, the hidden state `h` is getting updated with the most recent information, and therefore `h` might be getting "diluted" in information as it processes each token. Further, even with a relatively short sequence, the last token will always get the last say and therefore the thought vector will be somewhat biased/weighted towards that last word. To deal with this problem, we use an "attention" mechanism that allows the decoder to look not only at all of the hidden states from the input, but it also learns which hidden states, for each step in decoding, to put the most weight on. In this tutorial we will implement a sequence-to-sequence network that can be run either with or without attention enabled.
```
# Figure 3
Image(url="https://cntk.ai/jup/cntk204_s2s2.png", width=700)
```
The `Attention` layer above takes the current value of the hidden state in the Decoder, all of the hidden states in the Encoder, and calculates an augmented version of the hidden state to use. More specifically, the contribution from the Encoder's hidden states will represent a weighted sum of all of its hidden states where the highest weight corresponds both to the biggest contribution to the augmented hidden state and to the hidden state that will be most important for the Decoder to consider when generating the next word.
## Problem: Grapheme-to-Phoneme Conversion
The [grapheme](https://en.wikipedia.org/wiki/Grapheme) to [phoneme](https://en.wikipedia.org/wiki/Phoneme) problem is a translation task that takes the letters of a word as the input sequence (the graphemes are the smallest units of a writing system) and outputs the corresponding phonemes; that is, the units of sound that make up a language. In other words, the system aims to generate an unambigious representation of how to pronounce a given input word.
### Example
The graphemes or the letters are translated into corresponding phonemes:
> **Grapheme** : **|** T **|** A **|** N **|** G **|** E **|** R **|**
**Phonemes** : **|** ~T **|** ~AE **|** ~NG **|** ~ER **|**
## Task and Model Structure
As discussed above, the task we are interested in solving is creating a model that takes some sequence as an input, and generates an output sequence based on the contents of the input. The model's job is to learn the mapping from the input sequence to the output sequence that it will generate. The job of the encoder is to come up with a good representation of the input that the decoder can use to generate a good output. For both the encoder and the decoder, the LSTM does a good job at this.
Note that the LSTM is simply one of a whole set of different types of Blocks that can be used to implement an RNN. This is the code that is run for each step in the recurrence. In the Layers library, there are three built-in recurrent Blocks: the (vanilla) `RNN`, the `GRU`, and the `LSTM`. Each processes its input slightly differently and each has its own benefits and drawbacks for different types of tasks and networks. To get these blocks to run for each of the elements recurrently in a network, we create a `Recurrence` over them. This "unrolls" the network to the number of steps that are in the given input for the RNN layer.
## Importing CNTK and other useful libraries
CNTK is a Python module that contains several submodules like `io`, `learner`, `graph`, etc. We make extensive use of numpy as well.
```
from __future__ import print_function
import numpy as np
import os
import cntk as C
```
In the block below, we check if we are running this notebook in the CNTK internal test machines by looking for environment variables defined there. We then select the right target device (GPU vs CPU) to test this notebook. In other cases, we use CNTK's default policy to use the best available device (GPU, if available, else CPU).
```
# Define a test environment
def isTest():
return ('TEST_DEVICE' in os.environ)
# Select the right target device when this notebook is being tested:
if 'TEST_DEVICE' in os.environ:
if os.environ['TEST_DEVICE'] == 'cpu':
C.device.try_set_default_device(C.device.cpu())
else:
C.device.try_set_default_device(C.device.gpu(0))
```
## Downloading the data
In this tutorial we will use a lightly pre-processed version of the CMUDict (version 0.7b) dataset from http://www.speech.cs.cmu.edu/cgi-bin/cmudict. The CMUDict data refers to the Carnegie Mellon University Pronouncing Dictionary and is an open-source machine-readable pronunciation dictionary for North American English. The data is in the CNTKTextFormatReader format. Here is an example sequence pair from the data, where the input sequence (S0) is in the left column, and the output sequence (S1) is on the right:
```
0 |S0 3:1 |# <s> |S1 3:1 |# <s>
0 |S0 4:1 |# A |S1 32:1 |# ~AH
0 |S0 5:1 |# B |S1 36:1 |# ~B
0 |S0 4:1 |# A |S1 31:1 |# ~AE
0 |S0 7:1 |# D |S1 38:1 |# ~D
0 |S0 12:1 |# I |S1 47:1 |# ~IY
0 |S0 1:1 |# </s> |S1 1:1 |# </s>
```
The code below will download the required files (training, testing, the single sequence above for visual validation, and a small vocab file) and put them in a local folder (the training file is ~34 MB, testing is ~4MB, and the validation file and vocab file are both less than 1KB).
```
import requests
def download(url, filename):
""" utility function to download a file """
response = requests.get(url, stream=True)
with open(filename, "wb") as handle:
for data in response.iter_content():
handle.write(data)
MODEL_DIR = "."
DATA_DIR = os.path.join('..', 'Examples', 'SequenceToSequence', 'CMUDict', 'Data')
# If above directory does not exist, just use current.
if not os.path.exists(DATA_DIR):
DATA_DIR = '.'
dataPath = {
'validation': 'tiny.ctf',
'training': 'cmudict-0.7b.train-dev-20-21.ctf',
'testing': 'cmudict-0.7b.test.ctf',
'vocab_file': 'cmudict-0.7b.mapping',
}
for k in sorted(dataPath.keys()):
path = os.path.join(DATA_DIR, dataPath[k])
if os.path.exists(path):
print("Reusing locally cached:", path)
else:
print("Starting download:", dataPath[k])
url = "https://github.com/Microsoft/CNTK/blob/v2.0/Examples/SequenceToSequence/CMUDict/Data/%s?raw=true"%dataPath[k]
download(url, path)
print("Download completed")
dataPath[k] = path
```
## Reader
To efficiently collect our data, randomize it for training, and pass it to the network, we use the CNTKTextFormat reader. We will create a small function that will be called when training (or testing) that defines the names of the streams in our data, and how they are referred to in the raw training data.
```
# Helper function to load the model vocabulary file
def get_vocab(path):
# get the vocab for printing output sequences in plaintext
vocab = [w.strip() for w in open(path).readlines()]
i2w = { i:w for i,w in enumerate(vocab) }
w2i = { w:i for i,w in enumerate(vocab) }
return (vocab, i2w, w2i)
# Read vocabulary data and generate their corresponding indices
vocab, i2w, w2i = get_vocab(dataPath['vocab_file'])
def create_reader(path, is_training):
return MinibatchSource(CTFDeserializer(path, StreamDefs(
features = StreamDef(field='S0', shape=input_vocab_dim, is_sparse=True),
labels = StreamDef(field='S1', shape=label_vocab_dim, is_sparse=True)
)), randomize = is_training, max_sweeps = INFINITELY_REPEAT if is_training else 1)
input_vocab_dim = 69
label_vocab_dim = 69
# Print vocab and the correspoding mapping to the phonemes
print("Vocabulary size is", len(vocab))
print("First 15 letters are:")
print(vocab[:15])
print()
print("Print dictionary with the vocabulary mapping:")
print(i2w)
```
We will use the above to create a reader for our training data. Let's create it now:
```
def create_reader(path, is_training):
return C.io.MinibatchSource(C.io.CTFDeserializer(path, C.io.StreamDefs(
features = C.io.StreamDef(field='S0', shape=input_vocab_dim, is_sparse=True),
labels = C.io.StreamDef(field='S1', shape=label_vocab_dim, is_sparse=True)
)), randomize = is_training, max_sweeps = C.io.INFINITELY_REPEAT if is_training else 1)
# Train data reader
train_reader = create_reader(dataPath['training'], True)
# Validation data reader
valid_reader = create_reader(dataPath['validation'], True)
```
### Now let's set our model hyperparameters...
We have a number of settings that control the complexity of our network, the shapes of our inputs, and other options such as whether we will use an embedding (and what size to use), and whether or not we will employ attention. We set them now as they will be made use of when we build the network graph in the following sections.
```
hidden_dim = 512
num_layers = 2
attention_dim = 128
attention_span = 20
attention_axis = -3
use_attention = True
use_embedding = True
embedding_dim = 200
vocab = ([w.strip() for w in open(dataPath['vocab_file']).readlines()]) # all lines of vocab_file in a list
length_increase = 1.5
```
We will set two more parameters now: the symbols used to denote the start of a sequence (sometimes called 'BOS') and the end of a sequence (sometimes called 'EOS'). In this case, our sequence-start symbol is the tag $<s>$ and our sequence-end symbol is the end-tag $</s>$.
Sequence start and end tags are important in sequence-to-sequence networks for two reasons. The sequence start tag is a "primer" for the decoder; in other words, because we are generating an output sequence and RNNs require some input, the sequence start token "primes" the decoder to cause it to emit its first generated token. The sequence end token is important because the decoder will learn to output this token when the sequence is finished. Otherwise the network wouldn't know how long of a sequence to generate. For the code below, we setup the sequence start symbol as a `Constant` so that it can later be passed to the Decoder LSTM as its `initial_state`. Further, we get the sequence end symbol's index so that the Decoder can use it to know when to stop generating tokens.
```
sentence_start =C.Constant(np.array([w=='<s>' for w in vocab], dtype=np.float32))
sentence_end_index = vocab.index('</s>')
```
## Step 1: setup the input to the network
### Dynamic axes in CNTK (Key concept)
One of the important concepts in understanding CNTK is the idea of two types of axes:
- **static axes**, which are the traditional axes of a variable's shape, and
- **dynamic axes**, which have dimensions that are unknown until the variable is bound to real data at computation time.
The dynamic axes are particularly important in the world of recurrent neural networks. Instead of having to decide a maximum sequence length ahead of time, padding your sequences to that size, and wasting computation, CNTK's dynamic axes allow for variable sequence lengths that are automatically packed in minibatches to be as efficient as possible.
When setting up sequences, there are *two dynamic axes* that are important to consider. The first is the *batch axis*, which is the axis along which multiple sequences are batched. The second is the dynamic axis particular to that sequence. The latter is specific to a particular input because of variable sequence lengths in your data. For example, in sequence to sequence networks, we have two sequences: the **input sequence**, and the **output (or 'label') sequence**. One of the things that makes this type of network so powerful is that the length of the input sequence and the output sequence do not have to correspond to each other. Therefore, both the input sequence and the output sequence require their own unique dynamic axis.
We first create the `inputAxis` for the input sequence and the `labelAxis` for the output sequence. We then define the inputs to the model by creating sequences over these two unique dynamic axes. Note that `InputSequence` and `LabelSequence` are *type declarations*. This means that the `InputSequence` is a type that consists of a sequence over the `inputAxis` axis.
```
# Source and target inputs to the model
inputAxis = C.Axis('inputAxis')
labelAxis = C.Axis('labelAxis')
InputSequence = C.layers.SequenceOver[inputAxis]
LabelSequence = C.layers.SequenceOver[labelAxis]
```
## Step 2: define the network
As discussed before, the sequence-to-sequence network is, at its most basic, an RNN (LSTM) encoder followed by an RNN (LSTM) decoder, and a dense output layer. We will implement both the Encoder and the Decoder using the CNTK Layers library. Both of these will be created as CNTK Functions. Our `create_model()` Python function creates both the `encode` and `decode` CNTK Functions. The `decode` function directly makes use of the `encode` function and the return value of `create_model()` is the CNTK Function `decode` itself.
We start by passing the input through an embedding (learned as part of the training process). So that this function can be used in the `Sequential` block of the Encoder and the Decoder whether we want an embedding or not, we will use the `identity` function if the `use_embedding` parameter is `False`. We then declare the Encoder layers as follows:
First, we pass the input through our `embed` function and then we stabilize it. This adds an additional scalar parameter to the learning that can help our network converge more quickly during training. Then, for each of the number of LSTM layers that we want in our encoder, except the final one, we set up an LSTM recurrence. The final recurrence will be a `Fold` if we are not using attention because we only pass the final hidden state to the decoder. If we are using attention, however, then we use another normal LSTM `Recurrence` that the Decoder will put its attention over later on.
Below we see a diagram of how the layered version of the sequence-to-sequence network with attention works. As the code shows below, the output of each layer of the Encoder and Decoder is used as the input to the layer just above it. The Attention model focuses on the top layer of the Encoder and informs the first layer of the Decoder.
```
# Figure 4
Image(url="https://cntk.ai/jup/cntk204_s2s3.png", width=900)
```
For the decoder, we first define several sub-layers: the `Stabilizer` for the decoder input, the `Recurrence` blocks for each of the decoder's layers, the `Stabilizer` for the output of the stack of LSTMs, and the final `Dense` output layer. If we are using attention, then we also create an `AttentionModel` function `attention_model` which returns an augmented version of the decoder's hidden state with emphasis placed on the encoder hidden states that should be most used for the given step while generating the next output token.
We then build the CNTK Function `decode`. The decorator `@Function` turns a regular Python function into a proper CNTK Function with the given arguments and return value. The Decoder works differently during training than it does during test time. During training, the history (i.e. input) to the Decoder `Recurrence` consists of the ground-truth labels. This means that while generating $y^{(t=2)}$, for example, the input will be $y^{(t=1)}$. During evaluation, or "test time", however, the input to the Decoder will be the actual output of the model. For a greedy decoder -- which we are implementing here -- that input is therefore the `hardmax` of the final `Dense` layer.
The Decoder Function `decode` takes two arguments: (1) the `input` sequence; and (2) the Decoder `history`. First, it runs the `input` sequence through the Encoder function `encode` that we setup earlier. We then get the `history` and map it to its embedding if necessary. Then the embedded representation is stabilized before running it through the Decoder's `Recurrence`. For each layer of `Recurrence`, we run the embedded `history` (now represented as `r`) through the `Recurrence`'s LSTM. If we are not using attention, we run it through the `Recurrence` with its initial state set to the value of the final hidden state of the encoder (note that since we run the Encoder backwards when not using attention that the "final" hidden state is actually the first hidden state in chronological time). If we are using attention, however, then we calculate the auxiliary input `h_att` using our `attention_model` function and we splice that onto the input `x`. This augmented `x` is then used as input for the Decoder's `Recurrence`.
Finally, we stabilize the output of the Decoder, put it through the final `Dense` layer `proj_out`, and label the output using the `Label` layer which allows for simple access to that layer later on.
```
# create the s2s model
def create_model(): # :: (history*, input*) -> logP(w)*
# Embedding: (input*) --> embedded_input*
embed = C.layers.Embedding(embedding_dim, name='embed') if use_embedding else identity
# Encoder: (input*) --> (h0, c0)
# Create multiple layers of LSTMs by passing the output of the i-th layer
# to the (i+1)th layer as its input
# Note: We go_backwards for the plain model, but forward for the attention model.
with C.layers.default_options(enable_self_stabilization=True, go_backwards=not use_attention):
LastRecurrence = C.layers.Fold if not use_attention else C.layers.Recurrence
encode = C.layers.Sequential([
embed,
C.layers.Stabilizer(),
C.layers.For(range(num_layers-1), lambda:
C.layers.Recurrence(C.layers.LSTM(hidden_dim))),
LastRecurrence(C.layers.LSTM(hidden_dim), return_full_state=True),
(C.layers.Label('encoded_h'), C.layers.Label('encoded_c')),
])
# Decoder: (history*, input*) --> unnormalized_word_logp*
# where history is one of these, delayed by 1 step and <s> prepended:
# - training: labels
# - testing: its own output hardmax(z) (greedy decoder)
with C.layers.default_options(enable_self_stabilization=True):
# sub-layers
stab_in = C.layers.Stabilizer()
rec_blocks = [C.layers.LSTM(hidden_dim) for i in range(num_layers)]
stab_out = C.layers.Stabilizer()
proj_out = C.layers.Dense(label_vocab_dim, name='out_proj')
# attention model
if use_attention: # maps a decoder hidden state and all the encoder states into an augmented state
attention_model = C.layers.AttentionModel(attention_dim,
attention_span,
attention_axis,
name='attention_model') # :: (h_enc*, h_dec) -> (h_dec augmented)
# layer function
@C.Function
def decode(history, input):
encoded_input = encode(input)
r = history
r = embed(r)
r = stab_in(r)
for i in range(num_layers):
rec_block = rec_blocks[i] # LSTM(hidden_dim) # :: (dh, dc, x) -> (h, c)
if use_attention:
if i == 0:
@C.Function
def lstm_with_attention(dh, dc, x):
h_att = attention_model(encoded_input.outputs[0], dh)
x = C.splice(x, h_att)
return rec_block(dh, dc, x)
r = C.layers.Recurrence(lstm_with_attention)(r)
else:
r = C.layers.Recurrence(rec_block)(r)
else:
# unlike Recurrence(), the RecurrenceFrom() layer takes the initial hidden state as a data input
r = C.layers.RecurrenceFrom(rec_block)(*(encoded_input.outputs + (r,))) # :: h0, c0, r -> h
r = stab_out(r)
r = proj_out(r)
r = C.layers.Label('out_proj_out')(r)
return r
return decode
```
The network that we defined above can be thought of as an "abstract" model that must first be wrapped to be used. In this case, we will use it first to create a "training" version of the model (where the history for the Decoder will be the ground-truth labels), and then we will use it to create a greedy "decoding" version of the model where the history for the Decoder will be the `hardmax` output of the network. Let's set up these model wrappers next.
## Training
Before starting training, we will define the training wrapper, the greedy decoding wrapper, and the criterion function used for training the model. Let's start with the training wrapper.
```
def create_model_train(s2smodel):
# model used in training (history is known from labels)
# note: the labels must NOT contain the initial <s>
@C.Function
def model_train(input, labels): # (input*, labels*) --> (word_logp*)
# The input to the decoder always starts with the special label sequence start token.
# Then, use the previous value of the label sequence (for training) or the output (for execution).
past_labels = C.layers.Delay(initial_state=sentence_start)(labels)
return s2smodel(past_labels, input)
return model_train
```
Above, we create the CNTK Function `model_train` again using the `@Function` decorator. This function takes the input sequence `input` and the output sequence `labels` as arguments. The `past_labels` are setup as the `history` for the model we created earlier by using the `Delay` layer. This will return the previous time-step value for the input `labels` with an `initial_state` of `sentence_start`. Therefore, if we give the labels `['a', 'b', 'c']`, then `past_labels` will contain `['<s>', 'a', 'b', 'c']` and then return our abstract base model called with the history `past_labels` and the input `input`.
Let's go ahead and create the greedy decoding model wrapper now as well:
```
def create_model_greedy(s2smodel):
# model used in (greedy) decoding (history is decoder's own output)
@C.Function
@C.layers.Signature(InputSequence[C.layers.Tensor[input_vocab_dim]])
def model_greedy(input): # (input*) --> (word_sequence*)
# Decoding is an unfold() operation starting from sentence_start.
# We must transform s2smodel (history*, input* -> word_logp*) into a generator (history* -> output*)
# which holds 'input' in its closure.
unfold = C.layers.UnfoldFrom(lambda history: s2smodel(history, input) >> C.hardmax,
# stop once sentence_end_index was max-scoring output
until_predicate=lambda w: w[...,sentence_end_index],
length_increase=length_increase)
return unfold(initial_state=sentence_start, dynamic_axes_like=input)
return model_greedy
```
Above we create a new CNTK Function `model_greedy` which this time only takes a single argument. This is of course because when using the model at test time we don't have any labels -- it is the model's job to create them for us! In this case, we use the `UnfoldFrom` layer which runs the base model with the current `history` and funnels it into the `hardmax`. The `hardmax`'s output then becomes part of the `history` and we keep unfolding the `Recurrence` until the `sentence_end_index` has been reached. The maximum length of the output sequence (the maximum unfolding of the Decoder) is determined by a multiplier passed to `length_increase`. In this case we set `length_increase` to `1.5` above so the maximum length of each output sequence is 1.5x its input.
The last thing we will do before setting up the training loop is define the function that will create the criterion function for our model.
```
def create_criterion_function(model):
@C.Function
@C.layers.Signature(input=InputSequence[C.layers.Tensor[input_vocab_dim]],
labels=LabelSequence[C.layers.Tensor[label_vocab_dim]])
def criterion(input, labels):
# criterion function must drop the <s> from the labels
postprocessed_labels = C.sequence.slice(labels, 1, 0) # <s> A B C </s> --> A B C </s>
z = model(input, postprocessed_labels)
ce = C.cross_entropy_with_softmax(z, postprocessed_labels)
errs = C.classification_error(z, postprocessed_labels)
return (ce, errs)
return criterion
```
Above, we create the criterion function which drops the sequence-start symbol from our labels for us, runs the model with the given `input` and `labels`, and uses the output to compare to our ground truth. We use the loss function `cross_entropy_with_softmax` and get the `classification_error` which gives us the percent-error per-word of our generation accuracy. The CNTK Function `criterion` returns these values as a tuple and the Python function `create_criterion_function(model)` returns that CNTK Function.
Now let's move on to creating the training loop...
```
def train(train_reader, valid_reader, vocab, i2w, s2smodel, max_epochs, epoch_size):
# create the training wrapper for the s2smodel, as well as the criterion function
model_train = create_model_train(s2smodel)
criterion = create_criterion_function(model_train)
# also wire in a greedy decoder so that we can properly log progress on a validation example
# This is not used for the actual training process.
model_greedy = create_model_greedy(s2smodel)
# Instantiate the trainer object to drive the model training
minibatch_size = 72
lr = 0.001 if use_attention else 0.005
learner = C.fsadagrad(model_train.parameters,
lr = C.learning_rate_schedule([lr]*2+[lr/2]*3+[lr/4], C.UnitType.sample, epoch_size),
momentum = C.momentum_as_time_constant_schedule(1100),
gradient_clipping_threshold_per_sample=2.3,
gradient_clipping_with_truncation=True)
trainer = C.Trainer(None, criterion, learner)
# Get minibatches of sequences to train with and perform model training
total_samples = 0
mbs = 0
eval_freq = 100
# print out some useful training information
C.logging.log_number_of_parameters(model_train) ; print()
progress_printer = C.logging.ProgressPrinter(freq=30, tag='Training')
# a hack to allow us to print sparse vectors
sparse_to_dense = create_sparse_to_dense(input_vocab_dim)
for epoch in range(max_epochs):
while total_samples < (epoch+1) * epoch_size:
# get next minibatch of training data
mb_train = train_reader.next_minibatch(minibatch_size)
# do the training
trainer.train_minibatch({criterion.arguments[0]: mb_train[train_reader.streams.features],
criterion.arguments[1]: mb_train[train_reader.streams.labels]})
progress_printer.update_with_trainer(trainer, with_metric=True) # log progress
# every N MBs evaluate on a test sequence to visually show how we're doing
if mbs % eval_freq == 0:
mb_valid = valid_reader.next_minibatch(1)
# run an eval on the decoder output model (i.e. don't use the groundtruth)
e = model_greedy(mb_valid[valid_reader.streams.features])
print(format_sequences(sparse_to_dense(mb_valid[valid_reader.streams.features]), i2w))
print("->")
print(format_sequences(e, i2w))
# visualizing attention window
if use_attention:
debug_attention(model_greedy, mb_valid[valid_reader.streams.features])
total_samples += mb_train[train_reader.streams.labels].num_samples
mbs += 1
# log a summary of the stats for the epoch
progress_printer.epoch_summary(with_metric=True)
# done: save the final model
model_path = "model_%d.cmf" % epoch
print("Saving final model to '%s'" % model_path)
s2smodel.save(model_path)
print("%d epochs complete." % max_epochs)
```
In the above function, we created one version of the model for training (plus its associated criterion function) and one version of the model for evaluation. Normally this latter version would not be required but here we have done it so that we can periodically sample from the non-training model to visually understand how our model is converging by seeing the kinds of sequences that it generates as the training progresses.
We then setup some standard variables required for the training loop. We set the `minibatch_size` (which refers to the total number of elements -- NOT sequences -- in a minibatch), the initial learning rate `lr`, we initialize a `learner` using the `adam_sgd` algorithm and a `learning_rate_schedule` that slowly reduces our learning rate. We make use of gradient clipping to help control exploding gradients, and we finally create our `Trainer` object `trainer`.
We make use of CNTK's `ProgressPrinter` class which takes care of calculating average metrics per minibatch/epoch and we set it to update every 30 minibatches. And finally, before starting the training loop, we initialize a function called `sparse_to_dense` which we use to properly print out the input sequence data that we use for validation because it is sparse. That function is defined just below:
```
# dummy for printing the input sequence below. Currently needed because input is sparse.
def create_sparse_to_dense(input_vocab_dim):
I = C.Constant(np.eye(input_vocab_dim))
@C.Function
@C.layers.Signature(InputSequence[C.layers.SparseTensor[input_vocab_dim]])
def no_op(input):
return C.times(input, I)
return no_op
```
Inside the training loop, we proceed much like many other CNTK networks. We request the next bunch of minibatch data, we perform our training, and we print our progress to the screen using the `progress_printer`. Where we diverge from the norm, however, is where we run an evaluation using our `model_greedy` version of the network and run a single sequence, "ABADI" through to see what the network is currently predicting.
Another difference in the training loop is the optional attention window visualization. Calling the function `debug_attention` shows the weight that the Decoder put on each of the Encoder's hidden states for each of the output tokens that it generated. This function, along with the `format_sequences` function required to print the input/output sequences to the screen, are given below.
```
# Given a vocab and tensor, print the output
def format_sequences(sequences, i2w):
return [" ".join([i2w[np.argmax(w)] for w in s]) for s in sequences]
# to help debug the attention window
def debug_attention(model, input):
q = C.combine([model, model.attention_model.attention_weights])
#words, p = q(input) # Python 3
words_p = q(input)
words = words_p[0]
p = words_p[1]
seq_len = words[0].shape[attention_axis-1]
span = 7 #attention_span #7 # test sentence is 7 tokens long
p_sq = np.squeeze(p[0][:seq_len,:span,0,:]) # (batch, len, attention_span, 1, vector_dim)
opts = np.get_printoptions()
np.set_printoptions(precision=5)
print(p_sq)
np.set_printoptions(**opts)
```
Let's try training our network for a small part of an epoch. In particular, we'll run through 25,000 tokens (about 3% of one epoch):
```
model = create_model()
train(train_reader, valid_reader, vocab, i2w, model, max_epochs=1, epoch_size=25000)
```
As we can see above, while the loss has come down quite a ways, the output sequence is still quite a ways off from what we expect. Uncomment the code below to run for a full epoch (notice that we switch the `epoch_size` parameter to the actual size of the training data) and by the end of the first epoch you will already see a very good grapheme-to-phoneme translation model running!
```
# Uncomment the line below to train the model for a full epoch
#train(train_reader, valid_reader, vocab, i2w, model, max_epochs=1, epoch_size=908241)
```
## Testing the network
Now that we've trained a sequence-to-sequence network for graphme-to-phoneme translation, there are two important things we should do with it. First, we should test its accuracy on a held-out test set. Then, we should try it out in an interactive environment so that we can put in our own input sequences and see what the model predicts. Let's start by determining the test string error rate.
At the end of training, we saved the model using the line `s2smodel.save(model_path)`. Therefore, to test it, we will need to first `load` that model and then run some test data through it. Let's `load` the model, then create a reader configured to access our testing data. Note that we pass `False` to the `create_reader` function this time to denote that we are in testing mode so we should only pass over the data a single time.
```
# load the model for epoch 0
model_path = "model_0.cmf"
model = C.Function.load(model_path)
# create a reader pointing at our testing data
test_reader = create_reader(dataPath['testing'], False)
```
Now we need to define our testing function. We pass the `reader`, the learned `s2smodel`, and the vocabulary map `i2w` so that we can directly compare the model's predictions to the test set labels. We loop over the test set, evaluate the model on minibatches of size 512 for efficiency, and keep track of the error rate. Note that below we test *per-sequence*. This means that every single token in a generated sequence must match the tokens in the label for that sequence to be considered as correct.
```
# This decodes the test set and counts the string error rate.
def evaluate_decoding(reader, s2smodel, i2w):
model_decoding = create_model_greedy(s2smodel) # wrap the greedy decoder around the model
progress_printer = C.logging.ProgressPrinter(tag='Evaluation')
sparse_to_dense = create_sparse_to_dense(input_vocab_dim)
minibatch_size = 512
num_total = 0
num_wrong = 0
while True:
mb = reader.next_minibatch(minibatch_size)
if not mb: # finish when end of test set reached
break
e = model_decoding(mb[reader.streams.features])
outputs = format_sequences(e, i2w)
labels = format_sequences(sparse_to_dense(mb[reader.streams.labels]), i2w)
# prepend sentence start for comparison
outputs = ["<s> " + output for output in outputs]
num_total += len(outputs)
num_wrong += sum([label != output for output, label in zip(outputs, labels)])
rate = num_wrong / num_total
print("string error rate of {:.1f}% in {} samples".format(100 * rate, num_total))
return rate
```
Now we will evaluate the decoding using the above function. If you use the version of the model we trained above with just a small 50000 sample of the training data, you will get an error rate of 100% because we cannot possibly get every single token correct with such a small amount of training. However, if you uncommented the training line above that trains the network for a full epoch, you should have ended up with a much-improved model that showed approximately the following training statistics:
```
Finished Epoch[1 of 300]: [Training] loss = 0.878420 * 799303, metric = 26.23% * 799303 1755.985s (455.2 samples/s);
```
Now let's evaluate the model's test set performance below.
```
# print the string error rate
evaluate_decoding(test_reader, model, i2w)
```
If you did not run the training for the full first epoch, the output above will be a `1.0` meaning 100% string error rate. If, however, you uncommented the line to perform training for a full epoch, you should get an output of `0.569`. A string error rate of `56.9` is actually not bad for a single pass over the data. Let's now modify the above `evaluate_decoding` function to output the per-phoneme error rate. This means that we are calculating the error at a higher precision and also makes things easier in some sense because with the string error rate we could have every phoneme correct but one in each example and still end up with a 100% error rate. Here is the modified version of that function:
```
# This decodes the test set and counts the string error rate.
def evaluate_decoding(reader, s2smodel, i2w):
model_decoding = create_model_greedy(s2smodel) # wrap the greedy decoder around the model
progress_printer = C.logging.ProgressPrinter(tag='Evaluation')
sparse_to_dense = create_sparse_to_dense(input_vocab_dim)
minibatch_size = 512
num_total = 0
num_wrong = 0
while True:
mb = reader.next_minibatch(minibatch_size)
if not mb: # finish when end of test set reached
break
e = model_decoding(mb[reader.streams.features])
outputs = format_sequences(e, i2w)
labels = format_sequences(sparse_to_dense(mb[reader.streams.labels]), i2w)
# prepend sentence start for comparison
outputs = ["<s> " + output for output in outputs]
for s in range(len(labels)):
for w in range(len(labels[s])):
num_total += 1
if w < len(outputs[s]): # in case the prediction is longer than the label
if outputs[s][w] != labels[s][w]:
num_wrong += 1
rate = num_wrong / num_total
print("{:.1f}".format(100 * rate))
return rate
# print the phoneme error rate
test_reader = create_reader(dataPath['testing'], False)
evaluate_decoding(test_reader, model, i2w)
```
If you're using the model that was trained for one full epoch, then you should get a phoneme error rate of around 10%. Not bad! This means that for each of the 383,294 phonemes in the test set, our model predicted nearly 90% of them correctly (if you used the quickly-trained version of the model then you will get an error rate of around 45%). Now, let's work with an interactive session where we can input our own input sequences and see how the model predicts their pronunciation (i.e. phonemes). Additionally, we will visualize the Decoder's attention for these samples to see which graphemes in the input it deemed to be important for each phoneme that it produces. Note that in the examples below the results will only be good if you use a model that has been trained for at least one epoch.
## Interactive session
Here we will write an interactive function to make it easy to interact with the trained model and try out your own input sequences that do not appear in the test set. Please note that the results will be very poor if you just use the model that was trained for a very short amount of time. The model we used just above that was trained for one epoch does a good job, and if you have the time and patience to train the model for a full 30 epochs, it will perform very nicely.
We will first import some graphics libraries that make the attention visualization possible and then we will define the `translate` function that takes a numpy-based representation of the input and runs our model.
```
# imports required for showing the attention weight heatmap
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
def translate(tokens, model_decoding, vocab, i2w, show_attention=False):
vdict = {v:i for i,v in enumerate(vocab)}
try:
w = [vdict["<s>"]] + [vdict[c] for c in tokens] + [vdict["</s>"]]
except:
print('Input contains an unexpected token.')
return []
# convert to one_hot
query = C.Value.one_hot([w], len(vdict))
pred = model_decoding(query)
pred = pred[0] # first sequence (we only have one) -> [len, vocab size]
if use_attention:
pred = pred[:,0,0,:] # attention has extra dimensions
# print out translation and stop at the sequence-end tag
prediction = np.argmax(pred, axis=-1)
translation = [i2w[i] for i in prediction]
# show attention window (requires matplotlib, seaborn, and pandas)
if use_attention and show_attention:
q = C.combine([model_decoding.attention_model.attention_weights])
att_value = q(query)
# get the attention data up to the length of the output (subset of the full window)
att_value = att_value[0][0:len(prediction),0:len(w),0,0] # -> (len, span)
# set up the actual words/letters for the heatmap axis labels
columns = [i2w[ww] for ww in prediction]
index = [i2w[ww] for ww in w]
dframe = pd.DataFrame(data=np.fliplr(att_value.T), columns=columns, index=index)
sns.heatmap(dframe)
plt.show()
return translation
```
The `translate` function above takes a list of letters input by the user as `tokens`, the greedy decoding version of our model `model_decoding`, the vocabulary `vocab`, a map of index to vocab `i2w`, and the `show_attention` option which determines if we will visualize the attention vectors or not.
We convert our input into a `one_hot` representation, run it through the model with `model_decoding(query)` and, since each prediction is actually a probability distribution over the entire vocabulary, we take the `argmax` to get the most probable token for each step.
To visualize the attention window, we use `combine` to turn the `attention_weights` into a CNTK Function that takes the inputs that we expect. This way, when we run the function `q`, the output will be the values of the `attention_weights`. We do some data manipulation to get this data into the format that `sns` expects, and we show the visualization.
Finally, we need to write the user-interaction loop which allows a user to enter multiple inputs.
```
def interactive_session(s2smodel, vocab, i2w, show_attention=False):
model_decoding = create_model_greedy(s2smodel) # wrap the greedy decoder around the model
import sys
print('Enter one or more words to see their phonetic transcription.')
while True:
if isTest(): # Testing a prefilled text for routine testing
line = "psychology"
else:
line = input("> ")
if line.lower() == "quit":
break
# tokenize. Our task is letter to sound.
out_line = []
for word in line.split():
in_tokens = [c.upper() for c in word]
out_tokens = translate(in_tokens, model_decoding, vocab, i2w, show_attention=True)
out_line.extend(out_tokens)
out_line = [" " if tok == '</s>' else tok[1:] for tok in out_line]
print("=", " ".join(out_line))
sys.stdout.flush()
if isTest(): #If test environment we will test the translation only once
break
```
The above function simply creates a greedy decoder around our model and then continually asks the user for an input which we pass to our `translate` function. Visualizations of the attention will continue being appended to the notebook until you exit the loop by typing `quit`. Please uncomment the following line to try out the interaction session.
```
interactive_session(model, vocab, i2w, show_attention=True)
```
Notice how the attention weights show how important different parts of the input are for generating different tokens in the output. For tasks like machine translation, where the order of one-to-one words often changes due to grammatical differences between languages, this becomes very interesting as we see the attention window move further away from the diagonal that is mostly displayed in grapheme-to-phoneme translations.
## What's next
With the above model, you have the basics for training a powerful sequence-to-sequence model with attention in a number of distinct domains. The only major changes required are preparing a dataset with pairs input and output sequences and in general the rest of the building blocks will remain the same. Good luck, and have fun!
| true |
code
| 0.687945 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/GoogleCloudPlatform/tensorflow-without-a-phd/blob/master/tensorflow-mnist-tutorial/keras_02_mnist_dense.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### Parameters
```
BATCH_SIZE = 128
EPOCHS = 10
training_images_file = 'gs://mnist-public/train-images-idx3-ubyte'
training_labels_file = 'gs://mnist-public/train-labels-idx1-ubyte'
validation_images_file = 'gs://mnist-public/t10k-images-idx3-ubyte'
validation_labels_file = 'gs://mnist-public/t10k-labels-idx1-ubyte'
```
### Imports
```
import os, re, math, json, shutil, pprint
import PIL.Image, PIL.ImageFont, PIL.ImageDraw
import IPython.display as display
import numpy as np
import tensorflow as tf
from matplotlib import pyplot as plt
tf.enable_eager_execution()
print("Tensorflow version " + tf.__version__)
#@title visualization utilities [RUN ME]
"""
This cell contains helper functions used for visualization
and downloads only. You can skip reading it. There is very
little useful Keras/Tensorflow code here.
"""
# Matplotlib config
plt.ioff()
plt.rc('image', cmap='gray_r')
plt.rc('grid', linewidth=1)
plt.rc('xtick', top=False, bottom=False, labelsize='large')
plt.rc('ytick', left=False, right=False, labelsize='large')
plt.rc('axes', facecolor='F8F8F8', titlesize="large", edgecolor='white')
plt.rc('text', color='a8151a')
plt.rc('figure', facecolor='F0F0F0', figsize=(16,9))
# Matplotlib fonts
MATPLOTLIB_FONT_DIR = os.path.join(os.path.dirname(plt.__file__), "mpl-data/fonts/ttf")
# pull a batch from the datasets. This code is not very nice, it gets much better in eager mode (TODO)
def dataset_to_numpy_util(training_dataset, validation_dataset, N):
# get one batch from each: 10000 validation digits, N training digits
batch_train_ds = training_dataset.apply(tf.data.experimental.unbatch()).batch(N)
# eager execution: loop through datasets normally
if tf.executing_eagerly():
for validation_digits, validation_labels in validation_dataset:
validation_digits = validation_digits.numpy()
validation_labels = validation_labels.numpy()
break
for training_digits, training_labels in batch_train_ds:
training_digits = training_digits.numpy()
training_labels = training_labels.numpy()
break
else:
v_images, v_labels = validation_dataset.make_one_shot_iterator().get_next()
t_images, t_labels = batch_train_ds.make_one_shot_iterator().get_next()
# Run once, get one batch. Session.run returns numpy results
with tf.Session() as ses:
(validation_digits, validation_labels,
training_digits, training_labels) = ses.run([v_images, v_labels, t_images, t_labels])
# these were one-hot encoded in the dataset
validation_labels = np.argmax(validation_labels, axis=1)
training_labels = np.argmax(training_labels, axis=1)
return (training_digits, training_labels,
validation_digits, validation_labels)
# create digits from local fonts for testing
def create_digits_from_local_fonts(n):
font_labels = []
img = PIL.Image.new('LA', (28*n, 28), color = (0,255)) # format 'LA': black in channel 0, alpha in channel 1
font1 = PIL.ImageFont.truetype(os.path.join(MATPLOTLIB_FONT_DIR, 'DejaVuSansMono-Oblique.ttf'), 25)
font2 = PIL.ImageFont.truetype(os.path.join(MATPLOTLIB_FONT_DIR, 'STIXGeneral.ttf'), 25)
d = PIL.ImageDraw.Draw(img)
for i in range(n):
font_labels.append(i%10)
d.text((7+i*28,0 if i<10 else -4), str(i%10), fill=(255,255), font=font1 if i<10 else font2)
font_digits = np.array(img.getdata(), np.float32)[:,0] / 255.0 # black in channel 0, alpha in channel 1 (discarded)
font_digits = np.reshape(np.stack(np.split(np.reshape(font_digits, [28, 28*n]), n, axis=1), axis=0), [n, 28*28])
return font_digits, font_labels
# utility to display a row of digits with their predictions
def display_digits(digits, predictions, labels, title, n):
fig = plt.figure(figsize=(13,3))
digits = np.reshape(digits, [n, 28, 28])
digits = np.swapaxes(digits, 0, 1)
digits = np.reshape(digits, [28, 28*n])
plt.yticks([])
plt.xticks([28*x+14 for x in range(n)], predictions)
plt.grid(b=None)
for i,t in enumerate(plt.gca().xaxis.get_ticklabels()):
if predictions[i] != labels[i]: t.set_color('red') # bad predictions in red
plt.imshow(digits)
plt.grid(None)
plt.title(title)
display.display(fig)
# utility to display multiple rows of digits, sorted by unrecognized/recognized status
def display_top_unrecognized(digits, predictions, labels, n, lines):
idx = np.argsort(predictions==labels) # sort order: unrecognized first
for i in range(lines):
display_digits(digits[idx][i*n:(i+1)*n], predictions[idx][i*n:(i+1)*n], labels[idx][i*n:(i+1)*n],
"{} sample validation digits out of {} with bad predictions in red and sorted first".format(n*lines, len(digits)) if i==0 else "", n)
def plot_learning_rate(lr_func, epochs):
xx = np.arange(epochs+1, dtype=np.float)
y = [lr_decay(x) for x in xx]
fig, ax = plt.subplots(figsize=(9, 6))
ax.set_xlabel('epochs')
ax.set_title('Learning rate\ndecays from {:0.3g} to {:0.3g}'.format(y[0], y[-2]))
ax.minorticks_on()
ax.grid(True, which='major', axis='both', linestyle='-', linewidth=1)
ax.grid(True, which='minor', axis='both', linestyle=':', linewidth=0.5)
ax.step(xx,y, linewidth=3, where='post')
display.display(fig)
class PlotTraining(tf.keras.callbacks.Callback):
def __init__(self, sample_rate=1, zoom=1):
self.sample_rate = sample_rate
self.step = 0
self.zoom = zoom
self.steps_per_epoch = 60000//BATCH_SIZE
def on_train_begin(self, logs={}):
self.batch_history = {}
self.batch_step = []
self.epoch_history = {}
self.epoch_step = []
self.fig, self.axes = plt.subplots(1, 2, figsize=(16, 7))
plt.ioff()
def on_batch_end(self, batch, logs={}):
if (batch % self.sample_rate) == 0:
self.batch_step.append(self.step)
for k,v in logs.items():
# do not log "batch" and "size" metrics that do not change
# do not log training accuracy "acc"
if k=='batch' or k=='size':# or k=='acc':
continue
self.batch_history.setdefault(k, []).append(v)
self.step += 1
def on_epoch_end(self, epoch, logs={}):
plt.close(self.fig)
self.axes[0].cla()
self.axes[1].cla()
self.axes[0].set_ylim(0, 1.2/self.zoom)
self.axes[1].set_ylim(1-1/self.zoom/2, 1+0.1/self.zoom/2)
self.epoch_step.append(self.step)
for k,v in logs.items():
# only log validation metrics
if not k.startswith('val_'):
continue
self.epoch_history.setdefault(k, []).append(v)
display.clear_output(wait=True)
for k,v in self.batch_history.items():
self.axes[0 if k.endswith('loss') else 1].plot(np.array(self.batch_step) / self.steps_per_epoch, v, label=k)
for k,v in self.epoch_history.items():
self.axes[0 if k.endswith('loss') else 1].plot(np.array(self.epoch_step) / self.steps_per_epoch, v, label=k, linewidth=3)
self.axes[0].legend()
self.axes[1].legend()
self.axes[0].set_xlabel('epochs')
self.axes[1].set_xlabel('epochs')
self.axes[0].minorticks_on()
self.axes[0].grid(True, which='major', axis='both', linestyle='-', linewidth=1)
self.axes[0].grid(True, which='minor', axis='both', linestyle=':', linewidth=0.5)
self.axes[1].minorticks_on()
self.axes[1].grid(True, which='major', axis='both', linestyle='-', linewidth=1)
self.axes[1].grid(True, which='minor', axis='both', linestyle=':', linewidth=0.5)
display.display(self.fig)
```
### tf.data.Dataset: parse files and prepare training and validation datasets
Please read the [best practices for building](https://www.tensorflow.org/guide/performance/datasets) input pipelines with tf.data.Dataset
```
AUTO = tf.data.experimental.AUTOTUNE
def read_label(tf_bytestring):
label = tf.decode_raw(tf_bytestring, tf.uint8)
label = tf.reshape(label, [])
label = tf.one_hot(label, 10)
return label
def read_image(tf_bytestring):
image = tf.decode_raw(tf_bytestring, tf.uint8)
image = tf.cast(image, tf.float32)/256.0
image = tf.reshape(image, [28*28])
return image
def load_dataset(image_file, label_file):
imagedataset = tf.data.FixedLengthRecordDataset(image_file, 28*28, header_bytes=16)
imagedataset = imagedataset.map(read_image, num_parallel_calls=16)
labelsdataset = tf.data.FixedLengthRecordDataset(label_file, 1, header_bytes=8)
labelsdataset = labelsdataset.map(read_label, num_parallel_calls=16)
dataset = tf.data.Dataset.zip((imagedataset, labelsdataset))
return dataset
def get_training_dataset(image_file, label_file, batch_size):
dataset = load_dataset(image_file, label_file)
dataset = dataset.cache() # this small dataset can be entirely cached in RAM, for TPU this is important to get good performance from such a small dataset
dataset = dataset.shuffle(5000, reshuffle_each_iteration=True)
dataset = dataset.repeat() # Mandatory for Keras for now
dataset = dataset.batch(batch_size, drop_remainder=True) # drop_remainder is important on TPU, batch size must be fixed
dataset = dataset.prefetch(AUTO) # fetch next batches while training on the current one (-1: autotune prefetch buffer size)
return dataset
def get_validation_dataset(image_file, label_file):
dataset = load_dataset(image_file, label_file)
dataset = dataset.cache() # this small dataset can be entirely cached in RAM, for TPU this is important to get good performance from such a small dataset
dataset = dataset.batch(10000, drop_remainder=True) # 10000 items in eval dataset, all in one batch
dataset = dataset.repeat() # Mandatory for Keras for now
return dataset
# instantiate the datasets
training_dataset = get_training_dataset(training_images_file, training_labels_file, BATCH_SIZE)
validation_dataset = get_validation_dataset(validation_images_file, validation_labels_file)
# For TPU, we will need a function that returns the dataset
training_input_fn = lambda: get_training_dataset(training_images_file, training_labels_file, BATCH_SIZE)
validation_input_fn = lambda: get_validation_dataset(validation_images_file, validation_labels_file)
```
### Let's have a look at the data
```
N = 24
(training_digits, training_labels,
validation_digits, validation_labels) = dataset_to_numpy_util(training_dataset, validation_dataset, N)
display_digits(training_digits, training_labels, training_labels, "training digits and their labels", N)
display_digits(validation_digits[:N], validation_labels[:N], validation_labels[:N], "validation digits and their labels", N)
font_digits, font_labels = create_digits_from_local_fonts(N)
```
### Keras model
If you are not sure what cross-entropy, dropout, softmax or batch-normalization mean, head here for a crash-course: [Tensorflow and deep learning without a PhD](https://github.com/GoogleCloudPlatform/tensorflow-without-a-phd/#featured-code-sample)
```
model = tf.keras.Sequential(
[
tf.keras.layers.Input(shape=(28*28,)),
tf.keras.layers.Dense(200, activation='relu'),
tf.keras.layers.Dense(60, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
# print model layers
model.summary()
# utility callback that displays training curves
plot_training = PlotTraining(sample_rate=10, zoom=1)
```
### Train and validate the model
```
steps_per_epoch = 60000//BATCH_SIZE # 60,000 items in this dataset
print("Steps per epoch: ", steps_per_epoch)
history = model.fit(training_dataset, steps_per_epoch=steps_per_epoch, epochs=EPOCHS,
validation_data=validation_dataset, validation_steps=1, callbacks=[plot_training])
```
### Visualize predictions
```
# recognize digits from local fonts
probabilities = model.predict(font_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)
display_digits(font_digits, predicted_labels, font_labels, "predictions from local fonts (bad predictions in red)", N)
# recognize validation digits
probabilities = model.predict(validation_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)
display_top_unrecognized(validation_digits, predicted_labels, validation_labels, N, 7)
```
## License
---
author: Martin Gorner<br>
twitter: @martin_gorner
---
Copyright 2019 Google LLC
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
---
This is not an official Google product but sample code provided for an educational purpose
| true |
code
| 0.30562 | null | null | null | null |
|
# CX 4230, Spring 2016: [22] Input modeling
This notebook includes sample code to accompany the slides from the Monday, February 29 class. It does not contain any exercises.
```
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
%matplotlib inline
X = np.array ([105.84, 28.92, 98.64, 55.64,
128.04, 45.60, 67.80, 105.12,
48.48, 51.84, 173.40, 51.96,
54.12, 68.64, 93.12, 68.88,
84.12, 68.64, 41.52, 127.92,
42.12, 17.88, 33.00])
print (len (X), "observations:")
print (X)
```
For the next code cell, refer to the documentation for Scipy's [`linregress()`](http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.linregress.html).
```
from scipy.stats import linregress
T = np.arange (len (X))
slope, intercept, rvalue, pvalue, stderr = linregress (T, X)
print ("Slope:", slope)
print ("Intercept:", intercept)
print ("p-value:", pvalue)
```
For the next code cell, refer to the documentation for Numpy's [`pad()`](http://docs.scipy.org/doc/numpy/reference/generated/numpy.pad.html#numpy.pad) function.
```
# Running means (fixed w)
w = 2 # window size
n, r = len (X), len (X) % w
n_w = (n-r) / w
X_w = np.reshape (X if r == 0 else X[:-r], (n_w, w))
np.pad (X_w, ((0, 0), (0, 1)), 'mean')
def calc_windowed_mean (X, w):
n, r = len (X), len (X) % w
n_w = (n - r) / w
if r == 0:
X_w = np.reshape (X, (n_w, w))
else:
X_w = np.reshape (X[:-r], (n_w, w))
# Add column of mean values
X_w = np.pad (X_w, ((0, 0), (0, 1)), 'mean')
T_w = np.arange (0, n-r, w) + w/2
return X_w, T_w
# Demo
calc_windowed_mean (X, 2)
fig = plt.figure (figsize=(18, 6))
ax = fig.add_subplot (111)
for w in range (1, len (X)+1, 5):
X_w, T_w = calc_windowed_mean (X, w)
xp, yp = T_w, X_w[:, -1:]
ax.plot (xp, yp, 'o:', label=str (w))
ax.legend ()
def sample_mean (X):
return np.mean (X)
sample_mean (X)
def sample_autocovar (X, h):
n = len (X)
n_h = n - abs (h)
X_t = X[:n_h]
X_t_h = X[abs (h):n]
mu = sample_mean (X)
return np.sum ((X_t_h - mu) * (X_t - mu)) / n
# Demo
sample_autocovar (X, 3)
def sample_autocorr (X, h=None):
n = len (X)
if h is not None:
assert abs (h) < n
return sample_autocovar (X, h) / sample_autocovar (X, 0)
else:
C = np.zeros (2*n-1)
H = np.arange (-(n-1), n)
for h in H:
C[n-1+h] = sample_autocorr (X, h)
return C, H
assert False
# Demo
sample_autocorr (X)
def viz_autocorr (X):
C, H = sample_autocorr (X)
fig = plt.figure (figsize=(18, 6))
ax = fig.add_subplot (111)
ax.stem (H, C, '-.')
plt.title ('Lag autocorrelations')
ax.set_xlabel ('Lag')
return fig, ax, C, H
# Demo
_, _, _, _ = viz_autocorr (X)
```
The following code cell shows an alternative way to implement the sample autocorrelation measure using Scipy's built-in [`correlate()`](http://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.correlate.html) function.
```
from scipy.signal import correlate
def sample_autocorr2 (X, h=None):
n = len (X)
mu_X = np.mean (X)
Y = correlate ((X - mu_X)/n, (X - mu_X)/n)
C = Y / Y[int (len (Y)/2)]
H = np.arange (-(n-1), n)
if h is not None:
assert -n < h < n
return C[-(n-1)+h]
else:
return C, H
def viz_autocorr2 (X):
C, H = sample_autocorr2 (X)
fig = plt.figure (figsize=(18, 6))
ax = fig.add_subplot (111)
ax.stem (H, C, '-.')
plt.title ('Lag autocorrelations (Method 2)')
ax.set_xlabel ('Lag')
return fig, ax, C, H
# Demo
_, _, _, _ = viz_autocorr2 (X)
```
| true |
code
| 0.439146 | null | null | null | null |
|
```
import tensorflow as tf
import numpy as np
import random
import matplotlib.pyplot as plt
from zipfile import ZipFile
def unzip(nm):
with ZipFile(nm,"r") as zip:
zip.extractall()
unzip("archive.zip")
random.seed(123)
np.random.seed(123)
tf.random.set_seed(123)
train_ds = tf.keras.preprocessing.image_dataset_from_directory(
"TB_Chest_Radiography_Database",
validation_split = 0.2,
subset = "training",
seed = 123,
shuffle = True,
image_size = (224,224),
batch_size = 32,
)
val_ds = tf.keras.preprocessing.image_dataset_from_directory(
"TB_Chest_Radiography_Database",
validation_split = 0.2,
subset = "validation",
seed = 123,
shuffle = True,
image_size = (224,224),
batch_size = 32,
)
from tensorflow.data.experimental import cardinality
val_batches = cardinality(val_ds)
test_ds = val_ds.take(val_batches//5)
val_ds = val_ds.skip(val_batches//5)
class_names = train_ds.class_names
plt.figure(figsize=(12,12))
for images,labels in train_ds.take(1):
for i in range(4):
ax = plt.subplot(2,2,i+1)
plt.imshow(images[i].numpy().astype("uint8"))
plt.title(class_names[labels[i]])
plt.axis("off")
plt.show()
AUTOTUNE = tf.data.AUTOTUNE
train_ds = train_ds.prefetch(buffer_size=AUTOTUNE)
val_ds = val_ds.prefetch(buffer_size=AUTOTUNE)
test_ds = test_ds.prefetch(buffer_size=AUTOTUNE)
```
### Data Augmentation
```
from tensorflow.keras.layers import RandomZoom, RandomRotation
data_augmentation = tf.keras.Sequential([
RandomZoom(0.2),
RandomRotation(0.1),
])
```
### Model: CNN from Scratch
```
from tensorflow.keras import Input, Model
from tensorflow.keras.layers.experimental.preprocessing import Rescaling
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout
from tensorflow.keras.models import load_model
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.losses import SparseCategoricalCrossentropy
from tensorflow.keras.callbacks import ModelCheckpoint
from tensorflow.keras.models import load_model
class Tuber():
def model(self,input):
self.x = data_augmentation(input)
self.x = Rescaling(1./255)(self.x)
self.x = Conv2D(64,3,activation="relu",padding="same",strides=(2,2))(self.x)
self.x = MaxPooling2D()(self.x)
self.x = Conv2D(128,3,activation="relu",padding="same",strides=(2,2))(self.x)
self.x = Conv2D(128,3,activation="relu",padding="same",strides=(2,2))(self.x)
self.x = Conv2D(256,3,activation="relu",padding="same",strides=(2,2))(self.x)
self.x = MaxPooling2D()(self.x)
self.x = Flatten()(self.x)
self.x = Dense(128,activation="relu")(self.x)
self.x = Dropout(0.2,seed=123)(self.x)
self.x = Dense(64,activation="relu")(self.x)
self.x = Dropout(0.2,seed=123)(self.x)
self.outputs = Dense(2,activation="sigmoid")(self.x)
self.model = Model(input,self.outputs,name="Tuber")
return self.model
tuber = Tuber()
model = tuber.model(Input(shape=(224,224,3)))
model.summary()
model.compile(RMSprop(),SparseCategoricalCrossentropy(),metrics=["accuracy"])
```
### Train and evaluate the model
```
if __name__=="__main__":
initial_epochs = 50
loss0,accuracy0 = model.evaluate(val_ds)
checkpoint = ModelCheckpoint("tuberculosis.hdf5",save_weights_only=False,monitor="val_accuracy",save_best_only=True)
model.fit(train_ds,epochs=initial_epochs,validation_data=val_ds,callbacks=[checkpoint])
best = load_model("tuberculosis.hdf5")
val_loss,val_accuracy = best.evaluate(val_ds)
test_loss,test_accuracy = best.evaluate(test_ds)
print("\nVal accuracy: {:.2f} %".format(100*val_accuracy))
print("Val loss: {:.2f} %".format(100*val_loss))
print("\nTest accuracy: {:.2f} %".format(100*test_accuracy))
print("Test loss: {:.2f} %".format(100*test_loss))
```
| true |
code
| 0.748048 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/pachterlab/GFCP_2021/blob/main/notebooks/vcy_scvelo_comparison.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Figure 1: The user-facing workflows of `velocyto` and `scVelo`
In this notebook, we reanalyze the La Manno et al. forebrain dataset using the default settings in `velocyto` and `scVelo`. The resulting PCA velocity embeddings lead to different conclusions about the relationships between the cells.
# Dependencies
```
%%capture
pip install scvelo==0.2.3 --quiet
%%capture
pip install --upgrade git+https://github.com/meichenfang/velocyto.py.git
%%capture
pip install scanpy
%%capture
pip install umap-learn
!mkdir -p figure
!mkdir -p data
```
Obtain the data.
```
from google.colab import drive
drive.mount('/content/drive')
!cp -r /content/drive/MyDrive/rnavelocity/hgForebrainGlut.loom /content/data
# from urllib.request import urlretrieve
# urlretrieve("http://pklab.med.harvard.edu/velocyto/hgForebrainGlut/hgForebrainGlut.loom", "data/hgForebrainGlut.loom")
import matplotlib.pyplot as plt
import numpy as np
from sklearn.neighbors import NearestNeighbors
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.manifold import TSNE
import umap
import velocyto as vcy
import anndata as ad
import warnings
import scvelo as scv
from vis import *
```
## velocyto
```
vlm = vcy.VelocytoLoom(loom_filepath="data/hgForebrainGlut.loom")
vlm.ca
preprocess(vlm)
```
#### phasePlots
Display a sample phase plot for ELAVL4, with imputation using $k=30$ neighbors (as in `scVelo`).
```
gene_idx_spec=int(np.where(vlm.ra['Gene']=="ELAVL4")[0][0])
getImputed(vlm, knn_k=50)
def plotPhase2(ax, vlm, gene_idx):
'''
Plot phase portrait
Parameters
----------
Returns
-------
'''
y=vlm.Ux[gene_idx,:]
x=vlm.Sx[gene_idx,:]
k=vlm.gammas[gene_idx]
b=vlm.q[gene_idx]
ax.scatter(x, y, c=vlm.colors)
ax.set_xlabel('spliced')
ax.set_ylabel('unspliced')
x_=np.array([np.amin(x), np.amax(x)])
ax.plot(x_, x_*k+b, color='black',linewidth=4,linestyle='dashed')
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
return
fig, ax = plt.subplots(figsize=(5,5))
plotPhase2(ax, vlm, gene_idx_spec)
plt.setp(plt.gcf().get_axes(), xticks=[], yticks=[])
plt.savefig('phase.pdf')
```
### Velocity Grid Embedding
This workflow reproduces the [notebook](https://github.com/velocyto-team/velocyto-notebooks/blob/master/python/hgForebrainGlutamatergic.ipynb) used to generate Fig. 4 of "RNA Velocity of Single Cells."
```
vlm = vcy.VelocytoLoom("data/hgForebrainGlut.loom")
labels = vlm.ca["Clusters"]
manual_annotation = {str(i):[i] for i in labels}
annotation_dict = {v:k for k, values in manual_annotation.items() for v in values }
clusters = np.array([annotation_dict[i] for i in labels])
colors20 = np.vstack((plt.cm.tab20b(np.linspace(0., 1, 20))[::2], plt.cm.tab20c(np.linspace(0, 1, 20))[1::2]))
vlm.set_clusters(clusters, cluster_colors_dict={k:colors20[v[0] % 20,:] for k,v in manual_annotation.items()})
# just to find the initial cell size
vlm.normalize("S", size=True, log=False)
vlm.normalize("U", size=True, log=False)
vlm.score_detection_levels(min_expr_counts=30, min_cells_express=20,
min_expr_counts_U=0, min_cells_express_U=0)
vlm.filter_genes(by_detection_levels=True)
vlm.score_cv_vs_mean(2000, plot=True, max_expr_avg=50, winsorize=True, winsor_perc=(1,99.8), svr_gamma=0.01, min_expr_cells=50)
vlm.filter_genes(by_cv_vs_mean=True)
vlm.score_detection_levels(min_expr_counts=0, min_cells_express=0,
min_expr_counts_U=25, min_cells_express_U=20)
vlm.score_cluster_expression(min_avg_U=0.007, min_avg_S=0.06)
vlm.filter_genes(by_detection_levels=True, by_cluster_expression=True)
vlm.normalize_by_total(min_perc_U=0.5)
vlm.adjust_totS_totU(normalize_total=True, fit_with_low_U=False, svr_C=1, svr_gamma=1e-04)
vlm.perform_PCA()
#plt.plot(np.cumsum(vlm.pca.explained_variance_ratio_)[:100])
n_comps = np.where(np.diff(np.diff(np.cumsum(vlm.pca.explained_variance_ratio_))>0.0055))[0][0]
vlm.pcs[:,1] *= -1
!pip install igraph --quiet
from sklearn.neighbors import NearestNeighbors
import igraph
nn = NearestNeighbors(n_neighbors=50)
nn.fit(vlm.pcs[:,:4])
knn_pca = nn.kneighbors_graph(mode='distance')
knn_pca = knn_pca.tocoo()
G = igraph.Graph(list(zip(knn_pca.row, knn_pca.col)), directed=False, edge_attrs={'weight': knn_pca.data})
VxCl = G.community_multilevel(return_levels=False, weights="weight")
labels = np.array(VxCl.membership)
from numpy_groupies import aggregate, aggregate_np
k = 550
vlm.knn_imputation(n_pca_dims=n_comps,k=k, balanced=True,
b_sight=np.minimum(k*8, vlm.S.shape[1]-1),
b_maxl=np.minimum(k*4, vlm.S.shape[1]-1))
vlm.normalize_median()
vlm.fit_gammas(maxmin_perc=[2,95], limit_gamma=True)
vlm.normalize(which="imputed", size=False, log=True)
vlm.Pcs = np.array(vlm.pcs[:,:2], order="C")
vlm.predict_U()
vlm.calculate_velocity()
vlm.calculate_shift()
vlm.extrapolate_cell_at_t(delta_t=1)
vlm.estimate_transition_prob(hidim="Sx_sz", embed="Pcs", transform="log", psc=1,
n_neighbors=150, knn_random=True, sampled_fraction=1)
vlm.calculate_embedding_shift(sigma_corr = 0.05, expression_scaling=False)
vlm.calculate_grid_arrows(smooth=0.9, steps=(25, 25), n_neighbors=200)
# labels = vlm.ca["Clusters"]
# cluster_colors_dict={l:colors20[l % 20,:] for l in labels}
# vlm.colors=[cluster_colors_dict[label] for label in labels]
plt.figure(None,(9,9))
vlm.plot_grid_arrows(scatter_kwargs_dict={"alpha":0.7, "lw":0.7, "edgecolor":"0.4", "s":70, "rasterized":True},
min_mass=2.9, angles='xy', scale_units='xy',
headaxislength=2.75, headlength=5, headwidth=4.8, quiver_scale=0.35, scale_type="absolute")
# plt.plot(pc_obj.projections[pc_obj.ixsort,0], pc_obj.projections[pc_obj.ixsort,1], c="w", lw=6, zorder=1000000)
# plt.plot(pc_obj.projections[pc_obj.ixsort,0], pc_obj.projections[pc_obj.ixsort,1], c="k", lw=3, zorder=2000000)
plt.gca().invert_xaxis()
plt.axis("off")
plt.axis("equal");
```
## scvelo
```
# update to the latest version, if not done yet.
import scvelo as scv
scv.logging.print_version()
scv.settings.verbosity = 3 # show errors(0), warnings(1), info(2), hints(3)
scv.settings.presenter_view = True # set max width size for presenter view
scv.set_figure_params('scvelo') # for beautified visualization
adata = scv.read('data/hgForebrainGlut.loom', cache=True)
scv.pp.filter_and_normalize(adata, min_shared_counts=20, n_top_genes=2000)
scv.pp.moments(adata, n_pcs=30, n_neighbors=30)
scv.tl.velocity(adata)
adata
scv.tl.velocity_graph(adata)
#Get colors
labels = vlm.ca["Clusters"]
cluster_colors_dict={l:colors20[l % 20,:] for l in labels}
#colors=[cluster_colors_dict[label] for str(label) in labels]
cluster_colors_dict
scv.pl.velocity_embedding_stream(adata, basis='pca',color='Clusters',palette=cluster_colors_dict)
```
| true |
code
| 0.718397 | null | null | null | null |
|
```
%matplotlib inline
from pyvista import set_plot_theme
set_plot_theme('document')
```
Compare Field Across Mesh Regions
=================================
Here is some velocity data from a glacier modelling simulation that is
compared across nodes in the simulation. We have simplified the mesh to
have the simulation node value already on the mesh.
This was originally posted to
[pyvista/pyvista-support\#83](https://github.com/pyvista/pyvista-support/issues/83).
The modeling results are courtesy of [Urruty
Benoit](https://github.com/BenoitURRUTY) and are from the
[Elmer/Ice](http://elmerice.elmerfem.org) simulation software.
```
# sphinx_gallery_thumbnail_number = 2
import pyvista as pv
from pyvista import examples
import numpy as np
# Load the sample data
mesh = examples.download_antarctica_velocity()
mesh["magnitude"] = np.linalg.norm(mesh["ssavelocity"], axis=1)
mesh
```
Here is a helper to extract regions of the mesh based on the simulation
node.
```
def extract_node(node):
idx = mesh["node_value"] == node
return mesh.extract_points(idx)
p = pv.Plotter()
p.add_mesh(mesh, scalars="node_value")
for node in np.unique(mesh["node_value"]):
loc = extract_node(node).center
p.add_point_labels(loc, [f"Node {node}"])
p.show(cpos="xy")
vel_dargs = dict(scalars="magnitude", clim=[1e-3, 1e4], cmap='Blues', log_scale=True)
mesh.plot(cpos="xy", **vel_dargs)
a = extract_node(12)
b = extract_node(20)
pl = pv.Plotter()
pl.add_mesh(a, **vel_dargs)
pl.add_mesh(b, **vel_dargs)
pl.show(cpos='xy')
```
plot vectors without mesh
```
pl = pv.Plotter()
pl.add_mesh(a.glyph(orient="ssavelocity", factor=20), **vel_dargs)
pl.add_mesh(b.glyph(orient="ssavelocity", factor=20), **vel_dargs)
pl.camera_position = [(-1114684.6969340036, 293863.65389149904, 752186.603224546),
(-1114684.6969340036, 293863.65389149904, 0.0),
(0.0, 1.0, 0.0)]
pl.show()
```
Compare directions. Normalize them so we can get a reasonable direction
comparison.
```
flow_a = a.point_arrays['ssavelocity'].copy()
flow_a /= np.linalg.norm(flow_a, axis=1).reshape(-1, 1)
flow_b = b.point_arrays['ssavelocity'].copy()
flow_b /= np.linalg.norm(flow_b, axis=1).reshape(-1, 1)
# plot normalized vectors
pl = pv.Plotter()
pl.add_arrows(a.points, flow_a, mag=10000, color='b', label='flow_a')
pl.add_arrows(b.points, flow_b, mag=10000, color='r', label='flow_b')
pl.add_legend()
pl.camera_position = [(-1044239.3240694795, 354805.0268606294, 484178.24825854995),
(-1044239.3240694795, 354805.0268606294, 0.0),
(0.0, 1.0, 0.0)]
pl.show()
```
flow\_a that agrees with the mean flow path of flow\_b
```
agree = flow_a.dot(flow_b.mean(0))
pl = pv.Plotter()
pl.add_mesh(a, scalars=agree, cmap='bwr',
scalar_bar_args={'title': 'Flow agreement with block b'})
pl.add_mesh(b, color='w')
pl.show(cpos='xy')
agree = flow_b.dot(flow_a.mean(0))
pl = pv.Plotter()
pl.add_mesh(a, color='w')
pl.add_mesh(b, scalars=agree, cmap='bwr',
scalar_bar_args={'title': 'Flow agreement with block a'})
pl.show(cpos='xy')
```
| true |
code
| 0.646628 | null | null | null | null |
|
# Chapter 1, figures 3 and 4
This notebook will show you how to produce figures 1.3 and 1.4 after the predictive modeling is completed.
The predictive modeling itself, unfortunately, doesn't fit in a notebook. The number-crunching can take several hours, and although logistic regression itself is not complicated, the practical details -- dates, authors, multiprocessing to speed things up, etc -- turn it into a couple thousand lines of code. (If you want to dig into that, see ```chapter1/code/biomodel.py```, and the scripts in ```/logistic``` at the top level of the repo.)
Without covering those tangled details, this notebook can still explore the results of modeling in enough depth to give you a sense of some important choices made along the way.
### Define modeling parameters
I start by finding an optimal number of features for the model, and also a value for C (the regularization constant). To do this I run a "grid search" that tests different values of both parameters. (I use the "gridsearch" option in biomodel, aka: ```python3 biomodel.py gridsearch```.) The result looks like this:

where darker red squares indicate higher accuracies. I haven't labeled the axes correctly, but the vertical axis here is number of features (from 800 to 2500), and the horizontal axis is the C parameter (from .0012 to 10, logarithmically).
It's important to use the same sample size for this test that you plan to use in the final model: in this case a rather small group of 150 volumes (75 positive and 75 negative), because I want to be able to run models in periods as small as 20 years. With such a small sample, it's important to run the gridsearch several times, since the selection of a particular 150 volumes introduces considerable random variability into the process.
One could tune the C parameter for each sample, and I try that in a different chapter, but my experience is that it introduces complexity without actually changing results--plus I get anxious about overfitting through parameter selection. Probably better just to confirm results with multiple samples and multiple C settings. A robust result should hold up.
I've tested the differentiation of genres with multiple parameter settings, and it does hold up. But for figure 1.3, I settled on 1100 features (words) and C = 0.015 as settings that fairly consistently produce good results for the biography / fiction boundary. Then it's possible to
### Assess accuracy across time: Figure 1.3
I do this by running ```python3 biomodel.py usenewdata``` (the contrast between 'new' and 'old' metadata will become relevant later in this notebook). That produces a file of results visualized below.
```
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
import random
accuracy_df = pd.read_csv('../modeloutput/finalbiopredicts.csv')
accuracy_df.head()
# I "jitter" results horizontally because we often have multiple results with the same x and y coordinates.
def jitteraframe(df, yname):
jitter = dict()
for i in df.index:
x = df.loc[i, 'center']
y = df.loc[i, yname]
if x not in jitter:
jitter[x] = set()
elif y in jitter[x]:
dodge = random.choice([-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6])
x = x + dodge
df.loc[i, 'center'] = x
if x not in jitter:
jitter[x] = set()
jitter[x].add(y)
jitteraframe(accuracy_df, 'accuracy')
fig, ax = plt.subplots(figsize = (9, 9))
ax.margins(0.1)
ax.plot(accuracy_df.center, accuracy_df.accuracy, marker = 'o', linestyle = '', alpha = 0.5)
ax.annotate('accuracy', xy = (1700,1), fontsize = 16)
plt.show()
```
#### assessment
There's a lot of random variation with this small sample size, but it's still perfectly clear that accuracy rises across this timeline. It may not be a linear relationship: it looks like the boundary between fiction and biography may be sharpest around 1910, and rather than a smooth line, it might be two regimes divided around 1850. But it's still quite clear that accuracy rises: if we modeled it simply as a linear correlation, it would be strong and significant.
```
from scipy.stats import pearsonr
pearsonr(accuracy_df.floor, accuracy_df.accuracy)
```
The first number is the correlation coefficient; the second a p value.
### Plotting individual volume probabilities: Figure 1.4
In a sense plotting individual volumes is extremely simple. My modeling process writes files that record the metadata for each volume along with a column **logistic** that reports the predicted probability of being in the positive class (in this case, fiction). We can just plot the probabilities on the y axis, and dates used for modeling on the x axis. Have done that below.
```
root = '../modeloutput/'
frames = []
for floor in range(1700, 2000, 50):
sourcefile = root + 'theninehundred' + str(floor) + '.csv'
thisframe = pd.read_csv(sourcefile)
frames.append(thisframe)
df = pd.concat(frames)
df.head()
groups = df.groupby('realclass')
groupnames = {0: 'biography', 1: 'fiction'}
groupcolors = {0: 'k', 1: 'r'}
fig, ax = plt.subplots(figsize = (9, 9))
ax.margins(0.1)
for code, group in groups:
ax.plot(group.dateused, group.logistic, marker='o', linestyle='', ms=6, alpha = 0.66, color = groupcolors[code], label=groupnames[code])
ax.legend(numpoints = 1, loc = 'upper left')
plt.show()
```
#### caveats
The pattern you see above is real, and makes a nice visual emblem of generic differentiation. However, there are some choices involved worth reflection. The probabilities plotted above were produced by six models, trained on 50-year segments of the timeline, using 1100 features **and a C setting of 0.00008**. That C setting works fine, but it's much lower than the one I chose as optimal for assessing accuracy. What happens if we use instead C = 0.015, and in fact simply reuse the evidence from figure 1.3 unchanged?
The accuracies recorded in ```finalpredictbio.csv``` come from a series of models named ```cleanpredictbio``` (plus some more info). I haven't saved all of them, but we have the last model in each sequence of 15. We can plot those probabilities.
```
root = '../modeloutput/'
frames = []
for floor in range(1700, 2000, 20):
if floor == 1720:
continue
# the first model covers 40 years
sourcefile = root + 'cleanpredictbio' + str(floor) + '2017-10-15.csv'
thisframe = pd.read_csv(sourcefile)
frames.append(thisframe)
df = pd.concat(frames)
bio = []
fic = []
for i in range (1710, 1990):
segment = df[(df.dateused > (i - 10)) & (df.dateused < (i + 10))]
bio.append(np.mean(segment[segment.realclass == 0].logistic))
fic.append(np.mean(segment[segment.realclass == 1].logistic))
groups = df.groupby('realclass')
groupnames = {0: 'biography', 1: 'fiction'}
groupcolors = {0: 'k', 1: 'r'}
fig, ax = plt.subplots(figsize = (9, 9))
ax.margins(0.1)
for code, group in groups:
ax.plot(group.dateused, group.logistic, marker='o', linestyle='', ms=6, alpha = 0.5, color = groupcolors[code], label=groupnames[code])
ax.plot(list(range(1710,1990)), bio, c = 'k')
ax.plot(list(range(1710,1990)), fic, c = 'r')
ax.legend(numpoints = 1, loc = 'upper left')
plt.show()
```
Whoa, that's a different picture!
If you look closely, there's still a pattern of differentiation: probabilities are more dispersed in the early going, and probs of fiction and biography overlap more. Later on, a space opens up between the genres. I've plotted the mean trend lines to confirm the divergence.
But the picture *looks* very different. This model uses less aggressive regularization (the bigger C constant makes it more confident), so most probabilities hit the walls around 1.0 or 0.0.
This makes it less obvious, visually, that differentiation is a phenomenon affecting the whole genre. We actually *do* see a significant change in medians here, as well as means. But it would be hard to see with your eyeballs, because the trend lines are squashed toward the edges.
So I've chosen to use more aggressive regularization (and a smaller number of examples) for the illustration in the book. That's a debatable choice, and a consequential one: as I acknowledge above, it changes the way we understand the word *differentiation.* I think there are valid reasons for the choice. Neither of the illustrations above is "truer" than than the other; they are alternate, valid perspectives on the same evidence. But if you want to use this kind of visualization, it's important to recognize that tuning the regularization constant will very predictably give you this kind of choice. It can't make a pattern of differentiation appear out of thin air, but it absolutely does change the distribution of probabilities across the y axis. It's a visual-rhetorical choice that needs acknowledging.
| true |
code
| 0.436202 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/jonfisik/Projects/blob/master/VetoresPython.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import numpy as np
import matplotlib.pyplot as plt
u = [1,2]
v = [2,1]
# somou listas
u + v
u = np.array(u)
v = np.array(v)
# soma de vetores
u + v
#----------------------------------------------
w1 = np.array([2,3])
w2 = np.array([4,-1])
# Produto escalar ou interno função --> .dot()
w1.dot(w2)
w2.dot(w1)
# Módulo função --> .norm(vetor)
modulo_w1 = np.linalg.norm(w1) # foi atribuido o valor da norma a uma variável
modulo_w2 = np.linalg.norm(w2) # Idem
modulo_w1
modulo_w2
np.linalg.norm(w1)
#----------------------------------------------------- 15/10/2020
v = np.array([1,2,3,4])
v
type(v)
# Descrição de uma função
?np.array
lista = [3,5,66,20]
type(lista)
# Transformar uma lista em um vetor
v1 = np.array(lista)
v2 = np.array([1,2,3,4])
v3 = np.array((4,3,2,1))
v1
v2
v3
# Representação de vetores
e1 = np.array([1,0,0])
e2 = np.array([0,1,0])
e3 = np.array([0,0,1])
#------------------------------------------
def plotVectors(vecs, cols, alpha=2):
''' função para plotar vetores'''
plt.figure()
plt.axvline(x=0, color='#A9A9A9', zorder=0)
plt.axhline(y=0, color='#A9A9A9', zorder=0)
for i in range(len(vecs)):
x = np.concatenate([[0,0],vecs[i]])
plt.quiver([x[0]],
[x[1]],
[x[2]],
[x[3]],
angles='xy', scale_units='xy', scale=1, color=cols[i],
alpha=alpha)
laranja = '#FF9A13'
azul = '#1190FF'
resultante = '#11FFFF'
plotVectors([[2,3], [4,-1], [6,2]], [laranja, azul, resultante])
plt.xlim(-1,7)
plt.ylim(-2,7)
#Cores
cor1 = '#FF0000'
cor2 = '#FF0000'
corRes = '#11FFFF'
# Vetores
a = np.array([2,3])
b = np.array([3,1])
# Soma
r = a + b
# Função
plotVectors([a, b, r], [cor1, cor2, corRes])
# Plano cartesiano
plt.xlim(-1,6)
plt.ylim(-5,10)
plotVectors([e1,e2],[cor1,cor2])
plt.xlim(-1,1.5)
plt.ylim(-1,1.5)
# Ângulo entre vetores
def ang_2vetores(v,u):
v_escalar_u = v.dot(u)
vn = np.linalg.norm(v)
un = np.linalg.norm(u)
r = v_escalar_u/(vn*un) # cosseno do angulo
ang = np.arccos(r) # ang em radianos
return (180/np.pi)*ang # ang em graus
u = np.array([0,1])
v = np.array([1,0])
red = 'red'
blue = 'blue'
plotVectors([u,v], [red, blue])
plt.xlim(-1,1.5)
plt.ylim(-1,1.5)
ang_2vetores(u,v)
A = np.array([1,1])
B = np.array([1,0])
red = 'red'
blue = 'blue'
plotVectors([A, B], [red, blue])
plt.xlim(-1,1.5)
plt.ylim(-1,1.5)
ang_2vetores(A,B)
# Indexação de vetores
# vetor
x = [1,2,3,4,5]
vx = np.array(x)
# Tamanho do vetor
len(vx)
# posição inicial em python começa em "0"
posicao_2 = vx[2]
posicao_2
posicao_0 = vx[0]
posicao_0
```
| true |
code
| 0.30308 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.