prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
<a href="https://colab.research.google.com/github/JavaFXpert/qiskit4devs-workshop-notebooks/blob/master/grover_search_party.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Using Grover search for boolean satisfiability
### *Throwing a party while avoiding the drama*
Imagine you are inviting some friends to a party, some who are couples, and some who are not on speaking terms. Specifically, **Alice** and **Bob** are in a relationship, as are **Carol** and **David**. However, **Alice** and **David** had a bad breakup a while ago and haven't been civil with each other since. Armed with a quantum computer and Qiskit Aqua, how can you leverage Grover search algorithm to identify friendly combinations of people to invite?
Fortunately, Grover search may be used for [boolean satisfiability problems](https://en.wikipedia.org/wiki/Boolean_satisfiability_problem), and the constraints for our party planning problem may be formulated with the following boolean expression:
`((A and B) or (C and D)) and not (A and D)`
```
# Do the necessary import for our program
#!pip install qiskit-aqua
from qiskit import BasicAer
from qiskit.aqua.algorithms import Grover
from qiskit.aqua.components.oracles import LogicalExpressionOracle, TruthTableOracle
from qiskit.tools.visualization import plot_histogram
from qiskit.compiler import transpile
```
Let's go ahead and use our expression in a Grover search to find out compatible combinations of people to invite.
> Note: We'll represent `and` with `&`, `or` with `|`, `not` with `~` in our expression.
```
oracle_type = "Bit" #<-"Log" or "Bit"
#log_expr = '((A & B) | (C & D)) & ~(A & D) & (F | G)'
#log_expr = '(A & B & C)' #<- Oracle for |111>
#bitstr = '00000001'
#log_expr = '(~A & ~B & ~C)' #<- Oracle for |000>
#bitstr = '10000000'
#log_expr = '((~A & ~B & ~C) & (A & B & C))' #<- Oracle for |000> + |111>
#bitstr = '10000001'
log_expr = '(~A & B & C)' #<- Oracle for |110>
bitstr = '00000010'
if oracle_type=="Log":
algorithm = Grover(LogicalExpressionOracle(log_expr))
circuit = Grover(LogicalExpressionOracle(log_expr)).construct_circuit()
else:
algorithm = Grover(TruthTableOracle(bitstr))
circuit = Grover(TruthTableOracle(bitstr)).construct_circuit()
print(circuit)
```
Now we'll run the algorithm on a simulator, printing the result that occurred most often. This result is expressed as the numeric representations of our four friends; a minus sign indicating which ones Grover advised against inviting in that particular result.
```
# Run the algorithm on a simulator, printing the most frequently occurring result
backend = BasicAer.get_backend('qasm_simulator')
result = algorithm.run(backend)
print(result['top_measurement'])
print(result['measurement'])
```
Finally, we'll plot the results. Each basis state represents our four friends, with the least significant bit representing Alice. If a bit is 1, then the advice is to invite the person that the bit represents. If the bit is 0, then Grover advises not to send an invitation.
```
plot_histogram(result['measurement'])
"""Test"""
bitstr_test = '1000'
oracle_test = TruthTableOracle(bitstr_test)
display(oracle_test.circuit.draw(output='mpl'))
expression_test2 = ('(~A & ~B)')
oracle_test2 = LogicalExpressionOracle(expression_test2)
display(oracle_test2.circuit.draw(output='mpl'))
from qiskit.quantum_info.operators import Operator
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, IBMQ
from qiskit.compiler import transpile
%matplotlib inline
IBMQ.load_account()
provider = IBMQ.load_account()
unitary_oracle_0 = Operator([
[1, 0, 0, 0],
[0, -1, 0, 0],
[0, 0, -1, 0],
[0, 0, 0, -1]])
qr=QuantumRegister(2)
oracle_test3=QuantumCircuit(qr)
oracle_test3.append(unitary_oracle_0,qr)
display(oracle_test3.draw(output='mpl'))
device = provider.get_backend('ibmqx2')
trans_test = transpile(oracle_test3, device)
trans_test.draw()
trans_bell2 = transpile(bell2, device)
trans_bell2.draw()
print("Ch 8: Running “diagnostics” with the state vector simulator")
print("-----------------------------------------------------------")
# Import the required Qiskit classes
from qiskit import(
QuantumCircuit,
execute,
Aer,
IBMQ)
# Import Blochsphere visualization
from qiskit.visualization import *
# Import some math that we will need
from math import pi
# Set numbers display options
import numpy as np
np.set_printoptions(precision=3)
# Create a function that requests and display the state vector
# Use this function as a diagnositc tool when constructing your circuits
backend = Aer.get_backend('statevector_simulator')
def s_vec(circuit):
print(circuit.n_qubits, "qubit quantum circuit:\n------------------------")
print(circuit)
psi=execute(circuit, backend).result().get_statevector(circuit)
print("State vector for the",circuit.n_qubits,"qubit circuit:\n\n",psi)
print("\nState vector as Bloch sphere.\n")
display(plot_bloch_multivector(psi))
print("\nState vector as Q sphere.")
display(iplot_state_qsphere(psi,figsize=(5,5)))
input("Press enter to continue...\n")
# One qubit states
qc = QuantumCircuit(1,1)
s_vec(qc)
qc.h(0)
s_vec(qc)
qc.rz(pi/2,0)
s_vec(qc)
# Two qubit states
qc = QuantumCircuit(2,2)
s_vec(qc)
qc.h([0])
s_vec(qc)
qc.swap(0,1)
s_vec(qc)
# Entangled qubit states
qc = QuantumCircuit(2,2)
s_vec(qc)
qc.h(0)
s_vec(qc)
qc.cx(0,1)
s_vec(qc)
qc.rz(pi/4,0)
s_vec(qc)
# Three qubit states
qc = QuantumCircuit(3,3)
s_vec(qc)
qc.h(0)
s_vec(qc)
qc.h(1)
s_vec(qc)
qc.ccx(0,1,2)
s_vec(qc)
qc.rz(pi/4,0)
s_vec(qc)
# Notice how the Bloch sphere visualization doesn't lend itself very well to displaying entangled qubits, as they cannot be thought of as individual entities. And there is no good way of displaying multiple qubits on one Bloch sphere. A better option here is the density matrix, displayed as a state city.
# Measuring entangled qubits
qc.measure([0,1],[0,1])
print("Running the",qc.n_qubits,"qubit circuit on the qasm_simulator:\n")
print(qc)
backend_count = Aer.get_backend('qasm_simulator')
counts=execute(qc, backend_count,shots=10000).result().get_counts(qc)
print("Result:\n", counts)
```
#### Now it's you're turn to play!
Create and implement your own scenario that can be modeled as a boolean satisfiability problem using Grover search. Have fun with it, and carry on with your quantum computing journey!
| true |
code
| 0.462534 | null | null | null | null |
|
<small><small><i>
All the IPython Notebooks in this lecture series by Dr. Milan Parmar are available @ **[GitHub](https://github.com/milaan9/01_Python_Introduction)**
</i></small></small>
# Python Statement, Indentation and Comments
In this class, you will learn about Python statements, why indentation is important and use of comments in programming.
## 1. Python Statement
Instructions that a Python interpreter can execute are called statements. For example, **`a = 1`** is an assignment statement. **`if`** statement, **`for`** statement, **`while`** statement, etc. are other kinds of statements which will be discussed later.
### Multi-line statement
In Python, the end of a statement is marked by a newline character. But we can make a statement extend over multiple lines with the line continuation character **`\`**.
* Statements finish at the end of the line:
* Except when there is an open bracket or paranthesis:
```python
>>> 1+2
>>> +3 #illegal continuation of the sum
```
* A single backslash at the end of the line can also be used to indicate that a statement is still incomplete
```python
>>> 1 + \
>>> 2 + 3 # this is also okay
```
For example:
```
1+2 # assignment line 1
+3 # assignment line 2
# Python is only calculating assignment line 1
1+2\ # "\" means assignment line is continue to next line
+3
a = 1 + 2 + 3 + \
4 + 5 + 6 + \
7 + 8 + 9
print(a)
```
This is an explicit line continuation. In Python, line continuation is implied inside:
1. parentheses **`( )`**,
For Example:
```python
(1+2
+ 3) # perfectly OK even with spaces
```
2. brackets **`[ ]`**, and
3. braces **`{ }`**.
For instance, we can implement the above multi-line statement as:
```
(1+2
+3)
a = (1 + 2 + 3 +
4 + 5 + 6 +
7 + 8 + 9)
print(a)
```
Here, the surrounding parentheses **`( )`** do the line continuation implicitly. Same is the case with **`[ ]`** and **`{ }`**. For example:
```
colors = ['red',
'blue',
'green']
print(colors)
```
We can also put multiple statements in a single line using semicolons **`;`** as follows:
```
a = 1; b = 2; c = 3
print(a,b,c)
a,b,c
```
## 2. Python Indentation
No spaces or tab characters allowed at the start of a statement: Indentation plays a special role in Python (see the section on control statements). For now simply ensure that all statements start at the beginning of the line.
<div>
<img src="img/ind1.png" width="700"/>
</div>
Most of the programming languages like C, C++, and Java use braces **`{ }`** to define a block of code. Python, however, uses indentation.
A comparison of C & Python will help you understand it better.
<div>
<img src="img/ind2.png" width="700"/>
</div>
A code block (body of a **[function](https://github.com/milaan9/04_Python_Functions/blob/main/001_Python_Functions.ipynb)**, **[loop](https://github.com/milaan9/03_Python_Flow_Control/blob/main/005_Python_for_Loop.ipynb)**, etc.) starts with indentation and ends with the first unindented line. The amount of indentation is up to you, but it must be consistent throughout that block.
Generally, four whitespaces are used for indentation and are preferred over tabs. Here is an example.
> **In the case of Python, indentation is not for styling purpose. It is rather a requirement for your code to get compiled and executed. Thus it is mandatory!!!**
```
for i in range(1,11):
print(i) #press "Tab" one time for 1 indentation
if i == 6:
break
```
The enforcement of indentation in Python makes the code look neat and clean. This results in Python programs that look similar and consistent.
Indentation can be ignored in line continuation, but it's always a good idea to indent. It makes the code more readable. For example:
```
if True:
print('Hello')
a = 6
```
or
```
if True: print('Hello'); a = 6
```
both are valid and do the same thing, but the former style is clearer.
Incorrect indentation will result in **`IndentationError`**
.
## 3. Python Comments
Comments are very important while writing a program. They describe what is going on inside a program, so that a person looking at the source code does not have a hard time figuring it out.
You might forget the key details of the program you just wrote in a month's time. So taking the time to explain these concepts in the form of comments is always fruitful.
In Python, we use the hash **`#`** symbol to start writing a comment.
It extends up to the newline character. Comments are for programmers to better understand a program. Python Interpreter ignores comments.
Generally, comments will look something like this:
```python
#This is a Comment
```
Because comments do not **execute**, when you run a program you will not see any indication of the comment there. Comments are in the source code for **humans** to **read**, not for **computers to execute**.
```
#This is a Comment
```
### 1. Single lined comment:
In case user wants to specify a single line comment, then comment must start with **`#`**.
```python
#This is single line comment.
```
```
#This is single line comment.
```
### 2. Inline comments
If a comment is placed on the same line as a statement, it is called an inline comment. Similar to the block comment, an inline comment begins with a single hash (#) sign and followed by a space and comment.
It is recommended that an inline comment should separate from the statement at least **two spaces**. The following example demonstrates an inline comment
```python
>>>n+=1 # increase/add n by 1
```
```
n=9
n+=1 # increase/add n by 1
n
```
### 3. Multi lined comment:
We can have comments that extend up to multiple lines. One way is to use the hash **`#`** symbol at the beginning of each line. For example:
```
#This is a long comment
#and it extends
#to multiple lines
#This is a comment
#print out Hello
print('Hello')
```
Another way of doing this is to use triple quotes, either `'''` or `"""`.
These triple quotes are generally used for multi-line strings. But they can be used as a multi-line comment as well. Unless they are not docstrings, they do not generate any extra code.
```python
#single line comment
>>>print ("Hello Python"
'''This is
multiline comment''')
```
```
"""This is also a
perfect example of
multi-line comments"""
'''This is also a
perfect example of
multi-line comments'''
#single line comment
print ("Hello Python"
'''This is
multiline comment''')
```
### 4. Docstrings in Python
A docstring is short for documentation string.
**[Python Docstrings](https://github.com/milaan9/04_Python_Functions/blob/main/Python_Docstrings.ipynb)** (documentation strings) are the **[string](https://github.com/milaan9/02_Python_Datatypes/blob/main/002_Python_String.ipynb)** literals that appear right after the definition of a function, method, class, or module.
Triple quotes are used while writing docstrings. For example:
```python
>>>def double(num):
>>> """Function to double the value"""
>>> return 3*num
```
Docstrings appear right after the definition of a function, class, or a module. This separates docstrings from multiline comments using triple quotes.
The docstrings are associated with the object as their **`__doc__`** attribute.
So, we can access the docstrings of the above function with the following lines of code:
```
def double(num):
"""Function to double the value"""
return 3*num
print(double.__doc__)
```
To learn more about docstrings in Python, visit **[Python Docstrings](https://github.com/milaan9/04_Python_Functions/blob/main/Python_Docstrings.ipynb)** .
## Help topics
Python has extensive help built in. You can execute **`help()`** for an overview or **`help(x)`** for any library, object or type **`x`**. Try using **`help("topics")`** to get a list of help pages built into the help system.
`help("topics")`
```
help("topics")
```
| true |
code
| 0.225672 | null | null | null | null |
|
```
##### Import packages
# Basic packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Modelling packages
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVR
# To avoid warnings
import warnings
warnings.filterwarnings("ignore")
##### Import data
# Check the csv's path before running it
df_acc_final = pd.read_csv('df_final.csv')
df_acc_final
##### Creating Mean Absolute Percentage Error
def mean_absolute_percentage_error(y_true, y_pred):
y_true, y_pred = np.array(y_true), np.array(y_pred)
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
##### Format change to datetime on some energy columns
for col in ['date_Hr', 'startDate_energy', 'endDate_energy']:
df_acc_final[col] = pd.to_datetime(df_acc_final[col])
##### Creating new variables based on energy data
df_acc_final["time_elapsed"] = (df_acc_final["startDate_energy"] - df_acc_final["date_Hr"]).astype('timedelta64[s]')
df_acc_final["day"] = df_acc_final.date_Hr.apply(lambda x: x.day)
df_acc_final["month"] = df_acc_final.date_Hr.apply(lambda x: x.month)
df_acc_final["hour"] = df_acc_final.date_Hr.apply(lambda x: x.hour)
df_acc_final.drop(['date_Hr', 'startDate_energy', 'endDate_energy','totalTime_energy'], axis=1, inplace=True)
df_acc_final.head()
##### To avoid problems while using MAPE, I multiply whole target x 10
df_acc_final.value_energy = df_acc_final.value_energy.apply(lambda x: x*10)
```
# Modelling
```
##### Selecting all the columns to use to modelling (also the target)
# Before trying different models, it's important to keep in mind that the problem ask us for a model with not high computational
# costs and that does not occupy much in the memory. In addition, it's valued the simplicity, clarity and explicitness.
features = list(df_acc_final)
for col in ['id_', 'value_energy']:
features.remove(col)
print('Columns used on X:', features)
##### Creation of X and y
X = df_acc_final[features].values.astype('int')
y = df_acc_final['value_energy'].values.astype('int')
##### Creation of X and y split -- train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
```
## Decision Tree Regressor
```
##### Decision Tree Regressor
# This is a lightweight model related with memory usage and computationally
model = DecisionTreeRegressor()
params = {'criterion':['mae'],
'max_depth': [4,5,6,7],
'max_features': [7,8,9,10],
'max_leaf_nodes': [30,40,50],
'min_impurity_decrease' : [0.0005,0.001,0.005],
'min_samples_split': [2,4]}
# GridSearch
grid_solver = GridSearchCV(estimator = model,
param_grid = params,
scoring = 'neg_median_absolute_error',
cv = 10,
refit = 'neg_median_absolute_error',
verbose = 0)
model_result = grid_solver.fit(X_train,y_train)
reg = model_result.best_estimator_
reg.fit(X,y)
##### Mean Absolute Percentage Error
yhat = reg.predict(X_test)
print("Mean Absolute Percentage Error = %.2f" %mean_absolute_percentage_error(yhat,y_test),'%')
##### Feature Importance
features_importance = reg.feature_importances_
features_array = np.array(features)
features_array_ordered = features_array[(features_importance).argsort()[::-1]]
features_array_ordered
plt.figure(figsize=(16,10))
sns.barplot(y = features_array, x = features_importance, orient='h', order=features_array_ordered[:50])
plt.show()
```
## Random Forest Regressor
```
##### Random Forest Regressor
# Random Forest model should lower the metric further because it maintains the bias and reduces the variance by making
# combinations of models with low bias and high correlations but different from one value.
# The tree has a low bias but a high variance then I will try to combine models with low bias and that aren't completely correlated
# in order to to reduce the variance to its minimum value.
model = RandomForestRegressor()
params = {'bootstrap': [True],
'criterion':['mae'],
'max_depth': [8,10],
'max_features': [10,12],
'max_leaf_nodes': [10,20,30],
'min_impurity_decrease' : [0.001,0.01],
'min_samples_split': [2,4],
'n_estimators': [10,15]}
# GridSearch
grid_solver = GridSearchCV(estimator = model,
param_grid = params,
scoring = 'neg_median_absolute_error',
cv = 7,
refit = 'neg_median_absolute_error',
verbose = 0)
model_result = grid_solver.fit(X_train,y_train)
reg = model_result.best_estimator_
reg.fit(X,y)
##### Mean Absolute Percentage Error
yhat = reg.predict(X_test)
print("Mean Absolute Percentage Error = %.2f" %mean_absolute_percentage_error(yhat,y_test),'%')
##### Feature Importance
features_importance = reg.feature_importances_
features_array = np.array(features)
features_array_ordered = features_array[(features_importance).argsort()[::-1]]
features_array_ordered
plt.figure(figsize=(16,10))
sns.barplot(y = features_array, x = features_importance, orient='h', order=features_array_ordered[:50])
plt.show()
```
## SVM
```
##### SVM linear
# Although computationally it requires more effort, once the model is trained it takes up less memory space and it is very intuitive.
# After seeing graphs on EDA, it doesn't seem that the relations are linear but while trees have much flexibility, that algorithm is based on
# cuts by hyperplanes. I'll train different kernels for SVM to see if it fits better to the problem.
# Lineal Tuning
lineal_tuning = dict()
for c in [0.001,0.01, 1]:
svr = SVR(kernel = 'linear', C = c)
scores = cross_val_score(svr, X, y, cv = 5, scoring = 'neg_median_absolute_error')
lineal_tuning[c] = scores.mean()
best_score = min(lineal_tuning, key = lineal_tuning.get)
print(f'Best score = {lineal_tuning[best_score]} is achieved with c = {best_score}')
reg = SVR(kernel = 'linear', C = best_score)
reg.fit(X_train, y_train)
##### Mean Absolute Percentage Error
yhat = reg.predict(X_test)
print("Mean Absolute Percentage Error = %.2f" %mean_absolute_percentage_error(yhat,y_test),'%')
##### SVM poly
reg = SVR(kernel = 'linear', C = 0.01)
reg.fit(X_train, y_train)
##### Mean Absolute Percentage Error
yhat = reg.predict(X_test)
print("Mean Absolute Percentage Error = %.2f" %mean_absolute_percentage_error(yhat,y_test),'%')
##### SVM radial
reg = SVR(kernel = 'rbf', C = 0.01, gamma = 0.1)
reg.fit(X_train, y_train)
##### Mean Absolute Percentage Error
yhat = reg.predict(X_test)
print("Mean Absolute Percentage Error = %.2f" %mean_absolute_percentage_error(yhat,y_test),'%')
```
# Activity Intensity
```
##### Activity Intensity
# In addition to calculate the energy expenditure, for each time interval, the level of intensity of the activity carried out must be calculated.
# The classification of the intensity level is based on the metabolic equivalents or METS (kcal/kg*h) of the activity being:
# light activity < 3 METS, moderate 3 - 6 METS and intense > 6 METS.
# To estimate it, I consider a person of 75 kg. The model chosen is the Random Forest Regressor which has the lowest MAPE.
reg = RandomForestRegressor(criterion='mae', max_depth=8, max_features=12,
max_leaf_nodes=30, min_impurity_decrease=0.001,
n_estimators=15)
reg.fit(X,y)
yhat = reg.predict(X)
ids = df_acc_final['id_'].to_frame()
ids['yhat'] = yhat
ids['METs'] = ids["yhat"] / (75 * 62 / 3600)
conditions = [(ids["METs"] < 3 ),((3 < ids["METs"]) & (ids["METs"] < 6)),(ids["METs"] > 6)]
names = ['ligera', 'moderada', 'intensa']
ids['intensidad'] = np.select(conditions, names)
ids
##### Conclusions and Future Work
# The substantial improvement that can be seen when we introduce the non-linearity of the model is relevant to deduce that
# the relationships between the variables and the target are not linear.
# The dataset doesn't have full potential to establish a clear model then more efforts should be made to collect all the information on physical
# activity, I suggest signal treatment variables such as Zero Crossing Rate, Spectral Centroid, Spectral Rolloff and MFCC - Mel-Frequency Cepstral Coefficients.
# Additional information about individuals such as age, sex and weight would help to improve the MAPE of final model.
# Time was decisive on this project (3-4h only) so some workstreams couldn't be done and would be important to have a look on.
# Extra efforts should be made in the selection of predictive variables to analyze the L1 and L2 error, otherwise we would be
# losing explicitness, memory and battery.
```
| true |
code
| 0.814164 | null | null | null | null |
|
# Autokeras
[PCoE][pcoe]の No.6 Turbofan Engine Degradation Simulation Dataset に対して [Autokeras][autokeras] を利用したAutoMLの実行テスト。
[autokeras]: https://autokeras.com/
[pcoe]: https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/
# Install Autokeras
```
try:
import autokeras as ak
except ModuleNotFoundError:
# https://autokeras.com/install/
!pip install git+https://github.com/keras-team/keras-tuner.git
!pip install autokeras
import autokeras as ak
from autokeras import StructuredDataRegressor
```
# Preset
```
# default packages
import logging
import pathlib
import zipfile
from typing import Any, Dict, List, Sequence, Tuple
# third party packages
import IPython.display as display
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import seaborn as sns
import sklearn.model_selection as skmselection
import tensorflow.keras.models as tkmodels
import tensorflow.keras.callbacks as tkcallbacks
import tqdm.autonotebook as tqdm
# mode
MODE_DEBUG = False
# logger
_logger = logging.getLogger(__name__)
logging.basicConfig(level=logging.DEBUG if MODE_DEBUG else logging.INFO)
# seaborn
sns.set()
```
# Global parameters
```
PATH_ARCHIVE = pathlib.Path("turbofun.zip")
PATH_EXTRACT = pathlib.Path("turbofun")
# 利用する変数を定義
COLUMNS_ALL = [
*[f"op{i:02}" for i in range(3)],
*[f"sensor{i:02}" for i in range(26)],
]
COLUMNS_INVALID = [
"op02",
"sensor01",
"sensor04",
"sensor09",
"sensor15",
"sensor17",
"sensor18",
"sensor21",
"sensor22",
"sensor23",
"sensor24",
"sensor25",
]
COLUMNS_VALID = sorted(list(set(COLUMNS_ALL) - set(COLUMNS_INVALID)))
COLUMNS_TARGET = ["rul"]
```
# Load dataset
```
def download(filename: pathlib.Path) -> None:
"""zipファイルをダウンロード."""
if filename.exists():
return
url = "https://ti.arc.nasa.gov/c/6/"
res = requests.get(url, stream=True)
if res.status_code != 200:
_logger.error(res.status_code)
return
with open(filename, "wb") as f:
for chunk in tqdm.tqdm(res):
f.write(chunk)
download(PATH_ARCHIVE)
def extractall(src: pathlib.Path, dst: pathlib.Path) -> None:
"""zipファイルを解凍."""
if not src.exists():
_logger.error(f"{src} does not exist.")
return
if dst.exists():
_logger.error(f"{dst} exists.")
return
with zipfile.ZipFile(src) as zf:
zf.extractall(dst)
extractall(PATH_ARCHIVE, PATH_EXTRACT)
```
# Convert data shape
```
def get_unit_series(df: pd.DataFrame, unit: int) -> Dict[str, Any]:
"""unit単位のnumpy.arrayへ変換する."""
df_unit = df[df["unit"] == unit].copy()
df_unit.sort_values(by=["time"], ignore_index=True, inplace=True)
names_op = [f"op{i:02}" for i in range(3)]
names_sensor = [f"sensor{i:02}" for i in range(26)]
data = {
"unit": unit,
**{name: df_unit[name].to_numpy().ravel() for name in names_op},
**{name: df_unit[name].to_numpy().ravel() for name in names_sensor},
}
return data
def load_data(filename: pathlib.Path) -> pd.DataFrame:
"""データを読み取り、1セルに1unit分のデータをnumpy.arrayで保持するDataFrameとする."""
df = pd.read_csv(
filename,
header=None,
sep=" ",
names=[
"unit",
"time",
*[f"op{i:02d}" for i in range(3)],
*[f"sensor{i:02d}" for i in range(26)],
],
)
return df
DF_FD001_TRAIN = load_data(PATH_EXTRACT.joinpath("train_FD001.txt"))
DF_FD001_TEST = load_data(PATH_EXTRACT.joinpath("test_FD001.txt"))
display.display(DF_FD001_TRAIN)
display.display(DF_FD001_TEST)
def load_rul(filepath: pathlib.Path) -> pd.DataFrame:
"""テスト用のRULを読み込む."""
df = pd.read_csv(
filepath,
header=None,
sep=" ",
names=["rul", "none"],
)
df.drop(["none"], axis=1, inplace=True)
df["unit"] = range(len(df))
df.set_index(["unit"], inplace=True)
return df
DF_FD001_TEST_RUL = load_rul(PATH_EXTRACT.joinpath("RUL_FD001.txt"))
display.display(DF_FD001_TEST_RUL)
def create_train_rul(df: pd.DataFrame) -> pd.Series:
"""学習データに対するRULを算出する."""
df_rul = df.copy()
df_max_time = df.groupby(["unit"])["time"].max()
df_rul["rul"] = df_rul.apply(
lambda x: df_max_time.at[x["unit"]] - x["time"],
axis=1,
)
return df_rul
DF_FD001_TRAIN = create_train_rul(DF_FD001_TRAIN)
display.display(DF_FD001_TRAIN)
```
# Data split
```
def train_test_split(df: pd.DataFrame) -> Tuple[pd.DataFrame, pd.DataFrame]:
"""学習用データと検証用データを分割する."""
units = df["unit"].unique()
units_train, units_test = skmselection.train_test_split(
units,
test_size=0.2,
random_state=42,
)
df_train = df[df["unit"].isin(units_train)]
df_test = df[df["unit"].isin(units_test)]
return df_train, df_test
DF_TRAIN, DF_VALID = train_test_split(DF_FD001_TRAIN)
DF_TRAIN.info()
DF_VALID.info()
```
# Autokeras
```
def fit(df_feature: pd.DataFrame, df_target: pd.DataFrame) -> StructuredDataRegressor:
"""モデルの探索."""
max_trials = 3 if MODE_DEBUG else 100
epochs = 10 if MODE_DEBUG else 100
early_stopping = tkcallbacks.EarlyStopping(
monitor="val_loss",
min_delta=1e-4,
patience=10,
)
regressor = StructuredDataRegressor(
overwrite=True,
max_trials=max_trials,
loss="mean_squared_error",
metrics="mean_squared_error",
objective="val_loss",
seed=42,
)
regressor.fit(
df_feature.to_numpy(),
df_target.to_numpy(),
epochs=epochs,
validation_split=0.2,
callbacks=[early_stopping],
)
return regressor
REGRESSOR = fit(DF_TRAIN[COLUMNS_VALID], DF_TRAIN[COLUMNS_TARGET])
def export_model(regressor: StructuredDataRegressor, output: pathlib.Path) -> None:
"""モデルをファイルとして保存."""
model = regressor.export_model()
model.save(str(output), save_format="tf")
# test
loaded_model = tkmodels.load_model(str(output), custom_objects=ak.CUSTOM_OBJECTS)
export_model(REGRESSOR, pathlib.Path("model_autokeras"))
```
## Results
```
def predict(
regressor: StructuredDataRegressor,
df_info: pd.DataFrame,
df_feature: pd.DataFrame,
df_target: pd.DataFrame,
units: List[int],
) -> None:
"""予測結果を可視化する."""
results = regressor.predict(df_feature.to_numpy())
df_results = df_info.copy()
df_results["rul"] = df_target.to_numpy().ravel()
df_results["pred"] = results
for unit in units:
df_target = df_results[df_results["unit"] == unit]
fig, axes = plt.subplots(1, 1, figsize=(9, 4), tight_layout=True)
ax = axes
ax.plot(df_target["time"], df_target["rul"], label="rul")
ax.plot(df_target["time"], df_target["pred"], label="pred")
ax.set_title(f"unit{unit:02}")
plt.show()
plt.close()
fig.clf()
predict(
REGRESSOR,
DF_VALID[["unit", "time"]],
DF_VALID[COLUMNS_VALID],
DF_VALID[COLUMNS_TARGET],
DF_VALID["unit"].unique()[:3],
)
```
| true |
code
| 0.669664 | null | null | null | null |
|
# x-filter Overlay - Demostration Notebook
通过HLS高层次综合工具,可以很方便的通过C/C++语言将算法综合为可在Vivado中直接例化的硬件IP,利用FPGA并行计算的优势,帮助我们实现算法加速,提高系统响应速度。在本示例中通过HLS工具实现了一个阶数与系数均可实时修改的FIR滤波器IP。
x-filter Overlay实现了对该滤波器的系统集成,Block Design如下图所示,ARM处理器可通过AXI总线和DMA访问该IP。
<img src="./images/x-order_filter.PNG"/>
*注:Overlay可以理解为具体的FPGA比特流 + 相应的Python API驱动*
而在PYNQ框架下,通过Python API我们可以很方便的对Overlay中的IP进行调用。而基于Python的生态,导入数据分析库如numpy和图形库matplotlib,通过简单的几行代码即可对FIR滤波器进行分析和验证。在本notebook中我们展示了通过numpy库产生的多个频率的叠加信号作为FIR滤波器的输入,并对经过FIR滤波器滤波前后的信号在时域和频频进行了分析。
下表为HLS工具自动为IP产生的驱动头文件,在notebook中需要对照该头文件来对IP进行调用。
```
# ==============================================================
# File generated on Mon Oct 07 01:59:23 +0800 2019
# Vivado(TM) HLS - High-Level Synthesis from C, C++ and SystemC v2018.3 (64-bit)
# SW Build 2405991 on Thu Dec 6 23:38:27 MST 2018
# IP Build 2404404 on Fri Dec 7 01:43:56 MST 2018
# Copyright 1986-2018 Xilinx, Inc. All Rights Reserved.
# ==============================================================
# AXILiteS
# 0x00 : Control signals
# bit 0 - ap_start (Read/Write/COH)
# bit 1 - ap_done (Read/COR)
# bit 2 - ap_idle (Read)
# bit 3 - ap_ready (Read)
# bit 7 - auto_restart (Read/Write)
# others - reserved
# 0x04 : Global Interrupt Enable Register
# bit 0 - Global Interrupt Enable (Read/Write)
# others - reserved
# 0x08 : IP Interrupt Enable Register (Read/Write)
# bit 0 - Channel 0 (ap_done)
# bit 1 - Channel 1 (ap_ready)
# others - reserved
# 0x0c : IP Interrupt Status Register (Read/TOW)
# bit 0 - Channel 0 (ap_done)
# bit 1 - Channel 1 (ap_ready)
# others - reserved
# 0x10 : Data signal of coe
# bit 31~0 - coe[31:0] (Read/Write)
# 0x14 : reserved
# 0x18 : Data signal of ctrl
# bit 31~0 - ctrl[31:0] (Read/Write)
# 0x1c : reserved
# (SC = Self Clear, COR = Clear on Read, TOW = Toggle on Write, COH = Clear on Handshake)
```
为了帮助我们在notebook上对算法进行验证,我们通过matlab工具设计了2个滤波器,预设信号频率分量最高为750Hz,根据采样定理知采样频率要大于信号频率2倍,在设计的2个滤波器中,均设置扫描频率为1800Hz。
下图为在matlab中设计的的FIR低通滤波器幅频曲线,示例中设计了1个截至频率为500Hz的10阶FIR低通滤波器。
<img src="./images/MagnitudeResponse.PNG" width="70%" height="70%"/>
导出系数:[107,280,-1193,-1212,9334,18136,9334,-1212,-1193,280,107]
修改滤波器设置,重新设计1个截至频率为500Hz的15阶FIR高通滤波器.
<img src="./images/MagnitudeResponse_500Hz_HP.png" width="70%" height="70%"/>
导出系数:[-97,-66,435,0,-1730,1101,5506,-13305,13305,-5506,-1101,1730,0,-435,66,97]
# 步骤1 - 导入Python库,实例化用于控制FIR滤波器的DMA设备。
### 注:我们可以通过“Shift + Enter”组合键来逐一执行notebook中每一个cell内的python脚本。cell左边的"*"号表示脚本正在执行,执行完毕后会变为数字。
```
#导入必要的python库
import pynq.lib.dma #导入访问FPGA内侧DMA的库
import numpy as np #numpy为pyrhon的数值分析库
from pynq import Xlnk #Xlnk()可实现连续内存分配,访问FPGA侧的DMA需要该库
from scipy.fftpack import fft,ifft #python的FFT库
import matplotlib.pyplot as plt #python图表库
import scipy as scipy
#加载FPGA比特流
firn = pynq.Overlay("/usr/local/lib/python3.6/dist-packages/x-filter/bitstream/x-order_filter.bit")
#实例化Overlay内的DMA模块
dma = firn.axi_dma_0
led_4bits = firn.axi_gpio_0
rgb_leds = firn.axi_gpio_1
btn_4bits = firn.axi_gpio_2
fir_filter = firn.x_order_fir_0
led_4bits.write(0x04,0x00)
led_4bits.write(0x00,0x0A)
rgb_leds.write(0x04,0x00)
rgb_leds.write(0x00,0x0A)
#对Overlay内的DMA进行配置,每次传输1800个数据点。
xlnk = Xlnk()
in_buffer = xlnk.cma_array(shape=(1800,), dtype=np.int32)
out_buffer = xlnk.cma_array(shape=(1800,), dtype=np.int32)
#coe_buffer = xlnk.cma_array(shape=(11,), dtype=np.int32)
coe_buffer = xlnk.cma_array(shape=(16,), dtype=np.int32)
ctrl_buffer = xlnk.cma_array(shape=(2,), dtype=np.int32)
#coe = [107,280,-1193,-1212,9334,18136,9334,-1212,-1193,280,107]
coe = [-97,-66,435,0,-1730,1101,5506,-13305,13305,-5506,-1101,1730,0,-435,66,97]
for i in range (16):
coe_buffer[i] = coe[i]
ctrl_buffer[0] = 1
#ctrl_buffer[1] = 10
ctrl_buffer[1] = 16
coe_buffer.physical_address
fir_filter.write(0x10,coe_buffer.physical_address)
fir_filter.write(0x18,ctrl_buffer.physical_address)
fir_filter.write(0x00,0x81)
```
# 步骤2 - 叠加多个不同频率和幅值的信号,作为滤波器的输入信号。
```
#采样频率为1800Hz,即1秒内有1800个采样点,我们将采样点个数选择1800个。
x=np.linspace(0,1,1800)
#产生滤波器输入信号
f1 = 600 #设置第1个信号分量频率设置为600Hz
a1 = 100 #设置第1个信号分量幅值设置为100
f2 = 450 #设置第2个信号分量频率设置为450Hz
a2 = 100 #设置第2个信号分量幅值设置为100
f3 = 200 #设置第3个信号分量频率设置为200Hz
a3 = 100 #设置第3个信号分量幅值设置为100
f4 = 650 #设置第4个信号分量频率设置为650Hz
a4 = 100 #设置第5个信号分量幅值设置为100
#产生2个不同频率分量的叠加信号,将其作为滤波器的输入信号,我们还可以叠加更多信号。
#y=np.int32(a1*np.sin(2*np.pi*f1*x) + a2*np.sin(2*np.pi*f2*x))
y=np.int32(a1*np.sin(2*np.pi*f1*x) + a2*np.sin(2*np.pi*f2*x) + a3*np.sin(2*np.pi*f3*x) + a4*np.sin(2*np.pi*f4*x))
#绘制滤波器输入信号波形图
fig1 = plt.figure()
ax1 = fig1.gca()
plt.plot(y[0:50]) #为便于观察,这里仅显示前50个点的波形,如需要显示更多的点,请将50改为其它数值
plt.title('input signal',fontsize=10,color='b')
#通过DMA将数据发送in_buffer内的数值到FIR滤波器的输入端
for i in range(1800):
in_buffer[i] = y[i]
dma.sendchannel.transfer(in_buffer)
#获取滤波器的输出信号数据存储在out_buffer中
dma.recvchannel.transfer(out_buffer)
#绘制滤波器输出信号图
fig2 = plt.figure()
ax2 = fig2.gca()
plt.plot(out_buffer[0:50]/32768) #除于32768的原因是滤波器系数为16位有符号定点小数,运算过程中被当作整数计算。
plt.title('output signal',fontsize=10,color='b')
```
# 步骤3 - 对滤波器输入和输出信号做频域分析
```
#FFT变换函数体
def fft(signal_buffer,points):
yy = scipy.fftpack.fft(signal_buffer)
yreal = yy.real # 获取实部
yimag = yy.imag # 获取虚部
yf1 = abs(yy)/((len(points)/2)) #归一化处理
yf2 = yf1[range(int(len(points)/2))] #由于对称性,只取一半区间
xf1 = np.arange(len(signal_buffer)) # 频率
xf2 = xf1[range(int(len(points)/2))] #取一半区间
#混合波的FFT(双边频率范围)
#plt.subplot(222)
plt.plot(xf2,yf2,'r') #显示原始信号的FFT模值,本例只显示其中的750个点,如需要显示更多请调整750为其它数值
plt.title('FFT of Mixed wave',fontsize=10,color='r') #注意这里的颜色可以查询颜色代码
return
#对输入信号做FFT变换
fft(in_buffer,x)
#对输出信号做FFT变换
fft(out_buffer/32768,x)#除于32768的原因是滤波器系数为16位有符号定点小数,运算过程中被当作整数计算。
#dma.sendchannel.wait()
#dma.recvchannel.wait()
in_buffer.close()
out_buffer.close()
xlnk.xlnk_reset()
```
| true |
code
| 0.325474 | null | null | null | null |
|
## Write SEG-Y with `obspy`
Before going any further, you might like to know, [What is SEG-Y?](http://www.agilegeoscience.com/blog/2014/3/26/what-is-seg-y.html). See also the articles in [SubSurfWiki](http://www.subsurfwiki.org/wiki/SEG_Y) and [Wikipedia](https://en.wikipedia.org/wiki/SEG_Y).
We'll use the [obspy](https://github.com/obspy/obspy) seismology library to read and write SEGY data.
Technical SEG-Y documentation:
* [SEG-Y Rev 1](http://seg.org/Portals/0/SEG/News%20and%20Resources/Technical%20Standards/seg_y_rev1.pdf)
* [SEG-Y Rev 2 proposal](https://www.dropbox.com/s/txrqsfuwo59fjea/SEG-Y%20Rev%202.0%20Draft%20August%202015.pdf?dl=0) and [draft repo](http://community.seg.org/web/technical-standards-committee/documents/-/document_library/view/6062543)
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
ls -l ../data/*.sgy
```
## 2D data
```
filename = '../data/HUN00-ALT-01_STK.sgy'
from obspy.io.segy.segy import _read_segy
section = _read_segy(filename) # unpack_headers=True slows you down here
data = np.vstack([t.data for t in section.traces])
plt.figure(figsize=(16,8))
plt.imshow(data.T, cmap="Greys")
plt.colorbar(shrink=0.5)
plt.show()
```
Formatted header:
```
def chunk(string, width=80):
lines = int(np.ceil(len(string) / width))
result = ''
for i in range(lines):
line = string[i*width:i*width+width]
result += line + (width-len(line))*' ' + '\n'
return result
s = section.textual_file_header.decode()
print(chunk(s))
section.binary_file_header
section.traces[0].header
len(section.traces[0].data)
```
## Change the data
Let's scale the data.
```
scaled = data / 1000
scaled[np.isnan(scaled)] = 0
scaled
vm = np.percentile(scaled, 99)
plt.figure(figsize=(16,8))
plt.imshow(scaled.T, cmap="Greys", vmin=-vm, vmax=vm)
plt.colorbar(shrink=0.5)
plt.show()
```
## Write data
Let's write this all back to a new SEG-Y file.
```
from obspy.core import Trace, Stream, UTCDateTime
from obspy.io.segy.segy import SEGYTraceHeader
stream = Stream()
for i, trace in enumerate(scaled):
# Make the trace.
tr = Trace(trace)
# Add required data.
tr.stats.delta = 0.004
tr.stats.starttime = 0 # Not strictly required.
# Add yet more to the header (optional).
tr.stats.segy = {'trace_header': SEGYTraceHeader()}
tr.stats.segy.trace_header.trace_sequence_number_within_line = i + 1
tr.stats.segy.trace_header.receiver_group_elevation = 0
# Append the trace to the stream.
stream.append(tr)
stream
stream.write('../data/out.sgy', format='SEGY', data_encoding=5) # encode 5 for IEEE
```
## Add a file-wide header
So far we only attached metadata to the traces, but we can do more by attaching some filewide metadata, like a textual header. A SEGY file normally has a file wide text header. This can be attached to the stream object.
If this header and the binary header are not set, they will be autocreated with defaults.
```
from obspy.core import AttribDict
from obspy.io.segy.segy import SEGYBinaryFileHeader
# Text header.
stream.stats = AttribDict()
stream.stats.textual_file_header = '{:80s}'.format('This is the textual header.').encode()
stream.stats.textual_file_header += '{:80s}'.format('This file contains seismic data.').encode()
# Binary header.
stream.stats.binary_file_header = SEGYBinaryFileHeader()
stream.stats.binary_file_header.trace_sorting_code = 4
stream.stats.binary_file_header.seg_y_format_revision_number = 0x0100
import sys
stream.write('../data/out.sgy', format='SEGY', data_encoding=5, byteorder=sys.byteorder)
```
<hr />
<div>
<img src="https://avatars1.githubusercontent.com/u/1692321?s=50"><p style="text-align:center">© Agile Geoscience 2016</p>
</div>
| true |
code
| 0.363223 | null | null | null | null |
|
# Prepare and Deploy a TensorFlow Model to AI Platform for Online Serving
This Notebook demonstrates how to prepare a TensorFlow 2.x model and deploy it for serving with AI Platform Prediction. This example uses the pretrained [ResNet V2 101](https://tfhub.dev/google/imagenet/resnet_v2_101/classification/4) image classification model from [TensorFlow Hub](https://tfhub.dev/) (TF Hub).
The Notebook covers the following steps:
1. Downloading and running the ResNet module from TF Hub
2. Creating serving signatures for the module
3. Exporting the model as a SavedModel
4. Deploying the SavedModel to AI Platform Prediction
5. Validating the deployed model
## Setup
This Notebook was tested on **AI Platform Notebooks** using the standard TF 2.2 image.
### Import libraries
```
import base64
import os
import json
import requests
import time
import numpy as np
import tensorflow as tf
import tensorflow_hub as hub
import matplotlib.pyplot as plt
from typing import List, Optional, Text, Tuple
```
### Configure GCP environment settings
```
PROJECT_ID = 'jk-mlops-dev' # Set your project Id
BUCKET = 'labs-workspace' # Set your bucket name Id
REGION = 'us-central' # Set your region for deploying the model
MODEL_NAME = 'resnet_101'
MODEL_VERSION = 'v1'
GCS_MODEL_LOCATION = 'gs://{}/models/{}/{}'.format(BUCKET, MODEL_NAME, MODEL_VERSION)
THUB_MODEL_HANDLE = 'https://tfhub.dev/google/imagenet/resnet_v2_101/classification/4'
IMAGENET_LABELS_URL = 'https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt'
IMAGES_FOLDER = 'test_images'
!gcloud config set project $PROJECT_ID
```
### Create a local workspace
```
LOCAL_WORKSPACE = '/tmp/workspace'
if tf.io.gfile.exists(LOCAL_WORKSPACE):
print("Removing previous workspace artifacts...")
tf.io.gfile.rmtree(LOCAL_WORKSPACE)
print("Creating a new workspace...")
tf.io.gfile.makedirs(LOCAL_WORKSPACE)
```
## 1. Loading and Running the ResNet Module
### 1.1. Download and instantiate the model
```
os.environ["TFHUB_DOWNLOAD_PROGRESS"] = 'True'
local_savedmodel_path = hub.resolve(THUB_MODEL_HANDLE)
print(local_savedmodel_path)
!ls -la {local_savedmodel_path}
model = hub.load(THUB_MODEL_HANDLE)
```
The expected input to most TF Hub TF2 image classification models, including ResNet 101, is a rank 4 tensor conforming to the following tensor specification: `tf.TensorSpec([None, height, width, 3], tf.float32)`. For the ResNet 101 model, the expected image size is `height x width = 224 x 224`. The color values for all channels are expected to be normalized to the [0, 1] range.
The output of the model is a batch of logits vectors. The indices into the logits are the `num_classes = 1001` classes from the ImageNet dataset. The mapping from indices to class labels can be found in the [labels file](download.tensorflow.org/data/ImageNetLabels.txt) with class 0 for "background", followed by 1000 actual ImageNet classes.
We will now test the model on a couple of JPEG images.
### 1.2. Display sample images
```
image_list = [tf.io.read_file(os.path.join(IMAGES_FOLDER, image_path))
for image_path in os.listdir(IMAGES_FOLDER)]
ncolumns = len(image_list) if len(image_list) < 4 else 4
nrows = int(len(image_list) // ncolumns)
fig, axes = plt.subplots(nrows=nrows, ncols=ncolumns, figsize=(10,10))
for axis, image in zip(axes.flat[0:], image_list):
decoded_image = tf.image.decode_image(image)
axis.set_title(decoded_image.shape)
axis.imshow(decoded_image.numpy())
```
### 1.3. Preprocess the testing images
The images need to be preprocessed to conform to the format expected by the ResNet101 model.
```
def _decode_and_scale(image, size):
image = tf.image.decode_image(image, expand_animations=False)
image_height = image.shape[0]
image_width = image.shape[1]
crop_size = tf.minimum(image_height, image_width)
offset_height = ((image_height - crop_size) + 1) // 2
offset_width = ((image_width - crop_size) + 1) // 2
image = tf.image.crop_to_bounding_box(image, offset_height, offset_width, crop_size, crop_size)
image = tf.cast(tf.image.resize(image, [size, size]), tf.uint8)
return image
size = 224
raw_images = tf.stack(image_list)
preprocessed_images = tf.map_fn(lambda x: _decode_and_scale(x, size), raw_images, dtype=tf.uint8)
preprocessed_images = tf.image.convert_image_dtype(preprocessed_images, tf.float32)
print(preprocessed_images.shape)
```
### 2.4. Run inference
```
predictions = model(preprocessed_images)
predictions
```
The model returns a batch of arrays with logits. This is not a very user friendly output so we will convert it to the list of ImageNet class labels.
```
labels_path = tf.keras.utils.get_file(
'ImageNetLabels.txt',
IMAGENET_LABELS_URL)
imagenet_labels = np.array(open(labels_path).read().splitlines())
```
We will display the 5 highest ranked labels for each image
```
for prediction in list(predictions):
decoded = imagenet_labels[np.argsort(prediction.numpy())[::-1][:5]]
print(list(decoded))
```
## 2. Create Serving Signatures
The inputs and outputs of the model as used during model training may not be optimal for serving. For example, in a typical training pipeline, feature engineering is performed as a separate step preceding model training and hyperparameter tuning. When serving the model, it may be more optimal to embed the feature engineering logic into the serving interface rather than require a client application to preprocess data.
The ResNet V2 101 model from TF Hub is optimized for recomposition and fine tuning. Since there are no serving signatures in the model's metadata, it cannot be served with TF Serving as is.
```
list(model.signatures)
```
To make it servable, we need to add a serving signature(s) describing the inference method(s) of the model.
We will add two signatures:
1. **The default signature** - This will expose the default predict method of the ResNet101 model.
2. **Prep/post-processing signature** - Since the expected inputs to this interface require a relatively complex image preprocessing to be performed by a client, we will also expose an alternative signature that embeds the preprocessing and postprocessing logic and accepts raw unprocessed images and returns the list of ranked class labels and associated label probabilities.
The signatures are created by defining a custom module class derived from the `tf.Module` base class that encapsulates our ResNet model and extends it with a method implementing the image preprocessing and output postprocessing logic. The default method of the custom module is mapped to the default method of the base ResNet module to maintain the analogous interface.
The custom module will be exported as `SavedModel` that includes the original model, the preprocessing logic, and two serving signatures.
This technique can be generalized to other scenarios where you need to extend a TensorFlow model and you have access to the serialized `SavedModel` but you don't have access to the Python code implementing the model.
#### 2.1. Define the custom serving module
```
LABELS_KEY = 'labels'
PROBABILITIES_KEY = 'probabilities'
NUM_LABELS = 5
class ServingModule(tf.Module):
"""
A custom tf.Module that adds image preprocessing and output post processing to
a base TF 2 image classification model from TF Hub.
"""
def __init__(self, base_model, input_size, output_labels):
super(ServingModule, self).__init__()
self._model = base_model
self._input_size = input_size
self._output_labels = tf.constant(output_labels, dtype=tf.string)
def _decode_and_scale(self, raw_image):
"""
Decodes, crops, and resizes a single raw image.
"""
image = tf.image.decode_image(raw_image, dtype=tf.dtypes.uint8, expand_animations=False)
image_shape = tf.shape(image)
image_height = image_shape[0]
image_width = image_shape[1]
crop_size = tf.minimum(image_height, image_width)
offset_height = ((image_height - crop_size) + 1) // 2
offset_width = ((image_width - crop_size) + 1) // 2
image = tf.image.crop_to_bounding_box(image, offset_height, offset_width, crop_size, crop_size)
image = tf.image.resize(image, [self._input_size, self._input_size])
image = tf.cast(image, tf.uint8)
return image
def _preprocess(self, raw_inputs):
"""
Preprocesses raw inputs as sent by the client.
"""
# A mitigation for https://github.com/tensorflow/tensorflow/issues/28007
with tf.device('/cpu:0'):
images = tf.map_fn(self._decode_and_scale, raw_inputs, dtype=tf.uint8)
images = tf.image.convert_image_dtype(images, tf.float32)
return images
def _postprocess(self, model_outputs):
"""
Postprocesses outputs returned by the base model.
"""
probabilities = tf.nn.softmax(model_outputs)
indices = tf.argsort(probabilities, axis=1, direction='DESCENDING')
return {
LABELS_KEY: tf.gather(self._output_labels, indices, axis=-1)[:,:NUM_LABELS],
PROBABILITIES_KEY: tf.sort(probabilities, direction='DESCENDING')[:,:NUM_LABELS]
}
@tf.function(input_signature=[tf.TensorSpec([None, 224, 224, 3], tf.float32)])
def __call__(self, x):
"""
A pass-through to the base model.
"""
return self._model(x)
@tf.function(input_signature=[tf.TensorSpec([None], tf.string)])
def predict_labels(self, raw_images):
"""
Preprocesses inputs, calls the base model
and postprocesses outputs from the base model.
"""
# Call the preprocessing handler
images = self._preprocess(raw_images)
# Call the base model
logits = self._model(images)
# Call the postprocessing handler
outputs = self._postprocess(logits)
return outputs
serving_module = ServingModule(model, 224, imagenet_labels)
```
#### 2.2. Test the custom serving module
```
predictions = serving_module.predict_labels(raw_images)
predictions
```
## 3. Save the custom serving module as `SavedModel`
```
model_path = os.path.join(LOCAL_WORKSPACE, MODEL_NAME, MODEL_VERSION)
default_signature = serving_module.__call__.get_concrete_function()
preprocess_signature = serving_module.predict_labels.get_concrete_function()
signatures = {
'serving_default': default_signature,
'serving_preprocess': preprocess_signature
}
tf.saved_model.save(serving_module, model_path, signatures=signatures)
```
### 3.1. Inspect the `SavedModel`
```
!saved_model_cli show --dir {model_path} --tag_set serve --all
```
### 3.2. Test loading and executing the `SavedModel`
```
model = tf.keras.models.load_model(model_path)
model.predict_labels(raw_images)
```
### 3.3 Copy the model to Google Cloud Storage
```
!gsutil cp -r {model_path} {GCS_MODEL_LOCATION}
!gsutil ls {GCS_MODEL_LOCATION}
```
## License
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at [https://www.apache.org/licenses/LICENSE-2.0](https://www.apache.org/licenses/LICENSE-2.0)
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
| true |
code
| 0.622804 | null | null | null | null |
|
# 3D MNIST
https://medium.com/shashwats-blog/3d-mnist-b922a3d07334
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
from matplotlib import animation
# import seaborn as sns
import h5py
import os, sys
sys.path.append('data/')
from voxelgrid import VoxelGrid
from plot3D import *
%matplotlib inline
# plt.rcParams['image.interpolation'] = None
plt.rcParams['image.cmap'] = 'gray'
with h5py.File('./3d-mnist-kaggle/train_point_clouds.h5', 'r') as f:
# Reading digit at zeroth index
a = f["0"]
# Storing group contents of digit a
digit = (a["img"][:], a["points"][:], a.attrs["label"])
digits = []
with h5py.File("./3d-mnist-kaggle/train_point_clouds.h5", 'r') as h5:
for i in range(15):
d = h5[str(i)]
digits.append((d["img"][:],d["points"][:],d.attrs["label"]))
len(digits)
plt.imshow(digit[0])
# Plot some examples from original 2D-MNIST
fig, axs = plt.subplots(3,5, figsize=(12, 12), facecolor='w', edgecolor='k')
fig.subplots_adjust(hspace = .5, wspace=.2)
for ax, d in zip(axs.ravel(), digits):
ax.imshow(d[0][:])
ax.set_title("Digit: " + str(d[2]))
digit[0].shape, digit[1].shape
voxel_grid = VoxelGrid(digit[1], x_y_z = [16, 16, 16])
def count_plot(array):
cm = plt.cm.get_cmap('gist_rainbow')
n, bins, patches = plt.hist(array, bins=64)
bin_centers = 0.5 * (bins[:-1] + bins[1:])
# scale values to interval [0,1]
col = bin_centers - min(bin_centers)
col /= max(col)
for c, p in zip(col, patches):
plt.setp(p, 'facecolor', cm(c))
plt.show()
voxel_grid.structure[:, -1]
# Get the count of points within each voxel.
plt.title("DIGIT: " + str(digits[0][-1]))
plt.xlabel("VOXEL")
plt.ylabel("POINTS INSIDE THE VOXEL")
count_plot(voxel_grid.structure[:,-1])
voxels = []
for d in digits:
voxels.append(VoxelGrid(d[1], x_y_z=[16,16,16]))
# Visualizing the Voxel Grid sliced around the z-axis.
voxels[0].plot()
plt.show()
# Save Voxel Grid Structure as the scalar field of Point Cloud.
cloud_vis = np.concatenate((digit[1], voxel_grid.structure), axis=1)
np.savetxt('Cloud Visualization - ' + str(digit[2]) + '.txt', cloud_vis)
for i in range(cloud_vis.shape[1]):
plt.figure()
plt.plot(cloud_vis[:,i], '.')
```
# Train Classifier
```
with h5py.File("./3d-mnist-kaggle/full_dataset_vectors.h5", 'r') as h5:
X_train, y_train = h5["X_train"][:], h5["y_train"][:]
X_test, y_test = h5["X_test"][:], h5["y_test"][:]
X_train.shape, y_train.shape, X_test.shape, y_test.shape
np.max(X_train[0])
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import LinearSVC
from sklearn.neighbors import KNeighborsClassifier as KNN
from sklearn.ensemble import RandomForestClassifier
reg = LogisticRegression()
reg.fit(X_train,y_train)
print("LR-Accuracy: ", reg.score(X_test,y_test))
dt = DecisionTreeClassifier()
dt.fit(X_train,y_train)
print("DT-Accuracy: ", dt.score(X_test,y_test))
svm = LinearSVC()
svm.fit(X_train,y_train)
print("SVM-Accuracy: ", svm.score(X_test,y_test))
knn = KNN()
knn.fit(X_train,y_train)
print("KNN-Accuracy: ", knn.score(X_test,y_test))
rf = RandomForestClassifier(n_estimators=500)
rf.fit(X_train,y_train)
print("RF-Accuracy: ", rf.score(X_test,y_test))
```
| true |
code
| 0.558447 | null | null | null | null |
|
# Семинар 7 - Классификация методами машинного обучения
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.simplefilter('ignore')
plt.style.use('seaborn')
%matplotlib inline
```
# Логистическая регрессия
## Краткая теория

Где линейная модель - это: $$ \hat{y} = f(x) = \theta_0*1 + \theta_1*x_1 + ... + \theta_n*x_n = \theta^T*X$$
Функция активации $\sigma(x) = \frac{1}{1 + \exp^{-x}}$
```
from sklearn.datasets import fetch_olivetti_faces
# загрузим данные
data = fetch_olivetti_faces(shuffle=True)
X = data.data
y = data.target
print(X.shape, y.shape)
n_row, n_col = 2, 3
n_components = n_row * n_col
image_shape = (64, 64)
def plot_gallery(title, images, n_col=n_col, n_row=n_row, cmap=plt.cm.gray):
plt.figure(figsize=(2. * n_col, 2.26 * n_row))
plt.suptitle(title, size=16)
for i, comp in enumerate(images):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(comp.reshape(image_shape), cmap=cmap)
plt.axis('off')
plt.subplots_adjust(0.01, 0.05, 0.99, 0.93, 0.04, 0.)
plot_gallery("Olivetti faces", X[:n_components])
```
## Разделим выборку на две части: обучающую и тестовую
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
train_size=0.5,
test_size=0.5,
shuffle=True,
random_state=42)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
```
## Логистическая регрессия для многоклассовой классификации
```
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# Разделим выборку на тренировочную и тестовую
x_train, x_test, y_train, y_test = train_test_split(X, y, train_size=0.8, shuffle=True, random_state=42)
x_train.shape, x_test.shape, y_train.shape, y_test.shape
```
*Логистическая регрессия позволяет решать задачу многоклассовой классификации. Класс ``LogisticRegression`` позвляет это делать двумя способами:*
- Стандартный One vs Rest (т.е. каждый класс отделяется от всех других). Параметр `multi_class='ovr'`.*
- One vs One: Используя кросс-энтропию (оценивается сразу вектор вероятностей принадлежности классам). Параметр `multi_class='multinomial'`.*
#### One vs Rest
Find 𝐾 − 1 classifiers 𝑓 , 𝑓 , ... , 𝑓 12 𝐾−1
- 𝑓 classifies1𝑣𝑠{2,3,...,𝐾} 1
- 𝑓 classifies2𝑣𝑠{1,3,...,𝐾} 2
- ...
- 𝑓 classifies𝐾−1𝑣𝑠{1,2,...,𝐾−2}
- 𝐾−1
- Points not classified to classes {1,2, ... , 𝐾 − 1} are put to class 𝐾
#### Cross-entropy
В случае с бинарной классификацией функция потерь:
$$ \sum_{i=1}^l \bigl( y_i \log a_i - (1-y_i) \log (1-a_i) \bigr) \rightarrow min$$
$a_i$ – ответ (вероятность) алгоритма на i-м объекте на вопрос принадлежности к классу $y_i$
Обобщается для многомерного случая:
$$-\frac{1}{q} \sum_{i=1}^q \sum_{j=1}^l y_{ij} \log a_{ij} \rightarrow min $$
где
$q$ – число элементов в выборке,
$l$ – число классов,
$a_{ij}$ – ответ (вероятность) алгоритма на i-м объекте на вопрос принадлежности его к j-му классу
__Проблемы:__
- Сложности в поиске глобального минимума, так как присутствуют Локальные минимумы и плато
## Solvers

Source: [User Guide](https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression)
### Liblinear
Используется обычный покоординантный спуск.
Алгоритм:
- Инициализацируем любыми значениями вектор весов
- Повторяем для каждого i из пространства признаков:
- фиксируем значения всех переменных кроме $x_i$
- проводим одномерную оптимизацию по переменной $x_i$, любым методом одномерной оптимизации
- если достигнули минимума по одной координате, то возвращаем текущее значение вектора весов
Как это выглядит для минимизации функционала

__Недостатки:__
1. Не параллелится
2. Может "застрять" в локальном минимуме
3. Следствие п.2 - Не может использоваться кросс-энтропия для многомерного случая, так как легко "Застревает" в локальных минимумах. Вместо этого для каждого класса строит отдельный классификатор (One-vs-Rest)
```
from sklearn.model_selection import GridSearchCV
%%time
lr = LogisticRegression(solver='liblinear', multi_class='ovr')
lr.fit(x_train, y_train)
accuracy_score(lr.predict(x_test), y_test)
%%time
len_c = 10
param_grid = {
'C': np.linspace(0.01, 1, len_c),
'penalty': ['l1', 'l2']
}
gs = GridSearchCV(lr,param_grid=param_grid, cv=3, n_jobs=-1, scoring='accuracy')
gs.fit(x_train, y_train)
accuracy_score(gs.predict(x_test), y_test)
def print_cv_results(a, len_gs, params, param_r, param_sep):
d = len(params['param_grid'][param_sep])
ar = np.array(a).reshape(d, len_gs).T
df = pd.DataFrame(ar)
pen_par = params['param_grid'][param_sep]
c_par = params['param_grid'][param_r].tolist()
columns_mapper = dict(zip(range(0, len(pen_par)), pen_par))
row_mapper = dict(zip(range(0, len(c_par)), c_par))
df.rename(columns=columns_mapper, index=row_mapper, inplace=True)
plot = df.plot(title='Mean accuracy rating', grid=True)
plot.set_xlabel(param_r, fontsize=13)
plot.set_ylabel('acc', rotation=0, fontsize=13, labelpad=15)
print_cv_results(gs.cv_results_['mean_test_score'],
len_c, gs.get_params(), 'C','penalty')
```
### Stochatic Average Gradient (SAG)
Объединение градиентного спуска и стохастического.
При этом, он имеет низкую стоимость итерации свойственной SGD, но делает шаг градиента по отношению к аппроксимации полного градиента:
__Недостатки:__
- Нет L1
- Непрактичен для больших выборок, так как имеет высокую вычислительную сложность
```
%%time
lr = LogisticRegression(solver='sag', penalty='l2')
lr.fit(x_train, y_train)
accuracy_score(lr.predict(x_test), y_test)
%%time
len_c = 10
param_grid = {
'C': np.linspace(0.01, 1, len_c),
'multi_class': ['ovr', 'multinomial']
}
gs = GridSearchCV(lr,param_grid=param_grid, cv=3,
n_jobs=-1, scoring='accuracy')
gs.fit(x_train, y_train)
accuracy_score(gs.predict(x_test), y_test)
print_cv_results(gs.cv_results_['mean_test_score'],
len_c, gs.get_params(), 'C','multi_class')
```
### Stochatic Average Gradient Augmented (SAGA)
SAGA является вариантом SAG, но который поддерживает опцию non-smooth penalty=l1 (т. е. регуляризацию L1).
Кроме того, это единственный Solver, поддерживающий регуляризацию = "elasticnet".
[Подробнее: ](https://www.di.ens.fr/~fbach/Defazio_NIPS2014.pdf)
```
lr_clf = LogisticRegression(solver='saga', max_iter=1500)
%%time
len_c = 10
param_grid = {
'C': np.linspace(0.01, 1, len_c),
'penalty': ['l1', 'l2']
}
gs = GridSearchCV(lr_clf,param_grid=param_grid, cv=3,
n_jobs=-1, scoring='accuracy')
gs.fit(x_train, y_train)
print_cv_results(gs.cv_results_['mean_test_score'],
len_c, gs.get_params(), 'C','penalty')
accuracy_score(gs.predict(x_test), y_test)
```
# Support Vector Machine (SVM)
## Краткая теория
Задачу оптимизации линейной SVM можно сформулировать как
$$ \frac{1}{n} \sum_{i=1}^n \max(0, 1 - y_i (w X_i - b)) + \lambda ||w||_2 \to \min_w $$
Эта проблема может быть решена с помощью градиентных или субградиентных методов.
-----
Тогда как задача оптимизации формулируется следующим образом:
$$
\sum_{i=1}^n c_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n y_i c_i (X_i \cdot X_j ) y_j c_j \to \max_{c_1,...,c_n} \text{subject to}
\sum_{i=1}^n c_iy_i = 0
$$
$$
0 \leq c_i \leq \frac{1}{2n\lambda} \forall i
$$
$$f(x) = \sum_{i=1}^n \beta_i K(x_i, x)$$
$$K: K_{i,j} = K(x_i, x_j)$$
$$ \lambda \vec{\beta^T} K \vec{\beta} + \sum_{i=1}^n L(y_i, K_i^T \vec{\beta}) \to \min_{\vec{\beta}}$$
где L is Hinge loss: $L(y_i, K_i^T \vec{\beta}) = \max(0, 1 - y_i (K_i^T \vec{\beta}))$
## Playing with `sklearn`'s implementation
[original post](https://jakevdp.github.io/PythonDataScienceHandbook/05.07-support-vector-machines.html)
Сделаем данные
```
from sklearn.datasets import make_blobs
X, Y = make_blobs(n_samples=300, centers=2, random_state=45, cluster_std=0.6)
Y[Y == 0] = -1 # for convenience with formulas
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap='plasma')
from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear', C=1e5)
model.fit(X, Y)
def plot_svc_decision_function(model, ax=None, plot_support=True):
"""Plot the decision function for a 2D SVC"""
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
# plot decision boundary and margins
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)
plt.scatter(X[:, 0], X[:, 1], c=Y, s=50, cmap='autumn')
plot_svc_decision_function(model);
model.support_vectors_
```
### Эксперименты с разными ядрами
```
from sklearn.datasets import make_circles
X, y = make_circles(100, factor=.1, noise=.1)
y[y == 0] = -1
clf = SVC(kernel='linear', C=1e5).fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf, plot_support=False);
clf = SVC(kernel='poly', degree=20, C=1e6, max_iter=1e4)
y[y == 0] = -1
clf.fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=300, lw=1, facecolors='none');
```
### Different margins for nonseparable cases
```
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=1.2)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn');
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=1.2)
y[y == 0] = -1
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, C in zip(ax, [10.0, 0.005]):
model = SVC(kernel='linear', C=C).fit(X, y)
axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(model, axi)
axi.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, lw=1, facecolors='none');
axi.set_title('C = {0:.1f}'.format(C), size=14)
```
| true |
code
| 0.561936 | null | null | null | null |
|
# Comparing the performance of optimizers
```
import pennylane as qml
import numpy as np
from qiskit import IBMQ
import itertools
import matplotlib.pyplot as plt
import pickle
import scipy
```
## Hardware-friendly circuit
```
n_wires = 5
n_shots_list = [10, 100, 1000]
devs = [qml.device("default.qubit", wires=n_wires, shots=shots, analytic=False) for shots in n_shots_list]
devs.append(qml.device("default.qubit", wires=n_wires))
devs
def layers_circ(weights):
for i in range(n_wires):
qml.RX(weights[i], wires=i)
qml.CNOT(wires=[0, 1])
qml.CNOT(wires=[2, 1])
qml.CNOT(wires=[3, 1])
qml.CNOT(wires=[4, 3])
return qml.expval(qml.PauliZ(1))
layers = [qml.QNode(layers_circ, d) for d in devs]
seed = 2
weights = qml.init.basic_entangler_layers_uniform(n_layers=1, n_wires=5, seed=seed).flatten()
weights
grads = [qml.grad(l, argnum=0) for l in layers]
[l(weights) for l in layers]
g_exact = np.round(grads[-1](weights), 7)
g_exact
```
## Calculating the Hessian
```
s = 0.5 * np.pi
denom = 4 * np.sin(s) ** 2
shift = np.eye(len(weights))
LAMBDA = 0.2 # regulirization parameter for the Hessian
lr_gds = 0.15
lr_newton = 0.15
#weights[0] = 1.8
#weights[1] = 2.2
weights[0] = 0.1
weights[1] = 0.15
ARGS = 2
def is_pos_def(x):
return np.all(np.linalg.eigvals(x) > 0)
# First method
def regularize_hess(hess, lr):
return (1 / lr_newton) * (hess + LAMBDA * np.eye(len(hess)))
def regularize_diag_hess(hess, lr):
return (1 / lr_newton) * (hess + LAMBDA)
# Second method
def regularize_hess(hess, lr):
if is_pos_def(hess - LAMBDA * np.eye(len(hess))):
return (1 / lr_newton) * hess
return (1 / lr) * np.eye(len(hess))
def regularize_diag_hess(hess, lr):
if np.all(hess - LAMBDA > 0):
return (1 / lr_newton) * hess
return (1 / lr) * np.ones(len(hess))
# Third method
def regularize_hess(hess, lr):
abs_hess = scipy.linalg.sqrtm(hess @ hess)
return (1 / lr_newton) * (abs_hess + LAMBDA * np.eye(len(hess)))
def regularize_diag_hess(hess, lr):
return (1 / lr_newton) * (np.abs(hess) + LAMBDA)
# Forth method
def regularize_hess(hess, lr):
eig_vals, eig_vects = np.linalg.eig(hess)
epsilon = LAMBDA * np.ones(len(hess))
regul_eig_vals = np.max([eig_vals, epsilon], axis=0)
return (1 / lr_newton) * eig_vects @ np.diag(regul_eig_vals) @ np.linalg.inv(eig_vects)
def regularize_diag_hess(hess, lr):
epsilon = LAMBDA * np.ones(len(hess))
return (1 / lr_newton) * np.max([hess, epsilon], axis=0)
def hess_gen_results(func, weights, args=None):
results = {}
if not args:
args = len(weights)
for c in itertools.combinations(range(args), r=2):
weights_pp = weights + s * (shift[c[0]] + shift[c[1]])
weights_pm = weights + s * (shift[c[0]] - shift[c[1]])
weights_mp = weights - s * (shift[c[0]] - shift[c[1]])
weights_mm = weights - s * (shift[c[0]] + shift[c[1]])
f_pp = func(weights_pp)
f_pm = func(weights_pm)
f_mp = func(weights_mp)
f_mm = func(weights_mm)
results[c] = (f_pp, f_mp, f_pm, f_mm)
f = func(weights)
for i in range(args):
f_p = func(weights + 0.5 * np.pi * shift[i])
f_m = func(weights - 0.5 * np.pi * shift[i])
results[(i, i)] = (f_p, f_m, f)
return results
def hess_diag_gen_results(func, weights, args=None):
results = {}
if not args:
args = len(weights)
f = func(weights)
for i in range(args):
f_p = func(weights + 0.5 * np.pi * shift[i])
f_m = func(weights - 0.5 * np.pi * shift[i])
results[(i, i)] = (f_p, f_m, f)
return results
def grad_gen_results(func, weights, args=None):
results = {}
if not args:
args = len(weights)
for i in range(args):
f_p = func(weights + 0.5 * np.pi * shift[i])
f_m = func(weights - 0.5 * np.pi * shift[i])
results[i] = (f_p, f_m)
return results
def get_hess_diag(func, weights, args=None):
if not args:
args = len(weights)
hess = np.zeros(args)
results = hess_diag_gen_results(func, weights, args)
for i in range(args):
r = results[(i, i)]
hess[i] = (r[0] + r[1] - 2 * r[2]) / 2
grad = np.zeros(args)
for i in range(args):
r = results[(i, i)]
grad[i] = (r[0] - r[1]) / 2
return hess, results, grad
def get_grad(func, weights, args=None):
if not args:
args = len(weights)
grad = np.zeros(args)
results = grad_gen_results(func, weights, args)
for i in range(args):
r = results[i]
grad[i] = (r[0] - r[1]) / 2
return results, grad
def get_hess(func, weights, args=None):
if not args:
args = len(weights)
hess = np.zeros((args, args))
results = hess_gen_results(func, weights, args)
for c in itertools.combinations(range(args), r=2):
r = results[c]
hess[c] = (r[0] - r[1] - r[2] + r[3]) / denom
hess = hess + hess.T
for i in range(args):
r = results[(i, i)]
hess[i, i] = (r[0] + r[1] - 2 * r[2]) / 2
grad = np.zeros(args)
for i in range(args):
r = results[(i, i)]
grad[i] = (r[0] - r[1]) / 2
return hess, results, grad
```
## Visualizing optimization surface
```
grid = 200
xs = np.linspace(- 2 * np.pi, 2 * np.pi, grid)
ys = np.linspace(- 2 * np.pi, 2 * np.pi, grid)
xv, yv = np.meshgrid(xs, ys)
zv = np.zeros((grid, grid))
for i in range(grid):
for j in range(grid):
w = weights.copy()
w[0] = xv[i, j]
w[1] = yv[i, j]
zv[i, j] = layers[-1](w)
np.savez("grid.npz", xs=xs, ys=ys, zv=zv)
g = np.load("grid.npz")
xs = g["xs"]
ys = g["ys"]
zv = g["zv"]
weights
def gradient_descent(func, weights, reps, lr, i, args=ARGS):
ws = [weights.copy()]
res_dict = {}
gs = []
costs = [func(weights)]
for r in range(reps):
res, g = get_grad(func, ws[-1], args)
res_dict[r] = res
gs.append(g)
w_updated = ws[-1].copy()
w_updated[:args] -= lr * g
ws.append(w_updated)
costs.append(func(w_updated))
if r % 5 == 0:
print("Calculated for repetition {}".format(r))
with open("gds_results_{}.pickle".format(i), "wb") as f:
pickle.dump([ws, res, gs, costs], f)
return ws, res_dict, gs, costs
reps = 50
lr = lr_gds
args = ARGS
for i, l in enumerate(layers):
print("Calculating for layer {}".format(i))
ws, res, gs, costs = gradient_descent(l, weights, reps, lr, i)
def newton(func, weights, reps, lr, i, args=ARGS):
ws = [weights.copy()]
res_dict = {}
gs = []
hs = []
costs = [func(weights)]
for r in range(reps):
hess_r, res, g = get_hess(func, ws[-1], args)
res_dict[r] = res
gs.append(g)
hs.append(hess_r)
w_updated = ws[-1].copy()
hess_regul = regularize_hess(hess_r, lr)
h_inv = np.real(np.linalg.inv(hess_regul))
w_updated[:args] -= h_inv @ g
ws.append(w_updated)
costs.append(func(w_updated))
if r % 5 == 0:
print("Calculated for repetition {}".format(r))
with open("new_results_{}.pickle".format(i), "wb") as f:
pickle.dump([ws, res, gs, hs, costs], f)
return ws, res_dict, gs, hs, costs
reps = 50
lr = lr_gds
for i, l in enumerate(layers):
print("Calculating for layer {}".format(i))
ws, res, gs, hs, costs = newton(l, weights, reps, lr, i)
def newton_diag(func, weights, reps, lr, ii, args=ARGS):
ws = [weights.copy()]
res_dict = {}
gs = []
hs = []
costs = [func(weights)]
for r in range(reps):
hess_r, res, g = get_hess_diag(func, ws[-1], args)
res_dict[r] = res
gs.append(g)
hs.append(hess_r)
w_updated = ws[-1].copy()
hess_regul = regularize_diag_hess(hess_r, lr)
update = g / hess_regul
for i in range(len(update)):
if np.isinf(update[i]):
update[i] = 0
w_updated[:args] -= update
ws.append(w_updated)
costs.append(func(w_updated))
if r % 5 == 0:
print("Calculated for repetition {}".format(r))
with open("new_d_results_{}.pickle".format(ii), "wb") as f:
pickle.dump([ws, res, gs, hs, costs], f)
return ws, res_dict, gs, hs, costs
reps = 50
lr = lr_gds
for i, l in enumerate(layers):
print("Calculating for layer {}".format(i))
ws, res, gs, hs, costs = newton_diag(l, weights, reps, lr, i)
```
| true |
code
| 0.334909 | null | null | null | null |
|
# VQEによる量子化学計算
このチュートリアルでは、Amazon Braket で PennyLane を使用して量子化学の重要な問題、すなわち分子の基底状態エネルギーを見つける方法を説明します。この問題は、変分量子固有値ソルバー (VQE) アルゴリズムを実装することにより、近項量子ハードウェアを使用して対処できます。量子化学とVQEの詳細については、[Braket VQE ノートブック](../Hybrid_quantum_algorithms/vqe_Chemistry/vqe_Chemistry_braket.ipynb) や [PennyLane チュートリアル](https://pennylane.ai/qml/demos/tutorial_qubit_rotation.html) を参考にして下さい。
<div class="alert alert-block alert-info">
<b>注:</b> このノートブックの実行には PennyLane バージョン 0.16 以上が必要です。
</div>
## 量子化学から量子回路へ
まず最初のステップは、量子化学の問題を量子コンピュータで扱えるよう変換することです。PennyLane では ``qchem`` パッケージを使います。ローカルマシン上で実行している場合、``qchem`` パッケージは [これら](https://pennylane.readthedocs.io/en/stable/introduction/chemistry.html) の指示に従って別途インストールする必要があります。
```
import pennylane as qml
from pennylane import qchem
from pennylane import numpy as np
```
入力化学データは、多くの場合、分子に関する詳細を含むジオメトリファイルの形式で提供されます。ここで、[h2.xyz](./qchem/h2.xyz) ファイルに保存された $\mathrm {H} _2$ の原子構造を考えます。量子ビットハミルトニアンは ``qchem`` パッケージを使って構成されています。
```
symbols, coordinates = qchem.read_structure('qchem/h2.xyz')
h, qubits = qchem.molecular_hamiltonian(symbols, coordinates, name="h2")
print(h)
```
VQE アルゴリズムでは、変分量子回路上の上記のハミルトニアンの期待値を測定することにより、$\mathrm {H} _2$ 分子のエネルギーを計算します。我々の目的は、ハミルトニアンの期待値が最小になるように回路のパラメータを訓練し、それによって分子の基底状態エネルギーを見つけることです。
このチュートリアルでは、トータルスピンも計算します。そのために、``qchem`` パッケージを使ってトータルスピン演算子 $S^2$ を構築します。
```
electrons = 2 # Molecular hydrogen has two electrons
S2 = qchem.spin2(electrons, qubits)
print(S2)
```
## 回路の実行を減らすためにオブザーバブルをグループ化
電子ハミルトニアン ``h`` の期待値を測定したいとします。このハミルトニアンは、パウリ作用素のテンソル積である15の個々のオブザーバブルから構成されます。
```
print("Number of Pauli terms in h:", len(h.ops))
```
期待値を測定する簡単なアプローチは、回路を15回実装し、毎回ハミルトニアン ``h`` の一部を形成するパウリ項の1つを測定することです。しかし、もっと効率的な方法があるかもしれません。パウリ項は、単一の回路で同時に測定できるグループ(PennyLane の [グループ化](https://pennylane.readthedocs.io/en/stable/code/qml_grouping.html) モジュールを参照)に分けることができます。各グループの要素は、量子ビットごとに交換可能なオブザーバブルとして知られています。ハミルトニアン ``h`` は5つのグループに分けることができます:
```
groups, coeffs = qml.grouping.group_observables(h.ops, h.coeffs)
print("Number of qubit-wise commuting groups:", len(groups))
```
実際には、これは15の別々の回路を実行する代わりに、5つを実行するだけで済むことを意味します。この節約は、ハミルトニアンのパウリ項の数が増えるにつれて、さらに顕著になります。例えば、より大きな分子または異なる化学的基底集合に切り替えると、量子ビット数と項数の両方が増加する可能性があります。
幸い、PennyLane/Braket パイプラインには、デバイスの実行回数を最小限に抑えるためにオブザーバブルを事前にグループ化するための機能が組み込まれており、リモートデバイスを使用するときの実行時間とシミュレーション料金の両方を節約できます。このチュートリアルの残りの部分では、最適化されたオブザーバブルのグループ化を使用します。

## Ansatz 回路の定義
ここで、ハミルトニアンの基底状態を準備するために訓練される ansatz 回路を設定します。最初のステップは、ローカルの Braket デバイスを読み込むことです。
```
dev = qml.device("braket.local.qubit", wires=qubits)
```
このチュートリアルでは、[Delgado et al. (2020)](https://arxiv.org/abs/2106.13840) の [`AllSinglesDoubles`](https://pennylane.readthedocs.io/en/stable/code/api/pennylane.templates.subroutines.UCCSD.html) ansatz という化学インスパイアドな回路を使います。これを使用するには、量子化学の観点から追加の入力項目をいくつか定義する必要があります。
```
# Hartree-Fock state
hf_state = qchem.hf_state(electrons, qubits)
# generate single- and double-excitations
singles, doubles = qchem.excitations(electrons, qubits)
```
<div class="alert alert-block alert-info">
<b>注:</b> さまざまな ansatz とテンプレートが<a href="https://pennylane.readthedocs.io/en/stable/introduction/templates.html#quantum-chemistry-templates">利用可能で</a>、違うものを選ぶと、回路の深さや学習可能なパラメータ数が異なります。
</div>
この ansatz 回路は簡単に定義できます:
```
def circuit(params, wires):
qml.templates.AllSinglesDoubles(params, wires, hf_state, singles, doubles)
```
出力の測定はまだ定義されていないことに注意してください。これは次のステップで行います。
## エネルギーとトータルスピンの測定
先に説明したように、$\mathrm {H} _2$ のエネルギーに対応する量子ビットハミルトニアンの期待値を最小化したいと考えています。このハミルトニアンとトータルスピン $\hat {S} ^2$ 演算子の期待値は、以下を使用して定義できます。
```
energy_expval = qml.ExpvalCost(circuit, h, dev, optimize=True)
S2_expval = qml.ExpvalCost(circuit, S2, dev, optimize=True)
```
``optimize=True`` オプションに注意してください。これにより、PennyLane と Braket は、デバイスの実行効率を高めるために、各ハミルトニアンを量子ビットごとの交換可能なグループに分割するように指示します。
次に、ランダムな値をいくつか初期化し、エネルギーとスピンを評価しましょう。準備された状態のトータルスピン$S$は、$S=-\frac {1} {2} +\sqrt {\frac {1} {4} +\langle\hat {S} ^2\rangle}$ を用いて、期待値 $\langle \hat {S}^2 \rangle$ から得ることができます。$S$ を計算する関数はこのように定義することができます:
```
def spin(params):
return -0.5 + np.sqrt(1 / 4 + S2_expval(params))
np.random.seed(1967)
params = np.random.normal(0, np.pi, len(singles) + len(doubles))
```
エネルギーとトータルスピンは、
```
print("Energy:", energy_expval(params))
print("Spin: ", spin(params))
```
ランダムなパラメータを選んだので、測定されたエネルギーは基底状態エネルギーに対応しておらず、準備状態はトータルスピン演算子の固有状態ではありません。ここで、最小エネルギーを見つけるためにパラメータをトレーニングする必要があります。
## エネルギー最小化
エネルギーは、オプティマイザーを選択し、標準の最適化ループを実行することで最小化できます。
```
opt = qml.GradientDescentOptimizer(stepsize=0.4)
iterations = 40
energies = []
spins = []
for i in range(iterations):
params = opt.step(energy_expval, params)
e = energy_expval(params)
s = spin(params)
energies.append(e)
spins.append(s)
if (i + 1) % 5 == 0:
print(f"Completed iteration {i + 1}")
print("Energy:", e)
print("Total spin:", s)
print("----------------")
print(f"Optimized energy: {e} Ha")
print(f"Corresponding total spin: {s}")
```
水素分子の基底状態エネルギーの正確な値は ``-1.136189454088`` Hartrees (Ha) として理論的に計算されています。最適化されたエネルギーの誤差は、Hartree の $10^ {-5} $ 未満であることに注意してください。さらに、最適化された状態は、$\mathrm {H} _2$分子の基底状態に予想される固有値$S=0$を持つトータルスピン演算子の固有状態です。したがって、上記の結果は非常に有望に見えます!反復回数を増やすと、理論値にさらに近づきます。
最適化中に 2 つの量がどのように変化したかを視覚化してみましょう。
```
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import inset_axes
theory_energy = -1.136189454088
theory_spin = 0
plt.hlines(theory_energy, 0, 39, linestyles="dashed", colors="black")
plt.plot(energies)
plt.xlabel("Steps")
plt.ylabel("Energy")
axs = plt.gca()
inset = inset_axes(axs, width="50%", height="50%", borderpad=1)
inset.hlines(theory_spin, 0, 39, linestyles="dashed", colors="black")
inset.plot(spins, "r")
inset.set_xlabel("Steps")
inset.set_ylabel("Total spin");
```
このノートブックでは、Pennylane/Braket パイプラインを使用して、分子の基底状態エネルギーを効率的に見つける方法を学びました!
<div class="alert alert-block alert-info">
<b>次のステップは?</b> <code>qchem</code> フォルダには、水素分子の異なる原子間距離を表す追加の分子構造ファイルが含まれています。原子間距離の 1 つを選択し、基底状態のエネルギーを求めましょう。原子間距離によって基底状態のエネルギーはどのように変化するでしょう?
</div>
| true |
code
| 0.493226 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Inferencing with TensorFlow 2.0 on Azure Machine Learning Service
## Overview of Workshop
This notebook is Part 2 (Inferencing and Deploying a Model) of a four part workshop that demonstrates an end-to-end workflow for implementing a BERT model using Tensorflow 2.0 on Azure Machine Learning Service. The different components of the workshop are as follows:
- Part 1: [Preparing Data and Model Training](https://github.com/microsoft/bert-stack-overflow/blob/master/1-Training/AzureServiceClassifier_Training.ipynb)
- Part 2: [Inferencing and Deploying a Model](https://github.com/microsoft/bert-stack-overflow/blob/master/2-Inferencing/AzureServiceClassifier_Inferencing.ipynb)
- Part 3: [Setting Up a Pipeline Using MLOps](https://github.com/microsoft/bert-stack-overflow/tree/master/3-ML-Ops)
- Part 4: [Explaining Your Model Interpretability](https://github.com/microsoft/bert-stack-overflow/blob/master/4-Interpretibility/IBMEmployeeAttritionClassifier_Interpretability.ipynb)
This workshop shows how to convert a TF 2.0 BERT model and deploy the model as Webservice in step-by-step fashion:
* Initilize your workspace
* Download a previous saved model (saved on Azure Machine Learning)
* Test the downloaded model
* Display scoring script
* Defining an Azure Environment
* Deploy Model as Webservice (Local, ACI and AKS)
* Test Deployment (Azure ML Service Call, Raw HTTP Request)
* Clean up Webservice
## What is Azure Machine Learning Service?
Azure Machine Learning service is a cloud service that you can use to develop and deploy machine learning models. Using Azure Machine Learning service, you can track your models as you build, train, deploy, and manage them, all at the broad scale that the cloud provides.

#### How can we use Azure Machine Learning SDK for deployment and inferencing of a machine learning models?
Deployment and inferencing of a machine learning model, is often an cumbersome process. Once you a trained model and a scoring script working on your local machine, you will want to deploy this model as a web service.
To facilitate deployment and inferencing, the Azure Machine Learning Python SDK provides a high-level abstraction for model deployment of a web service running on your [local](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-deploy-and-where#local) machine, in Azure Container Instance ([ACI](https://azure.microsoft.com/en-us/services/container-instances/)) or Azure Kubernetes Service ([AKS](https://azure.microsoft.com/en-us/services/kubernetes-service/)), which allows users to easily deploy their models in the Azure ecosystem.
## Prerequisites
* Understand the [architecture and terms](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-azure-machine-learning-architecture) introduced by Azure Machine Learning
* If you are using an Azure Machine Learning Notebook VM, you are all set. Otherwise, go through the [configuration notebook](https://docs.microsoft.com/en-us/azure/machine-learning/service/tutorial-1st-experiment-sdk-setup) to:
* Install the AML SDK
* Create a workspace and its configuration file (config.json)
* For local scoring test, you will also need to have Tensorflow and Keras installed in the current Jupyter kernel.
* Please run through Part 1: [Working With Data and Training](1_AzureServiceClassifier_Training.ipynb) Notebook first to register your model
* Make sure you enable [Docker for non-root users](https://docs.docker.com/install/linux/linux-postinstall/) (This is needed to run Local Deployment). Run the following commands in your Terminal and go to the your [Jupyter dashboard](/tree) and click `Quit` on the top right corner. After the shutdown, the Notebook will be automatically refereshed with the new permissions.
```bash
sudo usermod -a -G docker $USER
newgrp docker
```
#### Enable Docker for non-root users
```
!sudo usermod -a -G docker $USER
!newgrp docker
```
Check if you have the correct permissions to run Docker. Running the line below should print:
```
CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
```
```
!docker ps
```
>**Note:** Make you shutdown your Jupyter notebook to enable this access. Go to the your [Jupyter dashboard](/tree) and click `Quit` on the top right corner. After the shutdown, the Notebook will be automatically refereshed with the new permissions.
## Azure Service Classification Problem
One of the key tasks to ensuring long term success of any Azure service is actively responding to related posts in online forums such as Stackoverflow. In order to keep track of these posts, Microsoft relies on the associated tags to direct questions to the appropriate support team. While Stackoverflow has different tags for each Azure service (azure-web-app-service, azure-virtual-machine-service, etc), people often use the generic **azure** tag. This makes it hard for specific teams to track down issues related to their product and as a result, many questions get left unanswered.
**In order to solve this problem, we will be building a model to classify posts on Stackoverflow with the appropriate Azure service tag.**
We will be using a BERT (Bidirectional Encoder Representations from Transformers) model which was published by researchers at Google AI Language. Unlike recent language representation models, BERT is designed to pre-train deep bidirectional representations from unlabeled text by jointly conditioning on both left and right context in all layers. As a result, the pre-trained BERT model can be fine-tuned with just one additional output layer to create state-of-the-art models for a wide range of natural language processing (NLP) tasks without substantial architecture modifications.
For more information about the BERT, please read this [paper](https://arxiv.org/pdf/1810.04805.pdf)
## Checking Azure Machine Learning Python SDK Version
If you are running this on a Notebook VM, the Azure Machine Learning Python SDK is installed by default. If you are running this locally, you can follow these [instructions](https://docs.microsoft.com/en-us/python/api/overview/azure/ml/install?view=azure-ml-py) to install it using pip.
This tutorial requires version 1.0.69 or higher. We can import the Python SDK to ensure it has been properly installed:
```
# Check core SDK version number
import azureml.core
print("SDK version:", azureml.core.VERSION)
```
## Connect To Workspace
Initialize a [Workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-azure-machine-learning-architecture#workspace) object from the existing workspace you created in the prerequisites step. Workspace.from_config() creates a workspace object from the details stored in config.json.
```
from azureml.core import Workspace
ws = Workspace.from_config()
print('Workspace name: ' + ws.name,
'Azure region: ' + ws.location,
'Subscription id: ' + ws.subscription_id,
'Resource group: ' + ws.resource_group, sep = '\n')
```
## Register Datastore
A [Datastore](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.datastore.datastore?view=azure-ml-py) is used to store connection information to a central data storage. This allows you to access your storage without having to hard code this (potentially confidential) information into your scripts.
In this tutorial, the model was been previously prepped and uploaded into a central [Blob Storage](https://azure.microsoft.com/en-us/services/storage/blobs/) container. We will register this container into our workspace as a datastore using a [shared access signature (SAS) token](https://docs.microsoft.com/en-us/azure/storage/common/storage-sas-overview).
We need to define the following parameters to register a datastore:
- `ws`: The workspace object
- `datastore_name`: The name of the datastore, case insensitive, can only contain alphanumeric characters and _.
- `container_name`: The name of the azure blob container.
- `account_name`: The storage account name.
- `sas_token`: An account SAS token, defaults to None.
```
from azureml.core.datastore import Datastore
datastore_name = 'tfworld'
container_name = 'azureml-blobstore-7c6bdd88-21fa-453a-9c80-16998f02935f'
account_name = 'tfworld6818510241'
sas_token = '?sv=2019-02-02&ss=bfqt&srt=sco&sp=rl&se=2020-11-02T06:01:06Z&st=2019-11-08T22:01:06Z&spr=https&sig=9XcJPwqp4c2cSgsGL1X7cXKO46bzhHCaX75N3gc98GU%3D'
datastore = Datastore.register_azure_blob_container(workspace=ws,
datastore_name=datastore_name,
container_name=container_name,
account_name=account_name,
sas_token=sas_token)
```
#### If the datastore has already been registered, then you (and other users in your workspace) can directly run this cell.
```
datastore = ws.datastores['tfworld']
```
### Download Model from Datastore
Get the trained model from an Azure Blob container. The model is saved into two files, ``config.json`` and ``model.h5``.
```
from azureml.core.model import Model
datastore.download('./',prefix="azure-service-classifier/model")
```
### Registering the Model with the Workspace
Register the model to use in your workspace.
```
model = Model.register(model_path = "./azure-service-classifier/model",
model_name = "azure-service-classifier", # this is the name the model is registered as
tags = {'pretrained': "BERT"},
workspace = ws)
model_dir = './azure-service-classifier/model'
```
### Downloading and Using Registered Models
> If you already completed Part 1: [Working With Data and Training](1_AzureServiceClassifier_Training.ipynb) Notebook.You can dowload your registered BERT Model and use that instead of the model saved on the blob storage.
```python
model = ws.models['azure-service-classifier']
model_dir = model.download(target_dir='.', exist_ok=True, exists_ok=None)
```
## Inferencing on the test set
Let's check the version of the local Keras. Make sure it matches with the version number printed out in the training script. Otherwise you might not be able to load the model properly.
```
import keras
import tensorflow as tf
print("Keras version:", keras.__version__)
print("Tensorflow version:", tf.__version__)
```
#### Install Transformers Library
We have trained BERT model using Tensorflow 2.0 and the open source [huggingface/transformers](https://github.com/huggingface/transformers) libary. So before we can load the model we need to make sure we have also installed the Transformers Library.
```
%pip install transformers
```
#### Load the Tensorflow 2.0 BERT model.
Load the downloaded Tensorflow 2.0 BERT model
```
from transformers import BertTokenizer, TFBertPreTrainedModel, TFBertMainLayer
from transformers.modeling_tf_utils import get_initializer
class TFBertForMultiClassification(TFBertPreTrainedModel):
def __init__(self, config, *inputs, **kwargs):
super(TFBertForMultiClassification, self).__init__(config, *inputs, **kwargs)
self.num_labels = config.num_labels
self.bert = TFBertMainLayer(config, name='bert')
self.dropout = tf.keras.layers.Dropout(config.hidden_dropout_prob)
self.classifier = tf.keras.layers.Dense(config.num_labels,
kernel_initializer=get_initializer(config.initializer_range),
name='classifier',
activation='softmax')
def call(self, inputs, **kwargs):
outputs = self.bert(inputs, **kwargs)
pooled_output = outputs[1]
pooled_output = self.dropout(pooled_output, training=kwargs.get('training', False))
logits = self.classifier(pooled_output)
outputs = (logits,) + outputs[2:] # add hidden states and attention if they are here
return outputs # logits, (hidden_states), (attentions)
max_seq_length = 128
labels = ['azure-web-app-service', 'azure-storage', 'azure-devops', 'azure-virtual-machine', 'azure-functions']
loaded_model = TFBertForMultiClassification.from_pretrained(model_dir, num_labels=len(labels))
tokenizer = BertTokenizer.from_pretrained('bert-base-cased')
print("Model loaded from disk.")
```
Feed in test sentence to test the BERT model. And time the duration of the prediction.
```
%%time
import json
# Input test sentences
raw_data = json.dumps({
'text': 'My VM is not working'
})
# Encode inputs using tokenizer
inputs = tokenizer.encode_plus(
json.loads(raw_data)['text'],
add_special_tokens=True,
max_length=max_seq_length
)
input_ids, token_type_ids = inputs["input_ids"], inputs["token_type_ids"]
# The mask has 1 for real tokens and 0 for padding tokens. Only real tokens are attended to.
attention_mask = [1] * len(input_ids)
# Zero-pad up to the sequence length.
padding_length = max_seq_length - len(input_ids)
input_ids = input_ids + ([0] * padding_length)
attention_mask = attention_mask + ([0] * padding_length)
token_type_ids = token_type_ids + ([0] * padding_length)
# Make prediction
predictions = loaded_model.predict({
'input_ids': tf.convert_to_tensor([input_ids], dtype=tf.int32),
'attention_mask': tf.convert_to_tensor([attention_mask], dtype=tf.int32),
'token_type_ids': tf.convert_to_tensor([token_type_ids], dtype=tf.int32)
})
result = {
'prediction': str(labels[predictions[0].argmax().item()]),
'probability': str(predictions[0].max())
}
print(result)
```
As you can see based on the sample sentence the model can predict the probability of the StackOverflow tags related to that sentence.
## Inferencing with ONNX
### ONNX and ONNX Runtime
**ONNX (Open Neural Network Exchange)** is an interoperable standard format for ML models, with support for both DNN and traditional ML. Models can be converted from a variety of frameworks, such as TensorFlow, Keras, PyTorch, scikit-learn, and more (see [ONNX Conversion tutorials](https://github.com/onnx/tutorials#converting-to-onnx-format)). This provides data teams with the flexibility to use their framework of choice for their training needs, while streamlining the process to operationalize these models for production usage in a consistent way.
In this section, we will demonstrate how to use ONNX Runtime, a high performance inference engine for ONNX format models, for inferencing our model. Along with interoperability, ONNX Runtime's performance-focused architecture can also accelerate inferencing for many models through graph optimizations, utilization of custom accelerators, and more. You can find more about performance tuning [here](https://github.com/microsoft/onnxruntime/blob/master/docs/ONNX_Runtime_Perf_Tuning.md).
#### Download ONNX Model
To visualize the model, we can use Netron. Click [here](https://lutzroeder.github.io/netron/) to open the browser version and load the model.
```
datastore.download('.',prefix="azure-service-classifier/model/bert_tf2.onnx")
```
#### Install ONNX Runtime
```
%pip install onnxruntime
```
#### Loading ONNX Model
Load the downloaded ONNX BERT model.
```
import numpy as np
import onnxruntime as rt
from transformers import BertTokenizer, TFBertPreTrainedModel, TFBertMainLayer
max_seq_length = 128
labels = ['azure-web-app-service', 'azure-storage', 'azure-devops', 'azure-virtual-machine', 'azure-functions']
tokenizer = BertTokenizer.from_pretrained('bert-base-cased')
sess = rt.InferenceSession("./azure-service-classifier/model/bert_tf2.onnx")
print("ONNX Model loaded from disk.")
```
#### View the inputs and outputs of converted ONNX model
```
for i in range(len(sess.get_inputs())):
input_name = sess.get_inputs()[i].name
print("Input name :", input_name)
input_shape = sess.get_inputs()[i].shape
print("Input shape :", input_shape)
input_type = sess.get_inputs()[i].type
print("Input type :", input_type)
for i in range(len(sess.get_outputs())):
output_name = sess.get_outputs()[i].name
print("Output name :", output_name)
output_shape = sess.get_outputs()[i].shape
print("Output shape :", output_shape)
output_type = sess.get_outputs()[i].type
print("Output type :", output_type)
```
#### Inferencing with ONNX Runtime
```
%%time
import json
# Input test sentences
raw_data = json.dumps({
'text': 'My VM is not working'
})
labels = ['azure-web-app-service', 'azure-storage', 'azure-devops', 'azure-virtual-machine', 'azure-functions']
# Encode inputs using tokenizer
inputs = tokenizer.encode_plus(
json.loads(raw_data)['text'],
add_special_tokens=True,
max_length=max_seq_length
)
input_ids, token_type_ids = inputs["input_ids"], inputs["token_type_ids"]
# The mask has 1 for real tokens and 0 for padding tokens. Only real tokens are attended to.
attention_mask = [1] * len(input_ids)
# Zero-pad up to the sequence length.
padding_length = max_seq_length - len(input_ids)
input_ids = input_ids + ([0] * padding_length)
attention_mask = attention_mask + ([0] * padding_length)
token_type_ids = token_type_ids + ([0] * padding_length)
# Make prediction
convert_input = {
sess.get_inputs()[0].name: np.array(tf.convert_to_tensor([token_type_ids], dtype=tf.int32)),
sess.get_inputs()[1].name: np.array(tf.convert_to_tensor([input_ids], dtype=tf.int32)),
sess.get_inputs()[2].name: np.array(tf.convert_to_tensor([attention_mask], dtype=tf.int32))
}
predictions = sess.run([output_name], convert_input)
result = {
'prediction': str(labels[predictions[0].argmax().item()]),
'probability': str(predictions[0].max())
}
print(result)
```
## Deploy models on Azure ML
Now we are ready to deploy the model as a web service running on your [local](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-deploy-and-where#local) machine, in Azure Container Instance [ACI](https://azure.microsoft.com/en-us/services/container-instances/) or Azure Kubernetes Service [AKS](https://azure.microsoft.com/en-us/services/kubernetes-service/). Azure Machine Learning accomplishes this by constructing a Docker image with the scoring logic and model baked in.
> **Note:** For this Notebook, we'll use the original model format for deployment, but the ONNX model can be deployed in the same way by using ONNX Runtime in the scoring script.

### Deploying a web service
Once you've tested the model and are satisfied with the results, deploy the model as a web service. For this Notebook, we'll use the original model format for deployment, but note that the ONNX model can be deployed in the same way by using ONNX Runtime in the scoring script.
To build the correct environment, provide the following:
* A scoring script to show how to use the model
* An environment file to show what packages need to be installed
* A configuration file to build the web service
* The model you trained before
Read more about deployment [here](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-deploy-and-where)
### Create score.py
First, we will create a scoring script that will be invoked by the web service call. We have prepared a [score.py script](code/scoring/score.py) in advance that scores your BERT model.
* Note that the scoring script must have two required functions, ``init()`` and ``run(input_data)``.
* In ``init()`` function, you typically load the model into a global object. This function is executed only once when the Docker container is started.
* In ``run(input_data)`` function, the model is used to predict a value based on the input data. The input and output to run typically use JSON as serialization and de-serialization format but you are not limited to that.
```
%pycat score.py
```
### Create Environment
You can create and/or use a Conda environment using the [Conda Dependencies object](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.conda_dependencies.condadependencies?view=azure-ml-py) when deploying a Webservice.
```
from azureml.core import Environment
from azureml.core.conda_dependencies import CondaDependencies
myenv = CondaDependencies.create(conda_packages=['numpy','pandas'],
pip_packages=['numpy','pandas','inference-schema[numpy-support]','azureml-defaults','tensorflow==2.0.0','transformers==2.0.0'])
with open("myenv.yml","w") as f:
f.write(myenv.serialize_to_string())
```
Review the content of the `myenv.yml` file.
```
%pycat myenv.yml
```
## Create Inference Configuration
We need to define the [Inference Configuration](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.model.inferenceconfig?view=azure-ml-py) for the web service. There is support for a source directory, you can upload an entire folder from your local machine as dependencies for the Webservice.
Note: in that case, your entry_script and conda_file paths are relative paths to the source_directory path.
Sample code for using a source directory:
```python
inference_config = InferenceConfig(source_directory="C:/abc",
runtime= "python",
entry_script="x/y/score.py",
conda_file="env/myenv.yml")
```
- source_directory = holds source path as string, this entire folder gets added in image so its really easy to access any files within this folder or subfolder
- runtime = Which runtime to use for the image. Current supported runtimes are 'spark-py' and 'python
- entry_script = contains logic specific to initializing your model and running predictions
- conda_file = manages conda and python package dependencies.
> **Note:** Deployment uses the inference configuration deployment configuration to deploy the models. The deployment process is similar regardless of the compute target. Deploying to AKS is slightly different because you must provide a reference to the AKS cluster.
```
from azureml.core.model import InferenceConfig
inference_config = InferenceConfig(source_directory="./",
runtime= "python",
entry_script="score.py",
conda_file="myenv.yml"
)
```
## Deploy as a Local Service
Estimated time to complete: **about 3-7 minutes**
Configure the image and deploy it locally. The following code goes through these steps:
* Build an image on local machine (or VM, if you are using a VM) using:
* The scoring file (`score.py`)
* The environment file (`myenv.yml`)
* The model file
* Define [Local Deployment Configuration](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.webservice.localwebservice?view=azure-ml-py#deploy-configuration-port-none-)
* Send the image to local docker instance.
* Start up a container using the image.
* Get the web service HTTP endpoint.
* This has a very quick turnaround time and is great for testing service before it is deployed to production
> **Note:** Make sure you enable [Docker for non-root users](https://docs.docker.com/install/linux/linux-postinstall/) (This is needed to run Local Deployment). Run the following commands in your Terminal and go to the your [Jupyter dashboard](/tree) and click `Quit` on the top right corner. After the shutdown, the Notebook will be automatically refereshed with the new permissions.
```bash
sudo usermod -a -G docker $USER
newgrp docker
```
#### Deploy Local Service
```
from azureml.core.model import InferenceConfig, Model
from azureml.core.webservice import LocalWebservice
# Create a local deployment for the web service endpoint
deployment_config = LocalWebservice.deploy_configuration()
# Deploy the service
local_service = Model.deploy(
ws, "mymodel", [model], inference_config, deployment_config)
# Wait for the deployment to complete
local_service.wait_for_deployment(True)
# Display the port that the web service is available on
print(local_service.port)
```
This is the scoring web service endpoint:
```
print(local_service.scoring_uri)
```
### Test Local Service
Let's test the deployed model. Pick a random samples about an issue, and send it to the web service. Note here we are using the run API in the SDK to invoke the service. You can also make raw HTTP calls using any HTTP tool such as curl.
After the invocation, we print the returned predictions.
```
%%time
import json
raw_data = json.dumps({
'text': 'My VM is not working'
})
prediction = local_service.run(input_data=raw_data)
```
### Reloading Webservice
You can update your score.py file and then call reload() to quickly restart the service. This will only reload your execution script and dependency files, it will not rebuild the underlying Docker image. As a result, reload() is fast.
```
%%writefile score.py
import os
import json
import tensorflow as tf
from transformers import TFBertPreTrainedModel, TFBertMainLayer, BertTokenizer
from transformers.modeling_tf_utils import get_initializer
import logging
logging.getLogger("transformers.tokenization_utils").setLevel(logging.ERROR)
class TFBertForMultiClassification(TFBertPreTrainedModel):
def __init__(self, config, *inputs, **kwargs):
super(TFBertForMultiClassification, self) \
.__init__(config, *inputs, **kwargs)
self.num_labels = config.num_labels
self.bert = TFBertMainLayer(config, name='bert')
self.dropout = tf.keras.layers.Dropout(config.hidden_dropout_prob)
self.classifier = tf.keras.layers.Dense(
config.num_labels,
kernel_initializer=get_initializer(config.initializer_range),
name='classifier',
activation='softmax')
def call(self, inputs, **kwargs):
outputs = self.bert(inputs, **kwargs)
pooled_output = outputs[1]
pooled_output = self.dropout(
pooled_output,
training=kwargs.get('training', False))
logits = self.classifier(pooled_output)
# add hidden states and attention if they are here
outputs = (logits,) + outputs[2:]
return outputs # logits, (hidden_states), (attentions)
max_seq_length = 128
labels = ['azure-web-app-service', 'azure-storage',
'azure-devops', 'azure-virtual-machine', 'azure-functions']
def init():
global tokenizer, model
# os.path.join(os.getenv('AZUREML_MODEL_DIR'), 'azure-service-classifier')
tokenizer = BertTokenizer.from_pretrained('bert-base-cased')
model_dir = os.path.join(os.getenv('AZUREML_MODEL_DIR'), 'model')
model = TFBertForMultiClassification \
.from_pretrained(model_dir, num_labels=len(labels))
print("hello from the reloaded script")
def run(raw_data):
# Encode inputs using tokenizer
inputs = tokenizer.encode_plus(
json.loads(raw_data)['text'],
add_special_tokens=True,
max_length=max_seq_length
)
input_ids, token_type_ids = inputs["input_ids"], inputs["token_type_ids"]
# The mask has 1 for real tokens and 0 for padding tokens.
# Only real tokens are attended to.
attention_mask = [1] * len(input_ids)
# Zero-pad up to the sequence length.
padding_length = max_seq_length - len(input_ids)
input_ids = input_ids + ([0] * padding_length)
attention_mask = attention_mask + ([0] * padding_length)
token_type_ids = token_type_ids + ([0] * padding_length)
# Make prediction
predictions = model.predict({
'input_ids': tf.convert_to_tensor([input_ids], dtype=tf.int32),
'attention_mask': tf.convert_to_tensor(
[attention_mask],
dtype=tf.int32),
'token_type_ids': tf.convert_to_tensor(
[token_type_ids],
dtype=tf.int32)
})
result = {
'prediction': str(labels[predictions[0].argmax().item()]),
'probability': str(predictions[0].max())
}
print(result)
return result
init()
run(json.dumps({
'text': 'My VM is not working'
}))
local_service.reload()
```
### Updating Webservice
If you do need to rebuild the image -- to add a new Conda or pip package, for instance -- you will have to call update(), instead (see below).
```python
local_service.update(models=[loaded_model],
image_config=None,
deployment_config=None,
wait=False, inference_config=None)
```
### View service Logs (Debug, when something goes wrong )
>**Tip: If something goes wrong with the deployment, the first thing to look at is the logs from the service by running the following command:** Run this cell
You should see the phrase **"hello from the reloaded script"** in the logs, because we added it to the script when we did a service reload.
```
import pprint
pp = pprint.PrettyPrinter(indent=4)
pp.pprint(local_service.get_logs())
```
## Deploy in ACI
Estimated time to complete: **about 3-7 minutes**
Configure the image and deploy. The following code goes through these steps:
* Build an image using:
* The scoring file (`score.py`)
* The environment file (`myenv.yml`)
* The model file
* Define [ACI Deployment Configuration](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.webservice.aciwebservice?view=azure-ml-py#deploy-configuration-cpu-cores-none--memory-gb-none--tags-none--properties-none--description-none--location-none--auth-enabled-none--ssl-enabled-none--enable-app-insights-none--ssl-cert-pem-file-none--ssl-key-pem-file-none--ssl-cname-none-)
* Send the image to the ACI container.
* Start up a container in ACI using the image.
* Get the web service HTTP endpoint.
```
%%time
from azureml.core.webservice import Webservice
from azureml.exceptions import WebserviceException
from azureml.core.webservice import AciWebservice, Webservice
## Create a deployment configuration file and specify the number of CPUs and gigabyte of RAM needed for your ACI container.
## If you feel you need more later, you would have to recreate the image and redeploy the service.
aciconfig = AciWebservice.deploy_configuration(cpu_cores=2,
memory_gb=4,
tags={"model": "BERT", "method" : "tensorflow"},
description='Predict StackoverFlow tags with BERT')
aci_service_name = 'asc-aciservice'
try:
# if you want to get existing service below is the command
# since aci name needs to be unique in subscription deleting existing aci if any
# we use aci_service_name to create azure ac
aci_service = Webservice(ws, name=aci_service_name)
if aci_service:
aci_service.delete()
except WebserviceException as e:
print()
aci_service = Model.deploy(ws, aci_service_name, [model], inference_config, aciconfig)
aci_service.wait_for_deployment(True)
print(aci_service.state)
```
This is the scoring web service endpoint:
```
print(aci_service.scoring_uri)
```
### Test the deployed model
Let's test the deployed model. Pick a random samples about an Azure issue, and send it to the web service. Note here we are using the run API in the SDK to invoke the service. You can also make raw HTTP calls using any HTTP tool such as curl.
After the invocation, we print the returned predictions.
```
%%time
import json
raw_data = json.dumps({
'text': 'My VM is not working'
})
prediction = aci_service.run(input_data=raw_data)
print(prediction)
```
### View service Logs (Debug, when something goes wrong )
>**Tip: If something goes wrong with the deployment, the first thing to look at is the logs from the service by running the following command:** Run this cell
```
import pprint
pp = pprint.PrettyPrinter(indent=4)
pp.pprint(aci_service.get_logs())
```
## Deploy in AKS (Single Node)
Estimated time to complete: **about 15-25 minutes**, 10-15 mins for AKS provisioning and 5-10 mins to deploy service
Configure the image and deploy. The following code goes through these steps:
* Provision a Production AKS Cluster
* Build an image using:
* The scoring file (`score.py`)
* The environment file (`myenv.yml`)
* The model file
* Define [AKS Provisioning Configuration](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.compute.akscompute?view=azure-ml-py#provisioning-configuration-agent-count-none--vm-size-none--ssl-cname-none--ssl-cert-pem-file-none--ssl-key-pem-file-none--location-none--vnet-resourcegroup-name-none--vnet-name-none--subnet-name-none--service-cidr-none--dns-service-ip-none--docker-bridge-cidr-none--cluster-purpose-none-)
* Provision an AKS Cluster
* Define [AKS Deployment Configuration](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.webservice.akswebservice?view=azure-ml-py#deploy-configuration-autoscale-enabled-none--autoscale-min-replicas-none--autoscale-max-replicas-none--autoscale-refresh-seconds-none--autoscale-target-utilization-none--collect-model-data-none--auth-enabled-none--cpu-cores-none--memory-gb-none--enable-app-insights-none--scoring-timeout-ms-none--replica-max-concurrent-requests-none--max-request-wait-time-none--num-replicas-none--primary-key-none--secondary-key-none--tags-none--properties-none--description-none--gpu-cores-none--period-seconds-none--initial-delay-seconds-none--timeout-seconds-none--success-threshold-none--failure-threshold-none--namespace-none--token-auth-enabled-none-)
* Send the image to the AKS cluster.
* Start up a container in AKS using the image.
* Get the web service HTTP endpoint.
#### Provisioning Cluster
```
from azureml.core.compute import AksCompute, ComputeTarget
# Use the default configuration (you can also provide parameters to customize this).
# For example, to create a dev/test cluster, use:
# prov_config = AksCompute.provisioning_configuration(cluster_purpose = AksCompute.ClusterPurpose.DEV_TEST)
prov_config = AksCompute.provisioning_configuration()
aks_name = 'myaks'
# Create the cluster
aks_target = ComputeTarget.create(workspace = ws,
name = aks_name,
provisioning_configuration = prov_config)
# Wait for the create process to complete
aks_target.wait_for_completion(show_output = True)
```
#### Deploying the model
```
from azureml.core.webservice import AksWebservice, Webservice
from azureml.core.model import Model
aks_target = AksCompute(ws,"myaks")
## Create a deployment configuration file and specify the number of CPUs and gigabyte of RAM needed for your cluster.
## If you feel you need more later, you would have to recreate the image and redeploy the service.
deployment_config = AksWebservice.deploy_configuration(cpu_cores = 2, memory_gb = 4)
aks_service = Model.deploy(ws, "myservice", [model], inference_config, deployment_config, aks_target)
aks_service.wait_for_deployment(show_output = True)
print(aks_service.state)
```
### Test the deployed model
#### Using the Azure SDK service call
We can use Azure SDK to make a service call with a simple function
```
%%time
import json
raw_data = json.dumps({
'text': 'My VM is not working'
})
prediction = aks_service.run(input_data=raw_data)
print(prediction)
```
This is the scoring web service endpoint:
```
print(aks_service.scoring_uri)
```
#### Using HTTP call
We will make a Jupyter widget so we can now send construct raw HTTP request and send to the service through the widget.
#### Test Web Service with HTTP call
```
import ipywidgets as widgets
from ipywidgets import Layout, Button, Box, FloatText, Textarea, Dropdown, Label, IntSlider, VBox
from IPython.display import display
import requests
text = widgets.Text(
value='',
placeholder='Type a query',
description='Question:',
disabled=False
)
button = widgets.Button(description="Get Tag!")
output = widgets.Output()
items = [text, button]
box_layout = Layout(display='flex',
flex_flow='row',
align_items='stretch',
width='70%')
box_auto = Box(children=items, layout=box_layout)
def on_button_clicked(b):
with output:
input_data = '{\"text\": \"'+ text.value +'\"}'
headers = {'Content-Type':'application/json'}
resp = requests.post(local_service.scoring_uri, input_data, headers=headers)
print("="*10)
print("Question:", text.value)
print("POST to url", local_service.scoring_uri)
print("Prediction:", resp.text)
print("="*10)
button.on_click(on_button_clicked)
#Display the GUI
VBox([box_auto, output])
```
Doing a raw HTTP request and send to the service through without a widget.
```
query = 'My VM is not working'
input_data = '{\"text\": \"'+ query +'\"}'
headers = {'Content-Type':'application/json'}
resp = requests.post(local_service.scoring_uri, input_data, headers=headers)
print("="*10)
print("Question:", query)
print("POST to url", local_service.scoring_uri)
print("Prediction:", resp.text)
print("="*10)
```
### View service Logs (Debug, when something goes wrong )
>**Tip: If something goes wrong with the deployment, the first thing to look at is the logs from the service by running the following command:** Run this cell
```
import pprint
pp = pprint.PrettyPrinter(indent=4)
pp.pprint(aks_service.get_logs())
```
## Summary of workspace
Let's look at the workspace after the web service was deployed. You should see
* a registered model named and with the id
* an AKS and ACI webservice called with some scoring URL
```
models = ws.models
for name, model in models.items():
print("Model: {}, ID: {}".format(name, model.id))
webservices = ws.webservices
for name, webservice in webservices.items():
print("Webservice: {}, scoring URI: {}".format(name, webservice.scoring_uri))
```
## Delete ACI to clean up
You can delete the ACI deployment with a simple delete API call.
```
local_service.delete()
aci_service.delete()
aks_service.delete()
```
| true |
code
| 0.504455 | null | null | null | null |
|
[Table of Contents](./table_of_contents.ipynb)
# The Extended Kalman Filter
```
#format the book
%matplotlib inline
from __future__ import division, print_function
from book_format import load_style
load_style()
```
We have developed the theory for the linear Kalman filter. Then, in the last two chapters we broached the topic of using Kalman filters for nonlinear problems. In this chapter we will learn the Extended Kalman filter (EKF). The EKF handles nonlinearity by linearizing the system at the point of the current estimate, and then the linear Kalman filter is used to filter this linearized system. It was one of the very first techniques used for nonlinear problems, and it remains the most common technique.
The EKF provides significant mathematical challenges to the designer of the filter; this is the most challenging chapter of the book. I do everything I can to avoid the EKF in favor of other techniques that have been developed to filter nonlinear problems. However, the topic is unavoidable; all classic papers and a majority of current papers in the field use the EKF. Even if you do not use the EKF in your own work you will need to be familiar with the topic to be able to read the literature.
## Linearizing the Kalman Filter
The Kalman filter uses linear equations, so it does not work with nonlinear problems. Problems can be nonlinear in two ways. First, the process model might be nonlinear. An object falling through the atmosphere encounters drag which reduces its acceleration. The drag coefficient varies based on the velocity the object. The resulting behavior is nonlinear - it cannot be modeled with linear equations. Second, the measurements could be nonlinear. For example, a radar gives a range and bearing to a target. We use trigonometry, which is nonlinear, to compute the position of the target.
For the linear filter we have these equations for the process and measurement models:
$$\begin{aligned}\dot{\mathbf x} &= \mathbf{Ax} + w_x\\
\mathbf z &= \mathbf{Hx} + w_z
\end{aligned}$$
Where $\mathbf A$ is the systems dynamic matrix. Using the state space methods covered in the **Kalman Filter Math** chapter these equations can be tranformed into
$$\begin{aligned}\bar{\mathbf x} &= \mathbf{Fx} \\
\mathbf z &= \mathbf{Hx}
\end{aligned}$$
where $\mathbf F$ is the *fundamental matrix*. The noise $w_x$ and $w_z$ terms are incorporated into the matrices $\mathbf R$ and $\mathbf Q$. This form of the equations allow us to compute the state at step $k$ given a measurement at step $k$ and the state estimate at step $k-1$. In earlier chapters I built your intuition and minimized the math by using problems describable with Newton's equations. We know how to design $\mathbf F$ based on high school physics.
For the nonlinear model the linear expression $\mathbf{Fx} + \mathbf{Bu}$ is replaced by a nonlinear function $f(\mathbf x, \mathbf u)$, and the linear expression $\mathbf{Hx}$ is replaced by a nonlinear function $h(\mathbf x)$:
$$\begin{aligned}\dot{\mathbf x} &= f(\mathbf x, \mathbf u) + w_x\\
\mathbf z &= h(\mathbf x) + w_z
\end{aligned}$$
You might imagine that we could proceed by finding a new set of Kalman filter equations that optimally solve these equations. But if you remember the charts in the **Nonlinear Filtering** chapter you'll recall that passing a Gaussian through a nonlinear function results in a probability distribution that is no longer Gaussian. So this will not work.
The EKF does not alter the Kalman filter's linear equations. Instead, it *linearizes* the nonlinear equations at the point of the current estimate, and uses this linearization in the linear Kalman filter.
*Linearize* means what it sounds like. We find a line that most closely matches the curve at a defined point. The graph below linearizes the parabola $f(x)=x^2−2x$ at $x=1.5$.
```
import kf_book.ekf_internal as ekf_internal
ekf_internal.show_linearization()
```
If the curve above is the process model, then the dotted lines shows the linearization of that curve for the estimate $x=1.5$.
We linearize systems by taking the derivative, which finds the slope of a curve:
$$\begin{aligned}
f(x) &= x^2 -2x \\
\frac{df}{dx} &= 2x - 2
\end{aligned}$$
and then evaluating it at $x$:
$$\begin{aligned}m &= f'(x=1.5) \\&= 2(1.5) - 2 \\&= 1\end{aligned}$$
Linearizing systems of differential equations is similar. We linearize $f(\mathbf x, \mathbf u)$, and $h(\mathbf x)$ by taking the partial derivatives of each to evaluate $\mathbf F$ and $\mathbf H$ at the point $\mathbf x_t$ and $\mathbf u_t$. We call the partial derivative of a matrix the [*Jacobian*](https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant). This gives us the the discrete state transition matrix and measurement model matrix:
$$
\begin{aligned}
\mathbf F
&= {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}} \\
\mathbf H &= \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}
\end{aligned}
$$
This leads to the following equations for the EKF. I put boxes around the differences from the linear filter:
$$\begin{array}{l|l}
\text{linear Kalman filter} & \text{EKF} \\
\hline
& \boxed{\mathbf F = {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}}} \\
\mathbf{\bar x} = \mathbf{Fx} + \mathbf{Bu} & \boxed{\mathbf{\bar x} = f(\mathbf x, \mathbf u)} \\
\mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q & \mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q \\
\hline
& \boxed{\mathbf H = \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}} \\
\textbf{y} = \mathbf z - \mathbf{H \bar{x}} & \textbf{y} = \mathbf z - \boxed{h(\bar{x})}\\
\mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} & \mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} \\
\mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} & \mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} \\
\mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}} & \mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}}
\end{array}$$
We don't normally use $\mathbf{Fx}$ to propagate the state for the EKF as the linearization causes inaccuracies. It is typical to compute $\bar{\mathbf x}$ using a suitable numerical integration technique such as Euler or Runge Kutta. Thus I wrote $\mathbf{\bar x} = f(\mathbf x, \mathbf u)$. For the same reasons we don't use $\mathbf{H\bar{x}}$ in the computation for the residual, opting for the more accurate $h(\bar{\mathbf x})$.
I think the easiest way to understand the EKF is to start off with an example. Later you may want to come back and reread this section.
## Example: Tracking a Airplane
This example tracks an airplane using ground based radar. We implemented a UKF for this problem in the last chapter. Now we will implement an EKF for the same problem so we can compare both the filter performance and the level of effort required to implement the filter.
Radars work by emitting a beam of radio waves and scanning for a return bounce. Anything in the beam's path will reflects some of the signal back to the radar. By timing how long it takes for the reflected signal to get back to the radar the system can compute the *slant distance* - the straight line distance from the radar installation to the object.
The relationship between the radar's slant range distance $r$ and elevation angle $\epsilon$ with the horizontal position $x$ and altitude $y$ of the aircraft is illustrated in the figure below:
```
ekf_internal.show_radar_chart()
```
This gives us the equalities:
$$\begin{aligned}
\epsilon &= \tan^{-1} \frac y x\\
r^2 &= x^2 + y^2
\end{aligned}$$
### Design the State Variables
We want to track the position of an aircraft assuming a constant velocity and altitude, and measurements of the slant distance to the aircraft. That means we need 3 state variables - horizontal distance, horizonal velocity, and altitude:
$$\mathbf x = \begin{bmatrix}\mathtt{distance} \\\mathtt{velocity}\\ \mathtt{altitude}\end{bmatrix}= \begin{bmatrix}x \\ \dot x\\ y\end{bmatrix}$$
### Design the Process Model
We assume a Newtonian, kinematic system for the aircraft. We've used this model in previous chapters, so by inspection you may recognize that we want
$$\mathbf F = \left[\begin{array}{cc|c} 1 & \Delta t & 0\\
0 & 1 & 0 \\ \hline
0 & 0 & 1\end{array}\right]$$
I've partioned the matrix into blocks to show the upper left block is a constant velocity model for $x$, and the lower right block is a constant position model for $y$.
However, let's practice finding these matrices. We model systems with a set of differential equations. We need an equation in the form
$$\dot{\mathbf x} = \mathbf{Ax} + \mathbf{w}$$
where $\mathbf{w}$ is the system noise.
The variables $x$ and $y$ are independent so we can compute them separately. The differential equations for motion in one dimension are:
$$\begin{aligned}v &= \dot x \\
a &= \ddot{x} = 0\end{aligned}$$
Now we put the differential equations into state-space form. If this was a second or greater order differential system we would have to first reduce them to an equivalent set of first degree equations. The equations are first order, so we put them in state space matrix form as
$$\begin{aligned}\begin{bmatrix}\dot x \\ \ddot{x}\end{bmatrix} &= \begin{bmatrix}0&1\\0&0\end{bmatrix} \begin{bmatrix}x \\
\dot x\end{bmatrix} \\ \dot{\mathbf x} &= \mathbf{Ax}\end{aligned}$$
where $\mathbf A=\begin{bmatrix}0&1\\0&0\end{bmatrix}$.
Recall that $\mathbf A$ is the *system dynamics matrix*. It describes a set of linear differential equations. From it we must compute the state transition matrix $\mathbf F$. $\mathbf F$ describes a discrete set of linear equations which compute $\mathbf x$ for a discrete time step $\Delta t$.
A common way to compute $\mathbf F$ is to use the power series expansion of the matrix exponential:
$$\mathbf F(\Delta t) = e^{\mathbf A\Delta t} = \mathbf{I} + \mathbf A\Delta t + \frac{(\mathbf A\Delta t)^2}{2!} + \frac{(\mathbf A \Delta t)^3}{3!} + ... $$
$\mathbf A^2 = \begin{bmatrix}0&0\\0&0\end{bmatrix}$, so all higher powers of $\mathbf A$ are also $\mathbf{0}$. Thus the power series expansion is:
$$
\begin{aligned}
\mathbf F &=\mathbf{I} + \mathbf At + \mathbf{0} \\
&= \begin{bmatrix}1&0\\0&1\end{bmatrix} + \begin{bmatrix}0&1\\0&0\end{bmatrix}\Delta t\\
\mathbf F &= \begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}
\end{aligned}$$
This is the same result used by the kinematic equations! This exercise was unnecessary other than to illustrate finding the state transition matrix from linear differential equations. We will conclude the chapter with an example that will require the use of this technique.
### Design the Measurement Model
The measurement function takes the state estimate of the prior $\bar{\mathbf x}$ and turn it into a measurement of the slant range distance. We use the Pythagorean theorem to derive:
$$h(\bar{\mathbf x}) = \sqrt{x^2 + y^2}$$
The relationship between the slant distance and the position on the ground is nonlinear due to the square root. We linearize it by evaluating its partial derivative at $\mathbf x_t$:
$$
\mathbf H = \frac{\partial{h(\bar{\mathbf x})}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}
$$
The partial derivative of a matrix is called a Jacobian, and takes the form
$$\frac{\partial \mathbf H}{\partial \bar{\mathbf x}} =
\begin{bmatrix}
\frac{\partial h_1}{\partial x_1} & \frac{\partial h_1}{\partial x_2} &\dots \\
\frac{\partial h_2}{\partial x_1} & \frac{\partial h_2}{\partial x_2} &\dots \\
\vdots & \vdots
\end{bmatrix}
$$
In other words, each element in the matrix is the partial derivative of the function $h$ with respect to the $x$ variables. For our problem we have
$$\mathbf H = \begin{bmatrix}{\partial h}/{\partial x} & {\partial h}/{\partial \dot{x}} & {\partial h}/{\partial y}\end{bmatrix}$$
Solving each in turn:
$$\begin{aligned}
\frac{\partial h}{\partial x} &= \frac{\partial}{\partial x} \sqrt{x^2 + y^2} \\
&= \frac{x}{\sqrt{x^2 + y^2}}
\end{aligned}$$
and
$$\begin{aligned}
\frac{\partial h}{\partial \dot{x}} &=
\frac{\partial}{\partial \dot{x}} \sqrt{x^2 + y^2} \\
&= 0
\end{aligned}$$
and
$$\begin{aligned}
\frac{\partial h}{\partial y} &= \frac{\partial}{\partial y} \sqrt{x^2 + y^2} \\
&= \frac{y}{\sqrt{x^2 + y^2}}
\end{aligned}$$
giving us
$$\mathbf H =
\begin{bmatrix}
\frac{x}{\sqrt{x^2 + y^2}} &
0 &
&
\frac{y}{\sqrt{x^2 + y^2}}
\end{bmatrix}$$
This may seem daunting, so step back and recognize that all of this math is doing something very simple. We have an equation for the slant range to the airplane which is nonlinear. The Kalman filter only works with linear equations, so we need to find a linear equation that approximates $\mathbf H$. As we discussed above, finding the slope of a nonlinear equation at a given point is a good approximation. For the Kalman filter, the 'given point' is the state variable $\mathbf x$ so we need to take the derivative of the slant range with respect to $\mathbf x$. For the linear Kalman filter $\mathbf H$ was a constant that we computed prior to running the filter. For the EKF $\mathbf H$ is updated at each step as the evaluation point $\bar{\mathbf x}$ changes at each epoch.
To make this more concrete, let's now write a Python function that computes the Jacobian of $h$ for this problem.
```
from math import sqrt
def HJacobian_at(x):
""" compute Jacobian of H matrix at x """
horiz_dist = x[0]
altitude = x[2]
denom = sqrt(horiz_dist**2 + altitude**2)
return array ([[horiz_dist/denom, 0., altitude/denom]])
```
Finally, let's provide the code for $h(\bar{\mathbf x})$:
```
def hx(x):
""" compute measurement for slant range that
would correspond to state x.
"""
return (x[0]**2 + x[2]**2) ** 0.5
```
Now let's write a simulation for our radar.
```
from numpy.random import randn
import math
class RadarSim(object):
""" Simulates the radar signal returns from an object
flying at a constant altityude and velocity in 1D.
"""
def __init__(self, dt, pos, vel, alt):
self.pos = pos
self.vel = vel
self.alt = alt
self.dt = dt
def get_range(self):
""" Returns slant range to the object. Call once
for each new measurement at dt time from last call.
"""
# add some process noise to the system
self.vel = self.vel + .1*randn()
self.alt = self.alt + .1*randn()
self.pos = self.pos + self.vel*self.dt
# add measurement noise
err = self.pos * 0.05*randn()
slant_dist = math.sqrt(self.pos**2 + self.alt**2)
return slant_dist + err
```
### Design Process and Measurement Noise
The radar measures the range to a target. We will use $\sigma_{range}= 5$ meters for the noise. This gives us
$$\mathbf R = \begin{bmatrix}\sigma_{range}^2\end{bmatrix} = \begin{bmatrix}25\end{bmatrix}$$
The design of $\mathbf Q$ requires some discussion. The state $\mathbf x= \begin{bmatrix}x & \dot x & y\end{bmatrix}^\mathtt{T}$. The first two elements are position (down range distance) and velocity, so we can use `Q_discrete_white_noise` noise to compute the values for the upper left hand side of $\mathbf Q$. The third element of $\mathbf x$ is altitude, which we are assuming is independent of the down range distance. That leads us to a block design of $\mathbf Q$ of:
$$\mathbf Q = \begin{bmatrix}\mathbf Q_\mathtt{x} & 0 \\ 0 & \mathbf Q_\mathtt{y}\end{bmatrix}$$
### Implementation
`FilterPy` provides the class `ExtendedKalmanFilter`. It works similarly to the `KalmanFilter` class we have been using, except that it allows you to provide a function that computes the Jacobian of $\mathbf H$ and the function $h(\mathbf x)$.
We start by importing the filter and creating it. The dimension of `x` is 3 and `z` has dimension 1.
```python
from filterpy.kalman import ExtendedKalmanFilter
rk = ExtendedKalmanFilter(dim_x=3, dim_z=1)
```
We create the radar simulator:
```python
radar = RadarSim(dt, pos=0., vel=100., alt=1000.)
```
We will initialize the filter near the airplane's actual position:
```python
rk.x = array([radar.pos, radar.vel-10, radar.alt+100])
```
We assign the system matrix using the first term of the Taylor series expansion we computed above:
```python
dt = 0.05
rk.F = eye(3) + array([[0, 1, 0],
[0, 0, 0],
[0, 0, 0]])*dt
```
After assigning reasonable values to $\mathbf R$, $\mathbf Q$, and $\mathbf P$ we can run the filter with a simple loop. We pass the functions for computing the Jacobian of $\mathbf H$ and $h(x)$ into the `update` method.
```python
for i in range(int(20/dt)):
z = radar.get_range()
rk.update(array([z]), HJacobian_at, hx)
rk.predict()
```
Adding some boilerplate code to save and plot the results we get:
```
from filterpy.common import Q_discrete_white_noise
from filterpy.kalman import ExtendedKalmanFilter
from numpy import eye, array, asarray
import numpy as np
dt = 0.05
rk = ExtendedKalmanFilter(dim_x=3, dim_z=1)
radar = RadarSim(dt, pos=0., vel=100., alt=1000.)
# make an imperfect starting guess
rk.x = array([radar.pos-100, radar.vel+100, radar.alt+1000])
rk.F = eye(3) + array([[0, 1, 0],
[0, 0, 0],
[0, 0, 0]]) * dt
range_std = 5. # meters
rk.R = np.diag([range_std**2])
rk.Q[0:2, 0:2] = Q_discrete_white_noise(2, dt=dt, var=0.1)
rk.Q[2,2] = 0.1
rk.P *= 50
xs, track = [], []
for i in range(int(20/dt)):
z = radar.get_range()
track.append((radar.pos, radar.vel, radar.alt))
rk.update(array([z]), HJacobian_at, hx)
xs.append(rk.x)
rk.predict()
xs = asarray(xs)
track = asarray(track)
time = np.arange(0, len(xs)*dt, dt)
ekf_internal.plot_radar(xs, track, time)
```
## Using SymPy to compute Jacobians
Depending on your experience with derivatives you may have found the computation of the Jacobian difficult. Even if you found it easy, a slightly more difficult problem easily leads to very difficult computations.
As explained in Appendix A, we can use the SymPy package to compute the Jacobian for us.
```
import sympy
sympy.init_printing(use_latex=True)
x, x_vel, y = sympy.symbols('x, x_vel y')
H = sympy.Matrix([sympy.sqrt(x**2 + y**2)])
state = sympy.Matrix([x, x_vel, y])
H.jacobian(state)
```
This result is the same as the result we computed above, and with much less effort on our part!
## Robot Localization
It's time to try a real problem. I warn you that this section is difficult. However, most books choose simple, textbook problems with simple answers, and you are left wondering how to solve a real world problem.
We will consider the problem of robot localization. We already implemented this in the **Unscented Kalman Filter** chapter, and I recommend you read it now if you haven't already. In this scenario we have a robot that is moving through a landscape using a sensor to detect landmarks. This could be a self driving car using computer vision to identify trees, buildings, and other landmarks. It might be one of those small robots that vacuum your house, or a robot in a warehouse.
The robot has 4 wheels in the same configuration used by automobiles. It maneuvers by pivoting the front wheels. This causes the robot to pivot around the rear axle while moving forward. This is nonlinear behavior which we will have to model.
The robot has a sensor that measures the range and bearing to known targets in the landscape. This is nonlinear because computing a position from a range and bearing requires square roots and trigonometry.
Both the process model and measurement models are nonlinear. The EKF accommodates both, so we provisionally conclude that the EKF is a viable choice for this problem.
### Robot Motion Model
At a first approximation an automobile steers by pivoting the front tires while moving forward. The front of the car moves in the direction that the wheels are pointing while pivoting around the rear tires. This simple description is complicated by issues such as slippage due to friction, the differing behavior of the rubber tires at different speeds, and the need for the outside tire to travel a different radius than the inner tire. Accurately modeling steering requires a complicated set of differential equations.
For lower speed robotic applications a simpler *bicycle model* has been found to perform well. This is a depiction of the model:
```
ekf_internal.plot_bicycle()
```
In the **Unscented Kalman Filter** chapter we derived these equations:
$$\begin{aligned}
\beta &= \frac d w \tan(\alpha) \\
x &= x - R\sin(\theta) + R\sin(\theta + \beta) \\
y &= y + R\cos(\theta) - R\cos(\theta + \beta) \\
\theta &= \theta + \beta
\end{aligned}
$$
where $\theta$ is the robot's heading.
You do not need to understand this model in detail if you are not interested in steering models. The important thing to recognize is that our motion model is nonlinear, and we will need to deal with that with our Kalman filter.
### Design the State Variables
For our filter we will maintain the position $x,y$ and orientation $\theta$ of the robot:
$$\mathbf x = \begin{bmatrix}x \\ y \\ \theta\end{bmatrix}$$
Our control input $\mathbf u$ is the velocity $v$ and steering angle $\alpha$:
$$\mathbf u = \begin{bmatrix}v \\ \alpha\end{bmatrix}$$
### Design the System Model
We model our system as a nonlinear motion model plus noise.
$$\bar x = f(x, u) + \mathcal{N}(0, Q)$$
Using the motion model for a robot that we created above, we can expand this to
$$\bar{\begin{bmatrix}x\\y\\\theta\end{bmatrix}} = \begin{bmatrix}x\\y\\\theta\end{bmatrix} +
\begin{bmatrix}- R\sin(\theta) + R\sin(\theta + \beta) \\
R\cos(\theta) - R\cos(\theta + \beta) \\
\beta\end{bmatrix}$$
We find The $\mathbf F$ by taking the Jacobian of $f(x,u)$.
$$\mathbf F = \frac{\partial f(x, u)}{\partial x} =\begin{bmatrix}
\frac{\partial f_1}{\partial x} &
\frac{\partial f_1}{\partial y} &
\frac{\partial f_1}{\partial \theta}\\
\frac{\partial f_2}{\partial x} &
\frac{\partial f_2}{\partial y} &
\frac{\partial f_2}{\partial \theta} \\
\frac{\partial f_3}{\partial x} &
\frac{\partial f_3}{\partial y} &
\frac{\partial f_3}{\partial \theta}
\end{bmatrix}
$$
When we calculate these we get
$$\mathbf F = \begin{bmatrix}
1 & 0 & -R\cos(\theta) + R\cos(\theta+\beta) \\
0 & 1 & -R\sin(\theta) + R\sin(\theta+\beta) \\
0 & 0 & 1
\end{bmatrix}$$
We can double check our work with SymPy.
```
import sympy
from sympy.abc import alpha, x, y, v, w, R, theta
from sympy import symbols, Matrix
sympy.init_printing(use_latex="mathjax", fontsize='16pt')
time = symbols('t')
d = v*time
beta = (d/w)*sympy.tan(alpha)
r = w/sympy.tan(alpha)
fxu = Matrix([[x-r*sympy.sin(theta) + r*sympy.sin(theta+beta)],
[y+r*sympy.cos(theta)- r*sympy.cos(theta+beta)],
[theta+beta]])
F = fxu.jacobian(Matrix([x, y, theta]))
F
```
That looks a bit complicated. We can use SymPy to substitute terms:
```
# reduce common expressions
B, R = symbols('beta, R')
F = F.subs((d/w)*sympy.tan(alpha), B)
F.subs(w/sympy.tan(alpha), R)
```
This form verifies that the computation of the Jacobian is correct.
Now we can turn our attention to the noise. Here, the noise is in our control input, so it is in *control space*. In other words, we command a specific velocity and steering angle, but we need to convert that into errors in $x, y, \theta$. In a real system this might vary depending on velocity, so it will need to be recomputed for every prediction. I will choose this as the noise model; for a real robot you will need to choose a model that accurately depicts the error in your system.
$$\mathbf{M} = \begin{bmatrix}\sigma_{vel}^2 & 0 \\ 0 & \sigma_\alpha^2\end{bmatrix}$$
If this was a linear problem we would convert from control space to state space using the by now familiar $\mathbf{FMF}^\mathsf T$ form. Since our motion model is nonlinear we do not try to find a closed form solution to this, but instead linearize it with a Jacobian which we will name $\mathbf{V}$.
$$\mathbf{V} = \frac{\partial f(x, u)}{\partial u} \begin{bmatrix}
\frac{\partial f_1}{\partial v} & \frac{\partial f_1}{\partial \alpha} \\
\frac{\partial f_2}{\partial v} & \frac{\partial f_2}{\partial \alpha} \\
\frac{\partial f_3}{\partial v} & \frac{\partial f_3}{\partial \alpha}
\end{bmatrix}$$
These partial derivatives become very difficult to work with. Let's compute them with SymPy.
```
V = fxu.jacobian(Matrix([v, alpha]))
V = V.subs(sympy.tan(alpha)/w, 1/R)
V = V.subs(time*v/R, B)
V = V.subs(time*v, 'd')
V
```
This should give you an appreciation of how quickly the EKF become mathematically intractable.
This gives us the final form of our prediction equations:
$$\begin{aligned}
\mathbf{\bar x} &= \mathbf x +
\begin{bmatrix}- R\sin(\theta) + R\sin(\theta + \beta) \\
R\cos(\theta) - R\cos(\theta + \beta) \\
\beta\end{bmatrix}\\
\mathbf{\bar P} &=\mathbf{FPF}^{\mathsf T} + \mathbf{VMV}^{\mathsf T}
\end{aligned}$$
This form of linearization is not the only way to predict $\mathbf x$. For example, we could use a numerical integration technique such as *Runge Kutta* to compute the movement
of the robot. This will be required if the time step is relatively large. Things are not as cut and dried with the EKF as for the Kalman filter. For a real problem you have to carefully model your system with differential equations and then determine the most appropriate way to solve that system. The correct approach depends on the accuracy you require, how nonlinear the equations are, your processor budget, and numerical stability concerns.
### Design the Measurement Model
The robot's sensor provides a noisy bearing and range measurement to multiple known locations in the landscape. The measurement model must convert the state $\begin{bmatrix}x & y&\theta\end{bmatrix}^\mathsf T$ into a range and bearing to the landmark. If $\mathbf p$
is the position of a landmark, the range $r$ is
$$r = \sqrt{(p_x - x)^2 + (p_y - y)^2}$$
The sensor provides bearing relative to the orientation of the robot, so we must subtract the robot's orientation from the bearing to get the sensor reading, like so:
$$\phi = \arctan(\frac{p_y - y}{p_x - x}) - \theta$$
Thus our measurement model $h$ is
$$\begin{aligned}
\mathbf z& = h(\bar{\mathbf x}, \mathbf p) &+ \mathcal{N}(0, R)\\
&= \begin{bmatrix}
\sqrt{(p_x - x)^2 + (p_y - y)^2} \\
\arctan(\frac{p_y - y}{p_x - x}) - \theta
\end{bmatrix} &+ \mathcal{N}(0, R)
\end{aligned}$$
This is clearly nonlinear, so we need linearize $h$ at $\mathbf x$ by taking its Jacobian. We compute that with SymPy below.
```
px, py = symbols('p_x, p_y')
z = Matrix([[sympy.sqrt((px-x)**2 + (py-y)**2)],
[sympy.atan2(py-y, px-x) - theta]])
z.jacobian(Matrix([x, y, theta]))
```
Now we need to write that as a Python function. For example we might write:
```
from math import sqrt
def H_of(x, landmark_pos):
""" compute Jacobian of H matrix where h(x) computes
the range and bearing to a landmark for state x """
px = landmark_pos[0]
py = landmark_pos[1]
hyp = (px - x[0, 0])**2 + (py - x[1, 0])**2
dist = sqrt(hyp)
H = array(
[[-(px - x[0, 0]) / dist, -(py - x[1, 0]) / dist, 0],
[ (py - x[1, 0]) / hyp, -(px - x[0, 0]) / hyp, -1]])
return H
```
We also need to define a function that converts the system state into a measurement.
```
from math import atan2
def Hx(x, landmark_pos):
""" takes a state variable and returns the measurement
that would correspond to that state.
"""
px = landmark_pos[0]
py = landmark_pos[1]
dist = sqrt((px - x[0, 0])**2 + (py - x[1, 0])**2)
Hx = array([[dist],
[atan2(py - x[1, 0], px - x[0, 0]) - x[2, 0]]])
return Hx
```
### Design Measurement Noise
It is reasonable to assume that the noise of the range and bearing measurements are independent, hence
$$\mathbf R=\begin{bmatrix}\sigma_{range}^2 & 0 \\ 0 & \sigma_{bearing}^2\end{bmatrix}$$
### Implementation
We will use `FilterPy`'s `ExtendedKalmanFilter` class to implement the filter. Its `predict()` method uses the standard linear equations for the process model. Ours is nonlinear, so we will have to override `predict()` with our own implementation. I'll want to also use this class to simulate the robot, so I'll add a method `move()` that computes the position of the robot which both `predict()` and my simulation can call.
The matrices for the prediction step are quite large. While writing this code I made several errors before I finally got it working. I only found my errors by using SymPy's `evalf` function. `evalf` evaluates a SymPy `Matrix` with specific values for the variables. I decided to demonstrate this technique to you, and used `evalf` in the Kalman filter code. You'll need to understand a couple of points.
First, `evalf` uses a dictionary to specify the values. For example, if your matrix contains an `x` and `y`, you can write
```python
M.evalf(subs={x:3, y:17})
```
to evaluate the matrix for `x=3` and `y=17`.
Second, `evalf` returns a `sympy.Matrix` object. Use `numpy.array(M).astype(float)` to convert it to a NumPy array. `numpy.array(M)` creates an array of type `object`, which is not what you want.
Here is the code for the EKF:
```
from filterpy.kalman import ExtendedKalmanFilter as EKF
from numpy import dot, array, sqrt
class RobotEKF(EKF):
def __init__(self, dt, wheelbase, std_vel, std_steer):
EKF.__init__(self, 3, 2, 2)
self.dt = dt
self.wheelbase = wheelbase
self.std_vel = std_vel
self.std_steer = std_steer
a, x, y, v, w, theta, time = symbols(
'a, x, y, v, w, theta, t')
d = v*time
beta = (d/w)*sympy.tan(a)
r = w/sympy.tan(a)
self.fxu = Matrix(
[[x-r*sympy.sin(theta)+r*sympy.sin(theta+beta)],
[y+r*sympy.cos(theta)-r*sympy.cos(theta+beta)],
[theta+beta]])
self.F_j = self.fxu.jacobian(Matrix([x, y, theta]))
self.V_j = self.fxu.jacobian(Matrix([v, a]))
# save dictionary and it's variables for later use
self.subs = {x: 0, y: 0, v:0, a:0,
time:dt, w:wheelbase, theta:0}
self.x_x, self.x_y, = x, y
self.v, self.a, self.theta = v, a, theta
def predict(self, u=0):
self.x = self.move(self.x, u, self.dt)
self.subs[self.theta] = self.x[2, 0]
self.subs[self.v] = u[0]
self.subs[self.a] = u[1]
F = array(self.F_j.evalf(subs=self.subs)).astype(float)
V = array(self.V_j.evalf(subs=self.subs)).astype(float)
# covariance of motion noise in control space
M = array([[self.std_vel*u[0]**2, 0],
[0, self.std_steer**2]])
self.P = dot(F, self.P).dot(F.T) + dot(V, M).dot(V.T)
def move(self, x, u, dt):
hdg = x[2, 0]
vel = u[0]
steering_angle = u[1]
dist = vel * dt
if abs(steering_angle) > 0.001: # is robot turning?
beta = (dist / self.wheelbase) * tan(steering_angle)
r = self.wheelbase / tan(steering_angle) # radius
dx = np.array([[-r*sin(hdg) + r*sin(hdg + beta)],
[r*cos(hdg) - r*cos(hdg + beta)],
[beta]])
else: # moving in straight line
dx = np.array([[dist*cos(hdg)],
[dist*sin(hdg)],
[0]])
return x + dx
```
Now we have another issue to handle. The residual is notionally computed as $y = z - h(x)$ but this will not work because our measurement contains an angle in it. Suppose z has a bearing of $1^\circ$ and $h(x)$ has a bearing of $359^\circ$. Naively subtracting them would yield a angular difference of $-358^\circ$, whereas the correct value is $2^\circ$. We have to write code to correctly compute the bearing residual.
```
def residual(a, b):
""" compute residual (a-b) between measurements containing
[range, bearing]. Bearing is normalized to [-pi, pi)"""
y = a - b
y[1] = y[1] % (2 * np.pi) # force in range [0, 2 pi)
if y[1] > np.pi: # move to [-pi, pi)
y[1] -= 2 * np.pi
return y
```
The rest of the code runs the simulation and plots the results, and shouldn't need too much comment by now. I create a variable `landmarks` that contains the landmark coordinates. I update the simulated robot position 10 times a second, but run the EKF only once per second. This is for two reasons. First, we are not using Runge Kutta to integrate the differental equations of motion, so a narrow time step allows our simulation to be more accurate. Second, it is fairly normal in embedded systems to have limited processing speed. This forces you to run your Kalman filter only as frequently as absolutely needed.
```
from filterpy.stats import plot_covariance_ellipse
from math import sqrt, tan, cos, sin, atan2
import matplotlib.pyplot as plt
dt = 1.0
def z_landmark(lmark, sim_pos, std_rng, std_brg):
x, y = sim_pos[0, 0], sim_pos[1, 0]
d = np.sqrt((lmark[0] - x)**2 + (lmark[1] - y)**2)
a = atan2(lmark[1] - y, lmark[0] - x) - sim_pos[2, 0]
z = np.array([[d + randn()*std_rng],
[a + randn()*std_brg]])
return z
def ekf_update(ekf, z, landmark):
ekf.update(z, HJacobian=H_of, Hx=Hx,
residual=residual,
args=(landmark), hx_args=(landmark))
def run_localization(landmarks, std_vel, std_steer,
std_range, std_bearing,
step=10, ellipse_step=20, ylim=None):
ekf = RobotEKF(dt, wheelbase=0.5, std_vel=std_vel,
std_steer=std_steer)
ekf.x = array([[2, 6, .3]]).T # x, y, steer angle
ekf.P = np.diag([.1, .1, .1])
ekf.R = np.diag([std_range**2, std_bearing**2])
sim_pos = ekf.x.copy() # simulated position
# steering command (vel, steering angle radians)
u = array([1.1, .01])
plt.figure()
plt.scatter(landmarks[:, 0], landmarks[:, 1],
marker='s', s=60)
track = []
for i in range(200):
sim_pos = ekf.move(sim_pos, u, dt/10.) # simulate robot
track.append(sim_pos)
if i % step == 0:
ekf.predict(u=u)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
std=6, facecolor='k', alpha=0.3)
x, y = sim_pos[0, 0], sim_pos[1, 0]
for lmark in landmarks:
z = z_landmark(lmark, sim_pos,
std_range, std_bearing)
ekf_update(ekf, z, lmark)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
std=6, facecolor='g', alpha=0.8)
track = np.array(track)
plt.plot(track[:, 0], track[:,1], color='k', lw=2)
plt.axis('equal')
plt.title("EKF Robot localization")
if ylim is not None: plt.ylim(*ylim)
plt.show()
return ekf
landmarks = array([[5, 10], [10, 5], [15, 15]])
ekf = run_localization(
landmarks, std_vel=0.1, std_steer=np.radians(1),
std_range=0.3, std_bearing=0.1)
print('Final P:', ekf.P.diagonal())
```
I have plotted the landmarks as solid squares. The path of the robot is drawn with a black line. The covariance ellipses for the predict step are light gray, and the covariances of the update are shown in green. To make them visible at this scale I have set the ellipse boundary at 6$\sigma$.
We can see that there is a lot of uncertainty added by our motion model, and that most of the error in in the direction of motion. We determine that from the shape of the blue ellipses. After a few steps we can see that the filter incorporates the landmark measurements and the errors improve.
I used the same initial conditions and landmark locations in the UKF chapter. The UKF achieves much better accuracy in terms of the error ellipse. Both perform roughly as well as far as their estimate for $\mathbf x$ is concerned.
Now let's add another landmark.
```
landmarks = array([[5, 10], [10, 5], [15, 15], [20, 5]])
ekf = run_localization(
landmarks, std_vel=0.1, std_steer=np.radians(1),
std_range=0.3, std_bearing=0.1)
plt.show()
print('Final P:', ekf.P.diagonal())
```
The uncertainly in the estimates near the end of the track are smaller. We can see the effect that multiple landmarks have on our uncertainty by only using the first two landmarks.
```
ekf = run_localization(
landmarks[0:2], std_vel=1.e-10, std_steer=1.e-10,
std_range=1.4, std_bearing=.05)
print('Final P:', ekf.P.diagonal())
```
The estimate quickly diverges from the robot's path after passing the landmarks. The covariance also grows quickly. Let's see what happens with only one landmark:
```
ekf = run_localization(
landmarks[0:1], std_vel=1.e-10, std_steer=1.e-10,
std_range=1.4, std_bearing=.05)
print('Final P:', ekf.P.diagonal())
```
As you probably suspected, one landmark produces a very bad result. Conversely, a large number of landmarks allows us to make very accurate estimates.
```
landmarks = array([[5, 10], [10, 5], [15, 15], [20, 5], [15, 10],
[10,14], [23, 14], [25, 20], [10, 20]])
ekf = run_localization(
landmarks, std_vel=0.1, std_steer=np.radians(1),
std_range=0.3, std_bearing=0.1, ylim=(0, 21))
print('Final P:', ekf.P.diagonal())
```
### Discussion
I said that this was a real problem, and in some ways it is. I've seen alternative presentations that used robot motion models that led to simpler Jacobians. On the other hand, my model of the movement is also simplistic in several ways. First, it uses a bicycle model. A real car has two sets of tires, and each travels on a different radius. The wheels do not grip the surface perfectly. I also assumed that the robot responds instantaneously to the control input. Sebastian Thrun writes in *Probabilistic Robots* that this simplified model is justified because the filters perform well when used to track real vehicles. The lesson here is that while you have to have a reasonably accurate nonlinear model, it does not need to be perfect to operate well. As a designer you will need to balance the fidelity of your model with the difficulty of the math and the CPU time required to perform the linear algebra.
Another way in which this problem was simplistic is that we assumed that we knew the correspondance between the landmarks and measurements. But suppose we are using radar - how would we know that a specific signal return corresponded to a specific building in the local scene? This question hints at SLAM algorithms - simultaneous localization and mapping. SLAM is not the point of this book, so I will not elaborate on this topic.
## UKF vs EKF
In the last chapter I used the UKF to solve this problem. The difference in implementation should be very clear. Computing the Jacobians for the state and measurement models was not trivial despite a rudimentary motion model. A different problem could result in a Jacobian which is difficult or impossible to derive analytically. In contrast, the UKF only requires you to provide a function that computes the system motion model and another for the measurement model.
There are many cases where the Jacobian cannot be found analytically. The details are beyond the scope of this book, but you will have to use numerical methods to compute the Jacobian. That undertaking is not trivial, and you will spend a significant portion of a master's degree at a STEM school learning techniques to handle such situations. Even then you'll likely only be able to solve problems related to your field - an aeronautical engineer learns a lot about Navier Stokes equations, but not much about modelling chemical reaction rates.
So, UKFs are easy. Are they accurate? In practice they often perform better than the EKF. You can find plenty of research papers that prove that the UKF outperforms the EKF in various problem domains. It's not hard to understand why this would be true. The EKF works by linearizing the system model and measurement model at a single point, and the UKF uses $2n+1$ points.
Let's look at a specific example. Take $f(x) = x^3$ and pass a Gaussian distribution through it. I will compute an accurate answer using a monte carlo simulation. I generate 50,000 points randomly distributed according to the Gaussian, pass each through $f(x)$, then compute the mean and variance of the result.
The EKF linearizes the function by taking the derivative to find the slope at the evaluation point $x$. This slope becomes the linear function that we use to transform the Gaussian. Here is a plot of that.
```
import kf_book.nonlinear_plots as nonlinear_plots
nonlinear_plots.plot_ekf_vs_mc()
```
The EKF computation is rather inaccurate. In contrast, here is the performance of the UKF:
```
nonlinear_plots.plot_ukf_vs_mc(alpha=0.001, beta=3., kappa=1.)
```
Here we can see that the computation of the UKF's mean is accurate to 2 decimal places. The standard deviation is slightly off, but you can also fine tune how the UKF computes the distribution by using the $\alpha$, $\beta$, and $\gamma$ parameters for generating the sigma points. Here I used $\alpha=0.001$, $\beta=3$, and $\gamma=1$. Feel free to modify them to see the result. You should be able to get better results than I did. However, avoid over-tuning the UKF for a specific test. It may perform better for your test case, but worse in general.
| true |
code
| 0.663369 | null | null | null | null |
|
# Functions (Magic spell boxes)
Functions are magic spell boxes, which store their own sleeping princesses and incantations.\
You can cast the spell with ()\
Casting the spell with () creates it own sub realm, which disappers after the sub realm returns an object to the main realm at the end of the spell\
The sleeping princess in the spell box might share the same name with a princess in the main realm but they are not the same princesses.
```
alice = 400
bella = 500
caroline = 600
daisy = 700
```
Now main realm has 4 princesses.
```
alice, bella, caroline, daisy
def add(alice, bella):
return alice+bella
```
Now the main realm has 4 princesses and 1 magic spell box called add. All are shown as below
```
alice, bella, caroline, daisy, add
```
Within the magic spell box called **add** we have 2 more sleeping princesses. These are not the same princesses as in main realm.
These are a different set of alice and bella and they are sleeping. They only wake up when the spell is cast.
When the spell is cast, Genie will need to give something for the princess to hold.
That could be objects directly such as **add(1,2)** or it could be objects in the main realm represented by the name of their princesses such as **add(alice, bella)**
```
add(1,2)
add(alice, bella)
```
In the above examples, the alice and bella are simply holding the objects, what their name sakes in main realm are holding, which are number objects 400 and 500 respectively.
```
add(caroline, daisy)
```
In the above example they are holding, what the other 2 princesses in the main realm are holding.\
Once the spell is cast and all the incantations in the spell are completed, the magic spell box returns something and the subrealm disappears, whcih means the the princesses in the magic spell box go back to sleep again.\
So after all this, in the main realm we still have 4 princesses and a magic spell box\
SO What happened to the 900 and 1300 number objects?
They were simply recycled as we havn't asked for a new princess or one of the existing princess to hold on to them.\
But if we
```
alice, bella, caroline, daisy, add
```
So after all this, in the main realm we still have 4 princesses and a magic spell box add
```
add
alice, bella, caroline, daisy, add
```
Now there is bit a twist, we have 2 more magic boxes called multiply and divide.
```
def multiply(alice, bella):
caroline = alice * bella
return caroline
```
This spell has 3 sleeping princess, who have similar names to main relam sprincess and not the same. They are currently sleeping.
```
def divide(alice, bella):
dot = alice / bella
return daisy
```
This spell has 3 more sleeping princess, who have similar names to main relam sprincess and princesses in other magic boxes but again they are not the same. They are again are currently sleeping.
```
multiply(alice, bella)
divide(alice, bella)
```
Now how many princes are there in the realm what are they holding?
```
alice, bella, caroline, daisy, add, multiply, divide
```
Where are the caroline and dot form the multiply and divide subrealms respectively.
They have diasspered, when their disappered after the relam reurned the object.
So, where are the objects 200000 and 0.8 which were retuned to the main realm living.
Well, these were recycled by Geneie as we have not asked Genie to give it to any princess
```
caroline = multiply(alice, bella)
gauri = divide(alice,bella)
alice, bella, caroline, daisy, gauri, add, multiply, divide
```
Let's have a look at another magic box
```
def surprise_subtract(alice , bella):
helena = 10
return alice - bella - helena
```
This magic box has 3 princesses. 2 of them are sleeping and they will need to be given some objects to hold, when the spell is cast and a sub realm is built.
The other princess helena is already awake as he is holding a number object, but she is in a limbo. She does not have a realm to live in, until teh spell is cast. She just lives in the box, with her object unseen by others, until her realm is cast. She goes back into the box with her object, after the spell is completed.
```
surprise_subtract(500, 400)
# Here the princess in the box alice and bella are given number objects directly
surprise_subtract(bella, alice)
# Here the princesses alice and bella in the magic box are holding
# the objects what princesses bella and alice in the main realm are holding respectively
```
| true |
code
| 0.465266 | null | null | null | null |
|
## Manual publication DB insertion from raw text using syntax features
### Publications and conferences of Dr. POP F. Horia, Profesor Universitar
#### http://www.cs.ubbcluj.ro/~hfpop
#### Text copied from professor's dynamic webpage.
```
text = """
Principal component analysis versus fuzzy principal component analysis: a case study: the quality of Danube water (1985–1996)
C Sarbu, HF Pop
Talanta 65 (5), 1215-1220 185 2005
Robust Fuzzy Principal Component Analysis (FPCA). A Comparative Study Concerning Interaction of Carbon− Hydrogen Bonds with Molybdenum− Oxo Bonds
TR Cundari, C Sârbu, HF Pop
Journal of chemical information and computer sciences 42 (6), 1363-1369 61 2002
A new fuzzy regression algorithm
HF Pop, C Sârbu
Analytical chemistry 68 (5), 771-778 57 1996
Introducere în algoritmi
TH Cormen, CE Leiserson, RR Rivest, HF Pop, S Motogna, PA Blaga
Computer Libris Agora 38 2004
A fuzzy classification of the chemical elements
HF Pop, C Sârbu, O Horowitz, D Dumitrescu
Journal of chemical information and computer sciences 36 (3), 465-482 32 1996
Fuzzy soft-computing methods and their applications in chemistry
C Sârbu, HF Pop
Reviews in Computational Chemistry 20, 249 26 2004
A fuzzy divisive hierarchical clustering algorithm for the optimal choice of sets of solvent systems
D Dumitrescu, C S [acaron] rbu, H Pop
Analytical letters 27 (5), 1031-1054 26 1994
Classical and fuzzy principal component analysis of some environmental samples concerning the pollution with heavy metals
HF Pop, JW Einax, C Sârbu
Chemometrics and Intelligent Laboratory Systems 97 (1), 25-32 25 2009
Structural Analysis of Transition Metal β-X Substituent Interactions. Toward the Use of Soft Computing Methods for Catalyst Modeling
TR Cundari, J Deng, HF Pop, C Sârbu
Journal of chemical information and computer sciences 40 (4), 1052-1061 24 2000
A study of Roman pottery (terra sigillata) using hierarchical fuzzy clustering
HF Pop, D Dumitrescu, C Sǎrbu
Analytica chimica acta 310 (2), 269-279 22 1995
Principal components analysis based on a fuzzy sets approach
H Pop
Mij 1 (2), 1 21 2001
Learning grammar weights using genetic algorithms
I Schröder, HF Pop, W Menzel, KA Foth
IN PROCEEDINGS RECENT ADVANCES IN NATURAL LANGUAGE PROCESSING, RANLP-2001 20 2001
Fuzzy clustering analysis of the first 10 MEIC chemicals
C Sârbu, HF Pop
Chemosphere 40 (5), 513-520 20 2000
A new component selection algorithm based on metrics and fuzzy clustering analysis
C Şerban, A Vescan, HF Pop
International Conference on Hybrid Artificial Intelligence Systems, 621-628 16 2009
The fuzzy hierarchical cross-clustering algorithm. Improvements and comparative study
HF Pop, C Sârbu
Journal of chemical information and computer sciences 37 (3), 510-516 16 1997
Fuzzy robust estimation of central location
C Sârbu, HF Pop
Talanta 54 (1), 125-130 15 2001
A Fuzzy cross-classification of the chemical elements, based on their physical, chemical, and structural features
C Sârbu, O Horowitz, HF Pop
Journal of chemical information and computer sciences 36 (6), 1098-1108 15 1996
Fuzzy hierarchical cross-classification of Greek muds
D Dumitrescu, HF Pop, C Sarbu
Journal of chemical information and computer sciences 35 (5), 851-857 15 1995
GFBA: a biclustering algorithm for discovering value-coherent biclusters
X Fei, S Lu, HF Pop, LR Liang
International Symposium on Bioinformatics Research and Applications, 1-12 14 2007
Degenerate and non-degenerate convex decomposition of finite fuzzy partitions—I
D Dumitrescu, HF Pop
Fuzzy sets and systems 73 (3), 365-376 14 1995
Data analysis with fuzzy sets: a short survey
HF Pop
Studia Universitatis Babes-Bolyai, Series Informatica 49 (2), 111-122 12 2004
A study of dependence of software attributes using data analysis techniques
M Frentiu, HF Pop
Studia Univ. Babes-Bolyai, Series Informatica 2, 53-66 12 2002
Selecting and optimally combining the systems of solvents in the thin film cromatography using the fuzzy sets theory
C Sârbu, D Dumitrescu, HF Pop
Rev. Chim.(Bucharest) 44, 450-459 12 1993
Software quality assessment using a fuzzy clustering approach
C Serban, HF POP
Studia Universitas Babes-Bolyai, Seria Informatica 53 (2), 27-38 9 2008
Evolutionary algorithms for the component selection problem
A Vescan, C Grosan, HF Pop
2008 19th International workshop on database and expert systems applications … 8 2008
Tehnici de Inteligenta Artificiala. Abordari bazate pe Agenti Inteligenti
G Serban, HF Pop
Ed. Mediamira, Cluj-Napoca 8 2004
Tehnici de Inteligenta Artificiala. Abordari bazate pe Agenti Inteligenti
G Serban, HF Pop
Ed. Mediamira, Cluj-Napoca 8 2004
An experiment on incremental analysis using robust parsing techniques
KA Foth, W Menzel, HF Pop, I Schroder
COLING 2000 Volume 2: The 18th International Conference on Computational … 8 2000
Intelligent Systems in Classification Problems
HF Pop
Ph. D. thesis," Babeş-Bolyai" University, Faculty of Mathematics and … 8 1995
A conceptual framework for component-based system metrics definition
C Şerban, A Vescan, HF Pop
9th RoEduNet IEEE International Conference, 73-78 7 2010
Intelligent disease identification based on discriminant analysis of clinical data
C Sarbu, HF Pop, R Elekes, G Covaci
Rev Chimie 59, 1237-1241 7 2008
The component selection problem as a constraint optimization problem
A Vescan, HF Pop
Software Engineering Techniques in Progress, Wroclaw University of … 7 2008
Learning weights for a natural language grammar using genetic algorithms
I Schröder, HF Pop, W Menzel, KA Foth
7 2002
Assessment of heart disease using fuzzy classification techniques
HF Pop, TL Pop, C Sârbu
TheScientificWorldJournal 1, 369-390 7 2001
A new fuzzy discriminant analysis method
HF Pop, C Sârbu
natural science (chemometrics, environmental sciences, biology, geology, etc … 6 2013
An experiment in incremental parsing using weighted constraints
K Foth, W Menzel, HF Pop, I Schröder
Proceedings of the 18th International Conference on Computational … 6 2000
Degenerate and non-degenerate convex decomposition of finite fuzzy partitions (II)
D Dumitrescu, HF Pop
Fuzzy sets and systems 96 (1), 111-118 6 1998
A formal model for component-based system assessment
C Serban, A Vescan, HF Pop
2010 Second International Conference on Computational Intelligence … 5 2010
An adaptive fuzzy agent clustering algorithm for search engines
RD Gaceanu, HF Pop
MACS2010: Proceedings of the 8th Joint Conference on Mathematics and … 5 2010
A study of licence examination results using Fuzzy Clustering techniques
M Frentiu, HF Pop
Babes-Bolyai University, Faculty of Mathematics and Computer Science … 5 2001
Fuzzy classification of the first 10 MEIC
C Sârbu, H Pop
Chemosphere 40 (513), e520 5 2000
Fuzzy regression. II. Outliers cases
HF Pop, C Sârbu
Revista de Chimie 48 (10-11), 888-891 5 1997
SAADI: Software for fuzzy clustering and related fields
HF Pop
Studia Universitatis Babes-Bolyai, Series Informatica 41 (1), 69-80 5 1996
Recognizing Emotions in Short Texts.
O Serban, A Pauchet, HF Pop
ICAART (1), 477-480 4 2012
An incremental ASM-based fuzzy clustering algorithm
RD Gaceanu, HF Pop
Informatics, 198-204 4 2011
A context-aware ASM-based clustering algorithm
RD GACEANU, HF Pop
Studia Universitatis Babes-Bolyai Series Informatica 56 (2), 55-61 4 2011
Automatic configuration for the component selection problem
A Vescan, HF Pop
Proceedings of the 5th international conference on Soft computing as … 4 2008
Component selection based on fuzzy clustering analysis
C Serban, A Vescan, HF Pop
Creative Mathematics and Informatics 17 (3), 505-510 4 2008
On Individual Projects in Software Engineering Education
M Frentiu, I Lazar, HF Pop
Studia Universitatis Babes-Bolyai Series Informatica 48 (2), 83-94 4 2003
Development of robust fuzzy regression techniques using a fuzzy clustering approach
HF Pop
Pure Mathematics and Applications 14 (3), 221-232 4 2003
Fuzzy classification and comparison of some Romanian and American coals
C Sârbu, HF Pop
MATCH-Communications in Mathematical and in Computer Chemistry, 387-400 4 2001
Fuzzy regression. 1. The heteroscedastic case
C Sârbu, H Pop
REVISTA DE CHIMIE 48 (8), 732-737 4 1997
DISCOVERING PATTERNS IN DATA USING ORDINAL DATA ANALYSIS.
AM COROIU, RD GĂCEANU, HF POP
Studia Universitatis Babes-Bolyai, Informatica 61 (1) 3 2016
Prognostic Factors in Liver Failure in Children by Discriminant Analysis of Clinical Data. A Chemometric Approach
HF Pop, C Sarbu, A Stefanescu, A Bizo, TL Pop
STUDIA UNIVERSITATIS BABES-BOLYAI CHEMIA 60 (2), 101-108 3 2015
Constraint optimization-based component selection problem
A Vescan, HF Pop
Studia Univ, Babes-Bolyai, Informatica 53 (2) 3 2008
Education for engineering students-The case of logic
H Pop, L Pop
Proceedings 6th International Conference on Electromechanical and Power … 3 2007
Tracking mistakes in software measurement using fuzzy data analysis
HF Pop, M Frenţiu
The 4-th International Conference RoEduNet Romania (Sovata, Târgu-Mures, 150-157 3 2005
Sisteme inteligente în probleme de clasificare
HF Pop
Mediamira 3 2004
Programare în inteligenţa artificială: LISP si PROLOG
HF Pop, G Şerban
Editura Albastră 3 2003
Rational Classification of the Chemical Elements
O Horovitz, C Sârbu, HF Pop
Dacia Publisher House, Cluj-Napoca 3 2000
Classification procedure for selectivity control in acrylonitrile electroreduction
DA Lowy, D Dumitrescu, L Oniciu, HF Pop, S Kiss-Szetsi
The 7th International Forum Process Analytical Chemistry (Process Analysis … 3 1993
Improving movement analysis in physical therapy systems based on kinect interaction
AD Călin, H F. Pop, R F. Boian
Proceedings of the 31st International BCS Human Computer Interaction … 2 2017
A fuzzy incremental clustering approach to hybrid data discovery
RD Gaceanu, HF Pop
Acta electrotechnica et informatica 12 (2), 16 2 2012
An incremental approach to the set covering problem
RD Gaceanu, HF Pop
Studia Universitatis Babes-Bolyai Series Informatica 47 (2), 61-72 2 2012
AP041 Joining the EuReCA–The Romanian Registry on Cardiac arrest–a year later
H Sabau, O Tudorache, H Pop, V Georgescu, V Strambu, I Dimitriu, ...
Resuscitation 82, S19 2 2011
A fuzzy clustering algorithm for dynamic environments
RD Gaceanu, HF POP
KEPT2011: Knowledge Engineering Principles and Techniques, Selected Papers … 2 2011
Romanian registry on cardiac arrest—A piece in the puzzle-Romanian contribution in the EuReCA project
V Georgescu, H Pop, O Tudorache, H Sabau, C Ciontu, I Dimitriu, ...
Resuscitation 81 (2), S39 2 2010
Effort Estimation by Analogy based on Soft Computing Methods, KEPT2009: Knowledge Engineering: Principles and Techniques, Selected Papers
HF Pop, M Frenţiu
Cluj University Press, Cluj-Napoca 2 2009
A New Component Selection Algorithm Based on Metrics and Fuzzy Clustering
C Serban, A Vescan, HF Pop
Creative Mathematics and Informatics 1 (3), 505-510 2 2009
Fundamentals of Programming
M Frenţiu, HF Pop
Cluj University Press 2 2006
Improving Virtual Team Performance: An Empirical Approach
D Radoiu, C Enachescu, HF Pop
A research paper of Sysgenic Sourcing, Available at sourcing. sysgenic. com … 2 2006
Supervised fuzzy classifiers
HF Pop
Studia Universitatis Babes-Bolyai, Series Mathematica 40 (3), 89-100 2 1995
OPTIMUM SELECTIONS AND COMBINATION OF SOLVENT SYSTEMS IN THIN-LAYER CHROMATOGRAPHY, USING THE FUZZY SET-THEORY
C Sârbu, D Dumitrescu, H Pop
Revista de Chimie 44 (5), 450-459 2 1993
Preliminary measurements in identifying design flaws
C SERBAN, A VESCAN, HF POP
Studia Universitatis Babes-Bolyai, Series Informatica 62 (1), 60-74 1 2017
AN AGENT BASED APPROACH FOR PARALLEL CONSTRAINT VERIFICATION
RD Gaceanu, HF Pop, SA Sotoc
Studia Universitatis Babes-Bolyai, Series Informatica 58 (3), 5-16 1 2013
An agent based approach for parallel constraint verification
RD Gaceanu, HF Pop, SA SOTOC
Studia Universitatis Babes-Bolyai Series Informatica 58 (3), 5-16 1 2013
Stereomatching using radiometric invariant measures
A Miron, S Ainouz, A Rogozan, A Bensrhair, HF POP
UNIVERSITATIS BABEŞ-BOLYAI INFORMATICA, 91 1 2011
Improving similarity join algorithms using fuzzy clustering technique
L Tan, F Fotouhi, W Grosky, HF Pop, N Mouaddib
2009 IEEE International Conference on Data Mining Workshops, 545-550 1 2009
OVERVIEW OF FUZZY METHODS FOR EFFORT ESTIMATION BY ANALOGY.
M Frenţiu, HF Pop
Studia Universitatis Babes-Bolyai, Informatica 1 2009
Lighting quality-component of indoor environment
F Pop, HF Pop, M Pop
LUX Eur, 499-506 1 2009
Applications of principal components methods
HF Pop, M Frentiu
2008 First International Conference on Complexity and Intelligence of the … 1 2008
Programming Fundamentals
M Frenţiu, HF Pop, G Şerban
Presa Universitară Clujeană 1 2006
Distance Learning and Supporting Tools at Babeş-Bolyai University
FM Boian, RF Boian, A Vancea, HF Pop
1
CHARACTERIZATION AND CLASSIFICATION OF MEDICINAL PLANT EXTRACTS ACCORDING TO THEIR ANTIOXIDANT ACTIVITY USING HIGH-PERFORMANCE LIQUID CHROMATOGRAPHY AND MULTIVARIATE ANALYSIS.
IM Simion, AC MOȚ, RD GĂCEANU, HF Pop, C Sarbu
Studia Universitatis Babes-Bolyai, Chemia 65 (1) 2020
A Comparison Study of Similarity Measures in Rough Sets Clustering
A Szederjesi-Dragomir, RD Găceanu, HF Pop, C Sârbu
2019 IEEE 15th International Scientific Conference on Informatics, 000037-000042 2019
A Machine Learning Perspective for Order Reduction in Electrical Motors Modeling
M Nutu, HF Pop, C Martis, SI Cosman, AM Nicorici
2019 21st International Symposium on Symbolic and Numeric Algorithms for … 2019
Principal Component Analysis for Computation of the Magnetization Characteristics of Synchronous Reluctance Machine
M Nutu, R Martis, HF Pop, C Martis
2018 AEIT International Annual Conference, 1-6 2018
SPECTROPHOTOMETRIC CHARACTERIZATION OF ROUMANIAN MEDICINAL HERBS ASSISTED BY ROBUST CHEMOMETRICS EXPERTISE
IM Simion, HF POPb, C Sarbu
Rev. Roum. Chim 63 (5-6), 489-496 2018
The Best Writing on Mathematics 2015
HF Pop
STUDIA UNIVERSITATIS BABES-BOLYAI MATHEMATICA 61 (1), 123-124 2016
PROGNOSTIC FACTORS IN LIVER FAILURE IN CHILDREN BY DISCRIMINANT ANALYSIS OF CLINICAL DATA. A CHEMOMETRIC APPROACH.
C SÂRBU, A BIZO, TL POP, HF POP, ANA ŞTEFANESCU
Studia Universitatis Babes-Bolyai, Chemia 60 2015
The Best Writing on Mathematics 2014
HF Pop
STUDIA UNIVERSITATIS BABES-BOLYAI MATHEMATICA 59 (3), 393-394 2014
Medical procedure breaches detection using a fuzzy clustering approach
R Găceanu, H Pop
Open Computer Science 4 (3), 127-140 2014
An incremental clustering approach to the set covering problem
RD Gaceanu, HF Pop
Zoltán Csörnyei (Ed.), 45 2012
Automatic criteria-based configuration for the component selection problem
A Vescan, HF Pop
International Journal of Computer Information Systems and Industrial … 2012
Recent developments in fuzzy statistical analysis
HF Pop
MaCS’10, 47 2010
PROCESSING ECG DATA USING MULTIVARIATE DATA ANALYSIS
MV PUŞCĂ, HF POP, NM ROMAN, V IANCU
ACADEMY OF ROMANIAN SCIENTISTS, 23 2010
M. Effort estimation by analogy based on soft computing methods
HF POP, M FRENTIU
KEPT 2009 International Conference Knowledge Engineering Principles and … 2009
Knowledge Engineering: Principles and Techniques: KEPT 2009: Cluj-Napoca, July 2-4, 2009
M Frențiu, HF Pop
Cluj University Press 2009
Iluminat eficient energetic în locuinţe
F Pop, D Beu, HF Pop, C Ciugudeanu
Revista Română de Informatică şi Automatică 18 (3), 101-112 2008
A Tutorial on Object-Oriented Functional Programming
HF Pop
Central European Functional Programming School, 228-249 2007
ON SOFTWARE ATTRIBUTES RELATIONSHIP USING A NEW FUZZY C-BIPARTITIONING METHOD
HF Pop, M Frentiu
Studia Universitatis Babes-Bolyai, Informatica Special Issue, 219-226 2007
Management of web pages using XML documents
L T ÂMBULEA, HF POP
Studia Universitatis Babes-Bolyai, Informatica Special Issue, 236-243 2007
Desired employment/Occupational field
N Italian, G Male
Cell 39, 081678652 2003
Appraisal of indoor lighting systems quality
M POP, HF POP, F POP
Ingineria Iluminatului, 37 2001
Papers from the 1999 Symposium on Mathematical Chemistry, Duluth, MN, May 1999-MOLECULAR MODELING-Structural Analysis of Transition Metal bX Substituent Interactions. Toward …
TR Cundari, J Deng, HF Pop, C Sarbu
Journal of Chemical Information and Computer Sciences 40 (4), 1052-1061 2000
Recognition of the forms applied to chemical elements
O Horowitz, C Sarbu, HF Pop
REVISTA DE CHIMIE 51 (1), 17-29 2000
REGRESIE FUZZY. II. CAZUL PUNCTELOR EXTREME (OUTLIERS)
HF POP, C SARBU
Revista de chimie 48 (10-11), 888-891 1997
REGRESIE FUZZY. I. CAZUL HETEROSCEDASTIC
C SARBU, H POP
Revista de chimie 48 (8), 732-737 1997
Desired employment Occupational field
F Horia
Education and training 1995 1992
KEPT2013: THE FOURTH INTERNATIONAL CONFERENCE ON KNOWLEDGE ENGINEERING, PRINCIPLES AND TECHNIQUES
M FRENTIU, HF POP, S MOTOGNA
UNIVERSITATIS BABEŞ-BOLYAI INFORMATICA, 5
Object-oriented logic programming
HF Pop, MM Dogaru
LSD–Lighting Systems Desing–un program pentru proiectarea sistemelor de iluminat
F Horia, POP Florin
SAADI: Software for Fuzzy Clustering and Related Fields
F Horia
Residential Energy Efficient Lighting
POP Florin, F Horia
A guide for writing a scientific paper
M Frenţiu, HF Pop
Metode de recunoastere a formelor bazate pe agenti
UBB Îndrumator, HF Pop
THE FIRST INTERNATIONAL CONFERENCE ON KNOWLEDGE ENGINEERING PRINCIPLES AND TECHNIQUES (KEPT 2007)
D TATAR, HF Pop, M FRENTIU, D Dumitrescu
COMMON MISTAKES IN WRITING A SCIENTIFIC PAPER
M FRENTIU, HF POP
"""
mylines = []
ctr = 0
title = ""
authors = ""
affiliations = ""
date = ""
for line in text.split('\n')[1:]:
# print(ctr, line)
if ctr == 0:
title = line
elif ctr == 1:
authors = line
elif ctr == 2:
affiliations = line.split('\t')[0]
date = line.split('\t')[-1]
ctr += 1
if ctr == 3:
mylines.append((title, authors, affiliations, date))
print(mylines[-1])
ctr = 0
title = ""
authors = ""
affiliations = ""
date = ""
for i, paper in enumerate(mylines):
print(i, paper[0])
errors_index = [113, 111]
for i, paper in enumerate(mylines):
if i in errors_index:
print(i, paper)
#mylines[i][0] = mylines[i][1]
```
# DB Storage (TODO)
Time to store the entries in the `papers` DB table.

```
import mariadb
import json
with open('../credentials.json', 'r') as crd_json_fd:
json_text = crd_json_fd.read()
json_obj = json.loads(json_text)
credentials = json_obj["Credentials"]
username = credentials["username"]
password = credentials["password"]
table_name = "publications_cache"
db_name = "ubbcluj"
mariadb_connection = mariadb.connect(user=username, password=password, database=db_name)
mariadb_cursor = mariadb_connection.cursor()
for paper in mylines:
title = ""
authors = ""
pub_date = ""
affiliations = ""
try:
title = paper[0].lstrip()
except:
pass
try:
authors = paper[1].lstrip()
except:
pass
try:
affiliations = paper[2].lstrip()
except AttributeError:
pass
try:
pub_date = paper[3].lstrip()
pub_date = str(pub_date) + "-01-01"
if len(pub_date) != 10:
pub_date = ""
except:
pass
insert_string = "INSERT INTO {0} SET ".format(table_name)
insert_string += "Title=\'{0}\', ".format(title)
insert_string += "ProfessorId=\'{0}\', ".format(5)
if pub_date != "":
insert_string += "PublicationDate=\'{0}\', ".format(str(pub_date))
insert_string += "Authors=\'{0}\', ".format(authors)
insert_string += "Affiliations=\'{0}\' ".format(affiliations)
print(insert_string)
print(paper)
try:
mariadb_cursor.execute(insert_string)
except mariadb.ProgrammingError as pe:
print("Error")
raise pe
except mariadb.IntegrityError:
continue
mariadb_connection.close()
```
# Conclusion
### In the end, the DB only required ~1 manual modifications with this code.
This was first stored in a DB cache table which is a duplicate of the main, reviewed, then inserted in the main table.

| true |
code
| 0.678114 | null | null | null | null |
|
# Overview
This notebook contains all experiment results exhibited in our paper.
```
%matplotlib inline
import glob
import numpy as np
import pandas as pd
import json
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib
sns.set(style='white')
matplotlib.rcParams['pdf.fonttype'] = 42
matplotlib.rcParams['ps.fonttype'] = 42
from tqdm.auto import tqdm
from joblib import Parallel, delayed
def func(x, N=80):
ret = x.ret.copy()
x = x.rank(pct=True)
x['ret'] = ret
diff = x.score.sub(x.label)
r = x.nlargest(N, columns='score').ret.mean()
r -= x.nsmallest(N, columns='score').ret.mean()
return pd.Series({
'MSE': diff.pow(2).mean(),
'MAE': diff.abs().mean(),
'IC': x.score.corr(x.label),
'R': r
})
ret = pd.read_pickle("data/ret.pkl").clip(-0.1, 0.1)
def backtest(fname, **kwargs):
pred = pd.read_pickle(fname).loc['2018-09-21':'2020-06-30'] # test period
pred['ret'] = ret
dates = pred.index.unique(level=0)
res = Parallel(n_jobs=-1)(delayed(func)(pred.loc[d], **kwargs) for d in dates)
res = {
dates[i]: res[i]
for i in range(len(dates))
}
res = pd.DataFrame(res).T
r = res['R'].copy()
r.index = pd.to_datetime(r.index)
r = r.reindex(pd.date_range(r.index[0], r.index[-1])).fillna(0) # paper use 365 days
return {
'MSE': res['MSE'].mean(),
'MAE': res['MAE'].mean(),
'IC': res['IC'].mean(),
'ICIR': res['IC'].mean()/res['IC'].std(),
'AR': r.mean()*365,
'AV': r.std()*365**0.5,
'SR': r.mean()/r.std()*365**0.5,
'MDD': (r.cumsum().cummax() - r.cumsum()).max()
}, r
def fmt(x, p=3, scale=1, std=False):
_fmt = '{:.%df}'%p
string = _fmt.format((x.mean() if not isinstance(x, (float, np.floating)) else x) * scale)
if std and len(x) > 1:
string += ' ('+_fmt.format(x.std()*scale)+')'
return string
def backtest_multi(files, **kwargs):
res = []
pnl = []
for fname in files:
metric, r = backtest(fname, **kwargs)
res.append(metric)
pnl.append(r)
res = pd.DataFrame(res)
pnl = pd.concat(pnl, axis=1)
return {
'MSE': fmt(res['MSE'], std=True),
'MAE': fmt(res['MAE'], std=True),
'IC': fmt(res['IC']),
'ICIR': fmt(res['ICIR']),
'AR': fmt(res['AR'], scale=100, p=1)+'%',
'VR': fmt(res['AV'], scale=100, p=1)+'%',
'SR': fmt(res['SR']),
'MDD': fmt(res['MDD'], scale=100, p=1)+'%'
}, pnl
```
# Preparation
You could prepare the source data as below for the backtest code:
1. Linear: see Qlib examples
2. LightGBM: see Qlib examples
3. MLP: see Qlib examples
4. SFM: see Qlib examples
5. ALSTM: `qrun` configs/config_alstm.yaml
6. Transformer: `qrun` configs/config_transformer.yaml
7. ALSTM+TRA: `qrun` configs/config_alstm_tra_init.yaml && `qrun` configs/config_alstm_tra.yaml
8. Tranformer+TRA: `qrun` configs/config_transformer_tra_init.yaml && `qrun` configs/config_transformer_tra.yaml
```
exps = {
'Linear': ['output/Linear/pred.pkl'],
'LightGBM': ['output/GBDT/lr0.05_leaves128/pred.pkl'],
'MLP': glob.glob('output/search/MLP/hs128_bs512_do0.3_lr0.001_seed*/pred.pkl'),
'SFM': glob.glob('output/search/SFM/hs32_bs512_do0.5_lr0.001_seed*/pred.pkl'),
'ALSTM': glob.glob('output/search/LSTM_Attn/hs256_bs1024_do0.1_lr0.0002_seed*/pred.pkl'),
'Trans.': glob.glob('output/search/Transformer/head4_hs64_bs1024_do0.1_lr0.0002_seed*/pred.pkl'),
'ALSTM+TS':glob.glob('output/LSTM_Attn_TS/hs256_bs1024_do0.1_lr0.0002_seed*/pred.pkl'),
'Trans.+TS':glob.glob('output/Transformer_TS/head4_hs64_bs1024_do0.1_lr0.0002_seed*/pred.pkl'),
'ALSTM+TRA(Ours)': glob.glob('output/search/finetune/LSTM_Attn_tra/K10_traHs16_traSrcLR_TPE_traLamb2.0_hs256_bs1024_do0.1_lr0.0001_seed*/pred.pkl'),
'Trans.+TRA(Ours)': glob.glob('output/search/finetune/Transformer_tra/K3_traHs16_traSrcLR_TPE_traLamb1.0_head4_hs64_bs512_do0.1_lr0.0005_seed*/pred.pkl')
}
res = {
name: backtest_multi(exps[name])
for name in tqdm(exps)
}
report = pd.DataFrame({
k: v[0]
for k, v in res.items()
}).T
report
# print(report.to_latex())
```
# RQ1
Case study
```
df = pd.read_pickle('output/search/finetune/Transformer_tra/K3_traHs16_traSrcLR_TPE_traLamb0.0_head4_hs64_bs512_do0.1_lr0.0005_seed1000/pred.pkl')
code = 'SH600157'
date = '2018-09-28'
lookbackperiod = 50
prob = df.iloc[:, -3:].loc(axis=0)[:, code].reset_index(level=1, drop=True).loc[date:].iloc[:lookbackperiod]
pred = df.loc[:,["score_0","score_1","score_2","label"]].loc(axis=0)[:, code].reset_index(level=1, drop=True).loc[date:].iloc[:lookbackperiod]
e_all = pred.iloc[:,:-1].sub(pred.iloc[:,-1], axis=0).pow(2)
e_all = e_all.sub(e_all.min(axis=1), axis=0)
e_all.columns = [r'$\theta_%d$'%d for d in range(1, 4)]
prob = pd.Series(np.argmax(prob.values, axis=1), index=prob.index).rolling(7).mean().round()
fig, axes = plt.subplots(1, 2, figsize=(7, 3))
e_all.plot(ax=axes[0], xlabel='', rot=30)
prob.plot(ax=axes[1], xlabel='', rot=30, color='red', linestyle='None', marker='^', markersize=5)
plt.yticks(np.array([0, 1, 2]), e_all.columns.values)
axes[0].set_ylabel('Predictor Loss')
axes[1].set_ylabel('Router Selection')
plt.tight_layout()
# plt.savefig('select.pdf', bbox_inches='tight')
plt.show()
```
# RQ2
You could prepared the source data for this test as below:
1. Random: Setting `src_info` = "NONE"
2. LR: Setting `src_info` = "LR"
3. TPE: Setting `src_info` = "TPE"
4. LR+TPE: Setting `src_info` = "LR_TPE"
```
exps = {
'Random': glob.glob('output/search/LSTM_Attn_tra/K10_traHs16_traSrcNONE_traLamb1.0_hs256_bs1024_do0.1_lr0.0001_seed*/pred.pkl'),
'LR': glob.glob('output/search/LSTM_Attn_tra/K10_traHs16_traSrcLR_traLamb1.0_hs256_bs1024_do0.1_lr0.0001_seed*/pred.pkl'),
'TPE': glob.glob('output/search/LSTM_Attn_tra/K10_traHs16_traSrcTPE_traLamb1.0_hs256_bs1024_do0.1_lr0.0001_seed*/pred.pkl'),
'LR+TPE': glob.glob('output/search/finetune/LSTM_Attn_tra/K10_traHs16_traSrcLR_TPE_traLamb2.0_hs256_bs1024_do0.1_lr0.0001_seed*/pred.pkl')
}
res = {
name: backtest_multi(exps[name])
for name in tqdm(exps)
}
report = pd.DataFrame({
k: v[0]
for k, v in res.items()
}).T
report
# print(report.to_latex())
```
# RQ3
Set `lamb` = 0 to obtain results without Optimal Transport(OT)
```
a = pd.read_pickle('output/search/finetune/Transformer_tra/K3_traHs16_traSrcLR_TPE_traLamb0.0_head4_hs64_bs512_do0.1_lr0.0005_seed3000/pred.pkl')
b = pd.read_pickle('output/search/finetune/Transformer_tra/K3_traHs16_traSrcLR_TPE_traLamb2.0_head4_hs64_bs512_do0.1_lr0.0005_seed3000/pred.pkl')
a = a.iloc[:, -3:]
b = b.iloc[:, -3:]
b = np.eye(3)[b.values.argmax(axis=1)]
a = np.eye(3)[a.values.argmax(axis=1)]
res = pd.DataFrame({
'with OT': b.sum(axis=0) / b.sum(),
'without OT': a.sum(axis=0)/ a.sum()
},index=[r'$\theta_1$',r'$\theta_2$',r'$\theta_3$'])
res.plot.bar(rot=30, figsize=(5, 4), color=['b', 'g'])
del a, b
```
# RQ4
You could prepared the source data for this test as below:
1. K=1: which is exactly the alstm model
2. K=3: Setting `num_states` = 3
3. K=5: Setting `num_states` = 5
4. K=10: Setting `num_states` = 10
5. K=20: Setting `num_states` = 20
```
exps = {
'K=1': glob.glob('output/search/LSTM_Attn/hs256_bs1024_do0.1_lr0.0002_seed*/info.json'),
'K=3': glob.glob('output/search/finetune/LSTM_Attn_tra/K3_traHs16_traSrcLR_TPE_traLamb2.0_hs256_bs1024_do0.1_lr0.0001_seed*/info.json'),
'K=5': glob.glob('output/search/finetune/LSTM_Attn_tra/K5_traHs16_traSrcLR_TPE_traLamb2.0_hs256_bs1024_do0.1_lr0.0001_seed*/info.json'),
'K=10': glob.glob('output/search/finetune/LSTM_Attn_tra/K10_traHs16_traSrcLR_TPE_traLamb2.0_hs256_bs1024_do0.1_lr0.0001_seed*/info.json'),
'K=20': glob.glob('output/search/finetune/LSTM_Attn_tra/K20_traHs16_traSrcLR_TPE_traLamb2.0_hs256_bs1024_do0.1_lr0.0001_seed*/info.json')
}
report = dict()
for k, v in exps.items():
tmp = dict()
for fname in v:
with open(fname) as f:
info = json.load(f)
tmp[fname] = (
{
"IC":info["metric"]["IC"],
"MSE":info["metric"]["MSE"]
})
tmp = pd.DataFrame(tmp).T
report[k] = tmp.mean()
report = pd.DataFrame(report).T
fig, axes = plt.subplots(1, 2, figsize=(6,3)); axes = axes.flatten()
report['IC'].plot.bar(rot=30, ax=axes[0])
axes[0].set_ylim(0.045, 0.062)
axes[0].set_title('IC performance')
report['MSE'].astype(float).plot.bar(rot=30, ax=axes[1], color='green')
axes[1].set_ylim(0.155, 0.1585)
axes[1].set_title('MSE performance')
plt.tight_layout()
# plt.savefig('sensitivity.pdf')
report
```
| true |
code
| 0.537102 | null | null | null | null |
|
```
%matplotlib inline
```
# K-means Clustering
The plots display firstly what a K-means algorithm would yield
using three clusters. It is then shown what the effect of a bad
initialization is on the classification process:
By setting n_init to only 1 (default is 10), the amount of
times that the algorithm will be run with different centroid
seeds is reduced.
The next plot displays what using eight clusters would deliver
and finally the ground truth.
```
print(__doc__)
# Code source: Gaël Varoquaux
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
# Though the following import is not directly being used, it is required
# for 3D projection to work
from mpl_toolkits.mplot3d import Axes3D
from sklearn.cluster import KMeans
from sklearn import datasets
np.random.seed(5)
iris = datasets.load_iris()
X = iris.data
y = iris.target
estimators = [('k_means_iris_8', KMeans(n_clusters=8)),
('k_means_iris_3', KMeans(n_clusters=3)),
('k_means_iris_bad_init', KMeans(n_clusters=3, n_init=1,
init='random'))]
fignum = 1
titles = ['8 clusters', '3 clusters', '3 clusters, bad initialization']
for name, est in estimators:
fig = plt.figure(fignum, figsize=(4, 3))
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
est.fit(X)
labels = est.labels_
ax.scatter(X[:, 3], X[:, 0], X[:, 2],
c=labels.astype(np.float), edgecolor='k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
ax.set_title(titles[fignum - 1])
ax.dist = 12
fignum = fignum + 1
# Plot the ground truth
fig = plt.figure(fignum, figsize=(4, 3))
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
for name, label in [('Setosa', 0),
('Versicolour', 1),
('Virginica', 2)]:
ax.text3D(X[y == label, 3].mean(),
X[y == label, 0].mean(),
X[y == label, 2].mean() + 2, name,
horizontalalignment='center',
bbox=dict(alpha=.2, edgecolor='w', facecolor='w'))
# Reorder the labels to have colors matching the cluster results
y = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=y, edgecolor='k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
ax.set_title('Ground Truth')
ax.dist = 12
fig.show()
```
| true |
code
| 0.641507 | null | null | null | null |
|
# Python cheatsheet
Inspired by [A Whirlwind Tour of Python](https://jakevdp.github.io/WhirlwindTourOfPython/) and [another Python Cheatsheet](https://www.pythoncheatsheet.org/).
Only covers Python 3.
```
import this
```
## Basics
```
# Print statement
print("Hello World!") # Python 3 - No parentheses in Python 2
# Optional separator
print(1, 2, 3)
print(1, 2, 3, sep='--')
# Variables (dynamically typed)
mood = "happy" # or 'happy'
print("I'm", mood)
```
## String formatting
```
# https://realpython.com/python-f-strings/
# https://cito.github.io/blog/f-strings/
name = "Garance"
age = 11
message = "My name is %s and I'm %s years old." % (name, age) # Original language syntax
print(message)
message = "My name is {} and I'm {} years old.".format(name, age) # Python 2.6+
print(message)
message = f"My name is {name} and I'm {age} years old." # Python 3.6+
print(message)
```
## Numbers and arithmetic
```
# Type: int
a = 4
# Type: float
b = 3.14
a, b = b, a
print(a, b)
print(13 / 2)
print(13 // 2)
# Exponential operator
print(3 ** 2)
print(2 ** 3)
```
## Flow control
### The if/elif/else statement
```
name = 'Bob'
age = 30
if name == 'Alice':
print('Hi, Alice.')
elif age < 12:
print('You are not Alice, kiddo.')
else:
print('You are neither Alice nor a little kid.')
```
### The while loop
```
num = 1
while num <= 10:
print(num)
num += 1
```
### The for/else loop
The optional `else`statement is only useful when a `break` condition can occur in the loop:
```
for i in [1, 2, 3, 4, 5]:
if i == 3:
print(i)
break
else:
print("No item of the list is equal to 3")
```
## Data structures
### Lists
```
countries = ["France", "Belgium", "India"]
print(len(countries))
print(countries[0])
print(countries[-1])
# Add element at end of list
countries.append("Ecuador")
print(countries)
```
### List indexing and slicing
```
spam = ['cat', 'bat', 'rat', 'elephant']
print(spam[1:3])
print(spam[0:-1])
print(spam[:2])
print(spam[1:])
print(spam[:])
print(spam[::-1])
```
### Tuples
Contrary to lists, tuples are immutable (read-only).
```
eggs = ('hello', 42, 0.5)
print(eggs[0])
print(eggs[1:3])
# TypeError: a tuple is immutable
# eggs[0] = 'bonjour'
```
### Dictionaries
```
numbers = {'one':1, 'two':2, 'three':3}
numbers['ninety'] = 90
print(numbers)
for key, value in numbers.items():
print(f'{key} => {value}')
```
### Sets
A set is an unordered collection of unique items.
```
# Duplicate elements are automatically removed
s = {1, 2, 3, 2, 3, 4}
print(s)
```
### Union, intersection and difference of sets
```
primes = {2, 3, 5, 7}
odds = {1, 3, 5, 7, 9}
print(primes | odds)
print(primes & odds)
print(primes - odds)
```
## Functions
### Function definition and function call
```
def square(x):
""" Returns the square of x """
return x ** 2
# Print function docstring
help(square)
print(square(0))
print(square(3))
```
### Default function parameters
```
def fibonacci(n, a=0, b=1):
""" Returns a list of the n first Fibonacci numbers"""
l = []
while len(l) < n:
a, b = b, a + b
l.append(a)
return l
print(fibonacci(7))
```
### Flexible function arguments
```
def catch_all(*args, **kwargs):
print("args =", args)
print("kwargs = ", kwargs)
catch_all(1, 2, 3, a=10, b='hello')
```
### Lambda (anonymous) functions
```
add = lambda x, y: x + y
print(add(1, 2))
```
## Iterators
### A unified interface
```
for element in [1, 2, 3]:
print(element)
for element in (4, 5, 6):
print(element)
for key in {'one':1, 'two':2}:
print(key)
for char in "baby":
print(char)
```
### Under the hood
- An **iterable** is a object that has an `__iter__` method which returns an **iterator** to provide iteration support.
- An **iterator** is an object with a `__next__` method which returns the next iteration element.
- A **sequence** is an iterable which supports access by integer position. Lists, tuples, strings and range objects are examples of sequences.
- A **mapping** is an iterable which supports access via keys. Dictionaries are examples of mappings.
- Iterators are used implicitly by many looping constructs.
### The range() function
It doesn't return a list, but a `range`object (which exposes an iterator).
```
for i in range(10):
if i % 2 == 0:
print(f"{i} is even")
else:
print(f"{i} is odd")
for i in range(0, 10, 2):
print(i)
for i in range(5, -1, -1):
print(i)
```
### The enumerate() function
```
supplies = ['pens', 'staplers', 'flame-throwers', 'binders']
for i, supply in enumerate(supplies):
print(f'Index {i} in supplies is: {supply}')
```
## Comprehensions
### Principle
- Provide a concise way to create sequences.
- General syntax: `[expr for var in iterable]`.
### List comprehensions
```
# Using explicit code
L = []
for n in range(12):
L.append(n ** 2)
print(L)
# Using a list comprehension
[n ** 2 for n in range(12)]
```
### Set and dictionary comprehensions
```
# Create an uppercase set
s = {"abc", "def"}
print({e.upper() for e in s})
# Obtains modulos of 4 (elimitaing duplicates)
print({a % 4 for a in range(1000)})
# Switch keys and values
d = {'name': 'Prosper', 'age': 7}
print({v: k for k, v in d.items()})
```
## Generators
### Principle
- A **generator** defines a recipe for producing values.
- A generator does not actually compute the values until they are needed.
- It exposes an iterator interface. As such, it is a basic form of iterable.
- It can only be iterated once.
### Generators expressions
They use parentheses, not square brackets like list comprehensions.
```
G1 = (n ** 2 for n in range(12))
print(list(G1))
print(list(G1))
```
### Generator functions
- A function that, rather than using `return` to return a value once, uses `yield` to yield a (potentially infinite) sequence of values.
- Useful when the generator algorithm gets complicated.
```
def gen():
for n in range(12):
yield n ** 2
G2 = gen()
print(list(G2))
print(list(G2))
```
## Object-oriented programming
### Classes and objects
```
class Vehicle:
def __init__(self, number_of_wheels, type_of_tank):
self.number_of_wheels = number_of_wheels
self.type_of_tank = type_of_tank
@property
def number_of_wheels(self):
return self.__number_of_wheels
@number_of_wheels.setter
def number_of_wheels(self, number):
self.__number_of_wheels = number
def make_noise(self):
print('VRUUUUUUUM')
tesla_model_s = Vehicle(4, 'electric')
tesla_model_s.number_of_wheels = 2 # setting number of wheels to 2
print(tesla_model_s.number_of_wheels)
tesla_model_s.make_noise()
```
### Class and instance attributes
```
class Employee:
empCount = 0
def __init__(self, name, salary):
self._name = name
self._salary = salary
Employee.empCount += 1
def count():
return f'Total employees: {Employee.empCount}'
def description(self):
return f'Name: {self._name}, salary: {self._salary}'
e1 = Employee('Ben', '30')
print(e1.description())
print(Employee.count())
```
### Inheritance
```
class Animal:
def __init__(self, species):
self.species = species
class Dog(Animal):
def __init__(self, name):
Animal.__init__(self, 'Mammal')
self.name = name
doggo = Dog('Fang')
print(doggo.name)
print(doggo.species)
```
## Modules and packages
```
# Importing all module content into a namespace
import math
print(math.cos(math.pi)) # -1.0
# Aliasing an import
import numpy as np
print(np.cos(np.pi)) # -1.0
# Importing specific module content into local namespace
from math import cos, pi
print(cos(pi)) # -1.0
# Importing all module content into local namespace (use with caution)
from math import *
print(sin(pi) ** 2 + cos(pi) ** 2) # 1.0
```
| true |
code
| 0.477981 | null | null | null | null |
|
# First a little bit of statistics review:
# Variance
Variance is a measure of the spread of numbers in a dataset. Variance is the average of the squared differences from the mean. So naturally, you can't find the variance of something unless you calculate it's mean first. Lets get some data and find its variance.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import random
# Lets generate two variables with 50 random integers each.
variance_one = []
variance_two = []
for x in range(50):
variance_one.append(random.randint(25,75))
variance_two.append(random.randint(0,100))
variance_data = {'v1': variance_one, 'v2': variance_two}
variance_df = pd.DataFrame(variance_data)
variance_df['zeros'] = pd.Series(list(np.zeros(50)))
variance_df.head()
# Now some scatter plots
plt.scatter(variance_df.v1, variance_df.zeros)
plt.xlim(0,100)
plt.title("Plot One")
plt.show()
plt.scatter(variance_df.v2, variance_df.zeros)
plt.xlim(0,100)
plt.title("Plot Two")
plt.show()
```
Now I know this isn't complicated, but each of the above plots has the same number of points, but we can tell visually that "Plot Two" has the greater variance because its points are more spread out. What if we didn't trust our eyes though? Lets calculate the variance of each of these variables to prove it to ourselves
$\overline{X}$ is the symbol for the mean of the dataset.
$N$ is the total number of observations.
$v$ or variance is sometimes denoted by a lowercase v. But you'll also see it referred to as $\sigma^{2}$.
\begin{align}
v = \frac{\sum{(X_{i} - \overline{X})^{2}} }{N}
\end{align}
How do we calculate a simple average? We add up all of the values and then divide by the total number of values. this is why there is a sum in the numerator and N in the denomenator.
However in this calculation, we're not just summing the values like we would if we were calculateing the mean, we are summing the squared difference between each point and the mean. (The squared distance between each point in the mean.)
```
# Since we generated these random values in a range centered around 50, that's
# about where their means should be.
# Find the means for each variable
v1_mean = variance_df.v1.mean()
print("v1 mean: ", v1_mean)
v2_mean = variance_df.v2.mean()
print("v2 mean: ", v2_mean)
# Find the distance between each point and its corresponding mean
variance_df['v1_distance'] = variance_df.v1-v1_mean
variance_df['v2_distance'] = variance_df.v2-v2_mean
variance_df.head()
# Now we'll square the distances from the means
variance_df['v1_squared_distance'] = variance_df.v1_distance**2
variance_df['v2_squared_distance'] = variance_df.v2_distance**2
# Notice that squaring the distances turns all of our negative values into positive ones?
variance_df.head()
# Now we'll sum the squared distances and divide by the number of observations.
observations = len(variance_df)
print("Number of Observations: ", observations)
Variance_One = variance_df.v1_squared_distance.sum()/observations
Variance_Two = variance_df.v2_squared_distance.sum()/observations
print("Variance One: ", Variance_One)
print("Variance Two: ", Variance_Two)
```
Woah, so what is the domain of V1 and V2?
Well, V1 goes from 25 to 75 so its range is ~50 and V2 goes from 0 to 100 so its range is about 100
So even though V2 is roughly twice as spread out, how much bigger is its variance than V1?
```
print("How many times bigger is Variance_One than Variance_Two? ", Variance_Two/Variance_One)
# About 3.86 times bigger! Why is that?
```
## A note about my code quality
Why did I go to the trouble of calculating all of that by hand, and add a bunch of extra useless rows to my dataframe? That is some bad code!
Because I wanted to make sure that you understood all of the parts of the equation. I didn't want the function to be some magic thing that you put numbers in and out popped a variance. Taking time to understand the equation will reinforce your intuition about the spread of the data. After all, I could have just done this:
```
print(variance_df.v1.var(ddof=1))
print(variance_df.v2.var(ddof=1))
```
But wait! Those variance values are different than the ones we calculated above, oh no! This is because variance is calculated slightly differently for a population vs a sample. Lets clarify this a little bit.
The **POPULATION VARIANCE** $\sigma^{2}$ is a **PARAMETER** (aspect, property, attribute, etc) of the population.
The **SAMPLE VARIANCE** $s^{2}$ is a **STATISTIC** (estimated attribute) of the sample.
We use the sample statistic to **estimate** the population parameter.
The sample variance $s^{2}$ is an estimate of the population variance $\sigma^{2}$.
Basically, if you're calculating a **sample** variance, you need to divide by $N-1$ or else your estimate will be a little biased. The equation that we were originally working from is for a **population variance**.
If we use the ddof=0 parameter (default is ddof=1) in our equation, we should get the same result. "ddof" stands for Denominator Degrees of Freedom.
```
print(variance_df.v1.var(ddof=0))
print(variance_df.v2.var(ddof=0))
```
# Standard Deviation
If you understand how variance is calculated, then standard deviation is a cinch. The standard deviation is the square root $\sqrt()$ of the variance.
## So why would we use one over the other?
Remember how we squared all of the distances from the mean before we added them all up? Well then taking the square root of the variance will put our measures back in the same units as the mean. So the Standard Deviation is a measure of spread of the data that is expressed in the same units as the mean of the data. Variance is the average squared distance from the mean, and the Standard Deviation is the average distance from the mean. You'll remember that when we did hypothesis testing and explored the normal distribution we talked in terms of standard deviations, and not in terms of variance for this reason.
```
print(variance_df.v1.std(ddof=0))
print(variance_df.v2.std(ddof=0))
```
# Covariance
Covariance is a measure of how changes in one variable are associated with changes in a second variable. It's a measure of how they Co (together) Vary (move) or how they move in relation to each other. For this topic we're not really going to dive into the formula, I just want you to be able to understand the topic intuitively. Since this measure is about two variables, graphs that will help us visualize things in two dimensions will help us demonstrate this idea. (scatterplots)

Lets look at the first scatterplot. the y variable has high values where the x variable has low values. This is a negative covariance because as one variable increases (moves), the other decreases (moves in the opposite direction).
In the second scatterplot we see no relation between high and low values of either variable, therefore this cloud of points has a near 0 covariance
In the third graph, we see that the y variable takes on low values in the same range where the x value takes on low values, and simiarly with high values. Because the areas of their high and low values match, we would expect this cloud of points to have a positive covariance.

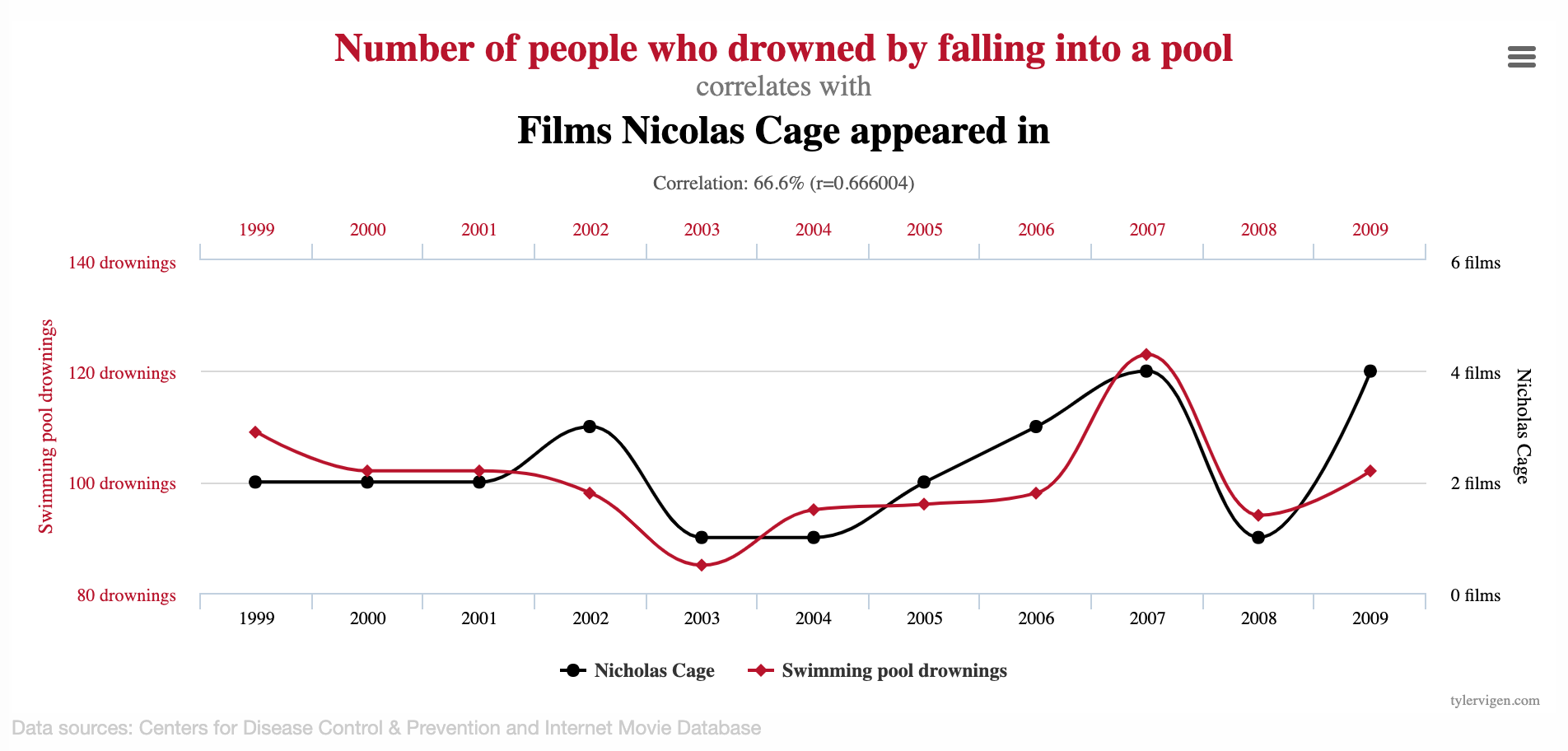
Check out how popular this site is:
<https://tylervigen.com>
<https://www.similarweb.com/website/tylervigen.com#overview>
## Interpeting Covariance
A large positive or negative covariance indicates a strong relationship between two variables. However, you can't necessarily compare covariances between sets of variables that have a different scale, since the covariance of variables that take on high values will always be higher than since covariance values are unbounded, they could take on arbitrarily high or low values. This means that you can't compare the covariances between variables that have a different scale. Two variablespositive covariance variable that has a large scale will always have a higher covariance than a variable with an equally strong relationship, yet smaller scale. This means that we need a way to regularlize
One of the challenges with covariance is that its value is unbounded and variables that take on larger values will have a larger covariance irrespective of
Let me show you what I mean:
```
a = [1,2,3,4,5,6,7,8,9]
b = [1,2,3,4,5,6,7,8,9]
c = [10,20,30,40,50,60,70,80,90]
d = [10,20,30,40,50,60,70,80,90]
fake_data = {"a": a, "b": b, "c": c, "d": d,}
df = pd.DataFrame(fake_data)
plt.scatter(df.a, df.b)
plt.xlim(0,100)
plt.ylim(0,100)
plt.show()
plt.scatter(df.c, df.d)
plt.xlim(0,100)
plt.ylim(0,100)
plt.show()
```
Which of the above sets of variables has a stronger relationship?
Which has the stronger covariance?
# The Variance-Covariance Matrix
In order to answer this problem we're going to use a tool called a variance-covariance matrix.
This is matrix that compares each variable with every other variable in a dataset and returns to us variance values along the main diagonal, and covariance values everywhere else.
```
df.cov()
```
What type of special square matrix is the variance-covariance matrix?
The two sets of variables above show relationships that are equal in their strength, yet their covariance values are wildly different.
How can we counteract this problem?
What if there was some statistic of a distribution that represented how spread out the data was that we could use to standardize the units/scale of the variables?
# Correlation Coefficient
Well, it just so happens that we do have such a measure of spread of a variable. It's called the Standard Deviation! And we already learned about it. If we divide our covariance values by the product of the standard deviations of the two variables, we'll end up with what's called the Correlation Coefficient. (Sometimes just referred to as the correlation).
Correlation Coefficients have a fixed range from -1 to +1 with 0 representing no linear relationship between the data.
In most use cases the correlation coefficient is an improvement over measures of covariance because:
- Covariance can take on practically any number while a correlation is limited: -1 to +1.
- Because of it’s numerical limitations, correlation is more useful for determining how strong the relationship is between the two variables.
- Correlation does not have units. Covariance always has units
- Correlation isn’t affected by changes in the center (i.e. mean) or scale of the variables
[Statistics How To - Covariance](https://www.statisticshowto.datasciencecentral.com/covariance/)
The correlation coefficient is usually represented by a lower case $r$.
\begin{align}
r = \frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}}
\end{align}
```
df.corr()
```
Correlation coefficients of 1 tell us that all of these varaibles have a perfectly linear positive correlation with one another.

Correlation and other sample statistics are somewhat limited in their ability to tell us about the shape/patterns in the data.
[Anscombe's Quartet](https://en.wikipedia.org/wiki/Anscombe%27s_quartet)

Or take it to the next level with the [Datasaurus Dozen](https://www.autodeskresearch.com/publications/samestats)
# Orthogonality
Orthogonality is another word for "perpendicularity" or things (vectors or matrices) existing at right angles to one another. Two vectors that are perpendicular to one another are orthogonal.
## How to tell if two vectors are orthogonal
Two vectors are orthogonal to each other if their dot product will be zero.
Lets look at a couple of examples to see this in action:
```
vector_1 = [0, 2]
vector_2 = [2, 0]
# Plot the Scaled Vectors
plt.arrow(0,0, vector_1[0], vector_1[1],head_width=.05, head_length=0.05, color ='red')
plt.arrow(0,0, vector_2[0], vector_2[1],head_width=.05, head_length=0.05, color ='green')
plt.xlim(-1,3)
plt.ylim(-1,3)
plt.title("Orthogonal Vectors")
plt.show()
```
Clearly we can see that the above vectors are perpendicular to each other, what does the formula say?
\begin{align}
a = \begin{bmatrix} 0 & 2\end{bmatrix}
\qquad
b = \begin{bmatrix} 2 & 0\end{bmatrix}
\\
a \cdot b = (0)(2) + (2)(0) = 0
\end{align}
```
vector_1 = [-2, 2]
vector_2 = [2, 2]
# Plot the Scaled Vectors
plt.arrow(0,0, vector_1[0], vector_1[1],head_width=.05, head_length=0.05, color ='red')
plt.arrow(0,0, vector_2[0], vector_2[1],head_width=.05, head_length=0.05, color ='green')
plt.xlim(-3,3)
plt.ylim(-1,3)
plt.title("Orthogonal Vectors")
plt.show()
```
Again the dot product is zero.
\begin{align}
a = \begin{bmatrix} -2 & 2\end{bmatrix}
\qquad
b = \begin{bmatrix} 2 & 2\end{bmatrix}
\\
a \cdot b = (-2)(2) + (2)(2) = 0
\end{align}
# Unit Vectors
In Linear Algebra a unit vector is any vector of "unit length" (1). You can turn any non-zero vector into a unit vector by dividing it by its norm (length/magnitude).
for example if I have the vector
\begin{align}
b = \begin{bmatrix} 1 \\ 2 \\ 2 \end{bmatrix}
\end{align}
and I want to turn it into a unit vector, first I will calculate its norm
\begin{align}
||b|| = \sqrt{1^2 + 2^2 + 2^2} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3
\end{align}
I can turn b into a unit vector by dividing it by its norm. Once something has been turned into a unit vector we'll put a ^ "hat" symbol over it to denote that it is now a unit vector.
\begin{align}
\hat{b} = \frac{1}{||b||}b = \frac{1}{3}\begin{bmatrix} 1 \\ 2 \\ 2 \end{bmatrix} = \begin{bmatrix} \frac{1}{3} \\ \frac{2}{3} \\ \frac{2}{3} \end{bmatrix}
\end{align}
You might frequently see mentioned the unit vectors used to denote a certain dimensional space.
$\mathbb{R}$ unit vector: $\hat{i} = \begin{bmatrix} 1 \end{bmatrix}$
$\mathbb{R}^2$ unit vectors: $\hat{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$, $\hat{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$
$\mathbb{R}^3$ unit vectors: $\hat{i} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$, $\hat{j} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}$, $\hat{k} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}$
You'll notice that in the corresponding space, these basis vectors are the rows/columns of the identity matrix.
```
# Axis Bounds
plt.xlim(-1,2)
plt.ylim(-1,2)
# Unit Vectors
i_hat = [1,0]
j_hat = [0,1]
# Fix Axes
plt.axes().set_aspect('equal')
# PLot Vectors
plt.arrow(0, 0, i_hat[0], i_hat[1], linewidth=3, head_width=.05, head_length=0.05, color ='red')
plt.arrow(0, 0, j_hat[0], j_hat[1], linewidth=3, head_width=.05, head_length=0.05, color ='blue')
plt.title("basis vectors in R^2")
plt.show()
```
## Vectors as linear combinations of scalars and unit vectors
Any vector (or matrix) can be be described in terms of a linear combination of scaled unit vectors. Lets look at an example.
\begin{align}
c = \begin{bmatrix} 2 \\ 3 \end{bmatrix}
\end{align}
We think about a vector that starts at the origin and extends to point $(2,3)$
Lets rewrite this in terms of a linear combination of scaled unit vectors:
\begin{align}
c = \begin{bmatrix} 2 \\ 3 \end{bmatrix} = 2\begin{bmatrix} 1 \\ 0 \end{bmatrix} + 3\begin{bmatrix} 0 \\ 1 \end{bmatrix} = 2\hat{i} + 3\hat{j}
\end{align}
This says that matrix $\begin{bmatrix} 2 \\ 3 \end{bmatrix}$ will result from scaling the $\hat{i}$ unit vector by 2, the $\hat{j}$ vector by 3 and then adding the two together.
We can describe any vector in $\mathbb{R}^2$ in this way. Well, we can describe any vector in any dimensionality this way provided we use all of the unit vectors for that space and scale them all appropriately. In this examply we just happen to be using a vector whose dimension is 2.
# Span
The span is the set of all possible vectors that can be created with a linear combination of two vectors (just as we described above).
A linear combination of two vectors just means that we're composing to vectors (via addition or subtraction) to create a new vector.
## Linearly Dependent Vectors
Two vectors that live on the same line are what's called linearly dependent. This means that there is no linear combination (no way to add, or subtract scaled version of these vectors from each other) that will ever allow us to create a vector that lies outside of that line.
In this case, the span of these vectors (lets say the green one and the red one for example - could be just those two or a whole set) is the line that they lie on, since that's what can be produced by scaling and composing them together.
The span is the graphical area that we're able to cover via a linear combination of a set of vectors.
## Linearly Independent Vectors
Linearly independent vectors are vectors that don't lie on the same line as each other. If two vectors are linearly independent, then there ought to be some linear combination of them that could represent any vector in the space ($\mathbb{R}^2$ in this case).
```
# Plot Linearly Dependent Vectors
# Axis Bounds
plt.xlim(-1.1,4)
plt.ylim(-1.1,4)
# Original Vector
v = [1,0]
# Scaled Vectors
v2 = np.multiply(3, v)
v3 = np.multiply(-1,v)
# Get Vals for L
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = 0*x_vals
# Plot Vectors and L
plt.plot(x_vals, y_vals, '--', color='b', linewidth=1)
plt.arrow(0,0, v2[0], v2[1], linewidth=3, head_width=.05, head_length=0.05, color ='yellow')
plt.arrow(0,0, v[0], v[1], linewidth=3, head_width=.05, head_length=0.05, color ='green')
plt.arrow(0,0, v3[0], v3[1], linewidth=3, head_width=.05, head_length=0.05, color ='red')
plt.title("Linearly Dependent Vectors")
plt.show()
# Plot Linearly Dependent Vectors
# Axis Bounds
plt.xlim(-2,3.5)
plt.ylim(-1,3)
# Original Vector
a = [-1.5,.5]
b = [3, 1]
# Plot Vectors
plt.arrow(0,0, a[0], a[1], linewidth=3, head_width=.05, head_length=0.05, color ='blue')
plt.arrow(0,0, b[0], b[1], linewidth=3, head_width=.05, head_length=0.05, color ='red')
plt.title("Linearly Independent Vectors")
plt.show()
```
# Basis
The basis of a vector space $V$ is a set of vectors that are linearly independent and that span the vector space $V$.
A set of vectors spans a space if their linear combinations fill the space.
For example, the unit vectors in the "Linearly Independent Vectors" plot above form a basis for the vector space $\mathbb{R}^2$ becayse they are linearly independent and span that space.
## Orthogonal Basis
An orthogonal basis is a set of vectors that are linearly independent, span the vector space, and are orthogonal to each other. Remember that vectors are orthogonal if their dot product equals zero.
## Orthonormal Basis
An orthonormal basis is a set of vectors that are linearly independent, span the vector space, are orthogonal to eachother and each have unit length.
For more on this topic (it's thrilling, I know) you might research the Gram-Schmidt process -which is a method for orthonormalizing a set of vectors in an inner product space.
The unit vectors form an orthonormal basis for whatever vector space that they are spanning.
# Rank
The rank of a matrix is the dimension of the vector space spanned by its columns. Just because a matrix has a certain number of rows or columns (dimensionality) doesn't neccessarily mean that it will span that dimensional space. Sometimes there exists a sort of redundancy within the rows/columns of a matrix (linear dependence) that becomes apparent when we reduce a matrix to row-echelon form via Gaussian Elimination.
## Gaussian Elimination
Gaussian Elimination is a process that seeks to take any given matrix and reduce it down to what is called "Row-Echelon form." A matrix is in Row-Echelon form when it has a 1 as its leading entry (furthest left) in each row, and zeroes at every position below that main entry. These matrices will usually wind up as a sort of upper-triangular matrix (not necessarly square) with ones on the main diagonal.

Gaussian Elimination takes a matrix and converts it to row-echelon form by doing combinations of three different row operations:
1) You can swap any two rows
2) You can multiply entire rows by scalars
3) You can add/subtract rows from each other
This takes some practice to do by hand but once mastered becomes the fastest way to find the rank of a matrix.
For example lets look at the following matrix:
\begin{align}
P = \begin{bmatrix}
1 & 0 & 1 \\
-2 & -3 & 1 \\
3 & 3 & 0
\end{bmatrix}
\end{align}
Now, lets use gaussian elimination to get this matrix in row-echelon form
Step 1: Add 2 times the 1st row to the 2nd row
\begin{align}
P = \begin{bmatrix}
1 & 0 & 1 \\
0 & -3 & -3 \\
3 & 3 & 0
\end{bmatrix}
\end{align}
Step 2: Add -3 times the 1st row to the 3rd row
\begin{align}
P = \begin{bmatrix}
1 & 0 & 1 \\
0 & -3 & 3 \\
0 & 3 & -3
\end{bmatrix}
\end{align}
Step 3: Multiply the 2nd row by -1/3
\begin{align}
P = \begin{bmatrix}
1 & 0 & 1 \\
0 & 1 & -1 \\
0 & 3 & -3
\end{bmatrix}
\end{align}
Step 4: Add -3 times the 2nd row to the 3rd row
\begin{align}
P = \begin{bmatrix}
1 & 0 & 1 \\
0 & 1 & -1 \\
0 & 0 & 0
\end{bmatrix}
\end{align}
Now that we have this in row-echelon form we can see that we had one row that was linearly dependent (could be composed as a linear combination of other rows). That's why we were left with a row of zeros in place of it. If we look closely we will see that the first row equals the second row plus the third row.
Because we had two rows with leading 1s (these are called pivot values) left after the matrix was in row-echelon form, we know that its Rank is 2.
What does this mean? This means that even though the original matrix is a 3x3 matrix, it can't span $\mathbb{R}^3$, only $\mathbb{R}^2$
# Linear Projections in $\mathbb{R}^{2}$
Assume that we have some line $L$ in $\mathbb{R}^{2}$.
```
# Plot a line
plt.xlim(-1,4)
plt.ylim(-1,4)
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = 0*x_vals
plt.plot(x_vals, y_vals, '--', color='b')
plt.title("A Line")
plt.show()
```
We know that if we have a vector $v$ that lies on that line, if we scale that vector in any direction, the resulting vectors can only exist on that line.
```
# Plot a line
# Axis Bounds
plt.xlim(-1.1,4)
plt.ylim(-1.1,4)
# Original Vector
v = [1,0]
# Scaled Vectors
v2 = np.multiply(3, v)
v3 = np.multiply(-1,v)
# Get Vals for L
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = 0*x_vals
# Plot Vectors and L
plt.plot(x_vals, y_vals, '--', color='b', linewidth=1)
plt.arrow(0,0, v2[0], v2[1], linewidth=3, head_width=.05, head_length=0.05, color ='yellow')
plt.arrow(0,0, v[0], v[1], linewidth=3, head_width=.05, head_length=0.05, color ='green')
plt.arrow(0,0, v3[0], v3[1], linewidth=3, head_width=.05, head_length=0.05, color ='red')
plt.title("v scaled two different ways")
plt.show()
```
Lets call the green vector $v$
This means that line $L$ is equal to vector $v$ scaled by all of the potential scalars in $\mathbb{R}$. We can represent this scaling factor by a constant $c$. Therefore, line $L$ is vector $v$ scaled by any scalar $c$.
\begin{align}
L = cv
\end{align}
Now, say that we have a second vector $w$ that we want to "project" onto line L
```
# Plot a line
# Axis Bounds
plt.xlim(-1.1,4)
plt.ylim(-1.1,4)
# Original Vector
v = [1,0]
w = [2,2]
# Get Vals for L
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = 0*x_vals
# Plot Vectors and L
plt.plot(x_vals, y_vals, '--', color='b', linewidth=1)
plt.arrow(0, 0, v[0], v[1], linewidth=3, head_width=.05, head_length=0.05, color ='green')
plt.arrow(0, 0, w[0], w[1], linewidth=3, head_width=.05, head_length=0.05, color ='red')
plt.title("vector w")
plt.show()
```
## Projection as a shadow cast onto the target vector at a right angle
This is the intuition that I want you to develop. Imagine that we are shining a light down onto lin $L$ from a direction that is exactly orthogonal to it. In this case shining a light onto $L$ from a direction that is orthogonal to it is as if we were shining a light down from directly above. How long will the shadow be?
Imagine that you're **projecting** light from above to cast a shadow onto the x-axis.
Well since $L$ is literally the x-axis you can probably tell that the length of the projection of $w$ onto $L$ is 2.
A projection onto an axis is the same as just setting the variable that doesn't match the axis to 0. in our case the coordinates of vector $w$ is $(2,2)$ so it projects onto the x-axis at (2,0) -> just setting the y value to 0.
### Notation
In linear algebra we write the projection of w onto L like this:
\begin{align}proj_{L}(\vec{w})\end{align}
```
# Axis Bounds
plt.xlim(-1.1,4)
plt.ylim(-1.1,4)
# Original Vector
v = [1,0]
w = [2,2]
proj = [2,0]
# Get Vals for L
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = 0*x_vals
# Plot Vectors and L
plt.plot(x_vals, y_vals, '--', color='b', linewidth=1)
plt.arrow(0, 0, proj[0], proj[1], linewidth=3, head_width=.05, head_length=0.05, color ='gray')
plt.arrow(0, 0, v[0], v[1], linewidth=3, head_width=.05, head_length=0.05, color ='green')
plt.arrow(0, 0, w[0], w[1], linewidth=3, head_width=.05, head_length=0.05, color ='red')
plt.title("Shadow of w")
plt.show()
```
The problem here is that we can't just draw a vector and call it a day, we can only define that vector in terms of our $v$ (green) vector.
Our gray vector is defined as:
\begin{align}
cv = proj_{L}(w)
\end{align}
But what if $L$ wasn't on the x-axis? How would calculate the projection?
```
# Axis Bounds
plt.xlim(-1.1,4)
plt.ylim(-1.1,4)
# Original Vector
v = [1,1/2]
w = [2,2]
proj = np.multiply(2.4,v)
# Set axes
axes = plt.gca()
plt.axes().set_aspect('equal')
# Get Vals for L
x_vals = np.array(axes.get_xlim())
y_vals = 1/2*x_vals
# Plot Vectors and L
plt.plot(x_vals, y_vals, '--', color='b', linewidth=1)
plt.arrow(0, 0, proj[0], proj[1], linewidth=3, head_width=.05, head_length=0.05, color ='gray')
plt.arrow(0, 0, v[0], v[1], linewidth=3, head_width=.05, head_length=0.05, color ='green')
plt.arrow(0, 0, w[0], w[1], linewidth=3, head_width=.05, head_length=0.05, color ='red')
plt.title("non x-axis projection")
plt.show()
```
Remember, that it doesn't matter how long our $v$ (green) vectors is, we're just looking for the c value that can scale that vector to give us the gray vector $proj_{L}(w)$.
```
# Axis Bounds
plt.xlim(-1.1,4)
plt.ylim(-1.1,4)
# Original Vector
v = [1,1/2]
w = [2,2]
proj = np.multiply(2.4,v)
x_minus_proj = w-proj
# Set axes
axes = plt.gca()
plt.axes().set_aspect('equal')
# Get Vals for L
x_vals = np.array(axes.get_xlim())
y_vals = 1/2*x_vals
# Plot Vectors and L
plt.plot(x_vals, y_vals, '--', color='b', linewidth=1)
plt.arrow(0, 0, proj[0], proj[1], linewidth=3, head_width=.05, head_length=0.05, color ='gray')
plt.arrow(0, 0, v[0], v[1], linewidth=3, head_width=.05, head_length=0.05, color ='green')
plt.arrow(0, 0, w[0], w[1], linewidth=3, head_width=.05, head_length=0.05, color ='red')
plt.arrow(proj[0], proj[1], x_minus_proj[0], x_minus_proj[1], linewidth=3, head_width=.05, head_length=0.05, color = 'yellow')
plt.title("non x-axis projection")
plt.show()
```
Lets use a trick. We're going to imagine that there is yellow vector that is orthogonal to $L$, that starts at the tip of our projection (gray) and ends at the tip of $w$ (red).
### Here's the hard part
This may not be intuitive, but we can define that yellow vector as $w-proj_{L}(w)$. Remember how two vectors added together act like we had placed one at the end of the other? Well this is the opposite, if we take some vector and subtract another vector, the tip moves to the end of the subtracted vector.
Since we defined $proj_{L}(w)$ as $cv$ (above). We then rewrite the yellow vector as:
\begin{align}
yellow = w-cv
\end{align}
Since we know that our yellow vector is orthogonal to $v$ we can then set up the following equation:
\begin{align}
v \cdot (w-cv) = 0
\end{align}
(remember that the dot product of two orthogonal vectors is 0)
Now solving for $c$ we get
1) Distribute the dot product
\begin{align}
v \cdot w - c(v \cdot v) = 0
\end{align}
2) add $c(v \cdot v)$ to both sides
\begin{align}
v \cdot w = c(v \cdot v)
\end{align}
3) divide by $v \cdot v$
\begin{align}
c = \frac{w \cdot v}{v \cdot v}
\end{align}
Since $cv = proj_{L}(w)$ we know that:
\begin{align}
proj_{L}(w) = \frac{w \cdot v}{v \cdot v}v
\end{align}
This is the equation for the projection of any vector $w$ onto any line $L$!
Think about if we were trying to project an already orthogonal vector onto a line:
```
# Axis Bounds
plt.xlim(-1.1,4)
plt.ylim(-1.1,4)
# Original Vector
# v = [1,0]
w = [0,2]
proj = [2,0]
# Get Vals for L
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = 0*x_vals
# Plot Vectors and L
plt.plot(x_vals, y_vals, '--', color='b', linewidth=1)
plt.arrow(0, 0, w[0], w[1], linewidth=3, head_width=.05, head_length=0.05, color ='red')
plt.title("Shadow of w")
plt.show()
```
Now that you have a feel for linear projections, you can see that the $proj_{L}(w)$ is 0 mainly because $w \cdot v$ is 0.
Why have I gone to all of this trouble to explain linear projections? Because I think the intuition behind it is one of the most important things to grasp in linear algebra. We can find the shortest distance between some data point (vector) and a line best via an orthogonal projection onto that line. We can now move data points onto any given line and be certain that they move as little as possible from their original position.
The square of the norm of a vector is equivalent to the dot product of a vector with itself.
The dot product of a vector and itself can be rewritten as that vector times the transpose of itself.
| true |
code
| 0.669988 | null | null | null | null |
|
## Wavelets
An increasingly popular family of basis functions is called **wavelets**. By construction, wavelets are localized in both frequency and time domains. Individual wavelets are specified by a set of wavelet filter coefficients. Given a wavelet, a complete
orthonormal set of basis functions can be constructed by scalings and translations. Different wavelet families trade the localization of a wavelet with its smoothness.
### Wavelet transform of Gaussian Noise
Below we have an example using a particular wavelet to compute a wavelet PSD as a
function of time $t_0$ and frequency $f_0$. The wavelet used is of the form
$$w(t|t_0,f_0,Q) = A exp[i2\pi f_0 (t-t_0)]exp[-f_0^2(t-t_0)^2/Q^2]$$
where $t_0$ is the central time, $f_0$ is the central frequency, and the dimensionless parameter Q is
a model parameter which controls the width of the frequency window.
The Fourier transform of this form is
$$W(f|t_0,f_0,Q)=(\frac{\pi}{f^2_0/Q^2})^{1/2} exp(-i2\pi f t_0) exp[\frac{-\pi^2Q^2(f-f_0)^2}{Qf^2_0}]$$
Note that the form given by above equations is not technically a wavelet because it
does not meet the admissibility criterion (the equivalent of orthogonality in Fourier transforms).
This form is closely related to a true wavelet, the *Morlet wavelet*, through a simple scaling and offset. Therefore, these equations should probaly be referred to as "matched filters" rather than "wavelets".
However, these functions display quite nicely one
main property of wavelets: the localization of power in both time and frequency. For this reason,
we will refer to these functions as "wavelets," and explore their ability to localize frequency signals.
#### Imput signal
We take a localized Gaussian noise as imput signal, as shown below.
```
import numpy as np
from matplotlib import pyplot as plt
from astroML.fourier import sinegauss, wavelet_PSD, FT_continuous, IFT_continuous
from astroML.plotting import setup_text_plots
setup_text_plots(usetex=True)
# Sample the function: localized noise
np.random.seed(0)
N = 1024
t = np.linspace(-5, 5, N)
x = np.ones(len(t))
h = np.random.normal(0, 1, len(t))
h *= np.exp(-0.5 * (t / 0.5) ** 2)
# Show signal
fig = plt.figure(figsize=(6, 2))
fig.subplots_adjust(hspace=0.05, left=0.12, right=0.95, bottom=0.08, top=0.95)
ax = fig.add_subplot(111)
ax.plot(t, h, '-k', lw=1)
ax.text(0.02, 0.95, ("Input Signal:\n"
"Localized Gaussian noise"),
ha='left', va='top', transform=ax.transAxes)
ax.set_xlim(-4, 4)
ax.set_ylim(-2.9, 2.9)
ax.set_ylabel('$h(t)$')
```
#### Compute wavelet
We compute the wavelet from sample data using *sinegauss* function in *astroML.fourier*.
Here we take Q=1.0 to control the width of the frequency window.
In the plot, solid line and dashed line show the real part and imaginary part respectively.
```
# Compute an example wavelet
W = sinegauss(t, 0, 1.5, Q=1.0)
# Show the example wavelet
fig = plt.figure(figsize=(6, 2))
fig.subplots_adjust(hspace=0.05, left=0.12, right=0.95, bottom=0.08, top=0.95)
ax = fig.add_subplot(111)
ax.plot(t, W.real, '-k', label='real part', lw=1)
ax.plot(t, W.imag, '--k', label='imag part', lw=1)
ax.text(0.02, 0.95, ("Example Wavelet\n"
"$t_0 = 0$, $f_0=1.5$, $Q=1.0$"),
ha='left', va='top', transform=ax.transAxes)
ax.text(0.98, 0.05,
(r"$w(t; t_0, f_0, Q) = e^{-[f_0 (t - t_0) / Q]^2}"
"e^{2 \pi i f_0 (t - t_0)}$"),
ha='right', va='bottom', transform=ax.transAxes)
ax.legend(loc=1)
ax.set_xlim(-4, 4)
ax.set_ylim(-1.4, 1.4)
ax.set_ylabel('$w(t; t_0, f_0, Q)$')
```
#### Compute PSD
The wavelet PSD (power spectral density) is defined by $PSD_w(f0, t0;Q) = |Hw(t_0; f_0,Q)|^2$. Unlike
the typical Fourier-transform PSD, the wavelet PSD allows detection of frequency information
which is localized in time.
Here we compute the wavelet PSD from sample wavelet using *wavelet_PSD* function in *astroML.fourier*.
The plot shows the PSD as a function of the frequency $f_0$ and the time $t_0$, for Q = 1.0.
```
# Compute the wavelet PSD
f0 = np.linspace(0.5, 7.5, 100)
wPSD = wavelet_PSD(t, h, f0, Q=1.0)
# Plot the results
fig = plt.figure(figsize=(6, 2))
fig.subplots_adjust(hspace=0.05, left=0.12, right=0.95, bottom=0.08, top=0.95)
# Third panel: the spectrogram
ax = plt.subplot(111)
ax.imshow(wPSD, origin='lower', aspect='auto',
extent=[t[0], t[-1], f0[0], f0[-1]])
ax.text(0.02, 0.95, ("Wavelet PSD"), color='w',
ha='left', va='top', transform=ax.transAxes)
ax.set_xlim(-4, 4)
ax.set_ylim(0.5, 7.5)
ax.set_xlabel('$t$')
ax.set_ylabel('$f_0$')
```
### Wavelet transform of a Noisy Spike
Here we use wavelet transform when the imput data is noisy spike rather than local Gaussian.
#### Define functions and construct imput noise
This example uses a Gaussian spike in the presence of white (Gaussian) noise as the imput noise. The imput signal is shown below.
```
def wavelet(t, t0, f0, Q):
return (np.exp(-(f0 / Q * (t - t0)) ** 2)
* np.exp(2j * np.pi * f0 * (t - t0)))
def wavelet_FT(f, t0, f0, Q):
# this is its fourier transform using
# H(f) = integral[ h(t) exp(-2pi i f t) dt]
return (np.sqrt(np.pi) * Q / f0
* np.exp(-2j * np.pi * f * t0)
* np.exp(-(np.pi * (f - f0) * Q / f0) ** 2))
def check_funcs(t0=1, f0=2, Q=3):
t = np.linspace(-5, 5, 10000)
h = wavelet(t, t0, f0, Q)
f, H = FT_continuous(t, h)
assert np.allclose(H, wavelet_FT(f, t0, f0, Q))
# Create the simulated dataset
np.random.seed(5)
t = np.linspace(-40, 40, 2001)[:-1]
h = np.exp(-0.5 * ((t - 20.) / 1.0) ** 2)
hN = h + np.random.normal(0, 0.5, size=h.shape)
# Plot the results
fig = plt.figure(figsize=(6, 2))
fig.subplots_adjust(hspace=0.05, left=0.12, right=0.95, bottom=0.08, top=0.95)
# plot the signal
ax = fig.add_subplot(111)
ax.plot(t, hN, '-k', lw=1)
ax.text(0.02, 0.95, ("Input Signal:\n"
"Localized spike plus noise"),
ha='left', va='top', transform=ax.transAxes)
ax.set_xlim(-40, 40)
ax.set_ylim(-1.2, 2.2)
ax.set_ylabel('$h(t)$')
```
#### Compute wavelet
Compute the convolution via the continuous Fourier transform. This is more exact than using the discrete transform, because we have an analytic expression for the FT of the wavelet. The wavelet transform applied to data h(t) is given by
$$H_w(t_0;f_0,Q)=\int^{\infty}_{\infty} h(t)w(t|t_0,f_0,Q)dt$$
By the convolution theorem $H(f) = A(f)B(f)$, we can write the Fourier transform
of $H_w$ as the pointwise product of the Fourier transforms of h(t) and $w*(t; t_0; f_0, Q)$. The first can
be approximated using the discrete Fourier transform as shown in appendix E in the textbook; the second can be found using the analytic formula for W(f) in the prevoius section. This allows us to quickly evaluate $H_w$ as a
function of $t_0$ and $f_0$, using two $O(N logN)$ fast Fourier transforms.
```
Q = 0.3
f0 = 2 ** np.linspace(-3, -1, 100)
f, H = FT_continuous(t, hN)
# Plot the results
fig = plt.figure(figsize=(6, 2))
fig.subplots_adjust(hspace=0.05, left=0.12, right=0.95, bottom=0.08, top=0.95)
# plot the wavelet
ax = fig.add_subplot(111)
W = wavelet(t, 0, 0.125, Q)
ax.plot(t, W.real, '-k', label='real part', lw=1)
ax.plot(t, W.imag, '--k', label='imag part', lw=1)
ax.legend(loc=1)
ax.text(0.02, 0.95, ("Example Wavelet\n"
"$t_0 = 0$, $f_0=1/8$, $Q=0.3$"),
ha='left', va='top', transform=ax.transAxes)
ax.text(0.98, 0.05,
(r"$w(t; t_0, f_0, Q) = e^{-[f_0 (t - t_0) / Q]^2}"
"e^{2 \pi i f_0 (t - t_0)}$"),
ha='right', va='bottom', transform=ax.transAxes)
ax.set_xlim(-40, 40)
ax.set_ylim(-1.4, 1.4)
ax.set_ylabel('$w(t; t_0, f_0, Q)$')
```
#### Compute spectrogram
We compute spectrogram using *IFT_continuous* in *astroML.fourier*.
The plot below shows the power spectral density as a function of the frequency $f_0$ and the time $t_0$, for Q = 0.3.
```
W = np.conj(wavelet_FT(f, 0, f0[:, None], Q))
t, HW = IFT_continuous(f, H * W)
# Plot the results
fig = plt.figure(figsize=(6, 2))
fig.subplots_adjust(hspace=0.05, left=0.12, right=0.95, bottom=0.08, top=0.95)
# plot the spectrogram
ax = fig.add_subplot(111)
ax.imshow(abs(HW) ** 2, origin='lower', aspect='auto', cmap=plt.cm.binary,
extent=[t[0], t[-1], np.log2(f0)[0], np.log2(f0)[-1]])
ax.set_xlim(-40, 40)
ax.text(0.02, 0.95, ("Wavelet PSD"), color='w',
ha='left', va='top', transform=ax.transAxes)
ax.set_ylim(np.log2(f0)[0], np.log2(f0)[-1])
ax.set_xlabel('$t$')
ax.set_ylabel('$f_0$')
ax.yaxis.set_major_locator(plt.MultipleLocator(1))
ax.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, *args: ("1/%i"
% (2 ** -x))))
```
### Examples of Wavelets
The resulting wavelets vary from different parameters Q and $f_0$.
Here we take several different parameters Q and $f_0$ and show the result wavelets, taking the prevoius Gaussian sample imput.
```
# Set up the wavelets
t0 = 0
t = np.linspace(-0.4, 0.4, 10000)
f0 = np.array([5, 5, 10, 10])
Q = np.array([1, 0.5, 1, 0.5])
# compute wavelets all at once
W = sinegauss(t, t0, f0[:, None], Q[:, None])
```
Solid lines show the real part and dashed lines show the imaginary part.
```
# Plot the wavelets
fig = plt.figure(figsize=(5, 3.75))
fig.subplots_adjust(hspace=0.05, wspace=0.05)
# in each panel, plot and label a different wavelet
for i in range(4):
ax = fig.add_subplot(221 + i)
ax.plot(t, W[i].real, '-k')
ax.plot(t, W[i].imag, '--k')
ax.text(0.04, 0.95, "$f_0 = %i$\n$Q = %.1f$" % (f0[i], Q[i]),
ha='left', va='top', transform=ax.transAxes)
ax.set_ylim(-1.2, 1.2)
ax.set_xlim(-0.35, 0.35)
ax.xaxis.set_major_locator(plt.MultipleLocator(0.2))
if i in (0, 1):
ax.xaxis.set_major_formatter(plt.NullFormatter())
else:
ax.set_xlabel('$t$')
if i in (1, 3):
ax.yaxis.set_major_formatter(plt.NullFormatter())
else:
ax.set_ylabel('$w(t)$')
```
| true |
code
| 0.803347 | null | null | null | null |
|
# Generative Adversarial Network in Tensorflow
**Generative Adversarial Networks**, introduced by Ian Goodfellow in 2014, are neural nets we can train to _produce_ new images (or other kinds of data) that look as though they came from our true data distribution. In this notebook, we'll implement a small GAN for generating images that look as though they come from the MNIST dataset.
The key insight behind the GAN is to pit two neural networks against each other. On the one hand is the **Generator**, a neural network that takes random noise as input and produces an image as output. On the other hand is the **Discriminator**, which takes in an image and classifies it as real (from MNIST) or fake (from our Generator). During training, we alternate between training the Generator to fool the Discriminator, and training the Discriminator to call the Generator's bluff.
Implementing a GAN in Tensorflow will give you practice turning more involved models into working code, and is also a great showcase for Tensorflow's **variable scope** feature. (Variable scope has made cameos in previous tutorials, but we'll discuss it in a bit more depth here. If you want to see how variable scope is used in TensorFlow Slim, definitely go revisit Kevin Liang's VAE tutorial!)
## Imports
```
%matplotlib inline
import tensorflow as tf
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import time
# Use if running on a GPU
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
config.log_device_placement = True
```
## Loading the data
As in previous examples, we'll use MNIST, because it's a small and easy-to-use dataset that comes bundled with Tensorflow.
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
```
## Utility functions
Let's define some utility functions that will help us quickly construct layers for use in our model. There are two things worth noting here:
1. Instead of `tf.Variable`, we use `tf.get_variable`.
The reason for this is a bit subtle, and you may want to skip this and come back to it once you've seen the rest of the code. Here's the basic explanation. Later on in this notebook, we will call `fully_connected_layer` from a couple different places. Sometimes, we will want _new variables_ to be added to the graph, because we are creating an entirely new layer of our network. Other times, however, we will want to use the same weights as an already-existing layer, but acting on different inputs.
For example, the Discriminator network will appear _twice_ in our computational graph; in one case, the input neurons will be connected to the "real data" placeholder (which we will feed MNIST images), and in the other, they will be connected to the output of the Generator. Although these networks form two separate parts of our computational graph, we want them to share the same weights: conceptually, there is _one_ Discriminator function that gets applied twice, not two different functions altogether. Since `tf.Variable` _always_ creates a new variable when called, it would not be appropriate for use here.
Variable scoping solves this problem. Whenever we are adding nodes to a graph, we are operating within a _scope_. Scopes can be named, and you can create a new scope using `tf.variable_scope('name')` (more on this later). When a scope is open, it can optionally be in _reuse mode_. The result of calling `tf.get_variable` depends on whether you are in reuse mode or not. If not (this is the default), `tf.get_variable` will create a new variable, or cause an error if a variable by the same name already exists in the current scope. If you _are_ in reuse mode, the behavior is the opposite: `tf.get_variable` will look up and return an existing variable (with the specified name) within your scope, or throw an error if it doesn't exist. By carefully controlling our scopes later on, we can create exactly the graph we want, with variables shared across the graph where appropriate.
2. The `variables_from_scope` function lists all variables created within a given scope. This will be useful later, when we want to update all "discriminator" variables, but no "generator" variables, or vice versa.
```
def shape(tensor):
"""
Get the shape of a tensor. This is a compile-time operation,
meaning that it runs when building the graph, not running it.
This means that it cannot know the shape of any placeholders
or variables with shape determined by feed_dict.
"""
return tuple([d.value for d in tensor.get_shape()])
def fully_connected_layer(in_tensor, out_units, activation_function=tf.nn.relu):
"""
Add a fully connected layer to the default graph, taking as input `in_tensor`, and
creating a hidden layer of `out_units` neurons. This should be called within a unique variable
scope. Creates variables W and b, and computes activation_function(in * W + b).
"""
_, num_features = shape(in_tensor)
W = tf.get_variable("weights", [num_features, out_units], initializer=tf.truncated_normal_initializer(stddev=0.1))
b = tf.get_variable("biases", [out_units], initializer=tf.constant_initializer(0.1))
return activation_function(tf.matmul(in_tensor, W) + b)
def variables_from_scope(scope_name):
"""
Returns a list of all variables in a given scope. This is useful when
you'd like to back-propagate only to weights in one part of the network
(in our case, the generator or the discriminator).
"""
return tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope=scope_name)
```
We'll also provide a simple function for displaying a few 28-pixel images. This will help us understand the progress of our GAN as it trains; we'll use it to visualize the generated 'fake digit' images.
```
def visualize_row(images, img_width=28, cmap='gray'):
"""
Takes in a tensor of images of given width, and displays them in a column
in a plot, using `cmap` to map from numbers to colors.
"""
im = np.reshape(images, [-1, img_width])
plt.figure()
plt.imshow(im, cmap=cmap)
plt.show()
```
## Generator
A GAN is made up of two smaller networks: a generator and a discriminator. The generator is responsible for sampling images from a distribution that we hope will get closer and closer, as we train, to the real data distribution.
Neural networks are deterministic, so in order to sample a new image from the generator, we first create some random noise `z` (in our case, `z` will be a 100-dimensional uniform random variable) and then feed that noise to the network. You can think of `z` as being a latent, low-dimensional representation of some image `G(z)`, though in a vanilla GAN, it is usually difficult to interpret `z`'s components in a meaningful way.
Our generator is a dead-simple multi-layer perceptron (feed-forward network), with 128 hidden units.
```
def generator(z):
"""
Given random noise `z`, use a simple MLP with 128 hidden units to generate a
sample image (784 values between 0 and 1, enforced with the sigmoid function).
"""
with tf.variable_scope("fc1"):
fc1 = fully_connected_layer(z, 128)
with tf.variable_scope("fc2"):
return fully_connected_layer(fc1, 784, activation_function=tf.sigmoid)
```
## Discriminator
Although it isn't necesssary, it makes some sense for our discriminator to mirror the generator's architecture, as we do here. The discriminator takes in an image (perhaps a real one from the MNIST dataset, perhaps a fake one from our generator), and attempts to classify it as real (1) or fake (0). Our architecture is again a simple MLP, taking 784 pixels down to 128 hidden units, and finally down to a probability.
```
def discriminator(x):
"""
This discriminator network takes in a tensor with shape [batch, 784], and classifies
each example image as real or fake. The network it uses is quite simple: a fully connected
layer with ReLU activation takes us down to 128 dimensions, then we collapse that to 1 number
in [0, 1] using a fully-connected layer with sigmoid activation. The result can be interpreted
as a probability, the discriminator's strength-of-belief that a sample is from the
real data distribution.
"""
with tf.variable_scope("fc1"):
fc1 = fully_connected_layer(x, 128)
with tf.variable_scope("fc2"):
return fully_connected_layer(fc1, 1, activation_function=tf.sigmoid)
```
## GAN
Given a generator and discriminator, we can now set up the GAN's computational graph.
We use Tensorflow's variable scope feature for two purposes.
1. First, it helps separate the variables used by the generator and by the discriminator; this is important, because when training, we want to alternate between updating each set of variables according to a different objective.
2. Second, scoping helps us reuse the same set of discriminator weights both for the operations we perform on _real_ images and for those performed on _fake_ images. To achieve this, after calling `discriminator` for the first time (and creating these weight variables), we tell our current scope to `reuse_variables()`, meaning that on our next call to `discriminator`, existing variables will be reused rather than creating new ones.
```
def gan(batch_size, z_dim):
"""
Given some details about the training procedure (batch size, dimension of z),
this function sets up the rest of the computational graph for the GAN.
It returns a dictionary containing six ops/tensors: `train_d` and `train_g`, the
optimization steps for the discriminator and generator, `real_data` and `noise`,
two placeholders that should be fed in during training, `d_loss`, the discriminator loss
(useful for estimating progress toward convergence), and `fake_data`, which can be
evaluated (with noise in the feed_dict) to sample from the generator's distribution.
"""
z = tf.placeholder(tf.float32, [batch_size, z_dim], name='z')
x = tf.placeholder(tf.float32, [batch_size, 784], name='x')
with tf.variable_scope('generator'):
fake_x = generator(z)
with tf.variable_scope('discriminator') as scope:
d_on_real = discriminator(x)
scope.reuse_variables()
d_on_fake = discriminator(fake_x)
g_loss = -tf.reduce_mean(tf.log(d_on_fake))
d_loss = -tf.reduce_mean(tf.log(d_on_real) + tf.log(1. - d_on_fake))
optimize_d = tf.train.AdamOptimizer().minimize(d_loss, var_list=variables_from_scope("discriminator"))
optimize_g = tf.train.AdamOptimizer().minimize(g_loss, var_list=variables_from_scope("generator"))
return {'train_d': optimize_d,
'train_g': optimize_g,
'd_loss': d_loss,
'fake_data': fake_x,
'real_data': x,
'noise': z}
```
## Training a GAN
Our training procedure is a bit more involved than in past demos. Here are the main differences:
1. Each iteration, we first train the generator, then (separately) the discriminator.
2. Each iteration, we need to feed in a batch of images, just as in previous notebooks. But we also need a batch of noise samples. For this, we use Numpy's `np.random.uniform` function.
3. Every 1000 iterations, we log some data to the console and visualize a few samples from our generator.
```
def train_gan(iterations, batch_size=50, z_dim=100):
"""
Construct and train the GAN.
"""
model = gan(batch_size=batch_size, z_dim=z_dim)
def make_noise():
return np.random.uniform(-1.0, 1.0, [batch_size, z_dim])
def next_feed_dict():
return {model['real_data']: mnist.train.next_batch(batch_size)[0],
model['noise']: make_noise()}
initialize_all = tf.global_variables_initializer()
with tf.Session(config=config) as sess:
sess.run(initialize_all)
start_time = time.time()
for t in range(iterations):
sess.run(model['train_g'], feed_dict=next_feed_dict())
_, d_loss = sess.run([model['train_d'], model['d_loss']], feed_dict=next_feed_dict())
if t % 1000 == 0 or t+1 == iterations:
fake_data = sess.run(model['fake_data'], feed_dict={model['noise']: make_noise()})
print('Iter [%8d] Time [%5.4f] d_loss [%.4f]' % (t, time.time() - start_time, d_loss))
visualize_row(fake_data[:5])
```
## Moment of truth
It's time to run our GAN! Watch as it learns to draw recognizable digits in about three minutes.
```
train_gan(25000)
```
| true |
code
| 0.879742 | null | null | null | null |
|
## Outlier Engineering
An outlier is a data point which is significantly different from the remaining data. “An outlier is an observation which deviates so much from the other observations as to arouse suspicions that it was generated by a different mechanism.” [D. Hawkins. Identification of Outliers, Chapman and Hall , 1980].
Statistics such as the mean and variance are very susceptible to outliers. In addition, **some Machine Learning models are sensitive to outliers** which may decrease their performance. Thus, depending on which algorithm we wish to train, we often remove outliers from our variables.
We discussed in section 3 of this course how to identify outliers. In this section, we we discuss how we can process them to train our machine learning models.
## How can we pre-process outliers?
- Trimming: remove the outliers from our dataset
- Treat outliers as missing data, and proceed with any missing data imputation technique
- Discrestisation: outliers are placed in border bins together with higher or lower values of the distribution
- Censoring: capping the variable distribution at a max and / or minimum value
**Censoring** is also known as:
- top and bottom coding
- winsorization
- capping
## Censoring or Capping.
**Censoring**, or **capping**, means capping the maximum and /or minimum of a distribution at an arbitrary value. On other words, values bigger or smaller than the arbitrarily determined ones are **censored**.
Capping can be done at both tails, or just one of the tails, depending on the variable and the user.
Check my talk in [pydata](https://www.youtube.com/watch?v=KHGGlozsRtA) for an example of capping used in a finance company.
The numbers at which to cap the distribution can be determined:
- arbitrarily
- using the inter-quantal range proximity rule
- using the gaussian approximation
- using quantiles
### Advantages
- does not remove data
### Limitations
- distorts the distributions of the variables
- distorts the relationships among variables
## In this Demo
We will see how to perform capping with the inter-quantile range proximity rule using the Boston House Dataset
## Important
When doing capping, we tend to cap values both in train and test set. It is important to remember that the capping values MUST be derived from the train set. And then use those same values to cap the variables in the test set
I will not do that in this demo, but please keep that in mind when setting up your pipelines
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# for Q-Q plots
import scipy.stats as stats
# boston house dataset for the demo
from sklearn.datasets import load_boston
from feature_engine.outliers import Winsorizer
# load the the Boston House price data
# load the boston dataset from sklearn
boston_dataset = load_boston()
# create a dataframe with the independent variables
# I will use only 3 of the total variables for this demo
boston = pd.DataFrame(boston_dataset.data,
columns=boston_dataset.feature_names)[[
'RM', 'LSTAT', 'CRIM'
]]
# add the target
boston['MEDV'] = boston_dataset.target
boston.head()
# function to create histogram, Q-Q plot and
# boxplot. We learned this in section 3 of the course
def diagnostic_plots(df, variable):
# function takes a dataframe (df) and
# the variable of interest as arguments
# define figure size
plt.figure(figsize=(16, 4))
# histogram
plt.subplot(1, 3, 1)
sns.histplot(df[variable], bins=30)
plt.title('Histogram')
# Q-Q plot
plt.subplot(1, 3, 2)
stats.probplot(df[variable], dist="norm", plot=plt)
plt.ylabel('Variable quantiles')
# boxplot
plt.subplot(1, 3, 3)
sns.boxplot(y=df[variable])
plt.title('Boxplot')
plt.show()
# let's find outliers in RM
diagnostic_plots(boston, 'RM')
# visualise outliers in LSTAT
diagnostic_plots(boston, 'LSTAT')
# outliers in CRIM
diagnostic_plots(boston, 'CRIM')
```
There are outliers in all of the above variables. RM shows outliers in both tails, whereas LSTAT and CRIM only on the right tail.
To find the outliers, let's re-utilise the function we learned in section 3:
```
def find_skewed_boundaries(df, variable, distance):
# Let's calculate the boundaries outside which sit the outliers
# for skewed distributions
# distance passed as an argument, gives us the option to
# estimate 1.5 times or 3 times the IQR to calculate
# the boundaries.
IQR = df[variable].quantile(0.75) - df[variable].quantile(0.25)
lower_boundary = df[variable].quantile(0.25) - (IQR * distance)
upper_boundary = df[variable].quantile(0.75) + (IQR * distance)
return upper_boundary, lower_boundary
# find limits for RM
RM_upper_limit, RM_lower_limit = find_skewed_boundaries(boston, 'RM', 1.5)
RM_upper_limit, RM_lower_limit
# limits for LSTAT
LSTAT_upper_limit, LSTAT_lower_limit = find_skewed_boundaries(boston, 'LSTAT', 1.5)
LSTAT_upper_limit, LSTAT_lower_limit
# limits for CRIM
CRIM_upper_limit, CRIM_lower_limit = find_skewed_boundaries(boston, 'CRIM', 1.5)
CRIM_upper_limit, CRIM_lower_limit
# Now let's replace the outliers by the maximum and minimum limit
boston['RM']= np.where(boston['RM'] > RM_upper_limit, RM_upper_limit,
np.where(boston['RM'] < RM_lower_limit, RM_lower_limit, boston['RM']))
# Now let's replace the outliers by the maximum and minimum limit
boston['LSTAT']= np.where(boston['LSTAT'] > LSTAT_upper_limit, LSTAT_upper_limit,
np.where(boston['LSTAT'] < LSTAT_lower_limit, LSTAT_lower_limit, boston['LSTAT']))
# Now let's replace the outliers by the maximum and minimum limit
boston['CRIM']= np.where(boston['CRIM'] > CRIM_upper_limit, CRIM_upper_limit,
np.where(boston['CRIM'] < CRIM_lower_limit, CRIM_lower_limit, boston['CRIM']))
# let's explore outliers in the trimmed dataset
# for RM we see much less outliers as in the original dataset
diagnostic_plots(boston, 'RM')
diagnostic_plots(boston, 'LSTAT')
diagnostic_plots(boston, 'CRIM')
```
We can see that the outliers are gone, but the variable distribution was distorted quite a bit.
## Censoring with Feature-engine
```
# load the the Boston House price data
# load the boston dataset from sklearn
boston_dataset = load_boston()
# create a dataframe with the independent variables
# I will use only 3 of the total variables for this demo
boston = pd.DataFrame(boston_dataset.data,
columns=boston_dataset.feature_names)[[
'RM', 'LSTAT', 'CRIM'
]]
# add the target
boston['MEDV'] = boston_dataset.target
boston.head()
# create the capper
windsoriser = Winsorizer(capping_method='iqr', # choose iqr for IQR rule boundaries or gaussian for mean and std
tail='both', # cap left, right or both tails
fold=1.5,
variables=['RM', 'LSTAT', 'CRIM'])
windsoriser.fit(boston)
boston_t = windsoriser.transform(boston)
diagnostic_plots(boston, 'RM')
diagnostic_plots(boston_t, 'RM')
# we can inspect the minimum caps for each variable
windsoriser.left_tail_caps_
# we can inspect the maximum caps for each variable
windsoriser.right_tail_caps_
```
| true |
code
| 0.67139 | null | null | null | null |
|
# Simple Toy Problem
This notebook contains a simple artificial experiment setup to illustrate optimal control.
```
%load_ext autoreload
%autoreload 2
%config IPCompleter.greedy=True
# Importing relevant libraries
import cvxpy as cp
import numpy as np
from solara.constants import PROJECT_PATH
EXPERIMENT_NAME = "experiment_01_penalty_grid"
PLOT_DIR = PROJECT_PATH + "/figures/experiments/"
OUT_FORMAT = ".svg" # Output format of figures
# Loading data
load_data = np.loadtxt(PROJECT_PATH + "/data/solar_trace_data_v2/load_5796.txt", delimiter=",")
pv_data = np.loadtxt(PROJECT_PATH + "/data/solar_trace_data_v2/PV_5796.txt", delimiter=",")
import matplotlib.pyplot as plt
plt.plot(load_data)
import scipy.interpolate
solar = [0,0,0,0,0,0,0,0.05,0.2,0.8,0.95,1,0.95,0.8,0.2,0.05,0,0,0,0,0,0,0,0,0]
load = [0.5] * 25
#load[6] = 0.9
load[19] = 1.4
pv_data = np.array(solar)
load_data = np.array(load)
print(len(y1))
x1 = np.linspace(0,24,num=len(solar))
plt.plot(x1,solar)
plt.plot(x1,load)
solar_trace(x2)
x_values
# Setting all the variables
## Given variables
### Basic
T_u = 1 # Time slot duration
T_h = 24 # Time horizon (hours)
### Grid
pi_b = 0.14 #0.14 # Base price per unit of energy purchased ($/kWh)
pi_d = 0.86 # Demand price penalty per unit of energy purchased with power demand exceeding Γ($/kWh)
Gamma = 1.00 # np.percentile(load_data, 80) # Threshold above which the demand price is paid (kW)
p_bar = 0.12 # Price per unit of energy sold at time t ($/kWh)
### Battery variables
size = 10
kWh_per_cell = 0.011284
num_cells = size / kWh_per_cell
nominal_voltage_c = 3.8793
nominal_voltage_d = 3.5967
u1 = 0.1920
v1_bar = 0.0
u2 = -0.4865
v2_bar = kWh_per_cell * num_cells
eta_d = 1 / 0.9 # taking reciprocal so that we don't divide by eta_d
eta_c = 0.9942
alpha_bar_d = (
v2_bar * 1
) # the 1 indicates the maximum discharging C-rate
alpha_bar_c = (
v2_bar * 1
) # the 1 indicates the maximum charging C-rate
# Given variables from data set
num_timesteps = T_h
start = 0#24*12
power_load = load_data[start:start+num_timesteps] #np.random.randn(num_timesteps) # Load at time t (kW)
power_solar = pv_data[start:start+num_timesteps] #np.random.randn(num_timesteps) # Power generated by solar panels at timet(kW)
# Variables that are being optimised over
power_direct = cp.Variable(num_timesteps) # Power flowing directly from PV and grid to meet the load or be sold at time t (kW) (P_dir)
power_charge = cp.Variable(num_timesteps) # Power used to charge the ESD at time t (kW) (P_c)
power_discharge = cp.Variable(num_timesteps) # Power from the ESD at time t (kW) (P_d)
power_grid = cp.Variable(num_timesteps) # Power drawn from the grid at time t (kW) (P_g)
power_sell = cp.Variable(num_timesteps) # Power sold to the grid at timet(kW) (P_sell)
power_over_thres = cp.Variable(num_timesteps) # Purchased power that exceeds Γ at time t (not in notation table) (P_over)
# Implicitly defined variable (not in paper in "given" or "optimized over" set of variables)
energy_battery = cp.Variable(num_timesteps+1) # the energy content of the ESD at the beginning of interval t (E_ESD)
base_constraints = [
0 <= power_grid, # from Equation (13)
0 <= power_direct,
0 <= power_sell,
0 <= power_charge, # Eq (18)
0 <= power_discharge, # Eq (19)
# Power flow
power_direct + power_discharge == power_load + power_sell, # from Equation (14)
0 <= power_charge + power_direct, # Eq (17)
power_charge + power_direct <= power_solar + power_grid, # Eq (17)
]
grid_constraints = [
0 <= power_over_thres,
power_grid - Gamma <= power_over_thres, # Eq (24)
power_sell == 0, # stopping selling to the grid
]
battery_constraints = [
energy_battery[0] == 0,
energy_battery[1:] == energy_battery[:-1] + eta_c*power_charge*T_u - eta_d * power_discharge * T_u,
energy_battery >= 0,
power_discharge <= alpha_bar_d,
power_charge <= alpha_bar_c, #equation (5)
u1 * ((power_discharge)/nominal_voltage_d) + v1_bar <= energy_battery[1:], # equation (4)
u2 * ((power_charge)/nominal_voltage_c) + v2_bar >= energy_battery[1:], # equation (4)
]
constraints = base_constraints + battery_constraints + grid_constraints
objective = cp.Minimize(cp.sum(pi_b*power_grid + pi_d*power_over_thres - cp.multiply(p_bar,power_sell)))
prob = cp.Problem(objective, constraints)
result = prob.solve(verbose=True)
charging_power = power_charge.value - power_discharge.value
episode_data = {
'load': power_load,
'pv_gen': power_solar,
'battery_cont': energy_battery.value,
'charging_power': charging_power,
'cost': pi_b*power_grid.value + pi_d*power_over_thres.value,
'price_threshold': np.ones(25) * Gamma,
'actions': charging_power / 10,
'rewards': - (pi_b*power_grid.value + pi_d*power_over_thres.value),
'power_diff': np.zeros(24),
}
import solara.utils.rllib
import solara.plot.widgets
initial_visibility = ['load','pv_gen','energy_cont','net_load',
'charging_power','cost','price_threshold',
'actions']
#initial_visibility = ['energy_cont', 'pv_gen', 'actions', 'charging_power', 'energy_cont']
solara.plot.widgets.InteractiveEpisodes([episode_data], initial_visibility=initial_visibility)
import matplotlib.pyplot as plt
# Plotting configuration
POLICY_PLOT_CONF = {
"selected_keys": ['load','pv_gen','energy_cont','net_load',
'charging_power','cost','price_threshold', #'battery_cont',
],
"y_min":-1.3,
"y_max":1.5,
"show_grid":False,
}
solara.plot.pyplot.plot_episode(episode_data,title=None, **POLICY_PLOT_CONF)
plt.savefig(fname=PLOT_DIR + EXPERIMENT_NAME + "_plot_09_convex_solution" + OUT_FORMAT, bbox_inches='tight')
plt.show()
import solara.envs.components.solar
import solara.envs.components.load
import solara.envs.components.grid
import solara.envs.components.battery
import solara.envs.battery_control
import solara.utils.logging
from solara.constants import PROJECT_PATH
def battery_env_creator(env_config=None):
"""Create a battery control environment."""
PV_DATA_PATH = PROJECT_PATH + "/data/solar_trace_data/PV_5796.txt"
LOAD_DATA_PATH = PROJECT_PATH + "/data/solar_trace_data/load_5796.txt"
# Setting up components of environment
battery_model = solara.envs.components.battery.LithiumIonBattery(size=10,
chemistry="NMC",
time_step_len=1)
pv_model = solara.envs.components.solar.DataPV(data_path=PV_DATA_PATH,
fixed_sample_num=12)
load_model = solara.envs.components.load.DataLoad(data_path=LOAD_DATA_PATH,
fixed_sample_num=12)
grid_model = solara.envs.components.grid.PeakGrid(peak_threshold=1.0)
# Fixing load and PV trace to single sample
episode_num = 12
load_model.fix_start(episode_num)
pv_model.fix_start(episode_num)
env = solara.envs.battery_control.BatteryControlEnv(
battery = battery_model,
solar = pv_model,
grid = grid_model,
load = load_model,
infeasible_control_penalty=True,
grid_charging=True,
logging_level = "WARNING",
)
return env
env = battery_env_creator()
solara.plot.widgets.InteractiveEpisodes([episode_data],
initial_visibility=initial_visibility,
manual_mode=True,
manual_start_actions=episode_data["actions"],
env=env)
episode_data["actions"][0]
```
| true |
code
| 0.512266 | null | null | null | null |
|
# Scale Seldon Deployments based on Prometheus Metrics.
This notebook shows how you can scale Seldon Deployments based on Prometheus metrics via KEDA.
[KEDA](https://keda.sh/) is a Kubernetes-based Event Driven Autoscaler. With KEDA, you can drive the scaling of any container in Kubernetes based on the number of events needing to be processed.
With the support of KEDA in Seldon, you can scale your seldon deployments with any scalers listed [here](https://keda.sh/docs/2.0/scalers/).
In this example we will scale the seldon deployment with Prometheus metrics as an example.
## Install Seldon Core
Install Seldon Core as described in [docs](https://docs.seldon.io/projects/seldon-core/en/latest/workflow/install.html)
Make sure add `--set keda.enabled=true`
## Install Seldon Core Analytic
seldon-core-analytics contains Prometheus and Grafana installation with a basic Grafana dashboard showing the default Prometheus metrics exposed by Seldon for each inference graph deployed.
Later we will use the Prometheus service installed to provide metrics in order to scale the Seldon models.
Install Seldon Core Analytics as described in [docs](https://docs.seldon.io/projects/seldon-core/en/latest/analytics/analytics.html)
```
!helm install seldon-core-analytics ../../helm-charts/seldon-core-analytics -n seldon-system --wait
```
## Install KEDA
```
!kubectl delete -f https://github.com/kedacore/keda/releases/download/v2.0.0/keda-2.0.0.yaml
!kubectl apply -f https://github.com/kedacore/keda/releases/download/v2.0.0/keda-2.0.0.yaml
!kubectl get pod -n keda
```
## Create model with KEDA
To create a model with KEDA autoscaling you just need to add a KEDA spec referring in the Deployment, e.g.:
```yaml
kedaSpec:
pollingInterval: 15 # Optional. Default: 30 seconds
minReplicaCount: 1 # Optional. Default: 0
maxReplicaCount: 5 # Optional. Default: 100
triggers:
- type: prometheus
metadata:
# Required
serverAddress: http://seldon-core-analytics-prometheus-seldon.seldon-system.svc.cluster.local
metricName: access_frequency
threshold: '10'
query: rate(seldon_api_executor_client_requests_seconds_count{seldon_app=~"seldon-model-example"}[10s]
```
The full SeldonDeployment spec is shown below.
```
VERSION = !cat ../../version.txt
VERSION = VERSION[0]
VERSION
%%writefile model_with_keda_prom.yaml
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: seldon-model
spec:
name: test-deployment
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/mock_classifier:1.5.0-dev
imagePullPolicy: IfNotPresent
name: classifier
resources:
requests:
cpu: '0.5'
kedaSpec:
pollingInterval: 15 # Optional. Default: 30 seconds
minReplicaCount: 1 # Optional. Default: 0
maxReplicaCount: 5 # Optional. Default: 100
triggers:
- type: prometheus
metadata:
# Required
serverAddress: http://seldon-core-analytics-prometheus-seldon.seldon-system.svc.cluster.local
metricName: access_frequency
threshold: '10'
query: rate(seldon_api_executor_client_requests_seconds_count{seldon_app=~"seldon-model-example"}[1m])
graph:
children: []
endpoint:
type: REST
name: classifier
type: MODEL
name: example
!kubectl create -f model_with_keda_prom.yaml
!kubectl rollout status deploy/$(kubectl get deploy -l seldon-deployment-id=seldon-model -o jsonpath='{.items[0].metadata.name}')
```
## Create Load
We label some nodes for the loadtester. We attempt the first two as for Kind the first node shown will be the master.
```
!kubectl label nodes $(kubectl get nodes -o jsonpath='{.items[0].metadata.name}') role=locust
!kubectl label nodes $(kubectl get nodes -o jsonpath='{.items[1].metadata.name}') role=locust
```
Before add loads to the model, there is only one replica
```
!kubectl get deployment seldon-model-example-0-classifier
!helm install seldon-core-loadtesting seldon-core-loadtesting --repo https://storage.googleapis.com/seldon-charts \
--set locust.host=http://seldon-model-example:8000 \
--set oauth.enabled=false \
--set locust.hatchRate=1 \
--set locust.clients=1 \
--set loadtest.sendFeedback=0 \
--set locust.minWait=0 \
--set locust.maxWait=0 \
--set replicaCount=1
```
After a few mins you should see the deployment scaled to 5 replicas
```
import json
import time
def getNumberPods():
dp = !kubectl get deployment seldon-model-example-0-classifier -o json
dp = json.loads("".join(dp))
return dp["status"]["replicas"]
scaled = False
for i in range(60):
pods = getNumberPods()
print(pods)
if pods > 1:
scaled = True
break
time.sleep(5)
assert scaled
!kubectl get deployment/seldon-model-example-0-classifier scaledobject/seldon-model-example-0-classifier
```
## Remove Load
```
!helm delete seldon-core-loadtesting
```
After 5-10 mins you should see the deployment replica number decrease to 1
```
!kubectl get pods,deployments,hpa,scaledobject
!kubectl delete -f model_with_keda_prom.yaml
```
| true |
code
| 0.500366 | null | null | null | null |
|
# Experiment 5.1 - Features extracted using Inception Resnet v2 + SVM
Reproduce Results of [Transfer learning with deep convolutional neural network for liver steatosis assessment in ultrasound images](https://pubmed.ncbi.nlm.nih.gov/30094778/). We used a pre-trained CNN to extract features based on B-mode images.
The CNNfeatures are extracted using the pretrained Inception-Resnet-v2 implemented in Keras.
See reference: https://jkjung-avt.github.io/keras-inceptionresnetv2/
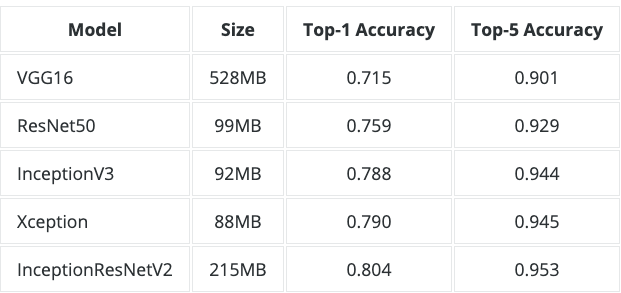
```
import sys
import random
sys.path.append('../src')
import warnings
warnings.filterwarnings("ignore")
from utils.compute_metrics import get_metrics, get_majority_vote,log_test_metrics
from utils.split import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.svm import LinearSVC
from sklearn.svm import SVC
from sklearn.model_selection import GroupKFold
from tqdm import tqdm
from pprint import pprint
from itertools import product
import pickle
import pandas as pd
import numpy as np
import mlflow
import matplotlib.pyplot as plt
```
## 1. Retrieve Extracted Features
```
with open('../data/03_features/inception_dict_tensor_avg_interpolation_pooling.pickle', 'rb') as handle:
features_dict = pickle.load(handle)
df_features = features_dict ['features']
interpolation = features_dict ['Interpolation']
```
# 2. Cross Validation using SVM Classification
> Methods that exclude outliers were used to normalize the features. Patient-specific leave-one-out cross-validation (LOOCV) was applied to evaluate the classification. In each case, the test set consisted of10 images from the same patient and the training set contained 540 images from the remaining 54 patients. For each training set, fivefold cross-validation and grid search were applied to indicate the optimal SVM classifier hyperparameters and the best kernel. To address the problem of class imbalance, the SVM hyperparameter C of each class was adjusted inversely proportional to that class frequency in the training set. Label 1 indicated the image containing a fatty liver and label −1 otherwise.
```
# Set the parameters by cross-validation
param_gamma = [1e-3, 1e-4]
param_C = [1, 10, 1000]
kernel = ['linear', 'poly', 'rbf', 'sigmoid']
params = list(product(kernel,param_gamma, param_C ))
def train_valid(param, X_train,X_valid,y_train, y_valid):
#The “balanced” mode uses the values of y to automatically adjust weights inversely
#proportional to class frequencies in the input data as n_samples / (n_classes * np.bincount(y)).
model = SVC(kernel =param[0], gamma=param[1], C=param[2], class_weight= 'balanced')#,probability = True)
model.fit(X_train, y_train)
predictions = model.predict(X_valid)
acc, auc, specificity, sensitivity = get_metrics(y_valid, predictions)
return acc, auc, specificity, sensitivity , predictions
def log_val_metrics(params, metrics, test_n_splits, num_components = 5):
mlflow.set_experiment('val_inception_avg_pooling_svm_experiment')
# log mlflow params
for param in params:
with mlflow.start_run():
#log params
mlflow.log_param('pca_n',pca_n_components)
mlflow.log_param('model',f'svm: {param[0]}')
mlflow.log_param('test K fold', test_n_splits)
mlflow.log_param('gamma',param[1])
mlflow.log_param('Num Components', num_components)
mlflow.log_param('C',param[2])
#log metrics
mlflow.log_metric('accuracy',np.array(metrics[str(param)]['acc']).mean())
mlflow.log_metric('AUC',np.array(metrics[str(param)]['auc']).mean())
mlflow.log_metric('specificity',np.array(metrics[str(param)]['specificity']).mean())
mlflow.log_metric('sensitivity',np.array(metrics[str(param)]['sensitivity']).mean())
print("Done logging validation params in MLFlow")
df = df_features
pca_n_components = 5
standardize = True
test_metrics={}
#majority vote results
test_metrics_mv={}
test_n_splits = 11
group_kfold_test = GroupKFold(n_splits=test_n_splits)
seed= 11
df_pid = df['id']
df_y = df['labels']
fold_c =1
predictions_prob =[]
labels =[]
for train_index, test_index in group_kfold_test.split(df,
df_y,
df_pid):
random.seed(seed)
random.shuffle(train_index)
X_train, X_test = df.iloc[train_index], df.iloc[test_index]
y_train, y_test = df_y.iloc[train_index], df_y.iloc[test_index]
X_test = X_test.drop(columns=['id', 'labels'])
X_train_pid = X_train.pop('id')
X_train = X_train.drop(columns=['labels'])
# Do cross-validation for hyperparam tuning
group_kfold_val = GroupKFold(n_splits=5)
metrics={}
#X_train_y = df.pop('class')
for subtrain_index, valid_index in group_kfold_val.split(X_train,
y_train,
X_train_pid):
X_subtrain, X_valid = X_train.iloc[subtrain_index], X_train.iloc[valid_index]
y_subtrain, y_valid = y_train.iloc[subtrain_index], y_train.iloc[valid_index]
#standardize
if standardize:
scaler = StandardScaler()
X_subtrain = scaler.fit_transform(X_subtrain)
X_valid = scaler.transform(X_valid)
pca = PCA(n_components=pca_n_components,random_state = seed)
X_subtrain = pca.fit_transform(X_subtrain)
X_valid = pca.transform(X_valid)
for param in tqdm(params):
if str(param) not in metrics.keys() :
metrics[str(param)] ={'acc':[], 'auc':[], 'sensitivity':[], 'specificity':[]}
acc, auc, specificity, sensitivity,_ = train_valid(param, X_subtrain,X_valid,y_subtrain, y_valid)
metrics[str(param)]['auc'].append(auc)
metrics[str(param)]['acc'].append(acc)
metrics[str(param)]['sensitivity'].append(sensitivity)
metrics[str(param)]['specificity'].append(specificity)
#log validation metrics for all combination of params
log_val_metrics(params, metrics, test_n_splits,pca_n_components, standardize)
#highest accuracy
index_param_max = np.array([np.array(metrics[str(param)]['auc']).mean() for param in params]).argmax()
print('From all the combinations, the highest accuracy was achieved with', params[index_param_max])
#standardize
if standardize:
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
pca = PCA(n_components=pca_n_components)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
#acc, auc, specificity, sensitivity, predictions = train_valid(params[index_param_max], X_train, X_test, y_train, y_test)
model = SVC(kernel ='sigmoid', gamma=0.001, C=1, class_weight= 'balanced',probability = True)
model.fit(X_train, y_train)
predictions_prob = predictions_prob + [probe[1] for probe in model.predict_proba(X_test)]
labels = labels + list(y_test)
#compute majority vote metrics
acc_mv, auc_mv, specificity_mv, sensitivity_mv = get_majority_vote(y_test, predictions)
print('FOLD '+ str(fold_c) + ': acc ' + str(acc) + ', auc ' + str(auc) + ', specificity '+ str(specificity)
+ ', sensitivity ' + str(sensitivity))
print('FOLD '+ str(fold_c) + ': MV acc ' + str(acc_mv) + ', MV auc ' + str(auc_mv) + ', MV specificity '+ str(specificity_mv)
+ ', MV sensitivity ' + str(sensitivity_mv))
test_metrics[fold_c]= {'acc':acc, 'auc':auc, 'sensitivity':sensitivity, 'specificity':specificity, 'param':params[index_param_max]}
test_metrics_mv[fold_c]= {'acc':acc_mv, 'auc':auc_mv, 'sensitivity':sensitivity_mv, 'specificity':specificity_mv, 'param':params[index_param_max]}
fold_c +=1
log_test_metrics(test_metrics, test_metrics_mv, test_n_splits, 'AVG Pooling Inception features + SVM', interpolation , seed, pca_n_components, standardize)
```
| true |
code
| 0.484563 | null | null | null | null |
|
# Bite Size Bayes
Copyright 2020 Allen B. Downey
License: [Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/)
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
## The "Girl Named Florida" problem
In [The Drunkard's Walk](https://www.goodreads.com/book/show/2272880.The_Drunkard_s_Walk), Leonard Mlodinow presents "The Girl Named Florida Problem":
>"In a family with two children, what are the chances, if [at least] one of the children is a girl named Florida, that both children are girls?"
I added "at least" to Mlodinow's statement of the problem to avoid a subtle ambiguity (which I'll explain at the end).
To avoid some real-world complications, let's assume that this question takes place in an imaginary city called Statesville where:
* Every family has two children.
* 50% of children are male and 50% are female.
* All children are named after U.S. states, and all state names are chosen with equal probability.
* Genders and names within each family are chosen independently.
To answer Mlodinow's question, I'll create a DataFrame with one row for each family in Statesville and a column for the gender and name of each child.
Here's a list of genders and a [dictionary of state names](https://gist.github.com/tlancon/9794920a0c3a9990279de704f936050c):
```
gender = ['B', 'G']
us_states = {
'Alabama': 'AL',
'Alaska': 'AK',
'Arizona': 'AZ',
'Arkansas': 'AR',
'California': 'CA',
'Colorado': 'CO',
'Connecticut': 'CT',
'Delaware': 'DE',
# 'District of Columbia': 'DC',
'Florida': 'FL',
'Georgia': 'GA',
'Hawaii': 'HI',
'Idaho': 'ID',
'Illinois': 'IL',
'Indiana': 'IN',
'Iowa': 'IA',
'Kansas': 'KS',
'Kentucky': 'KY',
'Louisiana': 'LA',
'Maine': 'ME',
'Maryland': 'MD',
'Massachusetts': 'MA',
'Michigan': 'MI',
'Minnesota': 'MN',
'Mississippi': 'MS',
'Missouri': 'MO',
'Montana': 'MT',
'Nebraska': 'NE',
'Nevada': 'NV',
'New Hampshire': 'NH',
'New Jersey': 'NJ',
'New Mexico': 'NM',
'New York': 'NY',
'North Carolina': 'NC',
'North Dakota': 'ND',
'Ohio': 'OH',
'Oklahoma': 'OK',
'Oregon': 'OR',
'Pennsylvania': 'PA',
'Rhode Island': 'RI',
'South Carolina': 'SC',
'South Dakota': 'SD',
'Tennessee': 'TN',
'Texas': 'TX',
'Utah': 'UT',
'Vermont': 'VT',
'Virginia': 'VA',
'Washington': 'WA',
'West Virginia': 'WV',
'Wisconsin': 'WI',
'Wyoming': 'WY'
}
```
To enumerate all possible combinations of genders and names, I'll use `from_product`, which makes a Pandas MultiIndex.
```
names = ['gender1', 'name1', 'gender2', 'name2']
index = pd.MultiIndex.from_product([gender, us_states]*2,
names=names)
```
Now I'll create a DataFrame with that index:
```
df = pd.DataFrame(index=index)
df.head()
```
It will be easier to work with if I reindex it so the levels in the MultiIndex become columns.
```
df = df.reset_index()
df.head()
```
This DataFrame contains one row for each family in Statesville; for example, the first row represents a family with two boys, both named Alabama.
As it turns out, there are 10,000 families in Statesville:
```
len(df)
```
## Probabilities
To compute probabilities, we'll use Boolean Series. For example, the following Series is `True` for each family where the first child is a girl:
```
girl1 = (df['gender1']=='G')
```
The following function takes a Boolean Series and counts the number of `True` values, which is the probability that the condition is true.
```
def prob(A):
"""Computes the probability of a proposition, A.
A: Boolean series
returns: probability
"""
assert isinstance(A, pd.Series)
assert A.dtype == 'bool'
return A.mean()
```
Not surprisingly, the probability is 50% that the first child is a girl.
```
prob(girl1)
```
And so is the probability that the second child is a girl.
```
girl2 = (df['gender2']=='G')
prob(girl2)
```
Mlodinow's question is a conditional probability: given that one of the children is a girl named Florida, what is the probability that both children are girls?
To compute conditional probabilities, I'll use this function, which takes two Boolean Series, `A` and `B`, and computes the conditional probability $P(A~\mathrm{given}~B)$.
```
def conditional(A, B):
"""Conditional probability of A given B.
A: Boolean series
B: Boolean series
returns: probability
"""
return prob(A[B])
```
For example, here's the probability that the second child is a girl, given that the first child is a girl.
```
conditional(girl2, girl1)
```
The result is 50%, which is the same as the unconditioned probability that the second child is a girl:
```
prob(girl2)
```
So that confirms that the genders of the two children are independent, which is one of my assumptions.
Now, Mlodinow's question asks about the probability that both children are girls, so let's compute that.
```
gg = (girl1 & girl2)
prob(gg)
```
In 25% of families, both children are girls. And that should be no surprise: because they are independent, the probability of the conjunction is the product of the probabilities:
```
prob(girl1) * prob(girl2)
```
While we're at it, we can also compute the conditional probability of two girls, given that the first child is a girl.
```
conditional(gg, girl1)
```
That's what we should expect. If we know the first child is a girl, and the probability is 50% that the second child is a girl, the probability of two girls is 50%.
## At least one girl
Before I answer Mlodinow's question, I'll warm up with a simpler version: given that at least one of the children is a girl, what is the probability that both are?
To compute the probability of "at least one girl" I will use the `|` operator, which computes the logical `OR` of the two Series:
```
at_least_one_girl = (girl1 | girl2)
prob(at_least_one_girl)
```
75% of the families in Statesville have at least one girl.
Now we can compute the conditional probability of two girls, given that the family has at least one girl.
```
conditional(gg, at_least_one_girl)
```
Of the families that have at least one girl, `1/3` have two girls.
If you have not thought about questions like this before, that result might surprise you. The following figure might help:
<img width="200" src="https://github.com/AllenDowney/BiteSizeBayes/raw/master/GirlNamedFlorida1.png">
In the top left, the gray square represents a family with two boys; in the lower right, the dark blue square represents a family with two girls.
The other two quadrants represent families with one girl, but note that there are two ways that can happen: the first child can be a girl or the second child can be a girl.
There are an equal number of families in each quadrant.
If we select families with at least one girl, we eliminate the gray square in the upper left. Of the remaining three squares, one of them has two girls.
So if we know a family has at least one girl, the probability they have two girls is 33%.
## What's in a name?
So far, we have computed two conditional probabilities:
* Given that the first child is a girl, the probability is 50% that both children are girls.
* Given that at least one child is a girl, the probability is 33% that both children are girls.
Now we're ready to answer Mlodinow's question:
* Given that at least one child is a girl *named Florida*, what is the probability that both children are girls?
If your intuition is telling you that the name of the child can't possibly matter, brace yourself.
Here's the probability that the first child is a girl named Florida.
```
gf1 = girl1 & (df['name1']=='Florida')
prob(gf1)
```
And the probability that the second child is a girl named Florida.
```
gf2 = girl2 & (df['name2']=='Florida')
prob(gf2)
```
To compute the probability that at least one of the children is a girl named Florida, we can use the `|` operator again.
```
at_least_one_girl_named_florida = (gf1 | gf2)
prob(at_least_one_girl_named_florida)
```
We can double-check it by using the disjunction rule:
```
prob(gf1) + prob(gf2) - prob(gf1 & gf2)
```
So, the percentage of families with at least one girl named Florida is a little less than 2%.
Now, finally, here is the answer to Mlodinow's question:
```
conditional(gg, at_least_one_girl_named_florida)
```
That's right, the answer is about 49.7%. To summarize:
* Given that the first child is a girl, the probability is 50% that both children are girls.
* Given that at least one child is a girl, the probability is 33% that both children are girls.
* Given that at least one child is a girl *named Florida*, the probability is 49.7% that both children are girls.
If your brain just exploded, I'm sorry.
Here's my best attempt to put your brain back together.
For each child, there are three possibilities: boy (B), girl not named Florida (G), and girl named Florida (GF), with these probabilities:
$P(B) = 1/2 $
$P(G) = 1/2 - x $
$P(GF) = x $
where $x$ is the percentage of people who are girls named Florida.
In families with two children, here are the possible combinations and their probabilities:
$P(B, B) = (1/2)(1/2)$
$P(B, G) = (1/2)(1/2-x)$
$P(B, GF) = (1/2)(x)$
$P(G, B) = (1/2-x)(1/2)$
$P(G, G) = (1/2-x)(1/2-x)$
$P(G, GF) = (1/2-x)(x)$
$P(GF, B) = (x)(1/2)$
$P(GF, G) = (x)(1/2-x)$
$P(GF, GF) = (x)(x)$
If we select only the families that have at least one girl named Florida, here are their probabilities:
$P(B, GF) = (1/2)(x)$
$P(G, GF) = (1/2-x)(x)$
$P(GF, B) = (x)(1/2)$
$P(GF, G) = (x)(1/2-x)$
$P(GF, GF) = (x)(x)$
Of those, if we select the families with two girls, here are their probabilities:
$P(G, GF) = (1/2-x)(x)$
$P(GF, G) = (x)(1/2-x)$
$P(GF, GF) = (x)(x)$
To get the conditional probability of two girls, given at least one girl named Florida, we can add up the last 3 probabilities and divide by the sum of the previous 5 probabilities.
With a little algebra, we get:
$P(\mathrm{two~girls} ~|~ \mathrm{at~least~one~girl~named~Florida}) = (1 - x) / (2 - x)$
As $x$ approaches $0$ the answer approaches $1/2$.
As $x$ approaches $1/2$, the answer approaches $1/3$.
Here's what all of that looks like graphically:
<img width="200" src="https://github.com/AllenDowney/BiteSizeBayes/raw/master/GirlNamedFlorida2.png">
Here `B` a boy, `Gx` is a girl with some property `X`, and `G` is a girl who doesn't have that property. If we select all families with at least one `Gx`, we get the five blue squares (light and dark). Of those, the families with two girls are the three dark blue squares.
If property `X` is common, the ratio of dark blue to all blue approaches `1/3`. If `X` is rare, the same ratio approaches `1/2`.
In the "Girl Named Florida" problem, `x` is 1/100, and we can compute the result:
```
x = 1/100
(1-x) / (2-x)
```
Which is what we got by counting all of the families in Statesville.
## Controversy
[I wrote about this problem in my blog in 2011](http://allendowney.blogspot.com/2011/11/girl-named-florida-solutions.html). As you can see in the comments, my explanation was not met with universal acclaim.
One of the issues that came up is the challenge of stating the question unambiguously. In this article, I rephrased Mlodinow's statement to clarify it.
But since we have come all this way, let me also answer a different version of the problem.
>Suppose you choose a house in Statesville at random and ring the doorbell. A girl (who lives there) opens the door and you learn that her name is Florida. What is the probability that the other child in this house is a girl?
In this version of the problem, the selection process is different. Instead of selecting houses with at least one girl named Florida, you selected a house, then selected a child, and learned that her name is Florida.
Since the selection of the child was arbitrary, we can say without loss of generality that the child you met is the first child in the table.
In that case, the conditional probability of two girls is:
```
conditional(gg, gf1)
```
Which is the same as the conditional probability, given that the first child is a girl:
```
conditional(gg, girl1)
```
So in this version of the problem, the girl's name is irrelevant.
| true |
code
| 0.628236 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/mengwangk/dl-projects/blob/master/04_02_auto_ml_4.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Automated ML
```
COLAB = True
if COLAB:
!sudo apt-get install git-lfs && git lfs install
!rm -rf dl-projects
!git clone https://github.com/mengwangk/dl-projects
#!cd dl-projects && ls -l --block-size=M
if COLAB:
!cp dl-projects/utils* .
!cp dl-projects/preprocess* .
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.stats as ss
import math
import matplotlib
from scipy import stats
from collections import Counter
from pathlib import Path
plt.style.use('fivethirtyeight')
sns.set(style="ticks")
# Automated feature engineering
import featuretools as ft
# Machine learning
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import Imputer, MinMaxScaler, StandardScaler
from sklearn.impute import SimpleImputer
from sklearn.metrics import precision_score, recall_score, f1_score, roc_auc_score, precision_recall_curve, roc_curve, mean_squared_error, accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.ensemble import RandomForestClassifier
from IPython.display import display
from utils import *
from preprocess import *
# The Answer to the Ultimate Question of Life, the Universe, and Everything.
np.random.seed(42)
%aimport
```
## Preparation
```
if COLAB:
from google.colab import drive
drive.mount('/content/gdrive')
GDRIVE_DATASET_FOLDER = Path('gdrive/My Drive/datasets/')
if COLAB:
DATASET_PATH = GDRIVE_DATASET_FOLDER
ORIGIN_DATASET_PATH = Path('dl-projects/datasets')
else:
DATASET_PATH = Path("datasets")
ORIGIN_DATASET_PATH = Path('datasets')
DATASET = DATASET_PATH/"feature_matrix_2.csv"
ORIGIN_DATASET = ORIGIN_DATASET_PATH/'4D.zip'
if COLAB:
!ls -l gdrive/"My Drive"/datasets/ --block-size=M
!ls -l dl-projects/datasets --block-size=M
data = pd.read_csv(DATASET, header=0, sep=',', quotechar='"', parse_dates=['time'])
origin_data = format_tabular(ORIGIN_DATASET)
data.info()
```
## Exploratory Data Analysis
```
feature_matrix = data
feature_matrix.columns
feature_matrix.head(4).T
origin_data[origin_data['LuckyNo']==911].head(10)
# feature_matrix.groupby('time')['COUNT(Results)'].mean().plot()
# plt.title('Average Monthly Count of Results')
# plt.ylabel('Strike Per Number')
```
## Feature Selection
```
from utils import feature_selection
%load_ext autoreload
%autoreload 2
feature_matrix_selection = feature_selection(feature_matrix.drop(columns = ['time', 'NumberId']))
feature_matrix_selection['time'] = feature_matrix['time']
feature_matrix_selection['NumberId'] = feature_matrix['NumberId']
feature_matrix_selection['Label'] = feature_matrix['Label']
feature_matrix_selection.columns
```
## Correlations
```
feature_matrix_selection.shape
corrs = feature_matrix_selection.corr().sort_values('TotalStrike')
corrs['TotalStrike'].head()
corrs['Label'].dropna().tail(8)
corrs['TotalStrike'].dropna().tail(8)
```
## Visualization
```
#pip install autoviz
#from autoviz.AutoViz_Class import AutoViz_Class
```
### XgBoost
```
import xgboost as xgb
model = xgb.XGBClassifier()
def predict_dt(dt, feature_matrix, return_probs = False):
feature_matrix['date'] = feature_matrix['time']
# Subset labels
test_labels = feature_matrix.loc[feature_matrix['date'] == dt, 'Label']
train_labels = feature_matrix.loc[feature_matrix['date'] < dt, 'Label']
print(f"Size of test labels {len(test_labels)}")
print(f"Size of train labels {len(train_labels)}")
# Features
X_train = feature_matrix[feature_matrix['date'] < dt].drop(columns = ['NumberId', 'time',
'date', 'Label', 'TotalStrike', 'month', 'year', 'index'], errors='ignore')
X_test = feature_matrix[feature_matrix['date'] == dt].drop(columns = ['NumberId', 'time',
'date', 'Label', 'TotalStrike', 'month', 'year', 'index'], errors='ignore')
print(f"Size of X train {len(X_train)}")
print(f"Size of X test {len(X_test)}")
feature_names = list(X_train.columns)
# Impute and scale features
pipeline = Pipeline([('imputer', SimpleImputer(strategy = 'median')),
('scaler', MinMaxScaler())])
# Fit and transform training data
X_train = pipeline.fit_transform(X_train)
X_test = pipeline.transform(X_test)
# Labels
y_train = np.array(train_labels).reshape((-1, ))
y_test = np.array(test_labels).reshape((-1, ))
print('Training on {} observations.'.format(len(X_train)))
print('Testing on {} observations.\n'.format(len(X_test)))
# Train
model.fit(X_train, y_train)
# Make predictions
predictions = model.predict(X_test)
probs = model.predict_proba(X_test)[:, 1]
# Total positive
positive = np.where((predictions==1))
print('Total predicted to be positive: ', len(positive[0]))
# Calculate metrics
p = precision_score(y_test, predictions)
r = recall_score(y_test, predictions)
f = f1_score(y_test, predictions)
auc = roc_auc_score(y_test, probs)
a = accuracy_score(y_test, predictions)
cm = confusion_matrix(y_test, predictions)
print(f'Precision: {round(p, 5)}')
print(f'Recall: {round(r, 5)}')
print(f'F1 Score: {round(f, 5)}')
print(f'ROC AUC: {round(auc, 5)}')
print(f'Accuracy: {round(a, 5)}')
#print('Probability')
#print(len(probs), probs)
# print('Probability >= Avg proba')
# avg_p = np.average(probs)
# print(f'Average probablity: {avg_p}')
# hp = np.where((probs >= avg_p * 2) & (predictions==1) )
# print(len(hp[0]), probs[hp[0]], hp[0])
print('Confusion matrix')
print(cm)
# Total predicted matches
print('Predicted matches')
m = np.where((predictions==1))
print(len(m[0]), m)
if len(positive[0]) > 0:
# Matching draws
print('Matched draws')
m = np.where((predictions==1) & (y_test == 1))
print(len(m[0]), m)
data = feature_matrix.loc[feature_matrix['date'] == dt]
display(data.iloc[m[0]][
['NumberId', 'Label', 'month', 'MODE(Results.PrizeType)_1stPrizeNo',
'MODE(Results.PrizeType)_2ndPrizeNo',
'MODE(Results.PrizeType)_3rdPrizeNo',
'MODE(Results.PrizeType)_ConsolationNo1',
'MODE(Results.PrizeType)_ConsolationNo10',
'MODE(Results.PrizeType)_ConsolationNo2',
'MODE(Results.PrizeType)_ConsolationNo3',
'MODE(Results.PrizeType)_ConsolationNo4',
'MODE(Results.PrizeType)_ConsolationNo5',
'MODE(Results.PrizeType)_ConsolationNo6',
'MODE(Results.PrizeType)_ConsolationNo7',
'MODE(Results.PrizeType)_ConsolationNo8',
'MODE(Results.PrizeType)_ConsolationNo9',
'MODE(Results.PrizeType)_SpecialNo1',
'MODE(Results.PrizeType)_SpecialNo10',
'MODE(Results.PrizeType)_SpecialNo2',
'MODE(Results.PrizeType)_SpecialNo3',
'MODE(Results.PrizeType)_SpecialNo4',
'MODE(Results.PrizeType)_SpecialNo5',
'MODE(Results.PrizeType)_SpecialNo6',
'MODE(Results.PrizeType)_SpecialNo7',
'MODE(Results.PrizeType)_SpecialNo8',
'MODE(Results.PrizeType)_SpecialNo9']].T)
else:
print('No luck this month')
# Feature importances
fi = pd.DataFrame({'feature': feature_names, 'importance': model.feature_importances_})
if return_probs:
return fi, probs
return fi
# All the months
len(feature_matrix_selection['time'].unique()), feature_matrix_selection['time'].unique()
```
### Prediction by months
```
from utils import plot_feature_importances
%time oct_2018 = predict_dt(pd.datetime(2018,10,1), feature_matrix_selection)
norm_oct_2018_fi = plot_feature_importances(oct_2018)
%time may_2019 = predict_dt(pd.datetime(2019,5,1), feature_matrix_selection)
norm_may_2019_fi = plot_feature_importances(may_2019)
%time june_2019 = predict_dt(pd.datetime(2019,6,1), feature_matrix_selection)
norm_june_2019_fi = plot_feature_importances(june_2019)
%time july_2019 = predict_dt(pd.datetime(2019,7,1), feature_matrix_selection)
norm_july_2019_fi = plot_feature_importances(july_2019)
%time aug_2019 = predict_dt(pd.datetime(2019,8,1), feature_matrix_selection)
norm_aug_2019_fi = plot_feature_importances(aug_2019)
%time oct_2019 = predict_dt(pd.datetime(2019,10,1), feature_matrix_selection)
norm_oct_2019_fi = plot_feature_importances(oct_2019)
%time sep_2019 = predict_dt(pd.datetime(2019,9,1), feature_matrix_selection)
```
## Tuning - GridSearchCV
## Check Raw Data
```
origin_data.tail(10)
origin_data[(origin_data['DrawDate'].dt.year == 2019) & (origin_data['DrawDate'].dt.month == 6)]['DrawNo'].nunique()
origin_data[(origin_data['DrawDate'].dt.year == 2019) & (origin_data['DrawDate'].dt.month == 10)]['DrawNo'].nunique()
print(15 * 45 + 14 * 45)
```
## Testing
```
import numpy as np
import pandas as pd
data = [['no_1', 1], ['no_2', 2], ['no_3', 3], ['no_4', 4], ['no_5', 5], ['no_6', 6], ['no_7', 7]]
# Create the pandas DataFrame
df = pd.DataFrame(data, columns = ['Name', 'Age'])
a = np.array([0,0,0,1,0,1, 1])
b = np.array([0,0,0,1,0,0, 1])
print(len(a))
m = np.where((a==1) & (b ==1))
print(len(m[0]), m[0], a[m[0]])
print(df.iloc[m[0]])
probs = np.array([0.03399902, 0.03295987, 0.03078781, 0.04921166, 0.03662422, 0.03233755])
print(np.average(probs))
mydict = [{'a': 1, 'b': 2, 'c': 3, 'd': 4},
{'a': 100, 'b': 200, 'c': 300, 'd': 400},
{'a': 1000, 'b': 2000, 'c': 3000, 'd': 4000 }]
df = pd.DataFrame(mydict)
df.iloc[[0]][['a','b']]
```
| true |
code
| 0.48054 | null | null | null | null |
|
# Chapter 5 - Commmunity Detection
In this notebook, we explore several algorithms to find communities in graphs.
In some cells, we use the ABCD benchmark to generate synthetic graphs with communities.
ABCD is written in Julia.
### Installing Julia and ABCD
We use the command line interface option to run ABCD below.
The following steps are required:
* install Julia (we used version 1.4.2) from https://julialang.org/downloads/
* download ABCD from https://github.com/bkamins/ABCDGraphGenerator.jl
* adjust the 'abcd_path' in the next cell to the location of the 'utils' subdirectory of ABCD
* run 'julia abcd_path/install.jl' to install the required packages
Also set the path(s) in the cell below. For Windows, you may need to use "\\" or "\\\\" as delimiters, for example 'C:\ABCD\utils\\\\'
### Directories
* Set the directories accordingly in the next cell
```
## set those accordingly
datadir = '../Datasets/'
abcd_path = '~/ABCD/utils/'
import igraph as ig
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.linear_model import LinearRegression
from collections import Counter
import os
import umap
import pickle
import partition_igraph
import subprocess
from sklearn.metrics import adjusted_mutual_info_score as AMI
## we used those for the book, but you can change to other colors
cls_edges = 'gainsboro'
cls = ['silver','dimgray','black']
```
# Zachary (karate) graph
A small graph with 34 nodes and two "ground-truth" communities.
Modularity-based algorithms will typically find 4 or 5 communities.
In the next cells, we look at this small graph from several different angles.
```
z = ig.Graph.Famous('zachary')
z.vs['size'] = 12
z.vs['name'] = [str(i) for i in range(z.vcount())]
z.vs['label'] = [str(i) for i in range(z.vcount())]
z.vs['label_size'] = 8
z.es['color'] = cls_edges
z.vs['comm'] = [0,0,0,0,0,0,0,0,1,1,0,0,0,0,1,1,0,0,1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,1]
z.vs['color'] = [cls[i] for i in z.vs['comm']]
#ig.plot(z, 'zachary_gt.eps', bbox=(0,0,300,200))
ig.plot(z, bbox=(0,0,350,250))
```
## Node Roles
We compute z(v) (normalized within module degree) and p(v) (participation coefficients) as defined in section 5.2 of the book for the Zachary graph. We identify 3 types of nodes, as described in the book.
* provincial hubs
* peripheral nodes (non-hubs)
* ultra peripheral nodes (non-hubs)
```
## compute internal degrees
in_deg_0 = z.subgraph_edges([e for e in z.es if z.vs['comm'][e.tuple[0]]==0 and z.vs['comm'][e.tuple[1]]==0],
delete_vertices=False).degree()
in_deg_1 = z.subgraph_edges([e for e in z.es if z.vs['comm'][e.tuple[0]]==1 and z.vs['comm'][e.tuple[1]]==1],
delete_vertices=False).degree()
## compute z (normalized within-module degree)
z.vs['in_deg'] = [in_deg_0[i] + in_deg_1[i] for i in range(z.vcount())]
mu = [np.mean([x for x in in_deg_0 if x>0]),np.mean([x for x in in_deg_1 if x>0])]
sig = [np.std([x for x in in_deg_0 if x>0],ddof=1),np.std([x for x in in_deg_1 if x>0],ddof=1)]
z.vs['z'] = [(v['in_deg']-mu[v['comm']])/sig[v['comm']] for v in z.vs]
## computing p (participation coefficient)
z.vs['deg'] = z.degree()
z.vs['out_deg'] = [v['deg'] - v['in_deg'] for v in z.vs]
z.vs['p'] = [1-(v['in_deg']/v['deg'])**2-(v['out_deg']/v['deg'])**2 for v in z.vs]
D = pd.DataFrame(np.array([z.vs['z'],z.vs['p']]).transpose(),columns=['z','p']).sort_values(by='z',ascending=False)
D.head()
```
Below, we plot the Zachary graph w.r.t. z where z>2.5 are hubs, which we show as square nodes.
The largest values are for node 0 (instructor), node 33 (president) and node 32.
Nodes 0 and 33 are the key nodes for the division of the group into two factions.
```
## Zachary graph w.r.t. roles
z.vs['color'] = 'black'
z.vs['shape'] = 'circle'
for v in z.vs:
if v['z']<2.5: ## non-hub
if v['p'] < .62 and v['p'] >= .05: ## peripheral
v['color'] = 'dimgrey'
if v['p'] < .05: ## ultra-peripheral
v['color'] = 'gainsboro'
if v['z']>=2.5 and v['p'] < .3: ## hubs (all provincial here)
v['color'] = 'silver'
v['shape'] = 'square'
#ig.plot(z, 'zachary_roles_1.eps', bbox=(0,0,350,250))
ig.plot(z, bbox=(0,0,350,250))
```
Code below is to generate Figure 5.3(b) in the book, again comparing node roles in the Zachary graph.
```
## Figure 5.3(b) -- comparing the roles
fig, ax = plt.subplots(figsize=(12,9))
ax.scatter(z.vs['p'],z.vs['z'],marker='o',s=75, color='k')
plt.plot([0, .5], [2.5, 2.5], color='k', linestyle='-', linewidth=2)
plt.plot([.05, .05], [-.5, 2.4], color='k', linestyle='-', linewidth=2)
ax.annotate('node 0', (z.vs['p'][0],z.vs['z'][0]-.05), xytext=(z.vs['p'][0]+.01,z.vs['z'][0]-.3),
fontsize=14,
arrowprops = dict( arrowstyle="-",connectionstyle="angle3,angleA=0,angleB=-90"))
ax.annotate('node 33', (z.vs['p'][33],z.vs['z'][33]-.05), xytext=(z.vs['p'][33]-.07,z.vs['z'][33]-.3),
fontsize=14,
arrowprops = dict( arrowstyle="-",connectionstyle="angle3,angleA=0,angleB=-90"))
ax.annotate('node 32', (z.vs['p'][32]-.005,z.vs['z'][32]), xytext=(z.vs['p'][32]-.07,z.vs['z'][32]),
fontsize=14,
arrowprops = dict( arrowstyle="-",connectionstyle="angle3,angleA=0,angleB=-90"))
ax.annotate('node 1', (z.vs['p'][1],z.vs['z'][1]-.05), xytext=(z.vs['p'][1]-.07,z.vs['z'][1]-.3),
fontsize=14,
arrowprops = dict( arrowstyle="-",connectionstyle="angle3,angleA=0,angleB=-90"))
ax.annotate('node 3', (z.vs['p'][3],z.vs['z'][3]-.05), xytext=(z.vs['p'][3]+.07,z.vs['z'][3]-.3),
fontsize=14,
arrowprops = dict( arrowstyle="-",connectionstyle="angle3,angleA=0,angleB=-90"))
ax.annotate('node 2', (z.vs['p'][2],z.vs['z'][2]-.05), xytext=(z.vs['p'][2]-.07,z.vs['z'][2]-.3),
fontsize=14,
arrowprops = dict( arrowstyle="-",connectionstyle="angle3,angleA=0,angleB=-90"))
ax.annotate('provincial hubs',(.3,3), fontsize=18)
ax.annotate('peripheral non-hubs',(.3,1.8), fontsize=18)
ax.annotate('ultra peripheral non-hubs',(0.025,0.0),xytext=(.1,0), fontsize=18,
arrowprops = dict( arrowstyle="->", connectionstyle="angle3,angleA=0,angleB=-90"))
plt.xlabel('participation coefficient (p)',fontsize=16)
plt.ylabel('normalized within module degree (z)',fontsize=16);
#plt.savefig('zachary_roles_2.eps')
```
## Strong and weak communities
Communities are defined as strong or weak as per (5.1) and (5.2) in the book.
For the Zachary graph, we verify if nodes within communities satisfy the strong criterion, then we verify is the two communities satisfy the weak definition.
For the strong definition (internal degree larger than external degree for each node), only two nodes do not qualify.
For the weak definition (total community internal degree > total community external degree), both communities satisfy this criterion.
```
## strong criterion
for i in range(z.vcount()):
c = z.vs[i]['comm']
n = [z.vs[v]['comm']==c for v in z.neighbors(i)]
if sum(n)<=len(n)-sum(n):
print('node',i,'has internal degree',sum(n),'external degree',len(n)-sum(n))
## weak criterion
I = [0,0]
E = [0,0]
for i in range(z.vcount()):
c = z.vs[i]['comm']
n = [z.vs[v]['comm']==c for v in z.neighbors(i)]
I[c] += sum(n)
E[c] += len(n)-sum(n)
print('community 0 internal degree',I[0],'external degree',E[0])
print('community 1 internal degree',I[1],'external degree',E[1])
```
## Hierarchical clustering and dendrogram
Girvan-Newman algorithm is described in section 5.5 of the book. We apply it to the Zachary graph and show the results of this divisive algorithm as a dendrogram.
```
## Girvan-Newman algorithm
gn = z.community_edge_betweenness()
#ig.plot(gn,'zachary_dendrogram.eps',bbox=(0,0,300,300))
ig.plot(gn,bbox=(0,0,300,300))
```
This is an example of a hierarchical clustering. In the next plot, we compute modularity for each possible cut of the dendrogram.
We see that we get strong modularity with 2 clusters, but maximal value is obtained with 5.
```
## compute modularity at each possible cut and plot
q = []
for i in np.arange(z.vcount()):
q.append(z.modularity(gn.as_clustering(n=i+1)))
plt.plot(np.arange(1,1+z.vcount()),q,'o-',color='black')
plt.xlabel('number of clusters',fontsize=14)
plt.ylabel('modularity',fontsize=14);
#plt.savefig('zachary_modularity.eps');
```
How are the nodes partitioned is we pick only 2 communities? How does this compare to the underlying ground truth?
From the plot below, we see that only 1 node is misclassified.
We also report the modularity of this partition, $q = 0.35996$. We also compare the partition with ground truth via AMI (adjusted mutual information), as defined in section 5.3 of the book; we got a high value AMI = 0.83276 showing strong concordance.
```
## show result with 2 clusters --
z.vs['gn'] = gn.as_clustering(n=2).membership
print('AMI:',AMI(z.vs['comm'],z.vs['gn'])) ## adjusted mutual information
print('q:',z.modularity(z.vs['gn'])) ## modularity
z.vs['size'] = 10
z.vs['name'] = [str(i) for i in range(z.vcount())]
z.vs['label'] = [str(i) for i in range(z.vcount())]
z.vs['label_size'] = 8
z.es['color'] = cls_edges
z.vs['comm'] = [0,0,0,0,0,0,0,0,1,1,0,0,0,0,1,1,0,0,1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,1]
#z.vs['color'] = [cls[i] for i in z.vs['comm']]
z.vs['color'] = [cls[i] for i in z.vs['gn']]
#ig.plot(z, 'zachary_2.eps',bbox=(0,0,300,200))
ig.plot(z,bbox=(0,0,300,200))
```
Same as above with 5 communities. We see higher modularity, but weaker AMI value.
```
## show result with optimal modularity (5 clusters)
z.vs['label'] = gn.as_clustering(n=5).membership
print('AMI:',AMI(z.vs['comm'],z.vs['label']))
print('q:',z.modularity(z.vs['label']))
z.vs['color'] = [cls[i] for i in z.vs['comm']]
z.vs['size'] = 10
z.vs['label_size'] = 8
#ig.plot(z, 'zachary_5.eps',bbox=(0,0,300,200))
ig.plot(z,bbox=(0,0,300,200))
```
# ABCD graph with 100 nodes
Next we look at a slightly larger graph generated with the ABCD benchmark model, which is described in section 5.3 of the book. This graph has 3 communities.
Using hierarchical clustering, we compare modularity and AMI for each possible cut.
ABCD parameters used to generate this graph are: $\gamma=3, \tau=2$, degree range [5,15], community size range [25,50], $\xi=.2$.
```
## read graph and communities; plot
g = ig.Graph.Read_Ncol(datadir+'ABCD/abcd_100.dat',directed=False)
c = np.loadtxt(datadir+'ABCD/abcd_100_comms.dat',dtype='uint16',usecols=(1))
g.vs['comm'] = [c[int(x['name'])-1]-1 for x in g.vs]
gt = {k:(v-1) for k,v in enumerate(g.vs['comm'])}
## map between int(name) to key
n2k = {int(v):k for k,v in enumerate(g.vs['name'])}
g.vs['size'] = 7
g.es['color'] = cls_edges
g.vs['color'] = [cls[i] for i in g.vs['comm']]
ig.plot(g, bbox=(0,0,300,200))
```
Girvan-Newman algorithm -- Modularity and AMI for each cut
In this case, both modularity and AMI are maximized with 3 communities.
```
q = []
a = []
gn = g.community_edge_betweenness()
for i in np.arange(g.vcount()):
q.append(g.modularity(gn.as_clustering(n=i+1)))
a.append(AMI(g.vs['comm'],gn.as_clustering(n=i+1).membership))
plt.plot(np.arange(1,1+g.vcount()),q,'.-',color='black',label='modularity')
plt.plot(np.arange(1,1+g.vcount()),a,'.-',color='grey',label='AMI')
plt.xlabel('number of clusters',fontsize=14)
plt.ylabel('modularity or AMI',fontsize=14)
plt.legend();
#plt.savefig('abcd_dendrogram.eps');
```
We see that with 3 communities, $q=0.502$ and AMI=1, so perfect recovery.
```
n_comm = np.arange(1,g.vcount()+1)
D = pd.DataFrame(np.array([n_comm,q,a]).transpose(),columns=['n_comm','q','AMI'])
df = D.head()
df
```
What would we get with 4 clusters, for which AMI = 0.95?
We see below that we have a few nodes splitted from one community.
```
## 4 communities
g.vs['gn'] = gn.as_clustering(n=4).membership
cls = ['silver','dimgray','black','white']
g.vs['color'] = [cls[i] for i in g.vs['gn']]
#ig.plot(g, 'abcd_4.eps', bbox=(0,0,300,200))
ig.plot(g, bbox=(0,0,300,200))
```
Those nodes form a triangle
```
sg = g.subgraph([v for v in g.vs() if v['gn']==3])
ig.plot(sg, bbox=(0,0,100,100))
```
# ABCD with varying $\xi$
Here we show a typical way to compare graph clustering algorithms using benchmark graphs.
We pick some model, here ABCD, and we vary the noise parameter $\xi$.
With ABCD, the larger $\xi$ is, the closer we are to a random Chung-Lu or configuration model graph (i.e. where only the degree distribution matters). For $\xi=0$, we get pure communities (all edges are internal).
For each choice of $\xi$, we generate 30 graphs, apply several different clustering algorithms,
and compute AMI for each algorithm, comparing with griund-truth communities.
The code below is commented out as it can take a while to run; a pickle file with results is included in the Data directory. To re-run from scratch, uncomment the cell below.
Parameters for the ABCD benchmark graphs are:
$\gamma=2.5, \tau=1.5$, degree range [10,50], community size range [50,100], $0.1 \le \xi \le 0.8$.
```
## load data generated with the code from above cell
with open(datadir+"ABCD/abcd_study.pkl","rb") as f:
L = pickle.load(f)
## store in dataframe and take averages
D = pd.DataFrame(L,columns=['algo','xi','AMI'])
## take average over 30 runs for each algorithm and every choice of xi
X = D.groupby(by=['algo','xi']).mean()
```
We plot the results in the following 2 cells.
We see good results with Louvain and Infomap, and even better results with ECG.
Label propagation is a fast algortihm, but it does collapse with moderate to high level of noise.
From the standard deviation plot, we see high variability around the value(s) for $\xi$ where the different
algorithms start to collapse. We see that this happen later and at a smaller scale with EGC, which is known to have better stability.
Such studies are useful to compare algorithms; using benchmarks, we can directly control parameters such as the noise level.
```
## plot average results foe each algorithm over range of xi
a = ['ECG','Louvain','Infomap','Label Prop.']
lt = ['-','--',':','-.','-.']
cl = ['blue','green','purple','red']
for i in range(len(a)):
## pick one - color or greyscale
plt.plot(X.loc[(a[i])].index,X.loc[(a[i])],lt[i],label=a[i],color=cl[i])
#plt.plot(X.loc[(a[i])].index,X.loc[(a[i])],lt[i],label=a[i],color='black')
plt.xlabel(r'ABCD noise ($\xi$)',fontsize=14)
plt.ylabel('AMI',fontsize=14)
plt.legend();
#plt.savefig('abcd_study.eps');
## Look at standard deviations
S = D.groupby(by=['algo','xi']).std()
a = ['ECG','Louvain','Infomap','Label Prop.']
#a = ['ECG','Louvain','Infomap','Label Prop.','Leiden','CNM']
lt = ['-','--',':','-.','--',':']
cl = ['blue','green','purple','red','red','blue']
for i in range(len(a)):
## pick one - color of greyscale
plt.plot(S.loc[(a[i])].index,S.loc[(a[i])],lt[i],label=a[i],color=cl[i])
#plt.plot(S.loc[(a[i])].index,S.loc[(a[i])],lt[i],label=a[i],color='black')
plt.xlabel(r'ABCD noise ($\xi$)',fontsize=14)
plt.ylabel('Standard Deviation (AMI)',fontsize=14)
plt.legend();
#plt.savefig('abcd_study_stdv.eps');
```
## Compare stability
This study is similar to the previous one, but we compare pairs of partitions for each algorithm on the same graph instead of comparing with the ground truth, so we look at the stability of algorithms. Note that an algorithm can be stable, but still be bad (ex: always cluster all nodes in a single community).
The code below can take a while to run; a pickle file with results is included in the Data directory. To re-run from scratch, uncomment the cell below.
```
## load L and train/val/test ids
with open(datadir+"ABCD/abcd_study_stability.pkl","rb") as f:
Ls = pickle.load(f)
## store in dataframe
D = pd.DataFrame(Ls,columns=['algo','xi','AMI'])
## take averages for each algorithm and each noise value xi
X = D.groupby(by=['algo','xi']).mean()
```
We plot the results below. The behaviour of algorithms can be clustered in two groups:
* For Louvain and ECG, stability is excellent and degrades gradually for high noise level, with ECG being the more stable algorithm.
* For Infomap and Label Propagation, stability is also good until the noise value where the results start to degrade, as we saw in the previous study. We see near perfect stability for very high noise values; those are values where the results were very bad in the previous study; this typically happens when the algorithm can't get any good clustering and returns some trivial parititon, such as putting all nodes together in the same community, thus a stable but bad result.
```
a = ['ECG','Louvain','Infomap','Label Prop.']
lt = ['-','--',':','-.']
for i in range(len(a)):
plt.plot(X.loc[(a[i])].index,X.loc[(a[i])],lt[i],label=a[i],color='black')
plt.xlabel(r'ABCD noise ($\xi$)',fontsize=14)
plt.ylabel('AMI between successive runs',fontsize=14)
plt.legend();
#plt.savefig('abcd_study_stability.eps');
```
# Modularity, resolution limit and rings of cliques
We illustrate issues with modularity with the famous ring of cliques examples.
For example below, we have a ring of 3-cliques connected ny a single (inter-clique) edge.
```
## n cliques of size s
def ringOfCliques(n,s):
roc = ig.Graph.Erdos_Renyi(n=n*s,p=0)
## cliques
for i in range(n):
for j in np.arange(s*i,s*(i+1)):
for k in np.arange(j+1,s*(i+1)):
roc.add_edge(j,k)
## ring
for i in range(n):
if i>0:
roc.add_edge(s*i-1,s*i)
else:
roc.add_edge(n*s-1,0)
roc.vs['size'] = 8
roc.vs['color'] = cls[2]
roc.es['color'] = cls_edges
return roc
## Ex: 10 3-cliques
roc = ringOfCliques(10,3)
#ig.plot(roc,'ring_3.eps',bbox=(0,0,300,300))
ig.plot(roc,bbox=(0,0,300,300))
```
We compare the number of cliques (the natural parts in a partition) with the actual number of communities found via 3 modularity based algorithms (Louvain, CNM, ECG).
We see that both Louvain and CNM return a smaller number of communities than the number of cliques; this is a known problem with modularity: merging cliques in the same community often lead to higher modularity.
A concensus algorithm like ECG can help a lot in such cases; here we see that the cliques are correctly recovered with ECG.
```
## Compare number of cliques and number of clusters found
L = []
s = 3
for n in np.arange(3,50,3):
roc = ringOfCliques(n,s)
ml = np.max(roc.community_multilevel().membership)+1
ec = np.max(roc.community_ecg().membership)+1
cnm = np.max(roc.community_fastgreedy().as_clustering().membership)+1
L.append([n,ml,ec,cnm])
D = pd.DataFrame(L,columns=['n','Louvain','ECG','CNM'])
plt.figure(figsize=(8,6))
plt.plot(D['n'],D['Louvain'],'--o',color='black',label='Louvain')
plt.plot(D['n'],D['ECG'],'-o',color='black',label='ECG')
plt.plot(D['n'],D['CNM'],':o',color='black',label='CNM')
plt.xlabel('number of '+str(s)+'-cliques',fontsize=14)
plt.ylabel('number of clusters found',fontsize=14)
plt.legend(fontsize=14);
#plt.savefig('rings.eps');
```
Let us look at a specific example: 10 cliques of size 3. Below we plot the communities found with Louvain; we clearly see that pairs of communities are systematically grouped into clusters.
```
## Louvain communities with 10 3-cliques
roc = ringOfCliques(n=10,s=3)
roc.vs['ml'] = roc.community_multilevel().membership
roc.vs['color'] = [cls[x%3] for x in roc.vs['ml']]
#ig.plot(roc,'ring_3_q.eps', bbox=(0,0,300,300))
ig.plot(roc,bbox=(0,0,300,300))
```
Why is ECG solving this problem? It is due to the first step, where we run an ensemble of level-1 Louvain and assign new weights to edges based on the proportion of times those edges are internal to a community.
We see below that there are exactly 30 edges with maximal edge weight of 1 (edges within cliques) and 10 edges with default minimal weight of 0.05 (edges between cliques).
With those new weights, the last clustering in ECG can easily recover the cliques as communities.
```
## ECG weights in this case: all 30 clique edges have max score
roc.es['W'] = roc.community_ecg().W
Counter(roc.es['W'])
```
# Ego nets and more
Suppose we want to look at node "near" some seed node $v$. One common way to do this is to look at its ego-net, i.e. the subgraph consisting of node $v$ and all other nodes that can be reached from $v$ in $k$ hops or less, where $k$ is small, typically 1 or 2.
Such subgraphs can become large quickly as we increase $k$. In the cells below, we look at ego-nets and compare with another approach to extract subgraph(s) around $v$ via clustering.
We consider the airport graph we already saw several times. We consider a simple, undirected version (no loops, directions or edge weights).
We compare ego-nets (1 and 2-hops subgraphs from a given node) with clusters obtained via graph clustering for some vertex $v$ with degree 11 (you can try other vertices).
```
## read edges and build simple undirected graph
D = pd.read_csv(datadir+'Airports/connections.csv')
g = ig.Graph.TupleList([tuple(x) for x in D.values], directed=True, edge_attrs=['weight'])
#df = D.head()
g = g.as_undirected()
g = g.simplify()
## read vertex attributes and add to graph
A = pd.read_csv(datadir+'Airports/airports_loc.csv')
lookup = {k:v for v,k in enumerate(A['airport'])}
l = [lookup[x] for x in g.vs()['name']]
g.vs()['layout'] = [(A['lon'][i],A['lat'][i]) for i in l]
g.vs()['state'] = [A['state'][i] for i in l]
g.vs()['city'] = [A['city'][i] for i in l]
## add a few more attributes for visualization
g.vs()['size'] = 6
g.vs()['color'] = cls[0]
g.es()['color'] = cls_edges
df = A.head()
## pick a vertex v
v = 207
print(g.vs[v])
print('degree:',g.degree()[v])
g.vs[v]['color'] = 'black'
## show its ego-net for k=1 (vertex v in black)
sg = g.subgraph([i for i in g.neighborhood(v,order=1)])
print(sg.vcount(),'nodes')
#ig.plot(sg,'airport_ego_1.eps',bbox=(0,0,300,300))
ig.plot(sg,bbox=(0,0,300,300))
## show its 2-hops ego-net ... this is already quite large!
sg = g.subgraph([i for i in g.neighborhood(v,order=2)])
sg.vs()['core'] = sg.coreness()
sg.delete_vertices([v for v in sg.vs if v['core']<2])
print(sg.vcount(),'nodes')
#ig.plot(sg,'airport_ego_2.eps',bbox=(0,0,300,300))
ig.plot(sg,bbox=(0,0,300,300))
## apply clustering and show the cluster containing the selected vertex
## recall that we ignore edge weights
## This result can vary somehow between runs
ec = g.community_ecg(ens_size=16)
g.es['W'] = ec.W
m = ec.membership[v]
sg = g.subgraph([i for i in range(g.vcount()) if ec.membership[i]==m])
sg.vs()['core'] = sg.coreness()
## display the 2-core
sg.delete_vertices([v for v in sg.vs if v['core']<2])
print(sg.vcount(),'nodes')
#ig.plot(sg,'airport_ecg.eps',bbox=(0,0,300,300))
ig.plot(sg,bbox=(0,0,300,300))
```
We see above that looking at the cluster with $v$ is smaller than the 2-hops ego-net, and several nodes are tightly connected.
Below we go further and look at the ECG edge weights, which we can use to prune the graph above, so we can look at the nodes most tightly connected to node $v$.
You can adjust the threshold below to get different zoomings.
```
## filter edges w.r.t. ECG votes (weights)
thresh = .85
tmp = sg.subgraph_edges([e for e in sg.es if e['W'] > thresh])
n = [i for i in range(tmp.vcount()) if tmp.vs[i]['color']=='black'][0]
tmp.vs['cl'] = tmp.clusters().membership
cl = tmp.vs[n]['cl']
ssg = tmp.subgraph([i for i in tmp.vs if i['cl']==cl])
ssg.vs()['core'] = ssg.coreness()
ssg.delete_vertices([v for v in ssg.vs if v['core']<2])
print(ssg.vcount(),'nodes')
#ig.plot(ssg,'airport_ecg_focus.eps',bbox=(0,0,300,300))
ig.plot(ssg,bbox=(0,0,300,300))
```
Most nodes in this subgraph are from the same state as node $v$ (MI) or nearby state (WI).
```
## states in the above subgraph
Counter(ssg.vs['state'])
```
# EXTRA CODE
The code below requires that Julia and ABCD are installed.
This is extra material not in the book.
# ABCD Properties
The cells below are for illustration purpose only, to show some ABCD graphs with different $\xi$ (noise) parameters,
and to show how you can run ABCD with Julia installed.
* notice the density of edges between communities as $\xi$ increases.
* most runs should yield 3 communities
Natural layouts for noisy graphs make it hard to distinguish communities, as the nodes will overlap a lot.
We use an ad-hoc method to "push away" nodes from the 3 different clusters to allow for better visualization.
```
## just for visualization -- push the layout apart given 3 communities
## adjust the 'push' factor with d
def push_layout(d=0):
if np.max(g.vs['comm'])>2:
return -1
ly = g.layout()
g.vs['ly'] = ly
x = [0,0,0]
y = [0,0,0]
for v in g.vs:
c = v['comm']
x[c] += v['ly'][0]
y[c] += v['ly'][1]
delta = [-d,0,d]
dx = [delta[i] for i in np.argsort(x)]
dy = [delta[i] for i in np.argsort(y)]
for v in g.vs:
c = v['comm']
v['ly'][0] += dx[c]
v['ly'][1] += dy[c]
return g.vs['ly']
## ABCD with very strong communities (xi = 0.05)
## results will vary, but we see 3 communities in most runs.
xi = 0.05
mc = 0
while mc != 3: ## run until we get 3 communities
## generate degree and community size values
cmd = 'julia '+abcd_path+'deg_sampler.jl deg.dat 2.5 5 15 100 1000'
os.system(cmd+' >/dev/null 2>&1')
cmd = 'julia '+abcd_path+'com_sampler.jl cs.dat 1.5 30 50 100 1000'
os.system(cmd+' >/dev/null 2>&1');
cmd = 'julia '+abcd_path+'graph_sampler.jl net.dat comm.dat deg.dat cs.dat xi '\
+str(xi)+' false false'
os.system(cmd+' >/dev/null 2>&1')
g = ig.Graph.Read_Ncol('net.dat',directed=False)
c = np.loadtxt('comm.dat',dtype='uint16',usecols=(1))
mc = max(c)
## plot
g.vs['comm'] = [c[int(x['name'])-1]-1 for x in g.vs]
g.vs['color'] = [cls[i] for i in g.vs['comm']]
g.vs['size'] = 5
g.es['color'] = 'lightgrey'
ly = push_layout(d=0) ## d=0, no need to push, communities are clear
ig.plot(g, layout=ly, bbox=(0,0,300,300))
## viz: ABCD with strong communities (xi = 0.15)
xi = 0.15
mc = 0
while mc != 3: ## run until we get 3 communities
## generate degree and community size values
cmd = 'julia '+abcd_path+'deg_sampler.jl deg.dat 2.5 5 15 100 1000'
os.system(cmd+' >/dev/null 2>&1')
cmd = 'julia '+abcd_path+'com_sampler.jl cs.dat 1.5 30 50 100 1000'
os.system(cmd+' >/dev/null 2>&1');
cmd = 'julia '+abcd_path+'graph_sampler.jl net.dat comm.dat deg.dat cs.dat xi '\
+str(xi)+' false false'
os.system(cmd+' >/dev/null 2>&1')
## compute AMI for various clustering algorithms
g = ig.Graph.Read_Ncol('net.dat',directed=False)
c = np.loadtxt('comm.dat',dtype='uint16',usecols=(1))
mc = max(c)
## plot
g.vs['comm'] = [c[int(x['name'])-1]-1 for x in g.vs]
g.vs['color'] = [cls[i] for i in g.vs['comm']]
g.vs['size'] = 5
g.es['color'] = 'lightgrey'
ly = push_layout(d=1) ## slightly push clusters apart for viz
ig.plot(g, layout=ly, bbox=(0,0,300,300))
## viz: ABCD with weak communities
## lots of edges between communities as expected
xi = 0.33
mc = 0
while mc != 3: ## run until we get 3 communities
## generate degree and community size values
cmd = 'julia '+abcd_path+'deg_sampler.jl deg.dat 2.5 5 15 100 1000'
os.system(cmd+' >/dev/null 2>&1')
cmd = 'julia '+abcd_path+'com_sampler.jl cs.dat 1.5 30 50 100 1000'
os.system(cmd+' >/dev/null 2>&1');
cmd = 'julia '+abcd_path+'graph_sampler.jl net.dat comm.dat deg.dat cs.dat xi '\
+str(xi)+' false false'
os.system(cmd+' >/dev/null 2>&1')
## compute AMI for various clustering algorithms
g = ig.Graph.Read_Ncol('net.dat',directed=False)
c = np.loadtxt('comm.dat',dtype='uint16',usecols=(1))
mc = max(c)
## plot
g.vs['comm'] = [c[int(x['name'])-1]-1 for x in g.vs]
g.vs['color'] = [cls[i] for i in g.vs['comm']]
g.vs['size'] = 5
g.es['color'] = 'lightgrey'
ly = push_layout(d=3) ## need to push more -- with d=0, communities can't be seen clearly
ig.plot(g, layout=ly, bbox=(0,0,300,300))
## viz: ABCD with very weak communities
xi = 0.5
mc = 0
while mc != 3: ## run until we get 3 communities
## generate degree and community size values
cmd = 'julia '+abcd_path+'deg_sampler.jl deg.dat 2.5 5 15 100 1000'
os.system(cmd+' >/dev/null 2>&1')
cmd = 'julia '+abcd_path+'com_sampler.jl cs.dat 1.5 30 50 100 1000'
os.system(cmd+' >/dev/null 2>&1');
cmd = 'julia '+abcd_path+'graph_sampler.jl net.dat comm.dat deg.dat cs.dat xi '\
+str(xi)+' false false'
os.system(cmd+' >/dev/null 2>&1')
## compute AMI for various clustering algorithms
g = ig.Graph.Read_Ncol('net.dat',directed=False)
c = np.loadtxt('comm.dat',dtype='uint16',usecols=(1))
mc = max(c)
## plot
g.vs['comm'] = [c[int(x['name'])-1]-1 for x in g.vs]
g.vs['color'] = [cls[i] for i in g.vs['comm']]
g.vs['size'] = 5
g.es['color'] = 'lightgrey'
ly = push_layout(5) ## need to push more -- with d=0, communities can't be seen clearly
ig.plot(g, layout=ly, bbox=(0,0,300,300))
```
## Measures to compare partitions
* We illustrate the importance of using proper adjusted measures when comparing partitions; this is why we use AMI (adjusted mutual information) or ARI (adjusted Rand index) in our experiments
* We generate some ABCD graph and compare ground truth with **random** partitions of different sizes
* Scores for random partitions should be close to 0 regardless of the number of parts
```
## RAND Index: given two clusterings u and v
def RI(u,v):
## build sets from A and B
a = np.max(u)+1
b = np.max(v)+1
n = len(u)
if n != len(v):
exit -1
A = [set() for i in range(a)]
B = [set() for i in range(b)]
for i in range(n):
A[u[i]].add(i)
B[v[i]].add(i)
## RAND index step by step
R = 0
for i in range(a):
for j in range(b):
s = len(A[i].intersection(B[j]))
if s>1:
R += s*(s-1)/2
R *= 2
for i in range(a):
s = len(A[i])
if s>1:
R -= s*(s-1)/2
for i in range(b):
s = len(B[i])
if s>1:
R -= s*(s-1)/2
R += n*(n-1)/2
R /= n*(n-1)/2
return R
## generate new degree and community size values
cmd = 'julia '+abcd_path+'deg_sampler.jl deg.dat 2.5 5 50 1000 1000'
os.system(cmd+' >/dev/null 2>&1')
cmd = 'julia '+abcd_path+'com_sampler.jl cs.dat 1.5 75 150 1000 1000'
os.system(cmd+' >/dev/null 2>&1')
xi = .1
cmd = 'julia '+abcd_path+'graph_sampler.jl net.dat comm.dat deg.dat cs.dat xi '\
+str(xi)+' false false'
os.system(cmd+' >/dev/null 2>&1')
g = ig.Graph.Read_Ncol('net.dat',directed=False)
c = np.loadtxt('comm.dat',dtype='uint16',usecols=(1))
## ground-truth communities
gt = [c[int(x['name'])-1]-1 for x in g.vs]
print('number of communities:',np.max(gt)+1)
## generate random clusterings and compute various measures w.r.t. ground truth
## this can take a few minutes to run
from sklearn.metrics import mutual_info_score as MI
from sklearn.metrics import adjusted_rand_score as ARI
from sklearn.metrics import normalized_mutual_info_score as NMI
L = []
n = g.vcount()
tc = {idx:part for idx,part in enumerate(gt)}
ar = np.arange(2,21)
for s in ar:
for i in range(100):
r = np.random.choice(s, size=n)
rd = {idx:part for idx,part in enumerate(r)}
L.append([s,MI(gt,r),NMI(gt,r),AMI(gt,r),RI(gt,r),ARI(gt,r),g.gam(tc,rd,adjusted=False),g.gam(tc,rd)])
D = pd.DataFrame(L,columns=['size','MI','NMI','AMI','RI','ARI','GRI','AGRI'])
R = D.groupby(by='size').mean()
```
Below we show results for 3 measures:
* Mutual information (MI) as is has strong bian w.r.t. number of clusters
* Normalized MI is better
* AMI is best, no bias w.r.t. number of clusters.
```
## Mutual information (MI), normalized MI (NMI) and adjusted MI (AMI)
plt.plot(ar,R['MI'],':',color='black',label='MI')
plt.plot(ar,R['NMI'],'--',color='black',label='NMI')
plt.plot(ar,R['AMI'],'-',color='black',label='AMI')
plt.xlabel('number of random clusters',fontsize=14)
plt.legend();
#plt.savefig('MI.eps');
```
Same below for Rand index (RI) and adjusted version.
GRI (graph RI) and AGRI (adjusted GRI) are variations of RI specifically for graph data.
```
## RAND index (RI) and adjusted (ARI)
## Also: Graph-aware RAND index (GRI) and adjusted version (AGRI)
## those measures are included in partition-igraph
## input are partitions of type 'igraph.clustering.VertexClustering'or a dictionaries of node:community.
plt.plot(ar,R['RI'],':',color='black',label='RI')
plt.plot(ar,R['GRI'],'--',color='black',label='GRI')
plt.plot(ar,R['ARI'],'-',color='black',label='ARI/AGRI')
plt.plot(ar,R['AGRI'],'-',color='black')
plt.xlabel('number of random clusters',fontsize=14)
plt.legend();
#plt.savefig('RI.eps');
```
| true |
code
| 0.502197 | null | null | null | null |
|
# Values and Variables
**CS1302 Introduction to Computer Programming**
___
```
%reload_ext mytutor
```
## Integers
**How to enter an [integer](https://docs.python.org/3/reference/lexical_analysis.html#integer-literals) in a program?**
```
15 # an integer in decimal
0b1111 # a binary number
0xF # hexadecimal (base 16) with possible digits 0, 1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
```
**Why all outputs are the same?**
- What you have entered are *integer literals*, which are integers written out literally.
- All the literals have the same integer value in decimal.
- By default, if the last line of a code cell has a value, the jupyter notebook (*IPython*) will store and display the value as an output.
```
3 # not the output of this cell
4 + 5 + 6
```
- The last line above also has the same value, `15`.
- It is an *expression* (but not a literal) that *evaluates* to the integer value.
**Exercise** Enter an expression that evaluates to an integer value, as big as possible.
(You may need to interrupt the kernel if the expression takes too long to evaluate.)
```
# There is no maximum for an integer for Python3.
# See https://docs.python.org/3.1/whatsnew/3.0.html#integers
11 ** 100000
```
## Strings
**How to enter a [string](https://docs.python.org/3/reference/lexical_analysis.html#string-and-bytes-literals) in a program?**
```
'\U0001f600: I am a string.' # a sequence of characters delimited by single quotes.
"\N{grinning face}: I am a string." # delimited by double quotes.
"""\N{grinning face}: I am a string.""" # delimited by triple single/double quotes.
```
- `\` is called the *escape symbol*.
- `\U0001f600` and `\N{grinning face}` are *escape sequences*.
- These sequences represent the same grinning face emoji by its Unicode in hexadecimal and its name.
**Why use different quotes?**
```
print('I\'m line #1.\nI\'m line #2.') # \n is a control code for line feed
print("I'm line #3.\nI'm line #4.") # no need to escape single quote.
print('''I'm line #5.
I'm line #6.''') # multi-line string
```
Note that:
- The escape sequence `\n` does not represent any symbol.
- It is a *control code* that creates a new line when printing the string.
- Another common control code is `\t` for tab.
Using double quotes, we need not escape the single quote in `I'm`.
Triple quotes delimit a multi-line string, so there is no need to use `\n`.
(You can copy and paste a multi-line string from elsewhere.)
In programming, there are often many ways to do the same thing.
The following is a one-line code ([one-liner](https://en.wikipedia.org/wiki/One-liner_program)) that prints multiple lines of strings without using `\n`:
```
print("I'm line #1", "I'm line #2", "I'm line #3", sep='\n') # one liner
```
- `sep='\n'` is a *keyword argument* that specifies the separator of the list of strings.
- By default, `sep=' '`, a single space character.
In IPython, we can get the *docstring* (documentation) of a function conveniently using the symbol `?`.
```
?print
print?
```
**Exercise** Print a cool multi-line string below.
```
print('''
(ง •̀_•́)ง
╰(●’◡’●)╮
(..•˘_˘•..)
(づ ̄ 3 ̄)づ
''')
# See also https://github.com/glamp/bashplotlib
# Star Wars via Telnet http://asciimation.co.nz/
```
## Variables and Assignment
It is useful to store a value and retrieve it later.
To do so, we assign the value to a variable:
```
x = 15
x # output the value of x
```
**Is assignment the same as equality?**
No because:
- you cannot write `15 = x`, but
- you can write `x = x + 1`, which increases the value of `x` by `1`.
**Exercise** Try out the above code yourself.
```
x = x + 1
x
```
Let's see the effect of assignment step-by-step:
1. Run the following cell.
1. Click `Next >` to see the next step of the execution.
```
%%mytutor -h 200
x = 15
x = x + 1
```
The following *tuple assignment* syntax can assign multiple variables in one line.
```
%%mytutor -h 200
x, y, z = '15', '30', 15
```
One can also use *chained assignment* to set different variables to the same value.
```
%%mytutor -h 250
x = y = z = 0
```
Variables can be deleted using `del`. Accessing a variable before assignment raises a Name error.
```
del x, y
x, y
```
## Identifiers
*Identifiers* such as variable names are case sensitive and follow certain rules.
**What is the syntax for variable names?**
1. Must start with a letter or `_` (an underscore) followed by letters, digits, or `_`.
1. Must not be a [keyword](https://docs.python.org/3.7/reference/lexical_analysis.html#keywords) (identifier reserved by Python):
<pre>False await else import pass
None break except in raise
True class finally is return
and continue for lambda try
as def from nonlocal while
assert del global not with
async elif if or yield</pre>
**Exercise** Evaluate the following cell and check if any of the rules above is violated.
```
from ipywidgets import interact
@interact
def identifier_syntax(assignment=['a-number = 15',
'a_number = 15',
'15 = 15',
'_15 = 15',
'del = 15',
'Del = 15',
'type = print',
'print = type',
'input = print']):
exec(assignment)
print('Ok.')
```
1. `a-number = 15` violates Rule 1 because `-` is not allowed. `-` is interpreted as an operator.
1. `15 = 15` violates Rule 1 because `15` starts with a digit instead of letter or _.
1. `del = 15` violates Rule 2 because `del` is a keyword.
What can we learn from the above examples?
- `del` is a keyword and `Del` is not because identifiers are case sensitive.
- Function/method/type names `print`/`input`/`type` are not keywords and can be reassigned.
This can useful if you want to modify the default implementations without changing their source code.
To help make code more readable, additional style guides such as [PEP 8](https://www.python.org/dev/peps/pep-0008/#function-and-variable-names) are available:
- Function names should be lowercase, with words separated by underscores as necessary to improve readability.
- Variable names follow the same convention as function names.
## User Input
**How to let the user input a value at *runtime*,
i.e., as the program executes?**
We can use the method `input`:
- There is no need to delimit the input string by quotation marks.
- Simply press `enter` after typing a string.
```
print('Your name is', input('Please input your name: '))
```
- The `input` method prints its argument, if any, as a [prompt](https://en.wikipedia.org/wiki/Command-line_interface#Command_prompt).
- It takes user's input and *return* it as its value. `print` takes in that value and prints it.
**Exercise** Explain whether the following code prints `'My name is Python'`. Does `print` return a value?
```
print('My name is', print('Python'))
```
- Unlike `input`, the function `print` does not return the string it is trying to print. Printing a string is, therefore, different from returning a string.
- `print` actually returns a `None` object that gets printed as `None`.
## Type Conversion
The following program tries to compute the sum of two numbers from user inputs:
```
num1 = input('Please input an integer: ')
num2 = input('Please input another integer: ')
print(num1, '+', num2, 'is equal to', num1 + num2)
```
**Exercise** There is a [bug](https://en.wikipedia.org/wiki/Software_bug) in the above code. Can you locate the error?
The two numbers are concatenated instead of added together.
`input` *returns* user input as a string.
E.g., if the user enters `12`, the input is
- not treated as the integer twelve, but rather
- treated as a string containing two characters, one followed by two.
To see this, we can use `type` to return the data type of an expression.
```
num1 = input('Please input an integer: ')
print('Your input is', num1, 'with type', type(num1))
```
**Exercise** `type` applies to any expressions. Try it out below on `15`, `print`, `print()`, `input`, and even `type` itself and `type(type)`.
```
type(15), type(print), type(print()), type(input), type(type), type(type(type))
```
**So what happens when we add strings together?**
```
'4' + '5' + '6'
```
**How to fix the bug then?**
We can convert a string to an integer using `int`.
```
int('4') + int('5') + int('6')
```
We can also convert an integer to a string using `str`.
```
str(4) + str(5) + str(6)
```
**Exercise** Fix the bug in the following cell.
```
num1 = input('Please input an integer: ')
num2 = input('Please input another integer: ')
# print(num1, '+', num2, 'is equal to', num1 + num2) # fix this line below
### BEGIN SOLUTION
print(num1, '+', num2, 'is equal to', int(num1) + int(num2))
### END SOLUTION
```
## Error
In addition to writing code, a programmer spends significant time in *debugging* code that contains errors.
**Can an error be automatically detected by the computer?**
- You have just seen an example of *logical error*, which is due to an error in the logic.
- The ability to debug or even detect such error is, unfortunately, beyond Python's intelligence.
Other kinds of error may be detected automatically.
As an example, note that we can omit `+` for string concatenation, but we cannot omit it for integer summation:
```
print('Skipping + for string concatenation')
'4' '5' '6'
print('Skipping + for integer summation')
4 5 6
```
Python interpreter detects the bug and raises a *syntax* error.
**Why Syntax error can be detected automatically?
Why is the print statement before the error not executed?**
- The Python interpreter can easily detect syntax error even before executing the code simply because
- the interpreter fails to interpret the code, i.e., translates the code to lower-level executable code.
The following code raises a different kind of error.
```
print("Evaluating '4' + '5' + 6")
'4' + '5' + 6 # summing string with integer
```
**Why Python throws a TypeError when evaluating `'4' + '5' + 6`?**
There is no default implementation of `+` operation on a value of type `str` and a value of type `int`.
- Unlike syntax error, the Python interpreter can only detect type error at runtime (when executing the code.)
- Hence, such error is called a *runtime error*.
**Why is TypeError a runtime error?**
The short answer is that Python is a [strongly-and-dynamically-typed](https://en.wikipedia.org/wiki/Strong_and_weak_typing) language:
- Strongly-typed: Python does not force a type conversion to avoid a type error.
- Dynamically-typed: Python allow data type to change at runtime.
The underlying details are more complicated than required for this course. It helps if you already know the following languages:
- JavaScript, which is a *weakly-typed* language that forces a type conversion to avoid a type error.
- C, which is a *statically-typed* language that does not allow data type to change at runtime.
```
%%javascript
alert('4' + '5' + 6) // no error because 6 is converted to a str automatically
```
A weakly-typed language may seem more robust, but it can lead to [more logical errors](https://www.oreilly.com/library/view/fluent-conference-javascript/9781449339203/oreillyvideos1220106.html).
To improve readability, [typescript](https://www.typescriptlang.org/) is a strongly-typed replacement of javascript.
**Exercise** Not all the strings can be converted into integers. Try breaking the following code by providing invalid inputs and record them in the subsequent cell. Explain whether the errors are runtime errors.
```
num1 = input('Please input an integer: ')
num2 = input('Please input another integer: ')
print(num1, '+', num2, 'is equal to', int(num1) + int(num2))
```
The possible invalid inputs are:
> `4 + 5 + 6`, `15.0`, `fifteen`
It raises a value error, which is a runtime error detected during execution.
Note that the followings are okay
> int('-1'), eval('4 + 5 + 6')
## Floating Point Numbers
Not all numbers are integers. In Enginnering, we often need to use fractions.
**How to enter fractions in a program?**
```
x = -0.1 # decimal number
y = -1.0e-1 # scientific notation
z = -1/10 # fraction
x, y, z, type(x), type(y), type(z)
```
**What is the type `float`?**
- `float` corresponds to the [*floating point* representation](https://en.wikipedia.org/wiki/Floating-point_arithmetic#Floating-point_numbers).
- A `float` in stored exactly the way we write it in scientific notation:
$$
\overbrace{-}^{\text{sign}} \underbrace{1.0}_{\text{mantissa}\kern-1em}e\overbrace{-1}^{\text{exponent}\kern-1em}=-1\times 10^{-1}
$$
- The [truth](https://www.h-schmidt.net/FloatConverter/IEEE754.html) is more complicated than required for the course.
Integers in mathematics may be regarded as a `float` instead of `int`:
```
type(1.0), type(1e2)
```
You can also convert an `int` or a `str` to a `float`.
```
float(1), float('1')
```
**Is it better to store an integer as `float`?**
Python stores a [floating point](https://docs.python.org/3/library/sys.html#sys.float_info) with finite precision (usually as a 64bit binary fraction):
```
import sys
sys.float_info
```
It cannot represent a number larger than the `max`:
```
sys.float_info.max * 2
```
The precision also affects the check for equality.
```
(1.0 == 1.0 + sys.float_info.epsilon * 0.5, # returns true if equal
1.0 == 1.0 + sys.float_info.epsilon * 0.6, sys.float_info.max + 1 == sys.float_info.max)
```
Another issue with float is that it may keep more decimal places than desired.
```
1/3
```
**How to [round](https://docs.python.org/3/library/functions.html#round) a floating point number to the desired number of decimal places?**
```
round(2.665,2), round(2.675,2)
```
**Why 2.675 rounds to 2.67 instead of 2.68?**
- A `float` is actually represented in binary.
- A decimal fraction [may not be represented exactly in binary](https://docs.python.org/3/tutorial/floatingpoint.html#tut-fp-issues).
The `round` function can also be applied to an integer.
```
round(150,-2), round(250,-2)
```
**Why 250 rounds to 200 instead of 300?**
- Python 3 implements the default rounding method in [IEEE 754](https://en.wikipedia.org/w/index.php?title=IEEE_754#Rounding_rules).
## String Formatting
**Can we round a `float` or `int` for printing but not calculation?**
This is possible with [*format specifications*](https://docs.python.org/3/library/string.html#format-specification-mini-language).
```
x = 10000/3
print('x ≈ {:.2f} (rounded to 2 decimal places)'.format(x))
x
```
- `{:.2f}` is a *format specification*
- that gets replaced by a string
- that represents the argument `x` of `format`
- as a decimal floating point number rounded to 2 decimal places.
**Exercise** Play with the following widget to learn the effect of different format specifications. In particular, print `10000/3` as `3,333.33`.
```
from ipywidgets import interact
@interact(x='10000/3',
align={'None':'','<':'<','>':'>','=':'=','^':'^'},
sign={'None':'','+':'+','-':'-','SPACE':' '},
width=(0,20),
grouping={'None':'','_':'_',',':','},
precision=(0,20))
def print_float(x,sign,align,grouping,width=0,precision=2):
format_spec = f"{{:{align}{sign}{'' if width==0 else width}{grouping}.{precision}f}}"
print("Format spec:",format_spec)
print("x ≈",format_spec.format(eval(x)))
print('{:,.2f}'.format(10000/3))
```
String formatting is useful for different data types other than `float`.
E.g., consider the following program that prints a time specified by some variables.
```
# Some specified time
hour = 12
minute = 34
second = 56
print("The time is " + str(hour) + ":" + str(minute) + ":" + str(second)+".")
```
Imagine you have to show also the date in different formats.
The code can become very hard to read/write because
- the message is a concatenation of multiple strings and
- the integer variables need to be converted to strings.
Omitting `+` leads to syntax error. Removing `str` as follows also does not give the desired format.
```
print("The time is ", hour, ":", minute, ":", second, ".") # note the extra spaces
```
To make the code more readable, we can use the `format` function as follows.
```
message = "The time is {}:{}:{}."
print(message.format(hour,minute,second))
```
- We can have multiple *place-holders* `{}` inside a string.
- We can then provide the contents (any type: numbers, strings..) using the `format` function, which
- substitutes the place-holders by the function arguments from left to right.
According to the [string formatting syntax](https://docs.python.org/3/library/string.html#format-string-syntax), we can change the order of substitution using
- indices *(0 is the first item)* or
- names inside the placeholder `{}`:
```
print("You should {0} {1} what I say instead of what I {0}.".format("do", "only"))
print("The surname of {first} {last} is {last}.".format(first="John", last="Doe"))
```
You can even put variables inside the format specification directly and have a nested string formatting.
```
align, width = "^", 5
print(f"{{:*{align}{width}}}".format(x)) # note the syntax f"..."
```
**Exercise** Play with the following widget to learn more about the formating specification.
1. What happens when `align` is none but `fill` is `*`?
1. What happens when the `expression` is a multi-line string?
```
from ipywidgets import interact
@interact(expression=r"'ABC'",
fill='*',
align={'None':'','<':'<','>':'>','=':'=','^':'^'},
width=(0,20))
def print_objectt(expression,fill,align='^',width=10):
format_spec = f"{{:{fill}{align}{'' if width==0 else width}}}"
print("Format spec:",format_spec)
print("Print:",format_spec.format(eval(expression)))
```
1. It returns a ValueError because align must be specified when fill is.
1. The newline character is simply regarded a character. The formatting is not applied line-by-line. E.g., try 'ABC\nDEF'.
| true |
code
| 0.453504 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Yazanmy/ML/blob/master/Exercises_(Important_Python_Packages).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
Ex1: Create a program that asks the user to enter their
name and their age. Print out a message addressed to them
that tells them the year that they will turn 100 years old.
```
```
import datetime
name = input("Your Name : ")
age = int(input("Your age : "))
date = datetime.datetime.now()
print ("Hello ",name, "in" , 100- age + int(date.year) )
```
```
Ex3: Take a list, say for example this one: a = [1, 1, 2, 3, 5, 8,
13, 21, 34, 55, 89] and write a program that prints out all
the elements of the list that are less than 5.
```
```
a = [1, 1, 2, 3, 5, 8,13, 21, 34, 55, 89]
for x in a :
if x<5 :
print (x)
```
```
Ex5: Take two lists, say for example these two: a = [1, 1, 2, 3,
5, 8, 13, 21, 34, 55, 89] and b = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13] and write a program that returns a list that
contains only the elements that are common between the
lists (without duplicates). Make sure your program works on
two lists of different sizes.
```
```
a = [1, 1, 2, 3,5, 8, 13, 21, 34, 55, 89]
b = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11, 12, 13]
print (set(a) & set(b))
both=[]
if len(a)<len(b) :
for i in b :
if i in a and i not in both :
both.append(i)
if len(b)<len(a):
for i in a :
if i in b and i not in both :
both.append(i)
print(both)
```
```
Ex28: Implement a function that takes as input three
variables, and returns the largest of the three. Do this
without using the Python max() function!
```
```
def fun(a,b,c):
if a>b and a>c:
return(a)
if b>a and b>c:
return(b)
if c>a and c>b:
return c
print(fun(5,9,7))
```
~~~
Class 9: Write a Python class which has two
methods get_String and print_String. get_String
accept a string from the user and print_String print
the string in upper case.
~~~
```
class myclass():
def __init__(self):
self.Name = ""
def get_String(self):
self.Name =input()
def print_String(self):
print(self.Name.upper())
S= myclass()
S.get_String()
S.print_String()
```
```
Class 10: Write a Python class named Rectangle
constructed by a length and width and a method
which will compute the area of a rectangle
```
```
class Rectangle():
def __init__(self,length,width):
self.length=length
self.width=width
def computeArea(self):
return self.length*self.width
Rectangle=Rectangle(5,10)
print(Rectangle.computeArea())
```
~~~
NumPy 3: Create a 3x3 matrix with values ranging from 2 to 10.
~~~
```
import numpy as np
array=np.arange(2,11,1).reshape(3,3)
print(array)
```
~~~
NumPy 73: Write a Python program to create an array of (3, 4) shape,
multiply every element value by 3 and display the new array.
~~~
```
import numpy as np
array=np.ones((3,4),np.int16)
print(array*3)
```
```
Pandas DataFrame 4 and 5: Write a Python program to get the first 3 rows
and the 'name' and 'score' columns from the following DataFrame.
```
```
import pandas as pd
exam_data = {'name': ['Anastasia', 'Dima', 'Katherine','James', 'Emily', 'Michael', 'Matthew', 'Laura', 'Kevin','Jonas'],
'score': [12.5, 9, 16.5, np.nan, 9, 20, 14.5, np.nan, 8,19],
'attempts': [1, 3, 2, 3, 2, 3, 1, 1, 2, 1],
'qualify': ['yes', 'no', 'yes', 'no', 'no', 'yes', 'yes','no', 'no', 'yes']}
labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
df=pd.DataFrame(exam_data)
print(df.ix[0:3,['name','score']])
```
| true |
code
| 0.263647 | null | null | null | null |
|
```
# load packages
import pandas as pd
import numpy as np
import seaborn as sns
import itertools
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.style.use('bmh')
import sys
import warnings
warnings.filterwarnings('ignore')
from IPython.display import display
# Further Markdown settings
# load libraries and set plot parameters
# specifying the path
import os
path = os.chdir(r'C:\Users\Mohamed Ahmed Warsam\Desktop\PythonScripts')
datapath1 = 'ts_modelling1.xlsx'
# import the data
data = pd.read_excel(datapath1, sheetname=0, index_col='Created')
# view data
display(data.head(10))
display(data.tail(10))
display(data.info())
# turning several columns into categories
data['Category'] = data['Category'].astype('category')
data['Priority'] = data['Priority'].astype('category')
data['Incident state'] = data['Incident state'].astype('category')
data['Urgency'] = data['Urgency'].astype('category')
data['Impact'] = data['Impact'].astype('category')
# checking change
data.info()
data.Priority.value_counts()
```
# Ticket Volume Forecasting Project - Pearson by Mohamed Warsame
This mini-project aims to provide ticket volume forecast over December 2016 and February 2017, on the basis of historical ticket volume recorded between July 2014 and November 2016. It is important to inspect and evaluate the dataset before delving into the modelling process. The underlying dataset has 7 columns in total, the date range starting on 2014-07-01 19:16:00 and ending on 2016-11-21 19:45:00. There are 25479 tickets recorded during that time period.
## Exploratory Data Analysis
The figure below provides a visual impression of the historical ticket volume (total) over the entire date range covered by the dataset. As can be seen, the series initially exhibits a moderate linear growth trend and roughly gains 5000 tickets every six months. However, there is an unprecedented jump in total ticket count occurring at the end of August 2016. The count of tickets gains over 1000 additional tickets on a single day. This event would be referred to as a structural break, or exogenous shock to the system in the terminology of statistical literature. The shape of the line also changes, displaying characteristics of a concave mathematical function with a very steep slope, rather than the moderate linear growth trend prior to that. To further examine this, we can zoom into the figure by only selecting a subset of the overall date range.
```
# explore the time series as visualisation
# Sample goes from July 2014 to November 2016
sns.set(font_scale = 1.25)
y = data['Number']
y.plot(linestyle='-.', figsize=(15, 8))
plt.xlabel('Date Created', fontsize=14)
plt.ylabel('Total Ticket Count', fontsize=14)
plt.title('Evolution of Ticket Count', fontsize=16)
plt.show()
fig = plt.figure()
fig.savefig('ETC.png', dpi=100)
plt.close(fig)
```
From the zoomed in perspective we can see that the extreme outlier day was the last day of August, 2016-08-31, after which the trend seems to indicate that roughly 1 thousand tickets come in every month. Contingent upon the hypothesis that this trend continues into the forecasting period this task aims to predict, we can already infer that total ticket count will reach close to 30,000 tickets by February 2017. However, further statistical analysis is required to establish the robustness of this rough estimate inferred from basic exploratory data analysis.
```
# Subset of ticket count of outburst
doubling = data.loc['2016-08-01': '2016-11-21',:]
y1 = doubling['Number']
y1.plot(linestyle='-.', figsize=(15, 8))
plt.xlabel('Date Created', fontsize=14)
plt.ylabel('Total Ticket Count', fontsize=14)
plt.title('Subset of Ticket Count', fontsize=16)
plt.show()
```
The following horizontal bar chart shows us the exact date of the outlier observed on the prior visualisations. Identified to be the last day of August, we can see that close to 1400 tickets have been recorded in that day alone. The prior day, 30th of August, 2016, also recorded an abnormally high number of tickets. To conclude on this point, those two days alone contributed close to 2000 tickets, a figure that is usually only reached over the course of several months. Perhaps, a system outage, or other technical problem with the overall technological infrastructure of Pearson failed around that time. In fact, after taking a closer look at that week, it appears that a ticket raised at around 11pm on the 29th August marked with the highest priority level 'critical' may have triggered the abnormally high ticket count of the following day. This supports my suspicion that a database, or systems related issue may have resulted in an outage of the entire technology infrastructure, severely limiting the actions of users.
```
# Showing the day
sns.set(font_scale = 1.25)
outlier = data.loc['2016-08-28':'2016-09-06','Number'].resample('D').count()
#data1 = data.loc['2016-08-28':'2016-09-06',:]
outlier.plot(x=outlier.index, y=outlier, kind='barh', figsize=(15, 8))
plt.xlabel('Total Ticket Count', fontsize=16)
plt.ylabel('Date', fontsize=16)
plt.title('Outlier Week Count', fontsize=18)
plt.show()
```
In order not to make erroneous decisions in the modelling process that follows, we need to exclude those two outliers from the sample. The line plot below shows the total ticket count grouped by day and not just the cumulative count of the 'Number' column in the dataset. It also perfectly illustrates the issue of outliers in forecasting, as they introduce a scaling problem of the axes and also misinform the statistical model, since they are not representative of the overall behaviour of the data generating process. With over 200 tickets, there is another day in March 2016 that has a value which is extremely different from neighbouring observations. For now, we can treat those three days that exhibit an abnormally high number of tickets as random bursts. The subsequent figure will show how the scales of the vertical axis will change after removing the extreme value in March and also the two more recent outliers.
```
# potential idea - I can use .resample() to resample by hour and count .mean to get average ticket volume
yd = data.loc[:,'Number'].resample('D').count()
#display(yd.head(20))
# plot daily count
yd.plot(linestyle='-.', figsize=(15, 8))
plt.xlabel('Date Created', fontsize=14)
plt.ylabel('Total Ticket Count', fontsize=14)
plt.title('Daily View of Ticket Count', fontsize=16)
plt.show()
# import changed excel
datapath2 = 'ts_modelling2.xlsx'
newdata = pd.read_excel(datapath2, sheetname=0, index_col='Created')
```
After removing those two outlier days, the scaling of our vertical axis changed significantly. The number of tickets coming in on a daily basis now range between 0 and 175, reaching this boundary only once in September 2016, when not taking into account those three outlier days that have been removed. The overall average for the entire date range gives us a figure of 26 tickets per day, again, this mean value does not take the 3 outlier days into consideration. A striking insight that one can derive from analysing the figure below is that the series becomes more volatile from January 2016 onwards, with a much larger variance and also containing more extreme values. In conclusion, the trend of daily ticket volume was more stable in 2015 than in 2016 and these characteristics indicate that a seasonal ARIMA (Auto-regressive Integrated Moving-average) model seems to be most suitable for the forecasting task. This would enable us to account for seasonal variation, the trend factor and the random noise component which is inherent in the underlying dataset.
```
# y2
y_ = newdata.loc[:,'Number'].resample('D').count()
y_.plot(linestyle='-', figsize=(15, 8))
#y_mean = [np.mean(y_)]*len(newdata.index)
plt.xlabel('Date Created', fontsize=14)
plt.ylabel('Total Ticket Count', fontsize=14)
plt.title('Daily View of Ticket Count', fontsize=16)
plt.show()
```
## Time Series Methodology and Analysis
The seasonal ARIMA model incorporates both non-seasonal and seasonal factors in a multiplicative model. One shorthand notation for the model is: $ARIMA(p, d, q) × (P, D, Q)S$ with with $p$ = non-seasonal AR order, $d$ = non-seasonal differencing, $q$ = non-seasonal MA order, $P$ = seasonal AR order, $D$ = seasonal differencing, $Q$ = seasonal MA order, and $S$ = time span of repeating seasonal pattern.
The regression output below shows the implementation of a **seasonal ARIMA** model, which suggests that all the selected parameters are statistically significant and of large magnitude, i.e., explaining the underlying time series. The **coef** column illustrates the weighting (i.e. importance) of each parameter and shows how each one affects daily ticket volume. The **P>|z|** column shows us the magnitude of each feature weight. Here, each weight has a **p-value** lower than 0.05, enabling us to infer that we can keep all of the parameters in our model.
```
# Fitting the model - ARIMA(1, 1, 1)x(1, 1, 1, 12)12
mod = sm.tsa.statespace.SARIMAX(y_,
order=(1, 1, 1),
seasonal_order=(1, 1, 1, 12),
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print(results.summary().tables[1])
```
However, when estimating and fitting seasonal ARIMA models, it is crucial to also compute model diagnostics. This ensures that none of the assumptions made by the statistical algorithm have been violated. The plot_diagnostics object enables us to quickly visualise model diagnostics and investigate for any unusual patterns.
```
# Plotting model diagnostics
results.plot_diagnostics(figsize=(15, 12))
plt.show()
```
The main point of concern for this modelling exercise is to verify whether the residuals of the seasonal ARIMA model are uncorrelated and normally distributed with zero-mean. If the model does not satisfy these properties, it simply means that it can be enhanced by additional hyperparameter tuning, i.e., tweaking the estimated equation such that our model achieves the desired statistical properties. Unfortunately, engaging in such painstaking manual steps is beyond the scope of this analysis. In the above case, our model diagnostics plots suggest that the residuals are approximately normally distributed. \begin{enumerate}
\item In the top right plot, we see that the green **KDE** line roughly follows the **N(0,1)** line (**where N(0,1)**) is the standard notation for a normal distribution with mean 0 and standard deviation of 1).
\item The qq-plot on the bottom left shows that the ordered distribution of residuals (blue dots) follows the linear trend of the samples taken from a standard normal distribution with **N(0, 1)**. Again, this is a strong indication that the model residuals are approximately normally distributed.
\item The residuals over time (top left plot) do not exhibit any obvious seasonality and appear to be white noise. The only cause for concern is the high variance towards the end of 2016. Also, the autocorrelation (i.e. correlogram) plot on the bottom right, shows that the time series residuals exhibit _some_ correlation with lagged versions of itself. This implies that there is a presence of autocorrelation.
\end{enumerate}
.
Taking these insights into consideration leads us to conclude that our model can indeed produce a satisfactory fit that could enable us to better understand our time series data and forecast future values. Another conclusion implicit in the observations elaborated on above is that 2016 is unlike 2015. Thus, it would be better to only feed the values of 2016 into our forecasting model.
### Validating the Model
As the discussion above has shown, we have obtained a rigorous methodology of a statistical model for our time series data of ticket volume that can now be used to produce forecasts. The first step of validating our seasonal ARIMA model is to compare the predicted values to the real values of the time series, which will aid us in understanding the accuracy of the forecast to come. The below plot shows the observed data of total ticket volume (blue colour) compared to our one-step ahead forecast (red colour) that was produced by the selected seasonal ARIMA methodology. The shaded area represents confidence intervals that provide us with a measure of certainty. Owing to the strong variability of the data for 2016, the confidence bounds are quite wide. Overall, the model forecasts align with the real observed values very well.
```
# comparing forecast values with actual values
pred = results.get_prediction(start=pd.to_datetime('01/01/2016'), dynamic=False)
pred_ci = pred.conf_int()
# Plotting original versus forecast
ax = y_['01/01/2016':].plot(label='observed', figsize=(15, 8))
pred.predicted_mean.plot(ax=ax, label='One-step ahead Forecast', color='r', alpha=.7, figsize=(15, 8))
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.2)
ax.set_xlabel('Date', fontsize=14)
ax.set_ylabel('Total Count of Tickets', fontsize=14)
plt.legend()
plt.show()
```
It is also useful to compute a measure of the accuracy of our forecasts. We will utilise the MSE (Mean Squared Error), which summarises the average error of the forecasts. For each predicted value, we compute its distance to the true value and square the result. The results need to be squared so that positive/negative differences do not cancel each other out when we compute the overall mean. As can be seen below, the MSE of our one-step ahead forecasts yields a value of 422.45, which is quite high as it should be close to 0. An MSE of 0 would mean that the estimator is predicting observations of the parameter with perfect accuracy, which would be an ideal scenario but it not typically possible. One reason for this high value of MSE is that our dataset for 2016 exhibits a very high variability, as could be seen by the confidence intervals in the graph above. In conclusion, this forecasting task may require a more advanced modelling methodology to reduce the MSE further.
```
# computing the MSE
y_forecasted = pred.predicted_mean
y_truth = y_['01/01/2016':]
# Compute the mean square error
mse = ((y_forecasted - y_truth) ** 2).mean()
print('The Mean Squared Error of our forecast is {}'.format(round(mse, 2)))
```
### Forecast for December-February 2017
As can be seen from the forecast for December, January and February, the seasonal ARIMA model provided us with an estimate of roughly 20-30 tickets per day, fluctuating around an average of 20 tickets. This is simply an extension of the lower daily average that started to decrease in September 2016. Prior visualisations have shown that there is a decreasing trend visible from the latter part of the second half of 2016. This feature is inherent in any seasonal ARIMA model, which picks up on the nearest seasonal patterns and adjusts its forecast accordingly. Another noticable characteristic of the forecast is that it exhibits less variability than the actual series, something that a more enhanced methodology could improve on. Furthermore, there are many other variables that impact ticket volume, such as: (1) the number of users that utilise a given software infrastructure, (2) the average number of bugs, and (3) the average number of technical staff that develop and maintain a given software infrastructure. Obtaining data on the number of users per day and hour of the day would remove a substantial amount of uncertainty from the errors and enhance the modelling results further.
```
# Forecast 99 days into the future, last date of sample is 21/11/2016
# Get forecast 500 steps ahead in future
pred_uc = results.get_forecast(steps=99)
# Get confidence intervals of forecasts
pred_ci = pred_uc.conf_int()
# plot forecast
sns.set(font_scale = 1.25)
ax = y_['11/01/2016':].plot(label='Observed', figsize=(15, 8))
pred_uc.predicted_mean.plot(ax=ax, label='Forecast', color='r', alpha=.7, figsize=(15, 8))
ax.set_xlabel('Date', fontsize=14)
ax.set_ylabel('Total Count of Tickets', fontsize=14)
plt.legend()
plt.title('Daily Ticket Count Forecast', fontsize=16)
plt.show()
# Time Series Modelling, DEFINING THE ARIMA TERMS
# Define the p, d and q parameters to take any value between 0 and 2
p = d = q = range(0, 2)
# Generate all different combinations of p, q and q triplets
pdq = list(itertools.product(p, d, q))
# Generate all different combinations of seasonal p, q and q triplets
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
#print('Examples of parameter combinations for Seasonal ARIMA...')
#print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[1]))
#print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[2]))
#print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[3]))
#print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[4]))
# Hyper Parameter tuning for our SARIMA model
# chosen model ARIMA(1, 1, 1)x(1, 1, 1, 12)12
import statsmodels.api as sm
warnings.filterwarnings("ignore") # specify to ignore warning messages
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(y_,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print('ARIMA{}x{}12 - AIC:{}'.format(param, param_seasonal, results.aic))
except:
continue
# calculating the mean of y_
y_mean = np.mean(y_)
print(y_mean)
# turning the index into a list
y_mean = [np.mean(y_)]*len(newdata.index)
# investigating the difference in the number of rows
#print(len(data))
#print(len(newdata))
# maybe you can count the number of rows (category) using the .count() on resample
# there must be a method
# the number of users that utilise a given software infrastructure
# the average number of bugs
# the average number of technical staff that develop and maintain a given software infrastructure
# Section 1 Exploratory data analysis
# Section 2 Methodology of modelling
# Section 3 Results and insights
# Characterize the growth trend and try to annotate the jump
# slice the index to further investigate the jump in ticket volume
# dropping outliers
#start_remove = '2016-08-30'
#end_remove = '2016-08-31'
#dropThis = data.loc['2016-08-30':'2016-08-31']
# newdata = data.drop(data.index[['2016-08-30','2016-08-31']])
#newdata1 = data[~data.index.isin(dropThis)]
```
| true |
code
| 0.605449 | null | null | null | null |
|
# Computing gradients in parallel with PennyLane-Braket
A central feature of the Amazon Braket SV1 simulator is that is can execute multiple circuits sent from PennyLane in parallel. This is crucial for scalable optimization, where each training step creates lots of variations of a circuit which need to be executed.
This tutorial will explain the importance of this feature and allow you to benchmark it yourself.
## Why is the training of circuits so expensive?
Quantum-classical hybrid optimization of quantum circuits is the workhorse algorithm of near-term quantum computing. It is not only fundamental for training variational quantum circuits but also more broadly for applications like quantum chemistry, quantum machine learning and, of course, for applications in "vanilla" quantum optimization. Today’s most powerful optimization algorithms rely on the efficient computation of gradients—which tell us how to adapt parameters a little bit at a time to improve the algorithm.
Training quantum circuits is tough! Each step during optimization requires evaluation of the circuit gradient. Calculating the gradient involves multiple device executions: for each trainable parameter we must execute our circuit on the device typically [more than once](https://pennylane.ai/qml/glossary/parameter_shift.html). Reasonable applications involve many trainable parameters (just think of a classical neural net with millions of tunable weights). The result is a huge number of device executions for each optimization step.

In the ``braket.local.qubit`` device, gradients are calculated in PennyLane through sequential device executions—in other words, all these circuits have to wait in the same queue until they can be evaluated. This approach is simpler, but quickly becomes slow as we scale the number of parameters. Moreover, as the number of qubits, or "width", of the circuit is scaled, each device execution will slow down and eventually become a noticeable bottleneck. In short—**the future of training quantum circuits relies on high-performance remote simulators and hardware devices that are highly parallelized**.
Fortunately, Amazon Braket provides a solution for scalable quantum circuit training with the SV1 simulator. The SV1 simulator is a high-performance state vector simulator that is designed with parallel execution in mind. Together with PennyLane, we can use SV1 to run in parallel all the circuits needed to compute a gradient!

## Loading the SV1 device
Let's load Braket's SV1 simulator in PennyLane with 25 qubits. Further details on loading Braket devices are provided in the [first tutorial](./0_Getting_started.ipynb). We begin with the standard imports and specification of the bucket and ARN:
```
import pennylane as qml
from pennylane import numpy as np
wires = 25
# Please enter the S3 bucket you created during onboarding
# (or any other S3 bucket starting with 'amazon-braket-' in your account) in the code below
my_bucket = f"amazon-braket-Your-Bucket-Name" # the name of the bucket
my_prefix = "Your-Folder-Name" # the name of the folder in the bucket
s3_folder = (my_bucket, my_prefix)
device_arn = "arn:aws:braket:::device/quantum-simulator/amazon/sv1"
```
Recall that all remote simulators and hardware on Braket are accessed through PennyLane using the ``braket.aws.qubit`` device name. The specific remote device is set using the ``device_arn`` argument.
```
dev_remote = qml.device(
"braket.aws.qubit",
device_arn=device_arn,
wires=wires,
s3_destination_folder=s3_folder,
parallel=True,
)
dev_local = qml.device("braket.local.qubit", wires=wires)
```
Note the ``parallel=True`` argument in ``dev_remote``. This setting allows us to unlock the power of parallel execution on SV1 for gradient calculations. The local Braket simulator has also been loaded for comparison.
## Benchmarking a circuit evaluation
We will now compare the execution time for the remote and local Braket devices. Our first step is to create a simple circuit:
```
def circuit(params):
for i in range(wires):
qml.RX(params[i], wires=i)
for i in range(wires):
qml.CNOT(wires=[i, (i + 1) % wires])
return qml.expval(qml.PauliZ(wires - 1))
```

In this circuit, each of the 25 qubits has a controllable rotation. A final block of two-qubit CNOT gates is added to entangle the qubits. Overall, this circuit has 25 trainable parameters. Although not particularly relevant for practical problems, we can use this circuit as a testbed in our comparison of the remote and local devices.
The next step is to convert the above circuit into a PennyLane QNode, which binds the circuit to a device for execution.
```
qnode_remote = qml.QNode(circuit, dev_remote)
qnode_local = qml.QNode(circuit, dev_local)
```
<div class="alert alert-block alert-info">
<b>Note</b> The above uses <code>qml.QNode</code> to convert the circuit. In previous tutorials, you may have seen the <code>@qml.qnode()</code> decorator being used. These approaches are interchangeable, but we use <code>qml.QNode</code> here because it allows us to pair the same circuit to different devices.
</div>
Let's now compare the execution time between the two devices:
```
import time
params = np.random.random(wires)
```
The following cell will result in 1 circuit being executed on SV1.
```
t_0_remote = time.time()
qnode_remote(params)
t_1_remote = time.time()
t_0_local = time.time()
qnode_local(params)
t_1_local = time.time()
print("Execution time on remote device (seconds):", t_1_remote - t_0_remote)
print("Execution time on local device (seconds):", t_1_local - t_0_local)
```
Nice! These timings highlight the advantage of using SV1 for simulations with large qubit numbers. In general, simulation times scale exponentially with the number of qubits, but SV1 is highly optimized and running on AWS remote servers. This allows SV1 to outperform the local simulator in this 25-qubit example. The time you see for the remote device will also depend on factors such as your distance to AWS servers.
<div class="alert alert-block alert-info">
<b>Note</b> Given these timings, why would anyone want to use the local simulator? You should consider using the local simulator when your circuit has few qubits. In this regime, the latency times of communicating the circuit to AWS dominate over simulation times, allowing the local simulator to be faster.
</div>
## Benchmarking gradient calculations
Now let us compare the gradient-calculation times between the two devices. Remember that when loading the remote device, we set ``parallel=True``. This allows the multiple device executions required during gradient calculations to be performed in parallel on SV1, so we expect the remote device to be much faster.
```
d_qnode_remote = qml.grad(qnode_remote)
d_qnode_local = qml.grad(qnode_local)
```
The following cell will result in 51 circuits being executed (in parallel) on SV1. We must execute the circuit twice to evaluate the partial derivative with respect to each parameter. Hence, for 25 parameters there are 50 circuit executions. The final circuit execution is due to a "forward pass" evaluation of the QNode before the gradient is calculated.
```
t_0_remote_grad = time.time()
d_qnode_remote(params)
t_1_remote_grad = time.time()
```
<div class="alert alert-block alert-warning">
<b>Caution:</b> Depending on your hardware, running the following cell can take 15 minutes or longer. Only uncomment it if you are happy to wait.
</div>
```
# t_0_local_grad = time.time()
# d_qnode_local(params)
# t_1_local_grad = time.time()
print("Gradient calculation time on remote device (seconds):", t_1_remote_grad - t_0_remote_grad)
# print("Gradient calculation time on local device (seconds):", t_1_local_grad - t_0_local_grad)
```
If you had the patience to run the local device, you will see times of around 15 minutes or more! Compare this to less than a minute spent calculating the gradient on SV1. This provides a powerful lesson in parallelization.
What if we had run on SV1 with ``parallel=False``? It would have taken around 3 minutes—still faster than a local device, but much slower than running SV1 in parallel.
<div class="alert alert-block alert-info">
<b>What's next?</b> Look into some applications, for example how to solve
<a href="./2_Graph_optimization_with_QAOA.ipynb">graph</a> or <a href="./3_Quantum_chemistry_with_VQE.ipynb">chemistry</a> problems with PennyLane and Braket.
</div>
| true |
code
| 0.278919 | null | null | null | null |
|
# Create trip statistics
# Purpose
Before looking at the dynamics of the ferries from the time series it is a good idea to first look at some longer term trends. Statistics for each trip will be generated and saved as a first data reduction, to spot trends over the day/week/month and year.
# Methodology
* Trip statistics will be generated for each trip containing:
* for all columns: min/mean/max/median/std
* energy consumption for all thrusters
* The statistics will be stored into a [xarray](http://xarray.pydata.org/en/stable/)
# Setup
```
# %load imports.py
#%load imports.py
%matplotlib inline
%load_ext autoreload
%autoreload 2
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (20,3)
#import seaborn as sns
import os
from collections import OrderedDict
from IPython.display import display
pd.options.display.max_rows = 999
pd.options.display.max_columns = 999
pd.set_option("display.max_columns", None)
import folium
import plotly.express as px
import plotly.graph_objects as go
import sys
import os
sys.path.append('../')
from src.visualization import visualize
from src.data import get_dataset
from src.data import trips
import scipy.integrate
import seaborn as sns
import xarray as xr
%%time
df = get_dataset.get(n_rows=None)
deltas = ['delta_%i' % i for i in range(1,5)]
df.drop(columns=deltas, inplace=True)
df['trip_time'] = pd.TimedeltaIndex(df['trip_time']).total_seconds()
mask = df['reversing'].copy()
df['reversing'].loc[mask] = 1
df['reversing'].loc[~mask] = 0
df.head()
groups = df.groupby(by='trip_no')
assert (groups.last()['sog'] < 0.3).all()
trip = df.groupby(by='trip_no').get_group(11)
visualize.plot_map(trip)
def integrate_time(trip):
trip_ = trip.copy()
t = pd.TimedeltaIndex(trip_['trip_time'],unit='s').total_seconds()
trip_.drop(columns=['trip_time'], inplace=True)
integral_trip = scipy.integrate.simps(y=trip_.T,x=t)
s = pd.Series(data=integral_trip, name='integral', index=trip_.columns)
return s
integrate_time(trip)
t = pd.TimedeltaIndex(trip['trip_time'], unit='s').total_seconds()
scipy.integrate.simps(y=trip['power_em_thruster_total'],x=t)
def trip_statistic(trip):
stats = trip.describe() # General statistics
integral_trip = integrate_time(trip)
stats = stats.append(integral_trip)
return stats
ds_stats = None
for trip_no, trip in df.groupby(by='trip_no'):
trip_ = trip.copy()
trip_direction = trip_.iloc[0]['trip_direction']
#trip_.drop(columns=['trip_no','trip_direction'], inplace=True)
trip_.drop(columns=['trip_no'], inplace=True)
stats = trip_statistic(trip_)
stats.index.name = 'statistic'
ds = xr.Dataset.from_dataframe(stats)
ds = ds.expand_dims('trip_no')
ds = ds.assign_coords(trip_no=np.array([trip_no],dtype=np.int64))
#ds.attrs['trip_direction'] = trip_direction
if ds_stats is None:
ds_stats = ds
else:
ds_stats = xr.concat([ds_stats,ds], dim="trip_no")
ds_stats
ds_stats.coords['statistic']
ds
ds_stats.sel(trip_no=2, statistic='mean')
ds_stats.sel(statistic='mean').plot.scatter(x="sog",y="trip_time")
ds_stats.sel(statistic='max').plot.scatter(x="sog",y="power_em_thruster_total")
ds_stats.sel(statistic=['min','mean','max']).plot.scatter(x="sog",y="power_em_thruster_total", hue='statistic');
xr.plot.hist(ds_stats.sel(statistic='mean')['sog'], bins=20);
xr.plot.hist(ds_stats.sel(statistic='integral')["power_em_thruster_total"], bins=20);
ds_stats.sel(statistic='integral').plot.scatter(x="sog",y="power_em_thruster_total")
df_mean = ds_stats.sel(statistic='mean').to_dataframe()
df_means = df_mean.groupby(by='trip_direction').mean()
df_stds = df_mean.groupby(by='trip_direction').std()
directions = pd.Series({
0 : 'Helsingör-Helsinborg',
1 : 'Helsinborg-Helsingör',
})
x = directions[df_means.index]
fig,ax=plt.subplots()
ax.bar(x=x, height=df_means['power_em_thruster_total'], yerr=df_stds['power_em_thruster_total'])
fig,ax=plt.subplots()
ax.bar(x=x, height=df_means['trip_time'], yerr=df_stds['trip_time'])
fig,ax=plt.subplots()
ax.bar(x=x, height=df_means['sog'], yerr=df_stds['sog'])
```
## Save statistics
```
df_mean = ds_stats.sel(statistic='mean').to_dataframe()
df_integral = ds_stats.sel(statistic='integral').to_dataframe()
df_std = ds_stats.sel(statistic='std').to_dataframe()
df_max = ds_stats.sel(statistic='max').to_dataframe()
df_stats = df_mean.drop(columns=['statistic'])
df_ = df.reset_index()
start_times = df_.groupby('trip_no').first()['time']
end_time = df_.groupby('trip_no').last()['time']
integral_columns = ['power_em_thruster_%i' %i for i in range(1,5)]
integral_columns+=['power_em_thruster_total','power_heeling']
df_stats[integral_columns] = df_integral[integral_columns]
max_columns = ['trip_time']
df_stats[max_columns] = df_max[max_columns]
df_stats['start_time'] = start_times
df_stats['end_time'] = end_time
df_stats.head()
from azureml.core import Workspace, Dataset
subscription_id = '3e9a363e-f191-4398-bd11-d32ccef9529c'
resource_group = 'demops'
workspace_name = 'D2E2F'
workspace = Workspace(subscription_id, resource_group, workspace_name)
def save():
df_stats_save = df_stats.copy()
df_stats_save.reset_index(inplace=True)
datastore = workspace.get_default_datastore()
dataset_2 = Dataset.Tabular.register_pandas_dataframe(dataframe=df_stats_save, target=datastore, name=new_name)
new_name = 'tycho_short_statistics'
if not new_name in workspace.datasets:
save()
columns = ['cos_pm%i' % i for i in range(1,5)]
df_std.mean()[columns]
columns = ['sin_pm%i' % i for i in range(1,5)]
df_std.mean()[columns]
```
| true |
code
| 0.399812 | null | null | null | null |
|
# Undertale & Deltarune Soundtrack Generator
---
## Table of Contents
0. [**Table of Contents**](#Table-of-Contents)
1. [**Imports**](#Imports)
2. [**Data Processing**](#Data-Processing)
2.1 [Data Loading](#Data-Loading)
2.2 [Data Preprocessing](#Data-Preprocessing)
2.3 [Dataset & Dataloader Definition](#Dataset-&-Dataloader-Definition)
3. [**Model Definition**](#Model-Definition)
4. [**Hyperparameters & Instantiation**](#Hyperparameters-&-Instantiation)
5. [**Training**](#Training)
---
## Imports
[(go to top)](#Undertale-&-Deltarune-Soundtrack-Generator)
Import required packages
```
import os # File handling
import itertools # chain() for merging lists
import random # Shuffling
import collections # Useful tools like Counter, OrderedDict
import math # For... math
from decimal import Decimal # Scientific notations in string formatting
from time import time # For use in progress bar
import tqdm.auto as tqdm # Progress bar
from IPython.display import clear_output
import torch # Deep Learning Framework
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
import matplotlib.pyplot as plt # Plotting training progress
from matplotlib.ticker import AutoLocator
%matplotlib inline
fig_bg_color = "lightsteelblue"
plot_bg_color = "slategray"
fontsize = 20
```
---
## Data Processing
[(go to top)](#Undertale-&-Deltarune-Soundtrack-Generator)
### Data Loading
[(go to top)](#Undertale-&-Deltarune-Soundtrack-Generator)
Read the text files in the target directory.
Do some processing to make sure the texts are clean.
```
def get_texts(texts_dir):
if not os.path.isdir(texts_dir):
raise FileNotFoundError("given text directory not found: {}".format(texts_dir))
texts = []
for text_path in (file.path for file in os.scandir(texts_dir) if file.is_file() and file.name.endswith(".txt")):
with open(file=text_path, mode='r', encoding="utf-8") as text_file:
text = text_file.read().strip()
if not text.replace(' ', '').isdigit():
raise RuntimeError("one or more characters other than digits and white spaces are detected: {}".format(text_path))
while " " in text:
text = text.replace(" ", ' ')
texts.append((text_path, text))
return dict(texts)
[(os.path.split(text_path)[1], text[:20]) for text_path, text in get_texts("./source/converted_texts").items()]
```
### Data Preprocessing
[(go to top)](#Undertale-&-Deltarune-Soundtrack-Generator)
Get integers out of the text and make lists of ints.
These lists can be used for the input of the models, or be further processed to compress or simplify the sequences.
In this notebook, I'll leave the data as it is and do note-by-note. (Similar to Character-By-Character approach)
```
def texts_to_intlists(text_list):
intlists = []
for i, text in enumerate(iterable=text_list):
int_strings = text.split(' ')
if not all(int_str.isdigit() for int_str in int_strings):
raise RuntimeError("non-digit string detected in text {}".format(i))
ints = [int(int_str) for int_str in int_strings]
intlists.append(ints)
return intlists
print([ints[:10] for ints in texts_to_intlists(get_texts("./source/converted_texts").values())])
```
### Dataset & Dataloader Definition
[(go to top)](#Undertale-&-Deltarune-Soundtrack-Generator)
Create a Dataset class from which training data can be sampled.
This Dataset should convert the encoded sequence above into tensors
and have a method for shuffling the order of multiple sequences while
leaving the patterns inside of each sequence untouched.
```
class UndertaleDeltaruneDataset(Dataset):
def __init__(self, texts_dir, batch_size=1):
self.texts = get_texts(texts_dir) # read and get a dictionary of {file_paths: text_contents}
self.sequences = texts_to_intlists(self.texts.values())
self.texts_dir = texts_dir
self.batch_size = batch_size
def __len__(self):
return self.batch_size
def data_len(self):
return sum([len(sequence) for sequence in self.sequences])
def __getitem__(self, index):
shuffled_list = list(itertools.chain(*random.sample(self.sequences, len(self.sequences))))
inputs = torch.LongTensor(shuffled_list[:-1])
labels = torch.LongTensor(shuffled_list[1:])
return inputs, labels
```
Create a custom class that loads the data from the dataset above and
allows iteration over the dataset, yielding a small sequence batch at a time.
```
class UDBatchLoader:
def __init__(self, ud_dataset, batch_size, sequence_len, drop_last=False, batch_first=True):
self.ud_dataset = ud_dataset
self.batch_size = batch_size
self.sequence_len = sequence_len
self.drop_last = drop_last
self.batch_first = batch_first
def __len__(self):
if self.drop_last:
return math.floor((self.ud_dataset.data_len() - 1) / self.sequence_len)
return math.ceil((self.ud_dataset.data_len() - 1) / self.sequence_len)
def generator(self):
seq_len = self.sequence_len
n_seq_batches = self.__len__()
batch_first = self.batch_first
input_batch, target_batch = next(iter(DataLoader(self.ud_dataset, self.batch_size)))
if not batch_first:
input_batch = input_batch.transpose(0, 1).contiguous()
target_batch = target_batch.transpose(0, 1).contiguous()
for start, end in zip(range(0, seq_len * n_seq_batches, seq_len), range(seq_len, (seq_len + 1) * n_seq_batches, seq_len)):
if batch_first:
yield (input_batch[:, start:end].contiguous(), target_batch[:, start:end].contiguous())
else:
yield (input_batch[start:end], target_batch[start:end])
def __iter__(self):
return self.generator()
```
---
## Model Definition
[(go to top)](#Undertale-&-Deltarune-Soundtrack-Generator)
Define the model architectures.
```
class UDNet(nn.Module):
def __init__(self, hidden_size, num_layers, dropout):
super(UDNet, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.dropout = dropout
self.init_hiddens = nn.Parameter(torch.randn(num_layers, 1, hidden_size))
self.init_cells = nn.Parameter(torch.randn(num_layers, 1, hidden_size))
self.embed = nn.Embedding(num_embeddings=129, embedding_dim=hidden_size)
self.lstm = nn.LSTM(input_size=hidden_size, hidden_size=hidden_size, num_layers=num_layers, dropout=dropout, batch_first=True)
self.fc0 = nn.Sequential(
nn.LayerNorm(hidden_size),
nn.Dropout(p=dropout),
nn.Linear(in_features=hidden_size, out_features=256)
)
self.fc1 = nn.Sequential(
nn.ReLU(),
nn.LayerNorm(256),
nn.Dropout(p=dropout),
nn.Linear(in_features=256, out_features=512)
)
self.fc2 = nn.Sequential(
nn.ReLU(),
nn.LayerNorm(512),
nn.Dropout(p=dropout),
nn.Linear(in_features=512, out_features=129)
)
def forward(self, x, hiddens=None):
if hiddens is None:
hiddens = self.get_init_hiddens(x.size(0))
x = self.embed(x)
x, new_hiddens = self.lstm(x, hiddens)
x = self.fc0(x)
x = self.fc1(x)
x = self.fc2(x)
return x, new_hiddens
def get_init_hiddens(self, n_batches):
return [self.init_hiddens.repeat(1, n_batches, 1), self.init_cells.repeat(1, n_batches, 1)]
```
---
## Training
[(go to top)](#Undertale-&-Deltarune-Soundtrack-Generator)
```
seed = 0
batch_size = 4
sequence_length = 12800
lr = 1e-3
factor = 0.5
patience = 5
n_logs = 30
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
random.seed(seed)
torch.manual_seed(seed)
ud_dataset = UndertaleDeltaruneDataset("./source/converted_texts", batch_size)
ud_loader = UDBatchLoader(ud_dataset, batch_size, sequence_length, drop_last=True, batch_first=True)
model = UDNet(hidden_size=256, num_layers=10, dropout=0.2).to(device)
optimizer = optim.Adam(model.parameters(), lr=lr)
lr_scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer, factor=factor, patience=patience, verbose=True)
print()
print('Data Sequence Total Length:', ud_dataset.data_len())
print()
print(model)
model.train()
logs = {'epoch': [], 'lr':[], 'loss_avg': [], 'acc_1': [], 'acc_5': []}
i_epoch = 0
while True:
hiddens = model.get_init_hiddens(batch_size)
running_loss = 0
n_top1_corrects = 0
n_top5_corrects = 0
n_instances = 0
for i, (inputs, labels) in enumerate(ud_loader):
print("{:d}/{:d}".format(i, len(ud_loader)-1), end='\r')
inputs = inputs.to(device)
labels = labels.view(-1).to(device)
outputs, hidden_states = model(inputs, hiddens)
outputs = outputs.view(-1, outputs.size(-1))
hiddens = [hiddens[0].detach(), hiddens[1].detach()]
loss = F.cross_entropy(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
n_instances += labels.size(0)
running_loss += loss.item() * labels.size(0)
top5_match = outputs.data.topk(k=5, dim=1)[1].eq(labels.unsqueeze(1))
n_top1_corrects += top5_match[:, 0].sum().item()
n_top5_corrects += top5_match.sum().item()
del top5_match
loss_avg = running_loss / n_instances
acc_1 = n_top1_corrects / n_instances
acc_5 = n_top5_corrects / n_instances
logs['epoch'].append(i_epoch)
logs['lr'].append(optimizer.param_groups[0]['lr'])
logs['loss_avg'].append(loss_avg)
logs['acc_1'].append(acc_1)
logs['acc_5'].append(acc_5)
clear_output(wait=True)
print('\n\n'.join(["Epoch {:d} - LR={:e}\n===============================================\n".format(i_e, lr)
+ "Average Loss: {:f}\nAverage Top-1 Accuracy: {:f}\nAverage Top-5 Accuracy: {:f}\n".format(l_a, a_1, a_5)
+ "==============================================="
for i_e, lr, l_a, a_1, a_5 in list(zip(*list(logs.values())))[-n_logs:]]), end='\n\n')
if (i_epoch + 1) % 10 == 0:
torch.save({'logs': logs, 'state_dict': model.state_dict(), 'optim_dict': optimizer.state_dict(), 'lr_dict': lr_scheduler.state_dict()},
"deep/{:d}.pth".format(i_epoch))
lr_scheduler.step(loss_avg)
i_epoch += 1
```
---
| true |
code
| 0.63273 | null | null | null | null |
|
For each of the following distributions:
1. --Bernoulli--
2. -Binomial-
3. -Poisson-
4. Gaussian
5. Uniform
6. Beta
A) Read up on what the formula for the probability distribution is and what sorts of problems it is used for
B) use Python, matplotlib and the scipy.stats to plot at least 2 unique parameters(or sets of parameters) for each distribution
C) Wrte a blog post summarizing A and B above for at least 3 of the distributions, post online, and provide a link to the comments by 6pm today.
You may use the entire internet to figure out what these distributions do.
**Note**: Here are examples of a sample short blog post here, just for reference:
- (http://muthu.co/poisson-distribution-with-python/)
- (http://hamelg.blogspot.com/2015/11/python-for-data-analysis-part-22.html).
You do not have to follow these models if you don't want to.
Also, you don't have to write the formula, you can just provide your simple graphing code and a reference link to the formula (for example, from wikipedia)
#### from team
Sean: other resources for probability distributions:
- (http://stattrek.com/probability-distributions/probability-distribution.aspx)
- (https://www.khanacademy.org/math/ap-statistics/random-variables-ap/binomial-random-variable/v/binomial-variables)
- (https://www.intmath.com/counting-probability/13-poisson-probability-distribution.php)
- Lingbin Jin Feb 24th at 12:37 PM
http://blog.cloudera.com/blog/2015/12/common-probability-distributions-the-data-scientists-crib-sheet/
- Sean Reed Feb 24th at 1:25 PM
- http://stattrek.com/probability-distributions/probability-distribution.aspx
- Sean Reed Feb 24th at 2:01 PM Using scipy.stats module in Python: https://docs.scipy.org/doc/scipy/reference/tutorial/stats.html
- Carolyn Chomik Feb 24th at 4:04 PM
https://medium.com/@carolynjjankowski/3-statistical-distributions-and-examples-of-how-they-are-used-e1c7cbf2134b
- Will Hall Yesterday at 4:14 PM
https://medium.com/@wcgopher/probability-distributions-7ac506dc2115
```
import numpy as np
from scipy.stats import bernoulli, binom, poisson, norm, uniform, beta
import matplotlib.pyplot as plt
def print_mvsk(*args):
t = args[0]
mean, var, skew, kurt, = float(t[0]),float(t[1]),float(t[2]),float(t[3])
sd = np.sqrt(var)
print(f'mean:{mean:.4f}\tvar:{var:.4f}\tskew:{skew:.4f}\nsd:{sd:.4f}\tkurt:{kurt:.4f}')
```
# Bernulli
Probability distribution witch takes value from 0 to 1
```
fig, ax = plt.subplots(1, 1)
p = 1/6
x = [0,1]
print_mvsk(bernoulli.stats(p, moments='mvsk'))
data = bernoulli.pmf(x, p)
print(x, data)
ax.vlines(x, 0, data, colors='y', lw=20)
###
plt.ylabel('Probability of winning in dice tos')
plt.xlabel('0 mean prob to lose \n 1 - chances to win')
plt.title('Bernulli Probability Distribution')
plt.grid(True)
plt.show()
p = 1/2
x = [0,1]
fig, ax = plt.subplots(1, 1)
data = bernoulli.pmf(x, p)
ax.vlines(x, 0, data, colors='y', lw=20)
plt.ylabel('Probability of winning in coin tos')
plt.xlabel('0 mean prob to lose \n 1 - chances to win')
plt.title('Bernulli Probability Distribution')
plt.grid(False)
plt.show()
```
### Binomial
A binomial experiment is one that possesses the following properties:
- The events that happens with “Success” or “Failure” results during the Bernoulli trial (испытание).
- The experiment consists of \mathbit{n} repeated trials.
- The probability of a success, denoted by \mathbit{p}, remain constant from trial to trial and repeated trial are independent.
Binomial random variable – X in n trials of binomial experiment
The probability distribution of the random variable X is called a binomial distribution, and is given by the formula:
```
fig, ax = plt.subplots(1, 1)
n = 100
p = 1/3
print_mvsk(binom.stats(n, p, moments='mvsk'))
start = binom.ppf(0.000001, n, p)
end = binom.ppf(1, n, p)
x = np.arange(start, end, step=1)
pmf_a = binom.pmf(x, n, p)
print(f'start:{start}\tend:{end}')
ax.plot(x, pmf_a, 'b-', ms=3, label='binom pmf')
plt.ylabel('Prob of Win unfair coin in coin tos')
plt.xlabel('0 mean prob to lose \n 1 - chances to win')
plt.title('Binomial Probability Distribution')
prob20 = binom.pmf([20], n, p)
ax.plot(20, prob20, 'ro', ms=7, label='binom pmf')
mean =int(binom.stats(n, p, moments='m'))
mean_y = binom.pmf([mean], n, p)
ax.vlines(mean, 0, mean_y, colors='y', lw=2)
plt.show()
plt.ylabel('Probability of car passing')
plt.xlabel('Number of cars')
plt.title('Probability Distribution Curve')
arr = []
rv = poisson(25)
for num in range(0,40):
arr.append(rv.pmf(num))
#print(rv.pmf(28))
prob = rv.pmf(28)
plt.grid(True)
plt.plot(arr, linewidth=2.0)
plt.plot([28], [prob], marker='o', markersize=6, color="red")
plt.show()
```
### Poisson
Suppose we are counting the number of occurrences of an event in a given unit of time, distance, area or volume.
For example:
- The number of car accidents in a day.
- The number of dandelions in a square meter plot pf land.
Suppose:
- Events are occurring independently
- The probability that an event occurs in a given length of time does not change through time. Events are occurring randomly and independently.
Then X, the number of events in a fixed unit of time, has a Poisson Distribution.
```
fig, ax = plt.subplots(1, 1)
mu = 4.6
print_mvsk(poisson.stats(mu, moments='mvsk'))
poisson.ppf(0.01, mu),
x = np.arange(poisson.ppf(0.00001, mu),
poisson.ppf(0.99999, mu))
data = poisson.pmf(x, mu)
data2 = [0]*len(data)
data2[3]= poisson.pmf(3, mu)
ax.vlines(x, 0, data, colors='r', lw=18, alpha=1)
ax.vlines(x, 0, data2, colors='b', lw=18, alpha=1)
ax.vlines(x, 0, data2, colors='b', lw=18, alpha=1)
plt.ylabel('Probability')
plt.xlabel('Number of Decays')
plt.title('Plutonium-239 prob of having 3 decays ')
plt.show()
```
## Normal / Gaussian
continues distribution
"The beta distribution can be understood as representing a probability distribution of probabilities"
Very popular distribution that is used to analyze random variables.
The random independent variables has Normal distribution
```
fig, ax = plt.subplots(1, 1)
print_mvsk(norm.stats(moments='mvsk'))
x = np.linspace(norm.ppf(0.00001),
norm.ppf(0.99999), 1000)
data = norm.pdf(x)
ax.plot(x, data, 'b-', ms=1)
ax.vlines(x, 0, data, colors='r', lw=1, alpha=1)
# 95 % of Normal Dist
x_sigma2 = np.linspace(norm.ppf(0.025),
norm.ppf(0.975), 1000)
sigma2 = norm.pdf(x_sigma2)
ax.vlines(x_sigma2,0, sigma2, color='b', lw=1, alpha=.5, label='asd')
p_sigma1 = norm.pdf(1)
x_sigma1 = np.linspace(norm.ppf(p_sigma1),
norm.ppf(1-p_sigma1), 1000)
sigma1 = norm.pdf(x_sigma1)
ax.vlines(x_sigma1,0, sigma1, color='g', lw=1, alpha=.5)
plt.ylabel('Prob')
plt.xlabel('Red 100%\nBlue 95%\nGreen=68.7')
plt.show()
```
## Uniform
# Beta distribution
Beta distribution describes the probability of probabilities
Continues, funtion
https://stats.stackexchange.com/questions/47916/bayesian-batting-average-prior/47921#47921
http://varianceexplained.org/statistics/beta_distribution_and_baseball/
```
fig, ax = plt.subplots(1, 1)
a, b = 81, 219
print_mvsk(beta.stats(a, b, moments='mvsk'))
x = np.linspace(beta.ppf(0, a, b),
beta.ppf(1, a, b), 100)
#print(x)
data = beta.pdf(x, a, b)
ax.plot(x, data,'r-', lw=2, alpha=.8, label='player @ begin')
rv = beta(a+100, b+100)
ax.plot(x, rv.pdf(x), 'k-', lw=2, label='Player @ end')
#Check accuracy of cdf and ppf:
vals = beta.ppf([0.1, 0.5, 0.999], a, b)
np.allclose([0.1, 0.5, 0.999], beta.cdf(vals, a, b))
#Generate random numbers:
#r = beta.rvs(a, b, size=1000)
#And compare the histogram:
#ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
```
| true |
code
| 0.585101 | null | null | null | null |
|
```
from IPython.display import Image
```
# CNTK 103: Part B - Feed Forward Network with MNIST
We assume that you have successfully completed CNTK 103 Part A.
In this tutorial we will train a fully connected network on MNIST data. This notebook provides the recipe using Python APIs. If you are looking for this example in BrainScript, please look [here](https://github.com/Microsoft/CNTK/tree/v2.0.beta15.0/Examples/Image/GettingStarted)
## Introduction
**Problem** (recap from the CNTK 101):
The MNIST data comprises of hand-written digits with little background noise.
```
# Figure 1
Image(url= "http://3.bp.blogspot.com/_UpN7DfJA0j4/TJtUBWPk0SI/AAAAAAAAABY/oWPMtmqJn3k/s1600/mnist_originals.png", width=200, height=200)
```
**Goal**:
Our goal is to train a classifier that will identify the digits in the MNIST dataset.
**Approach**:
The same 5 stages we have used in the previous tutorial are applicable: Data reading, Data preprocessing, Creating a model, Learning the model parameters and Evaluating (a.k.a. testing/prediction) the model.
- Data reading: We will use the CNTK Text reader
- Data preprocessing: Covered in part A (suggested extension section).
Rest of the steps are kept identical to CNTK 102.
```
# Import the relevant components
from __future__ import print_function
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import numpy as np
import sys
import os
import cntk as C
from cntk import UnitType
from cntk.io import CTFDeserializer, MinibatchSource, StreamDef, StreamDefs
from cntk.io import INFINITELY_REPEAT, FULL_DATA_SWEEP
from cntk.initializer import glorot_uniform
from cntk.layers import default_options, Input, Dense
# Select the right target device when this notebook is being tested:
if 'TEST_DEVICE' in os.environ:
import cntk
if os.environ['TEST_DEVICE'] == 'cpu':
cntk.device.try_set_default_device(cntk.device.cpu())
else:
cntk.device.try_set_default_device(cntk.device.gpu(0))
%matplotlib inline
```
## Data reading
In this section, we will read the data generated in CNTK 103 Part B.
```
# Ensure we always get the same amount of randomness
np.random.seed(0)
# Define the data dimensions
input_dim = 784
num_output_classes = 10
```
## Data reading
In this tutorial we are using the MNIST data you have downloaded using CNTK_103A_MNIST_DataLoader notebook. The dataset has 60,000 training images and 10,000 test images with each image being 28 x 28 pixels. Thus the number of features is equal to 784 (= 28 x 28 pixels), 1 per pixel. The variable `num_output_classes` is set to 10 corresponding to the number of digits (0-9) in the dataset.
The data is in the following format:
|labels 0 0 0 0 0 0 0 1 0 0 |features 0 0 0 0 ...
(784 integers each representing a pixel)
In this tutorial we are going to use the image pixels corresponding the integer stream named "features". We define a `create_reader` function to read the training and test data using the [CTF deserializer](https://cntk.ai/pythondocs/cntk.io.html?highlight=ctfdeserializer#cntk.io.CTFDeserializer). The labels are [1-hot encoded](https://en.wikipedia.org/wiki/One-hot).
```
# Read a CTF formatted text (as mentioned above) using the CTF deserializer from a file
def create_reader(path, is_training, input_dim, num_label_classes):
return MinibatchSource(CTFDeserializer(path, StreamDefs(
labels = StreamDef(field='labels', shape=num_label_classes, is_sparse=False),
features = StreamDef(field='features', shape=input_dim, is_sparse=False)
)), randomize = is_training, epoch_size = INFINITELY_REPEAT if is_training else FULL_DATA_SWEEP)
# Ensure the training and test data is generated and available for this tutorial.
# We search in two locations in the toolkit for the cached MNIST data set.
data_found = False
for data_dir in [os.path.join("..", "Examples", "Image", "DataSets", "MNIST"),
os.path.join("data", "MNIST")]:
train_file = os.path.join(data_dir, "Train-28x28_cntk_text.txt")
test_file = os.path.join(data_dir, "Test-28x28_cntk_text.txt")
if os.path.isfile(train_file) and os.path.isfile(test_file):
data_found = True
break
if not data_found:
raise ValueError("Please generate the data by completing CNTK 103 Part A")
print("Data directory is {0}".format(data_dir))
```
<a id='#Model Creation'></a>
## Model Creation
Our feed forward network will be relatively simple with 2 hidden layers (`num_hidden_layers`) with each layer having 400 hidden nodes (`hidden_layers_dim`).
```
# Figure 2
Image(url= "http://cntk.ai/jup/feedforward_network.jpg", width=200, height=200)
```
If you are not familiar with the terms *hidden_layer* and *number of hidden layers*, please refer back to CNTK 102 tutorial.
For this tutorial: The number of green nodes (refer to picture above) in each hidden layer is set to 200 and the number of hidden layers (refer to the number of layers of green nodes) is 2. Fill in the following values:
- num_hidden_layers
- hidden_layers_dim
Note: In this illustration, we have not shown the bias node (introduced in the logistic regression tutorial). Each hidden layer would have a bias node.
```
num_hidden_layers = 2
hidden_layers_dim = 400
```
Network input and output:
- **input** variable (a key CNTK concept):
>An **input** variable is a container in which we fill different observations in this case image pixels during model learning (a.k.a.training) and model evaluation (a.k.a. testing). Thus, the shape of the `input_variable` must match the shape of the data that will be provided. For example, when data are images each of height 10 pixels and width 5 pixels, the input feature dimension will be 50 (representing the total number of image pixels). More on data and their dimensions to appear in separate tutorials.
**Question** What is the input dimension of your chosen model? This is fundamental to our understanding of variables in a network or model representation in CNTK.
```
input = Input(input_dim)
label = Input(num_output_classes)
```
## Feed forward network setup
If you are not familiar with the feedforward network, please refer to CNTK 102. In this tutorial we are using the same network.
```
def create_model(features):
with default_options(init = glorot_uniform(), activation = C.ops.relu):
h = features
for _ in range(num_hidden_layers):
h = Dense(hidden_layers_dim)(h)
r = Dense(num_output_classes, activation = None)(h)
return r
z = create_model(input)
```
`z` will be used to represent the output of a network.
We introduced sigmoid function in CNTK 102, in this tutorial you should try different activation functions. You may choose to do this right away and take a peek into the performance later in the tutorial or run the preset tutorial and then choose to perform the suggested activity.
** Suggested Activity **
- Record the training error you get with `sigmoid` as the activation function
- Now change to `relu` as the activation function and see if you can improve your training error
*Quiz*: Different supported activation functions can be [found here][]. Which activation function gives the least training error?
[found here]: https://github.com/Microsoft/CNTK/wiki/Activation-Functions
```
# Scale the input to 0-1 range by dividing each pixel by 256.
z = create_model(input/256.0)
```
### Learning model parameters
Same as the previous tutorial, we use the `softmax` function to map the accumulated evidences or activations to a probability distribution over the classes (Details of the [softmax function][] and other [activation][] functions).
[softmax function]: http://cntk.ai/pythondocs/cntk.ops.html#cntk.ops.softmax
[activation]: https://github.com/Microsoft/CNTK/wiki/Activation-Functions
## Training
Similar to CNTK 102, we use minimize the cross-entropy between the label and predicted probability by the network. If this terminology sounds strange to you, please refer to the CNTK 102 for a refresher.
```
loss = C.cross_entropy_with_softmax(z, label)
```
#### Evaluation
In order to evaluate the classification, one can compare the output of the network which for each observation emits a vector of evidences (can be converted into probabilities using `softmax` functions) with dimension equal to number of classes.
```
label_error = C.classification_error(z, label)
```
### Configure training
The trainer strives to reduce the `loss` function by different optimization approaches, [Stochastic Gradient Descent][] (`sgd`) being one of the most popular one. Typically, one would start with random initialization of the model parameters. The `sgd` optimizer would calculate the `loss` or error between the predicted label against the corresponding ground-truth label and using [gradient-decent][] generate a new set model parameters in a single iteration.
The aforementioned model parameter update using a single observation at a time is attractive since it does not require the entire data set (all observation) to be loaded in memory and also requires gradient computation over fewer datapoints, thus allowing for training on large data sets. However, the updates generated using a single observation sample at a time can vary wildly between iterations. An intermediate ground is to load a small set of observations and use an average of the `loss` or error from that set to update the model parameters. This subset is called a *minibatch*.
With minibatches we often sample observation from the larger training dataset. We repeat the process of model parameters update using different combination of training samples and over a period of time minimize the `loss` (and the error). When the incremental error rates are no longer changing significantly or after a preset number of maximum minibatches to train, we claim that our model is trained.
One of the key parameter for optimization is called the `learning_rate`. For now, we can think of it as a scaling factor that modulates how much we change the parameters in any iteration. We will be covering more details in later tutorial.
With this information, we are ready to create our trainer.
[optimization]: https://en.wikipedia.org/wiki/Category:Convex_optimization
[Stochastic Gradient Descent]: https://en.wikipedia.org/wiki/Stochastic_gradient_descent
[gradient-decent]: http://www.statisticsviews.com/details/feature/5722691/Getting-to-the-Bottom-of-Regression-with-Gradient-Descent.html
```
# Instantiate the trainer object to drive the model training
learning_rate = 0.2
lr_schedule = C.learning_rate_schedule(learning_rate, UnitType.minibatch)
learner = C.sgd(z.parameters, lr_schedule)
trainer = C.Trainer(z, (loss, label_error), [learner])
```
First let us create some helper functions that will be needed to visualize different functions associated with training.
```
# Define a utility function to compute the moving average sum.
# A more efficient implementation is possible with np.cumsum() function
def moving_average(a, w=5):
if len(a) < w:
return a[:] # Need to send a copy of the array
return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)]
# Defines a utility that prints the training progress
def print_training_progress(trainer, mb, frequency, verbose=1):
training_loss = "NA"
eval_error = "NA"
if mb%frequency == 0:
training_loss = trainer.previous_minibatch_loss_average
eval_error = trainer.previous_minibatch_loss_average
if verbose:
print ("Minibatch: {0}, Loss: {1:.4f}, Error: {2:.2f}%".format(mb, training_loss, eval_error*100))
return mb, training_loss, eval_error
```
<a id='#Run the trainer'></a>
### Run the trainer
We are now ready to train our fully connected neural net. We want to decide what data we need to feed into the training engine.
In this example, each iteration of the optimizer will work on `minibatch_size` sized samples. We would like to train on all 60000 observations. Additionally we will make multiple passes through the data specified by the variable `num_sweeps_to_train_with`. With these parameters we can proceed with training our simple feed forward network.
```
# Initialize the parameters for the trainer
minibatch_size = 64
num_samples_per_sweep = 60000
num_sweeps_to_train_with = 10
num_minibatches_to_train = (num_samples_per_sweep * num_sweeps_to_train_with) / minibatch_size
# Create the reader to training data set
reader_train = create_reader(train_file, True, input_dim, num_output_classes)
# Map the data streams to the input and labels.
input_map = {
label : reader_train.streams.labels,
input : reader_train.streams.features
}
# Run the trainer on and perform model training
training_progress_output_freq = 500
plotdata = {"batchsize":[], "loss":[], "error":[]}
for i in range(0, int(num_minibatches_to_train)):
# Read a mini batch from the training data file
data = reader_train.next_minibatch(minibatch_size, input_map = input_map)
trainer.train_minibatch(data)
batchsize, loss, error = print_training_progress(trainer, i, training_progress_output_freq, verbose=1)
if not (loss == "NA" or error =="NA"):
plotdata["batchsize"].append(batchsize)
plotdata["loss"].append(loss)
plotdata["error"].append(error)
```
Let us plot the errors over the different training minibatches. Note that as we iterate the training loss decreases though we do see some intermediate bumps.
Hence, we use smaller minibatches and using `sgd` enables us to have a great scalability while being performant for large data sets. There are advanced variants of the optimizer unique to CNTK that enable harnessing computational efficiency for real world data sets and will be introduced in advanced tutorials.
```
# Compute the moving average loss to smooth out the noise in SGD
plotdata["avgloss"] = moving_average(plotdata["loss"])
plotdata["avgerror"] = moving_average(plotdata["error"])
# Plot the training loss and the training error
import matplotlib.pyplot as plt
plt.figure(1)
plt.subplot(211)
plt.plot(plotdata["batchsize"], plotdata["avgloss"], 'b--')
plt.xlabel('Minibatch number')
plt.ylabel('Loss')
plt.title('Minibatch run vs. Training loss')
plt.show()
plt.subplot(212)
plt.plot(plotdata["batchsize"], plotdata["avgerror"], 'r--')
plt.xlabel('Minibatch number')
plt.ylabel('Label Prediction Error')
plt.title('Minibatch run vs. Label Prediction Error')
plt.show()
```
## Evaluation / Testing
Now that we have trained the network, let us evaluate the trained network on the test data. This is done using `trainer.test_minibatch`.
```
# Read the training data
reader_test = create_reader(test_file, False, input_dim, num_output_classes)
test_input_map = {
label : reader_test.streams.labels,
input : reader_test.streams.features,
}
# Test data for trained model
test_minibatch_size = 512
num_samples = 10000
num_minibatches_to_test = num_samples // test_minibatch_size
test_result = 0.0
for i in range(num_minibatches_to_test):
# We are loading test data in batches specified by test_minibatch_size
# Each data point in the minibatch is a MNIST digit image of 784 dimensions
# with one pixel per dimension that we will encode / decode with the
# trained model.
data = reader_test.next_minibatch(test_minibatch_size,
input_map = test_input_map)
eval_error = trainer.test_minibatch(data)
test_result = test_result + eval_error
# Average of evaluation errors of all test minibatches
print("Average test error: {0:.2f}%".format(test_result*100 / num_minibatches_to_test))
```
Note, this error is very comparable to our training error indicating that our model has good "out of sample" error a.k.a. generalization error. This implies that our model can very effectively deal with previously unseen observations (during the training process). This is key to avoid the phenomenon of overfitting.
We have so far been dealing with aggregate measures of error. Let us now get the probabilities associated with individual data points. For each observation, the `eval` function returns the probability distribution across all the classes. The classifier is trained to recognize digits, hence has 10 classes. First let us route the network output through a `softmax` function. This maps the aggregated activations across the network to probabilities across the 10 classes.
```
out = C.softmax(z)
```
Let us a small minibatch sample from the test data.
```
# Read the data for evaluation
reader_eval = create_reader(test_file, False, input_dim, num_output_classes)
eval_minibatch_size = 25
eval_input_map = { input : reader_eval.streams.features }
data = reader_test.next_minibatch(eval_minibatch_size, input_map = test_input_map)
img_label = data[label].value
img_data = data[input].value
predicted_label_prob = [out.eval(img_data[i,:,:]) for i in range(img_data.shape[0])]
# Find the index with the maximum value for both predicted as well as the ground truth
pred = [np.argmax(predicted_label_prob[i]) for i in range(len(predicted_label_prob))]
gtlabel = [np.argmax(img_label[i,:,:]) for i in range(img_label.shape[0])]
print("Label :", gtlabel[:25])
print("Predicted:", pred)
```
Let us visualize some of the results
```
# Plot a random image
sample_number = 5
plt.imshow(img_data[sample_number].reshape(28,28), cmap="gray_r")
plt.axis('off')
img_gt, img_pred = gtlabel[sample_number], pred[sample_number]
print("Image Label: ", img_pred)
```
**Exploration Suggestion**
- Try exploring how the classifier behaves with different parameters - suggest changing the `minibatch_size` parameter from 25 to say 64 or 128. What happens to the error rate? How does the error compare to the logistic regression classifier?
- Suggest trying to increase the number of sweeps
- Can you change the network to reduce the training error rate? When do you see *overfitting* happening?
#### Code link
If you want to try running the tutorial from Python command prompt please run the [SimpleMNIST.py](https://github.com/Microsoft/CNTK/tree/v2.0.beta15.0/Examples/Image/Classification/MLP/Python) example.
| true |
code
| 0.722551 | null | null | null | null |
|
```
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
```
# Reflect Tables into SQLAlchemy ORM
```
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func
# create engine to hawaii.sqlite
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
# reflect an existing database into a new model
base = automap_base()
# reflect the tables
base.prepare(engine,reflect=True)
# View all of the classes that automap found
base.classes.keys()
# Save references to each table
measurement=base.classes.measurement
station=base.classes.station
# Create our session (link) from Python to the DB
session = Session(engine)
```
# Exploratory Precipitation Analysis
```
# Find the most recent date in the data set.
recent_date = session.query(measurement.date).\
order_by(measurement.date.desc()).first()
recent_date
# Design a query to retrieve the last 12 months of precipitation data and plot the results.
# Starting from the most recent data point in the database.
# Calculate the date one year from the last date in data set.
one_year=dt.date(2017,8,23)-dt.timedelta(days=365)
one_year
# Perform a query to retrieve the data and precipitation scores
pre_scores=session.query(measurement.date,measurement.prcp).\
filter(measurement.date > one_year).\
order_by(measurement.date).all()
pre_scores
# Save the query results as a Pandas DataFrame and set the index to the date column
precipitation_df=pd.DataFrame(pre_scores)
precipitation_df.head()
# Sort the dataframe by date
precipitation_df.set_index('date')
precipitation_df.head()
# Use Pandas Plotting with Matplotlib to plot the data
precipitation_df .plot(title="Precipitation Over The Last Year")
plt.savefig("Images/Precipitation.png")
plt.show()
# Use Pandas to calcualte the summary statistics for the precipitation data
precipitation_df.describe()
```
# Exploratory Station Analysis
```
# Design a query to calculate the total number stations in the dataset
stations=session.query(measurement).\
group_by(measurement.station).count()
print(f'stations: {stations}')
# Design a query to find the most active stations (i.e. what stations have the most rows?)
# List the stations and the counts in descending order.
actv_stations = session.query(measurement.station,
func.count(measurement.station)).\
group_by(measurement.station).\
order_by(func.count(measurement.station).desc()).all()
actv_stations
# Using the most active station id from the previous query, calculate the lowest, highest, and average temperature.
most_actv=actv_stations[0][0]
most_actv
temps = session.query(func.min(measurement.tobs), func.max(measurement.tobs),
func.avg(measurement.tobs)).filter(measurement.station == most_actv).all()
print(f'low: {temps[0][0]}')
print(f'high: {temps[0][1]}')
print(f'average: {temps[0][2]}')
# Using the most active station id
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram
most_actv
temperatures = session.query( measurement.tobs).filter(measurement.date >= one_year).\
filter(measurement.station == most_actv).all()
temperatures = pd.DataFrame(temperatures, columns=['temperature'])
temperatures_df=temperatures
temperatures_df.head()
plt.hist(temperatures_df['temperature'], bins =12)
plt.xlabel("temperature")
plt.ylabel("frequency")
plt.title("Frequency of Temp in Station USC00519281")
plt.savefig("Images/Temperature Frequency.png")
```
# Close session
```
# Close Session
session.close()
```
| true |
code
| 0.655612 | null | null | null | null |
|
# Training of a super simple model for celltype classification
```
import tensorflow as tf
!which python
!python --version
print(tf.VERSION)
print(tf.keras.__version__)
!pwd # start jupyter under notebooks/ for correct relative paths
import datetime
import inspect
import pandas as pd
import numpy as np
import seaborn as sns
from tensorflow.keras import layers
from tensorflow.keras.utils import to_categorical
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from depiction.models.examples.celltype.celltype import one_hot_encoding, one_hot_decoding
```
## a look at the data
labels are categories 1-20, here's the associated celltype:
```
meta_series = pd.read_csv('../data/single-cell/metadata.csv', index_col=0)
meta_series
```
There are 13 unbalanced classes, and over 80k samples
```
data_df = pd.read_csv('../data/single-cell/data.csv')
data_df.groupby('category').count()['CD45']
data_df.sample(n=10)
print(inspect.getsource(one_hot_encoding)) # from keras, but taking care of 1 indexed classes
print(inspect.getsource(one_hot_decoding))
classes = data_df['category'].values
labels = one_hot_encoding(classes)
#scale the data from 0 to 1
min_max_scaler = MinMaxScaler(feature_range=(0, 1), copy=True)
data = min_max_scaler.fit_transform(data_df.drop('category', axis=1).values)
data.shape
one_hot_decoding(labels)
data_train, data_test, labels_train, labels_test = train_test_split(
data, labels, test_size=0.33, random_state=42, stratify=data_df.category)
labels
batchsize = 32
dataset = tf.data.Dataset.from_tensor_slices((data_train, labels_train))
dataset = dataset.shuffle(2 * batchsize).batch(batchsize)
dataset = dataset.repeat()
testset = tf.data.Dataset.from_tensor_slices((data_test, labels_test))
testset = testset.batch(batchsize)
```
## I don't know how a simpler network would look like
```
model = tf.keras.Sequential()
# Add a softmax layer with output units per celltype:
model.add(layers.Dense(
len(meta_series), activation='softmax',
batch_input_shape=tf.data.get_output_shapes(dataset)[0]
))
model.summary()
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss='categorical_crossentropy',
metrics=[tf.keras.metrics.categorical_accuracy])
# evaluation on testset on every epoch
# log_dir="logs/fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
# tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir, histogram_freq=1)
model.fit(
dataset,
epochs=20, steps_per_epoch=np.ceil(data_train.shape[0]/batchsize),
validation_data=testset, # callbacks=[tensorboard_callback]
)
```
## Is such a simple model interpretable?
```
# Save entire model to a HDF5 file
model.save('./celltype_model.h5')
# tensorboard --logdir logs/fit
# To recreate the exact same model, including weights and optimizer.
# model = tf.keras.models.load_model('../data/models/celltype_dnn_model.h5')
```
# What is the effect of increasing model complexity?
Play around by adding some layers, train and save the model under some name to use with the other notebook.

```
model = tf.keras.Sequential()
# Adds a densely-connected layers with 64 units to the model:
model.add(layers.Dense(64, activation='relu', batch_input_shape=tf.data.get_output_shapes(dataset)[0])) #
# ...
# do whatever you want
# model.add(layers.Dense(64, activation='relu'))
# model.add(layers.Dropout(0.5))
# ...
# Add a softmax layer with output units per celltype:
model.add(layers.Dense(len(meta_series), activation='softmax'))
```
| true |
code
| 0.652878 | null | null | null | null |
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
Import Danych z Filmwebu
```
data_path='https://raw.githubusercontent.com/mateuszrusin/ml-filmweb-score/master/oceny.csv'
marks = pd.read_csv(data_path)
marks.head(10)
```
Scalamy tytuł oryginalny z polskim
```
marks['Tytuł oryginalny']=marks['Tytuł oryginalny'].fillna(marks['Tytuł polski']);
marks.head(10)
```
Tworzenie funkcji, która wybiera pierwszy kraj produkcji/nagrywania do dalszej analizy.
Hipotezą jest sprawdzenie czy jeżeli krajem produkcji są Stany Zjednoczone to użytkownik wyżej je ocenia
```
def firstValue(x, new_column, split_column, delimiter=','):
x[new_column]=[ y[0:y.find(delimiter)] if y.find(delimiter)>0 else y for y in x[split_column] ]
firstValue(marks, 'firstCountry', 'Kraj produkcji')
marks.head()
```
<b>Tworzenie lambda funkcji, która będzie tworzyć label. Plus konwersja typu danych</b>
```
converter = lambda x: 1 if x == 'USA' else 0
marks.dtypes
marks_Oceny=marks[marks['Ocena']!='brak oceny']
marks_Oceny['Ocena']=marks_Oceny['Ocena'].astype(int)
marks_Oceny['isUSA']= marks_Oceny['firstCountry'].apply(converter)
marks_Oceny.head()
country_dict= lambda x: 'USA' if x == 1 else 'Other'
```
<b>Piewrszy wykres</b> <br>
Sprawdzamy rozkład ocen dla IsUSA za pomocą barplot
```
a = marks_Oceny[['isUSA','Ocena']].groupby('isUSA').hist(alpha=0.4,by=marks_Oceny.isUSA.apply(country_dict))
```
Sprawdzamy rozkład zmiennej Oceny
```
marks_Oceny[['Ocena','isUSA']].plot(x='isUSA', y='Ocena', kind='kde', sharex=True, sharey=True)
a=marks_Oceny[['Ocena','isUSA']].groupby('isUSA').mean()
a.Ocena.at[1]
```
Wykres barplot dla porówania rozkładów. Ten Tutaj po niżej nie jest dobry, ponieważ nie sumuje się do 1 <br>
Nadal można wnioskować, że rozkłady są do siebie zbliżone
```
plt.hist(marks_Oceny[marks_Oceny.isUSA==1]['Ocena'], 50, density=1, facecolor='g', alpha=1,width=1.0)
plt.xlabel('Marks')
plt.title('Histogram of firstCountry=USA')
plt.text(3,1.2, r'$\mu1=%s$' % a.Ocena.at[1].round(3))
plt.show()
plt.xlabel('Marks')
plt.title('Histogram of firstCountry=Other')
plt.hist(marks_Oceny[marks_Oceny.isUSA==0]['Ocena'], 50, density=1, facecolor='r', alpha=1,width=1.0)
plt.text(3,1.7, r'$\mu0=%s$' % a.Ocena.at[0].round(3))
plt.axis([2, 10, 0, 2])
plt.show()
plt.xlabel('Marks')
plt.title('Histogram of firstCountry=Other')
plt.hist(marks_Oceny[marks_Oceny.isUSA==0]['Ocena'], 50, density=1, facecolor='r', alpha=1,width=1.0)
plt.hist(marks_Oceny[marks_Oceny.isUSA==1]['Ocena'], 50, density=1, facecolor='b', alpha=0.5,width=1.0)
plt.axis([2, 10, 0, 2])
plt.show()
marks_Oceny[['Ocena', 'isUSA']].groupby('isUSA').mean().plot(kind='bar', legend=True, ylim=5.2)
marks_Oceny.Gatunek.groupby(marks_Oceny.Gatunek).agg('count')
```
Wybranie pierwszego gatunku filmowego do dalszych analiz
```
firstValue(marks_Oceny,'firstGenrePL', 'Gatunek')
marks_Oceny[marks_Oceny.Gatunek=='Czarna komedia']
countGenre=marks_Oceny.firstGenrePL.groupby(marks_Oceny.firstGenrePL).agg('count')
countGenre.index
```
Wybranie pierwszych 5 najbardziej popularnych gatunków po zmapowaniu
```
genreMap=pd.DataFrame({'genre':countGenre.index,'value':countGenre.values})
firstFiveGenres=genreMap.sort_values(by='value' ,ascending=False).head()
firstFiveGenres
```
Zaczytanie słownika i łaczenie z naszym zbiorem
```
genres_map=pd.read_csv('genre.txt', sep=':')
genres_map.head()
marks_Oceny=marks_Oceny.merge(genres_map,how='left', left_on='firstGenrePL', right_on='Gatunek', suffixes=('_left','_right') )
marks_Oceny.head()
```
Stworzenie subsetu z pierwszych 5 najpopularniejszych gatunków
```
def subsets_create(x, column, by, by_column):
j=1
for i in by[by_column].index:
if j ==1 :
subset=x[x[column]==by.at[i,by_column]]
j=j+1
else:
subset=pd.concat([subset,x[x[column]==by.at[i,by_column]]], ignore_index=True )
return subset
New_set=subsets_create(marks_Oceny,'firstGenrePL',firstFiveGenres,'genre' )
New_set.head()
```
Import seaborn i tworzenie wykresów rozkładów
```
import seaborn as sns
p1=sns.kdeplot(New_set[New_set.Map=='Drama']['Ocena'], shade=True, color='c', label='Drama')
p1=sns.kdeplot(New_set[New_set.Map=='Thriller']['Ocena'], shade=True, color='r', label='Thriller')
p1=sns.kdeplot(New_set[New_set.Map=='Horror']['Ocena'], shade=True, color='b', label='Horror')
p1=sns.kdeplot(New_set[New_set.Map=='Comedy']['Ocena'], shade=True, color='y', label='Comedy')
p1=sns.kdeplot(New_set[New_set.Map=='Action']['Ocena'], shade=True, color='black', label='Action')
#p1=sns.kdeplot(df['sepal_length'], shade=True, color="b")
#sns.plt.show()
```
Merging with IMDB kod pochodzi z poprzedniego spotkania
```
import wget
import gzip
!wget https://datasets.imdbws.com/title.basics.tsv.gz
!wget https://datasets.imdbws.com/title.ratings.tsv.gz
!gzip -d -f title.basics.tsv.gz
!gzip -d -f title.ratings.tsv.gz
imdb_title = pd.read_csv('title.basics.tsv', sep='\t')
imdb_raiting = pd.read_csv('title.ratings.tsv', sep='\t')
imdb = pd.merge(imdb_title, imdb_raiting, how='left',on='tconst')
marks_Oceny['originalTitle'] = marks_Oceny['Tytuł oryginalny']
marks_Oceny['startYear'] =marks_Oceny['Rok produkcji'].astype(str)
match = {
'akcja': 'Action',
'animacja': 'Animation',
'biograficzny': 'Biography',
'czarna komedia': 'Comedy',
'dramat': 'Drama',
'dramat historyczny': 'Drama',
'dramat obyczajowy': 'Drama',
'dramat sądowy': 'Drama',
'erotyczny': 'Romance',
'familijny': 'Family',
'fantasy': 'Fantasy',
'gangsterski': 'Crime',
'horror': 'Horror',
'katastroficzny': 'Adventure',
'komedia': 'Comedy',
'komedia kryminalna': 'Comedy',
'komedia obycz.': 'Comedy',
'komedia rom.': 'Comedy',
'komediarom.': 'Comedy',
'kostiumowy': 'Kostiumowy',
'kryminał': 'Crime',
'melodramat': 'Melodramat',
'obyczajowy': 'Obyczajowy',
'przygodowy': 'Adventure',
'romans': 'Romance',
'sci-Fi': 'Sci-Fi',
'sensacyjny': 'Sensacyjny',
'surrealistyczny': 'Surrealistyczny',
'thriller': 'Thriller',
'western': 'Western',
'wojenny': 'War'
}
def to_list(textdata):
return "".join(textdata.lower().split()).split(',')
def change_type(t):
arr = [match[s.lower()] if s.lower() in match else s.lower() for s in to_list(t)]
return ", ".join(arr)
marks_Oceny['genre_eng'] = marks_Oceny.apply(lambda x: change_type(x['Gatunek']), axis=1)
marks_Oceny.head()
print(len(imdb))
imdb = imdb.dropna(subset=['startYear','originalTitle'])
imdb = imdb[imdb['titleType']=='movie']
imdb.head()
oceny_imdb = pd.merge(
marks_Oceny,
imdb,
how='inner',
on=['startYear','originalTitle'])
print(len(oceny_imdb))
oceny_imdb.head()
print('Zduplikowane: ', len(oceny_imdb[oceny_imdb.duplicated(subset=['originalTitle'])]))
oceny_imdb[oceny_imdb['originalTitle']=='Joker']
def get_similarity(row):
text_list_eng = to_list(row['genre_eng'])
text_list_genres = to_list(row['genres'])
# product of those lists
commons = set(text_list_eng) & set(text_list_genres)
return len(commons)
oceny_imdb['similarity'] = oceny_imdb.apply(get_similarity,axis=1)
oceny_duplicated = oceny_imdb[oceny_imdb.duplicated(subset=['originalTitle'], keep=False)]
oceny_duplicated
top1 = oceny_imdb.groupby(['ID']).apply(lambda x: x.sort_values(["similarity"], ascending = False)).reset_index(drop=True)
oceny_imdb2 = top1.groupby('ID').head(1).copy()
oceny_imdb2[oceny_imdb2['originalTitle']=='Joker']
oceny_imdb2.head()
```
Koniec kodu z poprzedniego Spotkania
Wykresy wiolinowe dla Oceny i średniej. Służą do porównania rozkładów w zależności od Grupy.
Zawiera takie informacje jak Min, Max, Mediana i Kwartyle
```
p1=sns.violinplot(x=oceny_imdb2['isUSA'], y=oceny_imdb2['Ocena'], palette=sns.color_palette("husl", 8) ,linewidth=5, inner='box')
p2=sns.violinplot(x=oceny_imdb2['isUSA'], y=oceny_imdb2['averageRating'], palette=sns.color_palette("Set1", n_colors=8, desat=.5),inner='box' ,linewidth=5)
p1=sns.violinplot(x=oceny_imdb2['isUSA'], y=oceny_imdb2['Ocena'], palette=sns.color_palette("husl", 8), inner=None ,linewidth=5)
p2=sns.violinplot(x=oceny_imdb2['isUSA'], y=oceny_imdb2['averageRating'], palette=sns.color_palette("Set1", n_colors=8, desat=.5), inner=None ,linewidth=5)
oceny_imdb2[['isUSA', 'Ocena', 'averageRating']].groupby('isUSA').agg(['mean','max','min'])
```
Porównanie rozkładów Ocen z filmweb i średniej użytkowników <br>
Patrz dystrybuantę dla OCeny wyżej. Widać, że kształt jest zachowany chodź minimalnie zniwelowany w zależnosci od gatunku
```
p1=sns.kdeplot(oceny_imdb2[oceny_imdb2.Map_right=='Drama']['Ocena'], shade=True, color='c', label='Drama_filmweb')
p1=sns.kdeplot(oceny_imdb2[oceny_imdb2.Map_right=='Drama']['averageRating'], shade=True, color='y', label='Drama_average')
p1=sns.kdeplot(oceny_imdb2[oceny_imdb2.Map_right=='Horror']['Ocena'], shade=True, color='g', label='Horror_filmweb')
p1=sns.kdeplot(oceny_imdb2[oceny_imdb2.Map_right=='Horror']['averageRating'], shade=True, color='y', label='Horror_average')
p1=sns.kdeplot(oceny_imdb2[oceny_imdb2.Map_right=='Comedy']['averageRating'], shade=True, color='y', label='Comedy_average')
p1=sns.kdeplot(oceny_imdb2[oceny_imdb2.Map_right=='Comedy']['Ocena'], shade=True, color='r', label='Comedy_filmweb')
p1=sns.kdeplot(oceny_imdb2[oceny_imdb2.Map_right=='Action']['averageRating'], shade=True, color='y', label='Action_average')
p1=sns.kdeplot(oceny_imdb2[oceny_imdb2.Map_right=='Action']['Ocena'], shade=True, color='black', label='Action_filmweb')
```
| true |
code
| 0.429489 | null | null | null | null |
|
(sec:hmm-ex)=
# Hidden Markov Models
In this section, we introduce Hidden Markov Models (HMMs).
## Boilerplate
```
# Install necessary libraries
try:
import jax
except:
# For cuda version, see https://github.com/google/jax#installation
%pip install --upgrade "jax[cpu]"
import jax
try:
import jsl
except:
%pip install git+https://github.com/probml/jsl
import jsl
try:
import rich
except:
%pip install rich
import rich
# Import standard libraries
import abc
from dataclasses import dataclass
import functools
import itertools
from typing import Any, Callable, NamedTuple, Optional, Union, Tuple
import matplotlib.pyplot as plt
import numpy as np
import jax
import jax.numpy as jnp
from jax import lax, vmap, jit, grad
from jax.scipy.special import logit
from jax.nn import softmax
from functools import partial
from jax.random import PRNGKey, split
import inspect
import inspect as py_inspect
from rich import inspect as r_inspect
from rich import print as r_print
def print_source(fname):
r_print(py_inspect.getsource(fname))
```
## Utility code
```
def normalize(u, axis=0, eps=1e-15):
'''
Normalizes the values within the axis in a way that they sum up to 1.
Parameters
----------
u : array
axis : int
eps : float
Threshold for the alpha values
Returns
-------
* array
Normalized version of the given matrix
* array(seq_len, n_hidden) :
The values of the normalizer
'''
u = jnp.where(u == 0, 0, jnp.where(u < eps, eps, u))
c = u.sum(axis=axis)
c = jnp.where(c == 0, 1, c)
return u / c, c
```
(sec:casino-ex)=
## Example: Casino HMM
We first create the "Ocassionally dishonest casino" model from {cite}`Durbin98`.
```{figure} /figures/casino.png
:scale: 50%
:name: casino-fig
Illustration of the casino HMM.
```
There are 2 hidden states, each of which emit 6 possible observations.
```
# state transition matrix
A = np.array([
[0.95, 0.05],
[0.10, 0.90]
])
# observation matrix
B = np.array([
[1/6, 1/6, 1/6, 1/6, 1/6, 1/6], # fair die
[1/10, 1/10, 1/10, 1/10, 1/10, 5/10] # loaded die
])
pi, _ = normalize(np.array([1, 1]))
pi = np.array(pi)
(nstates, nobs) = np.shape(B)
```
Let's make a little data structure to store all the parameters.
We use NamedTuple rather than dataclass, since we assume these are immutable.
(Also, standard python dataclass does not work well with JAX, which requires parameters to be
pytrees, as discussed in https://github.com/google/jax/issues/2371).
```
class HMM(NamedTuple):
trans_mat: jnp.array # A : (n_states, n_states)
obs_mat: jnp.array # B : (n_states, n_obs)
init_dist: jnp.array # pi : (n_states)
params = HMM(A, B, pi)
print(params)
print(type(params.trans_mat))
```
## Sampling from the joint
Let's write code to sample from this model. First we code it in numpy using a for loop. Then we rewrite it to use jax.lax.scan, which is faster.
```
def hmm_sample_numpy(params, seq_len, random_state=0):
def sample_one_step_(hist, a, p):
x_t = np.random.choice(a=a, p=p)
return np.append(hist, [x_t]), x_t
np.random.seed(random_state)
trans_mat, obs_mat, init_dist = params.trans_mat, params.obs_mat, params.init_dist
n_states, n_obs = obs_mat.shape
state_seq = np.array([], dtype=int)
obs_seq = np.array([], dtype=int)
latent_states = np.arange(n_states)
obs_states = np.arange(n_obs)
state_seq, zt = sample_one_step_(state_seq, latent_states, init_dist)
obs_seq, xt = sample_one_step_(obs_seq, obs_states, obs_mat[zt])
for _ in range(1, seq_len):
state_seq, zt = sample_one_step_(state_seq, latent_states, trans_mat[zt])
obs_seq, xt = sample_one_step_(obs_seq, obs_states, obs_mat[zt])
return state_seq, obs_seq
seq_len = 20
state_seq, obs_seq = hmm_sample_numpy(params, seq_len, random_state=0)
print(state_seq)
print(obs_seq)
```
Now let's write a JAX version.
```
#@partial(jit, static_argnums=(1,))
def hmm_sample(params, seq_len, rng_key):
trans_mat, obs_mat, init_dist = params.trans_mat, params.obs_mat, params.init_dist
n_states, n_obs = obs_mat.shape
initial_state = jax.random.categorical(rng_key, logits=logit(init_dist), shape=(1,))
obs_states = jnp.arange(n_obs)
def draw_state(prev_state, key):
logits = logit(trans_mat[:, prev_state])
state = jax.random.categorical(key, logits=logits.flatten(), shape=(1,))
return state, state
rng_key, rng_state, rng_obs = jax.random.split(rng_key, 3)
keys = jax.random.split(rng_state, seq_len - 1)
final_state, states = jax.lax.scan(draw_state, initial_state, keys)
state_seq = jnp.append(jnp.array([initial_state]), states)
def draw_obs(z, key):
obs = jax.random.choice(key, a=obs_states, p=obs_mat[z])
return obs
keys = jax.random.split(rng_obs, seq_len)
obs_seq = jax.vmap(draw_obs, in_axes=(0, 0))(state_seq, keys)
return state_seq, obs_seq
seq_len = 20
state_seq, obs_seq = hmm_sample(params, seq_len, PRNGKey(1))
print(state_seq)
print(obs_seq)
```
| true |
code
| 0.606906 | null | null | null | null |
|
## self-attention-cv : illustration of a training process with subvolume sampling for 3d segmentation
The dataset can be found here: https://iseg2019.web.unc.edu/ . i uploaded it and mounted from my gdrive
```
from google.colab import drive
drive.mount('/gdrive')
import zipfile
root_path = '/gdrive/My Drive/DATASETS/iSeg-2019-Training.zip'
!echo "Download and extracting folders..."
zip_ref = zipfile.ZipFile(root_path, 'r')
zip_ref.extractall("./")
zip_ref.close()
!echo "Finished"
!pip install torchio
!pip install self-attention-cv
```
## Training example
```
import glob
import torchio as tio
import torch
from torch.utils.data import DataLoader
paths_t1 = sorted(glob.glob('./iSeg-2019-Training/*T1.img'))
paths_t2 = sorted(glob.glob('./iSeg-2019-Training/*T2.img'))
paths_seg = sorted(glob.glob('./iSeg-2019-Training/*label.img'))
assert len(paths_t1) == len(paths_t2) == len(paths_seg)
subject_list = []
for pat in zip(paths_t1, paths_t2, paths_seg):
path_t1, path_t2, path_seg = pat
subject = tio.Subject(t1=tio.ScalarImage(path_t1,),
t2=tio.ScalarImage(path_t2,),
label=tio.LabelMap(path_seg))
subject_list.append(subject)
transforms = [tio.RescaleIntensity((0, 1)),tio.RandomAffine() ]
transform = tio.Compose(transforms)
subjects_dataset = tio.SubjectsDataset(subject_list, transform=transform)
patch_size = 24
queue_length = 300
samples_per_volume = 50
sampler = tio.data.UniformSampler(patch_size)
patches_queue = tio.Queue(
subjects_dataset,
queue_length,
samples_per_volume,sampler, num_workers=1)
patches_loader = DataLoader(patches_queue, batch_size=16)
from self_attention_cv.Transformer3Dsegmentation import Transformer3dSeg
def crop_target(img, target_size):
dim = img.shape[-1]
center = dim//2
start_dim = center - (target_size//2) - 1
end_dim = center + (target_size//2)
return img[:,0,start_dim:end_dim,start_dim:end_dim,start_dim:end_dim].long()
target_size = 3 # as in the paper
patch_dim = 8
num_epochs = 50
num_classes = 4
model = Transformer3dSeg(subvol_dim=patch_size, patch_dim=patch_dim,
in_channels=2, blocks=2, num_classes=num_classes).cuda()
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
print(len(patches_loader))
for epoch_index in range(num_epochs):
epoch_loss = 0
for c,patches_batch in enumerate(patches_loader):
optimizer.zero_grad()
input_t1 = patches_batch['t1'][tio.DATA]
input_t2 = patches_batch['t2'][tio.DATA]
input_tensor = torch.cat([input_t1, input_t2], dim=1).cuda()
logits = model(input_tensor) # 8x8x8 the 3d transformer-based approach
# for the 3d transformer-based approach the target must be cropped again to the desired size
targets = patches_batch['label'][tio.DATA]
cropped_target = crop_target(targets, target_size).cuda()
loss = criterion(logits, cropped_target)
loss.backward()
optimizer.step()
epoch_loss = epoch_loss+loss.cpu().item()
print(f'epoch {epoch_index} loss {epoch_loss/c}')
```
## Inference
```
import torch
import torch.nn as nn
import torchio as tio
patch_overlap = 0
patch_size = 24, 24, 24
target_patch_size = 3
#input sampling
grid_sampler = tio.inference.GridSampler(subject_list[0], patch_size, patch_overlap)
patch_loader = torch.utils.data.DataLoader(grid_sampler, batch_size=4)
# target vol sampling
grid_sampler_target = tio.inference.GridSampler(subject_list[0], target_patch_size, patch_overlap)
aggregator = tio.inference.GridAggregator(grid_sampler_target)
target_loader = torch.utils.data.DataLoader(grid_sampler_target, batch_size=4)
model.eval()
with torch.no_grad():
for patches_batch,target_patches in zip(patch_loader,target_loader):
input_t1 = patches_batch['t1'][tio.DATA]
input_t2 = patches_batch['t2'][tio.DATA]
input_tensor = torch.cat([input_t1, input_t2], dim=1).float().cuda()
locations = target_patches[tio.LOCATION]
logits = model(input_tensor)
labels = logits.argmax(dim=tio.CHANNELS_DIMENSION, keepdim=True)
outputs = labels
aggregator.add_batch(outputs.type(torch.int32), locations)
print('output tensor shape:',outputs.shape)
output_tensor = aggregator.get_output_tensor()
print(output_tensor.shape)
```
| true |
code
| 0.599368 | null | null | null | null |
|
```
"""Simple tutorial following the TensorFlow example of a Convolutional Network.
Parag K. Mital, Jan. 2016"""
# %% Imports
import tensorflow as tf
import tensorflow.examples.tutorials.mnist.input_data as input_data
from libs.utils import *
# %% Setup input to the network and true output label. These are
# simply placeholders which we'll fill in later.
mnist = input_data.read_data_sets('MNIST_data/', one_hot=True)
x = tf.placeholder(tf.float32, [None, 784])
y = tf.placeholder(tf.float32, [None, 10])
# %% Since x is currently [batch, height*width], we need to reshape to a
# 4-D tensor to use it in a convolutional graph. If one component of
# `shape` is the special value -1, the size of that dimension is
# computed so that the total size remains constant. Since we haven't
# defined the batch dimension's shape yet, we use -1 to denote this
# dimension should not change size.
x_tensor = tf.reshape(x, [-1, 28, 28, 1])
# %% We'll setup the first convolutional layer
# Weight matrix is [height x width x input_channels x output_channels]
filter_size = 5
n_filters_1 = 16
W_conv1 = weight_variable([filter_size, filter_size, 1, n_filters_1])
# %% Bias is [output_channels]
b_conv1 = bias_variable([n_filters_1])
# %% Now we can build a graph which does the first layer of convolution:
# we define our stride as batch x height x width x channels
# instead of pooling, we use strides of 2 and more layers
# with smaller filters.
h_conv1 = tf.nn.relu(
tf.nn.conv2d(input=x_tensor,
filter=W_conv1,
strides=[1, 2, 2, 1],
padding='SAME') +
b_conv1)
# %% And just like the first layer, add additional layers to create
# a deep net
n_filters_2 = 16
W_conv2 = weight_variable([filter_size, filter_size, n_filters_1, n_filters_2])
b_conv2 = bias_variable([n_filters_2])
h_conv2 = tf.nn.relu(
tf.nn.conv2d(input=h_conv1,
filter=W_conv2,
strides=[1, 2, 2, 1],
padding='SAME') +
b_conv2)
# %% We'll now reshape so we can connect to a fully-connected layer:
h_conv2_flat = tf.reshape(h_conv2, [-1, 7 * 7 * n_filters_2])
# %% Create a fully-connected layer:
n_fc = 1024
W_fc1 = weight_variable([7 * 7 * n_filters_2, n_fc])
b_fc1 = bias_variable([n_fc])
h_fc1 = tf.nn.relu(tf.matmul(h_conv2_flat, W_fc1) + b_fc1)
# %% We can add dropout for regularizing and to reduce overfitting like so:
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# %% And finally our softmax layer:
W_fc2 = weight_variable([n_fc, 10])
b_fc2 = bias_variable([10])
y_pred = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
# %% Define loss/eval/training functions
cross_entropy = -tf.reduce_sum(y * tf.log(y_pred))
optimizer = tf.train.AdamOptimizer().minimize(cross_entropy)
# %% Monitor accuracy
correct_prediction = tf.equal(tf.argmax(y_pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, 'float'))
# %% We now create a new session to actually perform the initialization the
# variables:
sess = tf.Session()
sess.run(tf.initialize_all_variables())
# %% We'll train in minibatches and report accuracy:
batch_size = 100
n_epochs = 5
for epoch_i in range(n_epochs):
for batch_i in range(mnist.train.num_examples // batch_size):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
sess.run(optimizer, feed_dict={
x: batch_xs, y: batch_ys, keep_prob: 0.5})
print(sess.run(accuracy,
feed_dict={
x: mnist.validation.images,
y: mnist.validation.labels,
keep_prob: 1.0
}))
# %% Let's take a look at the kernels we've learned
W = sess.run(W_conv1)
plt.imshow(montage(W / np.max(W)), cmap='coolwarm')
```
| true |
code
| 0.934185 | null | null | null | null |
|
## PHYS 105A: Introduction to Scientific Computing
# Random Numbers and Monte Carlo Methods
Chi-kwan Chan
* In physical science, students very often start with the concept that everything can be done exactly and deterministically.
* This can be one of the biggest misconcept!
* Many physical processes are non-deterministic by nature. Examples include:
* Radioactive decay
* Quantum mechanics
* Sometime, even when the governing equaitons are deterministic, the results are still non-deterministic. Examples include:
* 3-body problem
* Brownian motion
* Thermal noise
* Therefore, in computer we need some way to model these non-deterministic systems.
* For electronic computers, all operations are deterministic.
* Nevertheless, we can approximate random processes by *pseudo* random number generators.
* These pseudo random number generators can then be used to model non-deterministic systems.
* In addition, people started to realize, even for deterministic problems, randomizing them can still be a very powerful numerical method! Applications include
* Numerical integration of high-dimensional space
* Statistical inference
* This results a large number of random number based numerical methods.
* Monte Carlo is an area of Monaco well known for its world-famous Place du Casino.
* Monte Carlo methods are used to refer to random number based numerical methods.

```
# In order to understand the concept of a random number generator, let's implement one ourself.
mynext = 1
def myrand(): # NOT RECOMMENDED for real application.
global mynext
mynext = mynext * 1103515245 + 12345
return (mynext//65536) % 32768
# This random number generator would generate integers in the domain [0, 32768).
# This random is usually provided to user by
MYRAND_MAX = 32768-1
# There are reasons for choosing the strange constants. Take a look at
# https://en.wikipedia.org/wiki/Linear_congruential_generator
# if you are interested.
# Now, every time we run `rand()`, we will get a different number
myrand()
# For we may just print many of them at the same time:
Rs = [myrand() for i in range(100)]
print(Rs)
# We may even plot the random numbers
from matplotlib import pyplot as plt
plt.imshow([[myrand() for i in range(100)] for j in range(100)])
# Sometime it is useful to make sure your random number sequence remains the same.
# In our case, you may notice that we can simply reset the `mynext` global variable to reset the sequence.
# The value you put in `mynext` is often called the "seed".
print('The following two lists are not the same:')
print([myrand() for i in range(10)])
print([myrand() for i in range(10)])
print('We may ensure that they are the same by "seeding" the random number generator with a fixed value:')
mynext = 1234
print([myrand() for i in range(10)])
mynext = 1234
print([myrand() for i in range(10)])
```
* The above random number generator is very simple and is the *sample* implementation in many ANSI C libraries!
* However, because how the standard was written, this create a lot problems.
* The standard only require RAND_MAX be at least 32767. If one want to evulate 1e6 points (which is pretty small, as we will see below), you will actually be evaluating the same 32768 points 30 times each!
* Some implementation "tried" to imporve the algorithm, e.g., swapping the lower and higher bytes. But these tricks sometime ruins the generator!
* We mentioned that integrating high-dimension space is an important application of Monte Carlo methods. However, the above random number generator create correlation in k-space.
* Thankfully, `ptyhon`'s random number generator is based on the "more reliable" [Mersenne Twister algorithm](https://en.wikipedia.org/wiki/Mersenne_Twister).
* From now on, unless for demostration purpose, we will use python's built-in random number generators.
```
# Let's now try python's random number library
import random as rnd
print(rnd.random()) # return a random float in the range [0,1)
print(rnd.randrange(100)) # return a random int in the range [0, stop)
print(rnd.randint(a=0,b=99)) # return a random int in the range [a, b+1)
print(rnd.gauss(mu=0, sigma=1)) # sample from a Gaussian distribution
# We may plot the results of these random number generators
Rs = [rnd.random() for i in range(1000)]
plt.hist(Rs)
Rs = [rnd.randrange(100) for i in range(1000)]
plt.hist(Rs)
Rs = [rnd.gauss(0, 1) for i in range(1000)]
plt.hist(Rs)
# There is also a seed() function
rnd.seed(1234)
print([rnd.randrange(100) for i in range(10)])
rnd.seed(1234)
print([rnd.randrange(100) for i in range(10)])
```
* Once we have a (pseudo) random number generator, we are ready to develop Monte Carlo methods!
* We will start with a simple example of random walk. The model is very simple:
* We start with a (drunk) person at the center of the street.
* As the person step forward toward +t, the person random also step left +1 or right -1.
* The problem is, after n steps, how far away is the person away from the center of the street?
```
# We may step up this problem in the following way:
T = range(1, 1000+1)
X = [0] # initial position
for t in T:
last = X[-1] # last position
r = rnd.randint(0,1) # we generate 0 or 1 randomly
if r == 0: # depending on r, we step left or right
curr = last + 1
else:
curr = last - 1
X.append(curr) # append the current position to the list X
# We may plot this random walk
plt.plot(X)
# Awesome!
# But in order to find out how random walk behave statistically,
# we want to be able to run many simulations!
# It is convenient to define a function
def randomwalk(n_steps=1000):
X = [0] # initial position
for t in range(n_steps):
last = X[-1] # last position
r = rnd.randint(0,1) # we generate 0 or 1 randomly
if r == 0: # depending on r, we step left or right
curr = last + 1
else:
curr = last - 1
X.append(curr) # append the current position to the list X
return X # return the result
# And we can use this function in another loop.
for i in range(10):
plt.plot(randomwalk())
# We may now ask how far away the peron would walk depending on the number of stpes.
D = []
for t in T:
X = randomwalk(t)
D.append(abs(X[-1]))
plt.plot(D)
# Clearly, the distance gets farther when the number of steps increase.
# But this figure is too noise to read off the dependency.
# There are multiple ways to make the above figure less noise.
# One way is to simply do multiple numerical experiments for the same number of steps.
# And obtain the average distance.
n_trials = 100
D = []
for t in T:
M = 0
for trial in range(n_trials):
X = randomwalk(t)
M += abs(X[-1])
M /= n_trials
D.append(M)
plt.plot(D)
# The plot is much better!
# Later in the class, we will learn how to fit a curve.
# But for now, let's simply plot this in log-log scale.
# And compare it with the law of diffusion D ~ sqrt(T)
plt.loglog(T, D)
plt.plot(T, [t**0.5 for t in T])
```
* You may use this simple random walk model to model real physical process.
* For example, the Brownian motion, which describe how pollen is randomly pushed by water molecules.

* Einstein published a paper on Brownian motion in 1905, which is one of his first major scientific contributions.
```
# The simplest model of Brownian motion is simply a two-dimension random walk.
X = randomwalk()
Y = randomwalk()
plt.figure(figsize=(12,12))
plt.plot(X, Y)
plt.gca().set_aspect('equal')
# The resulting plot looks slightly funny because random walk forces x and y both to move at exactly one step.
# The final outcome is that the particle can only move in diagonal directions.
# But this artifact becomes irrelevant when we model random walk for many many more steps.
X = randomwalk(100000)
Y = randomwalk(100000)
plt.figure(figsize=(12,12))
plt.plot(X, Y)
plt.gca().set_aspect('equal')
# Here is a physics question: how far does a Brownian motion particle move as a function of time?
```
| true |
code
| 0.654702 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/IMOKURI/wandb-demo/blob/main/WandB_Baseline_Image.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 📔 About this notebook
Image classification baseline.
## 📝 Memo
# Check Environment
```
!free -m
!python --version
!nvidia-smi
!nvcc --version
```
# Prepare for Kaggle
- Add dataset [imokuri/wandbtoken](https://www.kaggle.com/imokuri/wandbtoken)
# Prepare for Colab
```
import os
import sys
import zipfile
if os.path.exists('init.txt'):
print("Already initialized.")
else:
if 'google.colab' in sys.modules:
from google.colab import drive
drive.mount('/content/drive')
dataset_dir = "/content/drive/MyDrive/Datasets"
# ====================================================
# Competition datasets
# ====================================================
with zipfile.ZipFile(f"{dataset_dir}/cassava-leaf-disease-classification-2021.zip", "r") as zp:
zp.extractall(path="./")
# for StratifiedGroupKFold
# !pip install -q -U scikit-learn
# for MultilabelStratifiedKFold
# !pip install -q iterative-stratification
# for CosineAnnealingWarmupRestarts
# !pip install -qU 'git+https://github.com/katsura-jp/pytorch-cosine-annealing-with-warmup'
!pip install -q wandb
# !pip install -q optuna
# ====================================================
# Competition specific libraries
# ====================================================
!pip install -q timm
!pip install -q albumentations==0.4.6
!touch init.txt
```
# 📚 Library
```
# General libraries
import collections
import glob
import json
import math
import os
import random
import re
import statistics
import time
import warnings
from contextlib import contextmanager
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
import torch
import torch.cuda.amp as amp
import torch.nn as nn
import torch.nn.functional as F
import wandb
# from cosine_annealing_warmup import CosineAnnealingWarmupRestarts
# from iterstrat.ml_stratifiers import MultilabelStratifiedKFold
from sklearn.metrics import accuracy_score, mean_squared_error
from sklearn.model_selection import KFold, StratifiedKFold # , StratifiedGroupKFold
from torch.optim import SGD, Adam
from torch.optim.lr_scheduler import CosineAnnealingLR, CosineAnnealingWarmRestarts
from torch.utils.data import DataLoader, Dataset
from tqdm.notebook import tqdm
# Competition specific libraries
import albumentations as A
import cv2
import timm
from albumentations.pytorch import ToTensorV2
warnings.filterwarnings("ignore")
netrc = "/content/drive/MyDrive/.netrc" if 'google.colab' in sys.modules else "../input/wandbtoken/.netrc"
!cp -f {netrc} ~/
!wandb login
wandb_tags = []
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
if torch.cuda.is_available():
wandb_tags.append(torch.cuda.get_device_name(0))
```
# Load Data
```
DATA_DIR = "./" if 'google.colab' in sys.modules else "../input/xxx/"
OUTPUT_DIR = "./"
MODEL_DIR = "./models/"
!rm -rf {MODEL_DIR}
os.makedirs(OUTPUT_DIR, exist_ok=True)
os.makedirs(MODEL_DIR, exist_ok=True)
train = pd.read_csv(DATA_DIR + "train.csv")
# test = pd.read_csv(DATA_DIR + "test.csv")
sub = pd.read_csv(DATA_DIR + "sample_submission.csv")
TRAIN_IMAGE_PATH = DATA_DIR + "train_images/"
TEST_IMAGE_PATH = DATA_DIR + "test_images/"
```
# 🤔 Config
```
# seed = random.randrange(10000)
seed = 440
print(seed)
class Config:
wandb_entity = "imokuri"
wandb_project = "baseline"
print_freq = 100
train = True
validate = False
inference = False
debug = False
num_debug_data = 1000
amp = True
config_defaults = {
"seed": seed,
"n_class": 5,
"n_fold": 5,
"epochs": 10,
"batch_size": 32,
"gradient_accumulation_steps": 1,
"max_grad_norm": 1000,
"criterion": "CrossEntropyLoss",
"optimizer": "Adam",
"scheduler": "CosineAnnealingWarmRestarts",
"lr": 1e-4,
"min_lr": 5e-6,
"weight_decay": 1e-6,
"model_name": "resnext50_32x4d", # "vit_base_patch16_384", "tf_efficientnetv2_m_in21k",
"size": 512,
}
if Config.debug:
config_defaults["n_fold"] = 3
config_defaults["epochs"] = 1
Config.print_freq = 10
if Config.train:
wandb_job_type = "training"
elif Config.inference:
wandb_job_type = "inference"
elif Config.validate:
wandb_job_type = "validation"
else:
wandb_job_type = ""
if Config.debug:
wandb_tags.append("debug")
if Config.amp:
wandb_tags.append("amp")
if Config.debug:
run = wandb.init(
entity=Config.wandb_entity,
project=Config.wandb_project,
config=config_defaults,
tags=wandb_tags,
mode="disabled",
)
else:
run = wandb.init(
entity=Config.wandb_entity,
project=Config.wandb_project,
config=config_defaults,
job_type=wandb_job_type,
tags=wandb_tags,
save_code=True,
)
config = wandb.config
```
# EDA 1
```
# for df in [train, test, sub]:
for df in [train, sub]:
print(f"=" * 120)
df.info()
display(df.head())
sns.distplot(train["label"], kde=False)
```
# Preprocess
```
def get_transforms(*, data):
if data == "train":
return A.Compose(
[
# A.Resize(config.size, config.size),
A.RandomResizedCrop(config.size, config.size),
A.Transpose(p=0.5),
A.HorizontalFlip(p=0.5),
A.VerticalFlip(p=0.5),
A.ShiftScaleRotate(p=0.5),
A.Normalize(
mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225],
),
ToTensorV2(),
]
)
elif data == "valid":
return A.Compose(
[
A.Resize(config.size, config.size),
# A.CenterCrop(config.size, config.size),
A.Normalize(
mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225],
),
ToTensorV2(),
]
)
```
# EDA 2
```
```
# 👑 Load Artifacts
```
if Config.debug:
train = train.sample(n=Config.num_debug_data, random_state=config.seed).reset_index(drop=True)
if len(sub) > Config.num_debug_data:
# test = test.sample(n=Config.num_debug_data, random_state=config.seed).reset_index(drop=True)
sub = sub.sample(n=Config.num_debug_data, random_state=config.seed).reset_index(drop=True)
```
# Utils
```
@contextmanager
def timer(name):
t0 = time.time()
LOGGER.info(f"[{name}] start")
yield
LOGGER.info(f"[{name}] done in {time.time() - t0:.0f} s.")
def init_logger(log_file=OUTPUT_DIR + "train.log"):
from logging import INFO, FileHandler, Formatter, StreamHandler, getLogger
logger = getLogger(__name__)
logger.setLevel(INFO)
handler1 = StreamHandler()
handler1.setFormatter(Formatter("%(message)s"))
handler2 = FileHandler(filename=log_file)
handler2.setFormatter(Formatter("%(message)s"))
logger.addHandler(handler1)
logger.addHandler(handler2)
return logger
LOGGER = init_logger()
def seed_torch(seed=42):
random.seed(seed)
os.environ["PYTHONHASHSEED"] = str(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.deterministic = True
seed_torch(seed=config.seed)
```
# Make Fold
```
Fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=seed)
for n, (train_index, val_index) in enumerate(Fold.split(train, train["label"])):
train.loc[val_index, "fold"] = int(n)
train["fold"] = train["fold"].astype(np.int8)
print(train.groupby(["fold", "label"]).size())
```
# Dataset
```
class BaseDataset(Dataset):
def __init__(self, df, transform=None, label=True):
self.df = df
self.file_names = df["image_id"].values
self.transform = transform
self.use_label = label
if self.use_label:
self.path = TRAIN_IMAGE_PATH
self.labels = df["label"].values
else:
self.path = TEST_IMAGE_PATH
def __len__(self):
return len(self.df)
def __getitem__(self, idx):
file_name = self.file_names[idx]
file_path = f"{self.path}/{file_name}"
image = cv2.imread(file_path)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
if self.transform:
augmented = self.transform(image=image)
image = augmented["image"]
if self.use_label:
label = torch.tensor(self.labels[idx])
return image, label
return image
train_ds = BaseDataset(train)
image, label = train_ds[0]
plt.imshow(image)
plt.title(f"label: {label}")
plt.show()
train_ds = BaseDataset(train, transform=get_transforms(data="train"))
image, label = train_ds[0]
plt.imshow(image[0])
plt.title(f"label: {label}")
plt.show()
```
# 🚗 Model
```
class BaseModel(nn.Module):
def __init__(self, model_name, pretrained=True):
super().__init__()
self.model_name = model_name
self.model = timm.create_model(model_name, pretrained=pretrained)
if "resnext50_32x4d" in model_name:
n_features = self.model.fc.in_features
self.model.fc = nn.Linear(n_features, config.n_class)
elif model_name.startswith("tf_efficientnet"):
n_features = self.model.classifier.in_features
self.model.classifier = nn.Linear(n_features, config.n_class)
elif model_name.startswith("vit_"):
n_features = self.model.head.in_features
self.model.head = nn.Linear(n_features, config.n_class)
def forward(self, x):
x = self.model(x)
return x
if config.model_name != "":
model = BaseModel(config.model_name)
print(model)
train_ds = BaseDataset(train, transform=get_transforms(data="train"))
train_loader = DataLoader(train_ds, batch_size=4, shuffle=True, num_workers=4, drop_last=True)
for image, label in train_loader:
output = model(image)
print(output)
break
```
# Optimizer
```
```
# Loss
```
```
# Scoring
```
def get_score(y_true, y_pred):
return accuracy_score(y_true, y_pred)
def get_result(result_df, fold=config.n_fold):
preds = result_df["preds"].values
labels = result_df["label"].values
score = get_score(labels, preds)
LOGGER.info(f"Score: {score:<.5f}")
if fold == config.n_fold:
wandb.log({"CV": score})
else:
wandb.log({f"CV_fold{fold}": score})
```
# Helper functions
```
class AverageMeter(object):
"""Computes and stores the average and current value"""
def __init__(self):
self.reset()
def reset(self):
self.val = 0
self.avg = 0
self.sum = 0
self.count = 0
def update(self, val, n=1):
self.val = val
self.sum += val * n
self.count += n
self.avg = self.sum / self.count
def asMinutes(s):
m = math.floor(s / 60)
s -= m * 60
return "%dm %ds" % (m, s)
def timeSince(since, percent):
now = time.time()
s = now - since
es = s / (percent)
rs = es - s
return "%s (remain %s)" % (asMinutes(s), asMinutes(rs))
def compute_grad_norm(parameters, norm_type=2.0):
"""Refer to torch.nn.utils.clip_grad_norm_"""
if isinstance(parameters, torch.Tensor):
parameters = [parameters]
parameters = [p for p in parameters if p.grad is not None]
norm_type = float(norm_type)
total_norm = 0
for p in parameters:
param_norm = p.grad.data.norm(norm_type)
total_norm += param_norm.item() ** norm_type
total_norm = total_norm ** (1. / norm_type)
return total_norm
def train_fn(train_loader, model, criterion, optimizer, scheduler, scaler, epoch, device):
losses = AverageMeter()
# switch to train mode
model.train()
start = time.time()
optimizer.zero_grad()
for step, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
batch_size = labels.size(0)
with amp.autocast(enabled=Config.amp):
y_preds = model(images)
loss = criterion(y_preds, labels)
losses.update(loss.item(), batch_size)
loss = loss / config.gradient_accumulation_steps
scaler.scale(loss).backward()
if (step + 1) % config.gradient_accumulation_steps == 0:
scaler.unscale_(optimizer)
grad_norm = torch.nn.utils.clip_grad_norm_(model.parameters(), config.max_grad_norm)
scaler.step(optimizer)
scaler.update()
scheduler.step()
optimizer.zero_grad()
else:
grad_norm = compute_grad_norm(model.parameters())
end = time.time()
if step % Config.print_freq == 0 or step == (len(train_loader) - 1):
print(
f"Epoch: [{epoch + 1}][{step}/{len(train_loader)}] "
f"Elapsed {timeSince(start, float(step + 1) / len(train_loader)):s} "
f"Loss: {losses.avg:.4f} "
f"Grad: {grad_norm:.4f} "
f"LR: {scheduler.get_lr()[0]:.6f} "
)
return losses.avg
def valid_fn(valid_loader, model, criterion, device):
losses = AverageMeter()
# switch to evaluation mode
model.eval()
preds = []
start = time.time()
for step, (images, labels) in enumerate(valid_loader):
images = images.to(device)
labels = labels.to(device)
batch_size = labels.size(0)
with torch.no_grad():
y_preds = model(images)
loss = criterion(y_preds, labels)
losses.update(loss.item(), batch_size)
preds.append(y_preds.softmax(1).to("cpu").numpy())
# preds.append(y_preds.to("cpu").numpy())
end = time.time()
if step % Config.print_freq == 0 or step == (len(valid_loader) - 1):
print(
f"EVAL: [{step}/{len(valid_loader)}] "
f"Elapsed {timeSince(start, float(step + 1) / len(valid_loader)):s} "
f"Loss: {losses.avg:.4f} "
)
predictions = np.concatenate(preds)
return losses.avg, predictions
```
# Postprocess
```
```
# 🏃♂️ Train loop
```
def train_loop(df, fold):
LOGGER.info(f"========== fold: {fold} training ==========")
# ====================================================
# Data Loader
# ====================================================
trn_idx = df[df["fold"] != fold].index
val_idx = df[df["fold"] == fold].index
train_folds = df.loc[trn_idx].reset_index(drop=True)
valid_folds = df.loc[val_idx].reset_index(drop=True)
train_dataset = BaseDataset(train_folds, transform=get_transforms(data="train"))
valid_dataset = BaseDataset(valid_folds, transform=get_transforms(data="valid"))
train_loader = DataLoader(
train_dataset,
batch_size=config.batch_size,
shuffle=True,
num_workers=4,
pin_memory=True,
drop_last=True,
)
valid_loader = DataLoader(
valid_dataset,
batch_size=config.batch_size,
shuffle=False,
num_workers=4,
pin_memory=True,
drop_last=False,
)
# ====================================================
# Optimizer
# ====================================================
def get_optimizer(model):
if config.optimizer == "Adam":
optimizer = Adam(model.parameters(), lr=config.lr, weight_decay=config.weight_decay)
elif config.optimizer == "AdamW":
optimizer = T.AdamW(model.parameters(), lr=config.lr, weight_decay=config.weight_decay)
return optimizer
# ====================================================
# Scheduler
# ====================================================
def get_scheduler(optimizer, train_dataset):
num_data = len(train_dataset)
num_steps = num_data // (config.batch_size * config.gradient_accumulation_steps) * config.epochs
if config.scheduler == "CosineAnnealingWarmRestarts":
scheduler = CosineAnnealingWarmRestarts(optimizer, T_0=num_steps, T_mult=1, eta_min=config.min_lr, last_epoch=-1)
elif config.scheduler == "CosineAnnealingLR":
scheduler = CosineAnnealingLR(optimizer, T_max=num_steps, eta_min=config.min_lr, last_epoch=-1)
elif config.scheduler == "CosineAnnealingWarmupRestarts":
scheduler = CosineAnnealingWarmupRestarts(
optimizer, first_cycle_steps=num_steps, max_lr=config.lr, min_lr=config.min_lr, warmup_steps=(num_steps // 10)
)
return scheduler
# ====================================================
# Model
# ====================================================
model = BaseModel(config.model_name)
model.to(device)
optimizer = get_optimizer(model)
scaler = amp.GradScaler(enabled=Config.amp)
scheduler = get_scheduler(optimizer, train_dataset)
# ====================================================
# Criterion
# ====================================================
def get_criterion():
if config.criterion == "CrossEntropyLoss":
criterion = nn.CrossEntropyLoss()
elif config.criterion == "BCEWithLogitsLoss":
criterion = nn.BCEWithLogitsLoss()
elif config.criterion == "MSELoss":
criterion = nn.MSELoss()
return criterion
criterion = get_criterion()
# ====================================================
# Loop
# ====================================================
best_score = -1
best_loss = np.inf
best_preds = None
for epoch in range(config.epochs):
start_time = time.time()
# train
avg_loss = train_fn(train_loader, model, criterion, optimizer, scheduler, scaler, epoch, device)
# eval
avg_val_loss, preds = valid_fn(valid_loader, model, criterion, device)
valid_labels = valid_folds["label"].values
# if config.criterion == "BCEWithLogitsLoss":
# preds = 1 / (1 + np.exp(-preds))
# scoring
score = get_score(valid_labels, preds.argmax(1))
# score = get_score(valid_labels, preds)
elapsed = time.time() - start_time
LOGGER.info(f"Epoch {epoch+1} - avg_train_loss: {avg_loss:.4f} avg_val_loss: {avg_val_loss:.4f} time: {elapsed:.0f}s")
LOGGER.info(f"Epoch {epoch+1} - Score: {score}")
wandb.log({
"epoch": epoch + 1,
f"loss/train_fold{fold}": avg_loss,
f"loss/valid_fold{fold}": avg_val_loss,
f"score/fold{fold}": score,
})
if avg_val_loss < best_loss:
best_score = score
best_loss = avg_val_loss
best_preds = preds
LOGGER.info(f"Epoch {epoch+1} - Save Best Model. score: {best_score:.4f}, loss: {best_loss:.4f}")
torch.save(
{"model": model.state_dict(), "preds": preds}, MODEL_DIR + f"{config.model_name.replace('/', '-')}_fold{fold}_best.pth"
)
# use artifacts instead
# wandb.save(MODEL_DIR + f"{config.model_name.replace('/', '-')}_fold{fold}_best.pth")
valid_folds[[str(c) for c in range(config.n_class)]] = best_preds
valid_folds["preds"] = best_preds.argmax(1)
# valid_folds["preds"] = best_preds
return valid_folds, best_score, best_loss
```
# Main function
```
def main():
# ====================================================
# Training
# ====================================================
if Config.train:
oof_df = pd.DataFrame()
oof_result = []
for fold in range(config.n_fold):
seed_torch(seed + fold)
_oof_df, score, loss = train_loop(train, fold)
oof_df = pd.concat([oof_df, _oof_df])
oof_result.append([fold, score, loss])
LOGGER.info(f"========== fold: {fold} result ==========")
get_result(_oof_df, fold)
# CV result
LOGGER.info(f"========== CV ==========")
get_result(oof_df)
loss = statistics.mean([d[2] for d in oof_result])
wandb.log({"loss": loss})
table = wandb.Table(data=oof_result, columns = ["fold", "score", "loss"])
run.log({"Fold Result": table})
# save result
oof_df.to_csv(OUTPUT_DIR + "oof_df.csv", index=False)
wandb.save(OUTPUT_DIR + "oof_df.csv")
artifact = wandb.Artifact(config.model_name, type='model')
artifact.add_dir(MODEL_DIR)
run.log_artifact(artifact)
```
# 🚀 Run
```
main()
wandb.finish()
```
| true |
code
| 0.445228 | null | null | null | null |
|
# Iris dataset example
Example of functional keras model with named inputs/outputs for compatability with the keras/tensorflow toolkit.
```
from sklearn.datasets import load_iris
from tensorflow import keras
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.utils import to_categorical
from sklearn.preprocessing import LabelEncoder
import pandas as pd
iris = load_iris()
data = pd.DataFrame(iris.data, columns=iris.feature_names)
data.columns = ["SepalLength", "SepalWidth", "PetalLength", "PetalWidth"]
data["Species"] = iris.target
data
train_dataset = data.sample(frac=0.8,random_state=0)
test_dataset = data.drop(train_dataset.index)
train_labels = train_dataset.pop('Species')
test_labels = test_dataset.pop('Species')
train_dataset.keys()
# encode class values as integers
encoder = LabelEncoder()
encoder.fit(train_labels)
encoded_Y = encoder.transform(train_labels)
# convert integers to dummy variables (i.e. one hot encoded)
dummy_y = to_categorical(encoded_Y)
# define model
def build_model():
# DEFINE INPUTS
sepal_length_input = keras.Input(shape=(1,), name="SepalLength")
sepal_width_input = keras.Input(shape=(1,), name="SepalWidth")
petal_length_input = keras.Input(shape=(1,), name="PetalLength")
petal_width_input = keras.Input(shape=(1,), name="PetalWidth")
# concatenate layer
inputs = [sepal_length_input, sepal_width_input, petal_length_input, petal_width_input]
merged = keras.layers.concatenate(inputs)
dense1 = Dense(8, activation='relu')(merged)
output = Dense(3, activation='softmax', name="Species")(dense1)
# Compile model
model = keras.Model(inputs=inputs, outputs=[output])
optimizer = tf.keras.optimizers.Adam()
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
return model
model = build_model()
train_stats = train_dataset.describe()
train_stats = train_stats.transpose()
train_stats
train_x = train_dataset.to_dict("series")
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=15)
history = model.fit(train_x, dummy_y, epochs=1000,
validation_split = 0.2, verbose=1, callbacks=[early_stop])
model.save("files/iris_model.h5")
#access input names
model.input_names
#access output names
model.output_names
test_item = train_dataset.iloc[[20]].to_dict("series")
# Output type softmax
model.predict([test_item])
```
| true |
code
| 0.833816 | null | null | null | null |
|
# Can we find zero in less than 20 iterations ?
## The Quest for the Ultimate Optimizer - Episode 2
-------------------------------------------------------------------
This notebook is a continuation of the first episode of my Quest for the Ultimate Optimizer series of notebooks, which was inspired by DeepMind’s paper [“Learning to learn by gradient descent by gradient descent”](https://arxiv.org/abs/1606.04474) and [Llion Jones's article on this paper](https://hackernoon.com/learning-to-learn-by-gradient-descent-by-gradient-descent-4da2273d64f2). I encourage you to read all of these if you want to understand how the following is set-up.
Being a continuation of the first episode, it contains quite a lot of setting-up that comes directly from it, and that I have positionned at the end to avoid repeating myself too much. This means that:
1. If you want to run this notebook, you need to start by running the appendix at the end before the rest of the notebook
2. If you haven't read the first notebook yet, go check it out, this one will make more sense if you start there.
### Appendix
I'll start with the same disclaimer as in the first notebook : the code in this section draws heavily from [Llion Jones's article](https://hackernoon.com/learning-to-learn-by-gradient-descent-by-gradient-descent-4da2273d64f2).
I encourage you to read, it if you want to understand how it is set-up.
For the rest you'll find a bit more explanations in the first notebook.
```
import tensorflow as tf
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import os
# If you have tensorflow for GPU but want to use your CPU
os.environ["CUDA_DEVICE_ORDER"]="PCI_BUS_ID"
os.environ["CUDA_VISIBLE_DEVICES"]=""
DIMS = 2 # Dimensions of the quadratic function, the simplest application problem in DeepMind's paper
scale = tf.random_uniform([DIMS], 0.5, 1.5)
# The scale vector gives a different shape to the quadratic function at each initialization
def quadratic(x):
x = scale*x
return tf.reduce_sum(tf.square(x))
# Some reference optimizers for benchmarking
def g_sgd(gradients, state, learning_rate=0.1):
# Vanilla Stochastic Gradient Descent
return -learning_rate*gradients, state
def g_rms(gradients, state, learning_rate=0.1, decay_rate=0.99):
# RMSProp
if state is None:
state = tf.zeros(DIMS)
state = decay_rate*state + (1-decay_rate)*tf.pow(gradients, 2)
update = -learning_rate*gradients / (tf.sqrt(state)+1e-5)
return update, state
TRAINING_STEPS = 20 # This is 100 in the paper
initial_pos = tf.random_uniform([DIMS], -1., 1.)
def learn(optimizer):
losses = []
x = initial_pos
state = None
# The loop below unrolls the 20 steps of the optimizer into a single tensorflow graph
for _ in range(TRAINING_STEPS):
loss = quadratic(x)
losses.append(loss)
grads, = tf.gradients(loss, x)
update, state = optimizer(grads, state)
x += update
return losses
sgd_losses = learn(g_sgd)
rms_losses = learn(g_rms)
# Now let's define the RNN optimizer
LAYERS = 2
STATE_SIZE = 20
cell = tf.contrib.rnn.MultiRNNCell(
[tf.contrib.rnn.LSTMCell(STATE_SIZE) for _ in range(LAYERS)])
cell = tf.contrib.rnn.InputProjectionWrapper(cell, STATE_SIZE)
cell = tf.contrib.rnn.OutputProjectionWrapper(cell, 1)
cell = tf.make_template('cell', cell)
def optimize(loss, learning_rate=0.1):
# "Meta optimizer" to be applied on the RNN defined above
optimizer = tf.train.AdamOptimizer(learning_rate)
gradients, v = zip(*optimizer.compute_gradients(loss))
gradients, _ = tf.clip_by_global_norm(gradients, 1.)
return optimizer.apply_gradients(zip(gradients, v))
def print_dict(*args):
# Prints variables in a dict format for easier reading
dict_name = dict((name,eval(name)) for name in args)
print(dict_name)
def graph_optimizers(f1, f2, f3, it=3, training_steps=TRAINING_STEPS):
# Graph to compare RNN to the 2 baseline optimizers
x = np.arange(training_steps)
for _ in range(it):
sgd_l, rms_l, rnn_l = sess.run([f1, f2, f3])
p1, = plt.semilogy(x, sgd_l, label='SGD')
p2, = plt.semilogy(x, rms_l, label='RMS')
p3, = plt.semilogy(x, rnn_l, label='RNN')
plt.legend(handles=[p1, p2, p3])
plt.title('Losses')
plt.show()
def rolling_log_average(array, L):
# Rolling average of the log of the array over a length of L
rolling_av = np.array([])
for i in range(array.size):
rolling_av = np.append(rolling_av, 10**(np.log10(array[:i+1][-L:] + 1e-38).mean()))
return rolling_av
import warnings
def draw_convergence(*args):
"""Draws the convergence of one or several meta optimizations
transparent area is the raw results, the plain line is the 500 rolling 'log average'"""
it = 0
for f in args:
it = max(eval(f).size, it)
handles = []
for f in args:
flist = eval(f)[np.logical_not(np.isnan(eval(f)))] #removes NaN
flist_rolling = rolling_log_average(flist, 500)
flist_size = flist.size
#matplotlib doesn't like graphs of different length so we fill the shorter graphs with None
if flist_size < it:
flist = np.append(flist, [None]*(it-flist_size))
flist_rolling = np.append(flist_rolling, [None]*(it-flist_size))
c1, = plt.semilogy(range(it), flist, alpha=0.3)
c2, = plt.semilogy(range(it), flist_rolling, color=c1.get_color(), label=f)
handles = handles + [c2]
plt.legend(handles=handles)
plt.title('End result of the optimizer')
#matplotlib still doesn't like graphs of different length so we filter associated warnings
warnings.filterwarnings("ignore",category =RuntimeWarning)
plt.show()
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
```
### Recap of the previous episode
In the first notebook, we reused [Llion Jones's implementation](https://hackernoon.com/learning-to-learn-by-gradient-descent-by-gradient-descent-4da2273d64f2) of [“Learning to learn by gradient descent by gradient descent”](https://arxiv.org/abs/1606.04474) which set-up a RNN (recurrent neural network) in tensorflow for use as an optimizer that works similarly to SGD or RMSProp, then unrolls 20 of its iterations (we'll call those the "base" iterations) within a single tensorflow graph so that we can iteratively modify the parameters of the RNN to minimize the result, thus optimizing the RNN optimizer (we'll call those the "meta" iterations).
The target was to beat RMSProp performance on the most simple problem you can think of : find the zero of a 2 dimension quadratic function.
To do that we tweaked a little bit the objective function to avoid the problem of vanishing gradient as the RNN gets better, finally settling on log of the RNN result as our objective function to minimize.
We also implemented what I will describe as a "liberal" interpretation of the preprocessing scheme for the RNN proposed in DeepMind's paper which is basically to also apply the log function on the gradients of the quadritic function before feeding the result into the RNN.
Let's re-run the last 2 RNNs proposed in the previous notebook.
```
def g_rnn_log15(gradients, state):
gradients = tf.expand_dims(gradients, axis=1)
# Casting of gradients from [exp(-15), 1] to [0, 1] and [-1, -exp(-15)] to [-1, 0]
min_log_gradient = -15
log_gradients = tf.log(tf.abs(gradients) + np.exp(min_log_gradient-5)) # residual added to avoid log(0)
sign_gradients = tf.sign(gradients)
trans_gradients = tf.multiply(sign_gradients,((log_gradients - min_log_gradient) / (- min_log_gradient)))
if state is None:
state = [[tf.zeros([DIMS, STATE_SIZE])] * 2] * LAYERS
update, state = cell(trans_gradients, state)
# Casting of output from [0, 1] to [exp(-15), 1] and [-1, 0] to [-1, -exp(-15)]
abs_update = tf.abs(update)
sign_update = tf.sign(update)
update = tf.multiply(sign_update, tf.exp(abs_update * (- min_log_gradient) + min_log_gradient))
return tf.squeeze(update, axis=[1]), state
rnn_losses = learn(g_rnn_log15)
log_loss = tf.log(rnn_losses[-1])
apply_update = optimize(log_loss, learning_rate=0.0003)
sess.run(tf.global_variables_initializer())
list_result = np.array([])
for it in range(50001):
errors, _ = sess.run([rnn_losses, apply_update])
list_result = np.append(list_result, errors[-1])
if it % 50000 == 0 :
optim_result = '{:.2E}'.format(errors[-1])
average_log_result = '{:.2f}'.format(np.log10(list_result[-5000:]).mean())
print_dict('it', 'optim_result', 'average_log_result')
RNN_log15_end_log_res = list_result
def g_rnn_log30(gradients, state):
gradients = tf.expand_dims(gradients, axis=1)
# Casting of gradients from [exp(-30), 1] to [0, 1] and [-1, -exp(-30)] to [-1, 0]
min_log_gradient = -30
log_gradients = tf.log(tf.abs(gradients) + np.exp(min_log_gradient-5))
sign_gradients = tf.sign(gradients)
trans_gradients = tf.multiply(sign_gradients,((log_gradients - min_log_gradient) / (- min_log_gradient)))
if state is None:
state = [[tf.zeros([DIMS, STATE_SIZE])] * 2] * LAYERS
update, state = cell(trans_gradients, state)
# Casting of output from [0, 1] to [exp(-30), 1] and [-1, 0] to [-1, -exp(-30)]
abs_update = tf.abs(update)
sign_update = tf.sign(update)
update = tf.multiply(sign_update, tf.exp(abs_update * (- min_log_gradient) + min_log_gradient))
return tf.squeeze(update, axis=[1]), state
rnn_losses = learn(g_rnn_log30)
log_loss = tf.log(rnn_losses[-1])
apply_update = optimize(log_loss, learning_rate=0.0003)
sess.run(tf.global_variables_initializer())
list_result = np.array([])
for it in range(100001):
errors, _ = sess.run([rnn_losses, apply_update])
list_result = np.append(list_result, errors[-1])
if it % 50000 == 0 :
optim_result = '{:.2E}'.format(errors[-1])
average_log_result = '{:.2f}'.format(np.log10(list_result[-5000:]).mean())
print_dict('it', 'optim_result', 'average_log_result')
RNN_log30_end_log_res = list_result
list_rms_errors = np.array([])
for it in range(1000):
sgd_errors, rms_errors = sess.run([sgd_losses, rms_losses])
list_rms_errors = np.append(list_rms_errors, rms_errors[-1])
Target_RMS = np.full(100001, rolling_log_average(list_rms_errors, 1000)[-1])
draw_convergence('Target_RMS', 'RNN_log15_end_log_res', 'RNN_log30_end_log_res')
graph_optimizers(sgd_losses, rms_losses, rnn_losses)
```
We concluded the last episode by declaring victory over RMSProp ... but is it the best we can do ?
### How about actually finding 0 ?
To do that we need to define what is 0 in our context.
It turns out Numpy offers an easy way to do that :
```
print(np.finfo(np.float32).tiny)
```
Now that we know what's our next target, let's give another look to the graph of convergences :
```
draw_convergence('RNN_log15_end_log_res', 'RNN_log30_end_log_res')
```
The obvious way to improve our RNN_log optimizer would be to continue the trend and try RNN_log50, however we can already see that the RNN_log30 had hard time starting it's convergence, so let's try to see if we can pinpoint what is the exact range of gradient we need to cast to [-1, 1] in the preprocessing of our RNN when we reach y = 1e-38.
We might even be able to explain why RNN_log15 and RNN_log30 both seems to be hitting a floor at respectively 1e-14 and 1e-28
```
# What's the log(gradient) when y = 1e-14, 1e-28 or 1 ? y = x**2 so y' = 2x = 2*(y**0.5)
print("log_gradient for 1e-14 : ", np.log(2*(1e-14**0.5)))
print("log_gradient for 1e-28 : ", np.log(2*(1e-28**0.5)))
print("log_gradient for 1e-38 : ", np.log(2*(1e-38**0.5)))
```
Bingo!
The floor that RNN_log15 is hitting (y = 1e-14) corresponds to when the log(gradient) of x reaches -15. Same for RNN_log15. So it looks like we need to go for -43 as our next min_log_gradient
```
def g_rnn_log43(gradients, state):
gradients = tf.expand_dims(gradients, axis=1)
# Casting of gradients from [exp(-43), 1] to [0, 1] and [-1, -exp(-43)] to [-1, 0]
min_log_gradient = -43
log_gradients = tf.log(tf.abs(gradients) + np.exp(min_log_gradient))
sign_gradients = tf.sign(gradients)
trans_gradients = tf.multiply(sign_gradients,((log_gradients - min_log_gradient) / (- min_log_gradient)))
if state is None:
state = [[tf.zeros([DIMS, STATE_SIZE])] * 2] * LAYERS
update, state = cell(trans_gradients, state)
# Casting of output from [0, 1] to [exp(-43), 1] and [-1, 0] to [-1, -exp(-43)]
abs_update = tf.abs(update)
sign_update = tf.sign(update)
update = tf.multiply(sign_update, tf.exp(abs_update * (- min_log_gradient) + min_log_gradient))
return tf.squeeze(update, axis=[1]), state
rnn_losses = learn(g_rnn_log43)
log_loss = tf.log(rnn_losses[-1])
apply_update = optimize(log_loss, learning_rate=0.0003)
sess.run(tf.global_variables_initializer())
list_result = np.array([])
for it in range(50001):
errors, _ = sess.run([rnn_losses, apply_update])
list_result = np.append(list_result, errors[-1])
if it % 5000 == 0 :
optim_result = '{:.2E}'.format(errors[-1])
average_log_result = '{:.2f}'.format(np.log10(list_result[-5000:]).mean())
print_dict('it', 'optim_result', 'average_log_result')
# Let's store the convergence for later comparison
RNN_log43_end_log_res = list_result
draw_convergence('RNN_log15_end_log_res', 'RNN_log30_end_log_res', 'RNN_log43_end_log_res')
```
The RNN is having trouble kick starting the convergence. The result is the same for RNN_log40, so we need some other way that extends the range of log(gradients) being correctly interpreted without completely freezing the convergence.
#### Variable gradient casting
The approach proposed below adapts the gradient range during the optimization, gradually lowering the floor of log(gradients) as the RNN gets more precise.
```
class Log_casting:
### Class used to cast logarithmically vectors from a variable range of scales below one to [-1, 1]
def __init__(self, init):
# scalar of the minimum log(gradient) encountered, initialized with init
self.min_log_value = tf.Variable(float(init), name="min_log_value", trainable=False)
# vector identity multiplied by min_log_value, initialized as None
self.min_log = None
def update_min_log(self, vector):
# This method is called at each iteration of the meta optimizer to adapt the min_log_value based on the
# last gradient (iteration 20) returned by the learn2 function (defined below)
log_vector = tf.log(tf.abs(vector) + 1e-38)
# update proposal based on the gradient, the factor 0.01 is to avoid confusing the RNN with a sudden big shift
update_proposal = 0.01*tf.reduce_min(log_vector) + 0.99*self.min_log_value
# the update is applied only if it is lower than the current value
new_value = tf.assign(self.min_log_value, tf.minimum(update_proposal, self.min_log_value))
return new_value
def preprocess(self, gradients):
# Casting of gradients from [exp(min_log_value), 1] to [0, 1] and [-1, -exp(min_log_value)] to [-1, 0]
self.min_log = tf.ones_like(gradients, name='MIN_LOG')*self.min_log_value
log_gradients = tf.log(tf.abs(gradients) + 1e-38)
sign_gradients = tf.sign(gradients)
inputs = tf.multiply(sign_gradients,((log_gradients - self.min_log) / (- self.min_log)))
return inputs
def postprocess(self, outputs):
# Casting back RNN output from [0, 1] to [exp(min_log_value), 1] and [-1, 0] to [-1, -exp(min_log_value)]
self.min_log = tf.ones_like(outputs, name='MIN_LOG')*self.min_log_value
abs_outputs = tf.abs(outputs)
sign_outputs = tf.sign(outputs)
update = tf.multiply(sign_outputs, tf.exp(abs_outputs * (- self.min_log) + self.min_log))
return update
def learn2(optimizer):
losses = []
x = initial_pos
state = None
# The loop below unrolls the 20 steps of the optimizer into a single tensorflow graph
for _ in range(TRAINING_STEPS):
loss = quadratic(x)
losses.append(loss)
grads, = tf.gradients(loss, x)
update, state = optimizer(grads, state)
x += update
return losses, grads # the last gradient is added to the ouptut for use by Log_casting
Log_casting_ = Log_casting(-5) # initializes our "log caster"
def g_rnn_logv(gradients, state):
gradients = tf.expand_dims(gradients, axis=1)
if state is None:
state = [[tf.zeros([DIMS, STATE_SIZE])] * 2] * LAYERS
inputs = Log_casting_.preprocess(gradients)
outputs, state = cell(inputs, state)
update = Log_casting_.postprocess(outputs)
return tf.squeeze(update, axis=[1]), state
rnn_losses, grads = learn2(g_rnn_logv) # grads output added for use by log_casting
log_loss = tf.log(rnn_losses[-1] + 1e-37) # residual added to prevent a log(0)... the price of success
apply_update = optimize(log_loss, learning_rate=0.0003)
# operation below added to gradually adapt the min_log value to the lowest gardient
update_log_casting = Log_casting_.update_min_log(grads)
sess.run(tf.global_variables_initializer())
list_result = np.array([])
list_sum_log_res = np.array([])
for it in range(100001):
errors, _, min_log = sess.run([rnn_losses, apply_update, update_log_casting])
list_result = np.append(list_result, errors[-1])
list_sum_log_res = np.append(list_sum_log_res, np.log10(np.array(errors) + 1e-38).sum()/20)
if it % 10000 == 0 :
optim_result = '{:.2E}'.format(errors[-1])
av_log_res = '{:.2f}'.format(np.log10(list_result[-10000:] + 1e-38).mean())
av_sum_log_res = '{:.2f}'.format(list_sum_log_res.mean())
min_log = '{:.2f}'.format(min_log)
print_dict('it', 'optim_result', 'av_log_res', 'av_sum_log_res', 'min_log')
RNN_logv_end_log_res = list_result
draw_convergence('RNN_log15_end_log_res', 'RNN_log30_end_log_res', 'RNN_logv_end_log_res')
```
So, on the plus side, the convergence is initially faster. We also seem to have removed the barrier preventing the RNN going lower than 1e-28. This allows the average result to continue improving, albeit very slowly.
On the minus side, well, we are still nowhere near 0 (ie 1e-38) on average.
Before exploring new RNN configurations, let's try one last trick : instead of minimizing the log of the last result, we can minimize the sum of log of all the iteration.
```
def optimize(loss, learning_rate=0.1):
# "Meta optimizer" to be applied on the RNN defined above
optimizer = tf.train.AdamOptimizer(learning_rate)
gradients, v = zip(*optimizer.compute_gradients(loss))
clipped_gradients, _ = tf.clip_by_global_norm(gradients, 1.)
checked_gradients = []
# The following loop is to remove any NaNs from the gradient as it would be introduced
# in the RNN weights and everything would stop working
for g in clipped_gradients:
checked_g = tf.where(tf.is_nan(g), tf.zeros_like(g), g)
checked_gradients = checked_gradients + [checked_g]
return optimizer.apply_gradients(zip(checked_gradients, v))
rnn_losses, grads = learn2(g_rnn_logv)
sum_log_losses = tf.reduce_sum(tf.log(tf.add(rnn_losses,1e-38)))
apply_update = optimize(sum_log_losses, learning_rate=0.0003)
update_log_casting = Log_casting_.update_min_log(grads)
sess.run(tf.global_variables_initializer())
list_result = np.array([])
list_sum_log_res = np.array([])
for it in range(100001):
errors, _, min_log = sess.run([rnn_losses, apply_update, update_log_casting])
list_result = np.append(list_result, errors[-1])
list_sum_log_res = np.append(list_sum_log_res, np.log10(np.array(errors) + 1e-38).sum()/20)
if it % 10000 == 0 :
optim_result = '{:.2E}'.format(errors[-1])
av_log_res = '{:.2f}'.format(np.log10(list_result[-10000:] + 1e-38).mean())
av_sum_log_res = '{:.2f}'.format(list_sum_log_res.mean())
min_log = '{:.2f}'.format(min_log)
print_dict('it', 'optim_result', 'av_log_res', 'av_sum_log_res', 'min_log')
RNN_logv_sum_log_res = list_result
draw_convergence('RNN_log15_end_log_res', 'RNN_log30_end_log_res', 'RNN_logv_end_log_res',
'RNN_logv_sum_log_res')
```
We are getting closer. Let's have a look at what the convergence looks like.
```
graph_optimizers(sgd_losses, rms_losses, rnn_losses)
```
Better, but we are still far from 1e-38
#### Scale Invariant RNN
The first problem we highlighted is that we are trying to design a RNN that works as well at y=1 as at y=1e-38, with gradient varying between 1 and exp(-43)≈1e-19 (I should mention that this python confusing convention of writting small numbers like 10-5 with 1e-5 is most unfortunate in our context).
The different implementations of logaritmic preprocessing of the gradients proposed above sort of address the problem by rescaling this huge variation of scale into a linear segment between 0 and 1 so that it is more or less interpretable by the RNN, but it's never truly scale invariant.
There is probably a much better implementation of this idea of logaritmic preprocessing, but instead of sinking more time into fine tuning this (or digging into Deepmind's code to see how they cracked this :-), we can try a simpler approach : since the RNN is being fed the past 20 inputs, why not feed it only the ratios of gradients between one step and the next and let it deal with it.
It's actually the first idea I tried. However, I was using the direct result of the RNN as the function to be minimized, and as we have seen, this leads to vanishing gradient if you're not applying log to the function.
```
def g_rnn_div(gradients, state):
gradients = tf.expand_dims(gradients, axis=1)
if state is None:
state_nn = [[tf.zeros([DIMS, STATE_SIZE])] * 2] * LAYERS
state = [state_nn, gradients]
inputs = tf.divide(gradients, tf.abs(state[1]) + 1e-38)
update, state[0] = cell(inputs, state[0])
outputs = tf.multiply(update, tf.abs(state[1]) + 1e-38)
state[1] = gradients
return tf.squeeze(outputs, axis=[1]), state
rnn_losses = learn(g_rnn_div)
end_loss = rnn_losses[-1]
apply_update = optimize(end_loss, learning_rate=0.0003)
sess.run(tf.global_variables_initializer())
list_result = np.array([])
list_sum_log_res = np.array([])
for it in range(50001):
errors, _ = sess.run([rnn_losses, apply_update])
list_result = np.append(list_result, errors[-1])
list_sum_log_res = np.append(list_sum_log_res, np.log10(np.array(errors) + 1e-38).sum()/20)
if it % 5000 == 0 :
optim_result = '{:.2E}'.format(errors[-1])
av_log_res = '{:.2f}'.format(np.log10(list_result[-5000:] + 1e-38).mean())
av_sum_log_res = '{:.2f}'.format(list_sum_log_res.mean())
print_dict('it', 'optim_result', 'av_log_res', 'av_sum_log_res')
RNN_div_end_res = list_result
draw_convergence('RNN_logv_sum_log_res', 'RNN_div_end_res')
rnn_losses = learn(g_rnn_div)
sum_log_losses = tf.reduce_sum(tf.log(tf.add(rnn_losses,1e-38)))
apply_update = optimize(sum_log_losses, learning_rate=0.0003)
sess.run(tf.global_variables_initializer())
list_result = np.array([])
list_sum_log_res = np.array([])
for it in range(100001):
errors, _ = sess.run([rnn_losses, apply_update])
list_result = np.append(list_result, errors[-1])
list_sum_log_res = np.append(list_sum_log_res, np.log10(np.array(errors) + 1e-38).sum()/20)
if it % 10000 == 0 :
optim_result = '{:.2E}'.format(errors[-1])
av_log_res = '{:.2f}'.format(np.log10(list_result[-10000:] + 1e-38).mean())
av_sum_log_res = '{:.2f}'.format(list_sum_log_res.mean())
print_dict('it', 'optim_result', 'av_log_res', 'av_sum_log_res')
RNN_div_sum_log_res = list_result
draw_convergence('RNN_logv_sum_log_res', 'RNN_div_end_res', 'RNN_div_sum_log_res')
graph_optimizers(sgd_losses, rms_losses, rnn_losses)
```
To be noted : the implementation above devides the gradient by the norm of the previous gradient. Dividing by the gradients yields more or less the same results
```
def optimize(loss, learning_rate=0.1):
# "Meta optimizer" to be applied on the RNN defined above
optimizer = tf.train.AdamOptimizer(learning_rate)
gradients, v = zip(*optimizer.compute_gradients(loss))
clipped_gradients, _ = tf.clip_by_global_norm(gradients, 1.)
checked_gradients = []
for g in clipped_gradients:
checked_g = tf.where(tf.is_nan(g), tf.zeros_like(g), g)
checked_gradients = checked_gradients + [checked_g]
return optimizer.apply_gradients(zip(checked_gradients, v))
Log_casting_ = Log_casting(-5)
def g_rnn_logdiv(gradients, state):
gradients = tf.expand_dims(gradients, axis=1)
if state is None:
state_nn = [[tf.zeros([DIMS, STATE_SIZE])] * 2] * LAYERS
state = [state_nn, gradients, gradients]
inputs_ = tf.divide(gradients, tf.abs(state[1]) + 1e-38)
inputs = Log_casting_.preprocess(inputs_)
outputs, state[0] = cell(inputs, state[0])
outputs_ = Log_casting_.postprocess(outputs)
update = tf.multiply(outputs_, tf.abs(state[1]) + 1e-38)
state[1] = gradients
state[2] = inputs_
return tf.squeeze(update, axis=[1]), state
def learn3(optimizer):
losses = []
x = initial_pos
state = None
for _ in range(TRAINING_STEPS):
loss = quadratic(x)
losses.append(loss)
grads, = tf.gradients(loss, x)
update, state = optimizer(grads, state)
x += update
return losses, state[2] # the last RNN input is added to the ouptut for use by Log_casting
rnn_losses, RNN_inputs = learn3(g_rnn_logdiv) # grads output added for use by log_casting
sum_log_losses = tf.reduce_sum(tf.log(tf.add(rnn_losses,1e-38)))
apply_update = optimize(sum_log_losses, learning_rate=0.0003)
# the operation below gradually adapts the min_log value to the lowest gardient ratio
update_log_casting = Log_casting_.update_min_log(RNN_inputs)
sess.run(tf.global_variables_initializer())
list_result = np.array([])
list_sum_log_res = np.array([])
for it in range(100001):
errors, _, min_log = sess.run([rnn_losses, apply_update, update_log_casting])
list_result = np.append(list_result, errors[-1])
list_sum_log_res = np.append(list_sum_log_res, np.log10(np.array(errors) + 1e-38).sum()/20)
if it % 10000 == 0 :
list_result_ = list_result[~np.isnan(list_result)]
list_sum_log_res_ = list_sum_log_res[~np.isnan(list_sum_log_res)]
NaN = list_result.size - list_result_.size
optim_result = '{:.2E}'.format(errors[-1])
av_log_res = '{:.2f}'.format(np.log10(list_result[-10000:] + 1e-38).mean())
av_sum_log_res = '{:.2f}'.format(list_sum_log_res.mean())
min_log = '{:.2f}'.format(min_log)
print_dict('it', 'optim_result', 'av_log_res', 'av_sum_log_res', 'min_log', 'NaN')
RNN_logdiv_sum_log_res = list_result
draw_convergence('RNN_logv_sum_log_res', 'RNN_div_sum_log_res', 'RNN_logdiv_sum_log_res')
graph_optimizers(sgd_losses, rms_losses, rnn_losses)
def g_rnn_log7div(gradients, state):
gradients = tf.expand_dims(gradients, axis=1)
if state is None:
state_nn = [[tf.zeros([DIMS, STATE_SIZE])] * 2] * LAYERS
state = [state_nn, gradients]
inputs_ = tf.divide(gradients, tf.abs(state[1]) + 1e-37)
# Casting of inputs from [exp(-43), 1] to [0, 1] and [-1, -exp(-43)] to [-1, 0]
min_log_gradient = -7
log_inputs_ = tf.log(tf.abs(inputs_) + np.exp(min_log_gradient-2))
sign_gradients = tf.sign(gradients)
inputs = tf.multiply(sign_gradients,((log_inputs_ - min_log_gradient) / (- min_log_gradient)))
outputs, state[0] = cell(inputs, state[0])
# Casting of output from [0, 1] to [exp(-43), 1] and [-1, 0] to [-1, -exp(-43)]
abs_outputs = tf.abs(outputs)
sign_outputs = tf.sign(outputs)
outputs_ = tf.multiply(sign_outputs, tf.exp(abs_outputs * (- min_log_gradient) + min_log_gradient))
update = tf.multiply(outputs_, tf.abs(state[1]) + 1e-37)
state[1] = gradients
return tf.squeeze(update, axis=[1]), state
rnn_losses = learn(g_rnn_logdiv)
sum_log_losses = tf.reduce_sum(tf.log(tf.add(rnn_losses,1e-37)))
apply_update = optimize(sum_log_losses, learning_rate=0.0001)
sess.run(tf.global_variables_initializer())
list_result = np.array([])
list_sum_log_res = np.array([])
for it in range(100001):
errors, _ = sess.run([rnn_losses, apply_update])
list_result = np.append(list_result, errors[-1])
list_sum_log_res = np.append(list_sum_log_res, np.log10(np.array(errors) + 1e-37).sum()/20)
if it % 10000 == 0 :
optim_result = '{:.2E}'.format(errors[-1])
av_log_res = '{:.2f}'.format(np.log10(list_result[-10000:] + 1e-37).mean())
av_sum_log_res = '{:.2f}'.format(list_sum_log_res.mean())
print_dict('it', 'optim_result', 'av_log_res', 'av_sum_log_res')
RNN_log7div_sum_log_res = list_result
draw_convergence('RNN_logv_sum_log_res', 'RNN_div_sum_log_res', 'RNN_logdiv_sum_log_res', 'RNN_log7div_sum_log_res')
```
| true |
code
| 0.588712 | null | null | null | null |
|
```
# Import Libraries
import numpy as np
import pandas as pd
from scipy.stats import iqr
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
import pickle
from sklearn.preprocessing import OneHotEncoder, LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import confusion_matrix
from sklearn import tree, metrics
import sklearn.metrics as metrics
from sklearn.model_selection import RandomizedSearchCV
from xgboost import XGBClassifier
from sklearn.inspection import permutation_importance
from sklearn.metrics import plot_confusion_matrix, classification_report
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from pdpbox.pdp import pdp_isolate, pdp_plot, pdp_interact, pdp_interact_plot
import shap
# Read In csv
df = pd.read_csv('ks-projects-201801.csv')
df.head()
```
## Doing some EDA
```
# Printing information about variables in Dataset
df.info()
# Checking for unique values for every column
for col in df:
print(df[col].unique())
# Base accuracy: failure rate is ~62%, success rate is 36%
df['state'].value_counts(normalize=True)
```
## Wrangle function to read and clean data
```
# loading data and cleaning dataset
def wrangle(file_path):
#reading in data, parsing the two date columns
df = pd.read_csv(file_path, parse_dates=['deadline', 'launched'], na_values=['N,0"'])
#dropping any live campaigns
df = df.query('state != "live"')
#creating new column 'success' will have a 1 if state is succesfull, else 0
df.loc[df['state'] == 'successful', 'success'] = 1
df.loc[df['state'] != 'successful', 'success'] = 0
#creating new columns for the dates
df = df.assign(hour=df.launched.dt.hour,
day=df.launched.dt.day,
month=df.launched.dt.month,
year=df.launched.dt.year)
return df
df = wrangle("ks-projects-201801.csv");
```
## Doing EDA on new Dataset
```
df.head()
# Get top 10 most frequent names
n=10
df['name'].value_counts()[:n].index.tolist()
# Summary statisticts about Dataset
df.describe()
```
## Checking for outliers
```
plt.boxplot(df['pledged'])
fig = plt.figure(figsize =(10, 7))
plt.show()
sns.boxplot(x=df['goal'])
Q1 = df['usd_pledged_real'].quantile(0.25)
Q3 = df['usd_pledged_real'].quantile(0.75)
IQR = Q3 - Q1
# Filtering values between Q1-1.5IQR and Q3+1.5IQR to exclude outliers
filtered = df.query('(@Q1 - 1.5 * @IQR) <= usd_pledged_real <= (@Q3 + 1.5 * @IQR)')
# Print a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean
print(filtered.skew())
filtered.head()
# Building scatterplot to see the correlation between two variables
fig, ax = plt.subplots(figsize=(20,10))
ax.scatter(filtered['goal'], filtered['usd_pledged_real'])
ax.set_xlabel('Goal')
ax.set_ylabel('Pledged')
plt.show()
#seeing how many unique values are there in the category column
filtered['category'].nunique()
# Base accuracy at this point: failure rate is ~72%, success rate is ~28%
filtered['success'].value_counts(normalize=True)
```
## Creating new columns with seasons and seasons_encoded values
```
def seasons(date_ranges):
season = ""
if date_ranges is pd.NaT:
return "NAN"
else:
#print(date_ranges)
str_date_range = date_ranges.strftime("%m-%d")
#print(date_ranges.strftime("%m-%d"))
#print(date_ranges.strftime("%m-%d") > "08-26")
if str_date_range >= "12-21" or str_date_range <= "03-20":
season = "Winter"
if str_date_range >= "03-21" and str_date_range <="06-20":
season = "Spring"
if str_date_range >="06-21" and str_date_range <="09-20":
season = "Summer"
if str_date_range >="09-21" and str_date_range <="12-20":
season = "Fall"
return season
filtered['launch_season'] = filtered['launched'].apply(seasons)
filtered['deadline_season'] = filtered['deadline'].apply(seasons)
def season_encoder(values):
inter = 0
if values == "Spring":
inter = 1
elif values == "Summer":
inter = 2
elif values == "Fall":
inter = 3
elif values == "Winter":
inter = 4
else:
inter = "NAN"
return inter
filtered['launch_season_encode'] = filtered['launch_season'].apply(season_encoder)
filtered['deadline_season_encode'] = filtered['deadline_season'].apply(season_encoder)
```
## Creating new column with duration in days
```
filtered['launched'] = pd.to_datetime(filtered['launched'])
filtered['deadline'] = pd.to_datetime(filtered['deadline'])
filtered['duration'] = filtered['deadline'] - filtered['launched']
filtered['duration'] = filtered['duration'].dt.days
filtered.head()
```
## After doing some feature selection below, creating new DataFrame
```
#choosing categorical features to be in the model
cat_features = ['country', 'currency', 'main_category']
#label encoding and creating new dataframe with encoded columns
encoder = LabelEncoder()
encoded = filtered[cat_features].apply(encoder.fit_transform)
encoded.head()
#choosing data columns to be in model and joining with categorical col above
data_features = ['goal', 'month', 'year', 'success', 'duration']
baseline = filtered[data_features].join(encoded)
baseline.head()
baseline_index = filtered['name']
baseline = baseline.join(baseline_index).set_index('name')
baseline.head()
# Creates a csv
baseline.to_csv(r'ks-projects-201801.csv')
# Printing the pairwise correlation of all columns in the DataFrame
baseline.corr()
# Creating target and feature variables
target = 'success'
X = baseline.drop(columns=target)
y = baseline[target]
# Splitting data into training and test data
X_train, X_val, y_train, y_val = train_test_split(X,y, test_size = .2, random_state = 42)
```
## Establishing Baseline
```
# The Baseline accuracy is the majority class in y_val and what percentage of the training observations it represents
baseline_acc = y_train.value_counts(normalize=True)[0]
print('Baseline Accuracy Score:', baseline_acc)
```
## Building Models
### We are building not one but few different models to see which one is the best to make predictions
```
# Creating and fitting model1 = XGBoost
model = XGBClassifier(label_encoder = False, random_state=42, n_estimators=50, n_jobs=-1, max_depth=15)
model.fit(X_train, y_train)
# Calculate the training and validation accuracy scores for model
training_accuracy = model.score(X_train, y_train)
val_accuracy = model.score(X_val, y_val)
print('Training Accuracy Score:', training_accuracy)
print('Validation Accuracy Score:', val_accuracy)
# Creating and fitting model2 = LogisticRegression
model2 = LogisticRegression(random_state=42, solver='newton-cg')
model2.fit(X_train, y_train)
# Calculate the training and validation accuracy scores for model2
training_accuracy2 = model2.score(X_train, y_train)
val_accuracy2 = model2.score(X_val, y_val)
print('Training Accuracy Score:', training_accuracy2)
print('Validation Accuracy Score:', val_accuracy2)
# Creating and fitting model3 = DecisionTree
model3 = tree.DecisionTreeClassifier(random_state=42)
model3.fit(X_train, y_train)
# Calculate the training and validation accuracy scores for model3
training_accuracy3 = model3.score(X_train, y_train)
val_accuracy3 = model3.score(X_val, y_val)
print('Training Accuracy Score:', training_accuracy3)
print('Validation Accuracy Score:', val_accuracy3)
# Creating and fitting model4 = RandomForestClassifer
model4 = RandomForestClassifier(random_state=42, n_estimators=50, n_jobs=-1)
model4.fit(X_train, y_train);
# Calculate the training and validation accuracy scores for model4
training_accuracy4 = model4.score(X_train, y_train)
val_accuracy4 = model4.score(X_val, y_val)
print('Training Accuracy Score:', training_accuracy4)
print('Validation Accuracy Score:', val_accuracy4)
# Creating and fitting model5 = GradientBoostingClassifer
model5 = GradientBoostingClassifier(random_state=42, n_estimators=150, min_samples_leaf=5, max_leaf_nodes=350, max_depth=4, learning_rate=0.25)
model5.fit(X_train, y_train);
# Calculate the training and validation accuracy scores for model5
training_accuracy5 = model5.score(X_train, y_train)
val_accuracy5 = model5.score(X_val, y_val)
print('Training Accuracy Score:', training_accuracy5)
print('Validation Accuracy Score:', val_accuracy5)
```
## Models Tuning
### To get better results we did hyperparameter tuning for each model and based on that we picked the model with the best score
```
#RandomizedSearchCV
#instead of choosing the hyperparameters manually, this helps you choose it
param_grid = {
'max_depth': [3, 4, 5],
'n_estimators': [150],
'min_samples_leaf': [3, 4, 5],
'max_leaf_nodes': [350, 370, 400],
'learning_rate': [0.25, 0.3,]
}
search = RandomizedSearchCV(model5,
param_distributions=param_grid,
n_iter=5,
n_jobs=-1,
cv=3,
verbose=1)
search.fit(X_train, y_train);
search.best_score_
search.best_params_
```
### Making some predictions
```
y_pred = model5.predict(X_val)
y_pred
```
## Communicate Results
## Making plot to show feature importances
```
coef = pd.DataFrame(data=model5.feature_importances_, index=X_train.columns, columns=['coefficients'])
# Interested in the most extreme coefficients
coef['coefficients'].abs().sort_values().plot(kind='barh');
plt.title('Most Important Features')
plt.show()
```
## Classification Report
```
print(classification_report(y_val, model5.predict(X_val), target_names=['Not successful', 'Successful']))
```
## Confusion Matrix to see how many predictions were made correct
```
plot_confusion_matrix(
model5,
X_val,
y_val,
values_format = '.0f',
display_labels = ['Not successful','Successful']
);
```
## Creating a partial dependence plot to show how a model prediction partially depends on two most important values of the input variables of interest
```
features = ['goal', 'main_category']
interact = pdp_interact(model5,
dataset=X_val,
model_features=X_val.columns,
features=features)
pdp_interact_plot(interact, plot_type='grid', feature_names=features);
```
## Shapley Plot
### - Showing the influence of features in *individual* predictions.
```
explainer = shap.TreeExplainer(model5)
shap_values = explainer.shap_values(X_val)
shap_values
shap.initjs()
shap.force_plot(explainer.expected_value[0], shap_values[-3], X_val.iloc[0,:])
```
## Picking most important features for model
```
#perm_imp is set to be permutation importance of boosting model on X_val and y_val
perm_imp = permutation_importance(model5, X_val, y_val, random_state=42)
#setting data as dict of the permutation importances mean and std.
data = {'imp_mean':perm_imp['importances_mean'],
'imp_std':perm_imp['importances_std']}
#setting permutation_importances to be data frame with columns in X val to be index and 'data' to be the other columns. Sorting by the mean importance from data.
permutation_importances5 = pd.DataFrame(data,index=X_val.columns).sort_values(by='imp_mean')
permutation_importances5
# Get feature importances
importances5 = pd.Series(model5.feature_importances_, X_train.columns)
# Plot feature importances
%matplotlib inline
import matplotlib.pyplot as plt
n = 20
plt.figure(figsize=(10,n/2))
plt.title(f'Top {n} features')
importances5.sort_values()[-n:].plot.barh(color='grey');
```
## Saving the model
```
pickle.dump(model5, open('Model', 'wb'))
```
| true |
code
| 0.591133 | null | null | null | null |
|
# Federated Learning of a Recurrent Neural Network for text classification
In this tutorial, you are going to learn how to train a Recurrent Neural Network (RNN) in a federated way with the purpose of *classifying* a person's surname to its most likely language of origin.
We will train two Recurrent Neural Networks residing on two remote workers based on a dataset containing approximately 20.000 surnames from 18 languages of origin, and predict to which language a name belongs based on the name's spelling.
A **character-level RNN** treats words as a series of characters - outputting a prediction and “hidden state” per character, feeding its previous hidden state into each next step. We take the final prediction to be the output, i.e. which class the word belongs to. Hence the training process proceeds sequentially character-by-character through the different hidden layers.
Following distributed training, we are going to be able to perform predictions of a surname's language of origin, as in the following example:
```python
predict(model_pointers["bob"], "Qing", alice) #alice is our worker
Qing
(-1.43) Korean
(-1.74) Vietnamese
(-2.18) Arabic
predict(model_pointers["alice"], "Daniele", alice)
Daniele
(-1.58) French
(-2.04) Scottish
(-2.07) Dutch
```
The present example is inspired by an official Pytorch [tutorial](https://pytorch.org/tutorials/intermediate/char_rnn_classification_tutorial.html), which I ported to PySyft with the purpose of learning a Recurrent Neural Network in a federated way.The present tutorial is self-contained, so there are no dependencies on external pieces of code apart from a few Python libraries.
**RNN Tutorial's author**: Daniele Gadler. [@DanyEle](https://github.com/danyele) on Github.
## 1. Step: Dependencies!
Make sure you have all the requires packages installed, or install them via the following command (assuming you didn't move the current Jupyter Notebook from its initial directory).
After installing new packages, you may have to restart this Jupyter Notebook from the tool bar Kernel -> Restart
```
!pip install -r "../../../requirements.txt"
from __future__ import unicode_literals, print_function, division
from torch.utils.data import Dataset
import torch
from io import open
import glob
import os
import numpy as np
import unicodedata
import string
import random
import torch.nn as nn
import time
import math
import pandas as pd
import random
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import urllib.request
from zipfile import ZipFile
#hide TF-related warnings in PySyft
import warnings
warnings.filterwarnings("ignore")
import syft as sy
from syft.frameworks.torch.federated import utils
from syft.workers.websocket_client import WebsocketClientWorker
```
## 2. Step: Data pre-processing and transformation
We are going to train our neural network based on a dataset containing surnames from 18 languages of origin. So let's run the following lines to automatically download the dataset and extract it. Afterwards, you'll be able to parse the dataset in Python following the initialization of a few basic functions for parsing the data
```
#create a function for checking if the dataset does indeed exist
def dataset_exists():
return (os.path.isfile('./data/eng-fra.txt') and
#check if all 18 files are indeed in the ./data/names/ directory
os.path.isdir('./data/names/') and
os.path.isfile('./data/names/Arabic.txt') and
os.path.isfile('./data/names/Chinese.txt') and
os.path.isfile('./data/names/Czech.txt') and
os.path.isfile('./data/names/Dutch.txt') and
os.path.isfile('./data/names/English.txt') and
os.path.isfile('./data/names/French.txt') and
os.path.isfile('./data/names/German.txt') and
os.path.isfile('./data/names/Greek.txt') and
os.path.isfile('./data/names/Irish.txt') and
os.path.isfile('./data/names/Italian.txt') and
os.path.isfile('./data/names/Japanese.txt') and
os.path.isfile('./data/names/Korean.txt') and
os.path.isfile('./data/names/Polish.txt') and
os.path.isfile('./data/names/Portuguese.txt') and
os.path.isfile('./data/names/Russian.txt') and
os.path.isfile('./data/names/Scottish.txt') and
os.path.isfile('./data/names/Spanish.txt') and
os.path.isfile('./data/names/Vietnamese.txt'))
#If the dataset does not exist, then proceed to download the dataset anew
if not dataset_exists():
#If the dataset does not already exist, let's download the dataset directly from the URL where it is hosted
print('Downloading the dataset with urllib2 to the current directory...')
url = 'https://download.pytorch.org/tutorial/data.zip'
urllib.request.urlretrieve(url, './data.zip')
print("The dataset was successfully downloaded")
print("Unzipping the dataset...")
with ZipFile('./data.zip', 'r') as zipObj:
# Extract all the contents of the zip file in current directory
zipObj.extractall()
print("Dataset successfully unzipped")
else:
print("Not downloading the dataset because it was already downloaded")
#Load all the files in a certain path
def findFiles(path):
return glob.glob(path)
# Read a file and split into lines
def readLines(filename):
lines = open(filename, encoding='utf-8').read().strip().split('\n')
return [unicodeToAscii(line) for line in lines]
#convert a string 's' in unicode format to ASCII format
def unicodeToAscii(s):
return ''.join(
c for c in unicodedata.normalize('NFD', s)
if unicodedata.category(c) != 'Mn'
and c in all_letters
)
all_letters = string.ascii_letters + " .,;'"
n_letters = len(all_letters)
#dictionary containing the nation as key and the names as values
#Example: category_lines["italian"] = ["Abandonato","Abatangelo","Abatantuono",...]
category_lines = {}
#List containing the different categories in the data
all_categories = []
for filename in findFiles('data/names/*.txt'):
print(filename)
category = os.path.splitext(os.path.basename(filename))[0]
all_categories.append(category)
lines = readLines(filename)
category_lines[category] = lines
n_categories = len(all_categories)
print("Amount of categories:" + str(n_categories))
```
Now we are going to format the data so as to make it compliant with the format requested by PySyft and Pytorch. Firstly, we define a dataset class, specifying how batches ought to be extracted from the dataset in order for them to be assigned to the different workers.
```
class LanguageDataset(Dataset):
#Constructor is mandatory
def __init__(self, text, labels, transform=None):
self.data = text
self.targets = labels #categories
#self.to_torchtensor()
self.transform = transform
def to_torchtensor(self):
self.data = torch.from_numpy(self.text, requires_grad=True)
self.labels = torch.from_numpy(self.targets, requires_grad=True)
def __len__(self):
#Mandatory
'''Returns:
Length [int]: Length of Dataset/batches
'''
return len(self.data)
def __getitem__(self, idx):
#Mandatory
'''Returns:
Data [Torch Tensor]:
Target [ Torch Tensor]:
'''
sample = self.data[idx]
target = self.targets[idx]
if self.transform:
sample = self.transform(sample)
return sample,target
#The list of arguments for our program. We will be needing most of them soon.
class Arguments():
def __init__(self):
self.batch_size = 1
self.learning_rate = 0.005
self.epochs = 10000
self.federate_after_n_batches = 15000
self.seed = 1
self.print_every = 200
self.plot_every = 100
self.use_cuda = False
args = Arguments()
```
We now need to unwrap data samples so as to have them all in one single list instead of a dictionary,where different categories were addressed by key.From now onwards, **categories** will be the languages of origin (Y) and **names** will be the data points (X).
```
%%latex
\begin{split}
names\_list = [d_1,...,d_n] \\
category\_list = [c_1,...,c_n]
\end{split}
Where $n$ is the total amount of data points
#Set of names(X)
names_list = []
#Set of labels (Y)
category_list = []
#Convert into a list with corresponding label.
for nation, names in category_lines.items():
#iterate over every single name
for name in names:
names_list.append(name) #input data point
category_list.append(nation) #label
#let's see if it was successfully loaded. Each data sample(X) should have its own corresponding category(Y)
print(names_list[1:20])
print(category_list[1:20])
print("\n \n Amount of data points loaded: " + str(len(names_list)))
```
We now need to turn our categories into numbers, as PyTorch cannot really understand plain text
For an example category: "Greek" ---> 0
```
#Assign an integer to every category
categories_numerical = pd.factorize(category_list)[0]
#Let's wrap our categories with a tensor, so that it can be loaded by LanguageDataset
category_tensor = torch.tensor(np.array(categories_numerical), dtype=torch.long)
#Ready to be processed by torch.from_numpy in LanguageDataset
categories_numpy = np.array(category_tensor)
#Let's see a few resulting categories
print(names_list[1200:1210])
print(categories_numpy[1200:1210])
```
We now need to turn every single character in each input line string into a vector, with a "1" marking the character present in that very character.
For example, in the case of a single character, we have:
"a" = array([[1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)
A word is just a vector of such character vectors: our Recurrent Neural Network will process every single character vector in the word, producing an output after passing through each of its hidden layers.
This technique, involving the encoding of a word as a vector of character vectors, is known as *word embedding*, as we embed a word into a vector of vectors.
```
def letterToIndex(letter):
return all_letters.find(letter)
# Just for demonstration, turn a letter into a <1 x n_letters> Tensor
def letterToTensor(letter):
tensor = torch.zeros(1, n_letters)
tensor[0][letterToIndex(letter)] = 1
return tensor
# Turn a line into a <line_length x 1 x n_letters>,
# or an array of one-hot letter vectors
def lineToTensor(line):
tensor = torch.zeros(len(line), 1, n_letters) #Daniele: len(max_line_size) was len(line)
for li, letter in enumerate(line):
tensor[li][0][letterToIndex(letter)] = 1
#Daniele: add blank elements over here
return tensor
def list_strings_to_list_tensors(names_list):
lines_tensors = []
for index, line in enumerate(names_list):
lineTensor = lineToTensor(line)
lineNumpy = lineTensor.numpy()
lines_tensors.append(lineNumpy)
return(lines_tensors)
lines_tensors = list_strings_to_list_tensors(names_list)
print(names_list[0])
print(lines_tensors[0])
print(lines_tensors[0].shape)
```
Let's now identify the longest word in the dataset, as all tensors need to have the same shape in order to fit into a numpy array. So, we append vectors containing just "0"s into our words up to the maximum word size, such that all word embeddings have the same shape.
```
max_line_size = max(len(x) for x in lines_tensors)
def lineToTensorFillEmpty(line, max_line_size):
tensor = torch.zeros(max_line_size, 1, n_letters) #notice the difference between this method and the previous one
for li, letter in enumerate(line):
tensor[li][0][letterToIndex(letter)] = 1
#Vectors with (0,0,.... ,0) are placed where there are no characters
return tensor
def list_strings_to_list_tensors_fill_empty(names_list):
lines_tensors = []
for index, line in enumerate(names_list):
lineTensor = lineToTensorFillEmpty(line, max_line_size)
lines_tensors.append(lineTensor)
return(lines_tensors)
lines_tensors = list_strings_to_list_tensors_fill_empty(names_list)
#Let's take a look at what a word now looks like
print(names_list[0])
print(lines_tensors[0])
print(lines_tensors[0].shape)
#And finally, from a list, we can create a numpy array with all our word embeddings having the same shape:
array_lines_tensors = np.stack(lines_tensors)
#However, such operation introduces one extra dimension (look at the dimension with index=2 having size '1')
print(array_lines_tensors.shape)
#Because that dimension just has size 1, we can get rid of it with the following function call
array_lines_proper_dimension = np.squeeze(array_lines_tensors, axis=2)
print(array_lines_proper_dimension.shape)
```
### Data unbalancing and batch randomization:
You may have noticed that our dataset is strongly unbalanced and contains a lot of data points in the "russian.txt" dataset. However, we would still like to take a random batch during our training procedure at every iteration. In order to prevent our neural network from classifying a data point as always belonging to the "Russian" category, we first pick a random category and then select a data point from that category. To do that, we construct a dictionary mapping a certain category to the corresponding starting index in the list of data points (e.g.: lines). Afterwards, we will take a datapoint starting from the starting_index identified
```
def find_start_index_per_category(category_list):
categories_start_index = {}
#Initialize every category with an empty list
for category in all_categories:
categories_start_index[category] = []
#Insert the start index of each category into the dictionary categories_start_index
#Example: "Italian" --> 203
# "Spanish" --> 19776
last_category = None
i = 0
for name in names_list:
cur_category = category_list[i]
if(cur_category != last_category):
categories_start_index[cur_category] = i
last_category = cur_category
i = i + 1
return(categories_start_index)
categories_start_index = find_start_index_per_category(category_list)
print(categories_start_index)
```
Let's define a few functions to take a random index from from the dataset, so that we'll be able to select a random data point and a random category.
```
def randomChoice(l):
rand_value = random.randint(0, len(l) - 1)
return l[rand_value], rand_value
def randomTrainingIndex():
category, rand_cat_index = randomChoice(all_categories) #cat = category, it's not a random animal
#rand_line_index is a relative index for a data point within the random category rand_cat_index
line, rand_line_index = randomChoice(category_lines[category])
category_start_index = categories_start_index[category]
absolute_index = category_start_index + rand_line_index
return(absolute_index)
```
## 3. Step: Model - Recurrent Neural Network
Hey, I must admit that was indeed a lot of data preprocessing and transformation, but it was well worth it!
We have defined almost all the function we'll be needing during the training procedure and our data is ready
to be fed into the neural network, which we're creating now:
```
#Two hidden layers, based on simple linear layers
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(RNN, self).__init__()
self.hidden_size = hidden_size
self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
self.i2o = nn.Linear(input_size + hidden_size, output_size)
self.softmax = nn.LogSoftmax(dim=1)
def forward(self, input, hidden):
combined = torch.cat((input, hidden), 1)
hidden = self.i2h(combined)
output = self.i2o(combined)
output = self.softmax(output)
return output, hidden
def initHidden(self):
return torch.zeros(1, self.hidden_size)
#Let's instantiate the neural network already:
n_hidden = 128
#Instantiate RNN
device = torch.device("cuda" if args.use_cuda else "cpu")
model = RNN(n_letters, n_hidden, n_categories).to(device)
#The final softmax layer will produce a probability for each one of our 18 categories
print(model)
#Now let's define our workers. You can either use remote workers or virtual workers
hook = sy.TorchHook(torch) # <-- NEW: hook PyTorch ie add extra functionalities to support Federated Learning
alice = sy.VirtualWorker(hook, id="alice")
bob = sy.VirtualWorker(hook, id="bob")
#charlie = sy.VirtualWorker(hook, id="charlie")
workers_virtual = [alice, bob]
#If you have your workers operating remotely, like on Raspberry PIs
#kwargs_websocket_alice = {"host": "ip_alice", "hook": hook}
#alice = WebsocketClientWorker(id="alice", port=8777, **kwargs_websocket_alice)
#kwargs_websocket_bob = {"host": "ip_bob", "hook": hook}
#bob = WebsocketClientWorker(id="bob", port=8778, **kwargs_websocket_bob)
#workers_virtual = [alice, bob]
#array_lines_proper_dimension = our data points(X)
#categories_numpy = our labels (Y)
langDataset = LanguageDataset(array_lines_proper_dimension, categories_numpy)
#assign the data points and the corresponding categories to workers.
federated_train_loader = sy.FederatedDataLoader(
langDataset
.federate(workers_virtual),
batch_size=args.batch_size)
```
## 4. Step - Model Training!
It's now time to train our Recurrent Neural Network based on the processed data. To do that, we need to define a few more functions
```
def categoryFromOutput(output):
top_n, top_i = output.topk(1)
category_i = top_i[0].item()
return all_categories[category_i], category_i
def timeSince(since):
now = time.time()
s = now - since
m = math.floor(s / 60)
s -= m * 60
return '%dm %ds' % (m, s)
def fed_avg_every_n_iters(model_pointers, iter, federate_after_n_batches):
models_local = {}
if(iter % args.federate_after_n_batches == 0):
for worker_name, model_pointer in model_pointers.items():
# #need to assign the model to the worker it belongs to.
models_local[worker_name] = model_pointer.copy().get()
model_avg = utils.federated_avg(models_local)
for worker in workers_virtual:
model_copied_avg = model_avg.copy()
model_ptr = model_copied_avg.send(worker)
model_pointers[worker.id] = model_ptr
return(model_pointers)
def fw_bw_pass_model(model_pointers, line_single, category_single):
#get the right initialized model
model_ptr = model_pointers[line_single.location.id]
line_reshaped = line_single.reshape(max_line_size, 1, len(all_letters))
line_reshaped, category_single = line_reshaped.to(device), category_single.to(device)
#Firstly, initialize hidden layer
hidden_init = model_ptr.initHidden()
#And now zero grad the model
model_ptr.zero_grad()
hidden_ptr = hidden_init.send(line_single.location)
amount_lines_non_zero = len(torch.nonzero(line_reshaped.copy().get()))
#now need to perform forward passes
for i in range(amount_lines_non_zero):
output, hidden_ptr = model_ptr(line_reshaped[i], hidden_ptr)
criterion = nn.NLLLoss()
loss = criterion(output, category_single)
loss.backward()
model_got = model_ptr.get()
#Perform model weights' updates
for param in model_got.parameters():
param.data.add_(-args.learning_rate, param.grad.data)
model_sent = model_got.send(line_single.location.id)
model_pointers[line_single.location.id] = model_sent
return(model_pointers, loss, output)
def train_RNN(n_iters, print_every, plot_every, federate_after_n_batches, list_federated_train_loader):
current_loss = 0
all_losses = []
model_pointers = {}
#Send the initialized model to every single worker just before the training procedure starts
for worker in workers_virtual:
model_copied = model.copy()
model_ptr = model_copied.send(worker)
model_pointers[worker.id] = model_ptr
#extract a random element from the list and perform training on it
for iter in range(1, n_iters + 1):
random_index = randomTrainingIndex()
line_single, category_single = list_federated_train_loader[random_index]
#print(category_single.copy().get())
line_name = names_list[random_index]
model_pointers, loss, output = fw_bw_pass_model(model_pointers, line_single, category_single)
#model_pointers = fed_avg_every_n_iters(model_pointers, iter, args.federate_after_n_batches)
#Update the current loss a
loss_got = loss.get().item()
current_loss += loss_got
if iter % plot_every == 0:
all_losses.append(current_loss / plot_every)
current_loss = 0
if(iter % print_every == 0):
output_got = output.get() #Without copy()
guess, guess_i = categoryFromOutput(output_got)
category = all_categories[category_single.copy().get().item()]
correct = '✓' if guess == category else '✗ (%s)' % category
print('%d %d%% (%s) %.4f %s / %s %s' % (iter, iter / n_iters * 100, timeSince(start), loss_got, line_name, guess, correct))
return(all_losses, model_pointers)
```
In order for the defined randomization process to work, we need to wrap the data points and categories into a list, from that we're going to take a batch at a random index.
```
#This may take a few seconds to complete.
print("Generating list of batches for the workers...")
list_federated_train_loader = list(federated_train_loader)
```
And finally,let's launch our training
```
start = time.time()
all_losses, model_pointers = train_RNN(args.epochs, args.print_every, args.plot_every, args.federate_after_n_batches, list_federated_train_loader)
#Let's plot the loss we got during the training procedure
plt.figure()
plt.ylabel("Loss")
plt.xlabel('Epochs (100s)')
plt.plot(all_losses)
```
## 5. Step - Predict!
Great! We have successfully created our two models for bob and alice in parallel using federated learning! I experimented with federated averaging of the two models, but it turned out that for a batch size of 1, as in the present case, the model loss was diverging. Let's try using our models for prediction now, shall we? This is the final reward for our endeavours.
```
def predict(model, input_line, worker, n_predictions=3):
model = model.copy().get()
print('\n> %s' % input_line)
model_remote = model.send(worker)
line_tensor = lineToTensor(input_line)
line_remote = line_tensor.copy().send(worker)
#line_tensor = lineToTensor(input_line)
#output = evaluate(model, line_remote)
# Get top N categories
hidden = model_remote.initHidden()
hidden_remote = hidden.copy().send(worker)
with torch.no_grad():
for i in range(line_remote.shape[0]):
output, hidden_remote = model_remote(line_remote[i], hidden_remote)
topv, topi = output.copy().get().topk(n_predictions, 1, True)
predictions = []
for i in range(n_predictions):
value = topv[0][i].item()
category_index = topi[0][i].item()
print('(%.2f) %s' % (value, all_categories[category_index]))
predictions.append([value, all_categories[category_index]])
```
Notice how the different models learned may perform different predictions, based on the data that was shown to them.
```
predict(model_pointers["alice"], "Qing", alice)
predict(model_pointers["alice"], "Daniele", alice)
predict(model_pointers["bob"], "Qing", alice)
predict(model_pointers["bob"], "Daniele", alice)
```
You may try experimenting with this example right now, for example by increasing or decreasing the amount of epochs and seeing how the two models perform. You may also try to de-commenting the part about federating averaging and check the new resulting loss function. There can be lots of other optimizations we may think of as well!
# Congratulations!!! - Time to Join the Community!
Congratulations on completing this notebook tutorial! If you enjoyed this and would like to join the movement toward privacy preserving, decentralized ownership of AI and the AI supply chain (data), you can do so in the following ways!
### Star PySyft on GitHub
The easiest way to help our community is just by starring the Repos! This helps raise awareness of the cool tools we're building.
- [Star PySyft](https://github.com/OpenMined/PySyft)
### Join our Slack!
The best way to keep up to date on the latest advancements is to join our community! You can do so by filling out the form at [http://slack.openmined.org](http://slack.openmined.org)
### Join a Code Project!
The best way to contribute to our community is to become a code contributor! At any time you can go to PySyft GitHub Issues page and filter for "Projects". This will show you all the top level Tickets giving an overview of what projects you can join! If you don't want to join a project, but you would like to do a bit of coding, you can also look for more "one off" mini-projects by searching for GitHub issues marked "good first issue".
- [PySyft Projects](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3AProject)
- [Good First Issue Tickets](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
### Donate
If you don't have time to contribute to our codebase, but would still like to lend support, you can also become a Backer on our Open Collective. All donations go toward our web hosting and other community expenses such as hackathons and meetups!
[OpenMined's Open Collective Page](https://opencollective.com/openmined)
| true |
code
| 0.567937 | null | null | null | null |
|
# Shor's Algorithm
Shor’s algorithm is famous for factoring integers in polynomial time. Since the best-known classical algorithm requires superpolynomial time to factor the product of two primes, the widely used cryptosystem, RSA, relies on factoring being impossible for large enough integers.
In this chapter we will focus on the quantum part of Shor’s algorithm, which actually solves the problem of _period finding_. Since a factoring problem can be turned into a period finding problem in polynomial time, an efficient period finding algorithm can be used to factor integers efficiently too. For now its enough to show that if we can compute the period of $a^x\bmod N$ efficiently, then we can also efficiently factor. Since period finding is a worthy problem in its own right, we will first solve this, then discuss how this can be used to factor in section 5.
```
import matplotlib.pyplot as plt
import numpy as np
from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.visualization import plot_histogram
from math import gcd
from numpy.random import randint
import pandas as pd
from fractions import Fraction
```
## 1. The Problem: Period Finding
Let’s look at the periodic function:
$$ f(x) = a^x \bmod{N}$$
<details>
<summary>Reminder: Modulo & Modular Arithmetic (Click here to expand)</summary>
The modulo operation (abbreviated to 'mod') simply means to find the remainder when dividing one number by another. For example:
$$ 17 \bmod 5 = 2 $$
Since $17 \div 5 = 3$ with remainder $2$. (i.e. $17 = (3\times 5) + 2$). In Python, the modulo operation is denoted through the <code>%</code> symbol.
This behaviour is used in <a href="https://en.wikipedia.org/wiki/Modular_arithmetic">modular arithmetic</a>, where numbers 'wrap round' after reaching a certain value (the modulus). Using modular arithmetic, we could write:
$$ 17 = 2 \pmod 5$$
Note that here the $\pmod 5$ applies to the entire equation (since it is in parenthesis), unlike the equation above where it only applied to the left-hand side of the equation.
</details>
where $a$ and $N$ are positive integers, $a$ is less than $N$, and they have no common factors. The period, or order ($r$), is the smallest (non-zero) integer such that:
$$a^r \bmod N = 1 $$
We can see an example of this function plotted on the graph below. Note that the lines between points are to help see the periodicity and do not represent the intermediate values between the x-markers.
```
N = 35
a = 3
# Calculate the plotting data
xvals = np.arange(35)
yvals = [np.mod(a**x, N) for x in xvals]
# Use matplotlib to display it nicely
fig, ax = plt.subplots()
ax.plot(xvals, yvals, linewidth=1, linestyle='dotted', marker='x')
ax.set(xlabel='$x$', ylabel='$%i^x$ mod $%i$' % (a, N),
title="Example of Periodic Function in Shor's Algorithm")
try: # plot r on the graph
r = yvals[1:].index(1) +1
plt.annotate('', xy=(0,1), xytext=(r,1), arrowprops=dict(arrowstyle='<->'))
plt.annotate('$r=%i$' % r, xy=(r/3,1.5))
except ValueError:
print('Could not find period, check a < N and have no common factors.')
```
## 2. The Solution
Shor’s solution was to use [quantum phase estimation](./quantum-phase-estimation.html) on the unitary operator:
$$ U|y\rangle \equiv |ay \bmod N \rangle $$
To see how this is helpful, let’s work out what an eigenstate of U might look like. If we started in the state $|1\rangle$, we can see that each successive application of U will multiply the state of our register by $a \pmod N$, and after $r$ applications we will arrive at the state $|1\rangle$ again. For example with $a = 3$ and $N = 35$:
$$\begin{aligned}
U|1\rangle &= |3\rangle & \\
U^2|1\rangle &= |9\rangle \\
U^3|1\rangle &= |27\rangle \\
& \vdots \\
U^{(r-1)}|1\rangle &= |12\rangle \\
U^r|1\rangle &= |1\rangle
\end{aligned}$$
```
ax.set(xlabel='Number of applications of U', ylabel='End state of register',
title="Effect of Successive Applications of U")
fig
```
So a superposition of the states in this cycle ($|u_0\rangle$) would be an eigenstate of $U$:
$$|u_0\rangle = \tfrac{1}{\sqrt{r}}\sum_{k=0}^{r-1}{|a^k \bmod N\rangle} $$
<details>
<summary>Click to Expand: Example with $a = 3$ and $N=35$</summary>
$$\begin{aligned}
|u_0\rangle &= \tfrac{1}{\sqrt{12}}(|1\rangle + |3\rangle + |9\rangle \dots + |4\rangle + |12\rangle) \\[10pt]
U|u_0\rangle &= \tfrac{1}{\sqrt{12}}(U|1\rangle + U|3\rangle + U|9\rangle \dots + U|4\rangle + U|12\rangle) \\[10pt]
&= \tfrac{1}{\sqrt{12}}(|3\rangle + |9\rangle + |27\rangle \dots + |12\rangle + |1\rangle) \\[10pt]
&= |u_0\rangle
\end{aligned}$$
</details>
This eigenstate has an eigenvalue of 1, which isn’t very interesting. A more interesting eigenstate could be one in which the phase is different for each of these computational basis states. Specifically, let’s look at the case in which the phase of the $k$th state is proportional to $k$:
$$\begin{aligned}
|u_1\rangle &= \tfrac{1}{\sqrt{r}}\sum_{k=0}^{r-1}{e^{-\tfrac{2\pi i k}{r}}|a^k \bmod N\rangle}\\[10pt]
U|u_1\rangle &= e^{\tfrac{2\pi i}{r}}|u_1\rangle
\end{aligned}
$$
<details>
<summary>Click to Expand: Example with $a = 3$ and $N=35$</summary>
$$\begin{aligned}
|u_1\rangle &= \tfrac{1}{\sqrt{12}}(|1\rangle + e^{-\tfrac{2\pi i}{12}}|3\rangle + e^{-\tfrac{4\pi i}{12}}|9\rangle \dots + e^{-\tfrac{20\pi i}{12}}|4\rangle + e^{-\tfrac{22\pi i}{12}}|12\rangle) \\[10pt]
U|u_1\rangle &= \tfrac{1}{\sqrt{12}}(|3\rangle + e^{-\tfrac{2\pi i}{12}}|9\rangle + e^{-\tfrac{4\pi i}{12}}|27\rangle \dots + e^{-\tfrac{20\pi i}{12}}|12\rangle + e^{-\tfrac{22\pi i}{12}}|1\rangle) \\[10pt]
U|u_1\rangle &= e^{\tfrac{2\pi i}{12}}\cdot\tfrac{1}{\sqrt{12}}(e^{\tfrac{-2\pi i}{12}}|3\rangle + e^{-\tfrac{4\pi i}{12}}|9\rangle + e^{-\tfrac{6\pi i}{12}}|27\rangle \dots + e^{-\tfrac{22\pi i}{12}}|12\rangle + e^{-\tfrac{24\pi i}{12}}|1\rangle) \\[10pt]
U|u_1\rangle &= e^{\tfrac{2\pi i}{12}}|u_1\rangle
\end{aligned}$$
(We can see $r = 12$ appears in the denominator of the phase.)
</details>
This is a particularly interesting eigenvalue as it contains $r$. In fact, $r$ has to be included to make sure the phase differences between the $r$ computational basis states are equal. This is not the only eigenstate with this behaviour; to generalise this further, we can multiply an integer, $s$, to this phase difference, which will show up in our eigenvalue:
$$\begin{aligned}
|u_s\rangle &= \tfrac{1}{\sqrt{r}}\sum_{k=0}^{r-1}{e^{-\tfrac{2\pi i s k}{r}}|a^k \bmod N\rangle}\\[10pt]
U|u_s\rangle &= e^{\tfrac{2\pi i s}{r}}|u_s\rangle
\end{aligned}
$$
<details>
<summary>Click to Expand: Example with $a = 3$ and $N=35$</summary>
$$\begin{aligned}
|u_s\rangle &= \tfrac{1}{\sqrt{12}}(|1\rangle + e^{-\tfrac{2\pi i s}{12}}|3\rangle + e^{-\tfrac{4\pi i s}{12}}|9\rangle \dots + e^{-\tfrac{20\pi i s}{12}}|4\rangle + e^{-\tfrac{22\pi i s}{12}}|12\rangle) \\[10pt]
U|u_s\rangle &= \tfrac{1}{\sqrt{12}}(|3\rangle + e^{-\tfrac{2\pi i s}{12}}|9\rangle + e^{-\tfrac{4\pi i s}{12}}|27\rangle \dots + e^{-\tfrac{20\pi i s}{12}}|12\rangle + e^{-\tfrac{22\pi i s}{12}}|1\rangle) \\[10pt]
U|u_s\rangle &= e^{\tfrac{2\pi i s}{12}}\cdot\tfrac{1}{\sqrt{12}}(e^{-\tfrac{2\pi i s}{12}}|3\rangle + e^{-\tfrac{4\pi i s}{12}}|9\rangle + e^{-\tfrac{6\pi i s}{12}}|27\rangle \dots + e^{-\tfrac{22\pi i s}{12}}|12\rangle + e^{-\tfrac{24\pi i s}{12}}|1\rangle) \\[10pt]
U|u_s\rangle &= e^{\tfrac{2\pi i s}{12}}|u_s\rangle
\end{aligned}$$
</details>
We now have a unique eigenstate for each integer value of $s$ where $$0 \leq s \leq r-1.$$ Very conveniently, if we sum up all these eigenstates, the different phases cancel out all computational basis states except $|1\rangle$:
$$ \tfrac{1}{\sqrt{r}}\sum_{s=0}^{r-1} |u_s\rangle = |1\rangle$$
<details>
<summary>Click to Expand: Example with $a = 7$ and $N=15$</summary>
For this, we will look at a smaller example where $a = 7$ and $N=15$. In this case $r=4$:
$$\begin{aligned}
\tfrac{1}{2}(\quad|u_0\rangle &= \tfrac{1}{2}(|1\rangle \hphantom{e^{-\tfrac{2\pi i}{12}}}+ |7\rangle \hphantom{e^{-\tfrac{12\pi i}{12}}} + |4\rangle \hphantom{e^{-\tfrac{12\pi i}{12}}} + |13\rangle)\dots \\[10pt]
+ |u_1\rangle &= \tfrac{1}{2}(|1\rangle + e^{-\tfrac{2\pi i}{4}}|7\rangle + e^{-\tfrac{\hphantom{1}4\pi i}{4}}|4\rangle + e^{-\tfrac{\hphantom{1}6\pi i}{4}}|13\rangle)\dots \\[10pt]
+ |u_2\rangle &= \tfrac{1}{2}(|1\rangle + e^{-\tfrac{4\pi i}{4}}|7\rangle + e^{-\tfrac{\hphantom{1}8\pi i}{4}}|4\rangle + e^{-\tfrac{12\pi i}{4}}|13\rangle)\dots \\[10pt]
+ |u_3\rangle &= \tfrac{1}{2}(|1\rangle + e^{-\tfrac{6\pi i}{4}}|7\rangle + e^{-\tfrac{12\pi i}{4}}|4\rangle + e^{-\tfrac{18\pi i}{4}}|13\rangle)\quad) = |1\rangle \\[10pt]
\end{aligned}$$
</details>
Since the computational basis state $|1\rangle$ is a superposition of these eigenstates, which means if we do QPE on $U$ using the state $|1\rangle$, we will measure a phase:
$$\phi = \frac{s}{r}$$
Where $s$ is a random integer between $0$ and $r-1$. We finally use the [continued fractions](https://en.wikipedia.org/wiki/Continued_fraction) algorithm on $\phi$ to find $r$. The circuit diagram looks like this (note that this diagram uses Qiskit's qubit ordering convention):
<img src="images/shor_circuit_1.svg">
We will next demonstrate Shor’s algorithm using Qiskit’s simulators. For this demonstration we will provide the circuits for $U$ without explanation, but in section 4 we will discuss how circuits for $U^{2^j}$ can be constructed efficiently.
## 3. Qiskit Implementation
In this example we will solve the period finding problem for $a=7$ and $N=15$. We provide the circuits for $U$ where:
$$U|y\rangle = |ay\bmod 15\rangle $$
without explanation. To create $U^x$, we will simply repeat the circuit $x$ times. In the next section we will discuss a general method for creating these circuits efficiently. The function `c_amod15` returns the controlled-U gate for `a`, repeated `power` times.
```
def c_amod15(a, power):
"""Controlled multiplication by a mod 15"""
if a not in [2,4,7,8,11,13]:
raise ValueError("'a' must be 2,4,7,8,11 or 13")
U = QuantumCircuit(4)
for iteration in range(power):
if a in [2,13]:
U.swap(0,1)
U.swap(1,2)
U.swap(2,3)
if a in [7,8]:
U.swap(2,3)
U.swap(1,2)
U.swap(0,1)
if a in [4, 11]:
U.swap(1,3)
U.swap(0,2)
if a in [7,11,13]:
for q in range(4):
U.x(q)
U = U.to_gate()
U.name = "%i^%i mod 15" % (a, power)
c_U = U.control()
return c_U
```
We will use 8 counting qubits:
```
# Specify variables
n_count = 8 # number of counting qubits
a = 7
```
We also import the circuit for the QFT (you can read more about the QFT in the [quantum Fourier transform chapter](./quantum-fourier-transform.html#generalqft)):
```
def qft_dagger(n):
"""n-qubit QFTdagger the first n qubits in circ"""
qc = QuantumCircuit(n)
# Don't forget the Swaps!
for qubit in range(n//2):
qc.swap(qubit, n-qubit-1)
for j in range(n):
for m in range(j):
qc.cp(-np.pi/float(2**(j-m)), m, j)
qc.h(j)
qc.name = "QFT†"
return qc
```
With these building blocks we can easily construct the circuit for Shor's algorithm:
```
# Create QuantumCircuit with n_count counting qubits
# plus 4 qubits for U to act on
qc = QuantumCircuit(n_count + 4, n_count)
# Initialize counting qubits
# in state |+>
for q in range(n_count):
qc.h(q)
# And auxiliary register in state |1>
qc.x(3+n_count)
# Do controlled-U operations
for q in range(n_count):
qc.append(c_amod15(a, 2**q),
[q] + [i+n_count for i in range(4)])
# Do inverse-QFT
qc.append(qft_dagger(n_count), range(n_count))
# Measure circuit
qc.measure(range(n_count), range(n_count))
qc.draw(fold=-1) # -1 means 'do not fold'
```
Let's see what results we measure:
```
aer_sim = Aer.get_backend('aer_simulator')
t_qc = transpile(qc, aer_sim)
results = aer_sim.run(t_qc).result()
counts = results.get_counts()
plot_histogram(counts)
```
Since we have 8 qubits, these results correspond to measured phases of:
```
rows, measured_phases = [], []
for output in counts:
decimal = int(output, 2) # Convert (base 2) string to decimal
phase = decimal/(2**n_count) # Find corresponding eigenvalue
measured_phases.append(phase)
# Add these values to the rows in our table:
rows.append([f"{output}(bin) = {decimal:>3}(dec)",
f"{decimal}/{2**n_count} = {phase:.2f}"])
# Print the rows in a table
headers=["Register Output", "Phase"]
df = pd.DataFrame(rows, columns=headers)
print(df)
```
We can now use the continued fractions algorithm to attempt to find $s$ and $r$. Python has this functionality built in: We can use the `fractions` module to turn a float into a `Fraction` object, for example:
```
Fraction(0.666)
```
Because this gives fractions that return the result exactly (in this case, `0.6660000...`), this can give gnarly results like the one above. We can use the `.limit_denominator()` method to get the fraction that most closely resembles our float, with denominator below a certain value:
```
# Get fraction that most closely resembles 0.666
# with denominator < 15
Fraction(0.666).limit_denominator(15)
```
Much nicer! The order (r) must be less than N, so we will set the maximum denominator to be `15`:
```
rows = []
for phase in measured_phases:
frac = Fraction(phase).limit_denominator(15)
rows.append([phase, f"{frac.numerator}/{frac.denominator}", frac.denominator])
# Print as a table
headers=["Phase", "Fraction", "Guess for r"]
df = pd.DataFrame(rows, columns=headers)
print(df)
```
We can see that two of the measured eigenvalues provided us with the correct result: $r=4$, and we can see that Shor’s algorithm has a chance of failing. These bad results are because $s = 0$, or because $s$ and $r$ are not coprime and instead of $r$ we are given a factor of $r$. The easiest solution to this is to simply repeat the experiment until we get a satisfying result for $r$.
### Quick Exercise
- Modify the circuit above for values of $a = 2, 8, 11$ and $13$. What results do you get and why?
## 4. Modular Exponentiation
You may have noticed that the method of creating the $U^{2^j}$ gates by repeating $U$ grows exponentially with $j$ and will not result in a polynomial time algorithm. We want a way to create the operator:
$$ U^{2^j}|y\rangle = |a^{2^j}y \bmod N \rangle $$
that grows polynomially with $j$. Fortunately, calculating:
$$ a^{2^j} \bmod N$$
efficiently is possible. Classical computers can use an algorithm known as _repeated squaring_ to calculate an exponential. In our case, since we are only dealing with exponentials of the form $2^j$, the repeated squaring algorithm becomes very simple:
```
def a2jmodN(a, j, N):
"""Compute a^{2^j} (mod N) by repeated squaring"""
for i in range(j):
a = np.mod(a**2, N)
return a
a2jmodN(7, 2049, 53)
```
If an efficient algorithm is possible in Python, then we can use the same algorithm on a quantum computer. Unfortunately, despite scaling polynomially with $j$, modular exponentiation circuits are not straightforward and are the bottleneck in Shor’s algorithm. A beginner-friendly implementation can be found in reference [1].
## 5. Factoring from Period Finding
Not all factoring problems are difficult; we can spot an even number instantly and know that one of its factors is 2. In fact, there are [specific criteria](https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.186-4.pdf#%5B%7B%22num%22%3A127%2C%22gen%22%3A0%7D%2C%7B%22name%22%3A%22XYZ%22%7D%2C70%2C223%2C0%5D) for choosing numbers that are difficult to factor, but the basic idea is to choose the product of two large prime numbers.
A general factoring algorithm will first check to see if there is a shortcut to factoring the integer (is the number even? Is the number of the form $N = a^b$?), before using Shor’s period finding for the worst-case scenario. Since we aim to focus on the quantum part of the algorithm, we will jump straight to the case in which N is the product of two primes.
### Example: Factoring 15
To see an example of factoring on a small number of qubits, we will factor 15, which we all know is the product of the not-so-large prime numbers 3 and 5.
```
N = 15
```
The first step is to choose a random number, $a$, between $1$ and $N-1$:
```
np.random.seed(1) # This is to make sure we get reproduceable results
a = randint(2, 15)
print(a)
```
Next we quickly check it isn't already a non-trivial factor of $N$:
```
from math import gcd # greatest common divisor
gcd(a, N)
```
Great. Next, we do Shor's order finding algorithm for `a = 7` and `N = 15`. Remember that the phase we measure will be $s/r$ where:
$$ a^r \bmod N = 1 $$
and $s$ is a random integer between 0 and $r-1$.
```
def qpe_amod15(a):
n_count = 8
qc = QuantumCircuit(4+n_count, n_count)
for q in range(n_count):
qc.h(q) # Initialize counting qubits in state |+>
qc.x(3+n_count) # And auxiliary register in state |1>
for q in range(n_count): # Do controlled-U operations
qc.append(c_amod15(a, 2**q),
[q] + [i+n_count for i in range(4)])
qc.append(qft_dagger(n_count), range(n_count)) # Do inverse-QFT
qc.measure(range(n_count), range(n_count))
# Simulate Results
aer_sim = Aer.get_backend('aer_simulator')
# Setting memory=True below allows us to see a list of each sequential reading
t_qc = transpile(qc, aer_sim)
result = aer_sim.run(t_qc, shots=1, memory=True).result()
readings = result.get_memory()
print("Register Reading: " + readings[0])
phase = int(readings[0],2)/(2**n_count)
print("Corresponding Phase: %f" % phase)
return phase
```
From this phase, we can easily find a guess for $r$:
```
phase = qpe_amod15(a) # Phase = s/r
Fraction(phase).limit_denominator(15) # Denominator should (hopefully!) tell us r
frac = Fraction(phase).limit_denominator(15)
s, r = frac.numerator, frac.denominator
print(r)
```
Now we have $r$, we might be able to use this to find a factor of $N$. Since:
$$a^r \bmod N = 1 $$
then:
$$(a^r - 1) \bmod N = 0 $$
which means $N$ must divide $a^r-1$. And if $r$ is also even, then we can write:
$$a^r -1 = (a^{r/2}-1)(a^{r/2}+1)$$
(if $r$ is not even, we cannot go further and must try again with a different value for $a$). There is then a high probability that the greatest common divisor of $N$ and either $a^{r/2}-1$, or $a^{r/2}+1$ is a proper factor of $N$ [2]:
```
guesses = [gcd(a**(r//2)-1, N), gcd(a**(r//2)+1, N)]
print(guesses)
```
The cell below repeats the algorithm until at least one factor of 15 is found. You should try re-running the cell a few times to see how it behaves.
```
a = 7
factor_found = False
attempt = 0
while not factor_found:
attempt += 1
print("\nAttempt %i:" % attempt)
phase = qpe_amod15(a) # Phase = s/r
frac = Fraction(phase).limit_denominator(N) # Denominator should (hopefully!) tell us r
r = frac.denominator
print("Result: r = %i" % r)
if phase != 0:
# Guesses for factors are gcd(x^{r/2} ±1 , 15)
guesses = [gcd(a**(r//2)-1, N), gcd(a**(r//2)+1, N)]
print("Guessed Factors: %i and %i" % (guesses[0], guesses[1]))
for guess in guesses:
if guess not in [1,N] and (N % guess) == 0: # Check to see if guess is a factor
print("*** Non-trivial factor found: %i ***" % guess)
factor_found = True
```
## 6. References
1. Stephane Beauregard, _Circuit for Shor's algorithm using 2n+3 qubits,_ [arXiv:quant-ph/0205095](https://arxiv.org/abs/quant-ph/0205095)
2. M. Nielsen and I. Chuang, _Quantum Computation and Quantum Information,_ Cambridge Series on Information and the Natural Sciences (Cambridge University Press, Cambridge, 2000). (Page 633)
```
import qiskit.tools.jupyter
%qiskit_version_table
```
| true |
code
| 0.597549 | null | null | null | null |
|
# REINFORCE in TensorFlow
Just like we did before for Q-learning, this time we'll design a TensorFlow network to learn `CartPole-v0` via policy gradient (REINFORCE).
Most of the code in this notebook is taken from approximate Q-learning, so you'll find it more or less familiar and even simpler.
```
import sys, os
if 'google.colab' in sys.modules:
%tensorflow_version 1.x
if not os.path.exists('.setup_complete'):
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/spring20/setup_colab.sh -O- | bash
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/coursera/grading.py -O ../grading.py
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/coursera/week5_policy_based/submit.py
!touch .setup_complete
# This code creates a virtual display to draw game images on.
# It will have no effect if your machine has a monitor.
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY")) == 0:
!bash ../xvfb start
os.environ['DISPLAY'] = ':1'
import gym
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
A caveat: we have received reports that the following cell may crash with `NameError: name 'base' is not defined`. The [suggested workaround](https://www.coursera.org/learn/practical-rl/discussions/all/threads/N2Pw652iEemRYQ6W2GuqHg/replies/te3HpQwOQ62tx6UMDoOt2Q/comments/o08gTqelT9KPIE6npX_S3A) is to install `gym==0.14.0` and `pyglet==1.3.2`.
```
env = gym.make("CartPole-v0")
# gym compatibility: unwrap TimeLimit
if hasattr(env, '_max_episode_steps'):
env = env.env
env.reset()
n_actions = env.action_space.n
state_dim = env.observation_space.shape
plt.imshow(env.render("rgb_array"))
```
# Building the network for REINFORCE
For REINFORCE algorithm, we'll need a model that predicts action probabilities given states.
For numerical stability, please __do not include the softmax layer into your network architecture__.
We'll use softmax or log-softmax where appropriate.
```
import tensorflow as tf
sess = tf.InteractiveSession()
# create input variables. We only need <s, a, r> for REINFORCE
ph_states = tf.placeholder('float32', (None,) + state_dim, name="states")
ph_actions = tf.placeholder('int32', name="action_ids")
ph_cumulative_rewards = tf.placeholder('float32', name="cumulative_returns")
from tensorflow import keras
from tensorflow.keras import layers as L
model = keras.models.Sequential()
model.add(L.InputLayer(input_shape=state_dim))
model.add(L.Dense(128, activation='relu'))
model.add(L.Dense(128, activation='relu'))
model.add(L.Dense(n_actions, activation='linear'))
logits = model(ph_states)
policy = tf.nn.softmax(logits)
log_policy = tf.nn.log_softmax(logits)
# Initialize model parameters
sess.run(tf.global_variables_initializer())
def predict_probs(states):
"""
Predict action probabilities given states.
:param states: numpy array of shape [batch, state_shape]
:returns: numpy array of shape [batch, n_actions]
"""
return policy.eval({ph_states: [states]})[0]
```
### Play the game
We can now use our newly built agent to play the game.
```
def generate_session(env, t_max=1000):
"""
Play a full session with REINFORCE agent.
Returns sequences of states, actions, and rewards.
"""
# arrays to record session
states, actions, rewards = [], [], []
s = env.reset()
for t in range(t_max):
# action probabilities array aka pi(a|s)
action_probs = predict_probs(s)
# Sample action with given probabilities.
a = np.random.choice([0, 1], p=action_probs)
new_s, r, done, info = env.step(a)
# record session history to train later
states.append(s)
actions.append(a)
rewards.append(r)
s = new_s
if done:
break
return states, actions, rewards
# test it
states, actions, rewards = generate_session(env)
```
### Computing cumulative rewards
$$
\begin{align*}
G_t &= r_t + \gamma r_{t + 1} + \gamma^2 r_{t + 2} + \ldots \\
&= \sum_{i = t}^T \gamma^{i - t} r_i \\
&= r_t + \gamma * G_{t + 1}
\end{align*}
$$
```
def get_cumulative_rewards(rewards, # rewards at each step
gamma=0.99 # discount for reward
):
"""
take a list of immediate rewards r(s,a) for the whole session
compute cumulative rewards R(s,a) (a.k.a. G(s,a) in Sutton '16)
R_t = r_t + gamma*r_{t+1} + gamma^2*r_{t+2} + ...
The simple way to compute cumulative rewards is to iterate from last to first time tick
and compute R_t = r_t + gamma*R_{t+1} recurrently
You must return an array/list of cumulative rewards with as many elements as in the initial rewards.
"""
rewards = rewards[::-1]
cumulative_rewards = [float(rewards[0])]
for i in rewards[1:]:
cumulative_rewards.append(i + gamma * cumulative_rewards[-1])
return cumulative_rewards[::-1]
assert len(get_cumulative_rewards(range(100))) == 100
assert np.allclose(get_cumulative_rewards([0, 0, 1, 0, 0, 1, 0], gamma=0.9),
[1.40049, 1.5561, 1.729, 0.81, 0.9, 1.0, 0.0])
assert np.allclose(get_cumulative_rewards([0, 0, 1, -2, 3, -4, 0], gamma=0.5),
[0.0625, 0.125, 0.25, -1.5, 1.0, -4.0, 0.0])
assert np.allclose(get_cumulative_rewards([0, 0, 1, 2, 3, 4, 0], gamma=0),
[0, 0, 1, 2, 3, 4, 0])
print("looks good!")
```
#### Loss function and updates
We now need to define objective and update over policy gradient.
Our objective function is
$$ J \approx { 1 \over N } \sum_{s_i,a_i} G(s_i,a_i) $$
REINFORCE defines a way to compute the gradient of the expected reward with respect to policy parameters. The formula is as follows:
$$ \nabla_\theta \hat J(\theta) \approx { 1 \over N } \sum_{s_i, a_i} \nabla_\theta \log \pi_\theta (a_i \mid s_i) \cdot G_t(s_i, a_i) $$
We can abuse Tensorflow's capabilities for automatic differentiation by defining our objective function as follows:
$$ \hat J(\theta) \approx { 1 \over N } \sum_{s_i, a_i} \log \pi_\theta (a_i \mid s_i) \cdot G_t(s_i, a_i) $$
When you compute the gradient of that function with respect to network weights $\theta$, it will become exactly the policy gradient.
```
# This code selects the log-probabilities (log pi(a_i|s_i)) for those actions that were actually played.
indices = tf.stack([tf.range(tf.shape(log_policy)[0]), ph_actions], axis=-1)
log_policy_for_actions = tf.gather_nd(log_policy, indices)
# Policy objective as in the last formula. Please use reduce_mean, not reduce_sum.
# You may use log_policy_for_actions to get log probabilities for actions taken.
# Also recall that we defined ph_cumulative_rewards earlier.
J = tf.reduce_mean(log_policy_for_actions * ph_cumulative_rewards)
```
As a reminder, for a discrete probability distribution (like the one our policy outputs), entropy is defined as:
$$ \operatorname{entropy}(p) = -\sum_{i = 1}^n p_i \cdot \log p_i $$
```
# Entropy regularization. If you don't add it, the policy will quickly deteriorate to
# being deterministic, harming exploration.
entropy = -tf.reduce_sum(policy * log_policy, 1, name='entropy')
# # Maximizing X is the same as minimizing -X, hence the sign.
loss = -(J + 0.1 * entropy)
update = tf.train.AdamOptimizer().minimize(loss)
def train_on_session(states, actions, rewards, t_max=1000):
"""given full session, trains agent with policy gradient"""
cumulative_rewards = get_cumulative_rewards(rewards)
update.run({
ph_states: states,
ph_actions: actions,
ph_cumulative_rewards: cumulative_rewards,
})
return sum(rewards)
# Initialize optimizer parameters
sess.run(tf.global_variables_initializer())
```
### The actual training
```
for i in range(100):
rewards = [train_on_session(*generate_session(env)) for _ in range(100)] # generate new sessions
print("mean reward: %.3f" % (np.mean(rewards)))
if np.mean(rewards) > 300:
print("You Win!") # but you can train even further
break
```
### Results & video
```
# Record sessions
import gym.wrappers
with gym.wrappers.Monitor(gym.make("CartPole-v0"), directory="videos", force=True) as env_monitor:
sessions = [generate_session(env_monitor) for _ in range(100)]
# Show video. This may not work in some setups. If it doesn't
# work for you, you can download the videos and view them locally.
from pathlib import Path
from IPython.display import HTML
video_names = sorted([s for s in Path('videos').iterdir() if s.suffix == '.mp4'])
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format(video_names[-1])) # You can also try other indices
from submit import submit_cartpole
submit_cartpole(generate_session, "rahulpathak263@gmail.com", "xKABD2rwFs5y19Zd")
```
That's all, thank you for your attention!
Not having enough? There's an actor-critic waiting for you in the honor section. But make sure you've seen the videos first.
| true |
code
| 0.648299 | null | null | null | null |
|
# TensorFlow Tutorial #03-B
# Layers API
by [Magnus Erik Hvass Pedersen](http://www.hvass-labs.org/)
/ [GitHub](https://github.com/Hvass-Labs/TensorFlow-Tutorials) / [Videos on YouTube](https://www.youtube.com/playlist?list=PL9Hr9sNUjfsmEu1ZniY0XpHSzl5uihcXZ)
## Introduction
It is important to use a builder API when constructing Neural Networks in TensorFlow because it makes it easier to implement and modify the source-code. This also lowers the risk of bugs.
Many of the other tutorials used the TensorFlow builder API called PrettyTensor for easy construction of Neural Networks. But there are several other builder APIs available for TensorFlow. PrettyTensor was used in these tutorials, because at the time in mid-2016, PrettyTensor was the most complete and polished builder API available for TensorFlow. But PrettyTensor is only developed by a single person working at Google and although it has some unique and elegant features, it is possible that it may become deprecated in the future.
This tutorial is about a small builder API that has recently been added to TensorFlow version 1.1. It is simply called *Layers* or the *Layers API* or by its Python name `tf.layers`. This builder API is automatically installed as part of TensorFlow, so you no longer have to install a separate Python package as was needed with PrettyTensor.
This tutorial is very similar to Tutorial #03 on PrettyTensor and shows how to implement the same Convolutional Neural Network using the Layers API. It is recommended that you are familiar with Tutorial #02 on Convolutional Neural Networks.
## Flowchart
The following chart shows roughly how the data flows in the Convolutional Neural Network that is implemented below. See Tutorial #02 for a more detailed description of convolution.

The input image is processed in the first convolutional layer using the filter-weights. This results in 16 new images, one for each filter in the convolutional layer. The images are also down-sampled using max-pooling so the image resolution is decreased from 28x28 to 14x14.
These 16 smaller images are then processed in the second convolutional layer. We need filter-weights for each of these 16 channels, and we need filter-weights for each output channel of this layer. There are 36 output channels so there are a total of 16 x 36 = 576 filters in the second convolutional layer. The resulting images are also down-sampled using max-pooling to 7x7 pixels.
The output of the second convolutional layer is 36 images of 7x7 pixels each. These are then flattened to a single vector of length 7 x 7 x 36 = 1764, which is used as the input to a fully-connected layer with 128 neurons (or elements). This feeds into another fully-connected layer with 10 neurons, one for each of the classes, which is used to determine the class of the image, that is, which number is depicted in the image.
The convolutional filters are initially chosen at random, so the classification is done randomly. The error between the predicted and true class of the input image is measured as the so-called cross-entropy. The optimizer then automatically propagates this error back through the Convolutional Network using the chain-rule of differentiation and updates the filter-weights so as to improve the classification error. This is done iteratively thousands of times until the classification error is sufficiently low.
These particular filter-weights and intermediate images are the results of one optimization run and may look different if you re-run this Notebook.
Note that the computation in TensorFlow is actually done on a batch of images instead of a single image, which makes the computation more efficient. This means the flowchart actually has one more data-dimension when implemented in TensorFlow.
## Imports
```
%matplotlib inline
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
from sklearn.metrics import confusion_matrix
import math
```
This was developed using Python 3.6 (Anaconda) and TensorFlow version:
```
tf.__version__
```
## Load Data
The MNIST data-set is about 12 MB and will be downloaded automatically if it is not located in the given path.
```
from tensorflow.examples.tutorials.mnist import input_data
data = input_data.read_data_sets('data/MNIST/', one_hot=True)
```
The MNIST data-set has now been loaded and consists of 70,000 images and associated labels (i.e. classifications of the images). The data-set is split into 3 mutually exclusive sub-sets. We will only use the training and test-sets in this tutorial.
```
print("Size of:")
print("- Training-set:\t\t{}".format(len(data.train.labels)))
print("- Test-set:\t\t{}".format(len(data.test.labels)))
print("- Validation-set:\t{}".format(len(data.validation.labels)))
```
The class-labels are One-Hot encoded, which means that each label is a vector with 10 elements, all of which are zero except for one element. The index of this one element is the class-number, that is, the digit shown in the associated image. We also need the class-numbers as integers for the test-set, so we calculate it now.
```
data.test.cls = np.argmax(data.test.labels, axis=1)
```
## Data Dimensions
The data dimensions are used in several places in the source-code below. They are defined once so we can use these variables instead of numbers throughout the source-code below.
```
# We know that MNIST images are 28 pixels in each dimension.
img_size = 28
# Images are stored in one-dimensional arrays of this length.
img_size_flat = img_size * img_size
# Tuple with height and width of images used to reshape arrays.
img_shape = (img_size, img_size)
# Number of colour channels for the images: 1 channel for gray-scale.
num_channels = 1
# Number of classes, one class for each of 10 digits.
num_classes = 10
```
### Helper-function for plotting images
Function used to plot 9 images in a 3x3 grid, and writing the true and predicted classes below each image.
```
def plot_images(images, cls_true, cls_pred=None):
assert len(images) == len(cls_true) == 9
# Create figure with 3x3 sub-plots.
fig, axes = plt.subplots(3, 3)
fig.subplots_adjust(hspace=0.3, wspace=0.3)
for i, ax in enumerate(axes.flat):
# Plot image.
ax.imshow(images[i].reshape(img_shape), cmap='binary')
# Show true and predicted classes.
if cls_pred is None:
xlabel = "True: {0}".format(cls_true[i])
else:
xlabel = "True: {0}, Pred: {1}".format(cls_true[i], cls_pred[i])
# Show the classes as the label on the x-axis.
ax.set_xlabel(xlabel)
# Remove ticks from the plot.
ax.set_xticks([])
ax.set_yticks([])
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show()
```
### Plot a few images to see if data is correct
```
# Get the first images from the test-set.
images = data.test.images[0:9]
# Get the true classes for those images.
cls_true = data.test.cls[0:9]
# Plot the images and labels using our helper-function above.
plot_images(images=images, cls_true=cls_true)
```
## TensorFlow Graph
The entire purpose of TensorFlow is to have a so-called computational graph that can be executed much more efficiently than if the same calculations were to be performed directly in Python. TensorFlow can be more efficient than NumPy because TensorFlow knows the entire computation graph that must be executed, while NumPy only knows the computation of a single mathematical operation at a time.
TensorFlow can also automatically calculate the gradients that are needed to optimize the variables of the graph so as to make the model perform better. This is because the graph is a combination of simple mathematical expressions so the gradient of the entire graph can be calculated using the chain-rule for derivatives.
TensorFlow can also take advantage of multi-core CPUs as well as GPUs - and Google has even built special chips just for TensorFlow which are called TPUs (Tensor Processing Units) and are even faster than GPUs.
A TensorFlow graph consists of the following parts which will be detailed below:
* Placeholder variables used for inputting data to the graph.
* Variables that are going to be optimized so as to make the convolutional network perform better.
* The mathematical formulas for the convolutional neural network.
* A so-called cost-measure or loss-function that can be used to guide the optimization of the variables.
* An optimization method which updates the variables.
In addition, the TensorFlow graph may also contain various debugging statements e.g. for logging data to be displayed using TensorBoard, which is not covered in this tutorial.
## Placeholder variables
Placeholder variables serve as the input to the TensorFlow computational graph that we may change each time we execute the graph. We call this feeding the placeholder variables and it is demonstrated further below.
First we define the placeholder variable for the input images. This allows us to change the images that are input to the TensorFlow graph. This is a so-called tensor, which just means that it is a multi-dimensional array. The data-type is set to `float32` and the shape is set to `[None, img_size_flat]`, where `None` means that the tensor may hold an arbitrary number of images with each image being a vector of length `img_size_flat`.
```
x = tf.placeholder(tf.float32, shape=[None, img_size_flat], name='x')
```
The convolutional layers expect `x` to be encoded as a 4-dim tensor so we have to reshape it so its shape is instead `[num_images, img_height, img_width, num_channels]`. Note that `img_height == img_width == img_size` and `num_images` can be inferred automatically by using -1 for the size of the first dimension. So the reshape operation is:
```
x_image = tf.reshape(x, [-1, img_size, img_size, num_channels])
```
Next we have the placeholder variable for the true labels associated with the images that were input in the placeholder variable `x`. The shape of this placeholder variable is `[None, num_classes]` which means it may hold an arbitrary number of labels and each label is a vector of length `num_classes` which is 10 in this case.
```
y_true = tf.placeholder(tf.float32, shape=[None, num_classes], name='y_true')
```
We could also have a placeholder variable for the class-number, but we will instead calculate it using argmax. Note that this is a TensorFlow operator so nothing is calculated at this point.
```
y_true_cls = tf.argmax(y_true, dimension=1)
```
## PrettyTensor Implementation
This section shows the implementation of a Convolutional Neural Network using PrettyTensor taken from Tutorial #03 so it can be compared to the implementation using the Layers API below. This code has been enclosed in an `if False:` block so it does not run here.
The basic idea is to wrap the input tensor `x_image` in a PrettyTensor object which has helper-functions for adding new computational layers so as to create an entire Convolutional Neural Network. This is a fairly simple and elegant syntax.
```
if False:
x_pretty = pt.wrap(x_image)
with pt.defaults_scope(activation_fn=tf.nn.relu):
y_pred, loss = x_pretty.\
conv2d(kernel=5, depth=16, name='layer_conv1').\
max_pool(kernel=2, stride=2).\
conv2d(kernel=5, depth=36, name='layer_conv2').\
max_pool(kernel=2, stride=2).\
flatten().\
fully_connected(size=128, name='layer_fc1').\
softmax_classifier(num_classes=num_classes, labels=y_true)
```
## Layers Implementation
We now implement the same Convolutional Neural Network using the Layers API that is included in TensorFlow version 1.1. This requires more code than PrettyTensor, although a lot of the following are just comments.
We use the `net`-variable to refer to the last layer while building the Neural Network. This makes it easy to add or remove layers in the code if you want to experiment. First we set the `net`-variable to the reshaped input image.
```
net = x_image
```
The input image is then input to the first convolutional layer, which has 16 filters each of size 5x5 pixels. The activation-function is the Rectified Linear Unit (ReLU) described in more detail in Tutorial #02.
```
net = tf.layers.conv2d(inputs=net, name='layer_conv1', padding='same',
filters=16, kernel_size=5, activation=tf.nn.relu)
```
One of the advantages of constructing neural networks in this fashion, is that we can now easily pull out a reference to a layer. This was more complicated in PrettyTensor.
Further below we want to plot the output of the first convolutional layer, so we create another variable for holding a reference to that layer.
```
layer_conv1 = net
```
We now do the max-pooling on the output of the convolutional layer. This was also described in more detail in Tutorial #02.
```
net = tf.layers.max_pooling2d(inputs=net, pool_size=2, strides=2)
```
We now add the second convolutional layer which has 36 filters each with 5x5 pixels, and a ReLU activation function again.
```
net = tf.layers.conv2d(inputs=net, name='layer_conv2', padding='same',
filters=36, kernel_size=5, activation=tf.nn.relu)
```
We also want to plot the output of this convolutional layer, so we keep a reference for later use.
```
layer_conv2 = net
```
The output of the second convolutional layer is also max-pooled for down-sampling the images.
```
net = tf.layers.max_pooling2d(inputs=net, pool_size=2, strides=2)
```
The tensors that are being output by this max-pooling are 4-rank, as can be seen from this:
```
net
```
Next we want to add fully-connected layers to the Neural Network, but these require 2-rank tensors as input, so we must first flatten the tensors.
The `tf.layers` API was first located in `tf.contrib.layers` before it was moved into TensorFlow Core. But even though it has taken the TensorFlow developers a year to move these fairly simple functions, they have somehow forgotten to move the even simpler `flatten()` function. So we still need to use the one in `tf.contrib.layers`.
```
net = tf.contrib.layers.flatten(net)
# This should eventually be replaced by:
# net = tf.layers.flatten(net)
```
This has now flattened the data to a 2-rank tensor, as can be seen from this:
```
net
```
We can now add fully-connected layers to the neural network. These are called *dense* layers in the Layers API.
```
net = tf.layers.dense(inputs=net, name='layer_fc1',
units=128, activation=tf.nn.relu)
```
We need the neural network to classify the input images into 10 different classes. So the final fully-connected layer has `num_classes=10` output neurons.
```
net = tf.layers.dense(inputs=net, name='layer_fc_out',
units=num_classes, activation=None)
```
The output of the final fully-connected layer are sometimes called logits, so we have a convenience variable with that name.
```
logits = net
```
We use the softmax function to 'squash' the outputs so they are between zero and one, and so they sum to one.
```
y_pred = tf.nn.softmax(logits=logits)
```
This tells us how likely the neural network thinks the input image is of each possible class. The one that has the highest value is considered the most likely so its index is taken to be the class-number.
```
y_pred_cls = tf.argmax(y_pred, dimension=1)
```
We have now created the exact same Convolutional Neural Network in a few lines of code that required many complex lines of code in the direct TensorFlow implementation.
The Layers API is perhaps not as elegant as PrettyTensor, but it has some other advantages, e.g. that we can more easily refer to intermediate layers, and it is also easier to construct neural networks with branches and multiple outputs using the Layers API.
### Loss-Function to be Optimized
To make the model better at classifying the input images, we must somehow change the variables of the Convolutional Neural Network.
The cross-entropy is a performance measure used in classification. The cross-entropy is a continuous function that is always positive and if the predicted output of the model exactly matches the desired output then the cross-entropy equals zero. The goal of optimization is therefore to minimize the cross-entropy so it gets as close to zero as possible by changing the variables of the model.
TensorFlow has a function for calculating the cross-entropy, which uses the values of the `logits`-layer because it also calculates the softmax internally, so as to to improve numerical stability.
```
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=y_true, logits=logits)
```
We have now calculated the cross-entropy for each of the image classifications so we have a measure of how well the model performs on each image individually. But in order to use the cross-entropy to guide the optimization of the model's variables we need a single scalar value, so we simply take the average of the cross-entropy for all the image classifications.
```
loss = tf.reduce_mean(cross_entropy)
```
### Optimization Method
Now that we have a cost measure that must be minimized, we can then create an optimizer. In this case it is the Adam optimizer with a learning-rate of 1e-4.
Note that optimization is not performed at this point. In fact, nothing is calculated at all, we just add the optimizer-object to the TensorFlow graph for later execution.
```
optimizer = tf.train.AdamOptimizer(learning_rate=1e-4).minimize(loss)
```
### Classification Accuracy
We need to calculate the classification accuracy so we can report progress to the user.
First we create a vector of booleans telling us whether the predicted class equals the true class of each image.
```
correct_prediction = tf.equal(y_pred_cls, y_true_cls)
```
The classification accuracy is calculated by first type-casting the vector of booleans to floats, so that False becomes 0 and True becomes 1, and then taking the average of these numbers.
```
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
```
### Getting the Weights
Further below, we want to plot the weights of the convolutional layers. In the TensorFlow implementation we had created the variables ourselves so we could just refer to them directly. But when the network is constructed using a builder API such as `tf.layers`, all the variables of the layers are created indirectly by the builder API. We therefore have to retrieve the variables from TensorFlow.
First we need a list of the variable names in the TensorFlow graph:
```
for var in tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES):
print(var)
```
Each of the convolutional layers has two variables. For the first convolutional layer they are named `layer_conv1/kernel:0` and `layer_conv1/bias:0`. The `kernel` variables are the ones we want to plot further below.
It is somewhat awkward to get references to these variables, because we have to use the TensorFlow function `get_variable()` which was designed for another purpose; either creating a new variable or re-using an existing variable. The easiest thing is to make the following helper-function.
```
def get_weights_variable(layer_name):
# Retrieve an existing variable named 'kernel' in the scope
# with the given layer_name.
# This is awkward because the TensorFlow function was
# really intended for another purpose.
with tf.variable_scope(layer_name, reuse=True):
variable = tf.get_variable('kernel')
return variable
```
Using this helper-function we can retrieve the variables. These are TensorFlow objects. In order to get the contents of the variables, you must do something like: `contents = session.run(weights_conv1)` as demonstrated further below.
```
weights_conv1 = get_weights_variable(layer_name='layer_conv1')
weights_conv2 = get_weights_variable(layer_name='layer_conv2')
```
## TensorFlow Run
### Create TensorFlow session
Once the TensorFlow graph has been created, we have to create a TensorFlow session which is used to execute the graph.
```
session = tf.Session()
```
### Initialize variables
The variables for the TensorFlow graph must be initialized before we start optimizing them.
```
session.run(tf.global_variables_initializer())
```
### Helper-function to perform optimization iterations
There are 55,000 images in the training-set. It takes a long time to calculate the gradient of the model using all these images. We therefore only use a small batch of images in each iteration of the optimizer.
If your computer crashes or becomes very slow because you run out of RAM, then you may try and lower this number, but you may then need to do more optimization iterations.
```
train_batch_size = 64
```
This function performs a number of optimization iterations so as to gradually improve the variables of the neural network layers. In each iteration, a new batch of data is selected from the training-set and then TensorFlow executes the optimizer using those training samples. The progress is printed every 100 iterations.
```
# Counter for total number of iterations performed so far.
total_iterations = 0
def optimize(num_iterations):
# Ensure we update the global variable rather than a local copy.
global total_iterations
for i in range(total_iterations,
total_iterations + num_iterations):
# Get a batch of training examples.
# x_batch now holds a batch of images and
# y_true_batch are the true labels for those images.
x_batch, y_true_batch = data.train.next_batch(train_batch_size)
# Put the batch into a dict with the proper names
# for placeholder variables in the TensorFlow graph.
feed_dict_train = {x: x_batch,
y_true: y_true_batch}
# Run the optimizer using this batch of training data.
# TensorFlow assigns the variables in feed_dict_train
# to the placeholder variables and then runs the optimizer.
session.run(optimizer, feed_dict=feed_dict_train)
# Print status every 100 iterations.
if i % 100 == 0:
# Calculate the accuracy on the training-set.
acc = session.run(accuracy, feed_dict=feed_dict_train)
# Message for printing.
msg = "Optimization Iteration: {0:>6}, Training Accuracy: {1:>6.1%}"
# Print it.
print(msg.format(i + 1, acc))
# Update the total number of iterations performed.
total_iterations += num_iterations
```
### Helper-function to plot example errors
Function for plotting examples of images from the test-set that have been mis-classified.
```
def plot_example_errors(cls_pred, correct):
# This function is called from print_test_accuracy() below.
# cls_pred is an array of the predicted class-number for
# all images in the test-set.
# correct is a boolean array whether the predicted class
# is equal to the true class for each image in the test-set.
# Negate the boolean array.
incorrect = (correct == False)
# Get the images from the test-set that have been
# incorrectly classified.
images = data.test.images[incorrect]
# Get the predicted classes for those images.
cls_pred = cls_pred[incorrect]
# Get the true classes for those images.
cls_true = data.test.cls[incorrect]
# Plot the first 9 images.
plot_images(images=images[0:9],
cls_true=cls_true[0:9],
cls_pred=cls_pred[0:9])
```
### Helper-function to plot confusion matrix
```
def plot_confusion_matrix(cls_pred):
# This is called from print_test_accuracy() below.
# cls_pred is an array of the predicted class-number for
# all images in the test-set.
# Get the true classifications for the test-set.
cls_true = data.test.cls
# Get the confusion matrix using sklearn.
cm = confusion_matrix(y_true=cls_true,
y_pred=cls_pred)
# Print the confusion matrix as text.
print(cm)
# Plot the confusion matrix as an image.
plt.matshow(cm)
# Make various adjustments to the plot.
plt.colorbar()
tick_marks = np.arange(num_classes)
plt.xticks(tick_marks, range(num_classes))
plt.yticks(tick_marks, range(num_classes))
plt.xlabel('Predicted')
plt.ylabel('True')
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show()
```
### Helper-function for showing the performance
Below is a function for printing the classification accuracy on the test-set.
It takes a while to compute the classification for all the images in the test-set, that's why the results are re-used by calling the above functions directly from this function, so the classifications don't have to be recalculated by each function.
Note that this function can use a lot of computer memory, which is why the test-set is split into smaller batches. If you have little RAM in your computer and it crashes, then you can try and lower the batch-size.
```
# Split the test-set into smaller batches of this size.
test_batch_size = 256
def print_test_accuracy(show_example_errors=False,
show_confusion_matrix=False):
# Number of images in the test-set.
num_test = len(data.test.images)
# Allocate an array for the predicted classes which
# will be calculated in batches and filled into this array.
cls_pred = np.zeros(shape=num_test, dtype=np.int)
# Now calculate the predicted classes for the batches.
# We will just iterate through all the batches.
# There might be a more clever and Pythonic way of doing this.
# The starting index for the next batch is denoted i.
i = 0
while i < num_test:
# The ending index for the next batch is denoted j.
j = min(i + test_batch_size, num_test)
# Get the images from the test-set between index i and j.
images = data.test.images[i:j, :]
# Get the associated labels.
labels = data.test.labels[i:j, :]
# Create a feed-dict with these images and labels.
feed_dict = {x: images,
y_true: labels}
# Calculate the predicted class using TensorFlow.
cls_pred[i:j] = session.run(y_pred_cls, feed_dict=feed_dict)
# Set the start-index for the next batch to the
# end-index of the current batch.
i = j
# Convenience variable for the true class-numbers of the test-set.
cls_true = data.test.cls
# Create a boolean array whether each image is correctly classified.
correct = (cls_true == cls_pred)
# Calculate the number of correctly classified images.
# When summing a boolean array, False means 0 and True means 1.
correct_sum = correct.sum()
# Classification accuracy is the number of correctly classified
# images divided by the total number of images in the test-set.
acc = float(correct_sum) / num_test
# Print the accuracy.
msg = "Accuracy on Test-Set: {0:.1%} ({1} / {2})"
print(msg.format(acc, correct_sum, num_test))
# Plot some examples of mis-classifications, if desired.
if show_example_errors:
print("Example errors:")
plot_example_errors(cls_pred=cls_pred, correct=correct)
# Plot the confusion matrix, if desired.
if show_confusion_matrix:
print("Confusion Matrix:")
plot_confusion_matrix(cls_pred=cls_pred)
```
## Performance before any optimization
The accuracy on the test-set is very low because the variables for the neural network have only been initialized and not optimized at all, so it just classifies the images randomly.
```
print_test_accuracy()
```
## Performance after 1 optimization iteration
The classification accuracy does not improve much from just 1 optimization iteration, because the learning-rate for the optimizer is set very low.
```
optimize(num_iterations=1)
print_test_accuracy()
```
## Performance after 100 optimization iterations
After 100 optimization iterations, the model has significantly improved its classification accuracy.
```
%%time
optimize(num_iterations=99) # We already performed 1 iteration above.
print_test_accuracy(show_example_errors=True)
```
## Performance after 1000 optimization iterations
After 1000 optimization iterations, the model has greatly increased its accuracy on the test-set to more than 90%.
```
%%time
optimize(num_iterations=900) # We performed 100 iterations above.
print_test_accuracy(show_example_errors=True)
```
## Performance after 10,000 optimization iterations
After 10,000 optimization iterations, the model has a classification accuracy on the test-set of about 99%.
```
%%time
optimize(num_iterations=9000) # We performed 1000 iterations above.
print_test_accuracy(show_example_errors=True,
show_confusion_matrix=True)
```
## Visualization of Weights and Layers
### Helper-function for plotting convolutional weights
```
def plot_conv_weights(weights, input_channel=0):
# Assume weights are TensorFlow ops for 4-dim variables
# e.g. weights_conv1 or weights_conv2.
# Retrieve the values of the weight-variables from TensorFlow.
# A feed-dict is not necessary because nothing is calculated.
w = session.run(weights)
# Get the lowest and highest values for the weights.
# This is used to correct the colour intensity across
# the images so they can be compared with each other.
w_min = np.min(w)
w_max = np.max(w)
# Number of filters used in the conv. layer.
num_filters = w.shape[3]
# Number of grids to plot.
# Rounded-up, square-root of the number of filters.
num_grids = math.ceil(math.sqrt(num_filters))
# Create figure with a grid of sub-plots.
fig, axes = plt.subplots(num_grids, num_grids)
# Plot all the filter-weights.
for i, ax in enumerate(axes.flat):
# Only plot the valid filter-weights.
if i<num_filters:
# Get the weights for the i'th filter of the input channel.
# See new_conv_layer() for details on the format
# of this 4-dim tensor.
img = w[:, :, input_channel, i]
# Plot image.
ax.imshow(img, vmin=w_min, vmax=w_max,
interpolation='nearest', cmap='seismic')
# Remove ticks from the plot.
ax.set_xticks([])
ax.set_yticks([])
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show()
```
### Helper-function for plotting the output of a convolutional layer
```
def plot_conv_layer(layer, image):
# Assume layer is a TensorFlow op that outputs a 4-dim tensor
# which is the output of a convolutional layer,
# e.g. layer_conv1 or layer_conv2.
# Create a feed-dict containing just one image.
# Note that we don't need to feed y_true because it is
# not used in this calculation.
feed_dict = {x: [image]}
# Calculate and retrieve the output values of the layer
# when inputting that image.
values = session.run(layer, feed_dict=feed_dict)
# Number of filters used in the conv. layer.
num_filters = values.shape[3]
# Number of grids to plot.
# Rounded-up, square-root of the number of filters.
num_grids = math.ceil(math.sqrt(num_filters))
# Create figure with a grid of sub-plots.
fig, axes = plt.subplots(num_grids, num_grids)
# Plot the output images of all the filters.
for i, ax in enumerate(axes.flat):
# Only plot the images for valid filters.
if i<num_filters:
# Get the output image of using the i'th filter.
img = values[0, :, :, i]
# Plot image.
ax.imshow(img, interpolation='nearest', cmap='binary')
# Remove ticks from the plot.
ax.set_xticks([])
ax.set_yticks([])
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show()
```
### Input Images
Helper-function for plotting an image.
```
def plot_image(image):
plt.imshow(image.reshape(img_shape),
interpolation='nearest',
cmap='binary')
plt.show()
```
Plot an image from the test-set which will be used as an example below.
```
image1 = data.test.images[0]
plot_image(image1)
```
Plot another example image from the test-set.
```
image2 = data.test.images[13]
plot_image(image2)
```
### Convolution Layer 1
Now plot the filter-weights for the first convolutional layer.
Note that positive weights are red and negative weights are blue.
```
plot_conv_weights(weights=weights_conv1)
```
Applying each of these convolutional filters to the first input image gives the following output images, which are then used as input to the second convolutional layer.
```
plot_conv_layer(layer=layer_conv1, image=image1)
```
The following images are the results of applying the convolutional filters to the second image.
```
plot_conv_layer(layer=layer_conv1, image=image2)
```
### Convolution Layer 2
Now plot the filter-weights for the second convolutional layer.
There are 16 output channels from the first conv-layer, which means there are 16 input channels to the second conv-layer. The second conv-layer has a set of filter-weights for each of its input channels. We start by plotting the filter-weigths for the first channel.
Note again that positive weights are red and negative weights are blue.
```
plot_conv_weights(weights=weights_conv2, input_channel=0)
```
There are 16 input channels to the second convolutional layer, so we can make another 15 plots of filter-weights like this. We just make one more with the filter-weights for the second channel.
```
plot_conv_weights(weights=weights_conv2, input_channel=1)
```
It can be difficult to understand and keep track of how these filters are applied because of the high dimensionality.
Applying these convolutional filters to the images that were ouput from the first conv-layer gives the following images.
Note that these are down-sampled to 14 x 14 pixels which is half the resolution of the original input images, because the first convolutional layer was followed by a max-pooling layer with stride 2. Max-pooling is also done after the second convolutional layer, but we retrieve these images before that has been applied.
```
plot_conv_layer(layer=layer_conv2, image=image1)
```
And these are the results of applying the filter-weights to the second image.
```
plot_conv_layer(layer=layer_conv2, image=image2)
```
### Close TensorFlow Session
We are now done using TensorFlow, so we close the session to release its resources.
```
# This has been commented out in case you want to modify and experiment
# with the Notebook without having to restart it.
# session.close()
```
## Conclusion
This tutorial showed how to use the so-called *Layers API* for easily building Convolutional Neural Networks in TensorFlow. The syntax is different and more verbose than that of PrettyTensor. Both builder API's have advantages and disadvantages, but since PrettyTensor is only developed by one person and the Layers API is now an official part of TensorFlow Core, it is possible that PrettyTensor will become deprecated in the future. If this happens, we might hope that some of its unique and elegant features will become integrated into TensorFlow Core as well.
I have been trying to get a clear answer from the TensorFlow developers for almost a year, on which of their APIs will be the main builder API for TensorFlow. They still seem to be undecided and very slow to implement it.
## Exercises
These are a few suggestions for exercises that may help improve your skills with TensorFlow. It is important to get hands-on experience with TensorFlow in order to learn how to use it properly.
You may want to backup this Notebook before making any changes.
* Change the activation function to sigmoid for some of the layers.
* Can you find a simple way of changing the activation function for all the layers?
* Add a dropout-layer after the fully-connected layer. If you want a different probability during training and testing then you will need a placeholder variable and set it in the feed-dict.
* Plot the output of the max-pooling layers instead of the conv-layers.
* Replace the 2x2 max-pooling layers with stride=2 in the convolutional layers. Is there a difference in classification accuracy? What if you optimize it again and again? The difference is random, so how would you measure if there really is a difference? What are the pros and cons of using max-pooling vs. stride in the conv-layer?
* Change the parameters for the layers, e.g. the kernel, depth, size, etc. What is the difference in time usage and classification accuracy?
* Add and remove some convolutional and fully-connected layers.
* What is the simplest network you can design that still performs well?
* Retrieve the bias-values for the convolutional layers and print them. See `get_weights_variable()` for inspiration.
* Remake the program yourself without looking too much at this source-code.
* Explain to a friend how the program works.
## License (MIT)
Copyright (c) 2016-2017 by [Magnus Erik Hvass Pedersen](http://www.hvass-labs.org/)
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
| true |
code
| 0.694613 | null | null | null | null |
|
# bulbea
> Deep Learning based Python Library for Stock Market Prediction and Modelling

A canonical way of importing the `bulbea` module is as follows:
```
import bulbea as bb
```
### `bulbea.Share`
In order to analyse a desired share, we use the `Share` object defined under `bulbea` which considers 2 arguments - *the **source code** for the economic data* and *the **ticker symbol** for a said company*.
```
source, ticker = 'YAHOO', 'INDEX_GSPC'
```
Go ahead and create a `Share` object as follows:
```
share = bb.Share(source, ticker)
```
By default, a `Share` object for a said source and symbol provides you historical data since a company's inception, as a `pandas.DataFrame` object. In order to access the same, use the `Share` object's member variable - `data` as follows:
```
data = share.data
nsamples = 5
data.tail(nsamples)
```
In order to analyse a given attribute, you could plot the same as follows:
```
figsize = (20, 15)
% matplotlib inline
share.plot(figsize = figsize)
share.plot(['Close', 'Adjusted Close'], figsize = figsize)
```
### Statistics
#### Global Mean
In order to plot the **global mean** of the stock, we could do the same as follows:
```
share.plot(figsize = (20, 15), global_mean = True)
```
#### Moving Averages and Bollinger Bands (R)
```
bands = share.bollinger_bands(period = 50, bandwidth = 2)
bands.tail(nsamples)
share.plot(['Close', 'Adjusted Close'], figsize = (20, 15), bollinger_bands = True, period = 100, bandwidth = 2)
```
### Training & Testing
```
from bulbea.learn.evaluation import split
scaler, Xtrain, Xtest, ytrain, ytest = split(share, 'Close', normalize = True)
import numpy as np
Xtrain = np.reshape(Xtrain, (Xtrain.shape[0], Xtrain.shape[1], 1))
Xtest = np.reshape(Xtest, ( Xtest.shape[0], Xtest.shape[1], 1))
```
### Modelling
```
layers = [1, 100, 100, 1] # number of neurons in each layer
nbatch = 512
epochs = 5
nvalidation = 0.05
from bulbea.learn.models import RNN
from bulbea.learn.models.ann import RNNCell
rnn = RNN(layers, cell = RNNCell.LSTM)
```
#### TRAINING
```
rnn.fit(Xtrain, ytrain,
batch_size = nbatch,
nb_epoch = epochs,
validation_split = nvalidation)
```
#### TESTING
```
predicted = rnn.predict(Xtest)
from sklearn.metrics import mean_squared_error
mean_squared_error(ytest, predicted)
from bulbea.entity.share import _plot_bollinger_bands
import pandas as pd
import matplotlib.pyplot as pplt
figsize = (20, 15)
figure = pplt.figure(figsize = figsize)
axes = figure.add_subplot(111)
series = pd.Series(data = scaler.inverse_transform(ytest))
# axes.plot(scaler.inverse_transform(ytest))
axes.plot(scaler.inverse_transform(predicted))
_plot_bollinger_bands(series, axes, bandwidth = 10)
```
### Sentiment Analysis
```
s = bb.sentiment(share)
s
```
| true |
code
| 0.628578 | null | null | null | null |
|
# Section 1.2 Model Fitting
```
import pymc3 as pm
import numpy as np
import arviz as az
import matplotlib.pyplot as plt
az.style.use('arviz-white')
```
## Activity 1: Estimate the Proportion of Water
Now it's your turn to work through an example inspired from Richard McElreath's excellent book [Statistical Rethinking](https://www.amazon.com/Statistical-Rethinking-Bayesian-Examples-Chapman/dp/1482253445/)
### How much of a planet is covered in water?
Good news: you're an astronomer that just discovered a new planet. Bad news: your telescope has a small field of view and you can only see one tiny point on the planet at a time. More bad news: you're also a starving grad student and you can only take 5 measurements on your monthly stipend.
**With 5 measurements what is your estimate for how much of the planet is covered in water?**
You are trying to estimate $\theta$ where
$$\theta = \text{Proportion of water on the planet}$$
Your model is formulated as follows
$$
\theta \sim \operatorname{Uniform}(0,1) \\
p_{\text{water}} \sim \operatorname{Binom}(\theta, N)
$$
(Note: the probability density function for $\operatorname{Uniform}(0, 1)$ is the same as for $\operatorname{Beta}(1, 1)$)
### Exercise 1
* What is the prior in this model? What does the prior intuitively mean?
$\theta \sim \operatorname{Uniform}(0,1) $
This means that prior to seeing any data we think that planet could have no surface water, be all water, or anything in between with equal probability. We just have no idea how much of the surface is water we just know it has to be somewhere between 0% and 100%.
In other words our prior is ¯\\\_(ツ)_/¯
### Exercise 2
* What is the likelihood in the model? What does the likelihood intuitively mean?
$p_{\text{water}} \sim \operatorname{Binom}(\theta, N)$
The likelihood is our Binomial model. This one is trickier, what it means is given our observations, how likely is a particular proportion of water. Remember here that $\theta$ is not just one number but a distribution of numbers.
### Exercise 3
Using the data provided below fit your model to estimate the proportion of water on the planet using PyStan or PyMC3. We have provided the PyMC3 model but please feel free to use the PPL you're more comfortable with.
After the fitting the model and plotting the posterior how "certain" are you about the proportion of water on this planet?
```
# A value of 0 signifies a land observation, a value of 1 signifies a water observation
observations = [0, 0, 1, 0, 1]
water_observations = sum(observations)
total_observations = len(observations)
with pm.Model() as planet_model:
# Prior
p_water = pm.Uniform("p_water", 0 ,1)
# Likelihood
w = pm.Binomial("w", p=p_water, n=total_observations, observed=water_observations)
# Inference Run/ Markov chain Monte Carlo
trace_5_obs = pm.sample(5000, chains=2)
az.plot_posterior(trace_5_obs)
```
### Exercise 4: Collect more data and get a new posterior
With some extra funding you're now able make 500 observations of this planet.
Using your inution, with more observations will you be more or less certain about the amount of water on a planet?
Do the results match your expectations?
```
one_hundred_times_the_observations = [0, 0, 1, 0, 1]*100
water_observations = sum(one_hundred_times_the_observations)
total_observations = len(one_hundred_times_the_observations)
with pm.Model() as planet_model_2:
p_water = pm.Uniform("p_water", 0 ,1)
w = pm.Binomial("w", p=p_water, n=total_observations, observed=water_observations)
trace_more_obs = pm.sample(5000, chains=2)
az.plot_posterior(trace_more_obs)
```
### Exercise 5: A new planet
During your research you encountered a new planet. Unfortunately you once again were only able to take 5 measurements, but in those 5 you only observed land, and no water.
Fit your model and see if the results look any different
```
desert_observations = [0, 0, 0, 0, 0]
water_observations = sum(desert_observations)
total_observations = len(desert_observations)
with pm.Model() as planet_model_3:
p_water = pm.Uniform("p_water", 0 ,1)
w = pm.Binomial("w", p=p_water, n=total_observations, observed=water_observations)
trace_new_planet = pm.sample(5000, chains=2)
az.plot_posterior(trace_new_planet)
```
### Exercise 5: Try out a couple ArviZ functions
Convert your inference data to `az.InferenceData` using the methods `az.from_pymc3` or `az.from_stan`. Then try a couple plots such as
* az.plot_trace
* az.plot_autocorr
* az.plot_forest
Try running a summary function such as
* az.summary
For now don't worry too much about how to interpret these plots and statistics. This will be covered as we continue in the tutorial.
```
# Convert PPL data to az.InferenceData
inference_data = az.from_pymc3(trace_5_obs)
az.summary(inference_data)
az.plot_trace(inference_data)
az.plot_autocorr(inference_data)
az.plot_forest([trace_5_obs, trace_more_obs, trace_new_planet], model_names=["5_observations", "100_observations", "new_planet"])
```
## Bonus:
Explore the ArviZ documentation to see what else is possible.
https://arviz-devs.github.io/arviz/
| true |
code
| 0.632418 | null | null | null | null |
|
```
!pip install scikit-learn==1.0.2 statsmodels yellowbrick python-slugify sagemaker==2.88.0 s3fs
```
# Data cleaning and Feature engineering
```
import os
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
import plotly.offline as py
import plotly.graph_objs as go
import plotly.tools as tls
from slugify import slugify
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from xgboost import XGBClassifier
import datetime as dt
churn_data = pd.read_csv("/content/telco-customer-churn.csv")
churn_data['TotalCharges'] = churn_data["TotalCharges"].replace(" ",np.nan)
churn_data = churn_data[churn_data["TotalCharges"].notnull()]
churn_data = churn_data.reset_index()[churn_data.columns]
churn_data["TotalCharges"] = churn_data["TotalCharges"].astype(float)
def tenure_label(churn_data) :
if churn_data["tenure"] <= 24 :
return "0-24"
elif (churn_data["tenure"] > 24) & (churn_data["tenure"] <= 48) :
return "24-48"
elif churn_data["tenure"] > 48:
return "48-end"
churn_data["tenure_group"] = churn_data.apply(lambda churn_data:tenure_label(churn_data),
axis = 1)
replace_cols = [ 'OnlineSecurity', 'OnlineBackup', 'DeviceProtection',
'TechSupport','StreamingTV', 'StreamingMovies']
for i in replace_cols :
churn_data[i] = churn_data[i].replace({'No internet service' : 'No'})
churn_data.sample(5)
churn_data.nunique()
bin_cols = churn_data.nunique()[churn_data.nunique() == 2].keys().tolist()
le = LabelEncoder()
for i in bin_cols :
churn_data[i] = le.fit_transform(churn_data[i])
all_categorical_cols = churn_data.nunique()[churn_data.nunique() <=4].keys().tolist()
multi_value_cols = [col for col in all_categorical_cols if col not in bin_cols]
churn_data = pd.get_dummies(data = churn_data, columns=multi_value_cols)
numerical_cols = ['tenure', 'MonthlyCharges', 'TotalCharges']
std = StandardScaler()
churn_data[numerical_cols] = std.fit_transform(churn_data[numerical_cols])
churn_data.columns = [slugify(col, lowercase=True, separator='_') for col in churn_data.columns]
sample = churn_data.head()
sample[['customerid', 'gender', 'seniorcitizen', 'partner', 'dependents',
'tenure', 'phoneservice', 'onlinesecurity', 'onlinebackup',
'deviceprotection', 'techsupport', 'streamingtv']]
sample[['streamingmovies', 'paperlessbilling', 'monthlycharges', 'totalcharges', 'churn',
'multiplelines_no', 'multiplelines_no_phone_service',
'multiplelines_yes', 'internetservice_dsl']]
sample[['internetservice_fiber_optic','internetservice_no',
'contract_month_to_month', 'contract_one_year', 'contract_two_year',
'paymentmethod_bank_transfer_automatic']]
sample[['paymentmethod_credit_card_automatic','paymentmethod_electronic_check',
'paymentmethod_mailed_check', 'tenure_group_0_24', 'tenure_group_24_48',
'tenure_group_48_end']]
```
# Featue group creation and ingestion
```
# import os
# os.environ["AWS_ACCESS_KEY_ID"] = "<aws_key_id>"
# os.environ["AWS_SECRET_ACCESS_KEY"] = "<aws_secret>"
# os.environ["AWS_DEFAULT_REGION"] = "us-east-1"
import boto3
FEATURE_GROUP_NAME = "telcom-customer-features"
feature_group_exist = False
client = boto3.client('sagemaker')
response = client.list_feature_groups(
NameContains=FEATURE_GROUP_NAME)
if FEATURE_GROUP_NAME in response["FeatureGroupSummaries"]:
feature_group_exist = True
import sagemaker
from sagemaker.session import Session
import time
role = "arn:aws:iam::<account_number>:role/sagemaker-iam-role"
sagemaker_session = sagemaker.Session()
region = sagemaker_session.boto_region_name
s3_bucket_name = "feast-demo-mar-2022"
from sagemaker.feature_store.feature_group import FeatureGroup
customers_feature_group = FeatureGroup(
name=FEATURE_GROUP_NAME, sagemaker_session=sagemaker_session
)
churn_data["event_timestamp"] = float(round(time.time()))
if not feature_group_exist:
customers_feature_group.load_feature_definitions(
churn_data[[col
for col in churn_data.columns
if col not in ["customerid"]]])
customer_id_def = FeatureDefinition(feature_name='customerid',
feature_type=FeatureTypeEnum.STRING)
customers_feature_group.feature_definitions = [customer_id_def] + customers_feature_group.feature_definitions
customers_feature_group.create(
s3_uri=f"s3://{s3_bucket_name}/{FEATURE_GROUP_NAME}",
record_identifier_name="customerid",
event_time_feature_name="event_timestamp",
role_arn=role,
enable_online_store=False
)
ingestion_results = customers_feature_group.ingest(churn_data, max_workers=1)
ingestion_results.failed_rows
```
| true |
code
| 0.358915 | null | null | null | null |
|
# Image augmentation strategies:
## Author: Dr. Rahul Remanan
### (CEO and Chief Imagination Officer, [Moad Computer](https://www.moad.computer))
### Demo data: [Kaggle Cats Vs. Dogs Redux](https://www.kaggle.com/c/dogs-vs-cats-redux-kernels-edition)
## Part 01 - [Using Keras pre-processing:](https://blog.keras.io/building-powerful-image-classification-models-using-very-little-data.html)
### Why perform image augmentation?
In order to make the most out of our few training image data, the process of "augmentation" of these images via a number of random transformations is helpful. This process feed the data to the neural network model, so that it would never see twice the exact same picture. The key advantage of implementation such an augmentation strategy is to help prevent overfitting and better generalization by the trained model.
In Keras this can be done via the keras.preprocessing.image.ImageDataGenerator class. This class allows you to:
* configure random transformations and normalization operations to be done on your image data during training
* instantiate generators of augmented image batches (and their labels) via .flow(data, labels) or .flow_from_directory(directory). These generators can then be used with the Keras model methods that accept data generators as inputs, fit_generator, evaluate_generator and predict_generator.
### Example implementation of image augmentation in Keras:
```
try:
import warnings
warnings.filterwarnings('ignore')
from keras.preprocessing.image import ImageDataGenerator
except:
print ("Please install Keras (cmd: $sudo pip3 install keras) to run this notebook ...")
datagen = ImageDataGenerator(rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
rescale=1./255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
```
### Image Augmentation in Keras -- Quick start:
For more information, see the [documentation](https://keras.io/preprocessing/image/).
* rotation_range is a value in degrees (0-180), a range within which to randomly rotate pictures
* width_shift and height_shift are ranges (as a fraction of total width or height) within which to randomly translate pictures vertically or horizontally
* rescale is a value by which we will multiply the data before any other processing. Our original images consist in RGB coefficients in the 0-255, but such values would be too high for our models to process (given a typical learning rate), so we target values between 0 and 1 instead by scaling with a 1/255. factor.
* shear_range is for randomly applying [shearing transformations](https://en.wikipedia.org/wiki/Shear_mapping)
* zoom_range is for randomly zooming inside pictures
* horizontal_flip is for randomly flipping half of the images horizontally --relevant when there are no assumptions of horizontal assymetry (e.g. real-world pictures).
* fill_mode is the strategy used for filling in newly created pixels, which can appear after a rotation or a width/height shift.
```
from keras.preprocessing.image import ImageDataGenerator, array_to_img, img_to_array, load_img
datagen = ImageDataGenerator(rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
img = load_img('./train/cats/cat.1.jpg')
x = img_to_array(img)
x = x.reshape((1,) + x.shape)
i = 0
for batch in datagen.flow(x, batch_size=1,
save_to_dir='./preview/', save_prefix='cat', save_format='jpeg'):
i += 1
if i > 20:
break
```
### Keras pre-processing overview:
* The load_img uses Pillow, a complete fork of PIL. This creates a PIL image.
* The img_to_array creates a Numpy array with shape (3, 150, 150).
* The reshape command creates a Numpy array with shape (1, 3, 150, 150).
* The .flow() command below generates batches of randomly transformed images and saves the results to the `../data/cats_dogs/preview/` directory
* The break function prevents the loop from iterating indefinitely.
```
import os
import matplotlib.image as mpl_image
import matplotlib.pyplot as plt
from IPython.display import Image as PyImage
def load_images(folder):
images = []
for filename in os.listdir(folder):
img = mpl_image.imread(os.path.join(folder, filename))
if img is not None:
images.append(img)
return images
def stack_plot(stack_size, folder):
rows, cols = stack_size, stack_size
fig,ax = plt.subplots(rows,cols,figsize=[24,24])
i = 0
try:
for filename in os.listdir(folder):
img = mpl_image.imread(os.path.join(folder, filename))
ax[int(i/rows),int(i % rows)].imshow(img)
ax[int(i/rows),int(i % rows)].axis('off')
i += 1
except:
print ("Failed to add an image to the stacked plot ...")
plt.show()
```
### Plotting augmented images:
* Using matplotlib library.
* The load_images function return a Numpy array of all the images in the folder specified in the function.
* The stack_plot generates a stack of images contained inside a specific folder of size: stack_size*stack_size
```
stack_plot(5, './preview/')
```
## Part 02 - Implementing a convolutional neural network that uses image augmentation:
### Importing dependent libraries:
```
try:
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D
from keras.layers import Activation, Dropout, Flatten, Dense
from keras import backend as K
except:
print ("Failed to load Keras modules. Verify if dependency requirements are satisfied ...")
```
* Importing preprocessing.image and models functions from Keras
* Importing layers function
* Importing keras backend
### Initialize some variables:
```
img_width, img_height = 150, 150
train_data_dir = './train/'
validation_data_dir = './validation/'
nb_train_samples = 20000
nb_validation_samples = 5000
epochs = 50
batch_size = 16
if K.image_data_format() == 'channels_first':
input_shape = (3, img_width, img_height)
else:
input_shape = (img_width, img_height, 3)
```
* Using img_width, img_height variables for specifying the dimensions of images to be consumed by the neural network
* Initilaizing variables for location pointers to training data, validation data, train data sample size, validation data sample size, number of training epochs, number of images to be processed in each batch
* Specifying a function to adjust input shape of the tensor if the image RGB data format is channels first or channels last
### Build and compile a neural network:
* Building a neural network model using the Sequential format in Keras
* Compile the model using binary cross entropy as the loss function, RMSProp as the optimizer and accuracy as the evaluation metrics
```
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape=input_shape))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(64))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(1))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
```
### Configuring data generators to process and feed the data to the neural network:
```
train_datagen = ImageDataGenerator(rescale=1. / 255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
```
* The image augmentation configuration for training
```
test_datagen = ImageDataGenerator(rescale=1. / 255)
```
* Image augmentation configuration to be used for testing
* This generator uses only rescaling
### Creating train and validation generators:
```
train_generator = train_datagen.flow_from_directory(train_data_dir,
target_size=(img_width, img_height),
batch_size=batch_size,
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(validation_data_dir,
target_size=(img_width, img_height),
batch_size=batch_size,
class_mode='binary')
```
### Creating a model fit generator function for training the neural network:
```
model.fit_generator(train_generator,
steps_per_epoch=nb_train_samples // batch_size,
epochs=epochs,
validation_data=validation_generator,
validation_steps=nb_validation_samples // batch_size)
```
### Saving model weights at the end of the training session:
```
model.save_weights('./model/first_try.h5')
```
## Part 03 - Improving classification accuracy of a neural network using transfer learning:
### Importing dependent libraries:
```
import numpy as np
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dropout, Flatten, Dense
from keras import applications
```
### Defining and initializing variables:
```
top_model_weights_path = './model/bottleneck_fc_model.h5'
train_data_dir = './train'
validation_data_dir = './validation'
bottleneck_train_path = './model/bottleneck_features_train.npy'
bottleneck_val_path = './model/bottleneck_features_validation.npy'
nb_train_samples = 2000
nb_validation_samples = 800
epochs = 50
batch_size = 16
```
### Specify the dimensions of images:
```
img_width, img_height = 150, 150
```
### Build the VGG16 network:
```
model = applications.VGG16(include_top=False, weights='imagenet', input_shape = (img_width, img_height,3))
```
### Define data generator:
```
datagen = ImageDataGenerator(rescale=1. / 255)
```
### Creating a function to save bottleneck features:
```
def save_train_bottlebeck_features(bottleneck_train_path=None):
generator = datagen.flow_from_directory(train_data_dir,
target_size=(img_width, img_height),
batch_size=batch_size,
class_mode="binary",
shuffle=False)
bottleneck_features_train = model.predict_generator(generator, nb_train_samples // batch_size)
np.save(open(bottleneck_train_path),
bottleneck_features_train)
def save_validation_bottlebeck_features(bottleneck_val_path=None):
generator = datagen.flow_from_directory(validation_data_dir,
target_size=(img_width, img_height),
batch_size=batch_size,
class_mode="binary",
shuffle=False)
bottleneck_features_validation = model.predict_generator(generator, nb_validation_samples // batch_size)
np.save(open(bottleneck_val_path),
bottleneck_features_validation)
```
### Saving bottleneck features:
```
save_train_bottlebeck_features(bottleneck_train_path = bottleneck_train_path)
save_validation_bottlebeck_features(bottleneck_val_path = bottleneck_val_path)
```
### Creating a function to train the top model:
```
def train_top_model(save_path=None, bottleneck_train_path = None, bottleneck_val_path = None):
top_model_weights_path = save_path
train_data = np.load(open(bottleneck_train_path, 'rb'))
train_labels = np.array([0] * (nb_train_samples // 2) + [1] * (nb_train_samples // 2))
validation_data = np.load(open(bottleneck_val_path, 'rb'))
validation_labels = np.array([0] * (nb_validation_samples // 2) + [1] * (nb_validation_samples // 2))
model = Sequential()
model.add(Flatten(input_shape=train_data.shape[1:]))
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy', metrics=['accuracy'])
model.fit(train_data, train_labels,
epochs=epochs,
batch_size=batch_size,
validation_data=(validation_data, validation_labels))
model.save_weights(top_model_weights_path)
```
### Intialize trainig session of the top model and save weights at the end of training:
```
train_top_model(save_path=top_model_weights_path, \
bottleneck_train_path = bottleneck_train_path, \
bottleneck_val_path = bottleneck_val_path)
```
### Fine tuning the model:
#### Load dependent libraries:
```
from keras import applications
from keras.preprocessing.image import ImageDataGenerator
from keras import optimizers
from keras.models import Sequential
from keras.layers import Dropout, Flatten, Dense
```
#### Specify dimensions of the images:
```
img_width, img_height = 150, 150
```
#### Load model weights:
```
weights_path = './model/vgg16_weights.h5'
top_model_weights_path = './model/bottleneck_fc_model.h5'
```
#### Initialize some variables:
```
train_data_dir = './train'
validation_data_dir = './validation'
nb_train_samples = 20000
nb_validation_samples = 5000
epochs = 50
batch_size = 16
checkpointer_savepath = './model/checkpointer.h5'
```
#### Build the VGG16 network:
```
model = Sequential()
model.add(applications.VGG16(weights='imagenet', include_top=False, input_shape = (img_width, img_height,3)))
print('Model loaded ...')
```
#### Build a classifier model to put on top of the V6616 convolutional model:
```
top_model = Sequential()
top_model.add(Flatten(input_shape=model.output_shape[1:]))
top_model.add(Dense(256, activation='relu'))
top_model.add(Dropout(0.5))
top_model.add(Dense(1, activation='sigmoid'))
```
#### Generate model summary:
```
model.summary()
from keras.utils import plot_model
import pydot
import graphviz # apt-get install -y graphviz libgraphviz-dev && pip3 install pydot graphviz
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
output_dir = './model'
plot_model(model, to_file= output_dir + '/model_top.png')
SVG(model_to_dot(model).create(prog='dot', format='svg'))
```
#### Load model weights:
* It is necessary to start with a fully-trained classifier
* This includes the top classifier
* Initializing model weights from zero may not train the train the network successfully
```
top_model.load_weights(top_model_weights_path)
```
#### Add top model top of the Vgg16 convolutional base:
```
model.add(top_model)
```
#### Generate sumary with base VGG16 model:
```
model.summary()
output_dir = './model'
plot_model(model, to_file= output_dir + '/model_full.png')
SVG(model_to_dot(model).create(prog='dot', format='svg'))
```
#### Freezing layers:
* Freeze the first 25 layers, up to the last conv block
* Weighhts become non-trainable and will not be updated
```
for layer in model.layers[:25]:
layer.trainable = False
```
#### Compile the model:
* With a SGD/momentum optimizer
* Very slow learning rate.
```
model.compile(loss='binary_crossentropy',
optimizer=optimizers.SGD(lr=1e-4, momentum=0.9),
metrics=['accuracy'])
```
#### Prepare data augmentation configuration:
```
train_datagen = ImageDataGenerator(rescale=1. / 255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
test_datagen = ImageDataGenerator(rescale=1. / 255)
```
#### Create generator functions to handle data:
```
train_generator = train_datagen.flow_from_directory(train_data_dir,
target_size=(img_height, img_width),
batch_size=batch_size,
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(validation_data_dir,
target_size=(img_height, img_width),
batch_size=batch_size,
class_mode='binary')
```
#### Implement a checkpoiting mechanism:
```
from keras.callbacks import EarlyStopping, ModelCheckpoint
early_stopper = EarlyStopping(patience=5, verbose=1)
checkpointer = ModelCheckpoint(checkpointer_savepath,\
verbose=1,\
save_best_only=True)
```
#### Load saved model:
```
from keras.models import Model, load_model
load_from_checkpoint = True
load_from_config = False
load_model_weights = False
if load_from_checkpoint == True:
model = load_model(checkpointer_savepath)
elif load_from_config == True:
model = load_prediction_model(args)
model = load_prediction_model_weights(args)
elif load_model_weights == True:
try:
model = load_prediction_model_weights(args)
except:
print ("An exception has occurred, while loading model weights ...")
else:
model = model
```
#### Train the model:
```
model.fit_generator(train_generator,
steps_per_epoch=nb_train_samples // batch_size,
epochs=epochs,
validation_data=validation_generator,
validation_steps=nb_validation_samples // batch_size,
callbacks=[early_stopper, checkpointer])
model.output_shape[1:]
```
#### Save the model:
```
model.save_weights('./model/vgg16_tl.h5')
```
## Part 04 - [Using radial image transformation:](https://arxiv.org/abs/1708.04347)
Deep learning models have a large number of free parameters that must be estimated by efficient training of the models on a large number of training data samples to increase their generalization performance. In real-world applications, the data available to train these networks is often limited or imbalanced. Hojjat Salehinejad et.al propose a sampling method based on the radial transform in a polar coordinate system for image augmentation. This facilitates the training of deep learning models from limited source data. The pixel-wise transformation implemeted here provides representations of the original image in the polar coordinate system by generating a new image from each pixel. This technique can generate radial transformed images up to the number of pixels in the original image to increase the diversity of poorly represented image classes. Our experiments show improved generalization performance in training deep convolutional neural networks using these radial transformed images.
```
from skimage import data
from skimage import io
import numpy as np
import math
import matplotlib.pyplot as plt
def to_gray(img):
w, h,_ = img.shape
ret = np.empty((w, h), dtype=np.uint8)
retf = np.empty((w, h), dtype=np.float)
imgf = img.astype(float)
retf[:, :] = ((imgf[:, :, 1] + imgf[:, :, 2] + imgf[:, :, 0])/3)
ret = retf.astype(np.uint8)
return ret
def radial_transform(img,w,h):
shape = im.shape
new_im = np.zeros(shape)
print(shape)
print(len(shape))
print('w',w)
print('h',h)
width = shape[1]
height = shape[0]
lens = len(shape)
for i in range(0,width):
xita = 2*3.14159*i/width
for a in range(0,height):
x = (int)(math.floor(a * math.cos(xita)))
y = (int)(math.floor(a * math.sin(xita)))
new_y = (int)(h+x)
new_x = (int)(w+y)
#print(h.dtype)
if new_x>=0 and new_x<width:
if new_y>=0 and new_y<height:
if lens==3:
new_im[a,i,0] = (im[new_y,new_x,0]-127.5)/128
new_im[a,i,1] = (im[new_y,new_x,1]-127.5)/128
new_im[a,i,2] = (im[new_y,new_x,2]-127.5)/128
else:
new_im[a,i] = (im[new_y,new_x]-127.5)/128
new_im[a,i] = (im[new_y,new_x]-127.5)/128
new_im[a,i] = (im[new_y,new_x]-127.5)/128
return new_im
im = io.imread('./preview/cat_0_1511.jpeg')
im = to_gray(im)
h = im.shape[0]
w = im.shape[1]
rt_im1 = radial_transform(im,(int)(w/2),(int)(h/2))
rt_im2 = radial_transform(im,(int)(w/4),(int)(h/4))
rt_im3 = radial_transform(im,(int)(w*0.5),(int)(h*0.75))
io.imshow(im)
io.imsave('./radial_transform/112.jpg',rt_im1)
io.imsave('./radial_transform/112.jpg',rt_im2)
io.imsave('./radial_transform/112.jpg',rt_im3)
io.show()
plt.figure(num='cats_dogs',figsize=(8,8))
plt.subplot(2,2,1)
plt.title('origin image')
plt.imshow(im,plt.cm.gray)
plt.subplot(2,2,2)
plt.title('0.5')
plt.imshow(rt_im1,plt.cm.gray)
plt.axis('off')
plt.subplot(2,2,3)
plt.title('0.25')
plt.imshow(rt_im2,plt.cm.gray)
plt.axis('off')
plt.subplot(2,2,4)
plt.title('0.75')
plt.imshow(rt_im3,plt.cm.gray)
plt.axis('off')
plt.show()
```
| true |
code
| 0.585931 | null | null | null | null |
|
# ResNet-50
- Landmark 분류 모델
# GPU 확인
```
import numpy as np
import pandas as pd
import keras
import tensorflow as tf
from IPython.display import display
import PIL
# How to check if the code is running on GPU or CPU?
from tensorflow.python.client import device_lib
print(device_lib.list_local_devices())
from keras import models, layers
from keras import Input
from keras.models import Model, load_model
from keras.preprocessing.image import ImageDataGenerator
from keras import optimizers, initializers, regularizers, metrics
from keras.callbacks import ModelCheckpoint, EarlyStopping
from keras.layers import BatchNormalization, Conv2D, Activation, Dense, GlobalAveragePooling2D, MaxPooling2D, ZeroPadding2D, Add
import os
import matplotlib.pyplot as plt
import numpy as np
import math
train_datagen = ImageDataGenerator(rescale=1./255)
val_datagen = ImageDataGenerator(rescale=1./255)
train_dir = os.path.join('훈련 클래스 데이터 경로')
val_dir = os.path.join('검증 클래스 데이터 경로')
train_generator = train_datagen.flow_from_directory(train_dir, batch_size=16, target_size=(224, 224), color_mode='rgb')
val_generator = val_datagen.flow_from_directory(val_dir, batch_size=16, target_size=(224, 224), color_mode='rgb')
# 클래스의 총 개수 (학습하는 렌드마크의 장소)
K = 392
input_tensor = Input(shape=(224, 224, 3), dtype='float32', name='input')
def conv1_layer(x):
x = ZeroPadding2D(padding=(3, 3))(x)
x = Conv2D(64, (7, 7), strides=(2, 2))(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = ZeroPadding2D(padding=(1,1))(x)
return x
def conv2_layer(x):
x = MaxPooling2D((3, 3), 2)(x)
shortcut = x
for i in range(3):
if (i == 0):
x = Conv2D(64, (1, 1), strides=(1, 1), padding='valid')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(64, (3, 3), strides=(1, 1), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(256, (1, 1), strides=(1, 1), padding='valid')(x)
shortcut = Conv2D(256, (1, 1), strides=(1, 1), padding='valid')(shortcut)
x = BatchNormalization()(x)
shortcut = BatchNormalization()(shortcut)
x = Add()([x, shortcut])
x = Activation('relu')(x)
shortcut = x
else:
x = Conv2D(64, (1, 1), strides=(1, 1), padding='valid')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(64, (3, 3), strides=(1, 1), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(256, (1, 1), strides=(1, 1), padding='valid')(x)
x = BatchNormalization()(x)
x = Add()([x, shortcut])
x = Activation('relu')(x)
shortcut = x
return x
def conv3_layer(x):
shortcut = x
for i in range(4):
if(i == 0):
x = Conv2D(128, (1, 1), strides=(2, 2), padding='valid')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(128, (3, 3), strides=(1, 1), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(512, (1, 1), strides=(1, 1), padding='valid')(x)
shortcut = Conv2D(512, (1, 1), strides=(2, 2), padding='valid')(shortcut)
x = BatchNormalization()(x)
shortcut = BatchNormalization()(shortcut)
x = Add()([x, shortcut])
x = Activation('relu')(x)
shortcut = x
else:
x = Conv2D(128, (1, 1), strides=(1, 1), padding='valid')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(128, (3, 3), strides=(1, 1), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(512, (1, 1), strides=(1, 1), padding='valid')(x)
x = BatchNormalization()(x)
x = Add()([x, shortcut])
x = Activation('relu')(x)
shortcut = x
return x
def conv4_layer(x):
shortcut = x
for i in range(6):
if(i == 0):
x = Conv2D(256, (1, 1), strides=(2, 2), padding='valid')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(256, (3, 3), strides=(1, 1), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(1024, (1, 1), strides=(1, 1), padding='valid')(x)
shortcut = Conv2D(1024, (1, 1), strides=(2, 2), padding='valid')(shortcut)
x = BatchNormalization()(x)
shortcut = BatchNormalization()(shortcut)
x = Add()([x, shortcut])
x = Activation('relu')(x)
shortcut = x
else:
x = Conv2D(256, (1, 1), strides=(1, 1), padding='valid')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(256, (3, 3), strides=(1, 1), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(1024, (1, 1), strides=(1, 1), padding='valid')(x)
x = BatchNormalization()(x)
x = Add()([x, shortcut])
x = Activation('relu')(x)
shortcut = x
return x
def conv5_layer(x):
shortcut = x
for i in range(3):
if(i == 0):
x = Conv2D(512, (1, 1), strides=(2, 2), padding='valid')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(512, (3, 3), strides=(1, 1), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(2048, (1, 1), strides=(1, 1), padding='valid')(x)
shortcut = Conv2D(2048, (1, 1), strides=(2, 2), padding='valid')(shortcut)
x = BatchNormalization()(x)
shortcut = BatchNormalization()(shortcut)
x = Add()([x, shortcut])
x = Activation('relu')(x)
shortcut = x
else:
x = Conv2D(512, (1, 1), strides=(1, 1), padding='valid')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(512, (3, 3), strides=(1, 1), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(2048, (1, 1), strides=(1, 1), padding='valid')(x)
x = BatchNormalization()(x)
x = Add()([x, shortcut])
x = Activation('relu')(x)
shortcut = x
return x
x = conv1_layer(input_tensor)
x = conv2_layer(x)
x = conv3_layer(x)
x = conv4_layer(x)
x = conv5_layer(x)
x = GlobalAveragePooling2D()(x)
output_tensor = Dense(K, activation='softmax')(x)
resnet50 = Model(input_tensor, output_tensor)
resnet50.summary()
resnet50.compile(optimizer='adamax',
loss='categorical_crossentropy',
metrics=['accuracy'])
```
# 조기 종료 수행
```
from keras.callbacks import EarlyStopping, ReduceLROnPlateau
earlystop = EarlyStopping(patience=100)
learning_rate_reduction = ReduceLROnPlateau(monitor='val_accuracy',
patience=30,
verbose=1,
factor=0.5,
min_lr=0.00001)
callbacks=[earlystop, learning_rate_reduction]
```
# 모델 학습
```
history=resnet50.fit_generator(
train_generator,
steps_per_epoch=15,
epochs=100000,
validation_data=val_generator,
validation_steps=5,
callbacks=callbacks
)
```
# 학습 결과
```
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.legend(['training','validation'], loc = 'upper left')
plt.show()
history.history['val_accuracy'].index(max(history.history['val_accuracy']))
max(history.history['val_accuracy'])
```
- epochs 644 수행 (최고 accuracy : 0.97083336 -552 Eopoch / 최고 val_accuracy : 0.987500011920929-641epoch)
# 모델 저장
```
resnet50.save("res_net50modelWpatience_camp7.h5")
resnet50.save_weights("res_net50modelWpatience_weight_camp7.h5")
```
---
# 모델 테스트
```
from keras.models import load_model
model = load_model('res_net50modelWpatience_camp7.h5')
test_datagen = ImageDataGenerator(rescale=1./255)
test_dir = os.path.join('테스트 클래스 데이터 경로')
test_generator = test_datagen.flow_from_directory(test_dir, batch_size=16, target_size=(224, 224), color_mode='rgb')
```
# 모델 예측 (분류)
# 라벨 인덱싱
```
test_generator.class_indices
labels = {value:key for key, value in train_generator.class_indices.items()}
labels
```
## 테스트 이미지 경로 설정
```
filenames = os.path.join('테스트 이미지 경로')
```
## 이미지 출력 확인
```
from keras.preprocessing.image import load_img
from keras.preprocessing.image import img_to_array
import random
# sample=random.choice(filenames)
image=load_img(filenames, target_size=(224,224))
image
```
## 테스트 이미지 전처리
```
img_to_array(image).shape
image=img_to_array(image)
image=image.reshape((1, image.shape[0], image.shape[1], image.shape[2]))
```
test_datagen = ImageDataGenerator(rescale=1./255)
test_dir = os.path.join('C:/Users/USER/Desktop/여기요/kbs')
test_generator = test_datagen.flow_from_directory(test_dir, batch_size=16, target_size=(224, 224), color_mode='rgb')
```
data=img_to_array(image)
data
data.shape
test_datagen = ImageDataGenerator(rescale=1./255)
test_dir = os.path.join('테스트 클래스 데이터 경로')
test_generator = test_datagen.flow_from_directory(test_dir, batch_size=16, target_size=(224, 224), color_mode='rgb')
```
## 예측 결과
```
output=model.predict_generator(test_generator)
print(output)
for out in output:
print(labels.get(out.argmax()))
place=labels.get(out.argmax())
```
| true |
code
| 0.53048 | null | null | null | null |
|
```
from __future__ import absolute_import, division, print_function, unicode_literals
import tensorflow as tf
tf.enable_eager_execution()
import numpy as np
import os
import time
# from lossT import sparse_categorical_crossentropy
```
### Parameters
```
# Spatially discretized data into 20 bins
bins=np.arange(-0.9, 1.1, 0.1)
num_bins=len(bins)
# Labels of all possible states in the ranges we considered.
# For 2d systems, this is not the same as the number of representative values.
all_combs = [i for i in range(num_bins)]
vocab=sorted(all_combs)
vocab_size = len(vocab)
# Sequence length and shift in step between past (input) & future (output)
seq_length = 100
shift=1
# Batch size
BATCH_SIZE = 64
# Buffer size to shuffle the dataset.
BUFFER_SIZE = 50000
# Model parameters
embedding_dim = 128
rnn_units = 1024
# Training epochs
EPOCHS=40
# Prediction
num_generate = 2000000
# Low temperatures results in more predictable text.
# Higher temperatures results in more surprising text.
# Experiment to find the best setting.
temperature = 1.0
def split_input_target(chunk):
"""
split sequences into input and target.
"""
input_text = chunk[:-shift]
target_text = chunk[shift:]
return input_text, target_text
def build_model(vocab_size, embedding_dim, rnn_units, batch_size):
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim,
batch_input_shape=[batch_size, None]),
rnn(rnn_units,
return_sequences=True,
recurrent_initializer='glorot_uniform',
stateful=True),
tf.keras.layers.Dense(vocab_size)
])
return model
def loss(labels, logits):
return tf.keras.losses.sparse_categorical_crossentropy(labels, logits, from_logits=True)
# return sparse_categorical_crossentropy(labels, logits, from_logits=True)
def generate_text(pmodel, num_generate, temperature, start_string):
"""
# Define function for generating prediction.
"""
# Converting the start string to numbers (vectorizing)
input_eval = [char2idx[s] for s in start_string]
input_eval = tf.expand_dims(input_eval, 0)
# Empty string to store the results
text_generated = np.empty(1)
# Here batch size = 1
pmodel.reset_states()
for i in range(num_generate):
predictions = pmodel(input_eval)
# remove the batch dimension
predictions = tf.squeeze(predictions, 0)
# using a multinomial distribution to predict the word returned by the model
predictions = predictions / temperature
predicted_id = tf.multinomial(predictions, num_samples=1)[-1,0].numpy()
# We pass the predicted word as the next input to the model
# along with the previous hidden state
input_eval = tf.expand_dims([predicted_id], 0)
text_generated = np.vstack((text_generated, idx2char[predicted_id].tolist()))
return text_generated
```
### Read data
```
infile = 'DATA_aladip/COLVAR_T450'
phi, psi=np.loadtxt(infile, unpack=True, usecols=(1,2), skiprows=7)
cos_phi=np.cos(phi)
sin_phi=np.sin(phi)
cos_psi=np.cos(psi)
sin_psi=np.sin(psi)
# Spatially discretized data
idx_sin_phi=np.digitize(sin_phi, bins)
idx_sin_psi=np.digitize(sin_psi, bins)
```
### Training data
```
idx_2d=list(idx_sin_phi[:10000])
text = idx_2d
char2idx = {u:i for i, u in enumerate(vocab)} # Mapping from characters to indices
idx2char = np.array(vocab)
text_as_int = np.array([char2idx[c] for c in text])
# Create training examples / targets
char_dataset = tf.data.Dataset.from_tensor_slices(text_as_int)
sequences = char_dataset.batch(seq_length+shift, drop_remainder=True)
dataset = sequences.map(split_input_target)
dataset = dataset.shuffle(BUFFER_SIZE).batch(BATCH_SIZE, drop_remainder=True)
```
### Use the same trajectory as the validation data
```
idx_sin_phi_v=np.digitize(sin_phi, bins)
idx_2dv=list(idx_sin_phi_v)
vali = idx_2dv[:200000]
vali_as_int = np.array([char2idx[c] for c in vali])
# Create validation examples/targets
vali_dataset = tf.data.Dataset.from_tensor_slices(vali_as_int)
sequences = vali_dataset.batch(seq_length+shift, drop_remainder=True)
vdataset = sequences.map(split_input_target)
vdataset = vdataset.shuffle(BUFFER_SIZE).batch(BATCH_SIZE, drop_remainder=True)
```
### Read the same trajectory and use the first few to activate the model for prediction
```
idx_sin_phi_p=np.digitize(sin_phi, bins)
idx_2dp=list(idx_sin_phi_p)
text4activation = idx_2dp[:100000]
```
### Decide whether to use GPU and build model of training
```
if tf.test.is_gpu_available():
rnn = tf.keras.layers.CuDNNLSTM
else:
import functools
rnn = functools.partial(
tf.keras.layers.LSTM, recurrent_activation='sigmoid')
model = build_model(vocab_size = vocab_size,
embedding_dim=embedding_dim,
rnn_units=rnn_units,
batch_size=BATCH_SIZE)
print(model.summary())
model.compile(optimizer = tf.train.AdamOptimizer(), loss = loss)
```
### Save checkpoint
```
# Directory where the checkpoints will be saved
checkpoint_dir = './training_checkpoints'
# Name of the checkpoint files
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt_{epoch}")
checkpoint_callback=tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_prefix, save_weights_only=True)
```
### Training
```
examples_per_epoch = len(text)//(seq_length+shift)
steps_per_epoch = examples_per_epoch//BATCH_SIZE
v_examples=len(vali_as_int)//(seq_length+shift)
v_steps_per_epoch=v_examples//BATCH_SIZE
history = model.fit(dataset.repeat(EPOCHS), epochs=EPOCHS, steps_per_epoch=steps_per_epoch, validation_data=vdataset.repeat(EPOCHS), validation_steps=v_steps_per_epoch, callbacks=[checkpoint_callback])
# Rebuild model with batch_size=1:
pmodel = build_model(vocab_size, embedding_dim, rnn_units, batch_size=1)
pmodel.load_weights(tf.train.latest_checkpoint(checkpoint_dir))
pmodel.build(tf.TensorShape([1, None]))
print(pmodel.summary())
# Print the length of seed for activating the model
print('length of seed: {}'.format(len(text4activation)))
```
### Generate prediction sequentially
```
start0 = time.time()
prediction=generate_text(pmodel, num_generate, temperature, start_string=text4activation)
print ('Time taken for total {} sec\n'.format(time.time() - start0))
```
### Save prediction
```
np.savetxt('prediction',prediction[1:])
```
| true |
code
| 0.881768 | null | null | null | null |
|
# Advanced SQL II: Subqueries
_**Author**: Boom Devahastin Na Ayudhya_
***
## Additional Learning Tools after the course
The dataset I've used for this lesson is from [Udemy's Master SQL for Data Science](https://www.udemy.com/master-sql-for-data-science/learn/lecture/9790570#overview) course. In the repo, you should copy and paste the database construction queries from the `employees_udemy.txt` script into PostgreSQL if you wish to explore the dataset on your own.
## What is a subquery?
Exactly what it sounds like: literally inception because **it's a query within a query**!
...What?! Sounds complicated...why do we need this?
**Motivation:** The `employees` table has a department column amongst other employee-specific information. The `departments` table shows information on each of the departments. However, some departments have recently turned over their entire team and so there may not be any employees listed in those departments. How can we figure out which departments did this?
TL;DR - How do we determine which departments exist in the `employees` table but not the `departments` table? Think through the logic in English first before you attempt to convert it to code.
_**DO NOT USE JOINS - we'll talk about why not in a bit!**_
_Answer:_
```MySQL
```
### Subqueries in `WHERE`
How did we think about this?
- The output of a subquery is a "dataframe" (or rather a subset of a table).
- If we choose to extract just one column from a table using a query, we essentially have a list
- We've written WHERE statements before with `IN` and `NOT IN` and compared results to a list
- Connecting the dots: we can replace the list in a WHERE clause with a subquery to make things more dynamic
**Exercise 1:** Write a query that returns all information about employees who work in the Electronics division.
_Answer:_
```MySQL
```
**Exercise 2:** Switching back to tables in the the `GoT_schema.txt` file now. Write a query that shows the name of characters (in the `people` table) who are not from any of the great noble houses (in the `houses` table).
_Answer:_
```MySQL
```
**Exercise 3:** You might have noticed there are some noble houses that do not have any bannermen. Write a query that shows the name of the great noble houses without any bannermen (vassal houses) serving them.
_Answer:_
```MySQL
```
_**Short Note on Efficient Queries**_
Some `JOIN` commands (especially `INNER JOIN`) can be very computationally intensive. This is why sometimes we would prefer to write subqueries.
_Example:_ Without using any kind of`JOIN`, find all employees who work in the Asia and Canada regions who make more than 13,000 dollars.
```MySQL
SELECT * from employees
WHERE salary > 13000
AND region_id IN (SELECT region_id
FROM regions
WHERE country IN ('Asia', 'Canada'))
```
### Subqueries in `SELECT`
Subqueries can show up almost anywhere in the query! If we want to compare values to a single value, we could include the result of a subquery in the `SELECT` clause. This is especially important when you want to construct some sort of **_benchmark_** (e.g. how much you have missed/beaten a sales target by, what the active returns of a mutual fund is compared to its benchmark index, etc.)
_Example:_ Show me the first_name, last_name, and salary of all employees next to the salary of the employee who earns the least at the company.
```MySQL
SELECT first_name,
department,
salary,
(SELECT MIN(salary) FROM employees) AS "lowest_salary"
FROM employees
```
#### _Short Note on Order of Execution in SQL Queries_
Across clauses, there is a sequence that queries follow. SQL queries will run FROM first, then WHERE and other filters, and then SELECT last. So in the exercise **below**, the `lowest_salary` is already going to be calculated based on Asia and Canada employees because WHERE executes before SELECT
However, within a clause (e.g. within SELECT) everything runs _**simultaneously**_, not sequentially! So you cannot use `lowest_salary` in say a calculation for "difference" -- you will need to use the actual subquery in the calculation.
**Exercise 4:** Among all employees who work in Asia and Canada, calculate the how much less each employee makes compared to the highest earner across those regions.
_Answer:_
```MySQL
```
### Subqueries using `ALL` keyword
**Motivation:** We've learned convenient functions like `MAX` and `MIN` which helps us find the highest or lowest value in a field/column.
```MySQL
SELECT MAX(salary) FROM employees
```
What if your interviewer asked you to find the highest salary of all employees in the company **WITHOUT** using any built in SQL functions though?
```MySQL
SELECT salary
FROM employees
WHERE salary >= ALL(SELECT salary
FROM employees)
```
Interview aside though, here's a more practical problem. You're not going to be able to use MAX or MIN when it comes to this situation:
**Exercise 5:** Find the mode salar(ies) of all employees in the company.
_Answer:_
```MySQL
```
### Challenge Interview Question \#1
A retailer store information about all of its products in a `Products` table, which contain the following columns:
- `id`: the unique identification number for the product
- `name`: the name the product
- `manuf_id`: the identification number of the manufacturer we acquired this from
- `grade`: the quality score on a scale of 1 (bad) to 100 (good) of the product according to reviews.
Write a SQL query that returns the names of all products (there are ties) that have the **_SECOND_ lowest** score.
_Answer:_
### Challenge Interview Question \#2
A table called `eval` has 3 columns: <br>
- case_id (int) <br>
- timestamp (datetime) <br>
- score (int) <br>
But case_id is not unique. For a given case_id, there may be scores on different dates.
Write a query to get the score for each case_id at most recent date.
_Answer:_
```MySQL
```
**_Need some help?_** While it is probably better that you do this under interview conditions (i.e. no help from pgAdmin), the option is there if you want to use this code to construct the database and visualize the outputs of your queries
```MySQL
create table eval (
case_id int,
timestamp date,
score int);
insert into eval values (123, '2019-05-09', 7);
insert into eval values (123, '2019-05-03', 6);
insert into eval values (456, '2019-05-07', 1);
insert into eval values (789, '2019-05-06', 3);
insert into eval values (456, '2019-05-02', 9);
insert into eval values (789, '2019-05-08', 2);```
| true |
code
| 0.739334 | null | null | null | null |
|
#Spectral clustering para documentos
El clustering espectral es una técnica de agrupamiento basada en la topología de gráficas. Es especialmente útil cuando los datos no son convexos o cuando se trabaja, directamente, con estructuras de grafos.
##Preparación d elos documentos
Trabajaremos con documentos textuales. Estos se limpiarán y se convertirán en vectores. Posteriormente, podremos aplicar el método de spectral clustering.
```
#Se importan las librerías necesarias
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from gensim.models.doc2vec import Doc2Vec, TaggedDocument
```
La librería de Natural Language Toolkit (nltk) proporciona algunos corpus con los que se puede trabajar. Por ejemplo, el cropus Gutenberg (https://web.eecs.umich.edu/~lahiri/gutenberg_dataset.html) del que usaremos algunos datos. Asimismo, obtendremos de esta librería herramientas de preprocesamiento: stemmer y lista de stopwords.
```
import nltk
#Descarga del corpus
nltk.download('gutenberg')
#Descarga de la lista de stopwords
nltk.download('stopwords')
from nltk.corpus import gutenberg
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
```
Definimos los nombres de los archivos (ids) y la lista de paro
```
#Obtiene ids de los archivos del corpus gutenberg
doc_labels = gutenberg.fileids()
#Lista de stopwords para inglés
lista_paro = stopwords.words('english')
```
Definiremos una función que se encargará de preprocesar los textos. Se eliminan símbolos, se quitan elementos de la lista de stopwords y se pasa todo a minúsculas.
```
def preprocess(document):
#Lista que guarda archivos limpios
text = []
for word in document:
#Minúsculas
word = word.lower()
#Elimina stopwords y símbolos
if word not in lista_paro and word.isalpha() == True:
#Se aplica stemming
text.append(PorterStemmer().stem(word))
return text
```
Por cada documento, obtenemos la lista de sus palabras (stems) aplicando un preprocesado. Cada documento, entonces, es de la forma $d_i = \{w_1, w_2, ..., w_{N_i}\}$, donde $w_k$ son los stems del documento.
```
docs = []
for doc in doc_labels:
#Lista de palabras del documentos
arx = gutenberg.words(doc)
#Aplica la función de preprocesado
arx_prep = preprocess(arx)
docs.append(arx_prep)
#Imprime el nombre del documento, su longitud original y su longitud con preproceso
print(doc,len(arx), len(arx_prep))
```
Posteriormente, convertiremos cada documento en un vector en $\mathbb{R}^d$. Para esto, utilizaremos el algoritmo Doc2Vec.
```
#Dimensión de los vectores
dim = 300
#tamaño de la ventana de contexto
windows_siz = 15
#Indexa los documentos con valores enteros
documents = [TaggedDocument(doc_i, [i]) for i, doc_i in enumerate(docs)]
#Aplica el modelo de Doc2Vec
model = Doc2Vec(documents, vector_size=dim, window=windows_siz, min_count=1)
#Matriz de datos
X = np.zeros((len(doc_labels),dim))
for j in range(0,len(doc_labels)):
#Crea la matriz con los vectores de Doc2Vec
X[j] = model.docvecs[j]
print(X)
```
###Visualización
```
#Función para plotear
def plot_words(Z,ids,color='blue'):
#Reduce a dos dimensiones con PCA
Z = PCA(n_components=2).fit_transform(Z)
r=0
#Plotea las dimensiones
plt.scatter(Z[:,0],Z[:,1], marker='o', c=color)
for label,x,y in zip(ids, Z[:,0], Z[:,1]):
#Agrega las etiquetas
plt.annotate(label, xy=(x,y), xytext=(-1,1), textcoords='offset points', ha='center', va='bottom')
r+=1
plot_words(X, doc_labels)
plt.show()
```
##Aplicación de spectral clustering
Una vez obtenidos los vectores d elos documentos. Podemos aplicar el algoritmo de spectral clustering. Lo primero que tenemos que hacer es crear un grafo a partir de los documentos.
```
#Importamos las librerías necesarias
from scipy import linalg
from itertools import combinations
from operator import itemgetter
import pandas as pd
import networkx as nx
```
Necesitamos definir un graph kernel:
```
#Kernel gaussiano
kernel = lambda weight: np.exp(-(weight**2)/2)
#Kernel euclidiano inverso
#kernel = lambda weight: 1./(1.+weight**2)
#Número de nodos
n = X.shape[0]
#Matriz de adyacencia del grafo
M = np.zeros((n,n))
for i,x in enumerate(X):
#Se hará una lista de candidatos
candidates_for_x = {}
for j,y in enumerate(X):
#Calcula la distancia euclideana
dist = linalg.norm(x-y)
#Determina los candidatos
candidates_for_x[j] = dist
#Criterio de selección
if dist < 3:
M[i,j] = kernel(dist)
#Se obtienen los k vecinos más cercanos
#closest_neighs = sorted(candidates_for_x.items(), key=itemgetter(1), reverse=False)[:3]
#for neigh, weight in closest_neighs:
#Se llenan las columnas de la matriz, esta es simétrica
#M[i,neigh] = kernel(weight)
#M[neigh,i] = kernel(weight)
#Elimina la diagonal (equivale a eliminar lazos)
M = M-np.identity(n)
#Comprueba que es simétrica
print((M == M.T).all())
print(M.shape)
```
####Visualización del grafo
Visualización en tabla:
```
df = pd.DataFrame(M, index=doc_labels, columns=doc_labels)
print(df.to_string())
```
Visualización en red:
```
#Indexado de labels
edges = {i:dat for i,dat in enumerate(doc_labels)}
nx.draw_networkx(nx.from_numpy_array(M), with_labels=True, labels=edges, font_size=8)
```
Obtenido el grafo, se obtienen la matriz Laplaciana, así como la descomposición espectral de ésta. Además, se ordena los eigen.
```
#Se obtiene la matriz Laplaciana
L = np.diag(M.sum(0)) - M
#Se calculan los eigen valores y eigen vectores de L
eig_vals, eig_vecs = linalg.eig(L)
#Se ordenan con respecto a los eigenvalores
values = sorted(zip(eig_vals.real,eig_vecs), key=itemgetter(0))
#Obtenemos ambos eigens
vals, vecs = zip(*values)
#Se crea una matriz de eigenvectores
matrix = np.array(vecs)
#Visualización de eigenvalores
plt.plot(np.array(vals),'o')
plt.show()
```
Finalmente, obtenemos la matriz a partir de los $k$ eigenvectores con eigenvalores más pequeños.
```
#Dimensión de los vectores resultantes
vec_siz = 2
#Obtiene la matriz
M_hat = matrix[1:vec_siz+1].T.real
print(M_hat.shape)
plot_words(M_hat,doc_labels)
```
Finalmente, aplicamos el algoritmo de k-means para clusterizar los datos.
```
from sklearn.cluster import KMeans
#Número de centroides
centroids=5
#Aplicación de kmenas
kmeans = KMeans(n_clusters=centroids).fit(M_hat)
#Obtención de los clusters
pred_lables = kmeans.predict(M_hat)
#Plot de clusters
plot_words(M_hat, doc_labels, color=pred_lables)
plt.show()
```
| true |
code
| 0.333018 | null | null | null | null |
|
## Programming Exercise 3: Multi-class Classification and Neural Networks
#### Author - Rishabh Jain
```
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
%matplotlib inline
from scipy.io import loadmat
```
### 1 Multi-class Classification
##### Problem Statement
For this exercise, we will use **logistic regression** and **neural networks** to recognize handwritten digits (from 0 to 9). In this part of the exercise we will extend our previous implementation of logistic regression and apply it to one-vs-all classification.
#### 1.1 Dataset
We are given a dataset in ex3data.mat that contains 5000 training examples of handwritten digits, where each training example is a 20 X 20 pixel grayscale image of the digit. Each pixel is repsented by a floating point number indicating the grayscale intensity at that location.
This 20 by 20 pixel grid is "unrolled" into 400-dimensional vector. Each of these training examples become a single row in our dataset. This gives us a 5000 X 400 design matrix X where every row is a training example for a handwritten digit image. The second part of the training set is a 5000-dimnesional vectory y that contains labels for the training set. Labels range from 1 to 10 where 10 reprsents digit '0'.
```
# Loading Mat file
mat=loadmat('./ex3data1.mat')
print(*mat.keys(),sep='\n')
# Loading data from mat to Dataframe
m,n=mat['X'].shape
data=pd.DataFrame()
for i in range(n):
data[f'x{i+1}']=mat['X'].T[i]
# Converting label 10 to label 0
data['y']=mat['y']
data.loc[data['y']==10,'y']=0
print('TRAINING DATASET SHAPE : {0} X {1}'.format(*data.shape))
data.sample(5)
```
#### 1.2 Visualizing the data
We will begin by visualizing a subset of the training set. We will randomly select 100 rows from X. This function maps each row to a 20 X 20 pixel image and displays together.
```
def displayData(X):
m,n=X.shape
width=int(np.sqrt(n))
height=int(n/width)
rows=int(np.floor(np.sqrt(m)))
cols=int(np.ceil(m/rows))
totalWidth=cols+cols*width
displayArray=np.zeros((1,totalWidth))
rowPadding=np.ones((1,totalWidth))
colPadding=np.ones((height,1))
index=0
for i in range(rows):
row=colPadding*0
for j in range(cols):
if index<m:
x=X[index].reshape((width,height)).T
index=index+1
else:
x=np.zeros((width,height)).T
row=np.column_stack((row,x))
if j<cols-1:
row=np.column_stack((row,colPadding))
displayArray=np.row_stack((displayArray,row))
if i<rows-1:
displayArray=np.row_stack((displayArray,rowPadding))
displayArray=np.row_stack((displayArray,rowPadding*0))
plt.imshow(displayArray,cmap='gray')
plt.axis('off')
displayData(data.sample(100).iloc[:,:-1].values)
```
#### 1.3 Vectorizing Logistic Regression
We will be using mutiple one-vs-all logistic regression models to build multi-class classifier. Since there are 10 classes, we wil need to train 10 separate logistic regression. To make this training efficient, it is important to ensure that our code is well vectorized. In this section, we will implement a vectorized version of logistic regression that does not employ any for loops.
**Formulae :**
$$ h_\theta(x)=g(\theta^Tx) $$
$$ g(z)=\frac{1}{1+e^{-z}} $$
$$ J(\theta)= \frac{-1}{m}\sum_{i=0}^m[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)})]+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2$$
$$ \theta_j:=\theta_j-\frac{\alpha}{m}(\sum_{i=0}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}+\lambda\sum_{j=1}^n\theta_j) $$
**From the previous notebook [Exercise-2](https://nbviewer.jupyter.org/github/rj425/ML-Coursera/blob/master/Exercise-2/ex2.ipynb), all these functions are already vectorized.**
```
def sigmoid(z):
sigma=1/(1+np.exp(-z))
return sigma
def predict(X,theta):
'''Predicts by applying logistic function on linear model'''
z=np.dot(X,theta.T)
h=sigmoid(z)
return h
def computeCost(h,y):
'''Computes the cost using Cross Entropy function'''
m=y.shape[0]
J=(-1/m)*np.sum(np.multiply(y,np.log(h))+np.multiply(1-y,np.log(1-h)))
return J
def regularizedGradientDescent(X,y,theta,alpha,lmbda,iterations):
'''Minimizes the cost function using Gradient Descent Optimization Algorithm'''
m=X.shape[0]
jHistory=[]
for i in range(iterations):
h=predict(X,theta)
# Computing cost
J=computeCost(h,y)
# Adding the regularized term
J=J+(lmbda/(2*m))*np.sum(np.power(theta[:,1:],2))
jHistory.append(J)
# Parameters update rule
gradient=(alpha/m)*(np.dot((h-y).T,X))
# Adding the regularized term
gradient=gradient+(alpha/m)*lmbda*np.column_stack((np.zeros((1,1)),theta[:,1:]))
theta=theta-gradient
return (theta,jHistory)
```
#### 1.4 One-vs-all Classification
In this part of the exercise, **we will implement One-vs-all classification by training multiple logistic regression classifiers, one for each of K classes in our dataset.**
```
def oneVsAll(X,Y,alpha,lmbda,iterations):
'''Returns all the classifier parameters in a matrix with shape of classes X features'''
m,n=X.shape
# Initializing theta
intialTheta=np.zeros(shape=(1,n))
labels=np.unique(Y)
thetas=np.zeros(shape=(len(labels),n))
i=0
print('Training classifiers...\n')
for label in labels:
y=np.zeros(shape=(m,1))
y[Y==label]=1
theta,jHistory=regularizedGradientDescent(X,y,intialTheta,alpha,lmbda,iterations)
thetas[i,:]=theta
print(f'For classifier{label} , J = {jHistory[iterations-1]:.3f}')
i+=1
return thetas
m=data.shape[0]
X=data.values[:,:-1]
# Adding intercept term to the design matrix
intercept=np.ones(shape=(m,1))
X=np.column_stack((intercept,X))
y=data['y'].values.reshape((m,1))
alpha=1
lmbda=0.3
iterations=3000
thetas=oneVsAll(X,y,alpha,lmbda,iterations)
```
#### 1.4.1 One-vs-all Prediction
After training One-vs-all classifier, we can use it to predict the digit contained in a given image. For each input, we should compute the 'probability' that it belongs to each class using the trained logistic regression classifiers.
```
def predictOneVsAll(thetas,X):
'''Predic the label for a trained One-vs-all classifier. The labels are in the range 0 to 9'''
h=predict(X,thetas)
labels=h.argmax(axis=1)
return labels.reshape((X.shape[0],1))
def calculateAccuracy(h,y):
'''Calculates the accuray between the target and prediction'''
m=y.shape[0]
unique,counts=np.unique(h==y,return_counts=True)
dic=dict(zip(unique,counts))
accuracy=(dic[True]/m)*100
return accuracy
h=predictOneVsAll(thetas,X)
accuracy=calculateAccuracy(h,y)
print(f'TRAINING ACCURACY : {accuracy:.2f}')
```
### 2 Neural Networks
In previous part of the exercise, we implemented multi-class logistic regression to recognize the handwritten digits. **However, logistic regression cannot form more complex hypotheses, as it is only a Linear Classifier.**
>**One may ask why is logistic regression a linear model if it can fit curves to our data??**
That's because the linearity of the model is concerned by the linearity of the parameters $\theta$. Here the target variable is a function of parameter ($\theta$) multiplied by the independent variable ($x_i$). And we can fit the curves to our data using the non linear transformation of independent variables or features but the parameters are still linear.
**Non Linear Hypotheses**
If the number of features are large which will ususally be the case, we will move towards the non linear hypotheses for a better fit for the data. So if $n=100$ :
- For quadratic hypotheses, $n\approx5000$ features
- For cubic hypotheses, $n\approx170000$ features
Solving such problems with logistic regression can cause two problems:
- Computationally expensive
- Time consuming
Not a good way to learn complex Non Linear hypthoses when feature space is large. Hence, **Neural Networks**.
#### 2.1 Model Representation
<table>
<tr>
<td>
<img src="images/neuron.png" width="300">
</td>
<td>
<img src="images/nn.png" width="300">
</td>
</tr>
</table>
$a_i^{(j)}=$ "activation" of unit $i$ in layer $j$
$\theta^{(j)}=$ matrix of weights controlling function mapping from layer $j$ to layer $j+1$
$g(x)=$ sigmoid activation function
**If network has $s_j$ units in layer $j$, $s_{j+1}$ units in layer $j+1$, then $\theta^{(j)}$ will be of dimension $s_{j+1}$ X $(s_j+1)$**
$$ a^{(2)}_1=g(\theta_{10}^{(1)}x_0+\theta_{11}^{(1)}x_1+\theta_{12}^{(1)}x_2+\theta_{13}^{(1)}x_3) $$
$$ a^{(2)}_2=g(\theta_{20}^{(1)}x_0+\theta_{21}^{(1)}x_1+\theta_{22}^{(1)}x_2+\theta_{23}^{(1)}x_3) $$
$$ a^{(2)}_3=g(\theta_{30}^{(1)}x_0+\theta_{31}^{(1)}x_1+\theta_{32}^{(1)}x_2+\theta_{33}^{(1)}x_3) $$
In this exercise, we will be using the parameters from a neural network that is already trained. Our goal is to implement the **Feed-Forward Progration** algorithm for prediction.
```
# Loading weights
weights=loadmat('./ex3weights.mat')
print(*weights.keys(),sep='\n')
```
The neural network we are about to use has 3 layers - an input layer ($L_1$), a hidden layer ($L_2$) and an output layer ($L_3$).
* L1 layer has 400 Neuron units (20 X 20 pixel image) excluding the extra bias unit that always output +1
* L2 layer has 25 Neuron units
* L3 layer has 10 Neuron Units
```
theta1=weights['Theta1']
theta2=weights['Theta2']
print(f'X : {X.shape}')
print(f'Theta1 : {theta1.shape}')
print(f'Theta2 : {theta2.shape}')
```
#### 2.2 Feedforward Propogation and Prediction
**Vectorized Implementation** for three layered Neural Network:
Step 0 : $a^{(1)}=x$
Step 1 : $z^{(2)}=\theta^{(1)}a^{(1)}$
Step 2 : $a^{(2)}=g(z^{(2)})$
Step 3 : Add $a^{(2)}_0=1$
Step 4 : $z^{(3)}=\theta^{(2)}a^{(2)}$
Step 5 : $a^{(3)}=g(z^{(3)})$
Step 6 : $h_\theta(x)=a^{(3)}$
```
def predictNN(theta1,theta2,X):
'''Predict the label of an input given a trained neural network'''
m,n=X.shape
# Feed Forward Propogation
a1=X
z2=np.dot(a1,theta1.T)
a2=sigmoid(z2)
a2=np.column_stack((np.ones(shape=(a2.shape[0],1)),a2))
z3=np.dot(a2,theta2.T)
a3=sigmoid(z3)
h=a3
labels=h.argmax(axis=1)
return labels.reshape((m,1))
# Using label 10 for digit 0
y=mat['y']
h=predictNN(theta1,theta2,X)
# Adding one to h because matlab indexing starts from 1 whereas python indexing starts from 0
h+=1
accuracy=calculateAccuracy(h,y)
print(f'TRAINING ACCURACY : {accuracy:.2f}')
```
<table>
<tr>
<td>
<img src="images/meme1.jpg" width="500">
</td>
<td>
<img src="images/meme2.jpg" width="300">
</td>
</tr>
</table>
| true |
code
| 0.436562 | null | null | null | null |
|
## Problem Statement
Previously, we considered the following problem:
>Given a positive integer `n`, write a function, `print_integers`, that uses recursion to print all numbers from `n` to `1`.
>
>For example, if `n` is `4`, the function shuld print `4 3 2 1`.
Our solution was:
```
def print_integers(n):
if n <= 0:
return
print(n)
print_integers(n - 1)
print_integers(5)
```
We have already discussed that every time a function is called, a new *frame* is created in memory, which is then pushed onto the *call stack*. For the current function, `print_integers`, the call stack with all the frames would look like this:
<img src='./recurrence-relation-resources/01.png'>
Note that in Python, the stack is displayed in an "upside down" manner. This can be seen in the illustration above—the last frame (i.e. the frame with `n = 0`) lies at the top of the stack (but is displayed last here) and the first frame (i.e., the frame with `n = 5`) lies at the bottom of the stack (but is displayed first).
But don't let this confuse you. The frame with `n = 0` is indeed the top of the stack, so it will be discarded first. And the frame with `n = 5` is indeed at the bottom of the stack, so it will be discarded last.
We define time complexity as a measure of amount of time it takes to run an algorithm. Similarly, the time complexity of our function `print_integers(5)`, would indicate the amount of time taken to exceute our function `print_integers`. But notice how when we call `print_integers()` with a particular value of `n`, it recursively calls itself multiple times.
In other words, when we call `print_integers(n)`, it does operations (like checking for base case, printing number) and then calls `print_integers(n - 1)`.
Therefore, the overall time taken by `print_integers(n)` to execute would be equal to the time taken to execute its own simple operations and the time taken to execute `print_integers(n - 1)`.
Let the time taken to execute the function `print_integers(n)` be $T(n)$. And let the time taken to exceute the function's own simple operations be represented by some constant, $k$.
In that case, we can say that
$$T(n) = T(n - 1) + k$$
where $T(n - 1)$ represents the time taken to execute the function `print_integers(n - 1)`.
Similarly, we can represent $T(n - 1)$ as
$$T(n - 1) = T(n - 2) + k$$
We can see that a pattern is being formed here:
1. $T(n)\ \ \ \ \ \ \ = T(n - 1) + k$
2. $T(n - 1) = T(n - 2) + k$
3. $T(n - 2) = T(n - 3) + k$
4. $T(n - 3) = T(n - 4) + k$
.<br>
.<br>
.<br>
.<br>
.<br>
.<br>
5. $T(2) = T(1) + k$
6. $T(1) = T(0) + k$
7. $T(0) = k1$
Notice that when `n = 0` we are only checking the base case and then returning. This time can be represented by some other constant, $k1$.
If we add the respective left-hand sides and right-hand sides of all these equations, we get:
$$T(n) = nk + k1$$
We know that while calculating time complexity, we tend to ignore these added constants because for large input sizes on the order of $10^5$, these constants become irrelevant.
Thus, we can simplify the above to:
$$T(n) = nk $$
We can see that the time complexity of our function `print_integers(n)` is a linear function of $n$. Hence, we can say that the time complexity of the function is $O(n)$.
## Binary Search
#### Overview
Given a **sorted** list (say `arr`), and a key (say `target`). The binary search algorithm returns the index of the `target` element if it is present in the given `arr` list, else returns -1. Here is an overview of how the the recursive version of binary search algorithm works:
1. Given a list with the lower bound (`start_index`) and the upper bound (`end_index`).
1. Find the center (say `mid_index`) of the list.
1. Check if the element at the center is your `target`? If yes, return the `mid_index`.<br><br>
1. Check if the `target` is greater than that element at `mid_index`? If yes, call the same function with right sub-array w.r.t center i.e., updated indexes as `mid_index + 1` to `end_index` <br><br>
1. Check if the `target` is less than that element at `mid_index`? If yes, call the same function with left sub-array w.r.t center i.e., updated indexes as `start_index` to `mid_index - 1` <br><br>
1. Repeat the step above until you find the target or until the bounds are the same or cross (the upper bound is less than the lower bound).
#### Complexity Analysis
Let's look at the time complexity of the recursive version of binary search algorithm.
>Note: The binary search function can also be written iteratively. But for the sake of understanding recurrence relations, we will have a look at the recursive algorithm.
Here's the binary search algorithm, coded using recursion:
```
def binary_search(arr, target):
return binary_search_func(arr, 0, len(arr) - 1, target)
def binary_search_func(arr, start_index, end_index, target):
if start_index > end_index:
return -1
mid_index = (start_index + end_index)//2
if arr[mid_index] == target:
return mid_index
elif arr[mid_index] > target:
return binary_search_func(arr, start_index, mid_index - 1, target)
else:
return binary_search_func(arr, mid_index + 1, end_index, target)
arr = [0, 1, 2, 3, 4, 5, 6, 7, 8]
print(binary_search(arr, 5))
```
Let's try to analyze the time complexity of the recursive algorithm for binary search by finding out the recurrence relation.
Our `binary_search()` function calls the `binary_search_func()` function. So the time complexity of the function is entirely dependent on the time complexity of the `binary_search_func()`.
The input here is an array, so our time complexity will be determined in terms of the size of the array.
Like we did earlier, let's say the time complexity of `binary_search_func()` is a function of the input size, `n`. In other words, the time complexity is $T(n)$.
Also keep in mind that we are usually concerned with the worst-case time complexity, and that is what we will calculate here. In the worst case, the `target` value will not be present in the array.
In the `binary_search_func()` function, we first check for the base case. If the base case does not return `True`, we calculate the `mid_index` and then compare the element at this `mid_index` with the `target` values. All the operations are independent of the size of the array. Therefore, we can consider all these independent operations as taking a combined time, $k$.
Apart from these constant time operations, we do just one other task. We either make a call on the left-half of the array, or on the right half of the array. By doing so, we are reducing the input size by $n/2$.
>Note: Remember that we usually consider large input sizes while calculating time complexity; there is no significant difference between $10^5$ and ($10^5 + 1$).
Thus, our new function call is only called with half the input size.
We said that $T(n)$ was the time complexity of our original function. The time complexity of the function when called with half the input size will be $T(n/2)$.
Therefore:
$$T(n) = T(n/2) + k$$
Similarly, in the next step, the time complexity of the function called with half the input size would be:
$$T(n/2) = T(n/4) + k$$
We can now form similar equations as we did for the last problem:
1. $T(n)\ \ \ = T(n/2) + k$
2. $T(n/2) = T(n/4) + k$
3. $T(n/4) = T(n/8) + k$
4. $T(n/8) = T(n/16) + k$
.<br>
.<br>
.<br>
.<br>
.<br>
.<br>
5. $T(4) = T(2) + k$
6. $T(2) = T(1) + k$
7. $T(1) = T(0) + k1$ $^{(1)}$
8. $T(0) = k1$
$^{(1)}$ If we have only one element, we go to 0 elements next
From our binary search section, we know that it takes $log(n)$ steps to go from $T(n)$ to $1$. Therefore, when we add the corresponding left-hand sides and right-hand sides, we can safely say that:
$$T(n) = log(n) * k + k1$$
As always, we can ignore the constant. Therefore:
$$T(n) = log(n) * k $$
Thus we see that the time complexity of the function is a logarithmic function of the input, $n$. Hence, the time complexity of the recursive algorithm for binary search is $log(n)$.
| true |
code
| 0.38027 | null | null | null | null |
|
# Estimating an AR Model
## Introduction to Autoregression Model
An autoregression model is a regression with a time series and itself, shifted by a time step or steps. These are called lags. I will demonstrate with five examples with the non-stationarized datasets so that you can see the results in the original dataset along with the forecasted dataset.
```
import pandas as pd
from pandas import read_csv
from matplotlib import pyplot
from pandas.plotting import lag_plot
from statsmodels.graphics.tsaplots import plot_acf
```
### Example 1: Vacation dataset
```
# Read in vacation dataset
vacation = read_csv('~/Desktop/section_3/df_vacation.csv', index_col=0, parse_dates=True)
vacation.head()
# Plot the time series against its lag
lag_plot(vacation)
pyplot.show()
from pandas import concat
values = pd.DataFrame(vacation.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t-1', 't+1']
result = dataframe.corr()
print(result)
# Plot the autocorrelation of the dataset
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(vacation)
pyplot.show()
# Plot the Autocorrelation Function, using candle sticks
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(vacation, lags=50)
pyplot.show()
# Estimating an AR Model
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Fit an AR(1) model to the first simulated data
mod = ARMA(vacation, order=(1,0)) # fit data to an AR1 model
res = mod.fit() # use fit() to estimate model
# Print out summary information on the fit
print(res.summary())
print(res.params)
# Estimated parameters are close to true parameters
```
The best model chosen is the one with the lowest Information Criterion. The AIC shows the lowest.
```
# Forecasting
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Forecast the first AR(1) model
mod = ARMA(vacation, order=(1,0))
res = mod.fit()
# Start the forecast 10 data points before the end of the point series at ,
#and end the forecast 10 data points after the end of the series at point
res.plot_predict(start='2015', end='2025')
pyplot.show()
```
### Example 2: Furniture dataset
```
furn = read_csv('~/Desktop/section_3/df_furniture.csv', index_col=0, parse_dates=True)
furn.head()
# Plot the time series against its lag
lag_plot(furn)
pyplot.show()
from pandas import concat
values = pd.DataFrame(furn.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t-1', 't+1']
result = dataframe.corr()
print(result)
# Plot the autocorrelation
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(furn)
pyplot.show()
# Plot the Autocorrelation Function, using candle sticks
from pandas import read_csv
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(furn, lags=50)
pyplot.show()
# Estimating an AR Model
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Fit an AR(1) model to the first simulated data
mod = ARMA(furn, order=(1,0)) # fit data to an AR1 model
res = mod.fit() # use fit() to estimate model
# Print out summary information on the fit
print(res.summary())
print(res.params)
# Estimated parameters are close to true parameters
# S.D. of innovations is standard deviation of errors
# L1 is lag1
# fitted model parameters
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Forecast the first AR(1) model
mod = ARMA(furn, order=(1,0))
res = mod.fit()
# Start the forecast 10 data points before the end of the point series at ,
#and end the forecast 10 data points after the end of the series at point
res.plot_predict(start='2015', end='2025')
pyplot.show()
```
### Example 3: Bank of America dataset
```
# Read in BOA dataset, this is original with resampling to monthly data
bac= read_csv('~/Desktop/section_3/df_bankofamerica.csv', index_col=0, parse_dates=True)
# convert daily data to monthly
bac= bac.resample(rule='M').last()
bac.head()
# Plot the time series against its lag
lag_plot(bac)
pyplot.show()
from pandas import concat
values = pd.DataFrame(bac.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t-1', 't+1']
result = dataframe.corr()
print(result)
# Plot the autocorrelation
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(bac)
pyplot.show()
# Plot the Autocorrelation Function, using candle sticks
from pandas import read_csv
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(bac, lags=50)
pyplot.show()
# Estimating an AR Model
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Fit an AR(1) model to the first simulated data
mod = ARMA(bac, order=(1,0)) # fit data to an AR1 model
res = mod.fit() # use fit() to estimate model
# Print out summary information on the fit
print(res.summary())
print(res.params)
# Estimated parameters are close to true parameters
# S.D. of innovations is standard deviation of errors
# L1 is lag1
# fitted model parameters
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Forecast the first AR(1) model
mod = ARMA(bac, order=(1,0))
res = mod.fit()
# Start the forecast 10 data points before the end of the point series at ,
#and end the forecast 10 data points after the end of the series at point
res.plot_predict(start='2015', end='2025')
pyplot.show()
```
### Example 4: J.P. Morgan dataset
```
# Read in JPM dataset
jpm = read_csv('~/Desktop/section_3/df_jpmorgan.csv', index_col=0, parse_dates=True)
# Convert the daily data to quarterly
jpm= jpm.resample(rule='Q').last() # resample to quarterly data
jpm.head()
# Plot the time series against its lag
lag_plot(jpm)
pyplot.show()
from pandas import concat
values = pd.DataFrame(jpm.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t-1', 't+1']
result = dataframe.corr()
print(result)
# Plot the autocorrelation
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(jpm)
pyplot.show()
# Plot the Autocorrelation Function, using candle sticks
from pandas import read_csv
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(jpm, lags=50)
pyplot.show()
# Estimating an AR Model
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Fit an AR(1) model to the first simulated data
mod = ARMA(jpm, order=(1,0)) # fit data to an AR1 model
res = mod.fit() # use fit() to estimate model
# Print out summary information on the fit
print(res.summary())
print(res.params)
# Estimated parameters are close to true parameters
# S.D. of innovations is standard deviation of errors
# L1 is lag1
# fitted model parameters
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Forecast the first AR(1) model
mod = ARMA(jpm, order=(1,0))
res = mod.fit()
# Start the forecast 10 data points before the end of the point series at ,
#and end the forecast 10 data points after the end of the series at point
res.plot_predict(start='2015', end='2025')
pyplot.show()
```
### Example 5: Average Temperature of St. Louis dataset
```
# Read in temp dataset
temp = read_csv('~/Desktop/section_3/df_temp.csv', index_col=0, parse_dates=True)
temp.head()
# Plot the time series against its lag
lag_plot(temp)
pyplot.show()
from pandas import concat
values = pd.DataFrame(temp.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t-1', 't+1']
result = dataframe.corr()
print(result)
# Plot the autocorrelation
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(temp)
pyplot.show()
# Plot the Autocorrelation Function, using candle sticks
from pandas import read_csv
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(temp, lags=50)
pyplot.show()
# Estimating an AR Model
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Fit an AR(1) model to the first simulated data
mod = ARMA(temp, order=(1,0)) # fit data to an AR1 model
res = mod.fit() # use fit() to estimate model
# Print out summary information on the fit
print(res.summary())
print(res.params)
# Estimated parameters are close to true parameters
# S.D. of innovations is standard deviation of errors
# L1 is lag1
# fitted model parameters
# Import the ARMA module from statsmodels
from statsmodels.tsa.arima_model import ARMA
# Forecast the first AR(1) model
mod = ARMA(temp, order=(1,0))
res = mod.fit()
# Start the forecast 10 data points before the end of the point series at ,
#and end the forecast 10 data points after the end of the series at point
res.plot_predict(start='2015', end='2025')
pyplot.show()
# end
```
| true |
code
| 0.665125 | null | null | null | null |
|
# SAS ODA and Python Integration to Analyze COVID-19 Data
The purpose of this notebook is to illustrate how Python code can be integrated with calls to SAS ODA in order to solve a particular problem of interest. In the course of this document, we will load the NYT COVID-19 data set. As the NYT data set contains raw cumulative values only, we will also load a census data set that contains estimates for the US population in 2019. We will combine the information from both data sets to calculate the number of cases and deaths per 1,000,000 residents of each state on each day for which we have data. Afterwards, we will use a few different techniques to visualize the cases per 100,000 for the various states.
## NYT Data Acquisition
Our first step is to start a connection with the SAS servers. We use the "SASPy" Python package (installed locally) and its [`SASsession` method](https://sassoftware.github.io/saspy/api.html#saspy.SASsession) to establish this connection.
```
import saspy
sas_session = saspy.SASsession()
```
With the connection established, we can use the [`submit` method](https://sassoftware.github.io/saspy/api.html#saspy.SASsession.submit) to run SAS code from our Python interface. This method returns the SAS output and log message as a Python dictionary which can then be queried for either component.
```
results_dict = sas_session.submitLST(
"""
filename nyt_url url 'https://raw.githubusercontent.com/nytimes/covid-19-data/master/us-counties.csv';
data us_counties_nyt;
length Date 8 County $ 30 statename $ 30 FIPS $ 6 Cases 8 Deaths 8 WeekOf 8;
format Date date9. WeekOf date9.;
infile nyt_url dlm=',' missover dsd firstobs=2;
input date : yymmdd10.
county
statename
FIPS
cases
deaths;
/* Adding Week ending value for easier summary later */
WeekOf = intnx('week',date,0,'E');
run;
""",
)
```
To view the SAS log of the previous operation, you would run the command ```print(results_dict["LOG"])``` in Python.
SAS has a built-in data set with information about the US, including the 2-letter state codes. We will use an inner join method using a `proc sql` in SAS to attach this 2-letter code to our data rows. We specifically use an inner join as the NYT data set includes data on some US territories which we wish to exclude from our analysis in order to focus only on the US states.
In the last line, we use the [`sd2df` method](https://sassoftware.github.io/saspy/api.html#saspy.SASsession.sd2df) on our SAS session to move the data from SAS to Python for further processing.
```
results_dict = sas_session.submit(
"""
proc sql noprint;
create table NYT_joined as
select nyt.Date, nyt.County, nyt.statename as State, usd.Statecode as StateCode, nyt.Cases, nyt.Deaths
from work.US_COUNTIES_NYT as nyt inner join sashelp.us_data as usd
on nyt.statename=usd.statename;
quit;
""",
)
nyt_df = sas_session.sd2df("NYT_joined")
```
Now that we have the data available in Python, we will load the various Python packages we will need.
```
# this is for type-hinting in function definitions:
from typing import List, Dict
# some standard imports from Python for this
# type of work
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# some nice imports to make life easier
# 1) make matplotlib aware of Pandas DateTime format
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
# 2) create nicer date formatting in plots
import matplotlib.dates as mdates
```
Since the source data set we imported lists data from various counties separately, we first want to simplify our work by adding up all the cases and deaths in each state so that we have only one row of data per state per date. Since this is a common class of problem, we will write a small function to do this task for us. This method is similar to writing and using a macro in SAS.
```
def make_state_summary(df: pd.DataFrame) -> pd.DataFrame:
"""
Function to process the initial data in two ways:
1) Filter down the columns to the important ones, dropping
columns that we don't need for our analysis.
2) Each state is broken down into counties in the NYT data set,
but we want state level information. We sum across the counties
in the state.
Overall, this function is comparable to a "proc freq"
in SAS.
"""
# filter out unnecessary information. Think of a SAS 'keep' statement.
df = df.filter(['Date', 'State','Cases','Deaths', 'StateCode'])
# sums up the data by 'Date', 'State, 'Statecode',
# - this returns state-level 'cases' and 'deaths'
short = df.groupby(['Date', 'State', 'StateCode'],
as_index=False).sum()
return short
# call our function to apply the manipulation from the
# `make_state_summary` function.
df = make_state_summary(nyt_df)
```
Let's verify the data types to make sure we have everything we need. It is important that the Date variable is listed as ```datetime64[ns]``` as opposed to as ```object```, which is a string format as opposed to the numeric date format we want. If this variable is listed as an object, we can run the line ```df.Date = pd.to_datetime(df.Date)``` to fix this problem. We run the conditional fix and print the data types of all columns to make sure we have the correct types for further analysis.
```
# verify that Date is not a string format,
# fix it otherwise.
if df["State"].dtype==df["Date"].dtype:
df.Date = pd.to_datetime(df.Date)
df.dtypes
```
## Updating our Data Set with the Census Information
Since we ultimately want to figure out the number of cases and deaths per 100,000 residents of each state, we use a data set from the census bureau which includes population estimates for 2019. We use the `filter` method (similar to a `keep` in SAS) to only load the columns we are interested in, including the actual values from the 2010 census, as well as the Census Bureau's estimates for the year 2019.
```
census_url = "http://www2.census.gov/programs-surveys/popest/datasets/2010-2019/national/totals/nst-est2019-alldata.csv?#"
pop_set = pd.read_csv(census_url).filter(['REGION', 'DIVISION', 'STATE', 'NAME', 'CENSUS2010POP',
'ESTIMATESBASE2010', 'POPESTIMATE2019'])
```
Now that we have both data sets available in memory, we will calculate the case-load and death-toll for each state and date given the 2019 estimate. The calculated values are appended as new columns to our data set.
```
def update_case_load(source : pd.DataFrame,
census : pd.DataFrame) -> pd.DataFrame:
"""
Function to update a dataframe to include case-load
and death-toll per 100,000 residents using a census
data set as look-up table for population values.
"""
# for loop iterates over all rows in the 'source' dataframe
for index, row in source.iterrows():
state = row["State"] # looks-up current statename of row
# then looks-up the "POPESTIMATE2019" column value associated with
# that state in the `census` dataframe.
pop = census[census.NAME==state]["POPESTIMATE2019"].to_numpy()[0]
# use the population value to calculate cases/deaths per 100.000 residents
cases_per_100k = 1e5*row["Cases"]/pop
deaths_per_100k = 1e5*row["Deaths"]/pop
# update `source` dataframe with three new column values
source.loc[index,"Population"] = pop
source.loc[index,"CPM"] = cases_per_100k
source.loc[index, "DPM"] = deaths_per_100k
return source
# run the functon to actually apply the calculations
# defined in the `update_case_load` function.
df = update_case_load(df, pop_set)
```
At this stage, we have two Pandas dataframes in memory - the `pop_set` dataframe which was used a look-up table for state population information, and the main dataframe `df` which contains the following columns of information we want for our visualizations:
```
df.dtypes
```
## Simple Plot Visualition
Let's start with a few simple visualizations to compare different states. To make it easier, we create a short function that subsets the necessary data, followed by a short function to do the plotting with the output data set.
```
def state_sets(df : pd.DataFrame, States: List) -> Dict:
"""
This function is similar to a data step in SAS. It takes
in a list of state-codes of interest together with the main
dataframe and returns a dictionary where each statecode is mapped
to a dataframe containing only the information from that state.
"""
# use a quick dictionary comprehension to subset the data
out_dict = {state : df[df.StateCode==state] for state in States }
return out_dict
def line_plot_states(states_of_interest : Dict,
min_date : str = "2020-03-01"):
"""
Convenience function to do the plotting.
Takes a dictionary of states and a start date and then
makes a line plot of the 'cases per 100,000' variable in
all states listed in the dictionary.
"""
# define plot size
fig, ax = plt.subplots(figsize=(10,5.625))
# iterates over the dictionary and adds each state's
# line to the plot
for key, data in states_of_interest.items():
subdata = data[data.Date>=pd.to_datetime(min_date)]
ax.plot(subdata.Date, subdata.CPM, label=key)
ax.legend() # turns on the legend
# make the axes pretty
fig.autofmt_xdate()
ax.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, loc: "{:,}".format(int(x))))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%m-%d'))
ax.set_ylabel('Cases per 100,000')
plt.show(fig) # necessary to display the plot
```
Now all we need to do is to create a list of states of interest and pass them to our function, along with an optional start date. Say we are interested in comparing the cases per 100,000 residents over time for several different states. Then our code would look as follows:
```
# list of states, sort it so that the legend is alphabetical
# Try out different states!
state_list = sorted(["AZ", "CA", "NC", "NJ", "AR"])
# get the dictionary of state data out
states_of_interest = state_sets(df, state_list)
# does the plotting
line_plot_states(states_of_interest, "2020-09-01")
```
## Making the Map
Making maps and plotting over them is hard. Luckily, SAS has a few special procedures available for this. To make our work easier, we will first collect the necessary information for the map from our Python data set and then export it to SAS for plotting. We'll pick data corresponding to a single date and upload the data set to SAS.
```
# list of dates of interest
# note that the SAS code below expects only one date,
# so if you choose to make a list of multiple dates here,
# please also update the SAS code below to pick a specific
# date for plotting.
# Use format 'YYYY-MM-DD' for the dates
dates_of_interest = ["2021-06-01"]
# uses the above list to subset the dataframe
sub_df = df[df.Date.isin(dates_of_interest)]
# uploads the dataframe to SAS under the name
# work.map_data
sas_session.df2sd(sub_df, table="map_data")
```
We first want to make a choropleth map of the situation. This would allow us to use a color scheme to differentiate between different classes of states, based on the CPM value. Well, `gmap` to the rescue. We will use the `midpoints=old` to use a the Nelder algorithm to determine the appropriate ranges and midpoints.
```
%%SAS sas_session
proc gmap data=work.map_data map=mapsgfk.us all;
id STATECODE;
format CPM COMMA10.;
choro CPM / midpoints=old;
run;
```
By changing the code slightly, we can also create a gradient map of cases.
```
%%SAS sas_session
proc sgmap mapdata=mapsgfk.us maprespdata=map_data;
choromap cpm / mapid=statecode name='choro';
format cpm COMMA10.;
gradlegend 'choro' / title='Cumulative Cases per 100,000' extractscale;
run;
```
| true |
code
| 0.716057 | null | null | null | null |
|
# ML for Trading: How to run an ML algorithm on Quantopian
The code in this notebook is written for the Quantopian Research Platform and uses the 'Algorithms' rather than the 'Research' option we used before.
To run it, you need to have a free Quantopian account, create a new algorithm and copy the content to the online development environment.
## Imports & Settings
### Quantopian Libraries
```
from quantopian.algorithm import attach_pipeline, pipeline_output, order_optimal_portfolio
from quantopian.pipeline import Pipeline, factors, filters, classifiers
from quantopian.pipeline.data.builtin import USEquityPricing
from quantopian.pipeline.data import Fundamentals
from quantopian.pipeline.data.psychsignal import stocktwits
from quantopian.pipeline.factors import (Latest,
CustomFactor,
SimpleMovingAverage,
AverageDollarVolume,
Returns,
RSI,
SimpleBeta,
MovingAverageConvergenceDivergenceSignal as MACD)
from quantopian.pipeline.filters import QTradableStocksUS
from quantopian.pipeline.experimental import risk_loading_pipeline, Size, Momentum, Volatility, Value, ShortTermReversal
import quantopian.optimize as opt
from quantopian.optimize.experimental import RiskModelExposure
```
### Other Python Libraries
```
from scipy.stats import spearmanr
import talib
import pandas as pd
import numpy as np
from time import time
from collections import OrderedDict
from scipy import stats
from sklearn import linear_model, preprocessing, metrics, cross_validation
from sklearn.pipeline import make_pipeline
```
### Strategy Positions
```
# strategy parameters
N_POSITIONS = 100 # Will be split 50% long and 50% short
TRAINING_PERIOD = 126 # past periods for training
HOLDING_PERIOD = 5 # predict returns N days into the future
# How often to trade, for daily, alternative is date_rules.every_day()
TRADE_FREQ = date_rules.week_start()
```
### Custom Universe
We define a custom universe to limit duration of training.
```
def Q250US():
"""Define custom universe"""
return filters.make_us_equity_universe(
target_size=250,
rankby=factors.AverageDollarVolume(window_length=200),
mask=filters.default_us_equity_universe_mask(),
groupby=classifiers.fundamentals.Sector(),
max_group_weight=0.3,
smoothing_func=lambda f: f.downsample('month_start'),
)
```
## Create Alpha Factors
```
def make_alpha_factors():
def PriceToSalesTTM():
"""Last closing price divided by sales per share"""
return Fundamentals.ps_ratio.latest
def PriceToEarningsTTM():
"""Closing price divided by earnings per share (EPS)"""
return Fundamentals.pe_ratio.latest
def DividendYield():
"""Dividends per share divided by closing price"""
return Fundamentals.trailing_dividend_yield.latest
def Capex_To_Cashflows():
return (Fundamentals.capital_expenditure.latest * 4.) / \
(Fundamentals.free_cash_flow.latest * 4.)
def EBITDA_Yield():
return (Fundamentals.ebitda.latest * 4.) / \
USEquityPricing.close.latest
def EBIT_To_Assets():
return (Fundamentals.ebit.latest * 4.) / \
Fundamentals.total_assets.latest
def Return_On_Total_Invest_Capital():
return Fundamentals.roic.latest
class Mean_Reversion_1M(CustomFactor):
inputs = [Returns(window_length=21)]
window_length = 252
def compute(self, today, assets, out, monthly_rets):
out[:] = (monthly_rets[-1] - np.nanmean(monthly_rets, axis=0)) / \
np.nanstd(monthly_rets, axis=0)
def MACD_Signal():
return MACD(fast_period=12, slow_period=26, signal_period=9)
def Net_Income_Margin():
return Fundamentals.net_margin.latest
def Operating_Cashflows_To_Assets():
return (Fundamentals.operating_cash_flow.latest * 4.) / \
Fundamentals.total_assets.latest
def Price_Momentum_3M():
return Returns(window_length=63)
class Price_Oscillator(CustomFactor):
inputs = [USEquityPricing.close]
window_length = 252
def compute(self, today, assets, out, close):
four_week_period = close[-20:]
out[:] = (np.nanmean(four_week_period, axis=0) /
np.nanmean(close, axis=0)) - 1.
def Returns_39W():
return Returns(window_length=215)
class Vol_3M(CustomFactor):
inputs = [Returns(window_length=2)]
window_length = 63
def compute(self, today, assets, out, rets):
out[:] = np.nanstd(rets, axis=0)
def Working_Capital_To_Assets():
return Fundamentals.working_capital.latest / Fundamentals.total_assets.latest
def sentiment():
return SimpleMovingAverage(inputs=[stocktwits.bull_minus_bear],
window_length=5).rank(mask=universe)
class AdvancedMomentum(CustomFactor):
""" Momentum factor """
inputs = [USEquityPricing.close,
Returns(window_length=126)]
window_length = 252
def compute(self, today, assets, out, prices, returns):
out[:] = ((prices[-21] - prices[-252])/prices[-252] -
(prices[-1] - prices[-21])/prices[-21]) / np.nanstd(returns, axis=0)
def SPY_Beta():
return SimpleBeta(target=sid(8554), regression_length=252)
return {
'Price to Sales': PriceToSalesTTM,
'PE Ratio': PriceToEarningsTTM,
'Dividend Yield': DividendYield,
# 'Capex to Cashflows': Capex_To_Cashflows,
# 'EBIT to Assets': EBIT_To_Assets,
# 'EBITDA Yield': EBITDA_Yield,
'MACD Signal Line': MACD_Signal,
'Mean Reversion 1M': Mean_Reversion_1M,
'Net Income Margin': Net_Income_Margin,
# 'Operating Cashflows to Assets': Operating_Cashflows_To_Assets,
'Price Momentum 3M': Price_Momentum_3M,
'Price Oscillator': Price_Oscillator,
# 'Return on Invested Capital': Return_On_Total_Invest_Capital,
'39 Week Returns': Returns_39W,
'Vol 3M': Vol_3M,
'SPY_Beta': SPY_Beta,
'Advanced Momentum': AdvancedMomentum,
'Size': Size,
'Volatitility': Volatility,
'Value': Value,
'Short-Term Reversal': ShortTermReversal,
'Momentum': Momentum,
# 'Materials': materials,
# 'Consumer Discretionary': consumer_discretionary,
# 'Financials': financials,
# 'Real Estate': real_estate,
# 'Consumer Staples': consumer_staples,
# 'Healthcare': health_care,
# 'Utilities': utilities,
# 'Telecom ': telecom,
# 'Energy': energy,
# 'Industrials': industrials,
# 'Technology': technology
}
```
## Custom Machine Learning Factor
Here we define a Machine Learning factor which trains a model and predicts forward returns
```
class ML(CustomFactor):
init = False
def compute(self, today, assets, out, returns, *inputs):
"""Train the model using
- shifted returns as target, and
- factors in a list of inputs as features;
each factor contains a 2-D array of shape [time x stocks]
"""
if (not self.init) or today.strftime('%A') == 'Monday':
# train on first day then subsequent Mondays (memory)
# get features
features = pd.concat([pd.DataFrame(data, columns=assets).stack().to_frame(i)
for i, data in enumerate(inputs)], axis=1)
# shift returns and align features
target = (pd.DataFrame(returns, columns=assets)
.shift(-HOLDING_PERIOD)
.dropna(how='all')
.stack())
target.index.rename(['date', 'asset'], inplace=True)
features = features.reindex(target.index)
# finalize features
features = (pd.get_dummies(features
.assign(asset=features
.index.get_level_values('asset')),
columns=['asset'],
sparse=True))
# train the model
self.model_pipe = make_pipeline(preprocessing.Imputer(),
preprocessing.MinMaxScaler(),
linear_model.LinearRegression())
# run pipeline and train model
self.model_pipe.fit(X=features, y=target)
self.assets = assets # keep track of assets in model
self.init = True
# predict most recent factor values
features = pd.DataFrame({i: d[-1] for i, d in enumerate(inputs)}, index=assets)
features = features.reindex(index=self.assets).assign(asset=self.assets)
features = pd.get_dummies(features, columns=['asset'])
preds = self.model_pipe.predict(features)
out[:] = pd.Series(preds, index=self.assets).reindex(index=assets)
```
## Create Factor Pipeline
Create pipeline with predictive factors and target returns
```
def make_ml_pipeline(alpha_factors, universe, lookback=21, lookahead=5):
"""Create pipeline with predictive factors and target returns"""
# set up pipeline
pipe = OrderedDict()
# Returns over lookahead days.
pipe['Returns'] = Returns(inputs=[USEquityPricing.open],
mask=universe,
window_length=lookahead + 1)
# Rank alpha factors:
pipe.update({name: f().rank(mask=universe)
for name, f in alpha_factors.items()})
# ML factor gets `lookback` datapoints on each factor
pipe['ML'] = ML(inputs=pipe.values(),
window_length=lookback + 1,
mask=universe)
return Pipeline(columns=pipe, screen=universe)
```
## Define Algorithm
```
def initialize(context):
"""
Called once at the start of the algorithm.
"""
set_slippage(slippage.FixedSlippage(spread=0.00))
set_commission(commission.PerShare(cost=0, min_trade_cost=0))
schedule_function(rebalance_portfolio,
TRADE_FREQ,
time_rules.market_open(minutes=1))
# Record tracking variables at the end of each day.
schedule_function(log_metrics,
date_rules.every_day(),
time_rules.market_close())
# Set up universe
# base_universe = AverageDollarVolume(window_length=63, mask=QTradableStocksUS()).percentile_between(80, 100)
universe = AverageDollarVolume(window_length=63, mask=QTradableStocksUS()).percentile_between(40, 60)
# create alpha factors and machine learning pipline
ml_pipeline = make_ml_pipeline(alpha_factors=make_alpha_factors(),
universe=universe,
lookback=TRAINING_PERIOD,
lookahead=HOLDING_PERIOD)
attach_pipeline(ml_pipeline, 'alpha_model')
attach_pipeline(risk_loading_pipeline(), 'risk_loading_pipeline')
context.past_predictions = {}
context.realized_rmse = 0
context.realized_ic = 0
context.long_short_spread = 0
```
## Evaluate Model
Evaluate model performance using past predictions on hold-out data
```
def evaluate_past_predictions(context):
"""Evaluate model performance using past predictions on hold-out data"""
# A day has passed, shift days and drop old ones
context.past_predictions = {k-1: v for k, v in context.past_predictions.items() if k-1 >= 0}
if 0 in context.past_predictions:
# Past predictions for the current day exist, so we can use todays' n-back returns to evaluate them
returns = pipeline_output('alpha_model')['Returns'].to_frame('returns')
df = (context
.past_predictions[0]
.to_frame('predictions')
.join(returns, how='inner')
.dropna())
# Compute performance metrics
context.realized_rmse = metrics.mean_squared_error(y_true=df['returns'], y_pred=df.predictions)
context.realized_ic, _ = spearmanr(df['returns'], df.predictions)
log.info('rmse {:.2%} | ic {:.2%}'.format(context.realized_rmse, context.realized_ic))
long_rets = df.loc[df.predictions >= df.predictions.median(), 'returns'].mean()
short_rets = df.loc[df.predictions < df.predictions.median(), 'returns'].mean()
context.long_short_spread = (long_rets - short_rets) * 100
# Store current predictions
context.past_predictions[HOLDING_PERIOD] = context.predictions
```
## Algo Execution
### Prepare Trades
```
def before_trading_start(context, data):
"""
Called every day before market open.
"""
context.predictions = pipeline_output('alpha_model')['ML']
context.predictions.index.rename(['date', 'equity'], inplace=True)
context.risk_loading_pipeline = pipeline_output('risk_loading_pipeline')
evaluate_past_predictions(context)
```
### Rebalance
```
def rebalance_portfolio(context, data):
"""
Execute orders according to our schedule_function() timing.
"""
predictions = context.predictions
predictions = predictions.loc[data.can_trade(predictions.index)]
# Select long/short positions
n_positions = int(min(N_POSITIONS, len(predictions)) / 2)
to_trade = (predictions[predictions>0]
.nlargest(n_positions)
.append(predictions[predictions < 0]
.nsmallest(n_positions)))
# Model may produce duplicate predictions
to_trade = to_trade[~to_trade.index.duplicated()]
# Setup Optimization Objective
objective = opt.MaximizeAlpha(to_trade)
# Setup Optimization Constraints
constrain_gross_leverage = opt.MaxGrossExposure(1.0)
constrain_pos_size = opt.PositionConcentration.with_equal_bounds(-.02, .02)
market_neutral = opt.DollarNeutral()
constrain_risk = RiskModelExposure(
risk_model_loadings=context.risk_loading_pipeline,
version=opt.Newest)
# Optimizer calculates portfolio weights and
# moves portfolio toward the target.
order_optimal_portfolio(
objective=objective,
constraints=[
constrain_gross_leverage,
constrain_pos_size,
market_neutral,
constrain_risk
],
)
```
### Track Performance
```
def log_metrics(context, data):
"""
Plot variables at the end of each day.
"""
record(leverage=context.account.leverage,
#num_positions=len(context.portfolio.positions),
realized_rmse=context.realized_rmse,
realized_ic=context.realized_ic,
long_short_spread=context.long_short_spread,
)
```
| true |
code
| 0.81492 | null | null | null | null |
|
# STUMPY Basics
[](https://mybinder.org/v2/gh/TDAmeritrade/stumpy/main?filepath=notebooks/Tutorial_STUMPY_Basics.ipynb)
## Analyzing Motifs and Anomalies with STUMP
This tutorial utilizes the main takeaways from the research papers: [Matrix Profile I](http://www.cs.ucr.edu/~eamonn/PID4481997_extend_Matrix%20Profile_I.pdf) & [Matrix Profile II](http://www.cs.ucr.edu/~eamonn/STOMP_GPU_final_submission_camera_ready.pdf).
To explore the basic concepts, we'll use the workhorse `stump` function to find interesting motifs (patterns) or discords (anomalies/novelties) and demonstrate these concepts with two different time series datasets:
1. The Steamgen dataset
2. The NYC taxi passengers dataset
`stump` is Numba JIT-compiled version of the popular STOMP algorithm that is described in detail in the original [Matrix Profile II](http://www.cs.ucr.edu/~eamonn/STOMP_GPU_final_submission_camera_ready.pdf) paper. `stump` is capable of parallel computation and it performs an ordered search for patterns and outliers within a specified time series and takes advantage of the locality of some calculations to minimize the runtime.
## Getting Started
Let's import the packages that we'll need to load, analyze, and plot the data.
```
%matplotlib inline
import pandas as pd
import stumpy
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as dates
from matplotlib.patches import Rectangle
import datetime as dt
plt.style.use('https://raw.githubusercontent.com/TDAmeritrade/stumpy/main/docs/stumpy.mplstyle')
```
## What is a Motif?
Time series motifs are approximately repeated subsequences found within a longer time series. Being able to say that a subsequence is "approximately repeated" requires that you be able to compare subsequences to each other. In the case of STUMPY, all subsequences within a time series can be compared by computing the pairwise z-normalized Euclidean distances and then storing only the index to its nearest neighbor. This nearest neighbor distance vector is referred to as the `matrix profile` and the index to each nearest neighbor within the time series is referred to as the `matrix profile index`. Luckily, the `stump` function takes in any time series (with floating point values) and computes the matrix profile along with the matrix profile indices and, in turn, one can immediately find time series motifs. Let's look at an example:
## Loading the Steamgen Dataset
This data was generated using fuzzy models applied to mimic a steam generator at the Abbott Power Plant in Champaign, IL. The data feature that we are interested in is the output steam flow telemetry that has units of kg/s and the data is "sampled" every three seconds with a total of 9,600 datapoints.
```
steam_df = pd.read_csv("https://zenodo.org/record/4273921/files/STUMPY_Basics_steamgen.csv?download=1")
steam_df.head()
```
## Visualizing the Steamgen Dataset
```
plt.suptitle('Steamgen Dataset', fontsize='30')
plt.xlabel('Time', fontsize ='20')
plt.ylabel('Steam Flow', fontsize='20')
plt.plot(steam_df['steam flow'].values)
plt.show()
```
Take a moment and carefully examine the plot above with your naked eye. If you were told that there was a pattern that was approximately repeated, can you spot it? Even for a computer, this can be very challenging. Here's what you should be looking for:
## Manually Finding a Motif
```
m = 640
fig, axs = plt.subplots(2)
plt.suptitle('Steamgen Dataset', fontsize='30')
axs[0].set_ylabel("Steam Flow", fontsize='20')
axs[0].plot(steam_df['steam flow'], alpha=0.5, linewidth=1)
axs[0].plot(steam_df['steam flow'].iloc[643:643+m])
axs[0].plot(steam_df['steam flow'].iloc[8724:8724+m])
rect = Rectangle((643, 0), m, 40, facecolor='lightgrey')
axs[0].add_patch(rect)
rect = Rectangle((8724, 0), m, 40, facecolor='lightgrey')
axs[0].add_patch(rect)
axs[1].set_xlabel("Time", fontsize='20')
axs[1].set_ylabel("Steam Flow", fontsize='20')
axs[1].plot(steam_df['steam flow'].values[643:643+m], color='C1')
axs[1].plot(steam_df['steam flow'].values[8724:8724+m], color='C2')
plt.show()
```
The motif (pattern) that we are looking for is highlighted above and yet it is still very hard to be certain that the orange and green subsequences are a match (upper panel), that is, until we zoom in on them and overlay the subsequences on top each other (lower panel). Now, we can clearly see that the motif is very similar! The fundamental value of computing the matrix profile is that it not only allows you to quickly find motifs but it also identifies the nearest neighbor for all subsequences within your time series. Note that we haven't actually done anything special here to locate the motif except that we grab the locations from the original paper and plotted them. Now, let's take our steamgen data and apply the `stump` function to it:
## Find a Motif Using STUMP
```
m = 640
mp = stumpy.stump(steam_df['steam flow'], m)
```
`stump` requires two parameters:
1. A time series
2. A window size, `m`
In this case, based on some domain expertise, we've chosen `m = 640`, which is roughly equivalent to half-hour windows. And, again, the output of `stump` is an array that contains all of the matrix profile values (i.e., z-normalized Euclidean distance to your nearest neighbor) and matrix profile indices in the first and second columns, respectively (we'll ignore the third and fourth columns for now). To identify the index location of the motif we'll need to find the index location where the matrix profile, `mp[:, 0]`, has the smallest value:
```
motif_idx = np.argsort(mp[:, 0])[0]
print(f"The motif is located at index {motif_idx}")
```
With this `motif_idx` information, we can also identify the location of its nearest neighbor by cross-referencing the matrix profile indices, `mp[:, 1]`:
```
nearest_neighbor_idx = mp[motif_idx, 1]
print(f"The nearest neighbor is located at index {nearest_neighbor_idx}")
```
Now, let's put all of this together and plot the matrix profile next to our raw data:
```
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Motif (Pattern) Discovery', fontsize='30')
axs[0].plot(steam_df['steam flow'].values)
axs[0].set_ylabel('Steam Flow', fontsize='20')
rect = Rectangle((motif_idx, 0), m, 40, facecolor='lightgrey')
axs[0].add_patch(rect)
rect = Rectangle((nearest_neighbor_idx, 0), m, 40, facecolor='lightgrey')
axs[0].add_patch(rect)
axs[1].set_xlabel('Time', fontsize ='20')
axs[1].set_ylabel('Matrix Profile', fontsize='20')
axs[1].axvline(x=motif_idx, linestyle="dashed")
axs[1].axvline(x=nearest_neighbor_idx, linestyle="dashed")
axs[1].plot(mp[:, 0])
plt.show()
```
What we learn is that the global minima (vertical dashed lines) from the matrix profile correspond to the locations of the two subsequences that make up the motif pair! And the exact z-normalized Euclidean distance between these two subsequences is:
```
mp[motif_idx, 0]
```
So, this distance isn't zero since we saw that the two subsequences aren't an identical match but, relative to the rest of the matrix profile (i.e., compared to either the mean or median matrix profile values), we can understand that this motif is a significantly good match.
## Find Potential Anomalies (Discords) using STUMP
Conversely, the index location within our matrix profile that has the largest value (computed from `stump` above) is:
```
discord_idx = np.argsort(mp[:, 0])[-1]
print(f"The discord is located at index {discord_idx}")
```
And the nearest neighbor to this discord has a distance that is quite far away:
```
nearest_neighbor_distance = mp[discord_idx, 0]
print(f"The nearest neighbor subsequence to this discord is {nearest_neighbor_distance} units away")
```
The subsequence located at this global maximum is also referred to as a discord, novelty, or "potential anomaly":
```
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Discord (Anomaly/Novelty) Discovery', fontsize='30')
axs[0].plot(steam_df['steam flow'].values)
axs[0].set_ylabel('Steam Flow', fontsize='20')
rect = Rectangle((discord_idx, 0), m, 40, facecolor='lightgrey')
axs[0].add_patch(rect)
axs[1].set_xlabel('Time', fontsize ='20')
axs[1].set_ylabel('Matrix Profile', fontsize='20')
axs[1].axvline(x=discord_idx, linestyle="dashed")
axs[1].plot(mp[:, 0])
plt.show()
```
Now that you've mastered the STUMPY basics and understand how to discover motifs and anomalies from a time series, we'll leave it up to you to investigate other interesting local minima and local maxima in the steamgen dataset.
To further develop/reinforce our growing intuition, let's move on and explore another dataset!
## Loading the NYC Taxi Passengers Dataset
First, we'll download historical data that represents the half-hourly average of the number of NYC taxi passengers over 75 days in the Fall of 2014.
We extract that data and insert it into a pandas dataframe, making sure the timestamps are stored as *datetime* objects and the values are of type *float64*. Note that we'll do a little more data cleaning than above just so you can see an example where the timestamp is included. But be aware that `stump` does not actually use or need the timestamp column at all when computing the matrix profile.
```
taxi_df = pd.read_csv("https://zenodo.org/record/4276428/files/STUMPY_Basics_Taxi.csv?download=1")
taxi_df['value'] = taxi_df['value'].astype(np.float64)
taxi_df['timestamp'] = pd.to_datetime(taxi_df['timestamp'])
taxi_df.head()
```
## Visualizing the Taxi Dataset
```
# This code is going to be utilized to control the axis labeling of the plots
DAY_MULTIPLIER = 7 # Specify for the amount of days you want between each labeled x-axis tick
x_axis_labels = taxi_df[(taxi_df.timestamp.dt.hour==0)]['timestamp'].dt.strftime('%b %d').values[::DAY_MULTIPLIER]
x_axis_labels[1::2] = " "
x_axis_labels, DAY_MULTIPLIER
plt.suptitle('Taxi Passenger Raw Data', fontsize='30')
plt.xlabel('Window Start Date', fontsize ='20')
plt.ylabel('Half-Hourly Average\nNumber of Taxi Passengers', fontsize='20')
plt.plot(taxi_df['value'])
plt.xticks(np.arange(0, taxi_df['value'].shape[0], (48*DAY_MULTIPLIER)/2), x_axis_labels)
plt.xticks(rotation=75)
plt.minorticks_on()
plt.margins(x=0)
plt.show()
```
It seems as if there is a general periodicity between spans of 1-day and 7-days, which can likely be explained by the fact that more people use taxis throughout the day than through the night and that it is reasonable to say most weeks have similar taxi-rider patterns. Also, maybe there is an outlier just to the right of the window starting near the end of October but, other than that, there isn't anything you can conclude from just looking at the raw data.
## Generating the Matrix Profile
Again, defining the window size, `m`, usually requires some level of domain knowledge but we'll demonstrate later on that `stump` is robust to changes in this parameter. Since this data was taken half-hourly, we chose a value `m = 48` to represent the span of exactly one day:
```
m = 48
mp = stumpy.stump(taxi_df['value'], m=m)
```
## Visualizing the Matrix Profile
```
plt.suptitle('1-Day STUMP', fontsize='30')
plt.xlabel('Window Start', fontsize ='20')
plt.ylabel('Matrix Profile', fontsize='20')
plt.plot(mp[:, 0])
plt.plot(575, 1.7, marker="v", markersize=15, color='b')
plt.text(620, 1.6, 'Columbus Day', color="black", fontsize=20)
plt.plot(1535, 3.7, marker="v", markersize=15, color='b')
plt.text(1580, 3.6, 'Daylight Savings', color="black", fontsize=20)
plt.plot(2700, 3.1, marker="v", markersize=15, color='b')
plt.text(2745, 3.0, 'Thanksgiving', color="black", fontsize=20)
plt.plot(30, .2, marker="^", markersize=15, color='b', fillstyle='none')
plt.plot(363, .2, marker="^", markersize=15, color='b', fillstyle='none')
plt.xticks(np.arange(0, 3553, (m*DAY_MULTIPLIER)/2), x_axis_labels)
plt.xticks(rotation=75)
plt.minorticks_on()
plt.show()
```
## Understanding the Matrix Profile
Let's understand what we're looking at.
### Lowest Values
The lowest values (open triangles) are considered a motif since they represent the pair of nearest neighbor subsequences with the smallest z-normalized Euclidean distance. Interestingly, the two lowest data points are *exactly* 7 days apart, which suggests that, in this dataset, there may be a periodicity of seven days in addition to the more obvious periodicity of one day.
### Highest Values
So what about the highest matrix profile values (filled triangles)? The subsequences that have the highest (local) values really emphasizes their uniqueness. We found that the top three peaks happened to correspond exactly with the timing of Columbus Day, Daylight Saving Time, and Thanksgiving, respectively.
## Different Window Sizes
As we had mentioned above, `stump` should be robust to the choice of the window size parameter, `m`. Below, we demonstrate how manipulating the window size can have little impact on your resulting matrix profile by running `stump` with varying windows sizes.
```
days_dict ={
"Half-Day": 24,
"1-Day": 48,
"2-Days": 96,
"5-Days": 240,
"7-Days": 336,
}
days_df = pd.DataFrame.from_dict(days_dict, orient='index', columns=['m'])
days_df.head()
```
We purposely chose spans of time that correspond to reasonably intuitive day-lengths that could be chosen by a human.
```
fig, axs = plt.subplots(5, sharex=True, gridspec_kw={'hspace': 0})
fig.text(0.5, -0.1, 'Subsequence Start Date', ha='center', fontsize='20')
fig.text(0.08, 0.5, 'Matrix Profile', va='center', rotation='vertical', fontsize='20')
for i, varying_m in enumerate(days_df['m'].values):
mp = stumpy.stump(taxi_df['value'], varying_m)
axs[i].plot(mp[:, 0])
axs[i].set_ylim(0,9.5)
axs[i].set_xlim(0,3600)
title = f"m = {varying_m}"
axs[i].set_title(title, fontsize=20, y=.5)
plt.xticks(np.arange(0, taxi_df.shape[0], (48*DAY_MULTIPLIER)/2), x_axis_labels)
plt.xticks(rotation=75)
plt.suptitle('STUMP with Varying Window Sizes', fontsize='30')
plt.show()
```
We can see that even with varying window sizes, our peaks stay prominent. But it looks as if all the non-peak values are converging towards each other. This is why having a knowledge of the data-context is important prior to running `stump`, as it is helpful to have a window size that may capture a repeating pattern or anomaly within the dataset.
## GPU-STUMP - Faster STUMP Using GPUs
When you have significantly more than a few thousand data points in your time series, you may need a speed boost to help analyze your data. Luckily, you can try `gpu_stump`, a super fast GPU-powered alternative to `stump` that gives speed of a few hundred CPUs and provides the same output as `stump`:
```
import stumpy
mp = stumpy.gpu_stump(df['value'], m=m) # Note that you'll need a properly configured NVIDIA GPU for this
```
In fact, if you aren't dealing with PII/SII data, then you can try out `gpu_stump` using the [this notebook on Google Colab](https://colab.research.google.com/drive/1FIbHQoD6mJInkhinoMehBDj2E1i7i2j7).
## STUMPED - Distributed STUMP
Alternatively, if you only have access to a cluster of CPUs and your data needs to stay behind your firewall, then `stump` and `gpu_stump` may not be sufficient for your needs. Instead, you can try `stumped`, a distributed and parallel implementation of `stump` that depends on [Dask distributed](https://distributed.dask.org/en/latest/):
```
import stumpy
from dask.distributed import Client
dask_client = Client()
mp = stumpy.stumped(dask_client, df['value'], m=m) # Note that a dask client is needed
```
## Bonus Section
### Understanding the Matrix Profile Columnar Output
For any 1-D time series, `T`, its matrix profile, `mp`, computed from `stumpy.stump(T, m)` will contain 4 explicit columns, which we'll describe in a moment. Implicitly, the `i`th row of the `mp` array corresponds to the set of (4) nearest neighbor values computed for the specific subsequence `T[i : i + m]`.
The first column of the `mp` contains the matrix profile (nearest neighbor distance) value, `P` (note that due to zero-based indexing, the "first column" has a column index value of zero).
The second column contains the (zero-based) index location, `I`, of where the (above) nearest neighbor is located along `T` (note that any negative index values are "bad" values and indicates that a nearest neighbor could not be found).
So, for the `i`th subsequence `T[i : i + m]`, its nearest neighbor (located somewhere along `T`) has a starting index location of `I = mp[i, 1]` and, assuming that `I >= 0`, this corresponds to the subsequence found at `T[I : I + m]`. And the matrix profile value for the `i`th subsequence, `P = [i, 0]`, is the exact (z-normalized Euclidean) distance between `T[i : i + m]` and `T[I : I + m]`. Note that the nearest neighbor index location, `I`, can be positioned ANYWHERE. That is, dependent upon the `i`th subsequence, its nearest neighbor, `I`, can be located before/to-the-"left" of `i` (i.e., `I <= i`) or come after/to-the-"right" of `i` (i.e., `I >= i`). In other words, there is no constraint on where a nearest neighbor is located. However, there may be a time when you might like to only know about a nearest neighbor that either comes before/after `i` and this is where columns 3 and 4 of `mp` come into play.
The third column contains the (zero-based) index location, `IL`, of where the "left" nearest neighbor is located along `T`. Here, there is a constraint that `IL < i` or that `IL` must come before/to-the-left of `i`. Thus, the "left nearest neighbor" for the `i`th subsequence would be located at `IL = mp[i, 2]` and corresponds to `T[IL : IL + m]`.
The fourth column contains the (zero-based) index location, `IR`, of where the "right" nearest neighbor is located along `T`. Here, there is a constraint that `IR > i` or that `IR` must come after/to-the-right of `i`. Thus, the "right nearest neighbor" for the `i`th subsequence would be located at `IR = mp[i, 3]` and corresponds to `T[IR : IR + m]`.
Again, note that any negative index values are "bad" values and indicates that a nearest neighbor could not be found.
To reinforce this more concretely, let's use the following `mp` array as an example:
```
array([[1.626257115121311, 202, -1, 202],
[1.7138456780667977, 65, 0, 65],
[1.880293454724256, 66, 0, 66],
[1.796922109741226, 67, 0, 67],
[1.4943082939628236, 11, 1, 11],
[1.4504278114808016, 12, 2, 12],
[1.6294354134867932, 19, 0, 19],
[1.5349365731102185, 229, 0, 229],
[1.3930265554289831, 186, 1, 186],
[1.5265881687159586, 187, 2, 187],
[1.8022253384245739, 33, 3, 33],
[1.4943082939628236, 4, 4, 118],
[1.4504278114808016, 5, 5, 137],
[1.680920620705546, 201, 6, 201],
[1.5625058007723722, 237, 8, 237],
[1.2860008417613522, 66, 9, -1]]
```
Here, the subsequence at `i = 0` would correspond to the `T[0 : 0 + m]` subsequence and the nearest neighbor for this subsequence is located at `I = 202` (i.e., `mp[0, 1]`) and corresponds to the `T[202 : 202 + m]` subsequence. The z-normalized Euclidean distance between `T[0 : 0 + m]` and `T[202 : 202 + m]` is actually `P = 1.626257115121311` (i.e., `mp[0, 0]`). Next, notice that the location of the left nearest neighbor is `IL = -1` (i.e., `mp[0, 2]`) and, since negative indices are "bad", this tells us that the left nearest neighbor could not be found. Hopefully, this makes sense since `T[0 : 0 + m]` is the first subsequence in `T` and there are no other subsequences that can possibly exist to the left of `T[0 : 0 + m]`! Conversely, the location of the right nearest neighbor is `IR = 202` (i.e., `mp[0, 3]`) and corresponds to the `T[202 : 202 + m]` subsequence.
Additionally, the subsequence at `i = 5` would correspond to the `T[5 : 5 + m]` subsequence and the nearest neighbor for this subsequence is located at `I = 12` (i.e., `mp[5, 1]`) and corresponds to the `T[12 : 12 + m]` subsequence. The z-normalized Euclidean distance between `T[5 : 5 + m]` and `T[12 : 12 + m]` is actually `P = 1.4504278114808016` (i.e., `mp[5, 0]`). Next, the location of the left nearest neighbor is `IL = 2` (i.e., `mp[5, 2]`) and corresponds to `T[2 : 2 + m]`. Conversely, the location of the right nearest neighbor is `IR = 12` (i.e., `mp[5, 3]`) and corresponds to the `T[12 : 12 + m]` subsequence.
Similarly, all other subsequences can be evaluated and interpreted using this approach!
### Find Top-K Motifs
Now that you've computed the matrix profile, `mp`, for your time series and identified the best global motif, you may be interested in discovering other motifs within your data. However, you'll immediately learn that doing something like `top_10_motifs_idx = np.argsort(mp[:, 0])[10]` doesn't actually get you what you want and that's because this only returns the index locations that are likely going to be close to the global motif! Instead, after identifying the best motif (i.e., the matrix profile location with the smallest value), you first need to exclude the local area (i.e., an exclusion zone) surrounding the motif pair by setting their matrix profile values to `np.inf` before searching for the next motif. Then, you'll need to repeat the "exclude-and-search" process for each subsequent motif. Luckily, STUMPY offers two additional functions, namely, `stumpy.motifs` and `stumpy.match`, that help simplify this process. While it is beyond the scope of this basic tutorial, we encourage you to check them out!
## Summary
And that's it! You have now loaded in a dataset, ran it through `stump` using our package, and were able to extract multiple conclusions of existing patterns and anomalies within the two different time series. You can now import this package and use it in your own projects. Happy coding!
## Resources
[Matrix Profile I](http://www.cs.ucr.edu/~eamonn/PID4481997_extend_Matrix%20Profile_I.pdf)
[Matrix Profile II](http://www.cs.ucr.edu/~eamonn/STOMP_GPU_final_submission_camera_ready.pdf)
[STUMPY Documentation](https://stumpy.readthedocs.io/en/latest/)
[STUMPY Matrix Profile Github Code Repository](https://github.com/TDAmeritrade/stumpy)
| true |
code
| 0.632645 | null | null | null | null |
|
#Traditional Value Factor Algorithm
By Gil Wassermann
Strategy taken from "130/30: The New Long-Only" by Andrew Lo and Pankaj Patel
Part of the Quantopian Lecture Series:
* www.quantopian.com/lectures
* github.com/quantopian/research_public
Notebook released under the Creative Commons Attribution 4.0 License. Please do not remove this attribution.
Before the crisis of 2007, 130/30 funds were all the rage. The idea of a 130/30 fund is simple: take a long position of 130% and a short position of 30%; this combination gives a net exposure of 100% (the same as a long-only fund) as well as the added benefit of the ability to short stocks. The ability to short in a trading strategy is crucial as it allows a fund manager to capitalize on a security's poor performance, which is impossible in a traditional, long-only strategy.
This notebook, using factors outlined by Andrew Lo and Pankaj Patel in "130/30: The New Long Only", will demonstrate how to create an algorithmic 130/30 strategy. It will also highlight Quantopian's Pipeline API which is a powerful tool for developing factor trading strategies.
First, let us import all necessary libraries and functions for this algorithm
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from quantopian.pipeline import Pipeline
from quantopian.pipeline.data.builtin import USEquityPricing
from quantopian.research import run_pipeline
from quantopian.pipeline.data import Fundamentals
from quantopian.pipeline.factors import CustomFactor
```
#Traditional Value
In this notebook, we will develop a strategy based on the "traditional value" metrics described in the Lo/Patel whitepaper. The factors employed in this strategy designate stocks as either cheap or expensive using classic fundamental analysis. The factors that Lo/Patel used are:
* Dividend Yield
* Price to Book Value
* Price to Trailing 12-Month Sales
* Price to Trainling 12-Month Cash Flows
##Dividend Yield
Dividend yield is calculated as:
$$Dividend\;Yield = \frac{Annual\;Dividends\;per\;share}{Price\;per\;share}$$
When a company makes profit, it faces a choice. It could either reinvest those profits in the company with an eye to increase efficiency, purchase new technology, etc. or it could pay dividends to its equity holders. While reinvestment may increase a company's future share price and thereby reward investors, the most concrete way equity holders are rewarded is through dividends. An equity with a high dividend yield is particularly attractive as the quantity of dividends paid to investors represent a larger proportion of the share price itself. Now we shall create a Dividend Yield factor using the Pipeline API framework and Pipeline's list of fundamental values.
```
# Custom Factor 1 : Dividend Yield
class Div_Yield(CustomFactor):
inputs = [Fundamentals.div_yield5_year]
window_length = 1
def compute(self, today, assets, out, d_y):
out[:] = d_y[-1]
```
While this factor could be calculated using other fundamental metrics, Fundamentals removes the need for any calculation. It is good practice to check the list of [fundamentals](https://www.quantopian.com/help/fundamentals) before creating a custom factor from scratch.
We will initialize a temporary Pipeline to get a sense of the values.
```
# create the pipeline
temp_pipe_1 = Pipeline()
# add the factor to the pipeline
temp_pipe_1.add(Div_Yield(), 'Dividend Yield')
# run the pipeline and get data for first 5 equities
run_pipeline(temp_pipe_1, start_date = '2015-11-11', end_date = '2015-11-11').dropna().head()
```
##Price to Book Value
Price to Book Value (a.k.a Price to Book Ratio) is calculated as:
$$P/B\;Ratio = \frac{Price\;per\;share}{Net\;Asset\;Value\;per\;share}$$
Net Asset Value per share can be thought of (very roughly) as a company's total assets less its total liabilities, all divided by the number of shares outstanding.
The P/B Ratio gives a sense of a stock being either over- or undervalued. A high P/B ratio suggests that a stock's price is overvalued, and should therefore be shorted, whereas a low P/B ratio is attractive as the stock gained by purchasing the equity is hypothetically "worth more" than the price paid for it.
We will now create a P/B Ratio custom factor and look at some of the results.
```
# Custom Factor 2 : P/B Ratio
class Price_to_Book(CustomFactor):
inputs = [Fundamentals.pb_ratio]
window_length = 1
def compute(self, today, assets, out, pbr):
out[:] = pbr[-1]
# create the Pipeline
temp_pipe_2 = Pipeline()
# add the factor to the Pipeline
temp_pipe_2.add(Price_to_Book(), 'P/B Ratio')
# run the Pipeline and get data for first 5 equities
run_pipeline(temp_pipe_2, start_date='2015-11-11', end_date='2015-11-11').head()
```
There are two points to make about this data series.
Firstly, AA_PR's P/B Ratio is given as NaN by Pipeline. NaN stands for "not a number" and occurs when a value can not be fetched by Pipeline. Eventually, we will remove these NaN values from the dataset as they often lead to confusing errors when manipulating the data.
Secondly, a low P/B Ratio and a high Dividend Yield are attractive for investors, whereas a a high P/B Ratio and a low Dividend Yield are unattractive. Therefore, we will "invert" the P/B ratio by making each value negative in the factor output so that, when the data is aggregated later in the algorithm, the maxima and minima have the same underlying "meaning".
##Price to Trailing 12-Month Sales
This is calculated as a simple ratio between price per share and trailing 12-month (TTM) sales.
TTM is a transformation rather than a metric and effectively calculates improvement or deterioration of a fundamental value from a particular quarter one year previously. For example, if one wanted to calculate today's TTM Sales for company XYZ, one would take the most recent quarter's revenue and divide it by the difference between this quarter's revenue and this quarter's revenue last year added to the revenue as given by the company's most recent fiscal year-end filing.
To calculate the exact TTM of a security is indeed possible using Pipeline; however, the code required is slow. Luckily, this value can be well approximated by the built-in Fundamental Morningstar ratios, which use annual sales to calculate the Price to Sales fundamental value. This slight change boosts the code's speed enormously yet has very little impact on the results of the strategy itself.
Price to TTM Sales is similar to the P/B Ratio in terms of function. The major difference in these two ratios is the fact that inclusion of TTM means that seasonal fluctuations are minimized, as previous data is used to smooth the value. In our case, annualized values accomplish this same smoothing.
Also, note that the values produced are negative; this factor requires the same inversion as the P/B Ratio.
```
# Custom Factor 3 : Price to Trailing 12 Month Sales
class Price_to_TTM_Sales(CustomFactor):
inputs = [Fundamentals.ps_ratio]
window_length = 1
def compute(self, today, assets, out, ps):
out[:] = -ps[-1]
# create the pipeline
temp_pipe_3 = Pipeline()
# add the factor to the pipeline
temp_pipe_3.add(Price_to_TTM_Sales(), 'Price / TTM Sales')
# run the pipeline and get data for first 5 equities
run_pipeline(temp_pipe_3, start_date='2015-11-11', end_date='2015-11-11').head()
```
##Price to Trailing 12-Month Cashflows
This is calculated as a simple ratio between price per share and TTM free cashflow (here using the built-in Fundamental Morningstar ratio as an approximaton).
This ratio serves a similar function to the previous two. A future notebook will explore the subtle differences in these metrics, but they largely serve the same purpose. Once again, low values are attractive and high values are unattractive, so the metric must be inverted.
```
# Custom Factor 4 : Price to Trailing 12 Month Cashflow
class Price_to_TTM_Cashflows(CustomFactor):
inputs = [Fundamentals.pcf_ratio]
window_length = 1
def compute(self, today, assets, out, pcf):
out[:] = -pcf[-1]
# create the pipeline
temp_pipe_4 = Pipeline()
# add the factor to the pipeline
temp_pipe_4.add(Price_to_TTM_Cashflows(), 'Price / TTM Cashflows')
# run the pipeline and get data for first 5 equities
run_pipeline(temp_pipe_4, start_date='2015-11-11', end_date='2015-11-11').head()
```
##The Full Pipeline
Now that each individual factor has been added, it is now time to get all the necessary data at once. In the algorithm, this will take place once every day.
Later in the process, we will need a factor in order to create an approximate S&P500, so we will also include another factor called SPY_proxy (SPY is an ETF that tracks the S&P500). The S&P500 is a collection of 500 of the largest companies traded on the stock market. Our interpretation of the S&P500 is a group of 500 companies with the greatest market capitalizations; however, the actual S&P500 will be slightly different as Standard and Poors, who create the index, have a more nuanced algorithm for calculation.
We will also alter our P/B Ratio factor in order to account for the inversion.
```
# This factor creates the synthetic S&P500
class SPY_proxy(CustomFactor):
inputs = [Fundamentals.market_cap]
window_length = 1
def compute(self, today, assets, out, mc):
out[:] = mc[-1]
# Custom Factor 2 : P/B Ratio
class Price_to_Book(CustomFactor):
inputs = [Fundamentals.pb_ratio]
window_length = 1
def compute(self, today, assets, out, pbr):
out[:] = -pbr[-1]
def Data_Pull():
# create the piepline for the data pull
Data_Pipe = Pipeline()
# create SPY proxy
Data_Pipe.add(SPY_proxy(), 'SPY Proxy')
# Div Yield
Data_Pipe.add(Div_Yield(), 'Dividend Yield')
# Price to Book
Data_Pipe.add(Price_to_Book(), 'Price to Book')
# Price / TTM Sales
Data_Pipe.add(Price_to_TTM_Sales(), 'Price / TTM Sales')
# Price / TTM Cashflows
Data_Pipe.add(Price_to_TTM_Cashflows(), 'Price / TTM Cashflow')
return Data_Pipe
# NB: Data pull is a function that returns a Pipeline object, so need ()
results = run_pipeline(Data_Pull(), start_date='2015-11-11', end_date='2015-11-11')
results.head()
```
##Aggregation
Now that we have all our data, we need to manipulate this in order to create a single ranking of the securities. Lo/Patel recommend the following algorithm:
* Extract the S&P500 from the set of equities and find the mean and standard deviation of each factor for this dataset (standard_frame_compute)
* Use these computed values to standardize each factor (standard_frame_compute)
* Replace values that are greater that 10 or less that -10 with 10 and -10 respectively in order to limit the effect of outliers (filter_fn)
* Sum these values for each equity and divide by the number of factors in order to give a value between -10 and 10 (composite score)
The code for this is shown below.
```
# limit effect of outliers
def filter_fn(x):
if x <= -10:
x = -10.0
elif x >= 10:
x = 10.0
return x
# standardize using mean and sd of S&P500
def standard_frame_compute(df):
# basic clean of dataset to remove infinite values
df = df.replace([np.inf, -np.inf], np.nan)
df = df.dropna()
# need standardization params from synthetic S&P500
df_SPY = df.sort(columns='SPY Proxy', ascending=False)
# create separate dataframe for SPY
# to store standardization values
df_SPY = df_SPY.head(500)
# get dataframes into numpy array
df_SPY = df_SPY.as_matrix()
# store index values
index = df.index.values
df = df.as_matrix()
df_standard = np.empty(df.shape[0])
for col_SPY, col_full in zip(df_SPY.T, df.T):
# summary stats for S&P500
mu = np.mean(col_SPY)
sigma = np.std(col_SPY)
col_standard = np.array(((col_full - mu) / sigma))
# create vectorized function (lambda equivalent)
fltr = np.vectorize(filter_fn)
col_standard = (fltr(col_standard))
# make range between -10 and 10
col_standard = (col_standard / df.shape[1])
# attach calculated values as new row in df_standard
df_standard = np.vstack((df_standard, col_standard))
# get rid of first entry (empty scores)
df_standard = np.delete(df_standard,0,0)
return (df_standard, index)
# Sum up and sort data
def composite_score(df, index):
# sum up transformed data
df_composite = df.sum(axis=0)
# put into a pandas dataframe and connect numbers
# to equities via reindexing
df_composite = pd.Series(data=df_composite,index=index)
# sort descending
df_composite.sort(ascending=False)
return df_composite
# compute the standardized values
results_standard, index = standard_frame_compute(results)
# aggregate the scores
ranked_scores = composite_score(results_standard, index)
# print the final rankings
ranked_scores
```
##Stock Choice
Now that we have ranked our securities, we need to choose a long basket and a short basket. Since we need to keep the ratio 130/30 between longs and shorts, why not have 26 longs and 6 shorts (in the algorithm we will weigh each of these equally, giving us our desired leverage and exposure).
On the graph below, we plot a histogram of the securities to get a sense of the distribution of scores. The red lines represent the cutoff points for the long and short buckets. One thing to notice is that the vast majority of equities are ranked near the middle of the histogram, whereas the tails are quite thin. This would suggest that there is something special about the securities chosen to be in these baskets, and -hopefully- these special qualities will yield positive alpha for the strategy.
```
# create histogram of scores
ranked_scores.hist()
# make scores into list for ease of manipulation
ranked_scores_list = ranked_scores.tolist()
# add labels to axes
plt.xlabel('Standardized Scores')
plt.ylabel('Quantity in Basket')
# show long bucket
plt.axvline(x=ranked_scores_list[25], linewidth=1, color='r')
# show short bucket
plt.axvline(x=ranked_scores_list[-6], linewidth=1, color='r');
```
Please see the full algorithm for backtested returns!
NB: In the implementation of the algorithm, a series of filters is used in order to ensure that only tradeable stocks are included. The methodology for this filter can be found in https://www.quantopian.com/posts/pipeline-trading-universe-best-practice.
*This presentation is for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation for any security; nor does it constitute an offer to provide investment advisory or other services by Quantopian, Inc. ("Quantopian"). Nothing contained herein constitutes investment advice or offers any opinion with respect to the suitability of any security, and any views expressed herein should not be taken as advice to buy, sell, or hold any security or as an endorsement of any security or company. In preparing the information contained herein, Quantopian, Inc. has not taken into account the investment needs, objectives, and financial circumstances of any particular investor. Any views expressed and data illustrated herein were prepared based upon information, believed to be reliable, available to Quantopian, Inc. at the time of publication. Quantopian makes no guarantees as to their accuracy or completeness. All information is subject to change and may quickly become unreliable for various reasons, including changes in market conditions or economic circumstances.*
| true |
code
| 0.557364 | null | null | null | null |
|
```
!conda upgrade scikit-learn -y
from azureml import services
from azureml import Workspace
from azure.servicebus import ServiceBusService
import warnings; warnings.filterwarnings('ignore')
import datetime
from dateutil import parser
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import cross_validation
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn import svm
#from sklearn.ensemble import VotingClassifier
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import f1_score
import requests
import urllib2
import json
from pylab import rcParams
rcParams['figure.figsize'] = 14, 3
%matplotlib inline
pd.options.display.max_colwidth = 500
ws = Workspace()
```
## Keys and Constants
```
Anomaly_Detection_KEY = 'put key here'
```
# Pull in and Pre-Process Data
**Import data**
```
vel_raw = ws.datasets['vel_raw'].to_dataframe().set_index('time').value
vel_edited = ws.datasets['vel_curated'].to_dataframe().set_index('time').value
df = pd.concat({'velocity': vel_raw, 'velocity_edited': vel_edited}, axis=1, join='inner')
df = df.reset_index()
df['time'] = pd.to_datetime(df['time'], format='%Y-%m-%d %H:%M')
df = df.set_index('time')
df
```
**Generate Velocity N window size of 4**
```
#create level channels
for i in range(1, 5):
df['velocity_{}'.format(i)] = df.velocity.shift(i)
df = df.dropna()
df.head(4)
```
**Tag Anomolies**
```
df['diff'] = np.abs(df.velocity - df.velocity_edited)
df['anomaly'] = df['diff'].apply(lambda x: 1 if x > 0 else 0)
df.head(4)
df[df['anomaly']>0].count()
```
# Visualize Data
**Check Few Points**
```
df['2013-04-02 02:30:00':'2013-04-02 02:50:00']
```
**Plot Sample Daily Pattern**
```
day_df = df['2013-09-03':'2013-09-03']
day_anomalies = day_df[day_df['anomaly']==1]
plt.plot(day_df['velocity'])
plt.scatter(day_anomalies.index, day_anomalies.velocity, color='r')
```
**Plot Sample Daily Pattern With Anomalies**
```
day_df = df['2013-09-02':'2013-09-02']
day_anomalies = day_df[day_df['anomaly']==1]
plt.plot(day_df['velocity'])
plt.scatter(day_anomalies.index, day_anomalies.velocity, color='r')
```
# Compare Anomaly Detection and Outlier Detection Models
**Define Metrics**
```
def print_report(expected, predicted):
target_names = ['Anomalies', 'Regular velocity']
print("Confusion Matrix")
print(confusion_matrix(expected, predicted))
print(classification_report(expected, predicted, target_names = target_names))
```
# Todo Update to reflect the new api
**Model #1 : Outlier Detection**
- Send the raw data to the [Anomaly Detection API](https://docs.microsoft.com/en-us/azure/machine-learning/machine-learning-apps-anomaly-detection-api) to tag outliers
- Score outlier model using [Anomaly Detection API](https://docs.microsoft.com/en-us/azure/machine-learning/machine-learning-apps-anomaly-detection-api) results against the 'manually tagged anomalies'
```
#Format data for processing
velDf = vel_raw.to_frame().reset_index()
velDf.value = velDf.value
values = [[parser.parse(t).strftime('%m/%d/%Y %H:%M:%S'),d] for t,d in velDf.values.tolist()]
values
def detectAnomalies(values):
data = {
"Inputs": {
"input1": {
"ColumnNames": ["Time", "Data"],
"Values": values
},
},
"GlobalParameters": {
"tspikedetector.sensitivity": "3",
"zspikedetector.sensitivity": "3",
"bileveldetector.sensitivity": "3.25",
"detectors.spikesdips": "Both"
}
}
body = str.encode(json.dumps(data))
url = 'https://europewest.services.azureml.net/subscriptions/13bbfab4b75b461c98963a55594775f2/services/eb7b355fe6534415ac983c6170756c3c/execute?api-version=2.0&details=true'
headers = {'Content-Type':'application/json', 'Authorization':('Bearer '+ Anomaly_Detection_KEY)}
req = urllib2.Request(url, body, headers)
try:
response = urllib2.urlopen(req)
result = response.read()
return result
except urllib2.HTTPError, error:
print("The request failed with status code: " + str(error.code))
# Print the headers - they include the requert ID and the timestamp, which are useful for debugging the failure
print(error.info())
print(json.loads(error.read()))
raw_outliers = json.loads(detectAnomalies(values))['Results']['output1']['value']
outliers = pd.DataFrame(raw_outliers['Values'], columns=raw_outliers['ColumnNames'])
outliers['detected_outliers'] = pd.to_numeric(outliers['rpscore']).apply(lambda x: 1 if x > 0 else 0)
print_report(df['anomaly'], outliers[4:]['detected_outliers'])
```
**Model #2: Binary Classifier**
- Create a historical window of the previous four velocity channel readings values at each time.
- Create a train and test set from a random split on the historical windows
- Train a random forest classifier on the train data
- Benchmark the random forest on the test data
```
#Define test and training set
columns = ['velocity', 'velocity_1','velocity_2','velocity_3','velocity_4']
X_train, X_test, y_train, y_test = cross_validation.train_test_split(df[columns], df.anomaly, test_size=0.3)
clf = RandomForestClassifier()
clf.fit(X_train, y_train)
xs = clf.predict(X_test)
print_report(y_test, xs)
```
**Model #3: Hybrid Classifier**
- Create a historical window of the previous four velocity channel readings values at each time using only the values marked as outliers.
- Create a train and test set from a random split on the historical windows.
- Train a random forest classifier on the train data.
- Benchmark the random forest on the test data.
- Benchmark the random forest on the entire velocity time series excluding the training set.
```
detected_outliers = pd.DataFrame({'time':outliers[4:]['Time'],'detected_outliers':outliers[4:]['detected_outliers']})
detected_outliers = detected_outliers[detected_outliers['detected_outliers'] == 1]
detected_outliers['time'] = pd.to_datetime(detected_outliers['time'])
df_outliers = df.loc[detected_outliers['time']]
X_train, X_test, y_train, y_test = cross_validation.train_test_split(df_outliers[columns], df_outliers.anomaly, test_size=0.3)
clf = RandomForestClassifier()
clf.fit(X_train, y_train)
xs = clf.predict(X_test)
print_report(y_test, xs)
unseenValues = pd.DataFrame({'time':outliers[4:]['Time'],'detected_outliers':outliers[4:]['detected_outliers']})
unseenValues = unseenValues[unseenValues['detected_outliers'] == 0]
unseenValues['time'] = pd.to_datetime(unseenValues['time'])
unseenValues = df.loc[unseenValues['time']]
oseries = clf.predict(unseenValues[columns])
print_report(unseenValues.anomaly, oseries)
```
The binary classification model was able to greatly help differentiate between the outliers, anomolies and regular values. While in this data set the anomolies are lineraly seperable in others this technique could be used to yield more accurate results across the 475 sensor errors in the dataset.
## Results
Though the anomoly detection API helped differentiate outliers for anomoly classification, in Carl Data's dataset the difference between anomalies and regular flow was linearly differentiable enough that a random forrest binary classifier was able to provide just as good results as the anomoly detection API without the overhead.
# Put Model Into Production
```
@services.publish(ws)
@services.types(curVel = float ,vel1 = float, vel2 = float,vel3 = float, vel4 = float)
@services.returns(int)
def detectAnomaly(curVel,vel1,vel2,vel3,vel4):
result = clf.predict([curVel,vel1,vel2,vel3,vel4])
return result[0]
# show information about the web service
serviceInfo = {
'service_url' : detectAnomaly.service.url,
'api_key' : detectAnomaly.service.api_key,
'help_url' : detectAnomaly.service.help_url,
'service_id' : detectAnomaly.service.service_id,
}
serviceInfo
```
**Test with anomaly**
```
print(detectAnomaly(0, 0, 0, 0, 10))
```
**Test with normal flow**
```
print(detectAnomaly(1.119, 1.162, 1.058, 1.065, 1.058))
```
# Create Event Hub For Visualization
**Create an [Eventhub namespace](https://docs.microsoft.com/en-us/azure/event-hubs/event-hubs-resource-manager-namespace-event-hub) from the azure portal and fill in the following**
```
servns = 'pyconil2017sb'
key_name = 'createandsend' # SharedAccessKeyName from Azure portal
key_value = '0fvHx77YIng4rn/SsxROp+1kFTd5GJ76WDzo5K5e8ps=' # SharedAccessKey from Azure portal
```
**Init Service Bus Service**
```
sbs = ServiceBusService(service_namespace=servns,
shared_access_key_name=key_name,
shared_access_key_value=key_value) # Create a ServiceBus Service Object
```
** Create Visualization Event Hub **
```
anomaly_visulization = sbs.create_event_hub('anomaly_visulization') # Create a Event Hub for the ServiceBus. If it exists then return true, else return false
print(anomaly_visulization)
def sendToEventHub(time, curVel, anomoaly):
event_data = json.dumps({ 'time': time,
'curVel': curVel,
'anomaly': anomoaly
})
sbs.send_event('anomaly_visulization', event_data)
```
**Link Visualization Eventhub to [Stream Analytics and PowerBI Embedded](https://docs.microsoft.com/en-us/azure/stream-analytics/stream-analytics-power-bi-dashboard)**
# Simulate a flow sensor and feed the data to our system
```
for index, row in df['2013-09-02':'2013-09-02'].iterrows():
anomaly = bool(detectAnomaly(row['velocity'], row['velocity_1'], row['velocity_2'], row['velocity_3'], row['velocity_4']))
time = (index.strftime("%Y-%m-%d %H:%M:%S"))
sendToEventHub(time,row['velocity'],anomaly)
```
| true |
code
| 0.490358 | null | null | null | null |
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/GetStarted/04_band_math.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/GetStarted/04_band_math.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=GetStarted/04_band_math.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/GetStarted/04_band_math.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# This function gets NDVI from Landsat 5 imagery.
def getNDVI(image):
return image.normalizedDifference(['B4', 'B3'])
# Load two Landsat 5 images, 20 years apart.
image1 = ee.Image('LANDSAT/LT05/C01/T1_TOA/LT05_044034_19900604')
image2 = ee.Image('LANDSAT/LT05/C01/T1_TOA/LT05_044034_20100611')
# Compute NDVI from the scenes.
ndvi1 = getNDVI(image1)
ndvi2 = getNDVI(image2)
# Compute the difference in NDVI.
ndviDifference = ndvi2.subtract(ndvi1)
ndviParams = {'palette': ['#d73027', '#f46d43', '#fdae61',
'#fee08b', '#d9ef8b', '#a6d96a', '#66bd63', '#1a9850']}
ndwiParams = {'min': -0.5, 'max': 0.5, 'palette': ['FF0000', 'FFFFFF', '0000FF']}
Map.centerObject(image1, 10)
Map.addLayer(ndvi1, ndviParams, 'NDVI 1')
Map.addLayer(ndvi2, ndviParams, 'NDVI 2')
Map.addLayer(ndviDifference, ndwiParams, 'NDVI difference')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
| true |
code
| 0.628806 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/hendradarwin/covid-19-prediction/blob/master/series-dnn_and_rnn/Forecast_2_dnn.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Pediction New Death Cases Global Covid-19 Cases
## Load Data and Import Libraries
```
# Use some functions from tensorflow_docs
!pip install -q git+https://github.com/tensorflow/docs
%tensorflow_version 2.x # make sure that collab use tensorflow 2
import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp
from tensorflow import keras
import pandas as pd
import seaborn as sns
from pylab import rcParams
import matplotlib.pyplot as plt
from matplotlib import rc
import os
import datetime
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
import tensorflow_docs.modeling
# from google.colab import drive
# drive.mount('/content/drive')
%matplotlib inline
%config InlineBackend.figure_format='retina'
sns.set(style='whitegrid', palette='muted', font_scale=1.5)
rcParams['figure.figsize'] = 16, 10
# !rm '/root/.keras/datasets/global_total.csv'
```
## Load Data
```
df_new_cases = pd.read_csv("https://raw.githubusercontent.com/virgiawan/covid-19-prediction/linear-regression/dataset/corona-virus/new_cases.csv")
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
step = 0;
times = []
series = []
for case in df_new_cases['World']:
times.append(step)
series.append(case)
step += 1
plot_series(times, series)
print('Total data {} series'.format(len(series)))
# Series 0 - 63 indicate flat data. Data not increased significantly.
# Try to ignore it first
skip = 63
used_series = series[skip:]
used_times = times[skip:]
plot_series(used_times, used_series)
print('Total data {} series'.format(len(used_series)))
split_percentage = 0.70
split_time = (int) (len(used_times) * split_percentage)
time_train = used_times[:split_time]
x_train = used_series[:split_time]
time_valid = used_times[split_time:]
x_valid = used_series[split_time:]
# create DNN window
def windowed_dataset_dnn(series, window_size, batch_size, shuffle_buffer):
series = tf.expand_dims(series, axis=-1)
dataset = tf.data.Dataset.from_tensor_slices(series)
dataset = dataset.window(window_size + 1, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_size + 1))
dataset = dataset.shuffle(shuffle_buffer)
dataset = dataset.map(lambda window: (window[:-1], window[-1]))
dataset = dataset.batch(batch_size).prefetch(1)
return dataset
# define hyper parameter
window_size = 20
batch_size = 2
shuffle_buffer_size = 10
epochs = 100
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
dataset = windowed_dataset_dnn(x_train, window_size, batch_size, shuffle_buffer_size)
l0 = tf.keras.layers.Conv1D(filters=32, kernel_size=5,
strides=1, padding="causal",
activation="relu",
input_shape=[None, 1])
l1 = tf.keras.layers.Dense(32, input_shape=[window_size], activation='relu')
l2 = tf.keras.layers.Dense(32, activation='relu')
l3 = tf.keras.layers.Dense(1)
l4 = tf.keras.layers.Lambda(lambda x: x * 10000)
model = tf.keras.models.Sequential([l0, l1, l2, l3, l4])
lr_schedule = tf.keras.callbacks.LearningRateScheduler(
lambda epoch: 1e-8 * 10**(epoch / 20))
optimizer = tf.keras.optimizers.SGD(lr=1e-8, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(), optimizer=optimizer, metrics=['mae'])
history = model.fit(dataset, epochs=epochs, callbacks=[lr_schedule], verbose=0)
len_data = 0
for window_dataset in dataset:
len_data += 1
print('Windows number: {}'.format(len_data))
plt.semilogx(history.history["lr"], history.history["loss"])
plt.axis([1e-8, 10, 0, 100000])
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
epochs = 10000
dataset = windowed_dataset_dnn(x_train, window_size, batch_size, shuffle_buffer_size)
l0 = tf.keras.layers.Conv1D(filters=32, kernel_size=5,
strides=1, padding="causal",
activation="relu",
input_shape=[None, 1])
l1 = tf.keras.layers.Dense(32, input_shape=[window_size], activation='relu')
l2 = tf.keras.layers.Dense(32, activation='relu')
l3 = tf.keras.layers.Dense(1)
l4 = tf.keras.layers.Lambda(lambda x: x * 10000)
model = tf.keras.models.Sequential([l0, l1, l2, l3, l4])
optimizer = tf.keras.optimizers.SGD(lr=1e-5, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(), optimizer=optimizer, metrics=['mae', 'acc'])
history = model.fit(dataset, epochs=epochs, verbose=2)
plt.semilogx(range(0, epochs), history.history["loss"])
plt.axis([0, 10000, 4000, 25000])
forecast = []
np_used_series = np.array(used_series)
np_used_series = tf.expand_dims(np_used_series, axis=-1)
for time in range(len(np_used_series) - window_size):
forecast.append(model.predict(np_used_series[time:time + window_size][np.newaxis]))
forecast = forecast[split_time-window_size:]
results = np.array(forecast)[:, 0, 0]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, results)
tf.keras.metrics.mean_absolute_error(x_valid, results).numpy()
```
| true |
code
| 0.724773 | null | null | null | null |
|
# Using Interact
The `interact` function (`ipywidgets.interact`) automatically creates user interface (UI) controls for exploring code and data interactively. It is the easiest way to get started using IPython's widgets.
```
from __future__ import print_function
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
```
## Basic `interact`
At the most basic level, `interact` autogenerates UI controls for function arguments, and then calls the function with those arguments when you manipulate the controls interactively. To use `interact`, you need to define a function that you want to explore. Here is a function that prints its only argument `x`.
```
def f(x):
return x
```
When you pass this function as the first argument to `interact` along with an integer keyword argument (`x=10`), a slider is generated and bound to the function parameter.
```
interact(f, x=10);
```
When you move the slider, the function is called, which prints the current value of `x`.
If you pass `True` or `False`, `interact` will generate a checkbox:
```
interact(f, x=True);
```
If you pass a string, `interact` will generate a text area.
```
interact(f, x='Hi there!');
```
`interact` can also be used as a decorator. This allows you to define a function and interact with it in a single shot. As this example shows, `interact` also works with functions that have multiple arguments.
```
@interact(x=True, y=1.0)
def g(x, y):
return (x, y)
```
## Fixing arguments using `fixed`
There are times when you may want to explore a function using `interact`, but fix one or more of its arguments to specific values. This can be accomplished by wrapping values with the `fixed` function.
```
def h(p, q):
return (p, q)
```
When we call `interact`, we pass `fixed(20)` for q to hold it fixed at a value of `20`.
```
interact(h, p=5, q=fixed(20));
```
Notice that a slider is only produced for `p` as the value of `q` is fixed.
## Widget abbreviations
When you pass an integer-valued keyword argument of `10` (`x=10`) to `interact`, it generates an integer-valued slider control with a range of `[-10,+3*10]`. In this case, `10` is an *abbreviation* for an actual slider widget:
```python
IntSlider(min=-10,max=30,step=1,value=10)
```
In fact, we can get the same result if we pass this `IntSlider` as the keyword argument for `x`:
```
interact(f, x=widgets.IntSlider(min=-10,max=30,step=1,value=10));
```
This examples clarifies how `interact` processes its keyword arguments:
1. If the keyword argument is a `Widget` instance with a `value` attribute, that widget is used. Any widget with a `value` attribute can be used, even custom ones.
2. Otherwise, the value is treated as a *widget abbreviation* that is converted to a widget before it is used.
The following table gives an overview of different widget abbreviations:
<table class="table table-condensed table-bordered">
<tr><td><strong>Keyword argument</strong></td><td><strong>Widget</strong></td></tr>
<tr><td>`True` or `False`</td><td>Checkbox</td></tr>
<tr><td>`'Hi there'`</td><td>Text</td></tr>
<tr><td>`value` or `(min,max)` or `(min,max,step)` if integers are passed</td><td>IntSlider</td></tr>
<tr><td>`value` or `(min,max)` or `(min,max,step)` if floats are passed</td><td>FloatSlider</td></tr>
<tr><td>`['orange','apple']` or `{'one':1,'two':2}`</td><td>Dropdown</td></tr>
</table>
Note that a dropdown is used if a list or a dict is given (signifying discrete choices), and a slider is used if a tuple is given (signifying a range).
You have seen how the checkbox and textarea widgets work above. Here, more details about the different abbreviations for sliders and dropdowns are given.
If a 2-tuple of integers is passed `(min,max)`, an integer-valued slider is produced with those minimum and maximum values (inclusively). In this case, the default step size of `1` is used.
```
interact(f, x=(0,4));
```
If a 3-tuple of integers is passed `(min,max,step)`, the step size can also be set.
```
interact(f, x=(0,8,2));
```
A float-valued slider is produced if the elements of the tuples are floats. Here the minimum is `0.0`, the maximum is `10.0` and step size is `0.1` (the default).
```
interact(f, x=(0.0,10.0));
```
The step size can be changed by passing a third element in the tuple.
```
interact(f, x=(0.0,10.0,0.01));
```
For both integer and float-valued sliders, you can pick the initial value of the widget by passing a default keyword argument to the underlying Python function. Here we set the initial value of a float slider to `5.5`.
```
@interact(x=(0.0,20.0,0.5))
def h(x=5.5):
return x
```
Dropdown menus are constructed by passing a list of strings. In this case, the strings are both used as the names in the dropdown menu UI and passed to the underlying Python function.
```
interact(f, x=['apples','oranges']);
```
If you want a dropdown menu that passes non-string values to the Python function, you can pass a list of (label, value) pairs.
```
interact(f, x=[('one', 10), ('two', 20)]);
```
## `interactive`
In addition to `interact`, IPython provides another function, `interactive`, that is useful when you want to reuse the widgets that are produced or access the data that is bound to the UI controls.
Note that unlike `interact`, the return value of the function will not be displayed automatically, but you can display a value inside the function with `IPython.display.display`.
Here is a function that returns the sum of its two arguments and displays them. The display line may be omitted if you don't want to show the result of the function.
```
from IPython.display import display
def f(a, b):
display(a + b)
return a+b
```
Unlike `interact`, `interactive` returns a `Widget` instance rather than immediately displaying the widget.
```
w = interactive(f, a=10, b=20)
```
The widget is an `interactive`, a subclass of `VBox`, which is a container for other widgets.
```
type(w)
```
The children of the `interactive` are two integer-valued sliders and an output widget, produced by the widget abbreviations above.
```
w.children
```
To actually display the widgets, you can use IPython's `display` function.
```
display(w)
```
At this point, the UI controls work just like they would if `interact` had been used. You can manipulate them interactively and the function will be called. However, the widget instance returned by `interactive` also gives you access to the current keyword arguments and return value of the underlying Python function.
Here are the current keyword arguments. If you rerun this cell after manipulating the sliders, the values will have changed.
```
w.kwargs
```
Here is the current return value of the function.
```
w.result
```
## Disabling continuous updates
When interacting with long running functions, realtime feedback is a burden instead of being helpful. See the following example:
```
def slow_function(i):
print(int(i),list(x for x in range(int(i)) if
str(x)==str(x)[::-1] and
str(x**2)==str(x**2)[::-1]))
return
%%time
slow_function(1e6)
```
Notice that the output is updated even while dragging the mouse on the slider. This is not useful for long running functions due to lagging:
```
from ipywidgets import FloatSlider
interact(slow_function,i=FloatSlider(min=1e5, max=1e7, step=1e5));
```
There are two ways to mitigate this. You can either only execute on demand, or restrict execution to mouse release events.
### `interact_manual`
The `interact_manual` function provides a variant of interaction that allows you to restrict execution so it is only done on demand. A button is added to the interact controls that allows you to trigger an execute event.
```
interact_manual(slow_function,i=FloatSlider(min=1e5, max=1e7, step=1e5));
```
### `continuous_update`
If you are using slider widgets, you can set the `continuous_update` kwarg to `False`. `continuous_update` is a kwarg of slider widgets that restricts executions to mouse release events.
```
interact(slow_function,i=FloatSlider(min=1e5, max=1e7, step=1e5, continuous_update=False));
```
### `interactive_output`
`interactive_output` provides additional flexibility: you can control how the UI elements are laid out.
Unlike `interact`, `interactive`, and `interact_manual`, `interactive_output` does not generate a user interface for the widgets. This is powerful, because it means you can create a widget, put it in a box, and then pass the widget to `interactive_output`, and have control over the widget and its layout.
```
a = widgets.IntSlider()
b = widgets.IntSlider()
c = widgets.IntSlider()
ui = widgets.HBox([a, b, c])
def f(a, b, c):
print((a, b, c))
out = widgets.interactive_output(f, {'a': a, 'b': b, 'c': c})
display(ui, out)
```
## Arguments that are dependent on each other
Arguments that are dependent on each other can be expressed manually using `observe`. See the following example, where one variable is used to describe the bounds of another. For more information, please see the [widget events example notebook](./Widget Events.ipynb).
```
x_widget = FloatSlider(min=0.0, max=10.0, step=0.05)
y_widget = FloatSlider(min=0.5, max=10.0, step=0.05, value=5.0)
def update_x_range(*args):
x_widget.max = 2.0 * y_widget.value
y_widget.observe(update_x_range, 'value')
def printer(x, y):
print(x, y)
interact(printer,x=x_widget, y=y_widget);
```
## Flickering and jumping output
On occasion, you may notice interact output flickering and jumping, causing the notebook scroll position to change as the output is updated. The interactive control has a layout, so we can set its height to an appropriate value (currently chosen manually) so that it will not change size as it is updated.
```
%matplotlib inline
from ipywidgets import interactive
import matplotlib.pyplot as plt
import numpy as np
def f(m, b):
plt.figure(2)
x = np.linspace(-10, 10, num=1000)
plt.plot(x, m * x + b)
plt.ylim(-5, 5)
plt.show()
interactive_plot = interactive(f, m=(-2.0, 2.0), b=(-3, 3, 0.5))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot
```
| true |
code
| 0.520862 | null | null | null | null |
|
# Tutorial Part 17: Training a Generative Adversarial Network on MNIST
In this tutorial, we will train a Generative Adversarial Network (GAN) on the MNIST dataset. This is a large collection of 28x28 pixel images of handwritten digits. We will try to train a network to produce new images of handwritten digits.
## Colab
This tutorial and the rest in this sequence are designed to be done in Google colab. If you'd like to open this notebook in colab, you can use the following link.
[](https://colab.research.google.com/github/deepchem/deepchem/blob/master/examples/tutorials/17_Training_a_Generative_Adversarial_Network_on_MNIST.ipynb)
## Setup
To run DeepChem within Colab, you'll need to run the following cell of installation commands. This will take about 5 minutes to run to completion and install your environment.
```
!curl -Lo conda_installer.py https://raw.githubusercontent.com/deepchem/deepchem/master/scripts/colab_install.py
import conda_installer
conda_installer.install()
!/root/miniconda/bin/conda info -e
!pip install --pre deepchem
import deepchem
deepchem.__version__
```
To begin, let's import all the libraries we'll need and load the dataset (which comes bundled with Tensorflow).
```
import deepchem as dc
import tensorflow as tf
from deepchem.models.optimizers import ExponentialDecay
from tensorflow.keras.layers import Conv2D, Conv2DTranspose, Dense, Reshape
import matplotlib.pyplot as plot
import matplotlib.gridspec as gridspec
%matplotlib inline
mnist = tf.keras.datasets.mnist.load_data(path='mnist.npz')
images = mnist[0][0].reshape((-1, 28, 28, 1))/255
dataset = dc.data.NumpyDataset(images)
```
Let's view some of the images to get an idea of what they look like.
```
def plot_digits(im):
plot.figure(figsize=(3, 3))
grid = gridspec.GridSpec(4, 4, wspace=0.05, hspace=0.05)
for i, g in enumerate(grid):
ax = plot.subplot(g)
ax.set_xticks([])
ax.set_yticks([])
ax.imshow(im[i,:,:,0], cmap='gray')
plot_digits(images)
```
Now we can create our GAN. Like in the last tutorial, it consists of two parts:
1. The generator takes random noise as its input and produces output that will hopefully resemble the training data.
2. The discriminator takes a set of samples as input (possibly training data, possibly created by the generator), and tries to determine which are which.
This time we will use a different style of GAN called a Wasserstein GAN (or WGAN for short). In many cases, they are found to produce better results than conventional GANs. The main difference between the two is in the discriminator (often called a "critic" in this context). Instead of outputting the probability of a sample being real training data, it tries to learn how to measure the distance between the training distribution and generated distribution. That measure can then be directly used as a loss function for training the generator.
We use a very simple model. The generator uses a dense layer to transform the input noise into a 7x7 image with eight channels. That is followed by two convolutional layers that upsample it first to 14x14, and finally to 28x28.
The discriminator does roughly the same thing in reverse. Two convolutional layers downsample the image first to 14x14, then to 7x7. A final dense layer produces a single number as output. In the last tutorial we used a sigmoid activation to produce a number between 0 and 1 that could be interpreted as a probability. Since this is a WGAN, we instead use a softplus activation. It produces an unbounded positive number that can be interpreted as a distance.
```
class DigitGAN(dc.models.WGAN):
def get_noise_input_shape(self):
return (10,)
def get_data_input_shapes(self):
return [(28, 28, 1)]
def create_generator(self):
return tf.keras.Sequential([
Dense(7*7*8, activation=tf.nn.relu),
Reshape((7, 7, 8)),
Conv2DTranspose(filters=16, kernel_size=5, strides=2, activation=tf.nn.relu, padding='same'),
Conv2DTranspose(filters=1, kernel_size=5, strides=2, activation=tf.sigmoid, padding='same')
])
def create_discriminator(self):
return tf.keras.Sequential([
Conv2D(filters=32, kernel_size=5, strides=2, activation=tf.nn.leaky_relu, padding='same'),
Conv2D(filters=64, kernel_size=5, strides=2, activation=tf.nn.leaky_relu, padding='same'),
Dense(1, activation=tf.math.softplus)
])
gan = DigitGAN(learning_rate=ExponentialDecay(0.001, 0.9, 5000))
```
Now to train it. As in the last tutorial, we write a generator to produce data. This time the data is coming from a dataset, which we loop over 100 times.
One other difference is worth noting. When training a conventional GAN, it is important to keep the generator and discriminator in balance thoughout training. If either one gets too far ahead, it becomes very difficult for the other one to learn.
WGANs do not have this problem. In fact, the better the discriminator gets, the cleaner a signal it provides and the easier it becomes for the generator to learn. We therefore specify `generator_steps=0.2` so that it will only take one step of training the generator for every five steps of training the discriminator. This tends to produce faster training and better results.
```
def iterbatches(epochs):
for i in range(epochs):
for batch in dataset.iterbatches(batch_size=gan.batch_size):
yield {gan.data_inputs[0]: batch[0]}
gan.fit_gan(iterbatches(100), generator_steps=0.2, checkpoint_interval=5000)
```
Let's generate some data and see how the results look.
```
plot_digits(gan.predict_gan_generator(batch_size=16))
```
Not too bad. Many of the generated images look plausibly like handwritten digits. A larger model trained for a longer time can do much better, of course.
# Congratulations! Time to join the Community!
Congratulations on completing this tutorial notebook! If you enjoyed working through the tutorial, and want to continue working with DeepChem, we encourage you to finish the rest of the tutorials in this series. You can also help the DeepChem community in the following ways:
## Star DeepChem on [GitHub](https://github.com/deepchem/deepchem)
This helps build awareness of the DeepChem project and the tools for open source drug discovery that we're trying to build.
## Join the DeepChem Gitter
The DeepChem [Gitter](https://gitter.im/deepchem/Lobby) hosts a number of scientists, developers, and enthusiasts interested in deep learning for the life sciences. Join the conversation!
| true |
code
| 0.712482 | null | null | null | null |
|
# Healthcare insurance fraud identification using PCA anomaly detection
1. [Background](#background)
1. [Setup](#setup)
1. [Data](#data)
1. [Obtain data](#datasetfiles)
1. [Feature Engineering](#feateng)
1. [Missing values](#missing)
1. [Categorical features](#catfeat)
1. [Gender](#gender)
1. [Age Group](#age)
1. [NLP for Textual features](#nlp)
1. [Diagnosis Descriptions](#diagnosis)
1. [Procedure Descriptions](#procedure)
1. [Split train & test data](#split)
1. [Standardize](#standardize)
1. [PCA](#pca)
1. [Calculate the Mahalanobis distance](#md)
1. [Unsupervised Anomaly Detection](#ad)
1. [Understanding Anomaly](#understandinganomaly)
1. [(Optional) Deploy PCA](#deployendpoint)
## 1. Background <a name="background"></a>
Medicare is a federal healthcare program created in 1965 with the passage of the Social Security Amendments to ensure that citizens 65 and older as well as younger persons with certain disabilities have access to quality healthcare. Medicare is administered by the Centers for Medicare and Medicaid Services (CMS). CMS manages Medicare programs by selecting official Medicare administrative contractors (MACs) to process the Medicare claims associated with various parts of Medicare. We propose a solution to apply unsupervised outlier techniques at post-payment stage to detect fraudulent patterns of received insurance claims.
Health care insurance fraud is a pressing problem, causing substantial and increasing costs in medical insurance programs. Due to large amounts of claims submitted, review of individual claims becomes a difficult task and encourages the employment of automated pre-payment controls and better post-payment decision support tools to enable subject matter expert analysis. We will demonstrate the unsupervised anomalous outlier techniques on a minimal set of metrics made available in the CMS Medicare inpatient claims from 2008. Once more data is available as extracts from different systems -Medicaid Information Management systems(MMIS), Medicaid Statistical Information Systems(MSIS), Medicaid Reference data such as Provider Files, Death Master Files, etc. - there is an opportunity to build a database of metrics to make the fraud detection technique more robust. The method can be used to flag claims as a targeting method for further investigation.
## 2. Setup <a name="setup"></a>
To begin, we'll install the Python libraries we'll need for the remainder of the exercise.
```
# Upgrade numpy to latest version. Should be numpy==1.15.0 or higher to use quantile attribute
import sys
!{sys.executable} -m pip install --upgrade numpy
#If thenumpy version prints less than 1.15.0
#Go to Jupyter notebook menu on the top, click on kernal and click "Restart and Clear Output". Start from the beginning again.
import numpy as np
print(np.__version__)
!{sys.executable} -m pip install columnize gensim
!{sys.executable} -m pip uninstall seaborn -y
!{sys.executable} -m pip install seaborn
```
Next, we'll import the Python libraries we'll need for the remainder of the exercise.
```
import numpy as np # For matrix operations and numerical processing
import pandas as pd # For munging tabular data
import boto3 #enables Python developers to create, configure, and manage AWS services
from IPython.display import display # For displaying outputs in the notebook
import matplotlib.pyplot as plt #for interactive plots and simple cases of programmatic plot generation
%matplotlib inline
from time import gmtime, strftime # For labeling SageMaker models, endpoints, etc.
import sys #provides access to some variables used or maintained by the interpreter
import os # For manipulating filepath names
import sagemaker #open source library for training and deploying machine-learned models on Amazon SageMaker
import time #provides various time-related functions
import warnings #allows you to handle all warnings with the standard logging
import io #interface to access files and streams
import sagemaker.amazon.common as smac #provides common function used for training and deploying machine-learned models on Amazon SageMaker
warnings.filterwarnings(action = 'ignore') #warnings filter controls whether warnings are ignored, displayed
from sklearn.model_selection import train_test_split #Quick utility to split data into train and test set
import gensim #topic modelling library for Python that provides access to Word2Vec
import columnize #format a simple (i.e. not nested) list into aligned columns.
from gensim.models import Word2Vec #topic modelling library for Python that provides access to Word2Vec
from sklearn.manifold import TSNE #containing T-SNE algorithms used to project high dimensional space into lower dimesional space
from numpy.linalg import inv #Compute the dot product of two or more arrays in a single function call
import scipy.stats #contains a large number of probability distributions for statistical analysis
import scipy as sp #collection of mathematical algorithms
import seaborn as sns #data visualization library based on matplotlib
import mxnet as mx #open-source deep learning software framework, used to train, and deploy deep neural networks.
from sklearn.manifold import TSNE
```
This notebook was created and tested on an ml.t2.medium instance.
Please specify a string that is unique to you, your name is fine! That way you can see your resources, in the event your AWS account is used by multiple people.
```
name = 'first-last'
import sagemaker
from sagemaker import get_execution_role
import boto3, os
s3 = boto3.resource('s3')
sess = sagemaker.Session()
role = get_execution_role()
# Assign a unique name to the bucket. S3 buckets should have unique global name.
bucket = sess.default_bucket()
prefix = 'aim302-30-may-2019/healthcare-fraud-detection/{}'.format(name)
print('Training input/output will be stored in {}/{}'.format(bucket, prefix))
print('\nIAM Role: {}'.format(role))
```
## 3. Data<a name="data"></a>
The dataset we'll be using in this example was downloaded from following link.
https://www.cms.gov/Research-Statistics-Data-and-Systems/Downloadable-Public-Use-Files/BSAPUFS/Inpatient_Claims.html
The data set is the public available Basic Stand Alone (BSA) Inpatient Public Use Files (PUF) named “CMS 2008 BSA Inpatient Claims PUF”. The file contains Medicare inpatient claims from 2008. Each record is an inpatient claim incurred by a 5% sample of Medicare beneficiaries. The file contains seven (7) variables: A primary claim key indexing the records and six (6) analytic variables. One of the analytic variables, claim cost, is provided in two forms, (a) as an integer category and (b) as a dollar average. There are some demographic and claim-related variables provided in this PUF.
However, as beneficiary identities are not provided, it is not possible to link claims that belong to the same beneficiary in the CMS 2008 BSA Inpatient Claims PUF. Without linking beneficiary Id to the claims, it is not possible to create features such as 'amount reimbursed over time', 'average reimbursement per visit' etc.
### 3A. Obtain data<a name="datasetfiles"></a>
We will use the following link to download claims dataset.
https://www.cms.gov/Research-Statistics-Data-and-Systems/Downloadable-Public-Use-Files/BSAPUFS/Downloads/2008_BSA_Inpatient_Claims_PUF.zip
The data dictionary required to interpret codes in dataset have been constructed from following pdf document.
https://www.cms.gov/Research-Statistics-Data-and-Systems/Downloadable-Public-Use-Files/BSAPUFS/Downloads/2008_BSA_Inpatient_Claims_PUF_DataDic_CB.pdf
Following dictionary files are already avaliable in data folder in the notebook.
- `ColumnNames.csv` - column description
- `DiagnosisRelatedGroupNames.csv` - dictionary for procedure codes
- `InternationalClassificationOfDiseasesNames.csv` - dictionary of diagnosis codes
- `LengthOfStayDays.csv` - dictionary of length of stay
- `AgeGroup.csv` - dictionary of age group
- `Gender.csv` - dictionary of gender
#### Download claims data file from CMS site.
```
#!wget https://www.cms.gov/Research-Statistics-Data-and-Systems/Downloadable-Public-Use-Files/BSAPUFS/Downloads/2008_BSA_Inpatient_Claims_PUF.zip
!unzip -o ./2008_BSA_Inpatient_Claims_PUF-backup.zip -d data
```
#### The data file have been extrcated under data folder locally on Sagemaker notebook volume in the data folder.
- `2008_BSA_Inpatient_Claims_PUF.csv` - claims data
#### Let's begin exploring data:
## 4. Feature Engineering <a name="feateng"></a>
```
# read the ColumnNames csv file to identify meaningful names for column labels in the claim data
colnames = pd.read_csv("./data/ColumnNames.csv")
colnames[colnames.columns[-1]] = colnames[colnames.columns[-1]].map(lambda x: x.replace('"','').strip())
display(colnames)
# read claims data file
df_cms_claims_data = pd.read_csv('./data/2008_BSA_Inpatient_Claims_PUF.csv')
df_cms_claims_data.columns = colnames[colnames.columns[-1]].ravel()
pd.set_option('display.max_columns', 500)
# print the shape of the data file
print('Shape:', df_cms_claims_data.shape)
# show the top few rows
display(df_cms_claims_data.head())
# describe the data object
display(df_cms_claims_data.describe())
# check the datatype for each column
display(df_cms_claims_data.dtypes)
# check null value for each column
display(df_cms_claims_data.isnull().mean())
```
#### You might have observed some 'NaN' and mean value(0.469985) for ICD9 primary procedure code in print results above.
We need fix to 'NaN' in ICD9 primary procedure code.
### 4A. Missing values<a name="missing"></a>
Do I have missing values? How are they expressed in the data? Should I withhold samples with missing values? Or should I replace them? If so, which values should they be replaced with?
Based on results of isnull.mean(), it is clear that 'ICD9 primary procedure code' has a non zero mean and it is so because it has NaN values. The NaN values corresponds to "No Procedure Performed" in the in the 'ICD9 primary procedure code' dictionary. Let's replace NaN values with a numeric code for "No Procedure Performed".
```
#Fill NaN with -1 for "No Procedure Performed"
procedue_na = -1
df_cms_claims_data['ICD9 primary procedure code'].fillna(procedue_na, inplace = True)
#convert procedure code from float to int64
df_cms_claims_data['ICD9 primary procedure code'] = df_cms_claims_data['ICD9 primary procedure code'].astype(np.int64)
#check count of null values to ensure dataframe is updated
display(df_cms_claims_data.isnull().mean())
```
### 4B. Categorical features <a name="catfeat"></a>
Munging categorical data is another essential process during data preprocessing. It is necessary to convert categorical features to a numerical representation.
#### a. Gender <a name="gender"></a>
Since gender is already binary and coded as 1 for Male and 2 for Female, no pre-processing is required.
```
def chart_balance(f_name, column_type):
if column_type == 'diagnosis':
data_dict = pd.read_csv(f_name, sep=', "', skiprows=1, names=['Base DRG code','Diagnosis related group']);
data_dict['Diagnosis related group'] = data_dict['Diagnosis related group'].map(lambda x: x.replace('"',''));
one, two, three = 'Base DRG code', 'Base DRG code', 'Base DRG code'
elif column_type == 'procedure':
data_dict = pd.read_csv(f_name, sep=', "', skiprows=1,
names=['ICD9 primary procedure code','International Classification of Diseases'])
data_dict = data_dict.applymap(lambda x: x.replace('"',''))
# replace -1 as code for 'No procedure performed'. In the dictionary the code is set as blank.
data_dict.iloc[0]['ICD9 primary procedure code'] = procedue_na
# convert procedure code from float to int64
data_dict['ICD9 primary procedure code'] = data_dict['ICD9 primary procedure code'].astype(np.int64)
one, two, three = 'ICD9 primary procedure code', 'ICD9 primary procedure code', 'ICD9 primary procedure code'
else:
# read dictionary csv file
data_dict = pd.read_csv(f_name)
data_dict.columns = data_dict.columns.to_series().apply(lambda x: x.strip())
if column_type == 'gender':
one = 'bene_sex_ident_cd'
two = 'Beneficiary gender code'
three = 'Beneficiary gender'
elif column_type == 'age':
one = 'BENE_AGE_CAT_CD'
two = 'Beneficiary Age category code'
three = 'Age Group'
elif column_type in ['procedure', 'diagnosis']:
plt.figure(figsize=(100,20))
plt.rc('xtick', labelsize=16)
display(data_dict.head())
display(data_dict.dtypes)
# join the beneficiary category code with group definition and describe the distribution amongst different groups in claims dataset
tmp_counts = data_dict.set_index(one).join( df_cms_claims_data[two].value_counts() )
tmp_counts['percentage'] = tmp_counts[two]/tmp_counts[two].sum()*100
# project gender distribution in the dataset on the bar graph
plt.bar(tmp_counts.index, tmp_counts['percentage'].tolist());
plt.xticks(tmp_counts.index, tmp_counts[three].tolist(), rotation=45)
plt.ylabel('Percentage claims')
if column_type in ['diagnosis', 'procedure']:
return data_dict
chart_balance("./data/Gender.csv", 'gender')
```
#### You may have observed a slight imbalance in claims distribution for male and female records in above bar graph.
Nothing concerning hear. But, we may use this information later in result analysis to justify our anomaly hypothesis.
#### b. Age Group <a name="age"></a>
```
chart_balance("./data/AgeGroup.csv", 'age')
```
#### You might have observed a slight imbalance in age group group distribution.
Nothing concerning in above distribution. Small imbalance is OK.
### 4B. NLP for Textual features <a name="nlp"></a>
All physician and hospital claims include one or more diagnosis codes. The ICD-9-CM diagnosis coding system is used since October, 2012.
Hospital inpatient claims also include one or more procedure codes that represent the services performed. The ICD-9-CM diagnosis coding system is used since October, 2012.
The codes are numeric number representing the phrases describing the diagnosis and the procedures itself. The code iteself is numberic but doesn't capture context of a word in a document, semantic and syntactic similarity, relation with other words, etc.
For diagnosis and procedure codes there is a option to consider it as categorical code and apply one hot encoding to it. That categorical data is defined as variables with a finite set of label values. We apply a technique called one hot encoding to do binarization of such values. In one hot encode we create one column for each label value and mark it as 0 or 1 as applicable to sample record. In case of dignosis code and procedure code it will give us a sparse matrix. Again, the code iteself will be numberic but doesn't capture context of a word in a document, semantic and syntactic similarity, relation with other words, etc.
Inorder to capture, capture context of a word in a document, semantic and syntactic similarity, relation with other words, etc. we use a technique called word embedding to convert every word in a phrase into a vector of floating point numbers. We then average the vector for each word in a phrase to derive vector for a phrase. We will use this approach for both diagnosis and procedure descriptions to extract features.
Word2Vec is a specific method to derieve word embeddings. It can be done using two methods (both involving Neural Networks): Skip Gram and Common Bag Of Words (CBOW)
CBOW Model: This method takes the context of each word as the input and tries to predict the word corresponding to the context.
Skip-Gram model: This method uses the target word (whose representation we want to generate) to predict the context and in the process, we produce the representations.
Both model have their own advantages and disadvantages. Skip Gram works well with small amount of data and is found to represent rare words well.
On the other hand, CBOW is faster and has better representations for more frequent words.
In our use case, we will use CBOW model to derieve wordtovec for pharases used to describe procedure and diagnosis code description.
#### a. Diagnosis Descriptions <a name="diagnosis"></a>
```
data_diagnosis = chart_balance('./data/DiagnosisRelatedGroupNames.csv', 'diagnosis')
```
#### b. Procedure Descriptions
```
data_procedures = chart_balance('./data/InternationalClassificationOfDiseasesNames.csv', 'procedure')
```
#### Observe the distribution of different diagnosis code in above bar graph printed from claims dataset.
Next, let's do text processing on diagnosis descriptions to make some of the acronyms more meaningful for word embeddings
```
# function to run pre processing on diagnosis descriptions
from nltk.tokenize import sent_tokenize, word_tokenize
def text_preprocessing(phrase):
phrase = phrase.lower()
phrase = phrase.replace('&', 'and')
#phrase = phrase.replace('non-', 'non') #This is to ensure non-critical, doesn't get handled as {'non', 'critical'}
phrase = phrase.replace(',','')
phrase = phrase.replace('w/o','without').replace(' w ',' with ').replace('/',' ')
phrase = phrase.replace(' maj ',' major ')
phrase = phrase.replace(' proc ', ' procedure ')
phrase = phrase.replace('o.r.', 'operating room')
sentence = phrase.split(' ')
return sentence
def get_embeddings(data_dict, column_type):
if column_type == 'procedure':
col = 'International Classification of Diseases'
elif column_type == 'diagnosis':
col = 'Diagnosis related group'
# perform tokenization
tmp_tokenized = data_dict[col].map(lambda x: text_preprocessing(x))
display(tmp_tokenized.head())
phrase_lengths = tmp_tokenized.map(lambda x: len(x)).value_counts().sort_index()
plt.bar(np.arange(1,1+len(phrase_lengths)), phrase_lengths)
plt.xlabel('Number of Tokens');
plt.ylabel('Phrases');
# traing wordtovec model on procedure description tokens
model_prc = Word2Vec(tmp_tokenized, min_count = 1, size = 72, window = 5, iter = 100)
print(model_prc)
words = list(model_prc.wv.vocab)
print(columnize.columnize(words, displaywidth=80, ljust=False))
return model_prc, words, tmp_tokenized
model_diagnosis, words_diagnosis, diagnosis_tokens = get_embeddings(data_diagnosis, 'diagnosis')
```
#### Word to vec hyperparameters explained
**size:** The size of the dense vector that is to represent each token or word. If you have very limited data, then size should be a much smaller value. If you have lots of data, its good to experiment with various sizes. A value of 100–150 has worked well for me for similarity lookups.
**window:** The maximum distance between the target word and its neighboring word. If your neighbor’s position is greater than the maximum window width to the left or the right, then some neighbors are not considered as being related to the target word. In theory, a smaller window should give you terms that are more related. If you have lots of data, then the window size should not matter too much, as long as its not overly narrow or overly broad. If you are not too sure about this, just use the default value.
**min_count:** Minimium frequency count of words. The model would ignore words that do not satisfy the min_count.Extremely infrequent words are usually unimportant, so its best to get rid of those. Unless your dataset is really tiny, this does not really affect the model.
**workers:** How many threads to use behind the scenes?
**iter:** How many epochs to train for? I typically use 10 or more for a small to medium dataset.
#### t-Distributed Stochastic Neighbor Embedding (t-SNE)
t-Distributed Stochastic Neighbor Embedding (t-SNE) is a non-linear technique for dimensionality reduction that is particularly well suited for the visualization of high-dimensional datasets.
```
# plot TSNE visualization
def tsne_plot(model):
"Creates and TSNE model and plots it"
labels = []
tokens = []
for word in model.wv.vocab:
tokens.append(model[word])
labels.append(word)
tsne_model = TSNE(perplexity=10, n_components=2, init='pca', n_iter=2500, random_state=10)
new_values = tsne_model.fit_transform(tokens)
x = []
y = []
for value in new_values:
x.append(value[0])
y.append(value[1])
plt.figure(figsize=(16, 16))
for i in range(len(x)):
plt.scatter(x[i],y[i])
plt.annotate(labels[i],
xy=(x[i], y[i]),
xytext=(5, 2),
textcoords='offset points',
ha='right',
va='bottom')
plt.show()
# plot t_SNE chart for diagnosis word to vector.
#2D visual plot of word embeddings derieved from diagnosis description.
tsne_plot(model_diagnosis)
# test most similiar for some word from model_drg.wv.keywords
model_diagnosis.most_similar('diagnosis')
# extract diagnosis words that starts with non
#display(tmp_diagnosis_tokenized.head())
series_diagnosis = pd.Series(words_diagnosis)
diagnosis_words_with_non = series_diagnosis[series_diagnosis.map(lambda x: 'non' in x)]
display(diagnosis_words_with_non)
# Check similarity between diagnosis words with opposite severity
for i in diagnosis_words_with_non:
a, not_a = i.replace('non-','').replace('non',''), i
if a in words_diagnosis:
print('Cosine similarity between', a, not_a, ':', model_diagnosis.wv.similarity(a, not_a))
print('')
```
#### b. Procedure Descriptions <a name="procedure"></a>
Apply the same process that we used for diagnosis description to procedure description to build a feature vector for procedure
```
model_procedure, words_procedure, tokens_procedure = get_embeddings(data_procedures, 'procedure')
# test most similiar for some word from model_prc.wv.keywords
model_procedure.most_similar('nonoperative')
# extract procedure words that starts with non
#display(tmp_procedure_tokenized.head())
series_procedure = pd.Series(words_procedure)
procedure_words_with_non = series_procedure[series_procedure.map(lambda x: 'non' in x)]
display(procedure_words_with_non)
# Check similarity between procedure words with opposite severity
for i in procedure_words_with_non:
a, not_a = i.replace('non-','').replace('non',''), i
if a in words_procedure:
print('Cosine similarity between', a, not_a, ':', model_procedure.wv.similarity(a, not_a))
print('')
def generate_features_from_embeddings(tokens, column_type, model):
if column_type == 'diagnosis':
one = 'Base DRG code'
two = 'DRG_VECTOR'
three = 'DRG_F'
elif column_type == 'procedure':
one = 'ICD9 primary procedure code'
two = 'PRC_VECTOR'
three = 'PRC_F'
values, index = [], []
# iterate through list of strings in each diagnosis phrase
for i, v in pd.Series(tokens).items():
#calculate mean of all word embeddings in each diagnosis phrase
values.append(model[v].mean(axis =0))
index.append(i)
tmp_phrase_vector = pd.DataFrame({one:index, two:values})
display(tmp_phrase_vector.head())
# expand tmp_diagnosis_phrase_vector into dataframe
# every scalar value in phrase vector will be considered a feature
features = tmp_phrase_vector[two].apply(pd.Series)
# rename each variable in diagnosis_features use DRG_F as prefix
features = features.rename(columns = lambda x : three + str(x + 1))
# view the diagnosis_features dataframe
display(features.head())
return features
# get diagnosis features
diagnosis_features = generate_features_from_embeddings(diagnosis_tokens, 'diagnosis', model_diagnosis)
# get procedure features
procedure_features = generate_features_from_embeddings(tokens_procedure, 'procedure', model_procedure)
#merge diagnosis word embeddings derived using word2vec in the base claims data as new features.
tmp_join_claim_diagnosis = pd.merge(df_cms_claims_data, diagnosis_features, how='inner', left_on = 'Base DRG code', right_index = True)
display(tmp_join_claim_diagnosis.head())
#merge procedure word embeddings derived using word2vec in the base claims data as new features.
tmp_join_claim_procedure = pd.merge(tmp_join_claim_diagnosis, procedure_features, how='inner', left_on = 'ICD9 primary procedure code', right_index = True)
display(tmp_join_claim_procedure.head())
#assign new feature set with procedure and diagnosis work embeddings to a new claims feature dataframe
#aggregate all the features extrcated so far to build a final claims feature set for training
claims_features = tmp_join_claim_procedure
```
## 5. Split train and test: train only on normal data <a name="split"></a>
We want to split our data into training and test sets. We want to ensure that in this random split we have samples that cover the distribution of payments. We perform a stratified shuffle split on the DRG quintile payment amount code, taking 30% of the data for testing and 70% for training.
```
from sklearn.model_selection import StratifiedShuffleSplit
X = claims_features.drop(['Encrypted PUF ID','ICD9 primary procedure code','Base DRG code'], axis=1)
strata = claims_features['DRG quintile payment amount code']
sss = StratifiedShuffleSplit(n_splits=1, test_size=0.3, random_state=0)
splits = sss.split(X, strata)
for train_index, test_index in splits:
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
display(X.head())
X.shape
```
## 5A. Standardize data based on training sample <a name="standardize"></a>
Because the PCA algorithm that we will use later for training maximizes the orthogonal variances of one's data, it is important to standardize the training data to have zero-mean and unit-variance prior to performing PCA. This way your PCA algorithm is idempotent to such rescalings, and prevent variables of large scale from dominating the PCA projection.
$$ \tilde{X} = \frac{X-\mu_x}{\sigma_z} $$
```
n_obs, n_features = X_train.shape
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_stndrd_train = scaler.transform(X_train)
X_stndrd_train = pd.DataFrame(X_stndrd_train, index=X_train.index, columns=X_train.columns)
```
### 5B. PCA <a name="pca"></a>
Principal Component Analysis (PCA) is an unsupervised method for taking a data set where features have multi-collinearity and creating a decorrelated data set, by finding the linear combination of vectors which maximize the data's variances in orthogonal dimensions.
#### PCA on Amazon SageMaker
The built-in PCA algorithm of SageMaker solves for the singular values, $s$, and for the Principal Components, $V$, of our data set. Here we'll perform SageMaker PCA on our standardized training dataset $\tilde{X}$, and then we'll use its outputs to project our correlated dataset into a decorrelated one.
$$ s, V = \rm{PCA}(\tilde{X})$$
```
# Convert data to binary stream.
matrx_train = X_stndrd_train.as_matrix().astype('float32')
import io
import sagemaker.amazon.common as smac
buf_train = io.BytesIO()
smac.write_numpy_to_dense_tensor(buf_train, matrx_train)
buf_train.seek(0)
```
Now we are ready to upload the file object to our Amazon S3 bucket. We specify two paths: one to where our uploaded matrix will reside, and one to where Amazon SageMaker will write the output. Amazon SageMaker will create folders within the paths that do not already exist.
```
%%time
key = 'healthcare_fraud_identification_feature_store'
boto3.resource('s3').Bucket(bucket).Object(os.path.join(prefix, 'train', key)).upload_fileobj(buf_train)
s3_train_data = 's3://{}/{}/train/{}'.format(bucket, prefix, key)
print('uploaded training data location: {}'.format(s3_train_data))
output_location = 's3://{}/{}/output/model'.format(bucket, prefix)
print('training artifacts will be uploaded to: {}'.format(output_location))
from sagemaker.amazon.amazon_estimator import get_image_uri
# select the algorithm container based on this notebook's current location
region_name = boto3.Session().region_name
container = get_image_uri(region_name, 'pca')
print('Using SageMaker PCA container: {} ({})'.format(container, region_name))
```
#### Start the Amazon Sagemaker Session and set training parameters for Estimator API
Instance type should be one of the following and number of instances can be greater than 1. Option to train on P instance type family to use GPUs for training
#### [ml.p2.xlarge, ml.m5.4xlarge, ml.m4.16xlarge, ml.p3.16xlarge, ml.m5.large, ml.p2.16xlarge, ml.c4.2xlarge, ml.c5.2xlarge, ml.c4.4xlarge, ml.c5.4xlarge, ml.c4.8xlarge, ml.c5.9xlarge, ml.c5.xlarge, ml.c4.xlarge, ml.c5.18xlarge, ml.p3.2xlarge, ml.m5.xlarge, ml.m4.10xlarge, ml.m5.12xlarge, ml.m4.xlarge, ml.m5.24xlarge, ml.m4.2xlarge, ml.p2.8xlarge, ml.m5.2xlarge, ml.p3.8xlarge, ml.m4.4xlarge]
```
num_obs, feature_dim = np.shape(matrx_train)
num_components = feature_dim-1
num_instances=2
instance_type = 'ml.c5.2xlarge'
algorithm_mode='regular'
platform='sagemaker'
start = time.time()
sess = sagemaker.Session()
pca = sagemaker.estimator.Estimator(container,
role,
train_instance_count=num_instances,
train_instance_type=instance_type,
output_path=output_location,
sagemaker_session=sess)
```
#### Specify the hyperparameters for your training job and start the training using Amazon SageMaker fit API call
Training will take approximately 4-5 minutes to complete.
```
pca.set_hyperparameters(feature_dim=feature_dim,
num_components=num_components,
subtract_mean=False,
algorithm_mode='regular',
mini_batch_size=200)
print('Start timestamp of launch: '+ str(start))
pca.fit({'train': s3_train_data})
stop = time.time()
total_time = stop-start
print('%2.2f minutes' %(total_time/60))
```
When the training job is complete, SageMaker writes the model artifact to the specified S3 output location. Let's download and unpack returned PCA model artifact.
```
job_name = pca.latest_training_job.name
os.system('aws s3 cp {}/{}/output/model.tar.gz ./'.format(output_location, job_name))
!tar xvzf model.tar.gz
pca_model = mx.ndarray.load('model_algo-1')
print('PCA model artifact:', pca_model.keys())
```
SageMaker PCA artifact contains $V$, the eigenvector principal components in *increasing* order of $s$, their singular values. A component's singular value is equal to the standard deviation that the component explains, i.e., the squared value of a singular component is equal to the variance that component explains. Therefore to calculate the proportion of variance of the data that each component explains, take the square of the singular value and divide it by the sum of all the singular values squared:
$$ \rm{component \,}i \% \rm{\,variance\, explained} = 100\cdot\frac{s_i^s}{\sum_{p=1}^P s_p^2} $$
First, we'll reverse this returned ordering, so that instead we have the components which explain the most variance come first, i.e., reorder the components in decreasing order of their singular values.
PCA can be further used to reduce the dimensionality of the problem. We have $P$ features and $P-1$ components, but we'll see in the plot below that many of the components don't contribute much to the explained variance of the data. We will keep only the $K$ leading components of $V$ which explain 95% of the variance in our data.
We will denote this reduced matrix as $V_K$.
```
singular_values = pca_model['s'].asnumpy()[::-1]
pc_reversedorder = pd.DataFrame(pca_model['v'].asnumpy())
pc = pc_reversedorder[list(pc_reversedorder.columns[::-1])]
eigenvalues = np.power(singular_values,2)
explained_var_pct = eigenvalues/np.sum(eigenvalues) *100
explained_var_cum = np.cumsum(explained_var_pct)
var_threshold = 95
n_components = np.min([np.where(explained_var_cum>=var_threshold)[0][0], n_features-1])
print('%i components explain %2.2f%% of the data\'s variance.' %(n_components+1, explained_var_cum[n_components]))
fig= plt.figure(figsize=[14,8])
width = 0.5
ax1 = fig.add_subplot(111)
ax1.bar(np.arange(0,len(singular_values)), singular_values, align='edge', color='darkgreen', label='Singular Values', alpha=0.5, width=width);
ax1.set_ylabel('Singular Values', fontsize=17);
ax1.set_xlabel('Principal Component', fontsize=17);
ax1.legend(loc='upper right', fontsize=14)
ax2 = ax1.twinx()
ax2.plot(np.arange(0,len(explained_var_cum)), explained_var_cum, color='black', label='Cumulative');
ax2.plot([0, n_components], [var_threshold, var_threshold], 'r:')
ax2.plot([n_components, n_components], [0, var_threshold], 'r:')
ax2.set_ylabel('% Variance Explained', fontsize=17);
ax2.legend(loc='right', fontsize=14)
ax2.set_ylim([0, 100])
ax2.set_xlim([0,len(eigenvalues)])
plt.title('Dimensionality Reduction', fontsize=20);
# We will now work with the reduced matrix that includes components that explains 95% of variance in the data
Vk = pc[pc.columns[:n_components+1]]
```
## 6. Calculate the Mahalanobis distance <a name="md"></a>
Above, we used the singular values returned by PCA to keep the $K$ principal component vectors that explain 95% of the data's variance, and stored them in dataframe $V_K$.
We use $V_K$ to tranform the data into an decorrelated dataset, by taking their matrix dot product:
$$ Z = \tilde{X} V_K $$
To detect anomaly data points, we want to measure how far a data point is from the distribution of the projected data. The farther a point lays from the distribution, the more anomalous it is.
Even though we have $K$ dimensions instead of $P$, this is still a multi-variate distribution. We will use the Mahalanobis distance [Mahalanobis, 1936](https://insa.nic.in/writereaddata/UpLoadedFiles/PINSA/Vol02_1936_1_Art05.pdf), which is a scalar measure of the multi-variate distance between a point $z$ and a distribution $D$. Distribution $D$ is defined by the mean and the inverse-covariance of the data in $Z$:
$$ \mu_Z = \rm{mean}(Z) $$
$$ \Sigma_Z = \rm{cov}(Z) $$
$$ \Sigma_Z^{-1} = \rm{inv}\big(\rm{cov}(Z)\big) $$
Mahalanobis distance is a measure of how many standard deviations away $z$ is from the mean of $D$ along each principal component axis.
We'll use the Mahalonobis distance of each point as its anomaly score. We take the top $\alpha$% of these points to consider as outliers, where $\alpha$ depends on how sensitive we want our detection to be. For this problem, we will take the top 1%, i.e. $\alpha=0.01$. Therefore we calculate the $(1-\alpha)$-quantile of Distribution $D$ as the threshold for considering a data point anomalous.
This method of PCA Anomaly Detection was developed in [A Novel Anomaly Detection Scheme Based on Principal Component Classifier](https://homepages.laas.fr/owe/METROSEC/DOC/FDM03.pdf).
```
# Z is the PCA-projected standardized data
pca_projected_X_train = pd.DataFrame(np.dot(X_stndrd_train, Vk), index=X_stndrd_train.index)
# Calculate Mahalanobis distance for multi-variate deviation
Zmean = pca_projected_X_train.mean()
covZ = pca_projected_X_train.cov()
invcovZ = inv(covZ)
M = pca_projected_X_train.apply(lambda x: sp.spatial.distance.mahalanobis(x, Zmean, invcovZ), axis=1)
# Threshold the training set's top alpha-%
alpha = 0.01
threshold = np.quantile(M, 1-alpha)
print(threshold)
# Plot the density graph for anomaly score and highlight the threshold calculated
plt.figure(figsize=[15,5]);
M.hist(bins=40, density=True);
plt.axvline(threshold, color='red', label='{}%-threshold = {}'.format(int(alpha*100), round(threshold,4)));
plt.legend();
plt.xlabel(r'Anomaly Score [based on Mahalanobis distance]', fontsize=14);
plt.ylabel('Density', fontsize=14);
```
## 7. Unsupervised Anomaly Detection <a name="ad"></a>
The above PCA-computed quantities - component matrix $V_K$, projected mean $\mu_Z$, inverse-covariance $\Sigma_Z^{-1}$, and threshold - have delivered us an unsupervised anomaly detection method.
We create a function below, which transforms the test data according the models fit on. the training data. The function **calcAnomalyScore**() performs the following:
* standardizes each test data point according to the training mean and training standard deviation
* projects each test data point using the PCs calculated from the training data
* measures the Mahalanobis distance of each test data point from the training distribution $D$
* a boolean if the test data point's anomaly score exceeds the threshold
```
def calcAnomalyScore(data, threshold, scaler=scaler, pc=Vk, Zmean=Zmean, invcovZ=invcovZ):
data_stndrd = pd.DataFrame(scaler.transform(data), index=data.index, columns=data.columns)
pc_projected_data = pd.DataFrame(np.dot(data_stndrd, Vk), index=data_stndrd.index)
anomaly_score = pc_projected_data.apply(lambda x: sp.spatial.distance.mahalanobis(x, Zmean, invcovZ), axis=1)
is_anomaly = (anomaly_score>threshold)
y = pd.concat([anomaly_score, is_anomaly], axis=1)
y.columns = ['anomaly_score','is_anomaly']
return y
y_test = calcAnomalyScore(X_test, threshold, scaler=scaler, pc=Vk, Zmean=Zmean, invcovZ=invcovZ)
print('Fraction of test data flagged as anomalous:', y_test['is_anomaly'].mean())
```
## 8. Understanding Anomaly<a name="understandinganomaly"></a>
Data points marked TRUE for "is_anomaly" can be passed on for inspection. Given that we now have separated norm data from anomalous data, we can contrast these to see if the differentiating reasons can be identified in the original feature space.
We attach the "is_anomaly" output as a label to the original claims feature data.
```
#list all claims with anomaly score and anomaly label(True)
y_test['anomalous'] = (y_test['is_anomaly']*1.).astype(int)
test_claims = claims_features.loc[y_test.index]
test_claims = y_test.merge(test_claims, how='outer', left_index=True, right_index=True)
test_claims = test_claims.filter(["anomalous","DRG quintile payment amount code","DRG quintile average payment amount","Inpatient days code","ICD9 primary procedure code","Base DRG code","Beneficiary Age category code","Beneficiary gender code"])
display(test_claims.head())
sns.pairplot(test_claims,hue ="anomalous", kind='scatter', plot_kws={'alpha':0.1})
```
#### In the above pair plot, look for following patterns
1. Plots where orange is asymmetrical with blue.
2. Orange appears in patches that doesn't overlap with the blue
The above patterns in the pairplot can be used a starting point to target investigation on specific cases.
## 9. Deploy PCA <a name="deployendpoint"></a>
This section is optional, but, in case, you are interested in learning how to do principal component analysis for a given claim record using Amazon SageMaker hosting. Follow the steps below.
You may find this step helpful if you want to use principal components of claims data to predict other variables of business significance. Example, find out length of stay based on diagnosis code, gender and age or predict the claims payment amount and quartile based on datapoints in the claims dataset.
Here we demonstrate how to deploy PCA model as an endpoint on Amazon Sagemaker for inference. But, to solve the example problems discussed in the above paragraph you will need to collect more data, label them and refactor your training based on the prediction problem.
```
#serialize test data to binary format for realtime inference for extracting principal components of claim features
X_stndrd_test = scaler.transform(X_test)
X_stndrd_test = pd.DataFrame(X_stndrd_test, index=X_test.index, columns=X_test.columns)
inference_input = X_stndrd_test.as_matrix().astype('float32')
buf = io.BytesIO()
smac.write_numpy_to_dense_tensor(buf, inference_input)
buf.seek(0)
#print the shape of inference_input matrix
inference_input.shape
```
#### Deploy the model using Amaazon SageMaker deploy API. AWS manages the highly avaliable and reliable infrastructure for it.
```
#deploy the Amazon Sagemaker PCA model trained above to create a hosted enpoint for realtime principal component extraction
pca_predictor = pca.deploy(initial_instance_count=1,
instance_type='ml.t2.medium')
from sagemaker.predictor import csv_serializer, json_deserializer
pca_predictor.content_type = 'text/csv'
pca_predictor.serializer = csv_serializer
pca_predictor.deserializer = json_deserializer
#run inference on first 500 claims. Avoid running it on large number of claims to avoid timeout on connection.
#For large dataset use Amazon Sagemaker batch inference
result = pca_predictor.predict(inference_input[0:500])
print(result)
#normalize above result in json format to more readable columar format with one principal component per column
from pandas.io.json import json_normalize
#result in json format and components are returned as a list under projections tag
result_normalized = json_normalize(result,'projections')
# expand df.tags into its own dataframe
pca_components = result_normalized['projection'].apply(pd.Series)
# rename each variable in pc
pca_components = pca_components.rename(columns = lambda x : 'PC_' + str(x))
#view the tags dataframe
pca_components
```
### Delete the Endpoint
If you're ready to be done with this notebook, please run the delete_endpoint line in the cell below. This will remove the hosted endpoint you created and avoid any charges from a stray instance being left turned on.
```
import sagemaker
sagemaker.Session().delete_endpoint(pca_predictor.endpoint)
```
| true |
code
| 0.465205 | null | null | null | null |
|
A very wide range of physical processes lead to wave motion, where
signals are propagated through a medium in space and time, normally
with little or no permanent movement of the medium itself.
The shape of the signals may undergo changes as they travel through
matter, but usually not so much that the signals cannot be recognized
at some later point in space and time.
Many types of wave motion can be described by the equation
$u_{tt}=\nabla\cdot (c^2\nabla u) + f$, which we will solve
in the forthcoming text by finite difference methods.
# Simulation of waves on a string
<div id="wave:string"></div>
We begin our study of wave equations by simulating one-dimensional
waves on a string, say on a guitar or violin.
Let the string in the undeformed state
coincide with the interval
$[0,L]$ on the $x$ axis, and let $u(x,t)$ be the displacement at
time $t$ in the $y$ direction of a point initially at $x$.
The displacement function $u$ is governed by the mathematical model
<!-- Equation labels as ordinary links -->
<div id="wave:pde1"></div>
$$
\begin{equation}
\frac{\partial^2 u}{\partial t^2} =
c^2 \frac{\partial^2 u}{\partial x^2}, \quad x\in (0,L),\ t\in (0,T]
\label{wave:pde1} \tag{1}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:ic:u"></div>
$$
\begin{equation}
u(x,0) = I(x), \quad x\in [0,L]
\label{wave:pde1:ic:u} \tag{2}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:ic:ut"></div>
$$
\begin{equation}
\frac{\partial}{\partial t}u(x,0) = 0, \quad x\in [0,L]
\label{wave:pde1:ic:ut} \tag{3}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:bc:0"></div>
$$
\begin{equation}
u(0,t) = 0, \quad t\in (0,T]
\label{wave:pde1:bc:0} \tag{4}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:bc:L"></div>
$$
\begin{equation}
u(L,t) = 0, \quad t\in (0,T]
\label{wave:pde1:bc:L} \tag{5}
\end{equation}
$$
The constant $c$ and the function $I(x)$ must be prescribed.
Equation ([1](#wave:pde1)) is known as the one-dimensional
*wave equation*. Since this PDE contains a second-order derivative
in time, we need *two initial conditions*. The condition
([2](#wave:pde1:ic:u)) specifies
the initial shape of the string, $I(x)$, and
([3](#wave:pde1:ic:ut)) expresses that the initial velocity of the
string is zero. In addition, PDEs need *boundary conditions*, given here as
([4](#wave:pde1:bc:0)) and ([5](#wave:pde1:bc:L)). These two
conditions specify that
the string is fixed at the ends, i.e., that the displacement $u$ is zero.
The solution $u(x,t)$ varies in space and time and describes waves that
move with velocity $c$ to the left and right.
Sometimes we will use a more compact notation for the partial derivatives
to save space:
<!-- Equation labels as ordinary links -->
<div id="_auto1"></div>
$$
\begin{equation}
u_t = \frac{\partial u}{\partial t}, \quad
u_{tt} = \frac{\partial^2 u}{\partial t^2},
\label{_auto1} \tag{6}
\end{equation}
$$
and similar expressions
for derivatives with respect to other variables. Then the
wave equation can be written compactly as $u_{tt} = c^2u_{xx}$.
The PDE problem ([1](#wave:pde1))-([5](#wave:pde1:bc:L)) will now be
discretized in space and time by a finite difference method.
## Discretizing the domain
<div id="wave:string:mesh"></div>
The temporal domain $[0,T]$ is represented by a finite number of mesh points
<!-- Equation labels as ordinary links -->
<div id="_auto2"></div>
$$
\begin{equation}
0 = t_0 < t_1 < t_2 < \cdots < t_{N_t-1} < t_{N_t} = T \label{_auto2} \tag{7}
\end{equation}
$$
Similarly, the spatial domain $[0,L]$ is replaced by a set of mesh points
<!-- Equation labels as ordinary links -->
<div id="_auto3"></div>
$$
\begin{equation}
0 = x_0 < x_1 < x_2 < \cdots < x_{N_x-1} < x_{N_x} = L \label{_auto3} \tag{8}
\end{equation}
$$
One may view the mesh as two-dimensional in the $x,t$ plane, consisting
of points $(x_i, t_n)$, with $i=0,\ldots,N_x$ and $n=0,\ldots,N_t$.
### Uniform meshes
For uniformly distributed mesh points we can introduce the constant
mesh spacings $\Delta t$ and $\Delta x$. We have that
<!-- Equation labels as ordinary links -->
<div id="_auto4"></div>
$$
\begin{equation}
x_i = i\Delta x,\ i=0,\ldots,N_x,\quad
t_n = n\Delta t,\ n=0,\ldots,N_t
\label{_auto4} \tag{9}
\end{equation}
$$
We also have that $\Delta x = x_i-x_{i-1}$, $i=1,\ldots,N_x$, and
$\Delta t = t_n - t_{n-1}$, $n=1,\ldots,N_t$. [Figure](#wave:pde1:fig:mesh)
displays a mesh in the $x,t$ plane with $N_t=5$, $N_x=5$, and constant
mesh spacings.
## The discrete solution
<div id="wave:string:numerical:sol"></div>
The solution $u(x,t)$ is sought at the mesh points. We introduce
the mesh function $u_i^n$, which approximates the exact
solution at the
mesh point $(x_i,t_n)$ for $i=0,\ldots,N_x$ and $n=0,\ldots,N_t$.
Using the finite difference method, we shall
develop algebraic equations for computing the mesh function.
## Fulfilling the equation at the mesh points
<div id="wave:string:samplingPDE"></div>
In the finite difference method, we relax
the condition that ([1](#wave:pde1)) holds at all points in
the space-time domain $(0,L)\times (0,T]$ to the requirement that the PDE is
fulfilled at the *interior* mesh points only:
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:step2"></div>
$$
\begin{equation}
\frac{\partial^2}{\partial t^2} u(x_i, t_n) =
c^2\frac{\partial^2}{\partial x^2} u(x_i, t_n),
\label{wave:pde1:step2} \tag{10}
\end{equation}
$$
for $i=1,\ldots,N_x-1$ and $n=1,\ldots,N_t-1$. For $n=0$ we have
the initial conditions $u=I(x)$ and $u_t=0$,
and at the boundaries $i=0,N_x$ we
have the boundary condition $u=0$.
## Replacing derivatives by finite differences
<div id="wave:string:fd"></div>
The second-order derivatives can be replaced by central
differences. The most widely used difference approximation of
the second-order derivative is
$$
\frac{\partial^2}{\partial t^2}u(x_i,t_n)\approx
\frac{u_i^{n+1} - 2u_i^n + u^{n-1}_i}{\Delta t^2}\
$$
mathcal{I}_t is convenient to introduce the finite difference operator notation
$$
[D_tD_t u]^n_i = \frac{u_i^{n+1} - 2u_i^n + u^{n-1}_i}{\Delta t^2}
$$
A similar approximation of the second-order derivative in the $x$
direction reads
$$
\frac{\partial^2}{\partial x^2}u(x_i,t_n)\approx
\frac{u_{i+1}^{n} - 2u_i^n + u^{n}_{i-1}}{\Delta x^2} = [D_xD_x u]^n_i
$$
### Algebraic version of the PDE
We can now replace the derivatives in ([10](#wave:pde1:step2))
and get
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:step3b"></div>
$$
\begin{equation}
\frac{u_i^{n+1} - 2u_i^n + u^{n-1}_i}{\Delta t^2} =
c^2\frac{u_{i+1}^{n} - 2u_i^n + u^{n}_{i-1}}{\Delta x^2},
\label{wave:pde1:step3b} \tag{11}
\end{equation}
$$
or written more compactly using the operator notation:
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:step3a"></div>
$$
\begin{equation}
[D_tD_t u = c^2 D_xD_x]^{n}_i
\label{wave:pde1:step3a} \tag{12}
\end{equation}
$$
### Interpretation of the equation as a stencil
A characteristic feature of ([11](#wave:pde1:step3b)) is that it
involves $u$ values from neighboring points only: $u_i^{n+1}$,
$u^n_{i\pm 1}$, $u^n_i$, and $u^{n-1}_i$. The circles in [Figure](#wave:pde1:fig:mesh) illustrate such neighboring mesh points that
contribute to an algebraic equation. In this particular case, we have
sampled the PDE at the point $(2,2)$ and constructed
([11](#wave:pde1:step3b)), which then involves a coupling of $u_1^2$,
$u_2^3$, $u_2^2$, $u_2^1$, and $u_3^2$. The term *stencil* is often
used about the algebraic equation at a mesh point, and the geometry of
a typical stencil is illustrated in [Figure](#wave:pde1:fig:mesh). One also often refers to the algebraic
equations as *discrete equations*, *(finite) difference equations* or
a *finite difference scheme*.
<!-- dom:FIGURE: [mov-wave/D_stencil_gpl/stencil_n_interior.png, width=500] Mesh in space and time. The circles show points connected in a finite difference equation. <div id="wave:pde1:fig:mesh"></div> -->
<!-- begin figure -->
<div id="wave:pde1:fig:mesh"></div>
<p>Mesh in space and time. The circles show points connected in a finite difference equation.</p>
<img src="mov-wave/D_stencil_gpl/stencil_n_interior.png" width=500>
<!-- end figure -->
### Algebraic version of the initial conditions
We also need to replace the derivative in the initial condition
([3](#wave:pde1:ic:ut)) by a finite difference approximation.
A centered difference of the type
$$
\frac{\partial}{\partial t} u(x_i,t_0)\approx
\frac{u^1_i - u^{-1}_i}{2\Delta t} = [D_{2t} u]^0_i,
$$
seems appropriate. Writing out this equation and ordering the terms give
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:step3c"></div>
$$
\begin{equation}
u^{-1}_i=u^{1}_i,\quad i=0,\ldots,N_x
\label{wave:pde1:step3c} \tag{13}
\end{equation}
$$
The other initial condition can be computed by
$$
u_i^0 = I(x_i),\quad i=0,\ldots,N_x
$$
## Formulating a recursive algorithm
<div id="wave:string:alg"></div>
We assume that $u^n_i$ and $u^{n-1}_i$ are available for
$i=0,\ldots,N_x$. The only unknown quantity in
([11](#wave:pde1:step3b)) is therefore $u^{n+1}_i$, which we now can
solve for:
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:step4"></div>
$$
\begin{equation}
u^{n+1}_i = -u^{n-1}_i + 2u^n_i + C^2
\left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right)
\label{wave:pde1:step4} \tag{14}
\end{equation}
$$
We have here introduced the parameter
<!-- Equation labels as ordinary links -->
<div id="_auto5"></div>
$$
\begin{equation}
C = c\frac{\Delta t}{\Delta x},
\label{_auto5} \tag{15}
\end{equation}
$$
known as the *Courant number*.
**$C$ is the key parameter in the discrete wave equation.**
We see that the discrete version of the PDE features only one
parameter, $C$, which is therefore the key parameter, together with
$N_x$, that governs the quality of the numerical solution (see the section [Analysis of the difference equations](wave_analysis.ipynb) for details). Both the primary physical
parameter $c$ and the numerical parameters $\Delta x$ and $\Delta t$
are lumped together in $C$. Note that $C$ is a dimensionless
parameter.
Given that $u^{n-1}_i$ and $u^n_i$ are known for $i=0,\ldots,N_x$,
we find new values at the next time level by applying the formula
([14](#wave:pde1:step4)) for $i=1,\ldots,N_x-1$. [Figure](#wave:pde1:fig:mesh) illustrates the points that are used to
compute $u^3_2$. For the boundary points, $i=0$ and $i=N_x$, we apply
the boundary conditions $u_i^{n+1}=0$.
Even though sound reasoning leads up to
([14](#wave:pde1:step4)), there is still a minor challenge with it that needs
to be resolved. Think of the very first computational step to be made.
The scheme ([14](#wave:pde1:step4)) is supposed to start at $n=1$, which means
that we compute $u^2$ from $u^1$ and $u^0$. Unfortunately, we do not know the
value of $u^1$, so how to proceed? A standard procedure in such cases is to
apply ([14](#wave:pde1:step4)) also for $n=0$. This immediately seems strange,
since it involves $u^{-1}_i$, which is an undefined
quantity outside the time mesh (and the time domain). However, we can
use the initial condition ([13](#wave:pde1:step3c)) in combination with
([14](#wave:pde1:step4)) when $n=0$ to eliminate $u^{-1}_i$ and
arrive at a special formula for $u_i^1$:
<!-- Equation labels as ordinary links -->
<div id="wave:pde1:step4:1"></div>
$$
\begin{equation}
u_i^1 = u^0_i - \frac{1}{2}
C^2\left(u^{0}_{i+1}-2u^{0}_{i} + u^{0}_{i-1}\right)
\label{wave:pde1:step4:1} \tag{16}
\end{equation}
$$
[Figure](#wave:pde1:fig:stencil:u1) illustrates how ([16](#wave:pde1:step4:1))
connects four instead of five points: $u^1_2$, $u_1^0$, $u_2^0$, and $u_3^0$.
<!-- dom:FIGURE: [mov-wave/D_stencil_gpl/stencil_n0_interior.png, width=500] Modified stencil for the first time step. <div id="wave:pde1:fig:stencil:u1"></div> -->
<!-- begin figure -->
<div id="wave:pde1:fig:stencil:u1"></div>
<p>Modified stencil for the first time step.</p>
<img src="mov-wave/D_stencil_gpl/stencil_n0_interior.png" width=500>
<!-- end figure -->
We can now summarize the computational algorithm:
1. Compute $u^0_i=I(x_i)$ for $i=0,\ldots,N_x$
2. Compute $u^1_i$ by ([16](#wave:pde1:step4:1)) for $i=1,2,\ldots,N_x-1$ and set $u_i^1=0$
for the boundary points given by $i=0$ and $i=N_x$,
3. For each time level $n=1,2,\ldots,N_t-1$
a. apply ([14](#wave:pde1:step4)) to find $u^{n+1}_i$ for $i=1,\ldots,N_x-1$
b. set $u^{n+1}_i=0$ for the boundary points having $i=0$, $i=N_x$.
The algorithm essentially consists of moving a finite difference
stencil through all the mesh points, which can be seen as an animation
in a [web page](mov-wave/D_stencil_gpl/index.html)
or a [movie file](mov-wave/D_stencil_gpl/movie.ogg).
## Sketch of an implementation
<div id="wave:string:impl"></div>
We start by defining some constants that will be used throughout our Devito code.
```
import numpy as np
# Given mesh points as arrays x and t (x[i], t[n]),
# constant c and function I for initial condition
x = np.linspace(0, 2, 101)
t = np.linspace(0, 2, 101)
c = 1
I = lambda x: np.sin(x)
dx = x[1] - x[0]
dt = t[1] - t[0]
C = c*dt/dx # Courant number
Nx = len(x)-1
Nt = len(t)-1
C2 = C**2 # Help variable in the scheme
L = 2.
```
Next, we define our 1D computational grid and create a function `u` as a symbolic `devito.TimeFunction`. We need to specify the `space_order` as 2 since our wave equation involves second-order derivatives with respect to $x$. Similarly, we specify the `time_order` as 2, as our equation involves second-order derivatives with respect to $t$. Setting these parameters allows us to use `u.dx2` and `u.dt2`.
```
from devito import Grid, TimeFunction
# Initialise `u` for space and time order 2, using initialisation function I
grid = Grid(shape=(Nx+1), extent=(L))
u = TimeFunction(name='u', grid=grid, time_order=2, space_order=2)
u.data[:,:] = I(x[:])
```
Now that we have initialised `u`, we can solve our wave equation for the unknown quantity $u^{n+1}_i$ using forward and backward differences in space and time.
```
from devito import Constant, Eq, solve
# Set up wave equation and solve for forward stencil point in time
pde = (1/c**2)*u.dt2-u.dx2
stencil = Eq(u.forward, solve(pde, u.forward))
print("LHS: %s" % stencil.lhs)
print("RHS: %s" % stencil.rhs)
```
Great! From these print statements, we can see that Devito has taken the wave equation in ([1](#wave:pde1)) and solved it for $u^{n+1}_i$, giving us equation ([14](#wave:pde1:step4)). Note that `dx` is denoted as `h_x`, while `u(t, x)`, `u(t, x - h_x)` and `u(t, x + h_x)` denote the equivalent of $u^{n}_{i}$, $u^{n}_{i-1}$ and $u^{n}_{i+1}$ respectively.
We also need to create a separate stencil for the first timestep, where we substitute $u^{1}_i$ for $u^{-1}_i$, as given in ([13](#wave:pde1:step3c)).
```
stencil_init = stencil.subs(u.backward, u.forward)
```
Now we can create expressions for our boundary conditions and build the operator. The results are plotted below.
```
#NBVAL_IGNORE_OUTPUT
from devito import Operator
t_s = grid.stepping_dim
# Boundary conditions
bc = [Eq(u[t_s+1, 0], 0)]
bc += [Eq(u[t_s+1, Nx], 0)]
# Defining one Operator for initial timestep and one for the rest
op_init = Operator([stencil_init]+bc)
op = Operator([stencil]+bc)
op_init.apply(time_M=1, dt=dt)
op.apply(time_m=1,time_M=Nt, dt=dt)
```
We can plot our results using `matplotlib`:
```
import matplotlib.pyplot as plt
plt.plot(x, u.data[-1])
plt.xlabel('x')
plt.ylabel('u')
plt.show()
```
# Verification
Before implementing the algorithm, it is convenient to add a source
term to the PDE ([1](#wave:pde1)), since that gives us more freedom in
finding test problems for verification. Physically, a source term acts
as a generator for waves in the interior of the domain.
## A slightly generalized model problem
<div id="wave:pde2:fd"></div>
We now address the following extended initial-boundary value problem
for one-dimensional wave phenomena:
<!-- Equation labels as ordinary links -->
<div id="wave:pde2"></div>
$$
\begin{equation}
u_{tt} = c^2 u_{xx} + f(x,t), \quad x\in (0,L),\ t\in (0,T]
\label{wave:pde2} \tag{17}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:ic:u"></div>
$$
\begin{equation}
u(x,0) = I(x), \quad x\in [0,L]
\label{wave:pde2:ic:u} \tag{18}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:ic:ut"></div>
$$
\begin{equation}
u_t(x,0) = V(x), \quad x\in [0,L]
\label{wave:pde2:ic:ut} \tag{19}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:bc:0"></div>
$$
\begin{equation}
u(0,t) = 0, \quad t>0
\label{wave:pde2:bc:0} \tag{20}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:bc:L"></div>
$$
\begin{equation}
u(L,t) = 0, \quad t>0
\label{wave:pde2:bc:L} \tag{21}
\end{equation}
$$
Sampling the PDE at $(x_i,t_n)$ and using the same finite difference
approximations as above, yields
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:fdop"></div>
$$
\begin{equation}
[D_tD_t u = c^2 D_xD_x u + f]^{n}_i
\label{wave:pde2:fdop} \tag{22}
\end{equation}
$$
Writing this out and solving for the unknown $u^{n+1}_i$ results in
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:step3b"></div>
$$
\begin{equation}
u^{n+1}_i = -u^{n-1}_i + 2u^n_i + C^2
(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}) + \Delta t^2 f^n_i
\label{wave:pde2:step3b} \tag{23}
\end{equation}
$$
The equation for the first time step must be rederived. The discretization
of the initial condition $u_t = V(x)$ at $t=0$
becomes
$$
[D_{2t}u = V]^0_i\quad\Rightarrow\quad u^{-1}_i = u^{1}_i - 2\Delta t V_i,
$$
which, when inserted in ([23](#wave:pde2:step3b)) for $n=0$, gives
the special formula
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:step3c"></div>
$$
\begin{equation}
u^{1}_i = u^0_i + \Delta t V_i + {\frac{1}{2}}
C^2
\left(u^{0}_{i+1}-2u^{0}_{i} + u^{0}_{i-1}\right) + \frac{1}{2}\Delta t^2 f^0_i
\label{wave:pde2:step3c} \tag{24}
\end{equation}
$$
## Using an analytical solution of physical significance
<div id="wave:pde2:fd:standing:waves"></div>
Many wave problems feature sinusoidal oscillations in time
and space. For example, the original PDE problem
([1](#wave:pde1))-([5](#wave:pde1:bc:L)) allows an exact solution
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:test:ue"></div>
$$
\begin{equation}
u_e(x,t) = A\sin\left(\frac{\pi}{L}x\right)
\cos\left(\frac{\pi}{L}ct\right)
\label{wave:pde2:test:ue} \tag{25}
\end{equation}
$$
This $u_e$ fulfills the PDE with $f=0$, boundary conditions
$u_e(0,t)=u_e(L,t)=0$, as well as initial
conditions $I(x)=A\sin\left(\frac{\pi}{L}x\right)$ and $V=0$.
**How to use exact solutions for verification.**
It is common to use such exact solutions of physical interest
to verify implementations. However, the numerical
solution $u^n_i$ will only be an approximation to $u_e(x_i,t_n)$.
We have no knowledge of the precise size of the error in
this approximation, and therefore we can never know if discrepancies
between $u^n_i$ and $u_e(x_i,t_n)$ are caused
by mathematical approximations or programming errors.
In particular, if plots of the computed solution $u^n_i$ and
the exact one ([25](#wave:pde2:test:ue)) look similar, many
are tempted to claim that the implementation works. However,
even if color plots look nice and the accuracy is "deemed good",
there can still be serious programming errors present!
The only way to use exact physical solutions like
([25](#wave:pde2:test:ue)) for serious and thorough verification is to
run a series of simulations on finer and finer meshes, measure the
integrated error in each mesh, and from this information estimate the
empirical convergence rate of the method.
An introduction to the computing of convergence rates is given in Section 3.1.6
in [[Langtangen_decay]](#Langtangen_decay).
There is also a detailed example on computing convergence rates in
the [verification section](../01_vib/vib_undamped.ipynb#vib:ode1:verify) of the Vibration ODEs chapter.
In the present problem, one expects the method to have a convergence rate
of 2 (see the section [Analysis of the difference equations](wave_analysis.ipynb)), so if the computed rates
are close to 2 on a sufficiently fine mesh, we have good evidence that
the implementation is free of programming mistakes.
## Manufactured solution and estimation of convergence rates
<div id="wave:pde2:fd:MMS"></div>
### Specifying the solution and computing corresponding data
One problem with the exact solution ([25](#wave:pde2:test:ue)) is
that it requires a simplification (${V}=0, f=0$) of the implemented problem
([17](#wave:pde2))-([21](#wave:pde2:bc:L)). An advantage of using
a *manufactured solution* is that we can test all terms in the
PDE problem. The idea of this approach is to set up some chosen
solution and fit the source term, boundary conditions, and initial
conditions to be compatible with the chosen solution.
Given that our boundary conditions in the implementation are
$u(0,t)=u(L,t)=0$, we must choose a solution that fulfills these
conditions. One example is
$$
u_e(x,t) = x(L-x)\sin t
$$
Inserted in the PDE $u_{tt}=c^2u_{xx}+f$ we get
$$
-x(L-x)\sin t = -c^2 2\sin t + f\quad\Rightarrow f = (2c^2 - x(L-x))\sin t
$$
The initial conditions become
$$
\begin{align*}
u(x,0) =& I(x) = 0,\\
u_t(x,0) &= V(x) = x(L-x)
\end{align*}
$$
### Defining a single discretization parameter
To verify the code, we compute the convergence rates in a series of
simulations, letting each simulation use a finer mesh than the
previous one. Such empirical estimation of convergence rates relies on
an assumption that some measure $E$ of the numerical error is related
to the discretization parameters through
$$
E = C_t\Delta t^r + C_x\Delta x^p,
$$
where $C_t$, $C_x$, $r$, and $p$ are constants. The constants $r$ and
$p$ are known as the *convergence rates* in time and space,
respectively. From the accuracy in the finite difference
approximations, we expect $r=p=2$, since the error terms are of order
$\Delta t^2$ and $\Delta x^2$. This is confirmed by truncation error
analysis and other types of analysis.
By using an exact solution of the PDE problem, we will next compute
the error measure $E$ on a sequence of refined meshes and see if
the rates $r=p=2$ are obtained. We will not be concerned with estimating
the constants $C_t$ and $C_x$, simply because we are not interested in
their values.
mathcal{I}_t is advantageous to introduce a single discretization parameter
$h=\Delta t=\hat c \Delta x$ for some constant $\hat c$. Since
$\Delta t$ and $\Delta x$ are related through the Courant number,
$\Delta t = C\Delta x/c$, we set $h=\Delta t$, and then $\Delta x =
hc/C$. Now the expression for the error measure is greatly
simplified:
$$
E = C_t\Delta t^r + C_x\Delta x^r =
C_t h^r + C_x\left(\frac{c}{C}\right)^r h^r
= Dh^r,\quad D = C_t+C_x\left(\frac{c}{C}\right)^r
$$
### Computing errors
We choose an initial discretization parameter $h_0$ and run
experiments with decreasing $h$: $h_i=2^{-i}h_0$, $i=1,2,\ldots,m$.
Halving $h$ in each experiment is not necessary, but it is a common
choice. For each experiment we must record $E$ and $h$. Standard
choices of error measure are the $\ell^2$ and $\ell^\infty$ norms of the
error mesh function $e^n_i$:
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:fd:MMS:E:l2"></div>
$$
\begin{equation}
E = ||e^n_i||_{\ell^2} = \left( \Delta t\Delta x
\sum_{n=0}^{N_t}\sum_{i=0}^{N_x}
(e^n_i)^2\right)^{\frac{1}{2}},\quad e^n_i = u_e(x_i,t_n)-u^n_i,
\label{wave:pde2:fd:MMS:E:l2} \tag{26}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:fd:MMS:E:linf"></div>
$$
\begin{equation}
E = ||e^n_i||_{\ell^\infty} = \max_{i,n} |e^n_i|
\label{wave:pde2:fd:MMS:E:linf} \tag{27}
\end{equation}
$$
In Python, one can compute $\sum_{i}(e^{n}_i)^2$ at each time step
and accumulate the value in some sum variable, say `e2_sum`. At the
final time step one can do `sqrt(dt*dx*e2_sum)`. For the
$\ell^\infty$ norm one must compare the maximum error at a time level
(`e.max()`) with the global maximum over the time domain: `e_max = max(e_max, e.max())`.
An alternative error measure is to use a spatial norm at one time step
only, e.g., the end time $T$ ($n=N_t$):
<!-- Equation labels as ordinary links -->
<div id="_auto6"></div>
$$
\begin{equation}
E = ||e^n_i||_{\ell^2} = \left( \Delta x\sum_{i=0}^{N_x}
(e^n_i)^2\right)^{\frac{1}{2}},\quad e^n_i = u_e(x_i,t_n)-u^n_i,
\label{_auto6} \tag{28}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="_auto7"></div>
$$
\begin{equation}
E = ||e^n_i||_{\ell^\infty} = \max_{0\leq i\leq N_x} |e^{n}_i|
\label{_auto7} \tag{29}
\end{equation}
$$
The important point is that the error measure ($E$) for the simulation is represented by a single number.
### Computing rates
Let $E_i$ be the error measure in experiment (mesh) number $i$
(not to be confused with the spatial index $i$) and
let $h_i$ be the corresponding discretization parameter ($h$).
With the error model $E_i = Dh_i^r$, we can
estimate $r$ by comparing two consecutive
experiments:
$$
\begin{align*}
E_{i+1}& =D h_{i+1}^{r},\\
E_{i}& =D h_{i}^{r}
\end{align*}
$$
Dividing the two equations eliminates the (uninteresting) constant $D$.
Thereafter, solving for $r$ yields
$$
r = \frac{\ln E_{i+1}/E_{i}}{\ln h_{i+1}/h_{i}}
$$
Since $r$ depends on $i$, i.e., which simulations we compare,
we add an index to $r$: $r_i$, where $i=0,\ldots,m-2$, if we
have $m$ experiments: $(h_0,E_0),\ldots,(h_{m-1}, E_{m-1})$.
In our present discretization of the wave equation we expect $r=2$, and
hence the $r_i$ values should converge to 2 as $i$ increases.
## Constructing an exact solution of the discrete equations
<div id="wave:pde2:fd:verify:quadratic"></div>
With a manufactured or known analytical solution, as outlined above,
we can estimate convergence rates and see if they have the correct
asymptotic behavior. Experience shows that this is a quite good
verification technique in that many common bugs will destroy the
convergence rates. A significantly better test though,
would be to check that the
numerical solution is exactly what it should be. This will in general
require exact knowledge of the numerical error, which we do not normally have
(although we in the section [Analysis of the difference equations](wave_analysis.ipynb) establish such knowledge
in simple cases).
However, it is possible to look for solutions where we can show that
the numerical error vanishes, i.e., the solution of the original continuous
PDE problem is
also a solution of the discrete equations. This property often arises
if the exact solution of the PDE
is a lower-order polynomial. (Truncation error
analysis leads to error measures that involve derivatives of the
exact solution. In the present problem, the truncation error involves
4th-order derivatives of $u$ in space and time. Choosing $u$
as a polynomial of degree three or less
will therefore lead to vanishing error.)
We shall now illustrate the construction of an exact solution to both the
PDE itself and the discrete equations.
Our chosen manufactured solution is quadratic in space
and linear in time. More specifically, we set
<!-- Equation labels as ordinary links -->
<div id="wave:pde2:fd:verify:quadratic:uex"></div>
$$
\begin{equation}
u_e (x,t) = x(L-x)(1+{\frac{1}{2}}t),
\label{wave:pde2:fd:verify:quadratic:uex} \tag{30}
\end{equation}
$$
which by insertion in the PDE leads to $f(x,t)=2(1+t)c^2$. This $u_e$
fulfills the boundary conditions $u=0$ and demands $I(x)=x(L-x)$
and $V(x)={\frac{1}{2}}x(L-x)$.
To realize that the chosen $u_e$ is also an exact
solution of the discrete equations,
we first remind ourselves that $t_n=n\Delta t$ so that
<!-- Equation labels as ordinary links -->
<div id="_auto8"></div>
$$
\begin{equation}
\lbrack D_tD_t t^2\rbrack^n = \frac{t_{n+1}^2 - 2t_n^2 + t_{n-1}^2}{\Delta t^2}
= (n+1)^2 -2n^2 + (n-1)^2 = 2,
\label{_auto8} \tag{31}
\end{equation}
$$
<!-- Equation labels as ordinary links -->
<div id="_auto9"></div>
$$
\begin{equation}
\lbrack D_tD_t t\rbrack^n = \frac{t_{n+1} - 2t_n + t_{n-1}}{\Delta t^2}
= \frac{((n+1) -2n + (n-1))\Delta t}{\Delta t^2} = 0
\label{_auto9} \tag{32}
\end{equation}
$$
Hence,
$$
[D_tD_t u_e]^n_i = x_i(L-x_i)[D_tD_t (1+{\frac{1}{2}}t)]^n =
x_i(L-x_i){\frac{1}{2}}[D_tD_t t]^n = 0
$$
Similarly, we get that
$$
\begin{align*}
\lbrack D_xD_x u_e\rbrack^n_i &=
(1+{\frac{1}{2}}t_n)\lbrack D_xD_x (xL-x^2)\rbrack_i\\
& =
(1+{\frac{1}{2}}t_n)\lbrack LD_xD_x x - D_xD_x x^2\rbrack_i \\
&= -2(1+{\frac{1}{2}}t_n)
\end{align*}
$$
Now, $f^n_i = 2(1+{\frac{1}{2}}t_n)c^2$, which results in
$$
[D_tD_t u_e - c^2D_xD_xu_e - f]^n_i = 0 +
c^2 2(1 + {\frac{1}{2}}t_{n}) +
2(1+{\frac{1}{2}}t_n)c^2 = 0
$$
Moreover, $u_e(x_i,0)=I(x_i)$,
$\partial u_e/\partial t = V(x_i)$ at $t=0$, and
$u_e(x_0,t)=u_e(x_{N_x},0)=0$. Also the modified scheme for the
first time step is fulfilled by $u_e(x_i,t_n)$.
Therefore, the exact solution $u_e(x,t)=x(L-x)(1+t/2)$ of the PDE
problem is also an exact solution of the discrete problem. This means
that we know beforehand what numbers the numerical algorithm should
produce. We can use this fact to check that the computed $u^n_i$
values from an implementation equals $u_e(x_i,t_n)$, within machine
precision. This result is valid *regardless of the mesh spacings*
$\Delta x$ and $\Delta t$! Nevertheless, there might be stability
restrictions on $\Delta x$ and $\Delta t$, so the test can only be run
for a mesh that is compatible with the stability criterion (which in
the present case is $C\leq 1$, to be derived later).
**Notice.**
A product of quadratic or linear expressions in the various
independent variables, as shown above, will often fulfill both the
PDE problem and the discrete equations, and can therefore be very useful
solutions for verifying implementations.
However, for 1D wave
equations of the type $u_{tt}=c^2u_{xx}$ we shall see that there is always
another much more powerful way of generating exact
solutions (which consists in just setting $C=1$ (!), as shown in
the section [Analysis of the difference equations](wave_analysis.ipynb)).
| true |
code
| 0.64919 | null | null | null | null |
|
# Non-linear dependencies amongst the SDGs and climate change by distance correlation
We start with investigating dependencies amongst the SDGs on different levels. The method how we investigate these dependencies should take as few assumptions as possible. So, a Pearson linear correlation coefficient or a rank correlation coefficient are not our choice since they assume linearity and/or monotony, respectively.
We choose to compute the [distance correlation](https://projecteuclid.org/euclid.aos/1201012979), precisely the [partial distance correlation](https://projecteuclid.org/download/pdfview_1/euclid.aos/1413810731), because of the following properties:
1. we have an absolute measure of dependence ranging from $0$ to $1$, $0 \leq \mathcal{R}(X,Y) \leq 1$
2. $\mathcal{R}(X,Y) = 0$ if and only if $X$ and $Y$ are independent,
3. $\mathcal{R}(X,Y) = \mathcal{R}(Y,X)$
4. we are able to investigate non-linear and non-monotone relationships,
5. we can find dependencies between indicators with differently many measurements,
6. the only assumptions we need to take is that probability distributions have finite first moments.
The conditional distance correlation has the advantage that we ignore the influence of any other targets or goals when we compute the correlation between any two targets or goals. This procedure is also called controlling for confounders.
The **distance correlation** is defined as:
$$
\mathcal{R}^2(X,Y) = \begin{cases}
\frac{\mathcal{V}^2 (X,Y)}{\sqrt{\mathcal{V}^2 (X)\mathcal{V}^2 (Y)}} &\text{, if $\mathcal{V}^2 (X)\mathcal{V}^2 (Y) > 0$} \\
0 &\text{, if $\mathcal{V}^2 (X)\mathcal{V}^2 (Y) = 0$}
\end{cases}
$$
where
$$
\mathcal{V}^2 (X,Y) = \| f_{X,Y}(t) - f_X(t)f_Y(t) \|^2
$$
is the distance covariance with **characteristic functions** $f(t)$. Bear in mind that characteristic functions include the imaginary unit $i$, $i^2 = -1$:
$$
f_X(t) = \mathbb{E}[e^{itX}]
$$
Thus, we are in the space of complex numbers $\mathbb{C}$. Unfortunately, this means we can most likely not find exact results, but we'll get back to this later under Estimators.
The **conditional distance correlation** is defined as:
$$
\mathcal{R}^2(X,Y \ | \ Z) = \begin{cases}
\frac{\mathcal{R}^2 (X,Y) - \mathcal{R}^2 (X,Z) \mathcal{R}^2 (Y,Z)}{\sqrt{1 - \mathcal{R}^4 (X,Z)} \sqrt{1 - \mathcal{R}^4 (Y,Z)}} &\text{, if $\mathcal{R}^4 (X,Z) \neq 1$ and $\mathcal{R}^4 (Y,Z) \neq 1$} \\
0 &\text{, if $\mathcal{R}^4 (X,Z) = 1$ and $\mathcal{R}^4 (Y,Z) = 1$}
\end{cases}
$$
# Distance covariance
Let's dismantle the distance covariance equation to know what we actually compute in the distance correlation:
$$
\mathcal{V}^2 (X,Y) = \| f_{X,Y}(t) - f_X(t) \ f_Y(t) \|^2 = \frac{1}{c_p c_q} \int_{\mathbb{R}^{p+q}} \frac{| f_{X,Y}(t) - f_X(t)f_Y(t) |^2}{| t |_p^{1+p} \ | t |_q^{1+q}} dt
$$
where
$$
c_d = \frac{\pi^{(1+d)/2}}{\Gamma \Big( (1+d)/2 \Big)}
$$
where the (complete) Gamma function $\Gamma$ is
$$
\Gamma (z) = \int_0^{\infty} x^{z-1} \ e^{-x} \ dx
$$
with $z \in \mathbb{R}^{+}$.
$p$ and $q$ are the samples of time-series. We can see this as a random vector with multiple samples available for each time point. However, the number of samples for time points must not vary over the same time-series. We can write this as:
$$X \ \text{in} \ \mathbb{R}^p$$
$$Y \ \text{in} \ \mathbb{R}^q$$
A preliminary conclusion of this formulation: **we can compute dependencies between time-series with different numbers of samples**.
But we still have some terms in the distance covariance $\mathcal{V}^2 (X,Y)$ which we need to define:
$ | t |_p^{1+p} $ is the Euclidean distance of $t$ in $\mathbb{R}^p$, $ | t |_q^{1+q} $ is the Euclidean distance of $t$ in $\mathbb{R}^q$.
The numerator in the integral of $\mathcal{V}^2 (X,Y)$ is:
$$
| f_{X,Y}(t) - f_X(t) \ f_Y(t) |^2 = \Big( 1- |f_X(t) | ^2 \Big) \ \Big( 1- |f_Y(t) |^2 \Big)
$$
where $|f_X(t) |$ and $|f_Y(t) |$ are absolute random vectors of the characteristic functions $f(t)$ with $p$ and $q$ samples, respectively.
## Estimators
Since the characteristic functions include the imaginary unit $i$, we cannot recover the exact solution for the distance covariance. However, we can estimate it by a quite simple form. We compute these estimators according to [Huo & Szekely, 2016](https://arxiv.org/abs/1410.1503).
We denote the pairwise distances of the $X$ observations by $a_{ij} := \|X_i - X_j \|$ and of the $Y$ observations by $b_{ij} = \|Y_i - Y_j \|$ for $i,j = 1, ..., n$, where $n$ is the number of measurements in $X$ and $Y$. The corresponding distance matrices are denoted by $(A_{ij})^n_{i,j=1}$ and $(B_{ij})^n_{i,j=1}$, where
$$
A_{ij} = \begin{cases}
a_{ij} - \frac{1}{n} \sum_{l=1}^n a_{il} - \frac{1}{n} \sum_{k=1}^n a_{kj} + \frac{1}{n^2} \sum_{k,l=1}^n a_{kl} & i \neq j; \\
0 & i = j.
\end{cases}
$$
and
$$
B_{ij} = \begin{cases}
b_{ij} - \frac{1}{n} \sum_{l=1}^n b_{il} - \frac{1}{n} \sum_{k=1}^n b_{kj} + \frac{1}{n^2} \sum_{k,l=1}^n b_{kl} & i \neq j; \\
0 & i = j.
\end{cases}
$$
Having computed these, we can estimate the sample distance covariance $\hat{\mathcal{V}}^2(X,Y)$ by
$$
\hat{\mathcal{V}}^2(X,Y) = \frac{1}{n^2} \sum_{i,j=1}^n A_{ij} \ B_{ij}
$$
The corresponding sample variance $\hat{\mathcal{V}}^2(X)$ is consequently:
$$
\hat{\mathcal{V}}^2(X) = \frac{1}{n^2} \sum_{i,j=1}^n A^2_{ij}
$$
Then, we can scale these covariances to finally arrive at the sample distance correlation $\hat{\mathcal{R}}^2(X,Y)$:
$$
\hat{\mathcal{R}}^2(X,Y) = \begin{cases}
\frac{\hat{\mathcal{V}}^2 (X,Y)}{\sqrt{\hat{\mathcal{V}}^2 (X)\hat{\mathcal{V}}^2 (Y)}} &\text{, if $\hat{\mathcal{V}}^2 (X)\mathcal{V}^2 (Y) > 0$} \\
0 &\text{, if $\hat{\mathcal{V}}^2 (X)\hat{\mathcal{V}}^2 (Y) = 0$}
\end{cases}
$$
### Unbiased estimators
These estimators are biased, but we can define unbiased estimators of the distance covariance $\hat{\mathcal{V}}^2(X,Y)$ and call them $\Omega_n(x,y)$. We must first redefine our distance matrices $(A_{ij})^n_{i,j=1}$ and $(B_{ij})^n_{i,j=1}$, which we will call $(\tilde{A}_{ij})^n_{i,j=1}$ and $(\tilde{B}_{ij})^n_{i,j=1}$:
$$
\tilde{A}_{ij} = \begin{cases}
a_{ij} - \frac{1}{n-2} \sum_{l=1}^n a_{il} - \frac{1}{n-2} \sum_{k=1}^n a_{kj} + \frac{1}{(n-1)(n-2)} \sum_{k,l=1}^n a_{kl} & i \neq j; \\
0 & i = j.
\end{cases}
$$
and
$$
\tilde{B}_{ij} = \begin{cases}
b_{ij} - \frac{1}{n-2} \sum_{l=1}^n b_{il} - \frac{1}{n-2} \sum_{k=1}^n b_{kj} + \frac{1}{(n-1)(n-2)} \sum_{k,l=1}^n b_{kl} & i \neq j; \\
0 & i = j.
\end{cases}
$$
Finally, we can compute the unbiased estimator $\Omega_n(X,Y)$ for $\mathcal{V}^2(X,Y)$ as the dot product $\langle \tilde{A}, \tilde{B} \rangle$:
$$
\Omega_n(X,Y) = \langle \tilde{A}, \tilde{B} \rangle = \frac{1}{n(n-3)} \sum_{i,j=1}^n \tilde{A}_{ij} \ \tilde{B}_{ij}
$$
Interestingly, [Lyons (2013)](https://arxiv.org/abs/1106.5758) found another solution how not only the sample distance correlation can be computed, but also the population distance correlation without characteristic functions. This is good to acknowledge, but it is not necessary to focus on it.
# Conditional distance covariance
We start with computing the unbiased distance matrices $(\tilde{A}_{ij})^n_{i,j=1}$, $(\tilde{B}_{ij})^n_{i,j=1}$, and $(\tilde{C}_{ij})^n_{i,j=1}$ for $X$, $Y$, and $Z$, respectively, as we have done previously for the distance covariance. We define the dot product
$$
\Omega_n(X,Y) = \langle \tilde{A}, \tilde{B} \rangle = \frac{1}{n(n-3)} \sum_{i,j=1}^n \tilde{A}_{ij} \tilde{B}_{ij}
$$
and project the sample $x$ onto $z$ as
$$
P_z (x) = \frac{\langle \tilde{A}, \tilde{C} \rangle}{\langle \tilde{C}, \tilde{C} \rangle} \tilde{C} .
$$
The complementary projection is consequently
$$
P_{z^{\bot}} (x) = \tilde{A} - P_z (x) = \tilde{A} - \frac{\langle \tilde{A}, \tilde{C} \rangle}{\langle \tilde{C}, \tilde{C} \rangle} \tilde{C} .
$$
Hence, the sample conditional distance covariance is
$$
\hat{\mathcal{V}}^2(X,Y \ | \ Z) = \langle P_{z^{\bot}} (x), P_{z^{\bot}} (y) \rangle .
$$
Then, we can scale these covariances to finally arrive at the sample conditional distance correlation $\hat{\mathcal{R}}^2(X,Y \ | \ Z)$:
$$
\hat{\mathcal{R}}^2(X,Y \ | \ Z) = \begin{cases}
\frac{\langle P_{z^{\bot}} (x), P_{z^{\bot}} (y) \rangle}{\| P_{z^{\bot}} (x) \| \ \| P_{z^{\bot}} (y) \|} &\text{, if} \ \| P_{z^{\bot}} (x) \| \ \| P_{z^{\bot}} (y) \| \neq 0 \\
0 &\text{, if} \ \| P_{z^{\bot}} (x) \| \ \| P_{z^{\bot}} (y) \| = 0
\end{cases}
$$
## Implementation
For our computations, we'll use the packages [`dcor`](https://dcor.readthedocs.io/en/latest/?badge=latest) for the partial distance correlation and [`community`](https://github.com/taynaud/python-louvain) for the clustering.
```
import dcor
import numpy as np
import pickle
import itertools
import pandas as pd
import os
import math
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt
import seaborn as sns
import networkx as nx
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
from matplotlib.offsetbox import OffsetImage, AnnotationBbox
from community import community_louvain as community
from scipy.spatial import distance
from dcor._dcor_internals import _u_distance_matrix, u_complementary_projection
from sklearn.manifold import MDS
import gc
import warnings
warnings.filterwarnings('ignore')
```
### Loading standardised imputed data set
We load first of all the standardised imputed data set which we have generated with the previous notebook.
```
#dict_all = pickle.load(open('utils/data/dict_all_wb.pkl', 'rb'))
dict_all_std = pickle.load(open('utils/data/dict_all_wb_std.pkl', 'rb'))
#indicators_values_i = pickle.load(open('utils/data/indicators_values_i_up_wb.pkl', 'rb'))
targets_values_i = pickle.load(open('utils/data/targets_values_i_up_arr_wb.pkl', 'rb'))
goals_values_i = pickle.load(open('utils/data/goals_values_i_up_arr_wb.pkl', 'rb'))
# check whether T appended
len(targets_values_i['Belgium'])
# read amended csv file
c = pd.read_csv('utils/countries_wb.csv', dtype=str, delimiter=';', header=None)
countries = list(c[0])
groups = pd.read_csv(r'utils/groups.csv')
groups.replace({"Democratic People's Republic of Korea": "Korea, Dem. People's Rep.", 'Gambia': 'Gambia, The', 'United Kingdom of Great Britain and Northern Ireland': 'United Kingdom', 'Congo': 'Congo, Rep.', 'Democratic Republic of the Congo': 'Congo, Dem. Rep.', 'Czechia': 'Czech Republic', 'Iran (Islamic Republic of)': 'Iran, Islamic Rep.', "Côte d'Ivoire": "Cote d'Ivoire", 'Kyrgyzstan': 'Kyrgyz Republic', "Lao People's Democratic Republic": 'Lao PDR', 'Republic of Moldova': 'Moldova', 'Micronesia (Federated States of)': 'Micronesia, Fed. Sts.', 'Slovakia': 'Slovak Republic', 'Viet Nam': 'Vietnam', 'Egypt': 'Egypt, Arab Rep.', 'United Republic of Tanzania': 'Tanzania','United States of America': 'United States', 'Venezuela (Bolivarian Republic of)': 'Venezuela, RB', 'Yemen': 'Yemen, Rep.', 'Bahamas': 'Bahamas, The', 'Bolivia (Plurinational State of)': 'Bolivia'}, inplace=True)
info = pd.read_csv(r'utils/wb_info.csv', header=None)
# removes some countries in-place
countries.remove('Micronesia, Fed. Sts.')
groups['Global South'].drop(index=1, inplace=True)
```
We later compute the correlations on an indicator level, but this is too detailed for any network visualisation and for an overarching understanding. Hence, we group here all sub-indicators first on an indicator-level. Then, we compute the distance correlations for the indicators, targets and goals.
We work with the `info` file again, so we don't need to assign all of this by hand.
```
# check
info
# check
#targets_values_i['France'].tail()
```
We would like to have values for targets, so we must, first of all, generate a list of all unique **targets**.
```
targets = list(info[4].unique())
dict_targets = {}
for target in targets:
t = info[0].where(info[4] == target)
dict_targets[target] = [i for i in t if str(i) != 'nan']
#check
dict_targets['1.2']
```
Finally we also generate a list of all unique **goals**.
```
goals = list(info[3].unique())
dict_goals = {}
for goal in goals:
g = info[4].where(info[3] == goal)
dict_goals[goal] = [t for t in g if str(t) != 'nan']
dict_goals[goal] = list(set(dict_goals[goal]))
#check
print(dict_goals['13'])
```
## Distance correlations between goals
The next step is to compute the distance correlations on a goal-level.
We work with the **concatenated time-series** to compute the conditioned distance correlation directly on goal-level data. Visually speaking, this means that we fit one non-linear function to the data for all targets of these two goals. Since goals often have diverse targets, this may end up in fitting a non-linear curve to very noisy data.
## Working with concatenated time-series
### Conditioning iteratively on subsets of joint distributions of all goals
We condition pairs of two goals iteratively on subsets of all remaining goals. We start with conditioning on the empty set, i.e. we compute the pairwise distance correlation first. Afterwards, we increase the set to condition on until we have reached the set of all remaining 15 goals to condition on. These sets are represented by the joint distributions of the goals entailed in them.
We need to condition on all **subsets** of these lists of SDGs we condition on to find the dependence which solely stems from either of the two SDGs we condition the others on:
```
def combinations(iterable, r):
# combinations('ABCD', 2) --> AB AC AD BC BD CD
# combinations(range(4), 3) --> 012 013 023 123
pool = tuple(iterable)
n = len(pool)
if r > n:
return
indices = list(range(r))
yield list(pool[i] for i in indices)
while True:
for i in reversed(range(r)):
if indices[i] != i + n - r:
break
else:
return
indices[i] += 1
for j in range(i+1, r):
indices[j] = indices[j-1] + 1
yield list(pool[i] for i in indices)
def combinations_tuple(iterable, r):
# combinations('ABCD', 2) --> AB AC AD BC BD CD
# combinations(range(4), 3) --> 012 013 023 123
pool = tuple(iterable)
n = len(pool)
if r > n:
return
indices = list(range(r))
yield tuple(pool[i] for i in indices)
while True:
for i in reversed(range(r)):
if indices[i] != i + n - r:
break
else:
return
indices[i] += 1
for j in range(i+1, r):
indices[j] = indices[j-1] + 1
yield tuple(pool[i] for i in indices)
def product(pool_0, pool_1):
#result = [[x, y]+[z] for x, y in pool_0 for z in pool_1 if x not in z and y not in z] # ~ 10 Mio rows
result = [[x, y]+[z] for x, y in pool_0 for z in pool_1] # ~ 40 Mio rows
for prod in result:
yield tuple(prod)
# create list out of all unique combinations of goals
g_combinations = list(combinations(goals, 2))
conditions_g = []
conditions_g_tuple = []
for i in range(1, 18):
conditions_g.extend(list(combinations(goals, i)))
conditions_g_tuple.extend(tuple(combinations_tuple(goals, i)))
# divide conditions_g_tuple into four sub-lists to save memory
conditions_g_tuple_1 = conditions_g_tuple[:int(len(conditions_g_tuple)/4)]
conditions_g_tuple_2 = conditions_g_tuple[int(len(conditions_g_tuple)/4)+1:2*int(len(conditions_g_tuple)/4)]
conditions_g_tuple_3 = conditions_g_tuple[2*int(len(conditions_g_tuple)/4)+1:3*int(len(conditions_g_tuple)/4)]
conditions_g_tuple_4 = conditions_g_tuple[3*int(len(conditions_g_tuple)/4)+1:]
pairs = list(product(g_combinations, conditions_g_tuple))
pairs_g0 = pd.DataFrame.from_records(pairs, columns=['pair_0', 'pair_1', 'condition'])
pairs_1 = list(product(g_combinations, conditions_g_tuple_1))
pairs_g0_1 = pd.DataFrame.from_records(pairs_1, columns=['pair_0', 'pair_1', 'condition'])
pairs_2 = list(product(g_combinations, conditions_g_tuple_2))
pairs_g0_2 = pd.DataFrame.from_records(pairs_2, columns=['pair_0', 'pair_1', 'condition'])
pairs_3 = list(product(g_combinations, conditions_g_tuple_3))
pairs_g0_3 = pd.DataFrame.from_records(pairs_3, columns=['pair_0', 'pair_1', 'condition'])
pairs_4 = list(product(g_combinations, conditions_g_tuple_4))
pairs_g0_4 = pd.DataFrame.from_records(pairs_4, columns=['pair_0', 'pair_1', 'condition'])
# how many rows?
print(len(pairs_g0))
print(len(pairs_g0_1), len(pairs_g0_2), len(pairs_g0_3), len(pairs_g0_4))
# adding empty condition set for pairwise dcor
pairs_g1 = pd.DataFrame.from_records(data=g_combinations, columns=['pair_0', 'pair_1'])
pairs_g1['condition'] = '0'
```
# Groups
```
# data preparation
groups_prep_g = {}
for group in groups:
print(group)
groups_prep_g[group] = np.empty(18, dtype=object)
for g, goal in enumerate(goals):
g_list = []
for country in groups[group].dropna():
g_list.append(np.asarray(goals_values_i[country][g]))
groups_prep_g[group][g] = np.asarray(g_list)
```
Now we call these data in our `dcor` computations. We first compute the pairwise distance covariance and correlation, then the partial ones with conditioning on all the previously defined sets in `pairs_g`.
### Preparations
Filtering out the conditions that contain goals $X$ (`pair_0`) or $Y$ (`pair_1`):
```
import multiprocessing as mp
print("Number of processors: ", mp.cpu_count())
# CHECKPOINT
pairs_g0_left_0 = pd.read_csv('utils/pairs_g0_left_0.zip', dtype=str, compression='zip')
pairs_g0_left_0_1 = pd.read_csv('utils/pairs_g0_left_0_1.zip', dtype=str, compression='zip')
pairs_g0_left_0_2 = pd.read_csv('utils/pairs_g0_left_0_2.zip', dtype=str, compression='zip')
pairs_g0_left_0_3 = pd.read_csv('utils/pairs_g0_left_0_3.zip', dtype=str, compression='zip')
pairs_g0_left_0_4 = pd.read_csv('utils/pairs_g0_left_0_4.zip', dtype=str, compression='zip')
# check
pairs_g0_left_0_3.tail()
pairs_g0_left_0.shape[0] / 153
len(g_combinations)
```
# With `multiprocessing` parallelisation
### Partial distance correlation
```
def partial_distance_cor(row):
pair_0, pair_1, cond = row
if pair_0=='T':
pair_0 = 18
if pair_1=='T':
pair_1 = 18
pair_0_array = groups_prep_g[group][int(pair_0)-1]
pair_1_array = groups_prep_g[group][int(pair_1)-1]
condition_array = conditions_dict[str(cond)].T
return dcor.partial_distance_correlation(pair_0_array, pair_1_array, condition_array)**2
#groups.drop(columns=['Global North', 'Global South'], inplace=True)
groups.columns
# groups
dict_cor_goals_groups_2_cond = {}
for group in ['Global South']:
print(group)
#dict_cor_goa_c = pairs_g0_left_0.copy(deep=True)
dict_cor_goa_c = pairs_g0_left_0_4.copy(deep=True) # pairs_g0_left_0 has all non-empty conditional sets
# preparing conditional set
conditions_dict = {}
#for cond in conditions_g_tuple:
for cond in conditions_g_tuple_4:
condition = []
for c in cond:
if c=='T':
condition.extend(groups_prep_g[group][17].T)
else:
condition.extend(groups_prep_g[group][int(c)-1].T)
conditions_dict[str(cond)] = np.asarray(condition)
# partial distance correlation
pool = mp.Pool(int(mp.cpu_count()/2))
dict_cor_goa_c_list = dict_cor_goa_c.values.tolist()
print('start dcor...')
cor_results = pool.map(partial_distance_cor, dict_cor_goa_c_list, chunksize=1000)
pool.close()
pool.join()
dict_cor_goa_c['dcor'] = cor_results
print('...dcor done')
# find minimum distance correlation between any two goals
dict_cor_goa_con = dict_cor_goa_c.groupby(['pair_0', 'pair_1'])['dcor'].apply(list).reset_index(name='list_dcor')
for i, row_con in dict_cor_goa_con.iterrows():
dict_cor_goa_con.loc[i, 'min_dcor'] = min(dict_cor_goa_con.loc[i, 'list_dcor'])
dict_cor_goa_con.drop(columns=['list_dcor'], inplace=True)
# finding conditional set of minimum partial distance correlation
dict_cor_goa_cond = dict_cor_goa_con.merge(dict_cor_goa_c, left_on='min_dcor', right_on='dcor').drop(['pair_0_y', 'pair_1_y', 'dcor'], axis=1).rename(columns={'pair_0_x': 'pair_0', 'pair_1_x': 'pair_1'})
dict_cor_goals_groups_2_cond[group] = dict_cor_goa_cond
# save every group separately to save memory
#g_cor = open('distance_cor/goals/dict_cor_goals_groups_2_cond_{}.pkl'.format(group), 'wb')
g_cor = open('distance_cor/goals/dict_cor_goals_groups_2_cond_{}_4.pkl'.format(group), 'wb')
pickle.dump(dict_cor_goals_groups_2_cond, g_cor)
g_cor.close()
gc.collect()
# for Global South (disaggregated because of memory restrictions)
dict_GS_1 = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Global South_1.pkl', 'rb'))
dict_GS_2 = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Global South_2.pkl', 'rb'))
dict_GS_3 = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Global South_3.pkl', 'rb'))
dict_GS_4 = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Global South_4.pkl', 'rb'))
cor_goals_continents_2_GS = pd.concat([dict_GS_1['Global South'], dict_GS_2['Global South'], dict_GS_3['Global South'], dict_GS_4['Global South']])
# find minimum distance correlation between any two goals
dict_cor_goa_con = cor_goals_continents_2_GS.groupby(['pair_0', 'pair_1'])['min_dcor'].apply(list).reset_index(name='list_dcor')
for i, row_c in dict_cor_goa_con.iterrows():
dict_cor_goa_con.loc[i, 'min_dcor'] = min(dict_cor_goa_con.loc[i, 'list_dcor'])
dict_cor_goa_con.drop(columns=['list_dcor'], inplace=True)
# finding conditional set of minimum partial distance correlation
dict_cor_goa_cond = dict_cor_goa_con.merge(cor_goals_continents_2_GS, left_on='min_dcor', right_on='min_dcor').drop(['pair_0_y', 'pair_1_y'], axis=1).rename(columns={'pair_0_x': 'pair_0', 'pair_1_x': 'pair_1'})
# save every entry region separately to save memory
g_cor = open('distance_cor/goals/dict_cor_goals_groups_2_cond_Global South.pkl', 'wb')
pickle.dump(dict_cor_goa_cond, g_cor)
g_cor.close()
dict_GN = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Global North.pkl', 'rb'))
dict_GS = {}
dict_GS['Global South'] = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Global South.pkl', 'rb'))
dict_LCD = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Least Developed Countries (LDC).pkl', 'rb'))
dict_LLDC = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Land Locked Developing Countries (LLDC).pkl', 'rb'))
dict_SIDS = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Small Island Developing States (SIDS).pkl', 'rb'))
dict_G20 = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_G20.pkl', 'rb'))
dict_EM = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Emerging Markets (BRICS + N-11).pkl', 'rb'))
dict_OPEC = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_OPEC.pkl', 'rb'))
dict_LI = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Low Income.pkl', 'rb'))
dict_LMI = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Lower middle Income.pkl', 'rb'))
dict_UMI = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_Upper middle Income.pkl', 'rb'))
dict_HI = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2_cond_High Income.pkl', 'rb'))
dict_cor_goals_groups_2_condition = {**dict_GN, **dict_GS, **dict_LCD, **dict_LLDC, **dict_SIDS, **dict_G20, **dict_EM, **dict_OPEC, **dict_LI, **dict_LMI, **dict_UMI, **dict_HI}
# check
print(dict_cor_goals_groups_2_condition.keys())
dict_cor_goals_groups_2_condition['Global South']
```
### Pairwise distance correlation
```
def distance_cor(row):
pair_0, pair_1 = row
if pair_0=='T':
pair_0 = 18
if pair_1=='T':
pair_1 = 18
pair_0_array = groups_prep_g[group][int(pair_0)-1]
pair_1_array = groups_prep_g[group][int(pair_1)-1]
return dcor.distance_correlation(pair_0_array, pair_1_array)**2
# groups
dict_cor_goals_groups_2_pair = {}
for group in groups:
print(group)
dict_cor_goa_c_pair = pairs_g1.drop(columns=['condition']).copy(deep=True) # pairs_g1 has empty conditional sets for pairwise dcor
pool = mp.Pool(int(mp.cpu_count()/2))
print('start dcor...')
dict_cor_goa_c_pair_list = dict_cor_goa_c_pair.values.tolist()
cor_results = pool.map(distance_cor, dict_cor_goa_c_pair_list, chunksize=1000)
pool.close()
pool.join()
dict_cor_goa_c_pair['min_dcor_pair'] = cor_results
print('...dcor done')
dict_cor_goals_groups_2_pair[group] = dict_cor_goa_c_pair
# check
dict_cor_goals_groups_2_pair['Least Developed Countries (LDC)']
# merge dictionaries
dict_cor_goals_groups_2 = {}
for group in dict_cor_goals_groups_2_condition.keys():
print(group)
dict_cor_goals_groups_2[group] = pd.DataFrame(index=range(153), columns=['pair_0', 'pair_1', 'min_dcor', 'condition'])
for i in dict_cor_goals_groups_2_pair[group].index:
for j in dict_cor_goals_groups_2_condition[group].index:
if dict_cor_goals_groups_2_pair[group].loc[i, 'pair_0']==dict_cor_goals_groups_2_condition[group].loc[j, 'pair_0'] and dict_cor_goals_groups_2_pair[group].loc[i, 'pair_1']==dict_cor_goals_groups_2_condition[group].loc[j, 'pair_1']:
dict_cor_goals_groups_2[group].loc[i, 'pair_0'] = dict_cor_goals_groups_2_pair[group].loc[i, 'pair_0']
dict_cor_goals_groups_2[group].loc[i, 'pair_1'] = dict_cor_goals_groups_2_pair[group].loc[i, 'pair_1']
dict_cor_goals_groups_2[group].loc[i, 'min_dcor'] = min(dict_cor_goals_groups_2_pair[group].loc[i, 'min_dcor_pair'], dict_cor_goals_groups_2_condition[group].loc[j, 'min_dcor'])
if dict_cor_goals_groups_2_pair[group].loc[i, 'min_dcor_pair'] < dict_cor_goals_groups_2_condition[group].loc[j, 'min_dcor']:
dict_cor_goals_groups_2[group].loc[i, 'condition'] = 0
else:
dict_cor_goals_groups_2[group].loc[i, 'condition'] = dict_cor_goals_groups_2_condition[group].loc[j, 'condition']
# CHECKPOINT
dict_cor_goals_groups_2 = pickle.load(open('distance_cor/goals/dict_cor_goals_groups_2.pkl', 'rb'))
```
### Testing for statistical significance
We calculate the p-values of our partial distance correlations, i.e., the probability that the null hypothesis of (partial) independence can be accepted.
```
for group in groups:
print(group)
dict_cor_goals_groups_2[group]['p-value'] = -1
for r, row in dict_cor_goals_groups_2[group].iterrows():
# preparing pair_0 and pair_1
if row.pair_1=='T':
row.pair_1 = 18
pair_0_array = groups_prep_g[group][int(row.pair_0)-1]
pair_1_array = groups_prep_g[group][int(row.pair_1)-1]
# extracting conditional variables from column 'condition'
cond_list = []
for i in row.condition.split():
newstr = ''.join((ch if ch in '0123456789.-eT' else ' ') for ch in i)
cond_list.extend([i for i in newstr.split()])
condition = []
for c in cond_list:
if c=='T':
condition.extend(groups_prep_g[group][17].T)
else:
condition.extend(groups_prep_g[group][int(c)-1].T)
cond_array = np.asarray(condition).T
dict_cor_goals_groups_2[group].iloc[r, 4] = dcor.independence.partial_distance_covariance_test(pair_0_array, pair_1_array, cond_array, num_resamples=10000).p_value
# save
if not os.path.exists('distance_cor'):
os.mkdir('distance_cor')
if not os.path.exists('distance_cor/goals'):
os.mkdir('distance_cor/goals')
g_cor = open('distance_cor/goals/dict_cor_goals_groups_2.pkl', 'wb')
pickle.dump(dict_cor_goals_groups_2, g_cor)
g_cor.close()
# saving as csv's
for group in groups:
dict_cor_goals_groups_2[group] = dict_cor_goals_groups_2[group][['pair_0', 'pair_1', 'min_dcor', 'p-value', 'condition']]
dict_cor_goals_groups_2[group]['p-value'] = dict_cor_goals_groups_2[group]['p-value'].astype(float).round(5)
dict_cor_goals_groups_2[group].min_dcor = dict_cor_goals_groups_2[group].min_dcor.astype(float).round(5)
dict_cor_goals_groups_2[group].to_csv('distance_cor/goals/conditions_{}.csv'.format(group))
```
We want to keep the minimum significant distance correlation of each pair of two goals, pairwise or conditioned on any potential subset.
The last step is to insert these values into the right cell in a matrix.
```
cor_goals_groups_2 = {}
for group in dict_cor_goals_groups_2.keys():
print(group)
cor_goals_groups_2[group] = pd.DataFrame(index=goals, columns=goals)
for i in list(dict_cor_goals_groups_2[group].index):
goal_0 = dict_cor_goals_groups_2[group].loc[i, 'pair_0']
goal_1 = dict_cor_goals_groups_2[group].loc[i, 'pair_1']
# take square root because we have previously squared the distance correlation
cor_goals_groups_2[group].loc[goal_1, goal_0] = np.sqrt(dict_cor_goals_groups_2[group].loc[i, 'min_dcor'])
```
In `cor_goals_groups_2` are the conditional distance correlations for all continents in a setting of 18 random vectors $X$, $Y$, and $Z_1, Z_2, ..., Z_{16}$, where $\boldsymbol{Z}$ is the array containing all random vectors we want to condition on.
```
# save
g_cor = open('distance_cor/goals/dcor_goals_groups_2.pkl', 'wb')
pickle.dump(cor_goals_groups_2, g_cor)
g_cor.close()
# CHECKPOINT
g_cor = pickle.load(open('distance_cor/goals/dcor_goals_groups_2.pkl', 'rb'))
```
## Visualisation on goal-level
Additionally to the matrices with numbers, we would also like to visualise these matrices and plot these correlations as networks.
```
# groups
for group in dict_cor_goals_groups_2.keys():
# generate a mask for the upper triangle
mask = np.zeros_like(cor_goals_groups_2[group].fillna(0), dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# set up the matplotlib figure
f, ax = plt.subplots(figsize=(25, 22))
# generate a custom diverging colormap
cmap = sns.color_palette("Reds", 100)
# draw the heatmap with the mask and correct aspect ratio
sns.heatmap(cor_goals_groups_2[group].fillna(0), mask=mask, cmap=cmap, vmax=1, center=0.5, vmin=0,
square=True, linewidths=.5, cbar_kws={"shrink": .8})
plt.title('{}'.format(group), fontdict={'fontsize': 52})
plt.savefig('distance_cor/goals/{}_cor_goals.png'.format(group))
# data preparation for networkX
dcor_dict_g = {}
for group in cor_goals_groups_2.keys():
dcor_dict_g[group] = {}
for goalcombination in g_combinations:
dcor_dict_g[group][tuple(goalcombination)] = [cor_goals_groups_2[group].loc[goalcombination[1], goalcombination[0]], float(dict_cor_goals_groups_2[group].loc[(dict_cor_goals_groups_2[group]['pair_0']=='{}'.format(goalcombination[0])) & (dict_cor_goals_groups_2[group]['pair_1']=='{}'.format(goalcombination[1]))]['p-value'])]
for group in cor_goals_groups_2.keys():
for key in dcor_dict_g[group].keys():
if key[1] == 'T':
dcor_dict_g[group][tuple((key[0], '18'))] = dcor_dict_g[group].pop(tuple((key[0], 'T')))
elif key[0] == 'T':
dcor_dict_g[group][tuple(('18', key[1]))] = dcor_dict_g[group].pop(tuple(('T', key[1])))
# plotting networks with weighted edges
layout = 'circular'
centrality_G = {} # dictionary to save centralities
degree_G = {} # dictionary to save degrees
density_G = {} # dictionary to save weighted densities
p_G = {} # auxiliary
partition_G = {} # dictionary to save clusters
for group in cor_goals_groups_2.keys():
G_G = nx.Graph()
for key, value in dcor_dict_g[group].items():
if value[1] <= 0.01:
w = value[0]
s = 'solid'
c = sns.color_palette('Reds', 100)[int(value[0]*100)]
elif 0.01 < value[1] <= 0.05:
w = value[0]
s = 'dashed'
c = sns.color_palette('Reds', 100)[int(value[0]*100)]
elif 0.05 < value[1] <= 0.1:
w = value[0]
s = 'dotted'
c = sns.color_palette('Reds', 100)[int(value[0]*100)]
else:
w = 0
s = 'solid'
c = 'white'
G_G.add_edge(int(key[0]), int(key[1]), style=s, weight=w, color=c, alpha=value[0])
if layout == 'circular':
pos = nx.circular_layout(G_G)
elif layout == 'spring':
pos = nx.spring_layout(G_G)
plt.figure(figsize=(24,16))
plt.tight_layout()
# nodes
nx.draw_networkx_nodes(G_G, pos, node_size=1000)
# labels
nx.draw_networkx_labels(G_G, pos, font_size=46, font_family='sans-serif')
nodes = G_G.nodes()
edges = G_G.edges()
colors = [G_G[u][v]['color'] for u,v in edges]
weights = [G_G[u][v]['weight'] for u,v in edges]
alphas = [G_G[u][v]['alpha'] for u,v in edges]
styles = [G_G[u][v]['style'] for u,v in edges]
nx.draw_networkx_nodes(G_G, pos, nodelist=nodes, node_color='white', node_size=1000)
for i, edge in enumerate(edges):
pos_edge = {edge[0]: pos[edge[0]], edge[1]: pos[edge[1]]}
nx.draw_networkx_edges(G_G, pos_edge, edgelist=[edge], edge_color=colors[i], style=styles[i], width=np.multiply(weights[i],25)) #alpha=np.multiply(alphas[i],2.5))
#nx.draw_networkx(G_G, pos, with_labels=False, edges=edges, edge_color=colors, node_color='white', node_size=1000, width=np.multiply(weights,25))
ax=plt.gca()
fig=plt.gcf()
trans = ax.transData.transform
trans_axes = fig.transFigure.inverted().transform
imsize = 0.08 # this is the image size
plt.title('{}'.format(group), y=1.05, fontdict={'fontsize': 52})
for node in G_G.nodes():
(x,y) = pos[node]
xx,yy = trans((x,y)) # figure coordinates
xa,ya = trans_axes((xx,yy)) # axes coordinates
a = plt.axes([xa-imsize/2.0,ya-imsize/2.0, imsize, imsize])
a.imshow(mpimg.imread('utils/images/E_SDG goals_icons-individual-rgb-{}.png'.format(node)))
a.axis('off')
plt.axis('off')
ax.axis('off')
plt.savefig('distance_cor/goals/{}_{}_network_logos_main.png'.format(group, layout), format='png')
plt.show()
# weighted centrality
centr = nx.eigenvector_centrality(G_G, weight='weight', max_iter=100000)
centrality_G[group] = sorted((v, '{:0.2f}'.format(c)) for v, c in centr.items())
degree_G[group] = dict(G_G.degree(weight='weight'))
# weighted density
density_G[group] = 2 * np.sum(weights) / (len(nodes) * (len(nodes) - 1))
# weighted clustering with Louvain algorithm
part_G = {}
modularity_G = {}
for i in range(100):
part_G[i] = community.best_partition(G_G, random_state=i)
modularity_G[i] = community.modularity(part_G[i], G_G)
p_G[group] = part_G[max(modularity_G, key=modularity_G.get)]
# having lists with nodes being in different clusters
partition_G[group] = {}
for com in set(p_G[group].values()) :
partition_G[group][com] = [nodes for nodes in p_G[group].keys() if p_G[group][nodes] == com]
# clusters
for group in cor_goals_groups_2.keys():
print(group)
print(partition_G[group])
print('-------------------------')
g_part = open('distance_cor/goals/partition_groups.pkl', 'wb')
pickle.dump(partition_G, g_part)
g_part.close()
# centralities
for group in cor_goals_groups_2.keys():
print(group)
print(centrality_G[group])
print('-------------------------')
g_cent = open('distance_cor/goals/centrality_groups.pkl', 'wb')
pickle.dump(centrality_G, g_cent)
g_cent.close()
# degrees
for group in cor_goals_groups_2.keys():
print(group)
print(degree_G[group])
print('-------------------------')
g_deg = open('distance_cor/goals/degree_groups.pkl', 'wb')
pickle.dump(degree_G, g_deg)
g_deg.close()
# densities
for group in cor_goals_groups_2.keys():
print(group)
print(density_G[group])
print('-------------------------')
g_dens = open('distance_cor/goals/density_groups.pkl', 'wb')
pickle.dump(degree_G, g_dens)
g_dens.close()
```
### Eigenvector visualisation
```
def get_image(goal):
return OffsetImage(plt.imread('utils/images/E_SDG goals_icons-individual-rgb-{}.png'.format(goal)), zoom=0.06)
for group in cor_goals_groups_2.keys():
# separating goals from their centralities
x = []
y = []
for cent in centrality_G[group]:
x.append(cent[0])
y.append(float(cent[1]))
fig, ax = plt.subplots(figsize=(24,16))
#plt.tight_layout()
plt.title('{}'.format(group), y=1.05, fontdict={'fontsize': 52})
ax.scatter(x, y)
# adding images
for x0, y0, goal in zip(x, y, list(nodes)):
ab = AnnotationBbox(get_image(goal), (x0, y0), frameon=False)
ax.add_artist(ab)
ax.set_xticks([])
ax.set_yticklabels([0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7], fontsize=28)
ax.yaxis.grid()
ax.set_ylim(0, 0.75)
ax.set_ylabel('Eigenvector centrality', labelpad=24, fontdict={'fontsize': 38})
ax.set_xlabel('Variables (SDGs + climate change)', labelpad=54, fontdict={'fontsize': 38})
plt.savefig('distance_cor/goals/{}_eigenvector_centrality.png'.format(group), format='png')
plt.show()
```
### Cluster visualisation
```
# plotting clusters in networks with weighted edges
from matplotlib.patches import Polygon
from matplotlib.collections import PatchCollection
layout = 'multipartite'
for group in cor_goals_groups_2.keys():
G_G = nx.Graph()
for key, value in dcor_dict_g[group].items():
G_G.add_edge(int(key[0]), int(key[1]), weight=value[0], color=sns.color_palette("Reds", 100)[int(np.around(value[0]*100))], alpha=value[0])
for node in nodes:
G_G.nodes[node]['subset'] = p_G[group][node]
if layout == 'circular':
pos = nx.circular_layout(G_G)
elif layout == 'spring':
pos = nx.spring_layout(G_G, iterations=100, seed=42)
elif layout == 'multipartite':
pos = nx.multipartite_layout(G_G)
plt.figure(figsize=(24,16))
# nodes
nx.draw_networkx_nodes(G_G, pos, node_size=1000)
# labels
nx.draw_networkx_labels(G_G, pos, font_size=46, font_family='sans-serif')
nodes = G_G.nodes()
edges = G_G.edges()
colors = [G_G[u][v]['color'] for u,v in edges]
weights = [G_G[u][v]['weight'] for u,v in edges]
nx.draw_networkx(G_G, pos, with_labels=False, edgelist=edges, edge_color=colors, node_color='white', node_size=1000, width=np.multiply(weights,25))
ax=plt.gca()
fig=plt.gcf()
trans = ax.transData.transform
trans_axes = fig.transFigure.inverted().transform
imsize = 0.08 # this is the image size
plt.title('{}'.format(group), y=1.05, fontdict={'fontsize': 52})
for node in G_G.nodes():
x,y = pos[node]
xx,yy = trans((x,y)) # figure coordinates
xa,ya = trans_axes((xx,yy)) # axes coordinates
a = plt.axes([xa-imsize/2.0,ya-imsize/2.0, imsize, imsize])
a.imshow(mpimg.imread('utils/images/E_SDG goals_icons-individual-rgb-{}.png'.format(node)))
a.axis('off')
# drawing polygon around nodes of clusters with maximum modularity
clusters = []
for com, goals in partition_G[group].items():
position = []
for goal in goals:
x,y = pos[goal]
position.append((x,y))
positions = []
for i in range(6000):
np.random.shuffle(position)
positions.extend(position)
# polygens
polygon = Polygon(positions, closed=False)
clusters.append(polygon)
np.random.seed(72)
colors = 100*np.random.rand(len(clusters))
p = PatchCollection(clusters, alpha=0.4)
p.set_array(np.array(colors))
ax.add_collection(p)
plt.axis('off')
ax.axis('off')
plt.savefig('distance_cor/goals/{}_{}_network_logos_cluster.png'.format(group, layout), format='png')
plt.show()
```
| true |
code
| 0.204819 | null | null | null | null |
|
# 7 - Functions
```
from scipy import *
from matplotlib.pyplot import *
%matplotlib inline
```
## Basics
```
def subtract(x1, x2):
return x1 - x2
r = subtract(5.0, 4.3)
r
```
## Parameters and Arguments
```
z = 3
e = subtract(5,z)
e
z = 3
e = subtract(x2 = z, x1 = 5)
e
```
### Changing Arguments
```
def subtract(x1, x2):
z = x1 - x2
x2 = 50.
return z
a = 20.
b = subtract(10, a) # returns -10.
b
a # still has the value 20
def subtract(x):
z = x[0] - x[1]
x[1] = 50.
return z
a = [10,20]
b = subtract(a) # returns -10
b
a # is now [10, 50.0]
```
### Access to variables defined outside the local namespace
```
import numpy as np # here the variable np is defined
def sqrt(x):
return np.sqrt(x) # we use np inside the function
a = 3
def multiply(x):
return a * x # bad style: access to the variable a defined outside
multiply(4) # returns 12
a=4
multiply(4) # returns 16
def multiply(x, a):
return a * x
```
### Default Arguments
```
import scipy.linalg as sl
sl.norm(identity(3))
sl.norm(identity(3), ord = 'fro')
sl.norm(identity(3), 'fro')
def subtract(x1, x2 = 0):
return x1 - x2
subtract(5)
def my_list(x1, x2 = []):
x2.append(x1)
return x2
my_list(1) # returns [1]
my_list(2) # returns [1,2]
```
### Variable Number of Arguments
```
data = [[1,2],[3,4]]
style = dict({'linewidth':3,'marker':'o','color':'green'})
plot(*data, **style)
```
## Return Values
```
def complex_to_polar(z):
r = sqrt(z.real ** 2 + z.imag ** 2)
phi = arctan2(z.imag, z.real)
return (r,phi) # here the return object is formed
z = 3 + 5j # here we define a complex number
a = complex_to_polar(z)
a
r = a[0]
r
phi = a[1]
phi
r,phi = complex_to_polar(z)
r,phi
def append_to_list(L, x):
L.append(x)
def function_with_dead_code(x):
return 2 * x
y = x ** 2 # these two lines ...
return y # ... are never executed!
```
## Recursive functions
```
def chebyshev(n, x):
if n == 0:
return 1.
elif n == 1:
return x
else:
return 2. * x * chebyshev(n - 1, x) \
- chebyshev(n - 2 ,x)
chebyshev(5, 0.52) # returns 0.39616645119999994
```
## Function Documentation
```
def newton(f, x0):
"""
Newton's method for computing a zero of a function
on input:
f (function) given function f(x)
x0 (float) initial guess
on return:
y (float) the approximated zero of f
"""
...
help(newton)
```
## Functions are Objects
```
def square(x):
"""Return the square of `x`"""
return x ** 2
square(4) # 16
sq = square # now sq is the same as square
sq(4) # 16
print(newton(sq, .2)) # passing as argument
del sq
```
### Partial Application
```
import functools
def sin_omega(t, freq):
return sin(2 * pi * freq * t)
def make_sine(frequency):
return functools.partial(sin_omega, freq = frequency)
sin1=make_sine(1)
sin1(2)
def make_sine(freq):
"Make a sine function with frequency freq"
def mysine(t):
return sin_omega(t, freq)
return mysine
sin1=make_sine(1)
sin1(2)
```
## Anonymous Functions - the `lambda` keyword
```
import scipy.integrate as si
si.quad(lambda x: x ** 2 + 5, 0, 1)
parabola = lambda x: x ** 2 + 5
parabola(3) # gives 14
def parabola(x):
return x ** 2 + 5
parabola(3)
import scipy.integrate as si
for iteration in range(3):
print(si.quad(lambda x: sin_omega(x, iteration * pi), 0, pi / 2.) )
```
## Functions as Decorators
```
def how_sparse(A):
return len(A.reshape(-1).nonzero()[0])
how_sparse([1,2,0]) # returns an error
def cast2array(f):
def new_function(obj):
fA = f(array(obj))
return fA
return new_function
@cast2array
def how_sparse(A):
return len(A.reshape(-1).nonzero()[0])
how_sparse([1,2,0]) # returns no error any more
```
| true |
code
| 0.607925 | null | null | null | null |
|
# Introduction to Random Forests
## Resources
This notebook is designed around the theory from the fast.ai lectures (course18) with added comments and details found in the lectures and online. The entire course can be found here: http://course18.fast.ai/ml.html.
### Links
- Lecture notebook: https://github.com/fastai/fastai/blob/master/courses/ml1/lesson1-rf.ipynb
## About Random Forests
"**Random forests** or **random decision forests** are an ensemble learning method for *classification*, *regression* and other tasks that operates by constructing a multitude of decision trees at training time and outputting the class that is the mode of the classes (classification) or mean prediction (regression) of the individual trees. Random decision forests correct for decision trees' habit of overfitting to their training set." - https://en.wikipedia.org/wiki/Random_forest
## Imports
```
# Notebook is automatically updated if the module source code is edited
%load_ext autoreload
%autoreload 2
# Show plots within the notebook
%matplotlib inline
import re
import math
import numpy as np
import pandas as pd
from os import makedirs
from dateutil.parser import parse
from pandas_summary import DataFrameSummary
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from IPython.display import display
from sklearn import metrics
PATH = '../data/bulldozers/'
```
## Fast.ai Methods
The following methods are designed by fast.ai and added to the notebook to work according to the details found in the lecture.
```
from sklearn_pandas import DataFrameMapper
from sklearn.preprocessing import LabelEncoder, Imputer, StandardScaler
from pandas.api.types import is_string_dtype, is_numeric_dtype, is_categorical_dtype
from sklearn.ensemble import forest
from sklearn.tree import export_graphviz
def set_plot_sizes(sml, med, big):
plt.rc('font', size=sml) # controls default text sizes
plt.rc('axes', titlesize=sml) # fontsize of the axes title
plt.rc('axes', labelsize=med) # fontsize of the x and y labels
plt.rc('xtick', labelsize=sml) # fontsize of the tick labels
plt.rc('ytick', labelsize=sml) # fontsize of the tick labels
plt.rc('legend', fontsize=sml) # legend fontsize
plt.rc('figure', titlesize=big) # fontsize of the figure title
def parallel_trees(m, fn, n_jobs=8):
return list(ProcessPoolExecutor(n_jobs).map(fn, m.estimators_))
def draw_tree(t, df, size=10, ratio=0.6, precision=0):
""" Draws a representation of a random forest in IPython.
Parameters:
-----------
t: The tree you wish to draw
df: The data used to train the tree. This is used to get the names of the features.
"""
s=export_graphviz(t, out_file=None, feature_names=df.columns, filled=True,
special_characters=True, rotate=True, precision=precision)
IPython.display.display(graphviz.Source(re.sub('Tree {',
f'Tree {{ size={size}; ratio={ratio}', s)))
def combine_date(years, months=1, days=1, weeks=None, hours=None, minutes=None,
seconds=None, milliseconds=None, microseconds=None, nanoseconds=None):
years = np.asarray(years) - 1970
months = np.asarray(months) - 1
days = np.asarray(days) - 1
types = ('<M8[Y]', '<m8[M]', '<m8[D]', '<m8[W]', '<m8[h]',
'<m8[m]', '<m8[s]', '<m8[ms]', '<m8[us]', '<m8[ns]')
vals = (years, months, days, weeks, hours, minutes, seconds,
milliseconds, microseconds, nanoseconds)
return sum(np.asarray(v, dtype=t) for t, v in zip(types, vals)
if v is not None)
def get_sample(df,n):
""" Gets a random sample of n rows from df, without replacement.
Parameters:
-----------
df: A pandas data frame, that you wish to sample from.
n: The number of rows you wish to sample.
Returns:
--------
return value: A random sample of n rows of df.
Examples:
---------
>>> df = pd.DataFrame({'col1' : [1, 2, 3], 'col2' : ['a', 'b', 'a']})
>>> df
col1 col2
0 1 a
1 2 b
2 3 a
>>> get_sample(df, 2)
col1 col2
1 2 b
2 3 a
"""
idxs = sorted(np.random.permutation(len(df))[:n])
return df.iloc[idxs].copy()
def add_datepart(df, fldname, drop=True, time=False, errors="raise"):
"""add_datepart converts a column of df from a datetime64 to many columns containing
the information from the date. This applies changes inplace.
Parameters:
-----------
df: A pandas data frame. df gain several new columns.
fldname: A string that is the name of the date column you wish to expand.
If it is not a datetime64 series, it will be converted to one with pd.to_datetime.
drop: If true then the original date column will be removed.
time: If true time features: Hour, Minute, Second will be added.
Examples:
---------
>>> df = pd.DataFrame({ 'A' : pd.to_datetime(['3/11/2000', '3/12/2000', '3/13/2000'], infer_datetime_format=False) })
>>> df
A
0 2000-03-11
1 2000-03-12
2 2000-03-13
>>> add_datepart(df, 'A')
>>> df
AYear AMonth AWeek ADay ADayofweek ADayofyear AIs_month_end AIs_month_start AIs_quarter_end AIs_quarter_start AIs_year_end AIs_year_start AElapsed
0 2000 3 10 11 5 71 False False False False False False 952732800
1 2000 3 10 12 6 72 False False False False False False 952819200
2 2000 3 11 13 0 73 False False False False False False 952905600
"""
fld = df[fldname]
fld_dtype = fld.dtype
if isinstance(fld_dtype, pd.core.dtypes.dtypes.DatetimeTZDtype):
fld_dtype = np.datetime64
if not np.issubdtype(fld_dtype, np.datetime64):
df[fldname] = fld = pd.to_datetime(fld, infer_datetime_format=True, errors=errors)
targ_pre = re.sub('[Dd]ate$', '', fldname)
attr = ['Year', 'Month', 'Week', 'Day', 'Dayofweek', 'Dayofyear',
'Is_month_end', 'Is_month_start', 'Is_quarter_end', 'Is_quarter_start', 'Is_year_end', 'Is_year_start']
if time: attr = attr + ['Hour', 'Minute', 'Second']
for n in attr: df[targ_pre + n] = getattr(fld.dt, n.lower())
df[targ_pre + 'Elapsed'] = fld.astype(np.int64) // 10 ** 9
if drop: df.drop(fldname, axis=1, inplace=True)
def is_date(x): return np.issubdtype(x.dtype, np.datetime64)
def train_cats(df):
"""Change any columns of strings in a panda's dataframe to a column of
categorical values. This applies the changes inplace.
Parameters:
-----------
df: A pandas dataframe. Any columns of strings will be changed to
categorical values.
Examples:
---------
>>> df = pd.DataFrame({'col1' : [1, 2, 3], 'col2' : ['a', 'b', 'a']})
>>> df
col1 col2
0 1 a
1 2 b
2 3 a
note the type of col2 is string
>>> train_cats(df)
>>> df
col1 col2
0 1 a
1 2 b
2 3 a
now the type of col2 is category
"""
for n,c in df.items():
if is_string_dtype(c): df[n] = c.astype('category').cat.as_ordered()
def apply_cats(df, trn):
"""Changes any columns of strings in df into categorical variables using trn as
a template for the category codes.
Parameters:
-----------
df: A pandas dataframe. Any columns of strings will be changed to
categorical values. The category codes are determined by trn.
trn: A pandas dataframe. When creating a category for df, it looks up the
what the category's code were in trn and makes those the category codes
for df.
Examples:
---------
>>> df = pd.DataFrame({'col1' : [1, 2, 3], 'col2' : ['a', 'b', 'a']})
>>> df
col1 col2
0 1 a
1 2 b
2 3 a
note the type of col2 is string
>>> train_cats(df)
>>> df
col1 col2
0 1 a
1 2 b
2 3 a
now the type of col2 is category {a : 1, b : 2}
>>> df2 = pd.DataFrame({'col1' : [1, 2, 3], 'col2' : ['b', 'a', 'a']})
>>> apply_cats(df2, df)
col1 col2
0 1 b
1 2 a
2 3 a
now the type of col is category {a : 1, b : 2}
"""
for n,c in df.items():
if (n in trn.columns) and (trn[n].dtype.name=='category'):
df[n] = c.astype('category').cat.as_ordered()
df[n].cat.set_categories(trn[n].cat.categories, ordered=True, inplace=True)
def fix_missing(df, col, name, na_dict):
""" Fill missing data in a column of df with the median, and add a {name}_na column
which specifies if the data was missing.
Parameters:
-----------
df: The data frame that will be changed.
col: The column of data to fix by filling in missing data.
name: The name of the new filled column in df.
na_dict: A dictionary of values to create na's of and the value to insert. If
name is not a key of na_dict the median will fill any missing data. Also
if name is not a key of na_dict and there is no missing data in col, then
no {name}_na column is not created.
Examples:
---------
>>> df = pd.DataFrame({'col1' : [1, np.NaN, 3], 'col2' : [5, 2, 2]})
>>> df
col1 col2
0 1 5
1 nan 2
2 3 2
>>> fix_missing(df, df['col1'], 'col1', {})
>>> df
col1 col2 col1_na
0 1 5 False
1 2 2 True
2 3 2 False
>>> df = pd.DataFrame({'col1' : [1, np.NaN, 3], 'col2' : [5, 2, 2]})
>>> df
col1 col2
0 1 5
1 nan 2
2 3 2
>>> fix_missing(df, df['col2'], 'col2', {})
>>> df
col1 col2
0 1 5
1 nan 2
2 3 2
>>> df = pd.DataFrame({'col1' : [1, np.NaN, 3], 'col2' : [5, 2, 2]})
>>> df
col1 col2
0 1 5
1 nan 2
2 3 2
>>> fix_missing(df, df['col1'], 'col1', {'col1' : 500})
>>> df
col1 col2 col1_na
0 1 5 False
1 500 2 True
2 3 2 False
"""
if is_numeric_dtype(col):
if pd.isnull(col).sum() or (name in na_dict):
df[name+'_na'] = pd.isnull(col)
filler = na_dict[name] if name in na_dict else col.median()
df[name] = col.fillna(filler)
na_dict[name] = filler
return na_dict
def numericalize(df, col, name, max_n_cat):
""" Changes the column col from a categorical type to it's integer codes.
Parameters:
-----------
df: A pandas dataframe. df[name] will be filled with the integer codes from
col.
col: The column you wish to change into the categories.
name: The column name you wish to insert into df. This column will hold the
integer codes.
max_n_cat: If col has more categories than max_n_cat it will not change the
it to its integer codes. If max_n_cat is None, then col will always be
converted.
Examples:
---------
>>> df = pd.DataFrame({'col1' : [1, 2, 3], 'col2' : ['a', 'b', 'a']})
>>> df
col1 col2
0 1 a
1 2 b
2 3 a
note the type of col2 is string
>>> train_cats(df)
>>> df
col1 col2
0 1 a
1 2 b
2 3 a
now the type of col2 is category { a : 1, b : 2}
>>> numericalize(df, df['col2'], 'col3', None)
col1 col2 col3
0 1 a 1
1 2 b 2
2 3 a 1
"""
if not is_numeric_dtype(col) and ( max_n_cat is None or len(col.cat.categories)>max_n_cat):
df[name] = pd.Categorical(col).codes+1
def scale_vars(df, mapper):
warnings.filterwarnings('ignore', category=sklearn.exceptions.DataConversionWarning)
if mapper is None:
map_f = [([n],StandardScaler()) for n in df.columns if is_numeric_dtype(df[n])]
mapper = DataFrameMapper(map_f).fit(df)
df[mapper.transformed_names_] = mapper.transform(df)
return mapper
def proc_df(df, y_fld=None, skip_flds=None, ignore_flds=None, do_scale=False, na_dict=None,
preproc_fn=None, max_n_cat=None, subset=None, mapper=None):
""" proc_df takes a data frame df and splits off the response variable, and
changes the df into an entirely numeric dataframe. For each column of df
which is not in skip_flds nor in ignore_flds, na values are replaced by the
median value of the column.
Parameters:
-----------
df: The data frame you wish to process.
y_fld: The name of the response variable
skip_flds: A list of fields that dropped from df.
ignore_flds: A list of fields that are ignored during processing.
do_scale: Standardizes each column in df. Takes Boolean Values(True,False)
na_dict: a dictionary of na columns to add. Na columns are also added if there
are any missing values.
preproc_fn: A function that gets applied to df.
max_n_cat: The maximum number of categories to break into dummy values, instead
of integer codes.
subset: Takes a random subset of size subset from df.
mapper: If do_scale is set as True, the mapper variable
calculates the values used for scaling of variables during training time (mean and standard deviation).
Returns:
--------
[x, y, nas, mapper(optional)]:
x: x is the transformed version of df. x will not have the response variable
and is entirely numeric.
y: y is the response variable
nas: returns a dictionary of which nas it created, and the associated median.
mapper: A DataFrameMapper which stores the mean and standard deviation of the corresponding continuous
variables which is then used for scaling of during test-time.
Examples:
---------
>>> df = pd.DataFrame({'col1' : [1, 2, 3], 'col2' : ['a', 'b', 'a']})
>>> df
col1 col2
0 1 a
1 2 b
2 3 a
note the type of col2 is string
>>> train_cats(df)
>>> df
col1 col2
0 1 a
1 2 b
2 3 a
now the type of col2 is category { a : 1, b : 2}
>>> x, y, nas = proc_df(df, 'col1')
>>> x
col2
0 1
1 2
2 1
>>> data = DataFrame(pet=["cat", "dog", "dog", "fish", "cat", "dog", "cat", "fish"],
children=[4., 6, 3, 3, 2, 3, 5, 4],
salary=[90, 24, 44, 27, 32, 59, 36, 27])
>>> mapper = DataFrameMapper([(:pet, LabelBinarizer()),
([:children], StandardScaler())])
>>>round(fit_transform!(mapper, copy(data)), 2)
8x4 Array{Float64,2}:
1.0 0.0 0.0 0.21
0.0 1.0 0.0 1.88
0.0 1.0 0.0 -0.63
0.0 0.0 1.0 -0.63
1.0 0.0 0.0 -1.46
0.0 1.0 0.0 -0.63
1.0 0.0 0.0 1.04
0.0 0.0 1.0 0.21
"""
#if not ignore_flds: ignore_flds=[]
if not skip_flds: skip_flds=[]
if subset: df = get_sample(df,subset)
#else: df = df.copy()
df = df.copy()
#ignored_flds = df.loc[:, ignore_flds]
#df.drop(ignore_flds, axis=1, inplace=True)
if preproc_fn: preproc_fn(df)
#if y_fld is None: y = None
#else:
# if not is_numeric_dtype(df[y_fld]): df[y_fld] = pd.Categorical(df[y_fld]).codes
# y = df[y_fld].values
# skip_flds += [y_fld]
y = df[y_fld].values
df.drop(skip_flds+[y_fld], axis=1, inplace=True)
if na_dict is None: na_dict = {}
else: na_dict = na_dict.copy()
#na_dict_initial = na_dict.copy()
for n,c in df.items(): na_dict = fix_missing(df, c, n, na_dict)
#if len(na_dict_initial.keys()) > 0:
# df.drop([a + '_na' for a in list(set(na_dict.keys()) - set(na_dict_initial.keys()))], axis=1, inplace=True)
if do_scale: mapper = scale_vars(df, mapper)
for n,c in df.items(): numericalize(df, c, n, max_n_cat)
#df = pd.get_dummies(df, dummy_na=True)
#df = pd.concat([ignored_flds, df], axis=1)
#res = [df, y, na_dict]
#if do_scale: res = res + [mapper]
#return res
res = [pd.get_dummies(df, dummy_na=True), y]
if not do_scale: return res
return res + [mapper]
def rf_feat_importance(m, df):
return pd.DataFrame({'cols':df.columns, 'imp':m.feature_importances_}
).sort_values('imp', ascending=False)
def set_rf_samples(n):
""" Changes Scikit learn's random forests to give each tree a random sample of
n random rows.
"""
forest._generate_sample_indices = (lambda rs, n_samples:
forest.check_random_state(rs).randint(0, n_samples, n))
def reset_rf_samples():
""" Undoes the changes produced by set_rf_samples.
"""
forest._generate_sample_indices = (lambda rs, n_samples:
forest.check_random_state(rs).randint(0, n_samples, n_samples))
def get_nn_mappers(df, cat_vars, contin_vars):
# Replace nulls with 0 for continuous, "" for categorical.
for v in contin_vars: df[v] = df[v].fillna(df[v].max()+100,)
for v in cat_vars: df[v].fillna('#NA#', inplace=True)
# list of tuples, containing variable and instance of a transformer for that variable
# for categoricals, use LabelEncoder to map to integers. For continuous, standardize
cat_maps = [(o, LabelEncoder()) for o in cat_vars]
contin_maps = [([o], StandardScaler()) for o in contin_vars]
```
## Load Dataset
Load the dataset as a DataFrame by reading the .csv file using pandas.
```
df_raw = pd.read_csv(f'{PATH}Train.csv', low_memory=False, parse_dates=["saledate"])
```
## Display Data
It is important to look at the data found in the dataset, to make sure that you understand the format, how it is stored, what type of values it holds, etc. Even if you have read descriptions about your data, the actual data may not be what you expect.
```
def display_all(df):
with pd.option_context("display.max_rows", 1000, "display.max_columns", 1000):
display(df)
display_all(df_raw.tail().T)
display_all(df_raw.describe(include='all').T)
```
## Metric
It is important to note what metric is being used for a project. Generally, selecting the metric(s) is an important part of the project setup. However, in this case - Kaggle tells us what metric to use: RMSLE (root mean squared log error) between the actual and predicted auction prices. Therefore we take the log of the prices, so that RMSE will give us what we need.
```
df_raw.SalePrice = np.log(df_raw.SalePrice)
```
## Feature Engineering
Feature engineering is an important part of all machine learning tasks. The dataset includes a limited amount of data and it is therefore important to expand the dataset with as much information as possible. This is done by feature engineering, which extends the dataset with relevant data.
```
df_raw['saledate']
add_datepart(df_raw, 'saledate')
df_raw.saleYear.head()
```
## Continuous and Categorical Variables
The dataset contains a mix of both continuous and categorical variables. This is not recommended for a random forest. The categorical variables are currently stored as strings, which is inefficient and does not provide the numeric coding required for a random forest. It is therefore important to convert the strings to pandas categories.
```
df_raw.head()
for col_name in df_raw.columns:
if(df_raw[col_name].dtype == 'object'):
df_raw[col_name] = df_raw[col_name].astype('category')
print('Process of changing data types has finished executing.')
```
The order of the categorical variables may affect the performance, it is therefore important to set the categories in a meaningful order.
```
df_raw.UsageBand.cat.categories
df_raw.UsageBand.cat.set_categories(['High', 'Medium', 'Low'], ordered=True, inplace=True)
```
## Missing Values
A dataset needs to be without missing values, which cannot be directly passed to a random forest.
```
display_all(df_raw.isnull().sum().sort_index()/len(df_raw))
```
## Store and Load DataFrames
After making changes to the dataframes in a dataset, the current state can be stored and loaded. This process avoids having to re-do all previous steps.
```
makedirs('dfs', exist_ok=True)
df_raw.to_feather('dfs/raw_bulldozers')
df_raw = pd.read_feather('dfs/raw_bulldozers')
```
## Pre-Processing
Before everything is ready for the fitting process, it is necessary to replace categories with their numeric codes, handle missing continuous values, and split the dependent variable into a separate variable.
```
df, y = proc_df(df_raw, y_fld='SalePrice')
df.columns
```
## Fit the Random Forest
Now that the dataset has been prepared, it is ready to fit.
```
m = RandomForestRegressor(n_jobs=-1)
m.fit(df, y)
m.score(df, y)
```
## Validation- and Training Set
An important idea in machine learning is to have separate training and validation data sets. As
```
def split_vals(a,n): return a[:n].copy(), a[n:].copy()
n_valid = 12000 # same as Kaggle's test set size
n_trn = len(df)-n_valid
raw_train, raw_valid = split_vals(df_raw, n_trn)
X_train, X_valid = split_vals(df, n_trn)
y_train, y_valid = split_vals(y, n_trn)
X_train.shape, y_train.shape, X_valid.shape
def rmse(x,y): return math.sqrt(((x-y)**2).mean())
def print_score(m):
res = [rmse(m.predict(X_train), y_train), rmse(m.predict(X_valid), y_valid),
m.score(X_train, y_train), m.score(X_valid, y_valid)]
if hasattr(m, 'oob_score_'): res.append(m.oob_score_)
print(res)
m = RandomForestRegressor(n_jobs=-1)
%time m.fit(X_train, y_train)
print_score(m)
```
| true |
code
| 0.801217 | null | null | null | null |
|
# Homework 1: Preprocessing and Text Classification
Student Name: Jun Luo
Student ID: 792597
Python version used: Python2.7
## General info
<b>Due date</b>: 11pm, Sunday March 18th
<b>Submission method</b>: see LMS
<b>Submission materials</b>: completed copy of this iPython notebook
<b>Late submissions</b>: -20% per day
<b>Marks</b>: 5% of mark for class
<b>Overview</b>: In this homework, you'll be using a corpus of tweets to do tokenisation of hashtags and build polarity classifers using bag of word (BOW) features.
<b>Materials</b>: See the main class LMS page for information on the basic setup required for this class, including an iPython notebook viewer and the python packages NLTK, Numpy, Scipy, Matplotlib, Scikit-Learn, and Gensim. In particular, if you are not using a lab computer which already has it installed, we recommend installing all the data for NLTK, since you will need various parts of it to complete this assignment. You can also use any Python built-in packages, but do not use any other 3rd party packages (the packages listed above are all fine to use); if your iPython notebook doesn't run on the marker's machine, you will lose marks.
<b>Evaluation</b>: Your iPython notebook should run end-to-end without any errors in a few minutes, and you must follow all instructions provided below, including specific implementation requirements and instructions for what needs to be printed (please avoid printing output we don't ask for). The amount each section is worth is given in parenthesis after the instructions. You will be marked not only on the correctness of your methods, but also the quality and efficency of your code: in particular, you should be careful to use Python built-in functions and operators when appropriate and pick descriptive variable names that adhere to <a href="https://www.python.org/dev/peps/pep-0008/">Python style requirements</a>. If you think it might be unclear what you are doing, you should comment your code to help the marker make sense of it.
<b>Extra credit</b>: Each homework has a task which is optional with respect to getting full marks on the assignment, but that can be used to offset any points lost on this or any other homework assignment (but not the final project or the exam). We recommend you skip over this step on your first pass, and come back if you have time: the amount of effort required to receive full marks (1 point) on an extra credit question will be substantially more than earning the same amount of credit on other parts of the homework.
<b>Updates</b>: Any major changes to the assignment will be announced via LMS. Minor changes and clarifications will be announced in the forum on LMS, we recommend you check the forum regularly.
<b>Academic Misconduct</b>: For most people, collaboration will form a natural part of the undertaking of this homework, and we encourge you to discuss it in general terms with other students. However, this ultimately is still an individual task, and so reuse of code or other instances of clear influence will be considered cheating. We will be checking submissions for originality and will invoke the University’s <a href="http://academichonesty.unimelb.edu.au/policy.html">Academic Misconduct policy</a> where inappropriate levels of collusion or plagiarism are deemed to have taken place.
## Preprocessing
<b>Instructions</b>: For this homework we will be using the tweets in the <i>twitter_samples</i> corpus included with NLTK. You should start by accessing these tweets. Use the <i>strings</i> method included in the NLTK corpus reader for <i>twitter_samples</i> to access the tweets (as raw strings). Iterate over the full corpus, and print out the average length, in characters, of the tweets in the corpus. (0.5)
```
import nltk
import nltk.corpus
import numpy
corpus = nltk.corpus.twitter_samples.strings()
total_characters = 0
for tweet in corpus:
total_characters += len(tweet)
print('Average Length:' + str(total_characters*1.0/len(corpus))+' characters')
```
<b>Instructions</b>: Hashtags (i.e. topic tags which start with #) pose an interesting tokenisation problem because they often include multiple words written without spaces or capitalization. You should use a regular expression to extract all hashtags of length 8 or longer which consist only of lower case letters (other than the # at the beginning, of course, though this should be stripped off as part of the extraction process). Do <b>not</b> tokenise the entire tweet as part of this process. The hashtag might occur at the beginning or the end of the tweet; you should double-check that you aren't missing any. After you have collected them into a list, print out number of hashtags you have collected: for full credit, you must get the exact number that we expect. (1.0)
```
"""
Daniel's post in the discussion board:
Assume the boundaries are whitespaces. So hashtags need to have whitespaces before and after
(unless they occur in the beginning or the end of the tweet).
Cases like #thisperson's should not be captured. Yes, in real world we would probably like to capture this phenomenon as well.
But to do this you need to assume some level of tokenisation already (splitting the 's) and you should not tokenise the tweet
in that question (this is in the instructions).
"""
import re
hashtags = []
# Collect all the hashtags into an array
for tweet in corpus:
array = re.findall(r"(?:^|(?<=\s))(?:#)([a-z]{8,})(?:$|(?=\s))", tweet)
for hashtag in array:
hashtags.append(hashtag)
print('Total Number of Hashtags:'+str(len(hashtags)))
```
<b>Instructions</b>: Now, tokenise the hashtags you've collected. To do this, you should implement a reversed version of the MaxMatch algorithm discussed in class (and in the reading), where matching begins at the end of the hashtag and progresses backwards. NLTK has a list of words that you can use for matching, see starter code below. Be careful about efficiency with respect to doing word lookups. One extra challenge you have to deal with is that the provided list of words includes only lemmas: your MaxMatch algorithm should match inflected forms by converting them into lemmas using the NLTK lemmatiser before matching. Note that the list of words is incomplete, and, if you are unable to make any longer match, your code should default to matching a single letter. Create a new list of tokenised hashtags (this should be a list of lists of strings) and use slicing to print out the last 20 hashtags in the list. (1.0)
```
from nltk import word_tokenize
from nltk.stem import WordNetLemmatizer
lemmatizer = WordNetLemmatizer()
def reverse_max_match(sentence, dictionary):
if len(sentence)==0:
return []
for i in reversed(range(1,len(sentence)+1)):
firstword = lemmatizer.lemmatize(sentence[-i:])
remainder = sentence[:-i]
if firstword in dictionary:
return reverse_max_match(remainder,dictionary)+[firstword]
# if no word was found, than make a one-character word
firstword = lemmatizer.lemmatize(sentence[-1:])
remainder = sentence[:-1]
return reverse_max_match(remainder,dictionary)+[firstword]
words = nltk.corpus.words.words() # words is a Python list
# print(reverse_max_match('flowers',words))
# print(len(hashtags))
counter = 0
result2 = []
for hashtag in hashtags:
counter+=1
# if(counter%100 == 0):
# print(counter)
result2.append(reverse_max_match(hashtag,words))
print(result2[-20:])
```
### Extra Credit (Optional)
<b>Instructions</b>: Implement the forward version of the MaxMatch algorithm as well, and print out all the hashtags which give different results for the two versions of MaxMatch. Your main task is to come up with a good way to select which of the two segmentations is better for any given case, and demonstrate that it works significantly better than using a single version of the algorithm for all hashtags. (1.0)
#### Answer:
The method I use to select the better segmentation is Maximum Known Matching (MKM).(http://cs.uccs.edu/~jkalita/work/reu/REU2015/FinalPapers/05Reuter.pdf)
The score is calculated using the formular below:
$ Score(s) = \sqrt[i]{\sum_{k=1}^i len(w_{k})^2}$
Where len(w) returns the length of a word w, and s is a segmentation into i words.
The higher the score is, the better a segmentation is.
It is obvious to see that max(score_a, score_b) >= score_a, max(score_a, score_b) >= score_b
To illustrate whether it is significantly better, 2 scores are calculated:
1. improvement_forward: Sum of improvement of using two segmentations comparing to only using the forward max_match
2. improvement_reverse: Sum of improvement of using two segmentations comparing to only using the reverse max_match
Then we will calculate the average improvement of score:
average_improve_reverse = improve_reverse/(length of the corpus)
average_improve_forward = improve_forward/(length of the corpus)
The result below shows that choosing the the matching sequence with the highest score is better than using only one single mathching algorithm.
##### It gets about 6% improvement to using single reversed maxMatch, and 4% improvement comparing to using single forward maxMatch.
The code below demonstrate the forward max_match algorithm and the score calculation process.
```
def max_match(sentence, dictionary):
if len(sentence)==0:
return []
for i in reversed(range(1,len(sentence)+1)):
firstword = lemmatizer.lemmatize(sentence[:i])
remainder = sentence[i:]
if firstword in dictionary:
return [firstword]+max_match(remainder,dictionary)
# if no word was found, than make a one-character word
firstword = lemmatizer.lemmatize(sentence[:1])
remainder = sentence[1:]
return [firstword]+max_match(remainder,dictionary)
words = nltk.corpus.words.words() # words is a Python list
# print(words[:100])
# print(len(hashtags))
counter = 0
result = []
for hashtag in hashtags:
counter+=1
# if(counter%100 == 0):
# print(counter)
result.append(max_match(hashtag,words))
print(result)
for index,value in enumerate(result2):
# print(result2[index])
if not result2[index] == result[index]:
print(result2[index])
print(result[index])
print('\r\n')
"""Select the best one among reverse and forwad"""
improvement_forward = 0
improvement_reverse = 0
def Score(arr):
sum_length_square = 0
for word in arr:
sum_length_square += len(word)**2
return (sum_length_square*1.0)**(1/float(len(arr)))
# print(Score([u'a', u'th', u'aba', u'ca']))
for index,value in enumerate(result2):
# print(hashtags[index])
# if result2[index] == result[index]:
# print(result2[index])
# print('\r\n')
# else:
# result2_1char = [ele for ele in result2[index] if len(ele)==1]
# print(result2[index])
# print(Score(result2[index]))
# print(result[index])
# print(Score(result[index]))
# print('\r\n')
improvement_reverse += max(Score(result[index]),Score(result2[index]))/Score(result[index])-1
improvement_forward += max(Score(result[index]),Score(result2[index]))/Score(result2[index])-1
# Score_B += max(Score(result[index]),Score(result2[index]))
# improve_reverse = Score_B*1.0/Score_R*1.0 - 1
# improve_forward = Score_B*1.0/Score_F*1.0 - 1
print('Improved Reverse:'+ str(improvement_reverse*100/len(result))+'%')
print('Improved Forward:'+ str(improvement_forward*100/len(result))+'%')
```
## Text classification (Not Optional)
<b>Instructions</b>: The twitter_sample corpus has two subcorpora corresponding to positive and negative tweets. You can access already tokenised versions using the <i> tokenized </i> method, as given in the code sample below. Iterate through these two corpora and build training, development, and test sets for use with Scikit-learn. You should exclude stopwords (from the built-in NLTK list) and tokens with non-alphabetic characters (this is very important you do this because emoticons were used to build the corpus, if you don't remove them performance will be artificially high). You should randomly split each subcorpus, using 80% of the tweets for training, 10% for development, and 10% for testing; make sure you do this <b>before</b> combining the tweets from the positive/negative subcorpora, so that the sets are <i>stratified</i>, i.e. the exact ratio of positive and negative tweets is preserved across the three sets. (1.0)
```
import numpy as np
positive_tweets = nltk.corpus.twitter_samples.tokenized("positive_tweets.json")
negative_tweets = nltk.corpus.twitter_samples.tokenized("negative_tweets.json")
np.random.shuffle(positive_tweets)
np.random.shuffle(negative_tweets)
train_positive = positive_tweets[:int(len(positive_tweets)*0.8)]
train_negative = negative_tweets[:int(len(negative_tweets)*0.8)]
dev_positive = positive_tweets[int(len(positive_tweets)*0.8):int(len(positive_tweets)*0.9)]
dev_negative = negative_tweets[int(len(negative_tweets)*0.8):int(len(negative_tweets)*0.9)]
test_positive = positive_tweets[int(len(positive_tweets)*0.9):]
test_negative = negative_tweets[int(len(negative_tweets)*0.9):]
from nltk.corpus import stopwords
stopwords = set(stopwords.words('english'))
from sklearn.feature_extraction import DictVectorizer
def get_BOW_lowered_no_stopwords(text):
BOW = {}
for word in text:
word = word.lower()
if word not in stopwords and len(re.findall(r"[^a-z]", word))== 0:
BOW[word] = BOW.get(word,0) + 1
return BOW
def prepare_data(datafile,feature_extractor):
feature_matrix = []
classifications = []
for tweet in datafile:
feature_dict = feature_extractor(tweet)
feature_matrix.append(feature_dict)
vectorizer = DictVectorizer()
dataset = vectorizer.fit_transform(feature_matrix)
return dataset,vectorizer
def fit_data(datafile,feature_extractor, vectorizer):
feature_matrix = []
classifications = []
for tweet in datafile:
feature_dict = feature_extractor(tweet)
feature_matrix.append(feature_dict)
dataset = vectorizer.transform(feature_matrix)
return dataset
dataset, vectorizer = prepare_data(np.concatenate((train_positive,train_negative)), get_BOW_lowered_no_stopwords)
# print(dataset[1])
# dataset._shape
vectorized_dev = fit_data(np.concatenate((dev_positive,dev_negative)), get_BOW_lowered_no_stopwords, vectorizer)
vectorized_test = fit_data(np.concatenate((test_positive,test_negative)), get_BOW_lowered_no_stopwords, vectorizer)
train_X = dataset
train_y = np.concatenate((np.zeros(len(train_positive)),np.ones(len(train_negative))))
from scipy.sparse import coo_matrix
train_X_sparse = coo_matrix(train_X)
from sklearn.utils import shuffle
train_X, train_X_sparse, train_y = shuffle(train_X, train_X_sparse, train_y, random_state=0)
# print(vectorized_dev_positive.shape)
from sklearn.feature_extraction.text import TfidfTransformer
transformer = TfidfTransformer(smooth_idf=False,norm=None)
train_X = transformer.fit_transform(train_X)
dev_X = vectorized_dev
dev_y = np.concatenate((np.zeros(len(dev_positive)),np.ones(len(dev_negative))))
dev_X_sparse = coo_matrix(dev_X)
dev_X, train_X_sparse, dev_y = shuffle(dev_X, dev_X_sparse, dev_y, random_state=0)
dev_X = transformer.transform(dev_X)
test_X = vectorized_test
test_y = np.concatenate((np.zeros(len(test_positive)),np.ones(len(test_negative))))
test_X_sparse = coo_matrix(test_X)
test_X, test_X_sparse, test_y = shuffle(test_X, test_X_sparse, test_y, random_state=0)
test_X = transformer.transform(test_X)
```
<b>Instructions</b>: Now, let's build some classifiers. Here, we'll be comparing Naive Bayes and Logistic Regression. For each, you need to first find a good value for their main regularisation (hyper)parameters, which you should identify using the scikit-learn docs or other resources. Use the development set you created for this tuning process; do <b>not</b> use crossvalidation in the training set, or involve the test set in any way. You don't need to show all your work, but you do need to print out the accuracy with enough different settings to strongly suggest you have found an optimal or near-optimal choice. We should not need to look at your code to interpret the output. (1.0)
```
%matplotlib inline
from sklearn.naive_bayes import MultinomialNB
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
alpha_list = []
score_list = []
for i in range(1,100):
alpha = i*0.1
alpha_list.append(alpha)
nb_cls = MultinomialNB(alpha = alpha)
nb_cls.fit(dev_X, dev_y)
f1 = nb_cls.score(dev_X, dev_y)
score_list.append(f1)
plt.xlabel('Alpha')
plt.ylabel('F1-Score')
plt.title('MultinomialNB Parameter Tuning: Alpha')
plt.plot(alpha_list,score_list,'b-')
plt.show()
optimal_alpha = alpha_list[np.argmax(np.array(score_list))]
print('Optimal value of alpha:'+str(optimal_alpha))
C = [0.001, 0.01, 0.1, 1, 10, 100, 1000]
score_list = []
for c in C:
nb_cls = LogisticRegression(C = c)
nb_cls.fit(train_X, train_y)
f1 = nb_cls.score(dev_X, dev_y)
score_list.append(f1)
plt.xlabel('C')
plt.ylabel('F1-Score')
plt.title('LogisticRegression Parameter Tuning: C, Penalty=L2')
plt.plot(C,score_list,'b-')
plt.show()
score_list_l1 = []
for c in C:
nb_cls = LogisticRegression(C = c,penalty = 'l1')
nb_cls.fit(train_X, train_y)
f1 = nb_cls.score(dev_X, dev_y)
score_list_l1.append(f1)
plt.xlabel('C')
plt.ylabel('F1-Score')
plt.title('LogisticRegression Parameter Tuning: C, Penalty=L1')
plt.plot(C,score_list_l1,'b-')
plt.show()
optimal_c = C[np.argmax(np.array(score_list))]
optimal_penalty = 'l2'
if(np.max(np.array(score_list))<np.max(np.array(score_list_l1))):
optimal_c = C[np.argmax(np.array(score_list_l1))]
optimal_penalty = 'l1'
print('Optimal value of C and Penalty:'+str(optimal_c)+' '+str(optimal_penalty))
```
<b>Instructions</b>: Using the best settings you have found, compare the two classifiers based on performance in the test set. Print out both accuracy and macroaveraged f-score for each classifier. Be sure to label your output. (0.5)
```
from sklearn.naive_bayes import MultinomialNB
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score
nb_cls = MultinomialNB(alpha = optimal_alpha)
nb_cls.fit(train_X, train_y)
y_pred = nb_cls.predict(test_X)
target_names = ['positive','negative']
print('MultinomialNB Classification Report:\r\n')
print(classification_report(test_y,y_pred, target_names=target_names))
print('Accuracy: '+str(accuracy_score(test_y,y_pred)))
lr_cls = LogisticRegression(C = optimal_c, penalty = optimal_penalty)
lr_cls.fit(train_X, train_y)
y_pred = lr_cls.predict(test_X)
print('-------------------------------------------------------------')
print('-------------------------------------------------------------')
print('\r\n\r\nLogisticRegression Classification Report:\r\n')
print(classification_report(test_y,y_pred, target_names=target_names))
print('Accuracy: '+str(accuracy_score(test_y,y_pred)))
```
| true |
code
| 0.278968 | null | null | null | null |
|
PPO Using VAE
# VAE classes
https://github.com/AntixK/PyTorch-VAE/blob/master/models/vanilla_vae.py
```
import torch
from torch import nn
from torch.nn import functional as F
import torch.optim as optim
class VAE(nn.Module):
# Use Linear instead of convs
def __init__(self,
in_channels: int,
latent_dim: int,
hidden_dims = None,
**kwargs) -> None:
super(VAE, self).__init__()
self.latent_dim = latent_dim
out_channels = in_channels
modules = []
if hidden_dims is None:
hidden_dims = [32, 64, 128, 256, 512]
# Build Encoder
for h_dim in hidden_dims:
modules.append(
nn.Sequential(
nn.Linear(in_channels, h_dim),
nn.LeakyReLU())
)
in_channels = h_dim
self.encoder = nn.Sequential(*modules)
self.fc_mu = nn.Linear(hidden_dims[-1], latent_dim)
self.fc_var = nn.Linear(hidden_dims[-1], latent_dim)
# Build Decoder
modules = []
self.decoder_input = nn.Linear(latent_dim, hidden_dims[-1])
hidden_dims.reverse()
for i in range(len(hidden_dims) - 1):
modules.append(
nn.Sequential(
nn.Linear(hidden_dims[i], hidden_dims[i+1]),
nn.LeakyReLU())
)
self.decoder = nn.Sequential(*modules)
self.final_layer = nn.Sequential(
nn.Linear(hidden_dims[-1],hidden_dims[-1]),
nn.LeakyReLU(),
nn.Linear(hidden_dims[-1],out_channels),
nn.Tanh())
def encode(self, input):
"""
Encodes the input by passing through the encoder network
and returns the latent codes.
:param input: (Tensor) Input tensor to encoder [N x C x H x W]
:return: (Tensor) List of latent codes
"""
result = self.encoder(input)
result = torch.flatten(result, start_dim=1)
# Split the result into mu and var components
# of the latent Gaussian distribution
mu = self.fc_mu(result)
log_var = self.fc_var(result)
return [mu, log_var]
def decode(self, z):
"""
Maps the given latent codes
onto the image space.
:param z: (Tensor) [B x D]
:return: (Tensor) [B x C x H x W]
"""
result = self.decoder_input(z)
#result = result.view(-1, 512, 2, 2)
result = self.decoder(result)
result = self.final_layer(result)
return result
def reparameterize(self, mu, logvar):
"""
Reparameterization trick to sample from N(mu, var) from
N(0,1).
:param mu: (Tensor) Mean of the latent Gaussian [B x D]
:param logvar: (Tensor) Standard deviation of the latent Gaussian [B x D]
:return: (Tensor) [B x D]
"""
std = torch.exp(0.5 * logvar)
eps = torch.randn_like(std)
return eps * std + mu
def forward(self, input, **kwargs):
mu, log_var = self.encode(input)
z = self.reparameterize(mu, log_var)
return self.decode(z), input, mu, log_var
def state_dim_reduction(self, state):
mu, log_var = self.encode(state)
z = self.reparameterize(mu, log_var)
return z
def loss_function(self, reconstruction, input, mu, log_var) -> dict:
"""
Computes the VAE loss function.
KL(N(\mu, \sigma), N(0, 1)) = \log \frac{1}{\sigma} + \frac{\sigma^2 + \mu^2}{2} - \frac{1}{2}
:param args:
:param kwargs:
:return:
"""
recons = reconstruction
input = input
mu = mu
log_var = log_var
recons_loss =F.mse_loss(recons, input)
kld_loss = torch.mean(-0.5 * torch.sum(1 + log_var - mu ** 2 - log_var.exp(), dim = 1), dim = 0)
loss = recons_loss + kld_loss
return {'loss': loss, 'Reconstruction_Loss':recons_loss, 'KLD':-kld_loss}
import pandas as pd
class VaeManager():
def __init__(self, vae_model, optimizer, obs_file, batch_size):
self.vae_model = vae_model
self.optimizer = optimizer
self.obs_file = obs_file
self.batch_size = batch_size
def train_step(self, batch):
reconstruction, input, mu, log_var = self.vae_model(batch)
loss = self.vae_model.loss_function(reconstruction, input, mu, log_var)['loss']
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
return loss
def train_with_file(self):
#TODO
df = pd.read_csv(self.fileNames[0])
for index, row in df.iterrows():
pass
def state_dim_reduction(self, state):
return self.vae_model.state_dim_reduction(state)
```
# PPO using VAE
```
# https://github.com/RPC2/PPO
import torch
import torch.nn as nn
class MlpPolicy(nn.Module):
def __init__(self, action_size, input_size=4):
super(MlpPolicy, self).__init__()
self.action_size = action_size
self.input_size = input_size
self.fc1 = nn.Linear(self.input_size, 24)
self.fc2 = nn.Linear(24, 24)
self.fc3_pi = nn.Linear(24, self.action_size)
self.fc3_v = nn.Linear(24, 1)
self.tanh = nn.Tanh()
self.relu = nn.ReLU()
self.softmax = nn.Softmax(dim=-1)
def pi(self, x):
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3_pi(x)
return self.softmax(x)
def v(self, x):
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3_v(x)
return x
class AgentConfig:
# Learning
gamma = 0.99
plot_every = 10
update_freq = 1
k_epoch = 3
learning_rate = 0.02
lmbda = 0.95
eps_clip = 0.2
v_coef = 1
entropy_coef = 0.01
# Memory
memory_size = 400
train_cartpole = True
import torch
import gym
import torch.optim as optim
import torch.nn as nn
import matplotlib.pyplot as plt
import pandas as pd
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
class Agent(AgentConfig):
def __init__(self, env, observation_space):
self.env = env
self.action_size = self.env.action_space.n # 2 for cartpole
if self.train_cartpole:
self.policy_network = MlpPolicy(action_size=self.action_size, input_size = observation_space).to(device)
self.optimizer = optim.Adam(self.policy_network.parameters(), lr=self.learning_rate)
self.scheduler = optim.lr_scheduler.StepLR(self.optimizer, step_size=self.k_epoch,
gamma=0.999)
self.loss = 0
self.criterion = nn.MSELoss()
self.memory = {
'state': [], 'action': [], 'reward': [], 'next_state': [], 'action_prob': [], 'terminal': [], 'count': 0,
'advantage': [], 'td_target': torch.tensor([], dtype=torch.float)
}
def new_random_game(self):
self.env.reset()
action = self.env.action_space.sample()
screen, reward, terminal, info = self.env.step(action)
return screen, reward, action, terminal
def train(self, vae_manager, vae_fit, num_episodes):
step = 0
reward_history = []
avg_reward = []
solved = False
# A new episode
for episode in range (1,num_episodes+1):
start_step = step
episode += 1
episode_length = 0
# Get initial state
state, reward, action, terminal = self.new_random_game()
state_mem = state
state = torch.tensor(state, dtype=torch.float, device=device)
if not vae_fit:
with torch.no_grad():
state = state.unsqueeze(dim=0)
state = vae_manager.state_dim_reduction(state).squeeze()
state_mem = state.tolist()
total_episode_reward = 1
# A step in an episode
while True:
step += 1
episode_length += 1
# Choose action
prob_a = self.policy_network.pi(state)
action = torch.distributions.Categorical(prob_a).sample().item()
# Act
new_state, reward, terminal, _ = self.env.step(action)
new_state_mem = new_state
new_state = torch.tensor(new_state, dtype=torch.float, device=device)
if not vae_fit:
print("Actual state and VAE state:")
print(new_state_mem)
with torch.no_grad():
new_state = new_state.unsqueeze(dim=0)
new_state = vae_manager.state_dim_reduction(new_state).squeeze()
new_state_mem = new_state.tolist()
print(new_state_mem)
reward = -1 if terminal else reward
self.add_memory(state_mem, action, reward/10.0, new_state_mem, terminal, prob_a[action].item())
state = new_state
state_mem = new_state_mem
total_episode_reward += reward
if vae_fit and episode % vae_manager.batch_size == 0:
vae_manager.train_step(torch.tensor(self.memory['state'][-10:], dtype=torch.float, device=device))
if terminal:
episode_length = step - start_step
reward_history.append(total_episode_reward)
avg_reward.append(sum(reward_history[-10:])/10.0)
self.finish_path(episode_length)
print('episode: %.2f, total step: %.2f, last_episode length: %.2f, last_episode_reward: %.2f, '
'loss: %.4f, lr: %.4f' % (episode, step, episode_length, total_episode_reward, self.loss,
self.scheduler.get_last_lr()[0]))
# if not vae_fit:
# print('episode: %.2f, total step: %.2f, last_episode length: %.2f, last_episode_reward: %.2f, '
# 'loss: %.4f, lr: %.4f' % (episode, step, episode_length, total_episode_reward, self.loss,
# self.scheduler.get_last_lr()[0]))
# else:
# print(f'Fitted vae for episode {episode} of {num_episodes}.')
self.env.reset()
break
if episode % self.update_freq == 0:
for _ in range(self.k_epoch):
self.update_network()
if episode % self.plot_every == 0 and not vae_fit:
plot_graph(reward_history, avg_reward)
self.env.close()
def update_network(self):
# get ratio
pi = self.policy_network.pi(torch.tensor(self.memory['state'], dtype=torch.float, device=device))
new_probs_a = torch.gather(pi, 1, torch.tensor(self.memory['action'], device=device))
old_probs_a = torch.tensor(self.memory['action_prob'], dtype=torch.float, device=device)
ratio = torch.exp(torch.log(new_probs_a) - torch.log(old_probs_a))
# surrogate loss
surr1 = ratio * torch.tensor(self.memory['advantage'], dtype=torch.float, device=device)
surr2 = torch.clamp(ratio, 1 - self.eps_clip, 1 + self.eps_clip) * torch.tensor(self.memory['advantage'], dtype=torch.float, device=device)
pred_v = self.policy_network.v(torch.tensor(self.memory['state'], dtype=torch.float, device=device))
v_loss = (0.5 * (pred_v - self.memory['td_target']).pow(2)).to('cpu') # Huber loss
entropy = torch.distributions.Categorical(pi).entropy()
entropy = torch.tensor([[e] for e in entropy])
self.loss = ((-torch.min(surr1, surr2)).to('cpu') + self.v_coef * v_loss - self.entropy_coef * entropy).mean()
self.optimizer.zero_grad()
self.loss.backward()
self.optimizer.step()
self.scheduler.step()
def add_memory(self, s, a, r, next_s, t, prob):
if self.memory['count'] < self.memory_size:
self.memory['count'] += 1
else:
self.memory['state'] = self.memory['state'][1:]
self.memory['action'] = self.memory['action'][1:]
self.memory['reward'] = self.memory['reward'][1:]
self.memory['next_state'] = self.memory['next_state'][1:]
self.memory['terminal'] = self.memory['terminal'][1:]
self.memory['action_prob'] = self.memory['action_prob'][1:]
self.memory['advantage'] = self.memory['advantage'][1:]
self.memory['td_target'] = self.memory['td_target'][1:]
self.memory['state'].append(s)
self.memory['action'].append([a])
self.memory['reward'].append([r])
self.memory['next_state'].append(next_s)
self.memory['terminal'].append([1 - t])
self.memory['action_prob'].append(prob)
def finish_path(self, length):
state = self.memory['state'][-length:]
reward = self.memory['reward'][-length:]
next_state = self.memory['next_state'][-length:]
terminal = self.memory['terminal'][-length:]
td_target = torch.tensor(reward, device=device) + \
self.gamma * self.policy_network.v(torch.tensor(next_state, dtype=torch.float,device=device)) * torch.tensor(terminal, device=device)
delta = (td_target - self.policy_network.v(torch.tensor(state, dtype=torch.float,device=device))).to('cpu')
delta = delta.detach().numpy()
# get advantage
advantages = []
adv = 0.0
for d in delta[::-1]:
adv = self.gamma * self.lmbda * adv + d[0]
advantages.append([adv])
advantages.reverse()
if self.memory['td_target'].shape == torch.Size([1, 0]):
self.memory['td_target'] = td_target.data
else:
self.memory['td_target'] = torch.cat((self.memory['td_target'].to(device), td_target.data), dim=0)
self.memory['advantage'] += advantages
def plot_graph(reward_history, avg_reward):
df = pd.DataFrame({'x': range(len(reward_history)), 'Reward': reward_history, 'Average': avg_reward})
plt.style.use('seaborn-darkgrid')
palette = plt.get_cmap('Set1')
plt.plot(df['x'], df['Reward'], marker='', color=palette(1), linewidth=0.8, alpha=0.9, label='Reward')
# plt.plot(df['x'], df['Average'], marker='', color='tomato', linewidth=1, alpha=0.9, label='Average')
# plt.legend(loc='upper left')
plt.title("CartPole", fontsize=14)
plt.xlabel("episode", fontsize=12)
plt.ylabel("score", fontsize=12)
plt.savefig('score.png')
environment = gym.make('CartPole-v0')
observation_space = environment.observation_space.shape[0]
#Hyperparameters
latent_space = 4 # Feature space after VAE transform
vae_lr = 0.0001
vae_batch_size = 10
existingFile = "" #"drive/MyDrive/Thesis/Code/RL_PCA/feature_data.csv" # Possible existing file name containing observations for VAE fitting
vae_model = VAE(in_channels = observation_space, latent_dim = latent_space).to(device)
vae_optimizer = optim.Adam(params=vae_model.parameters(), lr=vae_lr)
vae_manager = VaeManager(vae_model, vae_optimizer, existingFile, vae_batch_size)
#Fit PCA by getting demo trajectories
if existingFile is None or existingFile == "":
print("Demo Trajectories for fitting VAE")
num_episodes = 300
agent = Agent(environment, observation_space)
agent.train(vae_manager, vae_fit = True, num_episodes = num_episodes)
else:
vae_manager.train_with_file()
#Run actual Episodes
print("Actual trajectories")
num_episodes = 250
agent = Agent(environment, latent_space)
agent.train(vae_manager, vae_fit = False, num_episodes = num_episodes)
```
| true |
code
| 0.742913 | null | null | null | null |
|
# Model selection using hyperopt
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_moons
from sklearn.metrics import accuracy_score
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF, Matern
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
def plot_data(X_train, X_test, y_train, y_test, h=0.02):
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# just plot the dataset first
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
fig, ax = plt.subplots()
# Plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
# and testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
return fig, ax
# Show the decision surface of the optimal classifier
def plot_clf(X_train, X_test, y_train, y_test, clf, h=0.02):
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# just plot the dataset first
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
fig, ax = plt.subplots()
# Plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
# and testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
score = clf.score(X_test, y_test)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
if hasattr(clf, "decision_function"):
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
else:
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
# Put the result into a color plot
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=cm, alpha=.8)
# Plot also the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
# and testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright,
alpha=0.6)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
```
## Create an artificial data set
```
X, y = make_moons(n_samples=1000, noise=0.3, random_state=0)
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4, random_state=42)
plot_data(X_train, X_test, y_train, y_test)
from hyperopt import hp, fmin, rand, tpe, Trials, STATUS_FAIL, STATUS_OK
from hyperopt.pyll import scope
scope.define(KNeighborsClassifier)
scope.define(SVC)
scope.define(GaussianProcessClassifier)
```
## Define search space
```
C = hp.loguniform('svc_c', -4, 1)
search_space = hp.pchoice('estimator', [
(0.1, scope.KNeighborsClassifier(n_neighbors=1 + hp.randint('n_neighbors', 9))),
(0.1, scope.SVC(kernel='linear', C=C)),
(0.4, scope.SVC(kernel='rbf', C=C, gamma=hp.loguniform('svc_gamma', -4, 1))),
(0.4, scope.GaussianProcessClassifier(kernel=hp.choice('gp_kernel', [RBF(), Matern(nu=1.5), Matern(nu=2.5)])))
])
# Create logger using the Trials object supplied by hyperopt
trials = Trials()
def objective_function(estimator):
estimator.fit(X_train, y_train)
y_hat = estimator.predict(X_test)
return -1 * accuracy_score(y_test, y_hat)
# Call fmin
best = fmin(
fn=objective_function,
space=search_space,
algo=tpe.suggest,
max_evals=50
)
print(best)
clf = SVC(kernel='rbf', gamma=2.357247846608504, C=2.0908911442998437, probability=True)
clf.fit(X_train, y_train)
plot_clf(X_train, X_test, y_train, y_test, clf)
```
| true |
code
| 0.804483 | null | null | null | null |
|
# Train VAE for task2...
Then what if reconstruction is lower weighted?
Loss function is weighted as: $loss = 0.01 L_{Reconstruction} + L_{KLD}$
```
# public modules
from dlcliche.notebook import *
from dlcliche.utils import (
sys, random, Path, np, plt, EasyDict,
ensure_folder, deterministic_everything,
)
from argparse import Namespace
# private modules
sys.path.append('..')
import common as com
from pytorch_common import *
from model import VAE, VAE_loss_function
# loading parameters -> hparams (argparse compatible)
params = EasyDict(com.yaml_load('config.yaml'))
# create working directory
ensure_folder(params.model_directory)
# test directories
dirs = com.select_dirs(param=params, mode='development')
# fix random seeds
deterministic_everything(2020, pytorch=True)
# PyTorch device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
%load_ext tensorboard
%tensorboard --logdir lightning_logs/
# VAE Training class
class Task2VAELightning(Task2Lightning):
def training_step(self, batch, batch_nb):
x, y = batch
y_hat, z, mu, logvar = self.model.forward_all(x)
loss = VAE_loss_function(recon_x=y_hat, x=x, mu=mu, logvar=logvar,
reconst_loss='mse',
a_RECONST=.01, ############# Much less reconstruction loss
a_KLD=1.)
tensorboard_logs = {'train_loss': loss}
return {'loss': loss, 'log': tensorboard_logs}
# train models
for target_dir in dirs:
target = str(target_dir).split('/')[-1]
print(f'==== Start training [{target}] with {torch.cuda.device_count()} GPU(s). ====')
files = com.file_list_generator(target_dir)
model = VAE(device, x_dim=params.VAE.x_dim, h_dim=params.VAE.h_dim, z_dim=params.VAE.z_dim).to(device)
if target == 'ToyCar': summary(device, model)
task2 = Task2VAELightning(device, model, params, files, normalize=True)
trainer = pl.Trainer(max_epochs=10, # params.fit.epochs, ###### Simple try --> short epochs
gpus=torch.cuda.device_count())
trainer.fit(task2)
model_file = f'{params.model_directory}/model_{target}.pth'
torch.save(task2.model.state_dict(), model_file)
print(f'saved {model_file}.\n')
```
## Visualize
```
#load_weights(task2.model, 'model/model_ToyCar.pth')
show_some_predictions(task2.train_dataloader(), task2.model, 0, 3)
# Validation set samples
show_some_predictions(task2.val_dataloader(), task2.model, 0, 3)
```
## Model just learned mean signal as expected
```
plt.plot(task2.train_dataloader().dataset.X.mean(axis=0))
```
## Check model weights
Weights for bottleneck variables looks reasonable. But mean (fc21.weight) is almost zero...
```
summarize_weights(task2.model)
```
# Test the trained model
```
! python 01_test.py -d
def upto_6digits(cell):
if not cell[0].isdigit(): return cell
return f'{float(cell):.6f}'
with open('result/result.csv') as f:
for l in f.readlines():
l = l.strip() #replace('\n', '')
if ',' not in l:
print(l)
continue
ls = l.split(',')
print(f'{ls[0]}\t\t{upto_6digits(ls[1])}\t\t{upto_6digits(ls[2])}')
```
| true |
code
| 0.493042 | null | null | null | null |
|
## Introduction to matplotlib
`matplotlib` is the Python plotting package to rule them all. Not because it's the best. Or the easiest to use. Or the fastest. Or... wait, why is it the number 1 plotting package? Nobody knows! But it's everywhere, and making basic plots is... fine. It's really fine.
```
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
```
Let's get some well data to play with.
```
dt = np.load("../data/B-41_DT.npy")
rhob = np.load("../data/B-41_RHOB.npy")
depth = np.load("../data/B-41_DEPTH.npy")
```
## First steps
The first step is usually just a quick plot.
If we have a simple 1D array of numbers, we just pass `y`, and `x` will be generated from the indices of the elements.
```
plt.plot(dt)
```
If you have another parameter, you can do `plt.plot(x, y)`.
<div class="alert alert-success">
<b>Exercise</b>:
<ul>
<li>- Can you plot a smaller segment of the data?</li>
<li>- Try to plot the data vertically.</li>
<li>- Add `'r-o'` to your call to plot. It means 'red, line, circles'.</li>
<li>- What happens if you add another line with `plt.ylim(830, 880)`?</li>
<li>- Can you disply the whole well with 0 at the top?</li>
<li>- Try adding `plt.figure(figsize=(2,10))` at the start.</li>
</ul>
</div>
```
plt.plot(dt[3500:3600], depth[3500:3600], 'r-o')
plt.plot(dt, depth)
plt.ylim(830, 880)
plt.plot(dt, depth)
plt.fill_betweenx(depth, 0, dt)
plt.ylim(830, 880)
dtsm = np.convolve(np.ones(21)/21, dt, mode='same')
plt.plot(dt, depth, label='original')
plt.plot(dtsm, depth, label='smooth')
plt.legend()
plt.ylim(830, 880)
plt.figure(figsize=(2,10))
plt.plot(dt, depth, lw=0.5)
plt.ylim(depth[-1]+100, 0)
plt.figure(figsize=(2,10))
plt.plot(dt, depth, lw=0.5)
plt.ylim(depth[-1]+100, 0)
plt.xlabel('DT [µs/m]')
plt.ylabel('Depth [m]')
plt.title('DT log')
```
### `plt.scatter()`
It's also easy to make scatter plots:
```
plt.scatter(dt, rhob)
```
We can adjust how the points plot to make it more interesting:
```
plt.scatter(dt, rhob, c=dt*rhob, s=2, alpha=0.2)
plt.grid(c='k', alpha=0.1)
```
### `plt.hist()` and `plt.bar()`
```
hist = np.histogram(dt, bins=20)
dt.min(), dt.max()
rng = np.nanmin(dt), np.nanmax(dt)
```
It turns out that `np.histogram` struggles with NaNs, because it can't do the gt/lt comparisons it needs to do on the data. So now that we have the 'real' min and max, we can remove make a new DT curve without NaNs and they will be left out of the analysis.
```
dtn = dt[~np.isnan(dt)]
```
Luckily, `matplotlib` has a histogram plotting function:
```
n, bins, _ = plt.hist(dtn, bins='auto', range=rng)
```
Let's get the data and make our own bar chart. First, we have to compute the bin centres:
```
n.size, bins.size
bins = (bins[1:] + bins[:-1]) / 2
plt.bar(bins, n, width=2, color='g')
```
## `plt.imshow()` for raster data
For image-like data, such as slices of seismic, we need a different kind of visualization.
NB There's also `plt.pcolor` but it's very slow. Use `plt.pcolormesh` instead.
Let's load some seismic data from a SEG-Y flie.
```
import segyio
with segyio.open('../data/Penobscot_0-1000ms.sgy') as s:
vol = segyio.cube(s)
vol.shape
amp = vol[:, :, 200]
plt.imshow(amp)
```
We need to change the aspect ratio:
```
plt.imshow(amp, aspect=0.5)
plt.colorbar(shrink=0.75)
```
And fix the colorbar:
```
ma = np.percentile(vol, 98)
plt.imshow(amp, aspect=0.5, vmin=-ma, vmax=ma)
plt.colorbar(shrink=0.75)
```
<div class="alert alert-success">
<b>Exercise</b>:
<ul>
<li>- Try plotting a vertical section through the data. You'll need to think about indexing into `vol`.</li>
<li>- Can you make a histogram of the amplitudes? Remember the NaNs!</li>
</ul>
</div>
```
plt.imshow(vol[200, :, :].T)
ampn = amp[~np.isnan(amp)]
n, bins, _ = plt.hist(ampn, bins='auto', range=(-ma, ma))
plt.yscale('log', nonposy='clip')
```
## More `imshow` options
```
plt.imshow(amp[:50, :50], interpolation='bicubic')
```
We can choose new colourmaps easily, and post the colorbar.
```
plt.imshow(amp, aspect=0.5, cmap='gray', vmin=-ma, vmax=ma)
plt.colorbar()
```
Note too that matplotlib colourmaps all have reversed versions, just add `_r` to the end of the name.
```
plt.imshow(amp, aspect=0.5, cmap='RdBu_r', vmin=-ma, vmax=ma)
plt.colorbar()
```
We can give the image real-world extents:
```
plt.imshow(amp[:50, :50], extent=[10000, 11000, 200000, 201000])
plt.colorbar()
```
Notice that `plt.imshow()` assumes your pixels are sqaure. I find that I usually want to make this assumption.
## The other way to plot rasters: `pcolormesh()`
Sometimes you might have varying cell sizes or shapes, or want to render the edges of the cells. Then you can use `pcolormesh()`.
Read these articles to help figure out when to use what:
- http://thomas-cokelaer.info/blog/2014/05/matplotlib-difference-between-pcolor-pcolormesh-and-imshow/
- https://stackoverflow.com/questions/21166679/when-to-use-imshow-over-pcolormesh
```
plt.figure(figsize=(10,10))
plt.pcolormesh(amp[:20, :20], edgecolors=['white'], lw=1)
plt.show()
```
## Adding decoration
So far we've kept most of our calls to matplotlib to one line or so.
Things can get much, much more complicated... The good news is that plots are usually built up, bit by bit. So you start with the one-liner, then gradually add things:
```
hor = np.load("../data/Penobscot_Seabed.npy")
plt.imshow(vol[200, :, :].T, vmin=-ma, vmax=ma)
plt.imshow(vol[200, :, :].T, cmap="gray", vmin=-ma, vmax=ma)
plt.plot(hor[200, :], 'r', lw=2)
plt.colorbar(shrink=0.67)
inl, xl, ts = vol.shape
extent = [0, xl, ts*0.004, 0] # left, right, bottom, top
plt.imshow(vol[200, :, :].T, cmap="gray", vmin=-ma, vmax=ma, extent=extent, aspect='auto')
plt.plot(0.004 * hor[200, :], 'r', lw=2)
plt.colorbar(shrink=0.67)
plt.title("Penobscot, inline 200")
plt.xlabel("Crossline")
plt.ylabel("Time [ms]")
```
If things get more complicated than this, we need to switch to the so-called 'objected oriented' way to use matplotlib.
```
import matplotlib.patches as patches
fig, axs = plt.subplots(figsize=(15, 6), ncols=2)
ax = axs[0]
im = ax.imshow(vol[200, :, :].T, cmap="gray", vmin=-ma, vmax=ma, extent=extent, aspect='auto')
cb = fig.colorbar(im)
ax.plot(0.004 * hor[200, :], 'r', lw=2)
rect = patches.Rectangle((100, 100*0.004), 200, 100*0.004, lw=1, ec='b', fc='none')
ax.add_patch(rect)
ax.set_title("Penobscot, inline 200")
ax.set_xlabel("Crossline")
ax.set_ylabel("Time [ms]")
ax.text(10, 0.04, "peak = AI downward increase")
ax = axs[1]
ax.imshow(vol[200, 100:300, 100:200].T, extent=[100, 300, 0.8, 0.4], aspect='auto', cmap='gray', vmin=-ma, vmax=ma)
plt.setp(ax.spines.values(), color='b', lw=2)
ax.set_title('Zoomed area')
ax.set_xlabel("Crossline")
plt.savefig("../data/my_figure.png", dpi=300)
plt.savefig("../data/my_figure.svg")
plt.show()
```
## How complicated do you want to get?
It turns out you can do almost anything in `matplotlib`. This is a `matplotlib` figure:
```
from IPython.display import Image
Image('../data/t1.jpg')
```
The key method you need to make a tiled plot like this is [`gridspec`](https://matplotlib.org/users/gridspec.html). You will also need a lot of patience.
## Interactive plots
There are a few ways to achieve interactivity. We look at some of them in [`Intro_to_interactivity.ipynb`](Intro_to_interactivity.ipynb). Here's a quick example:
```
from ipywidgets import interact
@interact(t=(0, 450, 10))
def show(t):
plt.imshow(vol[:, :, t], vmin=-ma, vmax=ma, aspect=0.5)
plt.colorbar(shrink=0.75)
plt.show()
```
## Seaborn... KDE plots, better scatters, and more
Unfortunately, there's no density plot built into `matplotlib`, but the plotting library `seaborn` does have one. (So does `pandas`.)
Let's look again at [distributions uaing `seaborn`](https://seaborn.pydata.org/tutorial/distributions.html).
```
import seaborn as sns
sns.kdeplot(dtn)
```
We can change the bandwidth of the Gaussian:
```
sns.kdeplot(dtn, label="Default")
sns.kdeplot(dtn, bw=1, label="bw: 1")
sns.kdeplot(dtn, bw=10, label="bw: 10")
plt.legend();
sns.distplot(dtn[2000:2250], rug=True)
sns.jointplot(dt, rhob, s=2)
sns.jointplot(dt, rhob, kind='kde')
```
| true |
code
| 0.581778 | null | null | null | null |
|
# Introduction to Deep Learning with PyTorch
In this notebook, you'll get introduced to [PyTorch](http://pytorch.org/), a framework for building and training neural networks. PyTorch in a lot of ways behaves like the arrays you love from Numpy. These Numpy arrays, after all, are just tensors. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with Python and the Numpy/Scipy stack compared to TensorFlow and other frameworks.
## Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
<img src="assets/simple_neuron.png" width=400px>
Mathematically this looks like:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
With vectors this is the dot/inner product of two vectors:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## Tensors
It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
<img src="assets/tensor_examples.svg" width=600px>
With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
```
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 5 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
```
Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
`features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
`weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice benefits though such as GPU acceleration which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
> **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
```
## Calculate the output of this network using the weights and bias tensors
```
You can do the multiplication and sum in the same operation using a matrix multiplication. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
```python
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second column. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
**Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), and [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view).
* `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
* `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
* `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
> **Exercise**: Calculate the output of our little network using matrix multiplication.
```
## Calculate the output of this network using matrix multiplication
```
### Stack them up!
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
<img src='assets/multilayer_diagram_weights.png' width=450px>
The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on the right) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
```
> **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
```
## Your solution here
```
If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
The number of hidden units a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
## Numpy to Torch and back
Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
```
import numpy as np
a = np.random.rand(4,3)
a
b = torch.from_numpy(a)
b
b.numpy()
```
The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
```
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
```
| true |
code
| 0.642881 | null | null | null | null |
|
# Capital Allocation Problem
## Author: Snigdhayan Mahanta
In a large corporation the `capital allocation problem` is one of the biggest challenges for the corporate decision-makers. A `corporation` consists of several `business units`. From a high level perspective a corporation can choose to deploy its financial resources in the following different ways:
1. organic growth
2. M&A and portfolio diversification
3. debt reduction
4. shareholder dividends
5. share buyback
In this notebook I will focus solely on the organic growth option. A `business cycle` is a strategy execution period based on a fixed capital allocation. There are two extreme ways to allocate capital for organic growth:
1. `Inertial Corporation` - at the beginning of each business cycle the business units allocate their own capital according to the growth forecasts (each business unit allocates a fraction of its own capital into organic growth; higher growth forecast would imply higher probability of capital allocation toward organic growth)
2. `Dynamic Corporation` - at the beginning of each business cycle the corporation reallocates capital between the business units solely based on the growth forecasts of the business units (the corporation can reallocate capital from one business unit to another according to the growth forecasts of the individual business units).
I created an instance of an `Inertial Corporation` and an instance of a `Dynamic Corporation`. They both have identical organizational and financial structures but there is a slight variation in their business operations. The market periodically (at the beginning of each business cycle) updates the growth forecasts for their business units identically. Based on these assumptions I simulated and evaluated their financial performances across several business cycles mainly by tracking two financial metrics - `profits` and `profit margin`.
The metric `capital held` that I estimated below can be taken as an indicator for the capital that the corporation has decided to allocate for other purposes like inorganic growth. My analysis disregards the opportunity cost of inorganic growth at this point. For a more comprehensive analysis from the growth perspective one must also take the inorganic growth option into account.
```
from typing import Sequence
import copy
import numpy as np
import matplotlib.pyplot as plt
# Global parameters
n_BusinessUnits = 6 # no. of business units in the corporations
Forecast_options = [-1, 0, 1] # -1 = Dispose, 0 = Maintain, 1 = Grow
# Class definition of 'Business Unit'
class BusinessUnit:
'''
a business unit has its own P&L responsibility
'''
def __init__(self, label: str, forecast: int, capital: float, revenues: float, expenses: float) -> None:
self.label = label
self.forecast = forecast
self.capital = capital
self.revenues = revenues
self.expenses = expenses
@property
def profits(self) -> float:
return self.revenues - self.expenses
def update_forecast(self, forecast: int) -> None:
self.forecast = forecast
# Class definition of 'Corporation'
class Corporation:
'''
a corporation consists of multiple business units with aggregated P&L
'''
def __init__(self, label: str, BusinessUnits: Sequence[BusinessUnit]) -> None:
self.label = label
self.BusinessUnits = BusinessUnits
@property
def capital(self) -> float:
return sum([BusinessUnit.capital for BusinessUnit in self.BusinessUnits])
@property
def revenues(self) -> float:
return sum([BusinessUnit.revenues for BusinessUnit in self.BusinessUnits])
@property
def expenses(self) -> float:
return sum([BusinessUnit.expenses for BusinessUnit in self.BusinessUnits])
@property
def profits(self) -> float:
return sum([BusinessUnit.profits for BusinessUnit in self.BusinessUnits])
@property
def profit_margin(self) -> float:
return (self.profits/self.revenues)*100
def operate(self, cycle_length:int) -> None: # one iteration of business operations
for _ in range(cycle_length):
for BusinessUnit in self.BusinessUnits:
operational_change = np.random.choice([0, 1], p=[0.2, 0.8])
if (operational_change == 1):
organic1 = np.random.choice([0.3, 0.4, 0.5], p=[0.3, 0.4, 0.3])
organic2 = np.random.choice([0.3, 0.4, 0.5], p=[0.7, 0.2, 0.1])
delta1 = np.random.choice([0, 0.05, 0.1, 0.15, 0.2])
delta2 = np.random.choice([0, 0.01, 0.02])
new_revenues = BusinessUnit.revenues + delta1*BusinessUnit.forecast*organic1*BusinessUnit.capital
if (new_revenues > 0):
BusinessUnit.revenues = new_revenues
BusinessUnit.capital += -organic1*BusinessUnit.capital
new_expenses = BusinessUnit.expenses - organic2*BusinessUnit.capital + delta2*BusinessUnit.expenses
if (new_expenses > 0):
BusinessUnit.expenses = new_expenses
BusinessUnit.capital += -organic2*BusinessUnit.capital
class Inertial_Corporation(Corporation):
'''
incremental capital allocation within business unit ensuring business continuity
'''
def allocate_capital(self) -> float:
redeployed_capital = 0
for BusinessUnit in self.BusinessUnits:
if (BusinessUnit.profits > 0):
if (BusinessUnit.forecast == -1): fraction = np.random.choice(range(10, 30))/100
if (BusinessUnit.forecast == 0): fraction = np.random.choice(range(30, 50))/100
if (BusinessUnit.forecast == 1): fraction = np.random.choice(range(50, 70))/100
added_capital = fraction*BusinessUnit.profits
BusinessUnit.capital += added_capital
redeployed_capital += added_capital
return redeployed_capital
class Dynamic_Corporation(Corporation):
'''
cross business unit capital reallocation according to growth forecasts
'''
def allocate_capital(self) -> float:
BU_forecasts = [BusinessUnit.forecast for BusinessUnit in self.BusinessUnits]
redeployable_capital = self.profits
redeployed_capital = 0
allocation = []
for BusinessUnit in self.BusinessUnits:
if (BusinessUnit.forecast == -1):
reallocation = (np.random.choice(range(30, 40))/100)*BusinessUnit.capital
redeployable_capital += reallocation
BusinessUnit.capital += -reallocation
if (redeployable_capital > 0):
for BusinessUnit in self.BusinessUnits:
if (BusinessUnit.forecast == -1):
allocation.append(np.random.choice(range(10, 30))/100)
if (BusinessUnit.forecast == 0):
allocation.append(np.random.choice(range(30, 50))/100)
if (BusinessUnit.forecast == 1):
allocation.append(np.random.choice(range(50, 70))/100)
allocation = (np.random.choice(range(10, 80))/100)*(allocation/sum(allocation))
redeployed_capital = sum(allocation)*redeployable_capital
i = 0
for BusinessUnit in self.BusinessUnits:
BusinessUnit.capital += allocation[i]*redeployable_capital
i += 1
return redeployed_capital
# The market updates the growth forecasts of the business units (external factor)
def update_market_forecasts(Corporations: Sequence[Corporation]) -> None:
BU_pairs = zip(Corporations[0].BusinessUnits, Corporations[1].BusinessUnits)
for BU_pair in BU_pairs:
change_forecast = np.random.choice([0, 1], p=[0.8, 0.2])
if (change_forecast == 1):
new_forecast = np.random.choice(Forecast_options)
BU_pair[0].update_forecast(new_forecast)
BU_pair[1].update_forecast(new_forecast)
# Utility function to create a list of business units
def create_BU_list(n_BusinessUnits: int) -> Sequence[BusinessUnit]:
BusinessUnits = []
for i in range(1, n_BusinessUnits+1):
label = "BU_"+str(i) # label is a simple enuramation of the business units
forecast = np.random.choice(Forecast_options, p=[0.3, 0.4, 0.3])
capital = np.random.choice(a=range(10000, 20000))
revenues = np.random.choice(a=range(30000, 50000))
expenses = np.random.choice(a=range(30000, 40000))
BusinessUnits.append(BusinessUnit(label, forecast, capital, revenues, expenses))
return BusinessUnits
# Utility function to create a pair of corporations with identical structures
def create_corp_pair(n_BusinessUnits: int) -> Sequence[Corporation]:
BU_list1 = create_BU_list(n_BusinessUnits)
Corporation1 = Inertial_Corporation("Inertial Corporation", BU_list1)
BU_list2 = copy.deepcopy(BU_list1)
Corporation2 = Dynamic_Corporation("Dynamic Corporation", BU_list2)
return [Corporation1, Corporation2]
# Create a pair of corporations
Corporation1, Corporation2 = create_corp_pair(n_BusinessUnits)
# The initial financial metrics
BU_forecasts1 = [BusinessUnit.forecast for BusinessUnit in Corporation1.BusinessUnits]
BU_capitals1 = [BusinessUnit.capital for BusinessUnit in Corporation1.BusinessUnits]
BU_revenues1 = [BusinessUnit.revenues for BusinessUnit in Corporation1.BusinessUnits]
BU_expenses1 = [BusinessUnit.expenses for BusinessUnit in Corporation1.BusinessUnits]
BU_profits1 = [BusinessUnit.profits for BusinessUnit in Corporation1.BusinessUnits]
corporation_profits1 = Corporation1.profits
corporation_profit_margin1 = Corporation1.profit_margin
BU_forecasts2 = [BusinessUnit.forecast for BusinessUnit in Corporation2.BusinessUnits]
BU_capitals2 = [BusinessUnit.capital for BusinessUnit in Corporation2.BusinessUnits]
BU_revenues2 = [BusinessUnit.revenues for BusinessUnit in Corporation2.BusinessUnits]
BU_expenses2 = [BusinessUnit.expenses for BusinessUnit in Corporation2.BusinessUnits]
BU_profits2 = [BusinessUnit.profits for BusinessUnit in Corporation2.BusinessUnits]
corporation_profits2 = Corporation2.profits
corporation_profit_margin2 = Corporation2.profit_margin
# Simulate business cycles
n_cycles = 10 # no. of business cycles
cycle_length = 5 # no. of years in a business cycle
corporation1_capital = []
corporation1_redeployed_capital = []
corporation1_profits = []
corporation1_profit_margin = []
corporation2_capital = []
corporation2_redeployed_capital = []
corporation2_profits = []
corporation2_profit_margin = []
for _ in range(n_cycles):
#allocate capital
capital1 = Corporation1.allocate_capital()
corporation1_capital.append(Corporation1.capital)
corporation1_redeployed_capital.append(capital1)
capital2 = Corporation2.allocate_capital()
corporation2_capital.append(Corporation2.capital)
corporation2_redeployed_capital.append(capital2)
# operate business
Corporation1.operate(cycle_length)
corporation1_profits.append(Corporation1.profits)
corporation1_profit_margin.append(Corporation1.profit_margin)
Corporation2.operate(cycle_length)
corporation2_profits.append(Corporation2.profits)
corporation2_profit_margin.append(Corporation2.profit_margin)
# the market adjusts the growth forecasts for the next business cycle
update_market_forecasts([Corporation1, Corporation2])
# Visualize the changes in business unit capitals of 'Dynamic Corporation'
labels = [BusinessUnit.label for BusinessUnit in Corporation2.BusinessUnits]
x = np.arange(len(labels)) # the label locations
y1 = BU_capitals2
y2 = BU_revenues2
y3 = BU_expenses2
width = 0.35 # the width of the bars
fig, ax = plt.subplots(figsize=(15, 8), dpi=80, facecolor='w', edgecolor='k')
rects1 = ax.bar(x - width/2, y1, width, label='Capital')
rects2 = ax.bar(x, y2, width, label='Revenues', alpha=0.8)
rects3 = ax.bar(x + width/2, y3, width, label='Expenses', alpha=0.5)
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_xlabel(F'Business Unit')
ax.set_ylabel(F'Financial Structure')
ax.set_title(F'Initial Capital, Revenues and Expenses of Business Units')
ax.set_xticks(x)
ax.set_xticklabels(labels)
legends = [F'Capital',
F'Revenues',
F'Expenses']
ax.legend(legends, loc='upper right')
ax.margins(y=0.1)
plt.show()
# Pie charts of growth forecasts of business units - initial vs. current
fig, (ax1,ax2) = plt.subplots(1, 2, figsize=(18,12))
# Pie chart before trading period
labels = ["Dispose", "Maintain", "Grow"]
sizes1 = np.histogram(BU_forecasts1, bins=len(Forecast_options))[0]
ax1.pie(sizes1, labels=labels, autopct='%1.1f%%',
shadow=True, startangle=90, normalize=True)
ax1.axis('equal') # Equal aspect ratio ensures that pie is drawn as a circle.
ax1.set_title(F'Initial Forecasts of Business Units', size=20)
# Pie chart after trading period
Corporation_forecasts = [BusinessUnit.forecast for BusinessUnit in Corporation1.BusinessUnits]
sizes2 = np.histogram(Corporation_forecasts, bins=len(Forecast_options))[0]
ax2.pie(sizes2, labels=labels, autopct='%1.1f%%',
shadow=True, startangle=90, normalize=True)
ax2.axis('equal') # Equal aspect ratio ensures that pie is drawn as a circle.
ax2.set_title(F'Current Forecasts of Business Units', size=20)
plt.show()
# Visualize the comparison of the two capital allocation strategies - capital held
plt.figure(figsize=(15, 5), dpi=80, facecolor='w', edgecolor='k')
# Plot the points
# x-axis values
x = ["Cycle " + str(i) for i in range(1, n_cycles+1)]
# y-axis values
y1 = corporation1_capital
plt.plot(x, y1)
# x-axis values
# x = ["Cycle " + str(i) for i in range(1, n_cycles+1)]
# y-axis values
y2 = corporation2_capital
plt.plot(x, y2)
# x-axis label
plt.xlabel(F'Business Cycles')
# y-axis label
plt.ylabel(F'Capital Held')
# Title
plt.title(F'Capital Held Across Business Cycles - {Corporation1.label} vs. {Corporation2.label}')
legends = [F'{Corporation1.label} Average Capital Held = {round(sum(y1)/len(y1), 2)}',
F'{Corporation2.label} Average Capital Held = {round(sum(y2)/len(y2), 2)}']
plt.legend(legends, loc='upper right')
plt.margins(y=0.2)
plt.show()
# Visualize the comparison of the two capital allocation strategies - capital deployed
plt.figure(figsize=(15, 5), dpi=80, facecolor='w', edgecolor='k')
# Plot the points
# x-axis values
x = ["Cycle " + str(i) for i in range(1, n_cycles+1)]
# y-axis values
y1 = corporation1_redeployed_capital
plt.plot(x, y1)
# x-axis values
# x = ["Cycle " + str(i) for i in range(1, n_cycles+1)]
# y-axis values
y2 = corporation2_redeployed_capital
plt.plot(x, y2)
# x-axis label
plt.xlabel(F'Business Cycles')
# y-axis label
plt.ylabel(F'Capital Deployed')
# Title
plt.title(F'Capital Deployed Across Business Cycles - {Corporation1.label} vs. {Corporation2.label}')
legends = [F'{Corporation1.label} Cumulative Capital Deployed = {round(sum(y1), 2)}',
F'{Corporation2.label} Cumulative Capital Deployed = {round(sum(y2), 2)}']
plt.legend(legends, loc='upper right')
plt.margins(y=0.2)
plt.show()
# Visualize the comparison of the two capital allocation strategies - profits
plt.figure(figsize=(15, 5), dpi=80, facecolor='w', edgecolor='k')
# Plot the points
# x-axis values
x = ["Cycle " + str(i) for i in range(1, n_cycles+1)]
# y-axis values
y1 = corporation1_profits
plt.plot(x, y1)
# x-axis values
# x = ["Cycle " + str(i) for i in range(1, n_cycles+1)]
# y-axis values
y2 = corporation2_profits
plt.plot(x, y2)
# x-axis label
plt.xlabel(F'Business Cycles')
# y-axis label
plt.ylabel(F'Profits')
# Title
plt.title(F'Profits Across Business Cycles - {Corporation1.label} vs. {Corporation2.label}')
legends = [F'{Corporation1.label} Average Profits = {round(sum(y1)/len(y1), 2)}',
F'{Corporation2.label} Average Profits = {round(sum(y2)/len(y2), 2)}']
plt.legend(legends, loc='upper right')
plt.margins(y=0.2)
plt.show()
# Visualize the comparison of the two capital allocation strategies - profit margins
plt.figure(figsize=(15, 5), dpi=80, facecolor='w', edgecolor='k')
# Plot the points
# x-axis values
x = ["Cycle " + str(i) for i in range(1, n_cycles+1)]
# y-axis values
y1 = corporation1_profit_margin
plt.plot(x, y1)
# x-axis values
# x = ["Cycle " + str(i) for i in range(1, n_cycles+1)]
# y-axis values
y2 = corporation2_profit_margin
plt.plot(x, y2)
# x-axis label
plt.xlabel(F'Business Cycles')
# y-axis label
plt.ylabel(F'Profit Margin')
# Title
plt.title(F'Profit Margins Across Business Cycles - {Corporation1.label} vs. {Corporation2.label}')
legends = [F'{Corporation1.label} Average Profit Margin = {round(sum(y1)/len(y1), 2)}',
F'{Corporation2.label} Average Profit Margin = {round(sum(y2)/len(y2), 2)}']
plt.legend(legends, loc='upper right')
plt.margins(y=0.2)
plt.show()
# Comparison of the initial business unit revenues and profits
labels = [BusinessUnit.label for BusinessUnit in Corporation1.BusinessUnits]
x = np.arange(len(labels)) # the label locations
y1 = BU_revenues1
y2 = BU_profits1
width = 0.35 # the width of the bars
fig, ax = plt.subplots(figsize=(15, 8), dpi=80, facecolor='w', edgecolor='k')
rects1 = ax.bar(x - width/2, y1, width, label='{Corporation1.label}')
rects2 = ax.bar(x + width/2, y2, width, label='{Corporation2.label}')
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_xlabel(F'Business Unit')
ax.set_ylabel(F'Business Unit Revenues and Profits')
ax.set_title(F'Comparison of Initial Business Unit Revenues and Profits')
ax.set_xticks(x)
ax.set_xticklabels(labels)
legends = [F'Cumulative Revenues = {round(sum(y1), 2)}',
F'Cumulative Profits = {round(sum(y2), 2)}']
ax.legend(legends, loc='upper right')
ax.margins(y=0.1)
plt.show()
# Compare the current business unit revenues between the two corporations
labels = [BusinessUnit.label for BusinessUnit in Corporation1.BusinessUnits]
x = np.arange(len(labels)) # the label locations
y1 = [BusinessUnit.revenues for BusinessUnit in Corporation1.BusinessUnits]
y2 = [BusinessUnit.revenues for BusinessUnit in Corporation2.BusinessUnits]
width = 0.35 # the width of the bars
fig, ax = plt.subplots(figsize=(15, 8), dpi=80, facecolor='w', edgecolor='k')
rects1 = ax.bar(x - width/2, y1, width, label='{Corporation1.label}')
rects2 = ax.bar(x + width/2, y2, width, label='{Corporation2.label}')
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_xlabel(F'Business Unit')
ax.set_ylabel(F'Business Unit Revenues')
ax.set_title(F'Comparison of Current Business Unit Revenues')
ax.set_xticks(x)
ax.set_xticklabels(labels)
legends = [F'{Corporation1.label} Revenues = {round(Corporation1.revenues, 2)}',
F'{Corporation2.label} Revenues = {round(Corporation2.revenues, 2)}']
ax.legend(legends, loc='upper right')
ax.margins(y=0.1)
plt.show()
# Compare the current business unit profits between the two corporations
labels = [BusinessUnit.label for BusinessUnit in Corporation1.BusinessUnits]
x = np.arange(len(labels)) # the label locations
y1 = [BusinessUnit.profits for BusinessUnit in Corporation1.BusinessUnits]
y2 = [BusinessUnit.profits for BusinessUnit in Corporation2.BusinessUnits]
width = 0.35 # the width of the bars
fig, ax = plt.subplots(figsize=(15, 8), dpi=80, facecolor='w', edgecolor='k')
rects1 = ax.bar(x - width/2, y1, width, label='{Corporation1.label}')
rects2 = ax.bar(x + width/2, y2, width, label='{Corporation2.label}')
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_xlabel(F'Business Unit')
ax.set_ylabel(F'Business Unit Profits')
ax.set_title(F'Comparison of Current Business Unit Profits')
ax.set_xticks(x)
ax.set_xticklabels(labels)
legends = [F'{Corporation1.label} Profits = {round(Corporation1.profits, 2)}',
F'{Corporation2.label} Profits = {round(Corporation2.profits, 2)}']
ax.legend(legends, loc='upper right')
ax.margins(y=0.1)
plt.show()
# How many business cycles are under consideration?
n_cycles
# How many business units are there in the two corporations?
n_BusinessUnits
# What was the initial overall profit of the two corporations?
round(corporation_profits1, 2)
# What is the current overall profit of 'Inertial Corporation'?
round(Corporation1.profits, 2)
# What is the current overall profit of 'Dynamic Corporation'?
round(Corporation2.profits, 2)
# What was the initial profit margin of the two corporations?
round(corporation_profit_margin1, 2)
# What is the current overall profit margin of 'Inertial Corporation'?
round(Corporation1.profit_margin, 2)
# What is the current overall profit margin of 'Dynamic Corporation'?
round(Corporation2.profit_margin, 2)
```
| true |
code
| 0.802903 | null | null | null | null |
|
# Integration
```
import matplotlib.pyplot as plt
import numpy as np
```
## Contents
1.[Integral Calculus](#Integral_Calculus)
2.[Fundamental Theorem of Calculus](#Fundamental_Theorem_of_Calculus)
3.[Basic Integration](#Basic_Integration)
- [Integrating powers of x](#Integrating_powers_of_x)
- [Integrating other basic terms](#Integrating_other_basic_terms)
4.[Definite Integrals](#Definite_Integrals)
- [Area under graph](#Area_under_graph)
- [Area under graph for y axis](#Area_under_graph_for_y_axis)
- [Area between lines](#Area_between_lines)
- [Area between lines on y axis](#Area_between_lines_on_y_axis)
<a id='Integral_Calculus'></a>
## Integral Calculus
How to find area under curve between a specified x
$\lim_{n\to\infty}\sum_{i=1}^n f(x_i)\Delta x_i = \int^b_a f(x)dx$
- this is the area under the graph
- the left side sums as many values of y in the specified x data set and weights it with the difference in x
- the right side is the integral which is 1 function which takes the range of a to b
##### This is the Definite Integral
$\int f(x) dx$
##### This is the Indefinite Integral or anti-derivative
```
x = np.linspace(-10, 10, 201)
def f(x):
return x**2
y = f(x)
fig, ax = plt.subplots(1, figsize=(8,4))
ax.plot(x,y, 'g', label='line')
ax.fill_between(x,y, color='blue', alpha=0.3, label='area under graph')
ax.grid(True)
ax.legend()
plt.show()
```
<a id='Fundamental_Theorem_of_Calculus'></a>
## Fundamental Theorem of Calculus
$f(x)$ is continuous in $[a,b]$
$F(x) = \int^x_af(t)dt$
- where $x$ is in $[a,b]$
$\frac{dF}{dx} = \frac{d}{dx}\int^x_af(t)dt = f(x)$
#### Example:
$F(x) = \int^x_a\frac{\cos^2t}{-\sin t^2}dt$
$F\prime(x) = \frac{d}{dx}\int^x_a\frac{\cos^2t}{-\sin t^2}dt = \frac{\cos^2x}{-\sin x^2}$
#### Example 2:
$F(x) = \int^{x^2}_a\frac{\cos^2t}{-\sin t^2}dt$
$F\prime(x) = \frac{d}{dx}\int^{x^2}_a\frac{\cos^2t}{-\sin t^2}dt$
$= \frac{\cos^2x^2}{-\sin x^4}\times \frac{d}{dx}x^2$
$= 2\frac{\cos^2x^2}{-\sin x^4}$
<a id='Basic_Integration'></a>
## Basic Integration
<a id='Integrating_powers_of_x'></a>
### Integrating powers of x
$\int Ax^ndx = \frac{A}{n+1}x^{n+1} + C$
- to find the derivative we use $\frac{d}{dx}ax^n = anx^{n-1}$
- we do the opposite with $\int ax^ndx = a\frac{1}{n+1}x^{n+1}$
- we add $C$ as we cant find out the constant of the original function
#### Example
$\int 2x^5dx = \frac{1}{3}x^{6} + C$
<a id='Integrating_other_basic_terms'></a>
### Integrating other basic terms
#### Integrating $e^{kx}$
$\int Ae^{kx + b} dx = \frac{A}{k}e^{kx + b} + C$
- the derivative is $\frac{d}{dx}e^x = e^x$
- to differentiate, we would use the chain rule on the function of x and $\therefore$ multiply by k
#### Example
$\int 3e^{9x + 2} dx = \frac{1}{3}e^{9x + 2} + C$
#### Integrating $\frac{1}{x}$
$\int A\frac{n}{x} dx = An\ln x + C$
$\int A\frac{f\prime(x)}{f(x)} dx = A\ln|f(x)| + C$
- in the second rule, the top is caused by the chain rule
#### Example
$\int 2\frac{6}{x} dx = 12\ln x + C$
#### Example 2
$\int 2\frac{10x}{5x^2 + 3} dx = 2\ln |5x^2 + 3| + C$
#### Integrating $\sin x$
$\int A\sin(kx) dx = -A\frac{1}{k}\cos(kx) + C$
#### Example
$\int 4\sin(2x) dx = -2\cos(2x) + C$
#### Integrating $\cos x$
$\int A\cos(kx) dx = A\frac{1}{k}\sin(kx) + C$
#### Example
$\int 11\cos(3x) dx = \frac{11}{3}\sin(3x) + C$
<a id='Definite_Integrals'></a>
## Definite Integrals
This is where there are defined boundaries on the x or y axis
<a id='Area_under_graph'></a>
### Area under graph
$F(x) = \int f(x)dx$
$\int_a^b f(x)dx = F(b) - F(a)$
- if the graph is negative, the area can be negative
- the definite integral gives the net area
- to find area (not net area), split into positive and negative regions and find sum magnitudes of regions
#### Example
$f(x) = 6x^2$
$F(x) = 2x^3$
$\int_2^5 f(x)dx = F(5) - F(2)$
$= 2(5)^3 - 2(2)^3$
$= 234$
<a id='Area_under_graph_for_y_axis'></a>
### Area under graph for y axis
$F(y) = \int f^{-1}(y)dy$
$\int_c^d f^{-1}(y)dy = F(d) - F(c)$
- do the same but in terms of y
- this includes taking the inverse of the line function to get a function in terms of y
#### Example
$f(x) = 6x^2$
$f^{-1}(y) = \left(\frac{1}{6}y\right)^{\frac{1}{2}}$
$F(y) = 4\left(\frac{1}{6}y\right)^{\frac{3}{2}}$
$\int_2^5 f^{-1}(y)dy = F(5) - F(2)$
$= 4\left(\frac{5}{6}\right)^{\frac{3}{2}} - 4\left(\frac{1}{3}\right)^{\frac{3}{2}}$
$= 2.273$
<a id='Area_between_lines'></a>
### Area between lines
$\int_a^b(f(x) - g(x))dx = \int_a^bf(x)dx - \int_a^bg(x)dx$
#### Example
$= \int_0^1(\sqrt{x} - x^2)dx$
$= \left(\frac{2}{3}x^{\frac{3}{2}} - \frac{x^3}{3}\right)\mid^1_0$
$= \left(\frac{2}{3}1^{\frac{3}{2}} - \frac{1^3}{3}\right) - \left(\frac{2}{3}0^{\frac{3}{2}} - \frac{0^3}{3}\right)$
$= \left(\frac{2}{3} - \frac{1}{3}\right)$
$= \left(\frac{1}{3}\right)$
- if more lines, separate into sections on the x axis and sum
<a id='Area_between_lines_on_y_axis'></a>
### Area between lines on y axis
This works the same as area under graph on y axis but combined with the area between lines method
```
x = np.linspace(-5, 5, 201)
def f(x):
return 6*x**2 - 20
def F(x):
return 2*x**3 - 20*x
y = f(x)
start = 60
end = 160
section = x[start:end+1]
fig, ax = plt.subplots(1, figsize=(8,4))
ax.plot(x,y, 'g', label='y = 2x')
ax.fill_between(section,f(section), color='blue', alpha=0.3, label='area under graph')
ax.plot(x[start], 0, 'om', color='purple', label='a')
ax.plot(x[end], 0, 'om', color='r', label='b')
ax.grid(True)
ax.legend()
plt.show()
print 'shaded net area =', F(x[end]) - F(x[start])
```
| true |
code
| 0.544983 | null | null | null | null |
|
```
import numpy as np
from scipy import ndimage
from scipy import spatial
from scipy import io
from scipy import sparse
from scipy.sparse import csgraph
from scipy import linalg
from matplotlib import pyplot as plt
import seaborn as sns
from skimage import data
from skimage import color
from skimage import img_as_float
import graph3d
%matplotlib inline
```
# Load data
```
image = img_as_float(data.camera()[::2, ::2])
fig, ax = plt.subplots()
plt.imshow(image, cmap='gray')
plt.grid('off')
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])
ax.set_title('Original image')
plt.savefig('../img/tikhonov_regularization_0.pdf', bbox_inches='tight')
```
# Crop and add noise
```
image = image[40:80, 100:140]
noisy_image = image + 0.05*np.random.randn(*image.shape)
fig, ax = plt.subplots(1, 2, figsize=(8, 4))
ax[0].imshow(image, cmap='gray')
ax[1].imshow(noisy_image, cmap='gray')
ax[0].grid('off')
ax[1].grid('off')
ax[0].xaxis.set_ticks([])
ax[0].yaxis.set_ticks([])
ax[1].xaxis.set_ticks([])
ax[1].yaxis.set_ticks([])
ax[0].set_title('Cropped image')
ax[1].set_title('Noisy image')
plt.savefig('../img/tikhonov_regularization_1.pdf', bbox_inches='tight')
```
# Perform graph filtering
#### Given a signal $f_0$ corrupted by Gaussian noise $\eta$
\begin{equation}
\mathbf{y} = \mathbf{f_0} + \mathbf{\eta}
\end{equation}
#### Solve the regularization problem
\begin{equation}
\underset{f}{\text{argmin}} \{ ||f - y||_2^2 + \gamma f^T L f\}
\end{equation}
#### Solution is given by
\begin{equation}
f_{*}(i) = \sum_{l=0}^{N-1} \bigg[ \frac{1}{1 + \gamma \lambda_l} \bigg] \hat{y}
(\lambda_l) u_l(i)
\end{equation}
#### Or equivalently
\begin{equation}
\mathbf{f} = \hat{h}(L) \mathbf{y}
\end{equation}
#### Where L is the laplacian of the adjacency matrix defined by:
\begin{equation}
W_{i,j} =
\begin{cases}
\exp \bigg( - \frac{[dist(i, j)]^2}{2 \theta^2} \bigg) & \text{if $dist(i,j)$ < $\kappa$} \\
0 & \text{otherwise}
\end{cases}
\end{equation}
```
# Parameters
kappa = np.sqrt(2)
theta = 20
gamma = 10
# Query neighboring pixels for each pixel
yx = np.vstack(np.dstack(np.indices(noisy_image.shape)))
tree = spatial.cKDTree(yx)
q = tree.query_ball_point(yx, kappa)
# Get pixels I, and neighbors J
I = np.concatenate([np.repeat(k, len(q[k])) for k in range(len(q))])
J = np.concatenate(q)
# Distance metric is difference between neighboring pixels
dist_ij = np.sqrt(((noisy_image.flat[I] - noisy_image.flat[J])**2))
# Thresholded Gaussian kernel weighting function
W = np.exp(- ((dist_ij)**2 / 2*(theta**2)) )
# Construct sparse adjacency matrix
A = sparse.lil_matrix((noisy_image.size, noisy_image.size))
for i, j, w in zip(I, J, W):
A[i, j] = w
A[j, i] = w
A = A.todense()
# Compute Laplacian
L = csgraph.laplacian(A)
# Compute eigenvalues and eigenvectors of laplacian
l, u = linalg.eigh(L)
# Compute filtering kernel
h = u @ np.diag(1 / (1 + gamma*l)) @ u.T
# Filter the image using the kernel
graph_filtered_image = (h @ noisy_image.ravel()).reshape(noisy_image.shape)
# Filter the image using traditional gaussian filtering
traditional_filtered_image = ndimage.gaussian_filter(noisy_image, 0.8)
# Plot the result
fig, ax = plt.subplots(2, 2, figsize=(6, 6))
ax.flat[0].imshow(image, cmap='gray')
ax.flat[1].imshow(noisy_image, cmap='gray')
ax.flat[2].imshow(graph_filtered_image, cmap='gray')
ax.flat[3].imshow(traditional_filtered_image, cmap='gray')
ax.flat[0].grid('off')
ax.flat[1].grid('off')
ax.flat[2].grid('off')
ax.flat[3].grid('off')
ax.flat[0].xaxis.set_ticks([])
ax.flat[0].yaxis.set_ticks([])
ax.flat[1].xaxis.set_ticks([])
ax.flat[1].yaxis.set_ticks([])
ax.flat[2].xaxis.set_ticks([])
ax.flat[2].yaxis.set_ticks([])
ax.flat[3].xaxis.set_ticks([])
ax.flat[3].yaxis.set_ticks([])
ax.flat[0].set_title('Cropped Image')
ax.flat[1].set_title('Noisy Image')
ax.flat[2].set_title('Graph Filtered')
ax.flat[3].set_title('Gaussian Filtered')
plt.tight_layout()
plt.savefig('../img/tikhonov_regularization_2.pdf', bbox_inches='tight')
```
| true |
code
| 0.713531 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Tutorial: Azure Machine Learning Quickstart
In this tutorial, you learn how to quickly get started with Azure Machine Learning. Using a *compute instance* - a fully managed cloud-based VM that is pre-configured with the latest data science tools - you will train an image classification model using the CIFAR10 dataset.
In this tutorial you will learn how to:
* Create a compute instance and attach to a notebook
* Train an image classification model and log metrics
* Deploy the model
## Prerequisites
1. An Azure Machine Learning workspace
1. Familiar with the Python language and machine learning workflows.
## Create compute & attach to notebook
To run this notebook you will need to create an Azure Machine Learning _compute instance_. The benefits of a compute instance over a local machine (e.g. laptop) or cloud VM are as follows:
* It is a pre-configured with all the latest data science libaries (e.g. panads, scikit, TensorFlow, PyTorch) and tools (Jupyter, RStudio). In this tutorial we make extensive use of PyTorch, AzureML SDK, matplotlib and we do not need to install these components on a compute instance.
* Notebooks are seperate from the compute instance - this means that you can develop your notebook on a small VM size, and then seamlessly scale up (and/or use a GPU-enabled) the machine when needed to train a model.
* You can easily turn on/off the instance to control costs.
To create compute, click on the + button at the top of the notebook viewer in Azure Machine Learning Studio:
<img src="https://dsvmamlstorage127a5f726f.blob.core.windows.net/images/ci-create.PNG" width="500"/>
This will pop up the __New compute instance__ blade, provide a valid __Compute name__ (valid characters are upper and lower case letters, digits, and the - character). Then click on __Create__.
It will take approximately 3 minutes for the compute to be ready. When the compute is ready you will see a green light next to the compute name at the top of the notebook viewer:
<img src="https://dsvmamlstorage127a5f726f.blob.core.windows.net/images/ci-create2.PNG" width="500"/>
You will also notice that the notebook is attached to the __Python 3.6 - AzureML__ jupyter Kernel. Other kernels can be selected such as R. In addition, if you did have other instances you can switch to them by simply using the dropdown menu next to the Compute label.
## Import Data
For this tutorial, you will use the CIFAR10 dataset. It has the classes: airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck. The images in CIFAR-10 three-channel color images of 32x32 pixels in size.
The code cell below uses the PyTorch API to download the data to your compute instance, which should be quick (around 15 seconds). The data is divided into training and test sets.
* **NOTE: The data is downloaded to the compute instance (in the `/tmp` directory) and not a durable cloud-based store like Azure Blob Storage or Azure Data Lake. This means if you delete the compute instance the data will be lost. The [getting started with Azure Machine Learning tutorial series](https://docs.microsoft.com/azure/machine-learning/tutorial-1st-experiment-sdk-setup-local) shows how to create an Azure Machine Learning *dataset*, which aids durability, versioning, and collaboration.**
```
import torch
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='/tmp/data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='/tmp/data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
```
## Take a look at the data
In the following cell, you have some python code that displays the first batch of 4 CIFAR10 images:
```
import matplotlib.pyplot as plt
import numpy as np
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))
```
## Train model and log metrics
In the directory `model` you will see a file called [model.py](./model/model.py) that defines the neural network architecture. The model is trained using the code below.
* **Note: The model training take around 4 minutes to complete. The benefit of a compute instance is that the notebooks are separate from the compute - therefore you can easily switch to a different size/type of instance. For example, you could switch to run this training on a GPU-based compute instance if you had one provisioned. In the code below you can see that we have included `torch.device("cuda:0" if torch.cuda.is_available() else "cpu")`, which detects whether you are using a CPU or GPU machine.**
```
from model.model import Net
from azureml.core import Experiment
from azureml.core import Workspace
ws = Workspace.from_config()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device
exp = Experiment(workspace=ws, name="cifar10-experiment")
run = exp.start_logging(snapshot_directory=None)
# define convolutional network
net = Net()
net.to(device)
# set up pytorch loss / optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
run.log("learning rate", 0.001)
run.log("momentum", 0.9)
# train the network
for epoch in range(1):
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# unpack the data
inputs, labels = data[0].to(device), data[1].to(device)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999:
loss = running_loss / 2000
run.log("loss", loss)
print(f'epoch={epoch + 1}, batch={i + 1:5}: loss {loss:.2f}')
running_loss = 0.0
print('Finished Training')
```
Once you have executed the cell below you can view the metrics updating in real time in the Azure Machine Learning studio:
1. Select **Experiments** (left-hand menu)
1. Select **cifar10-experiment**
1. Select **Run 1**
1. Select the **Metrics** Tab
The metrics tab will display the following graph:
<img src="https://dsvmamlstorage127a5f726f.blob.core.windows.net/images/metrics-capture.PNG" alt="dataset details" width="500"/>
#### Understand the code
The code is based on the [Pytorch 60minute Blitz](https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html#sphx-glr-beginner-blitz-cifar10-tutorial-py) where we have also added a few additional lines of code to track the loss metric as the neural network trains.
| Code | Description |
| ------------- | ---------- |
| `experiment = Experiment( ... )` | [Experiment](https://docs.microsoft.com/python/api/azureml-core/azureml.core.experiment.experiment?view=azure-ml-py&preserve-view=true) provides a simple way to organize multiple runs under a single name. Later you can see how experiments make it easy to compare metrics between dozens of runs. |
| `run.log()` | This will log the metrics to Azure Machine Learning. |
## Version control models with the Model Registry
You can use model registration to store and version your models in your workspace. Registered models are identified by name and version. Each time you register a model with the same name as an existing one, the registry increments the version. Azure Machine Learning supports any model that can be loaded through Python 3.
The code below does:
1. Saves the model on the compute instance
1. Uploads the model file to the run (if you look in the experiment on Azure Machine Learning studio you should see on the **Outputs + logs** tab the model has been saved in the run)
1. Registers the uploaded model file
1. Transitions the run to a completed state
```
from azureml.core import Model
PATH = 'cifar_net.pth'
torch.save(net.state_dict(), PATH)
run.upload_file(name=PATH, path_or_stream=PATH)
model = run.register_model(model_name='cifar10-model',
model_path=PATH,
model_framework=Model.Framework.PYTORCH,
description='cifar10 model')
run.complete()
```
### View model in the model registry
You can see the stored model by navigating to **Models** in the left-hand menu bar of Azure Machine Learning Studio. Click on the **cifar10-model** and you can see the details of the model like the experiement run id that created the model.
## Deploy the model
The next cell deploys the model to an Azure Container Instance so that you can score data in real-time (Azure Machine Learning also provides mechanisms to do batch scoring). A real-time endpoint allows application developers to integrate machine learning into their apps.
* **Note: The deployment takes around 3 minutes to complete.**
```
from azureml.core import Environment, Model
from azureml.core.model import InferenceConfig
from azureml.core.webservice import AciWebservice
environment = Environment.get(ws, "AzureML-PyTorch-1.6-CPU")
model = Model(ws, "cifar10-model")
service_name = 'cifar-service'
inference_config = InferenceConfig(entry_script='score.py', environment=environment)
aci_config = AciWebservice.deploy_configuration(cpu_cores=1, memory_gb=1)
service = Model.deploy(workspace=ws,
name=service_name,
models=[model],
inference_config=inference_config,
deployment_config=aci_config,
overwrite=True)
service.wait_for_deployment(show_output=True)
```
### Understand the code
| Code | Description |
| ------------- | ---------- |
| `environment = Environment.get()` | [Environment](https://docs.microsoft.com/python/api/overview/azure/ml/?view=azure-ml-py#environment) specify the Python packages, environment variables, and software settings around your training and scoring scripts. In this case, you are using a *curated environment* that has all the packages to run PyTorch. |
| `inference_config = InferenceConfig()` | This specifies the inference (scoring) configuration for the deployment such as the script to use when scoring (see below) and on what environment. |
| `service = Model.deploy()` | Deploy the model. |
The [*scoring script*](score.py) file is has two functions:
1. an `init` function that executes once when the service starts - in this function you normally get the model from the registry and set global variables
1. a `run(data)` function that executes each time a call is made to the service. In this function, you normally deserialize the json, run a prediction and output the predicted result.
## Test the model service
In the next cell, you get some unseen data from the test loader:
```
dataiter = iter(testloader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
```
Finally, the next cell runs scores the above images using the deployed model service.
```
import json
input_payload = json.dumps({
'data': images.tolist()
})
output = service.run(input_payload)
print(output)
```
## Clean up resources
To clean up the resources after this quickstart, firstly delete the Model service using:
```
service.delete()
```
Next stop the compute instance by following these steps:
1. Go to **Compute** in the left-hand menu of the Azure Machine Learning studio
1. Select your compute instance
1. Select **Stop**
**Important: The resources you created can be used as prerequisites to other Azure Machine Learning tutorials and how-to articles.** If you don't plan to use the resources you created, delete them, so you don't incur any charges:
1. In the Azure portal, select **Resource groups** on the far left.
1. From the list, select the resource group you created.
1. Select **Delete resource group**.
1. Enter the resource group name. Then select **Delete**.
You can also keep the resource group but delete a single workspace. Display the workspace properties and select **Delete**.
## Next Steps
In this tutorial, you have seen how to run your machine learning code on a fully managed, pre-configured cloud-based VM called a *compute instance*. Having a compute instance for your development environment removes the burden of installing data science tooling and libraries (for example, Jupyter, PyTorch, TensorFlow, Scikit) and allows you to easily scale up/down the compute power (RAM, cores) since the notebooks are separated from the VM.
It is often the case that once you have your machine learning code working in a development environment that you want to productionize this by running as a **_job_** - ideally on a schedule or trigger (for example, arrival of new data). To this end, we recommend that you follow [**the day 1 getting started with Azure Machine Learning tutorial**](https://docs.microsoft.com/azure/machine-learning/tutorial-1st-experiment-sdk-setup-local). This day 1 tutorial is focussed on running jobs-based machine learning code in the cloud.
| true |
code
| 0.676126 | null | null | null | null |
|
## Различные графики
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
### Regular plot
```
n = 512
X = np.linspace(0, np.pi/2, n, endpoint=True)
Y = np.cos(20*X) * np.exp(-X)
plt.figure(figsize=(8,4), dpi=80)
# Plot upper sine wave
plt.plot(X, Y+2, color='green', alpha=1.00)
plt.fill_between(X, 2, Y+2, color='green', alpha=0.10)
# Plot lower sine wave
plt.plot(X, Y-1, color='orange', alpha=1.00)
plt.fill_between(X, -1, Y-1, (Y-1) > -1, color='#FFAA00', alpha=0.15)
plt.fill_between(X, -1, Y-1, (Y-1) < -1, color='#AAAA00', alpha=0.15)
plt.plot([0, np.pi/2], [0.5, 0.5], 'b--')
# Set x, y limits
plt.xlim(0, np.pi/2)
plt.ylim(-2.5, 3.5)
# Do not plot grids
plt.xticks([])
plt.yticks([])
# plt.grid(False)
```
### Scatter plot
```
# Create 2D random signal
n = 512
np.random.seed(1)
X = np.random.randn(n)
Y = np.random.randn(n)
T = np.arctan2(Y, X)
plt.figure(figsize=(6,6), dpi=80)
plt.scatter(X, Y, s=80, c=T, alpha=.60)
plt.xlim(-1.5,1.5), plt.xticks([])
plt.ylim(-1.5,1.5), plt.yticks([])
T.mean()
```
### Bar plot
```
n = 10
# Create two random vectors
X = np.arange(n)
np.random.seed(10)
Y1 = (1-X/float(n)) * np.random.uniform(0.5, 1.2, n)
Y2 = (1-X/float(n)) * np.random.uniform(0.5, 1.2, n)
# Plot two bars
plt.figure(figsize=(8,4), dpi=80)
plt.bar(X, +Y1, facecolor='#CCCCFF', edgecolor='red')
plt.bar(X, -Y2, facecolor='#FFCCCC', edgecolor='blue')
# Plot text into bars
for x,y in zip(X, Y1):
plt.text(x+0.2, +y+0.07, '%.2f' % y, ha='center', va='bottom')
for x,y in zip(X, Y2):
plt.text(x+0.2, -y-0.07, '%.2f' % y, ha='center', va='top')
plt.xlim(-1, n)
plt.ylim(-1.35, +1.35)
plt.grid()
```
### Contour Plots
```
# Create function
def f(x, y):
# return (x+x**4-y**5+y**2) * np.exp(-(0.95*x**2+0.65*y**2))
return (0.5-x+x**5+y**3-y) * np.exp(-(0.85*x**2+0.75*y**2))
# Create vectors and mesh
n = 200
x = np.linspace(-3, 3, n)
y = np.linspace(-3, 3, n)
X,Y = np.meshgrid(x,y)
# Plot
plt.figure(figsize=(6,6), dpi=80)
plt.contourf(X, Y, f(X,Y), 9, alpha=.75, cmap=plt.cm.hot)
C = plt.contour(X, Y, f(X,Y), 9, colors='black')
plt.clabel(C, inline=1, fontsize=8)
plt.grid(False)
```
### Imshow
```
# Create function
def f(x, y):
return (x+x**4-y**5+y**2) * np.exp(-(0.95*x**2+0.65*y**2))
# Create vectors and mesh
n = 200
x = np.linspace(-3, 3, n)
y = np.linspace(-3, 3, n)
X,Y = np.meshgrid(x,y)
Z = f(X,Y)
# Plot
plt.figure(figsize=(6,6), dpi=80)
plt.imshow(Z, interpolation='bicubic', cmap='bone', origin='lower')
plt.colorbar(shrink=.70)
plt.grid(False)
```
| true |
code
| 0.692499 | null | null | null | null |
|
# RNN Evaluation
From our paper on "Explainable Prediction of Acute Myocardial Infarction using Machine Learning and Shapley Values"
```
# Import libraries
from keras import optimizers, losses, activations, models
from keras.callbacks import ModelCheckpoint, EarlyStopping, LearningRateScheduler, ReduceLROnPlateau
from keras.layers import Layer, GRU, LSTM, Dense, Input, Dropout, Convolution1D, MaxPool1D, GlobalMaxPool1D, GlobalAveragePooling1D, \
concatenate
from keras.layers import LeakyReLU
from keras import regularizers, backend, initializers
from keras.models import Sequential
from keras.utils import to_categorical
from keras.initializers import Ones, Zeros
import keras.backend as K
from keras.models import load_model
from sklearn.metrics import f1_score, accuracy_score, roc_auc_score, confusion_matrix
from sklearn import preprocessing
import time
import gc
import pandas as pd
import numpy as np
import pylab as plt
import tensorflow as tf
from numpy import loadtxt
from numpy import savetxt
from tensorflow.python.framework import ops
print(tf.__version__)
# Visualization libraries
import seaborn as sns
```
# Loading Data
```
# Load data
train = loadtxt('train.csv', delimiter=',')
test = loadtxt('test.csv', delimiter=',')
# Split array
train_x = train[:,:11]
test_x = test[:,:11]
train_y = train[:,11]
test_y = test[:,11]
train_x_noageandsex = train_x[:,:9]
test_x_noageandsex = test_x[:,:9]
train_y_noageandsex = train_y
test_y_noageandsex = test_y
class LayerNormalization(Layer):
def __init__(self, eps=1e-6, **kwargs):
self.eps = eps
super(LayerNormalization, self).__init__(**kwargs)
def build(self, input_shape):
self.gamma = self.add_weight(name='gamma', shape=input_shape[-1:],
initializer=Ones(), trainable=True)
self.beta = self.add_weight(name='beta', shape=input_shape[-1:],
initializer=Zeros(), trainable=True)
super(LayerNormalization, self).build(input_shape)
def call(self, x):
mean = K.mean(x, axis=-1, keepdims=True)
std = K.std(x, axis=-1, keepdims=True)
return self.gamma * (x - mean) / (std + self.eps) + self.beta
def compute_output_shape(self, input_shape):
return input_shape
X_train_noageandsex = np.reshape(train_x_noageandsex, (train_x_noageandsex.shape[0], 1, train_x_noageandsex.shape[1]))
X_test_noageandsex = np.reshape(test_x_noageandsex, (test_x_noageandsex.shape[0], 1, test_x_noageandsex.shape[1]))
train_y_noageandsex = to_categorical(train_y_noageandsex)
```
# Model Evaluation + Confusion Matrix
```
model = load_model('model_noageandsex1_final.h5', custom_objects={'LayerNormalization': LayerNormalization})
model.summary()
# Test the model
start = time.clock()
pred_test = model.predict(X_test_noageandsex)
end = time.clock()
pred_test = np.argmax(pred_test, axis=-1)
print("Time for prediction: {} ".format((end-start)))
# Get f1 score
f1 = f1_score(test_y, pred_test, average="macro")
print("Test f1 score : %s "% f1)
# Get ROC AUC score
roc = roc_auc_score(test_y_noageandsex, pred_test)
print("Test ROC AUC Score : %s "% roc)
# Get the accuracy
acc = accuracy_score(test_y_noageandsex, pred_test)
print("Test accuracy score : %s "% acc)
# Get the specificity
tn, fp, fn, tp = confusion_matrix(test_y_noageandsex, pred_test).ravel()
specificity = tn / (tn+fp)
print("Specificity : %s "% specificity)
# Get the sensitivity
sensitivity= tp / (tp+fn)
print("Sensitivity: %s "% sensitivity)
# Confusion matrix
confusion = confusion_matrix(test_y_noageandsex, pred_test)
sns.heatmap(data=confusion, annot=True, xticklabels=["MI", "Not MI"], yticklabels=["MI", "Not MI"], fmt = "d", annot_kws={"fontsize":16})
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.yticks(va="center")
plt.show()
```
| true |
code
| 0.787768 | null | null | null | null |
|
```
from keras.datasets import mnist
(trainX, trainY), (testX, testY) = mnist.load_data()
from keras.models import Model
from keras.layers import Input, Reshape, Dense, Flatten, Dropout, LeakyReLU
class Autoencoder:
def __init__(self, img_shape=(28, 28), latent_dim=2, n_layers=2, n_units=128):
# encoder
h = i = Input(img_shape)
h = Flatten()(h)
for _ in range(n_layers):
h = Dense(n_units, activation='relu')(h)
o = Dense(latent_dim)(h)
self.encoder = Model(inputs=[i], outputs=[o])
# decoder
i = h = Input((latent_dim,))
for _ in range(n_layers):
h = Dense(n_units, activation='relu')(h)
h = Dense(img_shape[0] * img_shape[1])(h)
o = Reshape(img_shape)(h) # predict 1 frame
self.decoder = Model(inputs=[i], outputs=[o])
# stacked autoencoder
i = Input(img_shape)
z = self.encoder(i) # push observations into latent space
o = self.decoder(z) # project from latent space to feature space
self.auto = Model(inputs=[i], outputs=[o])
self.auto.compile(loss='mse', optimizer='adam')
model = Autoencoder()
model.auto.fit(trainX, trainX, validation_data=(testX[:100], testX[:100]), batch_size=100, epochs=10)
import matplotlib.pyplot as plt
%matplotlib inline
# transform each input image into the latent space
z = model.encoder.predict(trainX)
# color each point by its label
colors = trainY.tolist()
# plot the latent space
plt.scatter(z[:,0], z[:,1], marker='o', s=1, c=colors)
plt.colorbar()
import numpy as np
# sample from the region -50, -50
y = np.array([[60, -30]])
prediction = model.decoder.predict(y)
plt.imshow(prediction.squeeze())
```
# Create JS data structures
```
import json
with open('data/trainX-sample.json', 'w') as out:
json.dump(trainX[:50].tolist(), out)
with open('data/trainY.json', 'w') as out:
json.dump(trainY.tolist(), out)
import matplotlib.pyplot as plt
import numpy as np
import math
px_per_cell_side = 28
cells_per_axis = math.floor(2048/px_per_cell_side)
cells_per_atlas = cells_per_axis**2
n_atlases = math.ceil(trainX.shape[0] / cells_per_atlas)
# create a series of columns and suture them together
for i in range(n_atlases-1): # -1 to just create full atlas files (skip the remainder)
start = i * cells_per_atlas
end = (i+1) * cells_per_atlas
x = trainX[start:end]
cols = []
for j in range(cells_per_axis):
col_start = j*cells_per_axis
col_end = (j+1)*cells_per_axis
col = x[col_start:col_end].reshape(px_per_cell_side*cells_per_axis, px_per_cell_side)
cols.append(col)
im = np.hstack(cols)
im = 255-im # use 255- to flip black and white
plt.imsave('images/atlas-images/atlas-' + str(i) + '.jpg', im, cmap='gray')
# get a single row of images to render to ui
row = 255-x[col_start:col_end]
if False: plt.imsave('images/sample-row.jpg', np.hstack(row), cmap='gray')
print(' * total cells:', n_atlases * cells_per_atlas)
consumed = set()
for i in range(10):
for jdx, j in enumerate(trainY):
if j == i:
im = 255 - trainX[jdx].squeeze()
plt.imsave('images/digits/digit-' + str(i) + '.png', im, cmap='gray')
break
# create low dimensional embeddings
# from MulticoreTSNE import MulticoreTSNE as TSNE
from sklearn.manifold import TSNE, MDS, SpectralEmbedding, Isomap, LocallyLinearEmbedding
from umap import UMAP
from copy import deepcopy
import rasterfairy
import json
def center(arr):
'''Center an array to clip space -0.5:0.5 on all axes'''
arr = deepcopy(arr)
for i in range(arr.shape[1]):
arr[:,i] = arr[:,i] - np.min(arr[:,i])
arr[:,i] = arr[:,i] / np.max(arr[:,i])
arr[:,i] -= 0.5
return arr
def curate(arr):
'''Prepare an array for persistence to json'''
return np.around(center(arr), 4).tolist()
# prepare model inputs
n = 10000 #trainX.shape[0]
sampleX = trainX[:n]
flat = sampleX.reshape(sampleX.shape[0], sampleX.shape[1] * sampleX.shape[2])
# create sklearn outputs
for clf, label in [
#[SpectralEmbedding, 'se'],
#[Isomap, 'iso'],
#[LocallyLinearEmbedding, 'lle'],
#[MDS, 'mds'],
[TSNE, 'tsne'],
[UMAP, 'umap'],
]:
print(' * processing', label)
positions = clf(n_components=2).fit_transform(flat)
with open('data/mnist-positions/' + label + '_positions.json', 'w') as out:
json.dump(curate(positions), out)
import keras.backend as K
import numpy as np
import os, json
# create autoencoder outputs
model = Autoencoder(latent_dim=2)
lr = 0.005
for i in range(10):
lr *= 0.9
print(' * running step:', i, '-- lr:', lr)
K.set_value(model.auto.optimizer.lr, lr)
model.auto.fit(trainX, trainX, batch_size=250, epochs=10)
# save the auto latent positions to disk
auto_positions = model.encoder.predict(sampleX)
with open('data/mnist-positions/auto_positions.json', 'w') as out:
json.dump(curate(auto_positions), out)
# save the decoder to disk
model.decoder.save('data/model/decoder.h5')
os.system('tensorflowjs_converter --input_format keras \
data/model/decoder.h5 \
data/model/decoder')
# save the decoder domain to disk
domains = [[ float(np.min(z[:,i])), float(np.max(z[:,i])) ] for i in range(z.shape[1])]
with open('data/model/decoder-domains.json', 'w') as out:
json.dump(domains, out)
%matplotlib inline
import matplotlib.pyplot as plt
# plot the latent space
z = model.encoder.predict(trainX[:n]) # project inputs into latent space
colors = trainY[:n].tolist() # color points with labels
plt.scatter(z[:,0], z[:,1], marker='o', s=1, c=colors)
plt.colorbar()
import math
px_per_cell_side = 28
cells_per_axis = math.floor(2048/px_per_cell_side)
cells_per_atlas = cells_per_axis**2
n_atlases = math.ceil(trainX.shape[0] / cells_per_atlas)
print(' * total cells:', n_atlases * cells_per_atlas)
# create a series of columns and suture them together
for i in range(n_atlases-1): # -1 to just create full atlas files (skip the remainder)
start = i * cells_per_atlas
end = (i+1) * cells_per_atlas
x = trainX[start:end]
cols = []
for j in range(cells_per_axis):
col_start = j*cells_per_axis
col_end = (j+1)*cells_per_axis
col = x[col_start:col_end].reshape(px_per_cell_side*cells_per_axis, px_per_cell_side)
cols.append(col)
im = np.hstack(cols)
plt.imsave('atlas-' + str(i) + '.jpg', im, cmap='gray')
b = np.hstack(cols)
plt.imshow(b)
```
| true |
code
| 0.739553 | null | null | null | null |
|
# Neural Machine Translation with Attention: German to English
Here we implement a neural machine translator with attention using standard TensorFlow operations.
```
# These are all the modules we'll be using later. Make sure you can import them
# before proceeding further.
%matplotlib inline
from __future__ import print_function
import collections
import math
import numpy as np
import os
import random
import tensorflow as tf
import zipfile
from matplotlib import pylab
from six.moves import range
from six.moves.urllib.request import urlretrieve
import tensorflow as tf
from PIL import Image
from collections import Counter
import csv
import matplotlib.gridspec as gridspec
import word2vec
from nltk.translate.bleu_score import corpus_bleu
import nltk
```
## Loading Data
First, download the data from this [page](https://nlp.stanford.edu/projects/nmt/). The required files are:
* File containing German sentences: [`train.de`](https://nlp.stanford.edu/projects/nmt/data/wmt14.en-de/train.de)
* File containing English sentences: [`train.en`](https://nlp.stanford.edu/projects/nmt/data/wmt14.en-de/train.en)
* File containing German vocabulary: [`vocab.50K.de`](https://nlp.stanford.edu/projects/nmt/data/wmt14.en-de/vocab.50K.de)
* File containing English vocabulary: [`vocab.50K.en`](https://nlp.stanford.edu/projects/nmt/data/wmt14.en-de/vocab.50K.en)
### Loading Vocabulary
First we build the vocabulary dictionaries for both the source (German) and target (English) languages. The vocabularies are found in the `vocab.50K.de` (German) and `vocab.50K.en` files.
```
# ==========================================
# Building source language vocabulary
# Contains word string -> ID mapping
src_dictionary = dict()
# Read the vocabulary file
with open('vocab.50K.de', encoding='utf-8') as f:
# Read and store every line
for line in f:
#we are discarding last char as it is new line char
src_dictionary[line[:-1]] = len(src_dictionary)
# Build a reverse dictionary with the mapping ID -> word string
src_reverse_dictionary = dict(zip(src_dictionary.values(),src_dictionary.keys()))
# Print some of the words in the dictionary
print('Source')
print('\t',list(src_dictionary.items())[:10])
print('\t',list(src_reverse_dictionary.items())[:10])
print('\t','Vocabulary size: ', len(src_dictionary))
# ==========================================
# Building source language vocabulary
# Contains word string -> ID mapping
tgt_dictionary = dict()
# Read the vocabulary file
with open('vocab.50K.en', encoding='utf-8') as f:
# Read and store every line
for line in f:
#we are discarding last char as it is new line char
tgt_dictionary[line[:-1]] = len(tgt_dictionary)
# Build a reverse dictionary with the mapping ID -> word string
tgt_reverse_dictionary = dict(zip(tgt_dictionary.values(),tgt_dictionary.keys()))
# Print some of the words in the dictionary
print('Target')
print('\t',list(tgt_dictionary.items())[:10])
print('\t',list(tgt_reverse_dictionary.items())[:10])
print('\t','Vocabulary size: ', len(tgt_dictionary))
# Each language has 50000 words
vocabulary_size = 50000
```
### Loading Training and Testing Data
Here we load the data in the `train.de` and `train.en` files. And split the data in the files into two sets; training and testing data.
```
# Contains the training sentences
source_sent = [] # Input
target_sent = [] # Output
# Contains the testing sentences
test_source_sent = [] # Input
test_target_sent = [] # Output
# We grab around 100 lines of data that are interleaved
# in the first 50000 sentences
test_indices = [l_i for l_i in range(50,50001,500)]
# Read the source data file and read the first 250,000 lines (except first 50)
with open('train.de', encoding='utf-8') as f:
for l_i, line in enumerate(f):
# discarding first 50 translations as there was some
# english to english mappings found in the first few lines. which are wrong
if l_i<50:
continue
if len(source_sent)<250000 and l_i not in test_indices:
source_sent.append(line)
elif l_i in test_indices:
test_source_sent.append(line)
# Read the target data file and read the first 250,000 lines (except first 50)
with open('train.en', encoding='utf-8') as f:
for l_i, line in enumerate(f):
# discarding first 50 translations as there was some
# english to english mappings found in the first few lines. which are wrong
if l_i<50:
continue
if len(target_sent)<250000 and l_i not in test_indices:
target_sent.append(line)
elif l_i in test_indices:
test_target_sent.append(line)
# Make sure we extracted same number of both extracted source and target sentences
assert len(source_sent)==len(target_sent),'Source: %d, Target: %d'%(len(source_sent),len(target_sent))
# Print some source sentences
print('Sample translations (%d)'%len(source_sent))
for i in range(0,250000,10000):
print('(',i,') DE: ', source_sent[i])
print('(',i,') EN: ', target_sent[i])
# Print some target sentences
print('Sample test translations (%d)'%len(test_source_sent))
for i in range(0,100,10):
print('DE: ', test_source_sent[i])
print('EN: ', test_target_sent[i])
```
### Preprocessing text
Here we preprocess the text by replacing words not found in the dictionary with `<unk>` as well as remove punctuation marks (`.`,`,`) and new-line characters.
```
# Keep track of how many unknown words were encountered
src_unk_count, tgt_unk_count = 0, 0
def split_to_tokens(sent,is_source):
'''
This function takes in a sentence (source or target)
and preprocess the sentency with various steps (e.g. removing punctuation)
'''
global src_unk_count, tgt_unk_count
# Remove punctuation and new-line chars
sent = sent.replace(',',' ,')
sent = sent.replace('.',' .')
sent = sent.replace('\n',' ')
sent_toks = sent.split(' ')
for t_i, tok in enumerate(sent_toks):
if is_source:
# src_dictionary contain the word -> word ID mapping for source vocabulary
if tok not in src_dictionary.keys():
if not len(tok.strip())==0:
sent_toks[t_i] = '<unk>'
src_unk_count += 1
else:
# tgt_dictionary contain the word -> word ID mapping for target vocabulary
if tok not in tgt_dictionary.keys():
if not len(tok.strip())==0:
sent_toks[t_i] = '<unk>'
#print(tok)
tgt_unk_count += 1
return sent_toks
# Let us first look at some statistics of the sentences
# Train - source data
source_len = []
source_mean, source_std = 0,0
for sent in source_sent:
source_len.append(len(split_to_tokens(sent,True)))
print('(Source) Sentence mean length: ', np.mean(source_len))
print('(Source) Sentence stddev length: ', np.std(source_len))
# Let us first look at some statistics of the sentences
# Train - target data
target_len = []
for sent in target_sent:
target_len.append(len(split_to_tokens(sent,False)))
print('(Target) Sentence mean length: ', np.mean(target_len))
print('(Target) Sentence stddev length: ', np.std(target_len))
# Let us first look at some statistics of the sentences
# Test - source data
test_source_len = []
for sent in test_source_sent:
test_source_len.append(len(split_to_tokens(sent, True)))
print('(Test-Source) Sentence mean length: ', np.mean(test_source_len))
print('(Test-Source) Sentence stddev length: ', np.std(test_source_len))
# Let us first look at some statistics of the sentences
# Test - target data
test_target_len = []
test_tgt_mean, test_tgt_std = 0,0
for sent in test_target_sent:
test_target_len.append(len(split_to_tokens(sent, False)))
print('(Test-Target) Sentence mean length: ', np.mean(test_target_len))
print('(Test-Target) Sentence stddev length: ', np.std(test_target_len))
```
### Making training and testing data fixed length
Here we get all the source sentences and target sentences to a fixed length. This is, so that we can process the sentences as batches.
```
# ================================================================================
# Processing training data
src_unk_count, tgt_unk_count = 0, 0
train_inputs = []
train_outputs = []
# Chosen based on previously found statistics
src_max_sent_length = 41
tgt_max_sent_length = 61
print('Processing Training Data ...\n')
for s_i, (src_sent, tgt_sent) in enumerate(zip(source_sent,target_sent)):
# Break source and target sentences to word lists
src_sent_tokens = split_to_tokens(src_sent,True)
tgt_sent_tokens = split_to_tokens(tgt_sent,False)
# Append <s> token's ID to the beggining of source sentence
num_src_sent = [src_dictionary['<s>']]
# Add the rest of word IDs for words found in the source sentence
for tok in src_sent_tokens:
if tok in src_dictionary.keys():
num_src_sent.append(src_dictionary[tok])
# If the lenghth of the source sentence below the maximum allowed length
# append </s> token's ID to the end
if len(num_src_sent)<src_max_sent_length:
num_src_sent.extend([src_dictionary['</s>'] for _ in range(src_max_sent_length - len(num_src_sent))])
# If the length exceed the maximum allowed length
# truncate the sentence
elif len(num_src_sent)>src_max_sent_length:
num_src_sent = num_src_sent[:src_max_sent_length]
# Make sure the sentence is of length src_max_sent_length
assert len(num_src_sent)==src_max_sent_length,len(num_src_sent)
train_inputs.append(num_src_sent)
# Create the numeric target sentence with word IDs
# append <s> to the beginning and append actual words later
num_tgt_sent = [tgt_dictionary['<s>']]
for tok in tgt_sent_tokens:
if tok in tgt_dictionary.keys():
num_tgt_sent.append(tgt_dictionary[tok])
## Modifying the outputs such that all the outputs have max_length elements
if len(num_tgt_sent)<tgt_max_sent_length:
num_tgt_sent.extend([tgt_dictionary['</s>'] for _ in range(tgt_max_sent_length - len(num_tgt_sent))])
elif len(num_tgt_sent)>tgt_max_sent_length:
num_tgt_sent = num_tgt_sent[:tgt_max_sent_length]
train_outputs.append(num_tgt_sent)
print('Unk counts Src: %d, Tgt: %d'%(src_unk_count, tgt_unk_count))
print('Sentences ',len(train_inputs))
assert len(train_inputs) == len(source_sent),\
'Size of total elements: %d, Total sentences: %d'\
%(len(train_inputs),len(source_sent))
# Making inputs and outputs NumPy arrays
train_inputs = np.array(train_inputs, dtype=np.int32)
train_outputs = np.array(train_outputs, dtype=np.int32)
# Make sure number of inputs and outputs dividable by 100
train_inputs = train_inputs[:(train_inputs.shape[0]//100)*100,:]
train_outputs = train_outputs[:(train_outputs.shape[0]//100)*100,:]
print('\t Done processing training data \n')
# Printing some data
print('Samples from training data')
for ti in range(10):
print('\t',[src_reverse_dictionary[w] for w in train_inputs[ti,:].tolist()])
print('\t',[tgt_reverse_dictionary[w] for w in train_outputs[ti,:].tolist()])
print()
print('\tSentences ',train_inputs.shape[0])
# ================================================================================
# Processing Test data
src_unk_count, tgt_unk_count = 0, 0
print('Processing testing data ....\n')
test_inputs = []
test_outputs = []
for s_i, (src_sent,tgt_sent) in enumerate(zip(test_source_sent,test_target_sent)):
src_sent_tokens = split_to_tokens(src_sent,True)
tgt_sent_tokens = split_to_tokens(tgt_sent,False)
num_src_sent = [src_dictionary['<s>']]
for tok in src_sent_tokens:
if tok in src_dictionary.keys():
num_src_sent.append(src_dictionary[tok])
num_tgt_sent = [src_dictionary['<s>']]
for tok in tgt_sent_tokens:
if tok in tgt_dictionary.keys():
num_tgt_sent.append(tgt_dictionary[tok])
# Append </s> if the length is not src_max_sent_length
if len(num_src_sent)<src_max_sent_length:
num_src_sent.extend([src_dictionary['</s>'] for _ in range(src_max_sent_length - len(num_src_sent))])
# Truncate the sentence if length is over src_max_sent_length
elif len(num_src_sent)>src_max_sent_length:
num_src_sent = num_src_sent[:src_max_sent_length]
assert len(num_src_sent)==src_max_sent_length, len(num_src_sent)
test_inputs.append(num_src_sent)
# Append </s> is length is not tgt_max_sent_length
if len(num_tgt_sent)<tgt_max_sent_length:
num_tgt_sent.extend([tgt_dictionary['</s>'] for _ in range(tgt_max_sent_length - len(num_tgt_sent))])
# Truncate the sentence if length over tgt_max_sent_length
elif len(num_tgt_sent)>tgt_max_sent_length:
num_tgt_sent = num_tgt_sent[:tgt_max_sent_length]
assert len(num_tgt_sent)==tgt_max_sent_length, len(num_tgt_sent)
test_outputs.append(num_tgt_sent)
# Printing some data
print('Unk counts Tgt: %d, Tgt: %d'%(src_unk_count, tgt_unk_count))
print('Done processing testing data ....\n')
test_inputs = np.array(test_inputs,dtype=np.int32)
test_outputs = np.array(test_outputs,dtype=np.int32)
print('Samples from training data')
for ti in range(10):
print('\t',[src_reverse_dictionary[w] for w in test_inputs[ti,:].tolist()])
print('\t',[tgt_reverse_dictionary[w] for w in test_outputs[ti,:].tolist()])
```
## Learning word embeddings
In this section, we learn word embeddings for both the languages using the sentences we have. After learning word embeddings, this will create two arrays (`en-embeddings-tmp.npy` and `de-embeddings-tmp.npy`) and store them on disk. To use this in the successive computations, go ahead and change the names to `en-embeddings.npy` and `de-embeddings.npy` respectively. ** You can skip this if you have run the code previously. **
```
# Total number of sentences
tot_sentences = train_inputs.shape[0]
print('Total number of training sentences: ',tot_sentences)
# we keep a cursor for each sentence in the training set
sentence_cursors = [0 for _ in range(tot_sentences)]
batch_size = 64
embedding_size = 128 # Dimension of the embedding vector.
# Defining various things needed by the python script
word2vec.define_data_and_hyperparameters(
tot_sentences, src_max_sent_length, tgt_max_sent_length, src_dictionary, tgt_dictionary,
src_reverse_dictionary, tgt_reverse_dictionary, train_inputs, train_outputs, embedding_size,
vocabulary_size)
# Print some batches to make sure the data generator is correct
word2vec.print_some_batches()
# Define TensorFlow ops for learning word embeddings
word2vec.define_word2vec_tensorflow(batch_size)
# Run embedding learning for source language
# Stores the de-embeddings-tmp.npy into the disk
word2vec.run_word2vec_source(batch_size)
# Run embedding learning for target language
# Stores the en-embeddings-tmp.npy to the disk
word2vec.run_word2vec_target(batch_size)
```
## Flipping the Input Data
Changin the order of the sentence of the target language improves the performance of NMT systems. Because when reversed, it helps the NMT system to establish a strong connection as the last word of the source language and the last word of the target language will be closest to each other. *DON'T RUN THIS MULTIPLE TIMES as running two times gives original.*
```
## Reverse the Germen sentences
# Remember reversing the source sentence gives better performance
# DON'T RUN THIS MULTIPLE TIMES as running two times gives original
train_inputs = np.fliplr(train_inputs)
test_inputs = np.fliplr(test_inputs)
print('Training and Test source data after flipping ')
print('\t',[src_reverse_dictionary[w] for w in train_inputs[0,:].tolist()])
print('\t',[tgt_reverse_dictionary[w] for w in test_inputs[0,:].tolist()])
print()
print('\t',[src_reverse_dictionary[w] for w in train_inputs[10,:].tolist()])
print('\t',[tgt_reverse_dictionary[w] for w in test_inputs[10,:].tolist()])
print()
print('\nTesting data after flipping')
print('\t',[src_reverse_dictionary[w] for w in test_inputs[0,:].tolist()])
```
## Data Generations for MT
Now we define the data generator for our NMT.
```
emb_mat = np.load('de-embeddings.npy')
embedding_size = emb_mat.shape[1]
input_size = embedding_size
class DataGeneratorMT(object):
def __init__(self,batch_size,num_unroll,is_source, is_train):
# Number of data points in a batch
self._batch_size = batch_size
# Number of unrollings
self._num_unroll = num_unroll
# Cursors for each element in batch
self._cursor = [0 for offset in range(self._batch_size)]
# Loading the learnt word embeddings
self._src_word_embeddings = np.load('de-embeddings.npy')
self._tgt_word_embeddings = np.load('en-embeddings.npy')
# The sentence IDs being currently processed to create the
# current batch
self._sent_ids = None
# We want a batch of data from source or target?
self._is_source = is_source
# Is this training or testing data?
self._is_train = is_train
def next_batch(self, sent_ids):
# Depending on wheter we want source or target data
# change the maximum sentence length
if self._is_source:
max_sent_length = src_max_sent_length
else:
max_sent_length = tgt_max_sent_length
# Arrays to hold input and output data
# Word embeddings (current word)
batch_data = np.zeros((self._batch_size,input_size),dtype=np.float32)
# One-hot encoded label (next word)
batch_labels = np.zeros((self._batch_size,vocabulary_size),dtype=np.float32)
# Populate each index of the batch
for b in range(self._batch_size):
# Sentence IDs to get data from
sent_id = sent_ids[b]
# If generating data with source sentences
# use src_word_embeddings
if self._is_source:
# Depending on whether we need training data or testind data
# choose the previously created training or testing data
if self._is_train:
sent_text = train_inputs[sent_id]
else:
sent_text = test_inputs[sent_id]
# Populate the batch data arrays
batch_data[b] = self._src_word_embeddings[sent_text[self._cursor[b]],:]
batch_labels[b] = np.zeros((vocabulary_size),dtype=np.float32)
batch_labels[b,sent_text[self._cursor[b]+1]] = 1.0
# If generating data with target sentences
# use tgt_word_embeddings
else:
# Depending on whether we need training data or testind data
# choose the previously created training or testing data
if self._is_train:
sent_text = train_outputs[sent_id]
else:
sent_text = test_outputs[sent_id]
# We cannot avoid having two different embedding vectors for <s> token
# in soruce and target languages
# Therefore, if the symbol appears, we always take the source embedding vector
if sent_text[self._cursor[b]]!=tgt_dictionary['<s>']:
batch_data[b] = self._tgt_word_embeddings[sent_text[self._cursor[b]],:]
else:
batch_data[b] = self._src_word_embeddings[sent_text[self._cursor[b]],:]
# Populate the data arrays
batch_labels[b] = np.zeros((vocabulary_size),dtype=np.float32)
batch_labels[b,sent_text[self._cursor[b]+1]] = 1.0
# Update the cursor for each batch index
self._cursor[b] = (self._cursor[b]+1)%(max_sent_length-1)
return batch_data,batch_labels
def unroll_batches(self,sent_ids):
# Only if new sentence IDs if provided
# else it will use the previously defined
# sent_ids continuously
if sent_ids is not None:
self._sent_ids = sent_ids
# Unlike in the previous exercises we do not process a single sequence
# over many iterations of unrollings. We process either a source sentence or target sentence
# at a single go. So we reset the _cursor evrytime we generate a batch
self._cursor = [0 for _ in range(self._batch_size)]
unroll_data,unroll_labels = [],[]
# Unrolling data over time
for ui in range(self._num_unroll):
if self._is_source:
data, labels = self.next_batch(self._sent_ids)
else:
data, labels = self.next_batch(self._sent_ids)
unroll_data.append(data)
unroll_labels.append(labels)
# Return unrolled data and sentence IDs
return unroll_data, unroll_labels, self._sent_ids
def reset_indices(self):
self._cursor = [0 for offset in range(self._batch_size)]
# Running a tiny set to see if the implementation correct
dg = DataGeneratorMT(batch_size=5,num_unroll=20,is_source=True, is_train=True)
u_data, u_labels, _ = dg.unroll_batches([0,1,2,3,4])
print('Source data')
for _, lbl in zip(u_data,u_labels):
# the the string words for returned word IDs and display the results
print([src_reverse_dictionary[w] for w in np.argmax(lbl,axis=1).tolist()])
# Running a tiny set to see if the implementation correct
dg = DataGeneratorMT(batch_size=5,num_unroll=30,is_source=False, is_train=True)
u_data, u_labels, _ = dg.unroll_batches([0,2,3,4,5])
print('\nTarget data batch')
for d_i,(_, lbl) in enumerate(zip(u_data,u_labels)):
# the the string words for returned word IDs and display the results
print([tgt_reverse_dictionary[w] for w in np.argmax(lbl,axis=1).tolist()])
```
## Attention-Based NMT System
Here we define the attention based NMT system. Unlike the standard NMT attention based NMT has the ability to refer to any of the encoder states during any step of the decoding. This is achieved through the attention layer.
### Defining hyperparameters
Here we define various hyperparameters we use to define our model.
```
num_nodes = 128
batch_size = 10
# We unroll the full length at one go
# both source and target sentences
enc_num_unrollings = 40
dec_num_unrollings = 60
```
### Defining Input/Output Placeholders
Here we define the placeholder to feed in inputs/outputs. Additionally we define a mask placeholder that can mask certain outputs from the loss calculation.
```
tf.reset_default_graph()
tgt_word_embeddings = tf.convert_to_tensor(np.load('en-embeddings.npy'))
# Training Input data.
enc_train_inputs = []
# Defining unrolled training inputs
for ui in range(enc_num_unrollings):
enc_train_inputs.append(tf.placeholder(tf.float32, shape=[batch_size,input_size],name='train_inputs_%d'%ui))
# Training Input data.
dec_train_inputs, dec_train_labels = [],[]
dec_train_masks = []
# Defining unrolled training inputs
for ui in range(dec_num_unrollings):
dec_train_inputs.append(tf.placeholder(tf.float32, shape=[batch_size,input_size],name='dec_train_inputs_%d'%ui))
dec_train_labels.append(tf.placeholder(tf.float32, shape=[batch_size,vocabulary_size], name = 'dec_train_labels_%d'%ui))
dec_train_masks.append(tf.placeholder(tf.float32, shape=[batch_size,1],name='dec_train_masks_%d'%ui))
enc_test_input = [tf.placeholder(tf.float32, shape=[batch_size,input_size]) for _ in range(enc_num_unrollings)]
enc_test_mask = [tf.placeholder(tf.int32,shape=[batch_size]) for _ in range(enc_num_unrollings)]
dec_test_input = tf.nn.embedding_lookup(tgt_word_embeddings,[tgt_dictionary['<s>']])
```
### Defining the Encoder Model
We define the encoder model. The encoder model is a single LSTM cell with TensorFlow variables for the state and output variables.
```
print('Defining Encoder Parameters')
with tf.variable_scope('Encoder'):
# Input gate (i_t) - How much memory to write to cell state
enc_ix = tf.get_variable('ix',shape=[input_size, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
enc_im = tf.get_variable('im',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
enc_ib = tf.Variable(tf.random_uniform([1, num_nodes],-0.05, 0.05),name='ib')
# Forget gate (f_t) - How much memory to discard from cell state
enc_fx = tf.get_variable('fx',shape=[input_size, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
enc_fm = tf.get_variable('fm',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
enc_fb = tf.Variable(tf.random_uniform([1, num_nodes],-0.05, 0.05),name='fb')
# Candidate value (c~_t) - Used to compute the current cell state
enc_cx = tf.get_variable('cx',shape=[input_size, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
enc_cm = tf.get_variable('cm',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
enc_cb = tf.Variable(tf.random_uniform([1, num_nodes],-0.05,0.05),name='cb')
# Output gate (o_t) - How much memory to output from the cell state
enc_ox = tf.get_variable('ox',shape=[input_size, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
enc_om = tf.get_variable('om',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
enc_ob = tf.Variable(tf.random_uniform([1, num_nodes],-0.05,0.05),name='ob')
# Variables saving state across unrollings.
saved_output = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False, name='train_output')
saved_state = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False, name = 'train_cell')
# Variables for saving state for testing
saved_test_output = tf.Variable(tf.zeros([batch_size, num_nodes]),trainable=False, name='test_output')
saved_test_state = tf.Variable(tf.zeros([batch_size, num_nodes]),trainable=False, name='test_cell')
print('\tDone')
```
### Defining the Decoder Model
Decoder is a single LSTM cell with an additional softmax layer that can predict words.
```
print('Defining Decoder Parameters')
with tf.variable_scope('Decoder'):
# Input gate (i_t) - How much memory to write to cell state
dec_ix = tf.get_variable('ix',shape=[input_size, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_im = tf.get_variable('im',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_ic = tf.get_variable('ic',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_ib = tf.Variable(tf.random_uniform([1, num_nodes],-0.05, 0.05),name='ib')
# Forget gate (f_t) - How much memory to discard from cell state
dec_fx = tf.get_variable('fx',shape=[input_size, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_fm = tf.get_variable('fm',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_fc = tf.get_variable('fc',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_fb = tf.Variable(tf.random_uniform([1, num_nodes],-0.05, 0.05),name='fb')
# Candidate value (c~_t) - Used to compute the current cell state
dec_cx = tf.get_variable('cx',shape=[input_size, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_cm = tf.get_variable('cm',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_cc = tf.get_variable('cc',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_cb = tf.Variable(tf.random_uniform([1, num_nodes],-0.05,0.05),name='cb')
# Output gate (o_t) - How much memory to output from the cell state
dec_ox = tf.get_variable('ox',shape=[input_size, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_om = tf.get_variable('om',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_oc = tf.get_variable('oc',shape=[num_nodes, num_nodes],
initializer = tf.contrib.layers.xavier_initializer())
dec_ob = tf.Variable(tf.random_uniform([1, num_nodes],-0.05,0.05),name='ob')
# Softmax Classifier weights and biases.
# If we are using sampled softmax loss, the weights dims shouldbe [50000, 64]
# If not, then [64, 50000]
w = tf.get_variable('softmax_weights',shape=[num_nodes*2, vocabulary_size],
initializer = tf.contrib.layers.xavier_initializer())
b = tf.Variable(tf.random_uniform([vocabulary_size],-0.05,-0.05),name='softmax_bias')
print('\tDone')
```
### Attention Layer Related Variables
We define the weights used to compute the energy ($e_{ij}$) in the attention layer.
```
print('Defining Attention Variables ...')
with tf.variable_scope('Attention'):
# Used to calculate e_{ij} as
# e_{ij} = v_a' tanh(W_a . dec_output + U_a . enc_output)
# Then alpha_{ij} is the softmax output (normalized) of e_{ij}
W_a = tf.Variable(tf.truncated_normal([num_nodes,num_nodes],stddev=0.05),name='W_a')
U_a = tf.Variable(tf.truncated_normal([num_nodes,num_nodes],stddev=0.05),name='U_a')
v_a = tf.Variable(tf.truncated_normal([num_nodes,1],stddev=0.05),name='v_a')
print('\tDone')
```
### Defining Cell and Layer Computational Functions
We define several functions below:
* Encoder LSTM cell computations
* Decoder LSTM cell computations
* Attention layer computations.
```
# Definition of the cell computation (Encoder)
def enc_lstm_cell(i, o, state):
"""Create a LSTM cell"""
input_gate = tf.sigmoid(tf.matmul(i, enc_ix) + tf.matmul(o, enc_im) + enc_ib)
forget_gate = tf.sigmoid(tf.matmul(i, enc_fx) + tf.matmul(o, enc_fm) + enc_fb)
update = tf.matmul(i, enc_cx) + tf.matmul(o, enc_cm) + enc_cb
state = forget_gate * state + input_gate * tf.tanh(update)
output_gate = tf.sigmoid(tf.matmul(i, enc_ox) + tf.matmul(o, enc_om) + enc_ob)
return output_gate * tf.tanh(state), state
# Definition of the cell computation (Decoder)
def dec_lstm_cell(i, o, state, c):
"""Create a LSTM cell"""
input_gate = tf.sigmoid(tf.matmul(i, dec_ix) + tf.matmul(o, dec_im) + tf.matmul(c, dec_ic) + dec_ib)
forget_gate = tf.sigmoid(tf.matmul(i, dec_fx) + tf.matmul(o, dec_fm) + tf.matmul(c, dec_fc) + dec_fb)
update = tf.matmul(i, dec_cx) + tf.matmul(o, dec_cm) + tf.matmul(c, dec_cc) +dec_cb
state = forget_gate * state + input_gate * tf.tanh(update)
output_gate = tf.sigmoid(tf.matmul(i, dec_ox) + tf.matmul(o, dec_om) + tf.matmul(o, dec_oc) + dec_ob)
return output_gate * tf.tanh(state), state
def attn_layer(h_j_unrolled, s_i_minus_1):
'''
Computes attention values for a given decoding position
h_j_unrolled : all the unrolled encoder outputs [[batch_size, num_nodes], [batch_size, num_nodes], ....] => enc_num_unrolling-many
s_i_minus_1 : the previous decoder output [batch_size, num_nodes]
'''
# For the following four calculations we calculate by concatenating all encoder outputs (enc_num_unrollings)
# get the encoder logits
enc_logits = tf.concat(axis=0,values=h_j_unrolled)
# W_a . encoder_output
w_a_mul_s_i_minus_1 = tf.matmul(enc_logits,W_a) # of size [enc_num_unroll x batch_size, num_nodes]
# U_a . decoder_output
u_a_mul_h_j = tf.matmul(tf.tile(s_i_minus_1,[enc_num_unrollings,1]), U_a) # of size [enc_num_unroll x batch_size, num_nodes]
# calculate "energy"
e_j = tf.matmul(tf.nn.tanh(w_a_mul_s_i_minus_1 + u_a_mul_h_j),v_a) # of size [enc_num_unroll x batch_size ,1]
# we split the e_j s again into enc_num_unrollings batches
batched_e_j = tf.split(axis=0,num_or_size_splits=enc_num_unrollings,value=e_j) # list of enc_num_unroll elements, each element [batch_size, 1]
reshaped_e_j = tf.concat(axis=1,values=batched_e_j) # of size [batch_size, enc_num_unroll]
# Now we calculate alpha_i for all the enc_num_unrollings time steps
alpha_i = tf.nn.softmax(reshaped_e_j) # of size [batch_size, enc_num_unroll]
# break alpha_i into list of enc_num_unroll elemtns, each of size [batch_size,1]
alpha_i_list = tf.unstack(alpha_i,axis=1)
# list of enc_num_unroll elements, each of size [batch_size,num_nodes]
c_i_list = [tf.reshape(alpha_i_list[e_i],[-1,1])*h_j_unrolled[e_i] for e_i in range(enc_num_unrollings)]
# add_n batches all together
c_i = tf.add_n(c_i_list) # of size [batch_size, num_nodes]
return c_i,alpha_i
```
### Defining LSTM Computations
Here we define the computations to compute the final state variables of the encoder, feeding that into the decoder as the intial state, computing attention and finally computing the LSTM output, logit values and the predictions.
```
# ================================================
# Training related inference logic
# Store encoder outputs and decoder outputs across the unrolling
enc_outputs, dec_outputs = list(),list()
# Context vecs are the c_i values in the attention computation
context_vecs = list()
# These variables are initialized with saved_output and saved_sate
# values and then iteratively updated during unrollings
output = saved_output
state = saved_state
print('Calculating Encoder Output')
# update the output and state values for all the inputs we have
for i in enc_train_inputs:
output, state = enc_lstm_cell(i, output,state)
# Accumulate all the output values in to a list
enc_outputs.append(output)
print('Calculating Decoder Output with Attention')
# Before starting decoder computations, we make sure that
# the encoder outputs are computed
with tf.control_dependencies([saved_output.assign(output),
saved_state.assign(state)]):
# Iterate through the decoder unrollings
for ii,i in enumerate(dec_train_inputs):
# Compute attention value for each decode position
c_i,_ = attn_layer(enc_outputs, output)
# Accumulate c_i in a list
context_vecs.append(c_i)
output, state = dec_lstm_cell(i, output, state, c_i)
# Accumulate decoder outputs in a list
dec_outputs.append(output)
print('Calculating Softmax output')
# Compute the logit values
logits = tf.matmul(
tf.concat(axis=1, values=[
tf.concat(axis=0, values=dec_outputs),
tf.concat(axis=0, values=context_vecs)
]), w) + b
# Predictions.
train_prediction = tf.nn.softmax(logits)
# ================================================
# Testing related inference logic
# Initialize iteratively updated states with
# saved_test_output and saved_test_state
test_output = saved_test_output
test_state = saved_test_state
print("Calculations for test data")
test_predictions = []
test_enc_outputs = []
# Compute the encoder output iteratively
for i in enc_test_input:
test_output, test_state = enc_lstm_cell(i, test_output,test_state)
test_enc_outputs.append(test_output)
# This is used for visualization purposes
# To build the attention matrix discussed in the chapter
test_alpha_i_unrolled = []
# Make sure the encoder computations are done
with tf.control_dependencies([saved_test_output.assign(test_output),
saved_test_state.assign(test_state)]):
# Compute the decoder outputs iteratively
for i in range(dec_num_unrollings):
test_c_i,test_alpha = attn_layer(test_enc_outputs, test_output)
# Used for attention visualization purposes
test_alpha_i_unrolled.append(test_alpha)
test_output, test_state = dec_lstm_cell(dec_test_input, test_output, test_state, test_c_i)
# Compute predictions for each decoding step
test_prediction = tf.nn.softmax(
tf.nn.xw_plus_b(
tf.concat(axis=1,values=[test_output,test_c_i]), w, b
)
)
dec_test_input = tf.nn.embedding_lookup(tgt_word_embeddings,tf.argmax(test_prediction,axis=1))
test_predictions.append(tf.argmax(test_prediction,axis=1))
print('\tDone')
```
### Calculating the Loss
Here we calculate the loss. Loss is calculated by summing all the losses obtained across the time axis and averaging over the batch axis. You can see how the `dec_train_masks` is used to mask out irrelevant words from influencing loss
```
# Defining loss, cross-entropy loss summed across time axis averaged over batch axis
loss_batch = tf.concat(axis=0,values=dec_train_masks)*tf.nn.softmax_cross_entropy_with_logits_v2(
logits=logits, labels=tf.concat(axis=0, values=dec_train_labels))
loss = tf.reduce_mean(loss_batch)
```
### Optimizer
We define the model optimization specific operations. We use two optimizers here; Adam and SGD. I observed that using Adam only cause the model to exhibit some undesired behaviors in the long run. Therefore we use Adam to get a good initial estimate for the SGD and use SGD from that point onwards.
```
print('Defining Optimizer')
# These are used to decay learning rate over time
global_step = tf.Variable(0, trainable=False)
inc_gstep = tf.assign(global_step,global_step + 1)
# We use two optimizers, when the optimizer changes
# we reset the global step
reset_gstep = tf.assign(global_step,0)
# Calculate decaying learning rate
learning_rate = tf.maximum(
tf.train.exponential_decay(
0.005, global_step, decay_steps=1, decay_rate=0.95, staircase=True
), 0.0001)
sgd_learning_rate = tf.maximum(
tf.train.exponential_decay(
0.005, global_step, decay_steps=1, decay_rate=0.95, staircase=True
), 0.0001)
# We use two optimizers: Adam and naive SGD
# using Adam in the long run produced undesirable results
# (e.g.) sudden fluctuations in BLEU
# Therefore we use Adam to get a good starting point for optimizing
# and then switch to SGD from that point onwards
with tf.variable_scope('Adam'):
optimizer = tf.train.AdamOptimizer(learning_rate)
with tf.variable_scope('SGD'):
sgd_optimizer = tf.train.GradientDescentOptimizer(sgd_learning_rate)
# Calculates gradients with clipping for Adam
gradients, v = zip(*optimizer.compute_gradients(loss))
gradients, _ = tf.clip_by_global_norm(gradients, 25.0)
optimize = optimizer.apply_gradients(zip(gradients, v))
# Calculates gradients with clipping for SGD
sgd_gradients, v = zip(*sgd_optimizer.compute_gradients(loss))
sgd_gradients, _ = tf.clip_by_global_norm(sgd_gradients, 25.0)
sgd_optimize = optimizer.apply_gradients(zip(sgd_gradients, v))
# Make sure gradients exist flowing from decoder to encoder
print('Checking gradient flow from encoder-to-decoder')
for (g_i,v_i) in zip(gradients,v):
assert g_i is not None, 'Gradient none for %s'%(v_i.name)
print('\t Ok...')
print('\tDone')
```
### Resetting Train and Test States
We here define the state resetting functions
```
# Reset state
reset_train_state = tf.group(
tf.assign(saved_output, tf.zeros([batch_size, num_nodes])),
tf.assign(saved_state, tf.zeros([batch_size, num_nodes]))
)
reset_test_state = tf.group(
saved_test_output.assign(tf.zeros([batch_size, num_nodes])),
saved_test_state.assign(tf.zeros([batch_size, num_nodes]))
)
```
## Running the Neural Machine Translator with Attention
With all the relevant TensorFlow operations defined we move on to defining several functions related to executing our NMT model as well as runnning the model to obtain translations for previously unseen source sentences.
### Functions for Evaulating and Printing Results
Next we define two functions to print and save the prediction results for training data as well as testing data, and finally define a function to obtain candidate and reference data to calculate the BLEU score.
```
def print_and_save_train_predictions(du_labels, tr_pred, rand_idx, train_prediction_text_fname):
'''
Use this to print some predicted training samples and save it to file
du_labels: Decoder's unrolled labels (this is a list of dec_num_unrollings
where each item is [batch_size, vocabulary_size])
tr_pred: This is an array [dec_num_unrollings*batch_size, vocabulary_size] array
rand_idx: Some random index we use to pick a data point to print
train_prediction_text_fname: The file we save the prediction results into
'''
# This print_str will be written to the text file as well as printed here
print_str = 'Actual: '
# We can get each label corresponding to some sentence by traversing the
# concatenated labels array ([dec_num_unrollings*batch_size, vocabulary_size])
# with a batch_size stride
for w in np.argmax(np.concatenate(du_labels,axis=0)[rand_idx::batch_size],axis=1).tolist():
# Update the print_str
print_str += tgt_reverse_dictionary[w] + ' '
# When we encounter the end of sentence </s> we stop printing
if tgt_reverse_dictionary[w] == '</s>':
break
print(print_str)
# Write to file
with open(os.path.join(log_dir, train_prediction_text_fname),'a',encoding='utf-8') as fa:
fa.write(print_str+'\n')
# Now print the predicted data by following the same procedure as above
print()
print_str = 'Predicted: '
for w in np.argmax(tr_pred[rand_idx::batch_size],axis=1).tolist():
print_str += tgt_reverse_dictionary[w] + ' '
# When we encounter the end of sentence </s> we stop printing
if tgt_reverse_dictionary[w] == '</s>':
break
print(print_str)
with open(os.path.join(log_dir, train_prediction_text_fname),'a',encoding='utf-8') as fa:
fa.write(print_str+'\n')
def print_and_save_test_predictions(test_du_labels, test_pred_unrolled, batch_id, test_rand_idx, test_prediction_text_fname):
'''
Use this to print some predicted training samples and save it to file
test_du_labels: Decoder's unrolled labels (this is a list of dec_num_unrollings
where each item is [batch_size, vocabulary_size])
test_pred_unrolled: This is an array [dec_num_unrollings*batch_size, vocabulary_size] array
batch_id: We need this to retrieve the actual sentence for the predicted
test_rand_idx: Some random index we use to pick a data point to print
test_prediction_text_fname: The file we save the prediction results into
'''
# Print the actual sentence
print('DE: ',test_source_sent[(batch_id*batch_size)+test_rand_idx])
# print_str is the string we display as results and write to a file
print_str = '\t EN (TRUE):' + test_target_sent[(batch_id*batch_size)+test_rand_idx]
print(print_str + '\n')
# Printing predictions
print_str = '\t EN (Predicted): '
for test_pred in test_pred_unrolled:
print_str += tgt_reverse_dictionary[test_pred[test_rand_idx]] + ' '
if tgt_reverse_dictionary[test_pred[test_rand_idx]] == '</s>':
break
print(print_str + '\n')
# Write the results to text file
with open(os.path.join(log_dir, test_prediction_text_fname),'a',encoding='utf-8') as fa:
fa.write(print_str+'\n')
def create_bleu_ref_candidate_lists(all_preds, all_labels):
'''
Creates two lists (candidate list and reference list) for calcluating BLEU
all_preds: All the predictions
all_labels: Correspondign all the actual labels
Returns
cand_list: List (sentences) of lists (words in a sentence)
ref_list: List (sentences) of lists (words in a sentence)
'''
bleu_labels, bleu_preds = [],[]
# calculate bleu score:
# We iterate batch_size times as i=0,1,2,...,batch_size while grabbing
# i, i+batch_size, i+2*batch_size, i+3*batch_size elements from all_labels and all_preds
# This because the labels/predicitons belonging to same sentence are interleaved by batch_size
# due to the way concatenate labels and predictions
# Taking elements interleaved by batch_size gives the sequence of words belonging to the same sentence
ref_list, cand_list = [],[]
for b_i in range(batch_size):
tmp_lbl = all_labels[b_i::batch_size]
tmp_lbl = tmp_lbl[np.where(tmp_lbl != tgt_dictionary['</s>'])]
ref_str = ' '.join([tgt_reverse_dictionary[lbl] for lbl in tmp_lbl])
ref_list.append([ref_str])
tmp_pred = all_preds[b_i::batch_size]
tmp_pred = tmp_pred[np.where(tmp_pred != tgt_dictionary['</s>'])]
cand_str = ' '.join([tgt_reverse_dictionary[pre] for pre in tmp_pred])
cand_list.append(cand_str)
return cand_list, ref_list
```
### Defining a Single Step of Training
We now define a function to train the NMT model for a single step. It takes in encoder inputs, decoder inputs and decoder labels and train the NMT for a single step.
```
def train_single_step(eu_data, du_data, du_labels):
'''
Define a single training step
eu_data: Unrolled encoder inputs (word embeddings)
du_data: Unrolled decoder inputs (word embeddings)
du_labels: Unrolled decoder outputs (one hot encoded words)
'''
# Fill the feed dict (Encoder)
feed_dict = {}
for ui,dat in enumerate(eu_data):
feed_dict[enc_train_inputs[ui]] = dat
# Fill the feed dict (Decoder)
for ui,(dat,lbl) in enumerate(zip(du_data,du_labels)):
feed_dict[dec_train_inputs[ui]] = dat
feed_dict[dec_train_labels[ui]] = lbl
# The mask masks the </s> items from being part of the loss
d_msk = (np.logical_not(np.argmax(lbl,axis=1)==tgt_dictionary['</s>'])).astype(np.int32).reshape(-1,1)
feed_dict[dec_train_masks[ui]] = d_msk
# ======================= OPTIMIZATION ==========================
# Using Adam in long term gives very weird behaviors in loss
# so after 20000 iterations we change the optimizer to SGD
if (step+1)<20000:
_,l,tr_pred = sess.run([optimize,loss,train_prediction], feed_dict=feed_dict)
else:
_,l,tr_pred = sess.run([sgd_optimize,loss,train_prediction], feed_dict=feed_dict)
return l, tr_pred
```
### Defining Data Generators and Other Related Variables
Here we load the word embeddings and some other things as well as define a function to retrieve data generators
```
# This is where all the results will be logged into
log_dir = 'logs'
if not os.path.exists(log_dir):
os.mkdir(log_dir)
# Filenames of the logs
train_prediction_text_fname = 'train_predictions_attn.txt'
test_prediction_text_fname = 'test_predictions_attn.txt'
# Some configuration for the TensorFlow session
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
config.allow_soft_placement=True
sess = tf.InteractiveSession(config=config)
# Initialize global variables
tf.global_variables_initializer().run()
# Load the word embeddings
src_word_embeddings = np.load('de-embeddings.npy')
tgt_word_embeddings = np.load('en-embeddings.npy')
# Defining data generators
def define_data_generators(batch_size, enc_num_unrollings, dec_num_unrollings):
# Training data generators (Encoder and Decoder)
enc_data_generator = DataGeneratorMT(batch_size=batch_size,num_unroll=enc_num_unrollings,is_source=True, is_train=True)
dec_data_generator = DataGeneratorMT(batch_size=batch_size,num_unroll=dec_num_unrollings,is_source=False, is_train=True)
# Testing data generators (Encoder and Decoder)
test_enc_data_generator = DataGeneratorMT(batch_size=batch_size,num_unroll=enc_num_unrollings,is_source=True, is_train=False)
test_dec_data_generator = DataGeneratorMT(batch_size=batch_size,num_unroll=dec_num_unrollings,is_source=False, is_train=False)
return enc_data_generator,dec_data_generator,test_enc_data_generator,test_dec_data_generator
```
### Running Training and Testing for NMT
With all the TensorFlow operations, helper functions defined we train and test the NMT system.
```
# Training and test BLEU scores
attn_train_bleu_scores_over_time,attn_test_bleu_scores_over_time = [],[]
# Loss over time
loss_over_time = []
# Labels and predictions required to calculate the BLEU scores
# for both train and test data
train_bleu_refs, train_bleu_cands = [],[]
test_bleu_refs, test_bleu_cands = [],[]
# Training and test BLEU scores
num_steps = 100001
avg_loss = 0
# Defining data generators for encoder/decoder and training/testing
enc_data_generator, dec_data_generator, \
test_enc_data_generator, test_dec_data_generator = \
define_data_generators(batch_size, enc_num_unrollings, dec_num_unrollings)
print('Started Training')
for step in range(num_steps):
# input (encoder) unrolling length: 40
# output (decoder) unrolling length: 60
if (step+1)%10==0:
print('.',end='')
# Sample a random batch of IDs from training data
sent_ids = np.random.randint(low=0,high=train_inputs.shape[0],size=(batch_size))
# Getting an unrolled set of data batches for the encoder
eu_data, eu_labels, _ = enc_data_generator.unroll_batches(sent_ids=sent_ids)
# Getting an unrolled set of data batches for the decoder
du_data, du_labels, _ = dec_data_generator.unroll_batches(sent_ids=sent_ids)
# Train for single step
l, tr_pred = train_single_step(eu_data, du_data, du_labels)
# We don't calculate BLEU scores all the time as this is expensive,
# it slows down the code
if np.random.random()<0.1:
# all_labels are labels obtained by concatinating all the labels in batches
all_labels = np.argmax(np.concatenate(du_labels,axis=0),axis=1)
# all_preds are predictions for all unrolled steps
all_preds = np.argmax(tr_pred,axis=1)
# Get training BLEU candidates and references
batch_cands, batch_refs = create_bleu_ref_candidate_lists(all_preds, all_labels)
# Accumulate training candidates/references for calculating
# BLEU later
train_bleu_refs.extend(batch_refs)
train_bleu_cands.extend(batch_cands)
if (step+1)%500==0:
# Writing actual and predicte data to train_prediction.txt file for some random sentence
print('Step ',step+1)
with open(os.path.join(log_dir, train_prediction_text_fname),'a') as fa:
fa.write('============= Step ' + str(step+1) + ' =============\n')
rand_idx = np.random.randint(low=1,high=batch_size)
print_and_save_train_predictions(du_labels, tr_pred, rand_idx, train_prediction_text_fname)
# Calculating the BLEU score for the accumulated candidates/references
bscore = 0.0
bscore = corpus_bleu(train_bleu_refs,train_bleu_cands,smoothing_function=nltk.translate.bleu_score.SmoothingFunction().method4)
attn_train_bleu_scores_over_time.append(bscore)
print('(Train) BLEU (%d elements): '%(len(train_bleu_refs)),bscore)
# Reset the candidate/reference accumulators
train_bleu_refs, train_bleu_cands = [],[]
# Write BLEU score to file
with open(log_dir + os.sep +'blue_scores_attn.txt','a') as fa_bleu:
fa_bleu.write(str(step+1) +','+str(bscore)+'\n')
with open(os.path.join(log_dir, train_prediction_text_fname),'a') as fa:
fa.write('(Train) BLEU: %.5f\n'%bscore)
avg_loss += l # Update average loss
sess.run(reset_train_state) # resetting hidden state for each batch
# ============================= TEST PHASE ==================================
if (step+1)%1000==0:
# calculate average loss
print('============= Step ', str(step+1), ' =============')
print('\t Loss: ',avg_loss/1000.0)
loss_over_time.append(avg_loss/1000.0)
# write losses to file
with open(log_dir + os.sep + 'losses_attn.txt','a') as fa_loss:
fa_loss.write(str(step+1) +','+str(avg_loss/1000.0)+'\n')
with open(os.path.join(log_dir, train_prediction_text_fname),'a') as fa:
fa.write('============= Step ' + str(step+1) + ' =============\n')
fa.write('\t Loss: %.5f\n'%(avg_loss/1000.0))
avg_loss = 0.0
# Increase gstep to decay learning rate
sess.run(inc_gstep)
# reset global step when we change the optimizer
if (step+1)==20000:
sess.run(reset_gstep)
print('=====================================================')
print('(Test) Translating test sentences ...')
print('Processing test data ... ')
# ===================================================================================
# Predictions for Test data
for in_i in range(test_inputs.shape[0]//batch_size):
# Generate encoder / decoder data for testing data
test_eu_data, test_eu_labels, _ = test_enc_data_generator.unroll_batches(sent_ids=np.arange(in_i*batch_size,(in_i+1)*batch_size))
test_du_data, test_du_labels, _ = test_dec_data_generator.unroll_batches(sent_ids=np.arange(in_i*batch_size,(in_i+1)*batch_size))
# fill the feed dict
feed_dict = {}
for ui,(dat,lbl) in enumerate(zip(test_eu_data,test_eu_labels)):
feed_dict[enc_test_input[ui]] = dat
# Get predictions out with decoder
# run prediction calculation this returns a list of prediction dec_num_unrollings long
test_pred_unrolled = sess.run(test_predictions, feed_dict=feed_dict)
# We print a randomly selected sample from each batch
test_rand_idx = np.random.randint(0,batch_size) # used for printing test output
print_and_save_test_predictions(test_du_labels, test_pred_unrolled, in_i, test_rand_idx, test_prediction_text_fname)
# Things required to calculate test BLEU score
all_labels = np.argmax(np.concatenate(test_du_labels,axis=0),axis=1)
all_preds = np.concatenate(test_pred_unrolled, axis=0)
batch_cands, batch_refs = create_bleu_ref_candidate_lists(all_preds, all_labels)
test_bleu_refs.extend(batch_refs)
test_bleu_cands.extend(batch_cands)
# Reset the test state
sess.run(reset_test_state)
# Calculate test BLEU score
test_bleu_score = 0.0
test_bleu_score = corpus_bleu(test_bleu_refs,test_bleu_cands,
smoothing_function=nltk.translate.bleu_score.SmoothingFunction().method4)
attn_test_bleu_scores_over_time.append(test_bleu_score)
print('(Test) BLEU (%d elements): '%(len(test_bleu_refs)),test_bleu_score)
test_bleu_refs, test_bleu_cands = [],[]
print('=====================================================')
```
## Visualizing the Attention Model
Here we visualize the attention matrix for various translations the NMT system produced. The attention matrix is a `dec_num_unrollings x enc_num_unrollings` matrix. Where each cell denotes the $\alpha$ values obtained during attention calculation.
```
source_labels = []
target_labels = []
print('=====================================================')
print('(Test) Translating test sentences ...')
print('Processing test data ... ')
# Process each test input by batches
for in_i in range(test_inputs.shape[0]//batch_size):
# Generate test data
test_eu_data, test_eu_labels, _ = test_enc_data_generator.unroll_batches(sent_ids=np.arange(in_i*batch_size,(in_i+1)*batch_size))
test_du_data, test_du_labels, _ = test_dec_data_generator.unroll_batches(sent_ids=np.arange(in_i*batch_size,(in_i+1)*batch_size))
# Choose a random data point in the batch
test_rand_idx = np.random.randint(0,batch_size) # used for printing test output
# fill the feed dict
feed_dict = {}
source_labels = [] # This contains the source words of the test point considered
for ui,(dat,lbl) in enumerate(zip(test_eu_data,test_eu_labels)):
feed_dict[enc_test_input[ui]] = dat
source_labels.append(src_reverse_dictionary[test_inputs[(in_i*batch_size)+test_rand_idx,ui]])
# Print the true source sentence
print('DE: ',test_source_sent[(in_i*batch_size)+test_rand_idx])
print_str = '\t EN (TRUE):' + test_target_sent[(in_i*batch_size)+test_rand_idx]
print(print_str + '\n')
print_str = '\t EN (Predicted): '
# run prediction calculation this returns a list of prediction dec_num_unrollings long
# alpha_dec_unrolled is a list of dec_num_unrollings elements,
# where each element (another list) is num_enc_unrollings long
test_pred_unrolled, alpha_dec_unrolled = sess.run([test_predictions,test_alpha_i_unrolled], feed_dict=feed_dict)
target_labels = []
# Building the attention matrix
attention_matrix = []
r_i,c_i = 0, 0
# We build the attention matrix column by column
for u_i, (test_pred, alpha_enc_unrolled) in enumerate(zip(test_pred_unrolled, alpha_dec_unrolled)):
# Column index
c_i = 0
# Current target word
current_tgt = tgt_reverse_dictionary[test_pred[test_rand_idx]]
# Only add if the word is not <s> or </s> or <unk>
if current_tgt != '<s>' and current_tgt != '</s>' and current_tgt != '<unk>':
attention_matrix.append([])
target_labels.append(tgt_reverse_dictionary[test_pred[test_rand_idx]])
print_str += tgt_reverse_dictionary[test_pred[test_rand_idx]] + ' '
filtered_src_labels = []
# Fill each row position in that column
for u_ii in range(enc_num_unrollings):
# Only add if the word is not <s> or </s> or <unk>
if source_labels[u_ii] != '<s>' and source_labels[u_ii] != '</s>' and source_labels[u_ii] != '<unk>':
filtered_src_labels.append(source_labels[u_ii])
attention_matrix[r_i].append(alpha_enc_unrolled[test_rand_idx,u_ii])
c_i += 1
r_i += 1
assert r_i == len(target_labels)
# Make the above to a matrix
attention_matrix = np.array(attention_matrix)
if attention_matrix.ndim == 1:
attention_matrix = attention_matrix.reshape(1,-1)
# Reset test state after each batch
sess.run(reset_test_state)
# Plot
f,ax = pylab.subplots(1,1,figsize=(5.0 + 0.5*attention_matrix.shape[0],
5.0 + 0.5*attention_matrix.shape[1]))
# Repetitions are used to make the attention value to a set of image pixels
rep_attn = np.repeat(attention_matrix,5,axis=0)
rep_attn = np.repeat(rep_attn,5,axis=1)
# Correcting for source reversing
rep_attn = np.fliplr(rep_attn)
# Rendering image
ax.imshow(rep_attn,vmin=0.0,vmax=1.0,cmap='jet')
# Labels for columns
for s_i,src_text in enumerate(reversed(filtered_src_labels)):
ax.text(s_i*5+1,-2,src_text,rotation=90, verticalalignment='bottom',fontsize=18)
# Labels for rows
for t_i,tgt_text in enumerate(target_labels):
ax.text(-2, t_i*5+0.5,tgt_text, horizontalalignment = 'right', fontsize=18)
ax.axis('off')
f.savefig('attention_%d.png'%in_i)
pylab.close(f)
print('=====================================================')
```
| true |
code
| 0.39493 | null | null | null | null |
|
# AlexNet in Keras
In this notebook, we leverage an [AlexNet](https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks)-like deep, convolutional neural network to classify flowers into the 17 categories of the [Oxford Flowers](http://www.robots.ox.ac.uk/~vgg/data/flowers/17/) data set. Derived from [this earlier notebook](https://github.com/the-deep-learners/TensorFlow-LiveLessons/blob/master/notebooks/old/L3-3b__TFLearn_AlexNet.ipynb).
```
#load watermark
%load_ext watermark
%watermark -a 'Gopala KR' -u -d -v -p watermark,numpy,pandas,matplotlib,nltk,sklearn,tensorflow,theano,mxnet,chainer,seaborn,keras,tflearn
```
#### Set seed for reproducibility
```
#load watermark
%load_ext watermark
%watermark -a 'Gopala KR' -u -d -v -p watermark,numpy,pandas,matplotlib,nltk,sklearn,tensorflow,theano,mxnet,chainer,seaborn,keras
import numpy as np
np.random.seed(42)
```
#### Load dependencies
```
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPooling2D
from keras.layers.normalization import BatchNormalization
from keras.callbacks import TensorBoard # for part 3.5 on TensorBoard
```
#### Load *and preprocess* data
```
import tflearn.datasets.oxflower17 as oxflower17
X, Y = oxflower17.load_data(one_hot=True)
```
#### Design neural network architecture
```
model = Sequential()
model.add(Conv2D(96, kernel_size=(11, 11), strides=(4, 4), activation='relu', input_shape=(224, 224, 3)))
model.add(MaxPooling2D(pool_size=(3, 3), strides=(2, 2)))
model.add(BatchNormalization())
model.add(Conv2D(256, kernel_size=(5, 5), activation='relu'))
model.add(MaxPooling2D(pool_size=(3, 3), strides=(2, 2)))
model.add(BatchNormalization())
model.add(Conv2D(256, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(384, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(384, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(3, 3), strides=(2, 2)))
model.add(BatchNormalization())
model.add(Flatten())
model.add(Dense(4096, activation='tanh'))
model.add(Dropout(0.5))
model.add(Dense(4096, activation='tanh'))
model.add(Dropout(0.5))
model.add(Dense(17, activation='softmax'))
model.summary()
```
#### Configure model
```
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
```
#### Configure TensorBoard (for part 5 of lesson 3)
```
tensorbrd = TensorBoard('logs/alexnet')
```
#### Train!
```
model.fit(X, Y, batch_size=64, epochs=100, verbose=1, validation_split=0.1, shuffle=True,
callbacks=[tensorbrd])
```
| true |
code
| 0.695429 | null | null | null | null |
|
# T81-558: Applications of Deep Neural Networks
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), School of Engineering and Applied Science, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
**Module 10 Assignment: Time Series Neural Network**
**Student Name: Your Name**
# Assignment Instructions
For this assignment you will use a LSTM to predict a time series contained in the data file **[series-31-spring-2019.csv](http://data.heatonresearch.com/data/t81-558/datasets/series-31-spring-2019.csv)**. The code that you will use to complete this will be similar to the sunspots example from the course module. This data set contains two columns: *time* and *value*. Create a LSTM network and train it with a sequence size of 5 and a prediction window of 1. If you use a different sequence size, you will not have the correct number of submission rows. Train the neural network, the data set is fairly simple and you should easily be able to get a RMSE below 1.0. FYI, I generate this datasets by fitting a cubic spline to a series of random points.
This is a time series data set, do not randomize the order of the rows! For your training data use all *time* values less than 3000 and for test, use the remaining values greater than or equal to 3000. For the submit file, send me the results of your test evaluation. You should have two columns: *time* and *value*. The column *time* should be the time at the beginning of each predicted sequence. The *value* should be the next value that was predicted for each of your sequences.
Your submission file will look similar to:
# Helpful Functions
You will see these at the top of every module and assignment. These are simply a set of reusable functions that we will make use of. Each of them will be explained as the semester progresses. They are explained in greater detail as the course progresses. Class 4 contains a complete overview of these functions.
```
import base64
import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
from sklearn import preprocessing
# Encode text values to dummy variables(i.e. [1,0,0],[0,1,0],[0,0,1] for red,green,blue)
def encode_text_dummy(df, name):
dummies = pd.get_dummies(df[name])
for x in dummies.columns:
dummy_name = f"{name}-{x}"
df[dummy_name] = dummies[x]
df.drop(name, axis=1, inplace=True)
# Encode text values to a single dummy variable. The new columns (which do not replace the old) will have a 1
# at every location where the original column (name) matches each of the target_values. One column is added for
# each target value.
def encode_text_single_dummy(df, name, target_values):
for tv in target_values:
l = list(df[name].astype(str))
l = [1 if str(x) == str(tv) else 0 for x in l]
name2 = f"{name}-{tv}"
df[name2] = l
# Encode text values to indexes(i.e. [1],[2],[3] for red,green,blue).
def encode_text_index(df, name):
le = preprocessing.LabelEncoder()
df[name] = le.fit_transform(df[name])
return le.classes_
# Encode a numeric column as zscores
def encode_numeric_zscore(df, name, mean=None, sd=None):
if mean is None:
mean = df[name].mean()
if sd is None:
sd = df[name].std()
df[name] = (df[name] - mean) / sd
# Convert all missing values in the specified column to the median
def missing_median(df, name):
med = df[name].median()
df[name] = df[name].fillna(med)
# Convert all missing values in the specified column to the default
def missing_default(df, name, default_value):
df[name] = df[name].fillna(default_value)
# Convert a Pandas dataframe to the x,y inputs that TensorFlow needs
def to_xy(df, target):
result = []
for x in df.columns:
if x != target:
result.append(x)
# find out the type of the target column. Is it really this hard? :(
target_type = df[target].dtypes
target_type = target_type[0] if hasattr(
target_type, '__iter__') else target_type
# Encode to int for classification, float otherwise. TensorFlow likes 32 bits.
if target_type in (np.int64, np.int32):
# Classification
dummies = pd.get_dummies(df[target])
return df[result].values.astype(np.float32), dummies.values.astype(np.float32)
# Regression
return df[result].values.astype(np.float32), df[[target]].values.astype(np.float32)
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return f"{h}:{m:>02}:{s:>05.2f}"
# Regression chart.
def chart_regression(pred, y, sort=True):
t = pd.DataFrame({'pred': pred, 'y': y.flatten()})
if sort:
t.sort_values(by=['y'], inplace=True)
plt.plot(t['y'].tolist(), label='expected')
plt.plot(t['pred'].tolist(), label='prediction')
plt.ylabel('output')
plt.legend()
plt.show()
# Remove all rows where the specified column is +/- sd standard deviations
def remove_outliers(df, name, sd):
drop_rows = df.index[(np.abs(df[name] - df[name].mean())
>= (sd * df[name].std()))]
df.drop(drop_rows, axis=0, inplace=True)
# Encode a column to a range between normalized_low and normalized_high.
def encode_numeric_range(df, name, normalized_low=-1, normalized_high=1,
data_low=None, data_high=None):
if data_low is None:
data_low = min(df[name])
data_high = max(df[name])
df[name] = ((df[name] - data_low) / (data_high - data_low)) \
* (normalized_high - normalized_low) + normalized_low
# This function submits an assignment. You can submit an assignment as much as you like, only the final
# submission counts. The paramaters are as follows:
# data - Pandas dataframe output.
# key - Your student key that was emailed to you.
# no - The assignment class number, should be 1 through 1.
# source_file - The full path to your Python or IPYNB file. This must have "_class1" as part of its name.
# . The number must match your assignment number. For example "_class2" for class assignment #2.
def submit(data,key,no,source_file=None):
if source_file is None and '__file__' not in globals(): raise Exception('Must specify a filename when a Jupyter notebook.')
if source_file is None: source_file = __file__
suffix = '_class{}'.format(no)
if suffix not in source_file: raise Exception('{} must be part of the filename.'.format(suffix))
with open(source_file, "rb") as image_file:
encoded_python = base64.b64encode(image_file.read()).decode('ascii')
ext = os.path.splitext(source_file)[-1].lower()
if ext not in ['.ipynb','.py']: raise Exception("Source file is {} must be .py or .ipynb".format(ext))
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key':key}, json={'csv':base64.b64encode(data.to_csv(index=False).encode('ascii')).decode("ascii"),
'assignment': no, 'ext':ext, 'py':encoded_python})
if r.status_code == 200:
print("Success: {}".format(r.text))
else: print("Failure: {}".format(r.text))
```
# Assignment #10 Sample Code
The following code provides a starting point for this assignment.
```
import numpy as np
def to_sequences(seq_size, obs):
x = []
y = []
for i in range(len(obs)-seq_size):
#print(i)
window = obs[i:(i+seq_size)]
after_window = obs[i+seq_size]
window = [[x] for x in window]
#print("{} - {}".format(window,after_window))
x.append(window)
y.append(after_window)
return np.array(x),np.array(y)
# This is your student key that I emailed to you at the beginnning of the semester.
key = "ivYj3b2yJY2dvQ9MEQMLe5ECGenGc82p4dywJxtQ" # This is an example key and will not work.
# You must also identify your source file. (modify for your local setup)
# file='/resources/t81_558_deep_learning/assignment_yourname_class1.ipynb' # IBM Data Science Workbench
# file='C:\\Users\\jeffh\\projects\\t81_558_deep_learning\\t81_558_class1_intro_python.ipynb' # Windows
file='/Users/jheaton/projects/t81_558_deep_learning/assignments/assignment_yourname_class10.ipynb' # Mac/Linux
# Read from time series file
path = "./data/"
filename = os.path.join(path,"series-31-spring-2019.csv")
df = pd.read_csv(filename) # , index_col=False
print("Starting file:")
print(df[0:10])
print("Ending file:")
print(df[-10:])
df_train = df[df['time']<3000]
df_test = df[df['time']>=3000]
spots_train = df_train['value'].tolist()
spots_test = df_test['value'].tolist()
print("Training set has {} observations.".format(len(spots_train)))
print("Test set has {} observations.".format(len(spots_test)))
SEQUENCE_SIZE = 5
x_train,y_train = to_sequences(SEQUENCE_SIZE,spots_train)
x_test,y_test = to_sequences(SEQUENCE_SIZE,spots_test)
print("Shape of training set: {}".format(x_train.shape))
print("Shape of test set: {}".format(x_test.shape))
#submit(source_file=file,data=df,key=key,no=1)
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding
from keras.layers import LSTM
from keras.datasets import imdb
from keras.callbacks import EarlyStopping
import numpy as np
print('Build model...')
# Add assignment code here
submit(source_file=file,data=submit_df,key=key,no=10)
```
| true |
code
| 0.47591 | null | null | null | null |
|
# Fairness Metrics
This notebook implements the statistical fairness metrics from:
*Towards the Right Kind of Fairness in AI* by Boris Ruf and Marcin Detyniecki (2021)
https://arxiv.org/abs/2102.08453
Example with the `german-risk-scoring.csv` dataset.
Contributeurs : Xavier Lioneton & Francis Wolinski
## Imports
```
# imports
import numpy as np
import pandas as pd
from pandas.api.types import is_numeric_dtype
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
from IPython.display import display, Markdown
```
## Data Load
```
# dataset
data = pd.read_csv('german-risk-scoring.csv')
data.info()
# target
data['Cost Matrix(Risk)'].value_counts()
# Personal status and sex
data["Personal status and sex"].value_counts()
```
## Data Prep
```
# create sex column
data["sex"] = data["Personal status and sex"].apply(lambda x : x.split(":")[0])
# create X=features, y=target
X = data.drop(columns = 'Cost Matrix(Risk)')
y = data['Cost Matrix(Risk)'].map({"Good Risk": 1, "Bad Risk": 0})
# type modifications
cols_cat = [
'Status of existing checking account',
'Credit history',
'Purpose',
'Savings account/bonds',
'Present employment since',
'Personal status and sex',
'Other debtors / guarantors',
'Property',
'Other installment plans',
'Housing',
'Job',
'Telephone',
'foreign worker',
'sex'
]
cols_num = [
'Duration in month',
'Credit amount',
'Installment rate in percentage of disposable income',
'Present residence since',
'Age in years',
'Number of existing credits at this bank',
'Number of people being liable to provide maintenance for',
]
for col in cols_cat:
data[col] = data[col].astype(str)
for col in cols_num:
data[col] = data[col].astype(float)
cols = cols_cat + cols_num
# unique values of categorical columns
X[cols_cat].nunique()
# all to numbers
encoder = OneHotEncoder()
X_cat = encoder.fit_transform(X[cols_cat]).toarray()
X_num = X[cols_num]
X_prep = np.concatenate((X_num, X_cat), axis=1)
X_prep.shape
# data prepared
cols = data[cols_num].columns.tolist() + encoder.get_feature_names(input_features=X[cols_cat].columns).tolist()
data_prep = pd.DataFrame(X_prep, columns=cols)
data_prep.shape
# data prepared
data_prep.head()
```
## Machine Learning
```
# split train test
X_train, X_test, y_train, y_test = train_test_split(data_prep, y, test_size=0.2, random_state=42)
X_train = X_train.copy()
X_test = X_test.copy()
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
```
### Train Model
```
# train model
clf = LogisticRegression(random_state=0, n_jobs=8, max_iter=500)
clf.fit(X_train, y_train)
```
### Confusion mattrix
```
# Schema of confusion matrix
df = pd.DataFrame([['True negatives (TN)', 'False positives (FP)'], ['False negatives (FN)', 'True positives (TP)']], index=['Y = 0', 'Y = 1'], columns=['Ŷ = 0', 'Ŷ = 1'])
df = df.reindex(['Y = 1', 'Y = 0'])
df = df[['Ŷ = 1', 'Ŷ = 0']]
display(Markdown('**Schema of confusion matrix**'))
display(df)
# function pretty_confusion_mattrix()
def pretty_confusion_mattrix(y_label, y_pred, title=None):
"""Pretty print the confusion matrix computed by scikit-learn"""
_TN, _FP, _FN, _TP = confusion_matrix(y_label, y_pred).flatten()
array = [[_TP, _FN], [_FP, _TN]]
df = pd.DataFrame(array, index=['Y = 1', 'Y = 0'], columns=['Ŷ = 1', 'Ŷ = 0'])
if title is not None:
display(Markdown(title))
display(df)
# test dataset
y_pred = clf.predict(X_test)
pretty_confusion_mattrix(y_test, y_pred, title='**Confusion matrix for the test dataset**')
# function pretty_confusion_mattrix_by_subgroup()
def pretty_confusion_mattrix_by_subgroup(X, col, X_test, y_label, y_pred, q=4):
"""Pretty print the confusion matrices by subgroup
X: dataset
col: used for spliting in subgroups
X_test: test dataset
y_label: target for test dataset
y_pred: predictions for test dataset
q: quartile used for numerical column"""
# if col is numeric, use quantile
cat = pd.qcut(X[col], q) if is_numeric_dtype(X[col]) else X[col]
# select test data
cat = cat.loc[X_test.index]
# switch y_pred to Series so as to be able to select by subgroup
y_pred = pd.Series(y_pred, index=y_label.index)
# loop on subgroups
for value in sorted(cat.unique()):
X_select = X_test.loc[cat == value]
pretty_confusion_mattrix(y_label.loc[X_select.index],
y_pred.loc[X_select.index],
title=f'**Subgroup**: {col} = {value}')
pretty_confusion_mattrix_by_subgroup(X, 'sex', X_test, y_test, y_pred)
pretty_confusion_mattrix_by_subgroup(X, 'Age in years', X_test, y_test, y_pred)
```
### Metrics derived from confusion matrix
**Actual postitives**
This number is the sum of the true positives and the false negatives, which can be viewed as missed
true positives.
$P = TP + FN$
**Actual negatives**
This number is the sum of the true negatives and the false positives, which again can be viewed as missed true negatives.
$N = TN + FP$
**Base rate**
This number, sometimes also called the prevalence rate, represents the proportion of actual positives with respect to the entire data set.
$BR = \frac{P}{P + N}$
**Positive rate**
This number is the overall rate of positively classified instances, including both correct and incorrect decisions.
$PR = \frac{TP + FP}{P + N}$
**Negative rate**
This number is the ratio of negative classification, again irrespective of whether the decisions were correct or incorrect.
$NR = \frac{TN + FN}{P + N}$
**Accuracy**
This number is the ratio of the correctly classified instances (positive and negative) of all decisions.
$ACC = \frac{TP + TN}{P + N}$
**Misclassiffication rate**
This number is the ratio of the misclassified instances over all decisions.
$MR = \frac{FN + FP}{P + N}$
**True positive rate (recall)**
This number describes the proportions of correctly classified positive instances.
$TPR = \frac{TP}{P}$
**True negative rate**
This number describes the proportions of correctly classified negative instances.
$TNR = \frac{TN}{N}$
**False positive rate**
This number denotes the proportion of actual negatives which was falsely classified as positive.
$FPR = \frac{FP}{P}$
**False negative rate (silence)**
This number describes the proportion of actual positives which was misclassified as negative.
$FNR = \frac{FN}{N}$
**False discovery rate (noise)**
This number describes the share of misclassified positive classifications of all positive predictions.
$FDR = \frac{FP}{TP + FP}$
**Positive predicted value (precision)**
This number describes the ratio of samples which were correctly classified as positive from all the positive predictions.
$PPV = \frac{TP}{TP + FP}$
**False omission rate**
This number describes the proportion of false negative predictions of all negative predictions.
$FOR = \frac{FN}{TN + FN}$
**Negative predicted value**
This number describes the ratio of samples which were correctly classified as negative from all the negative predictions.
$NPV = \frac{TN}{TN + FN}$
```
# function pretty_confusion_mattrix()
def pretty_fairness_confusion_mattrix(y_label, y_pred, title=None):
"""Pretty print fairness confusion matrix
y_label: target for test dataset
y_pred: predictions for test dataset
title: string to display in Markdown"""
# compute fairness metrics
_TN, _FP, _FN, _TP = confusion_matrix(y_label, y_pred).flatten()
_P = _TP + _FN
_N = _FP + _TN
_BR = _P / (_P + _N)
_PR = (_TP + _FP) / (_P + _N)
_NR = (_TN + _FN) / (_P + _N)
_TPR = _TP / _P
_TNR = _TN / _N
_FDR = _FP / (_TP + _FP)
_FOR = _FN / (_TN + _FN)
# build the output dataframe
array = [[_TP, _FN, f'TPR = {_TPR:.2f}'],
[_FP, _TN, f'TNR = {_TNR:.2f}'],
[f'FDR = {_FDR:.2f}', f'FOR = {_FOR:.2f}', f'BR = {_BR:.2f}'],
[f'PR = {_PR:.2f}', f'NR = {_NR:.2f}', ''],
]
df = pd.DataFrame(array, index=['Y = 0', 'Y = 1', '', ' '], columns=['Ŷ = 0', 'Ŷ = 1', ''])
if title is not None:
display(Markdown(title))
display(df.style.set_table_styles([{'selector': 'td', 'props':[('text-align', 'center')]},
{'selector': 'th', 'props': [('text-align', 'center')]}],
overwrite=False))
pretty_fairness_confusion_mattrix(y_test, y_pred, title='**Fairness confusion matrix**')
# function pretty_fairness_confusion_mattrix_by_subgroup()
def pretty_fairness_confusion_mattrix_by_subgroup(X, col, X_test, y_label, y_pred, q=4):
"""Pretty print fairness confusion matrix by subgroup
X: dataset
col: used for spliting in subgroups
X_test: test dataset
y_label: target for test dataset
y_pred: predictions for test dataset
q: quartile used for numerical colum"""
# if col is numeric, use quantile
cat = pd.qcut(X[col], q) if is_numeric_dtype(X[col]) else X[col]
# select test data
cat = cat.loc[X_test.index]
# switch y_pred to Series so as to be able to select by subgroup
y_pred = pd.Series(y_pred, index=y_label.index)
# loop on subgroups
for value in sorted(cat.unique()):
X_select = X_test.loc[cat == value]
pretty_fairness_confusion_mattrix(y_label.loc[X_select.index],
y_pred.loc[X_select.index],
title=f'**Subgroup**: {col} = {value}')
pretty_fairness_confusion_mattrix_by_subgroup(X, 'sex', X_test, y_test, y_pred)
pretty_fairness_confusion_mattrix_by_subgroup(X, 'Age in years', X_test, y_test, y_pred)
```
| true |
code
| 0.518607 | null | null | null | null |
|
# Demonstrate the path of high probability and the orthogonal path on the pyloric rhythm for experimental data
```
# Note: this application requires a more recent version of dill.
# Other applications in this repository will require 0.2.7.1
# You might have to switch between versions to run all applications.
!pip install --upgrade dill
import numpy as np
import matplotlib.pylab as plt
import delfi.distribution as dd
import time
from copy import deepcopy
import sys
sys.path.append("model/setup")
sys.path.append("model/simulator")
sys.path.append("model/inference")
sys.path.append("model/visualization")
sys.path.append("model/utils")
import sys; sys.path.append('../')
from common import col, svg, plot_pdf, samples_nd
import netio
import viz
import importlib
import viz_samples
import train_utils as tu
import matplotlib as mpl
%load_ext autoreload
%autoreload 2
PANEL_A = 'illustration/panel_a.svg'
PANEL_B = 'svg/31D_panel_b.svg'
PANEL_C = 'svg/31D_panel_c.svg'
PANEL_C2 = 'svg/31D_panel_c2.svg'
PANEL_D = 'svg/31D_panel_d.svg'
PANEL_X1params = 'svg/31D_panel_App1_params.svg'
PANEL_X2params = 'svg/31D_panel_App2_params.svg'
PANEL_X1ss = 'svg/31D_panel_App1_ss.svg'
PANEL_X2ss = 'svg/31D_panel_App2_ss.svg'
PANEL_X = 'svg/31D_panel_x.svg'
```
### Load samples
```
params = netio.load_setup('train_31D_R1_BigPaper')
filedir = "results/31D_samples/pyloricsamples_31D_noNaN_3.npz"
pilot_data, trn_data, params_mean, params_std = tu.load_trn_data_normalize(filedir, params)
print('We use', len(trn_data[0]), 'training samples.')
stats = trn_data[1]
stats_mean = np.mean(stats, axis=0)
stats_std = np.std(stats, axis=0)
```
### Load network'
```
date_today = '1908208'
import dill as pickle
with open('results/31D_nets/191001_seed1_Exper11deg.pkl', 'rb') as file:
inf_SNPE_MAF, log, params = pickle.load(file)
params = netio.load_setup('train_31D_R1_BigPaper')
prior = netio.create_prior(params, log=True)
dimensions = np.sum(params.use_membrane) + 7
lims = np.asarray([-np.sqrt(3)*np.ones(dimensions), np.sqrt(3)*np.ones(dimensions)]).T
prior = netio.create_prior(params, log=True)
params_mean = prior.mean
params_std = prior.std
from find_pyloric import merge_samples, params_are_bounded
labels_ = viz.get_labels(params)
prior_normalized = dd.Uniform(-np.sqrt(3)*np.ones(dimensions), np.sqrt(3)*np.ones(dimensions), seed=params.seed)
```
### Load experimental data
```
summstats_experimental = np.load('results/31D_experimental/190807_summstats_prep845_082_0044.npz')['summ_stats']
```
### Calculate posterior
```
from find_pyloric import merge_samples, params_are_bounded
all_paths = []
all_posteriors = []
labels_ = viz.get_labels(params)
posterior_MAF = inf_SNPE_MAF.predict([summstats_experimental]) # given the current sample, we now predict the posterior given our simulation outcome. Note that this could just be overfitted.
```
### Load samples
```
samples_MAF = merge_samples("results/31D_samples/02_cond_vals", name='conductance_params')
samples_MAF = np.reshape(samples_MAF, (1000*2520, 31))
print(np.shape(samples_MAF))
```
### Load start and end point
```
num_to_watch = 3
infile = 'results/31D_pairs/similar_and_good/sample_pair_{}.npz'.format(num_to_watch) # 0 is shitty
npz = np.load(infile)
start_point = npz['params1']
end_point = npz['params2']
start_point_unnorm = start_point * params_std + params_mean
end_point_unnorm = end_point * params_std + params_mean
ratio = end_point_unnorm / start_point_unnorm
run_true = (ratio > np.ones_like(ratio) * 2.0) | (ratio < np.ones_like(ratio) / 2.0)
print(run_true)
```
### Calculate the high-probability path
```
from HighProbabilityPath import HighProbabilityPath
# number of basis functions used
num_basis_functions = 2
# number of timesteps
num_path_steps = 80
high_p_path = HighProbabilityPath(num_basis_functions, num_path_steps, use_sine_square=True)
#print('Starting to calculate path')
#high_p_path.set_start_end(start_point, end_point)
#high_p_path.set_pdf(posterior_MAF, dimensions)
#high_p_path.find_path(posterior_MAF, prior=prior_normalized, multiply_posterior=1,
# non_linearity=None, non_lin_param=3.0)
#high_p_path.get_travelled_distance()
#print('Finished calculating path')
#np.savez('results/31D_paths/high_p_path.npz', high_p_path=high_p_path)
high_p_path = np.load('results/31D_paths/high_p_path.npz', allow_pickle=True)['high_p_path'].tolist()
lims = np.asarray([-np.sqrt(3)*np.ones(dimensions), np.sqrt(3)*np.ones(dimensions)]).T
```
# Panel B: experimental data
Note: the full data is not contained in the repo. Therefore, this figure can not be created.
```
npz = np.load('results/31D_experimental/trace_data_845_082_0044.npz')
t = npz['t']
PD_spikes = npz['PD_spikes']
LP_spikes = npz['LP_spikes']
PY_spikes = npz['PY_spikes']
pdn = npz['pdn']
lpn = npz['lpn']
pyn = npz['pyn']
start_index = 219500 + 2100
end_index = 246500 + 2100 # 32000
height_offset = 200
shown_t = t[end_index] - t[start_index]
time_len = shown_t / 0.025 * 1000
dt = t[1] - t[0]
import matplotlib.patches as mp
with mpl.rc_context(fname='../.matplotlibrc'):
fig, ax = plt.subplots(1,1,figsize=(2.87, 2.08*3/4)) # (2.87, 2.08*3/4)
ax.plot(t[start_index:end_index], 2.5+pdn[start_index:end_index]*0.007, c=col['GT'], lw=0.8)
ax.plot(t[start_index:end_index], 1.2+lpn[start_index:end_index]*0.25, c=col['GT'], lw=0.8)
ax.plot(t[start_index:end_index], -0.1+pyn[start_index:end_index]*0.013, c=col['GT'], lw=0.8)
linew = 0.4
headl = 0.06
headw = 0.16
linelen = 0.17
circlefact = 0.8
# period arrow
height1 = 3.2
plt.arrow(t[start_index]+0.6, height1, 1.15, 0, shape='full', head_width=headw, head_length=headl, length_includes_head=True, color='k', lw=linew)
plt.arrow(t[start_index]+1.75, height1, -1.15, 0, shape='full', head_width=headw, head_length=headl, length_includes_head=True, color='k', lw=linew)
plt.plot([t[start_index]+0.6, t[start_index]+0.6], [height1-linelen,height1+linelen], c='k', lw=linew*1.5)
plt.plot([t[start_index]+1.75, t[start_index]+1.75], [height1-linelen,height1+linelen], c='k', lw=linew*1.5)
#patch =mp.Ellipse((t[start_index]+1.2, 3.65), 0.2*circlefact,0.6*circlefact, color='lightgray')
#ax.add_patch(patch)
# delay arrow
height2 = 1.64
plt.arrow(t[start_index]+0.6, height2, 0.48, 0, shape='full', head_width=headw, head_length=headl, length_includes_head=True, color='k', lw=linew)
plt.arrow(t[start_index]+1.08, height2, -0.48, 0, shape='full', head_width=headw, head_length=headl, length_includes_head=True, color='k', lw=linew)
plt.plot([t[start_index]+0.6, t[start_index]+0.6], [height2-linelen,height2+linelen], c='k', lw=linew*1.5)
plt.plot([t[start_index]+1.08, t[start_index]+1.08], [height2-linelen,height2+linelen], c='k', lw=linew*1.5)
#patch =mp.Ellipse((t[start_index]+0.94, 2.1), 0.2*circlefact,0.6*circlefact, color='lightgray')
#ax.add_patch(patch)
# gap arrow
plt.arrow(t[start_index]+1.98, height2, 0.27, 0, shape='full', head_width=headw, head_length=headl, length_includes_head=True, color='k', lw=linew)
plt.arrow(t[start_index]+2.25, height2, -0.27, 0, shape='full', head_width=headw, head_length=headl, length_includes_head=True, color='k', lw=linew)
plt.plot([t[start_index]+1.98, t[start_index]+1.98], [height2-linelen,height2+linelen], c='k', lw=linew*1.5)
plt.plot([t[start_index]+2.25, t[start_index]+2.25], [height2-linelen,height2+linelen], c='k', lw=linew*1.5)
#patch =mp.Ellipse((t[start_index]+2.1, 2.1), 0.2*circlefact,0.6*circlefact, color='lightgray')
#ax.add_patch(patch)
# duration arrow
height4 = 0.44
plt.arrow(t[start_index]+1.33, height4, 0.43, 0, shape='full', head_width=headw, head_length=headl, length_includes_head=True, color='k', lw=linew)
plt.arrow(t[start_index]+1.76, height4, -0.43, 0, shape='full', head_width=headw, head_length=headl, length_includes_head=True, color='k', lw=linew)
plt.plot([t[start_index]+1.33, t[start_index]+1.33], [height4-linelen,height4+linelen], c='k', lw=linew*1.5)
plt.plot([t[start_index]+1.76, t[start_index]+1.76], [height4-linelen,height4+linelen], c='k', lw=linew*1.5)
#patch =mp.Ellipse((t[start_index]+1.55, 0.9), radius=0.2, color='lightgray')
#ax.add_patch(patch)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.axes.get_yaxis().set_ticks([])
ax.axes.get_xaxis().set_ticks([])
ax.get_yaxis().set_visible(False)
ax.set_ylim([-0.95, 4.0])
duration = 0.5
number_of_timesteps = int(duration / dt)
t_scale = np.linspace(t[start_index], t[start_index + number_of_timesteps], 2)
ax.plot(t_scale, -0.8 * np.ones_like(t_scale), c='k', lw=1.0)
#plt.savefig(PANEL_B, facecolor='None', transparent=True)
plt.show()
```
# Panel C: posterior
```
from decimal import Decimal
all_labels = []
for dim_i in range(31):
if dim_i > len(params_mean) - 7.5: # synapses
if dim_i == 24: all_labels.append([r'$\mathdefault{0.01}$ ', r'$\mathdefault{10000}\;\;\;\;$ '])
else: all_labels.append([r'$\;\;\mathdefault{0.01}$', r'$\mathdefault{1000}\;\;\;\;$ '])
else: # membrane conductances
num_after_digits = -int(np.log10(lims[dim_i, 1] * params_std[dim_i] + params_mean[dim_i]))
if num_after_digits > 2:
num_after_digits=2
labels = [round(Decimal((lims[dim_i, num_tmp] * params_std[dim_i] + params_mean[dim_i]) / 0.628e-3), num_after_digits)
for num_tmp in range(2)]
new_labels = []
counter=0
for l in labels:
if counter == 0:
new_labels.append(r'$\mathdefault{'+str(l)+'}$')
else:
new_labels.append(r'$\mathdefault{'+str(l)+'}\;\;\;$ ')
counter+=1
all_labels.append(new_labels)
import matplotlib.patheffects as pe
with mpl.rc_context(fname='../.matplotlibrc'):
labels_ = viz.get_labels_8pt(params)
labels_[9] += ''
fig, axes = samples_nd(samples=[samples_MAF[:1260000], high_p_path.path_coords],
subset=[2,4,10,19,24,25,26,28],
limits=lims,
ticks=lims,
tick_labels=all_labels,
fig_size=(17.0*0.2435,17.0*0.2435),
labels=labels_,
points=[start_point, end_point],
scatter_offdiag={'rasterized':True, 'alpha':1.0},
points_offdiag={'marker':'o', 'markeredgecolor':'w', 'markersize':3.6, 'markeredgewidth':0.5, 'path_effects':[pe.Stroke(linewidth=1.2, foreground='k'), pe.Normal()]},
points_colors=[col['CONSISTENT1'], col['CONSISTENT2']],
samples_colors=[col['SNPE'], 'white'],
diag=['kde', 'None'],
upper=['hist', 'plot'],
hist_offdiag={'bins':50},
plot_offdiag={'linewidth': 1.6, 'path_effects':[pe.Stroke(linewidth=2.4, foreground='k'), pe.Normal()]})
# plt.savefig(PANEL_C, facecolor='None', transparent=True)
plt.show()
```
### Evaluate whether samples along path are identical according to Prinz
```
pyloric_sim = netio.create_simulators(params)
summ_stats = netio.create_summstats(params)
from viz import plot_posterior_over_path
high_p_path_mod = deepcopy(high_p_path)
# plots for the samples
num_cols = 2
num_rows = 5
scale = 'dist' # set this to 'dist' if you want to x-axis to be scale according to the travelled distance
num_steps = num_cols*num_rows
if scale == 'dist':
steps = np.linspace(0, high_p_path_mod.dists[-1], num_steps)
else:
steps = np.linspace(0, 1.0, num_steps)
```
# Inlet for Panel C
```
dimensions_to_use = [24,25]
high_p_path_mod = deepcopy(high_p_path)
num_paths = 10
path_start_positions = np.linspace(0, high_p_path_mod.dists[-1], num_paths)
high_p_indizes = high_p_path_mod.find_closest_index_to_dist(path_start_positions)
use_high_p_index = 45
high_p_indizes = [use_high_p_index]
from OrthogonalPath import OrthogonalPath
dimensions_to_use = [24,25]
high_p_path_mod = deepcopy(high_p_path)
start_point_ind = 23# 10
# ortho_path = OrthogonalPath(high_p_path_mod.path_coords, start_point_ind)
# ortho_path.find_orthogonal_path(posterior_MAF, max_distance=high_p_path_mod.dists[-1]/27, dim=dimensions, prior=prior_normalized)
# ortho_path.get_travelled_distance()
# print(len(ortho_path.path_coords))
#np.savez('results/31D_paths/ortho_path.npz', ortho_path=ortho_path)
ortho_path = np.load('results/31D_paths/ortho_path.npz', allow_pickle=True)['ortho_path'].tolist()
ortho_path_mod = deepcopy(ortho_path)
num_path_pos = 2
path_start_positions = np.linspace(0, ortho_path_mod.dists[-1], num_path_pos)
ortho_p_indizes = ortho_path_mod.find_closest_index_to_dist(path_start_positions)
ortho_p_indizes = [ortho_p_indizes[-1]]
labels_ = viz.get_labels_8pt(params)
labels_[9] += ''
color_mixture = 0.5 * (np.asarray(list(col['CONSISTENT1'])) + np.asarray(list(col['CONSISTENT2'])))
p1g = high_p_path.path_coords[int(high_p_indizes[0])]
p1b = ortho_path.path_coords[int(ortho_p_indizes[0])]
with mpl.rc_context(fname='../.matplotlibrc'):
_ = viz.plot_single_marginal_pdf(pdf1=posterior_MAF, prior=prior, resolution=200,
lims=lims, samples=np.transpose(samples_MAF), figsize=(1.5, 1.5),
ticks=False, no_contours=True, labels_params=labels_,
start_point=high_p_path.start_point, end_point=high_p_path.end_point,
path1=high_p_path.path_coords, display_axis_lims=True,
path2=ortho_path.path_coords, pointscale=0.5,
p1g=p1g, start_col=col['CONSISTENT1'], end_col=col['CONSISTENT2'],
p1b=p1b, current_col1=color_mixture,current_col=col['CONSISTENT2'],
current_col2=col['INCONSISTENT'],
path_steps1=1, path_steps2=1,
dimensions=dimensions_to_use)
#plt.savefig(PANEL_C2, facecolor='None', transparent=True, dpi=300, bbox_inches='tight')
plt.show()
```
# Panel D
```
dimensions_to_use = [6,7]
high_p_path_mod = deepcopy(high_p_path)
num_paths = 5
path_start_positions = np.linspace(0, high_p_path_mod.dists[-1], num_paths)
high_p_indizes = high_p_path_mod.find_closest_index_to_dist(path_start_positions)
indizes_show = high_p_indizes
high_p_indizes.pop(2)
high_p_indizes.pop(1)
current_point = high_p_path_mod.path_coords[high_p_indizes]
high_p_indizes = np.flip(high_p_indizes)
print(high_p_indizes)
high_p_indizes = [79, 0, use_high_p_index]
prior.mean
prior.std
labels_ = viz.get_labels_8pt(params)
high_p_path_mod = deepcopy(high_p_path)
seeds = [8, 8, 8, 8, 8]
offsets = 39000 * np.ones_like(seeds)
#offsets[0] = 47000
offsets[1] = 83500 # 75500
offsets[2] = 29000 # 21000
offsets[3] = 40500 # 40500
dimensions_to_use2D = [6,7]
with mpl.rc_context(fname='../.matplotlibrc'):
fig = viz.viz_path_and_samples_abstract_twoRows(posterior_MoG=posterior_MAF, high_p_path=high_p_path_mod, ortho_path=ortho_path_mod, prior=prior, lims=lims, samples=samples_MAF,
figsize=(5.87, 3.0), offsets=offsets, linescale=1.5, ticks=False, no_contours=True, labels_params=labels_, start_point=high_p_path.start_point,
end_point=high_p_path.end_point, ortho_p_indizes=ortho_p_indizes, high_p_indizes=high_p_indizes, mycols=col, time_len=int(time_len),
path1=high_p_path_mod.path_coords, path_steps1=1, path2=ortho_path_mod.path_coords, path_steps2=1, dimensions_to_use=dimensions_to_use2D, #ax=ax,
seeds=seeds, indizes=[0], hyperparams=params, date_today='190910_80start', case='ortho_p', save_fig=False)
#plt.savefig(PANEL_D, facecolor='None', transparent=True, dpi=300, bbox_inches='tight')
plt.show()
```
# Assemble figure
```
color_mixture = 0.5 * (np.asarray(list(col['CONSISTENT1'])) + np.asarray(list(col['CONSISTENT2'])))
import time
import IPython.display as IPd
def svg(img):
IPd.display(IPd.HTML('<img src="{}" / >'.format(img, time.time())))
from svgutils.compose import *
# > Inkscape pixel is 1/90 of an inch, other software usually uses 1/72.
# > http://www.inkscapeforum.com/viewtopic.php?f=6&t=5964
svg_scale = 1.25 # set this to 1.25 for Inkscape, 1.0 otherwise
factor_svg=5.5
# Panel letters in Helvetica Neue, 12pt, Medium
kwargs_text = {'size': '12pt', 'font': 'Arial', 'weight': '800'}
kwargs_consistent = {'size': '10pt', 'font': 'Arial', 'weight': '500', 'color': '#AF99EF'}
kwargs_consistent1 = {'size': '10pt', 'font': 'Arial', 'weight': '500', 'color': '#9E7DD5'}
kwargs_inconsistent = {'size': '10pt', 'font': 'Arial', 'weight': '500', 'color': '#D73789'}
kwargs_text8pt = {'size': '7.7pt', 'font': 'Arial'}
startx1 = 492
startx2 = 594
starty1 = 204
starty2 = 307
endx1 = 642
endx2 = 673
endy1 = 159
endy2 = 191
deltax1 = endx1-startx1
deltax2 = endx2-startx2
deltay1 = endy1-starty1
deltay2 = endy2-starty2
sizefactor = 1.0
dshift = 0.5*factor_svg
f = Figure("20.3cm", "9.1cm",
Line(((startx1,starty1+dshift),(startx1+deltax1*sizefactor,starty1+dshift+deltay1*sizefactor)), width=1.5, color='grey'),
Line(((startx2,starty2+dshift),(startx2+deltax2*sizefactor,starty2+dshift+deltay2*sizefactor)), width=1.5, color='grey'),
Panel(
SVG(PANEL_A).scale(svg_scale).scale(0.9).move(0, 15*factor_svg),
Text("a", -2.7*factor_svg, 16.9*factor_svg-dshift, **kwargs_text),
).move(2.7*factor_svg, -14.4*factor_svg+dshift),
Panel(
SVG(PANEL_B).scale(svg_scale).move(0*factor_svg, 0*factor_svg),
Text("b", -6.0*factor_svg, 5*factor_svg-dshift, **kwargs_text),
Text("PD", -1.*factor_svg+0.0, 8.2*factor_svg, **kwargs_text8pt),
Text("LP", -1.*factor_svg+0.0, 13.4*factor_svg, **kwargs_text8pt),
Text("PY", -1.*factor_svg+0.0, 18.6*factor_svg, **kwargs_text8pt),
#Text("Period", 15.5*factor_svg+0.0, 2.8*factor_svg, **kwargs_text8pt),
#Text("Delay", 11.3*factor_svg+0.0, 9.6*factor_svg, **kwargs_text8pt),
#Text("Gap", 27.5*factor_svg+0.0, 9.6*factor_svg, **kwargs_text8pt),
#Text("Duration", 19.2*factor_svg+0.0, 13.8*factor_svg, **kwargs_text8pt),
Text("1", 17.45*factor_svg+0.0, 4.5*factor_svg, **kwargs_text8pt),
Text("2", 13.1*factor_svg+0.0, 10.6*factor_svg, **kwargs_text8pt),
Text("3", 28.75*factor_svg+0.0, 10.6*factor_svg, **kwargs_text8pt),
Text("4", 21.7*factor_svg+0.0, 15.4*factor_svg, **kwargs_text8pt),
#Text("50 mV", 39.4*factor_svg, 25*factor_svg, **kwargs_text8pt),
#Text("50 mV", 32.0*factor_svg, 4.8*factor_svg, **kwargs_text8pt),
Text("500 ms", 3.2*factor_svg, 22.5*factor_svg, **kwargs_text8pt),
).move(37.8*factor_svg, -2.5*factor_svg+dshift),
Panel(
SVG(PANEL_C).scale(svg_scale).move(-10*factor_svg,0*factor_svg),
Text("c", -11.5*factor_svg, 2.7*factor_svg-dshift, **kwargs_text),
).move(90.1*factor_svg, -0.2*factor_svg+dshift),
Panel(
SVG(PANEL_C2).scale(svg_scale).move(-10*factor_svg,0*factor_svg),
#Text("1", 3.1*factor_svg, 5.2*factor_svg, **kwargs_consistent1),
Text("1", 11.2*factor_svg, 11.3*factor_svg, **kwargs_consistent1),
Text("2", 7.5*factor_svg, 6.7*factor_svg, **kwargs_inconsistent),
).move(90*factor_svg, 35.2*factor_svg+dshift),
Panel(
SVG(PANEL_D).scale(svg_scale).move(0*factor_svg, 0*factor_svg),
Text("d", 0*factor_svg, 3.5*factor_svg-dshift, **kwargs_text),
#Text("1", 41.5*factor_svg, 4*factor_svg, **kwargs_consistent),
Text("1", 4*factor_svg, 23.5*factor_svg, **kwargs_consistent1),
Text("2", 41.5*factor_svg, 23.5*factor_svg, **kwargs_inconsistent),
Text("50 mV", 68.4*factor_svg, 4*factor_svg, **kwargs_text8pt),
).move(0*factor_svg, 23.2*factor_svg+dshift)
)
!mkdir -p fig
f.save("fig/fig8_stg_31D.svg")
svg('fig/fig8_stg_31D.svg')
```
| true |
code
| 0.559892 | null | null | null | null |
|
```
#export
from fastai.basics import *
from fastai.text.core import *
from fastai.text.data import *
from fastai.text.models.core import *
from fastai.text.models.awdlstm import *
from fastai.callback.rnn import *
from fastai.callback.progress import *
#hide
from nbdev.showdoc import *
#default_exp text.learner
```
# Learner for the text application
> All the functions necessary to build `Learner` suitable for transfer learning in NLP
The most important functions of this module are `language_model_learner` and `text_classifier_learner`. They will help you define a `Learner` using a pretrained model. See the [text tutorial](http://docs.fast.ai/tutorial.text) for exmaples of use.
## Loading a pretrained model
In text, to load a pretrained model, we need to adapt the embeddings of the vocabulary used for the pre-training to the vocabulary of our current corpus.
```
#export
def match_embeds(old_wgts, old_vocab, new_vocab):
"Convert the embedding in `old_wgts` to go from `old_vocab` to `new_vocab`."
bias, wgts = old_wgts.get('1.decoder.bias', None), old_wgts['0.encoder.weight']
wgts_m = wgts.mean(0)
new_wgts = wgts.new_zeros((len(new_vocab),wgts.size(1)))
if bias is not None:
bias_m = bias.mean(0)
new_bias = bias.new_zeros((len(new_vocab),))
old_o2i = old_vocab.o2i if hasattr(old_vocab, 'o2i') else {w:i for i,w in enumerate(old_vocab)}
for i,w in enumerate(new_vocab):
idx = old_o2i.get(w, -1)
new_wgts[i] = wgts[idx] if idx>=0 else wgts_m
if bias is not None: new_bias[i] = bias[idx] if idx>=0 else bias_m
old_wgts['0.encoder.weight'] = new_wgts
if '0.encoder_dp.emb.weight' in old_wgts: old_wgts['0.encoder_dp.emb.weight'] = new_wgts.clone()
old_wgts['1.decoder.weight'] = new_wgts.clone()
if bias is not None: old_wgts['1.decoder.bias'] = new_bias
return old_wgts
```
For words in `new_vocab` that don't have a corresponding match in `old_vocab`, we use the mean of all pretrained embeddings.
```
wgts = {'0.encoder.weight': torch.randn(5,3)}
new_wgts = match_embeds(wgts.copy(), ['a', 'b', 'c'], ['a', 'c', 'd', 'b'])
old,new = wgts['0.encoder.weight'],new_wgts['0.encoder.weight']
test_eq(new[0], old[0])
test_eq(new[1], old[2])
test_eq(new[2], old.mean(0))
test_eq(new[3], old[1])
#hide
#With bias
wgts = {'0.encoder.weight': torch.randn(5,3), '1.decoder.bias': torch.randn(5)}
new_wgts = match_embeds(wgts.copy(), ['a', 'b', 'c'], ['a', 'c', 'd', 'b'])
old_w,new_w = wgts['0.encoder.weight'],new_wgts['0.encoder.weight']
old_b,new_b = wgts['1.decoder.bias'], new_wgts['1.decoder.bias']
test_eq(new_w[0], old_w[0])
test_eq(new_w[1], old_w[2])
test_eq(new_w[2], old_w.mean(0))
test_eq(new_w[3], old_w[1])
test_eq(new_b[0], old_b[0])
test_eq(new_b[1], old_b[2])
test_eq(new_b[2], old_b.mean(0))
test_eq(new_b[3], old_b[1])
#export
def _get_text_vocab(dls):
vocab = dls.vocab
if isinstance(vocab, L): vocab = vocab[0]
return vocab
#export
def load_ignore_keys(model, wgts):
"Load `wgts` in `model` ignoring the names of the keys, just taking parameters in order"
sd = model.state_dict()
for k1,k2 in zip(sd.keys(), wgts.keys()): sd[k1].data = wgts[k2].data.clone()
return model.load_state_dict(sd)
#export
def _rm_module(n):
t = n.split('.')
for i in range(len(t)-1, -1, -1):
if t[i] == 'module':
t.pop(i)
break
return '.'.join(t)
#export
#For previous versions compatibility, remove for release
def clean_raw_keys(wgts):
keys = list(wgts.keys())
for k in keys:
t = k.split('.module')
if f'{_rm_module(k)}_raw' in keys: del wgts[k]
return wgts
#export
#For previous versions compatibility, remove for release
def load_model_text(file, model, opt, with_opt=None, device=None, strict=True):
"Load `model` from `file` along with `opt` (if available, and if `with_opt`)"
distrib_barrier()
if isinstance(device, int): device = torch.device('cuda', device)
elif device is None: device = 'cpu'
state = torch.load(file, map_location=device)
hasopt = set(state)=={'model', 'opt'}
model_state = state['model'] if hasopt else state
get_model(model).load_state_dict(clean_raw_keys(model_state), strict=strict)
if hasopt and ifnone(with_opt,True):
try: opt.load_state_dict(state['opt'])
except:
if with_opt: warn("Could not load the optimizer state.")
elif with_opt: warn("Saved filed doesn't contain an optimizer state.")
#export
@log_args(but_as=Learner.__init__)
@delegates(Learner.__init__)
class TextLearner(Learner):
"Basic class for a `Learner` in NLP."
def __init__(self, dls, model, alpha=2., beta=1., moms=(0.8,0.7,0.8), **kwargs):
super().__init__(dls, model, moms=moms, **kwargs)
self.add_cbs([ModelResetter(), RNNRegularizer(alpha=alpha, beta=beta)])
def save_encoder(self, file):
"Save the encoder to `file` in the model directory"
if rank_distrib(): return # don't save if child proc
encoder = get_model(self.model)[0]
if hasattr(encoder, 'module'): encoder = encoder.module
torch.save(encoder.state_dict(), join_path_file(file, self.path/self.model_dir, ext='.pth'))
def load_encoder(self, file, device=None):
"Load the encoder `file` from the model directory, optionally ensuring it's on `device`"
encoder = get_model(self.model)[0]
if device is None: device = self.dls.device
if hasattr(encoder, 'module'): encoder = encoder.module
distrib_barrier()
wgts = torch.load(join_path_file(file,self.path/self.model_dir, ext='.pth'), map_location=device)
encoder.load_state_dict(clean_raw_keys(wgts))
self.freeze()
return self
def load_pretrained(self, wgts_fname, vocab_fname, model=None):
"Load a pretrained model and adapt it to the data vocabulary."
old_vocab = Path(vocab_fname).load()
new_vocab = _get_text_vocab(self.dls)
distrib_barrier()
wgts = torch.load(wgts_fname, map_location = lambda storage,loc: storage)
if 'model' in wgts: wgts = wgts['model'] #Just in case the pretrained model was saved with an optimizer
wgts = match_embeds(wgts, old_vocab, new_vocab)
load_ignore_keys(self.model if model is None else model, clean_raw_keys(wgts))
self.freeze()
return self
#For previous versions compatibility. Remove at release
@delegates(load_model_text)
def load(self, file, with_opt=None, device=None, **kwargs):
if device is None: device = self.dls.device
if self.opt is None: self.create_opt()
file = join_path_file(file, self.path/self.model_dir, ext='.pth')
load_model_text(file, self.model, self.opt, device=device, **kwargs)
return self
```
Adds a `ModelResetter` and an `RNNRegularizer` with `alpha` and `beta` to the callbacks, the rest is the same as `Learner` init.
This `Learner` adds functionality to the base class:
```
show_doc(TextLearner.load_pretrained)
```
`wgts_fname` should point to the weights of the pretrained model and `vocab_fname` to the vocabulary used to pretrain it.
```
show_doc(TextLearner.save_encoder)
```
The model directory is `Learner.path/Learner.model_dir`.
```
show_doc(TextLearner.load_encoder)
```
## Language modeling predictions
For language modeling, the predict method is quite different form the other applications, which is why it needs its own subclass.
```
#export
def decode_spec_tokens(tokens):
"Decode the special tokens in `tokens`"
new_toks,rule,arg = [],None,None
for t in tokens:
if t in [TK_MAJ, TK_UP, TK_REP, TK_WREP]: rule = t
elif rule is None: new_toks.append(t)
elif rule == TK_MAJ:
new_toks.append(t[:1].upper() + t[1:].lower())
rule = None
elif rule == TK_UP:
new_toks.append(t.upper())
rule = None
elif arg is None:
try: arg = int(t)
except: rule = None
else:
if rule == TK_REP: new_toks.append(t * arg)
else: new_toks += [t] * arg
return new_toks
test_eq(decode_spec_tokens(['xxmaj', 'text']), ['Text'])
test_eq(decode_spec_tokens(['xxup', 'text']), ['TEXT'])
test_eq(decode_spec_tokens(['xxrep', '3', 'a']), ['aaa'])
test_eq(decode_spec_tokens(['xxwrep', '3', 'word']), ['word', 'word', 'word'])
#export
@log_args(but_as=TextLearner.__init__)
class LMLearner(TextLearner):
"Add functionality to `TextLearner` when dealingwith a language model"
def predict(self, text, n_words=1, no_unk=True, temperature=1., min_p=None, no_bar=False,
decoder=decode_spec_tokens, only_last_word=False):
"Return `text` and the `n_words` that come after"
self.model.reset()
idxs = idxs_all = self.dls.test_dl([text]).items[0].to(self.dls.device)
if no_unk: unk_idx = self.dls.vocab.index(UNK)
for _ in (range(n_words) if no_bar else progress_bar(range(n_words), leave=False)):
with self.no_bar(): preds,_ = self.get_preds(dl=[(idxs[None],)])
res = preds[0][-1]
if no_unk: res[unk_idx] = 0.
if min_p is not None:
if (res >= min_p).float().sum() == 0:
warn(f"There is no item with probability >= {min_p}, try a lower value.")
else: res[res < min_p] = 0.
if temperature != 1.: res.pow_(1 / temperature)
idx = torch.multinomial(res, 1).item()
idxs = idxs_all = torch.cat([idxs_all, idxs.new([idx])])
if only_last_word: idxs = idxs[-1][None]
num = self.dls.train_ds.numericalize
tokens = [num.vocab[i] for i in idxs_all if num.vocab[i] not in [BOS, PAD]]
sep = self.dls.train_ds.tokenizer.sep
return sep.join(decoder(tokens))
@delegates(Learner.get_preds)
def get_preds(self, concat_dim=1, **kwargs): return super().get_preds(concat_dim=1, **kwargs)
show_doc(LMLearner, title_level=3)
show_doc(LMLearner.predict)
```
The words are picked randomly among the predictions, depending on the probability of each index. `no_unk` means we never pick the `UNK` token, `tempreature` is applied to the predictions, if `min_p` is passed, we don't consider the indices with a probability lower than it. Set `no_bar` to `True` if you don't want any progress bar, and you can pass a long a custom `decoder` to process the predicted tokens.
## `Learner` convenience functions
```
#export
from fastai.text.models.core import _model_meta
#export
def _get_text_vocab(dls):
vocab = dls.vocab
if isinstance(vocab, L): vocab = vocab[0]
return vocab
#export
@log_args(to_return=True, but_as=Learner.__init__)
@delegates(Learner.__init__)
def language_model_learner(dls, arch, config=None, drop_mult=1., backwards=False, pretrained=True, pretrained_fnames=None, **kwargs):
"Create a `Learner` with a language model from `dls` and `arch`."
vocab = _get_text_vocab(dls)
model = get_language_model(arch, len(vocab), config=config, drop_mult=drop_mult)
meta = _model_meta[arch]
learn = LMLearner(dls, model, loss_func=CrossEntropyLossFlat(), splitter=meta['split_lm'], **kwargs)
url = 'url_bwd' if backwards else 'url'
if pretrained or pretrained_fnames:
if pretrained_fnames is not None:
fnames = [learn.path/learn.model_dir/f'{fn}.{ext}' for fn,ext in zip(pretrained_fnames, ['pth', 'pkl'])]
else:
if url not in meta:
warn("There are no pretrained weights for that architecture yet!")
return learn
model_path = untar_data(meta[url] , c_key='model')
fnames = [list(model_path.glob(f'*.{ext}'))[0] for ext in ['pth', 'pkl']]
learn = learn.load_pretrained(*fnames)
return learn
```
You can use the `config` to customize the architecture used (change the values from `awd_lstm_lm_config` for this), `pretrained` will use fastai's pretrained model for this `arch` (if available) or you can pass specific `pretrained_fnames` containing your own pretrained model and the corresponding vocabulary. All other arguments are passed to `Learner`.
```
path = untar_data(URLs.IMDB_SAMPLE)
df = pd.read_csv(path/'texts.csv')
dls = TextDataLoaders.from_df(df, path=path, text_col='text', is_lm=True, valid_col='is_valid')
learn = language_model_learner(dls, AWD_LSTM)
```
You can then use the `.predict` method to generate new text.
```
learn.predict('This movie is about', n_words=20)
```
By default the entire sentence is feed again to the model after each predicted word, this little trick shows an improvement on the quality of the generated text. If you want to feed only the last word, specify argument `only_last_word`.
```
learn.predict('This movie is about', n_words=20, only_last_word=True)
#export
@log_args(to_return=True, but_as=Learner.__init__)
@delegates(Learner.__init__)
def text_classifier_learner(dls, arch, seq_len=72, config=None, backwards=False, pretrained=True, drop_mult=0.5, n_out=None,
lin_ftrs=None, ps=None, max_len=72*20, y_range=None, **kwargs):
"Create a `Learner` with a text classifier from `dls` and `arch`."
vocab = _get_text_vocab(dls)
if n_out is None: n_out = get_c(dls)
assert n_out, "`n_out` is not defined, and could not be infered from data, set `dls.c` or pass `n_out`"
model = get_text_classifier(arch, len(vocab), n_out, seq_len=seq_len, config=config, y_range=y_range,
drop_mult=drop_mult, lin_ftrs=lin_ftrs, ps=ps, max_len=max_len)
meta = _model_meta[arch]
learn = TextLearner(dls, model, splitter=meta['split_clas'], **kwargs)
url = 'url_bwd' if backwards else 'url'
if pretrained:
if url not in meta:
warn("There are no pretrained weights for that architecture yet!")
return learn
model_path = untar_data(meta[url], c_key='model')
fnames = [list(model_path.glob(f'*.{ext}'))[0] for ext in ['pth', 'pkl']]
learn = learn.load_pretrained(*fnames, model=learn.model[0])
learn.freeze()
return learn
```
You can use the `config` to customize the architecture used (change the values from `awd_lstm_clas_config` for this), `pretrained` will use fastai's pretrained model for this `arch` (if available). `drop_mult` is a global multiplier applied to control all dropouts. `n_out` is usually infered from the `dls` but you may pass it.
The model uses a `SentenceEncoder`, which means the texts are passed `seq_len` tokens at a time, and will only compute the gradients on the last `max_len` steps. `lin_ftrs` and `ps` are passed to `get_text_classifier`.
All other arguments are passed to `Learner`.
```
path = untar_data(URLs.IMDB_SAMPLE)
df = pd.read_csv(path/'texts.csv')
dls = TextDataLoaders.from_df(df, path=path, text_col='text', label_col='label', valid_col='is_valid')
learn = text_classifier_learner(dls, AWD_LSTM)
```
## Show methods -
```
#export
@typedispatch
def show_results(x: LMTensorText, y, samples, outs, ctxs=None, max_n=10, **kwargs):
if ctxs is None: ctxs = get_empty_df(min(len(samples), max_n))
for i,l in enumerate(['input', 'target']):
ctxs = [b.show(ctx=c, label=l, **kwargs) for b,c,_ in zip(samples.itemgot(i),ctxs,range(max_n))]
ctxs = [b.show(ctx=c, label='pred', **kwargs) for b,c,_ in zip(outs.itemgot(0),ctxs,range(max_n))]
display_df(pd.DataFrame(ctxs))
return ctxs
#export
@typedispatch
def show_results(x: TensorText, y, samples, outs, ctxs=None, max_n=10, trunc_at=150, **kwargs):
if ctxs is None: ctxs = get_empty_df(min(len(samples), max_n))
samples = L((s[0].truncate(trunc_at),*s[1:]) for s in samples)
ctxs = show_results[object](x, y, samples, outs, ctxs=ctxs, max_n=max_n, **kwargs)
display_df(pd.DataFrame(ctxs))
return ctxs
#export
@typedispatch
def plot_top_losses(x: TensorText, y:TensorCategory, samples, outs, raws, losses, trunc_at=150, **kwargs):
rows = get_empty_df(len(samples))
samples = L((s[0].truncate(trunc_at),*s[1:]) for s in samples)
for i,l in enumerate(['input', 'target']):
rows = [b.show(ctx=c, label=l, **kwargs) for b,c in zip(samples.itemgot(i),rows)]
outs = L(o + (TitledFloat(r.max().item()), TitledFloat(l.item())) for o,r,l in zip(outs, raws, losses))
for i,l in enumerate(['predicted', 'probability', 'loss']):
rows = [b.show(ctx=c, label=l, **kwargs) for b,c in zip(outs.itemgot(i),rows)]
display_df(pd.DataFrame(rows))
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| true |
code
| 0.741636 | null | null | null | null |
|
Air Quality Index
1)To identify the Most polluted City
2)Create a Model to Predict the quality of air
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df=pd.read_csv('https://raw.githubusercontent.com/tulseebisen/ML_Projects/main/AirQualityIndex/city_day.csv',parse_dates = ["Date"])
df
df.head()
df.tail()
sns.heatmap(df.isnull(),yticklabels=False,cbar=False,cmap='viridis')
print(df.isnull().sum())
(df.isnull().sum()/df.shape[0]*100).sort_values(ascending=False)
df.describe() # but it gives the information about all the cities alltogether
#converting dtype of date column to datetime
df['Date']=df['Date'].apply(pd.to_datetime)
#setting date column as index
df.set_index('Date',inplace=True)
df.columns
```
filling the Nan values present in the pollutants with mean (city wise)
```
df.iloc[:, 1:13] = df.groupby("City").transform(lambda x: x.fillna(x.mean()))
df
sns.heatmap(df.isnull(),yticklabels=False,cbar=False,cmap='viridis')
df.iloc[:, 1:13]=df.fillna(df.mean())
df
sns.heatmap(df.isnull(),yticklabels=False,cbar=False,cmap='viridis')
```
The AQI calculation uses 7 measures: PM2.5, PM10, SO2, NOx, NH3, CO and O3.
-->For PM2.5, PM10, SO2, NOx and NH3 the average value in last 24-hrs is used with the condition of having at least 16 values.
-->For CO and O3 the maximum value in last 8-hrs is used.
-->Each measure is converted into a Sub-Index based on pre-defined groups.
-->Sometimes measures are not available due to lack of measuring or lack of required data points.
-->Final AQI is the maximum Sub-Index with the condition that at least one of PM2.5 and PM10 should be available and at least three out of the seven should be available.
## calculating Sub-Index
```
# PM10 Sub-Index calculation
def get_PM10_subindex(x):
if x <= 50:
return x
elif x > 50 and x <= 100:
return x
elif x > 100 and x <= 250:
return 100 + (x - 100) * 100 / 150
elif x > 250 and x <= 350:
return 200 + (x - 250)
elif x > 350 and x <= 430:
return 300 + (x - 350) * 100 / 80
elif x > 430:
return 400 + (x - 430) * 100 / 80
else:
return 0
df["PM10_SubIndex"] = df["PM10"].astype(int).apply(lambda x: get_PM10_subindex(x))
# PM2.5 Sub-Index calculation
def get_PM25_subindex(x):
if x <= 30:
return x * 50 / 30
elif x > 30 and x <= 60:
return 50 + (x - 30) * 50 / 30
elif x > 60 and x <= 90:
return 100 + (x - 60) * 100 / 30
elif x > 90 and x <= 120:
return 200 + (x - 90) * 100 / 30
elif x > 120 and x <= 250:
return 300 + (x - 120) * 100 / 130
elif x > 250:
return 400 + (x - 250) * 100 / 130
else:
return 0
df["PM2.5_SubIndex"] = df["PM2.5"].astype(int).apply(lambda x: get_PM25_subindex(x))
# SO2 Sub-Index calculation
def get_SO2_subindex(x):
if x <= 40:
return x * 50 / 40
elif x > 40 and x <= 80:
return 50 + (x - 40) * 50 / 40
elif x > 80 and x <= 380:
return 100 + (x - 80) * 100 / 300
elif x > 380 and x <= 800:
return 200 + (x - 380) * 100 / 420
elif x > 800 and x <= 1600:
return 300 + (x - 800) * 100 / 800
elif x > 1600:
return 400 + (x - 1600) * 100 / 800
else:
return 0
df["SO2_SubIndex"] = df["SO2"].astype(int).apply(lambda x: get_SO2_subindex(x))
# NOx Sub-Index calculation
def get_NOx_subindex(x):
if x <= 40:
return x * 50 / 40
elif x > 40 and x <= 80:
return 50 + (x - 40) * 50 / 40
elif x > 80 and x <= 180:
return 100 + (x - 80) * 100 / 100
elif x > 180 and x <= 280:
return 200 + (x - 180) * 100 / 100
elif x > 280 and x <= 400:
return 300 + (x - 280) * 100 / 120
elif x > 400:
return 400 + (x - 400) * 100 / 120
else:
return 0
df["NOx_SubIndex"] = df["NOx"].astype(int).apply(lambda x: get_NOx_subindex(x))
# NH3 Sub-Index calculation
def get_NH3_subindex(x):
if x <= 200:
return x * 50 / 200
elif x > 200 and x <= 400:
return 50 + (x - 200) * 50 / 200
elif x > 400 and x <= 800:
return 100 + (x - 400) * 100 / 400
elif x > 800 and x <= 1200:
return 200 + (x - 800) * 100 / 400
elif x > 1200 and x <= 1800:
return 300 + (x - 1200) * 100 / 600
elif x > 1800:
return 400 + (x - 1800) * 100 / 600
else:
return 0
df["NH3_SubIndex"] = df["NH3"].astype(int).apply(lambda x: get_NH3_subindex(x))
# CO Sub-Index calculation
def get_CO_subindex(x):
if x <= 1:
return x * 50 / 1
elif x > 1 and x <= 2:
return 50 + (x - 1) * 50 / 1
elif x > 2 and x <= 10:
return 100 + (x - 2) * 100 / 8
elif x > 10 and x <= 17:
return 200 + (x - 10) * 100 / 7
elif x > 17 and x <= 34:
return 300 + (x - 17) * 100 / 17
elif x > 34:
return 400 + (x - 34) * 100 / 17
else:
return 0
df["CO_SubIndex"] = df["CO"].astype(int).apply(lambda x: get_CO_subindex(x))
# O3 Sub-Index calculation
def get_O3_subindex(x):
if x <= 50:
return x * 50 / 50
elif x > 50 and x <= 100:
return 50 + (x - 50) * 50 / 50
elif x > 100 and x <= 168:
return 100 + (x - 100) * 100 / 68
elif x > 168 and x <= 208:
return 200 + (x - 168) * 100 / 40
elif x > 208 and x <= 748:
return 300 + (x - 208) * 100 / 539
elif x > 748:
return 400 + (x - 400) * 100 / 539
else:
return 0
df["O3_SubIndex"] = df["O3"].astype(int).apply(lambda x: get_O3_subindex(x))
```
## Filling the Nan values of AQI column by taking maximum values out of sub-Indexes
```
df["AQI"] = df["AQI"].fillna(round(df[["PM2.5_SubIndex", "PM10_SubIndex", "SO2_SubIndex", "NOx_SubIndex","NH3_SubIndex", "CO_SubIndex", "O3_SubIndex"]].max(axis = 1)))
df
sns.heatmap(df.isnull(),yticklabels=False,cbar=False,cmap='viridis')
```
# AQI Bucket
```
from IPython import display
display.Image("/home/manikanta/Pictures/Screenshot from 2021-05-21 11-59-24.png",width = 400, height = 200)
```
### calculating AQI bucket and filling the NAN value present
```
## AQI bucketing
def get_AQI_bucket(x):
if x <= 50:
return "Good"
elif x > 50 and x <= 100:
return "Satisfactory"
elif x > 100 and x <= 200:
return "Moderate"
elif x > 200 and x <= 300:
return "Poor"
elif x > 300 and x <= 400:
return "Very Poor"
elif x > 400:
return "Severe"
else:
return '0'
df["AQI_Bucket"] = df["AQI_Bucket"].fillna(df["AQI"].apply(lambda x: get_AQI_bucket(x)))
df
sns.heatmap(df.isnull(),yticklabels=False,cbar=False,cmap='viridis')
df.columns
df_city_day = df.copy()
df_city_day.columns
plt.figure(figsize=(12,10))
sns.heatmap(df.corr(),cmap='coolwarm',annot=True);
pollutants = ['PM2.5', 'PM10', 'NO', 'NO2', 'NOx', 'NH3', 'CO', 'SO2','O3', 'Benzene', 'Toluene', 'Xylene']
df_city_day = df_city_day[pollutants]
print('Distribution of different pollutants in last 5 years')
df_city_day.plot(kind='line',figsize=(18,18),cmap='coolwarm',subplots=True,fontsize=10);
df[['City','AQI']].groupby('City').mean().sort_values('AQI').plot(kind='bar',cmap='Blues_r',figsize=(8,8))
plt.title('Average AQI in last 5 years');
```
### By above graph we can conclude that Ahmedabad is the heighest polluted city followed by Delhi and Gurugram
## Creating Model for predicting the Output
```
final_df= df[['AQI', 'AQI_Bucket']].copy()
final_df
final_df['AQI_Bucket'].unique()
#final_df = pd.get_dummies(final_df)
final_df['AQI_Bucket'] = final_df['AQI_Bucket'].map({'Good' :0, 'Satisfactory' :1, 'Moderate' :2, 'Poor' :3, 'Very Poor' :4, 'Severe' :5}).astype(int) #mapping numbers
final_df.head()
```
# Predicting the values of AQI_Bucket w.r.t values of AQI using Random Forest Classifier
```
X = final_df[['AQI']]
y = final_df[['AQI_Bucket']]
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)
clf = RandomForestClassifier(random_state = 0).fit(X_train, y_train)
y_pred = clf.predict(X_test)
print("Enter the value of AQI:")
AQI = float(input("AQI : "))
output = clf.predict([[AQI]])
output
#0-->Good
#1-->Satisfactory
#2-->moderate
#3-->poor
#4-->Very poor
#5-->Severe
from sklearn.metrics import accuracy_score,classification_report,confusion_matrix
print(accuracy_score(y_test, y_pred))
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
```
| true |
code
| 0.346403 | null | null | null | null |
|
# Systems Identification Model Fitting
Fit a Systems Identification model off based off of this [specification](https://hackmd.io/w-vfdZIMTDKwdEupeS3qxQ) and [spec](https://hackmd.io/XVaejEw-QaCghV1Tkv3eVQ) with data obtained in [data_acquisition.ipynb](data/data_acquisition.ipynb).
#### Process changes and decision points
* Create differenced linear regressor model for refining data formatting
* Fit VAR model off of differenced states with Yeo-Johnson power transformation
* Implemented coordinate transformations
* Created inverse transformations
* Fit one step forward VAR model that takes the difference between local arbitrager values and observed values and forcasts the errors within the coordinate transformation state.
* Fit VARMAX model with exogenous signal - error between redemption price and rai market price - retrain after every timestep
* Compare VARMAX vs VAR model (we chose VARMAX with an exogenous signal)
* VARMAX is too slow to retrain at each time step (25x slower than VAR). To determine which model performs better, we created a [validation notebook](VAR_vs_VARMAX_evaluation.ipynb)
* Refactor to functions for deployment
* Add back Yeo-Johnson power transformation
* Move from arbitrageur to exponentially weighted moving average of actual data
* Swept alpha of exponentially weighted moving average and found that a VAR(15) with an alpha of 0.8 performed best.
## Analyze and Prepare Data
```
# import libraries
import pandas as pd
import numpy as np
from scipy import stats
import math
import statsmodels.api as sm
from statsmodels.tsa.api import VAR, VARMAX
from sklearn.preprocessing import PowerTransformer
import matplotlib.pyplot as plt
import warnings
import os
warnings.filterwarnings("ignore")
os.chdir('..')
states = pd.read_csv('data/states.csv')
del states['Unnamed: 0']
states.head()
# add additional state variables
states['RedemptionPriceinEth'] = states['RedemptionPrice'] / states['ETH Price (OSM)']
states['RedemptionPriceError'] = states['RedemptionPrice'] - states['marketPriceUsd']
```
### Systems identification steps:
1. Calculate optimal state from APT model (updated to exponential weighted moving average of the real data)
2. Perform a coordinate transformation of data
3. Difference the local coordinate from the observed to get error
4. Perform a Yeo-Johnson power transformation
<!-- 4. Train VARMAX the errors + exogenous signal[s]
-->
5. Train a VAR(15) model
6. One step forecast
7. Invert the Yeo-Johnson power transformation
8. Convert forecasted values back from coordinate system
9. Add forecasted values to previous state to get new state
### Mapping of specification states to data
#### Initial vector
The quantity state variables of the system are as value, mathematical notation, and Graph and Big Query field names from [data_acquisition.ipynb](data/data_acquisition.ipynb).
* ETH in collateral = $Q$ = collateral
* ETH in Uniswap = $R_{ETH}$ = EthInUniswap
* RAI in Uniswap = $R_{RAI}$ = RaiInUniswap
* RAI drawn from SAFEs = $D$ = RaiDrawnFromSAFEs
<!-- (GlobalDebt won't equal total supply (create graphics around?)) -->
The metric state variables of the system are:
* Market Price of RAI in ETH = $p_{E/R} > 0$ = marketPriceEth
* Market Price of RAI in USD = $p_{U/R} > 0$ = marketPriceUsd
* Market Price of ETH in USD = $p_{U/E} > 0$ = ETH Price (OSM)
The metric control variables of the system are:
* Redemption Price of RAI in USD = $p^r_{U/R} > 0$ = RedemptionPrice
* Redemption Price of RAI in ETH = $p^r_{E/R} > 0$ = RedemptionPriceinEth
The system parameters are:
* Liquidation Ratio = $\bar{L} > 0$ = 1.45
* SAFE Debt Ceiling = $\bar{D} > 0$ = globalDebtCeiling
* Uniswap Fee = $\phi_U \in (0,1)$ = 0.003
* Gas Costs = $\bar{C}_{gas} \geq 0$ = 100e-9, # 100 gwei
The aggregate flow variables are:
* Collateral added or removed = $q \in \mathbb{R}$ (ETH)
* SAFE Debt drawn or repaid = $d \in \mathbb{R}$ (RAI)
* Uniswap RAI bought or sold = $r \in \mathbb{R}$ (RAI)
* Uniswap ETH bought or sold = $z \in \mathbb{R}$ (ETH)
### Model Formulation
There is an admissible action set of vectors:
(Graph values)
* ETH in collateral = $Q$ = collateral
* ETH in Uniswap = $R_{ETH}$ reserve1
* RAI in Uniswap = $R_{RAI}$ = reserve0
* RAI drawn from SAFEs = $D$ = erc20CoinTotalSupply
Action vector: $\vec{u} = (\Delta Q, \Delta R_{ETH}, \Delta R_{RAI}, \Delta D)$
Admissible action set: $\vec{u} \in \mathcal{U}$
Optimal Action Vector: $\vec{u^*} = (Q^*, R_{ETH}^*, \Delta R_{RAI}^*, \Delta D^*)$
```
# define constants (will come from cadCAD model but added here for calculations)
params = {
'liquidation_ratio': 1.45,
'debt_ceiling': 1e9,
'uniswap_fee': 0.003,
'arbitrageur_considers_liquidation_ratio': True,
}
```
## Create Arbtrageur data vector $u^*$
```
def get_aggregated_arbitrageur_decision(params, state):
# This Boolean indicates whether or not the arbitrageur is rationally considering
# borrowing to the liquidation ratio limit. If TRUE, arbitrage opportunities are less
# frequent when RAI is expensive and more frequent when RAI is cheap. If FALSE, only
# the difference in market and redemption prices (net of Uniswap fee) matters for trading,
# which may conform more to individual trader expectations and behavior.
consider_liquidation_ratio = params['arbitrageur_considers_liquidation_ratio']
# These are the states of the SAFE balances in aggregate & its fixed parameters
total_borrowed = state['SAFE_Debt'] # D
total_collateral = state['SAFE_Collateral'] # Q
liquidation_ratio = params['liquidation_ratio']
debt_ceiling = params['debt_ceiling']
# These are the states of the Uniswap secondary market balances and its fee
RAI_balance = state['RAI_balance'] # R_Rai
ETH_balance = state['ETH_balance'] # R_Eth
uniswap_fee = params['uniswap_fee']
# These are the prices of RAI in USD/RAI for SAFE redemption and the market price oracle, resp.
redemption_price = state['target_price'] # $p^r_{U/R}
market_price = state['market_price'] # p_{U/R} > 0
# This is the price of ETH in USD/ETH
eth_price = state['eth_price'] # p_{U/E}
# These functions define the optimal borrowing/repayment decisions of the aggregated arbitrageur
def g1(RAI_balance, ETH_balance, uniswap_fee, liquidation_ratio, redemption_price):
return ((eth_price * RAI_balance * ETH_balance * (1 - uniswap_fee)) / (liquidation_ratio * redemption_price)) ** 0.5
def g2(RAI_balance, ETH_balance, uniswap_fee, liquidation_ratio, redemption_price):
return (RAI_balance * ETH_balance * (1 - uniswap_fee) * liquidation_ratio * (redemption_price / eth_price)) ** 0.5
# This Boolean resolves to TRUE if the agg. arb. acts this timestep when RAI is expensive
# on the secondary market
expensive_RAI_on_secondary_market = \
redemption_price < ((1 - uniswap_fee) / liquidation_ratio) * market_price \
if consider_liquidation_ratio \
else redemption_price < (1 - uniswap_fee) * market_price
# This Boolean resolves to TRUE if the agg. arb. acts this timestep when RAI is cheap
# on the secondary market
cheap_RAI_on_secondary_market = \
redemption_price > (1 / ((1 - uniswap_fee) * liquidation_ratio)) * market_price \
if consider_liquidation_ratio \
else redemption_price > (1 / (1 - uniswap_fee)) * market_price
if expensive_RAI_on_secondary_market:
'''
Expensive RAI on Uni:
(put ETH from pocket into additional collateral in SAFE)
draw RAI from SAFE -> Uni
ETH from Uni -> into pocket
'''
_g1 = g1(RAI_balance, ETH_balance, uniswap_fee,
liquidation_ratio, redemption_price)
d = (_g1 - RAI_balance) / (1 - uniswap_fee) # should be \geq 0
q = ((liquidation_ratio * redemption_price) /
eth_price) * (total_borrowed + d) - total_collateral # should be \geq 0
z = -(ETH_balance * d * (1 - uniswap_fee)) / \
(RAI_balance + d * (1 - uniswap_fee)) # should be leq 0
r = d # should be \geq 0
elif cheap_RAI_on_secondary_market:
'''
Cheap RAI on Uni:
ETH out of pocket -> Uni
RAI from UNI -> SAFE to wipe debt
(and collect collateral ETH from SAFE into pocket)
'''
_g2 = g2(RAI_balance, ETH_balance, uniswap_fee,
liquidation_ratio, redemption_price)
z = (_g2 - ETH_balance) / (1 - uniswap_fee) # should be \geq 0
r = -(RAI_balance * z * (1 - uniswap_fee)) / \
(ETH_balance + z * (1 - uniswap_fee)) # should be \leq 0
d = r # should be \leq 0
q = ((liquidation_ratio * redemption_price /
eth_price) * (total_borrowed + d) - total_collateral) # should be \leq 0
else:
pass
return {
'q' : q,
'd' : d,
'r' : r,
'z' : z
}
# UPDATED: We will use an exponentially weighted moving average instead of this arbitrageur logic
# # subset state variables for arbitrageur vector
# state_subset = states[['marketPriceUsd','RedemptionPrice','ETH Price (OSM)','collateral',
# 'EthInUniswap','RaiInUniswap','RaiDrawnFromSAFEs']]
# # map state data to arbitrageur vector fields
# state_subset.columns = ['market_price','target_price','eth_price','SAFE_Collateral',
# 'ETH_balance','RAI_balance','SAFE_Debt']
# # create list of u^* vectors
# values = []
# # iterate through real data to create u^* and save to values
# for i in range(0,len(state_subset)):
# values.append(get_aggregated_arbitrageur_decision(params,state_subset.loc[i]))
# # create historic u^* dataframe
# local = pd.DataFrame(values)
# local.columns = ['Q','D','Rrai','Reth']
# local.head()
states
# subset state variables for arbitrageur vector
state_subset = states[['collateral','RaiDrawnFromSAFEs','RaiInUniswap','EthInUniswap']]
# map state data to vector fields
state_subset.columns = ['Q','D','Rrai','Reth']
# alpha is the smoothing factor
local = state_subset.ewm(alpha=0.8).mean()
local
```
## Coordinate Transformations
1. $\alpha := \frac{d}{\bar{D}}$
Constraint: $\bar{D} \geq D + d$
$ C_0 := \frac{p^r_{U/R}}{p_{U/E}}\bar{L} > 0$
$ C_0 D - Q =: C_1.$
2. $\beta := \frac{q - C_0 d}{C_1}$
3. $\gamma := \frac{r}{R_{RAI}}$
4. $\delta := \frac{z}{R_{ETH}}$
## Inverse Transformations
1. $d^* = \alpha * \bar{D}$.
2. $q^* = C_0 * \bar{D} * \alpha + C_1 * \beta$
3. $r^* = \gamma * {R_{RAI}}$
4. $z^* = \delta * {R_{ETH}}$
```
# function to create coordinate transformations
def coordinate_transformations(params,df,Q,R_eth,R_rai,D,RedemptionPrice,EthPrice):
'''
Description:
Function that takes in pandas dataframe and the names of columns
Parameters:
df: pandas dataframe containing states information
Q: dataframe column name
R_eth: dataframe column name
R_rai: dataframe column name
D: dataframe column name
RedemptionPrice: dataframe column name
EthPrice: dataframe column name
Returns: Pandas dataframe with alpha, beta, gamma, delta transformed values
Example:
coordinate_transformations(params,states,'collateral','EthInUniswap','RaiInUniswap',
'RaiDrawnFromSAFEs','RedemptionPrice','ETH Price (OSM)')[['alpha','beta','gamma','delta']]
'''
# Calculate alpha
d = df[D].diff()
d.fillna(0,inplace=True)
df['d'] = d
df['alpha'] = df['d'] / params['debt_ceiling']
# alpha constraint check
for i, row in df.iterrows():
#constraint
constraint = params['debt_ceiling'] >= row[D] + row['d']
if constraint == False:
print('For row index {}'.format(i))
print('Alpha constraint is not passed')
# calculate beta
df['C_o'] = (df[RedemptionPrice]/states[EthPrice]) * params['liquidation_ratio']
# C_0 constraint check
for i, row in df.iterrows():
#constraint
constraint = row['C_o'] > 0
if constraint == False:
print('For row index {}'.format(i))
print('C_0 constraint is not passed')
q = df[Q].diff()
q.fillna(0,inplace=True)
df['q'] = q
df['C_1'] = (df['C_o'] * df[D]) - df[Q]
df['beta'] = (df['q'] - (df['C_o']*df['d']))/ df['C_1']
# calculate gamma
r = df[R_rai].diff()
r.fillna(0,inplace=True)
df['r'] = r
df['gamma'] = df['r']/df[R_rai]
# calculate delta
z = df[R_eth].diff()
z.fillna(0,inplace=True)
df['z'] = z
df['delta'] = df['z']/df[R_eth]
return df
# transform historical data
transformed = coordinate_transformations(params,states,'collateral','EthInUniswap','RaiInUniswap',
'RaiDrawnFromSAFEs','RedemptionPrice','ETH Price (OSM)')[['alpha','beta','gamma','delta']]
transformed
# add additional signals to arbitrageur state
local['RedemptionPrice'] = states['RedemptionPrice']
local['ETH Price (OSM)'] = states['ETH Price (OSM)']
local
# transform u*
transformed_arbitrageur = coordinate_transformations(params,local,'Q','Reth','Rrai',
'D','RedemptionPrice','ETH Price (OSM)')[['alpha','beta','gamma','delta']]
transformed_arbitrageur
def create_transformed_errors(transformed_states,transformed_arbitrageur):
'''
Description:
Function for taking two pandas dataframes of transformed states and taking the difference
to produce an error dataframe.
Parameters:
transformed_states: pandas dataframe with alpha, beta, gamma, and delta features
transformed_arbitrageur: pandas dataframe with alpha, beta, gamma, and delta features
Returns:
error pandas dataframe and transformation object
'''
alpha_diff = transformed_states['alpha'] - transformed_arbitrageur['alpha']
beta_diff = transformed_states['beta'] - transformed_arbitrageur['beta']
gamma_diff = transformed_states['gamma'] - transformed_arbitrageur['gamma']
delta_diff = transformed_states['delta'] - transformed_arbitrageur['delta']
e_u = pd.DataFrame(alpha_diff)
e_u['beta'] = beta_diff
e_u['gamma'] = gamma_diff
e_u['delta'] = delta_diff
e_u = e_u.astype(float)
return e_u
e_u = create_transformed_errors(transformed,transformed_arbitrageur)
e_u.head()
e_u.describe()
e_u.hist()
```
When data isn't normal (as is shown above), it is best practice to do a transformation. For our initial transformation, we will use the Yeo-Johnson power transformation. The Yeo-Johnson power transformation is used to stabilize variance, and make data more Gausian. The Yeo-Johnson is an extension of Box-Cox that allows for both zero and negative values(https://en.wikipedia.org/wiki/Power_transform). You could use any other type of normalization tranformation as well, whichever fits the data the best.
Scikit-learn has a great implementation of the transformer, which we will use below.
```
pt = PowerTransformer()
yeo= pd.DataFrame(pt.fit_transform(e_u),columns=e_u.columns)
yeo.hist()
# transform back into coordinate system
pt.inverse_transform(yeo)
```
The data looks a little better, but we can always experiment with additional techniques
```
def power_transformation(e_u):
'''
Definition:
Function to perform a power transformation on the coordinate
transformed differenced data
Parameters:
e_u: Dataframe of coordinated transformed differenced data
Required:
import pandas as pd
from sklearn.preprocessing import PowerTransformer
Returns:
Transformed dataframe and transformation object
Example:
transformed_df, pt = power_transformation(e_u)
'''
pt = PowerTransformer()
yeo= pd.DataFrame(pt.fit_transform(e_u),columns=e_u.columns)
return yeo, pt
e_u,pt = power_transformation(e_u)
```
## Create model
```
# split data between train and test (in production deployment, can remove)
split_point = int(len(e_u) * .8)
train = e_u.iloc[0:split_point]
test = e_u.iloc[split_point:]
states_train = states.iloc[0:split_point]
states_test = states.iloc[split_point:]
```
<!-- Potential alternative transformations are as follows:
* sin
* log of the Yeo-Johnson
Both of which provide a better fit than the Yeo-Johnson (as seen below).
For the rest of this notebook, we will implement the model training, forecasting, and evaluation process which will allow us to iterate over different transformations until we find one that fits our use case the best. -->
<!-- ### Autogressive lag selection -->
```
aic = []
for i in range(1,25):
model = VAR(train)
results = model.fit(i,ic='aic')
aic.append(results.aic)
plt.figure(figsize=(10, 8))
plt.plot(aic, 'r+')
plt.legend(['AIC'])
plt.xlabel('Autocorrelation Lag')
plt.ylabel('AIC')
plt.title('Plot of sweeps over lag depths over AIC Loss functions')
plt.show()
# aic = []
# for i in range(1,16):
# model = VARMAX(endog=train.values,exog=states_train['RedemptionPriceError'].values,initialization='approximate_diffuse')
# results = model.fit(order=(i,0))
# aic.append(results.aic)
# plt.figure(figsize=(10, 8))
# plt.plot(aic, 'r+')
# plt.legend(['AIC'])
# plt.xlabel('Autocorrelation Lag')
# plt.ylabel('AIC')
# plt.title('Plot of sweeps over lag depths over AIC Loss functions')
# plt.show()
```
Given a set of candidate models for the data, **the preferred model is the one with the minimum AIC value, the sign of the data does not matter**. AIC optimizes for goodness of fit but also includes a penalty for each additional parameter, which discourages overfitting. In our case, this appears that a lag of ***15*** is optimal.
For a VARMAX model, which we have decided to use, an order of 1 is selected. To determine which model performs better overall for predictions, given the computational constraints that VARMAX is too slow to be retrained at each timestep, a [validation notebook](VAR_vs_VARMAX_evaluation.ipynb) was created to test if a VAR retrained every timestep vs a VARMAX retrained very 20 predictions. The result over 20 predictions was that VAR performed best for alpha, gamma, and delta but VARMAX performed better with beta by a higher magnitude than VAR.
```
def VARMAX_prediction(e_u,RedemptionPriceError,newRedemptionPriceError,steps=1,lag=1):
'''
Description:
Function to train and forecast a VARMAX model one step into the future
Parameters:
e_u: errors pandas dataframe
RedemptionPriceErrorPrevious: 1d Numpy array of RedemptionPriceError values
newRedemptionPriceError: exogenous latest redemption price error signal - float
steps: Number of forecast steps. Default is 1
lag: number of autoregressive lags. Default is 1
Returns:
Numpy array of transformed state changes
Example
Y_pred = VARMAX_prediction(train,states_train['RedemptionPriceError'],
states_test['RedemptionPriceError'][0:5],steps=5,lag=1)
'''
# instantiate the VARMAX model object from statsmodels
model = VARMAX(endog=e_u.values,exog=RedemptionPriceError,
initialization='approximate_diffuse',measurement_error=True)
# fit model with determined lag values
results = model.fit(order=(lag,0))
Y_pred = results.forecast(steps = steps, exog=newRedemptionPriceError)
return Y_pred.values
def VAR_prediction(e_u,lag=1):
'''
Description:
Function to train and forecast a VAR model one step into the future
Parameters:
e_u: errors pandas dataframe
lag: number of autoregressive lags. Default is 1
Returns:
Numpy array of transformed state changes
Example
VAR_prediction(e_u,6)
'''
# instantiate the VAR model object from statsmodels
model = VAR(e_u.values)
# fit model with determined lag values
results = model.fit(lag)
lag_order = results.k_ar
Y_pred = results.forecast(e_u.values[-lag_order:],1)
return Y_pred[0]
Y_pred = VAR_prediction(e_u,15)
Y_pred
def invert_power_transformation(pt,prediction):
'''
Definition:
Function to invert power transformation
Parameters:
pt: transformation object
prediction: Numpy array of model state coordinate transformed percentage changes
Required:
import pandas as pd
from sklearn.preprocessing import PowerTransformer
Returns:
inverted transformation numpy array
Example:
inverted_array = invert_power_transformation(pt,prediction)
'''
# transform back into coordinate system
inverted = pt.inverse_transform(prediction.reshape(1,-1))
return inverted
Y_pred = invert_power_transformation(pt,Y_pred)
Y_pred
```
# New states
## Inverse Transformations
1. $d^* = \alpha * \bar{D}$
2. $q^* = C_0 * \bar{D} * \alpha + C_1 * \beta$.
3. $r^* = \gamma * {R_{RAI}}$
4. $z^* = \delta * {R_{ETH}}$
```
Y_pred[0][0]*params['debt_ceiling']
def inverse_transformation_and_state_update(Y_pred,previous_state,params):
'''
Description:
Function to take system identification model prediction and invert transfrom and create new state
Parameters:
y_pred: numpy array of transformed state changes
previous_state: pandas dataframe of previous state or 'current' state
params: dictionary of system parameters
Returns:
pandas dataframe of new states
Example:
inverse_transformation_and_state_update(Y_pred,previous_state,params)
'''
d_star = Y_pred[0] * params['debt_ceiling']
q_star = previous_state['C_o'] * params['debt_ceiling'] * Y_pred[0] + previous_state['C_1'] * Y_pred[1]
r_star = Y_pred[2] * previous_state['gamma'] * previous_state['RaiInUniswap']
z_star = Y_pred[3] * previous_state['delta'] * previous_state['EthInUniswap']
new_state = pd.DataFrame(previous_state[['collateral','EthInUniswap','RaiInUniswap','RaiDrawnFromSAFEs']].to_dict(),index=[0])
new_state['Q'] = new_state['collateral'] + q_star
new_state['D'] = new_state['RaiDrawnFromSAFEs'] + d_star
new_state['R_Rai'] = new_state['RaiInUniswap'] + r_star
new_state['R_Eth'] = new_state['EthInUniswap'] + z_star
return new_state[['Q','D','R_Rai','R_Eth']]
previous_state = states.iloc[train.index[-1]]
print('Previous state:')
print(previous_state[['collateral','RaiDrawnFromSAFEs','RaiInUniswap','EthInUniswap']].to_dict())
print('\n New state:')
inverse_transformation_and_state_update(Y_pred[0],previous_state,params)
```
## Conclusion
In this notebook, we have iterated through several different models and decided on a VAR(15) model for us in the Rai Digital Twin.
| true |
code
| 0.427576 | null | null | null | null |
|
# Introduction to TensorFlow
## Computation graphs
In the first semester we used the NumPy-based `mlp` Python package to illustrate the concepts involved in automatically propagating gradients through multiple-layer neural network models. We also looked at how to use these calculated derivatives to do gradient-descent based training of models in supervised learning tasks such as classification and regression.
A key theme in the first semester's work was the idea of defining models in a modular fashion. There we considered models composed of a sequence of *layer* modules, the output of each of which fed into the input of the next in the sequence and each applying a transformation to map inputs to outputs. By defining a standard interface to layer objects with each defining a `fprop` method to *forward propagate* inputs to outputs, and a `bprop` method to *back propagate* gradients with respect to the output of the layer to gradients with respect to the input of the layer, the layer modules could be composed together arbitarily and activations and gradients forward and back propagated through the whole stack respectively.
<div style='margin: auto; text-align: center; padding-top: 1em;'>
<img style='margin-bottom: 1em;' src='res/pipeline-graph.png' width='30%' />
<i>'Pipeline' model composed of sequence of single input, single output layer modules</i>
</div>
By construction a layer was defined as an object with a single array input and single array output. This is a natural fit for the architectures of standard feedforward networks which can be thought of a single pipeline of transformations from user provided input data to predicted outputs as illustrated in the figure above.
<div style='margin: auto; text-align: center; padding-top: 1em;'>
<img style='display: inline-block; padding-right: 2em; margin-bottom: 1em;' src='res/rnn-graph.png' width='30%' />
<img style='display: inline-block; padding-left: 2em; margin-bottom: 1em;' src='res/skip-connection-graph.png' width='30%' /> <br />
<i>Models which fit less well into pipeline structure: left, a sequence-to-sequence recurrent network; right, a feed forward network with skip connections.</i>
</div>
Towards the end of last semester however we encountered several models which do not fit so well in to this pipeline-like structure. For instance (unrolled) recurrent neural networks tend to have inputs feeding in to and outputs feeding out from multiple points along a deep feedforward model corresponding to the updates of the hidden recurrent state, as illustrated in the left panel in the figure above. It is not trivial to see how to map this structure to our layer based pipeline. Similarly models with skip connections between layers as illustrated in the right panel of the above figure also do not fit particularly well in to a pipeline structure.
Ideally we would like to be able to compose modular components in more general structures than the pipeline structure we have being using so far. In particular it turns out to be useful to be able to deal with models which have structures defined by arbitrary [*directed acyclic graphs*](https://en.wikipedia.org/wiki/Directed_acyclic_graph) (DAGs), that is graphs connected by directed edges and without any directed cycles. Both the recurrent network and skip-connections examples can be naturally expressed as DAGs as well many other model structures.
When working with these more general graphical structures, rather than considering a graph made up of layer modules, it often more useful to consider lower level mathematical operations or *ops* that make up the computation as the fundamental building block. A DAG composed of ops is often termed a *computation graph*. THis terminolgy was covered briefly in [lecture 6](http://www.inf.ed.ac.uk/teaching/courses/mlp/2017-18/mlp06-enc.pdf), and also in the [MLPR course](http://www.inf.ed.ac.uk/teaching/courses/mlpr/2016/notes/w5a_backprop.html). The backpropagation rules we used to propagate gradients through a stack of layer modules can be naturally generalised to apply to computation graphs, with this method of applying the chain rule to automatically propagate gradients backwards through a general computation graph also sometimes termed [*reverse-mode automatic differentiation*](https://en.wikipedia.org/wiki/Automatic_differentiation#Reverse_accumulation).
<div style='margin: auto; text-align: center; padding-top: 1em;'>
<img style='margin-bottom: 1em;' src='res/affine-transform-graph.png' width='40%' />
<i>Computation / data flow graph for an affine transformation $\boldsymbol{y} = \mathbf{W}\boldsymbol{x} + \boldsymbol{b}$</i>
</div>
The figure above shows a very simple computation graph corresponding to the mathematical expression $\boldsymbol{y} = \mathbf{W}\boldsymbol{x} + \boldsymbol{b}$, i.e. the affine transformation we encountered last semester. Here the nodes of the graph are operations and the edges the vector or matrix values passed between operations. The opposite convention with nodes as values and edges as operations is also sometimes used. Note that just like there was ambiguity about what to define as a layer (as discussed previously at beginning of the [third lab notebook](03_Multiple_layer_models.ipynb), there are a range of choices for the level of abstraction to use in the op nodes in a computational graph. For instance, we could also have chosen to express the above computational graph with a single `AffineTransform` op node with three inputs (one matrix, two vector) and one vector output. Equally we might choose to express the `MatMul` op in terms of the underlying individual scalar addition and multiplication operations. What to consider an operation is therefore somewhat a matter of choice and what is convenient in a particular setting.
## TensorFlow
To allow us to work with models defined by more general computation graphs and to avoid the need to write `fprop` and `bprop` methods for each new model component we want to try out, this semester we will be using the open-source computation graph framework [TensorFlow](https://www.tensorflow.org/), originally developed by the Google Brain team:
> TensorFlow™ is an open source software library for numerical computation using data flow graphs. Nodes in the graph represent mathematical operations, while the graph edges represent the multidimensional data arrays (tensors) communicated between them. The flexible architecture allows you to deploy computation to one or more CPUs or GPUs
in a desktop, server, or mobile device with a single API.
TensorFlow allows complex computation graphs (also known as data flow graphs in TensorFlow parlance) to be defined via a Python interface, with efficient C++ implementations for running the corresponding operations on different devices. TensorFlow also includes tools for automatic gradient computation and a large and growing suite of pre-define operations useful for gradient-based training of machine learning models.
In this notebook we will introduce some of the basic elements of constructing, training and evaluating models with TensorFlow. This will use similar material to some of the [official TensorFlow tutorials](https://www.tensorflow.org/tutorials/) but with an additional emphasis of making links to the material covered in this course last semester. For those who have not used a computational graph framework such as TensorFlow or Theano before you may find the [basic usage tutorial](https://www.tensorflow.org/get_started/basic_usage) useful to go through.
### Installing TensorFlow
To install TensorFlow, open a terminal, activate your Conda `mlp` environment using
```
source activate mlp
```
and then run
```
pip install tensorflow # for CPU users
```
```
pip install tensorflow_gpu # for GPU users
```
This should locally install the stable release version of TensorFlow (currently 1.4.1) in your Conda environment. After installing TensorFlow you may need to restart the kernel in the notebook to allow it to be imported.
## Exercise 1: EMNIST softmax regression
As a first example we will train a simple softmax regression model to classify handwritten digit images from the EMNIST data set encountered last semester (for those fed up of working with EMNIST - don't worry you will soon be moving on to other datasets!). This is equivalent to the model implemented in the first exercise of the third lab notebook. We will walk through constructing an equivalent model in TensorFlow and explain new TensorFlow model concepts as we use them. You should run each cell as you progress through the exercise.
Similarly to the common convention of importing NumPy under the shortform alias `np` it is common to import the Python TensorFlow top-level module under the alias `tf`.
```
import tensorflow as tf
```
We begin by defining [*placeholder*](https://www.tensorflow.org/api_docs/python/io_ops/placeholders) objects for the data inputs and targets arrays. These are nodes in the computation graph to which we will later *feed* in external data, such as batches of training set inputs and targets. This abstraction allows us to reuse the same computation graph for different data inputs - we can think of placeholders as acting equivalently to the arguments of a function. It is actually possible to feed data into any node in a TensorFlow graph however the advantage of using a placeholder is that is *must* always have a value fed into it (an exception will be raised if a value isn't provided) and no arbitrary alternative values needs to be entered.
The `tf.placeholder` function has three arguments:
* `dtype` : The [TensorFlow datatype](https://www.tensorflow.org/api_docs/python/framework/tensor_types) for the tensor e.g. `tf.float32` for single-precision floating point values.
* `shape` (optional) : An iterable defining the shape (size of each dimension) of the tensor e.g. `shape=(5, 2)` would indicate a 2D tensor (matrix) with first dimension of size 5 and second dimension of size 2. An entry of `None` in the shape definition corresponds to the corresponding dimension size being left unspecified, so for example `shape=(None, 28, 28)` would allow any 3D inputs with final two dimensions of size 28 to be inputted.
* `name` (optional): String argument defining a name for the tensor which can be useful when visualising a computation graph and for debugging purposes.
As we will generally be working with batches of datapoints, both the `inputs` and `targets` will be 2D tensors with the first dimension corresponding to the batch size (set as `None` here to allow it to specified later) and the second dimension corresponding to the size of each input or output vector. As in the previous semester's work we will use a 1-of-K encoding for the class targets so for EMNIST each output corresponds to a vector of length 47 (number of digit/letter classes).
```
inputs = tf.placeholder(tf.float32, [None, 784], 'inputs')
targets = tf.placeholder(tf.float32, [None, 47], 'targets')
```
We now define [*variable*](https://www.tensorflow.org/api_docs/python/state_ops/variables) objects for the model parameters. Variables are stateful tensors in the computation graph - they have to be explicitly initialised and their internal values can be updated as part of the operations in a graph e.g. gradient updates to model parameter during training. They can also be saved to disk and pre-saved values restored in to a graph at a later time.
The `tf.Variable` constructor takes an `initial_value` as its first argument; this should be a TensorFlow tensor which specifies the initial value to assign to the variable, often a constant tensor such as all zeros, or random samples from a distribution.
```
weights = tf.Variable(tf.zeros([784, 47]))
biases = tf.Variable(tf.zeros([47]))
```
We now build the computation graph corresponding to producing the predicted outputs of the model (log unnormalised class probabilities) given the data inputs and model parameters. We use the TensorFlow [`matmul`](https://www.tensorflow.org/api_docs/python/math_ops/matrix_math_functions#matmul) op to compute the matrix-matrix product between the 2D array of input vectors and the weight matrix parameter variable. TensorFlow [overloads all of the common arithmetic operators](http://stackoverflow.com/a/35095052) for tensor objects so `x + y` where at least one of `x` or `y` is a tensor instance (both `tf.placeholder` and `tf.Variable` return (sub-classes) of `tf.Tensor`) corresponds to the TensorFlow elementwise addition op `tf.add`. Further elementwise binary arithmetic operators like addition follow NumPy style [broadcasting](https://docs.scipy.org/doc/numpy/user/basics.broadcasting.html), so in the expression below the `+ biases` sub-expression will correspond to creating an operation in the computation graph which adds the bias vector to each of the rows of the 2D tensor output of the `matmul` op.
```
outputs = tf.matmul(inputs, weights) + biases
```
While we could have defined `outputs` as the softmax of the expression above to produce normalised class probabilities as the outputs of the model, as discussed last semester when using a softmax output combined with a cross-entropy error function it usually desirable from a numerical stability and efficiency perspective to wrap the softmax computation in to the error computation (as done in the `CrossEntropySoftmaxError` class in our `mlp` framework).
In TensorFlow this can be achieved with the `softmax_cross_entropy_with_logits` op which is part of the `tf.nn` submodule which contains a number of ops specifically for neural network type models. This op takes as its first input log unnormalised class probabilities (sometimes termed logits) and as second input the class label targets which should be of the same dimension as the first input. By default the last dimension of the input tensors is assumed to correspond to the class dimension - this can be altered via an optional `dim` argument.
The output of the `softmax_cross_entropy_with_logits` op here is a 1D tensor with a cross-entropy error value for each data point in the batch. We wish to minimise the mean cross-entropy error across the full dataset and will use the mean of the error on the batch as a stochastic estimator of this value. In TensorFlow ops which *reduce* a tensor along a dimension(s), for example by taking a sum, mean, or product, are prefixed with `reduce`, with the default behaviour being to perform the reduction across all dimensions of the input tensor and return a scalar output. Therefore the second line below will take the per data point cross-entropy errors and produce a single mean value across the whole batch.
```
per_datapoint_errors = tf.nn.softmax_cross_entropy_with_logits(logits=outputs, labels=targets)
error = tf.reduce_mean(per_datapoint_errors)
```
Although for the purposes of training we will use the cross-entropy error as this is differentiable, for evaluation we will also be interested in the classification accuracy i.e. what proportion of all of the predicted classes correspond to the true target label. We can calculate this in TensorFlow similarly to how we used NumPy to do this previously - we use the TensorFlow `tf.argmax` op to find the index of along the class dimension corresponding to the maximum predicted class probability and check if this is equal to the index along the class dimension of the 1-of-$k$ encoded target labels. Analagously to the error computation above, this computes per-datapoint values which we then need to average across with a `reduce_mean` op to produce the classification accuracy for a batch.
```
per_datapoint_pred_is_correct = tf.equal(tf.argmax(outputs, 1), tf.argmax(targets, 1))
accuracy = tf.reduce_mean(tf.cast(per_datapoint_pred_is_correct, tf.float32))
```
As mentioned previously TensorFlow is able to automatically calculate gradients of scalar computation graph outputs with respect to tensors in the computation graph. We can explicitly construct a new sub-graph corresponding to the gradient of a scalar with respect to one or more tensors in the graph using the [`tf.gradients`](https://www.tensorflow.org/api_docs/python/train/gradient_computation) function.
TensorFlow also however includes a number of higher-level `Optimizer` classes in the `tf.train` module that internally deal with constructing graphs corresponding to the gradients of some scalar loss with respect to one or more `Variable` tensors in the graph (usually corresponding to model parameters) and then using these gradients to update the variables (roughly equivalent to the `LearningRule` classes in the `mlp` framework). The most basic `Optimizer` instance is the `GradientDescentOptimizer` which simply adds operations corresponding to basic (stochastic) gradient descent to the graph (i.e. no momentum, adaptive learning rates etc.). The `__init__` constructor method for this class takes one argument `learning_rate` corresponding to the gradient descent learning rate / step size encountered previously.
Usually we are not interested in the `Optimizer` object other than in adding operations in the graph corresponding to the optimisation steps. This can be achieved using the `minimize` method of the object which takes as first argument the tensor object corresponding to the scalar loss / error to be minimized. A further optional keyword argument `var_list` can be used to specify a list of variables to compute the gradients of the loss with respect to and update; by default this is set to `None` which indicates to use all trainable variables in the current graph. The `minimize` method returns an operation corresponding to applying the gradient updates to the variables - we need to store a reference to this to allow us to run these operations later. Note we do not need to store a reference to the optimizer as we have no further need of this object hence commonly the steps of constructing the `Optimizer` and calling `minimize` are commonly all applied in a single line as below.
```
train_step = tf.train.GradientDescentOptimizer(learning_rate=0.5).minimize(error)
```
We have now constructed a computation graph which can compute predicted outputs, use these to calculate an error value (and accuracy) and use the gradients of the error with respect to the model parameter variables to update their values with a gradient descent step.
Although we have defined our computation graph, we have not yet initialised any tensor data in memory - all of the tensor variables defined above are just symbolic representations of parts of the computation graph. We can think of the computation graph as a whole as being similar to a function - it defines a sequence of operations but does not directly run those operations on data itself.
To run the operations in (part of) a TensorFlow graph we need to create a [`Session`](https://www.tensorflow.org/api_docs/python/client/session_management) object:
> A `Session` object encapsulates the environment in which `Operation` objects are executed, and `Tensor` objects are evaluated.
A session object can be constructed using either `tf.Session()` or `tf.InteractiveSession()`. The only difference in the latter is that it installs itself as the default session on construction. This can be useful in interactive contexts such as shells or the notebook interface in which an alternative to running a graph operation using the session `run` method (see below) is to call the `eval` method of an operation e.g. `op.eval()`; generally a session in which the op runs needs to be passed to `eval`; however if an interactive session is used, then this is set as a default to use in `eval` calls.
```
sess = tf.InteractiveSession()
```
The key property of a session object is its `run` method. This takes an operation (or list of operations) in a defined graph as an argument and runs the parts of the computation graph necessary to evaluate the output(s) (if any) of the operation(s), and additionally performs any updates to variables states defined by the graph (e.g. gradient updates of parameters). The output values if any of the operation(s) are returned by the `run` call.
A standard operation which needs to be called before any other operations on a graph which includes variable nodes is a variable *initializer* operation. This, as the name suggests, initialises the values of the variables in the session to the values defined by the `initial_value` argument when adding the variables to the graph. For instance for the graph we have defined here this will initialise the `weights` variable value in the session to a 2D array of zeros of shape `(784, 10)` and the `biases` variable to a 1D array of shape `(10,)`.
We can access initializer ops for each variable individually using the `initializer` property of the variables in question and then individually run these, however a common pattern is to use the `tf.global_variables_initializer()` function to create a single initializer op which will initialise all globally defined variables in the default graph and then run this as done below.
```
init_op = tf.global_variables_initializer()
sess.run(init_op)
```
We are now almost ready to begin training our defined model, however as a final step we need to create objects for accessing batches of EMNIST input and target data. In the tutorial code provided in `tf.examples.tutorials.mnist` there is an `input_data` sub-module which provides a `read_data_sets` function for downloading the MNIST data and constructing an object for iterating over MNIST data. However in the `mlp` package we already have the MNIST and EMNIST data provider classes that we used extensively last semester, and corresponding local copies of the MNIST and EMNIST data, so we will use that here as it provides all the necessary functionality.
```
import data_providers as data_providers
train_data = data_providers.EMNISTDataProvider('train', batch_size=50, flatten=True)
valid_data = data_providers.EMNISTDataProvider('valid', batch_size=50, flatten=True)
```
We are now all set to train our model. As when training models last semester, the training procedure will involve two nested loops - an outer loop corresponding to multiple full-passes through the dataset or *epochs* and an inner loop iterating over individual batches in the training data.
The `init_op` we ran with `sess.run` previously did not depend on the placeholders `inputs` and `target` in our graph, so we simply ran it with `sess.run(init_op)`. The `train_step` operation corresponding to the gradient based updates of the `weights` and `biases` parameter variables does however depend on the `inputs` and `targets` placeholders and so we need to specify values to *feed* into these placeholders; as we wish the gradient updates to be calculated using the gradients with respect to a batch of inputs and targets, the values that we feed in are the input and target batches. This is specified using the keyword `feed_dict` argument to the session `run` method. As the name suggests this should be a Python dictionary (`dict`) with keys corresponding to references to the tensors in the graph to feed values in to and values the corresponding array values to feed in (typically NumPy `ndarray` instances) - here we have `feed_dict = {inputs: input_batch, targets: target_batch}`.
Another difference in our use of the session `run` method below is that we call it with a list of two operations - `[train_step, error]` rather than just a single operation. This allows the output (and variable updates) of multiple operations in a graph to be evaluated together - here we both run the `train_step` operation to update the parameter values and evaluate the `error` operation to return the mean error on the batch. Although we could split this into two separate session `run` calls, as the operations calculating the batch error will need to be evaluated when running the `train_step` operation (as this is the value gradients are calculated with respect to) this would involve redoing some of the computation and so be less efficient than combining them in a single `run` call.
As we are running two different operations, the `run` method returns two values here. The `train_step` operation has no outputs and so the first return value is `None` - in the code below we assign this to `_`, this being a common convention in Python code for assigning return values we are not interested in using. The second return value is the average error across the batch which we assign to `batch_error` and use to keep a running average of the dataset error across the epochs.
```
num_epoch = 20
for e in range(num_epoch):
running_error = 0.
for input_batch, target_batch in train_data:
_, batch_error = sess.run(
[train_step, error],
feed_dict={inputs: input_batch, targets: target_batch})
running_error += batch_error
running_error /= train_data.num_batches
print('End of epoch {0}: running error average = {1:.2f}'.format(e + 1, running_error))
```
To check your understanding of using sessions objects to evaluate parts of a graph and feeding values in to a graph, complete the definition of the function in the cell below. This should iterate across all batches in a provided data provider and calculate the error and classification accuracy for each, accumulating the average error and accuracy values across the whole dataset and returning these as a tuple.
```
def get_error_and_accuracy(data):
"""Calculate average error and classification accuracy across a dataset.
Args:
data: Data provider which iterates over input-target batches in dataset.
Returns:
Tuple with first element scalar value corresponding to average error
across all batches in dataset and second value corresponding to
average classification accuracy across all batches in dataset.
"""
err = 0
acc = 0
for input_batch, target_batch in data:
err += sess.run(error, feed_dict={inputs: input_batch, targets: target_batch})
acc += sess.run(accuracy, feed_dict={inputs: input_batch, targets: target_batch})
err /= data.num_batches
acc /= data.num_batches
return err, acc
```
Test your implementation by running the cell below - this should print the error and accuracy of the trained model on the validation and training datasets if implemented correctly.
```
print('Train data: Error={0:.2f} Accuracy={1:.2f}'
.format(*get_error_and_accuracy(train_data)))
print('Valid data: Error={0:.2f} Accuracy={1:.2f}'
.format(*get_error_and_accuracy(valid_data)))
```
## Exercise 2: Explicit graphs, name scopes, summaries and TensorBoard
In the exercise above we introduced most of the basic concepts needed for constructing graphs in TensorFlow and running graph operations. In an attempt to avoid introducing too many new terms and syntax at once however we skipped over some of the non-essential elements of creating and running models in TensorFlow, in particular some of the provided functionality for organising and structuring the computation graphs created and for monitoring the progress of training runs.
Now that you are hopefully more familiar with the basics of TensorFlow we will introduce some of these features as they are likely to provide useful when you are building and training more complex models in the rest of this semester.
Although we started off by motivating TensorFlow as a framework which builds computation graphs, in the code above we never explicitly referenced a graph object. This is because TensorFlow always registers a default graph at start up and all operations are added to this graph by default. The default graph can be accessed using `tf.get_default_graph()`. For example running the code in the cell below will assign a reference to the default graph to `default_graph` and print the total number of operations in the current graph definition.
```
default_graph = tf.get_default_graph()
print('Number of operations in graph: {0}'
.format(len(default_graph.get_operations())))
```
We can also explicitly create a new graph object using `tf.Graph()`. This may be useful if we wish to build up several independent computation graphs.
```
graph = tf.Graph()
```
To add operations to a constructed graph object, we use the `graph.as_default()` [context manager](http://book.pythontips.com/en/latest/context_managers.html). Context managers are used with the `with` statement in Python - `with context_manager:` opens a block in Python in which a special `__enter__` method of the `context_manager` object is called before the code in the block is run and a further special `__exit__` method is run after the block code has finished execution. This can be used to for example manage allocation of resources (e.g. file handles) but also to locally change some 'context' in the code - in the example here, `graph.as_default()` is a context manager which changes the default graph within the following block to be `graph` before returning to the previous default graph once the block code is finished running. Context managers are used extensively in TensorFlow so it is worth being familiar with how they work.
Another common context manager usage in TensorFlow is to define *name scopes*. As we encountered earlier, individual operations in a TensorFlow graph can be assigned names. As we will see later this is useful for making graphs interpretable when we use the tools provided in TensorFlow for visualising them. As computation graphs can become very big (even the quite simple graph we created in the first exercise has around 100 operations in it) even with interpretable names attached to the graph operations it can still be difficult to understand and debug what is happening in a graph. Therefore rather than simply allowing a single-level naming scheme to be applied to the individual operations in the graph, TensorFlow supports hierachical naming of sub-graphs. This allows sets of related operations to be grouped together under a common name, and thus allows both higher and lower level structure in a graph to be easily identified.
This hierarchical naming is performed by using the name scope context manager `tf.name_scope('name')`. Starting a block `with tf.name_scope('name'):`, will cause all the of the operations added to a graph within that block to be grouped under the name specified in the `tf.name_scope` call. Name scope blocks can be nested to allow finer-grained sub-groupings of operations. Name scopes can be used to group operations at various levels e.g. operations corresponding to inference/prediction versus training, grouping operations which correspond to the classical definition of a neural network layer etc.
The code in the cell below uses both a `graph.as_default()` context manager and name scopes to create a second copy of the computation graph corresponding to softmax regression that we constructed in the previous exercise.
```
with graph.as_default():
with tf.name_scope('data'):
inputs = tf.placeholder(tf.float32, [None, 784], name='inputs')
targets = tf.placeholder(tf.float32, [None, 47], name='targets')
with tf.name_scope('parameters'):
weights = tf.Variable(tf.zeros([784, 47]), name='weights')
biases = tf.Variable(tf.zeros([47]), name='biases')
with tf.name_scope('model'):
outputs = tf.matmul(inputs, weights) + biases
with tf.name_scope('error'):
error = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=outputs, labels=targets))
with tf.name_scope('train'):
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(error)
with tf.name_scope('accuracy'):
accuracy = tf.reduce_mean(tf.cast(
tf.equal(tf.argmax(outputs, 1), tf.argmax(targets, 1)), tf.float32))
```
As hinted earlier TensorFlow comes with tools for visualising computation graphs. In particular [TensorBoard](https://www.tensorflow.org/how_tos/summaries_and_tensorboard/) is an interactive web application for amongst other things visualising TensorFlow computation graphs (we will explore some of its other functionality in the latter part of the exercise). Typically TensorBoard in launched from a terminal and a browser used to connect to the resulting locally running TensorBoard server instance. However for the purposes of graph visualisation it is also possible to embed a remotely-served TensorBoard graph visualisation interface in a Jupyter notebook using the helper function below (a slight variant of the recipe in [this notebook](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/examples/tutorials/deepdream/deepdream.ipynb)).
<span style='color: red; font-weight: bold;'>Note: The code below seems to not work for some people when accessing the notebook in Firefox. You can either try loading the notebook in an alternative browser, or just skip this section for now and explore the graph visualisation tool when launching TensorBoard below.</span>
```
from IPython.display import display, HTML
import datetime
def show_graph(graph_def, frame_size=(900, 600)):
"""Visualize TensorFlow graph."""
if hasattr(graph_def, 'as_graph_def'):
graph_def = graph_def.as_graph_def()
timestamp = datetime.datetime.now().strftime("%Y-%m-%d_%H-%M-%S")
code = """
<script>
function load() {{
document.getElementById("{id}").pbtxt = {data};
}}
</script>
<link rel="import" href="https://tensorboard.appspot.com/tf-graph-basic.build.html" onload=load()>
<div style="height:{height}px">
<tf-graph-basic id="{id}"></tf-graph-basic>
</div>
""".format(height=frame_size[1], data=repr(str(graph_def)), id='graph'+timestamp)
iframe = """
<iframe seamless style="width:{width}px;height:{height}px;border:0" srcdoc="{src}"></iframe>
""".format(width=frame_size[0], height=frame_size[1] + 20, src=code.replace('"', '"'))
display(HTML(iframe))
```
Run the cell below to display a visualisation of the graph we just defined. Notice that by default all operations within a particular defined name scope are grouped under a single node; this allows the top-level structure of the graph and how data flows between the various components to be easily visualised. We can also expand these nodes however to interrogate the operations within them - simply double-click on one of the nodes to do this (double-clicking on the expanded node will cause it to collapse again). If you expand the `model` node you should see a graph closely mirroring the affine transform example given as a motivation above.
```
show_graph(graph)
```
To highlight how using name scopes can be very helpful in making these graph visualisations more interpretable, running the cell below will create a corresponding visualisation for the graph created in the first exercise, which contains the same operations but without the name scope groupings.
```
show_graph(tf.get_default_graph())
```
A common problem when doing gradient based training of complex models is how to monitor progress during training. In the `mlp` framework we used last semester we included some basic logging functionality for recording training statistics such as training and validation set error and classificaton accuracy at the end of each epoch. By printing the log output this allowed basic monitoring of how training was proceeding. However due to the noisiness of the the training procedures the raw values printed were often difficult to interpret. After a training run we often plotted training curves to allow better visualisation of how the run went but this could only be done after a run was completed and required a lot of boilerplate code to be written (or copied and pasted...).
TensorFlow [*summary* operations](https://www.tensorflow.org/api_docs/python/summary/) are designed to help deal with this issue. Summary operations can be added to the graph to allow summary statistics to be computed and serialized to event files. These event files can then be loaded in TensorBoard *during training* to allow continuous graphing of for example the training and validation set error during training. As well as summary operations for monitoring [scalar](https://www.tensorflow.org/api_docs/python/summary/generation_of_summaries_#scalar) values such as errors or accuracies, TensorFlow also includes summary operations for monitoring [histograms](https://www.tensorflow.org/api_docs/python/summary/generation_of_summaries_#histogram) of tensor quanties (e.g. the distribution of a set of weight parameters), displaying [images](https://www.tensorflow.org/api_docs/python/summary/generation_of_summaries_#image) (for example for checking if random augmentations being applied to image inputs are producing reasonable outputs) and even playing back [audio](https://www.tensorflow.org/api_docs/python/summary/generation_of_summaries_#audio).
The cell below adds two simple scalar summary operations to our new graph for monitoring the error and classification accuracy. While we can keep references to all of the summary ops we add to a graph and make sure to run them all individually in the session during training, as with variable initialisation, TensorFlow provides a convenience method to avoid having to write a lot of boilerplate code like this. The `tf.summary.merge_all()` function returns an merged op corresponding to all of the summary ops that have been added to the current default graph. We can then just run this one merged op in our session to generate all the summaries we have added.
```
with graph.as_default():
tf.summary.scalar('error', error)
tf.summary.scalar('accuracy', accuracy)
summary_op = tf.summary.merge_all()
```
In addition to the (merged) summary operation, we also need to define a *summary writer* object(s) to specify where the summaries should be written to on disk. The `tf.summary.FileWriter` class constructor takes a `logdir` as its first argument which should specify the path to a directory where event files should be written to. In the code below the log directory is specified as a local directory `tf-log` plus a timestamp based sub-directory within this to keep event files corresponding to different runs separated. The `FileWriter` constructor also accepts an optional `graph` argument which we here set to the graph we just populated with summaries. We construct separate writer objects for summaries on the training and validation datasets.
```
import os
import datetime
timestamp = datetime.datetime.now().strftime("%Y-%m-%d_%H-%M-%S")
train_writer = tf.summary.FileWriter(os.path.join('tf-log', timestamp, 'train'), graph=graph)
valid_writer = tf.summary.FileWriter(os.path.join('tf-log', timestamp, 'valid'), graph=graph)
```
The final step in using summaries is to run the merged summary op at the appropriate points in training and to add the outputs of the run summary operations to the writers. Here we evaluate the summary op on each training dataset batch and after every 100th batch evaluate the summary op on the whole validation dataset, writing the outputs of each to the relevant writers.
If you run the cell below, you should be able to visualise the resulting training run summaries by launching TensorBoard within a shell with
```bash
tensorboard --logdir=[path/to/tf-log]
```
where `[path/to/tf-log]` is replaced with the path to the `tf-log` directory specified abovem and then opening the URL `localhost:6006` in a browser.
```
with graph.as_default():
init = tf.global_variables_initializer()
sess = tf.InteractiveSession(graph=graph)
num_epoch = 5
valid_inputs = valid_data.inputs
valid_targets = valid_data.to_one_of_k(valid_data.targets)
sess.run(init)
for e in range(num_epoch):
for b, (input_batch, target_batch) in enumerate(train_data):
_, summary = sess.run(
[train_step, summary_op],
feed_dict={inputs: input_batch, targets: target_batch})
train_writer.add_summary(summary, e * train_data.num_batches + b)
if b % 100 == 0:
valid_summary = sess.run(
summary_op, feed_dict={inputs: valid_inputs, targets: valid_targets})
valid_writer.add_summary(valid_summary, e * train_data.num_batches + b)
```
That completes our basic introduction to TensorFlow. If you want more to explore more of TensorFlow before beginning your project for this semester, you may wish to go through some of the [official tutorials](https://www.tensorflow.org/tutorials/) or some of the many sites with unofficial tutorials e.g. the series of notebooks [here](https://github.com/aymericdamien/TensorFlow-Examples). If you have time you may also wish to have a go at the optional exercise below.
## Optional exercise: multiple layer EMNIST classifier using `contrib` modules
As well as the core officially supported codebase, TensorFlow is distributed with a series of contributed modules under [`tensorflow.contrib`](https://www.tensorflow.org/api_docs/python/tf/contrib). These tend to provide higher level interfaces for constructing and running common forms of computational graphs which can allow models to be constructed with much more concise code. The interfaces of the `contrib` modules tend to be less stable than the core TensorFlow Python interface and they are also more restricted in the sorts of models that can be created. Therefore it is worthwhile to also be familiar with constructing models with the operations available in the core TensorFlow codebase; you can also often mix and match use of 'native' TensorFlow and functions from `contrib` modules.
As an optional extension exercise, construct a deep EMNIST classifier model, either using TensorFlow operations directly as above or using one (or more) of the higher level interfaces defined in `contrib` modules such as [`tensorflow.contrib.learn`](https://www.tensorflow.org/tutorials/tflearn/), [`tensorflow.contrib.layers`](https://www.tensorflow.org/api_docs/python/tf/layers) or [`tensorflow.contrib.slim`](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/contrib/slim). You should choose an appropriate model architecture (number and width of layers) and choice of activation function based on your experience fitting models from last semester.
As well as exploring the use of the interfaces in `contrib` modules you may wish to explore the more advanced optimizers available in [`tensorflow.train`](https://www.tensorflow.org/api_docs/python/tf/train) - such as [`tensorflow.train.AdamOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/AdamOptimizer) and [`tensorflow.train.RMSPropOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/RMSPropOptimizer) corresponding to the adaptive learning rules implemented in the second coursework last semester.
```
```
| true |
code
| 0.866613 | null | null | null | null |
|
# Rhyming score experiments
This notebook is for rhyming score experiments. HAMR 2016.
```
from __future__ import print_function, unicode_literals
import string
import nltk
import numpy
# For plotting outputs, we'll need
import matplotlib.pyplot as plt
# To display the plotted images inside the notebook:
%matplotlib inline
# Plotting the figures at a reasonable size
import matplotlib
matplotlib.rcParams['figure.figsize'] = (30.0, 20.0)
# Dirty, dirty trick
import rhyme
reload(rhyme)
from rhyme import *
cmudict = collections.defaultdict(list)
for word, syl in nltk.corpus.cmudict.entries():
cmudict[word].append(syl)
bad_text = 'I see all I know all For i am the the oracle Give me your hand' \
' I see caked blood on concrete Dead bodies on grass' \
' Mothers crying seeing babies lowered caskets'
# bad_text = 'this thing does not rhyme even a little it is just normal text no rap'
good_text = 'Yeah, yeah It\'s the return of the Wild Style fashionist' \
' Smashin hits, make it hard to adapt to this Put pizazz and jazz in this, and cash in this' \
' Mastered this, flash this and make em clap to this DJ\'s throw on cuts and obey the crowd' \
' Just pump the volume up, and play it loud'
# good_text = 'take a step back hey really gonna hack a full stack in a day while on crack'
bad_words = tokenize(bad_text)
good_words = tokenize(good_text)
def pairwise_grid_stats(score_grid, words):
minimum = score_grid[score_grid != -1.0].min()
maximum = score_grid.max()
print('Range: {0} -- {1}'.format(minimum, maximum))
def pairwise_rhyme_visualization(score_grid, words, show=True):
fig, ax = plt.subplots()
heatmap = ax.pcolor(score_grid, cmap=plt.cm.Blues)
ax.set_xlim((0, len(words)))
ax.set_ylim((0, len(words)))
# put the major ticks at the middle of each cell
ax.set_xticks(numpy.arange(score_grid.shape[0])+0.5, minor=False)
ax.set_yticks(numpy.arange(score_grid.shape[1])+0.5, minor=False)
# want a more natural, table-like display
ax.invert_yaxis()
ax.xaxis.tick_top()
ax.set_xticklabels(words, minor=False)
ax.set_yticklabels(words, minor=False)
if show:
plt.show()
def score_words(words, prondict=cmudict):
score_grid = rhyme_score_grid(words, prondict=prondict)
aggregate = aggregate_score(score_grid)
return aggregate
def score_and_visualize_words(words, prondict=cmudict, **kwargs):
score_grid = rhyme_score_grid(words, prondict=prondict, **kwargs)
score = aggregate_score(score_grid)
print('Score: {0:.4f}'.format(score))
stats = pairwise_grid_stats(score_grid, words)
pairwise_rhyme_visualization(score_grid, words)
#score_and_visualize_words(bad_words)
#score_and_visualize_words(good_words)
```
### Assessing the metric: baseline
To get some understanding of how this metric works, we need to find a baseline. Let's use some random sequences from the Brown corpus.
Obvious limit of the metric: at some point, we will randomly get a rhyming word anyway. Tackled by a sliding window of max. 16 words.
```
bt_reader = nltk.corpus.brown.words()
brown_tokens = [t for i, t in enumerate(bt_reader) if i < 10000]
bad_text_max_length = 50
n_bad_texts = 100
bad_texts = []
for i in xrange(n_bad_texts):
# Choose a random start
start = numpy.random.randint(low=0, high=len(brown_tokens) - bad_text_max_length - 1)
text = brown_tokens[start:start + bad_text_max_length]
bad_texts.append(' '.join(text))
bad_text_words = [tokenize(t) for t in bad_texts]
bad_text_scores = numpy.array([score_words(w) for w in bad_text_words[:100]])
#n, bins, patches = plt.hist(bad_text_scores, 10, normed=True)
#plt.show()
import codecs
def parse_artist(filename):
with codecs.open(filename, 'r', 'utf-8') as hdl:
lines = [l.strip() for l in hdl]
texts = []
current_text = []
for l in lines:
if len(l) == 0:
texts.append(' '.join(current_text))
current_text = []
else:
current_text.append(l)
if len(current_text) > 0:
texts.append(' '.join(current_text))
return texts
rakim_texts = parse_artist('../examples_good_rhymes/rakim')
eminem_texts = parse_artist('../examples_good_rhymes/eminem')
aesop_texts = parse_artist('../examples_good_rhymes/aesop_rock')
lilwayne_texts = parse_artist('../examples_good_rhymes/lil_wayne')
good_texts = list(itertools.chain(rakim_texts, eminem_texts, aesop_texts, lilwayne_texts))
# print(len(good_texts))
good_text_words = [tokenize(t) for t in good_texts]
#good_text_scores = [score_words(w) for w in good_words]
score_and_visualize_words(good_text_words[0][:50], nonnegative=True)
score_and_visualize_words(bad_text_words[2][:50], nonnegative=True)
# n, bins, patches = plt.hist(bad_text_scores, 10, normed=True)
# plt.show()
# _, _, _ = plt.hist(good_text_scores, bins=bins, color='r')
# plt.show()
reload(rhyme)
from rhyme import *
good_score_grid = rhyme_score_grid(good_text_words[0], prondict=cmudict)
bad_score_grid = rhyme_score_grid(bad_text_words[0], prondict=cmudict)
gw = good_text_words[0]
bw = bad_text_words[0]
print(len(bw))
gsg = good_score_grid[:45,:45]
gw_part = gw[:45]
gsbg = binarize_grid(gsg)
pairwise_rhyme_visualization(gsbg, gw_part)
bsbg = binarize_grid(bad_score_grid)
pairwise_rhyme_visualization(bsbg, bw)
good_cliques = get_rhyme_groups(gsg, gw_part)
bad_cliques = get_rhyme_groups(good_score_grid, bw)
import pprint
good_graph = get_rhyme_graph(gsg, gw_part)
bad_graph = get_rhyme_graph(bad_score_grid, bw)
g_components = list(networkx.algorithms.connected.connected_components(good_graph))
g_nontrivial = [g for g in g_components if len(g) >= 2]
print(' '.join(gw_part))
pprint.pprint(g_nontrivial)
def nontrivial_components(G):
b_components = list(networkx.algorithms.connected.connected_components(G))
b_nontrivial = [g for g in b_components if len(g) >= 2]
pprint.pprint(b_nontrivial)
def triangle_analysis(G):
t = networkx.algorithms.cluster.triangles(G)
print('Triangles: {0}'.format({k: v for k, v in t.iteritems() if v >= 1}))
print(networkx.algorithms.cluster.average_clustering(G))
triangle_analysis(good_graph)
triangle_analysis(bad_graph)
def clique_analysis(cliques):
multi_cliques = [c for c in cliques if len(c) > 3]
multi_clique_ratio = float(len(multi_cliques)) / len(cliques)
cliques_by_level = collections.defaultdict(list)
for c in cliques:
cliques_by_level[len(c)].append(set([w.split('_')[0] for w in c]))
print(multi_clique_ratio)
pprint.pprint({k: len(v) for k, v in cliques_by_level.iteritems()})
if 3 in cliques_by_level:
pprint.pprint(cliques_by_level[3])
if 4 in cliques_by_level:
pprint.pprint(cliques_by_level[4])
else:
print('No cliques above 2 members')
return cliques_by_level
gcbl = clique_analysis(good_cliques)
bcbl = clique_analysis(bad_cliques)
print('-----------------')
g_overlap = find_overlapping_cliques(gcbl[3])
pprint.pprint(g_overlap)
print('---------------')
b_overlap = find_overlapping_cliques(bcbl[3])
pprint.pprint(b_overlap)
reload(rhyme)
from rhyme import *
other_gw = good_text_words[-1][:45]
other_good_score_grid = rhyme_score_grid(other_gw, prondict=cmudict)
ogsbg = binarize_grid(other_good_score_grid)
pairwise_rhyme_visualization(ogsbg, other_gw)
ograph = get_rhyme_graph(other_good_score_grid, other_gw)
triangle_analysis(ograph)
nontrivial_components(ograph)
k_cliques = list(networkx.k_clique_communities(ograph, 2))
print(k_cliques)
```
### Ideas on improving
* Disambiguate the indefinite article.
* Remove stopwords (count them as -1). Implemented as "weak" stopwords (if the other word is not a weak stopword, count normally) vs. "strong" (if one of the words is a strong stopword, the pair gets -1)
* Only count words within a relevant window (improves on randomness)
* Only retain nouns, verbs, adjectives and adverbs. (NOT IMPLEMENTED)
* Word count patterns:
| true |
code
| 0.522811 | null | null | null | null |
|
# Using multimetric experiments in SigOpt to identify multiple good solutions
If you have not yet done so, please make sure you are comfortable with the content in the [intro](multimetric_intro.ipynb) notebook.
Below we create the standard SigOpt [connection](https://sigopt.com/docs/overview/python) tool. If the `SIGOPT_API_TOKEN` is present in the environment variables, it is imported; otherwise, you need to copy and paste your key from the [API tokens page](https://sigopt.com/tokens).
```
import os
import numpy
from time import sleep
from matplotlib import pyplot as plt
%matplotlib inline
# Matplotlib stuff for generating plots
efficient_opts = {'linewidth': 0, 'marker': '+', 'color': 'r', 'markersize': 10, 'markeredgewidth': 2}
dominated_opts = {'linewidth': 0, 'marker': '.', 'color': 'k', 'alpha': .4}
from sigopt.interface import Connection
if 'SIGOPT_API_TOKEN' in os.environ:
SIGOPT_API_TOKEN = os.environ['SIGOPT_API_TOKEN']
else:
SIGOPT_API_TOKEN = None
assert SIGOPT_API_TOKEN is not None
conn = Connection(client_token=SIGOPT_API_TOKEN)
```
One natural situation for a multimetric experiment is in finding a second answer to an optimization problem. Given a function $f$ and domain $\Omega$ on which the maximum of $f$ occurs at $x^*$, the search for other points which have high values but are at least some distance away can be phrased as
\begin{align}
\text{value}:&\quad \max_{x\in\Omega} f(x) \\
\text{distance}:&\quad \max_{x\in\Omega} \|x - x^*\| \\
\end{align}
Here the norm is presumed to be the 2-norm, but could actually be any measurement of distance; that ambiguity is especially valuable in the situation where categorical parameters are present or a custom definition of distance is preferred.
### Finding $x^*$, the solution to the standard optimization of $f$
We start by defining a multimodal function $f$ which has multiple local optima below. The associated meta is for a standard, single metric experiment.
```
def multimodal_function(x1, x2):
return (
.5 * numpy.exp(-10 * ((x1 + .8) ** 2 + .3 * (x2 + .6) ** 2)) +
.5 * numpy.exp(-9 * (.4 * (x1 + .7) ** 2 + .4 * (x2 - .4) ** 2)) +
.5 * numpy.exp(-11 * (.2 * (x1 - .6) ** 2 + .5 * (x2 + .5) ** 2)) +
.5 * numpy.exp(-11 * (.6 * (x1) ** 2 + .5 * (x2 + .8) ** 2)) +
.5 * numpy.exp(-12 * (.4 * (x1 - .1) ** 2 + .7 * (x2 - .8) ** 2)) +
.5 * numpy.exp(-13 * (.8 * (x1) ** 2 + .7 * (x2) ** 2)) +
.5 * numpy.exp(-8 * (.3 * (x1 - .8) ** 2 + .6 * (x2 - .3) ** 2))
)
multimodal_first_solution_meta = {
'name': 'SigOpt Multimetric Demo - Single Metric Optimization (python)',
'project': 'sigopt-examples',
'metrics': [{'name': 'multimodal_function_value', 'objective': 'maximize'}],
'parameters': [
{'name': 'x1', 'bounds': {'min': -1.0, 'max': 1.0}, 'type': 'double'},
{'name': 'x2', 'bounds': {'min': -1.0, 'max': 1.0}, 'type': 'double'},
],
'type': 'offline',
'observation_budget': 40,
}
```
We can run the initial optimization to find this $x^*$ value which is the maximum of the function. The `sleep(2)` command helps simulate an actual experiment, where the cost of creating an observation is (significant) greater than the function we are studying here.
```
experiment = conn.experiments().create(**multimodal_first_solution_meta)
while experiment.progress.observation_count < experiment.observation_budget:
suggestion = conn.experiments(experiment.id).suggestions().create()
sleep(2)
value = multimodal_function(**suggestion.assignments)
conn.experiments(experiment.id).observations().create(suggestion=suggestion.id, value=value)
experiment = conn.experiments(experiment.id).fetch()
```
The solution to this problem $x^*$ must be extracted for identifying a second solution.
```
initial_optimization_best_assignments = conn.experiments(experiment.id).best_assignments().fetch()
x_star = initial_optimization_best_assignments.data[0].assignments
```
This contour plot shows that there is an amount of complexity in this function, and that choosing a diverse portfolio of solutions may be difficult. The initial solution $x^*$, as determined from the optimization above, is also plotted.
```
xplt = numpy.linspace(-1, 1, 40)
X1, X2 = numpy.meshgrid(xplt, xplt)
Y = multimodal_function(x1=X1, x2=X2)
plt.contour(X1, X2, Y)
plt.plot(x_star['x1'], x_star['x2'], '*k', markersize=20)
plt.xlabel('$x_1$', fontsize=15)
plt.ylabel('$x_2$', fontsize=15);
```
### Using the initial solution $x^*$ to search for a second solution
Now that we have this initial solution, we can define our multimetric experiment. Note that the distance we are using is the standard 2-norm. The multimetric function returns a list of dictionaries, one each per metric to be optimized.
```
def distance_function(assignments, x_star):
return numpy.sqrt((assignments['x1'] - x_star['x1']) ** 2 + (assignments['x2'] - x_star['x2']) ** 2)
def multimetric_value_distance_function(assignments, x_star):
function_value = multimodal_function(**assignments)
distance_from_x_star = distance_function(assignments, x_star)
return [
{'name': 'function value', 'value': function_value},
{'name': 'distance from x_star', 'value': distance_from_x_star},
]
multimetric_second_solution_meta = {
'name': 'SigOpt Multimetric Demo - Search for Second Solution (python)',
'metrics': [
{'name': 'function value', 'objective': 'maximize'},
{'name': 'distance from x_star', 'objective': 'maximize'},
],
'parameters': [
{'name': 'x1', 'bounds': {'min': -1.0, 'max': 1.0}, 'type': 'double'},
{'name': 'x2', 'bounds': {'min': -1.0, 'max': 1.0}, 'type': 'double'},
],
'type': 'offline',
'observation_budget': 100,
}
experiment = conn.experiments().create(**multimetric_second_solution_meta)
while experiment.progress.observation_count < experiment.observation_budget:
suggestion = conn.experiments(experiment.id).suggestions().create()
sleep(2)
values = multimetric_value_distance_function(suggestion.assignments, x_star)
conn.experiments(experiment.id).observations().create(suggestion=suggestion.id, values=values)
experiment = conn.experiments(experiment.id).fetch()
```
Extracting the solution to this multimetric optimization problem yields an array of points, each of which is [Pareto efficient](https://www.sigopt.com/docs/overview/pareto_efficiency). Plotting the metric values associated with these efficient points can help provide some guidance as to what possible solutions are available, and which might be preferred in an actual application.
Recall that metric evaluations are organized in **alphabetical order** when returned from SigOpt, which may differ from the order in which they were originally defined in the experiment. The loop below recovers the values in the same value in which they were defined initially.
We also, again, produce some random data to explore the full feasible domain.
```
pareto_efficient_results = conn.experiments(experiment.id).best_assignments().fetch()
efficient_points = numpy.empty((pareto_efficient_results.count, 2))
efficient_values = numpy.empty((pareto_efficient_results.count, 2))
for k, data in enumerate(pareto_efficient_results.data):
efficient_points[k, :] = [data.assignments['x1'], data.assignments['x2']]
dv = {d.name: d.value for d in data.values}
efficient_values[k, :] = [dv[m['name']] for m in multimetric_second_solution_meta['metrics']]
rand_pts = numpy.random.uniform(
[p['bounds']['min'] for p in multimetric_second_solution_meta['parameters']],
[p['bounds']['max'] for p in multimetric_second_solution_meta['parameters']],
(1000, 2)
)
random_values = numpy.empty((len(rand_pts), 2))
for k, pt in enumerate(rand_pts):
random_values[k, :] = [v['value'] for v in multimetric_value_distance_function({'x1': pt[0], 'x2': pt[1]}, x_star)]
```
The graph on the left again shows the SigOpt generated Pareto frontier with the red + signs.
As we can see for the contour plot associated with this multimetric experiment on the right, multiple regions of solutions emerge which have high values but are at least some distance away. This contour plot is only feasible for low dimensional problems -- for higher dimensional problems a different analysis of the efficient points will be necessary.
```
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
ax1.plot(random_values[:, 0], random_values[:, 1], **dominated_opts)
ax1.plot(efficient_values[:, 0], efficient_values[:, 1], **efficient_opts)
ax1.set_xlabel('function value', fontsize=15)
ax1.set_ylabel('distance to $x^*$', fontsize=15)
xplt = numpy.linspace(-1, 1, 40)
X1, X2 = numpy.meshgrid(xplt, xplt)
Y = multimodal_function(x1=X1, x2=X2)
ax2.contour(X1, X2, Y)
ax2.plot(x_star['x1'], x_star['x2'], '*k', markersize=20)
ax2.plot(efficient_points[:, 0], efficient_points[:, 1], **efficient_opts)
ax2.set_xlabel('$x_1$', fontsize=15)
ax2.set_ylabel('$x_2$', fontsize=15);
```
| true |
code
| 0.505981 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.