prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
<img src="http://hilpisch.com/tpq_logo.png" alt="The Python Quants" width="35%" align="right" border="0"><br>
# Python for Finance
**Analyze Big Financial Data**
O'Reilly (2014)
Yves Hilpisch
<img style="border:0px solid grey;" src="http://hilpisch.com/python_for_finance.png" alt="Python for Finance" width="30%" align="left" border="0">
**Buy the book ** |
<a href='http://shop.oreilly.com/product/0636920032441.do' target='_blank'>O'Reilly</a> |
<a href='http://www.amazon.com/Yves-Hilpisch/e/B00JCYHHJM' target='_blank'>Amazon</a>
**All book codes & IPYNBs** |
<a href="http://oreilly.quant-platform.com">http://oreilly.quant-platform.com</a>
**The Python Quants GmbH** | <a href='http://tpq.io' target='_blank'>http://tpq.io</a>
**Contact us** | <a href='mailto:pff@tpq.io'>pff@tpq.io</a>
# Volatility Options
```
from pylab import plt
plt.style.use('ggplot')
import matplotlib as mpl
mpl.rcParams['font.family'] = 'serif'
import warnings; warnings.simplefilter('ignore')
```
## The VSTOXX Data
```
import sys
sys.path.append('../python3/')
sys.path.append('../python3/dxa')
import numpy as np
import pandas as pd
```
### VSTOXX Index Data
```
url = 'http://www.stoxx.com/download/historical_values/h_vstoxx.txt'
vstoxx_index = pd.read_csv(url, index_col=0, header=2,
parse_dates=True, dayfirst=True,
sep=',')
vstoxx_index.info()
vstoxx_index = vstoxx_index[('2013/12/31' < vstoxx_index.index)
& (vstoxx_index.index < '2014/4/1')]
np.round(vstoxx_index.tail(), 2)
```
### VSTOXX Futures Data
```
vstoxx_futures = pd.read_excel('./source/vstoxx_march_2014.xlsx',
'vstoxx_futures')
vstoxx_futures.info()
del vstoxx_futures['A_SETTLEMENT_PRICE_SCALED']
del vstoxx_futures['A_CALL_PUT_FLAG']
del vstoxx_futures['A_EXERCISE_PRICE']
del vstoxx_futures['A_PRODUCT_ID']
columns = ['DATE', 'EXP_YEAR', 'EXP_MONTH', 'PRICE']
vstoxx_futures.columns = columns
import datetime as dt
import calendar
def third_friday(date):
day = 21 - (calendar.weekday(date.year, date.month, 1) + 2) % 7
return dt.datetime(date.year, date.month, day)
set(vstoxx_futures['EXP_MONTH'])
third_fridays = {}
for month in set(vstoxx_futures['EXP_MONTH']):
third_fridays[month] = third_friday(dt.datetime(2014, month, 1))
third_fridays
tf = lambda x: third_fridays[x]
vstoxx_futures['MATURITY'] = vstoxx_futures['EXP_MONTH'].apply(tf)
vstoxx_futures.tail()
```
### VSTOXX Options Data
```
vstoxx_options = pd.read_excel('./source/vstoxx_march_2014.xlsx',
'vstoxx_options')
vstoxx_options.info()
del vstoxx_options['A_SETTLEMENT_PRICE_SCALED']
del vstoxx_options['A_PRODUCT_ID']
columns = ['DATE', 'EXP_YEAR', 'EXP_MONTH', 'TYPE', 'STRIKE', 'PRICE']
vstoxx_options.columns = columns
vstoxx_options['MATURITY'] = vstoxx_options['EXP_MONTH'].apply(tf)
vstoxx_options.head()
vstoxx_options['STRIKE'] = vstoxx_options['STRIKE'] / 100.
save = False
if save is True:
import warnings
warnings.simplefilter('ignore')
h5 = pd.HDFStore('./source/vstoxx_march_2014.h5',
complevel=9, complib='blosc')
h5['vstoxx_index'] = vstoxx_index
h5['vstoxx_futures'] = vstoxx_futures
h5['vstoxx_options'] = vstoxx_options
h5.close()
```
## Model Calibration
### Relevant Market Data
```
pricing_date = dt.datetime(2014, 3, 31)
# last trading day in March 2014
maturity = third_fridays[10]
# October maturity
initial_value = vstoxx_index['V2TX'][pricing_date]
# VSTOXX on pricing_date
forward = vstoxx_futures[(vstoxx_futures.DATE == pricing_date)
& (vstoxx_futures.MATURITY == maturity)]['PRICE'].values[0]
tol = 0.20
option_selection = \
vstoxx_options[(vstoxx_options.DATE == pricing_date)
& (vstoxx_options.MATURITY == maturity)
& (vstoxx_options.TYPE == 'C')
& (vstoxx_options.STRIKE > (1 - tol) * forward)
& (vstoxx_options.STRIKE < (1 + tol) * forward)]
option_selection
```
### Option Modeling
```
from dxa import *
me_vstoxx = market_environment('me_vstoxx', pricing_date)
me_vstoxx.add_constant('initial_value', initial_value)
me_vstoxx.add_constant('final_date', maturity)
me_vstoxx.add_constant('currency', 'EUR')
me_vstoxx.add_constant('frequency', 'B')
me_vstoxx.add_constant('paths', 10000)
csr = constant_short_rate('csr', 0.01)
# somewhat arbitrarily chosen here
me_vstoxx.add_curve('discount_curve', csr)
# parameters to be calibrated later
me_vstoxx.add_constant('kappa', 1.0)
me_vstoxx.add_constant('theta', 1.2 * initial_value)
vol_est = vstoxx_index['V2TX'].std() \
* np.sqrt(len(vstoxx_index['V2TX']) / 252.)
me_vstoxx.add_constant('volatility', vol_est)
vol_est
vstoxx_model = square_root_diffusion('vstoxx_model', me_vstoxx)
me_vstoxx.add_constant('strike', forward)
me_vstoxx.add_constant('maturity', maturity)
payoff_func = 'np.maximum(maturity_value - strike, 0)'
vstoxx_eur_call = valuation_mcs_european('vstoxx_eur_call',
vstoxx_model, me_vstoxx, payoff_func)
vstoxx_eur_call.present_value()
option_models = {}
for option in option_selection.index:
strike = option_selection['STRIKE'].ix[option]
me_vstoxx.add_constant('strike', strike)
option_models[option] = \
valuation_mcs_european(
'eur_call_%d' % strike,
vstoxx_model,
me_vstoxx,
payoff_func)
def calculate_model_values(p0):
''' Returns all relevant option values.
Parameters
===========
p0 : tuple/list
tuple of kappa, theta, volatility
Returns
=======
model_values : dict
dictionary with model values
'''
kappa, theta, volatility = p0
vstoxx_model.update(kappa=kappa,
theta=theta,
volatility=volatility)
model_values = {}
for option in option_models:
model_values[option] = \
option_models[option].present_value(fixed_seed=True)
return model_values
calculate_model_values((0.5, 27.5, vol_est))
```
### Calibration Procedure
```
i = 0
def mean_squared_error(p0):
''' Returns the mean-squared error given
the model and market values.
Parameters
===========
p0 : tuple/list
tuple of kappa, theta, volatility
Returns
=======
MSE : float
mean-squared error
'''
global i
model_values = np.array(list(calculate_model_values(p0).values()))
market_values = option_selection['PRICE'].values
option_diffs = model_values - market_values
MSE = np.sum(option_diffs ** 2) / len(option_diffs)
# vectorized MSE calculation
if i % 20 == 0:
if i == 0:
print('%4s %6s %6s %6s --> %6s' %
('i', 'kappa', 'theta', 'vola', 'MSE'))
print('%4d %6.3f %6.3f %6.3f --> %6.3f' %
(i, p0[0], p0[1], p0[2], MSE))
i += 1
return MSE
mean_squared_error((0.5, 27.5, vol_est))
import scipy.optimize as spo
%%time
i = 0
opt_global = spo.brute(mean_squared_error,
((0.5, 3.01, 0.5), # range for kappa
(15., 30.1, 5.), # range for theta
(0.5, 5.51, 1)), # range for volatility
finish=None)
i = 0
mean_squared_error(opt_global)
%%time
i = 0
opt_local = spo.fmin(mean_squared_error, opt_global,
xtol=0.00001, ftol=0.00001,
maxiter=100, maxfun=350)
i = 0
mean_squared_error(opt_local)
calculate_model_values(opt_local)
pd.options.mode.chained_assignment = None
option_selection['MODEL'] = \
np.array(list(calculate_model_values(opt_local).values()))
option_selection['ERRORS'] = \
option_selection['MODEL'] - option_selection['PRICE']
option_selection[['MODEL', 'PRICE', 'ERRORS']]
round(option_selection['ERRORS'].mean(), 3)
import matplotlib.pyplot as plt
%matplotlib inline
fix, (ax1, ax2) = plt.subplots(2, sharex=True, figsize=(8, 8))
strikes = option_selection['STRIKE'].values
ax1.plot(strikes, option_selection['PRICE'], label='market quotes')
ax1.plot(strikes, option_selection['MODEL'], 'ro', label='model values')
ax1.set_ylabel('option values')
ax1.grid(True)
ax1.legend(loc=0)
wi = 0.25
ax2.bar(strikes - wi / 2., option_selection['ERRORS'],
label='market quotes', width=wi)
ax2.grid(True)
ax2.set_ylabel('differences')
ax2.set_xlabel('strikes')
# tag: vstoxx_calibration
# title: Calibrated model values for VSTOXX call options vs. market quotes
```
## American Options on the VSTOXX
### Modeling Option Positions
```
me_vstoxx = market_environment('me_vstoxx', pricing_date)
me_vstoxx.add_constant('initial_value', initial_value)
me_vstoxx.add_constant('final_date', pricing_date)
me_vstoxx.add_constant('currency', 'NONE')
# adding optimal parameters to environment
me_vstoxx.add_constant('kappa', opt_local[0])
me_vstoxx.add_constant('theta', opt_local[1])
me_vstoxx.add_constant('volatility', opt_local[2])
me_vstoxx.add_constant('model', 'srd')
payoff_func = 'np.maximum(strike - instrument_values, 0)'
shared = market_environment('share', pricing_date)
shared.add_constant('maturity', maturity)
shared.add_constant('currency', 'EUR')
option_positions = {}
# dictionary for option positions
option_environments = {}
# dictionary for option environments
for option in option_selection.index:
option_environments[option] = \
market_environment('am_put_%d' % option, pricing_date)
# define new option environment, one for each option
strike = option_selection['STRIKE'].ix[option]
# pick the relevant strike
option_environments[option].add_constant('strike', strike)
# add it to the environment
option_environments[option].add_environment(shared)
# add the shared data
option_positions['am_put_%d' % strike] = \
derivatives_position(
'am_put_%d' % strike,
quantity=100.,
underlying='vstoxx_model',
mar_env=option_environments[option],
otype='American',
payoff_func=payoff_func)
```
### The Options Portfolio
```
val_env = market_environment('val_env', pricing_date)
val_env.add_constant('starting_date', pricing_date)
val_env.add_constant('final_date', pricing_date)
# temporary value, is updated during valuation
val_env.add_curve('discount_curve', csr)
val_env.add_constant('frequency', 'B')
val_env.add_constant('paths', 25000)
underlyings = {'vstoxx_model' : me_vstoxx}
portfolio = derivatives_portfolio('portfolio', option_positions,
val_env, underlyings)
%time results = portfolio.get_statistics(fixed_seed=True)
results.sort_values(by='name')
results[['pos_value','pos_delta','pos_vega']].sum()
```
## Conclusions
## Further Reading
<img src="http://hilpisch.com/tpq_logo.png" alt="The Python Quants" width="35%" align="right" border="0"><br>
<a href="http://www.pythonquants.com" target="_blank">www.pythonquants.com</a> | <a href="http://twitter.com/dyjh" target="_blank">@dyjh</a>
<a href="mailto:analytics@pythonquants.com">analytics@pythonquants.com</a>
**Python Quant Platform** |
<a href="http://oreilly.quant-platform.com">http://oreilly.quant-platform.com</a>
**Derivatives Analytics with Python** |
<a href="http://www.derivatives-analytics-with-python.com" target="_blank">Derivatives Analytics @ Wiley Finance</a>
**Python for Finance** |
<a href="http://shop.oreilly.com/product/0636920032441.do" target="_blank">Python for Finance @ O'Reilly</a>
| true |
code
| 0.480235 | null | null | null | null |
|
## Part 1: LLE
Implement Locally Linear Embedding function
```
from sklearn.neighbors import kneighbors_graph
from scipy.sparse import csr_matrix
from numpy import matlib
import numpy as np
def csr_from_mat(W, NI):
n, k = W.shape
data = np.reshape(W, n*k)
cols = np.reshape(NI, n*k)
rows = np.floor(np.arange(0, n, 1/k))
return csr_matrix((data, (rows, cols)), shape=(n, n))
def lle_neighborhood(X, k):
n, d = X.shape
NN = kneighbors_graph(X, k, mode='connectivity')
return np.reshape(NN.indices, (n, k))
def lle_weights(X, NI):
n, d = X.shape
n, k = NI.shape
tol = 1e-3 if k>d else 0
W = np.zeros((n, k))
for i in range(n):
Z = (X[NI[i,:],:] - matlib.repmat(X[i,:], k, 1)).T
C = Z.T.dot(Z)
C = C + tol*np.trace(C)*np.identity(k)
w = np.linalg.inv(C).dot(np.ones((k, 1)))
w = w / np.sum(w)
W[i,:] = w.T
return W
def lle_embedding(W, m):
n, n = W.shape
I, W = np.identity(n), W
M = (I-W).T.dot(I-W)
w, v = np.linalg.eig(M)
i = np.argsort(w)
w, v = w[i].real, v[:,i].real
# did i do wrong here?
return v[:,1:m+1]
"""Args:
X: input samples, array (num, dim)
n_components: dimension of output data
n_neighbours: neighborhood size
Returns:
Y: output samples, array (num, n_components)
"""
def LLE(X, n_components=2, n_neighbours=10):
NI = lle_neighborhood(X, n_neighbours)
W = lle_weights(X, NI)
W = csr_from_mat(W, NI)
Y = lle_embedding(W, n_components)
return Y
```
## Part 2: Manifold Visualization
Visualize the S-shaped 3-d dataset using the LLE.
```
from sklearn import manifold, datasets
SX, St = datasets.make_s_curve(n_samples=1000, random_state=1337)
# SX: input data [n_samples, 3]
# St: univariate position along manifold [n_samples], use for coloring the plots
```
The code in the next cell should draw a single plot with the following subplots:
1. 3D S-shaped dataset
2. 2D Manifold learnt using LLE
Use the `St` variable to color the points in your visualizations. Use a color spectrum, and the position along the manifold to assign the color.
```
# Visualization code here
from matplotlib import pyplot as plt
%matplotlib notebook
LX = LLE(SX, 2)
fig = plt.figure(figsize=(6, 10))
axi = fig.add_subplot(211, projection='3d')
colorize = dict(c=St, cmap=plt.cm.get_cmap('rainbow', 4))
axi.scatter3D(SX[:, 0], SX[:, 1], SX[:, 2], **colorize)
axi.title.set_text('3D S-shaped dataset')
axi = fig.add_subplot(212)
axi.scatter([LX[:, 0]], [LX[:, 1]], **colorize)
axi.title.set_text('2D Manifold learnt using LLE')
```
## Part 3: Visualizing high-dimensional data
Visualize the Swiss roll dataset using LLE.
```
# Swiss roll dataset loading here
import numpy
d = []
with open('./swissroll.dat', 'r') as dat_file:
for line in dat_file:
line = line.strip().split()
line = [float(x.strip()) for x in line]
d.append(line)
swissroll = numpy.array(d)
print (swissroll.shape)
```
The code in the next cell should draw a single plot with the following subplots:
1. Visualize Swiss roll.
2. Unwrap the manifold in 2D and visualize using LLE.
```
import numpy as np
from matplotlib import pyplot as plt
%matplotlib notebook
X = swissroll
Xc = np.linspace(0, 1, X.shape[0])
LX = LLE(X, 2)
fig = plt.figure(figsize=(6, 10))
axi = fig.add_subplot(211, projection='3d')
colorize = dict(c=Xc, cmap=plt.cm.get_cmap('rainbow', 4))
axi.scatter3D(X[:, 0], X[:, 1], X[:, 2], **colorize)
axi.title.set_text('3D Swiss roll dataset')
axi = fig.add_subplot(212)
axi.scatter([LX[:, 0]], [LX[:, 1]], **colorize)
axi.title.set_text('Unwrap the manifold in 2D using LLE')
```
| true |
code
| 0.648717 | null | null | null | null |
|
# Contrast Effects
### Authors
Ndèye Gagnessiry Ndiaye and Christin Seifert
### License
This work is licensed under the Creative Commons Attribution 3.0 Unported License https://creativecommons.org/licenses/by/3.0/
This notebook illustrates 3 contrast effects:
- Simultaneous Brightness Contrast
- Chevreul Illusion
- Contrast Crispening
## Simultaneous Brightness Contrast
Simultaneous Brightness Contrast is the general effect where a gray patch placed on a dark background looks lighter than the same gray patch on a light background (foreground and background affect each other). The effect is based on lateral inhibition.
Also see the following video as an example:
https://www.youtube.com/watch?v=ZYh4SxE7Xp8
```
import numpy as np
import matplotlib.pyplot as plt
```
The following image shows a gray square on different backgrounds. The inner square always has the same color (84% gray), and is successively shown on 0%, 50%, 100%, and 150% gray background patches. Note, how the inner squares are perceived differently (square on the right looks considerably darker than the square on the left).
Suggestion: Change the gray values of the inner and outer squares and see what happens.
```
# defining the inner square as 3x3 array with an initial gray value
inner_gray_value = 120
inner_square = np.full((3,3), inner_gray_value, np.double)
# defining the outer squares and overlaying the inner square
a = np.zeros((5,5), np.double)
a[1:4, 1:4] = inner_square
b = np.full((5,5), 50, np.double)
b[1:4, 1:4] = inner_square
c = np.full((5,5), 100, np.double)
c[1:4, 1:4] = inner_square
d = np.full((5,5), 150, np.double)
d[1:4, 1:4] = inner_square
simultaneous=np.hstack((a,b,c,d))
im=plt.imshow(simultaneous, cmap='gray',interpolation='nearest',vmin=0, vmax=255)
#plt.rcParams["figure.figsize"] = (70,10)
plt.axis('off')
plt.colorbar(im, orientation='horizontal')
plt.show()
```
## Chevreul Illusion
The following images visualizes the Chevreul illusion. We use a sequence of gray bands (200%, 150%, 100%, 75% and 50% gray). One band has a uniform gray value. When putting the bands next to each other, the gray values seem to be darker at the edges. This is due to lateral inhibition, a feature of our visual system that increases edge contrasts and helps us to better detect outlines of shapes.
```
e = np.full((9,5), 200, np.double)
f = np.full((9,5), 150, np.double)
g = np.full((9,5), 100, np.double)
h = np.full((9,5), 75, np.double)
i = np.full((9,5), 50, np.double)
image1= np.hstack((e,f,g,h,i))
e[:,4] = 255
f[:,4] = 255
g[:,4] = 255
h[:,4] = 255
i[:,4] = 255
image2=np.hstack((e,f,g,h,i))
plt.subplot(1,2,1)
plt.imshow(image1, cmap='gray',vmin=0, vmax=255,interpolation='nearest',aspect=4)
plt.title('Bands')
plt.axis('off')
plt.subplot(1,2,2)
plt.imshow(image2, cmap='gray',vmin=0, vmax=255,interpolation='nearest',aspect=4)
plt.title('Bands with white breaks')
plt.axis('off')
plt.show()
```
## Contrast Crispening
The following images show the gray strips on a gray-scale background. Left image: All vertical gray bands are the same. Note how different parts of the vertical gray bands are enhanced (i.e., difference better perceivable) depending on the gray value of the background. In fact, differences are enhanced when the gray value in the foreground is closer to the gray value in the background. On the right, the same vertical bands are shown but without the background. In this image you can (perceptually) verify that all vertical gray bands are indeed the same.
```
strips = np.linspace( 0, 255, 10, np.double)
strips = strips.reshape((-1, 1))
M = np.linspace( 255, 0, 10, np.double)
n = np.ones((20, 10), np.double)
background = n[:,:]*M
background[5:15,::2] = strips
without_background = np.full((20,10), 255, np.double)
without_background[5:15,::2] = strips
plt.subplot(1,2,1)
plt.imshow(background, cmap='gray',vmin=0, vmax=255,interpolation='nearest')
plt.tick_params(axis='both', left='off', top='off', right='off', bottom='off', labelleft='off', labeltop='off', labelright='off', labelbottom='off')
plt.subplot(1,2,2)
plt.imshow(without_background, cmap='gray',vmin=0, vmax=255,interpolation='nearest')
plt.tick_params(axis='both', left='off', top='off', right='off', bottom='off', labelleft='off', labeltop='off', labelright='off', labelbottom='off')
plt.show()
```
| true |
code
| 0.667446 | null | null | null | null |
|
# Rasterio plotting of Landsat-8 scenes
In this notebook, we will download bands of a Landsat-8 scene, visualize them with [rasterio's plotting module]( https://rasterio.readthedocs.io/en/latest/topics/plotting.html), and write an RGB image as rendered GeoTIFF.
```
import os
import matplotlib.pyplot as plt
import numpy as np
import rasterio
from rasterio.plot import show
import requests
from skimage import exposure
%matplotlib inline
```
## Download and read bands
```
landsat_url_suffixes = {'red': 'B4', 'green': 'B3', 'blue': 'B2', 'qa': 'BQA'}
landsat_url_prefix = 'http://landsat-pds.s3.amazonaws.com/c1/L8/008/067/LC08_L1TP_008067_20190405_20190405_01_RT/LC08_L1TP_008067_20190405_20190405_01_RT_'
landsat_urls = {k: f'{landsat_url_prefix}{v}.TIF' for k, v in landsat_url_suffixes.items()}
def get_bands(band_urls, data_path='data', file_format='tif'):
"""Download and cache spectral bands of a satellite image
Parameters
----------
band_urls : dict
URLs of individual bands: {<band_name>: <url>}
data_path : string (optional)
Location to save the data
file_format : string (optional)
File format of band
Returns
-------
bands : dict
Band arrays and the profile
"""
if not os.path.exists(data_path):
os.makedirs(data_path)
bands = {}
for k, v in band_urls.items():
print(os.path.basename(v))
band_path = os.path.join(data_path, '{}.{}'.format(k, file_format))
if not os.path.exists(band_path):
print('Downloading...')
r = requests.get(v)
with open(band_path, 'wb') as f:
f.write(r.content)
else:
print('Already downloaded...')
with rasterio.open(band_path) as src:
print('Reading...\n')
bands[k] = src.read(1)
if 'profile' not in bands:
bands['profile'] = src.profile
return bands
landsat_bands = get_bands(landsat_urls, data_path='data', file_format='tif')
```
## Plot individual bands
Use `rasterio.plot.show()` to plot individual bands. The `transform` argument changes the image extent to the spatial bounds of the image.
```
def plot_rgb_bands(bands):
fig, (axr, axg, axb) = plt.subplots(1, 3, figsize=(21, 7))
transform = bands['profile']['transform']
show(bands['red'], ax=axr, cmap='Reds', title='Red band', transform=transform, vmax=np.percentile(bands['red'], 95))
show(bands['green'], ax=axg, cmap='Greens', title='Green band', transform=transform, vmax=np.percentile(bands['red'], 95))
show(bands['blue'], ax=axb, cmap='Blues', title='Blue band', transform=transform, vmax=np.percentile(bands['red'], 95))
plt.show()
plot_rgb_bands(landsat_bands)
```
## Create RGB stack
```
def create_rgb_stack(bands, method='rescaling', percentile=2, clip_limit=0.03):
"""Create RGB stack from RGB bands
Parameters
----------
bands : dict
Band arrays in {<band_name>: <array>} format, including 'red',
'green', 'blue', and 'qa' (optional) keys
method : string (optional)
Method for modifying the band intensities. 'rescaling' stretches
or shrinks the intensity range. 'clahe' applies Contrast Limited
Adaptive Histogram Equalization, which is an algorithm for
local contrast enhancement.
percentile : int (optional)
Shorthand for percentile range to compute (from percentile to
100 - percentile) for intensity rescaling. Required when
method='rescaling'.
clip_limit : float (optional)
Clipping limit. Required when method='clahe'.
Returns
-------
ndarray
RGB array (shape=(3, height, width), dtype='uint8')
"""
modified_bands = []
for band in [bands['red'], bands['green'], bands['blue']]:
if method == 'rescaling':
# Calculate percentiles, excluding fill pixels
try:
fill_mask = bands['qa'] == 1
masked_band = np.ma.masked_where(fill_mask, band)
masked_band = np.ma.filled(masked_band.astype('float'), np.nan)
except KeyError:
masked_band = band
vmin, vmax = np.nanpercentile(masked_band,
(percentile, 100 - percentile))
# Rescale to percentile range
modified_band = exposure.rescale_intensity(
band, in_range=(vmin, vmax), out_range='uint8')
modified_band = modified_band.astype(np.uint8)
elif method == 'clahe':
# Apply histogram equalization
modified_band = exposure.equalize_adapthist(
band, clip_limit=clip_limit)
modified_band = (modified_band * 255).astype(np.uint8)
modified_bands.append(modified_band)
return np.stack(modified_bands)
landsat_bands['rgb'] = create_rgb_stack(landsat_bands, method='clahe')
```
## Plot RGB image
```
def plot_rgb_image(bands):
plt.figure(figsize=(10, 10))
show(bands['rgb'], transform=bands['profile']['transform'])
plot_rgb_image(landsat_bands)
```
## Write RGB image
Write the RGB image as GeoTIFF and set 'RGB' color interpretation.
```
def write_rgb_image(bands, data_path='data'):
profile = bands['profile']
profile.update(driver='GTiff', dtype=rasterio.uint8, count=3, photometric='RGB')
rgb_path = os.path.join(data_path, 'rgb.tif')
with rasterio.open(rgb_path, 'w', **profile) as dst:
for i, band in enumerate(bands['rgb']):
dst.write_band(i + 1, band)
write_rgb_image(landsat_bands, data_path='data')
```
| true |
code
| 0.751677 | null | null | null | null |
|
(nm_heun_method)=
# Heun's method
```{index} Heun's method
```
{ref}`Euler's method <nm_euler_method>` is first-order accurate because it calculates the derivative using only the information available at the beginning of the time step. Higher-order convergence can be obtained if we also employ information from other points in the interval - the more points that we employ, the more accurate method for solving ODEs can be. [Heun's method](https://en.wikipedia.org/wiki/Heun%27s_method) uses 2 points compared to Euler's one single point, increasing accuracy.
Heun's method may be derived by attempting to use derivative information at both the start and the end of the interval:
\\[u(t+\Delta t)\approx u(t)+\frac{\Delta t}{2}\left(u'(t)+u'(t+\Delta t)\right),\\\\\\
u(t+\Delta t)\approx u(t)+\frac{\Delta t}{2}\big(f(u(t),t)+f(u(t+\Delta t),t+\Delta t)\big).\\]
The difficulty with this approach is that we now require \\(u(t+\Delta t)\\) in order to calculate the final term in the equation, and that's what we set out to calculate so we don't know it yet! So at this point we have an example of an implicit algorithm and at this stage the above ODE solver would be referred to as the trapezoidal method if we could solve it exactly for \\(u(t+\Delta t)\\).
Heun's method, unlike Euler method, is an implicit method, meaning that we do not have all of the information needed. While we have the information about \\(u(t)\\) and \\(f(u(t),t)\\), we lack information about \\(u(t+\Delta t)\\) and \\(f(u(t+\Delta t),t)\\), and we have to deal with not knowing these things somehow.
The simplest solution to this dilemma, the one adopted in Heun's method, is to use a first guess at \\(x(t+\Delta t)\\) calculated using Euler's method:
\\[ \tilde{u}(t+\Delta t)=u(t)+\Delta tf(u(t),t). \\]
This first guess is then used to solve for \\(u(t+\Delta t)\\) using:
\\[ u(t+\Delta t)\approx u(t)+\frac{\Delta t}{2}\big(f(u(t),t)+f(\tilde{u}(t+\Delta t),t+\Delta t)\big).\\]
The generic term for schemes of this type is **predictor-corrector**. The initial calculation of \\(\tilde{u}(t+\Delta t)\\) is used to predict the new value of \\(u\\) and then this is used in a more accurate calculation to produce a more correct value.
Note that Heun's method is \\(O(\Delta t^2)\\), i.e. **2nd order accurate**.
## Implementation
We will write a function `heun(f,u0,t0,t_max,dt)` that takes as arguments the function \\(f(u,t)\\) on the RHS of our ODE,
an initial value for \\(u\\), the start and end time of the integration, and the time step.
We will use it to integrate the following ODEs up to time \\(t=10\\)
\\[u'(t)=u(t),\quad u(0)=1,\\]
plot the results and compare them to Euler method.
First let's define the functions:
```
import matplotlib.pyplot as plt
import numpy as np
def euler(f,u0,t0,t_max,dt):
u=u0; t=t0; u_all=[u0]; t_all=[t0];
while t<t_max:
u = u + dt*f(u,t)
u_all.append(u)
t = t + dt
t_all.append(t)
return(u_all,t_all)
def heun(f,u0,t0,t_max,dt):
u=u0; t=t0; u_all=[u0]; t_all=[t0];
while t<t_max:
ue = u + dt*f(u,t) # euler guess
u = u + 0.5*dt*(f(u,t) + f(ue,t+dt))
u_all.append(u)
t = t + dt
t_all.append(t)
return(u_all,t_all)
def f1(u,t):
val = u
return val
def f2(u,t):
val = np.cos(u)
return val
```
Plot the solution for the first function:
```
dt = 0.4
u0 = 1.0
t0 = 0.0
tf = 10.0
# set up figure
fig = plt.figure(figsize=(7, 5))
ax1 = plt.subplot(111)
(u_all,t_all) = euler(f1,u0,t0,tf,dt)
ax1.plot(t_all, u_all,'b',label='euler')
(u_all,t_all) = heun(f1,u0,t0,tf,dt)
ax1.plot(t_all, u_all,'r',label='heun')
# exact solution
ax1.plot(t_all, np.exp(t_all),'k',label='exact')
ax1.set_xlabel('t', fontsize=14)
ax1.set_ylabel('u(t)', fontsize=14)
ax1.grid(True)
ax1.legend(loc='best')
plt.show()
```
| true |
code
| 0.75422 | null | null | null | null |
|
# Temporal-Difference Methods
In this notebook, you will write your own implementations of many Temporal-Difference (TD) methods.
While we have provided some starter code, you are welcome to erase these hints and write your code from scratch.
---
### Part 0: Explore CliffWalkingEnv
We begin by importing the necessary packages.
```
import sys
import gym
import numpy as np
from collections import defaultdict, deque
import matplotlib.pyplot as plt
%matplotlib inline
import check_test
from plot_utils import plot_values
```
Use the code cell below to create an instance of the [CliffWalking](https://github.com/openai/gym/blob/master/gym/envs/toy_text/cliffwalking.py) environment.
```
env = gym.make('CliffWalking-v0')
```
The agent moves through a $4\times 12$ gridworld, with states numbered as follows:
```
[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]]
```
At the start of any episode, state `36` is the initial state. State `47` is the only terminal state, and the cliff corresponds to states `37` through `46`.
The agent has 4 potential actions:
```
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
```
Thus, $\mathcal{S}^+=\{0, 1, \ldots, 47\}$, and $\mathcal{A} =\{0, 1, 2, 3\}$. Verify this by running the code cell below.
```
print(env.action_space)
print(env.observation_space)
```
In this mini-project, we will build towards finding the optimal policy for the CliffWalking environment. The optimal state-value function is visualized below. Please take the time now to make sure that you understand _why_ this is the optimal state-value function.
_**Note**: You can safely ignore the values of the cliff "states" as these are not true states from which the agent can make decisions. For the cliff "states", the state-value function is not well-defined._
```
# define the optimal state-value function
V_opt = np.zeros((4,12))
V_opt[0:13][0] = -np.arange(3, 15)[::-1]
V_opt[0:13][1] = -np.arange(3, 15)[::-1] + 1
V_opt[0:13][2] = -np.arange(3, 15)[::-1] + 2
V_opt[3][0] = -13
plot_values(V_opt)
```
### Part 1: TD Control: Sarsa
In this section, you will write your own implementation of the Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def epsilon_greedy_from_Q(env, Q, epsilon, state):
return np.argmax(Q[state]) if np.random.uniform() >= epsilon else env.action_space.sample()
def sarsa(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
epsilon = 1.0/i_episode
state = env.reset()
action = epsilon_greedy_from_Q(env, Q, epsilon, state)
while True:
next_state, reward, done, info = env.step(action)
if not done:
next_action = epsilon_greedy_from_Q(env, Q, epsilon, next_state)
Q[state][action] += alpha*(reward + gamma*Q[next_state][next_action] - Q[state][action])
state = next_state
action = next_action
else:
Q[state][action] += alpha*(reward - Q[state][action])
break
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsa = sarsa(env, 5000, .01)
# print the estimated optimal policy
policy_sarsa = np.array([np.argmax(Q_sarsa[key]) if key in Q_sarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_sarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsa)
# plot the estimated optimal state-value function
V_sarsa = ([np.max(Q_sarsa[key]) if key in Q_sarsa else 0 for key in np.arange(48)])
plot_values(V_sarsa)
```
### Part 2: TD Control: Q-learning
In this section, you will write your own implementation of the Q-learning control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def epsilon_greedy_from_Q(env, Q, epsilon, state):
return np.argmax(Q[state]) if np.random.uniform() >= epsilon else env.action_space.sample()
def q_learning(env, num_episodes, alpha, gamma=1.0):
# initialize empty dictionary of arrays
Q = defaultdict(lambda: np.zeros(env.nA))
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
epsilon = 1.0/i_episode
state = env.reset()
while True:
action = epsilon_greedy_from_Q(env, Q, epsilon, state)
next_state, reward, done, info = env.step(action)
if not done:
Q[state][action] += alpha*(reward + gamma*max(Q[next_state]) - Q[state][action])
state = next_state
else:
Q[state][action] += alpha*(reward - Q[state][action])
break
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsamax = q_learning(env, 5000, .01)
# print the estimated optimal policy
policy_sarsamax = np.array([np.argmax(Q_sarsamax[key]) if key in Q_sarsamax else -1 for key in np.arange(48)]).reshape((4,12))
check_test.run_check('td_control_check', policy_sarsamax)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsamax)
# plot the estimated optimal state-value function
plot_values([np.max(Q_sarsamax[key]) if key in Q_sarsamax else 0 for key in np.arange(48)])
```
### Part 3: TD Control: Expected Sarsa
In this section, you will write your own implementation of the Expected Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def update_Qs(env, Q, epsilon, gamma, alpha, nA, state, action, reward, next_state=None):
policy = np.ones(nA)*epsilon/nA
policy[np.argmax(Q[next_state])] = 1 - epsilon + epsilon/nA
return Q[state][action] + alpha*(reward + gamma*np.dot(Q[next_state], policy) - Q[state][action])
def expected_sarsa(env, num_episodes, alpha, gamma=1.0):
nA = env.action_space.n
# initialize empty dictionary of arrays
Q = defaultdict(lambda: np.zeros(env.nA))
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
epsilon = 1.0/i_episode
state = env.reset()
while True:
action = epsilon_greedy_from_Q(env, Q, epsilon, state)
next_state, reward, done, info = env.step(action)
Q[state][action] = update_Qs(env, Q, epsilon, gamma, alpha, nA, state, action, reward, next_state)
state = next_state
if done:
break
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_expsarsa = expected_sarsa(env, 50000, 1)
# print the estimated optimal policy
policy_expsarsa = np.array([np.argmax(Q_expsarsa[key]) if key in Q_expsarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_expsarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_expsarsa)
# plot the estimated optimal state-value function
plot_values([np.max(Q_expsarsa[key]) if key in Q_expsarsa else 0 for key in np.arange(48)])
```
| true |
code
| 0.474266 | null | null | null | null |
|
# Using `pyoscode` in cosmology
`pyoscode` is a fast numerical routine suitable for equations of the form
$$ \ddot{x} + 2\gamma(t)\dot{x} + \omega^2(t) = 0, $$
with
- $x(t)$: a scalar variable (e.g. curvature perturbation),
- $\omega(t)$: frequency,
- $\gamma(t)$: friction or first-derivative term.
In general $\gamma$, $\omega$ may not be explicit functions of time, and `pyoscode` can deal with them given as
- _in Python_: `numpy.array`s
- _in C++_: `array`s, `list`s, `std::vector`s, `Eigen::Vector`s, or functions.
Below we'll look at examples using the _Python_ interface, but first, let's look at the short summary of the relevant cosmology.
## Cosmology
We wish to calculate the primordial power spectrum of scalar perturbations in a universe with some spatial curvature. This involves
1. computing the isotropic, expanding "background" evolution,
2. then solving the equation of motion of the perturbations of varying lengthscales.
### Background evolution
The relevant equations are the Friedmann equations and the continuity equation. They can be cast into the following form:
$$ \frac{d\ln{\Omega_k}}{dN} = 4 + \Omega_k\big(4K - 2a^2V(\phi)\big), $$
$$ \Big(\frac{d\phi}{dN}\Big)^2 = 6 + \Omega_k\big(6K - 2a^2V(\phi)\big). $$
with
- $a$: scale factor of the universe
- $H$: Hubble parameter
- $N = \ln{a}$: number of e-folds, **the independent variable**
- $ \Omega_k = \frac{1}{(aH)^2}$, curvature density
- $K$: spatial curvature, $0, \pm1$ for flat, closed, and open universes
- $\phi$: inflaton field
- $ V$: inflationary potential
### Evolution of the perturbations
The equation of motion of the perturbations is given by the Mukhanov--Sasaki equation. It takes the form of a generalised oscillator, with frequency and damping terms given by (when written in terms of $N$):
$$ \omega^2 = \Omega_k\Bigg( (k_2 - K) - \frac{2Kk_2}{EK +k_2}\frac{\dot{E}}{E}\Bigg), $$
$$ 2\gamma = K\Omega_k + 3 - E + \frac{k_2}{EK + k_2}\frac{\dot{E}}{E}, $$
with
- $E = \frac{1}{2}\dot{\phi}^2$ (overdot is differentiation wrt $N$)
- $k_2 = k(k+2) - 3K$ if $K > 0$, and $k_2 = k^2 - 3K$ otherwise.
# Code
## A flat universe
```
import pyoscode
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import root_scalar
from scipy.integrate import solve_ivp
```
cosmological parameters:
- $m$: inflaton mass
- $mp$: Planck mass
- $nv$: exponent in inflationary potential
- $K$: curvature, $\pm1$, 0
```
m = 1
mp = 1
nv = 2
K = 0
```
Define the inflationary potential, its derivative, and the background equations. Also define initial conditions for the perturbations such that they start from the _Bunch-Davies_ vacuum.
```
def V(phi):
""" inflationary potential"""
return 0.5*m**2*phi**nv
def dV(phi):
""" derivative of the inflationary potential """
return 0.5*nv*m**2*phi**(nv-1)
def bgeqs(t, y):
""" System of equations describing the evolution of the cosmological
background """
dy = np.zeros(y.shape)
dy[0] = 4.0 + np.exp(y[0])*(4.0*K - 2.0*np.exp(2.0*t)*V(y[1]))
dy[1] = - np.sqrt(6.0 + np.exp(y[0])*(6.0*K -
2.0*np.exp(2.0*t)*V(y[1])))
return dy
def endinfl(t, y):
""" Crosses zero when inflation ends """
dphi = bgeqs(t,y)[1]
epsilon = 0.5*dphi**2
return epsilon - 1.
def bdic(k, phi, dphi, ddphi, N):
""" Defines the Bunch-Davies vacuum solution
for a given perturbation mode """
a0 = np.exp(N)
dz_z = ddphi/dphi + 1.
z = a0*dphi
R = 1./(np.sqrt(2.*k)*z) + 1j*0
dR = - R*dz_z - np.sqrt(k/2.*ok_i)/z*1j
return R,dR
def pps(k, rk1, rk2, x01, dx01, x02, dx02, x0, dx0):
""" Enforces x,dx as initial conditions by linear
combination of two solutions rk1 and rk2, which had
initial conditions x01, dx01 and x02, dx02 """
a = (x0*dx02 - dx0*x02)/(x01*dx02 - dx01*x02)
b = (x0*dx01 - dx0*x01)/(x02*dx01 - dx02*x01)
power = np.abs(a*rk1 + b*rk2)**2*k**3/(2*np.pi**2)
return power
```
Now solve the background with the help of `scipy.integrate`
```
# \Omega_k and N at the start of inflation fully
# parametrise the background.
ok_i = 2.1e-3
N_i = 1.
# Nominal end point of integration (we'll stop at the end of inflation)
N_f = 80.
# Points at which we'll obtain the background solution
Nbg = 10000 # This determines grid fineness, see note below.
N = np.linspace(N_i,N_f,Nbg)
# Initial conditions
phi_i = np.sqrt(4.*(1./ok_i + K)*np.exp(-2.0*N_i)/m**2)
logok_i = np.log(ok_i)
y_i = np.array([logok_i, phi_i])
# Solve for the background until the end of inflation
endinfl.terminal = True
endinfl.direction = 1
bgsol = solve_ivp(bgeqs, (N_i,N_f), y_i, events=endinfl, t_eval=N, rtol=1e-8, atol=1e-10)
```
**Note:** the most important parameter from a numerical perspective is $N_{\mathrm{bg}}$. This determines the fineness of the grid on which $\omega$ and $\gamma$ are defined. The speed of the method depends on how precisely numerical derivatives and integrals of $\omega$, $\gamma$ can be computed. If you experience slow-down, it is very likely that this grid was not fine enough.
The number of e-folds of inflation we got from this setup is
```
bgsol.t_events[0][0]-N_i
```
We're now ready to define the equation of motion of the perturbations. `pyoscode` takes the frequency and the damping term of the oscillator as `numpy.array`s.
```
logok = bgsol.y[0]
phi = bgsol.y[1]
N = bgsol.t
dphi = np.array([-np.sqrt(6.0 + np.exp(Logok)*(6.0*K -
2.0*np.exp(2.0*t)*V(Phi))) for Logok,Phi,t in zip(logok,phi,N) ])
dlogok = np.array([4.0 + np.exp(Logok)*(4.0*K - 2.0*np.exp(2.0*t)*V(Phi)) for Logok,Phi,t in zip(logok,phi,N) ])
dE_E = dlogok - 4. -2.*dV(phi)*np.exp(logok)*np.exp(2.*N)/dphi
E = 0.5*dphi**2
# Damping term
g = 0.5*(3 - E + dE_E)
# frequency
logw = 0.5*logok
```
Now we wish solve the Mukhanov--Sasaki equation in a loop, iterating over increasing values of $k$. We need to determine the range of integration for each: we'll start at a fixed $N$, and integrate until the mode is "well outside the Hubble horizon", $k < (aH)/100$.
```
# range of wavevectors
ks = np.logspace(0,4,1000)
end = np.zeros_like(ks,dtype=int)
endindex = 0
for i in range(len(ks)):
for j in range(endindex,Nbg):
if np.exp(-0.5*logok[j])/ks[i] > 100:
end[i] = j
endindex = j
break
```
We're now ready to solve the Mukhanov-Sasaki equation in a loop and generate a primordial power spectrum.
```
spectrum = np.zeros_like(ks,dtype=complex)
for i,k in enumerate(ks):
# Bunch-Davies i.c.
phi_0 = phi[0]
dphi_0 = dphi[0]
ddphi_0 = 0.5*dE_E[0]*dphi_0
N_0 = N_i
x0, dx0 = bdic(k, phi_0, dphi_0, ddphi_0, N_0)
x01 = 1.0
dx01 = 0.0
x02 = 0.0
dx02 = 1.0
# Linearly indep. solutions
sol1 = pyoscode.solve(N,logw+np.log(k),g,N_i,N[end[i]],x01,dx01,logw=True)
sol2 = pyoscode.solve(N,logw+np.log(k),g,N_i,N[end[i]],x02,dx02,logw=True)
rk1 = sol1["sol"][-1]
rk2 = sol2["sol"][-1]
spectrum[i] = pps(k, rk1, rk2, x01, dx01, x02, dx02, x0, dx0)
```
Plot the resulting spectrum:
```
plt.loglog(ks, spectrum)
plt.xlabel('comoving $k$')
plt.ylabel('$m^2 \\times P_{\mathcal{R}}(k)$')
plt.show()
plt.loglog(ks, spectrum)
plt.xlabel('comoving $k$')
plt.ylabel('$m^2 \\times P_{\mathcal{R}}(k)$')
plt.xlim((3e1,1e4))
plt.ylim((40,80))
plt.show()
```
## A closed universe
All we have to do differently is:
1. solve the background equations again with $K=1$,
```
K = 1
N_i = -1.74
ok_i = 1.0
N = np.linspace(N_i,N_f,Nbg)
# Initial conditions
phi_i = np.sqrt(4.*(1./ok_i + K)*np.exp(-2.0*N_i)/m**2)
logok_i = np.log(ok_i)
y_i = np.array([logok_i, phi_i])
# Solve for the background until the end of inflation
endinfl.terminal = True
endinfl.direction = 1
bgsol = solve_ivp(bgeqs, (N_i,N_f), y_i, events=endinfl, t_eval=N, rtol=1e-8, atol=1e-10)
```
Number of e-folds of inflation now is
```
bgsol.t_events[0][0]-N_i
```
2. Update the arrays storing the cosmological background:
```
logok = bgsol.y[0]
phi = bgsol.y[1]
N = bgsol.t
dphi = np.array([-np.sqrt(6.0 + np.exp(Logok)*(6.0*K -
2.0*np.exp(2.0*t)*V(Phi))) for Logok,Phi,t in zip(logok,phi,N) ])
dlogok = np.array([4.0 + np.exp(Logok)*(4.0*K - 2.0*np.exp(2.0*t)*V(Phi)) for Logok,Phi,t in zip(logok,phi,N) ])
dE_E = dlogok - 4. -2.*dV(phi)*np.exp(logok)*np.exp(2.*N)/dphi
E = 0.5*dphi**2
```
3. Update also the endpoint of integration for each mode:
```
# range of wavevectors
ks = np.concatenate((np.linspace(3,100,98), np.logspace(2,4,500)))
end = np.zeros_like(ks,dtype=int)
endindex = 0
for i in range(len(ks)):
for j in range(endindex,Nbg):
if np.exp(-0.5*logok[j])/ks[i] > 100:
end[i] = j
endindex = j
break
```
4. Solve the MS equation for each $k$. The frequency and the damping term now have non-trivial wavevector-dependence, so we'll compute them on the fly for each mode.
```
closed_spectrum = np.zeros_like(ks,dtype=complex)
for i,k in enumerate(ks):
# Bunch-Davies i.c.
phi_0 = phi[0]
dphi_0 = dphi[0]
ddphi_0 = 0.5*dE_E[0]*dphi_0
N_0 = N_i
x0, dx0 = bdic(k, phi_0, dphi_0, ddphi_0, N_0)
x01 = 1.0
dx01 = 0.0
x02 = 0.0
dx02 = 1.0
# wavenumber "squared"
k2 = complex(k*(k+2.)-3*K)
# Damping term
g = 0.5*(K*np.exp(logok) + 3 - E + dE_E*k2/(E*K+k2))
# frequency
logw = 0.5*(logok + np.log(k2 - K - 2.*K*k2*dE_E/(E*K + k2)))
# Linearly indep. solutions
sol1 = pyoscode.solve(N,logw,g,N_i,N[end[i]],x01,dx01,logw=True)
sol2 = pyoscode.solve(N,logw,g,N_i,N[end[i]],x02,dx02,logw=True)
rk1 = sol1["sol"][-1]
rk2 = sol2["sol"][-1]
closed_spectrum[i] = pps(k, rk1, rk2, x01, dx01, x02, dx02, x0, dx0)
```
Plot the resulting spectrum:
```
plt.loglog(ks, closed_spectrum)
plt.xlabel('comoving $k$')
plt.ylabel('$m^2 \\times P_{\mathcal{R}}(k)$')
plt.show()
```
Note that in the above spectrum, the jaggedness is due to the fact that the values $k$ takes are quantised (integers only).
| true |
code
| 0.585575 | null | null | null | null |
|
```
%load_ext watermark
%watermark -v -p numpy,sklearn,scipy,matplotlib,tensorflow
```
**14장 – 순환 신경망**
_이 노트북은 14장에 있는 모든 샘플 코드와 연습문제 해답을 가지고 있습니다._
# 설정
파이썬 2와 3을 모두 지원합니다. 공통 모듈을 임포트하고 맷플롯립 그림이 노트북 안에 포함되도록 설정하고 생성한 그림을 저장하기 위한 함수를 준비합니다:
```
# 파이썬 2와 파이썬 3 지원
from __future__ import division, print_function, unicode_literals
# 공통
import numpy as np
import os
# 일관된 출력을 위해 유사난수 초기화
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
# 맷플롯립 설정
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# 한글출력
plt.rcParams['font.family'] = 'NanumBarunGothic'
plt.rcParams['axes.unicode_minus'] = False
# 그림을 저장할 폴더
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "rnn"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
텐서플로를 임포트합니다:
```
import tensorflow as tf
```
# 기본 RNN
## 수동으로 RNN 만들기
```
reset_graph()
n_inputs = 3
n_neurons = 5
X0 = tf.placeholder(tf.float32, [None, n_inputs])
X1 = tf.placeholder(tf.float32, [None, n_inputs])
Wx = tf.Variable(tf.random_normal(shape=[n_inputs, n_neurons],dtype=tf.float32))
Wy = tf.Variable(tf.random_normal(shape=[n_neurons,n_neurons],dtype=tf.float32))
b = tf.Variable(tf.zeros([1, n_neurons], dtype=tf.float32))
Y0 = tf.tanh(tf.matmul(X0, Wx) + b)
Y1 = tf.tanh(tf.matmul(Y0, Wy) + tf.matmul(X1, Wx) + b)
init = tf.global_variables_initializer()
import numpy as np
X0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]]) # t = 0
X1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]]) # t = 1
with tf.Session() as sess:
init.run()
Y0_val, Y1_val = sess.run([Y0, Y1], feed_dict={X0: X0_batch, X1: X1_batch})
print(Y0_val)
print(Y1_val)
```
## `static_rnn()`을 사용하여 만들기
```
n_inputs = 3
n_neurons = 5
reset_graph()
X0 = tf.placeholder(tf.float32, [None, n_inputs])
X1 = tf.placeholder(tf.float32, [None, n_inputs])
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
output_seqs, states = tf.contrib.rnn.static_rnn(basic_cell, [X0, X1],
dtype=tf.float32)
Y0, Y1 = output_seqs
init = tf.global_variables_initializer()
X0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]])
X1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]])
with tf.Session() as sess:
init.run()
Y0_val, Y1_val = sess.run([Y0, Y1], feed_dict={X0: X0_batch, X1: X1_batch})
Y0_val
Y1_val
from tensorflow_graph_in_jupyter import show_graph
show_graph(tf.get_default_graph())
```
## 시퀀스 패딩
```
n_steps = 2
n_inputs = 3
n_neurons = 5
reset_graph()
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
X_seqs = tf.unstack(tf.transpose(X, perm=[1, 0, 2]))
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
output_seqs, states = tf.contrib.rnn.static_rnn(basic_cell, X_seqs,
dtype=tf.float32)
outputs = tf.transpose(tf.stack(output_seqs), perm=[1, 0, 2])
init = tf.global_variables_initializer()
X_batch = np.array([
# t = 0 t = 1
[[0, 1, 2], [9, 8, 7]], # 샘플 1
[[3, 4, 5], [0, 0, 0]], # 샘플 2
[[6, 7, 8], [6, 5, 4]], # 샘플 3
[[9, 0, 1], [3, 2, 1]], # 샘플 4
])
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
print(outputs_val)
print(np.transpose(outputs_val, axes=[1, 0, 2])[1])
```
## Using `dynamic_rnn()`
```
n_steps = 2
n_inputs = 3
n_neurons = 5
reset_graph()
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
init = tf.global_variables_initializer()
X_batch = np.array([
[[0, 1, 2], [9, 8, 7]], # instance 1
[[3, 4, 5], [0, 0, 0]], # instance 2
[[6, 7, 8], [6, 5, 4]], # instance 3
[[9, 0, 1], [3, 2, 1]], # instance 4
])
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
print(outputs_val)
show_graph(tf.get_default_graph())
```
## 시퀀스 길이 지정
```
n_steps = 2
n_inputs = 3
n_neurons = 5
reset_graph()
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
seq_length = tf.placeholder(tf.int32, [None])
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32,
sequence_length=seq_length)
init = tf.global_variables_initializer()
X_batch = np.array([
# 스텝 0 스텝 1
[[0, 1, 2], [9, 8, 7]], # 샘플 1
[[3, 4, 5], [0, 0, 0]], # 샘플 2 (0 벡터로 패딩)
[[6, 7, 8], [6, 5, 4]], # 샘플 3
[[9, 0, 1], [3, 2, 1]], # 샘플 4
])
seq_length_batch = np.array([2, 1, 2, 2])
with tf.Session() as sess:
init.run()
outputs_val, states_val = sess.run(
[outputs, states], feed_dict={X: X_batch, seq_length: seq_length_batch})
print(outputs_val)
print(states_val)
```
## 시퀀스 분류기 훈련하기
```
reset_graph()
n_steps = 28
n_inputs = 28
n_neurons = 150
n_outputs = 10
learning_rate = 0.001
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.int32, [None])
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
logits = tf.layers.dense(states, n_outputs)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
logits=logits)
loss = tf.reduce_mean(xentropy)
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
```
주의: `tf.examples.tutorials.mnist`은 삭제될 예정이므로 대신 `tf.keras.datasets.mnist`를 사용하겠습니다.
```
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
X_valid, X_train = X_train[:5000], X_train[5000:]
y_valid, y_train = y_train[:5000], y_train[5000:]
X_test = X_test.reshape((-1, n_steps, n_inputs))
X_valid = X_valid.reshape((-1, n_steps, n_inputs))
def shuffle_batch(X, y, batch_size):
rnd_idx = np.random.permutation(len(X))
n_batches = len(X) // batch_size
for batch_idx in np.array_split(rnd_idx, n_batches):
X_batch, y_batch = X[batch_idx], y[batch_idx]
yield X_batch, y_batch
# from tensorflow.examples.tutorials.mnist import input_data
# mnist = input_data.read_data_sets("/tmp/data/")
# X_test = mnist.test.images.reshape((-1, n_steps, n_inputs))
# y_test = mnist.test.labels
n_epochs = 100
batch_size = 150
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
X_batch = X_batch.reshape((-1, n_steps, n_inputs))
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_valid = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "배치 데이터 정확도:", acc_batch, "검증 세트 정확도:", acc_valid)
```
# 다층 RNN
```
reset_graph()
n_steps = 28
n_inputs = 28
n_outputs = 10
learning_rate = 0.001
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.int32, [None])
n_neurons = 100
n_layers = 3
layers = [tf.contrib.rnn.BasicRNNCell(num_units=n_neurons,
activation=tf.nn.relu)
for layer in range(n_layers)]
multi_layer_cell = tf.contrib.rnn.MultiRNNCell(layers)
outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)
states_concat = tf.concat(axis=1, values=states)
logits = tf.layers.dense(states_concat, n_outputs)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy)
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
n_epochs = 10
batch_size = 150
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
X_batch = X_batch.reshape((-1, n_steps, n_inputs))
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_valid = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "배치 데이터 정확도:", acc_batch, "검증 세트 정확도:", acc_valid)
```
# 시계열
```
t_min, t_max = 0, 30
resolution = 0.1
def time_series(t):
return t * np.sin(t) / 3 + 2 * np.sin(t*5)
def next_batch(batch_size, n_steps):
t0 = np.random.rand(batch_size, 1) * (t_max - t_min - n_steps * resolution)
Ts = t0 + np.arange(0., n_steps + 1) * resolution
ys = time_series(Ts)
return ys[:, :-1].reshape(-1, n_steps, 1), ys[:, 1:].reshape(-1, n_steps, 1)
t = np.linspace(t_min, t_max, int((t_max - t_min) / resolution))
n_steps = 20
t_instance = np.linspace(12.2, 12.2 + resolution * (n_steps + 1), n_steps + 1)
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.title("시계열 데이터 (인공 생성)", fontsize=14)
plt.plot(t, time_series(t), label=r"$t . \sin(t) / 3 + 2 . \sin(5t)$")
plt.plot(t_instance[:-1], time_series(t_instance[:-1]), "b-", linewidth=3, label="훈련 샘플")
plt.legend(loc="lower left", fontsize=14)
plt.axis([0, 30, -17, 13])
plt.xlabel("시간")
plt.ylabel("값", rotation=0)
plt.subplot(122)
plt.title("훈련 샘플", fontsize=14)
plt.plot(t_instance[:-1], time_series(t_instance[:-1]), "bo", markersize=12, label="샘플")
plt.plot(t_instance[1:], time_series(t_instance[1:]), "w*", markeredgewidth=0.5, markeredgecolor="b", markersize=14, label="타깃")
plt.legend(loc="upper left")
plt.xlabel("시간")
save_fig("time_series_plot")
plt.show()
X_batch, y_batch = next_batch(1, n_steps)
np.c_[X_batch[0], y_batch[0]]
```
## `OuputProjectionWrapper` 사용하기
RNN 하나를 만들어 보겠습니다. 이 신경망은 100개의 순환 뉴런을 가지고 있고 각 훈련 샘플은 20개의 입력 길이로 구성되므로 20개의 타임 스텝에 펼칠 것입니다. 각 입력은 하나의 특성을 가집니다(각 시간에서의 값 하나). 타깃도 20개의 입력 시퀀스이고 하나의 값을 가집니다:
```
reset_graph()
n_steps = 20
n_inputs = 1
n_neurons = 100
n_outputs = 1
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])
cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons, activation=tf.nn.relu)
outputs, states = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)
```
각 타임 스텝에서 크기가 100인 출력 벡터가 만들어 집니다. 하지만 각 타임 스텝에서 하나의 출력 값을 원합니다. 간단한 방법은 `OutputProjectionWrapper`로 셀을 감싸는 것입니다.
```
reset_graph()
n_steps = 20
n_inputs = 1
n_neurons = 100
n_outputs = 1
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])
cell = tf.contrib.rnn.OutputProjectionWrapper(
tf.contrib.rnn.BasicRNNCell(num_units=n_neurons, activation=tf.nn.relu),
output_size=n_outputs)
outputs, states = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)
learning_rate = 0.001
loss = tf.reduce_mean(tf.square(outputs - y)) # MSE
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_iterations = 1500
batch_size = 50
with tf.Session() as sess:
init.run()
for iteration in range(n_iterations):
X_batch, y_batch = next_batch(batch_size, n_steps)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
if iteration % 100 == 0:
mse = loss.eval(feed_dict={X: X_batch, y: y_batch})
print(iteration, "\tMSE:", mse)
saver.save(sess, "./my_time_series_model") # not shown in the book
with tf.Session() as sess: # 책에는 없음
saver.restore(sess, "./my_time_series_model") # 책에는 없음
X_new = time_series(np.array(t_instance[:-1].reshape(-1, n_steps, n_inputs)))
y_pred = sess.run(outputs, feed_dict={X: X_new})
y_pred
plt.title("모델 테스트", fontsize=14)
plt.plot(t_instance[:-1], time_series(t_instance[:-1]), "bo", markersize=12, label="샘플")
plt.plot(t_instance[1:], time_series(t_instance[1:]), "w*", markeredgewidth=0.5, markeredgecolor="b", markersize=14, label="타깃")
plt.plot(t_instance[1:], y_pred[0,:,0], "r.", markersize=10, label="예측")
plt.legend(loc="upper left")
plt.xlabel("시간")
save_fig("time_series_pred_plot")
plt.show()
```
## `OutputProjectionWrapper` 사용하지 않기
```
reset_graph()
n_steps = 20
n_inputs = 1
n_neurons = 100
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])
cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons, activation=tf.nn.relu)
rnn_outputs, states = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)
n_outputs = 1
learning_rate = 0.001
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurons])
stacked_outputs = tf.layers.dense(stacked_rnn_outputs, n_outputs)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])
loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_iterations = 1500
batch_size = 50
with tf.Session() as sess:
init.run()
for iteration in range(n_iterations):
X_batch, y_batch = next_batch(batch_size, n_steps)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
if iteration % 100 == 0:
mse = loss.eval(feed_dict={X: X_batch, y: y_batch})
print(iteration, "\tMSE:", mse)
X_new = time_series(np.array(t_instance[:-1].reshape(-1, n_steps, n_inputs)))
y_pred = sess.run(outputs, feed_dict={X: X_new})
saver.save(sess, "./my_time_series_model")
y_pred
plt.title("모델 테스트", fontsize=14)
plt.plot(t_instance[:-1], time_series(t_instance[:-1]), "bo", markersize=10, label="instance")
plt.plot(t_instance[1:], time_series(t_instance[1:]), "w*", markersize=10, label="target")
plt.plot(t_instance[1:], y_pred[0,:,0], "r.", markersize=10, label="prediction")
plt.legend(loc="upper left")
plt.xlabel("시간")
plt.show()
```
## 새로운 시퀀스 생성하기
```
with tf.Session() as sess: # 책에는 없음
saver.restore(sess, "./my_time_series_model") # 책에는 없음
sequence = [0.] * n_steps
for iteration in range(300):
X_batch = np.array(sequence[-n_steps:]).reshape(1, n_steps, 1)
y_pred = sess.run(outputs, feed_dict={X: X_batch})
sequence.append(y_pred[0, -1, 0])
plt.figure(figsize=(8,4))
plt.plot(np.arange(len(sequence)), sequence, "b-")
plt.plot(t[:n_steps], sequence[:n_steps], "b-", linewidth=3)
plt.xlabel("시간")
plt.ylabel("값")
plt.show()
with tf.Session() as sess:
saver.restore(sess, "./my_time_series_model")
sequence1 = [0. for i in range(n_steps)]
for iteration in range(len(t) - n_steps):
X_batch = np.array(sequence1[-n_steps:]).reshape(1, n_steps, 1)
y_pred = sess.run(outputs, feed_dict={X: X_batch})
sequence1.append(y_pred[0, -1, 0])
sequence2 = [time_series(i * resolution + t_min + (t_max-t_min/3)) for i in range(n_steps)]
for iteration in range(len(t) - n_steps):
X_batch = np.array(sequence2[-n_steps:]).reshape(1, n_steps, 1)
y_pred = sess.run(outputs, feed_dict={X: X_batch})
sequence2.append(y_pred[0, -1, 0])
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.plot(t, sequence1, "b-")
plt.plot(t[:n_steps], sequence1[:n_steps], "b-", linewidth=3)
plt.xlabel("시간")
plt.ylabel("값", rotation=0)
plt.subplot(122)
plt.plot(t, sequence2, "b-")
plt.plot(t[:n_steps], sequence2[:n_steps], "b-", linewidth=3)
plt.xlabel("시간")
save_fig("creative_sequence_plot")
plt.show()
```
# 심층 RNN
## MultiRNNCell
```
reset_graph()
n_inputs = 2
n_steps = 5
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
n_neurons = 100
n_layers = 3
layers = [tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
for layer in range(n_layers)]
multi_layer_cell = tf.contrib.rnn.MultiRNNCell(layers)
outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)
init = tf.global_variables_initializer()
X_batch = np.random.rand(2, n_steps, n_inputs)
with tf.Session() as sess:
init.run()
outputs_val, states_val = sess.run([outputs, states], feed_dict={X: X_batch})
outputs_val.shape
```
## 여러 GPU에 심층 RNN 분산하기
이렇게 사용해서는 **안됩니다**:
```
with tf.device("/gpu:0"): # 이 할당은 무시됩니다
layer1 = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
with tf.device("/gpu:1"): # 이 할당은 무시됩니다
layer2 = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
```
대신 `DeviceCellWrapper`를 사용합니다:
```
import tensorflow as tf
class DeviceCellWrapper(tf.contrib.rnn.RNNCell):
def __init__(self, device, cell):
self._cell = cell
self._device = device
@property
def state_size(self):
return self._cell.state_size
@property
def output_size(self):
return self._cell.output_size
def __call__(self, inputs, state, scope=None):
with tf.device(self._device):
return self._cell(inputs, state, scope)
reset_graph()
n_inputs = 5
n_steps = 20
n_neurons = 100
X = tf.placeholder(tf.float32, shape=[None, n_steps, n_inputs])
devices = ["/cpu:0", "/cpu:0", "/cpu:0"] # 만약 GPU가 세 개 있다면 ["/gpu:0", "/gpu:1", "/gpu:2"]로 바꿉니다
cells = [DeviceCellWrapper(dev,tf.contrib.rnn.BasicRNNCell(num_units=n_neurons))
for dev in devices]
multi_layer_cell = tf.contrib.rnn.MultiRNNCell(cells)
outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)
```
또 다른 방법으로 텐서플로 1.1부터 `tf.contrib.rnn.DeviceWrapper` 클래스를 사용할 수 있습니다(텐서플로 1.2부터는 `tf.nn.rnn_cell.DeviceWrapper`가 되었습니다).
```
init = tf.global_variables_initializer()
with tf.Session() as sess:
init.run()
print(sess.run(outputs, feed_dict={X: np.random.rand(2, n_steps, n_inputs)}))
```
## 드롭아웃
```
reset_graph()
n_inputs = 1
n_neurons = 100
n_layers = 3
n_steps = 20
n_outputs = 1
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])
```
노트: `input_keep_prob` 매개변수는 플레이스홀더로 훈련하는 동안에는 어느 값이나 가능하고 테스트할 때는 1.0으로 지정합니다(드롭아웃을 끕니다).
```
keep_prob = tf.placeholder_with_default(1.0, shape=())
cells = [tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
for layer in range(n_layers)]
cells_drop = [tf.contrib.rnn.DropoutWrapper(cell, input_keep_prob=keep_prob)
for cell in cells]
multi_layer_cell = tf.contrib.rnn.MultiRNNCell(cells_drop)
rnn_outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32)
learning_rate = 0.01
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurons])
stacked_outputs = tf.layers.dense(stacked_rnn_outputs, n_outputs)
outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])
loss = tf.reduce_mean(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_iterations = 1500
batch_size = 50
train_keep_prob = 0.5
with tf.Session() as sess:
init.run()
for iteration in range(n_iterations):
X_batch, y_batch = next_batch(batch_size, n_steps)
_, mse = sess.run([training_op, loss],
feed_dict={X: X_batch, y: y_batch,
keep_prob: train_keep_prob})
if iteration % 100 == 0: # not shown in the book
print(iteration, "훈련 MSE:", mse) # not shown
saver.save(sess, "./my_dropout_time_series_model")
with tf.Session() as sess:
saver.restore(sess, "./my_dropout_time_series_model")
X_new = time_series(np.array(t_instance[:-1].reshape(-1, n_steps, n_inputs)))
y_pred = sess.run(outputs, feed_dict={X: X_new})
plt.title("모델 테스트", fontsize=14)
plt.plot(t_instance[:-1], time_series(t_instance[:-1]), "bo", markersize=10, label="instance")
plt.plot(t_instance[1:], time_series(t_instance[1:]), "w*", markersize=10, label="target")
plt.plot(t_instance[1:], y_pred[0,:,0], "r.", markersize=10, label="prediction")
plt.legend(loc="upper left")
plt.xlabel("시간")
plt.show()
```
이런 드롭아웃이 이 경우엔 크게 도움이 안되네요. :/
# LSTM
```
reset_graph()
lstm_cell = tf.contrib.rnn.BasicLSTMCell(num_units=n_neurons)
n_steps = 28
n_inputs = 28
n_neurons = 150
n_outputs = 10
n_layers = 3
learning_rate = 0.001
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.int32, [None])
lstm_cells = [tf.contrib.rnn.BasicLSTMCell(num_units=n_neurons)
for layer in range(n_layers)]
multi_cell = tf.contrib.rnn.MultiRNNCell(lstm_cells)
outputs, states = tf.nn.dynamic_rnn(multi_cell, X, dtype=tf.float32)
top_layer_h_state = states[-1][1]
logits = tf.layers.dense(top_layer_h_state, n_outputs, name="softmax")
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
states
top_layer_h_state
n_epochs = 10
batch_size = 150
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
X_batch = X_batch.reshape((-1, n_steps, n_inputs))
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_valid = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print("에포크", epoch, "배치 데이터 정확도 =", acc_batch, "검증 세트 정확도 =", acc_valid)
acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})
print("테스트 세트 정확도 =", acc_test)
lstm_cell = tf.contrib.rnn.LSTMCell(num_units=n_neurons, use_peepholes=True)
gru_cell = tf.contrib.rnn.GRUCell(num_units=n_neurons)
```
# 임베딩
이 섹션은 텐서플로의 [Word2Vec 튜토리얼](https://www.tensorflow.org/versions/r0.11/tutorials/word2vec/index.html)을 기반으로 합니다.
## 데이터 추출
```
from six.moves import urllib
import errno
import os
import zipfile
WORDS_PATH = "datasets/words"
WORDS_URL = 'http://mattmahoney.net/dc/text8.zip'
def mkdir_p(path):
"""디렉토리 생성, 이미 있다면 그냥 통과
이 함수는 파이썬 2 버전을 지원하기 위해서입니다.
파이썬 3.2 이상이면 다음과 같이 쓸 수 있습니다:
>>> os.makedirs(path, exist_ok=True)
"""
try:
os.makedirs(path)
except OSError as exc:
if exc.errno == errno.EEXIST and os.path.isdir(path):
pass
else:
raise
def fetch_words_data(words_url=WORDS_URL, words_path=WORDS_PATH):
os.makedirs(words_path, exist_ok=True)
zip_path = os.path.join(words_path, "words.zip")
if not os.path.exists(zip_path):
urllib.request.urlretrieve(words_url, zip_path)
with zipfile.ZipFile(zip_path) as f:
data = f.read(f.namelist()[0])
return data.decode("ascii").split()
words = fetch_words_data()
words[:5]
```
## 사전 구축
```
from collections import Counter
vocabulary_size = 50000
vocabulary = [("UNK", None)] + Counter(words).most_common(vocabulary_size - 1)
vocabulary = np.array([word for word, _ in vocabulary])
dictionary = {word: code for code, word in enumerate(vocabulary)}
data = np.array([dictionary.get(word, 0) for word in words])
" ".join(words[:9]), data[:9]
" ".join([vocabulary[word_index] for word_index in [5241, 3081, 12, 6, 195, 2, 3134, 46, 59]])
words[24], data[24]
```
## 배치 생성
```
import random
from collections import deque
def generate_batch(batch_size, num_skips, skip_window):
global data_index
assert batch_size % num_skips == 0
assert num_skips <= 2 * skip_window
batch = np.ndarray(shape=(batch_size), dtype=np.int32)
labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32)
span = 2 * skip_window + 1 # [ skip_window target skip_window ]
buffer = deque(maxlen=span)
for _ in range(span):
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
for i in range(batch_size // num_skips):
target = skip_window # buffer 중간에 타깃 레이블을 둡니다
targets_to_avoid = [ skip_window ]
for j in range(num_skips):
while target in targets_to_avoid:
target = random.randint(0, span - 1)
targets_to_avoid.append(target)
batch[i * num_skips + j] = buffer[skip_window]
labels[i * num_skips + j, 0] = buffer[target]
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
return batch, labels
data_index=0
batch, labels = generate_batch(8, 2, 1)
batch, [vocabulary[word] for word in batch]
labels, [vocabulary[word] for word in labels[:, 0]]
```
## 모델 구성
```
batch_size = 128
embedding_size = 128 # 임베딩 벡터 차원
skip_window = 1 # 고려할 왼쪽과 오른쪽 단어의 개수
num_skips = 2 # 레이블을 생성하기 위한 입력의 재사용 횟수
# 가까운 이웃을 샘플링하기 위해 랜덤한 검증 세트를 만듭니다.
# 검증 샘플은 가장 흔한 단어인 낮은 ID 번호를 가진 것으로 제한합니다.
valid_size = 16 # 유사도를 평가하기 위해 랜덤하게 구성할 단어 세트 크기
valid_window = 100 # 검증 샘플을 전체 샘플의 앞 부분에서만 선택합니다
valid_examples = np.random.choice(valid_window, valid_size, replace=False)
num_sampled = 64 # 부정 샘플링(negative sampling)의 수
learning_rate = 0.01
reset_graph()
# 입력 데이터
train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1])
valid_dataset = tf.constant(valid_examples, dtype=tf.int32)
vocabulary_size = 50000
embedding_size = 150
# 입력을 위해 임베딩을 조회합니다
init_embeds = tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0)
embeddings = tf.Variable(init_embeds)
train_inputs = tf.placeholder(tf.int32, shape=[None])
embed = tf.nn.embedding_lookup(embeddings, train_inputs)
# NCE 손실을 위한 변수를 만듭니다
nce_weights = tf.Variable(
tf.truncated_normal([vocabulary_size, embedding_size],
stddev=1.0 / np.sqrt(embedding_size)))
nce_biases = tf.Variable(tf.zeros([vocabulary_size]))
# 배치에서 NCE 손실의 평균을 계산합니다.Compute the average NCE loss for the batch.
# tf.nce_loss는 자동으로 손실을 평가할 때마다 음성 레이블에서 새로운 샘플을 뽑습니다.
loss = tf.reduce_mean(
tf.nn.nce_loss(nce_weights, nce_biases, train_labels, embed,
num_sampled, vocabulary_size))
# Adam 옵티마이저
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
# 미니배치 샘플과 모든 임베딩 사이의 코사인 유사도를 계산합니다
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), axis=1, keepdims=True))
normalized_embeddings = embeddings / norm
valid_embeddings = tf.nn.embedding_lookup(normalized_embeddings, valid_dataset)
similarity = tf.matmul(valid_embeddings, normalized_embeddings, transpose_b=True)
# 초기화를 위한 연산
init = tf.global_variables_initializer()
```
## 모델 훈련
```
num_steps = 10001
with tf.Session() as session:
init.run()
average_loss = 0
for step in range(num_steps):
print("\r반복: {}".format(step), end="\t")
batch_inputs, batch_labels = generate_batch(batch_size, num_skips, skip_window)
feed_dict = {train_inputs : batch_inputs, train_labels : batch_labels}
# 훈련 연산을 평가하여 스텝을 한 단계를 업데이트합니다(session.run()에서 반환된 값을 사용합니다)
_, loss_val = session.run([training_op, loss], feed_dict=feed_dict)
average_loss += loss_val
if step % 2000 == 0:
if step > 0:
average_loss /= 2000
# 평균 손실은 2000개 배치에 대한 손실의 추정입니다.
print("스텝 ", step, "에서의 평균 손실: ", average_loss)
average_loss = 0
# 이 코드는 비용이 많이 듭니다 (500 스텝마다 ~20%씩 느려집니다)
if step % 10000 == 0:
sim = similarity.eval()
for i in range(valid_size):
valid_word = vocabulary[valid_examples[i]]
top_k = 8 # 가장 가까운 단어의 개수
nearest = (-sim[i, :]).argsort()[1:top_k+1]
log_str = "%s에 가장 가까운 단어:" % valid_word
for k in range(top_k):
close_word = vocabulary[nearest[k]]
log_str = "%s %s," % (log_str, close_word)
print(log_str)
final_embeddings = normalized_embeddings.eval()
```
마지막 임베딩을 저장합니다(물론 텐서플로의 `Saver`를 사용해도 됩니다):
```
np.save("./my_final_embeddings.npy", final_embeddings)
```
## 임베딩 그래프
```
def plot_with_labels(low_dim_embs, labels):
assert low_dim_embs.shape[0] >= len(labels), "임베딩보다 레이블이 많습니다."
plt.figure(figsize=(18, 18)) # 인치 크기
for i, label in enumerate(labels):
x, y = low_dim_embs[i,:]
plt.scatter(x, y)
plt.annotate(label,
xy=(x, y),
xytext=(5, 2),
textcoords='offset points',
ha='right',
va='bottom')
from sklearn.manifold import TSNE
tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000)
plot_only = 500
low_dim_embs = tsne.fit_transform(final_embeddings[:plot_only,:])
labels = [vocabulary[i] for i in range(plot_only)]
plot_with_labels(low_dim_embs, labels)
```
# 기계 번역
`basic_rnn_seq2seq()` 함수는 간단한 인코더/디코더 모델을 만듭니다. 먼저 `encoder_inputs`를 상태 벡터로 인코딩하는 RNN을 실행하고 그다음 `decoder_inputs`을 마지막 인코더 상태로 초기화시킨 디코더를 실행합니다. 인코더와 디코더는 같은 RNN 셀 타입을 사용하지만 파라미터를 공유하지는 않습니다.
```
import tensorflow as tf
reset_graph()
n_steps = 50
n_neurons = 200
n_layers = 3
num_encoder_symbols = 20000
num_decoder_symbols = 20000
embedding_size = 150
learning_rate = 0.01
X = tf.placeholder(tf.int32, [None, n_steps]) # 영어 문장
Y = tf.placeholder(tf.int32, [None, n_steps]) # 프랑스어 번역
W = tf.placeholder(tf.float32, [None, n_steps - 1, 1])
Y_input = Y[:, :-1]
Y_target = Y[:, 1:]
encoder_inputs = tf.unstack(tf.transpose(X)) # 1D 텐서의 리스트
decoder_inputs = tf.unstack(tf.transpose(Y_input)) # 1D 텐서의 리스트
lstm_cells = [tf.contrib.rnn.BasicLSTMCell(num_units=n_neurons)
for layer in range(n_layers)]
cell = tf.contrib.rnn.MultiRNNCell(lstm_cells)
output_seqs, states = tf.contrib.legacy_seq2seq.embedding_rnn_seq2seq(
encoder_inputs,
decoder_inputs,
cell,
num_encoder_symbols,
num_decoder_symbols,
embedding_size)
logits = tf.transpose(tf.unstack(output_seqs), perm=[1, 0, 2])
logits_flat = tf.reshape(logits, [-1, num_decoder_symbols])
Y_target_flat = tf.reshape(Y_target, [-1])
W_flat = tf.reshape(W, [-1])
xentropy = W_flat * tf.nn.sparse_softmax_cross_entropy_with_logits(labels=Y_target_flat, logits=logits_flat)
loss = tf.reduce_mean(xentropy)
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
```
# 연습문제 해답
## 1. to 6.
부록 A 참조.
## 7. 임베딩된 레버(Reber) 문법
먼저 문법에 맞는 문자열을 생성하는 함수가 필요합니다. 이 문법은 각 상태에서 가능한 전이 상태의 리스트입니다. 하나의 전이는 출력할 문자열(또는 생성할 문법)과 다음 상태를 지정합니다.
```
from random import choice, seed
# 일관된 출력을 위한 유사난수 초기화
seed(42)
np.random.seed(42)
default_reber_grammar = [
[("B", 1)], # (상태 0) =B=>(상태 1)
[("T", 2), ("P", 3)], # (상태 1) =T=>(상태 2) or =P=>(상태 3)
[("S", 2), ("X", 4)], # (상태 2) =S=>(상태 2) or =X=>(상태 4)
[("T", 3), ("V", 5)], # 등등..
[("X", 3), ("S", 6)],
[("P", 4), ("V", 6)],
[("E", None)]] # (상태 6) =E=>(종료 상태)
embedded_reber_grammar = [
[("B", 1)],
[("T", 2), ("P", 3)],
[(default_reber_grammar, 4)],
[(default_reber_grammar, 5)],
[("T", 6)],
[("P", 6)],
[("E", None)]]
def generate_string(grammar):
state = 0
output = []
while state is not None:
production, state = choice(grammar[state])
if isinstance(production, list):
production = generate_string(grammar=production)
output.append(production)
return "".join(output)
```
기본 레버 문법에 맞는 문자열을 몇 개 만들어 보겠습니다:
```
for _ in range(25):
print(generate_string(default_reber_grammar), end=" ")
```
좋습니다. 이제 임베딩된 레버 문법에 맞는 문자열을 몇 개 만들어 보겠습니다:
```
for _ in range(25):
print(generate_string(embedded_reber_grammar), end=" ")
```
좋네요, 이제 이 문법을 따르지 않는 문자열을 생성할 함수를 만듭니다. 무작위하게 문자열을 만들 수 있지만 그렇게 하면 너무 문제가 쉬워지므로 대신 문법을 따르는 문자열을 만든 후 하나의 문자만 바꾸어 놓도록 하겠습니다:
```
def generate_corrupted_string(grammar, chars="BEPSTVX"):
good_string = generate_string(grammar)
index = np.random.randint(len(good_string))
good_char = good_string[index]
bad_char = choice(list(set(chars) - set(good_char)))
return good_string[:index] + bad_char + good_string[index + 1:]
```
잘못된 문자열 몇 개를 만들어 보죠:
```
for _ in range(25):
print(generate_corrupted_string(embedded_reber_grammar), end=" ")
```
문자열을 바로 RNN에 주입할 수는 없습니다. 먼저 벡터의 연속으로 바꾸어야 합니다. 각 벡터는 원-핫 인코딩을 사용하여 하나의 문자를 나타냅니다. 예를 들어, 벡터 `[1, 0, 0, 0, 0, 0, 0]`는 문자 "B"를 나타내고 벡터 `[0, 1, 0, 0, 0, 0, 0]`는 문자 "E"를 나타내는 식입니다. 이런 원-핫 벡터의 연속으로 문자열을 바꾸는 함수를 작성해 보겠습니다. 문자열이 `n_steps`보다 짧으면 0 벡터로 패딩됩니다(나중에, 텐서플로에게 각 문자열의 실제 길이를 `sequence_length` 매개변수로 전달할 것입니다).
```
def string_to_one_hot_vectors(string, n_steps, chars="BEPSTVX"):
char_to_index = {char: index for index, char in enumerate(chars)}
output = np.zeros((n_steps, len(chars)), dtype=np.int32)
for index, char in enumerate(string):
output[index, char_to_index[char]] = 1.
return output
string_to_one_hot_vectors("BTBTXSETE", 12)
```
이제 50%는 올바른 문자열 50%는 잘못된 문자열로 이루어진 데이터셋을 만듭니다:
```
def generate_dataset(size):
good_strings = [generate_string(embedded_reber_grammar)
for _ in range(size // 2)]
bad_strings = [generate_corrupted_string(embedded_reber_grammar)
for _ in range(size - size // 2)]
all_strings = good_strings + bad_strings
n_steps = max([len(string) for string in all_strings])
X = np.array([string_to_one_hot_vectors(string, n_steps)
for string in all_strings])
seq_length = np.array([len(string) for string in all_strings])
y = np.array([[1] for _ in range(len(good_strings))] +
[[0] for _ in range(len(bad_strings))])
rnd_idx = np.random.permutation(size)
return X[rnd_idx], seq_length[rnd_idx], y[rnd_idx]
X_train, l_train, y_train = generate_dataset(10000)
```
첫 번째 훈련 샘플을 확인해 보겠습니다:
```
X_train[0]
```
데이터셋에서 가장 긴 문자열 때문에 패딩된 0 벡터가 많습니다. 문자열 길이가 얼마나 될까요?
```
l_train[0]
```
타깃 클래스는?
```
y_train[0]
```
아주 좋습니다! 올바른 문자열을 구분할 RNN을 만들 준비가 되었습니다. 앞서 MNIST 이미지를 분류하기 위해 만든 것과 매우 비슷한 시퀀스 분류기를 만듭니다. 차이점은 다음 두 가지입니다:
* 첫째, 입력 문자열이 가변 길이이므로 `dynamic_rnn()` 함수를 호출할 때 `sequence_length`를 지정해야 합니다.
* 둘째, 이진 분류기이므로 출력 뉴런은 하나만 필요합니다. 이 뉴런은 각 문자열에 대해 올바른 문자열일 추정 로그 확률을 출력할 것입니다. 다중 클래스 분류에서는 `sparse_softmax_cross_entropy_with_logits()`를 사용했지만 이진 분류에서는 `sigmoid_cross_entropy_with_logits()`를 사용합니다.
```
reset_graph()
possible_chars = "BEPSTVX"
n_inputs = len(possible_chars)
n_neurons = 30
n_outputs = 1
learning_rate = 0.02
momentum = 0.95
X = tf.placeholder(tf.float32, [None, None, n_inputs], name="X")
seq_length = tf.placeholder(tf.int32, [None], name="seq_length")
y = tf.placeholder(tf.float32, [None, 1], name="y")
gru_cell = tf.contrib.rnn.GRUCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(gru_cell, X, dtype=tf.float32,
sequence_length=seq_length)
logits = tf.layers.dense(states, n_outputs, name="logits")
y_pred = tf.cast(tf.greater(logits, 0.), tf.float32, name="y_pred")
y_proba = tf.nn.sigmoid(logits, name="y_proba")
xentropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate,
momentum=momentum,
use_nesterov=True)
training_op = optimizer.minimize(loss)
correct = tf.equal(y_pred, y, name="correct")
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
init = tf.global_variables_initializer()
saver = tf.train.Saver()
```
훈련하는 동안 진척 상황을 확인할 수 있도록 검증 세트를 만듭니다:
```
X_val, l_val, y_val = generate_dataset(5000)
n_epochs = 50
batch_size = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
X_batches = np.array_split(X_train, len(X_train) // batch_size)
l_batches = np.array_split(l_train, len(l_train) // batch_size)
y_batches = np.array_split(y_train, len(y_train) // batch_size)
for X_batch, l_batch, y_batch in zip(X_batches, l_batches, y_batches):
loss_val, _ = sess.run(
[loss, training_op],
feed_dict={X: X_batch, seq_length: l_batch, y: y_batch})
acc_train = accuracy.eval(feed_dict={X: X_batch, seq_length: l_batch, y: y_batch})
acc_val = accuracy.eval(feed_dict={X: X_val, seq_length: l_val, y: y_val})
print("{:4d} 훈련 손실: {:.4f}, 정확도: {:.2f}% 검증 세트 정확도: {:.2f}%".format(
epoch, loss_val, 100 * acc_train, 100 * acc_val))
saver.save(sess, "./my_reber_classifier")
```
이제 두 개의 문자열에 이 RNN을 테스트해 보죠. 첫 번째는 잘못된 것이고 두 번째는 올바른 것입니다. 이 문자열은 마지막에서 두 번째 글자만 다릅니다. RNN이 이를 맞춘다면 두 번째 문자가 항상 끝에서 두 번째 문자와 같아야 한다는 패턴을 알게 됐다는 것을 의미합니다. 이렇게 하려면 꽤 긴 단기 기억(long short-term memory)이 필요합니다(그래서 GRU 셀을 사용했습니다).
```
test_strings = [
"BPBTSSSSSSSSSSSSXXTTTTTVPXTTVPXTTTTTTTVPXVPXVPXTTTVVETE",
"BPBTSSSSSSSSSSSSXXTTTTTVPXTTVPXTTTTTTTVPXVPXVPXTTTVVEPE"]
l_test = np.array([len(s) for s in test_strings])
max_length = l_test.max()
X_test = [string_to_one_hot_vectors(s, n_steps=max_length)
for s in test_strings]
with tf.Session() as sess:
saver.restore(sess, "./my_reber_classifier")
y_proba_val = y_proba.eval(feed_dict={X: X_test, seq_length: l_test})
print()
print("레버 문자열일 추정 확률:")
for index, string in enumerate(test_strings):
print("{}: {:.2f}%".format(string, 100 * y_proba_val[index][0]))
```
쨘! 잘 작동하네요. 이 RNN이 완벽한 신뢰도로 정확한 답을 냈습니다. :)
## 8. 과 9.
Coming soon...
| true |
code
| 0.607081 | null | null | null | null |
|
# Discrete Bayes Animations
```
from __future__ import division, print_function
import matplotlib.pyplot as plt
import sys
sys.path.insert(0,'..') # allow us to format the book
sys.path.insert(0,'../code')
import book_format
book_format.load_style(directory='..')
```
This notebook creates the animations for the Discrete Bayesian filters chapter. It is not really intended to be a readable part of the book, but of course you are free to look at the source code, and even modify it. However, if you are interested in running your own animations, I'll point you to the examples subdirectory of the book, which contains a number of python scripts that you can run and modify from an IDE or the command line. This module saves the animations to GIF files, which is quite slow and not very interactive.
```
from matplotlib import animation
import matplotlib.pyplot as plt
import numpy as np
from book_plots import bar_plot
%matplotlib inline
# the predict algorithm of the discrete bayesian filter
def predict(pos, move, p_correct, p_under, p_over):
n = len(pos)
result = np.array(pos, dtype=float)
for i in range(n):
result[i] = \
pos[(i-move) % n] * p_correct + \
pos[(i-move-1) % n] * p_over + \
pos[(i-move+1) % n] * p_under
return result
def normalize(p):
s = sum(p)
for i in range (len(p)):
p[i] = p[i] / s
# the update algorithm of the discrete bayesian filter
def update(pos, measure, p_hit, p_miss):
q = np.array(pos, dtype=float)
for i in range(len(hallway)):
if hallway[i] == measure:
q[i] = pos[i] * p_hit
else:
q[i] = pos[i] * p_miss
normalize(q)
return q
import matplotlib
# make sure our matplotlibrc has been edited to use imagemagick
matplotlib.matplotlib_fname()
matplotlib.rcParams['animation.writer']
from gif_animate import animate
pos = [1.0,0,0,0,0,0,0,0,0,0]
def bar_animate(nframe):
global pos
bar_plot(pos)
plt.title('Step {}'.format(nframe + 1))
pos = predict(pos, 1, .8, .1, .1)
for i in range(10):
bar_animate(i)
fig = plt.figure(figsize=(6.5, 2.5))
animate('02_no_info.gif', bar_animate, fig=fig, frames=75, interval=75);
```
<img src="02_no_info.gif">
```
pos = np.array([.1]*10)
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])
def bar_animate(nframe):
global pos
#if nframe == 0:
# return
bar_plot(pos, ylim=(0,1.0))
plt.title('Step {}'.format(nframe + 1))
if nframe % 2 == 0:
pos = predict(pos, 1, .9, .05, .05)
else:
x = int((nframe/2) % len(hallway))
z = hallway[x]
pos = update(pos, z, .9, .2)
fig = plt.figure(figsize=(6.5, 2.5))
animate('02_simulate.gif', bar_animate, fig=fig, frames=40, interval=85);
```
<img src="02_simulate.gif">
| true |
code
| 0.487429 | null | null | null | null |
|
# nn explain
nn has two main parts : data and model components
containers are responsible for model components and parameters/buffers are responsible for model data
containers : Module, Sequential, ModuleList, ModuleDict, ParameterList, ParameterDict for module construction
parameters : parameter(...) for model training
buffers : parameter(...) for model aux
```
import torch
import torch.nn as nn
```
## 0.parameters and buffers
**parameter is just tensor with requires_grad=True and have their own space in model.parameters() and model ordered list**
**buffer is just tensor with requires_grad=True/False and have their own space in model.buffers() and model ordered list**
In one model,
parameter needs to backward and be updated by optimizer.step
buffer needs to be used in backward but not be updated by optimizer.step
both of these data are responsible for the whole module, thus they would be saved by model.state_dict() in form of OrderDict. Moreover, they would be loaded by model.load_state_dict(...)
nn.Parameter(...) should be used in the __init__ function in order to have init para at the first place.
```
class test(nn.Module):
def __init__(self):
super(test, self).__init__()
self.a = nn.Parameter(torch.randn(4,4))
self.linear = nn.Linear(4,5)
self.tensor_test = torch.rand((1,1), requires_grad=True)
print("Not added in nn.Module parameters : {}".format(self.tensor_test))
model = test()
print(model)
for para in model.parameters():
print(para)
class MyModule(nn.Module):
def __init__(self):
super(MyModule, self).__init__()
# fist way to have a parameter
# self.x = nn.Parameter(...) directly add one var into OrderDict
self.param1 = nn.Parameter(torch.tensor(1.))
# second way to have a parameter
# x = nn.Parameter(...) and self.register_parameter() in order to add normal parameter into OrderDict
param2 = nn.Parameter(torch.tensor(2.))
self.register_parameter('param2', param2)
# the only way to have buffer
# self.register_buffer in order to add normal tensor into OrderDict
buff = torch.tensor(3.)
self.register_buffer('buffer', buff)
def forward(self, x):
# ParameterList can act as an iterable, or be indexed using ints
x = self.param1
y = self.param2
z = torch.mm(x,y)
return z
model = MyModule()
print("=====para=====")
for para in model.parameters():
print(para)
print("=====buff=====")
for buff in model.buffers():
print(buff)
print("=====orderlist=====")
print(model.state_dict())
print("=====save&load=====")
# save model and load
PATH = './MyModule_dict'
torch.save(model.state_dict(), PATH)
model2 = MyModule()
model2.load_state_dict(torch.load(PATH))
print(model2.state_dict())
```
## 1. containers include Module, Sequential, ModuleList, ModuleDict, ParameterList, ParameterDict
Among them, nn.Module is the father class and the five following classes should be put under nn.Module class.
These containers can be used for adding module components.
**It is quite important to notice that nn supports nesting. Once there is one class from nn.Module, any nn.Linear or other nn.Module defined inside the nn.Module woulde automatically added to the whole nn.Module.**
```
class MyModule(nn.Module):
def __init__(self):
super(MyModule, self).__init__()
self.params = nn.ParameterList([nn.Parameter(torch.randn(10, 10)) for i in range(10)])
def forward(self, x):
# ParameterList can act as an iterable, or be indexed using ints
for i, p in enumerate(self.params):
x = self.params[i // 2].mm(x) + p.mm(x)
return x
model = MyModule()
for para in model.parameters():
print(para)
class MyModule(nn.Module):
def __init__(self):
super(MyModule, self).__init__()
self.params = nn.ParameterDict({
'left': nn.Parameter(torch.randn(5, 10)),
'right': nn.Parameter(torch.randn(5, 10))
})
def forward(self, x, choice):
# torch.mm() a@b
# torch.mul() a*b
x = self.params[choice].mm(x)
return x
model = MyModule()
model(torch.ones((10,10)), 'left')
class MyModule(nn.Module):
def __init__(self):
super(MyModule, self).__init__()
self.choices = nn.ModuleDict({
'conv': nn.Conv2d(10, 10, 3),
'pool': nn.MaxPool2d(3)
})
self.activations = nn.ModuleDict([
['lrelu', nn.LeakyReLU()],
['prelu', nn.PReLU()]
])
def forward(self, x, choice, act):
x = self.choices[choice](x)
x = self.activations[act](x)
return x
model = MyModule()
model(torch.ones((10,10,3,3)), 'conv', 'prelu')
```
## 2.difference between nn.Sequential and nn.Modulelist
both of them are subclasses of containers in torch.nn
The sequential class stores sequential list.
```
class seq_net(nn.Module):
def __init__(self):
super(seq_net, self).__init__()
self.seq = nn.Sequential(
nn.Conv2d(1,20,5),
nn.ReLU(),
nn.Conv2d(20,64,5),
nn.ReLU()
)
def forward(self, x):
return self.seq(x)
model = seq_net()
print(model)
```
The ModuleList can be used as list, all elements can be used as elements in the list, but the modules in the list are registered automatically to the whole net and the parameters are automatically put on the whole nn.Module model.
```
class modlist_net(nn.Module):
def __init__(self):
super(modlist_net, self).__init__()
self.modlist = nn.ModuleList([
nn.Conv2d(1, 20, 5),
nn.ReLU(),
nn.Conv2d(20, 64, 5),
nn.ReLU()
])
def forward(self, x):
for m in self.modlist:
x = m(x)
return x
model = modlist_net()
print(model)
```
Diff 1 : nn.ModuleList has no forward functions but nn.Sequential has default forward functions
Diff 2 : nn.Sequential can be named using OrderedDict but nn.ModuleList cannot.
```
from collections import OrderedDict
class seq_net(nn.Module):
def __init__(self):
super(seq_net, self).__init__()
self.seq = nn.Sequential(OrderedDict([
('conv1', nn.Conv2d(1,20,5)),
('relu1', nn.ReLU()),
('conv2', nn.Conv2d(20,64,5)),
('relu2', nn.ReLU())
]))
def forward(self, x):
return self.seq(x)
model = seq_net()
print(model)
```
Diff 3 : module in nn.ModuleList has no order, we can put modules in casual order.
Diff 4 : we can use "for" for duplicate modules in nn.ModuleList.
```
class modlist_net(nn.Module):
def __init__(self):
super(modlist_net, self).__init__()
self.modlist = nn.ModuleList([nn.Linear(10,10) for i in range(10)]
)
def forward(self, x):
for m in self.modlist:
x = m(x)
return x
model = modlist_net()
print(model)
```
## 3. Other APIs for nn.Module base class
collect other APIs not mentioned in the above.
train : effect Dropout & BatchNorm layers
eval : effect Dropout & BatchNorm layers ---> equivalent to self.train(false)
requires_grad_ : change if autograd should record operations on parameters
register_forward_pre_hook : be called every time before forward() is invoked
register_forward_hook : be called every time when forward() is invoked
named_parameters / named_buffers / named_modules / named_children
parameters / buffers / modules / children
add_module
apply
```
# when it comes to tensor we use requires_grad_() or requires_grad = False
x = torch.rand((4,4))
x.requires_grad_(False)
x.requires_grad = False
print(x)
# when it comes to nn.Module we use requires_grad_() or requires_grad = False
# this can be used for freezing parameters when fine tuning
# because the grad would not be changed when passing requires_grad_(False) layers
# ========= QUITE IMPORTANT ============
# since the grad in y = None, we just skip the whole step altogether
y = nn.Linear(2,2)
y.requires_grad_(False)
# or
y.requires_grad = False
print(y)
class MyModule(nn.Module):
def __init__(self):
super(MyModule, self).__init__()
# nn.Parameter actually transform the torch.tensor(requires_grad=True)
# --> torch.tensor(requires_grad=True) and add this parameter into the orderedlist of nn.Module
self.params = nn.ParameterList([nn.Parameter(torch.randn(10, 10)) for i in range(10)])
def forward(self, x):
# ParameterList can act as an iterable, or be indexed using ints
for i, p in enumerate(self.params):
x = self.params[i // 2].mm(x) + p.mm(x)
return x
model = MyModule()
x = model(torch.ones((10,10)))
model.requires_grad_(False)
loss = torch.sum(x)
loss.backward()
```
| true |
code
| 0.862901 | null | null | null | null |
|
# Contextual Bandit Content Personalization
In the Contextual Bandit(CB) introduction tutorial, we learnt about CB and different CB algorithms. In this tutorial we will simulate the scenario of personalizing news content on a site, using CB, to users. The goal is to maximize user engagement quantified by measuring click through rate (CTR).
Let's recall that in a CB setting, a data point has four components,
- Context
- Action
- Probability of choosing action
- Reward/cost for chosen action
In our simulator, we will need to generate a context, get an action/decision for the given context and also simulate generating a reward.
In our simulator, our goal is to maximize reward (click through rate/CTR) or minimize loss (-CTR)
- We have two website visitors: 'Tom' and 'Anna'
- Each of them may visit the website either in the morning or in the afternoon
The **context** is therefore (user, time_of_day)
We have the option of recommending a variety of articles to Tom and Anna. Therefore, **actions** are the different choices of articles: "politics", "sports", "music", "food", "finance", "health", "cheese"
The **reward** is whether they click on the article or not: 'click' or 'no click'
Let's first start with importing the necessary packages:
```
import vowpalwabbit
import random
import matplotlib.pyplot as plt
import pandas as pd
import itertools
```
## Simulate reward
In the real world, we will have to learn Tom and Anna's preferences for articles as we observe their interactions. Since this is a simulation, we will have to define Tom and Anna's preference profile. The reward that we provide to the learner will follow this preference profile. Our hope is to see if the learner can take better and better decisions as we see more samples which in turn means we are maximizing the reward.
We will also modify the reward function in a few different ways and see if the CB learner picks up the changes. We will compare the CTR with and without learning.
VW optimizes to minimize **cost which is negative of reward**. Therefore, we will always pass negative of reward as cost to VW.
```
# VW tries to minimize loss/cost, therefore we will pass cost as -reward
USER_LIKED_ARTICLE = -1.0
USER_DISLIKED_ARTICLE = 0.0
```
The reward function below specifies that Tom likes politics in the morning and music in the afternoon whereas Anna likes sports in the morning and politics in the afternoon. It looks dense but we are just simulating our hypothetical world in the format of the feedback the learner understands: cost. If the learner recommends an article that aligns with the reward function, we give a positive reward. In our simulated world this is a click.
```
def get_cost(context,action):
if context['user'] == "Tom":
if context['time_of_day'] == "morning" and action == 'politics':
return USER_LIKED_ARTICLE
elif context['time_of_day'] == "afternoon" and action == 'music':
return USER_LIKED_ARTICLE
else:
return USER_DISLIKED_ARTICLE
elif context['user'] == "Anna":
if context['time_of_day'] == "morning" and action == 'sports':
return USER_LIKED_ARTICLE
elif context['time_of_day'] == "afternoon" and action == 'politics':
return USER_LIKED_ARTICLE
else:
return USER_DISLIKED_ARTICLE
```
## Understanding VW format
There are some things we need to do to get our input into a format VW understands. This function handles converting from our context as a dictionary, list of articles and the cost if there is one into the text format VW understands.
```
# This function modifies (context, action, cost, probability) to VW friendly format
def to_vw_example_format(context, actions, cb_label = None):
if cb_label is not None:
chosen_action, cost, prob = cb_label
example_string = ""
example_string += "shared |User user={} time_of_day={}\n".format(context["user"], context["time_of_day"])
for action in actions:
if cb_label is not None and action == chosen_action:
example_string += "0:{}:{} ".format(cost, prob)
example_string += "|Action article={} \n".format(action)
#Strip the last newline
return example_string[:-1]
```
To understand what's going on here let's go through an example. Here, it's the morning and the user is Tom. There are four possible articles. So in the VW format there is one line that starts with shared, this is the shared context, followed by four lines each corresponding to an article.
```
context = {"user":"Tom","time_of_day":"morning"}
actions = ["politics", "sports", "music", "food"]
print(to_vw_example_format(context,actions))
```
## Getting a decision
When we call VW we get a _pmf_, [probability mass function](https://en.wikipedia.org/wiki/Probability_mass_function), as the output. Since we are incorporating exploration into our strategy, VW will give us a list of probabilities over the set of actions. This means that the probability at a given index in the list corresponds to the likelihood of picking that specific action. In order to arrive at a decision/action, we will have to sample from this list.
So, given a list `[0.7, 0.1, 0.1, 0.1]`, we would choose the first item with a 70% chance. `sample_custom_pmf` takes such a list and gives us the index it chose and what the probability of choosing that index was.
```
def sample_custom_pmf(pmf):
total = sum(pmf)
scale = 1/total
pmf = [x * scale for x in pmf]
draw = random.random()
sum_prob = 0.0
for index, prob in enumerate(pmf):
sum_prob += prob
if(sum_prob > draw):
return index, prob
```
We have all of the information we need to choose an action for a specific user and context. To use VW to achieve this, we will do the following:
1. We convert our context and actions into the text format we need
2. We pass this example to vw and get the pmf out
3. Now, we sample this pmf to get what article we will end up showing
4. Finally we return the article chosen, and the probability of choosing it (we are going to need the probability when we learn form this example)
```
def get_action(vw, context, actions):
vw_text_example = to_vw_example_format(context,actions)
pmf = vw.predict(vw_text_example)
chosen_action_index, prob = sample_custom_pmf(pmf)
return actions[chosen_action_index], prob
```
## Simulation set up
Now that we have done all of the setup work and know how to interface with VW, let's simulate the world of Tom and Anna. The scenario is they go to a website and are shown an article. Remember that the reward function allows us to define the worlds reaction to what VW recommends.
We will choose between Tom and Anna uniformly at random and also choose their time of visit uniformly at random. You can think of this as us tossing a coin to choose between Tom and Anna (Anna if heads and Tom if tails) and another coin toss for choosing time of day.
```
users = ['Tom', 'Anna']
times_of_day = ['morning', 'afternoon']
actions = ["politics", "sports", "music", "food", "finance", "health", "camping"]
def choose_user(users):
return random.choice(users)
def choose_time_of_day(times_of_day):
return random.choice(times_of_day)
# display preference matrix
def get_preference_matrix(cost_fun):
def expand_grid(data_dict):
rows = itertools.product(*data_dict.values())
return pd.DataFrame.from_records(rows, columns=data_dict.keys())
df = expand_grid({'users':users, 'times_of_day': times_of_day, 'actions': actions})
df['cost'] = df.apply(lambda r: cost_fun({'user': r[0], 'time_of_day': r[1]}, r[2]), axis=1)
return df.pivot_table(index=['users', 'times_of_day'],
columns='actions',
values='cost')
get_preference_matrix(get_cost)
```
We will instantiate a CB learner in VW and then simulate Tom and Anna's website visits `num_iterations` number of times. In each visit, we:
1. Decide between Tom and Anna
2. Decide time of day
3. Pass context i.e. (user, time of day) to learner to get action i.e. article recommendation and probability of choosing action
4. Receive reward i.e. see if user clicked or not. Remember that cost is just negative reward.
5. Format context, action, probability, reward in VW format
6. Learn from the example
- VW _reduces_ a CB problem to a cost sensitive multiclass classification problem.
This is the same for every one of our simulations, so we define the process in the `run_simulation` function. The cost function must be supplied as this is essentially us simulating how the world works.
```
def run_simulation(vw, num_iterations, users, times_of_day, actions, cost_function, do_learn = True):
cost_sum = 0.
ctr = []
for i in range(1, num_iterations+1):
# 1. In each simulation choose a user
user = choose_user(users)
# 2. Choose time of day for a given user
time_of_day = choose_time_of_day(times_of_day)
# 3. Pass context to vw to get an action
context = {'user': user, 'time_of_day': time_of_day}
action, prob = get_action(vw, context, actions)
# 4. Get cost of the action we chose
cost = cost_function(context, action)
cost_sum += cost
if do_learn:
# 5. Inform VW of what happened so we can learn from it
vw_format = vw.parse(to_vw_example_format(context, actions, (action, cost, prob)), vowpalwabbit.LabelType.CONTEXTUAL_BANDIT)
# 6. Learn
vw.learn(vw_format)
# We negate this so that on the plot instead of minimizing cost, we are maximizing reward
ctr.append(-1*cost_sum/i)
return ctr
```
We want to be able to visualize what is occurring, so we are going to plot the click through rate over each iteration of the simulation. If VW is showing actions the get rewards the ctr will be higher. Below is a little utility function to make showing the plot easier.
```
def plot_ctr(num_iterations, ctr):
plt.plot(range(1,num_iterations+1), ctr)
plt.xlabel('num_iterations', fontsize=14)
plt.ylabel('ctr', fontsize=14)
plt.ylim([0,1])
```
## Scenario 1
We will use the first reward function `get_cost` and assume that Tom and Anna do not change their preferences over time and see what happens to user engagement as we learn. We will also see what happens when there is no learning. We will use the "no learning" case as our baseline to compare to.
### With learning
```
# Instantiate learner in VW
vw = vowpalwabbit.Workspace("--cb_explore_adf -q UA --quiet --epsilon 0.2")
num_iterations = 5000
ctr = run_simulation(vw, num_iterations, users, times_of_day, actions, get_cost)
plot_ctr(num_iterations, ctr)
```
#### Aside: interactions
You'll notice in the arguments we supply to VW, **we include `-q UA`**. This is telling VW to create additional features which are the features in the (U)ser namespace and (A)ction namespaces multiplied together. This allows us to learn the interaction between when certain actions are good in certain times of days and for particular users. If we didn't do that, the learning wouldn't really work. We can see that in action below.
```
# Instantiate learner in VW but without -q
vw = vowpalwabbit.Workspace("--cb_explore_adf --quiet --epsilon 0.2")
num_iterations = 5000
ctr = run_simulation(vw, num_iterations, users, times_of_day, actions, get_cost)
plot_ctr(num_iterations, ctr)
```
### Without learning
Let's do the same thing again (with `-q`) but with do_learn set to False to show the effect if we don't learn from the rewards. The ctr never improves are we just hover around 0.2.
```
# Instantiate learner in VW
vw = vowpalwabbit.Workspace("--cb_explore_adf -q UA --quiet --epsilon 0.2")
num_iterations = 5000
ctr = run_simulation(vw, num_iterations, users, times_of_day, actions, get_cost, do_learn=False)
plot_ctr(num_iterations, ctr)
```
## Scenario 2
In the real world people's preferences change over time. So now in the simulation we are going to incorporate two different cost functions, and swap over to the second one halfway through. Below is a a table of the new reward function we are going to use, `get_cost_1`:
### Tom
| | `get_cost` | `get_cost_new1` |
|:---|:---:|:---:|
| **Morning** | Politics | Politics |
| **Afternoon** | Music | Sports |
### Anna
| | `get_cost` | `get_cost_new1` |
|:---|:---:|:---:|
| **Morning** | Sports | Sports |
| **Afternoon** | Politics | Sports |
This reward function is still working with actions that the learner has seen previously.
```
def get_cost_new1(context,action):
if context['user'] == "Tom":
if context['time_of_day'] == "morning" and action == 'politics':
return USER_LIKED_ARTICLE
elif context['time_of_day'] == "afternoon" and action == 'sports':
return USER_LIKED_ARTICLE
else:
return USER_DISLIKED_ARTICLE
elif context['user'] == "Anna":
if context['time_of_day'] == "morning" and action == 'sports':
return USER_LIKED_ARTICLE
elif context['time_of_day'] == "afternoon" and action == 'sports':
return USER_LIKED_ARTICLE
else:
return USER_DISLIKED_ARTICLE
get_preference_matrix(get_cost_new1)
```
To make it easy to show the effect of the cost function changing we are going to modify the `run_simulation` function. It is a little less readable now, but it supports accepting a list of cost functions and it will operate over each cost function in turn. This is perfect for what we need.
```
def run_simulation_multiple_cost_functions(vw, num_iterations, users, times_of_day, actions, cost_functions, do_learn = True):
cost_sum = 0.
ctr = []
start_counter = 1
end_counter = start_counter + num_iterations
for cost_function in cost_functions:
for i in range(start_counter, end_counter):
# 1. in each simulation choose a user
user = choose_user(users)
# 2. choose time of day for a given user
time_of_day = choose_time_of_day(times_of_day)
# Construct context based on chosen user and time of day
context = {'user': user, 'time_of_day': time_of_day}
# 3. Use the get_action function we defined earlier
action, prob = get_action(vw, context, actions)
# 4. Get cost of the action we chose
cost = cost_function(context, action)
cost_sum += cost
if do_learn:
# 5. Inform VW of what happened so we can learn from it
vw_format = vw.parse(to_vw_example_format(context, actions, (action, cost, prob)), vowpalwabbit.LabelType.CONTEXTUAL_BANDIT)
# 6. Learn
vw.learn(vw_format)
# We negate this so that on the plot instead of minimizing cost, we are maximizing reward
ctr.append(-1*cost_sum/i)
start_counter = end_counter
end_counter = start_counter + num_iterations
def run_simulation_multiple_cost_functions(vw, num_iterations, users, times_of_day, actions, cost_functions, do_learn = True):
cost_sum = 0.
ctr = []
start_counter = 1
end_counter = start_counter + num_iterations
for cost_function in cost_functions:
for i in range(start_counter, end_counter):
# 1. in each simulation choose a user
user = choose_user(users)
# 2. choose time of day for a given user
time_of_day = choose_time_of_day(times_of_day)
# Construct context based on chosen user and time of day
context = {'user': user, 'time_of_day': time_of_day}
# 3. Use the get_action function we defined earlier
action, prob = get_action(vw, context, actions)
# 4. Get cost of the action we chose
cost = cost_function(context, action)
cost_sum += cost
if do_learn:
# 5. Inform VW of what happened so we can learn from it
vw_format = vw.parse(to_vw_example_format(context, actions, (action, cost, prob)), vowpalwabbit.LabelType.CONTEXTUAL_BANDIT)
# 6. Learn
vw.learn(vw_format)
# We negate this so that on the plot instead of minimizing cost, we are maximizing reward
ctr.append(-1*cost_sum/i)
start_counter = end_counter
end_counter = start_counter + num_iterations
return ctr
```
### With learning
Let us now switch to the second reward function after a few samples (running the first reward function). Recall that this reward function changes the preferences of the web users but it is still working with the same action space as before. We should see the learner pick up these changes and optimize towards the new preferences.
```
# use first reward function initially and then switch to second reward function
# Instantiate learner in VW
vw = vowpalwabbit.Workspace("--cb_explore_adf -q UA --quiet --epsilon 0.2")
num_iterations_per_cost_func = 5000
cost_functions = [get_cost, get_cost_new1]
total_iterations = num_iterations_per_cost_func * len(cost_functions)
ctr = run_simulation_multiple_cost_functions(vw, num_iterations_per_cost_func, users, times_of_day, actions, cost_functions)
plot_ctr(total_iterations, ctr)
```
**Note:** The initial spike in CTR depends on the rewards received for the first few examples. When you run on your own, you may see something different initially because our simulator is designed to have randomness.
### Without learning
```
# Do not learn
# use first reward function initially and then switch to second reward function
# Instantiate learner in VW
vw = vowpalwabbit.Workspace("--cb_explore_adf -q UA --quiet --epsilon 0.2")
num_iterations_per_cost_func = 5000
cost_functions = [get_cost, get_cost_new1]
total_iterations = num_iterations_per_cost_func * len(cost_functions)
ctr = run_simulation_multiple_cost_functions(vw, num_iterations_per_cost_func, users, times_of_day, actions, cost_functions, do_learn=False)
plot_ctr(total_iterations, ctr)
```
## Scenario 3
In this scenario we are going to start rewarding actions that have never seen a reward previously when we change the cost function.
### Tom
| | `get_cost` | `get_cost_new2` |
|:---|:---:|:---:|
| **Morning** | Politics | Politics|
| **Afternoon** | Music | Food |
### Anna
| | `get_cost` | `get_cost_new2` |
|:---|:---:|:---:|
| **Morning** | Sports | Food|
| **Afternoon** | Politics | Food |
```
def get_cost_new2(context,action):
if context['user'] == "Tom":
if context['time_of_day'] == "morning" and action == 'politics':
return USER_LIKED_ARTICLE
elif context['time_of_day'] == "afternoon" and action == 'food':
return USER_LIKED_ARTICLE
else:
return USER_DISLIKED_ARTICLE
elif context['user'] == "Anna":
if context['time_of_day'] == "morning" and action == 'food':
return USER_LIKED_ARTICLE
elif context['time_of_day'] == "afternoon" and action == 'food':
return USER_LIKED_ARTICLE
else:
return USER_DISLIKED_ARTICLE
```
### With learning
Let us now switch to the third reward function after a few samples (running the first reward function). Recall that this reward function changes the preferences of the users and is working with a **different** action space than before. We should see the learner pick up these changes and optimize towards the new preferences
```
# use first reward function initially and then switch to third reward function
# Instantiate learner in VW
vw = vowpalwabbit.Workspace("--cb_explore_adf -q UA --quiet --epsilon 0.2")
num_iterations_per_cost_func = 5000
cost_functions = [get_cost, get_cost_new2]
total_iterations = num_iterations_per_cost_func * len(cost_functions)
ctr = run_simulation_multiple_cost_functions(vw, num_iterations_per_cost_func, users, times_of_day, actions, cost_functions)
plot_ctr(total_iterations, ctr)
```
### Without Learning
```
# Do not learn
# use first reward function initially and then switch to third reward function
# Instantiate learner in VW
vw = vowpalwabbit.Workspace("--cb_explore_adf -q UA --quiet --epsilon 0.2")
num_iterations_per_cost_func = 5000
cost_functions = [get_cost, get_cost_new2]
total_iterations = num_iterations_per_cost_func * len(cost_functions)
ctr = run_simulation_multiple_cost_functions(vw, num_iterations_per_cost_func, users, times_of_day, actions, cost_functions, do_learn=False)
plot_ctr(total_iterations, ctr)
```
## Summary
This tutorial aimed at showcasing a real world scenario where contextual bandit algorithms can be used. We were able to take a context and set of actions and learn what actions worked best for a given context. We saw that the learner was able to respond rapidly to changes in the world. We showed that allowing the learner to interact with the world resulted in higher rewards than the no learning baseline.
This tutorial worked with simplistic features. VW supports high dimensional sparse features, different exploration algorithms and policy evaluation approaches.
| true |
code
| 0.410845 | null | null | null | null |
|
# 01 Intro
- Introduction to Data Visualization
- Introduction to Matplotlib
- Basic Plotting with Matplotlib
- Dataset on Immigration to Canada
- Line Plots
# Introduction to Data Visualization
## Data visualization
> a way to show a
complex data in a form that is graphical and easy to understand.
>Transforming a visual into one which is more effective, attractive and impactive
## Why Build visuals
- For exploratory data analysis
- Communicate data clearly
- Share unbiased representation of data
- Support recommendations to different stakeholders
## Best Practices
### 3 Key points when creating a visual
1. Less is more effective.
2. Less is more attractive.
3. Less is more impactive.
Any feature or design you incorporate in your plot to make it more attractive or
pleasing should support the message that the plot is meant to get across and not
distract from it.
Simple, cleaner, less distracting, and much
easier to read graphs.
Bar graphs and charts are argued to be far
superior ways to quickly get a message across.
Reinforce the concept of less is more effective, attractive, and impactive.
# Introduction to Matplotlib
## Architecture of Matplotlib
Matplotlib's architecture is composed of
three main layers:
1. Back-end layer
2. Artist layer
3. Scripting layer
### 1. Back-end layer
Back-end layer has three built-in abstract interface classes:
1. FigureCanvas
2. Renderer
3. Event
### 2. Artist layer
Artist layer is composed of one main object,which is the Artist.
The Artist is the object that knows how to take the Renderer and use it to put ink on the canvas.
Everything you see on a Matplotlib figure is an Artist instance.
>The title, the lines, the tick labels, the
images, and so on, all correspond to an individual Artist.
There are two types of Artist objects.
1. Primitive type
> a line, a rectangle, a circle, or text.
2. Composite type
> figure or axes.

**Each composite artist may contain other composite
artists as well as primitive artists.**
### Use artist layer to generate histogram
>Use the artist layer to generate a histogram of 10,000 random numbers
```
import matplotlib.pyplot as plt
from matplotlib.backends.backend_agg import FigureCanvasAgg as FigureCanvas # import FigureCanvas
from matplotlib.figure import Figure # import Figure artist
fig = plt.figure() # an empty figure with no axes
canvas = FigureCanvas(fig) # attach the figure artist to figure canvas
# Create 10000 random numbers using numpy
import numpy as np
x = np.random.randn(10000)
ax = fig.add_subplot(111) # create an axes artist with one row and one column and uses the first cell in a grid
ax.hist(x, 100) # generate a histogram of the 10000 numbers with 100 bins
# add a title to the figure and save it
ax.set_title(r'Normal distribution with $\mu=0, \sigma=1$')
fig.savefig('../figs/01_Intro/matplotlib_histogram_artist.png')
plt.show()
```
### 3. Scripting layer
Developed for scientists who are not professional programmers to perform quick exploratory analysis of some data.
Matplotlib's scripting layer is essentially the Matplotlib.pyplot interface, which automates the process of defining a canvas and defining a figure artist instance and connecting them.
### Use scripting layer to generate histogram
>Use the scripting layer to generate a histogram of 10,000 random numbers
```
import matplotlib.pyplot as plt
import numpy as np
x = np.random.randn(10000)
plt.hist(x, 100)
plt.title(r'Normal distribution with $\mu=0, \sigma=1$')
plt.savefig('../figs/01_Intro/matplotlib_histogram_scripting.png')
plt.show()
```
# Basic Plotting with Matplotlib
```
# %matplotlib inline
import matplotlib.pyplot as plt
plt.plot(5, 5, 'o')
plt.show()
plt.plot(5, 5, 'o')
plt.ylabel("Y")
plt.xlabel("X")
plt.title("Plotting Example")
plt.show()
# Using pandas with matplotlib
import pandas as pd
india_china = {'1980': [8880, 5123],
'1981': [8670, 6682],
'1982': [8147, 3308],
'1983': [7338, 1863],
'1984': [5704, 1527]}
india_china
india_china_df = pd.DataFrame.from_dict(
india_china,
orient='index',
columns=['India', 'China'])
india_china_df
# Line plot
india_china_df.plot(kind="line");
# Histogram plot
india_china_df["India"].plot(kind="hist");
```
# Dataset on Immigration to Canada
## Immigration to Canada from 1980 to 2013 Dataset
>Dataset Source: International migration flows to and from selected countries - The 2015 revision.
>The dataset contains annual data on the flows of international immigrants as recorded by the countries of destination. The data presents both inflows and outflows according to the place of birth, citizenship or place of previous / next residence both for foreigners and nationals. The current version presents data pertaining to 45 countries.
>Get [the raw immigration data from United Nations Population Division Department of Economic and Social Affairs website](https://www.un.org/en/development/desa/population/migration/data/empirical2/data/UN_MigFlow_All_CountryFiles.zip)

> OR fetch Canada's immigration data that has been extracted and uploaded to one of IBM servers from [here](https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DV0101EN/labs/Data_Files/Canada.xlsx)
## Read Data into pandas Dataframe
```
import numpy as np
import pandas as pd
df_can = pd.read_excel('https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DV0101EN/labs/Data_Files/Canada.xlsx',
sheet_name='Canada by Citizenship',
skiprows=range(20),
skipfooter=2)
print ('Data read into a pandas dataframe!')
```
## Display Dataframe
```
df_can.head()
```
### Read Data into pandas Dataframe from local file
```
df_can = pd.read_excel('../data/Canada.xlsx',
sheet_name='Canada by Citizenship',
skiprows=range(20),
skipfooter=2)
print ('Data read into a pandas dataframe!')
df_can.head()
df_can.info()
# list of column headers
df_can.columns.values
# list of indicies
df_can.index.values
# type of index and columns
print(type(df_can.columns))
print(type(df_can.index))
# get the index and columns as lists
df_can.columns.tolist()
df_can.index.tolist()
print (type(df_can.columns.tolist()))
print (type(df_can.index.tolist()))
# size of dataframe (rows, columns)
df_can.shape
```
### Clean the data set
>Remove a few unnecessary columns
```
# in pandas axis=0 represents rows (default) and axis=1 represents columns.
df_can.drop(['AREA','REG','DEV','Type','Coverage'], axis=1, inplace=True)
df_can.head(2)
```
### Rename the columns
>Rename the columns by passing in a dictionary of old and new names
```
df_can.rename(columns={'OdName':'Country', 'AreaName':'Continent', 'RegName':'Region'}, inplace=True)
df_can.columns
```
### Sums up the total immigrants
>sums up the total immigrants by country over the entire period 1980 - 2013
```
# add a 'Total' column
df_can['Total'] = df_can.sum(axis=1)
df_can['Total']
```
### Check null objects
```
# check to see how many null objects we have in the dataset
df_can.isnull().sum()
# view a quick summary of each column in our dataframe
df_can.describe()
```
### Filtering list of countries
```
# filtering on the list of countries ('Country').
df_can.Country # returns a series
# filtering on the list of countries ('OdName') and the data for years: 1980 - 1985.
df_can[['Country', 1980, 1981, 1982, 1983, 1984, 1985]] # returns a dataframe
```
> notice that 'Country' is string, and the years are integers.
**Convert all column names to string later on.**
```
# setting the 'Country' column as the index
df_can.set_index('Country', inplace=True)
df_can.head(3)
```
## **loc** vs **iloc**
>df.loc[**label**]
- filters by the **labels** of the index/column
>df.iloc[**index**]
- filters by the **positions** of the index/column
```
# view the number of immigrants from Japan (row 87) for the following scenarios:
# 1. the full row data (all columns)
print(df_can.loc['Japan'])
# 2. for year 2013
print(df_can.loc['Japan', 2013])
# 3. for years 1980 to 1985
print(df_can.loc['Japan', [1980, 1981, 1982, 1983, 1984, 1984]])
print(df_can.iloc[87, [3, 4, 5, 6, 7, 8]])
```
### Convert the column names into strings: '1980' to '2013'.
```
df_can.columns = list(map(str, df_can.columns))
# converted years to string to easily call upon the full range of years for plotting
years = list(map(str, range(1980, 2014)))
years[:5]
```
### Filtering based on a criteria
> filter the dataframe based on a condition
> pass the condition as a boolean vector.
```
# filter the dataframe to show the data on Asian countries (AreaName = Asia).
# 1. create the condition boolean series
condition = df_can['Continent'] == 'Asia'
print(condition)
# 2. pass this condition into the dataFrame
df_can[condition]
# filter for AreaNAme = Asia and RegName = Southern Asia
df_can[(df_can['Continent']=='Asia') & (df_can['Region']=='Southern Asia')]
# review the changes we have made to our dataframe.
print('data dimensions:', df_can.shape)
print(df_can.columns)
df_can.head(2)
```
# Line Plots
## Plot a line graph of immigration from Haiti
```
# use the matplotlib inline backend
%matplotlib inline
# importing matplotlib.pyplot
import matplotlib.pyplot as plt
# converted the years to string to call upon the full range of years
years = list(map(str, range(1980, 2014)))
years[:5]
```
### Extract the data series for Haiti
```
# passing in years 1980 - 2013 to exclude the 'total' column
haiti = df_can.loc['Haiti',years]
haiti.head()
# plot a line plot by appending .plot() to the haiti dataframe
haiti.plot();
# change the index values of Haiti to type integer for plotting
haiti.index = haiti.index.map(int)
haiti.plot(kind='line')
plt.title('Immigration from Haiti')
plt.ylabel('Number of immigrants')
plt.xlabel('Years')
plt.show() # need this line to show the updates made to the figure
haiti.plot(kind='line')
plt.title('Immigration from Haiti')
plt.ylabel('Number of Immigrants')
plt.xlabel('Years')
# annotate the 2010 Earthquake.
# syntax: plt.text(x, y, label)
plt.text(2000, 6000, '2010 Earthquake') # see note below
plt.savefig('../figs/01_Intro/immigration_from_haiti.png')
plt.show()
```
### Add more countries to line plot
>Add more countries to line plot to make meaningful comparisons immigration from different countries.
### Compare the number of immigrants from India and China from 1980 to 2013.
### Step 1: Get the data set for China and India, and display dataframe.
```
china = df_can.loc['China',years]
china.head()
india = df_can.loc['India',years]
india.head()
df_china_india = df_can.loc[["China", "India"],years]
df_china_india.head()
```
### Step 2: Plot graph
```
df_china_india.plot(kind='line');
```
>Recall that pandas plots the indices on the x-axis and the columns as individual lines on the y-axis.
>As the dataframe with the country as the index and years as the columns, we must first transpose the dataframe using transpose() method to swap the row and columns.
```
df_china_india = df_china_india.transpose()
df_china_india.head()
# change the index values of df_china_india to type integer for plotting
df_china_india.index = df_china_india.index.map(int)
df_china_india.plot(kind='line')
plt.title('Immigration from China and India')
plt.ylabel('Number of Immigrants')
plt.xlabel('Years')
plt.savefig('../figs/01_Intro/immigration_from_china_india.png')
plt.show()
```
>From the above plot, we can observe that the China and India have very similar immigration trends through the years.
### Compare the trend of top 5 countries
>Compare the trend of top 5 countries that contributed the most to immigration to Canada.
### Step 1: Get the dataset.
>Recall that we created a Total column that calculates the cumulative immigration by country.
>We will sort on this column to get our top 5 countries using pandas sort_values() method.
>inplace = True paramemter saves the changes to the original df_can dataframe
```
df_can.sort_values(by='Total', ascending=False, axis=0, inplace=True)
# get the top 5 entries
df_top5 = df_can.head(5)
df_top5
# transpose the dataframe
df_top5 = df_top5[years].transpose()
print(df_top5)
```
### Step 2: Plot the dataframe.
>Change the size using the `figsize` parameter to make the plot more readeable
```
# let's change the index values of df_top5 to type integer for plotting
df_top5.index = df_top5.index.map(int)
# pass a tuple (x, y) size
df_top5.plot(kind='line', figsize=(14, 8))
plt.title('Immigration Trend of Top 5 Countries')
plt.ylabel('Number of Immigrants')
plt.xlabel('Years')
plt.savefig('../figs/01_Intro/immigration_trend_top5_countries.png')
plt.show()
```
| true |
code
| 0.622689 | null | null | null | null |
|
Notebook written by [Zhedong Zheng](https://github.com/zhedongzheng)

```
import tensorflow as tf
import numpy as np
import sklearn
VOCAB_SIZE = 20000
EMBED_DIM = 100
RNN_SIZE = 70
CLIP_NORM = 5.0
BATCH_SIZE = 32
LR = {'start': 5e-3, 'end': 5e-4, 'steps': 1500}
N_EPOCH = 2
N_CLASS = 2
def sort_by_len(x, y):
idx = sorted(range(len(x)), key=lambda i: len(x[i]))
return x[idx], y[idx]
def pad_sentence_batch(sent_batch, thres=400):
max_seq_len = max([len(sent) for sent in sent_batch])
if max_seq_len > thres:
max_seq_len = thres
sent_batch = [sent[-thres:] for sent in sent_batch]
padded_seqs = [(sent + [0]*(max_seq_len - len(sent))) for sent in sent_batch]
return padded_seqs
def next_train_batch(X_train, y_train):
for i in range(0, len(X_train), BATCH_SIZE):
padded_seqs = pad_sentence_batch(X_train[i : i+BATCH_SIZE])
yield padded_seqs, y_train[i : i+BATCH_SIZE]
def next_test_batch(X_test):
for i in range(0, len(X_test), BATCH_SIZE):
padded_seqs = pad_sentence_batch(X_test[i : i+BATCH_SIZE])
yield padded_seqs
def train_input_fn(X_train, y_train):
dataset = tf.data.Dataset.from_generator(
lambda: next_train_batch(X_train, y_train),
(tf.int32, tf.int64),
(tf.TensorShape([None,None]), tf.TensorShape([None])))
iterator = dataset.make_one_shot_iterator()
return iterator.get_next()
def predict_input_fn(X_test):
dataset = tf.data.Dataset.from_generator(
lambda: next_test_batch(X_test),
tf.int32,
tf.TensorShape([None,None]))
iterator = dataset.make_one_shot_iterator()
return iterator.get_next()
def rnn_cell():
return tf.nn.rnn_cell.GRUCell(RNN_SIZE, kernel_initializer=tf.orthogonal_initializer())
def forward(inputs, mode):
is_training = (mode == tf.estimator.ModeKeys.TRAIN)
x = tf.contrib.layers.embed_sequence(inputs, VOCAB_SIZE, EMBED_DIM)
x = tf.layers.dropout(x, 0.2, training=is_training)
bi_outs, bi_states = tf.nn.bidirectional_dynamic_rnn(
rnn_cell(), rnn_cell(), x, tf.count_nonzero(inputs, 1), dtype=tf.float32)
x = tf.concat(bi_states, -1)
logits = tf.layers.dense(x, N_CLASS)
return logits
def clip_grads(loss):
params = tf.trainable_variables()
grads = tf.gradients(loss, params)
clipped_grads, _ = tf.clip_by_global_norm(grads, CLIP_NORM)
return zip(clipped_grads, params)
def model_fn(features, labels, mode):
logits = forward(features, mode)
if mode == tf.estimator.ModeKeys.PREDICT:
preds = tf.argmax(logits, -1)
return tf.estimator.EstimatorSpec(mode, predictions=preds)
if mode == tf.estimator.ModeKeys.TRAIN:
global_step = tf.train.get_global_step()
lr_op = tf.train.exponential_decay(
LR['start'], global_step, LR['steps'], LR['end']/LR['start'])
loss_op = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
logits=logits, labels=labels))
train_op = tf.train.AdamOptimizer(lr_op).apply_gradients(
clip_grads(loss_op), global_step=global_step)
lth = tf.train.LoggingTensorHook({'lr': lr_op}, every_n_iter=100)
return tf.estimator.EstimatorSpec(
mode=mode, loss=loss_op, train_op=train_op, training_hooks=[lth])
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.imdb.load_data(num_words=VOCAB_SIZE)
X_train, y_train = sort_by_len(X_train, y_train)
X_test, y_test = sort_by_len(X_test, y_test)
estimator = tf.estimator.Estimator(model_fn)
for _ in range(N_EPOCH):
estimator.train(lambda: train_input_fn(X_train, y_train))
y_pred = np.fromiter(estimator.predict(lambda: predict_input_fn(X_test)), np.int32)
print("\nValidation Accuracy: %.4f\n" % (y_pred==y_test).mean())
```
| true |
code
| 0.672117 | null | null | null | null |
|
# NLP Learners
This module contains the main class to quickly define a `Learner` (and automatically generates an appropriate model) from your NLP data.
```
from fastai.gen_doc.nbdoc import *
from fastai.text import *
from fastai.docs import *
```
## Class RNNLearner
This is the class that handles the whole creation of a `Learner`, be it for a language model or an RNN classifier. It handles the conversion of weights from a pretrained model as well as saving or loading the encoder.
```
show_doc(RNNLearner, doc_string=False)
```
Creates an `RNNLearner` from `data` and a `model` with a text data using a certain `bptt`. The `split_func` is used to properly split the model in different groups for gradual unfreezing and differential learning rates. Gradient clipping of `clip` is optionnally applied. `adjust`, `alpha` and `beta` are all passed to create an instance of `RNNTrainer`.
### Factory methods
```
show_doc(RNNLearner.classifier, doc_string=False)
```
Create an RNNLearner with a classifier model from `data`. The model used is the encoder of an [AWD-LSTM](https://arxiv.org/abs/1708.02182) that is built with embeddings of size `emb_sz`, a hidden size of `nh`, and `nl` layers (the `vocab_size` is inferred from the `data`). All the dropouts are put to values that we found worked pretty well and you can control their strength by adjusting `drop_mult`. If `qrnn` is True, the model uses [QRNN cells](https://arxiv.org/abs/1611.01576) instead of LSTMs.
The input texts are fed into that model by bunch of `bptt` and only the last `max_len` activations are considerated. This gives us the backbone of our model. The head then consists of:
- a layer that concatenates the final outputs of the RNN with the maximum and average of all the intermediate outputs (on the sequence length dimension),
- blocks of [nn.BatchNorm1d, nn.Dropout, nn.Linear, nn.ReLU] layers.
The blocks are defined by the `lin_ftrs` and `drops` arguments. Specifically, the first block will have a number of inputs inferred from the backbone arch and the last one will have a number of outputs equal to data.c (which contains the number of classes of the data) and the intermediate blocks have a number of inputs/outputs determined by `lin_ftrs` (of course a block has a number of inputs equal to the number of outputs of the previous block). The dropouts all have a the same value ps if you pass a float, or the corresponding values if you pass a list. Default is to have an intermediate hidden size of 50 (which makes two blocks model_activation -> 50 -> n_classes) with a dropout of 0.1.
```
data = get_imdb(classifier=True)
learn = RNNLearner.classifier(data, drop_mult=0.5)
show_doc(RNNLearner.language_model, doc_string=False)
```
Create an RNNLearner with a language model from `data` of a certain `bptt`. The model used is an [AWD-LSTM](https://arxiv.org/abs/1708.02182) that is built with embeddings of size `emb_sz`, a hidden size of `nh`, and `nl` layers (the `vocab_size` is inferred from the `data`). All the dropouts are put to values that we found worked pretty well and you can control their strength by adjusting `drop_mult`. If `qrnn` is True, the model uses [QRNN cells](https://arxiv.org/abs/1611.01576) instead of LSTMs. The flag `tied_weights` control if we should use the same weights for the encoder and the decoder, the flag `bias` controls if the last linear layer (the decoder) has bias or not.
You can specify `pretrained_fnames` if you want to use the weights of a pretrained model. This should be a list of the name of the weight file and the name of the corresponding dictionary. The dictionary is needed because the function will internally convert the embeddings of the pretrained models to match the dictionary of the `data` passed (a word may have a different id for the pretrained model).
```
data = get_imdb()
learn = RNNLearner.language_model(data, pretrained_fnames=['lstm_wt103', 'itos_wt103'], drop_mult=0.5)
```
### Loading and saving
```
show_doc(RNNLearner.load_encoder)
show_doc(RNNLearner.save_encoder)
show_doc(RNNLearner.load_pretrained, doc_string=False)
```
Opens the weights in the `wgts_fname` of model diretory of the `RNNLearner` and the dictionary in `itos_fname` then adapts the pretrained weights to the vocabulary of the `data`.
## Utility functions
```
show_doc(lm_split)
show_doc(rnn_classifier_split)
show_doc(convert_weights, doc_string=False)
```
Convert the `wgts` from an old disctionary `stoi_wgts` (correspondance word to id) to a new dictionary `itos_new` (correspondans id to word).
| true |
code
| 0.638582 | null | null | null | null |
|
# AdaBoost
在做重要决定的时候,我们会考虑吸收多个专家的意见而不是一个人的意见,机器学习处理问题的时候也可以采用这种方法.这就是元算法(meta-algorithm)背后的思路.元算法是对其他算法进行组合的一种方式,我们会先建立一个**单层决策树(decision stump)**分类器,实际上它是一个单节点的决策树.AdaBoots算法将应用在上述单层决策树之上,然后将在一个难数据集上应用AdaBoots分类器,以了解该算法是如何迅速超越其他分类器的.
强可学习(strongly learnable)和弱可学习(weakly learnable)
- 强可学习:如果存在一个多项式学习算法,并且它的学习率很高,那么我们就称这个概念为**强可学习**.
- 弱可学习:如果存在一个多项式学习算法,它的学习率只比随机猜测略好,那么就称这个概念为**弱可学习**
AdaBoost algorithm 是将弱可学习变为强可学习算法中最具有代表性的算法.
对着提升方法来说,两个问题需要回答:一是在每一轮如何改变训练数据的权值或概率分布;二是如何将弱分类器组合成一个强分类器.关于第一个问题Adaboost的做法是,提高那些被前一轮弱分类器分类错误的样本权值,而降低那些被正确分类样本权值.这样一来,那些没有得到正确分类的数据,由于其权值的增大而获得更多的"关注".至于第2个问题,adaboost才用加权多数表决法的方法.具体的而言就是,加大分类错误率小的弱分类器权值,使其在表中起更大的作用,减小分类误差率大的弱分类器的权值,在表决中起较小的作用.
可以取看看[boosting和bagging](https://blog.csdn.net/u013709270/article/details/72553282)的不同之处
### AdaBoost 算法(boosting)
假定一个二分类分类的训练集
$T={(x_1,y_1),...,(x_n,y_n)}$
其中每一个点由实例和样本标签组成.实例$x_i \in X\subseteqq R^{n}$,标记$y_i \in Y={-1,+1}$,X是实例空间,Y是标记集合.Adaboost利用以下算法,从训练数据样本中学习一系列弱分类器或基本分类器,并将这些弱分类器线性组合成一个强分类器.
#### AdaBoost
输入:训练样本数据集$T={(x_1,y_1),...,(x_n,y_n)}$,其中$x_i \in X\subseteqq R^{n}$,$y_i \in Y={-1,+1}$;弱学习算法;
输出:最终分类器$G(x)$
(1) 初始化训练数据的权重值分布(在初始化的时候将所有样本的权重赋予相同值)
$D_1=(w_{11},w_{12},...w_{1i},w_{1N}),w_{1i} = \frac{1}{N},i=1,2,...N$
(2) 对$m=1,2,...,M$(需要执行人为定义的M轮)
(a) 使用具有权值分布的$D_m$的训练数据集学习,得到基本分类器
$G_m(x):X\rightarrow {+1,-1}$
(b) 计算$G_m(x)$在训练数据集上的分类错误率
$e_m = P(G_m(x_i) \neq y_i)=\sum_{i=1}^{N}w_{mi}I(G_m(x_i)\neq y_i)$
(c) 计算$G_m(x)$的系数
$\alpha_m=\frac{1}{2}log(\frac{1-e_m}{e_m})$,这里的log是自然对数
(d) 更新训练数据集的权值分布
$D_{m+1}=(w_{m+1,1},w_{m+1,2},...w_{m+1,i},w_{m+1,N})$
$w_{m+1,i}=\frac{w_{m,i}}{Z_{m}}exp(-\alpha_m \cdot y_i \cdot G(x_i)),i=1,2,...N$
这里,$Z_{m}$是规范化因子
$Z_{m}=\sum_{i=1}^{N}w_{mi}exp(-\alpha_m \cdot y_i \cdot G(x_i))$
它使$D_{m+1}$成为一个概率分布
(3) 构建基本分类器的线性组合
$f(x)=\sum_{m=1}^{M}\alpha_m G_{m}(x)$
最终得到分类器
$G(x)=sign(f(x))=sign\begin{pmatrix}
\sum_{m=1}^{M}\alpha_mG_m(x)
\end{pmatrix}$
<p style="color:blue">这里的sign是符号的意思,也就是说如果求出来为负,那么是一类,如果为正数,那么是另一类</p>
**对Adaboost的算法说明:**
步骤(1) 假设训练数据集具有均匀的权值分布,即每个训练样本在基本分类器的学习中作用是相同,这一假设保证第一步能够在原始数据集上学习基本分类器$G_1(x)$.
步骤(2) adaboost反复学习基本分类器,在每一轮$m=1,2,..,M$顺次的执行如下操作:
- (a) 使用当前分布$D_m$加权的训练数据,学习基本分类器$G_m(x)$
- (b) 计算基本分类器$G_m(x)$在加权训练数据集上的分类误差率:
- $e_m = P(G_m(x_i) \neq y_i)=\sum_{i=1}^{N}w_{mi}I(G_m(x_i)\neq y_i)$
- 这里,$w_{mi}$表示第m轮中第i个实例的权值,$\sum_{i=1}^{N}w_{mi}=1$
- (c) 计算基本分类器$G(x)$的系数$\alpha_m$,$\alpha_m$表示$G_m(x)$在最终分类器的权重性质.
- 当$e_m\leqslant \frac{1}{2}$,$\alpha \geqslant 0,$并且$a_m$随着$e_m$的减少而增大,所以分类误差率越小的基本分类器在最终的分类作用越大
- (d) 更新训练数据的权值分布为下一轮做准备.
- $\left\{\begin{matrix}
\frac{w_{mi}}{Z_m}e^{-\alpha}, &G_m(x_i)=y_i \\
\frac{w_{mi}}{Z_m}e^{\alpha}& G_m(x_i)\neq y_i
\end{matrix}\right.$
步骤(3) 线性组合$f(x)$实现M个基本分类器的加权表决.系数$\alpha_m$表示了$G_m(x)$的重要性,但是这里所有的$\alpha_m$之和并不为1.$f(x)$的符号决定了实例x的类,$f(x)$的绝对值表示了分类的确信度.
### AdaBoost的例子
给出如下表,假设多分类器是由$x<v$或者$x>v$产生,其中阈值为v使该分类器在训练数据集上分类错误率最低.

我们自定义选取的阈值为2.5,5.5,8.5
初始化数据权值分布
$D_1=(w_{11},w_{12},...,w_{110})$
$w_{1i}=\frac{1}{10} = 0.1,i=1,2,...,10$
**对m=1,**
(a) 在权值分布为$D_1$的训练数据集上,阈值v依次取值2.5,5.5,8.5时,且分别尝试**符号选择1,-1**时,错误率2.5或者8.5最低,那么我们先选取2.5,故基本分类器为:
$G_1(x)=\left\{\begin{matrix}
1, &x<2.5\\
-1,&x>2.5
\end{matrix}\right.$
**Note:**这里的符号选择是指,当我们选取某个阈值的时候,将其预测的分类分别使用1,-1尝试计算错误率,比如当我们选取阈值2.5时候,我们有两种选择方法:
- $\left\{\begin{matrix}
1, &x<2.5\\
-1,&x>2.5
\end{matrix}\right.$
- $\left\{\begin{matrix}
1, &x>2.5\\
-1,&x<2.5
\end{matrix}\right.$
$G_1(x)$的分类结果为:$[1,1,1,-1,-1,-1,-1,-1,-1,-1]$
$True\;labels:[1,1,1,-1,-1,-1,1,1,1,-1]$
(b) 计算$G_1(x)$在训练集上的错误率为$e_m = P(G_m(x_i) \neq y_i)=\sum_{i=1}^{N}w_{mi}I(G_m(x_i)\neq y_i)=0.1+0.1+0.1$这里分类错误的分别是x=6,7,8
(c) 计算$G_1(x)$的系数:$\alpha_1 = \frac{1}{2}log\frac{1-e_1}{e_1}=0.4236.$
(d) 更新训练样本的权值分布:
$D_2=(w_{21},...w_{210})$
$w_{wi}=\frac{w_{1i}}{Z_m}exp(-\alpha_1 y_i G_1(x_i)), i=1,2,...10$
$D_2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715)$
$f_1(x)=0.4236G_1(x)$
再使用分类器$sign[f_1(x)]$在训练数据集上进行分类,发现错误的点有3个.
**对m=2,**
(a) 在权值分布为 $D_2$ 的训练数据集上,阈值v依次取值2.5,5.5,8.5时,且分别尝试符号选择1,-1时,8.5最低,故基本分类器为:
$G_2(x)=\left\{\begin{matrix}
1, &x<8.5\\
-1,&x>8.5
\end{matrix}\right.$
$G_2(x)$的分类结果为:$[1,1,1,1,1,1,1,1,1,-1]$
$True\;labels:[1,1,1,-1,-1,-1,1,1,1,-1]$
(b) 计算$G_2(x)$在训练集上的错误率为$e_m = P(G_m(x_i) \neq y_i)=\sum_{i=1}^{N}w_{mi}I(G_m(x_i)\neq y_i)=0.0715+0.0715+0.0715=0.2145$这里分类错误的分别是x=3,4,5
(c) 计算$G_2(x)$的系数:$\alpha_2 = \frac{1}{2}log\frac{1-e_2}{e_2}=0.6496.$
(d) 更新训练样本的权值分布:
$D_3=(0.0455,0.0455,0.0455,0.1667,0.1667,0.1667,0.1060,0.1060,0.1060,0.0455)$
$f_2(x)=0.4236G_1(x)+0.6496G_2(x)$
再使用分类器$sign[f_2(x)]$在训练数据集上进行分类,发现错误的点有3个.
**对m=3,**
(a) 在权值分布为 $D_3$ 的训练数据集上,阈值v依次取值2.5,5.5,8.5时,且分别尝试符号选择1,-1时,5.5最低,故基本分类器为:
$G_3(x)=\left\{\begin{matrix}
-1, &x<5.5\\
1,&x>5.5
\end{matrix}\right.$
$G_3(x)$的分类结果为:$[-1,-1,-1,-1,-1,-1,1,1,1,1]$
$True\;labels:[1,1,1,-1,-1,-1,1,1,1,-1]$
(b) 计算$G_3(x)$在训练集上的错误率为$e_3=0.0455+0.0455+0.0455+0.0455=0.182$这里分类错误的分别是x=9,0,1,2
(c) 计算$G_3(x)$的系数:$\alpha_3 = \frac{1}{2}log\frac{1-e_3}{e_3}=0.7514.$
(d) 更新训练样本的权值分布:
$D_3=(0.125,0.125,0.125,0.102,0.102,0.102,0.065,0.065,0.065,0.125)$
$f_3(x)=0.4236G_1(x)+0.6496G_2(x)+0.7514G_3(x)$
再使用分类器$sign[f_3(x)]$在训练数据集上进行分类,发现错误的点有0个,分类完毕
所以最终的分类器为:
$G(x)=sign[f_3(x)=0.4236G_1(x)+0.6496G_2(x)+0.7514G_3(x)]$
## 下面将用Python代码实现
```
import numpy as np
```
1.首先我们创建一个模拟加载数据集,下面的为此例的数据集
```
def loadData():
"""
loading data set
Returns:
x: data set as x.
y: data set as y.
W: initialization weights.
"""
x = np.array([0,1,2,3,4,5,6,7,8,9])
y = np.array([1,1,1,-1,-1,-1,1,1,1,-1])
W = np.abs(y) / len(y)
return x,y,W
```
2.计算错误率,这里计算的错误率一定要走遍所有的阈值和方向的选取,最后返回出该轮最优阈值下的错误率最小的"基本分类器",这里的基本分类器是单层节点的决策分类器
$G_1(x)=\left\{\begin{matrix}
1, &x<thresh\\
-1,&x>thresh
\end{matrix}\right.$
-------------
$G_2(x)=\left\{\begin{matrix}
-1, &x<thresh\\
1,&x>thresh
\end{matrix}\right.$
```
def compute_error(threshs,x,y,W):
"""
compute error in every threshs.
Note:
1.Make sure the source data set is clean,we need copy x and y
2.initialization bestThresh_error is inf.
Returns:
bestThresh_error: The best error(minimum error) in some thresh.
bestGx: The best G(x) in best thresh and minimum error.
bestThresh_list: The best thresh,and split method.
"""
x_copy = x.copy()
G_x1 = y.copy()
G_x2 = y.copy()
bestThresh_error = np.inf
bestGx = None
bestThresh_list = None
for thresh in threshs:
index_gt = np.where(x_copy>thresh)[0] # find index in copy data
index_lt = np.where(x_copy<=thresh)[0]
G_x1[index_gt] = -1. # changed values in copy data,Implementate thresh split
G_x1[index_lt] = 1.
G_x2[index_gt] = 1. # we need try two situations.
G_x2[index_lt] = -1.
# compute error
G_W1 = np.where(G_x1 != y)
error_1 = np.sum(W[G_W1])
G_W2 = np.where(G_x2 != y)
error_2 = np.sum(W[G_W2])
# find the best error(minimum error),best thresh, best G(x)
if error_1 < bestThresh_error or error_2 < bestThresh_error:
if error_1 < error_2:
bestThresh_error = error_1.copy()
bestGx = G_x1.copy()
bestThresh_list = [thresh,"G_x1"]
else:
bestThresh_error = error_2.copy()
bestGx = G_x2.copy()
bestThresh_list = [thresh,"G_x2"]
return bestThresh_error,bestGx,bestThresh_list
```
3.计算G(x)的参数$\alpha$
```
def compute_alpha(error):
"""
Implement compute alpha value.
Returns:
alpha: parameters in G(x)
"""
alpha = 1./2. * (np.log((1.-error)/np.maximum(error,1e-16)))
return alpha
```
4.计算需要求出下一轮权重向量w的分母Z
```
def compute_Z(W,alpha,G_x,y):
"""
compute Z value to compute D
Returns:
Z:parameters in compute W or (D)
"""
return np.sum(W * np.exp(-alpha * y * G_x)),W
```
5.计算权重居中$D_{m+1}=(w_{m+1,1},w_{m+1,2},...w_{m+1,i},w_{m+1,N})$
```
def compute_W(W,Z,alpha,y,G_x):
"""
Implementate compute W(D)
returns:
W: weigths vector.
"""
W = W/Z * np.exp(-alpha * y * G_x)
return W
```
6.计算分类器$sign[f(x)]$
```
def compute_fx(alpha,G_x,y,thresh):
"""
build Classifier sign[f(x)]
Returns:
if fx equals label y,then we can break for loop,so we return False ,otherwise return True
"""
fx = np.multiply(alpha,G_x).sum(axis=0) # Implement f(x) = alpha_1G_1(x) + ... + alpha_nG_n(x)
fx[fx<0]=-1 # calculate "sign"
fx[fx>=0]=1
print("fx's result: ",fx)
if np.array_equal(fx,y):
print("划分结束")
return alpha[1:],thresh,False # alpha values is 0 when alpha index=1,so,alpha index start 1
else:
print("继续划分")
return alpha[1:],thresh,True
```
7.实现主函数
```
def main(epoch):
"""
Build main function, Implementate AdaBoost.
Returns:
1.classify parameters.
"""
x,y,W = loadData()
cache_alpha = np.zeros((1,1)) # cache alpha, this code must write.because every loop,we need append alpha value.
# The same reason as above
cache_Gx = np.zeros((1,len(x)))
cache_thresh = []
threshs = [2.5,5.5,8.5]
for i in range(epoch):
res_error,res_G_x,bestThresh_list = compute_error(threshs,x,y,W)
bestThresh = bestThresh_list[0]
cache_thresh.append(bestThresh_list)
print("error is: ",res_error,"G_x is: ",res_G_x,"best thresh: ",bestThresh)
cache_Gx = np.vstack((cache_Gx,np.array([res_G_x])))
alpha = compute_alpha(res_error)
cache_alpha = np.vstack((cache_alpha,np.array([[alpha]])))
Z,W = compute_Z(W=W,alpha=alpha,G_x=res_G_x,y=y)
W = compute_W(W,Z,alpha,y,res_G_x)
print("W is : ",W)
ALPHA,THRESH,result = compute_fx(alpha=cache_alpha,G_x=cache_Gx,y=y,thresh=cache_thresh)
if not result:
return ALPHA,THRESH
else:
print('程序执行完成,没有找到error=0的alpha.')
return ALPHA,THRESH
alphas,threshs = main(epoch=20)
print("alphas: ",alphas)
print("threshs: ",threshs)
```
由结果我们可以看出代码的结果是和例子中求出来的是一样的,阈值分别2.5采用第一种分割方式,8.5也是采用第一种分割方式,5.5采用第二种分割方式.
$\alpha_1=0.42364893,\alpha_2=0.64964149,\alpha_3=0.7520387$
实际上我们可以采取0.5步长的阈值进行测试.
```
def main_test(epoch):
"""
Build main function, Implementate AdaBoost.
Returns:
1.classify parameters.
"""
x,y,W = loadData()
cache_alpha = np.zeros((1,1)) # cache alpha, this code must write.because every loop,we need append alpha value.
# The same reason as above
cache_Gx = np.zeros((1,len(x)))
cache_thresh = []
threshs = np.arange(np.min(x),np.max(x),0.5)
for i in range(epoch):
res_error,res_G_x,bestThresh_list = compute_error(threshs,x,y,W)
bestThresh = bestThresh_list[0]
cache_thresh.append(bestThresh_list)
print("error is: ",res_error,"G_x is: ",res_G_x,"best thresh: ",bestThresh)
cache_Gx = np.vstack((cache_Gx,np.array([res_G_x])))
alpha = compute_alpha(res_error)
cache_alpha = np.vstack((cache_alpha,np.array([[alpha]])))
Z,W = compute_Z(W=W,alpha=alpha,G_x=res_G_x,y=y)
W = compute_W(W,Z,alpha,y,res_G_x)
print("W is : ",W)
ALPHA,THRESH,result = compute_fx(alpha=cache_alpha,G_x=cache_Gx,y=y,thresh=cache_thresh)
if not result:
return ALPHA,THRESH
else:
print('程序执行完成,没有找到error=0的alpha.')
return ALPHA,THRESH
alphas,threshs = main_test(epoch=10)
print("alphas: ",alphas)
print("threshs: ",threshs)
```
你会发现阈值结果和上面的会有些出入,但是也是正确的,因为化小数的阈值和化整数的阈值对于这个例子来说都是一样的
### 预测函数
$G(x)=sign[f(x)]=\alpha_1G_1(x) + \alpha_2G_2(x) + \cdots + \alpha_nG_n(x)$
```
def predict(test_x,alphas,threshs):
G_x = np.zeros(shape=(1,test_x.shape[0]))
for thresh_ in threshs:
G_x_single = np.ones(shape=(test_x.shape))
index_gt = np.where(test_x>thresh_[0])[0]
index_lt = np.where(test_x<=thresh_[0])[0]
if thresh_[1] == "G_x1":
G_x_single[index_gt] = -1.
G_x_single[index_lt] = 1.
G_x = np.vstack((G_x,G_x_single))
else:
G_x_single[index_gt] = 1.
G_x_single[index_lt] = -1.
G_x = np.vstack((G_x,G_x_single))
# compute fx
fx = np.multiply(alphas,G_x[1:]).sum(axis=0)
fx[fx<=0] = -1.
fx[fx>0] = 1
print(fx)
```
我们来看看测试的结果,我们分别尝试标签为1和-1的x的值

```
test_x = np.array([0])
predict(test_x=test_x,alphas=alphas,threshs=threshs)
test_x = np.array([5])
predict(test_x=test_x,alphas=alphas,threshs=threshs)
```
再来尝试一些其他的值
```
test_x = np.array([100])
predict(test_x=test_x,alphas=alphas,threshs=threshs)
```
最后我们来写出完整版的测试函数,返回训练样本的正确率
```
def predict_complete(test_x,test_y,alphas,threshs):
G_x = np.zeros(shape=(1,test_x.shape[0]))
for thresh_ in threshs:
G_x_single = np.ones(shape=(test_x.shape))
index_gt = np.where(test_x>thresh_[0])[0]
index_lt = np.where(test_x<=thresh_[0])[0]
if thresh_[1] == "G_x1":
G_x_single[index_gt] = -1.
G_x_single[index_lt] = 1.
G_x = np.vstack((G_x,G_x_single))
else:
G_x_single[index_gt] = 1.
G_x_single[index_lt] = -1.
G_x = np.vstack((G_x,G_x_single))
# compute fx
fx = np.multiply(alphas,G_x[1:]).sum(axis=0)
fx[fx<=0] = -1.
fx[fx>0] = 1
print("predict fx is : ",fx)
accurate = np.sum(fx==test_y)/len(test_y)
print("accurate is : ",accurate)
test_x = np.array([0,1,2,3,4,5,6,7,8,9])
test_y = np.array([1,1,1,-1,-1,-1,1,1,1,-1])
predict_complete(test_x=test_x,test_y=test_y,alphas=alphas,threshs=threshs)
```
### 现在使用大样本多特征进行测试
这里使用的样本是猫与非猫,其中猫是1,非猫是0
```
import h5py
import matplotlib.pyplot as plt
def load_data():
'''
create train set and test set
make sure you have .h5 file in your dataset
'''
train_dataset = h5py.File('data_set/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('data_set/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
train_x_orig, train_y, test_x_orig, test_y, classes = load_data()
train_x = train_x_orig.reshape(train_x_orig.shape[0],-1).T / 255
test_x = test_x_orig.reshape(test_x_orig.shape[0],-1).T / 255
print('Train_x\'s shape:{}'.format(train_x.shape))
print('Test_x\'s shape:{}'.format(test_x.shape))
print("Train_y's shape:{}".format(train_y.shape))
print("Test_y's shape:{}".format(test_y.shape))
index = 2
plt.imshow(train_x_orig[index])
print ("y = " + str(train_y[0,index]) + ". It's a " + classes[train_y[0,index]].decode("utf-8") + " picture.")
index = 3
plt.imshow(train_x_orig[index])
print ("y = " + str(train_y[0,index]) + ". It's a " + classes[train_y[0,index]].decode("utf-8") + " picture.")
```
根据AdaBoost的标签规则,更改y标签的值,从0,1改成-1,1.也就是说1为猫,-1为非猫。
```
train_y[train_y==0] = -1
print("New labels train_y is : ",train_y)
test_y[test_y==0] = -1
print("New labels test_y is : ",test_y)
def compute_error_big_data(threshs,x,y,W):
G_x1 = y.copy()
G_x2 = y.copy()
length_x = x.shape[0]
bestParameters = {'Thresh_error':np.inf}
for thresh in threshs:
for i in range(length_x):
# Try to split each feature.
index_gt = np.where(x[i,:]>thresh)[0] # find index in copy data
index_lt = np.where(x[i,:]<=thresh)[0]
G_x1[:,index_gt] = -1. # changed values in copy data,Implementate thresh split
G_x1[:,index_lt] = 1.
G_x2[:,index_gt] = 1. # we need try two situations.
G_x2[:,index_lt] = -1.
error_1 = np.sum(W[G_x1 !=y])
error_2 = np.sum(W[G_x2 != y])
if error_1 < error_2:
if error_1 < bestParameters['Thresh_error']:
bestParameters['Thresh_error'] = error_1.copy()
bestParameters['bestGx'] = G_x1.copy()
bestParameters['bestThresh'] = thresh
bestParameters['Feature_number'] = i
bestParameters['choose_split_method'] = "G_x1"
else:
if error_2 < bestParameters['Thresh_error']:
bestParameters['Thresh_error'] = error_2.copy()
bestParameters['bestGx'] = G_x2.copy()
bestParameters['bestThresh'] = thresh
bestParameters['Feature_number'] = i
bestParameters['choose_split_method'] = "G_x2"
return bestParameters
def compute_fx_for_big(alpha,G_x,y):
"""
build Classifier sign[f(x)]
Returns:
if fx equals label y,then we can break for loop,so we return False ,otherwise return True
"""
fx = np.multiply(alpha,G_x).sum(axis=0,keepdims=True) # Implement f(x) = alpha_1G_1(x) + ... + alpha_nG_n(x)
fx=np.sign(fx) # calculate "sign"
if np.array_equal(fx,y):
print("划分结束")
return alpha[1:],False # alpha values is 0 when alpha index=1,so,alpha index start 1
else:
return alpha[1:],True
def main_big_data(X,Y,epoch_num):
W = np.abs(Y)/Y.shape[1]
threshs = np.arange(np.min(X),np.max(X),0.1)
cache_alphas = np.zeros(shape=(1,1))
cache_Gx = np.zeros(Y.shape)
cache_Feature_number = []
cache_bestThresh = []
cache_choose_split_method = []
for epoch in range(epoch_num):
# select best thresh,error,Gx
bestParameters = compute_error_big_data(threshs=threshs,x=X,y=Y,W=W)
Thresh_error = bestParameters['Thresh_error']
bestGx = bestParameters['bestGx']
bestThresh = bestParameters['bestThresh']
Feature_number = bestParameters['Feature_number']
choose_split_method = bestParameters['choose_split_method']
# cache parameters
cache_Gx = np.vstack((cache_Gx,bestGx))
cache_Feature_number.append(Feature_number)
cache_bestThresh.append(bestThresh)
cache_choose_split_method.append(choose_split_method)
# compute alpha
alpha = compute_alpha(error=Thresh_error)
cache_alphas = np.vstack((cache_alphas,alpha))
# update weigths
Z,W = compute_Z(W=W,alpha=alpha,G_x=bestGx,y=Y)
W = compute_W(W=W,Z=Z,alpha=alpha,y=Y,G_x=bestGx)
ALPHA,result = compute_fx_for_big(alpha=cache_alphas,G_x=cache_Gx,y=Y)
if not result:
return ALPHA,cache_Feature_number,cache_bestThresh,cache_choose_split_method
else:
print('程序执行完成,没有找到error=0的alpha.')
return ALPHA,cache_Feature_number,cache_bestThresh,cache_choose_split_method
ALPHA,cache_Feature_number,cache_bestThresh,cache_choose_split_method = main_big_data(X=train_x,Y=train_y,epoch_num=10)
print("alphs is : ",ALPHA)
print("Feature_number is :",cache_Feature_number)
print("bestThresh is: ",cache_bestThresh)
print("choose split method is :",cache_choose_split_method)
def predict(test_X,test_Y,alphas,Feature_number,bestThresh,choose_split_method):
G_x = np.zeros(test_Y.shape)
for i in range(alphas.shape[0]):
G_x_single = np.ones(shape=(test_Y.shape))
# must choose one feature to split lable.
index_gt = np.where(test_X[Feature_number[i],:] > bestThresh[i])[0]
index_lt = np.where(test_X[Feature_number[i],:] <= bestThresh[i])[0]
if choose_split_method[i] == "G_x1":
G_x_single[:,index_gt] = -1.
G_x_single[:,index_lt] = 1.
G_x = np.vstack((G_x,G_x_single))
else:
G_x_single[:,index_gt] = 1.
G_x_single[:,index_lt] = -1.
G_x = np.vstack((G_x,G_x_single))
# Compute fx
fx = np.multiply(alphas,G_x[1:]).sum(axis=0,keepdims=True)
fx = np.sign(fx)
# calculate accurate.
accurate = np.sum(fx==test_Y) / test_Y.shape[1]
return accurate
accurate = predict(test_X=train_x,test_Y=train_y,alphas=ALPHA,Feature_number=cache_Feature_number,
bestThresh=cache_bestThresh,choose_split_method=cache_choose_split_method)
print("The train accurate is : ",accurate)
fx = predict(test_X=test_x,test_Y=test_y,alphas=ALPHA,Feature_number=cache_Feature_number,
bestThresh=cache_bestThresh,choose_split_method=cache_choose_split_method)
print("The f(x) is : ",fx)
def different_epoch_num():
plot_accurate = []
for i in range(1,50,5):
ALPHA,cache_Feature_number,cache_bestThresh,cache_choose_split_method = main_big_data(X=train_x,Y=train_y,epoch_num=i)
accurate = predict(test_X=train_x,test_Y=train_y,alphas=ALPHA,Feature_number=cache_Feature_number,
bestThresh=cache_bestThresh,choose_split_method=cache_choose_split_method)
print("After iter:{}, The Train set accurate is : ".format(i),accurate)
accurate = predict(test_X=test_x,test_Y=test_y,alphas=ALPHA,Feature_number=cache_Feature_number,
bestThresh=cache_bestThresh,choose_split_method=cache_choose_split_method)
print("After iter:{}, The Test set accurate is : ".format(i),accurate)
different_epoch_num()
```
| 迭代次数 | 训练样本正确率 | 测试样本正确率 |
| ------ | ------- | ------ |
| 1 | 0.68 | 0.58 |
| 6 | 0.77 | 0.58 |
| 11 | 0.88 | 0.64 |
| 16 | 0.89 | 0.58 |
| 21 | 0.96 | 0.66 |
| 26 | 0.97 | 0.58 |
| 31 | 0.99 | 0.58 |
| 36 | 0.99 | 0.6 |
| 41 | 0.99 | 0.66 |
| 46 | 1.0 | 0.58 |
可以看到随着迭代次数的增加,训练样本的正确率逐步升高,测试样本的正确率先升高然后降低(或者说在一定范围浮动),很明显在最大分类器46以后,再进行更多次数的迭代是毫无意义的,应该46已经是最大分类器的数量(实际上这里的最大分类器是44,也就是说训练样本误差为0),测试样本的正确率在分类器44以后都维持在0.58.所以按照上面的表格,我们应该选择分类器为41个左右的弱分类器所组成的强分类器是最好的
另外也可以看出随着分类器的个数的增加到一定限度,算法就开始呈现过拟合的状态.
实际在在运用过程中,不能总是想着训练样本的误差为0,因为这样模型就容易过拟合,再者,对于基本分类器$G_i(x)$,我们也可以选择其他的模型,比如:
Bagging + 决策树 = 随机森林
AdaBoost + 决策树 = 提升树
Gradient Boosting + 决策树 = GBDT
| true |
code
| 0.57326 | null | null | null | null |
|
## Computer Vision Interpret
[`vision.interpret`](/vision.interpret.html#vision.interpret) is the module that implements custom [`Interpretation`](/train.html#Interpretation) classes for different vision tasks by inheriting from it.
```
from fastai.gen_doc.nbdoc import *
from fastai.vision import *
from fastai.vision.interpret import *
show_doc(SegmentationInterpretation)
show_doc(SegmentationInterpretation.top_losses)
show_doc(SegmentationInterpretation._interp_show)
show_doc(SegmentationInterpretation.show_xyz)
show_doc(SegmentationInterpretation._generate_confusion)
show_doc(SegmentationInterpretation._plot_intersect_cm)
```
Let's show how [`SegmentationInterpretation`](/vision.interpret.html#SegmentationInterpretation) can be used once we train a segmentation model.
### train
```
camvid = untar_data(URLs.CAMVID_TINY)
path_lbl = camvid/'labels'
path_img = camvid/'images'
codes = np.loadtxt(camvid/'codes.txt', dtype=str)
get_y_fn = lambda x: path_lbl/f'{x.stem}_P{x.suffix}'
data = (SegmentationItemList.from_folder(path_img)
.split_by_rand_pct()
.label_from_func(get_y_fn, classes=codes)
.transform(get_transforms(), tfm_y=True, size=128)
.databunch(bs=16, path=camvid)
.normalize(imagenet_stats))
data.show_batch(rows=2, figsize=(7,5))
learn = unet_learner(data, models.resnet18)
learn.fit_one_cycle(3,1e-2)
learn.save('mini_train')
jekyll_warn("Following results will not make much sense with this underperforming model but functionality will be explained with ease")
```
### interpret
```
interp = SegmentationInterpretation.from_learner(learn)
```
Since `FlattenedLoss of CrossEntropyLoss()` is used we reshape and then take the mean of pixel losses per image. In order to do so we need to pass `sizes:tuple` to `top_losses()`
```
top_losses, top_idxs = interp.top_losses(sizes=(128,128))
top_losses, top_idxs
plt.hist(to_np(top_losses), bins=20);plt.title("Loss Distribution");
```
Next, we can generate a confusion matrix similar to what we usually have for classification. Two confusion matrices are generated: `mean_cm` which represents the global label performance and `single_img_cm` which represents the same thing but for each individual image in dataset.
Values in the matrix are calculated as:
\begin{align}
\ CM_{ij} & = IOU(Predicted , True | True) \\
\end{align}
Or in plain english: ratio of pixels of predicted label given the true pixels
```
learn.data.classes
mean_cm, single_img_cm = interp._generate_confusion()
mean_cm.shape, single_img_cm.shape
```
`_plot_intersect_cm` first displays a dataframe showing per class score using the IOU definition we made earlier. These are the diagonal values from the confusion matrix which is displayed after.
`NaN` indicate that these labels were not present in our dataset, in this case validation set. As you can imagine it also helps you to maybe construct a better representing validation set.
```
df = interp._plot_intersect_cm(mean_cm, "Mean of Ratio of Intersection given True Label")
```
Next let's look at the single worst prediction in our dataset. It looks like this dummy model just predicts everything as `Road` :)
```
i = top_idxs[0]
df = interp._plot_intersect_cm(single_img_cm[i], f"Ratio of Intersection given True Label, Image:{i}")
```
Finally we will visually inspect this single prediction
```
interp.show_xyz(i, sz=15)
jekyll_warn("""With matplotlib colormaps the max number of unique qualitative colors is 20.
So if len(classes) > 20 then close class indexes may be plotted with the same color.
Let's fix this together :)""")
interp.c2i
show_doc(ObjectDetectionInterpretation)
jekyll_warn("ObjectDetectionInterpretation is not implemented yet. Feel free to implement it :)")
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.715514 | null | null | null | null |
|
[](https://colab.research.google.com/github/giswqs/geemap/blob/master/examples/notebooks/tn_surface_water.ipynb)
# Automated mapping of surface water in the state of Tennessee using Google Earth Engine cloud computing
Author: Qiusheng Wu ([Website](https://wetlands.io) - [GitHub](https://github.com/giswqs))
<h1>Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Install-geemap" data-toc-modified-id="Install-geemap-1"><span class="toc-item-num">1 </span>Install geemap</a></span></li><li><span><a href="#Create-an-interactive-map" data-toc-modified-id="Create-an-interactive-map-2"><span class="toc-item-num">2 </span>Create an interactive map</a></span></li><li><span><a href="#Define-region-of-interest-(ROI)" data-toc-modified-id="Define-region-of-interest-(ROI)-3"><span class="toc-item-num">3 </span>Define region of interest (ROI)</a></span></li><li><span><a href="#Create-Landsat-timeseries" data-toc-modified-id="Create-Landsat-timeseries-4"><span class="toc-item-num">4 </span>Create Landsat timeseries</a></span></li><li><span><a href="#Calculate-Normalized-Difference-Water-Index-(NDWI)" data-toc-modified-id="Calculate-Normalized-Difference-Water-Index-(NDWI)-5"><span class="toc-item-num">5 </span>Calculate Normalized Difference Water Index (NDWI)</a></span></li><li><span><a href="#Extract-surface-water-extent" data-toc-modified-id="Extract-surface-water-extent-6"><span class="toc-item-num">6 </span>Extract surface water extent</a></span></li><li><span><a href="#Calculate-surface-water-areas" data-toc-modified-id="Calculate-surface-water-areas-7"><span class="toc-item-num">7 </span>Calculate surface water areas</a></span></li><li><span><a href="#Plot-temporal-trend" data-toc-modified-id="Plot-temporal-trend-8"><span class="toc-item-num">8 </span>Plot temporal trend</a></span></li></ul></div>
## Install geemap
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
import ee
import geemap
```
## Create an interactive map
```
Map = geemap.Map()
Map
```
## Define region of interest (ROI)
```
roi = ee.FeatureCollection('TIGER/2018/States').filter(
ee.Filter.eq('NAME', 'Tennessee')
)
Map.addLayer(roi, {}, "TN")
Map.centerObject(roi, 7)
```
## Create Landsat timeseries
```
images = geemap.landsat_timeseries(
roi=roi, start_year=1984, end_year=2020, start_date='01-01', end_date='12-31'
)
first = images.first()
vis_params = {'bands': ['NIR', 'Red', 'Green'], 'min': 0, 'max': 3000}
Map.addLayer(first, vis_params, 'First image')
```
## Calculate Normalized Difference Water Index (NDWI)
```
ndwi_images = images.map(
lambda img: img.normalizedDifference(['Green', 'SWIR1']).rename('ndwi')
)
ndwi_palette = [
'#ece7f2',
'#d0d1e6',
'#a6bddb',
'#74a9cf',
'#3690c0',
'#0570b0',
'#045a8d',
'#023858',
]
first_ndwi = ndwi_images.first()
Map.addLayer(first_ndwi, {'palette': ndwi_palette}, 'First NDWI')
```
## Extract surface water extent
```
water_images = ndwi_images.map(lambda img: img.gt(0).selfMask())
first_water = water_images.first()
Map.addLayer(first_water, {'palette': ['blue']}, 'First Water')
```
## Calculate surface water areas
```
def cal_area(img):
pixel_area = img.multiply(ee.Image.pixelArea()).divide(1e6)
img_area = pixel_area.reduceRegion(
**{
'geometry': roi.geometry(),
'reducer': ee.Reducer.sum(),
'scale': 1000,
'maxPixels': 1e12,
}
)
return img.set({'water_area': img_area})
water_areas = water_images.map(cal_area)
water_stats = water_areas.aggregate_array('water_area').getInfo()
water_stats
```
## Plot temporal trend
```
import matplotlib.pyplot as plt
x = list(range(1984, 2021))
y = [item.get('ndwi') for item in water_stats]
plt.bar(x, y, align='center', alpha=0.5)
# plt.xticks(y_pos, objects)
plt.ylabel('Area (km2)')
plt.title('Surface water dynamics in Tennessee')
plt.show()
Map.addLayerControl()
Map
```
| true |
code
| 0.606091 | null | null | null | null |
|

___
#### NAME:
#### STUDENT ID:
___
## Numpy Introduction
```
# Load required modules
import numpy as np
```
<br>
**1a) Create two numpy arrays called** ```a``` **and** ```b``` **where** ```a``` **should be all integers between 25-34 (inclusive), and** ```b``` **should be ten evenly spaced numbers between 1-6 (inclusive). Print** ```a``` **and** ```b```
```
# your work here
```
<br>
**1b) [Cube](https://numpy.org/doc/stable/reference/routines.math.html) (i.e. raise to the power of 3) all the elements in both** ```a``` **and** ```b``` **(element-wise). Store the results in two new arrays called** ```cubed_a``` **and** ```cubed_b```**. Print** ```cubed_a``` **and** ```cubed_b```
```
# your work here
```
<br>
**1c) [Add](https://numpy.org/doc/stable/reference/routines.math.html) the two cubed arrays (e.g.** ```[1,2] + [3,4] = [4,6]```**) and store the result in an array called** ```c```**. Print** ```c```
```
# your work here
```
<br>
**1d) [Sum](https://numpy.org/doc/stable/reference/routines.math.html) the elements with even indices of** ```c``` **and store the result in a variable called** ```d```**. Print** ```d```
```
# your work here
```
<br>
**1e) Take the element-wise [square root](https://numpy.org/doc/stable/reference/routines.math.html) of the** ```c``` **and store the result in an array called** ```e```**. Print** ```e```
```
# your work here
```
<br>
**1f) [Append](https://numpy.org/doc/stable/reference/routines.array-manipulation.html)** ```b``` **to** ```a```, **[reshape](https://numpy.org/doc/stable/reference/routines.array-manipulation.html) the appended array so that it is a 4x5, 2D array and store the results in a variable called** ```m```**. Print** ```m```
```
# your work here
```
<br>
**1g) Extract the third and the fourth column of the** ```m``` **matrix. Store the resulting 4x2 matrix in a new variable called** ```m2```**. Print** ```m2```
```
# your work here
```
<br>
**1h) Take the [dot product](https://numpy.org/doc/stable/reference/routines.array-manipulation.html) of** ```m``` **and** ```m2```**. Store the results in a matrix called** ```m3```**. Print** ```m3```
>**Note:** the Dot product of two matrices is given by
$$\large{A\cdot B = A^{T}B}$$
<br>
```
# your work here
```
<br>
**1i) [Round](https://numpy.org/doc/stable/reference/routines.math.html) the** ```m3``` **matrix to three decimal points. Store the result in place and print the new** ```m3```
```
# your work here
```
<br>
___
## NumPy and Masks
<br>
**2a) Create an array called** ```f``` **where the values are** ```cos(x)``` **for** ```x``` **from $0$ to $\pi$ with 50 [equally spaced values](https://numpy.org/doc/stable/reference/routines.array-creation.html) (inclusive). Print** ```f```
```
# your work here
```
<br>
**2b) Use a [mask](https://numpy.org/doc/stable/reference/maskedarray.html) to get an array that is** ```True``` **when** ```f >= 1/2``` **and** ```False``` **when** ```f < 1/2```**. Store the result in an array called** ```g```**. Print** ```g```
```
# your work here
```
<br>
**2c) Create an array called** ```h``` **that has only those values where** ```f>= 1/2```**. Print** ```h```
```
# your work here
```
<br>
___
## Exploratory Data Analysis (EDA) - Data Visualization
<br>
**3.1) Using the** ```df_google``` **data, plot the daily** ```High``` **value as a time series. Give your plot a title.**
>**Tip:**<br>
>* To view your current working directory enter ```%pwd``` in cell and run it.
>**To Do:**<br>
>1. Extract the data from the *'column'* ```high```<br>
>2. Use the datetime array, ```days``` with you extracted data to plot a lineplot (time series) using pyplot. Give your plot a tile.
<br>
**Note:** If you are having a hard time extracting the correct data, take a look at the *References and Additional Resources* section of the main notebook. In particular, the section titled *More on Multi-Dimensional Arrays* should have some valuable information.
```
# Plotting Set Up
import pandas as pd
import matplotlib.pyplot as plt
# jupyter notebook magic to display plots in output
%matplotlib inline
# make the plots bigger
plt.rcParams['figure.figsize'] = (10,8)
path_to_file = 'df_google.csv'
data = np.genfromtxt(path_to_file, delimiter=',')
# time stamps
index = pd.date_range('1/2/2018', periods=525)
# convert to np array include yyyy-mm-dd but not time
days = np.array(index, dtype = 'datetime64[D]')
# sanity check
days[:5]
# your work here
```
<br>
___
## NumPy and 2 Variable Prediction
<br>
**Below we have created 2 NumPy arrays each of size 100 that represent the following:**<br>
> ```x``` (number of miles) ranges from 1 to 10 with a uniform noise of $(0, 1/2)$<br>
> ```y``` (money spent in dollars) will be from 1 to 20 with a uniform noise $(0, 1)$
```
# seed the random number generator with a fixed value
import numpy as np
np.random.seed(500)
x=np.linspace(1, 10, 100) + np.random.uniform(low = 0, high = 0.5, size = 100)
y=np.linspace(1, 20, 100) + np.random.uniform(low = 0, high = 1.0, size = 100)
# sanity check
print ('x = ', x[:10])
print ('\ny = ', y[:10])
```
<br>
**3a) Find the [expected](https://numpy.org/doc/stable/reference/routines.statistics.html) value of** ```x``` **and the expected value of** ```y```**. Store the results in two variables called** ```ex``` **and** ```ey```
```
# your work here
```
<br>
**3b) Find [variance](https://numpy.org/doc/stable/reference/routines.statistics.html) of** ```x``` **and** ```y```**. Store the results in two variables called** ```varx``` **and** ```vary```
```
# your work here
```
<br>
**3c) Find [co-variance](https://numpy.org/doc/stable/reference/routines.statistics.html) of** ```x``` **and** ```y```**. Store the result in a variable called** ```cov```
```
# your work here
```
<br>
**3d) Assume that number of dollars spent in car fuel is only dependant on the miles driven -- a linear relationship. Write code that uses a linear predictor to calculate a predicted value of** ```y``` **for each** ```x``` **and store your predicitions in an array called** ```y_pred```**. Print first 5 elements in** ```y_pred```<br>
$$\large{y_{_{predicted}} = f(x) = y_0 + kx}$$
<br>
```
# your work here
```
<br>
**3e) Put the prediction error into an array called** ```y_error```**. Print first 5 elements in** ```y_error```
```
# your work here
```
<br>
**3f) Write code that calculates the root mean square error (RMSE). Store the result in a variable called** ```rmse```**. Print** ```rmse```
<br>
$$\large{RMSE = \sqrt{\frac{\sum_{i=1}^{n} \left(y_{_{predicted}} - y_{_{actual}}\right)^{^2}}{n}}} $$
<br>
```
# your work here
```
___
### Deliverables
Please submit your the following via the instructed method (lecture or Syllabus):
>(1) A copy of your work, either a downloaded notebook or a pdf, by the assignment deadline
<br>
**Note:** Don't gorget to restart your kernel prior to extracting your data.
>```Kernel --> Restart Kernel and Run all Cells```<br>
>```File --> Export Notebooks As --> PDF``` (or as instructed)
___
| true |
code
| 0.739414 | null | null | null | null |
|
---
_You are currently looking at **version 1.0** of this notebook. To download notebooks and datafiles, as well as get help on Jupyter notebooks in the Coursera platform, visit the [Jupyter Notebook FAQ](https://www.coursera.org/learn/python-data-analysis/resources/0dhYG) course resource._
---
# Merging Dataframes
```
import pandas as pd
df = pd.DataFrame([{'Name': 'Chris', 'Item Purchased': 'Sponge', 'Cost': 22.50},
{'Name': 'Kevyn', 'Item Purchased': 'Kitty Litter', 'Cost': 2.50},
{'Name': 'Filip', 'Item Purchased': 'Spoon', 'Cost': 5.00}],
index=['Store 1', 'Store 1', 'Store 2'])
df
df['Date'] = ['December 1', 'January 1', 'mid-May']
df
df['Delivered'] = True
df
df['Feedback'] = ['Positive', None, 'Negative']
df
adf = df.reset_index()
adf['Date'] = pd.Series({0: 'December 1', 2: 'mid-May'})
adf
staff_df = pd.DataFrame([{'Name': 'Kelly', 'Role': 'Director of HR'},
{'Name': 'Sally', 'Role': 'Course liasion'},
{'Name': 'James', 'Role': 'Grader'}])
staff_df = staff_df.set_index('Name')
student_df = pd.DataFrame([{'Name': 'James', 'School': 'Business'},
{'Name': 'Mike', 'School': 'Law'},
{'Name': 'Sally', 'School': 'Engineering'}])
student_df = student_df.set_index('Name')
print(staff_df.head())
print()
print(student_df.head())
pd.merge(staff_df, student_df, how='outer', left_index=True, right_index=True)
pd.merge(staff_df, student_df, how='inner', left_index=True, right_index=True)
pd.merge(staff_df, student_df, how='left', left_index=True, right_index=True)
pd.merge(staff_df, student_df, how='right', left_index=True, right_index=True)
staff_df = staff_df.reset_index()
student_df = student_df.reset_index()
pd.merge(staff_df, student_df, how='left', left_on='Name', right_on='Name')
staff_df = pd.DataFrame([{'Name': 'Kelly', 'Role': 'Director of HR', 'Location': 'State Street'},
{'Name': 'Sally', 'Role': 'Course liasion', 'Location': 'Washington Avenue'},
{'Name': 'James', 'Role': 'Grader', 'Location': 'Washington Avenue'}])
student_df = pd.DataFrame([{'Name': 'James', 'School': 'Business', 'Location': '1024 Billiard Avenue'},
{'Name': 'Mike', 'School': 'Law', 'Location': 'Fraternity House #22'},
{'Name': 'Sally', 'School': 'Engineering', 'Location': '512 Wilson Crescent'}])
pd.merge(staff_df, student_df, how='left', left_on='Name', right_on='Name')
staff_df = pd.DataFrame([{'First Name': 'Kelly', 'Last Name': 'Desjardins', 'Role': 'Director of HR'},
{'First Name': 'Sally', 'Last Name': 'Brooks', 'Role': 'Course liasion'},
{'First Name': 'James', 'Last Name': 'Wilde', 'Role': 'Grader'}])
student_df = pd.DataFrame([{'First Name': 'James', 'Last Name': 'Hammond', 'School': 'Business'},
{'First Name': 'Mike', 'Last Name': 'Smith', 'School': 'Law'},
{'First Name': 'Sally', 'Last Name': 'Brooks', 'School': 'Engineering'}])
staff_df
student_df
pd.merge(staff_df, student_df, how='inner', left_on=['First Name','Last Name'], right_on=['First Name','Last Name'])
```
# Idiomatic Pandas: Making Code Pandorable
```
import pandas as pd
df = pd.read_csv('census.csv')
df
(df.where(df['SUMLEV']==50)
.dropna()
.set_index(['STNAME','CTYNAME'])
.rename(columns={'ESTIMATESBASE2010': 'Estimates Base 2010'}))
df = df[df['SUMLEV']==50]
df.set_index(['STNAME','CTYNAME'], inplace=True)
df.rename(columns={'ESTIMATESBASE2010': 'Estimates Base 2010'})
import numpy as np
def min_max(row):
data = row[['POPESTIMATE2010',
'POPESTIMATE2011',
'POPESTIMATE2012',
'POPESTIMATE2013',
'POPESTIMATE2014',
'POPESTIMATE2015']]
return pd.Series({'min': np.min(data), 'max': np.max(data)})
df.apply(min_max, axis=1)
import numpy as np
def min_max(row):
data = row[['POPESTIMATE2010',
'POPESTIMATE2011',
'POPESTIMATE2012',
'POPESTIMATE2013',
'POPESTIMATE2014',
'POPESTIMATE2015']]
row['max'] = np.max(data)
row['min'] = np.min(data)
return row
df.apply(min_max, axis=1)
rows = ['POPESTIMATE2010',
'POPESTIMATE2011',
'POPESTIMATE2012',
'POPESTIMATE2013',
'POPESTIMATE2014',
'POPESTIMATE2015']
df.apply(lambda x: np.max(x[rows]), axis=1)
```
# Group by
```
import pandas as pd
import numpy as np
df = pd.read_csv('census.csv')
df = df[df['SUMLEV']==50]
df
%%timeit -n 10
for state in df['STNAME'].unique():
avg = np.average(df.where(df['STNAME']==state).dropna()['CENSUS2010POP'])
print('Counties in state ' + state + ' have an average population of ' + str(avg))
%%timeit -n 10
for group, frame in df.groupby('STNAME'):
avg = np.average(frame['CENSUS2010POP'])
print('Counties in state ' + group + ' have an average population of ' + str(avg))
df.head()
df = df.set_index('STNAME')
def fun(item):
if item[0]<'M':
return 0
if item[0]<'Q':
return 1
return 2
for group, frame in df.groupby(fun):
print('There are ' + str(len(frame)) + ' records in group ' + str(group) + ' for processing.')
df = pd.read_csv('census.csv')
df = df[df['SUMLEV']==50]
df.groupby('STNAME').agg({'CENSUS2010POP': np.average})
print(type(df.groupby(level=0)['POPESTIMATE2010','POPESTIMATE2011']))
print(type(df.groupby(level=0)['POPESTIMATE2010']))
(df.set_index('STNAME').groupby(level=0)['CENSUS2010POP']
.agg({'avg': np.average, 'sum': np.sum}))
(df.set_index('STNAME').groupby(level=0)['POPESTIMATE2010','POPESTIMATE2011']
.agg({'avg': np.average, 'sum': np.sum}))
(df.set_index('STNAME').groupby(level=0)['POPESTIMATE2010','POPESTIMATE2011']
.agg({'POPESTIMATE2010': np.average, 'POPESTIMATE2011': np.sum}))
```
# Scales
```
df = pd.DataFrame(['A+', 'A', 'A-', 'B+', 'B', 'B-', 'C+', 'C', 'C-', 'D+', 'D'],
index=['excellent', 'excellent', 'excellent', 'good', 'good', 'good', 'ok', 'ok', 'ok', 'poor', 'poor'])
df.rename(columns={0: 'Grades'}, inplace=True)
df
df['Grades'].astype('category').head()
grades = df['Grades'].astype('category',
categories=['D', 'D+', 'C-', 'C', 'C+', 'B-', 'B', 'B+', 'A-', 'A', 'A+'],
ordered=True)
grades.head()
grades > 'C'
df = pd.read_csv('census.csv')
df = df[df['SUMLEV']==50]
df = df.set_index('STNAME').groupby(level=0)['CENSUS2010POP'].agg({'avg': np.average})
pd.cut(df['avg'],10)
```
# Pivot Tables
```
#http://open.canada.ca/data/en/dataset/98f1a129-f628-4ce4-b24d-6f16bf24dd64
df = pd.read_csv('cars.csv')
df.head()
df.pivot_table(values='(kW)', index='YEAR', columns='Make', aggfunc=np.mean)
df.pivot_table(values='(kW)', index='YEAR', columns='Make', aggfunc=[np.mean,np.min], margins=True)
```
# Date Functionality in Pandas
```
import pandas as pd
import numpy as np
```
### Timestamp
```
pd.Timestamp('9/1/2016 10:05AM')
```
### Period
```
pd.Period('1/2016')
pd.Period('3/5/2016')
```
### DatetimeIndex
```
t1 = pd.Series(list('abc'), [pd.Timestamp('2016-09-01'), pd.Timestamp('2016-09-02'), pd.Timestamp('2016-09-03')])
t1
type(t1.index)
```
### PeriodIndex
```
t2 = pd.Series(list('def'), [pd.Period('2016-09'), pd.Period('2016-10'), pd.Period('2016-11')])
t2
type(t2.index)
```
### Converting to Datetime
```
d1 = ['2 June 2013', 'Aug 29, 2014', '2015-06-26', '7/12/16']
ts3 = pd.DataFrame(np.random.randint(10, 100, (4,2)), index=d1, columns=list('ab'))
ts3
ts3.index = pd.to_datetime(ts3.index)
ts3
pd.to_datetime('4.7.12', dayfirst=True)
```
### Timedeltas
```
pd.Timestamp('9/3/2016')-pd.Timestamp('9/1/2016')
pd.Timestamp('9/2/2016 8:10AM') + pd.Timedelta('12D 3H')
```
### Working with Dates in a Dataframe
```
dates = pd.date_range('10-01-2016', periods=9, freq='2W-SUN')
dates
df = pd.DataFrame({'Count 1': 100 + np.random.randint(-5, 10, 9).cumsum(),
'Count 2': 120 + np.random.randint(-5, 10, 9)}, index=dates)
df
df.index.weekday_name
df.diff()
df.resample('M').mean()
df['2017']
df['2016-12']
df['2016-12':]
df.asfreq('W', method='ffill')
import matplotlib.pyplot as plt
%matplotlib inline
df.plot()
```
| true |
code
| 0.22072 | null | null | null | null |
|
```
# for use in tutorial and development; do not include this `sys.path` change in production:
import sys ; sys.path.insert(0, "../")
```
# Vector embedding with `gensim`
Let's make use of deep learning through a technique called *embedding* – to analyze the relatedness of the labels used for recipe ingredients.
Among the most closely related ingredients:
* Some are very close synonyms and should be consolidated to improve data quality
* Others are interesting other ingredients that pair frequently, useful for recommendations
On the one hand, this approach is quite helpful for analyzing the NLP annotations that go into a knowledge graph.
On the other hand it can be used along with [`SKOS`](https://www.w3.org/2004/02/skos/) or similar vocabularies for ontology-based discovery within the graph, e.g., for advanced search UI.
## Curating annotations
We'll be working with the labels for ingredients that go into our KG.
Looking at the raw data, there are many cases where slightly different spellings are being used for the same entity.
As a first step let's define a list of synonyms to substitute, prior to running the vector embedding.
This will help produce better quality results.
Note that this kind of work comes of the general heading of *curating annotations* ... which is what we spend so much time doing in KG work.
It's similar to how *data preparation* is ~80% of the workload for data science teams, and for good reason.
```
SYNONYMS = {
"pepper": "black pepper",
"black pepper": "black pepper",
"egg": "egg",
"eggs": "egg",
"vanilla": "vanilla",
"vanilla extract": "vanilla",
"flour": "flour",
"all-purpose flour": "flour",
"onions": "onion",
"onion": "onion",
"carrots": "carrot",
"carrot": "carrot",
"potatoes": "potato",
"potato": "potato",
"tomatoes": "tomato",
"fresh tomatoes": "tomato",
"fresh tomato": "tomato",
"garlic": "garlic",
"garlic clove": "garlic",
"garlic cloves": "garlic",
}
```
## Analyze ingredient labels from 250K recipes
```
import csv
MAX_ROW = 250000 # 231638
max_context = 0
min_context = 1000
recipes = []
vocab = set()
with open("../dat/all_ind.csv", "r") as f:
reader = csv.reader(f)
next(reader, None) # remove file header
for i, row in enumerate(reader):
id = row[0]
ind_set = set()
# substitute synonyms
for ind in set(eval(row[3])):
if ind in SYNONYMS:
ind_set.add(SYNONYMS[ind])
else:
ind_set.add(ind)
if len(ind_set) > 1:
recipes.append([id, ind_set])
vocab.update(ind_set)
max_context = max(max_context, len(ind_set))
min_context = min(min_context, len(ind_set))
if i > MAX_ROW:
break
print("max context: {} unique ingredients per recipe".format(max_context))
print("min context: {} unique ingredients per recipe".format(min_context))
print("vocab size", len(list(vocab)))
```
Since we've performed this data preparation work, let's use `pickle` to save this larger superset of the recipes dataset to the `tmp.pkl` file:
```
import pickle
pickle.dump(recipes, open("tmp.pkl", "wb"))
recipes[:3]
```
Then we can restore the pickled Python data structure for usage later in other use cases.
The output shows the first few entries, to illustrated the format.
Now reshape this data into a vector of vectors of ingredients per recipe, to use for training a [*word2vec*](https://arxiv.org/abs/1301.3781) vector embedding model:
```
vectors = [
[
ind
for ind in ind_set
]
for id, ind_set in recipes
]
vectors[:3]
```
We'll use the [`Word2Vec`](https://radimrehurek.com/gensim/models/word2vec.html) implementation in the `gensim` library (i.e., *deep learning*) to train an embedding model.
This approach tends to work best if the training data has at least 100K rows.
Let's also show how to serialize the *word2vec* results, saving them to the `tmp.w2v` file so they could be restored later for other use cases.
NB: there is work in progress which will replace `gensim` with `pytorch` instead.
```
import gensim
MIN_COUNT = 2
model_path = "tmp.w2v"
model = gensim.models.Word2Vec(vectors, min_count=MIN_COUNT, window=max_context)
model.save(model_path)
```
The `get_related()` function takes any ingredient as input, using the embedding model to find the most similar other ingredients – along with calculating [`levenshtein`](https://github.com/toastdriven/pylev) edit distances (string similarity) among these labels. Then it calculates *percentiles* for both metrics in [`numpy`](https://numpy.org/) and returns the results as a [`pandas`](https://pandas.pydata.org/) DataFrame.
```
import numpy as np
import pandas as pd
import pylev
def term_ratio (target, description):
d_set = set(description.split(" "))
num_inter = len(d_set.intersection(target))
return num_inter / float(len(target))
def get_related (model, query, target, n=20, granularity=100):
"""return a DataFrame of the closely related items"""
try:
bins = np.linspace(0, 1, num=granularity, endpoint=True)
v = sorted(
model.wv.most_similar(positive=[query], topn=n),
key=lambda x: x[1],
reverse=True
)
df = pd.DataFrame(v, columns=["ingredient", "similarity"])
s = df["similarity"]
quantiles = s.quantile(bins, interpolation="nearest")
df["sim_pct"] = np.digitize(s, quantiles) - 1
df["levenshtein"] = [ pylev.levenshtein(d, query) / len(query) for d in df["ingredient"] ]
s = df["levenshtein"]
quantiles = s.quantile(bins, interpolation="nearest")
df["lev_pct"] = granularity - np.digitize(s, quantiles)
df["term_ratio"] = [ term_ratio(target, d) for d in df["ingredient"] ]
return df
except KeyError:
return pd.DataFrame(columns=["ingredient", "similarity", "percentile"])
```
Let's try this with `dried basil` as the ingredient to query, and review the top `50` most similar other ingredients returned as the DataFrame `df`:
```
pd.set_option("max_rows", None)
target = set([ "basil" ])
df = get_related(model, "dried basil", target, n=50)
df
```
Note how some of the most similar items, based on vector embedding, are *synonyms* or special forms of our query `dried basil` ingredient: `dried basil leaves`, `dry basil`, `dried sweet basil leaves`, etc. These tend to rank high in terms of levenshtein distance too.
Let's plot the similarity measures:
```
import matplotlib
import matplotlib.pyplot as plt
matplotlib.style.use("ggplot")
df["similarity"].plot(alpha=0.75, rot=0)
plt.show()
```
Notice the inflection points at approximately `0.56` and again at `0.47` in that plot.
We could use some statistical techniques (e.g., clustering) to segment the similarities into a few groups:
* highest similarity – potential synonyms for the query
* mid-range similarity – potential [hypernyms and hyponyms](https://en.wikipedia.org/wiki/Hyponymy_and_hypernymy) for the query
* long-tail similarity – other ingredients that pair well with the query
In this example, below a threshold of the 75th percentile for vector embedding similarity, the related ingredients are less about being synonyms and more about other foods that pair well with basil.
Let's define another function `rank_related()` which ranks the related ingredients based on a combination of these two metrics.
This uses a cheap approximation of a [*pareto archive*](https://www.cs.bham.ac.uk/~jdk/multi/) for the ranking -- which comes in handy for recommender systems and custom search applications that must combine multiple ranking metrics:
```
from kglab import root_mean_square
def rank_related (df):
df2 = df.copy(deep=True)
df2["related"] = df2.apply(lambda row: root_mean_square([ row[2], row[4] ]), axis=1)
return df2.sort_values(by=["related"], ascending=False)
df = rank_related(df)
df
```
Notice how the "synonym" cases tend to move up to the top now?
Meanwhile while the "pairs well with" are in the lower half of the ranked list: `fresh mushrooms`, `italian turkey sausage`, `cooked spaghetti`, `white kidney beans`, etc.
```
df.loc[ (df["related"] >= 50) & (df["term_ratio"] > 0) ]
```
---
## Exercises
**Exercise 1:**
Build a report for a *human-in-the-loop* reviewer, using the `rank_related()` function while iterating over `vocab` to make algorithmic suggestions for possible synonyms.
**Exercise 2:**
How would you make algorithmic suggestions for a reviewer about which ingredients could be related to a query, e.g., using the `skos:broader` and `skos:narrower` relations in the [`skos`](https://www.w3.org/2004/02/skos/) vocabulary to represent *hypernyms* and *hyponyms* respectively?
This could extend the KG to provide a kind of thesaurus about recipe ingredients.
| true |
code
| 0.498718 | null | null | null | null |
|
```
import nltk
```
# 1、Sentences Segment(分句)
```
sent_tokenizer = nltk.data.load('tokenizers/punkt/english.pickle')
paragraph = "The first time I heard that song was in Hawaii on radio. I was just a kid, and loved it very much! What a fantastic song!"
sentences = sent_tokenizer.tokenize(paragraph)
sentences
```
# 2、Tokenize sentences (分词)
```
from nltk.tokenize import WordPunctTokenizer
sentence = "Are you old enough to remember Michael Jackson attending the Grammys \
with Brooke Shields and Webster sat on his lap during the show?"
words = WordPunctTokenizer().tokenize(sentence)
words
text = 'That U.S.A. poster-print costs $12.40...'
pattern = r"""(?x) # set flag to allow verbose regexps
(?:[A-Z]\.)+ # abbreviations, e.g. U.S.A.
|\d+(?:\.\d+)?%? # numbers, incl. currency and percentages
|\w+(?:[-']\w+)* # words w/ optional internal hyphens/apostrophe
|\.\.\. # ellipsis
|(?:[.,;"'?():-_`]) # special characters with meanings
"""
nltk.regexp_tokenize(text, pattern)
```
# Tokenize and tag some text:
```
sentence = """At eight o'clock on Thursday morning
... Arthur didn't feel very good."""
tokens = nltk.word_tokenize(sentence)
tokens
tagged = nltk.pos_tag(tokens)
tagged
```
# Display a parse tree:
```
entities = nltk.chunk.ne_chunk(tagged)
entities
from nltk.corpus import treebank
t = treebank.parsed_sents('wsj_0001.mrg')[0]
t.draw()
from nltk.book import *
text1
text1.concordance("monstrous")
text1.similar("monstrous")
text2.common_contexts(["monstrous","very"])
text3.generate('luck')
text3.count('smote') / len(text3)
len(text3) / len(set(text3))
```
# 抽取词干 并归类
```
from pandas import DataFrame
import pandas as pd
d = ['pets insurance','pets insure','pet insurance','pet insur','pet insurance"','pet insu']
df = DataFrame(d)
df.columns = ['Words']
df
# 去除标点符号等特殊字符的正则表达式分词器
from nltk.stem import WordNetLemmatizer
from nltk.tokenize import word_tokenize
from nltk.stem.porter import *
stemmer = PorterStemmer()
wnl = WordNetLemmatizer()
tokenizer = nltk.RegexpTokenizer(r'w+')
df["Stemming Words"] = ""
df["Count"] = 1
j = 0
while (j <= 5):
for word in word_tokenize(df["Words"][j]): # 分词
df["Stemming Words"][j] = df["Stemming Words"][j] + " " + stemmer.stem(word) # stemming
j=j + 1
df
wnl.lemmatize('left')
tokenizer.tokenize( ' pets insur ')
uniqueWords = df.groupby(['Stemming Words'], as_index = False).sum()
uniqueWords
# Levenshtein edit-distance 有很多不同的计算距离的方法
from nltk.metrics import edit_distance
minDistance = 0.8
distance = -1
lastWord = ""
j = 0
while (j < 1):
lastWord = uniqueWords["Stemming Words"][j]
distance = edit_distance(uniqueWords["Stemming Words"][j], uniqueWords["Stemming Words"][j + 1])
if (distance > minDistance):
uniqueWords["Stemming Words"][j] = uniqueWords["Stemming Words"][j + 1]
j += 1
uniqueWords
uniqueWords = uniqueWords.groupby(['Stemming Words'], as_index = False).sum()
uniqueWords
```
# 停用词移除(Stop word removal)
```
from nltk.corpus import stopwords
stoplist = stopwords.words('english')
text = "This is just a test"
cleanwordlist = [word for word in text.split() if word not in stoplist]
print(cleanwordlist)
from nltk.metrics import edit_distance
print(edit_distance("rain", "rainbow"))
# 4.4 不同的解析器类型
# 4.4.1 递归下降解析器
# 4.4.2 移位-规约解析器
# 4.4.3 图表解析器
# 4.4.4 正则表达式解析器
import nltk
from nltk.chunk.regexp import *
chunk_rules = ChunkRule("<.*>+", "chunk everything")
reg_parser = RegexpParser('''
NP: {<DT>? <JJ>* <NN>*} # NP
P: {<IN>} # Preposition
V: {<V.*>} # Verb
PP: {<P> <NP>} # PP -> P NP
VP: {<V> <NP|PP>*} # VP -> V (NP|PP)*
''')
test_sent = "Mr. Obama played a big role in the Health insurance bill"
test_sent_pos = nltk.pos_tag(nltk.word_tokenize(test_sent))
paresed_out = reg_parser.parse(test_sent_pos)
print(paresed_out)
# 4.5 依存性文本解析(dependency parsing, DP)
# 基于概率的投射依存性解析器(probabilistic, projective dependency parser)
from nltk.parse.stanford import StanfordParser
# https://nlp.stanford.edu/software/stanford-parser-full-2017-06-09.zip
english_parser = StanfordParser()
english_parser.raw_parse_sents(("this is the english parser test"))
%pwd
```
# 文本分类
```
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
import csv
def preprocessing(text):
#text = text.decode("utf8")
# tokenize into words
tokens = [word for sent in nltk.sent_tokenize(text) for word in nltk.word_tokenize(sent)]
# remove stopwords
stop = stopwords.words('english')
tokens = [token for token in tokens if token not in stop]
# remove words less than three letters
tokens = [word for word in tokens if len(word) >= 3]
# lower capitalization
tokens = [word.lower() for word in tokens]
# lemmatize
lmtzr = WordNetLemmatizer()
tokens = [lmtzr.lemmatize(word) for word in tokens]
preprocessed_text = ' '.join(tokens)
return preprocessed_text
sms = open('./Machine-Learning-with-R-datasets-master/SMSSpamCollection.txt', encoding='utf8') # check the structure of this file!
sms_data = []
sms_labels = []
csv_reader = csv.reader(sms, delimiter = '\t')
for line in csv_reader:
# adding the sms_id
sms_labels.append(line[0])
# adding the cleaned text We are calling preprocessing method
sms_data.append(preprocessing(line[1]))
sms.close()
# 6.3 采样操作
import sklearn
import numpy as np
trainset_size = int(round(len(sms_data)*0.70))
# i chose this threshold for 70:30 train and test split.
print('The training set size for this classifier is ' + str(trainset_size) + '\n')
x_train = np.array([''.join(el) for el in sms_data[0: trainset_size]])
y_train = np.array([el for el in sms_labels[0: trainset_size]])
x_test = np.array([''.join(el) for el in sms_data[trainset_size+1:len(sms_data)]])
y_test = np.array([el for el in sms_labels[trainset_size+1:len(sms_labels)]])
#or el in sms_labels[trainset_size+1:len(sms_labels)]
print(x_train)
print(y_train)
from sklearn.feature_extraction.text import CountVectorizer
sms_exp = []
for line in sms_data:
sms_exp.append(preprocessing(line))
vectorizer = CountVectorizer(min_df = 1, encoding='utf-8')
X_exp = vectorizer.fit_transform(sms_exp)
print("||".join(vectorizer.get_feature_names()))
print(X_exp.toarray())
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(min_df = 2, ngram_range=(1, 2),
stop_words = 'english', strip_accents = 'unicode', norm = 'l2')
X_train = vectorizer.fit_transform(x_train)
X_test = vectorizer.transform(x_test)
# 6.3.1 朴素贝叶斯法
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
clf = MultinomialNB().fit(X_train, y_train)
y_nb_predicted = clf.predict(X_test)
print(y_nb_predicted)
print('\n confusion_matrix \n')
#cm = confusion_matrix(y_test, y_pred)
cm = confusion_matrix(y_test, y_nb_predicted)
print(cm)
print('\n Here is the classification report:')
print(classification_report(y_test, y_nb_predicted))
feature_names = vectorizer.get_feature_names()
coefs = clf.coef_
intercept = clf.intercept_
coefs_with_fns = sorted(zip(clf.coef_[0], feature_names))
n = 10
top = zip(coefs_with_fns[:n], coefs_with_fns[:-(n + 1):-1])
for (coef_1, fn_1), (coef_2, fn_2) in top:
print('\t%.4f\t%-15s\t\t%.4f\t%-15s' %(coef_1, fn_1, coef_2, fn_2))
# 6.3.2 决策树
from sklearn import tree
clf = tree.DecisionTreeClassifier().fit(X_train.toarray(), y_train)
y_tree_predicted = clf.predict(X_test.toarray())
print(y_tree_predicted)
print('\n Here is the classification report:')
print(classification_report(y_test, y_tree_predicted))
# 6.3.3 随机梯度下降法
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import confusion_matrix
clf = SGDClassifier(alpha = 0.0001, n_iter=50).fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('\n Here is the classification report:')
print(classification_report(y_test, y_pred))
print(' \n confusion_matrix \n')
cm = confusion_matrix(y_test, y_pred)
print(cm)
# 6.3.4 逻辑回归
# 6.3.5 支持向量机
from sklearn.svm import LinearSVC
svm_classifier = LinearSVC().fit(X_train, y_train)
y_svm_predicted = svm_classifier.predict(X_test)
print('\n Here is the classification report:')
print(classification_report(y_test, y_svm_predicted))
cm = confusion_matrix(y_test, y_pred)
print(cm)
# 6.4 随机森林
from sklearn.ensemble import RandomForestClassifier
RF_clf = RandomForestClassifier(n_estimators=10).fit(X_train, y_train)
predicted = RF_clf.predict(X_test)
print('\n Here is the classification report:')
print(classification_report(y_test, predicted))
cm = confusion_matrix(y_test, y_pred)
print(cm)
# 6.5 文本聚类
# K 均值法
from sklearn.cluster import KMeans, MiniBatchKMeans
from collections import defaultdict
true_k = 5
km = KMeans(n_clusters = true_k, init='k-means++', max_iter=100, n_init= 1)
kmini = MiniBatchKMeans(n_clusters=true_k, init='k-means++', n_init=1, init_size=1000, batch_size=1000, verbose=2)
km_model = km.fit(X_train)
kmini_model = kmini.fit(X_train)
print("For K-mean clustering ")
clustering = defaultdict(list)
for idx, label in enumerate(km_model.labels_):
clustering[label].append(idx)
print("For K-mean Mini batch clustering ")
clustering = defaultdict(list)
for idx, label in enumerate(kmini_model.labels_):
clustering[label].append(idx)
# 6.6 文本中的主题建模
# https://pypi.python.org/pypi/gensim#downloads
import gensim
from gensim import corpora, models, similarities
from itertools import chain
import nltk
from nltk.corpus import stopwords
from operator import itemgetter
import re
documents = [document for document in sms_data]
stoplist = stopwords.words('english')
texts = [[word for word in document.lower().split() if word not in stoplist] for document in documents]
print(texts)
dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]
tfidf = models.TfidfModel(corpus)
corpus_tfidf = tfidf[corpus]
lsi = models.LsiModel(corpus_tfidf, id2word = dictionary, num_topics = 100)
# print(lsi.print_topics(20))
n_topics = 5
lda = models.LdaModel(corpus_tfidf, id2word = dictionary, num_topics = n_topics)
for i in range(0, n_topics):
temp = lda.show_topic(i, 10)
terms = []
for term in temp:
terms.append(str(term[0]))
print("Top 10 terms for topic #" + str(i) + ": " + ",".join(terms))
```
# Getting Started with gensim
```
raw_corpus = ["Human machine interface for lab abc computer applications",
"A survey of user opinion of computer system response time",
"The EPS user interface management system",
"System and human system engineering testing of EPS",
"Relation of user perceived response time to error measurement",
"The generation of random binary unordered trees",
"The intersection graph of paths in trees",
"Graph minors IV Widths of trees and well quasi ordering",
"Graph minors A survey"]
# Create a set of frequent words
stoplist = set('for a of the and to in'.split(' '))
# Lowercase each document, split it by white space and filter out stopwords
texts = [[word for word in document.lower().split() if word not in stoplist]
for document in raw_corpus]
texts
# Count word frequencies
from collections import defaultdict
frequency = defaultdict(int)
# print(frequency['ddddd']) # 0 default
for text in texts:
for token in text:
frequency[token] += 1
frequency
# Only keep words that appear more than once
processed_corpus = [[token for token in text if frequency[token] > 1] for text in texts]
processed_corpus
'''
Before proceeding, we want to associate each word in the corpus with a unique integer ID.
We can do this using the gensim.corpora.Dictionary class. This dictionary defines the vocabulary of all words that our processing knows about.
'''
from gensim import corpora
dictionary = corpora.Dictionary(processed_corpus)
print(dictionary)
print(dictionary.token2id)
new_doc = "Human computer interaction"
new_vec = dictionary.doc2bow(new_doc.lower().split())
new_vec
bow_corpus = [dictionary.doc2bow(text) for text in processed_corpus]
bow_corpus
from gensim import models
# train the model
tfidf = models.TfidfModel(bow_corpus)
# transform the "system minors" string
tfidf[dictionary.doc2bow("system minors".lower().split())]
```
| true |
code
| 0.3863 | null | null | null | null |
|
<img src="https://drive.google.com/uc?id=1E_GYlzeV8zomWYNBpQk0i00XcZjhoy3S" width="100"/>
# DSGT Bootcamp Week 1: Introduction and Environment Setup
# Learning Objectives
1. Gain an understanding of Google Colab
2. Introduction to team project
3. Gain an understanding of Kaggle
4. Download and prepare dataset
5. Install dependencies
6. Gain an understanding of the basics of Python
7. Gain an understanding of the basics of GitHub / Git
# Google Colab
#### Google Colab is a cell-based Python text editor that allows you to run small snippets of code at a time. This is useful for data science; we can divide our work into manageable sections and run / debug independently of each other.
#### Colab lets you store and access data from your Google Drive account (freeing up local storage) and lets you use Google's servers for computing (allowing you to parse bigger datasets).
#### Any given cell will either be a **code cell** or a **markdown cell** (formatted text, like this one). We won't need to focus on using Markdown cells, because you can just use comments in code cells to convey any text that might be important.
---
# Basic Commands:
#### All of these commands assume that you have a cell highlighted. To do so, simply click on any cell.
#### `shift + enter (return)`: Runs the current cell, and highlights the next cell
#### `alt (option) + enter (return)`: Runs the current cell, and creates a new cell
#### `Top Bar -> Runtime -> Run all`: Runs entire notebook
#### `+Code or +Text`: Adds a code or text cell below your highlighted cell
### For more information, check out the resources at the end!
---
<img src="https://www.kaggle.com/static/images/site-logo.png" alt="kaggle-logo-LOL"/>
# Introducing Kaggle
#### [Kaggle](https://kaggle.com) is an online 'practice tool' that helps you become a better data scientist. They have various data science challenges, tutorials, and resources to help you improve your skillset.
#### For this bootcamp, we'll be trying to predict trends using the Kaggle Titanic Data Set. This dataset models variable related to the passengers and victims of the Titanic sinking incident. By the end of this bootcamp, you'll submit your machine learning model to the leaderboards and see how well it performs compared to others worldwide.
#### For more information on Kaggle, check out the resources section.
# Accessing the Titanic Dataset
#### To speed up the data download process, we've placed the data in this Google Folder where everyone will be making their notebooks. Let's go over the steps needed to import data into Google Colab.
**PLEASE READ THE STEPS!!!**
1. Go to your Google Drive (drive.google.com) and check **"Shared with me"**
2. Search for a folder named **"Spring 2021 Bootcamp Material"**
3. Enter the **Spring 2021 Bootcamp Material** folder, click the name of the folder (**Spring 2021 Bootcamp Material**) on the bar at the top of the folder to create a drop-down and select **"Add shortcut to Drive"**
4. Select **"My Drive"** and hit **"Add Shortcut"**
5. Enter the **Spring 2021 Bootcamp Material** folder you just made, and navigate to the **"Participants"** subfolder
6. Make a new folder within Participants in the format **"FirstName LastName"**.
7. Return to Google Colab.
8. Go to **"File -> Save a copy in Drive"**. Rename the file to **"firstname-lastname-week1.ipynb"**. It will be placed into a folder named **"Colab Notebooks"** in your Google Drive.
9. Move **"firstname-lastname-week1.ipynb"** to your **Participant** folder within Google Drive.
10. Return to Google Colab.
11. Hit the folder image on the left bar to expand the file system.
12. Hit **"Mount Drive"** to allow Colab to access your files. Click the link and copy the code provided into the textbox and hit Enter.
```
from google.colab import drive
drive.mount('/content/drive')
# This cell should appear once you hit "Mount Drive". Press Shift + Enter to run it.
from google.colab import drive
drive.mount('/content/drive')
"""
You can use the following commands in Colab code cells.
Type "%pwd" to list the folder you are currently in and "%ls" to list subfolders. Use "%cd [subfolder]"
to change your current directory into where the data is.
"""
%cd 'drive'
%ls
# Move into one subfolder ("change directory")
%cd 'drive'
%ls
# Move into a nested subfolder
%cd '/MyDrive/Spring 2021 Bootcamp Material/Participants/Data'
%pwd
```
As you can see here, we've now located our runtime at "../Participants/Data" where WICData.csv is located. This is the dataset for the WIC Program. For now, understand how you navigate the file system to move towards where your data is.
**Note:** The above code cells could also have simply been
`cd drive/MyDrive/Spring 2021 Bootcamp Material/Participants/Data`
It was done one step at a time to show the process of exploring a file system you might not be familiar with. If you know the file path before hand, you can move multiple subfolders at once.
# Project Presentation
Link to Google Slides: [Slides](https://docs.google.com/presentation/d/1QzomRX5kpJTKuy9j2JFvCo0siBEtkPNvacur2ZAxCiI/edit?usp=sharing)
# Read Data with Pandas
#### `!pip install` adds libraries (things that add more functionality to Python) to this environment as opposed to your machine.
#### We'll worry about importing and using these libraries later. For now, let's just make sure your environment has them installed.
#### Applied Data Science frequently uses core libraries to avoid "reinventing the wheel". One of these is pandas!
```
!pip install pandas
import pandas as pd #pd is the standard abbreviation for the library
```
#### Now that we're in the correct folder, we can use pandas to take a sneak peek at the data. Don't worry about these commands -- we'll cover them next week!
```
df = pd.read_csv("titanic_test.csv")
df.head()
```
# Introduction to the Python Programming Language
### **Why do we use Python?**
- Easy to read and understand
- Lots of libraries for Data Science
- One of the most popular languages for Data Science (alongside R)
# Primer on Variables, If Statements, and Loops
```
#You can create a variable by using an "=" sign. The value on the right gets
#assigned to the variable name of the left.
a = 5
b = 15
print(a + b)
c = "Data Science "
d = "is fun!"
print(c + d)
#If statements allow you to run certain lines of code based on certain conditions.
if (c + d) == "Data Science is fun!":
print("Correct!")
else: # this section is only triggered if (c + d) doesn't equal "Data Science is fun!"
print("False!")
#For loops are used to perform an action a fixed amount of times, or to go through each element in a list or string
for index in range(0, a):
print('DSGT')
#In this block of code, c+d is treated as a list of letters, with letter serving
#as each individual character as the for loop iterates through the string.
for letter in c + d:
print(letter)
```
# Lists, Tuples, and Dictionaries
```
# Let's start by creating a list (otherwise known as an array)
c = ["a", "b", "c"]
# We can retrieve an element by accessing its position in the array.
# Position counting starts at 0 in Python.
print("The 1st item in the array is " + c[0])
# Lists can have more than one type of element!
c[1] = 23
print(c)
# Tuples are lists but they don't like change
tup = ("car", True, 4)
tup[2] = 5 #would cause an error
# Dictionaries are unordered key, value pairs
d = {"Data Science": "Fun", "GPA": 4, "Best Numbers": [3, 4]}
# We can get values by looking up their corresponding key
print(d["Data Science"])
# We can also reassign the value of keys
d["Best Numbers"] = [99, 100]
# And add keys
d["Birds are Real"] = False
#We can also print out all the key value pairs
print(d)
```
## Functions
```
# Functions help improve code reusability and readability.
# You can define a series of steps and then use them multiple times.
def add(a, b):
sum = a + b
return sum
print(add(2, 4))
print(add(4, 7))
print(add(3 * 4, 6))
```
**Note**: A lot of Data Science is dependent on having a solid foundation in Python. If you aren't currently familiar, we *highly recommend* spending some time learning (tutorials available in resources). Otherwise, using the libraries and parsing data in a foreign language may make things rather difficult.
## **Introduction to the Version Control and GitHub**
What is Version Control?
* Tracks changes in computer files
* Coordinates work between multiple developers
* Allows you to revert back at any time
* Can have local & remote repositories
What is GitHub?
* cloud-based Git repository hosting service
* Allows users to use Git for version control
* **Git** is a command line tool
* **GitHub** is a web-based graphical user interface
# Set Up
If you do not already have Git on your computer, use the following link to install it:
[Install Git](https://git-scm.com/downloads)
**Setting Up a Repo**
* $git config
* $git config --global user.name "YOUR_NAME"
* $git config --global user.email "YOUR_EMAIL"
**Create a Repo**
* $git init
* $git clone [URL]
** You can use
https://github.gatech.edu with
YOUR_NAME = your username that you log into GitHub with
YOUR_EMAIL = your email that you log into GitHub with **
**GitHub GUI**
One person in each team will create a "New Repository" on GitHub. Once they add team members to the repo, anyone can clone the project to their local device using "$git clone [URL]" .
# Steps for Using Git
1. Check that you are up to date with Remote Repo -- **git fetch**
* check status -- **git status**
* if not up to date, pull down changes -- **git pull**
2. Make changes to code
3. Add all changes to the "stage" -- **git add .**
4. Commit any changes you want to make -- **git commit -m [message]**
5. Update the Remote Repo with your changes -- **git push**
**Summary**
3 stage process for making commits (after you have made a change):
1. ADD
2. COMMIT
3. PUSH
# Branching
By default when you create your project you will be on Master - however, it is good practice to have different branches for different features, people etc.
* To see all local branches -- **git branch**
* To create a branch -- **git branch [BRANCHNAME]**
* To move to a branch -- **git checkout [BRANCHNAME]**
* To create a new branch **and** move to it -- **git checkout -b [BRANCHNAME]**
# Merging
Merging allows you to carry the changes in one branch over to another branch. Github is your best friend for this - you can open and resolve merge conflicts through the GUI very easily. However, it is also good to know how to do it manually, in the event that you are unable to resolve conflicts.
**Manual Steps**
1. $git checkout [NAME_OF_BRANCH_TO_MERGE_INTO]
2. $git merge [NAME_OF_BRANCH_TO_BRING_IN]
# Helpful Resources
#### [Colab Overview](https://colab.research.google.com/notebooks/basic_features_overview.ipynb)
#### [Kaggle Courses](https://www.kaggle.com/learn/overview)
#### [Kaggle](https://www.kaggle.com/)
#### [Intro Python](https://pythonprogramming.net/introduction-learn-python-3-tutorials/)
#### [Pandas Documentation](https://pandas.pydata.org/docs/)
#### [Pandas Cheatsheet](https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf)
#### [Github Tutorial](https://guides.github.com/activities/hello-world/)
| true |
code
| 0.366434 | null | null | null | null |
|
## Figure 12
Similar to [Figure 5](https://github.com/EdwardJKim/astroclass/blob/master/paper/notebooks/figure05/purity_mag_integrated.ipynb)
but for the reduced training set.
```
from __future__ import division, print_function, unicode_literals
%matplotlib inline
import numpy as np
from scipy.special import gammaln
from scipy.integrate import quad
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.neighbors import KernelDensity
plt.rc('legend', fontsize=10)
truth_train = np.loadtxt('../../data/truth_train.dat')
truth_test = np.loadtxt('../../data/truth_test.dat')
mask_w1_train = np.loadtxt('../../data/vvds_w1_train.mask').astype(bool)
mag_i_train = np.loadtxt('../../data/mag_i.train.dat')
mag_i_test = np.loadtxt('../../data/mag_i.test.dat')
tpc_test = np.loadtxt('../../data/w1_22_0_tpc_test.mlz', unpack=True, usecols=(2,))
som_test = np.loadtxt('../../data/w1_22_0_som_test.mlz', unpack=True, usecols=(2,))
hbc_all = np.loadtxt('../../data/w1_22_0_median.hbc', unpack=True, usecols=(0,))
hbc_cv = hbc_all[:-len(truth_test)]
hbc_test = hbc_all[-len(truth_test):]
bmc_test = np.loadtxt('../../data/w1_22_0.bmc')
# read in FLUX_RADIUS and MAG_i and make a classification
def morph_class(magnitude, half_radius, cut=[0, 25, 1.0, 3.0]):
point_source = ((magnitude > cut[0]) & (magnitude < cut[1]) &
(half_radius > cut[2]) & (half_radius < cut[3]))
return point_source.astype(np.int)
mag_i_lower = 17
mag_i_upper = 21.0
r_h_lower = 1.4
r_h_upper = 2.8
r_h_test = np.loadtxt('../../data/flux_radius.test.dat')
mag_i_test = np.loadtxt('../../data/mag_i.test.dat')
morph_test = morph_class(mag_i_test, r_h_test, cut=[mag_i_lower, mag_i_upper, r_h_lower, r_h_upper])
hist_bins = np.arange(17, 25.5, 1)
# http://inspirehep.net/record/669498/files/fermilab-tm-2286.PDF
def calceff(N, k, conf=0.683, tol=1.0e-3, step=1.0e-3, a0=None, dx0=None, output=True):
epsilon = k / N
if a0 is None:
a0 = epsilon
if dx0 is None:
dx0 = step
bins = np.arange(0, 1 + step, step)
def get_log_p(N, k):
p = gammaln(N + 2) - gammaln(k + 1) - gammaln(N - k + 1) + k * np.log(bins) + (N - k) * np.log(1 - bins)
return p
alpha = np.arange(0, a0, step)
beta = np.arange(epsilon, 1, step)
log_p = get_log_p(N, k)
def func(x):
i = np.argmin(np.abs(bins - x))
return np.exp(log_p[i])
found = False
area_best = 1
alpha_best = alpha[-1]
beta_best = 1.0
dxs = np.arange(dx0, 1, step)
for ix, dx in enumerate(dxs):
for ia, a in enumerate(alpha[::-1]):
b = a + dx
#a = min(a, b)
#b = max(a, b)
if b > 1 or b < epsilon:
break
area, err = quad(func, a, b)
#print(area, a, b)
if np.abs(area - conf) < tol:
area_best = area
alpha_best = a
beta_best = b
found = True
break
if area > conf:
# go back a step, recalculate with smaller step
alpha_best, beta_best, area_best = calceff(N, k, step=0.8*step, a0=a + step, dx0=dx - step, output=False)
found = True
# exit the inner for loop for a
break
# exit the outer for loop for dx
if found:
break
if output:
print("Done. N = {0}, k = {1}, area: {2:.3f}, alpha: {3:.4f}, beta: {4:.4f}"
"".format(N, k, area_best, alpha_best, beta_best, step))
return alpha_best, beta_best, area_best
def calc_completeness_purity(truth, classif, mag, p_cut=0.001, bins=np.arange(16, 26, 0.5)):
'''
'''
bins = bins[1:]
result = {}
g_comp_bin = np.zeros(len(bins))
g_pur_bin = np.zeros(len(bins))
s_comp_bin = np.zeros(len(bins))
s_pur_bin = np.zeros(len(bins))
g_pur_lower_bin = np.zeros(len(bins))
g_pur_upper_bin = np.zeros(len(bins))
s_pur_upper_bin = np.zeros(len(bins))
s_pur_lower_bin = np.zeros(len(bins))
for i, b in enumerate(bins):
# true galaxies classified as stars
mask = (mag > -90) & (mag < b)
gs_bin = ((classif[mask] >= p_cut) & (truth[mask] == 0)).sum().astype(np.float)
# true galaxies classified as galaxies
gg_bin = ((classif[mask] < p_cut) & (truth[mask] == 0)).sum().astype(np.float)
# true stars classified as galaxies
sg_bin = ((classif[mask] < p_cut) & (truth[mask] == 1)).sum().astype(np.float)
# true stars classified as stars
ss_bin = ((classif[mask] >= p_cut) & (truth[mask] == 1)).sum().astype(np.float)
# galaxy completeness
g_comp_bin[i] = gg_bin / (gg_bin + gs_bin)
# galaxy purity
g_pur_bin[i] = gg_bin / (gg_bin + sg_bin)
# star completeness
s_comp_bin[i] = ss_bin / (ss_bin + sg_bin)
s_pur_bin[i] = ss_bin / (ss_bin + gs_bin)
print("Calculating completenss for {0}...".format(b))
g_pur_err = calceff(gg_bin + sg_bin, gg_bin)
g_pur_lower_bin[i] = g_pur_err[0]
g_pur_upper_bin[i] = g_pur_err[1]
print("Calculating purity for {0}...".format(b))
s_pur_err = calceff(ss_bin + gs_bin, ss_bin)
s_pur_lower_bin[i] = s_pur_err[0]
s_pur_upper_bin[i] = s_pur_err[1]
result['galaxy_completeness'] = g_comp_bin
result['galaxy_purity'] = g_pur_bin
result['galaxy_purity_lower'] = g_pur_lower_bin
result['galaxy_purity_upper'] = g_pur_upper_bin
result['star_completeness'] = s_comp_bin
result['star_purity'] = s_pur_bin
result['star_purity_lower'] = s_pur_lower_bin
result['star_purity_upper'] = s_pur_upper_bin
return result
def find_purity_at(truth_test, clf, step=0.001, gc=None, gp=None, sc=None, sp=None):
print("Finding the threshold value...")
if bool(gc) and bool(sc) and bool(gp) and bool(sp):
raise Exception('Specify only one of gp or sp parameter.')
pbin = np.arange(0, 1, step)
pure_all = np.zeros(len(pbin))
comp_all = np.zeros(len(pbin))
for i, p in enumerate(pbin):
# true galaxies classified as stars
gs = ((clf >= p) & (truth_test == 0)).sum()
# true galaxies classified as galaxies
gg = ((clf < p) & (truth_test == 0)).sum()
# true stars classified as galaxies
sg = ((clf < p) & (truth_test == 1)).sum()
# true stars classified as stars
ss = ((clf >= p) & (truth_test == 1)).sum()
if gc is not None or gp is not None:
if gg == 0 and sg == 0:
pure_all[i] = np.nan
else:
pure_all[i] = gg / (gg + sg)
if gg == 0 and gs == 0:
comp_all[i] = np.nan
else:
comp_all[i] = gg / (gg + gs)
if sc is not None or sp is not None:
if ss == 0 and sg == 0:
comp_all[i] = np.nan
else:
comp_all[i] = ss / (ss + sg)
if ss == 0 and gs == 0:
pure_all[i] = np.nan
else:
pure_all[i] = ss / (ss + gs)
if gc is not None:
ibin = np.argmin(np.abs(comp_all - gc))
return pbin[ibin], pure_all[ibin]
if gp is not None:
ibin = np.argmin(np.abs(pure_all - gp))
return pbin[ibin], comp_all[ibin]
if sc is not None:
ibin = np.argmin(np.abs(comp_all - sc))
return pbin[ibin], pure_all[ibin]
if sp is not None:
ibin = np.argmin(np.abs(pure_all - sp))
return pbin[ibin], comp_all[ibin]
morph = calc_completeness_purity(truth_test, morph_test, mag_i_test, p_cut=0.5, bins=hist_bins)
bmc_p_cut, _ = find_purity_at(truth_test, bmc_test, gc=0.9964, step=0.0001)
bmc_mg = calc_completeness_purity(truth_test, bmc_test, mag_i_test, p_cut=bmc_p_cut, bins=hist_bins)
bmc_p_cut, _ = find_purity_at(truth_test, bmc_test, sc=0.7145, step=0.0001)
bmc_ms = calc_completeness_purity(truth_test, bmc_test, mag_i_test, p_cut=bmc_p_cut, bins=hist_bins)
tpc_p_cut, _ = find_purity_at(truth_test, tpc_test, gc=0.9964, step=0.0001)
tpc_mg = calc_completeness_purity(truth_test, tpc_test, mag_i_test, p_cut=tpc_p_cut, bins=hist_bins)
tpc_p_cut, _ = find_purity_at(truth_test, tpc_test, sc=0.7145, step=0.0001)
tpc_ms = calc_completeness_purity(truth_test, tpc_test, mag_i_test, p_cut=tpc_p_cut, bins=hist_bins)
p = sns.color_palette()
sns.set_style("ticks")
fig = plt.figure(figsize=(6, 6))
ax0 = plt.subplot2grid((6, 3), (0, 0), colspan=3, rowspan=3)
ax1 = plt.subplot2grid((6, 3), (3, 0), colspan=3, rowspan=3)
plt.setp(ax0.get_xticklabels(), visible=False)
x_offset = 0.1
ax0.errorbar(hist_bins[1:], bmc_mg['galaxy_purity'],
yerr=[bmc_mg['galaxy_purity'] - bmc_mg['galaxy_purity_lower'],
bmc_mg['galaxy_purity_upper'] - bmc_mg['galaxy_purity']],
label='BMC', ls='-', marker='o', markersize=4)
ax0.errorbar(hist_bins[1:] - x_offset, tpc_mg['galaxy_purity'],
yerr=[tpc_mg['galaxy_purity'] - tpc_mg['galaxy_purity_lower'],
tpc_mg['galaxy_purity_upper'] - tpc_mg['galaxy_purity']],
label='TPC', ls='--', marker='o', markersize=4)
ax0.errorbar(hist_bins[1:] + x_offset, morph['galaxy_purity'],
yerr=[morph['galaxy_purity'] - morph['galaxy_purity_lower'],
morph['galaxy_purity_upper'] - morph['galaxy_purity']],
label='Morphology', ls='--', marker='o', markersize=4)
ax0.legend(loc='lower right')
ax0.set_xlim(17.5, 24.5)
ax0.set_ylim(0.875, 1.005)
#ax0.set_yticks([0.86, 0.91.0])
ax0.set_ylabel(r'$p_g\left(c_g=0.9964\right)$', fontsize=12)
ax1.errorbar(hist_bins[1:], bmc_ms['star_purity'],
yerr=[bmc_ms['star_purity'] - bmc_ms['star_purity_lower'],
bmc_ms['star_purity_upper'] - bmc_ms['star_purity']],
label='BMC', ls='-', marker='o', markersize=4)
ax1.errorbar(hist_bins[1:] - x_offset, tpc_ms['star_purity'],
yerr=[tpc_ms['star_purity'] - tpc_ms['star_purity_lower'],
tpc_ms['star_purity_upper'] - tpc_ms['star_purity']],
label='TPC', ls='--', marker='o', markersize=4)
ax1.errorbar(hist_bins[1:] + x_offset, morph['star_purity'],
yerr=[morph['star_purity'] - morph['star_purity_lower'],
morph['star_purity_upper'] - morph['star_purity']],
label='Morphology', ls='--', marker='o', markersize=4)
ax1.set_ylabel(r'$p_s\left(c_s=0.7145\right)$', fontsize=12)
ax1.set_xlim(17.5, 24.5)
ax1.set_ylim(0.55, 1.05)
ax1.set_yticks([0.6, 0.7, 0.8, 0.9, 1.0])
ax1.set_xlabel(r'$i$ (mag)')
plt.savefig('../../figures/purity_mag_cut_integrated.pdf')
plt.show()
```
| true |
code
| 0.371308 | null | null | null | null |
|
```
Copyright 2021 IBM Corporation
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
```
# Support Vector Machine on Avazu Dataset
## Background
This data is used in a competition on click-through rate prediction jointly hosted by Avazu and Kaggle in 2014. The participants were asked to learn a model from the first 10 days of advertising log, and predict the click probability for the impressions on the 11th day
## Source
The raw dataset can be obtained directly from the [Kaggle competition](https://www.kaggle.com/c/avazu-ctr-prediction/).
In this example, we download the pre-processed dataset from the [LIBSVM dataset repository](https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/).
## Goal
The goal of this notebook is to illustrate how Snap ML can accelerate training of a support vector machine model on this dataset.
## Code
```
cd ../../
CACHE_DIR='cache-dir'
import numpy as np
import time
from datasets import Avazu
from sklearn.svm import LinearSVC
from snapml import SupportVectorMachine as SnapSupportVectorMachine
from sklearn.metrics import accuracy_score as score
dataset= Avazu(cache_dir=CACHE_DIR)
X_train, X_test, y_train, y_test = dataset.get_train_test_split()
print("Number of examples: %d" % (X_train.shape[0]))
print("Number of features: %d" % (X_train.shape[1]))
print("Number of classes: %d" % (len(np.unique(y_train))))
# the dataset is highly imbalanced
labels, sizes = np.unique(y_train, return_counts=True)
print("%6.2f %% of the training transactions belong to class 0" % (sizes[0]*100.0/(sizes[0]+sizes[1])))
print("%6.2f %% of the training transactions belong to class 1" % (sizes[1]*100.0/(sizes[0]+sizes[1])))
model = LinearSVC(loss="hinge", class_weight="balanced", fit_intercept=False, random_state=42)
t0 = time.time()
model.fit(X_train, y_train)
t_fit_sklearn = time.time()-t0
score_sklearn = score(y_test, model.predict(X_test))
print("Training time (sklearn): %6.2f seconds" % (t_fit_sklearn))
print("Accuracy score (sklearn): %.4f" % (score_sklearn))
model = SnapSupportVectorMachine(n_jobs=4, class_weight="balanced", fit_intercept=False, random_state=42)
t0 = time.time()
model.fit(X_train, y_train)
t_fit_snapml = time.time()-t0
score_snapml = score(y_test, model.predict(X_test))
print("Training time (snapml): %6.2f seconds" % (t_fit_snapml))
print("Accuracy score (snapml): %.4f" % (score_snapml))
speed_up = t_fit_sklearn/t_fit_snapml
score_diff = (score_snapml-score_sklearn)/score_sklearn
print("Speed-up: %.1f x" % (speed_up))
print("Relative diff. in score: %.4f" % (score_diff))
```
## Disclaimer
Performance results always depend on the hardware and software environment.
Information regarding the environment that was used to run this notebook are provided below:
```
import utils
environment = utils.get_environment()
for k,v in environment.items():
print("%15s: %s" % (k, v))
```
## Record Statistics
Finally, we record the enviroment and performance statistics for analysis outside of this standalone notebook.
```
import scrapbook as sb
sb.glue("result", {
'dataset': dataset.name,
'n_examples_train': X_train.shape[0],
'n_examples_test': X_test.shape[0],
'n_features': X_train.shape[1],
'n_classes': len(np.unique(y_train)),
'model': type(model).__name__,
'score': score.__name__,
't_fit_sklearn': t_fit_sklearn,
'score_sklearn': score_sklearn,
't_fit_snapml': t_fit_snapml,
'score_snapml': score_snapml,
'score_diff': score_diff,
'speed_up': speed_up,
**environment,
})
```
| true |
code
| 0.853272 | null | null | null | null |
|
## YUV color space
Colors in images can be encoded in different ways. Most well known is perhaps the RGB-encoding, in which the image consists of a Red, Green, and Blue channel. However, there are many other encodings, which sometimes have arisen for historical reasons or to better comply with properties of human perception. The YUV color space has arisen in order to better deal with transmission or compression artifacts; when using YUV instead of RGB, these artifacts will less easily be detected by humans. YUV consists of one luma component (Y) and two chrominance (color) components (UV).
Many cameras used in robotics directly output YUV-encoded images. Although these images can be converted to RGB, this conversion costs computation time, so it is better to work directly in YUV-space. The YUV color space is aptly explained on <A HREF="https://en.wikipedia.org/wiki/YUV" TARGET="_blank">Wikipedia</A>. It also contains an image on the U and V axes, for a value of Y$=0.5$. However, using this image for determining thresholds on U and V for color detection may lead to suboptimal results.
<font color='red'><B>Exercise 1</B></font>
Generate slices of the YUV space below, with the help of the script `YUV_slices.py` <A HREF="https://github.com/guidoAI/YUV_notebook/blob/master/YUV_slices.py" TARGET="_blank">(link to file)</A>. You can change the number of slices (`n_slices`) and the height and width (`H`, `W`) of the generated images.
1. Why can determining thresholds at Y$=0.5$ lead to suboptimal results?
2. What U and V thresholds would you set for detecting orange? And for green?
3. Can you think of a better way than setting a threshold on U and V for determining if a pixel belongs to a certain color?
```
%matplotlib inline
import YUV_slices as YUV
n_slices = 5;
YUV.generate_slices_YUV(n_slices);
```
## Color filtering
The code below loads an image and filters the colors.
```
%matplotlib inline
import cv2;
import numpy as np;
import matplotlib.pyplot as plt
def filter_color(image_name = 'DelFly_tulip.jpg', y_low = 50, y_high = 200, \
u_low = 120, u_high = 130, v_low = 120, v_high = 130, resize_factor=1):
im = cv2.imread(image_name);
im = cv2.resize(im, (int(im.shape[1]/resize_factor), int(im.shape[0]/resize_factor)));
YUV = cv2.cvtColor(im, cv2.COLOR_BGR2YUV);
Filtered = np.zeros([YUV.shape[0], YUV.shape[1]]);
for y in range(YUV.shape[0]):
for x in range(YUV.shape[1]):
if(YUV[y,x,0] >= y_low and YUV[y,x,0] <= y_high and \
YUV[y,x,1] >= u_low and YUV[y,x,1] <= u_high and \
YUV[y,x,2] >= v_low and YUV[y,x,2] <= v_high):
Filtered[y,x] = 1;
plt.figure();
RGB = cv2.cvtColor(im, cv2.COLOR_BGR2RGB);
plt.imshow(RGB);
plt.title('Original image');
plt.figure()
plt.imshow(Filtered);
plt.title('Filtered image');
```
<font color='red'><B>Exercise 2</B></font>
Please answer the questions of this exercise, by changing and running the code block below. Note that Y, U, and V are all in the range $[0, 255]$.
1. Can you find an easy way to make the code run faster, while still being able to evaluate if your filter works?
2. Can you filter the colors, so that only the tulip remains?
3. Can you filter the colors, so that only the stem remains?
```
filter_color(y_low = 50, y_high = 200, u_low = 60, u_high = 160, v_low = 60, v_high = 160);
```
## Answers
Exercise 1:
1. Colors and color regions are different for different Y values. What is orange at one value of Y can be a different color (e.g., red) at another value of Y.
2. Green: low U, low V (e.g., [0,120], [0,120]). Orange: low U, relatively high V (e.g., [0,120], [160,220])
3. Include the Y in the selection of the threshold, e.g., as in a look-up table (different U and V depending on Y), or by determining a prototype pixel for each different "color" and when classifying a pixel, determining which prototype is closest in YUV-space.
Exercise 2:
1. Set the resize_factor to a factor larger than 1. Setting it to 4 makes the filtering faster, while it is still possible to evaluate the success of the filter.
2. ``y_low = 50, y_high = 200, u_low = 0, u_high = 120, v_low = 160, v_high = 220``
3. ``y_low = 50, y_high = 200, u_low = 0, u_high = 120, v_low = 0, v_high = 120``
| true |
code
| 0.365513 | null | null | null | null |
|
```
import os
os.environ['CASTLE_BACKEND'] = 'pytorch'
from collections import OrderedDict
import warnings
import numpy as np
import networkx as nx
import ges
from castle.common import GraphDAG
from castle.metrics import MetricsDAG
from castle.datasets import IIDSimulation, DAG
from castle.algorithms import PC, ICALiNGAM, GOLEM
import matplotlib.pyplot as plt
# Mute warnings - for the sake of presentation clarity
# Should be removed for real-life applications
warnings.simplefilter('ignore')
```
# Causal Discovery in Python
Over the last decade, causal inference gained a lot of traction in academia and in the industry. Causal models can be immensely helpful in various areas – from marketing to medicine and from finance to cybersecurity. To make these models work, we need not only data as in traditional machine learning, but also a causal structure. Traditional way to obtain the latter is through well-designed experiments. Unfortunately, experiments can be tricky – difficult to design, expensive or unethical. Causal discovery (also known as structure learning) is an umbrella term that describes several families of methods aiming at discovering causal structure from observational data. During the talk, we will review the basics of causal inference and introduce the concept of causal discovery. Next, we will discuss differences between various approaches to causal discovery. Finally, we will see a series of practical examples of causal discovery using Python.
## Installing the environment
* Using **Conda**:
`conda env create --file econml-dowhy-py38.yml`
* Installing `gcastle` only:
`pip install gcastle==1.0.3rc3`
```
def get_n_undirected(g):
total = 0
for i in range(g.shape[0]):
for j in range(g.shape[0]):
if (g[i, j] == 1) and (g[i, j] == g[j, i]):
total += .5
return total
```
## PC algorithm
**PC algorithm** starts with a **fully connected** graph and then performs a series of steps to remove edges, based on graph independence structure. Finally, it tries to orient as many edges as possible.
Figure 1 presents a visual representatrion of these steps.
<br><br>
<img src="img/glymour_et_al_pc.jpg">
<br>
<figcaption><center><b>Figure 1. </b>Original graph and PC algorithm steps. (Gylmour et al., 2019)</center></figcaption>
<br>
Interested in more details?
[Gylmour et al. - Review of Causal Discovery Methods Based on Graphical Models (2019)](https://www.frontiersin.org/articles/10.3389/fgene.2019.00524/full)
```
# Let's implement this structure
x = np.random.randn(1000)
y = np.random.randn(1000)
z = x + y + .1 * np.random.randn(1000)
w = .7 * z + .1 * np.random.randn(1000)
# To matrix
pc_dataset = np.vstack([x, y, z, w]).T
# Sanity check
pc_dataset, pc_dataset.shape
# Build the model
pc = PC()
pc.learn(pc_dataset)
pc.causal_matrix
# Get learned graph
learned_graph = nx.DiGraph(pc.causal_matrix)
# Relabel the nodes
MAPPING = {k: v for k, v in zip(range(4), ['X', 'Y', 'Z', 'W'])}
learned_graph = nx.relabel_nodes(learned_graph, MAPPING, copy=True)
# Plot the graph
nx.draw(
learned_graph,
with_labels=True,
node_size=1800,
font_size=18,
font_color='white'
)
```
## Let's do some more discovery!
### Generate datasets
We'll use a [scale-free](https://en.wikipedia.org/wiki/Scale-free_network) model to generate graphs.
Then we'll use three different causal models on this graph:
* linear Gaussian
* linear exp
* non-linear quadratic
```
# Data simulation, simulate true causal dag and train_data.
true_dag = DAG.scale_free(n_nodes=10, n_edges=15, seed=18)
DATA_PARAMS = {
'linearity': ['linear', 'nonlinear'],
'distribution': {
'linear': ['gauss', 'exp'],
'nonlinear': ['quadratic']
}
}
datasets = {}
for linearity in DATA_PARAMS['linearity']:
for distr in DATA_PARAMS['distribution'][linearity]:
datasets[f'{linearity}_{distr}'] = IIDSimulation(
W=true_dag,
n=2000,
method=linearity,
sem_type=distr)
# Sanity check
datasets
plt.figure(figsize=(16, 8))
for i, dataset in enumerate(datasets):
X = datasets[dataset].X
plt.subplot(4, 2, i + 1)
plt.hist(X[:, 0], bins=100)
plt.title(dataset)
plt.axis('off')
plt.subplot(4, 2, i + 5)
plt.scatter(X[:, 8], X[:, 4], alpha=.3)
plt.title(dataset)
plt.axis('off')
plt.subplots_adjust(hspace=.7)
plt.show()
```
### Visualize the true graph
```
nx.draw(
nx.DiGraph(true_dag),
node_size=1800,
alpha=.7,
pos=nx.circular_layout(nx.DiGraph(true_dag))
)
GraphDAG(true_dag)
plt.show()
```
## Method comparison
```
methods = OrderedDict({
'PC': PC,
'GES': ges,
'LiNGAM': ICALiNGAM,
'GOLEM': GOLEM
})
%%time
results = {}
for k, dataset in datasets.items():
print(f'************* Current dataset: {k}\n')
X = dataset.X
results[dataset] = {}
for method in methods:
if method not in ['GES', 'CORL']:
print(f'Method: {method}')
# Fit the model
if method == 'GOLEM':
model = methods[method](num_iter=2.5e4)
else:
model = methods[method]()
model.learn(X)
pred_dag = model.causal_matrix
elif method == 'GES':
print(f'Method: {method}')
# Fit the model
pred_dag, _ = methods[method].fit_bic(X)
# Get n undir edges
n_undir = get_n_undirected(pred_dag)
# Plot results
GraphDAG(pred_dag, true_dag, 'result')
mt = MetricsDAG(pred_dag, true_dag)
print(f'FDR: {mt.metrics["fdr"]}')
print(f'Recall: {mt.metrics["recall"]}')
print(f'Precision: {mt.metrics["precision"]}')
print(f'F1 score: {mt.metrics["F1"]}')
print(f'No. of undir. edges: {n_undir}\n')
print('-' * 50, '\n')
results[dataset][method] = pred_dag
print('\n')
```
| true |
code
| 0.540196 | null | null | null | null |
|
# Оценка pi ($\pi$) с использованием квантового алгоритма оценки фазы
# Оценка pi ($\pi$) с использованием квантового алгоритма оценки фазы.
## 1. Краткий обзор [квантового алгоритма оценки фазы](https://qiskit.org/textbook/ch-algorithms/quantum-phase-estimation.html)
Quantum Phase Estimation (QPE) is a quantum algorithm that forms the building block of many more complex quantum algorithms. At its core, QPE solves a fairly straightforward problem: given an operator $U$ and a quantum state $\vert\psi\rangle$ that is an eigenvalue of $U$ with $U\vert\psi\rangle = \exp\left(2 \pi i \theta\right)\vert\psi\rangle$, can we obtain an estimate of $\theta$?
Ответ положительный. Алгоритм QPE дает нам $2^n\theta$, где $n$ — количество кубитов, которое мы используем для оценки фазы $\theta$.
## 2. Оценка $\pi$
В этой демонстрации мы выбираем $$U = p(\theta), \vert\psi\rangle = \vert1\rangle$$, где $$ p(\theta) = \begin{bmatrix} 1 & 0\ 0 & \ exp(i\theta) \end{bmatrix} $$ — один из квантовых вентилей, доступных в Qiskit, а $$p(\theta)\vert1\rangle = \exp(i\theta)\vert1\rangle.$$
Выбрав фазу для нашего вентиля $\theta = 1$, мы можем найти $\pi$, используя следующие два соотношения:
1. На выходе алгоритма QPE мы измеряем оценку для $2^n\theta$. Тогда $\theta = \text{измерено} / 2^n$
2. Из приведенного выше определения вентиля $p(\theta)$ мы знаем, что $2\pi\theta = 1 \Rightarrow \pi = 1 / 2\theta$
Комбинируя эти два соотношения, $\pi = 1 / \left(2 \times (\text{(измерено)}/2^n)\right)$.
Для подробного понимания алгоритма QPE обратитесь к посвященной ему главе в учебнике Qiskit, расположенном по адресу [qiskit.org/textbook](https://qiskit.org/textbook/ch-algorithms/quantum-phase-estimation.html) .
## 3. Время писать код
Начнем с импорта необходимых библиотек.
```
## import the necessary tools for our work
from IPython.display import clear_output
from qiskit import *
from qiskit.visualization import plot_histogram
import numpy as np
import matplotlib.pyplot as plotter
from qiskit.tools.monitor import job_monitor
# Visualisation settings
import seaborn as sns, operator
sns.set_style("dark")
pi = np.pi
```
Функция `qft_dagger` вычисляет обратное квантовое преобразование Фурье. Для подробного понимания этого алгоритма см. посвященную ему главу в [учебнике Qiskit](https://qiskit.org/textbook/ch-algorithms/quantum-fourier-transform.html) .
```
## Code for inverse Quantum Fourier Transform
## adapted from Qiskit Textbook at
## qiskit.org/textbook
def qft_dagger(circ_, n_qubits):
"""n-qubit QFTdagger the first n qubits in circ"""
for qubit in range(int(n_qubits/2)):
circ_.swap(qubit, n_qubits-qubit-1)
for j in range(0,n_qubits):
for m in range(j):
circ_.cp(-np.pi/float(2**(j-m)), m, j)
circ_.h(j)
```
Следующая функция, `qpe_pre` , подготавливает начальное состояние для оценки. Обратите внимание, что начальное состояние создается путем применения вентиля Адамара ко всем кубитам, кроме последнего, и установки последнего кубита в $\vert1\rangle$.
```
## Code for initial state of Quantum Phase Estimation
## adapted from Qiskit Textbook at qiskit.org/textbook
## Note that the starting state is created by applying
## H on the first n_qubits, and setting the last qubit to |psi> = |1>
def qpe_pre(circ_, n_qubits):
circ_.h(range(n_qubits))
circ_.x(n_qubits)
for x in reversed(range(n_qubits)):
for _ in range(2**(n_qubits-1-x)):
circ_.cp(1, n_qubits-1-x, n_qubits)
```
Затем мы пишем быструю функцию `run_job` для запуска квантовой схемы и возврата результатов.
```
## Run a Qiskit job on either hardware or simulators
def run_job(circ, backend, shots=1000, optimization_level=0):
t_circ = transpile(circ, backend, optimization_level=optimization_level)
qobj = assemble(t_circ, shots=shots)
job = backend.run(qobj)
job_monitor(job)
return job.result().get_counts()
```
Затем загрузите свою учетную запись, чтобы использовать облачный симулятор или реальные устройства.
```
## Load your IBMQ account if
## you'd like to use the cloud simulator or real quantum devices
my_provider = IBMQ.load_account()
simulator_cloud = my_provider.get_backend('ibmq_qasm_simulator')
device = my_provider.get_backend('ibmq_16_melbourne')
simulator = Aer.get_backend('qasm_simulator')
```
Наконец, мы объединяем все вместе в функции `get_pi_estimate` , которая использует `n_qubits` для получения оценки $\pi$.
```
## Function to estimate pi
## Summary: using the notation in the Qiskit textbook (qiskit.org/textbook),
## do quantum phase estimation with the 'phase' operator U = p(theta) and |psi> = |1>
## such that p(theta)|1> = exp(2 x pi x i x theta)|1>
## By setting theta = 1 radian, we can solve for pi
## using 2^n x 1 radian = most frequently measured count = 2 x pi
def get_pi_estimate(n_qubits):
# create the circuit
circ = QuantumCircuit(n_qubits + 1, n_qubits)
# create the input state
qpe_pre(circ, n_qubits)
# apply a barrier
circ.barrier()
# apply the inverse fourier transform
qft_dagger(circ, n_qubits)
# apply a barrier
circ.barrier()
# measure all but the last qubits
circ.measure(range(n_qubits), range(n_qubits))
# run the job and get the results
counts = run_job(circ, backend=simulator, shots=10000, optimization_level=0)
# print(counts)
# get the count that occurred most frequently
max_counts_result = max(counts, key=counts.get)
max_counts_result = int(max_counts_result, 2)
# solve for pi from the measured counts
theta = max_counts_result/2**n_qubits
return (1./(2*theta))
```
Теперь запустите функцию `get_pi_estimate` с различным количеством кубитов и распечатайте оценки.
```
# estimate pi using different numbers of qubits
nqs = list(range(2,12+1))
pi_estimates = []
for nq in nqs:
thisnq_pi_estimate = get_pi_estimate(nq)
pi_estimates.append(thisnq_pi_estimate)
print(f"{nq} qubits, pi ≈ {thisnq_pi_estimate}")
```
И постройте все результаты.
```
plotter.plot(nqs, [pi]*len(nqs), '--r')
plotter.plot(nqs, pi_estimates, '.-', markersize=12)
plotter.xlim([1.5, 12.5])
plotter.ylim([1.5, 4.5])
plotter.legend(['$\pi$', 'estimate of $\pi$'])
plotter.xlabel('Number of qubits', fontdict={'size':20})
plotter.ylabel('$\pi$ and estimate of $\pi$', fontdict={'size':20})
plotter.tick_params(axis='x', labelsize=12)
plotter.tick_params(axis='y', labelsize=12)
plotter.show()
import qiskit
qiskit.__qiskit_version__
```
| true |
code
| 0.731478 | null | null | null | null |
|
# T81-558: Applications of Deep Neural Networks
**Module 6: Convolutional Neural Networks (CNN) for Computer Vision**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 6 Material
* Part 6.1: Image Processing in Python [[Video]](https://www.youtube.com/watch?v=4Bh3gqHkIgc&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_06_1_python_images.ipynb)
* Part 6.2: Keras Neural Networks for Digits and Fashion MNIST [[Video]](https://www.youtube.com/watch?v=-SA8BmGvWYE&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_06_2_cnn.ipynb)
* Part 6.3: Implementing a ResNet in Keras [[Video]](https://www.youtube.com/watch?v=qMFKsMeE6fM&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_06_3_resnet.ipynb)
* Part 6.4: Using Your Own Images with Keras [[Video]](https://www.youtube.com/watch?v=VcFja1fUNSk&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_06_4_keras_images.ipynb)
* **Part 6.5: Recognizing Multiple Images with YOLO Darknet** [[Video]](https://www.youtube.com/watch?v=oQcAKvBFli8&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_06_5_yolo.ipynb)
```
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return f"{h}:{m:>02}:{s:>05.2f}"
```
# Part 6.5: Recognizing Multiple Images with Darknet
Convolutional neural networks are great at recognizing classifying a single item that is centered in an image. However, as humans we are able to recognize many items in our field of view, in real-time. It is very useful to be able to recognize multiple items in a single image. One of the most advanced means of doing this is YOLO DarkNet (not to be confused with the Internet [Darknet](https://en.wikipedia.org/wiki/Darknet). YOLO is an acronym for You Only Look Once. This speaks to the efficency of the algorithm.
* Redmon, J., Divvala, S., Girshick, R., & Farhadi, A. (2016). [You only look once: Unified, real-time object detection](https://arxiv.org/abs/1506.02640). In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 779-788).
The following image shows YOLO tagging in action.

It is also possible to run YOLO on live video streams. The following frame is from the YouTube Video for this module.

As you can see it is classifying many things in this video. My collection of books behind me is adding considerable "noise", as DarkNet tries to classify every book behind me. If you watch the video you will note that it is less than perfect. The coffee mug that I pick up gets classified as a cell phone and at times a remote. The small yellow object behind me on the desk is actually a small toolbox. However, it gets classified as a book at times and a remote at other times. Currently this algorithm classifies each frame on its own. More accuracy could be gained by using multiple images together. Consider when you see an object coming towards you, if it changes angles, you might form a better opinion of what it was. If that same object now changes to an unfavorable angle, you still know what it is, based on previous information.
### How Does DarkNet/YOLO Work?
YOLO begins by resizing the image to an $S \times S$ grid. A single convolutional neural network is run against this grid that predicts bounding boxes and what might be contained by those boxes. Each bounding box also has a confidence in which item it believes the box contains. This is a regular convolution network, just like we've seen privously. The only difference is that a YOLO CNN outputs a number of prediction bounding boxes. At a high level this can be seen by the following diagram.

The output of the YOLO convolutional neural networks is essentially a multiple regression. The following values are generated for each of the bounding records that are generated.
* **x** - The x-coordinate of the center of a bounding rectangle.
* **y** - The y-coordinate of the center of a bounding rectangle.
* **w** - The width of each bounding rectangle.
* **h** - The height of each bounding rectangle.
* **labels** - The relative probabilities of each of the labels (1 value for each label)
* **confidence** - The confidence in this rectangle.
The output layer of a Keras neural network is a Tensor. In the case of YOLO, this output tensor is 3D and is of the following dimensions.
$ S \times S \times (B \cdot 5 + C) $
The constants in the above expression are:
* *S* - The dimensions of the YOLO grid that is overlaid across the source image.
* *B* - The number of potential bounding rectangles generated for each grid cell.
* *C* - The number of class labels that here are.
The value 5 in the above expression is simply the count of non-label components of each bounding rectangle ($x$, $y$, $h$, $w$, $confidence$.
Because there are $S^2 \cdot B$ total potential bounding rectangles, the image will get very full. Because of this it is important to drop all rectangles below some threshold of confidence. This is demonstrated by the image below.

The actual structure of the convolutional neural network behind YOLO is relatively simple and is shown in the following image. Because there is only one convolutional neural network, and it "only looks once," the performance is not impacted by how many objects are detected.

The following image shows some additional recognitions being performed by a YOLO.

### Using DarkFlow in Python
To make use of DarkFlow you have several options:
* **[DarkNet](https://pjreddie.com/darknet/yolo/)** - The original implementation of YOLO, written in C.
* **[DarkFlow](https://github.com/thtrieu/darkflow)** - Python package that implements YOLO in Python, using TensorFlow.
DarkFlow can be used from the command line. This allows videos to be produced from existing videos. This is how the YOLO videos used in the class module video were created.
It is also possible call DarkFlow directly from Python. The following code performs a classification of the image of my dog and I in the kitchen from above.
### Running DarkFlow (YOLO) from Google CoLab
Make sure you create the following folders on your Google drive and download yolo.weights, coco.names, and yolo.cfg into the correct locations. See the helper script below to set this up.
'/content/drive/My Drive/projects/yolo':
bin cfg
'/content/drive/My Drive/projects/yolo/bin':
yolo.weights
'/content/drive/My Drive/projects/yolo/cfg':
coco.names yolo.cfg
```
!git clone https://github.com/thtrieu/darkflow.git
!pip install ./darkflow/
# Note, if you are using Google CoLab, this can be used to mount your drive to load YOLO config and weights.
from google.colab import drive
drive.mount('/content/drive')
# The following helper script will create a projects/yolo folder for you
# and download the needed files.
!mkdir -p /content/drive/My\ Drive/projects
!mkdir -p /content/drive/My\ Drive/projects/yolo
!mkdir -p /content/drive/My\ Drive/projects/yolo/bin
!mkdir -p /content/drive/My\ Drive/projects/yolo/cfg
!wget https://raw.githubusercontent.com/thtrieu/darkflow/master/cfg/coco.names -O /content/drive/My\ Drive/projects/yolo/cfg/coco.names
!wget https://raw.githubusercontent.com/thtrieu/darkflow/master/cfg/yolo.cfg -O /content/drive/My\ Drive/projects/yolo/cfg/yolo.cfg
!wget https://pjreddie.com/media/files/yolov2.weights -O /content/drive/My\ Drive/projects/yolo/bin/yolo.weights
```
### Running DarkFlow (YOLO) Locally
If you wish to run YOLO from your own computer you will need to pip install cython and then follow the instructions [here](https://github.com/thtrieu/darkflow).
### Running DarkFlow (YOLO)
Regardless of which path you take above (Google CoLab or Local) you will run this code to continue. Make sure to uncomment the correct **os.chdir** command below.
```
from darkflow.net.build import TFNet
import cv2
import numpy as np
import requests
import os
from scipy import misc
from io import BytesIO
from urllib.request import urlopen
from PIL import Image, ImageFile
os.chdir('/content/drive/My Drive/projects/yolo') # Google CoLab
#os.chdir('/Users/jheaton/projects/darkflow') # Local
# For GPU (Google CoLab)
options = {"model": "./cfg/yolo.cfg", "load": "./bin/yolo.weights", "threshold": 0.1, "gpu": 1.0}
# For CPU
#options = {"model": "./cfg/yolo.cfg", "load": "./bin/yolo.weights", "threshold": 0.1}
tfnet = TFNet(options)
# Read image to classify
url = "https://raw.githubusercontent.com/jeffheaton/t81_558_deep_learning/master/images/cook.jpg"
response = requests.get(url)
img = Image.open(BytesIO(response.content))
img.load()
result = tfnet.return_predict(np.asarray(img))
for row in result:
print(row)
```
# Generate a YOLO Tagged Image
DarkFlow does not contain a built in "boxing function" for images. However, it is not difficult to create one using the results provided above. The following code demonstrates this process.
```
def box_image(img, pred):
array = np.asarray(img)
for result in pred:
top_x = result['topleft']['x']
top_y = result['topleft']['y']
bottom_x = result['bottomright']['x']
bottom_y = result['bottomright']['y']
confidence = int(result['confidence'] * 100)
label = f"{result['label']} {confidence}%"
if confidence > 0.3:
array = cv2.rectangle(array, (top_x, top_y), (bottom_x, bottom_y), (255,0,0), 3)
array = cv2.putText(array, label, (top_x, top_y-5), cv2.FONT_HERSHEY_COMPLEX_SMALL ,
0.45, (0, 255, 0), 1, cv2.LINE_AA)
return Image.fromarray(array, 'RGB')
boxed_image = box_image(img, result)
boxed_image
```
# Module 6 Assignment
You can find the first assignment here: [assignment 6](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/assignments/assignment_yourname_class1.ipynb)
| true |
code
| 0.424352 | null | null | null | null |
|
```
#This function gets the raw data and clean it
def data_clean(data):
print("Data shape before cleaning:" + str(np.shape(data)))
#Change the data type of any column if necessary.
print("Now it will print only those columns with non-numeric values")
print(data.select_dtypes(exclude=[np.number]))
#Now dropping those columns with zero values entirely or which sums to zero
data= data.loc[:, (data != 0).any(axis=0)]
#Now dropping those columns with NAN values entirely
data=data.dropna(axis=1, how='all')
data=data.dropna(axis=0, how='all')
#Keep track of the columns which are exculded after NAN and column zero sum operation above
print("Data shape after cleaning:" + str(np.shape(data)))
return data
#This function impute the missing values with features (column mean)
def data_impute(data):
#Seprating out the NAMES of the molecules column and ACTIVITY column because they are not the features to be normalized.
data_input=data.drop(['ACTIVITY', 'NAME'], axis=1)
data_labels= data.ACTIVITY
data_names = data.NAME
#Imputing the missing values with features mean values
fill_NaN = Imputer(missing_values=np.nan, strategy='mean', axis=1)
Imputed_Data_input = pd.DataFrame(fill_NaN.fit_transform(data_input))
print(np.shape(Imputed_Data_input))
print("Data shape after imputation:" + str(np.shape(Imputed_Data_input)))
return Imputed_Data_input, data_labels, data_names
#This function is to normalize features
def data_norm(Imputed_Data_input,data_labels,data_names):
#Calculatig the mean and STD of the imputed input data set
Imputed_Data_input_mean=Imputed_Data_input.mean()
Imputed_Data_input_std=Imputed_Data_input.std()
#z-score normalizing the whole input data:
Imputed_Data_input_norm = (Imputed_Data_input - Imputed_Data_input_mean)/Imputed_Data_input_std
#Adding names and labels to the data again
frames = [data_names,data_labels, Imputed_Data_input_norm]
full_data_norm = pd.concat(frames,axis=1)
return full_data_norm
#This function gives train-test-split
from sklearn.cross_validation import train_test_split as sk_train_test_split
def data_split(full_data_norm, test_size):
full_data_norm_input=full_data_norm.drop(['ACTIVITY', 'NAME'], axis=1)
target_attribute = full_data_norm['ACTIVITY']
# We call train set as train_cv as a part of it will be used for cross-validadtion
train_cv_x, test_x, train_cv_y, test_y = sk_train_test_split(full_data_norm_input, target_attribute, test_size=test_size, random_state=55)
return train_cv_x, test_x, train_cv_y, test_y
#Optimizing drop_out and threshold with 3 cross CV validation
def hybrid_model_opt():
class fs(TransformerMixin, BaseEstimator):
def __init__(self, n_estimators=1000, threshold='1.7*mean'):
self.ss=None
self.n_estimators = n_estimators
self.x_new = None
self. threshold= threshold
def fit(self, X, y):
m = ExtraTreesClassifier(n_estimators=self.n_estimators, random_state=0)
m.fit(X,y)
self.ss = SelectFromModel(m, threshold=self. threshold , prefit=True)
return self
def transform(self, X):
self.x_new=self.ss.transform(X)
global xx
xx=self.x_new.shape[1]
return self.x_new
def nn_model_opt(dropout_rate=0.5,init_mode='uniform', activation='relu'):
#n_x_new=xx # this is the number of features selected for current iteration
np.random.seed(200000)
model_opt = Sequential()
model_opt.add(Dense(xx,input_dim=xx ,kernel_initializer='he_normal', activation='relu'))
model_opt.add(Dense(10, kernel_initializer='he_normal', activation='relu'))
model_opt.add(Dropout(dropout_rate))
model_opt.add(Dense(1,kernel_initializer='he_normal', activation='sigmoid'))
model_opt.compile(loss='binary_crossentropy',optimizer='adam', metrics=['binary_crossentropy'])
return model_opt
clf=KerasClassifier(build_fn=nn_model_opt, epochs=250, batch_size=3000, verbose=-1)
hybrid_model = Pipeline([('fs', fs()),('clf', clf)])
return hybrid_model
#Getting fetaures importances of all the features using extra_tree classifier only
def feature_imp(train_cv_x,train_cv_y):
m = ExtraTreesClassifier(n_estimators=1000 )
m.fit(train_cv_x,train_cv_y)
importances = m.feature_importances_
return importances, m
def selected_feature_names(m, thr, train_cv_x):
sel = SelectFromModel(m,threshold=thr ,prefit=True)
feature_idx = sel.get_support()
feature_name = train_cv_x.columns[feature_idx]
feature_name =pd.DataFrame(feature_name )
return feature_name
def train_test_feature_based_selection(feature_name,train_cv_x,train_cv_y,test_x,test_y ):
feature_name=feature_name.T
feature_name.columns = feature_name.iloc[0]
feature_name.reindex(feature_name.index.drop(0))
train_selected_x=train_cv_x[train_cv_x.columns.intersection(feature_name.columns)]
test_selected_x=test_x[test_x.columns.intersection(feature_name.columns)]
train_selected_x=train_selected_x.as_matrix()
test_selected_x=test_selected_x.as_matrix()
train_selected_y=train_cv_y.as_matrix()
test_selected_y=test_y.as_matrix()
return train_selected_x, train_selected_y, test_selected_x, test_selected_y
def model_nn_final(train_selected_x, train_selected_y, test_selected_x, test_selected_y, x, drop_out):
model_final = Sequential()
#n_x_new=train_selected_x.shape[1]
n_x_new=train_selected_x.shape[1]
model_final.add(Dense(n_x_new, input_dim=n_x_new, kernel_initializer ='he_normal', activation='sigmoid'))
model_final.add(Dense(10, kernel_initializer='he_normal', activation='sigmoid'))
model_final.add(Dropout(drop_out))
model_final.add(Dense(1, kernel_initializer='he_normal', activation='sigmoid'))
model_final.compile(loss='binary_crossentropy', optimizer='adam', metrics=['binary_crossentropy'])
seed = 7000
np.random.seed(seed)
model_final.fit(train_selected_x, train_selected_y, epochs=250, batch_size=1064)
pred_test = model_final.predict(test_selected_x)
auc_test = roc_auc_score(test_selected_y, pred_test)
print ("AUROC_test: " + str(auc_test))
print(" ")
model_json = model_final.to_json()
with open(str(x)+"_model.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model_final.save_weights(str(x)+"_model.h5")
print("Saved model to disk")
print(" ")
return pred_test
```
## 1) Loading all packages needed
```
from keras.callbacks import ModelCheckpoint
from keras import backend as K
from keras import optimizers
from keras.layers import Dense
from keras.layers import Dense, Dropout
from keras.models import Sequential
from keras.wrappers.scikit_learn import KerasClassifier
from pandas import ExcelFile
from pandas import ExcelWriter
from PIL import Image
from scipy import ndimage
from scipy.stats import randint as sp_randint
from sklearn.base import BaseEstimator
from sklearn.base import TransformerMixin
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import SelectFromModel
from sklearn import datasets
from sklearn import metrics
from sklearn import pipeline
from sklearn.metrics import roc_auc_score, roc_curve
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import PredefinedSplit
from sklearn.model_selection import RandomizedSearchCV
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import FunctionTransformer
from sklearn.preprocessing import Imputer
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.utils import resample
from tensorflow.python.framework import ops
import h5py
import keras
import matplotlib.pyplot as plt
import numpy as np
import openpyxl
import pandas as pd
import scipy
import tensorflow as tf
import xlsxwriter
%load_ext autoreload
%matplotlib inline
```
## 2) Loading the data
The "NAME" Column is for naming the molecule. The "ACTIVITY" column is the Activity of molecule. Rest of the columns shows the features.
```
data = pd.read_excel(r'full_data.xlsx')
data
```
## 3) Cleaning the data
Removing NAN values from the data. Other attributes can also be added here to clean the data as per requirement. After executing this function, only those columns will be displayed which have non-numeric values in it. If these non-numeric values appear in numeric features columns, then these should be treated before going further. It will also print the data shape before and after cleaning.
```
#Cleaning the data
data= data_clean(data)
```
## 4) Imputing the missing data
Imputing the missin values in feature columns by means of respective feature.
```
#imputing the missing values
Imputed_Data_input, data_labels, data_names=data_impute(data)
```
## 5) Normalizing the data
Imputing the missin values in feature columns by means of respective feature.
```
#Normalizing the data
full_data_norm=data_norm(Imputed_Data_input, data_labels, data_names)
```
## 6) splitting the data the data
```
#Splitting the data into train and test
test_size=0.30
train_cv_x, test_x, train_cv_y, test_y=data_split(full_data_norm, test_size)
```
## 7) Hybrid Model optimization
Currently, only two variables are optimized (drop_out and threshold). This optimization search can be extended as per requiremnet. x-fold cross validation is used in random search setting.
```
xx=0 #This variable stores the number of features selected
hybrid_model=hybrid_model_opt() #calling the hybrid model for optimizattion
#Defining two important paramters of hybrid model to be optimized using random cv search
param_grid= {'fs__threshold': ['0.08*mean','0.09*mean','0.10*mean','0.2*mean','0.3*mean','0.4*mean','0.5*mean','0.6*mean','0.7*mean','0.8*mean','0.9*mean','1*mean','1.1*mean','1.2*mean','1.3*mean','1.4*mean','1.5*mean','1.6*mean','1.7*mean','1.8*mean','1.9*mean','2.0*mean','2.1*mean','2.2*mean','2.3*mean'],
'clf__dropout_rate': [0.1, 0.2, 0.3, 0.4, 0.5,0.6,0.7,0.8,0.9]}
#Random CV search
grid = RandomizedSearchCV(estimator=hybrid_model, param_distributions=param_grid,n_iter = 1,scoring='roc_auc',cv = 3 , n_jobs=1)
opt_result = grid.fit(train_cv_x, train_cv_y)
#Printing the optimization results
print("Best: %f using %s" % (opt_result.best_score_, opt_result.best_params_))
means = opt_result.cv_results_['mean_test_score']
stds = opt_result.cv_results_['std_test_score']
params = opt_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, stdev, param))
```
## 8) Gini_importances
```
#getting the importances of all the features
importances, m =feature_imp(train_cv_x,train_cv_y)
```
## 9) Features names
```
#getting the features names of the selected features based on optimized threshold
feature_name=selected_feature_names(m, opt_result.best_params_["fs__threshold"], train_cv_x)
```
## 10) Saving the gini-importance and selected features names
```
#saving gini-importance of all the featues
writer = pd.ExcelWriter('importances.xlsx',engine='xlsxwriter')
pd.DataFrame(importances).to_excel(writer,sheet_name='importances')
writer.save()
#Saving features names which are selected on the basis of optimized threshold
writer = pd.ExcelWriter('feature_name.xlsx',engine='xlsxwriter')
pd.DataFrame(feature_name).to_excel(writer,sheet_name='feature_name')
writer.save()
```
## 11) Features selection in train and test
```
#Selection of train and test features based on optimized value of threshold
train_selected_x, train_selected_y, test_selected_x, test_selected_y=train_test_feature_based_selection(feature_name,train_cv_x,train_cv_y,test_x,test_y )
```
## 12) Saving the test on the basis of selected features columns
```
#Saving the selected test set
writer = pd.ExcelWriter('test_selected.xlsx',engine='xlsxwriter')
pd.DataFrame(test_selected_x).to_excel(writer,sheet_name='test_selected_x')
pd.DataFrame(test_selected_y).to_excel(writer,sheet_name='test_selected_y')
writer.save()
```
## 13) Final prediction based on ensembling.
This will also save all the ensembled average models and weight matrix.
```
# At this point, we have obtained the optimized optimized values and selected the features in train and test based on
#optimized threshold value of feature selection module of hybrid framework
ensemb=4 #Number of ensembling average
pred_test=[] #To store the individual model test prediction
pred_test_final=np.zeros((test_selected_x.shape[0],1)) # To store the final test prediction after ensembling
#As per the above number of ensemble, the models will be saved in the directory
for x in range(ensemb):
pred_test.append(model_nn_final(train_selected_x, train_selected_y, test_selected_x, test_selected_y, x, opt_result.best_params_["clf__dropout_rate"]))
pred_test_final=pred_test[x]+pred_test_final
#ensemble averaging
pred_test_final=pred_test_final/ensemb
#Final Accuracy
auc_test_final = roc_auc_score(test_selected_y, pred_test_final)
print(auc_test_final)
```
| true |
code
| 0.688521 | null | null | null | null |
|
<!-- :Author: Arthur Goldberg <Arthur.Goldberg@mssm.edu> -->
<!-- :Date: 2020-07-13 -->
<!-- :Copyright: 2020, Karr Lab -->
<!-- :License: MIT -->
# DE-Sim tutorial
DE-Sim is an open-source, object-oriented, discrete-event simulation (OO DES) tool implemented in Python.
DE-Sim makes it easy to build and simulate discrete-event models.
This page introduces the basic concepts of discrete-event modeling and teaches you how to build and simulate discrete-event models with DE-Sim.
## Installation
Use `pip` to install `de_sim`.
```
!pip install de_sim
```

## DE-Sim model of a one-dimensional random walk
<font size="4">Three steps: define an event message class; define a simulation object class; and build and run a simulation.</font>
### 1: Create an event message class by subclassing [`EventMessage`](https://docs.karrlab.org/de_sim/master/source/de_sim.html#de_sim.event_message.EventMessage).
<font size="4">Each DE-Sim event contains an event message that provides data to the simulation object which executes the event.
The random walk model sends event messages that contain the value of a random step.</font>
```
import de_sim
class RandomStepMessage(de_sim.EventMessage):
"An event message class that stores the value of a random walk step"
step_value: float
```

### 2: Subclass `SimulationObject` to define a simulation object class
<font size="4">
Simulation objects are like threads: a simulation's scheduler decides when to execute them, and their execution is suspended when they have no work to do.
But a DES scheduler schedules simulation objects to ensure that events occur in simulation time order. Precisely, the fundamental invariant of discrete-event simulation:
<br>
<br>
1. All events in a simulation are executed in non-decreasing time order.
By guaranteeing this behavior, the DE-Sim scheduler ensures that causality relationships between events are respected.
This invariant has two consequences:
1. All synchronization between simulation objects is controlled by the simulation times of events.
2. Each simulation object executes its events in non-decreasing time order.
The Python classes that generate and handle simulation events are simulation object classes, subclasses of `SimulationObject` which uses a custom class creation method that gives special meaning to certain methods and attributes.
Below, we define a simulation object class that models a random walk which randomly selects the time delay between steps, and illustrates all key features of `SimulationObject`.
</font>
```
import random
class RandomWalkSimulationObject(de_sim.SimulationObject):
" A 1D random walk model, with random delays between steps "
def __init__(self, name):
super().__init__(name)
def init_before_run(self):
" Initialize before a simulation run; called by the simulator "
self.position = 0
self.history = {'times': [0],
'positions': [0]}
self.schedule_next_step()
def schedule_next_step(self):
" Schedule the next event, which is a step "
# A step moves -1 or +1 with equal probability
step_value = random.choice([-1, +1])
# The time between steps is 1 or 2, with equal probability
delay = random.choice([1, 2])
# Schedule an event `delay` in the future for this object
# The event contains a `RandomStepMessage` with `step_value=step_value`
self.send_event(delay, self, RandomStepMessage(step_value))
def handle_step_event(self, event):
" Handle a step event "
# Update the position and history
self.position += event.message.step_value
self.history['times'].append(self.time)
self.history['positions'].append(self.position)
self.schedule_next_step()
# `event_handlers` contains pairs that map each event message class
# received by this simulation object to the method that handles
# the event message class
event_handlers = [(RandomStepMessage, handle_step_event)]
# messages_sent registers all message types sent by this object
messages_sent = [RandomStepMessage]
```
<font size="4">
DE-Sim simulation objects employ special methods and attributes:
<br>
* Special `SimulationObject` methods:
1. **`init_before_run`** (optional): immediately before a simulation run, the simulator calls each simulation object’s `init_before_run` method. In this method simulation objects can send initial events and perform other initializations.
2. **`send_event`**: `send_event(delay, receiving_object, event_message)` schedules an event to occur `delay` time units in the future at simulation object `receiving_object`. `event_message` must be an [`EventMessage`](https://docs.karrlab.org/de_sim/master/source/de_sim.html#de_sim.event_message.EventMessage) instance. An event can be scheduled for any simulation object in a simulation.
The event will be executed at its scheduled simulation time by an event handler in the simulation object `receiving_object`.
The `event` parameter in the handler will be the scheduled event, which contains `event_message` in its `message` attribute.
3. **event handlers**: Event handlers have the signature `event_handler(self, event)`, where `event` is a simulation event. A subclass of `SimulationObject` must define at least one event handler, as illustrated by `handle_step_event` above.
<br>
<br>
* Special `SimulationObject` attributes:
1. **`event_handlers`**: a simulation object can receive arbitrarily many types of event messages, and implement arbitrarily many event handlers. The attribute `event_handlers` contains an iterator over pairs that map each event message class received to the event handler which handles the event message class.
2. **`time`**: `time` is a read-only attribute that always equals the current simulation time.
</font>

### 3: Execute a simulation by creating and initializing a [`Simulator`](https://docs.karrlab.org/de_sim/master/source/de_sim.html#de_sim.simulator.Simulator), and running the simulation.
<font size="4">
The `Simulator` class simulates models.
Its `add_object` method adds a simulation object to the simulator.
Each object in a simulation must have a unique `name`.
The `initialize` method, which calls each simulation object’s `init_before_run` method, must be called before a simulation starts.
At least one simulation object in a simulation must schedule an initial event--otherwise the simulation cannot start.
More generally, a simulation with no events to execute will terminate.
Finally, `run` simulates a model. It takes the maximum time of a simulation run. `run` also takes several optional configuration arguments.
</font>
```
# Create a simulator
simulator = de_sim.Simulator()
# Create a random walk simulation object and add it to the simulation
random_walk_sim_obj = RandomWalkSimulationObject('rand_walk')
simulator.add_object(random_walk_sim_obj)
# Initialize the simulation
simulator.initialize()
# Run the simulation until time 10
max_time = 10
simulator.run(max_time)
# Plot the random walk
import matplotlib.pyplot as plt
import matplotlib.ticker as plticker
fig, ax = plt.subplots()
loc = plticker.MultipleLocator(base=1.0)
ax.yaxis.set_major_locator(loc)
plt.step(random_walk_sim_obj.history['times'],
random_walk_sim_obj.history['positions'],
where='post')
plt.xlabel('Time')
plt.ylabel('Position')
plt.show()
```
<font size="4">
This example runs a simulation for `max_time` time units, and plots the random walk’s trajectory.
This trajectory illustrates two key characteristics of discrete-event models. First, the state changes at discrete times.
Second, since the state does not change between instantaneous events, the trajectory of any state variable is a step function.
</font>

## DE-Sim example with multiple object instances
<font size="4">
We show an DE-Sim implementation of the parallel hold (PHOLD) model, frequently used to benchmark parallel DES simulators.
<br>
<br>
We illustrate these DE-Sim features:
* Use multiple [`EventMessage`](https://docs.karrlab.org/de_sim/master/source/de_sim.html#de_sim.event_message.EventMessage) types
* Run multiple instances of a simulation object type
* Simulation objects scheduling events for each other
</font>
```
""" Messages for the PHOLD benchmark for parallel discrete-event simulators """
import random
class MessageSentToSelf(de_sim.EventMessage):
"A message that's sent to self"
class MessageSentToOtherObject(de_sim.EventMessage):
"A message that's sent to another PHold simulation object"
class InitMsg(de_sim.EventMessage):
"An initialization message"
MESSAGE_TYPES = [MessageSentToSelf, MessageSentToOtherObject, InitMsg]
class PholdSimulationObject(de_sim.SimulationObject):
""" Run a PHOLD simulation """
def __init__(self, name, args):
self.args = args
super().__init__(name)
def init_before_run(self):
self.send_event(random.expovariate(1.0), self, InitMsg())
@staticmethod
def record_event_header():
print('\t'.join(('Sender', 'Send', "Receivr",
'Event', 'Message type')))
print('\t'.join(('', 'time', '', 'time', '')))
def record_event(self, event):
record_format = '{}\t{:.2f}\t{}\t{:.2f}\t{}'
print(record_format.format(event.sending_object.name,
event.creation_time,
event.receiving_object.name,
self.time,
type(event.message).__name__))
def handle_simulation_event(self, event):
""" Handle a simulation event """
# Record this event
self.record_event(event)
# Schedule an event
if random.random() < self.args.frac_self_events or \
self.args.num_phold_objects == 1:
receiver = self
else:
# Send the event to another randomly selected object
obj_index = random.randrange(self.args.num_phold_objects - 1)
if int(self.name) <= obj_index:
obj_index += 1
receiver = self.simulator.simulation_objects[str(obj_index)]
if receiver == self:
message_type = MessageSentToSelf
else:
message_type = MessageSentToOtherObject
self.send_event(random.expovariate(1.0), receiver, message_type())
event_handlers = [(sim_msg_type, 'handle_simulation_event') \
for sim_msg_type in MESSAGE_TYPES]
messages_sent = MESSAGE_TYPES
```
<font size="4">
The PHOLD model runs multiple instances of `PholdSimulationObject`.
`create_and_run` creates the objects and adds them to the simulator.
Each `PholdSimulationObject` object is initialized with `args`, an object that defines two attributes used by all objects:
* `args.num_phold_objects`: the number of PHOLD objects running
* `args.frac_self_events`: the fraction of events sent to self
At time 0, each PHOLD object schedules an `InitMsg` event for itself that occurs after a random exponential time delay with mean = 1.0.
The `handle_simulation_event` method handles all events.
Each event schedules one more event.
A random value in [0, 1) is used to decide whether to schedule the event for itself (with probability `args.frac_self_events`) or for another PHOLD object.
If the event is scheduled for another PHOLD object, this gets a reference to the object:
receiver = self.simulator.simulation_objects[str(obj_index)]
The attribute `self.simulator` always references the running simulator, and `self.simulator.simulation_objects` is a dictionary that maps simulation object names to simulation objects.
</font>
<font size="4">
Each event is printed by `record_event`.
It accesses the DE-Sim `Event` object that is passed to all event handlers.
`de_sim.event.Event` contains five useful fields:
* `sending_object`: the object that created and sent the event
* `creation_time`: the simulation time when the event was created (a.k.a. its *send time*)
* `receiving_object`: the object that received the event
* `event_time`: the simulation time when the event must execute (a.k.a. its *receive time*)
* `message`: the [`EventMessage`](https://docs.karrlab.org/de_sim/master/source/de_sim.html#de_sim.event_message.EventMessage) carried by the event
However, rather than use the event's `event_time`, `record_event` uses `self.time` to report the simulation time when the event is being executed, as they are always equal.
</font>

### Execute the simulation
<font size="4">
Run a short simulation, and print all events:
</font>
```
def create_and_run(args):
# create a simulator
simulator = de_sim.Simulator()
# create simulation objects, and send each one an initial event message to self
for obj_id in range(args.num_phold_objects):
phold_obj = PholdSimulationObject(str(obj_id), args)
simulator.add_object(phold_obj)
# run the simulation
simulator.initialize()
PholdSimulationObject.record_event_header()
event_num = simulator.simulate(args.max_time).num_events
print("Executed {} events.\n".format(event_num))
from argparse import Namespace
args = Namespace(max_time=2,
frac_self_events=0.3,
num_phold_objects=6)
create_and_run(args)
```
| true |
code
| 0.699485 | null | null | null | null |
|
# First Steps with Huggingface
```
from IPython.display import display, Markdown
with open('../../doc/env_variables_setup.md', 'r') as fh:
content = fh.read()
display(Markdown(content))
```
## Import Packages
Try to avoid 'pip install' in the notebook. This can destroy dependencies in the env.
```
# only running this cell leads to problems when kernel has not been restarted
import tensorflow as tf
import tensorflow_datasets as tfds
from tensorflow.python.data.ops import dataset_ops
from tensorboard.backend.event_processing import event_accumulator
from absl import logging
from datetime import datetime
import os
import shutil
import numpy as np
from tqdm import tqdm
import re
#from transformers import *
from transformers import (BertTokenizer,
TFBertForSequenceClassification,
TFBertModel,
TFBertForPreTraining,
glue_convert_examples_to_features,
glue_processors,)
# local packages
import preprocessing.preprocessing as pp
import importlib
importlib.reload(pp);
```
### To Do:
- extend to other language models like gpt-2
- find out how to attach additional layers to the architecture
- find out at which point multilingualism can be introduced
## Define Paths
```
try:
data_dir=os.environ['PATH_DATASETS']
except:
print('missing PATH_DATASETS')
print(data_dir)
```
## 1. Loading the IMDb Dataset from Tensorflow
```
#import tensorflow_datasets as tfds
#from ipywidgets import IntProgress
train_data, validation_data, test_data = tfds.load(name="imdb_reviews",
data_dir=data_dir,
split=('train[:60%]', 'train[60%:]', 'test'),
as_supervised=True)
# trying to extract the info requires loading the data without splitting it
data_ex, data_ex_info = tfds.load(name="imdb_reviews",
data_dir=data_dir,
as_supervised=True,
with_info=True)
```
## 2. Exploring the Dataset
### 2.1. Getting a feeling of the data structure of the IMDb data
```
print(type(train_data))
# splitting features and labels up into separate objects and creating a batch with 10 entries
train_examples_batch, train_labels_batch = next(iter(train_data.batch(10)))
train_examples_batch[:2]
train_labels_batch
```
Converting the tf.Tensor objects into numpy arrays seems more manageable in the functions afterwards which is why it is done here.
```
train_examples_batch_np = tfds.as_numpy(train_examples_batch)
train_labels_batch_np = tfds.as_numpy(train_labels_batch)
data_ex_info
data_ex.keys()
data_ex['test']
data_ex_info.features
```
### 2.2. Experimenting with the Data Structure
```
# load as numpy
train_data_np = tfds.as_numpy(train_data)
#, validation_data_np, test_data_np
print(type(train_data_np))
# this data structure is a generator, but we need a tuple of strings / integers
# getting a sense of the structure inside the generator
for index, entry in enumerate(train_data_np):
if index < 10:
print(entry)
else:
break
# checking the data type of the main dataset
train_data
# different way of getting the entries
list(train_data.take(3).as_numpy_iterator())[0][0]
```
### 2.3. Cleaning
The data still contains non-word structures like \<br />\<br /> and \\ which have to be removed.
```
REPLACE_NO_SPACE = re.compile("[.;:!\'?,\"()\[\]]")
REPLACE_WITH_SPACE = re.compile("(<br\s*/><br\s*/>)|(\-)|(\/)")
REPLACE_NO_SPACE
#np.array(list(data_ex['train'].as_numpy_iterator()))
for line in np.array(list(train_data.as_numpy_iterator())):
print(line[0].decode("utf-8"))#.lower())
break
def preprocess_reviews(reviews):
#reviews = [REPLACE_NO_SPACE.sub("", line[0].decode("utf-8").lower()) for line in np.array(list(reviews.as_numpy_iterator()))]
reviews = [REPLACE_WITH_SPACE.sub(" ", line[0].decode("utf-8")) for line in np.array(list(reviews.as_numpy_iterator()))]# for line in reviews]
return reviews
reviews_train_clean = preprocess_reviews(train_data)
reviews_test_clean = preprocess_reviews(test_data)
for index, entry in enumerate(reviews_train_clean):
if index < 10:
print(entry)
else:
break
```
*Is it problematic that full stops got replaced?*
Yes -> took that part out again and even let capital letters in there
*What about stopwords?*
BERT was trained on full sentences and depends on word before and after -> eliminating stopwords would mess with this
### 2.4. Examining the Distribution of Labels
```
labels_train = [int(line[1].decode("utf-8")) for line in np.array(list(train_data.as_numpy_iterator()))]
labels_valid = [int(line[1].decode("utf-8")) for line in np.array(list(validation_data.as_numpy_iterator()))]
type(labels_train[0])
share_negative = sum(labels_train)/len(labels_train)
print(share_negative)
```
### 2.5. Comparisons to the MRPC Dataset
```
# testing the way the original code works by importing the other dataset
data_original, info_original = tfds.load('glue/mrpc', data_dir=data_dir, with_info=True)
info_original
info_original.features
print(type(data_original['train']))
print(type(train_data))
print(data_original['train'])
print(train_data)
```
### 2.5. Statistical Analysis
```
len_element = []
longest_sequences = []
for index, element in enumerate(train_data.as_numpy_iterator()):
len_element.append(len(element[0]))
if len(element[0])>7500:
longest_sequences.append(element[0])
continue
else:
continue
len(longest_sequences)
import statistics as st
print("Longest sequence: {:7}".format(max(len_element)))
print("Shortest sequence: {:7}".format(min(len_element)))
print("Average: {:10.{prec}f}".format(st.mean(len_element), prec=2))
print("Standard deviation: {:10.{prec}f}".format(st.stdev(len_element), prec=2))
# plot the distribution of the length of the sequences
import matplotlib.pyplot as plt
_ = plt.hist(len_element, bins='auto')
plt.title("Histogram of the sequence length")
plt.show()
```
Given the relatively large mean of the sequence length, choosing a max_length of 512 may not be appropriate and should be increased to 1024. This will increase the computation time, though.
*Is it an option to choose a relatively small max_length and still get good results?*
*Kick out outliers?*
```
# what do those really long sequences look like?
longest_sequences[1]
```
This little exploration shows that the longest sequences are simply really long summaries of the plot coupled with a recommendation of whether or not to watch it. We should experiment with just taking the beginning of the sequence and the end, or even better: snip out parts in the middle since the beginning and the and are somewhat summaries of the sentiment.
| true |
code
| 0.52208 | null | null | null | null |
|
Trees and diversity estimates for molecular markers. Env from 62_phylo_reduced.
After first run and evaluation, manually resolve problems with selected sequences (on plate fasta level):
- VBS00055 (aconitus) its2 trimmed 3' - weak signal, multipeaks
- VBS00021,VBS00022,VBS00023 (barbirostris) its2 re-trimmed to the same length - sequences too long, weak signal after 1000 bases
- VBS00024 (barbirostris) its2 removed - weak signal, multipeaks
- marshalli mis-identifications - remove all samples from analysis
- VBS00059, VBS00061 (minimus) coi trimmed 5' - retained variation is true
- VBS00145 (sundaicus) is rampae according to its2 and ampseq - removed from analysis
- vin.M0004, vin.B0009, vin.M0009 its2 removed - problem with amplification after ca 60 bases
After finalisation of sequences, need to re-run BLAST and 1_blast.ipynb
Higher than expexted variation left without changes:
- carnevalei its2 - legitimately highly variable
- coustani, tenebrosus, ziemannii - highly variable unresolved group with two branches according to all markers
- hyrcanus - two distinct lineages - VBS00082, VBS00083 and VBS00085,VBS00086 according to all markers
- nili - two distinct lineages - nil.237, nil.239 and nil.233, nil.236, nil.238 according to all markers
- paludis: Apal-81 within coustani group, while Apal-257 is an outgroup according to all markers
- VBS00113 (rampae) coi groups with maculatus (closest relative), while its2 and ampseq group it with rampae
- sundaicus coi - legitimately highly variable
- theileri its - multipeaks at the middle of all samples result in several bases mis-called, do not change
- vagus coi - legitimately highly variable
Other:
- brohieri, hancocki, demeilloni - single group of closely related individuals according to all markers
```
import os
from Bio import AlignIO, SeqIO
from Bio.Phylo.TreeConstruction import DistanceCalculator
from collections import defaultdict
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import ete3
# in
WD = '../../../data/phylo_ampl_dada2/coi_its2/work/'
PRD = '../../../data/phylo_ampl_dada2/phylo_reduced'
OD = 'data'
META = os.path.join(OD, 'species_predictions.csv')
FA = os.path.join(WD, 'seqman_fa/plate{}.fas')
AMPL_ALN = os.path.join(PRD,'aln_all/{}.fa')
AMPL_HAP = os.path.join(PRD,'0_haplotypes.csv')
TAXONOMY = '../7_species_id/data/0_taxonomy.csv'
# out
ALN = os.path.join(WD, 'phylo/{}.aln.fas')
TREE = os.path.join(OD, '{}.nwk')
TREE_FIG = os.path.join(OD, '{}.pdf')
TREE_FIG_UNFILTERED = os.path.join(WD, 'phylo/{}.all.pdf')
DIVERSITY = os.path.join(OD, 'diversity.csv')
! mkdir -p {os.path.join(WD, 'phylo')}
! mkdir -p {OD}
# mapping of markers used and plates
MARKER_PLATES = {
'coi':[1,2],
'its2':[3,4]
}
# samples with conflicting phylogenetic positions - to be removed from diversity estimates
CONFLICT_SAMPLES = ['Amar-3-1','Amar-42','Amar-5','VBS00145']
# minimum number of samples per species to be used in diversity plotting
MIN_SAMPLES_DIV = 2
# species labels containing multiple - hard filtering
MULTISP_LABELS = ['brohieri', 'hancocki', 'demeilloni',
'coustani','tenebrosus','ziemanni',
'hyrcanus','nili','paludis']
# species that are overly diverged - softer filtering
BAD_SPP = ['hyrcanus','nili','paludis']
MULTISP_LABELS = ['Anopheles_'+l for l in MULTISP_LABELS]
BAD_SPP = ['Anopheles_'+l for l in BAD_SPP]
```
## Metadata
```
meta = pd.read_csv(META, index_col=0)
meta.shape
# metadata table for use in diversity estimates - only include ampseq'd and non-conflicting samples
# remove non-ampseq'd
ampseq_meta = meta[~meta.ampseq_species.isna()]
# remove conflicting samples
# ampseq_meta = ampseq_meta[~ampseq_meta.index.isin(CONFLICT_SAMPLES)]
display(ampseq_meta.shape)
ampseq_meta.head(1)
# basic stats
meta[~meta.ampseq_species.isna()].COI_length.mean(), meta[~meta.ampseq_species.isna()].COI_length.std()
```
## Alignment and phylogeny
```
for marker, plates in MARKER_PLATES.items():
! cat {FA.format(plates[0])} {FA.format(plates[1])} | mafft - > {ALN.format(marker)}
for marker in MARKER_PLATES:
! fasttree -nt {ALN.format(marker)} > {TREE.format(marker)}
# draw trees
for marker in MARKER_PLATES:
t = ete3.Tree(TREE.format(marker))
# set outgroup to implexus
outgroups = []
for leaf in t:
if leaf.name.startswith('imp'):# or leaf.name.startswith('cou'):
outgroups.append(leaf.name)
# print(outgroups)
if len(outgroups) > 1:
t.set_outgroup(t.get_common_ancestor(*outgroups))
elif len(outgroups) == 1:
t.set_outgroup(outgroups[0])
# style
t.ladderize(direction=1)
ns = ete3.NodeStyle(size=0)
for n in t.traverse():
n.set_style(ns)
t.render(TREE_FIG_UNFILTERED.format(marker));
# remove non-ampseq samples from tree
pruned_taxa = [leaf.name for leaf in t if leaf.name in ampseq_meta[marker.upper() + '_seqid'].to_list()]
print(pruned_taxa)
t.prune(pruned_taxa)
t.render(TREE_FIG.format(marker));
'col.554_D08-ITS2A.ab1' in ampseq_meta.COI_seqid.to_list()
```
## Diversity estimates for Sanger sequencing
```
# variable sites
def distances(aln, seqids):
s_aln = [seq for seq in aln if seq.name in seqids]
s_aln = AlignIO.MultipleSeqAlignment(s_aln)
aln_len = len(s_aln[0].seq)
dist_matrix = DistanceCalculator('identity').get_distance(s_aln)
dists = []
for i, d in enumerate(dist_matrix):
dists.extend(d[:i])
dists = [int(d * aln_len) for d in dists]
return dists
def aln_stats(aln, seqids, verbose=False):
var_sites = 0
aln_len = 0
if len(seqids) == 0:
return var_sites, aln_len
# subset alignment to seqids
s_aln = [seq for seq in aln if seq.name in seqids]
s_aln = AlignIO.MultipleSeqAlignment(s_aln)
# iterate over alignment columns
for i in range(len(s_aln[0].seq)):
chars = s_aln[:,i]
charset = set(chars)
# any aligned bases
if charset != set('-'):
aln_len += 1
# any variable bases
if len(charset - set('-')) > 1:
if verbose:
print(i, chars)
var_sites += 1
return var_sites, aln_len
aln_div = defaultdict(dict)
for marker in MARKER_PLATES:
marker_aln = AlignIO.read(ALN.format(marker), format='fasta')
marker_aln = list(marker_aln)
for species, sp_meta in ampseq_meta.groupby('partner_species'):
# remove conflicting samples
sp_meta = sp_meta[~sp_meta.index.isin(CONFLICT_SAMPLES)]
# subset samples
sp_marker_samples = sp_meta[marker.upper()+'_seqid'].dropna().to_list()
# debug
if species == 'Anopheles_marshallii' and marker=='its2':
print(sp_marker_samples)
print(aln_stats(marker_aln, sp_marker_samples, verbose=True))
# skip small datasets
#if len(sp_marker_samples) < MIN_SAMPLES_DIV:
# continue
v, l = aln_stats(marker_aln, sp_marker_samples)
aln_div[marker + '_len'][species] = l
aln_div[marker + '_var'][species] = v
aln_div[marker + '_nseq'][species] = len(sp_marker_samples)
#aln_div[marker + '_samples'][species] = sp_marker_samples
#aln_div[marker + '_dists'][species] = distances(marker_aln, sp_marker_samples)
aln_div = pd.DataFrame(aln_div)
aln_div.head()
```
## Diversity estimates for ampseq
Use alignments generated for 62_phylo_reduced
```
ampl_haps = pd.read_csv(AMPL_HAP)
ampl_haps.head(1)
ampseq_var = defaultdict(dict)
ampseq_len = defaultdict(dict)
ampseq_nseq = dict()
for species, sp_meta in ampseq_meta.groupby('partner_species'):
# remove conflicting samples
sp_meta = sp_meta[~sp_meta.index.isin(CONFLICT_SAMPLES)]
# subset samples
sp_marker_samples = sp_meta.index.dropna().to_list()
# skip small datasets
#if len(sp_marker_aln) < MIN_SAMPLES_DIV:
# continue
ampseq_nseq[species] = len(sp_marker_samples)
for target in range(62):
target = str(target)
st_uids = ampl_haps.loc[ampl_haps.s_Sample.isin(sp_marker_samples)
& (ampl_haps.target == target),
'combUID'].to_list()
# no sequences - no divergent sites
if len(st_uids) == 0:
ampseq_var[target][species] = np.nan
# estimate divergent sites
else:
taln = AlignIO.read(AMPL_ALN.format(target), format='fasta')
ampseq_var[target][species], ampseq_len[target][species] = aln_stats(taln, st_uids)
ampseq_var = pd.DataFrame(ampseq_var)
ampseq_len = pd.DataFrame(ampseq_len)
ampseq_len.iloc[:3,:3]
comb_div = aln_div.copy()
comb_div['total_ampseq_len'] = ampseq_len.sum(axis=1).astype(int)
comb_div['total_ampseq_var'] = ampseq_var.sum(axis=1).astype(int)
comb_div['total_ampseq_nsamples'] = pd.Series(ampseq_nseq)
comb_div
comb_div.to_csv(DIVERSITY)
```
## Plot diversity
```
taxonomy = pd.read_csv(TAXONOMY, index_col=0)
taxonomy.head(1)
comb_div['series'] = taxonomy['series']
comb_div['subgenus'] = taxonomy['subgenus']
def region(species):
sp_data = ampseq_meta[ampseq_meta.partner_species == species]
if sp_data.index[0].startswith('VBS'):
return 'SE Asia'
elif sp_data.index[0].startswith('A'):
return 'Africa'
return 'Unknown'
comb_div['region'] = comb_div.index.map(region)
fig, axs = plt.subplots(1,2,figsize=(10,5))
for ax, marker in zip(axs, ('coi','its2')):
# exclude compromised species labels and species with insufficient sample size
d = comb_div[~comb_div.index.isin(BAD_SPP) & # harder filter - MULTISP_LABELS
(comb_div.total_ampseq_nsamples >= MIN_SAMPLES_DIV) &
(comb_div[marker+'_nseq'] >= MIN_SAMPLES_DIV)]
print(d[d[marker+'_var'] > 12].index)
sns.scatterplot(x=marker+'_var',y='total_ampseq_var',
hue='region',
size='total_ampseq_nsamples',
style='subgenus',
data=d,
ax=ax)
ax.legend().set_visible(False)
ax.legend(bbox_to_anchor=(1, 0.7), frameon=False);
sns.scatterplot(data=comb_div[~comb_div.index.isin(MULTISP_LABELS)],
x='coi_var',y='its2_var',hue='region',size='total_ampseq_nsamples');
# stats for good species (not multiple species with same label)
comb_div[~comb_div.index.isin(BAD_SPP) &
(comb_div.total_ampseq_nsamples >= MIN_SAMPLES_DIV)] \
.describe()
```
| true |
code
| 0.292381 | null | null | null | null |
|
<!-- dom:TITLE: PHY321: Two-body problems, gravitational forces, scattering and begin Lagrangian formalism -->
# PHY321: Two-body problems, gravitational forces, scattering and begin Lagrangian formalism
<!-- dom:AUTHOR: [Morten Hjorth-Jensen](http://mhjgit.github.io/info/doc/web/) at Department of Physics and Astronomy and Facility for Rare Ion Beams (FRIB), Michigan State University, USA & Department of Physics, University of Oslo, Norway -->
<!-- Author: -->
**[Morten Hjorth-Jensen](http://mhjgit.github.io/info/doc/web/)**, Department of Physics and Astronomy and Facility for Rare Ion Beams (FRIB), Michigan State University, USA and Department of Physics, University of Oslo, Norway
Date: **Mar 29, 2021**
Copyright 1999-2021, [Morten Hjorth-Jensen](http://mhjgit.github.io/info/doc/web/). Released under CC Attribution-NonCommercial 4.0 license
## Aims and Overarching Motivation
### Monday
1. Physical interpretation of various orbit types and summary gravitational forces, examples on whiteboard and handwritten notes
2. Start discussion two-body scattering
**Reading suggestion**: Taylor chapter 8 and sections 14.1-14.2 and Lecture notes
### Wednesday
1. Two-body scattering
**Reading suggestion**: Taylor and sections 14.3-14.6
### Friday
1. Lagrangian formalism
**Reading suggestion**: Taylor Sections 6.1-6.2
### Code example with gravitional force
The code example here is meant to illustrate how we can make a plot of the final orbit. We solve the equations in polar coordinates (the example here uses the minimum of the potential as initial value) and then we transform back to cartesian coordinates and plot $x$ versus $y$. We see that we get a perfect circle when we place ourselves at the minimum of the potential energy, as expected.
```
%matplotlib inline
# Common imports
import numpy as np
import pandas as pd
from math import *
import matplotlib.pyplot as plt
# Simple Gravitational Force -alpha/r
DeltaT = 0.01
#set up arrays
tfinal = 8.0
n = ceil(tfinal/DeltaT)
# set up arrays for t, v and r
t = np.zeros(n)
v = np.zeros(n)
r = np.zeros(n)
phi = np.zeros(n)
x = np.zeros(n)
y = np.zeros(n)
# Constants of the model, setting all variables to one for simplicity
alpha = 1.0
AngMom = 1.0 # The angular momentum
m = 1.0 # scale mass to one
c1 = AngMom*AngMom/(m*m)
c2 = AngMom*AngMom/m
rmin = (AngMom*AngMom/m/alpha)
# Initial conditions, place yourself at the potential min
r0 = rmin
v0 = 0.0 # starts at rest
r[0] = r0
v[0] = v0
phi[0] = 0.0
# Start integrating using the Velocity-Verlet method
for i in range(n-1):
# Set up acceleration
a = -alpha/(r[i]**2)+c1/(r[i]**3)
# update velocity, time and position using the Velocity-Verlet method
r[i+1] = r[i] + DeltaT*v[i]+0.5*(DeltaT**2)*a
anew = -alpha/(r[i+1]**2)+c1/(r[i+1]**3)
v[i+1] = v[i] + 0.5*DeltaT*(a+anew)
t[i+1] = t[i] + DeltaT
phi[i+1] = t[i+1]*c2/(r0**2)
# Find cartesian coordinates for easy plot
x = r*np.cos(phi)
y = r*np.sin(phi)
fig, ax = plt.subplots(3,1)
ax[0].set_xlabel('time')
ax[0].set_ylabel('radius')
ax[0].plot(t,r)
ax[1].set_xlabel('time')
ax[1].set_ylabel('Angle $\cos{\phi}$')
ax[1].plot(t,np.cos(phi))
ax[2].set_ylabel('y')
ax[2].set_xlabel('x')
ax[2].plot(x,y)
#save_fig("Phasespace")
plt.show()
```
## Changing initial conditions
Try to change the initial value for $r$ and see what kind of orbits you get.
In order to test different energies, it can be useful to look at the plot of the effective potential discussed above.
However, for orbits different from a circle the above code would need modifications in order to allow us to display say an ellipse. For the latter, it is much easier to run our code in cartesian coordinates, as done here. In this code we test also energy conservation and see that it is conserved to numerical precision. The code here is a simple extension of the code we developed for homework 4.
```
%matplotlib inline
# Common imports
import numpy as np
import pandas as pd
from math import *
import matplotlib.pyplot as plt
DeltaT = 0.01
#set up arrays
tfinal = 10.0
n = ceil(tfinal/DeltaT)
# set up arrays
t = np.zeros(n)
v = np.zeros((n,2))
r = np.zeros((n,2))
E = np.zeros(n)
# Constants of the model
m = 1.0 # mass, you can change these
alpha = 1.0
# Initial conditions as compact 2-dimensional arrays
x0 = 0.5; y0= 0.
r0 = np.array([x0,y0])
v0 = np.array([0.0,1.0])
r[0] = r0
v[0] = v0
rabs = sqrt(sum(r[0]*r[0]))
E[0] = 0.5*m*(v[0,0]**2+v[0,1]**2)-alpha/rabs
# Start integrating using the Velocity-Verlet method
for i in range(n-1):
# Set up the acceleration
rabs = sqrt(sum(r[i]*r[i]))
a = -alpha*r[i]/(rabs**3)
# update velocity, time and position using the Velocity-Verlet method
r[i+1] = r[i] + DeltaT*v[i]+0.5*(DeltaT**2)*a
rabs = sqrt(sum(r[i+1]*r[i+1]))
anew = -alpha*r[i+1]/(rabs**3)
v[i+1] = v[i] + 0.5*DeltaT*(a+anew)
E[i+1] = 0.5*m*(v[i+1,0]**2+v[i+1,1]**2)-alpha/rabs
t[i+1] = t[i] + DeltaT
# Plot position as function of time
fig, ax = plt.subplots(3,1)
ax[0].set_ylabel('y')
ax[0].set_xlabel('x')
ax[0].plot(r[:,0],r[:,1])
ax[1].set_xlabel('time')
ax[1].set_ylabel('y position')
ax[1].plot(t,r[:,0])
ax[2].set_xlabel('time')
ax[2].set_ylabel('y position')
ax[2].plot(t,r[:,1])
fig.tight_layout()
#save_fig("2DimGravity")
plt.show()
print(E)
```
## Scattering and Cross Sections
Scattering experiments don't measure entire trajectories. For elastic
collisions, they measure the distribution of final scattering angles
at best. Most experiments use targets thin enough so that the number
of scatterings is typically zero or one. The cross section, $\sigma$,
describes the cross-sectional area for particles to scatter with an
individual target atom or nucleus. Cross section measurements form the
basis for MANY fields of physics. BThe cross section, and the
differential cross section, encapsulates everything measurable for a
collision where all that is measured is the final state, e.g. the
outgoing particle had momentum $\boldsymbol{p}_f$. y studying cross sections,
one can infer information about the potential interaction between the
two particles. Inferring, or constraining, the potential from the
cross section is a classic {\it inverse} problem. Collisions are
either elastic or inelastic. Elastic collisions are those for which
the two bodies are in the same internal state before and after the
collision. If the collision excites one of the participants into a
higher state, or transforms the particles into different species, or
creates additional particles, the collision is inelastic. Here, we
consider only elastic collisions.
## Scattering: Coulomb forces
For Coulomb forces, the cross section is infinite because the range of
the Coulomb force is infinite, but for interactions such as the strong
interaction in nuclear or particle physics, there is no long-range
force and cross-sections are finite. Even for Coulomb forces, the part
of the cross section that corresponds to a specific scattering angle,
$d\sigma/d\Omega$, which is a function of the scattering angle
$\theta_s$ is still finite.
If a particle travels through a thin target, the chance the particle
scatters is $P_{\rm scatt}=\sigma dN/dA$, where $dN/dA$ is the number
of scattering centers per area the particle encounters. If the density
of the target is $\rho$ particles per volume, and if the thickness of
the target is $t$, the areal density (number of target scatterers per
area) is $dN/dA=\rho t$. Because one wishes to quantify the collisions
independently of the target, experimentalists measure scattering
probabilities, then divide by the areal density to obtain
cross-sections,
$$
\begin{eqnarray}
\sigma=\frac{P_{\rm scatt}}{dN/dA}.
\end{eqnarray}
$$
## Scattering, more details
Instead of merely stating that a particle collided, one can measure
the probability the particle scattered by a given angle. The
scattering angle $\theta_s$ is defined so that at zero the particle is
unscattered and at $\theta_s=\pi$ the particle is scattered directly
backward. Scattering angles are often described in the center-of-mass
frame, but that is a detail we will neglect for this first discussion,
where we will consider the scattering of particles moving classically
under the influence of fixed potentials $U(\boldsymbol{r})$. Because the
distribution of scattering angles can be measured, one expresses the
differential cross section,
<!-- Equation labels as ordinary links -->
<div id="_auto1"></div>
$$
\begin{equation}
\frac{d^2\sigma}{d\cos\theta_s~d\phi}.
\label{_auto1} \tag{1}
\end{equation}
$$
Usually, the literature expresses differential cross sections as
<!-- Equation labels as ordinary links -->
<div id="_auto2"></div>
$$
\begin{equation}
d\sigma/d\Omega=\frac{d\sigma}{d\cos\theta d\phi}=\frac{1}{2\pi}\frac{d\sigma}{d\cos\theta},
\label{_auto2} \tag{2}
\end{equation}
$$
where the last equivalency is true when the scattering does not depend
on the azimuthal angle $\phi$, as is the case for spherically
symmetric potentials.
The differential solid angle $d\Omega$ can be thought of as the area
subtended by a measurement, $dA_d$, divided by $r^2$, where $r$ is the
distance to the detector,
$$
\begin{eqnarray}
dA_d=r^2 d\Omega.
\end{eqnarray}
$$
With this definition $d\sigma/d\Omega$ is independent of the distance
from which one places the detector, or the size of the detector (as
long as it is small).
## Differential scattering cross sections
Differential scattering cross sections are calculated by assuming a
random distribution of impact parameters $b$. These represent the
distance in the $xy$ plane for particles moving in the $z$ direction
relative to the scattering center. An impact parameter $b=0$ refers to
being aimed directly at the target's center. The impact parameter
describes the transverse distance from the $z=0$ axis for the
trajectory when it is still far away from the scattering center and
has not yet passed it. The differential cross section can be expressed
in terms of the impact parameter,
<!-- Equation labels as ordinary links -->
<div id="_auto3"></div>
$$
\begin{equation}
d\sigma=2\pi bdb,
\label{_auto3} \tag{3}
\end{equation}
$$
which is the area of a thin ring of radius $b$ and thickness $db$. In
classical physics, one can calculate the trajectory given the incoming
kinetic energy $E$ and the impact parameter if one knows the mass and
potential.
## More on Differential Cross Sections
From the trajectory, one then finds the scattering angle
$\theta_s(b)$. The differential cross section is then
<!-- Equation labels as ordinary links -->
<div id="_auto4"></div>
$$
\begin{equation}
\frac{d\sigma}{d\Omega}=\frac{1}{2\pi}\frac{d\sigma}{d\cos\theta_s}=b\frac{db}{d\cos\theta_s}=\frac{b}{(d/db)\cos\theta_s(b)}.
\label{_auto4} \tag{4}
\end{equation}
$$
Typically, one would calculate $\cos\theta_s$ and $(d/db)\cos\theta_s$
as functions of $b$. This is sufficient to plot the differential cross
section as a function of $\theta_s$.
The total cross section is
<!-- Equation labels as ordinary links -->
<div id="_auto5"></div>
$$
\begin{equation}
\sigma_{\rm tot}=\int d\Omega\frac{d\sigma}{d\Omega}=2\pi\int d\cos\theta_s~\frac{d\sigma}{d\Omega}.
\label{_auto5} \tag{5}
\end{equation}
$$
Even if the total cross section is infinite, e.g. Coulomb forces, one
can still have a finite differential cross section as we will see
later on.
## Rutherford Scattering
This refers to the calculation of $d\sigma/d\Omega$ due to an inverse
square force, $F_{12}=\pm\alpha/r^2$ for repulsive/attractive
interaction. Rutherford compared the scattering of $\alpha$ particles
($^4$He nuclei) off of a nucleus and found the scattering angle at
which the formula began to fail. This corresponded to the impact
parameter for which the trajectories would strike the nucleus. This
provided the first measure of the size of the atomic nucleus. At the
time, the distribution of the positive charge (the protons) was
considered to be just as spread out amongst the atomic volume as the
electrons. After Rutherford's experiment, it was clear that the radius
of the nucleus tended to be roughly 4 orders of magnitude smaller than
that of the atom, which is less than the size of a football relative
to Spartan Stadium.
## Rutherford Scattering, more details
In order to calculate differential cross section, we must find how the
impact parameter is related to the scattering angle. This requires
analysis of the trajectory. We consider our previous expression for
the trajectory where we derived the elliptic form for the trajectory,
For that case we considered an attractive
force with the particle's energy being negative, i.e. it was
bound. However, the same form will work for positive energy, and
repulsive forces can be considered by simple flipping the sign of
$\alpha$. For positive energies, the trajectories will be hyperbolas,
rather than ellipses, with the asymptotes of the trajectories
representing the directions of the incoming and outgoing
tracks.
## Rutherford Scattering, final trajectories
We have
<!-- Equation labels as ordinary links -->
<div id="eq:ruthtraj"></div>
$$
\begin{equation}\label{eq:ruthtraj} \tag{6}
r=\frac{1}{\frac{m\alpha}{L^2}+A\cos\theta}.
\end{equation}
$$
Once $A$ is large enough, which will happen when the energy is
positive, the denominator will become negative for a range of
$\theta$. This is because the scattered particle will never reach
certain angles. The asymptotic angles $\theta'$ are those for which
the denominator goes to zero,
<!-- Equation labels as ordinary links -->
<div id="_auto6"></div>
$$
\begin{equation}
\cos\theta'=-\frac{m\alpha}{AL^2}.
\label{_auto6} \tag{7}
\end{equation}
$$
## Rutherford Scattering, Closest Approach
The trajectory's point of closest approach is at $\theta=0$ and the
two angles $\theta'$, which have this value of $\cos\theta'$, are the
angles of the incoming and outgoing particles. From
Fig (**to come**), one can see that the scattering angle
$\theta_s$ is given by,
<!-- Equation labels as ordinary links -->
<div id="eq:sthetover2"></div>
$$
\begin{eqnarray}
\label{eq:sthetover2} \tag{8}
2\theta'-\pi&=&\theta_s,~~~\theta'=\frac{\pi}{2}+\frac{\theta_s}{2},\\
\nonumber
\sin(\theta_s/2)&=&-\cos\theta'\\
\nonumber
&=&\frac{m\alpha}{AL^2}.
\end{eqnarray}
$$
Now that we have $\theta_s$ in terms of $m,\alpha,L$ and $A$, we wish
to re-express $L$ and $A$ in terms of the impact parameter $b$ and the
energy $E$. This will set us up to calculate the differential cross
section, which requires knowing $db/d\theta_s$. It is easy to write
the angular momentum as
<!-- Equation labels as ordinary links -->
<div id="_auto7"></div>
$$
\begin{equation}
L^2=p_0^2b^2=2mEb^2.
\label{_auto7} \tag{9}
\end{equation}
$$
## Rutherford Scattering, getting there
Finding $A$ is more complicated. To accomplish this we realize that
the point of closest approach occurs at $\theta=0$, so from
Eq. ([6](#eq:ruthtraj))
<!-- Equation labels as ordinary links -->
<div id="eq:rminofA"></div>
$$
\begin{eqnarray}
\label{eq:rminofA} \tag{10}
\frac{1}{r_{\rm min}}&=&\frac{m\alpha}{L^2}+A,\\
\nonumber
A&=&\frac{1}{r_{\rm min}}-\frac{m\alpha}{L^2}.
\end{eqnarray}
$$
Next, $r_{\rm min}$ can be found in terms of the energy because at the
point of closest approach the kinetic energy is due purely to the
motion perpendicular to $\hat{r}$ and
<!-- Equation labels as ordinary links -->
<div id="_auto8"></div>
$$
\begin{equation}
E=-\frac{\alpha}{r_{\rm min}}+\frac{L^2}{2mr_{\rm min}^2}.
\label{_auto8} \tag{11}
\end{equation}
$$
## Rutherford Scattering, More Manipulations
One can solve the quadratic equation for $1/r_{\rm min}$,
<!-- Equation labels as ordinary links -->
<div id="_auto9"></div>
$$
\begin{equation}
\frac{1}{r_{\rm min}}=\frac{m\alpha}{L^2}+\sqrt{(m\alpha/L^2)^2+2mE/L^2}.
\label{_auto9} \tag{12}
\end{equation}
$$
We can plug the expression for $r_{\rm min}$ into the expression for $A$, Eq. ([10](#eq:rminofA)),
<!-- Equation labels as ordinary links -->
<div id="_auto10"></div>
$$
\begin{equation}
A=\sqrt{(m\alpha/L^2)^2+2mE/L^2}=\sqrt{(\alpha^2/(4E^2b^4)+1/b^2}
\label{_auto10} \tag{13}
\end{equation}
$$
## Rutherford Scattering, final expression
Finally, we insert the expression for $A$ into that for the scattering angle, Eq. ([8](#eq:sthetover2)),
<!-- Equation labels as ordinary links -->
<div id="eq:scattangle"></div>
$$
\begin{eqnarray}
\label{eq:scattangle} \tag{14}
\sin(\theta_s/2)&=&\frac{m\alpha}{AL^2}\\
\nonumber
&=&\frac{a}{\sqrt{a^2+b^2}}, ~~a\equiv \frac{\alpha}{2E}
\end{eqnarray}
$$
## Rutherford Scattering, the Differential Cross Section
The differential cross section can now be found by differentiating the
expression for $\theta_s$ with $b$,
<!-- Equation labels as ordinary links -->
<div id="eq:rutherford"></div>
$$
\begin{eqnarray}
\label{eq:rutherford} \tag{15}
\frac{1}{2}\cos(\theta_s/2)d\theta_s&=&\frac{ab~db}{(a^2+b^2)^{3/2}}=\frac{bdb}{a^2}\sin^3(\theta_s/2),\\
\nonumber
d\sigma&=&2\pi bdb=\frac{\pi a^2}{\sin^3(\theta_s/2)}\cos(\theta_s/2)d\theta_s\\
\nonumber
&=&\frac{\pi a^2}{2\sin^4(\theta_s/2)}\sin\theta_s d\theta_s\\
\nonumber
\frac{d\sigma}{d\cos\theta_s}&=&\frac{\pi a^2}{2\sin^4(\theta_s/2)},\\
\nonumber
\frac{d\sigma}{d\Omega}&=&\frac{a^2}{4\sin^4(\theta_s/2)}.
\end{eqnarray}
$$
where $a= \alpha/2E$. This the Rutherford formula for the differential
cross section. It diverges as $\theta_s\rightarrow 0$ because
scatterings with arbitrarily large impact parameters still scatter to
arbitrarily small scattering angles. The expression for
$d\sigma/d\Omega$ is the same whether the interaction is positive or
negative.
## Rutherford Scattering, Example
Consider a particle of mass $m$ and charge $z$ with kinetic energy $E$
(Let it be the center-of-mass energy) incident on a heavy nucleus of
mass $M$ and charge $Z$ and radius $R$. We want to find the angle at which the
Rutherford scattering formula breaks down.
Let $\alpha=Zze^2/(4\pi\epsilon_0)$. The scattering angle in Eq. ([14](#eq:scattangle)) is
$$
\sin(\theta_s/2)=\frac{a}{\sqrt{a^2+b^2}}, ~~a\equiv \frac{\alpha}{2E}.
$$
The impact parameter $b$ for which the point of closest approach
equals $R$ can be found by using angular momentum conservation,
$$
\begin{eqnarray*}
p_0b&=&b\sqrt{2mE}=Rp_f=R\sqrt{2m(E-\alpha/R)},\\
b&=&R\frac{\sqrt{2m(E-\alpha/R)}}{\sqrt{2mE}}\\
&=&R\sqrt{1-\frac{\alpha}{ER}}.
\end{eqnarray*}
$$
## Rutherford Scattering, Example, wrapping up
Putting these together
$$
\theta_s=2\sin^{-1}\left\{
\frac{a}{\sqrt{a^2+R^2(1-\alpha/(RE))}}
\right\},~~~a=\frac{\alpha}{2E}.
$$
It was from this departure of the experimentally measured
$d\sigma/d\Omega$ from the Rutherford formula that allowed Rutherford
to infer the radius of the gold nucleus, $R$.
## Variational Calculus
The calculus of variations involves
problems where the quantity to be minimized or maximized is an integral.
The usual minimization problem one faces involves taking a function
${\cal L}(x)$, then finding the single value $x$ for which ${\cal L}$
is either a maximum or minimum. In multivariate calculus one also
learns to solve problems where you minimize for multiple variables,
${\cal L}(x_1,x_2,\cdots x_n)$, and finding the points $(x_1\cdots
y_n)$ in an $n$-dimensional space that maximize or minimize the
function. Here, we consider what seems to be a much more ambitious
problem. Imagine you have a function ${\cal L}(x(t),\dot{x}(t),t)$,
and you wish to find the extrema for an infinite number of values of
$x$, i.e. $x$ at each point $t$. The function ${\cal L}$ will not only
depend on $x$ at each point $t$, but also on the slope at each point,
plus an additional dependence on $t$. Note we are NOT finding an
optimum value of $t$, we are finding the set of optimum values of $x$
at each point $t$, or equivalently, finding the function $x(t)$.
## Variational Calculus, introducing the action
One treats the function $x(t)$ as being unknown while minimizing the action
$$
S=\int_{t_1}^{t_2}dt~{\cal L}(x(t),\dot{x}(t),t).
$$
Thus, we are minimizing $S$ with respect to an infinite number of
values of $x(t_i)$ at points $t_i$. As an additional criteria, we will
assume that $x(t_1)$ and $x(t_2)$ are fixed, and that that we will
only consider variations of $x$ between the boundaries. The dependence
on the derivative, $\dot{x}=dx/dt$, is crucial because otherwise the
solution would involve simply finding the one value of $x$ that
minimized ${\cal L}$, and $x(t)$ would equal a constant if there were no
explicit $t$ dependence. Furthermore, $x$ wouldn't need to be
continuous at the boundary.
## Variational Calculus, general Action
In the general case we have an integral of the type
$$
S[q]= \int_{t_1}^{t_2} {\cal L}(q(t),\dot{q}(t),t)dt,
$$
where $S$ is the quantity which is sought minimized or maximized. The
problem is that although ${\cal L}$ is a function of the general variables
$q(t),\dot{q}(t),t$ (note our change of variables), the exact dependence of $q$ on $t$ is not known.
This means again that even though the integral has fixed limits $t_1$
and $t_2$, the path of integration is not known. In our case the unknown
quantities are the positions and general velocities of a given number
of objects and we wish to choose an integration path which makes the
functional $S[q]$ stationary. This means that we want to find minima,
or maxima or saddle points. In physics we search normally for minima.
Our task is therefore to find the minimum of $S[q]$ so that its
variation $\delta S$ is zero subject to specific constraints. The
constraints can be treated via the technique of Lagrangian multipliers
as we will see below.
## Variational Calculus, Optimal Path
We assume the existence of an optimum path, that is a path for which
$S[q]$ is stationary. There are infinitely many such paths. The
difference between two paths $\delta q$ is called the variation of
$q$.
We call the variation $\eta(t)$ and it is scaled by a factor $\alpha$.
The function $\eta(t)$ is arbitrary except for
$$
\eta(t_1)=\eta(t_2)=0,
$$
and we assume that we can model the change in $q$ as
$$
q(t,\alpha) = q(t)+\alpha\eta(t),
$$
and
$$
\delta q = q(t,\alpha) -q(t,0)=\alpha\eta(t).
$$
## Variational Calculus, Condition for an Extreme Value
We choose $q(t,\alpha=0)$ as the unkonwn path that will minimize $S$. The value
$q(t,\alpha\ne 0)$ describes a neighbouring path.
We have
$$
S[q(\alpha)]= \int_{t_1}^{t_2} {\cal L}(q(t,\alpha),\dot{q}(t,\alpha),t)dt.
$$
The condition for an extreme of
$$
S[q(\alpha)]= \int_{t_1}^{t_2} {\cal L}(q(t,\alpha),\dot{q}(t,\alpha),t)dt,
$$
is
$$
\left[\frac{\partial S[q(\alpha)]}{\partial t}\right]_{\alpha=0} =0.
$$
## Variational Calculus. $\alpha$ Dependence
The $\alpha$ dependence is contained in $q(t,\alpha)$ and $\dot{q}(t,\alpha)$ meaning that
$$
\left[\frac{\partial E[q(\alpha)]}{\partial \alpha}\right]=\int_{t_1}^{t_2} \left( \frac{\partial {\cal l}}{\partial q}\frac{\partial q}{\partial \alpha}+\frac{\partial {\cal L}}{\partial \dot{q}}\frac{\partial \dot{q}}{\partial \alpha}\right)dt.
$$
We have defined
$$
\frac{\partial q(x,\alpha)}{\partial \alpha}=\eta(x)
$$
and thereby
$$
\frac{\partial \dot{q}(t,\alpha)}{\partial \alpha}=\frac{d(\eta(t))}{dt}.
$$
## INtegrating by Parts
Using
$$
\frac{\partial q(t,\alpha)}{\partial \alpha}=\eta(t),
$$
and
$$
\frac{\partial \dot{q}(t,\alpha)}{\partial \alpha}=\frac{d(\eta(t))}{dt},
$$
in the integral gives
$$
\left[\frac{\partial S[q(\alpha)]}{\partial \alpha}\right]=\int_{t_1}^{t_2} \left( \frac{\partial {\cal L}}{\partial q}\eta(t)+\frac{\partial {\cal L}}{\partial \dot{q}}\frac{d(\eta(t))}{dt}\right)dt.
$$
Integrating the second term by parts
$$
\int_{t_1}^{t_2} \frac{\partial {\cal L}}{\partial \dot{q}}\frac{d(\eta(t))}{dt}dt =\eta(t)\frac{\partial {\cal L}}{\partial \dot{q}}|_{t_1}^{t_2}-
\int_a^b \eta(t)\frac{d}{dx}\frac{\partial {\cal L}}{\partial \dot{q}}dt,
$$
and since the first term dissappears due to $\eta(a)=\eta(b)=0$, we obtain
$$
\left[\frac{\partial S[q(\alpha)]}{\partial \alpha}\right]=\int_{t_1}^{t_2} \left( \frac{\partial {\cal L}}{\partial q}-\frac{d}{dx}\frac{\partial {\cal L}}{\partial \dot{q}}
\right)\eta(t)dt=0.
$$
## Euler-Lagrange Equations
The latter can be written as
$$
\left[\frac{\partial S[q(\alpha)]}{\partial \alpha}\right]_{\alpha=0}=\int_{t_1}^{t_2} \left( \frac{\partial {\cal L}}{\partial q}-\frac{d}{\
dx}\frac{\partial {\cal L}}{\partial \dot{q}}\right)\delta q(t)dt=\delta S = 0.
$$
The condition for a stationary value is thus a partial differential equation
$$
\frac{\partial {\cal L}}{\partial q}-\frac{d}{dx}\frac{\partial {\cal L}}{\partial \dot{q}}=0,
$$
known as the **Euler-Lagrange** equation.
| true |
code
| 0.639652 | null | null | null | null |
|
ENS'IA - Session 4: Convolutional neural networks
-----
Today, we move on to **Convolutional neural networks (CNN)**!
These are neural networks specialized in image processing.
You will implement a basic CNN architecture and learn some techniques to boost your scores!
Let's load the libraries we will use along with the CIFAR-10 data
```
# We import some useful things for later
import tensorflow as tf
from tensorflow import keras
from keras.datasets import cifar10
import matplotlib.pyplot as plt
import numpy as np
print(tf.__version__)
(x_train, y_train), (x_test, y_test) = cifar10.load_data() # We load the dataset
# Let's visualize an example and its class
plt.imshow(x_train[0])
plt.show()
print(y_train[0])
# Dataset visualization
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
class_count = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_train == y)
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * class_count + y + 1
plt.subplot(samples_per_class, class_count, plt_idx)
plt.imshow(x_train[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()
```
Data preprocessing... Do you remember which ones? :)
```
# TODO... Many things possible!
# For example, you can transform your y using one hot encoding...
```
We now load the required libraries for the CNN
```
from keras.models import Sequential
from keras.layers import Dense, Conv2D, MaxPool2D , Flatten, Dropout
```
We then build our CNN. Here is the order On fabrique ensuite notre CNN.
Here is the order we recommend:
- Convolution, 32 filters, 3x3
- Convolution, 32 filters, 3x3
- MaxPool
- Dropout
<br>
- Convolution, 64 filters, 3x3
- Convolution, 64 filters, 3x3
- MaxPool
- Dropout
<br>
- Convolution, 128 filters, 3x3
- Convolution, 128 filters, 3x3
- MaxPool
- Dropout
<br>
- Flatten
- Dense
- Dropout
- Dense
```
model = Sequential([
# TODO... looks pretty empty to me!
])
model.summary() # To check our model!
```
We have at our disposal a training dataset of 50 000 images, which is... quite limited. Actually, we would like to have an infinity of images for our training and, to achieve this goal, we are going to do some **Data augmentation**.
In other words, we are going to create new images from the ones we have.
For that, Keras has a pretty handy "ImageDataGenerator" (look for its doc online!) which is going to do random modifications on the images we feed the neural network with.
Which modifications could be useful?
```
from keras.preprocessing.image import ImageDataGenerator
datagen = ImageDataGenerator(
width_shift_range=0.1,
height_shift_range=0.1,
fill_mode='nearest',
horizontal_flip=True,
)
```
In order to improve our score as much as possible, we will use a *callback*,
which is going to decrease the learning rate along in our training.
More precisely, if after X epochs the metric we chose (*accuracy*) has not
improved, then we decrease the learning rate.
```
from keras.callbacks import ReduceLROnPlateau
reduce_lr = ReduceLROnPlateau(
monitor = "val_accuracy",
factor=np.sqrt(0.1),
patience=3,
min_lr=0.5e-6)
```
Another callback will allow us to save the best version of our neural network
during the training. After each epoch, if the network improves its score on the validation set, we save it.
```
from keras.callbacks import ModelCheckpoint
checkpointer = ModelCheckpoint(filepath='model.hdf5', verbose=1, save_best_only=True)
```
Let's train the model! For that, we will use the functions we already saw together: *Adam* for the optimization and the loss function for the *cross entropy*.
```
model.compile(
# TODO :)
)
```
Quel batch size? Combien d'epochs? It's up to you! :P
```
history = model.fit(
# TODO
callbacks=[reduce_lr,checkpointer]
)
```
Let's now see in detail how our neural network training process went:
```
def plot_history(history):
"""
Plot the loss & accuracy
"""
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
plot_history(history)
```
Now that the training is done, we will load the saved model!
```
model.load_weights('model.hdf5')
```
You can now evaluate your model on the test set
```
model.evaluate(x_test, y_test)
```
To go further...
-----
Finished way too early?
Take this opportunity to discover https://keras.io/applications/!
You will find pre-trained and pre-built models that are very powerful and applicable to different tasks. Have fun!
To go even further...
-----
By now, you should have understood how convolution works and should have learned a few techniques to boost your score!
You should now be able to start working on bigger and more complex data sets!
We invite you to go to kaggle (www.kaggle.com) where you can find many datasets on which it is possible to work and to observe the work of other people on these data. It's really good for learning and it's perfect if you want to deepen your knowledge!
| true |
code
| 0.612715 | null | null | null | null |
|
# Kili Tutorial: How to leverage Counterfactually augmented data to have a more robust model
This recipe is inspired by the paper *Learning the Difference that Makes a Difference with Counterfactually-Augmented Data*, that you can find here on [arXiv](https://arxiv.org/abs/1909.12434)
In this study, the authors point out the difficulty for Machine Learning models to generalize the classification rules learned, because their decision rules, described as 'spurious patterns', often miss the key elements that affects most the class of a text. They thus decided to delete what can be considered as a confusion factor, by changing the label of an asset at the same time as changing the minimum amount of words so those **key-words** would be much easier for the model to spot.
We'll see in this tutorial :
1. How to create a project in Kili, both for [IMDB](##Data-Augmentation-on-IMDB-dataset) and [SNLI](##Data-Augmentation-on-SNLI-dataset) datasets, to reproduce such a data-augmentation task, in order to improve our model, and decrease its variance when used in production with unseen data.
2. We'll also try to [reproduce the results of the paper](##Reproducing-the-results), using similar models, to show how such a technique can be of key interest while working on a text-classification task.
We'll use the data of the study, both IMDB and Stanford NLI, publicly available [here](https://github.com/acmi-lab/counterfactually-augmented-data).
Additionally, for an overview of Kili, visit the [website](https://kili-technology.com), you can also check out the Kili [documentation](https://cloud.kili-technology.com/docs), or some other recipes.
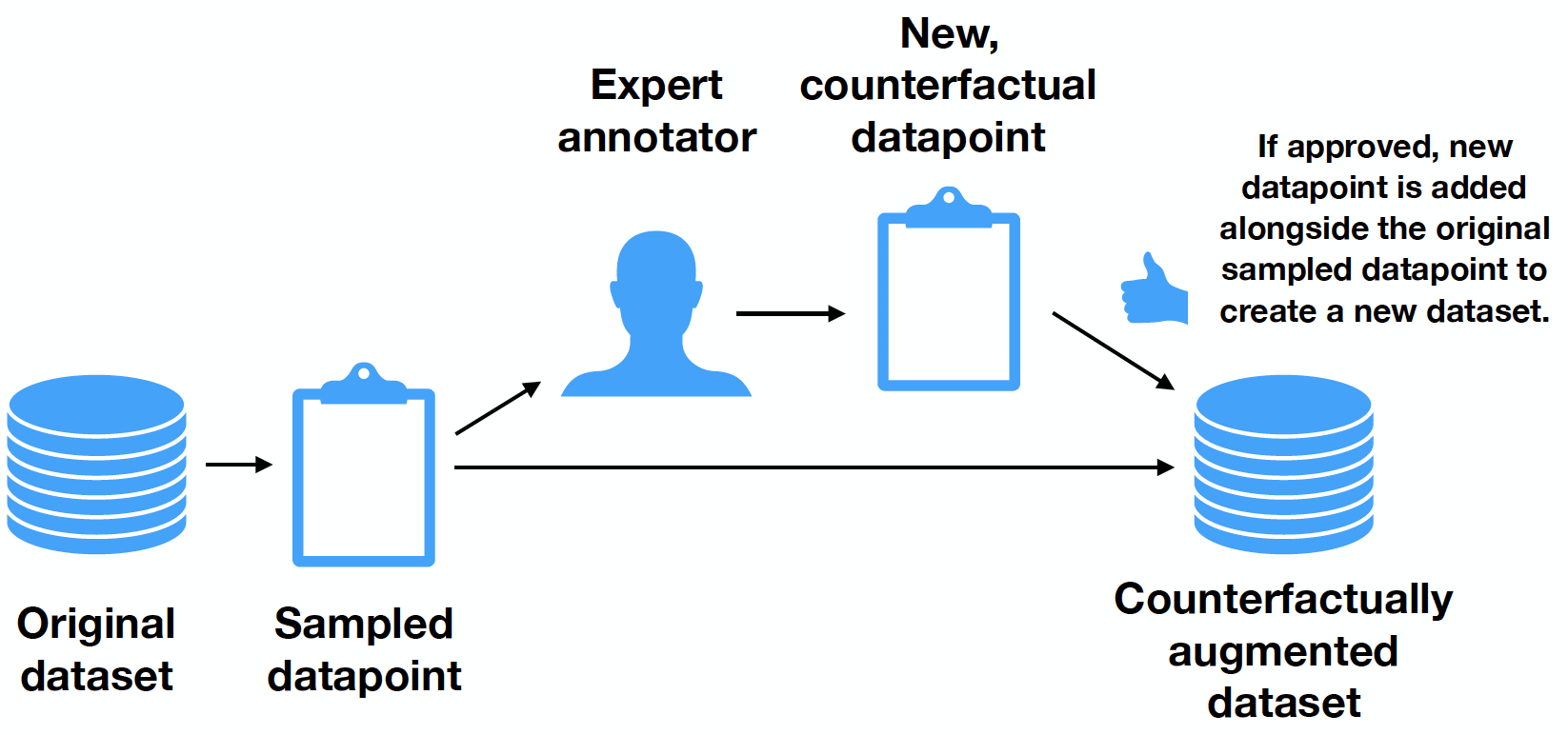
```
# Authentication
import os
# !pip install kili # uncomment if you don't have kili installed already
from kili.client import Kili
api_key = os.getenv('KILI_USER_API_KEY')
api_endpoint = os.getenv('KILI_API_ENDPOINT')
# If you use Kili SaaS, use the url 'https://cloud.kili-technology.com/api/label/v2/graphql'
kili = Kili(api_key=api_key, api_endpoint=api_endpoint)
user_id = kili.auth.user_id
```
## Data Augmentation on IMDB dataset
The data consists in reviews of films, that are classified as positives or negatives. State-of-the-art models performance is often measured against this dataset, making it a reference.
This is how our task would look like on Kili, into 2 different projects for each task, from Positive to Negative or Negative to Positive.
### Creating the projects
```
taskname = "NEW_REVIEW"
project_imdb_negative_to_positive = {
'title': 'Counterfactual data-augmentation - Negative to Positive',
'description': 'IMDB Sentiment Analysis',
'instructions': 'https://docs.google.com/document/d/1zhNaQrncBKc3aPKcnNa_mNpXlria28Ij7bfgUvJbyfw/edit?usp=sharing',
'input_type': 'TEXT',
'json_interface':{
"filetype": "TEXT",
"jobRendererWidth": 0.5,
"jobs": {
taskname : {
"mlTask": "TRANSCRIPTION",
"content": {
"input": None
},
"required": 1,
"isChild": False,
"instruction": "Write here the new review modified to be POSITIVE. Please refer to the instructions above before starting"
}
}
}
}
project_imdb_positive_to_negative = {
'title': 'Counterfactual data-augmentation - Positive to Negative',
'description': 'IMDB Sentiment Analysis',
'instructions': 'https://docs.google.com/document/d/1zhNaQrncBKc3aPKcnNa_mNpXlria28Ij7bfgUvJbyfw/edit?usp=sharing',
'input_type': 'TEXT',
'json_interface':{
"jobRendererWidth": 0.5,
"jobs": {
taskname : {
"mlTask": "TRANSCRIPTION",
"content": {
"input": None
},
"required": 1,
"isChild": False,
"instruction": "Write here the new review modified to be NEGATIVE. Please refer to the instructions above before starting"
}
}
}
}
for project_imdb in [project_imdb_positive_to_negative,project_imdb_negative_to_positive] :
project_imdb['id'] = kili.create_project(title=project_imdb['title'],
instructions=project_imdb['instructions'],
description=project_imdb['description'],
input_type=project_imdb['input_type'],
json_interface=project_imdb['json_interface'])['id']
```
We'll just create some useful functions for an improved readability :
```
def create_assets(dataframe, intro, objective, instructions, truth_label, target_label) :
return((intro + dataframe[truth_label] + objective + dataframe[target_label] + instructions + dataframe['Text']).tolist())
def create_json_responses(taskname,df,field="Text") :
return( [{taskname: { "text": df[field].iloc[k] }
} for k in range(df.shape[0]) ])
```
### Importing the data into Kili
```
import pandas as pd
datasets = ['dev','train','test']
for dataset in datasets :
url = f'https://raw.githubusercontent.com/acmi-lab/counterfactually-augmented-data/master/sentiment/combined/paired/{dataset}_paired.tsv'
df = pd.read_csv(url, error_bad_lines=False, sep='\t')
df = df[df.index%2 == 0] # keep only the original reviews as assets
for review_type,project_imdb in zip(['Positive','Negative'],[project_imdb_positive_to_negative,project_imdb_negative_to_positive]) :
dataframe = df[df['Sentiment']==review_type]
reviews_to_import = dataframe['Text'].tolist()
external_id_array = ('IMDB ' + review_type +' review ' + dataset + dataframe['batch_id'].astype('str')).tolist()
kili.append_many_to_dataset(
project_id=project_imdb['id'],
content_array=reviews_to_import,
external_id_array=external_id_array)
```
### Importing the labels into Kili
We will fill-in with the results of the study, as if they were predictions. In a real annotation project, we could fill in with the sentences as well so the labeler just has to write the changes.
```
model_name = 'results-arxiv:1909.12434'
for dataset in datasets :
url = f'https://raw.githubusercontent.com/acmi-lab/counterfactually-augmented-data/master/sentiment/combined/paired/{dataset}_paired.tsv'
df = pd.read_csv(url, error_bad_lines=False, sep='\t')
df = df[df.index%2 == 1] # keep only the modified reviews as predictions
for review_type,project_imdb in zip(['Positive','Negative'],[project_imdb_positive_to_negative,project_imdb_negative_to_positive]) :
dataframe = df[df['Sentiment']!=review_type]
external_id_array = ('IMDB ' + review_type +' review ' + dataset + dataframe['batch_id'].astype('str')).tolist()
json_response_array = create_json_responses(taskname,dataframe)
kili.create_predictions(project_id=project_imdb['id'],
external_id_array=external_id_array,
model_name_array=[model_name]*len(external_id_array),
json_response_array=json_response_array)
```
This is how our interface looks in the end, allowing to quickly perform the task at hand

## Data Augmentation on SNLI dataset
The data consists in a 3-class dataset, where, provided with two phrases, a premise and an hypothesis, the machine-learning task is to find the correct relation between those two sentences, that can be either entailment, contradiction or neutral.
Here is an example of a premise, and three sentences that could be the hypothesis for the three categories :

This is how our task would look like on Kili, this time keeping it as a single project. To do so, we strongly remind the instructions at each labeler.
### Creating the project
```
taskname = "SENTENCE_MODIFIED"
project_snli={
'title': 'Counterfactual data-augmentation NLI',
'description': 'Stanford Natural language Inference',
'instructions': '',
'input_type': 'TEXT',
'json_interface':{
"jobRendererWidth": 0.5,
"jobs": {
taskname: {
"mlTask": "TRANSCRIPTION",
"content": {
"input": None
},
"required": 1,
"isChild": False,
"instruction": "Write here the modified sentence. Please refer to the instructions above before starting"
}
}
}
}
project_snli['id'] = kili.create_project(title=project_snli['title'],
instructions=project_snli['instructions'],
description=project_snli['description'],
input_type=project_snli['input_type'],
json_interface=project_snli['json_interface'])['id']
print(f'Created project {project_snli["id"]}')
```
Again, we'll factorize our code a little, to merge datasets and differentiate properly all the cases of sentences :
```
def merge_datasets(dataset, sentence_modified) :
url_original = f'https://raw.githubusercontent.com/acmi-lab/counterfactually-augmented-data/master/NLI/original/{dataset}.tsv'
url_revised = f'https://raw.githubusercontent.com/acmi-lab/counterfactually-augmented-data/master/NLI/revised_{sentence_modified}/{dataset}.tsv'
df_original = pd.read_csv(url_original, error_bad_lines=False, sep='\t')
df_original = df_original[df_original.duplicated(keep='first')== False]
df_original['id'] = df_original.index.astype(str)
df_revised = pd.read_csv(url_revised, error_bad_lines=False, sep='\t')
axis_merge = 'sentence2' if sentence_modified=='premise' else 'sentence1'
# keep only one label per set of sentences
df_revised = df_revised[df_revised[[axis_merge,'gold_label']].duplicated(keep='first')== False]
df_merged = df_original.merge(df_revised, how='inner', left_on=axis_merge, right_on=axis_merge)
if sentence_modified == 'premise' :
df_merged['Text'] = df_merged['sentence1_x'] + '\nSENTENCE 2 :\n' + df_merged['sentence2']
instructions = " relation, by making a small number of changes in the FIRST SENTENCE\
such that the document remains coherent and the new label accurately describes the revised passage :\n\n\n\
SENTENCE 1 :\n"
else :
df_merged['Text'] = df_merged['sentence1'] + '\nSENTENCE 2 :\n' + df_merged['sentence2_x']
instructions = " relation, by making a small number of changes in the SECOND SENTENCE\
such that the document remains coherent and the new label accurately describes the revised passage :\n\n\n\
SENTENCE 1 : \n"
return(df_merged, instructions)
def create_external_ids(dataset,dataframe, sentence_modified):
return(('NLI ' + dataset + ' ' + dataframe['gold_label_x'] + ' to ' + dataframe['gold_label_y'] + ' ' + sentence_modified + ' modified ' + dataframe['id']).tolist())
```
### Importing the data into Kili
We'll add before each set of sentences a small precision of the task for the labeler :
```
datasets = ['dev','train','test']
sentences_modified = ['premise', 'hypothesis']
intro = "Those two sentences' relation is classified as "
objective = " to convert to a "
for dataset in datasets :
for sentence_modified in sentences_modified :
df,instructions = merge_datasets(dataset, sentence_modified)
sentences_to_import = create_assets(df, intro, objective, instructions, 'gold_label_x', 'gold_label_y')
external_id_array = create_external_ids(dataset, df, sentence_modified)
kili.append_many_to_dataset(project_id=project_snli['id'],
content_array=sentences_to_import,
external_id_array=external_id_array)
```
### Importing the labels into Kili
We will fill-in with the results of the study, as if they were predictions.
```
model_name = 'results-arxiv:1909.12434'
for dataset in datasets :
for sentence_modified in sentences_modified :
axis_changed = 'sentence1_y' if sentence_modified=='premise' else 'sentence2_y'
df,instructions = merge_datasets(dataset, sentence_modified)
external_id_array = create_external_ids(dataset, df, sentence_modified)
json_response_array = create_json_responses(taskname,df,axis_changed)
kili.create_predictions(project_id=project_snli['id'],
external_id_array=external_id_array,
model_name_array=[model_name]*len(external_id_array),
json_response_array=json_response_array)
```


## Conclusion
In this tutorial, we learned how Kili can be a great help in your data augmentation task, as it allows to set a simple and easy to use interface, with proper instructions for your task.
For the study, the quality of the labeling was a key feature in this complicated task, what Kili allows very simply. To monitor the quality of the results, we could set-up a consensus on a part or all of the annotations, or even keep a part of the dataset as ground truth to measure the performance of every labeler.
For an overview of Kili, visit [kili-technology.com](https://kili-technology.com). You can also check out [Kili documentation](https://cloud.kili-technology.com/docs).
| true |
code
| 0.51501 | null | null | null | null |
|
# Sales Analysis
Source: [https://github.com/d-insight/code-bank.git](https://github.com/d-insight/code-bank.git)
License: [MIT License](https://opensource.org/licenses/MIT). See open source [license](LICENSE) in the Code Bank repository.
-------------
#### Import libraries
```
import os
import pandas as pd
```
#### Merge data from each month into one CSV
```
path = "data"
files = [file for file in os.listdir(path) if not file.startswith('.')] # Ignore hidden files
all_months_data = pd.DataFrame()
for file in files:
current_data = pd.read_csv(path+"/"+file)
all_months_data = pd.concat([all_months_data, current_data])
all_months_data.to_csv(path + "/" + "all_data.csv", index=False)
```
#### Read in updated dataframe
```
all_data = pd.read_csv(path+"/"+"all_data.csv")
all_data.head()
all_data.shape
all_data.dtypes
# If you need to Fix Types (e.g. dates/times)
#time_cols=['Order Date']
#all_data = pd.read_csv(path+"/"+"all_data.csv", parse_dates=time_cols)
```
### Clean up the data!
The first step in this is figuring out what we need to clean. In practice, you find things you need to clean as you perform operations and get errors. Based on the error, you decide how you should go about cleaning the data
#### Drop missing values
```
# Find NAN
nan_df = all_months_data[all_months_data.isna().any(axis=1)] # Filter and get all rows with NaN
display(nan_df.head())
all_data = all_months_data.dropna(how='all')
all_data.head()
```
#### Get rid of unwanted text in order date column
```
all_data = all_data[all_data['Order Date'].str[0:2]!='Or']
```
#### Make columns correct type
```
all_data['Quantity Ordered'] = pd.to_numeric(all_data['Quantity Ordered'])
all_data['Price Each'] = pd.to_numeric(all_data['Price Each'])
```
### Augment data with additional columns
#### Add month column
```
all_data['Month'] = all_data['Order Date'].str[0:2] # Grab the first two chars of a string
all_data['Month'] = all_data['Month'].astype('int32') # Month should not be string
all_data.head()
```
#### Add month column (alternative method)
```
all_data['Month 2'] = pd.to_datetime(all_data['Order Date']).dt.month
all_data.head()
```
#### Add city column
```
def get_city(address):
return address.split(",")[1].strip(" ")
def get_state(address):
return address.split(",")[2].split(" ")[1]
all_data['City'] = all_data['Purchase Address'].apply(lambda x: f"{get_city(x)} ({get_state(x)})")
all_data.head()
```
## Data Exploration!
#### Question 1: What was the best month for sales? How much was earned that month?
```
all_data['Sales'] = all_data['Quantity Ordered'].astype('int') * all_data['Price Each'].astype('float')
all_data.groupby(['Month']).sum()
import matplotlib.pyplot as plt
months = range(1,13)
print(months)
plt.bar(months,all_data.groupby(['Month']).sum()['Sales'])
plt.xticks(months)
plt.ylabel('Sales in USD ($)')
plt.xlabel('Month')
plt.show()
```
#### Question 2: What city sold the most product?
```
all_data.groupby(['City']).sum()
all_data.groupby(['City']).sum()['Sales'].idxmax()
import matplotlib.pyplot as plt
keys = [city for city, df in all_data.groupby(['City'])]
plt.bar(keys,all_data.groupby(['City']).sum()['Sales'])
plt.ylabel('Sales in USD ($)')
plt.xlabel('Month number')
plt.xticks(keys, rotation='vertical', size=8)
plt.show()
```
#### Question 3: What time should we display advertisements to maximize likelihood of customer's buying product?
```
# Add hour column
all_data['Hour'] = pd.to_datetime(all_data['Order Date']).dt.hour
all_data['Minute'] = pd.to_datetime(all_data['Order Date']).dt.minute
all_data['Count'] = 1
all_data.head()
keys = [pair for pair, df in all_data.groupby(['Hour'])]
plt.plot(keys, all_data.groupby(['Hour']).count()['Count'])
plt.xticks(keys)
plt.grid()
plt.show()
# My recommendation is slightly before 11am or 7pm
```
#### Question 4: What products are most often sold together?
```
df.head()
# Keep rows with duplicated OrderID (i.e. items bought together)
df = all_data[all_data['Order ID'].duplicated(keep=False)]
# Create new column "Grouped" with items sold together joined and comma separated
df['Grouped'] = df.groupby('Order ID')['Product'].transform(lambda x: ','.join(x))
df2 = df[['Order ID', 'Grouped']].drop_duplicates()
# Referenced: https://stackoverflow.com/questions/52195887/counting-unique-pairs-of-numbers-into-a-python-dictionary
from itertools import combinations
from collections import Counter
count = Counter()
for row in df2['Grouped']:
row_list = row.split(',')
count.update(Counter(combinations(row_list, 2))) # Can edit 2 (couples) to 3, 4, ..etc.
for key,value in count.most_common(10):
print(key, value)
```
Maybe to get smarter for promotions!
#### Question 5: What product sold the most? Why?
```
product_group = all_data.groupby('Product')
quantity_ordered = product_group.sum()['Quantity Ordered']
print(quantity_ordered)
keys = [pair for pair, df in product_group]
plt.bar(keys, quantity_ordered)
plt.xticks(keys, rotation='vertical', size=8)
plt.show()
prices = all_data.groupby('Product').mean()['Price Each']
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.bar(keys, quantity_ordered, color='g')
ax2.plot(keys, prices, color='b')
ax1.set_xlabel('Product Name')
ax1.set_ylabel('Quantity Ordered', color='g')
ax2.set_ylabel('Price ($)', color='b')
ax1.set_xticklabels(keys, rotation='vertical', size=8)
fig.show()
```
| true |
code
| 0.441492 | null | null | null | null |
|
# Generative Adversarial Networks
This code is based on https://arxiv.org/abs/1406.2661 paper from Ian J. Goodfellow, Jean Pouget-Abadie, et all

```
from google.colab import drive
drive.mount('/content/drive')
# import All prerequisites
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.autograd import Variable
from torchvision.utils import save_image
import numpy as np
# Device configuration
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
ROOT = "/content/drive/My Drive/Colab Notebooks/DSC_UI_GAN/Batch1/W1/"
```
## Dataset
```
batch_size = 100
# MNIST Dataset
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5])])
train_dataset = datasets.MNIST(root='./mnist_data/', train=True, transform=transform, download=True)
# Data Loader (Input Pipeline)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
examples = enumerate(train_loader)
batch_idx, (example_data, example_targets) = next(examples)
## Print example
import matplotlib.pyplot as plt
fig = plt.figure()
for i in range(6):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(example_data[i][0], cmap='gray', interpolation='none')
plt.title("Ground Truth: {}".format(example_targets[i]))
plt.xticks([])
plt.yticks([])
fig
```
## Build Network

resource : https://medium.com/@jonathan_hui/gan-whats-generative-adversarial-networks-and-its-application-f39ed278ef09
```
class Discriminator(nn.Module):
def __init__(self, d_input_dim):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(d_input_dim, 512),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(512, 256),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(256, 1),
nn.Sigmoid(),
)
def forward(self, image):
img_flat = image.view(image.size(0), -1)
validity = self.model(img_flat)
return validity
class Generator(nn.Module):
def __init__(self, g_input_dim, g_output_dim):
super(Generator, self).__init__()
def block(in_feat, out_feat, normalize=True):
layers = [nn.Linear(in_feat, out_feat)]
if normalize:
layers.append(nn.BatchNorm1d(out_feat, 0.8))
layers.append(nn.LeakyReLU(0.2, inplace=True))
return layers
self.model = nn.Sequential(
*block(g_input_dim, 128, normalize=False),
*block(128, 256),
*block(256, 512),
*block(512, 1024),
nn.Linear(1024, g_output_dim),
nn.Tanh())
def forward(self, z):
image = self.model(z)
image = image.view(image.size(0), -1)
return image
# build network
z_dim = 100
mnist_dim = train_dataset.train_data.size(1) * train_dataset.train_data.size(2)
G = Generator(g_input_dim = z_dim, g_output_dim = mnist_dim).to(device)
D = Discriminator(mnist_dim).to(device)
print(G, D)
```
# Train Process
```
# loss
criterion = nn.BCELoss()
# optimizer
lr = 0.0002
b1 = 0.5
b2 = 0.999
G_optimizer = torch.optim.Adam(G.parameters(), lr=lr, betas=(b1, b2))
D_optimizer = torch.optim.Adam(D.parameters(), lr=lr, betas=(b1, b2))
```
### Discriminator Update

### Generator Update
### Before : <br>
 <br>
### Because Generator diminished gradient: <br>
In practice, equation 1 may not provide sufficient gradient for G to learn well. Early in learning, when G is poor,D can reject samples with high confidence because they are clearly different fromthe training data. In this case, log(1−D(G(z))) saturates. Rather than training G to minimize log(1−D(G(z))) we can train G to maximize logD(G(z)). This objective function results in thesame fixed point of the dynamics of G and D but provides much stronger gradients early in learning. (GAN Paper)<br>
 <br>

```
Tensor = torch.cuda.FloatTensor if torch.cuda.is_available() else torch.FloatTensor
epochs = 200
for epoch in range(epochs):
for i, (imgs, _) in enumerate(train_loader):
# Adversarial ground truths
valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train Generator
# -----------------
G_optimizer.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], z_dim))))
# Generate a batch of images
gen_imgs = G(z)
# Loss measures generator's ability to fool the discriminator
# g_loss = criterion(D(gen_imgs), fake) # Normal MinMax
g_loss = criterion(D(gen_imgs), valid) # Non Saturated
g_loss.backward()
G_optimizer.step()
# ---------------------
# Train Discriminator
# ---------------------
D_optimizer.zero_grad()
# Measure discriminator's ability to classify real from generated samples
real_loss = criterion(D(real_imgs), valid)
fake_loss = criterion(D(gen_imgs.detach()), fake)
d_loss = (real_loss + fake_loss) / 2
d_loss.backward()
D_optimizer.step()
if i % 300 == 0:
print(
"[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
% (epoch, epochs, i, len(train_loader), d_loss.item(), g_loss.item()))
if epoch % 5 == 0:
save_image(gen_imgs.view(gen_imgs.size(0), 1, 28, 28), ROOT + "sample/%d.png" % epoch, nrow=5, normalize=True)
torch.save(G, ROOT + 'G.pt')
torch.save(D, ROOT + 'D.pt')
```
| true |
code
| 0.864539 | null | null | null | null |
|
```
%matplotlib inline
"""This simpy model mimics the arrival and treatment of patients in an
emergency department with a limited number of doctors. Patients are generated,
wait for a doc (if none available), take up the doc resources for the time of
consulation, and exit the ED straight after seeing doc. Patients are of three
priorities (1=high to 3=low) and docs will always see higher priority patients
first (though they do not interrupt lower priority patients already being seen).
The model has four classes:
Global_vars: holds global variables
Model: holds model environemnt and th emain model run methods
Patient: each patient is an object instance of this class. This class also holds
a static variable (dictionary) containing all patient objects currently in
the simulation model.
Resources: defines the doc resources required to see/treat patient.
"""
import simpy
import random
import pandas as pd
import matplotlib.pyplot as plt
class Global_vars:
"""Storage of global variables. No object instance created. All times are
in minutes"""
# Simulation run time and warm-up (warm-up is time before audit results are
# collected)
sim_duration = 5000
warm_up = 1000
# Average time between patients arriving
inter_arrival_time = 10
# Number of doctors in ED
number_of_docs = 2
# Time between audits
audit_interval = 100
# Average and standard deviation of time patients spends being treated in ED
# (does not include any queuing time, this si the time a doc is occupied
# with a patient)
appointment_time_mean = 18
appointment_time_sd = 7
# Lists used to store audit results
audit_time = []
audit_patients_in_ED = []
audit_patients_waiting = []
audit_patients_waiting_p1 = []
audit_patients_waiting_p2 = []
audit_patients_waiting_p3 = []
audit_reources_used = []
# Set up dataframes to store results (will be transferred from lists)
patient_queuing_results = pd.DataFrame(
columns=['priority', 'q_time', 'consult_time'])
results = pd.DataFrame()
# Set up counter for number fo aptients entering simulation
patient_count = 0
# Set up running counts of patients waiting (total and by priority)
patients_waiting = 0
patients_waiting_by_priority = [0, 0, 0]
class Model:
"""
Model class contains the following methods:
__init__: constructor for initiating simpy simulation environment.
build_audit_results: At end of model run, transfers results held in lists
into a pandas DataFrame.
chart: At end of model run, plots model results using MatPlotLib.
perform_audit: Called at each audit interval. Records simulation time, total
patients waiting, patients waiting by priority, and number of docs
occupied. Will then schedule next audit.
run: Called immediately after initialising simulation object. This method:
1) Calls method to set up doc resources.
2) Initialises the two starting processes: patient admissions and audit.
3) Starts model envrionment.
4) Save individual patient level results to csv
5) Calls the build_audit_results metha and saves to csv
6) Calls the chart method to plot results
see_doc: After a patient arrives (generated in the trigger_admissions
method of this class), this see_doc process method is called (with
patient object passed to process method). This process requires a free
doc resource (resource objects held in this model class). The request is
prioritised by patient priority (lower priority numbers grab resources
first). The number of patients waiting is incremented, and doc resources
are requested. Once doc resources become available queuing times are
recorded (these are saved to global results if warm up period has been
completed). The patient is held for teh required time with doc (held in
patient object) and then time with doc recorded. The patient is then
removed from the Patient calss dictionary (which triggers Python to
remove the patient object).
trigger_admissions: Generates new patient admissions. Each patient is an
instance of the Patient obect class. This method allocates each
patient an ID, adds the patient to the dictionary of patients held by
the Patient class (static class variable), initiates a simpy process
(in this model class) to see a doc, and schedules the next admission.
"""
def __init__(self):
"""constructor for initiating simpy simulation environment"""
self.env = simpy.Environment()
def build_audit_results(self):
"""At end of model run, transfers results held in lists into a pandas
DataFrame."""
Global_vars.results['time'] = Global_vars.audit_time
Global_vars.results['patients in ED'] = Global_vars.audit_patients_in_ED
Global_vars.results['all patients waiting'] = \
Global_vars.audit_patients_waiting
Global_vars.results['priority 1 patients waiting'] = \
Global_vars.audit_patients_waiting_p1
Global_vars.results['priority 2 patients waiting'] = \
Global_vars.audit_patients_waiting_p2
Global_vars.results['priority 3 patients waiting'] = \
Global_vars.audit_patients_waiting_p3
Global_vars.results['resources occupied'] = \
Global_vars.audit_reources_used
def chart(self):
"""At end of model run, plots model results using MatPlotLib."""
# Define figure size and defintion
fig = plt.figure(figsize=(12, 4.5), dpi=75)
# Create two charts side by side
# Figure 1: patient perspective results
ax1 = fig.add_subplot(131) # 1 row, 3 cols, chart position 1
x = Global_vars.patient_queuing_results.index
# Chart loops through 3 priorites
markers = ['o', 'x', '^']
for priority in range(1, 4):
x = (Global_vars.patient_queuing_results
[Global_vars.patient_queuing_results['priority'] ==
priority].index)
y = (Global_vars.patient_queuing_results
[Global_vars.patient_queuing_results['priority'] ==
priority]['q_time'])
ax1.scatter(x, y,
marker=markers[priority - 1],
label='Priority ' + str(priority))
ax1.set_xlabel('Patient')
ax1.set_ylabel('Queuing time')
ax1.legend()
ax1.grid(True, which='both', lw=1, ls='--', c='.75')
# Figure 2: ED level queuing results
ax2 = fig.add_subplot(132) # 1 row, 3 cols, chart position 2
x = Global_vars.results['time']
y1 = Global_vars.results['priority 1 patients waiting']
y2 = Global_vars.results['priority 2 patients waiting']
y3 = Global_vars.results['priority 3 patients waiting']
y4 = Global_vars.results['all patients waiting']
ax2.plot(x, y1, marker='o', label='Priority 1')
ax2.plot(x, y2, marker='x', label='Priority 2')
ax2.plot(x, y3, marker='^', label='Priority 3')
ax2.plot(x, y4, marker='s', label='All')
ax2.set_xlabel('Time')
ax2.set_ylabel('Patients waiting')
ax2.legend()
ax2.grid(True, which='both', lw=1, ls='--', c='.75')
# Figure 3: ED staff usage
ax3 = fig.add_subplot(133) # 1 row, 3 cols, chart position 3
x = Global_vars.results['time']
y = Global_vars.results['resources occupied']
ax3.plot(x, y, label='Docs occupied')
ax3.set_xlabel('Time')
ax3.set_ylabel('Doctors occupied')
ax3.legend()
ax3.grid(True, which='both', lw=1, ls='--', c='.75')
# Create plot
plt.tight_layout(pad=3)
plt.show()
def perform_audit(self):
"""Called at each audit interval. Records simulation time, total
patients waiting, patients waiting by priority, and number of docs
occupied. Will then schedule next audit."""
# Delay before first aurdit if length of warm-up
yield self.env.timeout(Global_vars.warm_up)
# The trigger repeated audits
while True:
# Record time
Global_vars.audit_time.append(self.env.now)
# Record patients waiting by referencing global variables
Global_vars.audit_patients_waiting.append(
Global_vars.patients_waiting)
Global_vars.audit_patients_waiting_p1.append(
Global_vars.patients_waiting_by_priority[0])
Global_vars.audit_patients_waiting_p2.append(
Global_vars.patients_waiting_by_priority[1])
Global_vars.audit_patients_waiting_p3.append(
Global_vars.patients_waiting_by_priority[2])
# Record patients waiting by asking length of dictionary of all
# patients (another way of doing things)
Global_vars.audit_patients_in_ED.append(len(Patient.all_patients))
# Record resources occupied
Global_vars.audit_reources_used.append(
self.doc_resources.docs.count)
# Trigger next audit after interval
yield self.env.timeout(Global_vars.audit_interval)
def run(self):
"""Called immediately after initialising simulation object. This method:
1) Calls method to set up doc resources.
2) Initialises the two starting processes: patient admissions and audit.
3) Starts model envrionment.
4) Save individual patient level results to csv
5) Calls the build_audit_results metha and saves to csv
6) Calls the chart method to plot results
"""
# Set up resources using Resouces class
self.doc_resources = Resources(self.env, Global_vars.number_of_docs)
# Initialise processes that will run on model run
self.env.process(self.trigger_admissions())
self.env.process(self.perform_audit())
# Run
self.env.run(until=Global_vars.sim_duration)
# End of simulation run. Build and save results
Global_vars.patient_queuing_results.to_csv('patient results.csv')
self.build_audit_results()
Global_vars.results.to_csv('operational results.csv')
# plot results
self.chart()
def see_doc(self, p):
"""After a patient arrives (generated in the trigger_admissions
method of this class), this see_doc process method is called (with
patient object passed to process method). This process requires a free
doc resource (resource objects held in this model class). The request is
prioritised by patient priority (lower priority numbers grab resources
first). The number of patients waiting is incremented, and doc resources
are requested. Once doc resources become available queuing times are
recorded (these are saved to global results if warm up period has been
completed). The patient is held for teh required time with doc (held in
patient object) and then time with doc recorded. The patient is then
removed from the Patient calss dictionary (which triggers Python to
remove the patient object).
"""
# See doctor requires doc_resources
with self.doc_resources.docs.request(priority=p.priority) as req:
# Increment count of number of patients waiting. 1 is subtracted
# from priority to align priority (1-3) with zero indexed list.
Global_vars.patients_waiting += 1
Global_vars.patients_waiting_by_priority[p.priority - 1] += 1
# Wait for resources to become available
yield req
# Resources now available. Record time patient starts to see doc
p.time_see_doc = self.env.now
# Record patient queuing time in patient object
p.queuing_time = self.env.now - p.time_in
# Reduce count of number of patients (waiting)
Global_vars.patients_waiting_by_priority[p.priority - 1] -= 1
Global_vars.patients_waiting -= 1
# Create a temporary results list with patient priority and queuing
# time
_results = [p.priority, p.queuing_time]
# Hold patient (with doc) for consulation time required
yield self.env.timeout(p.consulation_time)
# At end of consultation add time spent with doc to temp results
_results.append(self.env.now - p.time_see_doc)
# Record results in global results data if warm-up complete
if self.env.now >= Global_vars.warm_up:
Global_vars.patient_queuing_results.loc[p.id] = _results
# Delete patient (removal from patient dictionary removes only
# reference to patient and Python then automatically cleans up)
del Patient.all_patients[p.id]
def trigger_admissions(self):
"""Generates new patient admissions. Each patient is an instance of the
Patient obect class. This method allocates each patient an ID, adds the
patient to the dictionary of patients held by the Patient class (static
class variable), initiates a simpy process (in this model class) to see
a doc, and then schedules the next admission"""
# While loop continues generating new patients throughout model run
while True:
# Initialise new patient (pass environment to be used to record
# current simulation time)
p = Patient(self.env)
# Add patient to dictionary of patients
Patient.all_patients[p.id] = p
# Pass patient to see_doc method
self.env.process(self.see_doc(p))
# Sample time for next asmissions
next_admission = random.expovariate(
1 / Global_vars.inter_arrival_time)
# Schedule next admission
yield self.env.timeout(next_admission)
class Patient:
"""The Patient class is for patient objects. Each patient is an instance of
this class. This class also holds a static dictionary which holds all
patient objects (a patient is removed after exiting ED).
Methods are:
__init__: constructor for new patient
"""
# The following static class dictionary stores all patient objects
# This is not actually used further but shows how patients may be tracked
all_patients = {}
def __init__(self, env):
"""Constructor for new patient object.
"""
# Increment global counts of patients
Global_vars.patient_count += 1
# Set patient id and priority (random between 1 and 3)
self.id = Global_vars.patient_count
self.priority = random.randint(1, 3)
# Set consultation time (time spent with doc) by random normal
# distribution. If value <0 then set to 0
self.consulation_time = random.normalvariate(
Global_vars.appointment_time_mean, Global_vars.appointment_time_sd)
self.consulation_time = 0 if self.consulation_time < 0 \
else self.consulation_time
# Set initial queuing time as zero (this will be adjusted in model if
# patient has to waiti for doc)
self.queuing_time = 0
# record simulation time patient enters simulation
self.time_in = env.now
# Set up variables to record simulation time that patient see doc and
# exit simulation
self.time_see_doc = 0
self.time_out = 0
class Resources:
"""Resources class for simpy. Only resource used is docs"""
def __init__(self, env, number_of_docs):
self.docs = simpy.PriorityResource(env, capacity=number_of_docs)
# Run model
if __name__ == '__main__':
# Initialise model environment
model = Model()
# Run model
model.run()
```
| true |
code
| 0.714914 | null | null | null | null |
|
# A study of bias in data on Wikipedia
The purpose of this study is to explore bias in data on Wikipedia by analyzing Wikipedia articles on politicians from various countries with respect to their populations. A further metric used for comparison is the quality of articles on politicians across different countries.
### Import libraries
```
# For getting data from API
import requests
import json
# For data analysis
import pandas as pd
import numpy as np
```
### Load datasets
**Data Sources:**
We will combine the below two datasets for our analysis of bias in data on Wikipedia:
1) **Wikipedia articles** : This dataset contains information on Wikipedia articles for politicians by country. Details include the article name, revision id (last edit id) and country. This dataset can be downloaded from [figshare](https://figshare.com/articles/Untitled_Item/5513449). A downloaded version "page_data.csv" (downloaded on 28th Oct 2018) is also uploaded to the [git](https://github.com/priyankam22/DATA-512-Human-Centered-Data-Science/tree/master/data-512-a2) repository.
2) **Country Population** : This dataset contains a list of countries and their populations till mid-2018 in millions. This dataset is sourced from the [Population Reference Bureau] (https://www.prb.org/data/). As the dataset is copyrighted, it is not available on this repository. The data might have changed when you extract it from the website. For reproducibility, i have included the intermediate merged file for the final analysis.
```
# Load the Wikipedia articles
wiki_articles = pd.read_csv('page_data.csv')
wiki_articles.head()
# Load the country population
country_pop = pd.read_csv('WPDS_2018_data.csv')
country_pop.head()
print("Number of records in Wikipedia articles dataset: ", wiki_articles.shape[0])
print("Number of records in country population dataset: ", country_pop.shape[0])
```
### Get the quality of Wikipedia articles
To get the quality score of Wikipedia articles, we will use the machine learning system called [ORES](https://www.mediawiki.org/wiki/ORES) ("Objective Revision Evaluation Service"). ORES estimates the quality of a given Wikipedia article by assigning a series of probabilities that the article belongs to one of the six quality categories and returns the most probable category as the prediction. The quality of an article (from best to worst) can be categorized into six categories as below.
1. FA - Featured article
2. GA - Good article
3. B - B-class article
4. C - C-class article
5. Start - Start-class article
6. Stub - Stub-class article
More details about these categories can be found at [Wikipedia: Content Assessment](https://en.wikipedia.org/wiki/Wikipedia:Content_assessment#Grades)
We will use a Wikimedia RESTful API endpoint for ORES to get the predictions for each of the Wikipedia articles. Documentation for the API can be found [here](https://ores.wikimedia.org/v3/#!/scoring/get_v3_scores_context_revid_model).
```
# Set the headers with your github ID and email address. This will be used for identification while making calls to the API
headers = {'User-Agent' : 'https://github.com/priyankam22', 'From' : 'mhatrep@uw.edu'}
# Function to get the predictions for Wikipedia articles using API calls
def get_ores_predictions(rev_ids, headers):
'''
Takes a list of revision ids of Wikipedia articles and returns the quality of each article.
Input:
rev_ids: A list of revision ids of Wikipedia articles
headers: a dictionary with identifying information to be passed to the API call
Output: a dictionary of dictionaries storing a final predicted label and probabilities for each of the categories
for every revision id passed.
'''
# Define the endpoint
endpoint = 'https://ores.wikimedia.org/v3/scores/{project}/?models={model}&revids={revids}'
# Specify the parameters for the endpoint
params = {'project' : 'enwiki',
'model' : 'wp10',
'revids' : '|'.join(str(x) for x in rev_ids) # A single string with all revision ids separated by '|'
}
# make the API call
api_call = requests.get(endpoint.format(**params))
# Get the response in json format
response = api_call.json()
return response
```
Lets look at the output of the API call by calling the function on a sample list of revision ids.
```
get_ores_predictions(list(wiki_articles['rev_id'])[0:5], headers)
```
We need to extract the prediction for each of the revision ids from the response. Note that the prediction is a key in one of the nested dictionaries.
We will call the API for all the Wikipedia articles in batches of 100 so that we do not overload the server with our requests. 100 was chosen after trial and error. Higher batchsize can throw an error.
```
# Make calls to the API in batches and append the scores portion of the dictionary response to the scores list.
scores = []
batch_size = 100
for begin_ind in range(0,len(wiki_articles),batch_size):
# set the end index by adding the batchsize except for the last batch.
end_ind = begin_ind+batch_size if begin_ind+batch_size <= len(wiki_articles) else len(wiki_articles)
# make the API call
output = get_ores_predictions(list(wiki_articles['rev_id'])[begin_ind:end_ind], headers)
# Append the scores extratced from the dictionary to scores list
scores.append(output['enwiki']['scores'])
```
Let us now extract the predicted labels for each revision_id from the list of scores.
```
# A list to store all the predicted labels
prediction = []
# Loop through all the scores dictionaries from the scores list.
for i in range(len(scores)):
# Get the predicted label from the value of all the keys(revision_ids)
for val in scores[i].values():
# Use the get function to get the value of 'score' key. If the score is not found (in case of no matches), none is returned.
prediction.append(val['wp10'].get('score')['prediction'] if val['wp10'].get('score') else None)
print("Number of predictions extracted : " , len(prediction))
```
This matches the number of revision ids we passed earlier.
```
print("Unique predictions extracted : " , set(prediction))
# Merging the predictions with the Wikipedia articles
wiki_articles['quality'] = prediction
wiki_articles.head()
```
### Merging the Wikipedia Quality data with the country population
```
# Create separate columns with lowercase country name so that we can join without mismatch
wiki_articles['country_lower'] = wiki_articles['country'].apply(lambda x: x.lower())
country_pop['Geography_lower'] = country_pop['Geography'].apply(lambda x: x.lower())
# Merge the two datasets on lowercase country name. Inner join will remove any countriess that do not have matching rows
dataset = wiki_articles.merge(country_pop, how='inner', left_on='country_lower', right_on='Geography_lower')
dataset.head()
```
### Data cleaning
```
# Drop the extra country columns.
dataset.drop(['country_lower','Geography','Geography_lower'], axis=1, inplace=True)
# Rename the remaining columns
dataset.columns = ['article_name','country','revision_id','article_quality','population']
# Remove columns where quality is None (not found from ORES)
quality_none_idx = dataset[dataset['article_quality'].isnull()].index
print("%d rows removed as ORES could not return the quality of the article" % len(quality_none_idx))
dataset.drop(quality_none_idx, inplace=True)
# Check the datatypes of the columns
dataset.info()
# Population is stored as text. Let us remove the commas used for separation and convert it to float
dataset['population'] = dataset['population'].apply(lambda x: float(x.replace(',','')))
dataset.shape
# Save the final dataset as a csv file for future reproducibility
dataset.to_csv('wiki_articles_country_pop.csv')
```
### Data Analysis
We will now perform some analysis on the number of articles on politicians with respect to a country's population and what proportion of these articles are good quality articles. By comparing the highest and lowest ranking countries in the list, we can get a fair idea of bias in the data on Wikipedia. Ideally we would expect to see similiar proportions in all countries.
```
# If you are skipping all the above steps then the prepared dataset can be loaded.
dataset = pd.read_csv('wiki_articles_country_pop.csv')
# Add a new binary column to classify the articles as good quality or not where good quality is defined as either FA or GA.
dataset['is_good_quality'] = dataset['article_quality'].apply(lambda x: 1 if x == 'FA' or x == 'GA' else 0)
```
To get an idea of the overall political coverage in Wikipedia by country, let us aggregate the data by country. We are interested in the total number of articles per country, the population of each country and the number of good articles per country.
```
output = dataset[['country','population','is_good_quality']].groupby(['country'], as_index=False).agg(['count','max','sum']).reset_index()
output.head()
# Drop the columns we dont need for the analysis.
output.drop(('population','count'), axis=1, inplace=True)
output.drop(('population','sum'), axis=1, inplace=True)
output.drop(('is_good_quality','max'), axis=1, inplace=True)
# Rename the useful columns
output.columns = ['country','population','total_articles','quality_articles']
output.head()
```
To be able to compare different countries, let us calculate the proportion of articles by unit population and the proportion of good quality articles.
```
# Create a new column with the proportion of articles per 100 ppl.
output['article_prop'] = np.round(output['total_articles']/(output['population']*10**4)*100,6)
# Create a new column for proportion of good quality articles
output['quality_prop'] = output['quality_articles']/output['total_articles']*100
```
### Results
### 10 highest-ranked countries in terms of number of politician articles as a proportion of country population
```
# Sort by article_prop and extract top 10 countries
high_art_prop = output.sort_values(by='article_prop',ascending=False)[0:10].drop(['quality_articles','quality_prop'], axis=1).reset_index(drop=True)
# Rename the columns
high_art_prop.columns = ['Country', 'Population till mid-2018 (in millions)', 'Total Articles', 'Articles Per 100 Persons']
high_art_prop
```
### 10 lowest-ranked countries in terms of number of politician articles as a proportion of country population
```
# Sort by article_prop and extract lowest 10 countries
low_art_prop = output.sort_values(by='article_prop',ascending=True)[0:10:].drop(['quality_articles','quality_prop'], axis=1).reset_index(drop=True)
# Rename the columns
low_art_prop.columns = ['Country', 'Population till mid-2018 (in millions)', 'Total Articles', 'Articles Per 100 Persons']
low_art_prop
```
As seen in above tables, there is a huge variation in the proportion of Wikipedia articles on politicians with respect to the population of the country. The highest ranking country is Tuvalu with a population of 0.01 million and 55 Wikipedia articles (55 articles per 100 persons) on politicians whereas the lowest ranking country is India with a population of 1371.3 million and only 986 Wikipedia articles on politicians (0.007% per 100 persons). One important trend to be noted here is that all the highest ranking countries (except Iceland) have extremely low populations (less than 100K). All the high ranking countries have very high populations. Most of the low ranking countries are developing countries which can explain the bias seen in the data.
### 10 highest-ranked countries in terms of number of GA and FA-quality articles as a proportion of all articles about politicians from that country
```
# Sort by quality_prop and extract highest 10 countries
high_qual_art = output.sort_values(by='quality_prop',ascending=False)[0:10].drop(['population','article_prop'], axis=1).reset_index(drop=True)
# Rename the columns
high_qual_art.columns = ['Country', 'Total Articles', 'Good Quality Articles', 'Proportion Of Good Quality Articles (%)']
high_qual_art
```
### 10 lowest-ranked countries in terms of number of GA and FA-quality articles as a proportion of all articles about politicians from that country
```
# Sort by quality_prop and extract highest 10 countries
low_qual_art = output.sort_values(by='quality_prop',ascending=True)[0:10].drop(['population','article_prop'], axis=1).reset_index(drop=True)
# Rename the columns
low_qual_art.columns = ['Country', 'Total Articles', 'Good Quality Articles', 'Proportion Of Good Quality Articles (%)']
low_qual_art
```
As seen in above two tables, the proportion of good quality articles is highest in North Korea at 17.94% and lowest at 0% in many countries like Sao Tome and Principe, Mozambique, Cameroon, etc. It seems like there are many countries with zero good quality articles. Lets find out all such countries.
```
no_good_quality_articles = list(output[output['quality_articles'] == 0]['country'])
len(no_good_quality_articles)
```
There are 37 countries with no good quality articles. All the countries are listed below.
```
no_good_quality_articles
```
| true |
code
| 0.418637 | null | null | null | null |
|
# Ensemble sorting of a Neuropixels recording
This notebook reproduces figures 1 and 4 from the paper [**SpikeInterface, a unified framework for spike sorting**](https://www.biorxiv.org/content/10.1101/796599v2).
The data set for this notebook is available on the Dandi Archive: [https://gui.dandiarchive.org/#/dandiset/000034](https://gui.dandiarchive.org/#/dandiset/000034)
The entire data archive can be downloaded with the command `dandi download https://gui.dandiarchive.org/#/dandiset/000034/draft` (about 75GB).
Files required to run the code are:
- the raw data: [sub-mouse412804_ecephys.nwb](https://girder.dandiarchive.org/api/v1/item/5f2b250fee8baa608594a166/download)
- two manually curated sortings:
- [sub-mouse412804_ses-20200824T155542.nwb](https://girder.dandiarchive.org/api/v1/item/5f43c74cbf3ae27e069e0aee/download)
- [sub-mouse412804_ses-20200824T155543.nwb](https://girder.dandiarchive.org/api/v1/item/5f43c74bbf3ae27e069e0aed/download)
These files should be in the same directory where the notebook is located (otherwise adjust paths below).
Author: [Matthias Hennig](http://homepages.inf.ed.ac.uk/mhennig/), University of Edinburgh, 24 Aug 2020
### Requirements
For this need you will need the following Python packages:
- numpy
- pandas
- matplotlib
- seaborn
- spikeinterface
- dandi
- matplotlib-venn
To run the MATLAB-based sorters, you would also need a MATLAB license.
For other sorters, please refer to the documentation on [how to install sorters](https://spikeinterface.readthedocs.io/en/latest/sortersinfo.html).
```
import os
# Matlab sorter paths:
# change these to match your environment
os.environ["IRONCLUST_PATH"] = "./ironclust"
os.environ["KILOSORT2_PATH"] = "./Kilosort2"
os.environ["HDSORT_PATH"] = "./HDsort"
import matplotlib.pyplot as plt
import numpy as np
from pathlib import Path
import pandas as pd
import seaborn as sns
from collections import defaultdict
from matplotlib_venn import venn3
import spikeinterface as si
import spikeextractors as se
import spiketoolkit as st
import spikesorters as ss
import spikecomparison as sc
import spikewidgets as sw
from spikecomparison import GroundTruthStudy, MultiSortingComparison
%matplotlib inline
def clear_axes(ax):
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
# print version information
si.print_spikeinterface_version()
ss.print_sorter_versions()
# where to find the data set
data_file = Path('./') / 'mouse412804_probeC_15min.nwb'
# results are stored here
study_path = Path('./')
# this folder will contain all results
study_folder = study_path / 'study_15min/'
# this folder will be used as temorary space, and hold the sortings etc.
working_folder = study_path / 'working_15min'
# sorters to use
sorter_list = ['herdingspikes', 'kilosort2', 'ironclust', 'tridesclous', 'spykingcircus', 'hdsort']
# pass the following parameters to the sorters
sorter_params = {
# 'kilosort2': {'keep_good_only': True}, # uncomment this to test the native filter for false positives
'spyking_circus': {'adjacency_radius': 50},
'herdingspikes': {'filter': True, }}
sorter_names = ['HerdingSpikes', 'Kilosort2', 'Ironclust','Tridesclous', 'SpykingCircus', 'HDSort']
sorter_names_short = ['HS', 'KS', 'IC', 'TDC', 'SC', 'HDS']
# create an extractor object for the raw data
recording = se.NwbRecordingExtractor(str(data_file))
print("Number of frames: {}\nSampling rate: {}Hz\nNumber of channels: {}".format(
recording.get_num_frames(), recording.get_sampling_frequency(),
recording.get_num_channels()))
```
# Run spike sorters and perform comparison between all outputs
```
# set up the study environment and run all sorters
# sorters are not re-run if outputs are found in working_folder
if not study_folder.is_dir():
print('Setting up study folder:', study_folder)
os.mkdir(study_folder)
# run all sorters
result_dict = ss.run_sorters(sorter_list=sorter_list, recording_dict_or_list={'rec': recording}, with_output=True,
sorter_params=sorter_params, working_folder=working_folder, engine='loop',
mode='keep', verbose=True)
# store sortings in a list for quick access
sortings = []
for s in sorter_list:
sortings.append(result_dict['rec',s])
# perform a multi-comparison, all to all sortings
# result is stored, and loaded from disk if the file is found
if not os.path.isfile(study_folder / 'multicomparison.gpickle'):
mcmp = sc.compare_multiple_sorters(sorting_list=sortings, name_list=sorter_names_short,
verbose=True)
print('saving multicomparison')
mcmp.dump(study_folder)
else:
print('loading multicomparison')
mcmp = sc.MultiSortingComparison.load_multicomparison(study_folder)
```
# Figure 1 - comparison of sorter outputs
```
# activity levels on the probe
plt.figure(figsize=(16,2))
ax = plt.subplot(111)
w = sw.plot_activity_map(recording, trange=(0,20), transpose=True, ax=ax, background='w', frame=True)
ax.plot((50,150),(-30,-30),'k-')
ax.annotate('100$\\mu m$',(100,-90), ha='center');
# example data traces
plt.figure(figsize=(16,6))
ax = plt.subplot(111)
w = sw.plot_timeseries(recording, channel_ids=range(20,28), color='k', ax=ax, trange=(1,2))
ax.axis('off')
p = ax.get_position()
p.y0 = 0.55
ax.set_position(p)
ax.set_xticks(())
ax.plot((1.01,1.11),(-1790,-1790),'k-')
ax.annotate('100ms',(1.051,-2900), ha='center');
ax.set_ylim((-2900,ax.set_ylim()[1]))
ax = plt.subplot(111)
ax.bar(range(len(sortings)), [len(s.get_unit_ids()) for s in sortings], color='tab:blue')
ax.set_xticks(range(len(sorter_names)))
ax.set_xticklabels(sorter_names_short, rotation=60, ha='center')
ax.set_ylabel('Units detected')
clear_axes(ax)
w = sw.plot_multicomp_agreement(mcmp, plot_type='pie')
w = sw.plot_multicomp_agreement_by_sorter(mcmp, show_legend=True)
# numbers for figure above
print('number of units detected:')
for i,s in enumerate(sortings):
print("{}: {}".format(sorter_names[i],len(s.get_unit_ids())))
sg_names, sg_units = mcmp.compute_subgraphs()
v, c = np.unique([len(np.unique(s)) for s in sg_names], return_counts=True)
df = pd.DataFrame(np.vstack((v,c,np.round(100*c/np.sum(c),2))).T,
columns=('in # sorters','# units','percentage'))
print('\nall sorters, all units:')
print(df)
df = pd.DataFrame()
for i, name in enumerate(sorter_names_short):
v, c = np.unique([len(np.unique(sn)) for sn in sg_names if name in sn], return_counts=True)
df.insert(2*i,name,c)
df.insert(2*i+1,name+'%',np.round(100*c/np.sum(c),1))
print('\nper sorter:')
print(df)
```
# Supplemental Figure - example unit templates
```
# show unit emplates and spike trains for two units/all sorters
sorting = mcmp.get_agreement_sorting(minimum_agreement_count=6)
get_sorting = lambda u: [mcmp.sorting_list[i] for i,n in enumerate(mcmp.name_list) if n==u[0]][0]
get_spikes = lambda u: [mcmp.sorting_list[i].get_unit_spike_train(u[1]) for i,n in enumerate(mcmp.name_list) if n==u[0]][0]
# one well matched and one not so well matched unit, all sorters
show_units = [2,17]
for i,unit in enumerate(show_units):
fig = plt.figure(figsize=(16, 2))
ax = plt.subplot(111)
ax.set_title('Average agreement: {:.2f}'.format(sorting.get_unit_property(sorting.get_unit_ids()[unit],'avg_agreement')))
units = sorting.get_unit_property(sorting.get_unit_ids()[unit], 'sorter_unit_ids')
cols = plt.cm.Accent(np.arange(len(units))/len(units))
for j,u in enumerate(dict(sorted(units.items())).items()):
s = get_sorting(u).get_units_spike_train((u[1],))[0]
s = s[s<20*get_sorting(u).get_sampling_frequency()]
ax.plot(s/get_sorting(u).get_sampling_frequency(), np.ones(len(s))*j, '|', color=cols[j], label=u[0])
ax.set_frame_on(False)
ax.set_xticks(())
ax.set_yticks(())
ax.plot((0,1),(-1,-1),'k')
ax.annotate('1s',(0.5,-1.75), ha='center')
ax.set_ylim((-2,len(units)+1))
fig = plt.figure(figsize=(16, 2))
units = sorting.get_unit_property(sorting.get_unit_ids()[unit], 'sorter_unit_ids')
print(units)
print('Agreement: {}'.format(sorting.get_unit_property(sorting.get_unit_ids()[unit],'avg_agreement')))
cols = plt.cm.Accent(np.arange(len(units))/len(units))
for j,u in enumerate(dict(sorted(units.items())).items()):
ax = plt.subplot(1, len(sorter_list), j+1)
w = sw.plot_unit_templates(recording, get_sorting(u), unit_ids=(u[1],), max_spikes_per_unit=10,
channel_locs=True, radius=75, show_all_channels=False, color=[cols[j]],
lw=1.5, ax=ax, plot_channels=False, set_title=False, axis_equal=True)
# was 100 spikes in original plot
ax.set_title(u[0])
```
# Figure 4 - comparsion between ensembe sortings and curated data
```
# perform a comparison with curated sortings (KS2)
curated1 = se.NwbSortingExtractor('sub-mouse412804_ses-20200824T155542.nwb', sampling_frequency=30000)
curated2 = se.NwbSortingExtractor('sub-mouse412804_ses-20200824T155543.nwb', sampling_frequency=30000)
comparison_curated = sc.compare_two_sorters(curated1, curated2)
comparison_curated_ks = sc.compare_multiple_sorters((curated1, curated2, sortings[sorter_list.index('kilosort2')]))
# consensus sortings (units where at least 2 sorters agree)
sorting = mcmp.get_agreement_sorting(minimum_agreement_count=2)
consensus_sortings = []
units_dict = defaultdict(list)
units = [sorting.get_unit_property(u,'sorter_unit_ids') for u in sorting.get_unit_ids()]
for au in units:
for u in au.items():
units_dict[u[0]].append(u[1])
for i,s in enumerate(sorter_names_short):
consensus_sortings.append(se.SubSortingExtractor(sortings[i], unit_ids=units_dict[s]))
# orphan units (units found by only one sorter)
sorting = mcmp.get_agreement_sorting(minimum_agreement_count=1, minimum_agreement_count_only=True)
unmatched_sortings = []
units_dict = defaultdict(list)
units = [sorting.get_unit_property(u,'sorter_unit_ids') for u in sorting.get_unit_ids()]
for au in units:
for u in au.items():
units_dict[u[0]].append(u[1])
for i,s in enumerate(sorter_names_short):
unmatched_sortings.append(se.SubSortingExtractor(sortings[i], unit_ids=units_dict[s]))
consensus_curated_comparisons = []
for s in consensus_sortings:
consensus_curated_comparisons.append(sc.compare_two_sorters(s, curated1))
consensus_curated_comparisons.append(sc.compare_two_sorters(s, curated2))
unmatched_curated_comparisons = []
for s in unmatched_sortings:
unmatched_curated_comparisons.append(sc.compare_two_sorters(s, curated1))
unmatched_curated_comparisons.append(sc.compare_two_sorters(s, curated2))
all_curated_comparisons = []
for s in sortings:
all_curated_comparisons.append(sc.compare_two_sorters(s, curated1))
all_curated_comparisons.append(sc.compare_two_sorters(s, curated2)) \
# count various types of units
count_mapped = lambda x : np.sum([u!=-1 for u in x.get_mapped_unit_ids()])
count_not_mapped = lambda x : np.sum([u==-1 for u in x.get_mapped_unit_ids()])
count_units = lambda x : len(x.get_unit_ids())
n_consensus_curated_mapped = np.array([count_mapped(c.get_mapped_sorting1()) for c in consensus_curated_comparisons]).reshape((len(sorter_list),2))
n_consensus_curated_unmapped = np.array([count_not_mapped(c.get_mapped_sorting1()) for c in consensus_curated_comparisons]).reshape((len(sorter_list),2))
n_unmatched_curated_mapped = np.array([count_mapped(c.get_mapped_sorting1()) for c in unmatched_curated_comparisons]).reshape((len(sorter_list),2))
n_all_curated_mapped = np.array([count_mapped(c.get_mapped_sorting1()) for c in all_curated_comparisons]).reshape((len(sorter_list),2))
n_all_curated_unmapped = np.array([count_not_mapped(c.get_mapped_sorting1()) for c in all_curated_comparisons]).reshape((len(sorter_list),2))
n_curated_all_unmapped = np.array([count_not_mapped(c.get_mapped_sorting2()) for c in all_curated_comparisons]).reshape((len(sorter_list),2))
n_all = np.array([count_units(s) for s in sortings])
n_consensus = np.array([count_units(s) for s in consensus_sortings])
n_unmatched = np.array([count_units(s) for s in unmatched_sortings])
n_curated1 = len(curated1.get_unit_ids())
n_curated2 = len(curated2.get_unit_ids())
# overlap between two manually curated data and the Kilosort2 sorting they were derived from
i = {}
for k in ['{0:03b}'.format(v) for v in range(1,2**3)]:
i[k] = 0
i['111'] = len(comparison_curated_ks.get_agreement_sorting(minimum_agreement_count=3).get_unit_ids())
s = comparison_curated_ks.get_agreement_sorting(minimum_agreement_count=2, minimum_agreement_count_only=True)
units = [s.get_unit_property(u,'sorter_unit_ids').keys() for u in s.get_unit_ids()]
for u in units:
if 'sorting1' in u and 'sorting2' in u:
i['110'] += 1
if 'sorting1' in u and 'sorting3' in u:
i['101'] += 1
if 'sorting2' in u and 'sorting3' in u:
i['011'] += 1
s = comparison_curated_ks.get_agreement_sorting(minimum_agreement_count=1, minimum_agreement_count_only=True)
units = [s.get_unit_property(u,'sorter_unit_ids').keys() for u in s.get_unit_ids()]
for u in units:
if 'sorting1' in u:
i['100'] += 1
if 'sorting2' in u:
i['010'] += 1
if 'sorting3' in u:
i['001'] += 1
colors = plt.cm.RdYlBu(np.linspace(0,1,3))
venn3(subsets = i,set_labels=('Curated 1', 'Curated 2', 'Kilosort2'),
set_colors=colors, alpha=0.6, normalize_to=100)
# overlaps betweem ensemble sortings (per sorter) and manually curated sortings
def plot_mcmp_results(data, labels, ax, ylim=None, yticks=None, legend=False):
angles = (np.linspace(0, 2*np.pi, len(sorter_list), endpoint=False)).tolist()
angles += angles[:1]
for i,v in enumerate(data):
v = v.tolist() + v[:1].tolist()
ax.bar(np.array(angles)+i*2*np.pi/len(sorter_list)/len(data)/2-2*np.pi/len(sorter_list)/len(data)/4,
v, label=labels[i],
alpha=0.8, width=np.pi/len(sorter_list)/2)
ax.set_thetagrids(np.degrees(angles), sorter_names_short)
if legend:
ax.legend(bbox_to_anchor=(1.0, 1), loc=2, borderaxespad=0., frameon=False, fontsize=8, markerscale=0.25)
ax.set_theta_offset(np.pi / 2)
ax.set_theta_direction(-1)
if ylim is not None:
ax.set_ylim(ylim)
if yticks is not None:
ax.set_yticks(yticks)
plt.figure(figsize=(14,3))
sns.set_palette(sns.color_palette("Set1"))
ax = plt.subplot(131, projection='polar')
plot_mcmp_results((n_all_curated_mapped[:,0]/n_all*100,
n_all_curated_mapped[:,1]/n_all*100),
('Curated 1','Curated 2'), ax, yticks=np.arange(20,101,20))
ax.set_title('Percent all units\nwith match in curated sets',pad=20);
plt.ylim((0,100))
ax = plt.subplot(132, projection='polar')
plot_mcmp_results((n_consensus_curated_mapped[:,0]/n_consensus*100,
n_consensus_curated_mapped[:,1]/n_consensus*100),
('Curated 1','Curated 2'), ax, yticks=np.arange(20,101,20))
ax.set_title('Percent consensus units\nwith match in curated sets',pad=20);
plt.ylim((0,100))
ax = plt.subplot(133, projection='polar')
plot_mcmp_results((n_unmatched_curated_mapped[:,0]/n_unmatched*100,
n_unmatched_curated_mapped[:,1]/n_unmatched*100),
('Curated 1','Curated 2'), ax, ylim=(0,30), yticks=np.arange(10,21,10), legend=True)
ax.set_title('Percent non-consensus units\nwith match in curated sets',pad=20);
# numbers for figure above
df = pd.DataFrame(np.vstack((n_all_curated_mapped[:,0]/n_all*100, n_all_curated_mapped[:,1]/n_all*100,
n_all_curated_mapped[:,0], n_all_curated_mapped[:,1])).T,
columns = ('C1 %', 'C2 %', 'C1', 'C2'), index=sorter_names_short)
print('Percent all units with match in curated sets')
print(df)
df = pd.DataFrame(np.vstack((n_consensus_curated_mapped[:,0]/n_consensus*100, n_consensus_curated_mapped[:,1]/n_consensus*100,
n_consensus_curated_mapped[:,0],n_consensus_curated_mapped[:,1])).T,
columns = ('C1 %', 'C2 %', 'C1', 'C2'), index=sorter_names_short)
print('\nPercent consensus units with match in curated sets')
print(df)
df = pd.DataFrame(np.vstack((n_unmatched_curated_mapped[:,0]/n_unmatched*100,
n_unmatched_curated_mapped[:,1]/n_unmatched*100,
n_unmatched_curated_mapped[:,0],n_unmatched_curated_mapped[:,1])).T,
columns = ('C1 %', 'C2 %', 'C1', 'C2'), index=sorter_names_short)
print('\nPercent non-consensus units with match in curated sets')
print(df)
```
| true |
code
| 0.402656 | null | null | null | null |
|
```
NAME = "Robina Shaheen"
DATE = "06242020"
COLLABORATORS = ""
```
# Wildfires in California: Causes and Consequences
The rising carbon dioxide in the atmosphere is contributing to constant increase in global temperatures. Over the last two decades, humanity has observed record-breaking extreme weather events. A comparison with the historical data indicates higher frequency, larger magnitude, longer duration, and timing of many of these events around the world has also changed singniciantly (Seneviratne et al., 2018). Wildfires are no exception, as seen in the recent years, devastating blazes across the globe (Amazon forest in 2019, California 2017-18 and Australia in 2019-2020. In the western U.S., wildfires are projected to increase in both frequency and intensity as the planet warms (Abatzoglou and Williams, 2016). The state of California with ~ 40 million residents and ~ 4.5 million housings and properties has experienced the most devastating economic, ecological and health consequences during and after wildfires (Baylis and Boomhower, 2019; Liao Y and Kousky C, 2020,).
During 2014 wildfires in San Diego, I volunteered to help people in the emergency shelters and watching the devastating effects of wildfires on children and adults emotional and physical health had a profound impact on me and moved me at a deeper level to search for potential markers/predictors of these events in the nature. This analysis is not only an academic endeavor but also a humble beginning to understand the complex interactions between atmosphere and biosphere in the nature and how we can plan for a better future for those who suffered the most during these catastrophic wildfires.
This goal of this study is to understand the weather data that can trigger wildfires and consequences of wildfires on the atmospheric chemistry and how we can predict and plan for a better future to mitigate disastrous consequences.
I have laid out this study in multiple sections:
1. Understanding weather pattern using advanced machine learning tools to identify certain markers that can be used to forecast future events.
2. Understanding changes in the chemical composition of the atmosphere and identify markers that can trigger respiratory stress and cardio-vascular diseases.
## Pictrue of an unprecdent wildfire near Camp Pendelton.
**Pulgas Fire 2014, San Diego, CA (source= wikimedia)**
<a href="https://en.wikipedia.org/wiki/May_2014_San_Diego_County_wildfires" target="_blank">May 2014 Wildfires</a>.

## Workflow
1. Import packages and modules
2. Import datetime conversion tools beteween panda and matplotlib for time series analysis
3. Download air quality data from the EPA website
4. Set working directory to "earth-analytics"
5. Define paths to download data files from data folder 'sd_fires_2014'
6. Import data into dataframes using appropriate functions(date-parser, indexing, remove missing values)
* weather data Jan-Dec. 2014
* Atmospheric gases and particulate matter data Jan - Dec. 2014
* Annual precipitation (2007-2020) San Diego, CA.
7. view nature and type of data
8. Use Scikit learn multivariate analysis to predict ozone levels.
9. Plot data to view any anomalies in data and identify source of the anomaly .
10. discuss plots and conclusions.
## Resources
* Environmental Protection Agency, USA. <a href="https://https://www.epa.gov/outdoor-air-quality-data//" target="_blank">EPA website/ User Guide to download data</a>.
* Precipitation Record (2007-2020), San Diego, CA. <a href="http://www.wx4mt.com/wxraindetail.php?year=2020//" target="_blank"> San Diego Weather, CA</a>.
## Import packages/ modules and Set Working Directory
```
# Import packages/ modules
import os
import numpy as np
import pandas as pd
from pandas.plotting import autocorrelation_plot
from pandas.plotting import lag_plot
import earthpy as et
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.dates import DateFormatter
import seaborn as sns
import datetime
from textwrap import wrap
from statsmodels.formula.api import ols
# Handle date time conversions between pandas and matplotlib
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
# Scikit learn to train model and make predictions.
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.linear_model import LinearRegression
# Use white grid plot background from seaborn
sns.set(font_scale=1.5, style="whitegrid")
# Set Working Directory
ea_path = os.path.join(et.io.HOME, 'earth-analytics')
# Set base path to download data
base_path = os.path.join(ea_path, "data")
base_path
```
# Data exploration and analysis
The EPA provides data for the entire state and it is a large data set, often slowing the processing time.
Therefore, it is important to select data required to check air quality and weather conditions.
I have selected ozone, oxides of nitrogen and carbon monoxide that are produced during wildfires.
Additionally, black carbon and particulate matter is emitted during wildfires which is dangerous to inhale.
These dataset will allow me to conduct my preliminary analysis of the effects of wildfires on the air quality in San Diego County.
```
file_path21 = os.path.join(base_path, "output_figures",
"sandiego_2014_fires", "air_quality_csv",
"sd_chemical_composition_2014_mean_v02.csv")
# To check if path is created
os.path.exists(file_path21)
# Define relative path to files
file_path1 = os.path.join(base_path, "output_figures",
"sandiego_2014_fires", "air_quality_csv",
"sd_weather_2014_mean_values_only.csv")
# To check if path is created
os.path.exists(file_path1)
# Import csv files into dataframe and ensure date time is imported properly.
sd_weather_2014_df = pd.read_csv(file_path1, parse_dates=['Date Local'],
index_col=['Date Local'])
sd_weather_2014_df.head(3)
# Use pandas scatter matrix function to view relationships between various components of weather system.
pd.plotting.scatter_matrix(sd_weather_2014_df, s=30, figsize=[
8, 6], marker='o', color='r')
plt.show()
```
The figure above shows a Gaussian distribution of temperature and pressure, whereas relative humidity data is skewed towards lower humidity levels.The wind pattern shows two distinct populations. Both relative humidity and wind pattern indicates extreme weather changes during Santa Ana events.
The correlation matrix graph shows inverse correlation between temperature and relative humidity. One can easily identify how extremely low relative humidity (<30%) can easily damage shrubs and other vegetations. The inverse relationship between pressure, temperature and winds is obvious from these graphs. A time series data has already shown that a high resolution record of temperature, relative humidity and wind can be used as a useful indicator of wildfire season.
# Autocorrelation plot and lag plot
Autocorrelation plots are often used for checking randomness in time series. This is done by computing autocorrelations for data values at varying time lags. If time series is random, such autocorrelations should be near zero for any and all time-lag separations. If time series is non-random then one or more of the autocorrelations will be significantly non-zero. The horizontal lines displayed in the plot correspond to 95% and 99% confidence bands. The dashed line is 99% confidence band.
1. The auto correlation plot shows the weather parameters are strongly related to each other.
2. A lag plot is a special type of scatter plot with the two variables (X,Y) and their frequency of occurrence. A lag plot is used to checks
a. Outliers (data points with extremely high or low values).
b. Randomness (data without a pattern).
c. Serial correlation (where error terms in a time series transfer from one period to another).
d. Seasonality (periodic fluctuations in time series data that happens at regular periods).
A lag plot of San Diego weather data shows two distinct populations, anomalous values during wildfires in the right upper corner and normal values are linearly correlated in the lag plot.
The lag plot help us to choose appropriate model for Machine learning.
```
# For this plot we need pandas.plotting import autocorrelation_plot function.
autocorrelation_plot(sd_weather_2014_df)
# For the lag plot we need to import pandas.plotting import lag_plot functions
plt.figure()
lag_plot(sd_weather_2014_df)
```
# The Chemical Composition of the Atmosphere
The atmosphere is composed of gases and aerosols (liquid and solid particles in the size range of few nanometer to micrometers).
In the cells below we are going to explore machine learning models and stats to understand the relations between various parameters. We will use Scikit learn multivariate analytical tools to predict the ozone concentrations. Ozone is a strong oxidant and very irritating gas. It can enter the respiratory system and damage thin linings of the respiratory system by producing free radicals.
# Scikit-learn
Scikit-learn is a simple and efficient tools for predictive data analysis.
It is designed for machine learning in python and built on NumPy, SciPy, and matplotlib.
In this notebook I have employed Scikkit-learn to understand relationship between ozone and its precursors.
Ozone formation depends on the presence of oxide of nitrogen, carbon monoxide and volatile organic compounds.
However, VOC's are not measured at all the stations and few stations have values measured for half of the year.
These msissing values cannot be predicted or filled due to spatial variability of its sources.
```
# Import dataframe and view columns
sd_atm_df = pd.read_csv(file_path21, parse_dates=['Date Local'],
index_col=['Date Local'])
sd_atm_df.head(2)
sd_atm_df.columns
# Understanding nature of the data
sd_atm_df.describe()
# To check empty columns, False means no empty colums
sd_atm_df.isnull().any()
# To fill empty cells with the nearest neighbour.
sd_atm_df = sd_atm_df.fillna(method='ffill')
# selected data frame for training
X = sd_atm_df[['NO2 (ppb)', 'CO_ppm', 'PM2.5 (ug/m3)']].values
y = sd_atm_df['O3 (ppb)'].values
X
# To view relaion between ozone and its precursor NOX.
sd_atm_df.plot(x='NO2 (ppb)', y='O3 (ppb)', style='o', c='r')
# sd_atm_df.plot(x2='NO2 (ppb)', y2='CO_ppm', style='o', c='b')
plt.title('Ozone vs Nitric oxide')
plt.xlabel('NO2 (ppb)')
plt.ylabel('O3 (ppb)')
plt.show()
# plt.savefig('data/output_figures/sandiego_2014_fires/air_quality_csv/O3_NOx_relation.png')
# To view relaion between ozone and its precursor NOX.
sd_atm_df.plot(x='PM2.5 (ug/m3)', y='O3 (ppb)', style='o', c='b')
plt.title('Ozone vs PM2.5')
plt.xlabel('PM2.5 (ug/m3)')
plt.ylabel('O3 (ppb)')
# plt.savefig('data/output_figures/sandiego_2014_fires/air_quality_csv/O3_PM2.5_relation.png')
plt.show()
# random state is a seed for data training
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
```
Our next step is to divide the data into “attributes” and “labels”.
Attributes are the independent variables while labels are dependent variables whose values are to be predicted. In our dataset, we only have two columns. We want to predict the oxide of nitrogen depending upon the carbon monoxide (CO) recorded.
Next, we will split 80% of the data to the training set while 20% of the data to test set using below code. The test_size variable is where we actually specify the proportion of the test set.
```
# random state is a seed for data training
indices = sd_atm_df.index.values
X_train, X_test, y_train, y_test, idx1, idx2 = train_test_split(
X, y, indices, test_size=0.2, random_state=0)
X
# Training Algorithm
regressor = LinearRegression()
regressor.fit(X_train, y_train)
#To retrieve the intercept:
print(regressor.intercept_)
#For retrieving the slope:
print(regressor.coef_)
y_pred = regressor.predict(X_test)
X_test
# print(y_pred)
type(y_pred)
# converted to DF
df2 = pd.DataFrame({'Date': idx2, 'Actual': y_test, 'Predicted': y_pred})
df2.head(2)
# Set index on date to identify anomalous events in the plot.
df3 = df2.set_index('Date')
df3.index = df3.index.date
# df3 = df2.set_index('Date')
df3.head(3)
# # Create figure and plot space
fig, ax = plt.subplots(figsize=(10, 6))
# printing only 20% values
df3 = df3.head(20)
df3.plot(ax=ax, kind='bar')
# plt.grid(which='major', linestyle='-', linewidth='0.5', color='green')
plt.grid(which='minor', linestyle=':', linewidth='0.5', color='black')
plt.title('Comparison of actual and predicted values of ozone')
plt.ylabel('O3 (ppb)')
# Rotate tick marks on x-axis
plt.setp(ax.get_xticklabels(), rotation=45)
# plt.savefig('data/output_figures/sandiego_2014_fires/air_quality_csv/O3_multivariate_analysis.png')
plt.show()
# Results:
print('Mean Absolute Error:', metrics.mean_absolute_error(y_test, y_pred))
print('Mean Squared Error:', metrics.mean_squared_error(y_test, y_pred))
print('Root Mean Squared Error:', np.sqrt(
metrics.mean_squared_error(y_test, y_pred)))
```
Mean O3 (ppb) = 30.693
RMSE = 6.51
# Conclusion
1. The ozone prediction from model = (6.51/30.69)*100 ~ 20% less than actual value. still reasonable model fit.
2. Bar grpah with predicted values indicated huge deviation on May 01, 2014 which is the wildfire day at its peak.
3. Taking wildfire days out will improve the relationship between normal parameters and hence MLR coefficents.
4. The ozone fromation depends on temp, pressure and destruction with OH radical, photolysis and collisons with air moleucles. The data for one of the important source of ozone formation VOC is incomplete and it can signficntly brings predicted values in alignment with the observed one.
5. A comparison with the rain in the previous years tells us an intersting story that good rainy season in 2011-12 resulted in huge biomass accumulation in San Diego.
6. Intense drought in 2012-2013 caused the biomass to turn into dry fuel for fire ignition.
7. In future studies, it would be valuable to compare rain patterns with wildfires in California.
# Future Outlook
There are many exciting avenues to expand this work to more wildfire events and comparison with weather and atmospheric conditions to test our model.
# Preliminary Analysis of Rain Patterns in San Diego.
**Figure . cumulative rain and number of rainy days in San Diego California, USA.**
<img src="http://drive.google.com/uc?export=view&id=12tON_T9EbfuwqyTGbNwcp60P65VEaHov" width="400" height="200">
The figure above shows that precipitation in 2010 was more than normal and resulted in rapid growth of shrubs, grasses and other vegetations which later served as tinder for fires in early 2014. The black line indicates exponential decrease in precipitation after heavy rains in 2010.
Tinder is an easily combustible material (dried grass and shrubs) and is used to ignite fires.
The black line indicates exponential decrease in precipitation after heavy rains in 2010. A further analysis of rain pattern in 2020 indicated 110mm of rain in Dec. 2020 which is almost half of the annual rain in San Diego. There was no rain from July-Aug. 2020 after deadly wildfires and had even worse consequences for the health of locals.
As climate is changing the populations are suffering not only from the immediate impact of wildfires but lingering effects of fine particulate matter and toxic gases are even worst especially for children and individuals suffering from respiratory diseases (Amy Maxman 2019).
# References
Abatzoglou, T. J., and Williams P. A., Proceedings of the National Academy of Sciences Oct 2016, 113 (42) 11770-11775; DOI: 10.1073/pnas.1607171113
Seneviratne, S. et al., ,Philos Trans A Math Phys Eng Sci. 2018 May 13; 376(2119): 20160450, doi: 10.1098/rsta.2016.0450
Baylis, P., and Boomhower, J., Moral hazard, wildfires, and the economic incidence of natural disasters, Posted: 2019, https://www.nber.org/papers/w26550.pdf
Liao, Yanjun and Kousky, Carolyn, The Fiscal Impacts of Wildfires on California Municipalities (May 27, 2020). https://ssrn.com/abstract=3612311 or http://dx.doi.org/10.2139/ssrn.3612311
Amy Maxman, California biologists are using wildfires to assess health risks of smoke. Nature 575, 15-16 (2019),doi: 10.1038/d41586-019-03345-2
| true |
code
| 0.651078 | null | null | null | null |
|
# Keras Basics
Welcome to the section on deep learning! We'll be using Keras with a TensorFlow backend to perform our deep learning operations.
This means we should get familiar with some Keras fundamentals and basics!
## Imports
```
import numpy as np
```
## Dataset
We will use the Bank Authentication Data Set to start off with. This data set consists of various image features derived from images that had 400 x 400 pixels. You should note **the data itself that we will be using ARE NOT ACTUAL IMAGES**, they are **features** of images. In the next lecture we will cover grabbing and working with image data with Keras. This notebook focuses on learning the basics of building a neural network with Keras.
_____
More info on the data set:
https://archive.ics.uci.edu/ml/datasets/banknote+authentication
Data were extracted from images that were taken from genuine and forged banknote-like specimens. For digitization, an industrial camera usually used for print inspection was used. The final images have 400x 400 pixels. Due to the object lens and distance to the investigated object gray-scale pictures with a resolution of about 660 dpi were gained. Wavelet Transform tool were used to extract features from images.
Attribute Information:
1. variance of Wavelet Transformed image (continuous)
2. skewness of Wavelet Transformed image (continuous)
3. curtosis of Wavelet Transformed image (continuous)
4. entropy of image (continuous)
5. class (integer)
## Reading in the Data Set
We've already downloaded the dataset, its in the DATA folder. So let's open it up.
```
from numpy import genfromtxt
data = genfromtxt('../DATA/bank_note_data.txt', delimiter=',')
data
labels = data[:,4]
labels
features = data[:,0:4]
features
X = features
y = labels
```
## Split the Data into Training and Test
Its time to split the data into a train/test set. Keep in mind, sometimes people like to split 3 ways, train/test/validation. We'll keep things simple for now. **Remember to check out the video explanation as to why we split and what all the parameters mean!**
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
X_train
X_test
y_train
y_test
```
## Standardizing the Data
Usually when using Neural Networks, you will get better performance when you standardize the data. Standardization just means normalizing the values to all fit between a certain range, like 0-1, or -1 to 1.
The scikit learn library also provides a nice function for this.
http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html
```
from sklearn.preprocessing import MinMaxScaler
scaler_object = MinMaxScaler()
scaler_object.fit(X_train)
scaled_X_train = scaler_object.transform(X_train)
scaled_X_test = scaler_object.transform(X_test)
```
Ok, now we have the data scaled!
```
X_train.max()
scaled_X_train.max()
X_train
scaled_X_train
```
## Building the Network with Keras
Let's build a simple neural network!
```
from keras.models import Sequential
from keras.layers import Dense
# Creates model
model = Sequential()
# 8 Neurons, expects input of 4 features.
# Play around with the number of neurons!!
model.add(Dense(4, input_dim=4, activation='relu'))
# Add another Densely Connected layer (every neuron connected to every neuron in the next layer)
model.add(Dense(8, activation='relu'))
# Last layer simple sigmoid function to output 0 or 1 (our label)
model.add(Dense(1, activation='sigmoid'))
```
### Compile Model
```
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
```
## Fit (Train) the Model
```
# Play around with number of epochs as well!
model.fit(scaled_X_train,y_train,epochs=50, verbose=2)
```
## Predicting New Unseen Data
Let's see how we did by predicting on **new data**. Remember, our model has **never** seen the test data that we scaled previously! This process is the exact same process you would use on totally brand new data. For example , a brand new bank note that you just analyzed .
```
scaled_X_test
# Spits out probabilities by default.
# model.predict(scaled_X_test)
model.predict_classes(scaled_X_test)
```
# Evaluating Model Performance
So how well did we do? How do we actually measure "well". Is 95% accuracy good enough? It all depends on the situation. Also we need to take into account things like recall and precision. Make sure to watch the video discussion on classification evaluation before running this code!
```
model.metrics_names
model.evaluate(x=scaled_X_test,y=y_test)
from sklearn.metrics import confusion_matrix,classification_report
predictions = model.predict_classes(scaled_X_test)
confusion_matrix(y_test,predictions)
print(classification_report(y_test,predictions))
```
## Saving and Loading Models
Now that we have a model trained, let's see how we can save and load it.
```
model.save('myfirstmodel.h5')
from keras.models import load_model
newmodel = load_model('myfirstmodel.h5')
newmodel.predict_classes(X_test)
```
Great job! You now know how to preprocess data, train a neural network, and evaluate its classification performance!
| true |
code
| 0.672036 | null | null | null | null |
|
<a href="https://kaggle.com/code/ritvik1909/siamese-network" target="_blank"><img align="left" alt="Kaggle" title="Open in Kaggle" src="https://kaggle.com/static/images/open-in-kaggle.svg"></a>
# Siamese Network
A Siamese neural network (sometimes called a twin neural network) is an artificial neural network that uses the same weights while working in tandem on two different input vectors to compute comparable output vectors.
Often one of the output vectors is precomputed, thus forming a baseline against which the other output vector is compared. This is similar to comparing fingerprints but can be described more technically as a distance function for locality-sensitive hashing.
It is possible to make a kind of structure that is functional similar to a siamese network, but implements a slightly different function. This is typically used for comparing similar instances in different type sets.
Uses of similarity measures where a twin network might be used are such things as recognizing handwritten checks, automatic detection of faces in camera images, and matching queries with indexed documents. The perhaps most well-known application of twin networks are face recognition, where known images of people are precomputed and compared to an image from a turnstile or similar. It is not obvious at first, but there are two slightly different problems. One is recognizing a person among a large number of other persons, that is the facial recognition problem.
Source: [Wikipedia](https://en.wikipedia.org/wiki/Siamese_neural_network)
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import random
import tensorflow as tf
import tensorflow.keras.backend as K
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Model, Sequential
from tensorflow.keras import layers, utils, callbacks
```
Lets start off by creating our dataset. Our input data will be consisting of pairs of images, and output will be either 1 or 0 indicating if the pair are similar or not
```
def make_pairs(images, labels, seed=19):
np.random.seed(seed)
pairImages = []
pairLabels = []
numClasses = len(np.unique(labels))
idx = [np.where(labels == i)[0] for i in range(numClasses)]
for idxA in range(len(images)):
currentImage = images[idxA]
label = labels[idxA]
idxB = np.random.choice(idx[label])
posImage = images[idxB]
pairImages.append([currentImage, posImage])
pairLabels.append([1])
negIdx = np.where(labels != label)[0]
negImage = images[np.random.choice(negIdx)]
pairImages.append([currentImage, negImage])
pairLabels.append([0])
return (np.array(pairImages), np.array(pairLabels))
```
We will be working with `MNIST` dataset in our notebook which comes along with the tensorflow library
```
(trainX, trainY), (testX, testY) = mnist.load_data()
trainX = 1 - (trainX / 255.0)
testX = 1 - (testX / 255.0)
trainX = np.expand_dims(trainX, axis=-1)
testX = np.expand_dims(testX, axis=-1)
(pairTrain, labelTrain) = make_pairs(trainX, trainY)
(pairTest, labelTest) = make_pairs(testX, testY)
print(f'\nTrain Data Shape: {pairTrain.shape}')
print(f'Test Data Shape: {pairTest.shape}\n\n')
```
Lets visualize the mnist images
```
fig, ax = plt.subplots(2, 6, figsize=(20, 6))
random.seed(19)
idx = random.choices(range(len(trainX)), k=12)
for i in range(12):
ax[i//6][i%6].imshow(np.squeeze(trainX[idx[i]]), cmap='gray')
ax[i//6][i%6].set_title(f'Label: {trainY[idx[i]]}', fontsize=18)
ax[i//6][i%6].set_axis_off()
fig.suptitle('MNIST Images', fontsize=24);
```
Here is a sample of our prepared dataset
```
fig, ax = plt.subplots(2, 6, figsize=(20, 6))
random.seed(19)
idx = random.choices(range(len(pairTrain)), k=6)
for i in range(0, 12, 2):
ax[i//6][i%6].imshow(np.squeeze(pairTrain[idx[i//2]][0]), cmap='gray')
ax[i//6][i%6+1].imshow(np.squeeze(pairTrain[idx[i//2]][1]), cmap='gray')
ax[i//6][i%6].set_title(f'Label: {labelTrain[idx[i//2]]}', fontsize=18)
ax[i//6][i%6].set_axis_off()
ax[i//6][i%6+1].set_axis_off()
fig.suptitle('Input Pair Images', fontsize=24);
```
Here we define some configurations for our model
```
class config():
IMG_SHAPE = (28, 28, 1)
EMBEDDING_DIM = 48
BATCH_SIZE = 64
EPOCHS = 500
```
Here we define a function to calculate euclidean distance between two vectors. This will be used by our model to calculate the euclidean distance between the vectors of the image pairs (image vectors will be created by the feature extractor of our model)
```
def euclidean_distance(vectors):
(featsA, featsB) = vectors
sumSquared = K.sum(K.square(featsA - featsB), axis=1, keepdims=True)
return K.sqrt(K.maximum(sumSquared, K.epsilon()))
```
With Siamese Network, the two most commonly used loss functions are:
* contrastive loss
* triplet loss
We will be using contrastive loss in this notebook ie:
```Contrastive loss = mean( (1-true_value) * square(prediction) + true_value * square( max(margin - prediction, 0)))```
```
def loss(margin=1):
def contrastive_loss(y_true, y_pred):
y_true = tf.cast(y_true, y_pred.dtype)
square_pred = tf.math.square(y_pred)
margin_square = tf.math.square(tf.math.maximum(margin - (y_pred), 0))
return tf.math.reduce_mean(
(1 - y_true) * square_pred + (y_true) * margin_square
)
return contrastive_loss
```
Finally we define our model architecture
* The model contains two input layers
* A feature extractor through which both the images will be passed to generate feature vectors, the feature extractor typically consists of Convolutional and Pooling Layers
* The feature vectors are passed through a custom layer to get euclidean distance between the vectors
* The final layer consists of a single sigmoid unit
```
class SiameseNetwork(Model):
def __init__(self, inputShape, embeddingDim):
super(SiameseNetwork, self).__init__()
imgA = layers.Input(shape=inputShape)
imgB = layers.Input(shape=inputShape)
featureExtractor = self.build_feature_extractor(inputShape, embeddingDim)
featsA = featureExtractor(imgA)
featsB = featureExtractor(imgB)
distance = layers.Lambda(euclidean_distance, name='euclidean_distance')([featsA, featsB])
outputs = layers.Dense(1, activation="sigmoid")(distance)
self.model = Model(inputs=[imgA, imgB], outputs=outputs)
def build_feature_extractor(self, inputShape, embeddingDim=48):
model = Sequential([
layers.Input(inputShape),
layers.Conv2D(64, (2, 2), padding="same", activation="relu"),
layers.MaxPooling2D(pool_size=2),
layers.Dropout(0.3),
layers.Conv2D(64, (2, 2), padding="same", activation="relu"),
layers.MaxPooling2D(pool_size=2),
layers.Dropout(0.3),
layers.Conv2D(128, (1, 1), padding="same", activation="relu"),
layers.Flatten(),
layers.Dense(embeddingDim, activation='tanh')
])
return model
def call(self, x):
return self.model(x)
model = SiameseNetwork(inputShape=config.IMG_SHAPE, embeddingDim=config.EMBEDDING_DIM)
model.compile(loss=loss(margin=1), optimizer="adam", metrics=["accuracy"])
es = callbacks.EarlyStopping(monitor='val_loss', patience=10, verbose=1, restore_best_weights=True, min_delta=1e-4)
rlp = callbacks.ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=3, min_lr=1e-6, mode='min', verbose=1)
history = model.fit(
[pairTrain[:, 0], pairTrain[:, 1]], labelTrain[:],
validation_data=([pairTest[:, 0], pairTest[:, 1]], labelTest[:]),
batch_size=config.BATCH_SIZE,
epochs=config.EPOCHS,
callbacks=[es, rlp]
)
fig, ax = plt.subplots(2, 6, figsize=(20, 6))
random.seed(19)
idx = random.choices(range(len(pairTest)), k=6)
preds = model.predict([pairTest[:, 0], pairTest[:, 1]])
for i in range(0, 12, 2):
ax[i//6][i%6].imshow(np.squeeze(pairTest[idx[i//2]][0]), cmap='gray')
ax[i//6][i%6+1].imshow(np.squeeze(pairTest[idx[i//2]][1]), cmap='gray')
ax[i//6][i%6].set_title(f'Label: {labelTest[idx[i//2]]}', fontsize=18)
ax[i//6][i%6+1].set_title(f'Predicted: {np.round(preds[idx[i//2]], 2)}', fontsize=18)
ax[i//6][i%6].set_axis_off()
ax[i//6][i%6+1].set_axis_off()
fig.suptitle('Test Pair Images', fontsize=24);
sns.set_style('darkgrid')
fig, ax = plt.subplots(2, 1, figsize=(20, 8))
df = pd.DataFrame(history.history)
df[['accuracy', 'val_accuracy']].plot(ax=ax[0])
df[['loss', 'val_loss']].plot(ax=ax[1])
ax[0].set_title('Model Accuracy', fontsize=12)
ax[1].set_title('Model Loss', fontsize=12)
fig.suptitle('Siamese Network: Learning Curve', fontsize=18);
```
# References
[Fisher Discriminant Triplet and Contrastive Losses for Training Siamese Networks](https://arxiv.org/pdf/2004.04674v1.pdf)
| true |
code
| 0.603465 | null | null | null | null |
|
# [Country Embedding](https://philippmuens.com/word2vec-intuition/)
```
import json
import pandas as pd
import seaborn as sns
import numpy as np
# prettier Matplotlib plots
import matplotlib.pyplot as plt
import matplotlib.style as style
style.use('seaborn')
```
# 1. Dataset
#### Download
```
%%bash
download=1
for FILE in "data/country-by-surface-area.json" "data/country-by-population.json"; do
if [[ ! -f ${FILE} ]]; then
download=0
fi
done
if [[ download -eq 0 ]]; then
mkdir -p data
wget -nc \
https://raw.githubusercontent.com/samayo/country-json/master/src/country-by-surface-area.json \
-O data/country-by-surface-area.json 2> /dev/null
wget -nc \
https://raw.githubusercontent.com/samayo/country-json/master/src/country-by-population.json \
-O data/country-by-population.json 2> /dev/null
fi
```
#### Build df
```
df_surface_area = pd.read_json("data/country-by-surface-area.json")
df_population = pd.read_json("data/country-by-population.json")
df_population.dropna(inplace=True)
df_surface_area.dropna(inplace=True)
df = pd.merge(df_surface_area, df_population, on='country')
df.set_index('country', inplace=True)
print(len(df))
df.head()
```
#### Visualize some countries
```
df_small = df[
(df['area'] > 100000) & (df['area'] < 600000) &
(df['population'] > 35000000) & (df['population'] < 100000000)
]
print(len(df_small))
df_small.head()
fig, ax = plt.subplots()
df_small.plot(
x='area',
y='population',
figsize=(10, 10),
kind='scatter', ax=ax)
for k, v in df_small.iterrows():
ax.annotate(k, v)
fig.canvas.draw()
```
# 2. Model
#### Euclidean distance
$$d(x,y)\ =\ \sqrt{\sum\limits_{i=1}^{N}(x_i\ -\ y_i)^2}$$
```
def euclidean_distance(x: (int, int), y: (int, int)) -> int:
'''
Note: cast the result into an int which makes it easier to compare
'''
x1, x2 = x
y1, y2 = y
result = np.sqrt((x1 - x2)**2 + (y1 - y2)**2)
return int(round(result, 0))
```
#### Finding similar countries based on population and area
```
from collections import defaultdict
similar_countries = defaultdict(list)
for country in df.iterrows():
name = country[0]
area = country[1]['area']
population = country[1]['population']
for other_country in df.iterrows():
other_name = other_country[0]
other_area = other_country[1]['area']
other_population = other_country[1]['population']
if other_name == name: continue
x = (area, other_area)
y = (population, other_population)
similar_countries[name].append(
(euclidean_distance(x, y), other_name))
for country in similar_countries.keys():
similar_countries[country].sort(key=lambda x: x[0], reverse=True)
# List of Vietnam similar countries based on population and area
similar_countries['Vietnam'][:10]
# List of Singapore similar countries based on population and area
similar_countries['Singapore'][:10]
```
| true |
code
| 0.392366 | null | null | null | null |
|
# 1. Regressão Linear
## 1.1. Univariada
Existem diversos problemas na natureza para os quais procura-se obter valores de saída dado um conjunto de dados de entrada. Suponha o problema de predizer os valores de imóveis de uma determinada cidade, conforme apresentado na Figura 1, em que podemos observer vários pontos que representam diferentes imóveis, cada qual com seu preço de acordo com o seu tamanho.
Em problemas de **regressão**, objetiva-se estimar valores de saída de acordo com um conjunto de valores de entrada. Desta forma, considerando o problema anterior, a ideia consiste em estimar o preço de uma casa de acordo com o seu tamanho, isto é, gostaríamos de encontrar uma **linha reta** que melhor se adequa ao conjunto de pontos na Figura 1.
```
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
from matplotlib import pyplot
import numpy
# gerando um conjunto de pontos aleatórios para um problema de regressão linear ***
x, y = make_regression(n_samples=100, n_features=1, noise=5.7)
# apresenta o conjunto de dados criado no passo anterior ***
fig = pyplot.figure(figsize=(15,7))
pyplot.subplot(1, 2, 1)
pyplot.scatter(x,y)
pyplot.xlabel("Tamanho ($m^2$)")
pyplot.ylabel("Preço (R\$x$10^3$)")
pyplot.title("(a)")
# executando regressor linear
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0) #criando partições
model = LinearRegression()
model.fit(x_train, y_train) # treinando o algoritmo
pyplot.subplot(1, 2, 2)
pyplot.scatter(x,y)
pyplot.plot(x, model.predict(x), color = 'red')
pyplot.xlabel("Tamanho ($m^2$)")
pyplot.ylabel("Preço (R\$x$10^3$)")
pyplot.title("(b)")
fig.tight_layout(pad=10)
fig.suptitle("Figura 1: Exemplo de conjunto de dados de valores imobiliários: (a) conjunto de dados de entrada e (b) linha reta estimada via regressão linear.", y=0.18)
pyplot.show()
```
Seja um conjunto de dados ${\cal D}=\{(x_1,y_1),(x_2,y_2),\ldots,(x_m,y_m)\}$ tal que $x_i\in\Re$ denota o conjunto dos dados de **entrada** (isto é, o tamanho da casa) e $y_i\in\Re$ representa o seu valor. Além disso, seja ${\cal D}_{tr}\subset {\cal D}$ o chamado **conjunto de treinamento** e ${\cal D}_{ts}\subset {\cal D}\backslash{\cal D}_{tr}$ o **conjunto de teste**. Usualmente, técnicas de aprendizado de máquina são avaliadas em conjuntos de treinamento e teste disjuntos, ou seja, temos que ${\cal D}_{tr}$ e ${\cal D}_{ts}$ são denominados **partições** do conjunto original ${\cal D}$. Em nosso exemplo, temos que $x_i$ e $y_i$ correspondem ao tamanho e preço do imóvel, respectivamente.
Basicamente, um algoritmo de regressão linear recebe como entrada um conjunto de dados de treinamento e objetiva estimar uma função linear (reta) a qual chamamos de **função hipótese**, dada por:
\begin{equation}
h_\textbf{w}(x) = w_0+w_1x,
\tag{1}
\end{equation}
em que $\textbf{w}=[w_0\ w_1]$ corresponde aos parâmetros do modelo, sendo que $w_0,w_1\in\Re$. Dependendo dos valores assumidos por $\textbf{w}$, a função hipótese pode assumir diferentes comportamentos, conforme ilustra a Figura 2.
```
fig = pyplot.figure(figsize=(15,7))
x = numpy.arange(-10, 10, 0.5)
pyplot.subplot(2, 2, 1)
y = 1.5 + 0*x #h_w(x) = 1.5 + w_1*0
pyplot.plot(x, y, color = "red")
pyplot.title("$h_w(x) = 1.5$ $(w_0 = 1$ e $w_1 = 1)$")
pyplot.subplot(2, 2, 2)
y = 0 + 0.5*x #h_w(x) = 0 + 0.5*x
pyplot.plot(x, y, color = "red")
pyplot.title("$h_w(x) = 0.5x$ $(w_0 = 0$ e $w_1 = 0.5)$")
pyplot.subplot(2, 2, 3)
y = 1 + 0.5*x #h_w(x) = 1 + 0.5*x
pyplot.plot(x, y, color = "red")
pyplot.title("$h_w(x) = 1 + 0.5x$ $(w_0 = 1$ e $w_1 = 0.5)$")
pyplot.subplot(2, 2, 4)
y = 0 - 0.5*x #h_w(x) = 0 - 0.5*x
pyplot.plot(x, y, color = "red")
pyplot.title("$h_w(x) = -0.5x$ $(w_0 = 0$ e $w_1 = -0.5)$")
fig.tight_layout(pad=2)
fig.suptitle("Figura 2: Exemplos de diferentes funções hipótese.", y=0.01)
pyplot.show()
```
De maneira geral, o objetivo da regressão linear é encontrar valores para $\textbf{w}=[w_0\ w_1]$ de tal forma que $h_w(x_i)$ é o mais próximo possível de $y_i$ considerando o conjunto de treinamento ${\cal D}_{tr}$, $\forall i\in\{1,2,\ldots,m^\prime\}$, em que $m^\prime=\left|{\cal D}_{tr}\right|$. Em outras palavras, o objetivo consiste em resolver o seguinte problema de minimização:
\begin{equation}
\label{e.mse}
\underset{\textbf{w}}{\operatorname{argmin}}\frac{1}{2m^\prime}\sum_{i=1}^{m^\prime}(h_\textbf{w}(x_i)-y_i)^2.
\tag{3}
\end{equation}
Essa equação é também conhecida por **erro médio quadrático**, do inglês *Minimum Square Error* (MSE). Uma outra denominação bastante comum é a de **função de custo**. Note que $h_w(x_i)$ representa o **preço estimado** do imóvel pela técnica de regressão linear, ao passo que $y_i$ denota o seu **valor rea**l dado pelo conjunto de treinamento.
Podemos simplificar a Equação \ref{e.mse} e reescrevê-la da seguinte maneira:
\begin{equation}
\label{e.mse_simplified}
\underset{\textbf{w}}{\operatorname{argmin}}J(\textbf{w}),
\tag{4}
\end{equation}
em que $J(\textbf{w})=\frac{1}{2m^\prime}\sum_{i=1}^{m^\prime}(h_\textbf{w}(x_i)-y_i)^2$. Partindo desta premissa, vamos simplificar um pouco mais a notação e assumir que nossa função hipótese cruza a origem do plano cartesiano:
\begin{equation}
\label{e.hypothesis_origin}
h_w(\textbf{x}) = w_1x,
\tag{5}
\end{equation}
ou seja, $w_0=0$. Neste caso, nosso problema de otimização restringe-se a encontrar $w_1$ que minimiza a seguinte equação:
\begin{equation}
\label{e.mse_simplified_origin}
\underset{w_1}{\operatorname{argmin}}J(w_1).
\tag{6}
\end{equation}
Como exemplo, suponha o seguinte conjunto de treinamento ${\cal D}_{tr}=\{(1,1),(2,2),(3,3)\}$, o qual é ilustrado na Figura 3a. Como pode ser observado, a função hipótese que modela esse conjunto de treinamento é dada por $h_\textbf{w}(x)=x$, ou seja, $\textbf{w}=[0\ 1]$, conforme apresentado na Figura 3b.
```
fig = pyplot.figure(figsize=(13,7))
x = numpy.arange(1, 4, 1)
pyplot.subplot(2, 2, 1)
y = x #h_w(x) = x
pyplot.scatter(x,y)
pyplot.title("(a)")
pyplot.subplot(2, 2, 2)
pyplot.scatter(x,y)
pyplot.plot(x, x, color = "red")
pyplot.title("(b)")
fig.suptitle("Figura 3: (a) conjunto de treinamento ($m^\prime=3$) e (b) função hipótese que intercepta os dados.", y=0.47)
pyplot.show()
```
Na prática, a ideia consiste em testar diferentes valores de $w_1$ e calcular o valor de $J(w_1)$. Aquele que minimizar a função de custo, é o valor de $w_1$ a ser utilizado no modelo (função hipótese). Suponha que tomemos como valor inicial $w_1 = 1$, ou seja, o "chute" correto. Neste caso, temos que:
\begin{equation}
\begin{split}
J(w_1) & =\frac{1}{2m^\prime}\sum_{i=1}^{m^\prime}(h_\textbf{w}(x_i)-y_i)^2 \\
& = \frac{1}{2m^\prime}\sum_{i=1}^{m^\prime}(w_1x_i-y_i)^2 \\
& = \frac{1}{2\times3}\left[(1-1)^2+(2-2)^2+(3-3)^2\right] \\
& = \frac{1}{6}\times 0 = 0.
\end{split}
\tag{7}
\end{equation}
Neste caso, temos que $J(w_1) = 0$ para $w_1 = 1$, ou seja, o custo é o menor possível dado que achamos a função hipótese **exata** que intercepta os dados. Agora, suponha que tivéssemos escolhido $w_1 = 0.5$. Neste caso, a funcão de custo seria calculada da seguinte forma:
\begin{equation}
\begin{split}
J(w_1) & =\frac{1}{2m^\prime}\sum_{i=1}^{m^\prime}(h_\textbf{w}(x_i)-y_i)^2 \\
& = \frac{1}{2m^\prime}\sum_{i=1}^{m^\prime}(w_1x_i-y_i)^2 \\
& = \frac{1}{2\times3}\left[(0.5-1)^2+(1-2)^2+(1.5-3)^2\right] \\
& = \frac{1}{6}\times (0.25+1+2.25) \approx 0.58.
\end{split}
\tag{8}
\end{equation}
Neste caso, nosso erro foi ligeiramente maior. Caso continuemos a calcular $J(w_1)$ para diferentes valores de $w_1$, obteremos o gráfico ilustrado na Figura 4.
```
def J(w_1, x, y):
error = numpy.zeros(len(w_1))
for i in range(len(w_1)):
error[i] = 0
for j in range(3):
error[i] = error[i] + numpy.power(w_1[i]*x[j]-y[j], 2)
return error
w_1 = numpy.arange(-7,10,1) #criando um vetor
error = J(w_1, x, y)
pyplot.plot(w_1, error, color = "red")
pyplot.xlabel("$w_1$")
pyplot.ylabel("$J(w_1)$")
pyplot.title("Figura 4: Comportamento da função de custo para diferentes valores de $w_1$.", y=-0.27)
pyplot.show()
```
Portanto, temos que $w_1=1$ é o valor que minimiza $J(w_1)$ para o exemplo citado anteriormente. Voltando à função de custo dada pela Equação \ref{e.mse}, a questão que temos agora é: como podemos encontrar valores plausíveis para o vetor de parâmetros $\textbf{w}=[w_0\ w_1]$. Uma abordagem simples seria testar uma combinação de valores aleatórios para $w_0$ e $w_1$ e tomar aqueles que minimizam $J(\textbf{w})$. Entretanto, essa heurística não garante que bons resultados sejam alcançados, principalmente em situações mais complexas.
Uma abordagem bastante comum para esse problema de otimização é fazer uso da ténica conhecida por **Gradiente Descentente** (GD), a qual consiste nos seguintes passos gerais:
1. Escolha valores aleatórios para $w_0$ e $w_1$.
2. Iterativamente, modifique os valores de $w_0$ e $w_1$ de tal forma a minimizar $J(\textbf{w})$.
A grande questão agora é qual heurística utilizar para atualizar os valores do vetor $\textbf{w}$. A técnica de GD faz uso das **derivadas parciais** da função de custo para guiar o processo de otimização no sentido do mínimo da função por meio da seguinte regra de atualização dos pesos:
\begin{equation}
\label{e.update_rule_GD}
w^{t+1}_j = w^{t}_j - \alpha\frac{\partial J(\textbf{w})}{\partial w_j},\ j\in\{0,1\},
\tag{9}
\end{equation}
em que $\alpha$ corresponde à chamada **taxa de aprendizado**.
Um questionamento bastante comum diz repeito ao termo derivativo, ou seja, como podemos calculá-lo. Para fins de explicação, suponha que tenhamos apenas o parâmetro $w_1$ para otimizar, ou seja, a nossa função hipótese é dada pela Equação \ref{e.hypothesis_origin}. Neste caso, o objetivo é minimizar $J(w_1)$ para algum valor de $w_1$. Na prática, o que significa a derivada em um dado ponto? A Figura \ref{f.derivada} ilustra melhor esta situação.
```
# Código basedo em https://stackoverflow.com/questions/54961306/how-to-plot-the-slope-tangent-line-of-parabola-at-any-point
# Definindo a parábola
def f(x):
return x**2
# Definindo a derivada da parábola
def slope(x):
return 2*x
# Definindo conjunto de dados para x
x = numpy.linspace(-5,5,100)
# Escolhendo pontos para traçar as retas tangentes
x1 = -3
y1 = f(x1)
x2 = 3
y2 = f(x2)
x3 = 0
y3 = f(x3)
# Definindo intervalo de dados em x para plotar a reta tangente
xrange1 = numpy.linspace(x1-1, x1+1, 10)
xrange2 = numpy.linspace(x2-1, x2+1, 10)
xrange3 = numpy.linspace(x3-1, x3+1, 10)
# Definindo a reta tangente
# y = m*(x - x1) + y1
def tangent_line(x, x1, y1):
return slope(x1)*(x - x1) + y1
# Desenhando as figuras
fig = pyplot.figure(figsize=(13,9))
pyplot.subplot2grid((2,4),(0,0), colspan = 2)
pyplot.title("Decaimento < 0.")
pyplot.plot(x, f(x))
pyplot.scatter(x1, y1, color='C1', s=50)
pyplot.plot(xrange1, tangent_line(xrange1, x1, y1), 'C1--', linewidth = 2)
pyplot.subplot2grid((2,4),(0,2), colspan = 2)
pyplot.title("Decaimento > 0.")
pyplot.plot(x, f(x))
pyplot.scatter(x2, y2, color='C1', s=50)
pyplot.plot(xrange2, tangent_line(xrange2, x2, y2), 'C1--', linewidth = 2)
pyplot.subplot2grid((2,4),(1,1), colspan = 2)
pyplot.title("Decaimento = 0.")
pyplot.plot(x, f(x))
pyplot.scatter(x3, y3, color='C1', s=50)
pyplot.plot(xrange3, tangent_line(xrange3, x3, y3), 'C1--', linewidth = 2)
```
| true |
code
| 0.724663 | null | null | null | null |
|
First we need to download the dataset. In this case we use a datasets containing poems. By doing so we train the model to create its own poems.
```
from datasets import load_dataset
dataset = load_dataset("poem_sentiment")
print(dataset)
```
Before training we need to preprocess the dataset. We tokenize the entries in the dataset and remove all columns we don't need to train the adapter.
```
from transformers import GPT2Tokenizer
def encode_batch(batch):
"""Encodes a batch of input data using the model tokenizer."""
encoding = tokenizer(batch["verse_text"])
# For language modeling the labels need to be the input_ids
#encoding["labels"] = encoding["input_ids"]
return encoding
tokenizer = GPT2Tokenizer.from_pretrained("gpt2")
# The GPT-2 tokenizer does not have a padding token. In order to process the data
# in batches we set one here
tokenizer.pad_token = tokenizer.eos_token
column_names = dataset["train"].column_names
dataset = dataset.map(encode_batch, remove_columns=column_names, batched=True)
```
Next we concatenate the documents in the dataset and create chunks with a length of `block_size`. This is beneficial for language modeling.
```
block_size = 50
# Main data processing function that will concatenate all texts from our dataset and generate chunks of block_size.
def group_texts(examples):
# Concatenate all texts.
concatenated_examples = {k: sum(examples[k], []) for k in examples.keys()}
total_length = len(concatenated_examples[list(examples.keys())[0]])
# We drop the small remainder, we could add padding if the model supported it instead of this drop, you can
# customize this part to your needs.
total_length = (total_length // block_size) * block_size
# Split by chunks of max_len.
result = {
k: [t[i : i + block_size] for i in range(0, total_length, block_size)]
for k, t in concatenated_examples.items()
}
result["labels"] = result["input_ids"].copy()
return result
dataset = dataset.map(group_texts,batched=True,)
dataset.set_format(type="torch", columns=["input_ids", "attention_mask", "labels"])
```
Next we create the model and add our new adapter.Let's just call it `poem` since it is trained to create new poems. Then we activate it and prepare it for training.
```
from transformers import AutoModelForCausalLM
model = AutoModelForCausalLM.from_pretrained("gpt2")
# add new adapter
model.add_adapter("poem")
# activate adapter for training
model.train_adapter("poem")
```
The last thing we need to do before we can start training is create the trainer. As trainingsargumnénts we choose a learningrate of 1e-4. Feel free to play around with the paraeters and see how they affect the result.
```
from transformers import Trainer, TrainingArguments
training_args = TrainingArguments(
output_dir="./examples",
do_train=True,
remove_unused_columns=False,
learning_rate=5e-4,
num_train_epochs=3,
)
trainer = Trainer(
model=model,
args=training_args,
tokenizer=tokenizer,
train_dataset=dataset["train"],
eval_dataset=dataset["validation"],
)
trainer.train()
```
Now that we have a trained udapter we save it for future usage.
```
model.save_adapter("adapter_poem", "poem")
```
With our trained adapter we want to create some poems. In order to do this we create a GPT2LMHeadModel wich is best suited for language generation. Then we load our trained adapter. Finally we have to choose the start of our poem. If you want your poem to start differently just change `PREFIX` accordingly.
```
from transformers import GPT2LMHeadModel, GPT2Tokenizer
model = GPT2LMHeadModel.from_pretrained("gpt2")
# You can also load your locally trained adapter
model.load_adapter("adapter_poem")
model.set_active_adapters("poem")
PREFIX = "In the night"
```
For the generation we need to tokenize the prefix first and then pass it to the model. In this case we create five possible continuations for the beginning we chose.
```
PREFIX = "In the night"
encoding = tokenizer(PREFIX, return_tensors="pt")
output_sequence = model.generate(
input_ids=encoding["input_ids"],
attention_mask=encoding["attention_mask"],
do_sample=True,
num_return_sequences=5,
max_length = 50,
)
```
Lastly we want to see what the model actually created. Too de this we need to decode the tokens from ids back to words and remove the end of sentence tokens. You can easily use this code with an other dataset. Don't forget to share your adapters at [AdapterHub](https://adapterhub.ml/).
```
for generated_sequence_idx, generated_sequence in enumerate(output_sequence):
print("=== GENERATED SEQUENCE {} ===".format(generated_sequence_idx + 1))
generated_sequence = generated_sequence.tolist()
# Decode text
text = tokenizer.decode(generated_sequence, clean_up_tokenization_spaces=True)
# Remove EndOfSentence Tokens
text = text[: text.find(tokenizer.eos_token)]
print(text)
model
```
| true |
code
| 0.790369 | null | null | null | null |
|

[](https://colab.research.google.com/github/JohnSnowLabs/spark-nlp-workshop/blob/master/tutorials/Certification_Trainings/Healthcare/20.SentenceDetectorDL_Healthcare.ipynb)
# 20. SentenceDetectorDL for Healthcare
`SentenceDetectorDL` (SDDL) is based on a general-purpose neural network model for sentence boundary detection. The task of sentence boundary detection is to identify sentences within a text. Many natural language processing tasks take a sentence as an input unit, such as part-of-speech tagging, dependency parsing, named entity recognition or machine translation.
In this model, we treated the sentence boundary detection task as a classification problem using a DL CNN architecture. We also modified the original implemenation a little bit to cover broken sentences and some impossible end of line chars.
```
import json
from google.colab import files
license_keys = files.upload()
with open(list(license_keys.keys())[0]) as f:
license_keys = json.load(f)
%%capture
for k,v in license_keys.items():
%set_env $k=$v
!wget https://raw.githubusercontent.com/JohnSnowLabs/spark-nlp-workshop/master/jsl_colab_setup.sh
!bash jsl_colab_setup.sh
import json
import os
from pyspark.ml import Pipeline,PipelineModel
from pyspark.sql import SparkSession
from sparknlp.annotator import *
from sparknlp_jsl.annotator import *
from sparknlp.base import *
import sparknlp_jsl
import sparknlp
params = {"spark.driver.memory":"16G",
"spark.kryoserializer.buffer.max":"2000M",
"spark.driver.maxResultSize":"2000M"}
spark = sparknlp_jsl.start(license_keys['SECRET'],params=params)
print (sparknlp.version())
print (sparknlp_jsl.version())
documenter = DocumentAssembler()\
.setInputCol("text")\
.setOutputCol("document")
sentencerDL_hc = SentenceDetectorDLModel.pretrained("sentence_detector_dl_healthcare","en","clinical/models") \
.setInputCols(["document"]) \
.setOutputCol("sentences")
sd_pipeline = PipelineModel(stages=[documenter, sentencerDL_hc])
sd_model = LightPipeline(sd_pipeline)
```
# **SetenceDetectorDL_HC** Performance and Comparison with **Spacy Sentence Splitter** on different **Clinical Texts**
```
def get_sentences_sddl(text):
print ('with Spark NLP SentenceDetectorDL_HC')
print ('=======================================')
for anno in sd_model.fullAnnotate(text)[0]["sentences"]:
print("{}\t{}\t{}\t{}".format(
anno.metadata["sentence"], anno.begin, anno.end, anno.result.replace('\n','')))
return
%%capture
!pip install spacy
!python3 -m spacy download en_core_web_sm
import spacy
import en_core_web_sm
nlp = en_core_web_sm.load()
def get_sentences_spacy(text):
print()
print ('with Spacy Sentence Detection')
print ('===================================')
for i,sent in enumerate(nlp(text).sents):
print(i, '\t',str(sent).replace('\n',''))# removing \n to beutify printing
return
```
### Text 1
```
text_1 = '''He was given boluses of MS04 with some effect, he has since been placed on a PCA - he take 80mg of oxycontin at home, his PCA dose is ~ 2 the morphine dose of the oxycontin, he has also received ativan for anxiety.Repleted with 20 meq kcl po, 30 mmol K-phos iv and 2 gms mag so4 iv. LASIX CHANGED TO 40 PO BID WHICH IS SAME AS HE TAKES AT HOME - RECEIVED 40 PO IN AM - 700CC U/O TOTAL FOR FLUID NEGATIVE ~ 600 THUS FAR TODAY, ~ 600 NEG LOS. pt initially hypertensive 160s-180s gave prn doses if IV hydralazine without effect, labetalol increased from 100 mg to 200 mg PO TID which kept SBP > 160 for rest of night.Transferred to the EW found to be hypertensive BP 253/167 HR 132 ST treated with IV NTG gtt 20-120mcg/ and captopril 12.5mg sl x3. During the day pt's resp status has been very tenuous, responded to lasix in the am but then became hypotensive around 1800 tx with 500cc NS bolus and a unit of RBC did improve her BP to 90-100/60 but also became increasingly more tachypneic, RR 30-40's crackles went from bases bilaterally to [**2-14**] way up bilaterally.Lasix given 10mg x 2 during the evening without much change in her respiratory status.10units iv insulin given, 1 amps of 50%dextrose, 1amp of sodium bicard, 2gm calc gluconate.LOPRESSOR 7MG IV Q6H, ENALAPRIL 0.625MG IV Q6H TOLERATED.
ID: Continues to receive flagyl, linazolid, pipercillin, ambisome, gent, and acyclovir, the acyclovir was changed from PO to IV-to be given after dialysis.Meds- Lipitor, procardia, synthroid, lisinopril, pepcid, actonel, calcium, MVI Social- Denies tobacco and drugs.'''
get_sentences_sddl(text_1)
get_sentences_spacy(text_1)
```
### Text 2
```
text_2 = '''ST 109-120 ST. Pt had two 10 beat runs and one 9 beat run of SVT s/p PICC line placement. Stable BP, VT nonsustained. Pt denies CP/SOB. EKG and echo obtained. Cyclying enzymes first CK 69. Cardiology consulted, awaiting echo report. Pt to be started on beta blocker for treatment of NSVT. ? secondary to severe illness.K+ 3.4 IV. IVF with 20meq KCL at 200cc/hr. S/p NSVT pt rec'd 40meq po and 40 meq IV KCL. K+ 3.9 repeat K+ at 8pm. Mg and Ca repleted. Please follow electrolyte SS.
'''
get_sentences_sddl(text_2)
get_sentences_spacy(text_2)
```
### Text 3
```
text_3 = '''PT. IS A 56 Y/O FEMALE S/P CRANIOTOMY ON 7/16 FOR REMOVAL OF BENIGN CYSTIC LESION. SURGERY PERFORMED AT BIDMC.STARTED ON DILANTIN POST-OP FOR SEIZURE PROPHYLAXIS. 2 DAYS PRIOR TO ADMISSION PT DEVELOPED BILAT. EYE DISCHARGE-- SEEN BY EYE MD AND TREATED WITH SULFATE OPTHALMIC DROPS.ALSO DEVELOPED ORAL SORES AND RASH ON CHEST AND RAPIDLY SPREAD TO TRUNK, ARMS, THIGHS, BUTTOCKS, AND FACE WITHIN 24 HRS.UNABLE TO EAT DUE TO MOUTH PAIN. + FEVER, + DIARRHEA, WEAKNESS. PRESENTED TO EW ON 8/4 WITH TEMP 104 SBP 90'S.GIVEN NS FLUID BOLUS, TYLENOL FOR TEMP. SHE PUSTULAR RED RASH ON FACE, RED RASH NOTED ON TRUNK, UPPER EXTREMITIES AND THIGHS. ALSO BOTH EYES DRAINING GREENISH-YELLOW DRAINAGE. ADMITTED TO CCU ( MICU BORDER) FOR CLOSE OBSERVATION.
'''
get_sentences_sddl(text_3)
get_sentences_spacy(text_3)
```
### Text 4
```
text_4 = '''Tylenol 650mg po q6h CVS: Aspirin 121.5mg po daily for graft patency, npn 7p-7a: ccu nsg progress note: s/o: does understand and speak some eng, family visiting this eve and states that pt is oriented and appropriate for them resp--ls w/crackles approx 1/2 up, rr 20's, appeared sl sob, on 4l sat when sitting straight up 95-99%, when lying flat or turning s-s sat does drop to 88-93%, pt does not c/o feeling sob, sat does come back up when sitting up, did rec 40mg iv lasix cardiac hr 90's sr w/occ pvc's, bp 95-106/50's, did not c/o any cp during the noc, conts on hep at 600u/hr, ptt during noc 79, am labs pnd, remains off pressors, at this time no further plans to swan pt or for her to go to cath lab, gi--abd soft, non tender to palpation, (+)bs, passing sm amt of brown soft stool, tol po's w/out diff renal--u/o cont'd low during the eve, team decided to give lasix 40mg in setting of crackles, decreased u/o and sob, did diuresis well to lasix, pt approx 700cc neg today access--pt has 3 peripheral iv's in place, all working, unable to draw bloods from pt d/t poor veins, pt is going to need access to draw bloods, central line or picc line social--son & dtr in visiting w/their famlies tonight, pt awake and conversing w/them a/p: cont to monitor/asses cvs follow resp status, additional lasix f/u w/team re: plan of care for her will need iv access for blood draws keep family & pt updated w/plan, Neuro:On propofol gtt dose increased from 20 to 40mcg/kg/min,moves all extrimities to pain,awaken to stimuly easily,purposeful movements.PERL,had an episode of seizure at 1815 <1min when neuro team in for exam ,responded to 2mg ativan on keprra Iv BID.2 grams mag sulfate given, IVF bolus 250 cc started, approx 50 cc in then dc'd d/t PAD's,2.5 mg IV lopressor given x 2 without effect. CCU NURSING 4P-7P S DENIES CP/SOB O. SEE CAREVUE FLOWSHEET FOR COMPLETE VS 1600 O2 SAT 91% ON 5L N/C, 1 U PRBC'S INFUSING, LUNGS CRACKLES BILATERALLY, LASIX 40MG IV ORDERED, 1200 CC U/O W/IMPROVED O2 SATS ON 4L N/C, IABP AT 1:1 BP 81-107/90-117/48-57, HR 70'S SR, GROIN SITES D+I, HEPARIN REMAINS AT 950 U/HR INTEGRELIN AT 2 MCGS/KG A: IMPROVED U/O AFTER LASIX, AWAITING CARDIAC SURGERY P: CONT SUPPORTIVE CARE, REPEAT HCT POST- TRANSFUSION, CHECK LYTES POST-DIURESIS AND REPLACE AS NEEDED, AWAITING CABG-DATE.Given 50mg IV benadryl and 2mg morphine as well as one aspirin PO and inch of NT paste. When pt remained tachycardic w/ frequent ectopy s/p KCL and tylenol for temp - Orders given by Dr. [**Last Name (STitle) 2025**] to increase diltiazem to 120mg PO QID and NS 250ml given X1 w/ moderate effect.Per team, the pts IV sedation was weaned over the course of the day and now infusing @ 110mcg/hr IV Fentanyl & 9mg/hr IV Verced c pt able to open eyes to verbal stimuli and nod head appropriately to simple commands (are you in pain?). A/P: 73 y/o male remains intubated, IVF boluses x2 for CVP <12, pt continues in NSR on PO amio 400 TID, dopamine gtt weaned down for MAPs>65 but the team felt he is overall receiving about the same amt fentanyl now as he has been in past few days, as the fentanyl patch 100 mcg was added a 48 hrs ago to replace the decrease in the IV fentanyl gtt today (fent patch takes at least 24 hrs to kick in).Started valium 10mg po q6hrs at 1300 with prn IV valium as needed.'''
get_sentences_sddl(text_4)
get_sentences_spacy(text_4)
```
# **SetenceDetectorDL_HC** Performance and Comparison with **Spacy Sentence Splitter** on **Broken Clinical Sentences**
### Broken Text 1
```
random_broken_text_1 = '''He was given boluses of MS04 with some effect, he has since been placed on a PCA
- he take 80mg of oxycontin at home, his PCA dose is ~ 2 the morphine dose of the oxycontin, he has also received ativan for anxiety.Repleted with 20 meq kcl po, 30 m
mol K-phos iv and 2 gms mag so4 iv. LASIX CHANGED TO 40 PO BID WHICH IS SAME AS HE TAKES AT HOME - RECEIVED 40 PO IN AM - 700CC U/O TOTAL FOR FLUID NEGATIVE ~ 600 THUS FAR TODAY, ~ 600 NEG LOS pt initially hypertensive 160s-180s gave prn doses if IV hydralazine without effect, labetalol increased from 100 mg to 200 mg PO TID which kept SBP > 160 for rest of night.Transferred to the EW found to be hypertensive BP 253/167 HR 132 ST treated with IV NTG gtt 20-120mcg/ and captopril 12.5mg sl x3. During the day pt's resp status has been very tenuous, responded to lasix in the am but then became hypotensive around 1800 tx with 500cc NS bolus and a unit of RBC did improve her BP to 90-100/60 but also became increasingly more tachypneic, RR 30-40's crackles went from bases bilaterally to [**2-14**] way up bilaterally.Lasix given 10
mg x 2 during the evening without much change in her respiratory status.10units iv insulin given, 1 amps of 50%dextrose, 1amp of sodium bicard, 2gm calc gluconate.LOPRESSOR 7MG IV Q6H, ENALAPRIL 0.625MG IV Q6H TOLERATED.
ID: Continues to receive flagyl, linazolid, pipercillin, ambisome, gent, and acyclovir, the acyclovir was changed from PO to IV-to be given after dialysis.Meds- Lipitor, procardia, synthroid, lisinopril, pepcid, actonel, calcium, MVI Social- Denies tobacco and drugs.'''
get_sentences_sddl(random_broken_text_1)
get_sentences_spacy(random_broken_text_1)
```
### Broken Text 2
```
random_broken_text_2 = '''A 28-year-
old female with a history of gestational diabetes mellitus diagnosed eight years prior to presentation and subsequent type two diabetes mellitus (
T2DM ),
one prior episode of HTG-induced pancreatitis three years prior to presentation, associated with an acute hepatitis , and obesity with a body mass index ( BMI ) of 33.5
kg/m2 , presented with a one-
week history of polyuria , polydipsia , poor appetite , and vomiting.Two weeks prior to presentation , she was treated with a five-day course of
amoxicillin for a respiratory tract infection.She was on metformin , glipizide , and dapagliflozin for T2DM and atorvastatin and gemfibrozil for HTG . She had been on dapagliflozin for six months at the time of
presentation. Physical examination on presentation was significant for dry oral mucosa ; significantly , her abdominal examination was benign with no tenderness , guarding , or rigidity .
Pertinent laboratory findings on admission were : serum glucose 111 mg
/dl , bicarbonate 18 mmol/l ,
anion gap 20 , creatinine 0.4 mg/dL , triglycerides 508 mg
/dL , total cholesterol 122
mg/dL , glycated hemoglobin ( HbA1c
) 10% , and venous pH 7.27 .Serum lipase was normal at 43U/L .Serum acetone levels could not be assessed as blood samples kept hemolyzing due to significant lipemia.The patient was initially admitted for starvation ketosis , as she reported poor oral intake for three days prior to admission.However , serum chemistry obtained six hours after presentation revealed her glucose was
186 mg/dL , the anion gap was still elevated at 21 , serum bicarbonate was 16 mmol/L , triglyceride level peaked at 2050
mg/dL , and lipase was 52 U/L.The β-hydroxybutyrate level was obtained and found to be elevated at 5.
29
mmol/L -
the original sample was centrifuged and the chylomicron layer removed prior to analysis due to interference from turbidity caused by lipemia again.The patient was treated with an insulin drip for euDKA
and HTG with a reduction in the anion gap to 13 and triglycerides to 1400 mg/
dL , within 24 hours.Her euDKA was thought to be precipitated by her respiratory tract infection in the setting of SGLT2 inhibitor use .
The patient was seen by the endocrinology service and she was discharged on 40
units of insulin glargine at night ,
12 units of insulin lispro with meals , and metformin 1000 mg two times a day.It was determined that all SGLT2 inhibitors should be discontinued indefinitely .'''
get_sentences_sddl(random_broken_text_2)
get_sentences_spacy(random_broken_text_2)
```
### Broken Text 3
```
random_broken_text_3 = ''' Tylenol 650mg po q6h CVS: Aspirin 121.5mg po daily for graft patency.npn 7p-7a: ccu nsg progress note: s/o: does understand and speak some eng, family visiting this eve and states that pt is oriented and appropriate for them resp--ls w/crackles approx 1/2 up, rr 20's, appeared sl sob, on 4l sat when sitting straight up 95-99%, when lying flat or turning s-s sat does drop to 88-93%, pt does not c/o feeling sob,
sat does come back up when sitting up, did rec 40
mg iv lasix cardiac--hr 90's sr w/occ pvc's, bp 95-
106/50's, did not c/o any cp during the noc, conts on hep at 600u/
hr, ptt during noc 79, am labs pnd, remains off pressors, at this time no further plans to swan pt or for her to go to cath lab, gi--abd soft, non tender to palpation, (+)bs, passing sm amt of brown soft stool, tol po's w/out diff renal--u/o cont'd low during the eve,
team decided to give lasix 40mg in setting of crackles, decreased u/o
and sob, did diuresis well to lasix, pt approx 700cc neg today access--pt has 3 peripheral iv's in place, all working, unable to draw bloods from pt d/t poor veins, pt is going to need access to draw bloods, ?central line or picc line social--son & dtr in visiting w/their famlies tonight, pt awake and conversing w/them a/p: cont to monitor/asses cvs follow resp status, additional
lasix f/u w/team re: plan of care for her will need iv access for blood draws keep family & pt updated w/plan, Neuro:On propofol gtt dose increased from 20 to 40mcg/kg/min,moves all extrimities to pain,awaken to stimuly easily,purposeful movements.PERL,had an episode of seizure at 1815 <1min when neuro team in for exam ,responded to 2mg ativan on keprra Iv BID.2 grams mag sulfate given, IVF bolus 250 cc started, approx 50 cc in then dc'd d/t PAD's,
2.5 mg IV lopressor given x 2 without effect. CCU NURSING 4P-7P S DENIES CP/SOB O. SEE CAREVUE FLOWSHEET FOR COMPLETE VS 1600 O2 SAT 91% ON 5L N/C, 1 U PRBC'S INFUSING, LUNGS CRACKLES BILATERALLY, LASIX 40MG IV ORDERED, 1200 CC U/O W/IMPROVED O2 SATS ON 4L N/C, IABP AT 1:1 BP 81-107/90-117/48-57, HR 70'S SR, GROIN SITES D+I, HEPARIN REMAINS AT 950 U/HR INTEGRELIN AT 2 MCGS/KG A: IMPROVED U/O AFTER LASIX, AWAITING CARDIAC SURGERY P: CONT SUPPORTIVE CARE,
REPEAT HCT POST-TRANSFUSION, CHECK LYTES POST-DIURESIS AND REPLACE AS NEEDED, AWAITING CABG -DATE.Given 50mg IV benadryl and 2mg morphine as well as one aspirin PO and inch of NT paste. When pt remained tachycardic w/ frequent ectopy s/p KCL and tylenol for temp - Orders given by Dr. [**Last Name (STitle) 2025**] to increase diltiazem to 120mg PO QID and NS 250ml given X1 w/ moderate effect.Per team, the pts IV sedation was weaned over the course of the
day and now infusing @ 110mcg/hr IV Fentanyl & 9mg/hr IV Verced c pt able to open eyes to verbal stimuli and nod head appropriately to simple commands (are you in pain?) . A/P: 73 y/o male remains intubated, IVF boluses x2 for CVP <12, pt continues in NSR on PO amio 400 TID, dopamine gtt weaned down for MAPs>65 but the team felt he is overall receiving about the same amt fentanyl now as he has been in past few days, as the fentanyl patch 100
mcg was added a 48 hrs ago to replace the decrease in the IV fentanyl gtt today (fent patch takes at least 24 hrs to kick in).Started valium 10mg po q6hrs at 1300 with prn IV valium as needed.'''
get_sentences_sddl(random_broken_text_3)
get_sentences_spacy(random_broken_text_3)
```
| true |
code
| 0.277975 | null | null | null | null |
|
```
# Imports / Requirements
import json
import numpy as np
import torch
import matplotlib.pyplot as plt
import torch.nn.functional as F
import torchvision
from torch import nn, optim
from torchvision import datasets, transforms, models
from torch.autograd import Variable
from collections import OrderedDict
from PIL import Image
%matplotlib inline
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
!python --version
print(f"PyTorch Version {torch.__version__}")
```
# Developing an AI application
Going forward, AI algorithms will be incorporated into more and more everyday applications. For example, you might want to include an image classifier in a smart phone app. To do this, you'd use a deep learning model trained on hundreds of thousands of images as part of the overall application architecture. A large part of software development in the future will be using these types of models as common parts of applications.
In this project, you'll train an image classifier to recognize different species of flowers. You can imagine using something like this in a phone app that tells you the name of the flower your camera is looking at. In practice you'd train this classifier, then export it for use in your application. We'll be using [this dataset](http://www.robots.ox.ac.uk/~vgg/data/flowers/102/index.html) of 102 flower categories, you can see a few examples below.
<img src='assets/Flowers.png' width=500px>
The project is broken down into multiple steps:
* Load and preprocess the image dataset
* Train the image classifier on your dataset
* Use the trained classifier to predict image content
We'll lead you through each part which you'll implement in Python.
When you've completed this project, you'll have an application that can be trained on any set of labeled images. Here your network will be learning about flowers and end up as a command line application. But, what you do with your new skills depends on your imagination and effort in building a dataset. For example, imagine an app where you take a picture of a car, it tells you what the make and model is, then looks up information about it. Go build your own dataset and make something new.
First up is importing the packages you'll need. It's good practice to keep all the imports at the beginning of your code. As you work through this notebook and find you need to import a package, make sure to add the import up here.
## Load the data
Here you'll use `torchvision` to load the data ([documentation](http://pytorch.org/docs/0.3.0/torchvision/index.html)). The data should be included alongside this notebook, otherwise you can [download it here](https://s3.amazonaws.com/content.udacity-data.com/nd089/flower_data.tar.gz). The dataset is split into three parts, training, validation, and testing. For the training, you'll want to apply transformations such as random scaling, cropping, and flipping. This will help the network generalize leading to better performance. You'll also need to make sure the input data is resized to 224x224 pixels as required by the pre-trained networks.
The validation and testing sets are used to measure the model's performance on data it hasn't seen yet. For this you don't want any scaling or rotation transformations, but you'll need to resize then crop the images to the appropriate size.
The pre-trained networks you'll use were trained on the ImageNet dataset where each color channel was normalized separately. For all three sets you'll need to normalize the means and standard deviations of the images to what the network expects. For the means, it's `[0.485, 0.456, 0.406]` and for the standard deviations `[0.229, 0.224, 0.225]`, calculated from the ImageNet images. These values will shift each color channel to be centered at 0 and range from -1 to 1.
```
data_dir = 'flowers'
train_dir = data_dir + '/train'
valid_dir = data_dir + '/valid'
test_dir = data_dir + '/test'
# pre-trained network expectations
# see: https://pytorch.org/docs/stable/torchvision/models.html
expected_means = [0.485, 0.456, 0.406]
expected_std = [0.229, 0.224, 0.225]
max_image_size = 224
batch_size = 32
# DONE: Define your transforms for the training, validation, and testing sets
data_transforms = {
"training": transforms.Compose([transforms.RandomHorizontalFlip(p=0.25),
transforms.RandomRotation(25),
transforms.RandomGrayscale(p=0.02),
transforms.RandomResizedCrop(max_image_size),
transforms.ToTensor(),
transforms.Normalize(expected_means, expected_std)]),
"validation": transforms.Compose([transforms.Resize(max_image_size + 1),
transforms.CenterCrop(max_image_size),
transforms.ToTensor(),
transforms.Normalize(expected_means, expected_std)]),
"testing": transforms.Compose([transforms.Resize(max_image_size + 1),
transforms.CenterCrop(max_image_size),
transforms.ToTensor(),
transforms.Normalize(expected_means, expected_std)])
}
# DONE: Load the datasets with ImageFolder
image_datasets = {
"training": datasets.ImageFolder(train_dir, transform=data_transforms["training"]),
"validation": datasets.ImageFolder(valid_dir, transform=data_transforms["validation"]),
"testing": datasets.ImageFolder(test_dir, transform=data_transforms["testing"])
}
# DONE: Using the image datasets and the trainforms, define the dataloaders
dataloaders = {
"training": torch.utils.data.DataLoader(image_datasets["training"], batch_size=batch_size, shuffle=True),
"validation": torch.utils.data.DataLoader(image_datasets["validation"], batch_size=batch_size),
"testing": torch.utils.data.DataLoader(image_datasets["testing"], batch_size=batch_size)
}
```
### Label mapping
You'll also need to load in a mapping from category label to category name. You can find this in the file `cat_to_name.json`. It's a JSON object which you can read in with the [`json` module](https://docs.python.org/2/library/json.html). This will give you a dictionary mapping the integer encoded categories to the actual names of the flowers.
```
import json
with open('cat_to_name.json', 'r') as f:
cat_to_name = json.load(f)
print(f"Images are labeled with {len(cat_to_name)} categories.")
```
# Building and training the classifier
Now that the data is ready, it's time to build and train the classifier. As usual, you should use one of the pretrained models from `torchvision.models` to get the image features. Build and train a new feed-forward classifier using those features.
We're going to leave this part up to you. If you want to talk through it with someone, chat with your fellow students! You can also ask questions on the forums or join the instructors in office hours.
Refer to [the rubric](https://review.udacity.com/#!/rubrics/1663/view) for guidance on successfully completing this section. Things you'll need to do:
* Load a [pre-trained network](http://pytorch.org/docs/master/torchvision/models.html) (If you need a starting point, the VGG networks work great and are straightforward to use)
* Define a new, untrained feed-forward network as a classifier, using ReLU activations and dropout
* Train the classifier layers using backpropagation using the pre-trained network to get the features
* Track the loss and accuracy on the validation set to determine the best hyperparameters
We've left a cell open for you below, but use as many as you need. Our advice is to break the problem up into smaller parts you can run separately. Check that each part is doing what you expect, then move on to the next. You'll likely find that as you work through each part, you'll need to go back and modify your previous code. This is totally normal!
When training make sure you're updating only the weights of the feed-forward network. You should be able to get the validation accuracy above 70% if you build everything right. Make sure to try different hyperparameters (learning rate, units in the classifier, epochs, etc) to find the best model. Save those hyperparameters to use as default values in the next part of the project.
```
# DONE: Build and train your network
# Get model Output Size = Number of Categories
output_size = len(cat_to_name)
# Using VGG16.
nn_model = models.vgg16(pretrained=True)
# Input size from current classifier
input_size = nn_model.classifier[0].in_features
hidden_size = [
(input_size // 8),
(input_size // 32)
]
# Prevent backpropigation on parameters
for param in nn_model.parameters():
param.requires_grad = False
# Create nn.Module with Sequential using an OrderedDict
# See https://pytorch.org/docs/stable/nn.html#torch.nn.Sequential
classifier = nn.Sequential(OrderedDict([
('fc1', nn.Linear(input_size, hidden_size[0])),
('relu1', nn.ReLU()),
('dropout', nn.Dropout(p=0.15)),
('fc2', nn.Linear(hidden_size[0], hidden_size[1])),
('relu2', nn.ReLU()),
('dropout', nn.Dropout(p=0.15)),
('output', nn.Linear(hidden_size[1], output_size)),
# LogSoftmax is needed by NLLLoss criterion
('softmax', nn.LogSoftmax(dim=1))
]))
# Replace classifier
nn_model.classifier = classifier
hidden_size
torch.cuda.is_available()
device
# hyperparameters
# https://en.wikipedia.org/wiki/Hyperparameter
epochs = 5
learning_rate = 0.001
chk_every = 50
# Start clean by setting gradients of all parameters to zero.
nn_model.zero_grad()
# The negative log likelihood loss as criterion.
criterion = nn.NLLLoss()
# Adam: A Method for Stochastic Optimization
# https://arxiv.org/abs/1412.6980
optimizer = optim.Adam(nn_model.classifier.parameters(), lr=learning_rate)
# Move model to perferred device.
nn_model = nn_model.to(device)
data_set_len = len(dataloaders["training"].batch_sampler)
total_val_images = len(dataloaders["validation"].batch_sampler) * dataloaders["validation"].batch_size
print(f'Using the {device} device to train.')
print(f'Training on {data_set_len} batches of {dataloaders["training"].batch_size}.')
print(f'Displaying average loss and accuracy for epoch every {chk_every} batches.')
for e in range(epochs):
e_loss = 0
prev_chk = 0
total = 0
correct = 0
print(f'\nEpoch {e+1} of {epochs}\n----------------------------')
for ii, (images, labels) in enumerate(dataloaders["training"]):
# Move images and labeles preferred device
# if they are not already there
images = images.to(device)
labels = labels.to(device)
# Set gradients of all parameters to zero.
optimizer.zero_grad()
# Propigate forward and backward
outputs = nn_model.forward(images)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# Keep a running total of loss for
# this epoch
e_loss += loss.item()
# Accuracy
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
# Keep a running total of loss for
# this epoch
itr = (ii + 1)
if itr % chk_every == 0:
avg_loss = f'avg. loss: {e_loss/itr:.4f}'
acc = f'accuracy: {(correct/total) * 100:.2f}%'
print(f' Batches {prev_chk:03} to {itr:03}: {avg_loss}, {acc}.')
prev_chk = (ii + 1)
# Validate Epoch
e_valid_correct = 0
e_valid_total = 0
# Disabling gradient calculation
with torch.no_grad():
for ii, (images, labels) in enumerate(dataloaders["validation"]):
# Move images and labeles perferred device
# if they are not already there
images = images.to(device)
labels = labels.to(device)
outputs = nn_model(images)
_, predicted = torch.max(outputs.data, 1)
e_valid_total += labels.size(0)
e_valid_correct += (predicted == labels).sum().item()
print(f"\n\tValidating for epoch {e+1}...")
correct_perc = 0
if e_valid_correct > 0:
correct_perc = (100 * e_valid_correct // e_valid_total)
print(f'\tAccurately classified {correct_perc:d}% of {total_val_images} images.')
print('Done...')
```
## Testing your network
It's good practice to test your trained network on test data, images the network has never seen either in training or validation. This will give you a good estimate for the model's performance on completely new images. Run the test images through the network and measure the accuracy, the same way you did validation. You should be able to reach around 70% accuracy on the test set if the model has been trained well.
```
# DONE: Do validation on the test set
correct = 0
total = 0
total_images = len(dataloaders["testing"].batch_sampler) * dataloaders["testing"].batch_size
# Disabling gradient calculation
with torch.no_grad():
for ii, (images, labels) in enumerate(dataloaders["testing"]):
# Move images and labeles perferred device
# if they are not already there
images = images.to(device)
labels = labels.to(device)
outputs = nn_model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print(f'Accurately classified {(100 * correct // total):d}% of {total_images} images.')
```
## Save the checkpoint
Now that your network is trained, save the model so you can load it later for making predictions. You probably want to save other things such as the mapping of classes to indices which you get from one of the image datasets: `image_datasets['train'].class_to_idx`. You can attach this to the model as an attribute which makes inference easier later on.
```model.class_to_idx = image_datasets['train'].class_to_idx```
Remember that you'll want to completely rebuild the model later so you can use it for inference. Make sure to include any information you need in the checkpoint. If you want to load the model and keep training, you'll want to save the number of epochs as well as the optimizer state, `optimizer.state_dict`. You'll likely want to use this trained model in the next part of the project, so best to save it now.
```
# DONE: Save the checkpoint
def save_checkpoint(model_state, file='checkpoint.pth'):
torch.save(model_state, file)
nn_model.class_to_idx = image_datasets['training'].class_to_idx
model_state = {
'epoch': epochs,
'state_dict': nn_model.state_dict(),
'optimizer_dict': optimizer.state_dict(),
'classifier': classifier,
'class_to_idx': nn_model.class_to_idx,
}
save_checkpoint(model_state, 'checkpoint.pth')
```
## Loading the checkpoint
At this point it's good to write a function that can load a checkpoint and rebuild the model. That way you can come back to this project and keep working on it without having to retrain the network.
```
# DONE: Write a function that loads a checkpoint and rebuilds the model
def load_checkpoint(file='checkpoint.pth'):
# Loading weights for CPU model while trained on GP
# https://discuss.pytorch.org/t/loading-weights-for-cpu-model-while-trained-on-gpu/1032
model_state = torch.load(file, map_location=lambda storage, loc: storage)
model = models.vgg16(pretrained=True)
model.classifier = model_state['classifier']
model.load_state_dict(model_state['state_dict'])
model.class_to_idx = model_state['class_to_idx']
return model
chkp_model = load_checkpoint()
```
# Inference for classification
Now you'll write a function to use a trained network for inference. That is, you'll pass an image into the network and predict the class of the flower in the image. Write a function called `predict` that takes an image and a model, then returns the top $K$ most likely classes along with the probabilities. It should look like
```python
probs, classes = predict(image_path, model)
print(probs)
print(classes)
> [ 0.01558163 0.01541934 0.01452626 0.01443549 0.01407339]
> ['70', '3', '45', '62', '55']
```
First you'll need to handle processing the input image such that it can be used in your network.
## Image Preprocessing
You'll want to use `PIL` to load the image ([documentation](https://pillow.readthedocs.io/en/latest/reference/Image.html)). It's best to write a function that preprocesses the image so it can be used as input for the model. This function should process the images in the same manner used for training.
First, resize the images where the shortest side is 256 pixels, keeping the aspect ratio. This can be done with the [`thumbnail`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) or [`resize`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) methods. Then you'll need to crop out the center 224x224 portion of the image.
Color channels of images are typically encoded as integers 0-255, but the model expected floats 0-1. You'll need to convert the values. It's easiest with a Numpy array, which you can get from a PIL image like so `np_image = np.array(pil_image)`.
As before, the network expects the images to be normalized in a specific way. For the means, it's `[0.485, 0.456, 0.406]` and for the standard deviations `[0.229, 0.224, 0.225]`. You'll want to subtract the means from each color channel, then divide by the standard deviation.
And finally, PyTorch expects the color channel to be the first dimension but it's the third dimension in the PIL image and Numpy array. You can reorder dimensions using [`ndarray.transpose`](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.ndarray.transpose.html). The color channel needs to be first and retain the order of the other two dimensions.
```
def process_image(image):
''' Scales, crops, and normalizes a PIL image for a PyTorch model,
returns an Numpy array
'''
expects_means = [0.485, 0.456, 0.406]
expects_std = [0.229, 0.224, 0.225]
pil_image = Image.open(image).convert("RGB")
# Any reason not to let transforms do all the work here?
in_transforms = transforms.Compose([transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize(expects_means, expects_std)])
pil_image = in_transforms(pil_image)
return pil_image
# DONE: Process a PIL image for use in a PyTorch model
chk_image = process_image(valid_dir + '/1/image_06739.jpg')
type(chk_image)
```
To check your work, the function below converts a PyTorch tensor and displays it in the notebook. If your `process_image` function works, running the output through this function should return the original image (except for the cropped out portions).
```
def imshow(image, ax=None, title=None):
if ax is None:
fig, ax = plt.subplots()
# PyTorch tensors assume the color channel is the first dimension
# but matplotlib assumes is the third dimension
image = image.transpose((1, 2, 0))
# Undo preprocessing
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
image = std * image + mean
# Image needs to be clipped between 0 and 1 or it looks like noise when displayed
image = np.clip(image, 0, 1)
ax.imshow(image)
return ax
imshow(chk_image.numpy())
```
## Class Prediction
Once you can get images in the correct format, it's time to write a function for making predictions with your model. A common practice is to predict the top 5 or so (usually called top-$K$) most probable classes. You'll want to calculate the class probabilities then find the $K$ largest values.
To get the top $K$ largest values in a tensor use [`x.topk(k)`](http://pytorch.org/docs/master/torch.html#torch.topk). This method returns both the highest `k` probabilities and the indices of those probabilities corresponding to the classes. You need to convert from these indices to the actual class labels using `class_to_idx` which hopefully you added to the model or from an `ImageFolder` you used to load the data ([see here](#Save-the-checkpoint)). Make sure to invert the dictionary so you get a mapping from index to class as well.
Again, this method should take a path to an image and a model checkpoint, then return the probabilities and classes.
```python
probs, classes = predict(image_path, model)
print(probs)
print(classes)
> [ 0.01558163 0.01541934 0.01452626 0.01443549 0.01407339]
> ['70', '3', '45', '62', '55']
```
```
def predict(image_path, model, topk=5):
''' Predict the class (or classes) of an image using a trained deep learning model.
'''
# DONE: Implement the code to predict the class from an image file
# evaluation mode
# https://pytorch.org/docs/stable/nn.html#torch.nn.Module.eval
model.eval()
# cpu mode
model.cpu()
# load image as torch.Tensor
image = process_image(image_path)
# Unsqueeze returns a new tensor with a dimension of size one
# https://pytorch.org/docs/stable/torch.html#torch.unsqueeze
image = image.unsqueeze(0)
# Disabling gradient calculation
# (not needed with evaluation mode?)
with torch.no_grad():
output = model.forward(image)
top_prob, top_labels = torch.topk(output, topk)
# Calculate the exponentials
top_prob = top_prob.exp()
class_to_idx_inv = {model.class_to_idx[k]: k for k in model.class_to_idx}
mapped_classes = list()
for label in top_labels.numpy()[0]:
mapped_classes.append(class_to_idx_inv[label])
return top_prob.numpy()[0], mapped_classes
```
## Sanity Checking
Now that you can use a trained model for predictions, check to make sure it makes sense. Even if the testing accuracy is high, it's always good to check that there aren't obvious bugs. Use `matplotlib` to plot the probabilities for the top 5 classes as a bar graph, along with the input image. It should look like this:
<img src='assets/inference_example.png' width=300px>
You can convert from the class integer encoding to actual flower names with the `cat_to_name.json` file (should have been loaded earlier in the notebook). To show a PyTorch tensor as an image, use the `imshow` function defined above.
```
# DONE: Display an image along with the top 5 classes
chk_image_file = valid_dir + '/55/image_04696.jpg'
correct_class = cat_to_name['55']
top_prob, top_classes = predict(chk_image_file, chkp_model)
label = top_classes[0]
fig = plt.figure(figsize=(6,6))
sp_img = plt.subplot2grid((15,9), (0,0), colspan=9, rowspan=9)
sp_prd = plt.subplot2grid((15,9), (9,2), colspan=5, rowspan=5)
image = Image.open(chk_image_file)
sp_img.axis('off')
sp_img.set_title(f'{cat_to_name[label]}')
sp_img.imshow(image)
labels = []
for class_idx in top_classes:
labels.append(cat_to_name[class_idx])
yp = np.arange(5)
sp_prd.set_yticks(yp)
sp_prd.set_yticklabels(labels)
sp_prd.set_xlabel('Probability')
sp_prd.invert_yaxis()
sp_prd.barh(yp, top_prob, xerr=0, align='center', color='blue')
plt.show()
print(f'Correct classification: {correct_class}')
print(f'Correct prediction: {correct_class == cat_to_name[label]}')
```
| true |
code
| 0.833189 | null | null | null | null |
|
## Eng+Wales well-mixed example model
This is the inference notebook. There are various model variants as encoded by `expt_params_local` and `model_local`, which are shared by the notebooks in a given directory.
Outputs of this notebook:
* `ewMod-inf.pik` : result of inference computation
* `ewMod-hess.npy` : hessian matrix of log-posterior
NOTE carefully : `Im` compartment is cumulative deaths, this is called `D` elsewhere
### Start notebook
(the following line is for efficient parallel processing)
```
%env OMP_NUM_THREADS=1
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
import pyross
import time
import pandas as pd
import matplotlib.image as mpimg
import pickle
import os
import pprint
import scipy.stats
# comment these before commit
#print(pyross.__file__)
#print(os.getcwd())
from ew_fns import *
import expt_params_local
import model_local
```
### switches etc
```
verboseMod=False ## print ancillary info about the model? (would usually be False, for brevity)
## Calculate things, or load from files ?
doInf = False ## do inference, or load it ?
doHes = False ## Hessian may take a few minutes !! does this get removed? what to do?
## time unit is one week
daysPerWeek = 7.0
## these are params that might be varied in different expts
exptParams = expt_params_local.getLocalParams()
pprint.pprint(exptParams)
## this is used for filename handling throughout
pikFileRoot = exptParams['pikFileRoot']
```
### convenient settings
```
np.set_printoptions(precision=3)
pltAuto = True
plt.rcParams.update({'figure.autolayout': pltAuto})
plt.rcParams.update({'font.size': 14})
```
## LOAD MODEL
```
loadModel = model_local.loadModel(exptParams,daysPerWeek,verboseMod)
## should use a dictionary but...
[ numCohorts, fi, N, Ni, model_spec, estimator, contactBasis, interventionFn,
modParams, priorsAll, initPriorsLinMode, obsDeath, fltrDeath,
simTime, deathCumulativeDat ] = loadModel
```
### Inspect most likely trajectory for model with prior mean params
```
x0_lin = estimator.get_mean_inits(initPriorsLinMode, obsDeath[0], fltrDeath)
guessTraj = estimator.integrate( x0_lin, exptParams['timeZero'], simTime, simTime+1)
## plots
yesPlot = model_spec['classes'].copy()
yesPlot.remove('S')
plt.yscale('log')
for lab in yesPlot :
indClass = model_spec['classes'].index(lab)
totClass = np.sum(guessTraj[:,indClass*numCohorts:(indClass+1)*numCohorts],axis=1)
plt.plot( N * totClass,'-',lw=3,label=lab)
plt.plot(N*np.sum(obsDeath,axis=1),'X',label='data')
plt.legend(fontsize=14,bbox_to_anchor=(1, 1.0))
plt.xlabel('time in weeks')
plt.ylabel('class population')
plt.show() ; plt.close()
indClass = model_spec['classes'].index('Im')
plt.yscale('log')
for coh in range(numCohorts):
plt.plot( N*guessTraj[:,coh+indClass*numCohorts],label='m{c:d}'.format(c=coh) )
plt.xlabel('time in weeks')
plt.ylabel('cumul deaths by age cohort')
plt.legend(fontsize=8,bbox_to_anchor=(1, 1.0))
plt.show() ; plt.close()
```
## INFERENCE
parameter count
* 32 for age-dependent Ai and Af (or beta and Af)
* 2 (step-like) or 3 (NPI-with-easing) for lockdown time and width (+easing param)
* 1 for projection of initial condition along mode
* 5 for initial condition in oldest cohort
* 5 for the gammas
* 1 for beta in late stage
total: 46 (step-like) or 47 (with-easing)
The following computation with CMA-ES takes some minutes depending on compute power, it should use multiple CPUs efficiently, if available. The result will vary (slightly) according to the random seed, can be controlled by passing `cma_random_seed` to `latent_infer`
```
def runInf() :
infResult = estimator.latent_infer(obsDeath, fltrDeath, simTime,
priorsAll,
initPriorsLinMode,
generator=contactBasis,
intervention_fun=interventionFn,
tangent=False,
verbose=True,
enable_global=True,
enable_local =True,
**exptParams['infOptions'],
)
return infResult
if doInf:
## do the computation
elapsedInf = time.time()
infResult = runInf()
elapsedInf = time.time() - elapsedInf
print('** elapsed time',elapsedInf/60.0,'mins')
# save the answer
opFile = pikFileRoot + "-inf.pik"
print('opf',opFile)
with open(opFile, 'wb') as f:
pickle.dump([infResult,elapsedInf],f)
else:
## load a saved computation
print(' Load data')
# here we load the data
# (this may be the file that we just saved, it is deliberately outside the if: else:)
ipFile = pikFileRoot + "-inf.pik"
print('ipf',ipFile)
with open(ipFile, 'rb') as f:
[infResult,elapsedInf] = pickle.load(f)
```
#### unpack results
```
epiParamsMAP = infResult['params_dict']
conParamsMAP = infResult['control_params_dict']
x0_MAP = infResult['x0']
CM_MAP = contactBasis.intervention_custom_temporal( interventionFn,
**conParamsMAP)
logPinf = -estimator.minus_logp_red(epiParamsMAP, x0_MAP, obsDeath, fltrDeath, simTime,
CM_MAP, tangent=False)
print('** measuredLikelihood',logPinf)
print('** logPosterior ',infResult['log_posterior'])
print('** logLikelihood',infResult['log_likelihood'])
```
#### MAP dominant trajectory
```
estimator.set_params(epiParamsMAP)
estimator.set_contact_matrix(CM_MAP)
trajMAP = estimator.integrate( x0_MAP, exptParams['timeZero'], simTime, simTime+1)
yesPlot = model_spec['classes'].copy()
yesPlot.remove('S')
plt.yscale('log')
for lab in yesPlot :
indClass = model_spec['classes'].index(lab)
totClass = np.sum(trajMAP[:,indClass*numCohorts:(indClass+1)*numCohorts],axis=1)
plt.plot( N * totClass,'-',lw=3,label=lab)
plt.plot(N*np.sum(obsDeath,axis=1),'X',label='data')
plt.xlabel('time in weeks')
plt.ylabel('class population')
plt.legend(fontsize=14,bbox_to_anchor=(1, 1.0))
plt.show() ; plt.close()
fig,axs = plt.subplots(1,2,figsize=(10,4.5))
cohRanges = [ [x,x+4] for x in range(0,75,5) ]
#print(cohRanges)
cohLabs = ["{l:d}-{u:d}".format(l=low,u=up) for [low,up] in cohRanges ]
cohLabs.append("75+")
ax = axs[0]
ax.set_title('MAP (average dynamics)')
mSize = 3
minY = 0.12
maxY = 1.0
indClass = model_spec['classes'].index('Im')
ax.set_yscale('log')
ax.set_ylabel('cumulative M (by cohort)')
ax.set_xlabel('time/weeks')
for coh in reversed(list(range(numCohorts))) :
ax.plot( N*trajMAP[:,coh+indClass*numCohorts],'o-',label=cohLabs[coh],ms=mSize )
maxY = np.maximum( maxY, np.max(N*trajMAP[:,coh+indClass*numCohorts]))
#ax.legend(fontsize=8,bbox_to_anchor=(1, 1.0))
maxY *= 1.6
ax.set_ylim(bottom=minY,top=maxY)
#plt.show() ; plt.close()
ax = axs[1]
ax.set_title('data')
ax.set_xlabel('time/weeks')
indClass = model_spec['classes'].index('Im')
ax.set_yscale('log')
for coh in reversed(list(range(numCohorts))) :
ax.plot( N*obsDeath[:,coh],'o-',label=cohLabs[coh],ms=mSize )
## keep the same as other panel
ax.set_ylim(bottom=minY,top=maxY)
ax.legend(fontsize=10,bbox_to_anchor=(1, 1.0))
#plt.show() ; plt.close()
#plt.savefig('ageMAPandData.png')
plt.show(fig)
```
#### sanity check : plot the prior and inf value for one or two params
```
(likFun,priFun,dim) = pyross.evidence.latent_get_parameters(estimator,
obsDeath, fltrDeath, simTime,
priorsAll,
initPriorsLinMode,
generator=contactBasis,
intervention_fun=interventionFn,
tangent=False,
)
def showInfPrior(xLab) :
fig = plt.figure(figsize=(4,4))
dimFlat = np.size(infResult['flat_params'])
## magic to work out the index of this param in flat_params
jj = infResult['param_keys'].index(xLab)
xInd = infResult['param_guess_range'][jj]
## get the range
xVals = np.linspace( *priorsAll[xLab]['bounds'], 100 )
#print(infResult['flat_params'][xInd])
pVals = []
checkVals = []
for xx in xVals :
flatP = np.zeros( dimFlat )
flatP[xInd] = xx
pdfAll = np.exp( priFun.logpdf(flatP) )
pVals.append( pdfAll[xInd] )
#checkVals.append( scipy.stats.norm.pdf(xx,loc=0.2,scale=0.1) )
plt.plot(xVals,pVals,'-',label='prior')
infVal = infResult['flat_params'][xInd]
infPdf = np.exp( priFun.logpdf(infResult['flat_params']) )[xInd]
plt.plot([infVal],[infPdf],'ro',label='inf')
plt.xlabel(xLab)
upperLim = 1.05*np.max(pVals)
plt.ylim(0,upperLim)
#plt.plot(xVals,checkVals)
plt.legend()
plt.show(fig) ; plt.close()
#print('**params\n',infResult['flat_params'])
#print('**logPrior\n',priFun.logpdf(infResult['flat_params']))
showInfPrior('gammaE')
```
## Hessian matrix of log-posterior
(this can take a few minutes, it does not make use of multiple cores)
```
if doHes:
## this eps amounts to a perturbation of approx 1% on each param
## (1/4) power of machine epsilon is standard for second deriv
xx = infResult['flat_params']
eps = 100 * xx*( np.spacing(xx)/xx )**(0.25)
#print('**params\n',infResult['flat_params'])
#print('** rel eps\n',eps/infResult['flat_params'])
CM_MAP = contactBasis.intervention_custom_temporal( interventionFn,
**conParamsMAP)
estimator.set_params(epiParamsMAP)
estimator.set_contact_matrix(CM_MAP)
start = time.time()
hessian = estimator.latent_hessian(obs=obsDeath, fltr=fltrDeath,
Tf=simTime, generator=contactBasis,
infer_result=infResult,
intervention_fun=interventionFn,
eps=eps, tangent=False, fd_method="central",
inter_steps=0)
end = time.time()
print('time',(end-start)/60,'mins')
opFile = pikFileRoot + "-hess.npy"
print('opf',opFile)
with open(opFile, 'wb') as f:
np.save(f,hessian)
else :
print('Load hessian')
# reload in all cases (even if we just saved it)
ipFile = pikFileRoot + "-hess.npy"
try:
print('ipf',ipFile)
with open(ipFile, 'rb') as f:
hessian = np.load(f)
except (OSError, IOError) :
print('... error loading hessian')
hessian = None
#print(hessian)
print("** param vals")
print(infResult['flat_params'],'\n')
if np.all(hessian) != None :
print("** naive uncertainty v1 : reciprocal sqrt diagonal elements (x2)")
print( 2/np.sqrt(np.diagonal(hessian)) ,'\n')
print("** naive uncertainty v2 : sqrt diagonal elements of inverse (x2)")
print( 2*np.sqrt(np.diagonal(np.linalg.inv(hessian))) ,'\n')
```
| true |
code
| 0.556942 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/mnslarcher/cs224w-slides-to-code/blob/main/notebooks/04-link-analysis-pagerank.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Link Analysis: PageRank
```
import random
from typing import Optional
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
def seed_everything(seed: Optional[int] = None) -> None:
random.seed(seed)
np.random.seed(seed)
seed_everything(42)
```
# Example: Flow Equations & M
```
def get_stochastic_adjacency_matrix(G: nx.Graph) -> np.ndarray:
nodes = list(G.nodes())
num_nodes = len(nodes)
M = np.zeros((num_nodes, num_nodes))
for j, node_j in enumerate(nodes):
in_edges = G.in_edges(node_j)
for in_edge in G.in_edges(node_j):
node_i = in_edge[0]
i = nodes.index(node_i)
M[j, i] += 1.0 / G.out_degree(node_i)
return M
# Or, more concise but slower:
# def get_stochastic_adjacency_matrix(G: nx.Graph) -> np.ndarray:
# A = nx.adjacency_matrix(G).todense().astype(float)
# out_degrees = np.array([degree[1] for degree in G.out_degree()])
# return np.divide(A, out_degrees, out=np.zeros_like(A), where=out_degrees != 0)
edge_list = [("y", "a"), ("y", "y"), ("a", "m"), ("a", "y"), ("m", "a")]
G = nx.DiGraph(edge_list)
M = get_stochastic_adjacency_matrix(G)
plt.figure(figsize=(4, 3))
# Self/multiple edges visualization sucks
nx.draw(G, node_color="tab:red", node_size=1500, with_labels=True)
plt.show()
print(f"\nStochastic Adjacency Matrix M (nodes {G.nodes()}):")
print(M)
```
# Summary: Page Rank Variants
```
def pagerank_example(
personalization: Optional[dict] = None,
spring_layout_k: float = 5.0,
label_rank_threshold: float = 0.02,
cmap_name: str = "viridis",
node_size_factor: float = 2e4,
width: float = 1.5,
font_size: int = 16,
seed: Optional[int] = 42,
) -> None:
edge_list = [
("B", "C"),
("C", "B"),
("D", "A"),
("D", "B"),
("E", "B"),
("E", "D"),
("E", "F"),
("F", "B"),
("F", "E"),
("G", "B"),
("G", "E"),
("H", "B"),
("H", "E"),
("I", "B"),
("I", "E"),
("J", "E"),
("K", "E"),
]
G = nx.DiGraph(edge_list)
ranks = nx.pagerank(G, personalization=personalization)
max_rank = max(ranks.values())
node_sizes = [max(100.0, node_size_factor * rank / max_rank) for node, rank in ranks.items()]
cmap = plt.get_cmap(cmap_name)
node_colors = [cmap(rank / max_rank) for node, rank in ranks.items()]
node_lables = {
node: f"{node}\n{100 * ranks[node]:.1f}" if ranks[node] > label_rank_threshold else "" for node in G.nodes
}
pos = nx.spring_layout(G, k=spring_layout_k, seed=seed)
nx.draw(
G,
pos=pos,
node_color=node_colors,
labels=node_lables,
edgecolors="black",
node_size=node_sizes,
width=1.5,
font_size=font_size,
)
```
## PageRank
```
personalization = None # Equivalent to {"A": 1 / num_nodes, "B": 1 / num_nodes, ...}
plt.figure(figsize=(6, 6))
pagerank_example(personalization=personalization)
plt.title("PageRank", fontsize=16)
plt.show()
```
## Personalized PageRank
```
personalization = {"A": 0.1, "D": 0.2, "G": 0.5, "J": 0.2}
plt.figure(figsize=(6, 6))
pagerank_example(personalization=personalization)
plt.title(f"Personalized PageRank\n(personalization = {personalization})", fontsize=16)
plt.show()
```
## Random Walk with Restarts
```
personalization = {"E": 1.0}
plt.figure(figsize=(6, 6))
pagerank_example(personalization=personalization)
plt.title(f"Random Walk with Restarts\n(personalization = {personalization})", fontsize=16)
plt.show()
```
| true |
code
| 0.787799 | null | null | null | null |
|
# Background
This notebook walks through the creation of a fastai [DataBunch](https://docs.fast.ai/basic_data.html#DataBunch) object. This object contains a pytorch dataloader for the train, valid and test sets. From the documentation:
```
Bind train_dl,valid_dl and test_dl in a data object.
It also ensures all the dataloaders are on device and applies to them dl_tfms as batch are drawn (like normalization). path is used internally to store temporary files, collate_fn is passed to the pytorch Dataloader (replacing the one there) to explain how to collate the samples picked for a batch.
```
Because we are training the language model, we want our dataloader to construct the target variable from the input data. The target variable for language models are the next word in a sentence. Furthermore, there are other optimizations with regard to the sequence length and concatenating texts together that avoids wasteful padding. Luckily the [TextLMDataBunch](https://docs.fast.ai/text.data.html#TextLMDataBunch) does all this work for us (and more) automatically.
```
from fastai.text import TextLMDataBunch as lmdb
from fastai.text.transform import Tokenizer
import pandas as pd
from pathlib import Path
```
### Read in Data
You can download the above saved dataframes (in pickle format) from Google Cloud Storage:
**train_df.hdf (9GB)**:
`https://storage.googleapis.com/issue_label_bot/pre_processed_data/2_partitioned_df/train_df.hdf`
**valid_df.hdf (1GB)**
`https://storage.googleapis.com/issue_label_bot/pre_processed_data/2_partitioned_df/valid_df.hdf`
```
# note: download the data and place in right directory before running this code!
valid_df = pd.read_hdf(Path('../data/2_partitioned_df/valid_df.hdf'))
train_df = pd.read_hdf(Path('../data/2_partitioned_df/train_df.hdf'))
print(f'rows in train_df:, {train_df.shape[0]:,}')
print(f'rows in valid_df:, {valid_df.shape[0]:,}')
train_df.head(3)
```
## Create The [DataBunch](https://docs.fast.ai/basic_data.html#DataBunch)
#### Instantiate The Tokenizer
```
def pass_through(x):
return x
# only thing is we are changing pre_rules to be pass through since we have already done all of the pre-rules.
# you don't want to accidentally apply pre-rules again otherwhise it will corrupt the data.
tokenizer = Tokenizer(pre_rules=[pass_through], n_cpus=31)
```
Specify path for saving language model artifacts
```
path = Path('../model/lang_model/')
```
#### Create The Language Model Data Bunch
**Warning**: this steps builds the vocabulary and tokenizes the data. This procedure consumes an incredible amount of memory. This took 1 hour on a machine with 72 cores and 400GB of Memory.
```
# Note you want your own tokenizer, without pre-rules
data_lm = lmdb.from_df(path=path,
train_df=train_df,
valid_df=valid_df,
text_cols='text',
tokenizer=tokenizer,
chunksize=6000000)
data_lm.save() # saves to self.path/data_save.hdf
```
### Location of Saved DataBunch
The databunch object is available here:
`https://storage.googleapis.com/issue_label_bot/model/lang_model/data_save.hdf`
It is a massive file of 27GB so proceed with caution when downlaoding this file.
| true |
code
| 0.512449 | null | null | null | null |
|
# Generative Adversarial Network
In this notebook, we'll be building a generative adversarial network (GAN) trained on the MNIST dataset. From this, we'll be able to generate new handwritten digits!
GANs were [first reported on](https://arxiv.org/abs/1406.2661) in 2014 from Ian Goodfellow and others in Yoshua Bengio's lab. Since then, GANs have exploded in popularity. Here are a few examples to check out:
* [Pix2Pix](https://affinelayer.com/pixsrv/)
* [CycleGAN](https://github.com/junyanz/CycleGAN)
* [A whole list](https://github.com/wiseodd/generative-models)
The idea behind GANs is that you have two networks, a generator $G$ and a discriminator $D$, competing against each other. The generator makes fake data to pass to the discriminator. The discriminator also sees real data and predicts if the data it's received is real or fake. The generator is trained to fool the discriminator, it wants to output data that looks _as close as possible_ to real data. And the discriminator is trained to figure out which data is real and which is fake. What ends up happening is that the generator learns to make data that is indistiguishable from real data to the discriminator.

The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector the generator uses to contruct it's fake images. As the generator learns through training, it figures out how to map these random vectors to recognizable images that can fool the discriminator.
The output of the discriminator is a sigmoid function, where 0 indicates a fake image and 1 indicates an real image. If you're interested only in generating new images, you can throw out the discriminator after training. Now, let's see how we build this thing in TensorFlow.
```
%matplotlib inline
import pickle as pkl
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data')
```
## Model Inputs
First we need to create the inputs for our graph. We need two inputs, one for the discriminator and one for the generator. Here we'll call the discriminator input `inputs_real` and the generator input `inputs_z`. We'll assign them the appropriate sizes for each of the networks.
>**Exercise:** Finish the `model_inputs` function below. Create the placeholders for `inputs_real` and `inputs_z` using the input sizes `real_dim` and `z_dim` respectively.
```
def model_inputs(real_dim, z_dim):
inputs_real = tf.placeholder(shape=(None, real_dim), dtype=tf.float32, name='inputs_real')
inputs_z = tf.placeholder(shape=(None, z_dim), dtype=tf.float32, name='inputs_z')
return inputs_real, inputs_z
```
## Generator network

Here we'll build the generator network. To make this network a universal function approximator, we'll need at least one hidden layer. We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.
#### Variable Scope
Here we need to use `tf.variable_scope` for two reasons. Firstly, we're going to make sure all the variable names start with `generator`. Similarly, we'll prepend `discriminator` to the discriminator variables. This will help out later when we're training the separate networks.
We could just use `tf.name_scope` to set the names, but we also want to reuse these networks with different inputs. For the generator, we're going to train it, but also _sample from it_ as we're training and after training. The discriminator will need to share variables between the fake and real input images. So, we can use the `reuse` keyword for `tf.variable_scope` to tell TensorFlow to reuse the variables instead of creating new ones if we build the graph again.
To use `tf.variable_scope`, you use a `with` statement:
```python
with tf.variable_scope('scope_name', reuse=False):
# code here
```
Here's more from [the TensorFlow documentation](https://www.tensorflow.org/programmers_guide/variable_scope#the_problem) to get another look at using `tf.variable_scope`.
#### Leaky ReLU
TensorFlow doesn't provide an operation for leaky ReLUs, so we'll need to make one . For this you can just take the outputs from a linear fully connected layer and pass them to `tf.maximum`. Typically, a parameter `alpha` sets the magnitude of the output for negative values. So, the output for negative input (`x`) values is `alpha*x`, and the output for positive `x` is `x`:
$$
f(x) = max(\alpha * x, x)
$$
#### Tanh Output
The generator has been found to perform the best with $tanh$ for the generator output. This means that we'll have to rescale the MNIST images to be between -1 and 1, instead of 0 and 1.
>**Exercise:** Implement the generator network in the function below. You'll need to return the tanh output. Make sure to wrap your code in a variable scope, with 'generator' as the scope name, and pass the `reuse` keyword argument from the function to `tf.variable_scope`.
```
def generator(z, out_dim, n_units=128, reuse=False, alpha=0.01):
''' Build the generator network.
Arguments
---------
z : Input tensor for the generator
out_dim : Shape of the generator output
n_units : Number of units in hidden layer
reuse : Reuse the variables with tf.variable_scope
alpha : leak parameter for leaky ReLU
Returns
-------
out:
'''
with tf.variable_scope(name_or_scope='generator', reuse=reuse):
# Hidden layer
h1 = tf.layers.dense(inputs=z, units=n_units, activation=tf.nn.leaky_relu)
# Leaky ReLU
# h1 =
# Logits and tanh output
logits = tf.layers.dense(inputs=h1, units=out_dim, activation=None)
out = tf.tanh(logits)
return out
```
## Discriminator
The discriminator network is almost exactly the same as the generator network, except that we're using a sigmoid output layer.
>**Exercise:** Implement the discriminator network in the function below. Same as above, you'll need to return both the logits and the sigmoid output. Make sure to wrap your code in a variable scope, with 'discriminator' as the scope name, and pass the `reuse` keyword argument from the function arguments to `tf.variable_scope`.
```
def discriminator(x, n_units=128, reuse=False, alpha=0.01):
''' Build the discriminator network.
Arguments
---------
x : Input tensor for the discriminator
n_units: Number of units in hidden layer
reuse : Reuse the variables with tf.variable_scope
alpha : leak parameter for leaky ReLU
Returns
-------
out, logits:
'''
with tf.variable_scope(name_or_scope='discriminator', reuse=reuse):
# Hidden layer
h1 = tf.layers.dense(inputs=x, units=n_units, activation=tf.nn.leaky_relu)
# Leaky ReLU
# h1 =
logits = tf.layers.dense(inputs=h1, units=1, activation=None)
out = tf.sigmoid(logits)
return out, logits
```
## Hyperparameters
```
# Size of input image to discriminator
input_size = 784 # 28x28 MNIST images flattened
# Size of latent vector to generator
z_size = 100
# Sizes of hidden layers in generator and discriminator
g_hidden_size = 128
d_hidden_size = 128
# Leak factor for leaky ReLU
alpha = 0.01
# Label smoothing
smooth = 0.1
```
## Build network
Now we're building the network from the functions defined above.
First is to get our inputs, `input_real, input_z` from `model_inputs` using the sizes of the input and z.
Then, we'll create the generator, `generator(input_z, input_size)`. This builds the generator with the appropriate input and output sizes.
Then the discriminators. We'll build two of them, one for real data and one for fake data. Since we want the weights to be the same for both real and fake data, we need to reuse the variables. For the fake data, we're getting it from the generator as `g_model`. So the real data discriminator is `discriminator(input_real)` while the fake discriminator is `discriminator(g_model, reuse=True)`.
>**Exercise:** Build the network from the functions you defined earlier.
```
tf.reset_default_graph()
# Create our input placeholders
input_real, input_z = model_inputs(input_size, z_size)
# Generator network here
g_model = generator(input_z, input_size, n_units=g_hidden_size)
# g_model is the generator output
# Disriminator network here
d_model_real, d_logits_real = discriminator(input_real, n_units=d_hidden_size, reuse=False)
d_model_fake, d_logits_fake = discriminator(g_model, n_units=d_hidden_size, reuse=True)
```
## Discriminator and Generator Losses
Now we need to calculate the losses, which is a little tricky. For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_loss_real + d_loss_fake`. The losses will by sigmoid cross-entropies, which we can get with `tf.nn.sigmoid_cross_entropy_with_logits`. We'll also wrap that in `tf.reduce_mean` to get the mean for all the images in the batch. So the losses will look something like
```python
tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))
```
For the real image logits, we'll use `d_logits_real` which we got from the discriminator in the cell above. For the labels, we want them to be all ones, since these are all real images. To help the discriminator generalize better, the labels are reduced a bit from 1.0 to 0.9, for example, using the parameter `smooth`. This is known as label smoothing, typically used with classifiers to improve performance. In TensorFlow, it looks something like `labels = tf.ones_like(tensor) * (1 - smooth)`
The discriminator loss for the fake data is similar. The logits are `d_logits_fake`, which we got from passing the generator output to the discriminator. These fake logits are used with labels of all zeros. Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.
Finally, the generator losses are using `d_logits_fake`, the fake image logits. But, now the labels are all ones. The generator is trying to fool the discriminator, so it wants to discriminator to output ones for fake images.
>**Exercise:** Calculate the losses for the discriminator and the generator. There are two discriminator losses, one for real images and one for fake images. For the real image loss, use the real logits and (smoothed) labels of ones. For the fake image loss, use the fake logits with labels of all zeros. The total discriminator loss is the sum of those two losses. Finally, the generator loss again uses the fake logits from the discriminator, but this time the labels are all ones because the generator wants to fool the discriminator.
```
# Calculate losses
d_loss_real = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_real,
labels=tf.ones_like(d_logits_real) * (1 - smooth)))
d_loss_fake = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake,
labels=tf.zeros_like(d_logits_real)))
d_loss = d_loss_real + d_loss_fake
g_loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake,
labels=tf.ones_like(d_logits_fake)))
```
## Optimizers
We want to update the generator and discriminator variables separately. So we need to get the variables for each part and build optimizers for the two parts. To get all the trainable variables, we use `tf.trainable_variables()`. This creates a list of all the variables we've defined in our graph.
For the generator optimizer, we only want to generator variables. Our past selves were nice and used a variable scope to start all of our generator variable names with `generator`. So, we just need to iterate through the list from `tf.trainable_variables()` and keep variables that start with `generator`. Each variable object has an attribute `name` which holds the name of the variable as a string (`var.name == 'weights_0'` for instance).
We can do something similar with the discriminator. All the variables in the discriminator start with `discriminator`.
Then, in the optimizer we pass the variable lists to the `var_list` keyword argument of the `minimize` method. This tells the optimizer to only update the listed variables. Something like `tf.train.AdamOptimizer().minimize(loss, var_list=var_list)` will only train the variables in `var_list`.
>**Exercise: ** Below, implement the optimizers for the generator and discriminator. First you'll need to get a list of trainable variables, then split that list into two lists, one for the generator variables and another for the discriminator variables. Finally, using `AdamOptimizer`, create an optimizer for each network that update the network variables separately.
```
# Optimizers
learning_rate = 0.002
# Get the trainable_variables, split into G and D parts
t_vars = tf.trainable_variables()
g_vars = tf.trainable_variables(scope='generator')
d_vars = tf.trainable_variables(scope='discriminator')
d_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(d_loss, var_list=d_vars)
g_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(g_loss, var_list=g_vars)
```
## Training
```
batch_size = 100
epochs = 100
samples = []
losses = []
saver = tf.train.Saver(var_list = g_vars)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for ii in range(mnist.train.num_examples//batch_size):
batch = mnist.train.next_batch(batch_size)
# Get images, reshape and rescale to pass to D
batch_images = batch[0].reshape((batch_size, 784))
batch_images = batch_images*2 - 1
# Sample random noise for G
batch_z = np.random.uniform(-1, 1, size=(batch_size, z_size))
# Run optimizers
_ = sess.run(d_train_opt, feed_dict={input_real: batch_images, input_z: batch_z})
_ = sess.run(g_train_opt, feed_dict={input_z: batch_z})
# At the end of each epoch, get the losses and print them out
train_loss_d = sess.run(d_loss, {input_z: batch_z, input_real: batch_images})
train_loss_g = g_loss.eval({input_z: batch_z})
print("Epoch {}/{}...".format(e+1, epochs),
"Discriminator Loss: {:.4f}...".format(train_loss_d),
"Generator Loss: {:.4f}".format(train_loss_g))
# Save losses to view after training
losses.append((train_loss_d, train_loss_g))
# Sample from generator as we're training for viewing afterwards
sample_z = np.random.uniform(-1, 1, size=(16, z_size))
gen_samples = sess.run(
generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),
feed_dict={input_z: sample_z})
samples.append(gen_samples)
saver.save(sess, './checkpoints/generator.ckpt')
# Save training generator samples
with open('train_samples.pkl', 'wb') as f:
pkl.dump(samples, f)
```
## Training loss
Here we'll check out the training losses for the generator and discriminator.
```
%matplotlib inline
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
losses = np.array(losses)
plt.plot(losses.T[0], label='Discriminator')
plt.plot(losses.T[1], label='Generator')
plt.title("Training Losses")
plt.legend()
```
## Generator samples from training
Here we can view samples of images from the generator. First we'll look at images taken while training.
```
def view_samples(epoch, samples):
fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)
for ax, img in zip(axes.flatten(), samples[epoch]):
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')
return fig, axes
# Load samples from generator taken while training
with open('train_samples.pkl', 'rb') as f:
samples = pkl.load(f)
```
These are samples from the final training epoch. You can see the generator is able to reproduce numbers like 5, 7, 3, 0, 9. Since this is just a sample, it isn't representative of the full range of images this generator can make.
```
_ = view_samples(-1, samples)
```
Below I'm showing the generated images as the network was training, every 10 epochs. With bonus optical illusion!
```
rows, cols = 10, 6
fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)
for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):
for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):
ax.imshow(img.reshape((28,28)), cmap='Greys_r')
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
```
It starts out as all noise. Then it learns to make only the center white and the rest black. You can start to see some number like structures appear out of the noise. Looks like 1, 9, and 8 show up first. Then, it learns 5 and 3.
## Sampling from the generator
We can also get completely new images from the generator by using the checkpoint we saved after training. We just need to pass in a new latent vector $z$ and we'll get new samples!
```
saver = tf.train.Saver(var_list=g_vars)
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))
sample_z = np.random.uniform(-1, 1, size=(16, z_size))
gen_samples = sess.run(
generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),
feed_dict={input_z: sample_z})
view_samples(0, [gen_samples])
```
| true |
code
| 0.815288 | null | null | null | null |
|
# Welcome to fastai
```
from fastai import *
from fastai.vision import *
from fastai.gen_doc.nbdoc import *
from fastai.core import *
from fastai.basic_train import *
```
The fastai library simplifies training fast and accurate neural nets using modern best practices. It's based on research in to deep learning best practices undertaken at [fast.ai](http://www.fast.ai), including "out of the box" support for [`vision`](/vision.html#vision), [`text`](/text.html#text), [`tabular`](/tabular.html#tabular), and [`collab`](/collab.html#collab) (collaborative filtering) models. If you're looking for the source code, head over to the [fastai repo](https://github.com/fastai/fastai) on GitHub. For brief examples, see the [examples](https://github.com/fastai/fastai/tree/master/examples) folder; detailed examples are provided in the full documentation (see the sidebar). For example, here's how to train an MNIST model using [resnet18](https://arxiv.org/abs/1512.03385) (from the [vision example](https://github.com/fastai/fastai/blob/master/examples/vision.ipynb)):
```
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
learn = create_cnn(data, models.resnet18, metrics=accuracy)
learn.fit(1)
jekyll_note("""This documentation is all built from notebooks;
that means that you can try any of the code you see in any notebook yourself!
You'll find the notebooks in the <a href="https://github.com/fastai/fastai/tree/master/docs_src">docs_src</a> folder of the
<a href="https://github.com/fastai/fastai">fastai</a> repo. For instance,
<a href="https://nbviewer.jupyter.org/github/fastai/fastai/blob/master/docs_src/index.ipynb">here</a>
is the notebook source of what you're reading now.""")
```
## Installation and updating
To install or update fastai, we recommend `conda`:
```
conda install -c pytorch -c fastai fastai pytorch-nightly cuda92
```
For troubleshooting, and alternative installations (including pip and CPU-only options) see the [fastai readme](https://github.com/fastai/fastai/blob/master/README.md).
## Reading the docs
To get started quickly, click *Applications* on the sidebar, and then choose the application you're interested in. That will take you to a walk-through of training a model of that type. You can then either explore the various links from there, or dive more deeply into the various fastai modules.
We've provided below a quick summary of the key modules in this library. For details on each one, use the sidebar to find the module you're interested in. Each module includes an overview and example of how to use it, along with documentation for every class, function, and method. API documentation looks, for example, like this:
### An example function
```
show_doc(rotate)
```
---
Types for each parameter, and the return type, are displayed following standard Python [type hint syntax](https://www.python.org/dev/peps/pep-0484/). Sometimes for compound types we use [type variables](/fastai_typing.html). Types that are defined by fastai or Pytorch link directly to more information about that type; try clicking *Image* in the function above for an example. The docstring for the symbol is shown immediately after the signature, along with a link to the source code for the symbol in GitHub. After the basic signature and docstring you'll find examples and additional details (not shown in this example). As you'll see at the top of the page, all symbols documented like this also appear in the table of contents.
For inherited classes and some types of decorated function, the base class or decorator type will also be shown at the end of the signature, delimited by `::`. For `vision.transforms`, the random number generator used for data augmentation is shown instead of the type, for randomly generated parameters.
## Module structure
### Imports
fastai is designed to support both interactive computing as well as traditional software development. For interactive computing, where convenience and speed of experimentation is a priority, data scientists often prefer to grab all the symbols they need, with `import *`. Therefore, fastai is designed to support this approach, without compromising on maintainability and understanding.
In order to do so, the module dependencies are carefully managed (see next section), with each exporting a carefully chosen set of symbols when using `import *`. In general, for interactive computing, you'll want to import from both `fastai`, and from one of the *applications*, such as:
```
from fastai import *
from fastai.vision import *
```
That will give you all the standard external modules you'll need, in their customary namespaces (e.g. `pandas as pd`, `numpy as np`, `matplotlib.pyplot as plt`), plus the core fastai libraries. In addition, the main classes and functions for your application ([`fastai.vision`](/vision.html#vision), in this case), e.g. creating a [`DataBunch`](/basic_data.html#DataBunch) from an image folder and training a convolutional neural network (with [`create_cnn`](/vision.learner.html#create_cnn)), are also imported.
If you wish to see where a symbol is imported from, either just type the symbol name (in a REPL such as Jupyter Notebook or IPython), or (in most editors) wave your mouse over the symbol to see the definition. For instance:
```
Learner
```
### Dependencies
At the base of everything are the two modules [`core`](/core.html#core) and [`torch_core`](/torch_core.html#torch_core) (we're not including the `fastai.` prefix when naming modules in these docs). They define the basic functions we use in the library; [`core`](/core.html#core) only relies on general modules, whereas [`torch_core`](/torch_core.html#torch_core) requires pytorch. Most type-hinting shortcuts are defined there too (at least the one that don't depend on fastai classes defined later). Nearly all modules below import [`torch_core`](/torch_core.html#torch_core).
Then, there are three modules directly on top of [`torch_core`](/torch_core.html#torch_core):
- [`data`](/vision.data.html#vision.data), which contains the class that will take a [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) or pytorch [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader) to wrap it in a [`DeviceDataLoader`](/basic_data.html#DeviceDataLoader) (a class that sits on top of a [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader) and is in charge of putting the data on the right device as well as applying transforms such as normalization) and regroup then in a [`DataBunch`](/basic_data.html#DataBunch).
- [`layers`](/layers.html#layers), which contains basic functions to define custom layers or groups of layers
- [`metrics`](/metrics.html#metrics), which contains all the metrics
This takes care of the basics, then we regroup a model with some data in a [`Learner`](/basic_train.html#Learner) object to take care of training. More specifically:
- [`callback`](/callback.html#callback) (depends on [`data`](/vision.data.html#vision.data)) defines the basis of callbacks and the [`CallbackHandler`](/callback.html#CallbackHandler). Those are functions that will be called every step of the way of the training loop and can allow us to customize what is happening there;
- [`basic_train`](/basic_train.html#basic_train) (depends on [`callback`](/callback.html#callback)) defines [`Learner`](/basic_train.html#Learner) and [`Recorder`](/basic_train.html#Recorder) (which is a callback that records training stats) and has the training loop;
- [`callbacks`](/callbacks.html#callbacks) (depends on [`basic_train`](/basic_train.html#basic_train)) is a submodule defining various callbacks, such as for mixed precision training or 1cycle annealing;
- `learn` (depends on [`callbacks`](/callbacks.html#callbacks)) defines helper functions to invoke the callbacks more easily.
From [`data`](/vision.data.html#vision.data) we can split on one of the four main *applications*, which each has their own module: [`vision`](/vision.html#vision), [`text`](/text.html#text) [`collab`](/collab.html#collab), or [`tabular`](/tabular.html#tabular). Each of those submodules is built in the same way with:
- a submodule named <code>transform</code> that handles the transformations of our data (data augmentation for computer vision, numericalizing and tokenizing for text and preprocessing for tabular)
- a submodule named <code>data</code> that contains the class that will create datasets specific to this application and the helper functions to create [`DataBunch`](/basic_data.html#DataBunch) objects.
- a submodule named <code>models</code> that contains the models specific to this application.
- optionally, a submodule named <code>learn</code> that will contain [`Learner`](/basic_train.html#Learner) speficic to the application.
Here is a graph of the key module dependencies:

| true |
code
| 0.818093 | null | null | null | null |
|
# The peaks over threshold method
This notebook continues with the dataset of the notebook about the `Dataset` object.
There are two main approaches in extreme value theory: the peaks over threshold approach and the block maxima approach.
In this notebook, the peaks over threshold approach will be illustrated.
In the notebook about the `Dataset` object, it was determined that the value 15 was a good guess for the threshold for our dataset.
First, generate the same dataset as in the notebook about the `Dataset` object.
```
from evt.dataset import Dataset
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.stats import pareto, norm
N_DATAPOINTS = 100000 # number of datapoints in the example set
NORMAL_STD = 5 # standard deviation of the normal distribution
PARETO_SHAPE = 2.5 # shape parameter of the Pareto distribution
EXAMPLE_NAME = 'Values' # for nicer plots
EXAMPLE_INDEX_NAME = 'Index'
np.random.seed(0) # enforce deterministic behaviour
series = pd.Series(
norm.rvs(scale=NORMAL_STD, size=N_DATAPOINTS) + pareto.rvs(PARETO_SHAPE, size=N_DATAPOINTS),
name=EXAMPLE_NAME
)
series.index.name = EXAMPLE_INDEX_NAME
dataset = Dataset(series)
```
Let's start by determining the peaks over threshold.
```
from evt.methods.peaks_over_threshold import PeaksOverThreshold
THRESHOLD = 15
peaks_over_threshold = PeaksOverThreshold(dataset, THRESHOLD)
```
The peaks are stored in the `.series_tail` attribute.
```
peaks_over_threshold.series_tail
```
To graphically show the peaks over threshold, we can plot the peaks.
The original dataset is shown for comparison.
```
fig, ax = plt.subplots()
peaks_over_threshold.plot_tail(ax)
fig.tight_layout()
plt.show()
```
A natural next question is whether the tail is fatter or lighter than an exponential.
The exponential distribution is a benchmark for tail behaviour.
```
fig, ax = plt.subplots()
peaks_over_threshold.plot_qq_exponential(ax)
fig.tight_layout()
plt.show()
```
The quantiles of the empirical survival function are not described well by an exponential.
High quantiles seem to lie under the diagonal.
This is a signal of a sub-exponential distribution.
Next, let's make a Zipf plot: a log-log diagram of the survival function against the values.
```
fig, ax = plt.subplots()
peaks_over_threshold.plot_zipf(ax)
fig.tight_layout()
plt.show()
```
Power laws will show as straight lines in the Zipf plot.
In following notebooks, the tail index in the peaks over threshold method will be estimated.
For example, using the Hill estimator, the moment estimator and maximum likelihood.
| true |
code
| 0.77193 | null | null | null | null |
|
```
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from keras import backend as K
import matplotlib.pyplot as plt
import pandas as pd
import datetime
```
# Load classification model
```
classification_model = tf.keras.models.load_model('TrainedModel/trainedModel.h5')
```
# Load dataset
### And convert it to numpy array
```
train_X = pd.read_csv('/home/ege/Repo/SideChannel-AdversarialAI/Tensorflow/DataSet/trainX13.csv', header=None)
train_Y = pd.read_csv('/home/ege/Repo/SideChannel-AdversarialAI/Tensorflow/DataSet/trainY13.csv', header=None)
trainY = train_Y.to_numpy()
trainX = train_X.to_numpy()
trainX = np.expand_dims(trainX,axis=2)
```
# Normalize dataset
```
minimum = np.amin(trainX)
maximum = np.amax(trainX)
trainX_normalized = (trainX-minimum)/(maximum-minimum)
#Uncomment below if you need to fit with a dataset for specific class
#classToCut = 6
#trainXCUT = trainX[classToCut::14]
#trainYCUT = trainY[classToCut::14]
```
# Define Sampling layer as a subclass of keras.layers.Layer
## Sampling layer: Layer that samples a random point in latent space from a distribution with a mean and variance
```
class Sampling(layers.Layer):
"""Uses (z_mean, z_log_var) to sample z, the vector encoding a digit."""
def call(self, inputs):
z_mean, z_log_var = inputs
batch = tf.shape(z_mean)[0]
dim = tf.shape(z_mean)[1]
epsilon = tf.keras.backend.random_normal(shape=(batch, dim))
return z_mean + tf.exp(0.5 * z_log_var) * epsilon
```
## Define latent space dimension
```
latent_dim = 2
```
# Encoder
```
encoder_inputs = keras.Input(shape=(6000,1))
x = layers.Conv1D(256,16,strides=2,padding='same',activation='relu')(encoder_inputs)#possibly update kernel_initializer
#x = layers.MaxPooling1D(pool_size = 4,strides = 4, padding = 'same')(x)
x = layers.Conv1D(128,16,strides=2,padding='same',activation='relu')(x)#possibly update kernel_initializer
#x = layers.MaxPooling1D(pool_size = 4,strides = 4, padding = 'same')(x)
x = layers.Conv1D(64,8,strides=2,padding='same',activation='relu')(x)#possibly update kernel_initializer
#x = layers.MaxPooling1D(pool_size = 4,strides = 4, padding = 'same')(x)
x = layers.Conv1D(32,8,strides=2,padding='same',activation='relu')(x)#possibly update kernel_initializer
#x = layers.MaxPooling1D(pool_size = 4,strides = 4, padding = 'same')(x)
shape_before_flattening = K.int_shape(x)
flatten_1 = layers.Flatten()(x)
#x = layers.LSTM(32,activation='tanh',recurrent_activation='hard_sigmoid',use_bias=True,kernel_initializer='VarianceScaling',recurrent_initializer = 'orthogonal',bias_initializer='Zeros', return_sequences = True)(flatten_1) #Variance Scaling
x = layers.Dense(64 , activation="relu")(flatten_1)
x = layers.Dense(32 , activation="relu")(x)
x = layers.Dense(16 , activation="relu")(x)
z_mean = layers.Dense(latent_dim, name="z_mean",kernel_initializer='Zeros',bias_initializer = 'Zeros')(x)
z_log_var = layers.Dense(latent_dim, name="z_log_var",kernel_initializer='Zeros',bias_initializer = 'Zeros')(x)
z = Sampling()([z_mean, z_log_var])
encoder = keras.Model(encoder_inputs, [z_mean, z_log_var, z], name="encoder")
encoder.summary()
```
# Decoder
```
#DECODER
latent_inputs = keras.Input(shape=(latent_dim,))
x = layers.Dense(16 , activation="relu")(latent_inputs)
x = layers.Dense(32 , activation="relu")(x)
x = layers.Dense(64 , activation="relu")(x)
#x = layers.LSTM(32,activation='tanh',recurrent_activation='hard_sigmoid',use_bias=True,kernel_initializer='VarianceScaling',recurrent_initializer = 'orthogonal',bias_initializer='Zeros', return_sequences = True)(x) #Variance Scaling
x = layers.Dense(np.prod(shape_before_flattening[1:]), activation="relu")(x)
x = layers.Reshape(shape_before_flattening[1:])(x)
x = layers.Conv1DTranspose(32, 8, activation="relu", strides=2,padding='same')(x)
x = layers.Conv1DTranspose(64, 8, activation="relu", strides=2,padding='same')(x)
x = layers.Conv1DTranspose(128, 16, activation="relu", strides=2,padding='same')(x)
x = layers.Conv1DTranspose(256, 16, activation="relu", strides=2,padding='same')(x)
decoder_outputs = layers.Conv1DTranspose(1, 16, padding="same",activation="sigmoid")(x)
decoder = keras.Model(latent_inputs, decoder_outputs, name="decoder")
decoder.summary()
```
# Defining subclass VAE
## VAE is a subclass of keras.Model class
```
class VAE(keras.Model):
def __init__(self, encoder, decoder, **kwargs):
super(VAE, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
self.reconstruction_loss_tracker = keras.metrics.Mean(
name="reconstruction_loss"
)
self.kl_loss_tracker = keras.metrics.Mean(name="kl_loss")
@property
def metrics(self):
return [
self.total_loss_tracker,
self.reconstruction_loss_tracker,
self.kl_loss_tracker,
]
def train_step(self, data):
with tf.GradientTape() as tape:
z_mean, z_log_var, z = self.encoder(data)
reconstruction = self.decoder(z)
reconstruction_loss = tf.reduce_mean(
tf.reduce_sum(
keras.losses.binary_crossentropy(data, reconstruction),axis=(1)
)
)
kl_loss = -1 * (1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var))
kl_loss = tf.reduce_mean(tf.reduce_sum(kl_loss, axis=0))
total_loss = reconstruction_loss + kl_loss
#total_loss = reconstruction_loss #ABSOLUTELY CHANGE!
grads = tape.gradient(total_loss, self.trainable_weights)
self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
self.total_loss_tracker.update_state(total_loss)
self.reconstruction_loss_tracker.update_state(reconstruction_loss)
self.kl_loss_tracker.update_state(kl_loss)
return {
"loss": self.total_loss_tracker.result(),
"reconstruction_loss": self.reconstruction_loss_tracker.result(),
"kl_loss": self.kl_loss_tracker.result(),
}
```
# Train model
```
vae = VAE(encoder, decoder)
vae.compile(optimizer=keras.optimizers.Adam())
history = vae.fit(trainX_normalized, epochs=25, batch_size=128)
```
# Test reconstructed dataset with the classification model
### Predict reconstructed dataset
```
sumOfAccuracy = 0
for j in range(14):
classPrediction = j
trainXCUT = trainX_normalized[classPrediction::14]
z_mean, z_log_var, z = vae.encoder.predict(trainXCUT)
reconstructed_x = vae.decoder.predict(z)
predictions = classification_model.predict(reconstructed_x)
#print(predictions)
correctPredAmt = 0
for i, y_i in enumerate(predictions):
firstHighest = np.argmax(y_i)
y_i[firstHighest] = 0
secondHighest = np.argmax(y_i)
y_i[secondHighest] = 0
thirdHighest = np.argmax(y_i)
if(firstHighest == classPrediction or secondHighest == classPrediction or thirdHighest == classPrediction):
correctPredAmt = correctPredAmt + 1
#print(str(firstHighest) +", "+str(secondHighest)+", "+str(thirdHighest))
accuracy = correctPredAmt/(len(predictions))
sumOfAccuracy = sumOfAccuracy + accuracy
print("Class "+str(j)+": "+str(accuracy))
averageAccuracy = sumOfAccuracy/14
print("Average: "+ str(averageAccuracy))
```
### Evaluate reconstructed dataset
```
for i in range(14):
trainXCUT = trainX_normalized[i::14]
trainYCUT = trainY[i::14]
z_mean, z_log_var, z = vae.encoder.predict(trainXCUT)
reconstructed_x = vae.decoder.predict(z)
classification_model.evaluate(reconstructed_x,trainYCUT)
classToCut = 6
trainXCUT = trainX_normalized[classToCut::14]
trainYCUT = trainY[classToCut::14]
z_mean, z_log_var, z = vae.encoder.predict(trainXCUT)
reconstructed_x = vae.decoder.predict(z)*(maximum-minimum)+minimum
fig = plt.figure(figsize=(40,5))
#plt.plot(results)
sampleToPredict = 15
plt.plot(reconstructed_x[sampleToPredict],label='Reconstruction')
plt.plot(trainXCUT[sampleToPredict]*(maximum-minimum)+minimum,label='Sample')
#plt.plot(data3[0],label=3)
#plt.plot(data4[0],label=4)
#plt.plot(averageArray[0])
plt.legend()
plt.yticks(np.arange(0, 9, 1))
plt.xticks(np.arange(0, 6000, 500))
plt.grid()
#plt.axhline(linewidth=1, color='r')
plt.xlabel("5 ms")
plt.ylabel("PnP timing")
#figure(figsize=(8, 6), dpi=80)
fig.savefig('vis_test.png',dpi=200)
```
| true |
code
| 0.80888 | null | null | null | null |
|
# Preliminary Analysis of Statement Sentiment by Lexicon
Analyse statement by Loughran and McDonald word list to see if the relationship between economy and net sentiment
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
import os
import pickle
import codecs
import re
from tqdm import tqdm_notebook as tqdm
#For tokenizing sentences
import nltk
nltk.download('punkt')
plt.style.use('seaborn-whitegrid')
```
### Reading the data in
```
file = open("../data/FOMC/statement.pickle", "rb")
Data = pickle.load(file)
Data['text'] = Data['contents'].apply(lambda x: x.replace('\n\n[SECTION]\n\n', '').replace('\n', ' ').replace('\r', ' ').strip())
Data.drop(columns=['title'], axis=1, inplace=True)
print('Date: ', Data.iloc[-1]['date'].strftime('%Y-%m-%d'))
print('Speaker: ', Data.iloc[-1]['speaker'])
print('Text: \n\n', Data.iloc[-1]['contents'].replace('\n[SECTION]\n', '')[1192:])
```
### Creating a Financial Dictionary based on Loughran and McDonald
```
#Dictionary tone assessment will compare them by Index (need the numbers back)
Data['Index'] = range(0, len(Data))
# Make 'date' column as the index of Data
Data.set_index(['date'], inplace=True)
Data.head()
import re
# Loughran and McDonald Sentiment Word Lists (https://sraf.nd.edu/textual-analysis/resources/)
lmdict = {'Negative': ['abandon', 'abandoned', 'abandoning', 'abandonment', 'abandonments', 'abandons', 'abdicated',
'abdicates', 'abdicating', 'abdication', 'abdications', 'aberrant', 'aberration', 'aberrational',
'aberrations', 'abetting', 'abnormal', 'abnormalities', 'abnormality', 'abnormally', 'abolish',
'abolished', 'abolishes', 'abolishing', 'abrogate', 'abrogated', 'abrogates', 'abrogating',
'abrogation', 'abrogations', 'abrupt', 'abruptly', 'abruptness', 'absence', 'absences',
'absenteeism', 'abuse', 'abused', 'abuses', 'abusing', 'abusive', 'abusively', 'abusiveness',
'accident', 'accidental', 'accidentally', 'accidents', 'accusation', 'accusations', 'accuse',
'accused', 'accuses', 'accusing', 'acquiesce', 'acquiesced', 'acquiesces', 'acquiescing',
'acquit', 'acquits', 'acquittal', 'acquittals', 'acquitted', 'acquitting', 'adulterate',
'adulterated', 'adulterating', 'adulteration', 'adulterations', 'adversarial', 'adversaries',
'adversary', 'adverse', 'adversely', 'adversities', 'adversity', 'aftermath', 'aftermaths',
'against', 'aggravate', 'aggravated', 'aggravates', 'aggravating', 'aggravation', 'aggravations',
'alerted', 'alerting', 'alienate', 'alienated', 'alienates', 'alienating', 'alienation',
'alienations', 'allegation', 'allegations', 'allege', 'alleged', 'allegedly', 'alleges',
'alleging', 'annoy', 'annoyance', 'annoyances', 'annoyed', 'annoying', 'annoys', 'annul',
'annulled', 'annulling', 'annulment', 'annulments', 'annuls', 'anomalies', 'anomalous',
'anomalously', 'anomaly', 'anticompetitive', 'antitrust', 'argue', 'argued', 'arguing',
'argument', 'argumentative', 'arguments', 'arrearage', 'arrearages', 'arrears', 'arrest',
'arrested', 'arrests', 'artificially', 'assault', 'assaulted', 'assaulting', 'assaults',
'assertions', 'attrition', 'aversely', 'backdating', 'bad', 'bail', 'bailout', 'balk', 'balked',
'bankrupt', 'bankruptcies', 'bankruptcy', 'bankrupted', 'bankrupting', 'bankrupts', 'bans',
'barred', 'barrier', 'barriers', 'bottleneck', 'bottlenecks', 'boycott', 'boycotted',
'boycotting', 'boycotts', 'breach', 'breached', 'breaches', 'breaching', 'break', 'breakage',
'breakages', 'breakdown', 'breakdowns', 'breaking', 'breaks', 'bribe', 'bribed', 'briberies',
'bribery', 'bribes', 'bribing', 'bridge', 'broken', 'burden', 'burdened', 'burdening', 'burdens',
'burdensome', 'burned', 'calamities', 'calamitous', 'calamity', 'cancel', 'canceled',
'canceling', 'cancellation', 'cancellations', 'cancelled', 'cancelling', 'cancels', 'careless',
'carelessly', 'carelessness', 'catastrophe', 'catastrophes', 'catastrophic', 'catastrophically',
'caution', 'cautionary', 'cautioned', 'cautioning', 'cautions', 'cease', 'ceased', 'ceases',
'ceasing', 'censure', 'censured', 'censures', 'censuring', 'challenge', 'challenged',
'challenges', 'challenging', 'chargeoffs', 'circumvent', 'circumvented', 'circumventing',
'circumvention', 'circumventions', 'circumvents', 'claiming', 'claims', 'clawback', 'closed',
'closeout', 'closeouts', 'closing', 'closings', 'closure', 'closures', 'coerce', 'coerced',
'coerces', 'coercing', 'coercion', 'coercive', 'collapse', 'collapsed', 'collapses',
'collapsing', 'collision', 'collisions', 'collude', 'colluded', 'colludes', 'colluding',
'collusion', 'collusions', 'collusive', 'complain', 'complained', 'complaining', 'complains',
'complaint', 'complaints', 'complicate', 'complicated', 'complicates', 'complicating',
'complication', 'complications', 'compulsion', 'concealed', 'concealing', 'concede', 'conceded',
'concedes', 'conceding', 'concern', 'concerned', 'concerns', 'conciliating', 'conciliation',
'conciliations', 'condemn', 'condemnation', 'condemnations', 'condemned', 'condemning',
'condemns', 'condone', 'condoned', 'confess', 'confessed', 'confesses', 'confessing',
'confession', 'confine', 'confined', 'confinement', 'confinements', 'confines', 'confining',
'confiscate', 'confiscated', 'confiscates', 'confiscating', 'confiscation', 'confiscations',
'conflict', 'conflicted', 'conflicting', 'conflicts', 'confront', 'confrontation',
'confrontational', 'confrontations', 'confronted', 'confronting', 'confronts', 'confuse',
'confused', 'confuses', 'confusing', 'confusingly', 'confusion', 'conspiracies', 'conspiracy',
'conspirator', 'conspiratorial', 'conspirators', 'conspire', 'conspired', 'conspires',
'conspiring', 'contempt', 'contend', 'contended', 'contending', 'contends', 'contention',
'contentions', 'contentious', 'contentiously', 'contested', 'contesting', 'contraction',
'contractions', 'contradict', 'contradicted', 'contradicting', 'contradiction', 'contradictions',
'contradictory', 'contradicts', 'contrary', 'controversial', 'controversies', 'controversy',
'convict', 'convicted', 'convicting', 'conviction', 'convictions', 'corrected', 'correcting',
'correction', 'corrections', 'corrects', 'corrupt', 'corrupted', 'corrupting', 'corruption',
'corruptions', 'corruptly', 'corruptness', 'costly', 'counterclaim', 'counterclaimed',
'counterclaiming', 'counterclaims', 'counterfeit', 'counterfeited', 'counterfeiter',
'counterfeiters', 'counterfeiting', 'counterfeits', 'countermeasure', 'countermeasures', 'crime',
'crimes', 'criminal', 'criminally', 'criminals', 'crises', 'crisis', 'critical', 'critically',
'criticism', 'criticisms', 'criticize', 'criticized', 'criticizes', 'criticizing', 'crucial',
'crucially', 'culpability', 'culpable', 'culpably', 'cumbersome', 'curtail', 'curtailed',
'curtailing', 'curtailment', 'curtailments', 'curtails', 'cut', 'cutback', 'cutbacks',
'cyberattack', 'cyberattacks', 'cyberbullying', 'cybercrime', 'cybercrimes', 'cybercriminal',
'cybercriminals', 'damage', 'damaged', 'damages', 'damaging', 'dampen', 'dampened', 'danger',
'dangerous', 'dangerously', 'dangers', 'deadlock', 'deadlocked', 'deadlocking', 'deadlocks',
'deadweight', 'deadweights', 'debarment', 'debarments', 'debarred', 'deceased', 'deceit',
'deceitful', 'deceitfulness', 'deceive', 'deceived', 'deceives', 'deceiving', 'deception',
'deceptions', 'deceptive', 'deceptively', 'decline', 'declined', 'declines', 'declining',
'deface', 'defaced', 'defacement', 'defamation', 'defamations', 'defamatory', 'defame',
'defamed', 'defames', 'defaming', 'default', 'defaulted', 'defaulting', 'defaults', 'defeat',
'defeated', 'defeating', 'defeats', 'defect', 'defective', 'defects', 'defend', 'defendant',
'defendants', 'defended', 'defending', 'defends', 'defensive', 'defer', 'deficiencies',
'deficiency', 'deficient', 'deficit', 'deficits', 'defraud', 'defrauded', 'defrauding',
'defrauds', 'defunct', 'degradation', 'degradations', 'degrade', 'degraded', 'degrades',
'degrading', 'delay', 'delayed', 'delaying', 'delays', 'deleterious', 'deliberate',
'deliberated', 'deliberately', 'delinquencies', 'delinquency', 'delinquent', 'delinquently',
'delinquents', 'delist', 'delisted', 'delisting', 'delists', 'demise', 'demised', 'demises',
'demising', 'demolish', 'demolished', 'demolishes', 'demolishing', 'demolition', 'demolitions',
'demote', 'demoted', 'demotes', 'demoting', 'demotion', 'demotions', 'denial', 'denials',
'denied', 'denies', 'denigrate', 'denigrated', 'denigrates', 'denigrating', 'denigration',
'deny', 'denying', 'deplete', 'depleted', 'depletes', 'depleting', 'depletion', 'depletions',
'deprecation', 'depress', 'depressed', 'depresses', 'depressing', 'deprivation', 'deprive',
'deprived', 'deprives', 'depriving', 'derelict', 'dereliction', 'derogatory', 'destabilization',
'destabilize', 'destabilized', 'destabilizing', 'destroy', 'destroyed', 'destroying', 'destroys',
'destruction', 'destructive', 'detain', 'detained', 'detention', 'detentions', 'deter',
'deteriorate', 'deteriorated', 'deteriorates', 'deteriorating', 'deterioration',
'deteriorations', 'deterred', 'deterrence', 'deterrences', 'deterrent', 'deterrents',
'deterring', 'deters', 'detract', 'detracted', 'detracting', 'detriment', 'detrimental',
'detrimentally', 'detriments', 'devalue', 'devalued', 'devalues', 'devaluing', 'devastate',
'devastated', 'devastating', 'devastation', 'deviate', 'deviated', 'deviates', 'deviating',
'deviation', 'deviations', 'devolve', 'devolved', 'devolves', 'devolving', 'difficult',
'difficulties', 'difficultly', 'difficulty', 'diminish', 'diminished', 'diminishes',
'diminishing', 'diminution', 'disadvantage', 'disadvantaged', 'disadvantageous', 'disadvantages',
'disaffiliation', 'disagree', 'disagreeable', 'disagreed', 'disagreeing', 'disagreement',
'disagreements', 'disagrees', 'disallow', 'disallowance', 'disallowances', 'disallowed',
'disallowing', 'disallows', 'disappear', 'disappearance', 'disappearances', 'disappeared',
'disappearing', 'disappears', 'disappoint', 'disappointed', 'disappointing', 'disappointingly',
'disappointment', 'disappointments', 'disappoints', 'disapproval', 'disapprovals', 'disapprove',
'disapproved', 'disapproves', 'disapproving', 'disassociates', 'disassociating',
'disassociation', 'disassociations', 'disaster', 'disasters', 'disastrous', 'disastrously',
'disavow', 'disavowal', 'disavowed', 'disavowing', 'disavows', 'disciplinary', 'disclaim',
'disclaimed', 'disclaimer', 'disclaimers', 'disclaiming', 'disclaims', 'disclose', 'disclosed',
'discloses', 'disclosing', 'discontinuance', 'discontinuances', 'discontinuation',
'discontinuations', 'discontinue', 'discontinued', 'discontinues', 'discontinuing', 'discourage',
'discouraged', 'discourages', 'discouraging', 'discredit', 'discredited', 'discrediting',
'discredits', 'discrepancies', 'discrepancy', 'disfavor', 'disfavored', 'disfavoring',
'disfavors', 'disgorge', 'disgorged', 'disgorgement', 'disgorgements', 'disgorges', 'disgorging',
'disgrace', 'disgraceful', 'disgracefully', 'dishonest', 'dishonestly', 'dishonesty', 'dishonor',
'dishonorable', 'dishonorably', 'dishonored', 'dishonoring', 'dishonors', 'disincentives',
'disinterested', 'disinterestedly', 'disinterestedness', 'disloyal', 'disloyally', 'disloyalty',
'dismal', 'dismally', 'dismiss', 'dismissal', 'dismissals', 'dismissed', 'dismisses',
'dismissing', 'disorderly', 'disparage', 'disparaged', 'disparagement', 'disparagements',
'disparages', 'disparaging', 'disparagingly', 'disparities', 'disparity', 'displace',
'displaced', 'displacement', 'displacements', 'displaces', 'displacing', 'dispose', 'dispossess',
'dispossessed', 'dispossesses', 'dispossessing', 'disproportion', 'disproportional',
'disproportionate', 'disproportionately', 'dispute', 'disputed', 'disputes', 'disputing',
'disqualification', 'disqualifications', 'disqualified', 'disqualifies', 'disqualify',
'disqualifying', 'disregard', 'disregarded', 'disregarding', 'disregards', 'disreputable',
'disrepute', 'disrupt', 'disrupted', 'disrupting', 'disruption', 'disruptions', 'disruptive',
'disrupts', 'dissatisfaction', 'dissatisfied', 'dissent', 'dissented', 'dissenter', 'dissenters',
'dissenting', 'dissents', 'dissident', 'dissidents', 'dissolution', 'dissolutions', 'distort',
'distorted', 'distorting', 'distortion', 'distortions', 'distorts', 'distract', 'distracted',
'distracting', 'distraction', 'distractions', 'distracts', 'distress', 'distressed', 'disturb',
'disturbance', 'disturbances', 'disturbed', 'disturbing', 'disturbs', 'diversion', 'divert',
'diverted', 'diverting', 'diverts', 'divest', 'divested', 'divesting', 'divestiture',
'divestitures', 'divestment', 'divestments', 'divests', 'divorce', 'divorced', 'divulge',
'divulged', 'divulges', 'divulging', 'doubt', 'doubted', 'doubtful', 'doubts', 'downgrade',
'downgraded', 'downgrades', 'downgrading', 'downsize', 'downsized', 'downsizes', 'downsizing',
'downsizings', 'downtime', 'downtimes', 'downturn', 'downturns', 'downward', 'downwards', 'drag',
'drastic', 'drastically', 'drawback', 'drawbacks', 'drop', 'dropped', 'drought', 'droughts', 'duress',
'dysfunction', 'dysfunctional', 'dysfunctions', 'easing', 'egregious', 'egregiously', 'embargo',
'embargoed', 'embargoes', 'embargoing', 'embarrass', 'embarrassed', 'embarrasses',
'embarrassing', 'embarrassment', 'embarrassments', 'embezzle', 'embezzled', 'embezzlement',
'embezzlements', 'embezzler', 'embezzles', 'embezzling', 'encroach', 'encroached', 'encroaches',
'encroaching', 'encroachment', 'encroachments', 'encumber', 'encumbered', 'encumbering',
'encumbers', 'encumbrance', 'encumbrances', 'endanger', 'endangered', 'endangering',
'endangerment', 'endangers', 'enjoin', 'enjoined', 'enjoining', 'enjoins', 'erode', 'eroded',
'erodes', 'eroding', 'erosion', 'erratic', 'erratically', 'erred', 'erring', 'erroneous',
'erroneously', 'error', 'errors', 'errs', 'escalate', 'escalated', 'escalates', 'escalating',
'evade', 'evaded', 'evades', 'evading', 'evasion', 'evasions', 'evasive', 'evict', 'evicted',
'evicting', 'eviction', 'evictions', 'evicts', 'exacerbate', 'exacerbated', 'exacerbates',
'exacerbating', 'exacerbation', 'exacerbations', 'exaggerate', 'exaggerated', 'exaggerates',
'exaggerating', 'exaggeration', 'excessive', 'excessively', 'exculpate', 'exculpated',
'exculpates', 'exculpating', 'exculpation', 'exculpations', 'exculpatory', 'exonerate',
'exonerated', 'exonerates', 'exonerating', 'exoneration', 'exonerations', 'exploit',
'exploitation', 'exploitations', 'exploitative', 'exploited', 'exploiting', 'exploits', 'expose',
'exposed', 'exposes', 'exposing', 'expropriate', 'expropriated', 'expropriates', 'expropriating',
'expropriation', 'expropriations', 'expulsion', 'expulsions', 'extenuating', 'fail', 'failed',
'failing', 'failings', 'fails', 'failure', 'failures', 'fallout', 'false', 'falsely',
'falsification', 'falsifications', 'falsified', 'falsifies', 'falsify', 'falsifying', 'falsity',
'fatalities', 'fatality', 'fatally', 'fault', 'faulted', 'faults', 'faulty', 'fear', 'fears',
'felonies', 'felonious', 'felony', 'fictitious', 'fined', 'fines', 'fired', 'firing', 'flaw',
'flawed', 'flaws', 'forbid', 'forbidden', 'forbidding', 'forbids', 'force', 'forced', 'forcing',
'foreclose', 'foreclosed', 'forecloses', 'foreclosing', 'foreclosure', 'foreclosures', 'forego',
'foregoes', 'foregone', 'forestall', 'forestalled', 'forestalling', 'forestalls', 'forfeit',
'forfeited', 'forfeiting', 'forfeits', 'forfeiture', 'forfeitures', 'forgers', 'forgery',
'fraud', 'frauds', 'fraudulence', 'fraudulent', 'fraudulently', 'frivolous', 'frivolously',
'frustrate', 'frustrated', 'frustrates', 'frustrating', 'frustratingly', 'frustration',
'frustrations', 'fugitive', 'fugitives', 'gratuitous', 'gratuitously', 'grievance', 'grievances',
'grossly', 'groundless', 'guilty', 'halt', 'halted', 'hamper', 'hampered', 'hampering',
'hampers', 'harass', 'harassed', 'harassing', 'harassment', 'hardship', 'hardships', 'harm',
'harmed', 'harmful', 'harmfully', 'harming', 'harms', 'harsh', 'harsher', 'harshest', 'harshly',
'harshness', 'hazard', 'hazardous', 'hazards', 'hinder', 'hindered', 'hindering', 'hinders',
'hindrance', 'hindrances', 'hostile', 'hostility', 'hurt', 'hurting', 'idle', 'idled', 'idling',
'ignore', 'ignored', 'ignores', 'ignoring', 'ill', 'illegal', 'illegalities', 'illegality',
'illegally', 'illegible', 'illicit', 'illicitly', 'illiquid', 'illiquidity', 'imbalance',
'imbalances', 'immature', 'immoral', 'impair', 'impaired', 'impairing', 'impairment',
'impairments', 'impairs', 'impasse', 'impasses', 'impede', 'impeded', 'impedes', 'impediment',
'impediments', 'impeding', 'impending', 'imperative', 'imperfection', 'imperfections', 'imperil',
'impermissible', 'implicate', 'implicated', 'implicates', 'implicating', 'impossibility',
'impossible', 'impound', 'impounded', 'impounding', 'impounds', 'impracticable', 'impractical',
'impracticalities', 'impracticality', 'imprisonment', 'improper', 'improperly', 'improprieties',
'impropriety', 'imprudent', 'imprudently', 'inability', 'inaccessible', 'inaccuracies',
'inaccuracy', 'inaccurate', 'inaccurately', 'inaction', 'inactions', 'inactivate', 'inactivated',
'inactivates', 'inactivating', 'inactivation', 'inactivations', 'inactivity', 'inadequacies',
'inadequacy', 'inadequate', 'inadequately', 'inadvertent', 'inadvertently', 'inadvisability',
'inadvisable', 'inappropriate', 'inappropriately', 'inattention', 'incapable', 'incapacitated',
'incapacity', 'incarcerate', 'incarcerated', 'incarcerates', 'incarcerating', 'incarceration',
'incarcerations', 'incidence', 'incidences', 'incident', 'incidents', 'incompatibilities',
'incompatibility', 'incompatible', 'incompetence', 'incompetency', 'incompetent',
'incompetently', 'incompetents', 'incomplete', 'incompletely', 'incompleteness', 'inconclusive',
'inconsistencies', 'inconsistency', 'inconsistent', 'inconsistently', 'inconvenience',
'inconveniences', 'inconvenient', 'incorrect', 'incorrectly', 'incorrectness', 'indecency',
'indecent', 'indefeasible', 'indefeasibly', 'indict', 'indictable', 'indicted', 'indicting',
'indictment', 'indictments', 'ineffective', 'ineffectively', 'ineffectiveness', 'inefficiencies',
'inefficiency', 'inefficient', 'inefficiently', 'ineligibility', 'ineligible', 'inequitable',
'inequitably', 'inequities', 'inequity', 'inevitable', 'inexperience', 'inexperienced',
'inferior', 'inflicted', 'infraction', 'infractions', 'infringe', 'infringed', 'infringement',
'infringements', 'infringes', 'infringing', 'inhibited', 'inimical', 'injunction', 'injunctions',
'injure', 'injured', 'injures', 'injuries', 'injuring', 'injurious', 'injury', 'inordinate',
'inordinately', 'inquiry', 'insecure', 'insensitive', 'insolvencies', 'insolvency', 'insolvent',
'instability', 'insubordination', 'insufficiency', 'insufficient', 'insufficiently',
'insurrection', 'insurrections', 'intentional', 'interfere', 'interfered', 'interference',
'interferences', 'interferes', 'interfering', 'intermittent', 'intermittently', 'interrupt',
'interrupted', 'interrupting', 'interruption', 'interruptions', 'interrupts', 'intimidation',
'intrusion', 'invalid', 'invalidate', 'invalidated', 'invalidates', 'invalidating',
'invalidation', 'invalidity', 'investigate', 'investigated', 'investigates', 'investigating',
'investigation', 'investigations', 'involuntarily', 'involuntary', 'irreconcilable',
'irreconcilably', 'irrecoverable', 'irrecoverably', 'irregular', 'irregularities',
'irregularity', 'irregularly', 'irreparable', 'irreparably', 'irreversible', 'jeopardize',
'jeopardized', 'justifiable', 'kickback', 'kickbacks', 'knowingly', 'lack', 'lacked', 'lacking',
'lackluster', 'lacks', 'lag', 'lagged', 'lagging', 'lags', 'lapse', 'lapsed', 'lapses',
'lapsing', 'late', 'laundering', 'layoff', 'layoffs', 'lie', 'limitation', 'limitations',
'lingering', 'liquidate', 'liquidated', 'liquidates', 'liquidating', 'liquidation',
'liquidations', 'liquidator', 'liquidators', 'litigant', 'litigants', 'litigate', 'litigated',
'litigates', 'litigating', 'litigation', 'litigations', 'lockout', 'lockouts', 'lose', 'loses',
'losing', 'loss', 'losses', 'lost', 'lying', 'malfeasance', 'malfunction', 'malfunctioned',
'malfunctioning', 'malfunctions', 'malice', 'malicious', 'maliciously', 'malpractice',
'manipulate', 'manipulated', 'manipulates', 'manipulating', 'manipulation', 'manipulations',
'manipulative', 'markdown', 'markdowns', 'misapplication', 'misapplications', 'misapplied',
'misapplies', 'misapply', 'misapplying', 'misappropriate', 'misappropriated', 'misappropriates',
'misappropriating', 'misappropriation', 'misappropriations', 'misbranded', 'miscalculate',
'miscalculated', 'miscalculates', 'miscalculating', 'miscalculation', 'miscalculations',
'mischaracterization', 'mischief', 'misclassification', 'misclassifications', 'misclassified',
'misclassify', 'miscommunication', 'misconduct', 'misdated', 'misdemeanor', 'misdemeanors',
'misdirected', 'mishandle', 'mishandled', 'mishandles', 'mishandling', 'misinform',
'misinformation', 'misinformed', 'misinforming', 'misinforms', 'misinterpret',
'misinterpretation', 'misinterpretations', 'misinterpreted', 'misinterpreting', 'misinterprets',
'misjudge', 'misjudged', 'misjudges', 'misjudging', 'misjudgment', 'misjudgments', 'mislabel',
'mislabeled', 'mislabeling', 'mislabelled', 'mislabels', 'mislead', 'misleading', 'misleadingly',
'misleads', 'misled', 'mismanage', 'mismanaged', 'mismanagement', 'mismanages', 'mismanaging',
'mismatch', 'mismatched', 'mismatches', 'mismatching', 'misplaced', 'misprice', 'mispricing',
'mispricings', 'misrepresent', 'misrepresentation', 'misrepresentations', 'misrepresented',
'misrepresenting', 'misrepresents', 'miss', 'missed', 'misses', 'misstate', 'misstated',
'misstatement', 'misstatements', 'misstates', 'misstating', 'misstep', 'missteps', 'mistake',
'mistaken', 'mistakenly', 'mistakes', 'mistaking', 'mistrial', 'mistrials', 'misunderstand',
'misunderstanding', 'misunderstandings', 'misunderstood', 'misuse', 'misused', 'misuses',
'misusing', 'monopolistic', 'monopolists', 'monopolization', 'monopolize', 'monopolized',
'monopolizes', 'monopolizing', 'monopoly', 'moratoria', 'moratorium', 'moratoriums',
'mothballed', 'mothballing', 'negative', 'negatively', 'negatives', 'neglect', 'neglected',
'neglectful', 'neglecting', 'neglects', 'negligence', 'negligences', 'negligent', 'negligently',
'nonattainment', 'noncompetitive', 'noncompliance', 'noncompliances', 'noncompliant',
'noncomplying', 'nonconforming', 'nonconformities', 'nonconformity', 'nondisclosure',
'nonfunctional', 'nonpayment', 'nonpayments', 'nonperformance', 'nonperformances',
'nonperforming', 'nonproducing', 'nonproductive', 'nonrecoverable', 'nonrenewal', 'nuisance',
'nuisances', 'nullification', 'nullifications', 'nullified', 'nullifies', 'nullify',
'nullifying', 'objected', 'objecting', 'objection', 'objectionable', 'objectionably',
'objections', 'obscene', 'obscenity', 'obsolescence', 'obsolete', 'obstacle', 'obstacles',
'obstruct', 'obstructed', 'obstructing', 'obstruction', 'obstructions', 'offence', 'offences',
'offend', 'offended', 'offender', 'offenders', 'offending', 'offends', 'omission', 'omissions',
'omit', 'omits', 'omitted', 'omitting', 'onerous', 'opportunistic', 'opportunistically',
'oppose', 'opposed', 'opposes', 'opposing', 'opposition', 'oppositions', 'outage', 'outages',
'outdated', 'outmoded', 'overage', 'overages', 'overbuild', 'overbuilding', 'overbuilds',
'overbuilt', 'overburden', 'overburdened', 'overburdening', 'overcapacities', 'overcapacity',
'overcharge', 'overcharged', 'overcharges', 'overcharging', 'overcome', 'overcomes',
'overcoming', 'overdue', 'overestimate', 'overestimated', 'overestimates', 'overestimating',
'overestimation', 'overestimations', 'overload', 'overloaded', 'overloading', 'overloads',
'overlook', 'overlooked', 'overlooking', 'overlooks', 'overpaid', 'overpayment', 'overpayments',
'overproduced', 'overproduces', 'overproducing', 'overproduction', 'overrun', 'overrunning',
'overruns', 'overshadow', 'overshadowed', 'overshadowing', 'overshadows', 'overstate',
'overstated', 'overstatement', 'overstatements', 'overstates', 'overstating', 'oversupplied',
'oversupplies', 'oversupply', 'oversupplying', 'overtly', 'overturn', 'overturned',
'overturning', 'overturns', 'overvalue', 'overvalued', 'overvaluing', 'panic', 'panics',
'penalize', 'penalized', 'penalizes', 'penalizing', 'penalties', 'penalty', 'peril', 'perils',
'perjury', 'perpetrate', 'perpetrated', 'perpetrates', 'perpetrating', 'perpetration', 'persist',
'persisted', 'persistence', 'persistent', 'persistently', 'persisting', 'persists', 'pervasive',
'pervasively', 'pervasiveness', 'petty', 'picket', 'picketed', 'picketing', 'plaintiff',
'plaintiffs', 'plea', 'plead', 'pleaded', 'pleading', 'pleadings', 'pleads', 'pleas', 'pled',
'poor', 'poorly', 'poses', 'posing', 'postpone', 'postponed', 'postponement', 'postponements',
'postpones', 'postponing', 'precipitated', 'precipitous', 'precipitously', 'preclude',
'precluded', 'precludes', 'precluding', 'predatory', 'prejudice', 'prejudiced', 'prejudices',
'prejudicial', 'prejudicing', 'premature', 'prematurely', 'pressing', 'pretrial', 'preventing',
'prevention', 'prevents', 'problem', 'problematic', 'problematical', 'problems', 'prolong',
'prolongation', 'prolongations', 'prolonged', 'prolonging', 'prolongs', 'prone', 'prosecute',
'prosecuted', 'prosecutes', 'prosecuting', 'prosecution', 'prosecutions', 'protest', 'protested',
'protester', 'protesters', 'protesting', 'protestor', 'protestors', 'protests', 'protracted',
'protraction', 'provoke', 'provoked', 'provokes', 'provoking', 'punished', 'punishes',
'punishing', 'punishment', 'punishments', 'punitive', 'purport', 'purported', 'purportedly',
'purporting', 'purports', 'question', 'questionable', 'questionably', 'questioned',
'questioning', 'questions', 'quit', 'quitting', 'racketeer', 'racketeering', 'rationalization',
'rationalizations', 'rationalize', 'rationalized', 'rationalizes', 'rationalizing',
'reassessment', 'reassessments', 'reassign', 'reassigned', 'reassigning', 'reassignment',
'reassignments', 'reassigns', 'recall', 'recalled', 'recalling', 'recalls', 'recession',
'recessionary', 'recessions', 'reckless', 'recklessly', 'recklessness', 'redact', 'redacted',
'redacting', 'redaction', 'redactions', 'redefault', 'redefaulted', 'redefaults', 'redress',
'redressed', 'redresses', 'redressing', 'refusal', 'refusals', 'refuse', 'refused', 'refuses',
'refusing', 'reject', 'rejected', 'rejecting', 'rejection', 'rejections', 'rejects',
'relinquish', 'relinquished', 'relinquishes', 'relinquishing', 'relinquishment',
'relinquishments', 'reluctance', 'reluctant', 'renegotiate', 'renegotiated', 'renegotiates',
'renegotiating', 'renegotiation', 'renegotiations', 'renounce', 'renounced', 'renouncement',
'renouncements', 'renounces', 'renouncing', 'reparation', 'reparations', 'repossessed',
'repossesses', 'repossessing', 'repossession', 'repossessions', 'repudiate', 'repudiated',
'repudiates', 'repudiating', 'repudiation', 'repudiations', 'resign', 'resignation',
'resignations', 'resigned', 'resigning', 'resigns', 'restate', 'restated', 'restatement',
'restatements', 'restates', 'restating', 'restructure', 'restructured', 'restructures',
'restructuring', 'restructurings', 'retaliate', 'retaliated', 'retaliates', 'retaliating',
'retaliation', 'retaliations', 'retaliatory', 'retribution', 'retributions', 'revocation',
'revocations', 'revoke', 'revoked', 'revokes', 'revoking', 'ridicule', 'ridiculed', 'ridicules',
'ridiculing', 'riskier', 'riskiest', 'risky', 'sabotage', 'sacrifice', 'sacrificed',
'sacrifices', 'sacrificial', 'sacrificing', 'scandalous', 'scandals', 'scrutinize',
'scrutinized', 'scrutinizes', 'scrutinizing', 'scrutiny', 'secrecy', 'seize', 'seized', 'seizes',
'seizing', 'sentenced', 'sentencing', 'serious', 'seriously', 'seriousness', 'setback',
'setbacks', 'sever', 'severe', 'severed', 'severely', 'severities', 'severity', 'sharply',
'shocked', 'shortage', 'shortages', 'shortfall', 'shortfalls', 'shrinkage', 'shrinkages', 'shut',
'shutdown', 'shutdowns', 'shuts', 'shutting', 'slander', 'slandered', 'slanderous', 'slanders',
'slippage', 'slippages', 'slow', 'slowdown', 'slowdowns', 'slowed', 'slower', 'slowest',
'slowing', 'slowly', 'slowness', 'sluggish', 'sluggishly', 'sluggishness', 'solvencies',
'solvency', 'spam', 'spammers', 'spamming', 'staggering', 'stagnant', 'stagnate', 'stagnated',
'stagnates', 'stagnating', 'stagnation', 'standstill', 'standstills', 'stolen', 'stoppage',
'stoppages', 'stopped', 'stopping', 'stops', 'strain', 'strained', 'straining', 'strains',
'stress', 'stressed', 'stresses', 'stressful', 'stressing', 'stringent', 'strong', 'subjected',
'subjecting', 'subjection', 'subpoena', 'subpoenaed', 'subpoenas', 'substandard', 'sue', 'sued',
'sues', 'suffer', 'suffered', 'suffering', 'suffers', 'suing', 'summoned', 'summoning',
'summons', 'summonses', 'susceptibility', 'susceptible', 'suspect', 'suspected', 'suspects',
'suspend', 'suspended', 'suspending', 'suspends', 'suspension', 'suspensions', 'suspicion',
'suspicions', 'suspicious', 'suspiciously', 'taint', 'tainted', 'tainting', 'taints', 'tampered',
'tense', 'terminate', 'terminated', 'terminates', 'terminating', 'termination', 'terminations',
'testify', 'testifying', 'threat', 'threaten', 'threatened', 'threatening', 'threatens',
'threats', 'tightening', 'tolerate', 'tolerated', 'tolerates', 'tolerating', 'toleration',
'tortuous', 'tortuously', 'tragedies', 'tragedy', 'tragic', 'tragically', 'traumatic', 'trouble',
'troubled', 'troubles', 'turbulence', 'turmoil', 'unable', 'unacceptable', 'unacceptably',
'unaccounted', 'unannounced', 'unanticipated', 'unapproved', 'unattractive', 'unauthorized',
'unavailability', 'unavailable', 'unavoidable', 'unavoidably', 'unaware', 'uncollectable',
'uncollected', 'uncollectibility', 'uncollectible', 'uncollectibles', 'uncompetitive',
'uncompleted', 'unconscionable', 'unconscionably', 'uncontrollable', 'uncontrollably',
'uncontrolled', 'uncorrected', 'uncover', 'uncovered', 'uncovering', 'uncovers', 'undeliverable',
'undelivered', 'undercapitalized', 'undercut', 'undercuts', 'undercutting', 'underestimate',
'underestimated', 'underestimates', 'underestimating', 'underestimation', 'underfunded',
'underinsured', 'undermine', 'undermined', 'undermines', 'undermining', 'underpaid',
'underpayment', 'underpayments', 'underpays', 'underperform', 'underperformance',
'underperformed', 'underperforming', 'underperforms', 'underproduced', 'underproduction',
'underreporting', 'understate', 'understated', 'understatement', 'understatements',
'understates', 'understating', 'underutilization', 'underutilized', 'undesirable', 'undesired',
'undetected', 'undetermined', 'undisclosed', 'undocumented', 'undue', 'unduly', 'uneconomic',
'uneconomical', 'uneconomically', 'unemployed', 'unemployment', 'unethical', 'unethically',
'unexcused', 'unexpected', 'unexpectedly', 'unfair', 'unfairly', 'unfavorability', 'unfavorable',
'unfavorably', 'unfavourable', 'unfeasible', 'unfit', 'unfitness', 'unforeseeable', 'unforeseen',
'unforseen', 'unfortunate', 'unfortunately', 'unfounded', 'unfriendly', 'unfulfilled',
'unfunded', 'uninsured', 'unintended', 'unintentional', 'unintentionally', 'unjust',
'unjustifiable', 'unjustifiably', 'unjustified', 'unjustly', 'unknowing', 'unknowingly',
'unlawful', 'unlawfully', 'unlicensed', 'unliquidated', 'unmarketable', 'unmerchantable',
'unmeritorious', 'unnecessarily', 'unnecessary', 'unneeded', 'unobtainable', 'unoccupied',
'unpaid', 'unperformed', 'unplanned', 'unpopular', 'unpredictability', 'unpredictable',
'unpredictably', 'unpredicted', 'unproductive', 'unprofitability', 'unprofitable', 'unqualified',
'unrealistic', 'unreasonable', 'unreasonableness', 'unreasonably', 'unreceptive',
'unrecoverable', 'unrecovered', 'unreimbursed', 'unreliable', 'unremedied', 'unreported',
'unresolved', 'unrest', 'unsafe', 'unsalable', 'unsaleable', 'unsatisfactory', 'unsatisfied',
'unsavory', 'unscheduled', 'unsellable', 'unsold', 'unsound', 'unstabilized', 'unstable',
'unsubstantiated', 'unsuccessful', 'unsuccessfully', 'unsuitability', 'unsuitable', 'unsuitably',
'unsuited', 'unsure', 'unsuspected', 'unsuspecting', 'unsustainable', 'untenable', 'untimely',
'untrusted', 'untruth', 'untruthful', 'untruthfully', 'untruthfulness', 'untruths', 'unusable',
'unwanted', 'unwarranted', 'unwelcome', 'unwilling', 'unwillingness', 'upset', 'urgency',
'urgent', 'usurious', 'usurp', 'usurped', 'usurping', 'usurps', 'usury', 'vandalism', 'verdict',
'verdicts', 'vetoed', 'victims', 'violate', 'violated', 'violates', 'violating', 'violation',
'violations', 'violative', 'violator', 'violators', 'violence', 'violent', 'violently',
'vitiate', 'vitiated', 'vitiates', 'vitiating', 'vitiation', 'voided', 'voiding', 'volatile',
'volatility', 'vulnerabilities', 'vulnerability', 'vulnerable', 'vulnerably', 'warn', 'warned',
'warning', 'warnings', 'warns', 'wasted', 'wasteful', 'wasting', 'weak', 'weaken', 'weakened',
'weakening', 'weakens', 'weaker', 'weakest', 'weakly', 'weakness', 'weaknesses', 'willfully',
'worries', 'worry', 'worrying', 'worse', 'worsen', 'worsened', 'worsening', 'worsens', 'worst',
'worthless', 'writedown', 'writedowns', 'writeoff', 'writeoffs', 'wrong', 'wrongdoing',
'wrongdoings', 'wrongful', 'wrongfully', 'wrongly',
'negative', 'negatives', 'fail', 'fails', 'failing', 'failure', 'weak', 'weakness', 'weaknesses',
'difficult', 'difficulty', 'hurdle', 'hurdles', 'obstacle', 'obstacles', 'slump', 'slumps',
'slumping', 'slumped', 'uncertain', 'uncertainty', 'unsettled', 'unfavorable', 'downturn',
'depressed', 'disappoint', 'disappoints', 'disappointing', 'disappointed', 'disappointment',
'risk', 'risks', 'risky', 'threat', 'threats', 'penalty', 'penalties', 'down', 'decrease',
'decreases', 'decreasing', 'decreased', 'decline', 'declines', 'declining', 'declined', 'fall',
'falls', 'falling', 'fell', 'fallen', 'drop', 'drops', 'dropping', 'dropped', 'deteriorate',
'deteriorates', 'deteriorating', 'deteriorated', 'worsen', 'worsens', 'worsening', 'weaken',
'weakens', 'weakening', 'weakened', 'worse', 'worst', 'low', 'lower', 'lowest', 'less', 'least',
'smaller', 'smallest', 'shrink', 'shrinks', 'shrinking', 'shrunk', 'below', 'under', 'challenge',
'challenges', 'challenging', 'challenged'
],
'Positive': ['able', 'abundance', 'abundant', 'acclaimed', 'accomplish', 'accomplished', 'accomplishes',
'accomplishing', 'accomplishment', 'accomplishments', 'achieve', 'achieved', 'achievement',
'achievements', 'achieves', 'achieving', 'adequately', 'advancement', 'advancements', 'advances',
'advancing', 'advantage', 'advantaged', 'advantageous', 'advantageously', 'advantages',
'alliance', 'alliances', 'assure', 'assured', 'assures', 'assuring', 'attain', 'attained',
'attaining', 'attainment', 'attainments', 'attains', 'attractive', 'attractiveness', 'beautiful',
'beautifully', 'beneficial', 'beneficially', 'benefit', 'benefited', 'benefiting', 'benefitted',
'benefitting', 'best', 'better', 'bolstered', 'bolstering', 'bolsters', 'boom', 'booming',
'boost', 'boosted', 'breakthrough', 'breakthroughs', 'brilliant', 'charitable', 'collaborate',
'collaborated', 'collaborates', 'collaborating', 'collaboration', 'collaborations',
'collaborative', 'collaborator', 'collaborators', 'compliment', 'complimentary', 'complimented',
'complimenting', 'compliments', 'conclusive', 'conclusively', 'conducive', 'confident',
'constructive', 'constructively', 'courteous', 'creative', 'creatively', 'creativeness',
'creativity', 'delight', 'delighted', 'delightful', 'delightfully', 'delighting', 'delights',
'dependability', 'dependable', 'desirable', 'desired', 'despite', 'destined', 'diligent',
'diligently', 'distinction', 'distinctions', 'distinctive', 'distinctively', 'distinctiveness',
'dream', 'easier', 'easily', 'easy', 'effective', 'efficiencies', 'efficiency', 'efficient',
'efficiently', 'empower', 'empowered', 'empowering', 'empowers', 'enable', 'enabled', 'enables',
'enabling', 'encouraged', 'encouragement', 'encourages', 'encouraging', 'enhance', 'enhanced',
'enhancement', 'enhancements', 'enhances', 'enhancing', 'enjoy', 'enjoyable', 'enjoyably',
'enjoyed', 'enjoying', 'enjoyment', 'enjoys', 'enthusiasm', 'enthusiastic', 'enthusiastically',
'excellence', 'excellent', 'excelling', 'excels', 'exceptional', 'exceptionally', 'excited',
'excitement', 'exciting', 'exclusive', 'exclusively', 'exclusiveness', 'exclusives',
'exclusivity', 'exemplary', 'fantastic', 'favorable', 'favorably', 'favored', 'favoring',
'favorite', 'favorites', 'friendly', 'gain', 'gained', 'gaining', 'gains', 'good', 'great',
'greater', 'greatest', 'greatly', 'greatness', 'happiest', 'happily', 'happiness', 'happy',
'highest', 'honor', 'honorable', 'honored', 'honoring', 'honors', 'ideal', 'impress',
'impressed', 'impresses', 'impressing', 'impressive', 'impressively', 'improve', 'improved',
'improvement', 'improvements', 'improves', 'improving', 'incredible', 'incredibly',
'influential', 'informative', 'ingenuity', 'innovate', 'innovated', 'innovates', 'innovating',
'innovation', 'innovations', 'innovative', 'innovativeness', 'innovator', 'innovators',
'insightful', 'inspiration', 'inspirational', 'integrity', 'invent', 'invented', 'inventing',
'invention', 'inventions', 'inventive', 'inventiveness', 'inventor', 'inventors', 'leadership',
'leading', 'loyal', 'lucrative', 'meritorious', 'opportunities', 'opportunity', 'optimistic',
'outperform', 'outperformed', 'outperforming', 'outperforms', 'perfect', 'perfected',
'perfectly', 'perfects', 'pleasant', 'pleasantly', 'pleased', 'pleasure', 'plentiful', 'popular',
'popularity', 'positive', 'positively', 'preeminence', 'preeminent', 'premier', 'premiere',
'prestige', 'prestigious', 'proactive', 'proactively', 'proficiency', 'proficient',
'proficiently', 'profitability', 'profitable', 'profitably', 'progress', 'progressed',
'progresses', 'progressing', 'prospered', 'prospering', 'prosperity', 'prosperous', 'prospers',
'rebound', 'rebounded', 'rebounding', 'receptive', 'regain', 'regained', 'regaining', 'resolve',
'revolutionize', 'revolutionized', 'revolutionizes', 'revolutionizing', 'reward', 'rewarded',
'rewarding', 'rewards', 'satisfaction', 'satisfactorily', 'satisfactory', 'satisfied',
'satisfies', 'satisfy', 'satisfying', 'smooth', 'smoothing', 'smoothly', 'smooths', 'solves',
'solving', 'spectacular', 'spectacularly', 'stability', 'stabilization', 'stabilizations',
'stabilize', 'stabilized', 'stabilizes', 'stabilizing', 'stable', 'strength', 'strengthen',
'strengthened', 'strengthening', 'strengthens', 'strengths', 'strong', 'stronger', 'strongest',
'succeed', 'succeeded', 'succeeding', 'succeeds', 'success', 'successes', 'successful',
'successfully', 'superior', 'surpass', 'surpassed', 'surpasses', 'surpassing', "sustainable", 'transparency',
'tremendous', 'tremendously', 'unmatched', 'unparalleled', 'unsurpassed', 'upturn', 'upturns',
'valuable', 'versatile', 'versatility', 'vibrancy', 'vibrant', 'win', 'winner', 'winners', 'winning', 'worthy',
'positive', 'positives', 'success', 'successes', 'successful', 'succeed', 'succeeds',
'succeeding', 'succeeded', 'accomplish', 'accomplishes', 'accomplishing', 'accomplished',
'accomplishment', 'accomplishments', 'strong', 'strength', 'strengths', 'certain', 'certainty',
'definite', 'solid', 'excellent', 'good', 'leading', 'achieve', 'achieves', 'achieved',
'achieving', 'achievement', 'achievements', 'progress', 'progressing', 'deliver', 'delivers',
'delivered', 'delivering', 'leader', 'leading', 'pleased', 'reward', 'rewards', 'rewarding',
'rewarded', 'opportunity', 'opportunities', 'enjoy', 'enjoys', 'enjoying', 'enjoyed',
'encouraged', 'encouraging', 'up', 'increase', 'increases', 'increasing', 'increased', 'rise',
'rises', 'rising', 'rose', 'risen', 'improve', 'improves', 'improving', 'improved', 'improvement',
'improvements', 'strengthen', 'strengthens', 'strengthening', 'strengthened', 'stronger',
'strongest', 'better', 'best', 'more', 'most', 'above', 'record', 'high', 'higher', 'highest',
'greater', 'greatest', 'larger', 'largest', 'grow', 'grows', 'growing', 'grew', 'grown', 'growth',
'expand', 'expands', 'expanding', 'expanded', 'expansion', 'exceed', 'exceeds', 'exceeded',
'exceeding', 'beat', 'beats', 'beating']
}
negate = ["aint", "arent", "cannot", "cant", "couldnt", "darent", "didnt", "doesnt", "ain't", "aren't", "can't",
"couldn't", "daren't", "didn't", "doesn't", "dont", "hadnt", "hasnt", "havent", "isnt", "mightnt", "mustnt",
"neither", "don't", "hadn't", "hasn't", "haven't", "isn't", "mightn't", "mustn't", "neednt", "needn't",
"never", "none", "nope", "nor", "not", "nothing", "nowhere", "oughtnt", "shant", "shouldnt", "wasnt",
"werent", "oughtn't", "shan't", "shouldn't", "wasn't", "weren't", "without", "wont", "wouldnt", "won't",
"wouldn't", "rarely", "seldom", "despite", "no", "nobody"]
def negated(word):
"""
Determine if preceding word is a negation word
"""
if word.lower() in negate:
return True
else:
return False
def tone_count_with_negation_check(dict, article):
"""
Count positive and negative words with negation check. Account for simple negation only for positive words.
Simple negation is taken to be observations of one of negate words occurring within three words
preceding a positive words.
"""
pos_count = 0
neg_count = 0
pos_words = []
neg_words = []
input_words = re.findall(r'\b([a-zA-Z]+n\'t|[a-zA-Z]+\'s|[a-zA-Z]+)\b', article.lower())
word_count = len(input_words)
for i in range(0, word_count):
if input_words[i] in dict['Negative']:
neg_count += 1
neg_words.append(input_words[i])
if input_words[i] in dict['Positive']:
if i >= 3:
if negated(input_words[i - 1]) or negated(input_words[i - 2]) or negated(input_words[i - 3]):
neg_count += 1
neg_words.append(input_words[i] + ' (with negation)')
else:
pos_count += 1
pos_words.append(input_words[i])
elif i == 2:
if negated(input_words[i - 1]) or negated(input_words[i - 2]):
neg_count += 1
neg_words.append(input_words[i] + ' (with negation)')
else:
pos_count += 1
pos_words.append(input_words[i])
elif i == 1:
if negated(input_words[i - 1]):
neg_count += 1
neg_words.append(input_words[i] + ' (with negation)')
else:
pos_count += 1
pos_words.append(input_words[i])
elif i == 0:
pos_count += 1
pos_words.append(input_words[i])
results = [word_count, pos_count, neg_count, pos_words, neg_words]
return results
print(len(Data))
temp = [tone_count_with_negation_check(lmdict,x) for x in Data.text]
temp = pd.DataFrame(temp)
Data['wordcount'] = temp.iloc[:,0].values
Data['NPositiveWords'] = temp.iloc[:,1].values
Data['NNegativeWords'] = temp.iloc[:,2].values
#Sentiment Score normalized by the number of words
Data['sentiment'] = (Data['NPositiveWords'] - Data['NNegativeWords']) / Data['wordcount'] * 100
Data['Poswords'] = temp.iloc[:,3].values
Data['Negwords'] = temp.iloc[:,4].values
temp.head()
Data.head()
```
### Plots of the sentiment analysis
Plot positive and negative word counts
```
NetSentiment = Data['NPositiveWords'] - Data['NNegativeWords']
plt.figure(figsize=(15,7))
ax = plt.subplot()
plt.plot(Data.index, Data['NPositiveWords'], c='green', linewidth= 1.0)
plt.plot(Data.index, Data['NNegativeWords']*-1, c='red', linewidth=1.0)
plt.plot(Data.index, NetSentiment, c='grey', linewidth=1.0)
plt.title('The number of positive/negative words in statement', fontsize=16)
plt.legend(['Positive Words', 'Negative Words', 'Net Sentiment'], prop={'size': 14}, loc=1)
ax.fill_between(Data.index, NetSentiment, where=(NetSentiment > 0), color='green', alpha=0.3, interpolate=True)
ax.fill_between(Data.index, NetSentiment, where=(NetSentiment <= 0), color='red', alpha=0.3, interpolate=True)
import matplotlib.dates as mdates
years = mdates.YearLocator() # every year
months = mdates.MonthLocator() # every month
years_fmt = mdates.DateFormatter('%Y')
# format the ticks
ax.xaxis.set_major_locator(years)
ax.xaxis.set_major_formatter(years_fmt)
ax.xaxis.set_minor_locator(months)
datemin = np.datetime64(Data.index[0], 'Y')
datemax = np.datetime64(Data.index[-1], 'Y') + np.timedelta64(1, 'Y')
ax.set_xlim(datemin, datemax)
ax.grid(True)
plt.show()
```
Positive and negative word counts highly correlate... probably because of the total number of words varies. Take the positive - negative as Net Sentiment.
```
NetSentiment = Data['NPositiveWords'] - Data['NNegativeWords']
fig, ax = plt.subplots(figsize=(15,7))
ax.plot(Data.index, NetSentiment,
c = 'red',
linewidth= 1.0)
plt.title('Net sentiment implied by BoW over time',size = 'medium')
# format the ticks
# round to nearest years.
datemin = np.datetime64(Data.index[0], 'Y')
datemax = np.datetime64(Data.index[-1], 'Y') + np.timedelta64(1, 'Y')
ax.set_xlim(datemin, datemax)
# format the coords message box
ax.format_xdata = mdates.DateFormatter('%Y-%m-%d')
ax.grid(True)
plt.show()
```
Plot derivative to see the changes in net sentiment
```
firstderivative = (NetSentiment.shift(1) - NetSentiment) / NetSentiment
fig, ax = plt.subplots(figsize=(15,7))
ax.plot(Data.index, firstderivative,
c = 'red')
plt.title('Change in sentiment over time (first derivative)')
# format the ticks
# round to nearest years.
datemin = np.datetime64(Data.index[0], 'Y')
datemax = np.datetime64(Data.index[-1], 'Y') + np.timedelta64(1, 'Y')
ax.set_xlim(datemin, datemax)
# format the coords message box
ax.format_xdata = mdates.DateFormatter('%Y-%m-%d')
ax.grid(True)
plt.show()
# Normalize data
NPositiveWordsNorm = Data['NPositiveWords'] / Data['wordcount'] * np.mean(Data['wordcount'])
NNegativeWordsNorm = Data['NNegativeWords'] / Data['wordcount'] * np.mean(Data['wordcount'])
NetSentimentNorm = (NPositiveWordsNorm - NNegativeWordsNorm)
fig, ax = plt.subplots(figsize=(15,7))
ax.plot(Data.index, NPositiveWordsNorm, c='green', linewidth= 1.0)
plt.plot(Data.index, NNegativeWordsNorm, c='red', linewidth=1.0)
plt.title('Counts normalized by the number of words', fontsize=16)
plt.legend(['Count of Positive Words', 'Count of Negative Words'],
prop={'size': 14},
loc = 1
)
# format the ticks
# round to nearest years.
import matplotlib.dates as mdates
years = mdates.YearLocator() # every year
months = mdates.MonthLocator() # every month
years_fmt = mdates.DateFormatter('%Y')
datemin = np.datetime64(Data.index[0], 'Y')
datemax = np.datetime64(Data.index[-1], 'Y') + np.timedelta64(1, 'Y')
ax.set_xlim(datemin, datemax)
# format the coords message box
ax.format_xdata = mdates.DateFormatter('%Y-%m-%d')
ax.grid(True)
plt.show()
fig, ax = plt.subplots(figsize=(15,7))
ax.plot(Data.index, NetSentimentNorm, c='red', linewidth=1.0)
plt.title('Net sentiment implied by BoW over time',size = 'medium')
# format the ticks
# round to nearest years.
datemin = np.datetime64(Data.index[0], 'Y')
datemax = np.datetime64(Data.index[-1], 'Y') + np.timedelta64(1, 'Y')
ax.set_xlim(datemin, datemax)
# format the coords message box
ax.format_xdata = mdates.DateFormatter('%Y-%m-%d')
ax.grid(True)
plt.show()
```
### Function for extracting the direction of the rate change (hike, keep, lower)
Gets Basis Points Move and End Rate Value for Fed Rate and Discount Rate as well as Preferred Fed Rate Move from Statement Text
```
import nltk.data
tokenizer = nltk.data.load('tokenizers/punkt/english.pickle')
def ExtractKeyValues(text):
'''
First, the text is tokenized in to sentences and the fed funds target rate sentence is extracted
Secondly, the decision whether the fed target rate was hiked, kept or lowered is retreived to RateHike variable
Third, the target rate range is extracted and saved in TargetRange (The max is extracted as it conveys most info)
'''
Potentials = [] #For storing the potential decision sentences
#Remove the \n and replace them with dots
text = text.replace('\\n','. ')
#Split the text in to a list of sentences
paragraph_sentence_list = tokenizer.tokenize(text)
#print('paragraph_sentence_list: ', paragraph_sentence_list)
#Finds the sentences with the decisions
for Sentence in paragraph_sentence_list:
#print('Sentence: ', Sentence)
#Make the text lower case
Sentence = Sentence.lower()
if 'federal funds ' in Sentence and 'target' in Sentence:
#Check if it contains a number
if bool(re.search(r'\d', Sentence)):
Potentials.append(Sentence)
Potentials = ''.join(Potentials)
#print('Potentials: ', Potentials)
#Look for decision words related to raising rates
r = Potentials.find('rais')
i = Potentials.find('increas')
upscore = max([r,i])
#Look for decision words related to keeping rates
k = Potentials.find('keep')
m = Potentials.find('maintain')
r = Potentials.find('remain')
c = Potentials.find('current')
keepscore = max([r,k,m,c])
#Look for decision words related to decreasing rates
l = Potentials.find('lower')
d = Potentials.find('decreas')
lowerscore = max([l,d])
Summary = {1:upscore,
0: keepscore,
-1:lowerscore
}
#take the key that was mentioned first in the text
RateHike = max(Summary.keys(), key=(lambda x: Summary[x]))
#For extracting the target range
def RangeReader(Nums):
def FractionReader(Fraction):
'''
Converts the fraction to a float
'''
i = 0
if '/' in Fraction:
if ' ' in Fraction:
i, Fraction = Fraction.split(' ')
if '-' in Fraction:
i, Fraction = Fraction.split('-')
if '‑' in Fraction:
i, Fraction = Fraction.split('‑')
N, D = Fraction.split('/')
return float(i) + float(N) / float(D)
else:
return float(i)+float(Fraction)
#Splits the range based on to or -
Splitters = [' to ','-']
for Splitter in Splitters:
if Splitter in Nums:
TargetRange = Nums.split(Splitter)
return FractionReader(TargetRange[0]), FractionReader(TargetRange[1])
#If there was no splitter in the range (no range)
return FractionReader(Nums)
#Find the percentage change and take the closest digits
Rate = Potentials[ : Potentials.find('percent') -1 ]
Rate = Rate[-16:]
# print(Rate)
if re.search("\d", Rate):
Rate = Rate[ re.search("\d", Rate).start() : ]
TargetRange = np.max(RangeReader(Rate))
else:
Rate = None
TargetRange = None
return RateHike, TargetRange
```
Appends decision, dummy and Moves and End Rate Values for Fed and Disc Rate also appends preferred fed rate Move while measuring the speed of the extraction
```
Data.tail()
#Data.drop(index=[pd.to_datetime("2020-03-03")], inplace=True)
```
Tried to take rate and decision from the statement text but it sometimes fails. Debugging takes time, so switch to use data instead of reading from text.
```
# import timeit
# start = timeit.timeit()
# #Append fed funds rates and decisions to dataframe
# Hikes = []
# TargetRate = []
# for i in range(len(Data)):
# if Data.iloc[i,1] == True:
# Hikes.append(np.nan)
# TargetRate.append(np.nan)
# else:
# Hikes.append( ExtractKeyValues( Data.iloc[i,0] )[0] )
# TargetRate.append( ExtractKeyValues( Data.iloc[i,0] )[1] )
# Data['RateDecision'] = Hikes
# Data['FedFundRateEndValue'] = TargetRate
# end = timeit.timeit()
# print (str ( end - start ) + ' seconds elapsed for ' + str(i) + ' statements')
# Data.tail()
# FRB changed to range from 2008. So use Upper side from 2008.
filename_till08 = '../data/MarketData/Quandl/FRED_DFEDTAR.csv'
filename_from08u = '../data/MarketData/Quandl/FRED_DFEDTARU.csv'
filename_from08l = '../data/MarketData/Quandl/FRED_DFEDTARL.csv'
fedtar = pd.read_csv(filename_till08, names=['Date', 'Rate'], header=0)
fedtaru = pd.read_csv(filename_from08u, names=['Date', 'Rate'], header=0)
fedtarl = pd.read_csv(filename_from08l, names=['Date', 'Rate'], header=0)
fedrate_df = pd.concat([fedtar, fedtaru], axis=0)
fedrate_df.index = pd.to_datetime(fedrate_df.Date, format="%Y-%m-%d")
fedrate_df.drop(columns=['Date'], inplace=True)
fedrate_df['Rate'] = fedrate_df['Rate'].map(lambda x: np.float(x))
fedrate_df
fig, ax = plt.subplots(figsize=(15,7))
ax.plot(fedrate_df.index, fedrate_df['Rate'].values, c = 'green', linewidth= 1.0)
ax.grid(True)
plt.show()
Data['RateDecision'] = None
Data['Rate'] = None
for i in range(len(Data)):
for j in range(len(fedrate_df)):
if Data.index[i] == fedrate_df.index[j]:
Data['Rate'][i] = float(fedrate_df['Rate'][j+1])
if fedrate_df['Rate'][j-1] == fedrate_df['Rate'][j+1]:
Data['RateDecision'][i] = 0
elif fedrate_df['Rate'][j-1] < fedrate_df['Rate'][j+1]:
Data['RateDecision'][i] = 1
elif fedrate_df['Rate'][j-1] > fedrate_df['Rate'][j+1]:
Data['RateDecision'][i] = -1
Data.head(10)
def pickle_dump(df, filename='no-filename.pickle'):
if filename:
with open(filename, "wb") as output_file:
pickle.dump(df, output_file)
```
### Plot the results and compare to the economical uncertainty / systemic risk periods
```
#Dot-com bubble
#https://en.wikipedia.org/wiki/Dot-com_bubble
DotCom = np.logical_and(Data.index > '2000-03', Data.index < '2002-10')
#Financial crisis of 2007–2008
#https://en.wikipedia.org/wiki/Financial_crisis_of_2007%E2%80%932008
FinCrisis = np.logical_and(Data.index > '2007-04', Data.index < '2009-03')
#European debt crisis
#https://en.wikipedia.org/wiki/European_debt_crisis
EuroDebt = np.logical_and(Data.index > '2010-09', Data.index < '2012-09')
#2015–16 Chinese stock market turbulence
#https://en.wikipedia.org/wiki/2015%E2%80%9316_Chinese_stock_market_turbulence
Asian = np.logical_and(Data.index > '2015-01', Data.index < '2016-06')
#2020- Covid-19 Pandemic
#https://en.wikipedia.org/wiki/COVID-19_pandemic
Covid = np.logical_and(Data.index > '2020-02', Data.index < '2021-12')
Recessions = np.logical_or.reduce((DotCom, FinCrisis, EuroDebt, Asian, Covid))
Window = 16
CompToMA = NetSentimentNorm.rolling(Window).mean()
fig, ax = plt.subplots(figsize=(15,7))
ax.plot(Data.index, CompToMA, c = 'r', linewidth= 2)
ax.plot(Data.index, NetSentimentNorm, c = 'green', linewidth= 1, alpha = 0.5)
# format the ticks
ax.xaxis.set_major_locator(years)
ax.xaxis.set_major_formatter(years_fmt)
ax.xaxis.set_minor_locator(months)
# round to nearest years.
datemin = np.datetime64(Data.index[0], 'Y')
datemax = np.datetime64(Data.index[-1], 'Y') + np.timedelta64(1, 'Y')
ax.set_xlim(datemin, datemax)
# format the coords message box
ax.format_xdata = mdates.DateFormatter('%Y-%m-%d')
ax.grid(True)
plt.title( str('Moving average of last ' + str(Window) + ' statements (~2 Year Window) seems to match with periods of economic uncertainty'))
ax.legend([str(str(Window) + ' statement MA'), 'Net sentiment of individual statements'],
prop={'size': 16},
loc = 2
)
import matplotlib.transforms as mtransforms
trans = mtransforms.blended_transform_factory(ax.transData, ax.transAxes)
theta = 0.9
ax.fill_between(Data.index, 0, 10, where = Recessions,
facecolor='darkblue', alpha=0.4, transform=trans)
# Add text
props = dict(boxstyle='round', facecolor='wheat', alpha=0.5)
ax.text(0.21, 0.15, "Dot Com Bubble", transform=ax.transAxes, fontsize=14, verticalalignment='top', bbox=props)
ax.text(0.46, 0.15, "Financial Crisis", transform=ax.transAxes, fontsize=14, verticalalignment='top', bbox=props)
ax.text(0.60, 0.15, "EU Debt Crisis", transform=ax.transAxes, fontsize=14, verticalalignment='top', bbox=props)
ax.text(0.76, 0.15, "China Crisis", transform=ax.transAxes, fontsize=14, verticalalignment='top', bbox=props)
ax.text(0.94, 0.15, "Covid-19", transform=ax.transAxes, fontsize=14, verticalalignment='top', bbox=props)
plt.show()
# Speaker window
Greenspan = np.logical_and(Data.index > '1987-08-11', Data.index < '2006-01-31')
Bernanke = np.logical_and(Data.index > '2006-02-01', Data.index < '2014-01-31')
Yellen = np.logical_and(Data.index > '2014-02-03', Data.index < '2018-02-03')
Powell = np.logical_and(Data.index > '2018-02-05', Data.index < '2022-02-05')
Speaker = np.logical_or.reduce((Greenspan, Yellen))
# Moving Average
Window = 8
CompToMA = NetSentimentNorm.rolling(Window).mean()
# Plotting Data
fig, ax = plt.subplots(figsize=(15,7))
plt.title('Sentiment goes down before monetary easing', fontsize=16)
ax.scatter(Data.index, Data['Rate']*3, c = 'g')
ax.plot(Data.index, CompToMA, c = 'r', linewidth= 2.0)
ax.plot(Data.index, NetSentimentNorm, c = 'green', linewidth= 1, alpha = 0.5)
ax.legend([str(str(Window) + ' statements moving average'),
'Net sentiment of individual statements',
'Fed Funds Rate'], prop={'size': 14}, loc = 1)
# Format X-axis
import matplotlib.dates as mdates
years = mdates.YearLocator() # every year
months = mdates.MonthLocator() # every month
years_fmt = mdates.DateFormatter('%Y')
ax.xaxis.set_major_locator(years)
ax.xaxis.set_major_formatter(years_fmt)
ax.xaxis.set_minor_locator(months)
# Set X-axis and Y-axis range
datemin = np.datetime64(Data.index[18], 'Y')
datemax = np.datetime64(Data.index[-1], 'Y') + np.timedelta64(1, 'Y')
ax.set_xlim(datemin, datemax)
ax.set_ylim(-10,30)
# format the coords message box
ax.format_xdata = mdates.DateFormatter('%Y-%m-%d')
ax.grid(True)
ax.tick_params(axis='both', which='major', labelsize=12)
# Fill speaker
import matplotlib.transforms as mtransforms
trans = mtransforms.blended_transform_factory(ax.transData, ax.transAxes)
theta = 0.9
ax.fill_between(Data.index, 0, 10, where = Speaker, facecolor='lightblue', alpha=0.5, transform=trans)
# Add text
props = dict(boxstyle='round', facecolor='wheat', alpha=0.5)
ax.text(0.13, 0.75, "Alan Greenspan", transform=ax.transAxes, fontsize=14, verticalalignment='top', bbox=props)
ax.text(0.46, 0.75, "Ben Bernanke", transform=ax.transAxes, fontsize=14, verticalalignment='top', bbox=props)
ax.text(0.73, 0.75, "Janet Yellen", transform=ax.transAxes, fontsize=14, verticalalignment='top', bbox=props)
ax.text(0.88, 0.75, "Jerome Powell", transform=ax.transAxes, fontsize=14, verticalalignment='top', bbox=props)
# Add annotations
arrow_style = dict(facecolor='black', edgecolor='white', shrink=0.05)
ax.annotate('QE1', xy=('2008-11-25', 0), xytext=('2008-11-25', -4), size=12, ha='right', arrowprops=arrow_style)
ax.annotate('QE1+', xy=('2009-03-18', 0), xytext=('2009-03-18', -6), size=12, ha='center', arrowprops=arrow_style)
ax.annotate('QE2', xy=('2010-11-03', 0), xytext=('2010-11-03', -4), size=12, ha='center', arrowprops=arrow_style)
ax.annotate('QE2+', xy=('2011-09-21', 0), xytext=('2011-09-21', -4.5), size=12, ha='center', arrowprops=arrow_style)
ax.annotate('QE2+', xy=('2012-06-20', 0), xytext=('2012-06-20', -6.5), size=12, ha='right', arrowprops=arrow_style)
ax.annotate('QE3', xy=('2012-09-13', 0), xytext=('2012-09-13', -8), size=12, ha='center', arrowprops=arrow_style)
ax.annotate('Tapering', xy=('2013-12-18', 0), xytext=('2013-12-18', -8), size=12, ha='center', arrowprops=arrow_style)
plt.show()
fig, ax = plt.subplots(figsize=(15,7))
Count = Data['wordcount']
ax.plot(Data.index, Count,
c = 'red',
linewidth= 1.5)
plt.title('Count of words per statement over time')
import matplotlib.dates as mdates
years = mdates.YearLocator() # every year
months = mdates.MonthLocator() # every month
years_fmt = mdates.DateFormatter('%Y')
# format the ticks
# round to nearest years.
datemin = np.datetime64(Data.index[0], 'Y')
datemax = np.datetime64(Data.index[-1], 'Y') + np.timedelta64(1, 'Y')
ax.set_xlim(datemin, datemax)
# format the coords message box
ax.format_xdata = mdates.DateFormatter('%Y-%m-%d')
ax.grid(True)
import matplotlib.transforms as mtransforms
trans = mtransforms.blended_transform_factory(ax.transData, ax.transAxes)
theta = 0.9
ax.fill_between(Data.index, 0, 10, where = Speaker,
facecolor='lightblue', alpha=0.5, transform=trans)
props = dict(boxstyle='round', facecolor='wheat', alpha=0.5)
ax.text(0.05, 0.95, "Alan Greenspan", transform=ax.transAxes, fontsize=14,
verticalalignment='top', bbox=props)
ax.text(0.50, 0.95, "Ben Bernanke", transform=ax.transAxes, fontsize=14,
verticalalignment='top', bbox=props)
ax.text(0.77, 0.95, "Janet Yellen", transform=ax.transAxes, fontsize=14,
verticalalignment='top', bbox=props)
ax.text(0.90, 0.95, "Jerome Powell", transform=ax.transAxes, fontsize=14,
verticalalignment='top', bbox=props)
plt.show()
```
| true |
code
| 0.245198 | null | null | null | null |
|
## http://scikit-learn.org/stable/auto_examples/manifold/plot_lle_digits.html
```
%matplotlib inline
# subset of http://scikit-learn.org/stable/_downloads/plot_lle_digits.py
# see Kyle Kastner at https://youtu.be/r-1XJBHot58?t=1335
# Authors: Fabian Pedregosa <fabian.pedregosa@inria.fr>
# Olivier Grisel <olivier.grisel@ensta.org>
# Mathieu Blondel <mathieu@mblondel.org>
# Gael Varoquaux
# License: BSD 3 clause (C) INRIA 2011
import matplotlib
matplotlib.rcParams['figure.figsize'] = (6.0, 6.0) # make plot larger in notebook
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
from matplotlib import offsetbox
import numpy as np
digits = load_digits(n_class=6)
X = digits.data
y = digits.target
n_img_per_row = 20
img = np.zeros((10 * n_img_per_row , 10 * n_img_per_row))
for i in range(n_img_per_row):
ix = 10 * i + 1
for j in range(n_img_per_row):
iy = 10 * j + 1
img[ix:ix +8 , iy:iy+8] = X[ i * n_img_per_row +j ].reshape((8,8))
plt.imshow(img,cmap=plt.cm.binary)
plt.xticks([])
plt.yticks([])
plt.title('A selection from the 64-dimensional digits datast')
#----------------------------------------------------------------------
# Scale and visualize the embedding vectors
def plot_embedding(X, title=None):
x_min, x_max = np.min(X, 0), np.max(X, 0)
X = (X - x_min) / (x_max - x_min)
plt.figure()
ax = plt.subplot(111)
for i in range(X.shape[0]):
plt.text(X[i, 0], X[i, 1], str(digits.target[i]),
color=plt.cm.Set1(y[i] / 10.),
fontdict={'weight': 'bold', 'size': 9})
if hasattr(offsetbox, 'AnnotationBbox'):
# only print thumbnails with matplotlib > 1.0
shown_images = np.array([[1., 1.]]) # just something big
for i in range(digits.data.shape[0]):
dist = np.sum((X[i] - shown_images) ** 2, 1)
if np.min(dist) < 4e-3:
# don't show points that are too close
continue
shown_images = np.r_[shown_images, [X[i]]]
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r),
X[i])
ax.add_artist(imagebox)
plt.xticks([]), plt.yticks([])
if title is not None:
plt.title(title)
plt.show()
X_tsne = TSNE(n_components=2, init="pca", random_state=1999).fit_transform(X)
plot_embedding(X_tsne, title="TSNE_embedding")
X_pca = PCA(n_components=2).fit_transform(X)
plot_embedding(X_pca, title="PCA_embedding")
```
| true |
code
| 0.726359 | null | null | null | null |
|
# Circuito cuántico para autoencoder
Propuesta para el hackathon es diseñar un circuito cuántico que pueda disminuir el número de variables de imagenes sin perder información y poder trabajar con menos qubits para una clasificación usando el conjunto de datos MNIST.
Se indican a continuación las dependencias necesarias para poder trabajar en este problema.
```
import numpy as np
# Bibliotecas necesarias de Qiskit
from qiskit import QuantumCircuit, transpile, Aer, IBMQ, execute, QuantumRegister, ClassicalRegister
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from qiskit.circuit import Parameter, ParameterVector
#Bliblioteca para la adquisición y preprocesamiento del conjunto MNIST.
import tensorflow as tf
#Bibliotecas para graficar
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme()
```
## Preprocesamiento
Inicializamos las carácteristicas de nuestro circuito cuántico que es el conjunto de datos MNIST, para esto nos apoyamos de tensorflow que ya tiene el conjunto de datos.
Cada conjunto tiene 10 clases : **[0,1,2,3,4,5,6,7,8,9]**,
y van de 0 a 255, por ello nosotros pasamos un proceso de **normalización que va de 0.0 a 1.0**, donde negro representa el fondo y el blanco y escala de gris a los números.
```
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train[..., np.newaxis]/255.0, x_test[..., np.newaxis]/255.0
print("Imagenes del conjunto de entrenamiento:", len(x_train))
print("Imagenes del conjunto de entrenamiento:", len(x_test))
def filter_01(x, y):
keep = (y == 0) | (y == 1)
x, y = x[keep], y[keep]
return x,y
x_train, y_train = filter_01(x_train, y_train)
x_test, y_test = filter_01(x_test, y_test)
print("Imagenes del conjunto de entrenamiento:", len(x_train))
print("Imagenes del conjunto de entrenamiento:", len(x_test))
```
Se representan las imagenes que tienen un tamaño original de 28x28
```
plt.imshow(x_train[0, :, :, 0])
plt.colorbar()
```
### Reducción de la imagen
Tensorflow tiene el método *tf.image.resize* que disminuye las imagenes a partir de los siguientes posibles criteros:
<ul>
<li><b>bilinear</b>: Bilinear interpolation. If antialias is true, becomes a hat/tent filter function with radius 1 when downsampling.</li>
<li><b>lanczos3</b>: Lanczos kernel with radius 3. High-quality practical filter but may have some ringing, especially on synthetic images.</li>
<li><b>lanczos5</b>: Lanczos kernel with radius 5. Very-high-quality filter but may have stronger ringing.</li>
<li><b>bicubic</b>: Cubic interpolant of Keys. Equivalent to Catmull-Rom kernel. Reasonably good quality and faster than Lanczos3Kernel, particularly when upsampling.</li>
<li><b>gaussian</b>: Gaussian kernel with radius 3, sigma = 1.5 / 3.0.</li>
<li><b>nearest</b>: Nearest neighbor interpolation. antialias has no effect when used with nearest neighbor interpolation.</li>
<li><b>area</b>: Anti-aliased resampling with area interpolation. antialias has no effect when used with area interpolation; it always anti-aliases.</li>
<li><b>mitchellcubic</b>: Mitchell-Netravali Cubic non-interpolating filter. For synthetic images (especially those lacking proper prefiltering), less ringing than Keys cubic kernel but less sharp.</li>
</ul>
Ejemplo de dicho preprocesamiento de reducción de datos se emplea a continuación con el método nearest y con el tamaño de imagen 8x8.
```
x_train_small = tf.image.resize(x_train, (8,8), method='nearest', preserve_aspect_ratio=True).numpy()
x_test_small = tf.image.resize(x_test, (8,8), method='nearest', preserve_aspect_ratio=True).numpy()
```
En este punto se tienen imagenes de tamaño 8x8 y se tienen que pasar como un estado de amplitud ya que $8x8 = 64$ y esto nos dará un vector de $2^6$ que recordando el valor 6 es el número de qubits a usar
```
plt.imshow(x_train_small[0,:,:,0], vmin=0, vmax=1)
plt.colorbar()
x_train = x_train_small.reshape(len(x_train_small), 64)
x_test = x_test_small.reshape(len(x_test_small), 64)
x_train.shape,x_test.shape
x_train_small[0]
```
## De imagen a qubits
Por las capacidades que actualmente se usa CPU para el diseño de circuitos cuánticos en Qiskit, no es posible ocupar todo el conjunto de imagenes, se diseñaron 8 experimentos por lo menos desde 10 iteraciones hasta 50, ocupando las siguientes entradas:
<ul>
<li>Las 5 primeras imagenes del conjunto de entrenamiento.</li>
<li>Las 10 primeras imagenes del conjunto de entrenamiento.</li>
<li>Las 12 primeras imagenes del conjunto de entrenamiento.</li>
<li>Las 50 primeras imagenes del conjunto de entrenamiento.</li>
<li>Las 70 primeras imagenes del conjunto de entrenamiento.</li>
<li>Las 100 primeras imagenes del conjunto de entrenamiento.</li>
<li>Las 200 primeras imagenes del conjunto de entrenamiento.</li>
<li>Las 500 primeras imagenes del conjunto de entrenamiento.</li>
</ul>
```
x_train = (x_train)
x_test = (x_test)
x_train.shape,x_test.shape
```
Se pasa de la matriz de tamaño 8x8 a un vector de tamaño 64x1 por cada imagen
```
x_train[0]
```
Se elimina las posibles imagenes que no tengan información, es decir, puros 0's para el conjutno de entrenamiento
```
k = 0
while k < len(x_train):
a = x_train[k].copy()
if np.sum(a) == 0.:
print(k,x_train[k])
x_train = np.delete(x_train, k, axis=0)
y_train = np.delete(y_train, k, axis=0)
k -= 1
k+=1
```
Se elimina las posibles imagenes que no tengan información, es decir, puros 0's para el conjutno de testeo
```
k = 0
while k < len(x_test):
a = x_test[k].copy()
if np.sum(a) == 0.:
print(k,x_test[k])
x_test = np.delete(x_test, k, axis=0)
y_test = np.delete(y_test, k, axis=0)
k -= 1
k+=1
```
Ahora se aplicara una renormalización para poder interpretar un vector de estado para pdoer aplicarse en nuestro modelo de circuito cuántico, siguiendo el critero:
$ \frac{vector-de-entrada}{\sqrt{\sum_{i=0}^{n-1} (vector-de-entrada_i)^2}}$,
donde vector-de-entrada es el vector de 64x1 que representa una imagen ya sea del conjunto de entrenamiento o de prueba con la finalidad de convertirse en un vector de estado $| \psi \rangle$.
```
import cmath
def Normalize(row):
suma = np.sqrt(np.sum(row**2))
if suma == 0.:
return 0.0
row = row/suma
return row
for i in range(len(x_train)):
x_train[i] = Normalize(x_train[i])
for i in range(len(x_test)):
x_test[i] = Normalize(x_test[i])
print("la suma de los estados de la imagen del conjunto de entrenamiento 0",np.sum(x_train[0]**2))
```
# Análisis y Diseño del Autoencoder
Para este trabajo se diseñará los circuitos necesarios para indicar el autoencoder en su versión cuántica.
Para este proceso se consideran 6 qubits que recordando equivalen al vector de estado 64x1, donde usaremos el mapeo por amplitud, y se ocupo por cuestiones de tiempo y recursos 1 sola capa por cada 1.
Más adelante se indicaran el circuito que se uso para esta aplicación pero requiere de 10 paramétros.
```
n=6
num_layers = 1
params = np.random.random(10*(num_layers))
```
Se valida que el vector de entrada con indice 0 este normalizado a un vector de estado
```
x_train[0]
```
Al ingresar el vector de estado como entrada a una función que genera un circuito cuántico de 6 qubits que usando el método
`initialize(vectorstate,qubits)` que genera la representación en términos de qubits.
Una observación de este método es que se puede variar el costo computacional por el tipo de método que se genere, y más si predominan estados con estados 0 de amplitud, generando que los equipos de computo de nuestro equipo fue limitado.
```
def input_data(n,inputs):
circuit = QuantumCircuit(n,1)
circuit.initialize(inputs,range(0,n,1))
circuit.barrier()
return circuit
input_data(n,x_train[0]).draw(output="mpl")
```
En este proceso generamos el circuito variacional cuántico que representa el autoencoder cuántico, consideramos de apoyo el circuito cuántico propuesto en [1], pero algunos problemas daban por el costo computacional por lo que consideramos [2],[3],[4],[5] para generar a partir de varias propuestas de redes tensoriales como peude ser MERA, para nuestro trabajo y con ciertas modificaciones para dejarlo en 6 qubits.
```
def vqc(n, num_layers,params):
#Set the number of layers and qubits
#ParameterVectors are initialized with a string identifier and an integer specifying the vector length
parameters = ParameterVector('θ', 10*(num_layers))
len_p = len(parameters)
circuit = QuantumCircuit(n, 1)
for layer in range(num_layers):
for i in range(n):
circuit.ry(parameters[(layer)+i], i)
circuit.barrier()
circuit.cx(2,0)
circuit.cx(3,1)
circuit.cx(5,4)
circuit.barrier()
circuit.ry(parameters[6+(layer)],0)
circuit.ry(parameters[7+(layer)],1)
circuit.ry(parameters[8+(layer)],4)
circuit.barrier()
circuit.cx(4,1)
circuit.barrier()
circuit.ry(parameters[9+(layer)], 1)
circuit.barrier()
params_dict = {}
i = 0
for p in parameters:
params_dict[p] = params[i]
i += 1
#Assign parameters using the assign_parameters method
circuit = circuit.assign_parameters(parameters = params_dict)
return circuit
```
El circuito de nuestra red tensorial se ve afectada por 10 compuertas $Ry(\theta)$ y 4 $C_{not}$, considerando como costo ligado al número de $C_{not}$ sería de 4.
```
vqc(n,num_layers,params).draw(output="mpl")
```
Considerando [6] se tiene la oportunidad de usar el Swap-test para buscar el valor de y se identifico de [7] la forma de trabajo de la Swap-Test se comparan dos estados $| \psi \rangle$ y $| \phi \rangle$, donde el primero es el vector de referencia $| 0 \rangle$ y el segundo los qubits que se quieren eliminar para disminuir variables, estos son $| \phi_0 \phi_1 \rangle$ donde al medirse el qubit que tiene la Hadamard del Swap-Test y este se acerque más al estado $|0 \rangle$ significa que se disminuyó de manera correcta la informacion en $| \phi_0 \phi_1 \rangle$.
```
def swap_test(n):
qubits_values = 2*n+1
qc = QuantumCircuit(qubits_values)
qc.h(0)
for i in range(n):
qc.cswap(0,i+1,2*n-i)
qc.h(0)
qc.barrier()
return qc
swap_test(2).draw(output="mpl")
```
El siguiente proceso indica el circuito cuántico variacional dle autoencoder para generar la disminución de dos qubits.
```
size_reduce = 2
circuit_init = input_data(n,x_train[0])
circuit_vqc = vqc(n,num_layers,params)
circuit_swap_test = swap_test(size_reduce)
circuit_full = QuantumCircuit(n+size_reduce+1,1)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(size_reduce+1,n+size_reduce+1)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(size_reduce+1,n+size_reduce+1)])
circuit_full = circuit_full.compose(circuit_swap_test,[i for i in range(2*size_reduce+1)])
circuit_full.draw(output="mpl")
```
Qiskit tiene la propeidad de generar de un circuito cuántico su inverso que es necesario para nosotros al momento de decodificar la disminuci´no de variables al tamaño original del vector de estado.
```
vqc(n,num_layers,params).inverse().draw(output = "mpl")
```
## Comprimir datos
En este trabajo al no encontrar una manera correecta de usar los optimziadores para un circuito cuántico que utiliza le mapeo por amplitud, se utilizo la libreria scikitlearn por su método de optimización que es el mismo que usan en Qiskit. y también se usa un shuffle para que en cada iteración logre ocupar algunas imagenes nuevas en cada iteración.
```
from random import shuffle
from scipy.optimize import minimize
```
Se uso para identificar el costo de cada entrada por el valor esperado en el eje z, es decir, $\langle z \rangle $, el cuál se define
$\langle Z \rangle = \langle q | Z | q\rangle =\langle q|0\rangle\langle 0|q\rangle - \langle q|1\rangle\langle 1|q\rangle
=|\langle 0 |q\rangle|^2 - |\langle 1 | q\rangle|^2 $
pero al adecuarl oal criterio del Swap test debe quedar como:
$1 -\langle Z \rangle = 1 - \langle q | Z | q\rangle = 1- [\langle q|0\rangle\langle 0|q\rangle - \langle q|1\rangle\langle 1|q\rangle] = 1 - [|\langle 0 |q\rangle|^2 - |\langle 1 | q\rangle|^2] = 1 - |\langle 0 |q\rangle|^2 + |\langle 1 | q\rangle|^2 $
para mayor información se puede observar en https://qiskit.org/textbook/ch-labs/Lab02_QuantumMeasurement.html
```
def objective_function(params):
costo = 0
shuffle(x_train)
lenght= 5
for i in range(lenght):
circuit_init = input_data(n,x_train[i])
circuit_vqc = vqc(n,num_layers,params)
circuit_swap_test = swap_test(size_reduce)
circuit_full = QuantumCircuit(n+size_reduce+1,1)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(size_reduce+1,n+size_reduce+1)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(size_reduce+1,n+size_reduce+1)])
circuit_full = circuit_full.compose(circuit_swap_test,[i for i in range(2*size_reduce+1)])
circuit_full.measure(0, 0)
#qc.draw()
shots= 8192
job = execute( circuit_full, Aer.get_backend('qasm_simulator'),shots=shots )
counts = job.result().get_counts()
probs = {}
for output in ['0','1']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
costo += (1 +probs['1'] - probs['0'])
return costo/lenght
for i in range(1):
minimum = minimize(objective_function, params, method='COBYLA', tol=1e-6)
params = minimum.x
print(" cost: ",objective_function(params))
print(params)
```
Al finalizar las iteraciones necesarias, depende del número del conjunto de instancia seleccionadas, se pasa por vector de estado por el complejo conjugado de nuestro circuito cuántico, dónde [6] y [7] mencionaban que nos debe dar la información original. Esto se realiza a todo el conjunto de entrenamiento como de prueba.
```
def compress_result_test(params):
reduce = []
for i in range(len(x_test)):
circuit_init = input_data(n,x_test[i])
circuit_vqc = vqc(n,num_layers,params)
circuit_full = QuantumCircuit(n,n-size_reduce)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(n)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(n)])
len_cf = len(circuit_full)
for i in range(n-size_reduce):
circuit_full.measure(size_reduce+i, i)
job = execute( circuit_full, Aer.get_backend('qasm_simulator'),shots=8192 )
result = job.result().get_counts()
probs = {k: np.sqrt(v / 8192) for k, v in result.items()}
reduce.append(probs)
return reduce
reduce_img =compress_result_test(params)
test_reduce = []
for i in reduce_img:
index_image = []
for j in range(16):
bin_index = bin(j)[2:]
while len(bin_index) <4:
bin_index = '0'+bin_index
try:
index_image.append(i[bin_index])
except:
index_image.append(0)
test_reduce.append(np.array(index_image))
def compress_result_train(params):
reduce = []
for i in range(len(x_train)):
circuit_init = input_data(n,x_train[i])
circuit_vqc = vqc(n,num_layers,params)
circuit_full = QuantumCircuit(n,n-size_reduce)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(n)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(n)])
len_cf = len(circuit_full)
for i in range(n-size_reduce):
circuit_full.measure(size_reduce+i, i)
job = execute( circuit_full, Aer.get_backend('qasm_simulator'),shots=8192 )
result = job.result().get_counts()
probs = {k: np.sqrt(v / 8192) for k, v in result.items()}
reduce.append(probs)
return reduce
reduce_img =compress_result_train(params)
train_reduce = []
for i in reduce_img:
index_image = []
for j in range(16):
bin_index = bin(j)[2:]
while len(bin_index) <4:
bin_index = '0'+bin_index
try:
index_image.append(i[bin_index])
except:
index_image.append(0)
train_reduce.append(np.array(index_image))
```
En este punto se muestra las primeras 5 imagenes del conjunto de prueba de tamaño 8x8 como se reducen a un tamaño de 4x4 cada una.
```
plt.figure()
#subplot(r,c) provide the no. of rows and columns
f, axarr = plt.subplots(5,1)
# use the created array to output your multiple images. In this case I have stacked 4 images vertically
axarr[0].imshow(x_test[0].reshape(8,8)*255)
axarr[1].imshow(x_test[1].reshape(8,8)*255)
axarr[2].imshow(x_test[2].reshape(8,8)*255)
axarr[3].imshow(x_test[3].reshape(8,8)*255)
axarr[4].imshow(x_test[4].reshape(8,8)*255)
#subplot(r,c) provide the no. of rows and columns
f, axarr = plt.subplots(5,1)
# use the created array to output your multiple images. In this case I have stacked 4 images vertically
axarr[0].imshow(test_reduce[0].reshape(4,4)*255)
axarr[1].imshow(test_reduce[1].reshape(4,4)*255)
axarr[2].imshow(test_reduce[2].reshape(4,4)*255)
axarr[3].imshow(test_reduce[3].reshape(4,4)*255)
axarr[4].imshow(test_reduce[4].reshape(4,4)*255)
```
### Descomprimir datos
Aquí recordando la aplicación del complejo conjugado de nuestra propuesta de red tensorial debemos acercarnos al valor original de entrada $|\phi \rangle$
```
vqc(n,num_layers,params).inverse().draw(output = "mpl")
def decoder_result_test(params):
reduce = []
for i in range(len(test_reduce)):
circuit_init = input_data(6,np.concatenate((np.zeros(48), test_reduce[i]), axis=0))
circuit_vqc = vqc(n,num_layers,params).inverse()
circuit_full = QuantumCircuit(n,n)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(n)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(n)])
job = execute( circuit_full, Aer.get_backend('statevector_simulator') )
result = job.result().get_statevector()
reduce.append(result)
return reduce
decoder =decoder_result_test(params)
plt.figure()
#subplot(r,c) provide the no. of rows and columns
f, axarr = plt.subplots(5,1)
# use the created array to output your multiple images. In this case I have stacked 4 images vertically
axarr[0].imshow(decoder[0].real.reshape(8,8)*255)
axarr[1].imshow(decoder[1].real.reshape(8,8)*255)
axarr[2].imshow(decoder[2].real.reshape(8,8)*255)
axarr[3].imshow(decoder[3].real.reshape(8,8)*255)
axarr[4].imshow(decoder[4].real.reshape(8,8)*255)
def decoder_result_train(params):
reduce = []
for i in range(len(train_reduce)):
circuit_init = input_data(n,np.concatenate((np.zeros(48), train_reduce[i]), axis=0))
circuit_vqc = vqc(n,num_layers,params).inverse()
circuit_full = QuantumCircuit(n,n)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(n)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(n)])
job = execute( circuit_full, Aer.get_backend('statevector_simulator') )
result = job.result().get_statevector()
reduce.append(result)
return reduce
decoder_train =decoder_result_train(params)
```
# métricas para comparar imagenes
De cada una de las imágenes tanto de prueba como entrenamiento se realizará las siguientes métricas para validar la capacidad de nuestro autoencoder entre las imagenes de entrada y descomprimidas.
- Error Cuadrático medio (o por sus siglas en inglés MSE)
$MSE=\frac{1}{m n} \sum_{i=0}^{m-1} \sum_{j=0}^{n-1}[I(i, j)-K(i, j)]^{2},$
donde $m$ es el alto de la imágen $I$, n el ancho de la imagen $K$ e $i$,$j$ las posiciones $x,y$ de los píxeles de las imágenes; entre más cercano a 0 sea su valor es mejor.
- Proporción Máxima de Señal a Ruido (o por sus siglas en inglés PSNR)
$PSNR = 10×log_{10}(\frac{(mxn)^2}{MSE},$
donde $m$ el alto de la imagen $I$, n el ancho de la imagen $K$ y $MSE$ el error cuadrático medio;entre más alto su valor es mejor.
- Semejanza Estructural (o por sus siglas en inglés SSIM)
$ \operatorname{SSIM}(x, y)=\frac{\left(2 \mu_{x} \mu_{y}+c_{1}\right)\left(2 \sigma_{x y}+c_{2}\right)}{\left(\mu_{x}^{2}+\mu_{y}^{2}+c_{1}\right)\left(\sigma_{x}^{2}+\sigma_{y}^{2}+c_{2}\right)},$
donde $\mu$ es el promedio, $\sigma$ es la varianza y $c$ es la covarianza \cite{c1}}; peor caso -1, mejor caso 1.
```
def mse(imageA, imageB):
err = np.sum((imageA.astype("float") - imageB.astype("float")) ** 2)
err /= float(imageA.shape[0] * imageA.shape[1])
return err
from skimage.metrics import structural_similarity as ssim
```
# Comparar el conjunto de entrenamiento
Se realiza los resultados de las tres métricas en el conjunto de entrenamiento
```
import math
ssim_list = []
mse_list = []
psnr_list = []
for i in range(len(x_train)):
test_img = x_train[i].reshape(8,8)*255
decoded_img = decoder_train[i].real.reshape(8,8)*255
Y = float(mse(decoded_img,test_img))
ssim_list.append(ssim(decoded_img.astype("float"),test_img.astype("float")))
mse_list.append(Y)
aux = (64**2)/Y
psnr_list.append(10*math.log10(aux))
from matplotlib import pyplot as plt
plt.plot(mse_list)
plt.show()
from matplotlib import pyplot as plt
plt.plot(psnr_list)
plt.show()
from matplotlib import pyplot as plt
plt.plot(ssim_list)
plt.show()
```
# Comparar el conjunto de prueba (Test)
Se realiza los resultados de las tres métricas en el conjunto de prueba
```
ssim_list = []
mse_list = []
psnr_list = []
for i in range(len(x_test)):
test_img = x_test[i].reshape(8,8)*255
decoded_img = decoder[i].real.reshape(8,8)*255
Y = float(mse(decoded_img,test_img))
ssim_list.append(ssim(decoded_img.astype("float"),test_img.astype("float")))
mse_list.append(Y)
aux = (64**2)/Y
psnr_list.append(10*math.log10(aux))
from matplotlib import pyplot as plt
plt.plot(mse_list)
plt.show()
from matplotlib import pyplot as plt
plt.plot(psnr_list)
plt.show()
from matplotlib import pyplot as plt
plt.plot(ssim_list)
plt.show()
```
Se repite el mis proceso pero ya con eentradas no aleatorias para guardar la información en archivos csv que se ocuapran para realizar una clasificación con las imagenes reducidas.
```
(x_train_c, y_train_c), (x_test_c, y_test_c) = tf.keras.datasets.mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train_c, x_test_c = x_train_c[..., np.newaxis]/255.0, x_test_c[..., np.newaxis]/255.0
x_train_c, y_train_c = filter_01(x_train_c, y_train_c)
x_test_c, y_test_c = filter_01(x_test_c, y_test_c)
x_train_c = tf.image.resize(x_train_c, (8,8), method='nearest', preserve_aspect_ratio=True).numpy()
x_test_c = tf.image.resize(x_test_c, (8,8), method='nearest', preserve_aspect_ratio=True).numpy()
for i in range(len(x_train_c)):
x_train_c[i] = Normalize(x_train_c[i])
for i in range(len(x_test)):
x_test_c[i] = Normalize(x_test_c[i])
x_train_c = x_train_c.reshape(len(x_train_small), 64)
x_test_c = x_test_c.reshape(len(x_test_small), 64)
x_train_c.shape
def compress_result_train(params):
reduce = []
for i in range(len(x_train_c)):
circuit_init = input_data(n,x_train_c[i])
circuit_vqc = vqc(n,num_layers,params)
circuit_full = QuantumCircuit(n,n-size_reduce)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(n)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(n)])
len_cf = len(circuit_full)
for i in range(n-size_reduce):
circuit_full.measure(size_reduce+i, i)
job = execute( circuit_full, Aer.get_backend('qasm_simulator'),shots=8192 )
result = job.result().get_counts()
probs = {k: np.sqrt(v / 8192) for k, v in result.items()}
reduce.append(probs)
return reduce
reduce_train_c = compress_result_train(params)
def compress_result_test(params):
reduce = []
for i in range(len(x_test_c)):
circuit_init = input_data(n,x_test_c[i])
circuit_vqc = vqc(n,num_layers,params)
circuit_full = QuantumCircuit(n,n-size_reduce)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(n)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(n)])
len_cf = len(circuit_full)
for i in range(n-size_reduce):
circuit_full.measure(size_reduce+i, i)
job = execute( circuit_full, Aer.get_backend('qasm_simulator'),shots=8192 )
result = job.result().get_counts()
probs = {k: np.sqrt(v / 8192) for k, v in result.items()}
reduce.append(probs)
return reduce
reduce_test_c = compress_result_test(params)
test_reduce = []
for i in reduce_test_c:
index_image = []
for j in range(16):
bin_index = bin(j)[2:]
while len(bin_index) <4:
bin_index = '0'+bin_index
try:
index_image.append(i[bin_index])
except:
index_image.append(0)
test_reduce.append(np.array(index_image))
train_reduce = []
for i in reduce_train_c:
index_image = []
for j in range(16):
bin_index = bin(j)[2:]
while len(bin_index) <4:
bin_index = '0'+bin_index
try:
index_image.append(i[bin_index])
except:
index_image.append(0)
train_reduce.append(np.array(index_image))
def decoder_result_train_c(params):
reduce = []
for i in range(len(train_reduce)):
circuit_init = input_data(n,np.concatenate((np.zeros(48), train_reduce[i]), axis=0))
circuit_vqc = vqc(n,num_layers,params).inverse()
circuit_full = QuantumCircuit(n,n)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(n)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(n)])
job = execute( circuit_full, Aer.get_backend('statevector_simulator') )
result = job.result().get_statevector()
reduce.append(result)
return reduce
decoder_train_c =decoder_result_train_c(params)
len(decoder_train_c)
def decoder_result_test_c(params):
reduce = []
for i in range(len(test_reduce)):
circuit_init = input_data(6,np.concatenate((np.zeros(48), test_reduce[i]), axis=0))
circuit_vqc = vqc(n,num_layers,params).inverse()
circuit_full = QuantumCircuit(n,n)
circuit_full = circuit_full.compose(circuit_init,[i for i in range(n)])
circuit_full = circuit_full.compose(circuit_vqc,[i for i in range(n)])
job = execute( circuit_full, Aer.get_backend('statevector_simulator') )
result = job.result().get_statevector()
reduce.append(result)
return reduce
decoder_c =decoder_result_test_c(params)
```
### Guardar los resultados
Se guardaron dos archivos train.csv y test.csv de las imágenes comprimidas obtenidas de nuestro autoencoder la primera para el conjunto de entrenamiento y la segunda para el conjunto de prueba
```
import pandas as pd
df = pd.DataFrame(train_reduce)
df[16] = y_train
df.to_csv("train_1.csv",index=False)
df = pd.DataFrame(test_reduce)
df[16] = y_test
df.to_csv("test_1.csv",index=False)
```
# Resultados del autoencoder cuántico
Siguiendo los resultados definimos en un histograma por métrica los mejores casos y nos dieron las siguientes gráficas
## MSE
Los resultados más cercanos al 0 son los mejores resultados, viendo de manera visual el mejor caso es con 200 imágenes.
<img src="mse.png">
## PSNR
Los resultados con un valor mayor en el eje de las ordenadas son los mejores resultados, observando de manera visual que el mejor caso es con 200 imágenes.
<img src="psnr.png">
## SSIM
Los resultados más cercanos a 1 son los mejores resultados, viendo de manera visual el mejor caso es con 200 imágenes.
<img src="ssim.png">
Por lo tanto consideraremos los resultados de 200 imagenes para realizar un clasificador binario.
# Parte del clasificador binario
Se importan las bibliotecas necesarias para esto usando qiskit meachine learning
```
# Scikit Imports
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler, MinMaxScaler
# Qiskit Imports
from qiskit import Aer, execute
from qiskit.circuit import QuantumCircuit, Parameter, ParameterVector
from qiskit.circuit.library import PauliFeatureMap, ZFeatureMap, ZZFeatureMap
from qiskit.circuit.library import TwoLocal, NLocal, RealAmplitudes, EfficientSU2
from qiskit.circuit.library import HGate, RXGate, RYGate, RZGate, CXGate, CRXGate, CRZGate
from qiskit_machine_learning.kernels import QuantumKernel
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import csv
```
Se obtiene los datos de los csv tanto para poder procesar los datos en el clasificador cuántico variacional. pasando un lado el vector de entrada de tamaño 16x1 y el otro la etiqueta
```
sample_train = []
label_train = []
with open('train.csv', newline='') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
next(reader, None)
for row in reader:
sample_train.append(row[0:-1])
label_train.append(row[-1])
sample_train = np.array(sample_train).astype(np.float)
label_train = np.array(label_train).astype(np.float)
sample_train.shape, label_train.shape
sample_test = []
label_test = []
with open('test.csv', newline='') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
next(reader, None)
for row in reader:
sample_test.append(row[0:-1])
label_test.append(row[-1])
sample_test = np.array(sample_test).astype(np.float)
label_test = np.array(label_test).astype(np.float)
sample_test.shape, label_test.shape
```
Se genera el vector de entrada para el conjunto de entrenamiento y prueba de tamañ0 16x1
```
sample_train = sample_train.reshape(len(sample_train), 16)
sample_test = sample_test.reshape(len(sample_test), 16)
```
Vamos a realizar un clasificador usando 4 qubits por lo cual hay disminuir el númeor de muestras para que nuestros dispositivos puedan correr los ejemplos, usando el método Hold-out 70-30, es decir, 70% entrenamiento y 30% de prueba.
```
train_size = 700
sample_train = sample_train[:train_size]
label_train = label_train[:train_size]
test_size = 300
sample_test = sample_test[:test_size]
label_test = label_test[:test_size]
```
Lo siguiente es mapear el vector clasico a un estado cuántico para ello usaremos la funcion ZZFeatureMap ("Se puede ocupar otro como PauliFeatureMap o ZFeatureMap").
Despues inicializaremos un Kernel cuántico del cual podemos calcular cada elemento de esta mátriz en una computadora cuántica calculando la amplitud de transición. Esto nos proporciona una estimación de la matriz cuántica del kernel, que luego podemos usar en un algoritmo de aprendizaje automático del kernel, es este caso se usara en una maquina de soporte vectorial
```
zz_map = ZZFeatureMap(feature_dimension=16, reps=1, entanglement='linear', insert_barriers=True)
zz_kernel = QuantumKernel(feature_map=zz_map, quantum_instance=Aer.get_backend('statevector_simulator'))
zz_map.draw(output="mpl")
```
Construimos las matrices de entrenamiento y prueba del kernel cuántico.
Para cada par de puntos de datos en el conjunto de datos de entrenamiento
```
matrix_train = zz_kernel.evaluate(x_vec=sample_train)
matrix_test = zz_kernel.evaluate(x_vec=sample_test, y_vec=sample_train)
```
Utilizamos las matrices de entrenamiento y prueba del kernel cuántico en un algoritmo de clasificación de máquina de vectores de soporte clásico.
```
zzpc_svc = SVC(kernel='precomputed')
zzpc_svc.fit(matrix_train, label_train)
zzpc_score = zzpc_svc.score(matrix_test, label_test)
print(f'Precomputed kernel classification test score: {zzpc_score}')
```
Probamos el algoritmo viendo que tal hace la clasificacion del set de prueba
```
predictions = zzpc_svc.predict(matrix_test)
```
Como se puede observar de 300 muestaras solo 6 no se clasificaron de manera correcta
```
for prediction,label in zip(predictions,label_test):
if(prediction != label):
print(prediction, label)
```
## Validar para el conjunto de 200 imagenes
Se repite el mismo proceso pero considerando que el método de validación hold-out se consideré válido se debe hacer la prueba con diferentes conjuntos de forma aleatoria que se realizará con el conjunto comprimido de 200 imágenes
```
sample_train = []
label_train = []
with open('train_200.csv', newline='') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
next(reader, None)
for row in reader:
sample_train.append(row[0:-1])
label_train.append(row[-1])
sample_train = np.array(sample_train).astype(np.float)
label_train = np.array(label_train).astype(np.float)
sample_test = []
label_test = []
with open('test_200.csv', newline='') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
next(reader, None)
for row in reader:
sample_test.append(row[0:-1])
label_test.append(row[-1])
sample_test = np.array(sample_test).astype(np.float)
label_test = np.array(label_test).astype(np.float)
sample_train.shape, label_train.shape, sample_test.shape, label_test.shape
```
Se genera 7 iteraciones con diferentes imagenes de rangos fijos
```
score = []
for i in range(7):
train_size = 700
sample_train_1 = sample_train[i*train_size:(i+1)*train_size]
label_train_1 = label_train[i*train_size:(i+1)*train_size]
test_size = 300
sample_test_1 = sample_test[i*test_size:(i+1)*test_size]
label_test_1 = label_test[i*test_size:(i+1)*test_size]
zz_map = ZZFeatureMap(feature_dimension=16, reps=1, entanglement='linear', insert_barriers=True)
zz_kernel = QuantumKernel(feature_map=zz_map, quantum_instance=Aer.get_backend('statevector_simulator'))
matrix_train = zz_kernel.evaluate(x_vec=sample_train_1)
matrix_test = zz_kernel.evaluate(x_vec=sample_test_1, y_vec=sample_train_1)
zzpc_svc = SVC(kernel='precomputed')
zzpc_svc.fit(matrix_train, label_train_1)
zzpc_score = zzpc_svc.score(matrix_test, label_test_1)
print(f'Precomputed kernel classification test score: {zzpc_score}')
score.append(zzpc_score)
del matrix_train, matrix_test
```
El valor promedio para el conjunto que se dio del auto encoder usando Hold-out 70-30 se obtuvo un valor de desempeño de
```
sum(score)/len(score)
```
## Autores
- Martínez Vázquez María Fernanda (undergraduate)
- Navarro Ambriz Ronaldo (undergraduate)
- Martinez Hernandez Luis Eduardo (undergraduate)
- Galindo Reyes Agustin (undergraduate)
- Alberto Maldonado Romo (master)
# Referencias
[1] Bravo-Prieto, Carlos. (2020). Quantum autoencoders with enhanced data encoding.
[2] Biamonte, Jacob. (2019). Lectures on Quantum Tensor Networks.
[3] Kardashin, Andrey & Uvarov, Aleksey & Biamonte, Jacob. (2021). Quantum Machine Learning Tensor Network States. Frontiers in Physics. 8. 586374. 10.3389/fphy.2020.586374.
[4] Stoudenmire, E. & Schwab, David. (2016). Supervised Learning with Quantum-Inspired Tensor Networks.
[5] Liu, Ding & Yao, Zekun & Zhang, Quan. (2020). Quantum-Classical Machine learning by Hybrid Tensor Networks
[6] Romero, Jonathan & Olson, Jonathan & Aspuru-Guzik, Alán. (2016). Quantum autoencoders for efficient compression of quantum data. Quantum Science and Technology. 2. 10.1088/2058-9565/aa8072.
[7] Foulds, Steph & Kendon, Viv & Spiller, Tim. (2020). The controlled SWAP test for determining quantum entanglement.
| true |
code
| 0.434941 | null | null | null | null |
|
# Comparison of the CNN filter combinations based on 5-fold cross-validation
Investigation into the effect of various filter combinations for the CNN model. To compare the different filter values, five-fold cross-validation was used. For each fold, one subject of the five total subjects (subject C being reserved for final evaluation) was withheld for evaluation whilst the model was trained on the remaining four subjects.
CNN model developed by A. Angelov, applied to the micro-Doppler spectrograms.
User c is completely removed as this is the test set.
The remaining users A, B, D, E and F make up each fold.
For example, fold 1 will train on users B, D, E and F then evaluate on A (and so on for each fold).
## Notebook setup
```
# Plot graphs inline
%matplotlib inline
```
The following cell is needed for compatibility when using both CoLab and Local Jupyter notebook. It sets the appropriate file path for the data.
```
import os
path = os.getcwd()
if path == '/content':
from google.colab import drive
drive.mount('/content/gdrive')
BASE_PATH = '/content/gdrive/My Drive/Level-4-Project/'
os.chdir('gdrive/My Drive/Level-4-Project/')
elif path == 'D:\\Google Drive\\Level-4-Project\\notebooks':
BASE_PATH = "D:/Google Drive/Level-4-Project/"
elif path == "/export/home/2192793m":
BASE_PATH = "/export/home/2192793m/Level-4-Project/"
DATA_PATH = BASE_PATH + 'data/processed/doppler_spectrograms/3/'
RESULTS_PATH = BASE_PATH + 'results/CNN_model_comparison/'
if not os.path.exists(RESULTS_PATH):
os.makedirs(RESULTS_PATH)
```
Import remaining packages
```
import numpy as np
from keras.optimizers import SGD
from keras.utils import np_utils
import pickle
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Convolution2D, MaxPooling2D
import matplotlib.pyplot as plt
# Needed as originally code was for theano backend but now using tensor flow
from keras import backend as K
K.set_image_dim_ordering('th')
```
## Experiment Setup
```
SAVE_GRAPHS_OVERFITTING = False # false to not override results
SAVE_GRAPHS_AVERAGES = False # save avg acc and avg loss graphs from k fold
SAVE_GRAPHS_DISTRIBUTIONS = False # save accuracy distribution across folds graphs
SAVE_RESULTS_OVERFITTING = False # false to not override results
SAVE_RESULTS_K_FOLD = False
SAVE_BOXPLOTS = False
target_names = ["walking", "pushing", "sitting", "pulling", "circling", "clapping", "bending"]
nb_classes = len(target_names)
batch_size = 64
# input image dimensions
img_rows, img_cols = 75, 75
# user c excluded as this is reserved for final evaluation
users = ["A", "B", "D", "E", "F"]
def load_data(user_letter):
"""
load the data and labels associated with a particular user/subject (interchangeable)
:param user_letter: Letter representing subject/user (A-F)
:type user_letter: str
:return: data and labels
:rtype: tuple of the form (data, labels)
"""
with open(DATA_PATH + user_letter + "_data.pkl", 'rb') as data_file:
data = pickle.load(data_file)
data = data.reshape(data.shape[0], 1, 75, 75)
with open(DATA_PATH + user_letter + "_labels.pkl", 'rb') as labels_file:
labels = pickle.load(labels_file)
labels = np.reshape(labels, (len(labels), 1))
return data, labels
datasets = {}
for user in users:
data, labels = load_data(user)
datasets[user] = {"data":data, "labels":labels}
def split_train_validation(validation_user):
"""
Splits the data into a train and validation set.
The validation set is composed of the subject specified, the training set of the remaining subjects.
:param validation_user: Subject to use for validation set (A-F)
:type validation_user: str
:return: data and labels for the train and validation set
:rtype: dictionary with keys "train_data", "train_labels", "validation_data" and "validation_labels"
"""
train_data = None
train_labels = None
first_round = True
validation_data = []
validation_labels = []
for user in users:
data = datasets[user]["data"]
labels = datasets[user]["labels"]
if user == validation_user:
validation_data = data
validation_labels = labels
else:
if first_round:
train_data = data
train_labels = labels
first_round = False
else:
train_data = np.concatenate((train_data, data))
train_labels = np.concatenate((train_labels, labels))
train_labels = np_utils.to_categorical(train_labels, nb_classes)
validation_labels = np_utils.to_categorical(validation_labels, nb_classes)
train_data = train_data.astype('float32')
validation_data = validation_data.astype('float32')
train_data /= 255
validation_data /= 255
return {
"train_data": train_data,
"train_labels": train_labels,
"validation_data": validation_data,
"validation_labels": validation_labels
}
```
## Define Models
```
def make_model(nb_filters, img_rows, img_cols, nb_classes):
"""
Make and return the CNN model
:param nb_filters: Number of filters to use in layers 1,2 and 3,4 respectively
:type nb_filters: str containing the number of filters for the first two layers followed by
the last two layers, for example: "16-32"
:param img_rows: image height
:type img_rows: int
:param img_cols: image width
:type img_cols: int
:param nb_classes: Number of classes to be predicted
:type nb_classes: int
:return: CNN model
:rtype: Keras sequential model
"""
model = Sequential(name=nb_filters)
nb_filters = nb_filters.split("-")
size_1 = int(nb_filters[0])
size_2 = int(nb_filters[1])
model.add(Convolution2D(size_1, (3, 3), padding='same', input_shape=(1, img_rows, img_cols), activation='relu'))
model.add(Convolution2D(size_1, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Convolution2D(size_2, (3, 3), padding='same', activation='relu'))
model.add(Convolution2D(size_2, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(nb_classes, activation='softmax'))
return model
model_types = ["2-4", "4-8", "8-16", "16-32", "32-64", "64-128"]
```
## Examining Overfitting
Train each model on 4 of the 5 users then evalaute on the 5th.
Compare at which epoch the model begins to overfit.
```
nb_epoch = 50
overfitting_results = {}
validation_user = "B" # use user B for validation
for model_type in model_types:
print("Model:", model_type)
data_split = split_train_validation(validation_user)
train_data = data_split["train_data"]
train_labels = data_split["train_labels"]
validation_data = data_split["validation_data"]
validation_labels = data_split["validation_labels"]
model = make_model(model_type, img_rows, img_cols, nb_classes)
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss='categorical_crossentropy',
optimizer=sgd,
metrics=['accuracy'])
history = model.fit(
train_data,
train_labels,
batch_size=batch_size,
epochs=nb_epoch,
shuffle=True,
validation_data=(validation_data, validation_labels),
verbose=0)
overfitting_results[model_type] = history.history
```
### Save Results
```
if SAVE_RESULTS_OVERFITTING:
with open(RESULTS_PATH + "overfitting_results.pkl", 'wb') as results_file:
pickle.dump(overfitting_results, results_file)
```
### Load Results
```
with open(RESULTS_PATH + "overfitting_results.pkl", 'rb') as results_file:
overfitting_results = pickle.load(results_file)
```
### Visualize Results
```
for model_type in model_types:
training_acc = np.array(overfitting_results[model_type]['acc'])*100
validation_acc = np.array(overfitting_results[model_type]['val_acc'])*100
# Create count of the number of epochs
epoch_count = range(1, len(training_acc) + 1)
# Visualize loss history
plt.plot(epoch_count, training_acc, 'b--', label='Training (Subjects A, D, E and F)')
plt.plot(epoch_count, validation_acc, 'r-', label='Validation (Subject B)')
plt.legend(loc='best')
plt.xlabel('Epoch')
plt.ylabel('Classification Accuracy (%)')
plt.title("Model: " + model_type)
plt.grid()
if SAVE_GRAPHS_OVERFITTING:
plt.savefig(RESULTS_PATH + model_type + "_overfitting.pdf", format='pdf')
plt.show()
```
## 5-Fold Cross-Validation
From the above graphs it would seem that all models have almost converged after 30 epochs. Therefore we will use this value for the k-fold comparison.
```
nb_epoch = 30
```
### Variables to save results
```
results = {}
for model_type in model_types:
results[model_type] = {}
for user in users:
results[model_type][user] = {}
```
### Run K-fold
```
for model_type in model_types:
print("Model:", model_type)
average_accuracy = 0
average_loss = 0
for user in users:
data_split = split_train_validation(user)
train_data = data_split["train_data"]
train_labels = data_split["train_labels"]
validation_data = data_split["validation_data"]
validation_labels = data_split["validation_labels"]
model = make_model(model_type, img_rows, img_cols, nb_classes)
# train the model using SGD + momentum.
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss='categorical_crossentropy',
optimizer=sgd,
metrics=['accuracy'])
model.fit(
train_data,
train_labels,
batch_size=batch_size,
epochs=nb_epoch,
shuffle=True,
verbose=0)
evaluation = model.evaluate(validation_data, validation_labels,
batch_size=batch_size, verbose=1)
results[model_type][user]["loss"] = evaluation[0]
results[model_type][user]["accuracy"] = evaluation[1]
average_loss += evaluation[0]
average_accuracy += evaluation[1]
results[model_type]["avg_loss"] = average_loss/len(users)
results[model_type]["avg_acc"] = average_accuracy/len(users)
print("Average Loss:", average_loss/len(users))
print("Average Accuracy:", average_accuracy/len(users))
```
## Save results
```
if SAVE_RESULTS_K_FOLD:
with open(RESULTS_PATH + "results_dictionary.pkl", 'wb') as results_file:
pickle.dump(results, results_file)
```
## Load previous results
```
with open(RESULTS_PATH + "results_dictionary.pkl", 'rb') as results_file:
results = pickle.load(results_file)
```
## Results Visualization
### Average Accuracy
```
accuracies = []
labels = []
for model_name, value in results.items():
accuracies.append(value["avg_acc"])
labels.append(model_name)
plt.bar(range(len(labels)), np.array(accuracies)*100, zorder=3)
plt.xticks(range(len(labels)), labels)
plt.xlabel("Model")
plt.ylabel("Average Classification Accuracy (%)")
plt.title("Average Accuracy Comparison from 5-Fold Cross-Validation")
plt.grid(axis='y', zorder=0)
if SAVE_GRAPHS_AVERAGES:
plt.savefig(RESULTS_PATH + "average_accuracy_comparison.pdf", format='pdf')
plt.show()
```
### Avererage Loss
```
loss = []
labels = []
for model_name, value in results.items():
loss.append(value["avg_loss"])
labels.append(model_name)
plt.bar(range(len(labels)), loss, zorder=3)
plt.xticks(range(len(labels)), labels)
plt.xlabel("Model")
plt.ylabel("Average Loss")
plt.title("Average Loss Comparison from 5-Fold Cross-Validation")
plt.grid(axis='y', zorder=0)
if SAVE_GRAPHS_AVERAGES:
plt.savefig(RESULTS_PATH + "average_loss_comparison.pdf", format='pdf')
plt.show()
```
### Box Plot Comparison
```
seperated_results = {}
for model_name, value in results.items():
accuracies = []
for user_label, res in value.items():
if len(user_label) > 1:
continue
accuracies.append(res["accuracy"] * 100)
seperated_results[model_name] = accuracies
labels = ["2-4", "4-8", "8-16", "16-32", "32-64", "64-128"]
data_to_plot = []
for label in labels:
data_to_plot.append(seperated_results[label])
plt.boxplot(data_to_plot, labels=labels, zorder=3)
plt.title("Five-Fold Cross-Validation Distribution Comparison")
plt.xlabel("Filter Combination")
plt.ylabel("Classification Accuracy (%)")
plt.ylim(0,100)
plt.grid(axis='y', zorder=0)
if SAVE_BOXPLOTS:
plt.savefig(RESULTS_PATH + "boxplot_all_models.pdf", format='pdf')
```
All the models above appear to be performing very similiar however due to its slightly higher mean and specifically its better minimum performance model "8-16" has been chosen to continue.
### Comparing Accuracy Across Folds
```
for model_name, value in results.items():
accuracies = []
labels = []
for user_label, res in value.items():
if len(user_label) > 1:
continue
accuracies.append(res["accuracy"]*100)
labels.append(user_label)
plt.bar(range(len(labels)), accuracies, zorder=3)
plt.xticks(range(len(labels)), labels)
plt.xlabel("Subject (fold)")
plt.ylabel("Classification Accuracy (%)")
plt.title("Model: " + model_name + " Fold Accuracy Distribution")
plt.grid(axis='y', zorder=0)
if SAVE_GRAPHS_DISTRIBUTIONS:
plt.savefig(RESULTS_PATH + model_name + "_fold_accuracy_distribution.pdf", format='pdf')
plt.show()
```
| true |
code
| 0.668312 | null | null | null | null |
|
# Deploy a Trained PyTorch Model
In this notebook, we walk through the process of deploying a trained model to a SageMaker endpoint. If you recently ran [the notebook for training](get_started_mnist_deploy.ipynb) with %store% magic, the `model_data` can be restored. Otherwise, we retrieve the
model artifact from a public S3 bucket.
```
# setups
import os
import json
import boto3
import sagemaker
from sagemaker.pytorch import PyTorchModel
from sagemaker import get_execution_role, Session
# Get global config
with open("code/config.json", "r") as f:
CONFIG = json.load(f)
sess = Session()
role = get_execution_role()
%store -r pt_mnist_model_data
try:
pt_mnist_model_data
except NameError:
import json
# copy a pretrained model from a public public to your default bucket
s3 = boto3.client("s3")
bucket = CONFIG["public_bucket"]
key = "datasets/image/MNIST/model/pytorch-training-2020-11-21-22-02-56-203/model.tar.gz"
s3.download_file(bucket, key, "model.tar.gz")
# upload to default bucket
pt_mnist_model_data = sess.upload_data(
path="model.tar.gz", bucket=sess.default_bucket(), key_prefix="model/pytorch"
)
print(pt_mnist_model_data)
```
## PyTorch Model Object
The `PyTorchModel` class allows you to define an environment for making inference using your
model artifact. Like `PyTorch` class we discussed
[in this notebook for training an PyTorch model](
get_started_mnist_train.ipynb), it is high level API used to set up a docker image for your model hosting service.
Once it is properly configured, it can be used to create a SageMaker
endpoint on an EC2 instance. The SageMaker endpoint is a containerized environment that uses your trained model
to make inference on incoming data via RESTful API calls.
Some common parameters used to initiate the `PyTorchModel` class are:
- entry_point: A user defined python file to be used by the inference image as handlers of incoming requests
- source_dir: The directory of the `entry_point`
- role: An IAM role to make AWS service requests
- model_data: the S3 location of the compressed model artifact. It can be a path to a local file if the endpoint
is to be deployed on the SageMaker instance you are using to run this notebook (local mode)
- framework_version: version of the PyTorch package to be used
- py_version: python version to be used
We elaborate on the `entry_point` below.
```
model = PyTorchModel(
entry_point="inference.py",
source_dir="code",
role=role,
model_data=pt_mnist_model_data,
framework_version="1.5.0",
py_version="py3",
)
```
### Entry Point for the Inference Image
Your model artifacts pointed by `model_data` is pulled by the `PyTorchModel` and it is decompressed and saved in
in the docker image it defines. They become regular model checkpoint files that you would produce outside SageMaker. This means in order to use your trained model for serving,
you need to tell `PyTorchModel` class how to a recover a PyTorch model from the static checkpoint.
Also, the deployed endpoint interacts with RESTful API calls, you need to tell it how to parse an incoming
request to your model.
These two instructions needs to be defined as two functions in the python file pointed by `entry_point`.
By convention, we name this entry point file `inference.py` and we put it in the `code` directory.
To tell the inference image how to load the model checkpoint, you need to implement a function called
`model_fn`. This function takes one positional argument
- `model_dir`: the directory of the static model checkpoints in the inference image.
The return of `model_fn` is an PyTorch model. In this example, the `model_fn`
looks like:
```python
def model_fn(model_dir):
model = Net().to(device)
model.eval()
return model
```
Next, you need to tell the hosting service how to handle the incoming data. This includes:
* How to parse the incoming request
* How to use the trained model to make inference
* How to return the prediction to the caller of the service
You do it by implementing 3 functions:
#### `input_fn` function
The SageMaker PyTorch model server will invoke an `input_fn` function in your inferece
entry point. This function handles data decoding. The `input_fn` have the following signature:
```python
def input_fn(request_body, request_content_type)
```
The two positional arguments are:
- `request_body`: the payload of the incoming request
- `request_content_type`: the content type of the incoming request
The return of `input_fn` is an object that can be passed to `predict_fn`
In this example, the `input_fn` looks like:
```python
def input_fn(request_body, request_content_type):
assert request_content_type=='application/json'
data = json.loads(request_body)['inputs']
data = torch.tensor(data, dtype=torch.float32, device=device)
return data
```
It requires the request payload is encoded as a json string and
it assumes the decoded payload contains a key `inputs`
that maps to the input data to be consumed by the model.
#### `predict_fn`
After the inference request has been deserialzed by `input_fn`, the SageMaker PyTorch
model server invokes `predict_fn` on the return value of `input_fn`.
The `predict_fn` function has the following signature:
```python
def predict_fn(input_object, model)
```
The two positional arguments are:
- `input_object`: the return value from `input_fn`
- `model`: the return value from `model_fn`
The return of `predict_fn` is the first argument to be passed to `output_fn`
In this example, the `predict_fn` function looks like
```python
def predict_fn(input_object, model):
with torch.no_grad():
prediction = model(input_object)
return prediction
```
Note that we directly feed the return of `input_fn` to `predict_fn`.
This means you should invoke the SageMaker PyTorch model server with data that
can be readily consumed by the model, i.e. normalized and has batch and channel dimension.
#### `output_fn`
After invoking `predict_fn`, the model server invokes `output_fn` for data post-process.
The `output_fn` has the following signature:
```python
def output_fn(prediction, content_type)
```
The two positional arguments are:
- `prediction`: the return value from `predict_fn`
- `content_type`: the content type of the response
The return of `output_fn` should be a byte array of data serialized to `content_type`.
In this exampe, the `output_fn` function looks like
```python
def output_fn(predictions, content_type):
assert content_type == 'application/json'
res = predictions.cpu().numpy().tolist()
return json.dumps(res)
```
After the inference, the function uses `content_type` to encode the
prediction into the content type of the response. In this example,
the function requires the caller of the service to accept json string.
For more info on handler functions, check the [SageMaker Python SDK document](https://sagemaker.readthedocs.io/en/stable/frameworks/pytorch/using_pytorch.html#process-model-output)
## Execute the inference container
Once the `PyTorchModel` class is initiated, we can call its `deploy` method to run the container for the hosting
service. Some common parameters needed to call `deploy` methods are:
- initial_instance_count: the number of SageMaker instances to be used to run the hosting service.
- instance_type: the type of SageMaker instance to run the hosting service. Set it to `local` if you want run the hosting service on the local SageMaker instance. Local mode are typically used for debugging.
- serializer: A python callable used to serialize (encode) the request data.
- deserializer: A python callable used to deserialize (decode) the response data.
Commonly used serializers and deserialzers are implemented in `sagemaker.serializers` and `sagemaker.deserializer`
submodules of the SageMaker Python SDK.
Since in the `transform_fn` we declared that the incoming requests are json-encoded, we need use a json serializer,
to encode the incoming data into a json string. Also, we declared the return content type to be json string, we
need to use a json deserializer to parse the response into a an (in this case, an
integer represeting the predicted hand-written digit).
<span style="color:red"> Note: local mode is not supported in SageMaker Studio </span>
```
from sagemaker.serializers import JSONSerializer
from sagemaker.deserializers import JSONDeserializer
# set local_mode to False if you want to deploy on a remote
# SageMaker instance
local_mode = False
if local_mode:
instance_type = "local"
else:
instance_type = "ml.c4.xlarge"
predictor = model.deploy(
initial_instance_count=1,
instance_type=instance_type,
serializer=JSONSerializer(),
deserializer=JSONDeserializer(),
)
```
The `predictor` we get above can be used to make prediction requests agaist a SageMaker endpoint. For more
information, check [the api reference for SageMaker Predictor](
https://sagemaker.readthedocs.io/en/stable/api/inference/predictors.html#sagemaker.predictor.Predictor)
Now, let's test the endpoint with some dummy data.
```
import random
import numpy as np
dummy_data = {"inputs": np.random.rand(16, 1, 28, 28).tolist()}
```
In `transform_fn`, we declared that the parsed data is a python dictionary with a key `inputs` and its value should
be a 1D array of length 784. Hence, the definition of `dummy_data`.
```
res = predictor.predict(dummy_data)
print("Predictions:", res)
```
If the input data does not look exactly like `dummy_data`, the endpoint will raise an exception. This is because
of the stringent way we defined the `transform_fn`. Let's test the following example.
```
dummy_data = [random.random() for _ in range(784)]
```
When the `dummy_data` is parsed in `transform_fn`, it does not have an `inputs` field, so `transform_fn` will crush.
```
# uncomment the following line to make inference on incorrectly formated input data
# res = predictor.predict(dummy_data)
```
Now, let's use real MNIST test to test the endpoint. We use helper functions defined in `code.utils` to
download MNIST data set and normalize the input data.
```
from utils.mnist import mnist_to_numpy, normalize
import random
import matplotlib.pyplot as plt
%matplotlib inline
data_dir = "/tmp/data"
X, _ = mnist_to_numpy(data_dir, train=False)
# randomly sample 16 images to inspect
mask = random.sample(range(X.shape[0]), 16)
samples = X[mask]
# plot the images
fig, axs = plt.subplots(nrows=1, ncols=16, figsize=(16, 1))
for i, splt in enumerate(axs):
splt.imshow(samples[i])
print(samples.shape, samples.dtype)
```
Before we invoke the SageMaker PyTorch model server with `samples`, we need to do
some pre-processing
- convert its data type to 32 bit floating point
- normalize each channel (only one channel for MNIST)
- add a channel dimension
```
samples = normalize(samples.astype(np.float32), axis=(1, 2))
res = predictor.predict({"inputs": np.expand_dims(samples, axis=1).tolist()})
```
The response is a list of probablity vector of each sample.
```
predictions = np.argmax(np.array(res, dtype=np.float32), axis=1).tolist()
print("Predicted digits: ", predictions)
```
## Test and debug the entry point before deployment
When deploying a model to a SageMaker endpoint, it is a good practice to test the entry
point. The following snippet shows you how you can test and debug the `model_fn` and
`transform_fn` you implemented in the entry point for the inference image.
```
!pygmentize code/test_inference.py
```
The `test` function simulates how the inference container works. It pulls the model
artifact and loads the model into
memory by calling `model_fn` and parse `model_dir` to it.
When it receives a request,
it calls `input_fn`, `predict_fn` and `output_fn` consecutively.
Implementing such a test function helps you debugging the entry point before put it into
the production. If `test` runs correctly, then you can be certain that if the incoming
data and its content type are what they suppose to be, then the endpoint point is going
to work as expected.
## (Optional) Clean up
If you do not plan to use the endpoint, you should delete it to free up some computation
resource. If you use local, you will need to manually delete the docker container bounded
at port 8080 (the port that listens to the incoming request).
```
import os
if not local_mode:
predictor.delete_endpoint()
else:
os.system("docker container ls | grep 8080 | awk '{print $1}' | xargs docker container rm -f")
```
| true |
code
| 0.438605 | null | null | null | null |
|
# LEARNING
This notebook serves as supporting material for topics covered in **Chapter 18 - Learning from Examples** , **Chapter 19 - Knowledge in Learning**, **Chapter 20 - Learning Probabilistic Models** from the book *Artificial Intelligence: A Modern Approach*. This notebook uses implementations from [learning.py](https://github.com/aimacode/aima-python/blob/master/learning.py). Let's start by importing everything from the module:
```
from learning import *
from notebook import *
```
## CONTENTS
* Machine Learning Overview
* Datasets
* Iris Visualization
* Distance Functions
* Plurality Learner
* k-Nearest Neighbours
* Decision Tree Learner
* Random Forest Learner
* Naive Bayes Learner
* Perceptron
* Learner Evaluation
## MACHINE LEARNING OVERVIEW
In this notebook, we learn about agents that can improve their behavior through diligent study of their own experiences.
An agent is **learning** if it improves its performance on future tasks after making observations about the world.
There are three types of feedback that determine the three main types of learning:
* **Supervised Learning**:
In Supervised Learning the agent observes some example input-output pairs and learns a function that maps from input to output.
**Example**: Let's think of an agent to classify images containing cats or dogs. If we provide an image containing a cat or a dog, this agent should output a string "cat" or "dog" for that particular image. To teach this agent, we will give a lot of input-output pairs like {cat image-"cat"}, {dog image-"dog"} to the agent. The agent then learns a function that maps from an input image to one of those strings.
* **Unsupervised Learning**:
In Unsupervised Learning the agent learns patterns in the input even though no explicit feedback is supplied. The most common type is **clustering**: detecting potential useful clusters of input examples.
**Example**: A taxi agent would develop a concept of *good traffic days* and *bad traffic days* without ever being given labeled examples.
* **Reinforcement Learning**:
In Reinforcement Learning the agent learns from a series of reinforcements—rewards or punishments.
**Example**: Let's talk about an agent to play the popular Atari game—[Pong](http://www.ponggame.org). We will reward a point for every correct move and deduct a point for every wrong move from the agent. Eventually, the agent will figure out its actions prior to reinforcement were most responsible for it.
## DATASETS
For the following tutorials we will use a range of datasets, to better showcase the strengths and weaknesses of the algorithms. The datasests are the following:
* [Fisher's Iris](https://github.com/aimacode/aima-data/blob/a21fc108f52ad551344e947b0eb97df82f8d2b2b/iris.csv): Each item represents a flower, with four measurements: the length and the width of the sepals and petals. Each item/flower is categorized into one of three species: Setosa, Versicolor and Virginica.
* [Zoo](https://github.com/aimacode/aima-data/blob/a21fc108f52ad551344e947b0eb97df82f8d2b2b/zoo.csv): The dataset holds different animals and their classification as "mammal", "fish", etc. The new animal we want to classify has the following measurements: 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 4, 1, 0, 1 (don't concern yourself with what the measurements mean).
To make using the datasets easier, we have written a class, `DataSet`, in `learning.py`. The tutorials found here make use of this class.
Let's have a look at how it works before we get started with the algorithms.
### Intro
A lot of the datasets we will work with are .csv files (although other formats are supported too). We have a collection of sample datasets ready to use [on aima-data](https://github.com/aimacode/aima-data/tree/a21fc108f52ad551344e947b0eb97df82f8d2b2b). Two examples are the datasets mentioned above (*iris.csv* and *zoo.csv*). You can find plenty datasets online, and a good repository of such datasets is [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets.html).
In such files, each line corresponds to one item/measurement. Each individual value in a line represents a *feature* and usually there is a value denoting the *class* of the item.
You can find the code for the dataset here:
```
%psource DataSet
```
### Class Attributes
* **examples**: Holds the items of the dataset. Each item is a list of values.
* **attrs**: The indexes of the features (by default in the range of [0,f), where *f* is the number of features). For example, `item[i]` returns the feature at index *i* of *item*.
* **attrnames**: An optional list with attribute names. For example, `item[s]`, where *s* is a feature name, returns the feature of name *s* in *item*.
* **target**: The attribute a learning algorithm will try to predict. By default the last attribute.
* **inputs**: This is the list of attributes without the target.
* **values**: A list of lists which holds the set of possible values for the corresponding attribute/feature. If initially `None`, it gets computed (by the function `setproblem`) from the examples.
* **distance**: The distance function used in the learner to calculate the distance between two items. By default `mean_boolean_error`.
* **name**: Name of the dataset.
* **source**: The source of the dataset (url or other). Not used in the code.
* **exclude**: A list of indexes to exclude from `inputs`. The list can include either attribute indexes (attrs) or names (attrnames).
### Class Helper Functions
These functions help modify a `DataSet` object to your needs.
* **sanitize**: Takes as input an example and returns it with non-input (target) attributes replaced by `None`. Useful for testing. Keep in mind that the example given is not itself sanitized, but instead a sanitized copy is returned.
* **classes_to_numbers**: Maps the class names of a dataset to numbers. If the class names are not given, they are computed from the dataset values. Useful for classifiers that return a numerical value instead of a string.
* **remove_examples**: Removes examples containing a given value. Useful for removing examples with missing values, or for removing classes (needed for binary classifiers).
### Importing a Dataset
#### Importing from aima-data
Datasets uploaded on aima-data can be imported with the following line:
```
iris = DataSet(name="iris")
```
To check that we imported the correct dataset, we can do the following:
```
print(iris.examples[0])
print(iris.inputs)
```
Which correctly prints the first line in the csv file and the list of attribute indexes.
When importing a dataset, we can specify to exclude an attribute (for example, at index 1) by setting the parameter `exclude` to the attribute index or name.
```
iris2 = DataSet(name="iris",exclude=[1])
print(iris2.inputs)
```
### Attributes
Here we showcase the attributes.
First we will print the first three items/examples in the dataset.
```
print(iris.examples[:3])
```
Then we will print `attrs`, `attrnames`, `target`, `input`. Notice how `attrs` holds values in [0,4], but since the fourth attribute is the target, `inputs` holds values in [0,3].
```
print("attrs:", iris.attrs)
print("attrnames (by default same as attrs):", iris.attrnames)
print("target:", iris.target)
print("inputs:", iris.inputs)
```
Now we will print all the possible values for the first feature/attribute.
```
print(iris.values[0])
```
Finally we will print the dataset's name and source. Keep in mind that we have not set a source for the dataset, so in this case it is empty.
```
print("name:", iris.name)
print("source:", iris.source)
```
A useful combination of the above is `dataset.values[dataset.target]` which returns the possible values of the target. For classification problems, this will return all the possible classes. Let's try it:
```
print(iris.values[iris.target])
```
### Helper Functions
We will now take a look at the auxiliary functions found in the class.
First we will take a look at the `sanitize` function, which sets the non-input values of the given example to `None`.
In this case we want to hide the class of the first example, so we will sanitize it.
Note that the function doesn't actually change the given example; it returns a sanitized *copy* of it.
```
print("Sanitized:",iris.sanitize(iris.examples[0]))
print("Original:",iris.examples[0])
```
Currently the `iris` dataset has three classes, setosa, virginica and versicolor. We want though to convert it to a binary class dataset (a dataset with two classes). The class we want to remove is "virginica". To accomplish that we will utilize the helper function `remove_examples`.
```
iris2 = DataSet(name="iris")
iris2.remove_examples("virginica")
print(iris2.values[iris2.target])
```
We also have `classes_to_numbers`. For a lot of the classifiers in the module (like the Neural Network), classes should have numerical values. With this function we map string class names to numbers.
```
print("Class of first example:",iris2.examples[0][iris2.target])
iris2.classes_to_numbers()
print("Class of first example:",iris2.examples[0][iris2.target])
```
As you can see "setosa" was mapped to 0.
Finally, we take a look at `find_means_and_deviations`. It finds the means and standard deviations of the features for each class.
```
means, deviations = iris.find_means_and_deviations()
print("Setosa feature means:", means["setosa"])
print("Versicolor mean for first feature:", means["versicolor"][0])
print("Setosa feature deviations:", deviations["setosa"])
print("Virginica deviation for second feature:",deviations["virginica"][1])
```
## IRIS VISUALIZATION
Since we will use the iris dataset extensively in this notebook, below we provide a visualization tool that helps in comprehending the dataset and thus how the algorithms work.
We plot the dataset in a 3D space using `matplotlib` and the function `show_iris` from `notebook.py`. The function takes as input three parameters, *i*, *j* and *k*, which are indicises to the iris features, "Sepal Length", "Sepal Width", "Petal Length" and "Petal Width" (0 to 3). By default we show the first three features.
```
iris = DataSet(name="iris")
show_iris()
show_iris(0, 1, 3)
show_iris(1, 2, 3)
```
You can play around with the values to get a good look at the dataset.
## DISTANCE FUNCTIONS
In a lot of algorithms (like the *k-Nearest Neighbors* algorithm), there is a need to compare items, finding how *similar* or *close* they are. For that we have many different functions at our disposal. Below are the functions implemented in the module:
### Manhattan Distance (`manhattan_distance`)
One of the simplest distance functions. It calculates the difference between the coordinates/features of two items. To understand how it works, imagine a 2D grid with coordinates *x* and *y*. In that grid we have two items, at the squares positioned at `(1,2)` and `(3,4)`. The difference between their two coordinates is `3-1=2` and `4-2=2`. If we sum these up we get `4`. That means to get from `(1,2)` to `(3,4)` we need four moves; two to the right and two more up. The function works similarly for n-dimensional grids.
```
def manhattan_distance(X, Y):
return sum([abs(x - y) for x, y in zip(X, Y)])
distance = manhattan_distance([1,2], [3,4])
print("Manhattan Distance between (1,2) and (3,4) is", distance)
```
### Euclidean Distance (`euclidean_distance`)
Probably the most popular distance function. It returns the square root of the sum of the squared differences between individual elements of two items.
```
def euclidean_distance(X, Y):
return math.sqrt(sum([(x - y)**2 for x, y in zip(X,Y)]))
distance = euclidean_distance([1,2], [3,4])
print("Euclidean Distance between (1,2) and (3,4) is", distance)
```
### Hamming Distance (`hamming_distance`)
This function counts the number of differences between single elements in two items. For example, if we have two binary strings "111" and "011" the function will return 1, since the two strings only differ at the first element. The function works the same way for non-binary strings too.
```
def hamming_distance(X, Y):
return sum(x != y for x, y in zip(X, Y))
distance = hamming_distance(['a','b','c'], ['a','b','b'])
print("Hamming Distance between 'abc' and 'abb' is", distance)
```
### Mean Boolean Error (`mean_boolean_error`)
To calculate this distance, we find the ratio of different elements over all elements of two items. For example, if the two items are `(1,2,3)` and `(1,4,5)`, the ration of different/all elements is 2/3, since they differ in two out of three elements.
```
def mean_boolean_error(X, Y):
return mean(int(x != y) for x, y in zip(X, Y))
distance = mean_boolean_error([1,2,3], [1,4,5])
print("Mean Boolean Error Distance between (1,2,3) and (1,4,5) is", distance)
```
### Mean Error (`mean_error`)
This function finds the mean difference of single elements between two items. For example, if the two items are `(1,0,5)` and `(3,10,5)`, their error distance is `(3-1) + (10-0) + (5-5) = 2 + 10 + 0 = 12`. The mean error distance therefore is `12/3=4`.
```
def mean_error(X, Y):
return mean([abs(x - y) for x, y in zip(X, Y)])
distance = mean_error([1,0,5], [3,10,5])
print("Mean Error Distance between (1,0,5) and (3,10,5) is", distance)
```
### Mean Square Error (`ms_error`)
This is very similar to the `Mean Error`, but instead of calculating the difference between elements, we are calculating the *square* of the differences.
```
def ms_error(X, Y):
return mean([(x - y)**2 for x, y in zip(X, Y)])
distance = ms_error([1,0,5], [3,10,5])
print("Mean Square Distance between (1,0,5) and (3,10,5) is", distance)
```
### Root of Mean Square Error (`rms_error`)
This is the square root of `Mean Square Error`.
```
def rms_error(X, Y):
return math.sqrt(ms_error(X, Y))
distance = rms_error([1,0,5], [3,10,5])
print("Root of Mean Error Distance between (1,0,5) and (3,10,5) is", distance)
```
## PLURALITY LEARNER CLASSIFIER
### Overview
The Plurality Learner is a simple algorithm, used mainly as a baseline comparison for other algorithms. It finds the most popular class in the dataset and classifies any subsequent item to that class. Essentially, it classifies every new item to the same class. For that reason, it is not used very often, instead opting for more complicated algorithms when we want accurate classification.

Let's see how the classifier works with the plot above. There are three classes named **Class A** (orange-colored dots) and **Class B** (blue-colored dots) and **Class C** (green-colored dots). Every point in this plot has two **features** (i.e. X<sub>1</sub>, X<sub>2</sub>). Now, let's say we have a new point, a red star and we want to know which class this red star belongs to. Solving this problem by predicting the class of this new red star is our current classification problem.
The Plurality Learner will find the class most represented in the plot. ***Class A*** has four items, ***Class B*** has three and ***Class C*** has seven. The most popular class is ***Class C***. Therefore, the item will get classified in ***Class C***, despite the fact that it is closer to the other two classes.
### Implementation
Below follows the implementation of the PluralityLearner algorithm:
```
psource(PluralityLearner)
```
It takes as input a dataset and returns a function. We can later call this function with the item we want to classify as the argument and it returns the class it should be classified in.
The function first finds the most popular class in the dataset and then each time we call its "predict" function, it returns it. Note that the input ("example") does not matter. The function always returns the same class.
### Example
For this example, we will not use the Iris dataset, since each class is represented the same. This will throw an error. Instead we will use the zoo dataset.
```
zoo = DataSet(name="zoo")
pL = PluralityLearner(zoo)
print(pL([1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 4, 1, 0, 1]))
```
The output for the above code is "mammal", since that is the most popular and common class in the dataset.
## K-NEAREST NEIGHBOURS CLASSIFIER
### Overview
The k-Nearest Neighbors algorithm is a non-parametric method used for classification and regression. We are going to use this to classify Iris flowers. More about kNN on [Scholarpedia](http://www.scholarpedia.org/article/K-nearest_neighbor).

Let's see how kNN works with a simple plot shown in the above picture.
We have co-ordinates (we call them **features** in Machine Learning) of this red star and we need to predict its class using the kNN algorithm. In this algorithm, the value of **k** is arbitrary. **k** is one of the **hyper parameters** for kNN algorithm. We choose this number based on our dataset and choosing a particular number is known as **hyper parameter tuning/optimising**. We learn more about this in coming topics.
Let's put **k = 3**. It means you need to find 3-Nearest Neighbors of this red star and classify this new point into the majority class. Observe that smaller circle which contains three points other than **test point** (red star). As there are two violet points, which form the majority, we predict the class of red star as **violet- Class B**.
Similarly if we put **k = 5**, you can observe that there are three yellow points, which form the majority. So, we classify our test point as **yellow- Class A**.
In practical tasks, we iterate through a bunch of values for k (like [1, 3, 5, 10, 20, 50, 100]), see how it performs and select the best one.
### Implementation
Below follows the implementation of the kNN algorithm:
```
psource(NearestNeighborLearner)
```
It takes as input a dataset and k (default value is 1) and it returns a function, which we can later use to classify a new item.
To accomplish that, the function uses a heap-queue, where the items of the dataset are sorted according to their distance from *example* (the item to classify). We then take the k smallest elements from the heap-queue and we find the majority class. We classify the item to this class.
### Example
We measured a new flower with the following values: 5.1, 3.0, 1.1, 0.1. We want to classify that item/flower in a class. To do that, we write the following:
```
iris = DataSet(name="iris")
kNN = NearestNeighborLearner(iris,k=3)
print(kNN([5.1,3.0,1.1,0.1]))
```
The output of the above code is "setosa", which means the flower with the above measurements is of the "setosa" species.
## DECISION TREE LEARNER
### Overview
#### Decision Trees
A decision tree is a flowchart that uses a tree of decisions and their possible consequences for classification. At each non-leaf node of the tree an attribute of the input is tested, based on which corresponding branch leading to a child-node is selected. At the leaf node the input is classified based on the class label of this leaf node. The paths from root to leaves represent classification rules based on which leaf nodes are assigned class labels.

#### Decision Tree Learning
Decision tree learning is the construction of a decision tree from class-labeled training data. The data is expected to be a tuple in which each record of the tuple is an attribute used for classification. The decision tree is built top-down, by choosing a variable at each step that best splits the set of items. There are different metrics for measuring the "best split". These generally measure the homogeneity of the target variable within the subsets.
#### Gini Impurity
Gini impurity of a set is the probability of a randomly chosen element to be incorrectly labeled if it was randomly labeled according to the distribution of labels in the set.
$$I_G(p) = \sum{p_i(1 - p_i)} = 1 - \sum{p_i^2}$$
We select a split which minimizes the Gini impurity in child nodes.
#### Information Gain
Information gain is based on the concept of entropy from information theory. Entropy is defined as:
$$H(p) = -\sum{p_i \log_2{p_i}}$$
Information Gain is difference between entropy of the parent and weighted sum of entropy of children. The feature used for splitting is the one which provides the most information gain.
#### Pseudocode
You can view the pseudocode by running the cell below:
```
pseudocode("Decision Tree Learning")
```
### Implementation
The nodes of the tree constructed by our learning algorithm are stored using either `DecisionFork` or `DecisionLeaf` based on whether they are a parent node or a leaf node respectively.
```
psource(DecisionFork)
```
`DecisionFork` holds the attribute, which is tested at that node, and a dict of branches. The branches store the child nodes, one for each of the attribute's values. Calling an object of this class as a function with input tuple as an argument returns the next node in the classification path based on the result of the attribute test.
```
psource(DecisionLeaf)
```
The leaf node stores the class label in `result`. All input tuples' classification paths end on a `DecisionLeaf` whose `result` attribute decide their class.
```
psource(DecisionTreeLearner)
```
The implementation of `DecisionTreeLearner` provided in [learning.py](https://github.com/aimacode/aima-python/blob/master/learning.py) uses information gain as the metric for selecting which attribute to test for splitting. The function builds the tree top-down in a recursive manner. Based on the input it makes one of the four choices:
<ol>
<li>If the input at the current step has no training data we return the mode of classes of input data received in the parent step (previous level of recursion).</li>
<li>If all values in training data belong to the same class it returns a `DecisionLeaf` whose class label is the class which all the data belongs to.</li>
<li>If the data has no attributes that can be tested we return the class with highest plurality value in the training data.</li>
<li>We choose the attribute which gives the highest amount of entropy gain and return a `DecisionFork` which splits based on this attribute. Each branch recursively calls `decision_tree_learning` to construct the sub-tree.</li>
</ol>
### Example
We will now use the Decision Tree Learner to classify a sample with values: 5.1, 3.0, 1.1, 0.1.
```
iris = DataSet(name="iris")
DTL = DecisionTreeLearner(iris)
print(DTL([5.1, 3.0, 1.1, 0.1]))
```
As expected, the Decision Tree learner classifies the sample as "setosa" as seen in the previous section.
## RANDOM FOREST LEARNER
### Overview

Image via [src](https://cdn-images-1.medium.com/max/800/0*tG-IWcxL1jg7RkT0.png)
#### Random Forest
As the name of the algorithm and image above suggest, this algorithm creates the forest with a number of trees. The more number of trees makes the forest robust. In the same way in random forest algorithm, the higher the number of trees in the forest, the higher is the accuray result. The main difference between Random Forest and Decision trees is that, finding the root node and splitting the feature nodes will be random.
Let's see how Rnadom Forest Algorithm work :
Random Forest Algorithm works in two steps, first is the creation of random forest and then the prediction. Let's first see the creation :
The first step in creation is to randomly select 'm' features out of total 'n' features. From these 'm' features calculate the node d using the best split point and then split the node into further nodes using best split. Repeat these steps until 'i' number of nodes are reached. Repeat the entire whole process to build the forest.
Now, let's see how the prediction works
Take the test features and predict the outcome for each randomly created decision tree. Calculate the votes for each prediction and the prediction which gets the highest votes would be the final prediction.
### Implementation
Below mentioned is the implementation of Random Forest Algorithm.
```
psource(RandomForest)
```
This algorithm creates an ensemble of decision trees using bagging and feature bagging. It takes 'm' examples randomly from the total number of examples and then perform feature bagging with probability p to retain an attribute. All the predictors are predicted from the DecisionTreeLearner and then a final prediction is made.
### Example
We will now use the Random Forest to classify a sample with values: 5.1, 3.0, 1.1, 0.1.
```
iris = DataSet(name="iris")
DTL = RandomForest(iris)
print(DTL([5.1, 3.0, 1.1, 0.1]))
```
As expected, the Random Forest classifies the sample as "setosa".
## NAIVE BAYES LEARNER
### Overview
#### Theory of Probabilities
The Naive Bayes algorithm is a probabilistic classifier, making use of [Bayes' Theorem](https://en.wikipedia.org/wiki/Bayes%27_theorem). The theorem states that the conditional probability of **A** given **B** equals the conditional probability of **B** given **A** multiplied by the probability of **A**, divided by the probability of **B**.
$$P(A|B) = \dfrac{P(B|A)*P(A)}{P(B)}$$
From the theory of Probabilities we have the Multiplication Rule, if the events *X* are independent the following is true:
$$P(X_{1} \cap X_{2} \cap ... \cap X_{n}) = P(X_{1})*P(X_{2})*...*P(X_{n})$$
For conditional probabilities this becomes:
$$P(X_{1}, X_{2}, ..., X_{n}|Y) = P(X_{1}|Y)*P(X_{2}|Y)*...*P(X_{n}|Y)$$
#### Classifying an Item
How can we use the above to classify an item though?
We have a dataset with a set of classes (**C**) and we want to classify an item with a set of features (**F**). Essentially what we want to do is predict the class of an item given the features.
For a specific class, **Class**, we will find the conditional probability given the item features:
$$P(Class|F) = \dfrac{P(F|Class)*P(Class)}{P(F)}$$
We will do this for every class and we will pick the maximum. This will be the class the item is classified in.
The features though are a vector with many elements. We need to break the probabilities up using the multiplication rule. Thus the above equation becomes:
$$P(Class|F) = \dfrac{P(Class)*P(F_{1}|Class)*P(F_{2}|Class)*...*P(F_{n}|Class)}{P(F_{1})*P(F_{2})*...*P(F_{n})}$$
The calculation of the conditional probability then depends on the calculation of the following:
*a)* The probability of **Class** in the dataset.
*b)* The conditional probability of each feature occurring in an item classified in **Class**.
*c)* The probabilities of each individual feature.
For *a)*, we will count how many times **Class** occurs in the dataset (aka how many items are classified in a particular class).
For *b)*, if the feature values are discrete ('Blue', '3', 'Tall', etc.), we will count how many times a feature value occurs in items of each class. If the feature values are not discrete, we will go a different route. We will use a distribution function to calculate the probability of values for a given class and feature. If we know the distribution function of the dataset, then great, we will use it to compute the probabilities. If we don't know the function, we can assume the dataset follows the normal (Gaussian) distribution without much loss of accuracy. In fact, it can be proven that any distribution tends to the Gaussian the larger the population gets (see [Central Limit Theorem](https://en.wikipedia.org/wiki/Central_limit_theorem)).
*NOTE:* If the values are continuous but use the discrete approach, there might be issues if we are not lucky. For one, if we have two values, '5.0 and 5.1', with the discrete approach they will be two completely different values, despite being so close. Second, if we are trying to classify an item with a feature value of '5.15', if the value does not appear for the feature, its probability will be 0. This might lead to misclassification. Generally, the continuous approach is more accurate and more useful, despite the overhead of calculating the distribution function.
The last one, *c)*, is tricky. If feature values are discrete, we can count how many times they occur in the dataset. But what if the feature values are continuous? Imagine a dataset with a height feature. Is it worth it to count how many times each value occurs? Most of the time it is not, since there can be miscellaneous differences in the values (for example, 1.7 meters and 1.700001 meters are practically equal, but they count as different values).
So as we cannot calculate the feature value probabilities, what are we going to do?
Let's take a step back and rethink exactly what we are doing. We are essentially comparing conditional probabilities of all the classes. For two classes, **A** and **B**, we want to know which one is greater:
$$\dfrac{P(F|A)*P(A)}{P(F)} vs. \dfrac{P(F|B)*P(B)}{P(F)}$$
Wait, **P(F)** is the same for both the classes! In fact, it is the same for every combination of classes. That is because **P(F)** does not depend on a class, thus being independent of the classes.
So, for *c)*, we actually don't need to calculate it at all.
#### Wrapping It Up
Classifying an item to a class then becomes a matter of calculating the conditional probabilities of feature values and the probabilities of classes. This is something very desirable and computationally delicious.
Remember though that all the above are true because we made the assumption that the features are independent. In most real-world cases that is not true though. Is that an issue here? Fret not, for the the algorithm is very efficient even with that assumption. That is why the algorithm is called **Naive** Bayes Classifier. We (naively) assume that the features are independent to make computations easier.
### Implementation
The implementation of the Naive Bayes Classifier is split in two; *Learning* and *Simple*. The *learning* classifier takes as input a dataset and learns the needed distributions from that. It is itself split into two, for discrete and continuous features. The *simple* classifier takes as input not a dataset, but already calculated distributions (a dictionary of `CountingProbDist` objects).
#### Discrete
The implementation for discrete values counts how many times each feature value occurs for each class, and how many times each class occurs. The results are stored in a `CountinProbDist` object.
With the below code you can see the probabilities of the class "Setosa" appearing in the dataset and the probability of the first feature (at index 0) of the same class having a value of 5. Notice that the second probability is relatively small, even though if we observe the dataset we will find that a lot of values are around 5. The issue arises because the features in the Iris dataset are continuous, and we are assuming they are discrete. If the features were discrete (for example, "Tall", "3", etc.) this probably wouldn't have been the case and we would see a much nicer probability distribution.
```
dataset = iris
target_vals = dataset.values[dataset.target]
target_dist = CountingProbDist(target_vals)
attr_dists = {(gv, attr): CountingProbDist(dataset.values[attr])
for gv in target_vals
for attr in dataset.inputs}
for example in dataset.examples:
targetval = example[dataset.target]
target_dist.add(targetval)
for attr in dataset.inputs:
attr_dists[targetval, attr].add(example[attr])
print(target_dist['setosa'])
print(attr_dists['setosa', 0][5.0])
```
First we found the different values for the classes (called targets here) and calculated their distribution. Next we initialized a dictionary of `CountingProbDist` objects, one for each class and feature. Finally, we iterated through the examples in the dataset and calculated the needed probabilites.
Having calculated the different probabilities, we will move on to the predicting function. It will receive as input an item and output the most likely class. Using the above formula, it will multiply the probability of the class appearing, with the probability of each feature value appearing in the class. It will return the max result.
```
def predict(example):
def class_probability(targetval):
return (target_dist[targetval] *
product(attr_dists[targetval, attr][example[attr]]
for attr in dataset.inputs))
return argmax(target_vals, key=class_probability)
print(predict([5, 3, 1, 0.1]))
```
You can view the complete code by executing the next line:
```
psource(NaiveBayesDiscrete)
```
#### Continuous
In the implementation we use the Gaussian/Normal distribution function. To make it work, we need to find the means and standard deviations of features for each class. We make use of the `find_means_and_deviations` Dataset function. On top of that, we will also calculate the class probabilities as we did with the Discrete approach.
```
means, deviations = dataset.find_means_and_deviations()
target_vals = dataset.values[dataset.target]
target_dist = CountingProbDist(target_vals)
print(means["setosa"])
print(deviations["versicolor"])
```
You can see the means of the features for the "Setosa" class and the deviations for "Versicolor".
The prediction function will work similarly to the Discrete algorithm. It will multiply the probability of the class occurring with the conditional probabilities of the feature values for the class.
Since we are using the Gaussian distribution, we will input the value for each feature into the Gaussian function, together with the mean and deviation of the feature. This will return the probability of the particular feature value for the given class. We will repeat for each class and pick the max value.
```
def predict(example):
def class_probability(targetval):
prob = target_dist[targetval]
for attr in dataset.inputs:
prob *= gaussian(means[targetval][attr], deviations[targetval][attr], example[attr])
return prob
return argmax(target_vals, key=class_probability)
print(predict([5, 3, 1, 0.1]))
```
The complete code of the continuous algorithm:
```
psource(NaiveBayesContinuous)
```
#### Simple
The simple classifier (chosen with the argument `simple`) does not learn from a dataset, instead it takes as input a dictionary of already calculated `CountingProbDist` objects and returns a predictor function. The dictionary is in the following form: `(Class Name, Class Probability): CountingProbDist Object`.
Each class has its own probability distribution. The classifier given a list of features calculates the probability of the input for each class and returns the max. The only pre-processing work is to create dictionaries for the distribution of classes (named `targets`) and attributes/features.
The complete code for the simple classifier:
```
psource(NaiveBayesSimple)
```
This classifier is useful when you already have calculated the distributions and you need to predict future items.
### Examples
We will now use the Naive Bayes Classifier (Discrete and Continuous) to classify items:
```
nBD = NaiveBayesLearner(iris, continuous=False)
print("Discrete Classifier")
print(nBD([5, 3, 1, 0.1]))
print(nBD([6, 5, 3, 1.5]))
print(nBD([7, 3, 6.5, 2]))
nBC = NaiveBayesLearner(iris, continuous=True)
print("\nContinuous Classifier")
print(nBC([5, 3, 1, 0.1]))
print(nBC([6, 5, 3, 1.5]))
print(nBC([7, 3, 6.5, 2]))
```
Notice how the Discrete Classifier misclassified the second item, while the Continuous one had no problem.
Let's now take a look at the simple classifier. First we will come up with a sample problem to solve. Say we are given three bags. Each bag contains three letters ('a', 'b' and 'c') of different quantities. We are given a string of letters and we are tasked with finding from which bag the string of letters came.
Since we know the probability distribution of the letters for each bag, we can use the naive bayes classifier to make our prediction.
```
bag1 = 'a'*50 + 'b'*30 + 'c'*15
dist1 = CountingProbDist(bag1)
bag2 = 'a'*30 + 'b'*45 + 'c'*20
dist2 = CountingProbDist(bag2)
bag3 = 'a'*20 + 'b'*20 + 'c'*35
dist3 = CountingProbDist(bag3)
```
Now that we have the `CountingProbDist` objects for each bag/class, we will create the dictionary. We assume that it is equally probable that we will pick from any bag.
```
dist = {('First', 0.5): dist1, ('Second', 0.3): dist2, ('Third', 0.2): dist3}
nBS = NaiveBayesLearner(dist, simple=True)
```
Now we can start making predictions:
```
print(nBS('aab')) # We can handle strings
print(nBS(['b', 'b'])) # And lists!
print(nBS('ccbcc'))
```
The results make intuitive sence. The first bag has a high amount of 'a's, the second has a high amount of 'b's and the third has a high amount of 'c's. The classifier seems to confirm this intuition.
Note that the simple classifier doesn't distinguish between discrete and continuous values. It just takes whatever it is given. Also, the `simple` option on the `NaiveBayesLearner` overrides the `continuous` argument. `NaiveBayesLearner(d, simple=True, continuous=False)` just creates a simple classifier.
## PERCEPTRON CLASSIFIER
### Overview
The Perceptron is a linear classifier. It works the same way as a neural network with no hidden layers (just input and output). First it trains its weights given a dataset and then it can classify a new item by running it through the network.
Its input layer consists of the the item features, while the output layer consists of nodes (also called neurons). Each node in the output layer has *n* synapses (for every item feature), each with its own weight. Then, the nodes find the dot product of the item features and the synapse weights. These values then pass through an activation function (usually a sigmoid). Finally, we pick the largest of the values and we return its index.
Note that in classification problems each node represents a class. The final classification is the class/node with the max output value.
Below you can see a single node/neuron in the outer layer. With *f* we denote the item features, with *w* the synapse weights, then inside the node we have the dot product and the activation function, *g*.

### Implementation
First, we train (calculate) the weights given a dataset, using the `BackPropagationLearner` function of `learning.py`. We then return a function, `predict`, which we will use in the future to classify a new item. The function computes the (algebraic) dot product of the item with the calculated weights for each node in the outer layer. Then it picks the greatest value and classifies the item in the corresponding class.
```
psource(PerceptronLearner)
```
Note that the Perceptron is a one-layer neural network, without any hidden layers. So, in `BackPropagationLearner`, we will pass no hidden layers. From that function we get our network, which is just one layer, with the weights calculated.
That function `predict` passes the input/example through the network, calculating the dot product of the input and the weights for each node and returns the class with the max dot product.
### Example
We will train the Perceptron on the iris dataset. Because though the `BackPropagationLearner` works with integer indexes and not strings, we need to convert class names to integers. Then, we will try and classify the item/flower with measurements of 5, 3, 1, 0.1.
```
iris = DataSet(name="iris")
iris.classes_to_numbers()
perceptron = PerceptronLearner(iris)
print(perceptron([5, 3, 1, 0.1]))
```
The correct output is 0, which means the item belongs in the first class, "setosa". Note that the Perceptron algorithm is not perfect and may produce false classifications.
## LEARNER EVALUATION
In this section we will evaluate and compare algorithm performance. The dataset we will use will again be the iris one.
```
iris = DataSet(name="iris")
```
### Naive Bayes
First up we have the Naive Bayes algorithm. First we will test how well the Discrete Naive Bayes works, and then how the Continuous fares.
```
nBD = NaiveBayesLearner(iris, continuous=False)
print("Error ratio for Discrete:", err_ratio(nBD, iris))
nBC = NaiveBayesLearner(iris, continuous=True)
print("Error ratio for Continuous:", err_ratio(nBC, iris))
```
The error for the Naive Bayes algorithm is very, very low; close to 0. There is also very little difference between the discrete and continuous version of the algorithm.
## k-Nearest Neighbors
Now we will take a look at kNN, for different values of *k*. Note that *k* should have odd values, to break any ties between two classes.
```
kNN_1 = NearestNeighborLearner(iris, k=1)
kNN_3 = NearestNeighborLearner(iris, k=3)
kNN_5 = NearestNeighborLearner(iris, k=5)
kNN_7 = NearestNeighborLearner(iris, k=7)
print("Error ratio for k=1:", err_ratio(kNN_1, iris))
print("Error ratio for k=3:", err_ratio(kNN_3, iris))
print("Error ratio for k=5:", err_ratio(kNN_5, iris))
print("Error ratio for k=7:", err_ratio(kNN_7, iris))
```
Notice how the error became larger and larger as *k* increased. This is generally the case with datasets where classes are spaced out, as is the case with the iris dataset. If items from different classes were closer together, classification would be more difficult. Usually a value of 1, 3 or 5 for *k* suffices.
Also note that since the training set is also the testing set, for *k* equal to 1 we get a perfect score, since the item we want to classify each time is already in the dataset and its closest neighbor is itself.
### Perceptron
For the Perceptron, we first need to convert class names to integers. Let's see how it performs in the dataset.
```
iris2 = DataSet(name="iris")
iris2.classes_to_numbers()
perceptron = PerceptronLearner(iris2)
print("Error ratio for Perceptron:", err_ratio(perceptron, iris2))
```
The Perceptron didn't fare very well mainly because the dataset is not linearly separated. On simpler datasets the algorithm performs much better, but unfortunately such datasets are rare in real life scenarios.
## AdaBoost
### Overview
**AdaBoost** is an algorithm which uses **ensemble learning**. In ensemble learning the hypotheses in the collection, or ensemble, vote for what the output should be and the output with the majority votes is selected as the final answer.
AdaBoost algorithm, as mentioned in the book, works with a **weighted training set** and **weak learners** (classifiers that have about 50%+epsilon accuracy i.e slightly better than random guessing). It manipulates the weights attached to the the examples that are showed to it. Importance is given to the examples with higher weights.
All the examples start with equal weights and a hypothesis is generated using these examples. Examples which are incorrectly classified, their weights are increased so that they can be classified correctly by the next hypothesis. The examples that are correctly classified, their weights are reduced. This process is repeated *K* times (here *K* is an input to the algorithm) and hence, *K* hypotheses are generated.
These *K* hypotheses are also assigned weights according to their performance on the weighted training set. The final ensemble hypothesis is the weighted-majority combination of these *K* hypotheses.
The speciality of AdaBoost is that by using weak learners and a sufficiently large *K*, a highly accurate classifier can be learned irrespective of the complexity of the function being learned or the dullness of the hypothesis space.
### Implementation
As seen in the previous section, the `PerceptronLearner` does not perform that well on the iris dataset. We'll use perceptron as the learner for the AdaBoost algorithm and try to increase the accuracy.
Let's first see what AdaBoost is exactly:
```
psource(AdaBoost)
```
AdaBoost takes as inputs: **L** and *K* where **L** is the learner and *K* is the number of hypotheses to be generated. The learner **L** takes in as inputs: a dataset and the weights associated with the examples in the dataset. But the `PerceptronLearner` doesnot handle weights and only takes a dataset as its input.
To remedy that we will give as input to the PerceptronLearner a modified dataset in which the examples will be repeated according to the weights associated to them. Intuitively, what this will do is force the learner to repeatedly learn the same example again and again until it can classify it correctly.
To convert `PerceptronLearner` so that it can take weights as input too, we will have to pass it through the **`WeightedLearner`** function.
```
psource(WeightedLearner)
```
The `WeightedLearner` function will then call the `PerceptronLearner`, during each iteration, with the modified dataset which contains the examples according to the weights associated with them.
### Example
We will pass the `PerceptronLearner` through `WeightedLearner` function. Then we will create an `AdaboostLearner` classifier with number of hypotheses or *K* equal to 5.
```
WeightedPerceptron = WeightedLearner(PerceptronLearner)
AdaboostLearner = AdaBoost(WeightedPerceptron, 5)
iris2 = DataSet(name="iris")
iris2.classes_to_numbers()
adaboost = AdaboostLearner(iris2)
adaboost([5, 3, 1, 0.1])
```
That is the correct answer. Let's check the error rate of adaboost with perceptron.
```
print("Error ratio for adaboost: ", err_ratio(adaboost, iris2))
```
It reduced the error rate considerably. Unlike the `PerceptronLearner`, `AdaBoost` was able to learn the complexity in the iris dataset.
| true |
code
| 0.469459 | null | null | null | null |
|
```
import sys
if 'google.colab' in sys.modules:
!wget https://raw.githubusercontent.com/yandexdataschool/Practical_RL/0ccb0673965dd650d9b284e1ec90c2bfd82c8a94/week08_pomdp/atari_util.py
!wget https://raw.githubusercontent.com/yandexdataschool/Practical_RL/0ccb0673965dd650d9b284e1ec90c2bfd82c8a94/week08_pomdp/env_pool.py
# If you are running on a server, launch xvfb to record game videos
# Please make sure you have xvfb installed
import os
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY")) == 0:
!bash ../xvfb start
os.environ['DISPLAY'] = ':1'
import numpy as np
from IPython.core import display
import matplotlib.pyplot as plt
%matplotlib inline
```
### Kung-Fu, recurrent style
In this notebook we'll once again train RL agent for for Atari [KungFuMaster](https://gym.openai.com/envs/KungFuMaster-v0/), this time using recurrent neural networks.

```
import gym
from atari_util import PreprocessAtari
def make_env():
env = gym.make("KungFuMasterDeterministic-v0")
env = PreprocessAtari(env, height=42, width=42,
crop=lambda img: img[60:-30, 15:],
color=False, n_frames=1)
return env
env = make_env()
obs_shape = env.observation_space.shape
n_actions = env.action_space.n
print("Observation shape:", obs_shape)
print("Num actions:", n_actions)
print("Action names:", env.env.env.get_action_meanings())
s = env.reset()
for _ in range(100):
s, _, _, _ = env.step(env.action_space.sample())
plt.title('Game image')
plt.imshow(env.render('rgb_array'))
plt.show()
plt.title('Agent observation')
plt.imshow(s.reshape([42, 42]))
plt.show()
```
### POMDP setting
The Atari game we're working with is actually a POMDP: your agent needs to know timing at which enemies spawn and move, but cannot do so unless it has some memory.
Let's design another agent that has a recurrent neural net memory to solve this. Here's a sketch.

```
import torch
import torch.nn as nn
import torch.nn.functional as F
# a special module that converts [batch, channel, w, h] to [batch, units]
class Flatten(nn.Module):
def forward(self, input):
return input.view(input.size(0), -1)
class SimpleRecurrentAgent(nn.Module):
def __init__(self, obs_shape, n_actions, reuse=False):
"""A simple actor-critic agent"""
super(self.__class__, self).__init__()
self.conv0 = nn.Conv2d(1, 32, kernel_size=(3, 3), stride=(2, 2))
self.conv1 = nn.Conv2d(32, 32, kernel_size=(3, 3), stride=(2, 2))
self.conv2 = nn.Conv2d(32, 32, kernel_size=(3, 3), stride=(2, 2))
self.flatten = Flatten()
self.hid = nn.Linear(512, 128)
self.rnn = nn.LSTMCell(128, 128)
self.logits = nn.Linear(128, n_actions)
self.state_value = nn.Linear(128, 1)
def forward(self, prev_state, obs_t):
"""
Takes agent's previous hidden state and a new observation,
returns a new hidden state and whatever the agent needs to learn
"""
# Apply the whole neural net for one step here.
# See docs on self.rnn(...).
# The recurrent cell should take the last feedforward dense layer as input.
<YOUR CODE>
new_state = <YOUR CODE>
logits = <YOUR CODE>
state_value = <YOUR CODE>
return new_state, (logits, state_value)
def get_initial_state(self, batch_size):
"""Return a list of agent memory states at game start. Each state is a np array of shape [batch_size, ...]"""
return torch.zeros((batch_size, 128)), torch.zeros((batch_size, 128))
def sample_actions(self, agent_outputs):
"""pick actions given numeric agent outputs (np arrays)"""
logits, state_values = agent_outputs
probs = F.softmax(logits)
return torch.multinomial(probs, 1)[:, 0].data.numpy()
def step(self, prev_state, obs_t):
""" like forward, but obs_t is a numpy array """
obs_t = torch.tensor(np.asarray(obs_t), dtype=torch.float32)
(h, c), (l, s) = self.forward(prev_state, obs_t)
return (h.detach(), c.detach()), (l.detach(), s.detach())
n_parallel_games = 5
gamma = 0.99
agent = SimpleRecurrentAgent(obs_shape, n_actions)
state = [env.reset()]
_, (logits, value) = agent.step(agent.get_initial_state(1), state)
print("action logits:\n", logits)
print("state values:\n", value)
```
### Let's play!
Let's build a function that measures agent's average reward.
```
def evaluate(agent, env, n_games=1):
"""Plays an entire game start to end, returns session rewards."""
game_rewards = []
for _ in range(n_games):
# initial observation and memory
observation = env.reset()
prev_memories = agent.get_initial_state(1)
total_reward = 0
while True:
new_memories, readouts = agent.step(
prev_memories, observation[None, ...])
action = agent.sample_actions(readouts)
observation, reward, done, info = env.step(action[0])
total_reward += reward
prev_memories = new_memories
if done:
break
game_rewards.append(total_reward)
return game_rewards
import gym.wrappers
with gym.wrappers.Monitor(make_env(), directory="videos", force=True) as env_monitor:
rewards = evaluate(agent, env_monitor, n_games=3)
print(rewards)
# Show video. This may not work in some setups. If it doesn't
# work for you, you can download the videos and view them locally.
from pathlib import Path
from base64 import b64encode
from IPython.display import HTML
video_paths = sorted([s for s in Path('videos').iterdir() if s.suffix == '.mp4'])
video_path = video_paths[-1] # You can also try other indices
if 'google.colab' in sys.modules:
# https://stackoverflow.com/a/57378660/1214547
with video_path.open('rb') as fp:
mp4 = fp.read()
data_url = 'data:video/mp4;base64,' + b64encode(mp4).decode()
else:
data_url = str(video_path)
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format(data_url))
```
### Training on parallel games
We introduce a class called EnvPool - it's a tool that handles multiple environments for you. Here's how it works:

```
from env_pool import EnvPool
pool = EnvPool(agent, make_env, n_parallel_games)
```
We gonna train our agent on a thing called __rollouts:__

A rollout is just a sequence of T observations, actions and rewards that agent took consequently.
* First __s0__ is not necessarily initial state for the environment
* Final state is not necessarily terminal
* We sample several parallel rollouts for efficiency
```
# for each of n_parallel_games, take 10 steps
rollout_obs, rollout_actions, rollout_rewards, rollout_mask = pool.interact(10)
print("Actions shape:", rollout_actions.shape)
print("Rewards shape:", rollout_rewards.shape)
print("Mask shape:", rollout_mask.shape)
print("Observations shape: ", rollout_obs.shape)
```
# Actor-critic objective
Here we define a loss function that uses rollout above to train advantage actor-critic agent.
Our loss consists of three components:
* __The policy "loss"__
$$ \hat J = {1 \over T} \cdot \sum_t { \log \pi(a_t | s_t) } \cdot A_{const}(s,a) $$
* This function has no meaning in and of itself, but it was built such that
* $ \nabla \hat J = {1 \over N} \cdot \sum_t { \nabla \log \pi(a_t | s_t) } \cdot A(s,a) \approx \nabla E_{s, a \sim \pi} R(s,a) $
* Therefore if we __maximize__ J_hat with gradient descent we will maximize expected reward
* __The value "loss"__
$$ L_{td} = {1 \over T} \cdot \sum_t { [r + \gamma \cdot V_{const}(s_{t+1}) - V(s_t)] ^ 2 }$$
* Ye Olde TD_loss from q-learning and alike
* If we minimize this loss, V(s) will converge to $V_\pi(s) = E_{a \sim \pi(a | s)} R(s,a) $
* __Entropy Regularizer__
$$ H = - {1 \over T} \sum_t \sum_a {\pi(a|s_t) \cdot \log \pi (a|s_t)}$$
* If we __maximize__ entropy we discourage agent from predicting zero probability to actions
prematurely (a.k.a. exploration)
So we optimize a linear combination of $L_{td}$ $- \hat J$, $-H$
```
```
```
```
```
```
__One more thing:__ since we train on T-step rollouts, we can use N-step formula for advantage for free:
* At the last step, $A(s_t,a_t) = r(s_t, a_t) + \gamma \cdot V(s_{t+1}) - V(s) $
* One step earlier, $A(s_t,a_t) = r(s_t, a_t) + \gamma \cdot r(s_{t+1}, a_{t+1}) + \gamma ^ 2 \cdot V(s_{t+2}) - V(s) $
* Et cetera, et cetera. This way agent starts training much faster since it's estimate of A(s,a) depends less on his (imperfect) value function and more on actual rewards. There's also a [nice generalization](https://arxiv.org/abs/1506.02438) of this.
__Note:__ it's also a good idea to scale rollout_len up to learn longer sequences. You may wish set it to >=20 or to start at 10 and then scale up as time passes.
```
def to_one_hot(y, n_dims=None):
""" Take an integer tensor and convert it to 1-hot matrix. """
y_tensor = y.to(dtype=torch.int64).view(-1, 1)
n_dims = n_dims if n_dims is not None else int(torch.max(y_tensor)) + 1
y_one_hot = torch.zeros(y_tensor.size()[0], n_dims).scatter_(1, y_tensor, 1)
return y_one_hot
opt = torch.optim.Adam(agent.parameters(), lr=1e-5)
def train_on_rollout(states, actions, rewards, is_not_done, prev_memory_states, gamma=0.99):
"""
Takes a sequence of states, actions and rewards produced by generate_session.
Updates agent's weights by following the policy gradient above.
Please use Adam optimizer with default parameters.
"""
# shape: [batch_size, time, c, h, w]
states = torch.tensor(np.asarray(states), dtype=torch.float32)
actions = torch.tensor(np.array(actions), dtype=torch.int64) # shape: [batch_size, time]
rewards = torch.tensor(np.array(rewards), dtype=torch.float32) # shape: [batch_size, time]
is_not_done = torch.tensor(np.array(is_not_done), dtype=torch.float32) # shape: [batch_size, time]
rollout_length = rewards.shape[1] - 1
# predict logits, probas and log-probas using an agent.
memory = [m.detach() for m in prev_memory_states]
logits = [] # append logit sequence here
state_values = [] # append state values here
for t in range(rewards.shape[1]):
obs_t = states[:, t]
# use agent to comute logits_t and state values_t.
# append them to logits and state_values array
memory, (logits_t, values_t) = <YOUR CODE>
logits.append(logits_t)
state_values.append(values_t)
logits = torch.stack(logits, dim=1)
state_values = torch.stack(state_values, dim=1)
probas = F.softmax(logits, dim=2)
logprobas = F.log_softmax(logits, dim=2)
# select log-probabilities for chosen actions, log pi(a_i|s_i)
actions_one_hot = to_one_hot(actions, n_actions).view(
actions.shape[0], actions.shape[1], n_actions)
logprobas_for_actions = torch.sum(logprobas * actions_one_hot, dim=-1)
# Now let's compute two loss components:
# 1) Policy gradient objective.
# Notes: Please don't forget to call .detach() on advantage term. Also please use mean, not sum.
# it's okay to use loops if you want
J_hat = 0 # policy objective as in the formula for J_hat
# 2) Temporal difference MSE for state values
# Notes: Please don't forget to call on V(s') term. Also please use mean, not sum.
# it's okay to use loops if you want
value_loss = 0
cumulative_returns = state_values[:, -1].detach()
for t in reversed(range(rollout_length)):
r_t = rewards[:, t] # current rewards
# current state values
V_t = state_values[:, t]
V_next = state_values[:, t + 1].detach() # next state values
# log-probability of a_t in s_t
logpi_a_s_t = logprobas_for_actions[:, t]
# update G_t = r_t + gamma * G_{t+1} as we did in week6 reinforce
cumulative_returns = G_t = r_t + gamma * cumulative_returns
# Compute temporal difference error (MSE for V(s))
value_loss += <YOUR CODE>
# compute advantage A(s_t, a_t) using cumulative returns and V(s_t) as baseline
advantage = <YOUR CODE>
advantage = advantage.detach()
# compute policy pseudo-loss aka -J_hat.
J_hat += <YOUR CODE>
# regularize with entropy
entropy_reg = <YOUR CODE: compute entropy regularizer>
# add-up three loss components and average over time
loss = -J_hat / rollout_length +\
value_loss / rollout_length +\
-0.01 * entropy_reg
# Gradient descent step
<YOUR CODE>
return loss.data.numpy()
# let's test it
memory = list(pool.prev_memory_states)
rollout_obs, rollout_actions, rollout_rewards, rollout_mask = pool.interact(10)
train_on_rollout(rollout_obs, rollout_actions,
rollout_rewards, rollout_mask, memory)
```
# Train
just run train step and see if agent learns any better
```
from IPython.display import clear_output
from tqdm import trange
from pandas import DataFrame
moving_average = lambda x, **kw: DataFrame(
{'x': np.asarray(x)}).x.ewm(**kw).mean().values
rewards_history = []
for i in trange(15000):
memory = list(pool.prev_memory_states)
rollout_obs, rollout_actions, rollout_rewards, rollout_mask = pool.interact(
10)
train_on_rollout(rollout_obs, rollout_actions,
rollout_rewards, rollout_mask, memory)
if i % 100 == 0:
rewards_history.append(np.mean(evaluate(agent, env, n_games=1)))
clear_output(True)
plt.plot(rewards_history, label='rewards')
plt.plot(moving_average(np.array(rewards_history),
span=10), label='rewards ewma@10')
plt.legend()
plt.show()
if rewards_history[-1] >= 10000:
print("Your agent has just passed the minimum homework threshold")
break
```
Relax and grab some refreshments while your agent is locked in an infinite loop of violence and death.
__How to interpret plots:__
The session reward is the easy thing: it should in general go up over time, but it's okay if it fluctuates ~~like crazy~~. It's also OK if it reward doesn't increase substantially before some 10k initial steps. However, if reward reaches zero and doesn't seem to get up over 2-3 evaluations, there's something wrong happening.
Since we use a policy-based method, we also keep track of __policy entropy__ - the same one you used as a regularizer. The only important thing about it is that your entropy shouldn't drop too low (`< 0.1`) before your agent gets the yellow belt. Or at least it can drop there, but _it shouldn't stay there for long_.
If it does, the culprit is likely:
* Some bug in entropy computation. Remember that it is $ - \sum p(a_i) \cdot log p(a_i) $
* Your agent architecture converges too fast. Increase entropy coefficient in actor loss.
* Gradient explosion - just [clip gradients](https://stackoverflow.com/a/56069467) and maybe use a smaller network
* Us. Or PyTorch developers. Or aliens. Or lizardfolk. Contact us on forums before it's too late!
If you're debugging, just run `logits, values = agent.step(batch_states)` and manually look into logits and values. This will reveal the problem 9 times out of 10: you'll likely see some NaNs or insanely large numbers or zeros. Try to catch the moment when this happens for the first time and investigate from there.
### "Final" evaluation
```
import gym.wrappers
with gym.wrappers.Monitor(make_env(), directory="videos", force=True) as env_monitor:
final_rewards = evaluate(agent, env_monitor, n_games=20)
print("Final mean reward", np.mean(final_rewards))
# Show video. This may not work in some setups. If it doesn't
# work for you, you can download the videos and view them locally.
from pathlib import Path
from base64 import b64encode
from IPython.display import HTML
video_paths = sorted([s for s in Path('videos').iterdir() if s.suffix == '.mp4'])
video_path = video_paths[-1] # You can also try other indices
if 'google.colab' in sys.modules:
# https://stackoverflow.com/a/57378660/1214547
with video_path.open('rb') as fp:
mp4 = fp.read()
data_url = 'data:video/mp4;base64,' + b64encode(mp4).decode()
else:
data_url = str(video_path)
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format(data_url))
```
| true |
code
| 0.705024 | null | null | null | null |
|
# PCA-tSNE-AE
```
%matplotlib notebook
import tensorflow as tf
import math
from sklearn import datasets
from sklearn.manifold import TSNE
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
iris_dataset = datasets.load_iris()
```
## PCA
```
class TF_PCA:
def __init__(self, data, target=None, dtype=tf.float32):
self.data = data
self.target = target
self.dtype = dtype
self.graph = None
self.X = None
self.u = None
self.singular_values = None
self.sigma = None
def fit(self):
self.graph = tf.Graph()
with self.graph.as_default():
self.X = tf.placeholder(self.dtype, shape=self.data.shape)
# Perform SVD
singular_values, u, _ = tf.svd(self.X)
# Create sigma matrix
sigma = tf.diag(singular_values)
with tf.Session(graph=self.graph) as session:
self.u, self.singular_values, self.sigma = session.run([u, singular_values, sigma],
feed_dict={self.X: self.data})
def reduce(self, n_dimensions=None, keep_info=None):
if keep_info:
# Normalize singular values
normalized_singular_values = self.singular_values / sum(self.singular_values)
# Create the aggregated ladder of kept information per dimension
ladder = np.cumsum(normalized_singular_values)
# Get the first index which is above the given information threshold
index = next(idx for idx, value in enumerate(ladder) if value >= keep_info) + 1
n_dimensions = index
with self.graph.as_default():
# Cut out the relevant part from sigma
sigma = tf.slice(self.sigma, [0, 0], [self.data.shape[1], n_dimensions])
# PCA
pca = tf.matmul(self.u, sigma)
with tf.Session(graph=self.graph) as session:
return session.run(pca, feed_dict={self.X: self.data})
tf_pca = TF_PCA(iris_dataset.data, iris_dataset.target)
tf_pca.fit()
pca = tf_pca.reduce(keep_info=0.9) # Results in two dimensions
color_mapping = {0: sns.xkcd_rgb['bright purple'], 1: sns.xkcd_rgb['lime'], 2: sns.xkcd_rgb['ochre']}
colors = list(map(lambda x: color_mapping[x], iris_dataset.target))
plt.scatter(pca[:, 0], pca[:, 1], c=colors)
plt.show()
```
## TSNE
```
plt.close()
model = TSNE(learning_rate=100, n_components=2, random_state=0, perplexity=5)
tsne5 = model.fit_transform(iris_dataset.data)
model = TSNE(learning_rate=100, n_components=2, random_state=0, perplexity=30)
tsne30 = model.fit_transform(iris_dataset.data)
model = TSNE(learning_rate=100, n_components=2, random_state=0, perplexity=50)
tsne50 = model.fit_transform(iris_dataset.data)
plt.figure(1)
plt.subplot(311)
plt.scatter(tsne5[:, 0], tsne5[:, 1], c=colors)
plt.subplot(312)
plt.scatter(tsne30[:, 0], tsne30[:, 1], c=colors)
plt.subplot(313)
plt.scatter(tsne50[:, 0], tsne50[:, 1], c=colors)
plt.show()
```
## Auto Encoder
```
plt.close()
def batch_generator(features, batch_size=50, n_epochs=1000):
"""
Batch generator for the iris dataset
"""
# Generate batches
for epoch in range(n_epochs):
start_index = 0
while start_index != -1:
# Calculate the end index of the batch to generate
end_index = start_index + batch_size if start_index + batch_size < n else -1
yield features[start_index:end_index]
start_index = end_index
# Auto Encoder
class TF_AutoEncoder:
def __init__(self, features, labels, dtype=tf.float32):
self.features = features
self.labels = labels
self.dtype = dtype
self.encoder = dict()
def fit(self, n_dimensions):
graph = tf.Graph()
with graph.as_default():
# Input variable
X = tf.placeholder(self.dtype, shape=(None, self.features.shape[1]))
# Network variables
encoder_weights = tf.Variable(tf.random_normal(shape=(self.features.shape[1], n_dimensions)))
encoder_bias = tf.Variable(tf.zeros(shape=[n_dimensions]))
decoder_weights = tf.Variable(tf.random_normal(shape=(n_dimensions, self.features.shape[1])))
decoder_bias = tf.Variable(tf.zeros(shape=[self.features.shape[1]]))
# Encoder part
encoding = tf.nn.sigmoid(tf.add(tf.matmul(X, encoder_weights), encoder_bias))
# Decoder part
predicted_x = tf.nn.sigmoid(tf.add(tf.matmul(encoding, decoder_weights), decoder_bias))
# Define the cost function and optimizer to minimize squared error
cost = tf.reduce_mean(tf.pow(tf.subtract(predicted_x, X), 2))
optimizer = tf.train.AdamOptimizer().minimize(cost)
with tf.Session(graph=graph) as session:
# Initialize global variables
session.run(tf.global_variables_initializer())
for batch_x in batch_generator(self.features):
self.encoder['weights'], self.encoder['bias'], _ = session.run([encoder_weights, encoder_bias, optimizer],
feed_dict={X: batch_x})
def reduce(self):
return np.add(np.matmul(self.features, self.encoder['weights']), self.encoder['bias'])
# Mix the data before training
n = len(iris_dataset.data)
random_idx = np.random.permutation(n)
features, labels = iris_dataset.data[random_idx], iris_dataset.target[random_idx]
# Create an instance and encode
tf_ae = TF_AutoEncoder(features, labels)
tf_ae.fit(n_dimensions=2)
auto_encoded = tf_ae.reduce()
colors = list(map(lambda x: color_mapping[x], labels))
plt.scatter(auto_encoded[:, 0], auto_encoded[:, 1], c=colors)
plt.show()
```
| true |
code
| 0.820073 | null | null | null | null |
|
# Self-Driving Car Engineer Nanodegree
## Deep Learning
## Project: Build a Traffic Sign Recognition Classifier
### Author: Sergey Morozov
In this notebook, a traffic sign classifier is implemented. [German Traffic Sign Dataset](http://benchmark.ini.rub.de/?section=gtsrb&subsection=dataset) is used to train the model. There is a [write-up](./Writeup.md) where different stages of the implementation are described including analysis of the pros and cons of the chosen approaches and suggestions for further improvements.
---
## Step 0: Load The Data
```
# Load pickled data
import pickle
import pandas as pd
# Data's location
training_file = "traffic-sign-data/train.p"
validation_file = "traffic-sign-data/valid.p"
testing_file = "traffic-sign-data/test.p"
with open(training_file, mode='rb') as f:
train = pickle.load(f)
with open(validation_file, mode='rb') as f:
valid = pickle.load(f)
with open(testing_file, mode='rb') as f:
test = pickle.load(f)
# features and labels
X_train, y_train = train['features'], train['labels']
X_valid, y_valid = valid['features'], valid['labels']
X_test, y_test = test['features'], test['labels']
# Sign id<->name mapping
sign_names = pd.read_csv('signnames.csv').to_dict(orient='index')
sign_names = { key : val['SignName'] for key, val in sign_names.items() }
```
---
## Step 1: Dataset Summary & Exploration
The pickled data is a dictionary with 4 key/value pairs:
- `'features'` is a 4D array containing raw pixel data of the traffic sign images, (num examples, width, height, channels).
- `'labels'` is a 1D array containing the label/class id of the traffic sign. The file `signnames.csv` contains id -> name mappings for each id.
- `'sizes'` is a list containing tuples, (width, height) representing the original width and height the image.
- `'coords'` is a list containing tuples, (x1, y1, x2, y2) representing coordinates of a bounding box around the sign in the image. THESE COORDINATES ASSUME THE ORIGINAL IMAGE. THE PICKLED DATA CONTAINS RESIZED VERSIONS (32 by 32) OF THESE IMAGES.
### A Basic Summary of the Dataset
```
import numpy as np
# Number of training examples
n_train = len(X_train)
# Number of testing examples.
n_test = len(X_test)
# Number of validation examples.
n_valid = len(X_valid)
# What's the shape of an traffic sign image?
image_shape = X_train.shape[1:]
# How many unique classes/labels there are in the dataset.
n_classes = len(np.unique(y_train))
print("Number of training examples =", n_train)
print("Number of testing examples =", n_test)
print("Number of validation examples =", n_valid)
print("Image data shape =", image_shape)
print("Number of classes =", n_classes)
```
### An Exploratory Visualization of the Dataset
#### Number of Samples in Each Category
The categories with minimum/maximum number of samples are marked with yellow/red color correspondingly.
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
plt.rcdefaults()
fig, ax = plt.subplots()
samples_per_category = [len(np.where(y_train==cat_id)[0]) for cat_id in sign_names.keys()]
category_names = tuple([val + " [ id:{id} ]".format(id=key) for key,val in sign_names.items()])
min_cnt = min(samples_per_category)
max_cnt = max(samples_per_category)
y_pos = np.arange(len(category_names))
rects = ax.barh(y_pos,
samples_per_category,
align='center',
color=['green' if val != min_cnt and val != max_cnt \
else 'yellow' if val == min_cnt \
else 'red' for val in samples_per_category])
# setting labels for each bar
for i in range(0,len(rects)):
ax.text(int(rects[i].get_width()),
int(rects[i].get_y()+rects[i].get_height()/2.0),
samples_per_category[i],
fontproperties=fm.FontProperties(size=5))
ax.set_yticks(y_pos)
ax.set_yticklabels(category_names,fontproperties=fm.FontProperties(size=5))
ax.invert_yaxis()
ax.set_title('Samples per Category')
plt.show()
```
#### Random Image from Each Category
Output a sample image from each category. Note, that images will be transformed before they are passed to neural network.
```
import random
import numpy as np
import matplotlib.pyplot as plt
import math
# Visualizations will be shown in the notebook.
%matplotlib inline
h_or_w = image_shape[0]
fig = plt.figure(figsize=(h_or_w,h_or_w))
for i in range(0, n_classes):
samples = np.where(y_train==i)[0]
index = random.randint(0, len(samples) - 1)
image = X_train[samples[index]]
ax = fig.add_subplot(math.ceil(n_classes/5), 5, i+1)
ax.set_title(sign_names[i])
ax.set_ylabel("id: {id}".format(id=i))
plt.imshow(image)
plt.show()
```
----
## Step 2: Design and Test a Model Architecture
Design and implement a deep learning model that learns to recognize traffic signs. The LeNet-5 CNN architecture is used here with minor modifications: dropout parameter added to the first fully connected layer.
### Pre-process the Data Set (normalization, grayscale, etc.)
#### Shuffle Data
```
from sklearn.utils import shuffle
X_train, y_train = shuffle(X_train, y_train)
```
#### Prepare Input Images
```
import cv2
def prepare_image(image_set):
"""Transform initial set of images so that they are ready to be fed to neural network.
(1) normalize image
(2) convert RGB image to gray scale
"""
# initialize empty image set for prepared images
new_shape = image_shape[0:2] + (1,)
prep_image_set = np.empty(shape=(len(image_set),) + new_shape, dtype=int)
for ind in range(0, len(image_set)):
# normalize
norm_img = cv2.normalize(image_set[ind], np.zeros(image_shape[0:2]), 0, 255, cv2.NORM_MINMAX)
# grayscale
gray_img = cv2.cvtColor(norm_img, cv2.COLOR_RGB2GRAY)
# set new image to the corresponding position
prep_image_set[ind] = np.reshape(gray_img, new_shape)
return prep_image_set
def equalize_number_of_samples(image_set, image_labels):
"""Make number of samples in each category equal.
The data set has different number of samples for each category.
This function will transform the data set in a way that each category
will contain the number of samples equal to maximum samples per category
from the initial set. This will provide an equal probability to meet
traffic sign of each category during the training process.
"""
num = max([len(np.where(image_labels==cat_id)[0]) for cat_id in sign_names.keys()])
equalized_image_set = np.empty(shape=(num * n_classes,) + image_set.shape[1:], dtype=int)
equalized_image_labels = np.empty(shape=(num * n_classes,), dtype=int)
j = 0
for cat_id in sign_names.keys():
cat_inds = np.where(y_train==cat_id)[0]
cat_inds_len = len(cat_inds)
for i in range(0, num):
equalized_image_set[j] = image_set[cat_inds[i % cat_inds_len]]
equalized_image_labels[j] = image_labels[cat_inds[i % cat_inds_len]]
j += 1
# at this stage data is definitely not randomly shuffled, so shuffle it
return shuffle(equalized_image_set, equalized_image_labels)
X_train_prep = prepare_image(X_train)
X_test_prep = prepare_image(X_test)
X_valid_prep = prepare_image(X_valid)
X_train_prep, y_train_prep = equalize_number_of_samples(X_train_prep, y_train)
# we do not need to transform labes for validation and test sets
y_test_prep = y_test
y_valid_prep = y_valid
image_shape_prep = X_train_prep[0].shape
```
### Model Architecture
```
# LeNet-5 architecture is used.
import tensorflow as tf
from tensorflow.contrib.layers import flatten
def LeNet(x, channels, classes, keep_prob, mu=0, sigma=0.01):
# Arguments used for tf.truncated_normal, randomly defines variables
# for the weights and biases for each layer
# Layer 1: Convolutional. Input = 32x32xchannels. Output = 28x28x6.
conv1_W = tf.Variable(tf.truncated_normal(shape=(5, 5, channels, 6), mean = mu, stddev = sigma))
conv1_b = tf.Variable(tf.zeros(6))
conv1 = tf.nn.conv2d(x, conv1_W, strides=[1, 1, 1, 1], padding='VALID') + conv1_b
# Layer 1: Activation.
conv1 = tf.nn.relu(conv1)
# Layer 1: Pooling. Input = 28x28x6. Output = 14x14x6.
conv1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# Layer 2: Convolutional. Output = 10x10x16.
conv2_W = tf.Variable(tf.truncated_normal(shape=(5, 5, 6, 16), mean = mu, stddev = sigma))
conv2_b = tf.Variable(tf.zeros(16))
conv2 = tf.nn.conv2d(conv1, conv2_W, strides=[1, 1, 1, 1], padding='VALID') + conv2_b
# Layer 2: Activation.
conv2 = tf.nn.relu(conv2)
# Layer 2: Pooling. Input = 10x10x16. Output = 5x5x16.
conv2 = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# Layer 2: Flatten. Input = 5x5x16. Output = 400.
fc0 = flatten(conv2)
fc0 = tf.nn.dropout(fc0, keep_prob=keep_prob)
# Layer 3: Fully Connected. Input = 400. Output = 120.
fc1_W = tf.Variable(tf.truncated_normal(shape=(400, 120), mean = mu, stddev = sigma))
fc1_b = tf.Variable(tf.zeros(120))
fc1 = tf.matmul(fc0, fc1_W) + fc1_b
# Layer 3: Activation.
fc1 = tf.nn.relu(fc1)
# Layer 4: Fully Connected. Input = 120. Output = 84.
fc2_W = tf.Variable(tf.truncated_normal(shape=(120, 84), mean = mu, stddev = sigma))
fc2_b = tf.Variable(tf.zeros(84))
fc2 = tf.matmul(fc1, fc2_W) + fc2_b
# Layer 4: Activation.
fc2 = tf.nn.relu(fc2)
# Layer 5: Fully Connected. Input = 84. Output = 10.
fc3_W = tf.Variable(tf.truncated_normal(shape=(84, classes), mean = mu, stddev = sigma))
fc3_b = tf.Variable(tf.zeros(classes))
logits = tf.matmul(fc2, fc3_W) + fc3_b
return logits
```
### Train, Validate and Test the Model
A validation set can be used to assess how well the model is performing. A low accuracy on the training and validation
sets imply underfitting. A high accuracy on the training set but low accuracy on the validation set implies overfitting.
#### Features and Labels
```
# x is a placeholder for a batch of input images
x = tf.placeholder(tf.float32, (None,) + image_shape_prep)
# y is a placeholder for a batch of output labels
y = tf.placeholder(tf.int32, (None))
one_hot_y = tf.one_hot(y, n_classes)
```
#### Training Pipeline
```
# hyperparameters of the training process
RATE = 0.0008
EPOCHS = 30
BATCH_SIZE = 128
KEEP_PROB = 0.7
STDDEV = 0.01
keep_prob = tf.placeholder(tf.float32)
logits = LeNet(x, image_shape_prep[-1], n_classes, keep_prob, sigma=STDDEV)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=one_hot_y, logits=logits)
loss_operation = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer(learning_rate = RATE)
training_operation = optimizer.minimize(loss_operation)
```
#### Model Evaluation
```
correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(one_hot_y, 1))
accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()
def evaluate(X_data, y_data):
num_examples = len(X_data)
total_accuracy = 0
sess = tf.get_default_session()
for offset in range(0, num_examples, BATCH_SIZE):
batch_x, batch_y = X_data[offset:offset+BATCH_SIZE], y_data[offset:offset+BATCH_SIZE]
accuracy = sess.run(accuracy_operation, feed_dict={x: batch_x, y: batch_y, keep_prob: 1})
total_accuracy += (accuracy * len(batch_x))
return total_accuracy / num_examples
```
#### Train the Model
```
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
num_examples = len(X_train_prep)
print("Training...")
print()
for i in range(EPOCHS):
X_train_prep, y_train_prep = shuffle(X_train_prep, y_train_prep)
for offset in range(0, num_examples, BATCH_SIZE):
end = offset + BATCH_SIZE
batch_x, batch_y = X_train_prep[offset:end], y_train_prep[offset:end]
sess.run(training_operation, feed_dict={x: batch_x, y: batch_y, keep_prob: KEEP_PROB})
train_accuracy = evaluate(X_train_prep, y_train_prep)
validation_accuracy = evaluate(X_valid_prep, y_valid_prep)
print("EPOCH {} ...".format(i+1))
print("Train Accuracy = {:.3f}".format(train_accuracy))
print("Validation Accuracy = {:.3f}".format(validation_accuracy))
print()
saver.save(sess, './model.ckpt')
print("Model saved")
```
#### Evaluate Trained Model Using Test Samples
```
with tf.Session() as sess:
saver.restore(sess, './model.ckpt')
test_accuracy = evaluate(X_test_prep, y_test_prep)
print("Test Accuracy = {:.3f}".format(test_accuracy))
```
---
## Step 3: Test a Model on New Images
It is time to apply the trained model to the German trafic sign images that were obtained from the Internet.
### Load and Output the Images
```
import os
import cv2
import matplotlib.image as mpimg
img_paths = os.listdir("traffic-sign-images")
images = list()
labels = list()
# read images and resize
for img_path in img_paths:
# read image from file
img = mpimg.imread(os.path.join("traffic-sign-images", img_path))
img = cv2.resize(img, image_shape[0:2], interpolation=cv2.INTER_CUBIC)
images.append(img)
# prefix of each image name is a number of its category
labels.append(int(img_path[0:img_path.find('-')]))
images = np.array(images)
labels = np.array(labels)
# output the resized images
h_or_w = image_shape[0]
fig = plt.figure(figsize=(h_or_w,h_or_w))
for i in range(0, len(images)):
ax = fig.add_subplot(1, len(images), i+1)
ax.set_title(sign_names[labels[i]])
ax.set_ylabel("id: {id}".format(id=labels[i]))
plt.imshow(images[i])
plt.show()
```
### Predict the Sign Type for Each Image
```
# preprocess images first
images_prep = prepare_image(images)
labels_prep = labels
# then make a prediction
with tf.Session() as sess:
saver.restore(sess, './model.ckpt')
sign_ids = sess.run(tf.argmax(logits, 1), feed_dict={x: images_prep, y: labels_prep, keep_prob: 1})
# output the results in the table
print('-' * 93)
print("| {p:^43} | {a:^43} |".format(p='PREDICTED', a='ACTUAL'))
print('-' * 93)
for i in range(len(sign_ids)):
print('| {p:^2} {strp:^40} | {a:^2} {stra:^40} |'.format(
p=sign_ids[i], strp=sign_names[sign_ids[i]], a=labels[i], stra=sign_names[labels[i]]))
print('-' * 93)
```
### Analyze Performance
```
# run evaluation on the new images
with tf.Session() as sess:
saver.restore(sess, './model.ckpt')
test_accuracy = evaluate(images_prep, labels_prep)
print("Accuracy = {:.3f}".format(test_accuracy))
```
### Top 5 Softmax Probabilities For Each Image Found on the Web
```
# Print out the top five softmax probabilities for the predictions on
# the German traffic sign images found on the web.
with tf.Session() as sess:
saver.restore(sess, './model.ckpt')
top_k = sess.run(tf.nn.top_k(tf.nn.softmax(logits), k=5),
feed_dict={x: images_prep, y: labels_prep, keep_prob: 1})
print(top_k)
plt.rcdefaults()
# show histogram of top 5 softmax probabilities for each image
h_or_w = image_shape[0]
fig = plt.figure()
for i in range(0, len(images)):
ax = fig.add_subplot(len(images), 1, i+1)
probabilities = top_k.values[i]
y_pos = np.arange(len(probabilities))
ax.set_ylabel("actual id: {id}".format(id=labels[i]), fontproperties=fm.FontProperties(size=5))
rects = ax.barh(y_pos,
probabilities,
align='center',
color='blue')
# setting labels for each bar
for j in range(0,len(rects)):
ax.text(int(rects[j].get_width()),
int(rects[j].get_y()+rects[j].get_height()/2.0),
probabilities[j],
fontproperties=fm.FontProperties(size=5), color='red')
ax.set_yticks(y_pos)
ax.set_yticklabels(top_k.indices[i], fontproperties=fm.FontProperties(size=5))
xticks = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
ax.set_xticks(xticks)
ax.set_xticklabels(xticks, fontproperties=fm.FontProperties(size=5))
ax.invert_yaxis()
plt.tight_layout()
plt.show()
```
| true |
code
| 0.589953 | null | null | null | null |
|
# Day 6
### Topics
1. Bit of a review
1. Read in Image data with Stitch Image
1. Colors in images with Stitch Image
1. Goodness/badness histogram
First, import our usual things:
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
```
## Bit of a review
Recall last time we played around with uploading data with Pandas and making some plots, with style!
```
gdp = pd.read_csv("https://raw.githubusercontent.com/UIUC-iSchool-DataViz/spring2020/master/week01/data/GDP.csv")
```
Our data formatting:
```
gdp['DATE'] = pd.to_datetime(gdp['DATE'])
```
We made a function to plot this dataset with different styles:
```
def make_gdp_plot(style): # note, "style" is something you can gooogle if you want more options
with plt.style.context(style):
fig, ax = plt.subplots(figsize=(10, 8))
ax.set_title("Style: " + style) # append 'Style:' and whatever style we chose
ax.plot(gdp["DATE"], gdp["GDP"], '-')
plt.show()
```
Now we can run our function. Let's remind ourselves of our choses:
```
plt.style.available
```
And then we made a few plots:
```
make_gdp_plot('seaborn-poster') ## change
```
Today we are going to play with an image dataset (the Stitch Image) and use it to learn about color space.
More info about image datasets can be found on Week 01 & Week 02 of the grad-level course: https://uiuc-ischool-dataviz.github.io/spring2020/
## Read in Image data with Stitch Image
Make sure you have the pillow package installed with:
```python
!conda install -c anaconda pillow
```
Or through using the Anaconda GUI.
Let's use the pillow library and its `Image` interface to load an image:
```
import PIL.Image as Image # note here we are using the Image set of functions *within* the PIL library
```
Now we'll read in image file, here I'm assuming the stitch image is stored in the same directory as this notebook:
```
im = Image.open("stitch_reworked.png", "r")
```
Note, we can take a quick look at this image:
```
im
```
The `im` variable is sort of like a "fig" object in that there is a method to display it to the screen in a Jupyter Notebook. Let's turn it into data:
```
data = np.array(im)
```
What is this data?
```
data
data.shape
```
This data is an image that is 483x430 in shape and has 4 color channels. Why 4 and not 3? The 4th channel is opacity -- how see through the image is. More on this in a moment.
Note we can also display this image with the `matplotlib` interface:
```
fig, ax = plt.subplots(1,1, figsize=(8,8))
ax.imshow(data)
plt.show()
```
We can see this way allows us to see some info about the # of pixels in the x/y directions.
Also, note that the y-direction starts at zero and *increases* going down. This is common for data in an image format.
## Colors in images with Stitch Image
One question we might ask at this point is how many unique colors are there in this image?
We could try using `np.unique` to do this for us:
```
np.unique(data)
```
Hmmm, but we know we are supposed to have channels that are like RGB triplets. By default, `np.unique` just looks for unique values across the entire data, so we have to be a little more careful. Before we get into it, what we know there are 4 channels: these are RGBA:
<img src="https://upload.wikimedia.org/wikipedia/commons/0/0b/RGBA_comp.png">
This is a nice representation of how the "A", or *alpha-channel* changes the look of the image. Here is a rainbow colormap with a checkered pattern behind it. As the alpha-channel decreases we are able to see more and more of the checkered background.
So what we *really* want to see is the number of unique RGBA combinations.
Let's first recall what the dimension of the data is:
```
data.shape
```
We might be tempted to try an "axis" argument:
```
len(np.unique(data, axis=0))
```
But that doens't really do what we want, so we have to be a little trickier.
Let's first see how many unique values are in each channel:
```
channel_labels = ['R', 'G', 'B', 'A']
for i in range(data.shape[2]): # this loops over the last entry of the shape array, so the #4
print('channel=', channel_labels[i],
'unique values=', np.unique( data[:,:,i] ) ) # print the unique elements in each channel
```
So this is still not giving us unique combinations of colors but it is telling us some very interesting stuff! Its saying for example, that there are likely very few colors because there are just not that many levels of any chanel (at most 3 of each). And its telling us that there are places on the image that are either perfectly solid (the alpha channel = 255) or perfectly see-through (alpha channel = 0).
What we really want to do is change our 483x430x4 dataset into a list of RGBA combinations. We can do this with `numpy.reshape` by saying "hey, let's collapse our dataset along the 3rd dimension -- index of 2":
```
data.reshape(-1, data.shape[2])
data.reshape(-1, data.shape[2]).shape
```
Now each pixel is represented by a row and we can, FINALLY, look for unique values along this first axis:
```
np.unique(data.reshape(-1, data.shape[2]), axis=0)
```
TahDah! So, we see that ther are only 4 colors in this image and 1 is just a totally transparent color -- RGBA = [0,0,0,0].
How to figure out where these colors are? Let's first start by trying to visualize where the transparent stuff is. While drawing a checkered pattern on the back of our image might be cool, we can also "set" a gray color to our background more easily and then plot on top of this with `matplotlib`.
```
fig, ax = plt.subplots(1,1, figsize=(8,8))
ax.set_facecolor('gray') # set background image
# plot on top!
ax.imshow(data)
plt.show()
```
What if I only wanted to plot the areas that are red regions? Or change the red areas to blue?
We can do this by doing something called a "boolean mask" -- this is basically making an array of booleans (True or False) that will be true ONLY when the image is transparent. Let's give this a shot:
```
image_boolean_mask = data[:,:,0] == 126 # from our understanding of RGB combinations this is the R channel that is redist
image_boolean_mask
```
So, this is very much like doing a boolean mask for one value:
```
126 == 126
```
So, let's first turn these parts of the image blue by "resetting" their values to be 255 in the blue channel and 0 otherwise.
```
data[image_boolean_mask] = [0,0,255,255]
```
Finally, let's plot!
```
fig, ax = plt.subplots(1,1, figsize=(8,8))
ax.set_facecolor('gray') # set background image
# plot on top!
ax.imshow(data)
plt.show()
```
A beautiful blue stitch!
You can also do more complex combinations of boolean searches for colors. What we'll do now is use a "user-defined" library to do some of these manipulations for us.
Make sure the `image_manipulations.py` file is in your current directory, and do:
```
from image_manipulations import my_boolean_mask
```
This is a little function I wrote myself that I stored in an external library. I put in some doc strings too so we can see a bit of info about this function:
```
my_boolean_mask?
```
Let's try it! Let's replace black lines by purple. We couldn't do this before -- why? Let's look at our data again:
```
np.unique(data.reshape(-1, data.shape[2]), axis=0)
```
If I tried to do a simple boolean mask with one of the channels for black -- [0,0,0,255] -- it would overlap with at least one more color so that won't work. The function does a full set of boolean operations to take this into account (you can check out the function yourself if you are interested):
```
myMask = my_boolean_mask(data, [0,0,0,255])
```
This time, let's not overwrite our original image. We can do this by copying the array:
```
newImageData = data.copy()
```
Now we can replace at will without changing the original data array!
```
newImageData[myMask] = [126, 0, 126, 255] # this will be a magenta looking thing!
```
Let's plot!
```
fig, ax = plt.subplots(1,1, figsize=(8,8))
ax.set_facecolor('gray') # set background image
ax.imshow(newImageData)
plt.show()
```
Cool! Now let's say we want to compare our modified image to the previous? We can do this by making side by size figures with a slight modificaiton to our matplotlib call:
```
fig, ax = plt.subplots(1,2, figsize=(16,8))
```
I haven't filled the figure with anything, just made some side-by-side plots. We can try other configurations and even call it with the number of rows and columns explicitly:
```
fig, ax = plt.subplots(nrows=3,ncols=2, figsize=(16,8))
```
Ok, let's go back to side by side plots:
```
fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(16,8))
```
How do we access the different sets of axis? Let's check what "ax" is now:
```
ax
```
`ax` is actually a an *array* of axis! We can access these axes the same way we would with any array:
```
ax[0]
ax[1]
```
Ok, let's actually put images on our plot:
```
fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(16,8))
ax[0].set_facecolor('gray') # set background image
ax[0].imshow(data) # original
ax[1].set_facecolor('gray') # set background image
ax[1].imshow(newImageData)
plt.show()
```
We can even add labels/titles in the usual way:
```
fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(16,8))
ax[0].set_facecolor('gray') # set background image
ax[0].imshow(data) # original
ax[0].set_title('Original')
ax[1].set_facecolor('gray') # set background image
ax[1].imshow(newImageData)
ax[1].set_title('Updated Image')
plt.show()
```
What if I just wanted to plot *just* the blue part and set the *rest* of the image to fully transparent?
Let's copy our dataset again:
```
onlyBlueData = data.copy()
```
And call a boolean mask for blues:
```
onlyBlueMask = my_boolean_mask(onlyBlueData, [0, 0, 255, 255])
```
What I want now is to turn all of the pixels that are *not* blue into transparent. So I do this with a "NOT-mask" which is basically a little twiddle in front of the mask instead of the mask itself:
```
onlyBlueData[~onlyBlueMask] = [0,0,0,0]
```
Let's plot and see what we did:
```
fig, ax = plt.subplots(1,1, figsize=(8,8)) # one fig again
ax.set_facecolor('gray') # set background image
ax.imshow(onlyBlueData)
plt.show()
```
## Goodness/badness histogram
Let's re-load our un-ultered image and take a quick look:
```
im = Image.open("stitch_reworked.png", "r")
data = np.array(im)
fig, ax = plt.subplots(1,1, figsize=(8,8)) # one fig again
ax.set_facecolor('gray') # set background image
ax.imshow(data)
plt.show()
```
So, when we first encountered this image we really wanted to measure the goodness and badness of Stitch, and now that we have masks we can do just this! Let's grab the measurement of Stitch's goodness which is the white parts of his upper head and ears and the "bad" parts which are the maroon parts using our masking.
First, what are the different colors again?
```
np.unique(data.reshape(-1, data.shape[2]), axis=0)
```
Ok, let's grab goodness and badness:
```
goodness_mask = my_boolean_mask(data, [255, 255, 255, 255])
badness_mask = my_boolean_mask(data, [126, 22, 33, 255])
```
And let's count pixels in each group:
```
npix_good = len(data[goodness_mask])
npix_bad = len(data[badness_mask])
npix_good, npix_bad
```
We could calculate a quick percentage of Stitch's "goodness":
```
npix_good/(npix_good + npix_bad)
```
So stitch is ~23% good. But! We can also make a histogram of this using a `matplotlib` bar-chart plot:
```
fig, ax = plt.subplots(figsize=(8,8))
# we'll turn these into arrays to make our lives easier down the road
labels = np.array(['badness', 'goodness'])
values = np.array([npix_bad, npix_good])
ax.bar(labels, values)
plt.show()
```
Ok this is fine, but wouldn't it be nice to be able to color these bars ourselves? We can do this by accessing the bar-chart's colors and setting them one by one:
```
fig, ax = plt.subplots(figsize=(8,8))
# we'll turn these into arrays to make our lives easier down the road
labels = np.array(['badness', 'goodness'])
values = np.array([npix_bad, npix_good])
myBarChart = ax.bar(labels, values)
plt.show()
myBarChart
myBarChart[0]
```
This is telling us we have 2 rectangles on this plot. Let's do a for loop and use the `set_color` function to pick their colors:
```
colors = ['maroon', 'lightgray'] # set badness = maroon & goodness = light gray
# set colors for each bar individually
for i in range(len(myBarChart)):
myBarChart[i].set_color(colors[i])
```
Re-show this figure:
```
fig
```
We can also set the colors by their RGBA values instead (with a normalization to 0-1 colorspace):
```
colors = np.array([(126, 22, 33, 255), (255, 255, 255, 255)])
# set colors for each bar individually
for i in range(len(myBarChart)):
myBarChart[i].set_color(colors[i]/255)
fig
```
Ah ha! But we have an issue! When we plot white we don't see the bar anymore. We can alleviate this with adding a black line around both of our bars:
```
colors = np.array([(126, 22, 33, 255), (255, 255, 255, 255)])
# set colors for each bar individually
for i in range(len(myBarChart)):
myBarChart[i].set_color(colors[i]/255)
# for the edges
myBarChart[i].set_edgecolor('black') # because one of our colors is white
myBarChart[i].set_linewidth(2) # so we can see the outlines clearly
fig
```
Let's put all this code in one place:
```
fig, ax = plt.subplots(figsize=(8,8))
# we'll turn these into arrays to make our lives easier down the road
labels = np.array(['badness', 'goodness'])
values = np.array([npix_bad, npix_good])
colors = np.array([(126, 22, 33, 255), (255, 255, 255, 255)])
myBarChart = ax.bar(labels, values)
# set colors for each bar individually
for i in range(len(myBarChart)):
myBarChart[i].set_color(colors[i]/255)
# for the edges
myBarChart[i].set_edgecolor('black') # because one of our colors is white
myBarChart[i].set_linewidth(2) # so we can see the outlines clearly
plt.show()
```
Of course, ideally, we'd like to do this for all colors in our image. We can do this with another function in `image_manipulations.py`:
```
from image_manipulations import color_components
colors, color_labels, color_rgb_labels, npix_of_a_color = color_components(data)
```
`colors` gives the array of unique colors, already scaled to 0-1
```
colors
```
`color_rgb_labels` gives the labels in terms of rgb values:
```
color_rgb_labels
```
And `npix_of_a_color` gives the number of pixels at each color:
```
npix_of_a_color
```
Which we can use with much the same code we had before to make histograms:
```
fig, ax = plt.subplots(figsize=(8,8))
myBarChart = ax.bar(color_rgb_labels, npix_of_a_color)
# set colors for each bar individually
for i in range(len(myBarChart)):
myBarChart[i].set_color(colors[i])
# for the edges
myBarChart[i].set_edgecolor('black') # because one of our colors is white
myBarChart[i].set_linewidth(2) # so we can see the outlines clearly
plt.show()
```
This is a nice histogram of the color distribution of the Stitch image showing that most of the pixels are actually transparent background!
| true |
code
| 0.558026 | null | null | null | null |
|
# DataSynthesizer Usage (correlated attribute mode)
> This is a quick demo to use DataSynthesizer in correlated attribute mode.
### Step 1 import packages
```
import os
from time import time
from DataSynthesizer.DataDescriber import DataDescriber
from DataSynthesizer.DataGenerator import DataGenerator
from DataSynthesizer.ModelInspector import ModelInspector
from DataSynthesizer.lib.utils import read_json_file, display_bayesian_network
import pandas as pd
```
## get run time
```
def get_runtime(input_data, na_values, mode):
description_file = f'./out/{mode}/description'
description_file = description_file + '_' + input_data.split('.')[0] + '.json'
synthetic_data = f'./out/{mode}/sythetic_data'
synthetic_data = synthetic_data + '_' + input_data
input_df = pd.read_csv(os.path.join('./data', input_data), skipinitialspace=True, na_values=na_values)
cols_dict = {col: False for col in input_df.columns}
categorical_attributes = (input_df.dtypes=='O').to_dict()
# Default values set here, change here if needed.
# An attribute is categorical if its domain size is less than this threshold.
# Here modify the threshold to adapt to the domain size of "education" (which is 14 in input dataset).
threshold_value = 20
# specify categorical attributes
categorical_attributes = categorical_attributes # {'native-country': True}
# specify which attributes are candidate keys of input dataset.
candidate_keys = cols_dict # {'index': True}
# A parameter in Differential Privacy. It roughly means that removing a row in the input dataset will not
# change the probability of getting the same output more than a multiplicative difference of exp(epsilon).
# Increase epsilon value to reduce the injected noises. Set epsilon=0 to turn off differential privacy.
epsilon = 1
# The maximum number of parents in Bayesian network, i.e., the maximum number of incoming edges.
degree_of_bayesian_network = 2
# Number of tuples generated in synthetic dataset.
num_tuples_to_generate = input_df.shape[0] # Here 32561 is the same as input dataset, but it can be set to another number.
### Step 3 DataDescriber
# 1. Instantiate a DataDescriber.
# 2. Compute the statistics of the dataset.
# 3. Save dataset description to a file on local machine.
start = time()
describer = DataDescriber(category_threshold=threshold_value, null_values=na_values)
describer.describe_dataset_in_correlated_attribute_mode(dataset_file=os.path.join('./data', input_data),
epsilon=epsilon,
k=degree_of_bayesian_network,
attribute_to_is_categorical=categorical_attributes,
attribute_to_is_candidate_key=candidate_keys)
describer.save_dataset_description_to_file(description_file)
duration_desc = time() - start
### Step 4 generate synthetic dataset
# 1. Instantiate a DataGenerator.
# 2. Generate a synthetic dataset.
# 3. Save it to local machine.
generator = DataGenerator()
generator.generate_dataset_in_correlated_attribute_mode(num_tuples_to_generate, description_file)
generator.save_synthetic_data(synthetic_data)
duration_tot = time() - start
print('took {} seconds'.format(duration_tot))
return duration_desc, duration_tot
```
### Step 2 user-defined parameteres
```
files = os.listdir('./data')
files = sorted([file for file in files if file.split('_')[0] == 'synth'])
files = sorted([file for file in files if file.split('_')[2] in ['10', '15', '25', '30']])
na_values = {}
mode = 'correlated_attribute_mode'
files
duration = []
for input_data in files:
duration_ = get_runtime(input_data, na_values, mode)
duration.append(duration_)
import numpy as np
df = pd.DataFrame(np.vstack([file.split('.csv')[0].split('_')[1:] for file in files]),
columns=['n_samples','n_features','n_informative',
'n_redundant','n_repeated','n_classes',
'ncat', 'nbins'])
for col in df.columns:
df[col] = df[col].astype(int)
#df[['duration_desc', 'duration_tot']] = np.vstack(duration)
df = df.iloc[:len(duration),:]
df[['duration_desc', 'duration_tot']] = np.vstack(duration)
df
#df.to_csv('./out/correlated_attribute_mode/duration_per_nfeat_ncat_10cls.csv', index=False)
df_old = pd.read_csv('./out/correlated_attribute_mode/duration_per_nfeat_ncat_10cls.csv')
df = pd.concat([df_old, df])
df.loc[df.ncat==0, ['n_features', 'duration_tot']] \
.sort_values('n_features') \
.multiply(1 / df.loc[df.ncat==0, ['n_features', 'duration_tot']].min()).plot(x='n_features', y='duration_tot')
df.loc[df.ncat==0, ['n_features', 'duration_tot']].sort_values('n_features')#.plot(x='n_features', y='duration_tot')
1 * (1 + .3)**(df.loc[df.ncat==0, ['n_features', 'duration_tot']].sort_values('n_features')).n_features
df.loc[df.ncat==0, ['n_features', 'duration_tot']] \
.sort_values('n_features')#\
#.multiply(1 / df.loc[df.ncat==0, ['n_features', 'duration_tot']].min())
```
| true |
code
| 0.501221 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/zaidalyafeai/Notebooks/blob/master/Unet.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Introduction
The U-Net model is a simple fully convolutional neural network that is used for binary segmentation i.e foreground and background pixel-wise classification. Mainly, it consists of two parts.
* Contracting Path: we apply a series of conv layers and downsampling layers (max-pooling) layers to reduce the spatial size
* Expanding Path: we apply a series of upsampling layers to reconstruct the spatial size of the input.
The two parts are connected using a concatenation layers among different levels. This allows learning different features at different levels. At the end we have a simple conv 1x1 layer to reduce the number of channels to 1.

# Imports
```
import numpy as np
import matplotlib.pyplot as plt
import os
from PIL import Image
import keras
from keras.models import Model
from keras.layers import Conv2D, MaxPooling2D, Input, Conv2DTranspose, Concatenate, BatchNormalization, UpSampling2D
from keras.layers import Dropout, Activation
from keras.optimizers import Adam, SGD
from keras.layers.advanced_activations import LeakyReLU
from keras.callbacks import ModelCheckpoint, ReduceLROnPlateau, EarlyStopping
from keras import backend as K
from keras.utils import plot_model
import tensorflow as tf
import glob
import random
import cv2
from random import shuffle
```
# Dataset
We will use the The Oxford-IIIT Pet Dataset. It contains 37 classes of dogs and cats with around 200 images per each class. The dataset contains labels as bounding boxes and segmentation masks. The total number of images in the dataset is a little more than 7K.

Download the images/masks and unzip the files
```
!wget http://www.robots.ox.ac.uk/~vgg/data/pets/data/images.tar.gz
!wget http://www.robots.ox.ac.uk/~vgg/data/pets/data/annotations.tar.gz
!tar -xvzf images.tar.gz && tar -xvzf annotations.tar.gz
!rm images/*.mat
```
Note that we have two foulders. The first one is `images` which contains the raw images and annotation which contains the masks as a `binary` foulder image.
# Generators
```
def image_generator(files, batch_size = 32, sz = (256, 256)):
while True:
#extract a random batch
batch = np.random.choice(files, size = batch_size)
#variables for collecting batches of inputs and outputs
batch_x = []
batch_y = []
for f in batch:
#get the masks. Note that masks are png files
mask = Image.open(f'annotations/trimaps/{f[:-4]}.png')
mask = np.array(mask.resize(sz))
#preprocess the mask
mask[mask >= 2] = 0
mask[mask != 0 ] = 1
batch_y.append(mask)
#preprocess the raw images
raw = Image.open(f'images/{f}')
raw = raw.resize(sz)
raw = np.array(raw)
#check the number of channels because some of the images are RGBA or GRAY
if len(raw.shape) == 2:
raw = np.stack((raw,)*3, axis=-1)
else:
raw = raw[:,:,0:3]
batch_x.append(raw)
#preprocess a batch of images and masks
batch_x = np.array(batch_x)/255.
batch_y = np.array(batch_y)
batch_y = np.expand_dims(batch_y,3)
yield (batch_x, batch_y)
batch_size = 32
all_files = os.listdir('images')
shuffle(all_files)
split = int(0.95 * len(all_files))
#split into training and testing
train_files = all_files[0:split]
test_files = all_files[split:]
train_generator = image_generator(train_files, batch_size = batch_size)
test_generator = image_generator(test_files, batch_size = batch_size)
x, y= next(train_generator)
plt.axis('off')
img = x[0]
msk = y[0].squeeze()
msk = np.stack((msk,)*3, axis=-1)
plt.imshow( np.concatenate([img, msk, img*msk], axis = 1))
```
# IoU metric
The intersection over union (IoU) metric is a simple metric used to evaluate the performance of a segmentation algorithm. Given two masks $x_{true}, x_{pred}$ we evaluate
$$IoU = \frac{y_{true} \cap y_{pred}}{y_{true} \cup y_{pred}}$$
```
def mean_iou(y_true, y_pred):
yt0 = y_true[:,:,:,0]
yp0 = K.cast(y_pred[:,:,:,0] > 0.5, 'float32')
inter = tf.count_nonzero(tf.logical_and(tf.equal(yt0, 1), tf.equal(yp0, 1)))
union = tf.count_nonzero(tf.add(yt0, yp0))
iou = tf.where(tf.equal(union, 0), 1., tf.cast(inter/union, 'float32'))
return iou
```
# Model
```
def unet(sz = (256, 256, 3)):
x = Input(sz)
inputs = x
#down sampling
f = 8
layers = []
for i in range(0, 6):
x = Conv2D(f, 3, activation='relu', padding='same') (x)
x = Conv2D(f, 3, activation='relu', padding='same') (x)
layers.append(x)
x = MaxPooling2D() (x)
f = f*2
ff2 = 64
#bottleneck
j = len(layers) - 1
x = Conv2D(f, 3, activation='relu', padding='same') (x)
x = Conv2D(f, 3, activation='relu', padding='same') (x)
x = Conv2DTranspose(ff2, 2, strides=(2, 2), padding='same') (x)
x = Concatenate(axis=3)([x, layers[j]])
j = j -1
#upsampling
for i in range(0, 5):
ff2 = ff2//2
f = f // 2
x = Conv2D(f, 3, activation='relu', padding='same') (x)
x = Conv2D(f, 3, activation='relu', padding='same') (x)
x = Conv2DTranspose(ff2, 2, strides=(2, 2), padding='same') (x)
x = Concatenate(axis=3)([x, layers[j]])
j = j -1
#classification
x = Conv2D(f, 3, activation='relu', padding='same') (x)
x = Conv2D(f, 3, activation='relu', padding='same') (x)
outputs = Conv2D(1, 1, activation='sigmoid') (x)
#model creation
model = Model(inputs=[inputs], outputs=[outputs])
model.compile(optimizer = 'rmsprop', loss = 'binary_crossentropy', metrics = [mean_iou])
return model
model = unet()
```
# Callbacks
Simple functions to save the model at each epoch and show some predictions
```
def build_callbacks():
checkpointer = ModelCheckpoint(filepath='unet.h5', verbose=0, save_best_only=True, save_weights_only=True)
callbacks = [checkpointer, PlotLearning()]
return callbacks
# inheritance for training process plot
class PlotLearning(keras.callbacks.Callback):
def on_train_begin(self, logs={}):
self.i = 0
self.x = []
self.losses = []
self.val_losses = []
self.acc = []
self.val_acc = []
#self.fig = plt.figure()
self.logs = []
def on_epoch_end(self, epoch, logs={}):
self.logs.append(logs)
self.x.append(self.i)
self.losses.append(logs.get('loss'))
self.val_losses.append(logs.get('val_loss'))
self.acc.append(logs.get('mean_iou'))
self.val_acc.append(logs.get('val_mean_iou'))
self.i += 1
print('i=',self.i,'loss=',logs.get('loss'),'val_loss=',logs.get('val_loss'),'mean_iou=',logs.get('mean_iou'),'val_mean_iou=',logs.get('val_mean_iou'))
#choose a random test image and preprocess
path = np.random.choice(test_files)
raw = Image.open(f'images/{path}')
raw = np.array(raw.resize((256, 256)))/255.
raw = raw[:,:,0:3]
#predict the mask
pred = model.predict(np.expand_dims(raw, 0))
#mask post-processing
msk = pred.squeeze()
msk = np.stack((msk,)*3, axis=-1)
msk[msk >= 0.5] = 1
msk[msk < 0.5] = 0
#show the mask and the segmented image
combined = np.concatenate([raw, msk, raw* msk], axis = 1)
plt.axis('off')
plt.imshow(combined)
plt.show()
```
# Training
```
train_steps = len(train_files) //batch_size
test_steps = len(test_files) //batch_size
model.fit_generator(train_generator,
epochs = 30, steps_per_epoch = train_steps,validation_data = test_generator, validation_steps = test_steps,
callbacks = build_callbacks(), verbose = 0)
```
# Testing
```
!wget http://r.ddmcdn.com/s_f/o_1/cx_462/cy_245/cw_1349/ch_1349/w_720/APL/uploads/2015/06/caturday-shutterstock_149320799.jpg -O test.jpg
raw = Image.open('test.jpg')
raw = np.array(raw.resize((256, 256)))/255.
raw = raw[:,:,0:3]
#predict the mask
pred = model.predict(np.expand_dims(raw, 0))
#mask post-processing
msk = pred.squeeze()
msk = np.stack((msk,)*3, axis=-1)
msk[msk >= 0.5] = 1
msk[msk < 0.5] = 0
#show the mask and the segmented image
combined = np.concatenate([raw, msk, raw* msk], axis = 1)
plt.axis('off')
plt.imshow(combined)
plt.show()
```
# References
1. http://deeplearning.net/tutorial/unet.html
2. https://github.com/ldenoue/keras-unet
| true |
code
| 0.643805 | null | null | null | null |
|
# Voltammetry Simulations
From Compton *et al.* "Understanding voltammetry: simulation of electrode processes", 2014
## Cyclic Voltammogram (reversible)
```
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
%matplotlib widget
def cv_rev(sigma):
#Specify simulation parameters
theta_i = 10.0
theta_v = -10.0
deltaX = 2e-3
deltaTheta = 0.02
#Calculate other parameters
deltaT = deltaTheta / sigma
maxT = 2 * np.abs(theta_v - theta_i) / sigma
maxX = 6*np.sqrt(maxT)
n = int( maxX / deltaX ) # number of spacesteps
m = int( maxT / deltaT ) # number of timesteps
# Calculate Thomas coefficients
wambda = deltaT / (deltaX**2)
alpha = -wambda
beta = 2.0*wambda + 1.0
gamma = -wambda
# Create containers
g_mod = np.zeros(n)
C = np.zeros(n)# concentration profile
Thetas = np.zeros(m)
fluxes = np.zeros(m)
#Modify gamma coefficients
g_mod[0] = 0 # boundary condition
for i in range(1,n):
g_mod[i] = gamma / (beta - g_mod[i-1] * alpha)
i+=1
# BEGIN SIMULATION
Theta = theta_i
for k in tqdm(range(m*2)):
if( k%m < m / 2 ):
Theta -= deltaTheta
else:
Theta += deltaTheta
# Forward sweep - create modified deltas
C[0] = (1.0 / (1.0 + np.exp(-Theta)))
for i in range(1,n-1):
C[i] = (( C[i] - C[i-1] * alpha ) / ( beta - g_mod[i-1] * alpha ))
i+=1
# Back Substitution
C[n-1] = 1.0
for i in np.arange(n-2,-1,-1):
C[i] = C[i] - g_mod[i] * C[i+1]
i-=1
#Output current
flux = -(-C[2] + 4*C[1] -3*C[0]) / (2*deltaX)
if(k>=m):
fluxes[k%m] = flux
Thetas[k%m] = Theta
k+=1
return Thetas, fluxes
# END SIMULATION
Thetas, Fluxes = cv_rev(100)
plt.plot(Thetas, Fluxes)
Thetas, Fluxes = cv_rev(1000)
plt.plot(Thetas, Fluxes)
Thetas, Fluxes = cv_rev(10000)
plt.plot(Thetas, Fluxes)
```
## Cyclic Voltammogram (irreversible)
```
def cv_irrev(K_0):
#Specify simulation parameters
theta_i = 10.0
theta_v = -10.0
sigma = 10e3
deltaX = 2e-3
deltaTheta = 0.02
alpha_BV = 0.5
C_Abulk = 0.5
C_Bbulk = 1 - C_Abulk
h = deltaX
def f_BV(Theta):
return np.exp(-alpha_BV*Theta)
#Calculate other parameters
deltaT = deltaTheta / sigma
maxT = 2 * np.abs(theta_v - theta_i) / sigma
maxX = 6*np.sqrt(maxT)
n = int( maxX / deltaX ) # number of spacesteps
m = int( maxT / deltaT ) # number of timesteps
# Calculate Thomas coefficients
alpha = 0
beta = 1 + h*f_BV(theta_i)*K_0*(1+np.exp(theta_i))
gamma = -1
delta = h*f_BV(theta_i)*K_0*np.exp(theta_i)
# Create containers
b_mod = np.zeros(n)
d_mod = np.zeros(n)
g_mod = np.zeros(n)
C_A = np.zeros(n)# concentration profile of A
C_B = np.zeros(n)# concentration profile of A
Thetas = np.zeros(m)
fluxes = np.zeros(m)
#Modify beta, delta coefficients
b_mod[0] = beta # boundary condition?
d_mod[0] = delta # boundary condition?
# BEGIN SIMULATION
Theta = theta_i
for k in tqdm(range(m*2)) :
if( k%m < m / 2 ):
Theta -= deltaTheta
else:
Theta += deltaTheta
g_mod[0] = 0 # boundary condition
for i in range(1,n):
g_mod[i] = gamma / (beta - g_mod[i-1] * alpha)
i+=1
# Forward sweep - create modified deltas
C_A[0] = (1.0 / (1.0 + np.exp(-Theta)))
for i in range(1,n-1):
beta = 1 + h*f_BV(Theta)*K_0*(1+np.exp(Theta))
delta = h*f_BV(Theta)*K_0*np.exp(Theta)
C_A[i] = C_A[i-1] * beta - delta * C_Bbulk
C_B[i] = 1 + C_Bbulk - C_A[i]
i+=1
# Back Substitution
C_A[n-1] = C_Abulk
C_B[n-1] = 1 + C_Bbulk - C_A[n-1]
for i in np.arange(n-2,-1,-1):
C_A[i] = C_A[i] - g_mod[i] * C_A[i+1]
i-=1
#Output current
flux = (C_A[1] - C_A[0]) / h
if(k>=m):
fluxes[k%m] = flux
Thetas[k%m] = Theta
k+=1
return Thetas, fluxes
# END SIMULATION
# Thetas, Fluxes = sim(10)
# plt.plot(Thetas, Fluxes)
# Thetas, Fluxes = sim(100)
# plt.plot(Thetas, Fluxes)
Thetas, Fluxes = cv_irrev(.1)
plt.plot(Thetas, Fluxes)
```
| true |
code
| 0.457137 | null | null | null | null |
|
```
# initial setup
try:
# settings colab:
import google.colab
except ModuleNotFoundError:
# settings local:
%run "../../../common/0_notebooks_base_setup.py"
```
---
<img src='../../../common/logo_DH.png' align='left' width=35%/>
#### Distribución Poisson
La distribución Poisson cuenta **cantidad de eventos en un período de tiempo dado**.
Podemos pensar esta distribución como la probabilidad de que ocurra un determinado número de eventos durante cierto período de tiempo.
Sea la variable aleatoria discreta X el número de veces que determinado evento ocurre en un intervalo de tiempo o espacio.
Entonces X puede ser una variable Poisson que toma valores $x=0,1,2,…$ si cumple con las siguientes condiciones:
1. El número de eventos que ocurren en períodos de tiempo, sin superposición entre períodos, es independiente.
2. La probabilidad de exactamente un evento en un intervalo de tiempo corto de duración h=1/n es aproximadamente h*λ donde n es la cantidad de intervalos dentro del período considerado.
3. La probabilidad de exactamente dos o más eventos en un intervalo de tiempo corto es esencialmente cero.
Si se cumplen esas condiciones X es una variable aleatoria que sigue un proceso de Poisson aproximado con parámetro $\lambda > 0$ por lo que su función de probabilidad puntual es
\begin{equation}
P(X = k) = \frac{\lambda^k . e^{-\lambda}}{k!} \\
\lambda > 0, \hspace{0.2cm} k = 0, 1, 2, ...
\end{equation}
Se puede mostrar que $\lambda$ es la media y la varianza de una variable Poisson.
<div>
<div>Función de densidad de probabilidad:</div><div>
<img src="img/prob_poisson.png" width="500"/></div>
</div>
**Ejemplos**:
* X: Cantidad de pacientes que ingresan en la guardia de un hospital en una hora
* X: Cantidad de autos que pasan por una cabina de peaje
* X: Cantidad de llamados que llegan a un operador en un call center en la mañana.
---
Vamos a ver ahora cómo generar datos con esta distibución de probabilidad.
Necesitamos un generador de números aleatorios, que expone métodos para generar números aleatorios con alguna distribución de probabilidad especificada. Construimos este generador de este modo `np.random.default_rng()`
https://docs.scipy.org/doc/numpy/reference/random/generator.html
Estas son las distribuciones de probabilidad disponibles:
https://docs.scipy.org/doc/numpy/reference/random/generator.html#distributions
Vamos a generar datos con distribución empleando el método `poisson`
https://docs.scipy.org/doc/numpy/reference/random/generated/numpy.random.Generator.poisson.html#numpy.random.Generator.poisson
```
import seaborn as sns
def distribution_plotter(data, label, bins=None):
sns.set(rc={"figure.figsize": (10, 7)})
sns.set_style("white")
dist = sns.distplot(data, bins= bins, hist_kws={'alpha':0.2}, kde_kws={'linewidth':5})
dist.set_title('Distribucion de ' + label + '\n', fontsize=16)
import numpy as np
random_generator = np.random.default_rng()
lambda_value = 10
sample_size = 10000
random_poisson_data = random_generator.poisson(lam=lambda_value, size = sample_size)
distribution_plotter(random_poisson_data, "Poisson")
```
#### Referencias
Gráficos: https://es.wikipedia.org/wiki/Distribuci%C3%B3n_de_Poisson
| true |
code
| 0.416826 | null | null | null | null |
|
# PyTorch Metric Learning
See the documentation [here](https://kevinmusgrave.github.io/pytorch-metric-learning/)
## Install the packages
```
!pip install pytorch-metric-learning
!pip install -q faiss-gpu
!git clone https://github.com/akamaster/pytorch_resnet_cifar10
```
## Import the packages
```
%matplotlib inline
from pytorch_resnet_cifar10 import resnet # pretrained models from https://github.com/akamaster/pytorch_resnet_cifar10
from pytorch_metric_learning.utils.inference import MatchFinder, InferenceModel
from pytorch_metric_learning.distances import CosineSimilarity
from pytorch_metric_learning.utils import common_functions as c_f
from torchvision import datasets, transforms
import torchvision
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.nn.init as init
import matplotlib.pyplot as plt
import numpy as np
```
## Create helper functions
```
def print_decision(is_match):
if is_match:
print("Same class")
else:
print("Different class")
mean = [0.485, 0.456, 0.406]
std = [0.229, 0.224, 0.225]
inv_normalize = transforms.Normalize(
mean= [-m/s for m, s in zip(mean, std)],
std= [1/s for s in std]
)
def imshow(img, figsize=(8, 4)):
img = inv_normalize(img)
npimg = img.numpy()
plt.figure(figsize = figsize)
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
```
## Create the dataset and load the trained model
```
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize(mean=mean, std=std)])
dataset = datasets.CIFAR10(root="CIFAR10_Dataset", train=False, transform=transform, download=True)
labels_to_indices = c_f.get_labels_to_indices(dataset.targets)
model = torch.nn.DataParallel(resnet.resnet20())
checkpoint = torch.load("pytorch_resnet_cifar10/pretrained_models/resnet20-12fca82f.th")
model.load_state_dict(checkpoint['state_dict'])
model.module.linear = c_f.Identity()
model.to(torch.device("cuda"))
print("done model loading")
```
## Create the InferenceModel wrapper
```
match_finder = MatchFinder(distance=CosineSimilarity(), threshold=0.7)
inference_model = InferenceModel(model, match_finder=match_finder)
# cars and frogs
classA, classB = labels_to_indices[1], labels_to_indices[6]
```
## Get nearest neighbors of a query
```
# create faiss index
inference_model.train_indexer(dataset)
# get 10 nearest neighbors for a car image
for img_type in [classA, classB]:
img = dataset[img_type[0]][0].unsqueeze(0)
print("query image")
imshow(torchvision.utils.make_grid(img))
indices, distances = inference_model.get_nearest_neighbors(img, k=10)
nearest_imgs = [dataset[i][0] for i in indices[0]]
print("nearest images")
imshow(torchvision.utils.make_grid(nearest_imgs))
```
## Compare two images of the same class
```
# compare two images of the same class
(x, _), (y, _) = dataset[classA[0]], dataset[classA[1]]
imshow(torchvision.utils.make_grid(torch.stack([x,y], dim=0)))
decision = inference_model.is_match(x.unsqueeze(0), y.unsqueeze(0))
print_decision(decision)
```
## Compare two images of different classes
```
# compare two images of a different class
(x, _), (y, _) = dataset[classA[0]], dataset[classB[0]]
imshow(torchvision.utils.make_grid(torch.stack([x,y], dim=0)))
decision = inference_model.is_match(x.unsqueeze(0), y.unsqueeze(0))
print_decision(decision)
```
## Compare multiple pairs of images
```
# compare multiple pairs of images
x = torch.zeros(20, 3, 32, 32)
y = torch.zeros(20, 3, 32, 32)
for i in range(0, 20, 2):
x[i] = dataset[classA[i]][0]
x[i+1] = dataset[classB[i]][0]
y[i] = dataset[classA[i+20]][0]
y[i+1] = dataset[classB[i+20]][0]
imshow(torchvision.utils.make_grid(torch.cat((x,y), dim=0), nrow=20), figsize=(30, 3))
decision = inference_model.is_match(x, y)
for d in decision:
print_decision(d)
print("accuracy = {}".format(np.sum(decision)/len(x)))
```
## Compare all pairs within a batch
```
# compare all pairs within a batch
match_matrix = inference_model.get_matches(x)
assert match_matrix[0,0] # the 0th image should match with itself
imshow(torchvision.utils.make_grid(torch.stack((x[3],x[4]), dim=0)))
print_decision(match_matrix[3,4]) # does the 3rd image match the 4th image?
```
## Compare all pairs between queries and references
```
# compare all pairs between queries and references
match_matrix = inference_model.get_matches(x, y)
imshow(torchvision.utils.make_grid(torch.stack((x[6],y[6]), dim=0)))
print_decision(match_matrix[6, 6]) # does the 6th query match the 6th reference?
```
# Get results in tuple form
```
# make a new model with high threshold
match_finder = MatchFinder(distance=CosineSimilarity(), threshold=0.95)
inference_model = InferenceModel(model, match_finder=match_finder)
# get all matches in tuple form
match_tuples = inference_model.get_matches(x, y, return_tuples=True)
print("MATCHING IMAGE PAIRS")
for i,j in match_tuples:
print(i,j)
imshow(torchvision.utils.make_grid(torch.stack((x[i],y[j]), dim=0)))
```
| true |
code
| 0.682759 | null | null | null | null |
|
# Count epitope mutations by trunk status for natural populations
For a given tree, classify each node as trunk or not and count the number of epitope and non-epitope mutations. Finally, summarize the number of mutations by category of trunk and mutation.
```
from augur.distance import read_distance_map
from augur.utils import json_to_tree
import Bio.Phylo
import json
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
```
## Load tree data
```
with open("../results/auspice/flu_natural_natural_sample_1_with_90_vpm_sliding_full_tree_2015-10-01_tree.json", "r") as fh:
tree_json = json.load(fh)
tree = json_to_tree(tree_json)
tree
```
## Load distance map
```
distance_map = read_distance_map("../config/distance_maps/h3n2/ha/luksza.json")
# Extract all epitope sites from the distance map, readjusting to one-based coordinates
# for comparison with one-based coordinates of amino acid mutations annotated on trees.
epitope_sites = [site + 1 for site in distance_map["map"]["HA1"].keys()]
np.array(epitope_sites)
", ".join([str(site) for site in epitope_sites[:-1]]) + ", and " + str(epitope_sites[-1])
```
## Annotate number of epitope and non-epitope mutations per node
```
for node in tree.find_clades():
epitope_mutations = 0
nonepitope_mutations = 0
if len(node.aa_muts) > 0:
for gene, muts in node.aa_muts.items():
for mut in muts:
if gene == "HA1" and int(mut[1:-1]) in epitope_sites:
epitope_mutations += 1
else:
nonepitope_mutations += 1
node.epitope_mutations = epitope_mutations
node.nonepitope_mutations = nonepitope_mutations
set([node.epitope_mutations for node in tree.find_clades() if node.epitope_mutations > 0])
```
## Assign trunk status
[Bedford et al. 2015](http://www.nature.com.offcampus.lib.washington.edu/nature/journal/v523/n7559/pdf/nature14460.pdf) defines trunk as "all branches ancestral to viruses
sampled within 1 year of the most recent sample". The algorithm for finding the trunk based on this definition is then:
1. Select all nodes in the last year
1. Select the parent of each selected node until the root
1. Create a unique set of nodes
1. Omit all nodes from the last year since resolution of the trunk is limited (note: this step is not implemented below)
Note that this definition was based on 12 years of flu data from 2000 to 2012.
```
max_date = max([tip.attr["num_date"] for tip in tree.find_clades(terminal=True)])
max_date
# Find all tips of the tree sampled within a year of the most recent sample in the tree.
recent_nodes = [node for node in tree.find_clades(terminal=True) if node.attr["num_date"] > (max_date - 1)]
len(recent_nodes)
# Find the last common ancestor of all recent nodes.
mrca = tree.common_ancestor(recent_nodes)
mrca
mrca.attr["num_date"]
# Label all nodes as not part of the trunk by default.
for node in tree.find_clades():
node.is_trunk = False
node.is_side_branch_ancestor = False
# Find all nodes that are ancestral to recent nodes.
# Label these ancestral nodes as part of the "trunk"
# and collect the set of distinct nodes in the trunk.
for recent_node in recent_nodes:
current_node = recent_node.parent
# Traverse from the current node to the tree's root.
while current_node != tree.root:
# Mark a node as part of the trunk if it was sampled
# before the MRCA of all recent nodes.
if current_node.attr["num_date"] < mrca.attr["num_date"]:
current_node.is_trunk = True
current_node = current_node.parent
def is_side_branch_ancestor(node):
"""Returns True if the current node belongs to a "side branch" clade
and is the immediate descendent from a trunk.
"""
return node.parent is not None and node.parent.is_trunk
trunk_path = [node for node in tree.find_clades(terminal=False)
if node.is_trunk]
# Find all nodes that are not on the trunk. These are
# side branch nodes.
side_branch_nodes = [node for node in tree.find_clades(terminal=False)
if not node.is_trunk and node.attr["num_date"] < mrca.attr["num_date"]]
len(trunk_path)
len(side_branch_nodes)
# Find all side branch nodes whose immediate parent is on the trunk.
side_branch_ancestors = []
for node in side_branch_nodes:
if is_side_branch_ancestor(node):
node.is_side_branch_ancestor = True
side_branch_ancestors.append(node)
len(side_branch_ancestors)
# Color nodes by status as on the trunk or as a side branch ancestor.
for node in tree.find_clades():
if node.is_trunk:
node.color = "green"
elif node.is_side_branch_ancestor:
node.color = "orange"
else:
node.color = "black"
# Draw tree with node colors instead of with node labels.
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)
Bio.Phylo.draw(tree, axes=ax, label_func=lambda node: "")
```
## Annotate mutations by trunk status
```
records = []
for node in tree.find_clades(terminal=False):
# Collect records for nodes that are on the trunk or that were sampled prior
# to the MRCA of recent nodes (i.e., side branch nodes).
if node.is_trunk or node.attr["num_date"] < mrca.attr["num_date"]:
records.append({
"node": node.name,
"branch type": "trunk" if node.is_trunk else "side branch",
"epitope mutations": node.epitope_mutations,
"non-epitope mutations": node.nonepitope_mutations
})
df = pd.DataFrame(records)
df.head()
counts_by_trunk_status = df.groupby("branch type").aggregate({"epitope mutations": "sum", "non-epitope mutations": "sum"})
counts_by_trunk_status["epitope-to-non-epitope ratio"] = round(
counts_by_trunk_status["epitope mutations"] / counts_by_trunk_status["non-epitope mutations"]
, 2)
counts_by_trunk_status
counts_by_trunk_status_table = counts_by_trunk_status.to_latex(escape=False)
with open("../manuscript/tables/mutations_by_trunk_status.tex", "w") as oh:
oh.write(counts_by_trunk_status_table)
```
| true |
code
| 0.567158 | null | null | null | null |
|
# Imports
We will be importing the following packages:
1. numpy
2. matplotlib
3. urllib
4. tqdm
5. imageio
6. glob
7. os
8. base64
9. IPython
10. **wandb**
```
%%capture
! pip install -q imageio
! pip install --upgrade wandb
! wandb login
import numpy as np
import matplotlib.pyplot as plt
import urllib.request
# import wandb
from tqdm import tqdm
import imageio
import glob
import os
import base64
from IPython import display
np.random.seed(666)
name_run = input('Enter name of the run')
wandb.init(entity="authors", project="rnn-viz", name=name_run)
```
# Data
We will be taking Shakespeare's work as our data. The data [url](https://storage.googleapis.com/download.tensorflow.org/data/shakespeare.txt) is fetched from this [tensorflow tutorial on text generation](https://www.tensorflow.org/tutorials/text/text_generation).
```
url = 'https://storage.googleapis.com/download.tensorflow.org/data/shakespeare.txt'
filename = 'input.txt'
urllib.request.urlretrieve(url, filename)
```
## Data processing
In this section we read the `input.txt` file that is downloaded. Vocabulary is the unique characters in the entire text file. This is extracted so that we can generate characters with a constraint.
```
text = open('input.txt','r').read()[:30000]
vocab = sorted(set(text))
text_size, vocab_size = len(text), len(vocab)
print('Number of characters: {}'.format(text_size))
print('Number of unique characters:{}'.format(vocab_size))
```
Let us look at the first 250 characters in the input text.
```
print(text[:250])
```
Here we map the unique characters to specific indices.
A -> 0
B -> 1
and so on
This process helps us in converting characters to numbers and also vice versa. The input text file which is read, is converted to numbers instead of characters. Computers are always better with numbers.
```
char_to_ix = {c:ix for ix,c in enumerate(vocab)}
ix_to_char = np.array(vocab)
text_as_int = np.array([char_to_ix[c] for c in text])
i = 1
print('The first 5 mappings of char_to_ix')
for key, value in char_to_ix.items():
print('{} : {}'.format(repr(key), value))
if i == 5:
break
i += 1
print('The first 5 mappings of ix_to_char')
for ix, value in enumerate(ix_to_char[:5]):
print('{} : {}'.format(ix, repr(value)))
print(text[:10])
print(text_as_int[:10])
```
# Hyperparameters
We are looking to have a hidden state of `100` dimensions. The recurrent neural network is to be unrolled for `25` time steps. The learning rate is chosen to be `0.1`.
```
hidden_size = 100 # size of hidden layer of neurons
seq_length = 25 # number of steps to unroll the RNN for
learning_rate = 1e-1
```
# Model Parameters
To get into this part let us have a look at the formulas governing the Recurrent Neural Nets.
$$
h^{l}_{t} =\tanh\begin{pmatrix}
h^{l-1}_{t}\\
h^{l}_{t-1}
\end{pmatrix}
$$
The above equation is a simple representation of the recurrence formula. This shows that the present hidden state of layer $(l)$, depends on the present hidden state of the immediate lower layer $(l-1)$ and the immediate past $(t-1)$ hidden layer of the same layer. A little nuance of the representation is that we consider $h^{0}_{t}$ as the input layer. We can write $h^{0}_{t}$ as $x_{t}$.
We can break down the above representation in the following way.
$$
raw\_h^{l}_{t} =W_{h\_prev\_layer}h^{l-1}_{t}+W_{h\_prev\_time}h^{l}_{t-1}+b_{h}\\
\boxed{h^{l}_{t} =\tanh raw\_h^{l}_{t}}\\
\boxed{y^{l+1}_{t} =W_{y}\times h^{l}_{t}+b_{y}}
$$
```
Wxh = np.random.normal(loc=0.0, scale=1e-2, size=(hidden_size, vocab_size))
Whh = np.random.normal(loc=0.0, scale=1e-2, size=(hidden_size, hidden_size))
Why = np.random.normal(loc=0.0, scale=1e-2, size=(vocab_size, hidden_size))
bh = np.random.normal(loc=0.0, scale=1e-2, size=(hidden_size, 1))
by = np.random.normal(loc=0.0, scale=1e-2, size=(vocab_size, 1))
print("Size of Wxh: {}".format(Wxh.shape))
print("Size of Whh: {}".format(Whh.shape))
print("Size of Why: {}".format(Why.shape))
print("Size of bh: {}".format(bh.shape))
print("Size of by: {}".format(by.shape))
def show_weights_hist(weight):
plt.hist(weight.reshape(-1),100)
plt.xlim(-1,1)
plt.show()
show_weights_hist(Why)
```
# Loss Function
In this section we will decipher the loss function and the back-propagation algorithm. In a recurrent sequence model, the back-propagation has a fancy term hooked to it, the **back propagation through time**.
```
def lossFun(inputs, target, hprev, hist_flag=False):
"""
This is the loss function
Inputs:
inputs- A list of integers for the input sequence
targets- A list of integers for the target sequence
hprev- The first hidden state h[t-1]
hist_flag- A bollean variable that holds the necessity of the histograms
Outputs:
returns the loss, gradients on model parameters, and last hidden state
"""
xs, hs= {}, {}
hs[-1] = hprev
# forward pass
for t in range(len(inputs)):
xs[t] = np.zeros((vocab_size,1))
xs[t][inputs[t],0] = 1
hs[t] = np.tanh(np.matmul(Wxh, xs[t]) + np.matmul(Whh, hs[t-1]) + bh)
# backward pass
y = np.matmul(Why, hs[t]) + by #projection
p = np.exp(y) / np.sum(np.exp(y)) #probability
loss = -np.log(p[target,0]) #softmax loss
dWxh, dWhh, dWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
dbh, dby = np.zeros_like(bh), np.zeros_like(by)
dy = np.copy(p)
dy[target] -= 1
dWhy = np.matmul(dy, hs[t].T)
dby = dy
dhnext = np.matmul(Why.T, dy)
if hist_flag:
dh_list = []
for t in reversed(range(len(inputs))):
if hist_flag:
dh_list.append(dhnext)
dh = dhnext
dhraw = (1 - hs[t] * hs[t]) * dh
dbh += dhraw
dWxh += np.matmul(dhraw, xs[t].T)
dWhh += np.matmul(dhraw, hs[t-1].T)
dhnext = np.matmul(Whh.T, dhraw)
if hist_flag:
return dh_list[::-1]
return loss, dWxh, dWhh, dWhy, dbh, dby, hs[len(inputs)-1]
```
# Text generation function
This function will be used for inference. We will provide a seed character, and will expect this function to return us with generated text of the sequence size mentioned.
```
def text_generate(inputs):
"""
A text generation function
Inputs:
Outputs:
"""
# forward pass
h = np.zeros((hidden_size,1))
for t in range(len(inputs)):
x = np.zeros((vocab_size,1))
x[inputs[t],0] = 1
h = np.tanh(np.matmul(Wxh, x) + np.matmul(Whh, h) + bh)
y = np.matmul(Why, h) + by #projection
p = np.exp(y) / np.sum(np.exp(y)) #probability
ix = np.random.choice(np.arange(vocab_size),p=p.ravel()) #this is to leak a little information, provides a soft bound
return ix
def imsave(dh, name, time_step):
'''
This function helps in saving the image
inputs:
image - Tensor
name - The name of the image
'''
fig = plt.figure(figsize=(5,5))
plt.hist(dh.reshape(-1),100)
plt.title('Time Step {}'.format(time_step))
plt.xlim(-1e-2, 1e-2)
plt.ylim(0,5)
plt.savefig(name)
plt.close()
def create_gif(path_to_images, name_gif):
filenames = glob.glob(path_to_images)
filenames = sorted(filenames,reverse=True)
images = []
for filename in tqdm(filenames):
images.append(imageio.imread(filename))
kargs = { 'duration': 0.50 }
imageio.mimsave(name_gif, images, 'GIF', **kargs)
def show_gif(fname):
with open(fname, 'rb') as fd:
b64 = base64.b64encode(fd.read()).decode('ascii')
return display.HTML(f'<img src="data:image/gif;base64,{b64}" />')
```
# Train
```
mWxh, mWhh, mWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
mbh, mby = np.zeros_like(bh), np.zeros_like(by) # memory variables for Adagrad
num_of_batches = text_size//(seq_length+1)
for iter in range(51):
seq_pointer = 0
hprev = np.zeros((hidden_size,1))
loss_avg = 0
# Inside an epoch
for batch in tqdm(range(num_of_batches)):
input = text_as_int[seq_pointer:seq_pointer+seq_length]
target = text_as_int[seq_pointer+seq_length]
# Create the histogram GIF
if seq_pointer == 0 and iter%10 == 0:
os.mkdir('RNN_hidden{:02d}'.format(iter))
dh_list = lossFun(input, target, hprev,hist_flag=True)
for time,dh in enumerate(dh_list):
imsave(dh, 'RNN_hidden{:02d}/time{:03d}.png'.format(iter,time), time)
create_gif('RNN_hidden{:02d}/time*.png'.format(iter), 'RNN_hidden{:02d}.gif'.format(iter))
# wandb.log({"video": wandb.Video('RNN_hidden{:02d}.gif'.format(iter), fps=2, format="gif")})
seq_pointer += seq_length
# forward seq_length characters through the net and fetch gradient
loss, dWxh, dWhh, dWhy, dbh, dby, hprev = lossFun(input, target, hprev)
loss_avg += loss
# perform parameter update with Adagrad
for param, dparam, mem in zip([Wxh, Whh, Why, bh, by],
[dWxh, dWhh, dWhy, dbh, dby],
[mWxh, mWhh, mWhy, mbh, mby]):
mem += dparam * dparam
param += -learning_rate * dparam / np.sqrt(mem + 1e-8) # adagrad update
# Outside an epoch
print('Epoch: {} loss: {:0.2f}'.format(iter, loss_avg/num_of_batches))
wandb.log({"loss":loss_avg/num_of_batches})
text_input = text_as_int[0:seq_length].tolist()
for index in range(200):
infer_char = text_generate(text_input)
text_input += [infer_char]
txt = ''.join(ix_to_char[ix] for ix in text_input)
print('----\n{}\n----'.format(txt))
```
# Vanishing and Exploding Gradients
The model has been trained. We will now try and look into the problems of a simple RNN. We will feed a single sequence to the network. The network produces the gradients for each time step. We will be plotting these gradient along the time step.
```
show_gif('RNN_hidden00.gif')
```
# Connectivity
$$
Connectivity\left( t,t^{'}\right) =\frac{\partial L_{t^{'}}}{\partial x_{t}}
$$
```
def connectivity(inputs, target, hprev):
xs, hs, ys, ps = {}, {}, {}, {}
hs[-1] = hprev
loss = 0
connections = []
# forward pass
for t in range(len(inputs)):
xs[t] = np.zeros((vocab_size,1))
xs[t][inputs[t],0] = 1
hs[t] = np.tanh(np.matmul(Wxh, xs[t]) + np.matmul(Whh, hs[t-1]) + bh)
# backward pass
ys = np.matmul(Why, hs[t]) + by
ps = np.exp(ys) / np.sum(np.exp(ys))
loss = -np.log(ps[target,0])
dWxh, dWhh, dWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
dbh, dby = np.zeros_like(bh), np.zeros_like(by)
dy = np.copy(ps)
dy[target] -= 1
dWhy += np.matmul(dy, hs[t].T)
dby += dy
dhnext = np.matmul(Why.T, dy)
heat = []
for t in reversed(range(len(inputs))):
dh = dhnext
dhraw = (1 - hs[t] * hs[t]) * dh
dbh += dhraw
dWxh += np.matmul(dhraw, xs[t].T)
dWhh += np.matmul(dhraw, hs[t-1].T)
dhnext = np.matmul(Whh.T, dhraw)
dx = np.matmul(Wxh.T, dhraw)
heat.append(np.sum(dx*dx))
return heat[::-1]
def coloring(value):
if value == -99:
return (0,1,0)
if value <= 0.5:
return (0,0,1,value)
else:
return (1,0,0,value-0.5)
def draw_text(text, heat_map):
'''
text is a list string
'''
fig, ax = plt.subplots()
counter_x = 0.0
counter_y = 1.0
for ch, heat in zip(text,heat_map):
if ch == '\n':
counter_x = 0.0
counter_y -= 0.1
continue
if ch == '\t':
counter_x += 0.05
continue
ax.text(x = 0.+counter_x,
y = 1.+counter_y,
s = ch,
color = 'black',
fontweight = 'bold',
fontsize=10,
backgroundcolor = coloring(heat)
)
counter_x += 0.05
ax.axis('off')
plt.show()
draw_text([0,1,2,3,4,5,6,7,8,9],[0, 0.1, 0.2, 0.3, 0.4, 0.5 ,0.6, 0.7, 0.8, 0.9])
index = 100
input = text_as_int[0:index]
target = text_as_int[index]
hprev = np.zeros((hidden_size,1))
connections = connectivity(input, target, hprev)
mi = min(connections)
ma = max(connections)
connections = [(value-mi)/(ma-mi) for value in connections]
draw_text(ix_to_char[text_as_int[:index+1]], connections+[-99])
```
| true |
code
| 0.515864 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/irahulcse/Data-Science-Work-For-Quora/blob/master/Copy_of_quora.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Quora Data Framework New
```
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from wordcloud import WordCloud as wc
from nltk.corpus import stopwords
import matplotlib.pylab as pylab
import matplotlib.pyplot as plt
from pandas import get_dummies
import matplotlib as mpl
import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib
import warnings
from sklearn.ensemble import RandomForestClassifier
import sklearn
import string
import scipy
import numpy
import nltk
import json
import sys
import csv
import os
nltk.download('averaged_perceptron_tagger')
nltk.download("stopwords")
```
# Version of the different libraries
```
print('matplotlib: {}'.format(matplotlib.__version__))
print('sklearn: {}'.format(sklearn.__version__))
print('scipy: {}'.format(scipy.__version__))
print('seaborn: {}'.format(sns.__version__))
print('pandas: {}'.format(pd.__version__))
print('numpy: {}'.format(np.__version__))
print('Python: {}'.format(sys.version))
```
# Getting alll the data from nltk stopwords
```
from nltk.tokenize import sent_tokenize,word_tokenize
from nltk.corpus import stopwords
data = "All work and no play makes jack dull boy. All work and no play makes jack a dull boy."
```
# Print the tokenize data
```
print(word_tokenize(data))
print(sent_tokenize(data))
# stopWords=set(stopwords.words('english'))
# words=word_tokenize(data)
# wordsFiltered=[]
# for w in words:
# if w in stopWords:
# wordsFiltered.append(w)
# print(wordsFiltered)
from nltk.stem import PorterStemmer
from nltk.tokenize import sent_tokenize,word_tokenize
words=["game","gaming","gamed","games"]
ps=PorterStemmer()
for word in words:
print(ps.stem(word))
from nltk.tokenize import PunktSentenceTokenizer
sentences=nltk.sent_tokenize(data)
for set in sentences:
print(nltk.pos_tag(nltk.word_tokenize(set)))
```
# How to make the use of the sns i am not able to get it in poproperly
```
sns.set(style='white',context='notebook',palette="deep")
```
# EDA
## I will be going to write the diffrent exploratoion technique which can be used to explore the dataset
```
train=pd.read_csv('/home/rahul/Desktop/Link to rahul_environment/Projects/Machine_Learning Projects/Quora_DataFramework/train.csv')
test=pd.read_csv('/home/rahul/Desktop/Link to rahul_environment/Projects/Machine_Learning Projects/Quora_DataFramework/test.csv')
print('shape of the train',train.shape)
print('shape of the test',test.shape)
train.size # finding the size of the training set
type(train) # tells us about the object type
train.describe() #describe use us about the data
train.sample(5)
```
# Data Cleaning
# for finding that there is any kind of the null element is present or not(sum of the null values)
```
train.isnull().sum()
# # but if we have the null values used it for finding the result in the dataset
print('Before Dropping the items',train.shape)
train=train.dropna()
print('After droping',train.shape)
```
# for finding the unique items for the target with command below:
# getting all the unique from the dataset
```
train_target=train['target'].values
np.unique(train_target)
train.head(5)
train.tail(5)
train.describe()
```
** Data preprocessing refers to the transformations applied to our data before feeding it to the algorithm.
Data Preprocessing is a technique that is used to convert the raw data into a clean data set. In other words, whenever the data is gathered from different sources it is collected in raw format which is not feasible for the analysis. there are plenty of steps for data preprocessing and we just listed some of them in general(Not just for Quora) :
removing Target column (id)
Sampling (without replacement)
Making part of iris unbalanced and balancing (with undersampling and SMOTE)
Introducing missing values and treating them (replacing by average values)
Noise filtering
Data discretization
Normalization and standardization
PCA analysis
Feature selection (filter, embedded, wrapper)
Etc.
now we will be going to perfrom some queries on the dataset**
```
train.where(train['target']==1).count()
train[train['target']>1]
train.where(train['target']==1).head(5)
```
** Imbalanced dataset is relevant primarily in the context of supervised machine learning involving two or more classes.
Imbalance means that the number of data points available for different the classes is different: If there are two classes, then balanced data would mean 50% points for each of the class. For most machine learning techniques, little imbalance is not a problem. So, if there are 60% points for one class and 40% for the other class, it should not cause any significant performance degradation. Only when the class imbalance is high, e.g. 90% points for one class and 10% for the other, standard optimization criteria or performance measures may not be as effective and would need modification.
Now we will be going to explore the exploreing question**
```
question=train['question_text']
i=0
for q in question[:5]:
i=i+1
print("Question came from the Quora Data_set=="+q)
train["num_words"] = train["question_text"].apply(lambda x: len(str(x).split()))
```
# Some Feature Engineering
eng_stopwords=set(stopwords.words("english"))
print(len(eng_stopwords))
print(eng_stopwords)
```
print(train.columns)
train.head()
# # Count Plot
ax=sns.countplot(x='target',hue='target',data=train,linewidth=5,edgecolor=sns.color_palette("dark",3))
plt.title('Is data set imbalance')
plt.show()
plt.savefig('targetsetimbalance')
ax=train['target'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',shadow=True)
ax.set_title('target')
ax.set_ylabel('')
plt.savefig('targetdiagramforpie')
plt.show()
# cf=RandomForestClassifier(n_estimators=)
```
# Histogram
f,ax=plt.subplots(1,2,figsize=(20,10))
train[train['target']==0].num_words.plot.hist(ax=ax[0],bins=20,edgecolor='black',color='red')
ax[0].set_title('target=0')
x1=list(range(0,85,5))
f,ax=plt.subplots(1,2,figsize=(18,8))
train[['target','num_words']].groupby(['target']).mean().plot().bar(ax=ax[0])
ax[0].set_title('num vs target')
sns.countplot('num_words',hue='target',data=train,ax=ax[1])
ax[1].set_title('num_words:target=0 vs target=1')
plt.show()
# histogram
```
train.hist(figsize=(15,20))
plt.figure()
# # Creating the histogram which can be used to make the
```
# Making the violin plot
```
sns.violinplot(data=train,x='target',y='num_words')
plt.savefig('violinplot')
```
# Making the kde plot
```
sns.FacetGrid(train,hue="target",size=5).map(sns.kdeplot,"num_words").add_legend()
plt.savefig('facetgrid-target')
plt.show()
```
# Box Plot
```
train['num_words'].loc[train['num_words']>60]=60
axes=sns.boxplot(x='target',y='num_words',data=train)
axes.set_xlabel('Target',fontsize=12)
axes.set_title("No of words in each class",fontsize=15)
plt.savefig('target-numwords')
plt.show()
# # How to Generate the Word Cloud in the d plotting we will be going to make the commit
# eng_stopwords=set(stopwords.words("english"))
# def generate_wordcloud(text):
# wordcloud = wc(relative_scaling = 1.0,stopwords = eng_stopwords).generate(text)
# fig,ax = plt.subplots(1,1,figsize=(10,10))
# ax.imshow(wordcloud, interpolation='bilinear')
# ax.axis("off")
# ax.margins(x=0, y=0)
# plt.show()
# text=' '.join(train.question_text)
# generate_wordcloud(text)
```
| true |
code
| 0.40295 | null | null | null | null |
|
# Lesson 1 - What's your pet
### Trying to pass pretrained weights into Learner created model, and making create_cnn working with custom models. I am using resnet50 only to make it comparable to the usual fastai resnet50 training scores to confirm that my method works.
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
```
We import all the necessary packages. We are going to work with the [fastai V1 library](http://www.fast.ai/2018/10/02/fastai-ai/) which sits on top of [Pytorch 1.0](https://hackernoon.com/pytorch-1-0-468332ba5163). The fastai library provides many useful functions that enable us to quickly and easily build neural networks and train our models.
```
from fastai import *
from fastai.vision import *
gpu_device = 1
defaults.device = torch.device(f'cuda:{gpu_device}')
torch.cuda.set_device(gpu_device)
path = untar_data(URLs.PETS); path
path.ls()
path_anno = path/'annotations'
path_img = path/'images'
```
The first thing we do when we approach a problem is to take a look at the data. We _always_ need to understand very well what the problem is and what the data looks like before we can figure out how to solve it. Taking a look at the data means understanding how the data directories are structured, what the labels are and what some sample images look like.
The main difference between the handling of image classification datasets is the way labels are stored. In this particular dataset, labels are stored in the filenames themselves. We will need to extract them to be able to classify the images into the correct categories. Fortunately, the fastai library has a handy function made exactly for this, `ImageDataBunch.from_name_re` gets the labels from the filenames using a [regular expression](https://docs.python.org/3.6/library/re.html).
```
fnames = get_image_files(path_img)
fnames[:5]
np.random.seed(2)
pat = re.compile(r'/([^/]+)_\d+.jpg$')
```
If you're using a computer with an unusually small GPU, you may get an out of memory error when running this notebook. If this happens, click Kernel->Restart, uncomment the 2nd line below to use a smaller *batch size* (you'll learn all about what this means during the course), and try again.
```
bs = 64
```
## Training: resnet50
Now we will train in the same way as before but with one caveat: instead of using resnet34 as our backbone we will use resnet50 (resnet34 is a 34 layer residual network while resnet50 has 50 layers. It will be explained later in the course and you can learn the details in the [resnet paper](https://arxiv.org/pdf/1512.03385.pdf)).
Basically, resnet50 usually performs better because it is a deeper network with more parameters. Let's see if we can achieve a higher performance here. To help it along, let's us use larger images too, since that way the network can see more detail. We reduce the batch size a bit since otherwise this larger network will require more GPU memory.
```
data = ImageDataBunch.from_name_re(path_img, fnames, pat, ds_tfms=get_transforms(),
size=299, bs=bs//2).normalize(imagenet_stats)
import pretrainedmodels
pretrainedmodels.model_names
# this works
def get_model(pretrained=True, model_name = 'resnet50', **kwargs ):
if pretrained:
arch = pretrainedmodels.__dict__[model_name](num_classes=1000, pretrained='imagenet')
else:
arch = pretrainedmodels.__dict__[model_name](num_classes=1000, pretrained=None)
return arch
# get_model() # uncomment if you want to see its arch
custom_head = create_head(nf=2048*2, nc=37, ps=0.5, bn_final=False)
# Although that original resnet50 last layer in_features=2048 as you can see below, but the modified fastai head should be in_features = 2048 *2 since it has 2 Pooling
# AdaptiveConcatPool2d((ap): AdaptiveAvgPool2d(output_size=1) + (mp): AdaptiveMaxPool2d(output_size=1)
children(models.resnet50())[-2:]
custom_head
fastai_resnet50=nn.Sequential(*list(children(get_model(model_name = 'resnet50'))[:-2]),custom_head)
learn = Learner(data, fastai_resnet50, metrics=error_rate) # It seems `Learner' is not using transfer learning. Jeremy: It’s better to use create_cnn, so that fastai will create a version you can use for transfer learning for your problem.
# https://forums.fast.ai/t/lesson-5-advanced-discussion/30865/21
# fastai_resnet50 # uncomment if you want to see its arch
learn.lr_find()
learn.recorder.plot()
learn.fit_one_cycle(5)
learn.unfreeze()
learn.lr_find()
learn.recorder.plot()
# learn.fit_one_cycle(3, max_lr=slice(1e-6,1e-4))
learn.fit_one_cycle(1, max_lr=slice(1e-6,1e-4))
```
### Comparing the previous learn scores (which seem did not use pretrained weights) with create_cnn method.
```
fastai_resnet50=nn.Sequential(*list(children(get_model(model_name = 'resnet50'))[:-2]),custom_head)
def get_fastai_model(pretrained=True, **kwargs ):
return fastai_resnet50
# get_fastai_model() # uncomment if you want to see its arch. You can see that it is identical to model.resnet50
learn = create_cnn(data, get_fastai_model, metrics=error_rate)
learn.lr_find()
learn.recorder.plot()
learn.fit_one_cycle(5)
learn.unfreeze()
learn.lr_find()
learn.recorder.plot()
# learn.fit_one_cycle(3, max_lr=slice(1e-6,1e-4))
learn.fit_one_cycle(1, max_lr=slice(1e-6,1e-4))
```
### Comparing the previous learn scores with the original fastai create_cnn method.
```
learn = create_cnn(data,models.resnet50, metrics=error_rate)
learn.lr_find()
learn.recorder.plot()
learn.fit_one_cycle(5)
learn.unfreeze()
learn.lr_find()
learn.recorder.plot()
# learn.fit_one_cycle(3, max_lr=slice(1e-6,1e-4))
learn.fit_one_cycle(1, max_lr=slice(1e-6,1e-4))
```
| true |
code
| 0.732563 | null | null | null | null |
|
# Generating Skewed Data for Prediction
This notebook helps generating skewed data based on the [covertype](https://archive.ics.uci.edu/ml/datasets/covertype) dataset from UCI Machine Learning Repository. The generated data is then used to simulate online prediction request workload to a deployed model version on the AI Platform Prediction.
The notebook covers the following steps:
1. Download the data
2. Define dataset metadata
3. Sample unskewed data points
4. Prepare skewed data points
5. Simulate serving workload to AI Platform Prediction
## Setup
### Install packages and dependencies
```
!pip install -U -q google-api-python-client
!pip install -U -q pandas
```
### Setup your GCP Project
```
PROJECT_ID = 'sa-data-validation'
BUCKET = 'sa-data-validation'
REGION = 'us-central1'
!gcloud config set project $PROJECT_ID
```
### Authenticate your GCP account
This is required if you run the notebook in Colab
```
try:
from google.colab import auth
auth.authenticate_user()
print("Colab user is authenticated.")
except: pass
```
### Import libraries
```
import os
from tensorflow import io as tf_io
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
```
### Define constants
You can change the default values for the following constants
```
LOCAL_WORKSPACE = './workspace'
LOCAL_DATA_DIR = os.path.join(LOCAL_WORKSPACE, 'data')
LOCAL_DATA_FILE = os.path.join(LOCAL_DATA_DIR, 'train.csv')
BQ_DATASET_NAME = 'data_validation'
BQ_TABLE_NAME = 'covertype_classifier_logs'
MODEL_NAME = 'covertype_classifier'
VERSION_NAME = 'v1'
MODEL_OUTPUT_KEY = 'probabilities'
SIGNATURE_NAME = 'serving_default'
```
## 1. Download Data
The covertype dataset is preprocessed, split, and uploaded to uploaded to the `gs://workshop-datasets/covertype` public GCS location.
We use this version of the preprocessed dataset in this notebook. For more information, see [Cover Type Dataset](https://github.com/GoogleCloudPlatform/mlops-on-gcp/tree/master/datasets/covertype)
```
if tf_io.gfile.exists(LOCAL_WORKSPACE):
print("Removing previous workspace artifacts...")
tf_io.gfile.rmtree(LOCAL_WORKSPACE)
print("Creating a new workspace...")
tf_io.gfile.makedirs(LOCAL_WORKSPACE)
tf_io.gfile.makedirs(LOCAL_DATA_DIR)
!gsutil cp gs://workshop-datasets/covertype/data_validation/training/dataset.csv {LOCAL_DATA_FILE}
!wc -l {LOCAL_DATA_FILE}
data = pd.read_csv(LOCAL_DATA_FILE)
print("Total number of records: {}".format(len(data.index)))
data.sample(10).T
```
## 2. Define Metadata
```
HEADER = ['Elevation', 'Aspect', 'Slope','Horizontal_Distance_To_Hydrology',
'Vertical_Distance_To_Hydrology', 'Horizontal_Distance_To_Roadways',
'Hillshade_9am', 'Hillshade_Noon', 'Hillshade_3pm',
'Horizontal_Distance_To_Fire_Points', 'Wilderness_Area', 'Soil_Type',
'Cover_Type']
TARGET_FEATURE_NAME = 'Cover_Type'
FEATURE_LABELS = ['0', '1', '2', '3', '4', '5', '6']
NUMERIC_FEATURE_NAMES = ['Aspect', 'Elevation', 'Hillshade_3pm',
'Hillshade_9am', 'Hillshade_Noon',
'Horizontal_Distance_To_Fire_Points',
'Horizontal_Distance_To_Hydrology',
'Horizontal_Distance_To_Roadways','Slope',
'Vertical_Distance_To_Hydrology']
CATEGORICAL_FEATURE_NAMES = ['Soil_Type', 'Wilderness_Area']
FEATURE_NAMES = CATEGORICAL_FEATURE_NAMES + NUMERIC_FEATURE_NAMES
HEADER_DEFAULTS = [[0] if feature_name in NUMERIC_FEATURE_NAMES + [TARGET_FEATURE_NAME] else ['NA']
for feature_name in HEADER]
NUM_CLASSES = len(FEATURE_LABELS)
for feature_name in CATEGORICAL_FEATURE_NAMES:
data[feature_name] = data[feature_name].astype(str)
```
## 3. Sampling Normal Data
```
normal_data = data.sample(2000)
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(20, 10))
normal_data['Elevation'].plot.hist(bins=15, ax=axes[0][0], title='Elevation')
normal_data['Aspect'].plot.hist(bins=15, ax=axes[0][1], title='Aspect')
normal_data['Wilderness_Area'].value_counts(normalize=True).plot.bar(ax=axes[1][0], title='Wilderness Area')
normal_data[TARGET_FEATURE_NAME].value_counts(normalize=True).plot.bar(ax=axes[1][1], title=TARGET_FEATURE_NAME)
```
## 4. Prepare Skewed Data
We are going to introduce the following skews to the data:
1. **Numerical Features**
* *Elevation - Feature Skew*: Convert the unit of measure from meters to kilometers for 1% of the data points
* *Aspect - Distribution Skew*: Decrease the value by randomly from 1% to 50%
2. **Categorical Features**
* *Wilderness_Area - Feature Skew*: Adding a new category "Others" for 1% of the data points
* *Wilderness_Area - Distribution Skew*: Increase of of the frequency of "Cache" and "Neota" values by 25%
```
skewed_data = data.sample(1000)
```
### 4.1 Skewing numerical features
#### 4.1.1 Elevation Feature Skew
```
ratio = 0.1
size = int(len(skewed_data.index) * ratio)
indexes = np.random.choice(skewed_data.index, size=size, replace=False)
skewed_data['Elevation'][indexes] = skewed_data['Elevation'][indexes] // 1000
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(20, 5))
normal_data['Elevation'].plot.hist(bins=15, ax=axes[0], title='Elevation - Normal')
skewed_data['Elevation'].plot.hist(bins=15, ax=axes[1], title='Elevation - Skewed')
```
#### 4.1.2 Aspect Distribution Skew
```
skewed_data['Aspect'] = skewed_data['Aspect'].apply(
lambda value: int(value * np.random.uniform(0.5, 0.99))
)
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(20, 5))
normal_data['Aspect'].plot.hist(bins=15, ax=axes[0], title='Aspect - Normal')
skewed_data['Aspect'].plot.hist(bins=15, ax=axes[1], title='Aspect - Skewed')
```
### 4.2 Skew categorical features
#### 4.2.1 Wilderness Area Feature Skew
Adding a new category "Others"
```
skewed_data['Wilderness_Area'] = skewed_data['Wilderness_Area'].apply(
lambda value: 'Others' if np.random.uniform() <= 0.1 else value
)
```
#### 4.2.2 Wilderness Area Distribution Skew
```
skewed_data['Wilderness_Area'] = skewed_data['Wilderness_Area'].apply(
lambda value: 'Neota' if value in ['Rawah', 'Commanche'] and np.random.uniform() <= 0.25 else value
)
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(20, 5))
normal_data['Wilderness_Area'].value_counts(normalize=True).plot.bar(ax=axes[0], title='Wilderness Area - Normal')
skewed_data['Wilderness_Area'].value_counts(normalize=True).plot.bar(ax=axes[1], title='Wilderness Area - Skewed')
```
## 5. Simulating serving workload
### 5.1 Implement the model API client
```
import googleapiclient.discovery
import numpy as np
service = googleapiclient.discovery.build('ml', 'v1')
name = 'projects/{}/models/{}/versions/{}'.format(PROJECT_ID, MODEL_NAME, VERSION_NAME)
print("Service name: {}".format(name))
def caip_predict(instance):
request_body={
'signature_name': SIGNATURE_NAME,
'instances': [instance]
}
response = service.projects().predict(
name=name,
body=request_body
).execute()
if 'error' in response:
raise RuntimeError(response['error'])
probability_list = [output[MODEL_OUTPUT_KEY] for output in response['predictions']]
classes = [FEATURE_LABELS[int(np.argmax(probabilities))] for probabilities in probability_list]
return classes
import time
def simulate_requests(data_frame):
print("Simulation started...")
print("---------------------")
print("Number of instances: {}".format(len(data_frame.index)))
i = 0
for _, row in data_frame.iterrows():
instance = dict(row)
instance.pop(TARGET_FEATURE_NAME)
for k,v in instance.items():
instance[k] = [v]
predicted_class = caip_predict(instance)
i += 1
print(".", end='')
if (i + 1) % 100 == 0:
print()
print("Sent {} requests.".format(i + 1))
time.sleep(0.5)
print("")
print("-------------------")
print("Simulation finised.")
```
### 5.2 Simulate AI Platform Prediction requests
```
simulate_requests(normal_data)
simulate_requests(skewed_data)
```
| true |
code
| 0.456349 | null | null | null | null |
|
<div style="text-align: right">Peter Norvig, 12 Feb 2016<br>Revised 17 Feb 2018</div>
# A Concrete Introduction to Probability (using Python)
In 1814, Pierre-Simon Laplace [wrote](https://en.wikipedia.org/wiki/Classical_definition_of_probability):
>*Probability theory is nothing but common sense reduced to calculation. ... [Probability] is thus simply a fraction whose numerator is the number of favorable cases and whose denominator is the number of all the cases possible ... when nothing leads us to expect that any one of these cases should occur more than any other.*

<center><a href="https://en.wikipedia.org/wiki/Pierre-Simon_Laplace">Pierre-Simon Laplace</a><br>1814</center>
Laplace nailed it. To untangle a probability problem, all you have to do is define exactly what the cases are, and careful count the favorable and total cases. Let's be clear on our vocabulary words:
- **[Trial](https://en.wikipedia.org/wiki/Experiment_(probability_theory%29):**
A single occurrence with an outcome that is uncertain until we observe it.
<br>*For example, rolling a single die.*
- **[Outcome](https://en.wikipedia.org/wiki/Outcome_(probability%29):**
A possible result of a trial; one particular state of the world. What Laplace calls a **case.**
<br>*For example:* `4`.
- **[Sample Space](https://en.wikipedia.org/wiki/Sample_space):**
The set of all possible outcomes for the trial.
<br>*For example,* `{1, 2, 3, 4, 5, 6}`.
- **[Event](https://en.wikipedia.org/wiki/Event_(probability_theory%29):**
A subset of outcomes that together have some property we are interested in.
<br>*For example, the event "even die roll" is the set of outcomes* `{2, 4, 6}`.
- **[Probability](https://en.wikipedia.org/wiki/Probability_theory):**
As Laplace said, the probability of an event with respect to a sample space is the "number of favorable cases" (outcomes from the sample space that are in the event) divided by the "number of all the cases" in the sample space (assuming "nothing leads us to expect that any one of these cases should occur more than any other"). Since this is a proper fraction, probability will always be a number between 0 (representing an impossible event) and 1 (representing a certain event).
<br>*For example, the probability of an even die roll is 3/6 = 1/2.*
This notebook will explore these concepts in a concrete way using Python code. The code is meant to be succint and explicit, and fast enough to handle sample spaces with millions of outcomes. If you need to handle trillions, you'll want a more efficient implementation. I also have [another notebook](http://nbviewer.jupyter.org/url/norvig.com/ipython/ProbabilityParadox.ipynb) that covers paradoxes in Probability Theory.
# `P` is for Probability
The code below implements Laplace's quote directly: *Probability is thus simply a fraction whose numerator is the number of favorable cases and whose denominator is the number of all the cases possible.*
```
from fractions import Fraction
def P(event, space):
"The probability of an event, given a sample space."
return Fraction(cases(favorable(event, space)),
cases(space))
favorable = set.intersection # Outcomes that are in the event and in the sample space
cases = len # The number of cases is the length, or size, of a set
```
# Warm-up Problem: Die Roll
What's the probability of rolling an even number with a single six-sided fair die? Mathematicians traditionally use a single capital letter to denote a sample space; I'll use `D` for the die:
```
D = {1, 2, 3, 4, 5, 6} # a sample space
even = { 2, 4, 6} # an event
P(even, D)
```
Good to confirm what we already knew. We can explore some other events:
```
prime = {2, 3, 5, 7, 11, 13}
odd = {1, 3, 5, 7, 9, 11, 13}
P(odd, D)
P((even | prime), D) # The probability of an even or prime die roll
P((odd & prime), D) # The probability of an odd prime die roll
```
# Card Problems
Consider dealing a hand of five playing cards. An individual card has a rank and suit, like `'J♥'` for the Jack of Hearts, and a `deck` has 52 cards:
```
suits = u'♥♠♦♣'
ranks = u'AKQJT98765432'
deck = [r + s for r in ranks for s in suits]
len(deck)
```
Now I want to define `Hands` as the sample space of all 5-card combinations from `deck`. The function `itertools.combinations` does most of the work; we than concatenate each combination into a space-separated string:
```
import itertools
def combos(items, n):
"All combinations of n items; each combo as a space-separated str."
return set(map(' '.join, itertools.combinations(items, n)))
Hands = combos(deck, 5)
len(Hands)
```
There are too many hands to look at them all, but we can sample:
```
import random
random.sample(Hands, 7)
random.sample(deck, 7)
```
Now we can answer questions like the probability of being dealt a flush (5 cards of the same suit):
```
flush = {hand for hand in Hands if any(hand.count(suit) == 5 for suit in suits)}
P(flush, Hands)
```
Or the probability of four of a kind:
```
four_kind = {hand for hand in Hands if any(hand.count(rank) == 4 for rank in ranks)}
P(four_kind, Hands)
```
# Urn Problems
Around 1700, Jacob Bernoulli wrote about removing colored balls from an urn in his landmark treatise *[Ars Conjectandi](https://en.wikipedia.org/wiki/Ars_Conjectandi)*, and ever since then, explanations of probability have relied on [urn problems](https://www.google.com/search?q=probability+ball+urn). (You'd think the urns would be empty by now.)

<center><a href="https://en.wikipedia.org/wiki/Jacob_Bernoulli">Jacob Bernoulli</a><br>1700</center>
For example, here is a three-part problem [adapted](http://mathforum.org/library/drmath/view/69151.html) from mathforum.org:
> *An urn contains 6 blue, 9 red, and 8 white balls. We select six balls at random. What is the probability of each of these outcomes:*
> - *All balls are red*.
- *3 are blue, and 1 is red, and 2 are white, *.
- *Exactly 4 balls are white*.
We'll start by defining the contents of the urn. A `set` can't contain multiple objects that are equal to each other, so I'll call the blue balls `'B1'` through `'B6'`, rather than trying to have 6 balls all called `'B'`:
```
def balls(color, n):
"A set of n numbered balls of the given color."
return {color + str(i)
for i in range(1, n + 1)}
urn = balls('B', 6) | balls('R', 9) | balls('W', 8)
urn
```
Now we can define the sample space, `U6`, as the set of all 6-ball combinations:
```
U6 = combos(urn, 6)
random.sample(U6, 5)
```
Define `select` such that `select('R', 6)` is the event of picking 6 red balls from the urn:
```
def select(color, n, space=U6):
"The subset of the sample space with exactly `n` balls of given `color`."
return {s for s in space if s.count(color) == n}
```
Now I can answer the three questions:
```
P(select('R', 6), U6)
P(select('B', 3) & select('R', 1) & select('W', 2), U6)
P(select('W', 4), U6)
```
## Urn problems via arithmetic
Let's verify these calculations using basic arithmetic, rather than exhaustive counting. First, how many ways can I choose 6 out of 9 red balls? It could be any of the 9 for the first ball, any of 8 remaining for the second, and so on down to any of the remaining 4 for the sixth and final ball. But we don't care about the *order* of the six balls, so divide that product by the number of permutations of 6 things, which is 6!, giving us
9 × 8 × 7 × 6 × 5 × 4 / 6! = 84. In general, the number of ways of choosing *c* out of *n* items is (*n* choose *c*) = *n*! / ((*n* - *c*)! × c!).
We can translate that to code:
```
from math import factorial
def choose(n, c):
"Number of ways to choose c items from a list of n items."
return factorial(n) // (factorial(n - c) * factorial(c))
choose(9, 6)
```
Now we can verify the answers to the three problems. (Since `P` computes a ratio and `choose` computes a count,
I multiply the left-hand-side by `N`, the length of the sample space, to make both sides be counts.)
```
N = len(U6)
N * P(select('R', 6), U6) == choose(9, 6)
N * P(select('B', 3) & select('W', 2) & select('R', 1), U6) == choose(6, 3) * choose(8, 2) * choose(9, 1)
N * P(select('W', 4), U6) == choose(8, 4) * choose(6 + 9, 2) # (6 + 9 non-white balls)
```
We can solve all these problems just by counting; all you ever needed to know about probability problems you learned from Sesame Street:

<center><a href="https://en.wikipedia.org/wiki/Count_von_Count">The Count</a><br>1972—</center>
# Non-Equiprobable Outcomes
So far, we have accepted Laplace's assumption that *nothing leads us to expect that any one of these cases should occur more than any other*.
In real life, we often get outcomes that are not equiprobable--for example, a loaded die favors one side over the others. We will introduce three more vocabulary items:
* [Frequency](https://en.wikipedia.org/wiki/Frequency_%28statistics%29): a non-negative number describing how often an outcome occurs. Can be a count like 5, or a ratio like 1/6.
* [Distribution](http://mathworld.wolfram.com/StatisticalDistribution.html): A mapping from outcome to frequency of that outcome. We will allow sample spaces to be distributions.
* [Probability Distribution](https://en.wikipedia.org/wiki/Probability_distribution): A probability distribution
is a distribution whose frequencies sum to 1.
I could implement distributions with `Dist = dict`, but instead I'll make `Dist` a subclass `collections.Counter`:
```
from collections import Counter
class Dist(Counter):
"A Distribution of {outcome: frequency} pairs."
```
Because a `Dist` is a `Counter`, we can initialize it in any of the following ways:
```
# A set of equiprobable outcomes:
Dist({1, 2, 3, 4, 5, 6})
# A collection of outcomes, with repetition indicating frequency:
Dist('THHHTTHHT')
# A mapping of {outcome: frequency} pairs:
Dist({'H': 5, 'T': 4})
# Keyword arguments:
Dist(H=5, T=4) == Dist({'H': 5}, T=4) == Dist('TTTT', H=5)
```
Now I will modify the code to handle distributions.
Here's my plan:
- Sample spaces and events can both be specified as either a `set` or a `Dist`.
- The sample space can be a non-probability distribution like `Dist(H=50, T=50)`; the results
will be the same as if the sample space had been a true probability distribution like `Dist(H=1/2, T=1/2)`.
- The function `cases` now sums the frequencies in a distribution (it previously counted the length).
- The function `favorable` now returns a `Dist` of favorable outcomes and their frequencies (not a `set`).
- I will redefine `Fraction` to use `"/"`, not `fractions.Fraction`, because frequencies might be floats.
- `P` is unchanged.
```
def cases(outcomes):
"The total frequency of all the outcomes."
return sum(Dist(outcomes).values())
def favorable(event, space):
"A distribution of outcomes from the sample space that are in the event."
space = Dist(space)
return Dist({x: space[x]
for x in space if x in event})
def Fraction(n, d): return n / d
```
For example, here's the probability of rolling an even number with a crooked die that is loaded to prefer 6:
```
Crooked = Dist({1: 0.1, 2: 0.1, 3: 0.1, 4: 0.1, 5: 0.1, 6: 0.5})
P(even, Crooked)
```
As another example, an [article](http://people.kzoo.edu/barth/math105/moreboys.pdf) gives the following counts for two-child families in Denmark, where `GB` means a family where the first child is a girl and the second a boy (I'm aware that not all births can be classified as the binary "boy" or "girl," but the data was reported that way):
GG: 121801 GB: 126840
BG: 127123 BB: 135138
```
DK = Dist(GG=121801, GB=126840,
BG=127123, BB=135138)
first_girl = {'GG', 'GB'}
P(first_girl, DK)
second_girl = {'GG', 'BG'}
P(second_girl, DK)
```
This says that the probability of a girl is somewhere between 48% and 49%. The probability of a girl is very slightly higher for the second child.
Given the first child, are you more likely to have a second child of the same sex?
```
same = {'GG', 'BB'}
P(same, DK)
```
Yes, but only by about 0.3%.
# Predicates as events
To calculate the probability of an even die roll, I originally said
even = {2, 4, 6}
But that's inelegant—I had to explicitly enumerate all the even numbers from one to six. If I ever wanted to deal with a twelve or twenty-sided die, I would have to go back and redefine `even`. I would prefer to define `even` once and for all like this:
```
def even(n): return n % 2 == 0
```
Now in order to make `P(even, D)` work, I'll allow an `Event` to be either a collection of outcomes or a `callable` predicate (that is, a function that returns true for outcomes that are part of the event). I don't need to modify `P`, but `favorable` will have to convert a callable `event` to a `set`:
```
def favorable(event, space):
"A distribution of outcomes from the sample space that are in the event."
if callable(event):
event = {x for x in space if event(x)}
space = Dist(space)
return Dist({x: space[x]
for x in space if x in event})
favorable(even, D)
P(even, D)
```
I'll define `die` to make a sample space for an *n*-sided die:
```
def die(n): return set(range(1, n + 1))
favorable(even, die(12))
P(even, die(12))
P(even, die(2000))
P(even, die(2001))
```
We can define more interesting events using predicates; for example we can determine the probability that the sum of rolling *d* 6-sided dice is prime:
```
def sum_dice(d): return Dist(sum(dice) for dice in itertools.product(D, repeat=d))
def is_prime(n): return (n > 1 and not any(n % i == 0 for i in range(2, n)))
for d in range(1, 9):
p = P(is_prime, sum_dice(d))
print("P(is_prime, sum_dice({})) = {}".format(d, round(p, 3)))
```
# Fermat and Pascal: The Unfinished Game
<table>
<tr><td><img src="https://upload.wikimedia.org/wikipedia/commons/thumb/9/98/Pierre_de_Fermat2.png/140px-Pierre_de_Fermat2.png"><center><a href="https://en.wikipedia.org/wiki/Pierre_de_Fermat">Pierre de Fermat</a><br>1654
<td><img src="https://www.umass.edu/wsp/images/pascal.jpg"><center><a href="https://en.wikipedia.org/wiki/Blaise_Pascal">Blaise Pascal]</a><br>1654
</table>
Consider a gambling game consisting of tossing a coin repeatedly. Player H wins the game as soon as a total of 10 heads come up, and T wins if a total of 10 tails come up before H wins. If the game is interrupted when H has 8 heads and T has 7 tails, how should the pot of money (which happens to be 100 Francs) be split? Here are some proposals, and arguments against them:
- It is uncertain, so just split the pot 50-50.
<br>*No, because surely H is more likely to win.*
- In proportion to each player's current score, so H gets a 8/(8+7) share.
<br>*No, because if the score was 0 heads to 1 tail, H should get more than 0/1.*
- In proportion to how many tosses the opponent needs to win, so H gets 3/(3+2).
<br>*This seems better, but no, if H is 9 away and T is only 1 away from winning, then it seems that giving H a 1/10 share is too much.*
In 1654, Blaise Pascal and Pierre de Fermat corresponded on this problem, with Fermat [writing](http://mathforum.org/isaac/problems/prob1.html):
>Dearest Blaise,
>As to the problem of how to divide the 100 Francs, I think I have found a solution that you will find to be fair. Seeing as I needed only two points to win the game, and you needed 3, I think we can establish that after four more tosses of the coin, the game would have been over. For, in those four tosses, if you did not get the necessary 3 points for your victory, this would imply that I had in fact gained the necessary 2 points for my victory. In a similar manner, if I had not achieved the necessary 2 points for my victory, this would imply that you had in fact achieved at least 3 points and had therefore won the game. Thus, I believe the following list of possible endings to the game is exhaustive. I have denoted 'heads' by an 'h', and tails by a 't.' I have starred the outcomes that indicate a win for myself.
> h h h h * h h h t * h h t h * h h t t *
> h t h h * h t h t * h t t h * h t t t
> t h h h * t h h t * t h t h * t h t t
> t t h h * t t h t t t t h t t t t
>I think you will agree that all of these outcomes are equally likely. Thus I believe that we should divide the stakes by the ration 11:5 in my favor, that is, I should receive (11/16)×100 = 68.75 Francs, while you should receive 31.25 Francs.
>I hope all is well in Paris,
>Your friend and colleague,
>Pierre
Pascal agreed with this solution, and [replied](http://mathforum.org/isaac/problems/prob2.html) with a generalization that made use of his previous invention, Pascal's Triangle. There's even [a book](https://smile.amazon.com/Unfinished-Game-Pascal-Fermat-Seventeenth-Century/dp/0465018963?sa-no-redirect=1) about it.
We can solve the problem with the tools we have:
```
def win_unfinished_game(h, t):
"The probability that H will win the unfinished game, given the number of points needed by H and T to win."
return P(at_least(h, 'h'), finishes(h, t))
def at_least(n, item):
"The event of getting at least n instances of item in an outcome."
return lambda outcome: outcome.count(item) >= n
def finishes(h, t):
"All finishes of a game where player H needs h points to win and T needs t."
tosses = ['ht'] * (h + t - 1)
return set(itertools.product(*tosses))
```
We can generate the 16 equiprobable finished that Pierre wrote about:
```
finishes(2, 3)
```
And we can find the 11 of them that are favorable to player `H`:
```
favorable(at_least(2, 'h'), finishes(2, 3))
```
Finally, we can answer the question:
```
100 * win_unfinished_game(2, 3)
```
We agree with Pascal and Fermat; we're in good company!
# Newton's Answer to a Problem by Pepys
<table>
<tr><td><img src="http://scienceworld.wolfram.com/biography/pics/Newton.jpg"><center><a href="https://en.wikipedia.org/wiki/Isaac_Newton">Isaac Newton</a><br>1693</center>
<td><img src="https://upload.wikimedia.org/wikipedia/commons/thumb/f/f8/Samuel_Pepys_portrait.jpg/148px-Samuel_Pepys_portrait.jpg"><center><a href="https://en.wikipedia.org/wiki/Samuel_Pepys">Samuel Pepys</a><br>1693</center>
</table>
Let's jump ahead from 1654 all the way to 1693, [when](http://fermatslibrary.com/s/isaac-newton-as-a-probabilist) Samuel Pepys wrote to Isaac Newton posing the problem:
> Which of the following three propositions has the greatest chance of success?
1. Six fair dice are tossed independently and at least one “6” appears.
2. Twelve fair dice are tossed independently and at least two “6”s appear.
3. Eighteen fair dice are tossed independently and at least three “6”s appear.
Newton was able to answer the question correctly (although his reasoning was not quite right); let's see how we can do. Since we're only interested in whether a die comes up as "6" or not, we can define a single die like this:
```
die6 = Dist({6: 1/6, '-': 5/6})
```
Next we can define the joint distribution formed by combining two independent distribution like this:
```
def joint(A, B, combine='{}{}'.format):
"""The joint distribution of two independent distributions.
Result is all entries of the form {'ab': frequency(a) * frequency(b)}"""
return Dist({combine(a, b): A[a] * B[b]
for a in A for b in B})
joint(die6, die6)
```
And the joint distribution from rolling *n* dice:
```
def dice(n, die):
"Joint probability distribution from rolling `n` dice."
if n == 1:
return die
else:
return joint(die, dice(n - 1, die))
dice(4, die6)
```
Now we are ready to determine which proposition is more likely to have the required number of sixes:
```
P(at_least(1, '6'), dice(6, die6))
P(at_least(2, '6'), dice(12, die6))
P(at_least(3, '6'), dice(18, die6))
```
We reach the same conclusion Newton did, that the best chance is rolling six dice.
# More Urn Problems: M&Ms and Bayes
Here's another urn problem (actually a "bag" problem) [from](http://allendowney.blogspot.com/2011/10/my-favorite-bayess-theorem-problems.html) prolific Python/Probability pundit [Allen Downey ](http://allendowney.blogspot.com/):
> The blue M&M was introduced in 1995. Before then, the color mix in a bag of plain M&Ms was (30% Brown, 20% Yellow, 20% Red, 10% Green, 10% Orange, 10% Tan). Afterward it was (24% Blue , 20% Green, 16% Orange, 14% Yellow, 13% Red, 13% Brown).
A friend of mine has two bags of M&Ms, and he tells me that one is from 1994 and one from 1996. He won't tell me which is which, but he gives me one M&M from each bag. One is yellow and one is green. What is the probability that the yellow M&M came from the 1994 bag?
To solve this problem, we'll first create distributions for each bag: `bag94` and `bag96`:
```
bag94 = Dist(brown=30, yellow=20, red=20, green=10, orange=10, tan=10)
bag96 = Dist(blue=24, green=20, orange=16, yellow=14, red=13, brown=13)
```
Next, define `MM` as the joint distribution—the sample space for picking one M&M from each bag. The outcome `'94:yellow 96:green'` means that a yellow M&M was selected from the 1994 bag and a green one from the 1996 bag. In this problem we don't get to see the actual outcome; we just see some evidence about the outcome, that it contains a yellow and a green.
```
MM = joint(bag94, bag96, '94:{} 96:{}'.format)
MM
```
We observe that "One is yellow and one is green":
```
def yellow_and_green(outcome): return 'yellow' in outcome and 'green' in outcome
favorable(yellow_and_green, MM)
```
Given this observation, we want to know "What is the probability that the yellow M&M came from the 1994 bag?"
```
def yellow94(outcome): return '94:yellow' in outcome
P(yellow94, favorable(yellow_and_green, MM))
```
So there is a 74% chance that the yellow comes from the 1994 bag.
Answering this question was straightforward: just like all the other probability problems, we simply create a sample space, and use `P` to pick out the probability of the event in question, given what we know about the outcome.
But in a sense it is curious that we were able to solve this problem with the same methodology as the others: this problem comes from a section titled **My favorite Bayes's Theorem Problems**, so one would expect that we'd need to invoke Bayes Theorem to solve it. The computation above shows that that is not necessary.

<center><a href="https://en.wikipedia.org/wiki/Thomas_Bayes">Rev. Thomas Bayes</a><br>1701-1761
</center>
Of course, we *could* solve it using Bayes Theorem. Why is Bayes Theorem recommended? Because we are asked about the probability of an outcome given the evidence—the probability the yellow came from the 94 bag, given that there is a yellow and a green. But the problem statement doesn't directly tell us the probability of that outcome given the evidence; it just tells us the probability of the evidence given the outcome.
Before we see the colors of the M&Ms, there are two hypotheses, `A` and `B`, both with equal probability:
A: first M&M from 94 bag, second from 96 bag
B: first M&M from 96 bag, second from 94 bag
P(A) = P(B) = 0.5
Then we get some evidence:
E: first M&M yellow, second green
We want to know the probability of hypothesis `A`, given the evidence:
P(A | E)
That's not easy to calculate (except by enumerating the sample space, which our `P` function does). But Bayes Theorem says:
P(A | E) = P(E | A) * P(A) / P(E)
The quantities on the right-hand-side are easier to calculate:
P(E | A) = 0.20 * 0.20 = 0.04
P(E | B) = 0.10 * 0.14 = 0.014
P(A) = 0.5
P(B) = 0.5
P(E) = P(E | A) * P(A) + P(E | B) * P(B)
= 0.04 * 0.5 + 0.014 * 0.5 = 0.027
And we can get a final answer:
P(A | E) = P(E | A) * P(A) / P(E)
= 0.04 * 0.5 / 0.027
= 0.7407407407
You have a choice: Bayes Theorem allows you to do less calculation at the cost of more algebra; that is a great trade-off if you are working with pencil and paper. Enumerating the sample space allows you to do less algebra at the cost of more calculation; usually a good trade-off if you have a computer. But regardless of the approach you use, it is important to understand Bayes theorem and how it works.
There is one important question that Allen Downey does not address: *would you eat twenty-year-old M&Ms*?
😨
<hr>
# Simulation
Sometimes it is inconvenient, difficult, or even impossible to explicitly enumerate a sample space. Perhaps the sample space is infinite, or perhaps it is just very large and complicated (perhaps with a bunch of low-probability outcomes that don't seem very important). In that case, we might feel more confident in writing a program to *simulate* a random outcome. *Random sampling* from such a simulation
can give an accurate estimate of probability.
# Simulating Monopoly
<center>[Mr. Monopoly](https://en.wikipedia.org/wiki/Rich_Uncle_Pennybags)<br>1940—
Consider [problem 84](https://projecteuler.net/problem=84) from the excellent [Project Euler](https://projecteuler.net), which asks for the probability that a player in the game Monopoly ends a roll on each of the squares on the board. To answer this we need to take into account die rolls, chance and community chest cards, and going to jail (from the "go to jail" space, from a card, or from rolling doubles three times in a row). We do not need to take into account anything about acquiring properties or exchanging money or winning or losing the game, because these events don't change a player's location.
A game of Monopoly can go on forever, so the sample space is infinite. Even if we limit the sample space to say, 1000 rolls, there are $21^{1000}$ such sequences of rolls, and even more possibilities when we consider drawing cards. So it is infeasible to explicitly represent the sample space. There are techniques for representing the problem as
a Markov decision problem (MDP) and solving it, but the math is complex (a [paper](https://faculty.math.illinois.edu/~bishop/monopoly.pdf) on the subject runs 15 pages).
The simplest approach is to implement a simulation and run it for, say, a million rolls. Here is the code for a simulation:
```
from collections import deque as Deck # a Deck of community chest or chance cards
# The Monopoly board, as specified by https://projecteuler.net/problem=84
(GO, A1, CC1, A2, T1, R1, B1, CH1, B2, B3,
JAIL, C1, U1, C2, C3, R2, D1, CC2, D2, D3,
FP, E1, CH2, E2, E3, R3, F1, F2, U2, F3,
G2J, G1, G2, CC3, G3, R4, CH3, H1, T2, H2) = board = range(40)
# A card is either a square, a set of squares meaning advance to the nearest,
# a -3 to go back 3 spaces, or None meaning no change to location.
CC_deck = Deck([GO, JAIL] + 14 * [None])
CH_deck = Deck([GO, JAIL, C1, E3, H2, R1, -3, {U1, U2}]
+ 2 * [{R1, R2, R3, R4}] + 6 * [None])
def monopoly(rolls):
"""Simulate given number of dice rolls of a Monopoly game,
and return the counts of how often each square is visited."""
counts = [0] * len(board)
doubles = 0 # Number of consecutive doubles rolled
random.shuffle(CC_deck)
random.shuffle(CH_deck)
goto(GO)
for _ in range(rolls):
d1, d2 = random.randint(1, 6), random.randint(1, 6)
doubles = (doubles + 1 if d1 == d2 else 0)
goto(here + d1 + d2)
if here == G2J or doubles == 3:
goto(JAIL)
doubles = 0
elif here in (CC1, CC2, CC3):
do_card(CC_deck)
elif here in (CH1, CH2, CH3):
do_card(CH_deck)
counts[here] += 1
return counts
def goto(square):
"Update 'here' to be this square (and handle passing GO)."
global here
here = square % len(board)
def do_card(deck):
"Take the top card from deck and do what it says."
card = deck.popleft() # The top card
deck.append(card) # Move top card to bottom of deck
if card == None: # Don't move
pass
elif card == -3: # Go back 3 spaces
goto(here - 3)
elif isinstance(card, set): # Advance to next railroad or utility
next1 = min({place for place in card if place > here} or card)
goto(next1)
else: # Go to destination named on card
goto(card)
```
Let's run the simulation for a million dice rolls:
```
counts = monopoly(10**6)
```
And print a table of square names and their percentages:
```
property_names = """
GO, A1, CC1, A2, T1, R1, B1, CH1, B2, B3,
JAIL, C1, U1, C2, C3, R2, D1, CC2, D2, D3,
FP, E1, CH2, E2, E3, R3, F1, F2, U2, F3,
G2J, G1, G2, CC3, G3, R4, CH3, H1, T2, H2""".replace(',', ' ').split()
for (c, n) in sorted(zip(counts, property_names), reverse=True):
print('{:4} {:.2%}'.format(n, c / sum(counts)))
```
There is one square far above average: `JAIL`, at a little over 6%. There are four squares far below average: the three chance squares, `CH1`, `CH2`, and `CH3`, at around 1% (because 10 of the 16 chance cards send the player away from the square), and the "Go to Jail" square, which has a frequency of 0 because you can't end a turn there. The other squares are around 2% to 3% each, which you would expect, because 100% / 40 = 2.5%.
# The Central Limit Theorem
We have covered the concept of *distributions* of outcomes. You may have heard of the *normal distribution*, the *bell-shaped curve.* In Python it is called `random.normalvariate` (also `random.gauss`). We can plot it with the help of the `repeated_hist` function defined below, which samples a distribution `n` times and displays a histogram of the results. (*Note:* in this section I am using "distribution" to mean a function that, each time it is called, returns a random sample from a distribution. I am not using it to mean a mapping of type `Dist`.)
```
%matplotlib inline
import matplotlib.pyplot as plt
from statistics import mean
from random import normalvariate, triangular, choice, vonmisesvariate, uniform
def normal(mu=0, sigma=1): return random.normalvariate(mu, sigma)
def repeated_hist(dist, n=10**6, bins=100):
"Sample the distribution n times and make a histogram of the results."
samples = [dist() for _ in range(n)]
plt.hist(samples, bins=bins, density=True)
plt.title('{} (μ = {:.1f})'.format(dist.__name__, mean(samples)))
plt.grid(axis='x')
plt.yticks([], '')
plt.show()
# Normal distribution
repeated_hist(normal)
```
Why is this distribution called *normal*? The **Central Limit Theorem** says that it is the ultimate limit of other distributions, as follows (informally):
- Gather *k* independent distributions. They need not be normal-shaped.
- Define a new distribution to be the result of sampling one number from each of the *k* independent distributions and adding them up.
- As long as *k* is not too small, and the component distributions are not super-pathological, then the new distribution will tend towards a normal distribution.
Here's a simple example: summing ten independent die rolls:
```
def sum10dice(): return sum(random.randint(1, 6) for _ in range(10))
repeated_hist(sum10dice, bins=range(10, 61))
```
As another example, let's take just *k* = 5 component distributions representing the per-game scores of 5 basketball players, and then sum them together to form the new distribution, the team score. I'll be creative in defining the distributions for each player, but [historically accurate](https://www.basketball-reference.com/teams/GSW/2016.html) in the mean for each distribution.
```
def SC(): return max(0, normal(12.1, 3) + 3 * triangular(1, 13, 4)) # 30.1
def KT(): return max(0, triangular(8, 22, 15.3) + choice((0, 3 * triangular(1, 9, 4)))) # 22.1
def DG(): return max(0, vonmisesvariate(30, 2) * 3.08) # 14.0
def HB(): return max(0, choice((normal(6.7, 1.5), normal(16.7, 2.5)))) # 11.7
def BE(): return max(0, normal(17, 3) + uniform(0, 40)) # 37.0
team = (SC, KT, DG, HB, BE)
def Team(team=team): return sum(player() for player in team)
for player in team:
repeated_hist(player, bins=range(70))
```
We can see that none of the players have a distribution that looks like a normal distribution: `SC` is skewed to one side (the mean is 5 points to the right of the peak); the three next players have bimodal distributions; and `BE` is too flat on top.
Now we define the team score to be the sum of the *k* = 5 players, and display this new distribution:
```
repeated_hist(Team, bins=range(50, 180))
```
Sure enough, this looks very much like a normal distribution. The **Central Limit Theorem** appears to hold in this case. But I have to say: "Central Limit" is not a very evocative name, so I propose we re-name this as the **Strength in Numbers Theorem**, to indicate the fact that if you have a lot of numbers, you tend to get the expected result.
# Conclusion
We've had an interesting tour and met some giants of the field: Laplace, Bernoulli, Fermat, Pascal, Bayes, Newton, ... even Mr. Monopoly and The Count.
The conclusion is: be methodical in defining the sample space and the event(s) of interest, and be careful in counting the number of outcomes in the numerator and denominator. and you can't go wrong. Easy as 1-2-3.
<hr>
# Appendix: Continuous Sample Spaces
Everything up to here has been about discrete, finite sample spaces, where we can *enumerate* all the possible outcomes.
But a reader asked about *continuous* sample spaces, such as the space of real numbers. The principles are the same: probability is still the ratio of the favorable cases to all the cases, but now instead of *counting* cases, we have to (in general) compute integrals to compare the sizes of cases.
Here we will cover a simple example, which we first solve approximately by simulation, and then exactly by calculation.
## The Hot New Game Show Problem: Simulation
Oliver Roeder posed [this problem](http://fivethirtyeight.com/features/can-you-win-this-hot-new-game-show/) in the 538 *Riddler* blog:
>Two players go on a hot new game show called *Higher Number Wins.* The two go into separate booths, and each presses a button, and a random number between zero and one appears on a screen. (At this point, neither knows the other’s number, but they do know the numbers are chosen from a standard uniform distribution.) They can choose to keep that first number, or to press the button again to discard the first number and get a second random number, which they must keep. Then, they come out of their booths and see the final number for each player on the wall. The lavish grand prize — a case full of gold bullion — is awarded to the player who kept the higher number. Which number is the optimal cutoff for players to discard their first number and choose another? Put another way, within which range should they choose to keep the first number, and within which range should they reject it and try their luck with a second number?
We'll use this notation:
- **A**, **B**: the two players.
- *A*, *B*: the cutoff values they choose: the lower bound of the range of first numbers they will accept.
- *a*, *b*: the actual random numbers that appear on the screen.
For example, if player **A** chooses a cutoff of *A* = 0.6, that means that **A** would accept any first number greater than 0.6, and reject any number below that cutoff. The question is: What cutoff, *A*, should player **A** choose to maximize the chance of winning, that is, maximize P(*a* > *b*)?
First, simulate the number that a player with a given cutoff gets (note that `random.random()` returns a float sampled uniformly from the interval [0..1]):
```
number= random.random
def strategy(cutoff):
"Play the game with given cutoff, returning the first or second random number."
first = number()
return first if first > cutoff else number()
strategy(.5)
```
Now compare the numbers returned with a cutoff of *A* versus a cutoff of *B*, and repeat for a large number of trials; this gives us an estimate of the probability that cutoff *A* is better than cutoff *B*:
```
def Pwin(A, B, trials=20000):
"The probability that cutoff A wins against cutoff B."
return mean(strategy(A) > strategy(B)
for _ in range(trials))
Pwin(0.6, 0.9)
```
Now define a function, `top`, that considers a collection of possible cutoffs, estimate the probability for each cutoff playing against each other cutoff, and returns a list with the `N` top cutoffs (the ones that defeated the most number of opponent cutoffs), and the number of opponents they defeat:
```
def top(N, cutoffs):
"Return the N best cutoffs and the number of opponent cutoffs they beat."
winners = Counter(A if Pwin(A, B) > 0.5 else B
for (A, B) in itertools.combinations(cutoffs, 2))
return winners.most_common(N)
from numpy import arange
top(10, arange(0.5, 1.0, 0.01))
```
We get a good idea of the top cutoffs, but they are close to each other, so we can't quite be sure which is best, only that the best is somewhere around 0.60. We could get a better estimate by increasing the number of trials, but that would consume more time.
## The Hot New Game Show Problem: Exact Calculation
More promising is the possibility of making `Pwin(A, B)` an exact calculation. But before we get to `Pwin(A, B)`, let's solve a simpler problem: assume that both players **A** and **B** have chosen a cutoff, and have each received a number above the cutoff. What is the probability that **A** gets the higher number? We'll call this `Phigher(A, B)`. We can think of this as a two-dimensional sample space of points in the (*a*, *b*) plane, where *a* ranges from the cutoff *A* to 1 and *b* ranges from the cutoff B to 1. Here is a diagram of that two-dimensional sample space, with the cutoffs *A*=0.5 and *B*=0.6:
<img src="http://norvig.com/ipython/probability2da.jpg" width=413>
The total area of the sample space is 0.5 × 0.4 = 0.20, and in general it is (1 - *A*) · (1 - *B*). What about the favorable cases, where **A** beats **B**? That corresponds to the shaded triangle below:
<img src="http://norvig.com/ipython/probability2d.jpg" width=413>
The area of a triangle is 1/2 the base times the height, or in this case, 0.4<sup>2</sup> / 2 = 0.08, and in general, (1 - *B*)<sup>2</sup> / 2. So in general we have:
Phigher(A, B) = favorable / total
favorable = ((1 - B) ** 2) / 2
total = (1 - A) * (1 - B)
Phigher(A, B) = (((1 - B) ** 2) / 2) / ((1 - A) * (1 - B))
Phigher(A, B) = (1 - B) / (2 * (1 - A))
And in this specific case we have:
A = 0.5; B = 0.6
favorable = 0.4 ** 2 / 2 = 0.08
total = 0.5 * 0.4 = 0.20
Phigher(0.5, 0.6) = 0.08 / 0.20 = 0.4
But note that this only works when the cutoff *A* ≤ *B*; when *A* > *B*, we need to reverse things. That gives us the code:
```
def Phigher(A, B):
"Probability that a sample from [A..1] is higher than one from [B..1]."
if A <= B:
return (1 - B) / (2 * (1 - A))
else:
return 1 - Phigher(B, A)
Phigher(0.5, 0.6)
```
We're now ready to tackle the full game. There are four cases to consider, depending on whether **A** and **B** gets a first number that is above or below their cutoff choices:
| first *a* | first *b* | P(*a*, *b*) | P(A wins | *a*, *b*) | Comment |
|:-----:|:-----:| ----------- | ------------- | ------------ |
| *a* > *A* | *b* > *B* | (1 - *A*) · (1 - *B*) | Phigher(*A*, *B*) | Both above cutoff; both keep first numbers |
| *a* < *A* | *b* < *B* | *A* · *B* | Phigher(0, 0) | Both below cutoff, both get new numbers from [0..1] |
| *a* > *A* | *b* < *B* | (1 - *A*) · *B* | Phigher(*A*, 0) | **A** keeps number; **B** gets new number from [0..1] |
| *a* < *A* | *b* > *B* | *A* · (1 - *B*) | Phigher(0, *B*) | **A** gets new number from [0..1]; **B** keeps number |
For example, the first row of this table says that the event of both first numbers being above their respective cutoffs has probability (1 - *A*) · (1 - *B*), and if this does occur, then the probability of **A** winning is Phigher(*A*, *B*).
We're ready to replace the old simulation-based `Pwin` with a new calculation-based version:
```
def Pwin(A, B):
"With what probability does cutoff A win against cutoff B?"
return ((1-A) * (1-B) * Phigher(A, B) # both above cutoff
+ A * B * Phigher(0, 0) # both below cutoff
+ (1-A) * B * Phigher(A, 0) # A above, B below
+ A * (1-B) * Phigher(0, B)) # A below, B above
Pwin(0.5, 0.6)
```
`Pwin` relies on a lot of algebra. Let's define a few tests to check for obvious errors:
```
def test():
assert Phigher(0.5, 0.5) == Phigher(0.75, 0.75) == Phigher(0, 0) == 0.5
assert Pwin(0.5, 0.5) == Pwin(0.75, 0.75) == 0.5
assert Phigher(.6, .5) == 0.6
assert Phigher(.5, .6) == 0.4
return 'ok'
test()
```
Let's repeat the calculation with our new, exact `Pwin`:
```
top(10, arange(0.5, 1.0, 0.01))
```
It is good to see that the simulation and the exact calculation are in rough agreement; that gives me more confidence in both of them. We see here that 0.62 defeats all the other cutoffs, and 0.61 defeats all cutoffs except 0.62. The great thing about the exact calculation code is that it runs fast, regardless of how much accuracy we want. We can zero in on the range around 0.6:
```
top(10, arange(0.5, 0.7, 0.001))
```
This says 0.618 is best, better than 0.620. We can get even more accuracy:
```
top(10, arange(0.617, 0.619, 0.000001))
```
So 0.618034 is best. Does that number [look familiar](https://en.wikipedia.org/wiki/Golden_ratio)? Can we prove that it is what I think it is?
To understand the strategic possibilities, it is helpful to draw a 3D plot of `Pwin(A, B)` for values of *A* and *B* between 0 and 1:
```
import numpy as np
from mpl_toolkits.mplot3d.axes3d import Axes3D
def map2(fn, A, B):
"Map fn to corresponding elements of 2D arrays A and B."
return [list(map(fn, Arow, Brow))
for (Arow, Brow) in zip(A, B)]
cutoffs = arange(0.00, 1.00, 0.02)
A, B = np.meshgrid(cutoffs, cutoffs)
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1, 1, 1, projection='3d')
ax.set_xlabel('A')
ax.set_ylabel('B')
ax.set_zlabel('Pwin(A, B)')
ax.plot_surface(A, B, map2(Pwin, A, B));
```
What does this [Pringle of Probability](http://fivethirtyeight.com/features/should-you-shoot-free-throws-underhand/) show us? The highest win percentage for **A**, the peak of the surface, occurs when *A* is around 0.5 and *B* is 0 or 1. We can confirm that, finding the maximum `Pwin(A, B)` for many different cutoff values of `A` and `B`:
```
cutoffs = (set(arange(0.00, 1.00, 0.01)) |
set(arange(0.500, 0.700, 0.001)) |
set(arange(0.61803, 0.61804, 0.000001)))
def Pwin_summary(A, B): return [Pwin(A, B), 'A:', A, 'B:', B]
max(Pwin_summary(A, B) for A in cutoffs for B in cutoffs)
```
So **A** could win 62.5% of the time if only **B** would chose a cutoff of 0. But, unfortunately for **A**, a rational player **B** is not going to do that. We can ask what happens if the game is changed so that player **A** has to declare a cutoff first, and then player **B** gets to respond with a cutoff, with full knowledge of **A**'s choice. In other words, what cutoff should **A** choose to maximize `Pwin(A, B)`, given that **B** is going to take that knowledge and pick a cutoff that minimizes `Pwin(A, B)`?
```
max(min(Pwin_summary(A, B) for B in cutoffs)
for A in cutoffs)
```
And what if we run it the other way around, where **B** chooses a cutoff first, and then **A** responds?
```
min(max(Pwin_summary(A, B) for A in cutoffs)
for B in cutoffs)
```
In both cases, the rational choice for both players in a cutoff of 0.618034, which corresponds to the "saddle point" in the middle of the plot. This is a *stable equilibrium*; consider fixing *B* = 0.618034, and notice that if *A* changes to any other value, we slip off the saddle to the right or left, resulting in a worse win probability for **A**. Similarly, if we fix *A* = 0.618034, then if *B* changes to another value, we ride up the saddle to a higher win percentage for **A**, which is worse for **B**. So neither player will want to move from the saddle point.
The moral for continuous spaces is the same as for discrete spaces: be careful about defining your sample space; measure carefully, and let your code take care of the rest.
| true |
code
| 0.686475 | null | null | null | null |
|
# Computer Vision
In this notebook we're going to cover the basics of computer vision using CNNs. So far we've explored using CNNs for text but their initial origin began with computer vision tasks.
<img src="figures/cnn_cv.png" width=650>
# Configuration
```
config = {
"seed": 1234,
"cuda": True,
"data_url": "data/surnames.csv",
"data_dir": "cifar10",
"shuffle": True,
"train_size": 0.7,
"val_size": 0.15,
"test_size": 0.15,
"vectorizer_file": "vectorizer.json",
"model_file": "model.pth",
"save_dir": "experiments",
"num_epochs": 5,
"early_stopping_criteria": 5,
"learning_rate": 1e-3,
"batch_size": 128,
"fc": {
"hidden_dim": 100,
"dropout_p": 0.1
}
}
```
# Set up
```
# Load PyTorch library
#!pip3 install torch
import os
import json
import numpy as np
import time
import torch
import uuid
```
### Components
```
def set_seeds(seed, cuda):
""" Set Numpy and PyTorch seeds.
"""
np.random.seed(seed)
torch.manual_seed(seed)
if cuda:
torch.cuda.manual_seed_all(seed)
print ("==> 🌱 Set NumPy and PyTorch seeds.")
def generate_unique_id():
"""Generate a unique uuid
preceded by a epochtime.
"""
timestamp = int(time.time())
unique_id = "{}_{}".format(timestamp, uuid.uuid1())
print ("==> 🔑 Generated unique id: {0}".format(unique_id))
return unique_id
def create_dirs(dirpath):
"""Creating directories.
"""
if not os.path.exists(dirpath):
os.makedirs(dirpath)
print ("==> 📂 Created {0}".format(dirpath))
def check_cuda(cuda):
"""Check to see if GPU is available.
"""
if not torch.cuda.is_available():
cuda = False
device = torch.device("cuda" if cuda else "cpu")
print ("==> 💻 Device: {0}".format(device))
return device
```
### Operations
```
# Set seeds for reproducability
set_seeds(seed=config["seed"], cuda=config["cuda"])
# Generate unique experiment ID
config["experiment_id"] = generate_unique_id()
# Create experiment directory
config["save_dir"] = os.path.join(config["save_dir"], config["experiment_id"])
create_dirs(dirpath=config["save_dir"])
# Expand file paths to store components later
config["vectorizer_file"] = os.path.join(config["save_dir"], config["vectorizer_file"])
config["model_file"] = os.path.join(config["save_dir"], config["model_file"])
print ("Expanded filepaths: ")
print ("{}".format(config["vectorizer_file"]))
print ("{}".format(config["model_file"]))
# Save config
config_fp = os.path.join(config["save_dir"], "config.json")
with open(config_fp, "w") as fp:
json.dump(config, fp)
# Check CUDA
config["device"] = check_cuda(cuda=config["cuda"])
```
# Load data
We are going to get CIFAR10 data which contains images from ten unique classes. Each image has length 32, width 32 and three color channels (RGB). We are going to save these images in a directory. Each image will have its own directory (name will be the class).
```
import matplotlib.pyplot as plt
import pandas as pd
from PIL import Image
import tensorflow as tf
```
### Components
```
def get_data():
"""Get CIFAR10 data.
"""
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
X = np.vstack([x_train, x_test])
y = np.vstack([y_train, y_test]).squeeze(1)
print ("==> 🌊 Downloading Cifar10 data using TensorFlow.")
return X, y
def create_class_dirs(data_dir, classes):
"""Create class directories.
"""
create_dirs(dirpath=data_dir)
for _class in classes.values():
classpath = os.path.join(data_dir, _class)
create_dirs(dirpath=classpath)
def visualize_samples(data_dir, classes):
"""Visualize sample images for
each class.
"""
# Visualize some samples
num_samples = len(classes)
for i, _class in enumerate(classes.values()):
for file in os.listdir(os.path.join(data_dir, _class)):
if file.endswith((".png", ".jpg", ".jpeg")):
plt.subplot(1, num_samples, i+1)
plt.title("{0}".format(_class))
img = Image.open(os.path.join(data_dir, _class, file))
plt.imshow(img)
plt.axis("off")
break
def img_to_array(fp):
"""Conver image file to NumPy array.
"""
img = Image.open(fp)
array = np.asarray(img, dtype="float32")
return array
def load_data(data_dir, classes):
"""Load data into Pandas DataFrame.
"""
# Load data from files
data = []
for i, _class in enumerate(classes.values()):
for file in os.listdir(os.path.join(data_dir, _class)):
if file.endswith((".png", ".jpg", ".jpeg")):
full_filepath = os.path.join(data_dir, _class, file)
data.append({"image": img_to_array(full_filepath), "category": _class})
# Load to Pandas DataFrame
df = pd.DataFrame(data)
print ("==> 🖼️ Image dimensions: {0}".format(df.image[0].shape))
print ("==> 🍣 Raw data:")
print (df.head())
return df
```
### Operations
```
# Get CIFAR10 data
X, y = get_data()
print ("X:", X.shape)
print ("y:", y.shape)
# Classes
classes = {0: 'plane', 1: 'car', 2: 'bird', 3: 'cat', 4: 'deer', 5: 'dog',
6: 'frog', 7: 'horse', 8: 'ship', 9: 'truck'}
# Create image directories
create_class_dirs(data_dir=config["data_dir"], classes=classes)
# Save images for each class
for i, (image, label) in enumerate(zip(X, y)):
_class = classes[label]
im = Image.fromarray(image)
im.save(os.path.join(config["data_dir"], _class, "{0:02d}.png".format(i)))
# Visualize each class
visualize_samples(data_dir=config["data_dir"], classes=classes)
# Load data into DataFrame
df = load_data(data_dir=config["data_dir"], classes=classes)
```
# Split data
Split the data into train, validation and test sets where each split has similar class distributions.
```
import collections
```
### Components
```
def split_data(df, shuffle, train_size, val_size, test_size):
"""Split the data into train/val/test splits.
"""
# Split by category
by_category = collections.defaultdict(list)
for _, row in df.iterrows():
by_category[row.category].append(row.to_dict())
print ("\n==> 🛍️ Categories:")
for category in by_category:
print ("{0}: {1}".format(category, len(by_category[category])))
# Create split data
final_list = []
for _, item_list in sorted(by_category.items()):
if shuffle:
np.random.shuffle(item_list)
n = len(item_list)
n_train = int(train_size*n)
n_val = int(val_size*n)
n_test = int(test_size*n)
# Give data point a split attribute
for item in item_list[:n_train]:
item['split'] = 'train'
for item in item_list[n_train:n_train+n_val]:
item['split'] = 'val'
for item in item_list[n_train+n_val:]:
item['split'] = 'test'
# Add to final list
final_list.extend(item_list)
# df with split datasets
split_df = pd.DataFrame(final_list)
print ("\n==> 🖖 Splits:")
print (split_df["split"].value_counts())
return split_df
```
### Operations
```
# Split data
split_df = split_data(
df=df, shuffle=config["shuffle"],
train_size=config["train_size"],
val_size=config["val_size"],
test_size=config["test_size"])
```
# Vocabulary
Create vocabularies for the image classes.
### Components
```
class Vocabulary(object):
def __init__(self, token_to_idx=None, add_unk=True, unk_token="<UNK>"):
# Token to index
if token_to_idx is None:
token_to_idx = {}
self.token_to_idx = token_to_idx
# Index to token
self.idx_to_token = {idx: token \
for token, idx in self.token_to_idx.items()}
# Add unknown token
self.add_unk = add_unk
self.unk_token = unk_token
if self.add_unk:
self.unk_index = self.add_token(self.unk_token)
def to_serializable(self):
return {'token_to_idx': self.token_to_idx,
'add_unk': self.add_unk, 'unk_token': self.unk_token}
@classmethod
def from_serializable(cls, contents):
return cls(**contents)
def add_token(self, token):
if token in self.token_to_idx:
index = self.token_to_idx[token]
else:
index = len(self.token_to_idx)
self.token_to_idx[token] = index
self.idx_to_token[index] = token
return index
def add_tokens(self, tokens):
return [self.add_token[token] for token in tokens]
def lookup_token(self, token):
if self.add_unk:
index = self.token_to_idx.get(token, self.unk_index)
else:
index = self.token_to_idx[token]
return index
def lookup_index(self, index):
if index not in self.idx_to_token:
raise KeyError("the index (%d) is not in the Vocabulary" % index)
return self.idx_to_token[index]
def __str__(self):
return "<Vocabulary(size=%d)>" % len(self)
def __len__(self):
return len(self.token_to_idx)
```
### Operations
```
# Vocabulary instance
category_vocab = Vocabulary(add_unk=False)
for index, row in df.iterrows():
category_vocab.add_token(row.category)
print (category_vocab) # __str__
print (len(category_vocab)) # __len__
index = category_vocab.lookup_token("bird")
print (index)
print (category_vocab.lookup_index(index))
```
# Sequence vocbulary
We will also create a vocabulary object for the actual images. It will store the mean and standard deviations for eahc image channel (RGB) which we will use later on for normalizing our images with the Vectorizer.
```
from collections import Counter
import string
```
### Components
```
class SequenceVocabulary(Vocabulary):
def __init__(self, train_means, train_stds):
self.train_means = train_means
self.train_stds = train_stds
def to_serializable(self):
contents = {'train_means': self.train_means,
'train_stds': self.train_stds}
return contents
@classmethod
def from_dataframe(cls, df):
train_data = df[df.split == "train"]
means = {0:[], 1:[], 2:[]}
stds = {0:[], 1:[], 2:[]}
for image in train_data.image:
for dim in range(3):
means[dim].append(np.mean(image[:, :, dim]))
stds[dim].append(np.std(image[:, :, dim]))
train_means = np.array((np.mean(means[0]), np.mean(means[1]),
np.mean(means[2])), dtype="float64").tolist()
train_stds = np.array((np.mean(stds[0]), np.mean(stds[1]),
np.mean(stds[2])), dtype="float64").tolist()
return cls(train_means, train_stds)
def __str__(self):
return "<SequenceVocabulary(train_means: {0}, train_stds: {1}>".format(
self.train_means, self.train_stds)
```
### Operations
```
# Create SequenceVocabulary instance
image_vocab = SequenceVocabulary.from_dataframe(split_df)
print (image_vocab) # __str__
```
# Vectorizer
The vectorizer will normalize our images using the vocabulary.
### Components
```
class ImageVectorizer(object):
def __init__(self, image_vocab, category_vocab):
self.image_vocab = image_vocab
self.category_vocab = category_vocab
def vectorize(self, image):
# Avoid modifying the actual df
image = np.copy(image)
# Normalize
for dim in range(3):
mean = self.image_vocab.train_means[dim]
std = self.image_vocab.train_stds[dim]
image[:, :, dim] = ((image[:, :, dim] - mean) / std)
# Reshape from (32, 32, 3) to (3, 32, 32)
image = np.swapaxes(image, 0, 2)
image = np.swapaxes(image, 1, 2)
return image
@classmethod
def from_dataframe(cls, df):
# Create vocabularies
image_vocab = SequenceVocabulary.from_dataframe(df)
category_vocab = Vocabulary(add_unk=False)
for category in sorted(set(df.category)):
category_vocab.add_token(category)
return cls(image_vocab, category_vocab)
@classmethod
def from_serializable(cls, contents):
image_vocab = SequenceVocabulary.from_serializable(contents['image_vocab'])
category_vocab = Vocabulary.from_serializable(contents['category_vocab'])
return cls(image_vocab=image_vocab,
category_vocab=category_vocab)
def to_serializable(self):
return {'image_vocab': self.image_vocab.to_serializable(),
'category_vocab': self.category_vocab.to_serializable()}
```
### Operations
```
# Vectorizer instance
vectorizer = ImageVectorizer.from_dataframe(split_df)
print (vectorizer.image_vocab)
print (vectorizer.category_vocab)
print (vectorizer.category_vocab.token_to_idx)
image_vector = vectorizer.vectorize(split_df.iloc[0].image)
print (image_vector.shape)
```
# Dataset
The Dataset will create vectorized data from the data.
```
import random
from torch.utils.data import Dataset, DataLoader
```
### Components
```
class ImageDataset(Dataset):
def __init__(self, df, vectorizer, infer=False):
self.df = df
self.vectorizer = vectorizer
# Data splits
if not infer:
self.train_df = self.df[self.df.split=='train']
self.train_size = len(self.train_df)
self.val_df = self.df[self.df.split=='val']
self.val_size = len(self.val_df)
self.test_df = self.df[self.df.split=='test']
self.test_size = len(self.test_df)
self.lookup_dict = {'train': (self.train_df, self.train_size),
'val': (self.val_df, self.val_size),
'test': (self.test_df, self.test_size)}
self.set_split('train')
# Class weights (for imbalances)
class_counts = df.category.value_counts().to_dict()
def sort_key(item):
return self.vectorizer.category_vocab.lookup_token(item[0])
sorted_counts = sorted(class_counts.items(), key=sort_key)
frequencies = [count for _, count in sorted_counts]
self.class_weights = 1.0 / torch.tensor(frequencies, dtype=torch.float32)
elif infer:
self.infer_df = self.df[self.df.split=="infer"]
self.infer_size = len(self.infer_df)
self.lookup_dict = {'infer': (self.infer_df, self.infer_size)}
self.set_split('infer')
@classmethod
def load_dataset_and_make_vectorizer(cls, df):
train_df = df[df.split=='train']
return cls(df, ImageVectorizer.from_dataframe(train_df))
@classmethod
def load_dataset_and_load_vectorizer(cls, df, vectorizer_filepath):
vectorizer = cls.load_vectorizer_only(vectorizer_filepath)
return cls(df, vectorizer)
def load_vectorizer_only(vectorizer_filepath):
with open(vectorizer_filepath) as fp:
return ImageVectorizer.from_serializable(json.load(fp))
def save_vectorizer(self, vectorizer_filepath):
with open(vectorizer_filepath, "w") as fp:
json.dump(self.vectorizer.to_serializable(), fp)
def set_split(self, split="train"):
self.target_split = split
self.target_df, self.target_size = self.lookup_dict[split]
def __str__(self):
return "<Dataset(split={0}, size={1})".format(
self.target_split, self.target_size)
def __len__(self):
return self.target_size
def __getitem__(self, index):
row = self.target_df.iloc[index]
image_vector = self.vectorizer.vectorize(row.image)
category_index = self.vectorizer.category_vocab.lookup_token(row.category)
return {'image': image_vector,
'category': category_index}
def get_num_batches(self, batch_size):
return len(self) // batch_size
def generate_batches(self, batch_size, shuffle=True, drop_last=True, device="cpu"):
dataloader = DataLoader(dataset=self, batch_size=batch_size,
shuffle=shuffle, drop_last=drop_last)
for data_dict in dataloader:
out_data_dict = {}
for name, tensor in data_dict.items():
out_data_dict[name] = data_dict[name].to(device)
yield out_data_dict
def sample(dataset):
"""Some sanity checks on the dataset.
"""
sample_idx = random.randint(0,len(dataset))
sample = dataset[sample_idx]
print ("\n==> 🔢 Dataset:")
print ("Random sample: {0}".format(sample))
print ("Unvectorized category: {0}".format(
dataset.vectorizer.category_vocab.lookup_index(sample['category'])))
```
### Operations
```
# Load dataset and vectorizer
dataset = ImageDataset.load_dataset_and_make_vectorizer(split_df)
dataset.save_vectorizer(config["vectorizer_file"])
vectorizer = dataset.vectorizer
print (dataset.class_weights)
# Sample checks
sample(dataset=dataset)
```
# Model
Basic CNN architecture for image classification.
```
import torch.nn as nn
import torch.nn.functional as F
```
### Components
```
class ImageModel(nn.Module):
def __init__(self, num_hidden_units, num_classes, dropout_p):
super(ImageModel, self).__init__()
self.conv1 = nn.Conv2d(3, 10, kernel_size=5) # input_channels:3, output_channels:10 (aka num filters)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv_dropout = nn.Dropout2d(dropout_p)
self.fc1 = nn.Linear(20*5*5, num_hidden_units)
self.dropout = nn.Dropout(dropout_p)
self.fc2 = nn.Linear(num_hidden_units, num_classes)
def forward(self, x, apply_softmax=False):
# Conv pool
z = self.conv1(x) # (N, 10, 28, 28)
z = F.max_pool2d(z, 2) # (N, 10, 14, 14)
z = F.relu(z)
# Conv pool
z = self.conv2(z) # (N, 20, 10, 10)
z = self.conv_dropout(z)
z = F.max_pool2d(z, 2) # (N, 20, 5, 5)
z = F.relu(z)
# Flatten
z = z.view(-1, 20*5*5)
# FC
z = F.relu(self.fc1(z))
z = self.dropout(z)
y_pred = self.fc2(z)
if apply_softmax:
y_pred = F.softmax(y_pred, dim=1)
return y_pred
def initialize_model(config, vectorizer):
"""Initialize the model.
"""
print ("\n==> 🚀 Initializing model:")
model = ImageModel(
num_hidden_units=config["fc"]["hidden_dim"],
num_classes=len(vectorizer.category_vocab),
dropout_p=config["fc"]["dropout_p"])
print (model.named_modules)
return model
```
### Operations
```
# Initializing model
model = initialize_model(config=config, vectorizer=vectorizer)
```
# Training
Training operations for image classification.
```
import torch.optim as optim
```
### Components
```
def compute_accuracy(y_pred, y_target):
_, y_pred_indices = y_pred.max(dim=1)
n_correct = torch.eq(y_pred_indices, y_target).sum().item()
return n_correct / len(y_pred_indices) * 100
def update_train_state(model, train_state):
""" Update train state during training.
"""
# Verbose
print ("[EPOCH]: {0} | [LR]: {1} | [TRAIN LOSS]: {2:.2f} | [TRAIN ACC]: {3:.1f}% | [VAL LOSS]: {4:.2f} | [VAL ACC]: {5:.1f}%".format(
train_state['epoch_index'], train_state['learning_rate'],
train_state['train_loss'][-1], train_state['train_acc'][-1],
train_state['val_loss'][-1], train_state['val_acc'][-1]))
# Save one model at least
if train_state['epoch_index'] == 0:
torch.save(model.state_dict(), train_state['model_filename'])
train_state['stop_early'] = False
# Save model if performance improved
elif train_state['epoch_index'] >= 1:
loss_tm1, loss_t = train_state['val_loss'][-2:]
# If loss worsened
if loss_t >= train_state['early_stopping_best_val']:
# Update step
train_state['early_stopping_step'] += 1
# Loss decreased
else:
# Save the best model
if loss_t < train_state['early_stopping_best_val']:
torch.save(model.state_dict(), train_state['model_filename'])
# Reset early stopping step
train_state['early_stopping_step'] = 0
# Stop early ?
train_state['stop_early'] = train_state['early_stopping_step'] \
>= train_state['early_stopping_criteria']
return train_state
class Trainer(object):
def __init__(self, dataset, model, model_file, device, shuffle,
num_epochs, batch_size, learning_rate, early_stopping_criteria):
self.dataset = dataset
self.class_weights = dataset.class_weights.to(device)
self.model = model.to(device)
self.device = device
self.shuffle = shuffle
self.num_epochs = num_epochs
self.batch_size = batch_size
self.loss_func = nn.CrossEntropyLoss(self.class_weights)
self.optimizer = optim.Adam(self.model.parameters(), lr=learning_rate)
self.scheduler = optim.lr_scheduler.ReduceLROnPlateau(
optimizer=self.optimizer, mode='min', factor=0.5, patience=1)
self.train_state = {
'done_training': False,
'stop_early': False,
'early_stopping_step': 0,
'early_stopping_best_val': 1e8,
'early_stopping_criteria': early_stopping_criteria,
'learning_rate': learning_rate,
'epoch_index': 0,
'train_loss': [],
'train_acc': [],
'val_loss': [],
'val_acc': [],
'test_loss': -1,
'test_acc': -1,
'model_filename': model_file}
def run_train_loop(self):
print ("==> 🏋 Training:")
for epoch_index in range(self.num_epochs):
self.train_state['epoch_index'] = epoch_index
# Iterate over train dataset
# initialize batch generator, set loss and acc to 0, set train mode on
self.dataset.set_split('train')
batch_generator = self.dataset.generate_batches(
batch_size=self.batch_size, shuffle=self.shuffle,
device=self.device)
running_loss = 0.0
running_acc = 0.0
self.model.train()
for batch_index, batch_dict in enumerate(batch_generator):
# zero the gradients
self.optimizer.zero_grad()
# compute the output
y_pred = self.model(batch_dict['image'])
# compute the loss
loss = self.loss_func(y_pred, batch_dict['category'])
loss_t = loss.item()
running_loss += (loss_t - running_loss) / (batch_index + 1)
# compute gradients using loss
loss.backward()
# use optimizer to take a gradient step
self.optimizer.step()
# compute the accuracy
acc_t = compute_accuracy(y_pred, batch_dict['category'])
running_acc += (acc_t - running_acc) / (batch_index + 1)
self.train_state['train_loss'].append(running_loss)
self.train_state['train_acc'].append(running_acc)
# Iterate over val dataset
# initialize batch generator, set loss and acc to 0; set eval mode on
self.dataset.set_split('val')
batch_generator = self.dataset.generate_batches(
batch_size=self.batch_size, shuffle=self.shuffle, device=self.device)
running_loss = 0.
running_acc = 0.
self.model.eval()
for batch_index, batch_dict in enumerate(batch_generator):
# compute the output
y_pred = self.model(batch_dict['image'])
# compute the loss
loss = self.loss_func(y_pred, batch_dict['category'])
loss_t = loss.to("cpu").item()
running_loss += (loss_t - running_loss) / (batch_index + 1)
# compute the accuracy
acc_t = compute_accuracy(y_pred, batch_dict['category'])
running_acc += (acc_t - running_acc) / (batch_index + 1)
self.train_state['val_loss'].append(running_loss)
self.train_state['val_acc'].append(running_acc)
self.train_state = update_train_state(model=self.model, train_state=self.train_state)
self.scheduler.step(self.train_state['val_loss'][-1])
if self.train_state['stop_early']:
break
def run_test_loop(self):
# initialize batch generator, set loss and acc to 0; set eval mode on
self.dataset.set_split('test')
batch_generator = self.dataset.generate_batches(
batch_size=self.batch_size, shuffle=self.shuffle, device=self.device)
running_loss = 0.0
running_acc = 0.0
self.model.eval()
for batch_index, batch_dict in enumerate(batch_generator):
# compute the output
y_pred = self.model(batch_dict['image'])
# compute the loss
loss = self.loss_func(y_pred, batch_dict['category'])
loss_t = loss.item()
running_loss += (loss_t - running_loss) / (batch_index + 1)
# compute the accuracy
acc_t = compute_accuracy(y_pred, batch_dict['category'])
running_acc += (acc_t - running_acc) / (batch_index + 1)
self.train_state['test_loss'] = running_loss
self.train_state['test_acc'] = running_acc
# Verbose
print ("==> 💯 Test performance:")
print ("Test loss: {0:.2f}".format(self.train_state['test_loss']))
print ("Test Accuracy: {0:.1f}%".format(self.train_state['test_acc']))
def plot_performance(train_state, save_dir, show_plot=True):
""" Plot loss and accuracy.
"""
# Figure size
plt.figure(figsize=(15,5))
# Plot Loss
plt.subplot(1, 2, 1)
plt.title("Loss")
plt.plot(train_state["train_loss"], label="train")
plt.plot(train_state["val_loss"], label="val")
plt.legend(loc='upper right')
# Plot Accuracy
plt.subplot(1, 2, 2)
plt.title("Accuracy")
plt.plot(train_state["train_acc"], label="train")
plt.plot(train_state["val_acc"], label="val")
plt.legend(loc='lower right')
# Save figure
plt.savefig(os.path.join(save_dir, "performance.png"))
# Show plots
if show_plot:
print ("==> 📈 Metric plots:")
plt.show()
def save_train_state(train_state, save_dir):
train_state["done_training"] = True
with open(os.path.join(save_dir, "train_state.json"), "w") as fp:
json.dump(train_state, fp)
print ("==> ✅ Training complete!")
```
### Operations
```
# Training
trainer = Trainer(
dataset=dataset, model=model, model_file=config["model_file"],
device=config["device"], shuffle=config["shuffle"],
num_epochs=config["num_epochs"], batch_size=config["batch_size"],
learning_rate=config["learning_rate"],
early_stopping_criteria=config["early_stopping_criteria"])
trainer.run_train_loop()
# Plot performance
plot_performance(train_state=trainer.train_state,
save_dir=config["save_dir"], show_plot=True)
# Test performance
trainer.run_test_loop()
# Save all results
save_train_state(train_state=trainer.train_state, save_dir=config["save_dir"])
```
~60% test performance for our CIFAR10 dataset is not bad but we can do way better.
# Transfer learning
In this section, we're going to use a pretrained model that performs very well on a different dataset. We're going to take the architecture and the initial convolutional weights from the model to use on our data. We will freeze the initial convolutional weights and fine tune the later convolutional and fully-connected layers.
Transfer learning works here because the initial convolution layers act as excellent feature extractors for common spatial features that are shared across images regardless of their class. We're going to leverage these large, pretrained models' feature extractors for our own dataset.
```
!pip install torchvision
from torchvision import models
model_names = sorted(name for name in models.__dict__
if name.islower() and not name.startswith("__")
and callable(models.__dict__[name]))
print (model_names)
model_name = 'vgg19_bn'
vgg_19bn = models.__dict__[model_name](pretrained=True) # Set false to train from scratch
print (vgg_19bn.named_parameters)
```
The VGG model we chose has a `features` and a `classifier` component. The `features` component is composed of convolution and pooling layers which act as feature extractors. The `classifier` component is composed on fully connected layers. We're going to freeze most of the `feature` component and design our own FC layers for our CIFAR10 task. You can access the default code for all models at `/usr/local/lib/python3.6/dist-packages/torchvision/models` if you prefer cloning and modifying that instead.
### Components
```
class ImageModel(nn.Module):
def __init__(self, feature_extractor, num_hidden_units,
num_classes, dropout_p):
super(ImageModel, self).__init__()
# Pretrained feature extractor
self.feature_extractor = feature_extractor
# FC weights
self.classifier = nn.Sequential(
nn.Linear(512, 250, bias=True),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(250, 100, bias=True),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(100, 10, bias=True),
)
def forward(self, x, apply_softmax=False):
# Feature extractor
z = self.feature_extractor(x)
z = z.view(x.size(0), -1)
# FC
y_pred = self.classifier(z)
if apply_softmax:
y_pred = F.softmax(y_pred, dim=1)
return y_pred
def initialize_model(config, vectorizer, feature_extractor):
"""Initialize the model.
"""
print ("\n==> 🚀 Initializing model:")
model = ImageModel(
feature_extractor=feature_extractor,
num_hidden_units=config["fc"]["hidden_dim"],
num_classes=len(vectorizer.category_vocab),
dropout_p=config["fc"]["dropout_p"])
print (model.named_modules)
return model
```
### Operations
```
# Initializing model
model = initialize_model(config=config, vectorizer=vectorizer,
feature_extractor=vgg_19bn.features)
# Finetune last few conv layers and FC layers
for i, param in enumerate(model.feature_extractor.parameters()):
if i < 36:
param.requires_grad = False
else:
param.requires_grad = True
# Training
trainer = Trainer(
dataset=dataset, model=model, model_file=config["model_file"],
device=config["device"], shuffle=config["shuffle"],
num_epochs=config["num_epochs"], batch_size=config["batch_size"],
learning_rate=config["learning_rate"],
early_stopping_criteria=config["early_stopping_criteria"])
trainer.run_train_loop()
# Plot performance
plot_performance(train_state=trainer.train_state,
save_dir=config["save_dir"], show_plot=True)
# Test performance
trainer.run_test_loop()
# Save all results
save_train_state(train_state=trainer.train_state, save_dir=config["save_dir"])
```
Much better performance! If you let it train long enough, we'll actually reach ~95% accuracy :)
## Inference
```
from pylab import rcParams
rcParams['figure.figsize'] = 2, 2
```
### Components
```
class Inference(object):
def __init__(self, model, vectorizer, device="cpu"):
self.model = model.to(device)
self.vectorizer = vectorizer
self.device = device
def predict_category(self, dataset):
# Batch generator
batch_generator = dataset.generate_batches(
batch_size=len(dataset), shuffle=False, device=self.device)
self.model.eval()
# Predict
for batch_index, batch_dict in enumerate(batch_generator):
# compute the output
y_pred = self.model(batch_dict['image'], apply_softmax=True)
# Top k categories
y_prob, indices = torch.topk(y_pred, k=len(self.vectorizer.category_vocab))
probabilities = y_prob.detach().to('cpu').numpy()[0]
indices = indices.detach().to('cpu').numpy()[0]
results = []
for probability, index in zip(probabilities, indices):
category = self.vectorizer.category_vocab.lookup_index(index)
results.append({'category': category, 'probability': probability})
return results
```
### Operations
```
# Load vectorizer
with open(config["vectorizer_file"]) as fp:
vectorizer = ImageVectorizer.from_serializable(json.load(fp))
# Load the model
model = initialize_model(config=config, vectorizer=vectorizer, feature_extractor=vgg_19bn.features)
model.load_state_dict(torch.load(config["model_file"]))
# Initialize
inference = Inference(model=model, vectorizer=vectorizer, device=config["device"])
# Get a sample
sample = split_df[split_df.split=="test"].iloc[0]
plt.imshow(sample.image)
plt.axis("off")
print ("Actual:", sample.category)
# Inference
category = list(vectorizer.category_vocab.token_to_idx.keys())[0] # random filler category
infer_df = pd.DataFrame([[sample.image, category, "infer"]], columns=['image', 'category', 'split'])
infer_dataset = ImageDataset(df=infer_df, vectorizer=vectorizer, infer=True)
results = inference.predict_category(dataset=infer_dataset)
results
```
# TODO
- segmentation
- interpretability via activation maps
- processing images of different sizes
| true |
code
| 0.482551 | null | null | null | null |
|
# Data description & Problem statement:
This data set contains a total 5820 evaluation scores provided by students from Gazi University in Ankara (Turkey). There is a total of 28 course specific questions and additional 5 attributes. Please check the description at: http://archive.ics.uci.edu/ml/datasets/turkiye+student+evaluation
* Dataset is imbalanced. The data has 5820 rows and 33 variables.
* This is a classification problem. The classification goal is to predict number of times the student is taking this course: 0 (passed) and >0 (failed).
# Workflow:
- Load the dataset, and define the required functions (e.g. for detecting the outliers)
- Data Cleaning/Wrangling: Manipulate outliers, missing data or duplicate values, Encode categorical variables, etc.
- Split data into training & test parts (utilize the training part for training and test part for the final evaluation of model)
# Model Training:
- Train an ensemble of Deep Neural Network models by Keras/Tensorflow, and finally aggregate the results (Note: I've utilized SMOTE technique via imblearn toolbox to synthetically over-sample the minority category and even the dataset imbalances.)
# Model Evaluation:
- Evaluate the Neural Network model on Test Dataset, by calculating:
- AUC score
- Confusion matrix
- ROC curve
- Precision-Recall curve
- Average precision
```
import keras
import sklearn
import tensorflow as tf
import numpy as np
from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import metrics
import random as rn
%matplotlib inline
import os
os.environ['PYTHONHASHSEED'] = '0'
# for the reproducable results:
np.random.seed(42)
rn.seed(42)
tf.set_random_seed(42)
from keras import backend as K
session_conf = tf.ConfigProto(intra_op_parallelism_threads=1, inter_op_parallelism_threads=1)
sess = tf.Session(graph=tf.get_default_graph(), config=session_conf)
K.set_session(sess)
import warnings
warnings.filterwarnings("ignore")
df=pd.read_csv('C:/Users/rhash/Documents/Datasets/wine quality/winequality-red.csv', sep=';')
df['quality']=df['quality'].map({3:'L', 4:'L', 5:'L', 6:'L', 7:'H', 8:'H'})
df['quality']=df['quality'].map({'L':0, 'H':1})
# To Shuffle the data:
np.random.seed(42)
df=df.reindex(np.random.permutation(df.index))
df.reset_index(inplace=True, drop=True)
df.head(5)
df.info()
# Removes outliers (all rows) by one of Z-score, MAD or IQR-based approaches:
def remove_outliers(df, name, thresh=3, method="Z_Score"):
L=[]
for name in name:
if method=="Z_Score":
drop_rows = df.index[(np.abs(df[name] - df[name].mean()) >= (thresh * df[name].std()))]
elif method=="MAD":
median = np.median(df[name], axis=0)
mad = np.median(np.abs(df[name] - median), axis=0)
modified_z_score = 0.6745 * (df[name]-median) / mad
drop_rows = df.index[modified_z_score >= 3.5]
elif method=="IQR":
quartile_1, quartile_3 = np.percentile(df[name], [25, 75])
iqr = np.abs(quartile_3 - quartile_1)
lower_bound = quartile_1 - (iqr * 1.5)
upper_bound = quartile_3 + (iqr * 1.5)
drop_rows = df.index[(df[name] > upper_bound) | (df[name] < lower_bound)]
L.extend(list(drop_rows))
df.drop(np.array(list(set(L))), axis=0, inplace=True)
remove_outliers(df, ['fixed acidity', 'volatile acidity', 'citric acid', 'residual sugar',
'chlorides', 'free sulfur dioxide', 'total sulfur dioxide', 'density',
'pH', 'sulphates', 'alcohol'], thresh=9)
X=df[['fixed acidity', 'volatile acidity', 'citric acid', 'residual sugar',
'chlorides', 'free sulfur dioxide', 'total sulfur dioxide', 'density',
'pH', 'sulphates', 'alcohol']]
y=df['quality']
from sklearn.preprocessing import StandardScaler, MinMaxScaler
scalor_X=MinMaxScaler().fit(X)
X=scalor_X.transform(X)
# we build a hold_out dataset for the final validation:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Resampling:
from imblearn.over_sampling import SMOTE, ADASYN, RandomOverSampler
#X_r, y_r = SMOTE().fit_sample(X_train, y_train)
X_r, y_r = RandomOverSampler(random_state=0).fit_sample(X_train, y_train)
from keras.utils import to_categorical
y_r=to_categorical(y_r)
y_test=to_categorical(y_test)
from sklearn.metrics import roc_curve, auc, confusion_matrix, classification_report, f1_score
class EarlyStopByAUC(keras.callbacks.Callback):
def __init__(self, value = 0, verbose = 0):
super(keras.callbacks.Callback, self).__init__()
self.value = value
self.verbose = verbose
def on_epoch_end(self, epoch, logs={}):
#score = f1_score(np.argmax(self.validation_data[1], axis=1), np.argmax(model.predict(self.validation_data[0]), axis=1))
score=roc_auc_score(self.validation_data[1], model.predict_proba(self.validation_data[0]))
L.append(score)
if score >= self.value:
if self.verbose >0:
print("Epoch %05d: early stopping Threshold" % epoch)
self.model.stop_training = True
# KNN with Cross-Validation:
from sklearn.metrics import roc_auc_score
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.regularizers import l2, l1
from keras.callbacks import EarlyStopping, ModelCheckpoint
from sklearn.utils.class_weight import compute_sample_weight
np.random.seed(42)
rn.seed(42)
tf.set_random_seed(42)
model = Sequential()
model.add(Dense(300, input_dim=X.shape[1], activation='relu', kernel_initializer = 'uniform',
activity_regularizer=l2(0.001))) # Hidden 1
model.add(Dropout(0.2))
model.add(Dense(400, activation='relu', kernel_initializer = 'uniform',
activity_regularizer=l2(0.001))) # Hidden 2
model.add(Dropout(0.2))
model.add(Dense(y_r.shape[1], activation='softmax', kernel_initializer='uniform')) # Output
L=[]
model.compile(loss='categorical_crossentropy', optimizer='adam')
monitor = EarlyStopByAUC(value =0.95, verbose =1) #EarlyStopping(monitor='loss', min_delta=0.001, patience=5, verbose=1, mode='auto')
checkpointer = ModelCheckpoint(filepath="best_weights.hdf5", verbose=0, save_best_only=True) # save best model
history=model.fit(X_r,y_r, epochs=100, batch_size=16, validation_data=(X_test, y_test), callbacks=[monitor, checkpointer], verbose=0)
model.load_weights('best_weights.hdf5')
# Measure this fold's accuracy
auc_test=roc_auc_score(y_test, model.predict_proba(X_test))
auc_train=roc_auc_score(to_categorical(y_train), model.predict_proba(X_train))
print('Training auc score: ', auc_train, "\n")
print('Validation auc score: ', auc_test)
# list all data in history
#print(history.history.keys())
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
from sklearn.metrics import roc_curve, auc, confusion_matrix, classification_report
# Plot a confusion matrix.
# cm is the confusion matrix, names are the names of the classes.
def plot_confusion_matrix(cm, names, title='Confusion matrix', cmap=plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(names))
plt.xticks(tick_marks, names, rotation=45)
plt.yticks(tick_marks, names)
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
class_names=["0", "1"]
# Compute confusion matrix
cm = confusion_matrix(np.argmax(y_test, axis=1), np.argmax(model.predict(X_test), axis=1))
np.set_printoptions(precision=2)
print('Confusion matrix, without normalization')
print(cm)
# Normalize the confusion matrix by row (i.e by the number of samples in each class)
cm_normalized = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print('Normalized confusion matrix')
print(cm_normalized)
plt.figure()
plot_confusion_matrix(cm_normalized, class_names, title='Normalized confusion matrix')
plt.show()
# Classification report:
report=classification_report(np.argmax(y_test, axis=1), np.argmax(model.predict(X_test), axis=1))
print(report)
# ROC curve & auc:
from sklearn.metrics import precision_recall_curve, roc_curve, roc_auc_score, average_precision_score
fpr, tpr, thresholds=roc_curve(np.array(y_test[:, 1]), model.predict_proba(X_test)[:, 1] , pos_label=1)
roc_auc=roc_auc_score(np.array(y_test), model.predict_proba(X_test))
plt.figure()
plt.step(fpr, tpr, color='darkorange', lw=2, label='ROC curve (auc = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', alpha=0.4, lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC curve')
plt.legend(loc="lower right")
plt.plot([cm_normalized[0,1]], [cm_normalized[1,1]], 'or')
plt.show()
# Precision-Recall trade-off:
precision, recall, thresholds=precision_recall_curve(y_test[:, 1], model.predict_proba(X_test)[:, 1], pos_label=1)
ave_precision=average_precision_score(y_test, model.predict_proba(X_test))
plt.step(recall, precision, color='navy')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.xlim([0, 1.001])
plt.ylim([0, 1.02])
plt.title('Precision-Recall curve: AP={0:0.2f}'.format(ave_precision))
plt.plot([cm_normalized[1,1]], [cm[1,1]/(cm[1,1]+cm[0,1])], 'ob')
plt.show()
```
| true |
code
| 0.591989 | null | null | null | null |
|
# Importing Necessary Modules
```
import sys
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use("ggplot")
plt.rcParams['figure.figsize'] = (12, 8)
import seaborn as sns
sns.set(style='whitegrid', color_codes=True)
import warnings
warnings.filterwarnings('ignore')
from sklearn.feature_selection import chi2,f_classif, mutual_info_classif, SelectKBest
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.model_selection import StratifiedKFold
from yellowbrick.model_selection import CVScores
from sklearn.metrics import confusion_matrix
```
# Load Dataset
```
df = pd.read_csv('../../datasets/PCOS_clean_data_without_infertility.csv')
df.head(12)
df.info()
X = df.drop(["PCOS (Y/N)",
"Blood Group",
"Height(Cm)",
"Pregnant(Y/N)",
"PRG(ng/mL)",
"RR (breaths/min)",
"No. of aborptions",
"FSH/LH",
"I beta-HCG(mIU/mL)",
"II beta-HCG(mIU/mL)",
"TSH (mIU/L)",
"FSH(mIU/mL)",
"LH(mIU/mL)",
"Waist:Hip Ratio",
"PRL(ng/mL)",
"BP _Diastolic (mmHg)",
"BP _Systolic (mmHg)",
"Reg.Exercise(Y/N)",
"RBS(mg/dl)"
],axis=1)
y = df[["PCOS (Y/N)"]]
```
# Data Augmentation
## Resampling on Complete Dataset
```
from imblearn.combine import SMOTEENN
resample = SMOTEENN(sampling_strategy="auto", random_state =0)
X, y = resample.fit_sample(X, y)
```
## Splitting
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify= y)
X_train, X_dev, y_train, y_dev = train_test_split(X_train, y_train, test_size=0.15, random_state=0, stratify= y_train)
X_train.shape
X_test.shape
X_dev.shape
```
## Scaling
```
from sklearn.preprocessing import RobustScaler, StandardScaler, MinMaxScaler
scaler = MinMaxScaler().fit(X_train)
X_train = scaler.transform(X_train)
X_train = pd.DataFrame(X_train)
X_dev = scaler.transform(X_dev)
X_dev = pd.DataFrame(X_dev)
X_test = scaler.transform(X_test)
X_test = pd.DataFrame(X_test)
# Setting Column Names from dataset
X_train.columns = X.columns
X_test.columns = X.columns
X_dev.columns = X.columns
```
# CNN
```
import tensorflow as tf
from tensorflow.keras import datasets, layers, models
X_train = X_train.to_numpy().reshape(X_train.shape[0], X_train.shape[1], 1)
# y_train = y_train.to_numpy().reshape(y_train.shape[0], 1)
X_test = X_test.to_numpy().reshape(X_test.shape[0], X_test.shape[1], 2)
# y_test = y_test.to_numpy().reshape(y_test.shape[0], 1)
X_dev = X_dev.to_numpy().reshape(X_dev.shape[0], X_dev.shape[1], 2)
# y_dev = y_dev.to_numpy().reshape(y_dev.shape[0], 1)
from keras.utils import to_categorical
y_train = to_categorical(y_train, 2)
y_test = to_categorical(y_test, 2)
y_dev = to_categorical(y_dev, 2)
X_train.shape[:]
model = models.Sequential()
model.add(layers.Conv2D(128, (3), activation='relu', input_shape=X_train.shape[1:]))
model.add(layers.Conv2D(64, (3), activation='relu'))
model.add(layers.Conv2D(32, (3), activation='relu'))
model.add(layers.Conv1D(64, (3), activation='relu'))
model.add(layers.Conv1D(64, (5), activation='relu'))
model.add(layers.Conv1D(32, (5), activation='relu'))
model.summary()
model.add(layers.Flatten())
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(2, activation='sigmoid'))
model.summary()
callbacks = [
tf.keras.callbacks.EarlyStopping(patience=50, monitor='val_loss', mode='min'),
tf.keras.callbacks.TensorBoard(log_dir='logs')]
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['AUC','accuracy', 'Precision', 'Recall'])
history = model.fit(X_train,y_train, epochs=200, validation_data= (X_dev,y_dev));
plt.plot(history.history['accuracy'], label='Accuracy')
plt.plot(history.history['val_accuracy'], label = 'Validation Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Scores')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.plot(history.history['loss'], label='Training Loss')
plt.plot(history.history['val_loss'], label = 'Validation Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(loc='upper right')
model.evaluate(X_test, y_test, verbose=1)
```
| true |
code
| 0.655364 | null | null | null | null |
|
## Data curation example
This notebook provides two data curation examples using data produced in the PV lab.
### 1. perovskite process data
The first example is the processing conditions for solution synthesizing perovsktie materials. We want to understand the relationship between the crystal dimensionality of perovsktie and process condtions.
Let's take a look at the data first
```
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
import numpy as np
from sklearn.preprocessing import MinMaxScaler
process_data = pd.read_excel('process.xlsx', index_col=0)
pd.set_option('display.max_rows', 104)
process_data
pd.set_option('display.max_rows', 10)
process_data.shape
```
We have 104 data points with different processing conditions. However,inputs are presented either in strings or dates. We also have missing labels (NaN). How do we convert it into machine readable format?
Firstly, we take remove the data points that are not labelled
```
process_data.isnull().sum(axis=0)
process_data = process_data.dropna(subset=['Phase '])
process_data.isnull().sum(axis=0)
```
Assign input and output
```
y = process_data['Phase ']
X = process_data.iloc[:,1:-1]
```
We can factorize the strings and dates to convert it to numbers, even for the NaNs. There a a number of methods to deal with missing data. In this case, we treat missing data as one categorical variable. Other methods include using average, nearest neighbours or zero fill NaNs. You can refer to this [tutorial](https://pandas.pydata.org/pandas-docs/stable/user_guide/missing_data.html)
```
X
for column in X:
X[column]= X[column].factorize()[0]
```
The NaNs are assigned to -1 using the factorize function from Pandas.
```
X
```
Now both input and output is machine readable, we can train a classifier to map process conditions to perovskite's phase. We first standardize the input data with zero mean and unit variance.
```
stdsc=StandardScaler()
X_std=stdsc.fit_transform(X)
X_std
X_train, X_test, y_train, y_test = train_test_split( X_std, y, test_size=0.33)
feat_labels = X.columns
forest=RandomForestClassifier(n_estimators=1000,n_jobs=-1)
forest.fit(X_train,y_train)
importances=forest.feature_importances_
indices=np.argsort(importances)[::-1]
for f in range(X_train.shape[1]):
print ('%2d) %-*s %f'%(f,30,feat_labels[indices[f]],importances[indices[f]]))
coefs=forest.feature_importances_
feat_labels = X.columns
# make importances relative to max importance
feature_importance = abs(100.0 * (coefs / abs(coefs).max()))
sorted_idx = np.argsort(feature_importance)[-10:]
pos = np.arange(sorted_idx.shape[0]) + .5
plt.subplot(1, 2, 2)
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos,feat_labels[sorted_idx])
plt.xlabel('Relative Importance')
plt.title('Variable Importance')
print ('RF train Accuracy:%f'%forest.score(X_train,y_train))
print ('RF test Accuracy:%f'%forest.score(X_test,y_test))
```
### 2. Silver nanoparticle process data
The second example for data curation is the processing conditions for solution synthesizing AgNPs. In this case study, the input are nicely arranged in numerical format. However, the output is an absorption spectra. We need to convert the output into scaler values.
Let's take a look at the data first
```
raw_input = pd.read_excel('AgNPs.xlsx','Sheet1')
raw_spectra = pd.read_excel('AgNPs.xlsx','Sheet2',index_col=0)
raw_input
```
We can remove certain features that are not useful
```
raw_input = raw_input.drop(raw_input.columns[[0,1,2]],axis=1)
raw_input
raw_spectra
plt.plot(raw_spectra.iloc[:,0:10])
plt.xlabel('wavelength (nm)')
plt.ylabel ('intensity (a.u)')
raw_target = pd.read_excel('AgNPs.xlsx','Target')
plt.plot(raw_target.iloc[:,0],raw_target.iloc[:,2])
```
To convert the output to a scaler value. We define a loss function that measures how similar the measured spectra is to the target spectra. We use the product of cosine similarity and a scaling function.
```
from sklearn.metrics.pairwise import cosine_similarity
#scaler the target spectra from 0 to 1
scaler = MinMaxScaler()
def step_int(x):
if x>1.2:
y = 0
elif 0.7<=x<=1.2:
y = 1
elif 0<x<0.7:
y = x/0.7
return y
def spectra_loss_function (spectra, target_spec_norm):
data = spectra.values
loss = []
for i in range(data.shape[1]):
step_coeff = step_int(max(data[:,i]))
data_col = scaler.fit_transform(data[:,i].reshape(-1,1))
cos_loss = cosine_similarity(target_spec_norm.T,data_col.T)
single_loss = cos_loss*step_coeff
loss.append(single_loss[0])
loss= 1- np.array(loss)
return loss
```
The target spectrum and the measured spectrum have different resolutions. We can use interpolation to unify the range
```
import scipy.interpolate as interp
wave = np.arange(380,801,1)
f = interp.interp1d(raw_target.iloc[:,0],raw_target.iloc[:,2],kind='slinear')
target_spec = f(wave)
scaler = MinMaxScaler()
target_spec_norm = scaler.fit_transform(target_spec.reshape(-1,1))
loss = spectra_loss_function (raw_spectra, target_spec_norm)
```
Now the output becomes a single scaler value
```
X= raw_input
y = loss
y
```
We can plot the spectra that has the lowest loss
```
a = np.argmin(loss)
b= np.argmax(loss)
plt.plot(raw_spectra.iloc[:,a], label ='lowest loss spectra')
plt.plot(raw_spectra.iloc[:,b],label ='highest loss spectra')
plt.plot(wave,target_spec_norm, label ='target')
plt.xlabel ('wavelength(nm)')
plt.ylabel ('intensites (a.u)')
plt.legend()
```
With 5D input and 1D output , we can train a regerssion model to map the processing conditions for AgNP to its spectral similarity value. This will be covered in the following lectures.
| true |
code
| 0.492859 | null | null | null | null |
|
# COMP 135 Fall 2019: HW1 STARTER
# Setup comp135_env package imports
```
import os
import numpy as np
import sklearn.neighbors
import sklearn.tree
from matplotlib import pyplot as plt
import seaborn as sns
%matplotlib inline
```
# Setup student-defined imports
```
from LeastSquaresLinearRegression import LeastSquaresLinearRegressor
from evaluate_perf_metrics import (
calc_perf_metric__absolute_error, calc_perf_metric__squared_error,
calc_perf_metrics_for_regressor_on_dataset)
```
# Load dataset
```
## TODO load all data (train/valid/test) into x_tr_NF, x_va_NF, x_te_NF, ...
y_tr_N = np.loadtxt('data_abalone/y_train.csv', delimiter=',', skiprows=1)
x_tr_NF = np.loadtxt('data_abalone/x_train.csv', delimiter=',', skiprows=1)
```
# 1a : Abalone histograms of response variable 'rings'
#### 1a(i): Produce one figure with three subplots, showing histograms of $y$ from train/valid/test
```
fig_h, axes_arr = plt.subplots(nrows=3, ncols=1, sharex=True)
## TODO plot histograms on the axes
## e.g. sns.distplot(y_tr_N, kde=False, rug=True, ax=axes_arr[0]);
```
#### 1a(ii): Describe the **train** distribution. Unimodal or multimodal? What shape? Are there noticeable outliers?
**TODO ANSWER HERE**
#### 1a(iii): Quantify train's descriptive statistics.
```
### TODO CODE HERE
```
# 1b : Scatterplots of 'rings' vs 'diam' and 'rings' vs 'shucked'
#### **1b(i):** Create figure with two subplots: scatter plot of `diam_mm` vs `rings` and scatter of `shucked_weight_g` vs `rings`.
```
## TODO CODE HERE
```
#### **1b(ii):** Describe the trends you between diameter and rings in a few sentences.
**TODO ANSWER HERE**
#### 1b(iii): Describe the trends you see between shucked weight and rings.
**TODO ANSWER HERE**
# Setup code for 1c
```
## Dummy class to perform "always guess training mean" prediction
class MeanPredictor():
def __init__(self):
self.yhat = None
def fit(self, x_tr_NF, y_tr_N):
self.yhat = np.mean(y_tr_N)
def predict(self, x_NF):
return self.yhat
## Dummy class to perform "always guess training median" prediction
class MedianPredictor():
def __init__(self):
self.yhat = None
def fit(self, x_tr_NF, y_tr_N):
self.yhat = np.median(y_tr_N)
def predict(self, x_NF):
return self.yhat
mean_value_predictor = MeanPredictor()
## TODO fit the predictor, like mean_value_predictor.fit(x_tr_N2, y_tr_N)
## TODO evaluate predictions on train, valid, and test
median_value_predictor = MedianPredictor()
## TODO fit the predictor
## TODO evaluate predictions on train, valid, and test
```
# 1c : Results Table for Abalone MSE
#### **1c:** Make a table of the **mean-squared-error** for each of the MeanPredictor and MedianPredictor predictors when evaluated on all 3 dataset splits (training, validation, and test).
**Mean Squared Error:**
| split | guess-mean | guess-median |
| ----- | ----------- | ------------ |
| train | | |
| valid | | |
| test | | |
# Model fitting code for 1d
```
linear_regressor_2feats = LeastSquaresLinearRegressor()
# TODO fit and evaluate
linear_regressor_8feats = LeastSquaresLinearRegressor()
# TODO fit and evaluate
```
# 1d : Results Table for Mean Squared Error on Abalone
### **1d(i)** and **1d(ii)** Add results to the table
**Mean Squared Error:**
| split | guess mean | guess median | linear regr (2 feats) | linear regr (8 feats)
| ----- | ----------- | ------------ | --------------------- | ---------------------
| train |
| valid |
| test |
### **1d(iii):** Does using more features seem worthwhile? Do you think the improvement on the test data is significant? Why or why not?
# 1e : Model selection for K-Nearest Neighbor Regressor
```
param_name = 'n_neighbors'
param_list = [1, 3, 5, 7, 11, 21, 41, 61, 81, 101, 201, 401, 801] # TODO ADD N
# Keep only values below total training size
param_list = [p for p in param_list if p <= param_list[-1]]
train_mse_list = []
valid_mse_list = []
test_mse_list = []
for n_neighbors in param_list:
knn_regr = sklearn.neighbors.KNeighborsRegressor(
n_neighbors=n_neighbors,
metric='euclidean',
algorithm='brute')
# TODO fit and predict and track performance metric values in the lists
```
#### **1e(i):** Make a line plot for mean-squared-error (MSE) vs $K$ on the validation set
```
# TODO
```
#### **1e(ii):** Which value do you recommend?
```
# TODO
```
#### **1e(iii):** Cumulative results table with K-Nearest Neighbor
**Mean Squared Error:**
| split | guess mean | guess median | linear regr (2 feats) | linear regr (8 feats) | k-NN (8 feats) |
| ----- | ----------- | ------------ | --------------------- | --------------------- | ----- |
| train |
| valid |
| test |
# <a name="problem-1-g"> 1g: Analyzing Residuals </a>
Bonus points possible. Not a required question. Feel free to skip
```
# TODO compute the predicted y values for linear regr and kNN
```
#### **1f(i):** Plot scatters of y vs yhat for linear regression and the best k-NN regressor
```
fig_h, ax_grid = plt.subplots(nrows=1, ncols=2, sharex=True, sharey=True)
plt.xlim([0, 26]); plt.ylim([0, 26]);
# ax_grid[0].plot(y_va_N, linear_yhat_va_N, 'k.', alpha=0.2);
ax_grid[0].set_title('Linear Regr.'); plt.xlabel('true y'); plt.ylabel('predicted y');
# ax_grid[1].plot(y_va_N, knn_yhat_va_N, 'k.', alpha=0.2);
plt.title('k-NN Regr.'); plt.xlabel('true y'); plt.ylabel('predicted y');
```
#### **1f(ii):** What kinds of systematic errors does each method make? What should be done about these?
TODO ANSWER HERE
# Problem 2 : Analysis of Doctor Visits
```
# TODO load data here
```
# 2a : Baseline predictions
#### **2a(i):** Given stakeholder's preferences, which error metric is most appropriate and why?
Because errors should scale linearly, we should use the *mean absolute error* metric.
If we used mean squared error, an error of 2 would cost 4x an error of 1.
```
mean_value_predictor = MeanPredictor()
## TODO fit and predict...
median_value_predictor = MedianPredictor()
## TODO fit and predict...
```
#### 2a(ii) : Results Table for Doctor Visits with Mean Absolute Error
**Mean Absolute Error:**
| split | guess-mean | guess-median |
| ----- | ----------- | ------------ |
| train |
| valid |
| test |
# Setup code for 2b
```
linear_regressor_2feats = LeastSquaresLinearRegressor()
# TODO fit and predict
linear_regressor_10feats = LeastSquaresLinearRegressor()
# TODO fit and predict
```
** 2b(i) and 2b(ii):** Add LR to Results Table for MAE on DoctorVisits
**Mean Absolute Error:**
| split | guess-mean | guess-median | linear regr (2 feats) | linear regr (10 feats) |
| ----- | ----------- | ------------ | --------------------- | ---------------------- |
| train |
| valid |
| test |
** 2b(iii):** Does using more features seem worthwhile? Why or why not?
# 2c : DecisionTreeRegressor
```
param_name = 'min_samples_leaf'
param_list = [1, 2, 3, 4, 5, 10, 20, 50, 100, 200, 500, 1000] # TODO add size of training set
train_mae_list = []
valid_mae_list = []
test_mae_list = []
for param in param_list:
tree_regr = sklearn.tree.DecisionTreeRegressor(
min_samples_leaf=param,
random_state=42)
# Fit, predict, and track performance metrics...
```
#### 2c(i): Line plot of mean absolute error vs min_samples_leaf
```
# TODO plot results
```
#### **2c(ii):** Which value of min_samples_leaf would you recommend?
TODO
#### 2c(iii): Add a column to the results table for MAE on DoctorVisits
**Mean Absolute Error:**
| split | guess-mean | guess-median | linear regr (2 feats) | linear regr (10 feats) | decision tree
| ----- | ----------- | ------------ | --------------------- | ---------------------- | --- |
| train |
| valid |
| test |
# 2d : DecisionTreeRegressor with MAE Training Criterion
```
train_mae_list = []
valid_mae_list = []
test_mae_list = []
for param in param_list:
tree_regr = sklearn.tree.DecisionTreeRegressor(
criterion='mae', # USE MEAN ABSOLUTE ERROR here
min_samples_leaf=param,
random_state=42)
# TODO fit, predict, and track performance metrics
```
#### 2d(i): Line plot of mean absolute error vs min_samples_leaf
```
# TODO
```
#### 2d(ii): Which value would you recommend?
```
# TODO
```
#### Setup for 2d(iii)
#### 2d(iii): Add a column to the results table for MAE on DoctorVisits
**Mean Absolute Error:**
| split | guess-mean | guess-median | linear regr (2 feats) | linear regr (10 feats) | decision tree (MSE) | decision tree (MAE)
| ----- | ----------- | ------------ | --------------------- | ---------------------- | --- | --- |
| train |
| valid |
| test |
# Problem 3: Concept questions
# 3a: Limits of $K$-NN
**Question**: When $K$ equals the total training set size $N$, the $K$-nearest-neighbor regression algorithm approaches the behavior of which other regression method discussed here?
#### 3a Answer:
TODO
# 3b: Modifications of $K$-NN
**Question**: Suppose in problem 2, when trying to minimize *mean absolute error* on heldout data, that instead of a DecisionTreeRegressor, we had used a $K$-NN regressor with Euclidean distance (as in Problem 1f).
Would we expect $K$-NN with large $K$ to always beat the strongest constant-prediction baseline (e.g. guess-median or guess-mean)?
To get better MAE values using a nearest-neighbor like approach, should we change the distance function used to compute neighbors? Would we need to change some other step of the $K$-NN prediction process?
#### 3b Answer:
TODO
# 3c: Linear Regression with Categorical Features
**Question:** Your colleague trains a linear regression model on a subset of the DoctorVisits data using only the `has_medicaid` and `has_private_insurance` features. Thus, all features in the vector have a binary categorical type and can be represented via a redundant one-hot encoding.
To your dismay, you discover that your colleague failed to include a bias term (aka intercept term) when training the weights. You recall from class that including a bias term can be important.
To be concrete, you wish each example $x_i$ was represented as a (bias-included) vector:
$$
x_i = [
\texttt{has_medicaid}
\quad \texttt{has_private_insurance}
\quad 1
] \quad \quad \quad ~
$$
However, your colleague used the following representation:
$$
\tilde{x}_i = [
\texttt{has_medicaid}
\quad \texttt{not(has_medicaid)}
\quad \texttt{has_private_insurance}
\quad \texttt{not(has_private_insurance)}
]
$$
Your colleague has delivered to you a length-4 feature vector $\tilde{w}$ for the 4 features above, but then left for vacation without giving you access to the training data.
Can you manipulate the $\tilde{w}$ vector to estimate an appropriate $w$ and $b$ such that for all possible inputs $x_i$:
$$
w^T x_i + b = \tilde{w}^T \tilde{x}_i
$$
#### 3c Answer:
TODO
| true |
code
| 0.452657 | null | null | null | null |
|
```
import numpy as np
from keras.models import Model
from keras.layers import Input
from keras.layers.convolutional import ZeroPadding2D
from keras import backend as K
import json
from collections import OrderedDict
def format_decimal(arr, places=6):
return [round(x * 10**places) / 10**places for x in arr]
DATA = OrderedDict()
```
### ZeroPadding2D
**[convolutional.ZeroPadding2D.0] padding (1,1) on 3x5x2 input, data_format='channels_last'**
```
data_in_shape = (3, 5, 2)
L = ZeroPadding2D(padding=(1, 1), data_format='channels_last')
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(250)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['convolutional.ZeroPadding2D.0'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[convolutional.ZeroPadding2D.1] padding (1,1) on 3x5x2 input, data_format='channels_first'**
```
data_in_shape = (3, 5, 2)
L = ZeroPadding2D(padding=(1, 1), data_format='channels_first')
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(251)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['convolutional.ZeroPadding2D.1'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[convolutional.ZeroPadding2D.2] padding (3,2) on 2x6x4 input, data_format='channels_last'**
```
data_in_shape = (2, 6, 4)
L = ZeroPadding2D(padding=(3, 2), data_format='channels_last')
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(252)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['convolutional.ZeroPadding2D.2'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[convolutional.ZeroPadding2D.3] padding (3,2) on 2x6x4 input, data_format='channels_first'**
```
data_in_shape = (2, 6, 4)
L = ZeroPadding2D(padding=(3, 2), data_format='channels_first')
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(253)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['convolutional.ZeroPadding2D.3'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[convolutional.ZeroPadding2D.4] padding ((1,2),(3,4)) on 2x6x4 input, data_format='channels_last'**
```
data_in_shape = (2, 6, 4)
L = ZeroPadding2D(padding=((1,2),(3,4)), data_format='channels_last')
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(254)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['convolutional.ZeroPadding2D.4'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[convolutional.ZeroPadding2D.5] padding 2 on 2x6x4 input, data_format='channels_last'**
```
data_in_shape = (2, 6, 4)
L = ZeroPadding2D(padding=2, data_format='channels_last')
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(255)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['convolutional.ZeroPadding2D.5'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
### export for Keras.js tests
```
print(json.dumps(DATA))
```
| true |
code
| 0.493775 | null | null | null | null |
|
# 3.4.4 Least Angle Regression
Least angle regression (LAR) uses a similar strategy to Forwarf stepwise regression, but only enters "as much" of a predictor as it deserves.
**Algorithm 3.2**
1. Standardize the predictors to have mean zero and unit norm. Start with the residual $\mathbf{r} = \mathbf{y} - \mathbf{\overline{y}}$ and $\beta_1,...,\beta_p = 0$
2. Find the predictor $\mathbf{x}_j$ most correlated with $\mathbf{r}$.
3. Move $\beta_j$ from 0 towards its least-squares coefficient $\langle \mathbf{x}_j, \mathbf{r} \rangle$, until some other competitor $\mathbf{x}_k$ has as much correlation with the current residual as does $\mathbf{x}_j$.
4. Move $\beta_j$ and $\beta_k$ in the direction defined by their joint least squares coefficient of the current residual on $\langle \mathbf{x}_j, \mathbf{x}_k \rangle$, until some other competitor $\mathbf{x}_l$ has as much correlation with the current residual.
5. Continue in this way until all $p$ predictors have been entered. After min(N - 1, p) steps, we arrive at the full least-squares solution.
Suppose at the beginning of the kth step:
- $\mathcal{A}_k$ is the active set of variables
- $\beta_{\mathcal{A}_k}$ be the coefficients
- $\mathbf{r}_k=\mathbf{y} - \mathbf{X}_{\mathcal{A}_k}\beta_{\mathcal{A}_k}$ is the current residual,
then the direction for this step is (3.55):
$$\delta_k = (\mathbf{X}_{\mathcal{A}_k}^T\mathbf{X}_{\mathcal{A}_k})^{-1}\mathbf{X}_{\mathcal{A}_k}^T\mathbf{r}_k$$
The coefficient profile then evolves as $\beta_{\mathcal{A}_k}(\alpha)=\beta_{\mathcal{A}_k} + \alpha \cdot \delta_k$ and the fit vector evolves as $\hat{f}_k(\alpha)=\hat{f}_k + \alpha \cdot \mathbf{u}_k$
```
import numpy as np
import pandas as pd
from scipy import stats
df = pd.read_csv('../data/prostate/prostate.data', delimiter='\t', index_col=0)
mask_train = df.pop('train')
df_y = df.pop('lpsa')
train_x = df[mask_train == 'T']
train_y = df_y[mask_train == 'T']
train_x_centered = train_x - train_x.mean(axis = 0)
train_x_centered /= np.linalg.norm(train_x_centered, axis=0)
train_y_centered = train_y - train_y.mean()
def lars(X, y):
n, p = X.shape
mu = np.zeros_like(y)
beta = np.zeros(p)
for _ in range(p):
c = X.T @ (y - mu)
c_abs = np.abs(c)
c_max = c_abs.max()
active = np.isclose(c_abs, c_max)
signs = np.where(c[active] > 0, 1, -1)
X_active = signs * X[:, active]
G = X_active.T @ X_active
Ginv = np.linalg.inv(G)
A = Ginv.sum() ** (-0.5)
w = A * Ginv.sum(axis = 1)
u = X_active @ w
gamma = c_max / A
if not np.all(active):
a = X.T @ u
complement = np.invert(active)
cc = c[complement]
ac = a[complement]
candidates = np.concatenate([(c_max - cc) / (A - ac),
(c_max + cc) / (A + ac)])
gamma = candidates[candidates >= 0].min()
mu += gamma * u
beta[active] += gamma * signs
return mu, beta
y_fit, beta = lars(train_x_centered.as_matrix(), train_y_centered.as_matrix())
train_error = np.mean((y_fit - train_y_centered) ** 2)
print ('Beta: ', beta)
print ('train error: ', train_error)
```
**Algorithm 3.2a**
4a. If a non-zero coefficient hits zero, drop its variable from the active set of variables and recompute the current joint least squares direction.
The LAR(lasso) algorithm is extremely efficient, requiring the same order of computation as that of a single least squares fit using the p predictors.
**Heuristic argument why LAR and Lasso are similar**
Suppose $\mathcal{A}$ is the active set of variables at some stage. We can express as (3.56):
$$\mathbf{x}_j^T(\mathbf{y}-\mathbf{X}\beta)=\lambda \cdot s_j, j \in \mathcal{A}$$
also $|\mathbf{x}_j^T(\mathbf{y}-\mathbf{X}\beta)| \le \lambda, j \notin \mathcal{A}$. Now consider the lasso criterian (3.57):
$$R(\beta)=\frac{1}{2}||\mathbf{y}-\mathbf{X}\beta||_2^2 + \lambda||\beta||_1$$
Let $\mathcal{B}$ be the active set of variables in the solution for a given value of $\lambda$, and $R(\beta)$ is differentiable, and the stationarity conditions give (3.58):
$$\mathbf{x}_j^T(\mathbf{y}-\mathbf{X}\beta)=\lambda \cdot sign(\beta_j), j \in \mathcal{B}$$
Comparing (3.56) and (3.58), we see that they are identical only if the sign of $\beta{j}$ matches the sign of the inner product. That is why the LAR algorithm and lasso starts to differ when an active coefficient passes through zero; The stationary conditions for the non-active variable require that (3.59):
$$|\mathbf{x}_j^T(\mathbf{y}-\mathbf{X}\beta)|\le \lambda, j \notin \mathcal{B}$$
# Degrees-of-Freedom Formula for LAR and Lasso
We define the degrees of freedom of the fitted vector $\hat{y}$ as:
$$
df(\hat{y})=\frac{1}{\sigma^2}\sum_{i=1}^N Cov(\hat{y}_i,y_i)
$$
This makes intuitive sense: the harder that we fit to the data, the larger this covariance and hence $df(\hat{\mathbf{y}})$.
| true |
code
| 0.430985 | null | null | null | null |
|
This notebook is part of the $\omega radlib$ documentation: https://docs.wradlib.org.
Copyright (c) 2018, $\omega radlib$ developers.
Distributed under the MIT License. See LICENSE.txt for more info.
# Converting Reflectivity to Rainfall
Reflectivity (Z) and precipitation rate (R) can be related in form of a power law $Z=a \cdot R^b$. The parameters ``a`` and ``b`` depend on the type of precipitation (i.e. drop size distribution and water temperature). $\omega radlib$ provides a couple of functions that could be useful in this context.
```
import wradlib as wrl
import matplotlib.pyplot as pl
import warnings
warnings.filterwarnings('ignore')
try:
get_ipython().magic("matplotlib inline")
except:
pl.ion()
import numpy as np
```
The following example demonstrates the steps to convert from the common unit *dBZ* (decibel of the reflectivity factor *Z*) to rainfall intensity (in the unit of mm/h). This is an array of typical reflectivity values (**unit: dBZ**)
```
dBZ = np.array([20., 30., 40., 45., 50., 55.])
print(dBZ)
```
Convert to reflectivity factor Z (**unit**: $mm^6/m^3$):
```
Z = wrl.trafo.idecibel(dBZ)
print(Z)
```
Convert to rainfall intensity (**unit: mm/h**) using the Marshall-Palmer Z(R) parameters:
```
R = wrl.zr.z_to_r(Z, a=200., b=1.6)
print(np.round(R, 2))
```
Convert to rainfall depth (**unit: mm**) assuming a rainfall duration of five minutes (i.e. 300 seconds)
```
depth = wrl.trafo.r_to_depth(R, 300)
print(np.round(depth, 2))
```
## An example with real radar data
The following example is based on observations of the DWD C-band radar on mount Feldberg (SW-Germany).
The figure shows a 15 minute accumulation of rainfall which was produced from three consecutive radar
scans at 5 minute intervals between 17:30 and 17:45 on June 8, 2008.
The radar data are read using [wradlib.io.read_dx](https://docs.wradlib.org/en/latest/generated/wradlib.io.radolan.read_dx.html) function which returns an array of dBZ values and a metadata dictionary (see also [Reading-DX-Data](../fileio/wradlib_reading_dx.ipynb#Reading-DX-Data)). The conversion is carried out the same way as in the example above. The plot is produced using
the function [wradlib.vis.plot_ppi](https://docs.wradlib.org/en/latest/generated/wradlib.vis.plot_ppi.html).
```
def read_data(dtimes):
"""Helper function to read raw data for a list of datetimes <dtimes>
"""
data = np.empty((len(dtimes),360,128))
for i, dtime in enumerate(dtimes):
f = wrl.util.get_wradlib_data_file('dx/raa00-dx_10908-{0}-fbg---bin.gz'.format(dtime))
data[i], attrs = wrl.io.read_dx(f)
return data
```
Read data from radar Feldberg for three consecutive 5 minute intervals and compute the accumulated rainfall depth.
```
# Read
dtimes = ["0806021735","0806021740","0806021745"]
dBZ = read_data(dtimes)
# Convert to rainfall intensity (mm/h)
Z = wrl.trafo.idecibel(dBZ)
R = wrl.zr.z_to_r(Z, a=200., b=1.6)
# Convert to rainfall depth (mm)
depth = wrl.trafo.r_to_depth(R, 300)
# Accumulate 15 minute rainfall depth over all three 5 minute intervals
accum = np.sum(depth, axis=0)
```
Plot PPI of 15 minute rainfall depth
```
pl.figure(figsize=(10,8))
ax, cf = wrl.vis.plot_ppi(accum, cmap="viridis")
pl.xlabel("Easting from radar (km)")
pl.ylabel("Northing from radar (km)")
pl.title("Radar Feldberg\n15 min. rainfall depth, 2008-06-02 17:30-17:45 UTC")
cb = pl.colorbar(cf, shrink=0.8)
cb.set_label("mm")
pl.xlim(-128,128)
pl.ylim(-128,128)
pl.grid(color="grey")
```
| true |
code
| 0.36771 | null | null | null | null |
|
# Setup
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn import (datasets,
dummy,
metrics,
model_selection as skms,
multiclass as skmulti,
naive_bayes,
neighbors,
preprocessing as skpre)
import warnings
warnings.filterwarnings("ignore")
np.random.seed(42)
```
# Multi-class Metric Averages
```
iris = datasets.load_iris()
tts = skms.train_test_split(iris.data, iris.target,
test_size=.33, random_state=21)
(iris_train_ftrs, iris_test_ftrs,
iris_train_tgt, iris_test_tgt) = tts
iris_preds = (neighbors.KNeighborsClassifier()
.fit(iris_train_ftrs, iris_train_tgt)
.predict(iris_test_ftrs))
print(metrics.classification_report(iris_test_tgt,
iris_preds))
# verify sums-across-rows
cm = metrics.confusion_matrix(iris_test_tgt, iris_preds)
print(cm)
print("row counts equal support:", cm.sum(axis=1))
macro_prec = metrics.precision_score(iris_test_tgt,
iris_preds,
average='macro')
print("macro:", macro_prec)
cm = metrics.confusion_matrix(iris_test_tgt, iris_preds)
print(cm)
n_labels = len(iris.target_names)
# remember:
# precision is about column of our confusion matrix
# diagonal is where we are correct
# 'macro' means "average over all classes"
# each_class_precision(correct / full column) [ add, divide n --> average]
manual_macro_prec = (np.diag(cm) / cm.sum(axis=0)).sum() / n_labels
print(manual_macro_prec)
print("should equal 'macro avg':", macro_prec == manual_macro_prec)
micro_prec = metrics.precision_score(iris_test_tgt,
iris_preds,
average='micro')
print("micro:", micro_prec)
cm = metrics.confusion_matrix(iris_test_tgt, iris_preds)
print(cm)
# 'micro' means over every prediction
# (3 in the confusion matrix means 3 predictions with that right/wrongness)
# TP.sum() / (TP&FP).sum() -->
# all correct / all preds
manual_micro_prec = np.diag(cm).sum() / cm.sum()
print(manual_micro_prec)
print("should equal avg='micro':", micro_prec==manual_micro_prec)
cr = metrics.classification_report(iris_test_tgt,
iris_preds,
digits=3)
print(cr)
# can get precision class-column with
# metrics.precision_score(actual, predicted, average=None)
# can get averages with average='macro'/'weighted'
# note: weighted is macro, but instead of dividing evenly
# (a + b + c) / 3
# it is weighted by occurance (support)
# a * (18/50) + b * (17/50) + c * (15/50)
```
# Multi-Class AUC: One-Versus-Rest
```
checkout = [0, 50, 100]
print("Original Encoding")
print(iris.target[checkout])
# instead of one target-label,
# create distinct target-label column for each target class
# (am i this or not?)
print("'Multi-label' Encoding")
print(skpre.label_binarize(iris.target, classes=[0,1,2])[checkout])
iris_multi_tgt = skpre.label_binarize(iris.target,
classes=[0,1,2])
# im --> "iris multi"
(im_train_ftrs, im_test_ftrs,
im_train_tgt, im_test_tgt) = skms.train_test_split(iris.data,
iris_multi_tgt,
test_size=.33,
random_state=21)
# knn wrapped up in one-versus-rest (3 classifiers)
knn = neighbors.KNeighborsClassifier(n_neighbors=5)
ovr_knn = skmulti.OneVsRestClassifier(knn)
pred_probs = (ovr_knn.fit(im_train_ftrs, im_train_tgt)
.predict_proba(im_test_ftrs))
# make ROC plots
lbl_fmt = "Class {} vs Rest (AUC = {:.2f})"
fig,ax = plt.subplots(figsize=(8,4))
for cls in [0,1,2]:
fpr, tpr, _ = metrics.roc_curve(im_test_tgt[:,cls],
pred_probs[:,cls])
label = lbl_fmt.format(cls, metrics.auc(fpr,tpr))
ax.plot(fpr, tpr, 'o--', label=label)
ax.legend()
ax.set_xlabel("FPR")
ax.set_ylabel("TPR");
fig,ax = plt.subplots(figsize=(6,3))
for cls in [0,1,2]:
prc = metrics.precision_recall_curve
precision, recall, _ = prc(im_test_tgt[:,cls],
pred_probs[:,cls])
prc_auc = metrics.auc(recall, precision)
label = "Class {} vs Rest (AUC) = {:.2f})".format(cls, prc_auc)
ax.plot(recall, precision, 'o--', label=label)
ax.legend()
ax.set_xlabel('Recall')
ax.set_ylabel('Precision');
```
# Multi-Class AUC: The Hand and Till Method
```
# pseudo-code
# 1. train a model
# 2. get classification scores for each example
# 3. create a blank table for each pair of classes
# (how tough is this pair of classes to distinguish with *this* classifier)
# auc is not symmetric b/c
# 4. for each pair (c_1, c_2) of classes:
# a. find AUC of c_1 against c_2 (c_1 POS, c_2 NEG)
# b. find AUC of c_2 against c_1 (c_2 POS, c_1 NEG)
# c. entry for c_1, c_2 is average of those AUCs
# 5. final value is average of the entries in the table
from mlwpy_video_extras import hand_and_till_M_statistic
knn = neighbors.KNeighborsClassifier()
knn.fit(iris_train_ftrs, iris_train_tgt)
test_probs = knn.predict_proba(iris_test_ftrs)
hand_and_till_M_statistic(iris_test_tgt, test_probs)
fig,ax = plt.subplots(1,1,figsize=(3,3))
htm_scorer = metrics.make_scorer(hand_and_till_M_statistic,
needs_proba=True)
cv_auc = skms.cross_val_score(knn,
iris.data, iris.target,
scoring=htm_scorer, cv=10)
sns.swarmplot(cv_auc, orient='v')
ax.set_title('10-Fold H&T Ms');
```
# Cumulative Response and Lift Curves
```
is_versicolor = iris.target == 1
tts_oc = skms.train_test_split(iris.data, is_versicolor,
test_size=.33, random_state = 21)
(oc_train_ftrs, oc_test_ftrs,
oc_train_tgt, oc_test_tgt) = tts_oc
# build, fit, predict (probability scores) for NB model
gnb = naive_bayes.GaussianNB()
prob_true = (gnb.fit(oc_train_ftrs, oc_train_tgt)
.predict_proba(oc_test_ftrs)[:,1]) # [:,1]=="True"
# what is the location of the "most likely true example"?
# negate b/c we want big values first
myorder = np.argsort(-prob_true)
# cumulative sum then to percent (last value is total)
realpct_myorder = oc_test_tgt[myorder].cumsum()
realpct_myorder = realpct_myorder / realpct_myorder[-1]
# convert counts of data into percents
N = oc_test_tgt.size
xs = np.linspace(1/N,1,N)
print(myorder[:3], realpct_myorder[:3])
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(8,4))
fig.tight_layout()
# cumulative response
ax1.plot(xs, realpct_myorder, 'r.')
ax1.plot(xs, xs, 'b-')
ax1.axes.set_aspect('equal')
ax1.set_title("Cumulative Response")
ax1.set_ylabel("Percent of Actual Hits")
ax1.set_xlabel("Percent Of Population\n" +
"Starting with Highest Predicted Hits")
# lift
# replace divide by zero with 1.0
ax2.plot(xs, realpct_myorder / np.where(xs > 0, xs, 1))
ax2.set_title("Lift Versus Random")
ax2.set_ylabel("X-Fold Improvement") # not cross-fold!
ax2.set_xlabel("Percent Of Population\n" +
"Starting with Highest Predicted Hits")
ax2.yaxis.tick_right()
ax2.yaxis.set_label_position('right');
```
# Case Study: A Classifier Comparison
```
classifiers = {'base' : dummy.DummyClassifier(strategy='most_frequent'),
'gnb' : naive_bayes.GaussianNB(),
'3-NN' : neighbors.KNeighborsClassifier(n_neighbors=10),
'10-NN' : neighbors.KNeighborsClassifier(n_neighbors=3)}
# define the one_class iris problem so we don't have random ==1 around
iris_onec_ftrs = iris.data
iris_onec_tgt = iris.target==1
msrs = ['accuracy', 'precision', 'roc_auc']
fig, axes = plt.subplots(len(msrs), 1, figsize=(8, 3*len(msrs)))
fig.tight_layout()
for mod_name, model in classifiers.items():
# abbreviate
cvs = skms.cross_val_score
cv_results = {msr:cvs(model, iris_onec_ftrs, iris_onec_tgt,
scoring=msr, cv=10) for msr in msrs}
for ax, msr in zip(axes, msrs):
msr_results = cv_results[msr]
my_lbl = "{:12s} {:.3f} {:.2f}".format(mod_name,
msr_results.mean(),
msr_results.std())
ax.plot(msr_results, 'o--', label=my_lbl)
ax.set_title(msr)
ax.legend(loc='lower left', ncol=2)
fig, axes = plt.subplots(2,2, figsize=(4,4), sharex=True, sharey=True)
fig.tight_layout()
for ax, (mod_name, model) in zip(axes.flat, classifiers.items()):
preds = skms.cross_val_predict(model,
iris_onec_ftrs, iris_onec_tgt,
cv=10)
cm = metrics.confusion_matrix(iris_onec_tgt, preds)
sns.heatmap(cm, annot=True, ax=ax,
cbar=False, square=True, fmt="d")
ax.set_title(mod_name)
axes[1,0].set_xlabel('Predicted')
axes[1,1].set_xlabel('Predicted')
axes[0,0].set_ylabel('Actual')
axes[1,0].set_ylabel('Actual');
fig, ax = plt.subplots(1, 1, figsize=(6,4))
cv_prob_true = {} # store these for use in next cell
for mod_name, model in classifiers.items():
cv_probs = skms.cross_val_predict(model,
iris_onec_ftrs, iris_onec_tgt,
cv=10, method='predict_proba')
cv_prob_true[mod_name] = cv_probs[:,1]
fpr, tpr, thresh = metrics.roc_curve(iris_onec_tgt,
cv_prob_true[mod_name])
auc = metrics.auc(fpr, tpr)
ax.plot(fpr, tpr, 'o--', label="{:7s}{}".format(mod_name, auc))
ax.set_title('ROC Curves')
ax.legend();
fig, (ax1,ax2) = plt.subplots(1, 2, figsize=(10,5))
N = len(iris_onec_tgt)
xs = np.linspace(1/N,1,N)
ax1.plot(xs, xs, 'b-')
for mod_name in classifiers:
# negate b/c we want big values first
myorder = np.argsort(-cv_prob_true[mod_name])
# cumulative sum then to percent (last value is total)
realpct_myorder = iris_onec_tgt[myorder].cumsum()
realpct_myorder = realpct_myorder / realpct_myorder[-1]
ax1.plot(xs, realpct_myorder, '.', label=mod_name)
ax2.plot(xs,
realpct_myorder / np.where(xs > 0, xs, 1),
label=mod_name)
ax1.legend()
ax2.legend()
ax1.set_title("Cumulative Response")
ax2.set_title("Lift versus Random");
```
| true |
code
| 0.608827 | null | null | null | null |
|
# EDA
Exploratory Data Analysis adalah proses yang memungkinkan analyst memahami isi data yang digunakan, mulai dari distribusi, frekuensi, korelasi dan lainnya.
Dalam proses ini pemahaman konteks data juga diperhatikan karena akan menjawab masalah - masalah dasar.
## 1. Import Libraries
Import library yang akan digunakan
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import string
```
## 2. Load Dataset
Load dataset hasil Crawling dengan menggunakan `tweepy` sebelumnya
```
# Load Dataset
data1 = pd.read_csv('../data/Crawling Twitter Jakarta 26 - 27.csv')
data2 = pd.read_csv('../data/Crawling Twitter Jakarta 25 - 23.csv')
data3 = pd.read_csv('../data/Crawling Twitter Jakarta 22 - 19 setengah.csv')
```
**Dataset info**
Menampilkan banyak data dan `Dtype` tiap kolomnya.
```
# Info
for i in [data1,data2,data3]:
i.info()
print()
```
## 3. Merge Dataset
Menyatukan dataset yang terpisah
```
# Merge Info
data = pd.concat([data1,data2,data3])
data.info()
```
## 4. EDA
Melakukan `Exploratory Data Analysis` pada data.
## 4.1. Tweet perhari
Mengecek banyaknya tweet perharinya
```
# Melihat banyak Tweet perhari
data['Tanggal'] = pd.to_datetime(data['Tanggal'])
tph = data['Tweets'].groupby(data['Tanggal'].dt.date).count()
frek = tph.values
h_index = {6:'Minggu',0:'Senin',1:'Selasa',2:'Rabu',3:'Kamis',4:'Jumat',5:"Sabtu"}
hari = [x.weekday() for x in tph.index]
hari = [h_index[x] for x in hari]
for i in range(len(hari)):
hari[i] = str(tph.index[i]) + f'\n{hari[i]}'
```
**Plotting** (Menampilkan hasil `EDA` lewat visual / Visualisasi Data)
```
# Plotting Line
plt.figure(figsize = (10,10))
sns.lineplot(range(len(frek)), frek)
for i, v in enumerate(frek.tolist()):
if i == 0 or i==2 or i ==4 or i == len(tph.values)-2:
plt.text(i-.25, v - 1000, str(v),fontsize=11)
elif i == 1 or i == 3 or i==6 or i == len(tph.values)-1:
plt.text(i-.25, v + 400, str(v),fontsize=11)
else :
plt.text(i+.07, v, str(v),fontsize=11)
plt.title('Banyak Tweet per Hari',fontsize=20)
plt.xticks(range(len(tph.values)), hari, rotation=45)
plt.xlabel('Tanggal',fontsize=16)
plt.ylabel('Frekuensi',fontsize=16)
plt.show()
```
**Insight**
Dapat dilihat jika jumlah tweet berada pada puncaknya di hari Sabtu dan Senin. Hal yang cukup mengejutkan yaitu terjadi penurunan jumlah tweet yang signifikan pada hari minggu.
## 4.2. Tweet perjam
Sekarang akan dilihat banyaknya tweet perjamnya.
```
# Melihat banyak Tweet perjam
tpj = []
for i in range(1,len(tph.index)) :
if i != len(tph.index)-1 :
tpj.append(data['Tanggal'][(data['Tanggal'] >= str(tph.index[i])) & (data['Tanggal']<str(tph.index[i+1]))])
else :
tpj.append(data['Tanggal'][data['Tanggal']>=str(tph.index[i])])
tpj = [x.groupby(x.dt.hour).count() for x in tpj]
```
**Plotting** (Menampilkan hasil `EDA` lewat visual / Visualisasi Data)
```
# Ploting Line
fig, axes = plt.subplots(nrows=2, ncols=4,figsize=(20,10))
for i in range(len(tpj)):
sns.lineplot(tpj[i].index.tolist(),tpj[i].values,ax=axes[i//4,i%4])
axes[i//4,i%4].set_title(f'{hari[i+1]}')
axes[i//4,i%4].set(xlabel = 'Jam', ylabel = 'Frekuensi')
plt.tight_layout()
#fig.suptitle('Banyak Tweet per Jam',fontsize=24)
plt.show()
```
**Insight**
Dapat dilihat bahwa user optimal melakukan tweet pada pukul 10 - pukul 15, selanjutnya akan terjadi penurunan jumlah tweet pada pukul 15 sampai dengan pukul 20. Selanjutnya jumlah tweet kembali naik pada pukul 20 dan kemudian menurun pada pukul 21 / 22.
## 4.3. Perbandingan Tweet dan Retweet
Akan dilihat perbandingan antara jumlah tweet dan retweet yang ada.
```
# Menghitung perbandingan tweet dan retweet
r_stat = data['Retweet Status'].groupby(data['Retweet Status']).count()
temp = r_stat.values
```
**Plotting** (Menampilkan hasil `EDA` lewat visual / Visualisasi Data)
```
# Plotting Pie
def func(pct, allvals):
absolute = int(pct/100.*np.sum(allvals))
return "{:.1f}%\n{:d}".format(pct, absolute)
plt.figure(figsize = (8,8))
plt.pie(temp,explode=(0.1,0),labels=['Tweet','Retweet'],shadow=True,colors=['#A3FBFF','#ADFFA3'],
autopct=lambda pct: func(pct, temp),startangle=90)
plt.title('Perbandingan Jumlah Tweet dan Retweet',fontsize=18)
plt.axis('equal')
plt.legend(fontsize=11)
plt.show()
```
## 4.4. Hashtag terbanyak
Dilihat hashtag terbanyak.
```
# Menghitung banyak hashtag terkait
hashtag = data['Hashtags'].tolist()
temp = []
freks = []
for x in hashtag:
if x != []:
x = x.translate(str.maketrans('', '', string.punctuation))
x = x.lower().split()
for i in x :
if i not in temp :
temp.append(i)
freks.append(1)
else :
freks[temp.index(i)] += 1
hashtag_ = pd.DataFrame({'Hashtag':temp,'Frekuensi':freks})
hashtag_ = hashtag_.sort_values(by='Frekuensi', ascending=False)
```
**Plotting** (Menampilkan hasil `EDA` lewat visual / Visualisasi Data)
```
# Plot 20 hashtag terbanyak
hmm = hashtag_.head(20)
plt.figure(figsize = (10,10))
sns.barplot(x = hmm['Hashtag'],y = hmm['Frekuensi'])
for i, v in enumerate(hmm['Frekuensi'].tolist()):
plt.text(i-len(str(v))/10, v + 50, str(v),fontsize=10)
plt.title('Hashtag Terbanyak',fontsize=20)
plt.xticks(rotation=90)
plt.xlabel('Hashtag',fontsize=16)
plt.ylabel('Frekuensi',fontsize=16)
plt.show()
```
## 4.5. Source (Device) Terbanyak
Dilihat Source/Device terbanyak yang digunakan oleh user.
```
# Source count
source = data['Source'].groupby(data['Source']).count()
source = pd.DataFrame({'Source' : source.index.tolist(),'Frekuensi' : source.values})
source = source.sort_values(by='Frekuensi', ascending=False)
```
**Plotting** (Menampilkan hasil `EDA` lewat visual / Visualisasi Data)
```
# Plot 20 Source terbanyak
hm = source.head(20)
plt.figure(figsize = (10,10))
sns.barplot(x = hm['Source'],y = hm['Frekuensi'])
for i, v in enumerate(hm['Frekuensi'].tolist()):
plt.text(i-len(str(v))/10, v + 1000, str(v),fontsize=10)
plt.title('Source Terbanyak',fontsize=20)
plt.xticks(rotation=90)
plt.xlabel('Source',fontsize=16)
plt.ylabel('Frekuensi',fontsize=16)
plt.show()
```
| true |
code
| 0.275081 | null | null | null | null |
|
... ***CURRENTLY UNDER DEVELOPMENT*** ...
## HyCReWW runup estimation
inputs required:
* Nearshore reconstructed historical storms
* Nearshore reconstructed simulated storms
* Historical water levels
* Synthetic water levels
in this notebook:
* HyCReWW runup estimation of historical and synthetic events
* Extreme value analysis and validation
### Workflow:
<div>
<img src="resources/nb02_04.png" width="400px">
</div>
**HyCReWW** provides wave-driven run-up estimations along coral reef-lined shorelines under a wide range of fringing reef morphologies and offshore forcing characteristics. The metamodel is based on two models: (a) a full factorial design of recent XBeach Non-Hydrostatic simulations under different reef configurations and offshore wave and water level conditions (Pearson et al, 2017); and (b) Radial Basis Functions (RBFs) for approximating the non-linear function of run-up for the set of multivariate parameters:
Runup = RBF($\eta_0$, $H_0$, ${H_0/L_0}$, $\beta_f$,$W_reef$, $\beta_b$, $c_f$ ); </center>
Where, the hydrodynamic variables defined are offshore water level ($\eta_0$), significant wave height ($H_0$), and wave steepness (${H_0/L_0}$); the reef morphologic parameters include fore reef slope ($\beta_f$), reef flat width ($W_reef$), beach slope ($\beta_b$), and seabed roughness ($c_f$). ${L_0}$ is the deep water wave length $L_0=gT_p^2/2pi$, and $T_p$ is the peak period. Beach crest elevation ($z_b$) was fixed at a height of 30 m to focus on run-up as a proxy for coastal inundation.
<img src="resources/nb02_04_profile.png">
```
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# common
import os
import os.path as op
# pip
import numpy as np
import pandas as pd
import xarray as xr
from scipy.interpolate import griddata
# DEV: override installed teslakit
import sys
sys.path.insert(0, op.join(os.path.abspath(''), '..', '..', '..'))
# teslakit
from teslakit.database import Database
from teslakit.rbf import RBF_Interpolation, RBF_Reconstruction
from teslakit.mda import Normalize, MaxDiss_Simplified_NoThreshold, nearest_indexes
from teslakit.plotting.extremes import Plot_ReturnPeriodValidation
```
## Database and Site parameters
```
# --------------------------------------
# Teslakit database
p_data = r'/Users/nico/Projects/TESLA-kit/TeslaKit/data'
db = Database(p_data)
# set site
db.SetSite('ROI')
```
## HyCReWW - RBFs configuration
runup has been calculated for a total of 15 scenarios (hs, hs_lo) and a set of reef characteristics
```
# 15 scenarios of runup model execution
# RBF wave conditions
rbf_hs = [1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5]
rbf_hs_lo = [0.005, 0.025, 0.05, 0.005, 0.025, 0.05, 0.005, 0.025, 0.05, 0.005, 0.025, 0.05, 0.005, 0.025, 0.05]
# load trained RBF coefficients and variables min. and max. limits
var_lims, rbf_coeffs = db.Load_HYCREWW()
# reef characteristics
reef_cs = {
'rslope': 0.0505,
'bslope': 0.1667,
'rwidth': 250,
'cf': 0.0105,
}
# rbf variables names: level is our teslakit input data
rbf_vns = ['level', 'rslope', 'bslope', 'rwidth', 'cf']
```
## HyCReWW methodology library
```
def HyCReWW_RU(df):
'''
Calculates runup using HyCReWW RBFs (level, reef variables)
and a linear interpolation (hs, hs_lo2) to input dataset
var_lims - HyCReWW variables min and max limits
rbf_coeffs - HyCReWW rbf coefficients
reef_cs - reef characteristics
rbf_vns - rbf variables
df - input pandas.dataframe (time,), vars: level, hs, tp, dir, hs_lo2
'''
# 1. Prepare input data
# -----------------------------------------------------------------
# add reef characteristics to input dataset
for p in reef_cs.keys(): df[p] = reef_cs[p]
# filter data: all variables inside limits
lp = []
for vn in var_lims.keys():
ps = (df[vn] > var_lims[vn][0]) & (df[vn] < var_lims[vn][1])
lp.append(ps)
ix_in = np.where(np.all(lp, axis=0))[0]
# select dataset to interpolate at RBFs
ds_in = df.iloc[ix_in]
ds_rbf_in = ds_in[rbf_vns]
# 2. Calculate RUNUP with input LEVEL for the 15 RBF scenarios
# -----------------------------------------------------------------
# parameters
ix_sc = [0, 1, 2, 3, 4]
ix_dr = []
minis = [var_lims[x][0] for x in rbf_vns]
maxis = [var_lims[x][1] for x in rbf_vns]
# Normalize data
ds_nm ,_ ,_ = Normalize(ds_rbf_in.values, ix_sc, ix_dr, minis=minis, maxis=maxis)
# RBF interpolate level for the 15 scenarios
aux_1 = []
for rc in rbf_coeffs:
ro = RBF_Interpolation(rc['constant'], rc['coeff'], rc['nodes'], ds_nm.T)
aux_1.append(ro)
ru_z = np.array(aux_1)
# 3. interpolate RUNUP for input WAVES with the 15 RBF scenarios
# -----------------------------------------------------------------
# RU linear interpolation (15 sets: hs, hs_lo -> runup)
#ru_in = np.zeros(ds_in.shape[0]) * np.nan
#for c, (_, r) in enumerate(ds_in.iterrows()):
# ru_in[c] = griddata((rbf_hs, rbf_hs_lo), ru_z[:,c], (r['hs'], r['hs_lo2']), method='linear')
# RU linear interpolation (15 sets: hs, hs_lo -> runup) (*faster than loop)
def axis_ipl_rbfs(inp):
return griddata((rbf_hs, rbf_hs_lo), inp[:15], (inp[15], inp[16]), method='linear')
inp = np.concatenate((ru_z, ds_in[['hs', 'hs_lo2']].T))
ru_in = np.apply_along_axis(axis_ipl_rbfs, 0, inp)
# 4. Prepare output
# -----------------------------------------------------------------
# add level to run_up
ru_in = ru_in + ds_in['level']
# return runup
ru_out = np.zeros(len(df.index)) * np.nan
ru_out[ix_in] = ru_in
xds_ru = xr.Dataset({'runup': (('time',), ru_out)}, coords={'time': df.index})
return xds_ru
```
## HyCReWW MDA-RBF statistical wrap
```
def mdarbf_HyCReWW(dataset):
'''
Solves HyCReWW methodology using a MDA-RBFs statistical wrap.
This results in a substantial reduce in computational cost.
A Statistical representative subset will be selected with MaxDiss algorithm from input dataset.
This subset will be solved using HyCReWW methodology.
This subset and its runup HyCReWW output will be used to fit Radial Basis Functions.
Using RBFs, the entire input dataset is statistically solved
'''
base_dataset = dataset.copy()
# 1. MaxDiss
# -----------------------------------------------------------------
vns_mda = ['hs', 'hs_lo2','level'] # variables used at classification
n_subset = 100
ix_scalar = [0, 1, 2]
ix_directional = []
# remove nan data from input dataset
dataset.dropna(inplace=True)
# data for MDA
data = dataset[vns_mda]
# MDA algorithm
sel = MaxDiss_Simplified_NoThreshold(data.values[:], n_subset, ix_scalar, ix_directional)
subset = pd.DataFrame(data=sel, columns=vns_mda)
# fill subset variables
ix_n = nearest_indexes(subset[vns_mda].values[:], data.values[:], ix_scalar, ix_directional)
vns_fill = ['tp', 'dir']
for vn in vns_fill:
subset[vn] = dataset[vn].iloc[ix_n].values[:]
# calculate runup with HyCReWW
ru_sel = HyCReWW_RU(subset)
target = ru_sel.runup.to_dataframe()
# clean subset variables
subset.drop(columns=['rslope', 'bslope', 'rwidth', 'cf'], inplace=True)
# clean nans from runup target and input subset
ix_rm = np.where(np.isnan(target.values))[0]
subset.drop(index=ix_rm, inplace=True)
target.drop(index=ix_rm, inplace=True)
# 2. RBF RunUp Reconstruction
# -----------------------------------------------------------------
vs_recon = ['hs', 'hs_lo2','level']
subset_r = subset[vs_recon]
dataset_r = base_dataset[vs_recon] # to maintain input indexes and put nan where there is no output
ix_scalar_subset = [0, 1, 2]
ix_scalar_target = [0]
recon = RBF_Reconstruction(
subset_r.values, ix_scalar_subset, [],
target.values, ix_scalar_target, [],
dataset_r.values
)
xds_ru = xr.Dataset({'runup': (('time',), recon.squeeze())}, coords={'time': base_dataset.index})
return xds_ru
```
## HyCReWW RBF Interpolation: Historical
```
# Load complete historical data and nearshore waves
# offshore level
level = db.Load_HIST_OFFSHORE(vns=['level'], decode_times=True)
# nearshore waves
waves = db.Load_HIST_NEARSHORE(vns=['Hs', 'Tp', 'Dir'], decode_times=True)
waves["time"] = waves["time"].dt.round("H") # fix waves times: round to nearest hour
# use same time for nearshore calculations
level = level.sel(time=waves.time)
# prepare data for HyCReWW
waves = waves.rename_vars({"Hs": "hs", "Tp": "tp", 'Dir':'dir'}) # rename vars
waves['hs_lo2'] = waves['hs']/(1.5613*waves['tp']**2) # calc. hs_lo2
waves['level'] = level['level'] # add level
dataset = waves[['hs', 'tp', 'dir', 'level', 'hs_lo2']].to_dataframe()
# calculate runup with HyCReWW
#ru_hist = HyCReWW_RU(dataset)
# calculate runup with HyCReWW MDA-RBF wrap
ru_hist = mdarbf_HyCReWW(dataset)
# store historical runup
db.Save_HIST_NEARSHORE(ru_hist)
```
## HyCREWW RBF Interpolation: Simulation
```
# offshore level
level = db.Load_SIM_OFFSHORE_all(vns=['level'], decode_times=False)
# nearshore waves
waves = db.Load_SIM_NEARSHORE_all(vns=['Hs', 'Tp', 'Dir', 'max_storms'], decode_times=False)
# prepare data for hycreww
waves = waves.rename_vars({"Hs": "hs", "Tp": "tp", 'Dir':'dir'}) # rename vars
waves['hs_lo2'] = waves['hs']/(1.5613*waves['tp']**2) # calc. hs_lo2
waves['level'] = level['level'] # add level
# fix simulation times (cftimes)
tmpt = db.Load_SIM_NEARSHORE_all(vns=['Hs'], decode_times=True, use_cftime=True)
waves['time'] = tmpt['time']
# iterate simulations
for n in waves.n_sim:
waves_n = waves.sel(n_sim=int(n))
dataset = waves_n[['hs', 'tp', 'dir', 'level', 'hs_lo2']].to_dataframe()
# calculate runup with HyCReWW
#ru_sim_n = HyCREWW_RU(dataset)
# calculate runup with HyCReWW MDA-RBF wrap
ru_sim_n = mdarbf_HyCReWW(dataset)
# store simulation runup
db.Save_SIM_NEARSHORE(ru_sim_n, int(n))
print('simulation {0} processed.'.format(int(n)))
```
## Methodology Validation: Annual Maxima
```
# load all simulations
ru_sims = db.Load_SIM_NEARSHORE_all(vns=['runup'], decode_times=True, use_cftime=True)
# compare historical and simulations runup annual maxima
hist_A = ru_hist['runup'].groupby('time.year').max(dim='time')
sim_A = ru_sims['runup'].groupby('time.year').max(dim='time')
# Return Period historical vs. simulations
Plot_ReturnPeriodValidation(hist_A, sim_A.transpose());
```
| true |
code
| 0.426979 | null | null | null | null |
|
# Monetary Economics: Chapter 4
### Preliminaries
```
# This line configures matplotlib to show figures embedded in the notebook,
# instead of opening a new window for each figure. More about that later.
# If you are using an old version of IPython, try using '%pylab inline' instead.
%matplotlib inline
import matplotlib.pyplot as plt
from pysolve.model import Model
from pysolve.utils import is_close,round_solution
```
### Model PC
```
def create_pc_model():
model = Model()
model.set_var_default(0)
model.var('Bcb', desc='Government bills held by the Central Bank')
model.var('Bh', desc='Government bills held by households')
model.var('Bs', desc='Government bills supplied by the government')
model.var('C', desc='Consumption goods')
model.var('Hh', desc='Cash held by households')
model.var('Hs', desc='Cash supplied by the central bank')
model.var('R', desc='Interest rate on government bills')
model.var('T', desc='Taxes')
model.var('V', desc='Household wealth')
model.var('Y', desc='Income = GDP')
model.var('YD', desc='Disposable income of households')
model.param('alpha1', desc='Propensity to consume out of income', default=0.6)
model.param('alpha2', desc='Propensity to consume out of wealth', default=0.4)
model.param('lambda0', desc='Parameter in asset demand function', default=0.635)
model.param('lambda1', desc='Parameter in asset demand function', default=5.0)
model.param('lambda2', desc='Parameter in asset demand function', default=0.01)
model.param('theta', desc='Tax rate', default=0.2)
model.param('G', desc='Government goods', default=20.)
model.param('Rbar', desc='Interest rate as policy instrument')
model.add('Y = C + G') # 4.1
model.add('YD = Y - T + R(-1)*Bh(-1)') # 4.2
model.add('T = theta*(Y + R(-1)*Bh(-1))') #4.3, theta < 1
model.add('V = V(-1) + (YD - C)') # 4.4
model.add('C = alpha1*YD + alpha2*V(-1)') # 4.5, 0<alpha2<alpha1<1
model.add('Hh = V - Bh') # 4.6
model.add('Bh = V*lambda0 + V*lambda1*R - lambda2*YD') # 4.7
model.add('Bs - Bs(-1) = (G + R(-1)*Bs(-1)) - (T + R(-1)*Bcb(-1))') # 4.8
model.add('Hs - Hs(-1) = Bcb - Bcb(-1)') # 4.9
model.add('Bcb = Bs - Bh') # 4.10
model.add('R = Rbar') # 4.11
return model
steady = create_pc_model()
steady.set_values({'alpha1': 0.6,
'alpha2': 0.4,
'lambda0': 0.635,
'lambda1': 5.0,
'lambda2': 0.01,
'G': 20,
'Rbar': 0.025})
for _ in range(100):
steady.solve(iterations=100, threshold=1e-5)
if is_close(steady.solutions[-2], steady.solutions[-1], atol=1e-4):
break
```
### Model PCEX
```
def create_pcex_model():
model = Model()
model.set_var_default(0)
model.var('Bcb', desc='Government bills held by the Central Bank')
model.var('Bd', desc='Demand for government bills')
model.var('Bh', desc='Government bills held by households')
model.var('Bs', desc='Government bills supplied by the government')
model.var('C', desc='Consumption goods')
model.var('Hd', desc='Demand for cash')
model.var('Hh', desc='Cash held by households')
model.var('Hs', desc='Cash supplied by the central bank')
model.var('R', desc='Interest rate on government bills')
model.var('T', desc='Taxes')
model.var('V', desc='Household wealth')
model.var('Ve', desc='Expected household wealth')
model.var('Y', desc='Income = GDP')
model.var('YD', desc='Disposable income of households')
model.var('YDe', desc='Expected disposable income of households')
model.set_param_default(0)
model.param('alpha1', desc='Propensity to consume out of income', default=0.6)
model.param('alpha2', desc='Propensity to consume o of wealth', default=0.4)
model.param('lambda0', desc='Parameter in asset demand function', default=0.635)
model.param('lambda1', desc='Parameter in asset demand function', default=5.0)
model.param('lambda2', desc='Parameter in asset demand function', default=0.01)
model.param('theta', desc='Tax rate', default=0.2)
model.param('G', desc='Government goods', default=20.)
model.param('Ra', desc='Random shock to expectations', default=0.0)
model.param('Rbar', desc='Interest rate as policy instrument', default=0.025)
model.add('Y = C + G') # 4.1
model.add('YD = Y - T + R(-1)*Bh(-1)') # 4.2
model.add('T = theta*(Y + R(-1)*Bh(-1))') #4.3, theta < 1
model.add('V = V(-1) + (YD - C)') # 4.4
model.add('C = alpha1*YDe + alpha2*V(-1)') # 4.5E
model.add('Bd = Ve*lambda0 + Ve*lambda1*R - lambda2*YDe') # 4.7E
model.add('Hd = Ve - Bd') # 4.13
model.add('Ve = V(-1) + (YDe - C)') # 4.14
model.add('Hh = V - Bh') # 4.6
model.add('Bh = Bd') # 4.15
model.add('Bs - Bs(-1) = (G + R(-1)*Bs(-1)) - (T + R(-1)*Bcb(-1))') # 4.8
model.add('Hs - Hs(-1) = Bcb - Bcb(-1)') # 4.9
model.add('Bcb = Bs - Bh') # 4.10
model.add('R = Rbar') # 4.11
model.add('YDe = YD * (1 + Ra)') # 4.16
return model
```
### Steady state and shocks
```
pcex_steady = create_pcex_model()
pcex_steady.set_values([('alpha1', 0.6),
('alpha2', 0.4),
('lambda0', 0.635),
('lambda1', 5.0),
('lambda2', 0.01),
('theta', 0.2),
('G', 20),
('Rbar', 0.025),
('Ra', 0),
('Bcb', 116.36),
('Bh', 363.59),
('Bs', 'Bh + Bcb'),
('Hh', 116.35),
('Hs', 'Hh'),
('V', 'Bh + Hh'),
('R', 'Rbar')])
for _ in range(100):
pcex_steady.solve(iterations=100, threshold=1e-5)
if is_close(pcex_steady.solutions[-2], pcex_steady.solutions[-1], atol=1e-4):
break
import random
random.seed(6)
shocks = create_pcex_model()
shocks.set_values(pcex_steady.solutions[-1], ignore_errors=True)
for _ in range(50):
shocks.parameters['Ra'].value = random.gauss(0,1) / 10.
shocks.solve(iterations=100, threshold=1e-3)
```
#### Figure 4.1
```
caption = '''
Figure 4.1 Money demand and held money balances, when the economy is subjected
to random shocks.'''
hddata = [s['Hd'] for s in shocks.solutions[25:]]
hhdata = [s['Hh'] for s in shocks.solutions[25:]]
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 1.1, 1.1])
axes.tick_params(top=False, right=False)
axes.spines['top'].set_visible(False)
axes.spines['right'].set_visible(False)
axes.set_ylim(min(hddata+hhdata)-2, max(hddata+hhdata)+2)
axes.plot(hhdata, 'b')
axes.plot(hddata, linestyle='--', color='r')
# add labels
plt.text(13, 35, 'Held money balances')
plt.text(13, 34, '(continuous line)')
plt.text(16, 12, 'Money demand')
plt.text(16, 11, '(dotted line)')
fig.text(0.1, -.05, caption);
```
###### Figure 4.2
```
caption = '''
Figure 4.2 Changes in money demand and in money balances held (first differences),
when the economy is subjected to random shocks. '''
hddata = [s['Hd'] for s in shocks.solutions[24:]]
hhdata = [s['Hh'] for s in shocks.solutions[24:]]
for i in range(len(hddata)-1, 0, -1):
hddata[i] -= hddata[i-1]
hhdata[i] -= hhdata[i-1]
hddata = hddata[1:]
hhdata = hhdata[1:]
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 1.1, 1.1])
axes.tick_params(top=False, right=False)
axes.spines['top'].set_visible(False)
axes.spines['right'].set_visible(False)
axes.set_ylim(min(hddata+hhdata)-2, max(hddata+hhdata)+2)
axes.plot(hhdata, 'b')
axes.plot(hddata, linestyle='--', color='r')
# add labels
plt.text(13, 20, 'Held money balances')
plt.text(13, 18, '(continuous line)')
plt.text(15, -18, 'Money demand')
plt.text(15, -20, '(dotted line)')
fig.text(0.1, -.05, caption);
```
### Scenario: Model PC, Steady state with increase in interest rate
```
rate_shock = create_pc_model()
rate_shock.set_values({'Bcb': 21.576,
'Bh': 64.865,
'Bs': 86.441,
'Hh': 21.62,
'Hs': 21.62,
'V': 86.485,
'alpha1': 0.6,
'alpha2': 0.4,
'lambda0': 0.635,
'lambda1': 5.0,
'lambda2': 0.01,
'G': 20,
'Rbar': 0.025})
# solve until stable
for i in range(50):
rate_shock.solve(iterations=100, threshold=1e-5)
if is_close(rate_shock.solutions[-2], rate_shock.solutions[-1], atol=1e-4):
break
rate_shock.parameters['Rbar'].value = 0.035
for i in range(40):
rate_shock.solve(iterations=100, threshold=1e-5)
```
###### Figure 4.3
```
caption = '''
Figure 4.3 Evolution of the shares of bills and money balances in the portfolio of
households, following an increase of 100 points in the rate of interest on bills.'''
hhdata = [s['Hh']/s['V'] for s in rate_shock.solutions[15:]]
bhdata = [s['Bh']/s['V'] for s in rate_shock.solutions[15:]]
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 1.1, 1.1])
axes.tick_params(top=False)
axes.spines['top'].set_visible(False)
axes.set_ylim(0.19, 0.26)
axes.plot(hhdata, 'b')
axes2 = axes.twinx()
axes2.tick_params(top=False)
axes2.spines['top'].set_visible(False)
axes2.set_ylim(0.74, 0.81)
axes2.plot(bhdata, linestyle='--', color='r')
plt.text(1, 0.81, 'Share of')
plt.text(1, 0.807, 'money balances')
plt.text(45, 0.81, 'Share of')
plt.text(45, 0.807, 'bills')
plt.text(15, 0.795, 'Share of bills in')
plt.text(15, 0.792, 'household portfolios')
plt.text(15, 0.755, 'Share of money balances')
plt.text(15, 0.752, 'in household portfolios')
fig.text(0.1, -.05, caption);
```
###### Figure 4.4
```
caption = '''
Figure 4.4 Evolution of disposable income and household consumption following an
increase of 100 points in the rate of interest on bills. '''
yddata = [s['YD'] for s in rate_shock.solutions[20:]]
cdata = [s['C'] for s in rate_shock.solutions[20:]]
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 1.1, 1.1])
axes.tick_params(top=False, right=False)
axes.spines['top'].set_visible(False)
axes.spines['right'].set_visible(False)
axes.set_ylim(86, 91)
axes.plot(yddata, 'b')
axes.plot(cdata, linestyle='--', color='r')
# add labels
plt.text(10, 90.2, 'Disposable')
plt.text(10, 90.0, 'Income')
plt.text(10, 88, 'Consumption')
fig.text(0.1, -0.05, caption);
```
### Model PCEX1
```
def create_pcex1_model():
model = Model()
model.set_var_default(0)
model.var('Bcb', desc='Government bills held by the Central Bank')
model.var('Bd', desc='Demand for government bills')
model.var('Bh', desc='Government bills held by households')
model.var('Bs', desc='Government bills supplied by the government')
model.var('C', desc='Consumption goods')
model.var('Hd', desc='Demand for cash')
model.var('Hh', desc='Cash held by households')
model.var('Hs', desc='Cash supplied by the central bank')
model.var('R', 'Interest rate on government bills')
model.var('T', desc='Taxes')
model.var('V', desc='Household wealth')
model.var('Ve', desc='Expected household wealth')
model.var('Y', desc='Income = GDP')
model.var('YD', desc='Disposable income of households')
model.var('YDe', desc='Expected disposable income of households')
model.set_param_default(0)
model.param('alpha1', desc='Propensity to consume out of income', default=0.6)
model.param('alpha2', desc='Propensity to consume o of wealth', default=0.4)
model.param('lambda0', desc='Parameter in asset demand function', default=0.635)
model.param('lambda1', desc='Parameter in asset demand function', default=5.0)
model.param('lambda2', desc='Parameter in asset demand function', default=0.01)
model.param('theta', desc='Tax rate', default=0.2)
model.param('G', desc='Government goods', default=20.)
model.param('Rbar', desc='Interest rate as policy instrument', default=0.025)
model.add('Y = C + G') # 4.1
model.add('YD = Y - T + R(-1)*Bh(-1)') # 4.2
model.add('T = theta*(Y + R(-1)*Bh(-1))') #4.3, theta < 1
model.add('V = V(-1) + (YD - C)') # 4.4
model.add('C = alpha1*YDe + alpha2*V(-1)') # 4.5E
model.add('Bd = Ve*lambda0 + Ve*lambda1*R - lambda2*YDe') # 4.7E
model.add('Hd = Ve - Bd') # 4.13
model.add('Ve = V(-1) + (YDe - C)') # 4.14
model.add('Hh = V - Bh') # 4.6
model.add('Bh = Bd') # 4.15
model.add('Bs - Bs(-1) = (G + R(-1)*Bs(-1)) - (T + R(-1)*Bcb(-1))') # 4.8
model.add('Hs - Hs(-1) = Bcb - Bcb(-1)') # 4.9
model.add('Bcb = Bs - Bh') # 4.10
model.add('R = Rbar') # 4.11
model.add('YDe = YD(-1)') # 4.16A
return model
pcex1 = create_pcex1_model()
pcex1.set_values({'Bcb': 21.576,
'Bh': 64.865,
'Bs': 86.441,
'Hh': 21.62,
'Hs': 21.62,
'V': 86.485,
'YD': 90,
'alpha1': 0.6,
'alpha2': 0.4,
'lambda0': 0.635,
'lambda1': 5.0,
'lambda2': 0.01,
'G': 20,
'Rbar': 0.025})
for i in range(10):
pcex1.solve(iterations=100, threshold=1e-5)
pcex1.parameters['alpha1'].value = 0.7
for i in range(40):
pcex1.solve(iterations=100, threshold=1e-5)
```
###### Figure 4.5
```
caption = '''
Figure 4.5 Rise and fall of national income (GDP) following an increase in the
propensity to consume out of expected disposable income ($\\alpha_1$) '''
ydata = [s['Y'] for s in pcex1.solutions[8:]]
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 1.1, 1.1])
axes.tick_params(top=False, right=False)
axes.spines['top'].set_visible(False)
axes.spines['right'].set_visible(False)
axes.set_ylim(104, 123)
axes.plot(ydata, 'b')
# add labels
plt.text(10, 116, 'National Income (GDP)')
fig.text(0.1, -0.05, caption);
```
###### Figure 4.6
```
caption = '''
Figure 4.6 Evolution of consumtion, expected disposable income and lagged wealth,
following an increase in the propensity to consume out of expected disposable
income ($\\alpha_1$).'''
vdata = [s['V'] for s in pcex1.solutions[8:]]
ydedata = [s['YDe'] for s in pcex1.solutions[8:]]
cdata = [s['C'] for s in pcex1.solutions[8:]]
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 1.1, 1.1])
axes.tick_params(top=False, right=False)
axes.spines['top'].set_visible(False)
axes.spines['right'].set_visible(False)
axes.set_ylim(60, 106)
axes.plot(cdata, linestyle=':', color='r')
axes.plot(ydedata, linestyle='--', color='b')
axes.plot(vdata, color='k')
# add labels
plt.text(5, 102, 'Consumption')
plt.text(5, 90, 'Expected')
plt.text(5, 88, 'disposable')
plt.text(5, 86, 'income')
plt.text(10, 70, 'Lagged wealth')
fig.text(0.1, -.1, caption);
```
### Model PCEX2
```
def create_pcex2_model():
model = Model()
model.set_var_default(0)
model.var('Bcb', desc='Government bills held by the Central Bank')
model.var('Bd', desc='Demand for government bills')
model.var('Bh', desc='Government bills held by households')
model.var('Bs', desc='Government bills supplied by the government')
model.var('C', desc='Consumption goods')
model.var('Hd', desc='Demand for cash')
model.var('Hh', desc='Cash held by households')
model.var('Hs', desc='Cash supplied by the central bank')
model.var('R', 'Interest rate on government bills')
model.var('T', desc='Taxes')
model.var('V', desc='Household wealth')
model.var('Ve', desc='Expected household wealth')
model.var('Y', desc='Income = GDP')
model.var('YD', desc='Disposable income of households')
model.var('YDe', desc='Expected disposable income of households')
model.var('alpha1', desc='Propensity to consume out of income')
model.set_param_default(0)
model.param('alpha2', desc='Propensity to consume out of wealth', default=0.6)
model.param('alpha10', desc='Propensity to consume out of income - exogenous')
model.param('iota', desc='Impact of interest rate on the propensity to consume out of income')
model.param('lambda0', desc='Parameter in asset demand function', default=0.635)
model.param('lambda1', desc='Parameter in asset demand function', default=5.0)
model.param('lambda2', desc='Parameter in asset demand function', default=0.01)
model.param('theta', desc='Tax rate', default=0.2)
model.param('G', desc='Government goods')
model.param('Rbar', desc='Interest rate as policy instrument')
model.add('Y = C + G') # 4.1
model.add('YD = Y - T + R(-1)*Bh(-1)') # 4.2
model.add('T = theta*(Y + R(-1)*Bh(-1))') #4.3, theta < 1
model.add('V = V(-1) + (YD - C)') # 4.4
model.add('C = alpha1*YDe + alpha2*V(-1)') # 4.5E
model.add('Bd = Ve*lambda0 + Ve*lambda1*R - lambda2*YDe') # 4.7E
model.add('Hd = Ve - Bd') # 4.13
model.add('Ve = V(-1) + (YDe - C)') # 4.14
model.add('Hh = V - Bh') # 4.6
model.add('Bh = Bd') # 4.15
model.add('Bs - Bs(-1) = (G + R(-1)*Bs(-1)) - (T + R(-1)*Bcb(-1))') # 4.8
model.add('Hs - Hs(-1) = Bcb - Bcb(-1)') # 4.9
model.add('Bcb = Bs - Bh') # 4.10
model.add('R = Rbar') # 4.11
model.add('YDe = YD(-1)') # 4.16A
model.add('alpha1 = alpha10 - iota*R(-1)')
return model
pcex2 = create_pcex2_model()
pcex2.set_values({'Bcb': 21.576,
'Bh': 64.865,
'Bs': 86.441, # Bs = Bh + Bcb
'Hh': 21.62,
'Hs': 21.62, # Hs = Hh
'R': 0.025,
'V': 86.485, # V = Bh + Hh
'YD': 90,
'alpha1': 0.6,
'alpha2': 0.4,
'alpha10': 0.7,
'iota': 4,
'lambda0': 0.635,
'lambda1': 5,
'lambda2': 0.01,
'theta': 0.2,
'G': 20,
'Rbar': 0.025})
for i in range(15):
pcex2.solve(iterations=100, threshold=1e-5)
# Introduce the rate shock
pcex2.parameters['Rbar'].value += 0.01
for i in range(40):
pcex2.solve(iterations=100, threshold=1e-5)
```
###### Figure 4.9
```
caption = '''
Figure 4.9 Evolution of GDP, disposable income, consumptiona and wealth,
following an increase of 100 points in the rate of interest on bills, in Model PCEX2
where the propensity to consume reacts negatively to higher interest rates'''
vdata = [s['V'] for s in pcex2.solutions[12:]]
ydata = [s['Y'] for s in pcex2.solutions[12:]]
yddata = [s['YD'] for s in pcex2.solutions[12:]]
cdata = [s['C'] for s in pcex2.solutions[12:]]
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 1.1, 1.1])
axes.tick_params(top=False, right=False)
axes.spines['top'].set_visible(False)
axes.spines['right'].set_visible(False)
axes.set_ylim(80, 116)
axes.plot(ydata, linestyle=':', color='b')
axes.plot(vdata, linestyle='-', color='r')
axes.plot(yddata, linestyle='-.', color='k')
axes.plot(cdata, linestyle='--', color='g')
# add labels
plt.text(15, 112, 'National income (GDP)')
plt.text(15, 101, 'Household wealth')
plt.text(8, 89, 'Disposable')
plt.text(8, 87.5, 'income')
plt.text(12, 84, 'Consumption')
fig.text(0.1, -0.1, caption);
```
###### Figure 4.10
```
caption = '''
Figure 4.10 Evolution of tax revenues and government expenditures including net
debt servicing, following an increase of 100 points in the rate of interest on bills,
in Model PCEX2 where the propensity to consume reacts negatively to higher
interest rates'''
tdata = list()
sumdata = list()
for i in range(12, len(pcex2.solutions)):
s = pcex2.solutions[i]
s_1 = pcex2.solutions[i-1]
sumdata.append( s['G'] + s_1['R']*s_1['Bh'])
tdata.append(s['T'])
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 1.1, 1.1])
axes.tick_params(top=False, right=False)
axes.spines['top'].set_visible(False)
axes.spines['right'].set_visible(False)
axes.set_ylim(20.5, 23)
axes.plot(sumdata, linestyle='-', color='r')
axes.plot(tdata, linestyle='--', color='k')
# add labels
plt.text(6, 22.9, 'Government expenditures plus net debt service')
plt.text(15, 22, 'Tax revenues')
fig.text(0.1, -0.15, caption);
```
| true |
code
| 0.576065 | null | null | null | null |
|
# Custom Mini-Batch and Training loop
### Imports
```
import Python
let request = Python.import("urllib.request")
let pickle = Python.import("pickle")
let gzip = Python.import("gzip")
let np = Python.import("numpy")
let plt = Python.import("matplotlib.pyplot")
import TensorFlow
```
### MNIST
Data
```
let result = request.urlretrieve(
"https://github.com/mnielsen/neural-networks-and-deep-learning/raw/master/data/mnist.pkl.gz",
"mnist.pkl.gz")
let filename = result[0]; filename
let mnist = pickle.load(gzip.open(filename), encoding:"latin-1")
// read train, validation and test datasets
let train_mnist = mnist[0]
let valid_mnist = mnist[1]
let test_mnist = mnist[2]
func unsequeeze(_ array: PythonObject, _ dtype: PythonObject = np.float32) -> PythonObject {
return np.expand_dims(array, axis:-1).astype(dtype)
}
// read training tuple into separate variables
let pyobj_train_x = train_mnist[0]
let pyobj_train_y = train_mnist[1].astype(np.int32) // expand dimension
// read validation tuple into separate variables
let pyobj_valid_x = valid_mnist[0]
let pyobj_valid_y = valid_mnist[1].astype(np.int32) // expand dimension
// read test tuple into separate variables
let pyobj_test_x = test_mnist[0]
let pyobj_test_y = test_mnist[1].astype(np.int32) // expand dimension
// read tensorflow arrays into Tensors
let X_train = Tensor<Float32>(numpy: pyobj_train_x)! // ! to unwrap optionals
let y_train = Tensor<Int32>(numpy: pyobj_train_y)! // ! to unwrap optionals
X_train.shape
```
Model
```
let m : Int = Int(X_train.shape[0]) // number of samples
let n_in: Int = Int(X_train.shape[1]) // number of features
let nh: Int = 50 // number of
let n_out: Int = 10 //number of classes
print("\(n_in) -> \(nh) -> \(n_out)")
struct Model: Layer {
var layer1 = Dense<Float>(inputSize: n_in, outputSize: nh, activation: relu)
var layer2 = Dense<Float>(inputSize: nh, outputSize: n_out)
@differentiable
func applied(to input: Tensor<Float>, in context: Context) -> Tensor<Float> {
return input.sequenced(in: context, through: layer1, layer2)
}
var description: String {
return "description here"
}
}
var model = Model()
let ctx = Context(learningPhase: .training)
// Apply the model to a batch of features.
let preds = model.applied(to: X_train, in: ctx)
preds[0..<2]
// test helper functions
func test_near_zero(_ val: Float32, _ msg: String) -> Void {
assert(val < 1e-3, msg)
}
func test_almost_eq(_ t1: Tensor<Float32>, _ t2: Tensor<Float32>, _ msg: String, _ epsilon: Float32 = 1e-3) -> Void {
assert(t1 - t2 < epsilon, msg)
}
```
### Custom loss function
We need to compute the softmax of our activations, then apply a log:
$$ i = \frac{e^{x_i}}{\sum_{0 \leq j \leq n-1} e^{x_j}} $$
```
func log_softmax(_ x: Tensor<Float>) -> Tensor<Float> {
let softmax = exp(x) / (exp(x).sum(alongAxes: -1))
return log(softmax)
}
```
with a sample check that our implementation is equal to tensorflow implementation
```
let x: Tensor<Float> = Tensor<Float>(arrayLiteral: [1, 2, 3, 4], [4, 3, 2, 1])
log_softmax(x)
logSoftmax(x)
test_almost_eq(log_softmax(x), logSoftmax(x), "Our impl should be same as Tensorflow impl")
let y_hat: Tensor<Float> = log_softmax(preds)
```
Given $x$ and its prediction $p(x)$, the **Cross Entropy** loss is:
$$ - \sum x \log p(x) $$
Now as the output of the NN is a 1-hot encoded array, we can rewrite the formula for the index $i$ of a desired target as follows:
$$-\log(p_{i})$$
Technically, if the predictions are of shape (m, 10) and target is (m, 1) then result should be `predictions[:, target]`.
```
let x1: Tensor<Float> = Tensor<Float>(arrayLiteral: [2], [3])
let x2: Tensor<Float> = log_softmax(x)
print("\(x1.shape) \(x2.shape)")
x2[1..<2]
let i: Int32 = 0
let pos: Int32 = Int32(x1[i][0].scalar!)
x2[i][pos].scalar!
```
Finnally a minually calculated loss looks like:
```
func nll(labels: Tensor<Int32>, logits: Tensor<Float>) -> Float {
let size = labels.shape[0]
var sum : Float = 0
for i in 0..<size {
let pos: Int32 = labels[i][0].scalar!
sum += logits[i][pos].scalar!
}
return sum / Float(size)
}
// our way
let loss1: Float = nll(labels: y_train, logits: y_hat)
// tensorflow-way
let loss2: Float = softmaxCrossEntropy(logits: preds, labels: y_train).scalar!
test_near_zero(loss1-loss2, "Loss manually calculated should be similar to Tensorflow-way")
```
Accuracy function:
```
func accuracy(_ logits: Tensor<Float>, _ labels: Tensor<Int32>) -> Float {
return Tensor<Float>(logits.argmax(squeezingAxis: -1) .== labels).mean().scalarized()
}
accuracy(preds, y_train)
```
### Basic training loop
- Grap a batch from the dataset
- Do a forward pass to get the output of the model on this batch
- compute a loss by comparint the output with the labels
- Do a backward pass to calculate the gradients of the loss
- update the model parameters with the gradients
```
let bs: Int32 = 64
// grap batch
let X_batch: Tensor<Float> = X_train[0..<bs]
let y_batch: Tensor<Int32> = y_train[0..<bs]
let ctx = Context(learningPhase: .training)
let (loss, grads) = model.valueWithGradient { model -> Tensor<Float> in
// forward pass
let preds = model.applied(to: X_batch, in: ctx)
// compute loss
return softmaxCrossEntropy(logits: preds, labels: y_batch)
}
// backward pass
/**
print("Current loss: \(loss)")
print("Current accuracy: \(accuracy(preds, y_batch))")
Continue from 47:00
*/
for l in model {
print(l)
}
```
| true |
code
| 0.663424 | null | null | null | null |
|
# Working with Unknown Dataset Sizes
This notebook demonstrates the features built into OpenDP to handle unknown or private dataset sizes.
### Load exemplar dataset
```
import os
data_path = os.path.join('.', 'data', 'PUMS_california_demographics_1000', 'data.csv')
with open(data_path) as data_file:
data = data_file.read()
```
By looking at the private data, we see this dataset has 1000 observations (rows).
Oftentimes the number of observations is public information.
For example, a researcher might run a random poll of 1000 respondents and publicly announce the sample size.
However, there are cases where simply the number of observations itself can leak private information.
For example, if a dataset contained all the individuals with a rare disease in a community,
then knowing the size of the dataset would reveal how many people in the community had that condition.
In general, any given dataset may be some well-defined subset of a population.
The given dataset's size is equivalent to a count query on that subset,
so we should protect the dataset size just as we would protect any other query we want to provide privacy guarantees for.
OpenDP assumes the sample size is private information.
If you know the dataset size (or any other parameter) is publicly available,
then you are free to make use of such information while building your measurement.
OpenDP will not assume you truthfully or correctly know the size of the dataset.
Moreover, OpenDP cannot respond with an error message if you get the size incorrect;
doing so would permit an attack whereby an analyst could repeatedly guess different dataset sizes until the error message went away,
thereby leaking the exact dataset size.
If we know the dataset size, we can incorporate it into the analysis as below,
where we provide `size` as an argument to the release of a sum on age.
While the "sum of ages" is not a particularly useful statistic, it's plenty capable of demonstrating the concept.
```
from opendp.trans import *
from opendp.meas import make_base_geometric
from opendp.mod import enable_features
enable_features("contrib")
# Define parameters up-front
# Each parameter is either a guess, a DP release, or public information
var_names = ["age", "sex", "educ", "race", "income", "married"] # public information
size = 1000 # public information
age_bounds = (0, 100) # an educated guess
constant = 38 # average age for entire US population (public information)
dp_sum = (
# Load data into a dataframe of string columns
make_split_dataframe(separator=",", col_names=var_names) >>
# Selects a column of df, Vec<str>
make_select_column(key="age", TOA=str) >>
# Cast the column as Vec<Int>
make_cast(TIA=str, TOA=int) >>
# Impute missing values to 0
make_impute_constant(constant) >>
# Clamp age values
make_clamp(bounds=age_bounds) >>
# Resize with the known `size`
make_bounded_resize(size=size, bounds=age_bounds, constant=constant) >>
# Aggregate
make_sized_bounded_sum(size=size, bounds=age_bounds) >>
# Noise
make_base_geometric(scale=1.)
)
release = dp_sum(data)
print("DP sum:", release)
```
### Providing incorrect dataset size values
However, if we provide an incorrect value of `n` we still receive an answer.
`make_sum_measurement` is just a convenience constructor for building a sum measurement from a `size` argument.
```
preprocessor = (
make_split_dataframe(separator=",", col_names=var_names) >>
make_select_column(key="age", TOA=str) >>
make_cast_default(TIA=str, TOA=int) >>
make_clamp(age_bounds)
)
def make_sum_measurement(size):
return make_bounded_resize(size=size, bounds=age_bounds, constant=constant) >> \
make_sized_bounded_sum(size=size, bounds=age_bounds) >> \
make_base_geometric(scale=1.0)
lower_n = (preprocessor >> make_sum_measurement(size=200))(data)
real_n = (preprocessor >> make_sum_measurement(size=1000))(data)
higher_n = (preprocessor >> make_sum_measurement(size=2000))(data)
print("DP sum (n=200): {0}".format(lower_n))
print("DP sum (n=1000): {0}".format(real_n))
print("DP sum (n=2000): {0}".format(higher_n))
```
### Analysis with no provided dataset size
If we do not believe we have an accurate estimate for `size` we can instead pay some of our privacy budget
to estimate the dataset size.
Then we can use that estimate in the rest of the analysis.
Here is an example:
```
# First, make the measurement
dp_count = (
make_split_dataframe(separator=",", col_names=var_names) >>
make_select_column(key="age", TOA=str) >>
make_count(TIA=str) >>
make_base_geometric(scale=1.)
)
dp_count_release = dp_count(data)
print("DP count: {0}".format(dp_count_release))
dp_sum = preprocessor >> make_sum_measurement(dp_count_release)
dp_sum_release = dp_sum(data)
print("DP sum: {0}".format(dp_sum_release))
```
Note that our privacy usage has increased because we apportioned some epsilon for both the release count of the dataset,
and the mean of the dataset.
### OpenDP `resize` vs. other approaches
The standard formula for the mean of a variable is:
$\bar{x} = \frac{\sum{x}}{n}$
The conventional, and simpler, approach in the differential privacy literature, is to:
1. compute a DP sum of the variable for the numerator
2. compute a DP count of the dataset rows for the denominator
3. take their ratio
This is sometimes called a 'plug-in' approach, as we are plugging-in differentially private answers for each of the
terms in the original formula, without any additional modifications, and using the resulting answer as our
estimate while ignoring the noise processes of differential privacy. While this 'plug-in' approach does result in a
differentially private value, the utility here is generally lower than the solution in OpenDP. Because the number of
terms summed in the numerator does not agree with the value in the denominator, the variance is increased and the
resulting distribution becomes both biased and asymmetrical, which is visually noticeable in smaller samples.
We have noticed that for the same privacy loss,
the distribution of answers from OpenDP's resizing approach to the mean is tighter around the true dataset value (thus lower in error) than the conventional plug-in approach.
*Note, in these simulations, we've shown equal division of the epsilon for all constituent releases,
but higher utility (lower error) can be generally gained by moving more of the epsilon into the sum,
and using less in the count of the dataset rows, as in earlier examples.*
| true |
code
| 0.464112 | null | null | null | null |
|
```
import glob
import os
import pickle
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
import datetime as dt
from ta import add_all_ta_features
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
```
#### Requirements
- pandas==0.25.1
- ta==0.4.7
- scikit-learn==21.3
#### Background on Trade Recommender Models
Trade recommender models were created with with the goal of predicting whether the price of a cryptocurrency will go up or down in the next time period (the period is determined by the specific model). If the time period for the model was 6hrs, and if the model predicted that the price will go up, that would mean that if you bought that cryptocurrency 6 hours after the prediction time (this time comes from the data point that the model is predicting off of), the price of the crypto should have gone up after 6 hours from the time that you bought it.
100s of iterations of models were generated in this notebook and the best ones were selected from each exchange/trading pair based on which iteration returned the highest net profit. When training the random forest classifier models, performance was highly varied with different periods and parameters so there was no one size fits all model, and that resulted in the models having unique periods and parameters. The data was obtained from the respective exchanges via their api, and models were trained on 1 hour candlestick data from 2015 - Oct 2018. The test set contained data from Jan 2019 - Oct 2019 with a two month gap left between the train and test sets to prevent data leakage. The models' predictions output 0 (sell) and 1 (buy) and profit was calculated by backtesting on the 2019 test set. The profit calculation incorporated fees like in the real world and considered any consecutive "buy" prediction as a "hold" trade instead so that fees wouldn't have to be paid on those transactions. The final models were all profitable with gains anywhere from 40% - 95% within the Jan 1, 2019 to Oct 30, 2019 time period. Visualizations for how these models performed given a $10K portfolio can be viewed at https://github.com/Lambda-School-Labs/cryptolytic-ds/blob/master/finalized_notebooks/visualization/tr_performance_visualization.ipynb
The separate models created for each exchange/trading pair combination were:
- Bitfinex BTC/USD
- Bitfinex ETH/USD
- Bitfinex LTC/USD
- Coinbase Pro BTC/USD
- Coinbase Pro ETH/USD
- Coinbase Pro LTC/USD
- HitBTC BTC/USD
- HitBTC ETH/USD
- HitBTC LTC/USD
##### Folder Structure:
├── trade_recommender/ <-- The top-level directory for all trade recommender work
│ │
│ ├── trade_rec_models.ipynb <-- Notebook for trade recommender models
│ │
│ ├── data/ <-- Directory for csv files of 1 hr candle data
│ │ └── data.csv
│ │
│ ├── pickles/ <-- Directory for all trade rec models
│ │ └── models.pkl
│ │
│ ├── tr_pickles/ <-- Directory for best trade rec models
└── models.pkl
### Get all csv filenames into a variable - 1 hr candles
```
csv_filenames = glob.glob('data/*.csv') # modify to your filepath for data
print(len(csv_filenames))
csv_filenames
```
# Functions
#### OHLCV Data Resampling
```
def resample_ohlcv(df, period):
""" Changes the time period on cryptocurrency ohlcv data.
Period is a string denoted by '{time_in_minutes}T'(ex: '1T', '5T', '60T')."""
# Set date as the index. This is needed for the function to run
df = df.set_index(['date'])
# Aggregation function
ohlc_dict = {'open':'first',
'high':'max',
'low':'min',
'close': 'last',
'base_volume': 'sum'}
# Apply resampling
df = df.resample(period, how=ohlc_dict, closed='left', label='left')
return df
```
#### Filling NaNs
```
# resample_ohlcv function will create NaNs in df where there were gaps in the data.
# The gaps could be caused by exchanges being down, errors from cryptowatch or the
# exchanges themselves
def fill_nan(df):
"""Iterates through a dataframe and fills NaNs with appropriate
open, high, low, close values."""
# Forward fill close column.
df['close'] = df['close'].ffill()
# Backward fill the open, high, low rows with the close value.
df = df.bfill(axis=1)
return df
```
#### Feature Engineering
```
def feature_engineering(df, period):
"""Takes in a dataframe of 1 hour cryptocurrency trading data
and returns a new dataframe with selected period, new technical analysis features,
and a target.
"""
# Add a datetime column to df
df['date'] = pd.to_datetime(df['closing_time'], unit='s')
# Convert df to selected period
df = resample_ohlcv(df, period)
# Add feature to indicate gaps in the data
df['nan_ohlc'] = df['close'].apply(lambda x: 1 if pd.isnull(x) else 0)
# Fill in missing values using fill function
df = fill_nan(df)
# Reset index
df = df.reset_index()
# Create additional date features
df['year'] = df['date'].dt.year
df['month'] = df['date'].dt.month
df['day'] = df['date'].dt.day
# Add technical analysis features
df = add_all_ta_features(df, "open", "high", "low", "close", "base_volume")
# Replace infinite values with NaNs
df = df.replace([np.inf, -np.inf], np.nan)
# Drop any features whose mean of missing values is greater than 20%
df = df[df.columns[df.isnull().mean() < .2]]
# Replace remaining NaN values with the mean of each respective column and reset index
df = df.apply(lambda x: x.fillna(x.mean()),axis=0)
# Create a feature for close price difference
df['close_diff'] = (df['close'] - df['close'].shift(1))/df['close'].shift(1)
# Function to create target
def price_increase(x):
if (x-(.70/100)) > 0:
return True
else:
return False
# Create target
target = df['close_diff'].apply(price_increase)
# To make the prediction before it happens, put target on the next observation
target = target[1:].values
df = df[:-1]
# Create target column
df['target'] = target
# Remove first row of dataframe bc it has a null target
df = df[1:]
# Pick features
features = ['open', 'high', 'low', 'close', 'base_volume', 'nan_ohlc',
'year', 'month', 'day', 'volume_adi', 'volume_obv', 'volume_cmf',
'volume_fi', 'volume_em', 'volume_vpt', 'volume_nvi', 'volatility_atr',
'volatility_bbh', 'volatility_bbl', 'volatility_bbm', 'volatility_bbhi',
'volatility_bbli', 'volatility_kcc', 'volatility_kch', 'volatility_kcl',
'volatility_kchi', 'volatility_kcli', 'volatility_dch', 'volatility_dcl',
'volatility_dchi', 'volatility_dcli', 'trend_macd', 'trend_macd_signal',
'trend_macd_diff', 'trend_ema_fast', 'trend_ema_slow',
'trend_adx_pos', 'trend_adx_neg', 'trend_vortex_ind_pos',
'trend_vortex_ind_neg', 'trend_vortex_diff', 'trend_trix',
'trend_mass_index', 'trend_cci', 'trend_dpo', 'trend_kst',
'trend_kst_sig', 'trend_kst_diff', 'trend_ichimoku_a',
'trend_ichimoku_b', 'trend_visual_ichimoku_a', 'trend_visual_ichimoku_b',
'trend_aroon_up', 'trend_aroon_down', 'trend_aroon_ind', 'momentum_rsi',
'momentum_mfi', 'momentum_tsi', 'momentum_uo', 'momentum_stoch',
'momentum_stoch_signal', 'momentum_wr', 'momentum_ao',
'others_dr', 'others_dlr', 'others_cr', 'close_diff', 'date', 'target']
df = df[features]
return df
```
#### Profit and Loss function
```
def performance(X_test, y_preds):
""" Takes in a test dataset and a model's predictions, calculates and returns
the profit or loss. When the model generates consecutive buy predictions,
anything after the first one are considered a hold and fees are not added
for the hold trades. """
fee_rate = 0.35
# creates dataframe for features and predictions
df_preds = X_test
df_preds['y_preds'] = y_preds
# creates column with 0s for False predictions and 1s for True predictions
df_preds['binary_y_preds'] = df_preds['y_preds'].shift(1).apply(lambda x: 1 if x == True else 0)
# performance results from adding the closing difference percentage of the rows where trades were executed
performance = ((10000 * df_preds['binary_y_preds']*df_preds['close_diff']).sum())
# calculating fees and improve trading strategy
# creates a count list for when trades were triggered
df_preds['preds_count'] = df_preds['binary_y_preds'].cumsum()
# feature that determines the instance of whether the list increased
df_preds['increase_count'] = df_preds['preds_count'].diff(1)
# feature that creates signal of when to buy(1), hold(0), or sell(-1)
df_preds['trade_trig'] = df_preds['increase_count'].diff(1)
# number of total entries(1s)
number_of_entries = (df_preds.trade_trig.values==1).sum()
# performance takes into account fees given the rate at the beginning of this function
pct_performance = ((df_preds['binary_y_preds']*df_preds['close_diff']).sum())
# calculate the percentage paid in fees
fees_pct = number_of_entries * 2 * fee_rate/100
# calculate fees in USD
fees = number_of_entries * 2 * fee_rate / 100 * 10000
# calculate net profit in USD
performance_net = performance - fees
# calculate net profit percent
performance_net_pct = performance_net/10000
return pct_performance, performance, fees, performance_net, performance_net_pct
```
#### Modeling Pipeline
```
def modeling_pipeline(csv_filenames, periods=['360T','720T','960T','1440T']):
"""Takes csv file paths of data for modeling, performs feature engineering,
train/test split, creates a model, reports train/test score, and saves
a pickle file of the model in a directory called /pickles. The best models
are moved to a directory called tr_pickles at the end"""
line = '------------'
performance_list = []
for file in csv_filenames:
# define model name
name = file.split('/')[1][:-9]
# read csv
csv = pd.read_csv(file, index_col=0)
for period in periods:
max_depth_list = [17]
# max_depth_list = [17, 20, 25, 27]
for max_depth in max_depth_list:
max_features_list = [40]
# max_features_list = [40, 45, 50, 55, 60]
for max_features in max_features_list:
print(line + name + ' ' + period + ' ' + str(max_depth) + ' ' + str(max_features) + line)
# create a copy of the csv
df = csv.copy()
# engineer features
df = feature_engineering(df, period)
# train test split
train = df[df['date'] < '2018-10-30 23:00:00'] # cutoff oct 30 2018
test = df[df['date'] > '2019-01-01 23:00:00'] # cutoff jan 01 2019
print('train and test shape ({model}):'.format(model=name), train.shape, test.shape)
# features and target
features = df.drop(columns=['target', 'date']).columns.tolist()
target = 'target'
# define X, y vectors
X_train = train[features]
X_test = test[features]
y_train = train[target]
y_test = test[target]
# instantiate model
model = RandomForestClassifier(max_features=max_features,
max_depth=max_depth,
n_estimators=100,
n_jobs=-1,
random_state=42)
try:
# filter out datasets that are too small
if X_test.shape[0] > 500:
# fit model
model.fit(X_train, y_train)
print('model fitted')
# train accuracy
train_score = model.score(X_train, y_train)
print('train accuracy:', train_score)
# make predictions
y_preds = model.predict(X_test)
print('predictions made')
# test accuracy
score = accuracy_score(y_test, y_preds)
print('test accuracy:', score)
# get profit and loss
a, b, c, d, e = performance(X_test, y_preds)
print(f'net profits: {str(round(d,2))}')
# formatting for filename
t = period[:-1]
# download pickle
(pickle.dump(model, open('pickles/{model}_{t}_{max_features}_{max_depth}.pkl'
.format(model=name, t=t,
max_features=str(max_features),
max_depth=str(max_depth)), 'wb')))
print('{model} pickle saved!\n'.format(model=name))
# save net performance to list
performance_list.append([f'{name}', period, max_features, max_depth, a, b, c , d, e])
else:
print('{model} does not have enough data!\n'.format(model=name))
except:
print('error with model')
# create dataframe for model performance
df = pd.DataFrame(performance_list, columns = ['ex_tp', 'period', 'max_features',
'max_depth','pct_gain','gain', 'fees',
'net_profit', 'pct_net_profit'])
# sort by net profit descending and drop duplicates
df2 = df.sort_values(by='net_profit', ascending=False).drop_duplicates(subset='ex_tp')
# get the names, periods, max_features, max_depth for best models
models = df2['ex_tp'].values
periods = df2['period'].values
max_features = df2['max_features'].values
max_depth = df2['max_depth'].values
# save the best models in a new directory /tr_pickles
for i in range(len(models)):
model_name = models[i] + '_' + periods[i][:-1] + '_' + str(max_features[i]) + '_' + str(max_depth[i])
os.rename(f'pickles/{model_name}.pkl', f'tr_pickles/{models[i]}.pkl')
# returning the dataframes for model performance
# df1 contains performance for all models trained
# df2 contains performance for best models
return df, df2
periods=['360T']
df, df2 = modeling_pipeline(csv_filenames, periods)
```
## training models with specific parameters
This part is not necessary if you do the above. It's for when you want to only train the best models if you know the parameters so you don't have to train 100s of models
```
def modeling_pipeline(csv_filenames, param_dict):
"""Takes csv file paths of data for modeling and parameters, performs feature engineering,
train/test split, creates a model, reports train/test score, and saves
a pickle file of the model in a directory called /pickles."""
line = '------------'
performance_list = []
for file in csv_filenames:
# define model name
name = file.split('/')[1][:-9]
# read csv
df = pd.read_csv(file, index_col=0)
params = param_dict[name]
print(params)
period = params['period']
print(period)
max_features = params['max_features']
max_depth = params['max_depth']
print(line + name + ' ' + period + line)
# engineer features
df = feature_engineering(df, period)
# train test split
train = df[df['date'] < '2018-10-30 23:00:00'] # cutoff oct 30 2018
test = df[df['date'] > '2019-01-01 23:00:00'] # cutoff jan 01 2019
print('train and test shape ({model}):'.format(model=name), train.shape, test.shape)
# features and target
features = df.drop(columns=['target', 'date']).columns.tolist()
target = 'target'
# define X, y vectors
X_train = train[features]
X_test = test[features]
y_train = train[target]
y_test = test[target]
# instantiate model
model = RandomForestClassifier(max_features=max_features,
max_depth=max_depth,
n_estimators=100,
n_jobs=-1,
random_state=42)
# fit model
if X_train.shape[0] > 500:
model.fit(X_train, y_train)
print('model fitted')
# train accuracy
train_score = model.score(X_train, y_train)
print('train accuracy:', train_score)
# make predictions
y_preds = model.predict(X_test)
print('predictions made')
# test accuracy
score = accuracy_score(y_test, y_preds)
print('test accuracy:', score)
# get profit and loss
a, b, c, d, e = performance(X_test, y_preds)
print(f'net profits: {str(round(d,2))}')
# formatting for filename
t = period[:-1]
# download pickle
pickle.dump(model, open('pickles/{model}_{t}.pkl'.format(model=name, t=t,), 'wb'))
print('{model} pickle saved!\n'.format(model=name))
# save net performance to list
performance_list.append([f'{name}', period, a, b, c , d, e])
else:
print('{model} does not have enough data!\n'.format(model=name))
# create df of model performance
df = pd.DataFrame(performance_list, columns = ['ex_tp', 'period', 'pct_gain',
'gain', 'fees', 'net_profit', 'pct_net_profit'])
# sort performance by net_profit and drop duplicates
df2 = df.sort_values(by='net_profit', ascending=False).drop_duplicates(subset='ex_tp')
models = df2['ex_tp'].values
periods = df2['period'].values
# move models to new dir tr_pickles
for i in range(len(models)):
model_name = models[i] + '_' + periods[i][:-1]
os.rename(f'pickles/{model_name}.pkl', f'tr_pickles/{models[i]}.pkl')
# returning the dataframes for model performance
# df1 contains performance for all models trained
# df2 contains performance for best models
return df, df2
param_dict = {'bitfinex_ltc_usd': {'period': '1440T', 'max_features': 50, 'max_depth': 20},
'hitbtc_ltc_usdt': {'period': '1440T', 'max_features': 45, 'max_depth': 27},
'coinbase_pro_ltc_usd': {'period': '960T', 'max_features': 50, 'max_depth': 17},
'hitbtc_btc_usdt': {'period': '360T', 'max_features': 40, 'max_depth': 17},
'coinbase_pro_btc_usd': {'period': '960T', 'max_features': 55, 'max_depth': 25},
'coinbase_pro_eth_usd': {'period': '960T', 'max_features': 50, 'max_depth': 27},
'bitfinex_btc_usd': {'period': '1200T', 'max_features': 55, 'max_depth': 25},
'bitfinex_eth_usd': {'period': '1200T', 'max_features': 60, 'max_depth': 20}
}
# 'hitbtc_eth_usdt': {'period': '1440T', 'max_depth': 50}
# ^ this cant go in param dict bc its trained differently
csv_paths = csv_filenames.copy()
del csv_paths[4]
print(csv_paths)
print(len(csv_paths))
len(csv_filenames)
df, df2 = modeling_pipeline(csv_paths)
```
#### train hitbtc eth_usdt model separately - was a special case where it performed better with less parameters
```
# for the hitbtc eth usdt model
def modeling_pipeline(csv_filenames):
"""Takes csv file paths of data for modeling, performs feature engineering,
train/test split, creates a model, reports train/test score, and saves
a pickle file of the model in a directory called /pickles."""
line = '------------'
performance_list = []
for file in csv_filenames:
# define model name
name = file.split('/')[1][:-9]
# read csv
df = pd.read_csv(file, index_col=0)
period = '1440T'
print(period)
print(line + name + ' ' + period + line)
# engineer features
df = feature_engineering(df, period)
# train test split
train = df[df['date'] < '2018-10-30 23:00:00'] # cutoff oct 30 2018
test = df[df['date'] > '2019-01-01 23:00:00'] # cutoff jan 01 2019
print('train and test shape ({model}):'.format(model=name), train.shape, test.shape)
# features and target
features = df.drop(columns=['target', 'date']).columns.tolist()
target = 'target'
# define X, y vectors
X_train = train[features]
X_test = test[features]
y_train = train[target]
y_test = test[target]
# instantiate model
model = RandomForestClassifier(max_depth=50,
n_estimators=100,
n_jobs=-1,
random_state=42)
# filter out datasets that are too small
if X_train.shape[0] > 500:
# fit model
model.fit(X_train, y_train)
print('model fitted')
# train accuracy
train_score = model.score(X_train, y_train)
print('train accuracy:', train_score)
# make predictions
y_preds = model.predict(X_test)
print('predictions made')
# test accuracy
score = accuracy_score(y_test, y_preds)
print('test accuracy:', score)
# get profit and loss
a, b, c, d, e = performance(X_test, y_preds)
print(f'net profits: {str(round(d,2))}')
# formatting for filename
t = period[:-1]
# download pickle
pickle.dump(model, open('pickles/{model}_{t}.pkl'.format(model=name, t=t,), 'wb'))
print('{model} pickle saved!\n'.format(model=name))
# save net performance to list
performance_list.append([f'{name}', period, a, b, c , d, e])
else:
print('{model} does not have enough data!\n'.format(model=name))
# create df of model performance
df = pd.DataFrame(performance_list, columns = ['ex_tp', 'period', 'pct_gain',
'gain', 'fees', 'net_profit', 'pct_net_profit'])
models = df2['ex_tp'].values
periods = df2['period'].values
# move model to new dir tr_pickles
for i in range(len(models)):
model_name = models[i] + '_' + periods[i][:-1]
os.rename(f'pickles/{model_name}.pkl', f'tr_pickles/{models[i]}.pkl')
# returning the dataframes for model performance
# df1 contains performance for all models trained
# df2 contains performance for best models
return df, df2
filepath = ['data/hitbtc_eth_usdt_3600.csv']
df, df2 = modeling_pipeline(filepath)
```
## What's next?
- neural networks
- implement NLP with data scraped from twitter to see how frequency of crypto discussion affects the predictions
- more exchange/trading pair support
| true |
code
| 0.594434 | null | null | null | null |
|
# Amazon sentiment analysis: Structural correspondence learning
Data downloaded from: processed_acl.tar.gz, processed for John Blitzer, Mark Dredze, Fernando Pereira. Biographies, Bollywood, Boom-boxes and Blenders: Domain Adaptation for Sentiment Classification. Association of Computational Linguistics (ACL), 2007
Method is based on the above paper and the [original SCL paper](http://john.blitzer.com/papers/emnlp06.pdf)
```
import numpy as np
import matplotlib.pyplot as plt
from read_funcs import organise_data, vectorise_data, select_high_freq_data
%matplotlib inline
from sklearn.preprocessing import Binarizer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import mutual_info_score
src = 'dvd'
tgt = 'kitchen'
XB, Y_src, XD, Y_tgt = organise_data(src, tgt)
# Vectorise the raw data
X_src, X_tgt, features = vectorise_data(XB, XD)
# Reduce the no. of features
N = 10000
X_src, X_tgt, features = select_high_freq_data(X_src, X_tgt, features, N)
# Visualise the difference in the frequent features
B_count = np.sum(X_src,0)
D_count = np.sum(X_tgt,0)
plt.plot(B_count[-3:-100:-1])
plt.plot(D_count[-3:-100:-1])
plt.legend([src, tgt])
```
## 1. Select pivot features
```
def compute_mutual_info(X, Y):
N = X.shape[1]
mutual_info = []
for i in range(N):
mutual_info.append(mutual_info_score(X[:,i], Y))
return mutual_info
mutual_info_src = compute_mutual_info(X_src, Y_src)
sort_idx = np.argsort(mutual_info_src)
m = 50
pivot_features = [features[i] for i in sort_idx[-m:]]
print(np.asarray(pivot_features[-1:-20:-1]))
```
## 2. Pivot predictor
```
# Binarise the data
X = np.r_[X_src, X_tgt]
binarizer = Binarizer().fit(X)
X_bin = binarizer.transform(X)
plt.plot(X_bin[:,10])
W = np.zeros((X.shape[1], m))
for i in range(m):
Y_pivot = X_bin[:, sort_idx[-i]]
model = LogisticRegression(C = 1)
model.fit(X_bin, Y_pivot)
W[:, i] = model.coef_
```
## 3. Low-dimensional feature space
```
u, s, vh = np.linalg.svd(W, full_matrices=False)
# Visualise low-dimensional space
u1 = u[:,2]
u1_sorted = sorted(range(len(u1)), key=lambda i: u1[i])
u1_pos_subspace = [features[i] for i in u1_sorted[-1:-21:-1]]
u1_neg_subspace = [features[i] for i in u1_sorted[:20]]
print(np.asarray(u1_pos_subspace))
print(np.asarray(u1_neg_subspace))
plt.plot(s[:10])
# The low dimensional subspace from the third components show confusing features
l = 50
theta = u[:,:l]
theta.shape
```
## 4. Prediction using enhanced feature space
```
# Baseline Classifier
model_BL= LogisticRegression(C = 1) # Regularisation parameter C
model_BL.fit(X_src, Y_src)
print('train {:s} acc: {:.3f}, test {:s} acc: {:.3f}'\
.format(src, model_BL.score(X_src, Y_src), tgt, model_BL.score(X_tgt,Y_tgt)))
def tune_reg_param_unsupervised(C_test, X_src_SCL, Y_src, X_tgt, Y_tgt, dev_size):
X_train, X_dev, Y_train, Y_dev = train_test_split(X_src_SCL, Y_src, test_size = dev_size, random_state = 3)
acc_train = []
acc_dev = []
for C in C_test:
model_SCL = LogisticRegression(C = C)
model_SCL.fit(X_train, Y_train)
acc_train.append(model_SCL.score(X_train, Y_train))
acc_dev.append(model_SCL.score(X_dev, Y_dev))
C_opt = C_test[np.argmax(acc_dev)]
model_SCL = LogisticRegression(C = C_opt)
model_SCL.fit(X_train, Y_train)
print('optimal alpha', C_opt, 'max acc', max(acc_dev),'test acc', model_SCL.score(X_tgt, Y_tgt))
plt.plot(C_test, acc_train)
plt.plot(C_test, acc_dev)
# Enhanced feature space
scale_factor = 1
# scale_factor = X_mean/X_SCL_mean*5
X_src_SCL = np.c_[X_src, scale_factor*np.dot(X_src, theta)]
X_tgt_SCL = np.c_[X_tgt, scale_factor*np.dot(X_tgt, theta)]
C_test = np.linspace(0.01,0.5,20)
tune_reg_param_unsupervised(C_test, X_src_SCL, Y_src, X_tgt_SCL, Y_tgt, 0.1)
```
## Scaling of enhanced feature in SCL
**The 2006 work scaled the enhanced feature such that their $\ell_1$ norm is 5 times the original features.**
```
X_l1 = np.sum(np.abs(X_src))
X_SCL_l1 = np.sum(np.abs(np.dot(X_src, theta)))
print(X_SCL_l1/X_l1)
scale_factor = X_l1/X_SCL_l1*5
print('scaling factor for 5 times l1 norm in enhanced feature space', scale_factor)
X_src_SCL = np.c_[X_src, scale_factor*np.dot(X_src, theta)]
X_tgt_SCL = np.c_[X_tgt, scale_factor*np.dot(X_tgt, theta)]
C_test = np.linspace(0.01,1,20)
tune_reg_param_unsupervised(C_test, X_src_SCL, Y_src, X_tgt_SCL, Y_tgt, 200)
# Try using only the low-dimensional space
X_src_SCL2 = np.dot(X_src, theta)
X_tgt_SCL2 = np.dot(X_tgt, theta)
C_test = np.linspace(0.01,1,20)
tune_reg_param_unsupervised(C_test, X_src_SCL2, Y_src, X_tgt_SCL2, Y_tgt, 200)
# Try out different scale factors
scale_list = [1]+[5*(i+1) for i in range(10)]
scale_acc = []
for i in range(11):
scale_factor = scale_list[i]
X_src_SCL = np.c_[X_src, scale_factor*np.dot(X_src, theta)]
X_tgt_SCL = np.c_[X_tgt, scale_factor*np.dot(X_tgt, theta)]
model_SCL= LogisticRegression(C = 0.06) # Regularisation parameter C
model_SCL.fit(X_src_SCL, Y_src)
scale_acc.append(model_SCL.score(X_tgt_SCL,Y_tgt))
plt.plot(scale_list, scale_acc)
# Weights of the pivot features
u_pivot = u[sort_idx[-m:],:]
u_non_pivot = u[sort_idx[:-m],:]
print('pivot mean/Non pivot mean: ', np.mean(abs(u_pivot))/np.mean(abs(u_non_pivot)))
```
## Finding the subspace of non-pivot feature only
Given the results above, the pivot features have 16 as much weight as the non-pivot ones. Is SCL simply enhancing the pivot features? Would the subspace trained on non-pivot features work too?
```
# Select non-pivot features
X_bin_non = X_bin[:, sort_idx[:-m]]
X_bin_non.shape
from sklearn.linear_model import LogisticRegression
W_non = np.zeros((X_bin_non.shape[1], m))
for i in range(m):
Y_pivot = X_bin[:, sort_idx[-i]]
model = LogisticRegression(C = 1)
model.fit(X_bin_non, Y_pivot)
W_non[:, i] = model.coef_
u_non, s, vh = np.linalg.svd(W_non, full_matrices=False)
non_pivot_features = [features[i] for i in sort_idx[:-m]]
u1 = u_non[:,3]
u1_sorted = sorted(range(len(u1)), key=lambda i: u1[i])
u1_pos_subspace = [non_pivot_features[i] for i in u1_sorted[-1:-21:-1]]
u1_neg_subspace = [non_pivot_features[i] for i in u1_sorted[:20]]
print(np.asarray(u1_pos_subspace))
print(np.asarray(u1_neg_subspace))
l = 50
theta = u_non[:,:l]
theta.shape
# Train a classifier with enhanced subspace
X_src_SCL_non = np.c_[X_src, np.dot(X_src[:, sort_idx[:-m]], theta)]
X_tgt_SCL_non = np.c_[X_tgt, np.dot(X_tgt[:, sort_idx[:-m]], theta)]
C_test = np.linspace(0.01,1,20)
tune_reg_param_unsupervised(C_test, X_src_SCL_non, Y_src, X_tgt_SCL_non, Y_tgt, 200)
```
| true |
code
| 0.487795 | null | null | null | null |
|
# Understanding Deepfakes with Keras
```
!pip3 install tensorflow==2.1.0 pillow matplotlib
!pip3 install git+https://github.com/am1tyadav/tfutils.git
%matplotlib notebook
import tensorflow as tf
import numpy as np
import os
import tfutils
from matplotlib import pyplot as plt
from tensorflow.keras.layers import Dense, Flatten, Conv2D, BatchNormalization
from tensorflow.keras.layers import Conv2DTranspose, Reshape, LeakyReLU
from tensorflow.keras.models import Model, Sequential
from PIL import Image
print('TensorFlow version:', tf.__version__)
```
# Importing and Plotting the Data
```
# download the MNIST dataset, unzip the data, pre-process it, normalize it
# this done by the code given in (https://github.com/am1tyadav/tfutils/tree/master/tfutils)
(x_train, y_train), (x_test, y_test) = tfutils.datasets.mnist.load_data(one_hot=False)
# eachc image is 28X28, we use only zeros
x_train = tfutils.datasets.mnist.load_subset([0], x_train, y_train)
x_test = tfutils.datasets.mnist.load_subset([0], x_test, y_test)
# combine both the training and testing sets
x = np.concatenate([x_train, x_test], axis=0)
# plot some training samples
tfutils.datasets.mnist.plot_ten_random_examples(plt, x, np.zeros((x.shape[0], 1))).show()
```
# Discriminator
```
# Using the same idea as mentioned in https://arxiv.org/pdf/1503.03832.pdf
size = 28
noise_dim = 1
discriminator = Sequential([
Conv2D(64, 3, strides=2, input_shape=(28, 28, 1)),
LeakyReLU(),
BatchNormalization(),
Conv2D(128, 5, strides=2),
LeakyReLU(),
BatchNormalization(),
Conv2D(256, 5, strides=2),
LeakyReLU(),
BatchNormalization(),
Flatten(),
Dense(1, activation='sigmoid')
])
opt = tf.keras.optimizers.Adam(lr=2e-4, beta_1=0.5)
discriminator.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
discriminator.summary()
```
# Generator
```
generator = Sequential([
Dense(256, activation='relu', input_shape=(noise_dim,)),
Reshape((1, 1, 256)),
Conv2DTranspose(256, 5, activation='relu'),
BatchNormalization(),
Conv2DTranspose(128, 5, activation='relu'),
BatchNormalization(),
Conv2DTranspose(64, 5, strides=2, activation='relu'),
BatchNormalization(),
Conv2DTranspose(32, 5, activation='relu'),
BatchNormalization(),
Conv2DTranspose(1, 4, activation='sigmoid')
])
generator.summary()
# visualize thegenrated image without training
noise = np.random.randn(1, noise_dim) # there is only one prediction
generated_images = generator.predict(noise) # there is only one prediction
gen_image = generated_images[0] # to bring the plotting sahpe to (28,28,1)
# gen_image = generator.predict(noise)[0]
plt.figure()
plt.imshow(np.reshape(gen_image, (28, 28)), cmap='binary')
```
# Generative Adversarial Network (GAN)
```
# We have discriminator and generator netoworks. The following will connect both the networks
input_layer = tf.keras.layers.Input(shape=(noise_dim,)) # noise input
gen_out = generator(input_layer) # create noise
disc_out = discriminator(gen_out) # ask the discriminator to determine if the input is real or fake
gan = Model(
input_layer,
disc_out
)
discriminator.trainable = False # to train the generator, later change this to True for
# training discriminator. Should train either Generator or
# discriminator and not both at the same time
gan.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
gan.summary()
```
# Training the GAN
```
%%time
epochs = 25
batch_size = 128
steps_per_epoch = int(2 * x.shape[0]/batch_size)
print('Steps per epoch=', steps_per_epoch)
dp = tfutils.plotting.DynamicPlot(plt, 5, 5, (8, 8))
for e in range(0, epochs):
dp.start_of_epoch(e)
for step in range(0, steps_per_epoch):
true_examples = x[int(batch_size/2)*step: int(batch_size/2)*(step + 1)]
true_examples = np.reshape(true_examples, (true_examples.shape[0], 28, 28, 1))
noise = np.random.randn(int(batch_size/2), noise_dim)
generated_examples = generator.predict(noise)
x_batch = np.concatenate([generated_examples, true_examples], axis=0)
y_batch = np.array([0] * int(batch_size/2) + [1] * int(batch_size/2))
indices = np.random.choice(range(batch_size), batch_size, replace=False)
x_batch = x_batch[indices]
y_batch = y_batch[indices]
# train the discriminator
discriminator.trainable = True
discriminator.train_on_batch(x_batch, y_batch) # first train disc, then set it to False
discriminator.trainable = False
# train the generator
loss, _ = gan.train_on_batch(noise, np.ones((int(batch_size/2), 1))) # to train the gan network (generator alone)
_, acc = discriminator.evaluate(x_batch, y_batch, verbose=False) # high acc - discriminator is doing good job
noise = np.random.randn(1, noise_dim)
generated_example = generator.predict(noise)[0]
dp.end_of_epoch(np.reshape(generated_example, (28, 28)), 'binary',
'DiscAcc:{:.2f}'.format(acc), 'GANLoss:{:.2f}'.format(loss))
```
| true |
code
| 0.85226 | null | null | null | null |
|
# Backtest a Single Model
The way to gauge the performance of a time-series model is through re-training models with different historic periods and check their forecast within certain steps. This is similar to a time-based style cross-validation. More often, we called it `backtest` in time-series modeling.
The purpose of this notebook is to illustrate how to do 'backtest' on a single model using `BackTester`
`BackTester` will compose a `TimeSeriesSplitter` within it, but `TimeSeriesSplitter` is useful as a standalone, in case there are other tasks to perform that requires splitting but not backtesting. You can also retrieve the composed `TimeSeriesSplitter` object from `BackTester` to utilize the additional methods in `TimeSeriesSplitter`
Currently, there are two schemes supported for the back-testing engine: expanding window and rolling window.
* expanding window: for each back-testing model training, the train start date is fixed, while the train end date is extended forward.
* rolling window: for each back-testing model training, the training window length is fixed but the window is moving forward.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from orbit.models import DLT
from orbit.diagnostics.backtest import BackTester, TimeSeriesSplitter
from orbit.diagnostics.plot import plot_bt_predictions
from orbit.diagnostics.metrics import smape, wmape
from orbit.utils.dataset import load_iclaims
from orbit.utils.plot import get_orbit_style
%load_ext autoreload
%autoreload 2
%reload_ext autoreload
```
## Load data
```
raw_data = load_iclaims()
data = raw_data.copy()
print(data.shape)
data.head(5)
```
## Create a BackTester
```
# instantiate a model
dlt = DLT(date_col='week',
response_col='claims',
regressor_col=['trend.unemploy', 'trend.filling', 'trend.job'],
seasonality=52,
estimator='stan-map')
bt = BackTester(model=dlt,
df=data,
min_train_len=100,
incremental_len=100,
forecast_len=20)
```
## Backtest Fit and Predict
The most expensive portion of backtesting is fitting the model iteratively. Thus, we separate the API calls for `fit_predict` and `score` to avoid redundant computation for multiple metrics or scoring methods.
```
bt.fit_predict();
```
Once `fit_predict()` is called, the fitted models and predictions can be easily retrieved from `BackTester`. Here the data is grouped by the date, split_key, and whether or not that observation is part of the training or test data.
```
predicted_df = bt.get_predicted_df()
predicted_df.head()
```
We also provide a plotting utility to visualize the predictions against the actuals for each split.
```
plot_bt_predictions(predicted_df, metrics=smape, ncol=2, include_vline=True);
```
Users might find this useful for any custom computations that may need to be performed on the set of predicted data. Note that the columns are renamed to generic and consistent names.
Sometimes, it might be useful to match the data back to the original dataset for ad-hoc diagnostics. This can easily be done by merging back to the orignal dataset
```
predicted_df.merge(data, left_on='date', right_on='week')
```
## Backtest Scoring
The main purpose of `BackTester` are the evaluation metrics. Some of the most widely used metrics are implemented and built into the `BackTester` API.
The default metric list is **smape, wmape, mape, mse, mae, rmsse**.
```
bt.score()
```
It is possible to filter for only specific metrics of interest, or even implement your own callable and pass into the `score()` method. For example, see this function that uses last observed value as a predictor and computes the `mse`. Or `naive_error` which computes the error as the delta between predicted values and the training period mean.
Note these are not really useful error metrics, just showing some examples of callables you can use ;)
```
def mse_naive(test_actual):
actual = test_actual[1:]
predicted = test_actual[:-1]
return np.mean(np.square(actual - predicted))
def naive_error(train_actual, test_predicted):
train_mean = np.mean(train_actual)
return np.mean(np.abs(test_predicted - train_mean))
bt.score(metrics=[mse_naive, naive_error])
```
It doesn't take additional time to refit and predict the model, since the results are stored when `fit_predict()` is called. Check docstrings for function criteria that is required for it to be supported with this API.
In some cases, we may want to evaluate our metrics on both train and test data. To do this you can call score again with the following indicator
```
bt.score(include_training_metrics=True)
```
## Backtest Get Models
In cases where `BackTester` doesn't cut it or for more custom use-cases, there's an interface to export the `TimeSeriesSplitter` and predicted data, as shown earlier. It's also possible to get each of the fitted models for deeper diving.
```
fitted_models = bt.get_fitted_models()
model_1 = fitted_models[0]
model_1.get_regression_coefs()
```
### Get TimeSeriesSplitter
BackTester composes a TimeSeriesSplitter within it, but TimeSeriesSplitter can also be created on its own as a standalone object. See section below on TimeSeriesSplitter for more details on how to use the splitter.
All of the additional TimeSeriesSplitter args can also be passed into BackTester on instantiation
```
ts_splitter = bt.get_splitter()
ts_splitter.plot()
plt.grid();
```
## Appendix
### Create a TimeSeriesSplitter
#### Expanding window
```
min_train_len = 380
forecast_len = 20
incremental_len = 20
ex_splitter = TimeSeriesSplitter(df=data,
min_train_len=min_train_len,
incremental_len=incremental_len,
forecast_len=forecast_len,
window_type='expanding',
date_col='week')
print(ex_splitter)
ex_splitter.plot()
plt.grid();
```
#### Rolling window
```
roll_splitter = TimeSeriesSplitter(df=data,
min_train_len=min_train_len,
incremental_len=incremental_len,
forecast_len=forecast_len,
window_type='rolling',
date_col='week')
roll_splitter.plot()
plt.grid();
```
#### Specifying number of splits
User can also define number of splits using `n_splits` instead of specifying minimum training length. That way, minimum training length will be automatically calculated.
```
ex_splitter2 = TimeSeriesSplitter(df=data,
min_train_len=min_train_len,
incremental_len=incremental_len,
forecast_len=forecast_len,
n_splits=5,
window_type='expanding',
date_col='week')
ex_splitter2.plot()
plt.grid();
```
| true |
code
| 0.575946 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/ksdkamesh99/LowLightEnhancer/blob/master/model_gradient.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive')
cd /content/drive/My Drive/LowLightEnhancement
import tensorflow as tf
import keras
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
img_high=np.load("image_high.npy")
img_low=np.load("image_low.npy")
img_low=img_low/255
img_high=img_high/255
img_high.shape
plt.imshow(img_low[0])
```
## Illumination Mask Network
```
input_layer_1=keras.layers.Input(shape=(96,96,3))
top=keras.layers.Conv2D(64,kernel_size=(3,3),input_shape=(96,96,3),padding='same')(input_layer_1)
top=keras.layers.Conv2D(64,kernel_size=(3,3),padding='same')(top)
top.get_shape
bottom_inp=input_layer_1
bottom_resize=tf.keras.layers.Lambda(
lambda img: tf.image.resize(img,(60,60))
)(bottom_inp)
bottom=keras.layers.Conv2D(64,kernel_size=(3,3),input_shape=(60,60,3),padding='same')(bottom_resize)
bottom=keras.layers.Conv2D(64,kernel_size=(3,3),padding='same')(bottom)
bottom=keras.layers.Conv2D(64,kernel_size=(3,3),padding='same')(bottom)
bottom.get_shape()
bottom=keras.layers.experimental.preprocessing.Resizing(96,96)(bottom)
bottom.get_shape()
top.get_shape()
merged=keras.layers.concatenate([top,bottom])
merged
merged=keras.layers.Conv2D(32,kernel_size=(7,7),padding='same')(merged)
merged=keras.layers.Conv2D(8,kernel_size=(1,1),padding='same')(merged)
merged=keras.layers.Conv2D(1,kernel_size=(5,5),activation='sigmoid',padding='same')(merged)
merged.get_shape()
model_illumination_mask=keras.models.Model(inputs=input_layer_1,outputs=merged)
model_illumination_mask.summary()
```
# Illumination Map
```
merged.get_shape
merged=keras.layers.Concatenate()([input_layer_1,merged])
merged
def ieb(input_feature):
ieb1=keras.layers.Conv2D(32,kernel_size=(3,3),activation='relu',padding='same')(input_feature)
ieb1=keras.layers.Conv2D(32,kernel_size=(3,3),activation='relu',padding='same')(ieb1)
max_pool=keras.layers.GlobalMaxPooling2D()(ieb1)
avg_pool=keras.layers.GlobalAveragePooling2D()(ieb1)
dense1=keras.layers.Dense(8,activation='relu')
dense2=keras.layers.Dense(32,activation='sigmoid')
max_pool=dense1(max_pool)
max_pool=dense2(max_pool)
avg_pool=dense1(avg_pool)
avg_pool=dense2(avg_pool)
'''max_pool=keras.layers.Lambda(
lambda image: keras.backend.expand_dims(keras.backend.expand_dims(image,axis=1),axis=1))(max_pool)
avg_pool=keras.layers.Lambda(
lambda image: keras.backend.expand_dims(keras.backend.expand_dims(image,axis=1),axis=1))(avg_pool)'''
channel=keras.layers.Add()([max_pool,avg_pool])
ieb1=keras.layers.Multiply()([ieb1,channel])
max_pool_s=tf.keras.layers.Lambda(
lambda x: keras.backend.max(x,axis=3,keepdims=True))(ieb1)
avg_pool_s=keras.layers.Lambda(
lambda x: keras.backend.mean(x,axis=3,keepdims=True))(ieb1)
concat_slayers=keras.layers.Concatenate(axis=3)([avg_pool_s,max_pool_s])
spacial=keras.layers.Conv2D(1,7,activation='sigmoid',padding='same')(concat_slayers)
#spacial=keras.layers.experimental.preprocessing.Resizing(92,92)(spacial)
ieb1=keras.layers.Multiply()([ieb1,spacial])
ieb1=keras.layers.BatchNormalization()(ieb1)
ieb1=keras.layers.Activation('relu')(ieb1)
#ieb1=keras.layers.experimental.preprocessing.Resizing(96,96)(ieb1)
return ieb1
ieb_1=ieb(merged)
ieb_2=ieb(ieb_1)
ieb_3=ieb(ieb_2)
ieb_4=ieb(ieb_3)
ieb_5=ieb(ieb_4)
added_ieb=keras.layers.concatenate([ieb_1,ieb_2,ieb_3,ieb_4,ieb_5])
added_ieb
impnet=keras.layers.Conv2D(32,(3,3),padding='same')(added_ieb)
impnet=keras.layers.Conv2D(8,(3,3),padding='same')(impnet)
impnet=keras.layers.Conv2D(1,(3,3),padding='same')(impnet)
```
# S/L Block
```
'''impnet=keras.layers.Lambda(
lambda x: x+keras.backend.constant(0.001)
)(impnet)'''
s_l=keras.layers.Lambda(
lambda input:input[0]/input[1]
)([input_layer_1,impnet])
s_l
```
# Correction Network
```
def correction_network(input_feature):
conv1=keras.layers.Conv2D(32,kernel_size=(3,3),strides=(1,1),activation='relu',padding='same')(input_feature)
conv2=keras.layers.Conv2D(32,kernel_size=(3,3),strides=(1,1),activation='relu',padding='same')(conv1)
conv3=keras.layers.Conv2D(16,kernel_size=(3,3),strides=(1,1),activation='relu',padding='same')(conv2)
conv4=keras.layers.Conv2D(16,kernel_size=(3,3),strides=(1,1),activation='relu',padding='same')(conv3)
conv5=keras.layers.Conv2D(3,kernel_size=(3,3),strides=(1,1),activation='sigmoid',padding='same')(conv4)
#conv5=keras.layers.experimental.preprocessing.Resizing(96,96)(conv5)
#conv5=keras.layers.multiply([impnet,conv5])
return conv5
final_output=correction_network(s_l)
```
# Custom Loss Function
```
import loss as l
import keras.backend as K
def enhancement_loss(x,y):
x=K.cast(x,dtype='float32')
y=K.cast(y,dtype='float32')
norm=tf.norm(x-y)
return norm
enhancement_loss(img_low[0],img_high[0])
def color_loss(x,y):
x=K.cast(x,dtype='float32')
y=K.cast(y,dtype='float32')
cosine_loss = keras.losses.CosineSimilarity()(x,y)
colorloss=1-cosine_loss
return colorloss
color_loss(img_low[0],img_high[0])
sobelFilter = K.variable([[[[1., 1.]], [[0., 2.]],[[-1., 1.]]],
[[[2., 0.]], [[0., 0.]],[[-2., 0.]]],
[[[1., -1.]], [[0., -2.]],[[-1., -1.]]]])
def expandedSobel(inputTensor):
inputChannels = K.reshape(K.ones_like(inputTensor[0,0,0,:]),(1,1,-1,1))
return sobelFilter * inputChannels
def squareSobelLoss(yTrue,yPred):
yTrue=K.cast(yTrue,dtype='float32')
yPred=K.cast(yPred,dtype='float32')
filt = expandedSobel(yTrue)
squareSobelTrue =K.square(K.depthwise_conv2d(yTrue,filt))
squareSobelPred =K.square(K.depthwise_conv2d(yPred,filt))
newShape = K.shape(squareSobelTrue)
newShape = K.concatenate([newShape[:-1],
newShape[-1:]//2,
K.variable([2],dtype='int32')])
squareSobelTrue = K.sum(K.reshape(squareSobelTrue,newShape),axis=-1)
squareSobelPred = K.sum(K.reshape(squareSobelPred,newShape),axis=-1)
return K.mean(K.abs(squareSobelTrue - squareSobelPred))
def MeanGradientError(outputs, targets):
outputs=tf.cast(outputs,dtype='float32')
targets=tf.cast(targets,dtype='float32')
filter_x = tf.tile(tf.expand_dims(tf.constant([[-1, -2, -2], [0, 0, 0], [1, 2, 1]], dtype = 'float32'), axis = -1), [1, 1, outputs.shape[-1]])
filter_x = tf.tile(tf.expand_dims(filter_x, axis = -1), [1, 1, 1, outputs.shape[-1]])
filter_y = tf.tile(tf.expand_dims(tf.constant([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]], dtype = 'float32'), axis = -1), [1, 1, targets.shape[-1]])
filter_y = tf.tile(tf.expand_dims(filter_y, axis = -1), [1, 1, 1, targets.shape[-1]])
# output gradient
output_gradient_x = tf.math.square(tf.nn.conv2d(outputs, filter_x, strides = 1, padding = 'SAME'))
output_gradient_y = tf.math.square(tf.nn.conv2d(outputs, filter_y, strides = 1, padding = 'SAME'))
#target gradient
target_gradient_x = tf.math.square(tf.nn.conv2d(targets, filter_x, strides = 1, padding = 'SAME'))
target_gradient_y = tf.math.square(tf.nn.conv2d(targets, filter_y, strides = 1, padding = 'SAME'))
# square
output_gradients = tf.math.sqrt(tf.math.add(output_gradient_x, output_gradient_y))
target_gradients = tf.math.sqrt(tf.math.add(target_gradient_x, target_gradient_y))
# compute mean gradient error
shape = output_gradients.shape[1:3]
mge = tf.math.reduce_sum(tf.math.squared_difference(output_gradients, target_gradients) / (shape[0] * shape[1]))
return mge
def max_rgb_filter(img):
# img=tf.keras.preprocessing.image.img_to_array(img)
r=img[:,:,:,0]
g=img[:,:,:,1]
b=img[:,:,:,2]
max_c=tf.maximum(K.maximum(r,g),b)
'''
b_broadcast = K.zeros(K.shape(r), dtype=r.dtype)
bool_r=K.less(r,max)
bool_g=K.less(g,max)
bool_b=K.less(b,max)
r=K.switch(bool_r,b_broadcast,r)
g=K.switch(bool_g,b_broadcast,g)
b=K.switch(bool_b,b_broadcast,b)
# print(K.shape(r))
r=K.expand_dims(r)
g=K.expand_dims(g)
b=K.expand_dims(b)
img=K.concatenate([r,g,b],axis=-1)
# print(K.shape(img))
# img_rgb_filter=tf.keras.preprocessing.image.array_to_img(img)
return img'''
return tf.expand_dims(max_c,axis=-1)
def light_mask_loss(input_img,pred_img,true_img):
pred_img=tf.cast(pred_img,tf.uint8)
true_img=tf.cast(true_img,tf.uint8)
input_img=tf.cast(input_img,tf.uint8)
m_i=max_rgb_filter(input_img)
m_t=max_rgb_filter(true_img)
# m_t=m_t+K.constant(0.001,shape=m_t.shape,dtype=m_t.dtype)
m_div_it=tf.divide(m_i,m_t)
m_div_it=tf.cast(m_div_it,tf.uint8)
light_mask=tf.subtract(pred_img,m_div_it)
light_mask=tf.cast(light_mask,tf.float32)
lightmask_loss=tf.norm(light_mask)
return lightmask_loss
a1=max_rgb_filter(tf.expand_dims(img_low[1],axis=0))
a2=max_rgb_filter(tf.expand_dims(img_high[1],axis=0))
b=a1/a2
img_low[0]-b
def custom_loss_wrapper(input_tensor):
def custom_loss(y_true,y_pred):
# lm_loss=light_mask_loss(input_img=input_tensor,pred_img=y_pred,true_img=y_true)
# print(lm_loss)
e_loss=enhancement_loss(y_true,y_pred)
c_loss=color_loss(y_true,y_pred)
s_loss=squareSobelLoss(y_true,y_pred)
total_loss=e_loss+s_loss*0.2+0.2*c_loss
# total_loss=total_loss+(10*lm_loss)
return total_loss
return custom_loss
```
# Model
```
model=keras.models.Model(inputs=[input_layer_1],outputs=final_output)
model.summary()
```
# Plot a DL Model
```
# keras.utils.plot_model(model,show_shapes=True,show_layer_names=True)
```
# Model Compile
```
opt=tf.optimizers.Adam()
EPOCHS=3
BATCH=28
import os
import random
for i in range(EPOCHS):
b=0
for j in range(0,img_high.shape[0],BATCH):
b=b+1
img_inp=img_low[j:j+BATCH]
img_out=img_high[j:j+BATCH]
with tf.GradientTape() as tape:
img_pred=model([img_inp])
lm_loss=light_mask_loss(input_img=img_inp,pred_img=img_pred,true_img=img_out)
e_loss=enhancement_loss(img_out,img_pred)
c_loss=color_loss(img_out,img_pred)
s_loss=MeanGradientError(img_out,img_pred)
total_loss=e_loss*4+s_loss*0.25+c_loss*1+lm_loss*5
# according to paper:- total_loss=e_loss*1+s_loss*0.2+c_loss*1+lm_loss*10
mse=tf.losses.mse(img_out,img_pred).numpy().sum()
# os.system('cls')
print(i,' ',b,' ',total_loss.numpy(),' ',mse)
grads = tape.gradient(total_loss, model.trainable_variables)
opt.apply_gradients(zip(grads, model.trainable_variables))
model.save('model_improved.h5')
```
# Inference
```
import matplotlib.pyplot as plt
model
def high_light(index):
img=np.expand_dims(img_low[index],axis=0)
a=model([img])
plt.imshow(img[0])
plt.show()
plt.imshow(a[0])
plt.show()
plt.imshow(img_high[index])
plt.show()
high_light(1443)
from tensorflow.keras.models import load_model
import tensorflow as tf
import keras
model=load_model('model_improved.h5')
model
```
| true |
code
| 0.703651 | null | null | null | null |
|
# Imports
The following packages will be used:
1. tensorflow
2. numpy
3. pprint
```
%%capture
!pip install --upgrade wandb
import wandb
from wandb.keras import WandbCallback
wandb.login()
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import Input, Model
from tensorflow.keras.layers import Conv2D, BatchNormalization, MaxPool2D, ReLU, ELU, LeakyReLU, Flatten, Dense, Add, AveragePooling2D, GlobalAveragePooling2D
import pprint
pp = pprint.PrettyPrinter(indent=4)
import numpy as np
np.random.seed(666)
tf.random.set_seed(666)
# Which GPU is being used?
!nvidia-smi
```
# Data
The data that is being used for this experiment is the CIFAR10.
The dataset has 60,000 images of dimensions 32,32,3.
```
# Load the training and testing set of CIFAR10
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.cifar10.load_data()
X_train = X_train.astype('float32')
X_train = X_train/255.
X_test = X_test.astype('float32')
X_test = X_test/255.
y_train = tf.reshape(tf.one_hot(y_train, 10), shape=(-1, 10))
y_test = tf.reshape(tf.one_hot(y_test, 10), shape=(-1, 10))
# Create TensorFlow dataset
BATCH_SIZE = 256
AUTOTUNE = tf.data.experimental.AUTOTUNE
train_ds = tf.data.Dataset.from_tensor_slices((X_train, y_train))
train_ds = train_ds.shuffle(1024).cache().batch(BATCH_SIZE).prefetch(AUTOTUNE)
test_ds = tf.data.Dataset.from_tensor_slices((X_test, y_test))
test_ds = test_ds.cache().batch(BATCH_SIZE).prefetch(AUTOTUNE)
```
# Organism
An organism contains the following:
1. phase - This denotes which phase does the organism belong to
2. chromosome - A dictionary of genes (hyperparameters)
3. model - The `tf.keras` model corresponding to the chromosome
4. prevBestOrganism - The best organism in the previous **phase**
```
options_phase0 = {
'a_filter_size': [(1,1), (3,3), (5,5), (7,7), (9,9)],
'a_include_BN': [True, False],
'a_output_channels': [8, 16, 32, 64, 128, 256, 512],
'activation_type': [ReLU, ELU, LeakyReLU],
'b_filter_size': [(1,1), (3,3), (5,5), (7,7), (9,9)],
'b_include_BN': [True, False],
'b_output_channels': [8, 16, 32, 64, 128, 256, 512],
'include_pool': [True, False],
'pool_type': [MaxPool2D, AveragePooling2D],
'include_skip': [True, False]
}
options = {
'include_layer': [True, False],
'a_filter_size': [(1,1), (3,3), (5,5), (7,7), (9,9)],
'a_include_BN': [True, False],
'a_output_channels': [8, 16, 32, 64, 128, 256, 512],
'b_filter_size': [(1,1), (3,3), (5,5), (7,7), (9,9)],
'b_include_BN': [True, False],
'b_output_channels': [8, 16, 32, 64, 128, 256, 512],
'include_pool': [True, False],
'pool_type': [MaxPool2D, AveragePooling2D],
'include_skip': [True, False]
}
class Organism:
def __init__(self,
chromosome={},
phase=0,
prevBestOrganism=None):
'''
chromosome is a dictionary of genes
phase is the phase that the individual belongs to
prevBestOrganism is the best organism of the previous phase
'''
self.phase = phase
self.chromosome = chromosome
self.prevBestOrganism=prevBestOrganism
if phase != 0:
# In a later stage, the model is made by
# attaching new layers to the prev best model
self.last_model = prevBestOrganism.model
def build_model(self):
'''
This is the function to build the keras model
'''
keras.backend.clear_session()
inputs = Input(shape=(32,32,3))
if self.phase != 0:
# Slice the prev best model
# Use the model as a layer
# Attach new layer to the sliced model
intermediate_model = Model(inputs=self.last_model.input,
outputs=self.last_model.layers[-3].output)
for layer in intermediate_model.layers:
# To make the iteration efficient
layer.trainable = False
inter_inputs = intermediate_model(inputs)
x = Conv2D(filters=self.chromosome['a_output_channels'],
padding='same',
kernel_size=self.chromosome['a_filter_size'],
use_bias=self.chromosome['a_include_BN'])(inter_inputs)
# This is to ensure that we do not randomly chose anothere activation
self.chromosome['activation_type'] = self.prevBestOrganism.chromosome['activation_type']
else:
# For PHASE 0 only
# input layer
x = Conv2D(filters=self.chromosome['a_output_channels'],
padding='same',
kernel_size=self.chromosome['a_filter_size'],
use_bias=self.chromosome['a_include_BN'])(inputs)
if self.chromosome['a_include_BN']:
x = BatchNormalization()(x)
x = self.chromosome['activation_type']()(x)
if self.chromosome['include_pool']:
x = self.chromosome['pool_type'](strides=(1,1),
padding='same')(x)
if self.phase != 0 and self.chromosome['include_layer'] == False:
# Except for PHASE0, there is a choice for
# the number of layers that the model wants
if self.chromosome['include_skip']:
y = Conv2D(filters=self.chromosome['a_output_channels'],
kernel_size=(1,1),
padding='same')(inter_inputs)
x = Add()([y,x])
x = GlobalAveragePooling2D()(x)
x = Dense(10, activation='softmax')(x)
else:
# PHASE0 or no skip
# in the tail
x = Conv2D(filters=self.chromosome['b_output_channels'],
padding='same',
kernel_size=self.chromosome['b_filter_size'],
use_bias=self.chromosome['b_include_BN'])(x)
if self.chromosome['b_include_BN']:
x = BatchNormalization()(x)
x = self.chromosome['activation_type']()(x)
if self.chromosome['include_skip']:
y = Conv2D(filters=self.chromosome['b_output_channels'],
padding='same',
kernel_size=(1,1))(inputs)
x = Add()([y,x])
x = GlobalAveragePooling2D()(x)
x = Dense(10, activation='softmax')(x)
self.model = Model(inputs=[inputs], outputs=[x])
self.model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
def fitnessFunction(self,
train_ds,
test_ds,
generation_number):
'''
This function is used to calculate the
fitness of an individual.
'''
wandb.init(entity="authors",
project="vlga",
group='KAGp{}'.format(self.phase),
job_type='g{}'.format(generation_number))
self.model.fit(train_ds,
epochs=3,
callbacks=[WandbCallback()],
verbose=0)
_, self.fitness = self.model.evaluate(test_ds,
verbose=0)
def crossover(self,
partner,
generation_number):
'''
This function helps in making children from two
parent individuals.
'''
child_chromosome = {}
endpoint = np.random.randint(low=0, high=len(self.chromosome))
for idx, key in enumerate(self.chromosome):
if idx <= endpoint:
child_chromosome[key] = self.chromosome[key]
else:
child_chromosome[key] = partner.chromosome[key]
child = Organism(chromosome= child_chromosome, phase=self.phase, prevBestOrganism=self.prevBestOrganism)
child.build_model()
child.fitnessFunction(train_ds,
test_ds,
generation_number=generation_number)
return child
def mutation(self, generation_number):
'''
One of the gene is to be mutated.
'''
index = np.random.randint(0, len(self.chromosome))
key = list(self.chromosome.keys())[index]
if self.phase != 0:
self.chromosome[key] = options[key][np.random.randint(len(options[key]))]
else:
self.chromosome[key] = options_phase0[key][np.random.randint(len(options_phase0[key]))]
self.build_model()
self.fitnessFunction(train_ds,
test_ds,
generation_number=generation_number)
def show(self):
'''
Util function to show the individual's properties.
'''
pp.pprint(self.chromosome)
def random_hyper(phase):
if phase == 0:
return {
'a_filter_size': options_phase0['a_filter_size'][np.random.randint(len(options_phase0['a_filter_size']))],
'a_include_BN': options_phase0['a_include_BN'][np.random.randint(len(options_phase0['a_include_BN']))],
'a_output_channels': options_phase0['a_output_channels'][np.random.randint(len(options_phase0['a_output_channels']))],
'activation_type': options_phase0['activation_type'][np.random.randint(len(options_phase0['activation_type']))],
'b_filter_size': options_phase0['b_filter_size'][np.random.randint(len(options_phase0['b_filter_size']))],
'b_include_BN': options_phase0['b_include_BN'][np.random.randint(len(options_phase0['b_include_BN']))],
'b_output_channels': options_phase0['b_output_channels'][np.random.randint(len(options_phase0['b_output_channels']))],
'include_pool': options_phase0['include_pool'][np.random.randint(len(options_phase0['include_pool']))],
'pool_type': options_phase0['pool_type'][np.random.randint(len(options_phase0['pool_type']))],
'include_skip': options_phase0['include_skip'][np.random.randint(len(options_phase0['include_skip']))]
}
else:
return {
'a_filter_size': options['a_filter_size'][np.random.randint(len(options['a_filter_size']))],
'a_include_BN': options['a_include_BN'][np.random.randint(len(options['a_include_BN']))],
'a_output_channels': options['a_output_channels'][np.random.randint(len(options['a_output_channels']))],
'b_filter_size': options['b_filter_size'][np.random.randint(len(options['b_filter_size']))],
'b_include_BN': options['b_include_BN'][np.random.randint(len(options['b_include_BN']))],
'b_output_channels': options['b_output_channels'][np.random.randint(len(options['b_output_channels']))],
'include_pool': options['include_pool'][np.random.randint(len(options['include_pool']))],
'pool_type': options['pool_type'][np.random.randint(len(options['pool_type']))],
'include_layer': options['include_layer'][np.random.randint(len(options['include_layer']))],
'include_skip': options['include_skip'][np.random.randint(len(options['include_skip']))]
}
def softmax(x):
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum()
```
# Generation
This is a class that hold generations of models.
1. fitSurvivalRate - The amount of fit individuals we want in the next generation.
2. unfitSurvivalProb - The probability of sending unfit individuals
3. mutationRate - The mutation rate to change genes in an individual.
4. phase - The phase that the generation belongs to.
5. population_size - The amount of individuals that the generation consists of.
6. prevBestOrganism - The best organism (individual) is the last phase
```
class Generation:
def __init__(self,
fitSurvivalRate,
unfitSurvivalProb,
mutationRate,
phase,
population_size,
prevBestOrganism):
self.population_size = population_size
self.population = []
self.generation_number = 0
self.mutationRate = mutationRate
self.fitSurvivalRate = fitSurvivalRate
self.unfitSurvivalProb = unfitSurvivalProb
self.prevBestOrganism = prevBestOrganism
self.phase = phase
# creating the first population: GENERATION_0
# can be thought of as the setup function
for idx in range(self.population_size):
org = Organism(chromosome=random_hyper(self.phase), phase=self.phase, prevBestOrganism=self.prevBestOrganism)
org.build_model()
org.fitnessFunction(train_ds,
test_ds,
generation_number=self.generation_number)
self.population.append(org)
# sorts the population according to fitness (high to low)
self.sortModel()
self.generation_number += 1
def sortModel(self):
'''
sort the models according to the
fitness in descending order.
'''
fitness = [ind.fitness for ind in self.population]
sort_index = np.argsort(fitness)[::-1]
self.population = [self.population[index] for index in sort_index]
def generate(self):
'''
Generate a new generation in the same phase
'''
number_of_fit = int(self.population_size * self.fitSurvivalRate)
new_pop = self.population[:number_of_fit]
for individual in self.population[number_of_fit:]:
if np.random.rand() <= self.unfitSurvivalProb:
new_pop.append(individual)
for index, individual in enumerate(new_pop):
if np.random.rand() <= self.mutationRate:
new_pop[index].mutation(generation_number=self.generation_number)
fitness = [ind.fitness for ind in new_pop]
children=[]
for idx in range(self.population_size-len(new_pop)):
parents = np.random.choice(new_pop, replace=False, size=(2,), p=softmax(fitness))
A=parents[0]
B=parents[1]
child=A.crossover(B, generation_number=self.generation_number)
children.append(child)
self.population = new_pop+children
self.sortModel()
self.generation_number+=1
def evaluate(self, last=False):
'''
Evaluate the generation
'''
fitness = [ind.fitness for ind in self.population]
wandb.log({'Best fitness': fitness[0]})
wandb.log({'Average fitness': sum(fitness)/len(fitness)})
self.population[0].show()
if last:
return self.population[0]
population_size = 10
number_generation = 3
fitSurvivalRate = 0.5
unfitSurvivalProb = 0.2
mutationRate = 0.1
number_of_phases = 5
prevBestOrganism = None
for phase in range(number_of_phases):
# print("PHASE {}".format(phase))
generation = Generation(fitSurvivalRate=fitSurvivalRate,
unfitSurvivalProb=unfitSurvivalProb,
mutationRate=mutationRate,
population_size=population_size,
phase=phase,
prevBestOrganism=prevBestOrganism)
while generation.generation_number < number_generation:
generation.generate()
if generation.generation_number == number_generation:
# Last generation is the phase
# print('I AM THE BEST IN THE PHASE')
prevBestOrganism = generation.evaluate(last=True)
keras.utils.plot_model(prevBestOrganism.model, to_file='best.png')
wandb.log({"best_model": [wandb.Image('best.png', caption="Best Model")]})
else:
generation.evaluate()
```
| true |
code
| 0.659021 | null | null | null | null |
|
# Iteratief ontwerpen
Overal herhalingen

Oneindige fractals ... Zie [Xaos](https://xaos-project.github.io/) voor de hypnotiserende ervaring!
## Herhalingen
`while` met ontsnapping!
```
from random import choice
def escape(hidden):
guess = 0
count = 0
while guess != hidden:
guess = choice(range(100))
count += 1
return count
```
## Simulaties
Monte Carlo simulaties ...
```
LC = [escape(42) for _ in range(1000)]
sum(LC) / len(LC)
```
## Verjaardagenparadox
Wat is de kans dat iemand op dezelfde dag jarig is?
Met hoeveel mensen bij elkaar is deze kans 50%?
Kan dit worden gesimuleerd?
### Aanpak?
Vul één voor één een kamer met mensen tot twee dezelfde verjaardag hebben.
**De ontsnapping?**
Bijf de kamer vullen zolang (`while`) de verjaardagen in de kamer uniek zijn!
De kamer? Een list!
```python
def until_a_repeat(high):
"""Fills a list of random values until a first repeat
Argument: high, the random value upper boundary
Return value: the number of elements in the list.
"""
```
### Hoe lang tot een herhaling?
Sneller dan je denkt!

```
def unique(L):
"""Returns whether all elements in L are unique.
Argument: L, a list of any elements.
Return value: True, if all elements in L are unique,
or False, if there is any repeated element
"""
if len(L) == 0:
return True
elif L[0] in L[1:]:
return False
else:
return unique(L[1:])
```
Deze hulpfunctie wordt gegeven!
### Een verjaardag is maar een dag
```
L = [bday for bday in range(365)]
L[:10]
```
Zet 1 Januari op 0, en verder tot 31 december (364) ...
```
unique(L)
```
### Toevallige verjaardagen
Simulatie met random!
```
%run simulate.py
LC = [until_a_repeat(365) for _ in range(1000)]
LC[:10]
min(LC)
max(LC)
sum(LC) / len(LC)
```
## Denken in lussen
`for`
```python
for x in range(42):
print(x)
```
`while`
```python
x = 1
while x < 42:
print(x)
x *= 2
```
### Verschillen
Wat zijn de verschillen in ontwerp tussen deze twee Python lussen?
`for` — eindige herhaling
Voor een bestaande list of bekend aantal herhalingen
`while` — oneindige herhaling
Voor een onbekend aantal herhalingen
## Pi met pijltjes
Pi of $\pi$ is een *constante*: de verhouding tussen de omtrek en de diameter van een cirkel
### Pithon?
```
import math
math.pi
```
### Pi bepalen?
Kan $\pi$ worden bepaald door middel van een simulatie?


### Algoritme
- gooi een aantal pijlen willekeurig (random!) op het vlak
- tel het aantal pijlen dat is geland in de cirkel
- bereken $\pi$ als volgt
$$
\pi = 4 \times \dfrac{\text{Pijlen in cirkel}}{\text{Pijlen totaal}}
$$

### Hoe werkt dit?
Verhoudingen!
$$
\dfrac{\text{Pijlen in cirkel}}{\text{Pijlen totaal}} \approx \dfrac{\text{Oppervlakte cirkel}}{\text{Oppervlakte vierkant}}
$$
Gegeven: het oppervlakte van een cirkel is gelijk aan $\pi \cdot r^2$
*Oppervlakte cirkel*
Straal $r$ is in dit geval 0.5, de oppervlakte van de cirkel is dus $\pi \cdot 0.25$, of $\dfrac{\pi}{4}$
*Oppervlakte vierkant*
De breedte van het vierkant is 1 dus de oppervlakte van het vierkant is 1
$$
\dfrac{\text{Oppervlakte cirkel}}{\text{Oppervlakte vierkant}} = \frac{\dfrac{\pi}{4}}{1}
$$
wat kan worden vereenvoudigd tot
$$
\dfrac{\text{Oppervlakte cirkel}}{\text{Oppervlakte vierkant}} = \dfrac{\pi}{4}
$$
en vervolgens vereenvoudigd kan worden tot
$$
\dfrac{\text{Oppervlakte cirkel}}{\text{Oppervlakte vierkant}} \times 4 = \pi
$$
### `for` of `while`?
Welke functie zal welk type lus gebruiken?
```python
pi_one(e)
```
`e` = hoe dichtbij we bij π moeten komen
`while`
```python
pi_two(n)
```
`n` = het aantal pijltjes dat gegooid moet worden
`for`
### Simuleer!
```python
def for_pi(n):
"""Calculate pi with a for loop
"""
...
```
```
for_pi(100000)
```
## Geneste lussen
Zijn heel erg bekend!

### Seconden tikken weg ...
```python
for minute in range(60):
for second in range(60):
tick()
```
### Tijd vliegt!
```python
for year in range(84):
for month in range(12):
for day in range(f(month, year)):
for hour in range(24):
for minute in range(60):
for second in range(60):
tick()
```
## Quiz
Wat zal worden geprint?
```python
for x in range(0, 1):
for y in range(x, 2):
print(x, y)
```
### Oplossing
```
for x in range(0, 1):
for y in range(x, 2):
print(x, y)
```
## Tweedimensionale structuren
Rijen en kolommen
Let op, als over "arrays" wordt gesproken (2D arrays): dit is wat je kent als lists!

### List comprehension
```
def mul_table(n):
"""Returns a multiplication table for n
"""
return [[x * y for x in range(1, n + 1)] for y in range(1, n + 1)]
mul_table(5)
```
### Iteratief
```
def mul_table(n):
"""Returns a multiplication table for n
"""
table = [] # start with an empty table
for x in range(1, n + 1): # for every row in this table ...
row = [] # start with an empty row
for y in range(1, n + 1): # for every column in this row ...
row += [x * y] # add the column value to the row
table += [row] # add the row to the table
return table # return table
mul_table(5)
```
### Een dozijn
```
def dozen(n):
"""Eggs by the dozen!
"""
for x in range(n):
row = ""
for y in range(12): # fixed, dozen is always 12!
row += "🥚"
print(row)
dozen(1)
dozen(12)
```
### Syntax
En semantiek...
```
row = ""
for y in range(12):
row += "🥚"
print(row)
print(12 * "🥚")
```

Python [ASCII Art](https://en.wikipedia.org/wiki/ASCII_art)!
### Rijen en kolommen
En nieuwe regels ...
```
for row in range(3):
for col in range(4):
print("#")
for row in range(3):
for col in range(4):
print("#", end="")
for row in range(3):
for col in range(4):
print("#", end="")
print()
```
```console
____ _
/ ___| _ _ ___ ___ ___ ___| |
\___ \| | | |/ __/ __/ _ \/ __| |
___) | |_| | (_| (_| __/\__ \_|
|____/ \__,_|\___\___\___||___(_)
```
| true |
code
| 0.475605 | null | null | null | null |
|
### 2. 학습 데이터 준비
```
# PyTorch 라이브러리 임포트
import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
# pandas 라이브러리 임포트
import pandas as pd
# NumPy 라이브러리 임포트
import numpy as np
# matplotlib 라이브러리 임포트
from matplotlib import pyplot as plt
%matplotlib inline
# 데이터를 읽어 들여 화면에 출력
dat = pd.read_csv('../data/weather_data.csv', skiprows=[0, 1, 2, 3, 4, 5], encoding="cp949")
dat
# 평균 기온값 추출 및 시각화
temp = dat['평균기온(℃)']
temp.plot()
plt.show()
# 데이터 집합을 훈련 데이터와 테스트 데이터로 분할
train_x = temp[:1461] # 2011년 1월 1일 ~ 2014년 12월 31일
test_x = temp[1461:] # 2015년 1월 1일 ~ 2016년 12월 31일
# NumPy 배열로 변환
train_x = np.array(train_x)
test_x = np.array(test_x)
# 설명 변수의 수
ATTR_SIZE = 180 # 6개월
tmp = []
train_X = []
# 데이터 점 1개 단위로 윈도우를 슬라이드시키며 훈련 데이터를 추출
for i in range(0, len(train_x) - ATTR_SIZE):
tmp.append(train_x[i:i+ATTR_SIZE])
train_X = np.array(tmp)
# 훈련 데이터를 데이터프레임으로 변환하여 화면에 출력
pd.DataFrame(train_X)
```
### 3. 신경망 구성
```
# 신경망 구성
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(180, 128)
self.fc2 = nn.Linear(128, 64)
self.fc3 = nn.Linear(64, 128)
self.fc4 = nn.Linear(128,180)
def forward(self, x):
x = F.relu(self.fc1(x))
x = self.fc2(x)
x = F.relu(self.fc3(x))
x = self.fc4(x)
return x
# 인스턴스 생성
model = Net()
```
### 4. 모형 학습
```
# 오차함수
criterion = nn.MSELoss()
# 최적화 기법 선택
optimizer = optim.Adam(model.parameters(), lr=0.001)
# 학습
for epoch in range(1000):
total_loss = 0
d = []
# 훈련 데이터를 미니배치로 분할
for i in range(100):
# 훈련 데이터에 인덱스 부여
index = np.random.randint(0, 1281)
# 미니배치 분할
d.append(train_X[index])
# NumPy 배열로 변환
d = np.array(d, dtype='float32')
# 계산 그래프 구성
d = Variable(torch.from_numpy(d))
# 경사 초기화
optimizer.zero_grad()
# 순전파 계산
output = model(d)
# 오차 계산
loss = criterion(output, d)
# 역전파 계산
loss.backward()
# 가중치 업데이트
optimizer.step()
# 오차 누적 계산
total_loss += loss.data[0]
# 100 에포크마다 누적 오차를 출력
if (epoch+1) % 100 == 0:
print(epoch+1, total_loss)
# 입력 데이터 플로팅
plt.plot(d.data[0].numpy(), label='original')
plt.plot(output.data[0].numpy(), label='output')
plt.legend(loc='upper right')
plt.show()
```
### 5. 이상 점수 계산
```
tmp = []
test_X = []
# 테스트 데이터를 6개월 단위로 분할
tmp.append(test_x[0:180])
tmp.append(test_x[180:360])
tmp.append(test_x[360:540])
tmp.append(test_x[540:720])
test_X = np.array(tmp, dtype="float32")
# 데이터를 데이터프레임으로 변환하여 화면에 출력
pd.DataFrame(test_X)
# 모형 적용
d = Variable(torch.from_numpy(test_X))
output = model(d)
# 입력 데이터 플로팅
plt.plot(test_X.flatten(), label='original')
plt.plot(output.data.numpy().flatten(), label='prediction')
plt.legend(loc='upper right')
plt.show()
# 이상 점수 계산
test = test_X.flatten()
pred = output.data.numpy().flatten()
total_score = []
for i in range(0, 720):
dist = (test[i] - pred[i])
score = pow(dist, 2)
total_score.append(score)
# 이상 점수를 [0,1] 구간으로 정규화
total_score = np.array(total_score)
max_score = np.max(total_score)
total_score = total_score / max_score
# 이상 점수 출력
total_score
# 이상 점수 플로팅
plt.plot(total_score)
plt.show()
```
| true |
code
| 0.668326 | null | null | null | null |
|
# Cálculo promedio de remuneración UNRC
Según datos oficiales extraídos del sistema de información de la UNRC y declaraciones públicas varias.
Se extrae de **Recursos humanos UNRC**: [Estadísticas Sireh](https://sisinfo.unrc.edu.ar/estadisticas/estadisticas_sireh.php) la cantidad de personal clasificados según *categoría* y *horas semanales*:
**AUTORIDADES**
| **Dedicación** | Exclusiva | Simple | Tiempo Completo | Tiempo Parcial |
|-----------------------|-----------|--------|-----------------|----------------|
| **Cantidad personas** | 41 | 39 | 2 | 1 |
| **Horas semanales** | 40 | 20 | 40 | 20 |
**DOCENTES**
| **Dedicación** | Exclusiva | Otra | Semi-Exclusiva | Simple |
|-----------------------|-----------|------|----------------|--------|
| **Cantidad personas** | 705 | 171 | 581 | 418 |
| **Horas semanales** | 40 | 20 | 20 | 10 |
**NO DOCENTES**
| **Categoría** | C1 | C2 | C3 | C4 | C5 | C6 | C7 |
|-----------------------|----|----|-----|-----|-----|----|-----|
| **Cantidad personas** | 16 | 45 | 110 | 104 | 144 | 49 | 122 |
| **Horas semanales** | 40 | 40 | 40 | 40 | 40 | 40 | 40 |
```
import matplotlib.pyplot as plt
import numpy as np
import math
%matplotlib inline
x = [0, 3, 4, 7, 8, 9]
y = [418, 752, 40, 705, 43, 590]
colors = ['green', 'green', 'blue', 'green', 'blue', 'orange']
bars = plt.bar(x, y, color=colors)
plt.xticks([0, 3.5, 8], [10, 20, 40], fontsize=12)
plt.yticks([40] + list(range(100, 800, 100)), fontsize=12)
plt.xlim(-1, 10)
plt.xlabel('Cantidad de horas semanales', fontsize=14)
plt.ylabel('Cantidad de personas', fontsize=14)
plt.title('Recursos humanos UNRC', fontsize=20)
plt.legend([bars[0], bars[2], bars[-1]], ['Docente', 'Autoridad', 'No docente'])
#plt.hlines(40, -1, 7.6, linestyles='--', alpha=0.3)
plt.grid(axis='y')
plt.savefig('../content/img/rrhh_unrc.png', dpi=100, bbox_inches='tight')
```
El sitio oficial de la UNRC **no publica** presupuesto para 2018, la última publicación al respecto data de 2016 *([Presupuesto UNRC](https://www.unrc.edu.ar/unrc/presupuesto.php))*. Una [noticia de puntal](http://www.puntal.com.ar/noticia/UNRC-el-presupuesto-para-2018-crece-25-y-llega-a--1.478-millones-20170920-0017.html) informa el monto de **$1.478** millones para el presupuesto 2018.
Según declaraciones públicas de autoridades de la UNRC en una [nota](https://www.unrc.edu.ar/unrc/n_comp.cdc?nota=32358) en el sitio oficial: **"*Los gastos de funcionamiento, que insumen entre el 10 y el 15 por ciento del presupuesto de la UNRC (el resto es para sueldos) fueron otro de los tópicos.*"**
Para un **85%** del presupuesto destinado a sueldos **(aproximadamente $1200 millones)**, se calcula un promedio por hora y así la supuesta remuneración por personal según su dedicación:
```
presupuesto_2018 = 1_478_000_000
presupuesto_sueldos_2018 = presupuesto_2018 * 0.85
total_horas = 3803800
pago_hora = presupuesto_sueldos_2018 / total_horas
pago_hora
pago_semana = []
pago_mes = []
horas = [10, 20, 30, 40]
for hora in horas:
semana = round(hora * pago_hora, 2)
pago_semana.append(semana)
mes = round(4 * hora * pago_hora, 2)
pago_mes.append(mes)
print(pago_semana)
print(pago_mes)
x = [10, 20, 30, 40]
y1 = pago_semana
y2 = pago_mes
#colors = ['green', 'green', 'blue', 'green', 'blue', 'orange']
bars = plt.bar(x, y1, width=4)#, color=colors)
#plt.xlim(-1, 45)
plt.xlabel('Cantidad de horas semanales', fontsize=14)
plt.ylabel('Remuneración en $', fontsize=14)
plt.title('Pago por semana', fontsize=20)
#plt.legend([bars[0], bars[2], bars[-1]], ['Docente', 'Autoridad', 'No docente'])
plt.xticks([10, 20, 30, 40])
plt.yticks([3000, 6500, 9500, 13000])
plt.grid(axis='y')
plt.savefig('../content/img/pago_semanal.png', dpi=100, bbox_inches='tight')
```
| Horas semanales | 10 | 20 | 30 | 40 |
|------------------|----------|----------|----------|----------|
| **Pago mensual** | \$13211.0 | \$26422.0 | \$39633.0 | \$52844.0 |
```
bars = plt.bar(x, y2, width=4)#, color=colors)
#plt.xlim(-1, 45)
plt.xlabel('Cantidad de horas semanales', fontsize=14)
plt.ylabel('Remuneración en $', fontsize=14)
plt.title('Pago por mes', fontsize=20)
#plt.legend([bars[0], bars[2], bars[-1]], ['Docente', 'Autoridad', 'No docente'])
plt.xticks([10, 20, 30, 40])
plt.yticks([13000, 25000, 40000, 50000])
plt.grid(axis='y')
plt.savefig('../content/img/pago_mensual.png', dpi=100, bbox_inches='tight')
# Cantidad de personas por dedicación exclusiva, semi-exclusiva, simple
autoridades = [43, 1, 40]
docentes = [705, 581, 418+171]
no_docentes = [16, 45, 110, 104, 144, 49, 122]
# Remuneración por dedicación/categoría
exclusiva_max = 77_410
exclusiva_promedio = (77_410 + 42_335) / 2
semi_exclusiva_max = 38_689
semi_exclusiva_promedio = (38_689 + 21_152) / 2
simple_max = 19_326
simple_promedio = (19_326 + 10_557) / 2
cat_no_docentes_max = [
52699 + 3074 + 10540 + 13175 + 527 + 5270 + 13649,
43916 + 3074 + 8783 + 10979 + 439 + 4391 + 6148,
36538 + 3074 + 7307 + 9134 + 365 + 3653 + 5164,
30390 + 3074 + 6078 + 7597 + 607 + 3039 + 4304,
25296 + 500 + 3074 + 5059 + 6324 + 505 +2529 + 3566,
21079 + 2500 + 3074 + 4216 + 5270 + 421 + 2108 + 2951,
17566 + 2500 + 3074 + 3513 + 4391 + 351 + 1756 + 2459
]
cat_no_docentes_promedio = [
52699 + 3074 + 10540 + 13175 + 527 + 5270 + ((13649 + 1949)/2),
43916 + 3074 + 8783 + 10979 + 439 + 4391 + ((6148 + 878)/2),
36538 + 3074 + 7307 + 9134 + 365 + 3653 + ((5164 + 737) /2),
30390 + 3074 + 6078 + 7597 + 607 + 3039 + ((4304 + 614) / 2),
25296 + 500 + 3074 + 5059 + 6324 + 505 +2529 + ((3566 + 509) /2),
21079 + 2500 + 3074 + 4216 + 5270 + 421 + 2108 + ((2951 + 421) /2),
17566 + 2500 + 3074 + 3513 + 4391 + 351 + 1756 + ((2459 + 351) /2)
]
remuneracion_autoridades_max = []
remuneracion_autoridades_promedio = []
remuneracion_docentes_max = []
remuneracion_docentes_promedio = []
remuneracion_no_docentes_max = []
remuneracion_no_docentes_promedio = []
# Aproximación para remuneración mensual promedio
remuneracion_autoridades_promedio.append(autoridades[0] * exclusiva_promedio * 12)
remuneracion_autoridades_promedio.append(autoridades[1] * semi_exclusiva_promedio * 12)
remuneracion_autoridades_promedio.append(autoridades[2] * simple_promedio * 12)
remuneracion_docentes_promedio.append(docentes[0] * exclusiva_promedio * 12)
remuneracion_docentes_promedio.append(docentes[1] * semi_exclusiva_promedio * 12)
remuneracion_docentes_promedio.append(docentes[2] * simple_promedio * 12)
for i, cant in enumerate(no_docentes):
remuneracion_no_docentes_promedio.append(cant * cat_no_docentes_promedio[i] * 12)
total_autoridades = sum(remuneracion_autoridades_promedio)
total_docentes = sum(remuneracion_docentes_promedio)
total_no_docentes = sum(remuneracion_no_docentes_promedio)
print('Total autoridades: $', total_autoridades)
print('Total docentes: $', total_docentes)
print('Total no docentes: $', total_no_docentes)
total_sueldos = total_autoridades + total_docentes + total_no_docentes
print('Total sueldos: $', total_sueldos)
presupuesto_2018 = 1_478_000_000
presupuesto_sueldos_2018 = presupuesto_2018 * 0.85
print(f'Presupuesto sueldos 2018: $ {presupuesto_sueldos_2018}')
resto = presupuesto_sueldos_2018 - total_sueldos
print('Resto: $', resto)
def div(a):
return a/1_000_000
y0 = [total_autoridades, total_docentes, total_no_docentes, resto]
y1 = [presupuesto_sueldos_2018]
y0 = list(map(div, y0))
y1 = list(map(div, y1))
#y_millones = list(map(div, y))
#y_millones
y0_cum = np.cumsum(y0)
y0_cum_shift = np.zeros_like(y0_cum)
y0_cum_shift[1:] = y0_cum[:-1]
colors = ['b', 'g', 'orange', 'r']
bars0 = plt.bar(x=0, height=y0, width=0.7, bottom=y0_cum_shift, color=colors)
bars1 = plt.bar(x=1, height=y1, color=['purple'])
plt.xlim(-3.25, 1.5)
plt.xlabel('Balance', fontsize=14)
plt.ylabel('Monto en millones de $', fontsize=14)
plt.title('Balance de sueldos con salario promedio', fontsize=20)
plt.yticks(y0_cum)
plt.xticks([])
plt.grid(axis='y')
plt.legend([bars[0], bars[1], bars[2], bars[3], bars[4]],
['Autoridad', 'Docente', 'No docente', 'Presupuesto para sueldos 2018', 'Resto'])
plt.savefig('../content/img/balance_promedio.png', dpi=100, bbox_inches='tight')
plt.show()
# Aproximación para remuneración mensual maximo
remuneracion_autoridades_max.append(autoridades[0] * exclusiva_max * 12)
remuneracion_autoridades_max.append(autoridades[1] * semi_exclusiva_max * 12)
remuneracion_autoridades_max.append(autoridades[2] * simple_max * 12)
remuneracion_docentes_max.append(docentes[0] * exclusiva_max * 12)
remuneracion_docentes_max.append(docentes[1] * semi_exclusiva_max * 12)
remuneracion_docentes_max.append(docentes[2] * simple_max * 12)
for i, cant in enumerate(no_docentes):
remuneracion_no_docentes_max.append(cant * cat_no_docentes_max[i] * 12)
total_autoridades = sum(remuneracion_autoridades_max)
total_docentes = sum(remuneracion_docentes_max)
total_no_docentes = sum(remuneracion_no_docentes_max)
print('Total autoridades: $', total_autoridades)
print('Total docentes: $', total_docentes)
print('Total no docentes: $', total_no_docentes)
total_sueldos = total_autoridades + total_docentes + total_no_docentes
print('Total sueldos: $', total_sueldos)
presupuesto_2018 = 1_478_000_000
presupuesto_sueldos_2018 = presupuesto_2018 * 0.85
print(f'Presupuesto sueldos 2018: $ {presupuesto_sueldos_2018}')
resto = presupuesto_sueldos_2018 - total_sueldos
print('Resto: $', resto)
colors
y0 = [total_autoridades, total_docentes, total_no_docentes, resto]
y1 = [presupuesto_sueldos_2018]
y0 = list(map(div, y0))
y1 = list(map(div, y1))
#y_millones = list(map(div, y))
#y_millones
y0_cum = np.cumsum(y0)
y0_cum_shift = np.zeros_like(y0_cum)
y0_cum_shift[1:] = y0_cum[:-1]
colors = ['b', 'g', 'orange', 'r']
bars0 = plt.bar(x=0, height=y0, width=0.7, bottom=y0_cum_shift, color=colors)
bars1 = plt.bar(x=1, height=y1, color=['purple'])
plt.xlim(-3.25, 1.5)
plt.xlabel('Balance', fontsize=14)
plt.ylabel('Monto en millones de $', fontsize=14)
plt.title('Balance de sueldos con salario promedio', fontsize=20)
plt.yticks(y0_cum)
plt.xticks([])
plt.grid(axis='y')
plt.legend([bars[0], bars[1], bars[2], bars[3], bars[4]],
['Autoridad', 'Docente', 'No docente', 'Presupuesto para sueldos 2018', 'Resto'])
plt.savefig('../content/img/balance_maximo.png', dpi=100, bbox_inches='tight')
plt.show()
```
| true |
code
| 0.205854 | null | null | null | null |
|
# FBSDE
Ji, Shaolin, Shige Peng, Ying Peng, and Xichuan Zhang. “Three Algorithms for Solving High-Dimensional Fully-Coupled FBSDEs through Deep Learning.” ArXiv:1907.05327 [Cs, Math], February 2, 2020. http://arxiv.org/abs/1907.05327.
```
%load_ext tensorboard
import os
from makers.gpu_utils import *
os.environ["CUDA_VISIBLE_DEVICES"] = str(pick_gpu_lowest_memory())
import numpy as np
import tensorflow as tf
from keras.layers import Input, Dense, Lambda, Reshape, concatenate, Layer
from keras import Model, initializers
from keras.callbacks import ModelCheckpoint
from keras.metrics import mean_squared_error
import matplotlib.pyplot as plt
from datetime import datetime
from keras.metrics import mse
from keras.optimizers import Adam
print("Num GPUs Available: ", len(tf.config.list_physical_devices("GPU")))
```
# Inputs
```
# numerical parameters
n_paths = 2 ** 18
n_timesteps = 16
n_dimensions = 4
n_diffusion_factors = 2
n_jump_factors = 2
T = 10.
dt = T / n_timesteps
batch_size = 128
epochs = 1000
learning_rate = 1e-5
# model parameters
nu = 0.1
eta = 1.
zeta = 0.1
epsilon = 0.1
lp = 0.2
lm = 0.2
k = 1.
phi = 1e-2
psi = 1e-2
# coefficients
def b(t, x, y, z, r):
ad = y[2] / y[3] - x[0]
dp = tf.maximum(0., 1./k + ad)
dm = tf.maximum(0., 1./k - ad)
return [
x[1],
-eta * x[1],
lm * tf.exp(-k * dm) - lp * tf.exp(-k * dp),
lp * (x[0] + dp) * tf.exp(-k * dp) - lm * (x[0] - dm) * tf.exp(-k * dm),
]
def s(t, x, y, z, r):
return [[nu, 0], [0, zeta], [0, 0], [0, 0]]
# - dH_dx
def f(t, x, y, z, r):
ad = y[2] / y[3] - x[0]
dp = tf.maximum(0., 1./k + ad)
dm = tf.maximum(0., 1./k - ad)
return [
-(y[3] * lp * tf.exp(-k * dp) - y[3] * lm * tf.exp(-k * dm)),
-(y[0] - eta * y[1]),
-(-2. * phi * x[2]),
-(0.)
]
def v(t, x, y, z, r):
return [[0, 0], [epsilon, -epsilon], [0, 0], [0, 0]]
# dg_dx
def g(x):
return [x[2], 0., x[0] - 2 * psi * x[2], 1.]
```
# Initial value layer
```
class InitialValue(Layer):
def __init__(self, y0, **kwargs):
super().__init__(**kwargs)
self.y0 = y0
def call(self, inputs):
return self.y0
```
# Model
```
def dX(t, x, y, z, r, dW, dN):
def drift(arg):
x, y, z, r = arg
return tf.math.multiply(b(t, x, y, z, r), dt)
a0 = tf.vectorized_map(drift, (x, y, z, r))
def noise(arg):
x, y, z, r, dW = arg
return tf.tensordot(s(t, x, y, z ,r), dW, [[1], [0]])
a1 = tf.vectorized_map(noise, (x, y, z, r, dW))
def jump(arg):
x, y, z, r, dN = arg
return tf.tensordot(v(t, x, y, z ,r), dN, [[1], [0]])
a2 = tf.vectorized_map(jump, (x, y, z, r, dN))
return a0 + a1 + a2
def dY(t, x, y, z, r, dW, dN):
def drift(arg):
x, y, z, r = arg
return tf.math.multiply(f(t, x, y, z, r), dt)
a0 = tf.vectorized_map(drift, (x, y, z, r))
def noise(arg):
x, y, z, r, dW = arg
return tf.tensordot(z, dW, [[1], [0]])
a1 = tf.vectorized_map(noise, (x, y, z, r, dW))
def jump(arg):
x, y, z, r, dN = arg
return tf.tensordot(r, dN, [[1], [0]])
a2 = tf.vectorized_map(jump, (x, y, z, r, dN))
return a0 + a1 + a2
paths = []
n_hidden_units = n_dimensions + n_diffusion_factors + n_jump_factors + 10
inputs_dW = Input(shape=(n_timesteps, n_diffusion_factors))
inputs_dN = Input(shape=(n_timesteps, n_jump_factors))
x0 = tf.Variable([[10., 0., 0., 0.]], trainable=False)
y0 = tf.Variable([g(x0[0])], trainable=True)
x = InitialValue(x0, name='x_0')(inputs_dW)
y = InitialValue(y0, name='y_0')(inputs_dW)
z = concatenate([x, y])
z = Dense(n_hidden_units, activation='relu', kernel_initializer=initializers.RandomNormal(stddev=1e-1), name='z1_0')(z)
z = Dense(n_dimensions * n_diffusion_factors, activation='relu', kernel_initializer=initializers.RandomNormal(stddev=1e-1), name='z2_0')(z)
z = Reshape((n_dimensions, n_diffusion_factors), name='zr_0')(z)
r = concatenate([x, y])
r = Dense(n_hidden_units, activation='relu', kernel_initializer=initializers.RandomNormal(stddev=1e-1), name='r1_0')(r)
r = Dense(n_dimensions * n_jump_factors, activation='relu', kernel_initializer=initializers.RandomNormal(stddev=1e-1), name='r2_0')(r)
r = Reshape((n_dimensions, n_jump_factors), name='rr_0')(r)
paths += [[x, y, z, r]]
# pre-compile lambda layers
@tf.function
def hx(args):
i, x, y, z, r, dW, dN = args
return x + dX(i * dt, x, y, z, r, dW, dN)
@tf.function
def hy(args):
i, x, y, z, r, dW, dN = args
return y + dY(i * dt, x, y, z, r, dW, dN)
for i in range(n_timesteps):
step = InitialValue(tf.Variable(i, dtype=tf.float32, trainable=False))(inputs_dW)
dW = Lambda(lambda x: x[0][:, tf.cast(x[1], tf.int32)])([inputs_dW, step])
dN = Lambda(lambda x: x[0][:, tf.cast(x[1], tf.int32)])([inputs_dN, step])
x, y = (
Lambda(hx, name=f'x_{i+1}')([step, x, y, z, r, dW, dN]),
Lambda(hy, name=f'y_{i+1}')([step, x, y, z, r, dW, dN]),
)
# we don't train z for the last time step; keep for consistency
z = concatenate([x, y])
z = Dense(n_hidden_units, activation='relu', name=f'z1_{i+1}')(z)
z = Dense(n_dimensions * n_diffusion_factors, activation='relu', name=f'z2_{i+1}')(z)
z = Reshape((n_dimensions, n_diffusion_factors), name=f'zr_{i+1}')(z)
# we don't train r for the last time step; keep for consistency
r = concatenate([x, y])
r = Dense(n_hidden_units, activation='relu', kernel_initializer=initializers.RandomNormal(stddev=1e-1), name=f'r1_{i+1}')(r)
r = Dense(n_dimensions * n_jump_factors, activation='relu', kernel_initializer=initializers.RandomNormal(stddev=1e-1), name=f'r2_{i+1}')(r)
r = Reshape((n_dimensions, n_jump_factors), name=f'rr_{i+1}')(r)
paths += [[x, y, z, r]]
outputs_loss = Lambda(lambda r: r[1] - tf.transpose(tf.vectorized_map(g, r[0])))([x, y])
outputs_paths = tf.stack(
[tf.stack([p[0] for p in paths[1:]], axis=1), tf.stack([p[1] for p in paths[1:]], axis=1)] +
[tf.stack([p[2][:, :, i] for p in paths[1:]], axis=1) for i in range(n_diffusion_factors)] +
[tf.stack([p[3][:, :, i] for p in paths[1:]], axis=1) for i in range(n_jump_factors)], axis=2)
adam = Adam(learning_rate=learning_rate)
model_loss = Model([inputs_dW, inputs_dN], outputs_loss)
model_loss.compile(loss='mse', optimizer=adam)
# (n_sample, n_timestep, x/y/z_k, n_dimension)
# skips the first time step
model_paths = Model([inputs_dW, inputs_dN], outputs_paths)
model_loss.summary()
```
# Transfer learning
```
# transfer weights right-to-left
model_loss.get_layer('y_0').set_weights(m_old.get_layer('y_0').get_weights())
n_small = 16
for i in range(n_small):
model_loss.get_layer(f'z1_{n_timesteps - n_small + i}').set_weights(m_old.get_layer(f'z1_{i}').get_weights())
model_loss.get_layer(f'z2_{n_timesteps - n_small + i}').set_weights(m_old.get_layer(f'z2_{i}').get_weights())
model_loss.get_layer(f'r1_{n_timesteps - n_small + i}').set_weights(m_old.get_layer(f'r1_{i}').get_weights())
model_loss.get_layer(f'r2_{n_timesteps - n_small + i}').set_weights(m_old.get_layer(f'r2_{i}').get_weights())
# try transfer learning from another starting point
model_loss.get_layer('y_0').set_weights(m_large.get_layer('y_0').get_weights())
for i in range(n_timesteps):
model_loss.get_layer(f'z1_{i}').set_weights(m_large.get_layer(f'z1_{i}').get_weights())
model_loss.get_layer(f'z2_{i}').set_weights(m_large.get_layer(f'z2_{i}').get_weights())
model_loss.get_layer(f'r1_{i}').set_weights(m_large.get_layer(f'r1_{i}').get_weights())
model_loss.get_layer(f'r2_{i}').set_weights(m_large.get_layer(f'r2_{i}').get_weights())
# transfer learning from cruder discretization
model_loss.get_layer('y_0').set_weights(m_small.get_layer('y_0').get_weights())
n_small = 4
for i in range(n_small):
for j in range(n_timesteps // n_small):
model_loss.get_layer(f'z1_{n_timesteps // n_small * i}').set_weights(m_small.get_layer(f'z1_{i}').get_weights())
model_loss.get_layer(f'z2_{n_timesteps // n_small * i}').set_weights(m_small.get_layer(f'z2_{i}').get_weights())
model_loss.get_layer(f'z1_{n_timesteps // n_small * i + j}').set_weights(m_small.get_layer(f'z1_{i}').get_weights())
model_loss.get_layer(f'z2_{n_timesteps // n_small * i + j}').set_weights(m_small.get_layer(f'z2_{i}').get_weights())
model_loss.get_layer(f'r1_{n_timesteps // n_small * i}').set_weights(m_small.get_layer(f'r1_{i}').get_weights())
model_loss.get_layer(f'r2_{n_timesteps // n_small * i}').set_weights(m_small.get_layer(f'r2_{i}').get_weights())
model_loss.get_layer(f'r1_{n_timesteps // n_small * i + j}').set_weights(m_small.get_layer(f'r1_{i}').get_weights())
model_loss.get_layer(f'r2_{n_timesteps // n_small * i + j}').set_weights(m_small.get_layer(f'r2_{i}').get_weights())
model_loss.save_weights('_models/weights0000.h5')
```
# Training
```
dW = tf.sqrt(dt) * tf.random.normal((n_paths, n_timesteps, n_diffusion_factors))
dN = tf.random.poisson((n_paths, n_timesteps), [dt * lp, dt * lm])
target = tf.zeros((n_paths, n_dimensions))
# check for exploding gradients before training
with tf.GradientTape() as tape:
loss = mse(model_loss([dW, dN]), target)
# bias of the last dense layer
variables = model_loss.variables[-1]
tape.gradient(loss, variables)
log_dir = "_logs/fit/" + datetime.now().strftime("%Y%m%d-%H%M%S")
checkpoint_callback = ModelCheckpoint('_models/weights{epoch:04d}.h5', save_weights_only=True, overwrite=True)
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir, histogram_freq=1)
history = model_loss.fit([dW, dN], target, batch_size=128, epochs=1000, callbacks=[checkpoint_callback, tensorboard_callback])
# validate
dW_test = tf.sqrt(dt) * tf.random.normal((n_paths//8, n_timesteps, n_diffusion_factors))
dN_test = tf.random.poisson((n_paths//8, n_timesteps), [dt * lp, dt * lm])
target_test = tf.zeros((n_paths//8, n_dimensions))
model_loss.evaluate([dW_test, dN_test], target_test)
```
# Display paths and loss
```
# load bad model
model_loss.load_weights('_models/weights0109.h5')
loss = model_loss([dW, dN]).numpy()
loss
paths = model_paths([dW, dN]).numpy()
def output(n0):
x = tf.transpose(paths[n0, :, 0, :], (1, 0))
dp = tf.maximum(0., 1./k + (paths[n0, :, 1, 2] / paths[n0, :, 1, 3] - paths[n0, :, 0, 0]))
dm = tf.maximum(0., 1./k - (paths[n0, :, 1, 2] / paths[n0, :, 1, 3] - paths[n0, :, 0, 0]))
return tf.concat([x, tf.expand_dims(dp, 0), tf.expand_dims(dm, 0)], axis=0)
for i in range(120, 140):
print(output(i))
fig, ax = plt.subplots(nrows=2, figsize=(10, 8))
out = output(502).numpy()
ax[0].set_title('midprice and d±')
ax[0].plot(out[0], c='b')
ax[0].plot(out[0] - out[5], c='r')
ax[0].plot(out[0] + out[4], c='r')
ax[1].set_title('alpha (red) and inventory (blue)')
ax[1].plot(out[1], c='r')
ax[1].twinx().plot(out[2], c='b')
# plt.plot(output(120).numpy().transpose())
```
| true |
code
| 0.713344 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.