prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import freqopttest.util as util
import freqopttest.data as data
import freqopttest.kernel as kernel
import freqopttest.tst as tst
import freqopttest.glo as glo
import sys
# sample source
m = 2000
dim = 200
n = m
seed = 11
#ss = data.SSGaussMeanDiff(dim, my=1.0)
ss = data.SSGaussVarDiff(dim)
#ss = data.SSBlobs()
dim = ss.dim()
tst_data = ss.sample(m, seed=seed+1)
tr, te = tst_data.split_tr_te(tr_proportion=0.5, seed=100)
#te = tst_data
```
## smooth CF test
```
J = 7
alpha = 0.01
smooth_cf = tst.SmoothCFTest.create_randn(te, J, alpha=alpha, seed=seed)
smooth_cf.perform_test(te)
```
## grid search to choose the best Gaussian width
```
def randn(J, d, seed):
rand_state = np.random.get_state()
np.random.seed(seed)
M = np.random.randn(J, d)
np.random.set_state(rand_state)
return M
T_randn = randn(J, dim, seed)
mean_sd = tr.mean_std()
scales = 2.0**np.linspace(-4, 4, 30)
#list_gwidth = mean_sd*scales*(dim**0.5)
list_gwidth = np.hstack( (mean_sd*scales*(dim**0.5), 2**np.linspace(-8, 8, 20) ))
list_gwidth.sort()
besti, powers = tst.SmoothCFTest.grid_search_gwidth(tr, T_randn, list_gwidth, alpha)
# plot
plt.plot(list_gwidth, powers, 'o-')
plt.xscale('log', basex=2)
plt.xlabel('Gaussian width')
plt.ylabel('Test power')
plt.title('Mean std: %.3g. Best chosen: %.2g'%(mean_sd, list_gwidth[besti]) )
med = util.meddistance(tr.stack_xy())
print('med distance xy: %.3g'%med)
# actual test
best_width = list_gwidth[besti]
scf_grid = tst.SmoothCFTest(T_randn, best_width, alpha)
scf_grid.perform_test(te)
```
## optimize test frequencies
```
op = {'n_test_freqs': J, 'seed': seed, 'max_iter': 300,
'batch_proportion': 1.0, 'freqs_step_size': 0.1,
'gwidth_step_size': 0.01, 'tol_fun': 1e-4}
# optimize on the training set
test_freqs, gwidth, info = tst.SmoothCFTest.optimize_freqs_width(tr, alpha, **op)
scf_opt = tst.SmoothCFTest(test_freqs, gwidth, alpha=alpha)
scf_opt_test = scf_opt.perform_test(te)
scf_opt_test
# plot optimization results
# trajectories of the Gaussian width
gwidths = info['gwidths']
fig, axs = plt.subplots(2, 2, figsize=(10, 9))
axs[0, 0].plot(gwidths)
axs[0, 0].set_xlabel('iteration')
axs[0, 0].set_ylabel('Gaussian width')
axs[0, 0].set_title('Gaussian width evolution')
# evolution of objective values
objs = info['obj_values']
axs[0, 1].plot(objs)
axs[0, 1].set_title('Objective $\lambda(T)$')
# trajectories of the test locations
# iters x J. X Coordinates of all test locations
locs = info['test_freqs']
for coord in [0, 1]:
locs_d0 = locs[:, :, coord]
J = locs_d0.shape[1]
axs[1, coord].plot(locs_d0)
axs[1, coord].set_xlabel('iteration')
axs[1, coord].set_ylabel('index %d of test_locs'%(coord))
axs[1, coord].set_title('evolution of %d test locations'%J)
print('optimized width: %.3f'%gwidth)
```
## SCF: optimize just the Gaussian width
```
op_gwidth = {'max_iter': 300,'gwidth_step_size': 0.1,
'batch_proportion': 1.0, 'tol_fun': 1e-4}
# optimize on the training set
rand_state = np.random.get_state()
np.random.seed(seed=seed)
T0_randn = np.random.randn(J, dim)
np.random.set_state(rand_state)
med = util.meddistance(tr.stack_xy())
gwidth, info = tst.SmoothCFTest.optimize_gwidth(tr, T0_randn, med**2, **op_gwidth)
# trajectories of the Gaussian width
gwidths = info['gwidths']
fig, axs = plt.subplots(1, 2, figsize=(10, 4))
axs[0].plot(gwidths)
axs[0].set_xlabel('iteration')
axs[0].set_ylabel('Gaussian width')
axs[0].set_title('Gaussian width evolution')
# evolution of objective values
objs = info['obj_values']
axs[1].plot(objs)
axs[1].set_title('Objective $\lambda(T)$')
```
| true |
code
| 0.621512 | null | null | null | null |
|
# T81-558: Applications of Deep Neural Networks
**Module 12: Deep Learning and Security**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module Video Material
Main video lecture:
* [Part 12.1: Security and Information Assurance with Deep Learning](https://www.youtube.com/watch?v=UI8HX5GzpGQ&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN&index=35)
* [Part 12.2: Programming KDD99 with Keras TensorFlow, Intrusion Detection System (IDS)](https://www.youtube.com/watch?v=2PAFVKA-OWY&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN&index=36)
* Part 12.3: Security Project (coming soon)
# Helpful Functions
You will see these at the top of every module. These are simply a set of reusable functions that we will make use of. Each of them will be explained as the semester progresses. They are explained in greater detail as the course progresses. Class 4 contains a complete overview of these functions.
```
import base64
import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
from sklearn import preprocessing
# Encode text values to dummy variables(i.e. [1,0,0],[0,1,0],[0,0,1] for red,green,blue)
def encode_text_dummy(df, name):
dummies = pd.get_dummies(df[name])
for x in dummies.columns:
dummy_name = f"{name}-{x}"
df[dummy_name] = dummies[x]
df.drop(name, axis=1, inplace=True)
# Encode text values to a single dummy variable. The new columns (which do not replace the old) will have a 1
# at every location where the original column (name) matches each of the target_values. One column is added for
# each target value.
def encode_text_single_dummy(df, name, target_values):
for tv in target_values:
l = list(df[name].astype(str))
l = [1 if str(x) == str(tv) else 0 for x in l]
name2 = f"{name}-{tv}"
df[name2] = l
# Encode text values to indexes(i.e. [1],[2],[3] for red,green,blue).
def encode_text_index(df, name):
le = preprocessing.LabelEncoder()
df[name] = le.fit_transform(df[name])
return le.classes_
# Encode a numeric column as zscores
def encode_numeric_zscore(df, name, mean=None, sd=None):
if mean is None:
mean = df[name].mean()
if sd is None:
sd = df[name].std()
df[name] = (df[name] - mean) / sd
# Convert all missing values in the specified column to the median
def missing_median(df, name):
med = df[name].median()
df[name] = df[name].fillna(med)
# Convert all missing values in the specified column to the default
def missing_default(df, name, default_value):
df[name] = df[name].fillna(default_value)
# Convert a Pandas dataframe to the x,y inputs that TensorFlow needs
def to_xy(df, target):
result = []
for x in df.columns:
if x != target:
result.append(x)
# find out the type of the target column. Is it really this hard? :(
target_type = df[target].dtypes
target_type = target_type[0] if hasattr(
target_type, '__iter__') else target_type
# Encode to int for classification, float otherwise. TensorFlow likes 32 bits.
if target_type in (np.int64, np.int32):
# Classification
dummies = pd.get_dummies(df[target])
return df[result].values.astype(np.float32), dummies.values.astype(np.float32)
# Regression
return df[result].values.astype(np.float32), df[[target]].values.astype(np.float32)
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return f"{h}:{m:>02}:{s:>05.2f}"
# Regression chart.
def chart_regression(pred, y, sort=True):
t = pd.DataFrame({'pred': pred, 'y': y.flatten()})
if sort:
t.sort_values(by=['y'], inplace=True)
plt.plot(t['y'].tolist(), label='expected')
plt.plot(t['pred'].tolist(), label='prediction')
plt.ylabel('output')
plt.legend()
plt.show()
# Remove all rows where the specified column is +/- sd standard deviations
def remove_outliers(df, name, sd):
drop_rows = df.index[(np.abs(df[name] - df[name].mean())
>= (sd * df[name].std()))]
df.drop(drop_rows, axis=0, inplace=True)
# Encode a column to a range between normalized_low and normalized_high.
def encode_numeric_range(df, name, normalized_low=-1, normalized_high=1,
data_low=None, data_high=None):
if data_low is None:
data_low = min(df[name])
data_high = max(df[name])
df[name] = ((df[name] - data_low) / (data_high - data_low)) \
* (normalized_high - normalized_low) + normalized_low
# This function submits an assignment. You can submit an assignment as much as you like, only the final
# submission counts. The paramaters are as follows:
# data - Pandas dataframe output.
# key - Your student key that was emailed to you.
# no - The assignment class number, should be 1 through 1.
# source_file - The full path to your Python or IPYNB file. This must have "_class1" as part of its name.
# . The number must match your assignment number. For example "_class2" for class assignment #2.
def submit(data,key,no,source_file=None):
if source_file is None and '__file__' not in globals(): raise Exception('Must specify a filename when a Jupyter notebook.')
if source_file is None: source_file = __file__
suffix = '_class{}'.format(no)
if suffix not in source_file: raise Exception('{} must be part of the filename.'.format(suffix))
with open(source_file, "rb") as image_file:
encoded_python = base64.b64encode(image_file.read()).decode('ascii')
ext = os.path.splitext(source_file)[-1].lower()
if ext not in ['.ipynb','.py']: raise Exception("Source file is {} must be .py or .ipynb".format(ext))
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key':key}, json={'csv':base64.b64encode(data.to_csv(index=False).encode('ascii')).decode("ascii"),
'assignment': no, 'ext':ext, 'py':encoded_python})
if r.status_code == 200:
print("Success: {}".format(r.text))
else: print("Failure: {}".format(r.text))
```
# The KDD-99 Dataset
The [KDD-99 dataset](http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html) is very famous in the security field and almost a "hello world" of intrusion detection systems in machine learning.
# Read in Raw KDD-99 Dataset
```
from keras.utils.data_utils import get_file
try:
path = get_file('kddcup.data_10_percent.gz', origin='http://kdd.ics.uci.edu/databases/kddcup99/kddcup.data_10_percent.gz')
except:
print('Error downloading')
raise
print(path)
# This file is a CSV, just no CSV extension or headers
# Download from: http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html
df = pd.read_csv(path, header=None)
print("Read {} rows.".format(len(df)))
# df = df.sample(frac=0.1, replace=False) # Uncomment this line to sample only 10% of the dataset
df.dropna(inplace=True,axis=1) # For now, just drop NA's (rows with missing values)
# The CSV file has no column heads, so add them
df.columns = [
'duration',
'protocol_type',
'service',
'flag',
'src_bytes',
'dst_bytes',
'land',
'wrong_fragment',
'urgent',
'hot',
'num_failed_logins',
'logged_in',
'num_compromised',
'root_shell',
'su_attempted',
'num_root',
'num_file_creations',
'num_shells',
'num_access_files',
'num_outbound_cmds',
'is_host_login',
'is_guest_login',
'count',
'srv_count',
'serror_rate',
'srv_serror_rate',
'rerror_rate',
'srv_rerror_rate',
'same_srv_rate',
'diff_srv_rate',
'srv_diff_host_rate',
'dst_host_count',
'dst_host_srv_count',
'dst_host_same_srv_rate',
'dst_host_diff_srv_rate',
'dst_host_same_src_port_rate',
'dst_host_srv_diff_host_rate',
'dst_host_serror_rate',
'dst_host_srv_serror_rate',
'dst_host_rerror_rate',
'dst_host_srv_rerror_rate',
'outcome'
]
# display 5 rows
df[0:5]
```
# Analyzing a Dataset
The following script can be used to give a high-level overview of how a dataset appears.
```
ENCODING = 'utf-8'
def expand_categories(values):
result = []
s = values.value_counts()
t = float(len(values))
for v in s.index:
result.append("{}:{}%".format(v,round(100*(s[v]/t),2)))
return "[{}]".format(",".join(result))
def analyze(filename):
print()
print("Analyzing: {}".format(filename))
df = pd.read_csv(filename,encoding=ENCODING)
cols = df.columns.values
total = float(len(df))
print("{} rows".format(int(total)))
for col in cols:
uniques = df[col].unique()
unique_count = len(uniques)
if unique_count>100:
print("** {}:{} ({}%)".format(col,unique_count,int(((unique_count)/total)*100)))
else:
print("** {}:{}".format(col,expand_categories(df[col])))
expand_categories(df[col])
# Analyze KDD-99
import tensorflow.contrib.learn as skflow
import pandas as pd
import os
import numpy as np
from sklearn import metrics
from scipy.stats import zscore
path = "./data/"
filename_read = os.path.join(path,"auto-mpg.csv")
```
# Encode the feature vector
Encode every row in the database. This is not instant!
```
# Now encode the feature vector
encode_numeric_zscore(df, 'duration')
encode_text_dummy(df, 'protocol_type')
encode_text_dummy(df, 'service')
encode_text_dummy(df, 'flag')
encode_numeric_zscore(df, 'src_bytes')
encode_numeric_zscore(df, 'dst_bytes')
encode_text_dummy(df, 'land')
encode_numeric_zscore(df, 'wrong_fragment')
encode_numeric_zscore(df, 'urgent')
encode_numeric_zscore(df, 'hot')
encode_numeric_zscore(df, 'num_failed_logins')
encode_text_dummy(df, 'logged_in')
encode_numeric_zscore(df, 'num_compromised')
encode_numeric_zscore(df, 'root_shell')
encode_numeric_zscore(df, 'su_attempted')
encode_numeric_zscore(df, 'num_root')
encode_numeric_zscore(df, 'num_file_creations')
encode_numeric_zscore(df, 'num_shells')
encode_numeric_zscore(df, 'num_access_files')
encode_numeric_zscore(df, 'num_outbound_cmds')
encode_text_dummy(df, 'is_host_login')
encode_text_dummy(df, 'is_guest_login')
encode_numeric_zscore(df, 'count')
encode_numeric_zscore(df, 'srv_count')
encode_numeric_zscore(df, 'serror_rate')
encode_numeric_zscore(df, 'srv_serror_rate')
encode_numeric_zscore(df, 'rerror_rate')
encode_numeric_zscore(df, 'srv_rerror_rate')
encode_numeric_zscore(df, 'same_srv_rate')
encode_numeric_zscore(df, 'diff_srv_rate')
encode_numeric_zscore(df, 'srv_diff_host_rate')
encode_numeric_zscore(df, 'dst_host_count')
encode_numeric_zscore(df, 'dst_host_srv_count')
encode_numeric_zscore(df, 'dst_host_same_srv_rate')
encode_numeric_zscore(df, 'dst_host_diff_srv_rate')
encode_numeric_zscore(df, 'dst_host_same_src_port_rate')
encode_numeric_zscore(df, 'dst_host_srv_diff_host_rate')
encode_numeric_zscore(df, 'dst_host_serror_rate')
encode_numeric_zscore(df, 'dst_host_srv_serror_rate')
encode_numeric_zscore(df, 'dst_host_rerror_rate')
encode_numeric_zscore(df, 'dst_host_srv_rerror_rate')
outcomes = encode_text_index(df, 'outcome')
num_classes = len(outcomes)
# display 5 rows
df.dropna(inplace=True,axis=1)
df[0:5]
# This is the numeric feature vector, as it goes to the neural net
```
# Train the Neural Network
```
import pandas as pd
import io
import requests
import numpy as np
import os
from sklearn.model_selection import train_test_split
from sklearn import metrics
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.callbacks import EarlyStopping
# Break into X (predictors) & y (prediction)
x, y = to_xy(df,'outcome')
# Create a test/train split. 25% test
# Split into train/test
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.25, random_state=42)
# Create neural net
model = Sequential()
model.add(Dense(10, input_dim=x.shape[1], kernel_initializer='normal', activation='relu'))
model.add(Dense(50, input_dim=x.shape[1], kernel_initializer='normal', activation='relu'))
model.add(Dense(10, input_dim=x.shape[1], kernel_initializer='normal', activation='relu'))
model.add(Dense(1, kernel_initializer='normal'))
model.add(Dense(y.shape[1],activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam')
monitor = EarlyStopping(monitor='val_loss', min_delta=1e-3, patience=5, verbose=1, mode='auto')
model.fit(x_train,y_train,validation_data=(x_test,y_test),callbacks=[monitor],verbose=2,epochs=1000)
# Measure accuracy
pred = model.predict(x_test)
pred = np.argmax(pred,axis=1)
y_eval = np.argmax(y_test,axis=1)
score = metrics.accuracy_score(y_eval, pred)
print("Validation score: {}".format(score))
```
| true |
code
| 0.521837 | null | null | null | null |
|
<img src="https://raw.githubusercontent.com/Qiskit/qiskit-tutorials/master/images/qiskit-heading.png" alt="Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook" width="500 px" align="left">
## _*The Vaidman Detection Test: Interaction Free Measurement*_
The latest version of this notebook is available on https://github.com/Qiskit/qiskit-tutorial.
***
### Contributors
Alex Breitweiser
***
### Qiskit Package Versions
```
import qiskit
qiskit.__qiskit_version__
```
## Introduction
One surprising result of quantum mechanics is the ability to measure something without ever directly "observing" it. This interaction-free measurement cannot be reproduced in classical mechanics. The prototypical example is the [Elitzur–Vaidman Bomb Experiment](https://en.wikipedia.org/wiki/Elitzur%E2%80%93Vaidman_bomb_tester) - in which one wants to test whether bombs are active without detonating them. In this example we will test whether an unknown operation is null (the identity) or an X gate, corresponding to a dud or a live bomb.
### The Algorithm
The algorithm will use two qubits, $q_1$ and $q_2$, as well as a small parameter, $\epsilon = \frac{\pi}{n}$ for some integer $n$. Call the unknown gate, which is either the identity or an X gate, $G$, and assume we have it in a controlled form. The algorithm is then:
1. Start with both $q_1$ and $q_2$ in the $|0\rangle$ state
2. Rotate $q_1$ by $\epsilon$ about the Y axis
3. Apply a controlled $G$ on $q_2$, conditioned on $q_1$
4. Measure $q_2$
5. Repeat (2-4) $n$ times
6. Measure $q_1$

### Explanation and proof of correctness
There are two cases: Either the gate is the identity (a dud), or it is an X gate (a live bomb).
#### Case 1: Dud
After rotation, $q_1$ is now approximately
$$q_1 \approx |0\rangle + \frac{\epsilon}{2} |1\rangle$$
Since the unknown gate is the identity, the controlled gate leaves the two qubit state separable,
$$q_1 \times q_2 \approx (|0\rangle + \frac{\epsilon}{2} |1\rangle) \times |0\rangle$$
and measurement is trivial (we will always measure $|0\rangle$ for $q_2$).
Repetition will not change this result - we will always keep separability and $q_2$ will remain in $|0\rangle$.
After n steps, $q_1$ will flip by $\pi$ to $|1\rangle$, and so measuring it will certainly yield $1$. Therefore, the output register for a dud bomb will read:
$$000...01$$
#### Case 2: Live
Again, after rotation, $q_1$ is now approximately
$$q_1 \approx |0\rangle + \frac{\epsilon}{2} |1\rangle$$
But, since the unknown gate is now an X gate, the combined state after $G$ is now
$$q_1 \times q_2 \approx |00\rangle + \frac{\epsilon}{2} |11\rangle$$
Measuring $q_2$ now might yield $1$, in which case we have "measured" the live bomb (obtained a result which differs from that of a dud) and it explodes. However, this only happens with a probability proportional to $\epsilon^2$. In the vast majority of cases, we will measure $0$ and the entire system will collapse back to
$$q_1 \times q_2 = |00\rangle$$
After every step, the system will most likely return to the original state, and the final measurement of $q_1$ will yield $0$. Therefore, the most likely outcome of a live bomb is
$$000...00$$
which will identify a live bomb without ever "measuring" it. If we ever obtain a 1 in the bits preceding the final bit, we will have detonated the bomb, but this will only happen with probability of order
$$P \propto n \epsilon^2 \propto \epsilon$$
This probability may be made arbitrarily small at the cost of an arbitrarily long circuit.
## Generating Random Bombs
A test set must be generated to experiment on - this can be done by classical (pseudo)random number generation, but as long as we have access to a quantum computer we might as well take advantage of the ability to generate true randomness.
```
# useful additional packages
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from collections import Counter #Use this to convert results from list to dict for histogram
# importing QISKit
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit import execute, Aer, IBMQ
from qiskit.providers.ibmq import least_busy
from qiskit.tools.visualization import plot_histogram
# To use IBMQ Quantum Experience
IBMQ.load_accounts()
```
We will generate a test set of 50 "bombs", and each "bomb" will be run through a 20-step measurement circuit. We set up the program as explained in previous examples.
```
# Use local qasm simulator
backend = Aer.get_backend('qasm_simulator')
# Use the IBMQ Quantum Experience
# backend = least_busy(IBMQ.backends())
N = 50 # Number of bombs
steps = 20 # Number of steps for the algorithm, limited by maximum circuit depth
eps = np.pi / steps # Algorithm parameter, small
# Prototype circuit for bomb generation
q_gen = QuantumRegister(1, name='q_gen')
c_gen = ClassicalRegister(1, name='c_gen')
IFM_gen = QuantumCircuit(q_gen, c_gen, name='IFM_gen')
# Prototype circuit for bomb measurement
q = QuantumRegister(2, name='q')
c = ClassicalRegister(steps+1, name='c')
IFM_meas = QuantumCircuit(q, c, name='IFM_meas')
```
Generating a random bomb is achieved by simply applying a Hadamard gate to a $q_1$, which starts in $|0\rangle$, and then measuring. This randomly gives a $0$ or $1$, each with equal probability. We run one such circuit for each bomb, since circuits are currently limited to a single measurement.
```
# Quantum circuits to generate bombs
qc = []
circuits = ["IFM_gen"+str(i) for i in range(N)]
# NB: Can't have more than one measurement per circuit
for circuit in circuits:
IFM = QuantumCircuit(q_gen, c_gen, name=circuit)
IFM.h(q_gen[0]) #Turn the qubit into |0> + |1>
IFM.measure(q_gen[0], c_gen[0])
qc.append(IFM)
_ = [i.qasm() for i in qc] # Suppress the output
```
Note that, since we want to measure several discrete instances, we do *not* want to average over multiple shots. Averaging would yield partial bombs, but we assume bombs are discretely either live or dead.
```
result = execute(qc, backend=backend, shots=1).result() # Note that we only want one shot
bombs = []
for circuit in qc:
for key in result.get_counts(circuit): # Hack, there should only be one key, since there was only one shot
bombs.append(int(key))
#print(', '.join(('Live' if bomb else 'Dud' for bomb in bombs))) # Uncomment to print out "truth" of bombs
plot_histogram(Counter(('Live' if bomb else 'Dud' for bomb in bombs))) #Plotting bomb generation results
```
## Testing the Bombs
Here we implement the algorithm described above to measure the bombs. As with the generation of the bombs, it is currently impossible to take several measurements in a single circuit - therefore, it must be run on the simulator.
```
# Use local qasm simulator
backend = Aer.get_backend('qasm_simulator')
qc = []
circuits = ["IFM_meas"+str(i) for i in range(N)]
#Creating one measurement circuit for each bomb
for i in range(N):
bomb = bombs[i]
IFM = QuantumCircuit(q, c, name=circuits[i])
for step in range(steps):
IFM.ry(eps, q[0]) #First we rotate the control qubit by epsilon
if bomb: #If the bomb is live, the gate is a controlled X gate
IFM.cx(q[0],q[1])
#If the bomb is a dud, the gate is a controlled identity gate, which does nothing
IFM.measure(q[1], c[step]) #Now we measure to collapse the combined state
IFM.measure(q[0], c[steps])
qc.append(IFM)
_ = [i.qasm() for i in qc] # Suppress the output
result = execute(qc, backend=backend, shots=1, max_credits=5).result()
def get_status(counts):
# Return whether a bomb was a dud, was live but detonated, or was live and undetonated
# Note that registers are returned in reversed order
for key in counts:
if '1' in key[1:]:
#If we ever measure a '1' from the measurement qubit (q1), the bomb was measured and will detonate
return '!!BOOM!!'
elif key[0] == '1':
#If the control qubit (q0) was rotated to '1', the state never entangled because the bomb was a dud
return 'Dud'
else:
#If we only measured '0' for both the control and measurement qubit, the bomb was live but never set off
return 'Live'
results = {'Live': 0, 'Dud': 0, "!!BOOM!!": 0}
for circuit in qc:
status = get_status(result.get_counts(circuit))
results[status] += 1
plot_histogram(results)
```
| true |
code
| 0.488405 | null | null | null | null |
|
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="figures/PDSH-cover-small.png">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
<!--NAVIGATION-->
< [In Depth: Naive Bayes Classification](05.05-Naive-Bayes.ipynb) | [Contents](Index.ipynb) | [In-Depth: Support Vector Machines](05.07-Support-Vector-Machines.ipynb) >
<a href="https://colab.research.google.com/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.06-Linear-Regression.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open and Execute in Google Colaboratory"></a>
# In Depth: Linear Regression
Just as naive Bayes (discussed earlier in [In Depth: Naive Bayes Classification](05.05-Naive-Bayes.ipynb)) is a good starting point for classification tasks, linear regression models are a good starting point for regression tasks.
Such models are popular because they can be fit very quickly, and are very interpretable.
You are probably familiar with the simplest form of a linear regression model (i.e., fitting a straight line to data) but such models can be extended to model more complicated data behavior.
In this section we will start with a quick intuitive walk-through of the mathematics behind this well-known problem, before seeing how before moving on to see how linear models can be generalized to account for more complicated patterns in data.
We begin with the standard imports:
```
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
```
## Simple Linear Regression
We will start with the most familiar linear regression, a straight-line fit to data.
A straight-line fit is a model of the form
$$
y = ax + b
$$
where $a$ is commonly known as the *slope*, and $b$ is commonly known as the *intercept*.
Consider the following data, which is scattered about a line with a slope of 2 and an intercept of -5:
```
rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
y = 2 * x - 5 + rng.randn(50)
plt.scatter(x, y);
```
We can use Scikit-Learn's ``LinearRegression`` estimator to fit this data and construct the best-fit line:
```
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model.fit(x[:, np.newaxis], y)
xfit = np.linspace(0, 10, 1000)
yfit = model.predict(xfit[:, np.newaxis])
plt.scatter(x, y)
plt.plot(xfit, yfit);
```
The slope and intercept of the data are contained in the model's fit parameters, which in Scikit-Learn are always marked by a trailing underscore.
Here the relevant parameters are ``coef_`` and ``intercept_``:
```
print("Model slope: ", model.coef_[0])
print("Model intercept:", model.intercept_)
```
We see that the results are very close to the inputs, as we might hope.
The ``LinearRegression`` estimator is much more capable than this, however—in addition to simple straight-line fits, it can also handle multidimensional linear models of the form
$$
y = a_0 + a_1 x_1 + a_2 x_2 + \cdots
$$
where there are multiple $x$ values.
Geometrically, this is akin to fitting a plane to points in three dimensions, or fitting a hyper-plane to points in higher dimensions.
The multidimensional nature of such regressions makes them more difficult to visualize, but we can see one of these fits in action by building some example data, using NumPy's matrix multiplication operator:
```
rng = np.random.RandomState(1)
X = 10 * rng.rand(100, 3)
y = 0.5 + np.dot(X, [1.5, -2., 1.])
model.fit(X, y)
print(model.intercept_)
print(model.coef_)
```
Here the $y$ data is constructed from three random $x$ values, and the linear regression recovers the coefficients used to construct the data.
In this way, we can use the single ``LinearRegression`` estimator to fit lines, planes, or hyperplanes to our data.
It still appears that this approach would be limited to strictly linear relationships between variables, but it turns out we can relax this as well.
## Basis Function Regression
One trick you can use to adapt linear regression to nonlinear relationships between variables is to transform the data according to *basis functions*.
We have seen one version of this before, in the ``PolynomialRegression`` pipeline used in [Hyperparameters and Model Validation](05.03-Hyperparameters-and-Model-Validation.ipynb) and [Feature Engineering](05.04-Feature-Engineering.ipynb).
The idea is to take our multidimensional linear model:
$$
y = a_0 + a_1 x_1 + a_2 x_2 + a_3 x_3 + \cdots
$$
and build the $x_1, x_2, x_3,$ and so on, from our single-dimensional input $x$.
That is, we let $x_n = f_n(x)$, where $f_n()$ is some function that transforms our data.
For example, if $f_n(x) = x^n$, our model becomes a polynomial regression:
$$
y = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots
$$
Notice that this is *still a linear model*—the linearity refers to the fact that the coefficients $a_n$ never multiply or divide each other.
What we have effectively done is taken our one-dimensional $x$ values and projected them into a higher dimension, so that a linear fit can fit more complicated relationships between $x$ and $y$.
### Polynomial basis functions
This polynomial projection is useful enough that it is built into Scikit-Learn, using the ``PolynomialFeatures`` transformer:
```
from sklearn.preprocessing import PolynomialFeatures
x = np.array([2, 3, 4])
poly = PolynomialFeatures(3, include_bias=False)
poly.fit_transform(x[:, None])
```
We see here that the transformer has converted our one-dimensional array into a three-dimensional array by taking the exponent of each value.
This new, higher-dimensional data representation can then be plugged into a linear regression.
As we saw in [Feature Engineering](05.04-Feature-Engineering.ipynb), the cleanest way to accomplish this is to use a pipeline.
Let's make a 7th-degree polynomial model in this way:
```
from sklearn.pipeline import make_pipeline
poly_model = make_pipeline(PolynomialFeatures(7),
LinearRegression())
```
With this transform in place, we can use the linear model to fit much more complicated relationships between $x$ and $y$.
For example, here is a sine wave with noise:
```
rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
y = np.sin(x) + 0.1 * rng.randn(50)
poly_model.fit(x[:, np.newaxis], y)
yfit = poly_model.predict(xfit[:, np.newaxis])
plt.scatter(x, y)
plt.plot(xfit, yfit);
```
Our linear model, through the use of 7th-order polynomial basis functions, can provide an excellent fit to this non-linear data!
### Gaussian basis functions
Of course, other basis functions are possible.
For example, one useful pattern is to fit a model that is not a sum of polynomial bases, but a sum of Gaussian bases.
The result might look something like the following figure:

[figure source in Appendix](#Gaussian-Basis)
The shaded regions in the plot are the scaled basis functions, and when added together they reproduce the smooth curve through the data.
These Gaussian basis functions are not built into Scikit-Learn, but we can write a custom transformer that will create them, as shown here and illustrated in the following figure (Scikit-Learn transformers are implemented as Python classes; reading Scikit-Learn's source is a good way to see how they can be created):
```
from sklearn.base import BaseEstimator, TransformerMixin
class GaussianFeatures(BaseEstimator, TransformerMixin):
"""Uniformly spaced Gaussian features for one-dimensional input"""
def __init__(self, N, width_factor=2.0):
self.N = N
self.width_factor = width_factor
@staticmethod
def _gauss_basis(x, y, width, axis=None):
arg = (x - y) / width
return np.exp(-0.5 * np.sum(arg ** 2, axis))
def fit(self, X, y=None):
# create N centers spread along the data range
self.centers_ = np.linspace(X.min(), X.max(), self.N)
self.width_ = self.width_factor * (self.centers_[1] - self.centers_[0])
return self
def transform(self, X):
return self._gauss_basis(X[:, :, np.newaxis], self.centers_,
self.width_, axis=1)
gauss_model = make_pipeline(GaussianFeatures(20),
LinearRegression())
gauss_model.fit(x[:, np.newaxis], y)
yfit = gauss_model.predict(xfit[:, np.newaxis])
plt.scatter(x, y)
plt.plot(xfit, yfit)
plt.xlim(0, 10);
```
We put this example here just to make clear that there is nothing magic about polynomial basis functions: if you have some sort of intuition into the generating process of your data that makes you think one basis or another might be appropriate, you can use them as well.
## Regularization
The introduction of basis functions into our linear regression makes the model much more flexible, but it also can very quickly lead to over-fitting (refer back to [Hyperparameters and Model Validation](05.03-Hyperparameters-and-Model-Validation.ipynb) for a discussion of this).
For example, if we choose too many Gaussian basis functions, we end up with results that don't look so good:
```
model = make_pipeline(GaussianFeatures(30),
LinearRegression())
model.fit(x[:, np.newaxis], y)
plt.scatter(x, y)
plt.plot(xfit, model.predict(xfit[:, np.newaxis]))
plt.xlim(0, 10)
plt.ylim(-1.5, 1.5);
```
With the data projected to the 30-dimensional basis, the model has far too much flexibility and goes to extreme values between locations where it is constrained by data.
We can see the reason for this if we plot the coefficients of the Gaussian bases with respect to their locations:
```
def basis_plot(model, title=None):
fig, ax = plt.subplots(2, sharex=True)
model.fit(x[:, np.newaxis], y)
ax[0].scatter(x, y)
ax[0].plot(xfit, model.predict(xfit[:, np.newaxis]))
ax[0].set(xlabel='x', ylabel='y', ylim=(-1.5, 1.5))
if title:
ax[0].set_title(title)
ax[1].plot(model.steps[0][1].centers_,
model.steps[1][1].coef_)
ax[1].set(xlabel='basis location',
ylabel='coefficient',
xlim=(0, 10))
model = make_pipeline(GaussianFeatures(30), LinearRegression())
basis_plot(model)
```
The lower panel of this figure shows the amplitude of the basis function at each location.
This is typical over-fitting behavior when basis functions overlap: the coefficients of adjacent basis functions blow up and cancel each other out.
We know that such behavior is problematic, and it would be nice if we could limit such spikes expliticly in the model by penalizing large values of the model parameters.
Such a penalty is known as *regularization*, and comes in several forms.
### Ridge regression ($L_2$ Regularization)
Perhaps the most common form of regularization is known as *ridge regression* or $L_2$ *regularization*, sometimes also called *Tikhonov regularization*.
This proceeds by penalizing the sum of squares (2-norms) of the model coefficients; in this case, the penalty on the model fit would be
$$
P = \alpha\sum_{n=1}^N \theta_n^2
$$
where $\alpha$ is a free parameter that controls the strength of the penalty.
This type of penalized model is built into Scikit-Learn with the ``Ridge`` estimator:
```
from sklearn.linear_model import Ridge
model = make_pipeline(GaussianFeatures(30), Ridge(alpha=0.1))
basis_plot(model, title='Ridge Regression')
```
The $\alpha$ parameter is essentially a knob controlling the complexity of the resulting model.
In the limit $\alpha \to 0$, we recover the standard linear regression result; in the limit $\alpha \to \infty$, all model responses will be suppressed.
One advantage of ridge regression in particular is that it can be computed very efficiently—at hardly more computational cost than the original linear regression model.
### Lasso regression ($L_1$ regularization)
Another very common type of regularization is known as lasso, and involves penalizing the sum of absolute values (1-norms) of regression coefficients:
$$
P = \alpha\sum_{n=1}^N |\theta_n|
$$
Though this is conceptually very similar to ridge regression, the results can differ surprisingly: for example, due to geometric reasons lasso regression tends to favor *sparse models* where possible: that is, it preferentially sets model coefficients to exactly zero.
We can see this behavior in duplicating the ridge regression figure, but using L1-normalized coefficients:
```
from sklearn.linear_model import Lasso
model = make_pipeline(GaussianFeatures(30), Lasso(alpha=0.001))
basis_plot(model, title='Lasso Regression')
```
With the lasso regression penalty, the majority of the coefficients are exactly zero, with the functional behavior being modeled by a small subset of the available basis functions.
As with ridge regularization, the $\alpha$ parameter tunes the strength of the penalty, and should be determined via, for example, cross-validation (refer back to [Hyperparameters and Model Validation](05.03-Hyperparameters-and-Model-Validation.ipynb) for a discussion of this).
## Example: Predicting Bicycle Traffic
As an example, let's take a look at whether we can predict the number of bicycle trips across Seattle's Fremont Bridge based on weather, season, and other factors.
We have seen this data already in [Working With Time Series](03.11-Working-with-Time-Series.ipynb).
In this section, we will join the bike data with another dataset, and try to determine the extent to which weather and seasonal factors—temperature, precipitation, and daylight hours—affect the volume of bicycle traffic through this corridor.
Fortunately, the NOAA makes available their daily [weather station data](http://www.ncdc.noaa.gov/cdo-web/search?datasetid=GHCND) (I used station ID USW00024233) and we can easily use Pandas to join the two data sources.
We will perform a simple linear regression to relate weather and other information to bicycle counts, in order to estimate how a change in any one of these parameters affects the number of riders on a given day.
In particular, this is an example of how the tools of Scikit-Learn can be used in a statistical modeling framework, in which the parameters of the model are assumed to have interpretable meaning.
As discussed previously, this is not a standard approach within machine learning, but such interpretation is possible for some models.
Let's start by loading the two datasets, indexing by date:
```
!sudo apt-get update
!apt-get -y install curl
!curl -o FremontBridge.csv https://data.seattle.gov/api/views/65db-xm6k/rows.csv?accessType=DOWNLOAD
# !wget -o FremontBridge.csv "https://data.seattle.gov/api/views/65db-xm6k/rows.csv?accessType=DOWNLOAD"
import pandas as pd
counts = pd.read_csv('FremontBridge.csv', index_col='Date', parse_dates=True)
weather = pd.read_csv('data/BicycleWeather.csv', index_col='DATE', parse_dates=True)
```
Next we will compute the total daily bicycle traffic, and put this in its own dataframe:
```
daily = counts.resample('d').sum()
daily['Total'] = daily.sum(axis=1)
daily = daily[['Total']] # remove other columns
```
We saw previously that the patterns of use generally vary from day to day; let's account for this in our data by adding binary columns that indicate the day of the week:
```
days = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun']
for i in range(7):
daily[days[i]] = (daily.index.dayofweek == i).astype(float)
```
Similarly, we might expect riders to behave differently on holidays; let's add an indicator of this as well:
```
from pandas.tseries.holiday import USFederalHolidayCalendar
cal = USFederalHolidayCalendar()
holidays = cal.holidays('2012', '2016')
daily = daily.join(pd.Series(1, index=holidays, name='holiday'))
daily['holiday'].fillna(0, inplace=True)
```
We also might suspect that the hours of daylight would affect how many people ride; let's use the standard astronomical calculation to add this information:
```
from datetime import datetime
def hours_of_daylight(date, axis=23.44, latitude=47.61):
"""Compute the hours of daylight for the given date"""
days = (date - datetime(2000, 12, 21)).days
m = (1. - np.tan(np.radians(latitude))
* np.tan(np.radians(axis) * np.cos(days * 2 * np.pi / 365.25)))
return 24. * np.degrees(np.arccos(1 - np.clip(m, 0, 2))) / 180.
daily['daylight_hrs'] = list(map(hours_of_daylight, daily.index))
daily[['daylight_hrs']].plot()
plt.ylim(8, 17)
```
We can also add the average temperature and total precipitation to the data.
In addition to the inches of precipitation, let's add a flag that indicates whether a day is dry (has zero precipitation):
```
# temperatures are in 1/10 deg C; convert to C
weather['TMIN'] /= 10
weather['TMAX'] /= 10
weather['Temp (C)'] = 0.5 * (weather['TMIN'] + weather['TMAX'])
# precip is in 1/10 mm; convert to inches
weather['PRCP'] /= 254
weather['dry day'] = (weather['PRCP'] == 0).astype(int)
daily = daily.join(weather[['PRCP', 'Temp (C)', 'dry day']],rsuffix='0')
```
Finally, let's add a counter that increases from day 1, and measures how many years have passed.
This will let us measure any observed annual increase or decrease in daily crossings:
```
daily['annual'] = (daily.index - daily.index[0]).days / 365.
```
Now our data is in order, and we can take a look at it:
```
daily.head()
```
With this in place, we can choose the columns to use, and fit a linear regression model to our data.
We will set ``fit_intercept = False``, because the daily flags essentially operate as their own day-specific intercepts:
```
# Drop any rows with null values
daily.dropna(axis=0, how='any', inplace=True)
column_names = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun', 'holiday',
'daylight_hrs', 'PRCP', 'dry day', 'Temp (C)', 'annual']
X = daily[column_names]
y = daily['Total']
model = LinearRegression(fit_intercept=False)
model.fit(X, y)
daily['predicted'] = model.predict(X)
```
Finally, we can compare the total and predicted bicycle traffic visually:
```
daily[['Total', 'predicted']].plot(alpha=0.5);
```
It is evident that we have missed some key features, especially during the summer time.
Either our features are not complete (i.e., people decide whether to ride to work based on more than just these) or there are some nonlinear relationships that we have failed to take into account (e.g., perhaps people ride less at both high and low temperatures).
Nevertheless, our rough approximation is enough to give us some insights, and we can take a look at the coefficients of the linear model to estimate how much each feature contributes to the daily bicycle count:
```
params = pd.Series(model.coef_, index=X.columns)
params
```
These numbers are difficult to interpret without some measure of their uncertainty.
We can compute these uncertainties quickly using bootstrap resamplings of the data:
```
from sklearn.utils import resample
np.random.seed(1)
err = np.std([model.fit(*resample(X, y)).coef_
for i in range(1000)], 0)
```
With these errors estimated, let's again look at the results:
```
print(pd.DataFrame({'effect': params.round(0),
'error': err.round(0)}))
```
We first see that there is a relatively stable trend in the weekly baseline: there are many more riders on weekdays than on weekends and holidays.
We see that for each additional hour of daylight, 129 ± 9 more people choose to ride; a temperature increase of one degree Celsius encourages 65 ± 4 people to grab their bicycle; a dry day means an average of 548 ± 33 more riders, and each inch of precipitation means 665 ± 62 more people leave their bike at home.
Once all these effects are accounted for, we see a modest increase of 27 ± 18 new daily riders each year.
Our model is almost certainly missing some relevant information. For example, nonlinear effects (such as effects of precipitation *and* cold temperature) and nonlinear trends within each variable (such as disinclination to ride at very cold and very hot temperatures) cannot be accounted for in this model.
Additionally, we have thrown away some of the finer-grained information (such as the difference between a rainy morning and a rainy afternoon), and we have ignored correlations between days (such as the possible effect of a rainy Tuesday on Wednesday's numbers, or the effect of an unexpected sunny day after a streak of rainy days).
These are all potentially interesting effects, and you now have the tools to begin exploring them if you wish!
<!--NAVIGATION-->
< [In Depth: Naive Bayes Classification](05.05-Naive-Bayes.ipynb) | [Contents](Index.ipynb) | [In-Depth: Support Vector Machines](05.07-Support-Vector-Machines.ipynb) >
<a href="https://colab.research.google.com/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.06-Linear-Regression.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open and Execute in Google Colaboratory"></a>
| true |
code
| 0.647185 | null | null | null | null |
|
# Analytics and demand forecasting for a multi-national retail store
## Notebook by Edward Warothe
### Introduction
General information about this analysis is in the readme file.
There are 4 datasets in these analysis: stores -has location, type and cluster information about the 54 stores in check; items which has family, class and perishable columns; transactions -has daily average transactions for each store; oil -has the daily average oil price per barrel; and train, which has date, store number, item number, unit sales and on promotion columns. We'll analyze all these to look for patterns and\or interesting features in the data.
At the moment of writing this article, I'm using a windows machine, core i7 with 8 GB RAM. Why is this information important? As you'll see the entire dataset takes around 5 GB in csv format which is too much for my machine to handle. My solution was to bucketize the train dataset into years (2013-2017). This method worked out especially well compared to several others I considered. I even have a short [medium article](https://eddywarothe.medium.com/is-your-data-too-big-for-your-ram-b3ed17a74095) comparing the different solutions I tried, results and compromises for each, and my choice, which is really important in case you come across a similar problem.
The images and charts are rendered using plotly's non-interactive renderer, (plotly.io svg). To get full plotly interactivity on your notebook (several hover tool capabilities), if you have an internet conection, delete the plotly.pio and pio.renderers.default='svg' lines below.
```
# Fisrt, we load the required python packages to use in the analyses.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import gc
import time
import pyarrow
from scipy.signal import savgol_filter
from fbprophet import Prophet
import plotly.graph_objects as go
import plotly.express as px
import plotly.io as pio
pio.renderers.default = 'svg'
import warnings
warnings.filterwarnings('ignore')
```
After loading the train dataset, I split it by year and persist it into my storage as a parquet file which preserves the data types I have preset and has approximately has read times 50% faster than csv. Before the split, I will separate the negative unit sale values from the positive ones. These negative values are from item returns. Later on, we'll analyze the returns data.
```
dtype = {'store_nbr':np.int16, 'item_nbr':np.int32, 'unit_sales':np.float32, 'onpromotion':object}
chunks = pd.read_csv('C:/favorita2/train.csv', parse_dates=['date'], dtype=dtype,
chunksize=1000000, usecols=[1,2,3,4,5])
# the below section is in comment form because running it consumes to much resources on my machine
'''
type(chunks)
train = pd.DataFrame()
count = 0
start = time.time()
for chunk in chunks:
train = pd.concat([train, chunk])
print('chunk', count, 'time taken', time.time()-start)
count += 1
returns = train[train['unit_sales']<0]
returns.to_csv('C:/returns.csv')
# then get the symmetric difference of the two
train = train.merge(returns,indicator = True, how='left').loc[lambda x: x['_merge']=='left_only']
# get the years by splitting
year1 = train[train['date'].between('2013-01-01', '2013-12-31')]
year2 = train[train['date'].between('2014-01-01', '2014-12-31')]
year3 = train[train['date'].between('2015-01-01', '2015-12-31')]
year4 = train[train['date'].between('2016-01-01', '2016-12-31')]
year5 = train[train['date'].between('2017-01-01', '2017-12-31')]
# it's failrly easy to save each as a parquet file for later reference and analysis
year1.to_parquet('C:/year1.parquet', engine = 'pyarrow', index=False)
# to load the dataset
year1 = pd.read_parquet('C:/year1.parquet')
'''
```
From this point, analysis becomes easier. Since our focus is on demand forecasting for certain items via time series analysis, we first answer some basic questions about our data :
1. Which items are getting popular as time goes? (so as to stock more of these items depending on the time thy're popular) 2. Which are getting less popular?
3. Which have consistently good sales?
4. What family do the preceding items belong to?
5. How does location affect sales?
6. How does oil price and transaction number affect sales?
7. Which items were returned most? How did returns affect sales?
8. What are the expected forecast sales for September 2017?
We answer these and many more in our quest to extract as much info as possible from the dataset.
Since loading the entire dataset takes up a lot of time and resources, we'll load the chunks, which have been split by year, from now on.
```
items = pd.read_csv('C:/favorita2/items.csv')
year1 = pd.read_parquet('C:/favorita2/year1.parquet')
year2 = pd.read_parquet('C:/favorita2/year2.parquet')
year3 = pd.read_parquet('C:/favorita2/year3.parquet')
year4 = pd.read_parquet('C:/favorita2/year4.parquet')
year5 = pd.read_parquet('C:/favorita2/year5.parquet')
```
#### 1. which items had increasing demand over the years? (increasing number of sales counts)
```
def get_counts(data):
# function to get item count in a particular year
item_count = data.item_nbr.value_counts().to_frame()
item_count = item_count.reset_index(level=0)
item_count.rename(columns={'index':'item_nbr', 'item_nbr':'counts'}, inplace=True)
return item_count
count1 = get_counts(year1)
count2 = get_counts(year2)
count3 = get_counts(year3)
count4 = get_counts(year4)
count5 = get_counts(year5)
count1.head()
```
Next we write a function to get the item count percentage difference, e.g between year1(2013) and year2(2014), for items featured in both years.
```
# get difference in item count for 2 consecutive years
def get_diff(data1, data2):
combined = data1.merge(data2, on = 'item_nbr', how = 'inner', suffixes = ('_a', '_b'))
combined['diff'] = ((combined['counts_b'] - combined['counts_a']) / combined['counts_a']).round(2)
return combined.sort_values(by='diff', ascending=False).merge(items, on='item_nbr', how='left')
diff = get_diff(count1, count2)
diff.head()
```
We can use the percentage differences between consecutive years to answer question 1. But we'll have to filter out other columns except item nbr and diff from the result returned by the get_diff function.
```
# get difference in item count for 2 consecutive years
def get_diff(data1, data2):
combined = data1.merge(data2, on = 'item_nbr', how = 'inner', suffixes = ('_a', '_b'))
combined['diff'] = ((combined['counts_b'] - combined['counts_a']) / combined['counts_a']).round(2)
return combined.sort_values(by='diff', ascending=False).merge(items, on='item_nbr', how='left')[['item_nbr', 'diff']]
diff1 = get_diff(count1,count2)
diff2 = get_diff(count2,count3)
diff3 = get_diff(count3,count4)
diff4 = get_diff(count4,count5)
dfs = [diff1, diff2, diff3, diff4]
from functools import reduce
df = reduce(lambda left,right: pd.merge(left,right, on='item_nbr'), dfs)
df.merge(items, on='item_nbr', how='inner').iloc[:,[0,1,2,3,4,5]].head(5)
```
The diff_x and diff_y keep repeating due to pandas merge behaviour for suffixes. In this case, the diff columns from left to right are percentage differences between the item counts from 2013 until 2017 respectively. That is, diff_x = 2014 item count - 2013 item count, and so on. Note we are limited in the number of items we can preview since the 'inner' parameter from the merge function only selects item numbers common to all the years. This will be remedied later by selecting the difference between the last 3 and 2 years.
#### 2. Which items were consistent perfomers? (those with consistent improvement in sales counts)
Note that since we're getting the differences between each year consecutively, positive values indicate an improvement from the previous year.
```
merged_counts = df.merge(items, on='item_nbr', how='inner').iloc[:,[0,1,2,3,4]]
merged_counts[(merged_counts > 0).all(1)].merge(items, on='item_nbr', how='left')
```
There are only three items that had increased transaction count over the years. The GroceryI item, 910928, is particularly interesting since it's constantly increasing in demand.
Lets have a look at the three years from 2014 since they had more common items.
```
dfs = [diff2, diff3, diff4]
from functools import reduce
df = reduce(lambda left,right: pd.merge(left,right, on='item_nbr'), dfs)
df.merge(items, on='item_nbr', how='inner').iloc[:,[0,1,2,3,4]].head(5)
merged_counts = df.merge(items, on='item_nbr', how='inner').iloc[:,[0,1,2,3]]
merged_counts[(merged_counts > 0).all(1)].merge(items, on='item_nbr', how='inner').sort_values(by=['diff','diff_y'], ascending=False).head(5)
```
There are 22 item that are on increasing demand from 2014 till 2017. We see that 2016 saw some big jumps in demand of select items as compared to the other years. The inventory and restocking options for this items should be a priority for the company.
Using this method, we can easily get the worst perfoming items across the last 4 years(2014 to 2017).
#### 3. Which items had consistently decreasing purchase counts? (which more or less equals demand)
```
merged_counts[(merged_counts.iloc[:,[1,2,3]] < 0).all(1)].merge(items, on='item_nbr', how='inner').family.value_counts()
```
There are 99 items which have had decreasing purchase counts over the last 4 years, with 64% of these items belonging to GroceryI and cleaning.
#### 4. Which items are in demand during the sales spikes?
The next question to answer in the demand planning process is when the spikes happen, and which items are in demand during these spikes. For this analysis, we'll make a time series object by averaging daily unit sales, and utilize the Savitsky-Golay filter to smooth our time series in order to get a view of the general trend and cyclical movements in the data.
```
items = pd.read_csv('C:/favorita2/items.csv')
year1 = pd.read_parquet('C:/favorita2/year1.parquet')
year2 = pd.read_parquet('C:/favorita2/year2.parquet')
year3 = pd.read_parquet('C:/favorita2/year3.parquet')
temp1 = pd.concat([data.groupby('date', as_index=False)['unit_sales'].mean() for data in [year1, year2, year3]])
del([year1, year2, year3])
import gc
gc.collect()
year4 = pd.read_parquet('C:/favorita2/year4.parquet')
year5 = pd.read_parquet('C:/favorita2/year5.parquet')
temp2 = pd.concat([data.groupby('date', as_index=False)['unit_sales'].mean() for data in [year4, year5]])
del([year4,year5])
df = pd.concat([temp1,temp2])
fig = go.Figure()
fig.add_trace(go.Scatter(x=df['date'], y=df['unit_sales']))
fig.add_trace(go.Scatter(x=df['date'],y=savgol_filter(df['unit_sales'],31,3)))
```
There 2 groups of spikes in the time series, one at 2/3rd of every mth-end mth, the other at
mid-mth period 15-17th. We filter spikes with a relatively high daily average unit sales value (12 and above) and see which items featured prominently during these days.
```
df['date'] = pd.to_datetime(df['date'])
spikes = df[df['unit_sales']>12]
spikes.info()
# since loading the entire dataset is out of the question, we 2013 and compare it to the spikes in 2016
y1_spikes = spikes[spikes['date'].dt.year == 2013].merge(year1, on='date', how='inner')
get_counts(y1_spikes).merge(items, on='item_nbr', how='left').iloc[:,[0,1,2]].head(200).family.value_counts()
```
Which stores were featured in these spikes?
```
y1_spikes.store_nbr.value_counts().head(5)
# lets compare to the spikes in 2016
y4_spikes = spikes[spikes['date'].dt.year == 2016].merge(year4, on='date', how='inner')
get_counts(y4_spikes).merge(items, on='item_nbr', how='left').iloc[:,[0,1,2]].head(200).family.value_counts()
y4_spikes.store_nbr.value_counts().head(5) # almost the same performance for stores compared
```
I also came across an interesting feature while looking at individual data spikes. During 2013 certain meat items were the most popular during these spikes as compared to beverage items during 2016.
```
topitems(year1, '2013-06-02').head(10)
topitems(year5, '2017-04-01').head(10)
```
#### 5. How does location affect sales? (What are the different sales trends in these locations)
The answer to this requires a visualization tool like streamlit, tableau or power BI to distinctly represent the different geographies. This is done at the end of this notebook.
#### 6. How did oil and transaction number affect sales?
We graph out a time series for both and look for changes in trend.
```
oil = pd.read_csv('C:/favorita2/oil.csv', parse_dates = [0])
oil.info() # dcoilwtico is the daily oil price
px.line(oil,x='date', y='dcoilwtico', color_discrete_map={'dcoilwtico':'ffa500'})
```
From the graph, we should see a increase in unit sales starting from mid-2014 but the general time series graph does not show a major increase in demand.
Although it would be better suited to look at each store individually, lets analyze the daily average transaction number.
```
transx = pd.read_csv('c:/favorita2/transactions.csv', parse_dates=[0])
transx.info()
grp_transx = transx.groupby('date', as_index=False)['transactions'].mean()
grp_transx.info()
fig = go.Figure()
fig.add_trace(go.Scatter(x=grp_transx['date'], y=grp_transx['transactions']))
fig.add_trace(go.Scatter(x=grp_transx['date'],y=savgol_filter(grp_transx['transactions'],29,3)))
```
The transactions are significant during the end of year holidays. Jan 1st 2014 shows an abnormal drop in average transactions and might warrant further analysis to ascertain the cause.
#### 7. How did returns affect sales?
Returns may signal problems with the items or delivery, and may cost the company in terms of lost revenue or even worse, lost customers. Questions to be answered in this analysis include: what items were returned mostwhen were they returned? is there a pattern in dates? common date? Are returns on the increase? decrease? Where? (a particular store? cluster?)
```
# to load the returns file
returns = pd.read_parquet('C:/favorita2/returns.parquet', engine='pyarrow')
returns.drop(['onpromotion'], axis=1, inplace=True) # do away with onpromotion col since it has only 8 items
returns.unit_sales = returns.unit_sales * -1
returns.info()
items = pd.read_csv('C:/favorita2/items.csv')
items_returned = returns.item_nbr.value_counts().to_frame() # might have defects: supplier or delivery/storage problem
items_returned.reset_index(level=0, inplace=True)
items_returned.rename(columns={'index':'item_nbr', 'item_nbr':'count'}, inplace=True)
items_returned.merge(items, on='item_nbr', how='left').head(15)
```
There were 2548 returns with 98% of those having been returned more than 10 times. The above table shows the top 15 returned items. Contrary to my expectation, most returns do not belong to the GroceryI or beverage item family but from Automotive and Home & Kitchen II. Since the specific items returned have been revealed, the next step for an analyst would be to find out the exact reason for the returns and avoid future errors if possible. Do the returns happen at a specific time? Let's find out:
```
import plotly.express as px
from scipy.signal import savgol_filter
return_date = returns.groupby('date', as_index=False)['item_nbr'].count()
px.line(return_date, x="date", y=savgol_filter(return_date.item_nbr, 29,3))
```
From the above plot, returns are certainly on the increase. This is not desirable since the transactions, and average unit sales time series graphs are almost constant through the five years in question. The causes for increasing trend should be checked and solutions delivered quickly to prevent lost revenue.
The days around April 23rd 2016 show an abnormally large increase in returns. These could be due to the effects of the earthquake on April 16th, as priorities changed for several people with regard to items needed from retail stores.
Which stores had most returned items?
```
store = pd.read_csv('C:/favorita2/stores.csv')
str_returns = returns.store_nbr.value_counts().to_frame().reset_index(level=0)
str_returns.rename(columns={'index':'store_nbr', 'store_nbr':'returns'}, inplace=True)
merged = str_returns.merge(store, on='store_nbr', how='left')
merged.head(7)
merged.type.value_counts()
```
store 18-type B, cluster 16 leads with 483 returns out of the top 27 stores with return counts exceeding 100. Type D and A stores are the majority of the stores with most returns. The states Pichincha and Quito led in terms of location, this could be because it has many stores per unit area as compared to other states.
Which stores lost the greatest revenue for returned items?
```
avg_returns = returns.groupby('store_nbr', as_index=False)['unit_sales'].sum().sort_values(by='unit_sales', ascending=False)
avg_returns.reset_index(drop=True, inplace=True)
avg_returns.merge(store, on='store_nbr', how='left').head(10)
```
Lets have a look into the first 3 stores:
stores that lead in the table had items with more monetary value as compared to the rest, returned
e.g a certain item could have been worth 10000 in unit sales as compared to most which had a unit sale value of 4.
It would be prudent to find out why these high value items are being returned to avoid future loss of revenue
The hight value in unit sales could also be an indicator that the item is popular and has many returns in a given time period.
e.g for store 18, 8 cleaning items led the count in terms of items returned
store 2 - groceryI items
#### 8. What are the forecast sales transactions for September 2017?
To answer this question we'll use the machine learning python algorithm Prophet which was developed by Facebook.
Why Prophet? Prophet is a great machine learning algorithm, it is fully automatic, light-weight, has holiday integration for time series, and relatively easy to understand since it explains the time series in terms of seasonality and trend.
We'll get the forecast for sales transactions as opposed to the forecast for the individual item sales because of a simple reason; computational power. The first week of January in train dataset contains over 1600 items with several having over 1000 counts over that single week. My machine takes over 10 minutes to fit and predict that one weeks worth of data. I'm working through better alternatives to prophet to handle that data.
In the meantime, let's predict the transaction volumes for the stores:
```
transx = pd.read_csv('C:/favorita2/transactions.csv', parse_dates=[0])
transx.rename(columns={'date':'ds', 'transactions':'y'}, inplace=True)
transx.info()
model = Prophet().fit(transx)
future = model.make_future_dataframe(periods=30)
forecast = model.predict(future)
model.plot(forecast);
model.plot_components(forecast);
```
The above graphs show the trends for our forecast according to each timeline;throughout the dataset timeframe, yearly and weekly.
Lets aggregate our visualization by store number for more actionable information.
```
import logging
logging.getLogger('fbprophet').setLevel(logging.WARNING)
grouped = transx.groupby('store_nbr')
final = pd.DataFrame()
for g in grouped.groups:
group = grouped.get_group(g)
m = Prophet(daily_seasonality=False)
m.fit(group)
future = m.make_future_dataframe(periods=30)
forecast = m.predict(future)
forecast = forecast.rename(columns={'yhat': 'store_'+str(g)})
final = pd.merge(final, forecast.set_index('ds'), how='outer', left_index=True, right_index=True)
final = final[['store_' + str(g) for g in grouped.groups.keys()]]
final = final.reset_index(level=0)
final.head()
final = final.replace(float('NaN'), 0)
stores = ['store_'+str(i) for i in range(1,55)]
px.line(final, x='ds', y=[store for store in final[stores]])
```
The above graph shows the daily transactions time series for each store, plus a 30 day forecast for the period between mid-August to mid-September. For better visibility, we'll use a smoothing function to get a glimpse of the trends for each store. I have created a [Power BI dashboard](https://github.com/Edwarothe/Demand-Planning-for-Corporacion-Favorita/blob/main/favorita.pbix) to show the trend dynamics of each store over the 5 year timeline. If you're not able to load the entire pbix file, [this](https://github.com/Edwarothe/Demand-Planning-for-Corporacion-Favorita/blob/main/favorita.pdf) is a pdf snapshot of the analysis.
| true |
code
| 0.33066 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/pabloderen/SightlineStudy/blob/master/Sightline.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#!/usr/bin/env python
# coding: utf-8
# # Collision analysis
import pandas as pd
import numpy as np
import itertools
import numba
from numba import vectorize
import os
import time
from numba import cuda
import multiprocessing as mp
from multiprocessing import Pool
from functools import partial
from numpy.lib import recfunctions as rfn
os.environ["OMP_NUM_THREADS"] = "10"
os.environ["OPENBLAS_MAIN_FREE"] = "10"
os.environ['NUMBAPRO_LIBDEVICE'] = "/usr/local/cuda-10.0/nvvm/libdevice"
os.environ['NUMBAPRO_NVVM'] = "/usr/local/cuda-10.0/nvvm/lib64/libnvvm.so"
```
# Main run:
Remember to upload the files
```
# Loger for python console
def log(message):
print('{} , {}'.format(time.time(), message))
@numba.jit(forceobj=True, parallel=True, nopython=True )
def FilterByBBX(Faces, line):
maxX = line[0]
maxY = line[1]
maxZ = line[2]
minX = line[3]
minY = line[4]
minZ = line[5]
midX = (Faces[:,0] + Faces[:,3])/2
mixY = (Faces[:,1] + Faces[:,4])/2
mixZ = (Faces[:,2] + Faces[:,5])/2
aa = np.where((midX >= minX) & ( mixY >= minY) & (mixZ >= minZ) & (midX <= maxX) & (mixY <= maxY) & (mixZ <= maxZ) )
return Faces[aa]
class BoundingBoxCreate():
def __init__(self, line):
XMax = max(line[3],line[0])
YMax = max(line[4],line[1])
ZMax = max(line[5],line[2])
XMin = min(line[3],line[0])
YMin = min(line[4],line[1])
ZMin = min(line[5],line[2])
self.box= np.array([XMax,YMax,ZMax,XMin,YMin,ZMin])
@numba.jit(nopython=True)
def split(aabb):
minX = aabb[3]
maxX = aabb[0]
minY = aabb[4]
maxY = aabb[1]
minZ = aabb[5]
maxZ = aabb[2]
centerX = (minX+ maxX)/2
centerY = (minY + maxY)/2
centerZ = (minZ+ maxY)/2
bbox0 = (maxX, maxY, maxZ, centerX, centerY, centerZ)
bbox1 = (centerX, maxY,maxZ, minX, centerY, centerZ)
bbox2 = (maxX, centerY, maxZ, centerX, minY, centerZ)
bbox3 = (centerX, centerY, maxZ, minX, minY, centerZ)
bbox4 = (maxX, maxY, centerZ, centerX, centerY, minZ)
bbox5 = (centerX, maxY,centerZ, minX, centerY, minZ)
bbox6 = (maxX, centerY, centerZ, centerX, minY, minZ)
bbox7 = (centerX, centerY, centerZ, minX, minY, minZ)
return bbox0, bbox1 , bbox2, bbox3, bbox4, bbox5, bbox6, bbox7
@numba.jit(nopython=True)
def XClipLine(d,vecMax, vecMin, v0, v1, f_low, f_high):
# Method for AABB vs line took from https://github.com/BSVino/MathForGameDevelopers/tree/line-box-intersection
# // Find the point of intersection in this dimension only as a fraction of the total vector
f_dim_low = (vecMin[d] - v0[d])/(v1[d] - v0[d] + 0.0000001)
f_dim_high = (vecMax[d] - v0[d])/(v1[d] - v0[d]+ 0.0000001)
# // Make sure low is less than high
if (f_dim_high < f_dim_low):
f_dim_high, f_dim_low = f_dim_low, f_dim_high
# // If this dimension's high is less than the low we got then we definitely missed.
if (f_dim_high < f_low):
return 0,0
# // Likewise if the low is less than the high.
if (f_dim_low > f_high):
return 0,0
# // Add the clip from this dimension to the previous results
f_low = max(f_dim_low, f_low)
f_high = min(f_dim_high, f_high)
if (f_low > f_high):
return 0,0
return f_low , f_high
@numba.jit(nopython=True)
def LineAABBIntersection(aabbBox,line):
# Method for AABB vs line took from https://github.com/BSVino/MathForGameDevelopers/tree/line-box-intersection
f_low = 0
f_high = 1
v0, v1 = (line[0], line[1], line[2]), (line[3], line[4], line[5])
vecMax = aabbBox[:3]
vecMin = aabbBox[-3:]
x = XClipLine(0, vecMax, vecMin , v0, v1, f_low, f_high)
if not x:
return False
x = XClipLine(1, vecMax, vecMin , v0, v1, x[0], x[1])
if x == (0,0) :
return False
x = XClipLine(2, vecMax, vecMin , v0, v1, x[0], x[1])
if x == (0,0):
return False
return True
# @numba.jit(forceobj=True, parallel=True)
def checkFaces(Faces, line):
for f in Faces:
if LineAABBIntersection(f,line):
return True
return False
# @numba.jit(forceobj=True, parallel=True)
def checklines(meshes, line):
global count
global totalLines
if (count % 10) == 0:
# print("=", end ="")
print("\r {} of {} total lines".format( str(count),totalLines ), end ="")
count = count + 1
for b in meshes:
#check if line line intersect with mesh
bbx = b.boundingBox
if LineAABBIntersection(bbx, line):
#if true split bbx in 4
splitted = b.parts
for s in splitted:
for ss in s.parts:
if LineAABBIntersection( ss.boundingBox , line):
for sss in ss.parts:
check = checkFaces(sss.faces,line)
if check:
return True
return False
from google.colab import drive
drive.mount('/content/drive')
```
# Mesh class
```
class Mesh():
def __init__(self, mesh, faces):
self.Id = mesh[6]
self.boundingBox = BoundingBoxCreate(mesh).box
self.parts = [MeshPart(self.Id, x, faces ) for x in split(self.boundingBox) ]
class MeshPart():
def __init__(self,Id, boundingBox,faces):
self.boundingBox = BoundingBoxCreate(boundingBox).box
ff = faces[faces[:,6] == Id]
filteredFaces = FilterByBBX(ff, boundingBox)
drop = np.delete(filteredFaces, np.s_[6:], axis=1)
self.parts = []
if drop.any():
self.parts = [MeshSubPart(Id, x, faces ) for x in split(self.boundingBox) ]
class MeshSubPart():
def __init__(self,Id, boundingBox,faces):
self.boundingBox = BoundingBoxCreate(boundingBox).box
ff = faces[faces[:,6] == Id]
filteredFaces = FilterByBBX(ff, boundingBox)
drop = np.delete(filteredFaces, np.s_[6:], axis=1)
self.parts = []
if drop.any():
self.parts = [MeshSubSubPart(Id, x, faces ) for x in split(self.boundingBox) ]
class MeshSubSubPart():
def __init__(self,Id, boundingBox,faces):
self.boundingBox = BoundingBoxCreate(boundingBox).box
ff = faces[faces[:,6] == Id]
filteredFaces = FilterByBBX(ff, boundingBox)
drop = np.delete(filteredFaces, np.s_[6:], axis=1)
self.faces =[ BoundingBoxCreate(d).box for d in drop]
def createObjects(meshes, faces):
objects = []
for m in meshes:
objects.append(Mesh(m, faces))
return objects
count = 0
if __name__ is '__main__':
start= time.time()
pov_ = pd.read_csv(r"/content/pov_.csv",header=None )
pov_.columns = ["x","y","z" ]
print('{} Points of View'.format(len(pov_)))
pov_.head(10)
# ## Reading targets (points over meshes)
target_ = pd.read_csv(r"/content/targets_.csv",header=None )
target_.columns = ["x1","y1","z1" ]
print('{} targets or points of interest'.format(len(target_)))
target_.head()
# ## Reading meshes bounding box
meshes_ = pd.read_csv(r"/content/context_.csv",header=None, index_col=0 )
meshes_.columns = ["xMax","yMax","zMax","xMin","yMin","zMin","id" ]
print('{} meshes in context set'.format(len(meshes_)))
meshes_.head()
# ## Reading meshes faces
mesh_faces = pd.read_csv(r"/content/mesh_faces.csv",header=None )
mesh_faces.columns = ["xMax","yMax","zMax","xMin","yMin","zMin", "id" ]
print('{} meshes faces in set'.format(len(mesh_faces)))
mesh_faces.head()
# ## Creating all cross product of points vs targets to represent the lines of view
lines = pov_
lines = lines.assign(foo=1).merge(target_.assign(foo=1)).drop('foo', 1)
lines = lines.drop_duplicates()
lines = lines.reset_index()
lines = lines.drop(['index'], axis=1)
totalLines = len(lines)
print('{} lines between POV and targets'.format(len(lines)))
# ## Finding mesh intersection
result = createObjects(meshes_.values, mesh_faces.values)
# funB = partial(checklines, result) # total time 211.28 seconds
# resultsB = pool.map(funB,lines.values)
resultsB = [checklines(result, x) for x in lines.values] # total time 192.399 seconds | 1378 lines between POV and targets
print("")
lines['hits']= resultsB
positive = len(lines[lines['hits'] == False])
print('{} lines with clean sight from POV to targets'.format(positive))
negative = len(lines[lines['hits'] == True])
print('{} lines with possible context intersection'.format(negative))
# ## Saving lines with no intersection
lines[ lines['hits'] == False].to_csv('miss.csv')
# ## Saving lines with possible intersection
lines[ lines['hits'] == True].to_csv('hits.csv')
end = time.time()
print('total time {} seconds'.format(round(end-start, 3)))
print('{},{},{},{},{},{},{},{},{} '.format("POV","Target","Meshes","Meshes faces", "Lines of sight", "Hits", "Miss","time", "Comments"))
data = '{},{},{},{},{},{},{},{},{}'.format(len(pov_), len(target_), len(meshes_), len(mesh_faces), len(lines), positive, negative, round(end-start, 3), "3 Level nesting + numba" )
with open('/content/drive/My Drive/sightlinelog.csv','a') as fd:
fd.write(data + "\n")
print(data)
```
| true |
code
| 0.307982 | null | null | null | null |
|
# Case Study 7
__Team Members:__ Amber Clark, Andrew Leppla, Jorge Olmos, Paritosh Rai
# Content
* [Objective](#objective)
* [Data Evaluation](#data-evaluation)
- [Loading Data](#loading-data)
- [Data Summary](#data-summary)
- [Missing Values](#missing-values)
- [Exploratory Data Analysis (EDA)](#eda)
* [Model Preparations](#model-preparations)
- [Sampling & Scaling Data](#sampling-scaling-data)
- [Evaluation Metrics](#proposed-metrics)
* [Model Building & Evaluations](#model-building)
- [Results](#performance-analysis)
* [Conclusion](#conclusion)
- [Final Model Proposal](#final_model)
- [Examining Feature Importance](#examining-feature-importance)
- [Future Considerations, Model Enhancements and Alternative Modeling Approaches](#model-enhancements)
## Objective: <a id='objective'>
The objective of this case study is to classify a binary target in an anonymous dataset with the goal of reducing monetary losses as much as possible for the customer.
# Data Evaluation <a id='data-evaluation'>
## Loading Data <a id='loading-data'>
```
# standard libraries
import os
import pandas as pd
import numpy as np
#import re
import os
from IPython.display import Image
from abc import ABC, abstractmethod
import time
import copy
#import sklearn
#import time
# visualization
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from tabulate import tabulate
from IPython.display import clear_output
import xgboost
# data pre-processing
from scipy.io import arff
#from sklearn.model_selection import train_test_split
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import SimpleImputer, KNNImputer, IterativeImputer
from sklearn.impute._base import _BaseImputer
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection._split import BaseShuffleSplit
from sklearn.datasets import load_digits
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from sklearn.preprocessing import LabelEncoder
from xgboost import XGBClassifier
# prediction models
import tensorflow as tf
from sklearn.svm import SVC
from sklearn.linear_model import SGDClassifier
from sklearn.svm._base import BaseSVC
from sklearn.model_selection import cross_val_score
from sklearn.metrics import f1_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import fbeta_score
from sklearn.metrics import roc_auc_score
from sklearn.linear_model import LogisticRegression
from tensorflow.keras.metrics import AUC
# import warnings filter
import warnings
warnings.filterwarnings('ignore')
from warnings import simplefilter
simplefilter(action='ignore', category=FutureWarning)
class FilePathManager:
def __init__(self, local_dir: str):
self.local_dir = local_dir
def retrieve_full_path(self):
return os.getcwd()+'/'+self.local_dir
class Loader:
df = pd.DataFrame()
def load_data(self, file_name):
pass
def get_df(self):
pass
def size(self):
return len(self.df)
from typing import Callable
class CSVLoader(Loader):
def __init__(self, file_path_manager: FilePathManager):
self.file_path_manager = file_path_manager
def load_data(self, _prepare_data: Callable[[pd.DataFrame], pd.DataFrame] = None):
self.df = pd.read_csv(self.file_path_manager.retrieve_full_path())
if _prepare_data:
self.df = _prepare_data(self.df)
def get_df(self):
return self.df;
def size(self):
return len(self.df)
def clean_data(df):
df['y'] = df['y'].astype(int)
df['x32'] = df['x32'].str.replace('%','').astype(float)
df['x37'] = df['x37'].str.replace('$','').astype(float)
return df
loader = CSVLoader(FilePathManager('final_project(5).csv'))
loader.load_data(clean_data)
```
## Data Summary <a id='data-summary'>
The dataset consists of fifty (50) features and a binary target class. There is no metadata or other descriptive information for the dataset, and the fifty feature labels are numbered from "x0" to "x49". There are 160,000 observations in the dataset; less than 0.03% of the features were missing data, and the imputation of these missing values is described below in the Missing Data section. Most of the features provided are numeric, but five were initially imported as text features.
Three of the five text features were identified as continents, months of the year, and days of the week. The values were cleaned up for spelling correction and consistency. The other two text object columns were numeric columns with a special character introduced in the data; column x32 had a trailing "%" and column x37 had a leading "$". These characters were removed so that these columns would be treated as numeric.
## Missing Values <a id='missing-values'>
All of the variables, except the target class, had missing values. The chart below depicts the number of observations missing values for each feature. Note: Even though the plot doesn't show missing values for categorical features, they do have missing values which are represented as nan's and so are missing from the plot.
<img src='https://raw.githubusercontent.com/olmosjorge28/QTW-SPRING-2022/main/ds7333_case_study_7/visuals/missing_values.png'></img>
The number of missing values was consistently around 20-40 missing observations for each column (less than 0.03% of 160,000 observations). For the logistic regression and neural network models, the mean of each column was used to impute the missing values for the numeric data, and the mode of each column was used for the missing categorical features.
For the XGBoost model, the algorithm can automatically handle missing values and find their optimal split for modeling, so no imputation was done prior to modeling.
## Exploratory Data Analysis (EDA) <a id='eda'>
The numeric data was examined to view the scales of the variables, and the data needs normalization to be effectively used in most types of models without issues.
For two model types, logistic regression and neural network, the categorical data for the three text columns were one-hot encoded to produce binary features for each of the values within those variables. In this data, there were three continents, twelve months, and five days of the week, so the one-hot encoding process did not contribute to creating an excess of sparsity in the dataframe that would be used for modeling. After one-hot encoding, the total number of explanatory features has increased to 67.
For the third model type, XGBoost, the categorical data were not one-hot encoded but rather label-encoded so the tree-based algorithm could split the data effectively.
### Balance of Target
The target classes are considered balanced in the dataset, with roughly 40:60 split between the positive and negative classes, as depicted below.
<img src='https://raw.githubusercontent.com/olmosjorge28/QTW-SPRING-2022/main/ds7333_case_study_7/visuals/y_dist.png'></img>
### Categorical Variables
The three categorical variables were x24 (continent), x29 (month), and x30 (weekday). Asia was disproportionately represented for continent, and months and weekday were both approximately normally distributed when ordered by time.
Looking at the target class, the categorical variables did not change. These are likely not strong predictors for the target variable.
<img src='https://raw.githubusercontent.com/olmosjorge28/QTW-SPRING-2022/main/ds7333_case_study_7/visuals/cat_feature_dist.png'></img>
<img src='https://raw.githubusercontent.com/olmosjorge28/QTW-SPRING-2022/main/ds7333_case_study_7/visuals/cat_feature_dist_by_y.png'></img>
### Continuous Variables - Scaling
Variable x37 (with \\$ values) had a very wide scale compared to other variables (-\\$5000 to \\$6000). The remaining variables still had varied scales based on the plot below. All continuous features were scaled using StandardScaler to ensure features were appropriately weighted for Logistic Regression feature importance. Scaling the data was less important for XGBoost (tree-based ensemble) and Neural Network models.
<img src='https://raw.githubusercontent.com/olmosjorge28/QTW-SPRING-2022/main/ds7333_case_study_7/visuals/box_plot_ex_x37.png'></img>
# Model Preparations <a id='model-preparations'/>
```
class BaseImputer:
def fit(self, X, y=None):
pass
def transform(self, X):
pass
class BaseModel:
def fit(self, X, y, sample_weight=None):
pass
def predict(self, X):
pass
class MeanModeSimpleImputer(BaseImputer):
defaults={}
def fit(self, X, y=None):
for col in ['x24','x29','x30']:
self.defaults[col]=X[col].mode()
for col in X.columns.difference(['x24','x29','x30', 'y']):
self.defaults[col]=X[col].mean()
def transform(self, X):
X_transform = copy.deepcopy(X)
for col in X.columns.difference(['y']):
X_transform[col].fillna(value=defaults[col], inplace=True)
return X_transform
```
## Sampling and Scaling Data <a id='sampling-scaling-data'/>
```
class Modeling:
_X_train_fitted = None
_X_test_fitted = None
_y_train = None
_y_test = None
_y_preds = None
_y_preds_proba = None
def __init__(self, data: pd.DataFrame,
target_name: str,
shuffle_splitter: BaseShuffleSplit,
imputer: BaseImputer,
model: BaseModel, scaler = None, encoder = None):
self._data = data
self._target_name = target_name
self._shuffle_splitter = shuffle_splitter
self._imputer = imputer
self._model = model
self._encoder = encoder
self._X, self._y = self._split_data()
self._scaler = scaler
@property
def X(self):
return self._X
@property
def y(self):
return self._y
@property
def model(self):
return self._model
@model.setter
def model(self, model):
self._model = model
@property
def X_train(self):
return self._X_train_fitted
@property
def X_test(self):
return self._X_test_fitted
@property
def y_train(self):
return self._y_train
@property
def y_test(self):
return self._y_test
@property
def y_preds(self):
return self._y_preds
def _split_data(self):
X = self._data.copy()
return X.drop([self._target_name], axis=1) , X[self._target_name]
def _shuffle_split(self):
X = self.X
y = self.y
for train_index, test_index in self._shuffle_splitter.split(X,y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
return X_train, X_test, y_train, y_test
def _fit_imputer(self, train):
if self._imputer is not None:
self._imputer.fit(train)
def _fit_scaler(self, train, cont_vars = None):
transfrom_cols = None
if cont_vars is None:
transform_cols = train.columns
else:
transform_cols = cont_vars
if self._scaler is not None:
self._scaler.fit(train[transform_cols])
def _impute_data(self, X: pd.DataFrame):
if self._imputer is not None:
return pd.DataFrame(self._imputer.transform(X), columns = self.X.columns, index = X.index)
return X
def _scale_data(self, X: pd.DataFrame, cont_vars = None):
transform_cols = None
if cont_vars is None:
transform_cols = X.columns
else:
transform_cols = cont_vars
scaled_data = X[transform_cols]
if self._scaler is not None:
scaled_data = pd.DataFrame(self._scaler.transform(scaled_data), columns = transform_cols, index =X.index)
X[transform_cols]=scaled_data
return X
def _encode_data(self):
df = self.X.copy()
cont_vars = df.describe().columns
cat_vars = set(df.columns) - set(cont_vars)
for column in [*cat_vars]:
df[column] = self._encoder.fit_transform(df[column].astype(str))
self._X = df
return cont_vars, cat_vars
def prepare(self):
cont_vars = None
if self._encoder is not None:
cont_vars, _ = self._encode_data()
X_train, X_test, y_train, y_test = self._shuffle_split()
self._fit_imputer(X_train)
X_train = self._impute_data(X_train)
X_test = self._impute_data(X_test)
self._fit_scaler(X_train, cont_vars)
self._X_train_fitted = self._scale_data(X_train, cont_vars)
self._X_test_fitted = self._scale_data(X_test, cont_vars)
self._y_train = y_train
self._y_test = y_test
def prepare_and_train(self):
self.prepare()
return self.train()
def train(self):
self._model.fit(self.X_train, self.y_train)
self._y_preds = self._model.predict(self.X_train)
self._y_preds_proba = self._model.predict_proba(self.X_train)
return self.metrics(self.y_train, self.y_preds, self._y_preds_proba)
def test(self):
return self.metrics(self.y_test, self._model.predict(self.X_test), self._model.predict_proba(self.X_test))
@abstractmethod
def metrics(self, y_true = None, y_pred = None, y_preds_proba = None):
pass
class ClassificationModeling(Modeling):
def __init__(self,
data: pd.DataFrame,
target_name: str,
shuffle_splitter: BaseShuffleSplit,
imputer: BaseImputer,
model: BaseModel,
scaler = None,
encoder = None,
beta: int = 1,
classification: str = 'binary'):
super().__init__(data, target_name, shuffle_splitter, imputer, model, scaler, encoder)
self.beta = beta
self.classification = classification
@abstractmethod
def metrics(self, y_true = None, y_pred = None, y_preds_proba=None):
pass
from typing import Type, TypeVar
class TuningClassificationModeling(ClassificationModeling):
TClass = None
all_models = [];
def __init__(self,
data: pd.DataFrame,
target_name: str,
shuffle_splitter: BaseShuffleSplit,
imputer: BaseImputer,
model: BaseModel,
scaler = None,
encoder = None,
beta: int = 1,
classification: str = 'binary',
classification_type: str = 'logistic'):
super().__init__(data, target_name, shuffle_splitter, imputer, model, scaler, encoder, beta, classification)
if classification_type == 'logistic':
TClass = TypeVar("TClass", bound=LogisticRegression)
elif classification_type == 'xgb':
TClass = TypeVar("TClass", bound=XGBClassifier)
elif classification_type == 'neural':
TClass = TypeVar("TClass", bound=NNModel)
def parameter_tuning(self, params, class_to_instantiate: Type[TClass]):
list_of_models = []
combination = []
params_base = {}
output = []
for key, value in params.items():
if isinstance(value, list):
combination.append((key,value))
else:
params_base[key]=value
result = {}
if len(combination) > 0:
result = TuningClassificationModeling.get_combinations(combination)
for r in result:
list_of_models.append(class_to_instantiate(**{**params_base, **r}))
for a_model in list_of_models:
self.model = a_model
startTrain = time.time()
train_metrics = self.train()
endTrain = time.time()
test_metrics = self.test()
endTest = time.time()
train_time = endTrain - startTrain
test_time = endTest - endTrain
output.append({'model': a_model, 'train_metrics': {**train_metrics,**{'elapsed_time':train_time}}, 'test_metrics': {**test_metrics,**{'elapsed_time':test_time}}})
self.all_models = output
return output
def find_best_model(self, metric):
max_accuracy = self.all_models[0]['test_metrics'][metric]
location = 0
for indx, output_metrics in enumerate(self.all_models):
if max_accuracy < output_metrics['test_metrics'][metric]:
max_accuracy = output_metrics['test_metrics'][metric]
location = indx
elif max_accuracy == output_metrics['test_metrics'][metric]:
if output_metrics['test_metrics']['elapsed_time'] < self.all_models[location]['test_metrics']['elapsed_time']:
location = indx
return self.all_models[location]
@staticmethod
def get_combinations(tuples):
length = len(tuples)
if length > 1:
total_params = []
tuple_copy = tuples.copy()
a_tuple = tuple_copy.pop(0)
params_list = TuningClassificationModeling.get_combinations(tuple_copy)
for value in a_tuple[1]:
for a_params in params_list:
temp = { a_tuple[0]: value}
total_params.append({**temp, **a_params})
return total_params
else:
params_list = []
a_tuple = tuples[0]
for value in a_tuple[1]:
temp = {}
temp[a_tuple[0]] = value
params_list.append(temp)
return params_list
def metrics(self, y_true = None, y_pred = None, y_pred_proba=None):
if y_true is None and y_pred is None:
y_true = self.y_train
y_pred = self.y_preds
conf_matrix = confusion_matrix(y_true, y_pred)
return {
'matrix': conf_matrix,
'auc': roc_auc_score(y_true, y_pred),
'accuracy': round(accuracy_score(y_true, y_pred), 5),
'precision': precision_score(y_true, y_pred, average=self.classification),
'recall': recall_score(y_true, y_pred, average=self.classification),
'f1': f1_score(y_true, y_pred),
'cost': TuningClassificationModeling.cost_calc(conf_matrix),
'y_pred': y_pred,
'y_pred_proba': y_pred_proba
}
@staticmethod
def cost_calc(conf_matrix):
cost_matrix = np.array([[0,-100],[-25,0]])
cost = np.sum(cost_matrix*conf_matrix)/np.sum(conf_matrix)
return cost
class NNModel:
model = None
epoch = 50
batch_size = 32
loss = 'BinaryCrossentropy',
metric = 'accuracy'
optimizer = 'adam'
def __init__(self,**inputs):
self.model = tf.keras.Sequential()
for arg, content in inputs.items():
if arg.startswith('input'):
self.model.add( tf.keras.layers.Input( shape=(content,) ) )
if arg.startswith('layer'):
self.model.add( tf.keras.layers.Dense(content['s'], activation = content['activation']) )
if arg == 'epoch':
self.epoch = content
if arg == 'bs':
self.batch_size = content
if arg == 'optimizer':
self.optimizer = content
if arg == 'loss':
self.loss = content
if arg == 'metric':
self.metric = content
self.model.compile(optimizer=self.optimizer, loss=self.loss, metrics=[self.metric])
print(self.model)
def fit(self, X, y):
self.model.fit(X, y, batch_size=self.batch_size, epochs=self.epoch)
def predict(self, X):
y_pred_proba = self.predict_proba(X)
return pd.Series( (y_pred_proba>0.5).astype(int))
def predict_proba(self, X):
y_pred_proba = self.model.predict(X)
return pd.Series(y_pred_proba.reshape((y_pred_proba.shape[1], y_pred_proba.shape[0]))[0])
def tune_cost_proba(train_proba, test_proba, y_train, y_test, conf_train, conf_test):
cost_results = pd.DataFrame()
thresh = 0
for i in range(11):
yhat_train = pd.Series(train_proba < thresh).astype(int)
yhat_test = pd.Series(test_proba < thresh).astype(int)
conf_train = confusion_matrix(y_train, yhat_train)
conf_test = confusion_matrix(y_test, yhat_test)
cost_results = cost_results.append({"Threshold": thresh,
"Train Cost": -TuningClassificationModeling.cost_calc(conf_train),
"Test Cost": -TuningClassificationModeling.cost_calc(conf_test),
"conf_train": conf_train,
"conf_test": conf_test
},
ignore_index=True)
thresh = thresh + 0.05
return cost_results
```
## Model Metrics <a id='proposed-metrics'/>
AUC (Area Under the Curve) and Cost Per Prediction were the model metrics. The final metric used for model evaluation was Cost per Prediction. This was calculated as follows:
__Cost per Prediction = (- \\$100×FP - \\$ 25×FN)/(Total # Predictions)__
where FP = false positive, FN = false negative.
The cost of a false positive (predicting 1 when it is actually 0) is \\$100, and the cost of a false negative (predicting 0 when it is actually 1) is \\$25. These costs are normalized by the total number of predictions so the costs can be compared between training and test sets and fairly assessed for any number of future predictions.
Before evaluating the model(s) for Cost per Prediction, the models were tuned to maximize ROC Area Under the Curve (AUC). The ROC (Receiver Operator Characteristic) curve plots the True Positive (TP) rate vs. the False Positive (FP) rate. The Area Under this Curve typically has a range of 0.5 to 1.0. A 50:50 random guess for classification would give an AUC = 0.5 with a diagonal line going from the lower left to upper right. A perfect (ideal) classifier would have an AUC = 1.0 with a line that goes straight up and then straight across.
<img src='https://raw.githubusercontent.com/olmosjorge28/QTW-SPRING-2022/main/ds7333_case_study_7/visuals/ROC_AUC_curve.png' height=400 width=400></img>
AUC was chosen as a standard metric that was quickly and easily implemented during initial model building and assessment. AUC was an appropriate metric given that the target classes are fairly balanced (40:60), and AUC is also independent of the prediction threshold which is discussed in the following paragraph.
Once the models were assessed for AUC, they were further tuned to minimize Cost per Prediction. This was done by adjusting the probability threshold for predicting a positive (1) vs. negative (0) class. The default threshold is 0.5 such that a probability < 0.5 is predicted as a negative class and ≥ 0.5 is predicted as a positive class. This threshold can be adjusted away from 0.5 such that more positive or negative classes are predicted. In this way, the number of FPs vs. FNs can be adjusted to minimize the Cost per Prediction.
# Model Building & Evaluations <a id='model-building'/>
Training and test sets were created from the data using the stratified splitting method to maintain the ratio of the binary outcome, although the class is relatively balanced between the two outcomes. 30% of the data was withheld for the test set, and the explanatory features were normalized using StandardScaler while avoiding data leakage into the test set.
## Naive Model
Given that false positives are 4 times more costly than false negatives (\\$100 vs. \\$25), a naive model would predict all negative classes to minimize cost. The naive model has a Cost per Prediction of __\\$10.03__.
```
base_model_matrix = [[28741, 0],[19259,0]]
```
#### Naive Cost
```
-TuningClassificationModeling.cost_calc(base_model_matrix)
```
## Logistic Model
Initially, logistic regression was run as a baseline model with fast implementation and high interpretability. This model did not necessarily satisfy the customer requirements of minimizing cost, but it served as a starting point to increase model complexity and improve the model performance. L1 (Lasso) regularization was used for feature selection with the logistic regression model.
### Logistic Regression
```
logistic_modeling = TuningClassificationModeling(loader.get_df(),'y',
StratifiedShuffleSplit(n_splits=1, test_size=0.3, random_state=12343),
MeanModeSimpleImputer(), LogisticRegression, StandardScaler(), LabelEncoder(), beta=1)
logistic_modeling.prepare()
logistic_result = logistic_modeling.parameter_tuning( {
'penalty':'l1',
'random_state':1,
'solver': 'liblinear',
'C': [0.001, 0.01, 1, 10],
}, LogisticRegression);
```
#### Selecting Best Logistic Regression Model
```
best_logistic_model = logistic_modeling.find_best_model('auc')
best_logistic_model['model']
{ metric: best_logistic_model['train_metrics'][metric] for metric in ['auc', 'cost', 'matrix'] }
{ metric: best_logistic_model['test_metrics'][metric] for metric in ['auc', 'cost', 'matrix'] }
```
### Feature Importance
```
lr_tuned = linear_modeling.find_best_model('auc')
feat_coef = []
feat = zip(linear_modeling.X_train.columns, lr_tuned['model'].coef_[0])
[feat_coef.append([i,j]) for i,j in feat]
feat_coef = pd.DataFrame(feat_coef, columns = ['feature','coef'])
top_feat_lr = feat_coef.loc[abs(feat_coef['coef'])>0].sort_values(by='coef')
feat_plot = sns.barplot(data=top_feat_lr, x='feature', y='coef', palette = "ch:s=.25,rot=-.25")
plt.xticks(rotation=90)
plt.title('LR Feature Importance with L1')
plt.show()
```
#### Tuning Threshold for Lowest Cost
```
def extract_best_model_metrics(model):
return (model.find_best_model('auc')['train_metrics']['y_pred_proba'],
model.find_best_model('auc')['test_metrics']['y_pred_proba'],
model.y_train,
model.y_test,
model.find_best_model('auc')['train_metrics']['matrix'],
model.find_best_model('auc')['test_metrics']['matrix'])
train_proba, test_proba, y_train, y_test, conf_train, conf_test = extract_best_model_metrics(logistic_modeling)
logistic_cost_results = tune_cost_proba(train_proba[:,0], test_proba[:,0], y_train, y_test, conf_train, conf_test)
logistic_cost_results[['Threshold', 'Train Cost','Test Cost' ]]
def plot_cost_tunning(cost_results, threshold):
sns.lineplot(data=cost_results, x='Threshold', y='Train Cost', color='blue')
sns.lineplot(data=cost_results, x='Threshold', y='Test Cost', color='red')
plt.title('Tuning Threshold')
plt.legend(['Train', 'Test'])
plt.axvline(threshold, color='black', ls='--')
plt.show()
plot_cost_tunning(logistic_cost_results, 0.15)
```
#### Best Logistic Model Metrics
LogisticRegression with C=0.001, penalty='l1', threshold=0.15 with and a cost of __\\$9.76__ per prediction and an AUC of __0.6708__ for the test set.
## XGB Model
Next, XGBoost (eXtreme Gradient Boosting) was used as a more complex nonlinear tree-based model. This model significantly improved performance while maintaining some interpretability with feature importances. However, the XGBoost model overfit the training set such that it achieved a perfect AUC=1.0, and this resulted in a maximum test __AUC=0.9434__.
### Extreme Gradient Boosting
```
xgb_classifier = TuningClassificationModeling(loader.get_df(),'y',
StratifiedShuffleSplit(n_splits=1, test_size=0.3, random_state=12343),
None, XGBClassifier, None, LabelEncoder(), beta=1,classification_type = 'xgb' )
xgb_classifier.prepare()
xgb_results = xgb_classifier.parameter_tuning( {
'max_depth': [3,6,10],
'learning_rate': [0.05, 0.1],
'n_estimators': [100, 500, 1000],
'colsample_bytree': [0.3, 0.7],
}, XGBClassifier);
```
#### Selecting Best XGB Model
```
best_xgb_model= xgb_classifier.find_best_model('auc')
best_xgb_model['model']
{ metric: best_xgb_model['train_metrics'][metric] for metric in ['auc', 'cost', 'matrix'] }
{ metric: best_xgb_model['test_metrics'][metric] for metric in ['auc', 'cost', 'matrix'] }
```
### Feature Importance
```
best_xgb_model = xgb_classifier.find_best_model('auc')['model']
xgboost.plot_importance(best_xgb_model, max_num_features=15)
plt.show()
```
#### Tuning Threshold for Lowest Cost
```
train_proba, test_proba, y_train, y_test, conf_train, conf_test = extract_best_model_metrics(xgb_classifier)
xgb_cost_results = tune_cost_proba(train_proba[:,0], test_proba[:,0], y_train, y_test, conf_train, conf_test)
xgb_cost_results[['Threshold', 'Train Cost','Test Cost' ]]
plot_cost_tunning(xgb_cost_results, 0.15)
```
#### Best XGB Model Metrics
XBG Classifier with max_depth= 10, learning_rate= 0.1, n_estimators= 1000, colsample_bytree= 0.7, threshold=0.15 with and a cost of __\\$2.40__ per prediction and an AUC of __0.9434__ for the test set.
## Neural Network Model
Finally, a Neural Network model was fit on the dataset, and its performance was compared against the rest of the models. This was the most complex model with the least interpretability.
### Neural Network
```
nn_modeling = TuningClassificationModeling(loader.get_df(),'y',
StratifiedShuffleSplit(n_splits=1, test_size=0.3, random_state=12343),
MeanModeSimpleImputer(), NNModel, StandardScaler(), LabelEncoder(), beta=1,classification_type='neural' )
nn_modeling.prepare()
nn_model_tunning = nn_modeling.parameter_tuning( {
'input':50,
'layer1':{'s':300, 'activation': 'relu'},
'layer2':{'s':200, 'activation': 'relu'},
'layer3':{'s':100, 'activation': 'relu'},
'layer4':{'s':1, 'activation':'sigmoid'},
'loss':'BinaryCrossentropy',
'metric': tf.keras.metrics.AUC(),
'epoch':[10,30,100],
'bs':[10,100,1000,10000],
'optimizer':'adam'
}, NNModel)
```
#### Selecting Best Neural Network Model
```
best_nn_model = nn_modeling.find_best_model('auc')
{
'batch_size': best_nn_model['model'].batch_size,
'epoch': best_nn_model['model'].epoch,
'loss': best_nn_model['model'].loss,
'metric': best_nn_model['model'].metric,
'optimizer': best_nn_model['model'].optimizer,
}
best_nn_model['model'].model.summary()
{ metric: best_nn_model['train_metrics'][metric] for metric in ['auc', 'cost', 'matrix'] }
{ metric: best_nn_model['test_metrics'][metric] for metric in ['auc', 'cost', 'matrix'] }
```
#### Tunning Treshold to for Lowest Cost
```
train_proba, test_proba, y_train, y_test, conf_train, conf_test = extract_best_model_metrics(nn_modeling)
nn_cost_results = tune_cost_proba(1-train_proba, 1-test_proba, y_train, y_test, conf_train, conf_test)
nn_cost_results[['Threshold', 'Train Cost','Test Cost' ]]
plot_cost_tunning(nn_cost_results, 0.05)
```
#### Best Neural Network Metrics
Neural Network Model with batch_size= 100, epoch=100, loss=BinaryCrossEntropy, metric=auc, optimizer=adam, with a threshold=0.05 with and a cost of __\\$1.96__ per prediction and an AUC of __0.9603__ for the test set.
### Results <a id='performance-analysis'>
Below are the results from the three models tried for this dataset and their comparison against predictions using the test dataset.
__Logistic Regression:__ This model was the quickest to train and had a result AUC of __0.6708__ and Cost per Prediction of __\\$9.76__ for the test dataset.
__XGBoost:__ This model was the longest to train and provided a significant improvement compared to the logistic regression. This model had a tendency to overfit showing difference in the train and test results. This model had a result AUC of __0.9434__ and Cost per Prediction of __\\$2.40__ for the test dataset.
__Neural Network:__ This model took significantly longer than the logistic, but much faster than XGB. It provided a slight improvement over the XGBModel and did not overfit to the training data. This model had a result AUC of __0.9603__ and Cost per Prediction of __\\$1.96__ for the test dataset.
#### Comparisions
The table below compares the key metrics between the models for the test dataset:
| Model |Cost Per Prediction | AUC | # False Positives | # False Negatives |
|-------|-----|-----|-------------------|-------------------|
|Logistic Regression | \\$9.76 | 0.6708 | 163 | 18043 |
|XGBoost | \\$2.40 | 0.9434 | 452 | 2797 |
|Neural Network | \\$1.96 | 0.9603 | 587 | 1422 |
```
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
models = ['Logistic Regression', 'XGBoost', 'Neural Network']
costs = [9.76, 2.40, 1.96]
ax.bar(models, costs)
plt.ylabel("Cost Per Prediction")
plt.show()
```
# Conclusion <a id='conclusion'>
## Final Model <a id='final_model'>
The team recommends using the Neural Network model. This model has an input layer and 3 hidden layers, with 300, 200, and 100 neurons, respectively, that use 'Relu' for the activation function and 1 output layer that uses sigmoid for its activation function. This model provided the best fit (AUC), which was then tuned for lowest overall cost.
### Monetary Outcome
The team recommends using the Neural Network model to minimize the Cost per Prediction. The Neural Network model had cost per prediction of \\$1.96. When compared to the naive model with a cost per prediction of \\$10.03 is an 80.4\% improvement in cost, compared to the Logistic Model that had a cost per prediction of \\$9.76 is a 79.9\% improvement, and compared to the XGBBoost model which had a cost per prediction of \\$2.40 it's an 18\% improvement. Using the recommended model yields an average cost per prediction of less than \\$2.00.
__If the customer were to make 1000 predictions using the recommended model vs. the naive approach, the customer would save over ~\\$8000.__
### Feature Importance <a id='examining-feature-importance'>
Even though the stakeholder is not interested in the key features for prediction, below are the feature importances according to the Logistic and XGB Models. The logistic feature importance accounts for features that have a linear relationship for predicting the target variable. The XGBoost feature importance differs significantly from the logistic model because the target variable is much better predicted by its non-linear terms. There were 50 total features, of which 7 appear to be the most important for the logistic model (abs coef > 0.01) vs. 14 features for the XGBoost (F-Score > 4000).
#### Logistic Feature Importance
```
lr_tuned = linear_modeling.find_best_model('auc')
feat_coef = []
feat = zip(linear_modeling.X_train.columns, lr_tuned['model'].coef_[0])
[feat_coef.append([i,j]) for i,j in feat]
feat_coef = pd.DataFrame(feat_coef, columns = ['feature','coef'])
top_feat_lr = feat_coef.loc[abs(feat_coef['coef'])>0].sort_values(by='coef')
feat_plot = sns.barplot(data=top_feat_lr, x='feature', y='coef', palette = "ch:s=.25,rot=-.25")
plt.xticks(rotation=90)
plt.title('LR Feature Importance with L1')
plt.show()
```
#### XGB Feature Importance
```
best_xgb_model = xgb_classifier.find_best_model('auc')['model']
xgboost.plot_importance(best_xgb_model, max_num_features=20)
plt.show()
```
### Future Considerations, Model Enhancements and Alternative Modeling Approaches <a id='model-enhancements'/>
To make the model more generalizable, the team recommend in the future using and tuning dropout rates for the neural network model. Also, a small improvement could be made by making an ensemble model. Lastly, the team recommends talking to domain experts to better understand features that could allow for better feature engineering to further reduce potential losses.
| true |
code
| 0.680268 | null | null | null | null |
|
# Methodological approach
### Models
- Baseline (TF-IDF + SVM with preprocessing): Train + Crossvalidation (default, 5-folds)
- Transformers: Validation is random sample of Train (10%). No cross-validation implemented yet, since not trivial
Both model classes use _class weights_ to address class imbalance problem and increase the effect on loss for minority classes. Uses the inverse of how many times a class is positive relative to negative, i.e. n_samples / (n_classes * np.bincount(y)
### Evaluation approach
1) Train the models on the train set
2) On each epoch, run evaluation with validation set and evaluation metric the Precision-Recall AuC
3) Load at the end of training the model at the best performing epoch checkpoint.
4) Do hyperparameter search and select the best model (of each model type)
5) Predict the class labels for the __entire__ train set (so train + validation) and calculate the ROC/PR curves and AuC.
6) Calculate the J-Stat (optimizing point in ROC space) and the F1 maximizing point in the Precision-Recall space
7) Set class thresholds according to the F1 maximizing point
8) Predict on the test set for model comparison (among model types)
### Scenarios
The following "scenarios" are defined:
- _optimistic_: Use only _positive_ labels for training, validation and test. This should give an "ceiling benchmark" of how good the _positive_ paragraphs can be separated/classified among themself.
- _efficient_realistic_: Use _Opportunities_ as _negative_ labels in training, use all negatives in test.
- _realistic_: Use all negatives (opportunities, "weak" and "strong" from labelling process) for train and test.
| scenarios | train | test |
| ------------- |:---------------:| --------------:|
| optimistic | P: 279 N: 0 | P: 56 N:0 |
| efficient | P: 279 N: 825 | P: 56 N: 28155 |
| realistic | P: 279 N: 27533| P: 56 N: 28155 |
--> Note: Positives are counts of paragraphs with at least one positive label and negatives are those with all 0's.
### Tasks
- _binary_: Identification of CR relevant/irrelevant as baseline task.
- _multi_label_cro_: Classification task of _Physical Risks_ and _Transition Risks_ with multi-labelling
- _multi_label_cro_sub_: Classification task of the 5 sub categories from _PR_ and _TR_
_multi_label_cro_sub_ is done as a second step after a _binary_ identification step. Train: All positives, Test: Overall Test dataset, where paragraphs that received a negative in the previous step are set to negative and included in the evaluation metrics to simulate a real word scenario, where the first step would act as a filter. Results are still pending here, since there seems to be an issue loading pretrained models https://github.com/huggingface/transformers/issues/8272.
# Results
Tables for each task below. As we know already, models perform well in the "naive" scenarios and bad once the negatives are considered. Performance improves once the full negative training data is provided. The relatively small and efficient distilbert-base-uncased performs best, beating the baseline but also roberta-large (in fact also other, bigger models. Needs certainly some investigation). Best PR AuC and F1-Score (at the threshold set according to the train results) for the test is at 48% for the binary task and at/below 40% for the
# Questions
- Cross-validation with Transformers: What do we gain? More robust estimates of the validation metrics? Which model do we load at the end?
- Step 3 in Evaluation approach. For some models/scenarios, if more than 2-3 epochs are used, the eval loss starts increasing while the ROC-AuC/PR-AuC also increase, suggesting overfitting. Should we switch back to "loss" for best model selection?
- Step 4/5, selection of the thresholds: Is that o.k to run it on the entire train set? Alternative: Only validation set...
# Way forward (not in scope of the thesis)
- More data: Maybe we can invert the problem, e.g. consider the train/test set as test set, since there we have "negatives" (and as such a ground truth) and then start collecting training data (were we do not really have to have the ground truth)
- Revisit the paragraph approach: Split paragraphs in sentences
- Investigate labelled data after prediction, i.e. look at the most confusing examples etc to maybe find a pattern or label correction
# Dataset
```
%load_ext autoreload
%autoreload 2
import sys
import os
import pandas as pd
sys.path.append('..')
from data import constants
from data import cro_dataset
from data.utils import tables
ds_pos = cro_dataset.prepare_datasets(
cro_category_level="cro_sub_type_combined", #cro_sub_type_combined
should_filter_op=True,
train_neg_sampling_strategy=None,
test_neg_sampling_strategy=None,
as_huggingface_ds=True
)
ds_neg = cro_dataset.prepare_datasets(
cro_category_level="cro_sub_type_combined", #cro_sub_type_combined
should_filter_op=True,
train_neg_sampling_strategy="all",
test_neg_sampling_strategy="all",
as_huggingface_ds=True
)
ds_op = cro_dataset.prepare_datasets(
cro_category_level="cro_sub_type_combined", #cro_sub_type_combined
should_filter_op=False,
train_neg_sampling_strategy=None,
test_neg_sampling_strategy=None,
as_huggingface_ds=True
)
# Also read the negatives from the adjunct fix
ds_train_neg = pd.read_pickle("/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Labelling/annual reports/Firm_AnnualReport_Labels_Training_Negative_incl_adjunct.pkl")
number_adjunct_fix = len(ds_train_neg.query("is_adjunct == True"))
class_labels = ds_pos['train'].features['labels'].feature.names
train_df = pd.DataFrame(data=ds_pos['train']['labels'], columns=class_labels)
test_df = pd.DataFrame(data=ds_pos['test']['labels'], columns=class_labels)
df_labels = pd.DataFrame(data={"Training": train_df.sum(), "Test": test_df.sum() })
df_labels.rename(index=constants.map_to_field(), inplace=True)
df_labels.loc["Positive paragraphs"] = [ ds_pos['train'].num_rows, ds_pos['test'].num_rows]
df_labels.loc['Negative paragraphs'] = [ ds_neg['train'].num_rows - ds_pos['train'].num_rows + number_adjunct_fix, ds_neg['test'].num_rows - ds_pos['test'].num_rows]
df_labels.loc['Opportunities'] = [ ds_op['train'].num_rows - ds_pos['train'].num_rows, ds_op['test'].num_rows - ds_pos['test'].num_rows ]
tables.export_to_latex(df_labels, filename="labels_dataset.tex")
```
# Results
```
import os
import re
import pandas as pd
RESULT_DIR = "/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Methodology/results"
try:
import google.colab
is_running_in_colab = True
except:
is_running_in_colab = False
if is_running_in_colab:
# Load Google drive where the data and models are stored
from google.colab import drive
drive.mount('/content/drive')
RESULT_DIR = "/content/drive/MyDrive/fin-disclosures-nlp/results/"
scenarios = ["optimistic", "efficient-realistic", "realistic"]
models = ["svm", "distilbert-base-uncased", "roberta-large"]
prefixes = ['test', 'train'] # 'eval' would also be there, however overlapping 'eval_roc_auc', 'eval_pr_auc',
report_columns = ['train_ROC AuC', 'train_PR AuC', 'test_ROC AuC', 'test_PR AuC', 'test_F1']
def sort_first_idx(idx):
mapper = {name: order for order, name in enumerate(scenarios)}
return idx.map(mapper)
def sort_second_idx(idx):
mapper = {name: order for order, name in enumerate(models)}
return idx.map(mapper)
def report_results(df):
df[['scenario', 'model']] = df.id.str.split('_', 1, expand=True)
# Set the row multi-index
df = df.set_index(['scenario', 'model'])
df = df.sort_index(key=sort_second_idx, level="model", sort_remaining=False).sort_index(key=sort_first_idx, level="scenario", sort_remaining=False)
df = df[[r for r in report_columns if r in df.columns ]]
# Set the column multi-index
first_lvl = []
second_lvl = []
for c in df.columns:
splits = c.split("_", 1)
first = splits[0] if splits[0] in prefixes else ""
second = splits[1] if splits[0] in prefixes else c
first_lvl.append(first)
second_lvl.append(second)
df.columns = [first_lvl, second_lvl]
df = df.round(3)
return df
binary_df = pd.read_csv(os.path.join(RESULT_DIR, "cro_sub_type_combined_binary_results.csv"))
multilabel_df = pd.read_csv(os.path.join(RESULT_DIR, "cro_multi-label_results.csv"))
print("Binary Task: ")
binary_report = report_results(binary_df)
binary_report
print("Multi-Label Task: ")
multilabel_report = report_results(multilabel_df)
multilabel_report
results_df = binary_report.merge(multilabel_report, left_index=True, right_index=True, suffixes=('_binary', '_multilabel'))
tables.export_to_latex(results_df, filename="methodology_results.tex")
results_df
import os
from IPython.display import Image
print("Note: These ROC and P-R curves are the plots after training, on the entire TRAIN set and are used to find the optimal threshold values (dot).")
path = "/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Methodology/results/figures/"
Image(filename = os.path.join(path, "cro_sub_type_combined_binary_realistic_distilbert-base-uncased_train_threshold.pdf.jpg"))
from IPython.display import Image
print("Confusion matrix on the test set...")
path = "/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Methodology/results/figures/"
Image(filename = os.path.join(path, "cro_sub_type_combined_binary_realistic_distilbert-base-uncased_test_evaluation.pdf.jpg"))
```
# 2 Stage: use the "test_predictions.pkl" in the labels folder, the thresholds from the results folders (or here:
1Stage: [0.69809985]
2Stage: [0.19047296, 0.25015372, 0.36645192, 0.27023202, 0.2140553])
1. Plot the confusion matrix of the first stage
2. Plot the decision threshold of the second stage
3. Plot the confusion matrix of the combined second stage of all 5 categories and converted to main categories
```
import pandas as pd
two_stage = pd.read_pickle("/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Methodology/data/labels/test_predictions.pkl")
two_stage.binary_pred_labels
two_stage.multilabel_pred_labels
```
| true |
code
| 0.511351 | null | null | null | null |
|
# Four Muon Spectrum
This code is another showcase of the awkward array toolset, and utilizing coffea histograms in addition to advanced functionality.
This shows the analysis object syntax implemented by coffea `JaggedCandidateArray`, along with a multi-tiered physics selection, and the usage of an accumulator class provided by FCAT. We now add in the concept of corrections as well in the case of a Monte-Carlo sample.
```
import time
from coffea import hist
from coffea.analysis_objects import JaggedCandidateArray
import coffea.processor as processor
from awkward import JaggedArray
import numpy as np
# uproot supports xrootd, but its nicer to have them local (about 7 GB)
!mkdir -p data
!xrdcp root://eospublic.cern.ch//eos/root-eos/cms_opendata_2012_nanoaod/Run2012B_DoubleMuParked.root data/
!xrdcp root://eospublic.cern.ch//eos/root-eos/cms_opendata_2012_nanoaod/Run2012C_DoubleMuParked.root data/
!xrdcp root://eospublic.cern.ch//eos/root-eos/cms_opendata_2012_nanoaod/ZZTo4mu.root data/
# Look at ProcessorABC to see the expected methods and what they are supposed to do
class FancyDimuonProcessor(processor.ProcessorABC):
def __init__(self):
dataset_axis = hist.Cat("dataset", "Primary dataset")
mass_axis = hist.Bin("mass", r"$m_{\mu\mu}$ [GeV]", 600, 0.25, 300)
pt_axis = hist.Bin("pt", r"$p_{T,\mu}$ [GeV]", 3000, 0.25, 300)
self._accumulator = processor.dict_accumulator({
'mass': hist.Hist("Counts", dataset_axis, mass_axis),
'mass_near': hist.Hist("Counts", dataset_axis, mass_axis),
'mass_far': hist.Hist("Counts", dataset_axis, mass_axis),
'pt_lead': hist.Hist("Counts", dataset_axis, pt_axis),
'pt_trail': hist.Hist("Counts", dataset_axis, pt_axis),
'cutflow': processor.defaultdict_accumulator(int),
})
@property
def accumulator(self):
return self._accumulator
def process(self, df):
output = self.accumulator.identity()
dataset = df['dataset']
muons = JaggedCandidateArray.candidatesfromcounts(
df['nMuon'],
pt=df['Muon_pt'],
eta=df['Muon_eta'],
phi=df['Muon_phi'],
mass=df['Muon_mass'],
charge=df['Muon_charge'],
softId=df['Muon_softId'],
tightId=df['Muon_tightId']
)
output['cutflow']['all events'] += muons.size
soft_id = (muons.softId > 0)
muons = muons[soft_id]
output['cutflow']['soft id'] += soft_id.any().sum()
twomuons = (muons.counts >= 2)
output['cutflow']['two muons'] += twomuons.sum()
dimuons = muons[twomuons].distincts()
twodimuons = (dimuons.counts >= 2)
output['cutflow']['>= two dimuons'] += twodimuons.sum()
dimuons = dimuons[twodimuons]
opposite_charge = (dimuons.i0['charge'] * dimuons.i1['charge'] == -1)
dimuons = dimuons[opposite_charge]
output['cutflow']['opposite charge'] += opposite_charge.any().sum()
mass_20GeV = (dimuons.mass > 35)
dimuons = dimuons[mass_20GeV]
exactlytwodimuons = (dimuons.counts == 2)
output['cutflow']['== two dimuons'] += exactlytwodimuons.sum()
dimuons = dimuons[exactlytwodimuons].compact()
leading_mu = (dimuons.i0.pt.content > dimuons.i1.pt.content)
pt_lead = JaggedArray.fromoffsets(dimuons.offsets, np.where(leading_mu,
dimuons.i0.pt.content, dimuons.i1.pt.content))
pt_trail = JaggedArray.fromoffsets(dimuons.offsets, np.where(~leading_mu,
dimuons.i0.pt.content, dimuons.i1.pt.content))
near_z = np.abs(dimuons.mass - 91.118).argmin()
far_z = np.abs(dimuons.mass - 91.118).argmax()
output['mass'].fill(dataset=dataset,
mass=dimuons.p4.sum().mass)
output['mass_near'].fill(dataset=dataset,
mass=dimuons.mass[near_z].flatten())
output['mass_far'].fill(dataset=dataset,
mass=dimuons.mass[far_z].flatten())
output['pt_lead'].fill(dataset=dataset,
pt=pt_lead.flatten())
output['pt_trail'].fill(dataset=dataset,
pt=pt_trail.flatten())
return output
def postprocess(self, accumulator):
return accumulator
tstart = time.time()
fileset = {
'DoubleMuon': [
'data/Run2012B_DoubleMuParked.root',
'data/Run2012C_DoubleMuParked.root',
],
'ZZ to 4mu': [
'data/ZZTo4mu.root'
]
}
output = processor.run_uproot_job(fileset,
treename='Events',
processor_instance=FancyDimuonProcessor(),
executor=processor.futures_executor,
executor_args={'workers': 6, 'flatten': True},
chunksize=500000,
)
elapsed = time.time() - tstart
print(output)
fig, ax, _ = hist.plot1d(output['mass'], overlay='dataset')
ax.set_xlim(70,150)
ax.set_ylim(0, 3000)
fig, ax, _ = hist.plot1d(output['mass_near'], overlay='dataset')
#ax.set_xscale('log')
#ax.set_yscale('log')
ax.set_xlim(60,120)
ax.set_ylim(0.1, 7500)
fig, ax, _ = hist.plot1d(output['mass_far'], overlay='dataset')
#ax.set_xscale('log')
#ax.set_yscale('log')
ax.set_ylim(0.1, 8000)
fig, ax, _ = hist.plot1d(output['pt_lead'], overlay='dataset')
#ax.set_xscale('log')
ax.set_yscale('log')
ax.set_ylim(0.1, 5e3)
fig, ax, _ = hist.plot1d(output['pt_trail'], overlay='dataset')
#ax.set_xscale('log')
ax.set_yscale('log')
ax.set_ylim(0.1, 2e4)
print("Events/s:", output['cutflow']['all events']/elapsed)
```
| true |
code
| 0.589185 | null | null | null | null |
|
# Neural Networks
G. Richards (2016,2018), where I found this video series particularly helpful in trying to simplify the explanation https://www.youtube.com/watch?v=bxe2T-V8XRs. Thanks also to Vince Baker (Drexel).
[Artificial Neural Networks](https://en.wikipedia.org/wiki/Artificial_neural_network) are a simplified computation architecture based loosely on the real neural networks found in brains.
In the image below the circles on the left represent the **attributes** of our input data, $X$, which here is 3 dimensional. The circles in the middle represent the neurons. They take in the information from the input and, based on some criterion decide whether or not to "fire". The collective results of the neurons in the hidden layer produce the output, $y$, which is represented by the circles on the right, which here is 2 dimensional result. The lines connecting the circles represent the synapses. This is a simple example with just one layer of neurons; however, there can be many layers of neurons.
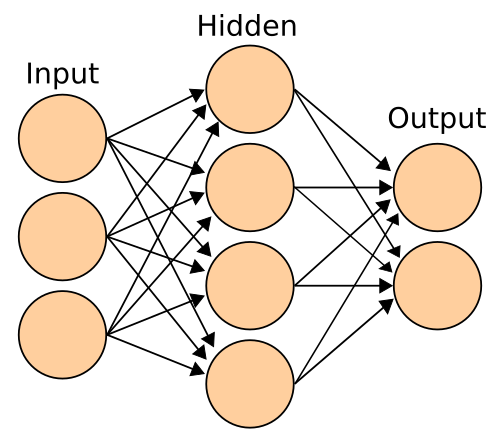
In more detail:
The job of a synapses is to take input values and multiply them by some weight before passing them to the neuron (hidden layer):
$$z = \sum_i w x_i$$
The neuron then sums up the inputs from all of the synapses connected to it and applies an "activation function". For example a [sigmoid](https://en.wikipedia.org/wiki/Sigmoid_function) activation function.
$$a = \frac{1}{1+e^{-z}}.$$

What the neural network does is to learn the weights of the synapses that are needed to produce an accurate model of $y_{\rm train}$.
Rather than think about the inputs individually, we can write this process in matrix form as
$$X W^{(1)} = Z^{(2)}.$$
If $D$ is the number of attributes (here 3) and $H$ is the number of neurons in the hidden layer (here 4), then $X$ is an $N\times D$ matrix, while $W^{(1)}$ is a $D\times H$ matrix. The result, $Z^{(2)}$, is then an $N\times H$ matrix.
We then apply the activation function to each entry of $Z^{(2)}$ independently:
$$A^{(2)} = f(Z^{(2)}),$$
where $A^{(2)}$ is the output of the neurons in the hidden layer and is also $N\times H$.
These values are then the inputs for the next set of synapses, where we multiply the inputs by another set of weights, $W^{(2)}:$
$$A^{(2)} W^{(2)} = Z^{(3)},$$
where $W^{(2)}$ is an $H\times O$ matrix and $Z^{(3)}$ is an $N\times O$ matrix with $O$-dimensional output.
Another activation function is then applied to $Z^{(3)}$ to give
$$\hat{y} = f(Z^{(3)}),$$
which is our estimator of $y$.
For example we might have $N=100$ people for which we have measured
* shoe size
* belt size
* hat size
for whom we know their height and weight.
Then we are going to use this to predict the height and weight for people where we only know shoe size, belt size, and hat size.
The neural network then essentially boils down to determining the weights, which are usually initialized randomly.
We do that by minimizing the cost function (which compares the true values of $y$ to our predicted values). Typically:
$$ {\rm Cost} = J = \sum\frac{1}{2}(y - \hat{y})^2.$$
If we just had 1 weight and we wanted to check 1000 possible values, that wouldn't be so bad. But we have 20 weights, which means checking $20^{1000}$ possible combinations. Remember the curse of dimensionality? That might take a while. Indeed, far, far longer than the age of the Universe.
How about just checking 3 points for each weight and see if we can at least figure out which way is "down hill"? That's a start.
We can rewrite $J$ as
$$ J = \sum\frac{1}{2}\left(y - f\left( f(X W^{(1)}) W^{(2)} \right) \right)^2$$
and then compute
$$\frac{\partial J}{\partial W}$$
in order to determine the slope of the cost function for each weight. This is the **gradient descent** method.
We'll want $\partial J/\partial W^{(1)}$ and $\partial J/\partial W^{(2)}$ separately. This allows us to [*backpropagate*](https://en.wikipedia.org/wiki/Backpropagation) the error contributions along each neuron and to change the weights where they most need to be changed. It is like each observations gets a vote on which way is "down hill". We compute the vector sum to decide the ultimate down hill direction.
Once we know the down hill direction from the derivative, we update the weights by subtracting a scalar times that derivative from the original weights. That's obviously much faster than randomly sampling all the possible combinations of weights. Once the weights are set, then you have your Neural Network classifier/regressor.

Scikit-Learn has both [unsupervised Neural Network](http://scikit-learn.org/stable/modules/neural_networks_unsupervised.html#neural-networks-unsupervised) and [supervised Neural Network](http://scikit-learn.org/stable/modules/neural_networks_supervised.html#neural-networks-supervised) examples. Apparently these are new as Jake VanderPlas didn't know about them.
Let's try to use the multi-layer perceptron classifier on the Boston House Price dataset (using 75% of the data for training and 25% for testing).
```
#Execute this cell after making the test set 25% of the total data set.
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
boston = load_boston()
#print boston.DESCR
X = boston.data
y = boston.target
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=___, random_state=42)
from sklearn.neural_network import MLPRegressor
clf = MLPRegressor(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=(5,2), random_state=1)
clf.fit(Xtrain, ytrain)
# Look at the weights
print [coef.shape for coef in clf.coefs_]
ypred = clf.predict(Xtest)
#print ypred, ytest
fig = plt.figure(figsize=(6, 6))
plt.scatter(ytest,ypred)
plt.xlabel("Actual Value [x$1000]")
plt.ylabel("Predicted Value [x$1000]")
plt.show()
```
Of course, that only predicts the value for a fraction of the data set. Again, we can use Scikit-Learn's [cross_val_predict](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_predict.html#sklearn.model_selection.cross_val_predict) to make predictions for the full data set.
```
from sklearn.model_selection import cross_val_predict
yCVpred = cross_val_predict(clf, X, y, cv=10) # Complete
fig = plt.figure(figsize=(6, 6))
plt.scatter(y,yCVpred)
plt.xlabel("Actual Value [x$1000]")
plt.ylabel("Predicted Value [x$1000]")
plt.show()
```
Recent interest in neural networks surged in 2012 when a team using a deep convolutional neural network acheived record results classifying objects in the [ImageNet](http://image-net.org/) data set.
This is clearly much more sophisticated than our basic perceptron. "Deep" networks consist of tens of layers with thousands of neurons. These large networks have become usabel thanks to two breakthroughs: the use of sparse layers and the power of graphics processing units (GPUs).
Many image processing tasks involve convolving an image with a 2-dimensional kernel as shown below.

The sparse layers or convolutional layers in a deep network contain a large number of hidden nodes but very few synapses. The sparseness arises from the relatively small size of a typical convolution kernel (15x15 is a large kernel), so a hidden node representing one output of the convolution is connected to only a few input nodes. Compare this the our previous perceptron, in which every hidden node was connected to every input node.
Even though the total number of connections is greatly reduced in the sparse layers, the total number of nodes and connections in a modern deep network is still enormous. Luckily, training these networks turns out to be a great task for GPU acceleration! Serious work using neural networks is almost always done usign specialized GPU-accelerated platforms.
| true |
code
| 0.607721 | null | null | null | null |
|
# Collaborative Filtering Algorithm
## Movie Recommemder System using Collaborative Filtering Algorithm
### This is an implementation of Collaborative Filtering Algorithm from scratch, based on the lecture of Andrew NG on the corresponding topic in Coursera.
### Dataset source: https://www.kaggle.com/grouplens/movielens-20m-dataset
```
# Import libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import os
from textwrap import wrap
# Set default fontsize and colors for graphs
SMALL_SIZE, MEDIUM_SIZE, BIG_SIZE = 8, 12, 16
plt.rc('font', size=MEDIUM_SIZE)
plt.rc('axes', titlesize=BIG_SIZE)
plt.rc('axes', labelsize=MEDIUM_SIZE)
plt.rc('xtick', labelsize=MEDIUM_SIZE)
plt.rc('ytick', labelsize=MEDIUM_SIZE)
plt.rc('legend', fontsize=SMALL_SIZE)
plt.rc('figure', titlesize=BIG_SIZE)
my_colors = 'rgbkymc'
# Disable scrolling for long output
from IPython.display import display, Javascript
disable_js = """
IPython.OutputArea.prototype._should_scroll = function(lines) {
return false;
}
"""
display(Javascript(disable_js))
```
## (1) Read and Prepare Data
### Read "movie" and "rating" dataset
```
# Read the input training data
input_data_file_movie = "C:\Study\DataSets\movielens-20m-dataset\\movie.csv"
input_data_file_rating = "C:\Study\DataSets\movielens-20m-dataset\\rating.csv"
movie_data_all = pd.read_csv(input_data_file_movie)
rating_data_all = pd.read_csv(input_data_file_rating)
movie_data_all.head(5)
rating_data_all.head(5)
print("Total number of movies =", movie_data_all.shape[0])
print("Total number of unique movies =", len(movie_data_all.movieId.unique()))
print("")
print("Total number of user ratings =", rating_data_all.shape[0])
print("Total number of unique users =", len(rating_data_all.userId.unique()))
# Keep only required columns
movie_data_all = movie_data_all.drop(['genres'], axis=1)
rating_data_all = rating_data_all.drop(['timestamp'], axis=1)
# Test with a subset of data
# Fetch num_movies number of movies
#num_movies = 10
#movie_data = movie_data_all.iloc[:num_movies, :]
# Fetch only ratings corresponding to above movies
#rating_data = rating_data_all[rating_data_all.movieId.isin(movie_data.movieId)]
#print("Total number of movies to be used to training =", movie_data.shape[0])
#print("Total number of user ratings to be used for training =", rating_data.shape[0])
# Test with a subset of data
#num_movies = 500
#num_ratings = 10000
#movie_data = movie_data.iloc[:num_movies, :]
#rating_data = rating_data.iloc[:num_ratings, :]
```
### Select few most popular movies, from two distinct genres. In this particular example, we considered movies of genres "Action" and "Romance".
### The objective is to find if collborative filtering algorithm can successfully learn the features of these movies based on user ratings, such that we can clearly distinguish their genres and recommend accordingly.
```
# Pick top movies
top_action_movies = ['Dark Knight, The', 'Lord of the Rings: The Return of the King',
'Inception', 'Star Wars: Episode V - The Empire Strikes Back',
'Matrix, The']
top_romantic_movies = ['Notting Hill', 'Love Story \(1970\)', 'When Harry Met Sally',
'Titanic \(1997\)', 'Pretty Woman']
top_movies = top_action_movies + top_romantic_movies
movie_data = movie_data_all[movie_data_all.title.str.contains('|'.join(top_movies))]
movie_data
# Pick all ratings
#num_ratings = 2000000
rating_data = rating_data_all.iloc[:, :]
```
### Merge movie and rating dataset based on movieId column
```
movie_rating_merged_data = movie_data.merge(rating_data, on='movieId', how='inner')
movie_rating_merged_data.head()
# Mean rating of a movie
movie_rating_merged_data[movie_rating_merged_data.title == 'Pretty Woman (1990)']['rating'].mean()
# Top 10 movies by mean rating
movie_rating_merged_data.groupby(['title'], sort=False)['rating'].mean().sort_values(ascending=False).head(10)
```
## (2) Build Collaborative Filtering Model
### Create a pivot table of movies (on rows) and corresponsing user ratings (on columns). The pivot table will contain the ratings of only selected movies.
### Thus, rows = movies and columns = users
```
movie_rating_merged_pivot = pd.pivot_table(movie_rating_merged_data,
index=['title'],
columns=['userId'],
values=['rating'],
dropna=False,
fill_value=0
)
movie_rating_merged_pivot.shape
Y = movie_rating_merged_pivot
```
### Create a matrix R, such that, R(i,j) = 1 iff User j has selected a rating for Movie i. R(i,j) = 0 otherwise.
```
R = np.ones(Y.shape)
no_rating_idx = np.where(Y == 0.0)
R[no_rating_idx] = 0
R
```
### Assign n_m (number of movies), n_u (number of users) and n_f (number of features)
```
n_u = Y.shape[1]
n_m = Y.shape[0]
n_f = 2
```
### Assign random initial values to movie and user parameters.
### X = parameters of movies (each row represent a movie)
### Theta = parameters of users (each row represent a user)
```
Initial_X = np.random.rand(n_m, n_f)
Initial_Theta = np.random.rand(n_u, n_f)
#print("Initial_X =", Initial_X)
#print("Initial_Theta =", Initial_Theta)
```
### Cost function or Objective function of collborative filtering algorithm
```
# Cost Function
def collabFilterCostFunction(X, Theta, Y, R, reg_lambda):
cost = 0
error = (np.dot(X, Theta.T) - Y) * R
error_sq = np.power(error, 2)
cost = np.sum(np.sum(error_sq)) / 2
cost = cost + (reg_lambda/2) * ( np.sum(np.sum((np.power(X, 2))))
+ np.sum(np.sum((np.power(Theta, 2)))) )
return cost
```
### Computation of Gradient Descent of collaborative filtering algorithm
```
# Gradient Descent
def collabFilterGradientDescent(X, Theta, Y, R, alpha, reg_lambda, num_iters):
cost_history = np.zeros([num_iters, 1])
for i in range(num_iters):
error = (np.dot(X, Theta.T) - Y) * R
X_grad = np.dot(error, Theta) + reg_lambda * X
Theta_grad = np.dot(error.T, X) + reg_lambda * Theta
X = X - alpha * X_grad
Theta = Theta - alpha * Theta_grad
cost_history[i] = collabFilterCostFunction(X, Theta, Y, R, reg_lambda)
return X, Theta, cost_history
```
## (3) Train the collborative filtering model
```
# Tune hyperparameters
alpha = 0.0001
num_iters = 25000
reg_lambda = 0
# Perform gradient descent to find optimal parameters
X, Theta = Initial_X, Initial_Theta
X, Theta, cost_history = collabFilterGradientDescent(X, Theta, Y, R, alpha, reg_lambda, num_iters)
cost = collabFilterCostFunction(X, Theta, Y, R, reg_lambda)
print("Find cost =", cost)
```
### Plot cost vs number of iterations
```
fig, axes = plt.subplots(figsize=(15,6))
axes.plot(cost_history, 'k--')
axes.set_xlabel('# of iterations')
axes.set_ylabel('Cost')
plt.show()
```
### Since we have considered only 2 genres (and hence 2 features), we plot the learned feature parameters of movies to visualize the pattern.
### We find below that the algorithm has learnt the features pretty well and hence the movies of same genre and clustered together.
### In this particular example, we considered movies of genres "Action" and "Romance". From the visualization, it can be concluded that X-axis represents "Degree of Action" and Y-axis represents "Degree of Romance".
### As a next step, we can run K-Means clustering to further verify our understanding.
```
fig, axes = plt.subplots(figsize=(10,10))
axes.scatter(X[:,0], X[:,1], color='red', marker='D')
for val, movie in zip(X, Y.index):
axes.text(val[0], val[1], movie)
axes.set_xlabel('Degree of Action')
axes.set_ylabel('Degree of Romance')
axes.set_title('Movie Matrix')
plt.show()
```
### For a random user, what are her preferred movies, and what is our recommendation for her based on result of collaborative filtering algorithm?
```
user_idx = np.random.randint(n_u)
pred_rating = []
print("Original rating of an user:\n", Y.iloc[:,user_idx].sort_values(ascending=False))
predicted_ratings = np.dot(X, Theta.T)
predicted_ratings = sorted(zip(predicted_ratings[:,user_idx], Y.index), reverse=True)
print("\nPredicted rating of the same user:")
_ = [print(rating, movie) for rating, movie in predicted_ratings]
```
| true |
code
| 0.48932 | null | null | null | null |
|
## Topic Modelling
The goal of this notebook is to find the topics on which people are talking within our dataset with tweets about vaccines. There are many models available for topic modelling, but in this Notebook we've focused only on **LDA (Latent Dirichlet Allocation)**.
For data protection purposes, the dataset used in this notebook is not provided here. If you want to replicate the notebook using this dataset, please contact the authors.
#### Input
- A dataset with tweets ready to be used by our LDA algorithm: `vacc_proc_for_topicMdl.csv`
#### Output
- An html where we can visualise the discovered topics: `Vaccs_Notts_topic_7.html`
- A dataset with tweets mapped to their main topic: `topics_mapped_Vaccs_Notts.csv`
```
# ----------------------------------------
# Libraries need to be installed
# ----------------------------------------
!pip install pyLDAvis
!pip install gensim
!pip install spacy
!python -m spacy download en_core_web_sm
# ----------------------------------------
# For File operations
# ----------------------------------------
import zipfile
import os
# ----------------------------------------
# Data read, write and other operations on Texts
# ----------------------------------------
import pandas as pd
import numpy as np
import string
import re
import unicodedata
from pprint import pprint
# ----------------------------------------
# For Libaries for NLP applications
# ----------------------------------------
import nltk
from nltk.corpus import stopwords
from nltk.util import ngrams
from nltk.tokenize import word_tokenize
from nltk.probability import FreqDist
import gensim
import spacy
spcy = spacy.load('/opt/conda/envs/Python-3.6-WMLCE/lib/python3.6/site-packages/en_core_web_sm/en_core_web_sm-2.3.1')
from gensim import corpora
from gensim.models import CoherenceModel
# ----------------------------------------
# For ignoring some warnings
# ----------------------------------------
import warnings
warnings.filterwarnings('ignore')
def wrng():
warnings.warn("deprecated", DeprecationWarning)
with warnings.catch_warnings():
warnings.simplefilter("ignore")
wrng()
# ----------------------------------------
# For Visualizations
# ----------------------------------------
import matplotlib
import matplotlib.pyplot as plt
import pyLDAvis
import pyLDAvis.gensim as pygen
pyLDAvis.enable_notebook()
# ----------------------------------------
# Need to download some extras
# ----------------------------------------
nltk.download('punkt')
nltk.download('stopwords')
```
### Load Dataset
Here the datset is used from the `TopicModelling_Vaccine_Preprocessing` notebook.
```
processed_tweets_Vaccs_ = pd.read_csv("/project_data/data_asset/vacc_proc_for_topicMdl.csv")
pd.set_option('display.max_columns', None) # Showing all columns for that dataframe
```
### Filtering data related to 'Nottingham'
```
notts_tweets_Vaccs_ = processed_tweets_Vaccs_[processed_tweets_Vaccs_["City"] == "Nottingham"]
```
### Part-of-Speech tagging
Filtering words based on particular part-of-speech as other parts of speech could generate noise for topics
```
sentences = []
for line in notts_tweets_Vaccs_["Clean_sentence_Comment"]:
pos_ = spcy(line)
sentence2 = " ".join([token.text for token in pos_ if (token.pos_ == "ADJ" or token.pos_ == "NOUN" or token.pos_ == "PROPN" or token.pos_ == "VERB")])
sentences.append(sentence2)
notts_tweets_Vaccs_["Clean_sentence_Comment"] = sentences
```
### Filtering words
Filtering the least and most frequent words (filters if less than 'no_below', more than 'no_above')
```
words = [text.split() for text in notts_tweets_Vaccs_["Clean_sentence_Comment"]]
dict_words = corpora.Dictionary(words)
dict_words.filter_extremes(no_below=5, no_above=0.2)
dict_words.compactify()
myCorpus_notts = [dict_words.doc2bow(word) for word in words]
```
### Training LDA Model
Here we train the LDA model and compute the coherence metric and log-perplexity for a range of topic numbers and other hyperparameters. Here, we've focused on coherence metric to choose the best model.
```
MulLda_coherent_scores = []
MulLda_topics_val = []
MulLda_perplexity_val = []
alpha_val = [0.05, 0.1, 0.3, 0.5, 0.8, 1]
MulLda_alphas = []
for topics in range(3, 15, 2):
for alph in alpha_val:
lda_model_multi_notts = gensim.models.LdaMulticore(corpus = myCorpus_notts,
id2word = dict_words,
random_state = 42,
num_topics = topics,
passes=10,
chunksize=512,
alpha=alph,
offset=64,
eta=None,
iterations=100,
per_word_topics=True,
workers=6)
coherence_model_MulLda_notts = CoherenceModel(model = lda_model_multi_notts,
texts = words,
dictionary = dict_words,
coherence = 'c_v')
coherence_MulLda = coherence_model_MulLda_notts.get_coherence()
perplexity_MulLda = lda_model_multi_notts.log_perplexity(myCorpus_notts)
MulLda_topics_val.append(topics)
MulLda_alphas.append(alph)
MulLda_coherent_scores.append(coherence_MulLda)
MulLda_perplexity_val.append(perplexity_MulLda)
df_mulLDA_notts = pd.DataFrame(list(zip(MulLda_topics_val, MulLda_alphas, MulLda_coherent_scores, MulLda_perplexity_val)),
columns = ["MulLda_Topic_Num", "MulLda_alpha_val", "MulLda_Coherent_score", "MulLda_Perplexity_val"])
df_mulLDA_notts.sort_values("MulLda_Coherent_score", axis = 0, ascending = False,
inplace = True)
df_mulLDA_notts.head()
```
### Final Model
After choosing best hyperparams from above dataframe based on coherence metric, we can train our final model. Note that we haven't just fully relied on the highest value for this metric, but we have rather chosen the model that makes the most sense based in our experience from the top models.
The cell below will output the words related to some topics and clusters of topics (visualization).
```
multi_lda_final_notts = gensim.models.LdaMulticore(corpus = myCorpus_notts,
id2word = dict_words,
random_state = 42,
num_topics = 7,
passes=10,
chunksize=512,
alpha=0.05,
offset=64,
eta=None,
iterations=100,
per_word_topics=True,
workers=6)
pprint(multi_lda_final_notts.print_topics(num_topics = 7, num_words=20))
print("\n\033[91m" + "\033[1m" +"------- Visualization -----------\n")
lda_Mul_vis_notts = pygen.prepare(multi_lda_final_notts, myCorpus_notts, dict_words)
pyLDAvis.display(lda_Mul_vis_notts)
```
### Saving Topics as html
```
pyLDAvis.save_html(lda_Mul_vis_notts, "/project_data/data_asset/Vaccs_Notts_topic_7.html")
```
### Mapping Tweets with Topics
```
topicss = []
probss = []
for i, row in enumerate(multi_lda_final_notts[myCorpus_notts]): # gives topics probablity
row = sorted(row[0], key=lambda x :(x[1]), reverse=True) # sorting according to higher probability
for j, (topic_num, probablity) in enumerate(row): # j=0 --> containing highest probablity, topic_num --> falls under which topic
if j == 0:
topicss.append(topic_num)
probss.append(probablity)
Notts_tweets_Vaccs_["Topic_Num"] = topicss
Notts_tweets_Vaccs_["Topic_prob"] = probss
Notts_tweets_Vaccs_.head()
```
### Final Dataset
we've given the topics some names and mapped with the tweets
```
"""
list_ - values of list needs to converted to string
"""
def ListToStr(list_):
str_val = ""
for item in list_:
str_val += item
return str_val
dts = []
for dttt in Notts_tweets_Vaccs_["Date"]:
yrs_ = re.findall(r"\d{4}", dttt)
dts.append(ListToStr(yrs_))
Notts_tweets_Vaccs_["year"] = dts
Notts_tweets_Vaccs_["Date"] = pd.to_datetime(Notts_tweets_Vaccs_["Date"]).dt.date
tpc_nms = []
for tpc_ in Notts_tweets_Vaccs_["Topic_Num"].values.tolist():
if tpc_ == 0:
tpc_nms.append("Effects of virus and vaccine")
if tpc_ == 1:
tpc_nms.append("Politics in US around vaccine")
if tpc_ == 2:
tpc_nms.append("Enforcement of vaccines")
if tpc_ == 3:
tpc_nms.append("Politics in UK around vaccine")
if tpc_ == 4:
tpc_nms.append("Science around Vaccine")
if tpc_ == 5:
tpc_nms.append("Public affairs")
if tpc_ == 6:
tpc_nms.append("Distribution of vaccine and logistics")
Notts_tweets_Vaccs_["Topic_Names"] = tpc_nms
tyms = []
for tym in Notts_tweets_Vaccs_["Date"].values.tolist():
tym_ = tym.strftime('%d-%b')
tyms.append(tym_)
Notts_tweets_Vaccs_["Date_month"] = tyms
```
### Saving Final dataset
```
Notts_tweets_Vaccs_.to_csv('/project_data/data_asset/topics_mapped_Vaccs_Notts.csv', index = False)
```
### Author:
- **Ananda Pal** is a Data Scientist and Performance Test Analyst at IBM, where he specialises in Data Science and Machine Learning Solutions
Copyright © IBM Corp. 2020. Licensed under the Apache License, Version 2.0. Released as licensed Sample Materials.
| true |
code
| 0.280407 | null | null | null | null |
|
# Writing OSEM (or another reconstruction algorithm) yourself with SIRF
This notebook invites you to write MLEM and OSEM yourself using SIRF functionality, i.e. Do It Yourself OSEM!
You should have completed the [OSEM_reconstruction notebook](OSEM_reconstruction.ipynb) first. The [ML_reconstruction notebook](ML_reconstruction.ipynb) might help as well.
The notebook is currently set-up to use prepared data with a single slice of an XCAT phantom, with a low resolution scanner, such that all results can be obtained easily on a laptop. Of course, your code will have to work for any data.
Authors: Kris Thielemans
First version: June 2021
CCP SyneRBI Synergistic Image Reconstruction Framework (SIRF).
Copyright 2021 University College London.
This is software developed for the Collaborative Computational Project in Synergistic Reconstruction for Biomedical Imaging (http://www.ccpsynerbi.ac.uk/).
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
# Initial set-up
```
#%% make sure figures appears inline and animations works
%matplotlib notebook
# Setup the working directory for the notebook
import notebook_setup
from sirf_exercises import cd_to_working_dir
cd_to_working_dir('PET', 'OSEM_reconstruction')
#%% Initial imports etc
import numpy
import matplotlib.pyplot as plt
import os
import sirf.STIR as pet
from sirf.Utilities import examples_data_path
from sirf_exercises import exercises_data_path
# define the directory with input files for this notebook
data_path = os.path.join(examples_data_path('PET'), 'thorax_single_slice')
# set-up redirection of STIR messages to files
msg_red = pet.MessageRedirector('info.txt', 'warnings.txt', 'errors.txt')
```
## We will first create some simulated data from ground-truth images
see previous notebooks for more information.
```
#%% Read in images
image = pet.ImageData(os.path.join(data_path, 'emission.hv'))
attn_image = pet.ImageData(os.path.join(data_path, 'attenuation.hv'))
#%% save max for future displays
im_slice = image.dimensions()[0]//2
cmax = image.max()*.6
#%% create acquisition model
acq_model = pet.AcquisitionModelUsingRayTracingMatrix()
template = pet.AcquisitionData(os.path.join(data_path, 'template_sinogram.hs'))
acq_model.set_up(template, image)
#%% simulate data using forward projection
acquired_data = acq_model.forward(image)
```
# Maximum Likelihood Expectatin Maximisation (MLEM)
Also called EMML. This is a standard algorithm, derived by using EM for the PET (or SPECT) problem. See the paper:
Shepp, L. A., and Y. Vardi. ‘Maximum Likelihood Reconstruction for Emission Tomography’. IEEE Transactions on Medical Imaging 1, no. 2 (1982): 113-122+.
Our notation here: $x$ is the image, $y$ the measured data with $A$ the system matrix. This is different from the Shepp and Vardi paper, which uses $\lambda$ for the image, $n^*$ for the measured data, $p(b,d)$ for the elements of the system matrix, and it has no background.
In our notation, the model for the mean of the data (i.e., modelling the expected measurement, given an image $x$) is
$$ \bar{y}=A x + b$$
The MLEM update is
$$ x^{\mathrm{new}} = \frac{x}{A^t 1} A^t \left(\frac{y}{A x + b}\right)$$
You hopefully recognise that the denominator of the factor on the right corresponds to the `forward` model applied ot the image $x$. Multiplication with the $A^t$ is the `backward` operation. So, we have used all the main operations already. We just need to do element-wise multiplication an division operation, but that's easy!
Let's first compute $A^t 1$, as this is a image that won't change over iterations. Note that the $1$ here represents a one-vector, i.e., an image filled with ones. It is often called the "sensivity image" as it is (proportional to) the probability that an event emitted in a voxel is detected by the scanner (without scattering).
```
sensitivity = acq_model.backward(acquired_data.get_uniform_copy(1))
```
Now we initialise the algorithm with a uniform image:
```
estimated_image = image.get_uniform_copy(1)
```
and we can do one MLEM iteration
```
quotient = acquired_data/acq_model.forward(estimated_image) # y / (Ax + b)
mult_update = acq_model.backward(quotient)/sensitivity # A^t * quotient / A^t1
estimated_image *= mult_update # update (in place)
```
And we can do some plots
```
plt.figure()
plt.subplot(1,2,1)
plt.imshow(estimated_image.as_array()[im_slice,:,:])
plt.subplot(1,2,2)
plt.imshow(mult_update.as_array()[im_slice,:,:])
```
Now you can of course duplicate some of these lines, or re-execute the above cells. However, it makes more sense to write a function to do this. Something like this:
```
def MLEM(acquired_data, acq_model, initial_image, num_iterations):
estimated_image = initial_image.clone()
# some stuff here
return estimated_image
```
And now you can run it!
```
estimated_image = MLEM(acquired_data, acq_model,image.get_uniform_copy(1), 40)
```
This was hopefully not too hard. Theree are a few problems though that you might encounter.
- your image might display nice, but on closer investigation will probably contain NaNs (Not a Number). These come from divisions: 0/0 is not defined. They can occur in 2 places:
- division in the acquisition data term. This should in theory not occur if you start with a strictly positive image that is large enough to "cover" all of the projection data. Of course, in practice it could happen that your image is smaller than the Field of View (FOV), and you might need to handle this anyway.
- division of the images. This will occur wherever the sensitivty image is zero. This difficulty is not a surprise: if a voxel cannot be measured, its ML estimate is undefined.
We have the second problem of course, as by default the projector uses a circular FOV. You might wat to add a post-processing step that sets those values to zero.
The STIR implementation of MLEM (`OSMAPOSL`) takes care of these corner cases, as well as any negatives in the data (arising when pre-correcting the data, as although this should not be done in theory, some people are interested in this anyway).
# Ordered Subsets Expectation Maximisation (OSEM)
Is discussed in previous notebooks, MLEM is great but slow. OSEM was introduced in
Hudson, H.M., and R.S. Larkin. ‘Accelerated Image Reconstruction Using Ordered Subsets of Projection Data’. IEEE Transactions on Medical Imaging 13, no. 4 (December 1994): 601–9. https://doi.org/10.1109/42.363108.
The update formula is exactly the same, except that at every update, only a subset of the data is used, i.e. restricting the data $y$, background $b$ and the matrix $A$ to a subset of all the rows. Clearly, for $N$ subsets, this reduces the number of computations for one image update with a factor $N$. While each update might be somewhat less accurate, it certainly works well in initial iterations.
So how do we implement this in SIRF? Luckily, an `sirf.STIR` acquisition model can be told to use only a subset of the data. The class documentation will show you that you can set `num_subsets` and `subset_num`.
(There is currently no way to change how the subsets are chosen, but only the number of subsets).
Note: the call to `forward` and `backward` also supports extra arguments for specifying the subsets. However, these are deprecated and will be removed in a future release.
Some interesting things to try:
- how does varying the `subset_num` affect the projection?
- how does varying the `num_subsets` affect the projection sparsity?
- what happens if you sum over all the subsets?
```
acq_model.num_subsets = 4
acq_model.subset_num = 0 # for 4 subsets, use a number between 0 and 3
data = acq_model.forward(image)
data.show(im_slice)
```
Unfortunately, SIRF currently has no way to restrict the data to a particular subset. There are 2 ways around that:
- ignore it and do the divisions over all of the data anyway. This will lead to 1/0 etc, but as those elements of the data are not backprojected, it won't change the final image.
- construct several "masks" as `AcquisitionData by forward projection an image full of ones for every subsets and doing some thresholding.
Clearly, the first option is easiest (although it does mean there is some overhead in computing extra additions/divisions). Let's see if it works ok!
```
check = acq_model.backward(acquired_data/data)
check.show(im_slice)
```
You should now be in a position to write your own OSEM algorithm. Don't forget that for a strict implementation of OSEM, you need to compute "subset sensitivities" for the division.
```
def OSEM(acquired_data, acq_model, initial_image, num_iterations):
estimated_image=initial_image.clone()
# some stuff here - hint, this will be similar to your solution for MLEM
# but you will have to additionally iterate over your subsets
return estimated_image
```
# Final remarks
Hopefully you have learned that taking an algorithm from a paper and implementing it yourself should be easy enough in SIRF. However, you probably also learned that you might encounter some subtleties that are often not so easy to spot when you read a paper.
The STIR `OSMAPOSL` implementation attempts to take care of these subtleties. It of course also avoids overheads such as the divisions with the subsets. Finally, it uses a multi-threaded implementation of the computation of the update that might be a bit faster than using calling the `forward` and `backward` operations directly (although these are multi-threaded as well).
When trying to implement an algorithm of a paper, there is often a choice at what "level" you choose for your code. In the above, we went to the projector-level. In the [ML_reconstruction notebook](ML_reconstruction.ipynb) we constructed an objective function and used the `update` and `objective_function_value` members to do a lot of the hard work. Similarly, the [MAP_EM notebook](MAP_EM.ipynb) that you could tackle now writes a MAP algorithm in terms of (OS)EM functionality. All choices will probably work ok, but there are various trade-offs between verbosity, flexibility, extendability to consider, but we won't go into that here.
| true |
code
| 0.45744 | null | null | null | null |
|
#**Part 1 - Data gathering and feature engineering**
**Libraries**
```
import numpy as np #Linear_Algebra
import matplotlib.pyplot as plt
import pandas as pd #Data_Processing
import pandas_datareader as pdr
from scipy import stats
%matplotlib inline
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
pip install -q yfinance --upgrade
#Import Yahoo Finance
import yfinance as yf
yf.pdr_override()
#CISCO data
SELECTED_STOCK = 'CSCO'
start = '2010-12-17'
end = '2018-12-17'
#Download NVIDIA stock price data for the past 10 yrs to date
stock_data = pdr.get_data_yahoo(SELECTED_STOCK, start, end)
stock_data.head(10)
```
**Feature Engineering**
```
#Getting the Open price
stock_data_open = stock_data.Open.values
reshaped_stock_data_open = np.reshape(stock_data_open, (-1, 1))
reshaped_stock_data_open
#validity check
np.mean(reshaped_stock_data_open)==np.mean(stock_data_open)
```
#**Indicators**
##**Moving Average**
```
# Moving Averages Code
# Load the necessary packages and modules
from pandas_datareader import data as pdr
import matplotlib.pyplot as plt
import fix_yahoo_finance
import pandas as pd
# Simple Moving Average
def SMA(data, ndays):
SMA = pd.Series(data['Close'], name = 'SMA').rolling(window=ndays).mean()
data = data.join(SMA)
return data
# Exponentially-weighted Moving Average
def EWMA(data, ndays):
EMA = pd.Series((data['Close'].ewm(span=ndays).mean()),
name = 'EWMA_' + str(ndays))
data = data.join(EMA)
return data
# Retrieve the CISCO data from Yahoo finance:
data = pdr.get_data_yahoo("CSCO", start="2010-01-01", end="2019-12-16")
data = pd.DataFrame(data)
close = data['Close']
# Compute the 50-day SMA for CISCO
n = 50
SMA_CISCO = SMA(data,n)
SMA_CISCO = SMA_CISCO.dropna()
SMA = SMA_CISCO['SMA']
# Compute the 200-day EWMA for CISCO
ew = 200
EWMA_CISCO = EWMA(data,ew)
EWMA_CISCO = EWMA_CISCO.dropna()
EWMA = EWMA_CISCO['EWMA_200']
# Plotting the CISCO Price Series chart and Moving Averages below
plt.figure(figsize=(9,5))
plt.plot(data['Close'],lw=1, label='NSE Prices')
plt.plot(SMA,'g',lw=1, label='50-day SMA (green)')
plt.plot(EWMA,'r', lw=1, label='200-day EWMA (red)')
plt.legend(loc=2,prop={'size':11})
plt.grid(True)
plt.setp(plt.gca().get_xticklabels(), rotation=30)
```
##**Commodity Channel Index (CCI)**
```
from pandas_datareader import data as pdr
import matplotlib.pyplot as plt
import fix_yahoo_finance
import pandas as pd
# Commodity Channel Index
def CCI(data, ndays):
TP = (data['High'] + data['Low'] + data['Close']) / 3
CCI = pd.Series((TP - pd.Series(TP).rolling(window=ndays).mean()) / (0.015 * pd.Series(TP).rolling(window=ndays).std()),
name = 'CCI')
data = data.join(CCI)
return data
# Retrieve the CISCO data from Yahoo finance:
data = pdr.get_data_yahoo("CSCO", start="2010-01-01", end="2019-12-16")
data = pd.DataFrame(data)
# Compute the Commodity Channel Index(CCI) for CISCO based on the 20-day Moving average
n = 20
CISCO_CCI = CCI(data, n)
CCI = CISCO_CCI['CCI']
# Plotting the Price Series chart and the Commodity Channel index below
fig = plt.figure(figsize=(7,5))
ax = fig.add_subplot(2, 1, 1)
ax.set_xticklabels([])
plt.plot(data['Close'],lw=1)
plt.title('NSE Price Chart')
plt.ylabel('Close Price')
plt.grid(True)
bx = fig.add_subplot(2, 1, 2)
plt.plot(CCI,'k',lw=0.75,linestyle='-',label='CCI')
plt.legend(loc=2,prop={'size':9.5})
plt.ylabel('CCI values')
plt.grid(True)
plt.setp(plt.gca().get_xticklabels(), rotation=30)
```
**Feature Scaling**
```
from sklearn.preprocessing import MinMaxScaler
sc = MinMaxScaler(feature_range = (0,1))
scaled_data = sc.fit_transform(reshaped_stock_data_open)
def timestamp(n_period, scaled_data):
x_train = []
y_train = [] #1 output to predict
for i in range(n_period,len(scaled_data)):
x_train.append(scaled_data[i-n_period:i,0])
y_train.append(scaled_data[i,0])
x_train, y_train = np.array(x_train), np.array(y_train)
#reshaping
x_train_ = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1))
return x_train_, x_train, y_train
x_train_, x_train, y_train = timestamp(60, scaled_data)
```
#**Part 2 - Model Identification**
##**Decision Tree (Regression)**
```
from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor
dt = DecisionTreeRegressor()
decision_tree_regr = BaggingRegressor(dt, n_estimators=10, random_state=0)
decision_tree_regr.fit(x_train, y_train)
```
##**Recurrent Neural Network (RNN)**
```
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
#Importing the keras libraries and packages
from tensorflow.python.keras.layers import Dense, LSTM, Dropout
from tensorflow.python.keras import Sequential
regressor = Sequential()
#Adding the first LSTM Layer and some Dropout regularisation
regressor.add(LSTM(units=50, return_sequences=True, input_shape = (x_train_.shape[1], 1)))
regressor.add(Dropout(rate = 0.2))
x_train.shape[1]
#Adding the second LSTM Layer and some Dropout regularisation
regressor.add(LSTM(units=50, return_sequences=True))
regressor.add(Dropout(rate = 0.2))
#Adding the third LSTM Layer and some Dropout regularisation
regressor.add(LSTM(units=50, return_sequences=True))
regressor.add(Dropout(rate = 0.2))
#Adding the fourth LSTM Layer and some Dropout regularisation
regressor.add(LSTM(units=50))
regressor.add(Dropout(rate = 0.2))
#Adding the output layer
regressor.add(Dense(units=1))
#compiling the RNN
regressor.compile(optimizer='adam', loss='mean_squared_error')
#fitting the RNN to the training set
regressor.fit(x_train_, y_train, epochs=50, batch_size = 32)
```
**Save the model**
```
regressor = regressor.save("regressor.h5")
```
**Load the model**
```
from tensorflow.python.keras.models import load_model
regressor = load_model("regressor.h5")
```
##**Making the predictions and visualising the results**
```
# Getting the real/test stock price of 2019
test_stock_data = pdr.get_data_yahoo(SELECTED_STOCK, start = '2018-12-18', end = '2019-12-17')
real_stock_price = test_stock_data.iloc[:, 1:2].values
dataset_total = pd.concat((stock_data['Open'], test_stock_data['Open']), axis = 0)
inputs = dataset_total[len(dataset_total) - len(test_stock_data) - 60:].values
inputs = inputs.reshape(-1,1)
inputs = sc.transform(inputs)
X_test = []
for i in range(60, 310): #80 because we're predicting 20 records
X_test.append(inputs[i-60:i, 0])
X_test = np.array(X_test)
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))
predicted_stock_price = regressor.predict(X_test)
predicted_stock_price = sc.inverse_transform(predicted_stock_price) #retranform the output because our input data was scaled between 0 and 1.
# Visualising the results
plt.plot(real_stock_price, color = 'red', label = 'Real CISCO Stock Price')
plt.plot(predicted_stock_price, color = 'blue', label = 'Predicted CISCO Stock Price')
plt.title('CISCO Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('CISCO Stock Price')
plt.legend()
plt.show()
```
| true |
code
| 0.591723 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/probml/probml-notebooks/blob/main/notebooks/numpyro_intro.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
[NumPyro](https://github.com/pyro-ppl/numpyro) is probabilistic programming language built on top of JAX. It is very similar to [Pyro](https://pyro.ai/), which is built on top of PyTorch.
However, the HMC algorithm in NumPyro
[is much faster](https://stackoverflow.com/questions/61846620/numpyro-vs-pyro-why-is-former-100x-faster-and-when-should-i-use-the-latter).
Both Pyro flavors are usually also [faster than PyMc3](https://www.kaggle.com/s903124/numpyro-speed-benchmark), and allow for more complex models, since Pyro is integrated into Python.
# Installation
```
import numpy as np
np.set_printoptions(precision=3)
import matplotlib.pyplot as plt
import math
# When running in colab pro (high RAM mode), you get 4 CPUs.
# But we need to force XLA to use all 4 CPUs
# This is generally faster than running in GPU mode
import os
os.environ["XLA_FLAGS"] = "--xla_force_host_platform_device_count=4"
# http://num.pyro.ai/en/stable/getting_started.html#installation
#CPU mode: often faster in colab!
!pip install numpyro
# GPU mode: as of July 2021, this does not seem to work
#!pip install numpyro[cuda111] -f https://storage.googleapis.com/jax-releases/jax_releases.html
import jax
print("jax version {}".format(jax.__version__))
print("jax backend {}".format(jax.lib.xla_bridge.get_backend().platform))
print(jax.lib.xla_bridge.device_count())
print(jax.local_device_count())
import jax.numpy as jnp
from jax import random
import numpyro
#numpyro.set_platform('gpu')
import numpyro.distributions as dist
from numpyro.distributions import constraints
from numpyro.distributions.transforms import AffineTransform
from numpyro.infer import MCMC, NUTS, Predictive
from numpyro.infer import SVI, Trace_ELBO, init_to_value
from numpyro.diagnostics import hpdi, print_summary
from numpyro.infer.autoguide import AutoLaplaceApproximation
rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)
```
# Example: 1d Gaussian with unknown mean.
We use the simple example from the [Pyro intro](https://pyro.ai/examples/intro_part_ii.html#A-Simple-Example). The goal is to infer the weight $\theta$ of an object, given noisy measurements $y$. We assume the following model:
$$
\begin{align}
\theta &\sim N(\mu=8.5, \tau^2=1.0)\\
y \sim &N(\theta, \sigma^2=0.75^2)
\end{align}
$$
Where $\mu=8.5$ is the initial guess.
## Exact inference
By Bayes rule for Gaussians, we know that the exact posterior,
given a single observation $y=9.5$, is given by
$$
\begin{align}
\theta|y &\sim N(m, s^s) \\
m &=\frac{\sigma^2 \mu + \tau^2 y}{\sigma^2 + \tau^2}
= \frac{0.75^2 \times 8.5 + 1 \times 9.5}{0.75^2 + 1^2}
= 9.14 \\
s^2 &= \frac{\sigma^2 \tau^2}{\sigma^2 + \tau^2}
= \frac{0.75^2 \times 1^2}{0.75^2 + 1^2}= 0.6^2
\end{align}
$$
```
mu = 8.5; tau = 1.0; sigma = 0.75;
hparams = (mu, tau, sigma)
y = 9.5
m = (sigma**2 * mu + tau**2 * y)/(sigma**2 + tau**2)
s2 = (sigma**2 * tau**2)/(sigma**2 + tau**2)
s = np.sqrt(s2)
print(m)
print(s)
def model(hparams, y=None):
prior_mean, prior_sd, obs_sd = hparams
theta = numpyro.sample("theta", dist.Normal(prior_mean, prior_sd))
y = numpyro.sample("y", dist.Normal(theta, obs_sd), obs=y)
return y
```
## Ancestral sampling
```
def model2(hparams):
prior_mean, prior_sd, obs_sd = hparams
theta = numpyro.sample("theta", dist.Normal(prior_mean, prior_sd))
yy = numpyro.sample("y", dist.Normal(theta, obs_sd))
return theta, yy
with numpyro.handlers.seed(rng_seed=0):
for i in range(5):
theta, yy = model2(hparams)
print([theta, yy])
```
## MCMC
See [the documentation](https://num.pyro.ai/en/stable/mcmc.html)
```
conditioned_model = numpyro.handlers.condition(model, {'y': y})
nuts_kernel = NUTS(conditioned_model)
mcmc = MCMC(nuts_kernel, num_warmup=200, num_samples=200, num_chains=4)
mcmc.run(rng_key_, hparams)
mcmc.print_summary()
samples = mcmc.get_samples()
print(type(samples))
print(type(samples['theta']))
print(samples['theta'].shape)
nuts_kernel = NUTS(model) # this is the unconditioned model
mcmc = MCMC(nuts_kernel, num_warmup=100, num_samples=1000)
mcmc.run(rng_key_, hparams, y) # we need to specify the observations here
mcmc.print_summary()
samples = mcmc.get_samples()
```
## Stochastic variational inference
See [the documentation](https://num.pyro.ai/en/stable/svi.html)
```
# the guide must have the same signature as the model
def guide(hparams, y):
prior_mean, prior_sd, obs_sd = hparams
m = numpyro.param("m", y) # location
s = numpyro.param("s", prior_sd, constraint=constraints.positive) # scale
return numpyro.sample("theta", dist.Normal(m, s))
# The optimizer wrap these, so have unusual keywords
#https://jax.readthedocs.io/en/latest/jax.experimental.optimizers.html
#optimizer = numpyro.optim.Adam(step_size=0.001)
optimizer = numpyro.optim.Momentum(step_size=0.001, mass=0.1)
#svi = SVI(model, guide, optimizer, Trace_ELBO(), hparams=hparams, y=y) # specify static args to model/guide
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
nsteps = 2000
svi_result = svi.run(rng_key_, nsteps, hparams, y) # or specify arguments here
print(svi_result.params)
print(svi_result.losses.shape)
plt.plot(svi_result.losses)
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
print([svi_result.params['m'], svi_result.params['s']])
```
## Laplace (quadratic) approximation
See [the documentation](https://num.pyro.ai/en/stable/autoguide.html#autolaplaceapproximation)
```
guide_laplace = AutoLaplaceApproximation(model)
svi = SVI(model, guide_laplace, optimizer, Trace_ELBO(), hparams=hparams, y=y)
svi_run = svi.run(rng_key_, 2000)
params = svi_run.params
losses = svi_result.losses
plt.figure()
plt.plot(losses)
# Posterior is an MVN
# https://num.pyro.ai/en/stable/distributions.html#multivariatenormal
post = guide_laplace.get_posterior(params)
print(post)
m = post.mean
s = jnp.sqrt(post.covariance_matrix)
print([m, s])
samples = guide_laplace.sample_posterior(rng_key_, params, (1000,))
print_summary(samples, 0.89, False)
```
# Example: Beta-Bernoulli model
Example is from [SVI tutorial](https://pyro.ai/examples/svi_part_i.html)
The model is
$$
\begin{align}
\theta &\sim \text{Beta}(\alpha, \beta) \\
x_i &\sim \text{Ber}(\theta)
\end{align}
$$
where $\alpha=\beta=10$. In the code, $\theta$ is called
`latent_fairness`.
```
alpha0 = 10.0
beta0 = 10.0
def model(data):
f = numpyro.sample("latent_fairness", dist.Beta(alpha0, beta0))
# loop over the observed data
for i in range(len(data)):
numpyro.sample("obs_{}".format(i), dist.Bernoulli(f), obs=data[i])
# create some data with 6 observed heads and 4 observed tails
data = jnp.hstack((jnp.ones(6), jnp.zeros(4)))
print(data)
N1 = jnp.sum(data==1)
N0 = jnp.sum(data==0)
print([N1, N0])
```
## Exact inference
The posterior is given by
$$
\begin{align}
\theta &\sim \text{Ber}(\alpha + N_1, \beta + N_0) \\
N_1 &= \sum_{i=1}^N [x_i=1] \\
N_0 &= \sum_{i=1}^N [x_i=0]
\end{align}
$$
```
alpha_q = alpha0 + N1
beta_q = beta0 + N0
print('exact posterior: alpha={:0.3f}, beta={:0.3f}'.format(alpha_q, beta_q))
post_mean = alpha_q / (alpha_q + beta_q)
post_var = (post_mean * beta_q)/((alpha_q + beta_q) * (alpha_q + beta_q + 1))
post_std = np.sqrt(post_var)
print([post_mean, post_std])
inferred_mean = alpha_q / (alpha_q + beta_q)
# compute inferred standard deviation
factor = beta_q / (alpha_q * (1.0 + alpha_q + beta_q))
inferred_std = inferred_mean * math.sqrt(factor)
print([inferred_mean, inferred_std])
```
## Variational inference
```
def guide(data):
alpha_q = numpyro.param("alpha_q", alpha0,
constraint=constraints.positive)
beta_q = numpyro.param("beta_q", beta0,
constraint=constraints.positive)
numpyro.sample("latent_fairness", dist.Beta(alpha_q, beta_q))
#optimizer = numpyro.optim.Adam(step_size=0.001)
optimizer = numpyro.optim.Momentum(step_size=0.001, mass=0.1)
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
nsteps = 2000
svi_result = svi.run(rng_key_, nsteps, data)
print(svi_result.params)
print(svi_result.losses.shape)
plt.plot(svi_result.losses)
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
# grab the learned variational parameters
alpha_q = svi_result.params["alpha_q"]
beta_q = svi_result.params["beta_q"]
print('variational posterior: alpha={:0.3f}, beta={:0.3f}'.format(alpha_q, beta_q))
post_mean = alpha_q / (alpha_q + beta_q)
post_var = (post_mean * beta_q)/((alpha_q + beta_q) * (alpha_q + beta_q + 1))
post_std = np.sqrt(post_var)
print([post_mean, post_std])
```
## MCMC
```
nuts_kernel = NUTS(model) # this is the unconditioned model
mcmc = MCMC(nuts_kernel, num_warmup=100, num_samples=1000)
mcmc.run(rng_key_, data)
mcmc.print_summary()
samples = mcmc.get_samples()
```
# Distributions
## 1d Gaussian
```
# 2 independent 1d gaussians (ie 1 diagonal Gaussian)
mu = 1.5
sigma = 2
d = dist.Normal(mu, sigma)
dir(d)
rng_key, rng_key_ = random.split(rng_key)
nsamples = 1000
ys = d.sample(rng_key_, (nsamples,))
print(ys.shape)
mu_hat = np.mean(ys,0)
print(mu_hat)
sigma_hat = np.std(ys, 0)
print(sigma_hat)
```
## Multivariate Gaussian
```
mu = np.array([-1, 1])
sigma = np.array([1, 2])
Sigma = np.diag(sigma)
d2 = dist.MultivariateNormal(mu, Sigma)
#rng_key, rng_key_ = random.split(rng_key)
nsamples = 1000
ys = d2.sample(rng_key_, (nsamples,))
print(ys.shape)
mu_hat = np.mean(ys,0)
print(mu_hat)
Sigma_hat = np.cov(ys, rowvar=False) #jax.np.cov not implemented
print(Sigma_hat)
```
## Shape semantics
[Numpyro](http://num.pyro.ai/en/stable/distributions.html), [Pyro](https://pyro.ai/examples/tensor_shapes.html) and [TFP](https://www.tensorflow.org/probability/examples/Understanding_TensorFlow_Distributions_Shapes)
and [Distrax](https://github.com/deepmind/distrax)
all distinguish between 'event shape' and 'batch shape'.
For a D-dimensional Gaussian, the event shape is (D,), and the batch shape
will be (), meaning we have a single instance of this distribution.
If the covariance is diagonal, we can view this as D independent
1d Gaussians, stored along the batch dimension; this will have event shape () but batch shape (2,).
When we sample from a distribution, we also specify the sample_shape.
Suppose we draw N samples from a single D-dim diagonal Gaussian,
and N samples from D 1d Gaussians. These samples will have the same shape.
However, the semantics of logprob differs.
We illustrate this below.
```
mu = np.array([-1, 1])
sigma = np.array([1, 2])
Sigma = np.diag(sigma)
d2 = dist.MultivariateNormal(mu, Sigma)
print(f'event shape {d2.event_shape}, batch shape {d2.batch_shape}')
nsamples = 3
ys2 = d2.sample(rng_key_, (nsamples,))
print('samples, shape {}'.format(ys2.shape))
print(ys2)
# 2 independent 1d gaussians (same as one 2d diagonal Gaussian)
d3 = dist.Normal(mu, scale=np.sqrt(np.diag(Sigma))) # scalar Gaussian needs std not variance
print(f'event shape {d3.event_shape}, batch shape {d3.batch_shape}')
ys3 = d3.sample(rng_key_, (nsamples,))
print('samples, shape {}'.format(ys3.shape))
print(ys3)
print(np.allclose(ys2, ys3))
y = ys2[0,:] # 2 numbers
print(d2.log_prob(y)) # log prob of a single 2d distribution on 2d input
print(d3.log_prob(y)) # log prob of two 1d distributions on 2d input
```
We can turn a set of independent distributions into a single product
distribution using the [Independent class](http://num.pyro.ai/en/stable/distributions.html#independent)
```
d4 = dist.Independent(d3, 1) # treat the first batch dimension as an event dimensions
# now d4 is just like d2
print(f'event shape {d4.event_shape}, batch shape {d4.batch_shape}')
print(d4.log_prob(y))
```
| true |
code
| 0.696655 | null | null | null | null |
|
## Description:
This script creates Figure S2
```
import numpy as np
import netCDF4 as nc
import datetime as dt
import pandas as pd
from sklearn.cluster import KMeans
#import mpl_toolkits.mplot3d as mpl3d
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import cartopy
import cartopy.crs as ccrs
# for shapefile
from cartopy.io.shapereader import Reader
from cartopy.feature import ShapelyFeature
%matplotlib inline
rootdir = '/raid1/chen423/serdp/archive/GRL2018/'
def get_nc_data(infile, var):
tmpgroup = nc.Dataset(infile, 'r', format='NETCDF4')
outdata = tmpgroup.variables[var][:]
tmpgroup.close()
return outdata
```
#### AR classification
```
def retrieve_ARclass(method):
file_ffeature = rootdir+'data/AR_features/part2/%s.AR_events_feature.1981-2015.nc' % (method)
ARfeature_full = get_nc_data(file_ffeature, 'AR_event_feature')
file_class = rootdir+'data/AR_classification/AR_3class.%s.nc' % (method)
AR_class_index = get_nc_data(file_class, 'ARclass_index')
ARfeature_norm = get_nc_data(file_class, 'ARfeature_norm')
return AR_class_index, ARfeature_full, ARfeature_norm
```
#### misc functions for data processing
```
def tindex_to_monthlyindex(index):
stime = dt.datetime(1981,1,1,0)
time_delta = dt.timedelta(hours=3*index)
etime = stime + time_delta
return (etime.year-1981)*12+etime.month-1 # -1 so it is conssistent with index that starts from 0 in 1981-01
def calc_lag_corraltion(clim_index, indata, lag=0):
outdata = np.zeros(1080)
full_len = clim_index.shape[0]
for i in np.arange(1080):
outdata[i] = np.corrcoef(clim_index[0:(full_len-lag)], indata[lag:(full_len),i])[0,1]
return outdata
```
#### AR statistics
```
def sub_AR_monthly_nevents(cclass, AR_class_index, ARfeature_fulldata):
outdata_counts = np.zeros(420)
for i in np.arange(AR_class_index.shape[0]):
mindex = tindex_to_monthlyindex(ARfeature_fulldata[i,8])
if cclass=='whole':
outdata_counts[mindex] = outdata_counts[mindex] + 1
else:
if AR_class_index[i]==cclass:
outdata_counts[mindex] = outdata_counts[mindex] + 1
outdata_sig = outdata_counts.copy()
outdata_sig[outdata_counts>=1] = 1
return outdata_counts, outdata_sig
def sub_AR_monthly_accum_IntDur(cclass, AR_class_index, ARfeature_fulldata):
# accumulation of Intensity*Duration
outdata = np.zeros(420)
for i in np.arange(AR_class_index.shape[0]):
mindex = tindex_to_monthlyindex(ARfeature_fulldata[i,8])
if cclass=='whole':
outdata[mindex] = outdata[mindex] + ARfeature_fulldata[i,3]*ARfeature_fulldata[i,7]
else:
if AR_class_index[i]==cclass:
outdata[mindex] = outdata[mindex] + ARfeature_fulldata[i,3]*ARfeature_fulldata[i,7]
return outdata
def sub_AR_monthly_accum_IntDurAre(cclass, AR_class_index, ARfeature_fulldata):
# accumulation of Intensity*Duration*Area_land
outdata = np.zeros(420)
for i in np.arange(AR_class_index.shape[0]):
mindex = tindex_to_monthlyindex(ARfeature_fulldata[i,8])
if cclass=='whole':
outdata[mindex] = outdata[mindex] + ARfeature_fulldata[i,3]*ARfeature_fulldata[i,7]*ARfeature_fulldata[i,1]
else:
if AR_class_index[i]==cclass:
outdata[mindex] = outdata[mindex] + ARfeature_fulldata[i,3]*ARfeature_fulldata[i,7]*ARfeature_fulldata[i,1]
return outdata
def sub_AR_monthly_accum_IntDurWid(cclass, AR_class_index, ARfeature_fulldata):
# accumulation of Intensity*Duration*Width_coast
outdata = np.zeros(420)
for i in np.arange(AR_class_index.shape[0]):
mindex = tindex_to_monthlyindex(ARfeature_fulldata[i,8])
if cclass=='whole':
outdata[mindex] = outdata[mindex] + ARfeature_fulldata[i,5]*ARfeature_fulldata[i,7]*ARfeature_fulldata[i,4]
else:
if AR_class_index[i]==cclass:
outdata[mindex] = outdata[mindex] + ARfeature_fulldata[i,5]*ARfeature_fulldata[i,7]*ARfeature_fulldata[i,4]
return outdata
def get_AR_stats(method):
AR_class_index, ARfeature_full, ARfeature_norm = retrieve_ARclass(method)
# on the first index: 0-2 are three AR types. 3 is the whole stats.
AR_monthly_nevents = np.zeros((4,420))
AR_monthly_sig = np.zeros((4,420))
AR_monthly_nevents[3,:], AR_monthly_sig[3,:] = sub_AR_monthly_nevents('whole', AR_class_index, ARfeature_full)
AR_monthly_nevents[0,:], AR_monthly_sig[0,:] = sub_AR_monthly_nevents(0, AR_class_index, ARfeature_full)
AR_monthly_nevents[1,:], AR_monthly_sig[1,:] = sub_AR_monthly_nevents(1, AR_class_index, ARfeature_full)
AR_monthly_nevents[2,:], AR_monthly_sig[2,:] = sub_AR_monthly_nevents(2, AR_class_index, ARfeature_full)
AR_mon_acc_ida = np.zeros((4,420))
AR_mon_acc_ida[3,:] = sub_AR_monthly_accum_IntDurAre('whole', AR_class_index, ARfeature_full)
AR_mon_acc_ida[0,:] = sub_AR_monthly_accum_IntDurAre(0, AR_class_index, ARfeature_full)
AR_mon_acc_ida[1,:] = sub_AR_monthly_accum_IntDurAre(1, AR_class_index, ARfeature_full)
AR_mon_acc_ida[2,:] = sub_AR_monthly_accum_IntDurAre(2, AR_class_index, ARfeature_full)
return AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida
def sub_AR_daily_sig(cclass, AR_class_index, ARfeature_full, totaldays, lag=0):
outdata = np.zeros(totaldays)
for i in np.arange(AR_class_index.shape[0]):
sindex = (dt.timedelta(hours=3*ARfeature_full[i,6])).days
eindex = (dt.timedelta(hours=3*(ARfeature_full[i,6])+ARfeature_full[i,7])).days + lag
if cclass=='whole':
outdata[sindex:(eindex+1)] = np.ones(np.minimum(eindex-sindex+1, totaldays-sindex))
else:
if AR_class_index[i]==cclass:
outdata[sindex:(eindex+1)] = np.ones(np.minimum(eindex-sindex+1, totaldays-sindex))
return outdata
```
##### hydrological data processing
```
def calc_extreme_sum_monthly(dailyinput, pvalue):
print(pvalue)
tindex_daily = pd.date_range('1/1/1981', periods=dailyinput.shape[0])
out_count = np.zeros((420,dailyinput.shape[1]))
for i in np.arange(dailyinput.shape[1]):
tmpdata = dailyinput[:,i].copy()
threshold = np.percentile(tmpdata, pvalue*100)
tmpdata[tmpdata<threshold]='NaN'
tmpdata_tagged = pd.Series(tmpdata, index=tindex_daily)
out_count[:,i] = tmpdata_tagged.resample('M').sum()
return out_count
def calc_extreme_daily_sig(dailyinput, pvalue):
print(pvalue)
out_sig = np.zeros(dailyinput.shape)
for i in np.arange(dailyinput.shape[1]):
tmpdata = dailyinput[:,i].copy()
threshold = np.percentile(tmpdata, pvalue*100)
tmpdata[tmpdata<threshold]=0
tmpdata[tmpdata>=threshold]=1
out_sig[:,i] = tmpdata
return out_sig
def gen_custom_positive_anomaly(indata, approach, pvalue=0.5):
# indata: ()
lens = indata.shape[0]
outdata = np.zeros(indata.shape)
for i in np.arange(indata.shape[1]): # loop over basins
if approach=='mean':
baseline = np.mean(indata[:,i])
elif approach=='percentile':
baseline = np.percentile(indata[:,i], pvalue*100)
outdata[:,i] = indata[:,i]-baseline
outdata[outdata<0] = 0
return outdata
```
#### computation of metrics
```
def compute_mean_correaltions_vlags(ARstats, hydrovar, lags=np.arange(7)):
sbasin = 734
ebasin = 1080
npts = lags.shape[0]
corr_stats = np.zeros((npts,5))
for i in np.arange(npts):
corrdata = calc_lag_corraltion(ARstats, hydrovar, lags[i])
corr_stats[i,0] = np.min(corrdata[sbasin:ebasin])
corr_stats[i,1] = np.percentile(corrdata[sbasin:ebasin], 25)
corr_stats[i,2] = np.mean(corrdata[sbasin:ebasin])
corr_stats[i,3] = np.percentile(corrdata[sbasin:ebasin], 75)
corr_stats[i,4] = np.max(corrdata[sbasin:ebasin])
return corr_stats
def calc_binary_scores(ARdata, hydrodata, metric):
tmpdata = hydrodata+ARdata
yy = (tmpdata==2).sum()
nn = (tmpdata==0).sum()
# yn, ARdata==1, hydrodata==0
tmpdata = ARdata-hydrodata
yn = (tmpdata==1).sum()
ny = (tmpdata==-1).sum()
if metric=='POD':
outvalue = yy/(yy + ny)
elif metric=='FAR':
outvalue = yn/(yy + yn)
elif metric=='Bias':
outvalue = (yy + yn)/(yy + ny)
elif metric=='HSS':
outvalue = 2*(yy*nn-yn*ny)/((yy+ny)*(ny+nn)+(yy+yn)*(yn+nn))
elif metric=='TS':
outvalue = yy/(yy + ny + yn)
elif metric=='GSS':
ets_tmp = (yy + yn)*(yy + ny)/(yy + ny + yn + nn)
outvalue= (yy - ets_tmp)/(yy + ny + yn - ets_tmp)
return outvalue
def wrap_calc_binary_score(AR_daily_sig, dailyhydro, metric):
outdata = np.zeros(dailyhydro.shape[1])
for i in np.arange(dailyhydro.shape[1]):
outdata[i] = calc_binary_scores(AR_daily_sig, dailyhydro[:,i], metric)
return outdata
```
#### plotting
```
def plot_single_range(axes, xdata, ydatas, color, location, title, yrange=[-1,1]):
axes.fill_between(xdata, ydatas[:,0], ydatas[:,4], facecolor=color, alpha=0.2)
axes.fill_between(xdata, ydatas[:,1], ydatas[:,3], facecolor=color, alpha=0.6)
axes.plot(ydatas[:,2], color, linewidth=4, alpha=1)
axes.plot(np.arange(10), np.zeros(10), color='black', linestyle='--')
axes.set_xlim(xrange)
axes.set_ylim(yrange)
# specific to locations
if location=='l':
axes.set_xticks([])
axes.set_ylabel('corr. coeff.', size=12)
elif location=='d':
axes.set_xlabel('lags (month)', size=12)
axes.set_yticks([])
elif location=='ld':
axes.set_xlabel('lags (month)', size=12)
axes.set_ylabel('corr. coeff.', size=12)
elif location=='o':
axes.set_xticks([])
axes.set_yticks([])
elif location=='s':
axes.set_ylabel('corr. coeff.', size=12)
axes.set_xlabel('lag (month)', size=12)
axes.text(xrange[1]/2, 0.8, title, horizontalalignment='center', size=10)
def panel_plot(axes, ARstats, hydrovar, lag):
mapdata = calc_lag_corraltion(ARstats[0], hydrovar, lag)
axes.plot(mapdata, color='royalblue', label='weak AR', zorder=0)
mapdata = calc_lag_corraltion(ARstats[2], hydrovar, lag)
axes.plot(mapdata, color='orange', label='prolonged AR', zorder=2)
mapdata = calc_lag_corraltion(ARstats[1], hydrovar, lag)
axes.plot(mapdata, color='lightseagreen', label='flash AR', zorder=1)
axes.plot(np.arange(1100), np.zeros(1100), 'black', linestyle='--')
axes.set_xlim(xrange)
axes.set_ylim(yrange)
axes.legend(loc='upper center', ncol=2, fontsize=10)
def panel_plot_1class(axes, ARstats, hydrovar, lag):
mapdata = calc_lag_corraltion(ARstats[3], hydrovar, lag)
axes.plot(mapdata, color='black', label='weak AR', alpha=0.8)
axes.plot(np.arange(1100), np.zeros(1100), 'blue', linestyle='--')
axes.set_xlim(xrange)
axes.set_ylim(yrange)
reffile = rootdir+'data/ref_data/HU8_wUS.red005.nc'
HU8_mask = get_nc_data(reffile, 'Band1')
HU8_mask = get_nc_data(reffile, 'Band1')
lat = get_nc_data(reffile, 'lat')
lon = get_nc_data(reffile, 'lon')
hu8_list = np.genfromtxt(rootdir+'data/ref_data/hu8_list')[:,1]
lons, lats = np.meshgrid(lon, lat)
def generate_plot_data_matrix(indata):
plot_data_matrix = np.ones(lons.shape)*9999
for i in np.arange(1080):
hu8id = hu8_list[i]
plot_data_matrix[HU8_mask==hu8id] = indata[i]
plot_data_matrix[plot_data_matrix==9999] = np.nan
return plot_data_matrix
```
#### hydrological data
```
# all the daily data
dailyP_file = rootdir+'data/hydro_data/PRISM/PRISM.HUC8.P.1981-2015.daily.nc'
dailyP = get_nc_data(dailyP_file, 'P')
monthly_p95P_sum = calc_extreme_sum_monthly(dailyP, 0.95)
daily_p95P_sig = calc_extreme_daily_sig(dailyP, 0.95)
```
## plotting
#### fig2. plot relationship between AR and P. So no lag is needed
```
xrange = [734,1080]
lag = 0
yrange = [-0.4,1]
Pdata = monthly_p95P_sum
title = 'corr(AR-IDA, 95% P total)'
fig2 = plt.figure(figsize=(12,8))
method = 'rutz'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
ax1 = plt.subplot(2,3,1)
panel_plot(ax1, AR_mon_acc_ida, Pdata, 0)
#panel_plot_1class(ax1, AR_mon_acc_ida, Pdata, 0)
ax1.plot((954,954), (-2,0.74), '-.', color='black')
ax1.text(800, -0.3, method, horizontalalignment='center', size=12)
ax1.set_title(title, size=12)
ax1.set_ylabel('corr. coeff.', size=12)
ax1.set_xticklabels([])
ax1.set_ylim(yrange)
method = 'gershunov'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
ax2 = plt.subplot(2,3,2)
panel_plot(ax2, AR_mon_acc_ida, Pdata, 0)
#panel_plot_1class(ax2, AR_mon_acc_ida, Pdata, 0)
ax2.plot((954,954), (-2,0.74), '-.', color='black')
ax2.text(800, -0.33, method, horizontalalignment='center', size=12)
ax2.set_title(title, size=12)
ax2.set_xticklabels([])
ax2.set_yticklabels([])
ax2.set_ylim(yrange)
method = 'guan'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
ax3 = plt.subplot(2,3,3)
panel_plot(ax3, AR_mon_acc_ida, Pdata, 0)
#panel_plot_1class(ax3, AR_mon_acc_ida, Pdata, 0)
ax3.plot((954,954), (-2,0.74), '-.', color='black')
ax3.text(800, -0.33, method, horizontalalignment='center', size=12)
ax3.set_title(title, size=12)
ax3.set_xticklabels([])
ax3.set_yticklabels([])
ax3.set_ylim(yrange)
method = 'goldenson'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
ax4 = plt.subplot(2,3,4)
panel_plot(ax4, AR_mon_acc_ida, Pdata, 0)
#panel_plot_1class(ax4, AR_mon_acc_ida, Pdata, 0)
ax4.plot((954,954), (-2,0.74), '-.', color='black')
ax4.text(800, -0.33, method, horizontalalignment='center', size=12)
ax4.set_title(title, size=12)
ax4.set_xticks([846,1017])
ax4.set_xlabel('HUC8 watersheds', size=13)
ax4.set_xticklabels({'PNW','California'})
ax4.set_ylabel('corr. coeff.', size=12)
ax4.set_ylim(yrange)
method = 'pnnl1'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
ax5 = plt.subplot(2,3,5)
panel_plot(ax5, AR_mon_acc_ida, Pdata, 0)
#panel_plot_1class(ax5, AR_mon_acc_ida, Pdata, 0)
ax5.plot((954,954), (-2,0.74), '-.', color='black')
ax5.text(800, -0.33, method, horizontalalignment='center', size=12)
ax5.set_title(title, size=12)
ax5.set_xticks([846,1017])
ax5.set_xlabel('HUC8 watersheds', size=13)
ax5.set_xticklabels({'PNW','California'})
ax5.set_yticklabels([])
ax5.set_ylim(yrange)
method = 'pnnl2'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
ax6 = plt.subplot(2,3,6)
panel_plot(ax6, AR_mon_acc_ida, Pdata, 0)
#panel_plot_1class(ax6, AR_mon_acc_ida, Pdata, 0)
ax6.plot((954,954), (-2,0.74), '-.', color='black')
ax6.text(800, -0.33, method, horizontalalignment='center', size=12)
ax6.set_title(title, size=12)
ax6.set_xticks([846,1017])
ax6.set_xlabel('HUC8 watersheds', size=13)
ax6.set_xticklabels({'PNW','California'})
ax6.set_yticklabels([])
ax6.set_ylim(yrange)
plt.show()
def visualize_wUS_map(axes, indata, location, title='', method='', ylim=[26,55], hu2bdy_flag=False, cmap='Blues', vmin=-0.6, vmax=0.6):
axes.pcolormesh(lons, lats, indata, cmap=cmap, vmin=vmin, vmax=vmax)
axes.set_xlim([-127, -100])
axes.set_ylim(ylim)
axes.add_feature(cartopy.feature.OCEAN, linewidth=0.5, facecolor='aliceblue', edgecolor='k', zorder=0)
axes.add_feature(cartopy.feature.LAND, linewidth=0.5, facecolor='none', edgecolor='k', zorder=1)
if hu2bdy_flag==True:
shpfile = rootdir+'data/ref_data/HUC/HU2_wUS_R07-R18.shp'
shape_feature = ShapelyFeature(Reader(shpfile).geometries(), ccrs.PlateCarree(),
facecolor='none', edgecolor='gray', linewidth=0.5)
axes.add_feature(shape_feature)
countries = cartopy.feature.NaturalEarthFeature(category='cultural', scale='10m', edgecolor='black', linewidth=0.25,\
facecolor='none', name='admin_0_countries')
axes.add_feature(countries, zorder=3)
gl = axes.gridlines(crs=ccrs.PlateCarree(), draw_labels=True, linestyle='-', alpha=1)
gl.xlabels_top = location[0]
gl.xlabels_bottom = location[1]
gl.ylabels_left = location[2]
gl.ylabels_right = location[3]
gl.xlocator = matplotlib.ticker.FixedLocator(np.arange(-180,-59,10))
gl.ylocator = matplotlib.ticker.FixedLocator(np.arange(0,81,5))
gl.xformatter = cartopy.mpl.gridliner.LONGITUDE_FORMATTER
gl.yformatter = cartopy.mpl.gridliner.LATITUDE_FORMATTER
axes.text(-108, 53, method, horizontalalignment='center', size=13, zorder=4)
axes.set_title(title, size=13)
Pdata = monthly_p95P_sum
fig3 = plt.figure(figsize=(12,8))
ax1 = plt.subplot2grid((2,10), (0,0), colspan=3, projection=ccrs.PlateCarree())
ax2 = plt.subplot2grid((2,10), (0,3), colspan=3, projection=ccrs.PlateCarree())
ax3 = plt.subplot2grid((2,10), (0,6), colspan=3, projection=ccrs.PlateCarree())
ax4 = plt.subplot2grid((2,10), (1,0), colspan=3, projection=ccrs.PlateCarree())
ax5 = plt.subplot2grid((2,10), (1,3), colspan=3, projection=ccrs.PlateCarree())
ax6 = plt.subplot2grid((2,10), (1,6), colspan=3, projection=ccrs.PlateCarree())
title = 'corr(AR-IDA, 95% P total)'
method = 'rutz'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
corrdata_raw = calc_lag_corraltion(AR_mon_acc_ida[3], Pdata, 0)
plot_data = generate_plot_data_matrix(corrdata_raw)
visualize_wUS_map(ax1, plot_data, location=[False,False,True,False], title=title, method=method, hu2bdy_flag=True, cmap='bwr_r')
print(method+' done')
method = 'gershunov'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
corrdata_raw = calc_lag_corraltion(AR_mon_acc_ida[3], Pdata, 0)
plot_data = generate_plot_data_matrix(corrdata_raw)
visualize_wUS_map(ax2, plot_data, location=[False,False,False,False], title=title, method=method, hu2bdy_flag=True, cmap='bwr_r')
print(method+' done')
method = 'guan'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
corrdata_raw = calc_lag_corraltion(AR_mon_acc_ida[3], Pdata, 0)
plot_data = generate_plot_data_matrix(corrdata_raw)
visualize_wUS_map(ax3, plot_data, location=[False,False,False,False], title=title, method=method, hu2bdy_flag=True, cmap='bwr_r')
print(method+' done')
method = 'goldenson'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
corrdata_raw = calc_lag_corraltion(AR_mon_acc_ida[3], Pdata, 0)
plot_data = generate_plot_data_matrix(corrdata_raw)
visualize_wUS_map(ax4, plot_data, location=[False,True,True,False], title=title, method=method, hu2bdy_flag=True, cmap='bwr_r')
print(method+' done')
method = 'pnnl1'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
corrdata_raw = calc_lag_corraltion(AR_mon_acc_ida[3], Pdata, 0)
plot_data = generate_plot_data_matrix(corrdata_raw)
visualize_wUS_map(ax5, plot_data, location=[False,True,False,False], title=title, method=method, hu2bdy_flag=True, cmap='bwr_r')
print(method+' done')
method = 'pnnl2'
AR_monthly_nevents, AR_monthly_sig, AR_mon_acc_ida = get_AR_stats(method)
corrdata_raw = calc_lag_corraltion(AR_mon_acc_ida[3], Pdata, 0)
plot_data = generate_plot_data_matrix(corrdata_raw)
visualize_wUS_map(ax6, plot_data, location=[False,True,False,False], title=title, method=method, hu2bdy_flag=True, cmap='bwr_r')
print(method+' done')
cbar_axes = fig3.add_axes([0.86, 0.15, 0.02, 0.7])
cb = matplotlib.colorbar.ColorbarBase(cbar_axes, cmap='bwr_r', ticks=[np.arange(0,1.01,0.25)], orientation='vertical')
cb.set_ticklabels(['-0.6', '-0.3', '0', '0.3', '0.6'])
cbar_axes.tick_params(labelsize=11)
#fig3.savefig(rootdir+'plots/misc05.map.corr.whole.PRISM.png', dpi=600)
plt.show()
plt.close()
del(fig3)
```
#### GSS/HSS plot
to check the possibility of using daily AR to forecast extreme P events
```
def panel_binary_score(axes, method, score, ylabel='', cat='none'):
AR_class_index, ARfeature_full, ARfeature_norm = retrieve_ARclass(method)
if cat=='single':
AR_daily_sig = sub_AR_daily_sig('whole', AR_class_index, ARfeature_full, totaldays, lag=0)
score_p95Pd_AR = wrap_calc_binary_score(AR_daily_sig, daily_p95P_sig, score)
axes.plot(score_p90Pd_AR, color='grey', label='90% P, AR')
axes.plot(score_p95Pd_AR, color='grey', linestyle='--', label='95% P, AR')
else:
AR0_daily_sig = sub_AR_daily_sig(0, AR_class_index, ARfeature_full, totaldays, lag=0)
AR1_daily_sig = sub_AR_daily_sig(1, AR_class_index, ARfeature_full, totaldays, lag=0)
AR2_daily_sig = sub_AR_daily_sig(2, AR_class_index, ARfeature_full, totaldays, lag=0)
score_p95Pd_AR0 = wrap_calc_binary_score(AR0_daily_sig, daily_p95P_sig, score)
score_p95Pd_AR1 = wrap_calc_binary_score(AR1_daily_sig, daily_p95P_sig, score)
score_p95Pd_AR2 = wrap_calc_binary_score(AR2_daily_sig, daily_p95P_sig, score)
axes.plot(score_p95Pd_AR0, color='royalblue', linestyle='--', label='95% P, w.AR')
axes.plot(score_p95Pd_AR1, color='lightseagreen', linestyle='--', label='95% P, f.AR')
axes.plot(score_p95Pd_AR2, color='orange', linestyle='--', label='95% P, p.AR')
axes.plot(np.arange(1080), np.zeros(1080), 'k')
if score=='HSS':
axes.plot((954,954), (-2,0.45), '-.', color='black')
elif score=='GSS':
axes.plot((954,954), (-2,0.25), '-.', color='black')
axes.set_xlim(xrange)
axes.set_ylim(yrange)
axes.legend(loc='upper center', ncol=2, fontsize=9, frameon=False)
axes.set_ylabel(ylabel, size=13)
axes.set_title('%s : %s' % (score, method), size=14)
xrange = [734,1080]
totaldays = dailyP.shape[0]
#score = 'GSS'
#ylabel = 'Gilbert Skill Score (GSS)'
#yrange = [-0.15, 0.35] # GSS
score = 'HSS'
ylabel = 'Heidke Skill Score (HSS)'
yrange = [-0.15,0.6] # HSS
fig4 = plt.figure(figsize=(12,8))
ax1 = plt.subplot2grid((2,3),(0,0))
ax2 = plt.subplot2grid((2,3),(0,1))
ax3 = plt.subplot2grid((2,3),(0,2))
ax4 = plt.subplot2grid((2,3),(1,0))
ax5 = plt.subplot2grid((2,3),(1,1))
ax6 = plt.subplot2grid((2,3),(1,2))
panel_binary_score(ax1, 'rutz', score, ylabel=ylabel, cat='none')
panel_binary_score(ax2, 'gershunov', score, cat='none')
panel_binary_score(ax3, 'guan', score, cat='none')
panel_binary_score(ax4, 'goldenson', score, ylabel=ylabel, cat='none')
panel_binary_score(ax5, 'pnnl1', score, cat='none')
panel_binary_score(ax6, 'pnnl2', score, cat='none')
ax1.set_xticks([])
ax2.set_xticks([])
ax3.set_xticks([])
ax2.set_yticks([])
ax3.set_yticks([])
ax5.set_yticks([])
ax6.set_yticks([])
ax4.set_xticks([846,1017])
ax4.set_xticklabels({'PNW','California'})
ax4.set_xlabel('HUC8 watersheds', size=13)
ax5.set_xticks([846,1017])
ax5.set_xticklabels({'PNW','California'})
ax5.set_xlabel('HUC8 watersheds', size=13)
ax6.set_xticks([846,1017])
ax6.set_xticklabels({'PNW','California'})
ax6.set_xlabel('HUC8 watersheds', size=13)
plt.tight_layout()
plt.show()
```
#### GSS/HSS map
see which regions are more predicable based on AR
```
def crt_MS_norm_colormap(cmapname):
full_info = {'precip3_9segs':['#ffffff', '#b5c9ff', '#7f96ff', '#0063ff', '#00c633', '#96ff00', '#ffff00', '#ffa000', '#ff1900']
}
if cmapname=='demo':
print(full_info.get('demo'))
else:
return matplotlib.colors.ListedColormap(full_info.get(cmapname))
def visualize_wUS_map_full_cus_cbar(axes, indata, location, cmap, norm, title='', method='', ylim=[26,55], hu2bdy_flag=False):
axes.pcolormesh(lons, lats, indata, cmap=cmap, norm=norm)
axes.set_xlim([-127, -100])
axes.set_ylim(ylim)
axes.add_feature(cartopy.feature.OCEAN, linewidth=0.5, facecolor='aliceblue', edgecolor='k', zorder=0)
axes.add_feature(cartopy.feature.LAND, linewidth=0.5, facecolor='none', edgecolor='k', zorder=1)
if hu2bdy_flag==True:
shpfile = rootdir+'data/ref_data/HUC/HU2_wUS_R07-R18.shp'
shape_feature = ShapelyFeature(Reader(shpfile).geometries(), ccrs.PlateCarree(),
facecolor='none', edgecolor='gray', linewidth=0.5)
axes.add_feature(shape_feature)
countries = cartopy.feature.NaturalEarthFeature(category='cultural', scale='10m', edgecolor='black', linewidth=0.25,\
facecolor='none', name='admin_0_countries')
axes.add_feature(countries, zorder=3)
gl = axes.gridlines(crs=ccrs.PlateCarree(), draw_labels=True, linestyle='-', alpha=1)
gl.xlabels_top = location[0]
gl.xlabels_bottom = location[1]
gl.ylabels_left = location[2]
gl.ylabels_right = location[3]
gl.xlocator = matplotlib.ticker.FixedLocator(np.arange(-180,-59,10))
gl.ylocator = matplotlib.ticker.FixedLocator(np.arange(0,81,5))
gl.xformatter = cartopy.mpl.gridliner.LONGITUDE_FORMATTER
gl.yformatter = cartopy.mpl.gridliner.LATITUDE_FORMATTER
axes.text(-108, 53, method, horizontalalignment='center', size=13, zorder=4)
axes.set_title(title, size=13)
totaldays = dailyP.shape[0]
score = 'GSS'
title = 'GSS (AR -> 95% daily P)'
fig5 = plt.figure(figsize=(12,8))
ax1 = plt.subplot2grid((2,10), (0,0), colspan=3, projection=ccrs.PlateCarree())
ax2 = plt.subplot2grid((2,10), (0,3), colspan=3, projection=ccrs.PlateCarree())
ax3 = plt.subplot2grid((2,10), (0,6), colspan=3, projection=ccrs.PlateCarree())
ax4 = plt.subplot2grid((2,10), (1,0), colspan=3, projection=ccrs.PlateCarree())
ax5 = plt.subplot2grid((2,10), (1,3), colspan=3, projection=ccrs.PlateCarree())
ax6 = plt.subplot2grid((2,10), (1,6), colspan=3, projection=ccrs.PlateCarree())
cmap = crt_MS_norm_colormap('precip3_9segs')
norm = matplotlib.colors.Normalize(vmin=-0.025,vmax=0.2)
method = 'rutz'
AR_class_index, ARfeature_full, ARfeature_norm = retrieve_ARclass(method)
AR_daily_sig = sub_AR_daily_sig('whole', AR_class_index, ARfeature_full, totaldays, lag=0)
scoredata = wrap_calc_binary_score(AR_daily_sig, daily_p95P_sig, score)
scoredata[scoredata<0] = -0.01
plot_data = generate_plot_data_matrix(scoredata)
visualize_wUS_map_full_cus_cbar(ax1, plot_data, location=[False,False,True,False], cmap=cmap, norm=norm,
title=title, method=method, hu2bdy_flag=True)
print(method+' done')
method = 'gershunov'
AR_class_index, ARfeature_full, ARfeature_norm = retrieve_ARclass(method)
AR_daily_sig = sub_AR_daily_sig('whole', AR_class_index, ARfeature_full, totaldays, lag=0)
scoredata = wrap_calc_binary_score(AR_daily_sig, daily_p95P_sig, score)
scoredata[scoredata<0] = -0.01
plot_data = generate_plot_data_matrix(scoredata)
visualize_wUS_map_full_cus_cbar(ax2, plot_data, location=[False,False,False,False], cmap=cmap, norm=norm,
title=title, method=method, hu2bdy_flag=True)
print(method+' done')
method = 'guan'
AR_class_index, ARfeature_full, ARfeature_norm = retrieve_ARclass(method)
AR_daily_sig = sub_AR_daily_sig('whole', AR_class_index, ARfeature_full, totaldays, lag=0)
scoredata = wrap_calc_binary_score(AR_daily_sig, daily_p95P_sig, score)
scoredata[scoredata<0] = -0.01
plot_data = generate_plot_data_matrix(scoredata)
visualize_wUS_map_full_cus_cbar(ax3, plot_data, location=[False,False,False,False], cmap=cmap, norm=norm,
title=title, method=method, hu2bdy_flag=True)
print(method+' done')
method = 'goldenson'
AR_class_index, ARfeature_full, ARfeature_norm = retrieve_ARclass(method)
AR_daily_sig = sub_AR_daily_sig('whole', AR_class_index, ARfeature_full, totaldays, lag=0)
scoredata = wrap_calc_binary_score(AR_daily_sig, daily_p95P_sig, score)
scoredata[scoredata<0] = -0.01
plot_data = generate_plot_data_matrix(scoredata)
visualize_wUS_map_full_cus_cbar(ax4, plot_data, location=[False,True,True,False], cmap=cmap, norm=norm,
title=title, method=method, hu2bdy_flag=True)
print(method+' done')
method = 'pnnl1'
AR_class_index, ARfeature_full, ARfeature_norm = retrieve_ARclass(method)
AR_daily_sig = sub_AR_daily_sig('whole', AR_class_index, ARfeature_full, totaldays, lag=0)
scoredata = wrap_calc_binary_score(AR_daily_sig, daily_p95P_sig, score)
scoredata[scoredata<0] = -0.01
plot_data = generate_plot_data_matrix(scoredata)
visualize_wUS_map_full_cus_cbar(ax5, plot_data, location=[False,True,False,False], cmap=cmap, norm=norm,
title=title, method=method, hu2bdy_flag=True)
print(method+' done')
method = 'pnnl2'
AR_class_index, ARfeature_full, ARfeature_norm = retrieve_ARclass(method)
AR_daily_sig = sub_AR_daily_sig('whole', AR_class_index, ARfeature_full, totaldays, lag=0)
scoredata = wrap_calc_binary_score(AR_daily_sig, daily_p95P_sig, score)
scoredata[scoredata<0] = -0.01
plot_data = generate_plot_data_matrix(scoredata)
visualize_wUS_map_full_cus_cbar(ax6, plot_data, location=[False,True,False,False], cmap=cmap, norm=norm,
title=title, method=method, hu2bdy_flag=True)
print(method+' done')
cbar_axes = fig5.add_axes([0.86, 0.15, 0.02, 0.7])
cb = matplotlib.colorbar.ColorbarBase(cbar_axes, cmap=cmap, ticks=[np.arange(0,1.01,1/9)], orientation='vertical')
#cb.set_ticklabels(['<0', '0', '0.05', '0.1', '0.15', '0.2', '0.25', '0.3', '0.35', '0.4'])
cb.set_ticklabels(['<0', '0', '0.025', '0.05', '0.075', '0.1', '0.125', '0.15', '0.175', '0.2'])
cbar_axes.tick_params(labelsize=11)
#fig5.savefig(rootdir+'plots/misc06.map.GSS.whole.PRISM.png', dpi=600)
plt.show()
plt.close()
del(fig5)
```
## verify PRISM and WRF P
```
# all the daily data
dailyP_file = rootdir+'data/hydro_data/PRISM/PRISM.HUC8.P.1981-2015.daily.nc'
dailyP_PRISM = get_nc_data(dailyP_file, 'P')
dailyP_file = rootdir+'data/hydro_data/WRF/NARR_hist.HUC8.P.nc'
dailyP_WRF = get_nc_data(dailyP_file, 'P')
p95P_PRISM = np.percentile(dailyP_PRISM, 95,axis=0)
p95P_WRF = np.percentile(dailyP_WRF, 95, axis=0)
mean_PRISM = np.mean(dailyP_PRISM, axis=0)
mean_WRF = np.mean(dailyP_WRF, axis=0)
fig6 = plt.figure(figsize=(7,3))
ax1 = plt.subplot2grid((10,7), (0,0), rowspan=9,colspan=3)
ax1.scatter(mean_PRISM, mean_WRF, s=0.5)
ax1.plot(np.arange(11), np.arange(11), linewidth=1, linestyle='--', color='black')
ax1.set_xlim([0,10])
ax1.set_ylim([0,10])
ax1.set_xlabel('PRISM P (mm)', size=12)
ax1.set_ylabel('WRF P (mm)', size=12)
ax1.set_title('(a) mean daily P over HUC8', size=12)
ax1.text(1,8.5, r'$R^2=%.2f$' % (np.corrcoef(mean_PRISM, mean_WRF)[0,1]**2), size=14)
ax2 = plt.subplot2grid((10,7), (0,4), rowspan=9, colspan=3)
ax2.scatter(p95P_PRISM, p95P_WRF, s=0.5)
ax2.plot(np.arange(51), np.arange(51), linewidth=1, linestyle='--', color='black')
ax2.set_xlim([0,50])
ax2.set_ylim([0,50])
ax2.set_xlabel('PRISM P (mm)', size=12)
ax2.set_ylabel('WRF P (mm)', size=12)
ax2.set_title('(b) 95% daily P over HUC8', size=12)
ax2.text(5,42, r'$R^2=%.2f$' % (np.corrcoef(p95P_PRISM, p95P_WRF)[0,1]**2), size=14)
#fig6.savefig(rootdir+'plots/figS2.png', dpi=600)
plt.show()
plt.close()
del(fig6)
print(np.corrcoef(mean_PRISM, mean_WRF)[0,1])
print(np.corrcoef(p95P_PRISM, p95P_WRF)[0,1])
```
| true |
code
| 0.215681 | null | null | null | null |
|
```
Copyright 2021 IBM Corporation
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
```
# Logistic Regression on Epsilon Dataset
## Background
This is a synthetic dataset from the [PASCAL Large Scale Learning Challenge](https://www.k4all.org/project/large-scale-learning-challenge/). This challenge is concerned with the scalability and efficiency of existing ML approaches with respect to computational, memory or communication resources, e.g. resulting from a high algorithmic complexity, from the size or dimensionality of the data set, and from the trade-off between distributed resolution and communication costs.
## Source
In this example, we download the dataset from the [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets.php).
## Goal
The goal of this notebook is to illustrate how Snap ML can accelerate training of a logistic regression model on this dataset.
## Code
```
cd ../../
CACHE_DIR='cache-dir'
import numpy as np
import time
from datasets import Epsilon
from sklearn.linear_model import LogisticRegression
from snapml import LogisticRegression as SnapLogisticRegression
from sklearn.metrics import roc_auc_score as score
dataset = Epsilon(cache_dir=CACHE_DIR)
X_train, X_test, y_train, y_test = dataset.get_train_test_split()
print("Number of examples: %d" % (X_train.shape[0]))
print("Number of features: %d" % (X_train.shape[1]))
print("Number of classes: %d" % (len(np.unique(y_train))))
model = LogisticRegression(fit_intercept=False, n_jobs=4)
t0 = time.time()
model.fit(X_train, y_train)
t_fit_sklearn = time.time()-t0
score_sklearn = score(y_test, model.predict_proba(X_test)[:,1])
print("Training time (sklearn): %6.2f seconds" % (t_fit_sklearn))
print("ROC AUC score (sklearn): %.4f" % (score_sklearn))
model = SnapLogisticRegression(fit_intercept=False, n_jobs=4)
t0 = time.time()
model.fit(X_train, y_train)
t_fit_snapml = time.time()-t0
score_snapml = score(y_test, model.predict_proba(X_test)[:,1])
print("Training time (snapml): %6.2f seconds" % (t_fit_snapml))
print("ROC AUC score (snapml): %.4f" % (score_snapml))
speed_up = t_fit_sklearn/t_fit_snapml
score_diff = (score_snapml-score_sklearn)/score_sklearn
print("Speed-up: %.1f x" % (speed_up))
print("Relative diff. in score: %.4f" % (score_diff))
```
## Disclaimer
Performance results always depend on the hardware and software environment.
Information regarding the environment that was used to run this notebook are provided below:
```
import utils
environment = utils.get_environment()
for k,v in environment.items():
print("%15s: %s" % (k, v))
```
## Record Statistics
Finally, we record the enviroment and performance statistics for analysis outside of this standalone notebook.
```
import scrapbook as sb
sb.glue("result", {
'dataset': dataset.name,
'n_examples_train': X_train.shape[0],
'n_examples_test': X_test.shape[0],
'n_features': X_train.shape[1],
'n_classes': len(np.unique(y_train)),
'model': type(model).__name__,
'score': score.__name__,
't_fit_sklearn': t_fit_sklearn,
'score_sklearn': score_sklearn,
't_fit_snapml': t_fit_snapml,
'score_snapml': score_snapml,
'score_diff': score_diff,
'speed_up': speed_up,
**environment,
})
```
| true |
code
| 0.843122 | null | null | null | null |
|
# Trax : Ungraded Lecture Notebook
In this notebook you'll get to know about the Trax framework and learn about some of its basic building blocks.
## Background
### Why Trax and not TensorFlow or PyTorch?
TensorFlow and PyTorch are both extensive frameworks that can do almost anything in deep learning. They offer a lot of flexibility, but that often means verbosity of syntax and extra time to code.
Trax is much more concise. It runs on a TensorFlow backend but allows you to train models with 1 line commands. Trax also runs end to end, allowing you to get data, model and train all with a single terse statements. This means you can focus on learning, instead of spending hours on the idiosyncrasies of big framework implementation.
### Why not Keras then?
Keras is now part of Tensorflow itself from 2.0 onwards. Also, trax is good for implementing new state of the art algorithms like Transformers, Reformers, BERT because it is actively maintained by Google Brain Team for advanced deep learning tasks. It runs smoothly on CPUs,GPUs and TPUs as well with comparatively lesser modifications in code.
### How to Code in Trax
Building models in Trax relies on 2 key concepts:- **layers** and **combinators**.
Trax layers are simple objects that process data and perform computations. They can be chained together into composite layers using Trax combinators, allowing you to build layers and models of any complexity.
### Trax, JAX, TensorFlow and Tensor2Tensor
You already know that Trax uses Tensorflow as a backend, but it also uses the JAX library to speed up computation too. You can view JAX as an enhanced and optimized version of numpy.
**Watch out for assignments which import `import trax.fastmath.numpy as np`. If you see this line, remember that when calling `np` you are really calling Trax’s version of numpy that is compatible with JAX.**
As a result of this, where you used to encounter the type `numpy.ndarray` now you will find the type `jax.interpreters.xla.DeviceArray`.
Tensor2Tensor is another name you might have heard. It started as an end to end solution much like how Trax is designed, but it grew unwieldy and complicated. So you can view Trax as the new improved version that operates much faster and simpler.
### Resources
- Trax source code can be found on Github: [Trax](https://github.com/google/trax)
- JAX library: [JAX](https://jax.readthedocs.io/en/latest/index.html)
## Installing Trax
Trax has dependencies on JAX and some libraries like JAX which are yet to be supported in [Windows](https://github.com/google/jax/blob/1bc5896ee4eab5d7bb4ec6f161d8b2abb30557be/README.md#installation) but work well in Ubuntu and MacOS. We would suggest that if you are working on Windows, try to install Trax on WSL2.
Official maintained documentation - [trax-ml](https://trax-ml.readthedocs.io/en/latest/) not to be confused with this [TraX](https://trax.readthedocs.io/en/latest/index.html)
```
#!pip install trax==1.3.1 Use this version for this notebook
```
## Imports
```
import numpy as np # regular ol' numpy
from trax import layers as tl # core building block
from trax import shapes # data signatures: dimensionality and type
from trax import fastmath # uses jax, offers numpy on steroids
# Trax version 1.3.1 or better
!pip list | grep trax
```
## Layers
Layers are the core building blocks in Trax or as mentioned in the lectures, they are the base classes.
They take inputs, compute functions/custom calculations and return outputs.
You can also inspect layer properties. Let me show you some examples.
### Relu Layer
First I'll show you how to build a relu activation function as a layer. A layer like this is one of the simplest types. Notice there is no object initialization so it works just like a math function.
**Note: Activation functions are also layers in Trax, which might look odd if you have been using other frameworks for a longer time.**
```
# Layers
# Create a relu trax layer
relu = tl.Relu()
# Inspect properties
print("-- Properties --")
print("name :", relu.name)
print("expected inputs :", relu.n_in)
print("promised outputs :", relu.n_out, "\n")
# Inputs
x = np.array([-2, -1, 0, 1, 2])
print("-- Inputs --")
print("x :", x, "\n")
# Outputs
y = relu(x)
print("-- Outputs --")
print("y :", y)
```
### Concatenate Layer
Now I'll show you how to build a layer that takes 2 inputs. Notice the change in the expected inputs property from 1 to 2.
```
# Create a concatenate trax layer
concat = tl.Concatenate()
print("-- Properties --")
print("name :", concat.name)
print("expected inputs :", concat.n_in)
print("promised outputs :", concat.n_out, "\n")
# Inputs
x1 = np.array([-10, -20, -30])
x2 = x1 / -10
print("-- Inputs --")
print("x1 :", x1)
print("x2 :", x2, "\n")
# Outputs
y = concat([x1, x2])
print("-- Outputs --")
print("y :", y)
```
## Layers are Configurable
You can change the default settings of layers. For example, you can change the expected inputs for a concatenate layer from 2 to 3 using the optional parameter `n_items`.
```
# Configure a concatenate layer
concat_3 = tl.Concatenate(n_items=3) # configure the layer's expected inputs
print("-- Properties --")
print("name :", concat_3.name)
print("expected inputs :", concat_3.n_in)
print("promised outputs :", concat_3.n_out, "\n")
# Inputs
x1 = np.array([-10, -20, -30])
x2 = x1 / -10
x3 = x2 * 0.99
print("-- Inputs --")
print("x1 :", x1)
print("x2 :", x2)
print("x3 :", x3, "\n")
# Outputs
y = concat_3([x1, x2, x3])
print("-- Outputs --")
print("y :", y)
```
**Note: At any point,if you want to refer the function help/ look up the [documentation](https://trax-ml.readthedocs.io/en/latest/) or use help function.**
```
#help(tl.Concatenate) #Uncomment this to see the function docstring with explaination
```
## Layers can have Weights
Some layer types include mutable weights and biases that are used in computation and training. Layers of this type require initialization before use.
For example the `LayerNorm` layer calculates normalized data, that is also scaled by weights and biases. During initialization you pass the data shape and data type of the inputs, so the layer can initialize compatible arrays of weights and biases.
```
# Uncomment any of them to see information regarding the function
help(tl.LayerNorm)
# help(shapes.signature)
# Layer initialization
norm = tl.LayerNorm()
# You first must know what the input data will look like
x = np.array([0, 1, 2, 3], dtype="float")
# Use the input data signature to get shape and type for initializing weights and biases
norm.init(shapes.signature(x)) # We need to convert the input datatype from usual tuple to trax ShapeDtype
print("Normal shape:",x.shape, "Data Type:",type(x.shape))
print("Shapes Trax:",shapes.signature(x),"Data Type:",type(shapes.signature(x)))
# Inspect properties
print("-- Properties --")
print("name :", norm.name)
print("expected inputs :", norm.n_in)
print("promised outputs :", norm.n_out)
# Weights and biases
print("weights :", norm.weights[0])
print("biases :", norm.weights[1], "\n")
# Inputs
print("-- Inputs --")
print("x :", x)
# Outputs
y = norm(x)
print("-- Outputs --")
print("y :", y)
```
## Custom Layers
This is where things start getting more interesting!
You can create your own custom layers too and define custom functions for computations by using `tl.Fn`. Let me show you how.
```
help(tl.Fn)
# Define a custom layer
# In this example you will create a layer to calculate the input times 2
def TimesTwo():
layer_name = "TimesTwo" #don't forget to give your custom layer a name to identify
# Custom function for the custom layer
def func(x):
return x * 2
return tl.Fn(layer_name, func)
# Test it
times_two = TimesTwo()
# Inspect properties
print("-- Properties --")
print("name :", times_two.name)
print("expected inputs :", times_two.n_in)
print("promised outputs :", times_two.n_out, "\n")
# Inputs
x = np.array([1, 2, 3])
print("-- Inputs --")
print("x :", x, "\n")
# Outputs
y = times_two(x)
print("-- Outputs --")
print("y :", y)
```
## Combinators
You can combine layers to build more complex layers. Trax provides a set of objects named combinator layers to make this happen. Combinators are themselves layers, so behavior commutes.
### Serial Combinator
This is the most common and easiest to use. For example could build a simple neural network by combining layers into a single layer using the `Serial` combinator. This new layer then acts just like a single layer, so you can inspect intputs, outputs and weights. Or even combine it into another layer! Combinators can then be used as trainable models. _Try adding more layers_
**Note:As you must have guessed, if there is serial combinator, there must be a parallel combinator as well. Do try to explore about combinators and other layers from the trax documentation and look at the repo to understand how these layers are written.**
```
# help(tl.Serial)
# help(tl.Parallel)
# Serial combinator
serial = tl.Serial(
tl.LayerNorm(), # normalize input
tl.Relu(), # convert negative values to zero
times_two, # the custom layer you created above, multiplies the input recieved from above by 2
### START CODE HERE
# tl.Dense(n_units=2), # try adding more layers. eg uncomment these lines
# tl.Dense(n_units=1), # Binary classification, maybe? uncomment at your own peril
# tl.LogSoftmax() # Yes, LogSoftmax is also a layer
### END CODE HERE
)
# Initialization
x = np.array([-2, -1, 0, 1, 2]) #input
serial.init(shapes.signature(x)) #initialising serial instance
print("-- Serial Model --")
print(serial,"\n")
print("-- Properties --")
print("name :", serial.name)
print("sublayers :", serial.sublayers)
print("expected inputs :", serial.n_in)
print("promised outputs :", serial.n_out)
print("weights & biases:", serial.weights, "\n")
# Inputs
print("-- Inputs --")
print("x :", x, "\n")
# Outputs
y = serial(x)
print("-- Outputs --")
print("y :", y)
```
## JAX
Just remember to lookout for which numpy you are using, the regular ol' numpy or Trax's JAX compatible numpy. Both tend to use the alias np so watch those import blocks.
**Note:There are certain things which are still not possible in fastmath.numpy which can be done in numpy so you will see in assignments we will switch between them to get our work done.**
```
# Numpy vs fastmath.numpy have different data types
# Regular ol' numpy
x_numpy = np.array([1, 2, 3])
print("good old numpy : ", type(x_numpy), "\n")
# Fastmath and jax numpy
x_jax = fastmath.numpy.array([1, 2, 3])
print("jax trax numpy : ", type(x_jax))
```
## Summary
Trax is a concise framework, built on TensorFlow, for end to end machine learning. The key building blocks are layers and combinators. This notebook is just a taste, but sets you up with some key inuitions to take forward into the rest of the course and assignments where you will build end to end models.
| true |
code
| 0.44571 | null | null | null | null |
|
PyGSLIB
========
Trans
---------------
The GSLIb equivalent parameter file is
```
Parameters for TRANS
********************
START OF PARAMETERS:
1 \1=continuous, 0=categorical
data/true.dat \file with reference distribution
1 0 \ columns for variable and weight(0=none)
data/cluster.dat \file with original distributions
3 0 \ columns for variable and weight(0=none)
-1.0e21 1.0e21 \trimming limits
trans.out \file for transformed distributions
1 \number of realizations or "sets" to trans
50 50 1 \categorical: nx, ny, nz: size of 3-D model
2 2 0 \ wx, wy, wz: window size for tie-breaking
1000 \continuous: number to transform per "set"
0.0 75.0 \ minimum and maximum values
1 1.0 \ lower tail: option, parameter
1 75.0 \ upper tail: option, parameter
1 \honor local data? (1=yes, 0=no)
data/kt3d.out \ file with estimation variance
2 \ column number
0.5 \ control parameter ( 0.33 < w < 3.0 )
69069 \ random number seed (conditioning cat.)
```
```
#general imports
import matplotlib.pyplot as plt
import pygslib
import numpy as np
import pandas as pd
#make the plots inline
%matplotlib inline
```
Getting the data ready for work
---------
If the data is in GSLIB format you can use the function `gslib.read_gslib_file(filename)` to import the data into a Pandas DataFrame.
```
#get the data in gslib format into a pandas Dataframe
true= pygslib.gslib.read_gslib_file('../data/true.dat')
cluster = pygslib.gslib.read_gslib_file('../data/cluster.dat')
kt3d = pygslib.gslib.read_gslib_file('../data/kt3d.out')
print ('\t\ttrue \n', true.tail())
print ('\n\t\tcluster \n',cluster.tail())
print ('\n\t\tkt3d \n',kt3d.tail())
```
### Some Stats
Here we check we are not incorporating undefined values (see minimum and max) and that we have the same number of rows in the reference distribution (*true.dat*) and in the file with estimation variance (*kt3d.out*)
```
print ('\t\ttrue \n', true.describe())
print ('\n\t\tcluster \n',cluster.describe())
print ('\n\t\tkt3d \n',kt3d.describe())
```
## Testing trans
```
print (pygslib.gslib.__trans.trans.__doc__)
true['Weight'] =1
cluster['NO-Weight']=1
parameters_trans = {
'ivtype' : 1, # 1=continuous, 0=categorical (in this case vo may have nxyza raws?)
'vr' : true['Primary'], # reference distribution (variable )
'wt' : true['Weight'], # reference distribution (weight)
'vo' : cluster['Primary'], # calibration scatterplot (secondary data)
'wo' : cluster['NO-Weight'], # calibration scatterplot (weight data)
'nx' : 50 , #categorical: nx, ny, nz: size of 3-D model
'ny' : 50,
'nz' : 1,
'wx' : 2, # wx, wy, wz: window size for tie-breaking
'wy' : 2,
'wz' : 0,
'nxyza' : 2500, # continuous: number to transform per "set"
'zmin' : 0 , # minimum and maximum values
'zmax' : 75,
'ltpar' : 1, # lower/upper tail: option, parameter
'utpar' : 75,
'ltail' : 1,
'utail' : 1,
'ldata' : 1, # honor local data?
'kv' : kt3d['EstimationVariance'].values,
'ef' : 0.5, # control parameter ( 0.33 < w < 3.0 )
'rseed' : 69069} # random number seed (conditioning cat.)
gmedian,rvr,rcdf,ncut,zval,error = pygslib.gslib.__trans.trans(**parameters_trans)
print ('error ? ', error != 0, error)
```
## Comparing results with gslib
```
print ('gmedian', gmedian)
print ('zval')
print (pd.DataFrame({'transformed variable':zval}).head(6))
print (pd.DataFrame({'transformed variable':zval}).tail(6))
```
**Results in GSLIB **
```
0.04457
0.03996
0.06228
0.07809
0.07216
0.08818
***
18.868
23.231
6.643
4.917
1.598
2.869
```
```
# not in gslib output, not used here because this is continuous
i= np.arange(len(rcdf))+1
print (pd.DataFrame({'i':i, 'rcdf': rcdf, 'rvr': rvr}). head())
print (pd.DataFrame({'i':i, 'rcdf': rcdf, 'rvr': rvr}). tail())
```
**expected results**
By adding this into GSLIB code
```
print *, 'i', 'rcdf(i)', 'rvr(i)'
do i=1,ncut
print *, i, rcdf(i), rvr(i)
end do
```
we get this results
```
1 1.99999995E-04 9.99999978E-03
2 5.99999970E-04 9.99999978E-03
3 9.99999931E-04 9.99999978E-03
4 1.39999995E-03 1.99999996E-02
5 1.79999997E-03 1.99999996E-02
******
2496 0.998214602 43.5000000
2497 0.998614550 46.5299988
2498 0.999014616 54.3899994
2499 0.999414563 58.3199997
2500 0.999814570 102.699997
```
```
parameters_probplt = {
'iwt' : 0, #int, 1 use declustering weight
'va' : true['Primary'], # array('d') with bounds (nd)
'wt' : true['Weight']} # array('d') with bounds (nd), wight variable (obtained with declust?)
binval,cl,xpt025,xlqt,xmed,xuqt,xpt975,xmin,xmax,xcvr,xmen,xvar,error = pygslib.gslib.__plot.probplt(**parameters_probplt)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
plt.plot (cl, binval, label = 'True')
parameters_probplt['va'] = cluster['Primary']
parameters_probplt['wt'] = cluster['NO-Weight']
binval,cl,xpt025,xlqt,xmed,xuqt,xpt975,xmin,xmax,xcvr,xmen,xvar,error = pygslib.gslib.__plot.probplt(**parameters_probplt)
plt.plot (cl, binval, label = 'Cluster not transformed')
parameters_probplt['va'] = zval
parameters_probplt['wt'] = cluster['NO-Weight']
binval,cl,xpt025,xlqt,xmed,xuqt,xpt975,xmin,xmax,xcvr,xmen,xvar,error = pygslib.gslib.__plot.probplt(**parameters_probplt)
plt.plot (cl, binval, label = 'Cluster transformed')
plt.grid(True)
ax.set_xscale('log')
#ax.set_yscale('log')
plt.legend(loc=4)
fig.show
```
| true |
code
| 0.735208 | null | null | null | null |
|
# k-Nearest Neighbors implementation
- Doesn't use any library to perform KNN.
- Uses scikit-learn library for calculating various metrics and confusion matrix.
It is possible to provide file name, k value and training-test data split ratio as arguments such as the following:
python knn.py data/iris.csv 5 0.67
It is tested with the following example data sets:
- [arrhythmia](./data/arrhythmia.csv): missed values replaced by -1 (https://archive.ics.uci.edu/ml/datasets/Arrhythmia)
- [banknote](./data/banknote.csv): nothing changed, converted to CSV (https://archive.ics.uci.edu/ml/datasets/banknote+authentication)
- [forestfires](./data/forestfires.csv): categorical values (mon, day) are converted to numeric values, all values larger than 0 are converted to 1 in burned area column (https://archive.ics.uci.edu/ml/datasets/Forest+Fires)
- [iris](./data/iris.csv): categorical result value are converted to numeric values (https://archive.ics.uci.edu/ml/datasets/Iris)
- [lung-cancer](./data/lung-cancer.csv): moved target values to the last column, missed values replaced by -1 (https://archive.ics.uci.edu/ml/datasets/Lung+Cancer)
- [phishing-websites](./data/phishing-websites.csv): nothing changed, converted to CSV without header (https://archive.ics.uci.edu/ml/datasets/Phishing+Websites)
The main source for the code is the following tutorial: [Develop k-Nearest Neighbors in Python From Scratch](http://machinelearningmastery.com/tutorial-to-implement-k-nearest-neighbors-in-python-from-scratch/)
```
from operator import itemgetter
from utility import display, euclidean, load_dataset, split_dataset
```
## Locate the most similar neighbors
```
def get_neighbors(training, test, k):
distances = {}
for x in range(len(training)):
dist = euclidean(test, training[x])
distances[x] = dist
distances = sorted(distances.items(), key=itemgetter(1))
neighbors = []
for _ in range(k):
neighbors.append(distances.pop()[0])
return neighbors
```
## Make a classification prediction with neighbors
```
def predict(neighbors, target):
class_votes = {}
for x in neighbors:
response = target[x]
if response in class_votes:
class_votes[response] += 1
else:
class_votes[response] = 1
sorted_votes = sorted(class_votes.items(),
key=itemgetter(1), reverse=True)
return sorted_votes[0][0]
```
## Load data
```
dataset, target = load_dataset("data/forestfires.csv")
```
## Split data
```
train_x, train_y, test_x, test_y = split_dataset(dataset, target, 0.8)
print("Training set size: %d" % (len(train_x)))
print("Testing set size: %d" % (len(test_x)))
```
## Predict
```
predictions = []
actual = []
for x in range(len(test_x)):
neighbors = get_neighbors(train_x, test_x[x], 5)
result = predict(neighbors, train_y)
predictions.append(result)
actual.append(test_y[x])
```
## Calculate and display scores
```
display(actual, predictions)
```
| true |
code
| 0.389053 | null | null | null | null |
|
# MOEA tutorial
In the previous assignments, we have been using sampling to investigate the uncertainty space and the lever space. However, we can also use optimization algorithms to search through these spaces. Most often, you would use optimization to search through the lever space in order to find promising policies. However, we can also use optimization to search through the uncertainty space in order to find for example a worst case scenario. In this assignment, we are going through the basics of using the optimization functionality of the workbench.
For optimization, the ema_workbench relies on a library called platypus-opt. *platypus-opt* is python package developed by David Hadka (http://platypus.readthedocs.io/en/latest/) for multi-objective optimization. It allows an explicit specification of the problem components (levers, objectives, constraints). The package includes several multi-objective evolutionary algorithms, therefore the users can choose the algorithm they wish to use.
you can use pip to install it:
```
pip install platypus-opt
```
Start with importing the lake model we have used in previous weeks and connecting it to the workbench. However, we need to make one change: for each outcome of interest we need to specify whether we want to maximize or minimize it, we can use the `kind` kwarg for this. `max_P` should be minimized, while all other outcomes are to be maximized. As a further simplification for this tutorial, we are ignoring the inertia objective. We do this by not setting the `kind` kwarg.
```
from lakemodel_function import lake_problem
from ema_workbench import (Model, RealParameter, ScalarOutcome,
MultiprocessingEvaluator, ema_logging,
Constant)
ema_logging.log_to_stderr(ema_logging.INFO)
#instantiate the model
lake_model = Model('lakeproblem', function=lake_problem)
lake_model.time_horizon = 100 # used to specify the number of timesteps
#specify uncertainties
lake_model.uncertainties = [RealParameter('mean', 0.01, 0.05),
RealParameter('stdev', 0.001, 0.005),
RealParameter('b', 0.1, 0.45),
RealParameter('q', 2.0, 4.5),
RealParameter('delta', 0.93, 0.99)]
# set levers, one for each time step
lake_model.levers = [RealParameter(str(i), 0, 0.1) for i in
range(lake_model.time_horizon)] # we use time_horizon here
#specify outcomes
lake_model.outcomes = [ScalarOutcome('max_P', kind=ScalarOutcome.MINIMIZE),
ScalarOutcome('utility', kind=ScalarOutcome.MAXIMIZE),
ScalarOutcome('inertia'),
ScalarOutcome('reliability', kind=ScalarOutcome.MAXIMIZE)]
lake_model.constantcs = [Constant('alpha', 0.41),
Constant('reps', 150)],
```
Instead of using `perform_experiments`, we will be using `optimize`. There is several kwargs that we need to provide, so let's go through all:
* **algorithm**; We can specify which algorithm we want to use. The default is $\epsilon$-NSGA2, a state of the art many-objective evolutionary algorithm. We can use any of the other algorithms that come with platypus-opt, or the GenerationalBorg algorithm that comes with the workbench. For now, we won't change this.
* **nfe**; the number of function evaluations, this is to be determined by analyzing whether the algorithm has converged
* **searchover**; are we optimizing over the uncertainties or the levers? Most often we will be searching over the levers, so we don't generally need to change this.
* **reference**; If we are searching over levers, what values should we assume for the uncertainties? Reference allows us to specify this. If searchover is set to levers, reference should be a `Scenario` or None, while if searchover is uncertainties, reference should be a `Policy` or None. In case of a None, the default values of the underlying model are unchanged
* **constraints**; see below
* **epsilons**; many state of the art MOEA's rely on a epsilon dominance. Basically, a grid is imposed on the objective space, and per grid cell a single solution is maintained. The granularity of the grid is specified through the epsilon values. Epsilon should be a list or array with a length equal to the number of outcomes. Below, we will see what the impact is of changing epsilon values.
* **convergence**; In order to track whether a MOEA has converged to the optimum solutions, we use convergence metrics. The workbench offers epsilon progress and hypervolume as two often used metrics for this. We will explore these below.
let's start with a simple optimization using 5000 nfe, and the 0.25, 0.1, and 0.1 as epsilon values.
```
with MultiprocessingEvaluator(lake_model) as evaluator:
results = evaluator.optimize(nfe=5000, epsilons=[0.25, 0.1, 0.1])
```
Since we are dealing with 3 outcomes of interest, we can still visualize our results in a 3d scatter plot. Alternatively, we can visualize it using a so-called parallel coordinate plot. In a parallel coordinate plot, the dimensions are visualized side by side. A line connecting the dimensions is a single point in the multidimensional space. For more than 3 dimensions, parallel coordiante plots are prefered over 3d scatter plots with additional visual encodings for the other dimensions. The workbench has support for parallel coordinate plots using `ema_workbench.analysis.parcoords`
```
from mpl_toolkits.mplot3d import Axes3D
outcomes = results.loc[:, ['max_P', 'utility', 'reliability']]
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(outcomes.max_P, outcomes.utility, outcomes.reliability)
ax.set_xlabel('max. P')
ax.set_ylabel('utility')
ax.set_zlabel('reliability')
plt.show()
from ema_workbench.analysis import parcoords
limits = parcoords.get_limits(outcomes)
axes = parcoords.ParallelAxes(limits)
axes.plot(outcomes)
# we invert this axis so direction of desirability is the same
axes.invert_axis('max_P')
plt.show()
```
As you can see, the parcoords figure is easier to interpret once you have learned how to read them. We can see a clear tradeoff between max_P and reliability on the one hand, and utility on the other. This is indicated by the crossing lines in between these respective dimensions.
for the remainder of this tutorial, we will be using a four objective formulation of the problem. We add the intertia objective and we want to maximize it.
```
#specify outcomes
lake_model.outcomes = [ScalarOutcome('max_P', kind=ScalarOutcome.MINIMIZE),
ScalarOutcome('utility', kind=ScalarOutcome.MAXIMIZE),
ScalarOutcome('inertia', kind=ScalarOutcome.MAXIMIZE),
ScalarOutcome('reliability', kind=ScalarOutcome.MAXIMIZE)]
```
## Exploring alternative epsilon values
Let's rerun the optimization, but with different epsilon values. Use \[0.5, 0.5, 0.5, 0.5\]
```
with MultiprocessingEvaluator(lake_model) as evaluator:
results = evaluator.optimize(nfe=5000, epsilons=[0.5, 0.5, 0.5, 0.5])
outcomes = results.loc[:, ['max_P', 'utility', 'reliability', 'inertia']]
limits = parcoords.get_limits(outcomes)
axes = parcoords.ParallelAxes(limits)
axes.plot(outcomes)
# we invert this axis so direction of desirability is the same
axes.invert_axis('max_P')
plt.show()
```
We see that by making our epsilons higher, we are coursening the grid, and thus are reducing the number of solutions we find. Let's test this by making our epsilons smaller. We now expect to find more solutions. Let's use \[0.125, 0.05, 0.05\]
```
with MultiprocessingEvaluator(lake_model) as evaluator:
results = evaluator.optimize(nfe=5000, epsilons=[0.125, 0.05, 0.05, 0.05])
outcomes = results.loc[:, ['max_P', 'utility', 'reliability', 'inertia']]
limits = parcoords.get_limits(outcomes)
axes = parcoords.ParallelAxes(limits)
axes.plot(outcomes)
# we invert this axis so direction of desirability is the same
axes.invert_axis('max_P')
plt.show()
```
And as expected, we now have many more solutions. Selecting appropriate epsilon values is tricky. It depends on case specific concerns (with what granularity do we want to find solutions?), as well as runtime considerations. The lower the epsilon values, the more solutions will be maintained in the Pareto set. Given how MOEA's work, this slows down the optimization.
## Assessing convergence
Next to selecting appropriate epsilon values, a second key issue is assessing convergence. In the foregoing, we have been running the MOEA for 5000 function evaluations. Is this sufficient? Has the algorithm converged? We have no idea. So, how can we add convergence assessment?
There exist a variety of metrics for assessing convergence of MOEAs. The workbench supports epsilong progress and hypervolume. Epsilon progress measures how often a solution in a new gridcel of the epsilon gridded output space is found. Early on, solutions in new grid cells are found quite frequently. Once the algorithm starts to converge, progress becomes more difficult and thus epsilon progress starts to stabilize. Hypervolume is a measure for how much of the objective space is covered by a given set of non-dominated solutions. THe higher the hypervolume, the larger the space is that is covered by the space. Again, hypervolume will grow quickly early on and starts to stabilize once the algorithm is converging. For a more elaborate description, have a look at [this blog](https://waterprogramming.wordpress.com/tag/hypervolume/).
Since hypervolume requires specifying the objective space within which we want to calculate the volume, we need to know this space. Sometimes it is known a priori. For example in the lake problem, reliability is scalled between 0 and 1. In contrast, the bounds on max_P are not known up front. To help with this, we can introduce a constraint saying that max_P must be below a particulare threshold.
```
from ema_workbench.em_framework.optimization import (HyperVolume,
EpsilonProgress)
from ema_workbench import Constraint
#specify outcomes
lake_model.outcomes = [ScalarOutcome('max_P', kind=ScalarOutcome.MINIMIZE,
expected_range=(0,5)),
ScalarOutcome('utility', kind=ScalarOutcome.MAXIMIZE,
expected_range=(0,2)),
ScalarOutcome('inertia', kind=ScalarOutcome.MAXIMIZE,
expected_range=(0,1)),
ScalarOutcome('reliability', kind=ScalarOutcome.MAXIMIZE,
expected_range=(0,1))]
convergence_metrics = [HyperVolume.from_outcomes(lake_model.outcomes),
EpsilonProgress()]
constraints = [Constraint("max pollution", outcome_names="max_P",
function=lambda x:max(0, x-5))]
with MultiprocessingEvaluator(lake_model) as evaluator:
results, convergence = evaluator.optimize(nfe=5000, searchover='levers',
epsilons=[0.125, 0.05, 0.01, 0.01],
convergence=convergence_metrics,
constraints=constraints)
fig, (ax1, ax2) = plt.subplots(ncols=2, sharex=True, figsize=(8,4))
ax1.plot(convergence.nfe, convergence.epsilon_progress)
ax1.set_ylabel('$\epsilon$-progress')
ax2.plot(convergence.nfe, convergence.hypervolume)
ax2.set_ylabel('hypervolume')
ax1.set_xlabel('number of function evaluations')
ax2.set_xlabel('number of function evaluations')
plt.show()
```
If we look at the above plots, we can see that neither hypervolume, nor $\epsilon$-progress has stablized. 5000 function evaluations is clearly not sufficient. Let's go to another extreme: 100.000. What happens in this case?
```
with MultiprocessingEvaluator(lake_model) as evaluator:
results, convergence = evaluator.optimize(nfe=100000, searchover='levers',
epsilons=[0.125, 0.05, 0.01, 0.01],
convergence=convergence_metrics,
constraints=constraints,
x)
fig, (ax1, ax2) = plt.subplots(ncols=2, sharex=True, figsize=(8,4))
ax1.plot(convergence.nfe, convergence.epsilon_progress)
ax1.set_ylabel('$\epsilon$-progress')
ax2.plot(convergence.nfe, convergence.hypervolume)
ax2.set_ylabel('hypervolume')
ax1.set_xlabel('number of function evaluations')
ax2.set_xlabel('number of function evaluations')
plt.show()
```
The runtime of this analysis has been substantial. Still, looking at the convergen graphs, hypervolume has more or less stablized, while $\epsilon$-progress only starts to stablize. This could be an argument for running the algorithm even longer (say 250.000 nfe). Establising the number of NFE is generally a form of trial and error.
# The role of stochasticity
MOEAs use stochastics in crossover and mutation. Thus, the specific set of results will vary from one run of the algorithm to the next. Analogous to how you deal with stochasticitiy in discrete event models, it is best practice to run an MOEA multiple times using a different random seed. Next, you would combine the results from the different runs into a combined pareto approximate set.
```
all_results = []
with MultiprocessingEvaluator(lake_model) as evaluator:
for rep in range(5):
# 5000 runs is clearly way to low, givent he convergence
# analysis above. this is only for demonstration purposes
results = evaluator.optimize(nfe=5000, searchover='levers',
epsilons=[0.125, 0.05, 0.01, 0.01],
constraints=constraints)
all_results.append(results)
limits = pd.DataFrame([[0,0,0,0],[5,2,1,1]], columns=['max_P', 'utility', 'reliability', 'inertia'])
axes = parcoords.ParallelAxes(limits)
for i, (result, color) in enumerate(zip(all_results, sns.color_palette())):
outcomes = result.loc[:, ['max_P', 'utility', 'reliability', 'inertia']]
axes.plot(outcomes, color=color, label='results {}'.format(i))
# we invert this axis so direction of desirability is the same
axes.invert_axis('max_P')
axes.legend()
plt.show()
```
# Using an alternative optimization algorithm
In this exercise, I recommend to use Platypus with the ε-NSGAII algorithm, since it is shown to outperform many MOEA’s. For other algortihms, see the documentation of Platypus. For a comparison of them, you can have a look at [Reed et al (2013)](http://dx.doi.org/10.1016/j.advwatres.2012.01.005).
```
from ema_workbench.em_framework.optimization import GenerationalBorg
with MultiprocessingEvaluator(lake_model) as evaluator:
results, convergence = evaluator.optimize(nfe=50000, searchover='levers',
epsilons=[0.125, 0.05, 0.01, 0.01],
convergence=convergence_metrics,
constraints=constraints,
algorithm=GenerationalBorg,
logging_freq=50)
fig, (ax1, ax2) = plt.subplots(ncols=2, sharex=True, figsize=(8,4))
ax1.plot(convergence.nfe, convergence.epsilon_progress)
ax1.set_ylabel('$\epsilon$-progress')
ax2.plot(convergence.nfe, convergence.hypervolume)
ax2.set_ylabel('hypervolume')
ax1.set_xlabel('number of function evaluations')
ax2.set_xlabel('number of function evaluations')
plt.show()
```
| true |
code
| 0.765095 | null | null | null | null |
|
# Introduction to Overfit and Underfit
### Learning objectives
1. Use the Higgs Dataset.
2. Demonstrate overfitting.
3. Strategies to prevent overfitting.
## Introduction
In this notebook, we'll explore several common regularization techniques, and use them to improve on a classification model.
As always, the code in this example will use the `tf.keras` API, which you can learn more about in the TensorFlow [Keras guide](https://www.tensorflow.org/guide/keras).
In both of the previous examples—[classifying text](https://www.tensorflow.org/tutorials/keras/text_classification_with_hub) and [predicting fuel efficiency](https://www.tensorflow.org/tutorials/keras/regression) — we saw that the accuracy of our model on the validation data would peak after training for a number of epochs, and would then stagnate or start decreasing.
In other words, our model would *overfit* to the training data. Learning how to deal with overfitting is important. Although it's often possible to achieve high accuracy on the *training set*, what we really want is to develop models that generalize well to a *testing set* (or data they haven't seen before).
The opposite of overfitting is *underfitting*. Underfitting occurs when there is still room for improvement on the train data. This can happen for a number of reasons: If the model is not powerful enough, is over-regularized, or has simply not been trained long enough. This means the network has not learned the relevant patterns in the training data.
If you train for too long though, the model will start to overfit and learn patterns from the training data that don't generalize to the test data. We need to strike a balance. Understanding how to train for an appropriate number of epochs as we'll explore below is a useful skill.
To prevent overfitting, the best solution is to use more complete training data. The dataset should cover the full range of inputs that the model is expected to handle. Additional data may only be useful if it covers new and interesting cases.
A model trained on more complete data will naturally generalize better. When that is no longer possible, the next best solution is to use techniques like regularization. These place constraints on the quantity and type of information your model can store. If a network can only afford to memorize a small number of patterns, the optimization process will force it to focus on the most prominent patterns, which have a better chance of generalizing well.
Each learning objective will correspond to a __#TODO__ in the [student lab notebook](../labs/overfit_and_underfit.ipynb) -- try to complete that notebook first before reviewing this solution notebook.
## Setup
Before getting started, import the necessary packages:
```
!pip install tensorflow==2.7.0
```
**NOTE**: Please ignore any incompatibility warnings and errors.
**NOTE**: Restart your kernel to use updated packages.
```
import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras import regularizers
print(tf.__version__)
!pip install git+https://github.com/tensorflow/docs
import tensorflow_docs as tfdocs
import tensorflow_docs.modeling
import tensorflow_docs.plots
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import pathlib
import shutil
import tempfile
logdir = pathlib.Path(tempfile.mkdtemp())/"tensorboard_logs"
shutil.rmtree(logdir, ignore_errors=True)
```
## The Higgs Dataset
The goal of this tutorial is not to do particle physics, so don't dwell on the details of the dataset. It contains 11 000 000 examples, each with 28 features, and a binary class label.
```
# TODO
# Downloads a file from a URL if it not already in the cache
gz = tf.keras.utils.get_file('HIGGS.csv.gz', 'http://mlphysics.ics.uci.edu/data/higgs/HIGGS.csv.gz')
FEATURES = 28
```
The `tf.data.experimental.CsvDataset` class can be used to read csv records directly from a gzip file with no intermediate decompression step.
```
# A Dataset comprising lines from one or more CSV files.
ds = tf.data.experimental.CsvDataset(gz,[float(),]*(FEATURES+1), compression_type="GZIP")
```
That csv reader class returns a list of scalars for each record. The following function repacks that list of scalars into a (feature_vector, label) pair.
```
def pack_row(*row):
label = row[0]
features = tf.stack(row[1:],1)
return features, label
```
TensorFlow is most efficient when operating on large batches of data.
So instead of repacking each row individually make a new `Dataset` that takes batches of 10000-examples, applies the `pack_row` function to each batch, and then splits the batches back up into individual records:
```
packed_ds = ds.batch(10000).map(pack_row).unbatch()
```
Have a look at some of the records from this new `packed_ds`.
The features are not perfectly normalized, but this is sufficient for this tutorial.
```
for features,label in packed_ds.batch(1000).take(1):
print(features[0])
plt.hist(features.numpy().flatten(), bins = 101)
```
To keep this tutorial relatively short use just the first 1000 samples for validation, and the next 10 000 for training:
```
N_VALIDATION = int(1e3)
N_TRAIN = int(1e4)
BUFFER_SIZE = int(1e4)
BATCH_SIZE = 500
STEPS_PER_EPOCH = N_TRAIN//BATCH_SIZE
```
The `Dataset.skip` and `Dataset.take` methods make this easy.
At the same time, use the `Dataset.cache` method to ensure that the loader doesn't need to re-read the data from the file on each epoch:
```
# Creates a Dataset with at most count elements from this dataset.
# Creates a Dataset that skips count elements from this dataset.
validate_ds = packed_ds.take(N_VALIDATION).cache()
train_ds = packed_ds.skip(N_VALIDATION).take(N_TRAIN).cache()
train_ds
```
These datasets return individual examples. Use the `.batch` method to create batches of an appropriate size for training. Before batching also remember to `.shuffle` and `.repeat` the training set.
```
validate_ds = validate_ds.batch(BATCH_SIZE)
train_ds = train_ds.shuffle(BUFFER_SIZE).repeat().batch(BATCH_SIZE)
```
## Demonstrate overfitting
The simplest way to prevent overfitting is to start with a small model: A model with a small number of learnable parameters (which is determined by the number of layers and the number of units per layer). In deep learning, the number of learnable parameters in a model is often referred to as the model's "capacity".
Intuitively, a model with more parameters will have more "memorization capacity" and therefore will be able to easily learn a perfect dictionary-like mapping between training samples and their targets, a mapping without any generalization power, but this would be useless when making predictions on previously unseen data.
Always keep this in mind: deep learning models tend to be good at fitting to the training data, but the real challenge is generalization, not fitting.
On the other hand, if the network has limited memorization resources, it will not be able to learn the mapping as easily. To minimize its loss, it will have to learn compressed representations that have more predictive power. At the same time, if you make your model too small, it will have difficulty fitting to the training data. There is a balance between "too much capacity" and "not enough capacity".
Unfortunately, there is no magical formula to determine the right size or architecture of your model (in terms of the number of layers, or the right size for each layer). You will have to experiment using a series of different architectures.
To find an appropriate model size, it's best to start with relatively few layers and parameters, then begin increasing the size of the layers or adding new layers until you see diminishing returns on the validation loss.
Start with a simple model using only `layers.Dense` as a baseline, then create larger versions, and compare them.
### Training procedure
Many models train better if you gradually reduce the learning rate during training. Use `optimizers.schedules` to reduce the learning rate over time:
```
# TODO
# A LearningRateSchedule that uses an inverse time decay schedule
lr_schedule = tf.keras.optimizers.schedules.InverseTimeDecay(
0.001,
decay_steps=STEPS_PER_EPOCH*1000,
decay_rate=1,
staircase=False)
def get_optimizer():
return tf.keras.optimizers.Adam(lr_schedule)
```
The code above sets a `schedules.InverseTimeDecay` to hyperbolically decrease the learning rate to 1/2 of the base rate at 1000 epochs, 1/3 at 2000 epochs and so on.
```
step = np.linspace(0,100000)
lr = lr_schedule(step)
plt.figure(figsize = (8,6))
plt.plot(step/STEPS_PER_EPOCH, lr)
plt.ylim([0,max(plt.ylim())])
plt.xlabel('Epoch')
_ = plt.ylabel('Learning Rate')
```
Each model in this tutorial will use the same training configuration. So set these up in a reusable way, starting with the list of callbacks.
The training for this tutorial runs for many short epochs. To reduce the logging noise use the `tfdocs.EpochDots` which simply prints a `.` for each epoch, and a full set of metrics every 100 epochs.
Next include `callbacks.EarlyStopping` to avoid long and unnecessary training times. Note that this callback is set to monitor the `val_binary_crossentropy`, not the `val_loss`. This difference will be important later.
Use `callbacks.TensorBoard` to generate TensorBoard logs for the training.
```
def get_callbacks(name):
return [
tfdocs.modeling.EpochDots(),
tf.keras.callbacks.EarlyStopping(monitor='val_binary_crossentropy', patience=200),
tf.keras.callbacks.TensorBoard(logdir/name),
]
```
Similarly each model will use the same `Model.compile` and `Model.fit` settings:
```
def compile_and_fit(model, name, optimizer=None, max_epochs=10000):
if optimizer is None:
optimizer = get_optimizer()
model.compile(optimizer=optimizer,
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[
tf.keras.losses.BinaryCrossentropy(
from_logits=True, name='binary_crossentropy'),
'accuracy'])
model.summary()
history = model.fit(
train_ds,
steps_per_epoch = STEPS_PER_EPOCH,
epochs=max_epochs,
validation_data=validate_ds,
callbacks=get_callbacks(name),
verbose=0)
return history
```
### Tiny model
Start by training a model:
```
# Sequential groups a linear stack of layers into a tf.keras.Model
# TODO
tiny_model = tf.keras.Sequential([
layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
layers.Dense(1)
])
size_histories = {}
size_histories['Tiny'] = compile_and_fit(tiny_model, 'sizes/Tiny')
```
Now check how the model did:
```
plotter = tfdocs.plots.HistoryPlotter(metric = 'binary_crossentropy', smoothing_std=10)
plotter.plot(size_histories)
plt.ylim([0.5, 0.7])
```
### Small model
To see if you can beat the performance of the small model, progressively train some larger models.
Try two hidden layers with 16 units each:
```
small_model = tf.keras.Sequential([
# `input_shape` is only required here so that `.summary` works.
layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
layers.Dense(16, activation='elu'),
layers.Dense(1)
])
size_histories['Small'] = compile_and_fit(small_model, 'sizes/Small')
```
### Medium model
Now try 3 hidden layers with 64 units each:
```
medium_model = tf.keras.Sequential([
layers.Dense(64, activation='elu', input_shape=(FEATURES,)),
layers.Dense(64, activation='elu'),
layers.Dense(64, activation='elu'),
layers.Dense(1)
])
```
And train the model using the same data:
```
size_histories['Medium'] = compile_and_fit(medium_model, "sizes/Medium")
```
### Large model
As an exercise, you can create an even larger model, and see how quickly it begins overfitting. Next, let's add to this benchmark a network that has much more capacity, far more than the problem would warrant:
```
large_model = tf.keras.Sequential([
layers.Dense(512, activation='elu', input_shape=(FEATURES,)),
layers.Dense(512, activation='elu'),
layers.Dense(512, activation='elu'),
layers.Dense(512, activation='elu'),
layers.Dense(1)
])
```
And, again, train the model using the same data:
```
size_histories['large'] = compile_and_fit(large_model, "sizes/large")
```
### Plot the training and validation losses
The solid lines show the training loss, and the dashed lines show the validation loss (remember: a lower validation loss indicates a better model).
While building a larger model gives it more power, if this power is not constrained somehow it can easily overfit to the training set.
In this example, typically, only the `"Tiny"` model manages to avoid overfitting altogether, and each of the larger models overfit the data more quickly. This becomes so severe for the `"large"` model that you need to switch the plot to a log-scale to really see what's happening.
This is apparent if you plot and compare the validation metrics to the training metrics.
* It's normal for there to be a small difference.
* If both metrics are moving in the same direction, everything is fine.
* If the validation metric begins to stagnate while the training metric continues to improve, you are probably close to overfitting.
* If the validation metric is going in the wrong direction, the model is clearly overfitting.
```
plotter.plot(size_histories)
a = plt.xscale('log')
plt.xlim([5, max(plt.xlim())])
plt.ylim([0.5, 0.7])
plt.xlabel("Epochs [Log Scale]")
```
Note: All the above training runs used the `callbacks.EarlyStopping` to end the training once it was clear the model was not making progress.
## Strategies to prevent overfitting
Before getting into the content of this section copy the training logs from the `"Tiny"` model above, to use as a baseline for comparison.
```
shutil.rmtree(logdir/'regularizers/Tiny', ignore_errors=True)
shutil.copytree(logdir/'sizes/Tiny', logdir/'regularizers/Tiny')
regularizer_histories = {}
regularizer_histories['Tiny'] = size_histories['Tiny']
```
### Add weight regularization
You may be familiar with Occam's Razor principle: given two explanations for something, the explanation most likely to be correct is the "simplest" one, the one that makes the least amount of assumptions. This also applies to the models learned by neural networks: given some training data and a network architecture, there are multiple sets of weights values (multiple models) that could explain the data, and simpler models are less likely to overfit than complex ones.
A "simple model" in this context is a model where the distribution of parameter values has less entropy (or a model with fewer parameters altogether, as we saw in the section above). Thus a common way to mitigate overfitting is to put constraints on the complexity of a network by forcing its weights only to take small values, which makes the distribution of weight values more "regular". This is called "weight regularization", and it is done by adding to the loss function of the network a cost associated with having large weights. This cost comes in two flavors:
* [L1 regularization](https://developers.google.com/machine-learning/glossary/#L1_regularization), where the cost added is proportional to the absolute value of the weights coefficients (i.e. to what is called the "L1 norm" of the weights).
* [L2 regularization](https://developers.google.com/machine-learning/glossary/#L2_regularization), where the cost added is proportional to the square of the value of the weights coefficients (i.e. to what is called the squared "L2 norm" of the weights). L2 regularization is also called weight decay in the context of neural networks. Don't let the different name confuse you: weight decay is mathematically the exact same as L2 regularization.
L1 regularization pushes weights towards exactly zero encouraging a sparse model. L2 regularization will penalize the weights parameters without making them sparse since the penalty goes to zero for small weights-one reason why L2 is more common.
In `tf.keras`, weight regularization is added by passing weight regularizer instances to layers as keyword arguments. Let's add L2 weight regularization now.
```
l2_model = tf.keras.Sequential([
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001),
input_shape=(FEATURES,)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(1)
])
regularizer_histories['l2'] = compile_and_fit(l2_model, "regularizers/l2")
```
`l2(0.001)` means that every coefficient in the weight matrix of the layer will add `0.001 * weight_coefficient_value**2` to the total **loss** of the network.
That is why we're monitoring the `binary_crossentropy` directly. Because it doesn't have this regularization component mixed in.
So, that same `"Large"` model with an `L2` regularization penalty performs much better:
```
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
```
As you can see, the `"L2"` regularized model is now much more competitive with the the `"Tiny"` model. This `"L2"` model is also much more resistant to overfitting than the `"Large"` model it was based on despite having the same number of parameters.
#### More info
There are two important things to note about this sort of regularization.
**First:** if you are writing your own training loop, then you need to be sure to ask the model for its regularization losses.
```
result = l2_model(features)
regularization_loss=tf.add_n(l2_model.losses)
```
**Second:** This implementation works by adding the weight penalties to the model's loss, and then applying a standard optimization procedure after that.
There is a second approach that instead only runs the optimizer on the raw loss, and then while applying the calculated step the optimizer also applies some weight decay. This "Decoupled Weight Decay" is seen in optimizers like `optimizers.FTRL` and `optimizers.AdamW`.
### Add dropout
Dropout is one of the most effective and most commonly used regularization techniques for neural networks, developed by Hinton and his students at the University of Toronto.
The intuitive explanation for dropout is that because individual nodes in the network cannot rely on the output of the others, each node must output features that are useful on their own.
Dropout, applied to a layer, consists of randomly "dropping out" (i.e. set to zero) a number of output features of the layer during training. Let's say a given layer would normally have returned a vector [0.2, 0.5, 1.3, 0.8, 1.1] for a given input sample during training; after applying dropout, this vector will have a few zero entries distributed at random, e.g. [0, 0.5,
1.3, 0, 1.1].
The "dropout rate" is the fraction of the features that are being zeroed-out; it is usually set between 0.2 and 0.5. At test time, no units are dropped out, and instead the layer's output values are scaled down by a factor equal to the dropout rate, so as to balance for the fact that more units are active than at training time.
In `tf.keras` you can introduce dropout in a network via the Dropout layer, which gets applied to the output of layer right before.
Let's add two Dropout layers in our network to see how well they do at reducing overfitting:
```
dropout_model = tf.keras.Sequential([
layers.Dense(512, activation='elu', input_shape=(FEATURES,)),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(1)
])
regularizer_histories['dropout'] = compile_and_fit(dropout_model, "regularizers/dropout")
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
```
It's clear from this plot that both of these regularization approaches improve the behavior of the `"Large"` model. But this still doesn't beat even the `"Tiny"` baseline.
Next try them both, together, and see if that does better.
### Combined L2 + dropout
```
combined_model = tf.keras.Sequential([
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu', input_shape=(FEATURES,)),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(1)
])
regularizer_histories['combined'] = compile_and_fit(combined_model, "regularizers/combined")
# TODO
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
```
This model with the `"Combined"` regularization is obviously the best one so far.
| true |
code
| 0.720626 | null | null | null | null |
|
## Keras rl-neural network models
# 1. Model
## Different models built on keras
```
# 1.1 Model
## DESCRIPTION : 6 layered Neural Network with dropout
from keras.models import Sequential
from keras.layers import Dense, Dropout
def create_model_1():
model = Sequential()
model.add(Dense(128, input_shape=(4,), activation='relu')) #Layer1 : 128 cells with relu activation function
model.add(Dropout(0.6))
model.add(Dense(256, activation="relu")) #Layer2 : 256 cells with relu activation function
model.add(Dropout(0.6))
model.add(Dense(512, activation="relu")) #Layer3 : 512 cells with relu activation function
model.add(Dropout(0.6))
model.add(Dense(256, activation="relu")) #Layer4 : 256 cells with relu activation function
model.add(Dropout(0.6))
model.add(Dense(128, activation="relu")) #Layer5 : 128 cells with relu activation function
model.add(Dropout(0.6))
model.add(Dense(2, activation="softmax")) #Layer5 : softmax last layer transformation
model.compile( #Layer6 : configure the learning process
loss="categorical_crossentropy",
optimizer="adam",
metrics=["accuracy"])
print(model.summary())
return model
# 1.2 Model
## DESCRIPTION : dqn_atari
from keras.models import Sequential
from keras.layers import Dense, Activation, Flatten, Convolution2D, Permute
def create_model_atari():
model_atari = Sequential()
model_atari.add(Convolution2D(32, 8, 8, subsample=(4, 4))) #Layer1 : convolutional layer 32 batch_size shape (8,8)
model_atari.add(Activation('relu'))
model_atari.add(Convolution2D(64, 4, 4, subsample=(2, 2)))
model_atari.add(Activation('relu'))
model_atari.add(Convolution2D(64, 3, 3, subsample=(1,1)))
model_atari.add(Activation('relu'))
model_atari.add(Flatten())
model_atari.add(Dense(512))
model_atari.add(Dense(nb_actions))
model_atari.add(Activation('linear'))
model.compile( #Layer6 : configure the learning process
loss="categorical_crossentropy",
optimizer="adam",
metrics=["accuracy"])
return model
```
# 2. Policies
## Different policies implemented for keras
#### LinearAnnealedPolicy . kudos to matthiasplappert
Wraps another policy and decreases a given parameter linearly.
(This policy can be used together within EpsGreedyQPolicy to transform eps-value from 1 to 0.1 )
#### EpsGreedyQPolicy
Epsilon greedy policy is a way of selecting random actions with uniform distributions
from a set of available actions. Using this policy either we can select random action
with epsilon probability and we can select an action with 1-epsilon prob that gives maximum
reward in a given state.
As parameters we will select
--epsilon (eps-val) : probability of an event should occur : from 0 to 1 ( makes an exploration-explotation that depends on this metric)
#### GreedyQPolicy
Epsilon greedy policy with epsilon value == 1
#### BolztmanQPolicy
Parameters
--epsilon :
#### MaxBoltzmanQPOlicy https://pure.uva.nl/ws/files/3153478/8461_UBA003000033.pdf
A combination of the eps-greedy and Boltzman q-policy.
#### BolztmannGumbelQPolicy https://arxiv.org/pdf/1705.10257.pdf
BGE is invariant with respect to the mean of the rewards but not their
variance. The parameter C, which defaults to 1, can be used to correct for
this, and should be set to the least upper bound on the standard deviation
of the rewards.
BGE is only available for training, not testing. For testing purposes, you
can achieve approximately the same result as BGE after training for N steps
on K actions with parameter C by using the BoltzmannQPolicy and setting
tau = C/sqrt(N/K).
| true |
code
| 0.733983 | null | null | null | null |
|
# Travel.State.Gov Visa Issuances
**Data Source:** [Monthly Immigrant Visa Issuance Statistics](https://travel.state.gov/content/travel/en/legal/visa-law0/visa-statistics/immigrant-visa-statistics/monthly-immigrant-visa-issuances.html) <br>
**Download the Output:** [here](../data/extracted_data/state-dept)
## Overview
This notebook provides functionality to "scrape" or extract all data from the PDF files found on the State Department Monthly Immigrant Visa Issuance Statistics page. The State Department releases monthly data on visa issuances, for both immigrant visas and non-immigrant visas.
The PDFs come in two forms.
* Posts --> Provides the counts of visas by post and class.
* FSC (Foreign State of Chargeability, or Place of Birth)--> Provides the counts of visas granted by FSC and by visa class.
<img src="../misc/images/monthly_visa_stats_pdf.png" width=500/>
In this notebook we will download these PDFs, extract structure data from the PDF and then create different data exports.
## Technical Approach
Using Python we will programattically download the PDFs, extract the information from them using [tabula](https://github.com/chezou/tabula-py) and finally we will combine the data sources to create a more comprehensive dataset.
## Skills Learned
1. How to download all PDF files to a local directory
2. How to extract structured data from all PDFs and recode the visa types to narrower categories.
3. How possibly summarize this data.
## The Code
**PLEASE NOTE**: We have made this notebook READ only to ensure you receive all updates we make to it. Do not edit this notebook directly, create a copy instead.
To customize and experiment with this notebook:
1. Create a copy: `Select File -> Make a Copy` at the top-left of the notebook
2. Unlock cells in your copy: Press `CMD + A` on your keyboard to select all cells, then click the small unlocked padlock button near the mid-top right of the notebook.
```
import logging
import logging.config
from pathlib import Path
import requests
from bs4 import BeautifulSoup
import pandas as pd
from PyPDF2 import PdfFileReader
import tabula
import time
from urllib.parse import urljoin, urlparse
pd.set_option("max_rows", 400)
today_date = time.strftime("%Y-%m-%d")
```
## 1. Download PDFs
**Functions**
```
def download_pdf(url: str, name: str, output_directory: str):
"""
Function to download a single PDF file from a provided link.
Parameters:
url: URL of the file you want to download
name: Label you want to apply to the file
output_folder: Folder path to save file
Returns:
Saves the file to the output directory, function itself returns nothing.
Example:
download_pdf(
'https://travel.state.gov/content/travel/en/legal/visa-law0/visa-statistics/immigrant-visa-statistics/monthly-immigrant-visa-issuances.html',
'July 2020 - IV Issuances by Post and Visa Class',
'state-dept/'
)
"""
output_directory = Path(output_directory)
response = requests.get(url)
if response.status_code == 200:
# Write content in pdf file
outpath = output_directory / f"{name}.pdf"
pdf = open(str(outpath), "wb")
pdf.write(response.content)
pdf.close()
print("File ", f"{name}.pdf", " downloaded")
else:
print("File ", f"{name}.pdf", " not found.")
def download_all_pdf_links(url: str, output_directory: str):
"""
Download all PDFs on a webpage where the PDFs
are presented as links. Uses the download_pdf function
defined above.
Parameters:
url (str): URL for website with links to many PDF documents, each PDF link
must be a direct download URL and not a URL to another website with PDF links.
output_directory: Folder path to savae file
Returns:
None, but saves many files to the output directory.
Examples:
download_all_pdf_links(
https://travel.state.gov/content/travel/en/legal/visa-law0/visa-statistics/immigrant-visa-statistics/monthly-immigrant-visa-issuances.html,
'state-dept')
"""
output_directory = Path(output_directory)
output_directory.mkdir(exist_ok=True, parents=True)
parse_url = urlparse(url)
base_url = f"{parse_url.scheme}://{parse_url.netloc}"
# Request URL and get response object
response = requests.get(url)
# Parse text obtained
soup = BeautifulSoup(response.text, "html.parser")
# Find all hyperlinks present on webpage
links = soup.find_all("a")
# Iterate through links we found,
# if it's a PDF link, download the PDF and save in output_directory
for link in links:
if ".pdf" in link.get("href", []):
name = link.text
url = f"{base_url}/{link.get('href')}"
download_pdf(url, name, output_directory)
print("All PDF files downloaded")
```
### Download Single Example File
Here we have the url for a single pdf and then pass that url (`example_pdf`) to the `download_pdf` function.
```
# July 2020 Post file https://travel.state.gov/content/dam/visas/Statistics/Immigrant-Statistics/MonthlyIVIssuances/JULY%202020%20-%20IV%20Issuances%20by%20Post%20and%20Visa%20Class.pdf
example_pdf = (
"https://travel.state.gov/content/dam/visas/Statistics/"
"Immigrant-Statistics/MonthlyIVIssuances/"
"JULY%202021%20-%20IV%20Issuances%20by%20Post%20and%20Visa%20Class.pdf"
)
download_pdf(
example_pdf,
"July 2020 - IV Issuances by Post and Visa Class",
"../data/raw_source_files/state-dept/",
)
```
### Download all files
Now let's download all PDFs on the State Department Visa Statistics page. We will pass the base url for that page to the `download_all_pdf_links` function, and then save them out to our `"../data/raw_source_files/state-dept"` folder.
```
url = "https://travel.state.gov/content/travel/en/legal/visa-law0/visa-statistics/immigrant-visa-statistics/monthly-immigrant-visa-issuances.html"
download_all_pdf_links(url, "../data/raw_source_files/state-dept")
```
----------------
## 2. Extract Data from PDFs
To extract structured data (in tabular format) from the PDFs we use a python package called [tabula-py](https://tabula-py.readthedocs.io/en/latest/). This package is a wrapper for a library written in the Java programming language called Tabula. It provides functionality to extract data from pdfs. We also use another python library called PdfFileReader to count the number of pages we need to process.
```
# Note below function not generalizable as has hard coded column names
def get_table_data(path: str, data_cols: list = ["Post", "Visa Class", "Issuances"]):
"""
Parameters:
path: path to specific PDF file to extract data from
data_cols: what the output data columns should be.
if processing the Post tables it is most likely:
["Post", "Visa Class", "Issuances"],
if processing the FSC tables it is most likley
["FSC", "Visa Class", "Issuances"]
Returns:
Pandas dataframe of structured (tabular) data extracted from the PDF
path provided.
Example:
get_table_data(
'data-repo-mvp/state-dept/April 2018 - IV Issuances by FSC or Place of Birth and Visa Class.pdf',
data_cols = ["FSC", "Visa Class", "Issuances"]
)
"""
# Read the PDF to get basic info on it
pdf = PdfFileReader(path)
# Data Holders
full_table = pd.DataFrame(columns=data_cols) # Will hold the combined data
# Processing PDF - we start with the first page (start)
# and go to the last page (stop)
start = 1
stop = pdf.getNumPages() + 1
for i in range(start, stop):
# Extract data from the specific PDF page using Tabula
df = tabula.read_pdf(
path,
pages=f"{i}",
lattice=True,
pandas_options={
"header": None
}, # none because some have headers and some dont
)[0]
# Edge case error correction - sometimes fully null extra columns
# are produced by Tabula
if df.shape[1] > 3:
full_null = df.isnull().all()
full_null_index = full_null[full_null].index[0]
if full_null_index:
df = df.drop(full_null_index, axis=1)
else:
print(f"ERROR on portion of table: {path}")
df.columns = data_cols
# Check if we have headers, if so drop 2 top rows
if not str(df.iloc[1][data_cols][2]).replace(",", "").isdigit():
df = df.loc[2:, :]
# Append this page of data to the full table
full_table = full_table.append(df)
# Clean up and validate the full table
# We validate by comparing the grand total column in the PDF
# to the sum of visas in the extracted table
full_table = full_table.reset_index(drop=True)
grand_total = full_table[
full_table[data_cols[0]].str.upper().str.contains("GRAND TOTAL")
]
full_table = full_table.drop(grand_total.index, axis=0)
full_table.loc[:, "Issuances"] = (
full_table.Issuances.astype(str).str.replace(",", "").astype(int)
)
table_grand_total = full_table.Issuances.sum()
row_grand_total = int(grand_total.Issuances.sum().replace(",", ""))
assert (
table_grand_total == row_grand_total
), f"Warning - Grand Total Row Does Not Equal Sum of Rows {row_grand_total} vs {table_grand_total}"
print("Data successfully extracted.")
return full_table
def extract_data_for_specific_year_month(
pdf_folder_path: str, year: int, month: str, report: str
):
"""
Helper function that allows you to extract data from a SINGLE PDF by passing
a folder path where PDF files are located and then retrieve a specific PDF based on a
year, named month (for example April or May) and report type of either fsc or post being present in the
PDF file name.
Parameters:
pdf_folder: path to folder holding PDFs
year: year of data to extract
month: month of data to extract
report: (options) --> posts | fsc
Returns:
Pandas dataframe of structured (tabular) data extracted from the PDF
path provided.
Example:
extract_data_for_specific_year_month('state-dept', 2019, 'August', 'fsc')
"""
pdf_folder = Path(pdf_folder_path)
report = report.lower()
target_filepath = None
data_cols = (
["Post", "Visa Class", "Issuances"]
if report == "post"
else ["FSC", "Visa Class", "Issuances"]
)
for file in pdf_folder.iterdir():
fn = file.name.lower()
if str(year).lower() in fn and str(month).lower() in fn and report in fn:
target_filepath = file
break
if target_filepath and target_filepath.exists():
return get_table_data(str(target_filepath), data_cols=data_cols)
def extract_data_from_many_pdfs(pdf_folder_path, start_year, stop_year, report):
"""
Helper function that allows you to extract data from MANY PDFs of a single
report type (FSC, POST) by passing a folder path where PDF files are located
and then retrieve data on all PDFs within a time range (start year to stop year)
and the report type
Parameters:
pdf_folder (str): path to folder holding PDFs
start_year (int | str): start year of data to extract
stop_year (int | str): stop year of data to extract
report (str): (options) --> posts | fsc
Returns:
Pandas dataframe of structured (tabular) data extracted from the PDF
path provided.
Example:
extract_data_for_specific_year_month('state-dept', 2019, 'August', 'fsc')
"""
months = [
"January",
"February",
"March",
"April",
"May",
"June",
"July",
"August",
"September",
"October",
"November",
"December",
]
visa_raw_data = []
for year in range(start_year, stop_year + 1):
for month in months:
data = extract_data_for_specific_year_month(
pdf_folder_path, year, month, report
)
if data is not None:
data["source"] = f"{year}-{month}"
visa_raw_data.append(data)
print(year, month, "- Processed")
else:
print(year, month, "- Not Available")
out_df = pd.concat(visa_raw_data, axis=0).reset_index(drop=True)
out_df["year_month"] = pd.to_datetime(out_df.source)
return out_df
```
### Extract data for years
Below we assign our paths to variables instead of writing them out in the function call, this is just to make the code more readable. We also apply Path(../path) to the paths as this provides some functionality for handling paths/folders etc.
```
downloaded_data_path = Path("../data/raw_source_files/state-dept/")
extracted_data_path = Path("../data/extracted_data/state-dept")
```
Below we call a function that was written a few cells above. This function leverages some additional functions to process each pdf and pull out the table data, then combine them together.
We will first extract all the data from the PDFs from 2019-2021, for the "Post and Visa Class" PDFs.
### Getting Posts
**Note this may take about 20 minutes to run**
Also, if processing 2017 -> 2021, then it may take even longer.
```
posts_data_2019_2021 = extract_data_from_many_pdfs(
downloaded_data_path, 2021, 2021, "post" # start year # end year # pdf type
)
```
**Now let's take a look at the data output**
We end up with a large table that has every row (Post, Visa class, issuances) from the pdfs aggregated together. We have also tagged each row with source data indicating the year and month of the data. We also have created a date field of that source info called `year_month` we can use to summarize data
```
posts_data_2019_2021.head()
```
### Getting FSC
**Note this may take about 20 minutes to run**
```
fsc_data_2019_2021 = extract_data_from_many_pdfs(
downloaded_data_path, 2021, 2021, "fsc"
)
```
**Now take a look at the output data**
This looks very much like the post data above, but instead of having a customs post as the first column we have the foriegn state of chargeability.
```
fsc_data_2019_2021.head()
```
### Export this data to csv
We can now call `to_csv` on each file to save it out.
```
posts_data_2019_2021.to_csv(extracted_data_path / f"raw_posts_extract-{today_date}.csv")
fsc_data_2019_2021.to_csv(extracted_data_path / f"raw_fsc_extract-{today_date}.csv")
```
------------
## 3. Analyze / Summarize Data
Now that we have this data in a structured format we will provide some examples of reformatting and summarizing this data to make it more useful
### Example 1: Get total visas by visa class per month for the Post data
```
summed_by_yearmonth_and_class_post = (
posts_data_2019_2021.groupby(["year_month", "Visa Class"]).sum().reset_index()
)
summed_by_yearmonth_and_class_post.pivot(
index="Visa Class", columns="year_month", values="Issuances"
).fillna(0)
```
### Example 2: Get total visas by visa class per month for the FSC data
```
summed_by_yearmonth_and_class_fsc = (
fsc_data_2019_2021.groupby(["year_month", "Visa Class"]).sum().reset_index()
)
summed_by_yearmonth_and_class_fsc.pivot(
index="Visa Class", columns="year_month", values="Issuances"
).fillna(0)
```
### Example 2: Get total visas by visa class per month with simplified coding
The state department uses many different visa class codes. From talking to experts in the field we understand that often codes change, new ones are added and olds ones are removed. That said, many of theses codes can be combined to summarized general families of visas which is helpful for analysis.
Below we have created and initial recoding of visas into a smaller number of classes. We are using a Python dictionary to recode different classes.
An example of the recoding is:
```
"IR": {
"1a": ["IR1", "CR1", "IB1", "IW1", "VI5", "IW"],
"1b": ["IR2", "CR2", "IB2", "IB3", "IW2"],
"1c": ["IR5"],
"1d": ["IR3", "IR4", "IH3", "IH4"],
},
```
Here we are saying that `["IR1", "CR1", "IB1", "IW1", "VI5", "IW"]` can all be recoded to a higher class of `1a` or an even higher level of `IR`.
We created this recode dictionary with some help from experts in the field but may have made mistakes or assumptions, therefore recognize that this recode is for example only.
```
recodes = {
"IR": {
"1a": ["IR1", "CR1", "IB1", "IW1", "VI5", "IW"],
"1b": ["IR2", "CR2", "IB2", "IB3", "IW2"],
"1c": ["IR5"],
"1d": ["IR3", "IR4", "IH3", "IH4"],
},
"FSP": {
"2a": ["F11", "F12", "B11", "B12", "F1"],
"2b": [
"F21",
"F22",
"F23",
"F24",
"F25",
"C21",
"C22",
"C23",
"C24",
"C25",
"B21",
"B22",
"B23",
"B24",
"B25",
"FX",
"FX1",
"FX2",
"FX3",
"CX",
"CX1",
"CX2",
"CX3",
"BX1",
"BX2",
"BX3",
],
"2c": ["F31", "F32", "F33", "C31", "C32", "C33", "B31", "B32", "B33", "F3"],
"2d": ["F41", "F42", "F43", "F4"],
},
"EB": {
"3a": ["E11", "E12", "E13", "E14", "E15", "E1"],
"3b": ["E21", "E22", "E23", "E2"],
"3c": ["E31", "E32", "E34", "E35", "EW3", "EW4", "EW5", "E3", "EW"],
"3d": [
"BC1",
"BC2",
"BC3",
"SD1",
"SD2",
"SD3",
"SE1",
"SE2",
"SE3",
"SF1",
"SF2",
"SG1",
"SG2",
"SH1",
"SH2",
"SJ1",
"SJ2",
"SK1",
"SK2",
"SK3",
"SK4",
"SL1",
"SN1",
"SN2",
"SN3",
"SN4",
"SR1",
"SR2",
"SR3",
"BC",
"E4",
"SD",
"SE",
"SF",
"SG",
"SH",
"SJ",
"SK",
"SN",
"SR",
],
"3e": [
"C51",
"C52",
"C53",
"T51",
"T52",
"T53",
"R51",
"R52",
"R53",
"I51",
"I52",
"I53",
"C5",
"T5",
"R5",
"I5",
],
},
"DI": ["DV1", "DV2", "DV3", "DV"],
"Other": [
"AM",
"AM1",
"AM2",
"AM3",
"SC2",
"SI1",
"SI2",
"SI3",
"SM1",
"SM2",
"SM3",
"SQ1",
"SQ2",
"SQ3",
"SU2",
"SU3",
"SU5",
"SB1",
"SC",
"SI",
"SM",
"SQ",
"SU",
],
}
```
**Create a coding lookup based on the `recode` dictonary above**
Now let's use some code to unpack these different recodings into a table format
```
unpack_codes = []
# iterate over the keys in the recode dictionary
for k in recodes:
next_level = recodes[k]
# if the value (next_level) is a dictionary then iterate over that as well
# this means that there is a sub level code such as `1a`
if isinstance(next_level, dict):
for sub_k in next_level:
unpack_codes += [[k, sub_k, val] for val in next_level[sub_k]]
else:
# if there are just detail values then we assign the `base_code`
# as the `sublevel code` as well
unpack_codes += [[k, k, val] for val in next_level]
coding_map = pd.DataFrame(
unpack_codes, columns=["base_code", "base_2_code", "detail_code"]
)
```
Below we see we have unpacked that information into a table with a row for each recode
The highest level is called the `base_code` and the sub code is called `base_2_code`, original code is called `detail_code`
```
coding_map
```
**Assign simplified codes to the dataframe**
We can merge the visa issuance data to the coding map to create different summaries
**Using the FSC data**
```
summary_data = coding_map.merge(
fsc_data_2019_2021, left_on="detail_code", right_on="Visa Class", how="right"
)
summary_data.base_code = summary_data.base_code.fillna("NA")
summary_data.detail_code = summary_data.detail_code.fillna("NA")
fsc_data_2019_2021.shape
summary_data
```
**Create a pivot table of simplified visa classes over time - using least granular coding**
We'll first summarize with the base code, after running the cell below you can see the most general visa class coding along with sums by year and month
```
base_code_summary_long = (
summary_data.groupby(["base_code", "year_month"]).Issuances.sum().reset_index()
)
print(base_code_summary_long.head())
base_code_summary_long.pivot(
index="base_code", columns="year_month", values="Issuances"
)
```
**Same as above but using the second level of coding as well**
```
base_code_summary_long = (
summary_data.groupby(["base_code", "base_2_code", "year_month"])
.Issuances.sum()
.reset_index()
)
print(base_code_summary_long.head())
base_code_summary_long_pivot = base_code_summary_long.pivot(
index=["base_code", "base_2_code"], columns="year_month", values="Issuances"
)
```
These summaries could then be exported to csv or excel using the `to_csv()` or `to_excel()` methods of the dataframe and used in additional analysis
```
base_code_summary_long_pivot.to_csv("../data/misc/state_dept_base_code_long_pivot.csv")
```
---------------------
## Appendix
# End
| true |
code
| 0.585871 | null | null | null | null |
|
# Using the GrainSizeTools script through JupyterLab or the notebook: first steps
> IMPORTANT NOTE: This Jupyter notebook example only applies to GrainSizeTools v3.0+ Please check your script version before using this notebook. You will be able to reproduce all the results shown in this tutorial using the dataset provided with the script, the ```file data_set.txt```
## Running the script in Jupyter lab/notebooks
The first step is to execute the code to get all the functionalities. JupyterLab (or Jupyter notebooks) allows you to run any code using the following code snippet: ``%run + the Python file to run``. In this case you must set the full filepath that indicates where the file ``GrainSizeTools_script.py`` is located in your system. If the script was executed correctly you will see that all GrainSizeTools (GST) modules have been loaded correctly and a welcome message as follows:
```
%run C:/Users/marco/Documents/GitHub/GrainSizeTools/grain_size_tools/GrainSizeTools_script.py
```
---
## Get information on the GrainSizeTools methods
First, to get a list of the main methods type
```
get.functions_list()
```
The script is implemented around several modules. To access a method within a module you will have to type the name of the module and then, separated by a dot, the name of the method.For example to access the method ``qq_plot`` of the plot module you should write
```python
plot.qq_plot()
```
and then provide the required parameters within the parenthesis.
To access the methods within a module, type the module name plus the dot and hit the tab key and a complete list of methods will pop up.
### Get detailed information on methods
You can get detailed information about any method or function of the script in different ways. The first is through the console using the character ? before the method
```
?conf_interval
```
Another option in Jupyter's lab is to get the information interactively without having to call it from the console. To do this, right-click on the mouse and select "Show Context Help" from the menu. Now, every time you write a method in the interactive console, all the information will automatically appear in the "Contextual help" window. In this case, you may prefer to rearrange the windows using drag and drop so that you can see the notebook and the contextual help in parallel.
---
# Importing tabular data
For this, [Pandas](https://pandas.pydata.org/about/index.html) is the de facto standard Python library for data analysis and manipulation of table-like datasets (CSV, excel or text files among others). The library includes several tools for reading files and handling of missing data and when running the GrainSizeTools script pandas is imported as ```pd``` for its general use.
All Pandas methods to read data are all named ```pd.read_*``` where * is the file type. For example:
```python
pd.read_csv() # read csv or txt files, default delimiter is ','
pd.read_table() # read general delimited file, default delimiter is '\t' (TAB)
pd.read_excel() # read excel files
pd.read_html() # read HTML tables
# etc.
```
For other supported file types see https://pandas.pydata.org/pandas-docs/stable/user_guide/io.html
The only mandatory argument for the reading methods is to define the path (local or URL) with the location of the file to be imported as follows.
```
# set the filepath, note that is enclosed in quotation marks
filepath = 'C:/Users/marco/Documents/GitHub/GrainSizeTools/grain_size_tools/DATA/data_set.txt'
# import the data
dataset = pd.read_table(filepath)
#display the data
dataset
```
Some important things to note about the code snippet used above are:
- We used the ``pd.read_table()`` method to import the file. By default, this method assumes that the data to import is stored in a text file separated by tabs. Alternatively you can use the ``pd.read_csv()`` method (note that csv means comma-separated values) and set the delimiter to ``'\t'`` as follows: ``pd.read_csv(filepath, sep='\t')``.
- When calling the variable ``dataset`` it returs a visualization of the dataset imported, which is a tabular-like dataset with 2661 entries and 11 columns with different grain properties.
In Python, this type of tabular-like objects are called (Pandas) *DataFrame* and allow a flexible and easy to use data analysis. Just for checking:
```
# show the variable type
type(dataset)
```
> 👉 Pandas' reading methods give you a lot of control over how a file is read. To keep things simple, I list the most commonly used arguments:
```python
sep # Delimiter/separator to use.
header # Row number(s) to use as the column names. By default it takes the first row as the column names (header=0). If there is no columns names in the file you must set header=None
skiprows # Number of lines to skip at the start of the file (an integer).
na_filter # Detect missing value markers. False by default.
sheet_name # Only excel files, the excel sheet name either a number or the full name.
```
> more details on Pandas csv read method: https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_csv.html
The GrainSizeTools script includes a method named ```get_filepath()``` to get the path of a file through a file selection dialog instead of directly writing it. This can be used in two ways:
```python
# store the path in a variable (here named filepath for convenience) and then use it when calling the read method
filepath = get_filepath()
dataset = pd.read_csv(filepath, sep='\t')
# use get_filepath() directly within the read method
dataset = pd.read_csv(get_filepath(), sep='\t')
```
Lastly, Pandas also allows to directly import tabular data from the clipboard (i.e. data copied using copy-paste commands). For example, after copying the table from a text file, excel spreadsheet or a website using:
```python
dataset = pd.read_clipboard()
```
---
## Basic data manipulation (using Pandas)
Let's first see how the data set looks like. Instead of calling the variable (as in the example before) we now use the ``head()`` and ``tail()`` methods so that it only shows us the first (or last) rows of the data set
```
dataset.head() # returns 5 rows by default, you can define any number within the parenthesis
```
The example dataset has 11 different columns (one without a name). To interact with one of the columns we must call its name in square brackets with the name in quotes as follows:
```
# get the column 'Area' and multiplied by two
dataset['Area'] * 2
```
If you want to remove one or more columns, you can do it with the ``drop()`` method. For example, let's remove the column without a name.
```
# Remove the column without a name from the DataFrame
dataset.drop(columns=' ', inplace=True)
dataset.head(3)
# If you want to remove more than one column pass a list of columns
dataset.drop(columns=['FeretX', 'FeretY'], inplace=True)
dataset.head(3)
```
### Create new columns
The example dataset does not contain any column with the grain diameters and therefore we have to estimate them. For example, assuming the data comes from a thin section, you can estimate the apparent diameters from the section areas using the equivalent circular diameter (ECD) formula which is
$ECD = 2 \cdot \sqrt{areas / \pi}$
we will call the new column ``'diameters'``
```
dataset['diameters'] = 2 * np.sqrt(dataset['Area'] / np.pi)
dataset.head()
```
You can see a new column named diameters.
> 👉 In the examples above we define the square root as ``np.sqrt``, the arithmetic mean as ``np.mean``, and pi as ``np.pi``. In this case, ``np.`` stems for NumPy or numerical Python, a core package for scientific computing with Python, and the keyword after the dot is the method or the scientific value to be applied. If you write in the console ``np.`` and then press the TAB key, you will see a large list of available methods. In general, the method names are equivalent to those used in MATLAB or R but always by adding the ``np.`` first.
### A list of useful Pandas methods
Some things you might want to try (just copy-paste in interactive cells below and explore):
```python
# Reduction
dataset.mean() # estimate the mean for all columns
dataset['Area'].mean() # estimate the mean only for the column Area
dataset.std() # estimate the (Bessel corrected) standard deviation
dataset.median() # estimate the median
dataset.mad() # estimate the mean absolute deviation
dataset.var() # estimate the unbiased variace
dataset.sem() # estimate the standard error of the mean
dataset.skew() # estimate the sample skewness
dataset.kurt() # estimate the sample kurtosis
dataset.quantile() # estimate the sample quantile
# Information
dataset.describe() # generate descriptive statistics
dataset.info() # display info of the DataFrame
dataset.shape() # (rows, columns)
dataset.count() # number of non-null values
dataset.dropna() # remove missing values from the data
# writing to disk
dataset.to_csv(filename) # save as csv file, the filename must be within quotes
dataset.to_excel(filename) # save as excel file
```
```
# estimate the mean of all columns
dataset.mean()
# Generate descriptive statistics
dataset.describe()
dataset[['Circ.', 'Round', 'Solidity']].boxplot()
```
| true |
code
| 0.680852 | null | null | null | null |
|
# Walmart data EDA
#### March 23, 2019
#### Luis Da Silva
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import datetime as dt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression, LassoCV, ElasticNetCV
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import cross_val_score
from joblib import dump, load
import sys
sys.path.insert(0, 'D:\\OneDrive\\Git\\scikit-learn-helpers')
import sklearnHelpers as skh
```
# Read in all data
```
features = pd.read_csv('../data/features.csv')
stores = pd.read_csv('../data/stores.csv')
train = pd.read_csv('../data/train.csv')
test = pd.read_csv('../data/test.csv')
```
# "features" EDA
```
features.tail()
features['Date'] = pd.to_datetime(features['Date'], dayfirst=True)
features['Date'].describe()
features.isnull().sum()
# Find out were missing values are
missings = features[['Promotion1', 'Promotion2', 'Promotion3', 'Promotion4', 'Promotion5',
'CPI', 'Unemployment']].isnull()
missings['Date'] = features['Date']
n = 0
plt.figure(figsize=(15, 4))
for v in missings.drop('Date', axis=1):
missings[v] += n
missings[v].replace(n, np.nan, inplace=True)
missings[v] += np.random.normal(0, 0.2, missings.shape[0])
sns.scatterplot(data=missings, x='Date', y=v, label=v)
n += 1
plt.axvline(x='11-02-2012', color='black')
plt.title('Points show where missing values are in time')
plt.xlim(('2010-02-05', '2013-07-26'))
plt.legend(loc='upper left')
plt.ylabel('')
cur_axes = plt.gca()
cur_axes.axes.get_yaxis().set_visible(False)
plt.savefig('../graphs/missingData.png')
plt.show()
# Average of missing values
features[['Promotion1', 'Promotion2', 'Promotion3', 'Promotion4', 'Promotion5',
'CPI', 'Unemployment']].isnull().mean()[:5].mean()
features.describe()
```
#### Adding holidays defined as important
```
def append_holiday(df, dates, name, lag=0):
holy = {'Date': dates}
holy = pd.DataFrame(holy)
holy['Date'] = pd.to_datetime(holy['Date'])
holy[name] = 1
if lag != 0:
holy['Date'] = holy['Date'].apply(lambda x: x - dt.timedelta(days=lag))
df = df.merge(holy, on='Date', how='left')
df[name].fillna(0, inplace=True)
return df
dates = {'Superbowl': ('12/02/2010', '11/02/2011', '10/02/2012', '08/02/2013'),
'Labor': ('10/09/2010', '09/09/2011', '07/09/2012', '06/09/2013'),
'ThanksGiving': ('26/11/2010', '25/11/2011', '23/11/2012', '29/11/2013'),
'Christmas': ('31/12/2010', '30/12/2011', "28/12/2012", '27/12/2013')}
for event, date in dates.items():
features = append_holiday(features, date, event)
features = append_holiday(features, date, event + '_l7', 7)
features = append_holiday(features, date, event + '_l14', 14)
features = append_holiday(features, date, event + '_l-7', -7)
```
#### Promotions EDA
```
plt.figure(figsize=(20, 10))
for i in range(1,6):
var = 'Promotion' + str(i)
plt.subplot(5, 3, (i-1)*3+1)
sns.distplot(features[var].dropna(), rug=True)
plt.subplot(5, 3, (i-1)*3+2)
sns.distplot(np.log(features[var].replace(0, 0.01)).dropna())
plt.xlabel("log({})".format(var))
plt.subplot(5, 3, i*3)
sns.lineplot(features.index, features[var], ci=None)
plt.xlim(['2011-10-01', '2014-01-01'])
plt.tight_layout()
plt.show()
features['Day'] = features['Date'].dt.day
features['Month'] = features['Date'].dt.month
features['Year'] = features['Date'].dt.year
features['Week'] = features['Date'].apply(lambda x: x.isocalendar()[1])
features['Date-1'] = features['Date'].apply(lambda x: x.replace(year= x.year-1))
features['Date-2'] = features['Date'].apply(lambda x: x.replace(year= x.year-2))
# Current year vs next year
plt.figure(figsize=(15,4))
for k in ['Date', 'Date-1']:
sns.lineplot(data=features, y='Promotion1', x=k, label=k)
plt.xlim(('2011-11-01', '2012-11-01'))
plt.legend()
plt.show()
# Correlation heatmap
plt.figure(figsize=(12,10))
sns.heatmap(features.corr(), cmap='bwr', center=0)
plt.savefig('../graphs/featuresHeatmap.png')
plt.show()
for i in range(1,6):
mean_promo = features.groupby('Store')['Promotion{}'.format(i)].mean()
for p, name in ((75, 'High'), (25, 'Low')):
p = np.percentile(mean_promo, p)
p = pd.DataFrame(mean_promo >= p)
p.columns = ['{}Promoter{}'.format(name, i)]
p.reset_index(inplace=True)
features = features.merge(p, on='Store', how='left')
```
#### Temperature
```
plt.figure(figsize=(15, 3))
sns.lineplot(features['Date'], features['Temperature'], ci=None)
plt.title('Temperature')
plt.xlim(['2010-01-01', '2014-01-01'])
plt.savefig('../graphs/temperature.png')
plt.show()
```
#### CPI
```
plt.figure(figsize=(15, 3))
sns.lineplot(features['Date'], features['CPI'], ci=None)
plt.xlim(['2010-01-01', '2014-01-01'])
plt.title('Consumer Price Index')
plt.savefig('../graphs/cpi.png')
plt.show()
features[features['CPI'].isnull()]['Date'].unique()
```
#### Unemployment
```
plt.figure(figsize=(15, 3))
sns.lineplot(features['Date'], features['Unemployment'], ci=None)
plt.xlim(['2010-01-01', '2014-01-01'])
plt.title('Unemployment')
plt.savefig('../graphs/unemployment.png')
plt.show()
```
# Model to fill missing values
### Now, add some predictive features
```
targets = ['Promotion{}'.format(i) for i in range(1,6)]
predictors =['Temperature', 'Fuel_Price', 'Promotion1', 'CPI', 'Unemployment', 'IsHoliday',
'Year', 'Month', 'ImportantHoliday'] + ['Store_{}'.format(i) for i in range(1, 46)] + \
['Week_{}'.format(i) for i in range(1, 53)]
def append_lag_price(df, promo, lag=-7):
ndf = df.loc[:,['Date', 'Store', promo]]
ndf2 = df[['Date', 'Store']]
ndf['Date'] = ndf.loc[:,'Date'].apply(lambda x: x - dt.timedelta(days=lag))
name = promo+str(lag)
ndf.columns = ['Date', 'Store', name]
return ndf2.merge(ndf, on=['Date', 'Store'], how='left')[name]
for i in (7, 14, 21):
features['Promotion1'+str(i)] = append_lag_price(features, 'Promotion1', i)
features = pd.get_dummies(features, prefix=['Store', 'Week', 'Month'],
columns=['Store', 'Week', 'Month'])
features['IsHoliday'] = features['IsHoliday'].astype(int)
features_train = features[features['Date'] >= '11-05-2011'].fillna(0)
features_predict = features[features['Date'] < '11-05-2011']
```
## Train Random Forest Model, predict promotions and fill missing data
```
for i in range(3,6):
target = 'Promotion{}'.format(i)
# Prepare datasets
drop_columns = ['Promotion{}'.format(j) for j in range(1,6) if j!=i] + \
['HighPromoter{}'.format(j) for j in range(1,6) if j!=i] + \
['LowPromoter{}'.format(j) for j in range(1,6) if j!=i] + \
['Promotion17','Promotion114','Promotion121']
temp = features_train.drop(drop_columns, axis=1)
temp.dropna(inplace=True)
y = temp[target]
X = temp.drop([target, 'Date', 'Day', 'Year', 'Date-1', 'Date-2'], axis=1)
# Train model
rf = RandomForestRegressor(n_estimators=100, max_depth=None)
param_grid = {'n_estimators':[50], 'max_depth':[50]}
results = skh.tune_fit_model(X, y, rf, forward_selection=True, cv=3, verbose=True,
scoring='neg_mean_squared_error', stopping=5, param_grid=param_grid)
# Save results for later use
tsubset = results['subset']
dump(results, '../models/RandomForests_{}.joblib'.format(target))
# Append predictions
features_predict.loc[:,target] = results['model'].predict(features_predict[tsubset])
print(target, 'finished.')
print('-'*20)
print()
# Consolidate new dataset
features = pd.concat([features_predict, features_train], sort=False)
features.to_csv('../data/Filled_features.csv')
# If re-running the notebook without fitting random forests
i=4
target = 'Promotion{}'.format(i)
drop_columns = ['Promotion{}'.format(j) for j in range(1,6) if j!=i] + \
['HighPromoter{}'.format(j) for j in range(1,6) if j!=i] + \
['LowPromoter{}'.format(j) for j in range(1,6) if j!=i] + \
['Promotion17','Promotion114','Promotion121']
temp = features_train.drop(drop_columns, axis=1)
temp.dropna(inplace=True)
y = temp[target]
X = temp.drop([target, 'Date', 'Day', 'Year', 'Date-1', 'Date-2'], axis=1)
results = load('../models/RandomForests_Promotion{}.joblib'.format(i))
tsubset = results['subset']
rf = results['model']
y_test = rf.predict(X[tsubset])
plt.figure(figsize=(15,4))
sns.barplot(x=tsubset, y=rf.feature_importances_)
plt.tight_layout()
plt.show()
filled_features = pd.read_csv('../data/Filled_features.csv').iloc[:,1:]
filled_features['Date'] = pd.to_datetime(filled_features['Date'], dayfirst=True)
filled_features = filled_features[filled_features['Date'] < '11-05-2011']
filled_features.head()
np.concatenate([filled_features['Promotion3'], y_test[mask]])
plt.figure(figsize=(15,3))
n = '21'
i = 4
mask = temp['Store_'+n] == 1
mask2 = features_train['Store_'+n] == 1
mask3 = filled_features['Store_'+n] == 1
y_to_plot = np.concatenate([filled_features[mask3]['Promotion'+str(i)], y_test[mask]])
date_to_plot = np.concatenate([filled_features[mask3]['Date'], temp['Date'][mask]])
sns.lineplot(date_to_plot, y_to_plot, label='Predicted', color='red')
sns.lineplot(features_train['Date'][mask2], features_train['Promotion'+str(i)][mask2], label='Real')
#plt.xlim(('2011-12-01', '2013-04-01'))
plt.title('Promotions {} for store {}'.format(i, n))
plt.legend()
plt.savefig('../graphs/promotions{}Store{}'.format(i,n))
plt.show()
mask = features_predict['Store'] == 'Store_25'
plt.plot(features_predict.loc[:,'Date'][mask], features_predict.loc[:,'Promotion1'][mask])
plt.show()
features['Store'] = features['Store_1']
for i in range(2,46):
features.loc[features['Store_{}'.format(i)]==1,'Store'] = i
features.to_csv('../data/Filled_features.csv')
np.percentile(train.Weekly_Sales, (1, 50, 75, 9, 95, 99))
```
# "stores" EDA
```
stores.head()
stores.isnull().sum()
stores.shape
fig, ax = plt.subplots(figsize = (7, 7))
size = 0.3
counts =stores['Type'].value_counts()
sizes = stores.groupby('Type').sum()['Size (sq ft)']
count_labels = ["No. of {} stores".format(k) for k in stores['Type'].unique()]
sizes_labels = ["Total size of {} stores".format(k) for k in stores['Type'].unique()]
cmap = plt.get_cmap("tab20c")
outer_colors = cmap([0, 4, 8])
inner_colors = cmap([2, 6, 10])
ax.pie(counts, radius=1, colors=outer_colors,
wedgeprops=dict(width=size, edgecolor='w'),
autopct='%1.1f%%', pctdistance=0.85)
ax.pie(sizes, radius=1-size, colors=inner_colors,
wedgeprops=dict(width=size, edgecolor='w'),
autopct='%1.1f%%', pctdistance=0.75)
ax.set(aspect="equal", title='Distribution of Stores')
plt.legend(count_labels + sizes_labels)
plt.tight_layout()
plt.savefig('../graphs/distributionStores.png')
plt.show()
mask = stores['Size (sq ft)']<50000
stores[mask].sort_values('Size (sq ft)')
sns.pairplot(stores.loc[:,['Type', 'Size (sq ft)']], hue='Type', height=5)
plt.legend()
plt.show()
```
# "train" EDA
```
train.head()
train['Date'] = pd.to_datetime(train['Date'], dayfirst = True)
train.shape
train.groupby(['Store', 'Dept']).IsHoliday.sum().max()
train.isnull().sum()
train['IsHoliday'].mean()
train_per_week = train.groupby('Date').mean()
sns.distplot(train_per_week[~train_per_week['IsHoliday']]['Weekly_Sales'], label='Regular week')
sns.distplot(train_per_week[train_per_week['IsHoliday']]['Weekly_Sales'], rug=True, label='Holiday')
plt.legend()
plt.savefig('../graphs/holidayDist.png')
plt.show()
train['ImportantHoliday'] = np.logical_and(train['Weekly_Sales'] > 19000, train['IsHoliday'])
train[train['ImportantHoliday']].Date.unique()
train['Year'] = train.Date.dt.year
train['Month'] = train.Date.dt.month
train['Week'] = train.Date.dt.week
train['Year'].unique()
nyear = train['Year'].nunique()
plt.figure(figsize=(10,6))
for i, year in enumerate(train['Year'].unique()):
if i == nyear-1:
break
plt.subplot(nyear - 1, 1, i+1)
mask = np.logical_and(train['Week'] >= 50, train['Year'] == year)
sns.violinplot(data=train[mask], y='Weekly_Sales', x='Week')
plt.ylabel('Sales')
plt.title('Year {}'.format(year))
plt.tight_layout()
plt.savefig('../graphs/christmasPerYear.png')
plt.show()
bydept = pd.pivot_table(data=train, index='Date', columns='Dept', values='Weekly_Sales', aggfunc='mean')
for i in (1, 14, 96):
mask_a = np.logical_and(train['Store'] == 10, train['Dept'] == i)
mask_b = np.logical_and(train['Store'] == 30, train['Dept'] == i)
plt.figure(figsize=(15,3))
sns.lineplot(data=bydept, x=bydept.index, y=i, label='Average')
sns.lineplot(data=train[mask_a], x='Date', y='Weekly_Sales', label='Store 10')
sns.lineplot(data=train[mask_b], x='Date', y='Weekly_Sales', label='Store 30')
plt.ylabel('Sales')
plt.title('Department '+str(i))
plt.legend()
plt.savefig('../graphs/avgDept{}.png'.format(i))
plt.show()
for i in (1, 96):
mask = np.logical_and(train['Store'] == 10, train['Dept'] == i)
pd.plotting.autocorrelation_plot(train[mask]['Weekly_Sales'])
plt.show()
sales_size = train.merge(stores, on='Store')
sales_size['SalesSize'] = sales_size['Weekly_Sales']/sales_size['Size (sq ft)']*52
sales_sqft = sales_size.groupby('Type')['SalesSize'].median()*52
sales_store = sales_size.groupby('Type')['Weekly_Sales'].median()*52
sns.violinplot(data=sales_size, x='Type', y='Weekly_Sales')
plt.ylabel('Weekly Sales')
plt.savefig('../graphs/weeklySales.png')
sns.violinplot(data=sales_size, x='Type', y='SalesSize')
plt.ylabel('Yearly Sales per Squared Feet')
plt.savefig('../graphs/yearlySalesSqf.png')
```
# "Test"
```
test['Date'] = pd.to_datetime(test['Date'], dayfirst = True)
test.Date.describe()
test.shape
test.isnull().sum()
test.Date.nunique()
```
# Merging
```
data = {}
for n, df in (('train', train), ('test', test)):
df = df.merge(features.drop('IsHoliday', axis=1), on=['Date', 'Store'])
df = df.merge(stores, on='Store')
df.to_csv('../data/merged_{}_data.csv'.format(n))
print(df.shape)
data[n] = df
data['train'].head()
plt.figure(figsize=(7, 6))
sns.heatmap(data['train'].loc[:,'Weekly_Sales':].corr(), cmap='bwr', center=0)
plt.title("Full Train Dataset correlation heatmap")
plt.show()
```
| true |
code
| 0.480174 | null | null | null | null |
|
# Testing a new contribution
```
import numpy as np
import pandas as pd
from deep_nilmtk.utils.templates import ExperimentTemplate
from deep_nilmtk.models.pytorch import Seq2Point
from deep_nilmtk.models.pytorch.layers import *
from deep_nilmtk.disaggregator import NILMExperiment
from deep_nilmtk.data.loader import GeneralDataLoader
import torch.nn as nn
DATA_PATH = '../../data/ukdale.h5'
EXPERIMENT_NAME = 'residual_seq2point'
RESULTS_PATH = '../../residual_seq2point'
```
## Defining the model
we will here extend the seq2point with a residal connection.
``` python
class seq2point_residual(Seq2point):
def __init__(self, params):
self.model = Seq
pass
def forward(self,x ):
y_pred = x
return y_pred
def step(self, batch):
x, y = batch
return loss, mae
def predict(self, model, test_dataloader):
return results
@staticmethod
def get_template():
params={}
return params
```
```
class residual_block(nn.Module):
def __init__(self, in_size, hidden_size, out_size, filter_size=5):
super(residual_block, self).__init__()
self.conv = nn.Sequential(create_conv1(in_size, hidden_size, filter_size, bias=True, stride=1, padding=(filter_size-1)//2),
create_conv1(hidden_size, out_size, filter_size, bias=True, stride=1, padding=(filter_size-1)//2),
nn.ReLU())
def forward(self,x):
out = x + self.conv(x)
return out
class ResidualSeq2Point(Seq2Point):
def __init__(self, params):
super(ResidualSeq2Point, self).__init__(params)
self.enc_net = nn.Sequential(
residual_block(self.in_size, hidden_size=32, out_size=50, filter_size=7),
residual_block(50, hidden_size=16, out_size=50, filter_size=7),
nn.AdaptiveAvgPool1d(self.pool_filter),
nn.Flatten())
```
## Defining the data loader
The interface for defining a custom model is as follows:
```python
class new_nilm_loader(torch.utils.data.Dataset):
def __init__(self, params):
pass
def __len__(self):
pass
def __getitem__(self, index):
pass
def __copy__(self):
return self
```
Nonethless, for the considered model we can directly use the pre-defined data loader as the model follows a learning seq2seq approach.
## Benchmarking with existing baselines
```
max_epochs = 5
template = ExperimentTemplate( data_path=DATA_PATH,
template_name='ukdale',
list_appliances=['washing machine'],
list_baselines_backends=[('Seq2Pointbaseline', 'pytorch')],
in_sequence=121,
out_sequence=1,
max_epochs=max_epochs)
res_seq2point_nilm = NILMExperiment({
"model_class": ResidualSeq2Point,
"loader_class": GeneralDataLoader,
"model_name": 'res_seq2point',
'backend':'pytorch',
'in_size': 121,
'out_size':1,
'custom_preprocess':None,
'feature_type':'mains',
'input_norm':'z-norm',
'target_norm':'z-norm',
'seq_type':'seq2point',
'point_position':'mid_position',
'learning_rate':10e-5,
'max_nb_epochs': max_epochs
})
template.extend_experiment({
'res_seq2point':res_seq2point_nilm
})
template.__print__()
template.run_template(EXPERIMENT_NAME,
RESULTS_PATH,
f'{RESULTS_PATH}/mlflow')
```
## Checking the results
```
template.extend_template()
```
| true |
code
| 0.532668 | null | null | null | null |
|
## Coding Exercise #0702
### 1. Linear regression:
```
import numpy as np
# import tensorflow as tf
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
```
#### 1.1. Data:
```
# Training data.
# hours of study (X) vs test score (y).
study = np.array([ 3, 4.5, 6, 1.2, 2, 6.9, 6.7, 5.5]) # Explanatory variable: X
score = np.array([ 88, 85, 90, 80, 81, 92, 95, 90]) # Response variable: y
```
#### 1.2. Define Variables and Placeholders:
```
b1 = tf.Variable(1.0) # A constant initial value.
b0 = tf.Variable(1.0) # A constant initial value.
X_ph = tf.placeholder(tf.float32, shape=(None)) # We don't need to fix the number of observations.
y_ph = tf.placeholder(tf.float32, shape=(None)) # We can just leave the size = None.
```
#### 1.3. Define the model:
```
y_model = b0 + b1*X_ph # Simple linear regression model.
```
#### 1.4. Define the loss function and the optimization method:
```
loss = tf.reduce_sum(tf.square(y_ph - y_model)) # L2 loss.
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.001)
# optimizer = tf.train.MomentumOptimizer(learning_rate = 0.001, momentum=0.9) # Momentum optimizer.
train = optimizer.minimize(loss) # Define training.
init = tf.global_variables_initializer() # Define Variable initialization.
```
#### 1.5. Training and Testing:
```
n_epochs = 5000 # N# of epochs (gradient descent steps).
with tf.Session() as sess:
# Variables initialization.
sess.run(init)
# Training.
my_feed = {X_ph:study, y_ph:score} # Prepare feed data as a dictionary.
for i in range(n_epochs):
sess.run(train, feed_dict = my_feed)
b0_model, b1_model = sess.run([b0, b1]) # Get the final values of the Variables.
# Testing.
mse = tf.reduce_mean(tf.square(y_ph - y_model)) # Define the test metric.
mse_value = sess.run(mse, feed_dict = my_feed) # Calculate the in-sample MSE.
```
#### 1.6. Display the result:
```
print("Parameters b0 = {:5.3f} , b1 = {:5.3f}".format(b0_model, b1_model))
print("MSE = {:5.3f}".format(mse_value))
print("RMSE = {:5.3f}".format(np.sqrt(mse_value)))
```
#### 1.7. Prediction:
```
# Define the testing data.
study_new = np.array([2.5, 3.3, 4.2]).reshape(-1,1)
X_ph = tf.placeholder(tf.float32, shape=(study_new.size,1))
y_model = b0_model + b1_model*X_ph # Define the prediction model.
with tf.Session() as sess:
my_feed = {X_ph:study_new}
y_pred_value = sess.run(y_model, feed_dict = my_feed)
# Predicted y values.
print(y_pred_value)
```
| true |
code
| 0.650828 | null | null | null | null |
|
```
import numpy as np
import math
import tensorflow as tf
from tensorflow.contrib.layers import fully_connected
import time
# import subprocess
import random
%matplotlib inline
```
## Utils
```
def alter_coord(action, position, g_coord, dx=0.1, change_nodes=list(range(1,9))):
if action==0:
g_coord[int(2*change_nodes[position])]+=dx
g_coord[int(2*change_nodes[position])+1]+=dx
elif action==1:
g_coord[int(2*change_nodes[position])]+=dx
g_coord[int(2*change_nodes[position])+1]-=dx
if action==2:
g_coord[int(2*change_nodes[position])]-=dx
g_coord[int(2*change_nodes[position])+1]+=dx
elif action==3:
g_coord[int(2*change_nodes[position])]-=dx
g_coord[int(2*change_nodes[position])+1]-=dx
elif action==4:
g_coord[int(2*change_nodes[position])+1]-=0
return g_coord
# this function must be tailored to different FE models
def observe(position, coord, displ):
return position, coord[0], coord[1],coord[2], coord[3], coord[4], coord[5],coord[6], \
coord[7], coord[8], coord[9],coord[10], coord[11], coord[12], coord[13],coord[14], coord[15],\
coord[16], coord[17],coord[18], coord[19], np.max(abs(displ))
#np.sum(abs(displ))
#displ[2]
# displ[0],displ[1],displ[2],displ[3],displ[4],\
# displ[5],displ[6],displ[7],displ[8],displ[9],displ[10],displ[11],displ[12],displ[13],\
# displ[14],displ[15],displ[16],displ[17],displ[18],displ[19],displ[20],displ[21],\
# displ[22],displ[23],displ[24],displ[25],displ[26],displ[27],displ[28],displ[29]
```
## Finite Element Model of the Plane Truss structure
```
def PlaneFrameElementLength(x1,y1,x2,y2):
return math.sqrt((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1))
def PlaneFrameElementStiffness(E,A,I,L,theta):
pi=3.14159265
x = theta*pi/180
C = math.cos(x)
S = math.sin(x)
w1 = A*C*C + 12*I*S*S/(L*L)
w2 = A*S*S + 12*I*C*C/(L*L)
w3 = (A-12*I/(L*L))*C*S
w4 = 6*I*S/L
w5 = 6*I*C/L
return E/L*np.array([[w1, w3, -w4, -w1, -w3, -w4],[ w3, w2, w5, -w3, -w2, w5],
[-w4, w5, 4*I, w4, -w5, 2*I],[ -w1, -w3, w4, w1, w3, w4],
[-w3, -w2, -w5, w3, w2, -w5], [-w4, w5, 2*I, w4, -w5, 4*I]])
def PlaneFrameAssemble(K,k,i,j):
K[3*i,3*i] = K[3*i,3*i] + k[0,0]
K[3*i,3*i+1] = K[3*i,3*i+1] + k[0,1]
K[3*i,3*i+2] = K[3*i,3*i+2] + k[0,2]
K[3*i,3*j] = K[3*i,3*j] + k[0,3]
K[3*i,3*j+1] = K[3*i,3*j+1] + k[0,4]
K[3*i,3*j+2] = K[3*i,3*j+2] + k[0,5]
K[3*i+1,3*i] = K[3*i+1,3*i] + k[1,0]
K[3*i+1,3*i+1] = K[3*i+1,3*i+1] + k[1,1]
K[3*i+1,3*i+2] = K[3*i+1,3*i+2] + k[1,2]
K[3*i+1,3*j] = K[3*i+1,3*j] + k[1,3]
K[3*i+1,3*j+1] = K[3*i+1,3*j+1] + k[1,4]
K[3*i+1,3*j+2] = K[3*i+1,3*j+2] + k[1,5]
K[3*i+2,3*i] = K[3*i+2,3*i] + k[2,0]
K[3*i+2,3*i+1] = K[3*i+2,3*i+1] + k[2,1]
K[3*i+2,3*i+2] = K[3*i+2,3*i+2] + k[2,2]
K[3*i+2,3*j] = K[3*i+2,3*j] + k[2,3]
K[3*i+2,3*j+1] = K[3*i,3*j+1] + k[2,4]
K[3*i+2,3*j+2] = K[3*i+2,3*j+2] + k[2,5]
K[3*j,3*i] = K[3*j,3*i] + k[3,0]
K[3*j,3*i+1] = K[3*j,3*i+1] + k[3,1]
K[3*j,3*i+2] = K[3*j,3*i+2] + k[3,2]
K[3*j,3*j] = K[3*j,3*j] + k[3,3]
K[3*j,3*j+1] = K[3*j,3*j+1] + k[3,4]
K[3*j,3*j+2] = K[3*j,3*j+2] + k[3,5]
K[3*j+1,3*i] = K[3*j+1,3*i] + k[4,0]
K[3*j+1,3*i+1] = K[3*j+1,3*i+1] + k[4,1]
K[3*j+1,3*i+2] = K[3*j+1,3*i+2] + k[4,2]
K[3*j+1,3*j] = K[3*j+1,3*j] + k[4,3]
K[3*j+1,3*j+1] = K[3*j+1,3*j+1] + k[4,4]
K[3*j+1,3*j+2] = K[3*j+1,3*j+2] + k[4,5]
K[3*j+2,3*i] = K[3*j+2,3*i] + k[5,0]
K[3*j+2,3*i+1] = K[3*j+2,3*i+1] + k[5,1]
K[3*j+2,3*i+2] = K[3*j+2,3*i+2] + k[5,2]
K[3*j+2,3*j] = K[3*j+2,3*j] + k[5,3]
K[3*j+2,3*j+1] = K[3*j+2,3*j+1] + k[5,4]
K[3*j+2,3*j+2] = K[3*j+2,3*j+2] + k[5,5]
return K
def FEA_u(coord, elcon, bc_u_elim, f_after_u_elim, I=5e-5, A=1e-4, E=210e6):
K=np.zeros(shape=(3*np.max(elcon)+3,3*np.max(elcon)+3))
pi=3.14159265
for el in elcon:
L=PlaneFrameElementLength(coord[el[0]][0],coord[el[0]][1],coord[el[1]][0],coord[el[1]][1])
theta=math.atan((coord[el[1]][1]-coord[el[0]][1])/(coord[el[1]][0]-coord[el[0]][0]+1e-13))*180/pi
k=PlaneFrameElementStiffness(E,A,I,L,theta)
K=PlaneFrameAssemble(K,k,el[0],el[1])
K=np.delete(K,bc_u_elim,0)
K=np.delete(K,bc_u_elim,1)
d=np.dot(np.linalg.inv(K),f_after_u_elim)
ans=np.zeros(shape=(3*len(coord)))
j=0
for i in range(len(ans)):
if i not in bc_u_elim:
ans[i]=d[j]
j+=1
if j>len(d)-1:
break
return ans
```
## Neural Network Policy - Policy Gradients
```
# Details of model can be found in the book:
# Hands-On Machine Learning with Scikit-Learn & TensorFlow. Aurйlien Gйron
# the NN architecture must be tailored to different FE models
n_inputs = 22
n_hidden = 70
n_outputs = 5
initializer = tf.contrib.layers.variance_scaling_initializer()
learning_rate = 0.001
# Build the neural network
X_ = tf.placeholder(tf.float64, shape=[None, n_inputs], name="X_")
hidden = fully_connected(X_, n_hidden, activation_fn=tf.nn.elu, weights_initializer=initializer)
hidden1 = fully_connected(hidden, n_hidden, activation_fn=tf.nn.elu, weights_initializer=initializer)
logits = fully_connected(hidden1, n_outputs, activation_fn=None, weights_initializer=initializer)
outputs = tf.nn.softmax(logits, name="Y_proba")
# Select a random action based on the estimated probabilities
action = tf.multinomial(tf.log(outputs), num_samples=1,output_dtype=tf.int32)
y=tf.reshape(tf.one_hot(action,depth=5,dtype=tf.float64),[5,1])
xentropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=tf.transpose(logits))
optimizer = tf.train.AdamOptimizer(learning_rate)
grads_and_vars = optimizer.compute_gradients(xentropy)
gradients = [grad for grad, variable in grads_and_vars]
gradient_placeholders = []
grads_and_vars_feed = []
for grad, variable in grads_and_vars:
gradient_placeholder = tf.placeholder(tf.float64, shape=grad.get_shape())
gradient_placeholders.append(gradient_placeholder)
grads_and_vars_feed.append((gradient_placeholder, variable))
training_op = optimizer.apply_gradients(grads_and_vars_feed)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
def discount_rewards(rewards, discount_rate=0.97):
discounted_rewards = np.empty(len(rewards))
cumulative_rewards = 0
for step in reversed(range(len(rewards))):
cumulative_rewards = rewards[step] + cumulative_rewards * discount_rate
discounted_rewards[step] = cumulative_rewards
return discounted_rewards
def discount_and_normalize_rewards(all_rewards, discount_rate=0.97):
all_discounted_rewards = [discount_rewards(rewards) for rewards in all_rewards]
flat_rewards = np.concatenate(all_discounted_rewards)
reward_mean = flat_rewards.mean()
reward_std = flat_rewards.std()
return [(discounted_rewards - reward_mean)/reward_std for discounted_rewards in all_discounted_rewards]
# this function must be tailored to different FE models
def reward_(obs_,obs):
# if np.max(abs(np.array(obs_[22:-1])))>np.max(abs(np.array(obs[22:-1]))):
# if sum(abs(np.array(obs_[22:-1])))>sum(abs(np.array(obs[22:-1]))):
# return sum(abs(np.array(obs_[22:-1]))>abs(np.array(obs[22:-1])))
# if abs(obs_[-1])>abs(obs[-1]):
if obs_[-1]>obs[-1]:
return 1
else:
return 0
# the training code must be tailored to different FE models
n_iterations =101 #251 # number of training iterations
n_max_steps = 500 #1000 # max steps per episode
n_games_per_update = 10 # train the policy every 10 episodes
save_iterations = 5 # save the model every 10 training iterations
with tf.Session() as sess:
start=time.time()
init.run()
# saver.restore(sess, tf.train.latest_checkpoint("./policy4/"))
# tf.get_default_graph()
for iteration in range(n_iterations):
all_rewards = [] # all sequences of raw rewards for each episode
all_gradients = [] # gradients saved at each step of each episode
for game in range(n_games_per_update):
current_rewards = [] # all raw rewards from the current episode
current_gradients = [] # all gradients from the current episode
pst=random.randint(0,7)
g_coord = alter_coord(4, pst, np.array([0.0,0,3,0,6,0,9,0,9,3,9,6,9,9,12,9,15,9,18,9]),
dx=0.1, change_nodes=list(range(1,9)))
displ = FEA_u(g_coord.reshape(10,2), elcon=np.array([[0,1],[1,2],[2,3],[3,4],[4,5],[5,6],[6,7],[7,8],[8,9]]),
bc_u_elim=[0,1,2],
f_after_u_elim=np.array([0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-10,0,0]),
I=5e-5, A=2e-2, E=210e6)
obs=observe(pst, g_coord,displ)
for step in range(n_max_steps):
action_val, gradients_val = sess.run([action, gradients],
feed_dict={X_: np.array(obs).reshape(1,n_inputs)})
obs_=obs
g_coord = alter_coord(action_val[0][0], pst, g_coord,
dx=0.1, change_nodes=list(range(1,9)))
pst=random.randint(0,7)
if PlaneFrameElementLength(g_coord[0],g_coord[1],g_coord[2],g_coord[3])<0.02:
break
if PlaneFrameElementLength(g_coord[2],g_coord[3],g_coord[4],g_coord[5])<0.02:
break
if PlaneFrameElementLength(g_coord[4],g_coord[5],g_coord[6],g_coord[7])<0.02:
break
if PlaneFrameElementLength(g_coord[6],g_coord[7],g_coord[8],g_coord[9])<0.02:
break
if PlaneFrameElementLength(g_coord[8],g_coord[9],g_coord[10],g_coord[11])<0.02:
break
if PlaneFrameElementLength(g_coord[10],g_coord[11],g_coord[12],g_coord[13])<0.02:
break
if PlaneFrameElementLength(g_coord[12],g_coord[13],g_coord[14],g_coord[15])<0.02:
break
if PlaneFrameElementLength(g_coord[14],g_coord[15],g_coord[16],g_coord[17])<0.02:
break
if PlaneFrameElementLength(g_coord[16],g_coord[17],g_coord[18],g_coord[19])<0.02:
break
displ = FEA_u(g_coord.reshape(10,2), elcon=np.array([[0,1],[1,2],[2,3],[3,4],[4,5],[5,6],[6,7],[7,8],[8,9]]),
bc_u_elim=[0,1,2],
f_after_u_elim=np.array([0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-10,0,0]),
I=5e-5, A=2e-2, E=210e6)
obs=observe(pst,g_coord,displ)
reward=reward_(obs_,obs)
current_rewards.append(reward)
current_gradients.append(gradients_val)
all_rewards.append(current_rewards)
all_gradients.append(current_gradients)
# At this point we have run the policy for 10 episodes, and we are
# ready for a policy update using the algorithm described earlier.
all_rewards = discount_and_normalize_rewards(all_rewards)
feed_dict = {}
for var_index, grad_placeholder in enumerate(gradient_placeholders):
# multiply the gradients by the action scores, and compute the mean
mean_gradients = np.mean([reward * all_gradients[game_index][step][var_index]
for game_index, rewards in enumerate(all_rewards)
for step, reward in enumerate(rewards)],axis=0)
feed_dict[grad_placeholder] = mean_gradients
sess.run(training_op, feed_dict=feed_dict)
if iteration % save_iterations == 0:
# print("Saving {} iteration".format(iteration))
print('Time taken for {} epoch {} sec\n'.format(iteration, time.time() - start))
saver.save(sess, "./policy4/pinjointed4.ckpt")
# end=time.time()
# print(end-start)
```
## AI designing the spool
```
def predict(coord):
with tf.Session() as sess:
saver = tf.train.import_meta_graph('./policy4/pinjointed4.ckpt.meta')
saver.restore(sess, "./policy4/pinjointed4.ckpt")
graph = tf.get_default_graph()
outputs = graph.get_tensor_by_name("Y_proba:0")
X_ = graph.get_tensor_by_name("X_:0")
# pst=random.randint(0,7)
j=0
pst=j%8
g_coord = alter_coord(4, pst, coord, dx=0.1, change_nodes=list(range(1,9)))
displ = FEA_u(g_coord.reshape(10,2), elcon=np.array([[0,1],[1,2],[2,3],[3,4],[4,5],[5,6],[6,7],[7,8],[8,9]]),
bc_u_elim=[0,1,2],
f_after_u_elim=np.array([0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-10,0,0]),
I=5e-5, A=2e-2, E=210e6)
obs=observe(pst, g_coord, displ)
print("before: ", np.max(abs(displ)))
for step in range(50):
action_val= sess.run([outputs],feed_dict={X_: np.array(obs).reshape(1,n_inputs)})
action_val=np.log(action_val)
g_coord = alter_coord( np.argmax(action_val), pst, g_coord, dx=0.1, change_nodes=list(range(1,9)))
# print(pst)
# pst=random.randint(0,7)
j+=1
pst=j%8
if PlaneFrameElementLength(g_coord[0],g_coord[1],g_coord[2],g_coord[3])<0.02:
break
if PlaneFrameElementLength(g_coord[2],g_coord[3],g_coord[4],g_coord[5])<0.02:
break
if PlaneFrameElementLength(g_coord[4],g_coord[5],g_coord[6],g_coord[7])<0.02:
break
if PlaneFrameElementLength(g_coord[6],g_coord[7],g_coord[8],g_coord[9])<0.02:
break
if PlaneFrameElementLength(g_coord[8],g_coord[9],g_coord[10],g_coord[11])<0.02:
break
if PlaneFrameElementLength(g_coord[10],g_coord[11],g_coord[12],g_coord[13])<0.02:
break
if PlaneFrameElementLength(g_coord[12],g_coord[13],g_coord[14],g_coord[15])<0.02:
break
if PlaneFrameElementLength(g_coord[14],g_coord[15],g_coord[16],g_coord[17])<0.02:
break
if PlaneFrameElementLength(g_coord[16],g_coord[17],g_coord[18],g_coord[19])<0.02:
break
displ = FEA_u(g_coord.reshape(10,2), elcon=np.array([[0,1],[1,2],[2,3],[3,4],[4,5],[5,6],[6,7],[7,8],[8,9]]),
bc_u_elim=[0,1,2],
f_after_u_elim=np.array([0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-10,0,0]),
I=5e-5, A=2e-2, E=210e6)
obs=observe(pst, g_coord, displ)
print("after: ", np.max(abs(displ)))
# print("after: ", abs(displ[2]))
return obs,g_coord
obs, g_coord = predict(np.array([0.0,0,3,0,6,0,9,0,9,3,9,6,9,9,12,9,15,9,18,9]))
g_coord
import matplotlib.pyplot as plt
def draw(coord,color,elcon):
coord=coord.reshape(np.max(elcon)+1,2)
plt.figure(figsize=(13,5))
for item in elcon:
plt.plot([coord[item[0]][0],coord[item[1]][0]],[coord[item[0]][1],coord[item[1]][1]],color=color)
plt.show()
```
### Initial Design
```
draw(np.array([0,0,3,0,6,0,9,0,9,3,9,6,9,9,12,9,15,9,18,9]),color="green",elcon=np.array([[0,1],[1,2],[2,3],[3,4],[4,5],[5,6],[6,7],[7,8],[8,9]]))
```
### Design by AI
```
draw(g_coord,color="blue",elcon=np.array([[0,1],[1,2],[2,3],[3,4],[4,5],[5,6],[6,7],[7,8],[8,9]]))
```
| true |
code
| 0.215722 | null | null | null | null |
|
# Introdução ao Python - Ana Beatriz Macedo<img src="https://octocat-generator-assets.githubusercontent.com/my-octocat-1626096942740.png" width="324" height="324" align="right">
## Link para download: https://github.com/AnabeatrizMacedo241/Python-101
## Github: https://github.com/AnabeatrizMacedo241
## Linkedin: www.linkedin.com/in/anabeatriz-macedo
<img src="https://cdn.jsdelivr.net/gh/devicons/devicon/icons/python/python-original.svg" alt="rails" width='150' height='150' style='max-width: 100%;'></img>

## Nessa oitava parte veremos:
- Filas
- Pilhas
### Filas
Em uma fila, seja ela do ônibus ou mercado, o primeiro da fila será o primeiro a sair. Faz sentido, não é? O termo de Filas em programação é igual, chamamos de `FIFO`: first in, first out. Ela servirá como uma estrutura de armazenamento de dados temporária.
```
#Um exemplo simples
fila = []
fila.append('Ana')
fila.append('Maria')
fila.append('Carlos')
fila.append('Marcelo')
fila
#Como 'Ana' foi a primeira a entrar, ela seria a primeira a sair.
fila.pop() #Ana
print(fila)
fila.pop() #Maria
print(fila)
```
Não foi isso que esperavamos... Isso acontece, porque listas não as melhores estruturas para criar Filas. O recomendado seria usar **deques**.
Suas operações principais são:
- `enqueue`: para inserir na fila
- `dequeue`: retirar da fila
```
#Exemplo
class Fila(object):
def __init__(self):
self.dados = []
def insere(self, elemento):
self.dados.append(elemento)
def retira(self):
return self.dados.pop()
def vazia(self):
return len(self.dados) == 0
class FilaDeque:
Capacidade = 25 #Definindo um número exato para armazenamento de dados
def __init__(self):
self.dados = [None] * FilaDeque.Capacidade
self.size = 0
self.front = 0
def __len__(self): #Quantidade de infos
return self.size
def vazia(self): #Chaca se está vazia
return self.size == 0
def primeiro(self):
if (self.vazia()): #Retorna o primeiro elemento
raise EmptyQueueException('A Fila está vazia')
return self.dados[self.front]
def dequeue(self):
if (self.vazia()): #Remove o primeiro elemento
raise EmptyQueueException('A Fila está vazia')
answer = self.dados[self.front]
self.dados[self.front] = None
self.front = (self.front + 1) % len(self.dados)
self.size -= 1
return answer
def enqueue(self, elemento): #Adiciona elementos
if (self.size == len(self.dados)):
self.resize(2 * len(self.dados))
avail = (self.front + self.size) % len(self.dados)
self.dados[avail] = elemento
self.size += 1
def __str__(self): #Retorna todos os valores
return str(self.dados)
Elementos = FilaDeque()
Elementos.enqueue(10)
Elementos.enqueue(9)
Elementos.enqueue(8)
print(Elementos.dequeue()) #10 é retirado e depois o 9 (FIFO)
print(Elementos.dequeue())
Elementos.enqueue(7)
print(Elementos) #25 espaços, apenas 8 e 7 restam em suas posições de entrada.
Elementos.vazia()
```
### Pilhas
Um exemplo do cotidiano para explicar **Pilhas** seriam pilhas de papéis, por exemplo. Quando vamos empilhando papéis, o último a ser colocado, será o priemiro a sair por ele estar em cima. Esse termo em programação seria `LIFO`: last in, first out.
Suas operações principais são:
- `push`: para inserir no topo da pilha
- `pop`: retirar do topo
- `top`: checar qual o elemento que está no topo
```
#Exemplo
class Pilha(object):
def __init__(self):
self.dados = []
def empilha(self, elemento):
self.dados.append(elemento)
def desempilha(self):
if not self.vazia():
return self.dados.pop()
def vazia(self):
return len(self.dados) == 0
```
Onde as pilhas são usadas?
Podem ser usadas em gerenciamento de chamadas de função de um programa com a finalidade de manter informações sobre as funções de um programa que estejam ativas, aguardando serem terminadas.
```
class Pilha:
def __init__(self):
self.dados = [] #Cria o armazenamento
def vazio(self):
return len(self.dados)==0 #Verifica se está vazio
def push(self, elemento):
self.dados.append(elemento) #Insere novos elementos
def pop(self):
if self.vazio():
raise Emptyexception('Pilha vazia')
return self.dados.pop() #Retira o elemento
def top(self):
if self.vazio():
raise Emptyexception('Pilha vazia')
return self.data[-1] #Retorna o elemento no topo, o último adicionado
def len_ (self):
return len(self.dados)
def __str__(self):
return str(self.dados) #Mostra o que tem dentro da pilha
Dados = Pilha()
Dados.push(10)
print(Dados)
Dados.push(9)
Dados.push(8)
Dados.push(7)
print(Dados)
Dados.pop()
print(Dados) #Retirou o último(LIFO)
```
### Conclusão:
**Filas e Pilhas** são usadas para a implementação de listas como estruturas para armazenamento dos dados.
### Faça seus próprios exemplos para praticar e bons estudos!
## Ana Beatriz Macedo

| true |
code
| 0.298159 | null | null | null | null |
|
<center>
<table style="border:none">
<tr style="border:none">
<th style="border:none">
<a href='https://colab.research.google.com/github/AmirMardan/ml_course/blob/main/3_pandas/0_intro_to_pandas.ipynb'><img src='https://colab.research.google.com/assets/colab-badge.svg'></a>
</th>
<th style="border:none">
<a href='https://github1s.com/AmirMardan/ml_course/blob/main/3_pandas/0_intro_to_pandas.ipynb'><img src='../imgs/open_vscode.svg' height=20px width=115px></a>
</th>
</tr>
</table>
</center>
This notebook is created by <a href='https://amirmardan.github.io'> Amir Mardan</a>. For any feedback or suggestion, please contact me via my <a href="mailto:mardan.amir.h@gmail.com">email</a>, (mardan.amir.h@gmail.com).
<center>
<img id='PYTHON' src='img/pandas.svg' width='300px'>
</center>
<a name='top'></a>
# Introduction to pandas
This notebook will cover the following topics:
- [Introduction](#introduction)
- [1. Introducing Pandas objects](#objects)
- [The pandas `Series` object](#series)
- [The pandas `DataFrame` object](#dataframe)
- [2. Data indexing and selection](#indexing)
- [Data selection in Series](#index_series)
- [Data selection in DataFrame](#index_df)
- [3. Handling missing data](#missing)
- [Detecting the missing values](#check_missing)
- [Dealing with missing values](#deal_missing)
- [4. IO in pandas](#import)
<a name='introduction'></a>
## Introduction
pandas is a library for data manipulation and analysis.
Created by **Wes McKinney**, first time released in January 2008.
<center><img src='./img/wes.png' alter='tavis' width=300px></center>
In this notebook, we learn the basic pandas. We learn
- What the pandas' objects are and how to create them,
- Data selection and indexing
- Handling missing data
```
# Ignore this cell
def letter_generator(n, random=True):
"""
random_letter generates characters
Parameters
----------
n : int
Number of required characters
random : Boolean
If True, the function returns structured random characters
Returns
-------
str
Random characters
"""
alphabet = 'abcdefghijklmnopqrstuvwxyz'
dis_alphabet = np.array([char for char in alphabet])
ind = np.random.randint(0, 26, n)
to_return = [dis_alphabet[ind[:n]] if random else dis_alphabet[:n]]
return to_return[0]
```
<a name='objects'></a>
## 1. Introducing pandas objects
At a basic level, pandas objects can be thought of as NumPy structured arrays in which the rows and columns are identified with labels rather than integer indices. There are three fundamental pandas structures:
- `Series`
- `DataFrame`
- `Index`
Let's import pandas and NumPy and discuss the mentioned structures.
```
import numpy as np
import pandas as pd
```
<a name='series'></a>
### 1.1 The pandas `Series` object
A pandas `Series` is a one-dimensional array.
```
# Creating a series from list
data = pd.Series([2, 1, 3.4, -8])
data
```
As we see, `Series` makes a sequence of values and a sequence of indices.
```
pd.Series(['k', 3, 2])
```
We can define the index
```
pd.Series([1, 2, 4], index=['a', 'x', 't'])
# Creating a series from dictionary
courses = {
'Math': 3.4,
'Literatur': 4,
'French': 3
}
pd.Series(courses)
# Creating a series from NumPy array
df = pd.Series(np.arange(3, 9, 1.2), index=['a', 'b', 'c', 'd', 'e'])
df
```
We have access to values and the indices using `values` and `index`
```
# Get the indices
df.index
# Get the values
df.values
```
Values are accessible using indices
```
# Creating homogenous series
pd.Series(50, index=[1, 2, 3])
```
<a name='dataframe'></a>
### 1.2 The pandas `DataFrame` object
A pandas `DataFrame` can be thought of NumPy array of a dictionary.
```
# Let's prepare some data
population_dict = {
'China': 1439323776,
'India': 1380004385,
'US': 331002651,
'Indonesia': 273523615,
'Pakistan': 220892340
}
land_area_dict = {
'China': 9388211,
'India': 2973190,
'US': 9147420,
'Indonesia': 1811570,
'Pakistan': 770880
}
# Creating DataFrame using Series
# 1. Creating Series
population = pd.Series(population_dict)
land_area = pd.Series(land_area_dict)
# 2. Combine the Series
countries = pd.DataFrame({'Population': population, 'Land Area': land_area})
countries
# Creating DataFrame using list
# 1. Creating the list
countries_list = []
population_list = []
land_area_list = []
for param in land_area_dict:
countries_list.append(param)
population_list.append(population_dict[param])
land_area_list.append(land_area_dict[param])
countries_list
# 2. Combine the lists
df = pd.DataFrame({"Population": population_list,
"Land Area": land_area_list},
index=countries_list)
df
# Adding another column.
# For example, let's calculate the density
df['Density']= df['Population'] /df['Land Area']
df
```
We use `index` and `columns` attributes to get the index and the name of columns.
```
df.index
df.columns
# Attribute values
df.values
# Creating DataFrame with missing values
pd.DataFrame([{'a': 0, 'b': 1},
{'a': 2, 'f':3, 'g':6}])
# Creating with 2-D NumPy array
pd.DataFrame(np.random.random((3, 4)),
columns=['col1', 'col2', 'col3', 'col4'],
index=[2, 4, 6])
```
<a name='indexing'></a>
## 2. Data indexing and selection
In this part, we learn how to get access to a part of data and modify it.
<a name='index_series'></a>
### 2.1 Data selection in Series
```
# Creating a series from NumPy array
a = np.arange(2.5, 12, 1.5)
df = pd.Series(a, index=letter_generator(len(a), False))
df
```
We can get a part of a `Series` with different methods:
- slicing
- masking
- fancy masking
For slicing, the data is accessible either with explicit indexing or implicit indexing.
```
# Explicit indexing to one element
df['a']
# Implicit indexing to one element
df[0]
# Explicit indexing
df['a': 'c']
# Explicit indexing
df[['a', 'd']]
# Masking
# Let's vreate a mask
mask = (df > 1) & (df % 2 == 0)
print("The create mask is:\n{}".format(mask))
# Index using the mask
masked = df[mask]
print("\nThe masked DataFrame is:\n{}".format(masked))
# Fancy indexing
df[[0, 3]]
```
#### Indexers, loc and iloc
Let's imagine a `Series` have integer indexing that doesn't start from zero. This can be the source of lots of confusion for explicit and implicit indexing.
```
df = pd.Series(letter_generator(5, random=False),
index=[4, 2, 3, 1, 6])
df
```
<hr>
<div>
<span style="color:#151D3B; font-weight:bold">Question: 🤔</span><p>
What's the result of
<code>df[2]</code>
Explicit indexing: 'b'
implicit indexing: 'c'
</div>
<hr>
```
# Answer
```
To avoid confusion, pandas provides some special *indexer*
- `loc`
- `iloc`
```
# loc for explicit indexing
df.loc[2]
# iloc for implicit indexing
df.iloc[2]
# Implicit slicing
df.iloc[2: 4]
# Implicit fancy indexing
df.loc[2: 1]
# Explicit fancy indexing
df.loc[[2, 4]]
```
<a name='index_df'></a>
### 2.2 Data selection in DataFrame
```
# Let's create a DataFrame
countries_list = ['China', 'India', 'US','Indonesia', 'Pakistan']
population_list = [1439323776, 1380004385, 331002651, 273523615, 220892340]
land_area_list = [9388211, 2973190, 9147420, 1811570, 770880]
density = list(map(np.divide, population_list, land_area_list))
df = pd.DataFrame({"Population": population_list,
"Land Area": land_area_list,
"Density": density},
index=countries_list)
df
```
An individual `Series` of the DataFrame can be accessed in attribute-style indexing.
```
df.Population
```
However, this might cause some confusion if DataFrame has a column with the name a reserved key. In this case, it's better to use dictionary-style indexing.
```
df['Population']
```
The other advantage of dictionary-style indexing is its functionality for picking more than one column.
```
df[['Population', 'Density']]
```
We can also use `loc` and `iloc`.
```
# Explicit indexing for DataFrame
df.loc['India', ['Population' ,'Density']]
```
<hr>
<div>
<span style="color:#151D3B; font-weight:bold">Question: 🤔</span><p>
Select the population and land area of Pakistan and India using explicit indexing.
</div>
<hr>
```
# Answer
df.loc[['Pakistan', 'India'],['Population', 'Land Area']]
# Answer using implicit indexing
df.iloc[[4, 1], [0, 1]]
```
#### Conditional indexing
```
# Get all columns based on a condition
df[df['Density'] < 120]
```
<hr>
<div>
<span style="color:#151D3B; font-weight:bold">Question: 🤔</span><p>
Get the population and land area of the countries with the density of at least twice the density of the US?
</div>
<hr>
```
# Answer
# df.loc[df['Density'] >= 2 * df.loc['US', 'Density'], ['Population', 'Land Area']]
```
$\color{red}{\text{Note:}}$
- Indexing refers to columns
- Slicing refers to rows
- Masking operations are row-wise
<a name='missing'></a>
## 3. Handling missing data
The data in the real world is rarely clean and homogenous. There are usually missing values in datasets. More complicated, there are different ways to indicate the missing data.
```
# Let's create a dataframe
population_dict = {
'China': 1439323776,
'India': 1380004385,
'US': 331002651,
'Indonesia': 273523615,
'Pakistan': 220892340,
}
land_area_dict = {
'China': 9388211,
'US': 9147420,
'Indonesia': 1811570,
'Pakistan': 770880,
'Brazil': 8358140
}
# 1. Creating Series
population = pd.Series(population_dict)
land_area = pd.Series(land_area_dict)
# 2. Combine the Series
df_missing = pd.DataFrame({'Population': population, 'Land Area': land_area})
df_missing
```
<a name='check_missing'></a>
### 3.1 Detecting the missing values
```
# Find the missing values using isna
df_missing.isna()
# Find the missing values using isnull
df_missing.isnull()
# Check the missing value
df_missing.notna()
# Number of missing values
df_missing.isnull().sum()
# Percentage of missing values
100 * df_missing.isnull().sum() / len(df_missing.isnull())
```
<a name='deal_missing'></a>
### 3.2 Dealing with missing values
Missing values can be either *ignored*, *dropped*, or *filled*.
#### Dropping
```
# Dropping the misisng values with axis = 0
df_missing.dropna()
# Dropping the misisng values with axis = 1
df_missing.dropna(axis=1)
# Dropping the misisng values with axis = 'rows'
df_missing.dropna(axis='rows')
# Drop specific column
df_missing['Population'].dropna()
df_missing
```
#### Filling
```
# Filling with a specific value
df_missing['Population'].fillna(df_missing['Population'].mean())
# Filling using forward or backward fill (ffill / bfill)
df_missing.fillna(method='ffill')
# Filling using forward or backward fill (ffill / bfill)
df_missing.fillna(method='bfill')
# Filling with axis
df_missing.fillna(method='bfill', axis='columns')
```
<a name='import'></a>
## 4. IO in pandas
Pandas has powerful functionality for dealing with different file formats. Here, we see how to import data files with CSV format or files from Excel
```
#Let's download the data
!curl -O https://raw.githubusercontent.com/AmirMardan/ml_course/main/data/house_intro_pandas.csv
!curl -O https://raw.githubusercontent.com/AmirMardan/ml_course/main/data/house_intro_pandas.xlsx
# Loading CSV file
df_csv = pd.read_csv('./house_intro_pandas.csv')
# We can use the method head() to see the five first rows of a dataframe
df_csv.head()
# Saving CSV file
df_csv.to_csv('./house_intro_pandas1.csv', index=False)
# Loading Excel file
df_xlsx = pd.read_excel('./house_intro_pandas.xlsx')
df_xlsx.head()
# Saving Excel file
df_csv.to_excel('./house_intro_pandas1.xlsx', index=False)
```
### [TOP ☝️](#top)
| true |
code
| 0.629262 | null | null | null | null |
|
# ModelList (Multi-Output) GP Regression
## Introduction
This notebook demonstrates how to wrap independent GP models into a convenient Multi-Output GP model using a ModelList.
Unlike in the Multitask case, this do not model correlations between outcomes, but treats outcomes independently. This is equivalent to setting up a separate GP for each outcome, but can be much more convenient to handle, in particular it does not require manually looping over models when fitting or predicting.
This type of model is useful if
- when the number of training / test points is different for the different outcomes
- using different covariance modules and / or likelihoods for each outcome
For block designs (i.e. when the above points do not apply), you should instead use a batch mode GP as described in the [batch independent multioutput example](./Batch_Independent_Multioutput_GP.ipynb). This will be much faster because it uses additional parallelism.
```
import math
import torch
import gpytorch
from matplotlib import pyplot as plt
%matplotlib inline
%load_ext autoreload
%autoreload 2
```
### Set up training data
In the next cell, we set up the training data for this example. We'll be using a different number of training examples for the different GPs.
```
train_x1 = torch.linspace(0, 0.95, 50) + 0.05 * torch.rand(50)
train_x2 = torch.linspace(0, 0.95, 25) + 0.05 * torch.rand(25)
train_y1 = torch.sin(train_x1 * (2 * math.pi)) + 0.2 * torch.randn_like(train_x1)
train_y2 = torch.cos(train_x2 * (2 * math.pi)) + 0.2 * torch.randn_like(train_x2)
```
## Set up the sub-models
Each individual model uses the `ExactGP` model from the [simple regression example](../01_Exact_GPs/Simple_GP_Regression.ipynb).
```
class ExactGPModel(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood):
super().__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
likelihood1 = gpytorch.likelihoods.GaussianLikelihood()
model1 = ExactGPModel(train_x1, train_y1, likelihood1)
likelihood2 = gpytorch.likelihoods.GaussianLikelihood()
model2 = ExactGPModel(train_x2, train_y2, likelihood2)
```
We now collect the submodels in an `IndependentMultiOutputGP`, and the respective likelihoods in a `MultiOutputLikelihood`. These are container modules that make it easy to work with multiple outputs. In particular, they will take in and return lists of inputs / outputs and delegate the data to / from the appropriate sub-model (it is important that the order of the inputs / outputs corresponds to the order of models with which the containers were instantiated).
```
model = gpytorch.models.IndependentModelList(model1, model2)
likelihood = gpytorch.likelihoods.LikelihoodList(model1.likelihood, model2.likelihood)
```
### Set up overall Marginal Log Likelihood
Assuming independence, the MLL for the container model is simply the sum of the MLLs for the individual models. `SumMarginalLogLikelihood` is a convenient container for this (by default it uses an `ExactMarginalLogLikelihood` for each submodel)
```
from gpytorch.mlls import SumMarginalLogLikelihood
mll = SumMarginalLogLikelihood(likelihood, model)
```
### Train the model hyperparameters
With the containers in place, the models can be trained in a single loop on the container (note that this means that optimization is performed jointly, which can be an issue if the individual submodels require training via very different step sizes).
```
# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
training_iterations = 2 if smoke_test else 50
# Find optimal model hyperparameters
model.train()
likelihood.train()
# Use the Adam optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.1) # Includes GaussianLikelihood parameters
for i in range(training_iterations):
optimizer.zero_grad()
output = model(*model.train_inputs)
loss = -mll(output, model.train_targets)
loss.backward()
print('Iter %d/%d - Loss: %.3f' % (i + 1, training_iterations, loss.item()))
optimizer.step()
```
### Make predictions with the model
```
# Set into eval mode
model.eval()
likelihood.eval()
# Initialize plots
f, axs = plt.subplots(1, 2, figsize=(8, 3))
# Make predictions (use the same test points)
with torch.no_grad(), gpytorch.settings.fast_pred_var():
test_x = torch.linspace(0, 1, 51)
# This contains predictions for both outcomes as a list
predictions = likelihood(*model(test_x, test_x))
for submodel, prediction, ax in zip(model.models, predictions, axs):
mean = prediction.mean
lower, upper = prediction.confidence_region()
tr_x = submodel.train_inputs[0].detach().numpy()
tr_y = submodel.train_targets.detach().numpy()
# Plot training data as black stars
ax.plot(tr_x, tr_y, 'k*')
# Predictive mean as blue line
ax.plot(test_x.numpy(), mean.numpy(), 'b')
# Shade in confidence
ax.fill_between(test_x.numpy(), lower.detach().numpy(), upper.detach().numpy(), alpha=0.5)
ax.set_ylim([-3, 3])
ax.legend(['Observed Data', 'Mean', 'Confidence'])
ax.set_title('Observed Values (Likelihood)')
None
```
| true |
code
| 0.795102 | null | null | null | null |
|
```
#hide
from utils import *
```
# Collaborative Filtering Deep Dive
## A First Look at the Data
```
from fastai.collab import *
from fastai.tabular.all import *
path = untar_data(URLs.ML_100k)
ratings = pd.read_csv(path/'u.data', delimiter='\t', header=None,
names=['user','movie','rating','timestamp'])
ratings.head()
last_skywalker = np.array([0.98,0.9,-0.9])
user1 = np.array([0.9,0.8,-0.6])
(user1*last_skywalker).sum()
casablanca = np.array([-0.99,-0.3,0.8])
(user1*casablanca).sum()
```
## Learning the Latent Factors
## Creating the DataLoaders
```
movies = pd.read_csv(path/'u.item', delimiter='|', encoding='latin-1',
usecols=(0,1), names=('movie','title'), header=None)
movies.head()
ratings = ratings.merge(movies)
ratings.head()
dls = CollabDataLoaders.from_df(ratings, item_name='title', bs=64)
dls.show_batch()
dls.classes
n_users = len(dls.classes['user'])
n_movies = len(dls.classes['title'])
n_factors = 5
user_factors = torch.randn(n_users, n_factors)
movie_factors = torch.randn(n_movies, n_factors)
one_hot_3 = one_hot(3, n_users).float()
user_factors.t() @ one_hot_3
user_factors[3]
```
## Collaborative Filtering from Scratch
```
class Example:
def __init__(self, a): self.a = a
def say(self,x): return f'Hello {self.a}, {x}.'
ex = Example('Sylvain')
ex.say('nice to meet you')
class DotProduct(Module):
def __init__(self, n_users, n_movies, n_factors):
self.user_factors = Embedding(n_users, n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return (users * movies).sum(dim=1)
x,y = dls.one_batch()
x.shape
model = DotProduct(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3)
class DotProduct(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0,5.5)):
self.user_factors = Embedding(n_users, n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
self.y_range = y_range
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return sigmoid_range((users * movies).sum(dim=1), *self.y_range)
model = DotProduct(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3)
class DotProductBias(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0,5.5)):
self.user_factors = Embedding(n_users, n_factors)
self.user_bias = Embedding(n_users, 1)
self.movie_factors = Embedding(n_movies, n_factors)
self.movie_bias = Embedding(n_movies, 1)
self.y_range = y_range
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
res = (users * movies).sum(dim=1, keepdim=True)
res += self.user_bias(x[:,0]) + self.movie_bias(x[:,1])
return sigmoid_range(res, *self.y_range)
model = DotProductBias(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3)
```
### Weight Decay
```
x = np.linspace(-2,2,100)
a_s = [1,2,5,10,50]
ys = [a * x**2 for a in a_s]
_,ax = plt.subplots(figsize=(8,6))
for a,y in zip(a_s,ys): ax.plot(x,y, label=f'a={a}')
ax.set_ylim([0,5])
ax.legend();
model = DotProductBias(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)
```
### Creating Our Own Embedding Module
```
class T(Module):
def __init__(self): self.a = torch.ones(3)
L(T().parameters())
class T(Module):
def __init__(self): self.a = nn.Parameter(torch.ones(3))
L(T().parameters())
class T(Module):
def __init__(self): self.a = nn.Linear(1, 3, bias=False)
t = T()
L(t.parameters())
type(t.a.weight)
def create_params(size):
return nn.Parameter(torch.zeros(*size).normal_(0, 0.01))
class DotProductBias(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0,5.5)):
self.user_factors = create_params([n_users, n_factors])
self.user_bias = create_params([n_users])
self.movie_factors = create_params([n_movies, n_factors])
self.movie_bias = create_params([n_movies])
self.y_range = y_range
def forward(self, x):
users = self.user_factors[x[:,0]]
movies = self.movie_factors[x[:,1]]
res = (users*movies).sum(dim=1)
res += self.user_bias[x[:,0]] + self.movie_bias[x[:,1]]
return sigmoid_range(res, *self.y_range)
model = DotProductBias(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)
```
## Interpreting Embeddings and Biases
```
movie_bias = learn.model.movie_bias.squeeze()
idxs = movie_bias.argsort()[:5]
[dls.classes['title'][i] for i in idxs]
idxs = movie_bias.argsort(descending=True)[:5]
[dls.classes['title'][i] for i in idxs]
g = ratings.groupby('title')['rating'].count()
top_movies = g.sort_values(ascending=False).index.values[:1000]
top_idxs = tensor([learn.dls.classes['title'].o2i[m] for m in top_movies])
movie_w = learn.model.movie_factors[top_idxs].cpu().detach()
movie_pca = movie_w.pca(3)
fac0,fac1,fac2 = movie_pca.t()
idxs = np.random.choice(len(top_movies), 50, replace=False)
idxs = list(range(50))
X = fac0[idxs]
Y = fac2[idxs]
plt.figure(figsize=(12,12))
plt.scatter(X, Y)
for i, x, y in zip(top_movies[idxs], X, Y):
plt.text(x,y,i, color=np.random.rand(3)*0.7, fontsize=11)
plt.show()
```
### Using fastai.collab
```
learn = collab_learner(dls, n_factors=50, y_range=(0, 5.5))
learn.fit_one_cycle(5, 5e-3, wd=0.1)
learn.model
movie_bias = learn.model.i_bias.weight.squeeze()
idxs = movie_bias.argsort(descending=True)[:5]
[dls.classes['title'][i] for i in idxs]
```
### Embedding Distance
```
movie_factors = learn.model.i_weight.weight
idx = dls.classes['title'].o2i['Silence of the Lambs, The (1991)']
distances = nn.CosineSimilarity(dim=1)(movie_factors, movie_factors[idx][None])
idx = distances.argsort(descending=True)[1]
dls.classes['title'][idx]
```
## Bootstrapping a Collaborative Filtering Model
## Deep Learning for Collaborative Filtering
```
embs = get_emb_sz(dls)
embs
class CollabNN(Module):
def __init__(self, user_sz, item_sz, y_range=(0,5.5), n_act=100):
self.user_factors = Embedding(*user_sz)
self.item_factors = Embedding(*item_sz)
self.layers = nn.Sequential(
nn.Linear(user_sz[1]+item_sz[1], n_act),
nn.ReLU(),
nn.Linear(n_act, 1))
self.y_range = y_range
def forward(self, x):
embs = self.user_factors(x[:,0]),self.item_factors(x[:,1])
x = self.layers(torch.cat(embs, dim=1))
return sigmoid_range(x, *self.y_range)
model = CollabNN(*embs)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.01)
learn = collab_learner(dls, use_nn=True, y_range=(0, 5.5), layers=[100,50])
learn.fit_one_cycle(5, 5e-3, wd=0.1)
@delegates(TabularModel)
class EmbeddingNN(TabularModel):
def __init__(self, emb_szs, layers, **kwargs):
super().__init__(emb_szs, layers=layers, n_cont=0, out_sz=1, **kwargs)
```
### Sidebar: kwargs and Delegates
### End sidebar
## Conclusion
## Questionnaire
1. What problem does collaborative filtering solve?
1. How does it solve it?
1. Why might a collaborative filtering predictive model fail to be a very useful recommendation system?
1. What does a crosstab representation of collaborative filtering data look like?
1. Write the code to create a crosstab representation of the MovieLens data (you might need to do some web searching!).
1. What is a latent factor? Why is it "latent"?
1. What is a dot product? Calculate a dot product manually using pure Python with lists.
1. What does `pandas.DataFrame.merge` do?
1. What is an embedding matrix?
1. What is the relationship between an embedding and a matrix of one-hot-encoded vectors?
1. Why do we need `Embedding` if we could use one-hot-encoded vectors for the same thing?
1. What does an embedding contain before we start training (assuming we're not using a pretained model)?
1. Create a class (without peeking, if possible!) and use it.
1. What does `x[:,0]` return?
1. Rewrite the `DotProduct` class (without peeking, if possible!) and train a model with it.
1. What is a good loss function to use for MovieLens? Why?
1. What would happen if we used cross-entropy loss with MovieLens? How would we need to change the model?
1. What is the use of bias in a dot product model?
1. What is another name for weight decay?
1. Write the equation for weight decay (without peeking!).
1. Write the equation for the gradient of weight decay. Why does it help reduce weights?
1. Why does reducing weights lead to better generalization?
1. What does `argsort` do in PyTorch?
1. Does sorting the movie biases give the same result as averaging overall movie ratings by movie? Why/why not?
1. How do you print the names and details of the layers in a model?
1. What is the "bootstrapping problem" in collaborative filtering?
1. How could you deal with the bootstrapping problem for new users? For new movies?
1. How can feedback loops impact collaborative filtering systems?
1. When using a neural network in collaborative filtering, why can we have different numbers of factors for movies and users?
1. Why is there an `nn.Sequential` in the `CollabNN` model?
1. What kind of model should we use if we want to add metadata about users and items, or information such as date and time, to a collaborative filtering model?
### Further Research
1. Take a look at all the differences between the `Embedding` version of `DotProductBias` and the `create_params` version, and try to understand why each of those changes is required. If you're not sure, try reverting each change to see what happens. (NB: even the type of brackets used in `forward` has changed!)
1. Find three other areas where collaborative filtering is being used, and find out what the pros and cons of this approach are in those areas.
1. Complete this notebook using the full MovieLens dataset, and compare your results to online benchmarks. See if you can improve your accuracy. Look on the book's website and the fast.ai forum for ideas. Note that there are more columns in the full dataset—see if you can use those too (the next chapter might give you ideas).
1. Create a model for MovieLens that works with cross-entropy loss, and compare it to the model in this chapter.
| true |
code
| 0.631083 | null | null | null | null |
|
# Fashion MNIST
-[Rishit Dagli](rishit.tech)
## About Me
[Twitter](https://twitter.com/rishit_dagli)
[GitHub](https://github.com/Rishit-dagli)
[Medium](https://medium.com/@rishit.dagli)
Note: Please unzip the files with the code in the cell below before you move forward
```
# !unzip /Fashion MNIST/fashionmnist.zip
```
# Some imports
```
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
import seaborn as sns
from tensorflow.keras.utils import to_categorical
from sklearn.model_selection import train_test_split
```
# Load the data
Let's now load the data using `pandas`
```
data_train = pd.read_csv('Fashion MNIST/fashion-mnist_train.csv')
data_test = pd.read_csv('Fashion MNIST/fashion-mnist_test.csv')
```
# Some preprocessing
Let's now specify the size of our image
```
img_rows, img_cols = 28, 28
input_shape = (img_rows, img_cols, 1)
```
Now we will split the feaures and labels
```
x_train = np.array(data_train.iloc[:, 1:])
y_train = np.array(data_train.iloc[:, 0])
y_train
x_test = np.array(data_test.iloc[:, 1:])
y_test = np.array(data_test.iloc[:, 0])
```
It is importnat to resize our data, we have 60000 train samples and 10000 test samples
```
x_train = x_train.reshape(60000, 28, 28, 1)
x_train = x_train / 255.0
x_test = x_test.reshape(10000, 28, 28, 1)
x_test = x_test/255.0
```
# Model
Let's define a few hyper parameters
```
num_classes = 10
epochs = 10
img_rows, img_cols = 28, 28
optimizer = 'adam'
loss = 'sparse_categorical_crossentropy'
```
And finally the model now
```
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(num_classes, activation='softmax')
])
```
You can try experimenting with different optimizers
```
model.compile(optimizer = optimizer,
loss = loss,
metrics=['accuracy'])
history = model.fit(x_train,
y_train,
epochs = epochs)
```
# Evaluating the model
Let's see the test accuracy of our model
```
test_loss, test_acc = model.evaluate(x_test,
y_test)
test_acc
```
# Seeing inside convolutions
Have fun with this code adapted from [Laurence Moroney](http://www.laurencemoroney.com/) which enables us too see an image being processed inside a CNN
```
import matplotlib.pyplot as plt
f, axarr = plt.subplots(3,4)
FIRST_IMAGE=0
SECOND_IMAGE=7
THIRD_IMAGE=26
CONVOLUTION_NUMBER = 1
from tensorflow.keras import models
layer_outputs = [layer.output for layer in model.layers]
activation_model = tf.keras.models.Model(inputs = model.input, outputs = layer_outputs)
for x in range(0,4):
f1 = activation_model.predict(x_test[FIRST_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[0,x].imshow(f1[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[0,x].grid(False)
f2 = activation_model.predict(x_test[SECOND_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[1,x].imshow(f2[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[1,x].grid(False)
f3 = activation_model.predict(x_test[THIRD_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[2,x].imshow(f3[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[2,x].grid(False)
```

```
predicted_classes = model.predict_classes(x_test)
y_true = data_test.iloc[:, 0]
correct = np.nonzero(predicted_classes==y_true)
incorrect = np.nonzero(predicted_classes!=y_true)
correct
```
A sample image
```
plt.imshow(x_test[0].reshape(28,28))
```
## Conclusion
We performed extremely well with a train accuracy of 97 % and a test of 93 % we did this in just 10 epochs which took us as low as 80 seconds to train! This is some pretty good success
| true |
code
| 0.61477 | null | null | null | null |
|
# M-Estimators for Robust Linear Modeling
```
%matplotlib inline
from __future__ import print_function
from statsmodels.compat import lmap
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import statsmodels.api as sm
```
* An M-estimator minimizes the function
$$Q(e_i, \rho) = \sum_i~\rho \left (\frac{e_i}{s}\right )$$
where $\rho$ is a symmetric function of the residuals
* The effect of $\rho$ is to reduce the influence of outliers
* $s$ is an estimate of scale.
* The robust estimates $\hat{\beta}$ are computed by the iteratively re-weighted least squares algorithm
* We have several choices available for the weighting functions to be used
```
norms = sm.robust.norms
def plot_weights(support, weights_func, xlabels, xticks):
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
ax.plot(support, weights_func(support))
ax.set_xticks(xticks)
ax.set_xticklabels(xlabels, fontsize=16)
ax.set_ylim(-.1, 1.1)
return ax
```
### Andrew's Wave
```
help(norms.AndrewWave.weights)
a = 1.339
support = np.linspace(-np.pi*a, np.pi*a, 100)
andrew = norms.AndrewWave(a=a)
plot_weights(support, andrew.weights, ['$-\pi*a$', '0', '$\pi*a$'], [-np.pi*a, 0, np.pi*a]);
```
### Hampel's 17A
```
help(norms.Hampel.weights)
c = 8
support = np.linspace(-3*c, 3*c, 1000)
hampel = norms.Hampel(a=2., b=4., c=c)
plot_weights(support, hampel.weights, ['3*c', '0', '3*c'], [-3*c, 0, 3*c]);
```
### Huber's t
```
help(norms.HuberT.weights)
t = 1.345
support = np.linspace(-3*t, 3*t, 1000)
huber = norms.HuberT(t=t)
plot_weights(support, huber.weights, ['-3*t', '0', '3*t'], [-3*t, 0, 3*t]);
```
### Least Squares
```
help(norms.LeastSquares.weights)
support = np.linspace(-3, 3, 1000)
lst_sq = norms.LeastSquares()
plot_weights(support, lst_sq.weights, ['-3', '0', '3'], [-3, 0, 3]);
```
### Ramsay's Ea
```
help(norms.RamsayE.weights)
a = .3
support = np.linspace(-3*a, 3*a, 1000)
ramsay = norms.RamsayE(a=a)
plot_weights(support, ramsay.weights, ['-3*a', '0', '3*a'], [-3*a, 0, 3*a]);
```
### Trimmed Mean
```
help(norms.TrimmedMean.weights)
c = 2
support = np.linspace(-3*c, 3*c, 1000)
trimmed = norms.TrimmedMean(c=c)
plot_weights(support, trimmed.weights, ['-3*c', '0', '3*c'], [-3*c, 0, 3*c]);
```
### Tukey's Biweight
```
help(norms.TukeyBiweight.weights)
c = 4.685
support = np.linspace(-3*c, 3*c, 1000)
tukey = norms.TukeyBiweight(c=c)
plot_weights(support, tukey.weights, ['-3*c', '0', '3*c'], [-3*c, 0, 3*c]);
```
### Scale Estimators
* Robust estimates of the location
```
x = np.array([1, 2, 3, 4, 500])
```
* The mean is not a robust estimator of location
```
x.mean()
```
* The median, on the other hand, is a robust estimator with a breakdown point of 50%
```
np.median(x)
```
* Analagously for the scale
* The standard deviation is not robust
```
x.std()
```
Median Absolute Deviation
$$ median_i |X_i - median_j(X_j)|) $$
Standardized Median Absolute Deviation is a consistent estimator for $\hat{\sigma}$
$$\hat{\sigma}=K \cdot MAD$$
where $K$ depends on the distribution. For the normal distribution for example,
$$K = \Phi^{-1}(.75)$$
```
stats.norm.ppf(.75)
print(x)
sm.robust.scale.mad(x)
np.array([1,2,3,4,5.]).std()
```
* The default for Robust Linear Models is MAD
* another popular choice is Huber's proposal 2
```
np.random.seed(12345)
fat_tails = stats.t(6).rvs(40)
kde = sm.nonparametric.KDEUnivariate(fat_tails)
kde.fit()
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
ax.plot(kde.support, kde.density);
print(fat_tails.mean(), fat_tails.std())
print(stats.norm.fit(fat_tails))
print(stats.t.fit(fat_tails, f0=6))
huber = sm.robust.scale.Huber()
loc, scale = huber(fat_tails)
print(loc, scale)
sm.robust.mad(fat_tails)
sm.robust.mad(fat_tails, c=stats.t(6).ppf(.75))
sm.robust.scale.mad(fat_tails)
```
### Duncan's Occupational Prestige data - M-estimation for outliers
```
from statsmodels.graphics.api import abline_plot
from statsmodels.formula.api import ols, rlm
prestige = sm.datasets.get_rdataset("Duncan", "car", cache=True).data
print(prestige.head(10))
fig = plt.figure(figsize=(12,12))
ax1 = fig.add_subplot(211, xlabel='Income', ylabel='Prestige')
ax1.scatter(prestige.income, prestige.prestige)
xy_outlier = prestige.loc['minister', ['income','prestige']]
ax1.annotate('Minister', xy_outlier, xy_outlier+1, fontsize=16)
ax2 = fig.add_subplot(212, xlabel='Education',
ylabel='Prestige')
ax2.scatter(prestige.education, prestige.prestige);
ols_model = ols('prestige ~ income + education', prestige).fit()
print(ols_model.summary())
infl = ols_model.get_influence()
student = infl.summary_frame()['student_resid']
print(student)
print(student.loc[np.abs(student) > 2])
print(infl.summary_frame().loc['minister'])
sidak = ols_model.outlier_test('sidak')
sidak.sort_values('unadj_p', inplace=True)
print(sidak)
fdr = ols_model.outlier_test('fdr_bh')
fdr.sort_values('unadj_p', inplace=True)
print(fdr)
rlm_model = rlm('prestige ~ income + education', prestige).fit()
print(rlm_model.summary())
print(rlm_model.weights)
```
### Hertzprung Russell data for Star Cluster CYG 0B1 - Leverage Points
* Data is on the luminosity and temperature of 47 stars in the direction of Cygnus.
```
dta = sm.datasets.get_rdataset("starsCYG", "robustbase", cache=True).data
from matplotlib.patches import Ellipse
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111, xlabel='log(Temp)', ylabel='log(Light)', title='Hertzsprung-Russell Diagram of Star Cluster CYG OB1')
ax.scatter(*dta.values.T)
# highlight outliers
e = Ellipse((3.5, 6), .2, 1, alpha=.25, color='r')
ax.add_patch(e);
ax.annotate('Red giants', xy=(3.6, 6), xytext=(3.8, 6),
arrowprops=dict(facecolor='black', shrink=0.05, width=2),
horizontalalignment='left', verticalalignment='bottom',
clip_on=True, # clip to the axes bounding box
fontsize=16,
)
# annotate these with their index
for i,row in dta.loc[dta['log.Te'] < 3.8].iterrows():
ax.annotate(i, row, row + .01, fontsize=14)
xlim, ylim = ax.get_xlim(), ax.get_ylim()
from IPython.display import Image
Image(filename='star_diagram.png')
y = dta['log.light']
X = sm.add_constant(dta['log.Te'], prepend=True)
ols_model = sm.OLS(y, X).fit()
abline_plot(model_results=ols_model, ax=ax)
rlm_mod = sm.RLM(y, X, sm.robust.norms.TrimmedMean(.5)).fit()
abline_plot(model_results=rlm_mod, ax=ax, color='red')
```
* Why? Because M-estimators are not robust to leverage points.
```
infl = ols_model.get_influence()
h_bar = 2*(ols_model.df_model + 1 )/ols_model.nobs
hat_diag = infl.summary_frame()['hat_diag']
hat_diag.loc[hat_diag > h_bar]
sidak2 = ols_model.outlier_test('sidak')
sidak2.sort_values('unadj_p', inplace=True)
print(sidak2)
fdr2 = ols_model.outlier_test('fdr_bh')
fdr2.sort_values('unadj_p', inplace=True)
print(fdr2)
```
* Let's delete that line
```
l = ax.lines[-1]
l.remove()
del l
weights = np.ones(len(X))
weights[X[X['log.Te'] < 3.8].index.values - 1] = 0
wls_model = sm.WLS(y, X, weights=weights).fit()
abline_plot(model_results=wls_model, ax=ax, color='green')
```
* MM estimators are good for this type of problem, unfortunately, we don't yet have these yet.
* It's being worked on, but it gives a good excuse to look at the R cell magics in the notebook.
```
yy = y.values[:,None]
xx = X['log.Te'].values[:,None]
%load_ext rpy2.ipython
%R library(robustbase)
%Rpush yy xx
%R mod <- lmrob(yy ~ xx);
%R params <- mod$coefficients;
%Rpull params
%R print(mod)
print(params)
abline_plot(intercept=params[0], slope=params[1], ax=ax, color='red')
```
### Exercise: Breakdown points of M-estimator
```
np.random.seed(12345)
nobs = 200
beta_true = np.array([3, 1, 2.5, 3, -4])
X = np.random.uniform(-20,20, size=(nobs, len(beta_true)-1))
# stack a constant in front
X = sm.add_constant(X, prepend=True) # np.c_[np.ones(nobs), X]
mc_iter = 500
contaminate = .25 # percentage of response variables to contaminate
all_betas = []
for i in range(mc_iter):
y = np.dot(X, beta_true) + np.random.normal(size=200)
random_idx = np.random.randint(0, nobs, size=int(contaminate * nobs))
y[random_idx] = np.random.uniform(-750, 750)
beta_hat = sm.RLM(y, X).fit().params
all_betas.append(beta_hat)
all_betas = np.asarray(all_betas)
se_loss = lambda x : np.linalg.norm(x, ord=2)**2
se_beta = lmap(se_loss, all_betas - beta_true)
```
#### Squared error loss
```
np.array(se_beta).mean()
all_betas.mean(0)
beta_true
se_loss(all_betas.mean(0) - beta_true)
```
| true |
code
| 0.729225 | null | null | null | null |
|
# Doubly Robust Models
Basically, different ensemble models that utilize a weight model to augment the outcome model.
This notebook presents different combinations of mixing outcome and propensity models,
but since the possible combination are a lot, it does not intend to show all of them.
```
%matplotlib inline
from sklearn.linear_model import LogisticRegression, LinearRegression
from causallib.datasets import load_smoking_weight
from causallib.estimation import IPW, Standardization, StratifiedStandardization
from causallib.estimation import DoublyRobustVanilla, DoublyRobustIpFeature, DoublyRobustJoffe
from causallib.evaluation import PropensityEvaluator, OutcomeEvaluator
```
#### Data:
The effect of quitting to smoke on weight loss.
Data example is taken from [Hernan and Robins Causal Inference Book](https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/)
```
data = load_smoking_weight()
data.X.join(data.a).join(data.y).head()
```
## Vanilla Doubly Robust
Used for average outcomes.
Its individual outcome estimation is directly its outcome model one's,
but for population outcome, it corrects the observed outcome using the individual outcome prediction before taking weighted average.
```
ipw = IPW(LogisticRegression(solver="liblinear"), truncate_eps=0.05)
std = StratifiedStandardization(LinearRegression())
dr = DoublyRobustVanilla(std, ipw)
dr.fit(data.X, data.a, data.y)
```
Doubly-robust corrected population outcomes:
```
pop_outcome = dr.estimate_population_outcome(data.X, data.a, data.y)
pop_outcome
effect = dr.estimate_effect(pop_outcome[1], pop_outcome[0])
effect
```
## Doubly Robust IP-Feature
Trains a weight model, and then use its output (predicted weights) as additional features to the outcome model.
If possible (like in IPW) the entire weight-matrix (weight of each individual for each treatment value) is used,
but usually, only a weight vector (according to the actual treatment assignment) is used.
```
ipw = IPW(LogisticRegression(solver="liblinear"))
std = Standardization(LinearRegression())
dr = DoublyRobustIpFeature(std, ipw)
dr.fit(data.X, data.a, data.y)
ind_outcomes = dr.estimate_individual_outcome(data.X, data.a)
ind_outcomes.head()
effect = dr.estimate_effect(ind_outcomes[1], ind_outcomes[0],
effect_types=["diff", "ratio"])
effect
```
## Doubly Robust Joffe
This uses an importance sampling using the estimated weights.
On the first step weight model is trained and used to predict weights.
These predicted weights are then provided as `sample_weights` to the outcome model.
```
ipw = IPW(LogisticRegression(solver="liblinear"))
std = Standardization(LinearRegression())
dr = DoublyRobustJoffe(std, ipw)
dr.fit(data.X, data.a, data.y)
ind_outcomes = dr.estimate_individual_outcome(data.X, data.a)
ind_outcomes.head()
pop_outcome = dr.estimate_population_outcome(data.X, data.a)
pop_outcome
effect = dr.estimate_effect(pop_outcome[1], pop_outcome[0])
effect
```
## Confounders, Instruments and Effect Modifiers
On general there are three main types of covariates in a graphical causal model:
1. Confounders: variables that affect both the outcome and treatment
2. Instruments: variables that affect the treatment assignment but not the outcome.
3. Effect mods: variables that affect the outcome but not the treatment assignment
For a Doubly Robust model that holds both outcome model and weight (treatment assignment prediction) model,
These can specified by a list of covariates `outcome_covariates` and `weight_covariates`,
which their intersection correspond to _confounders_ and their symmetric difference are the effect modifiers and instruments, respectively.
```
# Say smoke quitting does not depend on your weight and on your age
weight_covariates = [col for col in data.X.columns
if not col.startswith("wt") and not col.startswith("age")]
ipw = IPW(LogisticRegression(solver="liblinear"))
std = Standardization(LinearRegression())
dr = DoublyRobustIpFeature(std, ipw,
weight_covariates=weight_covariates)
# By not specifying `outcome_covariates` the model will use all covariates
dr.fit(data.X, data.a, data.y);
pop_outcome = dr.estimate_population_outcome(data.X, data.a)
pop_outcome
dr.estimate_effect(pop_outcome[1], pop_outcome[0])
```
## Refitting weight model
The doubly robust model has an outcome model and a weight model.
As noted, the weight model is used to augment the outcome model,
implying the outcome model is dependent on the weight model but not vice versa.
This allows us to save computation power when having a multi-outcome problem.
Since the weight model will be the same throughout, there's no need to refit it every time the model is trained for a different outcome.
The `refit_weight_model` can be turned off by providing `False`.
This way if provided with an already fitted weight model, it won't be refitted upon repeating `fit()` calls on the Doubly Robust object.
```
ipw = IPW(LogisticRegression(solver="liblinear"), truncate_eps=0.05)
std = Standardization(LinearRegression(), encode_treatment=True)
dr = DoublyRobustVanilla(std, ipw)
```
Let's imagine we have different outcomes, `y1` and `y2`.
Calling the first fit with whatever outcome will fit the weight model, as it is not fitted yet.
However, on the second call, it will not be fitted as we provide `refit_weight_model=False`.
```
y1, y2 = data.y, data.y
dr.fit(data.X, data.a, y1) # weight model is fitted since it is not yet fitted
dr.fit(data.X, data.a, y2) # weight model is fitted since we did not specify otherwise
dr.fit(data.X, data.a, y1, refit_weight_model=False); # weight model is not fitted.
```
## Evaluation
Evaluation is performed for the inner outcome model and weight model separately
```
ipw = IPW(LogisticRegression(solver="liblinear"))
std = Standardization(LinearRegression())
dr = DoublyRobustIpFeature(std, ipw)
dr.fit(data.X, data.a, data.y);
prp_evaluator = PropensityEvaluator(dr.weight_model)
results = prp_evaluator.evaluate_simple(data.X, data.a, data.y,
plots=["roc_curve", "weight_distribution"])
results.scores.prediction_scores
out_evaluator = OutcomeEvaluator(dr)
out_evaluator._regression_metrics.pop("msle") # Outcome has negative values, so log-error is not approproate
results = out_evaluator.evaluate_simple(data.X, data.a, data.y,
plots=["common_support", "continuous_accuracy"])
results.scores
```
| true |
code
| 0.708086 | null | null | null | null |
|
```
#import necessary libraries
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder
%matplotlib inline
```
### Business Understanding
As a soccer lover, I'm fascinated to explore on FIFA 18 complete player dataset. I took the dataset from Kaggle (https://www.kaggle.com/thec03u5/fifa-18-demo-player-dataset)
The dataset contains player personal attributes (such as Nationality, club, photo, age, value, etc.); Player performance attributes (Overall, Potential, Aggression, Agility) and Player preferred position and ratings at all positions
##### Project Motivation
The motivation behind the project is to study and understand the soccer players collected in FIFA 18 and analyze which Club or National Team has the best-rated players, co-relate between age and overall rating, nationality, potential, etc. and the results could add value to fantasy premier league enthusiasts. I would like to attempt the following questions to be addressed
1. Which Country has the maximum number of Soccer Players collected in FIFA 18 and List the top 20 countries?
2. What is the age distribution of the FIFA 18 Players?
3. Identify the top 10 clubs with the highest total player market value, and the highest average player wage?
4. Identify the best Squad?
5. Do Correlation between Age, Overall, Potential, Position, Club, Nationality, Special vs Value/Wage
### Data Understanding
I will use FIFA 18 Complete Player Dataset from kaggle. For this project, I will use the CompleteDataset.csv which contains all the information of the Players in FIFA 18.
```
# Read in the Complete Dataset
CompleteDataset = pd.read_csv('./CompleteDataset.csv')
CompleteDataset.head()
# Get the Basic info of the dataset
CompleteDataset.describe()
CompleteDataset.info()
num_rows = CompleteDataset.shape[0] #Provide the number of rows in the dataset
num_cols = CompleteDataset.shape[1] #Provide the number of columns in the dataset
print("Row number: {}".format(num_rows))
print("Column number: {}".format(num_cols))
# To check the column names in the dataset
CompleteDataset.columns
```
### Data Cleaning and Preparation
There are a few steps need to be adopted before using the dataset for exploration. The steps include are the following:
1. Leaving or dropping unused columns
2. Checking columns with missing values
2. Transforming string values into numbers for Value & Wage
3. One-Hot encoding for Categorical variables such as Club, Nationality, Preferred Positions etc.,
```
# Data Preparation Step 1: Drop the columns which will not be used in this project
CompleteDataset.drop('Photo', axis = 1,inplace=True)
CompleteDataset.drop('Flag', axis = 1,inplace=True)
CompleteDataset.drop('Club Logo', axis = 1,inplace=True)
CompleteDataset.drop('ID', axis = 1,inplace=True)
CompleteDataset.head()
# Data Preparation Step 2: Check whether any column has missing values
columns_with_missing_values = set(CompleteDataset.columns[CompleteDataset.isnull().mean()!=0])
print(columns_with_missing_values)
```
Coincidentally most of these columns with missing values are ratings at all positions. These columns are not used for my objectives except Club. For the club, a player with missing value in 'Club', the most likely explanation is that this player doesn't fit into any club for the moment meaning he is still vacant for transfer. Any club attentive in him may sign this player without paying any transfer fee
```
# Supporting function to convert string values into numbers
def str2number(amount):
"""
This function perform convertion from amount values in string type to float type numbers
Parameter:
amount(str): Amount values in string type with M & K as Abbreviation for Million and Thousands
Returns:
float: A float number represents the numerical value of the input parameter amount(str)
"""
if amount[-1] == 'M':
return float(amount[1:-1])*1000000
elif amount[-1] == 'K':
return float(amount[1:-1])*1000
else:
return float(amount[1:])
# Data Preparation Step 3: Convert string values into numbers for Value & Wage
# Create New Wage_Number column to store numerical type Wage info
CompleteDataset['Wage_Number'] = CompleteDataset['Wage'].map(lambda x: str2number(x))
#Create New Value_Number column to store numerical type Value info
CompleteDataset['Value_Number'] = CompleteDataset['Value'].map(lambda x: str2number(x))
# Data Preparation Step 4: One-Hot Encoding for Categorical variables such as Club, Nationality, Preferred Positions
# Select only one preferred position (first one) and stored in New 'Preferred Position' column
CompleteDataset['Preferred Position'] = CompleteDataset['Preferred Positions'].str.split().str[0]
# One-hot encode the feature: "Club" , "Nationality" and "Preferred Position"
le = LabelEncoder()
CompleteDataset['Club_onehot_encode'] = le.fit_transform(CompleteDataset['Club'].astype(str))
CompleteDataset['Nationality_onehot_encode'] = le.fit_transform(CompleteDataset['Nationality'].astype(str))
CompleteDataset['Preferred_Position_onehot_encode'] = le.fit_transform(CompleteDataset['Preferred Position'].astype(str))
```
### Addressing my objectives
Post the data cleaning and processing, I would like to attempt the key business questions jotted above
```
# 1. Which Country has the maximum number of Soccer Players collected in FIFA 18 and List the top 20 countries?
nationality_vals = CompleteDataset.Nationality.value_counts()
print(nationality_vals.head(20))
(nationality_vals.head(20)/CompleteDataset.shape[0]).plot(kind="bar");
plt.title("Top 20 FIFA 18 Players Nationality Distribution(in percentage)");
```
From the above result and plot; England, Germany, Spain, and France are the top 4 countries that have a maximum number of players in FIFA 18.
It’s sensible to see the results considering Barclays Premier League, La Liga, Bundesliga were among the 5 Football Leagues in Europe.
These leagues signify the finest football in Europe drawing maximum football stars and a lot attention, fuel soccer growth and fascination with the sports. The fifth and sixth ranking is Argentina and Brazil. My favorite players belong to Argentina and Brazil.
```
# 2. What is the age distribution of the FIFA 18 Players?
age_vals = CompleteDataset.Age.value_counts()
print(age_vals.head(20))
(age_vals.head(20)/CompleteDataset.shape[0]).plot(kind="bar");
plt.title("FIFA 18 Players Age Distribution (in percentage)");
```
It’s evident that the maximum number of players is at 25 years of age. Players older than thirty years of age are declining and it makes sense that this particular sport require more fitness versus other sports. Thus the number for players elder than 30 drops with the growth of age.
```
# 3. Identify the top clubs with the highest total player market value, and the highest average player wage?
Value_Wage_DF = CompleteDataset[["Name", "Club", "Value_Number", "Wage_Number"]]
Value_Wage_DF.head()
# Find out the top 10 clubs with the highest average wage
Value_Wage_DF.groupby("Club")["Wage_Number"].mean().sort_values(ascending=False).head(10).plot(kind="bar");
plt.title("Top 10 clubs with the highest average wage");
# Find out the top 10 clubs with the highest total player market value
Value_Wage_DF.groupby("Club")["Value_Number"].sum().sort_values(ascending=False).head(10).plot(kind="bar");
plt.title("Top 10 clubs with the highest total Value");
```
FC Barcelona, Real Madrid CF, and FC Bayern Munich are the highest-earning players comparing to any other clubs.
```
# 4. Identify the best squad
BestSquad_DF = CompleteDataset[['Name', 'Age', 'Overall', 'Potential', 'Preferred Position']]
BestSquad_DF.head()
```
I feel that the above analysis would be beneficial in choosing the best squad based on the player overall value.
I chose the best squad for two formations, Formation 4–3–3 and Formation 3–4–1–2
In addition, I remember for example in FIFA Ultimate Team Mode, the gamer needs to choose their team squad and try to collect the best players to win the matches. This sort of analytics could be potential gamechanger.
```
def find_best_squad(position):
"""
This function perform selection of the player with highest Overall Value for each provided position
Parameter:
position(str): a particular position of a certain footbal formation
Returns:
Position: The position from Input Parameter
Player: The Best Player Name for this Position
Overall: The Overall Value for this Best Player
"""
BestSquad_DF_copy = BestSquad_DF.copy()
BestSquad = []
for i in position:
BestSquad.append([i,BestSquad_DF_copy.loc[[BestSquad_DF_copy[BestSquad_DF_copy['Preferred Position'] == i]['Overall'].idxmax()]]['Name'].to_string(index = False), BestSquad_DF_copy[BestSquad_DF_copy['Preferred Position'] == i]['Overall'].max()])
BestSquad_DF_copy.drop(BestSquad_DF_copy[BestSquad_DF_copy['Preferred Position'] == i]['Overall'].idxmax(), inplace = True)
return pd.DataFrame(np.array(BestSquad).reshape(11,3), columns = ['Position', 'Player', 'Overall']).to_string(index = False)
# Formation 433
squad_Formation433 = ['GK', 'LB', 'CB', 'CB', 'RB', 'LM', 'CDM', 'RM', 'LW', 'ST', 'RW']
print ('Best Squad of Formation 4-3-3')
print (find_best_squad(squad_Formation433))
# Formation 3412
squad_Formation3412 = ['GK', 'CB', 'CB', 'CB', 'LM', 'CM', 'CM', 'RM', 'CAM', 'ST', 'ST']
print ('Best Squad of Formation 3-4-1-2')
print (find_best_squad(squad_Formation3412))
# 5. Do Correlation between Age, Overall, Potential, Position, Club, Nationality, Special vs Value/Wage
Correlation_DF = CompleteDataset[['Name', 'Age', 'Overall', 'Potential', 'Preferred_Position_onehot_encode', 'Club_onehot_encode', 'Nationality_onehot_encode', 'Special', 'Value_Number', 'Wage_Number']]
Correlation_DF.corr()
colormap = plt.cm.inferno
plt.figure(figsize=(16,12))
plt.title('Correlation between Age, Overall, Potential, Position, Club, Nationality, Special vs Value/Wage', y=1.05, size=15)
sns.heatmap(Correlation_DF.corr(),linewidths=0.1,vmax=1.0,
square=True, cmap=colormap, linecolor='white', annot=True)
```
As per the above heatmap, Overall and Potential are positively related to Wage & Value. Special have positive correlation as well with Wage & Value.
On the other side Club, Nationality and Position are not so important characteristic features that co-relate with Wage & Value.
Besides that, additionally found that Wage and Value are highly correlated to each other which is quite rational.
| true |
code
| 0.547283 | null | null | null | null |
|
#RepresentationSpace - Discovering Interpretable GAN Controls for Architectural Image Synthesis
Using [Ganspace]( https://github.com/armaank/archlectures/ganspace) to find latent directions in a StyleGAN2 model trained trained on the [ArchML dataset](http://165.227.182.79/)
## Instructions and Setup
1) Click the play button of the blocks titled "Initialization" and wait for it to finish the initialization.
2) In the Run PCA Analysis section, choose a model, the number of PCA components and the intermediate network layer in the 'Model Specification' cell. Then click the play button to run. The defaults are ok as is. This block will take a while (~5-10 mins) to run.
3) In the Explore Directions block, generate samples, play with the sliders, and name what you find. In the next block, compare the directions and generate videos.
```
%%capture
#@title Initialization - Setup
# Clone git
%tensorflow_version 1.x
%rm -rf archlectures
!git clone https://github.com/armaank/archlectures
%cd archlectures/generative/
%ls
#@title Initialization - Download Models
%%capture
%%sh
chmod 755 get_models.sh
./get_models.sh
ls
#@title Initilization - Install Requirements
%%capture
from IPython.display import Javascript
display(Javascript('''google.colab.output.setIframeHeight(0, true, {maxHeight: 200})'''))
!pip install fbpca boto3
!git submodule update --init --recursive
!python -c "import nltk; nltk.download('wordnet')"
%cd ./ganspace/
from IPython.utils import io
import torch
import PIL
import numpy as np
import ipywidgets as widgets
from PIL import Image
import imageio
from models import get_instrumented_model
from decomposition import get_or_compute
from config import Config
from skimage import img_as_ubyte
# Speed up computation
torch.autograd.set_grad_enabled(False)
torch.backends.cudnn.benchmark = True
# Custom OPs no longer required
#!pip install Ninja
#%cd models/stylegan2/stylegan2-pytorch/op
#!python setup.py install
#!python -c "import torch; import upfirdn2d_op; import fused; print('OK')"
#%cd "/content/ganspace"
```
## Run PCA Analysis
```
#@title Model Specification
model = "Adaily_B" #@param ["Adaily_A", "Adaily_B"]
num_components = 80#@param {type:"number"}
layer = 'style'#@param ["style","input","convs","upsamples","noises"]
model_class = model # this is the name of model
model_name = 'StyleGAN2'
!python visualize.py --model $model_name --class $model_class --use_w --layer=style -c $num_components
```
## Explore RepresentationSpace
After running the previous cell, your components will be stored in an npz file in `/content/ganspace/cache/components/` - below the npz file is unpacked, and a component/direction is chosen at random.
Using the UI, you can explore the latent direction and give it a name, which will be appeneded to the named_directions dictionary and saved as `direction_name.npy` for later use.
The variable `seed` controls the starting image
The `Truncation` slider controls the quality of the image sample, .7 is a good starting point
`Distance` is the main slider, it controls the strength/emphasis of the component
`start layer` and `end layer` control the number of layers used in the calculations, using all of them (0, 18) is a good start
```
#@title Load Model
config = Config(
model='StyleGAN2',
layer=layer,
output_class=model_class,
components=num_components,
use_w=True,
batch_size=5_000, # style layer quite small
)
inst = get_instrumented_model(config.model, config.output_class,
config.layer, torch.device('cuda'), use_w=config.use_w)
path_to_components = get_or_compute(config, inst)
model = inst.model
named_directions = {} #init named_directions dict to save directions
comps = np.load(path_to_components)
lst = comps.files
latent_dirs = []
latent_stdevs = []
load_activations = False
for item in lst:
if load_activations:
if item == 'act_comp':
for i in range(comps[item].shape[0]):
latent_dirs.append(comps[item][i])
if item == 'act_stdev':
for i in range(comps[item].shape[0]):
latent_stdevs.append(comps[item][i])
else:
if item == 'lat_comp':
for i in range(comps[item].shape[0]):
latent_dirs.append(comps[item][i])
if item == 'lat_stdev':
for i in range(comps[item].shape[0]):
latent_stdevs.append(comps[item][i])
#@title Load Random Component
#load one at random
num = np.random.randint(20)
if num in named_directions.values():
print(f'Direction already named: {list(named_directions.keys())[list(named_directions.values()).index(num)]}')
random_dir = latent_dirs[num]
random_dir_stdev = latent_stdevs[num]
print(f'Loaded Component No. {num}')
#@title Run UI (save component with Enter key)
from ipywidgets import fixed
# Taken from https://github.com/alexanderkuk/log-progress
def log_progress(sequence, every=1, size=None, name='Items'):
from ipywidgets import IntProgress, HTML, VBox
from IPython.display import display
is_iterator = False
if size is None:
try:
size = len(sequence)
except TypeError:
is_iterator = True
if size is not None:
if every is None:
if size <= 200:
every = 1
else:
every = int(size / 200) # every 0.5%
else:
assert every is not None, 'sequence is iterator, set every'
if is_iterator:
progress = IntProgress(min=0, max=1, value=1)
progress.bar_style = 'info'
else:
progress = IntProgress(min=0, max=size, value=0)
label = HTML()
box = VBox(children=[label, progress])
display(box)
index = 0
try:
for index, record in enumerate(sequence, 1):
if index == 1 or index % every == 0:
if is_iterator:
label.value = '{name}: {index} / ?'.format(
name=name,
index=index
)
else:
progress.value = index
label.value = u'{name}: {index} / {size}'.format(
name=name,
index=index,
size=size
)
yield record
except:
progress.bar_style = 'danger'
raise
else:
progress.bar_style = 'success'
progress.value = index
label.value = "{name}: {index}".format(
name=name,
index=str(index or '?')
)
def name_direction(sender):
if not text.value:
print('Please name the direction before saving')
return
if num in named_directions.values():
target_key = list(named_directions.keys())[list(named_directions.values()).index(num)]
print(f'Direction already named: {target_key}')
print(f'Overwriting... ')
del(named_directions[target_key])
named_directions[text.value] = [num, start_layer.value, end_layer.value]
save_direction(random_dir, text.value)
for item in named_directions:
print(item, named_directions[item])
def save_direction(direction, filename):
filename += ".npy"
np.save(filename, direction, allow_pickle=True, fix_imports=True)
print(f'Latent direction saved as {filename}')
def display_sample_pytorch(seed, truncation, direction, distance, start, end, disp=True, save=None, noise_spec=None, scale=2,):
# blockPrint()
with io.capture_output() as captured:
w = model.sample_latent(1, seed=seed).cpu().numpy()
model.truncation = truncation
w = [w]*model.get_max_latents() # one per layer
for l in range(start, end):
w[l] = w[l] + direction * distance * scale
#save image and display
out = model.sample_np(w)
final_im = Image.fromarray((out * 255).astype(np.uint8)).resize((500,500),Image.LANCZOS)
if disp:
display(final_im)
if save is not None:
if disp == False:
print(save)
final_im.save(f'out/{seed}_{save:05}.png')
def generate_mov(seed, truncation, direction_vec, layers, n_frames, out_name = 'out', scale = 2, noise_spec = None, loop=True):
"""Generates a mov moving back and forth along the chosen direction vector"""
# Example of reading a generated set of images, and storing as MP4.
%mkdir out
movieName = f'out/{out_name}.mp4'
offset = -10
step = 20 / n_frames
imgs = []
for i in log_progress(range(n_frames), name = "Generating frames"):
print(f'\r{i} / {n_frames}', end='')
w = model.sample_latent(1, seed=seed).cpu().numpy()
model.truncation = truncation
w = [w]*model.get_max_latents() # one per layer
for l in layers:
if l <= model.get_max_latents():
w[l] = w[l] + direction_vec * offset * scale
#save image and display
out = model.sample_np(w)
final_im = Image.fromarray((out * 255).astype(np.uint8))
imgs.append(out)
#increase offset
offset += step
if loop:
imgs += imgs[::-1]
with imageio.get_writer(movieName, mode='I') as writer:
for image in log_progress(list(imgs), name = "Creating animation"):
writer.append_data(img_as_ubyte(image))
seed = np.random.randint(0,100000)
style = {'description_width': 'initial'}
seed = widgets.IntSlider(min=0, max=100000, step=1, value=seed, description='Seed: ', continuous_update=False)
truncation = widgets.FloatSlider(min=0, max=2, step=0.1, value=0.7, description='Truncation: ', continuous_update=False)
distance = widgets.FloatSlider(min=-10, max=10, step=0.1, value=0, description='Distance: ', continuous_update=False, style=style)
# scale = widgets.FloatSlider(min=0, max=10, step=0.05, value=1, description='Scale: ', continuous_update=False)
start_layer = widgets.IntSlider(min=0, max=model.get_max_latents(), step=1, value=0, description='start layer: ', continuous_update=False)
end_layer = widgets.IntSlider(min=0, max=model.get_max_latents(), step=1, value=18, description='end layer: ', continuous_update=False)
# Make sure layer range is valid
def update_range_start(*args):
end_layer.min = start_layer.value
def update_range_end(*args):
start_layer.max = end_layer.value
start_layer.observe(update_range_start, 'value')
end_layer.observe(update_range_end, 'value')
text = widgets.Text(description="Name component here", style=style, width=200)
bot_box = widgets.HBox([seed, truncation, distance, start_layer, end_layer, text])
ui = widgets.VBox([bot_box])
out = widgets.interactive_output(display_sample_pytorch, {'seed': seed, 'truncation': truncation, 'direction': fixed(random_dir), 'distance': distance,'start': start_layer, 'end': end_layer})
display(ui, out)
text.on_submit(name_direction)
#@title Select from named directions
from IPython.display import display, clear_output
vardict = list(named_directions.keys())
select_variable = widgets.Dropdown(
options=vardict,
value=vardict[0],
description='Select variable:',
disabled=False,
button_style=''
)
def set_direction(b):
clear_output()
random_dir = latent_dirs[named_directions[select_variable.value][0]]
start_layer = named_directions[select_variable.value][1]
end_layer = named_directions[select_variable.value][2]
print(start_layer, end_layer)
out = widgets.interactive_output(display_sample_pytorch, {'seed': seed, 'truncation': truncation, 'direction': fixed(random_dir), 'distance': distance, 'scale': scale, 'start': fixed(start_layer), 'end': fixed(end_layer)})
display(select_variable)
display(ui, out)
random_dir = latent_dirs[named_directions[select_variable.value][0]]
start_layer = named_directions[select_variable.value][1]
end_layer = named_directions[select_variable.value][2]
seed = np.random.randint(0,100000)
style = {'description_width': 'initial'}
seed = widgets.IntSlider(min=0, max=100000, step=1, value=seed, description='Seed: ', continuous_update=False)
truncation = widgets.FloatSlider(min=0, max=2, step=0.1, value=0.7, description='Truncation: ', continuous_update=False)
distance = widgets.FloatSlider(min=-10, max=10, step=0.1, value=0, description='Distance: ', continuous_update=False, style=style)
scale = widgets.FloatSlider(min=0, max=10, step=0.05, value=1, description='Scale: ', continuous_update=False)
bot_box = widgets.HBox([seed, truncation, distance])
ui = widgets.VBox([bot_box])
out = widgets.interactive_output(display_sample_pytorch, {'seed': seed, 'truncation': truncation, 'direction': fixed(random_dir), 'distance': distance, 'scale': scale, 'start': fixed(start_layer), 'end': fixed(end_layer)})
display(select_variable)
display(ui, out)
select_variable.observe(set_direction, names='value')
#@title Generate Video from Representation (Optional)
direction_name = "c" #@param {type:"string"}
num_frames = 5 #@param {type:"number"}
truncation = 0.8 #@param {type:"number"}
num_samples = num_frames
assert direction_name in named_directions, \
f'"{direction_name}" not found, please save it first using the cell above.'
loc = named_directions[direction_name][0]
for i in range(num_samples):
s = np.random.randint(0, 10000)
generate_mov(seed = s, truncation = 0.8, direction_vec = latent_dirs[loc], scale = 2, layers=range(named_directions[direction_name][1], named_directions[direction_name][2]), n_frames = 20, out_name = f'{model_class}_{direction_name}_{i}', loop=True)
print('Video saved to ./ganspace/out/')
```
| true |
code
| 0.475971 | null | null | null | null |
|
# Representing Qubit States
You now know something about bits, and about how our familiar digital computers work. All the complex variables, objects and data structures used in modern software are basically all just big piles of bits. Those of us who work on quantum computing call these *classical variables.* The computers that use them, like the one you are using to read this article, we call *classical computers*.
In quantum computers, our basic variable is the _qubit:_ a quantum variant of the bit. These have exactly the same restrictions as normal bits do: they can store only a single binary piece of information, and can only ever give us an output of `0` or `1`. However, they can also be manipulated in ways that can only be described by quantum mechanics. This gives us new gates to play with, allowing us to find new ways to design algorithms.
To fully understand these new gates, we first need to understand how to write down qubit states. For this we will use the mathematics of vectors, matrices, and complex numbers. Though we will introduce these concepts as we go, it would be best if you are comfortable with them already. If you need a more in-depth explanation or a refresher, you can find the guide [here](../ch-prerequisites/linear_algebra.html).
## Contents
1. [Classical vs Quantum Bits](#cvsq)
1.1 [Statevectors](#statevectors)
1.2 [Qubit Notation](#notation)
1.3 [Exploring Qubits with Qiskit](#exploring-qubits)
2. [The Rules of Measurement](#rules-measurement)
2.1 [A Very Important Rule](#important-rule)
2.2 [The Implications of this Rule](#implications)
3. [The Bloch Sphere](#bloch-sphere)
3.1 [Describing the Restricted Qubit State](#bloch-sphere-1)
3.2 [Visually Representing a Qubit State](#bloch-sphere-2)
## 1. Classical vs Quantum Bits <a id="cvsq"></a>
### 1.1 Statevectors<a id="statevectors"></a>
In quantum physics we use _statevectors_ to describe the state of our system. Say we wanted to describe the position of a car along a track, this is a classical system so we could use a number $x$:

$$ x=4 $$
Alternatively, we could instead use a collection of numbers in a vector called a _statevector._ Each element in the statevector contains the probability of finding the car in a certain place:

$$
|x\rangle = \begin{bmatrix} 0\\ \vdots \\ 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}
\begin{matrix} \\ \\ \\ \leftarrow \\ \\ \\ \\ \end{matrix}
\begin{matrix} \\ \\ \text{Probability of} \\ \text{car being at} \\ \text{position 4} \\ \\ \\ \end{matrix}
$$
This isn’t limited to position, we could also keep a statevector of all the possible speeds the car could have, and all the possible colours the car could be. With classical systems (like the car example above), this is a silly thing to do as it requires keeping huge vectors when we only really need one number. But as we will see in this chapter, statevectors happen to be a very good way of keeping track of quantum systems, including quantum computers.
### 1.2 Qubit Notation <a id="notation"></a>
Classical bits always have a completely well-defined state: they are either `0` or `1` at every point during a computation. There is no more detail we can add to the state of a bit than this. So to write down the state of a of classical bit (`c`), we can just use these two binary values. For example:
c = 0
This restriction is lifted for quantum bits. Whether we get a `0` or a `1` from a qubit only needs to be well-defined when a measurement is made to extract an output. At that point, it must commit to one of these two options. At all other times, its state will be something more complex than can be captured by a simple binary value.
To see how to describe these, we can first focus on the two simplest cases. As we saw in the last section, it is possible to prepare a qubit in a state for which it definitely gives the outcome `0` when measured.
We need a name for this state. Let's be unimaginative and call it $0$ . Similarly, there exists a qubit state that is certain to output a `1`. We'll call this $1$. These two states are completely mutually exclusive. Either the qubit definitely outputs a ```0```, or it definitely outputs a ```1```. There is no overlap. One way to represent this with mathematics is to use two orthogonal vectors.
$$
|0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \, \, \, \, |1\rangle =\begin{bmatrix} 0 \\ 1 \end{bmatrix}.
$$
This is a lot of notation to take in all at once. First, let's unpack the weird $|$ and $\rangle$. Their job is essentially just to remind us that we are talking about the vectors that represent qubit states labelled $0$ and $1$. This helps us distinguish them from things like the bit values ```0``` and ```1``` or the numbers 0 and 1. It is part of the bra-ket notation, introduced by Dirac.
If you are not familiar with vectors, you can essentially just think of them as lists of numbers which we manipulate using certain rules. If you are familiar with vectors from your high school physics classes, you'll know that these rules make vectors well-suited for describing quantities with a magnitude and a direction. For example, the velocity of an object is described perfectly with a vector. However, the way we use vectors for quantum states is slightly different to this, so don't hold on too hard to your previous intuition. It's time to do something new!
With vectors we can describe more complex states than just $|0\rangle$ and $|1\rangle$. For example, consider the vector
$$
|q_0\rangle = \begin{bmatrix} \tfrac{1}{\sqrt{2}} \\ \tfrac{i}{\sqrt{2}} \end{bmatrix} .
$$
To understand what this state means, we'll need to use the mathematical rules for manipulating vectors. Specifically, we'll need to understand how to add vectors together and how to multiply them by scalars.
<p>
<details>
<summary>Reminder: Matrix Addition and Multiplication by Scalars (Click here to expand)</summary>
<p>To add two vectors, we add their elements together:
$$|a\rangle = \begin{bmatrix}a_0 \\ a_1 \\ \vdots \\ a_n \end{bmatrix}, \quad
|b\rangle = \begin{bmatrix}b_0 \\ b_1 \\ \vdots \\ b_n \end{bmatrix}$$
$$|a\rangle + |b\rangle = \begin{bmatrix}a_0 + b_0 \\ a_1 + b_1 \\ \vdots \\ a_n + b_n \end{bmatrix} $$
</p>
<p>And to multiply a vector by a scalar, we multiply each element by the scalar:
$$x|a\rangle = \begin{bmatrix}x \times a_0 \\ x \times a_1 \\ \vdots \\ x \times a_n \end{bmatrix}$$
</p>
<p>These two rules are used to rewrite the vector $|q_0\rangle$ (as shown above):
$$
\begin{aligned}
|q_0\rangle & = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle \\
& = \tfrac{1}{\sqrt{2}}\begin{bmatrix}1\\0\end{bmatrix} + \tfrac{i}{\sqrt{2}}\begin{bmatrix}0\\1\end{bmatrix}\\
& = \begin{bmatrix}\tfrac{1}{\sqrt{2}}\\0\end{bmatrix} + \begin{bmatrix}0\\\tfrac{i}{\sqrt{2}}\end{bmatrix}\\
& = \begin{bmatrix}\tfrac{1}{\sqrt{2}} \\ \tfrac{i}{\sqrt{2}} \end{bmatrix}\\
\end{aligned}
$$
</details>
</p>
<p>
<details>
<summary>Reminder: Orthonormal Bases (Click here to expand)</summary>
<p>
It was stated before that the two vectors $|0\rangle$ and $|1\rangle$ are orthonormal, this means they are both <i>orthogonal</i> and <i>normalised</i>. Orthogonal means the vectors are at right angles:
</p><p><img src="images/basis.svg"></p>
<p>And normalised means their magnitudes (length of the arrow) is equal to 1. The two vectors $|0\rangle$ and $|1\rangle$ are <i>linearly independent</i>, which means we cannot describe $|0\rangle$ in terms of $|1\rangle$, and vice versa. However, using both the vectors $|0\rangle$ and $|1\rangle$, and our rules of addition and multiplication by scalars, we can describe all possible vectors in 2D space:
</p><p><img src="images/basis2.svg"></p>
<p>Because the vectors $|0\rangle$ and $|1\rangle$ are linearly independent, and can be used to describe any vector in 2D space using vector addition and scalar multiplication, we say the vectors $|0\rangle$ and $|1\rangle$ form a <i>basis</i>. In this case, since they are both orthogonal and normalised, we call it an <i>orthonormal basis</i>.
</details>
</p>
Since the states $|0\rangle$ and $|1\rangle$ form an orthonormal basis, we can represent any 2D vector with a combination of these two states. This allows us to write the state of our qubit in the alternative form:
$$ |q_0\rangle = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle $$
This vector, $|q_0\rangle$ is called the qubit's _statevector,_ it tells us everything we could possibly know about this qubit. For now, we are only able to draw a few simple conclusions about this particular example of a statevector: it is not entirely $|0\rangle$ and not entirely $|1\rangle$. Instead, it is described by a linear combination of the two. In quantum mechanics, we typically describe linear combinations such as this using the word 'superposition'.
Though our example state $|q_0\rangle$ can be expressed as a superposition of $|0\rangle$ and $|1\rangle$, it is no less a definite and well-defined qubit state than they are. To see this, we can begin to explore how a qubit can be manipulated.
### 1.3 Exploring Qubits with Qiskit <a id="exploring-qubits"></a>
First, we need to import all the tools we will need:
```
from qiskit import QuantumCircuit, assemble, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi
```
In Qiskit, we use the `QuantumCircuit` object to store our circuits, this is essentially a list of the quantum operations on our circuit and the qubits they are applied to.
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
```
In our quantum circuits, our qubits always start out in the state $|0\rangle$. We can use the `initialize()` method to transform this into any state. We give `initialize()` the vector we want in the form of a list, and tell it which qubit(s) we want to initialise in this state:
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
initial_state = [0,1] # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
qc.draw() # Let's view our circuit
```
We can then use one of Qiskit’s simulators to view the resulting state of our qubit. To begin with we will use the statevector simulator, but we will explain the different simulators and their uses later.
```
svsim = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit
```
To get the results from our circuit, we use `execute` to run our circuit, giving the circuit and the backend as arguments. We then use `.result()` to get the result of this:
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
initial_state = [0,1] # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
qobj = assemble(qc) # Create a Qobj from the circuit for the simulator to run
result = svsim.run(qobj).result() # Do the simulation and return the result
```
from `result`, we can then get the final statevector using `.get_statevector()`:
```
out_state = result.get_statevector()
print(out_state) # Display the output state vector
```
**Note:** Python uses `j` to represent $i$ in complex numbers. We see a vector with two complex elements: `0.+0.j` = 0, and `1.+0.j` = 1.
Let’s now measure our qubit as we would in a real quantum computer and see the result:
```
qc.measure_all()
qc.draw()
```
This time, instead of the statevector we will get the counts for the `0` and `1` results using `.get_counts()`:
```
qobj = assemble(qc)
result = svsim.run(qobj).result()
counts = result.get_counts()
plot_histogram(counts)
```
We can see that we (unsurprisingly) have a 100% chance of measuring $|1\rangle$. This time, let’s instead put our qubit into a superposition and see what happens. We will use the state $|q_0\rangle$ from earlier in this section:
$$ |q_0\rangle = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle $$
We need to add these amplitudes to a python list. To add a complex amplitude, Python uses `j` for the imaginary unit (we normally call it "$i$" mathematically):
```
initial_state = [1/sqrt(2), 1j/sqrt(2)] # Define state |q_0>
```
And we then repeat the steps for initialising the qubit as before:
```
qc = QuantumCircuit(1) # Must redefine qc
qc.initialize(initial_state, 0) # Initialise the 0th qubit in the state `initial_state`
qobj = assemble(qc)
state = svsim.run(qobj).result().get_statevector() # Execute the circuit
print(state) # Print the result
qobj = assemble(qc)
results = svsim.run(qobj).result().get_counts()
plot_histogram(results)
```
We can see we have equal probability of measuring either $|0\rangle$ or $|1\rangle$. To explain this, we need to talk about measurement.
## 2. The Rules of Measurement <a id="rules-measurement"></a>
### 2.1 A Very Important Rule <a id="important-rule"></a>
There is a simple rule for measurement. To find the probability of measuring a state $|\psi \rangle$ in the state $|x\rangle$ we do:
$$p(|x\rangle) = | \langle x| \psi \rangle|^2$$
The symbols $\langle$ and $|$ tell us $\langle x |$ is a row vector. In quantum mechanics we call the column vectors _kets_ and the row vectors _bras._ Together they make up _bra-ket_ notation. Any ket $|a\rangle$ has a corresponding bra $\langle a|$, and we convert between them using the conjugate transpose.
<details>
<summary>Reminder: The Inner Product (Click here to expand)</summary>
<p>There are different ways to multiply vectors, here we use the <i>inner product</i>. The inner product is a generalisation of the <i>dot product</i> which you may already be familiar with. In this guide, we use the inner product between a bra (row vector) and a ket (column vector), and it follows this rule:
$$\langle a| = \begin{bmatrix}a_0^*, & a_1^*, & \dots & a_n^* \end{bmatrix}, \quad
|b\rangle = \begin{bmatrix}b_0 \\ b_1 \\ \vdots \\ b_n \end{bmatrix}$$
$$\langle a|b\rangle = a_0^* b_0 + a_1^* b_1 \dots a_n^* b_n$$
</p>
<p>We can see that the inner product of two vectors always gives us a scalar. A useful thing to remember is that the inner product of two orthogonal vectors is 0, for example if we have the orthogonal vectors $|0\rangle$ and $|1\rangle$:
$$\langle1|0\rangle = \begin{bmatrix} 0 , & 1\end{bmatrix}\begin{bmatrix}1 \\ 0\end{bmatrix} = 0$$
</p>
<p>Additionally, remember that the vectors $|0\rangle$ and $|1\rangle$ are also normalised (magnitudes are equal to 1):
$$
\begin{aligned}
\langle0|0\rangle & = \begin{bmatrix} 1 , & 0\end{bmatrix}\begin{bmatrix}1 \\ 0\end{bmatrix} = 1 \\
\langle1|1\rangle & = \begin{bmatrix} 0 , & 1\end{bmatrix}\begin{bmatrix}0 \\ 1\end{bmatrix} = 1
\end{aligned}
$$
</p>
</details>
In the equation above, $|x\rangle$ can be any qubit state. To find the probability of measuring $|x\rangle$, we take the inner product of $|x\rangle$ and the state we are measuring (in this case $|\psi\rangle$), then square the magnitude. This may seem a little convoluted, but it will soon become second nature.
If we look at the state $|q_0\rangle$ from before, we can see the probability of measuring $|0\rangle$ is indeed $0.5$:
$$
\begin{aligned}
|q_0\rangle & = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle \\
\langle 0| q_0 \rangle & = \tfrac{1}{\sqrt{2}}\langle 0|0\rangle + \tfrac{i}{\sqrt{2}}\langle 0|1\rangle \\
& = \tfrac{1}{\sqrt{2}}\cdot 1 + \tfrac{i}{\sqrt{2}} \cdot 0\\
& = \tfrac{1}{\sqrt{2}}\\
|\langle 0| q_0 \rangle|^2 & = \tfrac{1}{2}
\end{aligned}
$$
You should verify the probability of measuring $|1\rangle$ as an exercise.
This rule governs how we get information out of quantum states. It is therefore very important for everything we do in quantum computation. It also immediately implies several important facts.
### 2.2 The Implications of this Rule <a id="implications"></a>
### #1 Normalisation
The rule shows us that amplitudes are related to probabilities. If we want the probabilities to add up to 1 (which they should!), we need to ensure that the statevector is properly normalized. Specifically, we need the magnitude of the state vector to be 1.
$$ \langle\psi|\psi\rangle = 1 \\ $$
Thus if:
$$ |\psi\rangle = \alpha|0\rangle + \beta|1\rangle $$
Then:
$$ \sqrt{|\alpha|^2 + |\beta|^2} = 1 $$
This explains the factors of $\sqrt{2}$ you have seen throughout this chapter. In fact, if we try to give `initialize()` a vector that isn’t normalised, it will give us an error:
```
vector = [1,1]
qc.initialize(vector, 0)
```
#### Quick Exercise
1. Create a state vector that will give a $1/3$ probability of measuring $|0\rangle$.
2. Create a different state vector that will give the same measurement probabilities.
3. Verify that the probability of measuring $|1\rangle$ for these two states is $2/3$.
You can check your answer in the widget below (accepts answers ±1% accuracy, you can use numpy terms such as '`pi`' and '`sqrt()`' in the vector):
```
# Run the code in this cell to interact with the widget
from qiskit_textbook.widgets import state_vector_exercise
state_vector_exercise(target=1/3)
```
### #2 Alternative measurement
The measurement rule gives us the probability $p(|x\rangle)$ that a state $|\psi\rangle$ is measured as $|x\rangle$. Nowhere does it tell us that $|x\rangle$ can only be either $|0\rangle$ or $|1\rangle$.
The measurements we have considered so far are in fact only one of an infinite number of possible ways to measure a qubit. For any orthogonal pair of states, we can define a measurement that would cause a qubit to choose between the two.
This possibility will be explored more in the next section. For now, just bear in mind that $|x\rangle$ is not limited to being simply $|0\rangle$ or $|1\rangle$.
### #3 Global Phase
We know that measuring the state $|1\rangle$ will give us the output `1` with certainty. But we are also able to write down states such as
$$\begin{bmatrix}0 \\ i\end{bmatrix} = i|1\rangle.$$
To see how this behaves, we apply the measurement rule.
$$ |\langle x| (i|1\rangle) |^2 = | i \langle x|1\rangle|^2 = |\langle x|1\rangle|^2 $$
Here we find that the factor of $i$ disappears once we take the magnitude of the complex number. This effect is completely independent of the measured state $|x\rangle$. It does not matter what measurement we are considering, the probabilities for the state $i|1\rangle$ are identical to those for $|1\rangle$. Since measurements are the only way we can extract any information from a qubit, this implies that these two states are equivalent in all ways that are physically relevant.
More generally, we refer to any overall factor $\gamma$ on a state for which $|\gamma|=1$ as a 'global phase'. States that differ only by a global phase are physically indistinguishable.
$$ |\langle x| ( \gamma |a\rangle) |^2 = | \gamma \langle x|a\rangle|^2 = |\langle x|a\rangle|^2 $$
Note that this is distinct from the phase difference _between_ terms in a superposition, which is known as the 'relative phase'. This becomes relevant once we consider different types of measurement and multiple qubits.
### #4 The Observer Effect
We know that the amplitudes contain information about the probability of us finding the qubit in a specific state, but once we have measured the qubit, we know with certainty what the state of the qubit is. For example, if we measure a qubit in the state:
$$ |q\rangle = \alpha|0\rangle + \beta|1\rangle$$
And find it in the state $|0\rangle$, if we measure again, there is a 100% chance of finding the qubit in the state $|0\rangle$. This means the act of measuring _changes_ the state of our qubits.
$$ |q\rangle = \begin{bmatrix} \alpha \\ \beta \end{bmatrix} \xrightarrow{\text{Measure }|0\rangle} |q\rangle = |0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$$
We sometimes refer to this as _collapsing_ the state of the qubit. It is a potent effect, and so one that must be used wisely. For example, were we to constantly measure each of our qubits to keep track of their value at each point in a computation, they would always simply be in a well-defined state of either $|0\rangle$ or $|1\rangle$. As such, they would be no different from classical bits and our computation could be easily replaced by a classical computation. To achieve truly quantum computation we must allow the qubits to explore more complex states. Measurements are therefore only used when we need to extract an output. This means that we often place all the measurements at the end of our quantum circuit.
We can demonstrate this using Qiskit’s statevector simulator. Let's initialise a qubit in superposition:
```
qc = QuantumCircuit(1) # We are redefining qc
initial_state = [0.+1.j/sqrt(2),1/sqrt(2)+0.j]
qc.initialize(initial_state, 0)
qc.draw()
```
This should initialise our qubit in the state:
$$ |q\rangle = \tfrac{i}{\sqrt{2}}|0\rangle + \tfrac{1}{\sqrt{2}}|1\rangle $$
We can verify this using the simulator:
```
qobj = assemble(qc)
state = svsim.run(qobj).result().get_statevector()
print("Qubit State = " + str(state))
```
We can see here the qubit is initialised in the state `[0.+0.70710678j 0.70710678+0.j]`, which is the state we expected.
Let’s now measure this qubit:
```
qc.measure_all()
qc.draw()
```
When we simulate this entire circuit, we can see that one of the amplitudes is _always_ 0:
```
qobj = assemble(qc)
state = svsim.run(qobj).result().get_statevector()
print("State of Measured Qubit = " + str(state))
```
You can re-run this cell a few times to reinitialise the qubit and measure it again. You will notice that either outcome is equally probable, but that the state of the qubit is never a superposition of $|0\rangle$ and $|1\rangle$. Somewhat interestingly, the global phase on the state $|0\rangle$ survives, but since this is global phase, we can never measure it on a real quantum computer.
### A Note about Quantum Simulators
We can see that writing down a qubit’s state requires keeping track of two complex numbers, but when using a real quantum computer we will only ever receive a yes-or-no (`0` or `1`) answer for each qubit. The output of a 10-qubit quantum computer will look like this:
`0110111110`
Just 10 bits, no superposition or complex amplitudes. When using a real quantum computer, we cannot see the states of our qubits mid-computation, as this would destroy them! This behaviour is not ideal for learning, so Qiskit provides different quantum simulators: The `qasm_simulator` behaves as if you are interacting with a real quantum computer, and will not allow you to use `.get_statevector()`. Alternatively, `statevector_simulator`, (which we have been using in this chapter) does allow peeking at the quantum states before measurement, as we have seen.
## 3. The Bloch Sphere <a id="bloch-sphere"></a>
### 3.1 Describing the Restricted Qubit State <a id="bloch-sphere-1"></a>
We saw earlier in this chapter that the general state of a qubit ($|q\rangle$) is:
$$
|q\rangle = \alpha|0\rangle + \beta|1\rangle
$$
$$
\alpha, \beta \in \mathbb{C}
$$
(The second line tells us $\alpha$ and $\beta$ are complex numbers). The first two implications in section 2 tell us that we cannot differentiate between some of these states. This means we can be more specific in our description of the qubit.
Firstly, since we cannot measure global phase, we can only measure the difference in phase between the states $|0\rangle$ and $|1\rangle$. Instead of having $\alpha$ and $\beta$ be complex, we can confine them to the real numbers and add a term to tell us the relative phase between them:
$$
|q\rangle = \alpha|0\rangle + e^{i\phi}\beta|1\rangle
$$
$$
\alpha, \beta, \phi \in \mathbb{R}
$$
Finally, since the qubit state must be normalised, i.e.
$$
\sqrt{\alpha^2 + \beta^2} = 1
$$
we can use the trigonometric identity:
$$
\sqrt{\sin^2{x} + \cos^2{x}} = 1
$$
to describe the real $\alpha$ and $\beta$ in terms of one variable, $\theta$:
$$
\alpha = \cos{\tfrac{\theta}{2}}, \quad \beta=\sin{\tfrac{\theta}{2}}
$$
From this we can describe the state of any qubit using the two variables $\phi$ and $\theta$:
$$
|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle
$$
$$
\theta, \phi \in \mathbb{R}
$$
### 3.2 Visually Representing a Qubit State <a id="bloch-sphere-2"></a>
We want to plot our general qubit state:
$$
|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle
$$
If we interpret $\theta$ and $\phi$ as spherical co-ordinates ($r = 1$, since the magnitude of the qubit state is $1$), we can plot any single qubit state on the surface of a sphere, known as the _Bloch sphere._
Below we have plotted a qubit in the state $|{+}\rangle$. In this case, $\theta = \pi/2$ and $\phi = 0$.
(Qiskit has a function to plot a bloch sphere, `plot_bloch_vector()`, but at the time of writing it only takes cartesian coordinates. We have included a function that does the conversion automatically).
```
from qiskit_textbook.widgets import plot_bloch_vector_spherical
coords = [pi/2,0,1] # [Theta, Phi, Radius]
plot_bloch_vector_spherical(coords) # Bloch Vector with spherical coordinates
```
#### Warning!
When first learning about qubit states, it's easy to confuse the qubits _statevector_ with its _Bloch vector_. Remember the statevector is the vector discussed in [1.1](#notation), that holds the amplitudes for the two states our qubit can be in. The Bloch vector is a visualisation tool that maps the 2D, complex statevector onto real, 3D space.
#### Quick Exercise
Use `plot_bloch_vector()` or `plot_bloch_sphere_spherical()` to plot a qubit in the states:
1. $|0\rangle$
2. $|1\rangle$
3. $\tfrac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$
4. $\tfrac{1}{\sqrt{2}}(|0\rangle - i|1\rangle)$
5. $\tfrac{1}{\sqrt{2}}\begin{bmatrix}i\\1\end{bmatrix}$
We have also included below a widget that converts from spherical co-ordinates to cartesian, for use with `plot_bloch_vector()`:
```
from qiskit_textbook.widgets import bloch_calc
bloch_calc()
import qiskit
qiskit.__qiskit_version__
```
| true |
code
| 0.807366 | null | null | null | null |
|
# Computer vision data
```
%matplotlib inline
from fastai.gen_doc.nbdoc import *
from fastai import *
from fastai.vision import *
```
This module contains the classes that define datasets handling [`Image`](/vision.image.html#Image) objects and their tranformations. As usual, we'll start with a quick overview, before we get in to the detailed API docs.
## Quickly get your data ready for training
To get you started as easily as possible, the fastai provides two helper functions to create a [`DataBunch`](/basic_data.html#DataBunch) object that you can directly use for training a classifier. To demonstrate them you'll first need to download and untar the file by executing the following cell. This will create a data folder containing an MNIST subset in `data/mnist_sample`.
```
path = untar_data(URLs.MNIST_SAMPLE); path
```
There are a number of ways to create an [`ImageDataBunch`](/vision.data.html#ImageDataBunch). One common approach is to use *Imagenet-style folders* (see a ways down the page below for details) with [`ImageDataBunch.from_folder`](/vision.data.html#ImageDataBunch.from_folder):
```
tfms = get_transforms(do_flip=False)
data = ImageDataBunch.from_folder(path, ds_tfms=tfms, size=24)
```
Here the datasets will be automatically created in the structure of *Imagenet-style folders*. The parameters specified:
- the transforms to apply to the images in `ds_tfms` (here with `do_flip`=False because we don't want to flip numbers),
- the target `size` of our pictures (here 24).
As with all [`DataBunch`](/basic_data.html#DataBunch) usage, a `train_dl` and a `valid_dl` are created that are of the type PyTorch [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader).
If you want to have a look at a few images inside a batch, you can use [`ImageDataBunch.show_batch`](/vision.data.html#ImageDataBunch.show_batch). The `rows` argument is the number of rows and columns to display.
```
data.show_batch(rows=3, figsize=(5,5))
```
The second way to define the data for a classifier requires a structure like this:
```
path\
train\
test\
labels.csv
```
where the labels.csv file defines the label(s) of each image in the training set. This is the format you will need to use when each image can have multiple labels. It also works with single labels:
```
pd.read_csv(path/'labels.csv').head()
```
You can then use [`ImageDataBunch.from_csv`](/vision.data.html#ImageDataBunch.from_csv):
```
data = ImageDataBunch.from_csv(path, ds_tfms=tfms, size=28)
data.show_batch(rows=3, figsize=(5,5))
```
An example of multiclassification can be downloaded with the following cell. It's a sample of the [planet dataset](https://www.google.com/search?q=kaggle+planet&rlz=1C1CHBF_enFR786FR786&oq=kaggle+planet&aqs=chrome..69i57j0.1563j0j7&sourceid=chrome&ie=UTF-8).
```
planet = untar_data(URLs.PLANET_SAMPLE)
```
If we open the labels files, we seach that each image has one or more tags, separated by a space.
```
df =pd.read_csv(planet/'labels.csv')
df.head()
data = ImageDataBunch.from_csv(planet, folder='train', size=128, suffix='.jpg', sep=' ',
ds_tfms=get_transforms(flip_vert=True, max_lighting=0.1, max_zoom=1.05, max_warp=0.))
```
The `show_batch`method will then print all the labels that correspond to each image.
```
data.show_batch(rows=3, figsize=(10,8), ds_type=DatasetType.Valid)
```
You can find more ways to build an [`ImageDataBunch`](/vision.data.html#ImageDataBunch) without the factory methods in [`data_block`](/data_block.html#data_block).
```
show_doc(ImageDataBunch, doc_string=False)
```
### Factory methods
Normally we'll use one of the convenience wrappers below. However, these wrappers all accept a `kwargs` that is passed to the general [`DataBunch.create`](/basic_data.html#DataBunch.create) method (like `bs`, `num_workers`...)
If you quickly want to get a [`ImageDataBunch`](/vision.data.html#ImageDataBunch) and train a model, you should process your data to have it in one of the formats the following functions handle.
```
show_doc(ImageDataBunch.from_folder)
```
"*Imagenet-style*" datasets look something like this (note that the test folder is optional):
```
path\
train\
clas1\
clas2\
...
valid\
clas1\
clas2\
...
test\
```
For example:
```
data = ImageDataBunch.from_folder(path, ds_tfms=tfms, size=24)
```
Note that this (and all factory methods in this section) pass any `kwargs` to [`ImageDataBunch.create`](/vision.data.html#ImageDataBunch.create).
```
show_doc(ImageDataBunch.from_csv)
```
Create [`ImageDataBunch`](/vision.data.html#ImageDataBunch) from `path` by splitting the data in `folder` and labelled in a file `csv_labels` between a training and validation set. Use `valid_pct` to indicate the percentage of the total images for the validation set. An optional `test` folder contains unlabelled data and `suffix` contains an optional suffix to add to the filenames in `csv_labels` (such as '.jpg').
For example:
```
data = ImageDataBunch.from_csv(path, ds_tfms=tfms, size=24);
show_doc(ImageDataBunch.from_df)
```
Same as [`ImageDataBunch.from_csv`](/vision.data.html#ImageDataBunch.from_csv), but passing in a `DataFrame` instead of a csv file. E.gL
```
df = pd.read_csv(path/'labels.csv', header='infer')
df.head()
data = ImageDataBunch.from_df(path, df, ds_tfms=tfms, size=24)
```
Different datasets are labeled in many different ways. The following methods can help extract the labels from the dataset in a wide variety of situations. The way they are built in fastai is constructive: there are methods which do a lot for you but apply in specific circumstances and there are methods which do less for you but give you more flexibility.
In this case the hierachy is:
1. [`ImageDataBunch.from_name_re`](/vision.data.html#ImageDataBunch.from_name_re): Gets the labels from the filenames using a regular expression
2. [`ImageDataBunch.from_name_func`](/vision.data.html#ImageDataBunch.from_name_func): Gets the labels from the filenames using any function
3. [`ImageDataBunch.from_lists`](/vision.data.html#ImageDataBunch.from_lists): Labels need to be provided as an input in a list
```
show_doc(ImageDataBunch.from_name_re)
```
Creates an [`ImageDataBunch`](/vision.data.html#ImageDataBunch) from `fnames`, calling a regular expression (containing one *re group*) on the file names to get the labels, putting aside `valid_pct` for the validation. In the same way as [`ImageDataBunch.from_csv`](/vision.data.html#ImageDataBunch.from_csv), an optional `test` folder contains unlabelled data.
Our previously created dataframe contains the labels in the filenames so we can leverage it to test this new method. [`ImageDataBunch.from_name_re`](/vision.data.html#ImageDataBunch.from_name_re) needs the exact path of each file so we will append the data path to each filename before creating our [`ImageDataBunch`](/vision.data.html#ImageDataBunch) object.
```
fn_paths = [path/name for name in df['name']]; fn_paths[:2]
pat = r"/(\d)/\d+\.png$"
data = ImageDataBunch.from_name_re(path, fn_paths, pat=pat, ds_tfms=tfms, size=24)
data.classes
show_doc(ImageDataBunch.from_name_func)
```
Works in the same way as [`ImageDataBunch.from_name_re`](/vision.data.html#ImageDataBunch.from_name_re), but instead of a regular expression it expects a function that will determine how to extract the labels from the filenames. (Note that `from_name_re` uses this function in its implementation).
To test it we could build a function with our previous regex. Let's try another, similar approach to show that the labels can be obtained in a different way.
```
def get_labels(file_path): return '3' if '/3/' in str(file_path) else '7'
data = ImageDataBunch.from_name_func(path, fn_paths, label_func=get_labels, ds_tfms=tfms, size=24)
data.classes
show_doc(ImageDataBunch.from_lists)
```
The most flexible factory function; pass in a list of `labels` that correspond to each of the filenames in `fnames`.
To show an example we have to build the labels list outside our [`ImageDataBunch`](/vision.data.html#ImageDataBunch) object and give it as an argument when we call `from_lists`. Let's use our previously created function to create our labels list.
```
labels_ls = list(map(get_labels, fn_paths))
data = ImageDataBunch.from_lists(path, fn_paths, labels=labels_ls, ds_tfms=tfms, size=24)
data.classes
show_doc(ImageDataBunch.create_from_ll)
```
Create an [`ImageDataBunch`](/vision.data.html#ImageDataBunch) from `dss` with `bs`, `num_workers`, `collate_fn` and a potential `test` folder. `ds_tfms` is a tuple of two lists of transforms to be applied to the training and the validation (plus test optionally) set. `tfms` are the transforms to apply to the [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader). The `size` and the `kwargs` are passed to the transforms for data augmentation.
### Methods
```
show_doc(ImageDataBunch.show_batch)
```
Create a `rows` by `rows` grid of images from dataset `ds_type` for a `figsize` figure. This function works for all type of computer vision data (see [`data_block`](/data_block.html#data_block) for more examples).
Once you have your [`ImageDataBunch`](/vision.data.html#ImageDataBunch), you can have a quick look at your data by using this:
```
data.show_batch(rows=3, figsize=(6,6))
```
In the next two methods we will use a new dataset, CIFAR. This is because the second method will get the statistics for our dataset and we want to be able to show different statistics per channel. If we were to use MNIST, these statistics would be the same for every channel. White pixels are [255,255,255] and black pixels are [0,0,0] (or in normalized form [1,1,1] and [0,0,0]) so there is no variance between channels.
```
path = untar_data(URLs.CIFAR); path
show_doc(channel_view)
data = ImageDataBunch.from_folder(path, ds_tfms=tfms, valid='test', size=24)
def channel_view(x:Tensor)->Tensor:
"Make channel the first axis of `x` and flatten remaining axes"
return x.transpose(0,1).contiguous().view(x.shape[1],-1)
```
This function takes a tensor and flattens all dimensions except the channels, which it keeps as the first axis. This function is used to feed [`ImageDataBunch.batch_stats`](/vision.data.html#ImageDataBunch.batch_stats) so that it can get the pixel statistics of a whole batch.
Let's take as an example the dimensions our MNIST batches: 128, 3, 24, 24.
```
t = torch.Tensor(128, 3, 24, 24)
t.size()
tensor = channel_view(t)
tensor.size()
show_doc(ImageDataBunch.batch_stats)
```
Gets the statistics of each channel of a batch of data. If no functions are specified, default statistics are mean and standard deviation.
```
data.batch_stats()
show_doc(ImageDataBunch.normalize)
```
Adds the normalize transform to the set of transforms associated with the data. In the fast.ai library we have `imagenet_stats`, `cifar_stats` and `mnist_stats` so we can add normalization easily with any of these datasets. Let's see an example with our dataset of choice: MNIST.
```
data.normalize(cifar_stats)
data.batch_stats()
```
## Data normalization
You may also want to normalize your data, which can be done by using the following functions.
```
show_doc(normalize)
show_doc(denormalize)
show_doc(normalize_funcs, doc_string=False)
```
Create [`normalize`](/vision.data.html#normalize) and [`denormalize`](/vision.data.html#denormalize) functions using `mean` and `std`. `device` will store them on the device specified. `do_y` determines if the target should also be normaized or not.
On MNIST the mean and std are 0.1307 and 0.3081 respectively (looked on Google). If you're using a pretrained model, you'll need to use the normalization that was used to train the model. The imagenet norm and denorm functions are stored as constants inside the library named <code>imagenet_norm</code> and <code>imagenet_denorm</code>. If you're training a model on CIFAR-10, you can also use <code>cifar_norm</code> and <code>cifar_denorm</code>.
You may sometimes see warnings about *clipping input data* when plotting normalized data. That's because even although it's denormalized when plotting automatically, sometimes floating point errors may make some values slightly out or the correct range. You can safely ignore these warnings in this case.
```
data = ImageDataBunch.from_folder(untar_data(URLs.MNIST_SAMPLE),
ds_tfms=tfms, size=24)
data.normalize()
data.show_batch(rows=3, figsize=(6,6))
show_doc(get_annotations)
```
To use this dataset and collate samples into batches, you'll need to following function:
```
show_doc(bb_pad_collate)
```
Finally, to apply transformations to [`Image`](/vision.image.html#Image) in a [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset), we use this last class.
## ItemList specific to vision
The vision application adds a few subclasses of [`ItemList`](/data_block.html#ItemList) specific to images.
```
show_doc(ImageItemList, title_level=3)
```
Create a [`ItemList`](/data_block.html#ItemList) in `path` from filenames in `items`. `create_func` will default to [`open_image`](/vision.image.html#open_image). `label_cls` can be specified for the labels, `xtra` contains any extra information (usually in the form of a dataframe) and `processor` is applied to the [`ItemList`](/data_block.html#ItemList) after splitting and labelling.
```
show_doc(ImageItemList.from_folder)
show_doc(ImageItemList.from_df)
show_doc(get_image_files)
show_doc(ImageItemList.open)
```
Open the image in `fn`. Subclass and overwrite this function if you want to use a custom opening function.
```
show_doc(ImageItemList.show_xys)
show_doc(ImageItemList.show_xyzs)
show_doc(ObjectCategoryList, title_level=3)
show_doc(ObjectItemList, title_level=3)
show_doc(SegmentationItemList, title_level=3)
show_doc(SegmentationLabelList, title_level=3)
show_doc(PointsItemList, title_level=3)
show_doc(ImageImageList, title_level=3)
```
## Building your own dataset
This module also contains a few helper functions to allow you to build you own dataset for image classification.
```
show_doc(download_images)
show_doc(verify_images)
```
It will try if every image in this folder can be opened and has `n_channels`. If `n_channels` is 3 – it'll try to convert image to RGB. If `delete=True`, it'll be removed it this fails. If `resume` – it will skip already existent images in `dest`. If `max_size` is specifided, image is resized to the same ratio so that both sizes are less than `max_size`, using `interp`. Result is stored in `dest`, `ext` forces an extension type, `img_format` and `kwargs` are passed to PIL.Image.save. Use `max_workers` CPUs.
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(PointsItemList.get)
show_doc(SegmentationLabelList.new)
show_doc(ImageItemList.from_csv)
show_doc(ObjectCategoryList.get)
show_doc(ImageItemList.get)
show_doc(SegmentationLabelList.reconstruct)
show_doc(ImageImageList.show_xys)
show_doc(ImageImageList.show_xyzs)
show_doc(ImageItemList.open)
show_doc(PointsItemList.analyze_pred)
show_doc(SegmentationLabelList.analyze_pred)
show_doc(PointsItemList.reconstruct)
show_doc(SegmentationLabelList.open)
show_doc(ImageItemList.reconstruct)
show_doc(resize_to)
show_doc(ObjectCategoryList.reconstruct)
```
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.749909 | null | null | null | null |
|
# Random Forests
```
!pip install scikit-learn==0.23.2
import pandas as pd
import numpy as np
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, plot_confusion_matrix
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import plot_tree
data = load_digits(as_frame=True)
X, y, images = data.data, data.target, data.images
X.head()
X.describe()
y.value_counts().sort_index()
data.target_names
X_train, X_test, y_train, y_test, images_train, images_test = train_test_split(X, y, images, train_size=0.6, random_state=0)
fig, axes = plt.subplots(1, 4, figsize=(10, 4))
fig.suptitle("Dados de treino")
for ax, image, label in zip(axes, images_train, y_train):
ax.set_axis_off()
ax.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
ax.set_title('Label: %i' % label)
model = RandomForestClassifier(criterion="entropy", n_estimators=200, max_depth=3, random_state=0)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy_score(y_test, y_pred)
fig, ax = plt.subplots(figsize=(11, 10))
disp = plot_confusion_matrix(model, X_test, y_test, ax=ax)
disp.figure_.suptitle("Matriz de Confusão");
fig, axes = plt.subplots(1, 4, figsize=(10, 4))
fig.suptitle("Predições corretas")
for ax, image, pred, label in zip(axes, images_test[y_pred == y_test], y_pred[y_pred == y_test], y_test[y_pred == y_test]):
ax.set_axis_off()
ax.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
ax.set_title(f'Pred {pred}/Label {label}')
fig, axes = plt.subplots(1, 4, figsize=(10, 4))
fig.suptitle("Predições erradas")
for ax, image, pred, label in zip(axes, images_test[y_pred != y_test], y_pred[y_pred != y_test], y_test[y_pred != y_test]):
ax.set_axis_off()
ax.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
ax.set_title(f'Pred {pred}/Label {label}')
# This may not the best way to view each estimator as it is small
num_trees = 4
fn = data.feature_names
cn = [str(t) for t in data.target_names]
fig, axes = plt.subplots(num_trees, 1, figsize=(16,25))
for index in range(0, num_trees):
plot_tree(model.estimators_[index],
feature_names=fn,
class_names=cn,
filled=True,
ax=axes[index],
fontsize=9)
axes[index].set_title('Estimator: ' + str(index), fontsize=15)
fig, ax = plt.subplots(figsize=(9, 15))
ax.barh(data.feature_names, model.feature_importances_)
```
| true |
code
| 0.742452 | null | null | null | null |
|
In his blog post [Embedding Matplotlib Animations in IPython Notebooks](http://jakevdp.github.io/blog/2013/05/12/embedding-matplotlib-animations/), Jake VanderPlas presents a slick hack for embedding Matplotlib Animations in IPython Notebooks, which involves writing it as a video to a [tempfile](https://docs.python.org/2/library/tempfile.html), and then re-encoding it in Base64 as a HTML5 Video.
Unfortunately (or rather fortunately), this hack has been largely rendered obsolete by the heavy development efforts dedicated to both Matplotlib and IPython Notebook ([since renamed to Jupyter Notebook](https://blog.jupyter.org/2015/08/12/first-release-of-jupyter/)) in recent years. In particular, [Matplotlib 1.5.1](http://matplotlib.org/users/whats_new.html#new-in-matplotlib-1-5) now [supports inline display of animations in the notebook](http://matplotlib.org/users/whats_new.html#display-hook-for-animations-in-the-ipython-notebook) with the `to_html5_video` method, which converts the animation to an h264 encoded video and embeddeds it directly in the notebook.
In this notebook, we reproduce Jake VanderPlas' blog post with this new feature.
<!-- TEASER_END -->
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML
# First set up the figure, the axis, and the plot element we want to animate
fig, ax = plt.subplots()
ax.set_xlim(( 0, 2))
ax.set_ylim((-2, 2))
line, = ax.plot([], [], lw=2)
# initialization function: plot the background of each frame
def init():
line.set_data([], [])
return (line,)
# animation function. This is called sequentially
def animate(i):
x = np.linspace(0, 2, 1000)
y = np.sin(2 * np.pi * (x - 0.01 * i))
line.set_data(x, y)
return (line,)
# call the animator. blit=True means only re-draw the parts that have changed.
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=100, interval=20, blit=True)
HTML(anim.to_html5_video())
```
Note that [Animation](http://matplotlib.org/api/animation_api.html#matplotlib.animation.Animation) instances now have a `_repr_html_` method. However, it returns `None` by default.
```
anim._repr_html_() is None
```
This means we won't get any sort of animation from the inline display.
```
anim
```
The method used to display is controlled by the `animation.html` rc parameter, which currently supports values of `none` and `html5`. `none` is the default, performing no display. We simply need to set it to `html5`:
```
# equivalent to rcParams['animation.html'] = 'html5'
rc('animation', html='html5')
anim
```
And that's all there is to it!
| true |
code
| 0.553204 | null | null | null | null |
|
<img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# CCXT - Calculate Support and Resistance
<a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/CCXT/CCXT_Calculate_Support_and_Resistance.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
**Tags:** #ccxt #bitcoin #trading #investors #analytics #plotly
**Author:** [Jeremy Ravenel](https://www.linkedin.com/in/ACoAAAJHE7sB5OxuKHuzguZ9L6lfDHqw--cdnJg/)
## Input
```
!pip install trendln matplotlib==3.1.3 --user
import naas
import ccxt
import pandas as pd
from datetime import datetime
import naas_drivers
import trendln
import plotly.tools as tls
import plotly.graph_objects as go
```
### Setup Binance
👉 <a href='https://www.binance.com/en/support/faq/360002502072'>How to create API ?</a>
```
binance_api = ""
binance_secret = ""
```
### Variables
```
symbol = 'BTC/USDT'
limit = 180
timeframe = '4h'
```
## Model
### Get data
```
binance = ccxt.binance({
'apiKey': binance_api,
'secret': binance_secret
})
data = binance.fetch_ohlcv(symbol=symbol,
limit=limit,
timeframe=timeframe)
```
### Data cleaning
```
df = pd.DataFrame(data, columns=["Date", "Open", "High", "Low", "Close", "Volume"])
df['Date'] = [datetime.fromtimestamp(float(time)/1000) for time in df['Date']]
df
```
## Output
### Plotting figure
```
fig = trendln.plot_support_resistance(
df[-1000:].Close, #as per h for calc_support_resistance
xformatter = None, #x-axis data formatter turning numeric indexes to display output
# e.g. ticker.FuncFormatter(func) otherwise just display numeric indexes
numbest = 1, #number of best support and best resistance lines to display
fromwindows = True, #draw numbest best from each window, otherwise draw numbest across whole range
pctbound = 0.1, # bound trend line based on this maximum percentage of the data range above the high or below the low
extmethod = trendln.METHOD_NUMDIFF,
method=trendln.METHOD_PROBHOUGH,
window=125,
errpct = 0.005,
hough_prob_iter=50,
sortError=False,
accuracy=1)
plotly_fig = tls.mpl_to_plotly(fig)
layout = dict(
dragmode="pan",
xaxis_rangeslider_visible=False,
showlegend=True,
)
new_data = list(plotly_fig.data)
new_data.pop(2)
new_data.pop(2)
new_data.pop(1)
new_data.pop(1)
fig = go.Figure(data=new_data, layout=layout)
fig
```
| true |
code
| 0.728356 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/adasegroup/ML2021_seminars/blob/master/seminar3/seminar03-solution.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Measure quality of a classification model
This notebook explains how to measure quality of a classification machine learning model.
We provide definitions for various quality measures and try to find out if they are suitable or not for a particular machine learning classification problem.
The data is a subsample from the kaggle comptetion "Give me some credit"
https://www.kaggle.com/c/GiveMeSomeCredit#description
```
# Imports
# data processing tools: pandas and numpy
import numpy as np
import pandas as pd
# visualization tools: matplotlib, seaborn
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
# machine learning tools: various methods from scikit-learn
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix, roc_curve, precision_recall_curve, auc
from sklearn.metrics import f1_score, accuracy_score, average_precision_score
```
# Load data
```
# load the data
training_data = pd.read_csv('https://raw.githubusercontent.com/adasegroup/ML2021_seminars/master/seminar3/credit/training_data.csv')
test_data = pd.read_csv('https://raw.githubusercontent.com/adasegroup/ML2021_seminars/master/seminar3/credit/test_data.csv')
```
See some technical info about data
```
# print information about the data
training_data.info(verbose=True)
```
Let's look at some general statistics of data:
* **count** -- number of not `NaN` values;
* **mean**, **std** -- mean and standard deviation;
* other -- minimal, maximal values, quantiles.
```
training_data.describe().T
```
Choose randomly ten objects from dataset:
```
training_data.sample(10, random_state=123)
```
We see that there are `NaN`s in data. Let's calculate mean values of features on **training data** and fill them in instead of the missing values. We will do that both for **train** and **test**.
There are several ways to fill in skipped data:
* mean, median;
* regression predictions;
* in case of time series -- last known value,
* linear interpolation, etc.
If the number of skipped values is small, you can throw the corresponding objects away.
```
training_data["SeriousDlqin2yrs"].value_counts()
train_mean = training_data.mean()
train_mean
# fill NA values with mean training values
training_data.fillna(train_mean, inplace=True)
test_data.fillna(train_mean, inplace=True)
print(training_data.isnull().sum())
print(test_data.isnull().sum())
```
Compare train and test distributions
```
axes = training_data.hist(figsize=(16, 9), bins=25, alpha=0.75) # that will plot training data histograms
for plot in axes.flat: # that will draw test data on top of training histograms
column = plot.title.get_text()
if column:
test_data[column].hist(ax=plot, bins=25, alpha=0.55)
```
Pay attention to **SeriousDlqin2yrs** -- 90 days past due delinquency or worse in the last 2 years. We see that most of the borrowers pay in time.
```
# The data set is imbalanced: typically people return credits
training_data["SeriousDlqin2yrs"].value_counts()
```
# Classification algorithms
First of all, load data for learning as pairs $(X, y)$, where $X = (x_i)_{i=1}^n$ -- input features,
and $y=(y_i)_{i=1}^n$ corresponding labels.
```
training_X = training_data.drop("SeriousDlqin2yrs", axis=1)
training_y = training_data["SeriousDlqin2yrs"]
test_X = test_data.drop("SeriousDlqin2yrs", axis=1)
test_y = test_data["SeriousDlqin2yrs"]
```
Construct calssification algorithms and train them.
```
# Construct Decision Tree model
decision_tree = DecisionTreeClassifier(max_depth = 5)
decision_tree.fit(training_X, training_y)
!pip install graphviz
from graphviz import Source
from sklearn import tree
Source(tree.export_graphviz(decision_tree, out_file=None, feature_names=training_X.columns))
# Construct k Nearest Neighbors model
knn = KNeighborsClassifier(n_neighbors = 5)
knn.fit(training_X, training_y)
print("Training accuracy:")
print("\tDT accuracy:\t%.2f%%" % (100 * decision_tree.score(training_X, training_y)))
print("\tkNN accuracy:\t%.2f%%" % (100 * knn.score(training_X, training_y)))
print("\tNumber of '0' labels:\t%.2f%%" % (100 - 100 * np.mean(training_y)))
print()
print("Test accuracy:")
print("\tDT accuarcy:\t%.2f%%" % (100 * decision_tree.score(test_X, test_y)))
print("\tkNN accuarcy:\t%.2f%%" % (100 * knn.score(test_X, test_y)))
print("\tNumber of '0' labels:\t%.2f%%" % (100 - 100 * np.mean(test_y)))
test_predictions_dt = decision_tree.predict(test_X)
test_probabilities_dt = decision_tree.predict_proba(test_X)[:, 1]
training_predictions_dt = decision_tree.predict(training_X)
training_probabilities_dt = decision_tree.predict_proba(training_X)[:, 1]
test_predictions_knn = knn.predict(test_X)
test_probabilities_knn = knn.predict_proba(test_X)[:, 1]
training_predictions_knn = knn.predict(training_X)
training_probabilities_knn = knn.predict_proba(training_X)[:, 1]
np.unique(test_probabilities_dt)
np.unique(training_probabilities_knn)
```
# Classification quality measures
## Confusion matrix
Confusion matrix is table layout that allows visualization of the performance of an algorithm. Rows of this matrix correspond to actual classes of the test set, columns correspond to predicted labels. There are 4 types of elements if predictions are given:
* True Positive
* False Negative
* False Positive
* True Negative
| Variable | Predicted True | Predicted False |
| ------------- |-------------|-----|
| Actual True | TP | FN |
| Actual False | FP | TN |
```
confusion_dt = pd.DataFrame(confusion_matrix(test_y, test_predictions_dt))
confusion_knn = pd.DataFrame(confusion_matrix(test_y, test_predictions_knn))
print('Confusion for Decision Tree:')
print(confusion_dt)
print('Confusion for kNN:')
print(confusion_knn)
```
If we want to compare metrics on different data, we can use instead True Positive Rate and False Positive Rate:
* False Positive Rate is $\frac{FP}{FP + TN}$
* True Positive Rate is $\frac{TP}{TP + FN}$
## ROC curve
ROC stands for *Receiver Operating Characteristic*. This curve shows True Positive Rate (**TPR**) against False Positive Rate (**FPR**) as classifier's discrimination threshold is varied
Remember that classifiers are usually constructed based on some function
$f(x) \in [0, 1]$ and threshold $\tau$:
$$ \text{Classifier}\bigl(\text{object}\bigr)
= \begin{cases}
1 & \text{if}\, f(\text{object}) \geq \tau\,,\\
0 & \text{else}\,.
\end{cases}
$$
**roc_curve** function from *scikit-learn* allows to easily obtain ROC curve points and **threshold** values.
Detailed description of ROC-AUC by Alexander Dyakonov (in Russian)
https://dyakonov.org/2017/07/28/auc-roc-площадь-под-кривой-ошибок/
```
false_positive_rates_dt, true_positive_rates_dt, threshold_dt = roc_curve(test_y, test_probabilities_dt)
false_positive_rates_knn, true_positive_rates_knn, threshold_knn = roc_curve(test_y, test_probabilities_knn)
# create plot
fig = plt.figure(figsize=(14, 7))
# specify parameters for the first curve
plot_1 = fig.add_subplot(121,
xlabel="FPR", xlim=(-.01, 1.01),
ylabel="TPR", ylim=(-.01, 1.01), title = 'Decision Tree')
# draw the first curve
plot_1.plot(false_positive_rates_dt, true_positive_rates_dt,
color='darkorange', lw=2, label = 'ROC-curve on test')
plot_1.plot([0, 1], [0, 1], color='navy', lw=2, linestyle=':')
plt.legend(loc="lower right")
# specify parameters for the second curve
plot_2 = fig.add_subplot(122,
xlabel="FPR", xlim=(-.01, 1.01),
ylabel="TPR", ylim=(-.01, 1.01), title = 'k Nearest Neighbors')
# draw the second curve
plot_2.plot(false_positive_rates_knn, true_positive_rates_knn,
color='darkorange', lw=2, label = 'ROC-curve on test')
plot_2.plot([0, 1], [0, 1], color='navy', lw=2, linestyle=':')
plt.legend(loc="lower right")
plt.show()
```
The closer **ROC** curve to the **upper left** corner, the better classification is.
Despite being a good visual representation we usually need a number to make conclusions about calssification quality. In case of ROC curve this number is Area Under the Curve (**ROC-AUC**).
*scikit-learn* has a special function **auc(...)**:
```
roc_auc_dt = auc(false_positive_rates_dt, true_positive_rates_dt)
roc_auc_knn = auc(false_positive_rates_knn, true_positive_rates_knn)
print("DT ROC-AUC on test data:", roc_auc_dt)
print("kNN ROC-AUC on test data:", roc_auc_knn)
```
For the training set ROC curve and ROC-AUC look much better.
```
training_false_positive_rates_dt, training_true_positive_rates_dt, _ = roc_curve(training_y, training_probabilities_dt)
training_false_positive_rates_knn, training_true_positive_rates_knn, _ = roc_curve(training_y, training_probabilities_knn)
training_roc_auc_dt = auc(training_false_positive_rates_dt, training_true_positive_rates_dt)
training_roc_auc_knn = auc(training_false_positive_rates_knn, training_true_positive_rates_knn)
print("DT ROC-AUC on training data:", training_roc_auc_dt)
print("kNN ROC-AUC on training data:", training_roc_auc_knn)
fig = plt.figure(figsize=(14, 7))
plot_1 = fig.add_subplot(121,
xlabel="FPR", xlim=(-.01, 1.01),
ylabel="TPR", ylim=(-.01, 1.01), title = 'Decision Tree')
# draw the first curve
plot_1.plot(training_false_positive_rates_dt, training_true_positive_rates_dt,
color='darkgreen', lw=2, label = 'ROC-curve on train (AUC = %0.2f)' % training_roc_auc_dt)
plot_1.plot(false_positive_rates_dt, true_positive_rates_dt,
color='darkorange', lw=2, label = 'ROC-curve on test (AUC = %0.2f)' % roc_auc_dt)
plot_1.plot([0, 1], [0, 1], color='navy', lw=2, linestyle=':')
plt.legend(loc="lower right")
# specify parameters for the second curve
plot_2 = fig.add_subplot(122,
xlabel="FPR", xlim=(-.01, 1.01),
ylabel="TPR", ylim=(-.01, 1.01), title = 'k Nearest Neighbors')
# draw the second curve
plot_2.plot(training_false_positive_rates_knn, training_true_positive_rates_knn,
color='darkgreen', lw=2, label = 'ROC-curve on train (AUC = %0.2f)' % training_roc_auc_knn)
plot_2.plot(false_positive_rates_knn, true_positive_rates_knn,
color='darkorange', lw=2, label = 'ROC-curve on test (AUC = %0.2f)' % roc_auc_knn)
plot_2.plot([0, 1], [0, 1], color='navy', lw=2, linestyle=':')
plt.legend(loc="lower right")
plt.show()
```
Another ROC-AUC visualization http://www.navan.name/roc/
Area under ROC-curve = probability of pairs of objects from different classes being classified correctly.

$a_i$ - prediction at $i$-th object, $y_i$ - target (class), $q$- number of objects in test
## Precision and Recall
Precision and Recall are two other measures for evaluation of classification quality. Both of the metrics are calculated based on **confusion matrix**.
<img src="https://github.com/adasegroup/ML2021_seminars/blob/master/seminar3/figures/precision_recall.png?raw=1">
Note that Recall equals to True Positive Rate.
Although "accuracy" and "precision" have very similar meanings, they are completely different metrics. Look how Precision and Recall are evaluated for k Nearest Neighbors classifier:
```
confusion = confusion_matrix(test_y, test_predictions_knn)
TN, FP = confusion[0, 0], confusion[0, 1]
FN, TP = confusion[1, 0], confusion[1, 1]
```
**Recall** of a classifier is equal to True Positive Rate **TPR** ($\frac{TP}{TP + FN}$). This value may be interpreted as a sensitivity of a classifier to the objects with label `1`. If it is close to $100\%$, then a classifier rarely "miss" the object of class `1`.
```
recall = TP / (TP + FN)
print("Recall: %.2f%%" % (100 * recall))
```
**Precision** -- is a fraction $\frac{TP}{TP + FP}$. If this value is large, then a classifier assigns label `1` to objects with actual label `0` rarely.
See how it is different to Accuracy = $\frac{TP + TN}{TP + TN + FP + FN}$
```
precision = TP / (TP + FP)
print("Precision: %.2f%%" % (100 * precision))
```
A classifier with large Recall but small Precision produces many false positive predictions and tends to assign many `1` labels.
Vice versa, if a classifier has small Recall but large Precision, then it detects class `1` accurately, but misses many objects (many false negative predictions).
### Precision-Recall curve
In **precision-recall** space we may construct a curve similar to **ROC** curve in **FPR-TPR** space. PR curve also depicts the dependecy of Precision and Recall on threshold. *scikit* has the corresponding function: **precision_recall_curve(...)**.
Let's calculate PR curve points.
Note that unlike ROC curve, we cannot use interpolation for calculation of area under the curve. This may lead to larger values of the metric, which is not good. In this case we need to use **average_precision_score()** function instead of **auc()** function.
```
# generate values for Precision-Recall curve
precision_dt, recall_dt, _ = precision_recall_curve(test_y, test_probabilities_dt)
precision_knn, recall_knn, _ = precision_recall_curve(test_y, test_probabilities_knn)
# calculate value under Precision-Recall curve
pr_auc_dt = average_precision_score(test_y, test_probabilities_dt)
pr_auc_knn = average_precision_score(test_y, test_probabilities_knn)
print("DT PR-AUC on test data:", pr_auc_dt)
print("kNN PR-AUC on test data:", pr_auc_knn)
# generate values for training Precision Recall curve
training_precision_dt, training_recall_dt, _ = precision_recall_curve(training_y, training_probabilities_dt)
training_precision_knn, training_recall_knn, _ = precision_recall_curve(training_y, training_probabilities_knn)
# TODO calculate value under precision-recall curve
training_pr_auc_dt = average_precision_score(training_y, training_probabilities_dt)
training_pr_auc_knn = average_precision_score(training_y, training_probabilities_knn)
print("DT PR-AUC on training data:", training_pr_auc_dt)
print("kNN PR-AUC on training data:", training_pr_auc_knn)
fig = plt.figure(figsize=(14, 7))
plot_1 = fig.add_subplot(121,
xlabel="Recall", xlim=(-.01, 1.01),
ylabel="Precision", ylim=(-.01, 1.01), title = 'Decision Tree')
plot_1.plot(training_recall_dt, training_precision_dt,
color='darkgreen', lw=2, label = 'PR-curve on train (AUC = %0.2f)' % training_pr_auc_dt)
plot_1.plot(recall_dt, precision_dt,
color='darkorange', lw=2, label = 'PR-curve on test (AUC = %0.2f)' % pr_auc_dt)
plt.legend(loc="upper right")
plot_2 = fig.add_subplot(122,
xlabel="Recall", xlim=(-.01, 1.01),
ylabel="Precision", ylim=(-.01, 1.01), title = 'k Nearest Neighbors')
plot_2.plot(training_recall_knn, training_precision_knn,
color='darkgreen', lw=2, label = 'PR-curve on train (AUC = %0.2f)' % training_pr_auc_knn)
plot_2.plot(recall_knn, precision_knn,
color='darkorange', lw=2, label = 'PR-curve on test (AUC = %0.2f)' % pr_auc_knn)
plt.legend(loc="upper right")
plt.show()
```
The closer **PR** curve to the **upper right** corner, the better classification is.
Large AUC value means that Precision and Recall are also large. That means that classifier makes small number of both False Positives and False Negatives.
## F1 score
This metric allows to take into account a different cost for False Positive Errors and False Negative Errors.
General $F_\beta$ score is defined as follows:
$$
F_\beta = (1 + \beta^2) \frac{Precision \cdot Recall}{\beta^2 Precision + Recall} = \frac{1 + \beta^2}{\frac{\beta^2}{Recall} + \frac{1}{Precision}}= \frac{\beta + \beta^{-1}}{\beta\frac{1}{\text{Recall}} + \beta^{-1}\frac{1}{\text{Precision}}}
\,.
$$
Most commonly used is $F_1$ score:
$$
F_1 = 2 \frac{Precision \cdot Recall}{Precision + Recall}
$$
Harmonic mean is used in order to make metric value very small when Precision or Recall is close to zero. Note that $F_1$ score doesn't describe how classifier works for True Negative results (**TN**).
```
print("DT F1 score on training data", f1_score(training_y, training_predictions_dt))
print("kNN F1 score on training data", f1_score(training_y, training_predictions_knn))
print("DT F1 score on test data", f1_score(test_y, test_predictions_dt))
print("kNN F1 score on test data", f1_score(test_y, test_predictions_knn))
```
$F_1$ score is good for imbalanced classification, when a number of class `1` objects is **much** bigger than class `0` objects.
Let's compare **accuracy** and $F_1$ score of our classifiers with *random* classifier, which works as follows:
* estimate probability $\hat{p}$ of class `1` on training data (frequency of class `1` objects);
* for every test object predict randomly:
* label `1` with probability $\hat{p}$,
* label `0` with probability $1 - \hat{p}$.
```
training_prob = sum(training_y) / len(training_y)
random_predictions = np.random.binomial(1, training_prob, len(test_y))
print("Decision Tree accuracy\t\t", accuracy_score(test_y, test_predictions_dt))
print("kNN accuracy\t\t\t", accuracy_score(test_y, test_predictions_knn))
print("Random classifier accuracy\t", accuracy_score(test_y, random_predictions))
print('---')
print("Decision Tree F1 score\t\t", f1_score(test_y, test_predictions_dt))
print("kNN F1 score\t\t\t", f1_score(test_y, test_predictions_knn))
print("FRandom classifier F1 score\t", f1_score(test_y, random_predictions))
```
# Exercise 1
We have seen how some of classifiers work for this dataset. Now, try it yourself with Logistic Regression.
* Fisrt, **import** **LogisticRegression()** function and train it on training data.
* Then, calculate **ROC AUC**, **PR AUC** and **F1 score** on test data.
* Try to change parameters to improve results.
http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
```
from sklearn.linear_model import LogisticRegression
logistic_regression = LogisticRegression(penalty = 'l2', C = 100.0, max_iter = 1000)
logistic_regression.fit(training_X, training_y)
test_predictions = logistic_regression.predict(test_X)
test_probabilities = logistic_regression.predict_proba(test_X)[:, 1]
false_positive_rates, true_positive_rates, threshold = roc_curve(test_y, test_probabilities)
roc_auc = auc(false_positive_rates, true_positive_rates)
print(roc_auc)
precision, recall, _ = precision_recall_curve(test_y, test_probabilities)
pr_auc = average_precision_score(test_y, test_probabilities)
print(pr_auc)
print(f1_score(test_y, test_predictions))
```
# Cross-validation technique
In many cases test sample is not available or we have a small dataset, and we have only one sample: a training one. The most popular approach in this case is **cross-validation**.
The most common way is $k$-fold cross-validation. The idea is to divide training sample into $k$ blocks, one of them is treated as an artificial test sample and other $k-1$ are used for training.
*scikit* has several functions for dividing data into folds and for performing automated cross-validation. One of those functions is **GridSearchCV()**.
<img src="https://github.com/adasegroup/ML2021_seminars/blob/master/seminar3/figures/5-fold-cv.png?raw=1">
```
from sklearn.model_selection import GridSearchCV
parameters_knn = {'n_neighbors': [5, 10, 15, 20]}
knn_cv = GridSearchCV(knn, param_grid = parameters_knn)
knn_cv.fit(training_X, training_y)
knn_cv.best_params_
predictions_knn_cv = knn_cv.predict(test_X)
probabilities_knn_cv = knn_cv.predict_proba(test_X)[:,1]
false_positive_rates_knn_cv, true_positive_rates_knn_cv, _ = roc_curve(test_y, probabilities_knn_cv)
roc_auc_knn_cv = auc(false_positive_rates_knn_cv, true_positive_rates_knn_cv)
precision_knn_cv, recall_knn_cv, _ = precision_recall_curve(test_y, probabilities_knn_cv)
pr_auc_knn_cv = average_precision_score(test_y, probabilities_knn_cv)
f1_knn_cv = f1_score(test_y, predictions_knn_cv)
print('ROC AUC: ', roc_auc_knn_cv)
print('PR AUC: ', pr_auc_knn_cv)
print('F1_score: ', f1_knn_cv)
pd.DataFrame(confusion_matrix(test_y, predictions_knn_cv))
```
# Exercise 2
Now we know how to perform cross-validation. Try it yourself with Decision Tree.
* Using **GridSearchCV** choose parameter **min_samples_leaf**. Try several values from 1 to 100.
* Use **five**-fold cross-validation and **roc_auc** scoring. See the chosen parameters.
* Evaluate quality metrics and look how they changed. Try to make some plots.
http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html
http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html
HINT https://scikit-learn.org/stable/modules/generated/sklearn.metrics.make_scorer.html
```
from sklearn.metrics import roc_auc_score, make_scorer
parameters_dt = {'min_samples_leaf' : [1, 2, 4, 8, 16, 32, 64, 128]}
clf = DecisionTreeClassifier()
dt_cv = GridSearchCV(clf, param_grid = parameters_dt, scoring=make_scorer(roc_auc_score), cv=5)
dt_cv.fit(training_X, training_y)
dt_cv.best_params_
dt_cv.best_score_
dt_cv.cv_results_
fig,ax=plt.subplots(1,1)
plt.plot(dt_cv.cv_results_['param_min_samples_leaf'].data, dt_cv.cv_results_['mean_test_score'], axes = ax)
ax.set_xlabel('min_samples_leaf')
ax.set_ylabel('ROC AUC')
```
# Multiclass classification
Let's have a look how multiclass tasks are treated.
```
# import some modules
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.base import clone
from sklearn.linear_model import LogisticRegression
import zipfile
```
## Load data
We will use data from Kaggle contest *"Otto Group
Product Classification Challenge"*, which was created to predict class of an item by several features.
https://www.kaggle.com/c/otto-group-product-classification-challenge
Data are in ZIP, but we can load them easily
```
train_dataset = pd.read_csv('https://raw.githubusercontent.com/adasegroup/ML2021_seminars/master/seminar3/otto/train.csv', index_col='id')
test_dataset = pd.read_csv('https://raw.githubusercontent.com/adasegroup/ML2021_seminars/master/seminar3/otto/test.cutted.csv', index_col='id')
```
Data consist of the following:
* **id** -- anonymized identifier;
* **feat_1, ..., feat_93** -- features;
* **target** -- actual class of an item.
Number of objects for every class in **target**
```
train_dataset['target'].value_counts()
y = train_dataset["target"]
X = np.asarray(train_dataset.drop("target", axis = 1))
```
Let's see data description
```
train_dataset.describe().T
```
Divide data into input and output, transform labels from strings to numbers. **LabelEncoder** allows us to perform that transform nad obtain numbers from $0$ to $K-1$, where $K$ is the number of classes.
```
import xgboost
xgb = xgboost.XGBClassifier(objective='multi:softprob')
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
```
Split data into training sample and test sample
```
split = train_test_split(X, y, test_size=0.5,
random_state=42, stratify=y)
train_X, test_X, train_y, test_y = split
xgb.fit(train_X, train_y)
test_preds = xgb.predict(test_X)
accuracy_score(test_y, test_preds)
confusion_matrix(test_y, test_preds)
print(classification_report(test_y, test_preds))
```
| true |
code
| 0.708969 | null | null | null | null |
|
# Part 3: Create a model to serve the item embedding data
This notebook is the third of five notebooks that guide you through running the [Real-time Item-to-item Recommendation with BigQuery ML Matrix Factorization and ScaNN](https://github.com/GoogleCloudPlatform/analytics-componentized-patterns/tree/master/retail/recommendation-system/bqml-scann) solution.
Use this notebook to wrap the item embeddings data in a Keras model that can act as an item-embedding lookup, then export the model as a SavedModel.
Before starting this notebook, you must run the [02_export_bqml_mf_embeddings](02_export_bqml_mf_embeddings.ipynb) notebook to process the item embeddings data and export it to Cloud Storage.
After completing this notebook, run the [04_build_embeddings_scann](04_build_embeddings_scann.ipynb) notebook to create an approximate nearest neighbor index for the item embeddings.
## Setup
Import the required libraries, configure the environment variables, and authenticate your GCP account.
```
!pip install -q -U pip
!pip install -q tensorflow==2.2.0
!pip install -q -U google-auth google-api-python-client google-api-core
```
### Import libraries
```
import os
import tensorflow as tf
import numpy as np
print(f'Tensorflow version: {tf.__version__}')
```
### Configure GCP environment settings
Update the following variables to reflect the values for your GCP environment:
+ `PROJECT_ID`: The ID of the Google Cloud project you are using to implement this solution.
+ `BUCKET`: The name of the Cloud Storage bucket you created to use with this solution. The `BUCKET` value should be just the bucket name, so `myBucket` rather than `gs://myBucket`.
```
PROJECT_ID = 'yourProject' # Change to your project.
BUCKET = 'yourBucketName' # Change to the bucket you created.
EMBEDDING_FILES_PATH = f'gs://{BUCKET}/bqml/item_embeddings/embeddings-*'
MODEL_OUTPUT_DIR = f'gs://{BUCKET}/bqml/embedding_lookup_model'
!gcloud config set project $PROJECT_ID
```
### Authenticate your GCP account
This is required if you run the notebook in Colab. If you use an AI Platform notebook, you should already be authenticated.
```
try:
from google.colab import auth
auth.authenticate_user()
print("Colab user is authenticated.")
except: pass
```
## Create the embedding lookup model
You use the `EmbeddingLookup` class to create the item embedding lookup model. The `EmbeddingLookup` class inherits from [tf.keras.Model](https://www.tensorflow.org/api_docs/python/tf/keras/Model), and is implemented in the
[lookup_creator.py](embeddings_lookup/lookup_creator.py)
module.
The `EmbeddingLookup `class works as follows:
1. Accepts the `embedding_files_prefix` variable in the class constructor. This variable points to the Cloud Storage location of the CSV files containing the item embedding data.
1. Reads and parses the item embedding CSV files.
1. Populates the `vocabulary` and `embeddings` class variables. `vocabulary` is an array of item IDs, while `embeddings` is a Numpy array with the shape (*number of embeddings*, *embedding dimensions*).
1. Appends the `oov_embedding` variable to the `embeddings` variable. The `oov_embedding` variable value is all zeros, and it represents the out of vocabulary (OOV) embedding vector. The `oov_embedding` variable is used when an invalid ("out of vocabulary", or OOV) item ID is submitted, in which case an embedding vector of zeros is returned.
1. Writes the `vocabulary` value to a file, one array element per line, so it can be used as a model asset by the SavedModel.
1. Uses `token_to_idx`, a `tf.lookup.StaticHashTable` object, to map the
item ID to the index of the embedding vector in the `embeddings` Numpy array.
1. Accepts a list of strings with the `__call__` method of the model. Each string represents the item ID(s) for which the embeddings are to be retrieved. If the input list contains _N_ strings, then _N_ embedding vectors are returned.
Note that each string in the input list may contain one or more space-separated item IDs. If multiple item IDs are present, the embedding vectors of these item IDs are retrieved and _combined_ (by averaging) into a single embedding vector. This makes it possible to fetch an embedding vector representing a set of items (like a playlist) rather than just a single item.
### Clear the model export directory
```
if tf.io.gfile.exists(MODEL_OUTPUT_DIR):
print("Removing {} contents...".format(MODEL_OUTPUT_DIR))
tf.io.gfile.rmtree(MODEL_OUTPUT_DIR)
```
### Create the model and export the SavedModel file
Call the `export_saved_model` method, which uses the `EmbeddingLookup` class to create the model and then exports the resulting SavedModel file:
```
from embeddings_lookup import lookup_creator
lookup_creator.export_saved_model(EMBEDDING_FILES_PATH, MODEL_OUTPUT_DIR)
```
Inspect the exported SavedModel using the `saved_model_cli` command line tool:
```
!saved_model_cli show --dir {MODEL_OUTPUT_DIR} --tag_set serve --signature_def serving_default
```
### Test the SavedModel file
Test the SavedModel by loading it and then calling it with input item IDs:
```
loaded_model = tf.saved_model.load(MODEL_OUTPUT_DIR)
input_items = ['2114406', '2114402 2120788', 'abc123']
output = loaded_model(input_items)
print(f'Embeddings retrieved: {output.shape}')
for idx, embedding in enumerate(output):
print(f'{input_items[idx]}: {embedding[:5]}')
```
The output shows the output embedding vector (the first five elements of each vector) for each input item. Note the following:
+ The second entry in the input list contains two item IDs, `2114402` and `2120788`. The returned vector is the average of the embeddings of these two items.
+ The third entry in the input list, `abc123`, is an invalid item ID, so the returned embedding vector contains zeros.
## License
Copyright 2020 Google LLC
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License. You may obtain a copy of the License at: http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and limitations under the License.
**This is not an official Google product but sample code provided for an educational purpose**
| true |
code
| 0.50238 | null | null | null | null |
|
```
from __future__ import print_function
import sisl
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
First TranSiesta bias example.
In this example we will take the system from [TS 1](../TS_01/run.ipynb) and perform bias calculations on it. Note, however, that applying a bias to a *pristine* bulk system is non-physical and should thus **NEVER** be done. TranSiesta will *not* warn you about this and will happily calculate the non-equilibrium density for any bulk system with an applied bias. This is an ***extremely*** important point and once complete with this example you should carefully think through why this is the case.
Bias calculations are very heavy because of a full DFT+NEGF calculation *per bias-point*.
We will begin with creating the structures.
```
graphene = sisl.geom.graphene(1.44, orthogonal=True)
elec = graphene.tile(2, axis=0)
elec.write('STRUCT_ELEC.fdf')
device = elec.tile(3, axis=0)
device.write('STRUCT_DEVICE.fdf')
```
## Exercises
In this exercise you will be familiarized with the input options that define a bias calculation. The input options are *extremely elaborate*, yet they require little intervention when using default parameters.
As this is your first example of running TranSiesta with applied bias there are a few things you should know:
1. Do not start by performing any $V\neq0$ calculations until you are perfectly sure that your $V=0$ calculation is well converged and well behaved, i.e. a small `dQ` (see [TS 1](../TS_01/run.ipynb)).
2. When performing bias calculations your are recommended to create a new directory for each bias: `TS_<V>`.
3. *Any* bias calculation should be a restart by using the ***closests*** bias calculations TranSiesta density matrix. This can be ensured by copying the `siesta.TSDE` file from the ***closests*** bias calculation to the current simulation directory. I.e.
- First run $V=0$ in `TS_0`, ensure convergence etc.
- Second run $V=0.25\,\mathrm{eV}$ in `TS_0.25`, copy `TS_0/siesta.TSDE` to `TS_0.25/` and start run.
- Third run $V=0.5\,\mathrm{eV}$ in `TS_0.5`, copy `TS_0.25/siesta.TSDE` to `TS_0.5/` and start run.
- etc.
- $N$th run $V=-0.25\,\mathrm{eV}$ in `TS_-0.25`, copy `TS_0/siesta.TSDE` to `TS_-0.25/` and start run (note negative bias' can be performed in parallel to positive bias)
4. All the commands required for this example can be executed like this:
```
siesta --electrode RUN_ELEC.fdf > ELEC.out
cd TS_0
cp ../C.psf .
siesta ../RUN.fdf > TS.out
# Check that the charge is converged etc.
cp siesta.TSDE ../TS_0.5/
cd ../TS_0.5
cp ../C.psf .
siesta -V 0.5:eV ../RUN.fdf > TS.out
# Check that it has converged...
cp siesta.TSDE ../TS_1.0/
cd ../TS_1.0
cp ../C.psf .
siesta -V 1:eV ../RUN.fdf > TS.out
# Check that it has converged...
```
After every calculation go through the output to ensure everything is well behaved. Note that the output of a bias calculation is different from a non-bias calculation, they are more detailed.
5. An additional analysis (before going to the transport calculations) is to calculate the potential drop in the junction. In sisl this is easy:
```
v0 = sisl.Grid.read('TS_0/ElectrostaticPotential.grid.nc')
vd = (sisl.Grid.read('TS_0.5/ElectrostaticPotential.grid.nc') - v0)
```
`vd` then contains the potential profile (in eV). To save it as a linear average bias file (remember transport is along first lattice vector) you can execute the following:
```
vd = vd.average(1).average(2)
dv = (vd.dcell[0, :] ** 2).sum() ** .5
sisl.io.tableSile('potential_0.5.dat', 'w').write_data(dv * np.arange(vd.shape[0]), vd.grid[:, 0, 0])
```
This completes all non-equilibrium calculations for this example. However, we have only calculated the non-equilibrium density and thus, the non-equilibrium Hamiltonian. We still need to calculate the transport properties for all bias'. Basically we can only calculate the transport properties at the calculated bias values, but generally we are interested in a full $I(V)$ curve.
As a user, one has three options:
1. Calculate $I(V)$ for the calculated biases $V$ and perform an interpolation of $I(V)$, or
2. Interpolate the Hamiltonian to calculate $I(V)$ for all the required biases, or
3. Calculate all non-equilibrium Hamiltonians.
The first option is by far the fastests and easiest with a sometimes poor accuracy; the second option is relatively fast, and drastically improves the accuracy; while the last option is the most accurate but may sometimes be non-feasible due to insufficient computational resources.
In the following we will calculate all transmissions using option 2. Look in the manual for the options regarding the interpolation (there are two interpolation methods).
Go through `RUN.fdf` and find the respective block that tells TBtrans to interpolate the Hamiltonian, also notice how the energy-grid is defined in TBtrans. You will notice that this is the fastest way to calculate the $I(V)$ curve for *any* bias, it however, will not calculate any physical quantities outside the bias window.
Now complete the exercise by running TBtrans for $V\in\{0, 0.1, \dots, 1\}$ eV. Note that instead of changing the applied bias in the fdf-file, one can do:
tbtrans -V 0.4:eV RUN.fdf
to apply $V=0.4\,\mathrm{eV}$, *any* fdf-flag specified on the command line has precedence! The `:` is to denote an effective space, otherwise you will have to encapsulate in quotation marks `tbtrans -V "0.4 eV" RUN.fdf`.
If you do not want to run the commands manually, you may use this loop command:
```
for V in $(seq 0 0.1 1) ; do
d=TBT_${V//,/.}
mkdir $d
cd $d
tbtrans -V "${V//,/.}:eV" ../RUN.fdf > TBT.out
cd ../
done
```
**TIME**: A remark on this exercise. Think why applying a bias to a bulk system is wrong. If you can't immediately figure this out, try and create a longer system by replacing `device = elec.tile(3, axis=0)` with, say: `device = elec.tile(6, axis=0)` and redo the calculation for a given bias. Then compare the potential profiles.
### Plot the transmissions
Calculate the current for all $V$, then plot it.
```
V = np.arange(0, 1.05, 0.1)
I = np.empty([len(V)])
for i, v in enumerate(V):
I[i] = sisl.get_sile('TBT_{:.1f}/siesta.TBT.nc'.format(v)).current()
plt.plot(V, I * 1e6);
plt.xlabel('Bias [V]'); plt.ylabel(r'Current [$\mu\mathrm{A}$]');
```
Why is the current $0$ for $V<0.8$?
*Hint*: see [TB 1](../TB_01/run.ipynb).
| true |
code
| 0.613989 | null | null | null | null |
|
**Authors:** Peter Štrauch, Jozef Hanč, Martina Hančová <br>
**R consultant:** Andrej Gajdoš <br>
[Faculty of Science](https://www.upjs.sk/en/faculty-of-science/?prefferedLang=EN) *P. J. Šafárik University in Košice, Slovakia* <br>
email: [jozef.hanc@upjs.sk](mailto:jozef.hanc@upjs.sk)
***
**<font size=6 color=brown> Research study III: In-service teachers</font>**
**<font size=4> R Shiny $-$ UEQ (User Experience Questionary) evaluation and benchmark plot</font>**
<font size=4> Computational tool: </font> **<font size=4> R, CRAN libraries, own R functions </font>**
# Data and tools
## R libraries and functions
```
# use the following commands to install libraries, if it is needed
# packages = c('readxl', psychometric', 'repr', 'scale', 'Hmisc')
# install.packages(packages)
## load CRAN libraries
library(readxl) # read excel
library(psychometric) # measures - cronbach alpha
library(repr) # set up figures
require(scales) # transparent color
library(Hmisc) # weighted sd, var
# own UEQ functions
source('UEQ_functions.R')
```
## UEQ characteristics
```
## UEQ items
print(item_names())
## dimensions with items
dimensions()
## borders for levels in each dimension
benchmark_tab_borders()
```
## Data preprocesing
```
# load full results as dataframe
data_shiny <- as.data.frame(read_excel('../data/03_In-service_teachers_UEQ-weighted.xlsx'))
# types of data - structure
str(data_shiny, list.len = 5)
# select only UEQ data
data <- data_shiny[,4:29] # 1st column is timestamp, 2nd column is ID of teacher, 3rd column are weights
weights <- data_shiny$weight
## view data
head(weights,5)
head(data,5)
```
## Data wrangling for UEQ benchmark
```
## rescale data
DT <- rescale_data(data = data)
DT
```
# Analysis
## Consistency, inconsistency
```
## reliability
reliability(DT, spec = "whole")
reliability(DT, coef = "lambda")
## check data for inconstencies
inconsistencies(rescaled_data = DT, spec = "text")
## which responces are suggested to be deleted
remove_rows <- inconsistencies(rescaled_data = DT, spec = "remove")
remove_rows
## if we want we can remove suspicious responces - just delete "#" sign in the row below
#DT <- DT[-remove_rows,]; DT
#weights <- weights[-remove_rows]; weights
```
## Analysis of items
```
## mean values per item
item_mean(DT)
## plot of item means
options(repr.plot.width=8, repr.plot.height=6)
plot_items(rescaled_data = DT)
```
## Analysis of responses
```
## means per person
tab <- means_person(rescaled_data = DT)
tab
## mean, standard deviaton and variance for each dimension
dim_means <- dimensions_mean(data = tab, weights = weights)
dim_means
dimensions_deviation(data = tab, weights = weights)
dimensions_sderror(data=tab, weights = weights)
dimensions_variance(data = tab, weights = weights)
## means for grouped dimensions
grouped_dimensions_mean(tab, weights = weights)
```
## Vizualization and interpretation
```
## plot by dimensions
options(repr.plot.width=8, repr.plot.height=5)
plot_dimensions(data = tab, weights = weights)
## plot by grouped dimensions
options(repr.plot.width=7, repr.plot.height=5)
plot_grouped_dimensions(tab, weights = weights)
## plot with benchmarks
options(repr.plot.width=10, repr.plot.height=6)
plot_benchmarks(tab, weights = weights)
## interpretation of results
interpretation(dim_means)
```
## Weighted vs non-weighted
```
## duplicate data - with and without weights
data_merged <- merge_data(data_1 = data[,1:26], data_2 = data[,1:26], label_1 = "weighted", label_2 = "non-weighted")
weights_merged <- c(weights, rep(1, nrow(data)))
weights_merged
data_merged
## rescale data
DT_merged <- rescale_data(data = data_merged)
## calculate means for each dimension
tab_merged <- means_person(rescaled_data = DT_merged, grouping = TRUE)
dimensions_mean(data = tab_merged, grouping = TRUE, weights = weights_merged)
dimensions_deviation(data = tab_merged, grouping = TRUE, weights = weights_merged)
dimensions_sderror(data = tab_merged, grouping = TRUE, weights = weights_merged)
## plot with benchmarks
options(repr.plot.width=10, repr.plot.height=6)
plot_benchmarks(tab_merged, grouping = TRUE, weights = weights_merged)
## plot with benchmarks
options(repr.plot.width=10, repr.plot.height=6)
plot_benchmarks(tab_merged, grouping = TRUE, weights = weights_merged, ylim = c(1,1.6) )
```
| true |
code
| 0.609698 | null | null | null | null |
|
# Rotor Estimation using the Tensor Representation of Geometric Algebra
```
from __future__ import print_function
import sys
sys.path.append('../build/')
%pylab inline
np.set_printoptions(precision=2, suppress=True,threshold=np.inf)
import versor as vsr
```
## Dataset generation
```
r = vsr.Rot(vsr.Biv(0,1,0) * np.pi/6.0)
R = np.zeros((3,3))
for i in range(3):
for j in range(3):
a = vsr.Vec(0,0,0)
b = vsr.Vec(0,0,0)
a[j] = 1
b[i] = 1
R[i,j] = b <= a.spin(r)
R
vsr.Vec(1,0,0).spin(r)
vsr.Vec(0,1,0).spin(r)
vsr.Vec(0,0,1).spin(r)
n_points = 10
sigma = 0.09
points_a = [vsr.Vec(*np.random.normal(0.0, 0.8, 3))
for i in range(n_points)]
points_b = [point.spin(rotor) for point in points_a]
points_b_noisy = [vsr.Vec(*(np.array(point)[:3]
+ sigma * np.random.randn(3)))
for point in points_b]
rotor = vsr.Biv(0,-pi/8,0).exp()
print(rotor)
n_points = 3
sigma = 0.09
points_a = [vsr.Vec(*np.random.normal(0.0, 0.8, 3))
for i in range(n_points)]
points_b = [point.spin(rotor) for point in points_a]
points_b_noisy = [vsr.Vec(*(np.array(point)[:3]
+ sigma * np.random.randn(3)))
for point in points_b]
ega_a = [vsr.EGA(p) for p in points_a]
ega_b = [vsr.EGA(p) for p in points_b]
M = np.array([[1,0,0,0,0,0,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,1,0]])
print(M)
def matrix(a, b):
m = np.zeros((8,8))
for i in range(8):
ei = vsr.EGA(0,0,0,0,0,0,0,0)
ei[i] = i
m[i,:] = np.array(ei * a - b * ei)
return m
# m = np.row_stack([
# np.delete(np.delete(matrix(a,b),[0,4,5,6],0), [1,2,3,7],1)
# for a, b in zip(ega_a, ega_b)]).copy()
m = np.row_stack(np.dot(matrix(a,b),M.T) for a, b in zip(ega_a, ega_b))
U,s,Vt = np.linalg.svd(m)
# print(Vt.T)
print(vsr.Rot(*Vt[-1]))
# print(s)
```
## Solver
```
class Multivector(object):
def __init__(self, data=None):
if data is not None:
self._data = np.array(data).reshape(8,1)
else:
self._data = np.zeros((8,1))
self._grades = [0, 1, 1, 1, 2, 2, 2, 3]
self._gp_tensor = self._create_gp_tensor()
def __repr__(self):
return self._data.ravel().__repr__()
# @property
# def scalar(self):
# return self._data[0]
# @scalar.setter
def scalar(self, scalar):
self._data[0] = scalar
return Multivector(self._data)
# @property
gp_table = np.array([1, 2, 3, 4, 5, 6, 7, 8,
2, 1, 7, -6, 8, -4, 3, 5,
3, -7, 1, 5, 4, 8, -2, 6,
4, 6, -5, 1, -3, 2, 8, 7,
5, 8, -4, 3, -1, -7, 6, -2,
6, 4, 8, -2, 7, -1, -5, -3,
7, -3, 2, 8, -6, 5, -1, -4,
8, 5, 6, 7, -2, -3, -4, -1]).T.reshape(8,8)
# def vector(self):
# return self._data[1:4]
def vector(self, vector):
self._data[1:4] = np.array(vector).copy().reshape(-1,1)
return Multivector(self._data)
# @property
# def bivector(self):
# return self._data[4:7]
# @bivector.setter
def bivector(self, bivector):
self._data[4:7] = np.array(bivector).copy().reshape(-1,1)
return Multivector(self._data)
# @property
# def pseudoscalar(self):
# return self._data[7]
# @pseudoscalar.setter
def pseudoscalar(self, pseudoscalar):
self._data[7] = pseudoscalar
return Multivector(self._data)
def _create_gp_tensor(self):
M = np.zeros((8,8))
mask = np.array([1,2,3,4,5,6,7,8])
for i in range(8):
W = np.zeros((8,8))
for j in range(8):
a = vsr.EGA(0,0,0,0,0,0,0,0)
b = vsr.EGA(0,0,0,0,0,0,0,0)
a[i] = 1.
b[j] = 1.
M[i,j] = np.dot(mask, np.array(a * b))
gp_table = M.copy()
tensor = np.zeros((8,8,8))
for k in range(8):
for i in range(8):
for j in range(8):
val = gp_table[i,j]
if abs(val) == k + 1:
tensor[k,i,j] = np.sign(val)
return tensor
def gp_right_matrix(self):
return np.tensordot(self._gp_tensor.T,self._data,1).reshape(8,8)
def gp_left_matrix(self):
return np.tensordot(self._data.T, self._gp_tensor,1).reshape(8,8)
Multivector(vsr.EGA(vsr.Vec(1,2,3))).gp_left_matrix()
matrix(vsr.EGA(vsr.Vec(1,2,3)))
np.dot(Multivector(vsr.EGA(vsr.Vec(1,2,3))).gp_left_matrix(), vsr.EGA(vsr.Vec(-5,-5,-7)))
vsr.Vec(1,2,3) * vsr.Vec(-5,-5,-7)
vsr.Vec(-5,-5,-7) * vsr.Vec(1,2,3)
def matrix(a, left=True):
m = np.zeros((8,8))
for i in range(8):
ei = vsr.EGA(0,0,0,0,0,0,0,0)
ei[i] = 1.0
if left:
m[i,:] = np.array(a * ei)
else:
m[i,:] = np.array(ei * a)
return m
mask = [1,0,0,0,1,1,1,0]
mask= np.outer(mask,mask)
m = matrix(vsr.EGA(vsr.Vec(1,2,3))) - matrix(vsr.EGA(vsr.Vec(3,-1,5)),True)
print(m)
np.delete(np.delete(m,[0,4,5,6],0), [1,2,3,7],1)
motor
points_a = [vsr.EGA(vsr.Vec(1,0,0)),
vsr.EGA(vsr.Vec(0,0,1)),
vsr.EGA(vsr.Vec(1,2,3))]
points_b = [a.spin(vsr.EGA(rotor)) for a in points_a]
# n_points = 10
# sigma = 0.09
# points_a = [vsr.EGA(vsr.Vec(*np.random.normal(0.0, 0.8, 3)))
# for i in range(n_points)]
# points_b = [point.spin(vsr.EGA(rotor)) for point in points_a]
m = np.array([gp_a - gp_b for gp_a, gp_b in zip([Multivector(np.array(point)).gp_right_matrix()
for point in points_a],
[Multivector(np.array(point)).gp_left_matrix()
for point in points_b])]).reshape(-1,8)
U,s,Vt = np.linalg.svd(m)
print(s)
print(Vt.T)
print(rotor)
Multivector().vector(points_a[0]).gp_left_matrix()
class TensorRotorSolver(object):
def __init__(self):
self._gp_tensor = self._create_gp_tensor()
@property
def gp_tensor(self):
return self._gp_tensor
def _create_gp_tensor(self):
gp_table = np.array([1, 2, 3, 4, 5, 6, 7, 8,
2, 1, 7, -6, 8, -4, 3, 5,
3, -7, 1, 5, 4, 8, -2, 6,
4, 6, -5, 1, -3, 2, 8, 7,
5, 8, -4, 3, -1, -7, 6, -2,
6, 4, 8, -2, 7, -1, -5, -3,
7, -3, 2, 8, -6, 5, -1, -4,
8, 5, 6, 7, -2, -3, -4, -1]).T.reshape(8,8)
tensor = np.zeros((8,8,8))
for k in range(8):
for i in range(8):
for j in range(8):
val = gp_table[i,j]
if abs(val) == k + 1:
tensor[k,i,j] = np.sign(val)
return tensor
Gkij = TensorRotorSolver().gp_tensor
ai = np.array([0,1,2,3,0,0,0,0])
bj = np.array([0,0,0,0,1,2,3,0])
print(np.einsum('i,j,kij->k', ai, bj, Gkij))
print(np.einsum('j,kij->ki',bj, Ikij))
print(np.einsum('i,kij->kj', ai, Gkij))
vsr.EGA(0,1,0,0,0,0,0,0) * vsr.EGA(0,1,2,3,4,5,6,7)
B = vsr.EGA(0,0,0,0,5,6,7,0)
J = np.zeros((8,8))
for i in range(8):
ei = vsr.EGA(*np.zeros(8))
ei[i] = 1.
J[:,i] = ei <= B
print(J)
print(np.einsum('i,j,kij->k', ai, bj, Ikij))
print(np.einsum('i,j,kij->k', ai, bj, Okij))
vsr.EGA(1,2,3,4,5,6,7,8).rev()
Rji = np.array([1,0,0,0,0,0,0,0,
0,1,0,0,0,0,0,0,
0,0,1,0,0,0,0,0,
0,0,0,1,0,0,0,0,
0,0,0,0,-1,0,0,0,
0,0,0,0,0,-1,0,0,
0,0,0,0,0,0,-1,0,
0,0,0,0,0,0,0,-1
]).reshape(8,8)
rot = np.array([cos(pi/6),0,0,0,0,0,-sin(pi/6),0])
rotrev = np.einsum('i,ji->j', rot, Rji)
print(rot, rotrev)
print(np.einsum('i,j,m,kij,ml,pkl->p', rot, ai, rot,Gkij,Rji, Gkij))
print(np.einsum('i,j,m,lm,kij,pkl->p', rot, ai, rot,Rji,Gkij,Gkij))
print(np.einsum('j,m,ml,pkl->p', ai, rot,Rji,Gkij,Gkij))
print(np.einsum('j,m,ml,kij,pkl->pi', ai, rot,Rji,Gkij,Gkij) +
np.einsum('i,j,kij,pkl->pl', rot, ai, Gkij,Gkij))
print(np.einsum('i,j,lm,kij,pkl->pm', rot, ai,Rji,Gkij,Gkij) +
np.einsum('j,m,lm,kij,pkl->pi', ai, rot,Rji,Gkij,Gkij))
print(np.einsum('j,m,lm,kij,pkl->ip', ai, rot,Rji,Gkij,Gkij))
np.einsum('r,j,kij->')
Jac = np.zeros((3,4))
Jac[:,0] = np.array(vsr.EGA(1,0,0,0,0,0,0,0) * ae * Re.rev() + Re * ae * vsr.EGA(1,0,0,0,0,0,0,0))[1:4]
Jac[:,1] = np.array(vsr.EGA(0,0,0,0,1,0,0,0) * ae * Re.rev() + Re * ae * vsr.EGA(0,0,0,0,-1.,0,0,0))[1:4]
Jac[:,2] = np.array(vsr.EGA(0,0,0,0,0,1,0,0) * ae * Re.rev() + Re * ae * vsr.EGA(0,0,0,0,0,-1,0,0))[1:4]
Jac[:,3] = np.array(vsr.EGA(0,0,0,0,0,0,1.,0) * ae * Re.rev() + Re * ae * vsr.EGA(0,0,0,0,0,0,-1,0))[1:4]
print(Jac)
ae = vsr.EGA(0,1,0,0,0,0,0,0)
Re = vsr.EGA(cos(pi/6),0,0,0,-sin(pi/6),0,0,0)
Jac = np.zeros((8,8))
Jac[:,0] = np.array(vsr.EGA(1,0,0,0,0,0,0,0) * ae * Re.rev() + Re * ae * vsr.EGA(1,0,0,0,0,0,0,0))
Jac[:,1] = np.array(vsr.EGA(0,0,0,0,1,0,0,0) * ae * Re.rev() + Re * ae * vsr.EGA(0,0,0,0,-1.,0,0,0))
Jac[:,2] = np.array(vsr.EGA(0,0,0,0,0,1,0,0) * ae * Re.rev() + Re * ae * vsr.EGA(0,0,0,0,0,-1,0,0))
Jac[:,3] = np.array(vsr.EGA(0,0,0,0,0,0,1.,0) * ae * Re.rev() + Re * ae * vsr.EGA(0,0,0,0,0,0,-1,0))
print(Jac)
vsr.Vec(1,0,0).spin(vsr.Rot(cos(pi/6), -sin(pi/6),0,0))
def create_ip_tensor():
gp_table = np.array([0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, -4, 3, 5,
0, 0, 1, 0, 4, 0, -2, 6,
0, 0, 0, 1, -3, 2, 0, 7,
0, 0, -4, 3, -1, 0, 0, -2,
0, 4, 0, -2, 0, -1, 0, -3,
0, -3, 2, 0, 0, 0, -1, -4,
0, 5, 6, 7, -2, -3, -4, -1]).T.reshape(8,8)
tensor = np.zeros((8,8,8))
for k in range(8):
for i in range(8):
for j in range(8):
val = gp_table[i,j]
if abs(val) == k + 1:
tensor[k,i,j] = np.sign(val)
return tensor
def create_op_tensor():
gp_table = np.array([1, 2, 3, 4, 5, 6, 7, 8,
2, 0, 7, -6, 8, 0, 0, 0,
3, -7, 0, 5, 0, 8, 0, 0,
4, 6, -5, 0, 0, 0, 8, 0,
5, 8, 0, 0, 0, 0, 0, 0,
6, 0, 8, 0, 0, 0, 0, 0,
7, 0, 0, 8, 0, 0, 0, 0,
8, 0, 0, 0, 0, 0, 0, 0]).T.reshape(8,8)
tensor = np.zeros((8,8,8))
for k in range(8):
for i in range(8):
for j in range(8):
val = gp_table[i,j]
if abs(val) == k + 1:
tensor[k,i,j] = np.sign(val)
return tensor
Ikij = create_ip_tensor()
Okij = create_op_tensor()
BjIkij = np.einsum('j,kij->ki',B, Ikij)
print(BjIkij)
np.tensordot(a, BjIkij,1)
np.einsum('j,ijk->ki',B, Gkij)
Gkij = np.zeros((4,4,4))
Gkij[0] = np.array([1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,-1]).reshape(4,4)
Gkij[1] = np.array([0,1,0,0,1,0,0,0,0,0,0,-1,0,0,1,0]).reshape(4,4)
Gkij[2] = np.array([0,0,1,0,0,0,0,1,1,0,0,0,0,-1,0,0]).reshape(4,4)
Gkij[3] = np.array([0,0,0,1,0,0,1,0,0,-1,0,0,1,0,0,0]).reshape(4,4)
Gkij
ai = np.array([0,1,0,0])
bj = np.array([0,0,1,0])
np.einsum('i,j,kij->k',ai,bj,Gkij)
# Reduced tensor
Maji = Mbji = np.array([[0,1,0,0],[0,0,1,0]])
Mcji = np.array([[1,0,0,0],[0,0,0,1]])
Gwuv = np.einsum('wk,iu,jv,kij->wuv',Mcji,Maji.T, Mbji.T,Gkij)
aM = np.array([0,1]) # 0 e1 + 1 e2
bM = np.array([1,0]) # 1 e1 + 0 e2
cM = np.einsum('u,v,wuv->w',aM, bM, Gwuv)
np.einsum('w,wk',cM, Mcji)
np.tensordot(np.tensordot(a,B,0), Ikij,2)
np.tensordot(a, np.tensordot(B, Gkij,1),0)
np.einsum('i,j,kij->k',a, B, Gkij)
vsr.EGA(*a) * vsr.EGA(*B)
def rotor_estimation_ls_svd(points_a, points_b):
# gp_table = np.array([1, 2, 3, 4, 5, 6, 7, 8,
# 2, 1, 7, -6, 8, -4, 3, 5,
# 3, -7, 1, 5, 4, 8, -2, 6,
# 4, 6, -5, 1, -3, 2, 8, 7,
# 5, 8, -4, 3, -1, -7, 6, -2,
# 6, 4, 8, -2, 7, -1, -5, -3,
# 7, -3, 2, 8, -6, 5, -1, -4,
# 8, 5, 6, 7, -2, -3, -4, -1]).reshape(8,8)
M = np.zeros((8,8))
mask = np.array([1,2,3,4,5,6,7,8])
for i in range(8):
W = np.zeros((8,8))
for j in range(8):
a = vsr.EGA(0,0,0,0,0,0,0,0)
b = vsr.EGA(0,0,0,0,0,0,0,0)
a[i] = 1.
b[j] = 1.
M[i,j] = np.dot(mask, np.array(a * b))
gp_table = M.copy()
def gp_tensor():
dim = 8
tensor = np.zeros((8,8,8))
for k in range(dim):
for i in range(dim):
for j in range(dim):
val = gp_table[i,j]
if abs(val) == k + 1:
tensor[k,i,j] = np.sign(val)
return tensor
def gp_left_matrix(multivector):
tensor = gp_tensor()
matrix = np.zeros((8,8))
for i in range(8):
t = tensor[i,:,:]
matrix[i,:] = np.inner(t.T,np.array(multivector).T).reshape(-1)
return matrix
def gp_right_matrix(multivector):
tensor = gp_tensor()
matrix = np.zeros((8,8))
for i in range(8):
t = tensor[i,:,:]
matrix[i,:] = np.inner(np.array(multivector).T,t).reshape(-1)
return matrix
# A = [np.array([0.0, p[0], p[1], p[2], 0.0, 0.0, 0.0, 0.0]).reshape(8,1) for p in points_a]
# B = [np.array([0.0, p[0], p[1], p[2], 0.0, 0.0, 0.0, 0.0]).reshape(8,1) for p in points_b]
gp_a = np.row_stack([
np.delete(np.delete(gp_right_matrix(a),[0,4,5,6],0), [1,2,3,7],1)
for a in points_a])
b_gp = np.row_stack([
np.delete(np.delete(gp_left_matrix(b),[0,4,5,6],0), [1,2,3,7],1) for b in points_b])
m = gp_a - b_gp
[U,s,Vt] = np.linalg.svd(m)
print(Vt.T)
print(s)
names = ('sc', 'e1', 'e2', 'e3', 'e12', 'e13', 'e23', 'e123')
res = np.recarray(1, formats = 8*['f8'], names=names, buf=Vt.T[:,-2])
rotor = np.array([res['sc'], res['e12'], res['e13'], res['e23']])
return rotor, m
print(points_a)
print(points_b)
r,m2 = rotor_estimation_ls_svd(points_a, points_b)
vsr.Rot(*r)
print(rotor)
gp_table = np.array([1, 2, 3, 4, 5, 6, 7, 8,
2, 1, 7, -6, 8, -4, 3, 5,
3, -7, 1, 5, 4, 8, -2, 6,
4, 6, -5, 1, -3, 2, 8, 7,
5, 8, -4, 3, -1, -7, 6, -2,
6, 4, 8, -2, 7, -1, -5, -3,
7, -3, 2, 8, -6, 5, -1, -4,
8, 5, 6, 7, -2, -3, -4, -1]).T.reshape(8,8)
print(gp_table.T)
M = np.zeros((8,8))
mask = np.array([1,2,3,4,5,6,7,8])
for i in range(8):
W = np.zeros((8,8))
for j in range(8):
a = vsr.EGA(0,0,0,0,0,0,0,0)
b = vsr.EGA(0,0,0,0,0,0,0,0)
a[i] = 1.
b[j] = 1.
M[i,j] = np.dot(mask, np.array(a * b))
gp_table = M.T.copy()
print(gp_table.T)
print(Multivector().vector(points_a[0]).gp_right_matrix())
print(Multivector().vector(points_b[0]).gp_left_matrix())
print(m2[:8])
r = rotor
vsr.EGA(0,1,0,0,0,0,0,0).spin(vsr.EGA(r[0],0,0,0,r[1],r[2],r[3],0))
rotor = vsr.Biv(0,-pi/8,0).exp()
print(rotor)
n_points = 3
sigma = 0.09
points_a = [vsr.Vec(*np.random.normal(0.0, 0.8, 3))
for i in range(n_points)]
points_b = [point.spin(rotor) for point in points_a]
points_b_noisy = [vsr.Vec(*(np.array(point)[:3]
+ sigma * np.random.randn(3)))
for point in points_b]
ega_a = [vsr.EGA(p) for p in points_a]
ega_b = [vsr.EGA(p) for p in points_b]
def matrix(a, b):
m = np.zeros((8,8))
for i in range(8):
ei = vsr.EGA(0,0,0,0,0,0,0,0)
ei[i] = i
m[i,:] = np.array(ei * a - b * ei)
return m
m = np.row_stack([
np.delete(np.delete(matrix(a,b),[0,4,5,6],0), [1,2,3,7],1)
for a, b in zip(ega_a, ega_b)]).copy()
U,s,Vt = np.linalg.svd(m)
print(Vt.T)
print(s)
ega_a = [vsr.EGA(p) for p in points_a]
ega_b = [vsr.EGA(p) for p in points_b]
M = np.array([[1,0,0,0,0,0,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,1,0]])
print(M)
def matrix(a, b):
m = np.zeros((8,8))
for i in range(8):
ei = vsr.EGA(0,0,0,0,0,0,0,0)
ei[i] = i
m[i,:] = np.array(ei * a - b * ei)
return m
# m = np.row_stack([
# np.delete(np.delete(matrix(a,b),[0,4,5,6],0), [1,2,3,7],1)
# for a, b in zip(ega_a, ega_b)]).copy()
m = np.row_stack(np.dot(matrix(a,b),M.T) for a, b in zip(ega_a, ega_b))
U,s,Vt = np.linalg.svd(m)
# print(Vt.T)
print(vsr.Rot(*Vt[-1]))
# print(s)
matrix(ega_a[0], ega_b[0])
np.delete(np.delete(matrix(ega_a[0],ega_b[0]),[0,4,5,6],0), [1,2,3,7],1)
r = np.array([1,2,3,4,5,6,7,8]).T
vsr.CGA(vsr.Mot(1,2,3,4,5,6,7,8))
np.delete(matrix(ega_a[0],ega_b[0]),[0,4,5,6],0)
motor
Mrotij = np.array([[1,0,0,0,0,0,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,1,0]])
np.einsum('j,ij->i',r,Mrotij)
cga_a = [vsr.CGA(p.null()) for p in points_a]
cga_b = [vsr.CGA(p.null()) for p in points_b]
def matrix(a, b):
m = np.zeros((32,32))
for i in range(32):
ei = vsr.CGA(*np.zeros(32))
ei[i] = i
m[i,:] = np.array(ei * a - b * ei)
return m
k = matrix(cga_a[0], cga_b[0])
m = np.row_stack([matrix(a,b) for a,b in zip(cga_a, cga_b)])
U,s,Vt = np.linalg.svd(m)
print(Vt.T[-1])
import time
t1 = time.time()
vsr.CGA(vsr.Vec(1,2,3).null()).spin(vsr.CGA(motor))
t2 = time.time()
print(t2-t1)
t1 = time.time()
vsr.Vec(1,2,3).null().spin(motor)
t2 = time.time()
print(t2-t1)
np.set_printoptions(linewidth=200,precision=2)
motor = vsr.Vec(1,1,1).trs() * vsr.Rot(vsr.Biv(1,1,1).unit() * np.pi/6.0)
print(motor)
n_points = 10
sigma = 0.09
points_a = [vsr.Vec(*np.random.normal(0.0, 0.8, 3)).null()
for i in range(n_points)]
points_b = [point.spin(motor) for point in points_a]
points_b_noisy = [vsr.Vec(*(np.array(point)[:3]
+ sigma * np.random.randn(3))).null()
for point in points_b]
cga_a = [vsr.CGA(p) for p in points_a]
cga_b = [vsr.CGA(p) for p in points_b]
def set_idx(idx):
a = np.zeros(32)
a[idx] = 1.
return a
M = np.array([set_idx(0),
set_idx(6), set_idx(7), set_idx(8),
set_idx(12), set_idx(13), set_idx(14),
set_idx(27)])
def matrix(a, b):
m = np.zeros((32,32))
for i in range(32):
ei = vsr.CGA(*np.zeros(32))
ei[i] = i
m[i,:] = np.array(ei * a - b * ei)
return np.dot(m,M.T)[1:6,:]
# print(matrix(cga_a[0],cga_b[0])[1:6,:] )
m = np.row_stack([matrix(a,b) for a, b in zip(cga_a, cga_b)]).copy()
# print(m)
U,s,Vt = np.linalg.svd(m)
print(Vt.T)
print(s)
set_idx(1)
ega_a = [vsr.EGA(p) for p in points_a]
ega_b = [vsr.EGA(p) for p in points_b]
M = np.array([[1,0,0,0,0,0,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,1,0]])
print(M)
def matrix(a, b):
m = np.zeros((8,8))
for i in range(8):
ei = vsr.EGA(0,0,0,0,0,0,0,0)
ei[i] = i
m[i,:] = np.array(ei * a - b * ei)
return m
# m = np.row_stack([
# np.delete(np.delete(matrix(a,b),[0,4,5,6],0), [1,2,3,7],1)
# for a, b in zip(ega_a, ega_b)]).copy()
m = np.row_stack(np.dot(matrix(a,b),M.T) for a, b in zip(ega_a, ega_b))
U,s,Vt = np.linalg.svd(m)
# print(Vt.T)
print(vsr.Rot(*Vt[-1]))
# print(s)
e0 = vsr.CGA(vsr.Mot(1,0,0,0,0,0,0,0))
e12 = vsr.CGA(vsr.Mot(0,1,0,0,0,0,0,0))
e13 = vsr.CGA(vsr.Mot(0,0,1,0,0,0,0,0))
e23 = vsr.CGA(vsr.Mot(0,0,0,1,0,0,0,0))
e1i = vsr.CGA(vsr.Mot(0,0,0,0,1,0,0,0))
e2i = vsr.CGA(vsr.Mot(0,0,0,0,0,1,0,0))
e3i = vsr.CGA(vsr.Mot(0,0,0,0,0,0,1,0))
e123i = vsr.CGA(vsr.Mot(0,0,0,0,0,0,0,1))
a = cga_a[0]
b = cga_b[0]
e0 * a - b * e0
(lambda idx : [None for np.zeros(32); a[idx] = 1)(3)
(e12 * a - b * e12)
np.delete((e12 * a - b * e12),[0,6,7,8,9,10,11,12,13,14,15,26,27,28,29,30])
e13 * a - b * e13
e123i * a - b * e123i
vsr.CGA(vsr.Mot(1,2,3,4,5,6,7,8))
vsr.CGA(vsr.Mot(1,2,3,4,5,6,7,8))
vsr.Mot(vsr.CGA(vsr.Rot(1,2,3,4)) * vsr.CGA(vsr.Vec(1,2,3)))
import scipy.linalg as linalg
U,s,Vh = linalg.svd(m)
import scipy.io as io
io.savemat("/home/lars/m.mat", {"m":m})
M = io.loadmat("/home/lars/Downloads/M.mat")["M"]
print(M)
U,s,Vt = np.linalg.svd(M)
print(s)
print(m[:8])
print(M[:8])
matrix(vsr.EGA(1,0,0,0,0,0,0,0), vsr.EGA(0,0,0,0,0,0,0,0)).T
print(vsr.EGA(0,1,0,0,0,0,0,0) * vsr.EGA(1,0,0,0,0,0,0,0))
print(vsr.EGA(0,1,0,0,0,0,0,0) * vsr.EGA(0,1,0,0,0,0,0,0))
print(vsr.EGA(0,1,0,0,0,0,0,0) * vsr.EGA(0,0,1,0,0,0,0,0))
print(vsr.EGA(0,1,0,0,0,0,0,0) * vsr.EGA(0,0,0,1,0,0,0,0))
print(vsr.EGA(0,1,0,0,0,0,0,0) * vsr.EGA(0,0,0,0,1,0,0,0))
print(vsr.EGA(0,1,0,0,0,0,0,0) * vsr.EGA(0,0,0,0,0,1,0,0))
print(vsr.EGA(0,1,0,0,0,0,0,0) * vsr.EGA(0,0,0,0,0,0,1,0))
print(vsr.EGA(0,1,0,0,0,0,0,0) * vsr.EGA(0,0,0,0,0,0,0,1))
np.array([np.array(vsr.EGA(0,0,1,0,0,0,0,0) * vsr.EGA(1,0,0,0,0,0,0,0)),
np.array(vsr.EGA(0,0,1,0,0,0,0,0) * vsr.EGA(0,1,0,0,0,0,0,0)),
np.array(vsr.EGA(0,0,1,0,0,0,0,0) * vsr.EGA(0,0,1,0,0,0,0,0)),
np.array(vsr.EGA(0,0,1,0,0,0,0,0) * vsr.EGA(0,0,0,1,0,0,0,0)),
np.array(vsr.EGA(0,0,1,0,0,0,0,0) * vsr.EGA(0,0,0,0,1,0,0,0)),
np.array(vsr.EGA(0,0,1,0,0,0,0,0) * vsr.EGA(0,0,0,0,0,1,0,0)),
np.array(vsr.EGA(0,0,1,0,0,0,0,0) * vsr.EGA(0,0,0,0,0,0,1,0)),
np.array(vsr.EGA(0,0,1,0,0,0,0,0) * vsr.EGA(0,0,0,0,0,0,0,1))]).T
Multivector()._gp_tensor[2,:,:]
vsr.EGA(0,0,0,0,0,0,0,0) * vsr.EGA(0,a[0],a[1],0,a[2],0,0,0)
np.inner(matrix(vsr.EGA(vsr.Vec(1,2,3)), vsr.EGA(0,0,0,0,0,0,0,0)), vsr.EGA(vsr.Vec(-12,9,-13)))
vsr.Vec(1,2,3) * vsr.Vec(-12,9,-13)
motor = vsr.Vec(1,1,1).trs() * vsr.Rot(vsr.Biv(0,1,0) * np.pi/6.0)
a = vsr.CGA(motor)
print(a)
a = vsr.EGA(1,0,0,0,0,0,0,0)
m2 = np.zeros((8,8))
for i in range(8):
ei = vsr.EGA(*np.zeros(8))
ei[i] = 1.0
m2[:,i] = ei * vsr.EGA(1,0,0,0,0,0,0,0)
print(m)
np.sum(m2,0)
M = np.zeros((8,8))
for i in range(8):
W = np.zeros((8,8))
for j in range(8):
a = vsr.EGA(0,0,0,0,0,0,0,0)
b = vsr.EGA(0,0,0,0,0,0,0,0)
a[i] = 1.
b[j] = j + 1
W[i,:] = np.array(a * b)
print(np.sum(W,0))
M[i,:] = np.sum(W,0)
print(M)
M = np.zeros((8,8))
mask = np.array([1,2,3,4,5,6,7,8])
for i in range(8):
W = np.zeros((8,8))
for j in range(8):
a = vsr.EGA(0,0,0,0,0,0,0,0)
b = vsr.EGA(0,0,0,0,0,0,0,0)
a[i] = 1.
b[j] = 1.
M[i,j] = np.dot(mask, np.array(a <= b))
print(M.T)
def row(a):
M = np.zeros(8)
for i in range(8):
b = vsr.EGA(0,0,0,0,0,0,0,0)
b[i] = i + 1
M += np.array(a * b)
return M
for i in range(8):
ei = vsr.EGA(0,0,0,0,0,0,0,0)
ei[i] = 1.
print(row(ei))
np.dot([1,2,3,4,5,6,7,8], np.array(vsr.EGA(0,0,0,0,0,1,0,0) * vsr.EGA(0,0,0,0,0,0,0,1)))
```
| true |
code
| 0.561515 | null | null | null | null |
|
# Recommending movies: ranking
**Learning Objectives**
1. Get our data and split it into a training and test set.
2. Implement a ranking model.
3. Fit and evaluate it.
## Introduction
The retrieval stage is responsible for selecting an initial set of hundreds of candidates from all possible candidates. The main objective of this model is to efficiently weed out all candidates that the user is not interested in. Because the retrieval model may be dealing with millions of candidates, it has to be computationally efficient.
The ranking stage takes the outputs of the retrieval model and fine-tunes them to select the best possible handful of recommendations. Its task is to narrow down the set of items the user may be interested in to a shortlist of likely candidates.
Each learning objective will correspond to a _#TODO_ in this student lab notebook -- try to complete this notebook first and then review the [solution notebook](https://github.com/GoogleCloudPlatform/training-data-analyst/blob/master/courses/machine_learning/deepdive2/recommendation_systems/soulutions/basic_ranking.ipynb)
## Imports
Let's first get our imports out of the way.
```
!pip install -q tensorflow-recommenders
!pip install -q --upgrade tensorflow-datasets
```
**Note: Please ignore the incompatibility errors and re-run the above cell before proceeding for the lab.**
```
# You can use any Python source file as a module by executing an import statement in some other Python source file.
# The import statement combines two operations; it searches for the named module, then it binds the
# results of that search to a name in the local scope.
import os
import pprint
import tempfile
from typing import Dict, Text
import numpy as np
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_recommenders as tfrs
```
This notebook uses TF2.x.
Please check your tensorflow version using the cell below.
```
# Show the currently installed version of TensorFlow
print("TensorFlow version: ",tf.version.VERSION)
```
## Lab Task 1: Preparing the dataset
We're going to use the same data as the [retrieval](https://www.tensorflow.org/recommenders/examples/basic_retrieval) tutorial. This time, we're also going to keep the ratings: these are the objectives we are trying to predict.
```
ratings = tfds.load("movielens/100k-ratings", split="train")
ratings = ratings.map(lambda x: {
"movie_title": x["movie_title"],
"user_id": x["user_id"],
"user_rating": x["user_rating"]
})
```
As before, we'll split the data by putting 80% of the ratings in the train set, and 20% in the test set.
```
tf.random.set_seed(42)
shuffled = ratings.shuffle(100_000, seed=42, reshuffle_each_iteration=False)
# TODO 1a -- your code goes here
```
Let's also figure out unique user ids and movie titles present in the data.
This is important because we need to be able to map the raw values of our categorical features to embedding vectors in our models. To do that, we need a vocabulary that maps a raw feature value to an integer in a contiguous range: this allows us to look up the corresponding embeddings in our embedding tables.
```
movie_titles = ratings.batch(1_000_000).map(lambda x: x["movie_title"])
user_ids = ratings.batch(1_000_000).map(lambda x: x["user_id"])
unique_movie_titles = np.unique(np.concatenate(list(movie_titles)))
unique_user_ids = np.unique(np.concatenate(list(user_ids)))
```
## Lab Task 2: Implementing a model
### Architecture
Ranking models do not face the same efficiency constraints as retrieval models do, and so we have a little bit more freedom in our choice of architectures.
A model composed of multiple stacked dense layers is a relatively common architecture for ranking tasks. We can implement it as follows:
```
class RankingModel(tf.keras.Model):
def __init__(self):
super().__init__()
embedding_dimension = 32
# Compute embeddings for users.
# TODO 2a -- your code goes here
# Compute embeddings for movies.
# TODO 2b -- your code goes here
# Compute predictions.
self.ratings = tf.keras.Sequential([
# Learn multiple dense layers.
tf.keras.layers.Dense(256, activation="relu"),
tf.keras.layers.Dense(64, activation="relu"),
# Make rating predictions in the final layer.
tf.keras.layers.Dense(1)
])
def call(self, inputs):
user_id, movie_title = inputs
user_embedding = self.user_embeddings(user_id)
movie_embedding = self.movie_embeddings(movie_title)
return self.ratings(tf.concat([user_embedding, movie_embedding], axis=1))
```
This model takes user ids and movie titles, and outputs a predicted rating:
```
RankingModel()((["42"], ["One Flew Over the Cuckoo's Nest (1975)"]))
```
### Loss and metrics
The next component is the loss used to train our model. TFRS has several loss layers and tasks to make this easy.
In this instance, we'll make use of the `Ranking` task object: a convenience wrapper that bundles together the loss function and metric computation.
We'll use it together with the `MeanSquaredError` Keras loss in order to predict the ratings.
```
task = tfrs.tasks.Ranking(
loss = tf.keras.losses.MeanSquaredError(),
metrics=[tf.keras.metrics.RootMeanSquaredError()]
)
```
The task itself is a Keras layer that takes true and predicted as arguments, and returns the computed loss. We'll use that to implement the model's training loop.
### The full model
We can now put it all together into a model. TFRS exposes a base model class (`tfrs.models.Model`) which streamlines bulding models: all we need to do is to set up the components in the `__init__` method, and implement the `compute_loss` method, taking in the raw features and returning a loss value.
The base model will then take care of creating the appropriate training loop to fit our model.
```
class MovielensModel(tfrs.models.Model):
def __init__(self):
super().__init__()
self.ranking_model: tf.keras.Model = RankingModel()
self.task: tf.keras.layers.Layer = tfrs.tasks.Ranking(
loss = tf.keras.losses.MeanSquaredError(),
metrics=[tf.keras.metrics.RootMeanSquaredError()]
)
def compute_loss(self, features: Dict[Text, tf.Tensor], training=False) -> tf.Tensor:
rating_predictions = self.ranking_model(
(features["user_id"], features["movie_title"]))
# The task computes the loss and the metrics.
return self.task(labels=features["user_rating"], predictions=rating_predictions)
```
## Lab Task 3: Fitting and evaluating
After defining the model, we can use standard Keras fitting and evaluation routines to fit and evaluate the model.
Let's first instantiate the model.
```
model = MovielensModel()
model.compile(optimizer=tf.keras.optimizers.Adagrad(learning_rate=0.1))
```
Then shuffle, batch, and cache the training and evaluation data.
```
cached_train = train.shuffle(100_000).batch(8192).cache()
cached_test = test.batch(4096).cache()
```
Then train the model:
```
model.fit(cached_train, epochs=3)
```
As the model trains, the loss is falling and the RMSE metric is improving.
Finally, we can evaluate our model on the test set:
```
# TODO 3a -- your code goes here
```
The lower the RMSE metric, the more accurate our model is at predicting ratings.
## Next steps
The model above gives us a decent start towards building a ranking system.
Of course, making a practical ranking system requires much more effort.
In most cases, a ranking model can be substantially improved by using more features rather than just user and candidate identifiers. To see how to do that, have a look at the [side features](https://www.tensorflow.org/recommenders/examples/featurization) tutorial.
A careful understanding of the objectives worth optimizing is also necessary. To get started on building a recommender that optimizes multiple objectives, have a look at our [multitask](https://www.tensorflow.org/recommenders/examples/multitask) tutorial.
| true |
code
| 0.622172 | null | null | null | null |
|
```
!pip install d2l==0.17.2
```
# Concise Implementation of RNNs
Now we will see how to implement the same language model more efficiently
using functions provided by high-level PyTorch APIs.
We begin as before by reading the time machine dataset.
```
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
```
## [**Defining the Model**]
PyTorch APIs provide implementations of recurrent neural networks.
We construct the recurrent neural network layer `rnn_layer` with a single hidden layer and 256 hidden units.
```
num_hiddens = 256
rnn_layer = nn.RNN(len(vocab), num_hiddens)
```
We (**use a tensor to initialize the hidden state**),
whose shape is
(number of hidden layers, batch size, number of hidden units).
```
state = torch.zeros((1, batch_size, num_hiddens))
state.shape
```
[**With a hidden state and an input,
we can compute the output with
the updated hidden state.**]
Here, it should be emphasized that
the "output" (`Y`) of `rnn_layer`
does *not* involve computation of output layers:
it refers to
the hidden state at *each* time step,
and they can be used as the input
to the subsequent output layer.
```
X = torch.rand(size=(num_steps, batch_size, len(vocab)))
Y, state_new = rnn_layer(X, state)
Y.shape, state_new.shape
```
Similarly,
[**we define an `RNNModel` class
for a complete RNN model.**]
Note that `rnn_layer` only contains the hidden recurrent layers, we need to create a separate output layer.
```
class RNNModel(nn.Module):
"""The RNN model."""
def __init__(self, rnn_layer, vocab_size, **kwargs):
super(RNNModel, self).__init__(**kwargs)
self.rnn = rnn_layer
self.vocab_size = vocab_size
self.num_hiddens = self.rnn.hidden_size
# If the RNN is bidirectional (to be introduced later),
# `num_directions` should be 2, else it should be 1.
if not self.rnn.bidirectional:
self.num_directions = 1
self.linear = nn.Linear(self.num_hiddens, self.vocab_size)
else:
self.num_directions = 2
self.linear = nn.Linear(self.num_hiddens * 2, self.vocab_size)
def forward(self, inputs, state):
X = F.one_hot(inputs.T.long(), self.vocab_size)
X = X.to(torch.float32)
Y, state = self.rnn(X, state)
# The fully connected layer will first change the shape of `Y` to
# (`num_steps` * `batch_size`, `num_hiddens`). Its output shape is
# (`num_steps` * `batch_size`, `vocab_size`).
output = self.linear(Y.reshape((-1, Y.shape[-1])))
return output, state
def begin_state(self, device, batch_size=1):
if not isinstance(self.rnn, nn.LSTM):
# `nn.GRU` takes a tensor as hidden state
return torch.zeros((self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens),
device=device)
else:
# `nn.LSTM` takes a tuple of hidden states
return (torch.zeros((
self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device),
torch.zeros((
self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device))
```
## Training and Predicting
Before training the model, let us [**make a prediction with the a model that has random weights.**]
```
device = d2l.try_gpu()
net = RNNModel(rnn_layer, vocab_size=len(vocab))
net = net.to(device)
d2l.predict_ch8('time traveller', 10, net, vocab, device)
```
As is quite obvious, this model does not work at all. Next, we call `train_ch8` with the same hyperparameters defined before and [**train our model with PyTorch APIs**].
```
num_epochs, lr = 500, 1
d2l.train_ch8(net, train_iter, vocab, lr, num_epochs, device)
```
Compared the scratch implemention, this model achieves comparable perplexity,
albeit within a shorter period of time, due to the code being more optimized by
high-level PyTorch APIs.
| true |
code
| 0.885235 | null | null | null | null |
|
# Soccerstats Predictions v0.5
The changelog from v0.4:
* Try to implement the *MulticlassClassificationEvaluator* evaluator for the random-forest model.
* Use the *accuracy* metric to evaluate the random-forest model.
## A. Data Cleaning & Preparation
### 1. Read csv file
```
# load and cache data
stat_df = sqlContext.read\
.format("com.databricks.spark.csv")\
.options(header = True)\
.load("data/teamFixtures.csv")\
.cache()
# count hyphen nulls ("-") per column
def count_hyphen_null(df, col):
return df.where(df[col] == "-").count()
# count cols with "-" ie. null
total_rows = stat_df.count()
hyphen_rows = count_hyphen_null(stat_df, "gameFtScore")
to_remove = total_rows - hyphen_rows
print("Total rows: {}".format(total_rows))
print("Hyphen nulls: {}".format(hyphen_rows))
print("Rows to remove: {}".format(to_remove))
```
### 2. Filter-out "gameFtScore" column values
```
from pyspark.sql.functions import udf
from pyspark.sql.types import StringType
# replace non-"-" values with null
nullify_ft_column = udf(
lambda row_value: None if row_value != "-" else row_value,
StringType()
)
stat_df = (stat_df.withColumn("gameFtScore", nullify_ft_column(stat_df.gameFtScore)))
# drop Null values
stat_df = stat_df.dropna()
stat_df.select("gameFtScore").show(5)
print("Total rows: {}".format(stat_df.count()))
```
### 3. Write-out new dataframe to Json
```
# optional: save to file
# stat_df.coalesce(1).write.format('json').save('sstats_fixtures.json')
```
### 4. Read fixtures Json to dataframe
```
fx_df = spark.read.json('data/fixtures1.json')
fx_df.printSchema()
```
### 5. Encode "fixture_id" on stat_df dataframe
```
import hashlib
from pyspark.sql.functions import array
def encode_string(value):
return hashlib.sha1(
value.encode("utf-8")
).hexdigest()
# add an encoded col to "stat_df"; fixture_id
fxcol_df = udf(
lambda row_value: encode_string(u"".join([x for x in row_value])),
StringType()
)
stat_df = (stat_df.withColumn("fixture_id", fxcol_df(array(
"leagueName",
"leagueDivisionName",
"gamePlayDate",
"gameHomeTeamName",
"gameAwayTeamName"
))))
# display some encoded fixtures
stat_df.select("fixture_id").show(5, False)
```
### 6. Concat the two dataframes: "stat_df" and "fx_df"
```
from pyspark.sql.functions import col
# use "left-outer-join" to concat
full_df = stat_df.alias("a")\
.join(fx_df, stat_df.fixture_id == fx_df.fixture_id, "left_outer")\
.select(*[col("a."+c) for c in stat_df.columns] + [fx_df.ft_score])
full_df.select("leagueName", "leagueDivisionName", "gamePlayDate", "gameHomeTeamName", "gameAwayTeamName", "ft_score").show(5, False)
```
### 7. Assess damage on "ft_score " nulls
```
# count nulls per column
def count_null(df, col):
return df.where(df[col].isNull()).count()
print("Total rows: {}".format(full_df.count()))
print("Ft_score nulls: {}".format(count_null(full_df, "ft_score")))
# drop null values in ft_Score
full_df = full_df.dropna()
print("Total rows: {}".format(full_df.count()))
print("Ft_score nulls: {}".format(count_null(full_df, "ft_score")))
```
## B. Machine Learning
```
# print dataframe schema
# full_df.printSchema()
```
### 1. Clean data
```
# drop unnecessary columns
ml_df = full_df.drop(
"gameID", "gamePlayDate", "gamePlayTime", "gameHomeTeamName",
"gameAwayTeamName", "gameHomeTeamID","gameAwayTeamID", "leagueName",
"leagueDivisionName", "gameFtScore", "fixture_id"
)
# separate col types
all_cols = ml_df.columns
all_cols.remove(all_cols[-1])
# cast types to columns: string to double
ml_df = ml_df.select(*[col(c).cast("double").alias(c) for c in all_cols] + [ml_df.ft_score])
ml_df.printSchema()
# add extra column; over/under
over_under_udf = udf(
lambda r: "over" if (int(r.split("-")[0]) + int(r.split("-")[1])) > 2 else "under",
StringType()
)
ml_df = (ml_df.withColumn("over_under", over_under_udf(ml_df.ft_score)))
ml_df.select("ft_score", "over_under").show(5)
# drop "ft_score"
ml_df = ml_df.drop("ft_score")
```
### 2. Some featurization
```
from pyspark.ml.feature import StringIndexer
from pyspark.sql import Row
# index the label; "over_under"
si = StringIndexer(inputCol = "over_under", outputCol = "over_under_indx")
df_indexed = si\
.fit(ml_df)\
.transform(ml_df)\
.drop("over_under")\
.withColumnRenamed("over_under_indx", "over_under")
from pyspark.ml.feature import Normalizer
from pyspark.sql.functions import mean, stddev
# normalize feature columns; [(x - mean)/std_dev]
def normalize_col(df, cols):
# find mean & std for each column
aggExpr = []
aggStd = []
for col in cols:
aggExpr.append(mean(df[col]).alias(col))
aggStd.append(stddev(df[col]).alias(col + "_stddev"))
averages = df.agg(*aggExpr).collect()[0]
std_devs = df.agg(*aggStd).collect()[0]
# standardize dataframe
for col in cols:
df = df.withColumn(col + "_norm", ((df[col] - averages[col]) / std_devs[col + "_stddev"]))
return df, averages, std_devs
# normalize dataframe
df_indexed, averages, std_devs = normalize_col(df_indexed, all_cols)
# display some normalized column
df_indexed.select("HTS_teamPosition", "HTS_teamPosition_norm").show()
from pyspark.ml.linalg import Vectors
feature_cols = [col+"_norm" for col in all_cols]
df_indexed = df_indexed[feature_cols + ["over_under"]]
# vectorize labels and features
row = Row("label", "features")
label_fts = df_indexed.rdd.map(
lambda r: (row(r[-1], Vectors.dense(r[:-1])))
).toDF()
label_fts.show(5)
# split train/test values
train, test = label_fts.randomSplit([0.8, 0.2])
# split train/validate values
train, validate = train.randomSplit([0.9, 0.1])
print("Train values: '{}'".format(train.count()))
print("Test values: '{}'".format(test.count()))
print("Validate values: '{}'".format(validate.count()))
```
### 3. Apply some ML models
```
from pyspark.ml.classification import LogisticRegression, DecisionTreeClassifier, RandomForestClassifier
from pyspark.ml.evaluation import BinaryClassificationEvaluator
# 1. Logistic regression model
logr = LogisticRegression(
maxIter = 100,
regParam = 0.05,
labelCol="label"
)
# 2. decision tree model
d_tree = DecisionTreeClassifier(
maxDepth = 10,
labelCol = "label"
)
# 3. random forest model
r_forest = RandomForestClassifier(
numTrees = 100,
labelCol = "label"
)
from time import time
# start timer
start_time = time()
# fit models
lr_model = logr.fit(train)
dt_model = d_tree.fit(train)
rf_model = r_forest.fit(train)
print("Training time taken (min): {}".format((time() - start_time)/60))
# model evaluator
def testModel(model, df):
pred = model.transform(df)
evaluator = BinaryClassificationEvaluator(labelCol="label")
return evaluator.evaluate(pred)
# accuracy output
models = {
"Logistic regression": lr_model,
"Decision tree": dt_model,
"Random forest": rf_model
}
modelPerf = {k:testModel(v, test) for k,v in models.iteritems()}
print "Accuracy:", modelPerf
```
### 4. Try some hyper-parameter tuning
```
# from pyspark.ml.tuning import CrossValidator, ParamGridBuilder
# from pyspark.ml.evaluation import MulticlassClassificationEvaluator
# # tune best performing model: random forest
# paramGrid = ParamGridBuilder()\
# .addGrid(r_forest.maxDepth, [5, 10, 15, 20])\
# .addGrid(r_forest.numTrees, [30, 60, 90, 120])\
# .build()
# # define evaluation metric
# evaluator = MulticlassClassificationEvaluator(
# labelCol="label",
# predictionCol = "prediction",
# metricName="accuracy"
# )
# # start tuning
# cv = CrossValidator(
# estimator=r_forest,
# estimatorParamMaps=paramGrid,
# evaluator=evaluator,
# numFolds=5
# )
# # start timer
# cv_start_time = time()
# # fit tuned model
# cvModel = cv.fit(train)
# # calculate time taken to tune prameters
# print "Hyper-param tuning time taken (min): ", (time() - cv_start_time)/60
# # accuracy after tuning
# train_pred = cvModel.transform(train)
# test_pred = cvModel.transform(test)
# print("Random forest accuracy (train): {}".format(evaluator.evaluate(train_pred)))
# print("Random forest accuracy (test): {}".format(evaluator.evaluate(test_pred)))
```
| true |
code
| 0.289121 | null | null | null | null |
|
# Deep Q-learning
In this notebook, we'll build a neural network that can learn to play games through reinforcement learning. More specifically, we'll use Q-learning to train an agent to play a game called [Cart-Pole](https://gym.openai.com/envs/CartPole-v0). In this game, a freely swinging pole is attached to a cart. The cart can move to the left and right, and the goal is to keep the pole upright as long as possible.

We can simulate this game using [OpenAI Gym](https://gym.openai.com/). First, let's check out how OpenAI Gym works. Then, we'll get into training an agent to play the Cart-Pole game.
```
import gym
import tensorflow as tf
import numpy as np
```
>**Note:** Make sure you have OpenAI Gym cloned into the same directory with this notebook. I've included `gym` as a submodule, so you can run `git submodule --init --recursive` to pull the contents into the `gym` repo.
```
# Create the Cart-Pole game environment
env = gym.make('CartPole-v0')
```
We interact with the simulation through `env`. To show the simulation running, you can use `env.render()` to render one frame. Passing in an action as an integer to `env.step` will generate the next step in the simulation. You can see how many actions are possible from `env.action_space` and to get a random action you can use `env.action_space.sample()`. This is general to all Gym games. In the Cart-Pole game, there are two possible actions, moving the cart left or right. So there are two actions we can take, encoded as 0 and 1.
Run the code below to watch the simulation run.
```
env.reset()
rewards = []
for _ in range(100):
env.render()
state, reward, done, info = env.step(env.action_space.sample()) # take a random action
rewards.append(reward)
if done:
rewards = []
env.reset()
#Test
env.close()
```
To shut the window showing the simulation, use `env.close()`.
If you ran the simulation above, we can look at the rewards:
```
print(rewards[-20:])
```
The game resets after the pole has fallen past a certain angle. For each frame while the simulation is running, it returns a reward of 1.0. The longer the game runs, the more reward we get. Then, our network's goal is to maximize the reward by keeping the pole vertical. It will do this by moving the cart to the left and the right.
## Q-Network
We train our Q-learning agent using the Bellman Equation:
$$
Q(s, a) = r + \gamma \max{Q(s', a')}
$$
where $s$ is a state, $a$ is an action, and $s'$ is the next state from state $s$ and action $a$.
Before we used this equation to learn values for a Q-_table_. However, for this game there are a huge number of states available. The state has four values: the position and velocity of the cart, and the position and velocity of the pole. These are all real-valued numbers, so ignoring floating point precisions, you practically have infinite states. Instead of using a table then, we'll replace it with a neural network that will approximate the Q-table lookup function.
<img src="assets/deep-q-learning.png" width=450px>
Now, our Q value, $Q(s, a)$ is calculated by passing in a state to the network. The output will be Q-values for each available action, with fully connected hidden layers.
<img src="assets/q-network.png" width=550px>
As I showed before, we can define our targets for training as $\hat{Q}(s,a) = r + \gamma \max{Q(s', a')}$. Then we update the weights by minimizing $(\hat{Q}(s,a) - Q(s,a))^2$.
For this Cart-Pole game, we have four inputs, one for each value in the state, and two outputs, one for each action. To get $\hat{Q}$, we'll first choose an action, then simulate the game using that action. This will get us the next state, $s'$, and the reward. With that, we can calculate $\hat{Q}$ then pass it back into the $Q$ network to run the optimizer and update the weights.
Below is my implementation of the Q-network. I used two fully connected layers with ReLU activations. Two seems to be good enough, three might be better. Feel free to try it out.
```
class QNetwork:
def __init__(self, learning_rate=0.01, state_size=4,
action_size=2, hidden_size=10,
name='QNetwork'):
# state inputs to the Q-network
with tf.variable_scope(name):
self.inputs_ = tf.placeholder(tf.float32, [None, state_size], name='inputs')
# One hot encode the actions to later choose the Q-value for the action
self.actions_ = tf.placeholder(tf.int32, [None], name='actions')
one_hot_actions = tf.one_hot(self.actions_, action_size)
# Target Q values for training
self.targetQs_ = tf.placeholder(tf.float32, [None], name='target')
# ReLU hidden layers
self.fc1 = tf.contrib.layers.fully_connected(self.inputs_, hidden_size)
self.fc2 = tf.contrib.layers.fully_connected(self.fc1, hidden_size)
# Linear output layer
self.output = tf.contrib.layers.fully_connected(self.fc2, action_size,
activation_fn=None)
### Train with loss (targetQ - Q)^2
# output has length 2, for two actions. This next line chooses
# one value from output (per row) according to the one-hot encoded actions.
self.Q = tf.reduce_sum(tf.multiply(self.output, one_hot_actions), axis=1)
self.loss = tf.reduce_mean(tf.square(self.targetQs_ - self.Q))
self.opt = tf.train.AdamOptimizer(learning_rate).minimize(self.loss)
```
## Experience replay
Reinforcement learning algorithms can have stability issues due to correlations between states. To reduce correlations when training, we can store the agent's experiences and later draw a random mini-batch of those experiences to train on.
Here, we'll create a `Memory` object that will store our experiences, our transitions $<s, a, r, s'>$. This memory will have a maxmium capacity, so we can keep newer experiences in memory while getting rid of older experiences. Then, we'll sample a random mini-batch of transitions $<s, a, r, s'>$ and train on those.
Below, I've implemented a `Memory` object. If you're unfamiliar with `deque`, this is a double-ended queue. You can think of it like a tube open on both sides. You can put objects in either side of the tube. But if it's full, adding anything more will push an object out the other side. This is a great data structure to use for the memory buffer.
```
from collections import deque
class Memory():
def __init__(self, max_size = 1000):
self.buffer = deque(maxlen=max_size)
def add(self, experience):
self.buffer.append(experience)
def sample(self, batch_size):
idx = np.random.choice(np.arange(len(self.buffer)),
size=batch_size,
replace=False)
return [self.buffer[ii] for ii in idx]
```
## Exploration - Exploitation
To learn about the environment and rules of the game, the agent needs to explore by taking random actions. We'll do this by choosing a random action with some probability $\epsilon$ (epsilon). That is, with some probability $\epsilon$ the agent will make a random action and with probability $1 - \epsilon$, the agent will choose an action from $Q(s,a)$. This is called an **$\epsilon$-greedy policy**.
At first, the agent needs to do a lot of exploring. Later when it has learned more, the agent can favor choosing actions based on what it has learned. This is called _exploitation_. We'll set it up so the agent is more likely to explore early in training, then more likely to exploit later in training.
## Q-Learning training algorithm
Putting all this together, we can list out the algorithm we'll use to train the network. We'll train the network in _episodes_. One *episode* is one simulation of the game. For this game, the goal is to keep the pole upright for 195 frames. So we can start a new episode once meeting that goal. The game ends if the pole tilts over too far, or if the cart moves too far the left or right. When a game ends, we'll start a new episode. Now, to train the agent:
* Initialize the memory $D$
* Initialize the action-value network $Q$ with random weights
* **For** episode = 1, $M$ **do**
* **For** $t$, $T$ **do**
* With probability $\epsilon$ select a random action $a_t$, otherwise select $a_t = \mathrm{argmax}_a Q(s,a)$
* Execute action $a_t$ in simulator and observe reward $r_{t+1}$ and new state $s_{t+1}$
* Store transition $<s_t, a_t, r_{t+1}, s_{t+1}>$ in memory $D$
* Sample random mini-batch from $D$: $<s_j, a_j, r_j, s'_j>$
* Set $\hat{Q}_j = r_j$ if the episode ends at $j+1$, otherwise set $\hat{Q}_j = r_j + \gamma \max_{a'}{Q(s'_j, a')}$
* Make a gradient descent step with loss $(\hat{Q}_j - Q(s_j, a_j))^2$
* **endfor**
* **endfor**
## Hyperparameters
One of the more difficult aspects of reinforcememt learning are the large number of hyperparameters. Not only are we tuning the network, but we're tuning the simulation.
```
train_episodes = 1000 # max number of episodes to learn from
max_steps = 200 # max steps in an episode
gamma = 0.99 # future reward discount
# Exploration parameters
explore_start = 1.0 # exploration probability at start
explore_stop = 0.01 # minimum exploration probability
decay_rate = 0.0001 # exponential decay rate for exploration prob
# Network parameters
hidden_size = 64 # number of units in each Q-network hidden layer
learning_rate = 0.0001 # Q-network learning rate
# Memory parameters
memory_size = 10000 # memory capacity
batch_size = 20 # experience mini-batch size
pretrain_length = batch_size # number experiences to pretrain the memory
tf.reset_default_graph()
mainQN = QNetwork(name='main', hidden_size=hidden_size, learning_rate=learning_rate)
```
## Populate the experience memory
Here I'm re-initializing the simulation and pre-populating the memory. The agent is taking random actions and storing the transitions in memory. This will help the agent with exploring the game.
```
# Initialize the simulation
env.reset()
# Take one random step to get the pole and cart moving
state, reward, done, _ = env.step(env.action_space.sample())
memory = Memory(max_size=memory_size)
# Make a bunch of random actions and store the experiences
for ii in range(pretrain_length):
# Uncomment the line below to watch the simulation
# env.render()
# Make a random action
action = env.action_space.sample()
next_state, reward, done, _ = env.step(action)
if done:
# The simulation fails so no next state
next_state = np.zeros(state.shape)
# Add experience to memory
memory.add((state, action, reward, next_state))
# Start new episode
env.reset()
# Take one random step to get the pole and cart moving
state, reward, done, _ = env.step(env.action_space.sample())
else:
# Add experience to memory
memory.add((state, action, reward, next_state))
state = next_state
```
## Training
Below we'll train our agent. If you want to watch it train, uncomment the `env.render()` line. This is slow because it's rendering the frames slower than the network can train. But, it's cool to watch the agent get better at the game.
```
# Now train with experiences
saver = tf.train.Saver()
rewards_list = []
with tf.Session() as sess:
# Initialize variables
sess.run(tf.global_variables_initializer())
step = 0
for ep in range(1, train_episodes):
total_reward = 0
t = 0
while t < max_steps:
step += 1
# Uncomment this next line to watch the training
# env.render()
# Explore or Exploit
explore_p = explore_stop + (explore_start - explore_stop)*np.exp(-decay_rate*step)
if explore_p > np.random.rand():
# Make a random action
action = env.action_space.sample()
else:
# Get action from Q-network
feed = {mainQN.inputs_: state.reshape((1, *state.shape))}
Qs = sess.run(mainQN.output, feed_dict=feed)
action = np.argmax(Qs)
# Take action, get new state and reward
next_state, reward, done, _ = env.step(action)
total_reward += reward
if done:
# the episode ends so no next state
next_state = np.zeros(state.shape)
t = max_steps
print('Episode: {}'.format(ep),
'Total reward: {}'.format(total_reward),
'Training loss: {:.4f}'.format(loss),
'Explore P: {:.4f}'.format(explore_p))
rewards_list.append((ep, total_reward))
# Add experience to memory
memory.add((state, action, reward, next_state))
# Start new episode
env.reset()
# Take one random step to get the pole and cart moving
state, reward, done, _ = env.step(env.action_space.sample())
else:
# Add experience to memory
memory.add((state, action, reward, next_state))
state = next_state
t += 1
# Sample mini-batch from memory
batch = memory.sample(batch_size)
states = np.array([each[0] for each in batch])
actions = np.array([each[1] for each in batch])
rewards = np.array([each[2] for each in batch])
next_states = np.array([each[3] for each in batch])
# Train network
target_Qs = sess.run(mainQN.output, feed_dict={mainQN.inputs_: next_states})
# Set target_Qs to 0 for states where episode ends
episode_ends = (next_states == np.zeros(states[0].shape)).all(axis=1)
target_Qs[episode_ends] = (0, 0)
targets = rewards + gamma * np.max(target_Qs, axis=1)
loss, _ = sess.run([mainQN.loss, mainQN.opt],
feed_dict={mainQN.inputs_: states,
mainQN.targetQs_: targets,
mainQN.actions_: actions})
saver.save(sess, "checkpoints/cartpole.ckpt")
```
## Visualizing training
Below I'll plot the total rewards for each episode. I'm plotting the rolling average too, in blue.
```
%matplotlib inline
import matplotlib.pyplot as plt
def running_mean(x, N):
cumsum = np.cumsum(np.insert(x, 0, 0))
return (cumsum[N:] - cumsum[:-N]) / N
eps, rews = np.array(rewards_list).T
smoothed_rews = running_mean(rews, 10)
plt.plot(eps[-len(smoothed_rews):], smoothed_rews)
plt.plot(eps, rews, color='grey', alpha=0.3)
plt.xlabel('Episode')
plt.ylabel('Total Reward')
```
## Testing
Let's checkout how our trained agent plays the game.
```
test_episodes = 10
test_max_steps = 400
env.reset()
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))
for ep in range(1, test_episodes):
t = 0
while t < test_max_steps:
env.render()
# Get action from Q-network
feed = {mainQN.inputs_: state.reshape((1, *state.shape))}
Qs = sess.run(mainQN.output, feed_dict=feed)
action = np.argmax(Qs)
# Take action, get new state and reward
next_state, reward, done, _ = env.step(action)
if done:
t = test_max_steps
env.reset()
# Take one random step to get the pole and cart moving
state, reward, done, _ = env.step(env.action_space.sample())
else:
state = next_state
t += 1
env.close()
```
## Extending this
So, Cart-Pole is a pretty simple game. However, the same model can be used to train an agent to play something much more complicated like Pong or Space Invaders. Instead of a state like we're using here though, you'd want to use convolutional layers to get the state from the screen images.

I'll leave it as a challenge for you to use deep Q-learning to train an agent to play Atari games. Here's the original paper which will get you started: http://www.davidqiu.com:8888/research/nature14236.pdf.
| true |
code
| 0.658692 | null | null | null | null |
|
### Eco 100 diagrams
## Linear Demand and Supply Diagram
This is a jupyter notebook to generate a simple interactive supply and demand diagram using python and `ipywidgets` (interactive HTML widgets) to provide sliders and animations.
To run this notebook first run the code cells in the [code Section](#Code-Section) below and then return to run the cells below. If you are running this on Microsoft Azure notebook cloud service make sure you choose the kernel to be python 3.5 or above.
---
```
mkt(A=400, b=1, F=0, c=1)
```
### interactive plot
On the next cell move the sliders in the next cell to shift Supply or Demand in or out
Note: this will not display unless you are running this on a jupyter server
```
interact(mkt, A=(200,500,10),b=fixed(1),F=(0,300,10),c=fixed(1));
```
### Quantitative Restrictions
```
qrplot(150);
interact(qrplot, qr =(0,250,10));
```
End
## Code Section
We've put the code down here to keep the presentation uncluttered. Run the cells below first and then return to cells above where these functions are called.
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from ipywidgets import interact, fixed
```
The following is just styling for the graph
```
plt.style.use('bmh')
plt.rcParams["figure.figsize"] = [7,7]
plt.rcParams["axes.spines.right"] = False
plt.rcParams["axes.spines.top"] = False
plt.rcParams["font.size"] = 18
```
Now let's define simple linear (inverse) demand and supply functions:
```
def PD(Q, A, b):
return np.array(A - b * Q)
def PS(Q, F, c):
return np.array(F + c * Q)
def mkt(A=200, b=1, F=0, c=1):
'''Draw supply and demand diagram and calculate market equilibrium price and quantity'''
xmax = ymax = 500
xclip = 400
Q = np.arange(xmax)
# for aesthetic reasons we clip demand curve line to end above the x-axis by plotting over shorter Q_
d_end = np.round((A-50)/b)
Q_ = np.arange(0, d_end)
s_end = (xmax - F)/c # to keep S label inside box
plt.figure(figsize=(7.7,7.5))
plt.xlim(0,xmax)
plt.ylim(0, ymax)
plt.xlabel('Q - Quantity')
plt.ylabel('P - Price')
plt.plot(Q_,PD(Q_,A,b))
plt.text(d_end, PD(d_end, A,b)-4, 'D', fontsize = 18)
plt.plot(Q,PS(Q,F,c))
plt.text(s_end, PS(s_end, F,c)-20, 'S', fontsize = 18)
# market equilibrium
Qe = (A-F)/(c+b)
Pe = PD(Qe, A, b)
CS = (1/2)*(A-Pe)*Qe
plt.scatter(Qe, Pe)
plt.plot([0, Qe, Qe],[Pe, Pe, 0], ':')
return Qe, Pe
```
#### Notes: the simple math behind the diagram
A demand curve tells us the quantity $Q$ that will be demanded of a good at any given price. This suggests a relationship of the form $Q(P)$, i.e. $Q$ as a function of $P$.
However, by historical convention economists have almost always drawn demand curves with quantity $Q$ on the horizontal axis and price $P$ on the vertical axis. For some this might suggest we are plotting a function of the form $P(Q)$. This is an 'inverse' demand function (the maximum price at which quantity Q will be demanded).
In the diagram we use a linear (inverse) **demand curve** of the form:
$$P^D(Q) = A + b \cdot Q$$
this of course corresponds to a Demand curve of the form $Q^D(P) = \frac{A}{b} - \frac{1}{b}P$
The (inverse) **supply curve** curve is of the form:
$$P^S(Q) = F + c \cdot Q$$
As will be seen later in the course the market supply curve is a marginal cost curve.
The market equilibrium price $P^e$ can be found where supply meets demand.
$$P^S(Q) = P^e = P^D(Q)$$
With the linear demand and supply system above we can easily solve for the market equilibrium quantity $Q^e$
$$A+ b \cdot Q^e = F + c \cdot Q^e$$
which leads to:
$$Q^e = \frac{A-F}{c+b}$$
And the market equilibrium price $P^e$ is then easuily found from either $P^D(Q^e)$ or $P^S(Q^e)$
## Quantitative Restriction plot
```
def qrplot(qr):
A, b, F, c = 500, 1, 0, 1
qe, pe = mkt(A=500, b=1, F=0, c=1)
pd = PD(qr, A, b)
ps = PS(qr, F, c)
plt.scatter(qr, pd)
plt.scatter(qr, ps)
plt.axvline(qr, linestyle=':')
plt.vlines(qr, ymin= ps, ymax=480, linewidth =3.5)
plt.text(qr+10,480, "S\'")
plt.hlines(pd,xmin=0, xmax=qr)
plt.hlines(ps,xmin=0, xmax=qr, linestyle=':')
csurplus = (1/2) * qr*(A-pd)
psurplus = (1/2) * qr*(ps-F)
rents = qr *(pd-ps)
tsurplus = csurplus + psurplus + rents
dwl = (1/2)*(qe-qr)*(pd-ps)
plt.text(qr/6,pd+(A-pd)/5, 'CS')
plt.text(qr/6,ps-(ps-F)/4, 'PS')
if qr<80:
plt.text(qr/6,(ps+pd)/2, 'Rents', rotation=90)
elif qr == qe:
pass
else:
plt.text(qr/6,(ps+pd)/2, 'LR')
print( f'Pd = {pd:2.0f}, Ps = {ps:2.0f}, license rent = {pd-ps:2.0f}')
print(f'CS = {csurplus:2.0f}, PS = {psurplus:2.0f}, rents = {rents:2.0f}, TS = {tsurplus:2.0f} DWL = {dwl:2.0f}')
Q = np.arange(qr)
Q2 = np.arange(qr, qe)
plt.fill_between(Q, PD(Q,A,b), pd)
plt.fill_between(Q, PS(Q,F,c), ps)
plt.fill_between(Q, pd, ps)
plt.fill_between(Q2, PD(Q2,A,b), PS(Q2,F,c));
```
| true |
code
| 0.5047 | null | null | null | null |
|
# Plan:
* Prepare input with extracted UASTs
* Filter data from DB (if needed)
* Prepare pairs (provide specific requirements if needed)
* Statistics & visualization
* Export datasets
```
%matplotlib inline
from collections import defaultdict, deque
from datetime import datetime
from glob import glob
import os
import sys
import bblfsh
from bblfsh import BblfshClient
from bblfsh.sdkversion import VERSION
import Levenshtein
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.patches as patches
from matplotlib.pyplot import text as plt_text
import pandas as pd
from pyspark.sql import SparkSession
from pyspark.sql.functions import col, size, udf
from pyspark.sql.types import BooleanType
import seaborn as sns
from sqlalchemy import Column, String, Float
from sqlalchemy.ext.declarative import declarative_base
from sqlite3 import connect
from tqdm import tqdm_notebook as tqdm
```
## Initialize pyspark session
```
os.environ["PYSPARK_PYTHON"] = "python3"
os.environ['PYSPARK_SUBMIT_ARGS'] = '--conf "spark.tech.sourced.bblfsh.grpc.host=bblfshd" ' \
'--conf "spark.tech.sourced.engine.cleanup.skip=true" ' \
'--driver-memory 90g ' \
'--conf "spark.local.dir=/tmp/spark" ' \
'--conf "spark.driver.maxResultSize=22048" pyspark-shell '
spark = SparkSession.builder.appName("near_duplicates_dataset").master("local[26]")
spark = spark.getOrCreate()
```
## Prepare input with extracted UASTs
### Expected parquet file with fields: [blob_id, repository_id, content, path, commit_hash, uast]
```
base_path = "/storage/egor/tmp/"
data_loc = base_path + "dataset_with_uasts_full/"
print("data_loc:", data_loc)
## Read dataset
data = spark.read.parquet(data_loc)
print("number of rows:", data.count())
## Deduplicate by blob_id
data = data.drop_duplicates(["blob_id"])
print("number of rows after deduplication of blob_id:", data.count())
```
# Filter repositories and files to avoid duplications with DB
```
FILTER_REPOS = True
if FILTER_REPOS:
existing_db = base_path + "near_dupl_pairs/export_db/" + "2018-03-09T09_17_59Z-export.db"
query = "select repository_id_a, repository_id_b from file_pairs;"
ignore_repos = set()
with connect(existing_db) as conn:
repos_pairs = pd.read_sql_query(query, conn)
ignore_repos.update(repos_pairs["repository_id_a"].tolist())
ignore_repos.update(repos_pairs["repository_id_b"].tolist())
print("number of repos to ignore:", len(ignore_repos))
data = data[data.repository_id.isin(ignore_repos)== False]
print("number of rows after filtering repos:", data.count())
```
## Prepare pairs of similar files
```
def uast2sequence(root):
# hack for broken uast iterator
sequence = []
nodes = defaultdict(deque)
stack = [root]
nodes[id(root)].extend(root.children)
while stack:
if nodes[id(stack[-1])]:
child = nodes[id(stack[-1])].popleft()
nodes[id(child)].extend(child.children)
stack.append(child)
else:
sequence.append(stack.pop())
return sequence
def flatten_uast(uast):
seq = uast2sequence(uast)
res = [item.internal_type for item in seq]
return res
def uast_to_type_seq(uast):
from bblfsh import Node
return flatten_uast(Node.FromString(uast[0]))
def ratio_levenshtein(seq_a, seq_b):
return Levenshtein.ratio(seq_a, seq_b)
def calc_uast_sim(uast_a, uast_b):
type_seq_a = uast_to_type_seq(uast_a)
type_seq_b = uast_to_type_seq(uast_b)
res = ratio_levenshtein("".join(type_seq_a), "".join(type_seq_b))
return res
def extract_pairs(dataframe, filter_res=None):
if filter_res is None:
filter_res = lambda *args, **kwargs: True
elif not isinstance(filter_res, (list, tuple)):
raise ValueError("Expected list or tuple of filtering functions, got %s" % type(filter_res))
groups = dataframe.rdd.groupBy(lambda row: (row.repository_id, row.path))
n_groups = groups.count()
print("Number of groups:", n_groups)
def _extract_pairs(group):
key = group[0] # skip
rows = list(group[1])
if len(rows) < 2:
return
indices = list(range(len(rows)))
np.random.shuffle(indices)
n_pairs = 0
for a, b in zip(indices[:len(indices) // 2], indices[len(indices) // 2:]):
row_a = rows[a].asDict()
row_b = rows[b].asDict()
ratio = ratio_levenshtein(row_a["content"].decode("utf-8", "ignore"),
row_b["content"].decode("utf-8", "ignore"))
uast_ratio = calc_uast_sim(row_a["uast"], row_b["uast"])
if sum([fil(ratio, uast_ratio) for fil in filter_res]):
yield row_a, row_b, ratio, uast_ratio
return groups.flatMap(_extract_pairs)
```
## Sampling requirements
```
ranges = []
similarity_ranges = {"text_lower": 0.55,
"text_upper": 1.0,
"uast_lower": 0.45,
"uast_upper": 0.7}
ranges.append((similarity_ranges, 250))
similarity_ranges = {"text_lower": 0.55,
"text_upper": 0.7,
"uast_lower": 0.7,
"uast_upper": 1.}
ranges.append((similarity_ranges, 150))
similarity_ranges = {"text_lower": 0.3,
"text_upper": 0.55,
"uast_lower": 0.45,
"uast_upper": 1.}
ranges.append((similarity_ranges, 100))
def make_filter(sim_ranges):
def filter_similarity(text_sim, uast_sim):
return ((sim_ranges["text_lower"] <= text_sim <= sim_ranges["text_upper"]) and
(sim_ranges["uast_lower"] <= uast_sim <= sim_ranges["uast_upper"]))
return filter_similarity
```
## Select pairs that satisfy requirements above
```
filters = []
for sim_ranges, n_pairs in ranges:
filters.append(make_filter(sim_ranges))
pairs = extract_pairs(data, filter_res=filters).cache()
print("n_pairs extracted:", pairs.count())
all_pairs = pairs.collect()
xy = np.array([(row[2], row[3]) for row in all_pairs])
```
## Statistics
```
pairs_blobs = set()
for pair in all_pairs:
pairs_blobs.add(tuple(sorted((pair[0]["blob_id"], pair[0]["blob_id"]))))
print("number of unique blob id pairs:", len(pairs_blobs))
blobs = set()
for pair in all_pairs:
blobs.add(pair[0]["blob_id"])
blobs.add(pair[1]["blob_id"])
print("number of unique blob ids:", len(blobs))
```
### Lengths of texts
```
text_lengths = []
for pair in all_pairs:
text_lengths.append(len(pair[0]["content"]))
text_lengths.append(len(pair[1]["content"]))
sns.kdeplot(text_lengths, cut=0)
```
### Log lengths of texts
```
text_lengths = []
for pair in all_pairs:
text_lengths.append(np.log(len(pair[0]["content"])))
text_lengths.append(np.log(len(pair[1]["content"])))
sns.kdeplot(text_lengths, cut=0)
```
### Overall distribution
```
ax = sns.jointplot(x=xy[:, 0], y=xy[:, 1])
```
### Distribution with colorized length of texts
```
text_lengths = []
for pair in all_pairs:
text_lengths.append(np.log(max(len(pair[0]["content"]), len(pair[1]["content"]))))
colors = text_lengths
mymap = plt.get_cmap("Reds")
my_colors = mymap(colors)
plt.scatter(xy[:, 0], xy[:, 1], s=40, c=colors, edgecolors='None', cmap=mymap)
plt.colorbar()
```
## Sampling
### Select samples based on `abs(uast_score - text_score)` - the higher the higher probability to select
### The reason to make random sampling instead of selecting samples with highest diff - it creates unused ares (see below)
```
def dummy_sampler(similarity_ranges, xy):
res = []
for sim_range, n_samples in similarity_ranges:
fil_xy = xy[(sim_range["text_lower"] <= xy[:, 0]) & (xy[:, 0] <= sim_range["text_upper"]) &
(sim_range["uast_lower"] <= xy[:, 1]) & (xy[:, 1] <= sim_range["uast_upper"])]
# calculate pseudo probabilities based on distance
diff = np.abs(fil_xy[:, 0] - fil_xy[:, 1])
# select indicies
ind = np.arange(fil_xy.shape[0])[np.argsort(diff)[-min(n_samples, fil_xy.shape[0]):]]
xy_sample = fil_xy[ind]
res.append(xy_sample)
return np.vstack(res)
xy_final = dummy_sampler(ranges, xy)
ax = sns.jointplot(x=xy_final[:, 0], y=xy_final[:, 1])
```
### Proper random sampling
```
def sampler(similarity_ranges, xy):
res = []
input_ind = []
for sim_range, n_samples in similarity_ranges:
xy_ind = np.arange(xy.shape[0])[(sim_range["text_lower"] <= xy[:, 0]) &
(xy[:, 0] <= sim_range["text_upper"]) &
(sim_range["uast_lower"] <= xy[:, 1]) &
(xy[:, 1] <= sim_range["uast_upper"])]
fil_xy = xy[xy_ind]
# calculate pseudo probabilities based on distance
diff = np.abs(fil_xy[:, 0] - fil_xy[:, 1])
probas = np.log(diff + 1) / np.log(diff + 1).sum()
# select indicies
ind = np.random.choice(np.arange(fil_xy.shape[0]), size=n_samples, p=probas, replace=False)
input_ind.append(xy_ind[ind])
xy_sample = fil_xy[ind]
res.append(xy_sample)
return np.vstack(res), np.hstack(input_ind)
xy_final, list_ind = sampler(ranges, xy)
ax = sns.jointplot(x=xy_final[:, 0], y=xy_final[:, 1])
similar_pairs = [all_pairs[i] for i in list_ind.astype(int).tolist()]
print("total number of pairs to keep:", len(similar_pairs))
```
### Distribution with colorized length of texts
```
text_lengths = []
for pair in similar_pairs:
text_lengths.append(np.log(max(len(pair[0]["content"]), len(pair[1]["content"]))))
colors = text_lengths
mymap = plt.get_cmap("Reds")
my_colors = mymap(colors)
plt.scatter(xy_final[:, 0], xy_final[:, 1], s=40, c=colors, edgecolors='None', cmap=mymap)
plt.colorbar()
```
## Add dummy features to pairs (we don't compute them now)
```
for pair in similar_pairs:
pair[0]["bag"] = "no_features"
pair[1]["bag"] = "no_features"
```
## Export dataset
### Pickle
```
import pickle
save_loc = base_path + "near_dupl_pairs/" + str(datetime.now().date()) + "_500_pairs.pkl"
with open(save_loc, "wb") as f:
print("save similar pairs to", save_loc)
pickle.dump(similar_pairs, f)
```
### sqlite
```
Base = declarative_base()
fields = """blob_id_a TEXT, repository_id_a TEXT, commit_hash_a TEXT, path_a TEXT, content_a TEXT,
blob_id_b TEXT, repository_id_b TEXT, commit_hash_b TEXT, path_b TEXT, content_b TEXT,
score""".split()
fields = [field for field in fields if field != "TEXT,"]
start = "<Files("
end = "='%s')>"
repr_str = start + "='%s', ".join(fields) + end
class Files(Base):
extend_existing=True
__tablename__ = "files"
blob_id_a = Column(String, primary_key=True)
repository_id_a = Column(String)
commit_hash_a = Column(String)
path_a = Column(String)
content_a = Column(String)
blob_id_b = Column(String)
repository_id_b = Column(String)
commit_hash_b = Column(String)
path_b = Column(String)
content_b = Column(String)
score = Column(Float(precision="DOUBLE"))
def __repr__(self):
return repr_str % (self.blob_id_a,
self.repository_id_a,
self.commit_hash_a,
self.path_a,
self.content_a,
self.blob_id_b,
self.repository_id_b,
self.commit_hash_b,
self.path_b,
self.content_b,
self.score)
from sqlalchemy import create_engine
from sqlalchemy.orm import sessionmaker
# from https://www.pythoncentral.io/introductory-tutorial-python-sqlalchemy/
engine = create_engine("sqlite:///" + base_path + "near_dupl_pairs/" +
str(datetime.now().date()) + "_500_pairs.db")
Base.metadata.create_all(engine)
Base.metadata.bind = engine
DBSession = sessionmaker(bind=engine)
session = DBSession()
for pair in similar_pairs:
pair = Files(blob_id_a=pair[0]["blob_id"],
repository_id_a=pair[0]["repository_id"],
commit_hash_a=pair[0]["commit_hash"],
path_a=pair[0]["path"],
content_a=pair[0]["content"],
blob_id_b=pair[1]["blob_id"],
repository_id_b=pair[1]["repository_id"],
commit_hash_b=pair[1]["commit_hash"],
path_b=pair[1]["path"],
content_b=pair[1]["content"],
score=pair[2])
session.add(pair)
try:
session.commit()
except Exception as e:
import pdb;pdb.set_trace()
pass
```
| true |
code
| 0.261779 | null | null | null | null |
|
# Tutorial: Confidence Intervals
By Delaney Granizo-Mackenzie, Jeremiah Johnson, and Gideon Wulfsohn
Part of the Quantopian Lecture Series:
http://www.quantopian.com/lectures
http://github.com/quantopian/research_public
Notebook released under the Creative Commons Attribution 4.0 License.
## Sample Mean vs. Population Mean
Sample means and population means are different. Generally, we want to know about a population mean, but we can only calculate a sample mean. We then want to use the sample mean to estimate the population mean. We use confidence intervals in an attempt to determine how accurately our sample mean estimates the population mean.
## Confidence Interval
If I asked you to estimate the average height of a woman in the USA, you might do this by measuring 10 women and estimating that the mean of that sample was close to the population. Let's try that.
```
import numpy as np
import seaborn as sns
from scipy import stats
import matplotlib.pyplot as plt
# We'll set a seed here so our runs are consistent
np.random.seed(10)
# Let's define some 'true' population parameters, we'll pretend we don't know these.
POPULATION_MU = 64
POPULATION_SIGMA = 5
# Generate our sample by drawing from the population distribution
sample_size = 10
heights = np.random.normal(POPULATION_MU, POPULATION_SIGMA, sample_size)
print heights
mean_height = np.mean(heights)
print 'sample mean: ', mean_height
```
Unfortunately simply reporting the sample mean doesn't do much for us, as we don't know how it relates to the population mean. To get a sense for how it might relate, we can look for how much variance there is in our sample. Higher variance indicates instability and uncertainty.
```
print 'sample standard deviation: ', np.std(heights)
```
This still doesn't do that much for us, to really get a sense of how our sample mean relates to the population mean we need to compute a standard error. The standard error is a measure of the variance of the sample mean.
#### IMPORTANT
Computing a standard error involves assuming that the way you sample is unbaised, and that the data are normal and independent. If these conditions are violated, your standard error will be wrong. There are ways of testing for this and correcting.
The formula for standard error is.
$$SE = \frac{\sigma}{\sqrt{n}}$$
Where $\sigma$ is the sample standard deviation and $n$ is the number of samples.
```
SE = np.std(heights) / np.sqrt(sample_size)
print 'standard error: ', SE
```
There is a function in scipy's stats library for calculating the standard error. Note that this function by default contains a degrees-of-freedom correction that is often not necessary (for large enough samples, it is effectively irrelevant). You can omit the correction by setting the parameter ddof to 0.
```
stats.sem(heights, ddof=0)
```
Assuming our data are normally distributed, we can use the standard error to compute our confidence interval. To do this we first set our desired confidence level, say 95%, we then determine how many standard deviations contain 95% of the mass. Turns out that the 95% of the mass lies between -1.96 and 1.96 on a standard normal distribution. When the samples are large enough (generally > 30 is taken as a threshold) the Central Limit Theorem applies and normality can be safely assumed; if sample sizes are smaller, a safer approach is to use a $t$-distribution with appropriately specified degrees of freedom. The actual way to compute the values is by using a cumulative distribution function (CDF). If you are not familiar with CDFs, inverse CDFs, and their companion PDFs, you can read about them [here](https://en.wikipedia.org/wiki/Probability_density_function) and [here](https://en.wikipedia.org/wiki/Cumulative_distribution_function). Look [here](https://en.wikipedia.org/wiki/Student%27s_t-distribution) for information on the $t$-distribution. We can check the 95% number using one of the Python functions.
NOTE: Be careful when applying the Central Limit Theorem, however, as many datasets in finance are fundamentally non-normal and it is not safe to apply the theorem casually or without attention to subtlety.
We can visualize the 95% mass bounds here.
```
# Set up the x axis
x = np.linspace(-5,5,100)
# Here's the normal distribution
y = stats.norm.pdf(x,0,1)
plt.plot(x,y)
# Plot our bounds
plt.vlines(-1.96, 0, 1, colors='r', linestyles='dashed')
plt.vlines(1.96, 0, 1, colors='r', linestyles='dashed')
# Shade the area
fill_x = np.linspace(-1.96, 1.96, 500)
fill_y = stats.norm.pdf(fill_x, 0, 1)
plt.fill_between(fill_x, fill_y)
plt.xlabel('$\sigma$')
plt.ylabel('Normal PDF');
```
### Here's the trick
Now, rather than reporting our sample mean without any sense of the probability of it being correct, we can compute an interval and be much more confident that the population mean lies in that interval. To do this we take our sample mean $\mu$ and report $\left(\mu-1.96 SE , \mu+1.96SE\right)$.
This works because assuming normality, that interval will contain the population mean 95% of the time.
### SUBTLETY:
In any given case, the true value of the estimate and the bounds of the confidence interval are fixed. It is incorrect to say that "The national mean female height is between 63 and 65 inches with 95% probability," but unfortunately this is a very common misinterpretation. Rather, the 95% refers instead to the fact that over many computations of a 95% confidence interval, the true value will be in the interval in 95% of the cases (assuming correct calibration of the confidence interval, which we will discuss later). But in fact for a single sample and the single confidence interval computed from it, we have no way of assessing the probability that the interval contains the population mean. The visualization below demonstrates this.
In the code block below, there are two things to note. First, although the sample size is sufficiently large to assume normality, we're using a $t$-distribution, just to demonstrate how it is used. Second, the $t$-values needed (analogous to the $\pm1.96$ used above) are being calculated from the inverted cumulative density function, the ppf in scipy.stats. The $t$-distribution requires the extra parameter degrees of freedom (d.o.f), which is the size of the sample minus one.
```
np.random.seed(8309)
n = 100 # number of samples to take
samples = [np.random.normal(loc=0, scale=1, size=100) for _ in range(n)]
fig, ax = plt.subplots(figsize=(10, 7))
for i in np.arange(1, n, 1):
sample_mean = np.mean(samples[i]) # calculate sample mean
se = stats.sem(samples[i]) # calculate sample standard error
h = se*stats.t.ppf((1+0.95)/2, len(samples[i])-1) # calculate t; 2nd param is d.o.f.
sample_ci = [sample_mean - h, sample_mean + h]
if ((sample_ci[0] <= 0) and (0 <= sample_ci[1])):
plt.plot((sample_ci[0], sample_ci[1]), (i, i), color='blue', linewidth=1);
plt.plot(np.mean(samples[i]), i, 'bo');
else:
plt.plot((sample_ci[0], sample_ci[1]), (i, i), color='red', linewidth=1);
plt.plot(np.mean(samples[i]), i, 'ro');
plt.axvline(x=0, ymin=0, ymax=1, linestyle='--', label = 'Population Mean');
plt.legend(loc='best');
plt.title('100 95% Confidence Intervals for mean of 0');
```
### Further Reading
This is only a brief introduction, Wikipedia has excellent articles detailing these subjects in greater depth. Let's go back to our heights example. Since the sample size is small, we'll use a $t$-test.
```
# standard error SE was already calculated
t_val = stats.t.ppf((1+0.95)/2, 9) # d.o.f. = 10 - 1
print 'sample mean height:', mean_height
print 't-value:', t_val
print 'standard error:', SE
print 'confidence interval:', (mean_height - t_val * SE, mean_height + t_val * SE)
```
There is a built-in function in scipy.stats for computing the interval. Remember to specify the degrees of freedom.
```
print '99% confidence interval:', stats.t.interval(0.99, df=9,
loc=mean_height, scale=SE)
print '95% confidence interval:', stats.t.interval(0.95, df = 9,
loc=mean_height, scale=SE)
print '80% confidence interval:', stats.t.interval(0.8, df = 9,
loc=mean_height, scale=SE)
```
Note that as your confidence increases, the interval necessarily widens.
Assuming normality, there's also a built in function that will compute our interval for us. This time you don't need to specify the degrees of freedom. Note that at a corresponding level of confidence, the interval calculated using the normal distribution is narrower than the interval calcuated using the $t$-distribution.
```
print stats.norm.interval(0.99, loc=mean_height, scale=SE)
print stats.norm.interval(0.95, loc=mean_height, scale=SE)
print stats.norm.interval(0.80, loc=mean_height, scale=SE)
```
## What does this mean?
Confidence intervals allow us to set our desired confidence, and then report a range that will likely contain the population mean. The higher our desired confidence, the larger range we report. In general, one can never report a single point value, because the probability that any given point is the true population mean is incredibly small. Let's see how our intervals tighten as we change sample size.
```
np.random.seed(10)
sample_sizes = [10, 100, 1000]
for s in sample_sizes:
heights = np.random.normal(POPULATION_MU, POPULATION_SIGMA, s)
SE = np.std(heights) / np.sqrt(s)
print stats.norm.interval(0.95, loc=mean_height, scale=SE)
```
## Visualizing Confidence Intervals
Here is some code to visualize a confidence interval on a graph. Feel free to play around with it.
```
sample_size = 100
heights = np.random.normal(POPULATION_MU, POPULATION_SIGMA, sample_size)
SE = np.std(heights) / np.sqrt(sample_size)
(l, u) = stats.norm.interval(0.95, loc=np.mean(heights), scale=SE)
print (l, u)
plt.hist(heights, bins=20)
plt.xlabel('Height')
plt.ylabel('Frequency')
# Just for plotting
y_height = 5
plt.plot([l, u], [y_height, y_height], '-', color='r', linewidth=4, label='Confidence Interval')
plt.plot(np.mean(heights), y_height, 'o', color='r', markersize=10);
```
## Miscalibration and Violation of Assumptions
The computation of a standard deviation, standard error, and confidence interval all rely on certain assumptions. If these assumptions are violated then the 95% confidence interval will not necessarily contain the population parameter 95% of the time. We say that in this case the confidence interval is miscalibrated. Here is an example.
### Example: Autocorrelated Data
If your data generating process is autocorrelated, then estimates of standard deviation will be wrong. This is because autocorrelated processes tend to produce more extreme values than normally distributed processes. This is due to new values being dependent on previous values, series that are already far from the mean are likely to stay far from the mean. To check this we'll generate some autocorrelated data according to the following process.
$$X_t = \theta X_{t-1} + \epsilon$$
$$\epsilon \sim \mathcal{N}(0,1)$$
```
def generate_autocorrelated_data(theta, mu, sigma, N):
# Initialize the array
X = np.zeros((N, 1))
for t in range(1, N):
# X_t = theta * X_{t-1} + epsilon
X[t] = theta * X[t-1] + np.random.normal(mu, sigma)
return X
X = generate_autocorrelated_data(0.5, 0, 1, 100)
plt.plot(X);
plt.xlabel('t');
plt.ylabel('X[t]');
```
It turns out that for larger sample sizes, you should see the sample mean asymptotically converge to zero. This is because the process is still centered around zero, but let's check if that's true. We'll vary the number of samples drawn, and look for convergence as we increase sample size.
```
sample_means = np.zeros(200-1)
for i in range(1, 200):
X = generate_autocorrelated_data(0.5, 0, 1, i * 10)
sample_means[i-1] = np.mean(X)
plt.bar(range(1, 200), sample_means);
plt.xlabel('Sample Size');
plt.ylabel('Sample Mean');
```
Definitely looks like there's some convergence, we can also check what the mean of the sample means is.
```
np.mean(sample_means)
```
Pretty close to zero. We could also derive symbolically that the mean is zero, but let's assume that we've convinced ourselves with the simple empiral analysis. Now that we know the population mean, we can check the calibration of confidence intervals. First we'll write two helper functions which compute a naive interval for some input data, and check whether the interval contains the true mean, 0.
```
def compute_unadjusted_interval(X):
T = len(X)
# Compute mu and sigma MLE
mu = np.mean(X)
sigma = np.std(X)
SE = sigma / np.sqrt(T)
# Compute the bounds
return stats.norm.interval(0.95, loc=mu, scale=SE)
# We'll make a function that returns true when the computed bounds contain 0
def check_unadjusted_coverage(X):
l, u = compute_unadjusted_interval(X)
# Check to make sure l <= 0 <= u
if l <= 0 and u >= 0:
return True
else:
return False
```
Now we'll run many trials, in each we'll sample some data, compute a confidence interval, and then check if the confidence interval contains the population mean. We'll keep a running tally, and we should expect to see 95% of the trials succeed if the intervals are calibrated correctly.
```
T = 100
trials = 500
times_correct = 0
for i in range(trials):
X = generate_autocorrelated_data(0.5, 0, 1, T)
if check_unadjusted_coverage(X):
times_correct += 1
print 'Empirical Coverage: ', times_correct/float(trials)
print 'Expected Coverage: ', 0.95
```
Clearly the coverage is wrong. In this case we'd need to do what's known as a Newey-West correction on our standard error estimate to account for the autocorrelation. In practice it's important to check for the assumptions you make. It is quick and easy to check if your data are stationary (which implies not autocorrelated), and it can save you a lot of pain and suffering to do so. A normality test such as `Jarque Bera` will also be a good idea, as it may detect certain distribution properties which may violate assumptions of many following statistical analyses.
*This presentation is for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation for any security; nor does it constitute an offer to provide investment advisory or other services by Quantopian, Inc. ("Quantopian"). Nothing contained herein constitutes investment advice or offers any opinion with respect to the suitability of any security, and any views expressed herein should not be taken as advice to buy, sell, or hold any security or as an endorsement of any security or company. In preparing the information contained herein, Quantopian, Inc. has not taken into account the investment needs, objectives, and financial circumstances of any particular investor. Any views expressed and data illustrated herein were prepared based upon information, believed to be reliable, available to Quantopian, Inc. at the time of publication. Quantopian makes no guarantees as to their accuracy or completeness. All information is subject to change and may quickly become unreliable for various reasons, including changes in market conditions or economic circumstances.*
| true |
code
| 0.674024 | null | null | null | null |
|
# GOES-16 IR channel subregion plot (using reprojected data)
This jupyter notebook shows how to make a sub-region plot of a **reprojected** IR channel of GOES-16.
Import the GOES package.
```
import GOES
```
Set path and name of file that will be read.
```
path = '/home/joao/Downloads/GOES-16/ABI/'
file = 'OR_ABI-L2-CMIPF-M6C13_G16_s20200782000176_e20200782009496_c20200782010003.nc'
```
Reads the file.
```
ds = GOES.open_dataset(path+file)
```
Prints the contents of the file.
```
print(ds)
```
Set the map domain.
```
domain = [-90.0,-30.0,-60.0,15.0]
```
Gets image with the coordinates of corners of their pixels.
```
CMI, LonCen, LatCen = ds.image('CMI', lonlat='center', domain=domain)
```
Gets information about data.
```
sat = ds.attribute('platform_ID')
band = ds.variable('band_id').data[0]
wl = ds.variable('band_wavelength').data[0]
standard_name = CMI.standard_name
units = CMI.units
time_bounds = CMI.time_bounds
```
Creates a grid map with cylindrical equidistant projection and 2 km of spatial resolution.
```
LonCenCyl, LatCenCyl = GOES.create_gridmap(domain, PixResol=2.0)
```
Calculates the coordinates of corners of pixels.
```
LonCorCyl, LatCorCyl = GOES.calculate_corners(LonCenCyl, LatCenCyl)
```
Calculates the parameters for reprojection. For this we need install the **pyproj** and **pyresample** packages. Try with ***pip install pyproj*** and ***pip install pyresample***.
```
import pyproj as pyproj
Prj = pyproj.Proj('+proj=eqc +lat_ts=0 +lat_0=0 +lon_0=0 +x_0=0 +y_0=0 +a=6378.137 +b=6378.137 +units=km')
AreaID = 'cyl'
AreaName = 'cyl'
ProjID = 'cyl'
Proj4Args = '+proj=eqc +lat_ts=0 +lat_0=0 +lon_0=0 +x_0=0 +y_0=0 +a=6378.137 +b=6378.137 +units=km'
ny, nx = LonCenCyl.data.shape
SW = Prj(LonCenCyl.data.min(), LatCenCyl.data.min())
NE = Prj(LonCenCyl.data.max(), LatCenCyl.data.max())
area_extent = [SW[0], SW[1], NE[0], NE[1]]
from pyresample import utils
AreaDef = utils.get_area_def(AreaID, AreaName, ProjID, Proj4Args, nx, ny, area_extent)
```
Reprojects images.
```
from pyresample.geometry import SwathDefinition
from pyresample.kd_tree import resample_nearest
import numpy as np
SwathDef = SwathDefinition(lons=LonCen.data, lats=LatCen.data)
CMICyl = resample_nearest(SwathDef, CMI.data, AreaDef, radius_of_influence=6000,
fill_value=np.nan, epsilon=3, reduce_data=True)
```
Deletes unnecessary data.
```
del CMI, LonCen, LatCen, SwathDef, LonCenCyl, LatCenCyl
```
Creates a custom color palette using the [custom_color_palette](https://github.com/joaohenry23/custom_color_palette) package.
```
# import packages
import custom_color_palette as ccp
import matplotlib.pyplot as plt
# set the colors of the custom palette
lower_colors = ['maroon','red','darkorange','#ffff00','forestgreen','cyan','royalblue',(148/255,0/255,211/255)]
lower_palette = [lower_colors, ccp.range(180.0,240.0,1.0)]
upper_colors = plt.cm.Greys
upper_palette = [upper_colors, ccp.range(240.0,330.0,1.0), [ccp.range(180.0,330.0,1.0),240.0,330.0]]
# pass parameters to the creates_palette module
cmap, cmticks, norm, bounds = ccp.creates_palette([lower_palette, upper_palette], extend='both')
# creating colorbar labels
ticks = ccp.range(180,330,10)
```
Creates plot.
```
# import packages
import numpy as np
import cartopy.crs as ccrs
from cartopy.feature import NaturalEarthFeature
from cartopy.mpl.ticker import LatitudeFormatter, LongitudeFormatter
# calculates the central longitude of the plot
lon_cen = 360.0+(domain[0]+domain[1])/2.0
# creates the figure
fig = plt.figure('map', figsize=(4,4), dpi=200)
ax = fig.add_axes([0.1, 0.16, 0.80, 0.75], projection=ccrs.PlateCarree(lon_cen))
ax.outline_patch.set_linewidth(0.3)
# add the geographic boundaries
l = NaturalEarthFeature(category='cultural', name='admin_0_countries', scale='50m', facecolor='none')
ax.add_feature(l, edgecolor='gold', linewidth=0.25)
# plot the data
img = ax.pcolormesh(LonCorCyl.data, LatCorCyl.data, CMICyl.data, cmap=cmap, norm=norm,
transform=ccrs.PlateCarree())
# add the colorbar
cb = plt.colorbar(img, ticks=ticks, orientation='horizontal', extend='both',
cax=fig.add_axes([0.12, 0.05, 0.76, 0.02]))
cb.ax.tick_params(labelsize=5, labelcolor='black', width=0.5, length=1.5, direction='out', pad=1.0)
cb.set_label(label='{} [{}]'.format(standard_name, units), size=5, color='black', weight='normal')
cb.outline.set_linewidth(0.5)
# set the title
ax.set_title('{} - C{:02d} [{:.1f} μm]'.format(sat,band, wl), fontsize=7, loc='left')
ax.set_title(time_bounds.data[0].strftime('%Y/%m/%d %H:%M UTC'), fontsize=7, loc='right')
# Sets X axis characteristics
dx = 15
xticks = np.arange(domain[0], domain[1]+dx, dx)
ax.set_xticks(xticks, crs=ccrs.PlateCarree())
ax.xaxis.set_major_formatter(LongitudeFormatter(dateline_direction_label=True))
ax.set_xlabel('Longitude', color='black', fontsize=7, labelpad=3.0)
# Sets Y axis characteristics
dy = 15
yticks = np.arange(domain[2], domain[3]+dy, dy)
ax.set_yticks(yticks, crs=ccrs.PlateCarree())
ax.yaxis.set_major_formatter(LatitudeFormatter())
ax.set_ylabel('Latitude', color='black', fontsize=7, labelpad=3.0)
# Sets tick characteristics
ax.tick_params(left=True, right=True, bottom=True, top=True,
labelleft=True, labelright=False, labelbottom=True, labeltop=False,
length=0.0, width=0.05, labelsize=5.0, labelcolor='black')
# Sets grid characteristics
ax.gridlines(xlocs=xticks, ylocs=yticks, alpha=0.6, color='gray',
draw_labels=False, linewidth=0.25, linestyle='--')
# set the map limits
ax.set_extent([domain[0]+360.0, domain[1]+360.0, domain[2], domain[3]], crs=ccrs.PlateCarree())
plt.show()
```
| true |
code
| 0.591841 | null | null | null | null |
|
# Project 2: inverse kinematics and resolved rate control
In this project, we will implement an inverse kinematics algorithm and controllers for the Kuka iiwa 14 robot using the results from Project 1.
## Instructions
* Answer all questions in the notebook
* You will need to submit on Brightspace:
1. the code you wrote to answer the questions in a Jupyter Notebook. The code should be runnable as is.
2. a 2-3 pages report in pdf format (pdf only) detailing the methodology you followed to answer the questions as well as answers to the questions that require a typeset answer. You may add the plots in the report (does not count for the page limit) or in the Jupyter notebook.
As a reminder, the [Kuka iiwa 14 robot](https://www.kuka.com/en-us/products/robotics-systems/industrial-robots/lbr-iiwa) has 7 revolute joints and its kinematics is described in the picture below:

# Setup
Run the cell below only once when resetting the runtime in Colab - this will not do anything when running on a local Jupyter Notebook.
```
## check if we are in Google Colab
try:
import google.colab
RUNNING_IN_COLAB = True
print('detected Colab - setting up environment')
# then we need to install the conda environment
try:
import condacolab
condacolab.check()
except:
!pip install -q condacolab
import condacolab
condacolab.install()
except:
RUNNING_IN_COLAB = False
# after installing condalab, the runtime restarts
# -> need to check for colab env once more here
try:
import google.colab
RUNNING_IN_COLAB = True
except Exception as e:
RUNNING_IN_COLAB = False
if RUNNING_IN_COLAB:
try:
# Check if packages are installed or not. If not, install them.
import pinocchio
except:
# Install pinocchio, meschat-python
!conda install pinocchio meshcat-python
# get the class repo - first check if it exists
import os, sys
if not os.path.isdir('/content/ROB6003/Project2'):
print('cloning LAB repository')
os.chdir('/content')
!git clone https://github.com/righetti/ROB6003.git
print('cloning done')
else:
print('lab repos was found, skipping cloning')
print('done configuring for Colab')
sys.path.append('/content/ROB6003/Project2/')
os.chdir('/content/ROB6003/Project2/')
print('done adding system path and changing directory.')
```
# Starting the visualization environment
The following code will start a visualization environment (click on the printed address to see the robot)
You need to run this only ONCE. Each time you run this cell you will get a new display environment (so you need to close the previous one!)
This should work out of the box on Google Colab and you local Jupyter Notebook (make sure you have installed the right libraries in your local computer if you do not use Colab).
```
import numpy as np
import robot_visualizer
import time
import matplotlib.pyplot as plt
robot_visualizer.start_robot_visualizer()
```
# Displaying an arbitrary configuration
As in the previous project, you can use the following function to display arbitrary configurations of the robot
```
# here we display an arbitrary configuration of the robot
q = np.random.sample([7])
print(f'we show the configuration for the angles {q}')
robot_visualizer.display_robot(q)
```
## Question 1: inverse kinematics
* Write a function ``compute_IK_position`` that gets a desired end-effector 3D position (in spatial frame) and returns a vector of joint angles that solves the inverse kinematics problem
* The file ``desired_end_effector_positions.npy`` contains a sequence of 10 desired end-effector positions. For all the positions attainable by the robot, compute an inverse kinematics solution. For the positions for which an inverse kinematics solution does not exist, what is the issue and how close can you get the end-effector to the desired position?
* Write a function ``compute_IK_position_nullspace`` that solves the inverse kinematics problem and additionally uses joint redundancy (i.e. the nullspace) to try and keep the joints close to the following configuration $[1,1,-1,-1,1,1,1]$. Explain how you used the nullspace to implement this function.
* Use this new function to reach the positions set in the file ``desired_end_effector_positions.npy``, how do the solutions compare to the first ones you found?
```
## a script to load the desired end effector positions and display each of them every second
## you maybe modify this script to test your code
# load the file
with open('desired_end_effector_positions.npy', 'rb') as f:
desired_endeff = np.load(f)
# first we display the robot in 0 position
robot_visualizer.display_robot(np.zeros([7,1]))
# for each end-eff position
for i in range(desired_endeff.shape[1]):
# displays the desired endeff position
robot_visualizer.display_ball(desired_endeff[:,i])
time.sleep(1.)
```
## Question 2: Joint control and joint trajectories generation
We would like the robot to go from its initial configuration to the desired end-effector positions (in spatial coordinates) $[0.7, 0.2,0.7]$ in 5 seconds and then to the configuration $[0.3, 0.5,0.9]$ during the following 5 seconds.
* Compute inverse kinematics solutions to reach both goals
* Write a function ``get_point_to_point_motion`` that returns a desired position and velocity and takes as input the total motion duration T, the desired initial position and the desired final position. The generated trajectory needs to ensure that at t=0 and t=T both the velocity and acceleration are 0. You can use this function to interpolate between desired positions in both joint and end-effector space.
* Modify the ``robot_controller`` function below to move the robot from its initial configuration to reach the first goal (displayed in pink) at t=5 and the second goal ((in yellow) at t=10 by interpolating joint positions using the function ``get_point_to_point_motion`` you wrote above.
* Plot the resulting joint simulated and desired positions and velocities
* Plot the resulting end-effector positions and velocities
```
T = 10.
end_effector_goal1 = np.array([[0.7], [0.2],[0.7]])
end_effector_goal2 = np.array([[0.3], [0.5],[0.9]])
## this code is to save what the controller is doing for plotting and analysis after the simulation
global save_joint_positions, save_joint_velocities, save_t, ind
global save_des_joint_positions, save_des_joint_velocities
save_joint_positions = np.zeros([7,int(np.ceil(T / 0.001))+1])
save_joint_velocities = np.zeros_like(save_joint_positions)
save_des_joint_positions = np.zeros_like(save_joint_positions)
save_des_joint_velocities = np.zeros_like(save_joint_positions)
save_t = np.zeros([int(np.ceil(T / 0.001))+1])
ind=0
# end of saving code
def robot_controller(t, joint_positions, joint_velocities):
"""A typical robot controller
at every time t, this controller is called by the simulator. It receives as input
the current joint positions and velocities and needs to return a [7,1] vector
of desired torque commands
As an example, the current controller implements a PD controller and at time = 5s
it makes joint 2 and 3 follow sine curves
"""
desired_joint_positions = np.zeros([7,1])
desired_joint_velocities = np.zeros([7,1])
# when t>5. we generate sines for joint 2 and 3 as an example
if t > 5.:
desired_joint_positions[2] = 1. - np.cos(2*np.pi/5.*t)
desired_joint_velocities[2] = 2*np.pi/5. * np.sin(2*np.pi/5.*t)
desired_joint_positions[3] = .5 - 0.5*np.cos(2*np.pi/5.*t)
desired_joint_velocities[3] = np.pi/5. * np.sin(2*np.pi/5.*t)
# we compute the desired control commands using a PD controller
P = np.array([100., 100., 100., 100., 100., 100., 100.])
D = np.array([2.,2,2,2,2,2,2.])
desired_joint_torques = np.diag(P) @ (desired_joint_positions - joint_positions)
desired_joint_torques += np.diag(D) @ (desired_joint_velocities - joint_velocities)
## this code is to save what the controller is doing for plotting and analysis after the simulation
global save_joint_positions, save_joint_velocities, save_t, ind
global save_des_joint_positions, save_des_joint_velocities
save_joint_positions[:,ind] = joint_positions[:,0]
save_joint_velocities[:,ind] = joint_velocities[:,0]
save_des_joint_positions[:,ind] = desired_joint_positions[:,0]
save_des_joint_velocities[:,ind] = desired_joint_velocities[:,0]
save_t[ind] = t
ind += 1
## end of saving code
return desired_joint_torques
robot_visualizer.display_ball(end_effector_goal1[:,0])
robot_visualizer.display_ball2(end_effector_goal2[:,0])
robot_visualizer.simulate_robot(robot_controller, T=T)
# we plot the simulated vs. actual position of the robot
plt.figure(figsize=[9,12])
for i in range(7):
plt.subplot(7,1,i+1)
plt.plot(save_t, save_joint_positions[i,:])
plt.plot(save_t, save_des_joint_positions[i,:])
plt.ylim([-np.pi,np.pi])
plt.ylabel(f'q {i}')
plt.xlabel('Desired vs. actual joint positions - Time [s]')
# we plot the simulated vs. actual position of the robot
plt.figure(figsize=[9,12])
for i in range(7):
plt.subplot(7,1,i+1)
plt.plot(save_t, save_joint_velocities[i,:])
plt.plot(save_t, save_des_joint_velocities[i,:])
plt.ylim([-3,3])
plt.ylabel(f'dq {i}')
plt.xlabel('Desired vs. actual joint velocities - Time [s]')
```
## Question 3: End-effector control
As in Question 2, we would like the robot to go from its initial configuration to the desired end-effector positions (in spatial coordinates) $[0.7, 0.2,0.7]$ in 5 seconds and then to the configuration $[0.3, 0.5,0.9]$ during the following 5 seconds.
* Modify the ``robot_controller2`` function below to move the robot from its initial configuration to the first goal (reaching at t=5) and the second goal (t=10) by interpolating the desired end effector positions and directly mapping end-effector error to desired joint velocities (i.e. use P gains equal to 0 in joint space and do resolved-rate control).
* Plot the resulting joint simulated and desired positions and velocities
* Plot the resulting end-effector positions and velocities
* Compare results with Question 2
* Add a nullspace term to optimize a desired configuration of your choice and discuss the results
```
T = 10.
## this code is to save what the controller is doing for plotting and analysis after the simulation
global save_joint_positions, save_joint_velocities, save_t, ind
global save_des_joint_positions, save_des_joint_velocities
save_joint_positions = np.zeros([7,int(np.ceil(T / 0.001))+1])
save_joint_velocities = np.zeros_like(save_joint_positions)
save_des_joint_positions = np.zeros_like(save_joint_positions)
save_des_joint_velocities = np.zeros_like(save_joint_positions)
save_t = np.zeros([int(np.ceil(T / 0.001))+1])
ind=0
# end of saving code
def robot_controller2(t, joint_positions, joint_velocities):
"""A typical robot controller
at every time t, this controller is called by the simulator. It receives as input
the current joint positions and velocities and needs to return a [7,1] vector
of desired torque commands
As an example, the current controller implements a PD controller and at time = 5s
it makes joint 2 and 3 follow sine curves
"""
desired_joint_positions = np.zeros([7,1])
desired_joint_velocities = np.zeros([7,1])
# here we will only use a D controller (i.e. on the desired joint velocities)
# we increased the D gain for that purpose compared to the previous controller
D = np.array([4.,4,4,4,4,4,4.])
##TODO - find the desired joint velocities
desired_joint_torques = np.diag(D) @ (desired_joint_velocities - joint_velocities)
## this code is to save what the controller is doing for plotting and analysis after the simulation
global save_joint_positions, save_joint_velocities, save_t, ind
global save_des_joint_positions, save_des_joint_velocities
save_joint_positions[:,ind] = joint_positions[:,0]
save_joint_velocities[:,ind] = joint_velocities[:,0]
save_des_joint_positions[:,ind] = desired_joint_positions[:,0]
save_des_joint_velocities[:,ind] = desired_joint_velocities[:,0]
save_t[ind] = t
ind += 1
## end of saving code
return desired_joint_torques
robot_visualizer.display_ball(end_effector_goal1[:,0])
robot_visualizer.display_ball2(end_effector_goal2[:,0])
robot_visualizer.simulate_robot(robot_controller2, T=T)
```
## Question 4: Impedance control and gravity compensation
As in Question 2 and 3, we would like the robot to go from its initial configuration to the desired end-effector positions (in spatial coordinates) $[0.7, 0.2,0.7]$ in 5 seconds and then to the configuration $[0.3, 0.5,0.9]$ during the following 5 seconds.
In the previous questions, a gravity compensation controller was running "in the background" in addition to the control law you were computing. In this question, we remove this and implement a complete impedance controller with gravity compensation.
You are given a function ``robot_visualizer.rnea(q,dq,ddq)`` which implements the Recursive Newton Euler Algorithm (RNEA). It takes as arguments a vector of positions, velocities and accelerations, and computes (and returns) the following $M(q) \cdot \ddot{q} + C(q,\dot{q}) + G(q)$
* Modify the ``robot_controller3`` function below to implement an impedance controller with gravity compensation (add a small amount of joint damping, using a joint-space D gain of 0.1). Use this controller to move the robot from its initial configuration to the first goal (reaching at t=5) and the second goal (t=10) by interpolating the desired end effector positions as in the previous questions.
* Plot the resulting joint simulated and desired positions and velocities
* Plot the resulting end-effector positions and velocities
* Compare the controller when the small joint samping is on or off - can you explain the difference?
* Compare results with Question 2 and 3. Which controller would you rather choose and why?
```
T = 10.
## this code is to save what the controller is doing for plotting and analysis after the simulation
global save_joint_positions, save_joint_velocities, save_t, ind
global save_des_joint_positions, save_des_joint_velocities
save_joint_positions = np.zeros([7,int(np.ceil(T / 0.001))+1])
save_joint_velocities = np.zeros_like(save_joint_positions)
save_des_joint_positions = np.zeros_like(save_joint_positions)
save_des_joint_velocities = np.zeros_like(save_joint_positions)
save_t = np.zeros([int(np.ceil(T / 0.001))+1])
ind=0
# end of saving code
def robot_controller3(t, joint_positions, joint_velocities):
"""A typical robot controller
at every time t, this controller is called by the simulator. It receives as input
the current joint positions and velocities and needs to return a [7,1] vector
of desired torque commands
As an example, the current controller implements a PD controller and at time = 5s
it makes joint 2 and 3 follow sine curves
"""
desired_joint_positions = np.zeros([7,1])
desired_joint_velocities = np.zeros([7,1])
# here we will only use the D controller to inject small joint damping
D = np.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1])
##TODO - implement gravity compensation and impedance control
desired_joint_torques = -np.diag(D) @ joint_velocities
## this code is to save what the controller is doing for plotting and analysis after the simulation
global save_joint_positions, save_joint_velocities, save_t, ind
global save_des_joint_positions, save_des_joint_velocities
save_joint_positions[:,ind] = joint_positions[:,0]
save_joint_velocities[:,ind] = joint_velocities[:,0]
save_des_joint_positions[:,ind] = desired_joint_positions[:,0]
save_des_joint_velocities[:,ind] = desired_joint_velocities[:,0]
save_t[ind] = t
ind += 1
## end of saving code
return desired_joint_torques
robot_visualizer.display_ball([0.7, 0.2,0.7])
robot_visualizer.display_ball2([0.3, 0.5,0.9])
robot_visualizer.simulate_robot(robot_controller3, T=T, gravity_comp = False)
```
| true |
code
| 0.506774 | null | null | null | null |
|
# Gathering historical data about the addition of newspaper titles to Trove
The number of digitised newspapers available through Trove has increased dramatically since 2009. Understanding when newspapers were added is important for historiographical purposes, but there's no data about this available directly from Trove. This notebook uses web archives to extract lists of newspapers in Trove over time, and chart Trove's development.
Trove has always provided a browseable list of digitised newspaper titles. The url and format of this list has changed over time, but it's possible to find captures of this page in the Internet Archive and extract the full list of titles. The pages are also captured in the Australian Web Archive, but the Wayback Machine has a more detailed record.
The pages that I'm looking for are:
* [http://trove.nla.gov.au/ndp/del/titles](https://web.archive.org/web/*/http://trove.nla.gov.au/ndp/del/titles)
* [https://trove.nla.gov.au/newspaper/about](https://web.archive.org/web/*/https://trove.nla.gov.au/newspaper/about)
This notebook creates the following data files:
* [trove_newspaper_titles_2009_2021.csv](https://github.com/GLAM-Workbench/trove-newspapers/blob/master/trove_newspaper_titles_2009_2021.csv) – complete dataset of captures and titles
* [trove_newspaper_titles_first_appearance_2009_2021.csv](https://github.com/GLAM-Workbench/trove-newspapers/blob/master/trove_newspaper_titles_first_appearance_2009_2021.csv) – filtered dataset, showing only the first appearance of each title / place / date range combination
I've also created a [browseable list of titles](https://gist.github.com/wragge/7d80507c3e7957e271c572b8f664031a), showing when they first appeared in Trove.
```
import requests
import json
import re
from surt import surt
from bs4 import BeautifulSoup
import arrow
import pandas as pd
import altair as alt
from IPython.display import display, HTML
from pathlib import Path
```
## Code for harvesting web archive captures
We're using the Memento protocol to get a list of captures. See the [Web Archives section](https://glam-workbench.net/web-archives/) of the GLAM Workbench for more details.
```
# The code in this cell is copied from notebooks in the Web Archives section of the GLAM Workbench (https://glam-workbench.net/web-archives/)
# In particular see: https://glam-workbench.net/web-archives/#find-all-the-archived-versions-of-a-web-page
# These are the repositories we'll be using
TIMEGATES = {
'awa': 'https://web.archive.org.au/awa/',
'nzwa': 'https://ndhadeliver.natlib.govt.nz/webarchive/wayback/',
'ukwa': 'https://www.webarchive.org.uk/wayback/en/archive/',
'ia': 'https://web.archive.org/web/'
}
def convert_lists_to_dicts(results):
'''
Converts IA style timemap (a JSON array of arrays) to a list of dictionaries.
Renames keys to standardise IA with other Timemaps.
'''
if results:
keys = results[0]
results_as_dicts = [dict(zip(keys, v)) for v in results[1:]]
else:
results_as_dicts = results
for d in results_as_dicts:
d['status'] = d.pop('statuscode')
d['mime'] = d.pop('mimetype')
d['url'] = d.pop('original')
return results_as_dicts
def get_capture_data_from_memento(url, request_type='head'):
'''
For OpenWayback systems this can get some extra capture info to insert into Timemaps.
'''
if request_type == 'head':
response = requests.head(url)
else:
response = requests.get(url)
headers = response.headers
length = headers.get('x-archive-orig-content-length')
status = headers.get('x-archive-orig-status')
status = status.split(' ')[0] if status else None
mime = headers.get('x-archive-orig-content-type')
mime = mime.split(';')[0] if mime else None
return {'length': length, 'status': status, 'mime': mime}
def convert_link_to_json(results, enrich_data=False):
'''
Converts link formatted Timemap to JSON.
'''
data = []
for line in results.splitlines():
parts = line.split('; ')
if len(parts) > 1:
link_type = re.search(r'rel="(original|self|timegate|first memento|last memento|memento)"', parts[1]).group(1)
if link_type == 'memento':
link = parts[0].strip('<>')
timestamp, original = re.search(r'/(\d{14})/(.*)$', link).groups()
capture = {'urlkey': surt(original), 'timestamp': timestamp, 'url': original}
if enrich_data:
capture.update(get_capture_data_from_memento(link))
print(capture)
data.append(capture)
return data
def get_timemap_as_json(timegate, url, enrich_data=False):
'''
Get a Timemap then normalise results (if necessary) to return a list of dicts.
'''
tg_url = f'{TIMEGATES[timegate]}timemap/json/{url}/'
response = requests.get(tg_url)
response_type = response.headers['content-type']
if response_type == 'text/x-ndjson':
data = [json.loads(line) for line in response.text.splitlines()]
elif response_type == 'application/json':
data = convert_lists_to_dicts(response.json())
elif response_type in ['application/link-format', 'text/html;charset=utf-8']:
data = convert_link_to_json(response.text, enrich_data=enrich_data)
return data
```
## Harvest the title data from the Internet Archive
This gets the web page captures from the Internet Archive, scrapes the list of titles from the page, then does a bit of normalisation of the title data.
```
titles = []
# These are the pages that listed available titles.
# There was a change in 2016
pages = [{'url': 'http://trove.nla.gov.au/ndp/del/titles', 'path': '/ndp/del/title/'},
{'url': 'https://trove.nla.gov.au/newspaper/about', 'path': '/newspaper/title/'}]
for page in pages:
for capture in get_timemap_as_json('ia', page['url']):
if capture['status'] == '200':
url = f'https://web.archive.org/web/{capture["timestamp"]}id_/{capture["url"]}'
#print(url)
capture_date = arrow.get(capture['timestamp'][:8], 'YYYYMMDD').format('YYYY-MM-DD')
#print(capture_date)
response = requests.get(url)
soup = BeautifulSoup(response.content)
title_links = soup.find_all('a', href=re.compile(page['path']))
for title in title_links:
# Get the title text
full_title = title.get_text().strip()
# Get the title id
title_id = re.search(r'\/(\d+)\/?$', title['href']).group(1)
# Most of the code below is aimed at normalising the publication place and dates values to allow for easy grouping & deduplication
brief_title = re.sub(r'\(.+\)\s*$', '', full_title).strip()
try:
details = re.search(r'\((.+)\)\s*$', full_title).group(1).split(':')
except AttributeError:
place = ''
dates = ''
else:
try:
place = details[0].strip()
# Normalise states
try:
place = re.sub(r'(, )?([A-Za-z]+)[\.\s]*$', lambda match: f'{match.group(1) if match.group(1) else ""}{match.group(2).upper()}', place)
except AttributeError:
pass
# Normalise dates
dates = ' - '.join([d.strip() for d in details[1].strip().split('-')])
except IndexError:
place = ''
dates = ' - '.join([d.strip() for d in details[0].strip().split('-')])
titles.append({'title_id': title_id, 'full_title': full_title, 'title': brief_title, 'place': place, 'dates': dates, 'capture_date': capture_date, 'capture_timestamp': capture['timestamp']})
```
## Convert the title data to a DataFrame for analysis
```
df = pd.DataFrame(titles)
df
# Number of captures
len(df['capture_timestamp'].unique())
# Number of days on which the pages were captured
len(df['capture_date'].unique())
```
Save this dataset as a CSV file.
```
df.to_csv('trove_newspaper_titles_2009_2021.csv', index=False)
```
## How did the number of titles change over time?
```
# Drop duplicates in cases where there were mutiple captures on a single day
captures_df = df.drop_duplicates(subset=['capture_date', 'full_title'])
# Calculate totals per capture
capture_totals = captures_df['capture_date'].value_counts().to_frame().reset_index()
capture_totals.columns = ['capture_date', 'total']
capture_totals
alt.Chart(capture_totals).mark_line(point=True).encode(
x=alt.X('capture_date:T', title='Date captured'),
y=alt.Y('total:Q', title='Number of newspaper titles'),
tooltip=[alt.Tooltip('capture_date:T', format='%e %b %Y'), 'total:Q'],
).properties(width=700)
```
## When did titles first appear?
For historiographical purposes, its useful to know when a particular title first appeared in Trove. Here we'll only keep the first appearance of each title (or any subsequent changes to its date range / location).
```
first_appearance = df.drop_duplicates(subset=['title', 'place', 'dates'])
first_appearance
```
Find when a particular newspaper first appeared.
```
first_appearance.loc[first_appearance['title'] == 'Canberra Times']
```
Generate an alphabetical list for easy browsing. View the [results as a Gist](https://gist.github.com/wragge/7d80507c3e7957e271c572b8f664031a).
```
with Path('titles_list.md').open('w') as titles_list:
for title, group in first_appearance.groupby(['title', 'title_id']):
places = ' | '.join(group['place'].unique())
titles_list.write(f'<h4><a href="http://nla.gov.au/nla.news-title{title[1]}">{title[0]} ({places})</a></h4>')
titles_list.write(group.sort_values(by='capture_date')[['capture_date','dates', 'place']].to_html(index=False))
```
Save this dataset to CSV.
```
first_appearance.to_csv('trove_newspaper_titles_first_appearance_2009_2021.csv', index=False)
```
----
Created by [Tim Sherratt](https://timsherratt.org/) for the [GLAM Workbench](https://glam-workbench.github.io/).
Support this project by becoming a [GitHub sponsor](https://github.com/sponsors/wragge?o=esb).
| true |
code
| 0.345588 | null | null | null | null |
|
# Introduction to zfit
In this notebook, we will have a walk through the main components of zfit and their features. Especially the extensive model building part will be discussed separately.
zfit consists of 5 mostly independent parts. Other libraries can rely on this parts to do plotting or statistical inference, such as hepstats does. Therefore we will discuss two libraries in this tutorial: zfit to build models, data and a loss, minimize it and get a fit result and hepstats, to use the loss we built here and do inference.
<img src="attachment:screenshot%20from%202020-07-16%2014-29-15.png" style="max-width:50%">
## Data
This component in general plays a minor role in zfit: it is mostly to provide a unified interface for data.
Preprocessing is therefore not part of zfit and should be done beforehand. Python offers many great possibilities to do so (e.g. Pandas).
zfit `Data` can load data from various sources, most notably from Numpy, Pandas DataFrame, TensorFlow Tensor and ROOT (using uproot). It is also possible, for convenience, to convert it directly `to_pandas`. The constructors are named `from_numpy`, `from_root` etc.
```
import zfit
from zfit import z
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
```
A `Data` needs not only the data itself but also the observables: the human readable string identifiers of the axes (corresponding to "columns" of a Pandas DataFrame). It is convenient to define the `Space` not only with the observable but also with a limit: this can directly be re-used as the normalization range in the PDF.
First, let's define our observables
```
obs = zfit.Space('obs1', (-5, 10))
```
This `Space` has limits. Next to the effect of handling the observables, we can also play with the limits: multiple `Spaces` can be added to provide disconnected ranges. More importantly, `Space` offers functionality:
- limit1d: return the lower and upper limit in the 1 dimensional case (raises an error otherwise)
- rect_limits: return the n dimensional limits
- area(): calculate the area (e.g. distance between upper and lower)
- inside(): return a boolean Tensor corresponding to whether the value is _inside_ the `Space`
- filter(): filter the input values to only return the one inside
```
size_normal = 10000
data_normal_np = np.random.normal(size=size_normal, scale=2)
data_normal = zfit.Data.from_numpy(obs=obs, array=data_normal_np)
```
The main functionality is
- nevents: attribute that returns the number of events in the object
- data_range: a `Space` that defines the limits of the data; if outside, the data will be cut
- n_obs: defines the number of dimensions in the dataset
- with_obs: returns a subset of the dataset with only the given obs
- weights: event based weights
Furthermore, `value` returns a Tensor with shape `(nevents, n_obs)`.
To retrieve values, in general `z.unstack_x(data)` should be used; this returns a single Tensor with shape (nevents) or a list of tensors if `n_obs` is larger then 1.
```
print(f"We have {data_normal.nevents} events in our dataset with the minimum of {np.min(data_normal.unstack_x())}") # remember! The obs cut out some of the data
data_normal.n_obs
```
## Model
Building models is by far the largest part of zfit. We will therefore cover an essential part, the possibility to build custom models, in an extra chapter. Let's start out with the idea that you define your parameters and your observable space; the latter is the expected input data.
There are two types of models in zfit:
- functions, which are rather simple and "underdeveloped"; their usage is often not required.
- PDF that are function which are normalized (over a specified range); this is the main model and is what we gonna use throughout the tutorials.
A PDF is defined by
\begin{align}
\mathrm{PDF}_{f(x)}(x; \theta) = \frac{f(x; \theta)}{\int_{a}^{b} f(x; \theta)}
\end{align}
where a and b define the normalization range (`norm_range`), over which (by inserting into the above definition) the integral of the PDF is unity.
zfit has a modular approach to things and this is also true for models. While the normalization itself (e.g. what are parameters, what is normalized data) will already be pre-defined in the model, models are composed of functions that are transparently called inside. For example, a Gaussian would usually be implemented by writing a Python function `def gauss(x, mu, sigma)`, which does not care about the normalization and then be wrapped in a PDF, where the normalization and what is a parameter is defined.
In principle, we can go far by using simply functions (e.g. [TensorFlowAnalysis/AmpliTF](https://github.com/apoluekt/AmpliTF) by Anton Poluektov uses this approach quite successfully for Amplitude Analysis), but this design has limitations for a more general fitting library such as zfit (or even [TensorWaves](https://github.com/ComPWA/tensorwaves), being built on top of AmpliTF).
The main thing is to keep track of the different ordering of the data and parameters, especially the dependencies.
Let's create a simple Gaussian PDF. We already defined the `Space` for the data before, now we only need the parameters. This are a different object than a `Space`.
### Parameter
A `Parameter` (there are different kinds actually, more on that later) takes the following arguments as input:
`Parameter(human readable name, initial value[, lower limit, upper limit])` where the limits are recommended but not mandatory. Furthermore, `step_size` can be given (which is useful to be around the given uncertainty, e.g. for large yields or small values it can help a lot to set this). Also, a `floating` argument is supported, indicating whether the parameter is allowed to float in the fit or not (just omitting the limits does _not_ make a parameter constant).
Parameters have a unique name. This is served as the identifier for e.g. fit results. However, a parameter _cannot_ be retrieved by its string identifier (its name) but the object itself should be used. In places where a parameter maps to something, the object itself is needed, not its name.
```
mu = zfit.Parameter('mu', 1, -3, 3, step_size=0.2)
sigma_num = zfit.Parameter('sigma42', 1, 0.1, 10, floating=False)
```
These attributes can be changed:
```
print(f"sigma is float: {sigma_num.floating}")
sigma_num.floating = True
print(f"sigma is float: {sigma_num.floating}")
```
*PITFALL NOTEBOOKS: since the parameters have a unique name, a second parameter with the same name cannot be created; the behavior is undefined and therefore it raises an error.
While this does not pose a problem in a normal Python script, it does in a Jupyter-like notebook, since it is an often practice to "rerun" a cell as an attempt to "reset" things. Bear in mind that this does not make sense, from a logic point of view. The parameter already exists. Best practice: write a small wrapper, do not rerun the parameter creation cell or simply rerun the notebook (restart kernel & run all). For further details, have a look at the discussion and arguments [here](https://github.com/zfit/zfit/issues/186)*
Now we have everything to create a Gaussian PDF:
```
gauss = zfit.pdf.Gauss(obs=obs, mu=mu, sigma=sigma_num)
```
Since this holds all the parameters and the observables are well defined, we can retrieve them
```
gauss.n_obs # dimensions
gauss.obs
gauss.space
gauss.norm_range
```
As we've seen, the `obs` we defined is the `space` of Gauss: this acts as the default limits whenever needed (e.g. for sampling). `gauss` also has a `norm_range`, which equals by default as well to the `obs` given, however, we can explicitly change that with `set_norm_range`.
We can also access the parameters of the PDF in two ways, depending on our intention:
either by _name_ (the parameterization name, e.g. `mu` and `sigma`, as defined in the `Gauss`), which is useful if we are interested in the parameter that _describes_ the shape
```
gauss.params
```
or to retrieve all the parameters that the PDF depends on. As this now may sounds trivial, we will see later that models can depend on other models (e.g. sums) and parameters on other parameters. There is one function that automatically retrieves _all_ dependencies, `get_params`. It takes three arguments to filter:
- floating: whether to filter only floating parameters, only non-floating or don't discriminate
- is_yield: if it is a yield, or not a yield, or both
- extract_independent: whether to recursively collect all parameters. This, and the explanation for why independent, can be found later on in the `Simultaneous` tutorial.
Usually, the default is exactly what we want if we look for _all free parameters that this PDF depends on_.
```
gauss.get_params()
```
The difference will also be clear if we e.g. use the same parameter twice:
```
gauss_only_mu = zfit.pdf.Gauss(obs=obs, mu=mu, sigma=mu)
print(f"params={gauss_only_mu.params}")
print(f"get_params={gauss_only_mu.get_params()}")
```
## Functionality
PDFs provide a few useful methods. The main features of a zfit PDF are:
- `pdf`: the normalized value of the PDF. It takes an argument `norm_range` that can be set to `False`, in which case we retrieve the unnormalized value
- `integrate`: given a certain range, the PDF is integrated. As `pdf`, it takes a `norm_range` argument that integrates over the unnormalized `pdf` if set to `False`
- `sample`: samples from the pdf and returns a `Data` object
```
integral = gauss.integrate(limits=(-1, 3)) # corresponds to 2 sigma integral
integral
```
### Tensors
As we see, many zfit functions return Tensors. This is however no magical thing! If we're outside of models, than we can always safely convert them to a numpy array by calling `zfit.run(...)` on it (or any structure containing potentially multiple Tensors). However, this may not even be required often! They can be added just like numpy arrays and interact well with Python and Numpy:
```
np.sqrt(integral)
```
They also have shapes, dtypes, can be slices etc. So do not convert them except you need it. More on this can be seen in the talk later on about zfit and TensorFlow 2.0.
```
sample = gauss.sample(n=1000) # default space taken as limits
sample
sample.unstack_x()[:10]
sample.n_obs
sample.obs
```
We see that sample returns also a zfit `Data` object with the same space as it was sampled in. This can directly be used e.g.
```
probs = gauss.pdf(sample)
probs[:10]
```
**NOTE**: In case you want to do this repeatedly (e.g. for toy studies), there is a way more efficient way (see later on)
## Plotting
so far, we have a dataset and a PDF. Before we go for fitting, we can make a plot. This functionality is not _directly_ provided in zfit (but can be added to [zfit-physics](https://github.com/zfit/zfit-physics)). It is however simple enough to do it:
```
def plot_model(model, data, scale=1, plot_data=True): # we will use scale later on
nbins = 50
lower, upper = data.data_range.limit1d
x = tf.linspace(lower, upper, num=1000) # np.linspace also works
y = model.pdf(x) * size_normal / nbins * data.data_range.area()
y *= scale
plt.plot(x, y)
data_plot = zfit.run(z.unstack_x(data)) # we could also use the `to_pandas` method
if plot_data:
plt.hist(data_plot, bins=nbins)
plot_model(gauss, data_normal)
```
We can of course do better (and will see that later on, continuously improve the plots), but this is quite simple and gives us the full power of matplotlib.
### Different models
zfit offers a selection of predefined models (and extends with models from zfit-physics that contain physics specific models such as ARGUS shaped models).
```
print(zfit.pdf.__all__)
```
To create a more realistic model, we can build some components for a mass fit with a
- signal component: CrystalBall
- combinatorial background: Exponential
- partial reconstructed background on the left: Kernel Density Estimation
```
mass_obs = zfit.Space('mass', (0, 1000))
# Signal component
mu_sig = zfit.Parameter('mu_sig', 400, 100, 600)
sigma_sig = zfit.Parameter('sigma_sig', 50, 1, 100)
alpha_sig = zfit.Parameter('alpha_sig', 300, 100, 400)
n_sig = zfit.Parameter('n sig', 4, 0.1, 30)
signal = zfit.pdf.CrystalBall(obs=mass_obs, mu=mu_sig, sigma=sigma_sig, alpha=alpha_sig, n=n_sig)
# combinatorial background
lam = zfit.Parameter('lambda', -0.01, -0.05, -0.001)
comb_bkg = zfit.pdf.Exponential(lam, obs=mass_obs)
part_reco_data = np.random.normal(loc=200, scale=150, size=700)
part_reco_data = zfit.Data.from_numpy(obs=mass_obs, array=part_reco_data) # we don't need to do this but now we're sure it's inside the limits
part_reco = zfit.pdf.GaussianKDE1DimV1(obs=mass_obs, data=part_reco_data, bandwidth='adaptive')
```
## Composing models
We can also compose multiple models together. Here we'll stick to one dimensional models, the extension to multiple dimensions is explained in the "custom models tutorial".
Here we will use a `SumPDF`. This takes pdfs and fractions. If we provide n pdfs and:
- n - 1 fracs: the nth fraction will be 1 - sum(fracs)
- n fracs: no normalization attempt is done by `SumPDf`. If the fracs are not implicitly normalized, this can lead to bad fitting
behavior if there is a degree of freedom too much
```
sig_frac = zfit.Parameter('sig_frac', 0.3, 0, 1)
comb_bkg_frac = zfit.Parameter('comb_bkg_frac', 0.25, 0, 1)
model = zfit.pdf.SumPDF([signal, comb_bkg, part_reco], [sig_frac, comb_bkg_frac])
```
In order to have a corresponding data sample, we can just create one. Since we want to fit to this dataset later on, we will create it with slightly different values. Therefore, we can use the ability of a parameter to be set temporarily to a certain value with
```
print(f"before: {sig_frac}")
with sig_frac.set_value(0.25):
print(f"new value: {sig_frac}")
print(f"after 'with': {sig_frac}")
```
While this is useful, it does not fully scale up. We can use the `zfit.param.set_values` helper therefore.
(_Sidenote: instead of a list of values, we can also use a `FitResult`, the given parameters then take the value from the result_)
```
with zfit.param.set_values([mu_sig, sigma_sig, sig_frac, comb_bkg_frac, lam], [370, 34, 0.18, 0.15, -0.006]):
data = model.sample(n=10000)
plot_model(model, data);
```
Plotting the components is not difficult now: we can either just plot the pdfs separately (as we still can access them) or in a generalized manner by accessing the `pdfs` attribute:
```
def plot_comp_model(model, data):
for mod, frac in zip(model.pdfs, model.params.values()):
plot_model(mod, data, scale=frac, plot_data=False)
plot_model(model, data)
plot_comp_model(model, data)
```
Now we can add legends etc. Btw, did you notice that actually, the `frac` params are zfit `Parameters`? But we just used them as if they were Python scalars and it works.
```
print(model.params)
```
### Extended PDFs
So far, we have only looked at normalized PDFs that do contain information about the shape but not about the _absolute_ scale. We can make a PDF extended by adding a yield to it.
The behavior of the new, extended PDF does **NOT change**, any methods we called before will act the same. Only exception, some may require an argument _less_ now. All the methods we used so far will return the same values. What changes is that the flag `model.is_extended` now returns `True`. Furthermore, we have now a few more methods that we can use which would have raised an error before:
- `get_yield`: return the yield parameter (notice that the yield is _not_ added to the shape parameters `params`)
- `ext_{pdf,integrate}`: these methods return the same as the versions used before, however, multiplied by the yield
- `sample` is still the same, but does not _require_ the argument `n` anymore. By default, this will now equal to a _poissonian sampled_ n around the yield.
The `SumPDF` now does not strictly need `fracs` anymore: if _all_ input PDFs are extended, the sum will be as well and use the (normalized) yields as fracs
The preferred way to create an extended PDf is to use `PDF.create_extended(yield)`. However, since this relies on copying the PDF (which may does not work for different reasons), there is also a `set_yield(yield)` method that sets the yield in-place. This won't lead to ambiguities, as everything is supposed to work the same.
```
yield_model = zfit.Parameter('yield_model', 10000, 0, 20000, step_size=10)
model_ext = model.create_extended(yield_model)
```
alternatively, we can create the models as extended and sum them up
```
sig_yield = zfit.Parameter('sig_yield', 2000, 0, 10000, step_size=1)
sig_ext = signal.create_extended(sig_yield)
comb_bkg_yield = zfit.Parameter('comb_bkg_yield', 6000, 0, 10000, step_size=1)
comb_bkg_ext = comb_bkg.create_extended(comb_bkg_yield)
part_reco_yield = zfit.Parameter('part_reco_yield', 2000, 0, 10000, step_size=1)
part_reco.set_yield(part_reco_yield) # unfortunately, `create_extended` does not work here. But no problem, it won't change anyting.
part_reco_ext = part_reco
model_ext_sum = zfit.pdf.SumPDF([sig_ext, comb_bkg_ext, part_reco_ext])
```
# Loss
A loss combines the model and the data, for example to build a likelihood. Furthermore, it can contain constraints, additions to the likelihood. Currently, if the `Data` has weights, these are automatically taken into account.
```
nll_gauss = zfit.loss.UnbinnedNLL(gauss, data_normal)
```
The loss has several attributes to be transparent to higher level libraries. We can calculate the value of it using `value`.
```
nll_gauss.value()
```
Notice that due to graph building, this will take significantly longer on the first run. Rerun the cell above and it will be way faster.
Furthermore, the loss also provides a possibility to calculate the gradients or, often used, the value and the gradients.
We can access the data and models (and possible constraints)
```
nll_gauss.model
nll_gauss.data
nll_gauss.constraints
```
Similar to the models, we can also get the parameters via `get_params`.
```
nll_gauss.get_params()
```
### Extended loss
More interestingly, we can now build a loss for our composite sum model using the sampled data. Since we created an extended model, we can now also create an extended likelihood, taking into account a Poisson term to match the yield to the number of events.
```
nll = zfit.loss.ExtendedUnbinnedNLL(model_ext_sum, data)
nll.get_params()
```
# Minimization
While a loss is interesting, we usually want to minimize it. Therefore we can use the minimizers in zfit, most notably `Minuit`, a wrapper around the [iminuit minimizer](https://github.com/scikit-hep/iminuit).
The philosophy is to create a minimizer instance that is mostly _stateless_, e.g. does not remember the position (there are considerations to make it possible to have a state, in case you feel interested, [contact us](https://github.com/zfit/zfit#contact))
Given that iminuit provides us with a very reliable and stable minimizer, it is usually recommended to use this. Others are implemented as well and could easily be wrapped, however, the convergence is usually not as stable.
Minuit has a few options:
- `tolerance`: the Estimated Distance to Minimum (EDM) criteria for convergence (default 1e-3)
- `verbosity`: between 0 and 10, 5 is normal, 7 is verbose, 10 is maximum
- `use_minuit_grad`: if True, uses the Minuit numerical gradient instead of the TensorFlow gradient. This is usually more stable for smaller fits; furthermore the TensorFlow gradient _can_ (experience based) sometimes be wrong.
```
minimizer = zfit.minimize.Minuit(use_minuit_grad=True)
```
For the minimization, we can call `minimize`, which takes a
- loss as we created above
- optionally: the parameters to minimize
By default, `minimize` uses all the free floating parameters (obtained with `get_params`). We can also explicitly specify which ones to use by giving them (or better, objects that depend on them) to `minimize`; note however that non-floating parameters, even if given explicitly to `minimize` won 't be minimized.
## Pre-fit parts of the PDF
Before we want to fit the whole PDF however, it can be useful to pre-fit it. A way can be to fix the combinatorial background by fitting the exponential to the right tail.
Therefore we create a new data object with an additional cut and furthermore, set the normalization range of the background pdf to the range we are interested in.
```
values = z.unstack_x(data)
obs_right_tail = zfit.Space('mass', (700, 1000))
data_tail = zfit.Data.from_tensor(obs=obs_right_tail, tensor=values)
with comb_bkg.set_norm_range(obs_right_tail):
nll_tail = zfit.loss.UnbinnedNLL(comb_bkg, data_tail)
minimizer.minimize(nll_tail)
```
Since we now fit the lambda parameter of the exponential, we can fix it.
```
lam.floating = False
lam
result = minimizer.minimize(nll)
plot_comp_model(model_ext_sum, data)
```
# Fit result
The result of every minimization is stored in a `FitResult`. This is the last stage of the zfit workflow and serves as the interface to other libraries. Its main purpose is to store the values of the fit, to reference to the objects that have been used and to perform (simple) uncertainty estimation.
```
print(result)
```
This gives an overview over the whole result. Often we're mostly interested in the parameters and their values, which we can access with a `params` attribute.
```
print(result.params)
```
This is a `dict` which stores any knowledge about the parameters and can be accessed by the parameter (object) itself:
```
result.params[mu_sig]
```
'value' is the value at the minimum. To obtain other information about the minimization process, `result` contains more attributes:
- fmin: the function minimum
- edm: estimated distance to minimum
- info: contains a lot of information, especially the original information returned by a specific minimizer
- converged: if the fit converged
```
result.fmin
```
## Estimating uncertainties
The `FitResult` has mainly two methods to estimate the uncertainty:
- a profile likelihood method (like MINOS)
- Hessian approximation of the likelihood (like HESSE)
When using `Minuit`, this uses (currently) it's own implementation. However, zfit has its own implementation, which are likely to become the standard and can be invoked by changing the method name.
Hesse is also [on the way to implement](https://github.com/zfit/zfit/pull/244) the [corrections for weights](https://inspirehep.net/literature/1762842).
We can explicitly specify which parameters to calculate, by default it does for all.
```
result.hesse()
# result.hesse(method='hesse_np')
```
We get the result directly returned. This is also added to `result.params` for each parameter and is nicely displayed with an added column
```
print(result.params)
errors, new_result = result.errors(params=[sig_yield, part_reco_yield, mu_sig]) # just using three for speed reasons
# errors, new_result = result.errors(params=[yield_model, sig_frac, mu_sig], method='zfit_error')
print(errors)
print(result.params)
```
#### What is 'new_result'?
When profiling a likelihood, such as done in the algorithm used in `errors`, a new minimum can be found. If this is the case, this new minimum will be returned, otherwise `new_result` is `None`. Furthermore, the current `result` would be rendered invalid by setting the flag `valid` to `False`. _Note_: this behavior only applies to the zfit internal error estimator.
### A simple profile
There is no default function (yet) for simple profiling plot. However, again, we're in Python and it's simple enough to do that for a parameter. Let's do it for `sig_yield`
```
x = np.linspace(1600, 2000, num=50)
y = []
sig_yield.floating = False
for val in x:
sig_yield.set_value(val)
y.append(nll.value())
sig_yield.floating = True
zfit.param.set_values(nll.get_params(), result)
plt.plot(x, y)
```
We can also access the covariance matrix of the parameters
```
result.covariance()
```
# End of zfit
This is where zfit finishes and other libraries take over.
# Beginning of hepstats
`hepstats` is a library containing statistical tools and utilities for high energy physics. In particular you do statistical inferences using the models and likelhoods function constructed in `zfit`.
Short example: let's compute for instance a confidence interval at 68 % confidence level on the mean of the gaussian defined above.
```
from hepstats.hypotests.parameters import POIarray
from hepstats.hypotests.calculators import AsymptoticCalculator
from hepstats.hypotests import ConfidenceInterval
calculator = AsymptoticCalculator(input=result, minimizer=minimizer)
value = result.params[mu_sig]["value"]
error = result.params[mu_sig]["minuit_hesse"]["error"]
mean_scan = POIarray(mu_sig, np.linspace(value - 1.5*error, value + 1.5*error, 10))
ci = ConfidenceInterval(calculator, mean_scan)
ci.interval()
from utils import one_minus_cl_plot
ax = one_minus_cl_plot(ci)
ax.set_xlabel("mean")
```
There will be more of `hepstats` later.
| true |
code
| 0.64204 | null | null | null | null |
|
# Iterators and Generators
In the section on loops we introduced the `range` function, and said that you should think about it as creating a list of numbers. In Python `2.X` this is exactly what it does. In Python `3.X` this is *not* what it does. Instead it creates the numbers one at a time. The difference in speed and memory usage is enormous for very large lists - examples are given [here](http://justindailey.blogspot.se/2011/09/python-range-vs-xrange.html) and [here](https://asmeurer.github.io/python3-presentation/slides.html#42).
We can recreate one of the examples from [Meuer's slides](https://asmeurer.github.io/python3-presentation/slides.html#44) in detail:
```
def naivesum_list(N):
"""
Naively sum the first N integers
"""
A = 0
for i in list(range(N + 1)):
A += i
return A
```
We will now see how much memory this uses:
```
%load_ext memory_profiler
%memit naivesum_list(10**4)
%memit naivesum_list(10**5)
%memit naivesum_list(10**6)
%memit naivesum_list(10**7)
%memit naivesum_list(10**8)
```
We see that the memory usage is growing very rapidly - as the list gets large it's growing as $N$.
Instead we can use the `range` function that yields one integer at a time:
```
def naivesum(N):
"""
Naively sum the first N integers
"""
A = 0
for i in range(N + 1):
A += i
return A
%memit naivesum(10**4)
%memit naivesum(10**5)
%memit naivesum(10**6)
%memit naivesum(10**7)
%memit naivesum(10**8)
```
We see that the *memory* usage is unchanged with $N$, making it practical to run much larger calculations.
## Iterators
The `range` function is returning an [*iterator*](https://docs.python.org/3/glossary.html#term-iterator) here. This is an object - a general thing - that represents a stream, or a sequence, of data. The iterator knows how to create the first element of the stream, and it knows how to get the next element. It does not, in general, need to know all of the elements at once.
As we've seen above this can save a lot of memory. It can also save time: the code does not need to construct all of the members of the sequence before starting, and it's quite possible you don't need all of them (think about the "Shortest published mathematical paper" exercise).
An iterator such as `range` is very useful, and there's a lot more useful ways to work with iterators in the `itertools` module. These functions that return iterators, such as `range`, are called [*generators*](https://docs.python.org/3/glossary.html#term-generator), and it's useful to be able to make your own.
## Making your own generators
Let's look at an example: finding all primes less than $N$ that can be written in the form $4 k - 1$, where $k$ is an integer.
We're going to need to calculate all prime numbers less than or equal to $N$. We could write a function that returns all these numbers as a list. However, if $N$ gets large then this will be expensive, both in time and memory. As we only need one number at a time, we can use a generator.
```
def all_primes(N):
"""
Return all primes less than or equal to N.
Parameters
----------
N : int
Maximum number
Returns
-------
prime : generator
Prime numbers
"""
primes = []
for n in range(2, N+1):
is_n_prime = True
for p in primes:
if n%p == 0:
is_n_prime = False
break
if is_n_prime:
primes.append(n)
yield n
```
This code needs careful examination. First it defines the list of all prime numbers that it currently knows, `primes` (which is initially empty). Then it loops through all integers $n$ from $2$ to $N$ (ignoring $1$ as we know it's not prime).
Inside this loop it initially assumes that $n$ is prime. It then checks if any of the known primes exactly divides $n$ (`n%p == 0` checks if $n \bmod p = 0$). As soon as it finds such a prime divisor it knows that $n$ is not prime it resets the assumption with this new knowledge, then `break`s out of the loop. This statement stops the `for p in primes` loop early, as we don't need to look at later primes.
If no known prime ever divides $n$ then at the end of the `for p in primes` loop we will still have `is_n_prime` being `True`. In this case we must have $n$ being prime, so we add it to the list of known primes and return it.
It is precisely this point which makes the code above define a generator. We return the value of the prime number found
1. using the `yield` keyword, not the `return` keyword, and
2. we return the value as soon as it is known.
It is the use of the `yield` keyword that makes this function a generator.
This means that only the latest prime number is stored for return.
To use the iterator within a loop, we code it in the same way as with the `range` function:
```
print("All prime numbers less than or equal to 20:")
for p in all_primes(20):
print(p)
```
To see what the generator is actually doing, we can step through it one call at a time using the built in `next` function:
```
a = all_primes(10)
next(a)
next(a)
next(a)
next(a)
next(a)
```
So, when the generator gets to the end of its iteration it raises an exception. As seen in previous sections, we could surround the `next` call with a `try` block to capture the `StopIteration` so that we can continue after it finishes. This is effectively what the `for` loop is doing.
We can now find all primes (less than or equal to 100, for example) that have the form $4 k - 1$ using
```
for p in all_primes(100):
if (1+p)%4 == 0:
print("The prime {} is 4 * {} - 1.".format(p, int((1+p)/4)))
```
## Exercise : twin primes
A *twin prime* is a pair $(p_1, p_2)$ such that both $p_1$ and $p_2$ are prime and $p_2 = p_1 + 2$.
### Exercise 1
Write a generator that returns twin primes. You can use the generators above, and may want to look at the [itertools](https://docs.python.org/3/library/itertools.html) module together with [its recipes](https://docs.python.org/3/library/itertools.html#itertools-recipes), particularly the `pairwise` recipe.
### Exercise 2
Find how many twin primes there are with $p_2 < 1000$.
### Exercise 3
Let $\pi_N$ be the number of twin primes such that $p_2 < N$. Plot how $\pi_N / N$ varies with $N$ for $N=2^k$ and $k = 4, 5, \dots 16$. (You should use a logarithmic scale where appropriate!)
## Exercise : a basis for the polynomials
In the section on classes we defined a `Monomial` class to represent a polynomial with leading coefficient $1$. As the $N+1$ monomials $1, x, x^2, \dots, x^N$ form a basis for the vector space of polynomials of order $N$, $\mathbb{P}^N$, we can use the `Monomial` class to return this basis.
### Exercise 1
Define a generator that will iterate through this basis of $\mathbb{P}^N$ and test it on $\mathbb{P}^3$.
### Exercise 2
An alternative basis is given by the monomials
$$ \begin{aligned} p_0(x) &= 1, \\ p_1(x) &= 1-x, \\ p_2(x) &= (1-x)(2-x), \\ \dots & \quad \dots, \\ p_N(x) &= \prod_{n=1}^N (n-x). \end{aligned} $$
Define a generator that will iterate through this basis of $\mathbb{P}^N$ and test it on $\mathbb{P}^4$.
### Exercise 3
Use these generators to write another generator that produces a basis of $\mathbb{P}^3 \times \mathbb{P}^4$.
| true |
code
| 0.542318 | null | null | null | null |
|
# Object oriented programming
## Using an object
Below is the definition of an object. Run the cell and create at least two instances of it.
```
class Car:
def __init__(self, make, model, year, mpg=25, tank_capacity=30.0, miles=0):
self.make = make
self.model = model
self.year = year
self.mpg = mpg
self.gallons_in_tank = tank_capacity # cars start with a full tank
self.tank_capacity = tank_capacity
self.miles = miles
def __str__(self):
return "{} {} ({}), {} miles and {} gallons in tank".format(self.make,
self.model,
self.year,
self.miles,
self.gallons_in_tank)
def drive(self, new_miles):
"""Drive the car X miles and return number of miles driven.
If there is not enough fuel, drive 0 miles."""
fuel_need = new_miles/self.mpg
if fuel_need <= self.gallons_in_tank:
self.miles = self.miles + new_miles
self.gallons_in_tank = self.gallons_in_tank - fuel_need
return new_miles
else:
return 0
```
## Simple modification to class
OK, our car has a major problem: it can't be filled up.
Add a method called `fill_up()` to your class. It is up to you if you want to enable filling by an arbitary number or only back to the full state.
If you allow arbitary amounts of liquid remember to consider overfilling the tank.
Once you edit your class, the old objects do not automatically adopt to the changes you made. You will need to re-create them.
## Exceptions
Now make a modification to the `drive`-method: if an attempt is made to drive more than the gas will allow, create and raise an exception.
Instead of creating your own exception you may use a [ValueError](https://docs.python.org/3/library/exceptions.html#ValueError) for this case, as it is a logical choice.
Then add a try-except clause to the following:
```
suv = Car("Ford", "Escape", 2017, mpg=18, tank_capacity=30)
suv.drive(600)
```
## Bonus exercises
### Magic methods
Create a class called element for storing the following data
* name
* symbol
* atomic number
* molecular weight
You can use the following data for creating instances of a few elements:
| Element | symbol | atomic number | molecular weight |
|----------|--------|---------------|---------------|
| Hydrogen | H | 1 | 1.01 |
| Iron | Fe | 26 | 55.85 |
| Silver | Ag | 47 | 107.87 |
Next, we would like to be able to sort elements according to their atomic number. In order to do this, let's implement magic methods ``__lt__`` and ``__eq__`` as described [here](https://docs.python.org/3.5/reference/datamodel.html#object.__lt__).
Once finished, store few instances of a elements in a list, and try to sort it using list's ``sort`` method.
| true |
code
| 0.625467 | null | null | null | null |
|
# Model factory
Single-link models can be easily generated using a few parameters.
```
from pcg_gazebo.generators.creators import create_models_from_config
from pcg_gazebo.task_manager import Server
import os
# Start an empty world Gazebo simulation
server = Server()
server.create_simulation('default')
simulation = server.get_simulation('default')
simulation.create_gazebo_empty_world_task()
print(simulation.get_task_list())
print('Is Gazebo running: {}'.format(
simulation.is_task_running('gazebo')))
simulation.run_all_tasks()
# Create a Gazebo proxy
gazebo_proxy = simulation.get_gazebo_proxy()
import random
def create_and_spawn(config, pos=None):
models = create_models_from_config(config)
for model in models:
model.spawn(
gazebo_proxy=gazebo_proxy,
robot_namespace=model.name,
pos=pos if pos is not None else [
20 * random.random() - 10,
20 * random.random() - 10,
2 * random.random()
])
```
## Extruded models
```
from pcg_gazebo.generators.shapes import random_rectangle, \
random_points_to_triangulation, random_rectangles
config = [
dict(
type='extrude',
args=dict(
polygon=random_rectangle(),
height=0.2,
extrude_boundaries=False,
name='extruded_poly_random_rectangle',
color=None,
)
)
]
create_and_spawn(config, [-20, 0, 0.1])
config = [
dict(
type='extrude',
args=dict(
polygon=random_points_to_triangulation(),
height=0.8,
thickness=0.1,
extrude_boundaries=True,
name='extruded_poly_triangulation',
color='random'
)
)
]
create_and_spawn(config, [0, 0, 0.4])
config = [
dict(
type='extrude',
args=dict(
polygon=random_rectangles(),
height=0.5,
thickness=0.15,
extrude_boundaries=True,
name='extruded_poly_walls',
color='xkcd'
)
)
]
create_and_spawn(config, [20, 0, 0.25])
```
## Box-shaped models
```
config = [
dict(
type='box_factory',
args=dict(
size=[
[0.1, 0.4, 0.5],
[1, 2, 3]
],
name='box_static_var_size',
use_permutation=True,
color='xkcd'
)
),
dict(
type='box_factory',
args=dict(
size=[
[0.1, 0.4, 0.5],
[1, 2, 3]
],
mass=12,
name='box_dynamic_var_size',
use_permutation=False,
color='xkcd'
)
),
dict(
type='box_factory',
args=dict(
size=[
[0.2, 0.4, 0.15],
[1.2, 0.25, 0.7]
],
mass=[5, 2],
name='box_dynamic_permutate_size_mass',
use_permutation=True,
color='xkcd'
)
)
]
create_and_spawn(config)
```
Creating multiple boxes with lambda arguments
```
config = [
dict(
type='box_factory',
args=dict(
size="__import__('numpy').random.random((2, 3))",
use_permutation=True,
name='box_static_lambdas',
color='random'
)
),
dict(
type='box_factory',
args=dict(
size="__import__('numpy').random.random((4, 3))",
mass="__import__('numpy').arange(1, 10, 2)",
use_permutation=True,
name='box_dynamic_lambdas',
color='random'
)
)
]
create_and_spawn(config)
```
## Cylinder-shaped models
```
config = [
dict(
type='cylinder',
args=dict(
radius=3,
length=2,
mass=10,
name='cylinder',
pose=[0, 0, 1, 0, 0, 0]
)
),
dict(
type='cylinder_factory',
args=dict(
length=[0.3, 0.5],
radius=[0.2, 0.4],
mass=[5, 2],
name='cylinder_dynamic_permutate_radius_length_mass',
use_permutation=True,
color='xkcd'
)
),
dict(
type='cylinder_factory',
args=dict(
length="__import__('numpy').linspace(0.1, 10, 2)",
radius="__import__('numpy').random.random(2)",
mass="__import__('numpy').arange(1, 2, 1)",
use_permutation=True,
name='cylinder_dynamic_lambdas',
color='xkcd'
)
)
]
create_and_spawn(config)
```
## Sphere-shaped models
```
config = [
dict(
type='sphere',
args=dict(
radius=3,
mass=10,
name='sphere',
pose=[0, 0, 1.5, 0, 0, 0]
)
),
dict(
type='sphere_factory',
args=dict(
radius=[0.3, 0.9],
mass=[5, 2],
name='sphere_dynamic_permutate_radius_mass',
use_permutation=True,
color='xkcd'
)
),
dict(
type='sphere_factory',
args=dict(
radius="__import__('numpy').random.random(2) * 3",
mass="__import__('numpy').arange(1, 4, 1)",
use_permutation=True,
name='sphere_dynamic_lambdas',
color='xkcd'
)
)
]
create_and_spawn(config)
```
## Mesh models
```
mesh_filename = os.path.abspath('./meshes/monkey_offset.stl')
config = [
dict(
type='mesh',
args=dict(
visual_mesh=mesh_filename,
visual_mesh_scale=[1, 1, 1],
use_approximated_collision=False,
mass=10,
name='monkey_dynamic_no_approx_collision',
color='xkcd'
)
),
dict(
type='mesh',
args=dict(
visual_mesh=mesh_filename,
visual_mesh_scale=[1, 1, 1],
use_approximated_collision=True,
approximated_collision_model='box',
mass=20,
name='monkey_dynamic_with_approx_collision_box',
color='xkcd'
)
),
dict(
type='mesh',
args=dict(
visual_mesh=mesh_filename,
visual_mesh_scale=[1, 1, 1],
use_approximated_collision=True,
mass=15,
approximated_collision_model='cylinder',
name='monkey_dynamic_with_approx_collision_cylinder',
color='xkcd'
)
),
dict(
type='mesh',
args=dict(
visual_mesh=mesh_filename,
visual_mesh_scale=[1, 1, 1],
use_approximated_collision=True,
mass=3,
approximated_collision_model='sphere',
name='monkey_dynamic_with_approx_collision_sphere',
color='xkcd'
)
),
dict(
type='mesh',
args=dict(
visual_mesh=mesh_filename,
visual_mesh_scale=[1, 1, 1],
use_approximated_collision=True,
mass=3,
approximated_collision_model='sphere',
name='monkey_dynamic_defined_inertia',
color='xkcd',
use_approximated_inertia=False,
inertia=dict(
ixx=0.1,
iyy=0.1,
izz=0.1
)
)
)
]
create_and_spawn(config)
for name in gazebo_proxy.get_model_names():
print('\t - {}'.format(name))
simulation.kill_all_tasks()
```
The final result of the creation of models can be seen below

| true |
code
| 0.248397 | null | null | null | null |
|
# 20. Transfer Learning with Inception v3
```
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
from torchvision import models
import torchvision.utils
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
## 20.1 Prepare Data
```
# https://pytorch.org/docs/stable/torchvision/models.html
# https://github.com/pytorch/vision/tree/master/torchvision/models
# 미리 사용할 모델의 Input 파악 필수!
train_transform = transforms.Compose([
transforms.RandomResizedCrop(299),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(), # ToTensor : [0, 255] -> [0, 1]
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
])
test_transform = transforms.Compose([
transforms.Resize((299, 299)),
transforms.ToTensor(), # ToTensor : [0, 255] -> [0, 1]
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
])
train_data = dsets.ImageFolder('data/squir_chip_data/train/', train_transform)
test_data = dsets.ImageFolder('data/squir_chip_data/val/', test_transform)
batch_size = 5
train_loader = DataLoader(train_data,
batch_size=batch_size,
shuffle=True)
test_loader = DataLoader(test_data,
batch_size=batch_size,
shuffle=True)
def imshow(img, title):
img = torchvision.utils.make_grid(img, normalize=True)
npimg = img.numpy()
fig = plt.figure(figsize = (5, 15))
plt.imshow(np.transpose(npimg,(1,2,0)))
plt.title(title)
plt.axis('off')
plt.show()
dataiter = iter(train_loader)
images, labels = dataiter.next()
imshow(images, [train_data.classes[i] for i in labels])
```
## 20.2 Define Model
```
model = models.inception_v3(pretrained=True)
model
model.aux_logits = False
for parameter in model.parameters():
parameter.requires_grad = False
model.fc = nn.Sequential(
nn.Linear(model.fc.in_features, 10),
nn.Linear(10, 2)
)
model = model.cuda()
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.RMSprop(filter(lambda p: p.requires_grad, model.parameters()), lr=0.001)
```
## 20.3 Train Model
```
num_epochs = 30
for epoch in range(num_epochs):
total_batch = len(train_data)//batch_size
for i, (batch_images, batch_labels) in enumerate(train_loader):
X = batch_images.cuda()
Y = batch_labels.cuda()
pre = model(X)
cost = loss(pre, Y)
optimizer.zero_grad()
cost.backward()
optimizer.step()
if (i+1) % 5 == 0:
print('Epoch [%d/%d], lter [%d/%d] Loss: %.4f'
%(epoch+1, num_epochs, i+1, total_batch, cost.item()))
```
## 20.4 Test Model
```
model.eval()
correct = 0
total = 0
for images, labels in test_loader:
images = images.cuda()
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels.cuda()).sum()
print('Accuracy of test images: %f %%' % (100 * float(correct) / total))
classes = ["Squirrel", "Chipmunk"]
images, labels = iter(test_loader).next()
outputs = model(images.cuda())
_, predicted = torch.max(outputs.data, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]] for j in range(5)))
title = (' '.join('%5s' % classes[labels[j]] for j in range(5)))
imshow(torchvision.utils.make_grid(images, normalize=True), title)
```
| true |
code
| 0.820182 | null | null | null | null |
|
# Deconvolution Validation
Parameterized notebook to analyze a single dataset in a comparison between Flowdec and DeconvolutionLab2
```
import tempfile, os, warnings, timeit, math
import pandas as pd
import numpy as np
import papermill as pm
import matplotlib.pyplot as plt
import plotnine as pn
import io as pyio
from skimage import io
from flowdec import data as fd_data
from flowdec import psf as fd_psf
from flowdec.nb import utils as fd_nb_utils
from flowdec import restoration as fd_restoration
from skimage.exposure import rescale_intensity
from skimage.measure import compare_ssim, compare_psnr, compare_nrmse
from scipy.stats import describe
from collections import OrderedDict
```
<hr>
### Parameters
```
# Default Parameters
n_iter = 25
dl2_path = os.path.join(
os.path.expanduser('~'), 'repos', 'misc', 'DeconvolutionLab2',
'target', 'DeconcolutionLab2_-0.1.0-SNAPSHOT.jar')
downsample_factor = None
crop_slice = None
# Required Parameters
dataset_name = None
# Parameters
crop_slice = "(slice(48, 80), slice(96, 160), slice(192, 320))"
dataset_name = "microtubules"
n_iter = 25
# # Debugging
# dataset_name = 'bars'
# downsample_factor = .25
# crop_slice = '(slice(None), slice(None), slice(None))'
# dataset_name = 'celegans-dapi'
# downsample_factor = None
# crop_slice = '(slice(39, 65), slice(300, 600), slice(300, 600))'
# dataset_name = 'microtubules'
# downsample_factor = None
# crop_slice = '(slice(48, 80), slice(96, 160), slice(192, 320))'
assert dataset_name, 'Must set "dataset_name" parameter'
if crop_slice:
crop_slice = eval(crop_slice)
```
<hr>
### Dataset Prep
```
def prep(acq):
if crop_slice:
print('Applying crop slices {}'.format(crop_slice))
acq = acq.apply(lambda v: v[crop_slice])
if downsample_factor:
print('Downsampling dataset (factor = {})'.format(downsample_factor))
acq = acq.apply(lambda v: rescale_intensity(v.astype(np.float32), out_range=(-1., 1.)))
acq = fd_data.downsample_acquisition(acq, downsample_factor)
acq = acq.apply(lambda v: rescale_intensity(v.astype(np.float32), out_range=np.uint16).astype(np.uint16))
return acq
# Load dataset and run prep function to convert to uint16 and crop/downsample as configured
if dataset_name.startswith('celegans'):
acq = fd_data.load_celegans_channel(dataset_name.split('-')[1].upper())
else:
acq = eval('fd_data.load_' + dataset_name + '()')
print('Preparing raw dataset with shapes/types:')
print(acq.shape())
print(acq.dtype())
print()
acq = prep(acq)
print('\nPrepared dataset shapes/types:')
print(acq.shape())
print(acq.dtype())
print('\nDataset stats:')
print('\n'.join(map(str, acq.stats().items())))
# Visualize various projections/rotations of the volume to be deconvolved
fd_nb_utils.plot_rotations(acq.data)
```
<hr>
### Run Deconvolution
```
def to_uint(img):
tinfo = np.iinfo(np.uint16)
return img.clip(tinfo.min, tinfo.max).astype(np.uint16)
def run_flowdec(data, kernel, **kwargs):
algo = fd_restoration.RichardsonLucyDeconvolver(data.ndim, **kwargs)
acq = fd_data.Acquisition(data=data, kernel=kernel)
img = algo.initialize().run(acq, niter=n_iter).data
return to_uint(img)
def run_dl2(data, kernel, algo='RL {}'.format(n_iter), exargs='-constraint nonnegativity'):
# Generate temporary files to store image data within
data_file = tempfile.mktemp('.tif', 'data-')
kernel_file = tempfile.mktemp('.tif', 'kernel-')
output_file = tempfile.mktemp('', 'output-')
# Ignore low-contrast image warnings from skimage
with warnings.catch_warnings():
warnings.simplefilter("ignore")
io.imsave(data_file, acq.data)
io.imsave(kernel_file, acq.kernel)
# Setup system call to execute DL2 CLI
dl2_cmd = "java -Xmx32G -cp {jar} DeconvolutionLab2 Run -image file {data}"\
" -psf file {psf} -algorithm {algo} {exargs} -out stack {output_file} -path {output_path}"\
.format(
jar=dl2_path, data=data_file, psf=kernel_file, algo=algo, exargs=exargs,
output_file=os.path.basename(output_file), output_path=os.path.dirname(output_file)
)
!$dl2_cmd
img = io.imread(output_file + '.tif')
return to_uint(img)
acq_decon = OrderedDict()
%%capture
# Non-negative constraint
acq_decon[('dl2', 'rl-npad')] = run_dl2(acq.data, acq.kernel)
%%capture
# Power of 2 padding, non-negative constraint
acq_decon[('dl2', 'rl-wpad')] = run_dl2(acq.data, acq.kernel, exargs='-pad E2 E2 1 1 -constraint nonnegativity')
%%capture
# Naive-inverse Filtering
acq_decon[('dl2', 'nif')] = run_dl2(acq.data, acq.kernel, algo='NIF')
%%capture
# Regularized Richardson Lucy
acq_decon[('dl2', 'rltv')] = run_dl2(acq.data, acq.kernel, algo='RLTV 10 0.1')
%%capture
# Regularized Inverse Filtering
acq_decon[('dl2', 'rif')] = run_dl2(acq.data, acq.kernel, algo='RIF 0.001')
%%capture
# Landweber
acq_decon[('dl2', 'lw')] = run_dl2(acq.data, acq.kernel, algo='LW 25 1.0')
# Emulate DeconvolutionLab2 behavior with no padding
acq_decon[('flowdec', 'rl-npad')] = run_flowdec(acq.data, acq.kernel, start_mode='input', pad_mode='none')
# Emulate DeconvolutionLab2 behavior w/ padding noting that paddings must be with 0s rather
# than reflection of images (DL2 doesn't seem to support anything other than 0 padding)
acq_decon[('flowdec', 'rl-wpad')] = run_flowdec(acq.data, acq.kernel, start_mode='input', pad_mode='log2',
pad_min=[1,1,1], pad_fill='constant')
# Also include default flowdec settings w/ small minimum padding
acq_decon[('flowdec', 'rl-default')] = run_flowdec(acq.data, acq.kernel, pad_min=[1,1,1])
# Ensure that all results are of the same type
unique_types = {k: img.dtype for k, img in acq_decon.items()}
assert len(np.unique(unique_types.values())) == 1, \
'Results have differing data types; Data type by result: {}'.format(unique_types)
print('Data type of all results:', list(unique_types.values())[0])
```
<hr>
### Visualize Results
```
imgs = [('original', acq.data)]
if acq.actual is not None:
imgs += [('actual', acq.actual)]
imgs += [(k, img) for k, img in acq_decon.items()]
ncols = 2
nrows = math.ceil(len(imgs) / ncols)
fig, axs = plt.subplots(nrows, ncols)
fig.set_size_inches(ncols * 6, nrows * 4)
axs = axs.ravel()
for ax in axs:
ax.axis('off')
for i, (k, img) in enumerate(imgs):
axs[i].imshow(img.max(axis=0))
axs[i].set_title(k)
axs[i].axis('on')
plt.tight_layout()
score_fns = dict(
# Increase ssim window size to avoid obvious corner case w/ nearly completely saturated results
ssim=lambda it, ip: compare_ssim(it, ip, win_size=31),
# Use negative nrmse so that larger scores are better
nrmse=lambda it, ip: -compare_nrmse(it, ip),
psnr=compare_psnr
)
if acq.actual is not None:
comp_type = 'ground_truth'
img_true = acq.actual
else:
comp_type = 'original'
img_true = acq.data
def get_scores(img_pred):
return {k:fn(img_true, img_pred) for k, fn in score_fns.items()}
scores = pd.DataFrame(
{k: get_scores(img) for k, img in acq_decon.items()}
).T
scores.index.names = ['lib', 'algo']
scores = scores.reset_index().assign(comp_type=comp_type)
scores
(
pn.ggplot(
scores.melt(id_vars=['lib', 'algo', 'comp_type']),
pn.aes(x='algo', y='value', fill='lib')
) +
pn.geom_bar(stat='identity', position='dodge') +
pn.facet_wrap('~variable', ncol=1, scales='free') +
pn.ggtitle('Restoration Score Comparisons') +
pn.theme(figure_size=(12, 8))
)
```
<hr>
### Export
```
buf = pyio.StringIO()
scores.to_json(buf, orient='records')
pm.record('scores', buf.getvalue())
```
| true |
code
| 0.493958 | null | null | null | null |
|
# High-level PyTorch Example
```
import os
import sys
import numpy as np
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.utils.data as data_utils
import torch.nn.init as init
from torch.autograd import Variable
from common.params import *
from common.utils import *
# Big impact on training-time (from 350 to 165s)
torch.backends.cudnn.benchmark=True # enables cudnn's auto-tuner
print("OS: ", sys.platform)
print("Python: ", sys.version)
print("PyTorch: ", torch.__version__)
print("Numpy: ", np.__version__)
print("GPU: ", get_gpu_name())
class SymbolModule(nn.Module):
def __init__(self):
super(SymbolModule, self).__init__()
self.conv1 = nn.Conv2d(3, 50, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(50, 50, kernel_size=3, padding=1)
self.conv3 = nn.Conv2d(50, 100, kernel_size=3, padding=1)
self.conv4 = nn.Conv2d(100, 100, kernel_size=3, padding=1)
# feature map size is 8*8 by pooling
self.fc1 = nn.Linear(100*8*8, 512)
self.fc2 = nn.Linear(512, N_CLASSES)
def forward(self, x):
""" PyTorch requires a flag for training in dropout """
x = self.conv2(F.relu(self.conv1(x)))
x = F.relu(F.max_pool2d(x, kernel_size=2, stride=2))
x = F.dropout(x, 0.25, training=self.training)
x = self.conv4(F.relu(self.conv3(x)))
x = F.relu(F.max_pool2d(x, kernel_size=2, stride=2))
x = F.dropout(x, 0.25, training=self.training)
x = x.view(-1, 100*8*8) # reshape Variable
x = F.dropout(F.relu(self.fc1(x)), 0.5, training=self.training)
# nn.CrossEntropyLoss() contains softmax, don't apply twice
#return F.log_softmax(x)
return self.fc2(x)
def init_model(m):
# Implementation of momentum:
# v = \rho * v + g \\
# p = p - lr * v
opt = optim.SGD(m.parameters(), lr=LR, momentum=MOMENTUM)
criterion = nn.CrossEntropyLoss()
return opt, criterion
%%time
# Data into format for library
x_train, x_test, y_train, y_test = cifar_for_library(channel_first=True)
# Torch-specific
y_train = y_train.astype(np.int64)
y_test = y_test.astype(np.int64)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
print(x_train.dtype, x_test.dtype, y_train.dtype, y_test.dtype)
%%time
sym = SymbolModule()
sym.cuda() # CUDA!
%%time
optimizer, criterion = init_model(sym)
%%time
# 169s
# Sets training = True
sym.train()
for j in range(EPOCHS):
for data, target in yield_mb(x_train, y_train, BATCHSIZE, shuffle=True):
# Get samples
data = Variable(torch.FloatTensor(data).cuda())
target = Variable(torch.LongTensor(target).cuda())
# Init
optimizer.zero_grad()
# Forwards
output = sym(data)
# Loss
loss = criterion(output, target)
# Back-prop
loss.backward()
optimizer.step()
# Log
print(j)
%%time
# Test model
# Sets training = False
sym.eval()
n_samples = (y_test.shape[0]//BATCHSIZE)*BATCHSIZE
y_guess = np.zeros(n_samples, dtype=np.int)
y_truth = y_test[:n_samples]
c = 0
for data, target in yield_mb(x_test, y_test, BATCHSIZE):
# Get samples
data = Variable(torch.FloatTensor(data).cuda())
# Forwards
output = sym(data)
pred = output.data.max(1)[1].cpu().numpy().squeeze()
# Collect results
y_guess[c*BATCHSIZE:(c+1)*BATCHSIZE] = pred
c += 1
print("Accuracy: ", sum(y_guess == y_truth)/len(y_guess))
```
| true |
code
| 0.761527 | null | null | null | null |
|
```
%matplotlib inline
import os
import sys
# Modify the path
sys.path.append("..")
import yellowbrick as yb
import matplotlib.pyplot as plt
```
# Using Yellowbrick to Explore Book Reviews
This notebook is for the Yellowbrick user study.
About the data:
[Amazon book reviews Data Set](http://archive.ics.uci.edu/ml/datasets/Amazon+book+reviews)
Abstract:
213,335 book reviews for 8 different books.
Source:
Ahmet Taspinar, info '@' ataspinar.com, http://ataspinar.com
Data Set Information:
- Gone Girl: 41,974
- The Girl on the Train: 37,139
- The Fault in our Stars: 35,844
- Fifty Shades of Grey: 32,977
- Unbroken: 25,876
- The hunger games: 24,027
- The Goldfinch: 22,861
- The Martian: 22,571
Attribute Information:
Each entry is separated by a newline character. Each entry contains four attributes, which are separated by a space:
1. review score
2. tail of review url
3. review title
4. HTML of review text
After [downloading the data](http://archive.ics.uci.edu/ml/machine-learning-databases/00370/amazon_book_reviews.rar) in .rar archive form, I unpacked it with `unrar`:
_(if you don't have unrar)_
$ brew install unrar # or use apt-get or yum, depending on your system
$ urar e amazon_book_reviews.rar
The result is the following 8 csv files and a metadata.txt file:
- Andy-Weir-The-Martian.csv
- Laura-Hillenbrand-Unbroken.csv
- Donna-Tartt-The-Goldfinch.csv
- Paula_Hawkins-The-Girl-On-The-Train.csv
- EL-James-Fifty-Shades-of-Grey.csv
- Suzanne-Collins-The-Hunger-Games.csv
- Fillian_Flynn-Gone_Girl.csv
- John-Green-The-Fault-in-our-Stars.csv
- metadata.txt
```
from sklearn.datasets.base import Bunch
## The path to the test data sets
FIXTURES = os.path.join(os.getcwd(), "data")
## Dataset loading mechanisms
datasets = {
"reviews": os.path.join(FIXTURES, "reviews")
}
def load_data(name, download=True):
"""
Loads and wrangles the passed in text corpus by name.
If download is specified, this method will download any missing files.
"""
# Get the path from the datasets
path = datasets[name]
# Read the files in the directory as the categories.
categories = [
os.path.splitext(f)[0] for f in os.listdir(path)
if os.path.isfile(os.path.join(path, f))
and os.path.join(path, f).endswith(".csv")
]
files = [] # holds the file names relative to the root
data = [] # holds the text read from the file
target = [] # holds the string of the category
# Load the data from the files in the corpus
for cat in categories:
files.append(os.path.join(path, cat + '.csv'))
with open(os.path.join(path, cat + '.csv'), 'r') as f:
content = f.read()
docs = [s.strip() for s in content.splitlines()]
for doc in docs[:1000]: # limited size so nb won't crash
data.append(doc)
target.append(cat)
# Return the data bunch for use similar to the newsgroups example
return Bunch(
categories=categories,
files=files,
data=data,
target=target,
)
corpus = load_data('reviews')
```
### Visualizing Stopwords Removal
How much does stopwords removal impact a corpus of book reviews?
To visualize the transformation, we can compare the results before and after stopwords have been removed from the corpus using the Yellowbrick `FreqDistVisualizer`:
```
from yellowbrick.text.freqdist import FreqDistVisualizer
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
docs = vectorizer.fit_transform(corpus.data)
features = vectorizer.get_feature_names()
visualizer = FreqDistVisualizer()
visualizer.fit(docs, features)
visualizer.show()
vectorizer = CountVectorizer(stop_words='english')
docs = vectorizer.fit_transform(corpus.data)
features = vectorizer.get_feature_names()
visualizer = FreqDistVisualizer()
visualizer.fit(docs, features)
visualizer.show()
```
### Visualizing tokens across corpora
It is also interesting to explore the differences in tokens across a corpus. For example, do people say different things in reviews about books by men vs. books by women?
```
male = ['Andy-Weir-The-Martian',
'John-Green-The-Fault-in-our-Stars']
female = ['Laura-Hillenbrand-Unbroken',
'Paula_Hawkins-The-Girl-On-The-Train',
'Suzanne-Collins-The-Hunger-Games',
'Donna-Tartt-The-Goldfinch',
'EL-James-Fifty-Shades-of-Grey',
'Fillian_Flynn-Gone_Girl']
male_author_reviews = []
female_author_reviews = []
for book in male:
for idx in range(len(corpus.data)):
if corpus.target[idx] == book:
male_author_reviews.append(corpus.data[idx])
for book in female:
for idx in range(len(corpus.data)):
if corpus.target[idx] == book:
female_author_reviews.append(corpus.data[idx])
vectorizer = CountVectorizer(stop_words='english')
docs = vectorizer.fit_transform(text for text in female_author_reviews)
features = vectorizer.get_feature_names()
visualizer = FreqDistVisualizer()
visualizer.fit(docs, features)
visualizer.show()
vectorizer = CountVectorizer(stop_words='english')
docs = vectorizer.fit_transform(text for text in male_author_reviews)
features = vectorizer.get_feature_names()
visualizer = FreqDistVisualizer()
visualizer.fit(docs, features)
visualizer.show()
```
## t-SNE: Corpus Visualization
What patterns can we see if we project the book reviews into 2 dimensional space?
```
from yellowbrick.text import TSNEVisualizer
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf = TfidfVectorizer()
docs = tfidf.fit_transform(corpus.data)
labels = corpus.target
# Create the visualizer and draw the vectors
tsne = TSNEVisualizer()
tsne.fit(docs, labels)
tsne.show()
# Only visualize the books by female authors
tsne = TSNEVisualizer(classes=female)
tsne.fit(docs, labels)
tsne.show()
# Only visualize the books by male authors
tsne = TSNEVisualizer(classes=male)
tsne.fit(docs, labels)
tsne.show()
```
| true |
code
| 0.474936 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Cost-vs-qubits-size" data-toc-modified-id="Cost-vs-qubits-size-1"><span class="toc-item-num">1 </span>Cost vs qubits size</a></span></li></ul></div>
```
import numpy as np
import networkx as nx
from loguru import logger as log
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm import tqdm
import copy
import sys
sys.path.append('..')
sns.set_style('whitegrid')
import qtree
import utils
import utils_qaoa as qaoa
import utils_mproc as mputils
%load_ext autoreload
%autoreload 2
```
## Cost vs qubits size
```
def log_log_scale():
plt.yscale('log')
plt.xscale('log')
def minorticks():
plt.minorticks_on()
plt.grid(which='minor', alpha=0.3, linestyle='-', axis='both')
def get_est(xs, vals):
mem_est = np.polyfit(xs, np.log(vals), 2)
mem_est = np.poly1d(mem_est)
est = np.linspace(20,2e2, 100)
mem_est = mem_est(est)
return est, np.exp(mem_est)
sizes = np.arange(13,54,2)
results = [
qaoa.get_cost_of_task(s, 1, type='randomreg',degree=3) for s in sizes
]
def plot_theory(results, ns):
sums = [(max(y[0]), sum(y[1])) for y in results]
colors = [plt.cm.gnuplot2(x) for x in np.linspace(.8,.2,2)]
memsums, flopsums = zip(*sums)
est, mem_est = get_est(ns, memsums)
est, flop_est = get_est(ns, flopsums)
plt.plot(ns, flopsums, label='total FLOP', color=colors[1])
plt.plot(ns, np.array(memsums), label='maximum Memory', color=colors[0])
#plt.plot(est, mem_est, '--', label='mem log-log fit')
#plt.plot(est, flop_est, '--', label='flop log-log fit')
plt.xlabel('Number of qbits')
plt.yscale('log')
#plt.xscale('log')
#plt.suptitle('QAOA one amplitude simulation cost', fontsize=14)
#plt.title('MaxCut random regular graphs')
plt.legend()
plt.minorticks_on()
plt.grid(which='minor', alpha=0.3, linestyle='-', axis='both')
#ax = plt.gca().twinx()
#plt.grid(None)
#plt.plot(ns, nghssums, label='max ng', color='red')
import glob
import json
thread_folders = sorted(glob.glob('./contract_data/contr_profile_*thr'))
print(thread_folders)
thread_files = [sorted(glob.glob(folder+'/*.json')) for folder in thread_folders]
print(list(map(len, thread_files)))
thread_exps = [[json.load(open(f)) for f in files] for files in thread_files]
exp_results = [
(max(e['proc_buck memory'])
,1e9*np.array(e['proc_buck time']).sum()
)
for exps in thread_exps
for e in exps
]
print(len(exp_results))
sizes_exp = range(13,49,2)
threads_exp = [1, 16]
exp_results = np.array(exp_results).reshape(len(thread_exps), len(sizes_exp), 2)
print(exp_results.shape)
ns = list(zip(*results))[3]
#plot_theory(results, ns)
print(exp_results[0,:,1].shape)
plt.plot( exp_results[0,:,1])
plt.plot( exp_results[1,:,1])
result_rows = list(zip(*results))
plt.plot( list(map(sum, result_rows[1]))[:-2])
plt.yscale('log')
plt.savefig('figures/cost_vs_taskS_42d3.pdf')
plt.plot(thread_exps[0][-1]['proc_buck time'])
plt.yscale('log')
total_data = json.load(open('./contract_data/contr_profile_total_13_49_2_42d3.json'))
sim_sum = total_data['Total_sim']
new_data = json.load(open('./contract_data/contr_profile_data47_42d3.json'))
single_threaded_time = new_data['proc_buck time']
single_threaded_mem = new_data['proc_buck memory']
list(sizes_exp)
plt.plot(single_threaded_time[:100])
#plt.yscale('log')
colors = [plt.cm.gnuplot2(x) for x in np.linspace(.8,.2,2)]
lens = [len(x) for x in result_rows[0]]
def unpack_flops(all_flops, map_f=sum):
flops = []
for i, s in enumerate(sizes_exp):
prev = i
end = i+1
prev, end = [sum(lens[:x]) for x in (prev, end)]
flops.append(all_flops[prev:end])
sums_flops = [map_f(x) for x in flops]
return sums_flops
sums_flops = [ unpack_flops(thread_exps[i][-1]['proc_buck time'])
for i in range(len(thread_exps)) ]
sums_flops = 1e9*np.array(sums_flops)
print(sums_flops[0])
print(sums_flops.shape)
sums_flops_theory = [sum(x) for x in result_rows[1]]
sums_mems_theory = [max(x) for x in result_rows[0]]
#for sf in sums_flops: plt.plot(sf)
plt.plot(ns, sums_flops_theory, '--'
, color=colors[0]
, label='FLOP theory'
)
plt.plot(ns, 16*np.array(sums_mems_theory), '--'
, color=colors[1]
, label='Memory theory'
)
unp_flop = 1e9*np.array(unpack_flops(single_threaded_time, map_f=max))
unp_mem = unpack_flops(single_threaded_mem, map_f=max)
ns_exp = ns[:len(unp_mem)]
min_shift = lambda x: np.array(x) - .99*min(x)
flop_mem_shifted = (min_shift(x) for x in (unp_flop, unp_mem))
plt.plot(ns_exp, next(flop_mem_shifted), '-'
, color=colors[0]
, label='FLOP experiment'
)
plt.plot(ns_exp, next(flop_mem_shifted), '-'
, color=colors[1]
, label='Memory experiment'
)
plt.legend()
plt.yscale('log')
plt.minorticks_on()
plt.ylabel('Cost of contraction')
plt.xlabel('Number of qubits')
plt.savefig('figures/theory_vs_exp_tasks_')
```
| true |
code
| 0.341191 | null | null | null | null |
|
```
%matplotlib inline
```
# The double pendulum problem
This animation illustrates the double pendulum problem.
Double pendulum formula translated from the C code at
http://www.physics.usyd.edu.au/~wheat/dpend_html/solve_dpend.c
```
from numpy import sin, cos
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as integrate
import matplotlib.animation as animation
G = 9.8 # acceleration due to gravity, in m/s^2
L1 = 1.0 # length of pendulum 1 in m
L2 = 1.0 # length of pendulum 2 in m
M1 = 1.0 # mass of pendulum 1 in kg
M2 = 1.0 # mass of pendulum 2 in kg
def derivs(state, t):
dydx = np.zeros_like(state)
dydx[0] = state[1]
delta = state[2] - state[0]
den1 = (M1+M2) * L1 - M2 * L1 * cos(delta) * cos(delta)
dydx[1] = ((M2 * L1 * state[1] * state[1] * sin(delta) * cos(delta)
+ M2 * G * sin(state[2]) * cos(delta)
+ M2 * L2 * state[3] * state[3] * sin(delta)
- (M1+M2) * G * sin(state[0]))
/ den1)
dydx[2] = state[3]
den2 = (L2/L1) * den1
dydx[3] = ((- M2 * L2 * state[3] * state[3] * sin(delta) * cos(delta)
+ (M1+M2) * G * sin(state[0]) * cos(delta)
- (M1+M2) * L1 * state[1] * state[1] * sin(delta)
- (M1+M2) * G * sin(state[2]))
/ den2)
return dydx
# create a time array from 0..100 sampled at 0.05 second steps
dt = 0.05
t = np.arange(0, 20, dt)
# th1 and th2 are the initial angles (degrees)
# w10 and w20 are the initial angular velocities (degrees per second)
th1 = 120.0
w1 = 0.0
th2 = -10.0
w2 = 0.0
# initial state
state = np.radians([th1, w1, th2, w2])
# integrate your ODE using scipy.integrate.
y = integrate.odeint(derivs, state, t)
x1 = L1*sin(y[:, 0])
y1 = -L1*cos(y[:, 0])
x2 = L2*sin(y[:, 2]) + x1
y2 = -L2*cos(y[:, 2]) + y1
fig = plt.figure()
ax = fig.add_subplot(111, autoscale_on=False, xlim=(-2, 2), ylim=(-2, 2))
ax.set_aspect('equal')
ax.grid()
line, = ax.plot([], [], 'o-', lw=2)
time_template = 'time = %.1fs'
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
def init():
line.set_data([], [])
time_text.set_text('')
return line, time_text
def animate(i):
thisx = [0, x1[i], x2[i]]
thisy = [0, y1[i], y2[i]]
line.set_data(thisx, thisy)
time_text.set_text(time_template % (i*dt))
return line, time_text
ani = animation.FuncAnimation(fig, animate, range(1, len(y)),
interval=dt*1000, blit=True, init_func=init)
plt.show()
```
| true |
code
| 0.684027 | null | null | null | null |
|
## import modules
```
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
```
## define model architecture
```
class ConvNet(nn.Module):
def __init__(self):
super(ConvNet, self).__init__()
self.cn1 = nn.Conv2d(1, 16, 3, 1)
self.cn2 = nn.Conv2d(16, 32, 3, 1)
self.dp1 = nn.Dropout2d(0.10)
self.dp2 = nn.Dropout2d(0.25)
self.fc1 = nn.Linear(4608, 64) # 4608 is basically 12 X 12 X 32
self.fc2 = nn.Linear(64, 10)
def forward(self, x):
x = self.cn1(x)
x = F.relu(x)
x = self.cn2(x)
x = F.relu(x)
x = F.max_pool2d(x, 2)
x = self.dp1(x)
x = torch.flatten(x, 1)
x = self.fc1(x)
x = F.relu(x)
x = self.dp2(x)
x = self.fc2(x)
op = F.log_softmax(x, dim=1)
return op
```
## define training and inference routines
```
def train(model, device, train_dataloader, optim, epoch):
model.train()
for b_i, (X, y) in enumerate(train_dataloader):
X, y = X.to(device), y.to(device)
optim.zero_grad()
pred_prob = model(X)
loss = F.nll_loss(pred_prob, y) # nll is the negative likelihood loss
loss.backward()
optim.step()
if b_i % 10 == 0:
print('epoch: {} [{}/{} ({:.0f}%)]\t training loss: {:.6f}'.format(
epoch, b_i * len(X), len(train_dataloader.dataset),
100. * b_i / len(train_dataloader), loss.item()))
def test(model, device, test_dataloader):
model.eval()
loss = 0
success = 0
with torch.no_grad():
for X, y in test_dataloader:
X, y = X.to(device), y.to(device)
pred_prob = model(X)
loss += F.nll_loss(pred_prob, y, reduction='sum').item() # loss summed across the batch
pred = pred_prob.argmax(dim=1, keepdim=True) # us argmax to get the most likely prediction
success += pred.eq(y.view_as(pred)).sum().item()
loss /= len(test_dataloader.dataset)
print('\nTest dataset: Overall Loss: {:.4f}, Overall Accuracy: {}/{} ({:.0f}%)\n'.format(
loss, success, len(test_dataloader.dataset),
100. * success / len(test_dataloader.dataset)))
```
## create data loaders
```
# The mean and standard deviation values are calculated as the mean of all pixel values of all images in the training dataset
train_dataloader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1302,), (0.3069,))])), # train_X.mean()/256. and train_X.std()/256.
batch_size=32, shuffle=True)
test_dataloader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1302,), (0.3069,))
])),
batch_size=500, shuffle=False)
```
## define optimizer and run training epochs
```
torch.manual_seed(0)
device = torch.device("cpu")
model = ConvNet()
optimizer = optim.Adadelta(model.parameters(), lr=0.5)
```
## model training
```
for epoch in range(1, 3):
train(model, device, train_dataloader, optimizer, epoch)
test(model, device, test_dataloader)
```
## run inference on trained model
```
test_samples = enumerate(test_dataloader)
b_i, (sample_data, sample_targets) = next(test_samples)
plt.imshow(sample_data[0][0], cmap='gray', interpolation='none')
plt.show()
print(f"Model prediction is : {model(sample_data).data.max(1)[1][0]}")
print(f"Ground truth is : {sample_targets[0]}")
```
| true |
code
| 0.865934 | null | null | null | null |
|
<table>
<tr>
<td width=15%><img src="./img/UGA.png"></img></td>
<td><center><h1>Introduction to Python for Data Sciences</h1></center></td>
<td width=15%><a href="http://www.iutzeler.org" style="font-size: 16px; font-weight: bold">Franck Iutzeler</a> </td>
</tr>
</table>
<br/><br/>
<center><a style="font-size: 40pt; font-weight: bold">Chap. 4 - Scikit Learn </a></center>
<br/><br/>
# 2- Supervised Learning
In the session, we will investigate some *examples* on how to deal with popular learning problems using standard algorithms. Many other problems and algorithms exist so this course is not at all exhaustive.
## Classification
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
%matplotlib inline
# we create 40 separable points in R^2 around 2 centers (random_state=6 is a seed so that the set is separable)
X, y = make_blobs(n_samples=40, n_features=2, centers=2 , random_state=6)
print(X[:5,:],y[:5]) # print the first 5 points and labels
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
```
Support Vector Machines (SVM) are based on learning a vector $w$ and an intercept $b$ such that the hyperplane $w^T x - b = 0$ separates the data i.e. $a$ belongs to one class if $w^T a - b > 0$ and the other elsewhere.
They were later extended to *Kernel methods* that is $\kappa(w, a) - b = 0$ is now the separating *curve* where $\kappa$ is the *kernel*, typically:
* linear: $\kappa(x,y)= x^T y$ (original SVM)
* polynomial: $\kappa(x,y)= (x^T y)^d$
* Gaussian radial basis function (rfb): $\kappa(x,y)= \exp( - \gamma \| x - y \|^2 )$
```
from sklearn.svm import SVC # Support vector classifier i.e. Classifier by SVM
modelSVMLinear = SVC(kernel="linear")
modelSVMLinear.fit(X,y)
```
The following illustration can be found in the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas.
```
def plot_svc_decision_function(model, ax=None, plot_support=True):
"""Plot the decision function for a 2D SVC"""
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
# plot decision boundary and margins
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)
plt.scatter(X[:, 0], X[:, 1], c=y , cmap=plt.cm.Paired)
plot_svc_decision_function(modelSVMLinear)
```
We see clearly that the linear SVM seeks at maximizing the *margin* between the hyperplane and the two well defined classes from the data.
### Non-separable data
In real cases, the data is usually not linearly separable as before.
```
# we create points in R^2 around 2 centers (random_state=48443 is a seed so that the set is *not* separable)
X, y = make_blobs(n_samples=100, n_features=2, centers=2 , random_state=48443)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
```
Let us use the *same* linear SVM classifier. Obviously, there are *misclassified points*, the model is thus learnt not by maximizing the margin (which does not exist anymore) but by minimizing a penalty over misclassified data. This penalty takes the form of an allowance margin controlled by a parameter $C$. The smaller $C$ the more inclusive the margin. Finding a good value for $C$ is up to the data scientist.
```
from sklearn.model_selection import train_test_split # sklearn > ...
XTrain, XTest, yTrain, yTest = train_test_split(X,y,test_size = 0.5) # split data in two
model1 = SVC(kernel="linear",C=0.01)
model1.fit(XTrain,yTrain)
model2 = SVC(kernel="linear",C=100)
model2.fit(XTrain,yTrain)
plt.scatter(XTrain[:, 0], XTrain[:, 1], c=yTrain , cmap=plt.cm.Paired)
plot_svc_decision_function(model1)
plt.title("C = 0.01")
plt.scatter(XTrain[:, 0], XTrain[:, 1], c=yTrain , cmap=plt.cm.Paired)
plot_svc_decision_function(model2)
plt.title("C = 100")
```
To find out which value of $C$ to use or globally the performance of the classifier, one can use Scikit Learn's [classification metrics](http://scikit-learn.org/stable/modules/model_evaluation.html#classification-metrics), for instance the confusion matrix.
```
from sklearn.metrics import confusion_matrix
yFit1 = model1.predict(XTest)
yFit2 = model2.predict(XTest)
mat1 = confusion_matrix(yTest, yFit1)
mat2 = confusion_matrix(yTest, yFit2)
print('Model with C = 0.01')
print(mat1)
print("Model with C = 100")
print(mat2)
```
It can also be plotted in a fancier way with seaborn.
```
import seaborn as sns
sns.heatmap(mat1, square=True, annot=True ,cbar=False)
plt.ylabel('true label')
plt.xlabel('predicted label')
```
### Kernels
When the separation between classes is not *linear*, kernels may be used to draw separating curves instead of lines. The most popular is the Gaussian rbf.
```
from sklearn.datasets import make_moons
X,y = make_moons(noise=0.1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
modelLinear = SVC(kernel="linear")
modelLinear.fit(X,y)
modelRbf = SVC(kernel="rbf")
modelRbf.fit(X,y)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plot_svc_decision_function(modelLinear)
plot_svc_decision_function(modelRbf)
plt.title("The two models superposed")
```
Let us compare the linear and rbf training error using the zero one loss (the proportion of misclassified examples).
```
from sklearn.metrics import zero_one_loss
yFitLinear = modelLinear.predict(X)
yFitRbf = modelRbf.predict(X)
print("0/1 loss -- Linear: {:.3f} Rbf: {:.3f}".format(zero_one_loss(y, yFitLinear),zero_one_loss(y, yFitRbf)))
```
### Multiple classes
Where there are multiples classes (as in the *iris* dataset of the Pandas notebook), different strategies can be adopted:
* Transforming the multiclass problem into a binary one by looking at the *one-vs-rest* problem (for each class construct a binary classifier between it and the rest) or the *one-vs-one* one (where each couple of classes is considered separately). After this transformation, standard binary classifiers can be used.
* Using dedicated algorithms such as *decision trees*
The corresponding algorithms can be found in the [multiclass module documentation](http://scikit-learn.org/stable/modules/multiclass.html).
We are going to illustrate this by the iris 3-class classification problem using only the 2 petal features (width and length, this is only so that the feature vector is 2D and easy to visualize).
```
import pandas as pd
import numpy as np
iris = pd.read_csv('data/iris.csv')
classes = pd.DataFrame(iris["species"])
features = iris.drop(["species","sepal_length","sepal_width"],axis=1)
classes.sample(6)
features.sample(6)
XTrain, XTest, yTrain, yTest = train_test_split(features,classes,test_size = 0.5)
from sklearn.multiclass import OneVsRestClassifier
yPred = OneVsRestClassifier(SVC()).fit(XTrain, yTrain).predict(XTest)
print(yPred) # Note the classes are not number but everything went as expected
class_labels= ['virginica' , 'setosa' , 'versicolor']
sns.heatmap(confusion_matrix(yTest, yPred), square=True, annot=True ,cbar=False, xticklabels= class_labels, yticklabels=class_labels)
plt.ylabel('true label')
plt.xlabel('predicted label')
```
### Other classifiers
The main classifiers from Scikit learn are: *Linear SVM, RBF SVM (as already seen), Nearest Neighbors, Gaussian Process, Decision Tree, Random Forest, Neural Net, AdaBoost, Naive Bayes, QDA*.
Use is:
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
classifiers = [
KNeighborsClassifier(3),
SVC(kernel="linear", C=0.025),
SVC(gamma=2, C=1),
GaussianProcessClassifier(1.0 * RBF(1.0), warm_start=True),
DecisionTreeClassifier(max_depth=5),
RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1),
MLPClassifier(alpha=1),
AdaBoostClassifier(),
GaussianNB(),
QuadraticDiscriminantAnalysis()]
## Regression
Let consider the problem of predicting real values from a set of features.
We will consider the <a href="http://archive.ics.uci.edu/ml/datasets/Student+Performance">student performance</a> dataset. The goal is to predict the final grade from the other information, we get from the documentation:
```
import pandas as pd
import numpy as np
student = pd.read_csv('data/student-mat.csv')
student.head()
target = pd.DataFrame(student["G3"])
features = student.drop(["G3"],axis=1)
```
One immediate problem here is that the features are not *numeric* (not floats). Thankfully, Scikit Learn provides [encoders](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.LabelEncoder.html#sklearn.preprocessing.LabelEncoder) to convert categorical (aka nominal, discrete) features to numerical ones.
```
from sklearn.preprocessing import LabelEncoder
lenc = LabelEncoder()
num_features = features.apply(lenc.fit_transform)
num_features.head()
```
Even numerical values were encoded, as we are going to normalize, it is not really important.
The normalization is done by removing the mean and equalizing the variance per feature, in addition, we are going to add an intercept.
```
from sklearn.preprocessing import StandardScaler, add_dummy_feature
scaler = StandardScaler()
normFeatures = add_dummy_feature(scaler.fit_transform(num_features))
preproData = pd.DataFrame(normFeatures , columns=[ "intercept" ] + list(num_features.columns) )
preproData.describe().T
```
### Regression and Feature selection with the Lasso
The lasso problem is finding a regressor $w$ such that minimizes
$$ \frac{1}{2 n_{samples}} \|X w - y ||^2_2 + \alpha \|w\|_1 $$
and is popular for prediction as it simultaneously *selects features* thanks to the $\ell_1$-term. The greater $\alpha$ the fewer features.
```
from sklearn.model_selection import train_test_split # sklearn > ...
from sklearn.linear_model import Lasso
XTrain, XTest, yTrain, yTest = train_test_split(preproData,target,test_size = 0.25)
model = Lasso(alpha=0.1)
model.fit(XTrain,yTrain)
```
We can observe the regressor $w$ provided by the model, notice the sparsity.
```
model.coef_
```
We can observe which coefficients are put to $0$ and which ones are positively/negatively correlated.
```
print("Value Feature")
for idx,val in enumerate(model.coef_):
print("{:6.3f} {}".format(val,preproData.columns[idx]))
```
Let us take a look at our predictions.
```
targetPred = model.predict(XTest)
print("Predicted True")
for idx,val in enumerate(targetPred):
print("{:4.1f} {:.0f}".format(val,float(yTest.iloc[idx])))
```
### Regularization path
Selecting a good parameter $\alpha$ is the role of the data scientist. For instance, a easy way to do is the following.
```
n_test = 15
alpha_tab = np.logspace(-10,1,base=2,num = n_test)
print(alpha_tab)
trainError = np.zeros(n_test)
testError = np.zeros(n_test)
featureNum = np.zeros(n_test)
for idx,alpha in enumerate(alpha_tab):
model = Lasso(alpha=alpha)
model.fit(XTrain,yTrain)
yPredTrain = model.predict(XTrain)
yPredTest = model.predict(XTest)
trainError[idx] = np.linalg.norm(yPredTrain-yTrain["G3"].values)/yTrain.count()
testError[idx] = np.linalg.norm(yPredTest-yTest["G3"].values)/yTest.count()
featureNum[idx] = sum(model.coef_!=0)
alpha_opt = alpha_tab[np.argmin(testError)]
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline
plt.subplot(311)
plt.xscale("log")
plt.plot(alpha_tab, trainError,label="train error")
plt.xlim([min(alpha_tab),max(alpha_tab)])
plt.legend()
plt.xticks([])
plt.axvline(x=alpha_opt)
plt.ylabel("error")
plt.subplot(312)
plt.xscale("log")
plt.plot(alpha_tab, testError,'r',label="test error")
plt.xlim([min(alpha_tab),max(alpha_tab)])
#plt.ylim([0.19, 0.21])
plt.legend()
plt.axvline(x=alpha_opt)
plt.xticks([])
plt.ylabel("error")
plt.subplot(313)
plt.xscale("log")
plt.scatter(alpha_tab, featureNum)
plt.xlim([min(alpha_tab),max(alpha_tab)])
plt.ylim([0,28])
plt.axvline(x=alpha_opt)
plt.ylabel("nb. of features")
plt.xlabel("alpha")
```
## Exercises
> **Exercise:** a very popular binary classification exercise is the [survival prediction from Titanic shipwreck on Kaggle](https://www.kaggle.com/c/titanic)
>
> *The sinking of the RMS Titanic is one of the most infamous shipwrecks in history. On April 15, 1912, during her maiden voyage, the Titanic sank after colliding with an iceberg, killing 1502 out of 2224 passengers and crew. This sensational tragedy shocked the international community and led to better safety regulations for ships.*
>
> *One of the reasons that the shipwreck led to such loss of life was that there were not enough lifeboats for the passengers and crew. Although there was some element of luck involved in surviving the sinking, some groups of people were more likely to survive than others, such as women, children, and the upper-class.*
>
> *In this challenge, we ask you to complete the analysis of what sorts of people were likely to survive. In particular, we ask you to apply the tools of machine learning to predict which passengers survived the tragedy.*
>
>
> The data, taken from [Kaggle](https://www.kaggle.com/c/titanic) is located in `data/titanic/train.csv` and has the following form:
<table>
<tbody>
<tr><th><b>Feature</b></th><th><b>Definition</b></th><th><b>Comment</b></th></tr>
<tr>
<td>PassengerId</td>
<td>ID</td>
<td>numeric</td>
</tr>
<tr>
<td>Survival</td>
<td>Survival of the passenger</td>
<td>0 = No, 1 = Yes <b>target to predict</b></td>
</tr>
<tr>
<td>Pclass</td>
<td>Ticket class</td>
<td>1 = 1st, 2 = 2nd, 3 = 3rd</td>
</tr>
<tr>
<td>Name</td>
<td>Full name w/ Mr. Mrs. etc.</td>
<td>string</td>
</tr>
<tr>
<td>Sex</td>
<td>Sex</td>
<td><tt>male</tt> or <tt>female</tt></td>
</tr>
<tr>
<td>Age</td>
<td>Age in years</td>
<td>numeric</td>
</tr>
<tr>
<td>SibSp</td>
<td># of siblings / spouses aboard the Titanic</td>
<td>numeric</td>
</tr>
<tr>
<td>Parch</td>
<td># of parents / children aboard the Titanic</td>
<td></td>
</tr>
<tr>
<td>Ticket</td>
<td>Ticket number</td>
<td>quite messy</td>
</tr>
<tr>
<td>Fare</td>
<td>Passenger fare</td>
<td></td>
</tr>
<tr>
<td>cabin</td>
<td>Cabin number</td>
<td>letter + number (e.g. C85), often missing</td>
</tr>
<tr>
<td>Embarked</td>
<td>Port of Embarkation</td>
<td>C = Cherbourg, Q = Queenstown, S = Southampton</td>
</tr>
</tbody>
</table>
> * Load the dataset and preprocess the features. (you can remove features that seem uninteresting to you).
> * Perform binary classification to predict the survival of a passenger depending on its information.
> * Validate you method on the test set `data/titanic/test.csv`
> * Perform some feature engineering to improve the performance of you classifier (see e.g. https://triangleinequality.wordpress.com/2013/09/08/basic-feature-engineering-with-the-titanic-data/).
> **Exercise:** [House price prediction in Ames, Iowa on Kaggle](https://www.kaggle.com/c/house-prices-advanced-regression-techniques)
>
> The data, taken from [Kaggle](https://www.kaggle.com/c/house-prices-advanced-regression-techniques), is located in `data/house_prices/train.csv`.
>
> * Try to reach the best accurracy in terms of mean absolute error on the log of the prices:
$$Error = \frac{1}{n} \sum_{i=1}^n | \log(predicted_i) - \log(true_i) |$$
> on the test set `data/house_prices/test.csv`.
> * Which features (original or made up) are the most relevant? (see `data/house_prices/data_description.txt`)
| true |
code
| 0.617397 | null | null | null | null |
|
# Human Brain samples - MS Nature 2019 Rowitch dataset reprocessed
## Please download the input data before proceed
Please extract the tarball to current working directory, input data would be in **./data**
**Download link https://bit.ly/2F6o5n7**
```
import scanpy as sc
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
from matplotlib import colors
import seaborn as sb
import glob
import rpy2.rinterface_lib.callbacks
import logging
from rpy2.robjects import pandas2ri
import anndata2ri
from scipy.sparse.csc import csc_matrix
# Ignore R warning messages
#Note: this can be commented out to get more verbose R output
rpy2.rinterface_lib.callbacks.logger.setLevel(logging.ERROR)
# Automatically convert rpy2 outputs to pandas dataframes
pandas2ri.activate()
anndata2ri.activate()
%load_ext rpy2.ipython
plt.rcParams['figure.figsize']=(8,8) #rescale figures
sc.settings.verbosity = 3
#sc.set_figure_params(dpi=200, dpi_save=300)
sc.logging.print_versions()
results_file = './write/ms_nature_2019_rowitch_pp.h5ad'
```
## Load human brain snRNAseq samples
Here we load the pre-processed datasets (which has been annotated), and the raw matrices (which won't be filtered on the gene level).
### Raw data
```
wpath = "./data/"
metafile = "all_samples.txt"
meta = pd.read_csv( wpath + "/" + metafile, header = 0)
meta
# design
# Set up data loading
file_base = './data/'
adatas_raw = []
# Loop to load data
for i in range(len(meta['library_id'])):
#Parse filenames
sample = meta['library_id'][i]
h5_file = file_base+sample+'/outs/filtered_feature_bc_matrix.h5'
#Load data
adata_tmp = sc.read_10x_h5(h5_file)
adata_tmp.X = csc_matrix(adata_tmp.X)
#Annotate data
sampleID = sample.split('-rxn')[0]
adata_tmp.obs['sample'] = ['MSsnRNAseq2019_'+sample]*adata_tmp.n_obs
# adata_tmp.obs['study'] = ['MS_Nature_2019_Rowitch_snRNAseq']*adata_tmp.n_obs
# adata_tmp.obs['chemistry'] = ['v2_10X']*adata_tmp.n_obs
# adata_tmp.obs['tissue'] = ['Brain']*adata_tmp.n_obs
# adata_tmp.obs['species'] = ['Human']*adata_tmp.n_obs
# adata_tmp.obs['data_type'] = ['UMI']*adata_tmp.n_obs
# adata_tmp.obs
adata_tmp.var_names_make_unique()
#Append to main adata object
adatas_raw.append(adata_tmp)
meta['sample_id'] = meta['library_id'].copy()
meta['sample_id'] = meta['sample_id'].str.replace("_3PEE_ref", "")
meta
meta.shape
# Concatenate to unique adata object
adata_raw = adatas_raw[0].concatenate(adatas_raw[1:], batch_key='sample_ID',
batch_categories=meta['sample_id'])
adata_raw.obs['sample'] = adata_raw.obs['sample'].str.replace("_3PEE_ref", "")
adata_raw.obs.head()
adata_raw.obs.drop(columns=['sample_ID'], inplace=True)
adata_raw.obs.head()
adata_raw.obs.index.rename('barcode', inplace=True)
adata_raw.obs.head()
adata_raw.shape
type(adata_raw.X)
# adata_raw.X = csc_matrix(adata_raw.X)
# Save merged object
adata_raw.write(results_file)
```
# 1. Pre-processing and visualization
## 1.1 Quality control
```
adata_raw_copy = adata_raw.copy()
sc.pp.calculate_qc_metrics(adata_raw, inplace=True)
# Quality control - calculate QC covariates
adata_raw.obs['n_counts'] = adata_raw.X.sum(1)
adata_raw.obs['log_counts'] = np.log(adata_raw.obs['n_counts'])
adata_raw.obs['n_genes'] = (adata_raw.X > 0).sum(1)
# mt_gene_mask = [gene.startswith('MT-') for gene in adata_raw.var_names]
# adata_raw.obs['mt_frac'] = adata_raw.X[:, mt_gene_mask].sum(1)/adata_raw.obs['n_counts']
mito_genes = adata_raw.var_names.str.startswith('MT-')
adata_raw.obs['mt_frac'] = np.sum(adata_raw[:, mito_genes].X, axis=1) / np.sum(adata_raw.X, axis=1)
# Quality control - plot QC metrics
sc.pl.violin(adata_raw, ['n_genes', 'n_counts', 'mt_frac'],groupby='sample',
jitter=0.4, multi_panel=False)
sc.pl.scatter(adata_raw, x='n_counts', y='mt_frac')
sc.pl.scatter(adata_raw, x='n_counts', y='n_genes', color='mt_frac')
sc.pl.scatter(adata_raw[adata_raw.obs['n_counts'] < 20000], x='n_counts', y='n_genes', color='mt_frac')
#Thresholding decision: counts
p3 = sb.distplot(adata_raw.obs['n_counts'], kde=False, bins=200)
plt.show()
p4 = sb.distplot(adata_raw.obs['n_counts'][adata_raw.obs['n_counts']<4000], kde=False,bins=200)
plt.show()
p5 = sb.distplot(adata_raw.obs['n_counts'][adata_raw.obs['n_counts']>25000], kde=False, bins=60)
plt.show()
```
Zoom-in histograms of the number of counts per cell show that there's a group of cells with n_counts < 3500, this would remove 47k out of 65k cells. But paper said cut at 1000 reads, stick with 1000 reads. On the upper end of the distribution, we can see that the high peak centered around 5000 counts spans until around 40000 counts.
```
# Filter cells according to identified QC thresholds:
print('Total number of cells: {:d}'.format(adata_raw.n_obs))
sc.pp.filter_cells(adata_raw, min_counts = 1000)
print('Number of cells after min count filter: {:d}'.format(adata_raw.n_obs))
sc.pp.filter_cells(adata_raw, max_counts = 40000)
print('Number of cells after max count filter: {:d}'.format(adata_raw.n_obs))
adata_raw = adata_raw[adata_raw.obs['mt_frac'] < 0.2]
print('Number of cells after MT filter: {:d}'.format(adata_raw.n_obs))
# look at the effect of thresholding
sc.pl.scatter(adata_raw, x='n_counts', y='n_genes', color='mt_frac')
#Thresholding decision: genes
p6 = sb.distplot(adata_raw.obs['n_genes'], kde=False, bins=60)
plt.show()
p7 = sb.distplot(adata_raw.obs['n_genes'][adata_raw.obs['n_genes']<1500], kde=False, bins=60)
plt.show()
```
From the histograms of the number of genes per cell, we can notice that there still is a small population showing n_genes < 600 which should be filtered out. But paper said 500
```
# Thresholding on number of genes
print('Total number of cells: {:d}'.format(adata_raw.n_obs))
sc.pp.filter_cells(adata_raw, min_genes = 600)
print('Number of cells after gene filter: {:d}'.format(adata_raw.n_obs))
#Filter genes:
print('Total number of genes: {:d}'.format(adata_raw.n_vars))
# Min 20 cells - filters out 0 count genes
sc.pp.filter_genes(adata_raw, min_cells=20)
print('Number of genes after cell filter: {:d}'.format(adata_raw.n_vars))
# Save merged object
adata_raw.write('./write/ms_nature_2019_rowitch_done_QC_filter_46kcell_25kgene.h5ad')
```
### Normalization
```
adata_raw = sc.read_h5ad('./write/ms_nature_2019_rowitch_done_QC_filter_46kcell_25kgene.h5ad')
sc.pp.normalize_per_cell(adata_raw, counts_per_cell_after=1e6)
sc.pp.log1p(adata_raw)
# sc.pp.pca(adata_pp, n_comps=15, svd_solver='arpack')
# sc.pp.neighbors(adata_pp)
# sc.tl.louvain(adata_pp, key_added='groups', resolution=0.5)
adata_raw.write('./write/ms_nature_2019_rowitch_filtered_normalized_log1p_non_scaled.h5ad')
import gc
gc.collect()
infile = './write/ms_nature_2019_rowitch_filtered_normalized_log1p_non_scaled.h5ad'
adata_raw = sc.read_h5ad(infile)
def mod_index(meta):
meta['index'] = meta['index'].str.replace("_3PEE_ref", "")
return meta
# attach exisiting harmony and liger coordinates
# harmony
adata_harmony = sc.read_h5ad("./data/harmony_clustered.h5ad")
adata_harmony.obs.index = adata_harmony.obs.index.str.replace("_3PEE_ref", "")
adata_harmony.obs
# subset adata_raw to match same cells
cells = list(set(adata_raw.obs.index) & set(adata_harmony.obs.index))
adata_raw = adata_raw[cells]
xpca = pd.DataFrame(adata_harmony.obsm['X_pca']).set_index(adata_harmony.obs.index)
xtsne = pd.DataFrame(adata_harmony.obsm['X_tsne']).set_index(adata_harmony.obs.index)
xumap = pd.DataFrame(adata_harmony.obsm['X_umap']).set_index(adata_harmony.obs.index)
adata_raw.obsm['X_pca_harmony'] = np.array(xpca.loc[adata_raw.obs.index])
adata_raw.obsm['X_tsne_harmony'] = np.array(xtsne.loc[adata_raw.obs.index])
adata_raw.obsm['X_umap_harmony'] = np.array(xumap.loc[adata_raw.obs.index])
adata_raw.obs['louvain_harmony'] = adata_harmony.obs['louvain'].loc[adata_raw.obs.index]
adata_raw.obs = adata_raw.obs.astype({'louvain_harmony':'category'})
# liger
xtsne = pd.read_csv("./data/liger_runumap.tsne.coords.txt", sep='\t', encoding='utf-8')
xumap = pd.read_csv("./data/liger_runumap.umap.coords.txt", sep='\t', encoding='utf-8')
xlouvain = pd.read_csv("./data/liger_clusterID.txt", sep='\t', encoding='utf-8')
xtsne = mod_index(xtsne)
xumap = mod_index(xumap)
xlouvain['index'] = xlouvain['barcode']
xlouvain = mod_index(xlouvain)
xumap.set_index('index', inplace=True)
xtsne.set_index('index', inplace=True)
xlouvain.set_index('index', inplace=True)
adata_raw.obsm['X_tsne_liger'] = np.array(xtsne.loc[adata_raw.obs.index])
adata_raw.obsm['X_umap_liger'] = np.array(xumap.loc[adata_raw.obs.index])
adata_raw.obs['louvain_liger'] = np.array(xlouvain.loc[adata_raw.obs.index]['clusterID'])
adata_raw.obs = adata_raw.obs.astype({'louvain_liger':'category'})
outfile = infile
outfile = outfile.replace(".h5ad","")
adata_raw.write_h5ad(outfile+"_with_embedings.h5ad")
import gc
gc.collect()
```
# attach meta data from the paper
```
xmeta = pd.read_csv("./data/meta.tsv", sep='\t', encoding='utf-8')
xmeta.index = xmeta['cell'].str.replace("_.*_.*","")+"-"+xmeta['sample']+"_10x"
xmeta
xmeta.loc[set(set(xmeta.index) & set(adata_raw.obs.index))][['Capbatch','Seqbatch','cell_type','diagnosis','region','sample','sex','stage']]
features = ['Capbatch','Seqbatch','cell_type','diagnosis','region','sample','sex','stage']
bcodes = set(set(xmeta.index) & set(adata_raw.obs.index))
for f in features:
adata_raw.obs[f] = 'nan'
adata_raw.obs[f].loc[bcodes] = xmeta[f].loc[bcodes]
set(adata_raw.obs['cell_type'])
adata_raw.obs['>Description'] = ['Human brain snRNAseq 46k cells (MS Nature 2019 Schirmer et al.); data - normalized, log transformed UMI; platform - 10X v2 chemistry | embedding by umap_harmony; color by cell_type']*adata_raw.n_obs
outfile = infile
outfile = outfile.replace(".h5ad","")
adata_raw.write_h5ad(outfile+"_with_embedings_and_labels.h5ad")
```
| true |
code
| 0.378804 | null | null | null | null |
|
# Mimblewimble
## Resources:
### Software:
- Get rust at:
[www.rust-lang.org](https://www.rust-lang.org)
- Get jupyter notebook directly at [jupyter.org](https://www.jupyter.org) or through anaconda distribution at [anaconda.com](https://www.anaconda.com)
- get rust jupyter kernel at [https://github.com/google/evcxr/blob/master/evcxr_jupyter/README.md](https://github.com/google/evcxr/blob/master/evcxr_jupyter/README.md) or run the code normally
### Mimblewimble
- "Official" mimblewimble implementation [https://github.com/mimblewimble/grin/blob/master/doc/intro.md](https://github.com/mimblewimble/grin/blob/master/doc/intro.md)
- Helpful article expleining mimblewimble [https://medium.com/@brandonarvanaghi/grin-transactions-explained-step-by-step-fdceb905a853](https://medium.com/@brandonarvanaghi/grin-transactions-explained-step-by-step-fdceb905a853)
- Aggregate schnorr signatures [https://blockstream.com/2018/01/23/en-musig-key-aggregation-schnorr-signatures/](https://blockstream.com/2018/01/23/en-musig-key-aggregation-schnorr-signatures/)
# Mimblewimble History
In __2013__ Adam Back proposes confidential transactions in his bitcointalk post "bitcoins with homomorphic value" [https://bitcointalk.org/index.php?topic=305791.0](https://bitcointalk.org/index.php?topic=305791.0)
In __Aug. 2016__, Someone called Tom Elvis Jedusor (Voldemort's French name in J.K. Rowling's Harry Potter book series) placed the original MimbleWimble white paper on a bitcoin research channel, and then disappeared.
Tom's white paper "Mimblewimble" (a tongue-tying curse used in "The Deathly Hallows") was a blockchain proposal that could theoretically increase privacy, scalability and fungibility.
In __Oct. 2016__, Andrew Poelstra, a mathematician at Blockstream, wrote a precise paper, made precise Tom's original idea, and added further scaling improvements on it.
A __few days later__, Ignotus Peverell (name also came from "Harry Potter", the original owner of the invisibility cloak, if you know the Harry Potter characters) started a Github project called Grin, and began turning the MimbleWimble paper into something real.
And in __Mar. 2017__, Ignotus Peverell posted a technical introduction to MimbleWimble and Grin on Github.
# Mimblewimble deepdive
```
:dep curve25519-dalek = "1.1.3"
rand = "0.6.5"
sha2 = "0.8.0"
extern crate curve25519_dalek;
extern crate rand;
extern crate sha2;
use curve25519_dalek::constants;
use curve25519_dalek::ristretto::CompressedRistretto;
use curve25519_dalek::ristretto::RistrettoPoint;
use curve25519_dalek::scalar::Scalar;
use rand::prelude::*;
use sha2::{Sha256, Digest};
let mut rng = rand::thread_rng();
```
## Discrete logarithm problem

- given the Generator _G = 3_ and the point _P = 2_ (publlic key) it is extremely difficult (assuming large numbers) to get the multiplicator _r_ (private key) that satisfies
<div align="center">_P = r*G_</div>
- however, knowing _r_ it is easy to compute _P_
## Schnorr signatures
- private key _r_, public key _U_ with
<div align="center">_U = r*G_</div>
- signer generates random nonce _rt_ and computes commitment to nonce
<div align="center">_Ut = rt*G_</div>
- using challenge _c=H(m,Ut)_ (challenge has to be unique for message _m_ and nonce _rt_) signer computes
<div align="center">_rz = rt + c*r_</div>
- signer sends _(Ut,rz)_ to verifier
- verifier checks
<div align="center">_rz\*G = Ut + c\*U_</div>
- which can be expressed as
<div align="center">_rz\*G = rt\*G + c\*r\*G_</div>
```
//get generator for the elliptic curve points
let G = &constants::RISTRETTO_BASEPOINT_POINT;
//pick arbitrary private key
let r = Scalar::from_bytes_mod_order([2u8;32]);
//compute public key
let U = r*G;
//generate random nonce, has to be different every time
let mut temp: [u8;32] = [0u8;32];
temp.copy_from_slice((0..32).map(|x| rng.gen()).collect::<Vec<u8>>().as_slice());
let rt = Scalar::from_bytes_mod_order(temp);
//calculate commitment to nonce
let Ut = rt*G;
//generate challenge from hashfunction
let mut hasher = Sha256::new();
hasher.input("message".as_bytes());
hasher.input(Ut.compress().to_bytes());
temp.copy_from_slice(hasher.result().as_slice());
let c = Scalar::from_bytes_mod_order(temp);
let rz = rt + c*r;
//check whether signature is valid
assert_eq!(rz*G,Ut+c*U);
(rz*G).compress()
```
## Simple aggregate schnorr signatures (insecure!!!)
- two signers with private keys _r1,r2_ and public keys _U1,U2_ with
<div align="center">_U1 = r1\*G, U2 = r2\*G_</div>
- signers generate random nonces _rt1,rt2_ and compute commitments to the nonces
<div align="center">_Ut1 = rt1\*G, Ut2 = rt2\*G_</div>
- using challenge _c=H(m,Ut1+Ut2,U1+U2)_ (this is insecure!!!, see secure version [here](https://blockstream.com/2018/01/23/en-musig-key-aggregation-schnorr-signatures/)) signers compute
<div align="center">_rz1 = rt1 + c\*r1, rz2 = rt2 + c\*r2 _</div>
- signers send _(Ut1,rz1),(Ut2,rz2)_ to verifier
- verifier checks
<div align="center">_rz\*G = Ut + c\*U_</div>
<div align="center">_(rz1 + rz2)\*G = (Ut1 + Ut2) + c\*(U1 + U2)_</div>
- aggregate signatures allow to simply add puplic keys and signatures
<div align="center">_U = U1 + U2_</div>
<div align="center">_(Ut,rz) = (Ut1 + Ut2, rz1 + rz2)_</div>
```
//pick arbitrary private keys
let r1 = Scalar::from_bytes_mod_order([3u8;32]);
let r2 = Scalar::from_bytes_mod_order([4u8;32]);
//compute public key
let U1 = r1*G;
let U2 = r2*G;
//generate random nonces, has to be different every time
let mut temp: [u8;32] = [0u8;32];
temp.copy_from_slice((0..32).map(|x| rng.gen()).collect::<Vec<u8>>().as_slice());
let rt1 = Scalar::from_bytes_mod_order(temp);
let mut temp: [u8;32] = [0u8;32];
temp.copy_from_slice((0..32).map(|x| rng.gen()).collect::<Vec<u8>>().as_slice());
let rt2 = Scalar::from_bytes_mod_order(temp);
//calculate commitment to nonce
let Ut1 = rt1*G;
let Ut2 = rt2*G;
//generate challenge from hashfunction
let mut hasher = Sha256::new();
hasher.input("message".as_bytes());
hasher.input((Ut1+Ut2).compress().to_bytes());
hasher.input((U1+U2).compress().to_bytes());
temp.copy_from_slice(hasher.result().as_slice());
let c = Scalar::from_bytes_mod_order(temp);
let rz1 = rt1 + c*r1;
let rz2 = rt2 + c*r2;
let U = U1 + U2;
let rz = rz1 + rz2;
let Ut = Ut1 + Ut2;
//check whether signature is valid
assert_eq!(rz*G,Ut+c*U);
(rz*G).compress()
```
## UTXO transactions

## Example transaction
- Alice has 100 tokens and wants to pay Bob 60
- with the UTXO model Alice will use her input _vi0 = 100_ to pay herself the output _vo0 = 40_ and Bob the output _vo1 = 60_
- no transactions fees apply
- in order to not generate money out of nothing, the inputs must equal the ouputs
<div align="center">_vi0 = vo0 + vo1_</div>
```
let zeros: [u8;32] = [0u8;32];
let mut vi0 = zeros.clone();
vi0[0] = 100u8;
let vi0 = Scalar::from_bytes_mod_order(vi0);
let mut vo0 = zeros.clone();
vo0[0] = 40u8;
let vo0 = Scalar::from_bytes_mod_order(vo0);
let mut vo1 = zeros.clone();
vo1[0] = 60u8;
let vo1 = Scalar::from_bytes_mod_order(vo1);
//check whether input equals output
assert_eq!(vi0,vo0+vo1);
vi0
```
## Hiding
- in order to obscure the values of the transaction, one can multiply every term by the point _H_ on an elliptic curve, this yields
<div align="center">_vi0\*H = vo0\* H + vo1\*H_</div>
- similar to the dlog problem, for people not knowing _vi0, vo0, vo1_ it is almost impossible to obtain them now
- however, the inputs must still equal the outputs
```
//get point on the curve, it is important that the relation between G and H is unknown
let H = RistrettoPoint::random(&mut rng);
assert_eq!(vi0*H,vo0*H+vo1*H);
(vi0*H).compress()
```
## Blinding
- the problem now is that, the people that transacted with you know the value of the transactions values and it gets easy for them to deduce your following transactions (if they know you have 100, they can try every combination below 100 to see what you spend on your next output)
- the aim is to replace every input and output by its corresponding pedersen commitment
<div align="center">_v\*H -> r\*G + v\*H_</div>
- where _r_ is called blinding factor and _G_ is another point on the curve
- every input and ouput has its own blinding factor
- in the context of mimblewimble _r_ can be thought of as a private key to the corresponding output and it is only known by the owner of that output
## Main idea:
- each participant uses the sum of his pedersen commitments for the outputs minus the sum of the pedersen commitments for the inputs as his public key
<div align="center">_U1 = (ro0\*G + vo0\*H) - (ri0\*G + vi0\*H)_</div>
<div align="center">_U2 = (ro1\*G + vo1*H)_</div>
- the private key for each participant is then the sum of the blinding factors of the outputs minus the inputs
<div align="center">_r1 = (ro0 - ri0)_</div>
<div align="center">_r2 = ro1_</div>
## Validating transactions
- public key for sender is sum of pedersen commitments (output - input)
<div align="center">_U1 = (ro0 - ri0)\*G + (vo0 - vi0)\*H_</div>
- public key of reciever is sum of pedersen commitments (output - input)
<div align="center">_U2 = ro1\*G + vo1\*H_</div>
- both generate random nonces _rt1,rt2_ and compute commitments to the nonces
<div align="center">_Ut1 = rt1\*G, Ut2 = rt2\*G_</div>
- using challenge _c=H(m,Ut1+Ut2,U1+U2)_ signers compute
<div align="center">_rz1 = rt1 + c\*(ro0 - ri0), rz2 = rt2 + c\*ro1 _</div>
- signers send _(Ut1,rz1),(Ut2,rz2)_ to verifier
- verifier checks
<div align="center">_(rz1 + rz2)\*G = (Ut1 + Ut2) + c\*(U1 + U2)_</div>
- which is equal to
<div align="center">_(rz1 + rz2)\*G = (Ut1 + Ut2) + c\*((ro0 - ri0)\*G + (vo0 - vi0)\*H + ro1\*G + vo1\*H)_</div>
- if the following condition holds
<div align="center">_0 = vo0\* H - vi0\*H + vo1\*H_</div>
- this can be simplified to the valid aggregate schnorr signature
<div align="center">_(rz1 + rz2)\*G = (rt1\*G + rt2\*G) + c\*((ro0 - ri0)\*G + ro1\*G)_</div>
- vice versa, a valid signature means that the inputs and outputs cancel out
```
//initialize the blinding factors
let mut ri0 = zeros.clone();
ri0[0] = 10u8;
let ri0 = Scalar::from_bytes_mod_order(ri0);
let mut ro0 = zeros.clone();
ro0[0] = 20u8;
let ro0 = Scalar::from_bytes_mod_order(ro0);
let mut ro1 = zeros.clone();
ro1[0] = 30u8;
let ro1 = Scalar::from_bytes_mod_order(ro1);
//compute public key
let U1 = (ro0 - ri0)*G + (vo0 - vi0)*H;
let U2 = ro1*G + vo1*H;
//generate random nonces, has to be different every time
let mut temp: [u8;32] = [0u8;32];
temp.copy_from_slice((0..32).map(|x| rng.gen()).collect::<Vec<u8>>().as_slice());
let rt1 = Scalar::from_bytes_mod_order(temp);
let mut temp: [u8;32] = [0u8;32];
temp.copy_from_slice((0..32).map(|x| rng.gen()).collect::<Vec<u8>>().as_slice());
let rt2 = Scalar::from_bytes_mod_order(temp);
//calculate commitment to nonce
let Ut1 = rt1*G;
let Ut2 = rt2*G;
//generate challenge from hashfunction
let mut hasher = Sha256::new();
hasher.input("message".as_bytes());
hasher.input((Ut1+Ut2).compress().to_bytes());
hasher.input((U1+U2).compress().to_bytes());
temp.copy_from_slice(hasher.result().as_slice());
let c = Scalar::from_bytes_mod_order(temp);
let rz1 = rt1 + c*(ro0 - ri0);
let rz2 = rt2 + c*ro1;
let U = U1 + U2;
let rz = rz1 + rz2;
let Ut = Ut1 + Ut2;
//check whether signature is valid
assert_eq!(rz*G,Ut+c*U);
(rz*G).compress()
```
| true |
code
| 0.792926 | null | null | null | null |
|
# Module 6. Amazon SageMaker Deployment for EIA(Elastic Inference Accelerator)
---
***[주의] 본 모듈은 PyTorch EIA 1.3.1 버전에서 훈련을 수행한 모델만 배포가 가능합니다. 코드가 정상적으로 수행되지 않는다면, 프레임워크 버전을 동일 버전으로 맞춰 주시기 바랍니다.***
본 모듈에서는 Elastic Inference Accelerator(EIA)를 사용하여 모델을 배포해 보겠습니다.
### Elastic Inference Accelerator
훈련 인스턴스와 달리 실시간 추론 인스턴스는 계속 상시로 띄우는 경우가 많기에, 딥러닝 어플리케이션에서 low latency를 위해 GPU 인스턴스를 사용하면 많은 비용이 발생합니다.
Amazon Elastic Inference는 저렴하고 메모리가 작은 GPU 기반 가속기를 Amazon EC2, Amazon ECS, Amazon SageMaker에 연결할 수 있는 서비스로, Accelerator가 CPU 인스턴스에 프로비저닝되고 연결됩니다. EIA를 사용하면 GPU 인스턴스에 근접한 퍼포먼스를 보이면서 인스턴스 실행 비용을 최대 75%까지 절감할 수 있습니다.
모든 Amazon SageMaker 인스턴스 유형, EC2 인스턴스 유형 또는 Amazon ECS 작업을 지원하며, 대부분의 딥러닝 프레임워크를 지원하고 있습니다. 지원되는 프레임워크 버전은 AWS CLI로 확인할 수 있습니다.
```bash
$ aws ecr list-images --repository-name tensorflow-inference-eia --registry-id 763104351884
$ aws ecr list-images --repository-name pytorch-inference-eia --registry-id 763104351884
$ aws ecr list-images --repository-name mxnet-inference-eia --registry-id 763104351884
```
참조: https://aws.amazon.com/ko/blogs/korea/amazon-elastic-inference-gpu-powered-deep-learning-inference-acceleration/
<br>
## 1. Inference script
---
아래 코드 셀은 `src` 디렉토리에 SageMaker 추론 스크립트인 `inference_eia.py`를 저장합니다.<br>
Module 5의 코드와 대부분 동일하지만, `model_fn()` 메서드의 구현이 다른 점을 유의해 주세요.
```
import os
import time
import sagemaker
from sagemaker.pytorch.model import PyTorchModel
role = sagemaker.get_execution_role()
%%writefile ./src/inference_eia.py
from __future__ import absolute_import
import argparse
import json
import logging
import os
import sys
import time
import random
from os.path import join
import numpy as np
import io
import tarfile
import boto3
from PIL import Image
import torch
import torch.distributed as dist
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import lr_scheduler
import torch.optim as optim
import torchvision
import copy
import torch.utils.data
import torch.utils.data.distributed
from torchvision import datasets, transforms, models
from torch import topk
logger = logging.getLogger(__name__)
logger.setLevel(logging.DEBUG)
logger.addHandler(logging.StreamHandler(sys.stdout))
JSON_CONTENT_TYPE = 'application/json'
def model_fn(model_dir):
logger.info("==> model_dir : {}".format(model_dir))
traced_model = torch.jit.load(os.path.join(model_dir, 'model_eia.pth'))
return traced_model
# Deserialize the request body
def input_fn(request_body, request_content_type='application/x-image'):
print('An input_fn that loads a image tensor')
print(request_content_type)
if request_content_type == 'application/x-image':
img = np.array(Image.open(io.BytesIO(request_body)))
elif request_content_type == 'application/x-npy':
img = np.frombuffer(request_body, dtype='uint8').reshape(137, 236)
else:
raise ValueError(
'Requested unsupported ContentType in content_type : ' + request_content_type)
img = 255 - img
img = img[:,:,np.newaxis]
img = np.repeat(img, 3, axis=2)
test_transforms = transforms.Compose([
transforms.ToTensor()
])
img_tensor = test_transforms(img)
return img_tensor
# Predicts on the deserialized object with the model from model_fn()
def predict_fn(input_data, model):
logger.info('Entering the predict_fn function')
start_time = time.time()
input_data = input_data.unsqueeze(0)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model.to(device)
model.eval()
input_data = input_data.to(device)
result = {}
with torch.no_grad():
logits = model(input_data)
pred_probs = F.softmax(logits, dim=1).data.squeeze()
outputs = topk(pred_probs, 5)
result['score'] = outputs[0].detach().cpu().numpy()
result['class'] = outputs[1].detach().cpu().numpy()
print("--- Elapsed time: %s secs ---" % (time.time() - start_time))
return result
# Serialize the prediction result into the response content type
def output_fn(pred_output, accept=JSON_CONTENT_TYPE):
return json.dumps({'score': pred_output['score'].tolist(),
'class': pred_output['class'].tolist()}), accept
```
<br>
## 2. TorchScript Compile (Tracing)
---
PyTorch 프레임워크에서 EI를 사용하기 위해서는 [TorchScript](https://pytorch.org/docs/1.3.1/jit.html)로 모델을 컴파일해야 하며, 2020년 8월 시점에서는 PyTorch 1.3.1을 지원하고 있습니다. TorchScript는 PyTorch 코드에서 직렬화 및 최적화 가능한 모델로 컴파일하며 Python 인터프리터의 글로벌 인터프리터 잠금 (GIL)과 무관하기 때문에 Python 외의 언어에서 로드 가능하고 최적화가 용이합니다.
TorchScript로 변환하는 방법은 **tracing** 방식과 **scripting** 방식이 있으며, 본 핸즈온에서는 tracing 방식을 사용하겠습니다. <br>
참고로 tracing 방식은 샘플 입력 데이터를 모델에 입력 후 그 입력의 흐름(feedforward)을 기록하여 포착하는 메커니즘이며, scripting 방식은 모델 코드를 직접 분석해서 컴파일하는 방식입니다.
### Install dependencies
```
import sys
!{sys.executable} -m pip install --upgrade pip --trusted-host pypi.org --trusted-host files.pythonhosted.org
!{sys.executable} -m pip install https://download.pytorch.org/whl/cpu/torchvision-0.4.2%2Bcpu-cp36-cp36m-linux_x86_64.whl
!{sys.executable} -m pip install https://s3.amazonaws.com/amazonei-pytorch/torch_eia-1.3.1-cp36-cp36m-manylinux1_x86_64.whl
!{sys.executable} -m pip install graphviz==0.13.2
!{sys.executable} -m pip install mxnet-model-server==1.0.8
!{sys.executable} -m pip install pillow==7.1.0
!{sys.executable} -m pip install sagemaker_containers
!{sys.executable} -m pip install -U sagemaker
```
### Compile
Tracing 방식은 특정 input을 모델에 적용했을 때 수행되면서 operation이 저장하기 때문에, 이미지 사이즈와 동일한 크기의 랜덤 입력 데이터를 모델을 적용해야 합니다.
```
import torch, os
from torchvision import models
model_dir = './model'
print("==> model_dir : {}".format(model_dir))
model = models.resnet18(pretrained=True)
last_hidden_units = model.fc.in_features
model.fc = torch.nn.Linear(last_hidden_units, 186)
model.load_state_dict(torch.load(os.path.join(model_dir, 'model.pth')))
import torch
data = torch.rand(1,3,137,236)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model.to(device)
input_data = data.to(device)
with torch.jit.optimized_execution(True, {'target_device': 'eia:0'}):
traced_model = torch.jit.trace(model, input_data)
```
컴파일한 모델로 로컬 환경에서 추론을 수행해 보겠습니다.
```
from src.inference_eia import model_fn, input_fn, predict_fn, output_fn
from PIL import Image
import numpy as np
import json
file_path = 'test_imgs/test_0.jpg'
with open(file_path, mode='rb') as file:
img_byte = bytearray(file.read())
data = input_fn(img_byte)
result = predict_fn(data, traced_model)
print(result)
```
TorchScript 모델을 파일로 직렬화하여 저장합니다. 그런 다음, `tar.gz`로 압축하고 이 파일을 S3로 복사합니다.
```
torch.jit.save(traced_model, './model/model_eia.pth')
tar_filename = 'model_eia.tar.gz'
!cd model/ && tar -czvf $tar_filename model_eia.pth
artifacts_dir = 's3://sagemaker-us-east-1-143656149352/pytorch-training-2020-08-16-04-47-36-618/output/'
!aws s3 cp model/$tar_filename $artifacts_dir
```
<br>
## 3. SageMaker Hosted Endpoint Inference
---
SageMaker가 관리하는 배포 클러스터를 프로비저닝하는 시간이 소요되기 때문에 추론 서비스를 시작하는 데에는 약 5~10분 정도 소요됩니다.
```
import boto3
client = boto3.client('sagemaker')
runtime_client = boto3.client('sagemaker-runtime')
def get_model_path(sm_client, max_results=1, name_contains='pytorch'):
training_job = sm_client.list_training_jobs(MaxResults=max_results,
NameContains=name_contains,
SortBy='CreationTime',
SortOrder='Descending')
training_job_name = training_job['TrainingJobSummaries'][0]['TrainingJobName']
training_job_description = sm_client.describe_training_job(TrainingJobName=training_job_name)
model_path = training_job_description['ModelArtifacts']['S3ModelArtifacts']
return model_path
#model_path = get_model_path(client, max_results=3)
model_path = os.path.join(artifacts_dir, tar_filename)
print(model_path)
endpoint_name = "endpoint-bangali-classifier-eia-{}".format(int(time.time()))
pytorch_model = PyTorchModel(model_data=model_path,
role=role,
entry_point='./src/inference_eia.py',
framework_version='1.3.1',
py_version='py3')
predictor = pytorch_model.deploy(instance_type='ml.c5.large',
initial_instance_count=1,
accelerator_type='ml.eia2.large',
endpoint_name=endpoint_name,
wait=False)
# client = boto3.client('sagemaker')
# waiter = client.get_waiter('endpoint_in_service')
# waiter.wait(EndpointName=endpoint_name)
import boto3
client = boto3.client('sagemaker')
runtime_client = boto3.client('sagemaker-runtime')
endpoint_name = pytorch_model.endpoint_name
client.describe_endpoint(EndpointName = endpoint_name)
```
추론을 수행합니다. (`ContentType='application/x-image'`)
```
with open(file_path, mode='rb') as file:
img_byte = bytearray(file.read())
response = runtime_client.invoke_endpoint(
EndpointName=endpoint_name,
ContentType='application/x-image',
Accept='application/json',
Body=img_byte
)
print(response['Body'].read().decode())
%timeit runtime_client.invoke_endpoint(EndpointName=endpoint_name, ContentType='application/x-image', Accept='application/json', Body=img_byte)
```
### SageMaker Hosted Endpoint Clean-up
엔드포인트를 계속 사용하지 않는다면, 불필요한 과금을 피하기 위해 엔드포인트를 삭제해야 합니다.
SageMaker SDK에서는 `delete_endpoint()` 메소드로 간단히 삭제할 수 있으며, UI에서도 쉽게 삭제할 수 있습니다.
```
def delete_endpoint(client, endpoint_name):
response = client.describe_endpoint_config(EndpointConfigName=endpoint_name)
model_name = response['ProductionVariants'][0]['ModelName']
client.delete_model(ModelName=model_name)
client.delete_endpoint(EndpointName=endpoint_name)
client.delete_endpoint_config(EndpointConfigName=endpoint_name)
print(f'--- Deleted model: {model_name}')
print(f'--- Deleted endpoint: {endpoint_name}')
print(f'--- Deleted endpoint_config: {endpoint_name}')
delete_endpoint(client, endpoint_name)
```
| true |
code
| 0.709422 | null | null | null | null |
|
# OLS regressions - baseline for Capstone analysis
In this notebook, I perform OLS regressions using systemwide CaBi trips as the dependent variable.
```
from util_functions import *
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import seaborn as sns; sns.set_style('darkgrid')
import statsmodels.graphics.gofplots as gofplots
%matplotlib inline
set_env_path()
conn, cur = aws_connect()
query = """
SELECT *,
CASE day_of_week WHEN 5 THEN 1 WHEN 6 THEN 1 ELSE 0 END AS weekend_dummy,
from final_db"""
df = pd.read_sql(query, con=conn)
df.shape
```
### First specification attempt - theory based
A lot of the variation in daily CaBi rides can be explained by weather.
I decided on the following specification based on trial and error and intuition.
For our ML analysis, we will want to look into ways to perform feature selection algorithmically (I'm looking into this right now).
That said, the variables I've chosen are fairly arbitrary and could probably be improved, but we shouldn't spend a huge amount of time on baseline stuff. I made sure to try to avoid multicollinearity, for example high and low temperature, population and date, and all of the CaBi data are all highly correlated.
```
def fitOLS(equation, cov='nonrobust'):
'''
This function uses statsmodels.ols to estimate OLS regressions using R/patsy-style syntax.
Args:
equation (str): A patsy-style regression equation.
e.g. 'cabi_trips ~ apparenttemperaturehigh + daylight_hours + rain'
cov (str): A specific covariance matrix type. Default is 'nonrobust'.
HC0-HC3 available for heteroskedasticity-robust standard errors.
Returns:
results: A RegressionResults object which summarizes the fit of a linear regression model.
'''
model = smf.ols('{}'.format(equation), df)
results = model.fit(cov_type='{}'.format(cov), use_t=True)
return results
# Using the new weekend_dummy for demonstrative purposes
results = fitOLS('cabi_trips ~ year + daylight_hours + '
'apparenttemperaturehigh + rain + snow + '
'nats_games + weekend_dummy', cov='HC0')
results.summary()
# Fit the model and print results
# I wanted to use dc_pop instead of year (they're highly correlated)
# But there are 0s in dc_pop that throw off the analysis
results = fitOLS('cabi_trips ~ year + daylight_hours + '
'apparenttemperaturehigh + rain + snow + '
'nats_games + C(day_of_week)', cov='HC0')
results.summary()
```
Our results look good.
The R-squared tells us that about 74% of the variance in cabi_trips is explained by the variance in the explanatory variables.
The low p-values indicate that the results we found are all statistically significant.
Each of the coefficient estimates indicates the average change in daily CaBi trips associated with a one-unit increase in the explanatory variable, all else held equal. For dummy variables, this can be interpreted as an on-off switch, so on days when it snows, we should expect 1550 fewer rides.
There are other things to worry about, though. Statistical programming packages often include diagnostic plots by default, but statsmodels doesn't. I explain three of these plots below.
```
'''Homoskedasticity is when the variance/scatter/spread of the residuals is
constant for all values of the fitted values. It is an assumption under OLS.
Heteroskedasticity is when the variance of the residuals changes as the fitted values change.
If not addressed, it can lead to biased estimators.
If our residuals were heteroskedastic, we would expect a scatter plot to form a funnel shape,
and a regression line to have a slope.
'''
# Regplot fits a regression line to a scatterplot
plt.title('Residuals vs Fitted Values')
sns.regplot(results.fittedvalues, results.resid)
plt.xlabel('Y-hat')
plt.ylabel('Residuals')
plt.show()
```
It doesn't look like there's heteroskedasticity, and the regression line is flat. However I think given our sample size and the significance of our variables, it couldn't hurt to specify heteroskedasticity-robust standard errors (the cov=HC0 argument in fitOLS).
In practice I rarely see standard errors that aren't robust to either heteroskedasticity or clustering. (If we wanted to cluster, we would have to choose variables to cluster on, and I haven't looked into that for our data).
```
'''Normality of the residuals with mean 0 is another assumption under OLS.
If residuals are nonnormal and not approximately centered at 0, the model is probably misspecified.
The first chart is a kernel density estimation and the second is a Q-Q plot.
Q-Q plots compare two datasets to see whether or not they come from the same distribution.
If they do, the points should form a straight line.
Here, we have a Normal Q-Q plot, where our residuals are being compared against a normal distribution.
'''
# How are our residuals distributed?
plt.title('Density Plot of Residuals')
sns.kdeplot(results.resid)
plt.show()
# How close are our residuals to normal?
fig = gofplots.qqplot(results.resid, line='s')
plt.title("Normal Q-Q plot")
plt.show()
```
The residuals appear to be approximately centered around 0.
The third chart shows that our residuals are close to normal, but at the extreme ends of our distribution we get farther from a normal distribution.
### Second specification attempt - dockless?
Next, I add dless_trips_all to the specification to see if there's any effect.
```
results = fitOLS('cabi_trips ~ year + daylight_hours +'
'apparenttemperaturehigh + rain + snow + '
'nats_games + C(day_of_week) + dless_trips_all', cov='HC0')
results.summary()
```
R squared is slightly higher.
dless_trips_all is statistically significant, but its coefficient is small. An increase of 100 dockless trips is associated with 33 fewer CaBi trips. Its upper bound is also fairly close to 0.
For the sake of brevity I don't include the diagnostic plots here because they don't change much after adding just one independent variable.
### Third specification attempt - transformations
Next, I try taking the natural log of certain variables.
When you include a logged variable, its interpretation changes to percentage change instead of unit change. I get into specifics in the cell after the regression results.
Logging variables is also very good for dealing with outliers. OLS is sensitive to outliers - we saw this demonstrated in class when we removed one observation from the IQ ~ TVhours regression. Logging a variable with a long right tail will often make it approximately normal, which is better for OLS.
```
# I ran into errors trying to log cabi_trips because the log of 0 is undefined.
# Ended up having to drop the four observations where cabi_trips==0
df = df[df.cabi_trips != 0]
df.shape
results = fitOLS('np.log(cabi_trips) ~ year + daylight_hours + '
'np.log(apparenttemperaturehigh) + rain + snow + nats_games + C(day_of_week) + '
'dless_trips_all', cov='HC0')
results.summary()
```
Since we have some logged variables, the interpretation of the coefficients changes.
Before, the interpretation of apparenttemperaturehigh's effect on cabi_rides was basically "Holding all else equal, how many more cabi rides should we see if the feels-like temperature is one degree (F) higher?"
Now that both are logged, the coefficient of 0.8136 means "Holding all else equal, if feels-like temperature rises by 1%, we expect there to be a 0.81% increase in CaBi rides."
I explain the interpretation of the dummy coefficients below.
```
# When you have a logged dependent variable, be careful with dummies
# The effect is asymmetrical!
# more: https://davegiles.blogspot.com/2011/03/dummies-for-dummies.html
print('If rain switches from 0 to 1, the % impact on cabi_trips is ', 100*(np.exp(-0.2168) - 1))
print('If rain switches from 1 to 0, the % impact on cabi_trips is ', 100*(np.exp(0.2168) - 1))
print('If snow switches from 0 to 1, the % impact on cabi_trips is ', 100*(np.exp(-0.3684) - 1))
print('If snow switches from 1 to 0, the % impact on cabi_trips is ', 100*(np.exp(0.3684) - 1))
```
All in all, this third specification isn't that appealing. nats_games is no longer significant, the R squared is lower, and the dummy variables don't make as much intuitive sense.
Looking at the charts below you can see that things look worse than before. This particular specification is no good.
```
# Heteroskedasticity?
plt.title('Residuals vs Fitted Values')
sns.regplot(results.fittedvalues, results.resid)
plt.xlabel('Y-hat')
plt.ylabel('Residuals')
plt.show()
# How are our residuals distributed?
plt.title('Density Plot of Residuals')
sns.kdeplot(results.resid)
plt.show()
# How close are our residuals to normality?
fig = gofplots.qqplot(results.resid, line='s')
plt.title("Normal Q-Q plot")
plt.show()
```
| true |
code
| 0.755547 | null | null | null | null |
|
Copyright (c) 2020-2021. All rights reserved.
Licensed under the MIT License.
# Troubleshooting HPO for fine-tuning pre-trained language models
## 1. Introduction
In this notebook, we demonstrate a procedure for troubleshooting HPO failure in fine-tuning pre-trained language models (introduced in the following paper):
*[An Empirical Study on Hyperparameter Optimization for Fine-Tuning Pre-trained Language Models](https://arxiv.org/abs/2106.09204). Xueqing Liu, Chi Wang. To appear in ACL-IJCNLP 2021*
Notes:
*In this notebook, we only run each experiment 1 time for simplicity, which is different from the paper (3 times). To reproduce the paper's result, please run 3 repetitions and take the average scores.
*Running this notebook takes about one hour.
FLAML requires `Python>=3.6`. To run this notebook example, please install flaml with the `notebook` and `nlp` options:
```bash
pip install flaml[nlp]
```
Our paper was developed under transformers version 3.4.0. We uninstall and reinstall transformers==3.4.0:
```
!pip install flaml[nlp]
!pip install transformers==3.4.0
from flaml.nlp import AutoTransformers
```
## 2. Initial Experimental Study
### Load dataset
Load the dataset using AutoTransformer.prepare_data. In this notebook, we use the Microsoft Research Paraphrasing Corpus (MRPC) dataset and the Electra model as an example:
```
autohf = AutoTransformers()
preparedata_setting = {
"dataset_subdataset_name": "glue:mrpc",
"pretrained_model_size": "google/electra-base-discriminator:base",
"data_root_path": "data/",
"max_seq_length": 128,
}
autohf.prepare_data(**preparedata_setting)
```
### Running grid search
First, we run grid search using Electra. By specifying `algo_mode="grid"`, AutoTransformers will run the grid search algorithm. By specifying `space_mode="grid"`, AutoTransformers will use the default grid search configuration recommended by the Electra paper:
```
import transformers
autohf_settings = {
"resources_per_trial": {"gpu": 1, "cpu": 1},
"num_samples": 1,
"time_budget": 100000, # unlimited time budget
"ckpt_per_epoch": 5,
"fp16": True,
"algo_mode": "grid", # set the search algorithm to grid search
"space_mode": "grid", # set the search space to the recommended grid space
"transformers_verbose": transformers.logging.ERROR
}
validation_metric, analysis = autohf.fit(**autohf_settings)
```
Get the time for running grid search:
```
GST = autohf.last_run_duration
print("grid search for {} took {} seconds".format(autohf.jobid_config.get_jobid_full_data_name(), GST))
```
After the HPO run finishes, generate the predictions and save it as a .zip file to be submitted to the glue website. Here we will need the library AzureUtils which is for storing the output information (e.g., analysis log, .zip file) locally and uploading the output to an azure blob container (e.g., if multiple jobs are executed in a cluster). If the azure key and container information is not specified, the output information will only be saved locally.
```
predictions, test_metric = autohf.predict()
from flaml.nlp import AzureUtils
print(autohf.jobid_config)
azure_utils = AzureUtils(root_log_path="logs_test/", autohf=autohf)
azure_utils.write_autohf_output(valid_metric=validation_metric,
predictions=predictions,
duration=GST)
print(validation_metric)
```
The validation F1/accuracy we got was 92.4/89.5. After the above steps, you will find a .zip file for the predictions under data/result/. Submit the .zip file to the glue website. The test F1/accuracy we got was 90.4/86.7. As an example, we only run the experiment one time, but in general, we should run the experiment multiple repetitions and report the averaged validation and test accuracy.
### Running Random Search
Next, we run random search with the same time budget as grid search:
```
def tune_hpo(time_budget, this_hpo_space):
autohf_settings = {
"resources_per_trial": {"gpu": 1, "cpu": 1},
"num_samples": -1,
"time_budget": time_budget,
"ckpt_per_epoch": 5,
"fp16": True,
"algo_mode": "hpo", # set the search algorithm mode to hpo
"algo_name": "rs",
"space_mode": "cus", # customized search space (this_hpo_space)
"hpo_space": this_hpo_space,
"transformers_verbose": transformers.logging.ERROR
}
validation_metric, analysis = autohf.fit(**autohf_settings)
predictions, test_metric = autohf.predict()
azure_utils = AzureUtils(root_log_path="logs_test/", autohf=autohf)
azure_utils.write_autohf_output(valid_metric=validation_metric,
predictions=predictions,
duration=GST)
print(validation_metric)
hpo_space_full = {
"learning_rate": {"l": 3e-5, "u": 1.5e-4, "space": "log"},
"warmup_ratio": {"l": 0, "u": 0.2, "space": "linear"},
"num_train_epochs": [3],
"per_device_train_batch_size": [16, 32, 64],
"weight_decay": {"l": 0.0, "u": 0.3, "space": "linear"},
"attention_probs_dropout_prob": {"l": 0, "u": 0.2, "space": "linear"},
"hidden_dropout_prob": {"l": 0, "u": 0.2, "space": "linear"},
}
tune_hpo(GST, hpo_space_full)
```
The validation F1/accuracy we got was 93.5/90.9. Similarly, we can submit the .zip file to the glue website. The test F1/accuaracy we got was 81.6/70.2.
## 3. Troubleshooting HPO Failures
Since the validation accuracy is larger than grid search while the test accuracy is smaller, HPO has overfitting. We reduce the search space:
```
hpo_space_fixwr = {
"learning_rate": {"l": 3e-5, "u": 1.5e-4, "space": "log"},
"warmup_ratio": [0.1],
"num_train_epochs": [3],
"per_device_train_batch_size": [16, 32, 64],
"weight_decay": {"l": 0.0, "u": 0.3, "space": "linear"},
"attention_probs_dropout_prob": {"l": 0, "u": 0.2, "space": "linear"},
"hidden_dropout_prob": {"l": 0, "u": 0.2, "space": "linear"},
}
tune_hpo(GST, hpo_space_fixwr)
```
The validation F1/accuracy we got was 92.6/89.7, the test F1/accuracy was 85.9/78.7, therefore overfitting still exists and we further reduce the space:
```
hpo_space_min = {
"learning_rate": {"l": 3e-5, "u": 1.5e-4, "space": "log"},
"warmup_ratio": [0.1],
"num_train_epochs": [3],
"per_device_train_batch_size": [16, 32, 64],
"weight_decay": [0.0],
"attention_probs_dropout_prob": [0.1],
"hidden_dropout_prob": [0.1],
}
tune_hpo(GST, hpo_space_min)
```
The validation F1/accuracy we got was 90.4/86.7, test F1/accuracy was 83.0/73.0. Since the validation accuracy is below grid search, we increase the budget to 4 * GST:
```
hpo_space_min = {
"learning_rate": {"l": 3e-5, "u": 1.5e-4, "space": "log"},
"warmup_ratio": [0.1],
"num_train_epochs": [3],
"per_device_train_batch_size": [32],
"weight_decay": [0.0],
"attention_probs_dropout_prob": [0.1],
"hidden_dropout_prob": [0.1],
}
tune_hpo(4 * GST, hpo_space_min)
```
The validation F1/accuracy we got was 93.5/91.1, where the accuracy outperforms grid search. The test F1/accuracy was 90.1/86.1. As a result, random search with 4*GST and the minimum space overfits. We stop the troubleshooting process because the search space cannot be further reduced.
| true |
code
| 0.648578 | null | null | null | null |
|
# Cell
Problem:
In GDS format
- each cell must have a unique name. Ideally the name is also consitent from different run times, in case you want to merge GDS files that were created at different times or computers.
- two cells stored in the GDS file cannot have the same name. Ideally they will be references to the same Cell. See `References tutorial`. That way we only have to store that cell in memory once and all the references are just pointers to that cell.
- GDS cells info:
- `changed` used to create the cell
- `default` in function signature
- `full` full settings
- name
- function_name
- module
- child: (if any)
- simulation, testing, data analysis, derived properties (for example path length of the bend) ...
Solution: The decorator `@gf.cell` addresses all these issues:
1. Gives the cell a unique name depending on the parameters that you pass to it.
2. Creates a cache of cells where we use the cell name as the key. The first time the function runs, the cache stores the component, so the second time, you get the component directly from the cache, so you don't create the same cell twice.
For creating new Components you need to create them inside a function, and to make sure that the component gets a good name you just need to add the `@cell` decorator
Lets see how it works
```
import gdsfactory as gf
@gf.cell
def wg(length=10, width=1):
print("BUILDING waveguide")
c = gf.Component()
c.add_polygon([(0, 0), (length, 0), (length, width), (0, width)], layer=(1, 0))
c.add_port(name="o1", midpoint=[0, width / 2], width=width, orientation=180)
c.add_port(name="o2", midpoint=[length, width / 2], width=width, orientation=0)
return c
```
See how the cells get the name from the parameters that you pass them
```
c = wg()
print(c)
# The second time you will get this cell from the cache
c = wg()
print(c)
# If you call the cell with different parameters, the cell will get a different name
c = wg(width=0.5)
print(c)
c.info.changed
c.info.full
c.info.default
c.pprint()
```
thanks to `gf.cell` you can also add any metadata `info` relevant to the cell
```
c = wg(length=3, info=dict(polarization="te", wavelength=1.55))
c.pprint()
print(c.info.wavelength)
```
## Metadata
Together with the GDS files that you send to the foundry you can also store some metadata in YAML for each cell containing all the settings that we used to build the GDS.
the metadata will consists of all the parameters that were passed to the component function as well as derived properties
- info: includes all component metadata
- derived properties
- external metadata (test_protocol, docs, ...)
- simulation_settings
- function_name
- name: for the component
- name_long: for the component
- full: full list of settings
- changed: changed settings
- default: includes the default signature of the component
- ports: port name, width, orientation
How can you have add two different references to a cell with the same parameters?
```
import gdsfactory as gf
c = gf.Component("problem")
R1 = gf.components.rectangle(
size=(4, 2), layer=(0, 0)
) # Creates a rectangle (same Unique ID uid)
R2 = gf.components.rectangle(size=(4, 2), layer=(0, 0))
# Try Create a new rectangle that we want to change (but has the same name so we will get R1 from the cache)
r1r = c << R1 # Add the first rectangle to c
r2r = c << R2 # Add the second rectangle to c
r2r.move((4, 2))
c
print(R1 == R2)
print(R1)
print(R2)
# lets do it cleaner with references
import gdsfactory as gf
c = gf.Component("solution")
R = gf.components.rectangle(size=(4, 2), layer=(0, 0))
r1 = c << R # Add the first rectangle reference to c
r2 = c << R # Add the second rectangle reference to c
r2.rotate(45)
c
import gdsfactory as gf
c = gf.components.straight()
c.show()
c.plot()
```
We can even show ports of all references with `component.show(show_subports=True)`
```
c = gf.components.mzi_phase_shifter(length_x=50)
c
```
## Cache
To avoid that 2 exact cells are not references of the same cell the `cell` decorator has a
cache where if a component has already been built it will return the component
from the cache
```
@gf.cell
def wg(length=10, width=1):
c = gf.Component()
c.add_polygon([(0, 0), (length, 0), (length, width), (0, width)], layer=(1, 0))
print("BUILDING waveguide")
return c
gf.clear_cache()
wg1 = wg() # cell builds a straight
print(wg1)
wg2 = wg()
# cell returns the same straight as before without having to run the function
print(wg2) # notice that they have the same uuid (unique identifier)
wg2.plot()
from gdsfactory.cell import print_cache
```
Lets say that you change the code of the straight function in a jupyter notebook like this one. (I mostly use Vim/VsCode/Pycharm for creating new cells in python)
```
print_cache()
wg3 = wg()
wg4 = wg(length=11)
print_cache()
gf.clear_cache()
```
To enable nice notebook tutorials, every time we show a cell in Matplotlib or Klayout, you can clear the cache,
in case you want to develop cells in jupyter notebooks or an IPython kernel
```
print_cache() # cache is now empty
```
## Validate argument types
By default, also `@cell` validates arguments based on their type annotations.
To make sure you pass the correct arguments to the cell it runs a validator that checks the type annotations for the function.
For example this will be correct
```python
import gdsfactory as gf
@gf.cell
def straigth_waveguide(length:float):
return gf.components.straight(length=length)
component = straigth_waveguide(length=3)
```
While this will raise an error, because you are passing a length that is a string, so it cannot convert it to a float
```python
import gdsfactory as gf
@gf.cell
def straigth_waveguide(length:float):
return gf.components.straight(length=length)
component = straigth_waveguide(length='long')
```
by default `@cell` validates all arguments using [pydantic](https://pydantic-docs.helpmanual.io/usage/validation_decorator/#argument-types)
```
@gf.cell
def straigth_waveguide(length: float):
print(type(length))
return gf.components.straight(length=length)
# It will also convert an `int` to a `float`
straigth_waveguide(3)
```
| true |
code
| 0.469946 | null | null | null | null |
|
## Matching catalogues to the VAST Pilot Survey
This notebook gives an example of how to use vast-tools in a notebook environment to perform a crossmatch between a catalogue and the VAST Pilot Survey.
**Note** The settings and filters applied in this notebook, while sensible, are somewhat generic - always consider your science goals on what filters you want to make!
It is **highly recommended** that results from the VAST Pipeline are used and this is what will be primarily covered in this example. It is possible to run a search just using vast-tools but the results are nowhere near as rich as the pipeline - this is covered at the of this document.
### The VAST Pipeline
The pipeline hosted on the Nimbus server will contain the pipeline run for the full pilot survey. For a complete demo of what can be done with the vast-tools `Pipeline` class see the `vast-pipeline-example.ipynb` example notebook.
### The Imports
Below are the imports required for this example. The main imports required from vast-tools are the Pipeline and VASTMOCS objects. The Query object is for the vast-tools query option that is shown at the end of this notebook. Astropy objects are also imported as they are critical to perfoming the crossmatch.
```
from vasttools.moc import VASTMOCS
from vasttools.pipeline import Pipeline
from vasttools.query import Query
from mocpy import World2ScreenMPL
import matplotlib.pyplot as plt
from astropy import units as u
from astropy.coordinates import Angle, SkyCoord
```
### Catalogue selection
For this example we will be using the `Quasars and Active Galactic Nuclei (13th Ed.) (Veron+ 2010)` catalogue, which has the Vizier ID of `VII/258`.
_**Note:** Of course your catalogue doesn't have to come from Vizier. If you have a `csv` or `FITS` file then simply load this data into a DataFrame, create a SkyCoord object and you'll be good to go._
To start our search, the first question we want to answer is:
*What sources from the catalogue are in the VAST Pilot Survey footprint?*
This can be efficiently answered by using the `query_vizier_vast_pilot()` method in VASTMOCS.
First we initialise the VASTMOCS object:
```
mocs = VASTMOCS()
```
We then use the query vizier method to obtain all the sources from the Veron catalogue which are contained within the footprint. It will likely take a bit of time to complete.
```
veron_vast_sources = mocs.query_vizier_vast_pilot('VII/258', max_rows=200000)
veron_vast_sources
```
We see that 44,704 sources are within the VAST Pilot Survey footprint.
_**Tip:** The table returned above is an astropy.table. This can be converted to pandas by using `veron_vast_sources = veron_vast_sources.to_pandas()`._
These can be plotted along with the VAST Pilot Survey footprint using the MOC. See the vast-mocs-example notebook for more on using MOCS and the `Wordl2ScreenMPL` method.
```
from astropy.visualization.wcsaxes.frame import EllipticalFrame
fig = plt.figure(figsize=(16,8))
# Load the Epoch 1 MOC file to use
epoch1_moc = mocs.load_pilot_epoch_moc('1')
#
with World2ScreenMPL(
fig,
fov=320 * u.deg,
center=SkyCoord(0, 0, unit='deg', frame='icrs'),
coordsys="icrs",
rotation=Angle(0, u.degree),
) as wcs:
ax = fig.add_subplot(111, projection=wcs, frame_class=EllipticalFrame)
ax.set_title("Veron Catalogue Sources in the VAST Pilot Survey")
ax.grid(color="black", linestyle="dotted")
epoch1_moc.fill(ax=ax, wcs=wcs, alpha=0.5, fill=True, linewidth=0, color="#00bb00")
epoch1_moc.border(ax=ax, wcs=wcs, alpha=0.5, color="black")
ax.scatter(
veron_vast_sources['_RAJ2000'],
veron_vast_sources['_DEJ2000'],
transform=ax.get_transform('world'),
zorder=10,
s=3
)
fig
```
### Loading the VAST Pipeline Data
Now the results of the VAST Pipeline need to be loaded. This example will not give full details of the Pipeline class, but please refer to the `vast-pipeline-example.ipynb` example notebook for a full example and description.
We'll be using the full VAST Pilot Survey pipeline containing epochs 0–13 (a test version called `tiles_corrected`).
```
# below I suppress DeprecationWarnings due to ipykernel bug and an astropy warning due to FITS header warnings.
import warnings
from astropy.utils.exceptions import AstropyWarning
warnings.simplefilter('ignore', category=AstropyWarning)
warnings.filterwarnings("ignore", category=DeprecationWarning)
# define pipeline object
pipe = Pipeline()
# load the run
pipe_run = pipe.load_run('tiles_corrected')
```
We now have access to the unique sources found by the pipeline:
```
pipe_run.sources.head()
```
### Performing the Crossmatch
The crossmatch can be performed using the astropy `match_to_catalog_sky` function. The first step is to create the sky coord objects for each catalogue. First the Veron catalog which was already obtained above:
```
# Unfortunately we cannot use guess_from_table for the Vizier results, so we construct manually
veron_skycoord = SkyCoord(veron_vast_sources['_RAJ2000'], veron_vast_sources['_DEJ2000'], unit=(u.deg, u.deg))
veron_names = veron_vast_sources['Name'].tolist()
```
and then by default the pipeline run object has the default sources saved as a sky coord object as `pipe_run.sources_skycoord`:
```
pipe_run.sources_skycoord
```
Now the crossmatching can be performed. See https://docs.astropy.org/en/stable/coordinates/matchsep.html#astropy-coordinates-matching for details on the astropy functions and outputs.
```
idx, d2d, d3d = veron_skycoord.match_to_catalog_sky(pipe_run.sources_skycoord)
radius_limit = 15 * u.arcsec
(d2d <= radius_limit).sum()
```
From above we can see that 5048 Veron objects have a match to the pipeline sources. If you wish you could merge the results together:
```
# Convert Veron to pandas first
veron_vast_sources_pd = veron_vast_sources.to_pandas()
# Create a d2d mask
d2d_mask = d2d <= radius_limit
# Select the crossmatches less than 15 arcsec
veron_crossmatch_result_15asec = veron_vast_sources_pd.loc[d2d_mask].copy()
# Append the id and distance of the VAST crossmatch to the veron sources
veron_crossmatch_result_15asec['vast_xmatch_id'] = pipe_run.sources.iloc[idx[d2d_mask]].index.values
veron_crossmatch_result_15asec['vast_xmatch_d2d_asec'] = d2d[d2d_mask].arcsec
# Join the result
veron_crossmatch_result_15asec = veron_crossmatch_result_15asec.merge(pipe_run.sources, how='left', left_on='vast_xmatch_id', right_index=True, suffixes=("_veron", "_vast"))
veron_crossmatch_result_15asec
```
With the crossmatches in hand you can now start to do any kind of analysis you wish to perform. For example we can perform a quick check to see if the pipeline has picked out any of these sources as having significant two-epoch variability:
```
veron_crossmatch_result_15asec[veron_crossmatch_result_15asec['m_abs_significant_max_peak'] > 0.00]
```
And remember you can use the vast-toools source tools to view any source as in the other example notebooks:
```
# Get the first VAST source above from the table above
first_source_id = veron_crossmatch_result_15asec[veron_crossmatch_result_15asec['m_abs_significant_max_peak'] > 0.00].iloc[0].vast_xmatch_id
first_source = pipe_run.get_source(first_source_id)
first_source.plot_lightcurve(min_points=1)
first_source.show_all_png_cutouts(columns=5, figsize=(12,7), size=Angle(2. * u.arcmin))
```
### Filtering the Pipeline Sources (Optional)
The example above has used all the sources from the pipeline results, but these may need to be filtered further to improve results. For example Below is an example of how to filter the sources.
```
my_query_string = (
"n_measurements >= 3 "
"& n_selavy >= 2 "
"& n_neighbour_dist > 1./60. "
"& 0.8 < avg_compactness < 1.4 "
"& n_relations == 0 "
"& max_snr > 7.0"
)
pipe_run_filtered_sources = pipe_run.sources.query(my_query_string)
pipe_run_filtered_sources
```
You can either:
* apply this to the crossmatch results above, or
* substitute `pipe_run_filtered_sources` into the complete crossmatch process above in the place of `my_run.sources` (you need to create a new SkyCoord object first).
```
pipe_run_filtered_sources_skycoord = pipe_run.get_sources_skycoord(user_sources=pipe_run_filtered_sources)
pipe_run_filtered_sources_skycoord
```
### Finding All Crossmatches Between Sources
The crossmatch above only finds the nearest neighbour to the sources in your catalogue. Astropy also offers the functionality to find all matches between objects within a defined radius. See https://docs.astropy.org/en/stable/coordinates/matchsep.html#searching-around-coordinates for full details. This is done by performing the below, using the 15 arcsec radius:
```
idx_vast, idx_veron, d2d, d3d = veron_skycoord.search_around_sky(pipe_run.sources_skycoord, 15 * u.arcsec)
```
A merged dataframe of this crossmatch can be made like that below. Note there are multiple matches to sources so this will generate duplicate sources within the dataframe.
```
# Create a subset dataframe of the Veron sources with a match
veron_search_around_results_15asec = veron_vast_sources_pd.iloc[idx_veron].copy()
# Add the VAST d2d and match id columns
veron_search_around_results_15asec['vast_xmatch_d2d_asec'] = d2d.arcsec
veron_search_around_results_15asec['vast_xmatch_id'] = pipe_run.sources.iloc[idx_vast].index.values
# Perform the merge
veron_search_around_results_15asec = veron_search_around_results_15asec.merge(pipe_run.sources, how='left', left_on='vast_xmatch_id', right_index=True, suffixes=("_veron", "_vast"))
veron_search_around_results_15asec
```
This is the end of the example of performing a catalogue crossmatch using the VAST Pipeline. The information below this point is about using the vast-tools query method to find sources from the pilot survey if a pipeline run is not available. A pipeline run should be used whenever possible due to the superior quality of data it generates.
## Find VAST Matches Using VAST Tools
If a pipeline run isn't available you can use VAST Tools to match to the **VAST Pilot Survey only**.
Here the same Veron dataframe that was created in the pipeline section above is used.
The first step is to construct a Query to see how many sources have matches to selavy componentst in the VAST Pilot Survey. In the Query definition below we use the `matches_only` argument. This means that only those sources that have an actual match are returned. I also explicitly do not select RACS to search here, I'm only interested in the VAST Pilot data, so I select `all-vast`. Note you must pre-create the output directory for the query if you intend to use it.
```
veron_query = Query(
coords=veron_skycoord,
source_names=veron_names,
epochs='all-vast',
max_sep=1.5,
crossmatch_radius=10.0,
base_folder='/data/vast-survey/pilot/',
matches_only=True,
no_rms=True,
output_dir='veron-vast-crossmatching',
)
```
And run `find_sources` - again a warning that this will take a little while to process.
```
veron_query.find_sources()
```
We can check the results attribute to see how many sources return a match.
```
veron_query.results.shape[0]
```
### Using the results
4664 sources have returned a match in the VAST Pilot Survey in any epoch.
We can create new skycoord and name objects ready for a new query:
```
matches_mask = [i in (veron_query.results) for i in veron_vast_sources['Name']]
matched_names = veron_vast_sources['Name'][matches_mask].tolist()
matched_skycoords = veron_skycoord[matches_mask]
```
Or loop through and save all the measurements for each source.
```
# for i in veron_query.results:
# i.write_measurements()
```
While you can explore the sources as normal, for example
```
my_source = veron_query.results['1AXG J134412+0016']
lc = my_source.plot_lightcurve()
lc
cutout = my_source.show_png_cutout('1')
cutout
```
it's not recommended to produce cut outs for all sources in the notebook as this will start to take a lot of memory and be quite slow. If you'd like to do this then please use the `find_sources.py` script.
### VAST Tools Variability
Unlike the Pipeline, the sources returned using this method do not contain any of the caluclated metrics. However, you can also perform some rudimentary variablility analysis on the results if you wish.
I would recommened using the VAST Pipeline if possible for this kind of analysis as the associations will be much better and the you'll get a lot more information, but nevertheless this is an example of what you **can** do with the data from vast-tools.
In the code below I create a dataframe from the query results (which is a pandas series) and assign it to `variables_df` and define a function that returns the eta and V metrics for each source when passed through `.apply()`. These are then assigned to new `eta` and `v` columns in the `variables_df` dataframe.
```
import pandas as pd
def get_variable_metrics(row):
"""
Function to return the eta and v metrics using apply.
"""
return row['object'].calc_eta_and_v_metrics()
# create the variables_df dataframe, rename the column holding the objects as 'object'
variables_df = pd.DataFrame(veron_query.results).rename(columns={'name':'object'})
# obtain the metrics
variables_df[['eta', 'v']] = variables_df.apply(get_variable_metrics, result_type='expand', axis=1)
```
We can then, for example, plot the log eta distribution, making sure we choose sources that have more than 2 detections.
```
%matplotlib inline
mask = [i.detections > 2 for i in variables_df['object']]
import numpy as np
np.log10(variables_df.eta[mask]).hist(bins=100)
plt.show()
```
You could then do the same for `v` and start to fit Gaussians to the distributions and select candidates.
**Note** for large queries it is recommened to use the script version of `find_sources.py` to get cutouts for **all** results.
| true |
code
| 0.519156 | null | null | null | null |
|
# Name
Batch prediction using Cloud Machine Learning Engine
# Label
Cloud Storage, Cloud ML Engine, Kubeflow, Pipeline, Component
# Summary
A Kubeflow Pipeline component to submit a batch prediction job against a deployed model on Cloud ML Engine.
# Details
## Intended use
Use the component to run a batch prediction job against a deployed model on Cloud ML Engine. The prediction output is stored in a Cloud Storage bucket.
## Runtime arguments
| Argument | Description | Optional | Data type | Accepted values | Default |
|--------------------|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|----------|--------------|-----------------|---------|
| project_id | The ID of the Google Cloud Platform (GCP) project of the job. | No | GCPProjectID | | |
| model_path | The path to the model. It can be one of the following:<br/> <ul> <li>projects/[PROJECT_ID]/models/[MODEL_ID]</li> <li>projects/[PROJECT_ID]/models/[MODEL_ID]/versions/[VERSION_ID]</li> <li>The path to a Cloud Storage location containing a model file.</li> </ul> | No | GCSPath | | |
| input_paths | The path to the Cloud Storage location containing the input data files. It can contain wildcards, for example, `gs://foo/*.csv` | No | List | GCSPath | |
| input_data_format | The format of the input data files. See [REST Resource: projects.jobs](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#DataFormat) for more details. | No | String | DataFormat | |
| output_path | The path to the Cloud Storage location for the output data. | No | GCSPath | | |
| region | The Compute Engine region where the prediction job is run. | No | GCPRegion | | |
| output_data_format | The format of the output data files. See [REST Resource: projects.jobs](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#DataFormat) for more details. | Yes | String | DataFormat | JSON |
| prediction_input | The JSON input parameters to create a prediction job. See [PredictionInput](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#PredictionInput) for more information. | Yes | Dict | | None |
| job_id_prefix | The prefix of the generated job id. | Yes | String | | None |
| wait_interval | The number of seconds to wait in case the operation has a long run time. | Yes | | | 30 |
## Input data schema
The component accepts the following as input:
* A trained model: It can be a model file in Cloud Storage, a deployed model, or a version in Cloud ML Engine. Specify the path to the model in the `model_path `runtime argument.
* Input data: The data used to make predictions against the trained model. The data can be in [multiple formats](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#DataFormat). The data path is specified by `input_paths` and the format is specified by `input_data_format`.
## Output
Name | Description | Type
:--- | :---------- | :---
job_id | The ID of the created batch job. | String
output_path | The output path of the batch prediction job | GCSPath
## Cautions & requirements
To use the component, you must:
* Set up a cloud environment by following this [guide](https://cloud.google.com/ml-engine/docs/tensorflow/getting-started-training-prediction#setup).
* The component can authenticate to GCP. Refer to [Authenticating Pipelines to GCP](https://www.kubeflow.org/docs/gke/authentication-pipelines/) for details.
* Grant the following types of access to the Kubeflow user service account:
* Read access to the Cloud Storage buckets which contains the input data.
* Write access to the Cloud Storage bucket of the output directory.
## Detailed description
Follow these steps to use the component in a pipeline:
1. Install the Kubeflow Pipeline SDK:
```
%%capture --no-stderr
!pip3 install kfp --upgrade
```
2. Load the component using KFP SDK
```
import kfp.components as comp
mlengine_batch_predict_op = comp.load_component_from_url(
'https://raw.githubusercontent.com/kubeflow/pipelines/1.5.0-rc.0/components/gcp/ml_engine/batch_predict/component.yaml')
help(mlengine_batch_predict_op)
```
### Sample Code
Note: The following sample code works in an IPython notebook or directly in Python code.
In this sample, you batch predict against a pre-built trained model from `gs://ml-pipeline-playground/samples/ml_engine/census/trained_model/` and use the test data from `gs://ml-pipeline-playground/samples/ml_engine/census/test.json`.
#### Inspect the test data
```
!gsutil cat gs://ml-pipeline-playground/samples/ml_engine/census/test.json
```
#### Set sample parameters
```
# Required Parameters
PROJECT_ID = '<Please put your project ID here>'
GCS_WORKING_DIR = 'gs://<Please put your GCS path here>' # No ending slash
# Optional Parameters
EXPERIMENT_NAME = 'CLOUDML - Batch Predict'
OUTPUT_GCS_PATH = GCS_WORKING_DIR + '/batch_predict/output/'
```
#### Example pipeline that uses the component
```
import kfp.dsl as dsl
import json
@dsl.pipeline(
name='CloudML batch predict pipeline',
description='CloudML batch predict pipeline'
)
def pipeline(
project_id = PROJECT_ID,
model_path = 'gs://ml-pipeline-playground/samples/ml_engine/census/trained_model/',
input_paths = '["gs://ml-pipeline-playground/samples/ml_engine/census/test.json"]',
input_data_format = 'JSON',
output_path = OUTPUT_GCS_PATH,
region = 'us-central1',
output_data_format='',
prediction_input = json.dumps({
'runtimeVersion': '1.10'
}),
job_id_prefix='',
wait_interval='30'):
mlengine_batch_predict_op(
project_id=project_id,
model_path=model_path,
input_paths=input_paths,
input_data_format=input_data_format,
output_path=output_path,
region=region,
output_data_format=output_data_format,
prediction_input=prediction_input,
job_id_prefix=job_id_prefix,
wait_interval=wait_interval)
```
#### Compile the pipeline
```
pipeline_func = pipeline
pipeline_filename = pipeline_func.__name__ + '.zip'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
```
#### Submit the pipeline for execution
```
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
```
#### Inspect prediction results
```
OUTPUT_FILES_PATTERN = OUTPUT_GCS_PATH + '*'
!gsutil cat OUTPUT_FILES_PATTERN
```
## References
* [Component python code](https://github.com/kubeflow/pipelines/blob/master/components/gcp/container/component_sdk/python/kfp_component/google/ml_engine/_batch_predict.py)
* [Component docker file](https://github.com/kubeflow/pipelines/blob/master/components/gcp/container/Dockerfile)
* [Sample notebook](https://github.com/kubeflow/pipelines/blob/master/components/gcp/ml_engine/batch_predict/sample.ipynb)
* [Cloud Machine Learning Engine job REST API](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs)
## License
By deploying or using this software you agree to comply with the [AI Hub Terms of Service](https://aihub.cloud.google.com/u/0/aihub-tos) and the [Google APIs Terms of Service](https://developers.google.com/terms/). To the extent of a direct conflict of terms, the AI Hub Terms of Service will control.
| true |
code
| 0.553023 | null | null | null | null |
|
# Desafio 4
Neste desafio, vamos praticar um pouco sobre testes de hipóteses. Utilizaremos o _data set_ [2016 Olympics in Rio de Janeiro](https://www.kaggle.com/rio2016/olympic-games/), que contém dados sobre os atletas das Olimpíadas de 2016 no Rio de Janeiro.
Esse _data set_ conta com informações gerais sobre 11538 atletas como nome, nacionalidade, altura, peso e esporte praticado. Estaremos especialmente interessados nas variáveis numéricas altura (`height`) e peso (`weight`). As análises feitas aqui são parte de uma Análise Exploratória de Dados (EDA).
> Obs.: Por favor, não modifique o nome das funções de resposta.
## _Setup_ geral
```
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as sct
import seaborn as sns
import statsmodels.api as sm
#%matplotlib inline
from IPython.core.pylabtools import figsize
figsize(12, 8)
sns.set()
athletes = pd.read_csv("athletes.csv")
athletes.info()
athletes.head()
athletes[['height','weight']].describe()
athletes[['height','weight']].hist()
def get_sample(df, col_name, n=100, seed=42):
"""Get a sample from a column of a dataframe.
It drops any numpy.nan entries before sampling. The sampling
is performed without replacement.
Example of numpydoc for those who haven't seen yet.
Parameters
----------
df : pandas.DataFrame
Source dataframe.
col_name : str
Name of the column to be sampled.
n : int
Sample size. Default is 100.
seed : int
Random seed. Default is 42.
Returns
-------
pandas.Series
Sample of size n from dataframe's column.
"""
np.random.seed(seed)
random_idx = np.random.choice(df[col_name].dropna().index, size=n, replace=False) #retorna uma array com index das colunas
return df.loc[random_idx, col_name] #retorna uma series com index e valor da coluna
```
## Inicia sua análise a partir daqui
```
# Sua análise começa aqui.
```
## Questão 1
Considerando uma amostra de tamanho 3000 da coluna `height` obtida com a função `get_sample()`, execute o teste de normalidade de Shapiro-Wilk com a função `scipy.stats.shapiro()`. Podemos afirmar que as alturas são normalmente distribuídas com base nesse teste (ao nível de significância de 5%)? Responda com um boolean (`True` ou `False`).
```
def q1():
amostra_q1 = get_sample(athletes,'height', n=3000, seed=42)
stat, p = sct.shapiro(amostra_q1)
print('stat= {}, p={}'.format(stat,p))
return bool(p> 0.05)
q1()
```
__Para refletir__:
* Plote o histograma dessa variável (com, por exemplo, `bins=25`). A forma do gráfico e o resultado do teste são condizentes? Por que?
* Plote o qq-plot para essa variável e a analise.
* Existe algum nível de significância razoável que nos dê outro resultado no teste? (Não faça isso na prática. Isso é chamado _p-value hacking_, e não é legal).
```
amostra_q1 = get_sample(athletes,'height', n=3000, seed=42)
sns.distplot(amostra_q1, bins=25, hist_kws={"density": True})
plt.show ()
sm.qqplot(amostra_q1, fit=True, line="45")
plt.show ()
amostra_q1 = get_sample(athletes,'height', n=3000, seed=42)
stat, p = sct.shapiro(amostra_q1)
p > 0.0000001
```
## Questão 2
Repita o mesmo procedimento acima, mas agora utilizando o teste de normalidade de Jarque-Bera através da função `scipy.stats.jarque_bera()`. Agora podemos afirmar que as alturas são normalmente distribuídas (ao nível de significância de 5%)? Responda com um boolean (`True` ou `False`).
```
def q2():
amostra_q2 = get_sample(athletes,'height', n=3000, seed=42)
stat, p = sct.jarque_bera(amostra_q2)
print('stat= {}, p={}'.format(stat,p))
return bool(p> 0.05)
q2()
```
__Para refletir__:
* Esse resultado faz sentido?
```
amostra_q2 = get_sample(athletes,'height', n=3000, seed=42)
sm.qqplot(amostra_q2, fit=True, line="45")
plt.show ()
```
## Questão 3
Considerando agora uma amostra de tamanho 3000 da coluna `weight` obtida com a função `get_sample()`. Faça o teste de normalidade de D'Agostino-Pearson utilizando a função `scipy.stats.normaltest()`. Podemos afirmar que os pesos vêm de uma distribuição normal ao nível de significância de 5%? Responda com um boolean (`True` ou `False`).
```
def q3():
amostra_q3 = get_sample(athletes,'weight', n=3000, seed=42)
stat, p = sct.normaltest(amostra_q3)
print('stat= {}, p={}'.format(stat,p))
return bool(p> 0.05)
q3()
```
__Para refletir__:
* Plote o histograma dessa variável (com, por exemplo, `bins=25`). A forma do gráfico e o resultado do teste são condizentes? Por que?
* Um _box plot_ também poderia ajudar a entender a resposta.
```
amostra_q3 = get_sample(athletes,'weight', n=3000, seed=42)
sns.distplot(amostra_q3, bins=25, hist_kws={"density": True})
plt.show ()
sns.boxplot(data = amostra_q3)
```
## Questão 4
Realize uma transformação logarítmica em na amostra de `weight` da questão 3 e repita o mesmo procedimento. Podemos afirmar a normalidade da variável transformada ao nível de significância de 5%? Responda com um boolean (`True` ou `False`).
```
def q4():
amostra_q4 = get_sample(athletes,'weight', n=3000, seed=42)
amostra_q4_transformada = np.log(amostra_q4)
stat, p = sct.normaltest(amostra_q4_transformada)
print('stat= {}, p={}'.format(stat,p))
return bool(p> 0.05)
q4()
```
__Para refletir__:
* Plote o histograma dessa variável (com, por exemplo, `bins=25`). A forma do gráfico e o resultado do teste são condizentes? Por que?
* Você esperava um resultado diferente agora?
```
amostra_q4 = get_sample(athletes,'weight', n=3000, seed=42)
amostra_q4_transformada = np.log(amostra_q4)
sns.distplot(amostra_q4_transformada, bins=25, hist_kws={"density": True})
plt.show ()
sns.boxplot(data = amostra_q4_transformada)
```
> __Para as questão 5 6 e 7 a seguir considere todos testes efetuados ao nível de significância de 5%__.
## Questão 5
Obtenha todos atletas brasileiros, norte-americanos e canadenses em `DataFrame`s chamados `bra`, `usa` e `can`,respectivamente. Realize um teste de hipóteses para comparação das médias das alturas (`height`) para amostras independentes e variâncias diferentes com a função `scipy.stats.ttest_ind()` entre `bra` e `usa`. Podemos afirmar que as médias são estatisticamente iguais? Responda com um boolean (`True` ou `False`).
```
athletes.columns
athletes[(athletes.nationality == 'BRA') | (athletes.nationality == 'USA') | (athletes.nationality == 'CAN')]
bra = athletes[athletes.nationality == 'BRA']
usa = athletes[athletes.nationality == 'USA']
can = athletes[athletes.nationality == 'CAN']
bra['height'].describe()
bra.isna().sum()
usa['height'].describe()
usa.isna().sum()
can['height'].describe()
can.isna().sum()
def q5():
stat, p = sct.ttest_ind(bra['height'], usa['height'], equal_var = False, nan_policy = 'omit') #False: se falso, execute o teste t de Welch, que não assume igual variação populaciona
print('stat= {}, p={}'.format(stat,p))
return bool(p> 0.05)
q5()
sns.distplot(bra['height'], bins=25, hist=False, rug=True, label='BRA')
sns.distplot(usa['height'], bins=25, hist=False, rug=True, label='USA')
```
## Questão 6
Repita o procedimento da questão 5, mas agora entre as alturas de `bra` e `can`. Podemos afimar agora que as médias são estatisticamente iguais? Reponda com um boolean (`True` ou `False`).
```
def q6():
stat, p = sct.ttest_ind(bra['height'], can['height'], equal_var = False, nan_policy = 'omit') #False: se falso, execute o teste t de Welch, que não assume igual variação populaciona
print('stat= {}, p={}'.format(stat,p))
return bool(p> 0.05)
q6()
sns.distplot(bra['height'], bins=25, hist=False, rug=True, label='BRA')
sns.distplot(can['height'], bins=25, hist=False, rug=True, label='CAN')
```
## Questão 7
Repita o procedimento da questão 6, mas agora entre as alturas de `usa` e `can`. Qual o valor do p-valor retornado? Responda como um único escalar arredondado para oito casas decimais.
```
def q7():
stat, p = sct.ttest_ind(usa['height'], can['height'], equal_var = False, nan_policy = 'omit') #False: se falso, execute o teste t de Welch, que não assume igual variação populaciona
print('stat= {}, p={}'.format(stat,p))
if p > 0.05:
print('Probably the same distribution')
else:
print('Probably different distributions')
return float(np.round(p, 8))
q7()
```
__Para refletir__:
* O resultado faz sentido?
* Você consegue interpretar esse p-valor?
* Você consegue chegar a esse valor de p-valor a partir da variável de estatística?
```
stat, p = sct.ttest_ind(usa['height'], can['height'], equal_var = True, nan_policy = 'omit')
print('stat= {}, p={}'.format(stat,p))
#grau de liberdade para o teste t independente com variancias semelhantes: df = n1 + n2 - 2
gl = len(usa) + len(can) - 2
print(f"Graus de liberdade: {gl}")
q7_sf = sct.t.sf(stat, gl)*2 #Para Hipótese Bicaudal
print(q7_sf)
sns.distplot(usa['height'], bins=25, hist=False, rug=True, label='USA')
sns.distplot(can['height'], bins=25, hist=False, rug=True, label='CAN')
```
| true |
code
| 0.572065 | null | null | null | null |
|
# Amazon SageMaker で PyTorch の GNN を使ったノード分類を行う
このサンプルノートブックは、[PyTorch geometric のサンプルコード](https://pytorch-geometric.readthedocs.io/en/latest/notes/colabs.html)を参考にしました。
## Node Classification with Graph Neural Networks
[Previous: Introduction: Hands-on Graph Neural Networks](https://colab.research.google.com/drive/1h3-vJGRVloF5zStxL5I0rSy4ZUPNsjy8)
This tutorial will teach you how to apply **Graph Neural Networks (GNNs) to the task of node classification**.
Here, we are given the ground-truth labels of only a small subset of nodes, and want to infer the labels for all the remaining nodes (*transductive learning*).
To demonstrate, we make use of the `Cora` dataset, which is a **citation network** where nodes represent documents.
Each node is described by a 1433-dimensional bag-of-words feature vector.
Two documents are connected if there exists a citation link between them.
The task is to infer the category of each document (7 in total).
This dataset was first introduced by [Yang et al. (2016)](https://arxiv.org/abs/1603.08861) as one of the datasets of the `Planetoid` benchmark suite.
We again can make use [PyTorch Geometric](https://github.com/rusty1s/pytorch_geometric) for an easy access to this dataset via [`torch_geometric.datasets.Planetoid`](https://pytorch-geometric.readthedocs.io/en/latest/modules/datasets.html#torch_geometric.datasets.Planetoid):
## 準備
**このサンプルでは、カスタムコンテナを Amazon ECR に push する必要があります。**以下の操作でこのノートブックインスタンスで使用している IAM ロールに Amazon ECR にイメージを push するための権限を追加してください。
1. Amazon SageMaker コンソールからこのノートブックインスタンスの詳細画面を表示<br>(左側のメニューのインスタンス -> ノートブックインスタンス -> インスタンス名をクリック)
1. 「アクセス許可と暗号化」の「IAM ロール ARN」のリンクをクリック(IAM のコンソールに遷移します)
1. 「ポリシーをアタッチします」と書いてある青いボタンをクリック
1. 検索ボックスに ec2containerregistry と入力し AmazonEC2ContainerRegistryFullAccess のチェックボックスをチェックする
1. 「ポリシーのアタッチ」と書いてある青いボタンをクリック
以下のセルでは、Amazon SageMaker を使うためのセットアップを行います。ロールの情報、ノートブックインスタンスのリージョン、アカウントID などの情報を取得しています。
```
import boto3
import sys
import sagemaker
import numpy as np
from sagemaker import get_execution_role
role = get_execution_role()
region = boto3.session.Session().region_name
account_id = boto3.client('sts').get_caller_identity().get('Account')
session = sagemaker.Session()
bucket = session.default_bucket()
s3_output = session.default_bucket()
s3_prefix = 'gnn-byo'
!mkdir docker
!mkdir docker/processing
!mkdir docker/train
!mkdir docker/inference
%%writefile docker/processing/requirements.txt
boto3==1.17.35
torch-scatter -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
torch-sparse -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
torch-cluster -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
torch-spline-conv -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
torch-geometric==1.6.3
matplotlib==3.3.4
scikit-learn==0.24.1
!cp docker/processing/requirements.txt docker/train/requirements.txt
```
## Amazon SageMaker Experiments のセットアップ
Amazon SageMaker Experiments のライブラリをインストールします。
```
!{sys.executable} -m pip install sagemaker-experiments requests
```
前処理用、学習用の Expetiments を作成します。
```
from sagemaker.analytics import ExperimentAnalytics
from smexperiments.experiment import Experiment
from smexperiments.trial import Trial
from smexperiments.trial_component import TrialComponent
from smexperiments.tracker import Tracker
import time
gnn_experiment_preprocess = Experiment.create(
experiment_name=f"gnn-byo-preprocess-{int(time.time())}",
description="node classification using gnn (preprocess)",
sagemaker_boto_client=boto3.client('sagemaker'))
print(gnn_experiment_preprocess)
gnn_experiment_train = Experiment.create(
experiment_name=f"gnn-byo-train-{int(time.time())}",
description="node classification using gnn (train)",
sagemaker_boto_client=boto3.client('sagemaker'))
print(gnn_experiment_train)
```
このサンプルノートブックでは、データの前処理、前処理したデータを使ってモデルの学習、学習済みモデルを使ってバッチ推論、の順でおこないます。
これから 2種類のコンテナイメージを作成して Amazon ECR に push します。1つめのコンテナイメージはデータの前処理とバッチ推論で使用し、2つめのコンテナイメージはモデルの学習で使用します。
## データの前処理
データの前処理は Amazon SageMaker Processing の仕組みを使って行います。まずは前処理用のコンテナイメージを作成します。
```
ecr_repository = 'gnn-byo-proc'
tag = ':latest'
uri_suffix = 'amazonaws.com'
processing_repository_uri = '{}.dkr.ecr.{}.{}/{}'.format(account_id, region, uri_suffix, ecr_repository + tag)
%%writefile docker/processing/Dockerfile
FROM python:3.8-buster
WORKDIR /opt/app
RUN pip3 install torch==1.8.0
COPY requirements.txt /opt/app
RUN pip3 install -r requirements.txt
RUN pip3 install -U torch-sparse -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
RUN pip3 install jupyter
COPY . /opt/app
EXPOSE 8888
# jupyter notebook --allow-root --ip=* --no-browser -NotebookApp.token=''
```
上記 Dockerfile を使ってコンテナイメージをビルドし、Amazon ECR に push します。
```
# Create ECR repository and push docker image
!docker build -t $ecr_repository docker/processing
!$(aws ecr get-login --region $region --registry-ids $account_id --no-include-email)
!aws ecr create-repository --repository-name $ecr_repository
!docker tag {ecr_repository + tag} $processing_repository_uri
!docker push $processing_repository_uri
```
作成したイメージを使って ScriptProcessor を作成します。このとき、`instance_type` に `local` を設定するとローカルモードになり、ノートブックインスタンス上で Processing Job が実行されます。作成したコンテナイメージやスクリプトのデバッグをする際は、ローカルモードの利用がおすすめです。デバッグが完了したら、`instance_type` に インスタンスタイプを設定して Processing Job を実施します。
```
from sagemaker.processing import ScriptProcessor
script_processor = ScriptProcessor(command=['python3'],
image_uri=processing_repository_uri,
role=role,
sagemaker_session=session,
instance_count=1,
# instance_type='local')
instance_type='ml.c5.xlarge')
```
Processing Job で使用するスクリプトを作成します。前処理の内容を変更した場合は、前処理スクリプトを更新してから 2つしたのセル(script_processor.run)を再度実行すれば OK です。コンテナイメージの再作成は不要です。
```
%%writefile preprocessing.py
import sys
sys.path.append('/opt/app')
import boto3
from torch_geometric.transforms import NormalizeFeatures
from torch_geometric.datasets import Planetoid
import torch
import shutil
if __name__=='__main__':
aws_session = boto3.Session(profile_name=None)
dataset = Planetoid(root='data/Planetoid', name='Cora', transform=NormalizeFeatures())
print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')
data = dataset[0] # Get the first graph object.
print(data)
# Gather some statistics about the graph.
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
print(f'Number of training nodes: {data.train_mask.sum()}')
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}')
print(f'Contains isolated nodes: {data.contains_isolated_nodes()}')
print(f'Contains self-loops: {data.contains_self_loops()}')
print(f'Is undirected: {data.is_undirected()}')
# save to container directory for uploading to S3
import os
path = "./"
files = os.listdir(path)
print(files)
src = 'data/Planetoid/Cora'
dist = '/opt/ml/processing/output/Cora'
print(os.path.getsize(src))
import tarfile
# 圧縮
with tarfile.open('sample.tar.gz', 'w:gz') as t:
t.add(src)
files = os.listdir(path)
print(files)
shutil.copytree(src, dist)
from torch_geometric.io import read_planetoid_data
```
作成したスクリプトを使って `run` を実行して Processing Job を起動します。`run` の引数には以下を設定しています。
- code: 処理スクリプトのファイル名
- inputs: (入力データがある場合)入力データが保存されている Amazon S3 パスを `source` に、Processing 用インスタンスのどこに入力データをダウンロードするかを `destination` に設定します。今回はインターネット経由でデータをダウンロードするため使用しません。
- outputs: 出力データを保存する Processing 用インスタンスのパスを `source` で指定し、そこに処理済みのデータなどを保存しておくと、`destination` に設定した S3 パスにそれらのデータが自動的にアップロードされます。
- experiment_config: Processing Job を登録する Experiments があれば、その情報を指定します。
**以下をローカルモードで実行すると、最後に `PermissionError: [Errno 13] Permission denied: 'ind.cora.tx'` というエラーが出ますが、これはジョブがうまく動いていても出るので無視して構いません。インスタンスを使用した場合はこのエラーは出ません。**
```
from sagemaker.processing import ProcessingInput, ProcessingOutput
from time import gmtime, strftime
processing_job_name = "gnn-byo-process-{}".format(strftime("%d-%H-%M-%S", gmtime()))
output_destination = 's3://{}/{}/data'.format(s3_output, s3_prefix)
script_processor.run(code='preprocessing.py',
job_name=processing_job_name,
# inputs=[ProcessingInput(
# source=raw_s3,
# destination='/opt/ml/processing/input')],
outputs=[ProcessingOutput(output_name='output',
destination='{}/output'.format(output_destination),
source='/opt/ml/processing/output')],
experiment_config={
"ExperimentName": gnn_experiment_preprocess.experiment_name,
"TrialComponentDisplayName": "Processing",
}
)
preprocessing_job_description = script_processor.jobs[-1].describe()
```
## モデルの学習
ここまでで、データの前処理と、前処理済みデータの Amazon S3 へのアップロードが完了しました。次は、前処理済みのデータを使って GNN を学習します。
まずは学習用コンテナイメージを作成します。ベースイメージに、Amazon SageMaker が用意している PyTorch 1.8.0 のイメージを使用しました。
**この Dockerfile はノートブックインスタンスが `us-east-1 (バージニア北部)` の想定なので、他のリージョンをお使いの場合は FROM に書かれている Amazon ECR の URI の `us-east-1` の部分をお使いのリージョンに合わせて書き換えてください。**
```
%%writefile docker/train/Dockerfile
# FROM python:3.8-buster
FROM 763104351884.dkr.ecr.us-east-1.amazonaws.com/pytorch-training:1.8.0-cpu-py36-ubuntu18.04
WORKDIR /opt/app
RUN pip3 install torch==1.8.0
COPY requirements.txt /opt/app
RUN pip3 install -r requirements.txt
RUN pip3 install -U torch-sparse -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
RUN pip3 install jupyter
RUN pip3 install sagemaker-training
WORKDIR /
ecr_repository = 'gnn-byo-train'
tag = ':latest'
uri_suffix = 'amazonaws.com'
train_repository_uri = '{}.dkr.ecr.{}.{}/{}'.format(account_id, region, uri_suffix, ecr_repository + tag)
```
ベースイメージは Amazon SageMaker が用意している Amazon ECR リポジトリに保存されているため、そこへのアクセス権が必要です。以下のコマンドを実行します。
```
!$(aws ecr get-login --region $region --registry-ids 763104351884 --no-include-email)
```
学習スクリプトを作成します。学習スクリプトの内容を変更した場合は、`pytorch_estimator.fit()` を再度実行すれば OK です。学習スクリプトをコンテナイメージの中に入れておらず、Estimator 経由でコンテナに渡すようにしているため、コンテナイメージの再作成は不要です。
```
%%writefile train.py
import torch
from torch_geometric.nn import GCNConv
import torch.nn.functional as F
import json
import argparse
import os
class GCN(torch.nn.Module):
def __init__(self, hidden_channels, num_features, num_classes):
super(GCN, self).__init__()
torch.manual_seed(12345)
self.conv1 = GCNConv(num_features, hidden_channels)
self.conv2 = GCNConv(hidden_channels, num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
def train():
model.train()
optimizer.zero_grad() # Clear gradients.
out = model(data.x, data.edge_index) # Perform a single forward pass.
loss = criterion(out[data.train_mask], data.y[data.train_mask]) # Compute the loss solely based on the training nodes.
loss.backward() # Derive gradients.
optimizer.step() # Update parameters based on gradients.
return loss
def test():
model.eval()
out = model(data.x, data.edge_index)
pred = out.argmax(dim=1) # Use the class with highest probability.
test_correct = pred[data.test_mask] == data.y[data.test_mask] # Check against ground-truth labels.
test_acc = int(test_correct.sum()) / int(data.test_mask.sum()) # Derive ratio of correct predictions.
return test_acc
def _save_checkpoint(model, optimizer, epoch, loss, args):
# print("epoch: {} - loss: {}".format(epoch+1, loss))
checkpointing_path = args.checkpoint_path + '/checkpoint.pth'
print("Saving the Checkpoint: {}".format(checkpointing_path))
torch.save({
'epoch': epoch+1,
'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'loss': loss,
}, checkpointing_path)
def _load_checkpoint(model, optimizer, args):
print("--------------------------------------------")
print("Checkpoint file found!")
print("Loading Checkpoint From: {}".format(args.checkpoint_path + '/checkpoint.pth'))
checkpoint = torch.load(args.checkpoint_path + '/checkpoint.pth')
model.load_state_dict(checkpoint['model_state_dict'])
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
epoch_number = checkpoint['epoch']
loss = checkpoint['loss']
print("Checkpoint File Loaded - epoch_number: {} - loss: {}".format(epoch_number, loss))
print('Resuming training from epoch: {}'.format(epoch_number+1))
print("--------------------------------------------")
return model, optimizer, epoch_number
if __name__=='__main__':
parser = argparse.ArgumentParser()
# Data and model checkpoints directories
parser.add_argument('--features-num', type=int, default=64, metavar='N',
help='input feature size (default: 64)')
parser.add_argument('--classes-num', type=int, default=1, metavar='N',
help='input class size (default: 1)')
parser.add_argument('--epochs', type=int, default=10, metavar='N',
help='number of epochs to train (default: 10)')
parser.add_argument('--lr', type=float, default=0.01, metavar='LR',
help='learning rate (default: 0.01)')
parser.add_argument('--seed', type=int, default=1, metavar='S',
help='random seed (default: 1)')
parser.add_argument('--log-interval', type=int, default=100, metavar='N',
help='how many batches to wait before logging training status')
parser.add_argument('--backend', type=str, default=None,
help='backend for distributed training (tcp, gloo on cpu and gloo, nccl on gpu)')
# Container environment
parser.add_argument('--hosts', type=list, default=json.loads(os.environ['SM_HOSTS']))
parser.add_argument('--current-host', type=str, default=os.environ['SM_CURRENT_HOST'])
parser.add_argument('--model-dir', type=str, default=os.environ['SM_MODEL_DIR'])
parser.add_argument('--data-dir', type=str, default=os.environ['SM_CHANNEL_TRAIN'])
parser.add_argument('--num-gpus', type=int, default=os.environ['SM_NUM_GPUS'])
parser.add_argument("--checkpoint-path",type=str,default="/opt/ml/checkpoints")
args = parser.parse_args()
model = GCN(hidden_channels=16, num_features=args.features_num, num_classes=args.classes_num)
print(model)
optimizer = torch.optim.Adam(model.parameters(), lr=args.lr, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
path = args.data_dir
files = os.listdir(path)
print(files)
from torch_geometric.io import read_planetoid_data
data = read_planetoid_data(args.data_dir, 'Cora')
# Check if checkpoints exists
if not os.path.isfile(args.checkpoint_path + '/checkpoint.pth'):
epoch_number = 0
else:
model, optimizer, epoch_number = _load_checkpoint(model, optimizer, args)
for epoch in range(epoch_number, int(args.epochs)+1):
loss = train()
acc = test()
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}, Acc: {acc:.4f}')
if (epoch %100 == 0):
_save_checkpoint(model, optimizer, epoch, loss, args)
torch.save(model.state_dict(), args.model_dir+'/model.pth')
# Create ECR repository and push docker image
!docker build -t $ecr_repository docker/train
!$(aws ecr get-login --region $region --registry-ids $account_id --no-include-email)
!aws ecr create-repository --repository-name $ecr_repository
!docker tag {ecr_repository + tag} $train_repository_uri
!docker push $train_repository_uri
```
もし、上記コマンドでコンテナイメージをビルドする際に no space left というエラーが出ていたら、以下のコマンドのコメントアウトを解除して実行し、不要なファイルを削除してから再度コンテナイメージのビルドを実行してください。
```
# !docker system prune -a -f
```
Estimator を作成して `fit` で学習ジョブを起動します。ハイパーパラメタの設定や取得したいメトリクスの情報を指定することができます。Processing Job と同様にローカルモードを使用することができます。`fit` の引数には、学習データが保存されている S3 のパスを指定します。PyTorch の Estimator については [こちらのドキュメント](https://sagemaker.readthedocs.io/en/stable/frameworks/pytorch/sagemaker.pytorch.html#sagemaker.pytorch.estimator.PyTorch) をご参照ください。今回 PyTorch という名前の Estimator を使用しましたが、コンテナイメージの中に学習スクリプトを含めた状態で使用する場合は、Estimator という名前の Estimator を使用してください。
Estimator の `metric_definitions` に記録したいメトリクスの情報を指定することができます。`Regex` には、学習スクリプトが出力するログから取得したい数値を抽出するための正規表現を指定します。つまりメトリクスを記録したい場合は、学習スクリプトがメトリクスに関する情報をログに出力する必要があります。今回は Loss と Acc をメトリクスとして取得するよう設定しています。
Spot Instanceを用いて実行する場合は、下記のコードを Estimator の `instance_type`の次の行あたりに追加します。なお、`max_wait` は、`max_run` 以上の値である必要があります。
```python
max_run = 5000,
use_spot_instances = 'True',
max_wait = 10000,
```
チェックポイントの利用は必須ではありませんが、Spot Instance を使う場合は中断に備えてチェックポイントを有効にすることが推奨されています。チェックポイントの学習インスタンス上の保存パス(checkpoint_local_path)と、それらをアップロードする先のパス(checkpoint_s3_path)を設定し、学習スクリプトにチェックポイントを checkpoint_local_path に保存する記述を追加します。
保存したチェックポイントから学習を再開する場合は、新しく Estimator 定義して引数にチェックポイントが保存してある checkpoint_s3_path と チェックポイントをダウンロードしたいパス checkpoint_local_path を設定して fit を実行します。
チェックポイントの詳細については [こちらのドキュメント](https://docs.aws.amazon.com/sagemaker/latest/dg/model-checkpoints.html#model-checkpoints-enable) をご参照ください。
```
from sagemaker.estimator import Estimator
from sagemaker.pytorch.estimator import PyTorch
import uuid
import os
# Spot training をする場合は、チェックポイントの設定を推奨
checkpoint_suffix = str(uuid.uuid4())[:8]
checkpoint_s3_path = 's3://{}/checkpoint-{}'.format(bucket, checkpoint_suffix)
checkpoint_local_path="/opt/ml/checkpoints"
pytorch_estimator = PyTorch(
entry_point='train.py',
image_uri=train_repository_uri,
role=role,
instance_count=1,
# instance_type='local',
instance_type='ml.c4.2xlarge',
max_run = 5000,
use_spot_instances = 'True',
max_wait = 10000,
checkpoint_s3_uri=checkpoint_s3_path,
checkpoint_local_path=checkpoint_local_path,
output_path="s3://{}/output".format(bucket),
sagemaker_session=session,
hyperparameters = {'epochs': 200, 'features-num':1433, 'classes-num':7, 'lr':0.01},
enable_sagemaker_metrics=True,
metric_definitions = [dict(
Name = 'Loss',
Regex = 'Loss: ([0-9.]+)'
),
dict(
Name = 'Acc',
Regex = 'Acc: ([0-9.]+)'
)
]
)
pytorch_estimator.fit({'train': os.path.join(output_destination, 'output/Cora/raw/')},
experiment_config={
"ExperimentName": gnn_experiment_train.experiment_name,
"TrialComponentDisplayName": "Training",
})
```
## Amazon SageMaker Experiments でモデルを比較
SageMaker Experiments を使うと複数のモデルのメトリクスなどを比較することができます。上のセルの Estimator の引数で epochs や lr などのハイパーパラメタを変えて何度か学習を実行してから次のセル以降を実行してみましょう。Experiments 内の Trial のフィルタやソートなど方法については [ExperimentAnalytics のドキュメント](https://sagemaker.readthedocs.io/en/stable/api/training/analytics.html#sagemaker.analytics.ExperimentAnalytics) をご参照ください。
メトリクスに関して、DataFrame の列名は Loss - Min などと書かれていますが、ExperimentAnalytics の sort_by で Loss - Min を指定する場合は、metrics.loss.min となります。
```
search_expression = {
"Filters":[
{
"Name": "DisplayName",
"Operator": "Equals",
"Value": "Training",
}
],
}
trial_component_analytics = ExperimentAnalytics(
sagemaker_session=session,
experiment_name=gnn_experiment_train.experiment_name,
search_expression=search_expression,
sort_by="metrics.acc.max",
sort_order="Ascending",# Ascending or Descending
metric_names=['Loss', 'Acc'],
parameter_names=['epochs', 'lr'],
input_artifact_names=[]
)
import pandas as pd
df = trial_component_analytics.dataframe()
pd.set_option('display.max_columns', None)
df
print(df.columns.tolist())
```
## Processing Job を使ったバッチ推論
学習したモデルを使ってバッチ推論を行います。今回は、前処理で使用したコンテナイメージを流用してバッチ推論用 Processing Job を起動します。
まずは推論用スクリプトを作成します。<br>
推論結果をグラフにプロットし、その画像を Amazon S3 にアップロードするようにしました。
```
%%writefile inference.py
import torch
from torch_geometric.nn import GCNConv
import torch.nn.functional as F
import json
import argparse
import os
import tarfile
import matplotlib.pyplot as plt
class GCN(torch.nn.Module):
def __init__(self, hidden_channels, num_features, num_classes):
super(GCN, self).__init__()
torch.manual_seed(12345)
self.conv1 = GCNConv(num_features, hidden_channels)
self.conv2 = GCNConv(hidden_channels, num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
def test():
model.eval()
out = model(data.x, data.edge_index)
pred = out.argmax(dim=1) # Use the class with highest probability.
test_correct = pred[data.test_mask] == data.y[data.test_mask] # Check against ground-truth labels.
test_acc = int(test_correct.sum()) / int(data.test_mask.sum()) # Derive ratio of correct predictions.
return test_acc
from sklearn.manifold import TSNE
def visualize(h, color, path):
z = TSNE(n_components=2).fit_transform(out.detach().cpu().numpy())
fig = plt.figure(figsize=(10,10))
plt.xticks([])
plt.yticks([])
plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
# plt.show()
fig.savefig(os.path.join(path, "img.png"))
if __name__=='__main__':
parser = argparse.ArgumentParser()
# Data and model checkpoints directories
parser.add_argument('--features-num', type=str, default='1', metavar='N',
help='input feature size (default: 1)')
parser.add_argument('--classes-num', type=str, default='1', metavar='N',
help='input class size (default: 1)')
parser.add_argument('--model-dir', type=str, default='/opt/ml/model', metavar='N',
help='model data path (default: /opt/ml/model)')
parser.add_argument('--input-dir', type=str, default='/opt/ml/input', metavar='N',
help='input data path (default: /opt/ml/input)')
parser.add_argument('--output-dir', type=str, default='/opt/ml/output', metavar='N',
help='output data path (default: /opt/ml/output)')
args = parser.parse_args()
from torch_geometric.io import read_planetoid_data
data = read_planetoid_data(args.input_dir, 'Cora')
with tarfile.open(os.path.join(args.model_dir, 'model.tar.gz'), 'r:gz') as t:
t.extractall()
model = GCN(hidden_channels=16, num_features=int(args.features_num), num_classes=int(args.classes_num))
model.load_state_dict(torch.load('model.pth'))
# print(model)
test_acc = test()
print(f'Test Accuracy: {test_acc:.4f}')
model.eval()
out = model(data.x, data.edge_index)
visualize(out, color=data.y, path=args.output_dir)
from sagemaker.processing import ScriptProcessor
batch_inference_processor = ScriptProcessor(command=['python3'],
image_uri=processing_repository_uri,
role=role,
instance_count=1,
# instance_type='local')
instance_type='ml.c5.xlarge')
from sagemaker.processing import ProcessingInput, ProcessingOutput
from time import gmtime, strftime
processing_job_name = "gnn-byo-batch-inference-{}".format(strftime("%d-%H-%M-%S", gmtime()))
output_destination_inference = 's3://{}/{}/batch-inference'.format(s3_output, s3_prefix)
input_dir = '/opt/ml/processing/input'
model_dir = '/opt/ml/processing/model'
output_dir = '/opt/ml/processing/output'
model_s3 = pytorch_estimator.model_data
raw_s3 = os.path.join(output_destination, 'output/Cora/raw/')
batch_inference_processor.run(code='inference.py',
job_name=processing_job_name,
inputs=[ProcessingInput(
source=model_s3,
destination=model_dir),
ProcessingInput(
source=raw_s3,
destination=input_dir)],
outputs=[ProcessingOutput(output_name='output',
destination='{}/output'.format(output_destination_inference),
source=output_dir)],
arguments=['--model-dir', model_dir, '--input-dir', input_dir, '--output-dir', output_dir , '--features-num', '1433', '--classes-num', '7']
# experiment_config={
# "ExperimentName": gnn_experiment.experiment_name,
# "TrialComponentDisplayName": "Processing",
# }
)
preprocessing_job_description = batch_inference_processor.jobs[-1].describe()
```
バッチ推論で出力したプロットの画像をダウンロードして表示します。
```
!aws s3 cp $output_destination_inference/output/img.png ./
from IPython.display import Image
Image("./img.png")
```
## リソースの削除
利用が終わったら、このノートブックを実行したノートブックインスタンスの停止および削除を実施してください。ノートブックインスタンスを停止させると、ノートブックインスタンスの課金は止まりますがアタッチされている EBS ボリュームへの課金が継続しますので、完全に課金を止めるにはノートブックインスタンスの停止だけでなく削除まで実施してください。
また、Amazon S3 にアップロードした各種ファイルに対しても課金が発生するため、不要であれば削除してください。
```
sm = boto3.Session().client('sagemaker')
def cleanup(experiment):
for trial_summary in experiment.list_trials():
trial = Trial.load(sagemaker_boto_client=sm, trial_name=trial_summary.trial_name)
for trial_component_summary in trial.list_trial_components():
tc = TrialComponent.load(
sagemaker_boto_client=sm,
trial_component_name=trial_component_summary.trial_component_name)
trial.remove_trial_component(tc)
try:
# comment out to keep trial components
tc.delete()
except:
# tc is associated with another trial
continue
# to prevent throttling
time.sleep(.5)
trial.delete()
experiment.delete()
cleanup(gnn_experiment_preprocess)
cleanup(gnn_experiment_train)
```
| true |
code
| 0.395747 | null | null | null | null |
|
# ML algorithms: Logistic Regression
Source: https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
From the sklearn handbook:
>Logistic regression, despite its name, is a linear model for classification rather than regression. Logistic regression is also known in the literature as logit regression, maximum-entropy classification (MaxEnt) or the log-linear classifier. In this model, the probabilities describing the possible outcomes of a single trial are modeled using a logistic function.
Code: http://marcharper.codes/2016-06-27/Logistic+Regression.html
Slides: https://s3.amazonaws.com/assets.datacamp.com/production/course_15356/slides/chapter4.pdf
```
%matplotlib inline
%load_ext autoreload
%autoreload 2
import matplotlib.pyplot as plt
import pandas as pd
from scipy import stats
import seaborn as sns
distA = stats.norm(30, 5)
distB = stats.norm(15, 4)
data = []
for i in range(100):
data.append((distA.rvs(), "A"))
data.append((distB.rvs(), "B"))
df = pd.DataFrame(data, columns=["measurement", "class"])
df.head()
sns.violinplot(x="class", y="measurement", data=df);
sns.distplot(df[df["class"] == "A"]["measurement"])
sns.distplot(df[df["class"] == "B"]["measurement"]);
# convert categorical values to numbers
df["class_num"] = df['class'].apply(lambda x: 1 if x == 'A' else 0 )
df.head()
plt.scatter(df["measurement"], df["class_num"])
plt.show()
```
We could try to use a linear regression to separate the classes. With the best fit line we could label points above and below the line in seperate classes. This works ok (better than no classifier) but has a lot of drawbacks, and logistic regression typically gives a better solution.
```
from sklearn import linear_model
X = df[["measurement"]]
y = df["class_num"]
model = linear_model.LinearRegression()
model.fit(X, y)
plt.scatter(df["measurement"], df["class_num"])
plt.plot(df["measurement"], model.predict(X), color="r")
plt.show()
```
A logistic regression produces a classifier that separates the two classes much more sharply.
```
from sklearn import linear_model
df.sort_values(by="measurement", inplace=True)
X = df[["measurement"]]
y = df["class_num"]
model = linear_model.LogisticRegression()
model.fit(X, y)
plt.scatter(df["measurement"], df["class_num"])
plt.plot(df["measurement"], model.predict(X), color="r")
plt.xlabel("Measurement")
plt.show();
```
We can also plot the predicted probabilities and check the accuracy of the model.
```
from sklearn import linear_model
df.sort_values(by="measurement", inplace=True)
X = df[["measurement"]]
y = df["class_num"]
model = linear_model.LogisticRegression()
model.fit(X, y)
plt.scatter(df["measurement"], df["class_num"])
plt.plot(df["measurement"], model.predict_proba(X)[:, 1], color="r")
plt.xlabel("Measurement")
plt.ylabel("Probability of being in class B")
plt.show()
print("Accuracy", model.score(X, y))
```
Now let's try a set of data that is not so well separated.
```
distA = stats.norm(22, 5)
distB = stats.norm(15, 3)
data = []
for i in range(100):
data.append((distA.rvs(), "A"))
data.append((distB.rvs(), "B"))
df = pd.DataFrame(data, columns=["measurement", "class"])
df["class_num"] = df['class'].apply(lambda x: 1 if x == 'A' else 0 )
sns.distplot(df[df["class"] == "A"]["measurement"])
sns.distplot(df[df["class"] == "B"]["measurement"]);
from sklearn import linear_model
df.sort_values(by="measurement", inplace=True)
X = df[["measurement"]]
y = df["class_num"]
model = linear_model.LogisticRegression()
model.fit(X, y)
plt.scatter(df["measurement"], df["class_num"])
plt.plot(df["measurement"], model.predict_proba(X)[:, 1], color="r")
plt.show()
print("Accuracy", model.score(X, y))
```
# A more complex real-world example/ analysis
Source: https://github.com/carljv/Will_it_Python/tree/master/ARM/ch5
>Logistic models of well switching in Bangladesh
>Our data are information on about 3,000 respondent households in Bangladesh with wells having an unsafe amount of arsenic. The data record the amount of arsenic in the respondent's well, the distance to the nearest safe well (in meters), whether that respondent "switched" wells by using a neighbor's safe well instead of their own, as well as the respondent's years of education and a dummy variable indicating whether they belong to a community association.
>Our goal is to model well-switching decision. Since it's a binary variable (1 = switch, 0 = no switch), we'll use logistic regression.
>This analysis follows Gelman and Hill Data Analysis Using Regression and Multilevel/Hierarchical Models, chapter 5.4.
```
import numpy as np
from pandas import *
from statsmodels.formula.api import logit
import statsmodels.api as sm
import matplotlib.pyplot as plt
from patsy import dmatrix, dmatrices
df = read_csv('/data/ifu/summerschool/wells.dat', sep = ' ', header = 0, index_col = 0)
df.head()
```
### Model 1: Distance to a safe well
For our first pass, we'll just use the distance to the nearest safe well. Since the distance is recorded in meters, and the effect of one meter is likely to be very small, we can get nicer model coefficients if we scale it. Instead of creating a new scaled variable, we'll just do it in the formula description using the I() function.
```
model1 = logit('switch ~ I(dist/100.)', data = df).fit()
model1.summary()
def binary_jitter(x, jitter_amount = .05):
'''
Add jitter to a 0/1 vector of data for plotting.
'''
jitters = np.random.rand(*x.shape) * jitter_amount
x_jittered = x + np.where(x == 1, -1, 1) * jitters
return x_jittered
dist_logit_par = model1.params['I(dist / 100.)']
plt.plot(df['dist'], binary_jitter(df['switch'], .1), '.', alpha = .1)
plt.plot(np.sort(df['dist']), model1.predict()[np.argsort(df['dist'])], lw = 2)
plt.ylabel('Switched Wells')
plt.xlabel('Distance from safe well (meters)');
```
Another way to look at this is to plot the densities of distance for switchers and non-switchers. We expect the distribution of switchers to have more mass over short distances and the distribution of non-switchers to have more mass over long distances.
```
kde_sw = kde = sm.nonparametric.KDEUnivariate(df['dist'][df['switch'] == 1])
kde_nosw = sm.nonparametric.KDEUnivariate(df['dist'][df['switch'] == 0])
kde_sw.fit()
kde_nosw.fit()
plt.plot(kde_sw.support, kde_sw.density, label = 'Switch')
plt.plot(kde_nosw.support, kde_nosw.density, color = 'red', label = 'No Switch')
plt.xlabel('Distance (meters)')
plt.legend(loc = 'best');
```
#### Model 2: Distance to a safe well and the arsenic level of own well
Next, let's add the arsenic level as a regressor. We'd expect respondents with higher arsenic levels to be more motivated to switch.
```
model2 = logit('switch ~ I(dist / 100.) + arsenic', data = df).fit()
model2.summary()
```
Which is what we see. The coefficients are what we'd expect: the farther to a safe well, the less likely a respondent is to switch, but the higher the arsenic level in their own well, the more likely.
### Marginal effects
To see the effect of these on the probability of switching, let's calculate the marginal effects at the mean of the data.
```
argeff = model2.get_margeff(at = 'mean')
print(argeff.summary())
```
So, for the mean respondent, an increase of 100 meters to the nearest safe well is associated with a 22% lower probability of switching. But an increase of 1 in the arsenic level is associated with an 11% higher probability of switching.
#### Class separability
To get a sense of how well this model might classify switchers and non-switchers, we can plot each class of respondent in (distance-arsenic)-space.
We don't see very clean separation, so we'd expect the model to have a fairly high error rate. But we do notice that the short-distance/high-arsenic region of the graph is mostly comprised switchers, and the long-distance/low-arsenic region is mostly comprised of non-switchers.
```
logit_pars = model2.params
intercept = -logit_pars[0] / logit_pars[2]
slope = -logit_pars[1] / logit_pars[2]
dist_sw = df['dist'][df['switch'] == 1]
dist_nosw = df['dist'][df['switch'] == 0]
arsenic_sw = df['arsenic'][df['switch'] == 1]
arsenic_nosw = df['arsenic'][df['switch'] == 0]
plt.figure(figsize = (12, 8))
plt.plot(dist_sw, arsenic_sw, '.', mec = 'purple', mfc = 'None',
label = 'Switch')
plt.plot(dist_nosw, arsenic_nosw, '.', mec = 'orange', mfc = 'None',
label = 'No switch')
plt.plot(np.arange(0, 350, 1), intercept + slope * np.arange(0, 350, 1) / 100.,
'-k', label = 'Separating line')
plt.ylim(0, 10)
plt.xlabel('Distance to safe well (meters)')
plt.ylabel('Arsenic level')
plt.legend(loc = 'best');
```
### Model 3: Adding an interation
It's sensible that distance and arsenic would interact in the model. In other words, the effect of an 100 meters on your decision to switch would be affected by how much arsenic is in your well.
Again, we don't have to pre-compute an explicit interaction variable. We can just specify an interaction in the formula description using the : operator.
```
model3 = logit('switch ~ I(dist / 100.) + arsenic + I(dist / 100.):arsenic',
data = df).fit()
model3.summary()
```
The coefficient on the interaction is negative and significant. While we can't directly intepret its quantitative effect on switching, the qualitative interpretation gels with our intuition. Distance has a negative effect on switching, but this negative effect is reduced when arsenic levels are high. Alternatively, the arsenic level have a positive effect on switching, but this positive effect is reduced as distance to the nearest safe well increases.
### Model 4: Adding educuation, more interactions and centering variables
Respondents with more eduction might have a better understanding of the harmful effects of arsenic and therefore may be more likely to switch. Education is in years, so we'll scale it for more sensible coefficients. We'll also include interactions amongst all the regressors.
We're also going to center the variables, to help with interpretation of the coefficients. Once more, we can just do this in the formula, without pre-computing centered variables.
```
model_form = ('switch ~ center(I(dist / 100.)) + center(arsenic) + ' +
'center(I(educ / 4.)) + ' +
'center(I(dist / 100.)) : center(arsenic) + ' +
'center(I(dist / 100.)) : center(I(educ / 4.)) + ' +
'center(arsenic) : center(I(educ / 4.))'
)
model4 = logit(model_form, data = df).fit()
model4.summary()
```
#### Model assessment: Binned Residual plots
Plotting residuals to regressors can alert us to issues like nonlinearity or heteroskedasticity. Plotting raw residuals in a binary model isn't usually informative, so we do some smoothing. Here, we'll averaging the residuals within bins of the regressor. (A lowess or moving average might also work.)
```
model4.resid_response
def bin_residuals(resid, var, bins):
'''
Compute average residuals within bins of a variable.
Returns a dataframe indexed by the bins, with the bin midpoint,
the residual average within the bin, and the confidence interval
bounds.
'''
resid_df = DataFrame({'var': var, 'resid': resid})
resid_df['bins'] = qcut(var, bins)
bin_group = resid_df.groupby('bins')
bin_df = bin_group['var', 'resid'].mean()
bin_df['count'] = bin_group['resid'].count()
bin_df['lower_ci'] = -2 * (bin_group['resid'].std() /
np.sqrt(bin_group['resid'].count()))
bin_df['upper_ci'] = 2 * (bin_group['resid'].std() /
np.sqrt(bin_df['count']))
bin_df = bin_df.sort_values('var')
return(bin_df)
def plot_binned_residuals(bin_df):
'''
Plotted binned residual averages and confidence intervals.
'''
plt.plot(bin_df['var'], bin_df['resid'], '.')
plt.plot(bin_df['var'], bin_df['lower_ci'], '-r')
plt.plot(bin_df['var'], bin_df['upper_ci'], '-r')
plt.axhline(0, color = 'gray', lw = .5)
arsenic_resids = bin_residuals(model4.resid_response, df['arsenic'], 40)
dist_resids = bin_residuals(model4.resid_response, df['dist'], 40)
plt.figure(figsize = (12, 5))
plt.subplot(121)
plt.ylabel('Residual (bin avg.)')
plt.xlabel('Arsenic (bin avg.)')
plot_binned_residuals(arsenic_resids)
plt.subplot(122)
plot_binned_residuals(dist_resids)
plt.ylabel('Residual (bin avg.)')
plt.xlabel('Distance (bin avg.)');
```
#### Model 5: log-scaling arsenic
The binned residual plot indicates some nonlinearity in the arsenic variable. Note how the model over-estimated for low arsenic and underestimates for high arsenic. This suggests a log transformation or something similar.
We can again do this transformation right in the formula.
```
model_form = ('switch ~ center(I(dist / 100.)) + center(np.log(arsenic)) + ' +
'center(I(educ / 4.)) + ' +
'center(I(dist / 100.)) : center(np.log(arsenic)) + ' +
'center(I(dist / 100.)) : center(I(educ / 4.)) + ' +
'center(np.log(arsenic)) : center(I(educ / 4.))'
)
model5 = logit(model_form, data = df).fit()
model5.summary()
```
And the binned residual plot for arsenic now looks better.
```
arsenic_resids = bin_residuals(model5.resid_response, df['arsenic'], 40)
dist_resids = bin_residuals(model5.resid_response, df['dist'], 40)
plt.figure(figsize = (12, 5))
plt.subplot(121)
plot_binned_residuals(arsenic_resids)
plt.ylabel('Residual (bin avg.)')
plt.xlabel('Arsenic (bin avg.)')
plt.subplot(122)
plot_binned_residuals(dist_resids)
plt.ylabel('Residual (bin avg.)')
plt.xlabel('Distance (bin avg.)');
```
#### Model error rates
The pred_table() gives us a confusion matrix for the model. We can use this to compute the error rate of the model.
We should compare this to the null error rates, which comes from a model that just classifies everything as whatever the most prevalent response is. Here 58% of the respondents were switchers, so the null model just classifies everyone as a switcher, and therefore has an error rate of 42%.
```
print(model5.pred_table())
print(f'Model Error Rate: {1 - np.diag(model5.pred_table()).sum() / model5.pred_table().sum():2.0%}')
print(f' Null Error Rate: {1 - df.switch.mean():2.0%}')
```
# Using sklearn
```
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X = df.drop('switch', axis=1)
y = df['switch']
# no columns need to be converted to one-hot encoding...
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# not needed for logistic regression
# call fit_transform on the training set, but only transform on the test set!
#sc = StandardScaler()
#Xt_train = sc.fit_transform(X_train)
#Xt_test = sc.transform (X_test)
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)
print(f'Accuracy of logistic regression classifier on test set: {logreg.score(X_test, y_test):2.1%}')
```
| true |
code
| 0.582847 | null | null | null | null |
|
# Quantum Autoencoder
<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>
## Overview
This tutorial will show how to train a quantum autoencoder to compress and reconstruct a given quantum state (mixed state) [1].
### Theory
The form of the quantum autoencoder is very similar to the classical autoencoder, which is composed of an encoder $E$ and a decoder $D$. For the input quantum state $\rho_{in}$ of the $N$ qubit system (here we use the density operator representation of quantum mechanics to describe the mixed state), first use the encoder $E = U(\theta)$ to encode information into some of the qubits in the system. This part of qubits is denoted by **system $A$**. After measuring and discarding the remaining qubits (this part is denoted by **system $B$**), we get the compressed quantum state $\rho_{encode}$! The dimension of the compressed quantum state is the same as the dimension of the quantum system $A$. Suppose we need $N_A$ qubits to describe the system $A$, then the dimension of the encoded quantum state $\rho_{encode}$ is $2^{N_A}\times 2^{N_A}$. Note that the mathematical operation corresponding to the measure-and-discard operation in this step is partial trace. The reader can intuitively treat it as the inverse operation of the tensor product $\otimes$.
Let us look at a specific example. Given a quantum state $\rho_A$ of $N_A$ qubits and another quantum state $\rho_B$ of $N_B$ qubits, the quantum state of the entire quantum system composed of subsystems $A$ and $B$ is $\rho_{AB} = \rho_A \otimes \rho_B$, which is a state of $N = N_A + N_B$ qubits. Now we let the entire quantum system evolve under the action of the unitary matrix $U$ for some time to get a new quantum state $\tilde{\rho_{AB}} = U\rho_{AB}U^\dagger$. So if we only want to get the new quantum state $\tilde{\rho_A}$ of quantum subsystem A at this time, what should we do? We simply measure the quantum subsystem $B$ and then discard it. This step of the operation is completed by partial trace $\tilde{\rho_A} = \text{Tr}_B (\tilde{\rho_{AB}})$. With Paddle Quantum, we can call the built-in function `partial_trace(rho_AB, 2**N_A, 2**N_B, 2)` to complete this operation. **Note:** The last parameter is 2, which means that we want to discard quantum system $B$.

After discussing the encoding process, let us take a look at how decoding is done. To decode the quantum state $\rho_{encode}$, we need to introduce an ancillary system $C$ with the same dimension as the system $B$ and take its initial state as the $|0\dots0\rangle$ state. Then use the decoder $D = U^\dagger(\theta)$ to act on the entire quantum system $A+C$ to decode the compressed information in system A. We hope that the final quantum state $\rho_{out}$ and $\rho_{in}$ are as similar as possible and use Uhlmann-Josza fidelity $F$ to measure the similarity between them.
$$
F(\rho_{in}, \rho_{out}) = \left(\operatorname{tr} \sqrt{\sqrt{\rho_{in}} \rho_{out} \sqrt{\rho_{in}}} \right)^{2}.
\tag{1}
$$
Finally, by optimizing the encoder's parameters, we can improve the fidelity of $\rho_{in}$ and $\rho_{out}$ as much as possible.
## Paddle Quantum Implementation
Next, we will use a simple example to show the workflow of the quantum autoencoder. Here we first import the necessary packages.
```
from IPython.core.display import HTML
display(HTML("<style>pre { white-space: pre !important; }</style>"))
import numpy as np
from numpy import diag
import scipy
import scipy.stats
import paddle
from paddle import matmul, trace, kron, real
from paddle_quantum.circuit import UAnsatz
from paddle_quantum.utils import dagger, state_fidelity, partial_trace
```
### Generating the initial state
Let us consider the quantum state $\rho_{in}$ of $N = 3$ qubits. We first encode the information into the two qubits below (system $A$) through the encoder then measure and discard the first qubit (system $B$). Secondly, we introduce another qubit (the new reference system $C$) in state $|0\rangle$ to replace the discarded qubit $B$. Finally, through the decoder, the compressed information in A is restored to $\rho_{out}$. Here, we assume that the initial state is a mixed state and the spectrum of $\rho_{in}$ is $\lambda_i \in \{0.4, 0.2, 0.2, 0.1, 0.1, 0, 0, 0\}$, and then generate the initial state $\rho_{in}$ by applying a random unitary transformation.
```
N_A = 2 # Number of qubits in system A
N_B = 1 # Number of qubits in system B
N = N_A + N_B # Total number of qubits
scipy.random.seed(1) # Fixed random seed
V = scipy.stats.unitary_group.rvs(2**N) # Generate a random unitary matrix
D = diag([0.4, 0.2, 0.2, 0.1, 0.1, 0, 0, 0]) # Enter the spectrum of the target state rho
V_H = V.conj().T # Apply Hermitian transpose
rho_in = (V @ D @ V_H).astype('complex128') # Generate rho_in
# Initialize the quantum system C
rho_C = np.diag([1,0]).astype('complex128')
```
### Building a quantum neural network
Here, we use quantum neural networks (QNN) as encoders and decoders. Suppose system A has $N_A$ qubits, both system $B$ and $C$ have $N_B$ qubits, and the depth of the QNN is $D$. Encoder $E$ acts on the total system composed of systems A and B, and decoder $D$ acts on the total system composed of $A$ and $C$. In this example, $N_{A} = 2$ and $N_{B} = 1$.
```
# Set circuit parameters
cir_depth = 6 # Circuit depth
block_len = 2 # The length of each block
theta_size = N*block_len*cir_depth # The size of the circuit parameter theta
# Build the encoder E
def Encoder(theta):
# Initialize the network with UAnsatz
cir = UAnsatz(N)
# Build the network by layers
for layer_num in range(cir_depth):
for which_qubit in range(N):
cir.ry(theta[block_len*layer_num*N + which_qubit], which_qubit)
cir.rz(theta[(block_len*layer_num + 1)*N+ which_qubit], which_qubit)
for which_qubit in range(N-1):
cir.cnot([which_qubit, which_qubit + 1])
cir.cnot([N-1, 0])
return cir
```
### Configuring the training model: loss function
Here, we define the loss function to be
$$
Loss = 1-\langle 0...0|\rho_{trash}|0...0\rangle,
\tag{2}
$$
where $\rho_{trash}$ is the quantum state of the system $B$ discarded after encoding. Then we train the QNN through PaddlePaddle to minimize the loss function. If the loss function reaches 0, the input state and output state will be exactly the same state. This means that we have achieved compression and decompression perfectly, in which case the fidelity of the initial and final states is $F(\rho_{in}, \rho_{out}) = 1$.
```
# Set hyper-parameters
N_A = 2 # Number of qubits in system A
N_B = 1 # Number of qubits in system B
N = N_A + N_B # Total number of qubits
LR = 0.2 # Set the learning rate
ITR = 100 # Set the number of iterations
SEED = 15 # Fixed random number seed for initializing parameters
class NET(paddle.nn.Layer):
def __init__(self, shape, dtype='float64'):
super(NET, self).__init__()
# Convert Numpy array to Tensor supported in PaddlePaddle
self.rho_in = paddle.to_tensor(rho_in)
self.rho_C = paddle.to_tensor(rho_C)
self.theta = self.create_parameter(shape=shape,
default_initializer=paddle.nn.initializer.Uniform(low=0.0, high=2 * np.pi),
dtype=dtype, is_bias=False)
# Define loss function and forward propagation mechanism
def forward(self):
# Generate initial encoder E and decoder D
cir = Encoder(self.theta)
E = cir.U
E_dagger = dagger(E)
D = E_dagger
D_dagger = E
# Encode the quantum state rho_in
rho_BA = matmul(matmul(E, self.rho_in), E_dagger)
# Take partial_trace() to get rho_encode and rho_trash
rho_encode = partial_trace(rho_BA, 2 ** N_B, 2 ** N_A, 1)
rho_trash = partial_trace(rho_BA, 2 ** N_B, 2 ** N_A, 2)
# Decode the quantum state rho_out
rho_CA = kron(self.rho_C, rho_encode)
rho_out = matmul(matmul(D, rho_CA), D_dagger)
# Calculate the loss function with rho_trash
zero_Hamiltonian = paddle.to_tensor(np.diag([1,0]).astype('complex128'))
loss = 1 - real(trace(matmul(zero_Hamiltonian, rho_trash)))
return loss, self.rho_in, rho_out, cir
paddle.seed(SEED)
# Generate network
net = NET([theta_size])
# Generally speaking, we use Adam optimizer to get relatively good convergence
# Of course, it can be changed to SGD or RMS prop.
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=net.parameters())
# Optimization loops
for itr in range(1, ITR + 1):
# Forward propagation for calculating loss function
loss, rho_in, rho_out, cir = net()
# Use back propagation to minimize the loss function
loss.backward()
opt.minimize(loss)
opt.clear_grad()
# Calculate and print fidelity
fid = state_fidelity(rho_in.numpy(), rho_out.numpy())
if itr% 10 == 0:
print('iter:', itr,'loss:','%.4f'% loss,'fid:','%.4f'% np.square(fid))
if itr == ITR:
print("\nThe trained circuit:")
print(cir)
```
If the dimension of system A is denoted by $d_A$, it is easy to prove that the maximum fidelity can be achieved by quantum autoencoder is the sum of $d_A$ largest eigenvalues of $\rho_{in}$. In our case $d_A = 4$ and the maximum fidelity is
$$
F_{\text{max}}(\rho_{in}, \rho_{out}) = \sum_{j=1}^{d_A} \lambda_j(\rho_{in})= 0.4 + 0.2 + 0.2 + 0.1 = 0.9.
\tag{3}
$$
After 100 iterations, the fidelity achieved by the quantum autoencoder we trained reaches above 0.89, which is very close to the optimal value.
_______
## References
[1] Romero, J., Olson, J. P. & Aspuru-Guzik, A. Quantum autoencoders for efficient compression of quantum data. [Quantum Sci. Technol. 2, 045001 (2017).](https://iopscience.iop.org/article/10.1088/2058-9565/aa8072)
| true |
code
| 0.673675 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/yukinaga/bert_nlp/blob/main/section_4/02_fine_tuning_for_classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## ファインチューニングによる感情分析
ファインチューニングを活用し、文章の好悪感情を判別できるようにモデルを訓練します。
## ライブラリのインストール
ライブラリTransformers、およびnlpをインストールします。
```
!pip install transformers
!pip install nlp
```
## モデルとTokenizerの読み込み
事前学習済みのモデルと、これと紐づいたTokenizerを読み込みます。
```
from transformers import BertForSequenceClassification, BertTokenizerFast
sc_model = BertForSequenceClassification.from_pretrained("bert-base-uncased")
sc_model.cuda()
tokenizer = BertTokenizerFast.from_pretrained("bert-base-uncased")
```
## データセットの読み込み
ライブラリnlpを使用して、IMDbデータセットを読み込みます。
IMDbデータセットは、25000の映画レビューコメントに、ポジティブかネガティブの好悪感情を表すラベルが付随した、感情分析用のデータセットです。
https://www.imdb.com/interfaces/
読み込んだIMDbのデータはトークナイザーで処理し、形式を整えます。
```
from nlp import load_dataset
def tokenize(batch):
return tokenizer(batch["text"], padding=True, truncation=True)
train_data, test_data = load_dataset("imdb", split=["train", "test"])
print(train_data["label"][0], train_data["text"][0]) # 好意的なコメント
print(train_data["label"][20000], train_data["text"][20000]) # 否定的なコメント
train_data = train_data.map(tokenize, batched=True, batch_size=len(train_data))
train_data.set_format("torch", columns=["input_ids", "attention_mask", "label"])
test_data = test_data.map(tokenize, batched=True, batch_size=len(train_data))
test_data.set_format("torch", columns=["input_ids", "attention_mask", "label"])
```
## 評価用の関数
`sklearn.metrics`を使用し、モデルを評価するための関数を定義します。
```
from sklearn.metrics import accuracy_score
def compute_metrics(result):
labels = result.label_ids
preds = result.predictions.argmax(-1)
acc = accuracy_score(labels, preds)
return {
"accuracy": acc,
}
```
## Trainerの設定
Trainerクラス、およびTrainingArgumentsクラスを使用して、訓練を行うTrainerの設定を行います。
https://huggingface.co/transformers/main_classes/trainer.html
https://huggingface.co/transformers/main_classes/trainer.html#trainingarguments
```
from transformers import Trainer, TrainingArguments
training_args = TrainingArguments(
output_dir = "./results",
num_train_epochs = 1,
per_device_train_batch_size = 8,
per_device_eval_batch_size = 32,
per_gpu_train_batch_size = 8,
warmup_steps = 500, # 学習係数が0からこのステップ数で上昇
weight_decay = 0.01, # 重みの減衰率
# evaluate_during_training = True, # ここの記述はバージョンによっては必要ありません
logging_dir = "./logs",
)
trainer = Trainer(
model = sc_model,
args = training_args,
compute_metrics = compute_metrics,
train_dataset = train_data,
eval_dataset = test_data
)
```
## モデルの訓練
設定に基づきモデルを訓練します。
```
trainer.train()
```
## モデルの評価
Trainerの`evaluate()`メソッドによりモデルを評価します。
```
trainer.evaluate()
```
## TensorBoardによる結果の表示
TensorBoardを使って、logsフォルダに格納された学習過程を表示します。
```
%load_ext tensorboard
%tensorboard --logdir logs
```
| true |
code
| 0.539347 | null | null | null | null |
|
# Demagnetisation using periodic boundary conditions
## Setting the simulation
```
import dolfin as df
import numpy as np
import matplotlib.pyplot as plt
from finmag import Simulation as Sim
from finmag.energies import Demag
from finmag import MacroGeometry
%matplotlib inline
```
The mesh unit cell is a box with edge length $a$ and number of vertices along one dimension $N_{v}$.
```
a = 5 # edge length (nm)
Nv = 5 # number of verices along one direction
mesh = df.BoxMesh(-a/2., -a/2., -a/2., a/2., a/2., a/2., Nv, Nv, Nv)
```
The simulation object is created with saturation magnetisation $M_\text{s} = 10^6$ A/m.
```
Ms = 1e6 # saturation magnetisation (A/m)
sim = Sim(mesh, Ms, unit_length=1e-9)
```
Demag object is created using already defined lattice and added to the simulation:
```
n = 5
demag = Demag(macrogeometry=MacroGeometry(nx=n))
sim.add(demag)
```
Now, the demagnetisation field can be computed for different magnetisation configurations. For instance:
```
sim.set_m((0, 0, 1))
field = sim.llg.effective_field.get_dolfin_function('Demag')
```
At a particular point in the mesh, the field value can be extracted:
```
field_at_point = field(0, 0, 0)
print field_at_point
```
## Demagnetisation field for different number of elements in the lattice
An array of possible numbers of ellements in the lattice:
```
ns = np.arange(1, 30, 2)
print ns
```
The first part of this notebook implemented as a function which returns demagnetisation field for two different magnetisation configurations (0, 0, 1) and (1, 0, 0):
```
a = 10 # edge length (nm)
Nv = 10 # number of verices along one direction
mesh = df.BoxMesh(-a/2., -a/2., -a/2., a/2., a/2., a/2., Nv, Nv, Nv)
Ms = 1e6 # saturation magnetisation (A/m)
sim = Sim(mesh, Ms, unit_length=1e-9)
def compute_fields(n):
demag = Demag(macrogeometry=MacroGeometry(nx=n))
sim.add(demag)
sim.set_m((1, 0, 0))
field1 = sim.llg.effective_field.get_dolfin_function('Demag')
sim.set_m((0, 0, 1))
field2 = sim.llg.effective_field.get_dolfin_function('Demag')
sim.remove_interaction('Demag')
return field1(0, 0, 0)/Ms, field2(0, 0, 0)/Ms
```
Now, the field is computed for different values of $n$ and plotted:
```
field1_list = []
field2_list = []
for i in ns:
fields = compute_fields(i)
field1_list.append(fields[0][0])
field2_list.append(fields[1][2])
plt.figure(figsize=(10, 7))
plt.subplot(211)
plt.plot(ns, field1_list)
plt.xlabel('n')
plt.ylabel('Hx')
plt.grid()
plt.subplot(212)
plt.plot(ns, field2_list)
plt.xlabel('n')
plt.ylabel('Hz')
plt.grid()
```
| true |
code
| 0.361686 | null | null | null | null |
|
# Weather Underground Hurricane Data
-----
## Processed Data Research
A notebook for researching the processed Weather Underground data from the ```src/process_data.py``` script.
```
processed_data_dir = '../data/processed/'
media_dir = '../media'
figsize_width = 12
figsize_height = 8
output_dpi = 72
# Imports
import os
import pickle
import numpy as np
import pandas as pd
from datetime import datetime
import matplotlib.pyplot as plt
# Load Data
with open(os.path.join(processed_data_dir, 'region_data.pkl'), 'rb') as fin:
region_df = pickle.load(fin)
with open(os.path.join(processed_data_dir, 'region_yearly_data.pkl'), 'rb') as fin:
region_yearly_df = pickle.load(fin)
with open(os.path.join(processed_data_dir, 'storm_track_data.pkl'), 'rb') as fin:
storm_track_dict = pickle.load(fin)
# - Variable setup
default_fig_size = (figsize_width, figsize_height)
# - Plot data by region
regions = ['North Atlantic', 'East Pacific', 'Western Pacific', 'Indian Ocean']
stats = ['Storms', 'Hurricanes', 'Deaths', 'Damage']
colors = ['#2d758c', '#cf4917', '#f9ac3d', '#758c33']
color_dict = dict(zip(regions, colors))
fig, axs = plt.subplots(nrows=4, ncols=4, sharex=True, figsize=default_fig_size)
i_col = 0
for region in regions:
t_reg_df = region_df.loc[:, region]
i_row = 0
for statistic in stats:
ax = axs[i_row][i_col]
clr = color_dict[region]
t_reg_df.loc[:, statistic].plot(ax=ax, color=clr)
ax.grid(linestyle='--', color='grey', alpha=0.5)
ax.set_yticklabels([])
if i_col == 0:
ax.set_ylabel(statistic)
if i_row == 0:
ax.set_title(region)
i_row += 1
i_col += 1
fig.suptitle('Data by Region', fontweight='bold', va='top')
fig.savefig(os.path.join(media_dir, 'region_data_by_region_stat.png'), dpi=output_dpi)
plt.show();
# - Get common starting date
plt_start = region_df.first_valid_index()
for region in set(region_df.columns.get_level_values('Region')):
t_df = region_df.loc[:, pd.IndexSlice[region, 'Hurricanes']]
t_df[t_df == 0.] = np.nan
t_start_dt = t_df.first_valid_index()
if t_start_dt > plt_start:
plt_start = t_start_dt
print("Common starting date: {}".format(plt_start))
# - Total occurences over time
agg_data = region_df.groupby(level='Statistic', axis=1).sum().loc[plt_start:]
pct_hurricanes = agg_data.loc[:, 'Hurricanes'] / agg_data.loc[:, 'Storms']
avg_counts = agg_data.loc[:, ['Hurricanes', 'Storms']].mean().values
avg_pct = pct_hurricanes.mean()
# - Plot
plot_percentages = False
fig, ax = plt.subplots(figsize=default_fig_size)
agg_data.loc[:, 'Storms'].plot.area(ax=ax, alpha=1, color='#41a8c9', zorder=1)
agg_data.loc[:, 'Hurricanes'].plot.area(ax=ax, alpha=1, color='#ec8055', zorder=2)
ax.axhline(avg_counts[1], label='Storms Mean ({:.0f})'.format(avg_counts[1]),
color='#2d758c', alpha=0.9, linestyle='--', linewidth=2, zorder=3)
ax.axhline(avg_counts[0], label='Hurricanes Mean ({:.0f})'.format(avg_counts[0]),
color='#cf4917', alpha=0.9, linestyle='--', linewidth=2, zorder=3)
ax.set_title('Storms and Hurricanes over Time (All Regions)', fontweight='bold')
ax.set_ylabel('# of Occurrences');
ax.set_xlabel('')
lines, labels = ax.get_legend_handles_labels()
if plot_percentages:
ax2 = (pct_hurricanes * 100.).plot(ax=ax, secondary_y=True, zorder=4, linestyle='-',
color='#d0b285', linewidth=2.5,
label='Percent Hurricanes')
ax2.axhline(avg_pct*100., label='Percent Mean ({:.1f}%)'.format(100.*avg_pct),
color='#a2783c', alpha=0.9, linestyle='--', linewidth=2, zorder=5)
ax2.set_ylim((0, 100))
ax2.set_ylabel('Percent (%)')
lines_2, labels_2 = ax2.get_legend_handles_labels()
ax.legend(lines[::-1]+lines_2, labels[::-1]+labels_2, loc='upper right')
else:
ax.legend(lines[::-1], labels[::-1], loc='upper right')
fig.savefig(os.path.join(media_dir, 'storms_hurricanes_all_regions.png'),
dpi=output_dpi)
plt.show();
# - Get avg max winds data
start_dates = region_yearly_df.loc[:, ['Start Date']].set_index('Start Date').index
cut_region_yearly = region_yearly_df.loc[start_dates.year >= plt_start, :]
cut_start_dates = cut_region_yearly.loc[:, ['Start Date']].set_index('Start Date').index
avg_max_wind_speed = cut_region_yearly.loc[:, 'Max Winds'].groupby(cut_start_dates.year).mean()
# - Plot
fig, ax = plt.subplots(figsize=default_fig_size)
avg_max_wind_speed.plot(ax=ax, color='#2d758c')
ax.grid(linestyle='--', color='grey', alpha=0.5)
ax.set_ylim(0, 100)
ax.set_title('Average Max Wind Speed over Time (All Regions)', fontweight='bold')
ax.set_ylabel('Wind Speed (mph)')
ax.set_xlabel('')
fig.savefig(os.path.join(media_dir, 'avg_max_wind_speed_by_year.png'), dpi=output_dpi)
plt.show();
# - Avg Max Wind Speed by Region
reg_avgmaxwind = cut_region_yearly.groupby(['Region', cut_start_dates.year], axis=0) \
.mean().loc[:, 'Max Winds'].unstack('Region')
reg_counts = cut_region_yearly.groupby(['Region', cut_start_dates.year], axis=0).count() \
.loc[:, 'Max Winds'].unstack('Region')
# - Plot
fig, axs = plt.subplots(nrows=4, ncols=2, sharex=False,
figsize=(figsize_width, figsize_width))
i = 0
for reg in reg_avgmaxwind.columns:
ax = axs[i][0]
reg_avgmaxwind.loc[:, reg].plot(ax=ax, label=reg, color=color_dict[reg])
ax.set_ylim((0, 120))
ax.set_xlim((1960, 2016))
ax.grid(linestyle='--', color='grey', alpha=0.5)
ax.set_ylabel(reg)
ax.set_xlabel('')
ax = axs[i][1]
reg_counts.loc[:, reg].plot(ax=ax, kind='bar', label='Count', color=color_dict[reg])
ax.xaxis.set_major_locator(plt.MultipleLocator(10))
ax.xaxis.set_ticklabels([plt_start] + list(range(plt_start, 2015, 10)), rotation=0)
ax.set_xlabel('')
i += 1
axs[0][0].set_title('Avg Max Wind Speed by Year (mph)', fontweight='bold')
axs[0][1].set_title('Data Count by Year', fontweight='bold')
axs[-1][0].set_xlabel('')
axs[-1][1].set_xlabel('')
fig.savefig(os.path.join(media_dir, 'avg_max_winds_by_region.png'), dpi=output_dpi)
plt.show();
# - North Atlantic Specific Focus
allyr_avgmaxwind = region_yearly_df.groupby(['Region', start_dates.year], axis=0) \
.mean().loc[:, 'Max Winds'].unstack('Region')
allyr_counts = region_yearly_df.groupby(['Region', start_dates.year], axis=0) \
.count().loc[:, 'Max Winds'].unstack('Region')
fig, axs = plt.subplots(nrows=1, ncols=2,
figsize=(figsize_width, figsize_height/2))
ax = axs[0]
allyr_avgmaxwind.loc[:, 'North Atlantic'].plot(ax=ax, color=color_dict['North Atlantic'])
ax.set_ylim(0, 120)
ax.grid(True, color='grey', alpha=0.6, linestyle='--')
ax.set_title('')
ax.set_ylabel('Average Max Wind Speed (mph)')
ax.set_xlabel('')
ax = axs[1]
allyr_counts.loc[:, 'North Atlantic'].plot(ax=ax, kind='bar', label='Count',
color=color_dict['North Atlantic'])
disp_mult = 20
ax.xaxis.set_major_locator(plt.MultipleLocator(disp_mult))
ax.xaxis.set_ticklabels([allyr_counts.index[0]] +
list(range(allyr_counts.index[0], 2015, disp_mult)),
rotation=0)
ax.set_title('')
ax.set_ylabel('# of Data Points')
ax.set_xlabel('')
fig.suptitle('North Atlantic (All Data)', fontweight='bold')
fig.savefig(os.path.join(media_dir, 'north_atlantic_max_wind_speed_all.png'),
dpi=output_dpi)
plt.show();
# - 1945 Onward for North Atlantic
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(figsize_width, figsize_height/2))
ax = axs[0]
allyr_avgmaxwind.loc[1945:, 'North Atlantic'].plot(ax=ax,
color=color_dict['North Atlantic'])
ax.set_ylim(0, 120)
ax.grid(True, color='grey', alpha=0.6, linestyle='--')
ax.set_title('')
ax.set_ylabel('Average Max Wind Speed (mph)')
ax.set_xlabel('')
ax = axs[1]
allyr_counts.loc[1945:, 'North Atlantic'].plot(ax=ax, kind='bar', label='Count',
color=color_dict['North Atlantic'])
disp_mult = 10
ax.xaxis.set_major_locator(plt.MultipleLocator(disp_mult))
ax.xaxis.set_ticklabels([1945] + list(range(1945, 2015, disp_mult)),
rotation=0)
ax.set_title('')
ax.set_ylabel('# of Data Points')
ax.set_xlabel('')
fig.suptitle('North Atlantic (since 1945)', fontweight='bold')
fig.savefig(os.path.join(media_dir, 'north_atlantic_max_wind_speed_1945.png'),
dpi=output_dpi)
plt.show();
# - Tack on IsHurricane Columns to Regional-Yearly data
def _classify_helper(storm_name):
"""Helper function to classify 'hurricanes'"""
ret = False
designations = ['hurricane', 'typhoon']
storm_name = storm_name.lower()
all_words = storm_name.split(' ')
for designation in designations:
ret |= (designation in all_words)
return ret
regyr_wclass = region_yearly_df.copy()
is_hurricane = np.zeros((regyr_wclass.shape[0], 1))
for row_id, vals in enumerate(regyr_wclass.values):
is_hurricane[row_id] = 1 if _classify_helper(vals[1]) else 0
regyr_wclass['IsHurricane'] = regyr_wclass.loc[:, 'Max Winds'] >= 75.0
# - 1945 Onward for North Atlantic (Hurricanes Only)
hurricane_data = regyr_wclass.loc[regyr_wclass.loc[:, 'IsHurricane'] == 1] \
.drop('IsHurricane', axis=1)
hurricane_years = hurricane_data.loc[:, ['Start Date']].set_index('Start Date').index
regavg_hurricanes = hurricane_data.groupby(['Region', hurricane_years.year], axis=0) \
.mean().loc[:, 'Max Winds'].unstack('Region')
regcnt_hurricanes = hurricane_data.groupby(['Region', hurricane_years.year], axis=0) \
.count().loc[:, 'Max Winds'].unstack('Region')
# -- Plot
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(figsize_width, figsize_height/2))
ax = axs[0]
regavg_hurricanes.loc[1945:, 'North Atlantic'].plot(ax=ax,
color=color_dict['North Atlantic'])
ax.set_ylim(0, 140)
ax.grid(True, color='grey', alpha=0.6, linestyle='--')
ax.set_title('')
ax.set_ylabel('Average Max Wind Speed (mph)')
ax.set_xlabel('')
ax = axs[1]
regcnt_hurricanes.loc[1945:, 'North Atlantic'].plot(ax=ax, kind='bar', label='Count',
color=color_dict['North Atlantic'])
disp_mult = 10
ax.xaxis.set_major_locator(plt.MultipleLocator(disp_mult))
ax.xaxis.set_ticklabels([1945] + list(range(1945, 2015, disp_mult)),
rotation=0)
ax.set_title('')
ax.set_ylabel('# of Data Points')
ax.set_xlabel('')
fig.suptitle('North Atlantic Hurricanes', fontweight='bold')
fig.savefig(os.path.join(media_dir, 'north_atlantic_hurricanes_max_wind_speed_1945.png'),
dpi=output_dpi)
plt.show();
# - 1945 Onward for North Atlantic (Hurricanes Only)
non_hurr_data = regyr_wclass.loc[regyr_wclass.loc[:, 'IsHurricane'] == 0] \
.drop('IsHurricane', axis=1)
non_hurr_years = non_hurr_data.loc[:, ['Start Date']].set_index('Start Date').index
regavg_nonhurrs = non_hurr_data.groupby(['Region', non_hurr_years.year], axis=0) \
.mean().loc[:, 'Max Winds'].unstack('Region')
regcnt_nonhurrs = non_hurr_data.groupby(['Region', non_hurr_years.year], axis=0) \
.count().loc[:, 'Max Winds'].unstack('Region')
# -- Plot
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(figsize_width, figsize_height/2))
ax = axs[0]
regavg_nonhurrs.loc[1945:, 'North Atlantic'].plot(ax=ax,
color=color_dict['North Atlantic'])
ax.set_ylim(0, 140)
ax.grid(True, color='grey', alpha=0.6, linestyle='--')
ax.set_title('')
ax.set_ylabel('Average Max Wind Speed (mph)')
ax.set_xlabel('')
ax = axs[1]
regcnt_nonhurrs.loc[1945:, 'North Atlantic'].plot(ax=ax, kind='bar', label='Count',
color=color_dict['North Atlantic'])
disp_mult = 10
ax.xaxis.set_major_locator(plt.MultipleLocator(disp_mult))
ax.xaxis.set_ticklabels([1945] + list(range(1945, 2015, disp_mult)),
rotation=0)
ax.set_title('')
ax.set_ylabel('# of Data Points')
ax.set_xlabel('')
fig.suptitle('North Atlantic Non-Hurricanes', fontweight='bold')
fig.savefig(os.path.join(media_dir, 'north_atlantic_non_hurricanes_max_wind_speed_1945.png'),
dpi=output_dpi)
plt.show();
# - Hurricanes vs. Non-hurricanes by Region
hurr_prop = (regcnt_hurricanes.fillna(0) / (regcnt_nonhurrs + regcnt_hurricanes.fillna(0)))
# -- Plot
fig, axs = plt.subplots(nrows=4, ncols=3, figsize=(figsize_width, figsize_width/1.3))
for i_reg in range(len(regions)):
reg = regions[i_reg]
ax = axs[i_reg][0]
regavg_hurricanes.loc[1945:, reg].plot(ax=ax, color=color_dict[reg])
ax.set_ylim((0, 150))
ax.set_xlim((1944, 2016))
ax.grid(linestyle='--', color='grey', alpha=0.5)
ax.set_ylabel(reg)
ax.set_xlabel('')
ax = axs[i_reg][1]
regavg_nonhurrs.loc[1945:, reg].plot(ax=ax, color=color_dict[reg])
ax.set_ylim((0, 150))
ax.set_xlim((1944, 2016))
ax.grid(linestyle='--', color='grey', alpha=0.5)
ax.set_ylabel('')
ax.set_xlabel('')
ax = axs[i_reg][2]
(hurr_prop * 100.).loc[1945:, reg].plot(ax=ax, color=color_dict[reg])
ax.grid(linestyle='--', color='grey', alpha=0.5)
ax.set_ylim(0, 100)
ax.set_xlabel('')
axs[0][0].set_title('Hurricanes')
axs[0][1].set_title('Non-Hurricanes')
axs[0][2].set_title('Proportion Hurricanes (%)')
fig.suptitle('Hurricanes and Non-hurricanes by Region', fontweight='bold', va='top')
fig.savefig(os.path.join(media_dir, 'hurr_vs_non_hurr_stats_region.png'),
dpi=output_dpi)
plt.show();
```
| true |
code
| 0.656438 | null | null | null | null |
|
# Lecture 16: Classification
# Problem setting
## Review
In last few lectures we have learned the linear regression, where we explore the possibility of using a linear function (or higher degree polynomials) to represent the relation of the features in the samples (aka labels, $x$ values, or training data `X_train`) to a target value ($y$ values `y_train`), so that we can predict the target value $y$ (`y_pred` obtained by the model) based on testing data `X_test`.
However, linear regression is not appropriate in the case of a qualitative target value.
## Classification
Today, we will learn how to predict a discrete label such as
* predicting whether a grid of pixel intensities represents a "0" digit or a "1" digit;
* predicting whether tomorrow will have rain based on previous days' data.
* predicting whether a wine is good or mediocre based on its chemical components' data.
This is a classification problem. Logistic regression is a simple classification algorithm for learning to make such decisions for a binary label.
Reference: MATLAB tutorial in [Stanford Deep Learning tutorial](http://deeplearning.stanford.edu/tutorial/).
# Logistic Regression
----
## Heuristics
Recall the `winequality-red.csv` we have used in the last few lectures and labs. If the `quality` of a wine is $\geq 6$, relabel it as "favorable"; if the `quality` of a wine is $\leq 5$, relabel it as "mediocre".
For a certain sample $(\mathbf{x}^{(i)}, y^{(i)})$, where $\mathbf{x}^{(i)}$ is the vector representing its first 11 features, and $y^{(i)}$ is the quality score (label), if we know its score is 7, then
$$
P\big(i\text{-th sample is favorable} \big) = 1, \qquad
P\big(i\text{-th sample is mediocre} \big) = 0.
$$
If we relabel the "favorable" and "mediocre" into 1 and 0 as our values for $y^{(i)}$, then
$$
P\big(y^{(i)} = 1\big) = 1, \qquad P\big(y^{(i)} = 0\big) = 0.
$$
If some other sample, say $j$-th sample, has quality score 4, then
$$
P\big(y^{(i)} = 1\big) = 0, \qquad P\big(y^{(i)} = 0\big) = 1.
$$
We can use vector $[1,0]$ to represent the first sample's probability in each class, and vector $[0,1]$ to represent that of the second sample.
We want to build a model, so that given the first 11 features $\mathbf{x}$ of a certain sample, it can output an estimate, say, $[0.8, 0.2]$ to tell me that
$$
P\big(y = 1| \mathbf{x}\big) = 0.8, \qquad P\big(y = 0|\mathbf{x}\big) = 0.2,
$$
which is to say, this sample has 0.8 chance in Class 1, 0.2 chance in the Class 0. The predicted label $\hat{y}$ is then:
$$
\hat{y} = \operatorname{arg}\max_{j} P\big(y = j| \mathbf{x}\big),
$$
i.e., we use the biggest estimated probability's class as this sample's predicted label.
# Logistic regression
----
## Model function (hypothesis)
Weights vector $\mathbf{w}$, same shape with a sample's feature vector $\mathbf{x}$, $h(\mathbf{x})$ is our estimate of $ P(y=1|\mathbf{x})$ and $1 - h(\mathbf{x})$ is our estimate of $P(y=0|\mathbf{x}) = 1 - P(y=1|\mathbf{x})$.
$$
h(\mathbf{x}) = h(\mathbf{x};\mathbf{w}) = \frac{1}{1 + \exp(-\mathbf{w}^\top \mathbf{x})}
=: \sigma(\mathbf{w}^\top \mathbf{x})
$$
or more compactly, because $y = 0$ or $1$:
$$
P(y|\mathbf{x}) \text{ is estimated by } h(\mathbf{x})^y \big(1 - h(\mathbf{x}) \big)^{1-y}.
$$
----
## Loss function
$$
L (\mathbf{w}; X, \mathbf{y}) = - \frac{1}{N}\sum_{i=1}^N
\Bigl\{y^{(i)} \ln\big( h(\mathbf{x}^{(i)}; \mathbf{w}) \big)
+ (1 - y^{(i)}) \ln\big( 1 - h(\mathbf{x}^{(i)};\mathbf{w}) \big) \Bigr\}.
\tag{$\star$}
$$
----
## Training
The gradient of the loss function with respect to the weights $\mathbf{w}$ is:
$$
\nabla_{\mathbf{w}} \big( L (\mathbf{w}) \big)
=\frac{1}{N}\sum_{i=1}^N \big( h(\mathbf{x}^{(i)};\mathbf{w}) - y^{(i)} \big) \mathbf{x}^{(i)} . \tag{$\dagger$}
$$
```
import numpy as np
# model h(X; w) = sigma(-Xw)
# w: weights
# X: training data
# X.shape[0] is no. of samples, and X.shape[1] is the no. of features
def h(w,X):
z = np.matmul(X,w)
return 1.0 / (1.0 + np.exp(-z))
# loss function, modulo by N (size of training data), a vectorized implementation without for loop
def loss(w,X,y):
loss_components = np.log(h(w,X)) * y + (1.0 - y)* np.log(1 - h(w,X))
# above is a dimension (12665,) array
return -np.mean(loss_components) # same with loss_components.sum()/N
def gradient_loss(w,X,y):
gradient_for_all_training_data = (h(w,X) - y).reshape(-1,1)*X
# we should return a (n,) array, which is averaging all N training data's gradient
return np.mean(gradient_for_all_training_data, axis=0)
```
# Reading 1: Derivation of the logistic regression
For binary-valued labels, $y^{(i)} \in \{0,1\}$, we are trying to predict the probability that a given example belongs to the "1" class versus the probability that it belongs to the "0" class. Specifically, we will use the **logistic regression**, which tries to learn a function of the form:
$$
h(\mathbf{x}) = h(\mathbf{x};\mathbf{w}) = \frac{1}{1 + \exp(-\mathbf{w}^\top \mathbf{x})}
=: \sigma(\mathbf{w}^\top \mathbf{x})
$$
or more compactly, because $y = 0$ or $1$:
$$
P(y|\mathbf{x}) = h(\mathbf{x})^y \big(1 - h(\mathbf{x}) \big)^{1-y}
$$
----
## Sigmoid function
The function $\sigma(z) = 1/\big(1+\exp(−z)\big)$ is often called the "sigmoid" or "logistic" function, or "logistic/sigmoid" activation function in machine learning. It is an S-shaped function that "squashes" the value of $\mathbf{w}^\top \mathbf{x}$ into the range $[0,1]$ so that we may interpret $h(\mathbf{x})$ as a probability.
Our goal is to search for a value of the weights $\mathbf{w}$ so that:
> The probability $P(y=1|\mathbf{x})=h(\mathbf{x})$ is large when $x$ belongs to the "1" class, small when $x$ belongs to the "0" class (so that $P(y=0|\mathbf{x})=1- h(\mathbf{x})$ is large).
----
## Maximum likelihood
For a set of training examples with binary labels $\{(\mathbf{x}^{(i)},y^{(i)}):i=1,\dots,N\}$ the following likelihood estimator measures how well a given model $h(\mathbf{x};\mathbf{w})$ does this separating class job: assuming our training samples are independently Bernoulli distributed, we want to maximize the following quantity
$$
{\begin{aligned}
&P(\mathbf{y}\; | \; \mathbf{X};\mathbf{w} )\\
=&\prod _{i=1}^N P\left(y^{(i)}\mid \mathbf{x}^{(i)};\mathbf{w}\right)\\
=&\prod_{i=1}^N h\big(\mathbf{x}^{(i)} \big)^{y^{(i)}}
\Big(1-h\big(\mathbf{x}^{(i)}\big) \Big)^{\big(1-y^{(i)}\big)}
\end{aligned}}.
$$
This function is highly nonlinear on the weights $\mathbf{w}$ so we take the log and then average, lastly define our loss function to be minimized as follows:
$$
L (\mathbf{w}) = L (\mathbf{w}; X,\mathbf{y}) = - \frac{1}{N}\sum_{i=1}^N
\Bigl\{y^{(i)} \ln\big( h(\mathbf{x}^{(i)}) \big)
+ (1 - y^{(i)}) \ln\big( 1 - h(\mathbf{x}^{(i)}) \big) \Bigr\}.
\tag{$\star$}
$$
Note that only one of the two terms in the summation is non-zero for each training sample (depending on whether the label $y^{(i)}$ is 0 or 1). When $y^{(i)}=1$ minimizing the loss function means we need to make $h(x^{(i)})$ large, and when $y^{(i)}= 0$ we want to make $1- h(x^{(i)})$ large as explained above.
----
## Training and cross-validation
After the loss function $L (\mathbf{w})$ is set up, the training data is used by the gradient descent to minimize $L (\mathbf{w})$ to find the best choice of weights $\mathbf{w}$. Even though the cost function $(\star)$ looks quite complicated, due to the following special property of the Sigmoid function
$$
\frac{d}{dz} \big(\sigma(z)\big)
= \frac{d}{dz} \left(\frac{1}{1+\exp(−z)}\right) = \sigma(z)\cdot \big(1-\sigma(z)\big).
$$
Therefore recalling $h(\mathbf{x}) = \sigma(\mathbf{w}^\top \mathbf{x})$
$$
\begin{aligned}
\frac{\partial L (\mathbf{w})}{\partial w_k} & =
- \frac{1}{N}\sum_{i=1}^N
\Bigg\{y^{(i)} \frac{1}{h(\mathbf{x}^{(i)})} \frac{\partial}{\partial w_k} \sigma\big(\mathbf{w}^{\top} \mathbf{x}^{(i)} \big)
+ (1 - y^{(i)}) \frac{1}{1-h(\mathbf{x}^{(i)})} \frac{\partial}{\partial w_k}\Big(1- \sigma\big(\mathbf{w}^{\top} \mathbf{x}^{(i)}\big) \Big) \Bigg\}
\\
& = - \frac{1}{N}\sum_{i=1}^N
\Bigg\{y^{(i)} \frac{1}{h(\mathbf{x}^{(i)})}
\sigma\big(\mathbf{w}^{\top} \mathbf{x}^{(i)}\big)
\cdot \big(1-\sigma(\mathbf{w}^{\top} \mathbf{x}^{(i)})\big)
\frac{\partial}{\partial w_k} \sigma\big(\mathbf{w}^{\top} \mathbf{x}^{(i)} \big)
\\
& \qquad \qquad - (1 - y^{(i)}) \frac{1}{1-h(\mathbf{x}^{(i)})}
\sigma\big(\mathbf{w}^{\top} \mathbf{x}^{(i)}\big)
\cdot \big(1-\sigma(\mathbf{w}^{\top} \mathbf{x}^{(i)})\big)
\frac{\partial}{\partial w_k}\big(\mathbf{w}^{\top} \mathbf{x}^{(i)}\big) \Bigg\}
\\
& = - \frac{1}{N}\sum_{i=1}^N
\Bigg\{y^{(i)} \cdot \big(1-\sigma(\mathbf{w}^{\top} \mathbf{x}^{(i)})\big)
\frac{\partial}{\partial w_k} \sigma\big(\mathbf{w}^{\top} \mathbf{x}^{(i)} \big)
- (1 - y^{(i)}) \cdot
\sigma(\mathbf{w}^{\top} \mathbf{x}^{(i)})
\frac{\partial}{\partial w_k}\big(\mathbf{w}^{\top} \mathbf{x}^{(i)}\big) \Bigg\}
\\
& =\frac{1}{N}\sum_{i=1}^N \big(\sigma(\mathbf{w}^{\top} \mathbf{x}^{(i)}) - y^{(i)} \big) x^{(i)}_k.
\end{aligned}
$$
The final expression is pretty simple, basically the derivative of the Logistic loss function w.r.t. the $k$-th weight $w_k$ is the sum of the residuals $\big(\sigma(\mathbf{w}^{\top} \mathbf{x}^{(i)}) - y^{(i)} \big) $ multiply with the $k$-th component in the $i$-th training data $\mathbf{x}^{(i)}$.
Therefore the gradient for all the weights $\mathbf{w}$ is then:
$$
\nabla_{\mathbf{w}} \big( L (\mathbf{w}) \big) = \sum_{i=1}^N \big(\sigma(\mathbf{w}^{\top} \mathbf{x}^{(i)}) - y^{(i)} \big) \mathbf{x}^{(i)}
=\frac{1}{N}\sum_{i=1}^N \big( h(\mathbf{x}^{(i)}) - y^{(i)} \big) \mathbf{x}^{(i)} . \tag{$\dagger$}
$$
# Reading 2: Bayesian classification
What we have learned above, the logistic regression and softmax regression, are two classification methods that are closely related to Bayesian classifiers. Because essentially, we are trying minimize the following the error associated with a set of observations of the form in a way (by introducing some model with weights):
$$
\min_{\mathbf{w}} \Big[\text{Mean of } 1\big\{y^{(i), \text{Pred}} \neq y^{(i), \text{Actual}} \big\} \Big],
$$
If there is no model yet, let $K= \# \text{ classes}$. Keep in mind for now there are no weights involved, we simply want to classify the samples into $K$ classes, so that the minimization of problem above is *assigning each sample to the most likely class it belongs to*, given its values (feature vector), i.e., we want to compute
$$
\max_{j\in \{1,\dots ,K\}} P\big(y^{(i)}=j | \mathbf{x}^{(i)} \big) \tag{$\diamond$}
$$
where $P\big(y^{(i)}=j | \mathbf{x}^{(i)} \big)$ is the conditional probability that the label $y^{(i)}=j$ (the $i$-th sample is in the $j$-th class), given the observed vector $\mathbf{x}^{(i)}$ for the $i$-th sample. This is called the naive Bayes classifier.
----
### Naive Bayes classifier
Using the definition of the conditional probability: for an arbitrary sample and its label $(\mathbf{x},y)$
$$
P(y=j | \mathbf {x} )={\frac { P( y = j, \mathbf {x})}{P(\mathbf {x} )}} \tag{$\ast$}
$$
Assuming $\mathbf{x} = (x_1, x_2, \dots, x_n)$, i.e., each sample has $n$ features, then the numerator above is
$ P(y=j)\ P(\mathbf {x} | y = j)$, where $P(y=j)$ is the probability that an arbitrary sample is of class $j$ without any observation $\mathbf{x}$, i.e., $P(y=j)$ is the portion of class $j$ against all all samples. Now using the definition of conditional probability again:
$$
\begin{aligned}
P(y=j,x_{1},\dots ,x_{n}) &= P(x_{1},\dots ,x_{n},y=j)
\\
&= P(x_{1} | x_{2},\dots ,x_{n},y=j) P(x_{2},\dots ,x_{n},y=j)
\\
&= P(x_{1} | x_{2},\dots ,x_{n},y=j) P(x_{2} | x_{3},\dots ,x_{n},y=j) P(x_{3},\dots ,x_{n},y=j)
\\&=\dots
\\&= P(x_{1} | x_{2},\dots ,x_{n},y=j) P(x_{2} | x_{3},\dots ,x_{n},y=j)
\dots P(x_{n-1} | x_{n},y=j) P(x_{n}| y=j)P(y=j)\\
\end{aligned} \tag{$\ast\ast$}
$$
Assuming each feature is independent from one another, which means whether put $x_l$ ($l\neq i$) into the given observed conditions does not affect the probability of $x_i$:
$$
P(x_{i} | x_{i+1},\dots ,x_{n}, y =j) = P(x_{i}| y=j).
$$
Since $P(\mathbf{x}) = 1/N$ is a fixed value (assuming uniform distributed sample), we have by $(\ast)$ and $(\ast\ast)$
$$
\begin{aligned}
P(y=j | x_{1},\dots ,x_{n}) &\propto P(y=j,x_{1},\dots ,x_{n})
\\
&=P(y=j)\ P(x_{1} | y=j)\ P(x_{2}| y=j)\ P(x_{3} | y=j)\ \cdots
\\
&=P(y=j)\prod_{i=1}^{n}P(x_{i}| y=j),
\end{aligned}
$$
Now for training sample $\mathbf{x}^{(i)}$, the problem becomes:
$$
y^{(i), \text{Pred}}={\underset {j\in \{1,\dots ,K\}}{\operatorname {argmax} }}\ P(y = j)\displaystyle \prod _{i=1}^{n} P(x_{i} | y=j),
$$
where $y^{(i), \text{Pred}}$ is the class which the probability $(\diamond)$ is maximized.
----
### Pitfalls of naive Bayes classifier
In reality, there are two main reasons the method above is neither practical nor reasonable.
* there is no way $x_i$ and $x_l$ are independent when $i\neq l$ for a sample $\mathbf{x}$. Think in the handwritten digit classification example, $x_i$'s are the pixel intensity at $i$-th location (one of the pixel among 28x28 reshaped into a 784 array), any reasonable ansatz should not assume independency, because the pixel intensity are determined by the strokes.
* For real data, we do not know $P(y=j)$'s true value, i.e., percentage of the samples in class $k$, because new data may come in. For the same reason $P(x_{i} | y=j)$ is not known either.
Therefore, we introduce a model (an a priori assumption that the data can be described by such a model) with weights $\mathbf{w}$, and the problem changes to (softmax case) the following maximization of the log of the likehood function (or say cross entropy),
$$
\max_{\mathbf{w}}\sum_{i=1}^N \left\{\sum_{j=1}^K
1_{\{y^{(i)} = j\}} \ln P\big(y^{(i)}=j | \mathbf{x}^{(i)} ; \mathbf{w} \big) \right\},
$$
in Lecture 15, 16, 17, we will try using gradient descent to minimize the negative version of above.
| true |
code
| 0.604895 | null | null | null | null |
|
# Modeling and Simulation in Python
Milestone: Queueing theory
Copyright 2017 Allen Downey
License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
```
# If you want the figures to appear in the notebook,
# and you want to interact with them, use
# %matplotlib notebook
# If you want the figures to appear in the notebook,
# and you don't want to interact with them, use
# %matplotlib inline
# If you want the figures to appear in separate windows, use
# %matplotlib qt5
# To switch from one to another, you have to select Kernel->Restart
%matplotlib inline
from modsim import *
```
### One queue or two?
This notebook presents a solution to an exercise from *Modeling and Simulation in Python*. It uses features from the first four chapters to answer a question related to queueing theory, which is the study of systems that involve waiting in lines, also known as "queues".
Suppose you are designing the checkout area for a new store. There is room for two checkout counters and a waiting area for customers. You can make two lines, one for each counter, or one line that serves both counters.
In theory, you might expect a single line to be better, but it has some practical drawbacks: in order to maintain a single line, you would have to install rope barriers, and customers might be put off by what seems to be a longer line, even if it moves faster.
So you'd like to check whether the single line is really better and by how much. Simulation can help answer this question.
As we did in the bikeshare model, we'll assume that a customer is equally likely to arrive during any timestep. I'll denote this probability using the Greek letter lambda, $\lambda$, or the variable name `lam`. Since it's a new store, we don't know what the value of $\lambda$ will be, so we'll have to consider a range of possibilities.
Based on data from other stores, you know that it takes 5 minutes for a customer to check out, on average. But checkout times are highly variable: most customers take less than 5 minutes, but some take substantially more. A simple way to model this variability is to assume that when a customer is checking out, they have the same probability of finishing up during each time step. I'll denote this probability using the Greek letter mu, $\mu$, or the variable name `mu`.
If we choose $\mu=1/5$, the average number of time steps for each checkout will be 5 minutes, which is consistent with the data.
**Solution**
I'll start by defining a `System` object to contain the system parameters.
```
def make_system(lam, mu):
return System(lam=lam, mu=mu,
x=0, duration=8*60)
```
As an example, I'll set the arrival rate to one customer per 8 minutes.
```
interarrival_time = 8
service_time = 5
lam = 1 / interarrival_time
mu = 1 / service_time
system = make_system(lam, mu)
system
```
Here's a update function that simulates a single time step. During each time step, a customer can finish checking out (but only if there is a customer in the system), and a new customer can arrive.
```
def update_func1(system):
"""Simulate one time step.
system: System object
"""
# if there's a customer in service, check if they're done
if system.x > 0:
if flip(system.mu):
system.x -= 1
# check for an arrival
if flip(system.lam):
system.x += 1
```
Now we can run the simulation. `run_simulation` creates a `TimeSeries` that maps from each time step to the total number of customers in the store, including the one checking out.
After the simulation, we compute `L`, which is the average number of customers in the system, and `W`, which is the average time customers spend in the store. `L` and `W` are related by Little's Law:
$L = \lambda W$
Where $\lambda$ is the arrival rate.
```
def run_simulation(system, update_func):
"""Simulate a queueing system.
system: System object
update_func: function object
"""
results = TimeSeries()
for t in linrange(0, system.duration-1):
update_func(system)
results[t] = system.x
system.results = results
system.L = results.mean()
system.W = system.L / system.lam
```
Here are the results with the parameters we chose.
```
run_simulation(system, update_func1)
print(system.L, system.W)
plot(system.results)
```
Since we don't know the actual value of $\lambda$, we can sweep through a range of possibilities, from 10% to 80% of the completion rate.
If customers arrive faster than the completion rate, the queue grows without bound. In that case the metrics `L` and `W` just depend on how long the store is open.
```
mu = 1 / service_time
num_vals = 101
lam_array = linspace(0.1*mu, 0.8*mu, num_vals)
print(mu)
lam_array
```
The model I chose for this system is a common model in queueing theory, in part because many of its properties can be derived analytically. In particular, we expect the average time in the store to be:
$W = 1 / (\mu - \lambda)$
The following function plots the theoretical value of $W$ as a function of $\lambda$.
```
def plot_W(lam_array, mu):
"""Plot the theoretical mean wait time.
lam_array: array of values for `lam`
mu: probability of finishing a checkout
"""
W = 1 / (mu - lam_array)
plot(lam_array, W, 'g-')
plot_W(lam_array, mu)
```
Now let's run the simulation with a range of values for $\lambda$ and plot the observed value of `W` versus `lam`:
```
def sweep_lam(lam_array, mu, update_func):
"""Run simulations with a range of values for `lam`
Plots wait time, W, versus lam, and
prints the average of W across runs.
lam_array: array of values for `lam`
mu: probability of finishing a checkout
update_func: passed along to run_simulation
"""
total = 0
for lam in lam_array:
system = make_system(lam, mu)
run_simulation(system, update_func)
total += system.W
plot(lam, system.W)
W_avg = total / len(lam_array)
print('Average of averages = ', W_avg, 'minutes')
```
If we imagine that this range of values represents arrival rates on different days, we can use the average value of `W`, for a range of values of `lam`, to compare different queueing strategies.
Here are the results for a single queue with a single checkout counter.
```
plot_W(lam_array, mu)
sweep_lam(lam_array, mu, update_func1)
decorate(xlabel='Arrival rate (per minute)',
ylabel='Average time in system')
```
The results on any simulated day are highly variable, but looks like the theoretical result is plausible. The simulated results tend to be lower, partly because they include a cold start at the beginning of each day.
Now let's try the other two queueing strategies:
1. One queue with two checkout counters.
2. Two queues, one for each counter.
The following figure shows the three scenarios:

Here's the update function for a single queue with two servers.
```
def update_func2(system):
"""Simulate a single queue with two servers.
system: System object
"""
# if both servers are busy, check whether the
# second is complete
if system.x > 1 and flip(system.mu):
system.x -= 1
# check whether the first is complete
if system.x > 0 and flip(system.mu):
system.x -= 1
# check for an arrival
if flip(system.lam):
system.x += 1
```
Here are the results for a single run.
```
system = make_system(lam, mu)
run_simulation(system, update_func2)
print(system.L, system.W)
plot(system.results)
```
Since we have two counters now, we can consider a wider range of values for $\lambda$
```
lam_array = linspace(0.1*mu, 1.6*mu, num_vals)
```
Here's what the results look like. With two counters, the average time in the store is lower, even for higher values of $\lambda$
```
sweep_lam(lam_array, mu, update_func2)
decorate(xlabel='Arrival rate (per minute)',
ylabel='Average time in system')
```
Finally, here's the update function for the scenario with two separate queues.
```
def update_func3(system):
"""Simulate two queues with one server each.
system: System object
"""
# if the first servers is busy, check it it's done
if system.q1 > 0 and flip(system.mu):
system.q1 -= 1
# if the second queue is busy, check if it's done
if system.q2 > 0 and flip(system.mu):
system.q2 -= 1
# check for an arrival
if flip(system.lam):
# join whichever queue is shorter
if system.q1 < system.q2:
system.q1 += 1
else:
system.q2 += 1
system.x = system.q1 + system.q2
```
Since we added `q1` and `q2` as system variables, we need a new version of `make_system`
```
def make_system(lam, mu):
return System(lam=lam, mu=mu,
x=0, duration=8*60,
q1=0, q2=0)
```
Here are the results for a single run
```
system = make_system(lam, mu)
run_simulation(system, update_func3)
print(system.L, system.W)
plot(system.results)
```
And here are the results for a range of values of `lam`
```
sweep_lam(lam_array, mu, update_func3)
decorate(xlabel='Arrival rate (per minute)',
ylabel='Average time in system')
```
With two queues, the average of averages is slightly higher, most of the time. But the difference is small.
The two configurations are equally good as long as both servers are busy; the only time two lines is worse is if one queue is empty and the other contains more than one customer. In real life, if we allow customers to change lanes, that disadvantage can be eliminated.
From a theoretical point of view, one line is better. From a practical point of view, the difference is small and can be mitigated. So the best choice depends on practical considerations.
On the other hand, you can do substantially better with an express line for customers with short service times. But that's a topic for another notebook.
| true |
code
| 0.623004 | null | null | null | null |
|
## Grid Manipulations (merge, split, refine, transform)
### Notes
Most grid transformations such as `merge` and `transpose` return a new object, allowing consecutive operations to be chained together.
Optionally, you can pass `inplace=True` to the call signature to modify the existing object and return `None`.
Both approaches are demonstrated below.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas
from shapely.geometry import Point, Polygon
import geopandas
import pygridgen as pgg
import pygridtools as pgt
```
### Basic merging operations
The function below create our 3 test model grids moving counter-clockwise in the figure shown two cells down.
```
def to_gdf(df):
return (
df.assign(geometry=df.apply(lambda r: Point(r.x, r.y), axis=1))
.drop(columns=['x', 'y'])
.pipe(geopandas.GeoDataFrame)
)
def make_test_grids():
domain1 = pandas.DataFrame({'x': [2, 5, 5, 2], 'y': [6, 6, 4, 4], 'beta': [1, 1, 1, 1]})
domain2 = pandas.DataFrame({'x': [6, 11, 11, 5], 'y': [5, 5, 3, 3], 'beta': [1, 1, 1, 1]})
domain3 = pandas.DataFrame({'x': [7, 9, 9, 7], 'y': [2, 2, 0, 0], 'beta': [1, 1, 1, 1]})
grid1 = pgt.make_grid(domain=to_gdf(domain1), nx=6, ny=5, rawgrid=False)
grid2 = pgt.make_grid(domain=to_gdf(domain2), nx=8, ny=7, rawgrid=False)
grid3 = pgt.make_grid(domain=to_gdf(domain3), nx=4, ny=10, rawgrid=False)
return grid1, grid2, grid3
```
Display positions of grids relative to each other
```
grid1, grid2, grid3 = make_test_grids()
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = grid1.plot_cells(ax=ax, cell_kws=dict(cmap='Blues'))
_ = grid2.plot_cells(ax=ax, cell_kws=dict(cmap='Greens'))
_ = grid3.plot_cells(ax=ax, cell_kws=dict(cmap='Reds'))
```
#### Merge grids 1 and 2 together, horizontally
By default, the bottom rows are aligned and the cell mask is not updated. We do that manually for now.
```
one_two = grid1.merge(grid2, how='horiz')
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = one_two.plot_cells(ax=ax, cell_kws=dict(cmap='BuPu'))
_ = grid3.plot_cells(ax=ax, cell_kws=dict(cmap='Reds'))
```
#### Use the shift parameter to center grid 2
Use `shift=-1` since we're sliding grid 2's i-j indexes downward relative to grid 1
```
one_two = grid1.merge(grid2, how='horiz', shift=-1)
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = one_two.plot_cells(ax=ax, cell_kws=dict(cmap='BuPu'))
_ = grid3.plot_cells(ax=ax, cell_kws=dict(cmap='Reds'))
```
#### Vertically merge grid 2 and grid 3
Notice that by default, the grids are left-aligned and the *bottom* of grid 3 ties into the *top* of grid 2
```
two_three = grid2.merge(grid3, how='vert', shift=2)
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = grid1.plot_cells(ax=ax, cell_kws=dict(cmap='Blues'))
_ = two_three.plot_cells(ax=ax, cell_kws=dict(cmap='YlOrBr'))
```
#### Try again, switching the order of the grids
Notice the change in sign of the `shift` parameter.
```
two_three = grid3.merge(grid2, how='vert', shift=-2)
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = grid1.plot_cells(ax=ax, cell_kws=dict(cmap='Blues'))
_ = two_three.plot_cells(ax=ax, cell_kws=dict(cmap='YlOrBr'))
```
#### Alternatively, you can switch the arguments and use `where='-'` to indicate that the "other" grid is below the first.
And the sign of the `shift` parameter returns to its original value.
```
two_three = grid2.merge(grid3, how='vert', where='-', shift=2)
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = grid1.plot_cells(ax=ax, cell_kws=dict(cmap='Blues'))
_ = two_three.plot_cells(ax=ax, cell_kws=dict(cmap='YlOrBr'))
```
#### Now merge all three in a single chained operation (`inplace=False`).
```
grid1, grid2, grid3 = make_test_grids()
all_grids = (
grid2.merge(grid3, how='vert', where='-', shift=2)
.merge(grid1, how='horiz', where='-', shift=11)
)
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = all_grids.plot_cells(ax=ax, cell_kws=dict(cmap='GnBu'))
```
### Split the final grid into two vertical parts
`grid.split(<index of split>, axis=0)`
```
grid_bottom, grid_top = all_grids.split(14, axis=0)
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = grid_bottom.plot_cells(ax=ax, cell_kws=dict(cmap='OrRd'))
_ = grid_top.plot_cells(ax=ax, cell_kws=dict(cmap='BuPu'))
```
### Splitting and linearly refining columns and rows
#### Split the final grid into two horizontal parts
`grid.split(<index of split>, axis=1)`
```
grid_left, grid_right = all_grids.split(8, axis=1)
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = grid_left.plot_cells(ax=ax, cell_kws=dict(cmap='Oranges'))
_ = grid_right.plot_cells(ax=ax, cell_kws=dict(cmap='Blues'))
```
#### Refine individual rows of the grid cells
`grid.refine(<index of cell>, axis=0, n_points=<num. of divisions>)`
```
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = (
all_grids
.insert(13, axis=0, n_nodes=2)
.plot_cells(ax=ax, cell_kws=dict(cmap='Blues'))
)
```
#### Refine individual columns of the grid cells
`grid.refine(<index of cell>, axis=1, n_points=<num. of divisions>)`
```
fig, ax = plt.subplots(figsize=(7.5, 7.5))
_ = (
all_grids
.insert(10, axis=1, n_nodes=4)
.plot_cells(ax=ax, cell_kws=dict(cmap='Blues'))
)
```
### Chained operations
#### One big chained operation for fun
```
def make_fake_bathy(grid):
j_cells, i_cells = grid.cell_shape
y, x = np.mgrid[:j_cells, :i_cells]
z = (y - (j_cells // 2))** 2 - x
return z
fig, ax = plt.subplots(figsize=(7.5, 7.5))
g = (
grid2.merge(grid3, how='vert', where='-', shift=2)
.merge(grid1, how='horiz', where='-', shift=11)
.insert(10, axis=1, n_nodes=4)
.insert(13, axis=0, n_nodes=2)
.transform(lambda x: x*5 + 2)
)
bathy = make_fake_bathy(g)
_ = g.plot_cells(ax=ax, cell_kws=dict(cmap='Blues', colors=bathy))
```
| true |
code
| 0.630315 | null | null | null | null |
|
# TASK #1: UNDERSTAND VARIABLES ASSIGNMENT
```
# Define a variable named "x" and assign a number (integer) to it
# integer is a whole number (no decimals) that could be positive or negative
x = 20
# Let's view "x"
print(x)
# Define a variable named "y" and assign a number (float) to it
# Float are real numbers with a decimal point dividing the integer and fractional parts
y = 35.20
# Let's view "y"
print(y)
# Let's overwrite "y" (assume your portfolio value increased)
y= y + 20
# Notice that "y" will only contain the most recent value
print(y)
# Get the type of "x" which is integer
# integer is a whole number (no decimals) that could be positive or negative
type(x)
# Get the type of "y" which is float
# Float are real numbers with a decimal point dividing the integer and fractional parts
type(y)
```
MINI CHALLENGE #1:
- We defined a variable z and we assigned these 4 values listed below to it. Without executing any code cells, what will these lines of code generate?
- Verify your answer by executing the code cells
```
z = 1000
z = 2000
z = 5000
z = 6000
z
```
```
z = 1000
z = 2000
z = 5000
z = 6000
print(z)
```
# TASK #2: PERFORM MATH OPERATIONS IN PYTHON
```
# Define a variable named i and initialize it with 20
# Let's assume that we want to increment the value by 4
i = 20
i += 4
i
# Let's assume that you own a little grocery store
# The price of 1 bottle of milk is $3 and we currently have 50 bottles
# We can calculate the total dollar value of our inventory as follows:
milk = 3
Total_bottle = 50
total_value = milk * Total_bottle
total_value
# Let's assume you have $550 USD in our bank account
# We want to buy x number of IBM stocks using the total amount
# each IBM stock is priced at $128 each
Account_balance = 550
IBM_stock = 128
X_unit = Account_balance / IBM_stock
X_unit
# Divide the account balance by Amazon stock price and place the answer in units
Account_balance = 600
Amazon_share = 2200
unit = Account_balance / Amazon_share
unit
```
MINI CHALLENGE #2:
- Write a code that takes in APPLE (AAPL) stock prices at two days and calculate the return:
- AAPL price on day 1 = \$135
- AAPL price on day 2 = \$150
```
Apple_day1 = 135
Apple_day2 = 150
Profite = Apple_day2 / Apple_day1
print(Profite)
Difference = Apple_day2 - Apple_day1
Percentage = (Difference / Apple_day1)*100
print(Percentage)
```
# TASK #3: UNDERSTAND PRINT AND INPUT OPERATIONS
```
# Print function is used to print elements on the screen
# Define a string x
# A string in Python is a sequence of characters
# String in python are surrounded by single or double quotation marks
x = 'Roshan'
# Obtain the data type for 'x'
print(x)
type(x)
# The format() method formats the specified value and insert it in the placeholder
# The placeholder is defined using curly braces: {}
company_name = "Amazon"
shares = 200
print("I own {}'s total shares of {}".format(shares,company_name))
# input is a built-in function in python
# Obtain client data such as name, country and e-mail and print them all out on the screen
name = input("Enter your name: ")
country = input("Enter the country: ")
email = input("Enter your email: ")
print("my name is {}, I am from {} and my email is {}".format(name,country,email))
```
MINI CHALLENGE #3:
- Write a code that takes in the name of the stock, price at which it is selling, the number of stocks that you want to own and prints out the total funds required to buy this stock. Find a sample expected output below:
- Enter the price of the stock you want to buy: 3000
- Enter the number of stocks that you want to buy: 5
- Enter the name of the stock that you want to buy: AMZN
- The total funds required to buy 5 number of AMZN stocks at 3000 is: 15000
```
stock_name = input("ENTER THE NAME OF THE STOCK ")
STOCK_PRICE = int(input("Enter the stock's price "))
stocks_buy = int(input("How many stocks you want? "))
total_fund = STOCK_PRICE * stocks_buy
print(total_fund)
print("You need total of {} amount to buy unit {} of {} shares at the rate of {}".format(total_fund,stocks_buy,stock_name,STOCK_PRICE))
```
# TASK #4: UNDERSTAND LISTS DATA TYPES
```
# A list is a collection which is ordered and changeable.
# List allows duplicate members.
List1 = ["name", "email" , 25]
print(List1)
# Obtain the datatype
type(List1)
# Access specific elements in the list with Indexing
# Note that the first element in the list has an index of 0 (little confusing but you'll get used to it!)
print(List1[2])
```
MINI CHALLENGE #4:
- Print the first, second and last element in the list below
```
grocery_list = ['milk', 'rice', 'eggs', 'bread', 'oranges', 'water']
```
```
grocery_list = ['milk', 'rice', 'eggs', 'bread', 'oranges', 'water']
print(grocery_list[0])
print(grocery_list[1:3][0][2])
print(grocery_list[-1])
print(grocery_list[5])
```
# TASK #5: UNDERSTAND COMPARISON OPERATORS AND CONDITIONAL STATEMENTS
```
# Comparison Operator output could be "True" or "False"
# Let's cover equal '==' comparison operator first
# It's simply a question: "Is x equals y or not?"
# "True" output means condition is satisfied
# "False" output means Condition is not satisfied (condition is not true)
x = 50
y = 60
x == y
# Greater than or equal operator '>='
x = 40
y = 30
x >= y
# Note that '==' is a comparison operator
# Note that '=' is used for variable assignment (put 10 in x)
x = 10
x == 10
```
- A simple if-else statement is written in Python as follows:
```
if condition:
statement #1
else:
statement #2
```
- If the condition is true, execute the first indented statement
- if the condition is not true, then execute the else indented statements.
- Note that Python uses indentation (whitespace) to indicate code sections and scope.
```
# Let's take an input from the user and grant or deny access accordingly
user_input = int(input("Enter the number:"))
if (user_input <= 50):
print("You have been granted the access")
else:
print("You have been denied the acces")
x = int(input(" Enter an integer from 1 to 1000: "))
if x%2 == 0:
print("Number is even")
else:
print("Number is odd")
```
MINI CHALLENGE #5:
- Write a code that takes a number from the user and indicates if it's positive or negative
```
number = float(input("Enter the number: "))
if number < 0:
print("Number is negative")
elif number == 0:
print("Number is zero")
else:
print("Number is positive")
```
# TASK #6: DEVELOP FUNCTIONS IN PYTHON
```
# Define a function that takes in two argument x and y and returns their multiplication
def multiply(x,y):
z = x*y
return z
# Call the function
multiply(2,8)
```
MINI CHALLENGE #6:
- Write a code that takes in three inputs from the user and calculate their sum
```
def sum():
a=int(input("Enter the number: "))
b=int(input("Enter the second number: "))
c=int(input("Enter the third number: "))
return a+b+c
sum()
def sum(e,f,j):
return e+f+j
a=int(input("Enter the number: "))
b=int(input("Enter the second number: "))
c=int(input("Enter the third number: "))
sum(a,b,c)
```
# TASK #7: UNDERSTAND FOR AND WHILE LOOPS
```
# List of strings
for i in range(10):
print(i)
g_list= ["milk", "eggs", "rice", "toothpaste", "bread", "oranges", "water"]
for i in g_list:
print(i)
print("Hello {}".format(i))
# Range() generates a list of numbers, which is used to iterate over with for loops.
# range() is 0-index based, meaning list indexes start at 0, not 1.
# The last integer generated by range() is up to, but not including, last element.
# Example: range(0, 7) generates integers from 0 up to, but not including, 7.
for i in range(1,6):
print()
# While loop can be used to execute a set of statements as long as a certain condition holds true.
i = 6
while(i<10):
print(i)
i=i+1
```
MINI CHALLENGE #7:
- Write a code that displays numbers from 1 to 10 using for and while loops
```
for num in range(1,11):
print(num)
i = 1
while i <= 10:
print(i)
i+=1
```
# TASK #8: CAPSTONE PROJECT
Develop a guessing game that performs the following:
- The system will automatically generate a random number between 1 and 100.
- Users can insert any number between 1 and 100
- The program shall be able to compare the number generated by the system and the number that has been entered by the user. The program shall print out one of the following options to help the user improve their next guess:
- You are right, great job!
- Your guess is low, try again!
- your guess is high, try again!
- The program exits when the user guess matches the number generated by the system
```
import random
sys_number = random.randint(1,100)
sys_number
number= int(input("Enter your number between 1 and 100: "))
number
```
```
while (True):
if sys_number == number:
print("You are right, great job!")
break
elif sys_number > number:
print(" Your guess is low, try again!")
number= int(input("Enter your number between 1 and 100: "))
else:
print("Your guess is high, try again")
number = int(input("Enter your number between 1 and 100: "))
```
| true |
code
| 0.412353 | null | null | null | null |
|
# Sample Size Experiment using Random Forest and Deep Networks
### Random Forest (RF) vs. Deep Networks (DN)
Random forest is inherently a non-parametric model, meaning that the algorithm requires no assumptions about the data distribution. With infinitely many trees and n → $\infty$, RF will follow non-parametric behavior and will guarantee convergence.
Deep Networks with a fixed architecture are entirely parametric. As presented by [Vogelstein, et al. (2020)](https://www.biorxiv.org/content/10.1101/2020.04.29.068460v1), there is a visible bias variance tradeoff between DNs of varying complexity. This is evident by testing each model over a range of sample sizes. At a large enough sample size, a RF model will surpass any parametric DN.
The goal of this tutorial is to identify a joint distribution (X,Y) that demonstrates this relationship. RF should profuce a smaller generalization error as small sample sizes, a specific parametric DN should produce a smaller generalization error at medium sample sizes, and RF should once again produce a smaller generalization error at large sample sizes.
### Import necessary packages and modules
```
from functions.sample_size_functions import *
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline
```
### Sparse Parity Distribution
The joint distribution used to demonstrate RF convergence is sparse parity. Sparse parity is a _p_-dimensional binary classification problem that generalizes the noisy XOR distribution.
Data is generated from a _p_-dimensional feature vector, where each _X_<sub>1</sub>, ... , _X_<sub>p</sub> ~ i.i.d. _U_(-1,1). A parameter _p_* represents the number of informative dimensions, where _p_* < _p_. Class label _Y_ = 0 if there are an even number of positive values among the first _p_* < _p_ dimensions, and _Y_ = 1 if not.
Mathematically, we can let _Q_ = $\sum_{j=1}^{p*}$I ( X<sub>j</sub> > 0 ) where _p_* < _p_. The function I ( _X_<sub>j</sub> > 0 ) represents the indicator that the feature at position _j_ is greater than 0. Class label _Y_ returns 1 if _Q_ is odd, and 0 if _Q_ is even.
```
X, y = sparse_parity(num_samples=500, p=5, p_star=2)
```
### Visualize Sparse Parity
Plot the first and second dimensions of the sparse parity distribution. For this plot, `p` = 5 and `p_star` = 2. With only 2 informative dimensions, this plot is equivalent to that of the noisy XOR distribution.
```
fig = plt.figure(figsize=(9, 9))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="coolwarm")
plt.ylabel("X2", fontsize=24)
plt.xlabel("X1", fontsize=24)
plt.yticks([-1, 0, 1], fontsize=20)
plt.xticks([-1, 0, 1], fontsize=20)
plt.title("sparse parity: p=5, p*=2", fontsize=24);
```
### Define Experiment Parameters and Model Hyperparameters
#### The cell below defines the sparse parity distribution parameters:
`p`: The number of total dimensions in the sparse parity distribution
`p_star`: The number of informative dimensions in the sparse parity distribution
```
# Sparse parity parameters
p = 14
p_star = 3
```
#### The cell below defines the RF and DF hyperparameters:
`num_trees`: The number of trees in the RF model
`max_depth`: Max depth of the RF model
`rf_verbose`: The printed output of the RF model
`hidden_nodes`: The number of nodes in the hidden layer of the DN
`batch_size`: The batch size of the DN
`dnn_verbose`: The printed output of the DN model
```
# RF hyperparameters
num_trees = 500
max_depth = None
rf_verbose = 0
# DN hyperparameters
hidden_nodes = 4
batch_size = 3
dn_verbose = 0
```
#### The cell below defines experiment parameters:
`training_sample_sizes`: A list of training set sample sizes to iterate over while training the model
`testing_sample_size`: An integer designating the size of the test set
`trials`: Number of trials to run the experiment
```
# Experiment parameters
training_sample_sizes = [
500,
1000,
2000,
3000,
5000,
7000,
10000,
12000,
14000,
17000,
20000,
]
testing_sample_size = 8000
trials = 5
```
### Run the Testing Suite
The testing suite trains RF and DN models across all sample sizes and averages accuracies across trials
```
rf_evolution, dn_evolution = test_suite(
training_sample_sizes=training_sample_sizes,
testing_sample_size=testing_sample_size,
trials=trials,
p=p,
p_star=p_star,
num_trees=num_trees,
max_depth=None,
rf_verbose=rf_verbose,
hidden_nodes=hidden_nodes,
batch_size=batch_size,
dn_verbose=dn_verbose,
)
```
### Plot and Visualize the Results
```
plot_sample_size_experiment(rf_evolution, dn_evolution, training_sample_sizes, 14, 3)
```
### Load the Stored Model (Trained with 100 Trials)
Increasing the number of trials improves the smoothness of the output, but takes additional time to run. The below cell loads in a model trained with 100 trials.
```
%store -r rf_evolution_100_trials
%store -r dn_evolution_100_trials
```
### Plot and Visualize the Results of 100 Trial Output
```
plot_sample_size_experiment(
rf_evolution_100_trials, dn_evolution_100_trials, training_sample_sizes, 14, 3
)
```
### Plot and Visualize Alternate Solution
An equivalent solution was found using sparse parity parameters `p` = 20 and `p_star` = 2. This leads to a faster convergence and reduced training time. Parameters for this experimental setting are shown below:
#### Sparse parity parameters:
`p` = 20
`p_star` = 2
#### RF hyperparameters:
`num_trees` = 500
`max_depth` = None
#### DN hyperparameters:
`hidden_nodes` = 36
`batch_size` = 2
#### Experimental parameters:
`training_sample_sizes` = [ 200, 300, 400, 500, 700, 1000, 1500, 2000, 2500, 3000, 4000 ]
`testing_sample_size` = 2000
`trials` = 100
```
%store -r rf_evolution_alt
%store -r dn_evolution_alt
training_sample_sizes = [200,300,400,500,700,1000,1500,2000,2500,3000,4000]
plot_sample_size_experiment(
rf_evolution_alt, dn_evolution_alt, training_sample_sizes, 20, 2
)
```
| true |
code
| 0.807309 | null | null | null | null |
|
# Ch `10`: Concept `02`
## Recurrent Neural Network
Import the relevant libraries:
```
import numpy as np
import tensorflow as tf
from tensorflow.contrib import rnn
```
Define the RNN model:
```
class SeriesPredictor:
def __init__(self, input_dim, seq_size, hidden_dim=10):
# Hyperparameters
self.input_dim = input_dim
self.seq_size = seq_size
self.hidden_dim = hidden_dim
# Weight variables and input placeholders
self.W_out = tf.Variable(tf.random_normal([hidden_dim, 1]), name='W_out')
self.b_out = tf.Variable(tf.random_normal([1]), name='b_out')
self.x = tf.placeholder(tf.float32, [None, seq_size, input_dim])
self.y = tf.placeholder(tf.float32, [None, seq_size])
# Cost optimizer
self.cost = tf.reduce_mean(tf.square(self.model() - self.y))
self.train_op = tf.train.AdamOptimizer().minimize(self.cost)
# Auxiliary ops
self.saver = tf.train.Saver()
def model(self):
"""
:param x: inputs of size [T, batch_size, input_size]
:param W: matrix of fully-connected output layer weights
:param b: vector of fully-connected output layer biases
"""
cell = rnn.BasicLSTMCell(self.hidden_dim)
outputs, states = tf.nn.dynamic_rnn(cell, self.x, dtype=tf.float32)
num_examples = tf.shape(self.x)[0]
W_repeated = tf.tile(tf.expand_dims(self.W_out, 0), [num_examples, 1, 1])
out = tf.matmul(outputs, W_repeated) + self.b_out
out = tf.squeeze(out)
return out
def train(self, train_x, train_y):
with tf.Session() as sess:
tf.get_variable_scope().reuse_variables()
sess.run(tf.global_variables_initializer())
for i in range(1000):
_, mse = sess.run([self.train_op, self.cost], feed_dict={self.x: train_x, self.y: train_y})
if i % 100 == 0:
print(i, mse)
save_path = self.saver.save(sess, 'model.ckpt')
print('Model saved to {}'.format(save_path))
def test(self, test_x):
with tf.Session() as sess:
tf.get_variable_scope().reuse_variables()
self.saver.restore(sess, './model.ckpt')
output = sess.run(self.model(), feed_dict={self.x: test_x})
return output
```
Now, we'll train a series predictor. Let's say we have a sequence of numbers `[a, b, c, d]` that we want to transform into `[a, a+b, b+c, c+d]`. We'll give the RNN a couple examples in the training data. Let's see how well it learns this intended transformation:
```
if __name__ == '__main__':
predictor = SeriesPredictor(input_dim=1, seq_size=4, hidden_dim=10)
train_x = [[[1], [2], [5], [6]],
[[5], [7], [7], [8]],
[[3], [4], [5], [7]]]
train_y = [[1, 3, 7, 11],
[5, 12, 14, 15],
[3, 7, 9, 12]]
predictor.train(train_x, train_y)
test_x = [[[1], [2], [3], [4]], # 1, 3, 5, 7
[[4], [5], [6], [7]]] # 4, 9, 11, 13
actual_y = [[[1], [3], [5], [7]],
[[4], [9], [11], [13]]]
pred_y = predictor.test(test_x)
print("\nLets run some tests!\n")
for i, x in enumerate(test_x):
print("When the input is {}".format(x))
print("The ground truth output should be {}".format(actual_y[i]))
print("And the model thinks it is {}\n".format(pred_y[i]))
tested; Gopal
```
| true |
code
| 0.678593 | null | null | null | null |
|
# Demo
This notebook demonstrates the basic functionality of the `perfectns` package; for background see the dynamic nested sampling paper [(Higson at al., 2019a)](https://doi.org/10.1007/s11222-018-9844-0).
### Running nested sampling calculations
The likelihood $\mathcal{L}(\theta)$, prior $\pi(\theta)$ and calculation settings are specified in a PerfectNSSettings object. For this example we will use a 10-dimensional spherically symmetric Gaussian likelihood with size $\sigma_\mathcal{L}=1$ and a Gaussian prior with size $\sigma_{\pi}=10$.
```
import perfectns.settings
import perfectns.likelihoods as likelihoods
import perfectns.priors as priors
# Input settings
settings = perfectns.settings.PerfectNSSettings()
settings.likelihood = likelihoods.Gaussian(likelihood_scale=1)
settings.prior = priors.Gaussian(prior_scale=10)
settings.n_dim = 10
settings.ninit = 10
settings.nlive_const = 100
```
The "dynamic_goal" setting determines if dynamic nested sampling should be used and, if so, how to split the computational effort between increasing parameter estimation accuracy and evidence calculation accuracy. dynamic_goal=1 optimises purely for parameter estimation and dynamic_goal=0 optimises purely for calculating the Bayesian evidence $\mathcal{Z}$.
Lets try running standard nested sampling and dynamic nested sampling calculation:
```
import perfectns.nested_sampling as nested_sampling
# Perform standard nested sampling
settings.dynamic_goal = None
standard_ns_run = nested_sampling.generate_ns_run(settings, random_seed=0) # set random_seed for reproducible results
# Perform dynamic nested sampling
settings.dynamic_goal = 1 # optimise for parameter estimation accuracy
dynamic_ns_run = nested_sampling.generate_ns_run(settings, random_seed=0) # set random_seed for reproducible results
```
We can now make posterior inferences using the samples generated by the nested sampling calculations using the utility functions from ``nestcheck``. Here we calculate:
1\. the log Bayesian evidence $\log \mathcal{Z}=\log \left( \int \mathcal{L}(\theta) \pi(\theta) \mathrm{d}\theta \right)$,
2\. the mean of the first parameter $\theta_1$,
3\. the second moment of the posterior distribution of $\theta_1$,
4\. the median of $\theta_1$,
5\. the 84% one-tailed credible interval on $\theta_1$.
For the Gaussian likelihood and prior we can calculate the posterior distribution analytically, so we first calculate the analytic values of each quantity for comparison. The results are displayed in a `pandas` DataFrame.
```
import perfectns.estimators as e
import nestcheck.ns_run_utils
import pandas as pd
estimator_list = [e.LogZ(),
e.ParamMean(),
e.ParamSquaredMean(),
e.ParamCred(0.5),
e.ParamCred(0.84)]
estimator_names = [est.latex_name for est in estimator_list]
results = pd.DataFrame([nestcheck.ns_run_utils.run_estimators(standard_ns_run, estimator_list),
nestcheck.ns_run_utils.run_estimators(dynamic_ns_run, estimator_list)],
columns=estimator_names, index=['standard run', 'dynamic run'])
# Add true values for comparison
results.loc['true values'] = e.get_true_estimator_values(estimator_list, settings)
results
```
### Estimating sampling errors
You can estimate the numerical uncertainties on these results by calculating the standard deviation of the sampling errors distributions each run using the bootstrap resampling approach described in [Higson et al. (2018)](https://doi.org/10.1214/17-BA1075) (implemented in `nestcheck`).
```
import numpy as np
import nestcheck.error_analysis
np.random.seed(0)
results.loc['standard unc'] = nestcheck.error_analysis.run_std_bootstrap(
standard_ns_run, estimator_list, n_simulate=200)
results.loc['dynamic unc'] = nestcheck.error_analysis.run_std_bootstrap(
dynamic_ns_run, estimator_list, n_simulate=200)
results.loc[['standard unc', 'dynamic unc']]
```
This approach works for both dynamic and standard nested sampling. In addition as `perfectns` can perform the nested sampling algorithm "perfectly" there are no additional errors from implementation-specific effects such as correlated samples (see [Higson et al., 2019b](http://doi.org/10.1093/mnras/sty3090) for a detailed discussion).
### Generating and analysing runs in parallel
Multiple nested sampling runs can be generated and analysed in parallel (using `parallel_utils` from `nestcheck`).
```
import numpy as np
import nestcheck.parallel_utils as pu
import nestcheck.pandas_functions as pf
# Generate 100 nested sampling runs
run_list = nested_sampling.get_run_data(settings, 100, save=False, load=False, random_seeds=list(range(100)))
# Calculate posterior inferences for each run
values = pu.parallel_apply(nestcheck.ns_run_utils.run_estimators, run_list,
func_args=(estimator_list,))
# Show the mean and standard deviation of the calculation results
multi_run_tests = pf.summary_df_from_list(values, estimator_names)
multi_run_tests
```
### Comparing dynamic and standard nested sampling performance
Lets now compare the performance of dynamic and standard nested sampling, using the 10-dimensional Gaussian likelihood and prior.
```
import perfectns.results_tables as rt
# Input settings
settings = perfectns.settings.PerfectNSSettings()
settings.likelihood = likelihoods.Gaussian(likelihood_scale=1)
settings.prior = priors.Gaussian(prior_scale=10)
settings.ninit = 10
settings.nlive_const = 100
settings.n_dim = 10
# Run results settings
dynamic_results_table = rt.get_dynamic_results(100, [0, 1], estimator_list, settings, save=False, load=False)
dynamic_results_table[estimator_names]
```
Looking at the `std efficiency gain` rows, you should see that dynamic nested sampling targeted at parameter estimation (dynamic goal=1) has an efficiency gain (equivalent computational speedup) for parameter estimation (columns other than $\log \mathcal{Z}$) of factor of around 3 compared to standard nested sampling.
Similar results tables for different likelihoods can be found in the dynamic nested sampling paper [(Higson at al., 2019a)](https://doi.org/10.1007/s11222-018-9844-0). For more information about the get_dynamic_results function look at its documentation.
### Comparing bootstrap error estimates to observed distributions of results
We can check if the bootstrap estimates of parameter estimation sampling errors are accurate, using a 3d Gaussian likelihood and Gaussian prior.
```
settings.likelihood = likelihoods.Gaussian(likelihood_scale=1)
settings.prior = priors.Gaussian(prior_scale=10)
settings.n_dim = 3
bootstrap_results_table = rt.get_bootstrap_results(50, 50, # 100, 200,
estimator_list, settings,
n_run_ci=20,
n_simulate_ci=200, # n_simulate_ci=1000,
add_sim_method=False,
cred_int=0.95,
ninit_sep=True,
parallel=True)
bootstrap_results_table
```
Note that every second column gives an estimated numerical uncertainty on the values in the previous column.
You should see that the ratio of the bootstrap error estimates to bootstrap_results the standard deviation of results (row 4 of bootstrap_results_table) has values close to 1 given the estimated numerical uncertainties. Similar results are given in the appendix of the dynamic nested sampling paper [(Higson, 2019a)](https://doi.org/10.1007/s11222-018-9844-0); see the paper and the get_bootstrap_results function's documentation for more details.
| true |
code
| 0.664812 | null | null | null | null |
|
<small><small><i>
All the IPython Notebooks in **[Python Seaborn Module](https://github.com/milaan9/12_Python_Seaborn_Module)** lecture series by **[Dr. Milaan Parmar](https://www.linkedin.com/in/milaanparmar/)** are available @ **[GitHub](https://github.com/milaan9)**
</i></small></small>
<a href="https://colab.research.google.com/github/milaan9/12_Python_Seaborn_Module/blob/main/008_Seaborn_Distribution_Plots.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# What is Distribution Plots?
- Flexibly plot a univariate distribution of observations.
- This function combines the matplotlib hist function (with automatic calculation of a good default bin size) with the seaborn **`kdeplot()`** and **`rugplot()`** functions. It can also fit scipy.stats distributions and plot the estimated PDF over the data.
### Let's discuss some plots that allow us to visualize the distribution of a dataset. These plots are:
- **`distplot()`**
- **`jointplot()`**
- **`pairplot()`**
- **`rugplot()`**
- **`kdeplot()`**
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
%matplotlib inline
num = np.random.randn(150)
sns.distplot(num,color ='green')
label_dist = pd.Series(num,name = " Variable x")
sns.distplot(label_dist,color = "red")
# Plot the distribution with a kenel density. estimate and rug plot:
sns.distplot(label_dist,hist = False,color = "red")
# Plot the distribution with a kenel density estimate and rug plot:
sns.distplot(label_dist,rug = True,hist = False,color = "red")
# Plot the distribution with a histogram and maximum likelihood gaussian distribution fit:
from scipy.stats import norm
sns.distplot(label_dist, fit=norm, kde=False)
```
### Plot the distribution on the vertical axis:
```
sns.distplot(label_dist, vertical =True)
```
## Let's implement with dataset
### Data
Seaborn comes with built-in data sets!
```
tips = sns.load_dataset('tips')
tips.head()
```
### 1 `distplot()`
The **`distplot()`** shows the distribution of a univariate set of observations.
```
sns.distplot(tips['total_bill'])
# Safe to ignore warnings
sns.distplot(tips['total_bill'],kde=False,bins=30)
```
### 2 `jointplot()`
`jointplot()` allows you to basically match up two distplots for bivariate data. With your choice of what kind parameter to compare with:
- `scatter`
- `reg`
- `resid`
- `kde`
- `hex`
```
# 'scatter'
sns.jointplot(x='total_bill',y='tip',data=tips,kind='scatter')
# 'hex'
sns.jointplot(x='total_bill',y='tip',data=tips,kind='hex')
# 'reg'
sns.jointplot(x='total_bill',y='tip',data=tips,kind='reg')
```
### 3 `pairplot()`
`pairplot()` will plot pairwise relationships across an entire dataframe (for the numerical columns) and supports a color hue argument (for categorical columns).
```
sns.pairplot(tips)
sns.pairplot(tips,hue='sex',palette='coolwarm')
```
### 4 `rugplot()`
`rugplots()` are actually a very simple concept, they just draw a dash mark for every point on a univariate distribution. They are the building block of a KDE plot:
```
sns.rugplot(tips['total_bill'])
```
### 5 `kdeplot()`
`kdeplots()` are **[Kernel Density Estimation plots](http://en.wikipedia.org/wiki/Kernel_density_estimation#Practical_estimation_of_the_bandwidth)**. These KDE plots replace every single observation with a Gaussian (Normal) distribution centered around that value. For example:
```
# Don't worry about understanding this code!
# It's just for the diagram below
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
#Create dataset
dataset = np.random.randn(25)
# Create another rugplot
sns.rugplot(dataset);
# Set up the x-axis for the plot
x_min = dataset.min() - 2
x_max = dataset.max() + 2
# 100 equally spaced points from x_min to x_max
x_axis = np.linspace(x_min,x_max,100)
# Set up the bandwidth, for info on this:
url = 'http://en.wikipedia.org/wiki/Kernel_density_estimation#Practical_estimation_of_the_bandwidth'
bandwidth = ((4*dataset.std()**5)/(3*len(dataset)))**.2
# Create an empty kernel list
kernel_list = []
# Plot each basis function
for data_point in dataset:
# Create a kernel for each point and append to list
kernel = stats.norm(data_point,bandwidth).pdf(x_axis)
kernel_list.append(kernel)
#Scale for plotting
kernel = kernel / kernel.max()
kernel = kernel * .4
plt.plot(x_axis,kernel,color = 'grey',alpha=0.5)
plt.ylim(0,1)
# To get the kde plot we can sum these basis functions.
# Plot the sum of the basis function
sum_of_kde = np.sum(kernel_list,axis=0)
# Plot figure
fig = plt.plot(x_axis,sum_of_kde,color='indianred')
# Add the initial rugplot
sns.rugplot(dataset,c = 'indianred')
# Get rid of y-tick marks
plt.yticks([])
# Set title
plt.suptitle("Sum of the Basis Functions")
sns.kdeplot(tips['total_bill'])
sns.rugplot(tips['total_bill'])
sns.kdeplot(tips['tip'])
sns.rugplot(tips['tip'])
```
Alright! Since we've finished with Distribution Plots in our next lecture where we shall be discussing few other plots which deal quite heavily with **[Categorical Data Plots](https://github.com/milaan9/12_Python_Seaborn_Module/blob/main/009_Seaborn_Categorical_Swarm_Plot.ipynb)**, that is commonly seen across.
| true |
code
| 0.613758 | null | null | null | null |
|
# Quick Start
This notebook demonstrates how to use MARO's reinforcement learning (RL) toolkit to solve the container inventory management ([CIM](https://maro.readthedocs.io/en/latest/scenarios/container_inventory_management.html)) problem. It is formalized as a multi-agent reinforcement learning problem, where each port acts as a decision agent. When a vessel arrives at a port, these agents must take actions by transfering a certain amount of containers to / from the vessel. The objective is for the agents to learn policies that minimize the cumulative container shortage.
```
import numpy as np
# Common info
common_config = {
"port_attributes": ["empty", "full", "on_shipper", "on_consignee", "booking", "shortage", "fulfillment"],
"vessel_attributes": ["empty", "full", "remaining_space"],
"action_space": list(np.linspace(-1.0, 1.0, 21)),
# Parameters for computing states
"look_back": 7,
"max_ports_downstream": 2,
# Parameters for computing actions
"finite_vessel_space": True,
"has_early_discharge": True,
# Parameters for computing rewards
"reward_time_window": 99,
"fulfillment_factor": 1.0,
"shortage_factor": 1.0,
"time_decay": 0.97
}
```
## Shaping
```
from collections import defaultdict
import numpy as np
from maro.rl import Trajectory
from maro.simulator.scenarios.cim.common import Action, ActionType
class CIMTrajectory(Trajectory):
def __init__(
self, env, *, port_attributes, vessel_attributes, action_space, look_back, max_ports_downstream,
reward_time_window, fulfillment_factor, shortage_factor, time_decay,
finite_vessel_space=True, has_early_discharge=True
):
super().__init__(env)
self.port_attributes = port_attributes
self.vessel_attributes = vessel_attributes
self.action_space = action_space
self.look_back = look_back
self.max_ports_downstream = max_ports_downstream
self.reward_time_window = reward_time_window
self.fulfillment_factor = fulfillment_factor
self.shortage_factor = shortage_factor
self.time_decay = time_decay
self.finite_vessel_space = finite_vessel_space
self.has_early_discharge = has_early_discharge
def get_state(self, event):
vessel_snapshots, port_snapshots = self.env.snapshot_list["vessels"], self.env.snapshot_list["ports"]
tick, port_idx, vessel_idx = event.tick, event.port_idx, event.vessel_idx
ticks = [max(0, tick - rt) for rt in range(self.look_back - 1)]
future_port_idx_list = vessel_snapshots[tick: vessel_idx: 'future_stop_list'].astype('int')
port_features = port_snapshots[ticks: [port_idx] + list(future_port_idx_list): self.port_attributes]
vessel_features = vessel_snapshots[tick: vessel_idx: self.vessel_attributes]
return {port_idx: np.concatenate((port_features, vessel_features))}
def get_action(self, action_by_agent, event):
vessel_snapshots = self.env.snapshot_list["vessels"]
action_info = list(action_by_agent.values())[0]
model_action = action_info[0] if isinstance(action_info, tuple) else action_info
scope, tick, port, vessel = event.action_scope, event.tick, event.port_idx, event.vessel_idx
zero_action_idx = len(self.action_space) / 2 # index corresponding to value zero.
vessel_space = vessel_snapshots[tick:vessel:self.vessel_attributes][2] if self.finite_vessel_space else float("inf")
early_discharge = vessel_snapshots[tick:vessel:"early_discharge"][0] if self.has_early_discharge else 0
percent = abs(self.action_space[model_action])
if model_action < zero_action_idx:
action_type = ActionType.LOAD
actual_action = min(round(percent * scope.load), vessel_space)
elif model_action > zero_action_idx:
action_type = ActionType.DISCHARGE
plan_action = percent * (scope.discharge + early_discharge) - early_discharge
actual_action = round(plan_action) if plan_action > 0 else round(percent * scope.discharge)
else:
actual_action, action_type = 0, None
return {port: Action(vessel, port, actual_action, action_type)}
def get_offline_reward(self, event):
port_snapshots = self.env.snapshot_list["ports"]
start_tick = event.tick + 1
ticks = list(range(start_tick, start_tick + self.reward_time_window))
future_fulfillment = port_snapshots[ticks::"fulfillment"]
future_shortage = port_snapshots[ticks::"shortage"]
decay_list = [
self.time_decay ** i for i in range(self.reward_time_window)
for _ in range(future_fulfillment.shape[0] // self.reward_time_window)
]
tot_fulfillment = np.dot(future_fulfillment, decay_list)
tot_shortage = np.dot(future_shortage, decay_list)
return np.float32(self.fulfillment_factor * tot_fulfillment - self.shortage_factor * tot_shortage)
def on_env_feedback(self, event, state_by_agent, action_by_agent, reward):
self.trajectory["event"].append(event)
self.trajectory["state"].append(state_by_agent)
self.trajectory["action"].append(action_by_agent)
def on_finish(self):
training_data = {}
for event, state, action in zip(self.trajectory["event"], self.trajectory["state"], self.trajectory["action"]):
agent_id = list(state.keys())[0]
data = training_data.setdefault(agent_id, {"args": [[] for _ in range(4)]})
data["args"][0].append(state[agent_id]) # state
data["args"][1].append(action[agent_id][0]) # action
data["args"][2].append(action[agent_id][1]) # log_p
data["args"][3].append(self.get_offline_reward(event)) # reward
for agent_id in training_data:
training_data[agent_id]["args"] = [
np.asarray(vals, dtype=np.float32 if i == 3 else None)
for i, vals in enumerate(training_data[agent_id]["args"])
]
return training_data
```
## [Agent](https://maro.readthedocs.io/en/latest/key_components/rl_toolkit.html#agent)
The out-of-the-box ActorCritic is used as our agent.
```
import torch.nn as nn
from torch.optim import Adam, RMSprop
from maro.rl import ActorCritic, ActorCriticConfig, FullyConnectedBlock, OptimOption, SimpleMultiHeadModel
# We consider the port in question as well as two downstream ports.
# We consider the states of these ports over the past 7 days plus the current day, hence the factor 8.
input_dim = (
(common_config["look_back"] + 1) *
(common_config["max_ports_downstream"] + 1) *
len(common_config["port_attributes"]) +
len(common_config["vessel_attributes"])
)
agent_config = {
"model": {
"actor": {
"input_dim": input_dim,
"output_dim": len(common_config["action_space"]),
"hidden_dims": [256, 128, 64],
"activation": nn.Tanh,
"softmax": True,
"batch_norm": False,
"head": True
},
"critic": {
"input_dim": input_dim,
"output_dim": 1,
"hidden_dims": [256, 128, 64],
"activation": nn.LeakyReLU,
"softmax": False,
"batch_norm": True,
"head": True
}
},
"optimization": {
"actor": OptimOption(optim_cls=Adam, optim_params={"lr": 0.001}),
"critic": OptimOption(optim_cls=RMSprop, optim_params={"lr": 0.001})
},
"hyper_params": {
"reward_discount": .0,
"critic_loss_func": nn.SmoothL1Loss(),
"train_iters": 10,
"actor_loss_coefficient": 0.1, # loss = actor_loss_coefficient * actor_loss + critic_loss
"k": 1, # for k-step return
"lam": 0.0 # lambda return coefficient
}
}
def get_ac_agent():
actor_net = FullyConnectedBlock(**agent_config["model"]["actor"])
critic_net = FullyConnectedBlock(**agent_config["model"]["critic"])
ac_model = SimpleMultiHeadModel(
{"actor": actor_net, "critic": critic_net}, optim_option=agent_config["optimization"],
)
return ActorCritic(ac_model, ActorCriticConfig(**agent_config["hyper_params"]))
```
## Training
This code cell demonstrates a typical single-threaded training workflow.
```
from maro.simulator import Env
from maro.rl import Actor, MultiAgentWrapper, OnPolicyLearner
from maro.utils import set_seeds
set_seeds(1024) # for reproducibility
env = Env("cim", "toy.4p_ssdd_l0.0", durations=1120)
agent = MultiAgentWrapper({name: get_ac_agent() for name in env.agent_idx_list})
actor = Actor(env, agent, CIMTrajectory, trajectory_kwargs=common_config)
learner = OnPolicyLearner(actor, 40) # 40 episodes
learner.run()
```
| true |
code
| 0.63341 | null | null | null | null |
|
## SimCLR: A Simple Framework for Contrastive Learning of Visual Representations
This colab demonstrates how to load pretrained/finetuned SimCLR models from checkpoints or hub modules. It contains two parts:
* Part I - Load checkpoints and print parameters (count)
* Part II - Load hub module for inference
The checkpoints are accessible in the following Google Cloud Storage folders.
* Pretrained SimCLRv2 models with a linear classifier: [gs://simclr-checkpoints/simclrv2/pretrained](https://console.cloud.google.com/storage/browser/simclr-checkpoints/simclrv2/pretrained)
* Fine-tuned SimCLRv2 models on 1% of labels: [gs://simclr-checkpoints/simclrv2/finetuned_1pct](https://console.cloud.google.com/storage/browser/simclr-checkpoints/simclrv2/finetuned_1pct)
* Fine-tuned SimCLRv2 models on 10% of labels: [gs://simclr-checkpoints/simclrv2/finetuned_10pct](https://console.cloud.google.com/storage/browser/simclr-checkpoints/simclrv2/finetuned_10pct)
* Fine-tuned SimCLRv2 models on 100% of labels: [gs://simclr-checkpoints/simclrv2/finetuned_100pct](https://console.cloud.google.com/storage/browser/simclr-checkpoints/simclrv2/finetuned_100pct)
* Supervised models with the same architectures: [gs://simclr-checkpoints/simclrv2/pretrained](https://console.cloud.google.com/storage/browser/simclr-checkpoints/simclrv2/pretrained)
Use the corresponding checkpoint / hub-module paths for accessing the model. For example, to use a pre-trained model (with a linear classifier) with ResNet-152 (2x+SK), set the path to `gs://simclr-checkpoints/simclrv2/pretrained/r152_2x_sk1`.
## Part I - Load checkpoints and print parameters (count)
```
import re
import numpy as np
import tensorflow.compat.v1 as tf
tf.disable_eager_execution()
import tensorflow_hub as hub
import tensorflow_datasets as tfds
import matplotlib
import matplotlib.pyplot as plt
def count_params(checkpoint, excluding_vars=[], verbose=True):
vdict = checkpoint.get_variable_to_shape_map()
cnt = 0
for name, shape in vdict.items():
skip = False
for evar in excluding_vars:
if re.search(evar, name):
skip = True
if skip:
continue
if verbose:
print(name, shape)
cnt += np.prod(shape)
cnt = cnt / 1e6
print("Total number of parameters: {:.2f}M".format(cnt))
return cnt
checkpoint_path = 'gs://simclr-checkpoints/simclrv2/finetuned_100pct/r50_1x_sk0/'
checkpoint = tf.train.load_checkpoint(checkpoint_path)
_ = count_params(checkpoint, excluding_vars=['global_step', "Momentum", 'ema', 'memory', 'head'], verbose=False)
```
## Part II - Load hub module for inference
```
#@title Load class id to label text mapping from big_transfer (hidden)
# Code snippet credit: https://github.com/google-research/big_transfer
!wget https://storage.googleapis.com/bit_models/ilsvrc2012_wordnet_lemmas.txt
imagenet_int_to_str = {}
with open('ilsvrc2012_wordnet_lemmas.txt', 'r') as f:
for i in range(1000):
row = f.readline()
row = row.rstrip()
imagenet_int_to_str.update({i: row})
tf_flowers_labels = ['dandelion', 'daisy', 'tulips', 'sunflowers', 'roses']
#@title Preprocessing functions from data_util.py in SimCLR repository (hidden).
FLAGS_color_jitter_strength = 0.3
CROP_PROPORTION = 0.875 # Standard for ImageNet.
def random_apply(func, p, x):
"""Randomly apply function func to x with probability p."""
return tf.cond(
tf.less(tf.random_uniform([], minval=0, maxval=1, dtype=tf.float32),
tf.cast(p, tf.float32)),
lambda: func(x),
lambda: x)
def random_brightness(image, max_delta, impl='simclrv2'):
"""A multiplicative vs additive change of brightness."""
if impl == 'simclrv2':
factor = tf.random_uniform(
[], tf.maximum(1.0 - max_delta, 0), 1.0 + max_delta)
image = image * factor
elif impl == 'simclrv1':
image = random_brightness(image, max_delta=max_delta)
else:
raise ValueError('Unknown impl {} for random brightness.'.format(impl))
return image
def to_grayscale(image, keep_channels=True):
image = tf.image.rgb_to_grayscale(image)
if keep_channels:
image = tf.tile(image, [1, 1, 3])
return image
def color_jitter(image,
strength,
random_order=True):
"""Distorts the color of the image.
Args:
image: The input image tensor.
strength: the floating number for the strength of the color augmentation.
random_order: A bool, specifying whether to randomize the jittering order.
Returns:
The distorted image tensor.
"""
brightness = 0.8 * strength
contrast = 0.8 * strength
saturation = 0.8 * strength
hue = 0.2 * strength
if random_order:
return color_jitter_rand(image, brightness, contrast, saturation, hue)
else:
return color_jitter_nonrand(image, brightness, contrast, saturation, hue)
def color_jitter_nonrand(image, brightness=0, contrast=0, saturation=0, hue=0):
"""Distorts the color of the image (jittering order is fixed).
Args:
image: The input image tensor.
brightness: A float, specifying the brightness for color jitter.
contrast: A float, specifying the contrast for color jitter.
saturation: A float, specifying the saturation for color jitter.
hue: A float, specifying the hue for color jitter.
Returns:
The distorted image tensor.
"""
with tf.name_scope('distort_color'):
def apply_transform(i, x, brightness, contrast, saturation, hue):
"""Apply the i-th transformation."""
if brightness != 0 and i == 0:
x = random_brightness(x, max_delta=brightness)
elif contrast != 0 and i == 1:
x = tf.image.random_contrast(
x, lower=1-contrast, upper=1+contrast)
elif saturation != 0 and i == 2:
x = tf.image.random_saturation(
x, lower=1-saturation, upper=1+saturation)
elif hue != 0:
x = tf.image.random_hue(x, max_delta=hue)
return x
for i in range(4):
image = apply_transform(i, image, brightness, contrast, saturation, hue)
image = tf.clip_by_value(image, 0., 1.)
return image
def color_jitter_rand(image, brightness=0, contrast=0, saturation=0, hue=0):
"""Distorts the color of the image (jittering order is random).
Args:
image: The input image tensor.
brightness: A float, specifying the brightness for color jitter.
contrast: A float, specifying the contrast for color jitter.
saturation: A float, specifying the saturation for color jitter.
hue: A float, specifying the hue for color jitter.
Returns:
The distorted image tensor.
"""
with tf.name_scope('distort_color'):
def apply_transform(i, x):
"""Apply the i-th transformation."""
def brightness_foo():
if brightness == 0:
return x
else:
return random_brightness(x, max_delta=brightness)
def contrast_foo():
if contrast == 0:
return x
else:
return tf.image.random_contrast(x, lower=1-contrast, upper=1+contrast)
def saturation_foo():
if saturation == 0:
return x
else:
return tf.image.random_saturation(
x, lower=1-saturation, upper=1+saturation)
def hue_foo():
if hue == 0:
return x
else:
return tf.image.random_hue(x, max_delta=hue)
x = tf.cond(tf.less(i, 2),
lambda: tf.cond(tf.less(i, 1), brightness_foo, contrast_foo),
lambda: tf.cond(tf.less(i, 3), saturation_foo, hue_foo))
return x
perm = tf.random_shuffle(tf.range(4))
for i in range(4):
image = apply_transform(perm[i], image)
image = tf.clip_by_value(image, 0., 1.)
return image
def _compute_crop_shape(
image_height, image_width, aspect_ratio, crop_proportion):
"""Compute aspect ratio-preserving shape for central crop.
The resulting shape retains `crop_proportion` along one side and a proportion
less than or equal to `crop_proportion` along the other side.
Args:
image_height: Height of image to be cropped.
image_width: Width of image to be cropped.
aspect_ratio: Desired aspect ratio (width / height) of output.
crop_proportion: Proportion of image to retain along the less-cropped side.
Returns:
crop_height: Height of image after cropping.
crop_width: Width of image after cropping.
"""
image_width_float = tf.cast(image_width, tf.float32)
image_height_float = tf.cast(image_height, tf.float32)
def _requested_aspect_ratio_wider_than_image():
crop_height = tf.cast(tf.rint(
crop_proportion / aspect_ratio * image_width_float), tf.int32)
crop_width = tf.cast(tf.rint(
crop_proportion * image_width_float), tf.int32)
return crop_height, crop_width
def _image_wider_than_requested_aspect_ratio():
crop_height = tf.cast(
tf.rint(crop_proportion * image_height_float), tf.int32)
crop_width = tf.cast(tf.rint(
crop_proportion * aspect_ratio *
image_height_float), tf.int32)
return crop_height, crop_width
return tf.cond(
aspect_ratio > image_width_float / image_height_float,
_requested_aspect_ratio_wider_than_image,
_image_wider_than_requested_aspect_ratio)
def center_crop(image, height, width, crop_proportion):
"""Crops to center of image and rescales to desired size.
Args:
image: Image Tensor to crop.
height: Height of image to be cropped.
width: Width of image to be cropped.
crop_proportion: Proportion of image to retain along the less-cropped side.
Returns:
A `height` x `width` x channels Tensor holding a central crop of `image`.
"""
shape = tf.shape(image)
image_height = shape[0]
image_width = shape[1]
crop_height, crop_width = _compute_crop_shape(
image_height, image_width, height / width, crop_proportion)
offset_height = ((image_height - crop_height) + 1) // 2
offset_width = ((image_width - crop_width) + 1) // 2
image = tf.image.crop_to_bounding_box(
image, offset_height, offset_width, crop_height, crop_width)
image = tf.image.resize_bicubic([image], [height, width])[0]
return image
def distorted_bounding_box_crop(image,
bbox,
min_object_covered=0.1,
aspect_ratio_range=(0.75, 1.33),
area_range=(0.05, 1.0),
max_attempts=100,
scope=None):
"""Generates cropped_image using one of the bboxes randomly distorted.
See `tf.image.sample_distorted_bounding_box` for more documentation.
Args:
image: `Tensor` of image data.
bbox: `Tensor` of bounding boxes arranged `[1, num_boxes, coords]`
where each coordinate is [0, 1) and the coordinates are arranged
as `[ymin, xmin, ymax, xmax]`. If num_boxes is 0 then use the whole
image.
min_object_covered: An optional `float`. Defaults to `0.1`. The cropped
area of the image must contain at least this fraction of any bounding
box supplied.
aspect_ratio_range: An optional list of `float`s. The cropped area of the
image must have an aspect ratio = width / height within this range.
area_range: An optional list of `float`s. The cropped area of the image
must contain a fraction of the supplied image within in this range.
max_attempts: An optional `int`. Number of attempts at generating a cropped
region of the image of the specified constraints. After `max_attempts`
failures, return the entire image.
scope: Optional `str` for name scope.
Returns:
(cropped image `Tensor`, distorted bbox `Tensor`).
"""
with tf.name_scope(scope, 'distorted_bounding_box_crop', [image, bbox]):
shape = tf.shape(image)
sample_distorted_bounding_box = tf.image.sample_distorted_bounding_box(
shape,
bounding_boxes=bbox,
min_object_covered=min_object_covered,
aspect_ratio_range=aspect_ratio_range,
area_range=area_range,
max_attempts=max_attempts,
use_image_if_no_bounding_boxes=True)
bbox_begin, bbox_size, _ = sample_distorted_bounding_box
# Crop the image to the specified bounding box.
offset_y, offset_x, _ = tf.unstack(bbox_begin)
target_height, target_width, _ = tf.unstack(bbox_size)
image = tf.image.crop_to_bounding_box(
image, offset_y, offset_x, target_height, target_width)
return image
def crop_and_resize(image, height, width):
"""Make a random crop and resize it to height `height` and width `width`.
Args:
image: Tensor representing the image.
height: Desired image height.
width: Desired image width.
Returns:
A `height` x `width` x channels Tensor holding a random crop of `image`.
"""
bbox = tf.constant([0.0, 0.0, 1.0, 1.0], dtype=tf.float32, shape=[1, 1, 4])
aspect_ratio = width / height
image = distorted_bounding_box_crop(
image,
bbox,
min_object_covered=0.1,
aspect_ratio_range=(3. / 4 * aspect_ratio, 4. / 3. * aspect_ratio),
area_range=(0.08, 1.0),
max_attempts=100,
scope=None)
return tf.image.resize_bicubic([image], [height, width])[0]
def gaussian_blur(image, kernel_size, sigma, padding='SAME'):
"""Blurs the given image with separable convolution.
Args:
image: Tensor of shape [height, width, channels] and dtype float to blur.
kernel_size: Integer Tensor for the size of the blur kernel. This is should
be an odd number. If it is an even number, the actual kernel size will be
size + 1.
sigma: Sigma value for gaussian operator.
padding: Padding to use for the convolution. Typically 'SAME' or 'VALID'.
Returns:
A Tensor representing the blurred image.
"""
radius = tf.to_int32(kernel_size / 2)
kernel_size = radius * 2 + 1
x = tf.to_float(tf.range(-radius, radius + 1))
blur_filter = tf.exp(
-tf.pow(x, 2.0) / (2.0 * tf.pow(tf.to_float(sigma), 2.0)))
blur_filter /= tf.reduce_sum(blur_filter)
# One vertical and one horizontal filter.
blur_v = tf.reshape(blur_filter, [kernel_size, 1, 1, 1])
blur_h = tf.reshape(blur_filter, [1, kernel_size, 1, 1])
num_channels = tf.shape(image)[-1]
blur_h = tf.tile(blur_h, [1, 1, num_channels, 1])
blur_v = tf.tile(blur_v, [1, 1, num_channels, 1])
expand_batch_dim = image.shape.ndims == 3
if expand_batch_dim:
# Tensorflow requires batched input to convolutions, which we can fake with
# an extra dimension.
image = tf.expand_dims(image, axis=0)
blurred = tf.nn.depthwise_conv2d(
image, blur_h, strides=[1, 1, 1, 1], padding=padding)
blurred = tf.nn.depthwise_conv2d(
blurred, blur_v, strides=[1, 1, 1, 1], padding=padding)
if expand_batch_dim:
blurred = tf.squeeze(blurred, axis=0)
return blurred
def random_crop_with_resize(image, height, width, p=1.0):
"""Randomly crop and resize an image.
Args:
image: `Tensor` representing an image of arbitrary size.
height: Height of output image.
width: Width of output image.
p: Probability of applying this transformation.
Returns:
A preprocessed image `Tensor`.
"""
def _transform(image): # pylint: disable=missing-docstring
image = crop_and_resize(image, height, width)
return image
return random_apply(_transform, p=p, x=image)
def random_color_jitter(image, p=1.0):
def _transform(image):
color_jitter_t = functools.partial(
color_jitter, strength=FLAGS_color_jitter_strength)
image = random_apply(color_jitter_t, p=0.8, x=image)
return random_apply(to_grayscale, p=0.2, x=image)
return random_apply(_transform, p=p, x=image)
def random_blur(image, height, width, p=1.0):
"""Randomly blur an image.
Args:
image: `Tensor` representing an image of arbitrary size.
height: Height of output image.
width: Width of output image.
p: probability of applying this transformation.
Returns:
A preprocessed image `Tensor`.
"""
del width
def _transform(image):
sigma = tf.random.uniform([], 0.1, 2.0, dtype=tf.float32)
return gaussian_blur(
image, kernel_size=height//10, sigma=sigma, padding='SAME')
return random_apply(_transform, p=p, x=image)
def batch_random_blur(images_list, height, width, blur_probability=0.5):
"""Apply efficient batch data transformations.
Args:
images_list: a list of image tensors.
height: the height of image.
width: the width of image.
blur_probability: the probaility to apply the blur operator.
Returns:
Preprocessed feature list.
"""
def generate_selector(p, bsz):
shape = [bsz, 1, 1, 1]
selector = tf.cast(
tf.less(tf.random_uniform(shape, 0, 1, dtype=tf.float32), p),
tf.float32)
return selector
new_images_list = []
for images in images_list:
images_new = random_blur(images, height, width, p=1.)
selector = generate_selector(blur_probability, tf.shape(images)[0])
images = images_new * selector + images * (1 - selector)
images = tf.clip_by_value(images, 0., 1.)
new_images_list.append(images)
return new_images_list
def preprocess_for_train(image, height, width,
color_distort=True, crop=True, flip=True):
"""Preprocesses the given image for training.
Args:
image: `Tensor` representing an image of arbitrary size.
height: Height of output image.
width: Width of output image.
color_distort: Whether to apply the color distortion.
crop: Whether to crop the image.
flip: Whether or not to flip left and right of an image.
Returns:
A preprocessed image `Tensor`.
"""
if crop:
image = random_crop_with_resize(image, height, width)
if flip:
image = tf.image.random_flip_left_right(image)
if color_distort:
image = random_color_jitter(image)
image = tf.reshape(image, [height, width, 3])
image = tf.clip_by_value(image, 0., 1.)
return image
def preprocess_for_eval(image, height, width, crop=True):
"""Preprocesses the given image for evaluation.
Args:
image: `Tensor` representing an image of arbitrary size.
height: Height of output image.
width: Width of output image.
crop: Whether or not to (center) crop the test images.
Returns:
A preprocessed image `Tensor`.
"""
if crop:
image = center_crop(image, height, width, crop_proportion=CROP_PROPORTION)
image = tf.reshape(image, [height, width, 3])
image = tf.clip_by_value(image, 0., 1.)
return image
def preprocess_image(image, height, width, is_training=False,
color_distort=True, test_crop=True):
"""Preprocesses the given image.
Args:
image: `Tensor` representing an image of arbitrary size.
height: Height of output image.
width: Width of output image.
is_training: `bool` for whether the preprocessing is for training.
color_distort: whether to apply the color distortion.
test_crop: whether or not to extract a central crop of the images
(as for standard ImageNet evaluation) during the evaluation.
Returns:
A preprocessed image `Tensor` of range [0, 1].
"""
image = tf.image.convert_image_dtype(image, dtype=tf.float32)
if is_training:
return preprocess_for_train(image, height, width, color_distort)
else:
return preprocess_for_eval(image, height, width, test_crop)
#@title Load tensorflow datasets: we use tensorflow flower dataset as an example
batch_size = 5
dataset_name = 'tf_flowers'
tfds_dataset, tfds_info = tfds.load(
dataset_name, split='train', with_info=True)
num_images = tfds_info.splits['train'].num_examples
num_classes = tfds_info.features['label'].num_classes
def _preprocess(x):
x['image'] = preprocess_image(
x['image'], 224, 224, is_training=False, color_distort=False)
return x
x = tfds_dataset.map(_preprocess).batch(batch_size)
x = tf.data.make_one_shot_iterator(x).get_next()
tfds_dataset, x
#@title Load module and get the computation graph
hub_path = 'gs://simclr-checkpoints/simclrv2/finetuned_100pct/r50_1x_sk0/hub/'
module = hub.Module(hub_path, trainable=False)
key = module(inputs=x['image'], signature="default", as_dict=True)
logits_t = key['logits_sup'][:, :]
key # The accessible tensor in the return dictionary
sess = tf.Session()
sess.run(tf.global_variables_initializer())
image, labels, logits = sess.run((x['image'], x['label'], logits_t))
pred = logits.argmax(-1)
#@title Plot the images and predictions
fig, axes = plt.subplots(5, 1, figsize=(15, 15))
for i in range(5):
axes[i].imshow(image[i])
true_text = tf_flowers_labels[labels[i]]
pred_text = imagenet_int_to_str[pred[i]]
if i == 0:
axes[i].text(0, 0, 'Attention: the predictions here are inaccurate as they are constrained among 1000 ImageNet classes.\n', c='r')
axes[i].axis('off')
axes[i].text(256, 128, 'Truth: ' + true_text + '\n' + 'Pred: ' + pred_text)
# aa = hub.Module(hub_path)
a = module(image)
logitss = tf.layers.dense(a, 1000)
prob = tf.nn.softmax(logitss)
a.shape
from keras import layers
key['block_group4'].shape
print(np.min(sess.run(afaf)[2][:1000]))
print(np.min(sess.run(logits_t)))
print(len(module.variable_map))
model = tf.keras.Sequential([
module(inputs=x['image'], signature="default"),
layers.Dense(1000, activation='softmax')
])
afaf = module(image)
print("names:", module.get_signature_names())
print("input:", module.get_input_info_dict())
print("output:", module.get_output_info_dict())
module.get_output_info_dict(), afaf.shape
afaf = module(image)
sess.run(afaf).shape
print(module.get_signature_names)
# https://e3oroush.github.io/tsne-visualization/
import numpy as np
import tensorflow as tf
from PIL import Image
from sklearn.manifold import TSNE
import os, re, glob2, pickle
from keras.engine import Model
from keras.layers import Input
# from keras_vggface.vggface import VGGFace
from keras.preprocessing import image
# from keras_vggface import utils
import matplotlib.pyplot as plt
%pylab inline
# custom paramers: change these parameters to properly run on your machine
image_path = '/home/esoroush/Datasets/MSRC/MSRC/' # addres of images
no_of_images = 1600 # number of images. It is recommended to use a square of 2 number
ellipside =False # elipsoid or rectangular visualization
image_width = 64 # width and height of each visualized images
# choices are: inception, raw and vggfaces
feature_extraction = 'inception' # feature extraction method
# find all images
image_names = glob2.glob(image_path + "**/*.png")
image_names +=glob2.glob(image_path + "**/*.jpg")
image_names +=glob2.glob(image_path + "**/*.gif")
# suffle images
np.random.seed(3)
np.random.shuffle(image_names)
if no_of_images > len(image_names):
no_of_images = len(image_names)
image_names = image_names[:no_of_images]
# Google inception pre-trained network
if feature_extraction == 'inception':
print('using %s network/method for feature extraction'%feature_extraction)
import sys, tarfile
from six.moves import urllib
model_dir = os.path.join(os.environ['HOME'], '.tensorflow/models')
DATA_URL = 'http://download.tensorflow.org/models/image/imagenet/inception-2015-12-05.tgz'
def create_graph():
"""Creates a graph from saved GraphDef file and returns a saver."""
# Creates graph from saved graph_def.pb.
with tf.gfile.FastGFile(os.path.join(
model_dir, 'classify_image_graph_def.pb'), 'rb') as f:
graph_def = tf.GraphDef()
graph_def.ParseFromString(f.read())
_ = tf.import_graph_def(graph_def, name='')
def run_inference_on_image(image):
"""Runs forward path on an image.
Args:
image: Image file name.
Returns:
off the shelf 2048 feature vector
"""
if not tf.gfile.Exists(image):
tf.logging.fatal('File does not exist %s', image)
image_data = tf.gfile.FastGFile(image, 'rb').read()
with tf.Session() as sess:
# Some useful tensors:
# 'softmax:0': A tensor containing the normalized prediction across
# 1000 labels.
# 'pool_3:0': A tensor containing the next-to-last layer containing 2048
# float description of the image.
# 'DecodeJpeg/contents:0': A tensor containing a string providing JPEG
# encoding of the image.
# Runs the softmax tensor by feeding the image_data as input to the graph.
pool3 = sess.graph.get_tensor_by_name('pool_3:0')
features = sess.run(pool3,
{'DecodeJpeg/contents:0': image_data})
return features
def maybe_download_and_extract():
"""Download and extract model tar file."""
dest_directory = model_dir
if not os.path.exists(dest_directory):
os.makedirs(dest_directory)
filename = DATA_URL.split('/')[-1]
filepath = os.path.join(dest_directory, filename)
if not os.path.exists(filepath):
def _progress(count, block_size, total_size):
sys.stdout.write('\r>> Downloading %s %.1f%%' % (
filename, float(count * block_size) / float(total_size) * 100.0))
sys.stdout.flush()
filepath, _ = urllib.request.urlretrieve(DATA_URL, filepath, _progress)
print()
statinfo = os.stat(filepath)
print('Successfully downloaded', filename, statinfo.st_size, 'bytes.')
tarfile.open(filepath, 'r:gz').extractall(dest_directory)
maybe_download_and_extract()
# Creates graph from saved GraphDef.
create_graph()
feature_filename = '%s-feature-inception-%d.p'%(image_path.split('/')[-2], no_of_images)
if os.path.exists(feature_filename):
with open(feature_filename, 'rb') as f:
features, image_names = pickle.load(f)
else:
features = np.zeros([no_of_images, 2048])
for i in xrange(no_of_images):
print('image name: %s index: %d/%d' %(image_names[i], i, no_of_images))
features[i, :] = run_inference_on_image(image=image_names[i]).squeeze()
with open(feature_filename, 'wb') as f:
pickle.dump((features, image_names), f)
# raw image pixels resized to 100x100
if feature_extraction == 'raw':
print('using %s network/method for feature extraction'%feature_extraction)
features = np.zeros([no_of_images, 100*100])
for i, name in enumerate(image_names):
features[i, :] = np.asarray(Image.open(name).resize((100, 100)).convert('L')).reshape(-1,)
# vgg face pretrained network
if feature_extraction == 'vggfaces':
print('using %s network/method for feature extraction'%feature_extraction)
# Convolution Features
features = np.zeros([no_of_images, 2048])
vgg_model_conv = VGGFace(include_top=False, input_shape=(224, 224, 3), pooling='avg') # pooling: None, avg or max
# FC7 Features
vgg_model = VGGFace() # pooling: None, avg or max
out = vgg_model.get_layer('fc7').output
vgg_model_fc7 = Model(vgg_model.input, out)
feature_filename = '%s-feature-vggfaces-%d.p'%(image_path.split('/')[-2], no_of_images)
if os.path.exists(feature_filename):
with open(feature_filename, 'rb') as f:
features, image_names = pickle.load(f)
else:
features = np.zeros([no_of_images, 4096])
for i, name in enumerate(image_names):
img = image.load_img(name, target_size=(224, 224))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = utils.preprocess_input(x)
print('image name: %s progress: %d/%d'%(name, i, no_of_images))
features[i, :] = vgg_model_fc7.predict(x)
with open(feature_filename, 'wb') as f:
pickle.dump((features, image_names), f)
# use tsne to cluster images in 2 dimensions
tsne = TSNE()
reduced = tsne.fit_transform(features)
reduced_transformed = reduced - np.min(reduced, axis=0)
reduced_transformed /= np.max(reduced_transformed, axis=0)
image_xindex_sorted = np.argsort(np.sum(reduced_transformed, axis=1))
# draw all images in a merged image
merged_width = int(np.ceil(np.sqrt(no_of_images))*image_width)
merged_image = np.zeros((merged_width, merged_width, 3), dtype='uint8')
for counter, index in enumerate(image_xindex_sorted):
# set location
if ellipside:
a = np.ceil(reduced_transformed[counter, 0] * (merged_width-image_width-1)+1)
b = np.ceil(reduced_transformed[counter, 1] * (merged_width-image_width-1)+1)
a = int(a - np.mod(a-1,image_width) + 1)
b = int(b - np.mod(b-1,image_width) + 1)
if merged_image[a,b,0] != 0:
continue
image_address = image_names[counter]
img = np.asarray(Image.open(image_address).resize((image_width, image_width)))
merged_image[a:a+image_width, b:b+image_width,:] = img[:,:,:3]
else:
b = int(np.mod(counter, np.sqrt(no_of_images)))
a = int(np.mod(counter//np.sqrt(no_of_images), np.sqrt(no_of_images)))
image_address = image_names[index]
img = np.asarray(Image.open(image_address).resize((image_width, image_width)))
merged_image[a*image_width:(a+1)*image_width, b*image_width:(b+1)*image_width,:] = img[:,:,:3]
plt.imshow(merged_image)
plt.show()
merged_image = Image.fromarray(merged_image)
if ellipside:
merged_image.save('merged-%s-ellipsoide-inception.png'%image_path.split('/')[-2])
else:
merged_image.save('merged-%s.png'%image_path.split('/')[-2])
a = np.array([[1,2], [2,6], [3,9], [9,3], [1,5]], dtype=float)
print(a)
normalized_a = a - np.min(a, axis=0)
normalized_a /= np.max(normalized_a, axis=0)
print(normalized_a)
# reduced_transformed = reduced - np.min(reduced, axis=0)
# reduced_transformed /= np.max(reduced_transformed, axis=0)
# image_xindex_sorted = np.argsort(np.sum(reduced_transformed, axis=1))
```
| true |
code
| 0.733165 | null | null | null | null |
|
# <div style="text-align: center"> Santander ML Explainability </div>
### <div style="text-align: center">CLEAR DATA. MADE MODEL. </div>
<img src='https://galeria.bankier.pl/p/b/5/215103d7ace468-645-387-261-168-1786-1072.jpg' width=600 height=600>
<div style="text-align:center"> last update: <b> 10/03/2019</b></div>
You can Fork code and Follow me on:
> ###### [ GitHub](https://github.com/mjbahmani/10-steps-to-become-a-data-scientist)
> ###### [Kaggle](https://www.kaggle.com/mjbahmani/)
-------------------------------------------------------------------------------------------------------------
<b>I hope you find this kernel helpful and some <font color='red'>UPVOTES</font> would be very much appreciated.</b>
-----------
<a id="top"></a> <br>
## Notebook Content
1. [Introduction](#1)
1. [Load packages](#2)
1. [import](21)
1. [Setup](22)
1. [Version](23)
1. [Problem Definition](#3)
1. [Problem Feature](#31)
1. [Aim](#32)
1. [Variables](#33)
1. [Evaluation](#34)
1. [Exploratory Data Analysis(EDA)](#4)
1. [Data Collection](#41)
1. [Visualization](#42)
1. [Data Preprocessing](#43)
1. [Machine Learning Explainability for Santander](#5)
1. [Permutation Importance](#51)
1. [How to calculate and show importances?](#52)
1. [What can be inferred from the above?](#53)
1. [Partial Dependence Plots](#54)
1. [Model Development](#6)
1. [lightgbm](#61)
1. [RandomForestClassifier](#62)
1. [DecisionTreeClassifier](#63)
1. [CatBoostClassifier](#64)
1. [Funny Combine](#65)
1. [References](#7)
<a id="1"></a> <br>
## 1- Introduction
At [Santander](https://www.santanderbank.com) their mission is to help people and businesses prosper. they are always looking for ways to help our customers understand their financial health and identify which products and services might help them achieve their monetary goals.
<img src='https://www.smava.de/kredit/wp-content/uploads/2015/12/santander-bank.png' width=400 height=400>
In this kernel we are going to create a **Machine Learning Explainability** for **Santander** based this perfect [course](https://www.kaggle.com/learn/machine-learning-explainability) in kaggle.
><font color="red"><b>Note: </b></font>
how to extract **insights** from models?
<a id="2"></a> <br>
## 2- A Data Science Workflow for Santander
Of course, the same solution can not be provided for all problems, so the best way is to create a **general framework** and adapt it to new problem.
**You can see my workflow in the below image** :
<img src="http://s8.picofile.com/file/8342707700/workflow2.png" />
**You should feel free to adjust this checklist to your needs**
###### [Go to top](#top)
<a id="2"></a> <br>
## 2- Load packages
<a id="21"></a> <br>
## 2-1 Import
```
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedKFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from catboost import CatBoostClassifier,Pool
from IPython.display import display
import matplotlib.patches as patch
import matplotlib.pyplot as plt
from sklearn.svm import NuSVR
from scipy.stats import norm
from sklearn import svm
import lightgbm as lgb
import xgboost as xgb
import seaborn as sns
import pandas as pd
import numpy as np
import warnings
import time
import glob
import sys
import os
import gc
```
<a id="22"></a> <br>
## 2-2 Setup
```
# for get better result chage fold_n to 5
fold_n=5
folds = StratifiedKFold(n_splits=fold_n, shuffle=True, random_state=10)
%matplotlib inline
%precision 4
warnings.filterwarnings('ignore')
plt.style.use('ggplot')
np.set_printoptions(suppress=True)
pd.set_option("display.precision", 15)
```
<a id="23"></a> <br>
## 2-3 Version
```
print('pandas: {}'.format(pd.__version__))
print('numpy: {}'.format(np.__version__))
print('Python: {}'.format(sys.version))
```
<a id="3"></a>
<br>
## 3- Problem Definition
In this **challenge**, we should help this **bank** identify which **customers** will make a **specific transaction** in the future, irrespective of the amount of money transacted. The data provided for this competition has the same structure as the real data we have available to solve this **problem**.
<a id="31"></a>
### 3-1 Problem Feature
1. train.csv - the training set.
1. test.csv - the test set. The test set contains some rows which are not included in scoring.
1. sample_submission.csv - a sample submission file in the correct format.
<a id="32"></a>
### 3-2 Aim
In this competition, The task is to predict the value of **target** column in the test set.
<a id="33"></a>
### 3-3 Variables
We are provided with an **anonymized dataset containing numeric feature variables**, the binary **target** column, and a string **ID_code** column.
The task is to predict the value of **target column** in the test set.
<a id="34"></a>
## 3-4 evaluation
**Submissions** are evaluated on area under the [ROC curve](http://en.wikipedia.org/wiki/Receiver_operating_characteristic) between the predicted probability and the observed target.
<img src='https://upload.wikimedia.org/wikipedia/commons/6/6b/Roccurves.png' width=300 height=300>
```
from sklearn.metrics import roc_auc_score, roc_curve
```
<a id="4"></a>
## 4- Exploratory Data Analysis(EDA)
In this section, we'll analysis how to use graphical and numerical techniques to begin uncovering the structure of your data.
* Data Collection
* Visualization
* Data Preprocessing
* Data Cleaning
<img src="http://s9.picofile.com/file/8338476134/EDA.png" width=400 height=400>
<a id="41"></a> <br>
## 4-1 Data Collection
```
print(os.listdir("../input/"))
# import Dataset to play with it
train= pd.read_csv("../input/train.csv")
test = pd.read_csv('../input/test.csv')
sample_submission = pd.read_csv('../input/sample_submission.csv')
sample_submission.head()
train.shape, test.shape, sample_submission.shape
train.head(5)
```
# Reducing memory size by ~50%
Because we make a lot of calculations in this kernel, we'd better reduce the size of the data.
1. 300 MB before Reducing
1. 150 MB after Reducing
```
#Based on this great kernel https://www.kaggle.com/arjanso/reducing-dataframe-memory-size-by-65
def reduce_mem_usage(df):
start_mem_usg = df.memory_usage().sum() / 1024**2
print("Memory usage of properties dataframe is :",start_mem_usg," MB")
NAlist = [] # Keeps track of columns that have missing values filled in.
for col in df.columns:
if df[col].dtype != object: # Exclude strings
# Print current column type
print("******************************")
print("Column: ",col)
print("dtype before: ",df[col].dtype)
# make variables for Int, max and min
IsInt = False
mx = df[col].max()
mn = df[col].min()
# Integer does not support NA, therefore, NA needs to be filled
if not np.isfinite(df[col]).all():
NAlist.append(col)
df[col].fillna(mn-1,inplace=True)
# test if column can be converted to an integer
asint = df[col].fillna(0).astype(np.int64)
result = (df[col] - asint)
result = result.sum()
if result > -0.01 and result < 0.01:
IsInt = True
# Make Integer/unsigned Integer datatypes
if IsInt:
if mn >= 0:
if mx < 255:
df[col] = df[col].astype(np.uint8)
elif mx < 65535:
df[col] = df[col].astype(np.uint16)
elif mx < 4294967295:
df[col] = df[col].astype(np.uint32)
else:
df[col] = df[col].astype(np.uint64)
else:
if mn > np.iinfo(np.int8).min and mx < np.iinfo(np.int8).max:
df[col] = df[col].astype(np.int8)
elif mn > np.iinfo(np.int16).min and mx < np.iinfo(np.int16).max:
df[col] = df[col].astype(np.int16)
elif mn > np.iinfo(np.int32).min and mx < np.iinfo(np.int32).max:
df[col] = df[col].astype(np.int32)
elif mn > np.iinfo(np.int64).min and mx < np.iinfo(np.int64).max:
df[col] = df[col].astype(np.int64)
# Make float datatypes 32 bit
else:
df[col] = df[col].astype(np.float32)
# Print new column type
print("dtype after: ",df[col].dtype)
print("******************************")
# Print final result
print("___MEMORY USAGE AFTER COMPLETION:___")
mem_usg = df.memory_usage().sum() / 1024**2
print("Memory usage is: ",mem_usg," MB")
print("This is ",100*mem_usg/start_mem_usg,"% of the initial size")
return df, NAlist
```
Reducing for train data set
```
train, NAlist = reduce_mem_usage(train)
print("_________________")
print("")
print("Warning: the following columns have missing values filled with 'df['column_name'].min() -1': ")
print("_________________")
print("")
print(NAlist)
```
Reducing for test data set
```
test, NAlist = reduce_mem_usage(test)
print("_________________")
print("")
print("Warning: the following columns have missing values filled with 'df['column_name'].min() -1': ")
print("_________________")
print("")
print(NAlist)
```
<a id="41"></a> <br>
## 4-1-1Data set fields
```
train.columns
print(len(train.columns))
print(train.info())
```
<a id="422"></a> <br>
## 4-2-2 numerical values Describe
```
train.describe()
```
<a id="42"></a> <br>
## 4-2 Visualization
<a id="421"></a>
## 4-2-1 hist
```
train['target'].value_counts().plot.bar();
f,ax=plt.subplots(1,2,figsize=(20,10))
train[train['target']==0].var_0.plot.hist(ax=ax[0],bins=20,edgecolor='black',color='red')
ax[0].set_title('target= 0')
x1=list(range(0,85,5))
ax[0].set_xticks(x1)
train[train['target']==1].var_0.plot.hist(ax=ax[1],color='green',bins=20,edgecolor='black')
ax[1].set_title('target= 1')
x2=list(range(0,85,5))
ax[1].set_xticks(x2)
plt.show()
```
<a id="422"></a> <br>
## 4-2-2 Mean Frequency
```
train[train.columns[2:]].mean().plot('hist');plt.title('Mean Frequency');
```
<a id="423"></a>
## 4-2-3 countplot
```
f,ax=plt.subplots(1,2,figsize=(18,8))
train['target'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('target')
ax[0].set_ylabel('')
sns.countplot('target',data=train,ax=ax[1])
ax[1].set_title('target')
plt.show()
```
<a id="424"></a>
## 4-2-4 hist
If you check histogram for all feature, you will find that most of them are so similar
```
train["var_0"].hist();
train["var_81"].hist();
train["var_2"].hist();
```
<a id="426"></a>
## 4-2-6 distplot
The target in data set is **imbalance**
```
sns.set(rc={'figure.figsize':(9,7)})
sns.distplot(train['target']);
```
<a id="427"></a>
## 4-2-7 violinplot
```
sns.violinplot(data=train,x="target", y="var_0")
sns.violinplot(data=train,x="target", y="var_81")
```
<a id="43"></a> <br>
## 4-3 Data Preprocessing
Before we start this section let me intrduce you, some other compitation that they were similar to this:
1. https://www.kaggle.com/artgor/how-to-not-overfit
1. https://www.kaggle.com/c/home-credit-default-risk
1. https://www.kaggle.com/c/porto-seguro-safe-driver-prediction
<a id="431"></a> <br>
## 4-3-1 Check missing data for test & train
```
def check_missing_data(df):
flag=df.isna().sum().any()
if flag==True:
total = df.isnull().sum()
percent = (df.isnull().sum())/(df.isnull().count()*100)
output = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
data_type = []
# written by MJ Bahmani
for col in df.columns:
dtype = str(df[col].dtype)
data_type.append(dtype)
output['Types'] = data_type
return(np.transpose(output))
else:
return(False)
check_missing_data(train)
check_missing_data(test)
```
<a id="432"></a> <br>
## 4-3-2 Binary Classification
```
train['target'].unique()
```
<a id="433"></a> <br>
## 4-3-3 Is data set imbalance?
A large part of the data is unbalanced, but **how can we solve it?**
```
train['target'].value_counts()
def check_balance(df,target):
check=[]
# written by MJ Bahmani for binary target
print('size of data is:',df.shape[0] )
for i in [0,1]:
print('for target {} ='.format(i))
print(df[target].value_counts()[i]/df.shape[0]*100,'%')
```
1. **Imbalanced dataset** is relevant primarily in the context of supervised machine learning involving two or more classes.
1. **Imbalance** means that the number of data points available for different the classes is different
<img src='https://www.datascience.com/hs-fs/hubfs/imbdata.png?t=1542328336307&width=487&name=imbdata.png'>
[Image source](http://api.ning.com/files/vvHEZw33BGqEUW8aBYm4epYJWOfSeUBPVQAsgz7aWaNe0pmDBsjgggBxsyq*8VU1FdBshuTDdL2-bp2ALs0E-0kpCV5kVdwu/imbdata.png)
```
check_balance(train,'target')
```
## 4-3-4 skewness and kurtosis
```
#skewness and kurtosis
print("Skewness: %f" % train['target'].skew())
print("Kurtosis: %f" % train['target'].kurt())
```
<a id="5"></a> <br>
# 5- Machine Learning Explainability for Santander
In this section, I want to try extract **insights** from models with the help of this excellent [**Course**](https://www.kaggle.com/learn/machine-learning-explainability) in Kaggle.
The Goal behind of ML Explainability for Santander is:
1. All features are senseless named.(var_1, var2,...) but certainly the importance of each one is different!
1. Extract insights from models.
1. Find the most inmortant feature in models.
1. Affect of each feature on the model's predictions.
<img src='http://s8.picofile.com/file/8353215168/ML_Explain.png'>
As you can see from the above, we will refer to three important and practical concepts in this section and try to explain each of them in detail.
<a id="51"></a> <br>
## 5-1 Permutation Importance
In this section we will answer following question:
1. What features have the biggest impact on predictions?
1. how to extract insights from models?
### Prepare our data for our model
```
cols=["target","ID_code"]
X = train.drop(cols,axis=1)
y = train["target"]
X_test = test.drop("ID_code",axis=1)
```
### Create a sample model to calculate which feature are more important.
```
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
rfc_model = RandomForestClassifier(random_state=0).fit(train_X, train_y)
```
<a id="52"></a> <br>
## 5-2 How to calculate and show importances?
### Here is how to calculate and show importances with the [eli5](https://eli5.readthedocs.io/en/latest/) library:
```
import eli5
from eli5.sklearn import PermutationImportance
perm = PermutationImportance(rfc_model, random_state=1).fit(val_X, val_y)
eli5.show_weights(perm, feature_names = val_X.columns.tolist(), top=150)
```
<a id="53"></a> <br>
## 5-3 What can be inferred from the above?
1. As you move down the top of the graph, the importance of the feature decreases.
1. The features that are shown in green indicate that they have a positive impact on our prediction
1. The features that are shown in white indicate that they have no effect on our prediction
1. The features shown in red indicate that they have a negative impact on our prediction
1. The most important feature was **Var_110**.
<a id="54"></a> <br>
## 5-4 Partial Dependence Plots
While **feature importance** shows what **variables** most affect predictions, **partial dependence** plots show how a feature affects predictions.[6][7]
and partial dependence plots are calculated after a model has been fit. [partial-plots](https://www.kaggle.com/dansbecker/partial-plots)
```
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
tree_model = DecisionTreeClassifier(random_state=0, max_depth=5, min_samples_split=5).fit(train_X, train_y)
```
For the sake of explanation, I use a Decision Tree which you can see below.
```
features = [c for c in train.columns if c not in ['ID_code', 'target']]
from sklearn import tree
import graphviz
tree_graph = tree.export_graphviz(tree_model, out_file=None, feature_names=features)
graphviz.Source(tree_graph)
```
As guidance to read the tree:
1. Leaves with children show their splitting criterion on the top
1. The pair of values at the bottom show the count of True values and False values for the target respectively, of data points in that node of the tree.
><font color="red"><b>Note: </b></font>
Yes **Var_81** are more effective on our model.
<a id="55"></a> <br>
## 5-5 Partial Dependence Plot
In this section, we see the impact of the main variables discovered in the previous sections by using the [pdpbox](https://pdpbox.readthedocs.io/en/latest/).
```
from matplotlib import pyplot as plt
from pdpbox import pdp, get_dataset, info_plots
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=tree_model, dataset=val_X, model_features=features, feature='var_81')
# plot it
pdp.pdp_plot(pdp_goals, 'var_81')
plt.show()
```
<a id="56"></a> <br>
## 5-6 Chart analysis
1. The y axis is interpreted as change in the prediction from what it would be predicted at the baseline or leftmost value.
1. A blue shaded area indicates level of confidence
```
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=tree_model, dataset=val_X, model_features=features, feature='var_82')
# plot it
pdp.pdp_plot(pdp_goals, 'var_82')
plt.show()
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=tree_model, dataset=val_X, model_features=features, feature='var_139')
# plot it
pdp.pdp_plot(pdp_goals, 'var_139')
plt.show()
# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=tree_model, dataset=val_X, model_features=features, feature='var_110')
# plot it
pdp.pdp_plot(pdp_goals, 'var_110')
plt.show()
```
<a id="57"></a> <br>
## 5-7 SHAP Values
**SHAP** (SHapley Additive exPlanations) is a unified approach to explain the output of **any machine learning model**. SHAP connects game theory with local explanations, uniting several previous methods [1-7] and representing the only possible consistent and locally accurate additive feature attribution method based on expectations (see the SHAP NIPS paper for details).
<img src='https://raw.githubusercontent.com/slundberg/shap/master/docs/artwork/shap_diagram.png' width=400 height=400>
[image credits](https://github.com/slundberg/shap)
><font color="red"><b>Note: </b></font>
Shap can answer to this qeustion : **how the model works for an individual prediction?**
```
row_to_show = 5
data_for_prediction = val_X.iloc[row_to_show] # use 1 row of data here. Could use multiple rows if desired
data_for_prediction_array = data_for_prediction.values.reshape(1, -1)
rfc_model.predict_proba(data_for_prediction_array);
import shap # package used to calculate Shap values
# Create object that can calculate shap values
explainer = shap.TreeExplainer(rfc_model)
# Calculate Shap values
shap_values = explainer.shap_values(data_for_prediction)
```
If you look carefully at the code where we created the SHAP values, you'll notice we reference Trees in **shap.TreeExplainer(my_model)**. But the SHAP package has explainers for every type of model.
1. shap.DeepExplainer works with Deep Learning models.
1. shap.KernelExplainer works with all models, though it is slower than other Explainers and it offers an approximation rather than exact Shap values.
```
shap.initjs()
shap.force_plot(explainer.expected_value[1], shap_values[1], data_for_prediction)
```
<a id="6"></a> <br>
# 6- Model Development
So far, we have used two models, and at this point we add another model and we'll be expanding it soon.
in this section you will see following model:
1. lightgbm
1. RandomForestClassifier
1. DecisionTreeClassifier
1. CatBoostClassifier
## 6-1 lightgbm
```
# params is based on following kernel https://www.kaggle.com/brandenkmurray/nothing-works
params = {'objective' : "binary",
'boost':"gbdt",
'metric':"auc",
'boost_from_average':"false",
'num_threads':8,
'learning_rate' : 0.01,
'num_leaves' : 13,
'max_depth':-1,
'tree_learner' : "serial",
'feature_fraction' : 0.05,
'bagging_freq' : 5,
'bagging_fraction' : 0.4,
'min_data_in_leaf' : 80,
'min_sum_hessian_in_leaf' : 10.0,
'verbosity' : 1}
%%time
y_pred_lgb = np.zeros(len(X_test))
num_round = 1000000
for fold_n, (train_index, valid_index) in enumerate(folds.split(X,y)):
print('Fold', fold_n, 'started at', time.ctime())
X_train, X_valid = X.iloc[train_index], X.iloc[valid_index]
y_train, y_valid = y.iloc[train_index], y.iloc[valid_index]
train_data = lgb.Dataset(X_train, label=y_train)
valid_data = lgb.Dataset(X_valid, label=y_valid)
lgb_model = lgb.train(params,train_data,num_round,#change 20 to 2000
valid_sets = [train_data, valid_data],verbose_eval=1000,early_stopping_rounds = 3500)##change 10 to 200
y_pred_lgb += lgb_model.predict(X_test, num_iteration=lgb_model.best_iteration)/5
```
<a id="62"></a> <br>
## 6-2 RandomForestClassifier
```
y_pred_rfc = rfc_model.predict(X_test)
```
<a id="63"></a> <br>
## 6-3 DecisionTreeClassifier
```
y_pred_tree = tree_model.predict(X_test)
```
<a id="64"></a> <br>
## 6-4 CatBoostClassifier
```
train_pool = Pool(train_X,train_y)
cat_model = CatBoostClassifier(
iterations=3000,# change 25 to 3000 to get best performance
learning_rate=0.03,
objective="Logloss",
eval_metric='AUC',
)
cat_model.fit(train_X,train_y,silent=True)
y_pred_cat = cat_model.predict(X_test)
```
Now you can change your model and submit the results of other models.
```
submission_rfc = pd.DataFrame({
"ID_code": test["ID_code"],
"target": y_pred_rfc
})
submission_rfc.to_csv('submission_rfc.csv', index=False)
submission_tree = pd.DataFrame({
"ID_code": test["ID_code"],
"target": y_pred_tree
})
submission_tree.to_csv('submission_tree.csv', index=False)
submission_cat = pd.DataFrame({
"ID_code": test["ID_code"],
"target": y_pred_cat
})
submission_cat.to_csv('submission_cat.csv', index=False)
# good for submit
submission_lgb = pd.DataFrame({
"ID_code": test["ID_code"],
"target": y_pred_lgb
})
submission_lgb.to_csv('submission_lgb.csv', index=False)
```
<a id="65"></a> <br>
## 6-5 Funny Combine
```
submission_rfc_cat = pd.DataFrame({
"ID_code": test["ID_code"],
"target": (y_pred_rfc +y_pred_cat)/2
})
submission_rfc_cat.to_csv('submission_rfc_cat.csv', index=False)
submission_lgb_cat = pd.DataFrame({
"ID_code": test["ID_code"],
"target": (y_pred_lgb +y_pred_cat)/2
})
submission_lgb_cat.to_csv('submission_lgb_cat.csv', index=False)
submission_rfc_lgb = pd.DataFrame({
"ID_code": test["ID_code"],
"target": (y_pred_rfc +y_pred_lgb)/2
})
submission_rfc_lgb.to_csv('submission_rfc_lgb.csv', index=False)
```
you can follow me on:
> ###### [ GitHub](https://github.com/mjbahmani/)
> ###### [Kaggle](https://www.kaggle.com/mjbahmani/)
<b>I hope you find this kernel helpful and some <font color='red'>UPVOTES</font> would be very much appreciated.<b/>
<a id="7"></a> <br>
# 7- References & credits
Thanks fo following kernels that help me to create this kernel.
1. [https://www.kaggle.com/dansbecker/permutation-importance](https://www.kaggle.com/dansbecker/permutation-importance)
1. [https://www.kaggle.com/dansbecker/partial-plots](https://www.kaggle.com/dansbecker/partial-plots)
1. [https://www.kaggle.com/miklgr500/catboost-with-gridsearch-cv](https://www.kaggle.com/miklgr500/catboost-with-gridsearch-cv)
1. [https://www.kaggle.com/dromosys/sctp-working-lgb](https://www.kaggle.com/dromosys/sctp-working-lgb)
1. [https://www.kaggle.com/gpreda/santander-eda-and-prediction](https://www.kaggle.com/gpreda/santander-eda-and-prediction)
1. [https://www.kaggle.com/dansbecker/permutation-importance](https://www.kaggle.com/dansbecker/permutation-importance)
1. [https://www.kaggle.com/dansbecker/partial-plots](https://www.kaggle.com/dansbecker/partial-plots)
1. [https://www.kaggle.com/dansbecker/shap-values](https://www.kaggle.com/dansbecker/shap-values)
1. [https://docs.microsoft.com/en-us/azure/machine-learning/studio/algorithm-choice](https://docs.microsoft.com/en-us/azure/machine-learning/studio/algorithm-choice)
1. [kernel https://www.kaggle.com/arjanso/reducing-dataframe-memory-size-by-65](kernel https://www.kaggle.com/arjanso/reducing-dataframe-memory-size-by-65)
1. [https://www.kaggle.com/brandenkmurray/nothing-works](https://www.kaggle.com/brandenkmurray/nothing-works)
| true |
code
| 0.352202 | null | null | null | null |
|
```
import numpy as np
from numpy import random
import matplotlib.pyplot as plt
```
# Uniform distribution
```
# get a single random number between 0 and 100
x = random.uniform(0, 100)
print(x)
# get 10 random numbers
x = random.uniform(0, 100, size=10)
print(x)
# improve readability by writing all parameter names
x = random.uniform(low=0, high=100, size=10000)
print(x)
plt.hist(x, bins=100)
plt.show()
# make a 2 dimensional distribution of random numbers and plot it
x = random.uniform(low=0, high=100, size=100)
y = random.uniform(low=0, high=100, size=100)
plt.plot(x, y, ".")
plt.show()
```
# Gaussian / Normal distribution
```
import math
def normal_distribution(x, mean, standard_deviation):
return math.exp(-0.5 * pow( (x - mean) / standard_deviation, 2)) / standard_deviation / math.sqrt(2 * math.pi)
mean = 0
standard_deviation = 1
x_array = np.arange(-4, 4, 0.1)
y_array = []
for x in x_array:
y = normal_distribution(x, mean, standard_deviation)
y_array = y_array + [y]
fig, ax = plt.subplots()
ax.plot(x_array, y_array, "-")
ax.set_xlabel("x")
ax.set_ylabel("probability")
plt.show()
# generate random numbers following a normal distribution
x = random.normal(loc=0, scale=2, size=10000)
print(x)
plt.hist(x, bins=100)
plt.show()
# make a 2 dimensional distribution of random numbers and plot it
x = random.normal(loc=0, scale=2, size=1000)
y = random.normal(loc=0, scale=2, size=1000)
plt.plot(x, y, ".")
plt.show()
x = random.normal(loc=0, scale=2, size=1000)
y = random.normal(loc=0, scale=2, size=1000)
data = [x, y]
fig1, ax1 = plt.subplots()
ax1.set_title('Box Plot')
ax1.boxplot(data)
plt.show()
```
# Biomodal distribution
```
# generate random numbers following a bi-modal distribution
a = random.normal(loc=0, scale=2, size=10000)
b = random.normal(loc=8, scale=2, size=10000)
x = np.concatenate([a, b])
print(x)
plt.hist(x, bins=100)
plt.show()
```
# Paired/related samples
```
number_of_samples = 100
x = random.uniform(low=0, high=100, size=number_of_samples)
x1 = x + random.normal(loc=0, scale=2, size=number_of_samples)
x2 = x + random.normal(loc=0, scale=2, size=number_of_samples)
plt.plot(x1, x2, ".")
plt.show()
```
## Recap: Descriptive statistics
```
# we setup an array of normal distributed values and
# measure their mean and standard deviation.
x = random.normal(loc=0, scale=2, size=1000000) # <-- increase and decrease
# the size here!
mean = np.mean(x)
standard_deviation = np.std(x)
print("Mean: " + str(mean))
print("standard_deviation: " + str(standard_deviation))
```
# Central limit theorem
```
def normal_random_plots(num_random_numbers):
x = random.normal(loc=0, scale=1, size=num_random_numbers)
data = [x]
fig1, ax1 = plt.subplots()
ax1.set_title('Probability distribution of ' + str(num_random_numbers) + ' normal distributed random numbers')
ax1.set_xlabel("x");
ax1.set_ylabel("probability");
ax1.hist(data)
plt.show()
for i in [1, 5, 10, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000]:
normal_random_plots(i)
def normal_random_box_plots(num_random_numbers):
x = random.normal(loc=0, scale=1, size=num_random_numbers)
y = random.normal(loc=0, scale=1, size=num_random_numbers)
data = [x, y]
fig1, ax1 = plt.subplots()
ax1.set_title('Box Plot of ' + str(num_random_numbers) + ' normal distributed random numbers')
ax1.boxplot(data)
plt.show()
for i in [1, 5, 10, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000]:
normal_random_box_plots(i)
def uniform_random_box_plots(num_random_numbers):
x = random.uniform(low=0, high=10, size=num_random_numbers)
y = random.uniform(low=0, high=10, size=num_random_numbers)
data = [x, y]
fig1, ax1 = plt.subplots()
ax1.set_title('Box Plot of ' + str(num_random_numbers) + ' normal distributed random numbers')
ax1.boxplot(data)
plt.show()
for i in [1, 5, 10, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000]:
uniform_random_box_plots(i)
```
# Students grades
```
from numpy import random
import matplotlib.pyplot as plt
student_count = 60
grades = random.normal(loc=3, scale=1, size=student_count)
fig1, ax1 = plt.subplots()
ax1.set_title('Probability distribution grades')
ax1.set_xlabel("grade");
ax1.set_ylabel("count");
ax1.hist(grades, range=(1,6), bins=6)
plt.show()
student_count = 60
grades = random.normal(loc=2.5, scale=0.8, size=student_count)
fig1, ax1 = plt.subplots()
ax1.set_title('Probability distribution grades')
ax1.set_xlabel("grade");
ax1.set_ylabel("likelihood");
ax1.hist(grades, range=(1,6), bins=6, density=True)
plt.show()
student_count = 10000
grades = random.normal(loc=3, scale=1, size=student_count)
fig1, ax1 = plt.subplots()
ax1.set_title('Probability distribution grades')
ax1.set_xlabel("grade");
ax1.set_ylabel("probability");
ax1.hist(grades, range=(1,6), bins=6, density=True)
plt.show()
```
| true |
code
| 0.668826 | null | null | null | null |
|
## Demonstrates some common TensorFlow errors
This notebook demonstrates some common TensorFlow errors, how to find them, and how to fix them.
```
import tensorflow as tf
print(tf.__version__)
```
# Shape error
```
def some_method(data):
a = data[:,0:2]
c = data[:,1]
s = (a + c)
return tf.sqrt(tf.matmul(s, tf.transpose(s)))
with tf.Session() as sess:
fake_data = tf.constant([
[5.0, 3.0, 7.1],
[2.3, 4.1, 4.8],
[2.8, 4.2, 5.6],
[2.9, 8.3, 7.3]
])
print(sess.run(some_method(fake_data)))
def some_method(data):
a = data[:,0:2]
print(a.get_shape())
c = data[:,1]
print(c.get_shape())
s = (a + c)
return tf.sqrt(tf.matmul(s, tf.transpose(s)))
with tf.Session() as sess:
fake_data = tf.constant([
[5.0, 3.0, 7.1],
[2.3, 4.1, 4.8],
[2.8, 4.2, 5.6],
[2.9, 8.3, 7.3]
])
print(sess.run(some_method(fake_data)))
def some_method(data):
a = data[:,0:2]
print(a.get_shape())
c = data[:,1:3]
print(c.get_shape())
s = (a + c)
return tf.sqrt(tf.matmul(s, tf.transpose(s)))
with tf.Session() as sess:
fake_data = tf.constant([
[5.0, 3.0, 7.1],
[2.3, 4.1, 4.8],
[2.8, 4.2, 5.6],
[2.9, 8.3, 7.3]
])
print(sess.run(some_method(fake_data)))
import tensorflow as tf
x = tf.constant([[3, 2],
[4, 5],
[6, 7]])
print("x.shape", x.shape)
expanded = tf.expand_dims(x, 1)
print("expanded.shape", expanded.shape)
sliced = tf.slice(x, [0, 1], [2, 1])
print("sliced.shape", sliced.shape)
with tf.Session() as sess:
print("expanded: ", expanded.eval())
print("sliced: ", sliced.eval())
```
# Vector vs scalar
```
def some_method(data):
print(data.get_shape())
a = data[:,0:2]
print(a.get_shape())
c = data[:,1:3]
print(c.get_shape())
s = (a + c)
return tf.sqrt(tf.matmul(s, tf.transpose(s)))
with tf.Session() as sess:
fake_data = tf.constant([5.0, 3.0, 7.1])
print(sess.run(some_method(fake_data)))
def some_method(data):
print(data.get_shape())
a = data[:,0:2]
print(a.get_shape())
c = data[:,1:3]
print(c.get_shape())
s = (a + c)
return tf.sqrt(tf.matmul(s, tf.transpose(s)))
with tf.Session() as sess:
fake_data = tf.constant([5.0, 3.0, 7.1])
fake_data = tf.expand_dims(fake_data, 0)
print(sess.run(some_method(fake_data)))
```
# Type error
```
def some_method(a, b):
s = (a + b)
return tf.sqrt(tf.matmul(s, tf.transpose(s)))
with tf.Session() as sess:
fake_a = tf.constant([
[5.0, 3.0, 7.1],
[2.3, 4.1, 4.8],
])
fake_b = tf.constant([
[2, 4, 5],
[2, 8, 7]
])
print(sess.run(some_method(fake_a, fake_b)))
def some_method(a, b):
b = tf.cast(b, tf.float32)
s = (a + b)
return tf.sqrt(tf.matmul(s, tf.transpose(s)))
with tf.Session() as sess:
fake_a = tf.constant([
[5.0, 3.0, 7.1],
[2.3, 4.1, 4.8],
])
fake_b = tf.constant([
[2, 4, 5],
[2, 8, 7]
])
print(sess.run(some_method(fake_a, fake_b)))
```
# TensorFlow debugger
Wrap your normal Session object with tf_debug.LocalCLIDebugWrapperSession
```
import tensorflow as tf
from tensorflow.python import debug as tf_debug
def some_method(a, b):
b = tf.cast(b, tf.float32)
s = (a / b)
s2 = tf.matmul(s, tf.transpose(s))
return tf.sqrt(s2)
with tf.Session() as sess:
fake_a = [
[5.0, 3.0, 7.1],
[2.3, 4.1, 4.8],
]
fake_b = [
[2, 0, 5],
[2, 8, 7]
]
a = tf.placeholder(tf.float32, shape=[2, 3])
b = tf.placeholder(tf.int32, shape=[2, 3])
k = some_method(a, b)
# Note: won't work without the ui_type="readline" argument because
# Datalab is not an interactive terminal and doesn't support the default "curses" ui_type.
# If you are running this a standalone program, omit the ui_type parameter and add --debug
# when invoking the TensorFlow program
# --debug (e.g: python debugger.py --debug )
sess = tf_debug.LocalCLIDebugWrapperSession(sess, ui_type="readline")
sess.add_tensor_filter("has_inf_or_nan", tf_debug.has_inf_or_nan)
print(sess.run(k, feed_dict = {a: fake_a, b: fake_b}))
```
In the tfdbg> window that comes up, try the following:
* run -f has_inf_or_nan
* Notice that several tensors are dumped once the filter criterion is met
* List the inputs to a specific tensor:
* li transpose:0
* Print the value of a tensor
* pt transpose:0
* Where is the inf?
Visit https://www.tensorflow.org/programmers_guide/debugger for usage details of tfdbg
## tf.Print()
Create a python script named debugger.py with the contents shown below.
```
%%writefile debugger.py
import tensorflow as tf
def some_method(a, b):
b = tf.cast(b, tf.float32)
s = (a / b)
print_ab = tf.Print(s, [a, b])
s = tf.where(tf.is_nan(s), print_ab, s)
return tf.sqrt(tf.matmul(s, tf.transpose(s)))
with tf.Session() as sess:
fake_a = tf.constant([
[5.0, 3.0, 7.1],
[2.3, 4.1, 4.8],
])
fake_b = tf.constant([
[2, 0, 5],
[2, 8, 7]
])
print(sess.run(some_method(fake_a, fake_b)))
```
### Execute the python script
```
%%bash
python debugger.py
```
| true |
code
| 0.479138 | null | null | null | null |
|
# Milestone Project 2 - Complete Walkthrough Solution
This notebook walks through a proposed solution to the Blackjack Game milestone project. The approach to solving and the specific code used are only suggestions - there are many different ways to code this out, and yours is likely to be different!
## Game Play
To play a hand of Blackjack the following steps must be followed:
1. Create a deck of 52 cards
2. Shuffle the deck
3. Ask the Player for their bet
4. Make sure that the Player's bet does not exceed their available chips
5. Deal two cards to the Dealer and two cards to the Player
6. Show only one of the Dealer's cards, the other remains hidden
7. Show both of the Player's cards
8. Ask the Player if they wish to Hit, and take another card
9. If the Player's hand doesn't Bust (go over 21), ask if they'd like to Hit again.
10. If a Player Stands, play the Dealer's hand. The dealer will always Hit until the Dealer's value meets or exceeds 17
11. Determine the winner and adjust the Player's chips accordingly
12. Ask the Player if they'd like to play again
## Playing Cards
A standard deck of playing cards has four suits (Hearts, Diamonds, Spades and Clubs) and thirteen ranks (2 through 10, then the face cards Jack, Queen, King and Ace) for a total of 52 cards per deck. Jacks, Queens and Kings all have a rank of 10. Aces have a rank of either 11 or 1 as needed to reach 21 without busting. As a starting point in your program, you may want to assign variables to store a list of suits, ranks, and then use a dictionary to map ranks to values.
## The Game
### Imports and Global Variables
** Step 1: Import the random module. This will be used to shuffle the deck prior to dealing. Then, declare variables to store suits, ranks and values. You can develop your own system, or copy ours below. Finally, declare a Boolean value to be used to control <code>while</code> loops. This is a common practice used to control the flow of the game.**
suits = ('Hearts', 'Diamonds', 'Spades', 'Clubs')
ranks = ('Two', 'Three', 'Four', 'Five', 'Six', 'Seven', 'Eight', 'Nine', 'Ten', 'Jack', 'Queen', 'King', 'Ace')
values = {'Two':2, 'Three':3, 'Four':4, 'Five':5, 'Six':6, 'Seven':7, 'Eight':8, 'Nine':9, 'Ten':10, 'Jack':10,
'Queen':10, 'King':10, 'Ace':11}
```
import random
suits = ('Hearts', 'Diamonds', 'Spades', 'Clubs')
ranks = ('Two', 'Three', 'Four', 'Five', 'Six', 'Seven', 'Eight', 'Nine', 'Ten', 'Jack', 'Queen', 'King', 'Ace')
values = {'Two':2, 'Three':3, 'Four':4, 'Five':5, 'Six':6, 'Seven':7, 'Eight':8, 'Nine':9, 'Ten':10, 'Jack':10,
'Queen':10, 'King':10, 'Ace':11}
playing = True
```
### Class Definitions
Consider making a Card class where each Card object has a suit and a rank, then a Deck class to hold all 52 Card objects, and can be shuffled, and finally a Hand class that holds those Cards that have been dealt to each player from the Deck.
**Step 2: Create a Card Class**<br>
A Card object really only needs two attributes: suit and rank. You might add an attribute for "value" - we chose to handle value later when developing our Hand class.<br>In addition to the Card's \_\_init\_\_ method, consider adding a \_\_str\_\_ method that, when asked to print a Card, returns a string in the form "Two of Hearts"
```
class Card:
def __init__(self,suit,rank):
self.suit = suit
self.rank = rank
def __str__(self):
return self.rank + ' of ' + self.suit
```
**Step 3: Create a Deck Class**<br>
Here we might store 52 card objects in a list that can later be shuffled. First, though, we need to *instantiate* all 52 unique card objects and add them to our list. So long as the Card class definition appears in our code, we can build Card objects inside our Deck \_\_init\_\_ method. Consider iterating over sequences of suits and ranks to build out each card. This might appear inside a Deck class \_\_init\_\_ method:
for suit in suits:
for rank in ranks:
In addition to an \_\_init\_\_ method we'll want to add methods to shuffle our deck, and to deal out cards during gameplay.<br><br>
OPTIONAL: We may never need to print the contents of the deck during gameplay, but having the ability to see the cards inside it may help troubleshoot any problems that occur during development. With this in mind, consider adding a \_\_str\_\_ method to the class definition.
```
class Deck:
def __init__(self):
self.deck = [] # start with an empty list
for suit in suits:
for rank in ranks:
self.deck.append(Card(suit,rank)) # build Card objects and add them to the list
def __str__(self):
deck_comp = '' # start with an empty string
for card in self.deck:
deck_comp += '\n '+card.__str__() # add each Card object's print string
return 'The deck has:' + deck_comp
def shuffle(self):
random.shuffle(self.deck)
def deal(self):
single_card = self.deck.pop()
return single_card
```
TESTING: Just to see that everything works so far, let's see what our Deck looks like!
```
test_deck = Deck()
print(test_deck)
```
Great! Now let's move on to our Hand class.
**Step 4: Create a Hand Class**<br>
In addition to holding Card objects dealt from the Deck, the Hand class may be used to calculate the value of those cards using the values dictionary defined above. It may also need to adjust for the value of Aces when appropriate.
```
class Hand:
def __init__(self):
self.cards = [] # start with an empty list as we did in the Deck class
self.value = 0 # start with zero value
self.aces = 0 # add an attribute to keep track of aces
def add_card(self,card):
self.cards.append(card)
self.value += values[card.rank]
def adjust_for_ace(self):
pass
```
TESTING: Before we tackle the issue of changing Aces, let's make sure we can add two cards to a player's hand and obtain their value:
```
test_deck = Deck()
test_deck.shuffle()
test_player = Hand()
test_player.add_card(test_deck.deal())
test_player.add_card(test_deck.deal())
test_player.value
```
Let's see what these two cards are:
```
for card in test_player.cards:
print(card)
```
Great! Now let's tackle the Aces issue. If a hand's value exceeds 21 but it contains an Ace, we can reduce the Ace's value from 11 to 1 and continue playing.
```
class Hand:
def __init__(self):
self.cards = [] # start with an empty list as we did in the Deck class
self.value = 0 # start with zero value
self.aces = 0 # add an attribute to keep track of aces
def add_card(self,card):
self.cards.append(card)
self.value += values[card.rank]
if card.rank == 'Ace':
self.aces += 1 # add to self.aces
def adjust_for_ace(self):
while self.value > 21 and self.aces:
self.value -= 10
self.aces -= 1
```
We added code to the add_card method to bump self.aces whenever an ace is brought into the hand, and added code to the adjust_for_aces method that decreases the number of aces any time we make an adjustment to stay under 21.
**Step 5: Create a Chips Class**<br>
In addition to decks of cards and hands, we need to keep track of a Player's starting chips, bets, and ongoing winnings. This could be done using global variables, but in the spirit of object oriented programming, let's make a Chips class instead!
```
class Chips:
def __init__(self):
self.total = 100 # This can be set to a default value or supplied by a user input
self.bet = 0
def win_bet(self):
self.total += self.bet
def lose_bet(self):
self.total -= self.bet
```
A NOTE ABOUT OUR DEFAULT TOTAL VALUE:<br>
Alternatively, we could have passed a default total value as an parameter in the \_\_init\_\_. This would have let us pass in an override value at the time the object was created rather than wait until later to change it. The code would have looked like this:
def __init__(self,total=100):
self.total = total
self.bet = 0
Either technique is fine, it only depends on how you plan to start your game parameters.
### Function Defintions
A lot of steps are going to be repetitive. That's where functions come in! The following steps are guidelines - add or remove functions as needed in your own program.
**Step 6: Write a function for taking bets**<br>
Since we're asking the user for an integer value, this would be a good place to use <code>try</code>/<code>except</code>. Remember to check that a Player's bet can be covered by their available chips.
```
def take_bet(chips):
while True:
try:
chips.bet = int(input('How many chips would you like to bet? '))
except ValueError:
print('Sorry, a bet must be an integer!')
else:
if chips.bet > chips.total:
print("Sorry, your bet can't exceed",chips.total)
else:
break
```
We used a <code>while</code> loop here to continually prompt the user for input until we received an integer value that was within the Player's betting limit.
A QUICK NOTE ABOUT FUNCTIONS:<br>
If we knew in advance what we were going to call our Player's Chips object, we could have written the above function like this:
def take_bet():
while True:
try:
player_chips.bet = int(input('How many chips would you like to bet? '))
except ValueError:
print('Sorry, a bet must be an integer!')
else:
if player_chips.bet > player_chips.total:
print("Sorry, your bet can't exceed",player_chips.total)
else:
break
and then we could call the function without passing any arguments. This is generally not a good idea! It's better to have functions be self-contained, able to accept any incoming value than depend on some future naming convention. Also, this makes it easier to add players in future versions of our program!
**Step 7: Write a function for taking hits**<br>
Either player can take hits until they bust. This function will be called during gameplay anytime a Player requests a hit, or a Dealer's hand is less than 17. It should take in Deck and Hand objects as arguments, and deal one card off the deck and add it to the Hand. You may want it to check for aces in the event that a player's hand exceeds 21.
```
def hit(deck,hand):
hand.add_card(deck.deal())
hand.adjust_for_ace()
```
**Step 8: Write a function prompting the Player to Hit or Stand**<br>
This function should accept the deck and the player's hand as arguments, and assign playing as a global variable.<br>
If the Player Hits, employ the hit() function above. If the Player Stands, set the playing variable to False - this will control the behavior of a <code>while</code> loop later on in our code.
```
def hit_or_stand(deck,hand):
global playing # to control an upcoming while loop
while True:
x = input("Would you like to Hit or Stand? Enter 'h' or 's' ")
if x[0].lower() == 'h':
hit(deck,hand) # hit() function defined above
elif x[0].lower() == 's':
print("Player stands. Dealer is playing.")
playing = False
else:
print("Sorry, please try again.")
continue
break
```
**Step 9: Write functions to display cards**<br>
When the game starts, and after each time Player takes a card, the dealer's first card is hidden and all of Player's cards are visible. At the end of the hand all cards are shown, and you may want to show each hand's total value. Write a function for each of these scenarios.
```
def show_some(player,dealer):
print("\nDealer's Hand:")
print(" <card hidden>")
print('',dealer.cards[1])
print("\nPlayer's Hand:", *player.cards, sep='\n ')
def show_all(player,dealer):
print("\nDealer's Hand:", *dealer.cards, sep='\n ')
print("Dealer's Hand =",dealer.value)
print("\nPlayer's Hand:", *player.cards, sep='\n ')
print("Player's Hand =",player.value)
```
QUICK NOTES ABOUT PRINT STATEMENTS:<br>
* The asterisk <code>*</code> symbol is used to print every item in a collection, and the <code>sep='\n '</code> argument prints each item on a separate line.
* In the fourth line where we have
print('',dealer.cards[1])
the empty string and comma are there just to add a space.
- Here we used commas to separate the objects being printed in each line. If you want to concatenate strings using the <code>+</code> symbol, then you have to call each Card object's \_\_str\_\_ method explicitly, as with
print(' ' + dealer.cards[1].__str__())
**Step 10: Write functions to handle end of game scenarios**<br>
Remember to pass player's hand, dealer's hand and chips as needed.
```
def player_busts(player,dealer,chips):
print("Player busts!")
chips.lose_bet()
def player_wins(player,dealer,chips):
print("Player wins!")
chips.win_bet()
def dealer_busts(player,dealer,chips):
print("Dealer busts!")
chips.win_bet()
def dealer_wins(player,dealer,chips):
print("Dealer wins!")
chips.lose_bet()
def push(player,dealer):
print("Dealer and Player tie! It's a push.")
```
### And now on to the game!!
```
while True:
# Print an opening statement
print('Welcome to BlackJack! Get as close to 21 as you can without going over!\n\
Dealer hits until she reaches 17. Aces count as 1 or 11.')
# Create & shuffle the deck, deal two cards to each player
deck = Deck()
deck.shuffle()
player_hand = Hand()
player_hand.add_card(deck.deal())
player_hand.add_card(deck.deal())
dealer_hand = Hand()
dealer_hand.add_card(deck.deal())
dealer_hand.add_card(deck.deal())
# Set up the Player's chips
player_chips = Chips() # remember the default value is 100
# Prompt the Player for their bet
take_bet(player_chips)
# Show cards (but keep one dealer card hidden)
show_some(player_hand,dealer_hand)
while playing: # recall this variable from our hit_or_stand function
# Prompt for Player to Hit or Stand
hit_or_stand(deck,player_hand)
# Show cards (but keep one dealer card hidden)
show_some(player_hand,dealer_hand)
# If player's hand exceeds 21, run player_busts() and break out of loop
if player_hand.value > 21:
player_busts(player_hand,dealer_hand,player_chips)
break
# If Player hasn't busted, play Dealer's hand until Dealer reaches 17
if player_hand.value <= 21:
while dealer_hand.value < 17:
hit(deck,dealer_hand)
# Show all cards
show_all(player_hand,dealer_hand)
# Run different winning scenarios
if dealer_hand.value > 21:
dealer_busts(player_hand,dealer_hand,player_chips)
elif dealer_hand.value > player_hand.value:
dealer_wins(player_hand,dealer_hand,player_chips)
elif dealer_hand.value < player_hand.value:
player_wins(player_hand,dealer_hand,player_chips)
else:
push(player_hand,dealer_hand)
# Inform Player of their chips total
print("\nPlayer's winnings stand at",player_chips.total)
# Ask to play again
new_game = input("Would you like to play another hand? Enter 'y' or 'n' ")
if new_game[0].lower()=='y':
playing=True
continue
else:
print("Thanks for playing!")
break
```
And that's it! Remember, these steps may differ significantly from your own solution. That's OK! Keep working on different sections of your program until you get the desired results. It takes a lot of time and patience! As always, feel free to post questions and comments to the QA Forums.
# Good job!
| true |
code
| 0.307769 | null | null | null | null |
|
# PROJECT 2 : TEAM 11
Members: Talia Tandler, SeungU Lyu
```
# Configure Jupyter so figures appear in the notebook
%matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
%config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import functions from the modsim.py module
from modsim import *
import math
```
http://www.worldometers.info/world-population/us-population/
US pop in 2017 = 324,459,463
https://wwwnc.cdc.gov/travel/yellowbook/2018/infectious-diseases-related-to-travel/measles-rubeola
Measles incubation period 11 days average, infectious period 2-4 days before rash to after rash.
https://www.cdc.gov/vaccines/imz-managers/coverage/childvaxview/data-reports/mmr/trend/index.html
MMR immunization rate in 2017 = 90.7%
```
#population
pop = 999
#initial immunity of the US population
init_im = 0.907
#assumed contact rate
beta = 0.9
#US recovery rate from measles
gamma = 1/7
#US rate from exposure period of 11 days to infected
sigma = 0.091;
```
## Question
### What is the result of lowering the measles immunity rate in a small community during a outbreak?
Measles is a highly infectious disease that can infect about 90% of people that come into contact with the patient. However, the disease is not common these days because of the MMR vaccination, which can effectively prevent people getting the disease. Due to the high vaccination rate, the United States was declared free of circulating measles in 2000. However there were 911 cases of measles between 2001 and 2011. These occurences arose due to individuals from other countries entering the U.S. with measles. Because of the disease's high infectious rate upon contact, herd immunity is considered very important for measles.
In 2015, a measles outbreak occured at Disney World causing more than 159 people to be infected during a single outbreak. Only 50~86% people exposed to this outbreak were vaccinated, causing an even bigger outbreak. This vaccination was lower than it should have been due to Anti-Vaccination Movements in the U.S. These lower rates lowered the population immunity rate and caused the herd immunity to not function as expected. The starter of this movement, Andrew Wakefield, stated that the MMR vaccination can cause autism in newborn children because of the mercury content inside the specific vaccine. Due to this false research, many parents became concerned with the side effects of the vaccination and opted to not vaccinate their children with MMR. As a result, there was a decently sized generation of children susceptible to measles because they did not receive the vaccination at birth.
This simulation utilizes an SEIR model to understand how varying the measles immunity rate in a community effects herd immunity.
## Methodology
In order to create this model, we:
1. Did background research on the MMR vaccination and the measles diseases and found a set of constants we would implement in our model.
2. Put the variables into a state function.
3. Set the total population to 1000, with initial infection number as one person infected with measles.
4. Ran the simulation based on the number measles infections every day.
5. Set a condition where the measles outbreak ends when the number infected people is less than one person.
6. Created graphs to visually represent our results.
```
def make_system (pop, init_im, beta, gamma, sigma):
"""Make a system object for the SCIR model
pop: Total US population
init_im: Initial Population Immunity
beta: effective contact number for patient
gamma: recovery rate for infected people
sigma: rate of incubation group moving to infectious group
return: System object"""
#S: susceptible, E: exposed period, I: infected, R: recovered(immune to disease)
init = State(S = int(pop*(1 - init_im)), E = 0, I = 1, R = int(pop*init_im))
init /= np.sum(init)
t0 = 0
#number of days in 1 year
t_end = 365
return System(init = init,
beta = beta,
gamma = gamma,
sigma = sigma,
t0 = t0,
t_end = t_end,
init_im = init_im)
```
make_system function sets the initial values for the state and returns it with other necessary variables. Since the model is a SEIR model, initial state init contains four values, S, E, I, R where S and R is determined by the initial size and immunization rate of the community, and I is set to 1 to show that one person is infected at the start. Time span for the simulation was set to a year, since every outbreak in this simulation ends within the period.
```
def update_func(state, time, system):
"""Update the SEIR model
state: starting variables of SEIR
t: time step
system: includes alpha,beta,gamma,omega rates
contact: current contact number for the state
"""
unpack(system)
s,e,i,r = state
#current population
total_pop = s+e+i+r
#change rate for each status
#change in number of people susceptible
ds = (-beta*s*i)/total_pop
#change in number of people moving to exposed period
de = ((beta*s*i)/total_pop) - sigma*e
#change in people moving to infectious period
di = sigma*e - gamma*i
#change in people recovered
dr = gamma*i
s += ds
e += de
i += di
r += dr
return State(S=s, E=e, I=i, R=r)
```
update_func function updates the state with four different differential equations. System object was unpacked at the beginning of the code to make it easy to read. Change in susceptible group is affected only by the number of people in infected group, which will raise the number of people in exposed group. There is no direct transition from susceptible group to the infected group, because measles have average of 11 days incubation period, where the person does not spread the disease during that period. Therefore, about 1/11 (sigma value) of people in the exposed group move to the infected group every day, showing that their incubatoin period has ended. It takes about 7 days in average for people to get recoverd, so 1/7 (gamma) of people infected is recovered every day.
```
def run_simulation(system, update_func):
"""Runs a simulation of the system.
system: System object
update_func: function that updates state
returns: TimeFrame
"""
unpack(system)
#creates timeframe to save daily states
frame = TimeFrame(columns=init.index)
frame.row[t0] = init
for time in linrange(t0, t_end):
frame.row[time+1] = update_func(frame.row[time], time, system)
return frame
```
run_simulation function takes a system object with a update_func function, and simulates the state for the duration of the time span set at the make_system function. It returns a TimeFrame object with all the state values for each time step.
```
def plot_results (S,E,I,R):
plot(S, '--', label = 'Susceptible')
plot(E, '-', label = 'Exposed')
plot(I, '.', label = 'Infected')
plot(R, ':', label = 'Recovered')
decorate(xlabel='Time (days)',
ylabel = 'Fraction of population')
```
A plotting function was made for convenience.
```
init_im = 0.907
system = make_system(pop, init_im, beta, gamma, sigma)
results = run_simulation(system, update_func);
```
The code was tested with 2017 average immunization rate for the U.S (90.7%), testing out what will happen if a measles infected person is introduced to a community of 1000 people in a real world situation.
```
plot_results(results.S, results.E, results.I, results.R)
decorate(title ='Figure 1')
```
The result shows that even though measles is a highly contagious disease, the measles outbreak ends without infecting number of people due high immunity rate. We call this herd immunity, because immunized people acts as a barrier that prevents disease to spread among the susceptible people. For each disease, there is specific percentage of people needed to create a herd immunity. Lowering the immunity rate will show abrupt change in infected people, once the herd immunity stops working.
```
init_im2 = 0.3
system = make_system(pop, init_im2, beta, gamma, sigma)
results2 = run_simulation(system, update_func)
results2;
```
Next, the code was tested with lowered initial immunity rate of 30%.
```
plot_results(results2.S, results2.E, results2.I, results2.R)
decorate (title = 'Figure 2')
```
The result is a lot different from the one above, showing that most of susceptible people become infected before the outbreak ends. This shows that the community with only 30% immunity rate has lost their herd immunity, because the number of immuned (recovered) people is too small to act as a barrier that protects the susceptible people. Seeing the result, we can assume that there must be a point between immunity rate of 30% to 90% where the herd immunity fails to function.
```
def calc_highest_infected(results):
"""Fraction of population infected during the simulation.
results: DataFrame with columns S, E, I, R
returns: fraction of population
"""
return max(results.I)
def sweep_init_im(imun_rate_array):
"""Sweep a range of values for beta.
beta_array: array of beta values
gamma: recovery rate
returns: SweepSeries that maps from beta to total infected
"""
sweep = SweepSeries()
for init_im in imun_rate_array:
system = make_system(pop, init_im, beta, gamma, sigma)
results = run_simulation(system, update_func)
sweep[system.init_im] = calc_highest_infected(results)*pop
return sweep
```
To carefully check out the impact due to the change of initial immunity for the community, a sweep_init_im function was created. The function checks out the highest number of people infected to the disease during the simulation. Since the number of people being infected at a day is proportional to the number of currently infected people, higher numbers means that the disease is spreading faster.
```
imun_rate_array = linspace(0, 1, 21)
sweep = sweep_init_im(imun_rate_array)
sweep
plot(sweep)
decorate(xlabel='Immunity Rate',
ylabel = 'Highest number of people infected during 1 outbreak',
title = 'Figure 3')
```
Looking at the table and the plot, we can examine that the speed of infection decreases almost linearly until the immunity rate reachs 80%. Actually, the table states that the maximum number of people infected after the initial immunization rate of 85% is 1, meaning that no one except for the initially infected person was infected during the outbreak. We guessed that the herd immunity for measles in this simulation must be around 80~85% range.
```
def calc_fraction_infected(results):
"""Fraction of susceptible population infected during the simulation.
results: DataFrame with columns S, E, I, R
returns: fraction of susceptible group population
"""
return (get_first_value(results.S) - get_last_value(results.S))/get_first_value(results.S)
def sweep_init_im2(imun_rate_array):
"""Sweep a range of values for beta.
beta_array: array of beta values
gamma: recovery rate
returns: SweepSeries that maps from beta to total infected
"""
sweep = SweepSeries()
for init_im in imun_rate_array:
system = make_system(pop, init_im, beta, gamma, sigma)
results = run_simulation(system, update_func)
sweep[system.init_im] = calc_fraction_infected(results) * 100
return sweep
```
To do a deeper analysis, another sweep_init_im function was created to check out the percentage of people in the susceptible group infected during the outbreak. It will give us more clear view toward the herd immunity for measles and hopefully reveal the danger of lowering immunity rate for a community.
```
imun_rate_array = linspace(0, 0.99, 34)
sweep2 = sweep_init_im2(imun_rate_array)
sweep2
plot(sweep2)
decorate(xlabel='Immunity Rate',
ylabel = '% of susceptible people getting measles during an outbreak',
title = 'Figure 4')
```
Until the immunity rate reaches 60%, more than 90% of people in the susceptible group is infected by the measles. However, the percentage drops abruptly after that, hitting less than 10% on immunity rate of 84%. This graph clearly shows the importance of herd immunity, and the threat people can face due to the lowering of the immunity rate.
## Results
This model uses SEIR methodology to examine how measels would spread throughout a community of 1000 individuals with varying immunity rates. Figure 1 depicts an SEIR representation based on a 90.7% measles immunity rate, equivalent to that of the immunity rate in the United States. Due to the high immunity rate, susceptible people are protected by the herd immunity, and the number of individuals in each of the categories, susceptible, recovered, and infected remains constant throughout the simulated outbreak.
Figure 2 represents an example of the SEIR model with an immunity rate of 30%. In this model, we can see that as the number of susceptible individuals decreases, the number of recovered individuals increases at an equal and opposite rate. The entire population get infected and later recovered from this measles outbreak within 150 days of the start.
Figure 3 depicts the predicted outcome of this model that as the immunity rate in a community increases, rate of infection decreases, thus the number of people infected during an outbreak will decrease. We see the number of infected individuals plateau around 80%~85% immunity.
Figure 4 depicts the percent of susceptible individuals that do contact measles during an outbreak. At low immunity rates (without herd immunity) a large percent of susceptible individuals do contact measles. As the immunity rate increases, this percentage decreases.
## Interpretation
As expected, as the immunity rate in the community increased, the highest number of people infected with measles during an outbreak decreased. The number of people infected with measles begins to plateau between an 80 - 85% immunity rate. From the data that Figure 4 is based on we can see that the ideal immunity rate for a community should be more than 80 - 85%, because the herd immunity is lost at the lowered immunity rate. Between these 2 numbers, the percent of susceptible individuals that contract measles drops sharply from 36% to 6%.
Our model does have several limitations:
1. We were unable to find an effective contact number or contact rate for measles within the United States. Having this number would have enabled us to calculate beta instead of just assuming it to be 0.9.
2. The model gets to a point where less than 1 person is infected with measles. This is physically impossible as you cannot have less than one person. In our results, we interpreted less than 1 to mean the individual did not have measles.
3. The outbreak usually happens country wide, not restricted into a single community. Due to the fact that the simulation was done in a close community, the results may vary in real world situation.
4. People who get measles are usually quarantined before they start infecting other people. One special feature about measles is the rash, which usuaully appears 14 days after exposure. In real world, people get quarantined right away when they get the rash. In this simulation, the factor was ignored. People can also get a MMR vaccination while they are exposed, meaning that not every exposed people move to the infected stage.
5. Measles spread differently among different age groups. Usually, it spread easily among the younger children. The age factor was ignored in this simulation due to its complexity.
## Abstract
In this model, we were seeking to find out the result of lowering the measles immunity rate in a small community during a outbreak. As predicted, we found that as the immunity rate in a community is lowered, the number of infections in a community increases. We also found that when immunity is between 80-85%, the number of individuals infected in a population begins to plateau. This finding indicated that the ideal immunity rate for a community of 1000 individuals is between 80-85%.
```
plot(sweep)
decorate(xlabel='Immunity Rate',
ylabel = 'Highest number of people infected during 1 outbreak',
title = 'Figure 3')
plot(sweep2)
decorate(xlabel='Immunity Rate',
ylabel = '% of susceptible people getting measles during an outbreak',
title = 'Figure 4')
```
| true |
code
| 0.731547 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.