prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
```
#!pip install git+https://github.com/JoaquinAmatRodrigo/skforecast#master --upgrade
%load_ext autoreload
%autoreload 2
import sys
#sys.path.insert(1, '/home/ximo/Documents/GitHub/skforecast')
# Libraries
# ==============================================================================
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from skforecast.model_selection import grid_search_forecaster
from skforecast.model_selection import backtesting_forecaster
%config Completer.use_jedi = False
import session_info
session_info.show(html=False, write_req_file=False)
```
# Data
```
# Download data
# ==============================================================================
url = ('https://raw.githubusercontent.com/JoaquinAmatRodrigo/skforecast/master/data/h2o_exog.csv')
data = pd.read_csv(url, sep=',')
# data preprocessing
# ==============================================================================
data['fecha'] = pd.to_datetime(data['fecha'], format='%Y/%m/%d')
data = data.set_index('fecha')
data = data.rename(columns={'x': 'y'})
data = data.asfreq('MS')
data = data.sort_index()
# Plot
# ==============================================================================
fig, ax=plt.subplots(figsize=(9, 4))
data.plot(ax=ax);
# Split train-test
# ==============================================================================
steps = 36
data_train = data.iloc[:-steps, :]
data_test = data.iloc[-steps:, :]
```
# ForecasterAutoregCustom without exogenous variables
```
def create_predictors(y):
'''
Create first 10 lags of a time series.
Calculate moving average with window 20.
'''
lags = y[-1:-11:-1]
mean = np.mean(y[-20:])
predictors = np.hstack([lags, mean])
return predictors
# Create and fit forecaster
# ==============================================================================
from sklearn.pipeline import make_pipeline
forecaster = ForecasterAutoregCustom(
regressor = make_pipeline(StandardScaler(), Ridge()),
fun_predictors = create_predictors,
window_size = 20
)
forecaster.fit(y=data_train.y)
forecaster
# Predict
# ==============================================================================
predictions = forecaster.predict(steps)
# Prediction error
# ==============================================================================
error_mse = mean_squared_error(
y_true = data_test.y,
y_pred = predictions
)
print(f"Test error (mse): {error_mse}")
# Plot
# ==============================================================================
fig, ax=plt.subplots(figsize=(9, 4))
data_train.y.plot(ax=ax, label='train')
data_test.y.plot(ax=ax, label='test')
predictions.plot(ax=ax, label='predictions')
ax.legend();
# Grid search hiperparameters
# ==============================================================================
forecaster = ForecasterAutoregCustom(
regressor = RandomForestRegressor(random_state=123),
fun_predictors = create_predictors,
window_size = 20
)
# Regressor hiperparameters
param_grid = {'n_estimators': [50, 100],
'max_depth': [5, 10]}
results_grid = grid_search_forecaster(
forecaster = forecaster,
y = data_train.y,
param_grid = param_grid,
steps = 10,
metric = 'mean_squared_error',
refit = False,
initial_train_size = int(len(data_train)*0.5),
return_best = True,
verbose = False
)
# Results grid search
# ==============================================================================
results_grid
# Predictors importance
# ==============================================================================
forecaster.get_feature_importance()
# Backtesting
# ==============================================================================
steps = 36
n_backtest = 36 * 3 + 1
data_train = data[:-n_backtest]
data_test = data[-n_backtest:]
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 20
)
metrica, predicciones_backtest = backtesting_forecaster(
forecaster = forecaster,
y = data.y,
initial_train_size = len(data_train),
steps = steps,
metric = 'mean_squared_error',
verbose = True
)
print(metrica)
# Gráfico
# ==============================================================================
fig, ax = plt.subplots(figsize=(9, 4))
data_train.y.plot(ax=ax, label='train')
data_test.y.plot(ax=ax, label='test')
predicciones_backtest.plot(ax=ax)
ax.legend();
predicciones_backtest
forecaster.fit(y=data_train.y)
predictions_1 = forecaster.predict(steps=steps)
predictions_2 = forecaster.predict(steps=steps, last_window=data_test.y[:steps])
predictions_3 = forecaster.predict(steps=steps, last_window=data_test.y[steps:steps*2])
predictions_4 = forecaster.predict(steps=1, last_window=data_test.y[steps*2:steps*3])
np.allclose(predicciones_backtest.pred, np.concatenate([predictions_1, predictions_2, predictions_3, predictions_4]))
```
# ForecasterAutoregCustom with 1 exogenous variables
```
# Split train-test
# ==============================================================================
steps = 36
data_train = data.iloc[:-steps, :]
data_test = data.iloc[-steps:, :]
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 20
)
forecaster
# Create and fit forecaster
# ==============================================================================
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 20
)
forecaster.fit(y=data_train.y, exog=data_train.exog_1)
# Predict
# ==============================================================================
steps = 36
predictions = forecaster.predict(steps=steps, exog=data_test.exog_1)
# Plot
# ==============================================================================
fig, ax=plt.subplots(figsize=(9, 4))
data_train.y.plot(ax=ax, label='train')
data_test.y.plot(ax=ax, label='test')
predictions.plot(ax=ax, label='predictions')
ax.legend();
# Error prediction
# ==============================================================================
error_mse = mean_squared_error(
y_true = data_test.y,
y_pred = predictions
)
print(f"Test error (mse): {error_mse}")
# Grid search hiperparameters and lags
# ==============================================================================
forecaster = ForecasterAutoregCustom(
regressor = RandomForestRegressor(random_state=123),
fun_predictors = create_predictors,
window_size = 20
)
# Regressor hiperparameters
param_grid = {'n_estimators': [50, 100],
'max_depth': [5, 10]}
results_grid = grid_search_forecaster(
forecaster = forecaster,
y = data_train.y,
exog = data_train.exog_1,
param_grid = param_grid,
steps = 10,
metric = 'mean_squared_error',
refit = False,
initial_train_size = int(len(data_train)*0.5),
return_best = True,
verbose = False
)
# Results grid Search
# ==============================================================================
results_grid.head(4)
# Backtesting
# ==============================================================================
steps = 36
n_backtest = 36 * 3 + 1
data_train = data[:-n_backtest]
data_test = data[-n_backtest:]
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 20
)
metrica, predicciones_backtest = backtesting_forecaster(
forecaster = forecaster,
y = data.y,
exog = data.exog_1,
initial_train_size = len(data_train),
steps = steps,
metric = 'mean_squared_error',
verbose = True
)
print(metrica)
# Verificar predicciones de backtesting
forecaster.fit(y=data_train.y, exog=data_train.exog_1)
predictions_1 = forecaster.predict(steps=steps, exog=data_test.exog_1[:steps])
predictions_2 = forecaster.predict(steps=steps, last_window=data_test.y[:steps], exog=data_test.exog_1[steps:steps*2])
predictions_3 = forecaster.predict(steps=steps, last_window=data_test.y[steps:steps*2], exog=data_test.exog_1[steps*2:steps*3])
predictions_4 = forecaster.predict(steps=1, last_window=data_test.y[steps*2:steps*3], exog=data_test.exog_1[steps*3:steps*4])
np.allclose(predicciones_backtest.pred, np.concatenate([predictions_1, predictions_2, predictions_3, predictions_4]))
```
# ForecasterAutoregCustom with multiple exogenous variables
```
# Split train-test
# ==============================================================================
steps = 36
data_train = data.iloc[:-steps, :]
data_test = data.iloc[-steps:, :]
# Create and fit forecaster
# ==============================================================================
forecaster = ForecasterAutoregCustom(
regressor = RandomForestRegressor(random_state=123),
fun_predictors = create_predictors,
window_size = 20
)
forecaster.fit(y=data_train.y, exog=data_train[['exog_1', 'exog_2']])
# Predict
# ==============================================================================
steps = 36
predictions = forecaster.predict(steps=steps, exog=data_test[['exog_1', 'exog_2']])
# Plot
# ==============================================================================
fig, ax=plt.subplots(figsize=(9, 4))
data_train.y.plot(ax=ax, label='train')
data_test.y.plot(ax=ax, label='test')
predictions.plot(ax=ax, label='predictions')
ax.legend();
# Error
# ==============================================================================
error_mse = mean_squared_error(
y_true = data_test.y,
y_pred = predictions
)
print(f"Test error (mse): {error_mse}")
# Grid search hiperparameters and lags
# ==============================================================================
forecaster = ForecasterAutoregCustom(
regressor = RandomForestRegressor(random_state=123),
fun_predictors = create_predictors,
window_size = 20
)
# Regressor hiperparameters
param_grid = {'n_estimators': [50, 100],
'max_depth': [5, 10]}
# Lags used as predictors
lags_grid = [3, 10, [1,2,3,20]]
results_grid = grid_search_forecaster(
forecaster = forecaster,
y = data_train['y'],
exog = data_train[['exog_1', 'exog_2']],
param_grid = param_grid,
lags_grid = lags_grid,
steps = 10,
metric = 'mean_squared_error',
refit = False,
initial_train_size = int(len(data_train)*0.5),
return_best = True,
verbose = False
)
# Results grid Search
# ==============================================================================
results_grid
```
# Unit testing
```
# Unit test create_train_X_y
# ==============================================================================
import pytest
import numpy as np
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_create_train_X_y_output_when_y_is_series_10_and_exog_is_None():
'''
Test the output of create_train_X_y when y=pd.Series(np.arange(10)) and
exog is None.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
results = forecaster.create_train_X_y(y=pd.Series(np.arange(10)))
expected = (pd.DataFrame(
data = np.array([[4, 3, 2, 1, 0],
[5, 4, 3, 2, 1],
[6, 5, 4, 3, 2],
[7, 6, 5, 4, 3],
[8, 7, 6, 5, 4]]),
index = np.array([5, 6, 7, 8, 9]),
columns = ['custom_predictor_0', 'custom_predictor_1',
'custom_predictor_2', 'custom_predictor_3',
'custom_predictor_4']
),
pd.Series(
np.array([5, 6, 7, 8, 9]),
index = np.array([5, 6, 7, 8, 9]))
)
assert (results[0] == expected[0]).all().all()
assert (results[1] == expected[1]).all()
def test_create_train_X_y_output_when_y_is_series_10_and_exog_is_series():
'''
Test the output of create_train_X_y when y=pd.Series(np.arange(10)) and
exog is a pandas series
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
results = forecaster.create_train_X_y(
y = pd.Series(np.arange(10)),
exog = pd.Series(np.arange(100, 110), name='exog')
)
expected = (pd.DataFrame(
data = np.array([[4, 3, 2, 1, 0, 105],
[5, 4, 3, 2, 1, 106],
[6, 5, 4, 3, 2, 107],
[7, 6, 5, 4, 3, 108],
[8, 7, 6, 5, 4, 109]]),
index = np.array([5, 6, 7, 8, 9]),
columns = ['custom_predictor_0', 'custom_predictor_1',
'custom_predictor_2', 'custom_predictor_3',
'custom_predictor_4', 'exog']
),
pd.Series(
np.array([5, 6, 7, 8, 9]),
index = np.array([5, 6, 7, 8, 9]))
)
assert (results[0] == expected[0]).all().all()
assert (results[1] == expected[1]).all()
def test_create_train_X_y_output_when_y_is_series_10_and_exog_is_dataframe():
'''
Test the output of create_train_X_y when y=pd.Series(np.arange(10)) and
exog is a pandas dataframe with two columns.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
results = forecaster.create_train_X_y(
y = pd.Series(np.arange(10)),
exog = pd.DataFrame({
'exog_1' : np.arange(100, 110),
'exog_2' : np.arange(1000, 1010)
})
)
expected = (pd.DataFrame(
data = np.array([[4, 3, 2, 1, 0, 105, 1005],
[5, 4, 3, 2, 1, 106, 1006],
[6, 5, 4, 3, 2, 107, 1007],
[7, 6, 5, 4, 3, 108, 1008],
[8, 7, 6, 5, 4, 109, 1009]]),
index = np.array([5, 6, 7, 8, 9]),
columns = ['custom_predictor_0', 'custom_predictor_1',
'custom_predictor_2', 'custom_predictor_3',
'custom_predictor_4', 'exog_1', 'exog_2']
),
pd.Series(
np.array([5, 6, 7, 8, 9]),
index = np.array([5, 6, 7, 8, 9])
)
)
assert (results[0] == expected[0]).all().all()
assert (results[1] == expected[1]).all()
def test_create_train_X_y_exception_when_y_and_exog_have_different_length():
'''
Test exception is raised when length of y and length of exog are different.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
with pytest.raises(Exception):
forecaster.fit(y=pd.Series(np.arange(50)), exog=pd.Series(np.arange(10)))
with pytest.raises(Exception):
forecaster.fit(y=pd.Series(np.arange(10)), exog=pd.Series(np.arange(50)))
with pytest.raises(Exception):
forecaster.fit(
y=pd.Series(np.arange(10)),
exog=pd.DataFrame(np.arange(50).reshape(25,2))
)
def test_create_train_X_y_exception_when_y_and_exog_have_different_index():
'''
Test exception is raised when y and exog have different index.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
with pytest.raises(Exception):
forecaster.fit(
y=pd.Series(np.arange(50)),
exog=pd.Series(np.arange(10), index=np.arange(100, 110))
)
test_create_train_X_y_output_when_y_is_series_10_and_exog_is_None()
test_create_train_X_y_output_when_y_is_series_10_and_exog_is_series()
test_create_train_X_y_output_when_y_is_series_10_and_exog_is_dataframe()
test_create_train_X_y_exception_when_y_and_exog_have_different_length()
test_create_train_X_y_exception_when_y_and_exog_have_different_index()
from pytest import approx
import numpy as np
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_estimate_boot_interval_output_when_forecaster_is_LinearRegression_steps_is_1_in_sample_residuals_is_True():
'''
Test output of _estimate_boot_interval when regressor is LinearRegression and
1 step is predicted using in-sample residuals.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(10)))
forecaster.in_sample_residuals = np.full_like(forecaster.in_sample_residuals, fill_value=10)
expected = np.array([[20., 20.]])
results = forecaster._estimate_boot_interval(steps=1, in_sample_residuals=True, n_boot=2)
assert results == approx(expected)
test_estimate_boot_interval_output_when_forecaster_is_LinearRegression_steps_is_1_in_sample_residuals_is_True()
import numpy as np
import pandas as pd
from pytest import approx
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_fit_last_window_stored():
'''
Test that values of last window are stored after fitting.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(50)))
expected = pd.Series(np.array([45, 46, 47, 48, 49]), index=[45, 46, 47, 48, 49])
assert (forecaster.last_window == expected).all()
def test_in_sample_residuals_stored_when_fit_forecaster():
'''
Test that values of in_sample_residuals are stored after fitting.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(7)))
expected = np.array([0, 0])
results = forecaster.in_sample_residuals
assert results.values == approx(expected)
test_fit_last_window_stored()
test_in_sample_residuals_stored_when_fit_forecaster()
from pytest import approx
import numpy as np
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_output_get_coef_when_regressor_is_LinearRegression():
'''
Test output of get_coef when regressor is LinearRegression with lags=3
and it is trained with y=pd.Series(np.arange(5)).
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(7)))
expected = pd.DataFrame({
'feature': ['custom_predictor_0', 'custom_predictor_1',
'custom_predictor_2', 'custom_predictor_3',
'custom_predictor_4'],
'coef': np.array([0.2, 0.2, 0.2, 0.2, 0.2])
})
results = forecaster.get_coef()
assert (results['feature'] == expected['feature']).all()
assert results['coef'].values == approx(expected['coef'].values)
def test_get_coef_when_regressor_is_RandomForest():
'''
Test output of get_coef when regressor is RandomForestRegressor with lags=3
and it is trained with y=pd.Series(np.arange(5)).
'''
forecaster = ForecasterAutoregCustom(
regressor = RandomForestRegressor(n_estimators=1, max_depth=2),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(6)))
expected = None
results = forecaster.get_coef()
assert results is expected
test_output_get_coef_when_regressor_is_LinearRegression()
test_get_coef_when_regressor_is_RandomForest()
from pytest import approx
import numpy as np
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.ensemble import RandomForestRegressor
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_output_get_feature_importance_when_regressor_is_RandomForest():
'''
'''
forecaster = ForecasterAutoregCustom(
regressor = RandomForestRegressor(n_estimators=1, max_depth=2, random_state=123),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(10)))
expected = np.array([0.82142857, 0., 0.17857143, 0., 0.])
expected = pd.DataFrame({
'feature': ['custom_predictor_0', 'custom_predictor_1',
'custom_predictor_2', 'custom_predictor_3',
'custom_predictor_4'],
'importance': np.array([0.82142857, 0., 0.17857143, 0., 0.])
})
results = forecaster.get_feature_importance()
assert (results['feature'] == expected['feature']).all()
assert results['importance'].values == approx(expected['importance'].values)
def test_output_get_feature_importance_when_regressor_is_linear_model():
'''
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(6)))
expected = None
results = forecaster.get_feature_importance()
assert results is expected
test_output_get_feature_importance_when_regressor_is_RandomForest()
test_output_get_feature_importance_when_regressor_is_linear_model()
import pytest
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_init_exception_when_window_size_argument_is_string():
with pytest.raises(Exception):
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = '5'
)
def test_init_exception_when_fun_predictors_argument_is_string():
with pytest.raises(Exception):
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = 'create_predictors',
window_size = 5
)
test_init_exception_when_window_size_argument_is_string()
test_init_exception_when_fun_predictors_argument_is_string()
import numpy as np
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_predict_interval_output_when_forecaster_is_LinearRegression_steps_is_1_in_sample_residuals_is_True():
'''
Test output when regressor is LinearRegression and one step ahead is predicted
using in sample residuals.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(10)))
forecaster.in_sample_residuals = np.full_like(forecaster.in_sample_residuals, fill_value=10)
expected = pd.DataFrame(
np.array([[10., 20., 20.]]),
columns = ['pred', 'lower_bound', 'upper_bound'],
index = pd.RangeIndex(start=10, stop=11, step=1)
)
results = forecaster.predict_interval(steps=1, in_sample_residuals=True, n_boot=2)
pd.testing.assert_frame_equal(results, expected)
def test_predict_interval_output_when_forecaster_is_LinearRegression_steps_is_2_in_sample_residuals_is_True():
'''
Test output when regressor is LinearRegression and two step ahead is predicted
using in sample residuals.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(10)))
forecaster.in_sample_residuals = np.full_like(forecaster.in_sample_residuals, fill_value=10)
expected = pd.DataFrame(
np.array([[10., 20., 20.],
[11., 23., 23.]]),
columns = ['pred', 'lower_bound', 'upper_bound'],
index = pd.RangeIndex(start=10, stop=12, step=1)
)
results = forecaster.predict_interval(steps=2, in_sample_residuals=True, n_boot=2)
pd.testing.assert_frame_equal(results, expected)
def test_predict_interval_output_when_forecaster_is_LinearRegression_steps_is_1_in_sample_residuals_is_False():
'''
Test output when regressor is LinearRegression and one step ahead is predicted
using out sample residuals.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(10)))
forecaster.out_sample_residuals = np.full_like(forecaster.in_sample_residuals, fill_value=10)
expected = pd.DataFrame(
np.array([[10., 20., 20.]]),
columns = ['pred', 'lower_bound', 'upper_bound'],
index = pd.RangeIndex(start=10, stop=11, step=1)
)
results = forecaster.predict_interval(steps=1, in_sample_residuals=False, n_boot=2)
pd.testing.assert_frame_equal(results, expected)
def test_predict_interval_output_when_forecaster_is_LinearRegression_steps_is_2_in_sample_residuals_is_False():
'''
Test output when regressor is LinearRegression and two step ahead is predicted
using out sample residuals.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(10)))
forecaster.out_sample_residuals = np.full_like(forecaster.in_sample_residuals, fill_value=10)
expected = pd.DataFrame(
np.array([[10., 20., 20.],
[11., 23., 23.]]),
columns = ['pred', 'lower_bound', 'upper_bound'],
index = pd.RangeIndex(start=10, stop=12, step=1)
)
results = forecaster.predict_interval(steps=2, in_sample_residuals=False)
pd.testing.assert_frame_equal(results, expected)
test_predict_interval_output_when_forecaster_is_LinearRegression_steps_is_1_in_sample_residuals_is_True()
test_predict_interval_output_when_forecaster_is_LinearRegression_steps_is_2_in_sample_residuals_is_True()
test_predict_interval_output_when_forecaster_is_LinearRegression_steps_is_1_in_sample_residuals_is_False()
test_predict_interval_output_when_forecaster_is_LinearRegression_steps_is_2_in_sample_residuals_is_False()
from pytest import approx
import numpy as np
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_predict_output_when_regressor_is_LinearRegression():
'''
Test predict output when using LinearRegression as regressor.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(50)))
results = forecaster.predict(steps=5)
expected = pd.Series(
data = np.array([50., 51., 52., 53., 54.]),
index = pd.RangeIndex(start=50, stop=55, step=1),
name = 'pred'
)
pd.testing.assert_series_equal(results, expected)
test_predict_output_when_regressor_is_LinearRegression()
# Unit test _recursive_predict
# ==============================================================================
from pytest import approx
import numpy as np
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_recursive_predict_output_when_regressor_is_LinearRegression():
'''
Test _recursive_predict output when using LinearRegression as regressor.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.fit(y=pd.Series(np.arange(50)))
predictions = forecaster._recursive_predict(
steps = 5,
last_window = forecaster.last_window.values,
exog = None
)
expected = np.array([50., 51., 52., 53., 54.])
assert (predictions == approx(expected))
test_recursive_predict_output_when_regressor_is_LinearRegression()
import pytest
import numpy as np
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_set_out_sample_residuals_exception_when_residuals_is_not_array():
'''
Test exception is raised when residuals argument is not numpy array.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
with pytest.raises(Exception):
forecaster.set_out_sample_residuals(residuals=[1, 2, 3])
def test_set_out_sample_residuals_when_residuals_length_is_less_than_1000_and_no_append():
'''
Test residuals stored when its length is less than 1000 and append is False.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.set_out_sample_residuals(residuals=np.arange(10), append=False)
expected = np.arange(10)
results = forecaster.out_sample_residuals
assert (results == expected).all()
def test_set_out_sample_residuals_when_residuals_length_is_less_than_1000_and_append():
'''
Test residuals stored when its length is less than 1000 and append is True.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.set_out_sample_residuals(residuals=np.arange(10), append=True)
forecaster.set_out_sample_residuals(residuals=np.arange(10), append=True)
expected = np.hstack([np.arange(10), np.arange(10)])
results = forecaster.out_sample_residuals
assert (results == expected).all()
def test_set_out_sample_residuals_when_residuals_length_is_greater_than_1000():
'''
Test residuals stored when its length is greater than 1000.
'''
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(),
fun_predictors = create_predictors,
window_size = 5
)
forecaster.set_out_sample_residuals(residuals=np.arange(2000))
assert len(forecaster.out_sample_residuals) == 1000
test_set_out_sample_residuals_exception_when_residuals_is_not_array()
test_set_out_sample_residuals_when_residuals_length_is_less_than_1000_and_no_append()
test_set_out_sample_residuals_when_residuals_length_is_less_than_1000_and_append()
test_set_out_sample_residuals_when_residuals_length_is_greater_than_1000()
import pandas as pd
from skforecast.ForecasterAutoregCustom import ForecasterAutoregCustom
from sklearn.linear_model import LinearRegression
def create_predictors(y):
'''
Create first 5 lags of a time series.
'''
lags = y[-1:-6:-1]
return lags
def test_set_paramns():
forecaster = ForecasterAutoregCustom(
regressor = LinearRegression(fit_intercept=True),
fun_predictors = create_predictors,
window_size = 5
)
new_params = {'fit_intercept': False}
forecaster.set_params(**new_params)
expected = {'copy_X': True,
'fit_intercept': False,
'n_jobs': None,
'normalize': 'deprecated',
'positive': False
}
results = forecaster.regressor.get_params()
assert results == expected
test_set_paramns()
```
| true |
code
| 0.692798 | null | null | null | null |
|
```
import pandas as pd
from matplotlib import pyplot as plt
from functools import partial
% matplotlib inline
# Given these coordenates
x_points = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
y_points = [1, 2, 3, 1, 4, 5, 4, 6, 7, 10, 15]
# Let's plot to display how they are located
plt.plot(x_points, y_points, 'bo')
# remeber the straight line equation? We will use it to find `y` and plot a straight line.
def straight_line_equation(m, x, b):
'''Calculate Y based on straight line equation.
:m: slope or gradient (how steep the line is)
:x: how far along
:b: the Y intercept (where the line crosses the Y axis)
:returns: calculated y
'''
return m * x + b
# now define a function to plot a straight line
def plot_straight_line(data_points, m, b):
'''Use matplotlib to plot a straight line.
:data_points: x points used to a the straight line
:m: how far along
:b: the Y intercept (where the line crosses the Y axis)
:returns: None(plot a graph)
'''
x_values = range(int(min(data_points)) - 1, int(max(data_points) +2))
y_values = [straight_line_equation(x, m, b) for x in x_values]
plt.plot(x_values, y_values, 'r')
# To test our function, let's plot a initial straight line
plot_straight_line(x_points, m=0, b=0)
plt.plot(x_points, y_points, 'bo')
def Σ(lower_bound, upper_bound, function):
'''Summation is a math operator to easily represent a great sum of terms,
even infinity.
It's represented with the greek letter sigma.
Sum terms from lower_bound until upper_bound, applying some function on
each term.
>>> Σ(1,5,lambda x:x) # 1 + 2 + 3 + 4 + 5 = 15
15
'''
return sum(function(index) for index in range(lower_bound,
upper_bound + 1))
LEARN = .001 # mean standard error
def derived_at_point_A(index, x_points, y_points, m, b):
'Derived from the equation of the plane at point A.'
return straight_line_equation(x_points[index],m,b) - y_points[index]
def derived_at_point_B(index, x_points, y_points, m, b):
'Derived from the equation of the plane at point B.'
return (straight_line_equation(x_points[index],m,b) - y_points[index]) * x_points[index]
def separate_points(x_points, y_points, *, intermediate_lines=False):
'''Divide some points into 2 classes.
Obs: 80 is an arbitrary point, because we need logistic regression to obtain that perfect number.
'''
m = 0
b = 0
for i in range(80):
mean1 = Σ(1, len(x_points) -1, partial(derived_at_point_A, x_points=x_points, y_points=y_points, m=m, b=b)) / len(x_points)
mean2 = Σ(1, len(x_points) -1, partial(derived_at_point_B, x_points=x_points, y_points=y_points, m=m, b=b)) / len(x_points)
m -= mean2 * LEARN
b -= mean1 * LEARN
if intermediate_lines:
plot_straight_line(x_points, m, b)
plot_straight_line(x_points, m, b)
plt.plot(x_points, y_points, 'bo')
separate_points(x_points, y_points, intermediate_lines=True)
separate_points(x_points, y_points)
# homework
df = pd.read_csv('tabela.csv')
x_points, y_points = df['faturamento'], df['tempo']
separate_points(x_points, y_points)
```
| true |
code
| 0.74344 | null | null | null | null |
|
# Fuzzy Water Observations from Space <img align="right" src="../../../Supplementary_data/dea_logo.jpg">
* [**Sign up to the DEA Sandbox**](https://docs.dea.ga.gov.au/setup/sandbox.html) to run this notebook interactively from a browser
* **Compatibility:** Notebook currently compatible with both the `NCI` and `DEA Sandbox` environments
* **Products used:**
[wofs_albers](https://explorer.sandbox.dea.ga.gov.au/wofs_albers),
[ga_ls8c_ard_3](https://explorer.sandbox.dea.ga.gov.au/ga_ls7e_ard_3),
[DEA Waterbodies](https://www.ga.gov.au/dea/products/dea-waterbodies)
## Description
This notebook demonstrates FuzzyWOfS, a reimplementation of [the WOfS classifier](https://github.com/GeoscienceAustralia/wofs/blob/master/wofs/classifier.py) over distributions. FuzzyWOfS estimates the probability that each pixel in a Landsat image is wet.
We will:
1. Show how to visualise the FuzzyWOfS classifier;
2. Show how to use FuzzyWOfS to find the probability that each pixel in a Landsat image is wet;
3. Compare the FuzzyWOfS results to MNDWI and TCW, which are band indices often used to estimate wetness.
***
## Getting started
Choose a waterbody in the "Analysis parameters" section and then run all cells.
### Load packages
Import Python packages that are used for the analysis.
```
%matplotlib inline
import sys
import datacube
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import xarray as xr
import geopandas as gpd
import matplotlib.colors
import IPython.display
import matplotlib.patches
sys.path.append("../../../Scripts")
from dea_plotting import rgb
from dea_datahandling import mostcommon_crs
from dea_waterbodies import get_waterbody
from dea_bandindices import calculate_indices
import fuzzy_wofs
```
### Connect to the datacube
Connect to the datacube so we can access DEA data.
The `app` parameter is a unique name for the analysis which is based on the notebook file name.
```
dc = datacube.Datacube(app="FuzzyWOfS")
```
### Analysis parameters
Specify the geohash for a waterbody:
```
geohash = "r38psere6" # Lake Cullivel
```
A product:
```
product = "ga_ls7e_ard_3"
```
A date with observations:
```
date = "2002-02-21" # Lake Cullivel
```
And a buffer radius in metres:
```
buffer = 500
```
### Load the waterbody polygon
```
wb = get_waterbody(geohash)
wb.geometry[0]
```
## Load the image to classify
We'll load a Landsat image to apply FuzzyWOfS to. Set up the waterbody polygon so we can use it to query:
```
gpg = datacube.utils.geometry.Geometry(wb.geometry[0], crs=wb.crs)
```
Identify the correct CRS for the output:
```
best_crs = mostcommon_crs(dc, product=product, query=dict(geopolygon=gpg, time=date))
```
Query the Landsat image:
```
bands = [
"nbart_blue",
"nbart_green",
"nbart_red",
"nbart_nir",
"nbart_swir_1",
"nbart_swir_2",
]
da = dc.load(
product,
geopolygon=datacube.utils.geometry.Geometry(
wb.geometry[0].buffer(buffer), crs=wb.crs
),
time=date,
output_crs=best_crs,
resolution=(-30, 30),
resampling="cubic",
measurements=bands + ["fmask"],
)
```
Then we can have a look at the image.
```
landsat = da.isel(time=0)
rgb(landsat)
```
## Visualise the FuzzyWOfS classifier
The structure of FuzzyWOfS is exactly the same as WOfS. The implementation, however, is a tree, so we can perform tree operations that are hard to do with WOfS. One such operation is visualising the tree. We can construct a tree diagram of WOfS:
```
dot = fuzzy_wofs.wofs.build_graphviz()
dot.render("wofs_tree", format="gif")
IPython.display.Image('wofs_tree.gif')
```
Dry leaf nodes are in red, and wet leaf nodes are in blue. A pixel travels probabilistically down each branch depending on its value, and ends up in a mixture of leaf nodes. The probability of the pixel being wet is then the weighted sum of the probabilities that each leaf node is wet.
We can even turn this tree into a single Python equation:
```
print(fuzzy_wofs.wofs.to_string())
```
## Running FuzzyWOfS on an image
First convert your xarray from `dc.load` into a numpy array:
```
def xr_to_cube(landsat):
"""Convert an Landsat xarray Dataset to a DataArray for WOfS."""
return landsat[bands].to_array(dim="band")
landsat_cube = np.array(xr_to_cube(landsat))
```
We can then run `wofs.predict` on this cube to predict whether each pixel is water. This should be equivalent to WOfS.
```
hard_predictions = fuzzy_wofs.wofs.predict(landsat_cube)
plt.imshow(hard_predictions, interpolation="nearest", cmap='Blues')
patches = [matplotlib.patches.Patch(color=matplotlib.cm.Blues([0, 255])[v], label=['Dry', 'Wet'][v]) for v in [0, 1]]
plt.legend(handles=patches)
plt.axis('off');
```
If we want probabilities, we can run `wofs.fuzzy_predict` instead. Before we can estimate probabilities, though, we need to estimate uncertainty in Landsat. For example, let's assume (fairly arbitrarily) that the noise is 11% of the median (for which there is a function to estimate the noise included in `fuzzy_wofs`).
```
landsat_noise = fuzzy_wofs.guess_noise(landsat_cube)
```
Then we can predict.
```
fuzzy_predictions = fuzzy_wofs.wofs.fuzzy_predict(landsat_cube, landsat_noise)
plt.figure()
plt.imshow(
fuzzy_predictions, vmin=0, vmax=1, cmap="coolwarm_r", interpolation="nearest"
)
cb = plt.colorbar(label="Uncalibrated probability")
cb.ax.axhline(0.2, c="white")
cb.ax.axhline(0.5, c="grey")
cb.ax.axhline(0.8, c="black")
plt.contour(fuzzy_predictions, [0.2, 0.5, 0.8], colors=["white", "grey", "black"])
```
We now get an estimate of the probability that each pixel is wet. A probability of 0 means that WOfS is entirely sure that the pixel is not water. A probability of 1 means that WOfS is entirely sure that the pixel is water. The average value of the probability—and the probability in the limit of infinite noise—is the probability that any given pixel in the WOfS training set is wet, about 30%.
This value contains more information than WOfS by itself. WOfS can determine only whether a pixel is wet or dry. FuzzyWOfS can indicate how close WOfS was to classifying each pixel as wet or dry.
In WOfS, a pixel can only end up in a single leaf node: each decision is binary, and each pixel travels down one branch until it reaches a leaf. In FuzzyWOfS, pixels are split between multiple branches based on their probability of the (unobserved) true pixel value belonging in each branch. Each pixel can end up in multiple leaf nodes. The final result for a given pixel is the average of the marginal probabilities at each leaf, weighted by how much of that pixel ended up in each leaf. We decide how much of each pixel to send down each branch by modelling the probability distribution of the surface reflectance of each pixel, which we choose to model as a Gaussian.
What if the noise was really really high? For example, what if we have no SWIR bands at all? We could imagine these SWIR bands take the value of the median of some similar, known image as an assumed expected value and have really high noise.
```
median_swir = np.median(landsat_cube[-2:], axis=(1, 2))
median_swir
landsat_noswir = landsat_cube.copy()
landsat_noswir[-2:] = median_swir[:, None, None]
```
WOfS will output dry for every pixel in this no-SWIR case:
```
hard_predictions_noswir = fuzzy_wofs.wofs.predict(landsat_noswir)
plt.imshow(hard_predictions_noswir, interpolation="nearest")
```
But FuzzyWOfS can account for the fact that we don't know the SWIR, and evaluate WOfS over _all_ possible SWIR values:
```
really_high_noise = landsat_noise.copy()
really_high_noise[-2:] = 1000
fuzzy_predictions_noswir = fuzzy_wofs.wofs.fuzzy_predict(
landsat_noswir, really_high_noise
)
plt.figure()
plt.imshow(
fuzzy_predictions_noswir, vmin=0, vmax=1, cmap="coolwarm_r", interpolation="nearest"
)
cb = plt.colorbar(label="Uncalibrated probability")
cb.ax.axhline(0.2, c="white")
plt.contour(fuzzy_predictions_noswir, [0.2], colors=["white"])
```
We get a low probability prediction of water.
## Visualise how WOfS classifies an image
We can also use FuzzyWOfS to investigate which leaf nodes contribute to the classification in each part of the image. Each pixel ends up in a leaf node which classifies it. Which leaf does each pixel end up in?
```
leaves = fuzzy_wofs.wofs.get_leaf(landsat_cube)
plt.figure(figsize=(12, 8))
for i in range(23):
plt.subplot(4, 6, i + 1)
plt.imshow(leaves == i, cmap="Greys", interpolation="gaussian")
plt.axis("off")
plt.title(i)
```
The dry areas in this image are mostly classified by leaf 22, while the wet areas are mostly classified by leaf 0. The areas in between are classified with a few other leaves.
What about the fuzzy classification? Each pixel now partly ends up in each leaf. We can visualise how much of each pixel ends up in each leaf:
```
fuzzy_leaves = fuzzy_wofs.wofs.get_fuzzy_leaf(landsat_cube, landsat_noise)
plt.figure(figsize=(12, 8))
for i in range(23):
plt.subplot(4, 6, i + 1)
plt.imshow(fuzzy_leaves[i], cmap="Greys", interpolation="gaussian", vmin=0, vmax=1)
plt.axis("off")
plt.title(i)
```
We can see that all leaves contribute to the prediction in different amounts. This is the key difference between WOfS and FuzzyWOfS: in FuzzyWOfS, all leaves contribute to the prediction, while in WOfS, each prediction is based only on one leaf.
## Comparison to other wetness measures
How does FuzzyWOfS compare to Tasseled Cap Wetness (TCW) and the Modified Normalised Difference Water Index (MNDWI), as well as the all-time summary of WOfS?
Load TCW, MNDWI, and the WOfS summary:
```
tcw = calculate_indices(da, index="TCW", collection="ga_ls_3")
mndwi = calculate_indices(da, index="MNDWI", collection="ga_ls_3")
wofs_summary = dc.load("wofs_filtered_summary", like=da.drop("time"))
```
Then we can plot them all together. We'll outline the 5% maximum extent that DEA Waterbodies uses, and also the 50% mark for FuzzyWOfS.
```
plt.figure(figsize=(10, 10))
plt.subplot(2, 2, 1)
plt.title("FuzzyWOfS")
plt.imshow(fuzzy_predictions, cmap="Blues")
plt.colorbar(label='p(wet)')
plt.contour(fuzzy_predictions, [0.5], colors="black", linestyles=":")
plt.contour(wofs_summary.wofs_filtered_summary.isel(time=0), [0.05], colors="black")
plt.subplot(2, 2, 2)
plt.title("TCW")
plt.imshow(tcw.isel(time=0).TCW, cmap="Blues")
plt.colorbar(label='TCW')
plt.contour(fuzzy_predictions, [0.5], colors="black", linestyles=":")
plt.contour(wofs_summary.wofs_filtered_summary.isel(time=0), [0.05], colors="black")
plt.subplot(2, 2, 3)
plt.title("MNDWI")
plt.imshow(mndwi.isel(time=0).MNDWI, cmap="Blues")
plt.colorbar(label='MNDWI')
plt.contour(fuzzy_predictions, [0.5], colors="black", linestyles=":")
plt.contour(wofs_summary.wofs_filtered_summary.isel(time=0), [0.05], colors="black")
plt.subplot(2, 2, 4)
plt.title("WOfS all-time summary")
plt.imshow(wofs_summary.wofs_filtered_summary.isel(time=0), vmin=0, cmap="Blues")
plt.colorbar(label='p(wet)')
plt.contour(fuzzy_predictions, [0.5], colors="black", linestyles=":")
plt.contour(wofs_summary.wofs_filtered_summary.isel(time=0), [0.05], colors="black")
```
Bluer regions of the above maps indicate a higher likelihood of open water. All of the different scene-based measures show different amounts of water, though the water they show tends to be within the boundaries of the lake. TCW shows much more water, while MNDWI shows sparser water. This shows how FuzzyWOfS provides an alternative to TCW and MNDWI for continuous (i.e. non-binary) water predictions on a scene-by-scene basis in a way that is consistent with, and augments, the existing WOfS product.
***
## Additional information
**License:** The code in this notebook is licensed under the [Apache License, Version 2.0](https://www.apache.org/licenses/LICENSE-2.0).
Digital Earth Australia data is licensed under the [Creative Commons by Attribution 4.0](https://creativecommons.org/licenses/by/4.0/) license.
**Contact:** If you need assistance, please post a question on the [Open Data Cube Slack channel](http://slack.opendatacube.org/) or on the [GIS Stack Exchange](https://gis.stackexchange.com/questions/ask?tags=open-data-cube) using the `open-data-cube` tag (you can view previously asked questions [here](https://gis.stackexchange.com/questions/tagged/open-data-cube)).
If you would like to report an issue with this notebook, you can file one on [Github](https://github.com/GeoscienceAustralia/dea-notebooks).
**Last modified:** November 2020
**Compatible datacube version:**
```
print(datacube.__version__)
```
## Tags
Browse all available tags on the DEA User Guide's [Tags Index](https://docs.dea.ga.gov.au/genindex.html)
| true |
code
| 0.616647 | null | null | null | null |
|
# 数据迭代
`Ascend` `GPU` `CPU` `数据准备`
[](https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/master/programming_guide/zh_cn/mindspore_dataset_usage.py) [](https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/master/programming_guide/zh_cn/mindspore_dataset_usage.ipynb) [](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/programming_guide/source_zh_cn/dataset_usage.ipynb)
## 概述
原始数据集通过数据集加载接口读取到内存,再通过数据增强操作进行数据变换,得到的数据集对象有两种常规的数据迭代方法:
- 创建迭代器进行数据迭代。
- 传入Model接口(如`model.train`、`model.eval`等)进行迭代训练或推理。
## 创建迭代器进行数据迭代
数据集对象通常可以创建两种不同的迭代器来遍历数据,分别为元组迭代器和字典迭代器。
创建元组迭代器的接口为`create_tuple_iterator`,创建字典迭代器的接口为`create_dict_iterator`,具体使用方法如下。
首先,任意创建一个数据集对象作为演示说明。
```
import mindspore.dataset as ds
np_data = [[[1, 2], [3, 4]], [[5, 6], [7, 8]]]
dataset = ds.NumpySlicesDataset(np_data, column_names=["data"], shuffle=False)
```
则可使用以下方法创建数据迭代器。
```
# 创建元组迭代器
print("\n create tuple iterator")
for item in dataset.create_tuple_iterator():
print("item:\n", item[0])
# 创建字典迭代器
print("\n create dict iterator")
for item in dataset.create_dict_iterator():
print("item:\n", item["data"])
# 直接遍历数据集对象(等同于创建元组迭代器)
print("\n iterate dataset object directly")
for item in dataset:
print("item:\n", item[0])
# 使用enumerate方式遍历(等同于创建元组迭代器)
print("\n iterate dataset using enumerate")
for index, item in enumerate(dataset):
print("index: {}, item:\n {}".format(index, item[0]))
```
此外,如果需要产生多个Epoch的数据,可以相应地调整入参`num_epochs`的取值。相比于多次调用迭代器接口,直接设置Epoch数可以提高数据迭代的性能。
```
# 创建元组迭代器产生2个Epoch的数据
epoch = 2
iterator = dataset.create_tuple_iterator(num_epochs=epoch)
for i in range(epoch):
print("epoch: ", i)
for item in iterator:
print("item:\n", item[0])
```
迭代器默认输出的数据类型为`mindspore.Tensor`,如果希望得到`numpy.ndarray`类型的数据,可以设置入参`output_numpy=True`。
```
# 默认输出类型为mindspore.Tensor
for item in dataset.create_tuple_iterator():
print("dtype: ", type(item[0]), "\nitem:", item[0])
# 设置输出类型为numpy.ndarray
for item in dataset.create_tuple_iterator(output_numpy=True):
print("dtype: ", type(item[0]), "\nitem:", item[0])
```
更详细的说明,请参考[create_tuple_iterator](https://www.mindspore.cn/docs/api/zh-CN/master/api_python/dataset/mindspore.dataset.NumpySlicesDataset.html#mindspore.dataset.NumpySlicesDataset.create_tuple_iterator) 和[create_dict_iterator](https://www.mindspore.cn/docs/api/zh-CN/master/api_python/dataset/mindspore.dataset.NumpySlicesDataset.html#mindspore.dataset.NumpySlicesDataset.create_dict_iterator)的API文档。
## 传入Model接口进行迭代训练或推理
数据集对象创建后,可通过传入`Model`接口,由接口内部进行数据迭代,并送入网络执行训练或推理。
```
import numpy as np
from mindspore import ms_function
from mindspore import context, nn, Model
import mindspore.dataset as ds
import mindspore.ops as ops
def create_dataset():
np_data = [[[1, 2], [3, 4]], [[5, 6], [7, 8]]]
np_data = np.array(np_data, dtype=np.float16)
dataset = ds.NumpySlicesDataset(np_data, column_names=["col1"], shuffle=False)
return dataset
class Net(nn.Cell):
def __init__(self):
super(Net, self).__init__()
self.relu = ops.ReLU()
self.print = ops.Print()
@ms_function
def construct(self, x):
self.print(x)
return self.relu(x)
if __name__ == "__main__":
# it is supported to run in CPU, GPU or Ascend
context.set_context(mode=context.GRAPH_MODE)
dataset = create_dataset()
network = Net()
model = Model(network)
# do training, sink to device defaultly
model.train(epoch=1, train_dataset=dataset, dataset_sink_mode=True)
```
Model接口中的`dataset_sink_mode`参数用于设置是否将数据下沉到Device。若设置为不下沉,则内部会创建上述迭代器,逐条遍历数据并送入网络;若设置为下沉,则内部会将数据直接发送给Device,并送入网络进行迭代训练或推理。
更加详细的使用方法,可参见[Model基本使用](https://www.mindspore.cn/docs/programming_guide/zh-CN/master/model_use_guide.html#id3)。
| true |
code
| 0.480174 | null | null | null | null |
|
# Linear Regression
##### Examining the relationship between a player's pass volume and completion percentage
---
```
import requests
import pandas as pd
from tqdm import tqdm
import matplotlib.pyplot as plt
```
Same as in previous Notebook, but we're adding:
- `matplotlib.pyplot as plt`. which is the commonly-used convention for importing `matplotlib`
---
```
base_url = "https://raw.githubusercontent.com/statsbomb/open-data/master/data/"
comp_url = base_url + "matches/{}/{}.json"
match_url = base_url + "events/{}.json"
def parse_data(competition_id, season_id):
matches = requests.get(url=comp_url.format(competition_id, season_id)).json()
match_ids = [m['match_id'] for m in matches]
all_events = []
for match_id in tqdm(match_ids):
events = requests.get(url=match_url.format(match_id)).json()
passes = [x for x in events if x['type']['name'] == "Pass"]
for a in passes:
attributes = {
"player_id": a['player']['id'],
"outcome": 0 if 'outcome' in a['pass'].keys() else 1,
}
all_events.append(attributes)
return pd.DataFrame(all_events)
```
The `parse_data` function has been adjusted such that `player_id` and `outcome` are the only attributes being collected.
The StatsBomb data has this weird quirk of only presenting an `outcome` key on event objects that are incomplete. This bit of code handles that:
`"outcome": 0 if 'outcome' in a['pass'].keys() else 1`
---
```
competition_id = 43
season_id = 3
df = parse_data(competition_id, season_id)
df.head(15)
total_passes = df.groupby('player_id')['outcome'].sum()
percentage = df.groupby('player_id')['outcome'].mean()
```
In `Pandas` DataFrames, you can do some basic grouping and aggregation.
Here, we're grouping on `player_id`, and applying a `sum()` or a `mean()` to the `outcome` attribute.
---
```
plt.scatter(total_passes, percentage, alpha=0.8)
plt.show()
```
This is a basic scatter plot via `Matplotlib`, with the x and y axes set to `total_passes` and `percentage`
`alpha=0.8` sets the opacity of each scatter point.
---
```
from sklearn.linear_model import LinearRegression
```
This imports LinearRegression from `scikit-learn`'s `linear_model` module.
---
```
model = LinearRegression()
fit = model.fit([[x] for x in total_passes], percentage)
print("Coefficients: {}".format(fit.coef_))
print("Intercept: {}".format(fit.intercept_))
```
This builds a LinearRegression model, and attempts to predict `percentage` with the features in the `total_passes` variable.
The list comprehension (`[[x] for x in total_passes]`) that surrounds `total_passes` is worth an explanation. Since `model.fit()` allows for multiple features, it requires a nested list as the first argument.
---
```
xfit = [0, 500] # This is the x-axis range of the chart
yfit = model.predict([[x] for x in xfit])
```
This builds the regression line such that it can be plotted in the next step.
---
```
plt.scatter(total_passes, percentage, alpha=0.3)
plt.plot(xfit, yfit, 'r')
plt.show()
```
This plots the previous chart, but also overlays the calculated regression line in red. The color is adjusted with the `'r'` in the `plt.plot()` function.
---
Devin Pleuler 2020
| true |
code
| 0.519278 | null | null | null | null |
|
# TensorFlow Distributions: A Gentle Introduction
>[TensorFlow Distributions: A Gentle Introduction](#scrollTo=DcriL2xPrG3_)
>>[Basic Univariate Distributions](#scrollTo=QD5lzFZerG4H)
>>[Multivariate Distributions](#scrollTo=ztM2d-N9nNX2)
>>[Multiple Distributions](#scrollTo=57lLzC7MQV-9)
>>[Using Independent To Aggregate Batches to Events](#scrollTo=t52ptQXvUO07)
>>[Batches of Multivariate Distirbutions](#scrollTo=INu1viAVXz93)
>>[Broadcasting, aka Why Is This So Confusing?](#scrollTo=72uiME85SmEH)
>>[Going Farther](#scrollTo=JpjjIGThrj8Q)
In this notebook, we'll explore TensorFlow Distributions (TFD for short). The goal of this notebook is to get you gently up the learning curve, including understanding TFD's handling of tensor shapes. This notebook tries to present examples before rather than abstract concepts. We'll present canonical easy ways to do things first, and save the most general abstract view until the end. If you're the type who prefers a more abstract and reference-style tutorial, check out [Understanding TensorFlow Distributions Shapes](https://github.com/tensorflow/probability/blob/master/tensorflow_probability/examples/jupyter_notebooks/Understanding_TensorFlow_Distributions_Shapes.ipynb). If you have any questions about the material here, don't hesitate to contact (or join) [the TensorFlow Probability mailing list](https://groups.google.com/a/tensorflow.org/forum/#!forum/tfprobability). We're happy to help.
Before we start, we need to import the appropriate libraries. Our overall library is `tensorflow_probability`. By convention, we generally refer to the distributions library as `tfd`.
[Tensorflow Eager](https://www.tensorflow.org/guide/eager) is an imperative execution environment for TensorFlow. In TensorFlow eager, every TF operation is immediately evaluated and produces a result. This is in contrast to TensorFlow's standard "graph" mode, in which TF operations add nodes to a graph which is later executed. This entire notebook is written using TF Eager, although none of the concepts presented here rely on that, and TFP can be used in graph mode.
```
import collections
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
tfe = tf.contrib.eager
tfe.enable_eager_execution()
import matplotlib.pyplot as plt
from __future__ import print_function
```
## Basic Univariate Distributions
Let's dive right in and create a normal distribution:
```
n = tfd.Normal(loc=0., scale=1.)
n
```
We can draw a sample from it:
```
n.sample()
```
We can draw multiple samples:
```
n.sample(3)
```
We can evaluate a log prob:
```
n.log_prob(0.)
```
We can evaluate multiple log probabilities:
```
n.log_prob([0., 2., 4.])
```
We have a wide range of distributions. Let's try a Bernoulli:
```
b = tfd.Bernoulli(probs=0.7)
b
b.sample()
b.sample(8)
b.log_prob(1)
b.log_prob([1, 0, 1, 0])
```
## Multivariate Distributions
We'll create a multivariate normal with a diagonal covariance:
```
nd = tfd.MultivariateNormalDiag(loc=[0., 10.], scale_diag=[1., 4.])
nd
```
Comparing this to the univariate normal we created earlier, what's different?
```
tfd.Normal(loc=0., scale=1.)
```
We see that the univariate normal has an `event_shape` of `()`, indicating it's a scalar distribution. The multivariate normal has an `event_shape` of `2`, indicating the basic [event space](https://en.wikipedia.org/wiki/Event_(probability_theory)) of this distribution is two-dimensional.
Sampling works just as before:
```
nd.sample()
nd.sample(5)
nd.log_prob([0., 10])
```
Multivariate normals do not in general have diagonal covariance. TFD offers multiple ways to create multivariate normals, including a full-covariance specification, which we use here.
```
nd = tfd.MultivariateNormalFullCovariance(
loc = [0., 5], covariance_matrix = [[1., .7], [.7, 1.]])
data = nd.sample(200)
plt.scatter(data[:, 0], data[:, 1], color='blue', alpha=0.4)
plt.axis([-5, 5, 0, 10])
plt.title("Data set")
plt.show()
```
## Multiple Distributions
Our first Bernoulli distribution represented a flip of a single fair coin. We can also create a batch of independent Bernoulli distributions, each with their own parameters, in a single `Distribution` object:
```
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
b3
```
It's important to be clear on what this means. The above call defines three independent Bernoulli distributions, which happen to be contained in the same Python `Distribution` object. The three distributions cannot be manipulated individually. Note how the `batch_shape` is `(3,)`, indicating a batch of three distributions, and the `event_shape` is `()`, indicating the individual distributions have a univariate event space.
If we call `sample`, we get a sample from all three:
```
b3.sample()
b3.sample(6)
```
If we call `prob`, (this has the same shape semantics as `log_prob`; we use `prob` with these small Bernoulli examples for clarity, although `log_prob` is usually preferred in applications) we can pass it a vector and evaluate the probability of each coin yielding that value:
```
b3.prob([1, 1, 0])
```
Why does the API include batch shape? Semantically, one could perform the same computations by creating a list of distributions and iterating over them with a `for` loop (at least in Eager mode, in TF graph mode you'd need a `tf.while` loop). However, having a (potentially large) set of identically parameterized distributions is extremely common, and the use of vectorized computations whenever possible is a key ingredient in being able to perform fast computations using hardware accelerators.
## Using Independent To Aggregate Batches to Events
In the previous section, we created `b3`, a single `Distribution` object that represented three coin flips. If we called `b3.prob` on a vector $v$, the $i$'th entry was the probability that the $i$th coin takes value $v[i]$.
Suppose we'd instead like to specify a "joint" distribution over independent random variables from the same underlying family. This is a different object mathematically, in that for this new distribution, `prob` on a vector $v$ will return a single value representing the probability that the entire set of coins matches the vector $v$.
How do we accomplish this? We use a "higher-order" distribution called `Independent`, which takes a distribution and yields a new distribution with the batch shape moved to the event shape:
```
b3_joint = tfd.Independent(b3, reinterpreted_batch_ndims=1)
b3_joint
```
Compare the shape to that of the original `b3`:
```
b3
```
As promised, we see that that `Independent` has moved the batch shape into the event shape: `b3_joint` is a single distribution (`batch_shape = ()`) over a three-dimensional event space (`event_shape = (3,)`).
Let's check the semantics:
```
b3_joint.prob([1, 1, 0])
```
An alternate way to get the same result would be to compute probabilities using `b3` and do the reduction manually by multiplying (or, in the more usual case where log probabilities are used, summing):
```
tf.reduce_prod(b3.prob([1, 1, 0]))
```
`Indpendent` allows the user to more explicitly represent the desired concept. We view this as extremely useful, although it's not strictly necessary.
Fun facts:
* `b3.sample` and `b3_joint.sample` have different conceptual implementations, but indistinguishable outputs: the difference between a batch of independent distributions and a single distribution created from the batch using `Independent` shows up when computing probabilites, not when sampling.
* `MultivariateNormalDiag` could be trivially implemented using the scalar `Normal` and `Independent` distributions (it isn't actually implemented this way, but it could be).
## Batches of Multivariate Distirbutions
Let's create a batch of three full-covariance two-dimensional multivariate normals:
```
ndb = tfd.MultivariateNormalFullCovariance(
loc = [[0., 0.], [1., 1.], [2., 2.]],
covariance_matrix = [[[1., .1], [.1, 1.]],
[[1., .3], [.3, 1.]],
[[1., .5], [.5, 1.]]])
nd_batch
```
We see `batch_shape = (3,)`, so there are three independent multivariate normals, and `event_shape = (2,)`, so each multivariate normal is two-dimensional. In this example, the individual distributions do not have independent elements.
Sampling works:
```
ndb.sample(4)
```
Since `batch_shape = (3,)` and `event_shape = (2,)`, we pass a tensor of shape `(3, 2)` to `log_prob`:
```
nd_batch.log_prob([[0., 0.], [1., 1.], [2., 2.]])
```
## Broadcasting, aka Why Is This So Confusing?
Abstracting out what we've done so far, every distribution has an batch shape `B` and an event shape `E`. Let `BE` be the concatenation of the event shapes:
* For the univariate scalar distributions `n` and `b`, `BE = ().`.
* For the two-dimensional multivariate normals `nd`. `BE = (2).`
* For both `b3` and `b3_joint`, `BE = (3).`
* For the batch of multivariate normals `ndb`, `BE = (3, 2).`
The "evaluation rules" we've been using so far are:
* Sample with no argument returns a tensor with shape `BE`; sampling with a scalar n returns an "n by `BE`" tensor.
* `prob` and `log_prob` take a tensor of shape `BE` and return a result of shape `B`.
The actual "evaluation rule" for `prob` and `log_prob` is more complicated, in a way that offers potential power and speed but also complexity and challenges. The actual rule is (essentially) that **the argument to `log_prob` *must* be [broadcastable](https://docs.scipy.org/doc/numpy/user/basics.broadcasting.html) against `BE`; any "extra" dimensions are preserved in the output.**
Let's explore the implications. For the univariate normal `n`, `BE = ()`, so `log_prob` expects a scalar. If we pass `log_prob` a tensor with non-empty shape, those show up as batch dimensions in the output:
```
n = tfd.Normal(loc=0., scale=1.)
n
n.log_prob(0.)
n.log_prob([0.])
n.log_prob([[0., 1.], [-1., 2.]])
```
Let's turn to the two-dimensional multivariate normal `nd` (parameters changed for illustrative purposes):
```
nd = tfd.MultivariateNormalDiag(loc=[0., 1.], scale_diag=[1., 1.])
nd
```
`log_prob` "expects" an argument with shape `(2,)`, but it will accept any argument that broadcasts against this shape:
```
nd.log_prob([0., 0.])
```
But we can pass in "more" examples, and evaluate all their `log_prob`'s at once:
```
nd.log_prob([[0., 0.],
[1., 1.],
[2., 2.]])
```
Perhaps less appealingly, we can broadcast over the event dimensions:
```
nd.log_prob([0.])
nd.log_prob([[0.], [1.], [2.]])
```
Broadcasting this way is a consequence of our "enable broadcasting whenever possible" design; this usage is somewhat controversial and could potentially be removed in a future version of TFP.
Now let's look at the three coins example again:
```
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
```
Here, using broadcasting to represent the probability that *each* coin comes up heads is quite intuitive:
```
b3.prob([1])
```
(Compare this to `b3.prob([1., 1., 1.])`, which we would have used back where `b3` was introduced.)
Now suppose we want to know, for each coin, the probability the coin comes up heads *and* the probability it comes up tails. We could imagine trying:
`b3.log_prob([0, 1])`
Unfortunately, this produces an error with a long and not-very-readable stack trace. `b3` has `BE = (3)`, so we must pass `b3.prob` something broadcastable against `(3,)`. `[0, 1]` has shape `(2)`, so it doesn't broadcast and creates an error. Instead, we have to say:
```
b3.prob([[0], [1]])
```
Why? `[[0], [1]]` has shape `(2, 1)`, so it broadcasts against shape `(3)` to make a broadcast shape of `(2, 3)`.
Broadcasting is quite powerful: there are cases where it allows order-of-magnitude reduction in the amount of memory used, and it often makes user code shorter. However, it can be challenging to program with. If you call `log_prob` and get an error, a failure to broadcast is nearly always the problem.
## Going Farther
In this tutorial, we've (hopefully) provided a simple introduction. A few pointers for going further:
* `event_shape`, `batch_shape` and `sample_shape` can be arbitrary rank (in this tutorial they are always either scalar or rank 1). This increases the power but again can lead to programming challenges, especially when broadcasting is involved. For an additional deep dive into shape manipulation, see the [Understanding TensorFlow Distributions Shapes](https://github.com/tensorflow/probability/blob/master/tensorflow_probability/examples/jupyter_notebooks/Understanding_TensorFlow_Distributions_Shapes.ipynb).
* TFP includes a powerful abstraction known as `Bijectors`, which in conjunction with `TransformedDistribution`, yields a flexible, compositional way to easily create new distributions that are invertible transformations of existing distributions. We'll try to write a tutorial on this soon, but in the meantime, check out [the documentation](https://www.tensorflow.org/api_docs/python/tf/contrib/distributions/TransformedDistribution)
| true |
code
| 0.702141 | null | null | null | null |
|
# Introduction/Business Problem
Car accidents are one of the most common issues found across the globe to be severe.Accidents might sometimes be due to our negligence or due to natural reasons or anything.Sometimes, we might be too lazy or negligent to drive costing our lives as well as the others.Whereas sometimes, due to heavy rain or heavy gales etc. we might unknowingly droop into an accident with the other car.Whatever the reason maybe, car accidents not only lead to property damage but cause injuries and sometimes even leading to people's death.In our project we decide how these accidents occur due to weather conditions.So, the main problem or question arising in this depressing situation is
"What is the severity of these car accidents?What are their causes?And How to curb or slow down them?"
# Data section
We have several attributes in our dataset which tell us about the severity of these accidents.attributes like WEATHER, ROADCOND, LIGHTCOND, JUNCTIONTYPE can tell us about the accidents which happen naturally.And attributes like SEVERITYDESC and COLLISIONTYPE help us decide how these accidents take place.
Our predictor or target variable will be 'SEVERITYCODE' because it is used measure the severity of an accident from 0 to 5 within the dataset. Attributes used to weigh the severity of an accident are 'WEATHER', 'ROADCOND' and 'LIGHTCOND'.
* 0 : Little to no Probability (Clear Weather Conditions)
* 1 : Very Low Probability - Chance or Property Damage
* 2 : Low Probability - Chance of Injury
* 3 : Mild Probability - Chance of Serious Injury
* 4 : High Probability - Chance of Fatality
So depending on these severity codes, we decide the extent of severity of accidents due to these these weather conditions
# Methodology
UK Road Safety data: Total accident counts with accident severity as Slight, Serious and Fatal
Normalized accident counts each month for slight and (Serious and Fatal clubbed)
Plotting importance of each feature for considered features
Data Pre-processing techniques: The dataset is imputed by replacing NaN and missing values with most frequent values of the corresponding column. All the categorical values have been labeled by integers from 0 to n for each column. Time has been converted to categorial feature with 2 values i.e., daytime and night time.
The data is visualized for correlation. Negatively correlated features are selected to be dropped. Feature importance is plotted to visualize and only features with high importance are taken into consideration for predicting accident severity.
The multi class label is converted to binary class by merging “Serious” and “Fatal” to Serious class.
Feature Selection: The dataset has 34 attributes describing the incident of an accident. There are mixed types of data such as continuous and categorical. Manually dropped few columns due to its inconsistency in values such as Accident ID, and Location ID. For selecting the best features, below functions are used from sklearn library.
* 1. SelectKBest: SelectKBest is a sci-kit learn library provides the k best features by performing statistical tests i.e., chi squared computation between two non-negative features. Using chi squared function filters out the features which are independent of target attribute.
* 2. Recursive Feature Elimination (RFE): RFE runs the defined model by trying out different possible combinations of features, and it removes the features recursively which are not impacting the class label. Logistic regression algorithm is used as a parameter for RFE to decide on features.
```
import pandas as pd
import numpy as np
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
df = pd.read_csv('Accident_Information.csv', sep=',')
encoding = {
"Carriageway_Hazards": {"None": 0, "Other object on road": 1, "Any animal in carriageway (except ridden horse)": 1, "Pedestrian in carriageway - not injured": 1, "Previous accident": 1, "Vehicle load on road": 1, "Data missing or out of range": 0 }
}
df.replace(encoding, inplace=True)
print(df['Carriageway_Hazards'].value_counts())
print(df['Light_Conditions'].value_counts())
encoding_light = {"Light_Conditions": {"Daylight": 0, "Darkness - lights lit": 1, "Darkness - no lighting": 1, "Darkness - lighting unknown": 1, "Darkness - lights unlit": 1, "Data missing or out of range": 0}}
df.replace(encoding_light, inplace=True)
print(df['Light_Conditions'].value_counts())
print(df['Day_of_Week'].value_counts())
encoding_day_of_week = {"Day_of_Week": {"Saturday": 1, "Sunday": 1, "Monday": 0, "Tuesday": 0, "Wednesday": 0, "Thursday": 0, "Friday": 0}}
df.replace(encoding_day_of_week, inplace=True)
print(df['Day_of_Week'].value_counts())
print(df['Special_Conditions_at_Site'].value_counts())
encoding_Special_Conditions_at_Site = {"Special_Conditions_at_Site": {"None": 0, "Roadworks": 1, "Oil or diesel": 1, "Mud": 1, "Road surface defective": 1, "Auto traffic signal - out": 1, "Road sign or marking defective or obscured": 1, "Auto signal part defective": 1, "Data missing or out of range": 0}}
df.replace(encoding_Special_Conditions_at_Site, inplace=True)
print(df['Special_Conditions_at_Site'].value_counts())
encoding_1st_road_class = {"1st_Road_Class": {"A": 1, "A(M)": 1, "B": 2, "C": 3, "Motorway": 4, "Unclassified": 1}}
df.replace(encoding_1st_road_class, inplace=True)
df['1st_Road_Class'].value_counts()
#replacing 'Data missing or out of range' with most occured value 'Give way or uncontrolled'
df['Junction_Control'] = df['Junction_Control'].replace(['Data missing or out of range'], 'Give way or uncontrolled')
df['Junction_Control'].value_counts()
encoding_junction_detail = {"Junction_Control":
{"Give way or uncontrolled": 1,
"Auto traffic signal": 2,
"Not at junction or within 20 metres": 3,
"Stop sign": 4,
"Authorised person": 5,
}}
df.replace(encoding_junction_detail, inplace=True)
df['Junction_Control'].value_counts()
encoding_junction_detail = {"Junction_Detail":
{"Not at junction or within 20 metres": 1,
"T or staggered junction": 2,
"Crossroads": 3,
"Roundabout": 4,
"Private drive or entrance": 5,
"Other junction": 6,
"Slip road": 7,
"More than 4 arms (not roundabout)": 8,
"Mini-roundabout": 9,
"Data missing or out of range": 1 }}
df.replace(encoding_junction_detail, inplace=True)
df['Junction_Detail'].value_counts()
encoding_road_surface_cond = {"Road_Surface_Conditions":
{"Dry": 1,
"Wet or damp": 2,
"Frost or ice": 3,
"Snow": 4,
"Flood over 3cm. deep": 5,
"Data missing or out of range": 1 }}
df.replace(encoding_road_surface_cond, inplace=True)
df['Road_Surface_Conditions'].value_counts()
encoding_road_type = {"Road_Type":
{"Single carriageway": 1,
"Dual carriageway": 2,
"Roundabout": 3,
"One way street": 4,
"Slip road": 5,
"Unknown": 0,
"Data missing or out of range": 1 }}
df.replace(encoding_road_type, inplace=True)
df['Road_Type'].value_counts()
encoding_urban_rural = {"Urban_or_Rural_Area":
{"Urban": 1,
"Rural": 2,
"Unallocated": 1 }}
df.replace(encoding_urban_rural, inplace=True)
df['Urban_or_Rural_Area'].value_counts()
encoding_weather = {"Weather_Conditions":
{"Fine no high winds": 1,
"Raining no high winds": 2,
"Raining + high winds": 3,
"Fine + high winds": 4,
"Snowing no high winds": 5,
"Fog or mist": 6,
"Snowing + high winds": 7,
"Unknown": 1,
"Other": 1,
"Data missing or out of range": 1 }}
df.replace(encoding_weather, inplace=True)
df['Weather_Conditions'].value_counts()
np.where(np.isnan(df['Speed_limit']))
df['Speed_limit'].fillna((df['Speed_limit'].mean()), inplace=True)
df['Time'].fillna(0, inplace=True)
def period(row):
rdf = []
if(type(row) == float):
row = str(row)
rdf = row.split(".")
else:
rdf = str(row).split(":"); # day -- 8am-8pm
hr = rdf[0]
if int(hr) > 8 and int(hr) < 20:
return 1;
else:
return 2;
df['Time'] = df['Time'].apply(period)
df_train1 = df[['1st_Road_Class','Carriageway_Hazards','Junction_Control','Day_of_Week','Junction_Detail','Light_Conditions','Road_Surface_Conditions','Road_Type','Special_Conditions_at_Site','Speed_limit','Time','Urban_or_Rural_Area','Weather_Conditions','Accident_Severity']]
df_slight = df_train1[df_train1['Accident_Severity']=='Slight']
df_serious = df_train1[df_train1['Accident_Severity']=='Serious']
df_fatal = df_train1[df_train1['Accident_Severity']=='Fatal']
df_serious['Accident_Severity'].value_counts()
random_subset = df_slight.sample(n=3)
random_subset.head()
df_fatal['Accident_Severity'].value_counts()
df_slight_sampling = df_slight.sample(n=45000) #Matched the combined number of records for Fatal and Serious(As we are going to club fatal&serious to Serious)
df_serious_sampling = df_serious.sample(n=24693) #Matched number of records with the rarer class (Fatal#24693)
df_final_sampling = pd.concat([df_serious_sampling,df_slight_sampling,df_fatal])
df_final_sampling.head()
df_test = df_final_sampling[['Accident_Severity']]
#replacing 'Data missing or out of range' with most occured value 'None'
df_test['Accident_Severity'] = df_test['Accident_Severity'].replace(['Fatal'], 'Serious')
df_train = df_final_sampling[['1st_Road_Class','Carriageway_Hazards','Junction_Control','Day_of_Week','Junction_Detail','Light_Conditions','Road_Surface_Conditions','Road_Type','Special_Conditions_at_Site','Speed_limit','Time','Urban_or_Rural_Area','Weather_Conditions']]
df_test['Accident_Severity'].value_counts()
```
# Results
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(df_train, df_test, test_size=0.2)
from sklearn.ensemble import RandomForestClassifier
#class_weight = dict({2:1, 1:15, 0:50})
rdf = RandomForestClassifier(n_estimators=300,random_state=35)
rdf.fit(X_train,y_train)
y_pred=rdf.predict(X_test)
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
from sklearn.ensemble import RandomForestClassifier
#class_weight = dict({2:1, 1:15, 0:50})
rdf = RandomForestClassifier(bootstrap=True,
class_weight="balanced_subsample",
criterion='gini',
max_depth=8, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=4, min_samples_split=10,
min_weight_fraction_leaf=0.0, n_estimators=300,
oob_score=True,
random_state=35,
verbose=0, warm_start=False)
rdf.fit(X_train,y_train)
y_pred=rdf.predict(X_test)
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
pip install xgboost
from xgboost import XGBClassifier
model = XGBClassifier(learning_rate =0.07, n_estimators=300,
class_weight="balanced_subsample",
max_depth=8, min_child_weight=1,
scale_pos_weight=7,
seed=27,subsample=0.8,colsample_bytree=0.8)
model.fit(X_train,y_train)
y_pred=model.predict(X_test)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
# import the class
from sklearn.neighbors import KNeighborsClassifier
# instantiate the model (with the default parameters)
knn = KNeighborsClassifier(n_neighbors=3,weights='distance')
# fit the model with data (occurs in-place)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
from sklearn.linear_model import LogisticRegression
logisticRegr = LogisticRegression()
logisticRegr.fit(X_train, y_train)
y_pred = logisticRegr.predict(X_test)
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
gnb = GaussianNB()
y_pred = gnb.fit(X_train, y_train).predict(X_test)
print(accuracy_score(y_test, y_pred))
confusion_matrix(y_test, y_pred)
print(format(classification_report(y_test, y_pred)))
from sklearn.ensemble import GradientBoostingClassifier
gbc = GradientBoostingClassifier(loss="deviance", learning_rate=0.1,
n_estimators=100, subsample=1.0, criterion="friedman_mse",
min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0,
max_depth=3, min_impurity_decrease=0.0, min_impurity_split=None, init=None,
random_state=None, max_features=None, verbose=0, max_leaf_nodes=None, warm_start=False,
presort="auto")
y_pred = gbc.fit(X_train, y_train.values.ravel()).predict(X_test)
print(format(classification_report(y_test, y_pred)))
print(accuracy_score(y_test, y_pred))
```
# Discussion
Our main aim was to predict the severity of the accident when it is “serious” and “fatal”. It was very difficult to handle this large-sized data. Using HPC we were able to run most of our algorithms. Data is highly imbalanced so even though most of our algorithms were giving > 89% accuracies, it was of no use. It was predicting all the accidents as slight accidents. After checking on all these algorithms, the team even tried dimensionality reduction techniques and but the results were not improved. Then the team decided to use the undersampled dataset as it was giving better results in predicting the severe/fatal accidents. This decision was made on trying out oversampling, undersampling, test and train data with an equal ratio of classification classes.
# Conclusion
In conclusion, most of the algorithms are biased towards most frequent class. However, efficient pre-processing and corresponding imbalanced data techniques should give optimal results. Based on the current known conditions of weather, light, traffic signal, road surface, speed limit etc., accident severity can be classified. But there is no one feature, that influences the accident severity.
| true |
code
| 0.245831 | null | null | null | null |
|
문장을 입력해서 이진분류하는 모델에 대해서 알아보겠습니다. 언어가 시계열적인 의미가 있으므로, 이 언어를 문자로 표현한 문장도 시계열적인 의미가 있습니다. 모델에 입력하기 위해서 문장을 시계열수치로 인코딩하는 방법과 여러가지 이진분류 모델을 구성해보고, 학습 결과를 살펴보겠습니다. 이 모델들은 문장 혹은 시계열수치로 양성/음성을 분류하거나 이벤트 발생 유무를 감지하는 문제를 풀 수 있습니다.
---
### 데이터셋 준비
IMDB에서 제공하는 영화 리뷰 데이터셋을 이용하겠습니다. 이 데이터셋은 훈련셋 25,000개, 시험셋 25,000개의 샘플을 제공합니다. 라벨은 1과 0으로 좋아요/싫어요로 지정되어 있습니다. 케라스에서 제공하는 imdb의 load_data() 함수을 이용하면 데이터셋을 쉽게 얻을 수 있습니다. 데이터셋은 이미 정수로 인코딩되어 있으며, 정수값은 단어의 빈도수를 나타냅니다. 모든 단어를 고려할 수 없으므로 빈도수가 높은 단어를 위주로 데이터셋을 생성합니다. 20,000번째로 많이 사용하는 단어까지만 데이터셋으로 만들고 싶다면, num_words 인자에 20000이라고 지정하면 됩니다.
```
from keras.datasets import imdb
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=20000)
```
훈련셋의 데이터가 어떻게 구성되어 있는 지 살펴보겠습니다. x_train을 출력하면 다음과 같습니다.
```
print(x_train)
```
총 25000개의 샘플이 있으며, 각 샘플은 영화 리뷰 한 건을 의미하며, 단어의 인덱스로 구성되어 있습니다. 'num_words=20000'으로 지정했기 때문에 빈도수가 20,000을 넘는 단어는 보이지가 않습니다. 훈련셋 25,000개를 다시 훈련셋 20,000개와 검증셋 5,000개로 분리합니다.
```
x_val = x_train[20000:]
y_val = y_train[20000:]
x_train = x_train[:20000]
y_train = y_train[:20000]
```
리뷰의 길이가 다르니 각 샘플의 길이가 다르겠죠? 적개는 수십 단어로 많게는 천 개 이상의 단어로 구성되어 있습니다. 모델의 입력으로 사용하려면 고정된 길이로 만들어야 하므로 케라스에서 제공되는 전처리 함수인 sequence의 pad_sequences() 함수를 사용합니다. 이 함수는 두 가지 역할을 수행합니다.
* 문장을 maxlen 인자로 지정된 길이로 맞춰줍니다. 예를 들어 200으로 지정했다면 200보다 짧은 문장은 0으로 채워서 200단어로 맞춰주고 200보다 긴 문장은 200단어까지만 잘라냅니다.
* (num_samples, num_timesteps)으로 2차원의 numpy 배열로 만들어줍니다. maxlen을 200으로 지정하였다면, num_timesteps도 200이 됩니다.
```
from keras.preprocessing import sequence
x_train = sequence.pad_sequences(x_train, maxlen=200)
x_val = sequence.pad_sequences(x_val, maxlen=200)
x_test = sequence.pad_sequences(x_test, maxlen=200)
```
---
### 레이어 준비
본 장에서 새롭게 소개되는 블록들은 다음과 같습니다.
|블록|이름|설명|
|:-:|:-:|:-|
||Embedding|단어를 의미론적 기하공간에 매핑할 수 있도록 벡터화시킵니다.|
||Conv2D|필터를 이용하여 영상 특징을 추출하는 컨볼루션 레이어입니다.|
||MaxPooling2D|영상에서 사소한 변화가 특징 추출에 크게 영향을 미치지 않도록 해주는 맥스풀링 레이어입니다.|
||Flatten|2차원의 특징맵을 전결합층으로 전달하기 위해서 1차원 형식으로 바꿔줍니다.
||relu|활성화 함수로 주로 Conv2D 은닉층에 사용됩니다.|
---
### 모델 준비
영상을 입력하여 다중클래스분류를 하기 위해 `다층퍼셉트론 신경망 모델`, `컨볼루션 신경망 모델`, `깊은 컨볼루션 신경망 모델`을 준비했습니다.
#### 다층퍼셉트론 신경망 모델
model = Sequential()
model.add(Embedding(20000, 128, input_length=200))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
임베딩 레이어 인자의 의미는 다음과 같습니다.
* 첫번째 인자(input_dim) : 단어 사전의 크기를 말하며 총 20,000개의 단어 종류가 있다는 의미입니다. 이 값은 앞서 imdb.load_data() 함수의 num_words 인자값과 동일해야 합니다.
* 두번째 인자(output_dim) : 단어를 인코딩 한 후 나오는 벡터 크기 입니다. 이 값이 128이라면 단어를 128차원의 의미론적 기하공간에 나타낸다는 의미입니다. 단순하게 빈도수만으로 단어를 표시한다면, 10과 11은 빈도수는 비슷하지만 단어로 볼 때는 전혀 다른 의미를 가지고 있습니다. 하지만 의미론적 기하공간에서는 거리가 가까운 두 단어는 의미도 유사합니다. 즉 임베딩 레이어는 입력되는 단어를 의미론적으로 잘 설계된 공간에 위치시켜 벡터로 수치화 시킨다고 볼 수 있습니다.
* input_length : 단어의 수 즉 문장의 길이를 나타냅니다. 임베딩 레이어의 출력 크기는 샘플 수 * output_dim * input_lenth가 됩니다. 임베딩 레이어 다음에 Flatten 레이어가 온다면 반드시 input_lenth를 지정해야 합니다. 플래튼 레이어인 경우 입력 크기가 알아야 이를 1차원으로 만들어서 Dense 레이어에 전달할 수 있기 때문입니다.

#### 순환 신경망 모델
model = Sequential()
model.add(Embedding(max_features, 128))
model.add(LSTM(128))
model.add(Dense(1, activation='sigmoid'))
```
# 0. 사용할 패키지 불러오기
from keras.datasets import imdb
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding
from keras.layers import Flatten
max_features = 20000
text_max_words = 200
# 2. 모델 구성하기
model = Sequential()
model.add(Embedding(max_features, 128, input_length=text_max_words))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
# 3. 모델 학습과정 설정하기
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
%matplotlib inline
SVG(model_to_dot(model, show_shapes=True).create(prog='dot', format='svg'))
# 0. 사용할 패키지 불러오기
from keras.datasets import imdb
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding, LSTM
from keras.layers import Flatten
max_features = 20000
text_max_words = 200
# 1. 데이터셋 생성하기
# 2. 모델 구성하기
model = Sequential()
model.add(Embedding(max_features, 128))
model.add(LSTM(128))
model.add(Dense(1, activation='sigmoid'))
# 3. 모델 학습과정 설정하기
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
%matplotlib inline
SVG(model_to_dot(model, show_shapes=True).create(prog='dot', format='svg'))
# 0. 사용할 패키지 불러오기
from keras.datasets import imdb
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding, LSTM
from keras.layers import Flatten
max_features = 20000
text_max_words = 200
# 1. 데이터셋 생성하기
# 2. 모델 구성하기
model = Sequential()
model.add(Embedding(max_features, 128))
model.add(LSTM(128, dropout=0.2, recurrent_dropout=0.2))
model.add(Dense(1, activation='sigmoid'))
# 3. 모델 학습과정 설정하기
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
%matplotlib inline
SVG(model_to_dot(model, show_shapes=True).create(prog='dot', format='svg'))
# 0. 사용할 패키지 불러오기
from keras.datasets import imdb
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding, LSTM
from keras.layers import Flatten, Dropout
from keras.layers import Conv1D, GlobalMaxPooling1D
max_features = 20000
text_max_words = 200
# 2. 모델 구성하기
model = Sequential()
model.add(Embedding(max_features, 128, input_length=text_max_words))
model.add(Dropout(0.2))
model.add(Conv1D(256,
3,
padding='valid',
activation='relu',
strides=1))
model.add(GlobalMaxPooling1D())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(1, activation='sigmoid'))
# 3. 모델 학습과정 설정하기
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
%matplotlib inline
SVG(model_to_dot(model, show_shapes=True).create(prog='dot', format='svg'))
# 0. 사용할 패키지 불러오기
from keras.datasets import imdb
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding, LSTM
from keras.layers import Flatten, Dropout
from keras.layers import Conv1D, MaxPooling1D
max_features = 20000
text_max_words = 200
# 1. 데이터셋 생성하기
# 2. 모델 구성하기
model = Sequential()
model.add(Embedding(max_features, 128, input_length=text_max_words))
model.add(Dropout(0.2))
model.add(Conv1D(256,
3,
padding='valid',
activation='relu',
strides=1))
model.add(MaxPooling1D(pool_size=4))
model.add(LSTM(128, dropout=0.2, recurrent_dropout=0.2))
model.add(Dense(1, activation='sigmoid'))
# 3. 모델 학습과정 설정하기
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
%matplotlib inline
SVG(model_to_dot(model, show_shapes=True).create(prog='dot', format='svg'))
```
---
### 데이터셋 준비
입력 x에 대해 2를 곱해 두 배 정도 값을 갖는 출력 y가 되도록 데이터셋을 생성해봤습니다. 선형회귀 모델을 사용한다면 Y = w * X + b 일 때, w가 2에 가깝고, b가 0.16에 가깝게 되도록 학습시키는 것이 목표입니다.
```
import numpy as np
# 데이터셋 생성
x_train = np.random.random((1000, 1))
y_train = x_train * 2 + np.random.random((1000, 1)) / 3.0
x_test = np.random.random((100, 1))
y_test = x_test * 2 + np.random.random((100, 1)) / 3.0
# 데이터셋 확인
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(x_train, y_train, 'ro')
plt.plot(x_test, y_test, 'bo')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
```
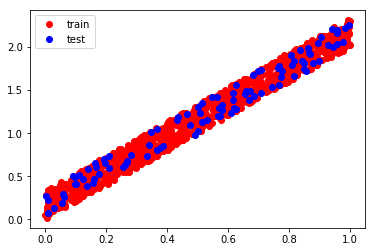
---
### 레이어 준비
수치예측 모델에 사용할 레이어는 `Dense`와 `Activation`입니다. `Activation`에는 은닉층(hidden layer)에 사용할 `relu`를 준비했습니다. 데이터셋은 일차원 벡터만 다루도록 하겠습니다.
|종류|구분|상세구분|브릭|
|:-:|:-:|:-:|:-:|
|데이터셋|Vector|-||
|레이어|Dense|||
|레이어|Activation|relu||
---
### 모델 준비
수치예측을 하기 위해 `선형회귀 모델`, `퍼셉트론 모델`, `다층퍼셉트론 모델`, `깊은 다층퍼셉트론 모델`을 준비했습니다.
#### 선형회귀 모델
가장 간단한 1차 선형회귀 모델로 수치예측을 해보겠습니다. 아래 식에서 x, y는 우리가 만든 데이터셋이고, 회귀분석을 통해서, w와 b값을 구하는 것이 목표입니다.
Y = w * X + b
w와 b값을 구하게 되면, 임의의 입력 x에 대해서 출력 y가 나오는 데 이것이 예측 값입니다. w, b 값은 분산, 공분산, 평균을 이용하여 쉽게 구할 수 있습니다.
w = np.cov(X, Y, bias=1)[0,1] / np.var(X)
b = np.average(Y) - w * np.average(X)
간단한 수식이지만 이 수식을 도출하기란 꽤나 복잡습니다. 오차를 최소화하는 극대값을 구하기 위해 편미분을 수행하고, 다시 식을 전개하는 등등의 과정이 필요합니다.

#### 퍼셉트론 모델
Dense 레이어가 하나이고, 뉴런의 수도 하나인 가장 기본적인 퍼셉트론 모델입니다. 즉 웨이트(w) 하나, 바이어스(b) 하나로 전형적인 Y = w * X + b를 풀기 위한 모델입니다. 수치 예측을 하기 위해서 출력 레이어에 별도의 활성화 함수를 사용하지 않았습니다. w, b 값이 손으로 푼 선형회귀 최적해에 근접하려면 경우에 따라 만번이상의 에포크가 필요합니다. 실제로 사용하지는 않는 모델이지만 선형회귀부터 공부하시는 분들에게는 입문 모델로 나쁘지 않습니다.
model = Sequential()
model.add(Dense(1, input_dim=1))

#### 다층퍼셉트론 모델
Dense 레이어가 두 개인 다층퍼셉트론 모델입니다. 첫 번째 레이어는 64개의 뉴런을 가진 Dense 레이어이고 오류역전파가 용이한 `relu` 활성화 함수를 사용하였습니다. 출력 레이어인 두 번째 레이어는 하나의 수치값을 예측을 하기 위해서 1개의 뉴런을 가지며, 별도의 활성화 함수를 사용하지 않았습니다.
model = Sequential()
model.add(Dense(64, input_dim=1, activation='relu'))
model.add(Dense(1))

#### 깊은 다층퍼셉트론 모델
Dense 레이어가 총 세 개인 다층퍼셉트론 모델입니다. 첫 번째, 두 번째 레이어는 64개의 뉴런을 가진 Dense 레이어이고 오류역전파가 용이한 `relu` 활성화 함수를 사용하였습니다. 출력 레이어인 세 번째 레이어는 하나의 수치값을 예측을 하기 위해서 1개의 뉴런을 가지며, 별도의 활성화 함수를 사용하지 않았습니다.
model = Sequential()
model.add(Dense(64, input_dim=1, activation='relu'))
model.add(Dense(64, activation='relu'))
model.add(Dense(1))

---
### 전체 소스
앞서 살펴본 `선형회귀 모델`, `퍼셉트론 모델`, `다층퍼셉트론 모델`, `깊은 다층퍼셉트론 모델`의 전체 소스는 다음과 같습니다.
#### 다층퍼셉트론 모델
```
# 다층퍼셉트론 모델로 수치예측하기
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
import random
# 1. 데이터셋 준비하기
x_train = np.random.random((1000, 1))
y_train = x_train * 2 + np.random.random((1000, 1)) / 3.0
x_test = np.random.random((100, 1))
y_test = x_test * 2 + np.random.random((100, 1)) / 3.0
# 2. 모델 구성하기
model = Sequential()
model.add(Dense(64, input_dim=1, activation='relu'))
model.add(Dense(1))
# 3. 모델 학습과정 설정하기
model.compile(optimizer='rmsprop', loss='mse')
# 4. 모델 학습시키기
hist = model.fit(x_train, y_train, epochs=50, batch_size=64)
# 5. 모델 평가하기
loss = model.evaluate(x_test, y_test, batch_size=32)
print('loss : ' + str(loss))
# 6. 학습과정 확인하기
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(hist.history['loss'])
plt.ylim(0.0, 1.5)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
```
#### 깊은 다층퍼셉트론 모델
```
# 깊은 다층퍼셉트론 모델로 수치예측하기
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
import random
# 1. 데이터셋 준비하기
x_train = np.random.random((1000, 1))
y_train = x_train * 2 + np.random.random((1000, 1)) / 3.0
x_test = np.random.random((100, 1))
y_test = x_test * 2 + np.random.random((100, 1)) / 3.0
# 2. 모델 구성하기
model = Sequential()
model.add(Dense(64, input_dim=1, activation='relu'))
model.add(Dense(64, activation='relu'))
model.add(Dense(1))
# 3. 모델 학습과정 설정하기
model.compile(optimizer='rmsprop', loss='mse')
# 4. 모델 학습시키기
hist = model.fit(x_train, y_train, epochs=50, batch_size=64)
# 5. 모델 평가하기
loss = model.evaluate(x_test, y_test, batch_size=32)
print('loss : ' + str(loss))
# 6. 학습과정 확인하기
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(hist.history['loss'])
plt.ylim(0.0, 1.5)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
```
---
### 학습결과 비교
퍼셉트론 > 다층퍼셉트론 > 깊은 다층퍼셉트론 순으로 학습이 좀 더 빨리 되는 것을 확인할 수 있습니다.
|퍼셉트론|다층퍼셉트론|깊은 다층퍼셉트론|
|:-:|:-:|:-:|
||||
---
### 결론
수치예측을 위한 퍼셉트론, 다층퍼셉트론, 깊은 다층퍼셉트론 모델을 살펴보고, 그 성능을 확인 해봤습니다.

---
### 같이 보기
* [강좌 목차](https://tykimos.github.io/lecture/)
| true |
code
| 0.737205 | null | null | null | null |
|
# Scalable Batch GP Classification in 1D (w/ SVGP)
This example shows how to use grid interpolation based variational classification with an `ApproximateGP` using a `VariationalStrategy` module while learning the inducing point locations.
**Note:** The performance of this notebook is substantially improved by using a GPU and casting your tensors with `.cuda()`. See our other GPU example notebooks for how to do this.
```
import math
import torch
import gpytorch
from matplotlib import pyplot as plt
from math import exp
%matplotlib inline
%load_ext autoreload
%autoreload 2
train_x = torch.linspace(0, 1, 260).unsqueeze(-1)
train_y_cos = torch.cos(train_x * (2 * math.pi)).squeeze() + 0.1 * torch.randn(260)
train_y_sin = torch.sin(train_x * (2 * math.pi)).squeeze() + 0.1 * torch.randn(260)
# Make train_x (2 x 260 x 1) and train_y (2 x 260)
train_x = torch.cat([train_x, train_x], dim=1).transpose(-2, 1).unsqueeze(-1)
train_y = torch.cat([train_y_cos.unsqueeze(-1), train_y_sin.unsqueeze(-1)], dim=1).transpose(-2, -1)
from gpytorch.models import ApproximateGP
from gpytorch.variational import CholeskyVariationalDistribution
from gpytorch.variational import VariationalStrategy
class SVGPRegressionModel(ApproximateGP):
def __init__(self, inducing_points):
variational_distribution = CholeskyVariationalDistribution(inducing_points.size(-2), batch_size=2)
variational_strategy = VariationalStrategy(self,
inducing_points,
variational_distribution,
learn_inducing_locations=True)
super(SVGPRegressionModel, self).__init__(variational_strategy)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
def forward(self,x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
latent_pred = gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
return latent_pred
# We'll initialize the inducing points to evenly span the space of train_x
inducing_points = torch.linspace(0, 1, 25).unsqueeze(-1).repeat(2, 1, 1)
model = SVGPRegressionModel(inducing_points)
likelihood = gpytorch.likelihoods.GaussianLikelihood()
from gpytorch.mlls.variational_elbo import VariationalELBO
# Find optimal model hyperparameters
model.train()
likelihood.train()
# Use the adam optimizer
optimizer = torch.optim.Adam([
{'params': model.parameters()},
{'params': likelihood.parameters()}
], lr=0.01)
# "Loss" for GPs - the marginal log likelihood
# n_data refers to the number of training datapoints
mll = VariationalELBO(likelihood, model, train_y.size(-1), combine_terms=False)
def train():
num_iter = 200
for i in range(num_iter):
optimizer.zero_grad()
output = model(train_x)
# Calc loss and backprop gradients
log_lik, kl_div, log_prior = mll(output, train_y)
loss = -(log_lik - kl_div + log_prior)
loss = loss.sum()
loss.backward()
if i % 50 == 0:
print('Iter %d - Loss: %.3f [%.3f, %.3f, %.3f]' % (i + 1, loss.item(), log_lik.sum().item(), kl_div.sum().item(), log_prior.sum().item()))
optimizer.step()
# Get clock time
%time train()
# Set into eval mode
model.eval()
likelihood.eval()
# Initialize plots
f, (y1_ax, y2_ax) = plt.subplots(2, 1, figsize=(8, 8))
# Test points every 0.02 in [0,1]
# Make predictions
with torch.no_grad():
test_x = torch.linspace(0, 1, 51).view(1, -1, 1).repeat(2, 1, 1)
observed_pred = likelihood(model(test_x))
# Get mean
mean = observed_pred.mean
# Get lower and upper confidence bounds
lower, upper = observed_pred.confidence_region()
# Plot training data as black stars
y1_ax.plot(train_x[0].detach().numpy(), train_y[0].detach().numpy(), 'k*')
# Predictive mean as blue line
y1_ax.plot(test_x[0].squeeze().numpy(), mean[0, :].numpy(), 'b')
# Shade in confidence
y1_ax.fill_between(test_x[0].squeeze().numpy(), lower[0, :].squeeze().numpy(), upper[0, :].squeeze().numpy(), alpha=0.5)
y1_ax.set_ylim([-3, 3])
y1_ax.legend(['Observed Data', 'Mean', 'Confidence'])
y1_ax.set_title('Observed Values (Likelihood)')
y2_ax.plot(train_x[1].detach().numpy(), train_y[1].detach().numpy(), 'k*')
y2_ax.plot(test_x[1].squeeze().numpy(), mean[1, :].numpy(), 'b')
y2_ax.fill_between(test_x[1].squeeze().numpy(), lower[1, :].squeeze().numpy(), upper[1, :].squeeze().numpy(), alpha=0.5)
y2_ax.set_ylim([-3, 3])
y2_ax.legend(['Observed Data', 'Mean', 'Confidence'])
y2_ax.set_title('Observed Values (Likelihood)')
```
| true |
code
| 0.800634 | null | null | null | null |
|
```
# data retrieval
import requests
# data storage and manipulation
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# functional tools to allow for model fine tuning
from functools import partial, update_wrapper
# modeling and validation
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, \
precision_score, \
recall_score, \
confusion_matrix, \
f1_score
# from my modeling repo
from indoorplants.analysis import exploratory
from indoorplants.validation import crossvalidate, curves
%matplotlib inline
```
### --------------------------------------------------------------
# Census Data Analysis
### --------------------------------------------------------------
# 0. Overview
### Prerequisites
This notebook contains the results of a quick exercise in data analysis and prediction, with the goal being to develop a model to predict whether a given person, based on the provided data, makes more than $50K per year.
Depending on which version of Jupyter Notebook you are running, you may have to increase your data transmission limits in order to be able to download the dataset within the confines of the notebook, which is what I have done here. This can be achieved through passing a new limit to the *NotebookApp.iopub_data_rate_limit* option while launching Jupyter Notebook from the command line:
jupyter notebook --NotebookApp.iopub_data_rate_limit=10000000
The original dataset and description can be found at: https://archive.ics.uci.edu/ml/datasets/Adult
### Analysis Description
I put together this analysis in an effort to showcase some analysis & ML-validation modules that I have been working on. The Notebook has 3 parts:
1) Get Data
- Pull dataset from the UC Irvine website
- Check for and deal with duplicates and nulls
- Carry out a slight reworking of table
2) Exploratory Data Analaysis
- Investigate certain features, looking for relationships with income level
- The approach taken here is visual (and also pretty casual)
- Additionally, provide some descriptions of the dataset
3) Modeling
- Fit a Random Forest Classifier to the data
- Leverage cross-validationTune to depth parameter to reduce overfitting
- Introduce example business logic and develop custom score function
# 1. Get Data
### Retrieve
```
def get_census_data():
cols = ['age', 'workclass', 'fnlwgt', 'education',
'education_num', 'marital_status', 'occupation',
'relationship', 'race', 'sex', 'capital_gain',
'capital_loss', 'hours_per_week', 'native_country',
'over_fifty_k']
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data'
with requests.get(url, stream=True) as r:
results = [l.decode().split(',') for l in r.iter_lines()]
return pd.DataFrame(results, columns=cols)
table = get_census_data()
table.head()
table.to_csv("cencus_data.csv")
len(table)
```
### Check for problems
#### Duplicates
```
len(table[table.duplicated()])
table = table.drop_duplicates()
```
#### Nulls
```
table.isnull().sum()
table[table.workclass.isnull()]
table[~table.index.isin((32561,))].isnull().sum()
table = table[~table.index.isin((32561,))].reset_index(drop=True)
```
### Set up data types
```
table.dtypes
int_cols = ['age', 'fnlwgt', 'capital_gain', 'capital_loss', 'hours_per_week']
table.loc[:, int_cols] = table.loc[:, int_cols].astype(int)
```
### Set up response column
```
table.over_fifty_k.value_counts()
table.over_fifty_k.unique()
table.over_fifty_k = table.over_fifty_k.map(lambda _:
1 if _ == ' >50K'
else 0)
```
# 2. Exploratory Data Analysis
```
table.over_fifty_k.value_counts() / len(table)
```
#### Notes
The classes are imbalanced, appearing here at a ratio of roughly 3: 1 negative: postitive.
### Age
```
table.age.head()
table.age.isnull().sum()
table.age = table.age.astype(int)
table.age.nunique()
ax = table.age.value_counts().sort_index().plot.bar(figsize=(15, 8), color="steelblue")
ax.title.set_text('age: counts by age')
```
#### Notes
The *age* data looks to be positively skewed, and has a floor of 17.
We can look, in more detail, at the distribution of the *age* data, this time with overlays for the data's mean and strandard deviation, using the `center_scale_plot` function from the **exploratory** module.
```
ax = exploratory.center_scale_plot(table.age, np.mean, np.std, bins=73)
len(table[table.age > 79]) / len(table)
```
#### Notes
A couple of observations:
- roughly 99.6% of the data falls within 3 standard deviations of the mean, which is 38.6 years
- the concentration of data with age 90 might indicate that age was cut off at 90
```
ax = exploratory.qq_plot(table.age.astype(int))
```
#### Notes
We can use a Q-Q, or quantile-quantile, plot (which in this case plots the quantiles of our data against the quantiles of a Normal distribution with the same mean and standard deviation as the data) to assess whether the data is Normally distributed.
We have an $R^2$ of over 98%, as the vast majority of the data, particularly the data close to the mean, fits the Normal distribution (the straight red line) quite well. However, we can see clearly the deviation from the Normal distribution that occurs in the tails, particularly in the left tail.
The positive skewness makes sense given that the data does not seem to include those under the age of 17.
```
ax = exploratory.feature_value_counts_by_class(table, 'over_fifty_k', 'age', figsize=(15, 8))
```
#### Notes
Breaking down age by income, we can see that the bulk of the $50K-or-higher earners are middle-aged.
### Education
```
table.education.nunique()
ed = table[['education', 'education_num']
].drop_duplicates().set_index('education',
drop=True)
ed['education_num'] = ed['education_num'].astype(int)
ed.sort_values('education_num')
```
#### Notes
There is a one-to-one mapping of *education* to *education_num*. We can retain the ordering here for future analysis of the *education* field.
```
table.education = pd.Categorical(table.education,
ed.sort_values('education_num').index)
ax = table['education'].value_counts(
).sort_index(
).plot.bar(figsize=(11, 8), rot=40, color="steelblue")
ax.title.set_text('education: counts')
ax = exploratory.feature_value_counts_by_class(table, 'over_fifty_k','education', rot=40)
table['education_num'] = table.education_num.astype(int)
```
#### Notes
High income is much more prevalent amongst those who went at least as far as to complete high school.
### Education vs. age, by income class
```
ax = exploratory.scatter_by_class(table, 'over_fifty_k', 'age', 'education_num')
```
#### Notes
The more brownish regions in the above plot indicate an overlap between the classes. The bright orange here could indicate some pockets of predominantly over-$50K earners. Let us continue examining other variables to see if a decision boundary becomes more clear.
### Work class
```
table.workclass.nunique()
ax = table['workclass'].value_counts(
).sort_index(
).plot.bar(figsize=(11, 8), rot=40, color="steelblue")
t = ax.title.set_text('workclass: histogram')
ax = exploratory.feature_value_counts_by_class(table, 'over_fifty_k', 'workclass', rot=40)
```
#### Notes
The *Private* employment bucket seem to hold the bulk of the high earners, though most of the people in this bucket in fact do not eclipse $50K in income.
### Final weight
#### Notes
The UCI documentation describes this column as reflecting a by-state population demographic weight. Let's take a look at how this data is distributed.
```
table.fnlwgt.nunique()
table.fnlwgt = table.fnlwgt.astype(int)
ax = exploratory.center_scale_plot(table.fnlwgt, np.mean, np.std, bins=100)
len(table[table.fnlwgt > 506445]) / len(table)
```
#### Notes
The final weight data exhibits strong positive skewness.
```
ax = exploratory.center_scale_plot(np.log(table.fnlwgt), np.mean, np.std, bins=100)
```
#### Notes
Taking the log transform has yielded a more symmetrical dataset that sits almost entirely within 3 standard deviation bands.
```
ax = exploratory.qq_plot(np.log(table.fnlwgt))
```
#### Notes
Plotting the ordered final weight data against the quantiles of a Normal distribution with the same location and center as the data, we achieve a high goodness-of-fit measure. The unusual lump in the data's left tail stands out on this QQ plot as it did on the above histogram.
```
table['fnlwgt_log'] = np.log(table.fnlwgt)
```
### Final weight vs. education, by income class
```
ax = exploratory.scatter_by_class(table, 'over_fifty_k', 'education_num', 'fnlwgt_log')
```
# 2. Modeling
#### Notes
I am going to keep it simple: one-hot encode the categorical variables, leave the rest in their original states, and see what kind of results can be achieved using a Random Forest Classifier.
A Decision Tree works by repeatedly splitting a dataset, 20-questions-style, in an effort to find feature values by which the dataset can be seperated into its proper classes. At a high-level, a Random Forest works by creating many different Decision Trees and then averaging its trees predictions to obtain a single value.
RFCs are capable of finding complex decision boundaries, require little with respect to data prep and hyperparameter tuning, and can handle class imbalances in a straightforward manner, through a weighting of the class counts when evaluating splits and making predictions. We will in this case opt for a _balanced subsample_ class weighting. See sklearn [docs](http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html) for more detail.
### Function to get modeling data
```
def get_model_data(table, features, dont_dummy):
cols = ['over_fifty_k'] + features
for_modeling = table[cols]
to_dummy = list(filter(lambda _: _ not in dont_dummy, cols))
return pd.get_dummies(for_modeling, columns=to_dummy)
```
### Prep
```
table.columns
table.dtypes
table[['capital_gain',
'capital_loss',
'hours_per_week']] = table[['capital_gain',
'capital_loss',
'hours_per_week']
].astype(int)
int_cols = list(table.dtypes[table.dtypes=='int64'].index.values)
int_cols
X = ['age', 'workclass', 'fnlwgt', 'education_num',
'marital_status', 'occupation', 'relationship',
'race', 'sex', 'capital_gain', 'capital_loss',
'hours_per_week', 'native_country']
```
### Get data
```
for_modeling = get_model_data(table, X, int_cols)
len(for_modeling.columns)
X_model = [col for col in for_modeling.columns if col != 'over_fifty_k']
cv, final = train_test_split(for_modeling.index, test_size=.20,
stratify=for_modeling.over_fifty_k)
final = for_modeling.loc[final, :]
for_modeling = for_modeling.loc[cv, :]
```
### Cross validate
#### Notes
Cross validation involves slicing the data into *k* pieces (in this case 5) and, for each of the *k* folds, holding that fold out as a test set (which the model will not be trained on) and training on the rest.
The results for the tests on each of the folds are then averaged. This methodology solves 2 common problems in model selection:
- performance figures that stem from predicting the data the model is trained on will be overly optimistic
- the particular subset of the data the model is trained on can bias the hyper-parameter tuning process
We will perform cross validation on 80% of the data (saved into the `for_modeling` table) and we will perform our final tests on the remaining 20% (`final`) so as to avoid reporting final test results based on the data that is used for model selection.
```
results = crossvalidate.cv_score(model_obj=RandomForestClassifier(n_estimators=100,
class_weight='balanced_subsample'),
X=for_modeling[X_model],
y=for_modeling.over_fifty_k,
score_funcs=[accuracy_score,
precision_score,
recall_score])
results
```
#### Analysis
We've trained and tested a Random Forest classifier with 2 hyper parameters passed:
- `n_estimators` determines the number of Decision Trees built
- `class_weight` of *balanced_subsample* tells the algorithm to weight class counts, within each tree, inversely to the prevalence of the classes in the subsample of the data that the tree was built on
Our test *accuracy* of ~85% is on par with the results posted by this dataset's curator. But there are a couple of issues with these results:
- there is a large disparity between train and test results for all 3 of the scores we've calculated
- *accuracy*, especially when dealing with imbalanced classes, can be very misleading
I've included *accuracy* as a sort of quick-n-dirty guide, but the *precision* and *recall* scores here are more important as they are based off of the results for the positive (over-$50K annual income) class, which is less prevalent in the dataset.
*Precision* tells us how reckless the model was in making its positive predictions. The higher the score, the more careful the model. *Recall* tells us how much money was left on the table, so to speak. The higher the *recall*, the greater the percent of all positive class instances identified.
We can introduce some prepruning, which means limiting the growth of the RFC's internal Decision Trees, so as to curb the overfitting.
```
curves.validation_curve(model_type=RandomForestClassifier,
X=for_modeling[X_model],
y=for_modeling.over_fifty_k,
param_name='max_depth',
param_range=np.linspace(4, 16, 7),
other_params={'class_weight':'balanced_subsample',
'n_estimators':100},
score=f1_score)
curves.learning_curve(model_type=RandomForestClassifier,
X=for_modeling[X_model],
y=for_modeling.over_fifty_k,
model_params={'class_weight':'balanced_subsample',
'n_estimators':100,
"max_depth": 14},
score=f1_score)
curves.calibration_curve(model_type=RandomForestClassifier,
X=for_modeling[X_model],
y=for_modeling.over_fifty_k,
model_params={'class_weight':'balanced_subsample',
'n_estimators':100,
"max_depth": 14})
```
#### Analysis
The above validation curve plots cross validation performance for the model across different levels of prepruning. The lower `max_depth` is, the stronger the prepruning. As `max_depth` increases, the train and test scores diverge, which is a good sign of overfitting.
The performance metric being used here is called *f1 score*. f1 is the harmonic mean of precision and recall, which means that if you have to choose one number, this can be a good choice as it accounts for both care and thoroughness, so to speak. Additionally, this measure is calculated on the positive class, which means that we will know if our model is simply dumping all predictions into the negative class bucket, a common "gotcha" when dealing with imbalanced classes.
I am going to continue validation with a `max_depth` of 14, as the train and test divergence is still pretty tame (within 5%), and there does appear to be a gain in validation performance between a `max_depth` of 12 and 14.
```
r = crossvalidate.cv_conf_mat(model_obj=RandomForestClassifier(n_estimators=100,
class_weight='balanced_subsample',
max_depth=14),
X=for_modeling[X_model],
y=for_modeling.over_fifty_k,
splits=3)
r
```
#### Analysis
To really come to an opinion on how a model's working, it is good to take a look at what's being put where, which is what the above confusion matrices show us (1 for each of 3 trials). It doesn't seem like anything crazy is happening - these numbers reflect what we'd expect from the aggregate scores we looked at above.
### Test situation
Taking the confusion matrix further, one can put a value on each type of correct or incorrect prediction. This can make a performance score less abstract and more aligned with a business objective.
Example: you are selling insurance, and a potential client will buy your insurance if the following conditions hold:
1. potential client makes at least $50K annually
2. potential client is exposed to your insurance product via advertising
It will cost you \$100 to advertise this insurance to a potential client, and you will generate $1000 in revenue if a potential client converts. You need to build a model that will help you decide who to advertise to in order to maximize your simplified gross income of *sales revenue* - *advertising costs*.
#### Set up cost funcs
```
def cost(true, pred):
# true negative, no cost
if true == 0 and pred == 0:
return 0
# false positive, lose $100 to advertising
elif true == 0 and pred == 1:
return 100
# false negative, miss out on a grand
elif true == 1 and pred == 0:
return 1000
# true positive, spend $100 to get $1000
elif true == 1 and pred == 1:
return -900
def model_cost(y_true, y_pred):
func = np.vectorize(cost)
return func(y_true, y_pred).sum()
```
#### Cross validate
```
results = crossvalidate.cv_score(model_obj=RandomForestClassifier(
n_estimators=100,
class_weight='balanced_subsample',
max_depth=14),
X=for_modeling[X_model],
y=for_modeling.over_fifty_k,
score_funcs=[model_cost])
results
```
#### Analysis
We've set up an aggressive cost function here where poor *recall* is heavily penalized, which makes sense given the business model. Fortunately, our model is coming in on the right side of zero (this is a measurement of cost so negative is good).
It's worth noting that there's a large disparity between train and test error. This could be an indication of overfitting. That said, the standard deviation, proportionately speaking, is quite small. Both of these qualities - overfitting but also consistency - were revealed to us in our learning curve analysis above.
#### Train / test disparity
I wonder if the disparity between train and test costs may have something to do with the larger size of the training set? (this is an absolute, not %, cost)
```
results.loc[('model_cost', 'test'), 'mean'
] / results.loc[('model_cost', 'train'), 'mean']
```
Our train data sets used in the CV contained 4 times as much data as our test set did (5-fold validation), and our train score is about 5 times our test score. So we are overfitting, but only by, let's say, 5 or so percent.
#### Next steps
One thing we can do to optimize our cost here is tweak our decision boundary. **sklearn's** models default to a boundary of .5 for binary classification. Since we are much more interested in *recall* than *precision* (we want to nail as many positives as possible and are OK with some false positives) we can lower that decision bounday a bit. In other words, we're going to tell the model to be a little more aggressive in looking for positive classifications.
We will start with a decision boundary of 40%.
### Adjust boundaries
#### New RF Classifier that predicts probabilities
To do this, we are going to have to put a wrapper around the **sklearn** `RandomForestClassifier` class. These cross-validation tools expect models with an API similar to that of the **sklearn** models, which means they are looking for every model to have a predict method. However, we can change the functionality of a model's predict method so that it predicts class probabilities instead of labels.
*Note*: I have left this boundary analysis broken out into pieces here in the notebook, but the **indoorplants.validation.boundaries** module provides tools for evaluating binary classifier performance using adjusted decision boundaries.
```
class RFProb(RandomForestClassifier):
def predict(self, X):
return self.predict_proba(X)
```
#### Modify cost mechanisms to convert probability to label
```
def prob_to_class(func):
def convert(y_true, y_pred):
pos_class = y_pred[:, 1]
conv = np.vectorize(lambda _: 1 if _ > .4 else 0)
return func(y_true, conv(pos_class))
return convert
@prob_to_class
def model_cost(y_true, y_pred):
func = np.vectorize(cost)
return func(y_true, y_pred).sum()
```
#### Cross validate
```
results40 = crossvalidate.cv_score(model_obj=RFProb(n_estimators=100,
class_weight='balanced_subsample',
max_depth=14),
X=for_modeling[X_model],
y=for_modeling.over_fifty_k,
score_funcs=[model_cost])
results40
results40.loc[('convert', 'test'), 'mean'
] / results.loc[('model_cost', 'test'), 'mean']
```
#### Notes
We have seen an improvement here, subtracting roughly 16% from our test cost. We can push this boundary even further if we'd like.
#### Rework functions to allow for testing across passed thresholds
```
def cost(true, pred):
if true == 0 and pred == 0:
return 0
elif true == 0 and pred == 1:
return 100
elif true == 1 and pred == 0:
return 1000
elif true == 1 and pred == 1:
return -900
def model_cost(y_true, y_pred):
func = np.vectorize(cost)
return func(y_true, y_pred).sum()
def prob_to_class(t, func):
def convert(t, y_true, y_pred):
pos_class = y_pred[:, 1]
conv = np.vectorize(lambda _: 1 if _ > t else 0)
return func(y_true, conv(pos_class))
def threshold(t):
partial_func = partial(convert, t)
update_wrapper(partial_func, convert)
return partial_func
return threshold(t)
def boundary_cost(t):
return prob_to_class(t, model_cost)
```
#### Function to cross validate over multiple boundaries: 5% to 55%
```
def test_boundaries():
i, results = .55, {}
while i > .05:
results[i] = crossvalidate.cv_score(
model_obj=RFProb(n_estimators=100,
class_weight='balanced_subsample',
max_depth=14),
X=for_modeling[X_model],
y=for_modeling.over_fifty_k,
score_funcs=[boundary_cost(i)])
i -= .05
return pd.concat(results)
```
#### Run cross validation
```
results = test_boundaries()
results
```
#### Analysis
The minimum cost (test) was produced with a decision boundary of 15%. However, we see a drastically reduced standard deviation for a decision boundary of 10%.
Of course, whether or not we'd actually want a model this aggressive would depend upon our real-world use case. Seeing as how this is not a real business model, I will continue with a decision threshold of 10%.
This means that we will advertise to anyone to whom the model assigns at least a 10% probability of earning at least $50K per year.
### Train and test final model
#### Instantiate model
```
model = RFProb(n_estimators=100,
class_weight='balanced_subsample',
max_depth=14)
```
#### Train
```
model = model.fit(for_modeling[X_model], for_modeling.over_fifty_k)
```
#### Predict
```
y_pred = model.predict(final[X_model])
```
#### Threshold
```
def convert(t, y_pred):
pos_class = y_pred[:, 1]
conv = np.vectorize(lambda _: 1 if _ > t else 0)
return conv(pos_class)
y_pred_class = convert(.1, y_pred)
```
#### Analysis
```
conf_mat = confusion_matrix(final.over_fifty_k, y_pred_class)
conf_mat
boundary_cost(.1)(final.over_fifty_k, y_pred)
'recall: {}'.format(conf_mat[1][1] / conf_mat[1, :].sum())
'precision: {}'.format(conf_mat[1][1] / conf_mat[:, 1].sum())
```
Testing on our held-out 20% (stratified & randomly selected) of the dataset, we've achieved a positive-class *recall* score of roughly 99%, and a a positive-class *precision* of roughly 37%.
To put it differently, we can see (looking at the above confusion matrix) that we had almost no false negatives, with a whole lot of false positives - about as many (a bit more actually) than there were true negatives.
In a real business situation, you would have to think carefully about how you wanted to score your model's performance. However, we've seen in this exercise that, depending on your situation, it can be worth thinking outside the box (or in the case of the confusion matrix - reinterpreting the box).
| true |
code
| 0.509886 | null | null | null | null |
|
# Steam Data Cleaning - Optimising Cleaning of the Release Date Column
*This forms part of a larger series of posts for my [blog](http://nik-davis.github.io) on downloading, processing and analysing data from the steam store. [See all posts here](http://nik-davis.github.io/tag/steam).*
```
# view software version information
# http://raw.github.com/jrjohansson/version_information/master/version_information.py
%load_ext version_information
# %reload_ext version_information
%version_information numpy, pandas
```
<!-- PELICAN_BEGIN_SUMMARY -->
In my [previous post](https://nik-davis.github.io/posts/2019/steam-data-cleaning/), we took an in-depth look at cleaning data downloaded from the Steam Store. We followed the process from start to finish, omitting just one column, which we will look at today.
The final column to clean, `release_date`, provides some interesting optimisation and learning challenges. We encountered columns with a similar structure previously, so we can use what we learned there, but now we will also have dates to handle. We're going to approach this problem with the goal of optimisation in mind - we'll start by figuring out how to solve the task, getting to the point of a functional solution, then we'll test parts of the code to see where the major slowdowns are, using this to develop a framework for improving the efficiency of the code. By iteratively testing, rewriting and rerunning sections of code, we can gradually move towards a more efficienct solution.
<!-- PELICAN_END_SUMMARY -->
## Importing Local Functions
When cleaning the data, we wrote a `print_steam_links` function to easily create links from a dataframe. To use it again, we could copy the code and define it here, but instead we will use a handy trick in jupyter notebook. If we place the function in a separate python (.py) file inside a folder at the root of the project directory (in this case, the 'src' folder), we can tell python to look there for local modules using `sys.path.append`. Then we can import the function directly, where the file name (datacleaning) is the module name, as seen below.
```
import sys
sys.path.append('../src/')
from datacleaning import print_steam_links
```
## Import and Inspect Data
We begin by importing the necessary libraries and inspecting the data, with every column cleaned except release date.
```
# standard library imports
from ast import literal_eval
import time
import re
import sys
sys.path.append('../src/')
# third-party imports
import numpy as np
import pandas as pd
# local imports
from datacleaning import print_steam_links
# customisations
pd.set_option("max_columns", 100)
imported_steam_data = pd.read_csv('../data/exports/steam_partially_clean.csv')
print('Rows:', imported_steam_data.shape[0])
print('Columns:', imported_steam_data.shape[1])
imported_steam_data.head()
```
Checking the null counts, we see there are no columns with missing values. This means we did our job properly previously, and we should just be able to focus on cleaning and formatting the column.
```
imported_steam_data.isnull().sum()
```
## Checking the Format
First we shall inspect the raw format of the column. As we can see below, it is stored as a dictionary-like string object containing values for `coming_soon` and `date`. From the first few rows it would appear that the dates are stored in a uniform format - day as an integer, month as a 3-character string abbreviation, a comma, then the year as a four-digit number. We can parse this either using the python built-in datetime module, or as we already have pandas imported, we can use the [pd.to_datetime](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.to_datetime.html) function.
Also, as our analysis will involve looking at ownership and sales data, looking at games that are not released yet will not be useful to us. Intuitively, we can drop any titles which are marked as coming soon, presumably having this value set to true. As a side note, once parsed it may be worth checking that no release dates in our data are beyond the current date, just to make doubly sure none slip through.
```
display(imported_steam_data['release_date'][0])
imported_steam_data[['name', 'release_date']].head()
```
We can explore the data a little further using the `value_counts` method. Whilst it looks like most dates are in the format `dd mmm, yyyy`, there at least a couple of rows in the format `mmm yyyy`, such as 'Jun 2009'. This means that all the dates aren't stored uniformly, so we will have to take care when parsing them.
```
print(imported_steam_data['release_date'].value_counts().head())
imported_steam_data.loc[imported_steam_data['release_date'].str.contains('Jun 2009'), 'release_date']
```
There are also a number of rows that have a blank string for the date value. We'll have to treat these as missing values, and decide if we want to remove them from the dataset. We can use the imported `print_steam_links` function to inspect some of the rows, using `sample` to randomly select a few.
```
no_release_date = imported_steam_data[imported_steam_data['release_date'].str.contains("'date': ''")]
print('Rows with no release date:', no_release_date.shape[0], '\n')
print_steam_links(no_release_date.sample(5, random_state=0))
```
It looks like some are special re-releases, like anniversary or game of the year editions, some are early access and not officially released yet, and others simply have a missing date. Apart from that there don't appear to be any clear patterns emerging, so as there are only 26 rows it may be best to remove them.
## Parsing the dates
Taking a look at the format of the column, we'll need to be using `literal_eval` as we did before. Apart from that it should be straightforward enough to extract the date.
```
print(type(imported_steam_data['release_date'].iloc[0]))
imported_steam_data['release_date'].iloc[0]
print(type(literal_eval(imported_steam_data['release_date'].iloc[0])))
literal_eval(imported_steam_data['release_date'].iloc[0])['date']
```
Once extracted, we can use the `pd.to_datetime` functon to interpret and store dates as `datetime` objects. This is useful as it will allow us to search and sort the dataset by year when it comes to performing analysis. Say for example we only wish to examine games released in 2010, by converting our dates to a python-recognisable format this will be very easy to achieve.
As seen below, we can supply the `to_datetime` function with a date and pandas will automatically interpret the format. We can then inspect it or print an attribute like the year. We can also provide pandas with the format explicitly, so it knows what to look for and how to parse it, which may be [quicker for large sets of data](https://stackoverflow.com/questions/32034689/why-is-pandas-to-datetime-slow-for-non-standard-time-format-such-as-2014-12-31).
```
timestamp = pd.to_datetime(literal_eval(imported_steam_data['release_date'].iloc[0])['date'])
print(timestamp)
print(timestamp.year)
pd.to_datetime(literal_eval(imported_steam_data['release_date'].iloc[0])['date'], format='%d %b, %Y')
```
## Initial Function Definition
Now we are ready to begin defining a function. As we only want to keep unreleased games, we first evaluate values from the `coming_soon` key, and keep only those where the value is `False`. Next we extract the release date, and set missing dates to np.nan, the default way of storing null values in pandas.
Then, using the formats we learned previously, we interpret those dates using the `to_datetime` function. Once complete we pass over the dataframe once more with a general call to `to_datetime`, catching any dates we missed.
Finally we drop the columns we no longer need and return the dataframe.
```
def process_release_date(df):
df = df.copy()
df['coming_soon'] = df['release_date'].apply(lambda x: literal_eval(x)['coming_soon'])
# Only want to keep released games
df = df[df['coming_soon'] == False].copy()
# extract release date and set missing dates to null
df['date'] = df['release_date'].apply(lambda x: literal_eval(x)['date'])
df.loc[df['date'] == '', 'date'] = np.nan
# Parse the date formats we have discovered
df['datetime'] = pd.to_datetime(df['date'], format='%d %b, %Y', errors='ignore')
df['datetime'] = pd.to_datetime(df['datetime'], format='%b %Y', errors='ignore')
# Parse the rest of the date formats
df['release_date'] = pd.to_datetime(df['datetime'])
df = df.drop(['coming_soon', 'date', 'datetime'], axis=1)
return df
result = process_release_date(imported_steam_data)
result[['steam_appid', 'release_date']].head()
```
Whilst functional, the process is quite slow. The easiest way to measure the efficiency of code is by timing how long it takes to run, and that is the method we'll use here. By running this code inside of jupyter notebook, we can take advanted of IPython magics, and use the [%timeit](https://ipython.readthedocs.io/en/stable/interactive/magics.html#magic-timeit) magic to easily test how long it takes to run the function.
```
%timeit process_release_date(imported_steam_data)
```
We can see that, on average, it takes about 3.5 seconds. Whilst manageable, we could certainly benefit from optimising our code, as this could quickly add up in larger data sets, where increasing efficiency can prove invaluable.
There are a few areas we can investigate to make improvements. When initially parsing the date, we end up calling `literal_eval` twice, which may be a source of slowdown. We also loop over the entire dataset multiple times when calling the `to_datetime` function.
We can be pretty confident that reducing the number of traversals over the dataset will provide some gains, but first, let's find out which part is causing the greatest slowdown. Targetting the slowest part of the code and improving it will lead to the most noticeable gains, and beyond that we can tweak other parts until we're happy.
We just used the %timeit magic to time our function - the function is run multiple times and the average execution time is given - but we can also use the built-in `time` module of python to easily inspect specific sections of code.
```
# begin timing
start_time = time.time()
# do something
x = 1
for i in range(1000):
x += 1
for j in range(1000):
x += 1
# stop timing
end_time = time.time()
# calculate time difference
execution_time = end_time - start_time
print(execution_time)
```
We'll break down the function into different sections which we think may be causing slowdown, and see which takes the longest to execute.
```
def process_release_date(df):
df = df.copy()
# first section
eval_start = time.time()
df['coming_soon'] = df['release_date'].apply(lambda x: literal_eval(x)['coming_soon'])
df = df[df['coming_soon'] == False].copy()
df['date'] = df['release_date'].apply(lambda x: literal_eval(x)['date'])
print('Evaluation run-time:', time.time() - eval_start)
df.loc[df['date'] == '', 'date'] = None
# second section
first_parse_start = time.time()
df['datetime'] = pd.to_datetime(df['date'], format='%d %b, %Y', errors='ignore')
df['datetime'] = pd.to_datetime(df['datetime'], format='%b %Y', errors='ignore')
print('First parse run-time:', time.time() - first_parse_start)
# third section
second_parse_start = time.time()
df['release_date'] = pd.to_datetime(df['datetime'])
print('Second parse run-time:', time.time() - second_parse_start)
df = df.drop(['coming_soon', 'date', 'datetime'], axis=1)
return df
function_start = time.time()
process_release_date(imported_steam_data)
print('\nTotal run-time:', time.time() - function_start)
```
Immediately we can see that the majority of run-time is taken up by the second call to `pd.to_datetime`. This suggests that the first two calls are not functioning as expected - they are possibly terminating after the first error instead of skipping over it as desired - and most of the work is being done by the final call. Now it makes sense why it is slow - pandas has to figure out how each date is formatted, and since we know we have some variations this may be slowing it down considerably.
Whilst the evaluation run-time is much shorter, multiple calls to `literal_eval` may be slowing the function as well, so we may wish to investigate that. As we know the biggest slowdown, we will begin there.
We now know that handling our dates in their current form is slow, and we know that we have some different formats mixed in there. Whilst there are likely many possible solutions to this problem, using regular expressions (or regex) comes to mind as they tend to excel at pattern matching in strings.
We know for sure two of the patterns, so let's build a regex for each of those. Then we can iteratively add more as we discover any other patterns. A powerful and useful tool for building and testing regex can be found at [regexr.com](https://regexr.com/).
```
pattern = r'[\d]{1,2} [A-Za-z]{3}, [\d]{4}'
string = '13 Jul, 2018'
print(re.search(pattern, string))
pattern = r'[A-Za-z]{3} [\d]{4}'
string = 'Apr 2016'
print(re.search(pattern, string))
```
Using these two patterns we can start building out a function. We're going to apply a function to the date column which searches for each pattern, returning a standardised date string which we will then feed into the `to_datetime` function.
The first search matches the 'mmm yyyy' pattern, like 'Apr 2019'. As we don't know the particular day for these matches we will assume it is the first of the month, returning '1 Apr 2019' in this example.
If we don't match this, we'll check for the second case. The second match will be the 'dd mmm, yyyy' pattern, like '13 Jul, 2018'. In this case we will simply return the match with the comma removed, to become '13 Jul 2018'.
If neither of these match, we'll check for the empty string, and return it as it is for now.
For anything else we'll simply print the string so we know what else we should be searching for.
```
def process_release_date(df):
df = df.copy()
df['coming_soon'] = df['release_date'].apply(lambda x: literal_eval(x)['coming_soon'])
df = df[df['coming_soon'] == False].copy()
df['date'] = df['release_date'].apply(lambda x: literal_eval(x)['date'])
def parse_date(x):
if re.search(r'[A-Za-z]{3} [\d]{4}', x):
return '1 ' + x
elif re.search(r'[\d]{1,2} [A-Za-z]{3}, [\d]{4}', x):
return x.replace(',', '')
elif x == '':
return x
else:
print(x)
df['date'] = df['date'].apply(parse_date)
df['release_date'] = pd.to_datetime(df['date'], infer_datetime_format=True)
df = df.drop(['coming_soon', 'date'], axis=1)
return df
result = process_release_date(imported_steam_data)
```
As no other rows we're printed out, we can be confident that we caught all of the patterns, and don't have any extra to take care of.
We just used the `infer_datetime_format` parameter of `to_datetime`, which, according to the documentation, can speed up the process. However, as we now know the exact format the dates will be in, we can explicitly set it ourselves, and this should be the fastest way of doing things.
We also need to decide how to handle the missing dates - those with the empty strings. For now let's set the way the function handles errors as `coerce`, which returns `NaT` (not a time).
We can now rewrite the function and time it as we did before.
```
def process_release_date_old(df):
df = df.copy()
df['coming_soon'] = df['release_date'].apply(lambda x: literal_eval(x)['coming_soon'])
df = df[df['coming_soon'] == False].copy()
df['date'] = df['release_date'].apply(lambda x: literal_eval(x)['date'])
# Simple parsing
df['release_date'] = pd.to_datetime(df['date'])
df = df.drop(['coming_soon', 'date'], axis=1)
return df
def process_release_date_new(df):
df = df.copy()
df['coming_soon'] = df['release_date'].apply(lambda x: literal_eval(x)['coming_soon'])
df = df[df['coming_soon'] == False].copy()
df['date'] = df['release_date'].apply(lambda x: literal_eval(x)['date'])
# Complex parsing
def parse_date(x):
if re.search(r'[A-Za-z]{3} [\d]{4}', x):
return '1 ' + x
elif re.search(r'[\d]{1,2} [A-Za-z]{3}, [\d]{4}', x):
return x.replace(',', '')
elif x == '':
return x
df['date'] = df['date'].apply(parse_date)
df['release_date'] = pd.to_datetime(df['date'], format='%d %b %Y', errors='coerce')
df = df.drop(['coming_soon', 'date'], axis=1)
return df
print('Testing date parsing:\n')
%timeit process_release_date_old(imported_steam_data)
%timeit process_release_date_new(imported_steam_data)
```
Our results show that the new method is almost four times faster, so we're on the right track.
Another optimisation we can make here is checking which part of the if/else statements has the most matches. It makes sense to order our statements from most matches to least, so for the majority of rows we only have to search through once.
To do this, instead of returning the date we'll return a number for each match. We can then print the value counts for the column and see which is the most frequent.
```
def optimise_regex_order(df):
df = df.copy()
df['coming_soon'] = df['release_date'].apply(lambda x: literal_eval(x)['coming_soon'])
df = df[df['coming_soon'] == False].copy()
df['date'] = df['release_date'].apply(lambda x: literal_eval(x)['date'])
def parse_date(x):
if re.search(r'[A-Za-z]{3} [\d]{4}', x):
return '0: mmm yyyy' # '1 ' + x
elif re.search(r'[\d]{1,2} [A-Za-z]{3}, [\d]{4}', x):
return '1: dd mmm, yyyy' # x.replace(',', '')
elif x == '':
return '2: empty' # pass
df['release_date'] = df['date'].apply(parse_date)
return df
result = optimise_regex_order(imported_steam_data)
result['release_date'].value_counts()
```
By far the majority of dates are in the 'dd mmm, yyyy' format, which is second in our if/else statements. This means that for all these rows we are unnecessarily searching the string twice. Simply by reordering our searches we should see a performance improvement.
```
def process_release_date_unordered(df):
df = df.copy()
df['coming_soon'] = df['release_date'].apply(lambda x: literal_eval(x)['coming_soon'])
df = df[df['coming_soon'] == False].copy()
df['date'] = df['release_date'].apply(lambda x: literal_eval(x)['date'])
def parse_date(x):
if re.search(r'[A-Za-z]{3} [\d]{4}', x):
return '1 ' + x
elif re.search(r'[\d]{1,2} [A-Za-z]{3}, [\d]{4}', x):
return x.replace(',', '')
elif x == '':
return x
df['release_date'] = df['date'].apply(parse_date)
df['release_date'] = pd.to_datetime(df['date'], format='%d %b %Y', errors='coerce')
df = df.drop(['coming_soon', 'date'], axis=1)
return df
def process_release_date_ordered(df):
df = df.copy()
df['coming_soon'] = df['release_date'].apply(lambda x: literal_eval(x)['coming_soon'])
df = df[df['coming_soon'] == False].copy()
df['date'] = df['release_date'].apply(lambda x: literal_eval(x)['date'])
def parse_date(x):
if re.search(r'[\d]{1,2} [A-Za-z]{3}, [\d]{4}', x):
return x.replace(',', '')
elif re.search(r'[A-Za-z]{3} [\d]{4}', x):
return '1 ' + x
elif x == '':
return x
df['release_date'] = df['date'].apply(parse_date)
df['release_date'] = pd.to_datetime(df['date'], format='%d %b %Y', errors='coerce')
df = df.drop(['coming_soon', 'date'], axis=1)
return df
%timeit process_release_date_unordered(imported_steam_data)
%timeit process_release_date_ordered(imported_steam_data)
```
It's an improvement, if only slightly, so we'll keep it. If anything this goes to show how fast regex pattern matching is, as there was hardly any slowdown in searching most of the strings twice.
Now parsing is well-optimised we can move on to the evaluation section.
```
# Testing evaluation methods
def evaluation_method_original(df):
df = df.copy()
df['coming_soon'] = df['release_date'].apply(lambda x: literal_eval(x)['coming_soon'])
df = df[df['coming_soon'] == False].copy()
df['release_date'] = df['release_date'].apply(lambda x: literal_eval(x)['date'])
return df
def evaluation_method_1(df):
df = df.copy()
df['release_date'] = df['release_date'].apply(lambda x: literal_eval(x))
df['coming_soon'] = df['release_date'].apply(lambda x: x['coming_soon'])
df = df[df['coming_soon'] == False].copy()
df['release_date'] = df['release_date'].apply(lambda x: x['date'])
return df
def evaluation_method_2(df):
df = df.copy()
df['release_date'] = df['release_date'].apply(lambda x: literal_eval(x))
df_2 = df['release_date'].transform([lambda x: x['coming_soon'], lambda x: x['date']])
df = pd.concat([df, df_2], axis=1)
return df
def evaluation_method_3(df):
df = df.copy()
def eval_date(x):
x = literal_eval(x)
if x['coming_soon']:
return np.nan
else:
return x['date']
df['release_date'] = df['release_date'].apply(eval_date)
df = df[df['release_date'].notnull()]
return df
print('Original method:\n')
%timeit evaluation_method_original(imported_steam_data)
print('\nNew methods:\n')
%timeit evaluation_method_1(imported_steam_data)
%timeit evaluation_method_2(imported_steam_data)
%timeit evaluation_method_3(imported_steam_data)
```
It looks like we may have been right in our assumption that multiple calls to `literal_eval` were slowing down the function - by calling it once instead of twice we almost halved the run-time.
Of the new methods the final one was just about the fastest, which is useful because it contains flexible custom logic we can modify if needed. Let's put everything together into the final function, and time it once more to see the improvements we've made.
We'll make a couple of changes so we can easily remove missing values at the end, which should mean we end up with clean release dates.
```
def process_release_date(df):
df = df.copy()
def eval_date(x):
x = literal_eval(x)
if x['coming_soon']:
return '' # return blank string so can drop missing at end
else:
return x['date']
df['release_date'] = df['release_date'].apply(eval_date)
def parse_date(x):
if re.search(r'[\d]{1,2} [A-Za-z]{3}, [\d]{4}', x):
return x.replace(',', '')
elif re.search(r'[A-Za-z]{3} [\d]{4}', x):
return '1 ' + x
elif x == '':
return np.nan
df['release_date'] = df['release_date'].apply(parse_date)
df['release_date'] = pd.to_datetime(df['release_date'], format='%d %b %Y', errors='coerce')
df = df[df['release_date'].notnull()]
return df
%timeit process_release_date(imported_steam_data)
```
Referring back to the original time of 3.5s, we've achieved a 7x speed increase. That's pretty close to an order of magnitude improvement. With a dataset like this, we're only talking a matter of seconds, but in a much larger dataset with millions of rows, spending the time to improve code efficiency could shave hours off of run time.
As I'm sure you're aware if you have some familiarity with writing code, for most tasks there are a million and one ways of approaching and solving the problem. Hopefully this helps lay out a simple methodology for testing, improving and thinking about code. Plus, it can be fun and interesting to figure out different ways of achieving the same output. Speaking of which, let's look at a final little challenge.
## Bonus: Vanilla Python Solution
In our final solution to cleaning the `release_date` column, we relied heavily on the pandas library. Often using libraries such as this is a good idea as it contains vectorised and optimised methods for dealing with data, plus it's generally quicker to develop a working solution.
As a small challenge, let's have a look at performing the above cleaning process entirely with vanilla python functions, as in those available by default using python and its built-in packages.
First we need to convert the data from a pandas dataframe into a native python format. We have a few options but let's store the data as a list of lists. We'll also only include the AppID and release date columns, for the sake of demonstration.
```
date_list = []
for i, row in imported_steam_data.iterrows():
date_list.append([row['steam_appid'], row['release_date']])
date_list[:5]
```
The process is actually very similar. We have to loop through the data, rather than using pandas `apply`, and we parse the dates using `strptime` from the `datetime` module. We can generate the output using regex pattern matching, as we did before, and we can store the results in a new list of lists.
We also display the first few rows of the output, and time how long it takes to run so we can compare.
```
from datetime import datetime as dt
def python_only(ls):
processed_rows = []
for i, date in ls:
eval_row = literal_eval(date)
if eval_row['coming_soon'] == False:
if re.search(r'[\d]{1,2} [A-Za-z]{3}, [\d]{4}', eval_row['date']):
output = dt.strptime(eval_row['date'], '%d %b, %Y')
elif re.search(r'[A-Za-z]{3} [\d]{4}', eval_row['date']):
output = dt.strptime(eval_row['date'], '%b %Y')
elif eval_row['date'] == '':
output = 'none'
else:
print('Not matched:', eval_row['date'])
processed_rows.append([i, output])
else:
processed_rows.append([i, 'none'])
return processed_rows
start = time.time()
display(python_only(date_list)[:5])
end = time.time() - start
print(f'\nTime taken: {end:.2f}s')
```
Impressively, this method only took twice as long as our optimised method using pandas. It would probably take a bit longer if we had to deal with all the columns in the dataset, but this is still a viable solution. Also, we didn't properly handle the missing values, and the data is populated with some amount of 'none' values.
| true |
code
| 0.233684 | null | null | null | null |
|
# Generates images from text prompts with CLIP guided diffusion.
By Katherine Crowson (https://github.com/crowsonkb, https://twitter.com/RiversHaveWings). It uses a 512x512 unconditional ImageNet diffusion model fine-tuned from OpenAI's 512x512 class-conditional ImageNet diffusion model (https://github.com/openai/guided-diffusion) together with CLIP (https://github.com/openai/CLIP) to connect text prompts with images.
```
# @title Licensed under the MIT License
# Copyright (c) 2021 Katherine Crowson
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
# THE SOFTWARE.
```
Note: This notebook requires 16 GB of GPU memory to work, if you are unable to get a 16 GB GPU consistently, try the [256x256 version](https://colab.research.google.com/drive/12a_Wrfi2_gwwAuN3VvMTwVMz9TfqctNj).
```
# Check the GPU
!nvidia-smi
# Install dependencies
!git clone https://github.com/openai/CLIP
!git clone https://github.com/crowsonkb/guided-diffusion
!pip install -e ./CLIP
!pip install -e ./guided-diffusion
!pip install lpips
# Download the diffusion model
!curl -OL --http1.1 'https://the-eye.eu/public/AI/models/512x512_diffusion_unconditional_ImageNet/512x512_diffusion_uncond_finetune_008100.pt'
# Imports
import gc
import io
import math
import sys
from IPython import display
import lpips
from PIL import Image
import requests
import torch
from torch import nn
from torch.nn import functional as F
from torchvision import transforms
from torchvision.transforms import functional as TF
from tqdm.notebook import tqdm
sys.path.append('./CLIP')
sys.path.append('./guided-diffusion')
import clip
from guided_diffusion.script_util import create_model_and_diffusion, model_and_diffusion_defaults
# Define necessary functions
def fetch(url_or_path):
if str(url_or_path).startswith('http://') or str(url_or_path).startswith('https://'):
r = requests.get(url_or_path)
r.raise_for_status()
fd = io.BytesIO()
fd.write(r.content)
fd.seek(0)
return fd
return open(url_or_path, 'rb')
def parse_prompt(prompt):
if prompt.startswith('http://') or prompt.startswith('https://'):
vals = prompt.rsplit(':', 2)
vals = [vals[0] + ':' + vals[1], *vals[2:]]
else:
vals = prompt.rsplit(':', 1)
vals = vals + ['', '1'][len(vals):]
return vals[0], float(vals[1])
class MakeCutouts(nn.Module):
def __init__(self, cut_size, cutn, cut_pow=1.):
super().__init__()
self.cut_size = cut_size
self.cutn = cutn
self.cut_pow = cut_pow
def forward(self, input):
sideY, sideX = input.shape[2:4]
max_size = min(sideX, sideY)
min_size = min(sideX, sideY, self.cut_size)
cutouts = []
for _ in range(self.cutn):
size = int(torch.rand([])**self.cut_pow * (max_size - min_size) + min_size)
offsetx = torch.randint(0, sideX - size + 1, ())
offsety = torch.randint(0, sideY - size + 1, ())
cutout = input[:, :, offsety:offsety + size, offsetx:offsetx + size]
cutouts.append(F.adaptive_avg_pool2d(cutout, self.cut_size))
return torch.cat(cutouts)
def spherical_dist_loss(x, y):
x = F.normalize(x, dim=-1)
y = F.normalize(y, dim=-1)
return (x - y).norm(dim=-1).div(2).arcsin().pow(2).mul(2)
def tv_loss(input):
"""L2 total variation loss, as in Mahendran et al."""
input = F.pad(input, (0, 1, 0, 1), 'replicate')
x_diff = input[..., :-1, 1:] - input[..., :-1, :-1]
y_diff = input[..., 1:, :-1] - input[..., :-1, :-1]
return (x_diff**2 + y_diff**2).mean([1, 2, 3])
def range_loss(input):
return (input - input.clamp(-1, 1)).pow(2).mean([1, 2, 3])
# Model settings
model_config = model_and_diffusion_defaults()
model_config.update({
'attention_resolutions': '32, 16, 8',
'class_cond': False,
'diffusion_steps': 1000,
'rescale_timesteps': True,
'timestep_respacing': '1000', # Modify this value to decrease the number of
# timesteps.
'image_size': 512,
'learn_sigma': True,
'noise_schedule': 'linear',
'num_channels': 256,
'num_head_channels': 64,
'num_res_blocks': 2,
'resblock_updown': True,
'use_fp16': True,
'use_scale_shift_norm': True,
})
# Load models
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print('Using device:', device)
model, diffusion = create_model_and_diffusion(**model_config)
model.load_state_dict(torch.load('512x512_diffusion_uncond_finetune_008100.pt', map_location='cpu'))
model.requires_grad_(False).eval().to(device)
for name, param in model.named_parameters():
if 'qkv' in name or 'norm' in name or 'proj' in name:
param.requires_grad_()
if model_config['use_fp16']:
model.convert_to_fp16()
clip_model = clip.load('ViT-B/16', jit=False)[0].eval().requires_grad_(False).to(device)
clip_size = clip_model.visual.input_resolution
normalize = transforms.Normalize(mean=[0.48145466, 0.4578275, 0.40821073],
std=[0.26862954, 0.26130258, 0.27577711])
lpips_model = lpips.LPIPS(net='vgg').to(device)
```
## Settings for this run:
```
prompts = ['alien friend by Odilon Redon']
image_prompts = []
batch_size = 1
clip_guidance_scale = 1000 # Controls how much the image should look like the prompt.
tv_scale = 150 # Controls the smoothness of the final output.
range_scale = 50 # Controls how far out of range RGB values are allowed to be.
cutn = 32
cut_pow = 0.5
n_batches = 1
init_image = None # This can be an URL or Colab local path and must be in quotes.
skip_timesteps = 0 # This needs to be between approx. 200 and 500 when using an init image.
# Higher values make the output look more like the init.
init_scale = 0 # This enhances the effect of the init image, a good value is 1000.
seed = 0
```
### Actually do the run...
```
def do_run():
if seed is not None:
torch.manual_seed(seed)
make_cutouts = MakeCutouts(clip_size, cutn, cut_pow)
side_x = side_y = model_config['image_size']
target_embeds, weights = [], []
for prompt in prompts:
txt, weight = parse_prompt(prompt)
target_embeds.append(clip_model.encode_text(clip.tokenize(txt).to(device)).float())
weights.append(weight)
for prompt in image_prompts:
path, weight = parse_prompt(prompt)
img = Image.open(fetch(path)).convert('RGB')
img = TF.resize(img, min(side_x, side_y, *img.size), transforms.InterpolationMode.LANCZOS)
batch = make_cutouts(TF.to_tensor(img).unsqueeze(0).to(device))
embed = clip_model.encode_image(normalize(batch)).float()
target_embeds.append(embed)
weights.extend([weight / cutn] * cutn)
target_embeds = torch.cat(target_embeds)
weights = torch.tensor(weights, device=device)
if weights.sum().abs() < 1e-3:
raise RuntimeError('The weights must not sum to 0.')
weights /= weights.sum().abs()
init = None
if init_image is not None:
init = Image.open(fetch(init_image)).convert('RGB')
init = init.resize((side_x, side_y), Image.LANCZOS)
init = TF.to_tensor(init).to(device).unsqueeze(0).mul(2).sub(1)
cur_t = None
def cond_fn(x, t, y=None):
with torch.enable_grad():
x = x.detach().requires_grad_()
n = x.shape[0]
my_t = torch.ones([n], device=device, dtype=torch.long) * cur_t
out = diffusion.p_mean_variance(model, x, my_t, clip_denoised=False, model_kwargs={'y': y})
fac = diffusion.sqrt_one_minus_alphas_cumprod[cur_t]
x_in = out['pred_xstart'] * fac + x * (1 - fac)
clip_in = normalize(make_cutouts(x_in.add(1).div(2)))
image_embeds = clip_model.encode_image(clip_in).float()
dists = spherical_dist_loss(image_embeds.unsqueeze(1), target_embeds.unsqueeze(0))
dists = dists.view([cutn, n, -1])
losses = dists.mul(weights).sum(2).mean(0)
tv_losses = tv_loss(x_in)
range_losses = range_loss(out['pred_xstart'])
loss = losses.sum() * clip_guidance_scale + tv_losses.sum() * tv_scale + range_losses.sum() * range_scale
if init is not None and init_scale:
init_losses = lpips_model(x_in, init)
loss = loss + init_losses.sum() * init_scale
return -torch.autograd.grad(loss, x)[0]
if model_config['timestep_respacing'].startswith('ddim'):
sample_fn = diffusion.ddim_sample_loop_progressive
else:
sample_fn = diffusion.p_sample_loop_progressive
for i in range(n_batches):
cur_t = diffusion.num_timesteps - skip_timesteps - 1
samples = sample_fn(
model,
(batch_size, 3, side_y, side_x),
clip_denoised=False,
model_kwargs={},
cond_fn=cond_fn,
progress=True,
skip_timesteps=skip_timesteps,
init_image=init,
randomize_class=True,
)
for j, sample in enumerate(samples):
cur_t -= 1
if j % 100 == 0 or cur_t == -1:
print()
for k, image in enumerate(sample['pred_xstart']):
filename = f'progress_{i * batch_size + k:05}.png'
TF.to_pil_image(image.add(1).div(2).clamp(0, 1)).save(filename)
tqdm.write(f'Batch {i}, step {j}, output {k}:')
display.display(display.Image(filename))
gc.collect()
do_run()
```
| true |
code
| 0.778923 | null | null | null | null |
|
## Chapter 2: Refresher of OOP concepts in Python
### Classes and Objects
```
class ClassName:
'''attributes...'''
'''methods...'''
objName = ClassName()
class Branch:
'''attributes...'''
'''methods...'''
class Branch:
'''attributes'''
branchID = None
branchStreet = None
branchCity = None
branchState = None
branchZip = None
'''methods'''
def getProduct(self):
return 'product'
def getSales(self):
return 'sales'
def getInvoice(self):
return 'invoice'
branchAlbany = Branch()
branchAlbany.branchID = 123
branchAlbany.branchStreet = '123 Main Street'
branchAlbany.branchCity = 'Albany'
branchAlbany.branchState = 'New York'
branchAlbany.branchZip = 12084
branchAlbany.branchID
branchAlbany.branchStreet
branchAlbany.branchCity
branchAlbany.branchState
branchAlbany.branchZip
branchAlbany.getInvoice()
branchNevada = Branch()
branchNevada.branchID
branchNevada.branchID = 456
branchNevada.branchID
class Branch:
def __init__(self, branchID, branchStreet, branchCity, branchState, branchZip):
self.branchID = branchID
self.branchStreet = branchStreet
self.branchCity = branchCity
self.branchState = branchState
self.branchZip = branchZip
def getProduct(self):
return 'product'
def getSales(self):
return 'sales'
def getInvoice(self):
return 'invoice'
objectAlbany = Branch(101,'123 Main Street','Albany','New York', 12084)
print (objectAlbany.branchID, objectAlbany.branchStreet,\
objectAlbany.branchCity,objectAlbany.branchState,\
objectAlbany.branchZip)
```
### Methods
```
class Branch:
def __init__(self, branchID, branchStreet, branchCity, branchState, branchZip):
self.branchID = branchID
self.branchStreet = branchStreet
self.branchCity = branchCity
self.branchState = branchState
self.branchZip = branchZip
def getProduct(self):
return 'product'
def getSales(self):
return 'sales'
def getInvoice(self):
return 'invoice'
objectAlbany = Branch(101,'123 Main Street','Albany','New York', 12084)
objectAlbany.getInvoice()
objectAlbany.getSales()
objectAlbany.getProduct()
class Branch:
def setBranch(self, **branch):
return branch
def setSales(self, **sales):
return sales
def setProduct(self, **product):
return product
def calcTax(self):
branch = self.branch
product = self.product
sales = self.sales
pricebeforetax = sales['purchasePrice'] + sales['purchasePrice'] * sales['profitMargin']
finalsellingprice = pricebeforetax + (pricebeforetax * sales['taxRate'])
sales['sellingPrice'] = finalsellingprice
return branch, product, sales
branchNyc = Branch()
branchNyc.branch = branchNyc.setBranch(branchID = 202,
branchStreet = '234 3rd Main Street',
branchCity = 'New York City',
branchState = 'New York',
branchZip = 11005)
branchNyc.branch
branchNyc.product = branchNyc.setProduct(
productId = 100001,
productName = 'Refrigerator',
productBrand = 'Whirlpool'
)
branchNyc.product
branchNyc.sales = branchNyc.setSales(
purchasePrice = 300,
profitMargin = 0.20,
taxRate = 0.452
)
branchNyc.sales
branchNyc.calcTax()
```
### Inheritance
```
class Parent:
'''attributes...'''
'''methods...'''
class Child(Parent):
'''attributes...'''
'''methods...'''
class NYC(Branch):
def setManagement(self, **intercitybranch):
return intercitybranch
def calcTaxNYC(self):
branch = self.branch
intercitybranch = self.intercitybranch
product = self.product
sales = self.sales
pricebeforetax = sales['purchasePrice'] + sales['purchasePrice'] * sales['profitMargin']
finalsellingprice = pricebeforetax + (pricebeforetax * (sales['taxRate'] + sales['localRate']))
sales['sellingPrice'] = finalsellingprice
return branch,intercitybranch, product, sales
branchManhattan = NYC()
branchManhattan.branch = branchManhattan.setBranch(branchID = 2021,
branchStreet = '40097 5th Main Street',
branchBorough = 'Manhattan',
branchCity = 'New York City',
branchState = 'New York',
branchZip = 11007)
branchManhattan.branch
branchManhattan.intercitybranch = branchManhattan.setManagement(
regionalManager = 'John M',
branchManager = 'Tom H',
subBranchID = '2021-01'
)
branchManhattan.intercitybranch
branchManhattan.product = branchManhattan.setProduct(
productId = 100002,
productName = 'WashingMachine',
productBrand = 'Whirlpool'
)
branchManhattan.product
branchManhattan.sales = branchManhattan.setSales(
purchasePrice = 450,
profitMargin = 0.19,
taxRate = 0.4,
localRate = 0.055
)
branchManhattan.sales
branchManhattan.calcTax()
branchManhattan.calcTaxNYC()
```
### Polymorphism
```
class NYC(Branch):
def setManagement(self, **intercitybranch):
return intercitybranch
def calcTax(self):
branch = self.branch
intercitybranch = self.intercitybranch
product = self.product
sales = self.sales
pricebeforetax = sales['purchasePrice'] + sales['purchasePrice'] * sales['profitMargin']
finalsellingprice = pricebeforetax + (pricebeforetax * (sales['taxRate'] + sales['localRate']))
sales['sellingPrice'] = finalsellingprice
return branch,intercitybranch, product, sales
branchManhattan = NYC()
branchManhattan.branch = branchManhattan.setBranch(branchID = 2021,
branchStreet = '40097 5th Main Street',
branchBorough = 'Manhattan',
branchCity = 'New York City',
branchState = 'New York',
branchZip = 11007)
branchManhattan.intercitybranch = branchManhattan.setManagement(
regionalManager = 'John M',
branchManager = 'Tom H',
subBranchID = '2021-01'
)
branchManhattan.product = branchManhattan.setProduct(
productId = 100002,
productName = 'WashingMachine',
productBrand = 'Whirlpool'
)
branchManhattan.sales = branchManhattan.setSales(
purchasePrice = 450,
profitMargin = 0.19,
taxRate = 0.4,
localRate = 0.055
)
branchManhattan.calcTax()
class Brooklyn:
def maintenanceCost(self, productType, quantity):
self.productType = productType
self.quantity = quantity
coldstorageCost = 100
if (productType == 'FMCG'):
maintenanceCost = self.quantity * 0.25 + coldstorageCost
return maintenanceCost
else:
return "We don't stock this product"
class Queens:
def maintenanceCost(self, productType, quantity):
self.productType = productType
self.quantity = quantity
if (productType == 'Electronics'):
maintenanceCost = self.quantity * 0.05
return maintenanceCost
else:
return "We don't stock this product"
objectBrooklyn = Brooklyn()
objectQueens = Queens()
objectBrooklyn.maintenanceCost('FMCG', 2000)
objectQueens.maintenanceCost('Electronics', 2000)
```
### Multiple Inheritance
```
class Product:
_productID = 100902
_productName = 'Iphone X'
_productCategory = 'Electronics'
_unitPrice = 700
def getProduct(self):
return self._productID, self._productName, self._productCategory, self._unitPrice
class Branch:
_branchID = 2021
_branchStreet = '40097 5th Main Street'
_branchBorough = 'Manhattan'
_branchCity = 'New York City'
_branchState = 'New York'
_branchZip = 11007
def getBranch(self):
return self._branchID, self._branchStreet, self._branchBorough, self._branchCity, self._branchState, self._branchZip
class Sales(Product, Branch):
date = '08/02/2021'
def getSales(self):
return self.date, Product.getProduct(self), Branch.getBranch(self)
sales = Sales()
sales.getSales()
```
### Abstraction
```
class Branch():
def maintenanceCost(self):
pass
class Brooklyn(Branch):
def maintenanceCost(self, productType, quantity):
self.productType = productType
self.quantity = quantity
coldstorageCost = 100
if (productType == 'FMCG'):
maintenanceCost = self.quantity * 0.25 + coldstorageCost
return maintenanceCost
else:
return "We don't stock this product"
class Queens(Branch):
def maintenanceCost(self, productType, quantity):
self.productType = productType
self.quantity = quantity
if (productType == 'Electronics'):
maintenanceCost = self.quantity * 0.05
return maintenanceCost
else:
return "We don't stock this product"
branch = Branch()
branch.maintenanceCost()
from abc import ABC,abstractmethod
class Branch(ABC):
@abstractmethod
def maintenanceCost(self):
pass
class Brooklyn(Branch):
def maintenanceCost(self, productType, quantity):
self.productType = productType
self.quantity = quantity
coldstorageCost = 100
if (productType == 'FMCG'):
maintenanceCost = self.quantity * 0.25 + coldstorageCost
return maintenanceCost
else:
return "We don't stock this product"
class Queens(Branch):
def maintenanceCost(self, productType, quantity):
self.productType = productType
self.quantity = quantity
if (productType == 'Electronics'):
maintenanceCost = self.quantity * 0.05
return maintenanceCost
else:
return "We don't stock this product"
branch = Branch()
branchBrooklyn = Brooklyn()
branchBrooklyn.maintenanceCost('FMCG', 5000)
branchQueens = Queens()
branchQueens.maintenanceCost('Electronics', 5000)
```
### Encapsulation
```
class Branch():
branchID = 2021
regionalManager = 'John M'
branchManager = 'Tom H'
__productId = None
__productName = None
__productBrand = None
__purchasePrice = None
__profitMargin = None
def __displayProductDetails(self):
self.__productId = 100002
self.__productName = 'Washing Machine'
self.__productBrand = 'Whirlpool'
self.__purchasePrice = 450
self.__profitMargin = 0.19
print('Product ID: ' + str(self.__productId) + ', Product Name: ' + self.__productName +
', Product Brand: ' + self.__productBrand + ', Purchase Price: ' + str(self.__purchasePrice)
+ ', Profit Margin: ' + str(self.__profitMargin))
def __init__(self):
self.__displayProductDetails()
branch = Branch()
branch.branchID
branch.__profitMargin
branch.__displayProductDetails()
class Branch():
branchID = 2022
regionalManager = 'Ron D'
__branchManager = 'Sam J'
_productId = None
_productName = None
_productBrand = None
_purchasePrice = None
_profitMargin = None
def _displayProductDetails(self):
self._productId = 100003
self._productName = 'Washing Machine'
self._productBrand = 'Samsung'
self._purchasePrice = 430
self._profitMargin = 0.18
print('Product ID: ' + str(self._productId) + ', Product Name: ' + self._productName +
', Product Brand: ' + self._productBrand + ', Purchase Price: ' + str(self._purchasePrice)
+ ', Profit Margin: ' + str(self._profitMargin))
def __init__(self):
self._displayProductDetails()
branch = Branch()
class Brooklyn(Branch):
def __init__(self):
print(self._productId)
self._displayProductDetails()
branchBrooklyn = Brooklyn()
class Brooklyn(Branch):
def __init__(self):
print(self._productId)
self._displayProductDetails()
print(self.__branchManager)
branchBrooklyn = Brooklyn()
```
### These are all the examples covered in this chapter.
| true |
code
| 0.434161 | null | null | null | null |
|
Deep Learning
=============
Assignment 5
------------
The goal of this assignment is to train a Word2Vec skip-gram model over [Text8](http://mattmahoney.net/dc/textdata) data.
```
# These are all the modules we'll be using later. Make sure you can import them
# before proceeding further.
%matplotlib inline
from __future__ import print_function
import collections
import math
import numpy as np
import os
import random
import tensorflow as tf
import zipfile
from matplotlib import pylab
from six.moves import range
from six.moves.urllib.request import urlretrieve
from sklearn.manifold import TSNE
```
Download the data from the source website if necessary.
```
url = 'http://mattmahoney.net/dc/'
def maybe_download(filename, expected_bytes):
"""Download a file if not present, and make sure it's the right size."""
if not os.path.exists(filename):
filename, _ = urlretrieve(url + filename, filename)
statinfo = os.stat(filename)
if statinfo.st_size == expected_bytes:
print('Found and verified %s' % filename)
else:
print(statinfo.st_size)
raise Exception(
'Failed to verify ' + filename + '. Can you get to it with a browser?')
return filename
filename = maybe_download('text8.zip', 31344016)
```
Read the data into a string.
```
def read_data(filename):
"""Extract the first file enclosed in a zip file as a list of words"""
with zipfile.ZipFile(filename) as f:
data = tf.compat.as_str(f.read(f.namelist()[0])).split()
return data
words = read_data(filename)
print('Data size %d' % len(words))
```
Build the dictionary and replace rare words with UNK token.
```
vocabulary_size = 50000
def build_dataset(words):
count = [['UNK', -1]]
count.extend(collections.Counter(words).most_common(vocabulary_size - 1))
dictionary = dict()
for word, _ in count:
dictionary[word] = len(dictionary)
data = list()
unk_count = 0
for word in words:
if word in dictionary:
index = dictionary[word]
else:
index = 0 # dictionary['UNK']
unk_count = unk_count + 1
data.append(index)
count[0][1] = unk_count
reverse_dictionary = dict(zip(dictionary.values(), dictionary.keys()))
return data, count, dictionary, reverse_dictionary
data, count, dictionary, reverse_dictionary = build_dataset(words)
print('Most common words (+UNK)', count[:5])
print('Sample data', data[:10])
del words # Hint to reduce memory.
```
Function to generate a training batch for the skip-gram model.
```
data_index = 0
def generate_batch(batch_size, num_skips, skip_window):
global data_index
assert batch_size % num_skips == 0
assert num_skips <= 2 * skip_window
batch = np.ndarray(shape=(batch_size), dtype=np.int32)
labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32)
span = 2 * skip_window + 1 # [ skip_window target skip_window ]
buffer = collections.deque(maxlen=span)
for _ in range(span):
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
for i in range(batch_size // num_skips):
target = skip_window # target label at the center of the buffer
targets_to_avoid = [ skip_window ]
for j in range(num_skips):
while target in targets_to_avoid:
target = random.randint(0, span - 1)
targets_to_avoid.append(target)
batch[i * num_skips + j] = buffer[skip_window]
labels[i * num_skips + j, 0] = buffer[target]
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
return batch, labels
print('data:', [reverse_dictionary[di] for di in data[:8]])
for num_skips, skip_window in [(2, 1), (4, 2)]:
data_index = 0
batch, labels = generate_batch(batch_size=8, num_skips=num_skips, skip_window=skip_window)
print('\nwith num_skips = %d and skip_window = %d:' % (num_skips, skip_window))
print(' batch:', [reverse_dictionary[bi] for bi in batch])
print(' labels:', [reverse_dictionary[li] for li in labels.reshape(8)])
```
Train a skip-gram model.
```
batch_size = 128
embedding_size = 128 # Dimension of the embedding vector.
skip_window = 1 # How many words to consider left and right.
num_skips = 2 # How many times to reuse an input to generate a label.
# We pick a random validation set to sample nearest neighbors. here we limit the
# validation samples to the words that have a low numeric ID, which by
# construction are also the most frequent.
valid_size = 16 # Random set of words to evaluate similarity on.
valid_window = 100 # Only pick dev samples in the head of the distribution.
valid_examples = np.array(random.sample(range(valid_window), valid_size))
num_sampled = 64 # Number of negative examples to sample.
graph = tf.Graph()
with graph.as_default(), tf.device('/cpu:0'):
# Input data.
train_dataset = tf.placeholder(tf.int32, shape=[batch_size])
train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1])
valid_dataset = tf.constant(valid_examples, dtype=tf.int32)
# Variables.
embeddings = tf.Variable(
tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0))
softmax_weights = tf.Variable(
tf.truncated_normal([vocabulary_size, embedding_size],
stddev=1.0 / math.sqrt(embedding_size)))
softmax_biases = tf.Variable(tf.zeros([vocabulary_size]))
# Model.
# Look up embeddings for inputs.
embed = tf.nn.embedding_lookup(embeddings, train_dataset)
# Compute the softmax loss, using a sample of the negative labels each time.
loss = tf.reduce_mean(
tf.nn.sampled_softmax_loss(weights=softmax_weights, biases=softmax_biases, inputs=embed,
labels=train_labels, num_sampled=num_sampled, num_classes=vocabulary_size))
# Optimizer.
# Note: The optimizer will optimize the softmax_weights AND the embeddings.
# This is because the embeddings are defined as a variable quantity and the
# optimizer's `minimize` method will by default modify all variable quantities
# that contribute to the tensor it is passed.
# See docs on `tf.train.Optimizer.minimize()` for more details.
optimizer = tf.train.AdagradOptimizer(1.0).minimize(loss)
# Compute the similarity between minibatch examples and all embeddings.
# We use the cosine distance:
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims=True))
normalized_embeddings = embeddings / norm
valid_embeddings = tf.nn.embedding_lookup(
normalized_embeddings, valid_dataset)
similarity = tf.matmul(valid_embeddings, tf.transpose(normalized_embeddings))
num_steps = 100001
with tf.Session(graph=graph) as session:
tf.global_variables_initializer().run()
print('Initialized')
average_loss = 0
for step in range(num_steps):
batch_data, batch_labels = generate_batch(
batch_size, num_skips, skip_window)
feed_dict = {train_dataset : batch_data, train_labels : batch_labels}
_, l = session.run([optimizer, loss], feed_dict=feed_dict)
average_loss += l
if step % 2000 == 0:
if step > 0:
average_loss = average_loss / 2000
# The average loss is an estimate of the loss over the last 2000 batches.
print('Average loss at step %d: %f' % (step, average_loss))
average_loss = 0
# note that this is expensive (~20% slowdown if computed every 500 steps)
if step % 10000 == 0:
sim = similarity.eval()
for i in range(valid_size):
valid_word = reverse_dictionary[valid_examples[i]]
top_k = 8 # number of nearest neighbors
nearest = (-sim[i, :]).argsort()[1:top_k+1]
log = 'Nearest to %s:' % valid_word
for k in range(top_k):
close_word = reverse_dictionary[nearest[k]]
log = '%s %s,' % (log, close_word)
print(log)
final_embeddings = normalized_embeddings.eval()
num_points = 400
tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000, method='exact')
two_d_embeddings = tsne.fit_transform(final_embeddings[1:num_points+1, :])
def plot(embeddings, labels):
assert embeddings.shape[0] >= len(labels), 'More labels than embeddings'
pylab.figure(figsize=(15,15)) # in inches
for i, label in enumerate(labels):
x, y = embeddings[i,:]
pylab.scatter(x, y)
pylab.annotate(label, xy=(x, y), xytext=(5, 2), textcoords='offset points',
ha='right', va='bottom')
pylab.show()
words = [reverse_dictionary[i] for i in range(1, num_points+1)]
plot(two_d_embeddings, words)
```
---
Problem
-------
An alternative to skip-gram is another Word2Vec model called [CBOW](http://arxiv.org/abs/1301.3781) (Continuous Bag of Words). In the CBOW model, instead of predicting a context word from a word vector, you predict a word from the sum of all the word vectors in its context. Implement and evaluate a CBOW model trained on the text8 dataset.
---
| true |
code
| 0.746083 | null | null | null | null |
|
# VQGAN JAX Encoding for `webdataset`
This notebook shows how to pre-encode images to token sequences using JAX, VQGAN and a dataset in the [`webdataset` format](https://webdataset.github.io/webdataset/).
This example uses a small subset of YFCC100M we created for testing, but it should be easy to adapt to any other image/caption dataset in the `webdataset` format.
```
import numpy as np
from tqdm import tqdm
import torch
import torchvision.transforms as T
import torchvision.transforms.functional as TF
from torchvision.transforms import InterpolationMode
import math
import webdataset as wds
import jax
from jax import pmap
```
## Dataset and Parameters
The following is the list of shards we'll process. We hardcode the length of data so that we can see nice progress bars using `tqdm`.
```
shards = 'https://huggingface.co/datasets/dalle-mini/YFCC100M_OpenAI_subset/resolve/main/data/shard-{0000..0008}.tar'
length = 8320
```
If we are extra cautious or our server is unreliable, we can enable retries by providing a custom `curl` retrieval command:
```
# Enable curl retries to try to work around temporary network / server errors.
# This shouldn't be necessary when using reliable servers.
# shards = f'pipe:curl -s --retry 5 --retry-delay 5 -L {shards} || true'
from pathlib import Path
# Output directory for encoded files
encoded_output = Path.home()/'data'/'wds'/'encoded'
batch_size = 128 # Per device
num_workers = 8 # For parallel processing
bs = batch_size * jax.device_count() # You can use a smaller size while testing
batches = math.ceil(length / bs)
```
Image processing
```
def center_crop(image, max_size=256):
# Note: we allow upscaling too. We should exclude small images.
image = TF.resize(image, max_size, interpolation=InterpolationMode.LANCZOS)
image = TF.center_crop(image, output_size=2 * [max_size])
return image
preprocess_image = T.Compose([
center_crop,
T.ToTensor(),
lambda t: t.permute(1, 2, 0) # Reorder, we need dimensions last
])
```
Caption preparation.
Note that we receive the contents of the `json` structure, which will be replaced by the string we return.
If we want to keep other fields inside `json`, we can add `caption` as a new field.
```
def create_caption(item):
title = item['title_clean'].strip()
description = item['description_clean'].strip()
if len(title) > 0 and title[-1] not in '.!?': title += '.'
return f'{title} {description}'
```
When an error occurs (a download is disconnected, an image cannot be decoded, etc) the process stops with an exception. We can use one of the exception handlers provided by the `webdataset` library, such as `wds.warn_and_continue` or `wds.ignore_and_continue` to ignore the offending entry and keep iterating.
**IMPORTANT WARNING:** Do not use error handlers to ignore exceptions until you have tested that your processing pipeline works fine. Otherwise, the process will continue trying to find a valid entry, and it will consume your whole dataset without doing any work.
We can also create our custom exception handler as demonstrated here:
```
# UNUSED - Log exceptions to a file
def ignore_and_log(exn):
with open('errors.txt', 'a') as f:
f.write(f'{repr(exn)}\n')
return True
# Or simply use `wds.ignore_and_continue`
exception_handler = wds.warn_and_continue
dataset = wds.WebDataset(shards,
length=batches, # Hint so `len` is implemented
shardshuffle=False, # Keep same order for encoded files for easier bookkeeping. Set to `True` for training.
handler=exception_handler, # Ignore read errors instead of failing.
)
dataset = (dataset
.decode('pil') # decode image with PIL
# .map_dict(jpg=preprocess_image, json=create_caption, handler=exception_handler) # Process fields with functions defined above
.map_dict(jpg=preprocess_image, json=create_caption) # Process fields with functions defined above
.to_tuple('__key__', 'jpg', 'json') # filter to keep only key (for reference), image, caption.
.batched(bs)) # better to batch in the dataset (but we could also do it in the dataloader) - this arg does not affect speed and we could remove it
%%time
keys, images, captions = next(iter(dataset))
images.shape
T.ToPILImage()(images[0].permute(2, 0, 1))
```
### Torch DataLoader
```
dl = torch.utils.data.DataLoader(dataset, batch_size=None, num_workers=num_workers)
```
## VQGAN-JAX model
```
from vqgan_jax.modeling_flax_vqgan import VQModel
```
We'll use a VQGAN trained with Taming Transformers and converted to a JAX model.
```
model = VQModel.from_pretrained("flax-community/vqgan_f16_16384")
```
## Encoding
Encoding is really simple using `shard` to automatically distribute "superbatches" across devices, and `pmap`. This is all it takes to create our encoding function, that will be jitted on first use.
```
from flax.training.common_utils import shard
from functools import partial
@partial(jax.pmap, axis_name="batch")
def encode(batch):
# Not sure if we should `replicate` params, does not seem to have any effect
_, indices = model.encode(batch)
return indices
```
### Encoding loop
```
import os
import pandas as pd
def encode_captioned_dataset(dataloader, output_dir, save_every=14):
output_dir.mkdir(parents=True, exist_ok=True)
# Saving strategy:
# - Create a new file every so often to prevent excessive file seeking.
# - Save each batch after processing.
# - Keep the file open until we are done with it.
file = None
for n, (keys, images, captions) in enumerate(tqdm(dataloader)):
if (n % save_every == 0):
if file is not None:
file.close()
split_num = n // save_every
file = open(output_dir/f'split_{split_num:05x}.jsonl', 'w')
images = shard(images.numpy().squeeze())
encoded = encode(images)
encoded = encoded.reshape(-1, encoded.shape[-1])
encoded_as_string = list(map(lambda item: np.array2string(item, separator=',', max_line_width=50000, formatter={'int':lambda x: str(x)}), encoded))
batch_df = pd.DataFrame.from_dict({"key": keys, "caption": captions, "encoding": encoded_as_string})
batch_df.to_json(file, orient='records', lines=True)
```
Create a new file every 318 iterations. This should produce splits of ~500 MB each, when using a total batch size of 1024.
```
save_every = 318
encode_captioned_dataset(dl, encoded_output, save_every=save_every)
```
----
| true |
code
| 0.613294 | null | null | null | null |
|
# Simulating Language 5, Simple Innate Signalling (walkthrough)
This is a line-by-line walkthrough of the code for lab on simple signalling.
### Data Structures: a signalling matrix represented as a list of lists
A production system can be thought of as a matrix which maps meanings to signals. We are representing this as a list. Each member of the list is itself a list containing the association strengths for *one particular meaning*. Look at the example below:
```python
psys = [[1, 0, 0], [1, 2, 1], [3, 4, 4]]
```
Here, a production system called `psys` is defined: it has three members, representing three meanings. The length of the system `len(psys)` is equivalent to the number of meanings in the system. `psys[0]` is `[1, 0, 0]`, which are the association strengths for the first meaning (remember python indexes start from 0!). Each of these sub-lists has three members, representing three possible signals. So `psys[0][0]` is the strength of association between the first meaning and the first signal. We sometimes refer to these association strengths as "weights".
We can do the same thing to model a reception system, but in this case we are dealing with a system which maps from signals to meanings: so, if `rsys` is a reception system then each member of `rsys` is itself a list that contains the association strengths between a signal and several meanings.
- Create a variable containing the following production matrix:
|. | s1 | s2 | s3 |
|----|----|----|----|
| m1 | 1 | 0 | 2 |
| m2 | 2 | 2 | 0 |
| m3 | 0 | 1 | 3 |
- Print the weights for meaning m1
- Print the weight for the connection between meaning m2 and signal s3
- Create a variable containing the following reception matrix:
|. | m1 | m2 | m3 |
|----|----|----|----|
| s1 | 1 | 2 | 0 |
| s2 | 0 | 2 | 1 |
| s3 | 2 | 0 | 3 |
- Print the weights for signal s3
- Print the weight of the connection between signal s1 and meaning m2
## The code proper
The code begins by importing various random number and plotting modules:
```
import random
%matplotlib inline
import matplotlib.pyplot as plt
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg', 'pdf')
```
### Function wta
The function `wta` ("winner takes all") takes a list of numbers (`items`) as its argument. This represents a row of a production or reception matrix. The function returns the index of the largest number in the list `items`. If there are multiple equally large numbers, then one of them is chosen at random.
```
def wta(items):
maxweight = max(items)
candidates = []
for i in range(len(items)):
if items[i] == maxweight:
candidates.append(i)
return random.choice(candidates)
```
`maxweight == max(items)` uses the built-in function `max` to calculate the maximum value of `items` and allocates this value to the variable `maxweight`.
`candidates = []` creates an empty list.
`for i in range(len(items)):` lets us look at each item in the list in turn, keeping track of where it is in the list. `range(len(items))` creates a sequence of numbers from 0 up to (but not including) the length of the list `items`. These represent each possible index of `items`, and in the the for loop, we go through each of these in turn, allocating it to the variable, `i`, and then carrying out everything in the next code block for each value of `i`:
```python
if items[i] == maxweight:
candidates.append(i)
```
This block of code checks each member of `items` in turn; if its value is equal to `maxweight`, then the index `i` is appended to (added to) the list of `candidates`.
After this loop has been completed, `candidates` will contain the indices of all the largest numbers.
`return random.choice(candidates)` returns a random choice from the numbers in the list, `candidates`. If there is only one number in `candidates`, then this is returned.
- Using the `wta` function and the variables you created above to store the production and reception matrices:
- find the preferred signal for each meaning in turn
- find the preferred meaning for each signal in turn
For example, if you called your production system `my_psys`, you could find the preferred signal for meaning 1 like this:
```python
wta(my_psys[0])
```
This takes the first row of the production system we defined earlier (`my_psys[0]`), then uses `wta` to find the index of the preferred signal for that row. Note that the `wta` function will only work if you pressed SHIFT+ENTER on the cell in the notebook above, otherwise the computer doesn't know what `wta` means.
### Function communicate
The function `communicate` plays a communication episode; it takes three arguments:
- `speaker_system`, the production matrix of the speaker;
- `hearer_system`, the reception matrix of the hearer; and
- `meaning`, the index of the meanign which is to be communicated.
```
def communicate(speaker_system, hearer_system, meaning):
speaker_signal = wta(speaker_system[meaning])
hearer_meaning = wta(hearer_system[speaker_signal])
if meaning == hearer_meaning:
return 1
else:
return 0
```
In a communication episode, the speaker chooses a signal it uses to communicate `meaning`, and expresses this signal to the hearer; the hearer then chooses the meaning it understands by the speaker's signal. If the hearer's meaning is the same as the speaker's meaning, then the communication episode succeeds, otherwise it fails.
`speaker_signal = wta(speaker_system[meaning])` uses `speaker_system[meaning]` to extract a list of association strengths from the speaker's production matrix (`speaker_system`) for `meaning`, and then uses `wta` (see above) to find the index corresponding to the largest of these weights. This value is then stored in the variable `speaker_signal`.
`hearer_meaning = wta(hearer_system[speaker_signal])` uses `hearer_system[speaker_signal]` to extract a list of association strengths from the hearer's reception matrix (`hearer_system`) for `speaker_signal`, and then uses `wta` (see above) to find the index corresponding to the largest of these weights. This value is then stored in the variable `hearer_meaning`.
```python
if meaning == hearer_meaning:
return 1
else:
return 0
```
If the hearer's interpretation of the speaker's signal (`hearer_meaning`) equals the original value of `meaning` (i.e. the meaning the speaker was trying to convey) and thus the communication episode succeeds, then the function returns 1 (indicating success), otherwise (`else`) it returns 0 (indicating failure).
- Using the same matrices you created earlier, find out which of the meanings can be successfully communicated using these production and reception matrices.
### Function ca_monte
The function `ca_monte` (standing for "Communicative Accuracy Monte Carlo") is the main function in this program. It performs a Monte Carlo simulation, which runs a set number of communication episodes between a production system and a reception system, calculates how many of them were communicatively successful, and returns a trial-by-trial list of results. It takes three arguments:
- `speaker_system`, the production matrix of the speaker;
- `hearer_system`, the reception matrix of the hearer; and
- `trials`, the number of trials of the simulation, or the number of communicative episodes over which communicative accuracy should be calculated.
```
def ca_monte(speaker_system, hearer_system, trials):
total = 0.
accumulator = []
for n in range(trials):
total += communicate(speaker_system, hearer_system,
random.randrange(len(speaker_system)))
accumulator.append(total / (n + 1))
return accumulator
```
`total = 0.` creates a variable called total, which will store the number of successful communicative episodes. We use `0.` rather than `0` as a shorthand for `0.0`, which indicates that the eventual result isn't going to be a round number. In fact, this isn't strictly necessary for the version of Python we're using, but you're likely to see something like this in a lot of code you read.
`accumulator = []` creates a variable called `accumulator`, which will be used to build up a list of trial-by-trial success rates. We initialise the accumulator with an empty list: before we have conducted any trials, we don't have any results for success or failure.
`for n in range(trials):` sets up a loop to allow us to test communicative accuracy over and over again. `range(trials)` creates a sequence of numbers from 0 up to (but not including) `trials`, which is then traversed by the for loop.
`total += communicate(speaker_system, hearer_system, random.randrange(len(speaker_system)))` updates a running total of the number of communicative episodes that were successful. On each communicative episode, we choose a random meaning (that's what `random.randrange(len(speaker_system))` does - the length of `speaker_system` is the number of rows in their production matrix, which is the same as the number of meanings). Then we use the function `communicate` to see whether the speaker can successfully communicate this meaning to the hearer (`hearer_system`). We add the value returned by `communicate` (i.e. 0 or 1) to the existing value in `total`, which therefore contains the number of successful communicative episodes.
`accumulator.append(total / (n + 1))` builds up a list of exposure-by-exposure proportions of communicative episodes so far which have been successful. `total / (n + 1)` gives the total number of events so far that have been successful (stored in `total`) divided by the number of times we've been round the loop at this point. Note that the number of trials conducted so far is `n + 1`, not just `n`, because of the way `range` works. The first trial has `n` equal to 0, the second 1 and so on, so we have to add 1 to this number to get the number of trials completed. We then use `append` to add this value to `accumulator`, which is our building list of trial-by-trial success proportions.
`return accumulator` simply returns this list. Note that this line of code is outside of the the for loop. `accumulator` is only returned one the loop has run the necessary number of trials.
- What is the overall communicative accuracy for the matrices you defined earlier?
- create another matrix (maybe with more meanings and/or signals). What is its communicative accuracy?
| true |
code
| 0.229168 | null | null | null | null |
|
# Natural Language Processing with `nltk`
`nltk` is the most popular Python package for Natural Language processing, it provides algorithms for importing, cleaning, pre-processing text data in human language and then apply computational linguistics algorithms like sentiment analysis.
## Inspect the Movie Reviews Dataset
It also includes many easy-to-use datasets in the `nltk.corpus` package, we can download for example the `movie_reviews` package using the `nltk.download` function:
```
import nltk
nltk.download("movie_reviews")
```
You can also list and download other datasets interactively just typing:
nltk.download()
in the Jupyter Notebook.
Once the data have been downloaded, we can import them from `nltk.corpus`
```
from nltk.corpus import movie_reviews
```
The `fileids` method provided by all the datasets in `nltk.corpus` gives access to a list of all the files available.
In particular in the movie_reviews dataset we have 2000 text files, each of them is a review of a movie, and they are already split in a `neg` folder for the negative reviews and a `pos` folder for the positive reviews:
```
len(movie_reviews.fileids())
movie_reviews.fileids()[:5]
movie_reviews.fileids()[-5:]
```
`fileids` can also filter the available files based on their category, which is the name of the subfolders they are located in. Therefore we can have lists of positive and negative reviews separately.
```
negative_fileids = movie_reviews.fileids('neg')
positive_fileids = movie_reviews.fileids('pos')
len(negative_fileids), len(positive_fileids)
```
We can inspect one of the reviews using the `raw` method of `movie_reviews`, each file is split into sentences, the curators of this dataset also removed from each review from any direct mention of the rating of the movie.
```
print(movie_reviews.raw(fileids=positive_fileids[0]))
```
## Tokenize Text in Words
```
romeo_text = """Why then, O brawling love! O loving hate!
O any thing, of nothing first create!
O heavy lightness, serious vanity,
Misshapen chaos of well-seeming forms,
Feather of lead, bright smoke, cold fire, sick health,
Still-waking sleep, that is not what it is!
This love feel I, that feel no love in this."""
```
The first step in Natural Language processing is generally to split the text into words, this process might appear simple but it is very tedious to handle all corner cases, see for example all the issues with punctuation we have to solve if we just start with a split on whitespace:
```
romeo_text.split()
```
`nltk` has a sophisticated word tokenizer trained on English named `punkt`, we first have to download its parameters:
```
nltk.download("punkt")
```
Then we can use the `word_tokenize` function to properly tokenize this text, compare to the whitespace splitting we used above:
```
romeo_words = nltk.word_tokenize(romeo_text)
romeo_words
```
Good news is that the `movie_reviews` corpus already has direct access to tokenized text with the `words` method:
```
movie_reviews.words(fileids=positive_fileids[0])
```
## Build a bag-of-words model
The simplest model for analyzing text is just to think about text as an unordered collection of words (bag-of-words). This can generally allow to infer from the text the category, the topic or the sentiment.
From the bag-of-words model we can build features to be used by a classifier, here we assume that each word is a feature that can either be `True` or `False`.
We implement this in Python as a dictionary where for each word in a sentence we associate `True`, if a word is missing, that would be the same as assigning `False`.
```
{word:True for word in romeo_words}
type(_)
def build_bag_of_words_features(words):
return {word:True for word in words}
build_bag_of_words_features(romeo_words)
```
This is what we wanted, but we notice that also punctuation like "!" and words useless for classification purposes like "of" or "that" are also included.
Those words are named "stopwords" and `nltk` has a convenient corpus we can download:
```
nltk.download("stopwords")
import string
string.punctuation
```
Using the Python `string.punctuation` list and the English stopwords we can build better features by filtering out those words that would not help in the classification:
```
useless_words = nltk.corpus.stopwords.words("english") + list(string.punctuation)
#useless_words
#type(useless_words)
def build_bag_of_words_features_filtered(words):
return {
word:1 for word in words \
if not word in useless_words}
build_bag_of_words_features_filtered(romeo_words)
```
## Plotting Frequencies of Words
It is common to explore a dataset before starting the analysis, in this section we will find the most common words and plot their frequency.
Using the `.words()` function with no argument we can extract the words from the entire dataset and check that it is about 1.6 millions.
```
all_words = movie_reviews.words()
len(all_words)/1e6
```
First we want to filter out `useless_words` as defined in the previous section, this will reduce the length of the dataset by more than a factor of 2:
```
filtered_words = [word for word in movie_reviews.words() if not word in useless_words]
type(filtered_words)
len(filtered_words)/1e6
```
The `collection` package of the standard library contains a `Counter` class that is handy for counting frequencies of words in our list:
```
from collections import Counter
word_counter = Counter(filtered_words)
```
It also has a `most_common()` method to access the words with the higher count:
```
most_common_words = word_counter.most_common()[:10]
most_common_words
```
Then we would like to have a visualization of this using `matplotlib`.
First we want to use the Jupyter magic function
%matplotlib inline
to setup the Notebook to show the plot embedded into the Jupyter Notebook page, you can also test:
%matplotlib notebook
for a more interactive plotting interface which however is not as well supported on all platforms and browsers.
```
%matplotlib inline
import matplotlib.pyplot as plt
```
We can sort the word counts and plot their values on Logarithmic axes to check the shape of the distribution. This visualization is particularly useful if comparing 2 or more datasets, a flatter distribution indicates a large vocabulary while a peaked distribution a restricted vocabulary often due to a focused topic or specialized language.
```
sorted_word_counts = sorted(list(word_counter.values()), reverse=True)
plt.loglog(sorted_word_counts)
plt.ylabel("Freq")
plt.xlabel("Word Rank");
```
Another related plot is the histogram of `sorted_word_counts`, which displays how many words have a count in a specific range.
Of course the distribution is highly peaked at low counts, i.e. most of the words appear which a low count, so we better display it on semilogarithmic axes to inspect the tail of the distribution.
```
plt.hist(sorted_word_counts, bins=50);
plt.hist(sorted_word_counts, bins=50, log=True);
```
## Train a Classifier for Sentiment Analysis
Using our `build_bag_of_words_features` function we can build separately the negative and positive features.
Basically for each of the 1000 negative and for the 1000 positive review, we create one dictionary of the words and we associate the label "neg" and "pos" to it.
```
negative_features = [
(build_bag_of_words_features_filtered(movie_reviews.words(fileids=[f])), 'neg') \
for f in negative_fileids
]
print(negative_features[3])
positive_features = [
(build_bag_of_words_features_filtered(movie_reviews.words(fileids=[f])), 'pos') \
for f in positive_fileids
]
print(positive_features[6])
from nltk.classify import NaiveBayesClassifier
```
One of the simplest supervised machine learning classifiers is the Naive Bayes Classifier, it can be trained on 80% of the data to learn what words are generally associated with positive or with negative reviews.
```
split = 800
sentiment_classifier = NaiveBayesClassifier.train(positive_features[:split]+negative_features[:split])
```
We can check after training what is the accuracy on the training set, i.e. the same data used for training, we expect this to be a very high number because the algorithm already "saw" those data. Accuracy is the fraction of the data that is classified correctly, we can turn it into percent:
```
nltk.classify.util.accuracy(sentiment_classifier, positive_features[:split]+negative_features[:split])*100
```
The accuracy above is mostly a check that nothing went very wrong in the training, the real measure of accuracy is on the remaining 20% of the data that wasn't used in training, the test data:
```
nltk.classify.util.accuracy(sentiment_classifier, positive_features[split:]+negative_features[split:])*100
```
Accuracy here is around 70% which is pretty good for such a simple model if we consider that the estimated accuracy for a person is about 80%.
We can finally print the most informative features, i.e. the words that mostly identify a positive or a negative review:
```
sentiment_classifier.show_most_informative_features()
```
| true |
code
| 0.446495 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Mukilan-Krishnakumar/NLP_With_Disaster_Tweets/blob/main/NLP_with_Disaster_Tweets_Part_2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
This is the part 2 of **NLP with Disaster Tweets Series**. The previous [Part](https://github.com/Mukilan-Krishnakumar/NLP_With_Disaster_Tweets/blob/main/NLP_with_Disaster_Tweets_Part_1.ipynb) along with the blogpost can be found in [this link](https://medium.com/@mukilankrishnakumar2002/natural-language-processing-with-disaster-tweets-part-1-db31c9ad07).
In the previous part, we created a baseline nlp model, we covered the basics of building a NLP model and ended up with an accuracy which is far from good. In this part, we are going to implement NLP model with LSTM architecture.
We will be seeing in detail, how a LSTM model works and how to implement it in our code.
Let's get started.
```
# Prerequisite Block 1
! pip install kaggle
! mkdir ~/.kaggle
! cp kaggle.json ~/.kaggle/
! chmod 600 ~/.kaggle/kaggle.json
! kaggle competitions download nlp-getting-started
# ! unzip nlp-getting-started.zip
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import re
import tensorflow as tf
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
def cleaningText(df):
df['text'] = [re.sub(r'http\S+', '', x, flags=re.MULTILINE) for x in df['text']]
df['text'] = df['text'].str.lower()
df = pd.read_csv('/content/train.csv')
df_test = pd.read_csv('/content/train.csv')
df.head()
cleaningText(df)
df.head()
sentences = [x for x in df['text']]
labels = [x for x in df['target']]
print(sentences)
labels = np.array(labels)
training_sentences = sentences[:6090]
training_labels = labels[:6090]
testing_sentences = sentences[6090:]
testing_labels = labels[6090:]
```
Now that we have taken the data from the table and converted it into sequences and labels. We will now convert the labels into numpy arrays. Then we will tokenize the words in sequences. The max length of a tweet is 280 characters. We will fix `max_length` to be **280**. The we will pad all the sentence to length. We will do `post_trunc`.
```
vocab_size = 10000
embedding_dim = 16
max_length = 280
trunc_type='post'
oov_tok = "<OOV>"
tokenizer = Tokenizer(num_words = vocab_size, oov_token=oov_tok)
tokenizer.fit_on_texts(training_sentences)
word_index = tokenizer.word_index
sequences = tokenizer.texts_to_sequences(training_sentences)
padded = pad_sequences(sequences,maxlen=max_length, truncating=trunc_type)
testing_sequences = tokenizer.texts_to_sequences(testing_sentences)
testing_padded = pad_sequences(testing_sequences,maxlen=max_length)
reverse_word_index = dict([(v, k) for (k, v) in word_index.items()])
def decode_tweet(text):
return ' '.join([reverse_word_index.get(i, '?') for i in text])
print(decode_tweet(padded[3]))
print(training_sentences[3])
```
Before we get to building our model, we need to understand what is an LSTM.
LSTM is a type of Recurrent Neural Network (RNN).
Traditional neural networks are called Feed-Forward Networks, information only flows in one direction.
Let us consider an example to see, why feed forward networks are not useful for NLP.
Consider the sentence:
"Hello, I am Gakuto Kajiwara, I am from Japan... I speak"
When we read this sentence, we can correctly predict that the next word is **japanese**.
This is possible because the word **japan** has importance on the prediction even though it is not the last word before prediction. It might even be a few sentences ahead.
The ability of a network to remember information learned in previous words to use it in future predictions is embedded in something called a **cell state**.
Cell state is implemented in RNN where the hidden layers are connected and information flows between them.
LSTMs are much better modifications on RNN, they leverage few activation functions and **gates**.
Gates have the ability to add or remove information from cell state.
For a much better deep dive read colah's blog on [LSTM](https://colah.github.io/posts/2015-08-Understanding-LSTMs/).
```
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size,embedding_dim,input_length = max_length),
tf.keras.layers.Dropout(rate = 0.25),
tf.keras.layers.LSTM(16,
activation = 'tanh',
recurrent_activation = 'sigmoid',
recurrent_dropout = 0.0),
tf.keras.layers.Dropout(rate = 0.25),
tf.keras.layers.Dense(1, activation = "sigmoid")
])
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
model.summary()
num_epochs = 10
model.fit( padded, training_labels,epochs = num_epochs, validation_data = (testing_padded, testing_labels))
```
We were able to get 75% validation accuracy, which is really good compared to our previous model.
| true |
code
| 0.549761 | null | null | null | null |
|
# Transformer的Keras实现
参考tensorflow的官方教程:[transformer](https://www.tensorflow.org/alpha/tutorials/sequences/transformer)
* tensorflow==2.0.0a
```
!pip install -q tensorflow==2.0.0a
!pip install -q matplotlib
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
tf.__version__
```
## positional encoding
$$PE_{pos, 2i} = sin(\frac{pos}{10000^{2i/d}})$$
$$PE_{pos, 2i+1} = cos(\frac{pos}{10000^{2i/d}})$$
```
def get_angles(pos, i, d_model):
angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
return pos * angle_rates
def positional_encoding(position, d_model):
angle_rads = get_angles(np.arange(position)[:, np.newaxis],
np.arange(d_model)[np.newaxis, :],
d_model)
# apply sin to even indices in the array; 2i
sines = np.sin(angle_rads[:, 0::2])
# apply cos to odd indices in the array; 2i+1
cosines = np.cos(angle_rads[:, 1::2])
pos_encoding = np.concatenate([sines, cosines], axis=-1)
pos_encoding = pos_encoding[np.newaxis, ...]
return tf.cast(pos_encoding, dtype=tf.float32)
pos_encoding = positional_encoding(50, 512)
print (pos_encoding.shape)
plt.pcolormesh(pos_encoding[0], cmap='RdBu')
plt.xlabel('Depth')
plt.xlim((0, 512))
plt.ylabel('Position')
plt.colorbar()
plt.show()
```
## Masking
maksing分为两种:
* padding masking,为了屏蔽对齐的时候补全的位置的词语的影响
* look ahead masking,为了屏蔽未来时间步的词语的影响
```
def create_padding_mask(seq):
seq = tf.cast(tf.math.equal(seq, 0), tf.float32)
# add extra dimensions so that we can add the padding
# to the attention logits.
return seq[:, tf.newaxis, tf.newaxis, :] # (batch_size, 1, 1, seq_len)
def create_look_ahead_mask(size):
mask = 1 - tf.linalg.band_part(tf.ones((size, size)), -1, 0)
return mask # (seq_len, seq_len)
print('padding mask test:')
x = tf.constant([[7, 6, 0, 0, 1], [1, 2, 3, 0, 0], [0, 0, 0, 4, 5]])
padding_mask = create_padding_mask(x)
print(padding_mask.shape)
print(padding_mask)
print('look ahead mask test:')
x = tf.random.uniform((1, 3))
temp = create_look_ahead_mask(x.shape[1])
print(temp.shape)
print(temp)
```
## Scaled dot-product attention
```
def scaled_dot_product_attention(q, k, v, mask):
"""Calculate the attention weights.
q, k, v must have matching leading dimensions.
The mask has different shapes depending on its type(padding or look ahead)
but it must be broadcastable for addition.
Args:
q: query shape == (..., seq_len_q, depth)
k: key shape == (..., seq_len_k, depth)
v: value shape == (..., seq_len_v, depth)
mask: Float tensor with shape broadcastable
to (..., seq_len_q, seq_len_k). Defaults to None.
Returns:
output, attention_weights
"""
matmul_qk = tf.matmul(q, k, transpose_b=True) # (..., seq_len_q, seq_len_k)
# scale matmul_qk
dk = tf.cast(tf.shape(k)[-1], tf.float32)
scaled_attention_logits = matmul_qk / tf.math.sqrt(dk)
# add the mask to the scaled tensor.
if mask is not None:
scaled_attention_logits += (mask * -1e9)
# softmax is normalized on the last axis (seq_len_k) so that the scores
# add up to 1.
attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1) # (..., seq_len_q, seq_len_k)
output = tf.matmul(attention_weights, v) # (..., seq_len_v, depth)
return output, attention_weights
def print_out(q, k, v):
temp_out, temp_attn = scaled_dot_product_attention(
q, k, v, None)
print ('Attention weights are:')
print (temp_attn)
print ('Output is:')
print (temp_out)
np.set_printoptions(suppress=True)
temp_k = tf.constant([[10,0,0],
[0,10,0],
[0,0,10],
[0,0,10]], dtype=tf.float32) # (4, 3)
temp_v = tf.constant([[ 1,0],
[ 10,0],
[ 100,5],
[1000,6]], dtype=tf.float32) # (4, 3)
# This `query` aligns with the second `key`,
# so the second `value` is returned.
temp_q = tf.constant([[0, 10, 0]], dtype=tf.float32) # (1, 3)
print_out(temp_q, temp_k, temp_v)
print()
# This query aligns with a repeated key (third and fourth),
# so all associated values get averaged.
temp_q = tf.constant([[0, 0, 10]], dtype=tf.float32) # (1, 3)
print_out(temp_q, temp_k, temp_v)
print()
# This query aligns equally with the first and second key,
# so their values get averaged.
temp_q = tf.constant([[10, 10, 0]], dtype=tf.float32) # (1, 3)
print_out(temp_q, temp_k, temp_v)
print()
temp_q = tf.constant([[0, 0, 10], [0, 10, 0], [10, 10, 0]], dtype=tf.float32) # (3, 3)
print_out(temp_q, temp_k, temp_v)
```
## Multi-head attention
```
class MultiHeadAttention(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads):
super(MultiHeadAttention, self).__init__()
self.num_heads = num_heads
self.d_model = d_model
assert d_model % self.num_heads == 0
self.depth = d_model // self.num_heads
self.wq = tf.keras.layers.Dense(d_model)
self.wk = tf.keras.layers.Dense(d_model)
self.wv = tf.keras.layers.Dense(d_model)
self.dense = tf.keras.layers.Dense(d_model)
def split_heads(self, x, batch_size):
"""Split the last dimension into (num_heads, depth).
Transpose the result such that the shape is (batch_size, num_heads, seq_len, depth)
"""
x = tf.reshape(x, (batch_size, -1, self.num_heads, self.depth))
return tf.transpose(x, perm=[0, 2, 1, 3])
def call(self, v, k, q, mask):
batch_size = tf.shape(q)[0]
q = self.wq(q) # (batch_size, seq_len, d_model)
k = self.wk(k) # (batch_size, seq_len, d_model)
v = self.wv(v) # (batch_size, seq_len, d_model)
q = self.split_heads(q, batch_size) # (batch_size, num_heads, seq_len_q, depth)
k = self.split_heads(k, batch_size) # (batch_size, num_heads, seq_len_k, depth)
v = self.split_heads(v, batch_size) # (batch_size, num_heads, seq_len_v, depth)
# scaled_attention.shape == (batch_size, num_heads, seq_len_v, depth)
# attention_weights.shape == (batch_size, num_heads, seq_len_q, seq_len_k)
scaled_attention, attention_weights = scaled_dot_product_attention(
q, k, v, mask)
scaled_attention = tf.transpose(scaled_attention, perm=[0, 2, 1, 3]) # (batch_size, seq_len_v, num_heads, depth)
concat_attention = tf.reshape(scaled_attention,
(batch_size, -1, self.d_model)) # (batch_size, seq_len_v, d_model)
output = self.dense(concat_attention) # (batch_size, seq_len_v, d_model)
return output, attention_weights
temp_mha = MultiHeadAttention(d_model=512, num_heads=8)
y = tf.random.uniform((1, 60, 512)) # (batch_size, encoder_sequence, d_model)
out, attn = temp_mha(y, k=y, q=y, mask=None)
out.shape, attn.shape
```
## Feed forward network
```
def point_wise_feed_forward_network(d_model, dff):
return tf.keras.Sequential([
tf.keras.layers.Dense(dff, activation='relu'), # (batch_size, seq_len, dff)
tf.keras.layers.Dense(d_model) # (batch_size, seq_len, d_model)
])
class PointWiseFeedForwardNetwork(tf.keras.Model):
def __init__(self, d_model, dff):
super(PointWiseFeedForwardNetwork, self).__init__(name='ffn')
self.d_model = d_model
self.dense_1 = tf.keras.layers.Dense(dff, activation='relu')
self.dense_2 = tf.keras.layers.Dense(d_model)
def call(self, x):
x = self.dense_1(x)
return self.dense_2(x)
def compute_output_shape(self, input_shape):
shapes = tf.shape(input_shape).as_list()
shapes[-1] = self.d_model
return tf.TensorShape(shapes)
sample_ffn = point_wise_feed_forward_network(512, 2048)
print(sample_ffn(tf.random.uniform((64, 50, 512))).shape)
print()
ffn = PointWiseFeedForwardNetwork(512, 2048)
print(ffn(tf.random.uniform((64, 50, 256))).shape)
```
## Encoder layer
```
class LayerNormalization(tf.keras.layers.Layer):
def __init__(self, epsilon=1e-6, **kwargs):
self.eps = epsilon
super(LayerNormalization, self).__init__(**kwargs)
def build(self, input_shape):
self.gamma = self.add_weight(name='gamma', shape=input_shape[-1:],
initializer=tf.keras.initializers.Ones(), trainable=True)
self.beta = self.add_weight(name='beta', shape=input_shape[-1:],
initializer=tf.keras.initializers.Zeros(), trainable=True)
super(LayerNormalization, self).build(input_shape)
def call(self, x):
mean = tf.keras.backend.mean(x, axis=-1, keepdims=True)
std = tf.keras.backend.std(x, axis=-1, keepdims=True)
return self.gamma * (x - mean) / (std + self.eps) + self.beta
def compute_output_shape(self, input_shape):
return input_shape
class EncoderLayer(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads, dff, rate=0.1):
super(EncoderLayer, self).__init__()
self.mha = MultiHeadAttention(d_model, num_heads)
self.ffn = point_wise_feed_forward_network(d_model, dff)
self.layernorm1 = LayerNormalization(epsilon=1e-6)
self.layernorm2 = LayerNormalization(epsilon=1e-6)
self.dropout1 = tf.keras.layers.Dropout(rate)
self.dropout2 = tf.keras.layers.Dropout(rate)
def call(self, x, training, mask):
attn_output, _ = self.mha(x, x, x, mask) # (batch_size, input_seq_len, d_model)
attn_output = self.dropout1(attn_output, training=training)
out1 = self.layernorm1(x + attn_output) # (batch_size, input_seq_len, d_model)
ffn_output = self.ffn(out1) # (batch_size, input_seq_len, d_model)
ffn_output = self.dropout2(ffn_output, training=training)
out2 = self.layernorm2(out1 + ffn_output) # (batch_size, input_seq_len, d_model)
return out2
sample_encoder_layer = EncoderLayer(512, 8, 2048)
sample_encoder_layer_output = sample_encoder_layer(
tf.random.uniform((64, 43, 512)), False, None)
sample_encoder_layer_output.shape # (batch_size, input_seq_len, d_model)
class Encoder(tf.keras.layers.Layer):
def __init__(self, num_layers, d_model, num_heads, dff, input_vocab_size,
rate=0.1):
super(Encoder, self).__init__()
self.d_model = d_model
self.num_layers = num_layers
self.embedding = tf.keras.layers.Embedding(input_vocab_size, d_model)
self.pos_encoding = positional_encoding(input_vocab_size, self.d_model)
self.enc_layers = [EncoderLayer(d_model, num_heads, dff, rate)
for _ in range(num_layers)]
self.dropout = tf.keras.layers.Dropout(rate)
def call(self, x, training, mask):
seq_len = tf.shape(x)[1]
# adding embedding and position encoding.
x = self.embedding(x) # (batch_size, input_seq_len, d_model)
x *= tf.math.sqrt(tf.cast(self.d_model, tf.float32))
x += self.pos_encoding[:, :seq_len, :]
x = self.dropout(x, training=training)
for i in range(self.num_layers):
x = self.enc_layers[i](x, training, mask)
return x # (batch_size, input_seq_len, d_model)
sample_encoder = Encoder(num_layers=2, d_model=512, num_heads=8,
dff=2048, input_vocab_size=8500)
sample_encoder_output = sample_encoder(tf.random.uniform((64, 62)),
training=False, mask=None)
print (sample_encoder_output.shape) # (batch_size, input_seq_len, d_model)
```
## Decoder layer
```
class DecoderLayer(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads, dff, rate=0.1):
super(DecoderLayer, self).__init__()
self.mha1 = MultiHeadAttention(d_model, num_heads)
self.mha2 = MultiHeadAttention(d_model, num_heads)
self.ffn = point_wise_feed_forward_network(d_model, dff)
self.layernorm1 = LayerNormalization(epsilon=1e-6)
self.layernorm2 = LayerNormalization(epsilon=1e-6)
self.layernorm3 = LayerNormalization(epsilon=1e-6)
self.dropout1 = tf.keras.layers.Dropout(rate)
self.dropout2 = tf.keras.layers.Dropout(rate)
self.dropout3 = tf.keras.layers.Dropout(rate)
def call(self, x, enc_output, training,
look_ahead_mask, padding_mask):
# enc_output.shape == (batch_size, input_seq_len, d_model)
attn1, attn_weights_block1 = self.mha1(x, x, x, look_ahead_mask) # (batch_size, target_seq_len, d_model)
attn1 = self.dropout1(attn1, training=training)
out1 = self.layernorm1(attn1 + x)
attn2, attn_weights_block2 = self.mha2(
enc_output, enc_output, out1, padding_mask) # (batch_size, target_seq_len, d_model)
attn2 = self.dropout2(attn2, training=training)
out2 = self.layernorm2(attn2 + out1) # (batch_size, target_seq_len, d_model)
ffn_output = self.ffn(out2) # (batch_size, target_seq_len, d_model)
ffn_output = self.dropout3(ffn_output, training=training)
out3 = self.layernorm3(ffn_output + out2) # (batch_size, target_seq_len, d_model)
return out3, attn_weights_block1, attn_weights_block2
sample_decoder_layer = DecoderLayer(512, 8, 2048)
sample_decoder_layer_output, _, _ = sample_decoder_layer(
tf.random.uniform((64, 50, 512)), sample_encoder_layer_output,
False, None, None)
sample_decoder_layer_output.shape # (batch_size, target_seq_len, d_model)
class Decoder(tf.keras.layers.Layer):
def __init__(self, num_layers, d_model, num_heads, dff, target_vocab_size,
rate=0.1):
super(Decoder, self).__init__()
self.d_model = d_model
self.num_layers = num_layers
self.embedding = tf.keras.layers.Embedding(target_vocab_size, d_model)
self.pos_encoding = positional_encoding(target_vocab_size, self.d_model)
self.dec_layers = [DecoderLayer(d_model, num_heads, dff, rate)
for _ in range(num_layers)]
self.dropout = tf.keras.layers.Dropout(rate)
def call(self, x, enc_output, training,
look_ahead_mask, padding_mask):
seq_len = tf.shape(x)[1]
attention_weights = {}
x = self.embedding(x) # (batch_size, target_seq_len, d_model)
x *= tf.math.sqrt(tf.cast(self.d_model, tf.float32))
x += self.pos_encoding[:, :seq_len, :]
x = self.dropout(x, training=training)
for i in range(self.num_layers):
x, block1, block2 = self.dec_layers[i](x, enc_output, training,
look_ahead_mask, padding_mask)
attention_weights['decoder_layer{}_block1'.format(i+1)] = block1
attention_weights['decoder_layer{}_block2'.format(i+1)] = block2
# x.shape == (batch_size, target_seq_len, d_model)
return x, attention_weights
sample_decoder = Decoder(num_layers=2, d_model=512, num_heads=8,
dff=2048, target_vocab_size=8000)
output, attn = sample_decoder(tf.random.uniform((64, 26)),
enc_output=sample_encoder_output,
training=False, look_ahead_mask=None,
padding_mask=None)
output.shape, attn['decoder_layer2_block2'].shape
```
## Transformer
```
class Transformer(tf.keras.Model):
def __init__(self, num_layers, d_model, num_heads, dff, input_vocab_size,
target_vocab_size, rate=0.1):
super(Transformer, self).__init__()
self.encoder = Encoder(num_layers, d_model, num_heads, dff,
input_vocab_size, rate)
self.decoder = Decoder(num_layers, d_model, num_heads, dff,
target_vocab_size, rate)
self.final_layer = tf.keras.layers.Dense(target_vocab_size)
def call(self, inp, tar, training, enc_padding_mask,
look_ahead_mask, dec_padding_mask):
enc_output = self.encoder(inp, training, enc_padding_mask) # (batch_size, inp_seq_len, d_model)
# dec_output.shape == (batch_size, tar_seq_len, d_model)
dec_output, attention_weights = self.decoder(
tar, enc_output, training, look_ahead_mask, dec_padding_mask)
final_output = self.final_layer(dec_output) # (batch_size, tar_seq_len, target_vocab_size)
return final_output, attention_weights
sample_transformer = Transformer(
num_layers=2, d_model=512, num_heads=8, dff=2048,
input_vocab_size=8500, target_vocab_size=8000)
temp_input = tf.random.uniform((64, 62))
temp_target = tf.random.uniform((64, 26))
fn_out, _ = sample_transformer(temp_input, temp_target, training=False,
enc_padding_mask=None,
look_ahead_mask=None,
dec_padding_mask=None)
fn_out.shape # (batch_size, tar_seq_len, target_vocab_size)
```
## HParams
```
num_layers = 4
d_model = 128
dff = 512
num_heads = 8
input_vocab_size = 100
target_vocab_size = 100
dropout_rate = 0.1
```
## Optimizer
```
class CustomSchedule(tf.keras.optimizers.schedules.LearningRateSchedule):
def __init__(self, d_model, warmup_steps=4000):
super(CustomSchedule, self).__init__()
self.d_model = d_model
self.d_model = tf.cast(self.d_model, tf.float32)
self.warmup_steps = warmup_steps
def __call__(self, step):
arg1 = tf.math.rsqrt(step)
arg2 = step * (self.warmup_steps ** -1.5)
return tf.math.rsqrt(self.d_model) * tf.math.minimum(arg1, arg2)
learning_rate = CustomSchedule(d_model)
optimizer = tf.keras.optimizers.Adam(learning_rate, beta_1=0.9, beta_2=0.98,
epsilon=1e-9)
temp_learning_rate_schedule = CustomSchedule(d_model)
plt.plot(temp_learning_rate_schedule(tf.range(40000, dtype=tf.float32)))
plt.ylabel("Learning Rate")
plt.xlabel("Train Step")
```
| true |
code
| 0.733874 | null | null | null | null |
|
# Metric learning for MIR coding demo (2)
# Training
## Enabling and testing the GPU
First, you'll need to enable GPUs for the notebook:
- Navigate to **Edit→Notebook** Settings
- select **GPU** from the **Hardware Accelerator** drop-down
Next, we'll confirm that we can connect to the GPU with tensorflow:
> Source: https://colab.research.google.com/notebooks/gpu.ipynb
```
%tensorflow_version 2.x
import tensorflow as tf
device_name = tf.test.gpu_device_name()
if device_name != '/device:GPU:0':
raise SystemError('GPU device not found')
print('Found GPU at: {}'.format(device_name))
print(f'TensorFlow version: {tf.__version__}')
```
## Preparing the dataset
```
# Install a Google Drive downloading tool
!pip install gdown
# Download the dataset
!gdown --id 1MycZ6p3Y4OPtQVQXddqbOOTi7f7Wh_8f
!gdown --id 17Yl_K84dbADoHude6v_ON6pGqsPCMPPA
# Extract mel-spectrograms
!tar zxf dim-sim_mel.tar.gz
```
## Importing packages
```
import json
import numpy as np
import tensorflow as tf
import tensorflow.keras.backend as K
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.callbacks import EarlyStopping, ReduceLROnPlateau, ModelCheckpoint, CSVLogger
from tensorflow.keras.layers import (Conv1D, MaxPool1D, BatchNormalization, GlobalAvgPool1D, Dense, dot,
Activation, Input, Flatten, Lambda, Embedding, Concatenate, Layer, Reshape)
from sklearn.preprocessing import normalize
```
## Loading the metadata
```
# Load json metadata
def load_json(file_name):
"""Load json."""
with open(file_name, 'r') as f:
data = json.load(f)
return data
trainset = load_json('dim-sim_all.json')
print(f'The number of training examples: {len(trainset)}')
```
## Creating data loaders
```
# Setup the batch size and compute steps
batch_size = 10
steps_per_epoch = int(len(trainset) / batch_size)
def data_loader(dataset):
"""Data loader."""
# IDs for dataset.
triplet_ids = list(dataset.keys())
# Generator.
count_triplet = 0
while True:
for batch_iter in range(0, steps_per_epoch * batch_size, batch_size):
if count_triplet > len(dataset) - batch_size:
count_triplet = 0
batch_x, batch_y = batch_triplet_loader(dataset, triplet_ids[count_triplet: count_triplet + batch_size])
count_triplet += batch_size
yield batch_x, batch_y
def mel_normalization(mel):
"""Normalization mel value."""
mel -= 0.20
mel /= 0.25
return mel
def batch_triplet_loader(dataset, triplet_ids):
"""Batch loader."""
anchor_col = []
positive_col = []
negative_col = []
for triplet_id in triplet_ids:
triplet = dataset[triplet_id]
anchor_mel = np.load('./dim-sim_mel/' + triplet['anchor']['id'] + '.npy')
positive_mel = np.load('./dim-sim_mel/' + triplet['positive']['id'] + '.npy')
negative_mel = np.load('./dim-sim_mel/' + triplet['negative']['id'] + '.npy')
# Normalize mel.
anchor_mel = mel_normalization(anchor_mel)
positive_mel = mel_normalization(positive_mel)
negative_mel = mel_normalization(negative_mel)
# Stack batch data.
anchor_col.append(anchor_mel)
positive_col.append(positive_mel)
negative_col.append(negative_mel)
# To array.
anchor_col = np.array(anchor_col)
positive_col = np.array(positive_col)
negative_col = np.array(negative_col)
batch_x = {
'anchor_input': anchor_col,
'positive_input': positive_col,
'negative_input': negative_col
}
batch_y = np.zeros((batch_size, 2))
batch_y[:, 0] = 1
return batch_x, batch_y
```
## Creating a backbone model
```
# Basic block.
def basic_block(x, num_features, fp_length):
x = Conv1D(num_features, fp_length, padding='same', use_bias=True, kernel_initializer='he_uniform')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = MaxPool1D(pool_size=fp_length, padding='valid')(x)
return x
# Backbone model.
num_frames = 130
x_in = Input(shape = (num_frames, 128))
x = basic_block(x_in, 64, 4)
x = basic_block(x, 64, 4)
x = basic_block(x, 64, 4)
x = basic_block(x, 64, 2)
x = GlobalAvgPool1D()(x)
backbone_model = Model(inputs=[x_in], outputs=[x], name='backbone')
backbone_model.summary()
```
## Creating a triplet model
```
# Triplet model.
anchor = Input(shape = (num_frames, 128), name='anchor_input')
positive = Input(shape = (num_frames, 128), name='positive_input')
negative = Input(shape = (num_frames, 128), name='negative_input')
anchor_embedding = backbone_model(anchor)
positive_embedding = backbone_model(positive)
negative_embedding = backbone_model(negative)
# Cosine similarity.
dist_fn = Lambda(lambda x: dot(x, axes=1, normalize=True))
dist_anchor_positive = dist_fn([anchor_embedding, positive_embedding])
dist_anchor_negative = dist_fn([anchor_embedding, negative_embedding])
# Stack the similarity scores [1,0] and triplet model.
similarity_scores = Lambda(lambda vects: K.stack(vects, axis=1))([dist_anchor_positive, dist_anchor_negative])
tripletmodel = Model(inputs=[anchor, positive, negative], outputs=similarity_scores, name='triplet')
tripletmodel.summary()
```
## Defining the triplet loss function
```
# Define the loss function
def triplet_hinge_loss(y_true, y_pred):
"""Triplet hinge loss."""
# Always the first dimension of the similarity score is true.
# Margin is set to 0.1
y_pos = y_pred[:, 0]
y_neg = y_pred[:, 1]
loss = K.mean(K.maximum(0., 0.1 + y_neg - y_pos))
return loss
```
## Training!
```
# Create an optimizer
optimizer = Adam(lr=0.001)
# Compile the model with the loss
tripletmodel.compile(optimizer, loss=triplet_hinge_loss)
# Kick off the training!
tripletmodel.fit(data_loader(trainset),
epochs=20,
verbose=1,
steps_per_epoch=steps_per_epoch,
)
```
---
# Evaluation
## Preparing input data
```
# Collect unique tracks.
track_ids = []
triplet_ids = list(trainset.keys())
for triplet_id in triplet_ids:
triplet = trainset[triplet_id]
anchor = triplet['anchor']['id']
positive = triplet['positive']['id']
negative = triplet['negative']['id']
track_ids.append(anchor)
track_ids.append(positive)
track_ids.append(negative)
# Load mel.
track_id_to_mel = {}
for track_id in track_ids:
mel = np.load('./dim-sim_mel/' + track_id + '.npy')
# Normalize mel.
mel = mel_normalization(mel)
mel = np.expand_dims(mel, axis=0)
track_id_to_mel[track_id] = mel
# Prepare input mel-spectrograms
mels = np.squeeze(np.array(list(track_id_to_mel.values())))
```
## Extracting embedding features
```
# Extract embedding features of the tracks
embedding_features = backbone_model.predict(mels, batch_size=64)
# Collect the embedding features
track_id_to_features = {}
for i, track_id in enumerate(track_ids):
track_id_to_features[track_id] = embedding_features[i]
```
## Computing distances and scores (triplet prediction)
```
# Define a distance function
def euclidean_distance(x1, x2):
return np.sqrt(np.maximum(np.sum(np.square(x1 - x2)), 1e-07))
# Define an evaluation metric
def calculate_accuracy(prediction, groundtruth):
y_true = np.argmax(groundtruth, axis=-1)
y_pred = np.argmin(prediction, axis=-1)
accuracy = float(sum(y_true == y_pred))/len(groundtruth)
return accuracy
# A placeholder array for triplet prediction
prediction = np.zeros((len(triplet_ids), 2))
# A placeholder array for the baseline
mel_prediction = np.zeros((len(triplet_ids), 2))
# Create a groundtruth array
groundtruth = np.zeros_like(prediction)
groundtruth[:, 0] = 1
# Compute distances and scores
for i in range(len(triplet_ids)):
triplet = trainset[triplet_ids[i]]
anchor = triplet['anchor']['id']
positive = triplet['positive']['id']
negative = triplet['negative']['id']
prediction[i, 0] = euclidean_distance(
np.squeeze(normalize(track_id_to_features[anchor].reshape(1, -1), 'l2')),
np.squeeze(normalize(track_id_to_features[positive].reshape(1, -1), 'l2'))
)
prediction[i, 1] = euclidean_distance(
np.squeeze(normalize(track_id_to_features[anchor].reshape(1, -1), 'l2')),
np.squeeze(normalize(track_id_to_features[negative].reshape(1, -1), 'l2'))
)
# mel similarity
mel_prediction[i, 0] = euclidean_distance(
np.squeeze(normalize(track_id_to_mel[anchor].flatten().reshape(1, -1), 'l2')),
np.squeeze(normalize(track_id_to_mel[positive].flatten().reshape(1, -1), 'l2'))
)
mel_prediction[i, 1] = euclidean_distance(
np.squeeze(normalize(track_id_to_mel[anchor].flatten().reshape(1, -1), 'l2')),
np.squeeze(normalize(track_id_to_mel[negative].flatten().reshape(1, -1), 'l2'))
)
accuracy = calculate_accuracy(prediction, groundtruth)
mel_accuracy = calculate_accuracy(mel_prediction, groundtruth)
print(f'Triplet model accuracy: {accuracy:.2f}')
print(f'Baseline accuracy : {mel_accuracy:.2f}')
```
| true |
code
| 0.727558 | null | null | null | null |
|
# Simple Line Plots
Perhaps the simplest of all plots is the visualization of a single function $y = f(x)$.
Here we will take a first look at creating a simple plot of this type.
As with all the following sections, we'll start by setting up the notebook for plotting and importing the packages we will use:
```
%matplotlib inline #magic Funcation
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np
plt.style.available
li = ['Solarize_Light2',
'_classic_test_patch', 'bmh', 'classic', 'dark_background', 'fast', 'fivethirtyeight', 'ggplot',
'grayscale', 'seaborn', 'seaborn-bright', 'seaborn-colorblind', 'seaborn-dark', 'seaborn-dark-palette',
'seaborn-darkgrid', 'seaborn-deep',
'seaborn-muted',
'seaborn-notebook',
'seaborn-paper',
'seaborn-pastel',
'seaborn-poster',
'seaborn-talk',
'seaborn-ticks',
'seaborn-white',
'seaborn-whitegrid',
'tableau-colorblind10']
for i in li:
fig = plt.figure()
plt.style.use(i)
ax=plt.axes()
```
For all Matplotlib plots, we start by creating a figure and an axes.
In their simplest form, a figure and axes can be created as follows:
```
fig = plt.figure()
ax = plt.axes()
```
In Matplotlib, the *figure* (an instance of the class ``plt.Figure``) can be thought of as a single container that contains all the objects representing axes, graphics, text, and labels.
The *axes* (an instance of the class ``plt.Axes``) is what we see above: a bounding box with ticks and labels, which will eventually contain the plot elements that make up our visualization.
Throughout this book, we'll commonly use the variable name ``fig`` to refer to a figure instance, and ``ax`` to refer to an axes instance or group of axes instances.
Once we have created an axes, we can use the ``ax.plot`` function to plot some data. Let's start with a simple sinusoid:
```
fig = plt.figure()
ax = plt.axes()
x = np.linspace(0, 10, 1000)
ax.plot(x, np.sin(x));
```
Alternatively, we can use the pylab interface and let the figure and axes be created for us in the background
(see [Two Interfaces for the Price of One](04.00-Introduction-To-Matplotlib.ipynb#Two-Interfaces-for-the-Price-of-One) for a discussion of these two interfaces):
```
plt.plot(x, np.sin(x));
```
If we want to create a single figure with multiple lines, we can simply call the ``plot`` function multiple times:
```
plt.plot(x, np.sin(x))
plt.plot(x, np.cos(x));
```
That's all there is to plotting simple functions in Matplotlib!
We'll now dive into some more details about how to control the appearance of the axes and lines.
## Adjusting the Plot: Line Colors and Styles
The first adjustment you might wish to make to a plot is to control the line colors and styles.
The ``plt.plot()`` function takes additional arguments that can be used to specify these.
To adjust the color, you can use the ``color`` keyword, which accepts a string argument representing virtually any imaginable color.
The color can be specified in a variety of ways:
```
plt.plot(x, np.sin(x - 0), color='blue') # specify color by name
plt.plot(x, np.sin(x - 1), color='g') # short color code (rgbcmyk)
plt.plot(x, np.sin(x - 2), color='0.75') # Grayscale between 0 and 1
plt.plot(x, np.sin(x - 3), color='#FFDD44') # Hex code (RRGGBB from 00 to FF)
plt.plot(x, np.sin(x - 4), color=(1.0,0.2,0.3)) # RGB tuple, values 0 to 1
plt.plot(x, np.sin(x - 5), color='chartreuse'); # all HTML color names supported
```
If no color is specified, Matplotlib will automatically cycle through a set of default colors for multiple lines.
Similarly, the line style can be adjusted using the ``linestyle`` or ``ls`` keyword:
```
plt.plot(x, x + 0, linestyle='solid')
plt.plot(x, x + 1, linestyle='dashed')
plt.plot(x, x + 2, linestyle='dashdot')
plt.plot(x, x + 3, linestyle='dotted');
# For short, you can use the following codes:
plt.plot(x, x + 4, linestyle='-') # solid
plt.plot(x, x + 5, linestyle='--') # dashed
plt.plot(x, x + 6, linestyle='-.') # dashdot
plt.plot(x, x + 7, linestyle=':'); # dotted
```
If you would like to be extremely terse, these ``linestyle`` and ``color`` codes can be combined into a single non-keyword argument to the ``plt.plot()`` function:
```
plt.plot(x, x + 0, '-g') # solid green
plt.plot(x, x + 1, '--c') # dashed cyan
plt.plot(x, x + 2, '-.k') # dashdot black
plt.plot(x, x + 3, ':r'); # dotted red
```
These single-character color codes reflect the standard abbreviations in the RGB (Red/Green/Blue) and CMYK (Cyan/Magenta/Yellow/blacK) color systems, commonly used for digital color graphics.
There are many other keyword arguments that can be used to fine-tune the appearance of the plot; for more details, I'd suggest viewing the docstring of the ``plt.plot()`` function using IPython's help tools (See [Help and Documentation in IPython](01.01-Help-And-Documentation.ipynb)).
## Adjusting the Plot: Axes Limits
Matplotlib does a decent job of choosing default axes limits for your plot, but sometimes it's nice to have finer control.
The most basic way to adjust axis limits is to use the ``plt.xlim()`` and ``plt.ylim()`` methods:
```
plt.plot(x, np.sin(x))
plt.xlim(-1, 11)
plt.ylim(-1.5, 1.5);
```
If for some reason you'd like either axis to be displayed in reverse, you can simply reverse the order of the arguments:
```
plt.plot(x, np.sin(x))
plt.xlim(10, 0)
plt.ylim(1.2, -1.2);
```
A useful related method is ``plt.axis()`` (note here the potential confusion between *axes* with an *e*, and *axis* with an *i*).
The ``plt.axis()`` method allows you to set the ``x`` and ``y`` limits with a single call, by passing a list which specifies ``[xmin, xmax, ymin, ymax]``:
```
plt.plot(x, np.sin(x))
plt.axis([-1, 11, -1.5, 1.5]);
```
The ``plt.axis()`` method goes even beyond this, allowing you to do things like automatically tighten the bounds around the current plot:
```
plt.plot(x, np.sin(x))
plt.axis('tight');
```
It allows even higher-level specifications, such as ensuring an equal aspect ratio so that on your screen, one unit in ``x`` is equal to one unit in ``y``:
```
plt.plot(x, np.sin(x))
plt.axis('equal');
```
For more information on axis limits and the other capabilities of the ``plt.axis`` method, refer to the ``plt.axis`` docstring.
## Labeling Plots
As the last piece of this section, we'll briefly look at the labeling of plots: titles, axis labels, and simple legends.
Titles and axis labels are the simplest such labels—there are methods that can be used to quickly set them:
```
plt.plot(x, np.sin(x))
plt.title("A Sine Curve")
plt.xlabel("x")
plt.ylabel("sin(x)");
```
The position, size, and style of these labels can be adjusted using optional arguments to the function.
For more information, see the Matplotlib documentation and the docstrings of each of these functions.
When multiple lines are being shown within a single axes, it can be useful to create a plot legend that labels each line type.
Again, Matplotlib has a built-in way of quickly creating such a legend.
It is done via the (you guessed it) ``plt.legend()`` method.
Though there are several valid ways of using this, I find it easiest to specify the label of each line using the ``label`` keyword of the plot function:
```
plt.plot(x, np.sin(x), '-g', label='sin(x)')
plt.plot(x, np.cos(x), ':b', label='cos(x)')
plt.axis('equal')
plt.legend();
```
As you can see, the ``plt.legend()`` function keeps track of the line style and color, and matches these with the correct label.
More information on specifying and formatting plot legends can be found in the ``plt.legend`` docstring; additionally, we will cover some more advanced legend options in [Customizing Plot Legends](04.06-Customizing-Legends.ipynb).
## Aside: Matplotlib Gotchas
While most ``plt`` functions translate directly to ``ax`` methods (such as ``plt.plot()`` → ``ax.plot()``, ``plt.legend()`` → ``ax.legend()``, etc.), this is not the case for all commands.
In particular, functions to set limits, labels, and titles are slightly modified.
For transitioning between MATLAB-style functions and object-oriented methods, make the following changes:
- ``plt.xlabel()`` → ``ax.set_xlabel()``
- ``plt.ylabel()`` → ``ax.set_ylabel()``
- ``plt.xlim()`` → ``ax.set_xlim()``
- ``plt.ylim()`` → ``ax.set_ylim()``
- ``plt.title()`` → ``ax.set_title()``
In the object-oriented interface to plotting, rather than calling these functions individually, it is often more convenient to use the ``ax.set()`` method to set all these properties at once:
```
ax = plt.axes()
ax.plot(x, np.sin(x))
ax.set(xlim=(0, 10), ylim=(-2, 2),
xlabel='x', ylabel='sin(x)',
title='A Simple Plot');
```
| true |
code
| 0.643945 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Tutorial #3: Deploy an image classification model for encrypted inferencing in Azure Container Instance (ACI)
This tutorial is **a new addition to the two-part series**. In the [previous tutorial](img-classification-part1-training.ipynb), you trained machine learning models and then registered a model in your workspace on the cloud.
Now, you're ready to deploy the model as a encrypted inferencing web service in [Azure Container Instances](https://docs.microsoft.com/azure/container-instances/) (ACI). A web service is an image, in this case a Docker image, that encapsulates the scoring logic and the model itself.
In this part of the tutorial, you use Azure Machine Learning service (Preview) to:
> * Set up your testing environment
> * Retrieve the model from your workspace
> * Test the model locally
> * Deploy the model to ACI
> * Test the deployed model
ACI is a great solution for testing and understanding the workflow. For scalable production deployments, consider using Azure Kubernetes Service. For more information, see [how to deploy and where](https://docs.microsoft.com/azure/machine-learning/service/how-to-deploy-and-where).
## Prerequisites
Complete the model training in the [Tutorial #1: Train an image classification model with Azure Machine Learning](train-models.ipynb) notebook.
```
# If you did NOT complete the tutorial, you can instead run this cell
# This will register a model and download the data needed for this tutorial
# These prerequisites are created in the training tutorial
# Feel free to skip this cell if you completed the training tutorial
# register a model
from azureml.core import Workspace
ws = Workspace.from_config()
from azureml.core.model import Model
model_name = "sklearn_mnist"
model = Model.register(model_path="sklearn_mnist_model.pkl",
model_name=model_name,
tags={"data": "mnist", "model": "classification"},
description="Mnist handwriting recognition",
workspace=ws)
```
### Setup the Environment
Add `encrypted-inference` package as a conda dependency
```
from azureml.core.environment import Environment
from azureml.core.conda_dependencies import CondaDependencies
# to install required packages
env = Environment('tutorial-encryption-env')
cd = CondaDependencies.create(pip_packages=['azureml-dataset-runtime[pandas,fuse]', 'azureml-defaults', 'azure-storage-blob', 'encrypted-inference==0.9'], conda_packages = ['scikit-learn==0.22.1'])
env.python.conda_dependencies = cd
# Register environment to re-use later
env.register(workspace = ws)
```
## Set up the environment
Start by setting up a testing environment.
### Import packages
Import the Python packages needed for this tutorial.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import azureml.core
# display the core SDK version number
print("Azure ML SDK Version: ", azureml.core.VERSION)
```
#### Install Homomorphic Encryption based library for Secure Inferencing
Our library is based on [Microsoft SEAL](https://github.com/Microsoft/SEAL) and pubished to [PyPi.org](https://pypi.org/project/encrypted-inference) as an easy to use package
```
!pip install encrypted-inference==0.9
```
## Deploy as web service
Deploy the model as a web service hosted in ACI.
To build the correct environment for ACI, provide the following:
* A scoring script to show how to use the model
* A configuration file to build the ACI
* The model you trained before
### Create scoring script
Create the scoring script, called score_encrypted.py, used by the web service call to show how to use the model.
You must include two required functions into the scoring script:
* The `init()` function, which typically loads the model into a global object. This function is run only once when the Docker container is started.
* The `run(input_data)` function uses the model to predict a value based on the input data. Inputs and outputs to the run typically use JSON for serialization and de-serialization, but other formats are supported. The function fetches homomorphic encryption based public keys that are uploaded by the service caller.
```
%%writefile score_encrypted.py
import json
import os
import pickle
import joblib
from azure.storage.blob import BlobServiceClient, BlobClient, ContainerClient, PublicAccess
from encrypted.inference.eiserver import EIServer
def init():
global model
# AZUREML_MODEL_DIR is an environment variable created during deployment.
# It is the path to the model folder (./azureml-models/$MODEL_NAME/$VERSION)
# For multiple models, it points to the folder containing all deployed models (./azureml-models)
model_path = os.path.join(os.getenv('AZUREML_MODEL_DIR'), 'sklearn_mnist_model.pkl')
model = joblib.load(model_path)
global server
server = EIServer(model.coef_, model.intercept_, verbose=True)
def run(raw_data):
json_properties = json.loads(raw_data)
key_id = json_properties['key_id']
conn_str = json_properties['conn_str']
container = json_properties['container']
data = json_properties['data']
# download the Galois keys from blob storage
#TODO optimize by caching the keys locally
blob_service_client = BlobServiceClient.from_connection_string(conn_str=conn_str)
blob_client = blob_service_client.get_blob_client(container=container, blob=key_id)
public_keys = blob_client.download_blob().readall()
result = {}
# make prediction
result = server.predict(data, public_keys)
# you can return any data type as long as it is JSON-serializable
return result
```
### Create configuration file
Create a deployment configuration file and specify the number of CPUs and gigabyte of RAM needed for your ACI container. While it depends on your model, the default of 1 core and 1 gigabyte of RAM is usually sufficient for many models. If you feel you need more later, you would have to recreate the image and redeploy the service.
```
from azureml.core.webservice import AciWebservice
aciconfig = AciWebservice.deploy_configuration(cpu_cores=1,
memory_gb=1,
tags={"data": "MNIST", "method" : "sklearn"},
description='Encrypted Predict MNIST with sklearn + SEAL')
```
### Deploy in ACI
Estimated time to complete: **about 2-5 minutes**
Configure the image and deploy. The following code goes through these steps:
1. Create environment object containing dependencies needed by the model using the environment file (`myenv.yml`)
1. Create inference configuration necessary to deploy the model as a web service using:
* The scoring file (`score_encrypted.py`)
* envrionment object created in previous step
1. Deploy the model to the ACI container.
1. Get the web service HTTP endpoint.
```
%%time
import uuid
from azureml.core.webservice import Webservice
from azureml.core.model import InferenceConfig
from azureml.core.environment import Environment
from azureml.core import Workspace
from azureml.core.model import Model
ws = Workspace.from_config()
model = Model(ws, 'sklearn_mnist')
myenv = Environment.get(workspace=ws, name="tutorial-encryption-env")
inference_config = InferenceConfig(entry_script="score_encrypted.py", environment=myenv)
service_name = 'sklearn-mnist-svc-' + str(uuid.uuid4())[:4]
service = Model.deploy(workspace=ws,
name=service_name,
models=[model],
inference_config=inference_config,
deployment_config=aciconfig)
service.wait_for_deployment(show_output=True)
```
Get the scoring web service's HTTP endpoint, which accepts REST client calls. This endpoint can be shared with anyone who wants to test the web service or integrate it into an application.
```
print(service.scoring_uri)
```
## Test the model
### Download test data
Download the test data to the **./data/** directory
```
import os
from azureml.core import Dataset
from azureml.opendatasets import MNIST
data_folder = os.path.join(os.getcwd(), 'data')
os.makedirs(data_folder, exist_ok=True)
mnist_file_dataset = MNIST.get_file_dataset()
mnist_file_dataset.download(data_folder, overwrite=True)
```
### Load test data
Load the test data from the **./data/** directory created during the training tutorial.
```
from utils import load_data
import os
import glob
data_folder = os.path.join(os.getcwd(), 'data')
# note we also shrink the intensity values (X) from 0-255 to 0-1. This helps the neural network converge faster
X_test = load_data(glob.glob(os.path.join(data_folder,"**/t10k-images-idx3-ubyte.gz"), recursive=True)[0], False) / 255.0
y_test = load_data(glob.glob(os.path.join(data_folder,"**/t10k-labels-idx1-ubyte.gz"), recursive=True)[0], True).reshape(-1)
```
### Predict test data
Feed the test dataset to the model to get predictions.
The following code goes through these steps:
1. Create our Homomorphic Encryption based client
1. Upload HE generated public keys
1. Encrypt the data
1. Send the data as JSON to the web service hosted in ACI.
1. Use the SDK's `run` API to invoke the service. You can also make raw calls using any HTTP tool such as curl.
#### Create our Homomorphic Encryption based client
Create a new EILinearRegressionClient and setup the public keys
```
from encrypted.inference.eiclient import EILinearRegressionClient
# Create a new Encrypted inference client and a new secret key.
edp = EILinearRegressionClient(verbose=True)
public_keys_blob, public_keys_data = edp.get_public_keys()
```
#### Upload HE generated public keys
Upload the public keys to the workspace default blob store. This will allow us to share the keys with the inference server
```
import azureml.core
from azureml.core import Workspace, Datastore
import os
ws = Workspace.from_config()
datastore = ws.get_default_datastore()
container_name=datastore.container_name
# Create a local file and write the keys to it
public_keys = open(public_keys_blob, "wb")
public_keys.write(public_keys_data)
public_keys.close()
# Upload the file to blob store
datastore.upload_files([public_keys_blob])
# Delete the local file
os.remove(public_keys_blob)
```
#### Encrypt the data
```
#choose any one sample from the test data
sample_index = 1
#encrypt the data
raw_data = edp.encrypt(X_test[sample_index])
```
#### Send the test data to the webservice hosted in ACI
Feed the test dataset to the model to get predictions. We will need to send the connection string to the blob storage where the public keys were uploaded
```
import json
from azureml.core import Webservice
service = Webservice(ws, service_name)
#pass the connection string for blob storage to give the server access to the uploaded public keys
conn_str_template = 'DefaultEndpointsProtocol={};AccountName={};AccountKey={};EndpointSuffix=core.windows.net'
conn_str = conn_str_template.format(datastore.protocol, datastore.account_name, datastore.account_key)
#build the json
data = json.dumps({"data": raw_data, "key_id" : public_keys_blob, "conn_str" : conn_str, "container" : container_name })
data = bytes(data, encoding='ASCII')
print ('Making an encrypted inference web service call ')
eresult = service.run(input_data=data)
print ('Received encrypted inference results')
```
#### Decrypt the data
Use the client to decrypt the results
```
import numpy as np
results = edp.decrypt(eresult)
print ('Decrypted the results ', results)
#Apply argmax to identify the prediction result
prediction = np.argmax(results)
print ( ' Prediction : ', prediction)
print ( ' Actual Label : ', y_test[sample_index])
```
## Clean up resources
To keep the resource group and workspace for other tutorials and exploration, you can delete only the ACI deployment using this API call:
```
service.delete()
```
If you're not going to use what you've created here, delete the resources you just created with this quickstart so you don't incur any charges. In the Azure portal, select and delete your resource group. You can also keep the resource group, but delete a single workspace by displaying the workspace properties and selecting the Delete button.
## Next steps
In this Azure Machine Learning tutorial, you used Python to:
> * Set up your testing environment
> * Retrieve the model from your workspace
> * Test the model locally
> * Deploy the model to ACI
> * Test the deployed model
You can also try out the [regression tutorial](regression-part1-data-prep.ipynb).

| true |
code
| 0.345312 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/ariG23498/G-SimCLR/blob/master/Imagenet_Subset/Vanilla_SimCLR/Linear_Evaluation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Imports and setup
```
import tensorflow as tf
print(tf.__version__)
!nvidia-smi
!pip install -q wandb
# Other imports
from sklearn.preprocessing import LabelEncoder
from tensorflow.keras.layers import *
from tensorflow.keras.models import *
import matplotlib.pyplot as plt
from imutils import paths
from tqdm import tqdm
import tensorflow as tf
import seaborn as sns
import numpy as np
import cv2
# Random seed fixation
tf.random.set_seed(666)
np.random.seed(666)
# Authorize wandb
import wandb
wandb.login()
from wandb.keras import WandbCallback
```
## Dataset gathering and preparation
```
# Gather dataset
!git clone https://github.com/thunderInfy/imagenet-5-categories
# Train and test image paths
train_images = list(paths.list_images("imagenet-5-categories/train"))
test_images = list(paths.list_images("imagenet-5-categories/test"))
print(len(train_images), len(test_images))
def prepare_images(image_paths):
images = []
labels = []
for image in tqdm(image_paths):
image_pixels = plt.imread(image)
image_pixels = cv2.resize(image_pixels, (224, 224))
image_pixels = image_pixels/255.
label = image.split("/")[2].split("_")[0]
images.append(image_pixels)
labels.append(label)
images = np.array(images)
labels = np.array(labels)
print(images.shape, labels.shape)
return images, labels
X_train, y_train = prepare_images(train_images)
X_test, y_test = prepare_images(test_images)
le = LabelEncoder()
y_train_enc = le.fit_transform(y_train)
y_test_enc = le.transform(y_test)
```
## Utilities
```
# Architecture utils
def get_resnet_simclr(hidden_1, hidden_2, hidden_3):
base_model = tf.keras.applications.ResNet50(include_top=False, weights=None, input_shape=(224, 224, 3))
base_model.trainable = True
inputs = Input((224, 224, 3))
h = base_model(inputs, training=False)
h = GlobalAveragePooling2D()(h)
projection_1 = Dense(hidden_1)(h)
projection_1 = Activation("relu")(projection_1)
projection_2 = Dense(hidden_2)(projection_1)
projection_2 = Activation("relu")(projection_2)
projection_3 = Dense(hidden_3)(projection_2)
resnet_simclr = Model(inputs, projection_3)
return resnet_simclr
!wget https://github.com/ariG23498/G-SimCLR/releases/download/v3.0/ImageNet_Subset_Deep_Autoencoder.zip
!unzip -qq ImageNet_Subset_Deep_Autoencoder.zip
resnet_simclr = tf.keras.models.load_model('ImageNet_Subset_Deep_Autoencoder/vanilla_simclr_imagenet_subset.h5')
resnet_simclr.summary()
def plot_training(H):
with plt.xkcd():
plt.plot(H.history["loss"], label="train_loss")
plt.plot(H.history["val_loss"], label="val_loss")
plt.plot(H.history["accuracy"], label="train_acc")
plt.plot(H.history["val_accuracy"], label="val_acc")
plt.title("Training Loss and Accuracy")
plt.xlabel("Epoch #")
plt.ylabel("Loss/Accuracy")
plt.legend(loc="lower left")
plt.show()
def get_linear_model(features):
linear_model = Sequential([Dense(5, input_shape=(features, ), activation="softmax")])
return linear_model
```
## Evaluation
```
resnet_simclr.layers[1].trainable = False
resnet_simclr.summary()
# Early Stopping to prevent overfitting
es = tf.keras.callbacks.EarlyStopping(monitor="val_loss", patience=2, verbose=2, restore_best_weights=True)
# These layers will not be trained during linear evaluation
resnet_simclr.layers[3].trainable = False
resnet_simclr.layers[5].trainable = False
# Encoder model with non-linear projections
projection = Model(resnet_simclr.input, resnet_simclr.layers[-2].output)
print(projection.summary())
# Extract train and test features
train_features = projection.predict(X_train)
test_features = projection.predict(X_test)
print(train_features.shape, test_features.shape)
# Initialize wandb
wandb.init(entity="g-simclr", project="g-simclr", id="imagenet-s-simclr-le-1")
# Linear model
linear_model = get_linear_model(128)
linear_model.compile(loss="sparse_categorical_crossentropy", metrics=["accuracy"],
optimizer="adam")
history = linear_model.fit(train_features, y_train_enc,
validation_data=(test_features, y_test_enc),
batch_size=64,
epochs=100,
callbacks=[es, WandbCallback()])
plot_training(history)
# Encoder model with lesser non-linearity
projection = Model(resnet_simclr.input, resnet_simclr.layers[-4].output)
print(projection.summary())
# Extract train and test features
train_features = projection.predict(X_train)
test_features = projection.predict(X_test)
print(train_features.shape, test_features.shape)
# Initialize wandb
wandb.init(entity="g-simclr", project="g-simclr", id="imagenet-s-simclr-le-2")
linear_model = get_linear_model(256)
linear_model.compile(loss="sparse_categorical_crossentropy", metrics=["accuracy"],
optimizer="adam")
history = linear_model.fit(train_features, y_train_enc,
validation_data=(test_features, y_test_enc),
batch_size=64,
epochs=35,
callbacks=[es, WandbCallback()])
plot_training(history)
# Encoder model with no projection
projection = Model(resnet_simclr.input, resnet_simclr.layers[-6].output)
print(projection.summary())
# Extract train and test features
train_features = projection.predict(X_train)
test_features = projection.predict(X_test)
print(train_features.shape, test_features.shape)
# Initialize wandb
wandb.init(entity="g-simclr", project="g-simclr", id="imagenet-s-simclr-le-3")
linear_model = get_linear_model(2048)
linear_model.compile(loss="sparse_categorical_crossentropy", metrics=["accuracy"],
optimizer="adam")
history = linear_model.fit(train_features, y_train_enc,
validation_data=(test_features, y_test_enc),
batch_size=64,
epochs=35,
callbacks=[es, WandbCallback()])
plot_training(history)
```
| true |
code
| 0.752289 | null | null | null | null |
|
```
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from decimal import *
import scipy.special
import scipy.stats
import scipy
import numpy
import math
import itertools
import sys
sys.version
```
# Out-of-band P2W attack evaluation
## P2W attack success probability within $ N $ total blocks (no attacker hash rate $\alpha$ )
* $\omega$ This denotes the hash rate of all bribed miners (or the hashrate of the attacker if applicable)
* $\beta = 1 -
\omega$ The hash rate of the nodes that keep on mining on the main chain i.e., Bob if all others switch
* $k$ The number of conirmations blocks required to catch up
* $N$ The total number of blocks that can be rewarded
A new block is appended to the *main chain* with probability:
$$
\dfrac{\beta}{\omega+\beta} = \beta
$$
A new block is appended to the *attack cahin* with probability:
$$
\dfrac{\omega}{\omega+\beta} = \omega
$$
All successful series of blocks up to the maximum number of blocks $ N - n $ are given by:
$$
\sum_{i=0}^{i \le N - k -1}
{
\left(\binom{k+2i}{i} - \binom{k+2i}{i-1}\right)
\cdot
{ \omega }^{k+1+i}
\cdot
{ \beta }^{i}
}
\,\,.
$$
```
# Attack probability of catching-up k blocks within N total blocks
def attack_prob(k,N,omega,beta=None):
if beta is None:
beta = 1 - omega
p = 0
#for i in range(0,N-k):
i = 0
while i <= N-k-1:
p += ( scipy.special.binom(k+2*i, i) - scipy.special.binom(k+2*i, i-1) ) * omega**(k+i+1) * beta**i
#print(i,p)
i += 1
return p
assert math.isclose(attack_prob(2,3,0.8,0.2),0.512)
assert math.isclose(attack_prob(2,4,0.8,0.2),0.7577600000000001)
assert math.isclose(attack_prob(2,5,0.8,0.2),0.8757248000000003)
assert math.isclose(attack_prob(2,6,0.8,0.2),0.9344450560000004)
assert math.isclose(attack_prob(2,7,0.8,0.2),0.9646440448000003)
attack_prob(2,3,0.8,0.2)
attack_prob(1,200,0.1)
attack_prob(k=6,N=6,omega=0.670)
attack_prob(k=6,N=7,omega=0.670)
# Get number of required total blocks s.t. attack success probability is met
def attack_N(k,omega,success_prob):
N = 0
prob = 0
while prob < success_prob:
#prob = probCalc_optimized.compute_prob(k, N, omega,beta=1-omega)
prob = attack_prob(k, N, omega,beta=1-omega)
N += 1
# the last N value produces the right prob not the current one, therefore -1
return N - 1
attack_N(k=6,omega=0.532,success_prob=0.995)
attack_N(k=6,omega=0.67,success_prob=0.995)
attack_N(k=6,omega=0.67,success_prob=1)
# calculate expected number of blocks in which attack is successful i.e., target sucess probability is reached with this amount of N
def attack_expected_estimate(k,N,omega,beta=None):
if beta is None:
beta = 1 - omega
P = 0
p = 0
e = 0
i = 0
while i <= N-k-1:
# Current success probability:
p = ( scipy.special.binom(k+2*i, i) - scipy.special.binom(k+2*i, i-1) ) * omega**(k+i+1) * beta**i
# Overall target success probability:
P += p
# Expected value:
# y is the real current value of blocks passed
# this is why we need to add k+1 to y
# to account for the k+1 in the formular and the loop condition
y = i+k+1
if math.isnan(p):
print("p isnan P=",P," e=",e)
return e
e += p * y
#print(P,p,i,y,e)
i += 1
p = 0
return e
math.ceil(attack_expected_estimate(k=6,N=41,omega=0.670))
math.ceil(attack_expected_estimate(k=6,N=265,omega=0.670))
math.ceil(attack_expected_estimate(k=6,N=500,omega=0.670))
math.ceil(attack_expected_estimate(k=6,N=500,omega=0.764))
math.ceil(attack_expected_estimate(k=6,N=500,omega=0.828))
math.ceil(attack_expected_estimate(k=6,N=500,omega=0.887))
import numpy as py
def simulate_race(p_omega = 0.670, # rational hashrate
k_v = 6,
runs = 1):
p_beta = 1-p_omega
i=0
results={"mblk":0,
"ablk":0,
"N":0}
while (i<runs):
achain = 0
mchain = k_v
#results["mblk"] = k_v
while(achain <= mchain):
values = np.random.choice([0,1],1,p=[p_beta,p_omega])
for v in values:
if v == 0:
mchain += 1
results["mblk"] += 1
else:
achain +=1
results["ablk"] += 1
results["N"] += 1
i += 1
return results
simulate_race()
runs=10**4
%time simulate_race(p_omega=0.532,runs=runs)["N"]/runs
runs=10**5
%time simulate_race(p_omega=0.670,runs=runs)["N"]/runs
runs=10**5
%time simulate_race(p_omega=0.764,runs=runs)["N"]/runs
runs=10**5
%time simulate_race(p_omega=0.828,runs=runs)["N"]/runs
runs=10**5
%time simulate_race(p_omega=0.887,runs=runs)["N"]/runs
runs=10**5
%time simulate_race(p_omega=0.999,runs=runs)["N"]/runs
def attack_expected(k,N,omega,beta=None,runs=10**3):
return math.ceil(simulate_race(p_omega=omega,runs=runs)["N"]/runs)
attack_expected(k=6,N=265,omega=0.670)
```
### Compare with classical catch-up
General catch up condition $ a_z $ from:
* https://arxiv.org/pdf/1402.2009.pdf
* https://bitcoin.org/bitcoin.pdf
Classical parameter names:
* $p$ = hashrate of the honest network
* $q$ = hashrate of the attacker
$$
p + q = 1
$$
* $n$ = number of confirmation blocks, including and on top of the block which includes the respective transaction which needs to be confirmed or double-spend respectively
The probability to **ever** catch-up if $ z $ blocks behind, where one block is added to $z$ when the honest miners find a block and one block is substracted from $ z $ when the attacker finds a block i.e.,
The catch-up probability is a simplification of the *recurrance relation*, where $ q = \alpha $ and $ p = \beta $, given as:
$$
\begin{align}
a_z &= p \cdot a_{z+1} + q \cdot a_{z-1} \\
&= min(q/q,1)^{max(z+1,0)}
\end{align}
$$
```
def catch_up(q,z):
if q >= 0.5:
return 1.0
return ( q/(1-q) )**(z+1)
```
With $ p \geq 0.5 $ of hashpower the attacker will always catch up:
```
assert catch_up(0.5,100)*100 == 100.0
catch_up(0.5,100)*100
```
With $ p < 0.5 $ of hashpower the probability drops exponentially with $ z $:
```
catch_up(0.49,6)*100
catch_up(0.49,12.5)*100
catch_up(0.49,25)*100
catch_up(0.49,50)*100
catch_up(0.49,100)*100
```
#### Comparision
```
# Probability to catch up 1 blocks i.e., 1 block behind in unlimited time/blocks
catch_up(q=0.33,z=1)*100
# Probability to catch up 1 blocks i.e., 1 block behind in (large) limited time/blocks
attack_prob(1,100,0.33)*100
# Probability to catch up 1 blocks i.e., 1 block behind in unlimited time/blocks
catch_up(q=0.66,z=1)*100
# Probability to catch up 1 blocks i.e., 1 block behind in limited time/blocks i.e., 12
attack_prob(1,12,0.66)*100
```
### Comparison of catching-up within $ N $ total blocks vs catching-up after $ \infty $ blocks
```
def fig_prob_to_catch_up():
fig, ax = plt.subplots(figsize=(16, 9))
# https://matplotlib.org/api/markers_api.html
marker = itertools.cycle(('o','v', '+', 's','.', ',', '*','1','D','x','^'))
omega = [ 0.1, 0.2, 0.33, 0.4, 0.5, 0.66 ]
N = np.arange(0,33)
color = itertools.cycle(( 'b','orange','c','r', 'g','darkviolet',))
"""
NUM_COLORS = len(omega)
cm = plt.get_cmap('gist_rainbow')
colors = [cm(1.*i/NUM_COLORS) for i in range(NUM_COLORS)]
color = iter(colors)
#ax.set_color_cycle([cm(1.*i/NUM_COLORS) for i in range(NUM_COLORS)])
"""
for o in reversed(omega):
current_color=next(color)
plt.plot(N, [ attack_prob(1,n,o)*100 for n in N ] , color=current_color, marker=next(marker), label=" $\omega$=" + str(o))
P = catch_up(o,1)*100
plt.plot([0, len(N)], [P, P], color=current_color, linestyle='--', linewidth=2)
plt.plot([2, 2], [-2, 100], color='k', linestyle='-', linewidth=4)
plt.plot([0, 100], [100, 100], color='k', linestyle='-', linewidth=4)
#plt.plot([0, 50], [50, 50], color='k', linestyle='--', linewidth=3)
# tidy up the figure
ax.grid(True)
#ax.legend(loc='center right', bbox_to_anchor=(0.8, 0.57))
ax.legend(loc='center right', bbox_to_anchor=(0.90, 0.30), framealpha=1, prop={'size': 24} )
#ax.set_title("Probability of catching-up 1 block after $ N $ total blocks")
ax.set_ylabel("Probability of catching-up in $ \% $ ", fontsize=28)
ax.set_xlabel("Number of blocks till catching up ($ N $)", fontsize=28)
ax.set_yscale('log'),
#ax.set_ylim([-1,81])
ax.set_yticks([1,5,10,25,50,75,100])
ax.get_yaxis().set_major_formatter(matplotlib.ticker.ScalarFormatter())
ax.set_xlim([0,len(N)-1])
# draw line at 0
#plt.plot([x1, x2], [y1, y2], color='k', linestyle='-', linewidth=2)
#plt.plot([0, 100], [0, 0], color='k', linestyle='--', linewidth=2)
#plt.yticks(np.arange(-1, 15, step=1))
plt.xticks(np.arange(0, len(N), step=2))
#plt.yscale('log')
plt.rcParams.update({'font.size': 23})
plt.rc('xtick', labelsize=24)
plt.rc('ytick', labelsize=24)
plt.savefig("plots/number_of_blocks_for_catching-up_z=1.png", bbox_inches='tight',dpi=100)
plt.show()
fig_prob_to_catch_up()
```
### P2W attack success probability plot
```
def fig_probability_success_after_at_most_N_steps():
fig, ax = plt.subplots(figsize=(16, 9))
# https://matplotlib.org/api/markers_api.html
marker = itertools.cycle((',','v', '+', 's','.', 'o', '*','1','D','x','^'))
x = np.arange(0, 36)
for omega in [0.33, 0.40, 0.49, 0.51, 0.6, 0.66, 0.75, 0.90, 1 ]:
plt.plot(x, [ attack_prob(6, N, omega,beta=1-omega) for N in x ] , marker=next(marker), label=" ω=" + str(omega))
# tidy up the figure
ax.grid(True)
#ax.legend(loc='center right', bbox_to_anchor=(0.8, 0.57))
ax.legend(loc='center right', bbox_to_anchor=(0.185, 0.57), framealpha=1, prop={'size': 20})
#ax.set_title("Attack success probability")
ax.set_xlabel("Number of steps/blocks (N) that the attack is funded", fontsize=28)
ax.set_ylabel("Attack success probability",fontsize=28)
ax.set_ylim([1e-10, 1])
ax.set_xlim([0,35])
#plt.yscale('log')
plt.rcParams.update({'font.size': 17})
plt.rc('xtick', labelsize=17)
plt.rc('ytick', labelsize=17)
plt.savefig("plots/attack_probability_no-hashrate_n=6_N=35.png", bbox_inches='tight', dpi=100) # sage image
plt.show()
fig_probability_success_after_at_most_N_steps()
# This figure compares against the probabilities mentioned in the whale attack paper
# https://www.cs.umd.edu/~jkatz/papers/whale-txs.pdf
def fig_probability_success_after_at_most_N_steps():
fig, ax = plt.subplots(figsize=(16, 9))
# https://matplotlib.org/api/markers_api.html
marker = itertools.cycle((',','v', '+', 's','.', 'o', '*','1','D','x','^'))
x = np.arange(0, 64)
for omega in [0.532, 0.670, 0.764, 0.828, 0.887, 0.931, 0.968, 0.999 ]:
plt.plot(x, [ attack_prob(6, N, omega,beta=1-omega) for N in x ] , marker=next(marker), label=" ω=" + "{:.3f}".format(omega))
# tidy up the figure
ax.grid(True)
#ax.legend(loc='center right', bbox_to_anchor=(0.8, 0.57))
ax.legend(loc='center right', bbox_to_anchor=(0.80, 0.30))
#ax.set_title("Attack success probability")
ax.set_xlabel("Max steps (N) that the attack can be funded")
ax.set_ylabel("Attack success probability")
ax.set_ylim([1e-10, 1])
ax.set_xlim([0,63])
#plt.yscale('log')
plt.rcParams.update({'font.size': 17})
plt.rc('xtick', labelsize=17)
plt.rc('ytick', labelsize=17)
plt.savefig("plots/attack_probability_no-hashrate_n=6_N=60.png", dpi=100) # sage image
plt.show()
fig_probability_success_after_at_most_N_steps()
```
## Costs of the attack
Transaction exclusion and ordering attack costs for $ \omega = 1 $:
```
N = 6 # duration of the attack
#reward = 12.5 # block reward
reward = 6.25 # block reward
fee = 2 # average fees rounded to 1 (see other notebook)
r_b = reward + fee
epsilon = 1 # bribe
c_operational = 0.5 # operational costs
f_B = N * ( r_b + epsilon ) + c_operational # required funds of the attacker which are payed in Ethereum
c_fail = N * r_b + c_operational
c_success = N * epsilon + c_operational
print("N = ",N)
print("c_operational = ",c_operational)
print("r_b = ",r_b)
print("epsilon = ",epsilon)
print("f_B = ",f_B)
print("c_fail = ",c_fail)
print("c_success = ",c_success)
```
Transaction revision,exclusion and ordering attack costs for $ \omega = 1 $:
https://en.bitcoin.it/wiki/Controlled_supply
```
k = 6 # security parameter of victim
N = k+1 # minimum N
#reward = 12.5 # block reward
#fee = 1 # average fees rounded to 1 (see other notebook)
reward = 6.25 # block reward
#reward = 12.5
fee = 2
r_b = reward + fee
epsilon = 1 # bribe per block
# epsilon = 0.0002 # min. bribe in BTC (smalest transferable value w.r. to tx fees)
c_operational = 0.5 # operational costs
exchangerate = 13_077.50
f_B = k * r_b + N * ( r_b + epsilon ) + c_operational # required funds of the attacker which are payed in Ethereum
c_fail = N * r_b + c_operational
c_success = k * r_b + N * epsilon + c_operational
print("k = ",k)
print("N = ",N)
print("c_operational = ",c_operational)
print("r_b = ",r_b)
print("epsilon = ",epsilon)
print("f_B = ",f_B, " BTC")
print(" = ","{:,}".format(f_B*exchangerate), " USD")
print("c_fail = ",c_fail, " BTC")
print(" = ","{:,}".format(c_fail*exchangerate), " USD")
print("c_success = ",c_success, " BTC")
print(" = ","{:,}".format(c_success*exchangerate), " USD")
```
We compare against https://www.cs.umd.edu/~jkatz/papers/whale-txs.pdf
```
# costs of an 0.532 percent whale attack transactions
# taken from https://www.cs.umd.edu/~jkatz/papers/whale-txs.pdf
print("{:.0f}".format(2.93e+23))
print("{:.2e}".format(2.93e+23))
```
### Big Table of P2W attack costs vs whale attack costs
```
bribe_per_block=1 # additional bribe epsilon
block_reward=6.25 # current block reward
#block_reward=12.5 # current block reward
#block_reward=25 # current block reward
block_fees_average=2 # current average fees per block
operational_costs=0.5
block_total= block_reward + block_fees_average
block_total_plus_bribe = block_total + bribe_per_block
success_prob = 0.9950
# success_prob = 0.99510916
print("""
\\begin{table}[]
\\centering
\\label{tab:costs}
\\begin{tabular}{c|c|c|c|c|c|c|c|c|c}
""")
print("$\omega$ \t& whale costs \t& \\makecell{p2w costs\\\\ fail} \t& \% whale \t& \\makecell{p2w costs\\\\ success} \t& \% whale \t& \\makecell{p2w costs\\\\ expected} & \\% whale & \\makecell{N\\\\ (w.c.)} & \makecell{N\\\\ (avg.)} \\\\")
print("\\hline")
# data from https://www.cs.umd.edu/~jkatz/papers/whale-txs.pdf
# (omega,k,BTC)
whale_omega_k_costs = [ (0.532,6,2.93e+23),
(0.670,6,999.79),
(0.764,6,768.09),
(0.828,6,1265.14),
(0.887,6,1205.00),
(0.931,6,1806.67),
(0.968,6,2178.58),
(0.999,6,2598.64) ]
# test values
"""
whale_omega_k_costs = [ (0.532,0,1),
(0.670,0,1),
(0.764,0,1),
(0.828,0,1),
(0.887,0,1),
(0.931,0,1),
(0.968,0,1),
(0.999,0,1),
(1.0,0,1)]
"""
for whale in whale_omega_k_costs:
N = 0
prob = 0
omega=whale[0]
k=whale[1]
whale_costs=whale[2]
N = attack_N(k,omega,success_prob)
# costs of failed attack
c_p2w_fail = N * block_total + operational_costs
# costs of successful p2w attack
c_p2w_succ = N*bribe_per_block + k*block_total + operational_costs
# calculated number of expected blocks
expected = math.ceil(attack_expected(k,N,omega,beta=1-omega))
c_p2w_exp = expected*bribe_per_block + k*block_total + operational_costs
"""
print("omega = {:.3f} prob = {:.3f} N = {:3.0f} c_p2w_succ = {:.8f} c_p2w_fail = {:.8f} bribe_per_block = {:2.0f}".format(omega,
prob,
N,
c_p2w_succ,
c_p2w_fail,
bribe_per_block))
"""
print("{:.3f} \t\t& {:.2f} \t& {:.0f} \t\t& {:.0f} \t\t& {:.2f} \t\t& {:2.0f} \t\t& {:.0f} \t\t& {:.2f} \t& {:2.0f} \\\\".format(omega,
whale_costs,
c_p2w_fail,
c_p2w_succ,
(c_p2w_succ/whale_costs)*100,
N,
c_p2w_exp,
(c_p2w_exp/whale_costs)*100,
expected ) )
N = 0
prob = 0
print("\end{tabular}")
print("\\caption{{Comparison of attack costs whale attack~\cite{{liao2017incentivizing}} for $ k_V = {:d} $, all costs given in BTC. For comparision different Bitcoin block reward epochs (12.5 and 6.25 BTC) are provided for our P2W attack, all with $ c_{{operational}} = {:.1f} $ BTC, and average fee per block of {:.0f} BTC and $ \epsilon = {:.0f} $ BTC.}}".format(k,operational_costs,block_fees_average,bribe_per_block))
print("\end{table}")
```
### Small Table of P2W attack costs vs whale attack costs
```
bribe_per_block=1 # additional bribe epsilon
block_fees_average=2 # current average fees per block
operational_costs=0.5 # operational costs of attack
success_prob = 0.9950 # success_prob = 0.99510916
# current block reward epoch
block_total_6= 6.25 + block_fees_average
block_total_6_plus_bribe = block_total_6 + bribe_per_block
# previous block reward epoch
block_total_12= 12.5 + block_fees_average
block_total_12_plus_bribe = block_total_12 + bribe_per_block
print("""
\\begin{table*}[]
\\centering
\\scriptsize
\\label{tab:costs}
\\begin{tabular}{c|c||c|c|c||c}
""")
print("""
\makecell{Rational \\\\ hashrate \\\\ $\\omega$} &
\makecell{Average whale attack costs \\\\ epoch reward $ 12.5 $ \\\\ $ c_{whale} $ in BTC} &
\makecell{P2W \\\\ epoch reward $ 12.5 $ \\\\ $ c_{expected} $ in BTC} &
\makecell{P2W cost \\\\ compared to whale } &
\makecell{P2W \\\\ $ N $ \\\\ average} &
\makecell{P2W \\\\ epoch reward $ 6.25 $ \\\\ $ c_{expected} $ in BTC} \\\\
""")
print("\\hline")
# data from https://www.cs.umd.edu/~jkatz/papers/whale-txs.pdf
# (omega,k,BTC)
whale_omega_k_costs = [ (0.532,6,2.93e+23),
(0.670,6,999.79),
(0.764,6,768.09),
(0.828,6,1265.14),
(0.887,6,1205.00),
(0.931,6,1806.67),
(0.968,6,2178.58),
(0.999,6,2598.64) ]
for whale in whale_omega_k_costs:
N = 0
prob = 0
omega=whale[0]
k=whale[1]
whale_costs=whale[2]
# calculate number of required block to reach target success_probability (close to one)
N = attack_N(k,omega,success_prob)
# calculated number of expected blocks
expected = math.ceil(attack_expected(k,N,omega,beta=1-omega))
# costs for block reward epoch 12.5
c_p2w_exp_12 = expected*bribe_per_block + k*block_total_12 + operational_costs
# costs for block reward epoch 6.25
c_p2w_exp_6 = expected*bribe_per_block + k*block_total_6 + operational_costs
print("{:.3f} \t\t& {:.2f} \t& {:.2f} \t\t& {:.2f}\% \t\t& {:d} \t\t& {:.2f} \\\\".format(
omega,
whale_costs,
c_p2w_exp_12,
(c_p2w_exp_12/whale_costs)*100,
expected,
c_p2w_exp_6) )
N = 0
prob = 0
print("\end{tabular}")
print("\\caption{{Comparison of attack costs for $ k_V = {:d} $, all costs given in BTC. The costs for the whale attack are the average from $ 10^6 $ simulation results provided in~\cite{{liao2017incentivizing}}. For comparision different Bitcoin block reward epochs (12.5 and 6.25 BTC) are provided for our P2W attack, all with $ c_{{operational}} = {:.1f} $ BTC, and average fee per block of {:.0f} BTC and a bribe $ \epsilon = {:.0f} $ BTC.}}".format(k,operational_costs,block_fees_average,bribe_per_block))
print("\end{table*}")
```
## Probability of Out-of-Band attack desynchronization
What is the probability that the two chains (funding and attack chain) desynchronize during an attack i.e.,
that two (or more) Bitcoin blocks are mined in close succession without an Ethereum block in between.
The time between Bitcoin as well as the time between Ethereum blocks is exponentially distributed.
Assuming constant difficulty and overall hashrate, Ethereum has a mean block interval i.e., an expected value $E(x)$ of $ 15 $ seconds, whereas Bitcoin has a mean block interval of $ 10\cdot 60 $ seconds.
$$
\begin{align}
E_{ETH}(x) &= 15 \\
E_{BTC}(x) &= 600
\end{align}
$$
$$
\begin{align}
P(X < x) &=
\begin{cases}
1 - \exp(-\lambda x) & x \geq 0, \\
0 & x < 0
\end{cases} \\
P(X \geq x) &= exp(-\lambda x)
\end{align}
$$
#### What is th probability that the time between two Bitcoin blocks is smaller than the mean Etheruem block interval?
What is the probability that the time between two Bitcoin blocks is less than the Ethereum mean block interval of 15 seconds?
<a id='p2in1'></a>
$$
\begin{align}
E_{BTC}(x) &= 600 \\
E_{ETH}(x) &= 15 \\
x &= 15 \\
\lambda &= \frac{1}{E_{BTC}(x)} \\
P(X < 15) &= 1 - e^{-\lambda \cdot x} \\
\end{align}
$$
```
import math
vlambda = 1/(10*60)
x = 15
P_leq_eth = 1 - math.e**( -vlambda * x)
print("The probability that the time between two Bitcoin blocks is less than 15 seconds is\n{} %".format(P_leq_eth * 100))
```
What is the probability that this happens within $ N $ Bitcoin blocks i.e.,
what is the probability that the time between two Bitcoin blocks is smaller than $ 16 $ seconds during $ N $ total Bitcoin blocks?
$$
\begin{align}
P(N) &= 1 - ( 1 - P(X < 15) ) ^ {N-1}
\end{align}
$$
```
N = 32
P_within_N_btc = 1 - ( 1 - P_leq_eth )**(N-1)
P_within_N_btc * 100
```
What is the probability that two new Bitcoin blocks arrive within less than 15 seconds each?
```
P_leq_eth * P_leq_eth * 100
```
#### What is the probability that $2,3,...$ Bitcoin blocks are found within the Ethereum mean block interval of 15 seconds?
We use a Poission point process, where the poission distribution parameter $ \Lambda = E(N=n) = \frac{t}{E_{BTC}(x)} $ referres to the expected value of the number of events happening within $ t $ time.
$$
\begin{align}
P(N=n) &= \frac{\Lambda^n}{n!} \cdot e^{-\Lambda} \\
\lambda &= \frac{1}{E_{BTC}(x)} = 1/600 \\
\Lambda &= E(N=n) = t/600 \\
t &= 15 \\
n &\in \{1,2,3,...\}
\end{align}
$$
Note that $ n=1 $ already stands for two sequential Bitcoin blocks since we assume Bitcoin and Ethereum start at the same point in time ($ n = 0 $) with a new block each. So if the first Bitcoin block is found before the mean Ethereum block interval we have it that two Bitcoin blocks have been found without a Ethereum block in between.
What is the probability that **exaclty** $ n $ Bitcoin blocks are found within the mean Etheruem block interval of $15$ seconds?
```
def P_n_within_t(n,t,E_x):
Lambda = t/E_x
P_n_within_t = ( ( Lambda**n )/( math.factorial(n) ) ) * math.e**( - Lambda )
return P_n_within_t
n = 1
E_x = 600
t = 15
P_n_within_t(n,t,E_x) * 100
# Double check with scipy
n = 1
E_x = 600
mu = t/E_x
assert scipy.stats.poisson.pmf(n,mu)*100 == P_n_within_t(n,t,E_x)*100
scipy.stats.poisson.pmf(n,mu) * 100
n = 2
t = 15
E_x = 600
P_n_within_t(n,t,E_x) * 100
```
What is the probability that **at least** $ n $ Bitcoin blocks are found within the mean Etheruem block interval of $15$ seconds?
Lets approximate the result first by iterating and adding the next values of $ n $ to get
the value for at least $ n $ blocks within time $ t $.
For $ n = 1 $ this should be approximately the same value as calculated previously for the probability that the time between two Bitcoin blocks is smaller than the Ethereum block intervall of $ 15 $ seconds i.e., $ 2.4690087971667385 \% $
[see here](#p2in1)
```
P_n_within_t(n,t,E_x) * 100 + P_n_within_t(2,15,600) * 100 # ...
# approximate the result by iterating and adding the next values of n
def P_at_least_n_within_t_approx(n,t,E_x,iterations=10):
p = 0
for i in range(n,n+iterations):
p += P_n_within_t(i,t,E_x)
return p
n = 1
t = 15
E_x = 600
P_at_least_n_within_t_approx(n,t,E_x) * 100
P_at_least_n_within_t_approx(2,15,600) * 100
P_n_within_t(2,15,600) * 100 # for comparison
P_at_least_n_within_t_approx(3,15,600) * 100
P_at_least_n_within_t_approx(4,15,600) * 100
P_at_least_n_within_t_approx(5,15,600) * 100
```
To accurately capture this case we use the complementary probability of the CDF of the Poisson Distribution.
We calulate the probability to find at least $ n $ blocks within time $ t $ and expected value $ E[x] $ as mean time between Bitcoin blocks.
Therefore $ \lambda = t/E[x] $ is the average number of events per interval.
We calculate the complementary probability for finding at most $ n-1 $ blocks as follows.
$$
\begin{align}
P(X > n) &= 1 - P(X \leq n-1) \\
P(X \leq n) &= F(x) = e^{-\lambda } \sum_{i=0}^{n-1} \frac{\lambda ^i}{i!}
\end{align}
$$
```
def P_at_least_n_within_t(n,t,E_x):
Lambda = t/E_x
p = 0
for i in range(0,n): # is equal to {0,...,n-1}
p += ( Lambda**i ) / ( math.factorial(i) )
return 1 - ( math.e**(-Lambda) * p )
n = 1
t = 15
E_x = 600
P_at_least_n_within_t(n,t,E_x) * 100
# Double check with scipy and complementary probability of cdf(0).
# i.e., the complement of the probability that 0 (or less) blocks are found during 15 seconds?
n = 0
E_x = 600
t = 15
mu = t/E_x
assert P_at_least_n_within_t(1,t,E_x) == (1 - scipy.stats.poisson(mu).cdf(0))
(1 - scipy.stats.poisson(mu).cdf(n)) * 100
# Double check with probability that the time between two Bitcoin blocks is
# less than 15 seconds.
n = 1
t = x = 15
E_x = 600
vlambda = 1/E_x
assert P_at_least_n_within_t(n,t,E_x) * 100 == (1 - math.e**( -vlambda * x) )*100
P_at_least_n_within_t(n,t,E_x) * 100
```
Double check this case by using the continous Erlang distribution.
We calulate the probability to find at least $ n $ blocks within time $ t $ and expected value $ E[x] $ as mean time between Bitcoin blocks as follows.
The probability that $ n $ (sometimes denoted $ k $ and refered to as "shape") events happen in time $ x $ when $ \lambda = 1/E[x] $ is the rate at which events happen. $ \mu = 1/\lambda $ is the reciprocal of the rate and sometimes refered to as "scale".
$$
\begin{align}
F(x) &= \begin{cases}
1 - e^{-\lambda x} \sum_{i=0}^{n-1} \frac{(\lambda x)^i}{i!} & x \geq 0, \\
0 & x < 0
\end{cases} \\
\end{align}
$$
```
def P_at_least_n_within_t_erlang(n,t,E_x):
Lambda = 1/E_x
x = t
p = 0
for i in range(0,n): # is equal to {0,...,n-1}
p += ( ( Lambda * x )**i ) / ( math.factorial(i) )
return 1 - ( math.e**(-Lambda*x) * p )
n = 1
t = 15
E_x = 600
assert P_at_least_n_within_t(n,t,E_x) * 100 == P_at_least_n_within_t_erlang(n,t,E_x) * 100
P_at_least_n_within_t_erlang(n,t,E_x) * 100
# Double check with scipy
n = 1
t = 15
E_x = 600
assert scipy.stats.erlang(a=n, scale=1/(1/E_x)).cdf(t) * 100 == scipy.stats.erlang(a=n, scale=E_x).cdf(t) * 100
scipy.stats.erlang(a=n, scale=E_x).cdf(t) * 100
n = 2
E_x = 600
t = 15
scipy.stats.erlang(a=n, scale=E_x).cdf(t) * 100
# Double check against complement of Poisson cdf
n = 2
E_x = 600
t = 15
mu = t/E_x
(1 - scipy.stats.poisson(mu).cdf(n-1)) * 100
n = 2
E_x = 600
t = 15
P_at_least_n_within_t_erlang(n,t,E_x) * 100
n = 2
t = 15
E_x = 600
P_at_least_n_within_t(n,t,E_x) * 100
n = 3
t = 15
E_x = 600
P_at_least_n_within_t(n,t,E_x) * 100
n = 4
t = 15
E_x = 600
P_at_least_n_within_t(n,t,E_x) * 100
```
What is the probability that this happens within $ N $ Bitcoin blocks i.e.,
what is the probability that the time between three Bitcoin blocks is smaller than $ 15 $ seconds during $ N $ total Bitcoin blocks.
$$
\begin{align}
P(N) &= 1 - ( 1 - P(n) ) ^ {\lceil N/n \rceil}
\end{align}
$$
Recall both chains start at the same moment in time therefore $ n = 1 $ already stands for two sequential Bitcoin blocks
```
N = 32
n = 1
P_at_leat_n_within_N = 1 - ( 1 - P_at_least_n_within_t(n,15,600) )**(math.ceil((N-1)/n))
P_at_leat_n_within_N * 100
# for comparision the less accurate value
N = 32
n = 1
P_n_within_N = 1 - ( 1 - P_n_within_t(n,15,600) )**(math.ceil((N-1)/n))
P_n_within_N * 100
# 3 Bitcoin blocks within 15 seconds over N total Bitcoin blocks
N = 32
n = 2
P_at_leat_n_within_N = 1 - ( 1 - P_at_least_n_within_t(n,15,600) )**(math.ceil((N-1)/n))
P_at_leat_n_within_N * 100
# 3 Bitcoin blocks within 15 seconds over N total Bitcoin blocks
N = 32
n = 2
P_at_least_n_within_N = 1 - ( 1 - P_at_least_n_within_t_erlang(n,15,600) )**(math.ceil((N-1)/n))
P_at_least_n_within_N * 100
N = 32
n = 3
P_at_leat_n_within_N = 1 - ( 1 - P_at_least_n_within_t(n,15,600) )**(math.ceil((N-1)/n))
P_at_leat_n_within_N * 100
N = 32
n = 4
P_at_leat_n_within_N = 1 - ( 1 - P_at_least_n_within_t(n,15,600) )**(math.ceil((N-1)/n))
P_at_leat_n_within_N * 100
```
#### Probability that the time between two Ethereum blocks is larger than the mean Bitcoin block interval
What is the probability that the time between two Ethereum blocks is larger than the Bitcoin mean block interval of 600 seconds?
$$
\begin{align}
E_{BTC}(x) &= 600 \\
E_{ETH}(x) &= 15 \\
x &= 600 \\
\lambda &= \frac{1}{E_{ETH}(x)} \\
P(X \geq x) &= e^{-\lambda \cdot x} \\
\end{align}
$$
```
import math
vlambda = 1/(15)
x = 600
P_gt_btc = math.e**( - vlambda * x )
P_gt_btc * 100
```
#### Probability that during a time period $ t $, a Bitcoin block is mined before an Ethereum block
Assuming both chains are synchronized and miners start their search for the next block at the same time on the respective chains.
What is that probability that during the whole time period the next Bitcoin block is mined before the next Etheruem block.
$$
\begin{align}
P_{ETH}(X \geq x) &= e^{-\frac{1}{15} \cdot x} \\
P_{BTC}(X < x) &= 1 - e^{-\frac{1}{600} \cdot (x+1)} \\
P(t) &= \sum_{i=0}^{t} P_{ETH}(X \geq x) \cdot P_{BTC}(X < x)
\end{align}
$$
```
# P_e(X >= x_1) * P_b(X < (x_1 + 1) ) + P_e(X >= x_2) * P_b(X < (x_2 + 1) + ...
def P_e(x,vbeta):
# P(X >= x)
vlambda = 1/vbeta
return math.e**( - vlambda * x )
def P_b(x,vbeta):
# P(X < (x+1))
vlambda = 1/vbeta
return 1 - math.e**( - vlambda * (x+1) )
t = 200
P = 0
for i in range(1,t):
#print("{:3}: {:8.7f}".format(i,P))
P += P_e(i,15) * P_b(i,600)
print("\nThe probability that a Bitcoin block arrives before an Ethereum block in an interval of {} seconds is\n {} %".format(t,P * 100))
```
### Simulation of desynchronization
Simulate the two chains and check if there ever occures a case where a sequence of Bitcoin blocks are mined without any Ethereuem block in between.
```
import numpy
vbeta_btc = 10*60 # mean time between Bitcoin blocks (whole network)
N_btc = 32 # Total number of Bitcoin block events for the attack
vlambda_btc = 1/vbeta_btc
rand_btc = numpy.random.exponential(vbeta_btc,N_btc)
print(rand_btc)
#print(np.cumsum(rand)) # sort values ascending
print(" lambda = ",vlambda_btc)
print(" E(x) (beta) = ",vbeta_btc)
print(" Var(x) = ",vbeta_btc**2)
import numpy
vbeta_eth = 15 # mean time between Ethereum blocks
N_eth = int( (sum(rand_btc).item() / vbeta_eth) + (sum(rand_btc).item() / vbeta_eth)*0.1 ) # Total number of Ethereum block events for the attack plus some extra margin
vlambda_eth = 1/vbeta_eth
rand_eth = numpy.random.exponential(vbeta_eth,N_eth)
print(rand_eth)
#print(np.cumsum(rand)) # sort values ascending
print(" len(rand_eth)= ",len(rand_eth))
print(" lambda = ",vlambda_eth)
print(" E(x) (beta) = ",vbeta_eth)
print(" Var(x) = ",vbeta_eth**2)
def find_block_in_the_middle(begin,end,input_list):
t = 0
for k in input_list:
t += k
if t > begin and t < end:
return True
if t > end:
return False
return False
def compare_chains(rand_btc_list,rand_eth_list,verbose=False,sequence=2):
"""
Check if a sequence of n bitcoin blocks exists which
is not interrupted by a ethereum block somewhere in between
"""
btc_time = 0
btc_blkcnt = 0
eth_time = 0
eth_blkcnt = 0
fail_cnt = 0
blkgap = 0
sequence = sequence - 1 # reduce sequence by one since we count additional blocks starting from current
begin_btc = 0
for i in range(0,len(rand_btc_list)):
begin_btc += rand_btc_list[i]
end_btc = begin_btc
if i+sequence < len(rand_btc_list):
for j in range(1,sequence+1):
pos = i+j
end_btc += rand_btc_list[pos]
if begin_btc != end_btc and not find_block_in_the_middle(begin_btc,end_btc,rand_eth_list):
if verbose:
esum = 0
for num,entry in enumerate(rand_eth_list):
esum += entry
if esum > begin_btc*0.8:
print("ETH: {:4d} : {:8.4f} += {:10.4f}".format(num,entry,esum))
if esum > end_btc:
break
print("inter: {} - {} begin: [{}] = {} end: [{}] = {}".format(begin_btc,
end_btc,
i,
rand_btc_list[i],
pos,
rand_btc_list[pos]))
esum = 0
for num,entry in enumerate(rand_btc_list):
esum += entry
if num >= i:
print("\tBTC: {:4d} : {:8.4f} += {:10.4f}".format(num,entry,esum))
if num > pos:
break
return "fail"
return "success"
rand_btc_list = rand_btc.tolist()
rand_eth_list = rand_eth.tolist()
compare_chains(rand_btc_list,rand_eth_list,True,sequence=1)
def simulate_chains(vbeta_btc,vbeta_eth,N_btc,verbose=False,sequence=2):
rand_btc = numpy.random.exponential(vbeta_btc,N_btc)
N_eth = int( (sum(rand_btc).item() / vbeta_eth) + (sum(rand_btc).item() / vbeta_eth)*0.33 ) # Total number of Ethereum block events for the attack plus some
rand_eth = numpy.random.exponential(vbeta_eth,N_eth)
rand_btc_list = rand_btc.tolist()
rand_eth_list = rand_eth.tolist()
return compare_chains(rand_btc_list,rand_eth_list,verbose,sequence)
simulate_chains(600,15,32,False)
from collections import Counter
def simulation_run(iterations,N_btc,sequence):
cnt = Counter()
for i in range(0,iterations):
cnt[simulate_chains(600,15,N_btc,False,sequence)] += 1
k1 = cnt.most_common(2)[0][0]
v1 = (cnt.most_common(2)[0][1]/iterations)*100
if len(cnt.most_common(2)) > 1:
k2 = cnt.most_common(2)[1][0]
v2 = (cnt.most_common(2)[1][1]/iterations)*100
else:
k2 = "fail"
v2 = 0
print("{:10}: {}\n{:10}: {}".format(k1,v1,k2,v2))
iterations = 100
N_btc = 32
sequence = 2
simulation_run(iterations,N_btc,sequence)
iterations = 10000
N_btc = 32
sequence = 2
simulation_run(iterations,N_btc,sequence)
# compare with calculated approximation
N = 32
P_within_N_btc = 1 - ( 1 - (1 - math.e**( -vlambda * x)) )**(N-1)
P_within_N_btc * 100
# compare with other calculated approximation
N = 32
n = 1
P_at_least_n_within_N = 1 - ( 1 - P_at_least_n_within_t(n,15,600) )**(math.ceil((N-1)/n))
P_at_least_n_within_N * 100
iterations = 10000
N_btc = 32
sequence = 3
simulation_run(iterations,N_btc,sequence)
# compare with calculated approximation
N = 32
n = 2
P_at_least_n_within_N = 1 - ( 1 - P_at_least_n_within_t(n,15,600) )**(math.ceil((N-1)/n))
P_at_least_n_within_N * 100
iterations = 10000
N_btc = 32
sequence = 4
simulation_run(iterations,N_btc,sequence)
# compare with calculated approximation
N = 32
n = 3
P_at_least_n_within_N = 1 - ( 1 - P_at_least_n_within_t(n,15,600) )**(math.ceil((N-1)/n))
P_at_least_n_within_N * 100
iterations = 10000
N_btc = 32
sequence = 5
simulation_run(iterations,N_btc,sequence)
iterations = 10000
N_btc = 32
sequence = 6
simulation_run(iterations,N_btc,sequence)
```
## Calculate some concreate values for P2W attacks
### precision limits
```
# approx smallest target probability (99,510916 %) which can be calculated for smallest omega form the
# whale attack paper (53,2%)
attack_N(k=6,omega=0.532,success_prob=0.99510916)
# for k=1 max target is 99,89713 %
attack_N(k=1,omega=0.532,success_prob=0.9989713)
# approx smallest omega which can be calculated with floats and target probability 99%
attack_N(k=1,omega=0.517,success_prob=0.99)
math.ceil(attack_expected(k=1,N=492,omega=0.52)) # expected number of blocks for this value
attack_prob(k=1,N=21,omega=0.517)*100 # Probability of success after that many extra rewarded blocks
21 * 10 / 60 # duration of the attack in hours (Bitcoin)
21 * 15 / 60 # duration of the attack in min. (Ethereum)
catch_up(0.33,1)
attack_N(k=1,omega=0.33,success_prob=0.24)
attack_expected(k=1,N=18,omega=0.24)
def attack_limits(k,omega):
if omega > 0.5:
max_P = 0.99
else:
max_P = round(catch_up(omega,k) - 0.005,3) # round down to xx.xx precent
max_N = attack_N(k,omega,success_prob=max_P)
exp_N = math.ceil(attack_expected(k,max_N,omega))
P = attack_prob(k,max_N,omega)
exp_P = attack_prob(k,exp_N,omega)
return (max_P,max_N,P,exp_N,exp_P)
attack_limits(k=1,omega=0.75)
attack_limits(k=1,omega=0.70)
attack_limits(k=1,omega=0.66)
attack_limits(k=1,omega=0.60)
attack_limits(k=1,omega=0.55)
attack_limits(k=1,omega=0.517)
attack_limits(k=1,omega=0.479)
attack_limits(k=1,omega=0.33)
attack_limits(k=2,omega=0.33)
attack_limits(k=1,omega=0.15)
attack_limits(k=1,omega=0.10)
```
| true |
code
| 0.487002 | null | null | null | null |
|
# Circuit optimization using PatternManager - example of QAOA for MaxCut
This notebook provides an example of minimizing the duration of a quantum circuit. In this notebook, a quantum circuit implementing an instance of Q.A.O.A. is used and the `PatternManager` tool will be used to minimize the duration of this circuit. Since the purpose of this notebook is to explain the optimization tool `PatternManager`, details on the implementation of the circuit are not explained.
In this notebook, a variational circuit is used to solve MaxCut for the graph printed below. Solving MaxCut for a graph $\mathcal{G} = (\mathcal{V}, \mathcal{E})$ consists in finding a subset $S$ of $\mathcal{V}$ such as the number of edges in $\mathcal{E}$ linking a vertex of $S$ to a vertex of $\mathcal{V} \backslash S$ is maximal.
<img src="images/graph.png" width="500px" height="auto" alt="Graph of interaction" title="Graph of interaction"/>
The circuit used in this example can be split in 3 parts:
1. An Hadamard gate on each qubit
2. For each pair of qubits $i$ and $j$, there is an E gate if and only if $i$ and $j$ are connected in the graph above
3. An $R_X$ on each qubit
An E gate can be defined by the following pattern:
<img src="images/E_gate.png" width="500px" height="auto" alt="Porte E" title="E gate definition"/>
Our circuit (limited to the first 8 qubits) looks like:
<img src="images/algo.png" width="750px" height="auto" alt="Algorithm" title="Algorithm limited to the first 8 qubits"/>
## Initial circuit
The circuit should be created before starting the optimization. The following code defines an abstract gate `E` corresponding to the definition above. The circuit is then defined using these `E` gates. Since `PatternManager` is used to optimize the depth of the circuit, the initial order of `E` corresponds to the order which maximize the duration of the circuit.
```
from qat.lang.AQASM import Program, H, CNOT, PH, RX, QRoutine
from qat.lang.AQASM.misc import build_gate
from qat.pbo.utils import depth
import numpy as np
# Define an abstract gate E
@build_gate("E", [float], 2)
def E(alpha):
"""
Build a E gate
"""
routine = QRoutine()
routine.apply(CNOT, [0, 1])
routine.apply(PH(alpha), [1])
routine.apply(CNOT, [0, 1])
# Define the worst order of E gates
edges = [(10, 15), (9, 15), (9, 14), (4, 9), (0, 4), (0, 5),
(1, 5), (5, 10), (10, 16), (11, 16), (11, 17),
(6, 11), (1, 6), (2, 6), (2, 7), (7, 12), (12, 17),
(12, 18), (13, 18), (8, 13), (3, 8)]
# Define program
prog = Program()
qbits = prog.qalloc(19)
alpha = prog.new_var(float, r"\alpha")
beta = prog.new_var(float, r"\beta")
# Wall of hadamard
for qb in qbits:
prog.apply(H, qb)
# E gates
for vertex_1, vertex_2 in edges:
prog.apply(E(alpha), qbits[vertex_1], qbits[vertex_2])
# Wall of RX
for qb in qbits:
prog.apply(RX(beta), qb)
# Get initial circ
initial_circ = prog.to_circ()
%qatdisplay initial_circ
```
## Using metrics
The tool `PatternManager` is used to optimize any *score function* given by the user. A *score function* is a function that that the user wants to maximize. The `qat.nnize` modules provide tools to define score functions.
The `DurationMetric` class can be used as a *score function*, this class will compute the opposite of the duration of the circuit (this tool computes the opposite of the duration because maximizing the opposite of the duration is equivalent to minimizing the duration: the opposition of the duration is then the metric we want to maximize).
In our example, each gate will have the same duration: 1 unit of time.
```
from qat.nnize.metrics import DurationMetric
# Define the metric
duration_metric = DurationMetric()
# Define the default duration
duration_metric.set_gate_time({"-DEFAULT-": 1})
# The metric have to compute the duration of the circuit
duration_metric.minimize_overall_time()
# Duration of the initial circuit
print("Duration of the initial circuit:",
-duration_metric(initial_circ))
```
## Circuit optimization
The optimization problem consists in maximizing the function `duration_metric`. This function is called **global metric**, the tool `PatternManager` will use this metric to perform the optimization.
Since E gates commutes on any qubits, few rules will be defined. The tool `PatternManager` will uses these rules to optimize the duration of the circuit. The rules are defined by:
<img src="images/patterns.png" width="500px" height="auto" alt="Rewriting rules" title="Patterns"/>
There are 3 commutation rules above, so 3 groups will be defined for the optimizer. A group is a set of equivalent patterns (i.e. a small subcircuit), the optimizer can replace any pattern in the circuit by a pattern of the same group. Groups define the action space of the optimizer.
`PatternManager` will use an heuristic to solve this optimization. Two different methods may be used:
- The gradient descent (use `"gradient"`) $\rightarrow$ Used by default
- The simulated annealing (use `"annealing"`) $\rightarrow$ Used here
```
from qat.pbo import PatternManager, VAR
from qat.lang.AQASM import AbstractGate
# Define the optimizer
manager = PatternManager(global_metric=duration_metric)
# Define abstract variables
theta = VAR()
gamma = VAR()
# Group 1 - first commutation rule
group1 = manager.new_group()
group1.add_pattern([('E', [1, 2], theta), ('E', [0, 1], gamma)])
group1.add_pattern([('E', [0, 1], gamma), ('E', [1, 2], theta)])
# Group 2 - second commutation rule
group2 = manager.new_group()
group2.add_pattern([('E', [0, 1], theta), ('E', [0, 2], gamma)])
group2.add_pattern([('E', [0, 2], gamma), ('E', [0, 1], theta)])
# Group 3 - third commutation rule
group3 = manager.new_group()
x3 = VAR()
group3.add_pattern([('E', [0, 2], theta), ('E', [1, 2], gamma)])
group3.add_pattern([('E', [1, 2], gamma), ('E', [0, 2], theta)])
```
The optimizer can be then called on the circuit to minimize the duration of the circuit. A trace can be passed to the optimizer to log the values of the metric during the optimization.
Since the E gate is not a common gate, the constructor of the E gate should be given to the optimizer.
```
# Create a trace list
trace = list()
# Add E gate constructor
manager.add_abstract_gate(E)
# Start optimization
final_circ = manager.replace_pattern(initial_circ, method='annealing', trace=trace)
# Print final circuit
print("Final duration:", -duration_metric(final_circ))
```
The trace of the optimization can be plotted using matplotlib.
```
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 5))
plt.xlabel("Nb iterations")
plt.ylabel("Duration")
plt.plot(range(len(trace)), [-depth for depth in trace])
plt.show()
```
# Compilation
Before starting compilation, E gates must be replaced by their implementation. The `GraphCircuit` tool will be used to replace `E` gates.
```
from qat.pbo import GraphCircuit
# Init graph circuit
theta = VAR()
graph = GraphCircuit()
graph.load_circuit(final_circ)
# Replace pattern
graph.replace_pattern(
[("E", [0, 1], theta)],
[("CNOT", [0, 1]), ("PH", [1], theta), ("CNOT", [0, 1])],
pos=all
)
# Get circuit
final_circ = graph.to_circ()
```
One wants to compile this optimized circuit on the Rigetti Forest 19Q. Only few gates may be used on this quantum computer. The allowed gates are:
- Gate $R_Z(x)$ for $x \in \mathbb{R}$
- Gate $R_X(x)$ for $x \in \left\{ \pm \pi, \pm \frac{\pi}{2} \right\}$ (these $R_X$ gates are called "compliant $R_X$")
- Gate $CZ$
Since our algorithm does not use these gates, some changes may be defined. `PatternManager` may be used to solve this optimization problem. It is possible to define patterns which must disappear.
- The gate $PH$ must disappear: $PH(x) \rightarrow R_Z(x)$
- The gate $H$ must disappear: $H \rightarrow R_Z \left (\frac{\pi}{2} \right) \cdot R_X \left (\frac{\pi}{2} \right) \cdot R_Z \left (\frac{\pi}{2} \right)$
- The gate $CNOT$ must disappear $CNOT \rightarrow \left(\mathbb{1} \otimes H \right) \cdot CZ \cdot \left(\mathbb{1} \otimes H \right)$
### Groups
**Group 1** Only non-compliant $R_X(x)$ are transformed into $H \cdot R_Z(x) \cdot H$
**Group 2** $PH(x)$ gates are replaced by $R_Z(x)$ gates
**Group 3** $CNOT$ gates are replaced by $(\mathbb{1} \otimes H) \cdot CZ \cdot (\mathbb{1} \otimes H)$
**Group 4** $H$ gates are replaced by $R_Z \left (\frac{\pi}{2} \right) \cdot R_X \left (\frac{\pi}{2} \right) \cdot R_Z \left (\frac{\pi}{2} \right)$
```
from math import pi
# Define a compiler: no metric needed
compiler = PatternManager()
theta = VAR()
# Group 1: remove non compliant RX gates
constraint_angle = VAR()
for angle in [pi, -pi, pi/2, -pi/2]:
constraint_angle.add_prohibited_value(angle)
group_1 = compiler.new_group()
group_1.pattern_to_remove([("RX", [0], constraint_angle)])
group_1.add_pattern([("H", [0]), ("RZ", [0], constraint_angle), ("H", [0])])
# Group 2: remove PH gate
group_2 = compiler.new_group()
group_2.pattern_to_remove([("PH", [0], theta)])
group_2.add_pattern([("RZ", [0], theta)])
# Group 3: remove CNOT
group_3 = compiler.new_group()
group_3.pattern_to_remove([("CNOT", [0, 1])])
group_3.add_pattern([("H", [1]), ("CSIGN", [0, 1]), ("H", [1])])
# Group 4: remove H
group_4 = compiler.new_group()
group_4.pattern_to_remove([("H", [0])])
group_4.add_pattern([("RZ", [0], pi/2), ("RX", [0], pi/2), ("RZ", [0], pi/2)])
```
The object `compiler` can used to compile our circuit. Moreover, this object is also a plugin, it can be linked to any QPU.
## Checking compilation
First, a function which print the gate set will be used to check the compilation output:
```
from qat.core.util import extract_syntax
def print_gate_set(circuit):
gate_set = set()
for operator in circuit.ops:
name, params = extract_syntax(
circuit.gateDic[operator.gate],
circuit.gateDic
)
gate_set.add((name, *params))
print(gate_set)
```
Then, our compiler can compile our circuit using:
- in the first example, RX gates with accepted angles
- in the second example, RX gates with non-accepted angles
```
# Case 1: using RX gates with accepted angles
first_circ = compiler.replace_pattern(
final_circ.bind_variables({r"\alpha": pi/4, r"\beta": pi})
)
print("\nCase 1 with compliant RX")
print_gate_set(first_circ)
# Case 2: using RX gates with non accepted angles
second_circ = compiler.replace_pattern(
final_circ.bind_variables({r"\alpha": pi/4, r"\beta": pi/6})
)
print("\nCase 2 with non-compliant RX")
print_gate_set(second_circ)
```
| true |
code
| 0.580114 | null | null | null | null |
|
# Simple Reinforcement Learning in Tensorflow Part 1:
## The Multi-armed bandit
This tutorial contains a simple example of how to build a policy-gradient based agent that can solve the multi-armed bandit problem. For more information, see this [Medium post](https://medium.com/@awjuliani/super-simple-reinforcement-learning-tutorial-part-1-fd544fab149).
For more Reinforcement Learning algorithms, including DQN and Model-based learning in Tensorflow, see my Github repo, [DeepRL-Agents](https://github.com/awjuliani/DeepRL-Agents).
```
import tensorflow as tf
import tensorflow.contrib.slim as slim
import numpy as np
```
### The Bandit
Here we define our bandit. For this example we are using a four-armed bandit. The pullBandit function generates a random number from a normal distribution with a mean of 0. The lower the bandit number, the more likely a positive reward will be returned. We want our agent to learn to always choose the arm that will give that positive reward.
```
#List out our bandit arms.
#Currently arm 4 (index #3) is set to most often provide a positive reward.
bandit_arms = [0.2,0,-0.2,-2]
num_arms = len(bandit_arms)
def pullBandit(bandit):
#Get a random number.
result = np.random.randn(1)
if result > bandit:
#return a positive reward.
return 1
else:
#return a negative reward.
return -1
```
### The Agent
The code below established our simple neural agent. It consists of a set of values for each of the bandit arms. Each value is an estimate of the value of the return from choosing the bandit. We use a policy gradient method to update the agent by moving the value for the selected action toward the recieved reward.
```
tf.reset_default_graph()
#These two lines established the feed-forward part of the network.
weights = tf.Variable(tf.ones([num_arms]))
output = tf.nn.softmax(weights)
#The next six lines establish the training proceedure. We feed the reward and chosen action into the network
#to compute the loss, and use it to update the network.
reward_holder = tf.placeholder(shape=[1],dtype=tf.float32)
action_holder = tf.placeholder(shape=[1],dtype=tf.int32)
responsible_output = tf.slice(output,action_holder,[1])
loss = -(tf.log(responsible_output)*reward_holder)
optimizer = tf.train.AdamOptimizer(learning_rate=1e-3)
update = optimizer.minimize(loss)
```
### Training the Agent
We will train our agent by taking actions in our environment, and recieving rewards. Using the rewards and actions, we can know how to properly update our network in order to more often choose actions that will yield the highest rewards over time.
```
total_episodes = 1000 #Set total number of episodes to train agent on.
total_reward = np.zeros(num_arms) #Set scoreboard for bandit arms to 0.
init = tf.global_variables_initializer()
# Launch the tensorflow graph
with tf.Session() as sess:
sess.run(init)
i = 0
while i < total_episodes:
#Choose action according to Boltzmann distribution.
actions = sess.run(output)
a = np.random.choice(actions,p=actions)
action = np.argmax(actions == a)
reward = pullBandit(bandit_arms[action]) #Get our reward from picking one of the bandit arms.
#Update the network.
_,resp,ww = sess.run([update,responsible_output,weights], feed_dict={reward_holder:[reward],action_holder:[action]})
#Update our running tally of scores.
total_reward[action] += reward
if i % 50 == 0:
print "Running reward for the " + str(num_arms) + " arms of the bandit: " + str(total_reward)
i+=1
print "\nThe agent thinks arm " + str(np.argmax(ww)+1) + " is the most promising...."
if np.argmax(ww) == np.argmax(-np.array(bandit_arms)):
print "...and it was right!"
else:
print "...and it was wrong!"
```
| true |
code
| 0.459925 | null | null | null | null |
|
## Largest Product of Three from List
Given a list of integers, return the largest product that can be made by multiplying any three integers. For example, if the list is [-10,-10,5,2] you should return 500. You can assume that the list has at least three integers.
```
# If the list is all positive, then it's trivial. Just sort and then multiply
import numpy as np
lst = [np.random.randint(1,30) for i in range(50)]
print(lst)
# Could use number_list.sort() if you want without assigning to a new_list
def product_naive(number_list):
new_list = sorted(number_list, reverse = True)
product = new_list[0] * new_list[1] * new_list[2]
return product
product_naive(lst) # nice works
```
Now what can you do if there are negative numbers? Maybe start from the beginning and end of a sorted list .. Because we know that there are three numbers, we know that we need at least two negative numbers or else we're in trouble.
```
def product_three(number_list):
new_list = sorted(number_list, reverse = True)
# there are really only two combinations here that make sense...
# the product has to be the last 2 negative numbers and the largest positive
# or it has to be the three largest numbers in the front
positive_product = new_list[0] * new_list[1] * new_list[2]
mixed_product = new_list[0] * new_list[len(new_list)-1] * new_list[len(new_list)-2]
# alternatively you could use new_list[-1] instead of len(new_list)-1 .....
if positive_product > mixed_product:
return positive_product
else:
return mixed_product
product_three(lst)
if product_three(lst) == product_naive(lst):
print("TRUE")
example = [-10,-10,5,2]
product_three(example)
```
### This is kind of unsatisfying because it abuses the fact that we have three numbers.
And so it might not generalize well outside ...
### This also runs in O(N logN) time since we have to sort the input array... yikes
To do this faster you should use select. This requires us to use the math library.
```
from math import inf
def maximum_product(lst):
max1, max2, max3, min1, min2 = -inf, -inf, -inf, inf, inf
for x in lst:
if x > max1:
max3 = max2
max2 = max1
max1 = x
elif x > max2:
max3 = max2
max2 = x
elif x > max3:
max3 = x
if x < min1:
min2 = min1
min1 = x
elif x < min2:
min2 = x
return max(max1 * max2 * max3, max1 * min1 * min2)
```
| true |
code
| 0.320422 | null | null | null | null |
|
# Importing the libraries
```
import numpy as np
import pandas as pd
import statsmodels.formula.api as sm
```
# Load Data
```
dataset=pd.read_csv('OnlineRetail.csv',encoding='latin1')
dataset.head()
dataset.describe()
dataset.info()
```
# Data Preprocessing
We are going to analysis the Customers based on below 3 factors:
+ R (Recency): Number of days since last purchase
+ F (Frequency): Number of tracsactions
+ M (Monetary): Total amount of transactions (revenue contributed)
```
# Add New attribute Amount
dataset['Amount']= dataset['Quantity']*dataset['UnitPrice']
dataset.head()
```
Pandas datetimeindex provides efficient way to extract year, month or day from string format date.
docs: https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DatetimeIndex.html
You can also use the formula (dataset['InvoiceDate'] - pd.Timestamp("1970-01-01")) // pd.Timedelta('1s') to calculate unixtime
```
# Convert date to unixtime
dataset['InvoiceDate']= pd.to_datetime(dataset['InvoiceDate'])
dataset['InvoiceDate']=(dataset['InvoiceDate'] - pd.Timestamp("1970-01-01")) // pd.Timedelta('1s')
dataset.head()
# Add New attribute Recency
max_date=max(dataset['InvoiceDate'])
print(max_date)
dataset['timeDiff']= max_date - dataset['InvoiceDate']
dataset.head()
# drop columns which are not used for segmentation
df = dataset.drop(['StockCode', 'Description','Quantity', 'UnitPrice','InvoiceDate'], axis=1)
df.head()
# aggregate amount based on CustomerID
amt_df = df.groupby('CustomerID')['Amount'].sum()
amt_df.head()
# get count of Invoices for the CustomerID
fre_df = df.groupby('CustomerID')['InvoiceNo'].count()
fre_df.head()
# get most recent transation of the customer
rec_df = df.groupby('CustomerID')['timeDiff'].min() # last transaction
rec_df.head()
# Create a dataframe with only required fields. We do this by merging the amt_df, fre_df and rec_df dataframe
data = pd.merge(amt_df,fre_df,on='CustomerID',how='inner')
data.head()
data = pd.merge(data,rec_df,on='CustomerID',how='inner')
data.head()
# Rename the columns to Frequency and Recency
data = data.rename(columns={"InvoiceNo": "Frequency", "timeDiff": "Recency"})
data.head()
# verify the data type
numerical = [var for var in data.columns if data[var].dtype!='O']
print('There are {} numerical variables : \n'.format(len(numerical)), numerical)
categorical = [var for var in data.columns if data[var].dtype=='O']
print('There are {} categorical variables : \n'.format(len(categorical)), categorical)
# view summary statistics in numerical variables
print(round(data[numerical].describe()),2)
# Check for Nan
data[data.isnull().any(axis=1)]
```
# Build Model
```
# Encoding data
from sklearn.preprocessing import StandardScaler
scaleddata = StandardScaler().fit_transform(data)
```
# K-means clustering
```
from sklearn.cluster import KMeans
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score
#for loop to run k means with different no of clusters. we will find WCSS for all of them. WSCC =sum of square of the diff of each point to the centroid of the cluster. And draw graph with WCSS vs no of clusters
wcss=[]
for clusterCount in range(2,12):
kmeans = KMeans(n_clusters=clusterCount, init='k-means++',random_state=42)
kmeans.fit(scaleddata)
wcss.append(kmeans.inertia_)#get wcss
clusterLabels = kmeans.labels_
silhouette_avg = silhouette_score(scaleddata,clusterLabels)
print("For n_clusters={0}, the silhouette score is {1}".format(clusterCount, silhouette_avg))
plt.plot(range(2,12) # x axis
,wcss) # y axis
plt.title('The Elbow Curve')
plt.xlabel('Number of Clusters')
plt.ylabel('WCSS')
plt.show()
```
Max silhouette score is for 2 clusters. we pick the next highest score which is for 5 clusters.
```
cluster = KMeans(n_clusters=5, init='k-means++', max_iter=100, n_init=1)
cluster.fit(scaleddata)
cluster_labels=cluster.labels_
print(cluster_labels)
score = silhouette_score(scaleddata, cluster_labels)
print(score)
# Add cluster labels to preprocessed data
data['kcluster']=cluster_labels
data.head()
fig, ax = plt.subplots(figsize=(18,18))
sns.scatterplot(ax=ax, data=data, x="Frequency", y="Recency",size="Amount", hue="kcluster", palette="deep")
```
# Hierarchical clustering
```
from sklearn.neighbors import kneighbors_graph
from sklearn.cluster import AgglomerativeClustering
connectivity = kneighbors_graph(scaleddata, n_neighbors=10, include_self=False)
model = AgglomerativeClustering(n_clusters=6, connectivity=connectivity,
linkage='ward')
model = model.fit(scaleddata)
cluster_labels=model.labels_
score = silhouette_score(scaleddata, cluster_labels)
print(score)
# Add cluster labels to preprocessed data
data['hcluster']=cluster_labels
data.head()
fig, ax = plt.subplots(figsize=(18,18))
sns.scatterplot(ax=ax, data=data, x="Frequency", y="Recency",size="Amount", hue="hcluster", palette="deep")
```
# MeanShift clustering
```
from sklearn.cluster import MeanShift
model = MeanShift(bandwidth=2)
model = model.fit(scaleddata)
cluster_labels=model.labels_
score = silhouette_score(scaleddata, cluster_labels)
print(score)
# Add cluster labels to preprocessed data
data['acluster']=cluster_labels
data.head()
fig, ax = plt.subplots(figsize=(18,18))
sns.scatterplot(ax=ax, data=data, x="Frequency", y="Recency",size="Amount", hue="acluster", palette="deep")
```
# SpectralClustering
```
from sklearn.cluster import SpectralClustering
model = SpectralClustering(n_clusters=5,assign_labels="discretize", random_state=0)
model = model.fit(scaleddata)
cluster_labels=model.labels_
cluster_labels=model.labels_
score = silhouette_score(scaleddata, cluster_labels)
print(score)
# Add cluster labels to preprocessed data
data['scluster']=cluster_labels
data.head()
fig, ax = plt.subplots(figsize=(18,18))
sns.scatterplot(ax=ax, data=data, x="Frequency", y="Recency",size="Amount", hue="scluster", palette="deep")
```
# MiniBatchKMeans Clustering
```
from sklearn.cluster import MiniBatchKMeans
model = MiniBatchKMeans(n_clusters=5)
model = model.fit(scaleddata)
cluster_labels=model.labels_
score = silhouette_score(scaleddata, cluster_labels)
print(score)
# Add cluster labels to preprocessed data
data['mcluster']=cluster_labels
data.head()
fig, ax = plt.subplots(figsize=(18,18))
sns.scatterplot(ax=ax, data=data, x="Frequency", y="Recency",size="Amount", hue="mcluster", palette="deep")
```
# DBSCAN Clustering
```
from sklearn.cluster import DBSCAN
model = DBSCAN(eps=3)
model = model.fit(scaleddata)
cluster_labels=model.labels_
score = silhouette_score(scaleddata, cluster_labels)
print(score)
# Add cluster labels to preprocessed data
data['dcluster']=cluster_labels
data.head()
fig, ax = plt.subplots(figsize=(18,18))
sns.scatterplot(ax=ax, data=data, x="Frequency", y="Recency",size="Amount", hue="dcluster", palette="deep")
```
| true |
code
| 0.618492 | null | null | null | null |
|
```
import time
import toml
import numpy as np
import matplotlib.pyplot as plt
from ref_trajectory import generate_trajectory as traj
%matplotlib inline
```
There are a lot of configuration parameters. It is a good idea to separate it from the main code. At some point you will be doing parameter tuning.
We will use toml format to store parameters. Open config.toml and go over the description of the different parameters we may use here
Read the config parameters, default output is a dictionary. You have to then store them as local variables.
You have 2 options for this
1. update locals() directly - a little bit dangerous
2. You can use itemgetter
```
config_params = toml.load("config.toml")['params']
print(config_params)
locals().update(config_params)
print(dt, V_MAX)
```
There are 3 functions we need to write for DWA
1. Simulate unicyle - we will slightly modify it to simulate $N$ steps
2. Command Window - Entire set of acceptable $(v, \omega)$ in that time instant given current $(v, \omega)$$
3. track - get $(v, \omega )$ for path with the lowest cost
In the first iteration, let us not integrate collision checking. Let us integrate these pieces, make sure DWA works for a few paths!
```
v_min, v_max = 0.0, 0.2
w_min, w_max = -0.1, 0.1
vs = np.linspace(v_min, v_max, num=11)
ws = np.linspace(w_min, w_max, num=11)
cmd = np.transpose([np.tile(vs, len(ws)), np.repeat(ws, len(vs))])
print(vs)
def simulate_unicycle(pose, v,w, N=1, dt=0.1):
x, y, t = pose
poses = []
for _ in range(N):
x += v*np.cos(t)*dt
y += v*np.sin(t)*dt
t += w*dt
poses.append([x,y,t])
return np.array(poses)
def command_window(v, w, dt=0.1):
"""Returns acceptable v,w commands given current v,w"""
# velocity can be (0, V_MAX)
# ACC_MAX = max linear acceleration
v_max = min(V_MAX, v + ACC_MAX*dt)
v_min = max(0, v - ACC_MAX*dt)
# omega can be (-W_MAX, W_MAX)
#W_DOT_MAX = max angular acceleration
epsilon = 1e-6
w_max = min(W_MAX, w + W_DOT_MAX*dt)
w_min = max(-W_MAX, w - W_DOT_MAX*dt)
#generate quantized range for v and omega
vs = np.linspace(v_min, v_max, num=11)
ws = np.linspace(w_min, w_max, num=21)
#cartesian product of [vs] and [ws]
#remember there are 0 velocity entries which have to be discarded eventually
commands = np.transpose([np.tile(vs, len(ws)), np.repeat(ws, len(vs))])
#calculate kappa for the set of commands
kappa = commands[:,1]/(commands[:,0]+epsilon)
#returning only commands < max curvature
return commands[(kappa < K_MAX) & (commands[:, 0] != 0)]
def track(ref_path, pose, v, w, dt=0.1):
commands = command_window(v, w, dt)
#initialize path cost
best_cost, best_command = np.inf, None
for i, (v, w) in enumerate(commands):
local_path = simulate_unicycle(pose, v, w) #Number of steps = prediction horizon
#if circle_collision_check(grid, local_path): #ignore colliding paths
# print("local path has a collision")
# continue
#calculate cross-track error
#can use a simplistic definition of
#how close is the last pose in local path from the ref path
cte = np.sqrt(((local_path[-1][0]-local_ref_path[-1][0])**2 + (local_path[-1][1]-local_ref_path[-1][1])**2))
#other cost functions are possible
#can modify collision checker to give distance to closest obstacle
cost = w_cte*cte + w_speed*(V_MAX - v)**2
#check if there is a better candidate
if cost < best_cost:
best_cost, best_command = cost, (v, w)
if best_command:
return best_command
else:
return [0, 0]
grid_res = 0.05
def circle_collision_check(grid, local_traj):
xmax, ymax = grid.shape
all_x = np.arange(xmax)
all_y = np.arange(ymax)
X, Y = np.meshgrid(all_x, all_y)
for xl, yl, tl in local_traj:
rot = np.array([[np.sin(tl), -np.cos(tl)],[np.cos(tl), np.sin(tl)]])
for xc, yc, rc in circles:
xc_rot, yc_rot = rot @ np.array([xc, yc]) + np.array([xl, yl])
xc_pix, yc_pix = int(xc_rot/grid_res), int(yc_rot/ grid_res)
rc_pix = (rc/ grid_res)
inside_circle = ((X-xc_pix)**2 +(Y-yc_pix)**2 - rc_pix**2 < 0)
occupied_pt = grid[X, Y] == 1
if np.sum(np.multiply(inside_circle, occupied_pt)):
return True
return False
start_pose = np.array([0, 0, np.pi/2])
route = [("straight", 5),("turn", -90),("straight", 6),("turn", 90)]
ref_path = traj(route, start_pose).T
pose = [start_pose]
logs = []
path_index = 0
v, w = 0.0, 0.0
while path_index < len(ref_path)-1:
t0 = time.time()
local_ref_path = ref_path[path_index:path_index+pred_horizon]
# update path_index using current pose and local_ref_path
pose=pose[0]
dist = np.sqrt(((pose[0]-ref_path[-1][0])**2 + (pose[1]-ref_path[-1][1])**2))
if dist > goal_threshold*10:
path_index = path_index+1
# get next command
v, w = track(local_ref_path, pose, v, w)
#simulate vehicle for 1 step
# remember the function now returns a trajectory, not a single pose
pose = simulate_unicycle(pose, v, w)
#update logs
logs.append([*pose, v, w])
t1 = time.time() #simplest way to time-profile your code
print(f"idx:{path_index}, v:{v:0.3f}, w:{w:0.3f}, time:{(t1-t0) * 1000:0.1f}ms")
poses = np.array(logs)[:,:3]
plt.figure()
plt.axes().set_aspect('equal', 'datalim')
plt.plot(ref_path[:,0], ref_path[:,1], '.', c='g')
plt.plot(poses[:,0], poses[:,1], c='r')
```
Now it should be relatively straight-forward to integrate collision checking in the grid environment the robot is going to navigate
```
```
| true |
code
| 0.430207 | null | null | null | null |
|
# AutoGluon Tabular with SageMaker
[AutoGluon](https://github.com/awslabs/autogluon) automates machine learning tasks enabling you to easily achieve strong predictive performance in your applications. With just a few lines of code, you can train and deploy high-accuracy deep learning models on tabular, image, and text data.
This notebook shows how to use AutoGluon-Tabular with Amazon SageMaker by creating custom containers.
## Prerequisites
If using a SageMaker hosted notebook, select kernel `conda_mxnet_p36`.
```
# Make sure docker compose is set up properly for local mode
!./setup.sh
import os
import boto3
import sagemaker
from time import sleep
from collections import Counter
import numpy as np
import pandas as pd
from sagemaker import get_execution_role, local, Model, utils, s3
from sagemaker.estimator import Estimator
from sagemaker.predictor import Predictor
from sagemaker.serializers import CSVSerializer
from sagemaker.deserializers import StringDeserializer
from sklearn.metrics import accuracy_score, classification_report
from IPython.core.display import display, HTML
from IPython.core.interactiveshell import InteractiveShell
# Print settings
InteractiveShell.ast_node_interactivity = "all"
pd.set_option('display.max_columns', 500)
pd.set_option('display.max_rows', 10)
# Account/s3 setup
session = sagemaker.Session()
local_session = local.LocalSession()
bucket = session.default_bucket()
prefix = 'sagemaker/autogluon-tabular'
region = session.boto_region_name
role = get_execution_role()
client = session.boto_session.client(
"sts", region_name=region, endpoint_url=utils.sts_regional_endpoint(region)
)
account = client.get_caller_identity()['Account']
registry_uri_training = sagemaker.image_uris.retrieve('mxnet', region, version= '1.7.0', py_version='py3', instance_type='ml.m5.2xlarge', image_scope='training')
registry_uri_inference = sagemaker.image_uris.retrieve('mxnet', region, version= '1.7.0', py_version='py3', instance_type='ml.m5.2xlarge', image_scope='inference')
ecr_uri_prefix = account +'.'+'.'.join(registry_uri_training.split('/')[0].split('.')[1:])
```
### Build docker images
Build the training/inference image and push to ECR
```
training_algorithm_name = 'autogluon-sagemaker-training'
inference_algorithm_name = 'autogluon-sagemaker-inference'
!/bin/bash ./container-training/build_push_training.sh {account} {region} {training_algorithm_name} {ecr_uri_prefix} {registry_uri_training.split('/')[0].split('.')[0]} {registry_uri_training}
!/bin/bash ./container-inference/build_push_inference.sh {account} {region} {inference_algorithm_name} {ecr_uri_prefix} {registry_uri_training.split('/')[0].split('.')[0]} {registry_uri_inference}
```
### Get the data
In this example we'll use the direct-marketing dataset to build a binary classification model that predicts whether customers will accept or decline a marketing offer.
First we'll download the data and split it into train and test sets. AutoGluon does not require a separate validation set (it uses bagged k-fold cross-validation).
```
# Download and unzip the data
!aws s3 cp --region {region} s3://sagemaker-sample-data-{region}/autopilot/direct_marketing/bank-additional.zip .
!unzip -qq -o bank-additional.zip
!rm bank-additional.zip
local_data_path = './bank-additional/bank-additional-full.csv'
data = pd.read_csv(local_data_path)
# Split train/test data
train = data.sample(frac=0.7, random_state=42)
test = data.drop(train.index)
# Split test X/y
label = 'y'
y_test = test[label]
X_test = test.drop(columns=[label])
```
##### Check the data
```
train.head(3)
train.shape
test.head(3)
test.shape
X_test.head(3)
X_test.shape
```
Upload the data to s3
```
train_file = 'train.csv'
train.to_csv(train_file,index=False)
train_s3_path = session.upload_data(train_file, key_prefix='{}/data'.format(prefix))
test_file = 'test.csv'
test.to_csv(test_file,index=False)
test_s3_path = session.upload_data(test_file, key_prefix='{}/data'.format(prefix))
X_test_file = 'X_test.csv'
X_test.to_csv(X_test_file,index=False)
X_test_s3_path = session.upload_data(X_test_file, key_prefix='{}/data'.format(prefix))
```
## Hyperparameter Selection
The minimum required settings for training is just a target label, `init_args['label']`.
Additional optional hyperparameters can be passed to the `autogluon.tabular.TabularPredictor.fit` function via `fit_args`.
Below shows a more in depth example of AutoGluon-Tabular hyperparameters from the example [Predicting Columns in a Table - In Depth](https://auto.gluon.ai/stable/tutorials/tabular_prediction/tabular-indepth.html). Please see [fit parameters](https://auto.gluon.ai/stable/_modules/autogluon/tabular/predictor/predictor.html#TabularPredictor) for further information. Note that in order for hyperparameter ranges to work in SageMaker, values passed to the `fit_args['hyperparameters']` must be represented as strings.
```python
nn_options = {
'num_epochs': "10",
'learning_rate': "ag.space.Real(1e-4, 1e-2, default=5e-4, log=True)",
'activation': "ag.space.Categorical('relu', 'softrelu', 'tanh')",
'layers': "ag.space.Categorical([100],[1000],[200,100],[300,200,100])",
'dropout_prob': "ag.space.Real(0.0, 0.5, default=0.1)"
}
gbm_options = {
'num_boost_round': "100",
'num_leaves': "ag.space.Int(lower=26, upper=66, default=36)"
}
model_hps = {'NN': nn_options, 'GBM': gbm_options}
init_args = {
'eval_metric' : 'roc_auc'
'label': 'y'
}
fit_args = {
'presets': ['best_quality', 'optimize_for_deployment'],
'time_limits': 60*10,
'hyperparameters': model_hps,
'hyperparameter_tune': True,
'search_strategy': 'skopt'
}
hyperparameters = {
'fit_args': fit_args,
'feature_importance': True
}
```
**Note:** Your hyperparameter choices may affect the size of the model package, which could result in additional time taken to upload your model and complete training. Including `'optimize_for_deployment'` in the list of `fit_args['presets']` is recommended to greatly reduce upload times.
<br>
```
# Define required label and optional additional parameters
init_args = {
'label': 'y'
}
# Define additional parameters
fit_args = {
'label': 'y',
# Adding 'best_quality' to presets list will result in better performance (but longer runtime)
'presets': ['optimize_for_deployment'],
}
# Pass fit_args to SageMaker estimator hyperparameters
hyperparameters = {
# 'init_args': init_args,
'fit_args': fit_args,
'feature_importance': True
}
tags = [{
'Key' : 'AlgorithmName',
'Value' : 'AutoGluon-Tabular'
}]
```
## Train
For local training set `train_instance_type` to `local` .
For non-local training the recommended instance type is `ml.m5.2xlarge`.
**Note:** Depending on how many underlying models are trained, `train_volume_size` may need to be increased so that they all fit on disk.
```
%%time
instance_type = 'ml.m5.2xlarge'
#instance_type = 'local'
ecr_image = f'{ecr_uri_prefix}/{training_algorithm_name}:latest'
estimator = Estimator(image_uri=ecr_image,
role=role,
instance_count=1,
instance_type=instance_type,
hyperparameters=hyperparameters,
volume_size=100,
tags=tags)
# Set inputs. Test data is optional, but requires a label column.
inputs = {'training': train_s3_path, 'testing': test_s3_path}
estimator.fit(inputs)
```
### Review the performance of the trained model
```
from utils.ag_utils import launch_viewer
launch_viewer(is_debug=False)
```
### Create Model
```
# Create predictor object
class AutoGluonTabularPredictor(Predictor):
def __init__(self, *args, **kwargs):
super().__init__(*args,
serializer=CSVSerializer(),
deserializer=StringDeserializer(), **kwargs)
ecr_image = f'{ecr_uri_prefix}/{inference_algorithm_name}:latest'
if instance_type == 'local':
model = estimator.create_model(image_uri=ecr_image, role=role)
else:
#model_uri = os.path.join(estimator.output_path, estimator._current_job_name, "output", "model.tar.gz")
model_uri = estimator.model_data
model = Model(ecr_image, model_data=model_uri, role=role, sagemaker_session=session, predictor_cls=AutoGluonTabularPredictor)
```
### Batch Transform
For local mode, either `s3://<bucket>/<prefix>/output/` or `file:///<absolute_local_path>` can be used as outputs.
By including the label column in the test data, you can also evaluate prediction performance (In this case, passing `test_s3_path` instead of `X_test_s3_path`).
```
output_path = f's3://{bucket}/{prefix}/output/'
# output_path = f'file://{os.getcwd()}'
transformer = model.transformer(instance_count=1,
instance_type=instance_type,
strategy='MultiRecord',
max_payload=6,
max_concurrent_transforms=1,
output_path=output_path)
transformer.transform(test_s3_path, content_type='text/csv', split_type='Line')
transformer.wait()
```
### Endpoint
##### Deploy remote or local endpoint
```
instance_type = 'ml.m5.2xlarge'
#instance_type = 'local'
predictor = model.deploy(initial_instance_count=1,
instance_type=instance_type)
```
##### Attach to endpoint (or reattach if kernel was restarted)
```
# Select standard or local session based on instance_type
if instance_type == 'local':
sess = local_session
else:
sess = session
# Attach to endpoint
predictor = AutoGluonTabularPredictor(predictor.endpoint, sagemaker_session=sess)
```
##### Predict on unlabeled test data
```
results = predictor.predict(X_test.to_csv(index=False)).splitlines()
# Check output
print(Counter(results))
```
##### Predict on data that includes label column
Prediction performance metrics will be printed to endpoint logs.
```
results = predictor.predict(test.to_csv(index=False)).splitlines()
# Check output
print(Counter(results))
```
##### Check that classification performance metrics match evaluation printed to endpoint logs as expected
```
y_results = np.array(results)
print("accuracy: {}".format(accuracy_score(y_true=y_test, y_pred=y_results)))
print(classification_report(y_true=y_test, y_pred=y_results, digits=6))
```
##### Clean up endpoint
```
predictor.delete_endpoint()
```
| true |
code
| 0.521593 | null | null | null | null |
|
# Q-learning applied to FrozenLake
#### **Remember**: Q-learning is a model free, off-policy algorithm that can be used to find an optimal action using a Q function. Q can be represented as a table that contains a value for each pair state-action
To review Q-learning watch [Q learning explained by Siraj](https://www.youtube.com/watch?v=aCEvtRtNO-M)
#### Q-learning pipeline is quite easy an can be summarised in 5 blocks:

## WHAT'S THE ENVIRONMENT?
#### We'll apply Q-learning on a [Gym](http://gym.openai.com/) game called [FrozenLake](https://gym.openai.com/envs/FrozenLake-v0/)

## LET'S START TO CODE
```
import gym
import random
from collections import namedtuple
import collections
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
### BASIC FUNCTION TO CHOOSE AN ACTION FOLLOWING DIFFERENT POLICIES
```
def select_eps_greedy_action(table, obs, n_actions):
'''
Select the action using a ε-greedy policy (add a randomness ε for the choice of the action)
'''
value, action = best_action_value(table, obs)
if random.random() < epsilon:
return random.randint(0,n_actions-1)
else:
return action
def select_greedy_action(table, obs, n_actions):
'''
Select the action using a greedy policy (take the best action according to the policy)
'''
value, action = best_action_value(table, obs)
return action
def best_action_value(table, state):
'''
Exploring the table, take the best action that maximize Q(s,a)
'''
best_action = 0
max_value = 0
for action in range(n_actions):
if table[(state, action)] > max_value:
best_action = action
max_value = table[(state, action)]
return max_value, best_action
```

```
def Q_learning(table, obs0, obs1, reward, action):
'''
Q-learning. Update Q(obs0,action) according to Q(obs1,*) and the reward just obtained
'''
# Take the best value reachable from the state obs1
best_value, _ = best_action_value(table, obs1)
# Calculate Q-target value
Q_target = reward + GAMMA * best_value
# Calculate the Q-error between the target and the previous value
Q_error = Q_target - table[(obs0, action)]
# Update Q(obs0,action)
table[(obs0, action)] += LEARNING_RATE * Q_error
```
### TEST THE POLICY
```
def test_game(env, table):
'''
Test the new table playing TEST_EPISODES games
'''
n_actions = env.action_space.n
reward_games = []
for _ in range(TEST_EPISODES):
obs = env.reset()
rewards = 0
while True:
# Act greedly
next_obs, reward, done, _ = env.step(select_greedy_action(table, obs, n_actions))
obs = next_obs
rewards += reward
if done:
reward_games.append(rewards)
break
return np.mean(reward_games)
```
### MAIN PROCEDURE
```
# Some hyperparameters..
GAMMA = 0.95
# NB: the decay rate allow to regulate the Exploration - Exploitation trade-off
# start with a EPSILON of 1 and decay until reach 0
EPS_DECAY_RATE = 0.9993
LEARNING_RATE = 0.8
# .. and constants
TEST_EPISODES = 100
MAX_GAMES = 15000
# Create the environment
#env = gym.make('Taxi-v2')
env = gym.make("FrozenLake-v0")
obs = env.reset()
obs_length = env.observation_space.n
n_actions = env.action_space.n
reward_count = 0
games_count = 0
# Create and initialize the table with 0.0
table = collections.defaultdict(float)
test_rewards_list = []
# Reinitialize epsilon after each session
epsilon = 1.0
while games_count < MAX_GAMES:
# Select the action following an ε-greedy policy
action = select_eps_greedy_action(table, obs, n_actions)
next_obs, reward, done, _ = env.step(action)
# Update the Q-table
Q_learning(table, obs, next_obs, reward, action)
reward_count += reward
obs = next_obs
if done:
epsilon *= EPS_DECAY_RATE
# Test the new table every 1k games
if (games_count + 1) % 1000 == 0:
test_reward = test_game(env, table)
print('\tEp:', games_count, 'Test reward:', test_reward, np.round(epsilon,2))
test_rewards_list.append(test_reward)
obs = env.reset()
reward_count = 0
games_count += 1
# Plot the accuracy over the number of steps
plt.figure(figsize=(18,9))
plt.xlabel('Steps')
plt.ylabel('Accurracy')
plt.plot(test_rewards_list)
plt.show()
```
#### NB: in case you want to apply Q-learning to continuous state and actions games, you have to quantize the state and action spaces
| true |
code
| 0.638835 | null | null | null | null |
|
# Interactive Widget: Front End Code: Bagging Classifier
This is our official final version of the widget.
Throughout this workbook, we used steps from the following web pages to inform our widgets.
- https://ipywidgets.readthedocs.io/en/latest/examples/Widget%20Basics.html
- https://ipywidgets.readthedocs.io/en/latest/examples/Widget%20List.html
- https://ipywidgets.readthedocs.io/en/latest/examples/Using%20Interact.html
### Set Up
```
# Import the necessary data libraries.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split as tts
from sklearn.ensemble import BaggingClassifier
import scipy.stats as stats
# The following are for Classification Accuracy.
from sklearn import metrics
# The following are for Jupyter Widgets.
import ipywidgets as widgets
from IPython.display import display
from __future__ import print_function
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from ipywidgets import FloatSlider
```
Although the URLs say they were for the K-Neighbors widget, we did not change anything in the resampling or testing data, so we will still use these files.
```
# Set up datasets.
X_resampled_url = 'https://raw.githubusercontent.com/georgetown-analytics/Formula1/main/data/interim/X_resampled_forKNeighborWidget.csv'
X_resampled = pd.read_csv(X_resampled_url, sep = ',', engine = 'python')
y_resampled_url = 'https://raw.githubusercontent.com/georgetown-analytics/Formula1/main/data/interim/y_resampled_forKNeighborWidget.csv'
y_resampled = pd.read_csv(y_resampled_url, sep = ',', engine = 'python')
X_test_url = 'https://raw.githubusercontent.com/georgetown-analytics/Formula1/main/data/interim/X_test_forKNeighborWidget.csv'
X_test = pd.read_csv(X_test_url, sep = ',', engine = 'python')
y_test_url = 'https://raw.githubusercontent.com/georgetown-analytics/Formula1/main/data/interim/y_test_forKNeighborWidget.csv'
y_test = pd.read_csv(y_test_url, sep = ',', engine = 'python')
```
We know from testing the type of `y_resampled` in `InteractiveWidget_BackEnd.ipynb` that `y_resampled` and `y_test` need to be a series in order for our model to run correctly. We also know from this site (https://datatofish.com/pandas-dataframe-to-series/) how to change a dataframe into a series.
```
# Change the y_resampled dataframe into a y_resampled series.
y_resampled = y_resampled.squeeze()
# Change the y_test dataframe into a y_test series.
y_test = y_test.squeeze()
```
### Create the Modeling Functions
```
# Create the function score_model.
def widgetpred(X_resampled, y_resampled, X_test, y_test, input_test, estimator, **kwargs):
"""
Test various estimators.
"""
# Instantiate the classification model and visualizer.
estimator.fit(X_resampled, y_resampled, **kwargs)
expected = y_test
predicted = estimator.predict(X_test)
inputpred = estimator.predict(input_test)
# Compute and return the prediction.
return [predicted, inputpred]
# Create the function conmatrix.
def conmatrix(y_test, predicted, inputpred):
"""
Compute the confusion matrix and return the results.
"""
confusion = metrics.confusion_matrix(y_test, predicted)
TP = confusion[1, 1]
TN = confusion[0, 0]
FP = confusion[0, 1]
FN = confusion[1, 0]
# When the prediction is positive, how often is it correct? Define truepositive_rate.
truepositive_rate = round((TP / (TP + FP)) * 100, 2)
# When the prediction is negative, how often is it correct? Define truenegative_rate.
truenegative_rate = round((TN / (TN + FN)) * 100, 2)
# Use an if-else statement to print a statement about the true positive or negative rate, depending on the prediction.
if inputpred == 1:
print("When our model predicts that a car will finish the race, it is correct", truepositive_rate, "% of the time.")
else:
print("When our model predicts that a car will not finish the race, it is correct", truenegative_rate, "% of the time.")
```
### Create the Widget
```
"""
Establish function "predict" which allows selection of two track types, whether
the track is historic or not, and how popular the circuit is,
as well as the input of one of each of the following values:
year, grid, alt, average_lap_time, minimum_lap_time, PRCP, TAVG.
Place these values in the dataframe input_df and display the dataframe.
Create prediction based on widgetpred function and display the prediction:
0 for did not finish, 1 for did finish.
"""
def predictfinish(trackType, historic, circuit, year, grid, alt, average_lap_time, normalized_minLapTime, PRCP, TAVG):
# Use an if-else statement to determine the output based on the input track.
if trackType == "Race":
trackType = 0
else:
trackType = 1
# Use an if-else statement to determine the output based on the input historic.
if historic == "Not Historic":
isHistoric = 0
else:
isHistoric = 1
# Use an if-else statement to determine the output based on the input circuit.
if circuit == "Used 500+ times":
oneHot_circuits_1 = 1
oneHot_circuits_2 = 0
oneHot_circuits_3 = 0
oneHot_circuits_4 = 0
oneHot_circuits_5 = 0
oneHot_circuits_6 = 0
elif circuit == "Used 400-499 times":
oneHot_circuits_1 = 0
oneHot_circuits_2 = 1
oneHot_circuits_3 = 0
oneHot_circuits_4 = 0
oneHot_circuits_5 = 0
oneHot_circuits_6 = 0
elif circuit == "Used 300-399 times":
oneHot_circuits_1 = 0
oneHot_circuits_2 = 0
oneHot_circuits_3 = 1
oneHot_circuits_4 = 0
oneHot_circuits_5 = 0
oneHot_circuits_6 = 0
elif circuit == "Used 200-299 times":
oneHot_circuits_1 = 0
oneHot_circuits_2 = 0
oneHot_circuits_3 = 0
oneHot_circuits_4 = 1
oneHot_circuits_5 = 0
oneHot_circuits_6 = 0
elif circuit == "Used 100-199 times":
oneHot_circuits_1 = 0
oneHot_circuits_2 = 0
oneHot_circuits_3 = 0
oneHot_circuits_4 = 0
oneHot_circuits_5 = 1
oneHot_circuits_6 = 0
elif circuit == "Used less than 100 times":
oneHot_circuits_1 = 0
oneHot_circuits_2 = 0
oneHot_circuits_3 = 0
oneHot_circuits_4 = 0
oneHot_circuits_5 = 0
oneHot_circuits_6 = 1
# Transform average_lap_time.
normalized_avgLapTime = np.log(average_lap_time)
# Use an if-else statement to move any potential outliers from average_lap_time.
avgQ1 = -0.019303
avgQ3 = 0.006690
avgIQR = avgQ3 - avgQ1
avglowertail = avgQ1 - 2.5 * avgIQR
avguppertail = avgQ3 + 2.5 * avgIQR
avgmedian = -0.005962837883204569
if normalized_avgLapTime > avguppertail or normalized_avgLapTime < avglowertail:
normalized_avgLapTime = avgmedian
# Use an if-else statement to move any potential outliers from normalized_minLapTime.
minQ1 = 0.984717
minQ3 = 1.006281
minIQR = minQ3 - minQ1
minlowertail = minQ1 - 2.0 * minIQR
minuppertail = minQ3 + 2.0 * minIQR
minmedian = 0.995628475361378
if normalized_minLapTime > minuppertail or normalized_minLapTime < minlowertail:
normalized_minLapTime = minmedian
# Transform altitude.
alt_trans = np.log(alt + 1 - (-7))
# Transform precipitation.
PRCP_trans = np.log(PRCP + 1)
# Establish the data of our input_df dataframe.
inputdata = [[grid, trackType, year, TAVG, isHistoric, oneHot_circuits_1, oneHot_circuits_2,
oneHot_circuits_3, oneHot_circuits_4, oneHot_circuits_5, oneHot_circuits_6, alt_trans,
PRCP_trans, normalized_minLapTime, normalized_avgLapTime]]
# Establish the dataframe input_df itself with pd.DataFrame.
input_df = pd.DataFrame(inputdata, columns =
['grid', 'trackType', 'year', 'TAVG',
'isHistoric', 'oneHot_circuits_1', 'oneHot_circuits_2',
'oneHot_circuits_3', 'oneHot_circuits_4', 'oneHot_circuits_5',
'oneHot_circuits_6', 'alt_trans', 'PRCP_trans', 'normalized_minLapTime',
'normalized_avgLapTime'])
display(input_df)
# Using the widgetpred function, predict whether the car will finish the race or not given input_df.
pred = widgetpred(X_resampled, y_resampled, X_test, y_test, input_df, BaggingClassifier())
# Using an if-else statement, determine what interactors will see given the data they input.
if pred[1] == 1:
writtenpred = "finish the race."
else:
writtenpred = "not finish the race."
# Print the model's prediction.
print("According to our Bagging Classifier model, your car is predicted to", writtenpred)
"""
Using the conmatrix function, print out a statement about
the true positive or negative rate, depending on the prediction.
"""
conmatrix(y_test, pred[0], pred[1])
# Create a widget that will interact with the predictfinish function.
interact(predictfinish, trackType = widgets.Dropdown(options = ["Race", "Street"], value = "Race", description = 'Track Type'),
historic = widgets.Dropdown(options = ["Not Historic", "Historic"], value = "Not Historic", description = 'Historic?'),
circuit = widgets.Dropdown(options = ["Used 500+ times", "Used 400-499 times", "Used 300-399 times", "Used 200-299 times", "Used 100-199 times", "Used less than 100 times"], value = "Used less than 100 times", description = 'Circuit'),
year = widgets.IntSlider(min = 1996, max = 2021, description = 'Year', disabled = False, continuous_update = False),
grid = widgets.IntSlider(min = 0, max = 30, description = 'Grid', disabled = False, continuous_update = False),
alt = widgets.BoundedFloatText(min = -100, max = 2500, description = 'Altitude', disabled = False, continuous_update = False),
average_lap_time = widgets.FloatSlider(min = 0.1, max = 6.0, value = 0.1, description = 'Avg Lap Time', disabled = False, continuous_update = False),
normalized_minLapTime = widgets.FloatSlider(min = 0.1, max = 6.0, value = 0.1, description = 'Min Lap Time', disabled = False, continuous_update = False),
PRCP = widgets.FloatSlider(min = 0, max = 10, description = 'Precipitation', disabled = False, continuous_update = False),
TAVG = widgets.FloatSlider(min = 0, max = 110, description = 'Avg Temp (F)', disabled = False, continuous_update = False));
```
| true |
code
| 0.654619 | null | null | null | null |
|
# TV Script Generation
In this project, I have tried to generate my own [Seinfeld](https://en.wikipedia.org/wiki/Seinfeld) TV scripts using RNNs. I have used part of the [Seinfeld dataset](https://www.kaggle.com/thec03u5/seinfeld-chronicles#scripts.csv) of scripts from 9 seasons. The Neural Network will generate a new ,"fake" TV script, based on patterns it recognizes in this training data.
## Get the Data
```
# load in data
import helper
data_dir = './data/Seinfeld_Scripts.txt'
text = helper.load_data(data_dir)
```
## Explore the Data
```
view_line_range = (0, 10)
import numpy as np
print('Dataset Stats')
print('Roughly the number of unique words: {}'.format(len({word: None for word in text.split()})))
lines = text.split('\n')
print('Number of lines: {}'.format(len(lines)))
word_count_line = [len(line.split()) for line in lines]
print('Average number of words in each line: {}'.format(np.average(word_count_line)))
print()
print('The lines {} to {}:'.format(*view_line_range))
print('\n'.join(text.split('\n')[view_line_range[0]:view_line_range[1]]))
```
---
## Implement Pre-processing Functions
The first thing to do to any dataset is pre-processing. I will implement the following pre-processing functions below:
- Lookup Table
- Tokenize Punctuation
### Lookup Table
To create a word embedding, you first need to transform the words to ids. In this function, create two dictionaries:
- Dictionary to go from the words to an id, we'll call `vocab_to_int`
- Dictionary to go from the id to word, we'll call `int_to_vocab`
```
import problem_unittests as tests
from collections import Counter
def create_lookup_tables(text):
words = Counter(text)
vocab = sorted(words, key = words.get, reverse = True)
vocab_to_int = {word : ii for ii, word in enumerate(vocab)}
int_to_vocab = {ii : word for ii, word in enumerate(vocab)}
# return tuple
return (vocab_to_int, int_to_vocab)
tests.test_create_lookup_tables(create_lookup_tables)
```
### Tokenize Punctuation
```
def token_lookup():
#getting the key-value pair in a dict
punctuation = {'.': "||Period||", ',': "||Comma||", '"': "||Quotation_Mark||", ';': "||Semicolon||",
'!': "||Exclamation_Mark||", '?': "||Question_Mark||", '(': "||Left_Parentheses||",
')': "||Right_Parentheses||", '-': "||Dash||", '\n': "||Return||"
}
return punctuation
tests.test_tokenize(token_lookup)
```
## Pre-process all the data and save it
Running the code cell below will pre-process all the data and save it to file.
```
# pre-process training data
helper.preprocess_and_save_data(data_dir, token_lookup, create_lookup_tables)
import helper
import problem_unittests as tests
int_text, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
```
## Build the Neural Network
```
import torch
# Check for a GPU
train_on_gpu = torch.cuda.is_available()
if not train_on_gpu:
print('No GPU found. Please use a GPU to train your neural network.')
from torch.utils.data import TensorDataset, DataLoader
def batch_data(words, sequence_length, batch_size):
num_featues = len(words) - sequence_length #this is how many total features we can have at given sequence length
X_train = np.zeros((num_featues, sequence_length), dtype = int) #num_features gives us shape of complete X_train
y_train = np.zeros(num_featues) #num of labels is equal to num of rows in X_train
#now, we will ommit the zeros with our words with this logic
for i in range(0, num_featues):
X_train[i] = words[i:i+sequence_length]
y_train[i] = words[i+sequence_length]
#changing dtype
feature_array = np.asarray(X_train, np.int64)
target_array = np.asarray(y_train, np.int64)
data = TensorDataset(torch.from_numpy(feature_array), torch.from_numpy(target_array))
dataloader = DataLoader(data, batch_size = batch_size, shuffle = True)
return dataloader
words = np.array([99,88,77,66,55,44,33,22,11,0])
loader = batch_data(words, 5, 3)
dataiter = iter(loader)
dataiter.next()
# test dataloader
test_text = range(50)
t_loader = batch_data(test_text, sequence_length=5, batch_size=10)
data_iter = iter(t_loader)
sample_x, sample_y = data_iter.next()
print(sample_x.shape)
print(sample_x)
print()
print(sample_y.shape)
print(sample_y)
print(len(t_loader))
```
---
## Build the Neural Network
```
import torch.nn as nn
class RNN(nn.Module):
def __init__(self, vocab_size, output_size, embedding_dim, hidden_dim, n_layers, dropout=0.5):
super(RNN, self).__init__()
# set class variables
self.hidden_dim = hidden_dim
self.output_size = output_size
self.n_layers = n_layers
#embedding layer
self.embedding = nn.Embedding(vocab_size, embedding_dim)
#lstm layer
self.lstm = nn.LSTM(embedding_dim, hidden_dim, n_layers, dropout=dropout, batch_first=True)
# dropout layer
self.dropout = nn.Dropout(p=0.2)
#fully connected layer
self.fc = nn.Linear(hidden_dim, output_size)
def forward(self, nn_input, hidden):
batch_size = nn_input.size(0)
embeds = self.embedding(nn_input)
lstm_output, hidden = self.lstm(embeds, hidden)
#stack the outputs of the lstm to pass to your fully-connected layer - kinda flattening step
lstm_output = lstm_output.contiguous().view(-1, self.hidden_dim)
output = self.dropout(lstm_output)
output = self.fc(lstm_output)
output = output.view(batch_size, -1, self.output_size)
#getting the last batch of outputs
output = output[:,-1]
# return one batch of output word scores and the hidden state
return output, hidden
def init_hidden(self, batch_size):
#hidden state of dims (n_layers, batch_size, hidden_dim)
weight = next(self.parameters()).data
# initialize hidden state with zero weights, and move to GPU if available
if train_on_gpu:
hidden = (weight.new(self.n_layers, batch_size, self.hidden_dim).zero_().cuda(),
weight.new(self.n_layers, batch_size, self.hidden_dim).zero_().cuda())
else:
hidden = (weight.new(self.n_layers, batch_size, self.hidden_dim).zero_(),
weight.new(self.n_layers, batch_size, self.hidden_dim).zero_())
return hidden
```
### Define forward and backpropagation
```
def forward_back_prop(rnn, optimizer, criterion, inp, target, hidden):
# move data to GPU, if available
if train_on_gpu:
inp, target = inp.cuda(), target.cuda()
# perform backpropagation and optimization
hidden = tuple([i.data for i in hidden])
rnn.zero_grad()
output, hidden = rnn(inp, hidden)
loss = criterion(output, target)
loss.backward()
#useing gradient clipping to prevent exploding gradients problem
nn.utils.clip_grad_norm_(rnn.parameters(), 5)
optimizer.step()
# return the loss over a batch and the hidden state produced by our model
return loss.item(), hidden
```
## Neural Network Training
With the structure of the network complete and data ready to be fed in the neural network, it's time to train it.
```
def train_rnn(rnn, batch_size, optimizer, criterion, n_epochs, show_every_n_batches=100):
batch_losses = []
rnn.train()
print("Training for %d epoch(s)..." % n_epochs)
for epoch_i in range(1, n_epochs + 1):
# initialize hidden state
hidden = rnn.init_hidden(batch_size)
for batch_i, (inputs, labels) in enumerate(train_loader, 1):
# making sure to iterate over completely full batches, only
n_batches = len(train_loader.dataset)//batch_size
if(batch_i > n_batches):
break
# forward, back prop
loss, hidden = forward_back_prop(rnn, optimizer, criterion, inputs, labels, hidden)
# record loss
batch_losses.append(loss)
# printing loss stats
if batch_i % show_every_n_batches == 0:
print('Epoch: {:>4}/{:<4} Loss: {}\n'.format(
epoch_i, n_epochs, np.average(batch_losses)))
batch_losses = []
# returns a trained rnn
return rnn
```
### Hyperparameters
```
# Data params
# Sequence Length - [5, 7, 10, 15, 20, 25]
sequence_length = 15 # of words in a sequence
# Batch Size - [64, 128, 256]
batch_size = 128
# data loader - do not change
train_loader = batch_data(int_text, sequence_length, batch_size)
# Training parameters
# Number of Epochs
num_epochs = 25
# Learning Rate - [0.001 - 0.005, 0.01, 0.1]
learning_rate = 0.001
# Model parameters
# Vocab size
vocab_size = len(int_to_vocab)
# Output size
output_size = vocab_size
# Embedding Dimension - [200, 400, 600]
embedding_dim = 128
# Hidden Dimension - [300, 500, 1000]
hidden_dim = 500
# Number of RNN Layers - [2,3]
n_layers = 2
# Show stats for every n number of batches
show_every_n_batches = 500
```
### Train
```
import time
t0 = time.time()
from workspace_utils import active_session
with active_session():
# create model and move to gpu if available
rnn = RNN(vocab_size, output_size, embedding_dim, hidden_dim, n_layers, dropout=0.5)
if train_on_gpu:
rnn.cuda()
# defining loss and optimization functions for training
optimizer = torch.optim.Adam(rnn.parameters(), lr=learning_rate)
criterion = nn.CrossEntropyLoss()
# training the model
trained_rnn = train_rnn(rnn, batch_size, optimizer, criterion, num_epochs, show_every_n_batches)
# saving the trained model
helper.save_model('./save/trained_rnn', trained_rnn)
print('Model Trained and Saved')
t1 = time.time()
print('Time taken:', (t1-t0)/3600, 'hours')
```
---
# Checkpoint
```
import torch
import helper
import problem_unittests as tests
_, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
trained_rnn = helper.load_model('./save/trained_rnn')
```
## Generate TV Script
With the network trained and saved, I can use it to generate a new, "fake" Seinfeld TV script.
### Generate Text
To generate the text, the network needs to start with a single word and repeat its predictions until it reaches a set length. It takes a word id to start with, `prime_id`, and generates a set length of text, `predict_len`. Also note that it uses topk sampling to introduce some randomness in choosing the most likely next word, given an output set of word scores!
```
import torch.nn.functional as F
def generate(rnn, prime_id, int_to_vocab, token_dict, pad_value, predict_len=100):
rnn.eval()
# create a sequence (batch_size=1) with the prime_id
current_seq = np.full((1, sequence_length), pad_value)
current_seq[-1][-1] = prime_id
predicted = [int_to_vocab[prime_id]]
for _ in range(predict_len):
if train_on_gpu:
current_seq = torch.LongTensor(current_seq).cuda()
else:
current_seq = torch.LongTensor(current_seq)
# initialize the hidden state
hidden = rnn.init_hidden(current_seq.size(0))
# get the output of the rnn
output, _ = rnn(current_seq, hidden)
# get the next word probabilities
p = F.softmax(output, dim=1).data
if(train_on_gpu):
p = p.cpu() # move to cpu
# use top_k sampling to get the index of the next word
top_k = 5
p, top_i = p.topk(top_k)
top_i = top_i.numpy().squeeze()
# select the likely next word index with some element of randomness
p = p.numpy().squeeze()
word_i = np.random.choice(top_i, p=p/p.sum())
# retrieve that word from the dictionary
word = int_to_vocab[word_i]
predicted.append(word)
# the generated word becomes the next "current sequence" and the cycle can continue
current_seq = np.roll(current_seq, -1, 1)
current_seq[-1][-1] = word_i
gen_sentences = ' '.join(predicted)
# Replace punctuation tokens
for key, token in token_dict.items():
ending = ' ' if key in ['\n', '(', '"'] else ''
gen_sentences = gen_sentences.replace(' ' + token.lower(), key)
gen_sentences = gen_sentences.replace('\n ', '\n')
gen_sentences = gen_sentences.replace('( ', '(')
# return all the sentences
return gen_sentences
```
### Generate a New Script
It's time to generate the text.
```
gen_length = 400
prime_word = 'jerry' # name for starting the script
pad_word = helper.SPECIAL_WORDS['PADDING']
generated_script = generate(trained_rnn, vocab_to_int[prime_word + ':'], int_to_vocab, token_dict, vocab_to_int[pad_word], gen_length)
print(generated_script)
```
#### Save your favorite scripts
Once you have a script that you like (or find interesting), save it to a text file!
```
# save script to a text file
f = open("generated_script_1.txt","w")
f.write(generated_script)
f.close()
```
| true |
code
| 0.676273 | null | null | null | null |
|
```
import panel as pn
pn.extension('plotly')
```
The ``HoloViews`` pane renders HoloViews plots with one of the plotting backends supported by HoloViews. It supports the regular HoloViews widgets for exploring the key dimensions of a ``HoloMap`` or ``DynamicMap``, but is more flexible than the native HoloViews widgets since it also allows customizing widget types and their position relative to the plot.
#### Parameters:
For layout and styling related parameters see the [customization user guide](../../user_guide/Customization.ipynb).
* **``backend``** (str): Any of the supported HoloViews backends ('bokeh', 'matplotlib', or 'plotly')
* **``center``** (boolean, default=False): Whether to center the plot
* **``linked_axes``** (boolean, default=True): Whether to link axes across plots in a panel layout
* **``object``** (object): The HoloViews object being displayed
* **``widget_location``** (str): Where to lay out the widget relative to the plot
* **``widget_layout``** (ListPanel type): The object to lay the widgets out in, one of ``Row``, ``Column`` or ``WidgetBox``
* **``widget_type``** (str): Whether to generate individual widgets for each dimension, or to use a global linear scrubber with dimensions concatenated.
* **``widgets``** (dict): A mapping from dimension name to a widget class, instance, or dictionary of overrides to modify the default widgets.
##### Display
* **``default_layout``** (pn.layout.Panel, default=Row): Layout to wrap the plot and widgets in
___
The `panel` function will automatically convert any ``HoloViews`` object into a displayable panel, while keeping all of its interactive features:
```
import numpy as np
import holoviews as hv
box = hv.BoxWhisker((np.random.randint(0, 10, 100), np.random.randn(100)), 'Group').sort()
hv_layout = pn.panel(box)
hv_layout
```
By setting the pane's ``object`` the plot can be updated like all other pane objects:
```
hv_layout.object = hv.Violin(box).opts(violin_color='Group', cmap='Category20')
```
### Widgets
HoloViews natively renders plots with widgets if a HoloMap or DynamicMap declares any key dimensions. Unlike Panel's ``interact`` functionality, this approach efficiently updates just the data inside a plot instead of replacing it entirely. Calling ``pn.panel`` on the DynamicMap will return a ``Row`` layout (configurable via the ``default_layout`` option), which is equivalent to calling ``pn.pane.HoloViews(dmap).layout``:
```
import pandas as pd
import hvplot.pandas
import holoviews.plotting.bokeh
def sine(frequency=1.0, amplitude=1.0, function='sin'):
xs = np.arange(200)/200*20.0
ys = amplitude*getattr(np, function)(frequency*xs)
return pd.DataFrame(dict(y=ys), index=xs).hvplot()
dmap = hv.DynamicMap(sine, kdims=['frequency', 'amplitude', 'function']).redim.range(
frequency=(0.1, 10), amplitude=(1, 10)).redim.values(function=['sin', 'cos', 'tan'])
hv_panel = pn.panel(dmap)
hv_panel.pprint()
```
We can see the widgets generated for each of the dimensions and arrange them any way we like, e.g. by unpacking them into a ``Row``:
```
widgets = hv_panel[1]
pn.Column(
pn.Row(*widgets),
hv_panel[0])
```
However, more conveniently the HoloViews pane offers options to lay out the plot and widgets in a number of preconfigured arrangements using the ``center`` and ``widget_location`` parameters.
```
pn.panel(dmap, center=True, widget_location='right_bottom')
```
The ``widget_location`` parameter accepts all of the following options:
['left', 'bottom', 'right', 'top', 'top_left', 'top_right', 'bottom_left',
'bottom_right', 'left_top', 'left_bottom', 'right_top', 'right_bottom']
#### Customizing widgets
As we saw above, the HoloViews pane will automatically try to generate appropriate widgets for the type of data, usually defaulting to ``DiscreteSlider`` and ``Select`` widgets. This behavior can be modified by providing a dictionary of ``widgets`` by dimension name. The values of this dictionary can override the default widget in one of three ways:
* Supplying a ``Widget`` instance
* Supplying a compatible ``Widget`` type
* Supplying a dictionary of ``Widget`` parameter overrides
``Widget`` instances will be used as they are supplied and are expected to provide values matching compatible with the values defined on HoloMap/DynamicMap. Similarly if a ``Widget`` type is supplied it should be discrete if the parameter space defines a discrete set of values. If the defined parameter space is continuous, on the other hand, it may supply any valid value.
In the example below the 'amplitude' dimension is overridden with an explicit ``Widget`` instance, the 'function' dimension is overridden with a RadioButtonGroup letting us toggle between the different functions, and lastly the 'value' parameter on the 'frequency' widget is overridden to change the initial value:
```
hv_panel = pn.pane.HoloViews(dmap, widgets={
'amplitude': pn.widgets.LiteralInput(value=1., type=(float, int)),
'function': pn.widgets.RadioButtonGroup,
'frequency': {'value': 5}
}).layout
```
### Switching backends
The ``HoloViews`` pane will default to the Bokeh backend if no backend has been loaded, but you can override the backend as needed.
```
import holoviews.plotting.mpl
import holoviews.plotting.plotly
hv_pane = pn.pane.HoloViews(dmap, backend='matplotlib')
hv_pane
```
The ``backend``, like all other parameters, can be modified after the fact. To demonstrate, we can set up a select widget to toggle between backends for the above plot:
```
backend_select = pn.widgets.RadioButtonGroup(name='Backend Selector:', options=['bokeh', 'matplotlib', 'plotly'])
backend_select.link(hv_pane[0], value='backend')
backend_select
```
| true |
code
| 0.37108 | null | null | null | null |
|
# scatter_selector widget
A set of custom matplotlib widgets that allow you to select points on a scatter plot as use that as input to other interactive plots. There are three variants that differ only in what they pass to their callbacks:
1. {obj}`.scatter_selector`: callbacks will receive `index, (x, y)` where `index` is the position of the point in the of the points.
2. {obj}`.scatter_selector_value`: callbacks will receive `x, y`
3. {obj}`.scatter_selector_index`: callbacks will receive `index`
In this example we will use {obj}`.scatter_selector_index` along with the `indexer` convenience function to make line plots of stock data. However, you can use custom functions for the interactive plots, or even attach your own callbacks to the scatter_selector widgets.
## PCA of Stock Data
For this example we will plot companies in SP500 in a scatter plot by principle components extracted from principal components analysis (PCA) an interactive visualization of companies in SP500 using [PCA](https://towardsdatascience.com/a-one-stop-shop-for-principal-component-analysis-5582fb7e0a9c). The data was originally obtained from <https://www.kaggle.com/camnugent/sandp500> and the data was cleaned using code derived from <https://github.com/Hekstra-Lab/scientific-python-bootcamp/tree/master/day3>
```
%matplotlib ipympl
import pickle
import ipywidgets as widgets
import matplotlib.pyplot as plt
import numpy as np
import mpl_interactions.ipyplot as iplt
from mpl_interactions import indexer, panhandler, zoom_factory
from mpl_interactions.utils import indexer
from mpl_interactions.widgets import scatter_selector_index
```
### Data loading/cleaning
For this example we have pre-cleaned data that we will just load. If you are curious on how the data was originally processed you see the full code at the bottom of this notebook.
The datafiles that we load for this example are available for download at <https://github.com/ianhi/mpl-interactions/tree/master/docs/examples/data>
```
import pickle
with open("data/stock-metadata.pickle", "rb") as f:
meta = pickle.load(f)
prices = np.load("data/stock-prices.npz")["prices"]
names = meta["names"]
good_idx = meta["good_idx"] # only plot the ones for which we were able to parse sector info
data_colors = meta["data_colors"]
# calculate the daily price difference
price_changes = np.diff(prices)
# Below is a pretty standard way of normalizing numerical data
normalized_price_changes = price_changes - price_changes.mean(axis=-1, keepdims=True)
normalized_price_changes /= price_changes.std(axis=-1, keepdims=True)
# calculate the covariance matrix
covariance = np.cov(normalized_price_changes.T)
# Calculate the eigenvectors (i.e. the principle components)
evals, evecs = np.linalg.eig(covariance)
evecs = np.real(evecs)
# project the companies onto the principle components
transformed = normalized_price_changes @ evecs
# take only the first two components for plotting
# we also take only the subset of companies for which it was easy to extract a sector and a name
x, y = transformed[good_idx][:, 0], transformed[good_idx][:, 1]
```
### Making the plot
We create the left scatter plot using the `scatter_selector_index` which will tell use the index of the company that was clicked on. Since this is just a Matplotlib `AxesWidget` it can be passed directly to `iplt.plot` as a kwarg and the `controls` object will handle it appropriately.
In this example we also make use of the function `mpl_interactions.utils.indexer`. This is a convenience function that handles indexing an array for you. So these two statements are equivalent:
```python
# set up data
arr = np.random.randn(4,100).cumsum(-1)
def f(idx):
return arr[idx]
iplt.plot(f, idx=np.arange(4))
# or equivalently
iplt.plot(indexer(arr), idx=np.arange(4))
```
```
fig, axs = plt.subplots(1, 2, figsize=(10, 5), gridspec_kw={"width_ratios": [1.5, 1]})
index = scatter_selector_index(axs[0], x, y, c=data_colors, cmap="tab20")
# plot all the stock traces in light gray
plt.plot(prices.T, color="k", alpha=0.05)
# add interactive components to the subplot on the right
# note the use of indexer
controls = iplt.plot(indexer(prices), idx=index, color="r")
iplt.title(indexer(names), controls=controls["idx"])
# styling + zooming
axs[0].set_xlabel("PC-1")
axs[0].set_ylabel("PC-2")
axs[1].set_xlabel("days")
axs[1].set_ylabel("Price in $")
axs[1].set_yscale("log")
cid = zoom_factory(axs[0])
ph = panhandler(fig)
```

### Datacleaning
Below is the code we used to clean and save the datasets. While we start out with 500 companies we end up with only 468 as some of them we were unable to easily and correctly parse so they were thrown away.
```
# NBVAL_SKIP
# Download the data from https://www.kaggle.com/camnugent/sandp500
# and save it into a folder named `data`
import glob
test = np.loadtxt("data/A_data.csv", delimiter=",", skiprows=1, usecols=1)
sp500_glob = glob.glob(
"data/*.csv",
)
names = []
prices = np.zeros((len(sp500_glob), test.shape[0]))
prices_good = []
fails = []
for i, f in enumerate(sp500_glob):
fname = f.split("/")[-1]
names.append(fname.split("_")[0])
try:
prices[i] = np.loadtxt(f, delimiter=",", skiprows=1, usecols=1)
prices_good.append(True)
except:
fails.append(fname.split("_")[0])
prices_good.append(False)
pass
prices = prices[prices_good]
np.savez_compressed("data/stock-prices.npz", prices=prices)
# processing names and sector info
arr = np.loadtxt("data/SP500_names.csv", delimiter="|", skiprows=1, dtype=str, encoding="utf-8")
name_dict = {a[0].strip(): a[[1, 2, 3]] for a in arr}
# idx_to_info = {i:name_dict[real_names[i]] for i in range(468)}
good_names = []
primary = []
secondary = []
good_idx = np.zeros(real_names.shape[0], dtype=bool)
for i, name in enumerate(real_names):
try:
info = name_dict[name]
good_idx[i] = True
good_names.append(info[0])
primary.append(info[1])
secondary.append(info[2])
except:
pass
psector_dict = {val: i for i, val in enumerate(np.unique(primary))}
data_colors = np.array([psector_dict[val] for val in primary], dtype=int)
import pickle
meta = {
"good_idx": good_idx,
"names": good_names,
"sector": psector_dict,
"data_colors": data_colors,
}
with open("data/stock-metadata.pickle", "wb") as outfile:
pickle.dump(meta, outfile)
```
| true |
code
| 0.617282 | null | null | null | null |
|
# Calculating Thermodynamics Observables with a quantum computer
```
# imports
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from functools import partial
from qiskit.utils import QuantumInstance
from qiskit import Aer
from qiskit.algorithms import NumPyMinimumEigensolver, VQE
from qiskit_nature.drivers import UnitsType, Molecule
from qiskit_nature.drivers.second_quantization import (
ElectronicStructureDriverType,
ElectronicStructureMoleculeDriver,
)
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import JordanWignerMapper
from qiskit_nature.algorithms import GroundStateEigensolver
import qiskit_nature.constants as const
from qiskit_nature.algorithms.pes_samplers import BOPESSampler, EnergySurface1DSpline
from thermodynamics_utils.thermodynamics import constant_volume_heat_capacity
from thermodynamics_utils.vibrational_structure_fd import VibrationalStructure1DFD
from thermodynamics_utils.partition_function import DiatomicPartitionFunction
from thermodynamics_utils.thermodynamics import Thermodynamics
import warnings
warnings.simplefilter("ignore", np.RankWarning)
```
A preliminary draft with more information related to this tutorial can be found in preprint: Stober et al, arXiv 2003.02303 (2020)
### Calculation of the Born Oppenheimer Potential Energy Surface (BOPES)
To compute thermodynamic observables we begin with single point energy calculation which calculates the wavefunction and charge density and therefore the energy of a particular arrangement of nuclei. Here we compute the Born-Oppenheimer potential energy surface of a hydrogen molecule, as an example, which is simply the electronic energy as a function of bond length.
```
qubit_converter = QubitConverter(mapper=JordanWignerMapper())
quantum_instance = QuantumInstance(backend=Aer.get_backend("aer_simulator_statevector"))
solver = VQE(quantum_instance=quantum_instance)
me_gss = GroundStateEigensolver(qubit_converter, solver)
stretch1 = partial(Molecule.absolute_distance, atom_pair=(1, 0))
mol = Molecule(
geometry=[("H", [0.0, 0.0, 0.0]), ("H", [0.0, 0.0, 0.2])],
degrees_of_freedom=[stretch1],
masses=[1.6735328e-27, 1.6735328e-27],
)
# pass molecule to PSYCF driver
driver = ElectronicStructureMoleculeDriver(mol, driver_type=ElectronicStructureDriverType.PYSCF)
es_problem = ElectronicStructureProblem(driver)
# BOPES sampler testing
bs = BOPESSampler(gss=me_gss, bootstrap=True)
points = np.linspace(0.45, 5, 50)
res = bs.sample(es_problem, points)
energies = []
bs_res_full = res.raw_results
for point in points:
energy = bs_res_full[point].computed_energies + bs_res_full[point].nuclear_repulsion_energy
energies.append(energy)
fig = plt.figure()
plt.plot(points, energies)
plt.title("Dissociation profile")
plt.xlabel("Interatomic distance")
plt.ylabel("Energy")
energy_surface = EnergySurface1DSpline()
xdata = res.points
ydata = res.energies
energy_surface.fit(xdata=xdata, ydata=ydata)
plt.plot(xdata, ydata, "kx")
x = np.arange(min(xdata) - 0.25, max(xdata) + 0.25, 0.05)
plt.plot(x, energy_surface.eval(x), "r-")
plt.xlabel(r"distance, $\AA$")
plt.ylabel("energy, Hartree")
dist = max(ydata) - min(ydata)
plt.ylim(min(ydata) - 0.1 * dist, max(ydata) + 0.1 * dist)
```
### Calculation of the molecular Vibrational Energy levels
The Born-Oppeheimer approximation removes internuclear vibrations from the molecular Hamiltonian and the energy computed from quantum mechanical ground-state energy calculations using this approximation contain only the electronic energy. Since even at absolute zero internuclear vibrations still occur, a correction is required to obtain the true zero-temperature energy of a molecule. This correction is called the zero-point vibrational energy (ZPE), which is computed by summing the contribution from internuclear vibrational modes. Therefore, the next step in computing thermodynamic observables is determining the vibrational energy levels. This can be done by constructing the Hessian matrix based on computed single point energies close to the equilibrium bond length. The eigenvalues of the Hessian matrix can then be used to determine the vibrational energy levels and the zero-point vibrational energy
\begin{equation}
{\rm ZPE} = \frac{1}{2}\, \sum_i ^M \nu_i \, ,
\end{equation}
with $\nu_i$ being the vibrational frequencies, $M = 3N − 6$ or $M = 3N − 5$ for non-linear or linear molecules, respectively, and $N$ is number of the particles.
Here we fit a "full" energy surface using a 1D spline potential and use it to evaluate molecular vibrational energy levels.
```
vibrational_structure = VibrationalStructure1DFD(mol, energy_surface)
plt.plot(xdata, ydata, "kx")
x = np.arange(min(xdata) - 0.25, max(xdata) + 0.25, 0.05)
plt.plot(x, energy_surface.eval(x), "r-")
plt.xlabel(r"distance, $\AA$")
plt.ylabel("energy, Hartree")
dist = max(ydata) - min(ydata)
plt.ylim(min(ydata) - 0.1 * dist, max(ydata) + 0.1 * dist)
for N in range(15):
on = np.ones(x.shape)
on *= energy_surface.eval(
energy_surface.get_equilibrium_geometry()
) + vibrational_structure.vibrational_energy_level(N)
plt.plot(x, on, "g:")
on = np.ones(x.shape)
plt.show()
```
### Create a partition function for the calculation of heat capacity
The partition function for a molecule is the product of contributions from translational, rotational, vibrational, electronic, and nuclear degrees of freedom. Having the vibrational frequencies, now we can obtain the vibrational partition function $q_{\rm vibration}$ to compute the whole molecular partition function
\begin{equation}
q_{\rm vibration} = \prod_{i=1} ^M \frac{\exp\,(-\Theta_{\nu_i}/2T)}{1-\exp\,(-\Theta_{\nu_i}/2T} \, .
\end{equation}
Here $\Theta_{\nu_i}= h\nu_i/k_B$, $T$ is the temperature and $k_B$ is the Boltzmann constant.
The single-point energy calculations and the resulting partition function can be used to calculate the (constant volume or constant pressure) heat capacity of the molecules. The constant volume heat capacity, for example, is given by
\begin{equation}
C_v = \left.\frac{\partial U}{\partial T}\right|_{N,V}\, ,
\qquad
{\rm with} \quad
U=k_B T^2 \left.\frac{\partial {\rm ln} Q}{\partial T}\right|_{N,V} .
\end{equation}
$U$ is the internal energy, $V$ is the volume and $Q$ is the partition function.
Here we illustrate the simplest usage of the partition function, namely creating a Thermodynamics object to compute properties like the constant pressure heat capacity defined above.
```
Q = DiatomicPartitionFunction(mol, energy_surface, vibrational_structure)
P = 101350 # Pa
temps = np.arange(10, 1050, 5) # K
mol.spins = [1 / 2, 1 / 2]
td = Thermodynamics(Q, pressure=101350)
td.set_pressure(101350)
temps = np.arange(10, 1500, 5)
ymin = 5
ymax = 11
plt.plot(temps, td.constant_pressure_heat_capacity(temps) / const.CAL_TO_J)
plt.xlim(0, 1025)
plt.ylim(ymin, ymax)
plt.xlabel("Temperature, K")
plt.ylabel("Cp, cal mol$^{-1}$ K$^{-1}$")
plt.show()
```
Here we demonstrate how to access particular components (the rotational part) of the partition function, which in the H2 case we can further split to para-hydrogen and ortho-hydrogen components.
```
eq = Q.get_partition(part="rot", split="eq")
para = Q.get_partition(part="rot", split="para")
ortho = Q.get_partition(part="rot", split="ortho")
```
We will now plot the constant volume heat capacity (of the rotational part) demonstrating how we can call directly the functions in the 'thermodynamics' module, providing a callable object for the partition function (or in this case its rotational component). Note that in the plot we normalize the plot dividing by the universal gas constant R (Avogadro's number times Boltzmann's constant) and we use crossed to compare with experimental data found in literature.
```
# REFERENCE DATA from literature
df_brink_T = [80.913535, 135.240157, 176.633783, 219.808499, 246.226899]
df_brink_Cv = [0.118605, 0.469925, 0.711510, 0.833597, 0.895701]
df_eucken_T = [
25.120525,
30.162485,
36.048121,
41.920364,
56.195875,
62.484934,
72.148692,
73.805910,
73.804236,
92.214423,
180.031917,
230.300866,
]
df_eucken_Cv = [
0.012287,
0.012354,
0.008448,
0.020478,
0.032620,
0.048640,
0.048768,
0.076678,
0.078670,
0.170548,
0.667731,
0.847681,
]
df_gia_T = [
190.919338,
195.951254,
202.652107,
204.292585,
209.322828,
225.300754,
234.514217,
243.747768,
]
df_gia_Cv = [0.711700, 0.723719, 0.749704, 0.797535, 0.811546, 0.797814, 0.833793, 0.845868]
df_parting_T = [80.101665, 86.358919, 185.914204, 239.927797]
df_parting_Cv = [0.084730, 0.138598, 0.667809, 0.891634]
df_ce_T = [
80.669344,
135.550569,
145.464190,
165.301153,
182.144856,
203.372528,
237.993108,
268.696642,
294.095771,
308.872014,
]
df_ce_Cv = [
0.103048,
0.467344,
0.541364,
0.647315,
0.714078,
0.798258,
0.891147,
0.944848,
0.966618,
0.985486,
]
HeatCapacity = constant_volume_heat_capacity
R = const.N_A * const.KB_J_PER_K
plt.plot(temps, HeatCapacity(eq, temps) / R, "-k", label="Cv_rot Equilibrium")
plt.plot(temps, HeatCapacity(para, temps) / R, "-b", label="Cv_rot Para")
plt.plot(temps, HeatCapacity(ortho, temps) / R, "-r", label="Cv_rot Ortho")
plt.plot(
temps,
0.25 * HeatCapacity(para, temps) / R + 0.75 * HeatCapacity(ortho, temps) / R,
"-g",
label="Cv_rot 1:3 para:ortho",
)
plt.plot(df_brink_T, df_brink_Cv, "+g")
plt.plot(df_eucken_T, df_eucken_Cv, "+g")
plt.plot(df_gia_T, df_gia_Cv, "+g")
plt.plot(df_parting_T, df_parting_Cv, "+g")
plt.plot(df_ce_T, df_ce_Cv, "+g", label="experimental data")
plt.legend(loc="upper right", frameon=False)
plt.xlim(10, 400)
plt.ylim(-0.1, 2.8)
plt.xlabel("Temperature, K")
plt.ylabel("Cv (rotational)/R")
plt.tight_layout()
plt.show()
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
```
| true |
code
| 0.610744 | null | null | null | null |
|
## Explore The Data: Explore Continuous Features
Using the Titanic dataset from [this](https://www.kaggle.com/c/titanic/overview) Kaggle competition.
This dataset contains information about 891 people who were on board the ship when departed on April 15th, 1912. As noted in the description on Kaggle's website, some people aboard the ship were more likely to survive the wreck than others. There were not enough lifeboats for everybody so women, children, and the upper-class were prioritized. Using the information about these 891 passengers, the challenge is to build a model to predict which people would survive based on the following fields:
- **Name** (str) - Name of the passenger
- **Pclass** (int) - Ticket class (1st, 2nd, or 3rd)
- **Sex** (str) - Gender of the passenger
- **Age** (float) - Age in years
- **SibSp** (int) - Number of siblings and spouses aboard
- **Parch** (int) - Number of parents and children aboard
- **Ticket** (str) - Ticket number
- **Fare** (float) - Passenger fare
- **Cabin** (str) - Cabin number
- **Embarked** (str) - Port of embarkation (C = Cherbourg, Q = Queenstown, S = Southampton)
**This section focuses on exploring the `Pclass`, `Age`, `SibSp`, `Parch`, and `Fare` features.**
### Read In Data
```
# Read in our data
import pandas as pd
from scipy import stats
titanic_df = pd.read_csv('../Data/titanic.csv')
titanic_df.head()
# Drop all categorical features
cat_feat = ['PassengerId', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked']
titanic_df.drop(cat_feat, axis=1, inplace=True)
titanic_df.head()
```
### Explore Continuous Features
```
# Look at the general distribution of these features
titanic_df.describe()
# Look at the correlation matrix
titanic_df.corr()
```
- as from the data above, we can see correlation between `Survived` and `Pclass`, `Fare` are pretty strong. Note that negative correlation still counts. so we might need to dig further.
- there is also strong negative correlation between `Pclass` and `Fare`, which makes sense, such as 3rd class is much cheaper fare than 1st class.
```
# Look at fare by different passenger class levels
titanic_df.groupby('Pclass')['Fare'].describe()
def describe_cont_features(feature):
print('\n*** Results for {} ***'.format(feature))
print(titanic_df.groupby('Survived')[feature].describe())
print(ttest(feature))
def ttest(feature):
# seperate between Survival and Non-Survival Groups
survived = titanic_df[titanic_df['Survived'] == 1][feature]
not_survived = titanic_df[titanic_df['Survived'] == 0][feature]
tstat, pval = stats.ttest_ind(survived, not_survived, equal_var=False)
print('t-statistics: {:.1f}, p-value: {:.3}'.format(tstat, pval))
# Look at the distribution of each feature at each level of the target variable
for feature in ['Pclass', 'Age', 'SibSp', 'Parch', 'Fare']:
describe_cont_features(feature)
```
based on the statistics above, we can se that mean and median values of `Pclass` and `Fare` pretty stand out. There is significant difference between Survived and Non Survived groups in those values. But we have to keep in mind that there is a negative correlation between those 2 features.
```
# Look at the average value of each feature based on whether Age is missing
titanic_df.groupby(titanic_df['Age'].isnull()).mean()
```
looking at the above chart, `True` is for the group of missing Age. `False` is for the group with Age.
We can see that mean Age for Non Survived group is much lower than Survived group. Maybe they didn't record for passengers who were travelling in bowels of the ships. We can also see that Pclass is a bit lower and more Siblings, Spouses and much lower Fare.
| true |
code
| 0.412382 | null | null | null | null |
|
## This notebook contains prototyping work for implementing the viterbi decode algorithm
```
import numpy as np
import librosa
import matplotlib.pyplot as plt
def redistribute_trans_table(A):
for i in range(5,A.shape[1]):
current_col = A[:,i]
idx = (-current_col).argsort()[:2]
second_max_val = current_col[idx[1]]
current_col[idx[0]] = second_max_val
new_array = (current_col/current_col.sum(axis=0))
A[:,i] = new_array
for i in range(0,5):
current_col = A[:,i]
idx = (-current_col).argsort()[:1]
max_val = current_col[idx[0]]
new_array = np.zeros_like(A[5:,i])
new_array = np.random.uniform(low=0,high=max_val,size=new_array.shape[0])
A[5:,i] = new_array
A[:,i] = A[:,i]/(A[:,i].sum(axis=0))
return A
def viterbi(A, B, sequence, B_weight=1):
'''
~~~~ ARGUMENTS ~~~~
sequence : list
- a sequence of labels
A : numpy array
- transition table
- shape = [number of notes + 1 for <start>, number of notes]
- NOTE: the <start> token should be indexed at the last row
B : numpy array
- emission table
- shape = [number of notes, number of possible labels]
'''
# let's work in log space
A = np.log(A)
B = np.log(B*B_weight)
num_notes = B.shape[0]
# create empty viterbi matrix and backpointer matrix
viterbi = np.full((num_notes, len(sequence)), None)
bp = np.full((num_notes, len(sequence)), None)
# Compute the first column
first_label = sequence[0]
start_token = A.shape[0]
for n in range(num_notes):
viterbi[n,0] = A[-1,n] + B[n,first_label]
bp[n,0] = start_token
for w in range(1, len(sequence)):
for n in range(num_notes):
viterbi[n,w], bp[n,w] = compute_viterbi_val(n=n, w=w, viterbi=viterbi, A_prev=A[:,n], B_prev=B[n,w]) #transitions from previous note to current note
# Find maximum value of last column of viterbi
max_idx = np.argmax(viterbi[:,-1])
# Trace back maximum indices in backpointer table
note_sequence = [max_idx]
next_note = bp[max_idx,-1]
for i in range(1,len(sequence)):
reverse_i = len(sequence)-i
# print('reverse_i : {}'.format(reverse_i))
note_sequence.append(bp[next_note, reverse_i])
next_note = bp[next_note, reverse_i]
# print('next_note: {}'.format(next_note))
# for i in range(0,len(sequence)):
# reverse_i = len(sequence)-i-1
# print(f'[{i-1},{reverse_i}]')
# note_sequence.append(bp[note_sequence[i-1], reverse_i])
note_sequence.reverse()
return note_sequence, viterbi, bp
def compute_viterbi_val(n, w, viterbi, A_prev, B_prev):
# Compute first viterbi value
current_val = viterbi[0,w-1] + A_prev[0] + B_prev
max_val = current_val
bp = 0
# Loop through rest of values
for i, v in enumerate(list(viterbi[:,w-1])):
current_val = v + A_prev[i] + B_prev
if current_val > max_val:
max_val = current_val
bp = i
return max_val, bp
def make_emission_table():
# Numpy array
em_table = np.random.uniform(0,1,(32,12000))
new_array = (em_table/em_table.sum(axis=0))
return new_array
def onset_label(onset, spectrogram=None):
'''
Function that takes in 1D onset array and spectrogram and labels each onset with the spectrogram that most closely
matches the emission probability table
INPUTS: 1D Onset Array , computed spectrogram
OUTPUTS: 1D Array of same length as onset array corresponding to column indices of emission probability table
'''
# X will probably need to be determined by spectrogram clusters , set locally just to highlight
X = 12000
return np.random.randint(0,X,len(onset))
def onset_time(processed_path):
# Load the songs and the notes arrays one at a time
# for idx in range (len(song_paths)):
# Load the song
y, sr = librosa.load(processed_path)
# resample the song if it isn't sr=22050 (for consistent sizing)
if not sr == 22050:
y = librosa.resample(y, sr, 22050)
sr = 22050
#source seperation, margin can be tuned
y_harmonic, y_percussive = librosa.effects.hpss(y, margin=2.0)
# Set Hop_len
hop_len = 520
onset_frame_backtrack = librosa.onset.onset_detect(y_harmonic, sr = sr, hop_length = hop_len, backtrack=True)
onset_times = librosa.frames_to_time(onset_frame_backtrack)
return y_harmonic, onset_times
# Load and modify transition table
A = np.load('trans_prob_table.npy')
# A_redistributed = redistribute_trans_table(A)
# Display
plt.figure()
plt.imshow(A)
plt.title('Transition Table')
plt.figure()
plt.imshow(A)
plt.title('Redistributed')
song_path = r'X:\Training Data\Unprocessed\Angevil Hero II\1. John 5 - 27 Needles\song.ogg'
_, onset_times = onset_time(song_path)
print(onset_times)
onset = [0 for _ in range(1000)]
B = make_emission_table()
sequence = onset_label(onset)
note_sequence, v, bp = viterbi(A_redistributed, B, sequence)
# print(note_sequence)
def onset_time_bins(onset_times):
otb = [int(x) for x in onset_times*100]
return otb
otb = onset_time_bins(onset_times)
print(otb)
note_sequence
import matplotlib.pyplot as plt
def make_emission_table():
# Numpy array
em_table = np.random.uniform(0,1,(32,12000))
new_array = (em_table/em_table.sum(axis=0))
return new_array
def onset_label(onset, spectrogram=None):
'''
Function that takes in 1D onset array and spectrogram and labels each onset with the spectrogram that most closely
matches the emission probability table
INPUTS: 1D Onset Array , computed spectrogram
OUTPUTS: 1D Array of same length as onset array corresponding to column indices of emission probability table
'''
# X will probably need to be determined by spectrogram clusters , set locally just to highlight
X = 12000
return np.random.randint(0,X,len(onset))
onset = [0 for _ in range(1000)]
A = np.load('trans_prob_table.npy')
B = make_emission_table()
sequence = onset_label(onset)
note_sequence = viterbi(A, B, sequence)
print(note_sequence)
plt.imshow(A)
def redistribute_trans_table(A):
for i in range(5,A.shape[1]):
current_col = A[:,i]
idx = (-current_col).argsort()[:2]
second_max_val = current_col[idx[1]]
current_col[idx[0]] = second_max_val
new_array = (current_col/current_col.sum(axis=0))
A[:,i] = new_array
for i in range(0,5):
current_col = A[:,i]
idx = (-current_col).argsort()[:1]
max_val = current_col[idx[0]]
new_array = np.zeros_like(A[5:,i])
new_array = np.random.uniform(low=0,high=max_val,size=new_array.shape[0])
A[5:,i] = new_array
A[:,i] = A[:,i]/(A[:,i].sum(axis=0))
return A
# A_fully_redistributed = redistribute_trans_table(A)
A_redistributed = redistribute_trans_table(A)
plt.imshow(A_redistributed)
print(np.max(A_redistributed))
```
| true |
code
| 0.422683 | null | null | null | null |
|
# Example: CanvasXpress scatter2d Chart No. 4
This example page demonstrates how to, using the Python package, create a chart that matches the CanvasXpress online example located at:
https://www.canvasxpress.org/examples/scatter2d-4.html
This example is generated using the reproducible JSON obtained from the above page and the `canvasxpress.util.generator.generate_canvasxpress_code_from_json_file()` function.
Everything required for the chart to render is included in the code below. Simply run the code block.
```
from canvasxpress.canvas import CanvasXpress
from canvasxpress.js.collection import CXEvents
from canvasxpress.render.jupyter import CXNoteBook
cx = CanvasXpress(
render_to="scatter2d4",
data={
"y": {
"vars": [
"s1",
"s2",
"s3",
"s4",
"s5",
"s6",
"s7",
"s8",
"s9",
"s10",
"s11",
"s12",
"s13",
"s14",
"s15",
"s16",
"s17",
"s18",
"s19",
"s20",
"s21"
],
"smps": [
"U-Trial 1",
"U-Trial 2",
"U-Trial 3",
"S-Trial 1",
"S-Trial 2",
"S-Trial 3"
],
"data": [
[
38.4,
27.7,
25.7,
53.1,
30.6,
30.2
],
[
46.2,
57.2,
41.9,
54.7,
43.3,
56.7
],
[
72.5,
57.9,
51.9,
74.2,
53.4,
42.4
],
[
38,
38,
32.2,
49.6,
37.4,
34.4
],
[
82.8,
57.9,
64.7,
53.6,
48.6,
44.8
],
[
33.9,
32,
31.4,
51.3,
35.5,
42.9
],
[
50.4,
40.6,
40.1,
44.1,
46.9,
42.7
],
[
35,
33.1,
43.2,
34,
26.4,
24.8
],
[
32.8,
26.8,
33.9,
34.5,
25.1,
25.1
],
[
60.1,
53.2,
40.4,
59.1,
87.1,
59.2
],
[
75.1,
63.1,
58,
67.3,
43.8,
42.2
],
[
57.6,
57.7,
61.5,
75.5,
126.6,
48.4
],
[
55.5,
63.3,
44.6,
41.1,
41.8,
32
],
[
49.5,
45.8,
35.3,
52.2,
53.8,
48.1
],
[
40.9,
35.7,
37.2,
28.3,
26,
33.7
],
[
44.3,
46.8,
39.4,
74.9,
45.3,
42.6
],
[
93.8,
91.9,
77.4,
77.5,
55.8,
54.9
],
[
47.9,
59.9,
52.8,
50.9,
58.6,
64.5
],
[
75.2,
54.1,
63.6,
70.1,
44,
43.1
],
[
46.2,
39.3,
56.6,
60.3,
47.8,
52.8
],
[
56.3,
45.8,
58.9,
59.9,
36.8,
44.3
]
]
},
"m": {
"Name": "Scents",
"Description": "Data on the time subjects required to complete a pencil and paper maze when they were smelling a floral scent and when they were not.",
"Reference": "Hirsch, A. R., and Johnston, L. H. Odors and Learning, Smell & Taste Treatment and Research Foundation, Chicago."
},
"z": {
"Sex": [
"M",
"F",
"M",
"M",
"M",
"F",
"F",
"F",
"M",
"F",
"F",
"F",
"F",
"M",
"M",
"M",
"M",
"M",
"F",
"F",
"M"
],
"Smoker": [
"N",
"Y",
"N",
"N",
"N",
"Y",
"N",
"N",
"N",
"N",
"Y",
"Y",
"Y",
"Y",
"N",
"N",
"Y",
"N",
"Y",
"N",
"N"
],
"Opinion": [
"pos",
"neg",
"pos",
"neg",
"neg",
"pos",
"pos",
"pos",
"pos",
"indiff",
"pos",
"indiff",
"pos",
"indiff",
"indiff",
"pos",
"neg",
"neg",
"pos",
"neg",
"neg"
],
"Age": [
23,
43,
43,
32,
15,
37,
26,
35,
26,
31,
35,
55,
25,
39,
25,
26,
33,
62,
54,
38,
65
],
"Order": [
1,
2,
1,
2,
1,
2,
1,
2,
1,
2,
1,
2,
1,
2,
1,
2,
1,
2,
1,
2,
1
]
}
},
config={
"citation": "Hirsch, A. R., and Johnston, L. H. Odors and Learning, Smell & Taste Treatment and Research Foundation, Chicago.",
"graphType": "Scatter2D",
"histogramStat": "count",
"legendBox": True,
"setMaxX": 100,
"setMaxY": 150,
"setMinX": 0,
"setMinY": 0,
"shapeBy": "Smoker",
"showTransition": False,
"sizeBy": "Age",
"theme": "CanvasXpress",
"title": "Data on the time subjects required to complete a pencil and paper mazewhen they were smelling a floral scent and when they were not.",
"xAxis": [
"U-Trial 1",
"U-Trial 2",
"U-Trial 3"
],
"xAxisExact": True,
"xAxisHistogramShow": True,
"yAxis": [
"S-Trial 1",
"S-Trial 2",
"S-Trial 3"
],
"yAxisExact": True,
"yAxisHistogramShow": True
},
width=613,
height=613,
events=CXEvents(),
after_render=[],
other_init_params={
"version": 35,
"events": False,
"info": False,
"afterRenderInit": False,
"noValidate": True
}
)
display = CXNoteBook(cx)
display.render(output_file="scatter2d_4.html")
```
| true |
code
| 0.626867 | null | null | null | null |
|
# MNIST
```
import torch
from torch import nn, optim
from torchvision import datasets, transforms
import numpy as np
%matplotlib inline
from matplotlib import pyplot as plt
```
### Description
Classification of hand-written digits (MNIST dataset) using a simple multi-layer perceptorn architecture implemented in PyTorch with the `nn.Sequential` module.
### Content
1. Loading a training dataset
1. Apply transformations
2. Creating a data loader
2. Defining a sequential neural network
3. Training a neural network
## Data Set
### MNIST
The MNIST data set is a large database of handwritten digits, often used as toy model to validate machine learning and deep learning algorithms in image recognition and classification.
### Loading the Data Set
Let's start by loading the MNIST dataset. Since we want to use the data (both images and associated labels) with PyTorch we have to load the dataset into `torch.tensor`s. Additionally we want our data to be normalised in order to avoid large variations in the data; we can compose the two transformations and apply them directly when loading the dataset.
```
transform = transforms.Compose(
[
transforms.ToTensor(), # Array to PyTorch tensor
transforms.Normalize((0.5,), (0.5,)), # Normalisation (mean and std)
]
)
trainset = datasets.MNIST('data', download=True, train=True, transform=transform)
```
*Note*: some `torchvision.transforms` apply directly to the loaded image and therefore go before `transforms.ToTensor()` while other `torchvision.transforms` are applied directly to `torch.tensors` and therefore go after `transforms.ToTensor()`.
Once the dataset is loaded and transformed, we can define a `DataLoader`. This is an utility class that allows to split the dataset in *minibatches*, used for training.
```
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True, drop_last=True)
```
### Visualizing Images and Labels
Let's look at the first batch of images:
```
dataiter = iter(trainloader) # Create an iterator from trainloader
images, labels = next(dataiter)
fig = plt.figure(figsize=(8,8))
for idx in range(64):
ax = fig.add_subplot(8, 8, idx + 1, xticks=[], yticks=[])
# Un-normalize image
img = images[idx].numpy().squeeze() * 0.5 + 0.5
plt.imshow(img, cmap='Greys')
ax.set_title(labels[idx].item(), fontdict={"fontsize": 12})
plt.tight_layout()
plt.show()
```
*Note*: Images have been normalised when loading the dataset. In order to visualise the original images we have to (manually) undo this transformation.
## Sequential Neural Network with PyTorch
### Define a Sequential NN
PyTorch allows to define simple (sequential) NN architectures very easily using `nn.Sequential`. `nn.Sequential` takes a list of layers and automatically build a sequential NN. The following architecture defines a multi-layer perceptron (MLP) with an input layer, a hidden layer and an output layer and using ReLU activation functions between layers:
```
model = nn.Sequential(nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 64),
nn.ReLU(),
nn.Linear(64, 10))
```
Printing the model will show its composition:
```
print(model)
```
### Test Forward Pass
In order to check that the model is defined correctly we can perfom a forward pass with a batch of images. We can also visualize how the model performs before training by plotting predicting class probabilities:
```
images, labels = next(dataiter)
def showclassp(images, labels, model):
"""
Plot class probabilities for a batch of images and labels.
"""
# Defint a figure
fig = plt.figure(figsize=(12,12))
# Flatten image for forward pass
images = images.view(images.shape[0], -1)
# Compute predictions
with torch.no_grad(): # Do not track gradients
# Perform forward pass
out = model(images)
# Compute class probabilities
p = nn.functional.softmax(out, dim=1).numpy()
# Loop over images and labels in a batch
for idx in range(64):
# Create subplot
ax = fig.add_subplot(8, 8, idx + 1, xticks=range(10), yticks=[0, 1])
# Plot all class probabilities for given image
for i in range(10):
if labels[idx] == i:
if labels[idx] == np.argmax(p[idx]):
plt.bar(i, p[idx,i], color="g")
else:
plt.bar(i, p[idx,i], color="r")
else:
plt.bar(i, p[idx,i], color="k")
plt.ylim([0,1.25])
ax.set_title(labels[idx].item(), fontdict={"fontsize": 12})
plt.tight_layout()
plt.show()
showclassp(images, labels, model)
```
The graph show the predicted probability for each class (before training). Green bars represent a correct classification while red bars represent an incorrect classification. Since the weights of the network are initialised at random, every class has a similar probability, close to $\frac{1}{10}$.
### Training
To train our model we need to define a loss function. For this multi-class classification problem we can use the cross-entropy loss:
```
cross_entropy_loss = nn.CrossEntropyLoss()
```
*Note*: the `nn.CrossEntropyLoss()` loss function composes `nn.LogSoftmax()` and `nn.NLLLoss()`. If the model outputs raw values `nn.CrossEntropyLoss()` should be used, while if the model output `nn.LogSoftmax()` then `nn.NLLLoss()` should be used as loss function.
In order to update the weights of our network we also need to define an optimiser. Here we use the simple stocastic gradient descent (SGD) optimiser:
```
# Learning rate
learning_rate = 0.003
# Define optimizer and link with model parameters
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
```
Finally we can train our model by looping over the batches and updating the weights of our network using backpropagation. The backpropagation algorithm works as follows:
1. Initialize gradients to zero
2. Perform a forward pass
3. Compute the loss
4. Perform backpropagation to compute the gradients
5. Update the paramerters of the model (weights)
```
# Define the number of training. epochs
epochs = 10
# Loop over epochs
for epoch in range(epochs):
# Initialize total epoch loss
epoch_loss = 0
# Loop over batches
for images, labels in trainloader:
# Flatten input image
images = images.view(images.shape[0], -1)
# Initialize the gradients to zero
optimizer.zero_grad()
# Perform forward pass
output = model(images)
# Compute the loss
loss = cross_entropy_loss(output, labels)
# Perform backpropagation
loss.backward()
# Update the weights
optimizer.step()
# Accumulate total epoch loss
epoch_loss += loss.item()
else:
print(f"Loss #{epoch+1}: {epoch_loss/len(trainloader)}")
```
Finally, we can plot class probabilities after training for a single batch:
```
images, labels = next(dataiter)
showclassp(images, labels, model)
```
We see that after training the model gives reasonable results (compared to the class probabilities obtained before trasining).
## Comments
Here we visualised the model predictions on one batch of the training dataset. This is not a fair evaluation of our model performance since this btach has been used multiple times to change the model weights. NN are known to easily overfit the training data and therefore one has to use regularization rechniques (such as *dropouts*, *eraly stopping*, ...) and validate the model on a different test set.
| true |
code
| 0.844056 | null | null | null | null |
|
# Inference only Text Models in `arcgis.learn`
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc">
<ul class="toc-item">
<li><span><a href="#Introduction" data-toc-modified-id="Introduction-1">Introduction</a></span></li>
<li><span><a href="#Transformer-Basics" data-toc-modified-id="Transformer-Basics-2">Transformer Basics</a></span></li>
<li><span><a href="#Prerequisites" data-toc-modified-id="Prerequisites-3">Prerequisites</a></span></li>
<li><span><a href="#Inference-only-models" data-toc-modified-id="Inference-only-models-4">Inference only models</a></span></li>
<ul class="toc-item">
<li><span><a href="#ZeroShotClassifier" data-toc-modified-id="ZeroShotClassifier-4.1">ZeroShotClassifier</a></span></li>
<li><span><a href="#QuestionAnswering" data-toc-modified-id="QuestionAnswering-4.2">QuestionAnswering</a></span></li>
<li><span><a href="#TextSummarizer" data-toc-modified-id="TextSummarizer-4.3">TextSummarizer</a></span></li>
<li><span><a href="#TextTranslator" data-toc-modified-id="TextTranslator-4.4">TextTranslator</a></span></li>
<li><span><a href="#TextGenerator" data-toc-modified-id="TextGenerator-4.5">TextGenerator</a></span></li>
<li><span><a href="#FillMask" data-toc-modified-id="FillMask-4.6">FillMask</a></span></li>
</ul>
<li><span><a href="#References" data-toc-modified-id="References-5">References</a></span></li>
</ul>
</div>
# Introduction
The pretrained/inference-only models available in `arcgis.learn.text` submodule are based on [Hugging Face Transformers](https://huggingface.co/transformers/v3.3.0/index.html) library. This library provides transformer models like `BERT` [[1]](#References), `RoBERTa`, `XLM`, `DistilBert`, `XLNet` etc., for **Natural Language Understanding (NLU)** with over 32+ pretrained models in 100+ languages. [This page](https://huggingface.co/transformers/v3.0.2/pretrained_models.html) mentions different transformer architectures [[2]](#References) which come in different sizes (model parameters), trained on different languages/corpus, having different attention heads, etc.
These inference-only classes offers a simple API dedicated to several **Natural Language Processing (NLP)** tasks including **Masked Language Modeling**, **Text Generation**, **Sentiment Analysis**, **Summarization**, **Machine Translation** and **Question Answering**.
The usage of these models differs from rest of the models available in `arcgis.learn` module in the sense that these models do not need to be trained on a given dataset before they can be used for inferencing. Therefore, these model do not have methods like `fit()`, `lr_find()` etc., which are required to train an `arcgis.learn` model.
Instead these model classes follow the following pattern:
- A model constructor where user can pass a pretrained model name to initialize the model.
- A `supported_backbones` attribute which tells the supported transformer architectures for that particular model.
- A method where user can pass input text and appropriate arguments to generate the model inference.
# Transformer Basics
Transformers in **Natural Language Processing (NLP)** are novel architectures that aim to solve [sequence-to-sequence](https://towardsdatascience.com/understanding-encoder-decoder-sequence-to-sequence-model-679e04af4346) tasks while handling [long-range dependencies](https://medium.com/tech-break/recurrent-neural-network-and-long-term-dependencies-e21773defd92) with ease. The transformers are the latest and advanced models that give state of the art results for a wide range of tasks such as **text/sequence classification**, **named entity recognition (NER)**, **question answering**, **machine translation**, **text summarization**, **text generation** etc.
The Transformer architecture was proposed in the paper [Attention Is All You Need](https://arxiv.org/pdf/1706.03762.pdf). A transformer consists of an **encoding component**, a **decoding component** and **connections** between them.
- The **Encoding component** is a stack of encoders (the paper stacks six of them on top of each other).
- The **Decoding component** is a stack of decoders of the same number.
<img src="data:image/jpeg;base64,/9j/4AAQSkZJRgABAQEAeAB4AAD/4QCCRXhpZgAATU0AKgAAAAgAAYdpAAQAAAABAAAAGgAAAAAABJADAAIAAAAUAAAAUJAEAAIAAAAUAAAAZJKRAAIAAAADNjkAAJKSAAIAAAADNjkAAAAAAAAyMDIwOjEyOjAyIDE1OjI0OjM4ADIwMjA6MTI6MDIgMTU6MjQ6MzgAAAD/4QGgaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLwA8P3hwYWNrZXQgYmVnaW49J++7vycgaWQ9J1c1TTBNcENlaGlIenJlU3pOVGN6a2M5ZCc/Pg0KPHg6eG1wbWV0YSB4bWxuczp4PSJhZG9iZTpuczptZXRhLyI+PHJkZjpSREYgeG1sbnM6cmRmPSJodHRwOi8vd3d3LnczLm9yZy8xOTk5LzAyLzIyLXJkZi1zeW50YXgtbnMjIj48cmRmOkRlc2NyaXB0aW9uIHJkZjphYm91dD0idXVpZDpmYWY1YmRkNS1iYTNkLTExZGEtYWQzMS1kMzNkNzUxODJmMWIiIHhtbG5zOnhtcD0iaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLyI+PHhtcDpDcmVhdGVEYXRlPjIwMjAtMTItMDJUMTU6MjQ6MzguNjkwPC94bXA6Q3JlYXRlRGF0ZT48L3JkZjpEZXNjcmlwdGlvbj48L3JkZjpSREY+PC94OnhtcG1ldGE+DQo8P3hwYWNrZXQgZW5kPSd3Jz8+/9sAQwAGBAUGBQQGBgUGBwcGCAoQCgoJCQoUDg8MEBcUGBgXFBYWGh0lHxobIxwWFiAsICMmJykqKRkfLTAtKDAlKCko/9sAQwEHBwcKCAoTCgoTKBoWGigoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgo/8AAEQgBoQJWAwEiAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A+qaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAI5pEhieSQhUUZJPYVgxatqV6PM07Tgbc/dklfbuHrirXi4lfDt4QcfKB+orRskWO0hVBhQigD04q1ZRuylormP9q1/wD6B9t/3+o+1a//ANA+2/7/AFb9FHMuwc3kYH2rX/8AoH23/f6j7Vr/AP0D7b/v9W/RRzLsHN5GB9q1/wD6B9t/3+o+1a//ANA+2/7/AFb9FHMuwc3kYH2rX/8AoH23/f6j7Vr/AP0D7b/v9W/RS5l2Dm8jA+1a/wD9A+2/7/Ufatf/AOgfbf8Af6t+ijmXYObyMD7Vr/8A0D7b/v8AUfatf/6B9t/3+rfoo5l2Dm8jA+1a/wD9A+2/7/Ufatf/AOgfbf8Af6t+inzLsHN5GB9q1/8A6B9t/wB/qPtWv/8AQPtv+/1b9FHMuwc3kYBvNeXk6bAw9Fm5NXdH1RdQWRWjaG4iOJIn6qf8K0q5+3GzxldBeA1spPuc0K0k9BrU6CiiioICiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMJtSu2t7i8ijhNrC7DaSdzKpwTnoKsQ6i8kl+Aq7YFVkPrlc80yTR2IliS6kS1lYs8QUd+oB7A0650pnmle3uXgWZQsihQcgDHGehxV+6VoQNf3zNY+X9nC3S5G5T8p25Pemtq86XrxnyCqzrDsBO85x8w9uf0rSawQyWbISq2udq46gjFLaWMcE1xLwzzSeZkjkcAY/SjmiF0Uv7Uk/suW62LuSfygO2PMC06O5vjqxtibfywgkztOdpJGOvXikOj/vGQXL/AGRpfOMO0ctnPX0zV1bULqButxyYxHtx6EnNF0F10KPi7/kXLz/dH8xWpbf8e8f+6P5Vl+L/APkXbz/dH8xWpb/8e8f+6P5Un8AdCvNdmPUra12585Xbdnptx/jV2s64tpH1mznUDy40kVjnoTtx/KtGiVrKwnYM1Sn1S0gult5ZSsjEAfKcZPQZxirhrltUstTu5po2RmTz0eNxKFQICDjHUng06cVJ+8OKTepsza3p8MzRS3KqytsbIOFPoT0FTWOoW19v+zSbihwwIII9ODWPc6XPJZahGEUvNdLKvPVQV5/Q1oW1rImuXNwQBC8EaKc9SC2f5iqlGFtH/Wg2o20NOmTSLDE0khwijJOOgp9UtZW6bT5BY/6/IxyBkZ5xnvjNZxV3Ylbj7HULa+Dm2ctsOGBUqR+Bq1WHodpcxXt3PcRvGsqoFDyb24znP51uVU0k7Ickk9CleapaWcyxTyESMM7VUsQPU4HA+tV49csjPeRszp9lP7xmQhegPX8ara5bXT3Xm6fBItzs2rOsgC/RlPUVBdWF3Kur2/lArdLvSXcMBtgXBHXtVxjBpXZSjG2pvPdwJMInkCuUMmD/AHR1P61mRa5BcalBb2rq6OjuzEEEAYwRnqOetUbizv8AUrh2mgFshs3gGXDHcSPTtxTns769uoGmthbIltJAW3hjlgORjtxTUIJasajHqa9vq9jOZBFOD5alzwR8o6keo9xTE1uwk3iObcUQvwp+ZR3Hr+FYtnpU4gaOW2lE8ds8KSGfchJXHAz34+laEmnymfTCiqEghdH56ZUAfrQ4U09xOMbmhpeoQ6laLcW+4I3ZlII/OsyH/kc7j/r1X+dXdASaHTIYbmLy3iUR/eBDYHUVSh/5HO4/69V/nUpJOSQrWbsb9FFFZEBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGN4vBPh28x/dB/UVpWbBrWEqcgoCD+FPuIUnhkilG5HUqw9qwItO1iwQQ2F3BJbr9wTqSyj0yKtaqxS1VjoqKwPL8Rf89dP/75ajy/Ef8Az10//vlqOTzDl8zforA8vxH/AM9dP/75ajy/Ef8Az10//vlqOTzDl8zforA8vxH/AM9dP/75ajy/Ef8Az10//vlqOTzDl8zforA8vxH/AM9dP/75ajy/EX/PXT/++Wo5PMOXzN+iuatZtcuoy9tdaZKgZkLIGIDA4I/A1N5fiP8A566f/wB8tS5PMOXzN+isDy/Ef/PXT/8AvlqPL8R/89dP/wC+Wp8nmHL5m/RWB5fiP/nrp/8A3y1Hl+I/+eun/wDfLUcnmHL5m/RWB5fiP/nrp/8A3y1Hl+I/+eun/wDfLUcnmHL5m/WDAd3jO5x/DaqD7c0nleIjwZ7BR6hGJFXNG0v7D5ss8xnu5jmSQjGfQAdhQrRT1DY1KKKKgkKKKKACiiigAooooAKKKKACjNITiuR1f4gaFp141oss17drw0VnEZSp9CRxWlKjUrO1OLZE6kKavJ2OvzRXBf8ACxof4fD3iBvcWn/16X/hY0f/AELviH/wE/8Ar10fUMR/L+Rl9bpdzvKK4P8A4WNH/wBC74h/8BP/AK9H/Cxo/wDoXfEP/gJ/9ej6hiP5fxX+YfW6Pc7yiuD/AOFjR/8AQu+If/AT/wCvR/wsaP8A6F3xD/4Cf/Xo+oYj+X8V/mH1uj3O8org/wDhY0f/AELviH/wE/8Ar0f8LGj/AOhd8Q/+An/16PqGI/l/Ff5h9bo9zvKK4P8A4WNH/wBC74h/8BP/AK9H/Cxo/wDoXfEP/gJ/9ej6hiP5fxX+YfW6Pc7yiuD/AOFjR/8AQu+If/AT/wCvR/wsaP8A6F3xD/4Cf/Xo+oYj+X8V/mH1uj3O8org/wDhY0f/AELviH/wE/8Ar0f8LGj/AOhd8Q/+An/16PqGI/l/Ff5h9bo9zvKK4P8A4WNH/wBC74h/8BP/AK9H/Cxo/wDoXfEP/gJ/9ej6hiP5fxX+YfW6Pc7yiuD/AOFjR/8AQu+If/AT/wCvR/wsaP8A6F3xD/4Cf/Xo+oYj+X8V/mH1uj3O8org/wDhY0f/AELviH/wE/8Ar0f8LGj/AOhd8Q/+An/16PqGI/l/Ff5h9bo9zvKK4P8A4WNH/wBC74h/8BP/AK9H/Cxo/wDoXfEP/gJ/9ej6hiP5fxX+YfW6Pc7yiuD/AOFjR/8AQu+If/AT/wCvR/wsaP8A6F3xD/4Cf/Xo+oYj+X8V/mH1uj3O8org/wDhY0f/AELviH/wE/8Ar0f8LGj/AOhd8Q/+An/16PqGI/l/Ff5h9bo9zvKK4P8A4WNH/wBC74h/8BP/AK9H/Cxo/wDoXfEP/gJ/9ej6hiP5fxX+YfW6Pc7yiuD/AOFjR/8AQu+If/AT/wCvR/wsaP8A6F3xD/4Cf/Xo+oYj+X8V/mH1uj3O8org/wDhY0f/AELviH/wE/8Ar0f8LGj/AOhd8Q/+An/16PqGI/l/Ff5h9bo9zvKK4P8A4WNH/wBC74h/8BP/AK9H/Cxo/wDoXfEP/gJ/9ej6hiP5fxX+YfW6Pc7yiuD/AOFjR/8AQu+If/AT/wCvR/wsaP8A6F3xD/4Cf/Xo+oYj+X8V/mH1uj3O8org/wDhY0f/AELviH/wE/8Ar0f8LGj/AOhd8Q/+An/16PqGI/l/Ff5h9bo9zvKK4P8A4WNH/wBC74h/8BP/AK9H/Cxo/wDoXfEP/gJ/9ej6hiP5fxX+YfW6Pc7yiuD/AOFjR/8AQu+If/AT/wCvR/wsaP8A6F3xD/4Cf/Xo+oYj+X8V/mH1uj3O8org/wDhY0f/AELviH/wE/8Ar0f8LGj/AOhd8Q/+An/16PqGI/l/Ff5h9bo9zvKK4P8A4WNH/wBC74h/8BP/AK9H/Cxo/wDoXfEP/gJ/9ej6hiP5fxX+YfW6Pc7ykrhP+FjR/wDQu+If/AT/AOvR/wALGj/6F3xD/wCAn/16PqGI/l/Ff5h9bo9zu6K4T/hY0f8A0LviH/wE/wDr0f8ACxo/+hd8Q/8AgJ/9ej6hiP5fxX+YfW6Pc7uiuE/4WNH/ANC74h/8BP8A69H/AAsaP/oXfEP/AICf/Xo+oYj+X8V/mH1uj3O7rJ8VzahB4fvH0e3a41AxlYUUgfMeM8+nX8K5r/hY0f8A0LviH/wE/wDr0jfEWMj/AJF3xD/4Cf8A16PqGI/l/FB9bo9zmvgI+tQx6jb31tI2ntKxWcuDtmBwykZzz/SvYa8Z+HfjNNL0i7hOi6xcb72WXdBb7lGT0Jz1rq/+FjR/9C74h/8AAT/69H1GvLVR/IPrVJaNnd0tcH/wsaP/AKF3xD/4Cf8A16P+FjR/9C74h/8AAT/69H1DEfy/iv8AMPrdHud3RXCf8LGj/wChd8Q/+An/ANej/hY0f/Qu+If/AAE/+vR9QxH8v4r/ADD63R7nd0Vwn/Cxo/8AoXfEP/gJ/wDXo/4WNH/0LviH/wABP/r0fUMR/L+K/wAw+t0e53dLXB/8LGj/AOhd8Q/+An/16P8AhY0f/Qu+If8AwE/+vR9QxH8v4r/MPrdHud5RXB/8LGj7+HfEH/gJ/wDXo/4WZpcRH9oWGrWKd3ntWCj64zR9QxHSILF0f5jvM0VS0zUrTVLRLrT7iK4t35V42yKujpXI04u0lqbppq6CiiikMKKKKACiiigDiPiTqF2YtO0PTZTBdatN5BmHWOMDLMPfFXok0DwHoAL+Va2yYBcjLyt/Niay/FPzfFLwah6eXdN+SVV1SFNW+K0cF3+8t9NsRPFG3KiRmxux64rtrydOhTgtmrvzd2v0OWnaVScn00/BFofEm1fm38PeI7iPs8djkH9aX/hY8f8A0K3ij/wA/wDsq6fGOmPTpRXn+08jbmZzH/Cx4/8AoVvFH/gB/wDZUf8ACx4/+hW8Uf8AgB/9lXT0Ue08h8xzH/Cx4/8AoVvFH/gB/wDZUf8ACx4/+hW8Uf8AgB/9lXT0Ue08g5jmP+Fjx/8AQreKP/AD/wCyo/4WPH/0K3ij/wAAP/sq6eij2nkHMcx/wseP/oVvFH/gB/8AZUf8LHj/AOhW8Uf+AH/2VdPRR7TyDmZzH/Cx4/8AoVvFH/gB/wDZUf8ACx4/+hW8Uf8AgB/9lXT0Ue08g5mcx/wseP8A6FbxR/4Af/ZUf8LHj/6FbxR/4Af/AGVdPRR7TyDmZzH/AAseP/oVvFH/AIAf/ZUf8LHj/wChW8Uf+AH/ANlXT0Ue08g5jmP+Fjx/9Ct4o/8AAD/7Kj/hY8f/AEK3ij/wA/8Asq6eij2nkHMcx/wseP8A6FbxR/4Af/ZUf8LHj/6FbxR/4Af/AGVdPRR7TyDmOY/4WPH/ANCt4o/8AP8A7Kj/AIWPH38L+KB/24f/AGVdPRR7TyDmMjQPHWkaxfCxAubK+YZW3vITEzfTsa6yvPPidYxz+Fri8QBLyxxcQSjhkZSD/Ku30a6N9pNldkYM8KSY9MqDVJ3Vxp3LmKMUUUygxRiiigAxRiiigAxRiiigAxRiiigAxRiiigAxRiiigAxRiiigAxRiiigDM8Qa5p+gWDXeqXCwxA7RkZLH0AHJNcqPiVav81v4e8STxno8djlT9PmqrqUSav8AFjybweZb6bYrLFG3KiRm+9j1xXZdOlMuMOZXOY/4WPH/ANCt4o/8AP8A7Kj/AIWPH/0K3in/AMAP/sq6eigr2RzH/Cx4/wDoVvFH/gB/9lR/wseP/oVvFH/gB/8AZV09FAeyOY/4WPH/ANCt4o/8AP8A7Kj/AIWPH/0K3ij/AMAP/sq6eigPZHMf8LHj/wChW8U/+AH/ANlR/wALHj/6FbxR/wCAH/2VdPRQHsjmP+Fjx/8AQreKP/AD/wCypG+I0ZH/ACK/ij/wA/8Asq6iimHsjzPwL4pl0DS7q2vPDXiJ5JbuScGKxJG1jkdSOa6X/hY8f/QreKf/AAA/+yrp6KA9kcx/wseP/oVvFH/gB/8AZUf8LHj/AOhW8Uf+AH/2VdPRQHsjmP8AhY8f/QreKf8AwA/+yo/4WPH/ANCt4o/8AP8A7KunopB7I5j/AIWPH/0K3ij/AMAP/sqP+Fjx/wDQreKf/AD/AOyrp6KA9kcx/wALHj/6FbxR/wCAH/2VH/Cx4/8AoVvFH/gB/wDZV09FAeyOY/4WPF38L+KAP+vD/wCyq/onjXRtduzp7JcWt4wOLW9h8tmHsDwfpWxXH/FGyjl8LTX6DZe2BW4gmH3kII7015ClTsiO+tE8FeMtOu9O/c6Rq0v2a5t1+4kp+66jtnvXpI6V5v8AEy4Nz4N0K8PDPfWkox2yf/r16QOldeJbqUqdWW7uvW2352OKilGpOC20f3hRRRXEdIUUUUAFFFFAHBeJv+Sr+Df+uV3/AOi6hi/5K9qn/YMi/wDQjU3ib/kq/g3/AK5Xf/ouoYv+Su6p/wBg2L/0OuvF/wAOn/h/9ukclH4qnr+iOuooorzDYKKKKBBRRRQAVQ167ksND1C7h2mW3t5JV3DIyqkjNX6ranaJqGm3VnKzKlxE0TMvUBgRkfnTW4zjW8San/wj5u7O4s766aaKNY1gaMDd1HJ6+9WpvGSrHNcwxh7ZNP8AtOzo4k37dp9MHitaPQWNrDBdahcXCQyxyx7lQY2HgcDoart4R09r/U7hjJ5eoQmKWAHCDPUj0JOD9aq6Agu9R1rS9LN1fNZzzTGOKGGJCoWR2AAJycgZ/SmXOs6rpVzNa6ibad3s5bmCWJCoVkHKsCT6jmr7eHjPp0llfajdXMJCiMsEDRlTlWBA5II6mkHhtJZJpr6+ubueS3e1WRwo8tG64AAGT6mi6AoWet6pbyaaNT+yzR6jCXieFChjcJu2kEnIxnn2rLs/Ft/L4VvNUN3ZyTxQrIIVgZRGS2OSTyK6Ox8NRwTW8lze3N21tEYYBJtCxgjBIAA5xxmoIfCoXQ5NJl1G5ls2jEaqyoCgBB4IHt3ovEB/hHWbnVJLyOd7e4igKBLq3UhHJGSvJPI4710dZ2n6TFYX11PbyOqXG0tDxsDAY3D0JGM/StGpl5CCiiikAUUUUAFFFFAHPfED/kStZ/69n/lV7TNZsdC8C6Re6pOILYWsClypOCUGOBVH4g/8iXrP/Xs/8qv6dpNrrXw+0/T79A8E1jEpBHQ7Bgj3FbQ2LjsUR8T/AAkemrKf+2L/AOFL/wALN8J/9BUf9+ZP8K+edQ0rUPCviybTzcPbzxvhJFfYJFP3Tntn8q9T8K69r0pMEa6bqd1GMyWN5ELa5I/2SPlYe9aOKKudp/ws3wn/ANBUf9+JP8KP+Fm+E/8AoKj/AL8Sf4VUg8aaTbyCLxDpFxospON1zbgxE+gdQRXV6fJpOow+bYGzuY/70W1h+lKwHP8A/CzfCf8A0FR/34k/wo/4Wb4T/wCgqP8AvxJ/hXVfYrb/AJ94f++BS/YrX/n3h/74FGgzlP8AhZvhP/oKj/vxJ/hR/wALN8J/9BUf9+JP8K6v7Fa/8+8P/fAo+xWv/PvD/wB8CjQDlP8AhZvhP/oKj/vxJ/hR/wALN8J/9BUf9+JP8K6v7Fa/8+8P/fAo+xWv/PvD/wB8CjQDlP8AhZvhP/oKj/vxJ/hR/wALN8J/9BUf9+JP8K6v7Fa/8+8P/fAo+xWv/PvD/wB8CjQDlP8AhZvhP/oKj/vxJ/hR/wALN8J/9BUf9+JP8K6v7Fa/8+8P/fAo+xWv/PvD/wB8CjQDlP8AhZvhP/oKj/vxJ/hR/wALN8J/9BUf9+JP8K6v7Fa/8+8P/fAo+xWv/PvD/wB8CjQDgvEPxX0Gy0uSfS7lby6UrthKOm4ZGeSOOM1reCfHuk+LV2WTSRXarueCQcj6Hoa1tf8ADena5pklheQhYJCpYxgK3BB6/hU+i6Jp2iWot9LtIraIDHyLyfqepo0A422/5K5rP/XhD/6FXX1yFt/yVzWf+vCH+ddfTN6fwhRRRSLCiiigAooooAralO1tp1zOgBaOJnGemQM1zOma7qcTaOdU+yzQ6pHmNoUKGN9m7BBJyMZ5rqryAXVrNAxIWVChI6gEYrE07wzHay2clxeXN2bOPy7dZNoWPjGcADJx600J36GHpHi65k0W61G4uLa4eOHeLWOFkIYtgAsSQecVpX2oa1pOmie9eynnuJI4II40ZQkjtjk5OQOtWbPwykOlSaZPfXFxYvEYhE4UbQe4IAORT5PDxuNPa0v9RurmP5TGzBFaNlOQwIHXI70E6mfd63qmkTXVpqH2aeY2Ul3BLEhUZTqrAk+o5zS22tanaz2Mep/ZpUv4WeKSFSux1TdtYEnjHfNXf+EaSZ7mW+vbi7uJrdrUSOFHlo3XaAMZPrS2fhuOKeKa6vLm8kghMMPmBQI1IwSAAOcdzQFmc7beLL5/Ct1qhu7OSdIUfyxAyiMswBySeR9K3/CWsXOqNepO1vcRwMqpdW4KpJkZIwc8joabF4XA0RtKm1G5mtNixorKgKBSCOQOenetPTtKi0+8u5rd3WO5IZoeNisBgsPc96Bq5o0UUUigooooAKKKKACub+I3/Ik6v/1wNdJXN/Eb/kSNX/64mmhS2ZkePP8AknHhv/r4sv6V6gOgry/x5/yTjw3/ANfFl/SvUB0FdVX/AHan6y/Q82n/ABp/L9QooorjOkKKKKACiiigDgvE/wDyVfwd/wBcrv8A9F1V8XSN4b8cW/iG4jZtLurYWdxIoJ8lg2Qxx27Va8Tf8lX8G/8AXK7/APRddzLEk0bRyorxsMMrDIIrrxXwUv8AD/7dI5aCvKp6/ojm7fX9JuIxJDqdk6EZBEy8/rUv9r6b/wBBC0/7/L/jUdx4C8L3EheXRbMs3JIXb/Kov+FdeEv+gJa/r/jXDyI35Cz/AGvpv/QQtP8Av8v+NH9r6b/0ELT/AL/L/jVb/hXXhP8A6Alr+v8AjR/wrrwn/wBAS1/X/Gj2a7hyFn+19N/6CFp/3+X/ABo/tfTf+ghaf9/l/wAarf8ACuvCX/QEtf1/xo/4V14T/wCgJa/r/jRyLuHIWf7X03/oIWn/AH+X/Gj+19N/6CFp/wB/l/xqt/wrrwn/ANAS1/X/ABo/4V14T/6Alr+v+NHs13DkLP8Aa+m/9BC0/wC/y/40f2vpv/QQtP8Av8v+NVv+FdeE/wDoCWv6/wCNH/CuvCf/AEBLX9f8aPZruHIyz/a+m/8AQQs/+/y/40f2vpv/AEELT/v8v+NcT8TtA8JeGPCtzcxaLai7l/c2/X7579ewyab8LtB8JeKPCsFxLo1qbyH91cAgglh369xz9c0/ZrcXKdx/a+m/9BC0/wC/y/40f2vpv/QQtP8Av8v+NVv+FdeE/wDoCWv6/wCNH/CuvCf/AEBLX9f8aXs13HyFn+19N/6CFp/3+X/Gj+19N/6CFp/3+X/Gq3/CuvCX/QEtf1/xo/4V14T/AOgJa/r/AI0ci7hyFn+19N/6CFp/3+X/ABo/tfTf+ghaf9/l/wAarf8ACuvCf/QEtf1/xo/4V14T/wCgJa/r/jRyLuHIWf7X03/oIWn/AH+X/Gj+19N/6CFp/wB/l/xqt/wrrwn/ANAS1/X/ABo/4V14T/6Alr+v+NHs13DkLP8Aa+m/9BC0/wC/y/40f2xpo66haf8Af5f8arf8K68J/wDQEtf1/wAaUfDvwmOmiWv6/wCNHs13DkOY8ba7b61Zt4d0GVb3Ub4iNvJO9YUyNzMRwOK9K0+2Wzsba2T7kMaxj6AYqtpOiabpEZTS7G3tVPXykAJ+prRqkrKyKSseZfG7wl/bGijVbKMG/sAWIC58yPuPw6/nXn/he+sb7S7dNZ806ejCOK+jYifTpOwLdfLPbP8ASvoxlDKQ3IPBB714H4k0STwZ4yleyg8/TL5WYWzDKzp1kh+o+8tWn0Bo7YazqPh2NbfxbEuqaI4xHqkSB/lPTzV/qK0G8E+HdUjS/wBCkewkcZS502bYD+A4P5VgaDqy+GraBjIb7wXff6mZhvayY/8ALN/9nPHtWxceF7vR5TqngW5jjST95Jp7tm3n91P8J+nFIB/2LxrovFjf2muWo6R3a+VMB/vDg/jT4/iBDZuIvEul3+jy9C8kZkiPuHXtWh4Z8YWmrTtY3cb6frEf+ss7jhvqp/iH0rpJYkmQrKiuh6qwyDQBV0zVbDVIRLp95BcoRkGKQNV3iuT1P4faDeTGe3gk0666iaxcwkH6Dj9Kpf2X4y0XnTtVt9Zt1/5Y3yeXIR6Bxx+dAandUVwyePhp7eX4o0e/0l+hl2ebCf8Aga/4V1Ola1purRCTTb23uV/6ZyBsfX0pDNCijNFABRRRQAUUUUAFFFFAHm/iyU+GvHUWv3MbnSry2FpPKoz5Lg5BPsa6GDXtJnjDxanZsrDIPnL/AI10c0Mc8TRzIkkbDDKwyCPcVzc/gDwtPIXk0Sz3E5O1do/IU7lxm46Ev9sab/0ELP8A7/L/AI0f2xpv/QQs/wDv8v8AjVb/AIV34T/6Adr+v+NH/Cu/Cf8A0A7X9f8AGi6H7Rln+2NN/wCghZ/9/l/xo/tjTf8AoIWf/f5f8arf8K78J/8AQDtf1/xo/wCFd+E/+gHa/r/jRdB7Rln+2NN/6CFn/wB/l/xo/tjTf+ghZ/8Af5f8arf8K78J/wDQDtf1/wAaP+Fd+E/+gHa/+Pf40XQe0ZZ/tjTf+ghZ/wDf5f8AGj+2NN/6CFn/AN/l/wAarf8ACu/Cf/QDtf1/xo/4V34T/wCgHa/r/jRdB7Vln+2NN/6CFn/3+X/Gj+2NN/6CFp/3+X/Gq3/Cu/Cf/QDtf1/xrP8AEHg/wboujXeo3OiWgit4y5HPzHsOvc4oug9qzZ/tfTf+ghZ/9/l/xo/tjTf+ghZ/9/l/xryr4O2XhnxPFfWup6PaG+ikMqDBGYyeg57Hj6Yr0z/hXfhP/oB2v6/409A9qyz/AGxpv/QQs/8Av8v+NH9sab/0ELP/AL/L/jVb/hXfhP8A6Adr+v8AjR/wrvwn/wBAO1/8e/xpaB7Rln+2NN/6CFn/AN/l/wAaP7Y03/oIWf8A3+X/ABqt/wAK78J/9AO1/X/Gj/hXfhP/AKAdr+v+NF0HtGWf7Y03/oIWf/f5f8aP7Y03/oIWf/f5f8arf8K78J/9AO1/X/Gj/hXfhP8A6Adr+v8AjRdB7Rln+2NN/wCghZ/9/l/xo/tjTf8AoIWf/f5f8arf8K78J/8AQDtf/Hv8aP8AhXfhP/oB2v6/40XQe0ZY/tjTBydRs/8Av8v+Nch431qDXbX/AIRzQJVvdQvWVH8k7lhjyCzMRwOK6hfh34TByNDtR+f+NbelaNp2kRlNMsre1U9fLQAn6nqaLoTqNqxxfxWt1tPB+k26fdiv7VB9AcV6IOgrgvjJ/wAi3Yf9hK2/9CrvR0FddX/dqfrL9Djp/wAafy/UKKKK4zpCiiigAooooA4LxN/yVfwb/wBcrv8A9F10HirxLZeG7SOW88ySWZtkFvEu6SVvRRXPeJv+SreDf+uV3/6LqC5UXnxek88b1stNVoQeQrM3JHvXXinanS/w/wDt0jlo/FU9f0RKPF/imT5ovBsgQ8jfeorfiMUf8JX4t/6E7/yfT/Curorg9obczOU/4Svxb/0J3/k+n+FH/CV+Lf8AoTv/ACfT/Curoo5w5mcp/wAJX4t/6E7/AMn0/wAKP+Er8W/9Cd/5Pp/hXV0Uc4czOU/4Svxb/wBCd/5Pp/hR/wAJX4t/6E7/AMn0/wAK6uijnDmZyn/CV+Lf+hO/8n0/wo/4Svxb/wBCd/5Pp/hXV0Uc4czPP/Emo+JNd0q4s7nwVCWkjZI5Xuo3MRIxuHFJ4Yv/ABHoGk21nbeCoQ8cSpJKl3GhlIGNxwOteg0Ue0YczOU/4Svxb/0J3/k+n+FH/CV+Lf8AoTv/ACfT/Curoo5w5mcp/wAJX4t/6E7/AMn0/wAKP+Er8W/9Cd/5Pp/hXV0Uc4czOU/4Svxb/wBCd/5Pp/hR/wAJX4t/6E7/AMn0/wAK6uijnDmZyn/CV+Lf+hO/8n0/wo/4Svxb/wBCd/5Pp/hXV0Uc4czOU/4Svxb/ANCd/wCT6f4Uf8JX4s/6E7/yfT/Curoo5w5mc9pPjotqUOn+IdLn0e5nO2FpGDxSH0Djofau2rgfiZaR3PgvUWYfvIE8+Jh1VlOciuv0C5a90PTrmT781vHI31Kg1ad1cqLuX6wPGugr4g0SS3RvLu4z51tN0Mcq8qc1v0HpTKPFPDeqLpXmvfwAaJeym01S1YZFpddC2P7jdfbPtXSQy3Pw+uljmd7rwnO37uXO5rInoD6p79qTx1p0Oi61/bMkQk0fUVFnqsWOADwsv1B71L4XuP7LvW8Ja4y3NlMhbTp5MMJ4f+eZPcgfpVCOk1/w9pPiixia4RWYDfBdQth4/QqwrnV1fXPBrCHxEr6powOF1KJMyRD/AKar3+oqJTc/Du8Ct5tz4TmfhuWaxY9vdP5V6BFJDeWyyRsk0Eq5Ug5Vgf50gI9Nv7XUrSO6sZ457eQZV0bINWq4bUvCF1pV1JqXgy4WzuGO6Wyfm3n/AA/hPuKveHPGVvqN1/ZuqQPpesr961n43+6N0YUDOpZFdSHUMD1BGa5fVvAegX8xnSz+xXXUT2bGFwfX5eP0rqQc0tIDhf7F8X6L82j61FqkK9LbUk+bH/XReSfrTh45uNNOzxToV9p3/TeJfPh+pZeR+VdxSMoYYYAj0NO4rGZo3iDStai36Zf29wO4VxuH1XqK1K5nWfA2gatJ509ikNz/AM97Y+U/5r1/Gss+HvFOjn/iReIBewL9221NN5+m8c4oA7qiuFHjW/0s7fE/h+8tEXhrm1/fxD345ArotG8S6PrQ/wCJZqFvO39wNhv++TzRYLmxRSFgOtGc0hmH4q8TWPhu1jku/MlnmbZBbwruklb0A/rXODxf4pkG6Lwa+09N96in8sVFKgvPi9cmYBxZacvlA87Szcke9dhTNIw5lc5T/hK/Fv8A0J3/AJPp/hR/wlfi3/oTv/J9P8K6uigr2SOU/wCEr8W/9Cd/5Pp/hR/wlfi3/oTv/J9P8K6uigPZI5T/AISvxb/0J3/k+n+FH/CV+Lf+hO/8n0/wrq6KA9kjlP8AhK/Fv/Qnf+T6f4Uf8JX4t/6E7/yfT/CurooD2SOU/wCEr8W/9Cd/5Pp/hUF54h8S3sDQ3fgeKeI9UlvI2U/gRXZUUB7JHl/g1fEPhqGYR+C4JZ5JnkEwuY1ZVY/cBxnArpf+Er8W/wDQnf8Ak+n+FdXRTD2SOU/4Svxb/wBCd/5Pp/hR/wAJX4t/6E7/AMn0/wAK6uikHskcp/wlfi3/AKE7/wAn0/wo/wCEr8W/9Cd/5Pp/hXV0UB7JHKf8JX4t/wChO/8AJ9P8KP8AhK/Fv/Qnf+T6f4V1dFAeyRyn/CV+Lf8AoTv/ACfT/Cj/AISvxb/0J3/k+n+FdXRQHskcp/wlni3/AKE7/wAnk/wq1pHjrzNUh07xBpk+j3c5xCZGDxSH0Djv7V0Ncn8ULVLjwXfyMMSW4WaNx1VlIwRQJ00lck+Mf/It2H/YSt//AEKu9HQV5r8SZ2uvAeh3D/elvLNz9SQa9KXoK66v+7U/WX6HDT/jT+X6hRRRXGdIUUUUAFFFFAHBeJv+SreDf+uV3/6LqGL/AJK9qn/YMi/9CqbxN/yVfwb/ANcrv/0XUMZx8XtTz/0DIv8A0KurF/w6X+H/ANukclH4qnr+iOuooorzTYKKKKACiiigArN8SXEtp4e1O5t22TQ20kiNjOGCkg1pVBfWsV9ZT2twpaGeNo3AOMqRg0IDhpL/AFgeHEltL2+F7NPCiNewIijd1AwOQfXrT5vF9xsvLmEYNvp5d7Zx/q5xJtIPfjP5V0tt4etIYFhaS7mjSRJUE07PtKnjGeg9qcfD2mnUL28NuDLexeVOCfldfcVd0Bj6lJqmi6OLltUe7uLl4oV8yJRHCzsBuGBnAz0JqK/vtS0W8ls5NQe8E1hNcRySRqHidB/sjBBz3HUVsw+GrGOzmtXa6nt5ECeXNOzhAOm3J4xgcjnii28N2EH2gt9onkmiMDSTzM7BD/CCTwKLoDFtNQ1KxfR/tN+17HqULEiSNVaJxHvyNoGR259RWRaa3qv/AAhN5qb3uom7ECsrS26LGGLAEphfm49fWux03w3p9hIJIxNLIsZiRp5WkKJ6Lnp+FRW/hTT4NPlsQ929pIgTynuGZVAOeAelF0BW8F6jeX8l+s1xLdWkLKsUs8Qil3YywKgDgcY4HWuoqnbadb219PdwqyyzqqyfMcNjoceuOM1cqXvoAUUUUgCiiigAooooA574g/8AIlaz/wBez/yrf8H/APIqaN/15xf+gCsD4hHHgrWc/wDPs4/St/wiCPCujg8EWcQ/8cFaw2Kia9FFFWWVtSsodRsZ7O6QSQTIUdT3BrzKx0tr61uvB2qytFqemET6XdnhjGPuMD7dDXq1cd8QdJuJIbfW9IX/AIm2mHzUA/5ax/xxn1yKaAk8H60ddsbrStbhRdWs/wBzeQOPlcf3wO6msbF18PLzKiS58JzPyB8z2LH+afyp2sRnWtP0/wAZeFv+QlDHuaPp58f8cTD1HOPcV1mh6pY+JtCjuYAslvOpWSJxnaehRh7UCNO1niuoI54HWSGRQyOpyCD0NZniTw7p3iC18nUYNzLzHMnyyRn1VuorkJI7r4eXjSwCS48KzNmSMfM1kxPJH+x/KvQbO5hu7WO4tZFlhkG5HU5BBpDODXUNe8F4TWBLq+hDhb2NczwD/pov8QHqK7bSdSs9Wso7rT7iO4gcZDocj/6xq26hlwQCD1BritU8HTWN5Jqng+5GnXzHdJbHm3n9dy9j7imB21Fcj4e8ZRXN4NM123bStZHHkyn5JfeNujD9a67NIAoxRRQAm0elc7rPgvQdWYvc6dEk/UTwfu5AfXK966OigDyTxxoXiHw/4enTQtY1PUILj9x9jki86QA9w45GK2vhTqPiWTTvsXibTbmLyl/dXUowWH91h1z74r0GincDzu2/5K5rP/YPh/nXX1yNuMfFzWc99PiI/wC+q66mb0/hCiiikWFFFFABRRRQBV1WV4dLu5Ym2yJEzKfQgcVyem6jqdmfD73V+17HqkfzpJGqtE3l78qVA47cjvXZXEKXFvJDKMxyKUYZxkGsnS/DWn6bJHJCJpZIk8uJp5Wk8tfRcnj8KaJab2OV0nXtRj8NXWqTz3886wblFxAqQbi2AVIAJArW1R9U0XS45Tqkl3c3csVurSRIFiZ2ALAADjnofatOx8M2Fnby26tcy20kZiME07OgU9gD0oi8NWKWU1pK11cW0ihdk87OEA6bcngj1HPFAWZiajqGpaJd3Vk+oPeB9Omuo5ZEUPE6Y/ujBBz3FPh1DUtOudLiuL5r2PULd2/eRqrxOqbsjaACO3IrZt/DVhClyG+0TvcRGB5J5mkcIf4QSeBzS6d4csLGTzEWaaXyzErzzNIUQ9lyeB9KBWZx9vrWqDwVdak17qRufIjcPNboqAlgCUwvPXvXR+C7+7vjf+dcSXNpFIqRSzRCOQtj5gy4HQ+wqe38K2EOnyWW+7ktXVV8qSdmVQDkYyeOladtp1vbX1xdQqyyXAUSDd8p2jAOPX3o0Gk7lyiiikUFFFFABRRRQAVzfxG/5EnV/wDrga6Sua+I5x4I1fP/ADxP9KaFLZmT48/5Jx4b/wCviy/pXqA6CvL/AB6MfDnw4D1FzZD+VeoDoK6qv+7U/WX6Hm0/40/l+oUUUVxnSFFFFABRRRQBwXif/kq/g7/rld/+i6Txrp+oab4htvE+k2z3oWA215bJ99o85DL6kGl8Tf8AJV/Bv/XK7/8ARdd4K68V8FL/AA/+3SOWhrKp6/ojzhfiRoOP3v22Ju6vauCP0pf+FkeHv+et1/4DP/hXopjQ9VB/Ck8pP7q/lXFyROjlPO/+FkeHv+et1/4DP/hR/wALI8Pf89br/wABn/wr0Tyk/ur+VHlJ/dX8qOSIcp53/wALI8Pf89br/wABn/wo/wCFkeHv+et1/wCAz/4V6J5Sf3V/Kjyk/ur+VHJEOU87/wCFkeHv+et1/wCAz/4Uf8LI8Pf89br/AMBn/wAK9E8pP7q/lR5Sf3V/KjkiHKed/wDCyPD3/PW6/wDAZ/8ACj/hZHh7/nrdf+Az/wCFeieUn91fyo8pP7q/lRyRDlPOv+Fk+HR/y1uv/AZ/8KX/AIWT4d/563X/AIDP/hVz4va7/YHhKf7LGTd3X7mMqv3AR8zfgP5034O65/b3hGBbqMi7tAIXLD74A+VvxH8qPZxFylX/AIWR4e/563X/AIDP/hR/wsjw9/z1uv8AwGf/AAr0Tyk/ur+VHlJ/dX8qOSI+U87/AOFkeHv+et1/4DP/AIUf8LI8Pf8APW6/8Bn/AMK9E8pP7q/lR5Sf3V/KjkiHKed/8LI8Pf8APW6/8Bn/AMKP+FkeHv8Anrdf+Az/AOFeieUn91fyo8pP7q/lRyRDlPO/+FkeHv8Anrdf+Az/AOFH/CyPD3/PW6/8Bn/wr0Tyk/ur+VHlJ/dX8qOSIcp53/wsjw9/z1uv/AZ/8KP+FkeHv+et1/4DP/hXonlJ/dX8qPKj/uL+VHJEOU8r1bU7jx5CNH0Kzuk0+V1+2Xs0ZjVUByVXPUmvUraJIII4YxhI1CqPQAVIoAGAAB7UtUkkrIaVgooooGFIRxS0UAee2Y/4Q3xm1o3y6HrTmSE9FguMcr7Bu1JrEb+CPED63aKToV84GoQqOIXPSUD09a6rxdokPiDQ57GY7WYbopB1jkH3WH0NZXgzVP7f0S503WolOpWhNrfQuOGPTd9GFMR06mG8tQfkmglTPqrKR+orgJoLr4e3rXNmslx4VmfM0ABZrJj1Zf8AY9u1S+HLiXwfrg8Oai7NpdwS2mXLnp6wsfUdq76SNZY2SRQyMMFSMgigCOyu4L61jubSVZYJFDI6nIIqevObq3uvh/eveWCSXPheZs3FsvzNaE/xp/seo7V31he29/ZxXVnKs1vKu5HU5BFIZT8QaDp2v2X2bU7ZZVHKN0aM+qnqDXIi41/wQdt75ut6AvS4UZuLdf8AaH8QHr1r0KkIzweRQBR0XVrLWbJLvTbmO4gYfeU9PYjsav1xWseDHhvX1XwpcjS9TY5kQDMFx7Onb6ipNC8ZK96uleI7Y6Tq/RUkP7qb3jbofpTA7GijOaKQBRRRQBwHjSw1DSvEkHifSrZ7xBAba8to/vlM5Dr6kVWX4kaDj94b2Nu6vauCP0r0imeWndV/KncpSa2PO/8AhZHh7/nrdf8AgM/+FH/CyPD3/PW6/wDAZ/8ACvRPKT+6v5UeUn91fyouh+0ked/8LI8Pf89br/wGf/Cj/hZHh7/nrdf+Az/4V6J5Sf3V/Kjyk/ur+VF0HtJHnf8Awsjw9/z1uv8AwGf/AApP+FkeHv8Anrdf+Az/AOFei+Un91fyo8pP7q/lRdB7SR53/wALI8Pf89br/wABn/wo/wCFkeHv+et1/wCAz/4V6J5Sf3V/Kjyk/ur+VF0HtJHnf/CyPD3/AD1uv/AZ/wDCj/hZHh7/AJ63X/gM/wDhXonlJ/dX8qyfFepRaFoF5qDRbzChKIFyWY8KPzxRdB7SRyA+JPh09Jrn/wAB3/wpf+FkeHv+et1/4DP/AIVj/AvxRPqiX2napvecSNcRSMvBBPzLn2Jz+NeueUn91fypuwKpI87/AOFkeHv+et1/4DP/AIUn/CyPD3/PW6/8Bn/wr0Xyk/ur+VHlJ/dX8qV0HtJHnf8Awsjw9/z1uv8AwGf/AAo/4WR4e/563X/gM/8AhXonlJ/dX8qPKT+6v5UXQe0ked/8LI8Pf89br/wGf/Cj/hZHh7/nrdf+Az/4V6J5Sf3V/Kjyk/ur+VF0HtJHnX/CyPD3/PW6/wDAZ/8ACl/4WR4e/wCet1/4DP8A4V6J5Sf3V/Kjyk/ur+VF0HtJHnX/AAsjw92luj/27P8A4Vn6rqNx49jXR9CtLlNOkdTeXs8ZjVUBB2rnqTXqvlIOir+VOAC9AAKLic21Y8/+Lkaw+FdNjjGETUbZQPQBq9BHQVwXxj/5Fuw/7CVt/wChV3o6Cuur/u1P1l+hyU/40/l+oUUUVxnSFFFFABRRRQBwXib/AJKv4N/65Xf/AKLrX8YeKU0AW1vbW73uqXZ229rGcFsdWJ7AVkeJv+Sr+Df+uV3/AOi6gZRN8YLsyc+RpaCPP8OX5rrxX8Ok/wC7/wC3SOWh8VT1/RCjUPiHL8y2vh2EH+CR5WI/EcUv2z4if88/DP5zV1tFef7Rm3MzkvtnxE/55+Gfzmo+2fET/nn4Z/Oautoo9ow5mcl9s+In/PPwz+c1H2z4if8APPwz+c1dbRR7RhzM5L7Z8RP+efhn85qPtnxE/wCefhn85q62ij2jDmZyX2z4if8APPwz+c1H2z4if88/DP5zV1tFHOw5mcPq0fj/AFTTbqynTw0sVxG0TMrTZAIwccU3Ro/H+laXaWNunhsxW8SxKztLkgDjPvXdUUe0YXZyX2z4if8APPwz+c1H2z4if88/DP5zV1tFHtGHMzkvtnxE/wCefhn85qPtnxE/55+GfzmrraKOdhzM5L7Z8RP+efhn85qPtnxE/wCefhn85q62ij2jDmZyX2z4if8APPwz+c1H2z4if88/DP5zV1tFHtGHMzkvtnxE/wCefhn85qPtnxE/55eGT+M1dbRR7RhzM5S18Y6xpWoW1t4w063t4LlxHHe2jlog56BgeRn1r0AciuE+JMCXHgjVhIAdkPmL7FTkH9K6nw1O9z4e0yeU5eS2jdj6kqK0i7q5UXc0qKKKZQUUUUAFcF40hfw5rlt4rslPkDEGpRr/ABxHo/1Wu9qK6t47q3lguEWSKRSjqw4IPUUAY/iHSLPxToJgdgUkUSQTp1jbqrqazfA2u3Nw0+ia3hNasAFk/wCm8f8ADIPr3ql4HuJNA1e68J37krEDPp8rf8tISfu/VT+lXvHOg3F4sGsaLiPXNPy8J7TL3jb1Bp+QjrJEV0ZHUMrDBBGQRXnl7aXXgC9kv9Kje48NzNuurNeTak9XjH931FdZ4U1638Q6THeQZSQEpNC33opB95TWuyh1IYAqRgg96QyDTb631Kyhu7KZJreZdyOpyCKs153f2V34Dv5dT0iJ5/D0zbryxTk25PWSMenqK7rTb+21Kxiu7GZZreVdyOp4NAFqs3XdE0/XbJrTVLZJ4jyNw5U+oPUGtKigDz3Ov+CDz52uaAv43Nsv/s4FdhoWt2Gu2K3Wl3KTxHg46qfQjqDWkeRXHa74MD3rar4buDpWsdSyD91N7OnQ/WmB2NFcVo/jPyLsab4stxpWogfLIx/cT47o/wDQ10uh6xZa5YC802YTW5ZkDDjkHBpWAyfGHildBNta2ls99q12SLe1Q4JA6sx7AVhf2h8Q5PmW18Owg8hHeVmH1I4pFAn+L+os/Jt9OjVM/wAOW5rr6o0hBSV2cj9s+Iv/ADz8M/nNR9s+Iv8Azz8M/nNXXUUFeyRyP2z4i/8APPwz+c1H2z4i/wDPPwz+c1ddRQHskcj9s+Iv/PPwz+c1H2z4i/8APPwz+c1ddRQHskcj9s+Iv/PPwz+c1H2z4i/88/DP5zV11Jmi4ezRyX2z4i/88/DP5zUNdfERhgxeGfzmrrc0tAezied+HNN8d+H7SW3s18POkkzzkyNKTuY5I4A4rW+2fEX/AJ5+GfzmrrqTNFw9lE5L7Z8Rf+efhn85qPtnxF/55+GfzmrrqKA9mjkftnxF/wCefhn85qPtnxF/55+GfzmrrqKA9kjkftnxF/55+Gfzmo+2fEX/AJ5+GfzmrrqKA9kjkftnxF/55+Gfzmo+2fEX/nn4Z/OauuooD2SOR+2/EQdYvDX5zU+z8Y6vpeoW9r4w063tobhxHFe2rlot56BgeRn1rq65b4nQpP4H1QOM7EEin0IIINApU0ldC/GM58N2H/YStv8A0Ku9HQV5n8RZmuPh/oEznLyXVmxPucV6YOgrqq/7tT9ZfocNP+NP5fqFFFFcZ0hRRRQAUUUUAcF4m/5Kv4N/65Xf/ouoYv8Akr2qf9gyL/0I1N4m/wCSr+Df+uV3/wCi6hT5fi9qWe+mRkf99114v+HT/wAP/t0jko/FU9f0R11FFFeYbBRRRQIKKKKACsrxVI8PhjVpInZJEtJWVlOCCEOCDWrUc8MdxBJDOiyRSKUdGGQynqDQgPPriC9HhmBYWvbC4ubi3VZmvDMTnvyeB7VHceJb8/2m6lo76z00rND1EcofBfH05B9K7i00PTLSPZbWUEa71fCrxuXofwqcadZi8muvs0X2iZBHJJtGXX0PqKvmQ7nJ6rb/ANkeHRcWOo3byXLQxS3MlwX2q7gNIATgHB7VBqRk0bUZ7TT7y6kgm02eZ1kmaQxuoG1wx5Gc11VtoOl20cyQWFvHHMu2RAgww9KdZ6JpllHLHa2UESTLtkCp95fQ+1HMgucnZvLptxoYtb65m+3W7NcQyzGTbiPd5gySRzx+NZVrJeR/D28vmF7HO9upW4N6zlyWGSFz8pr0LT9F03TyxsrG3gLLtYogBI9PpUUHh7SLeKWOHTrZI5VCuoThgDnB/EUcyC5j+BpLhrrVEke5S3jZES2upfMljO3JOcng5GOT3rragS0gjunuEiRZ3UI0gHLAdAanqW7u4gooopAFFFFABRRRQBz3xB/5ErWf+vZ/5Vv+EP8AkVdG/wCvOL/0AVz/AMQ2CeCdYLHA+zsPz4rofCalPC+kKwwVtIgf++BW0PhLia1FFFUWFFFFABRRRQBynxA0SbUdPhvtLO3WNOfz7Vv7xHVD7EcVp+Fdbg8QaHb6hb/LvGJI+8bjhlP0NbBGa8/mH/CG+NhMvy6Hrcm2QfwwXP8Ae9g386Yg8S203hPXD4l0yNn0+chdTtkHb/nsB6jvXc2NzDe2kVzayLLBKodHXowPSpJo1miaN1V43GGUjIINef6W7+BvEC6RcsT4fv3JspWPFvIesRPoe1Az0J1DKVYAgjBB7157qVhd+Br+XVdEie40KZt95YJ1h9ZIx/MV6HmggEYPIpAVNJ1G11axivLCZJreVdysv+etW6891TTbzwVqEusaBE0+jynfe6cnOz1kjHr6iu10fU7TV9PivdPmWa3lGVZf5H3oAu0UUUAc5468OHxRoMmnCeO3LsD5rRCQrjnj0PvXPfDXwXq3g26uYZL+C70ucbtoBVkcdCB05HXn0r0SinfoB53a/wDJXNZ/7B8P/oVdfXIQfL8XNXB43afER7/NXX0zen8IUUUUiwooooAKKKKAKessyaReuhKusLkEHkHBri9Lkm0+Tw0bW9uZjqMObmGWYyD/AFe7eM5K849ua76RFljZJFDIwKlT0INUdP0XTdOYtY2Nvbuw2lo0AOPTNMlps4PSbm/tfB11qSx3S3BtyVuZbsyg5bBYITxgc9O1a2tW39j6FHJYahds11LBDNcvcGTajsA0gzwDz1HHNdJZ6Fpdk0htLGCLzFKvtTG4HqDSW2g6VawzRW9hbpFMu2RQgww9MelAcrOU1ZpdG1C9srC8uZLeTS5rhlkmMhideFYMTkZyfy4p1vJLpl9pMVne3MyX1pI88Msxk2YTcHBPK8nHXHNdXaaJplnDNFbWMEccy7ZAqj5x6H2pbDRdN0/f9hsbeAuu1iiYLD0PtRcXKzz+B7yPwBc3pW9jnkgiInN8ZDJlhkqN3yn/ABrpfA8k7zaoryXC28cqpHbXUvmSxHbkknJ4Ocjk1rW/h7SbeKSKHT7dI5AA6heGwcgH8avR2sEd1JcJEizyKFdwMFgOgNA1Fk9FFFIoKKKKACiiigArm/iN/wAiTq//AFwNdJXNfEhgvgfV8nH7nH600KWzMnx5/wAk48N/9fFl/SvUB0FeYePlK/Dnw6pGCLmyB/SvTx0FdVX/AHan6y/Q82n/ABp/L9QooorjOkKKKKACiiigDgvE3/JV/Bv/AFyu/wD0XU3jXQtR/ta08Q+HQkmo28Zhmt3OFniPOM9iDyKh8Tf8lX8G/wDXK7/9F13grrxXwUv8P/t0jlofFU9f0R50PGOoRjbc+D/ESyDqIrcSL+eaP+E0uv8AoUPE/wD4B/8A169Gori5UdHKjzn/AITS6/6FDxP/AOAf/wBej/hNLr/oUPE//gH/APXr0aijliHIec/8Jpdf9Ch4n/8AAP8A+vR/wml1/wBCh4n/APAP/wCvXo1FHLEOQ85/4TS6/wChQ8T/APgH/wDXo/4TS6/6FDxP/wCAf/169Goo5YhyHnP/AAml1/0KHif/AMA//r0f8Jpdf9Ch4n/8A/8A69ejUUcsQ5DzeTxvPFE8kvhPxKiICzM1oAAPU80Q+OZpoklh8J+JXjcBlZbMEMD0I5q98Y5dVHg26i0eBpPMB+0yBgPLiAyx5Pfp+dM+DEuqt4MtotXt2RYwDbSlgfMiIyvQ9un5U+RWuHKit/wml1/0KHif/wAA/wD69H/CaXX/AEKHif8A8A//AK9ejUUuWIch5z/wml1/0KHif/wD/wDr0f8ACaXX/QoeJ/8AwD/+vXo1FHLEOQ85/wCE0uv+hQ8T/wDgH/8AXo/4TS6/6FDxP/4B/wD169Goo5YhyHnP/CaXX/QoeJ//AAD/APr0f8Jpdf8AQoeJ/wDwD/8Ar16NRRyxDkPOf+E0uv8AoUPE/wD4B/8A16P+E0uv+hQ8T/8AgH/9evRqM0csQ5UeX3lvrvjdorGfSp9H0TeHuHuSBLKAc7Ao6AmvTo0WONUQYVQAB6CnZoppW2GlYKKKKYwooooAKKKKACszxHo9vrujXWn3Q+SZMBu6N2Ye4NadFAHI/D7WJ7q0uNJ1UgavpbeRMD1kX+GQexFbniHR7XXdJuLC+XdFKMAjqjdmHuDXL+PLSfSNQtfFmmozS2g8q9iX/lrbk8/ivWuysLuC+sobq0dZIJkDoy9CD0p+YHJeB9Yure6m8Na8+dVsl/dTH/l6h7OPfsa7UVy/jfw9Jq9rDeaa4g1qxPm2k3v3Q/7J6VZ8G+Io/EGl+ayGC9hbyrq3P3opB1B9vSgDfIyMGvPtY0y78HajLrXh6Fp9MlO+/wBOXt6yxj19RXoNHWkBR0XVbTWdPivdPmWW3lGQR1HsR2PtV6vP9Y0i98JajLrnhuIzWMp3X+mr0b1kj9G9R3rsNC1ez1vTIr7TpllgkGQR1B7gjsaANCiiigDiPGmhakutW3iLw6qTX8EZgmtpG2ieLOcA9iDVBfGOoIMT+D/EQkHXyrcSL+BzXo1IOadylJrY87/4TS6/6FHxP/4Bf/Xo/wCE0uv+hR8T/wDgF/8AXr0Sii4/aSPO/wDhNLr/AKFHxP8A+AX/ANej/hNLr/oUfE//AIBf/Xr0Sii4e0ked/8ACaXX/Qo+J/8AwD/+vR/wml1/0KPif/wC/wDr16JRRcPaSPO/+E0uv+hR8T/+Af8A9ej/AITS6/6FHxP/AOAX/wBevRKKLh7SR53/AMJpdf8AQo+J/wDwC/8Ar0n/AAml1/0KPif/AMA//r16LWT4qm1C30C8fR7drjUDGVhRSB8x4zzxx1/Ci4ueRxlv48kuUL2/hbxHKgYqWS0BAIOCPvdQRUv/AAml1/0KPif/AMAv/r1hfAN9Zhj1G3vreRtPaVmWcuDtlBwynnPPH5V7DTYKcjzv/hNLr/oUfE//AIBf/Xo/4TS6/wChR8T/APgF/wDXr0SilcftJHnf/CaXX/Qo+J//AAD/APr0f8Jpdf8AQo+J/wDwC/8Ar16JRRcPaSPO/wDhNLr/AKFHxP8A+AX/ANej/hNLr/oUfE//AIB//Xr0Sii4e0ked/8ACaXX/Qo+J/8AwC/+vR/wml1/0KPif/wC/wDr16JRRcPaSPOv+E0u+3hDxP8A+Af/ANeql3ba744eKyudKn0fQxIr3DXJAlmAOQoXtXqFFFxObejOB+MChPDGnqowq6lbAAdhurvx0FcF8ZP+RbsP+wlbf+hV3o6Cuur/ALtT9ZfoclP+PP5fqFFFFcZ0hRRRQAUUUUAcF4n/AOSr+Dv+uV3/AOi6teNPEN/BqVpoXh5Izq10pkaWQZW3iHG8juc9BVXxN/yVfwb/ANcrv/0XUKjf8X9RLfw6ZGB7ZeuvFaU6T/u/+3SOWj8VT1/REf8Awi+vTfPdeMdTEh6+Qiov4Cj/AIRHVv8Aocta/wC+lrsqK8/nZrdnG/8ACI6t/wBDlrf/AH0tH/CI6t/0OWtf99LXZUUc8u4XZxv/AAiOrf8AQ5a1/wB9LR/wiOrf9Dlrf/fS12VFHPLuF2cb/wAIjq3/AEOWtf8AfS0f8Ijq3/Q5a3/30tdlSOwRCzsFVRkknAAo55Duzjv+ER1b/octb/76Wj/hEdW/6HLWv++lrqUv7N0Lpd27KCAWEgIBPQdetT+YvmbNy78btuecetHPILs4q68E6jdW8kFx4u1mSGRSjoxXDKeCDRa+CdRtLaO3tvF2sRQxKERFK4UDoBXXw3trMziG5hkMf3wjg7fr6UsN3bzo7w3EUiJ95kcEL9aOeQXZyn/CI6t/0OWtf99LR/wiOrf9Dlrf/fS11lvdQXCk288UoXqUcNj8qjTULN1dku7dlQZYiQHaPejnkF2cv/wiOrf9DlrX/fS0f8Ijq3/Q5a1/30tddBPFOm6CVJFzjKMGH6VJRzy7iuzjf+ER1b/octb/AO+lo/4RHVv+hy1r/vpa7Kijnl3C7ON/4RHVv+hy1v8A76Wj/hEdW/6HLWv++lrsqKXPILs43/hEdW/6HLWv++lo/wCER1ft4y1rPuVrsqKOdhdnDT6j4h8Fyw3OqagNY0NnEczvGFlgycBsjqM9a9NRg6KynKsMg1xHxFQP4J1gMAR9nZvy5ro/CjmTwzpDuSWa0iJJ/wBwVpF3Vy4s1aKKKooKKKKACiiigAooooAZNGksTRyKGRgVZSMgiuE8JyN4X8ST+F7lj9hmzcaY7HIC9Wiz6jtXfVzXjvQX1vSQ1kwi1OzYXFpN0KyLzjPoelNAdKRmuD8Y2NxoGrf8JVo0ZfaNuo2y/wDLaL++P9pa3/Buup4g0OK72+XcrmO4hPWKVeGUitxlDKQwBBpAVtLv7fVLCC8spFlt5lDow9KtV53GW8A+IRExI8MalL8hzxaTnsfRDXoanK5HIPSgBSMjmuB1zR7zwvqcuveGImlt5Duv9OXpKO8iDsw/Wu+ooAztB1mz13TYr7TpRJDIPoVPcEdjWjXnvifTZ/CV5P4l0DaLY/PqFiW2pKP76dg3860vAPji18YtqH2WF4RbOoUOfmdSPvfmDTt1AZ408Q6hDqlroPh5YzqlyhleaUZS3jzjcR3PoKy/+EW12b5rnxlqYkPXyVVF/AdqfB8/xc1YtyU06ID2y1dfTNYRTV2cb/wiOrf9DnrX/fQo/wCER1b/AKHPWv8AvoV2VFFyvZx7HG/8Ijq3/Q561/30KP8AhEdW/wChz1r/AL6FdlRRcPZx7HG/8Ijq3/Q561/30KP+ER1b/oc9a/76FdlRRcPZx7HG/wDCI6t/0Oetf99Cj/hEdW/6HPWv++hXYsQqlmIAAySe1RW91b3AJt54pQOuxw2PyouHJHscn/wiOrf9DnrX/fQo/wCER1b/AKHPWv8AvoV1UF7azuUguYJGAyQkgYj8qIb21m3+TcwyeX9/a4O36+lAckTjNP8AAN5p0Tx2PivVoI3cyMqFQCx6n61Z/wCER1b/AKHPWv8AvoV1cN3bTRtJDcQyRr95lcED60sF1BcKWgnilUdSjBgPyo1Dkicn/wAIjq3/AEOetf8AfQo/4RHVv+hz1r/voV1CahZOrsl3bsqDLkSAhfrU0E0U6b4JEkTpuRgw/SjUOSJyP/CI6t/0Oetf99Cj/hEdW/6HPWv++hXZUUXD2cexxv8AwiOrf9DnrX/fQo/4RHVv+hz1r/voV2VFFw9nHscb/wAIjq3/AEOetf8AfQo/4RHVv+hz1r/voV2VFFw9nHscb/wiWrjp4z1nPbJFQzal4g8GTQXGrX/9saG8ixSyPGFlt8nAbI6j1ruK5n4lIH8D6uGGcQ5/EEGgUoK2hH8YWD+GdPZTkHUrYg/8Crv16CvMPH7F/h34dZjktc2RJ/KvTx0FdVX/AHan6y/Q4Kf8efy/UKKKK4zpCiiigAooooA4LxN/yVfwb/1yu/8A0XUMX/JXtU/7BkX/AKEam8T/APJVvBv/AFyu/wD0XUAOz4v6gG6yaXGV98PXXi/4dP8Aw/8At0jko/FU9f0R19FFFeYbBRRRQIKKKKACsjxeM+FNZAGc2cwx/wAANa9BGRg9KadhnmP2Swv/AAxBaRS6fMJbq2SX7FD5RXP97k5PXmmXDarLc61Yusp1K00swiRBgzLvyGU+pX9a9QCKOigd+lAUA5AGafOB59qI0WfwyV0CCD5fJN3HBFiTyQ43q2BnOOoPNRXg0+e/upPDkUQs10udblrePZGWx8gOMAt1969GCKOigZ68UBFUYCgD2FHMB5xpC2EtzoreH4UV47VxfSQx7UK+XgKxHBbdj3rIsUtT8Or5IJNOkujbIHjhg2yr84/1hyd35CvXlUL0AH0pBGg6Kvp0p8wHIeB7X7Fqmrw3EcFtdN5beRbpsiKbeHUep5B+ldjSYGc4GaWpbuIKKKKQBRRRQAUUUUAc98Qf+RK1n/r2f+Vb/g//AJFTRv8Arzi/9AFc78RpFi8D6wzkAGAqCfU8D+ddL4WjaHw1pMbgh0tYlIPYhRW0PhLialFFFUWFFFFABRRRQAUUUUAFFFFAHn2sA+D/ABimsJldG1Z1ivQOkU38MnsD0NegKQy5HI7GqWuabb6vpVzYXiB4J0KMPT0I9wea5n4falcIt14e1ZydT0w7A5P+uh/gcfhxTEdPrGmW2r6ZcWF9GJLeddjg/wAx7iuT8G6ldaRqT+FdbkL3EK7rG4b/AJeIewz/AHl713Nc7418O/2/p6fZ38jUrVvOtLgdY5B/Q9DSGdFRXN+CfEJ1uxkivU8jVbNvJvID1V/UexxkGukoAp6tpdnq9i9nqUC3Fs/3o26Gua8M+AdM8Ma5LqGjS3EKTIY5Ldm3IR1GO/H1rsaDQB53a/8AJXNZ/wCwfD/6FXX1yEX7v4vaqrcGTTomX3w1dfTN6fwhRRRQWFFFFABRRRQBS1wZ0a+H/TB//QTXA6CtlLP4bOgxIJ44P9Pkgj2rs8v7rkDBO7HvXpfXrSKoXoAPpTTE1c8q0NFfwbex6fLZPqBtTuitoNlwBu+YM2ck4yOgrV1YaNN4dH9gQW5jSSE3sdtFhzAHG5WAGenUda79UVfuqo+goCKM4VRnrgUXFynm98LGa81KTw3HEtgulTLctbx7Y2f+AccFsZ+lP04WUt/pb+HYUVY7OQX8kEe1CCg2qxxgtu/HrXowVQMAAD0xQqgdAB9BRcOU8ks0tn+Hl1HbSabJc/ZoQ8cFvtkX514kOTn8q6zwNb/Y9R1eGeOG2uyyMYLdNkWzbhXUe/f3FdcEUZwq89eKXAznAz60XBR6i0UUUigooooAKKKKACub+I3/ACJOr/8AXA10lcx8SpFj8D6sXOMxbRn1JA/rTQpbMy/Hn/JOPDf/AF8WX9K9QHQV5j8QUaL4e+Ho3GGS6slI9CMV6cOgrqq/7tT9ZfoebT/jT+X6hRRRXGdIUUUUAFFFFAHBeJv+Sr+Df+uV3/6Lq/4y8M3OpXVrq2iXCWus2gKozjKSoeqN7f4mqHib/kq/g3/rld/+i67wV14r4KX+H/26Ry0Piqev6I86GpeN4/lk8LW0jDqyXygH86X+1fGn/Qoxf+B6V6JkUZHrXHyrsdHKjzz+1fGn/Qoxf+B6Uf2r40/6FGL/AMD0r0PI9aMj1pcsewciPPP7V8af9CjF/wCB6Uf2r40/6FGL/wAD0r0PI9aMj1o5Y9g5Eeef2r40/wChRi/8D0o/tXxp/wBCjF/4HpXoeR60ZHrRyx7ByI88/tXxp/0KMX/gelH9q+NP+hRi/wDA9K9DyPWjI9aOWPYORHmt5r/i+ytZrm68KwxwQoXdjfpwAMmksfEHi6/s4bq08KwyW8yB43F+nzKehrS+MVpqd94Mu4tLkhjiVTLcs7EExqM7Rx3xTPgza6nZeDbWPU5IpIHUS2pViSI252nI7E/rT5I2vYOVEH9q+NP+hRi/8D0o/tXxp/0KMX/geleh5HrRketLlj2DkR55/avjT/oUYv8AwPSj+1fGn/Qoxf8Ageleh5HrRketHLHsHIjzz+1fGn/Qoxf+B6Uf2r40/wChRi/8D0r0PI9aMj1o5Y9g5Eeef2r40/6FGL/wPSj+1fGn/Qoxf+B6V6HketGR60csewciPPP7V8af9CjF/wCB6Uf2r41/6FGL/wAD0r0PI9aMj1p8sewciPN/7B8ReKrqBfE0VvpukwusjWkMnmPOQcgM3THtXpCgKoA6AYFHFLTGlYKKKKBhRRRQAUUUUAFFFFABRRRQAGuJ+INhcWklr4m0pN1/po/exqOZ4D95fw6iu2pGUMCGAIPUGgCppOo2+q6db3tm4e3nQOjD37fWrlef6Ex8H+LZdDlJGkakzT2DHpHJ/FF/UV6AKAOI8a6TdWF9H4n0FC19bLtuoB/y8w9x/vDtXT6DqtrrWlW9/YSeZBMu4HuD3B9xV9hkdK88vlbwH4ia/iB/4RvUZP8ASkA4tZj0cD+6e9MD0Simo6uoZGDKwyCDkEU6kByPjLwzdaheW2r6HcJbazagqpkGUmT+43t71kDU/G6fK/ha3kYcFkvlAP516IcUZFO41JrY87/tXxr/ANClF/4HpR/avjX/AKFKL/wPSvRMj2oz9KLj55dzzv8AtXxr/wBClF/4HpR/avjX/oUov/A9K9Ez9KM/Si4c8u553/avjX/oUov/AAPSj+1fGv8A0KUX/geleiZ+lGfpRcOeXc87/tXxr/0KUX/gelH9q+Nf+hSi/wDA9K9Ez9KM/Si4c8u553/avjX/AKFKL/wPSj+1fGg6+Eosf9f6V6Jn6Vk+Kor+40G8g0dokvpUKRvIxULnqcgHkDNFw55dzhdL8U+KNVgeaw8MwTxpI0TMt+vDKcEVc/tXxr/0KUX/AIHpWH8BdP1bT4dRM0kD6a8zRkByWWVDgkDHQj+Qr2DP0pvQFOXc87/tXxr/ANClF/4HpR/avjX/AKFKL/wPSvRM/SjP0pXDnl3PO/7V8a/9ClF/4HpR/avjX/oUov8AwPSvRM/SjP0ouHPLued/2r41/wChSi/8D0o/tXxr/wBClF/4HpXomfpRn6UXDnl3PO/7V8a/9ClF/wCB6Uf2r41/6FKL/wAD0r0TP0oz9KLhzy7nnf8AavjX/oUoh/2/pTBoHiHxVd2//CTxW+naTDIJDZwyeY87A5G5umPavR8iii4nJs4L4xAL4bsAOn9pW3/oVd8vQVwXxj/5Fuw/7CVt/wChV3o6Cuur/u1P1l+hy0/40/l+oUUUVxnSFFFFABRRRQBwXif/AJKv4N/65Xf/AKLp3jXVdSu9etfDWhTm0mlhNxdXQGWiizjC+5P9KZ4m/wCSreDf+uV3/wCi6ij5+L2p57aZEB/33XXi/wCHS/w/+3SOWj8VT1/REQ+HmnPzd6hq1zL/ABSPdsC35Uf8K50X/ntqf/gY9dnRXnczNbnGf8K50X/ntqf/AIGPR/wrnRf+e2p/+Bj12dFHM+4XOM/4Vzov/PbU/wDwMej/AIVzov8Az21P/wADHrs6KOZ9wucZ/wAK60X/AJ7an/4GPR/wrnRf+e2p/wDgY9dnUdxPHbW8k07rHFGpd3Y4CgDJNHM+4XOQ/wCFc6L/AM9tT/8AAx6P+FdaL/z21P8A8DHrfXxBpTWrXH26EQKyqXLYUFugzVxry3WYxGaMSLH5pBbon976Uc0gOTf4b6G6lXk1JlIwQbxyDQnw30SNAiSaiqqMAC7cAV0Ntr2l3Mc0kN9A0cK73fdgBfXPTFOtNb027SZre8hcQrvk+blV9fp70c0g1Od/4Vzov/PbU/8AwMej/hXOi/8APbU//Ax66Ox1rTr9itneQysq7yobnb649Kii8Q6TLbyzx30JhiXc754UZxnNHNIDB/4Vzov/AD21P/wMej/hXOi/89tT/wDAx66jT9Ss9SV2sbmKcIcNsbJU+/pVujmkFzjP+Fc6L/z21P8A8DHo/wCFdaL/AM9tT/8AAx67OijmfcLnGf8ACudF/wCe2p/+Bj0f8K50X/ntqf8A4GPXZ0Ucz7hc4z/hXWi/89tT/wDAx6P+FdaMOk+pg/8AX49dnRRzPuFzgNRt9R8BomqafqV3eaRG6rdWd0/mFUJxuQ9eK9RgkWaFJIyCjqGUjuDXF/EIA+CtZz/z7Mf0rofCJLeFtHJ5JtIj/wCOCtIO6uy4mtRRRVFBRRRQAUUUUAFFFFABRRRQAUUUUAYHjTQBr+iPbo/lXkRE1rMODHKvIOaj8D6+dc0UNcp5Wo2zGC7iPBSReDx6HrXRmuA8TI3hTxRB4jgBGnXhW31JB0U/wy/h0NNAd/VbULKDULOa1u41lt5kKOjDIINTxusiKyMGVhkEHIIp1IDgfCd5P4Z1n/hFtWkZ7dstply//LRP+eZP94fyrvc1y/xG0+0vfC9zLdiZZLUedBLAhaSOQdCoHNcj8JfH2o+KNZurLVPKXybZWQIuCzA4Yn3OaYjb8Z6rqV94gtvDWh3H2OSSI3F3dgZaOPOAF9yapj4eaa/N3f6vcS/xSPeMCT+FSW/Pxc1jPbT4gP8Avquvpm0Ipq7OM/4Vzov/AD21P/wMej/hXOi/89tT/wDAx67OikacqOM/4Vzov/PbU/8AwMej/hXOi/8APbU//Ax67OigOVdjjP8AhXOi/wDPbU//AAMej/hXOi/89tT/APAx67OigOVdjjP+Fc6L/wA9tT/8DHo/4Vzov/PbU/8AwMeuxlkWKJ5JGCooLMx7AVQ0/WtN1B9lneQTPt37Vbkr649KYuWJzv8AwrnRf+e2p/8AgY9H/CudF/57an/4GPXQ2euabeeYba8hkEal2IbgKOpz6Ulvr+lzxTSxX0DRQrud92AB659KA5YnOR/DTQYlIifUUBOSFu2GTT/+Fc6L/wA9tT/8DHrorXXNNuo5pILyF1hXfJ83Kr6kelLY61p18XFpeQSsi72VW5C+uPSgOWJzn/CudF/57an/AOBj0f8ACudF/wCe2p/+Bj1uxeItJlt5bhL6EwxKGd88AE4HNW9P1Gz1GN2sbiOcIcNsbO0+9AcsTl/+Fc6L/wA9tT/8DHo/4Vzov/PbU/8AwMeuzopD5V2OM/4Vzov/AD21P/wMej/hXOi/89tT/wDAx67OigOVdjjP+Fc6L/z21P8A8DHo/wCFc6L/AM9tT/8AAx67OigOVdjjP+FdaN2n1QH1F49UtRg1LwGseqWGo3d7o6uqXVpdPvKITjch6jFegVzXxHAPgfVwf+eJP60yZQViH4vSLL4X06RDlG1G2YH1BavQB0FeX+PST8OfDhPU3Nl/SvUB0FdVX/dqfrL9Dz6f8afy/UKKKK4zpCiiigAooooA4LxN/wAlX8G/9crv/wBF1DF/yV7VP+wZF/6Eam8Tf8lX8G/9crv/ANF1A7CD4wXYk48/S0Mf+1hua68X/Dpf4f8A26RyUfiqev6I6+iiivMNgooooAKKKKACsvxVFJP4Z1aKFWeR7SVVVRksSpAAFalFAHnq2kmpeH4LOf8AtK7UXNuJEu7by9i9GA+UZHvVWTR9Xln1jTWilk8nTvs9tcMCFmXflV3f3tvymvTKKvnA4zVZX1jw6Lay068jltnhkkt5YSm5UYFkBPB4Hb0qvqiz61qE95ZWV1DBDps8DGaIxtI7fdQA8nGP1ru6KXMBwdlHPqU2htDYXVuNPt3E800RjLEx7dgB5PPPpwKybK2vH8A3dgBqr3Yt0AgmtSqoQ44Q7Rn9elepUU+cDlvClncWWr6r/aPmzXUvlst0Y9qSRgYC4AwCCTkV1NHPvRUt3dwCiiikAUUUUAFFFFAHPfEH/kStZ/69n/lW/wCD/wDkVNG/684v/QBXN/EqdLfwRqxkON8XlqPVmOAP1rqfDcD2vh7TIJBh4raNGHoQoFaw2KiaVFFFWWFFFFABRRRQAUUUUAFFFFABRRRQAVW1Kyg1Gxns7tA8E6GN1PcGrNFAHD+AL2fTbu68Lao5a5sRutZG/wCW1ufun6joa7iuO+IWk3EkFtrmkL/xNtLbzUA/5ax/xIfXIroPD+rW+t6Pa6jaNmGdNwB6qe4PuDTYGjWRH4d0uHWhq0FpHDf7WRpIxt3g9dwHBrXopAed23/JXNa/68If/Qq6+uQBEHxe1BZDg3GnRsmf4sNg119Ub09gooopFhRRRQAUUUUAU9YVpNJvUjUs7QuAAMknBrjtMiudRbw0IrG6t/7Nh/0iWeIx/wDLPbsAPJ5/Diu9oppktXPM9Isb258I3enK2pm6+z4FtcW/lxjDZ2qxUZz05J61saxM+taDHHZafeKbWaGaS3lhMe9UYFkGeGOB244rtKOtFw5TgtWSfWb68vrKyu4YI9Mmtz5sRjaV25ChTycYP50+CK41S80ia3sbm3jsbWRZpZ4jGXJTaEAPJ55ruqKLi5TzC0tryXwJcWKnVZLlYYl8ie12LGQ65CHaC2Pqa6fwnZ3NlqmrDUPNlu5WRvtJj2pJGBhQMDAI5BH411FFFxqKQUUUUigooooAKKKKACub+I3/ACJOr/8AXA10lct8Tpkh8D6pvON8YjX3YkAU0KWzM3x5/wAk48N/9fFl/SvUB0FeZ/EWFrfwBoMMgw8d3ZqR6EYr0wdBXVV/3an6y/Q82n/Gn8v1CiiiuM6QooooAKKKKAOC8T/8lX8G/wDXK7/9F1seL/C8evrbzwXL2Op2h3W91GMlfUEdwfSsfxN/yVfwb/1yu/8A0XXefWuvFfBS/wAP/t0jmofFU9f0R58NM+IMI2pfeHZwOA80cqsfqF4pfsPxE/57eFv++Z67ObV9NgcpNqFnG44KvMoI/Wmf27pH/QUsP/AhP8a5OVdjosjj/sPxE/57eFv++Z6PsPxE/wCe3hb/AL5nrsP7d0j/AKClh/4EJ/jR/bukf9BSw/8AAhP8aOVdgsjj/sPxE/57eFv++Z6PsPxE/wCe3hb/AL5nrsP7d0j/AKClh/4EJ/jR/bukf9BSw/8AAhP8aOVdgsjj/sPxE/57eFv++Z6PsPxE/wCe3hb/AL5nrsP7d0j/AKClh/4EJ/jR/bukf9BSw/8AAhP8aOVdgsjj/sPxE/57eFv++Z6PsPxE/wCe3hb/AL5nrsP7d0j/AKClh/4EJ/jR/bukf9BSw/8AAhP8aOVdgsjg9Wfx5pWm3N9eXHhdYLdDI5Cz9B/Wk0aTx5q+l21/Z3Hhdre4QOhKz557H3qb4ttba54TuIbLXbGFIQZ5IxKrNNtGQgwfWm/B9rbRPCcEV7rljJHOBPHE0qq0G4ZKHJ9aOVW2FZXLP2H4if8APbwt/wB8z0fYfiJ/z28Lf98z12H9u6R/0FLD/wACE/xo/t3SP+gpYf8AgQn+NHKuw7I4/wCw/ET/AJ7eFv8Avmej7D8RP+e3hb/vmeuw/t3SP+gpYf8AgQn+NH9u6R/0FLD/AMCE/wAaOVdgsjj/ALD8RP8Ant4W/wC+Z6PsPxE/57eFv++Z67D+3dI/6Clh/wCBCf40f27pH/QUsP8AwIT/ABo5V2CyOP8AsPxE/wCe3hb/AL5no+w/ET/nt4W/75nrsP7d0j/oKWH/AIEJ/jR/bukf9BSw/wDAhP8AGjlXYLI4/wCw/ET/AJ7eFv8Avmej7D8Q/wDnv4XH/AZ67D+3dI/6Clh/4EJ/jR/bmknpqlj/AOBCf40WXYLI5G08G6tqmoW914w1OG6ht3EkdlaoVh3DoSTycV344FRwTxTxh4JUkQ9GRgw/SpKASCiiigYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAjDIwa8/sx/wAIb40ayb5dE1pzJB2WC47p9G7V6DWN4u0OLxDodxYyko7DfFIOscg5Vh+NMDZorl/AOuTarpkltqIEer2D/Z7uM8HcOjfQjmuopAcz4w8LJrv2e5trp7DVLUk293GMlc9VI7g1hrpnxBiGxL/w7Oo6PLHKrH8F4r0LIqjNq+mQuVm1CzjcdQ06gj9ad2O7Rxn2L4if89/C/wD3zPR9i+In/Pfwt/3zPXYf27pH/QUsP/AhP8aP7d0j/oKWH/gQn+NF2HM+5x/2L4if89/C3/fM9H2L4if89/C3/fM9dh/bukf9BSw/8CE/xo/t3SP+gpYf+BCf40XYcz7nH/YviJ/z38Lf98z0fYviJ/z28Lf98z12H9u6R/0FLD/wIT/Gj+3dI/6Clh/4EJ/jRdhzPucf9i+In/Pfwt/3zPR9i+In/Pfwt/3zPXYf27pH/QUsP/AhP8aP7d0j/oKWH/gQn+NF2HM+5x/2L4if89vC3/fM9I1p8QlUs0/hYKBknbPxXY/27pH/AEFLD/wIT/GsnxTfWeqaDeWVhrun2s06eX5pmVtqnrxnrjNO7Dmfc47w3qnjTxHZy3OmXfhh445WhbKzZyp/keo+ta/2L4if89/C3/fM9cr8EbePRRf3E+t2S2skjQtbO6qSyHhxk9DzXrX9u6R/0FLD/wACE/xobYKb7nH/AGL4if8APfwt/wB8z0fYviJ/z28Lf98z12H9u6R/0FLD/wACE/xo/t3SP+gpYf8AgQn+NK7Dmfc4/wCxfET/AJ7+Fv8Avmej7F8RP+e3hb/vmeuw/t3SP+gpYf8AgQn+NH9u6R/0FLD/AMCE/wAaLsOZ9zj/ALF8RP8Ant4W/wC+Z6PsXxE/57+Fv++Z67D+3dI/6Clh/wCBCf40f27pH/QUsP8AwIT/ABouw5n3OP8AsXxE/wCe3hb/AL5no+xfET/nt4W/75nrsP7d0j/oKWH/AIEJ/jR/bukf9BSw/wDAhP8AGi7Dmfc4/wCw/ET/AJ+PDA+iz06z8G6pqWo2934w1KC7jt3EkVnaxlIt46Mc8nFdd/bmknpqlj/4EJ/jV2CaKeMSQSJIh6MjAg/iKLsG29zhvjGMeG7D/sJW3/oVd6OgrgvjH/yLdh/2Erb/ANCrvR0FddX/AHan6y/Q5af8afy/UKKKK4zpCiiigAooooA4LxP/AMlX8Hf9crv/ANF1F40nu9c8VW3hi2uZbSzWD7VeyRNtd1zgID2qXxN/yVfwb/1yu/8A0XUMf/JXtT/7BkX/AKFXXiv4dJ/3f/bpHLR+Kp6/oiSD4f8AhiJAp0mCQjjdISxP61L/AMIJ4X/6Alp/3yf8a6WivN5ma6nNf8IJ4X/6Alp/3yf8aP8AhBPC/wD0BLT/AL5P+NdLRRzMLs5r/hBPC/8A0BLT/vk/40f8IJ4X/wCgJaf98n/Guloo5mF2c1/wgnhf/oCWn/fJ/wAaP+EE8L/9AS0/75P+NdLUF/dxWNjcXdxkQwRtK+0ZOAMnijmYXZg/8IJ4X/6Alp/3yf8AGj/hBPC//QEtP++T/jT38W2EWmNf3UN7b2yui7poCud3QgdxWjLrNjFM8ckoULb/AGpnI+UR5xnNP3g1Mr/hA/C//QEtP++T/jR/wgfhf/oC2n/fJ/xqxB4ospLWe5khvLe2iQP5k1uyhwTgbfUnsKda+JrGcXAdLm3lgiM5inhKMyDqyg9RReQalb/hBPC//QEtP++T/jR/wgnhf/oCWn/fJ/xqzpviawv5ViVbmCR4zLGs8LRmRQMkrnrUEHi6xl0yfUPIvktIk8wyPAQHGcfL69aLyDUb/wAIJ4X/AOgJaf8AfJ/xo/4QTwv/ANAS0/75P+NaWja1a6sZlgE0csO3zIpoyjrkZBwex9a06G2guzmv+EE8L/8AQEtP++T/AI0f8IJ4X/6Alp/3yf8AGulopczC7Oa/4QTwv/0BLT/vk/40f8IJ4X/6Alp/3yf8a6WijmYXZzX/AAgnhf8A6Alp/wB8n/GkPgPwv/0BbT8j/jXTUUcz7hdnnniDQ18Fw/2/4ZaS3Fuym5tN5McseQDwehFep2k6XNrFPEcxyoHU+xGa474g8+CtZz/z7P8Ayrf8If8AIq6P/wBecX/oArWDbWpUTXoooqiwooooAKKKKACiiigAooooAKKKKACiiigAooooA4LxlDJ4c1628V2SMYDi31KNR96Mnh8eqmu4t5o7iBJoWDxyKGVlOQQelV9aiebSbyKK2S6d4mUQSNtWTI6E9q8Z+Ed/rtp44Gh62bmGCG2kWG2kPyp8wPHr3wae6Edh4ymute8WQ+GLe5ktbFLf7VeyRHa8gJwEB7D1qWL4f+GI0C/2TDIR1aQlifxzUNtz8XNZ/wCwfD/Ouvpm9OKauzmv+EE8L/8AQEtP++T/AI0f8IJ4X/6Alp/3yf8AGulopF8qOa/4QTwv/wBAS0/75P8AjR/wgnhf/oCWn/fJ/wAa6WigOVHNf8IJ4X/6Alp/3yf8aP8AhBPC/wD0BLT/AL5P+NdLRQHKjmv+EE8L/wDQEtP++T/jR/wgnhf/AKAlp/3yf8a6C5mW3t5ZpM7I1LtgdhzWRpPiew1KWKNBcQPKnmRC4hMfmrjOVJ4NPUVkVv8AhBPC/wD0BLT/AL5P+NJ/wgnhf/oC2n/fJ/xqzp/ieyvbeW5WO7htI4zIZ5oSiFR6HvSQ+KbJ7Sa5mhvbeCNQwea3ZA+eBt9SfSjUNCv/AMIH4X/6Atp/3yf8aX/hBPC//QEtP++T/jVi38T2Msd0ZEuraS3iM7xXEJRyg/iAPUcU7TfEtjfSeUFuIJTGZUS4hMZdB1K560ahaJV/4QTwv/0BLT/vk/40f8IJ4X/6Alp/3yf8adD4usZNMm1D7PfpaRxrJve3K7wSANvr1FaOj6za6t5y24mjlhIEkU0ZjdcjI4PY0ahoZn/CCeF/+gJaf98n/Gj/AIQTwv8A9AS0/wC+T/jXS0Uh8qOa/wCEE8L/APQEtP8Avk/40f8ACCeF/wDoCWn/AHyf8a6WigOVHNf8IJ4X/wCgJaf98n/Gj/hBPC//AEBLT/vk/wCNdLRQHKjmT4D8Ln/mC2v4A/41heINFXwTGNf8MvLbxwOpurPeWjljJAPBPBFeh1zfxH/5EnV/+uBp3JlFWK3xamW48J6ZNHykmoWrqfYtmvQl6CvL/HnPw48Of9fFl/SvUB0FdVX/AHan6y/Q8+n/ABp/L9QooorjOkKKKKACiiigDgvE3/JV/Bv/AFyu/wD0XUMf/JXtU/7BkX/oVTeJ/wDkq3g3/rld/wDouq2oSrpvxaEl0fLi1DTxFC56M6vkr9cV1Yv+HT/w/wDt0jko/FU9f0R2NFFFeabBRRRQIKKKKACs7xHbS3nh/U7a3XdNNbSRoucZYqQBWjRQgOJh0q5uNItrU6fdxGO5geUXNwJQyj72PmOB7VSbwpqTXGrWOVNg1kYLKZm7FtwRu/HTPpivQ6KrmGclqUOp6xoYgbTWtbq2eKdQ8i7JXRgdoI7HHUiodQsdT1q8lu5bFrRYrGa3jjkkUtK7genAAx+tdnRRzAcXZ6dqd/JpH2qx+xw6bCwy8il5XMezAA6L36+lZlroeoN4KutL+wXkV20CpukuQ6MQwPyjccfpXo9FHMBznhnSrjStR1BZxJOs2x0u5H3OwAxsb6dvY10dFFJu4gooopAFFFFABRRRQBz3xB/5ErWf+vZ/5Vv+D/8AkVNG/wCvOL/0AVyvxOvY7bwjeQZ3XF2Bbwxjq7McYH612eh2psdGsbV+WggSM/UKBW0PhLiXqKKKosKKKKACiiigAooooAKKKKACiiigAooooAKKKKACq8lpBJcxXEkMbTxZ2SEfMuRg4NWKKAPO7b/krms/9g+H+ddfXHXjrpvxbd7o7I9RsFSFm4DOjcrn1xXY0zen8IUUUUFhRRRQAUUUUAVdViefS7uKMZeSJlUepINcnp2m6peHQku7I2cOlxfMzyBmlfy9mABnA78121FO4mrnnumaDeP4YudLksrq3ujBtEk1xviZg2QAu44/KtXVYtU1rSEjOmta3VrLFcIkkilJWRgSoIPTjqa62igXKcVqGnalrV1d3r2TWezT5baKJ5FLyO/04AGB+dPg07UtRutNkurL7FDp9u6gPIrPK7JtxgcAe9dlRRcOVHnVtol+3g240z7Bew3ZhjQtLch0YhhnYNxC9z0FdJ4Z0y40u+1GOcPMkrLIl3I+53GMbG/3e3sa6GigajYKKKKQwooooAKKKKACub+I3/Ikav8A9cDXSVyPxRvEg8I3VtkG5vCtvDGPvOzEDgU0KWzKXjz/AJJv4b/6+LL+leoDoK82+JlubTwPols33ory0jP4HFekjoK6qv8Au1P1l+h5tP8AjT+X6hRRRXGdIUUUUAFFFFAHn/jxxYeM/COqTfLbpPJbOx6KZFwM11HiDQNP8RWH2XUod6K25HU7XRvVT2NS+IdGtNe0mewv03QyjGR1U9iPcVx1rN4z8MRi1axj8QWMfyxTRyiOYL2DA9a7lFYilGMWlKOmrtdXvu/U5daM5Nq6ZL/wgN/F8ln4t1aOIcKr7XI/Gj/hBtY/6HHUv+/a0v8AwmuvD73gjVc+0imj/hN9d/6EjV/++1qfqNbsvvj/AJj+s0vP7n/kJ/wg2sf9DjqX/ftaP+EG1j/ocdS/79rS/wDCb67/ANCRq/8A32tH/Cb67/0JGr/99rR9Qrdl98f8xfWKXn9z/wAhP+EG1j/ocdS/79rR/wAINrH/AEOOpf8AftaX/hN9d/6EjV/++1o/4TfXf+hI1f8A77Wj6hW7L74/5h9Ypef3P/IT/hBtY/6HHUv+/a0f8INrH/Q46l/37Wl/4TfXf+hI1f8A77Wj/hN9d/6EjV/++1o+oVuy++P+YfWKXn9z/wAhP+EG1j/ocdS/79rR/wAINrH/AEOOpf8AftaX/hN9d/6EjV/++1o/4TfXf+hI1f8A77Wj6hW7L74/5h9Ypef3P/IyvE3h7UtB0G91K48Y6iUt4ywXYo3N2H4nAqPwloWo+I9BtNStvGOogTL8yhFOxu6/gapfEDU9V8TaDJbXvhPW7WGLM25ZE25AOC3HQdarfDLUtR8O6Cg07wvrV5FchZWfzEKM2MblGOAf6UvqNXbS/qv8x/WKdr6/c/8AI67/AIQbWP8AocdS/wC/a0f8INrH/Q46l/37Wl/4TfXf+hI1f/vtaP8AhN9d/wChI1f/AL7Wn9Qrdl98f8xfWKXn9z/yE/4QbWP+hx1L/v2tH/CDax/0OOpf9+1pf+E313/oSNX/AO+1o/4TfXf+hI1f/vtaPqFbsvvj/mH1il5/c/8AIT/hBtY/6HHUv+/a0f8ACDax/wBDjqX/AH7Wl/4TfXf+hI1f/vtaP+E313/oSNX/AO+1o+oVuy++P+YfWKXn9z/yE/4QbWP+hx1L/v2tH/CDax/0OOpf9+1pf+E313/oSNX/AO+1o/4TfXf+hI1f/vtaPqFbsvvj/mH1il5/c/8AIT/hBtY/6HHUv+/a0f8ACC6wevjHU/wjWl/4TfXf+hI1f/vtaP8AhN9d/wChI1f/AL7Wj6hW7L74/wCYfWKXn9z/AMi/oXgOx0/UU1G+urvVL9PuS3cm4R/7q9BXX1wP/Cb67/0JGr/99rR/wm+u/wDQkav/AN9rR9QreX3x/wAx/Wqfn9z/AMjvqK4H/hN9d/6EjV/++1o/4TfXf+hI1f8A77Wj6hW8v/Ao/wCY/rVPz+5/5HfUVwP/AAm+u/8AQkav/wB9rR/wm+u/9CRq/wD32tH1Gt5f+BR/zD61T8/uf+R31FcD/wAJvrv/AEJGr/8Afa0f8Jvrv/Qkav8A99rR9QreX/gUf8w+tU/P7n/kd9RXA/8ACb67/wBCRq//AH2tH/Cb67/0JGr/APfa0fUK3l/4FH/MPrVPz+5/5HfUVwP/AAm+u/8AQkav/wB9rR/wm+u/9CRq/wD32tH1Ct5f+BR/zD61T8/uf+R31FcD/wAJvrv/AEJGr/8Afa0f8Jvrv/Qkav8A99rR9QreX/gUf8w+tU/P7n/kd9RXA/8ACb67/wBCRq//AH2tH/Cb67/0JGr/APfa0fUa3l/4FH/MPrVPz+5/5HfUVwP/AAm+u/8AQkav/wB9rR/wm+u/9CRq/wD32tH1Gt5f+BR/zD61T8/uf+R31FcD/wAJvrv/AEJGr/8Afa0f8Jvrv/Qkav8A99rR9QreX/gUf8w+tU/P7n/kdP4k8Paf4isfs2pxF1U7kdTteNvVT2Ncv/wgOoRfLaeLtWjiH3VkxIQPqaX/AITbXf8AoSNX/wC+1o/4TbXf+hI1f/vtaPqNby/8Cj/mH1qn5/c/8hP+EG1j/ocdS/79rR/wg2sf9DjqX/ftaX/hNtd/6EjV/wDvtaP+E213/oSNX/77Wn9RreX/AIFH/MPrcPP7n/kJ/wAINrH/AEOOpf8AftaP+EG1j/ocdS/79rS/8Jtrv/Qkav8A99rR/wAJtrv/AEJGr/8Afa0fUa3l/wCBR/zD63Dz+5/5Cf8ACDax/wBDjqX/AH7Wj/hBtY/6HHUv+/a0v/Cba7/0JGr/APfa0f8ACba7/wBCRq//AH2tH1Gt5f8AgUf8w+tw8/uf+Qn/AAg2sf8AQ46l/wB+1o/4QbWP+hx1L/v2tL/wm2u/9CRq/wD32tH/AAm2u/8AQkav/wB9rR9RreX/AIFH/MPrcPP7n/kJ/wAINrH/AEOOpf8AftaP+EG1j/ocdS/79rS/8Jtrv/Qkav8A99rR/wAJtrv/AEJGr/8Afa0fUa3l/wCBR/zD63Dz+5/5Cf8ACDax/wBDjqX/AH7Wj/hBtY/6HHUv+/a0v/Cba7/0JGr/APfa0f8ACba7/wBCRq//AH2tH1Gt5f8AgUf8w+tw8/uf+Qn/AAg2sf8AQ46l/wB+1o/4QbWP+hx1L/v2tL/wm2u/9CRq/wD32tH/AAm2u/8AQkav/wB9rR9Rr+X/AIFH/MPrcPP7n/kJ/wAINrH/AEOOpf8AftaP+EG1j/ocdS/79rS/8Jtrv/Qkav8A99rR/wAJtrv/AEJGr/8Afa0fUa3l/wCBR/zD63Dz+5/5Cf8ACDax/wBDjqX/AH7Wj/hBtY/6HHUv+/a0v/Cba7/0JGr/APfa0f8ACba7/wBCRq//AH2tH1Gt5f8AgUf8w+tw8/uf+Qn/AAg2sf8AQ46l/wB+1o/4QbWP+hx1L/v2tL/wm2u/9CRq/wD32tH/AAm2u/8AQkav/wB9rR9RreX/AIFH/MPrcPP7n/kJ/wAINq/fxjqZHtGorQ0LwLY6bqCajeXV3qmop9ya7k3CP/dXoKof8Jtrv/Qkat/32tDeKfFl4pjsPB80EjcCS7uFVF9yByaX1Kr1t/4FH/MPrUH3+5jfiewvbnw7o0PzXFzqEcxUdo4+WNegDoK47wp4YurbU5da8QXK3msyrsBQYjgT+6g/rXYjpSxM4JRpQd1Hr5vew6MZXlUkrXCiiiuQ3CiiigAooooAKTFLRQAmOaKWmSSLGheRgqjkkngUAPxRisRvEunhiEaWQA4ykZIo/wCElsf7tx/36NTzIj2ke5t4oxWJ/wAJLY/3bj/v0aP+Elsf7tx/36NHMu4e0j3NvFGKxP8AhJbH+7cf9+jR/wAJLY/3bj/v0aOZB7SPc28UYrE/4SWx/u3H/fo0f8JLY/3bj/v0aOZdw9pHuW9eTfouoLj71vIP/HTWL8L23+A9GP8A0wA/Imrc3iHT5oXjdbja6lT+6PQ1V0TUtJ0fTILCzS6FvCu1A0ZJ60c0e4c8e51OKMVif8JLY/3bj/v0aP8AhJbH+7cf9+jRzLuHtI9zbxRisT/hJbH+7cf9+jR/wktj/duP+/Ro5l3D2ke5t4oxWJ/wktj/AHbj/v0aP+Elsf7tx/36NHMg9pHubeKMVif8JLY/3bj/AL9GhfEunkgO0sYPd4yBRzIPaR7m1S4pkUiyxh42DIwyCDkGn1RYYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYoxRRQAYpMUtFACYpaKKACiiigAoopGYKpJ4AGaAFoqnHqVrJJAiTIWnUvGP7w9qbNqtnAu6WYAbzHwCfmHUUXFdF6iqsF/bztGIpVcyKWTHcDr/ADqCfWbGBS0k4ADFCdpOCDgilcLo0TWF4r+e3soD9y4uo439wf8A9Va9tcR3MIlhbcjdDjFZHif7+k/9f0f9aUtianwmzFCkUapGiqqjAAHSn7R6CjNQR3UclzNAM74gC2Rxz0p3RWhPtHoKNo9BSI6uMqQR6g06mMTaPQUbR6ClpsjqgyxAHuaT0FoLtHoKNo9BSBwehHTNRmcCRUwSGBO4dBii6DQl2j0FG0egpqSK/wB1g3rg0+mGgm0ego2j0FBbHWqaahH9naaYGGPfsBfvzgGk2luDsi5tHoKNo9BTVkB6EHvSNKqrksPbnrRdWuGg/aPQUbR6CqlnfLdRwuiOFlTeCRwPb61YEqnJDqQOvPShNPVBdbj9o9BTJokkjZHRWVhggjrTXuI0jZ2kUKgyxz0p0ciyoGQgqeQRRdbBoYvhX93FfW4z5cF06IPQccVvVheGf9dq3/X6/wDSt2lHYmn8IUUUVRYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABUc43QuBySpH6VJRQByVvpU81vYqyPFNDa/I5H3JAwIH+e1EFpf3CWjNG9tMbuWRyVDbAQea63FGKnlRPIjn/sZ0q5s3ijmniVJFdlGWDMQckfhURsrg+H7tTC4lmufNWPHzBS4P8hXS4oxT5UHKhAMCsPxP9/Sf+v6P+tbtYXif7+k/wDX9H/WlLYmp8JuVy+qRzS3GrC2yT+53ADOV7jHfiuoxkVXtLOC03iBNu87mJOST9TUVIc9kVKPMZvh2ERvcOkmVfb8ghMSgjuAfw/Ktukx0pauEeWNgirKwVkeIoUlhhLsQyPuUGIyK3HQgVr0honHmjYbV1Y5yznaG4tp57Z4Ea3KBEjJAIbpgDjPXmobOB3t7QTxzRobacOQpyuWGPxrqMUYrL2N92R7PzMTw6PLkmiWFfLULiZYTFv68EHuPWt2m4Ap1aQjyqxUVZWMvxFHPLpUy2wJfjIAySuRnjvxmsKSyVrK4dR5yeZCxiW2ZANrDJAPU49K7Gm7aidJTd2KUOZ3OeWRbe9u2jil8ma3QQhIjgkbuOnHUdaq20Kqbc6jbyOgtESMGMttb+IYxweldXgUYpex8xcnmcnZpcW1vauttKxjsGXYyn72RwfeoWglaPUBDGdklqAPKt2iUtk9j1NdlilxU/V+l/62F7Lpc5u/05UkkjtrcBZLN1YKnDNxjPv1rW0byv7PhEEflqFAK7NmD34xV3FLitI0lF3RShZ3MPw1/rtW/wCv1/6Vu1heGv8AXat/1+v/AErdq47Cp/CFFFFUaBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFZmvWMl7ZqICBPE4ljJ6bhWnRik1dCaurMwE1u5iULc6VeeYOD5ahl/A07+33/6BWo/9+v8A69buKTFKz7k8su5h/wBvv/0CtR/79f8A16P7ff8A6BWo/wDfr/69bmKMUWl3Dll3MP8At9/+gVqP/fr/AOvR/b7/APQK1H/v1/8AXrcxRiiz7hyy7mH/AG+//QK1H/v1/wDXo/t9/wDoFaj/AN+v/r1uYoxRZ9w5ZdzD/t9/+gVqP/fr/wCvR/b7/wDQK1H/AL9f/XrcxRii0u4csu5h/wBvv/0CtR/79f8A16P7ff8A6BWo/wDfr/69bmKMUWl3Dll3MP8At9/+gVqP/fr/AOvR/b7/APQK1H/v1/8AXrcxRiiz7hyy7mH/AG+//QK1H/v1/wDXo/t9/wDoFaj/AN+v/r1uYoxRaXcOWXcw/wC33/6BWo/9+v8A69NbXLiRStvpN75h6eYu1fxNb2KMUWfcOWXczNBsZLK1f7QQbiaQyyY6AmtSjFFNaFJWVkFFFFMYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAf/Z
">
<center>Figure1: High level view of a <a href="https://jalammar.github.io/illustrated-transformer/">transformer</a></center>
1. The **encoders** are all identical in structure (yet they do not share weights). Each one is broken down into two sub-layers:
- **Self-Attention Layer**
- Say the following sentence is an input sentence we want to translate:
**The animal didn't cross the street because it was too tired.**
What does **"it"** in this sentence refer to? Is it referring to the **street** or to the **animal**? It's a simple question to a human, but not as simple to an algorithm. When such data is fed into a transformer model, the model processes the word **"it"** and the **self-attention layer** allows the model to associate **"it"** with **"animal"**. As each word in the input sequence is processed, **self-attention** looks at other words in the input sequence for clues that can lead to a better encoding for this word.
- **Feed Forward Layer**
- The outputs of the self-attention layer are fed to a feed-forward neural network. The exact same feed-forward network is independently applied to each position.
2. The **decoder** has both those layers (**self-attention** & **feed forward layer**), but between them is an **attention layer** (sometimes called **encoder-decoder** attention) that helps the decoder focus on relevant parts of the input sentence.
<img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAA28AAAEXCAYAAAA6IXx5AAAYJ2lDQ1BJQ0MgUHJvZmlsZQAAWIWVeQdUFE2zds/OBliWJeeck+QMknPOGYEl55xRiSJBRRBQBFRQQVDBQBIxIYgoIqiAAZGgZBUUUATkDkHf7773P/89t8+ZmWerq6uf7qruntoBgI2ZFB4ejKIGICQ0OtLaQJvb0cmZGzcOMIAckAEVQE/yigrXsrQ0BUj58/zvZWUQQFvPl+Jbtv5n/f+30Hj7RHkBAFki2NM7yisEwQ0AoFm9wiOjAcD0IXK+uOjwLbyEYPpIhCAAWLIt7LeD2bew5w6W2taxtdZBsC4AZAQSKdIPAOKWfe5YLz/EDjEcqaMN9Q4IRVQzEKzu5U/yBoC1A9HZExIStoUXECzs+R92/P6bTc+/Nkkkv794ZyzbhUw3ICo8mJTwf5yO/72EBMf86YMXuQj+kYbWW2NG5u1SUJjJFiYguC3U09wCwbQIfhzgva2/hd/6xxja7erPe0XpIHMGGAFAAW+SrgmCkblEMcYE2WntYhlS5HZbRB9lHhBtZLuLPSPDrHfto2JDg81Nd+1k+fsY/cFnfKL0bP7o+AboGyEYiTRUQ6K/rcMOT1RHbIC9OYKJCO6LCrIx2W07kuivY/5HJzLGeoszP4KXfCP1rXd0YOaQqD/jgiW8SNt9MSNYM9rf1nCnLezoE+Vo+oeDt4+u3g4H2Nsn1G6XG4xEl7b1btvM8GDLXX34jE+wgfXOPMPXomJt/rR9EY0E2M48wOOBJGPLHf7wSni0pe0ONzQamAIdoAu4QQxyeYIwEAgCeueb55FfOzX6gAQigR/wAeK7kj8tHLZrQpG7DUgEnxHkA6L+ttPervUBsYh846905y4OfLdrY7dbBIFJBIegWdHqaFW0KXLXRC4ZtBJa+U87bqo/vWL1sLpYQ6w+VuQvDy+EdTByRYKA/4fMBHn6IKPb4hL6Zwz/2MNMYvox45gBzCjmDbAHH7et7Gq5B6RF/os5NzADo4g1/d3ReSI2Z/7ooAUR1vJobbQawh/hjmZEswJxtBwyEi20BjI2eUT6nwxj/nL7Zy7/3d8W6/8cz66cKEqU32Xh+dczOn+1/m1F5z/myBt5mvxbE86Cb8Jd8AO4G26DmwE3fA9ugXvgO1v4byR83I6EP71Zb3MLQuwE/NGRuiw1I7X+P3on7TKI3PY3iPaJj95aEDph4QmRAX7+0dxayI7sw20U6iWxh1tGSloJgK39fWf7+G69vW9DjM//kflMA7AXiXHyvn9kgScAqO0EgCnnH5mgCwAsewC4/sIrJjJ2R4beumEAHlAhK4MFcAI+IIyMSQYoAFWgCfSAMbAAtsAJuCGz7g9CENZxYD9IBZkgFxwHReA0OAvOg0vgKrgBmkEbeAAegaegDwyAd0hsfAJzYAGsgDUIgnAQJUQHsUBckAAkBslASpA6pAeZQtaQE+QB+UGhUAy0H0qHcqEC6DRUAdVA16Fb0AOoG+qH3kBj0Az0DfqFglEEFD2KAyWIkkQpobRQJihb1D6UHyoClYjKQB1DnUJVoq6gmlAPUE9RA6hR1BxqGQYwBcwI88DisBKsA1vAzrAvHAkfhHPgYrgSroNbEV+/hEfheXgVjUXTobnR4kh8GqLt0F7oCPRB9BH0afQldBO6A/0SPYZeQP/GUGLYMWIYFYwRxhHjh4nDZGKKMVWYRkwnsnY+YVawWCwjVgiriKxNJ2wgNgl7BFuOrcfex/ZjJ7DLOByOBSeGU8NZ4Ei4aFwmrgR3BXcP9wL3CfeTjIKMi0yGTJ/MmSyULI2smKyW7C7ZC7IpsjVyanIBchVyC3Jv8gTyPPIL5K3kz8k/ka/hafBCeDW8LT4Qn4o/ha/Dd+KH8d8pKCh4KZQprCgCKFIoTlFco3hMMUaxSqAliBJ0CK6EGMIxQjXhPuEN4TslJaUgpSalM2U05THKGsqHlCOUP4l0RAmiEdGbmEwsJTYRXxC/UJFTCVBpUblRJVIVU92kek41T01OLUitQ02iPkhdSn2Leoh6mYaORprGgiaE5ghNLU03zTQtjlaQVo/WmzaD9jztQ9oJOpiOj06Hzosune4CXSfdJ3osvRC9EX0gfS79Vfpe+gUGWgY5BnuGeIZShjsMo4wwoyCjEWMwYx7jDcZBxl9MHExaTD5M2Ux1TC+YfjCzMWsy+zDnMNczDzD/YuFm0WMJYslnaWZ5z4pmFWW1Yo1jPcPayTrPRs+myubFlsN2g+0tO4pdlN2aPYn9PHsP+zIHJ4cBRzhHCcdDjnlORk5NzkDOQs67nDNcdFzqXAFchVz3uGa5Gbi1uIO5T3F3cC/wsPMY8sTwVPD08qzxCvHa8abx1vO+58PzKfH58hXytfMt8HPxm/Hv57/M/1aAXEBJwF/gpECXwA9BIUEHwcOCzYLTQsxCRkKJQpeFhoUphTWEI4QrhV+JYEWURIJEykX6RFGi8qL+oqWiz8VQYgpiAWLlYv17MHuU94TuqdwzJE4Q1xKPFb8sPibBKGEqkSbRLPFFkl/SWTJfskvyt5S8VLDUBal30rTSxtJp0q3S32REZbxkSmVeyVLK6ssmy7bILsqJyfnInZF7LU8nbyZ/WL5dfkNBUSFSoU5hRpFf0UOxTHFIiV7JUumI0mNljLK2crJym/KqioJKtMoNla+q4qpBqrWq03uF9vrsvbB3Qo1XjaRWoTaqzq3uoX5OfVSDR4OkUakxrsmn6a1ZpTmlJaIVqHVF64u2lHakdqP2Dx0VnQM693VhXQPdHN1ePVo9O73TeiP6vPp++pf1FwzkDZIM7htiDE0M8w2HjDiMvIxqjBaMFY0PGHeYEExsTE6bjJuKmkaatpqhzIzNTpgNmwuYh5o3WwALI4sTFu8thSwjLG9bYa0srUqtJq2lrfdbd9nQ2bjb1Nqs2Grb5tm+sxO2i7Frt6eyd7Wvsf/hoOtQ4DDqKOl4wPGpE6tTgFOLM87Z3rnKedlFz6XI5ZOrvGum6+A+oX3x+7rdWN2C3e64U7mT3G96YDwcPGo91kkWpErSsqeRZ5nngpeO10mvOW9N70LvGR81nwKfKV813wLfaT81vxN+M/4a/sX+8wE6AacDFgMNA88G/giyCKoO2gx2CK4PIQvxCLkVShsaFNoRxhkWH9YfLhaeGT4aoRJRFLEQaRJZFQVF7YtqiaZHXnV6YoRjDsWMxarHlsb+jLOPuxlPEx8a35MgmpCdMJWon3gxCZ3kldS+n2d/6v6xA1oHKg5CBz0PtifzJWckf0oxSLmUik8NSn2WJpVWkLaU7pDemsGRkZIxccjg0OVMYmZk5tBh1cNns9BZAVm92bLZJdm/c7xznuRK5Rbnrh/xOvLkqPTRU0c3j/ke681TyDtzHHs89Phgvkb+pQKagsSCiRNmJ5oKuQtzCpeK3Iu6i+WKz57En4w5OXrK9FRLCX/J8ZL10/6nB0q1S+vL2Muyy36Ue5e/OKN5pu4sx9ncs7/OBZx7XWFQ0VQpWFl8Hns+9vzkBfsLXReVLtZUsVblVm1Uh1aPXrK+1FGjWFNTy16bdxl1OebyzBXXK31Xda+21InXVdQz1udeA9dirs1e97g+eMPkRvtNpZt1DQINZY10jTlNUFNC00Kzf/Noi1NL/y3jW+2tqq2NtyVuV7fxtJXeYbiTdxd/N+Pu5r3Ee8v3w+/PP/B7MNHu3v7uoePDVx1WHb2dJp2PH+k/etil1XXvsdrjtm6V7ltPlJ40P1V42tQj39P4TP5ZY69Cb9Nzxectfcp9rf17++++0Hjx4KXuy0evjF49HTAf6B+0G3w95Do0+tr79fSb4DeLb2Pfrr1LGcYM57ynfl88wj5S+UHkQ/2owuidMd2xnnGb8XcTXhNzH6M+rn/KmKScLJ7imqqZlplum9Gf6Zt1mf00Fz63Np/5meZz2RfhLw1fNb/2LDgufFqMXNz8duQ7y/fqJbml9mXL5ZGVkJW1Hzk/WX5eWlVa7frl8GtqLW4dt35qQ2Sj9bfJ7+HNkM3NcFIkaftVAEYulK8vAN+qAaB0AoAOyePwxJ38a7fA0FbaAYA9pIfSgpXQzBg8lgwnReZEno6/R8BSkojN1HiaYNon9PIMZUyAOYill02B/TjHHJcmdx5PPx+eX1nASTBIKETYVURblEN0UezRnhLxIAk1SUrJD1L10ikyVrI8sp/lbskfUrBSZFf8pFSnHK+ipYpXfbm3TM1bfY/6N41mzf1a2toE7Q86d3Vr9cr18w0OGpKMNIyZjRdNekzrzMrNKyzaLCesMTYstqx21Paw/brDmhNwJnchulLuQ+9bdht37/O4T7rpWeVV4p3jk+Dr52frrx0gFygaxBPMEkIVCocuhY2H90XcjrwQdSw6OSYztjEeneCTeH8/OCB4UCXZKMUlNSbtWHpRRtIhuUMTmXmHLbMEsilyQC7qCM1R4WPqeebHHfKdC5xPOBbaF9kWW500P2VSYnBau1S9TLlc9oz4WdFzUhUmlennRy8aVV2pnquhqRW4LH1F9apunVm9wzX36/43wm/GNRxsTGs61JzVknsrr7Xodllb1Z2Gu533hu6PPhhsr3/o28Hc8biz+FFcl+/jfd0OT6yemvQYPDPstX0e0Xeu/81LileSAzqDRkN6r5XeCLwlvl19Nz38+v2DkfMf0kf9xuzGzSfMPlp8spg0nlKeZpoencmZlZsdnbs0n/jZ8AvZl5qvBl8nFs4vxn9z+26xZLYcuNL+8/Cv5g3dzc1d/0vDaHgGPYqZwC6QweQKeH+KMsIoUZQqjvoRLQtdAv0rRhmmNOb3rPJsmex9nKxcjtz5PG28w3zL/CsCs4LPhM4LR4qoi5KJvhI7uydQXF78t8QjyWNSDtJc0lMydbKxcmrykHynQo6ihRKd0qByiYqLKofqMBIFruos6kMaJzVdtAS11rQHdK7rHtHz0d9rQGMwadhmVGQca+Jj6mnmbx5mEWLpaWVhrWojastmR7RH2a84TDkOOj10rnMpdc3Zl+gW4O7ooUuS9GT2grxmvQd8Onwb/ar8iwMyAsOCnII1Q4RCKZFIGAsfiViK4ol2jymJfRD3On4iYT5xdT/FAc6DwsncKdiUD6mNaXnpkRluh+wyHQ8HZKVnl+dczW080nS04dj1vKvHa/IvFpw7UVpYVJRXnH0y7VRCSdhpv9KAspTye2dFzl2qFDpfcOHlxdVq4iXWGr5aUSQOFK+q1+nWm11zuh58I/Pm+Ya7jf1NI83TLd9b4dtMbWJ3VO9q3lO8z/MA9WC8vethY0d1Z+mj412HHid2Rz6Jfprd09bL+PxA3/sXrC81XtkO+A6mDF18/fzN0jvaYfH3piPhH06O3h57MT4yMf5xbhKDeD91pn+OZl7qs/wXwa9UX38uTC4OfXvy/dZSxXLyiv0PoR8rP9tWE3+prhHWdTdmdv0vAc2hymE3tAgGh1nEzuBmycbJFynwBAFKLaIzVSr1FZp+2k16AQY9xkCmQ8xnWRpYO9kesz/iuM1ZwRXPrc39i+cCrwnvHF8WvxB/u4CbwKpgoZCU0BNhPxGcSLWooeiUWOYe4T2d4l4SQKJccq/ka6kY5O2mXsZUZlo2XY5TrkXeWn5e4ZAil2Iz8tYyrZyswqhyWVVL9cVer71f1JLUceqlGnIag5qJWpxaLdoW2m90/HU2dSv1LPXJ9R8a7DeUM5w1qjR2NWE2GTQtMrMxpzLvtki3VLVcsqq3DrIRsvloW2G3z57F/pVDnqOh46ZTo3OwC7/Le9fifeb7VtwK3QXcGzy0PN6S4j15PV8j+4i/j4Gvop+yv1EAKTAkiBSsEUIdMhx6MSwkXD58PeJhZE6UZTRD9LuYs7HecYJxk/FnEvQShhODk+iTXu6/feDuwY7khym3UmvSitPTM8IOuWTqHRbNwmS9yi7Jcc7lz107Mnr02bFbeeeOH8x3KVA5wXpitXCw6EbxyZNHTxWUVJy+Wfqo7HX57Jm1c5QV3JWy5w0vuF4MqzpYnX3pSE1KLemy4hXilW9XP9etXiNc57whc9OyIamxoelni/Kt8NaS29faWu7cvtt9b/mBQfutDpvO5a7ibtknr3qO9nr0Gb3QeqU9GPyGODw33ju7vLS65f+d/+G2ClYBgBOpSIaaCYCdBgD5HUieOYDknXgALCkBsFUGKEFfgCL0AEhl7O/5ASGnDRZQABrADLiAEJACKkhubAGcgS+SE6eCPHAG1IG74DkYA0tI5sgOSUMGkDsUB+VDV6DH0CQKixJGmaKiUOVInreJ5HWx8C34N9oAfQI9jpHFZGE+YFWwJdg1JMN6QqZIVk3ORp6Pp8BnU+ApjhNYCdWUcpRtRDViK5US1W1qQ+p3NNG01LRX6XTp+ult6fsZLBheMLoz/mQqYVZjHmE5wMrG2srmxk7O3sYRyynH+Z3rBnckjzzPOm8XXzG/v8BeQaLgqNBN4SwRT1EtMcE9xD1r4l8kPkoOSDVKJ8lIy4zIZsnJy32Vb1EoUExQ8lY2VZFSZdpLVJNQL9UU0zqq3a3zVY9Mn8GAxZDdiN9YzsTcNMLslHmHxTcrPmsHm2O2XfZoB13HTKceF0ZXz321bh89sCQaT6znstcn72GfWT8qf5OAosCp4L0hhaFfwo0jaqMI0RExb+P041sSxZOqDnAfLE1hTM1Px2ekHlo+HJg1l5N7JORYYz7NCdbCz8U1p9xPM5b2lR89a3BuuTLvAv3FrKqVS0E13y4fv6pXT3Nt8cZkw3TTXMtU60Tb4j2mBzoP3To9umy6NZ5KPhN5rtAf+vLnEPot+fDZD3Rjdz8Rp/fPaX2u/7r2TWFJfwX/4+jPJ6vTvz6tvVlv2Dj+23NTanv/2PI/DhAALWABPEAUyAI1YAhsgQcIAUkgG5SAGnALPAXvwQKEgVghqW3vJ0CF0DWoF/qMokLJopxR6agbqE8wF+wOX4Dn0QroDPQARgSTihlGfF+KAzh/3ACZHlkLuSR5LV4Ef4VCjuIewZIwQRlPJCcWUfFQXUPy13c0cbSMtM109nSf6Q8w4BlOMYozPmEKY2Zivs8SwErPep8tjJ2ffZijhNORi5nrDXc5jzevFB/ge8V/WSBD0FVIDsnlZkV6RG8ip1ieeLrEfsloKS9pTRmCTK9sjpyJPJP8osIbxS6lJuVKlSOqiXtj1bLVWzR+aMlqe+vk6lbpNenfNrhteMeo23jMFGUmam5vcciy2Wreht/W3a7cfsSR1ynQuckVt8/B7bR7p0c/qd2zxivLO8DH2tfQz8k/LeB+EGWwZ0hbGGt4YsT7KO3omliquPD4p4k8SbH7+w7KJ19IZUsrzMAfSsqczyJlj+cmHpXKQx1/X3C9MLZY7uS3kuulMeUqZ36dq6qUOV9+YapKqNr/0rVapstlV9XqPl8ruaF8s7eR1LTWUtlq1Qbu1Nwzvb/YfrbD85HKY54n6KfPnsU+x/blvCC8rBxwHzJ7E/yu+v3UKNe45cfUybszTHPHvwguPPteuHJk1WhNZv3Mxsffi7v+RwNyQI2sfh4gBhSADrAEbojvDyArvwI0gMdgBFn3BEgQ0oT2QUlQKXQHGkORI14noYpQfTAD7APfQbOjU9CzGCfMM6wO9g5ODfeAzJTsPXkUngp/jcKeABOaKSOI0sSfVJ3UJTQxtE50RvTGDFaMxkyKzCIs8qzubAns0RyenLZc5txmPGa8pnxm/NYC7oJRQkeFa0Uei87soRRXlPCVPC01KMMq6y1XL7+maKn0TCV7r5M6RuO45rq2iU464sFm/TaDu4a9RmsmJqZN5hIWV6wkrJtsdewGHUKc8M5XXO3daDwoPN29XXw++qn65wZMBlkH94Sahb2IcImcjk6K5YwbSXiUdP9AebJdyq+0igz7TK7DC9l3co8c9c0zyGcpeFroW7RyMr2E5nRlmUL5s7O+FVBl2QWliwPVMTVstY+vJNcZXJO8od+Q3FTZktfq1MZ0Z+he6QOnh7iOi4/kum536z0Z6onvleyD+xdeTg/0D+W/EXpb/u73e72RnA9Px6jG7SbOfZyZlJ4Kmj4383h2dh7zmf2L1FfdBYdF0jfv75ZLvEvLy0dX2Fdqfyj/OP1j9afDz6ZVxtXI1abVtV+avzJ+da8R12zWTq71rZOta67Hr19fn9ng2XDaKNh4srHxW/q39++Tv5/+/r0pvemzeWqzZ8v/Ub6yMtvHB0TQBgAzsrn5XRAAXAEAG/mbm2uVm5sb55FkYxiA+8E733a2zxpqAMq2vvGApy2/Uv79jeW/AP1xyAFVitPKAAABnWlUWHRYTUw6Y29tLmFkb2JlLnhtcAAAAAAAPHg6eG1wbWV0YSB4bWxuczp4PSJhZG9iZTpuczptZXRhLyIgeDp4bXB0az0iWE1QIENvcmUgNS40LjAiPgogICA8cmRmOlJERiB4bWxuczpyZGY9Imh0dHA6Ly93d3cudzMub3JnLzE5OTkvMDIvMjItcmRmLXN5bnRheC1ucyMiPgogICAgICA8cmRmOkRlc2NyaXB0aW9uIHJkZjphYm91dD0iIgogICAgICAgICAgICB4bWxuczpleGlmPSJodHRwOi8vbnMuYWRvYmUuY29tL2V4aWYvMS4wLyI+CiAgICAgICAgIDxleGlmOlBpeGVsWERpbWVuc2lvbj44Nzk8L2V4aWY6UGl4ZWxYRGltZW5zaW9uPgogICAgICAgICA8ZXhpZjpQaXhlbFlEaW1lbnNpb24+Mjc5PC9leGlmOlBpeGVsWURpbWVuc2lvbj4KICAgICAgPC9yZGY6RGVzY3JpcHRpb24+CiAgIDwvcmRmOlJERj4KPC94OnhtcG1ldGE+Csfa0rMAAEAASURBVHgB7J0HfBzVtf+Peu+y1S3JlmW54W5MbIoLrmBsisGFGvLoCZCQ8gKP8JL/S3h5CSEQICF0jGnGFDcMtnED914ky13Fsq1m9a7/PXd1Z2elXRV7d7S7+h1/VnNn5s4t31nf2TPn3HM9moUQBARAAARAAARAAARAAARAAARAwKkJeDp169A4EAABEAABEAABEAABEAABEAABSQDKG74IIAACIAACIAACIAACIAACIOACBKC8ucBNQhNBAARAAARAAARAAARAAARAAMobvgMgAAIgAAIgAAIgAAIgAAIg4AIEoLy5wE1CE0EABEAABEAABEAABEAABEAAyhu+AyAAAiAAAiAAAiAAAiAAAiDgAgSgvLnATUITQQAEQAAEQAAEQAAEQAAEQADKG74DIAACIAACIAACIAACIAACIOACBKC8ucBNQhNBAARAAARAAARAAARAAARAAMobvgMgAAIgAAIgAAIgAAIgAAIg4AIEoLy5wE1CE0EABEAABEAABEAABEAABEAAyhu+AyAAAiAAAiAAAiAAAiAAAiDgAgSgvLnATUITQQAEQAAEQAAEQAAEQAAEQADKG74DIAACIAACIAACIAACIAACIOACBKC8ucBNQhNBAARAAARAAARAAARAAARAAMobvgMgAAIgAAIgAAIgAAIgAAIg4AIEoLy5wE1CE0EABEAABEAABEAABEAABEAAyhu+AyAAAiAAAiAAAiAAAiAAAiDgAgSgvLnATUITQQAEQAAEQAAEQAAEQAAEQADKG74DIAACIAACIAACIAACIAACIOACBKC8ucBNQhNBAARAAARAAARAAARAAARAAMobvgMgAAIgAAIgAAIgAAIgAAIg4AIEvF2gjWgiCIAACIAACICAHQgU7TpG5ccKTCV5EPmEBJBfZAiFZiSQb1iQRQ3Fe09QWVa+xTHeCRuURBFDk7Xj9RXVVH40nypzCqm2qJz8e4dRYEIUhaTFyfI5Y2NdAxVtO0pVZ4upvrSSfEIDyT8mjKKvHEDegX5aWQ3VtZT75Q5t39PXW7QvmALiIiikfzx5eIhGt0hjbT3lfL5N7Zq3IkvKvAly//zmw1SVVyzTHl4e5B0cQIGJURQ2MIk8vfD+2gwNKRAAAVchAOXNVe4U2gkCIAACIAACl0mgtriCKk+fl8qQh4+XVLhKD5ym81sOU++rB1P0mP5aDXUtef1jwomVKE2am7VkfXk1nVy8gerLqoQyFk5+USFSgbt4OIeC+vSS+WqLy+n0x1tkHr9eYeQfG0H1F6uoaMcxKj2UQ8m3XCXaEynzNjc0yfZ5CYXOv1cocfnc3qZtDRSQEEmJN44lX6H4sTQ3teQN8CW/6FB5rPWfmgsXTf0V1zZVNVDFyXNUuv8UcZ9Tbr+aPDzNymDra7EPAiAAAs5IQDcaO2Pz0CYQAAEQAAEQAAF7E4ifMYr8WxQetpblfrWdzq0/IBSmMApO6W1RXfy0ERQgFK7W0lTfSKc/EUqZULCS5lxJoekJWhY+xlY9loK1+6XiFjdlGEWO7KflKT92ls4s+4Hyv95Dfe+eZGFVC07uJRU1zsxKWuH2bDq/8RDlr9xFKXdcrZXBicDEaOozd5zFsdY7ybf8iLz8faUF8OTi76hKWAn5EyTqgYAACICAKxGAz4Ar3S20FQRAAARAAATsTICtZQmzRstSz2082OnSq4ULZG1hGYULF0q94sYFKMWttqhMWrvYsqZX3DgPu1XydTXn2Tp2gQ9ZFQ9PT+o1boBwm4yjyjMXqOLUOav5OnPQS1gQVVvrK2s6cwnygAAIgIBTEYDy5lS3A40BARAAARAAAeMJsMXNNyKIai+UUbPOLZJbwopVWVae9mmoqpUNrD5bIrehQgmzJWzVY7Fl4dJcK4WS15GEpMXLLKzs6aVBzLnTt68yt1B/2iLN8+TKxPw8FrbuQbqXwNLPl3dvA1A7CLggAbhNuuBNQ5NBAARAAARAwN4EfEICqa6kkhoqajTLGddxboOlNS5l/jUyyEjN+VLZBJ9Qk3uktfbUl1XLw97B/tZOiwAipuMqn9VMLQdVPTxfTi+sROZ8YQ5cEiTcPoNaApaofGc++4HYzbPmXCl5eHtSnHAF9Q6y3iZ1DbaOJXAk8yh98NFSGpSRTgPFBwICINA5AlDeOscJuUAABEAABEDArQk0CDdCDuDRWqlJmjOO/ETwECXKJZLnkLE01tSrU2223kGmSJKN1XVtzvGBxhrTcX3ESasZxUFWKlm8W+bSyR3xh5W1uOuHq13y9PbS0irhISJLerYEJ4kc3pcih6WqU9h2E4GPPv1c1szb3z39y25qBaoFAdcjALdJ17tnaDEIgAAIgAAI2JUABxipK6kQrpPBbSIwssXLTxxXH6Uc+YSblhaoFtYsW+Lbkqe1q6PKr46zy2ZHwgFGWHiOnl48fcRyArr2KeVSnyfppisp9Y5rhPtmbyrec0JGxNSfR9pYAmx1O3DoiKyUt7wPAQEQ6BwBKG+d44RcIAACIAACIOCWBHgeGEd8bG5qpqgrO+++Fpou1l0T1iwO+a/mwbUG5B8TIZWt8ux8qi4wzZFTeerE8gIcsp8tfcEpMeqw1S1Hpiw5cEouCRDSN9Zqns4c5IiXYlIf5a/e3WZuX2euRx77EFBWN1Va6311HFsQAIG2BOA22ZYJjoAACIAACICAWxMo2XdShs6vEwtmV4rojQ2VtabFt4eYF99WAErEumjlJ1oW9hYHg0Rofg40wot6R41Np8KtWXT87bUy6iQfY0WuOr9Yhvr3FGvJxU4eRmc+3UInP9hIkcNTyVdYznih7pJ9p6hJLN4dN3WE5Tpyoo6awnK6IMplV062zrHVjdd+SxBLHLALpF7qxDpy5783WXH4uIf41+tHGfosWpqtdlFiLbtCsWB4yd6TFDmir3YOCWMI6K1uqkZlfcPcN0UEWxCwTQDKm202OAMCIAACIAACbkmgeNdxaTVj10deNDtKrL8WnGrd+sVKjl6aRdh+FSUy5prB5BsZTIXfZ1LhD1kym5e/j2nR7Jb1r3nduL53TaSz3+6jYlFWc0OjVMB4we6kSeOkMqgvn9O1YnHt8+LDChu7XkYLi2C0qNfLz6d1VukCeWGzWXnjDLaUN3nuqgwqFYuIcyAWXq7Amptlm0pwwG4EbFnZMPfNbohRkJsT8BAhgZvdvI/oHgiAAAiAAAiAgIMJcDTHprr6NgFP9NXyTw4OPMKukuxyCelZBNjq9vRzf7TZ6T88+xtEnrRJBydAwETA0vcAVEAABEAABEAABEDgEgiwi2TrSJWti/Hw8JCWLihurcn0jH1bVjfV+47Oq3zYgkBPJgDlrSffffQdBEAABEAABEAABAwgYG2uW+tq1dy31sexDwIgYCYAt0kzC6RAAARAAARAAARAAAQcQKDg3HkqLCrWSn72989r6eee+ZWWjo6KpNiY3to+EiAAApYEELDEkgf2QAAEQAAEQAAEQAAE7EyAFTJbStmQQdajg9q5CSgOBNyCANwm3eI2ohMgAAIgAAIgAAIgAAIgAALuTgDKm7vfYfQPBEAABEAABEAABEAABEDALQjAbdItbiM6AQIgAAIg0CMJNDQRFVaKTxXRxRqiqjqxSFojkQjbT3yuSawGxCsC8RYCAs5K4IO9ztoytKunEuClTER0XOKtt7B1iWi65Cc+gb5EYf5E0YHiE2Q6ZzAjKG8GA0d1IAACIAACIHDZBHIvEmUXEhWUC+XssktDASAAAiAAAnoC8oWXGFzFezD5Mqy6vuWseFmmhJeqjA0h6h9NlBimjjp8C+XN4YhRAQiAAAiAAAjYiQBb2XbmEhVX26lAFAMCIAACIHBJBPjF2VnxAo0/kcISNyqBqJewxjlYoLw5GDCKBwEQAAEQAAG7ENh3lujQubZFRQSYfjDwj4cg4dLjLx7t7OLDrj5e4sNvh+WH/0BAwEkIfKVrx4Lhuh0kQcAJCEiXc9GORuF+zi7o7Ipe00BUKVzTi4Wb+gXxIq1E9xKNj32TTTQ4huiKWJPLpYO6AeXNQWBRLAiAAAiAAAjYhQD/iNh8iohdJZWwYpYuXHXSe4k5GD7qKLYgAAIgAAL2IMBz3Vi8xIswX/EhMc4qz8i+kfIUVQlXSnZfz7pgUvD4KL9gKxPzj8enmObLmXLa9a8Y/SEgAAIgAAIgAAJOSYCDjWw5Zam4xYcS3TiQaHg8FDenvGloFAiAQI8gwC/OhsWZxmMel5XkiBdt/MLNQQLlzUFgUSwIgAAIgAAIXDYBdpXkHwJK2CXnur5EAbC2KSTYggAIgEC3EuDxmMdlHp+VsKcEj98OEChvDoCKIkEABEAABEDgsgnwnIrD583F8A8DfssLAQEQAAEQcD4CPD4P6m1uF7tQcpApO4tHsxA7l4niQAAEQAAEQAAELpfA6qOmifFcDrvk8JvdLkpFRSUdyTxKx06cpPyzBVRcXELlFRVUWVVNdXV11FDfIObjN1GT+ODnQBfhIjsIgIBLEvAQ67d5enqKeE6e5O3jTb6+vhQYEEChIcEUFRlJCQlxNCA9jdLT+lFgoAgI1VX57gRRfpnpqkhx/fQBXS2h3fxQ3trFg5MgAAIgAAIg0A0E2OVm40lTxRychOe4ddJVkhWxHTv30Ko1a+nQ4UyxPjfe0XbDHUSVIAACLk7AUyh5gwdl0PSpk2js6JFS4etUlziQyfIj5iAm16TadR04KG+dugvIBAIgAAIgAAIGElh/3LR2EFfZBXfJQ0ey6M13FtOp0zkGNhZVgQAIgIB7E0juk0j33b2QhghlrlOyN9/s9h4nFvKe2K9Tl3UmE5S3zlBCHhAAARAAARAwigCvJ/TpASJlMJszuMOokuz6uHjJJ/TF8tVtWpmY1If6DxhICYlJFBkdRcHBIRQQEEi+fr4iCra3+HiRciNqczEOgAAIgICbEWAXcfZQaGxsFJ8Gqquto+rqKqqoKKeiCxcoN+cMHT+WTXli29qdfPas6bRowW3S5bJdLGx9+/yQKQuvOnDrUNP6m+1e1LmTUN46xwm5QAAEQAAEQMAYAjxXgudMsISL+RIz258vUSvmrv3lb6/Qrj37TNeIv35+/nTdlOtpwjUTKSw8XDuOBAiAAAiAQOcIlF0spU0b1tOGtd9QTY1Yu61FRo0YRj9//GHyE3Pl2pVVWeaFvK8VrpMJaqG4dq/q8CSUtw4RIQMIgAAIgAAIGEjgQAERf1gGiEW4RyWY0lb+ssXt+f/7u4XiNnjoMJp/1z0UGmqfHwpWqsUhEAABEOgxBMrLymjJ+2/TwX17tT6PHjmcfvnzx9q3wO3KMy3gzVcNjTV9tBIuPYGlAi6dHa4EARAAARAAAfsTKKs1lxnhb05bSb3/wScWitv0WbPpgUd/BsXNCiscAgEQAIFLIRASGkr/8fBPicdXJTt375Wu6mrf6lY/fuvHdauZO38QylvnWSEnCIAACIAACDieQFWduY4gP3O6VeqgiCT55QrzHDf+YTFz9pxWubALAiAAAiBgDwI8vk6bdaNWFM8x5iBRNkU/fuvHdZsXdO4ElLfOcUIuEAABEAABEDCGQJ0IWKLE31ulLLY82Z6jSioZMmw4FDcFA1sQAAEQcBCBWbPnErumK+FxmMdjq6Ifv/XjutXMnT8I5a3zrJATBEAABEAABBxPQP+Q9/GyWt/2nbvp9Jlcec7f35/mL7rHaj4cBAEQAAEQsC8BnlPMQaFYeFkWXlfTqujHb/24bjVz5w9Cees8K+QEARAAARAAAccTaNC9xfWx/phevWad1o5rJ19PPCcDAgIgAAIg4HgCHAyKo/kqWbVmrUpabr1147d+XLfM1eU9XaldvhYXgAAIgAAIgAAI2JtAk1rgTRTs2fYxXVVVTYfEfDcWXp/t6msnyjT+gAAIgAAIGEOAl2Hh8ZeFx2Mel9uIl278tuVa2eaijg/oSu04M3KAAAiAAAiAAAg4mIBYQFYT028DbZcTWdnHqKklT2KfZAoNwzpuFoCwAwIgAAIOJsDrZyYk9ZG18Hh89NjxtjXqx2/dsN42Y9eOQHnrGi/kBgEQAAEQAAHHErCwvOmf/qZqj2abfyT07Zfm2LagdBAAARAAAasE+qX1145nHT2mpbWEfviG8qZhQQIEQAAEQAAEehSB3Lx8rb9seYOAAAiAAAgYTyCxxfLGNeflnW3bgBa3SnlC71HRNmeXjsDy1iVcyAwCIAACIAAC3UugqKhEa0BUdLSWRgIEQAAEQMA4AlG9emmVFRUXa2lHJ6C8OZowygcBEAABEAABOxIoKy/XSgsJQZRJDQYSIAACIGAggeDgEK22svIKLe3oBJQ3RxNG+SAAAiAAAiBgRwLVNTVaaf7+AVoaCRAAARAAAeMIBAQEapVVVVuJNqmdtW8Cypt9eaI0EAABEAABEHAogbq6Oq18Xz9fLY0ECIAACICAcQT0429drXlcdnQLoLw5mjDKBwEQAAEQAAE7Emiob9BK8/b20dJIgAAIgAAIGEfAy8tbq6yhwTwuawcdlIDy5iCwKBYEQAAEQAAEHEGgUbfYq6eVRbwdUSfKBAEQAAEQsCTg5eWlHdCPy9pBByWgvDkILIoFARAAARAAAUcQaILy5gisKBMEQAAEukRA//JMPy53qZBLyAzl7RKg4RIQAAEQAAEQ6C4Czbr1gjz06wh1V4NQb48jUFxcRBvXr6XcnDM9ru/c4crKCtn/49lHe2T/0WkTAf34qx+XHc3H7Kzp6JpQPgiAAAiAAAiAAAiAgN0IbFz3LR3Yv69NeePGT6BRY65sc9xeB86dzadPP1xMN90yj/QLFevL/8ff/qLf1dI/efhR8vX10/ZdMVFWelH2/9rJ11O//umu2AW02YUJwPLmwjcPTQcBEAABEAABEOi5BAoKCijryCGqqqqihsYG7dPc3NTtULhdp0+d0Nqk2qczHHd7G9EAEHBFArC8ueJdQ5tBAARAAARAAARAoIXAXffdTzGxcTZ5lJeVUVHhBYqK7kUhoW0Xduf5OoUXzlNtbY0oJ15YxtouQVF28SKVlhRTbHwC6d3FbFYqTiT1SaHHnnzKZhZVb41YuzA2Lq6NRa6kpIgCA4PJz8+PysvLqPD8ednPGtHOsNAw8vI2/YytFsprdU01BQcHa2XU1tZK90b9MXZ3LBL9DA2LoPCICIt2VVdXUb0I9x4aHk7cLnYJDQ+PEHnDZL7KigrJKCY+njw8PSyuxQ4IGEkAypuRtFEXCIAACIAACIAACBhEgBWSxe+8Rfv37NJqvPKq8XT7orvJu0XxOX3yBL39+mtUVFQo8/j7+9O8BXfS6CuvkvuNjY308eJ36Yctm+S+j48vTbp+mlbepSayj2bS+2/+m0qEQsjiKSL3zbzxJrp++ixNOXz2108J18zbqLS0lNhFNDgkhKaK80s/XkL3P/AIXTFylLz2rX+9SpnC0nf99Bvoxrk3y2NrVi6nb1avoKd++6xQIpPpnX//k3bv3E5qblJ8QiLdesdCSksfIPOv/Xo1bdqwjh7/xa/p5Rf/QuVCWZ1/5z101YRr6KtlS2VZnJGDVEy/Yba8Bn9AoDsIQHnrDuqoEwRAAARAAARAAAQcTGDZpx9LxW3OrfNo6LARtHXLFqGELKdeMTE0dcYNwtJWS/965e/kKxSyBx97XChHobTskw+FwvcmJSWnSCvX9h+2SMWN57bNEMrVOeGquf7bry+r5WwJfP0ffycfYeHjeXO9e8fQ2m9W0/LPP6PIyChNceRKvv16lVS4Jk6ZSn3T+gsLXTyRUN6OZmVK5Y37kJ2dJaxkkZR5+ICmvGUeOSytjGpO3uArhtHwUaNEv1LpfMFZeuPVf9A60Q+lvHFdbMF76a9/pjih2M26cQ6lDxxERw4flIpbL9HGWTfNpcqKclq35vL6z3VBQOBSCUB5u1RyuA4EQAAEQAAEQAAEnIDA3//yvLQIqaY89NgTFNWrN20X1rLk1L7CUjZdnpo5+ybasnE97du9Sypve3btIFakbp53Bw0acoXMM2XaDPrnyy/Swf17pfK2Y+sP8vj8u+6VFqyhw4j8/P3okw/eV9XZ3J44nk3P/OpJ7XxiUjI98OjPaPvWLcSukmzBUm1LSk6m//r1L4RiuMZCeWN3xV8+/TuLwChRUdFCeTsiyz2aeZgaGxpo0tSp9NnHH8r+sFUx78wpGiWsh8rFc/TYcVo7WEFkxezQwf1SgWW3TCVp6Rl03wMPqV1a8cUymVYKMO+ER0TS66+8pOVBAgSMJADlzUjaqAsEQAAEQAAEQAAE7Eygf/8M8g8M1ErlNM9haxLRQfJzc+g/f/4z7VyNmBvGof5ZLpw7J7crv/qC1qxcIdNqvariIlOeYuFO6efnT/GJSfI8/4mLS9DS7SWCxBy0wUOHa1mie0XJ9PmWevulmSM1skLEc/LOC8ueXtjSpqxn6vjAwUNps1BCeR7e4YMHiK1iI0aOkcpbprCU+Yr2ct8HDRmqLqFt32+mXdu30QXBhee+1QmLHfe1ob5ezqlTGUeNtYzSWSzmCrKw1U9JnJj3BwGB7iIA5a27yKNeEAABEAABEAABELADgRnCotY6YMnZ6mpZch/hJnjtpMkWtXh5mX7+KavUhGsmUh9h+dILW+5YPMQcL+G3qD9F9fV1Fvu2dmJi4uiORXe1OR0QYFI061qVU99QTx5eloHQw8LC21yfMXiwVN5OnjguXCUPSSUtTAQgiRXBRNhdMlQEZeG+ZQwcLK9du2Y1fbH0YxqQMUi4Ps6hhIQ+9OWyT+nQgbbLLEREWNYn+8+l6BDU19W3aRMOgIBRBKC8GUUa9YAACIAACIAACICAQQTYGuUlgoAUFOTT0OEjZbp11XEJJgsSBzYZPmpM69NyP1pYwzhSZX7uGRk9kg9mZ2VZzdvZg8mpqTJrtpi31l+4KbJcOH+OykRgktS+aXK/vT/pGQNlgJPDwu2R2zZIWOJYBg4aSgf27aEIYcXrk5JKbPljYescy/y775Vz6hqFxS0n57Q81tEf7j8vxn3iWLbgOEJm52ArEBDoLgJQ3rqLPOoFARAAARAAARAAAQcR8PbxoSnTZtLXK7+iV178K10lFu4OCgqmvLxcGVJ/3PirafiIUbRaLDHAQUmam5pp2MiRVFdXK+aTZdF1k6ZId8RxV19NWWJe2Vv/eo0mT5suQu1foO83b7ysVg8cPEQGBVknLGKVlZUUExNLG0Q0SZYp02d0WLa/fwD1FUre7h3bydvHm/pnmBRAtsh9t3aNcKcspclTzeX0Ey6P2WKO3NbNmyi1Xz/asW0rVZSXd1gPZxgnok1uE3w+WvKeiMh5gaqFRfP7TRs6dS0ygYAjCFjaph1RA8oEARAAARAAARAAARAwnAAHBJk5ew7liOAd7775Or360gsieuNKzQrH66Q98vjPacCgwUJB2Uyv/v0FeuO1V4Sik6mtoTZy1FiaNvNGEa6/mD56/13aK4Kd3P/goxYBUrraMVa+Hvnpk9Sv/wDaJoKqfPrhYhHApJoW3n2fjIrZmfIGDR0i16VLSxugre3GaS9vL6GA1hEriErGTbiaMgYNoTWrlstgLM3C8nbnvfer0+1uWfG79fYFVFtVLefUbRGK2yJxrbLqtXsxToKAAwh4iPUudF68DqgBRYIACIAACIAACHSewAd7zXkXmIM9qIO3LrhPW6vqxdfe0KLpqfPYgoA1AhzcgxeXZusbr1XWWng9t4vCYsXz0QICAlqfJj5fVVVJIWI5AXsKR4qsEm6b9i7XWht5KQAfYZFkq2RXhYObsLVOLdrd1euR3/0IsAr1swd/LDvGcyw//eDNtp3sYDxve0HHR+A22TEj5AABEAABEAABpyHAP7z5hzQL/6DkeU0QEOiIQEdKB3+POIS+LeHzjlCw2PrniHKt9SNAF5HT2vn2jvH/u44Ytnc9zrkfARWZlXtm7YWIo3rc9tWLo2pCuSAAAiAAAiAAApdNwEtnNdH/eLjsglEACIAACIBApwmol2h8gX5c7nQBl5gRytslgsNlIAACIAACINAdBDhAg5IGEVodAgIgAAIgYDyBxsYGrVL9uKwddFACypuDwKJYEAABEAABEHAEAV9fX63YutrOrbelXYAECIAACICAXQjox1/9uGyXwtspBMpbO3BwCgRAAARAAAScjUBQoDmYBK/PBQEBEAABEDCegH78DfD3N6wBZt8Lw6q8/Iq2n9xDR8+daFPQsKTBNDQhg4oqSmjVwXXivAfdOOx6CgsIsci7bM9qCvYLpOsHXWNxvODiBco+f4JOF+VRdX01JYTHUZ/IeMqITSNvLxOqkspS+v7ELjpfVkiVdVUUHRRJydGJdGXKCIvJiicunKbvj+/Uyg/0DaCo4Ejq1yuZEiPitOOcOF2US5uyt1kc453YsN40ZeDV8viHO76ghhbzrI+XD4UGBIt29afU6KQ21+EACIAACICA+xIIaVl4mHtYUdG5tarclwZ6BgIgAALdQ0A//oaFWuoajmyRS1reCiuK6UThGaFg1VJjU6P2aW5ukqxqG+rk+ROFp2n1wfVt+OUU59HZi+ctjp8U5b2xZYlUohqbG4XCF0rHLpyitZmbNaXsyNlsem3je7TnzEEZmjk2tDcVVZbQN4c3ims/pOq6Gq3MitpK2YaymgoZ0vlceSFtPrad3hT5vty3RrZZZa6srZJ5S6ouan3hfuknop8szKGckrPy/LmyC7Tj1D56b+un9F3WD6oYbEEABEAABHoAgcjICK2XxYVFWhoJEAABEAAB4wgUFRZqlUVFRmppRydc0vKmoNw0fCr1DolWu222of7BlHXuOGUVHKcBsf3anFcH2Ir20Y4vKcg3kBZeOZd6hZhD5ZYL5cvTw5NqhaK44sBaobR50j0/ulWznvEaD98e2UQ/CGvcRmE9mzb4WlWs3F7VdxSN6GNaKLKqrppW7P+W9uYcovDAMLqm/5UWecf1HUljUtqu6aMyRQVF0N0/mid3WYF9bcN7tOX4DlmOkSFKVXuwBQEQAAEQMJ5AfFysVmlebo6WRgIEQAAEQMA4ArlnTmuVJSRYetVpJxyQcEnLW2c5TEgbS37evsKFcj3VtROR69DZo1TXWC9cFCdYKG5cT4hQAFn25x0hVr7GCuVK7/bIi/JNyhgv8gUJa9heqtdFnpEX6v6w6+RNw6cLl80gaeGrF3VeqkQLF0xuB1voquvNFr9LLQ/XgQAIgAAIuAaBtL6pWkOzs45oaSRAAARAAASMI3Di+DGtsvT+to1EWiY7JVxaeeN5ZYeFK6P66N0WmY+fjx9NHDCeymrKacNR2+6F+aUFEmd6jG3wbOliSbEyx8zL04uSIuKpSbhtllSVyny2/vh6+4h5an2k0qXKVHnZlVP1hbc8d8+WXCgvEm6U+dLyGCTm70GMJ7D08+XGV4oaQQAEejyBgRnpwiPEQ3LIzTlDF0vbf+70eGAAAAIgAAJ2JlB2sZSU5Y3H4wH90+xcg+3iXNptco2Ya6aXH4+fTwm+ZncSDvAxJmUY7cs9TFtP7qYrEgdSTGgv/SUyXSDmkPkLRY8VK1tysdo0KTxEWM2sCVvTWDhfe66cnEcFUCmtKqO4sBg+JIXdKfmjZHLGBBqfNkbtUrGYX/fuD5+KOsqEknhRzsu74Yop2nkkjCNwJPMoffDRUhokfkTxDykICIAACBhFIDg4iAYPyqADh0xWt80b19Os2XONqh71gAAIgECPJ7Bpw3oZ04JB8HgcqIsC7Gg4Lq28zR87h3gemBKe46aXZmqWgUVmDZ1M/978gZhvtpbuHX+7FoBE5Q3w8ZeBR9hyxvPbrImybtlyUVTHed5cR8LBTFhCW0XBvKb/OKlgqusDfVuFHRWavbew8vm0RL6cOWSShQunug5bxxP46NPPZSW8/d3Tv3R8hagBBEAABHQEZkydrClv3337DV193SQKDQ3T5UASBEAABEDAEQTKy8pow9pvtKKnT52kpY1IWNdUjKjZDnWwBSsyKFz7qHD+rYuOD4+RgUByS8/S7jMHpAKkzxMhgodw4BEOXGJLIgPD5SleTsCacARIFm5Pe8IRJHOK82WWaJ3iyQeC/AK0vnA5/kKp1Au3YYEIqHL3VfOIFc5vjmyU7pf6PEg7ngBb3dQbb97yPgQEQAAEjCQwZvQISkk2LRVTW1tDS95928jqURcIgAAI9FgCS95/m2pqTPEmkvsk0tjRIw1l4dLKW1dITRrwIxkohEP/tw4qMiR+gCyKw+7rw/Pryx8Un048t43dL1vPreP5aefFHLQBYs4cu1/aErbsrc/6Xlr5RiVfIefk2crb3vEAYZGbLIKr8Jw5a+vDtXctzl0+AWV1UyW13lfHsQUBEAABRxHgCMP33bVAK/7QgX208kuTR4B2EAkQAAEQAAG7EuBx9uC+vVqZ9929sI1Hn3bSQQmXdpvcdXq/DO+v2CRHJRJ/rAkHL+Ew/kt3r6QaEfaf13FTMkQs7L3j9D46KhbofvP7D2mgWPyaI0OWinllNQ21NEO4J7J1bny/MWI5gK30+qbFwr1xkIwwyUFGeN03P28/bUFtVS5vs8+fpHLhJlkm5sKdEevLscLF68NNEfPZWsux86csFENeToDn6VmTEUlDpBVx87EdNFgon/rlDazlxzH7ENBb3VSJyvqGuW+KCLYgAAJGEOB5FjfdMJ2+WL5aVrd6xZdyO3P2HCOqRx0gAAIg0KMIsOKmxlnu+OxZ02mIGIeNFpdW3nihar1cJ6xrtpQ3zsdKDgcEOS6iVOqFw/3fNe5WaRU7kJcpF+bm8zyHTh+B8roBVwklKVJErtwqLV48p46XIkiP6SsUvIlt5rBxGZkFx+TH5OIZQVemjqCRfYbKuXh8Xi+s6PFHSWpUkk3ljdvMc97+vXkJfbX/G7r3R7dbLVOVha19CNiysmHum334ohQQAIGuEVg4/zbKyy+gnbtNb4L5h0Vu7hmav+geCgk1v6TsWqnIDQIgAAIgoAiUlV2Uruns4aBk1IhhtGjBbWrX0K2HmOvVbGiNLlAZu0WySworZrZErq8m8gWL9d0gPYMAW92efu6PNjv7h2d/g8iTNungBAiAQKcJfGB2yaEFwzu8rLaujv7yt1do1x7zDwt/f3+6dvL1dPW14sViWHiHZSADCIAACICAJQFehoWj+XJQKJ5brGT0yOH05M8eIj9f23qCyktdHM+169pJQHlrBw5OgYCewO/+8L9aoBL9cZUeOnggIk8qGNiCAAhcOoFLeNg3imBY73/wCX25wuRCqSpnL43EPsnUt1+a3EZFR1NwcAgFBASSr58veYslcvhlJX84LwQEQAAE3J0A2604xgV/Ghrqqa62jqqrq6iiopyKC4soLzeHsrOOEK+j2VrYVZ09HrzEmNkpuYTxvKNyXdptsqPO4TwI2IuAtblurcvG3LfWRLAPAiBgFAH+IXH3ottp1Mhh9OY7i+n0mVxZNf9IyTl9Sn6MagvqAQEQAAF3I8DRfTk4yeCBpiCH3dk/WN66kz7qdhkCBefOU2FRsdbeZ3//vJZ+7plfaenoqEiKjemt7SMBAiAAAl0mcJlvavlt8vadu2n1mnV06HAmNWF2RJdvAS4AARAAAU/hjcCBoXhdTV6ehT0UuiyXOZ5bqw+WN2tUcAwEWhFghcyWUtYdkYZaNQ+7IAACIKAR4B8Y48aOlp+qqmrKyj5GR7OPU17eWSoqLqaLZeVULdYoqhNz5RrqG8R6oSb3IUyB1xAiAQIg4MYE2EWcx0n2WPD28SZfMXctKDCAQoKDKTIyguLjYimtb6qMYxAc7HyxLaC8ufGXE10DARAAARDo2QQCxQ+SEcOGyk/PJoHeOyOBpZ8vp1vm3OCMTUObQMBpCXS78lYr1lzj9c94vbSiymKxHloFVdfXiLXYaqi+QbwRbG4ULh9NxG8E5cdpUaJhPZXA75e/0FO7jn47GQEVboLfKHp6iLeKHl7k4+0t16HktStDA4IpOjiSEiPixSeOfLx8nKwHaA4IgEBPIcBzyT/4aCkNykhHpOaectPRT7sQ6Dbl7WjBcdopFsY+WXgG/vh2uZUoBARAoKcTUOu+sBuceO1F9dRANQ21VE6VbdCwL39qdB8anTLMYj3LNhlxAARAAAQcQECtm4p1Uh0AF0W6NQHDlbfcknxafXC9tLS5NVl0DgRAAAScmAAHsTh+4bT8xIX1pmmDr6OkyAQnbjGaBgIg4C4E9BGcEanZXe4q+mEUAUOVt/WZW2jLse2k3g5zJ9nNJya0FyVHJcpteGAYBfkFSDcfX7H+DLv9sPsPTy7EGjRGfS1QT0cEbll8r5blmRue0NJIgIAzEJDr1wh384amBqpvbCB2T6+sq6bSqovixdk5yinOp3NlF7SxmN3W3/n+YxqfNpauG/AjjLXOcBPRBhBwYwLK6qa6COubIoEtCHRMwBDlrbGpkT7bvZIyC45pLfIVcy3GpAynManDKcQ/WDuOBAiAAAiAwOURkHPeSETR8vImfzGtjcfYaFEkvyQbljRYFl5eU0E7T+2j7Sf3UF1jvVTkNouXa4UVxXTzyJkiCpfX5TUCV4MACICAFQJ6q5s6DeubIoEtCHRM4BIWLOi4UH0ODjLSWnFL651Cj0y6lyYNnADFTQ8LaRAAARAwiAArdBMzxsuxuH/vVK1WfsnGYzYEBEAABBxBoLXVTdVh67g6jy0IgICJgMOVN3aV1FvcJgi3nPlj51Kwn/Otm4AvBQiAAAj0NAI8Ft8xdg7x2KyEx2weuyEgAAIgYE8C1qxuqnxlfVP72IIACFgn4FDlLUcsAfD98R1azfzjgN/0QkAABEAABJyLAI/N4/uN0RrF85M5wBQEBEAABOxFoCPrWkfn7dUOlAMCrkzAocrb14e+0ybEs1sOFDdX/qqg7SAAAu5OgF3Z2a2dhQNLcWRgCAiAAAjYg0B7VjdVPqxvigS2IGCbgMMClhw9d1xbDoCDk9xwxfW2W2HjTGVVFWVmZtOxEycpL/8sFRWXUHl5BVVVV1NtbS01NDRSY2MjNYs1jTjsNQQEuoPALfPNkSe7o37U2fMI8BptHmIhbi8vL/L29iI/Pz8KDAigkBARmCQqkuLjYimtXyoNHJBOgYEBXQLEY/Ur69+WQUw4CiWvyZke269LZSAzCIAACLQmEBERTs898yvt8LO/f15L649zPggIgIBtAg5T3jiKmZKxqSMo2L9zc9w4wMnO3Xtp9Zp1tP/gYeKQ1xAQAAEQAAEzAfmySry44pdXdXVEVVXVVFJSas7QkmLlbsigDJoxdTKNHjW8U0sAcCATjgS8pcXlfefpfVDe2pDFARAAga4SiI3pTfyxJjxOQUAABDpHwCHKG68pdLLwjGwBr+M2OmVYp1qTeTSb3nh7MZ04ebpT+ZEJBEAABEDANgFW7vYdOCQ/qSnJ9OO7F9DAjHTbF7Sc4SVceL4y+zPwWF4vlhLwER4UENcjwB4s7K52/MQpeLC43u3rMS2GB0uPudVO0dH2vFeiIiMoIT6O0vqmUkZGfwoKDHSKNusb4RDlLUdMcldujL1DoztcDoCtax9+sow++2IFseVNLwmJSdR/QAbxNiq6FwWHhJC/v1jE299PuAx5S7chXryb1zWCgAAIgEBPIMBjJo+VrJw1NDRQnXAjr6mppvKyMiouKqTcnDOUnZVJ+Xm5Go6Tp07TM//9J5o7exbNnze33TGTrW8xob2oQCzkzWN5bslZSo3uo5WFhHMTkB4su/bSqjVriecQwYPFue8XWgcCIGAsgc56r7BuMXTwQJo+dRKNHjm83eemkT1wiPKWX1qg9SElKklLW0vU1dXTCy+/Rtt37NZO+/r60rWTptDV102i8IhI7TgSIAACIAACpD1A2C2Sx8tA+WYwgmLj4iWeK1sglZaW0Kbv1tGGdd9KBY9/1H/2xXLKzc+nJx97kHx8bFvTkiLjpfLGRXHUSShvLVCdfHMkK5vefAceLE5+m9A8EAABFyDAL77M3it9hPfKwk55rzi6aw5R3ooqS7R289tbW8JQWituAwcPpfl33iOUtghbl+E4CIAACIBAJwiEh0fQjXNuoWuum0xL3nuLDh88IK/il2UvvPRP+sXjD2uKYOvi4sJitEOFFcVaGgnnJMDP0yUff0bLvlzZxoMlJTGWhqQnU3JiDMVERVBYaBAF+PuSv58veYsXAF5enuTpIT6ePNEBAgIgAALuTaCpqVl4lTQJ75UmGfywRkwer66po9KyCjpfVEqncgro4NHTdDrvnAbi5KkzLd4rM+mOeTeTVzd6/DlEeSurrtA6Gx4YpqVbJ/hBo7e4XT99Jt0499bW2bAPAiAAAiBwGQTCwsPpwceeoK+WfUrfrF4pS9q2Y5d0V19w+y1WS9aP3fox3WpmHOxWAtY8WFgxm3HdGPEZS1HhId3aPlQOAiAAAs5EgF9UiXjN8uWVn6+PmNfmL5uXGBttauZVpk1RaTl9vWEHrVi/nWpq6+SLMZ7ilZuXT0889pDwfLHtveLI/jpkolh1fY3W5iA/62GqeQI1vyFUAsVNkcAWBEAABBxDgF+OTZk2UyucH0IcKMqa6Mfuqrpqa1lwzAkINLIHy0uvWrwIHTE4jV763SO0aM5kKG5OcI/QBBAAAdckwC++Ftw0SY6nI4f01zqxfece6TnYXfOJHaK81eiUNz9vP62zKsGdfeOdDzTXjkFDhsLipuBgCwIgAAIOJDD75lspY9AQWQPPgeMIv7xtLfqxu7ahtvVp7DsJgSUfLSX+IaHk5ukT6OlHF1AkrG0KCbYgAAIgcFkEeDz97SPzicdXJew5uOTjZWrX0K1DlLd6Ef1Mia93W5Pirt37iCOfsfiKxWXn33mvyo4tCIAACICAgwksuOteGeiEq+GlWXhtzdbiI6L5KtGP6eoYtt1PgD1YPv9qldYQ/mGxULwlhoAACIAACNifAI+vc6eN1wpe9uUK4iBRRotDlLfG5katH14eXlpaJTh8sRKOKsnzMSAgAAIgAALGEOCAUDz2Klm9Zp1KaltvT7Pyph/TtQxIdCsBkweL2WrKLj1Q3Lr1lqByEACBHkCA3dHZNZ2FvVY4uq817xVHonCI8sYRXJRwBCu9VFdXy3Vn1DFeDgACAiAAAiBgLAH92Lv/4GHixZz1oh+79WO6Pg/S3UeAraUc/YyFg5M8vOjG7msMagYBEACBHkTgoUU3yHGXuyy9V8S6mkaKpWZlp5r1E/haL5599NgJbcHQxKQ+xKGsISAAAiAAAsYS4DU0ExJN63DymJ2Zaen64eFhDhuvH9ONbSVqs0VAby2dNXEsRYQF28qK4yAAAiAAAnYkEBUeKqP5qiL1HoXqmCO3DlHe2mtw1tFj2unUfiazo3YACRAAARAAAcMIpKUP0Oo6duKkluaEXnmzOIGdbifAVtIDh45o7Zh27RgtjQQIgAAIgIDjCfAyLEp4PG7tvaLOOWLrEOWtbdwyc9N5bQQlfZJTVBJbEAABEAABgwmw94OSvPyzKtlm296Y3iYzDjicAFtJlTU0OSEGywE4nDgqAAEQAAFLAryMQEpirDzI4zEHkDJKHKK8tdf4ouIS7XRUdC8tjQQIgAAIgICxBPRjsH5sNrYVqK2rBPRW0iHpyV29HPlBAARAAATsQEA//h4/ccoOJXauCMOVt7Kycq1lwSEhWhoJEAABEAABYwnox+Dy8gpjK0dtl0xAbyVNSTK9+b3kwnAhCIAACIDAJRFITozRrtOPy9pBByUMV96qRLRJJf7+ASqJLQiAAAiAgMEE9GOwfmw2uBmorosE9FbSmCgE/eoiPmQHARAAAbsQ0I+/+nHZLoW3U4jhyltdXZ3WHD9/Py2NBAiAAAiAgLEEfP3MY3Btba2xlaO2Syagt5KGhQZdcjm4EARAAARA4NIJ6Mdf/bh86SV27krDlbeG+gatZV5e5kVgtYNIgAAIgAAIGELA29s8Bjc0NBpSJyq5fAJ6K2mAv+/lF4gSQAAEQAAEukxAP/7qx+UuF9TFCwxX3hpFRBYlXl5eKoktCIAACICAwQT063A2NkJ5Mxj/JVent5LyAt0QEAABEAAB4wn4+5rHX/247OiWGK68qfDG3DH9DwdHdxTlgwAIgAAIWBLQj8HNuhdrlrmw52wE9B4s3ngJ6my3B+0BARDoIQS8vc1GKCO9VwxX3pqbzSsGYRHYHvLtdrJuFhcX0cb1ayk354yTtcyY5lRWVsj+H882bk0SY3qGWrpKQK+8NenG5q6Wg/zGErD0YDH8MW5sZ1EbCIAACDgpAS9P8/hrpPeKecKDk4JBs9yXwMZ139KB/fvadHDc+Ak0asyVbY7b68C5s/n06YeL6aZb5pF+kWJ9+f/421/0u1r6Jw8/Sr6+5iAP2gkXSpSVXpT9v3by9dSvf7oLtRxNBQEQYAJ6Dxb9jwfQAQEQAAEQMI6A/gWokd4rZpXRuL6iJhCQBAoKCijryCGqqqqihsYG7dPcbJ4X2V2ouF2nT53Q2qTaB+NEd90R1AsCIKAIwINFkXDfbWNjE636bgftPpTtvp3sRM9yCy5IDmfPF3cid8/JUnChxOIlTs/puXP11NPTQ2uQkd4rsLxp2JHoLgJ33Xc/xcTG2ay+vKyMigovUFR0LwoJDW2Tj99CF144T7W1NaKceGEZM08gVZnLLl6k0pJiio1PoM666yb1SaHHnnxKFdFmq+qtqamh2Li4Nha5kpIiCgwMJj8Rjr28vIwKz5+X/awR7QwLDSOvlkh/1UJ5ra6ppuDgYK0MnvjK7o36Y7xfJPoZGhZB4RGWaztVV1dRfW0dhYaHywGdXULDwyNE3jDZ7sqKCskoJj6ePHSDTZtO4QAIgAAI9BACK9dvpx0H2rqPT7xqGF0zZmi3UqhvaKB/f7SKxg4bQCMH93dIWz5avoEyT+TIsj09PKhXZBjFx0TJvoeHBTukzq4Wmnk8V3J44sc3U1zvyK5e3un8327eTWu/30uD+vehO+dO6fR13ZFx7+Hj9PuXFtM9t06lGyeP644moM5uJgDlrZtvAKq3TYAVksXvvEX79+zSMl151Xi6fdHdpEKcnz55gt5+/TUqKiqUefz9/Wnegjtp9JVXyX32Qf548bv0w5ZNct/Hx5cmXT9NK+9SE9lHM+n9N/9NJUIhZPEUQQNm3ngTXT99lqYcPvvrp4Rr5m1UWlpK7CIaHBJCU8X5pR8vofsfeISuGDlKXvvWv16lTGHpu376DXTj3JvlsTUrl9M3q1fQU799lpL6JNM7//4n7d65ndQb9/iERLr1joWUlj5A5l/79WratGEdPf6LX9PLL/6FyoWyOv/Oe+iqCdfQV8uWyrI4I5v4p98wW16DPyAAAiDQkwnkFhTS/iMnqF9yHPnpXvo1NZnn5rszn1O5BbL/g9L6kHhwESsF3wgl5pOVG+m+26bRxKuGu3P3Lfr21dptdPZCEZ3KKaCbp0+goAB/i/PM5Oy5IvrpvXMtjr/+4Ury9fGmu2+ZanHcXjtLV2+iM3nn6Ykf36IVmZIQQ9OuHkVXZKRqx5DoWQSgvPWs++1SvV326cdScZtz6zwaOmwEbd2yRSghy6lXTAxNnXGDsLTV0r9e+bsYOH3pwcceF8pRKC375EOh8L1JSckp0sq1/YctUnHjuW0zhHJ1Trhqrv/268viwJbA1//xd/IRD3ueN9e7dwyt/WY1Lf/8M4qMjNIUR67k269XSYVr4pSp1Detv7DQxRMJ5e1oVqZU3rgP2dlZwkoWSZmHD2jKW+aRw9LKqObkDb5iGA0fNUr0K5XOF5ylN179B60T/VDKG9fFFryX/vpnihOK3awb51D6wEF05PBBqbj1Em2cddNcqqwop3VrLq//XBcEBEAABNyFwKN3zaE+8b3adKdGeDNUVFVTdEQYsRtjztnzwjoVTkGBlj/s1YUXyyrpXGGJtBCFBAeqw3JbL9a4zRM//vkFWoKwbnl5tZ21UlVdS3lCoWQLk4+v7Z9nxaXCk6O4jOJiIikkyFwPR7srKaugiNBg8YLTiwouFFOdqLdPfG+LtrTe+dWDt1NwUIA8fOxUPv31jU/plfe/otSkWEpJjLXIXnKxnC4UXbTaR87IHinnCkuFN0kNJcXHkI8uGh+fL6+sEkpQMUVFhMoPH2stF4ovUnlFlbi+N7FF0Jpw0J78c4XyviTERJOPUKCUVFbVUJ2wXDIHznfyTIG4h6Fky5p47FQesXsmW7G+WruVvt95mK6/eqQqTjJc/8Neiu0VSdw2FrZS8v3atOOgsIymyePsQhcVbvYOYva54jvjL7xvYnpFkH5+6sXyStk3/p5UVtfQOeEGmZwYY5GHvzPrf9gnOenrDRTfv7lCwQxu9T3kl7vni0qprLyKEuOiKcDfcn5+kfjeBIpjfLz0YgWViXvR0XdDg4CEUxEwf9udqlloTE8i8Pe/PG+xbMRDjz1BUb1603ZhLUtO7SssZdMljpmzb6ItG9fTvt27pPK2Z9cOYkXq5nl30KAhV8g8U6bNoH++/CId3L9XKm87tv4gj8+/615pwRo6jMhPDFyffPB+h4hPHM+mZ371pJYvMSmZHnj0Z7R96xZiV0m2YKm2JSUn03/9+hdCMVxjobyxu+Ivn/6dRWCUqKhoobwdkeUezTxMjeIhM2nqVPrs4w9lf9iqmHfmFI0S1kPl4jl6rNk1ghVEVswOHdwvFVh2y1SSlp5B9z3wkNqlFV8sk2mlAPNOeEQkvf7KS1oeJEAABEAABNoS2LLzkFRifnrPHHrz46+lIuctlK5hA/vRz+6bq1lnWGH6xztf0p7Dx7RCfjRqEP38/lvl/ppNu+jtT9dQbV293GdF6eFFN9KVwzO0/Ks37KA3Pl4tlB+T1e+2mdcIhcQchpwz8g/uF99eRvszT8rr+Pkwc+JYule4z3E65+wF+sX//Iv+85H5xC6hbEkbMSiNnn5sgVZPR4m0lHh6cOGN9NyL79GSr76j3zx0h7yElY0X31pG+4SlUsmM68ZIC50K2sDtevmdz6motFxmYVaPCXYTRg8Rypx42bpkJW3cfkBdTgNSkwTHORQTbZoGwMryC29+Rjv3m1xZmdMkK9a/A6Kev4m2lAruLCHBAfTInbNpzBUmT5TPvt5C677fQ8/+bBH9t3AvZKX6sbtvouvGiR8AVmT91n1Skbp52gTavi+Lvtu6V1PemPkv//S67BMrpQ/+9kVZwovPPkzP/OVtYkWRFTj+hIUG0ZvP/1ye53v+lvjOsBLJwgr7k+L7kCIUNBZuf21NPQ1OT6bPvt4sj/H1s8T9vGX61cS8f/nH16mwpIx4vp+q9+OXn6ZDR0/RH17+wMJt8vjps+L+fCZfEHBh/H2YPWUcLbxpsvai4ClR3kjxfagR38Mfdh+WdcZEh9P82ZPo6jFD5D7+uAYBKG+ucZ/cupX9+2eQf6D57SGneQ4bT/7Mz82h//z5z7T+14i5YRzqn+XCuXNyu/KrL2jNyhUyraKwFReZ8hQLd0o/P3+KT0yS5/lPXFyClm4vESTmoA0eanYbie4VJbOfb6m3X5o5UiMrRDwn77yw7OmFLW3KeqaODxw8lDYLJZTn4R0+eIDYKjZi5BipvGUKS5mvaC/3fdAQ85yLbd9vpl3bt9EFwYXnvtUJix33taG+Xs6pU2WPGmsZpbNYzBVkYaufkjgx7w8CAiAAAiBgIrDvyHFp8VI8hg5I0SxRfOyfH6yQP6qHCwvLN+JHOf9QZwXj2itNLw1fW7xcKm78A5hdDc+LH/m9o8JkcfxDm69PiutFN8+YQHV1DbRM/Fj/y78/pb8+/SAlxkYLq0+hmNe1msJCgmj+jddJK9IX33xP9fWNqkly++oHy+mgKO+hhTeIuVnJtHzdNlohPmz9NgxQAAA9PklEQVQ9mTJ+hJb3JaFABYopBAtumkQZ/czPPi1DBwl2x/P39aHTuaZnLGfnPrDS9MCCWTQkPUUqhxxQpY/o19RrRksF6fnXPpIWvztEH7jeoyfz6IoBfWVt7y1bKxW38aMG05QJI4VieYxWrd8hOTz/q/ulsvHltz9Irty3m6eNp6wTuaKPWy1ay0rN8//8SFpDHxcKNFvc/v3havrbG5/RS889QpEtlq8yYbl77sX3KTmhN024caJQklIsylE79cJauXnHIRoi7nloSCCNF0o3K3+sMLEFlK2sP//JrfSff36LBot23SvcSVnYkvfIXbPpj698SONGDqRbhcLlJaZPsBw5niN5sUVu4ZxJ0lLJ9+4F0ca/Pv2ApkxlncyRLwQeEop8mKj7vc++lS6rMydeSYHCbfOp/7iNfvX8GzSwXx/68e3TZdnWLLa1dXX0p1c/FEpZHd1+w7XUPyVBfje++OYHUW4w3XS9aRoJF8CKKrvJ/lKUXS2UOFYwP1mxEcqbpOs6f6C8uc69ctuWzhAWtdYBS85WV8v+9hFugtdOmmzRdy8v09dWWaUmXDOR+gjLl17YcsfiwWtwCEVIL/X1dfpdm+mYmDi6Y9Fdbc4HBJgUzbpW5dQ31JNHK1eYsLDwNtdnDB4slbeTJ44LV8lDUkkLEwFIYkUwEXaXDBVBWbhvGQMHy2vXrllNXyz9mAZkDBKuj3MoIaEPfbnsUzp0YF+bsiMiLOuT/edcOgT1LW9/21yMAyAAAiDQAwmwVUwvf/rlj6l/qvklF7vQLZxjeg7FCisRK2/b92VK5a1IWEZYkWMF6vH7THOW9WWt/G673H1w0Q2U0dekSAUJ74//E8rbKnHuJ3fMpE3CGsUub7cIVzhWbFjYQvPkH/4p0/yH3ea4ntFXpGt5Fok2rd2ym7buPmKhvNULBfGvf3hAuOv5atd3NcFujflCgeGXhGzh2rY3U7oHThVzrVgWzp1M336/m34Qx1l5+27bPmLL2YLpE6XliPMMHWCak8UK0jebd1FkWIiwPt3Cp+R8rfPC/ZItQIePnZGK0YZt++W5XwhliRXZEUL5YXdVZZnik98J5aO6pk7OS1Pl3zBpLL30zhe0V1gF9ZY6VkL1c8Vk4a3+MFN2jR0vrIMsvGXljeuZP3uiVA6VtYwVKnYlVcKKNwu7ruqPrxJWT5a7hUWU87Dr6b7MEzJqZp5w9dS7KrJFUH3X8oVb7btCgdt78BhdJZTI5BaX1YAAX4vyZeG6P1v3ZFKxcGdlJW3erGvlGRl45cn/peXCDVSvvLE77a8fvkOzGu8X1tkN4vvHdXOwGohrEIDy5hr3qce1kq1R/BaroCCfhg4fqb3R0oOISzA9XDmwyfBRY/SntHS0sIZxpMr83DPCbTJFHs/OytLOX0oiOdX0QMoW89b6CzdFlgvnz1GZCEyS2jetwyLTMwbKACeHhdsjt22QsMSxDBw0lA7s20MRworXJyWV2PLHwtY5lvl33yvn1LEPf07OaXmsoz/cf16M+8SxbMHR9GaWg61AQAAEQAAETAR+++h8imvxrOAjbFXRS58485wxVmrYHZDnFbHknzd5ebD7mzXJF/O72P2xX5947fSglrw8v42F58mx6K1kibGWc/D4xzXL/iMn6d6n/k+m+U+jcLNU86HUwTEiQqVecdu25wh9KX7EK5knXDKHDeqndq1u2RU0MixYTmlgJY7l4NHTlnU3NAmrUqk8x5YqFmsWLu4fu4MO5MAoOmFLFitvzGGgsNRxP9jaxYqbkqSEVhxaeHMkzrc+Mc3fbhCByVhUW9S1V481e6+oY623rKSx8HxGDkrC4uvjQ6xIsgVRvSSWJzr5R30n2K1SSV3LS1OeL6hX3vro+scvBlguirloXRH13WALnRIOwJPWJ4HYulctlOqAFkU+KjxEU9w4L8/FY7koLJVQ3iQKl/gD5c0lblPPa6S3GDynTJtJX6/8il558a90lVi4OygomPLycmX4/HHjr6bhI0bRarHEAAclaRYPhmEjRwqXlFoxnyyLrps0Rbojjrv6asoS88re+tdrNHnadBFq/wJ9v9k0QF8q1YGDh8igIOuERayyspJiYmJpw7pvZXFTps/osFh//wDqK5S83Tu2k7dw+eifYVIA2SL33do1wp2ylCZPNZfTT7g8Zos5cls3b6LUfv1ox7atVFFe3mE9nGGciDa5TfD5aMl7IiLnBaoWFs3vN23o1LXIBAIgAAI9gUC08FhoLwy9n5+PTQzqxz1biKxJYICftB6xgqGCd/AyACzKzU7NGdO7SNQJl3hVNudVgTvYpXNiq7lb/v6WFjZWMPXC86i5HUq8WgURUcfV9pRwl+RgHGnC/Y5FtYOVrck/Mk8l4HN+/i1shLcIS6OwsrWWoJa61Zw/dZ4DerB4ixe1XIeqR53nLbuZ6sXDQ3jTCGFrUrxO4eZjCcKFUy9s6WtPeC6cWkdvuYg2qRdWJA9mnaKhlxDRkVHw/WIXS58WV0pVdmqSac6b2tdHOVXHurpliyBLrfjO6EXNt9OvRaZX6vV5kXYtAlDeXOt+9ajWckAQfsis++Zrqbxw5wODguiWefMlB14n7ZHHfy6CN74vFJTNQikzKSW8ltvkqdNlnpGjxlJBXr6IBrmKPnr/XYoW7pT3P/govfzCn+X5S/nDytcjP32SFr/7Fm3bskk8XOpkZMiFd98no2J2psxBQ4fQMRFlkl0jfX1ND9W0tAGyv1weK4hKxk24mk6dPEFrVi2Xh0YIK+Od994vlw9QeWxtWfG79fYFcrkADojC68Dxtby8AgQEQAAEQODyCCilj+eiWROef5Qp5kBlCtdAdgNkOSQsWCw8D46Fg0awHDmWQ31bLHSHs89oS8PwucSWaJhs1WGXuq7IqKH9iT+dEZ5TxnP4WOZMuUpu2fWPFav884U2644TkRhZ2DrX2voWIZQotvgcPnZaumEqZfVwtomDKj8mKlwG3GClioN3sPCcQb2oqKCs1HWVg74cTm/ccUBaBGVQFTEXT8lJsVzAr//3DTk/jJU3T08vqYyxQq0XFeFSWdXUuT4iyuYJEeHSXyj9Y4eZXs6qc13ZsgLIipdScm1d2z/VZNXl7xUHh2Fh5ZuXguBgMH7iZTjEvQhAeXOv++lSvZm3YJFYk22RzTbzW8nps2bLDwf34MWl2fqmBn6+kAOF/MfDPxVvNhvporBY8Xy0gIAArUx+4HCIfFYEq6oqKSTE9Ebyb6/+W8tjLfH3f75p7bB2jJWgh376hIwUWSXcNlW5WgaRaK+MKdNmCcviLH12ERrah/768r8sjvEOR5d8+GdPyqUAfMQgzFZJllFjzMFJbphzM/HHmlwjrJATrpskrXVq0e4//uXv1rLiGAiAAAj0OAJrNu7UlAXuPLtADkqz7gbZGg6HhueokTwn7NkX3pXz4NgFj59TvNjzlAkjaJ0IM//yu1/KyJAc/n2ViCzpK14+zppkGsM5yMmnqzbRRys2UJWIyugnngUcrVAvHPb+ejEfjtdh+59/LJGRE9kieOLMWTGvqhddJYJmXKpweHwWDle/WwQS4QiKs4Xiplwr2Y2R57p9LTj9PxHlkKM2srWPlZz43lHEkTXZGvjJyg30uZgvxnPk+iXHS8Xr6rFD5CLjN13/I3pTuDn+9v/elvPzOGrl7oPZcq5bet9EWf/k8SPFnK9vRITI9yWb46fzabvgqhdmxXVwsBZmNXpIfxFqv1ZE4Dwh56jpXS7111lLcxh+dpEcJ+4fzwVTwnPQODrkVuFu+pP5M6XLIbt8svLJSwbwS2W+53zvOR9b73geJE9puE4EsZk77Udi/4AIpLJKKFDnZMARDtPPAVg44EtnhYOTcHAYnhPI3yFu45XCJba19E9JlEFIOMImW3jTxf6qDaZ1YedOHd86O/bdgIDhyhv/mFYLDfPWmpncDbiiC3YmoJQOW8WyosdKji3h89YULFv5O3ucrX+OKNda/QG6iJzWzrd3jH9IdMSwvetxzj0JqOis3DuMxe55j9GrjgmwMqUXnuvUWeWNr3tIBCNh179te4/IaJD8f4nDtLOwYsWh+9/+ZA19+NV6aelJEmtwPSDC8fNaYSy9hcXpyftuodeWrBB5vpMRDv9DKA2fr/lenld/7p03Tbo/fr1xF+0Sig9LuFDquP7LEVYceV4ez7lit0xW3Aa0BFdR5d4jgm/w+mC8pMHuQ8fk4XBhHVPKCEdqfOaxhfTq+8tNiqdQPnlNscktUTBZUWULEiufvIYczxu8csRA+g8RsEUJL3twVqxNx0rIP4Syy0FAfiGiInJYfCU8d+t3j99FvDg2t4WXRGDp2yfWYo00ld/WlhXP03nnhKVqsMX8QJX/GqGELflyvZyTx0FQ5giF7N2l30olnNs+QswZZIvWbSJACN/Xv4klDjhCJytvfM+f/ekiGUH0o+UmjyC2oKmlDFQdndnyvSgVlkjmwfUO++MTbS5jd1wOQvLKe1/K4DXrvt8r1oALkEtI8MsDiPsR8BAKVLO9u/X75S9oRT5zg+UXbd6i+6WVhDO88Mrrms+3dgESIAACIAAChhBgi/UTD/9E1sUvOD5+39Ii3d5YbkgDe2olH+w193yB5RwjPnHL/Hu180tf/S8tjUT3EuB5byVl5fKHs7W5RRw4gqMft148Wd9qDhQSLixdHb1M4YW6vUXkZV7jrKO8+vLtke6obl7Tja1i4SJMvbXQ9uwWyWu4WTvH7WPrJIe91y9Abq3dHMWSrXxclgrIYS2fPY/xIuVBQjHy1S0KzuWzZS00OEib16jqVAu9h/G5VteoPJ3Z2qq39bVs/SsXwXRsLUjeOj/2L5/ALQ/9t1bI0iVvaWkt0cF4ruXrQsJwyxuvMM8/GFh4yz8YICAAAiAAAsYTUGMx18xjM8Q1CPCPdfXelaP46QMSuEYP3LOVrIxER5isadZ62BkFg90jOyNqPbPO5LV3no7qZuW0PQVVzWez1S5Wcjqj6LDFSVkvbZVl7+M8f8+asAulNWEl3poiby1ve8ds1dv6Gh7Hobi1puK4fR5/lRj5EsXwpzVHPVLS0BJxSe1jCwIgAAIgYBwB/RjMkU8hrkFAP++3qdl6lEPX6AlaCQIgAAKuS0A//urHZUf3yHDlzVe3aGRdba2j+4fyQQAEQAAEbBDQj8G+Yl0giGsQ0FtJbYWod42eoJUgAAIg4LoE9OOvflx2dI8MV94CdZEAa2qqHd0/lA8CIAACIGCDgH4M1o/NNrLjsJMQ0FtJ1QLFTtI0NAMEQAAEegyBBt26hvpx2dEADFfeQkPN/sKdXWjY0RBQPgiAAAj0RAL6MVg/NvdEFq7UZz8/84LLHBABAgIgAAIgYDwBDqyjxEjvFcOVt6jICNVPKiq8oKWRAAEQAAEQMJaAfgzWj83GtgK1dZVAYIC/dkl1jfnHg3YQCRAAARAAAYcTqBZrDCox0nvFcOUtMSFe9ZPOnD6lpZEAARAAARAwloB+DNaPzca2ArV1lUBIiNmDhcOuQ0AABEAABIwncFEsy6DESO8Vw5W3Aelpqp908rhpoUftABIgAAIgAAKGEdCPwfqx2bAGoKJLIhAVYfZgOVdUckll4CIQAAEQAIHLI3C+qFQrwEjvFcOVt/T+/cSaNKZqc3POUGkpHjzanUcCBEAABAwiwGMvj8EsPCbz2AxxDQIJCXFaQ0/nntPSSIAACIAACBhH4PjpfK0yI71XDFfeAvz9aejggVpnN61fq6WRAAEQAAEQMIbApu/WaRXxmMxjM8Q1CPTrm6I19ODR01oaCRAAARAAAeMIZJ7I0Soz0nvFcOWNezlj2mStsxvWfUulJbC+aUCQAAEQAAEHE7hYWko89iqZMdU8Jqtj2DovgYEZ6ZoHy6ncAioqLXfexqJlIAACIOCGBIpKy+hkToHsmfReSetrWC+7RXkbPXI49U1Nlp2sE2E2l7z3tmEdRkUgAAIg0NMJLHnvLVILdKemJNPoUcN7OhKX6n9QYKCFB8uq77a7VPvRWBAAARBwdQJfb9ipdUF6r+jWsdZOOCjRLcqbh4cH/fiehcRbliOHDtBXyz51UBdRLAiAAAiAgCLAY+3hgwfkrhyL716gjcUqD7bOT0BvLV313Q4qhvXN+W8aWggCIOAWBHi8XbHe/NJs+tRJhvarW5Q37mFGen+6+aZZWme/Wb0SCpxGAwkQAAEQsD8BVtx4rFUyd/ZMYhc8iOsRYGup8mDhhbpfef8r1+sEWgwCIAACLkjg1cXLicddltSUPsQehUZKtylv3Mk7bptLY8eM1PrLPypee+kF4vkYEBAAARAAAfsQ4HnFr/79BQvFjcfe+fNutk8FKMVwAmw1ve9uswfLnkPHaPEX5iA0hjcIFYIACIBADyDA4+zug9mypybvlYXaHGSjut+tyhtP8Hvi0QctFDh25/n9f/2Gvvp8KZYRMOpbgHpAAATckkBpSbH0aPiDGFPZPV3JlWNG0ZOPPWj4A0fVj619CAwc0J/mzjZ7sHy2ejMUOPugRSkgAAIg0IYAK248zirpLu8Vb9WA7tr6+vrQU48/Qks+/ow++2KFbAZPpP9m1Qr5SUzqQ6n90qhPcgpFRfei4JAQ8vcPID9/P/Ly8hYfL/kDRM2f665+oF4QAAEQMIpAU1MTNTc3U2Njo/g0UG1NLdXUVFNFeTkVFV6gvNwcys7KlFt9m3icZHd19npQ623qzyPtegTmz5tLufn5tH3Hbtl4/mFxSqz99vCiGykiLNj1OoQWgwAIgICTEeA5buyazh4OSsaOHkF3dJP3SrcrbwyBf0QsvONWGjn8CnrjnQ/o5CnzujW8iKxaSFYBwxYEQAAEQKBrBHh+FAeK4vnGEPchoDxYXnjpVdq+c4/sGLv0PPrsyzRr4liadu0YigoPcZ8OoycgAAIgYBABXoaFo/lyUCg1x42r5mkH7DnoJfSX7hCnUN5Ux3ni/P/+v/+iXbv30ao1a+nAoSPEb5ghIAACIAACXSfAP+yvGDKIOBIWT6iGh0LXGbrCFezB8osnHqUlHy2lZV+aAtLwD42lwgrHn+SEGBqSnkwpSbEUExVBYaFBYlF2X/L38yVv4b3i5eUpf4Tg++EKdxttBAEQuFwC0nNF6BeNjU3UIDxYeLysrqmji2WVdK6ohE4L74WDR08LLwbTOm6qPh4j2VWdPR6603vFqZQ3hsMwxghTJH+qa2roaPZxyjp6jHLz8qmouITKysqpqrqaeH24hvoGahTwlQuRgostCBhBgP/z48eOEaRRR2sC/L3jsZLdxr29vcjPz48CxRozISHBFBUZQQnxcdSvb4qMJMlrgkHcnwC/AV40/zYaOeIKelN6sJzROn067xzxBwICIAACIHBpBNh7hYNE8Vzj7hanU970QAL8/WnY0MHyoz+ONAh0N4EjmUfp6ef+SH949jcItd7dNwP1g4ALESg4d55KSi867AfAoIwBwoPlWdq5ey+tXrMOHiwu9N1AU0EABJyLAL8k5QW4eV1NXp7FWV7YO7Xy5ly3EK0BATOBjz79XO7w9ndP/9J8AikQAAEQaIdAYVExPfv756U767xb5zhEieMfHGNHj5SfyqoqyszMpmMnTlJe/lnpwVJeXiE9WGpFcDB4sLRzs3AKBEDALQlY917xF94rIS7hvQLlzS2/luiUIwmw1Y3nY7Lwlvex0LEjiaNsEHA/AvsPHib+8JxERylxTI3dZkeNHCY/7kcRPXJlAvBgceW7h7Z3J4HuCZPSnT1G3SBwmQSU1U0V03pfHccWBEAABDoiwArc07/7H3ru//2ZjmSZFn7t6BqcBwF3IKCenWrrDn1CH0DACAKwvBlBGXW4DQG91U11CtY3RQJbdySwd/F+2a1bFt/rjt1zmj7pLXEPh4ykXtFRTtM2NAQE7E1A/yzFM9TedFGeuxOA5c3d7zD6Z1cCtt4Q2jpu18pRGAiAgNsTYCVu7fqNdFi4Y0NAwF0JtH5mtt53136jXyBgDwJQ3uxBEWX0CAL6N4WtO6zeHLY+jn0QAAEQ6AoBjmw2eeI1NEisewoBAXckYO1ZimeoO95p9MlRBOA26SiyKNftCHT0ZpDPI/Kk2932Ht+h4QuvkAyeueGJHs/CHgAOHs6U0SZbl8VK2+0cfZKVtg/2tj6NfRBwGwK2nqV4hrrNLUZHHEwAypuDAaN49yBg7U1h656pN4eIPNmaDPZBAARsEbBQ2mxlwnEQcBMC7T1L8Qx1k5uMbjicAJQ3hyNGBe5AICIinJ575ldaV3idJiX645wPAgIgAAIdEYDS1hEhnHdHArasbqqvsL4pEtiCgG0CUN5ss8EZENAIxMb0Jv5YkyGDMqwdxjEQAAEQaEMgOiqS/vDsb7A2ZBsyOODuBNqzuqm+w/qmSGALArYJQHmzzQZnQAAEQAAEQMCuBNp7EWTXilAYCDgZAXiwONkNQXNcloBTK2/VNTV0NPs4ZR09Rrl5+VRUXEJlZeXEx2tra6mhvoEam5qoSXyam5td9iag4a5N4Jb5WP/Kte+g67Xe08ODPDw9ycvLi7y9vcjPz48CAwIoJCSY2LITHxdLaf1SaeCAdAoMDHC9DqLFdiNQWVVFbPE4fuIU5eWflc/R8vIKqqquNj1HGxqpsbGRmvlZiueo3bijoK4R0E9F6NqVyA0CXSfQ3jM0KjKCEuLjKK1vKmVk9KegwMCuV+DgK5xOeWMlbOfuvbR6zTri9W5YMYOAAAiAAAiYCcgf2eIHN//orqsjqqqqppKSUnOGlhQrd+zWO2PqZBo9ajh5CKUP4v4E5HN0115atWYtsRsanqPuf8/RQxAAgc4T6Owz1FO8JOX5ydOnTqLRI4cT7zuDOJXylnk0m954ezGdOHnaGdigDSAAAiDg0gRYudt34JD8pKYk04/vXoC5Vi59Rztu/JGsbHrzHTxHOyaFHCAAAiDQPgF+8WV+hvYRz9CFTvEMdQrljeF8+Mky+uyLFW3cH1OTYimjbxL1S46n3lHhFBYaRAH+vuTv6yvdhby8PMnTQ3w88Ua5/a8gzoIACLgLgaamZuHi1iQsb03UINzeaoT5rbqmjkrLKuhC0UU6mXOWDh49RafzzmtdPnnqND3z33+iubNn0fx5c53mDaLWQCQuiwA/R5d8/Bkt+3Jlm+doSmIsDUlPpuTEGIqJijA/R/3Ec1RYZ/EcvSz0uBgEQMDFCLT3DD1fVEqncgrEM/S0eIae03p28tSZlmfoTLpj3s3k1Y1WuG5X3urq6umFl1+j7Tt2a4D8fH1o5sSxNOO6sRQVHqIdRwIEQAAEQIDkyyox403+8ObxMijQX2JJjI2W24lXDZPbotJyWr1hB61cv51qauvkj/rPvlhOufn59ORjD5KPjw9wugEBa89Rf6GYzbhuDJ6jbnB/0QUQAAH7EmCDT3vPULrKVB8/Q78Wz9AVFs/QFTIOxxOPPUS+4vnbHdKtzpv8prC14jZicBq99NwjtGjOZChu3fGNQJ0gAAJuQ4Bffi28aRK99LtHaKQYW5Xwy7IXXvon5kIpIC685aBdL7z0qsULUPkcFfccz1EXvrFoOgiAQLcT4GfoAvUMHdJfa8/2nXuk/sJ6THdItypv7OKht7jNnTaenn50gVDaQruDBeoEARAAAbckECkeQL8VYyuPsUq27dgl3dXVPrauSWDJR0uJf0gouXn6BPkc5XsOAQEQAAEQuHwC8hn6yHzi8VUJ6y9LPl6mdg3ddpvyxqGL2TdfCf+o4LeEEBAAARAAAccQ4DF27lSzAsfzjDlQFMQ1CfBz9POvVmmN5x8WbGmFgAAIgAAI2J8Aj6/6l6DLvlxBHCTKaOkW5Y3NjG+884E2qZrdeaC4GX3rUR8IgEBPJLBo7mQaPqif7DqHlOcIv1gn0/W+CabnqPnejRQuPVDcXO8+osUgAAKuRYD1FXZNZ+FnJ0f3NfoZ2i3K267d+4gjn7HwpOqHFt0o0/gDAiAAAiDgeAIP33kjcaATFl6ahdfWhLgWAb5nHP2MhZ+jD+M56lo3EK0FARBwWQIPLbpBjrvcAfkMFetqGindorzxwqFKOKokfPMVDWxBAARAwPEEeF4xj71KVq9Zp5LYuggB/T2bJe5lRFiwi7QczQQBEAAB1ybAz1CO5qtEr9eoY47cGq68VVdX04FDR7Q+Tb/W3HntIBIgAAIgAAIOJTBDN/buP3iYKquqHFofCrcfAb5X+ufoNN29tF8tKAkEQAAEQMAWAV7OTAmPx9U1NWrX4VvDlbejx05o4al5AW6s4+bwe4wKQAAEQKANgaiIUEpOiJHHef5UZqbxk67bNAoHOkWA75UKUc33EM/RTmFDJhAAARCwGwEed1mPYeHx+Gj2cbuV3VFBhitvWUePaW3K6JukpZEAARAAARAwlsCQ9GStwmMnTmppJJybgP5e6e+hc7carQMBEAAB9yKg12P0+o2je2m48pabl6/1qV9yvJZGAgRAAARAwFgCKS1vDbnWvPyzxlaO2i6ZgP5e6e/hJReIC0EABEAABLpMQK/H6PWbLhfUxQsMV96Kiku0JvaOCtfSSIAACIAACBhLICYqQqtQPzZrB5FwSgL6e6W/h07ZWDQKBEAABNyUgF6P0Y/Lju6u4cpbWVm51qewkEAtjQQIgAAIgICxBMJCg7QKy8srtDQSzk1Af6/099C5W43WgQAIgIB7EdCPv3r9xtG9NFx5qxLRJpUEBPipJLYgAAIgAAIGEwjw99Vq1I/N2kEknJKA/l7p76FTNhaNAgEQAAE3JaAff/XjsqO7a7jyVldXp/WJFxaFgAAIgAAIdA8Bf1/zGFxbW9s9jUCtXSagv1d4jnYZHy4AARAAAbsQ0D9D9fqNXQpvpxDDlbeG+gatOd5eXloaCRAAARAAAWMJeHubx+CGhkZjK0dtl0wAz9FLRocLQQAEQMBuBCyeoTr9xm4V2CjIcOWtUayFoMTLy/DqVdXYggAIgECPJ+DlaR6DGxuhvLnKFwLPUVe5U2gnCICAOxPQ6zH6cdnRfTY/uR1dU0v5amFR3tX/cDCoelQDAiAAAiDQQsBTp7w1616sAZBzE8Bz1LnvD1oHAiDQMwh4epjVKP247Ojem2t1dE0t5Tc3N2s1eXh4aGkkQOBSCGzccYC+27qvzaWncgvoq7VbaeueI1RTa55n2Sajix3gNzsFF4pdrNVorrMS8PQ0j8FNurHZWduLdpkI4DmKb4K9COAZai+SKKcnEtA/Q/XjsqNZeDu6ApQPArYI1An/4N0Hs2nn/qN0IucsJSfE0IC+iTRm2ACKCg+1dZnF8U9WbKS6unq6btww7fifX/+Etu4+Qr4+PsT/sd7888+1c9YSb37yNWWfzKNp146m6668wloWpzm2dNUm+mj5Bvqfp+4VrJKcpl1oCAiAAAiAgLEE8AztOm88Q7vODFc4HwEob853T3pMi15+5wvasusQxfaKoKS43nQg6xRt3H6ABqcnd1p5aw2rsrqGduzLotFXpP//9s4EPKoqy+MHslT2kBASSICELCyyaLMpi7SiKOLGIoJb02hri35q6zc9ozM66LQzfs7Y46czNtOfbas9CuoA4oKyKSiLzdoo+yZbEsgeslc2555bea9uVaUqVaFeVT3qf7+vePfdd9+79/1uuKdO3XPPod8+OJfafmoni1Di3KXaugZa881Oefnzr7Z3qry9tOQDGjkkh26ZepXDY55++S26eeqVdPW4EQ7l/jr59z9+REPzBtBt10/QHzl6eAFV19RTVkaaXoYMCIAACIBA+BGADPU85pChnvngqnkJQHkz79iZuueNwpRx256DlNM/g37/T7/W36W86gKlpSTr55zhukXnyigxIY44mr0nc9uDR09TW1s7ZWemU1VNHSXExzo8y/lk8879sv6t110lzSxPF5XIFUCtXmlFNe3Zd4z69+1DZZUXKEp4SO2VnEDHTxXTsVNFVFldK8tZQUxSgs6zEll0rpxSUxJd3qeiqobi4mIoVoTKqLpQS3UNjVJ51drkI3PY+cMRykhLkc9nj0YpSQnULyOVZt04iSxOYTbYU+C5sgr5Llmir1GKF0E2teR+9kqMp6ioSGF2WSVXJJklEgiAAAiAgPkIQIZChprvrxY99hcBKG/+Ionn+EQgUjhKsERHEccoYjthTSFTFTcuXy7MBD9a/Q21t9v2ShYMyqKnHpgjlTjnBleu3UoffLZRFq9Ys4X48+D8m2j6z8c5V9XPN/51L/VLT6Xbb5hIn3+9Xe6fWzDnBnn9wNFT9G9vLCPeC7Rq3Vb54fZnTptIr/55pazzl5XriT/jRg2hpxfNI1ai/rJyA63euF1v4/JhufSbhbN15e7xF/5AU8aPpEqhuLHJKKfMjN50z+1T6aqfDaNDx8/Qi/+9VL7zpxu+I/7kDuxL//HMQ8Srg8xDNZvctvsg/XHpaqkE8rNiBNcH5t1EUydewafEyuKiZ1+nu2+/lrjuqcISWZ6fk0kPzptBfEQCARAAARAwDwHIUMhQ8/y1oqf+JhBwhyX+fgE8z5wEeAVovNjbdvjEWakg8UqWc9qy64BQxjYJs8SR9NriRfTE/bPo9NkSWvLeZ85V5TmbLy6YPU3mb582gV75x4do4ujhndblwjPFpfTjmfM0acxwuao1vCBbmm3yyh0n3oO34A6bIjfj2vHyeY8vmEnD8gbSnTdPkXXm3fJzWb5wrq3e6o07pOLG5pT/9fyj9Ou7ZtD3h36kd1ask/W1f9Zt3k1WsaL49MPz6NH7bpMrcCvWbJaXB/TrQwvn3ijzN04ZK5//5P1ztFsdjmeKy+jVt1ZQfJyFHr77FvrN/bMpQ5ihvvG/n0olUK289JONYoWvDy1+4j66d+ZUuXq45lubyahaD3kQAAEQAIHQJgAZChka2n+h6J2RBLDyZiRdPNsjgYeEYsOKEu9723PguFy9unfWdcJE0baf6wuhCEVFRdD9QpFh80c2Xdy266A0J2xotFJcrMXh+X1Sk6XiwoWpvRJp0IC+DtedTzZ+Z/NSOWmsbc/apLHD5QrW3oMnaMzIAtlmvz6p8raUZMfn9ekwOUwTbartfLlpByUJ885fzLqe2NSRV9Q2bNtL24XXS/rlTL0LvDr2zCPzxepjtCzbvf+o8Ix5WJpL8uojrwZyShEmmurzZaHyz1qhfPHK4C+E0sqrdpzSUpLo2d+/I1YS/0rD8gfqtVkZZeWO06ihg+gr0a+d3x91WPnUKyMDAiAAAiAQ0gQgQyFDQ/oPFJ0zjACUN8PQ4sFdEYiNsdBTv5pDc26aLEwSt8lVLzYZfPnpB4QTk1QqLhV7uFrb6bHn39Af1WRtkXnei8b75bxJ7HCkrr5RVmUvltwm7wP7dscP0sRw+95DxJ/aOludjSL0ACtvvib2/MX74jho44PPvKrf3mi1UktLm3h+g9y3xxfSxV42TXHjc35fTjW1DS575OQFN/8Ul9rCBvBqoJbyc7IoOjKSis6Xa0XyODCzj8M576c7J+5n5S8CYTsc2OAEBEAABEKdAGSo7cdPHifI0FD/a0X//EkAyps/aeJZ3SLAK0JPLJxFrFy8t+prYicic2dMoZ5CoYgVq2sPzZ/h8lxeZfM2xQklUQueGBNjm+x5dY29NnJi00w1saMQVva6cnai3sN5jpjFe/d45ey+mdc5X5b7+7RC3u/nj6StPlpbbEotP7O9vU162YwQzlXUxPsLkUAABEAABC4tApCh3R9PyNDus8OdwSMA5S147MO6ZVamegqnJWoaKJQ4Ti1iBYvTQOExcr9wGsJ7uHIH9pNl3fmHFUPnpAX2fn3xI9Kjo3ad96K99dEa2iJMOaeL/WaRYm8eJ44lp6aoiI7yjr7yNd6DwOaOvJo1JK+/MN30Llad+lwtz14tOTU321ho5c7HguwsGdOOnaukT7A5KDl8olCaow4QZqZIIAACIAAClx4ByFDPYwoZ6pkPrpqbAJQ3c4+faXu/X7j0f1c48RgzokAqT2wGyStuHFSbPTdyuuOmq6Xy9p/CIce0yWMoV+xhKymvEq7uK+lesaesu6m+oYl2iFhw7Dkyq2N/nfasyWL/GzsXYeWOlbf87EyKFat1m3fu00MITBg9jEaIWHS8Mrhhyx7p7CRSKFtsaskrhq+9/TH9q/BSOe3qMcR75opLKqihyUpzpk/WmunymCfajRfhBHg/IL83pwljLnO5j520rBZeMt9Zvl4qjWxGw05TeAWQPWgigQAIgAAIXHoEIEM9jylkqGc+uGpuAlDezD1+pu19aq8EShZxx9YL5adG7AXjlCWce/ydCKzNShWnkcKpxt8/NJfeFa732R0/J3YCMm3yaJnv7j9bdu2XLv2v7nBUoj6HY7VdMSyPdu8/RoVizxg7T5l/yzW0av139Mqb/ye9NbLyxjHnZgtlbO3mXcSBQNkBCCtvHAKAVw6XCVPMN5d9IR/NJpIcm82XxPvmuN2PRfiDV/60XLLpTHnrLZyTPPf4vaKt1fTJ+m3UKhzA8F42dobiydGJL31BXRAAARAAgdAiABnqeTwgQz3zwVVzE+ghYmnZAmj58T1+97ndWcNztzzp8OQ5dy3Uz1cs+Wc9j0z4Eqi+UEcWsbrFQavdJQ563SRc6ycnxEsFzl09o8rZRKVK9JMDdEco5p7sLbO6tk6uvjmbgbKDkta2NuF9Ml46MelO3/R2RYBuFkaeEu97axFmlr7u1fP0TFy79AnMWfQv+kuuWPa2nueMp7ncoSJO/Etg6V778+62mUPbC4ggR1UayEOGuv8bgAx1zwZX/EPAkwyVLXQxn3enFwFfeWNTM/Zux4kDL7OZHFJ4E2CFqKsUHxtD/AlWYsWMV7mcEytU7MGys8Srcxeb3LXb2XMtUVHEHyQQ8JYAz8FaYlNbJHMQ4LHSfneFHDXHmBnZS8hQ93QhQ92zwZWLJ6DKUNZvApU8/5RvQC96KKsW7T+1G9ACHgkCIAACIOANAXUOdl459uZ+1AkOAXWs1DEMTm/QKgiAAAiEJwFe2dWSqt9oZUYdA668qe7L2eQMCQRAAARAIDgE1DlYNQcOTm/QqrcE1LFSx9Db+1EPBEAABEDg4glwzGAtqfqNVmbUMeDKGzuc0BLvB0ICARAAARAIDoHWVvscrIXFCE5P0KovBNSxghz1hRzqggAIgID/CDjIUEW/8V8LnT8p4MqbxWLRe8IOKJBAAARAAASCQ6Cp2T4HR0e7dxgUnN6hVXcE1LGCHHVHCeUgAAIgYCwBVYaq+o2xrRIFXHmLi43V36mxyf7FQS9EBgRAAARAICAE1DlYnZsD0jga6TaB+DjI0W7Dw40gAAIg4CcCwZKhAVfeEhPtngUv1NT7CR8eAwIgAAIg4CsBdQ5OSkr09XbUDxKBxET7WKljGKTuoFkQAAEQCEsC1TV1+nur+o1eaFDGEOXNk7PM3qkp+quUVFTpeWRAAARAAAQCS6C0olpvUJ2b9cKOjKc53bkuzo0noI4V5KjxvNECCIAACHRGoKzigl6szst6oUEZQ5Q3ta9aLBqtLCuzn5al04Uleh4ZEAABEACBwBI4cbpYb7B/Vqae54zz3O1wESeBI9ARF1VtEHJUpYE8CIAACASHwMmz5/SG1XlZL1Tnbz/GgTNEeVNj0Dh/AcjLzdHfad+RU3oeGRAAARAAgcASOPzjWb3BIYPz9Txn1LlbndMdKuHEGAI9lbVOexx1vS1Vju4/elovRwYEQAAEQCBwBNT5Nz93kGvD6vytTOuuFX0rMUZ562F/rHMA0WFDB5P2ReB0UQlVVNX41mPUBgEQAAEQuGgCFdW1dPLsefkcnpMHF+Q5PFOdu3sqc7pDJZwYQ0D9hVYV/h2tqXL0VOF54rFEAgEQAAEQCBwBnndZj+HEMnTo0ALXxtX5O9SVt4ge9lhubT/Z4wjxW8XHxdGoEZfpL/jlNzv1PDIgAAIgAAKBIbBGmXtHDh9GsTExDg23trfq5+qcrhciYxwBdeVNCQKrNchylMdMS19u2qFlcQQBEAABEAgAgbVOMpTnZZfUZg/iLTQ8l8vdLfDfk5QeREVG6mfNrS16XstMv2GqlqUvNu4Qvxpi9U0HggwIgAAIGEygUvxiyHOvlm664Totqx9b2uzKmzqn6xWQMY5ApCKaWxThr7SojtmXm3YSjykSCIAACICA8QR4vl2tyFBVr3FovVWZv9V53aGS7yeKhPD9Znd3WCLtgbitrVaXamNHX0G5g7JlubW5hZa897lLHRSAAAiAAAgYQ2DJe5+RFtx5UE42jR1zhUtD1hb73K3O6S4VUeB/AlGKaG5xtF7RGuMx0+Qoj+UfxJgigQAIgAAIGE9gyfufKzJ0ILFe02lS5+9ou1Vip3V9KFQkhA93dVE1LtoeQLTe2uhSu4ew53/gl/cQHzn97cBxem/VVy71UAACIAACIOBfAjzX7hFzLic5Fy+4W5+L1Zbqm+1ztzqnq3WQN4iAxW69Qk32FVC1NR67+xc4ytH3P/larYI8CIAACICAnwnwPLtn/zH5VJsMvUf35eHSlDp/h7rylhgTr/e/usEeA0EvFJmhgwto9u0360Ufr90KBU6ngQwIgAAI+J8AK24812pp1m0ziJ1fdJbUuTspNqGzKigzikBctP3J9fYVUHuhLTdsSAHNus0uR1eu2UJQ4Jwp4RwEQAAE/EOA51eeZ7XkSYbKOvXNWlUidV63l3Yrp/y81637O70pLaG3Xl5SU6bnnTPz586is0XFtGPnHnmJv1Rw7LdF995Kqb0SnavjHARAAARAoBsEeF8xm6ezlYOWxo8bTXfdOVs7dTmeu2CPw5mWkOpyHQUGEkiybz2gqiaPDd115ywqLLbLUf5icUrI0UeEHE1JhtLtER4uggAIgIAXBHiPG5umO8jQsT+j+R5kqHxsld2ChdR53Ys2PVWJeF4kTxW6c625tZn2Fx+Rt7a1t9GY7FGdPoaXG8ePGS0UuCIqKrYFujtXVknrt+yRtqRZfdMoLkYRYp0+BYUgAAIgAAKdEeBQLCvXbqHX315FhefL9SpXjhtDTz32MEUqzqX0ix2ZjYe3Up21QZ5NLriSUuKSnavg3CgCrWKf2+lq29Pbha/pgjS3LelytLBQyFFb6IdzpZW0bvNusoq9cJmQo27Z4QIIgAAIeCLA4QD4B7HX3xEy9Jx9MYp//HzysUXUpTOvvUK30UwnL0snSvSPTtNDBGJVoxB4egevr/FG91fWLaF28Wje1fbE9Q9SYoz7XwDbhSvkZR+tpJWfrHZpY9CAvjQ0dwDlZWdSeu9elJwYR7GxFoqxRFNkRARFRPSkCOF+kwUYEgiAAAiEA4F28YWe47C1CTfErW1t8seuxqZmulBTTyUVVdKCYd+RU3oMGo0Jz5Nsrs5WD1q8Te2aeqxtqqPXNrxJLBx6int+e+MjFB2pmPKplZH3PwHe5L58n4iU3vHomcOFyU2Ux3baWI5+uII+/vQLl3rZWRk0YnA25Qh5mtE7hZKT4kVoiGjIURdSKAABEAgHAqz68JzpSYZyAG6Oo6kmlqFsqs4WD55kqLynQXjbX3XAdjurKHeMJIryj9MSQ5Q37unS7SvpRNlp2enJ+ePp2qGTZN7TP4cOH6W33l1KJ0/Z7vNUF9dAAARAAAS8J8CeCdlRFO837irxqtuW47ZQAnl9sunuK92bV3b1LFzvJoGNJ4jOdbj/H55BdHk/rx508PAR+rOUo2e8qo9KIAACIAACXRNgGcpOonivsVfpe7HqdqBj+0E/sRXs2jyvbvOmkmHK29HzJ+jDXZ/KPkRHRNGjUxdSgiW+yz7xKtzuPd/Tl+u+on0HDhGfI4EACIAACPhOgH8ZHDXiMuIYNOzK2BsLhTprPb3x9dvU3GaL0Tlv3G00OMN/Qsf3twjTOwqFs69vT9penuMD3SqCcsd6Xn3TSLHc3LVnL61Z9zXkqAYFRxAAARDwkQDL0JHDhxHH1eTwLN7IUNlEo5Cfnx0i0uK8TRlE1N9/Ww8MU96483/a/D6du1Aq3yM/PYfuGj9L5r39p7GpiY4eO0FHjh6nQuHYpKKyimpqaqmhsZGam5uptaVVLnuyoDLA+tPbbqJemBJgiyZeCUcCgUATYAHCQiVCmI5HRkaQxWKhuNhYSkxMoN6pKZSV2Y/ycnOkJ8n4uDifuvfBjlV0rNSmNPRLTqdfXX2PT/ejsh8JrBF7xys7NrxnJhFdk+vzw+sbGujw4WN0/MeTcm85y9Ha2jopR61WK+Soz0Rxgz8JQI76kyae5S2BzmVojJChiRctQ2UfNv1IVFxj606qkMHTO/fq7G1/nesZqrwVVhXTO1s/1M32vTWfdO4kzkEg1Aiwie+zL7xELy5+xq2r9VDrM/oDAl0RUM0l+YeJBRPvpAGpWV3dhutGESivJ1p3zP50H8wn7TchBwKhSQByNDTHBb26SAKquSQ/apows+zTteWhL60aEqRb60D/lEyaJPa7aYn3UPCXAyQQMDuBD5evkq/w0YpPzP4q6D8ISAKq4sYFPHdDcQvyH0eaEPissGmJ90/wFwMkELgECECOXgKDiFdwJOCsuPH87WfFjRs0VHnjBthRydC++ZyViRU4NsupaxK/KCKBgAkJ8K+FvB+T0w/7DxKfI4GAWQnwHrdlOz7WHZTwe/Ccfc2QiWZ9pUur3+yoRN0rwQocm+TwngokEDApAchRkw4cut05AZ6PeV7WHJRwrQFij9uovp3Xv8hSQ+K8OfeJvwiU1VZQeV2lvFRZX017Tv9ALWJDPAd/tcAFtTMynIcwgTf+5y0qLbPHzCqvqKRrpkwK4R6jayDgSoDDAWw9toNW/W0NlXXMzVyL5+vZo2d07QbZ9ZEoMYrAgF5EF0Sw7hqrrYVacTxeYdsMnxTjN/fTRnUfzwUBZwKQo85EcG5KAhwOgBW2787Y5mjtJfgHt8k5HGtHK/Hr0dA9b2pP2aEIm+VsO7FT3wPH1/m10pPSKKf3AMpI6kO9RCDYeEusUOgsIq5QFEX0iBDv3hNfJFSYyAeNgGaj79wB7H1zJoLzYBJgJ04yDtxPbdTc2kLWVivVWxupuuECldSU0emKQnlkZwFa4rmYTSW9Ceui3YNjAAkIGSpNJg/anIA5tMwb4tPEh4/xIh5fTKRNoYsSxjXCsY0UtAZ9iXDoB05AwAsCkKNeQEKV4BMQ8VSlwiLiqUqvkRx/kwNu1zcLR1INRGXCgrCqw6GU2tsA7E0OmPKmvdfZyiJae2CT7oVSK8cRBMxA4PiGE1RX4mrym9g3gfKuyzXDK6CPIOBCgL1KTh9xLfE+ZaQQJ8BfGHYX2b48hHhX0T0Q6IzA89tW0D7xA5JzGpU2gBZPQExJZy44NwmB1Fiisf3FD2n+dU7S2dsHXHnTOnG05ATtOvU9nSw/I34hVn//1WrgCAKhRaCutJ6OrxeBc92k/Gl5lJBu/H9aN82jGAR8ItBThBsYlDaQxmZfToP7Io6bT/BCoTLHgTsqzLdLRCBviNBQGBH0wQsChyqK6Nlty93WfHHiHTSsd5bb67gAAiFFgE1W+ooA3AVpjnuTDe5k0JQ37b2sLVY6K0IKFFefp4p6EcetsU7sw26iJvFpaRVx3ITZD5v/aMG6IaM0cjgGmoC7VTetH1h900jgGCwCmnU9x4Bjc3M2O4+KjJRm6HHRsZQUK+LAxacSr7QNFCEALFGWYHUV7fqLAJvyVAgTnnLx4X1xbNLTLMq4nAPEStMfITn5iAQCQSbgbtVN6xZW3zQSOAadAJuaix855b61SGF+HhVBZBGfOGGaniz2GrOpem/x4fIAJ2EYH9zEXx7y0wfJT3B7gtZBwD0BaaP//kvuK4grtefr6I78mxH3zSMlXAQBEPArAf7iwL/88gcJBEKYgPQw+ZmruaTa5R/Kz9Kh0XGQoyoU5EHAiUDQV96c+oNTEAhJAudLSom9Smpp8e9e1rL0wnP/oOfTeqdS34x0/RwZEAABEAABEAABIshR/BWAgH8IBH3lzT+vgaeAgLEEWCFzp5SNuGyosY3j6SAAAiAAAiBgcgKQoyYfQHQ/ZAgII04kEAABEAABEAABEAABEAABEACBUCcA5S3URwj9AwEQAAEQAAEQAAEQAAEQAAFBAMob/gxAAARAAARAAARAAARAAARAwAQEoLyZYJDQRRAAARAAARAAARAAARAAARCA8oa/ARAAARAAARAAARAAARAAARAwAQEobyYYJHQRBEAABEAABEAABEAABEAABKC84W8ABEAABEAABEAABEAABEAABExAAMqbCQYJXQQBEAABEAABEAABEAABEAABKG/4GwABEAABEAABEAABEAABEAABExCA8maCQUIXQQAEQAAEQAAEQAAEQAAEQADKG/4GQAAEQAAEQAAEQAAEQAAEQMAEBHr8JJIJ+okuggAIgAAIgAAIgAAIgAAIgEBYE8DKW1gPP14eBEAABEAABEAABEAABEDALASgvJllpNBPEAABEAABEAABEAABEACBsCYA5S2shx8vDwIgAAIgAAIgAAIgAAIgYBYCUN7MMlLoJwiAAAiAAAiAAAiAAAiAQFgTgPIW1sOPlwcBEAABEAABEAABEAABEDALAShvZhkp9BMEQAAEQAAEQAAEQAAEQCCsCUB5C+vhx8uDAAiAAAiAAAiAAAiAAAiYhQCUN7OMFPoJAiAAAiAAAiAAAiAAAiAQ1gSgvIX18OPlQQAEQAAEQAAEQAAEQAAEzEIAyptZRgr9BAEQAAEQAAEQAAEQAAEQCGsCUN7Cevjx8iAAAiAAAiAAAiAAAiAAAmYhAOXNLCOFfoIACIAACIAACIAACIAACIQ1AShvYT38eHkQAAEQAAEQAAEQAAEQAAGzEIDyZpaRQj9BAARAAARAAARAAARAAATCmgCUt7Aefrw8CIAACIAACIAACIAACICAWQj8P13QZpfKgqvLAAAAAElFTkSuQmCC">
<center>Figure2: Different types of layers in encoder and decoder component of a <a href="https://jalammar.github.io/illustrated-transformer/">transformer</a></center>
To get a more detailed explanation on **different forms of attention** visit [this](https://towardsdatascience.com/attention-and-its-different-forms-7fc3674d14dc) page. Also there is a great blog post on [Visualizing attention in machine translation model](https://jalammar.github.io/visualizing-neural-machine-translation-mechanics-of-seq2seq-models-with-attention/) that can help in understanding the attention mechanism in a better way.
An **“annotated”** [[3]](#References) version of the paper is also present in the form of a line-by-line implementation of the transformer architecture.
# Prerequisites
- Inferencing workflows for pretrained text models of `arcgis.learn.text` submodule is based on [Hugging Face Transformers](https://huggingface.co/transformers/v3.0.2/index.html) library.
- Refer to the section [Install deep learning dependencies of arcgis.learn module](https://developers.arcgis.com/python/guide/install-and-set-up/#Install-deep-learning-dependencies) for detailed explanation about deep learning dependencies.
- **Choosing a pretrained model**: Depending on the task and the language of the input text, user might need to choose an appropriate transformer backbone to generate desired inference. This [link](https://huggingface.co/models) lists out all the pretrained models offered by [Hugging Face Transformers](https://huggingface.co/transformers/v3.0.2/index.html) library.
# Inference only models
The `arcgis.learn.text` submodule offers the following models pretrained on unstructured text:
- **ZeroShotClassifier**
- **QuestionAnswering**
- **TextSummarizer**
- **TextTranslator**
- **TextGenerator**
- **FillMask**
These models can be imported using the below command
```
from arcgis.learn.text import ZeroShotClassifier, QuestionAnswering, TextSummarizer, \
TextTranslator, TextGenerator, FillMask
```
## ZeroShotClassifier
[Zero-shot learning](https://towardsdatascience.com/applications-of-zero-shot-learning-f65bb232963f) is a specific area of machine learning where we want the model to classify data based on very few or even no training example. In **Zero-shot learning** the classes covered in the training data and the classes we wish to classify are completely different.
The **ZeroShotClassifier** model of `arcgis.learn.text` submodule **classifies an input sequence from a list of candidate labels**. The transformer model is trained on the task of **Natural Language Inference (NLI)**, which takes in two sequences and determines whether they contradict each other, entail each other, or neither.
The model assumes by default that only one of the candidate labels is true, and returns a list of scores for each label which add up to 1. Visit [this link](https://huggingface.co/models?search=nli) to learn more about the available models for **zero-shot-classification** task. To get a list of supported transformer backbones for this model use the below command.
```
print(ZeroShotClassifier.supported_backbones)
```
The command below creates a model object by calling the `ZeroShotClassifier` class.
```
classifier = ZeroShotClassifier()
```
A sample code for performing **single-label classification** task.
```
sequence = "Who are you voting for in 2020?"
candidate_labels = ["politics", "public health", "economics"]
classifier.predict(sequence, candidate_labels)
```
For **multi-label classification**, we simply need to pass `multi_class=True` in the `predict()` method of the model. The resulting per label scores for multi-label classification are independent probabilities and fall in the (0, 1) range.
```
sequence_list = [
"TAKE THIS MAP DOWN! YOU DO NOT OWN THIS MAP PROJECT OR DATA!",
"This imagery was great but is not available now"
]
candidate_labels = ["toxic", "severe_toxic", "threat", "insult", "identity_hate"]
from pprint import pprint
pprint(classifier.predict(sequence_list, candidate_labels, multi_class=True))
```
The **ZeroShotClassifier** model has been fine-tuned on [XNLI](https://cims.nyu.edu/~sbowman/xnli/) corpus which includes 15 languages: Arabic, Bulgarian, Chinese, English, French, German, Greek, Hindi, Russian, Spanish, Swahili, Thai, Turkish, Urdu, and Vietnamese. So this model can be used to classify **multi-lingual** text as well.
Below example shows how this model can be used to classify an input sequence written in Spanish language.
```
# Classification on spanish data
sequence = "¿A quién vas a votar en 2020?" # translation: "Who are you voting for in 2020?"
candidate_labels = ["Europa", "salud pública", "política"] # ["Europe", "public health", "politics"]
classifier.predict(sequence, candidate_labels)
```
This model can be used with any combination of languages. For example, we can classify a Russian sentence with English candidate labels:
```
# Russian with english candidate labels
sequence = "За кого вы голосуете в 2020 году?" # translation: "Who are you voting for in 2020?"
candidate_labels = ["economics", "public health", "politics"]
classifier.predict(sequence, candidate_labels)
```
## QuestionAnswering
**QuestionAnswering** model can be used to extract the answers for an input question from a given context. The model has been fine-tuned on a question answering task like [SQuAD](https://rajpurkar.github.io/SQuAD-explorer/). SQuAD belongs to a subdivision of **question-answering** system known as [extractive question-answering](https://medium.com/deepset-ai/going-beyond-squad-part-1-question-answering-in-different-languages-8eac6cf56f21#:~:text=SQuAD%20belongs%20to%20a%20subdivision,referred%20to%20as%20reading%20comprehension.&text=When%20an%20extractive%20QA%20system,the%20question%20(see%20diagram).), also referred to as reading comprehension. Its training data is formed from triples of question, passage and answer. When an **extractive question-answering** system is presented a question and a passage, it is tasked with returning the string sequence from the passage which answers the question.
Visit [this](https://huggingface.co/models?filter=question-answering) link to learn more about the available models for **question-answering** task. To get a list of supported transformer backbones for this model use the below command.
```
print(QuestionAnswering.supported_backbones)
```
Use the below command to instantiate a model object.
```
model = QuestionAnswering()
```
A sample code to **extract answers** from a given context for a list of questions.
```
context = r"""
The arcgis.learn module includes PointCNN model to efficiently classify and segment points from a point cloud dataset.
Point cloud datasets are typically collected using Lidar sensors ( light detection and ranging ) – an optical
remote-sensing technique that uses laser light to densely sample the surface of the earth, producing highly
accurate x, y, and z measurements. These Lidar sensor produced points, once post-processed and spatially
organized are referred to as a 'Point cloud' and are typically collected using terrestrial (both mobile or static)
and airborne Lidar.
"""
question_list = ["What is PointCNN?", "How is Point cloud dataset collected?", "What is Lidar?"]
model.get_answer(question_list, context=context)
```
## TextSummarizer
Text summarization [[4]](#References) refers to a technique of shortening long pieces of text. The intent is to create a coherent and concise sequence of text keeping only the main points outlined in the input sentence or paragraph. It's a common problem in **Natural Language Processing (NLP)** domain. Machine learning models are usually trained on documents to distill the useful information before outputting the required summarized texts.
The **TextSummarizer** model can be used generate summary for a given text. These models have been fine-tuned on **summarization** task. Visit [this link](https://huggingface.co/models?filter=summarization) to learn more about the available models for **summarization** task. To get a list of supported transformer backbones for this model use the below command.
```
print(TextSummarizer.supported_backbones)
```
Sample code to instantiate the model object and summarize a given text.
```
summarizer = TextSummarizer()
summary_text = """
This deep learning model is used to extract building footprints from high resolution (30-50 cm) satellite imagery.
Building footprint layers are useful in preparing base maps and analysis workflows for urban planning and development,
insurance, taxation, change detection, infrastructure planning and a variety of other applications.
Digitizing building footprints from imagery is a time consuming task and is commonly done by digitizing features
manually. Deep learning models have a high capacity to learn these complex workflow semantics and can produce
superior results. Use this deep learning model to automate this process and reduce the time and effort required
for acquiring building footprints.
"""
summarizer.summarize(summary_text, max_length=100)
```
## TextTranslator
Machine translation is a sub-field of computational linguistics that deals with the problem of translating an input text or speech from one language to another. The **TextTranslator** model is a class of inference only models that are fine-tuned on a translation task. Visit [this](https://jalammar.github.io/visualizing-neural-machine-translation-mechanics-of-seq2seq-models-with-attention/) link to get a more detailed explanation on how machine translation model works. These models uses technique called **Attention**, which highly improves the quality of machine translation systems. **Attention** allows the model to focus on the relevant parts of the input sequence as needed.
<img src="data:image/jpeg;base64,/9j/4AAQSkZJRgABAQEAeAB4AAD/4QCCRXhpZgAATU0AKgAAAAgAAYdpAAQAAAABAAAAGgAAAAAABJADAAIAAAAUAAAAUJAEAAIAAAAUAAAAZJKRAAIAAAADMzEAAJKSAAIAAAADMzEAAAAAAAAyMDIwOjEyOjAzIDE1OjM1OjIwADIwMjA6MTI6MDMgMTU6MzU6MjAAAAD/4QGgaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLwA8P3hwYWNrZXQgYmVnaW49J++7vycgaWQ9J1c1TTBNcENlaGlIenJlU3pOVGN6a2M5ZCc/Pg0KPHg6eG1wbWV0YSB4bWxuczp4PSJhZG9iZTpuczptZXRhLyI+PHJkZjpSREYgeG1sbnM6cmRmPSJodHRwOi8vd3d3LnczLm9yZy8xOTk5LzAyLzIyLXJkZi1zeW50YXgtbnMjIj48cmRmOkRlc2NyaXB0aW9uIHJkZjphYm91dD0idXVpZDpmYWY1YmRkNS1iYTNkLTExZGEtYWQzMS1kMzNkNzUxODJmMWIiIHhtbG5zOnhtcD0iaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLyI+PHhtcDpDcmVhdGVEYXRlPjIwMjAtMTItMDNUMTU6MzU6MjAuMzEwPC94bXA6Q3JlYXRlRGF0ZT48L3JkZjpEZXNjcmlwdGlvbj48L3JkZjpSREY+PC94OnhtcG1ldGE+DQo8P3hwYWNrZXQgZW5kPSd3Jz8+/9sAQwAGBAUGBQQGBgUGBwcGCAoQCgoJCQoUDg8MEBcUGBgXFBYWGh0lHxobIxwWFiAsICMmJykqKRkfLTAtKDAlKCko/9sAQwEHBwcKCAoTCgoTKBoWGigoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgo/8AAEQgB8QH2AwEiAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A+qaKKa2SwAJH0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU3af77fpRtP99v0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU3af77fpRtP99v0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU3af77fpRtP99v0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU3af77fpRtP99v0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU3af77fpRtP99v0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU3af77fpRtP99v0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU3af77fpRtP99v0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU3af77fpRtP99v0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU3af77fpRtP99v0oAdRTdp/vt+lG0/32/SgB1FN2n++36UbT/fb9KAHUU1M5YE5wadQAUUUUAFNb/WL9DTqa3+sX6GgB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUE4oqK6hS4t5IZQTHIpRgDjIIweaAKthqdvf3V9BbsxezlEMuRjDbQ3Hrwwpmh6va6zDcS2TMyQXEtq+5cYeNirD6ZB5rxK88IeGLbXtVstC8Ha9rJgmAuJotReONJCo+QEyAscYzXrfw/to7LwxbW0GiSaHFGXC2cjh2XLEliwJySSTnNAHSUUUUAFFFFABRRRQAUUUUAFFFFABRRmkzQAtFAooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAav3n+v9KdTV+8/1/pTqACiiigAprf6xfoadTW/1i/Q0AOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDyHXGOnfEa6tdK8bHTb3VpI86emnrOqybMAsx+6SB3IzXoHgueSfRv3+rrq80U0sMlwIBD8yuVKlR0IIxXn3i7QvE+neJXvNE0i21a0n1OLUtxukgkjZU2lG34yvGQQePSu3+HujXejaNcf2m0R1C+vJr64WE5SN5HLbFPcAYGe9AHUUUUUAFFFFABRRRQAV538TNTuodd0HS/+EgHh7Tr3zjNeL5YdnUDbGC+QoOTzjtivRK86+LOrwWP2W2Xw9Y63feRPdqt7gRxRRAFznaTk5AAAoA0fAtnFbX1wYvGlz4hJjAMMs8Mgj5+9iMA+1dpXmPw2vLmPxNPYah4a0LRpJbBLyCXTnLGeNjg5+RcbTjIPqK9OoA434hPfWU2h6taWl1e2un3TSXdta8yNGyMoYLn5tpIOKzNH1mfxZ400y+0ux1W00qwt51uJb23e3Ervs2oqNgnG0nOKteOls9JsHl1LxJr9kLu6zClid8pbb/qo0VGJXjOMfjWb8P7q2m1/bDqvjW6byWPl6xbPHB1HOTGvzenPrQB6aOlFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADV+8/wBf6U6mr95/r/SnUAFFFFABTW/1i/Q06mt/rF+hoAdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBopDQB4brC+GZ/iB4ki8TaFqHiOeOSMxyW9s9wlumxf3RA4U9+Oua9Q8AxaVF4eiXQdKn0qyDtttpoDCynPJ2nnk1xGrnXNE8eX8GieJvDNodXlWWLTr2F3lL7AC3ysDzt+nFd/wCD7i/udIDateafeXayujy2ClYsq2CuCScggg89RQBt0UUUAFFFFABRRRQAVwvxF1DS9OvbGS40u51XVmguEgtoGCkwlR5pYkhQuMde+K7qvOvi/b2sNvZar/b0Gi6jCstvDJNCZ1mSRfnj8tfmPQHI5GKAIPh1YaLpviKH7K2qTX15pEdzbve3BlENsW/1SemCRn145r0yvKvgzb211M+oTeIrfWdRtbOPT0igt2txawL0BR/nyxGSx649q9VoA8/+KhvxdeGBoa266w2oEW1xck+TF+7bfvA5OVyABg5rW8Or4vXUM+IJtBey2HiyjlWTdxj7xIx1rM+LsOk3Oj2Nrq+m32qzzXSizs7KYxSSSgE53ZGABkkk8VhfDu2sdL8WJa3mia1o2qS27vbi81N7uGdARuCncQGGR1H0oA9aooHSigAooooAKKKKACkJA6kClrifil4Yg1zw7e3SwXM+p2lrK1okNzJHl8ZAwrDPPrQB2u4eo/Olr5un07wX/wAI/py+HNT1m78ULJAY7U3dwZXk3LuWVCcKOua+j4siNNwwcDIoAdRRRQAVFdXEVtC0txKkUajJd2CgfialqpqljaajZS22o2sN3ayL88MyB0Ye4PBoAxNN8a6NfaKdRF9axIPMPlvOgb5GI9e+M1r6DqSaxo1lqMUbxx3USzKj9QCMjNeKxwaNJYaJaeF/BnhV9Wvmurgi9tldIIYZCCWIG7cSQB2B9hXsXhHU01nw1p2oxQiBLiBXES9E45A9hQBr0UUUAFFFFABRRRQAVzvjbxbp3g/T7e81YyeVPcJbKI13HLd/oBkk10VcDr+hy+J/HUkWoQONGsdMkijLrhZZ58qxB77UUf8AfdAHeowdQynIIyDS1zPw5bUB4SsrbWYpI7+zDWshcY8zyyVDj2IAP4101ADV+8/1/pTqav3n+v8ASnUAFFFFABTW/wBYv0NOprf6xfoaAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFZJ8SaMNcGj/wBpWx1QqW+zB8uABk5HbigDWpDUNjeW1/ax3NlNHPbyDKSRnKsPY1MaAPGfFmmazpHjGS9t/DVzq8U2qQ36Xdo0ZkCLHtMTBmBGD07YPau7+G2l32m6LdSatELe9v724v3tlcOIPMcsEyOCQMZxxkmvMfGmoWOk/EiO+8SXF1b3cOqwtaPJ5nkC08vnYB8ud2c984r0f4VtczeH7u6uFnS3u9QurmzScEOsDyEpkHkZ5IHoRQB2dFFFABRRRQAUUZozQAV598RbTWofE3h/W9A0aLVnslmjliluUhCK4X5gW/i4/nXoNeZfFyO2bVtBPiGK8l8Kjzfti24cqJcDyzIE5Kfe9s4oAzbC58aP46k8QSeCoUR7QWQWHUoiSu/cXc9yOw+vrXrynI54PpXlXwwj00eMtRfwXDdxeFjZr5m8OsDXO7jyg/8As/exx0r1agDh/iqunwaPaalf66NCuLG48y1vdnmYcggps6uGBIIHNcx8PdZ03xH4xiubzxaNc1W3t5FtoIdMktIolJXe3zA5Y4XqfpXVfEjTtUuBouoaHaWl3e6bdmbZdTCOPYUKtkkHnB49Kn8K61r+p3uNR0fT7az2HM9tfrOd3YYA+v5UAdcOlIxx16Utcp8SNOudV0azsoEme2mvoFvEhYqzQb/nGRzj19s0AdMtxEzYWRGPYBgTUteA+CfDNpo/jLR7ez8O3tvrVlfXQu7toW+ztas0hjYOflJwYwMcjBr36gAorO1/V7XQ9Nkvr9mWBGVTtXcSWYKAB9SKwL3x9pdp4qGhPFePKJI4ZblISYIZZBlI2bsxGPzFAHYVkeL9Tm0bwtq2pW0PnTWttJMkZ/iKqSBWuKzvEepwaNoOoaldo0kFrA8zooyWCgkigDyKDXdS0nR9fvZNdg1C+22M9rMsMahmmIzGgAyQegySa9siJaNSwwSORXjXh/wtdR6vba5Y/DzQbN5Ssys19l4gechQu0Ng9q9mX7ozxQAtFFFABSNS0jdKAPIrmx8R6JfazqOlfD7RXNx5gkki1PbJPGSSeNnBPUgHrXofgq4guvCekzWkEVvA9shSGJtyxjH3QT1x0rx/WPEmiyTap9p8V+ORaQzSRXKwWTiOPkgoHCcDt1r1L4e61oOo6LHZ+HHdYLBEiME0bRyxDHy7lYA8gZz3oA2PEOsWmgaNd6pqLlLW1jMjlV3H6AdyemK5/wAO+PLXVNTj03UNN1LRdQmTzbeHUI1T7QncoysVJHdc7h3FaXjvSINd8J6jp93ci0hljybhsYiKncGOewIFcL4k8c/DzxHaro2o+ILdrlMPHdxhlMMo6SK+MAg++KAPQ/C+tw+ItGj1G2ikiikeRAsmNwKOUPQnuta1c58PNFXw/wCELDT0vv7QVA7i6wB5u9y27jj+KujoAKKKKAIrqNpbeSOORonZSBIoyVPqM+lePrpHiBvHF1oknxG1W3jgs47lRJFb+ZMXZwduUxtXbz15PbjPsteZeP7eTxN4kfRLTwzouqyWMEdxJcaq5VU8wsAqbVLfwEntQBf+Fdzfm48R6fqOtz679gvFjjvZERQQUDFBtAGVJwfwrvq5rwFp9/pekG01DTNH01I2/cwaWW8sL3JyBzmuloAav3n+v9KdTV+8/wBf6U6gAooooAKa3+sX6GnU1v8AWL9DQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigBGGRXiUtjr/hnxTE8Hha61TZqF3eLe2rx/v1mUhBIWIKlSdv0HFewa5qtnommy3+pzeRaxEb32lsZIA4AJ6kV4TpuqeDNbv8AVrnxZrurNfG8k8oxzXMcPk5/d7AgA+7jPfOaAPX/AIdaPdaF4PsLHUPKF4N8sqRHKI8js5VT6Ddj8K6U1i+Dxpw8OWI0SWWbTtp8mSV2ZiMnqW5POetbRoA80uL/AMXaN4o1pLbwrNrelTzLNbTG/ijKHYoZQrHgZHtXb+G76+1HTEn1TTH0u6JINu8yykAHg7l45ryHXrfwrJ468SN4412/0icyJ9liOoS20TxeWvzx4IDHOcgdKn+E9pf6bqWiy2dxq82m6j9tEq3jyOGijk/cTfNyjMvbv1xQB7XSZx1pRXjXji50F/iJeWvjTVNThtFtYnsY7WSZIlPO/d5f8ROMZ7UAeyAg+lKa5L4br4fXR5/+EVubm5s/PO9p5JHYPgcZk5xjHtXW9qAPK/ix4i1yzubyy0TU00n7HpraiZTCsj3BDY8td3AA7nBPIrq9E1ia78ba7pwnSe0tYLaRdgH7mRg25CR1OArf8CrnPidHZ+INWg8OjwvHrt4lubpmluRbrBGTt+/1yTngDtzW38ONKn0ewntZfD1nokW8Mot7r7QZiepZsA5+uaAOxrhfHqeI7XxDomqeGbBdRWBZorm2kvBAjKwXB56sCOPxruq4X4mjwqVsf+EtF4RlvI+zxzt6Zz5QPt1oA0/Cer+INQupo9c8PRaVCqbkkS+Wfec9MADH1rp68h+F1tpSeP8AUZ/Cdvqf9iNYKJZrxJ0QT7/up5oBPy8nAxx7169QBwHxctftFlpLX1ld3+hRXe/Ura1Us7x7DtJUcsobBKjqKwPA8Gjy+Ora68CaRdabpKW0q6izWsltDMx2+WAjgZYfNyB0rrPiFqs+iTaHqLm6/siC7Jvzbxs5VCjBWYKM7Q2M1n6b4qh8T+OtNHhe6lutKtbaY30qRsINzFfLXcQAXyG6dBnNAHoVcd8Vb24sfDCPDeTWFvJdQxXd5B9+CBmAdgcHHHftXYjpXJfEy71Gx8PRXWk2d3fyRXUTS2drGJHni3fOmD2xQB5/4C8RrcN4f0rS9bm1G5TWb4Sg3BmY2avKFaQ+n+rwT+Fe21554N1+wfVI7Ww8C63ojXGfMuJdMSCMHGfmZTXodAHPeP7LTr7wnqMWsXbWVkI/Ma5UgGEqdyuM55BA4ryzQNZ8LXJtNHOu6te6nfaxHdz3U+lyR/apk24T7gVAAidOgFemfEqzt7/wheQ3l9BYQq0chuLhtsa7XDDcfQ4x+NclHoWo6xrJbRdS0W68OS6nHqhnhlLzxsAu6NcZXkjrkcEjFAHqi1l+K0t5PDOqpfSSxWrW0glkhTc6rtOSowckDpwa1FrG8XWkOqeH9S0qW9S0e8tpIxIWAKgqQWx6DvQB4hpOs+G9NtdP+z+O/iB9iBVYFeyYxyAdFB8jkY44Ne7+H9ZsNe0yK+0m4FxauSA4BByDggg8gg9jXmE//CQ65pdh4f1CXwtaWcUkPm3trf73dY2BHlxbRtJ2jvxnvXofhXRH0YapvkR/tl9JdqEUgIrBQB9fl59yaAN6imyOqIWchVAyST0FcKPir4bdj9m/ta7izgTW2l3Esb+6uEwR7igDvKRxlSMkZ7imQSCaJJF3BXUMAwwcH2p7dDxmgDx5ZvEWi2N54dsLjwpcWLvMsd9dX+yREkZifMiwdzDce/OOcV2Hg3woNH1MahHfJcxNpltYLsX7/l7jvJzzndx6AVxPiJ/DV42oWrfDDXrm4lZ081NKCLI5J+YSEjAJ53fjXpngi0u7HwlpNrqKJHdw2yJKiYwpA6ccUAQfELRbjxD4N1TS7N40nuIsJ5hOxiCDtbH8Jxg+xrjtNs9a8ReJNJk1zwxYaHZ6bFIjj7UkzXG5dvlqFHEffn0HFdd8Sjqa+B9XbQ/O+3iE7PIGZMZG7Z/tbc4968c0/wAK+CfEni3SE8L2+sSOI5DqNxKbiMwjb8pLvjEu7sPegD2b4e6Nc6B4TtdNvDH5kLy7VjYsqIZGKKD7KQPwro65n4bSajJ4Osv7YMzXcbSRF512u6rIyozD1KgH8a6agAooooAK8g+KC6LF4wiupb3xVDqSwQwzHRpljjhieQqjSEjHLE+p46V6/XmPxD8J6treqXsnhbVNOinnit0vrW7Ut/q5C8bArypPI5GCKAOi8CRWtjNq+mQanq+oXFnMizNqUwkZdyBl2kAfKQfzzXWVyfw/0iexj1K+1LULW/1a/n3XUloMRIUG1Y1BJPygd+ck11lADV+8/wBf6U6mr95/r/SnUAFFFFABTW/1i/Q06mt/rF+hoAdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBx/xcv7jTPAGpXlm8yTxNCVMJ+c/vUyB7kcfjWXH8QJDGpPgrxQ3A5+wg/wBa6zxJZ6brelT6bqFwiwyMpcLKFYFWDD9QKvR3loFAFzBxx/rBQBDod6dS0y3uzaXFl5oJ+z3CbJE5Iww7GtCq/wBstP8An5g/7+Cj7ba/8/MH/fwUAeT+Ltf8S3/igWek3WmafYrqQ0xXuLQTuXMXmbjkgAZwAB9a7D4X6pqOqeHpv7auobrUrO8ns55IYgiFo3I+UA9MYrR1bR/Dmr2l3bajb2M0V0yvN8wUuy8BiwIORjg5zVnRLXRtD02HT9JFpa2cWdkaOMDJyTknJJPJJ5NAGtXnWvTa1r/jS+0XS9bi0SCwgikZlgSWa4LgnI3cBRjH1rvfttr/AM/MH/fwVz3ifwv4U8USRSa5bWtzLENqSicxuB6bkYHHtnFAEHw61O/u4tXsNVube+uNLvPsv2yCMIs4KK+So4DDfg47iuvYEoQDgkdR2rJ0Oz0TQtPjsdHWztLRMlY42AGT1J55Puav/bbX/n5g/wC/goA8iuPDIk8beS/xD1+PUoLUyCbdbKBGXwUPyc8jODXX+AybXV9X0x/EWo67LbLC7S3RiKx7w2FUoo54yc+1NuvAfga61ebUrnSdKluplw7OFIY5znHrnvW9oen+H9Bt3h0W306xidtzrbhEDH1OOpoA2TXk1542urXQdWlfUbdb2DX/ALGiyFQywecq4x6bSea9S+22v/PzB/38Fc1feD/BF/eS3d9omg3FzMxeSWWCNmdj3JI5NAFez157v4qPplpfRz6aujrcGONlYCXzipOR3xiu1rndC0Lwt4fmkm0PT9I0+WRdrvbRpGWHXBI61tfbbX/n5g/7+CgDzXxJ4wutNtPiB/p8Edzppj+xRyFcrmJW4B68k1tTa6JPiB4f07T72CSzuLO6mnjhZWBZfK2k46feNX9W8LeDdXvnvdV0jRLy7kxvmnhjd2xwMk80/RfDfhHQ7z7Xo2l6NY3W0p5tvFHG209RkduBQB03avM/iP411rQNYisLWzisNOljDNrd1C80MbE/d2oOvuxAr0T7ba/8/MH/AH8FI91ZupV57dlPBBcEGgDyv4W239ueJNa1LUvElz4gfTbqOOzmWbZb7XgRyVjU7ersM8nivXa5GLwp4VtvEMWtWMNtZaghO57WXyllz/fRTtb6kZrpvttr/wA/MH/fwUAUfFR1EaDenRLa0utQ8s+TDdkiJz6NjtXgXhm00S2+I2lSeKZJ9I8RyTr5FppkEUVtI+eAxiJLD/er37WYdK1jTprHUZYpLWYbZEWcpkfVSDVTRdF8M6GoGk2Wl2mP4olQMfct1J9zQBviuZ8fRabZ+H9S1q+0y3vpbKymwsiglkKncmewI4Nb/wBttf8An5g/7+Co7mawureWC5ltpYZVKOjupDKeCCPSgDxPW4NB0vVDLpXgnw5NaaXb211qE2wB42lbhYsDBIHzc9iK92jIMakdCMiuUsfCPhCw0efS7O0tIrCeVZpY1uG+dlIK5bdkgbRxnGBjGK6X7ZaAY+0wY6f6wUAN1Dy5LWWCRkBmRkVWbG7IPFeY+Grjxromi2elq3hKaG0jEMTm7dWKDhQccZAwK9FvYdIvpYJbwWc8luxaJpGUlCRgkenBxXP/APCDeAy2ToWhZ658pKAOut2ZoUMm3eVBbacjOOce1YvjnWNQ0Lw3dahpGlS6teRbdtrGcFgTgn14HPFasVzZRRqkc9uqKAqqHAAA7U77Zaf8/MH/AH8FAHgsniG/8W61oVpe+L0ijvbw291pGmo1rJEvls3zs37zqoGeBXvOm2cOn2MFpagiCFAiBmLHA9zyawvEvh7wv4lh2aza2Fw4+7LuCyofVXBDA/Q1qaWbHT9Pgs4LtWigQRqZJg7YHTJJyaAIPGGux+GvDeoavPby3MdpEZWiixuYD0zxXJw+OteeNZIvh7reyQbgRPBznv8Af9K7i7k068tpLe7ktZoJVKPHIysrqeoIPUU+O6so0VEnt1RRgKHAAFAHPfC7Wb3X/BVlqOqDbeSvMHUgArtlZQpxxwAB+FdXVO3l0+2hEVtJaxRgkhEZVAycnge9SfbbX/n5g/7+CgCxmobW7t7tC9rNHMisULRsGAYdRx3ppvbQ9bmD/v4Kraemk6dE8enixto3cyMsO1AzHqxx3PrQBo15f8SNSPgrxRD4mGTbX9lJp0ygdZ1y9v8AmS6/iK9I+22v/PzB/wB/BVa+XStQiWK++xXMausirKVcBlOQwB7g9DQBnfD/AEZtB8JafZTNuutnm3Dd2lc7nJ/4ETXRVX+22v8Az8wf9/BUsU0cozFIjgcZVgaAFX7z/X+lOpq/ef6/0p1ABRRRQAU1v9Yv0NOprf6xfoaAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBQtNYsbvVr3TbecPe2ao08eD8gfJX88GmXGqWj3l5pscw+3QWwuHjAOVRtwU56dVP5VxfhN0j+LvjkMyr+5ssZOM/I9ddNpNmmpX+sxhjeXFotu7bsqUQsVwPq5oA+RtF0m01KxN3fCWa5lllLyNK+Sd7e9SXXh2xW7sxHBL5bO3mYlfGNpxnn1o8K3FwNMjRbN2j82QeZvUD/WNzjrXR0AY3/CNaX3gf/v6/wDjXmPiSL7Nrd3DBJMkaPhVErcfrXs1eO+Lf+Rivv8ArpQBjSvNhNs9x94Z/et0/On7pP8AnvP/AN/W/wAaSigDI1G7uo7kql1cAY6ea3+NVPt95/z+XP8A39apdV/4/G+lUqALP2+8/wCfu5/7+t/jTW1C9/5/Ln/v63+NQUxutAFn+0L3/n8uf+/rf40f2he/8/lz/wB/W/xqrRQBZOo3v/P5c/8Af1v8aP7Rvf8An8uf+/rf41VNJQBb/tG9/wCfy5/7+t/jR/aN7/z+XP8A39b/ABqpRQBb/tG9/wCfy5/7+t/jR/aN7/z+XP8A39b/ABqpRQBcXUb0tzeXP/f1v8al+3Xn/P3c/wDf1v8AGqCfeFTUAWBf3n/P5c/9/W/xpft15/z+XP8A39b/ABqtRQBZ+3Xn/P5c/wDf1v8AGj7feZP+l3P/AH9b/Gq1LQBZW+vNwzd3PX/nq3+NbgeTb/r5+n/PVv8AGuaX76/WukXoKADfL5rfv7jbgY/et/jTt8n/AD3n/wC/rf40lFAGVLeXQkYC6uMZ/wCerf40z7bd7uLq5xj/AJ6t/jUc3+tf60ygCx9suv8An6uf+/rf41E19ebv+Pu5/wC/rf40wVE/3jQBMb+84/0u5/7+t/jS/brz/n8uf+/rf41WooAsfb7z/n7uf+/rf40G/vO13c/9/W/xqsaKALP2+8/5+7n/AL+t/jSG/vP+fy5/7+t/jVekNAFj7fef8/lz/wB/W/xpft95/wA/dz/39b/Gq1FAFuO/vCebu5/7+t/jT2vbvHF3c/8Af1v8apx9T9KkoAsfbbvH/H3c/wDf1v8AGvpv9i26uZ7rxNHNcSyRqkTBXcsAcn1r5cP0zX05+xMf9O8Uf9c4f5mgD6qX7z/X+lOpq/ef6/0p1ABRRRQAU1v9Yv0NOprf6xfoaAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBy2teAPDGt6lJqGqaRDcXsihXlLMGYDoDgjpWzDY2+maJ9isohDbQQlI4wSQqgcDmtCs6bUbWea/sYp0a7tog8sQ6oGB2k/XBoA+SfCs8K6LGGljBEkvBYD/lo1a/2mD/ntF/32K+cdVlkXVr4LI4H2iTof9o1W8+X/nq//fRoA+l/tMH/AD2i/wC+xXlHii1uJtevHigldGfIZUJB/GvPvPl/56P/AN9Gvuf4L28Mnww8PtJFG7G3BLMoJPJoA+RfsN3/AM+s/wD37NH2G7/59Z/+/Zr7v+yW3/PCL/vgUfZLb/n3i/74FAH52a1G8V8yyoyNgcMMGs/NeqftOIkfxUu1jVVX7PGcAY7GvJ6AJM01qbRQAUUlFACmkoooAKKKWgBKKdRQAJ94VPioovvirFADMUU+kk+4aAGZozUFFAFhfvr9a6NWGByPzrlAeasZPrQB0m4eo/OjcPUfnXN5PrRk+tAFiYjzW5HWm5HqKoknJoyaAL2R6ioXI3VXyaWgCbNGahooAlzRmoc0ZoAmzSGos0UASZozUdFAE8fU1JkVUHWl/GgC1kV9OfsTH/TvFH/XOH+Zr5Z/GvqP9iH/AI/PE/8A1zi/maAPq1fvP9f6U6mr95/r/SnUAFFFFABTW/1i/Q06mt/rF+hoAdRRRQAUUUUAFFFFABXk3xA1rUW1bWF8P3mvvPpkKmZbQQrb277N4D7+WJBBIz0+tes1yGt/D7RdY1W6vrlr+NrxVS7ht7uSKK5CjaPMVSAeOPoOaAOVsfEOseLr7wlp0OoyaTHfaM2q3ctuq+ZKQyKI0JBAGWJNaevNq9vrHhvwrba9eR/bPPmn1F1QzskYyI1+XAPI5x0FbN54A0S50rSrJFurb+y4/Ksrm2uHinhXABAcHJBA5BzUl54G0m80a00+6k1CQ2khlgvGvJPtMbnOWEud3fp07YoA5/xVJq2kXHhrw5aa5el9YvZEfUJQjSxxpGX2KduMnGASM1h654g17QLHxzpMWrTXdxplpbXVlezKpkj81iCj4GDjbxxnBru5vA2lXGhppl3LqNyI5vtEd1Ndu1xHJ/fWTOQfpxSWngLRbfRdQ01lurhNQKtdz3Fw0k0xUjG5yc8Y4FAHL6uNcsLvw3oY8RXzTa3OzXF6yoGjVI9xSIbcLk/XjNHgm1ubH4geOba81F9RaO1tNk0oAk2lHIDYABIz1x0xXceI/DOneILGC2v1mX7O4kt5oJWjlhccBlcHIOKpaJ4Q0vw0up3WnC5e6vYwLme4naV5SoOGYsTzz/kUAfnNq5/4m19/18Sf+hGqlW9W/wCQtff9fEn/AKEaq0AIelfeHwU/5Jb4e/69h/M18IYzX3d8E2H/AAq3w9yP+PYfzNAHcUUmR6ijI9RQB8WftP8A/JVrz/r3i/ka8kr1v9p7n4rXn/XvF/KvJcGgBKKXBoxigBKKKKACilooASlFFFAC0UUUAOj++KsVXi++Ks0AJSP9w06mv9w0AVaSlpKAFHWp6gFT0AFFFFAEB6mkpT1pKACnUlFAC0UUUAIaSlpKACiiigAooooAUdaWkFLQAV9R/sQ/8fnif/rnF/M18uV9R/sQ/wDH54n/AOucX8zQB9Wr95/r/SnU1fvP9f6U6gAooooAKa3+sX6GnU1v9Yv0NADqKKKACiiigAooooAKKKKACiig0AGaM1wnxO1zV9F/ss6e09tp8sji8vYLT7U8AC/L8noT3waq2fiqdpfBiWWr2+rW+qX89vPdJAE3KlvK4XaPusGQZoA9FqG8P+hzf7jfyrzPxd4z1bTR4++xtBnRrS3mtN6Zwzgk7vUcCuv8PwaumhzTa7qEd5PcReYEjgEaw5XlR3Ye5oA/OTVv+Qrff9fEn/oRqrirWrH/AIm16P8Ap4k/9CNVaADFdDp/ifXLO0jt7XVr2GGMYVElICj6Vz1WY/uCgDoP+Ew8R/8AQb1D/v8AtR/wmHiP/oN6h/3/AGrBooA9y8AW0Gu+HY73WYkvrtnZTNON7EDoMmuj/wCEe0f/AKBtp/36FYPwl/5E+H/rq/8AOuyoAy/+Ee0f/oG2n/foV458arG1sdasks7eKBWhJIjXGTmvd68R+O//ACHbD/rgf50AeY4oxRRQAqgelPwPSmrTqADApGApaRqAG4oxS0UAKg+apKjXrUlABSrywz60lKn3x9aALPlp/dH5UnlJ/dH5U+igBhjTB+UflVSrrdDVKgBKKKKAIyKMUtJQAYqxGo2jiq9WY/uCgBdo9KNo9KWigCrOMPxUVS3H+sqKgAooooAKKKKALenqGZtwB4q95af3R+VUtO+8/wBKv0AM8tP7o/KvpT9i0BdS8TgDA8uH+Zr5tYgda+kv2LTu1LxOR/zyh/maAPqZfvP9f6U6mr95/r/SnUAFFFFABTW/1i/Q06mt/rF+hoAdRRRQAUUUUAFFFFABRRRQAUUUUAYviLRrrVfJNnreoaU8ecm0EZDg/wB4OjfpisA/DjTY9EtbO1vtQt7u2vX1GPUEdfPFw4Id+V28hiCNuMV3NFAHBL8NdPNj4ggu9R1O7l1yOOO8nmdN52DAK4UAfTGPauzljEWmvGpJVIioJ9hVhXVs7SDg4OD0qO9/485v9xv5UAfmPqv/ACFb7/r4k/8AQjVWn605GsXwB4+0Sf8AoRqn5jetAFmrMf3BWb5jetOE8gH3qANKis3z5P71L9ok/vUAfRHwl/5E+H/rq/8AOuyr5e0vxdrWl2otrK9eKEHIUAVb/wCE/wDEn/QSk/IUAfS1eI/Hf/kO2H/XA/zrl/8AhP8AxJ/0EpPyFej/AAysoPG2m3V34mjF9cQyeXG78bVxnFAHiVFfUH/CvPDP/QMj/M0f8K88M/8AQMj/ADNAHzCtOr1X4y+G9K0K101tLtVgaV2DkHrgCvLMUANpGp+KkhRWf5hQBXorQ8iP+7R5Ef8AdoAoL1qStjRbOCfUI0kQMpzkV1P9iaf/AM+6/nQB59Sp98fWvQP7E0//AJ91/OquqaRZQ6dcSRQKrqhIOelAHKUVnefJ/epPPk/vUAaLdDVKo/Pk/vUzefWgCaiod5o3mgB9JTNx9aNx9aAH1Zj+4KqZNKJGAxmgC5RVTzW9aPNb1oAW4/1lRUrEscmkoAKKKKACiiigC5p33n+lX6x45GjPynGaf9ol/v0AatfSX7F//IU8Uf8AXKH+Zr5Y+0S/3q+oP2I3L3vicscny4v5mgD6sX7z/X+lOpq/ef6/0p1ABRRRQAU1v9Yv0NOprf6xfoaAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB5VoOryaP4f8W3aXthZuviC5RZr4sY1y4GMLyT6AVo+BfGc/iC51zSb2WzubixgjmW5tY3jSRJAwGVfkEFD7VPe/D/zLOUWmpPDef2w2sQStEHVJGOdrLn5l/HNWND8J3el63rmvapq7ahfajaRwOohEUcQj3kBACSB83ck55zQB+dut/wDIZvv+u8n/AKEapVd1v/kM3/8A13k/9CNUqACiiigAooooAKKKKACvev2fP+Rf1D/ruP5V4LXvX7Pf/Iv6h/13H8qAPVqKKKAPJP2gf+PLSP8Aro/8hXite1ftA/8AHlpH/XR/5CvFaACpbf7/AOFRVLb/AOs/CgC1RRRQBo+H/wDkKRfjXZ1xnh//AJCkX412dABVLWf+QTd/9czV2qWtH/iU3f8A1zNAHl1FLSUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfUv7EH/AB+eJ/8ArnF/M18tV9S/sQf8fnif/rnF/M0AfVq/ef6/0p1NX7z/AF/pTqACiiigAprf6xfoadTW/wBYv0NADqKKKACiiigAooooAKKKKACikYkDjrXnf/CZeI4fGGn6Fd6JYNJckySm3vS7QQjrI42jA9OeTQB6LRXmLfEjUfsL68miI3hNLgwG7+0fviofyzKI8Y2Z9845q5qnjTW31zW9O8PaHDejSo4ppJprnyldXQtheCS3FAHoVQ3v/HnN/uN/KvP734kpLpvh9tGtYZL7Wbc3Ucd5ciCOGMAbi7fU4AA5rY8JeKD4k0vVkuII7e/0+Rre5SKYSx7igZWRx1UqwPr2oA/ObW/+Qzf/APXeT/0I1Sq7rf8AyGb7/rvJ/wChGqVABRRRQAUUUUAFFFFABXV+EfGuq+GbSa303yfLkfe29M84rlKkjoA9F/4W34j9bX/v3R/wtvxH62v/AH7rz2igDpPFnjLU/E8VumpeViAkpsXHWua3GhqbQA7ea1fDlul5fNHLnaEJ4rIrd8If8hJv+uZoA6H+xLX/AG/zo/sS1/2/zrUooAt+BfDVjeeJrWGbzNjZzhvavYP+FeaL/wBN/wDvuvO/hv8A8jdZ/wDAv5V7rQBx3/CvNF/6b/8AfdYnjXwLpNn4S1a5i87zIrZ3XL8ZAr0yue+IX/Ij65/16SfyoA+L6SlpKACnYptPoATFGKWigBtJS0lABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABX1L+xB/x+eJ/wDrnF/M18tV9S/sQf8AH54n/wCucX8zQB9Wr95/r/SnU1fvP9f6U6gAooooAKa3+sX6GnU1v9Yv0NADqKKKACiiigAooooAKKKKAGyBijBMBscE9M15x4L8L+LNDv7ifUbnQ7yS+n8y9u9kvnyL2VecAAcAdK9JooA8qb4fa8NGk8KpqWnDwo9yZA3kv9qWEyeZ5PXb143enaut0zw1JY614kvBMhi1SOGOJMHMflxsnP511FFAHlP/AArO7tdK8MvZzaXcapo1s1o6X1uZLe4jbkgjqpB5BrsPDemXunaNerqNvpFtLIWYR6ZAY4wNvfPLH34rpqhvf+POf/cb+VAH5fa3/wAhm/8A+u8n/oRqlV3W/wDkM3//AF3k/wDQjVKgAooooAKKKKACiiigAqSOo6epxQBJRTN/tRv9qAHNTa0dHsF1B5A7lNozwK1P+Edj/wCezflQBzVbvhD/AJCTf9czVj/hHY/+ezflXZ/CvwRBq3iCSCS6eMCEtkLnuKAIaK9f/wCFTWf/AEEpv++BR/wqaz/6CU3/AHwKAOH+G/8AyN1n/wAC/lXuteY+IPDcfw+0uXxFazvdy2uMQyLtDZOOo+tcX/wvnUP+gPb/APfw/wCFAH0FXPfEL/kR9c/69JP5V49/wvnUP+gPbf8Afw/4Vn6/8aL7VtFvdPfSoI1uYmiLiQkjI69KAPIKSlNJQAU+mUuaAHUU3NGaACkoooAKKKKACiiigAooooAKKKKACiiigAooooAK+pf2IP8Aj88T/wDXOL+Zr5ar6l/Yg/4/PE//AFzi/maAPq1fvP8AX+lOpq/ef6/0p1ABRRRQAU1v9Yv0NOprf6xfoaAHVmeI9Zs/D+jz6jqLMtvCBkIMsxJwFUdySQBWnXKfE7w3N4p8KS2FqyLdJLHcRCRiquyMGCsRyAcYyKAMXwd4n3a5qUPiBdTsNQuUa8hivlCRi3TgiMKxA25BbPPNa3h3xr/bs8D2uh6tHpk4ZotQljVImUDO7G7cAexIrmNI8JvqM1yl/wCEzpDSWM9qL19TNy6eYu1ginOAR3OOgrY8JDxLBp1p4f1nQoYraCD7NJqMN2pR1C4DLHjcCeOD0oALT4mafcTW0p07UotGurj7Nb6rJEBbyMThSOdwUngEjBpdV+JFrZX2sW8Gj6tejSJNt7JbxLsiXaG3ZJGeD0HPBrmLfwv4on8KaR4JutNtotOsJ4Q+rLcgiWGJw67Y8ZDnaAc8Dmups/Dd/Da+PEZI92rTSPa/MPmBt1QZ9PmBoAt6r46srWXTYNNs73V7y/t/tcMFmgLCHj52JIAHOOvWqs/xL0iPQLHVEt7+UXd6dPFskP76O4GQY2XPByuPxFYWmeHfEXhefw9qmn6bFqc0GiRaVeWn2gRsrIQwZGPBGcg03T/BGtLbaVc3aW4vpfET6zeRRyZSFHDDap/iIyvPfmgDWj+JiSz3lnH4b119VswHnsRCm9IyMiTO7aQecYOSQa0o/E1nqWpeE57K8uFttUimmjjVF2SqI93zk8jHt3qTT9Fu4PHXiLU5FUWl7Z20MLBuSyeZuyO33xXO+GPB2q2MPgRLuONf7JguY7va4O0uhC49eaALN38VNOt7d77+ydWk0f7QLWLUUiBhlcvs45zt3Z5IxxXWWmv211qusWEaSibS0jeYkDDB1LDH4LXjPifT/Efhv4XJ4ZuNLtzpun3MCDU/tAPmwi4UriPGQ/IBzxwTXb6hYeJdK8Wa7d6LpUGo2utW0CCR7oRfZpI1ZfmBBLKQwPHPFAGm3xC059H0a8srO+vLjV1Z7SyhQGV1X7xOTgAdyTWnoPiS38RaZqJjt7m0urRmgubW5ULJC+3cAcEgggggg8g15qvw91e10LwdcTWMWoXukWklrd2KXbQFw5zujkGOQR0PBrufBWl/2fpeqSvoI0WW4bc0bXZuXlwmAzNz9MZ6CgD87Nb/AOQzf/8AXeT/ANCNUqu63/yGb7/rvJ/6EapUAFFFFABRRRQAUUUUAFKKSlFAC0UUUAdB4R/1tx9BXS1zXhH/AFtx9BXS0AFeifA//kbJf+vdv5ivO69E+B//ACNkv/Xu38xQB7vRRRQBwHx0/wCSa6p/wD/0IV8iV9d/HT/kmuqf8A/9CFfIlABSN900tI33TQBDSUtJQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV9S/sQf8fnif8A65xfzNfLVfUv7EH/AB+eJ/8ArnF/M0AfVq/ef6/0p1NX7z/X+lOoAKKKKACmt/rF+hp1Nb/WL9DQA6iignFABRXHzfEXQIrx4WlujAk4tnvRbObZJScbDLjGcnHpmt601uyu9Q1KzglLT6eUFwNpwu5dw578UAaVFcfdfETw/b2Oj3XnzyJq8Rlskigd3mAAOAoBOeelGo/ELRdPmEM6ag1wsC3M8MVo7vbRno0oA+T8aAOworlNU8faDp/9lbriW4bVYmlsVtoWlM4GPugDr8w4qS38caFP4futYN00NrayGGdZo2SSKTIGwoRndyMDvmgDp80Vw3gnxNHf3WrjUr2eO6X/AEoWl1btbi3tuisAwBYcZLepq7pHj7RNVv7a1t2u0+15FpNPbPHFckDJ8t2GG45oA6a6tobuExXMMc0RIJSRQwJByODUoGBXFTfE3w5FPOhmumjt7lrO4nS2cxW8ofZtd8YXn/GrmteO9H0jVpNMm+2XGoJCtwbe0tnmbyzn5vlHTg0AdVUN7/x5zf7jfyrn5/HGhxaDYasty89tqBC2iwxM8k7f3VQDJPBz6YqfSPEdh4g06/axMySWxaKeCeJopIm25AZWGRwQaAPzX1v/AJDN/wD9d5P/AEI1Sq7rf/IZv/8ArvJ/6EapUAFFFFABRRRQAUUUUAFLSUUALmjNJRQB6v8AAjwDc+O7zVYrS7itjaxox8wE5yT6fSvYf+GetV/6DFn/AN8NWD+xP/yFvE3/AFxh/m1fWNAHzZ/wz1qv/QYtP++Gqlqvhib4MW48Q6nOmoQyN9mEUAKsC3OefpX1BXhf7X//ACTW2/6/U/kaAPPf+GgdL/6A93/32tH/AA0Dpn/QHu/++1r5yooA9p+IfxhsPE3hS80uDTbiGSbbh3YEDBzXifme1Ok+4agoAl8welIz5HSo6KAFpKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvqX9iD/j88T/8AXOL+Zr5ar6l/Yg/4/PE//XOL+ZoA+rV+8/1/pTqav3n+v9KdQAUUUUAFNb/WL9DTqa3+sX6GgB1NkXchUEjIxkdqdRQB4FYeDp7PTZvD2u6Z4svUa4kx9hvV+yTI0hcNgsNvXkEdRXXSR6z4c8XeJHtdDvNRg1eKE20sDJtR0j2FZCSCvQHODxXp9FAHkPg3wvq9m/wzN7YOn9labNDd52/uZCigA89evTNaMy6t4W8Y+J7yLQbvV7bWVhkt5LbYcOiFTHJuIwvQg8jk16bRQB4JDYah4O1/4aWk1hJqF7aadfefDbkMy7thOzJAO3OOoyM1e1zwhrniTS9c1dLK5sprvVra/h08zCOZ4oUVD8wyFdsEj04zXsM+mWc+qW2oywI17bI8cMp6orY3AfXAq5QB45b+Ex4gh1pYrTxTaahPpU9jHd6xch0TzMfIAGJPIBz0wD61F4V8Ol73QbXV9J8XfatOkjk3T3qvaRSIMBx83K9cADPNe0UUAeT3XhnVW+FHi/TEsG/tG+vb6aCIbd0gedmQ9ccrg9a3/DujX1t8RNU1K4tmS1l0q0t45Tjl1L7l9eMiu5ooA8HbwTrcHh7wndSWmpB9Kubz7RaWM4iuBHK7bXQ5wSOOM9Ca7jwHpcFtFrWoR2WvW890qo8mrzCR5QqnBGCcAZxzXoFQ3v8Ax5zf7jfyoA/L7W/+Qzff9d5P/QjVKrut/wDIZv8A/rvJ/wChGqVABRRRQAUUUUAFFLRigBKKXFFACUUUtAH0z+xP/wAhbxN/1xh/m1fWNfEH7NPxA0XwFqGtS681wFuo41j8qPfyCc5/Ovev+GjPA3/PTUP/AAH/APr0Aey14X+1/wD8k1tv+v1P5Gr/APw0Z4G/v6h/4D//AF68w/aC+LPhvxx4Mh03Q2ujcrcrKfNi2jaAe+aAPnCinbTRtNADJPuGoKsSKdpqLyzQAyin+Was6bYTahfwWlvt82Zwi5OBk0AU6K9C/wCFSeJv7lp/3+/+tR/wqTxN/ctP+/3/ANagDz2ivQX+E3iVEZilrhRk/vv/AK1cwfDd+CQRHkcfeoAxaK2v+EcvvSP/AL6o/wCEcvvSP/vqgDFop8sbRyMjdVODTcUAJRS4ooASiiigAooooAKKKKACiiigAooooAK+pf2IP+PzxP8A9c4v5mvlqvqX9iD/AI/PE/8A1zi/maAPq1fvP9f6U6mr95/r/SnUAFFFFABTW/1i/Q06mt/rF+hoAdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGbr2tWeh2YudQd1QsEURxtIzN6BVBJqrpXiDTfEWk3VxpVx5yxho5VKlHjbGdrKQCDgg81hfE6bV44tIGnHUI9Oe6xqMunoGnSLacbQQeN2MkDOKx/hrZX0Gr+Mrq4tNVgsrowtbPqTbpZgItpY/iOnXGKAPgnW/wDkM33/AF3k/wDQjVKrut/8hm+/67yf+hGqVABRRRQAUUUUAOXpS0i9KWgApGpaRqAG0tJS0AWLXq1WarWvU/SrNABTX7U6mvQA2iiigBr/AHaZT3+7UdAC1teCf+Ru0j/r5T+dYlbfgn/kbtI/6+U/nQB9VUtIKWgCK6/49Zf9xv5V4RL/AKx/qa93uv8Aj1l/3G/lXhEv+tf/AHjQAyiiigDzq/8A+Pyf/fNQVPf/APH7P/vmoKACkpaSgAooooAQ0lKaSgApRSUooAWiiigAooooAK+o/wBiH/j88T/9c4v5mvlyvqP9iH/j88T/APXOL+ZoA+rV+8/1/pTqav3n+v8ASnUAFFFFABTW/wBYv0NOprf6xfoaAHUUUUAFFFFABRRRQAUUUUAFFFFABRWfr2rWeiaXNfajPFBBEM7pHCAnsMnjJrj2+IVnpngD/hJdVu7C4QzLHss5gVUu4ATcTyyg5P0NAHf4qG8GLOf/AHG/lWJfeMNFt/DkutRalZzWShgjrOu2Rx/AGzjOeKXwzqh1jwlHeyXVndSyxMzvZvujU8/KDnnHSgD82tb/AOQzf/8AXeT/ANCNUsVe1r/kMX//AF8Sf+hGqdADcUYp1FADcUYp1FACDijNI3WkoAdmkJpKKAClpKKAJ7dwpO44qfzk/vCqNFAF7zk/vCmtKh/iFU6KALfmr60eYvrVSigC00iletR7xUNFAE28VteDJUTxXpTOcKLhCT+Nc/Wn4a/5GDT/APrsv86APqz+1rL/AJ7rR/a1l/z3WuKooA7KfVLN4JFWZSzKQB+FeUSaDqZkYi1fBOe1dPH99frXSr0FAHmP9gan/wA+j/pR/YGp/wDPo/6V6fRQB8talE6ahcK64ZZCCKrbG9K1te/5Dd9/12b+dUKAIdjelMxg81Zqu/3jQAlFFFACGkpTSUAFKKSnLQAYopaKAEooNFABX1H+xD/x+eJ/+ucX8zXy5X1H+xD/AMfnif8A65xfzNAH1av3n+v9KdTV+8/1/pTqACiiigAprf6xfoadTW/1i/Q0AOooooAKKKKACiiigAooooAKKKKAPLfjFbXY1jwrqJkkj0qzmlNzItr9pELsmEkaPuByM9s1zeraVbX/AIK8Y3mk302syXEtlNIkWn+SimKVWZkXHzMUBzj+6K92IB6jNIFAGAAPwoA8W8b3UN/rnhXXtOmeDw/bi4ikmGnGRbeYgYZ4yMjgEbscfjXUfDm1so7TxFeadqT36Xs3myMLT7NGHEQU7FwBzjkjvXoO0YxgY+lQ3gAs5sAD5G6fSgD8wda/5DF//wBfEn/oRqnVzWv+Qxf/APXxJ/6Eap0AFFFOCsegNADaKdsb+6aNjf3TQBG3WkpzAg802gAooooAKKKKACiiigAooooAKKKKACiiigArT8Nf8jBp/wD12X+dZlaPh11j1yxd2Cqsykk9BzQB7zRVL+1bD/n8g/77FH9q2H/P5B/32KAL6ffX610q9BXHQ6nYtKirdwFiwAAcc13q6XfFQRaTkEf3DQBUoq5/ZV//AM+c/wD3waX+yr//AJ85/wDvg0AfLWvf8hu+/wCuzfzqhV/xF8mvX6vwwnYEHtzWfuHrQAtV3+8an3D1qBj81ACUUlFAAaSlpKACnLTaVaAHUUZozQAhooJpKAFr6j/Yh/4/PE//AFzi/ma+W6+pP2If+PzxP/1zi/maAPq1fvP9f6U6mr95/r/SnUAFFFFABTW/1i/Q06mt/rF+hoAdRRRQAUUUUAFFFFABRRRQBHNPHAu6aRI0/vOwAqpcagY7+xt47aWaO537p0wUi2rkbvr0FcB8VdIhv9e0i8mudDuDaQzf8SrWJNkUwYr+8U54YYxkgjDGsrw/qdrql/8ADm50vThptuf7QRLVW3IpWIj5T3XIyD6UAevfaYfMMfmx7xyV3DIpJLmKL/WyInOPmYCvmbUF8PN8L47rUZIh46e/T7ad5+1Gf7QA6tznZjt0xivQ/wDhGdJ8R/Ejxr/bVqLyOGxsVjjkYlELJLlgOm7jg9RzQB6jqF9FY2M91PnyoULttGTgDsKp6Ze3Go+HFu7u2FrLNEz+Tv3lAc4BPrjGfevCPtN5qOg/DiDVJLObSZLedX/tORxbyzIcRrIR1O0HAPBNelfDXTf7L0/xBFBe6ZLZSTeZFa6dK0kVofLG5RknGSC2OgzQB+f2tf8AIYv/APr4k/8AQjVOrms/8hi//wCviT/0I1ToAKv2/wDqlqhV+3/1K0ASUUUUAULr/XGoKnuv9cagoAKKKKACiiigAooooAKKKKACiiigBaWkpaACjNFJQA7J9aMn1NFFAFzRz/xNrLn/AJbp/wChCv0iswPskHH8C/yr83dH/wCQtZf9d0/9CFfpFZ/8ekH+4v8AKgCbA9BRgelFFAH5zeOv+Ry1v/r8l/8AQjWFW546/wCRy1v/AK/Jf/QjWFQAtJRRQAUUUUAFFFFABRRRQAUUUUAFFFFABX1L+xB/x+eJ/wDrnF/M18tV9S/sQf8AH54n/wCucX8zQB9Wr95/r/SnU1fvP9f6U6gAooooAKa3+sX6GnU1v9Yv0NADqKKKACiiigAooooAKKKKAM/VNG03VvL/ALTsLS78v7nnxK+36ZFWEsrePyNkEK+QCItqAeWCMHb6cVYooA4PVvAEmsaqZtT1SOSwa4WdoI7KOOSTa25UeUclQQOwziu2W3iSWSRYoxJIAHcLywHQE98ZNTUhOOvFAFOfSrCex+xTWVtJZ9PIaMFPy6VHFptnpmmTwadaW9rDsY7IYwi5x6CtEnFQXhzZzEHI2N/KgD8wda/5DF//ANfEn/oRqnVvWv8AkMX/AP18Sf8AoRqnQAtX4P8AUryKz6TJ9TQBqZHqKMj1FZeT6mjJ9TQBNdf641BS0lABRRSigBKKdRQA2inUUANop1IaAEooooAWlpF61JigBlFPxSr94UAMoqzgUYFAD9I/5C1ln/nun/oQr9HrOeH7JD+9j+4v8Q9K/N9RggjgitUalff8/lx/38NAH6IfaIf+esf/AH0KXz4f+esf/fQr87v7Svv+fy4/7+Gj+0r7/n8uP+/hoAb45ic+MNaIRiDdyEHB/vGsPyZP+eb/APfJr7G8N2ltJoOnvJBEztAhJKAk8CtH7Baf8+0P/fAoA+KPJk/55v8A98mmsjKcEEH6V9tfYLT/AJ9of++BXzp8RIo08ZamqIqqJOAB04oA8vwfQ0YPoa6zYv8AdH5UbF/uj8qAOTxRWnqgAuiAAOKp4oAgoqfFMk60ARUU/FGKAG0U4UtADK+pP2IP+PzxP/1zi/ma+Xq+ov2Iv+P3xP8A9c4f5mgD6sX7z/X+lOpq/ef6/wBKdQAUUUUAFNb/AFi/Q06mt/rF+hoAdRRRQAUUUUAFFFFABRRRQAUUUUAFeL+MRqOsfFbUNMmtbO8s7bT4ZLW2vNSktEJYtvkUIp3sCAM9vxr2isvW/D+ka6qLrGnW14IzlPOjDFfoetAHkZ0rUpG+H+ja/qLTBry6SU2d67iWJUYqjSDaWxwD9K6zwTbJpWu+N9Hs2kGnWssMlvC8rSCLzLdWYKWJIG7Jx712ltoum2qWiW9jbxLaZ+zhIwPKz12+mcmnz2dvCl7cRRIk06ZlcLgvhcDJ74FAH5ja1/yGL/8A6+JP/QjVOrmtf8hi/wD+viT/ANCNU6ACkpaSgBKKKKACiiigApRSUooAWiiigAooooAKQ0tIaAEooooAcv3qkqNfvVJQAUL94UUL94UATUUUUAKKtVVFWqACijijigD668L/APIu6b/1wT+QrTrM8Mf8i7pv/XBP5CtOgAr5v+I//I6ap/11/pX0hXzf8Rv+R01T/rr/AEoA5qijFGKAMTVf+Ps/QVTq7qv/AB9n6CqVABTJOtPpknWgBtFFFAAKdSCigAr6i/Yi/wCP3xP/ANc4v5mvl2vqL9iL/j98T/8AXOH+ZoA+rF+8/wBf6U6mr95/r/SnUAFFFFABTW/1i/Q06mt/rF+hoAdRRRQAUUUUAFFFFABRRRQAUZFFeSeP7qfUtc1qLR/7a+0aRbq000Oq/ZLeBihdTs5DnHJyCO1AHreagvryCxs57q6cJBCjSOx7KBk15DpWsaj4yfwNY6hqd1Y2+o6O+oXLWcpge5lXYu0OvIHzFiBjr6VTuNb1WzsBp/8Aat1c29h4vtdOF275aW3baTHIw+9gttJPXHNAHq+h+JLDV9Klv4jJbxQlhMlynlvFjk7genHP0q+1xDd6Ubi1kWWCWHfHIhyGUjIIPoa828aXD3viXxNpK3kq2q+HDM0UMhUrJvOG47kAD6Vt/DLS4tP+HWmyRXV5P9o0+KQi4uGlC/uxwoP3R7CgD88tb/5DN/8A9d5P/QjVKrmt/wDIZvv+u8n/AKEapUALSUUUAFFFFABRRRQAUtJRQAtFJRQAopaQUtABSGlpDQAlFFFAC0ZNJRQAuTRk+tJRQA7e3qaN7epptFAD97f3jS+a/wDeP51HTqAHea/94/nR5r/3j+dNooA24vF2vwxrHFrF6qKNqqJTgCn/APCZeI/+g1ff9/TXP0UAdB/wmXiL/oNX3/f019m/Brwxomu/DXQ9S1nS7S9v7iHdLcTRhnc5PJNfCdfoL+z/AP8AJIfDn/Xv/wCzGgDc/wCEB8Kf9C/pv/fkUf8ACA+FP+hf03/vyK6aigD4Y/aZ0ux0j4ly22mWsVrbi3Q+XEu0ZNeTV7L+1d/yVab/AK9o68aoAKjl+9UlRy/eoAZmjNJRQAuaM0lFAC5r6k/Yg/4/PE//AFzi/ma+Wq+pf2IP+PzxP/1zi/maAPq1fvP9f6U6mr95/r/SnUAFFFFABTW/1i/Q06mt/rF+hoAdRRRQAUUUUAFFFFABRRRQAVzeseCfD+r6lLf6hpyy3MqhJSJHUSqOgdQQGx75rpCcVnWGuaXqF1Na2Go2lzcwDMsUMyuyfUA5FAGZdeCtAutLsNOm05Pstgu21COyNCOmFZSGH51J/wAIfoI8PPoY0yEaY7b2h55bOd27Od2ec5zVq/8AEejadfx2V/qllbXkuNkMsyq7Z6cE5qXWNc0zRYEm1e/trKJ22q88gQMfQZoAoaL4P0LRriafT9PWOeaLyJZHdpGkTOdrFiSfxp+l+HdM8PafdxaPbfZoZEJKB2KjAOMAk4HsKuXGt6XbaWupXGoWkensAVuGlURsD0w2cGorPWdN1rS7ifSL62vYVVlLwSBwDjocdDQB+Z2t/wDIZvv+u8n/AKEapVd1v/kM3/8A13k/9CNUqACiiigAooooAKKKKACiiigAooooAUUtNpaAFpDRSUAFFFFABRRRQAUUUUAFFFFABTqbS0ALRSUUAJRRRQAtfoL+z/8A8kh8Of8AXv8A1Nfn1XoXh/4w+M9A0e20zS9U8qzt12xp5YOBQB+gtFfBf/C+fiB/0Gf/ACEv+FH/AAvn4gf9Bn/yEv8AhQBs/tXf8lWm/wCvaOvGq+wfhD4Q0f4s+EU8SeOLb7fq7StCZtxT5V6DArt/+FB/D7/oDf8AkVv8aAPgeo5etffn/Cg/h9/0Bv8AyK3+NfNv7UXgrQ/BXiLSbbw9afZop7cu43FsndjvQB4jRRRQAUUUUAFfUv7EH/H54n/65xfzNfLVfUv7EH/H54n/AOucX8zQB9Wr95/r/SnU1fvP9f6U6gAooooAKa3+sX6GnU1v9Yv0NADqKKKACiiigAooooAKKKKAEYBgQeQa8w8PaZY6V8ctag02zt7SFtEgdkgjCAsZnySB1PvXp5Ga4i1+G+mW3iQ66l/rLagcBma9YqyhtwQjuuSeKAOC8T6dcaNH8RBqvhqfVG1SR7m0v1RGjWPylCq7k5TYVJ/HirOlW2p/aPBXiTVtHutasv7BFq8MMayyQTNtbzNjEZ3KME9q7/XfAthrl/LPqN5qcltMVMtiLphbvgAcqO3HTODV3xD4Yh1mO2QX2oWCW6lFFjOYsqcZBwPYY9KAPP8A4USWk3hrxK3iHT7a00ex1m4lggulVkt1B3Y7qNpJ6dDmtPwFYm81nxH4ptbH+zdK1K3jhtINnlmdYw3+kMo6Ft2BnnABre1L4e6Ff+EofDbRzw6ZHIJdsMxVnYHOWbq2Tyc9asaL4Xg8Pw3bwX+p3QkhKbbu5MqrgHoD0oA/N/W/+Qzff9d5P/QjVKrut/8AIZv/APrvJ/6EapUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFLQAlFLRQAlFLRQAlFLRQAlFLRQAlOpKWgAooooA+5/wBkf/kksX/XzJXtdeKfsj/8klh/6+ZK9roAK+PP22P+Rt0L/r0b/wBCNfYdfHv7bH/I26F/16N/6EaAPm2ilxRigBKKWkoAK+pf2IP+PzxP/wBc4v5mvlqvqX9iD/j88T/9c4v5mgD6tX7z/X+lOpq/ef6/0p1ABRRRQAU1v9Yv0NOprf6xfoaAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVDe/wDHnN/uN/Kpqhvjizm/3G/lQB+Y+rQq+rXzEn/j4k/9CNVfs6+pq7qbD+1L0f8ATxJ/6EagoAh+zr6moHjAYgVdqrJ980ARbKNlPooAaIx70vlj3pw6UtADPLHvTWXBqWo5PvUAMxRilooAMUYoFLQAmKUKDRSr1oANg96Nn1p9FACJGCwBzUvkJ6mmx/fFT0AReQnqadHbI0ijJ5OKfUkH+uT60AWP7Lh7s/50f2XB/ef86v0UAZ50uHH3n/Oov7Pi/vNWo3Q1BQBS/s+L+81H9nxf3mq7RQA1dGgKgln/ADpf7Gt/77/nWnH/AKtfpTqAMv8Asa3/AL7/AJ1j3kCw3DxrkhTjmusrmdT/AOP6X60AU9lGynUUAeqfDr41+IPAvh1dI0q3spLdXaQNMhLZPXvXUf8ADUHjD/nz0z/v2f8AGvBBRQB73/w1B4w/589M/wC/Z/xrm/E/ie7+LVxFf+IFihmtF8lBbDAIPPNeUV3Xw/8A+PG5/wCun9KAH/8ACGaf/wA9Jvzo/wCEMsP+ek35109LQB534n0G20uOFoGkbeSDuNc/5K+tdv4+/wBRa/7x/lXG0AReSvrX09+xIoW+8Tgf884f5mvmUnFfTn7E5/07xR/1zh/maAPqlfvP9f6U6mr95/r/AEp1ABRRRQAU1v8AWL9DTqa3+sX6GgB1FFFABRRRQAUUUUAFFFFABRRRQAUUZFISAMkgD3oAWsi506RNSvdQN9cNFJaiEWhP7pCNx3gf3jnB+la9Q3v/AB5z/wC438qAPzL1L/kKXv8A18Sf+hGq9WNS/wCQpe/9d5P/AEI1XoAKqyffNWqpytiQ0AFFM3+1G/2oAkHSlqPzPajzPagCSo5PvUeZ7U1mzQAUUlFACilpopaAFpV602lBxQBJRUe+jfQBNH98VPVRZMN0qTz/APZoAnqSD/XJ9aqef/s05Lna4bb0OaAOgorK/tU/88/1o/tU/wDPP9aANRuhqCqX9qnB/dj86i/tI/8APMfnQBpUVm/2kf8AnmPzo/tI/wDPMfnQB0kf+rX6U6sVNYIUDyu3rS/2yf8Anl+tAGzXM6l/x/S/Wrv9sn/nl+tVJV+0yNKeNxzigCnRVn7P/tUfZ/8AaoAriinum1sUmKAG13Xw/wD+PG5/66f0rh8V0fhjVTp1vKgjD7mz1oA7+lrmf+Emb/n3H50f8JM3/PuPzoAg8ff6i1/3j/KuNr1Pw34fHxBkmhknNn9lAbIXduzxW7/wo6P/AKDDf9+v/r0AeH19N/sT/wDH/wCKP+ucP8zXKf8ACjo/+gw3/fr/AOvXp/7M/hoeFfF3ijTluDOBb28m8jHUmgD6FX7z/X+lOpq/ef6/0p1ABRRRQAU1v9Yv0NOprf6xfoaAHUUUUAFFFFABRRRQAE4rz3/hZCazeXFh4K0yXWLqBzFLLJILeCJh1yW+Y49lr0Kub8QeCtB1tjLdWKxXnVbq2YwzKfUOuD+eaAMXxZ4xvvCXh/TH1ldMGsahdC2jUSMlvGSGbczHJwFX8TjpmsWH4ozLpnifemm395o9iL6OWxkYwTqcjac8qwI6ZPFdJrPgf+0NE0y0GqXTX2mXP2q0vrpVmdWwy7XHAddrEH885qK48I6tqnhvWdL1nU7AnULc26NZ2HlCLPVjliW+nFAENl4r1y08Q6LZ+IbGxhtdYikeD7PIzPAyIHKPnhuM8jHSuN8ceJvEGv8Aw3uNXisLOHQrq7gjiCyP9oWMXSASE/dwSMbeoB616Zq/hkajrXhzUGudn9kGU+X5eRLvj2evGOveuRvPhpqc2gt4dh8RCLw8lwtxDD9k3TKBKJBGz7uVyD2B6fiAdT4iv/EumXXnaZpdnqmmBAWiE/k3CnvjdlG/SofDPjnSfFcepWth9oiv7JMXNtOmGiJBxyMqfwNT6/4Ns/EGopPq13qE1qqhRYpcGOAkd2C4LficVq2+k6fpOlzQaXZW9pEIz8kMYQdPagD82NTI/tS95/5eJP8A0I1BVjUv+Qpe/wDXxJ/6EarZ5HvQAtUZv9YavVRn/wBYaAI6KKKACiiigAooooAKKKKAFFLSCloAKQ0tIaAEooooAUdadTRTqACiiigAooooAKZT6ZQAUtJS0ATr90UUL0FFABVyH/ViqlW4f9WKAH0UmeQPWloArzffqOpJvv1GTigAq9p/3X+tUavaf91vrQBbopGIXr9KWgD1v4A/8f2q/wDXNf517NXjPwB/4/tV/wCua/zr2C8uYrO2ae4bbGuMkDPU4/mRQAXV1BaR+ZdTRxJnG52AGatfBm5gu/iN4pktpUlj+yWw3I2R/FUMkaSriRFcdcMM1a+D8aR/EjxSsaKi/Y7XhRj+9QB7Kv3n+v8ASnU1fvP9f6U6gAooooAKa331+hp1Iy57kfSgBaKbsP8Afb9KNn+236UAOopuz/bb9KNn+236UAOopuz/AG2/SjZ/tt+lADqKbs/22/SjZ/tt+lADqKbs/wBtv0o2f7bfpQA6im7P9tv0o2f7bfpQA6o54/NidM43KVz9ads/22/SjZ/tt+lAHyLqH7MHiea/upYda0jypJXdd3mA4JyM8dar/wDDLfirj/ic6Nx/10/+Jr7C2n++36f4UbT/AH2/SgD49/4Zc8Vf9BnRv/In/wATUTfsq+KWYk61o/8A5E/+Jr7H2n++36UbT/fb9KAPjb/hlPxR/wBBvR//ACJ/8TR/wyn4o/6Dej/+RP8A4mvsnaf77fpRtP8Afb9KAPjb/hlPxR/0G9H/APIn/wATR/wyn4o/6Dej/wDkT/4mvsnaf77fpRtP99v0oA+Nv+GU/FH/AEG9H/8AIn/xNH/DKfij/oN6P/5E/wDia+ydp/vt+lG0/wB9v0oA+Nv+GU/FH/Qb0f8A8if/ABNH/DKfij/oN6P/AORP/ia+ydp/vt+lG0/32/SgD42/4ZT8Uf8AQa0f/wAif/E0v/DKnij/AKDWj/8AkT/4mvsjaf77fpRtP99v0oA+N/8AhlTxR/0GtH/8if8AxNH/AAyp4o/6DWj/APkT/wCJr7I2n++36UbT/fb9KAPjb/hlPxR/0G9H/wDIn/xNH/DKfij/AKDej/8AkT/4mvsnaf77fpRtP99v0oA+N/8AhlTxR/0GtH/8if8AxNH/AAyp4p/6DWj/APkT/wCJr7I2n++36UbT/fb9KAPjf/hlTxT/ANBrR/8AyJ/8TR/wyp4p/wCg1o//AJE/+Jr7I2n++36UbT/fb9KAPjf/AIZU8U/9BrR//In/AMTR/wAMqeKf+g1o/wD5E/8Aia+yNp/vt+lG0/32/SgD43/4ZU8U/wDQa0f/AMif/E0n/DKfij/oN6P/AORP/ia+ydp/vt+lG0/32/SgD42/4ZT8Uf8AQb0f/wAif/E0f8Mp+KP+g3o//kT/AOJr7J2n++36UbT/AH2/SgD45/4ZX8Uj/mNaP/5E/wDiaP8AhlfxTn/kNaP/AORP/ia+xtp/vt+lG0/32/SgD45/4ZX8U/8AQa0f/wAif/E1Kv7LvitVwNZ0b/yJ/wDE19g7T/fb9KNp/vt+lAHx+f2XfFRIP9s6Nx/10/8AiaP+GXvFf/QZ0b/yJ/8AE19gbT/fb9KNp/vt+lAHx4/7LXipjk6zo3/kT/4mm/8ADLHin/oNaP8A+RP/AImvsXaf77fpRtP99v0oA+Ov+GWPFX/Qa0f/AMif/E1PD+zB4riBC6zoxz6+Z/8AE19fbT/fb9KNp/vt+lAHyI37MfixgM6xovBz/wAtP/iaX/hmXxZ/0GNF/wDIn/xNfXW0/wB9v0o2n++36UAfNXgv4J+NvCk1xJaX/h6czgKRKZuMfQV0WpfD7x/f2clvJP4YVXwcqZ88EH09q9z2n++36UbT/fb9KAPFR4J+IWP9b4X/ADn/AMK6X4Y+DNa0DXNY1bxBcae9xexxRJHZB9qqmeSW5zzXou0/32/Sjaf77fpQAJ95/r/SnUirjPJOeeaWgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD//2Q== ">
<center>Figure3: The model paid attention correctly when outputing "European Economic Area". In French, the order of these words is reversed ("européenne économique zone") as compared to English.</center>
This [link](https://huggingface.co/models?search=helsinki) lists out the models that allows translation from a source language to one or more target languages. To get a list of supported transformer backbones for this model use the below command.
```
print(TextTranslator.supported_backbones)
```
Sample code to instantiate the model object and translate a Spanish language text in German language.
```
translator_german = TextTranslator(target_language="de")
text = """La cobertura terrestre describe la superficie de la tierra. Son útiles para comprender la planificación
urbana, la gestión de recursos, la detección de cambios, la agricultura y una variedad de otras aplicaciones."""
print(translator_german.translate(text))
```
Sample code for translating English language text to French language.
```
translator_french = TextTranslator(source_language="en", target_language="fr")
text_list = """Land cover describes the surface of the earth. They are useful for understanding urban planning,
resource management, change detection, agriculture and a variety of other applications."""
print(translator_french.translate(text_list))
```
## TextGenerator
**TextGenerator** model can be used to generate sequence of text for a given incomplete text sequence or paragraph. These models are trained with an autoregressive language modeling objective and is therefore powerful at predicting the next token in a sequence. Visit [this](https://huggingface.co/models?search=&filter=lm-head) link to learn more about the available models for **text-generation** task. To get a list of supported transformer backbones for this model use the below command.
```
print(TextGenerator.supported_backbones)
```
Sample code to instantiate the model object and using it to generate sequence of text for a given incomplete sentence
```
text_gen = TextGenerator()
text_list = ["Hundreds of thousands of organizations in virtually every field are using GIS to make maps that"]
pprint(text_gen.generate_text(text_list, num_return_sequences=2, max_length=30))
```
## FillMask
**FillMask** model can be used to provide suggestion for a missing token/word in a sentence. These models have been trained with a [Masked Language Modeling (MLM)](https://huggingface.co/transformers/task_summary.html#masked-language-modeling) objective, which includes the bi-directional models in the library. Visit this [link](https://huggingface.co/models?filter=lm-head) to learn more about the available models for **fill-mask** task. To get a list of supported transformer backbones for this model use the below command.
```
print(FillMask.supported_backbones)
```
Sample usage to get suggestions for a missing word in a sentence
```
fill_mask = FillMask()
# original text - This deep learning model is used to extract building footprints from high resolution satellite imagery
text_list = ["This deep learning model is used to extract building footprints from high resolution satellite __."]
fill_mask.predict_token(text_list, num_suggestions=4)
```
# References
[1] [BERT Paper](https://arxiv.org/pdf/1810.04805.pdf)
[2] [Summary of the models](https://huggingface.co/transformers/summary.html)
[3] [The Annotated Transformer](http://nlp.seas.harvard.edu/2018/04/03/attention.html)
[4] [Text Summarization with Machine Learning](https://medium.com/luisfredgs/automatic-text-summarization-with-machine-learning-an-overview-68ded5717a25)
| true |
code
| 0.606003 | null | null | null | null |
|
# MNIST Dataset & Database
In the [MNIST tutorial](https://github.com/caffe2/caffe2/blob/master/caffe2/python/tutorials/MNIST.ipynb) we use an lmdb database. You can also use leveldb or even minidb by changing the type reference when you get ready to read from the dbs. In this tutorial, we will go over how to download, extract, and generate lmdb and leveldb variants of the MNIST dataset.
## Dataset:
You can download the raw [MNIST dataset](https://download.caffe2.ai/datasets/mnist/mnist.zip), g/unzip the dataset and labels, and make the database yourself.
## Databases:
We provide a few database formats for you to try with the MNIST tutorial. The default is lmdb.
* [MNIST-nchw-lmdb](https://download.caffe2.ai/databases/mnist-lmdb.zip) - contains both the train and test lmdb MNIST databases in NCHW format
* [MNIST-nchw-leveldb](https://download.caffe2.ai/databases/mnist-leveldb.zip) - contains both the train and test leveldb MNIST databases in NCHW format
* [MNIST-nchw-minidb](https://download.caffe2.ai/databases/mnist-minidb.zip) - contains both the train and test minidb MNIST databases in NCHW format
## Tools:
### make_mnist_db
If you like LevelDB you can use Caffe2's `make_mnist_db` binary to generate leveldb databases. This binary is found in `/caffe2/build/caffe2/binaries/` or depending on your OS and installation, in `/usr/local/bin/`.
Here is an example call to `make_mnist_db`:
```
./make_mnist_db --channel_first --db leveldb --image_file ~/Downloads/train-images-idx3-ubyte --label_file ~/Downloads/train-labels-idx1-ubyte --output_file ~/caffe2/caffe2/python/tutorials/tutorial_data/mnist/mnist-train-nchw-leveldb
./make_mnist_db --channel_first --db leveldb --image_file ~/Downloads/t10k-images-idx3-ubyte --label_file ~/Downloads/t10k-labels-idx1-ubyte --output_file ~/caffe2/caffe2/python/tutorials/tutorial_data/mnist/mnist-test-nchw-leveldb
```
Note leveldb can get deadlocked if more than one user attempts to open the leveldb at the same time. This is why there is logic in the Python below to delete LOCK files if they're found.
### Python script
You can use the Python in the code blocks below to download and extract the dataset with `DownloadResource`, call the `make_mnist_db` binary, and generate your database with `GenerateDB`.
First, we will define our functions.
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
from __future__ import unicode_literals
import os
def DownloadResource(url, path):
'''Downloads resources from s3 by url and unzips them to the provided path'''
import requests, zipfile, StringIO
print("Downloading... {} to {}".format(url, path))
r = requests.get(url, stream=True)
z = zipfile.ZipFile(StringIO.StringIO(r.content))
z.extractall(path)
print("Completed download and extraction.")
def GenerateDB(image, label, name):
'''Calls the make_mnist_db binary to generate a leveldb from a mnist dataset'''
name = os.path.join(data_folder, name)
print('DB: ', name)
if not os.path.exists(name):
syscall = "/usr/local/bin/make_mnist_db --channel_first --db leveldb --image_file " + image + " --label_file " + label + " --output_file " + name
# print "Creating database with: ", syscall
os.system(syscall)
else:
print("Database exists already. Delete the folder if you have issues/corrupted DB, then rerun this.")
if os.path.exists(os.path.join(name, "LOCK")):
# print "Deleting the pre-existing lock file"
os.remove(os.path.join(name, "LOCK"))
```
Now that we have our functions for loading, extracting, and generating our dbs, we will put these functions to use and generate the MNIST data in both lmdb and leveldb formats (if they do not already exist).
First, we **download and extract the MNIST dataset (train and test) in lmdb format** using:
```python
DownloadResource("http://download.caffe2.ai/databases/mnist-lmdb.zip", data_folder)
```
Next, we focus on **downloading, extracting, and generating MNIST train and test leveldbs**. We start by downloading and extracting the raw MNIST dataset (in ubyte format). This will ultimately extract four files, consisting of training images and labels, and testing images and labels.
```python
DownloadResource("http://download.caffe2.ai/datasets/mnist/mnist.zip", data_folder)
```
Finally, we **generate the leveldb train and test databases** (or regenerate; it can get locked with multi-user setups or abandoned threads). We do this by passing our `GenerateDB` function the names of the corresponding ubyte files along with an output file name.
```python
GenerateDB(image_file_train, label_file_train, "mnist-train-nchw-leveldb")
GenerateDB(image_file_test, label_file_test, "mnist-test-nchw-leveldb")
```
```
current_folder = os.path.join(os.path.expanduser('~'), 'caffe2_notebooks')
data_folder = os.path.join(current_folder, 'tutorial_data', 'mnist')
# If the data_folder does not already exist, create it
if not os.path.exists(data_folder):
os.makedirs(data_folder)
# Downloads and extracts the lmdb databases of MNIST images - both test and train
if not os.path.exists(os.path.join(data_folder,"mnist-train-nchw-lmdb")):
DownloadResource("http://download.caffe2.ai/databases/mnist-lmdb.zip", data_folder)
else:
print("mnist-lmdb already downloaded and extracted")
# Downloads and extracts the MNIST data set
if not os.path.exists(os.path.join(data_folder, "train-images-idx3-ubyte")):
DownloadResource("http://download.caffe2.ai/datasets/mnist/mnist.zip", data_folder)
else:
print("Raw mnist ubyte data already downloaded and extracted")
# (Re)generate the leveldb database (it can get locked with multi-user setups or abandoned threads)
# Requires the download of the dataset (mnist.zip) - see DownloadResource above.
# You also need to change references in the MNIST tutorial code where you train or test from lmdb to leveldb
image_file_train = os.path.join(data_folder, "train-images-idx3-ubyte")
label_file_train = os.path.join(data_folder, "train-labels-idx1-ubyte")
image_file_test = os.path.join(data_folder, "t10k-images-idx3-ubyte")
label_file_test = os.path.join(data_folder, "t10k-labels-idx1-ubyte")
GenerateDB(image_file_train, label_file_train, "mnist-train-nchw-leveldb")
GenerateDB(image_file_test, label_file_test, "mnist-test-nchw-leveldb")
```
## Code Changes for Other DBs
If you chose to use a format other than lmdb you will need to change a couple lines of code. When you use `ModelHelper` to instantiate the CNN, you pass in the `db` parameter with a path and the `db_type` with the type of db. You would need to update both of these values. Since you create two networks, one for training and one for testing, you would need to update the code for both of these.
**Default code using lmdb**
```python
train_model = model_helper.ModelHelper(name="mnist_train", arg_scope=arg_scope)
data, label = AddInput(
train_model, batch_size=64,
db=os.path.join(data_folder, 'mnist-train-nchw-lmdb'),
db_type='lmdb')
```
**Updated code using leveldb**
```python
train_model = model_helper.ModelHelper(name="mnist_train", arg_scope=arg_scope)
data, label = AddInput(
train_model, batch_size=64,
db=os.path.join(data_folder, 'mnist-train-nchw-leveldb'),
db_type='leveldb')
```
| true |
code
| 0.432603 | null | null | null | null |
|
# Machine Learning Foundation
## Section 2, Part d: Regularization and Gradient Descent
## Introduction
We will begin with a short tutorial on regression, polynomial features, and regularization based on a very simple, sparse data set that contains a column of `x` data and associated `y` noisy data. The data file is called `X_Y_Sinusoid_Data.csv`.
```
import os
data_path = ['data']
```
## Question 1
* Import the data.
* Also generate approximately 100 equally spaced x data points over the range of 0 to 1. Using these points, calculate the y-data which represents the "ground truth" (the real function) from the equation: $y = sin(2\pi x)$
* Plot the sparse data (`x` vs `y`) and the calculated ("real") data.
```
import pandas as pd
import numpy as np
filepath = os.sep.join(data_path + ['X_Y_Sinusoid_Data.csv'])
data = pd.read_csv(filepath)
X_real = np.linspace(0, 1.0, 100)
Y_real = np.sin(2 * np.pi * X_real)
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set_style('white')
sns.set_context('talk')
sns.set_palette('dark')
# Plot of the noisy (sparse)
ax = data.set_index('x')['y'].plot(ls='', marker='o', label='data')
ax.plot(X_real, Y_real, ls='--', marker='', label='real function')
ax.legend()
ax.set(xlabel='x data', ylabel='y data');
```
## Question 2
* Using the `PolynomialFeatures` class from Scikit-learn's preprocessing library, create 20th order polynomial features.
* Fit this data using linear regression.
* Plot the resulting predicted value compared to the calculated data.
Note that `PolynomialFeatures` requires either a dataframe (with one column, not a Series) or a 2D array of dimension (`X`, 1), where `X` is the length.
```
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# Setup the polynomial features
degree = 20
pf = PolynomialFeatures(degree)
lr = LinearRegression()
# Extract the X- and Y- data from the dataframe
X_data = data[['x']]
Y_data = data['y']
# Create the features and fit the model
X_poly = pf.fit_transform(X_data)
lr = lr.fit(X_poly, Y_data)
Y_pred = lr.predict(X_poly)
# Plot the result
plt.plot(X_data, Y_data, marker='o', ls='', label='data', alpha=1)
plt.plot(X_real, Y_real, ls='--', label='real function')
plt.plot(X_data, Y_pred, marker='^', alpha=.5, label='predictions w/ polynomial features')
plt.legend()
ax = plt.gca()
ax.set(xlabel='x data', ylabel='y data');
```
## Question 3
* Perform the regression on using the data with polynomial features using ridge regression ($\alpha$=0.001) and lasso regression ($\alpha$=0.0001).
* Plot the results, as was done in Question 1.
* Also plot the magnitude of the coefficients obtained from these regressions, and compare them to those obtained from linear regression in the previous question. The linear regression coefficients will likely need a separate plot (or their own y-axis) due to their large magnitude.
What does the comparatively large magnitude of the data tell you about the role of regularization?
```
# Mute the sklearn warning about regularization
import warnings
warnings.filterwarnings('ignore', module='sklearn')
from sklearn.linear_model import Ridge, Lasso
# The ridge regression model
rr = Ridge(alpha=0.001)
rr = rr.fit(X_poly, Y_data)
Y_pred_rr = rr.predict(X_poly)
# The lasso regression model
lassor = Lasso(alpha=0.0001)
lassor = lassor.fit(X_poly, Y_data)
Y_pred_lr = lassor.predict(X_poly)
# The plot of the predicted values
plt.plot(X_data, Y_data, marker='o', ls='', label='data')
plt.plot(X_real, Y_real, ls='--', label='real function')
plt.plot(X_data, Y_pred, label='linear regression', marker='^', alpha=.5)
plt.plot(X_data, Y_pred_rr, label='ridge regression', marker='^', alpha=.5)
plt.plot(X_data, Y_pred_lr, label='lasso regression', marker='^', alpha=.5)
plt.legend()
ax = plt.gca()
ax.set(xlabel='x data', ylabel='y data');
# let's look at the absolute value of coefficients for each model
coefficients = pd.DataFrame()
coefficients['linear regression'] = lr.coef_.ravel()
coefficients['ridge regression'] = rr.coef_.ravel()
coefficients['lasso regression'] = lassor.coef_.ravel()
coefficients = coefficients.applymap(abs)
coefficients.describe() # Huge difference in scale between non-regularized vs regularized regression
colors = sns.color_palette()
# Setup the dual y-axes
ax1 = plt.axes()
ax2 = ax1.twinx()
# Plot the linear regression data
ax1.plot(lr.coef_.ravel(),
color=colors[0], marker='o', label='linear regression')
# Plot the regularization data sets
ax2.plot(rr.coef_.ravel(),
color=colors[1], marker='o', label='ridge regression')
ax2.plot(lassor.coef_.ravel(),
color=colors[2], marker='o', label='lasso regression')
# Customize axes scales
ax1.set_ylim(-2e14, 2e14)
ax2.set_ylim(-25, 25)
# Combine the legends
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax1.legend(h1+h2, l1+l2)
ax1.set(xlabel='coefficients',ylabel='linear regression')
ax2.set(ylabel='ridge and lasso regression')
ax1.set_xticks(range(len(lr.coef_)));
```
## Question 4
For the remaining questions, we will be working with the [data set](https://www.kaggle.com/c/house-prices-advanced-regression-techniques) from last lesson, which is based on housing prices in Ames, Iowa. There are an extensive number of features--see the exercises from week three for a discussion of these features.
To begin:
* Import the data with Pandas, remove any null values, and one hot encode categoricals. Either Scikit-learn's feature encoders or Pandas `get_dummies` method can be used.
* Split the data into train and test sets.
* Log transform skewed features.
* Scaling can be attempted, although it can be interesting to see how well regularization works without scaling features.
```
filepath = os.sep.join(data_path + ['Ames_Housing_Sales.csv'])
data = pd.read_csv(filepath, sep=',')
```
Create a list of categorial data and one-hot encode. Pandas one-hot encoder (`get_dummies`) works well with data that is defined as a categorical.
```
# Get a Pd.Series consisting of all the string categoricals
one_hot_encode_cols = data.dtypes[data.dtypes == np.object] # filtering by string categoricals
one_hot_encode_cols = one_hot_encode_cols.index.tolist() # list of categorical fields
# Here we see another way of one-hot-encoding:
# Encode these columns as categoricals so one hot encoding works on split data (if desired)
for col in one_hot_encode_cols:
data[col] = pd.Categorical(data[col])
# Do the one hot encoding
data = pd.get_dummies(data, columns=one_hot_encode_cols)
```
Next, split the data in train and test data sets.
```
from sklearn.model_selection import train_test_split
train, test = train_test_split(data, test_size=0.3, random_state=42)
```
There are a number of columns that have skewed features--a log transformation can be applied to them. Note that this includes the `SalePrice`, our predictor. However, let's keep that one as is.
```
# Create a list of float colums to check for skewing
mask = data.dtypes == np.float
float_cols = data.columns[mask]
skew_limit = 0.75
skew_vals = train[float_cols].skew()
skew_cols = (skew_vals
.sort_values(ascending=False)
.to_frame()
.rename(columns={0:'Skew'})
.query('abs(Skew) > {0}'.format(skew_limit)))
skew_cols
```
Transform all the columns where the skew is greater than 0.75, excluding "SalePrice".
```
# OPTIONAL: Let's look at what happens to one of these features, when we apply np.log1p visually.
field = "BsmtFinSF1"
fig, (ax_before, ax_after) = plt.subplots(1, 2, figsize=(10, 5))
train[field].hist(ax=ax_before)
train[field].apply(np.log1p).hist(ax=ax_after)
ax_before.set(title='before np.log1p', ylabel='frequency', xlabel='value')
ax_after.set(title='after np.log1p', ylabel='frequency', xlabel='value')
fig.suptitle('Field "{}"'.format(field));
# a little bit better
# Mute the setting wtih a copy warnings
pd.options.mode.chained_assignment = None
for col in skew_cols.index.tolist():
if col == "SalePrice":
continue
train[col] = np.log1p(train[col])
test[col] = test[col].apply(np.log1p) # same thing
```
Separate features from predictor.
```
feature_cols = [x for x in train.columns if x != 'SalePrice']
X_train = train[feature_cols]
y_train = train['SalePrice']
X_test = test[feature_cols]
y_test = test['SalePrice']
```
## Question 5
* Write a function **`rmse`** that takes in truth and prediction values and returns the root-mean-squared error. Use sklearn's `mean_squared_error`.
```
from sklearn.metrics import mean_squared_error
def rmse(ytrue, ypredicted):
return np.sqrt(mean_squared_error(ytrue, ypredicted))
```
* Fit a basic linear regression model
* print the root-mean-squared error for this model
* plot the predicted vs actual sale price based on the model.
```
from sklearn.linear_model import LinearRegression
linearRegression = LinearRegression().fit(X_train, y_train)
linearRegression_rmse = rmse(y_test, linearRegression.predict(X_test))
print(linearRegression_rmse)
f = plt.figure(figsize=(6,6))
ax = plt.axes()
ax.plot(y_test, linearRegression.predict(X_test),
marker='o', ls='', ms=3.0)
lim = (0, y_test.max())
ax.set(xlabel='Actual Price',
ylabel='Predicted Price',
xlim=lim,
ylim=lim,
title='Linear Regression Results');
```
## Question 6
Ridge regression uses L2 normalization to reduce the magnitude of the coefficients. This can be helpful in situations where there is high variance. The regularization functions in Scikit-learn each contain versions that have cross-validation built in.
* Fit a regular (non-cross validated) Ridge model to a range of $\alpha$ values and plot the RMSE using the cross validated error function you created above.
* Use $$[0.005, 0.05, 0.1, 0.3, 1, 3, 5, 10, 15, 30, 80]$$ as the range of alphas.
* Then repeat the fitting of the Ridge models using the range of $\alpha$ values from the prior section. Compare the results.
Now for the `RidgeCV` method. It's not possible to get the alpha values for the models that weren't selected, unfortunately. The resulting error values and $\alpha$ values are very similar to those obtained above.
```
from sklearn.linear_model import RidgeCV
alphas = [0.005, 0.05, 0.1, 0.3, 1, 3, 5, 10, 15, 30, 80]
ridgeCV = RidgeCV(alphas=alphas,
cv=4).fit(X_train, y_train)
ridgeCV_rmse = rmse(y_test, ridgeCV.predict(X_test))
print(ridgeCV.alpha_, ridgeCV_rmse)
```
## Question 7
Much like the `RidgeCV` function, there is also a `LassoCV` function that uses an L1 regularization function and cross-validation. L1 regularization will selectively shrink some coefficients, effectively performing feature elimination.
The `LassoCV` function does not allow the scoring function to be set. However, the custom error function (`rmse`) created above can be used to evaluate the error on the final model.
Similarly, there is also an elastic net function with cross validation, `ElasticNetCV`, which is a combination of L2 and L1 regularization.
* Fit a Lasso model using cross validation and determine the optimum value for $\alpha$ and the RMSE using the function created above. Note that the magnitude of $\alpha$ may be different from the Ridge model.
* Repeat this with the Elastic net model.
* Compare the results via table and/or plot.
Use the following alphas:
`[1e-5, 5e-5, 0.0001, 0.0005]`
```
from sklearn.linear_model import LassoCV
alphas2 = np.array([1e-5, 5e-5, 0.0001, 0.0005])
lassoCV = LassoCV(alphas=alphas2,
max_iter=5e4,
cv=3).fit(X_train, y_train)
lassoCV_rmse = rmse(y_test, lassoCV.predict(X_test))
print(lassoCV.alpha_, lassoCV_rmse) # Lasso is slower
```
We can determine how many of these features remain non-zero.
```
print('Of {} coefficients, {} are non-zero with Lasso.'.format(len(lassoCV.coef_),
len(lassoCV.coef_.nonzero()[0])))
```
Now try the elastic net, with the same alphas as in Lasso, and l1_ratios between 0.1 and 0.9
```
from sklearn.linear_model import ElasticNetCV
l1_ratios = np.linspace(0.1, 0.9, 9)
elasticNetCV = ElasticNetCV(alphas=alphas2,
l1_ratio=l1_ratios,
max_iter=1e4).fit(X_train, y_train)
elasticNetCV_rmse = rmse(y_test, elasticNetCV.predict(X_test))
print(elasticNetCV.alpha_, elasticNetCV.l1_ratio_, elasticNetCV_rmse)
```
Comparing the RMSE calculation from all models is easiest in a table.
```
rmse_vals = [linearRegression_rmse, ridgeCV_rmse, lassoCV_rmse, elasticNetCV_rmse]
labels = ['Linear', 'Ridge', 'Lasso', 'ElasticNet']
rmse_df = pd.Series(rmse_vals, index=labels).to_frame()
rmse_df.rename(columns={0: 'RMSE'}, inplace=1)
rmse_df
```
We can also make a plot of actual vs predicted housing prices as before.
```
f = plt.figure(figsize=(6,6))
ax = plt.axes()
labels = ['Ridge', 'Lasso', 'ElasticNet']
models = [ridgeCV, lassoCV, elasticNetCV]
for mod, lab in zip(models, labels):
ax.plot(y_test, mod.predict(X_test),
marker='o', ls='', ms=3.0, label=lab)
leg = plt.legend(frameon=True)
leg.get_frame().set_edgecolor('black')
leg.get_frame().set_linewidth(1.0)
ax.set(xlabel='Actual Price',
ylabel='Predicted Price',
title='Linear Regression Results');
```
## Question 8
Let's explore Stochastic gradient descent in this exercise.
Recall that Linear models in general are sensitive to scaling.
However, SGD is *very* sensitive to scaling.
Moreover, a high value of learning rate can cause the algorithm to diverge, whereas a too low value may take too long to converge.
* Fit a stochastic gradient descent model without a regularization penalty (the relevant parameter is `penalty`).
* Now fit stochastic gradient descent models with each of the three penalties (L2, L1, Elastic Net) using the parameter values determined by cross validation above.
* Do not scale the data before fitting the model.
* Compare the results to those obtained without using stochastic gradient descent.
```
# Import SGDRegressor and prepare the parameters
from sklearn.linear_model import SGDRegressor
model_parameters_dict = {
'Linear': {'penalty': 'none'},
'Lasso': {'penalty': 'l2',
'alpha': lassoCV.alpha_},
'Ridge': {'penalty': 'l1',
'alpha': ridgeCV_rmse},
'ElasticNet': {'penalty': 'elasticnet',
'alpha': elasticNetCV.alpha_,
'l1_ratio': elasticNetCV.l1_ratio_}
}
new_rmses = {}
for modellabel, parameters in model_parameters_dict.items():
# following notation passes the dict items as arguments
SGD = SGDRegressor(**parameters)
SGD.fit(X_train, y_train)
new_rmses[modellabel] = rmse(y_test, SGD.predict(X_test))
rmse_df['RMSE-SGD'] = pd.Series(new_rmses)
rmse_df
```
Notice how high the error values are! The algorithm is diverging. This can be due to scaling and/or learning rate being too high. Let's adjust the learning rate and see what happens.
* Pass in `eta0=1e-7` when creating the instance of `SGDClassifier`.
* Re-compute the errors for all the penalties and compare.
```
# Import SGDRegressor and prepare the parameters
from sklearn.linear_model import SGDRegressor
model_parameters_dict = {
'Linear': {'penalty': 'none'},
'Lasso': {'penalty': 'l2',
'alpha': lassoCV.alpha_},
'Ridge': {'penalty': 'l1',
'alpha': ridgeCV_rmse},
'ElasticNet': {'penalty': 'elasticnet',
'alpha': elasticNetCV.alpha_,
'l1_ratio': elasticNetCV.l1_ratio_}
}
new_rmses = {}
for modellabel, parameters in model_parameters_dict.items():
# following notation passes the dict items as arguments
SGD = SGDRegressor(eta0=1e-7, **parameters)
SGD.fit(X_train, y_train)
new_rmses[modellabel] = rmse(y_test, SGD.predict(X_test))
rmse_df['RMSE-SGD-learningrate'] = pd.Series(new_rmses)
rmse_df
```
Now let's scale our training data and try again.
* Fit a `MinMaxScaler` to `X_train` create a variable `X_train_scaled`.
* Using the scaler, transform `X_test` and create a variable `X_test_scaled`.
* Apply the same versions of SGD to them and compare the results. Don't pass in a eta0 this time.
```
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
new_rmses = {}
for modellabel, parameters in model_parameters_dict.items():
# following notation passes the dict items as arguments
SGD = SGDRegressor(**parameters)
SGD.fit(X_train_scaled, y_train)
new_rmses[modellabel] = rmse(y_test, SGD.predict(X_test_scaled))
rmse_df['RMSE-SGD-scaled'] = pd.Series(new_rmses)
rmse_df
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
new_rmses = {}
for modellabel, parameters in model_parameters_dict.items():
# following notation passes the dict items as arguments
SGD = SGDRegressor(**parameters)
SGD.fit(X_train_scaled, y_train)
new_rmses[modellabel] = rmse(y_test, SGD.predict(X_test_scaled))
rmse_df['RMSE-SGD-scaled'] = pd.Series(new_rmses)
rmse_df
```
---
### Machine Learning Foundation (C) 2020 IBM Corporation
| true |
code
| 0.647297 | null | null | null | null |
|
# Basic training functionality
```
from fastai.basic_train import *
from fastai.gen_doc.nbdoc import *
from fastai.vision import *
from fastai.distributed import *
```
[`basic_train`](/basic_train.html#basic_train) wraps together the data (in a [`DataBunch`](/basic_data.html#DataBunch) object) with a pytorch model to define a [`Learner`](/basic_train.html#Learner) object. This is where the basic training loop is defined for the [`fit`](/basic_train.html#fit) function. The [`Learner`](/basic_train.html#Learner) object is the entry point of most of the [`Callback`](/callback.html#Callback) functions that will customize this training loop in different ways (and made available through the [`train`](/train.html#train) module), notably:
- [`Learner.lr_find`](/train.html#lr_find) will launch an LR range test that will help you select a good learning rate
- [`Learner.fit_one_cycle`](/train.html#fit_one_cycle) will launch a training using the 1cycle policy, to help you train your model fast.
- [`Learner.to_fp16`](/train.html#to_fp16) will convert your model in half precision and help you launch a training in mixed precision.
```
show_doc(Learner, title_level=2)
```
The main purpose of [`Learner`](/basic_train.html#Learner) is to train `model` using [`Learner.fit`](/basic_train.html#Learner.fit). After every epoch, all *metrics* will be printed, and will also be available to callbacks.
The default weight decay will be `wd`, which will be handled using the method from [Fixing Weight Decay Regularization in Adam](https://arxiv.org/abs/1711.05101) if `true_wd` is set (otherwise it's L2 regularization). If `bn_wd` is False then weight decay will be removed from batchnorm layers, as recommended in [Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour](https://arxiv.org/abs/1706.02677). You can ensure that batchnorm layer learnable params are trained even for frozen layer groups, by enabling `train_bn`.
To use [discriminative layer training](#Discriminative-layer-training) pass an [`nn.Module`](https://pytorch.org/docs/stable/nn.html#torch.nn.Module) for each layer group to be optimized with different settings.
Any model files created will be saved in `path`/`model_dir`.
You can pass a list of [`callbacks`](/callbacks.html#callbacks) that you have already created, or (more commonly) simply pass a list of callback functions to `callback_fns` and each function will be called (passing `self`) on object initialization, with the results stored as callback objects. For a walk-through, see the [training overview](/training.html) page. You may also want to use an `application` to fit your model, e.g. using the [`create_cnn`](/vision.learner.html#create_cnn) method:
```
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
learn = create_cnn(data, models.resnet18, metrics=accuracy)
learn.fit(1)
```
### Model fitting methods
```
show_doc(Learner.fit)
```
Uses [discriminative layer training](#Discriminative-layer-training) if multiple learning rates or weight decay values are passed. To control training behaviour, use the [`callback`](/callback.html#callback) system or one or more of the pre-defined [`callbacks`](/callbacks.html#callbacks).
```
show_doc(Learner.fit_one_cycle)
```
Uses the [`OneCycleScheduler`](/callbacks.one_cycle.html#OneCycleScheduler) callback.
```
show_doc(Learner.lr_find)
```
Runs the learning rate finder defined in [`LRFinder`](/callbacks.lr_finder.html#LRFinder), as discussed in [Cyclical Learning Rates for Training Neural Networks](https://arxiv.org/abs/1506.01186).
### See results
```
show_doc(Learner.get_preds)
show_doc(Learner.validate)
show_doc(Learner.show_results)
show_doc(Learner.predict)
show_doc(Learner.pred_batch)
show_doc(Learner.interpret, full_name='interpret')
jekyll_note('This function only works in the vision application.')
```
### Model summary
```
show_doc(Learner.summary)
```
### Test time augmentation
```
show_doc(Learner.TTA, full_name = 'TTA')
```
Applies Test Time Augmentation to `learn` on the dataset `ds_type`. We take the average of our regular predictions (with a weight `beta`) with the average of predictions obtained through augmented versions of the training set (with a weight `1-beta`). The transforms decided for the training set are applied with a few changes `scale` controls the scale for zoom (which isn't random), the cropping isn't random but we make sure to get the four corners of the image. Flipping isn't random but applied once on each of those corner images (so that makes 8 augmented versions total).
### Gradient clipping
```
show_doc(Learner.clip_grad)
```
### Mixed precision training
```
show_doc(Learner.to_fp16)
```
Uses the [`MixedPrecision`](/callbacks.fp16.html#MixedPrecision) callback to train in mixed precision (i.e. forward and backward passes using fp16, with weight updates using fp32), using all [NVIDIA recommendations](https://docs.nvidia.com/deeplearning/sdk/mixed-precision-training/index.html) for ensuring speed and accuracy.
```
show_doc(Learner.to_fp32)
```
### Distributed training
```
show_doc(Learner.distributed, full_name='distributed')
```
### Discriminative layer training
When fitting a model you can pass a list of learning rates (and/or weight decay amounts), which will apply a different rate to each *layer group* (i.e. the parameters of each module in `self.layer_groups`). See the [Universal Language Model Fine-tuning for Text Classification](https://arxiv.org/abs/1801.06146) paper for details and experimental results in NLP (we also frequently use them successfully in computer vision, but have not published a paper on this topic yet). When working with a [`Learner`](/basic_train.html#Learner) on which you've called `split`, you can set hyperparameters in four ways:
1. `param = [val1, val2 ..., valn]` (n = number of layer groups)
2. `param = val`
3. `param = slice(start,end)`
4. `param = slice(end)`
If we chose to set it in way 1, we must specify a number of values exactly equal to the number of layer groups. If we chose to set it in way 2, the chosen value will be repeated for all layer groups. See [`Learner.lr_range`](/basic_train.html#Learner.lr_range) for an explanation of the `slice` syntax).
Here's an example of how to use discriminative learning rates (note that you don't actually need to manually call [`Learner.split`](/basic_train.html#Learner.split) in this case, since fastai uses this exact function as the default split for `resnet18`; this is just to show how to customize it):
```
# creates 3 layer groups
learn.split(lambda m: (m[0][6], m[1]))
# only randomly initialized head now trainable
learn.freeze()
learn.fit_one_cycle(1)
# all layers now trainable
learn.unfreeze()
# optionally, separate LR and WD for each group
learn.fit_one_cycle(1, max_lr=(1e-4, 1e-3, 1e-2), wd=(1e-4,1e-4,1e-1))
show_doc(Learner.lr_range)
```
Rather than manually setting an LR for every group, it's often easier to use [`Learner.lr_range`](/basic_train.html#Learner.lr_range). This is a convenience method that returns one learning rate for each layer group. If you pass `slice(start,end)` then the first group's learning rate is `start`, the last is `end`, and the remaining are evenly geometrically spaced.
If you pass just `slice(end)` then the last group's learning rate is `end`, and all the other groups are `end/10`. For instance (for our learner that has 3 layer groups):
```
learn.lr_range(slice(1e-5,1e-3)), learn.lr_range(slice(1e-3))
show_doc(Learner.unfreeze)
```
Sets every layer group to *trainable* (i.e. `requires_grad=True`).
```
show_doc(Learner.freeze)
```
Sets every layer group except the last to *untrainable* (i.e. `requires_grad=False`).
```
show_doc(Learner.freeze_to)
show_doc(Learner.split)
```
A convenience method that sets `layer_groups` based on the result of [`split_model`](/torch_core.html#split_model). If `split_on` is a function, it calls that function and passes the result to [`split_model`](/torch_core.html#split_model) (see above for example).
### Saving and loading models
Simply call [`Learner.save`](/basic_train.html#Learner.save) and [`Learner.load`](/basic_train.html#Learner.load) to save and load models. Only the parameters are saved, not the actual architecture (so you'll need to create your model in the same way before loading weights back in). Models are saved to the `path`/`model_dir` directory.
```
show_doc(Learner.load)
show_doc(Learner.save)
```
### Deploying your model
When you are ready to put your model in production, export the minimal state of your [`Learner`](/basic_train.html#Learner) with
```
show_doc(Learner.export)
```
Then you can load it with the following function.
```
show_doc(load_learner)
```
You can find more information and multiple examples in [this tutorial](/tutorial.inference.html)
### Other methods
```
show_doc(Learner.init)
```
Initializes all weights (except batchnorm) using function `init`, which will often be from PyTorch's [`nn.init`](https://pytorch.org/docs/stable/nn.html#torch-nn-init) module.
```
show_doc(Learner.mixup)
```
Uses [`MixUpCallback`](/callbacks.mixup.html#MixUpCallback).
```
show_doc(Learner.backward)
show_doc(Learner.create_opt)
```
You generally won't need to call this yourself - it's used to create the [`optim`](https://pytorch.org/docs/stable/optim.html#module-torch.optim) optimizer before fitting the model.
```
show_doc(Learner.dl)
show_doc(Recorder, title_level=2)
```
A [`Learner`](/basic_train.html#Learner) creates a [`Recorder`](/basic_train.html#Recorder) object automatically - you do not need to explicitly pass it to `callback_fns` - because other callbacks rely on it being available. It stores the smoothed loss, hyperparameter values, and metrics for each batch, and provides plotting methods for each. Note that [`Learner`](/basic_train.html#Learner) automatically sets an attribute with the snake-cased name of each callback, so you can access this through `Learner.recorder`, as shown below.
### Plotting methods
```
show_doc(Recorder.plot)
```
This is mainly used with the learning rate finder, since it shows a scatterplot of loss vs learning rate.
```
learn = create_cnn(data, models.resnet18, metrics=accuracy)
learn.lr_find()
learn.recorder.plot()
show_doc(Recorder.plot_losses)
```
Note that validation losses are only calculated once per epoch, whereas training losses are calculated after every batch.
```
learn.fit_one_cycle(2)
learn.recorder.plot_losses()
show_doc(Recorder.plot_lr)
learn.recorder.plot_lr(show_moms=True)
show_doc(Recorder.plot_metrics)
```
Note that metrics are only collected at the end of each epoch, so you'll need to train at least two epochs to have anything to show here.
```
learn.recorder.plot_metrics()
```
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
```
show_doc(Recorder.on_backward_begin)
show_doc(Recorder.on_batch_begin)
show_doc(Recorder.on_epoch_end)
show_doc(Recorder.on_train_begin)
```
### Inner functions
The following functions are used along the way by the [`Recorder`](/basic_train.html#Recorder) or can be called by other callbacks.
```
show_doc(Recorder.add_metrics)
show_doc(Recorder.add_metric_names)
show_doc(Recorder.format_stats)
```
## Module functions
Generally you'll want to use a [`Learner`](/basic_train.html#Learner) to train your model, since they provide a lot of functionality and make things easier. However, for ultimate flexibility, you can call the same underlying functions that [`Learner`](/basic_train.html#Learner) calls behind the scenes:
```
show_doc(fit)
```
Note that you have to create the `Optimizer` yourself if you call this function, whereas [`Learn.fit`](/basic_train.html#fit) creates it for you automatically.
```
show_doc(train_epoch)
```
You won't generally need to call this yourself - it's what [`fit`](/basic_train.html#fit) calls for each epoch.
```
show_doc(validate)
```
This is what [`fit`](/basic_train.html#fit) calls after each epoch. You can call it if you want to run inference on a [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader) manually.
```
show_doc(get_preds)
show_doc(loss_batch)
```
You won't generally need to call this yourself - it's what [`fit`](/basic_train.html#fit) and [`validate`](/basic_train.html#validate) call for each batch. It only does a backward pass if you set `opt`.
## Other classes
```
show_doc(LearnerCallback, title_level=3)
show_doc(RecordOnCPU, title_level=3)
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(Learner.tta_only)
show_doc(Learner.TTA)
show_doc(RecordOnCPU.on_batch_begin)
```
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.866302 | null | null | null | null |
|
<small><small><i>
All the IPython Notebooks in this **Python Examples** series by Dr. Milaan Parmar are available @ **[GitHub](https://github.com/milaan9/90_Python_Examples)**
</i></small></small>
# Python Program to Make a Simple Calculator
In this example you will learn to create a simple calculator that can add, subtract, multiply or divide depending upon the input from the user.
To understand this example, you should have the knowledge of the following **[Python programming](https://github.com/milaan9/01_Python_Introduction/blob/main/000_Intro_to_Python.ipynb)** topics:
* **[Python Functions](https://github.com/milaan9/04_Python_Functions/blob/main/001_Python_Functions.ipynb)**
* **[Python Function Arguments](https://github.com/milaan9/04_Python_Functions/blob/main/004_Python_Function_Arguments.ipynb)**
* **[Python User-defined Functions](https://github.com/milaan9/04_Python_Functions/blob/main/Python_User_defined_Functions.ipynb)**
* **[Python if-elif-else Statement](https://github.com/milaan9/03_Python_Flow_Control/blob/main/003_Python_if_elif_else_statement%20.ipynb)**
```
# Example 1: Simple Calculator by Using Functions
# This function adds two numbers
def add(x, y):
return x + y
# This function subtracts two numbers
def subtract(x, y):
return x - y
# This function multiplies two numbers
def multiply(x, y):
return x * y
# This function divides two numbers
def divide(x, y):
return x / y
print("Select operation.")
print("1.Add")
print("2.Subtract")
print("3.Multiply")
print("4.Divide")
while True:
# Take input from the user
choice = input("Enter choice(1/2/3/4): ")
# Check if choice is one of the four options
if choice in ('1', '2', '3', '4'):
num1 = float(input("Enter first number: "))
num2 = float(input("Enter second number: "))
if choice == '1':
print(num1, "+", num2, "=", add(num1, num2))
elif choice == '2':
print(num1, "-", num2, "=", subtract(num1, num2))
elif choice == '3':
print(num1, "*", num2, "=", multiply(num1, num2))
elif choice == '4':
print(num1, "/", num2, "=", divide(num1, num2))
break
else:
print("Invalid Input")
'''
>>Output/Runtime Test Cases:
Select operation.
1.Add
2.Subtract
3.Multiply
4.Divide
Enter choice(1/2/3/4): 3
Enter first number: 3
Enter second number: 9
3.0 * 9.0 = 27.0
'''
```
**Explanation:**
In this program, we ask the user to choose an operation. Options **`1`**, **`2`**, **`3`**, and **`4`** are valid. If any other input is given, **`Invalid Input`** is displayed and the loop continues until a valid option is selected.
Two numbers are taken and an **`if-elif-else`** branching is used to execute a particular section. User-defined functions **`add()`**, **`subtract()`**, **`multiply()`** and **`divide()`** evaluate respective operations and display the output.
| true |
code
| 0.519704 | null | null | null | null |
|
```
# default_exp inference
```
# Inference
> This contains the code required for inference.
```
# export
from fastai.learner import load_learner
from fastai.callback.core import GatherPredsCallback
from fastai.learner import Learner
from fastcore.basics import patch
from fastcore.meta import delegates
#export
@patch
def get_X_preds(self: Learner, X, y=None, bs=64, with_input=False, with_decoded=True, with_loss=False):
if with_loss and y is None:
print("cannot find loss as y=None")
with_loss = False
dl = self.dls.valid.new_dl(X, y=y)
if bs: setattr(dl, "bs", bs)
else: assert dl.bs, "you need to pass a bs != 0"
output = list(self.get_preds(dl=dl, with_input=with_input, with_decoded=with_decoded, with_loss=with_loss, reorder=False))
if with_decoded and len(self.dls.tls) >= 2 and hasattr(self.dls.tls[-1], "tfms") and hasattr(self.dls.tls[-1].tfms, "decodes"):
output[2 + with_input] = self.dls.tls[-1].tfms.decode(output[2 + with_input])
return tuple(output)
```
Get the predictions and targets, optionally with_input and with_loss.
with_decoded will also return the decoded predictions (it reverses the transforms applied).
The order of the output is the following:
- input (optional): if with_input is True
- **probabiblities** (for classification) or **predictions** (for regression)
- **target**: if y is provided. Otherwise None.
- **predictions**: predicted labels. Predictions will be decoded if with_decoded=True.
- loss (optional): if with_loss is set to True and y is not None.
```
from tsai.data.external import get_UCR_data
dsid = 'OliveOil'
X, y, splits = get_UCR_data(dsid, split_data=False)
X_test = X[splits[1]]
y_test = y[splits[1]]
learn = load_learner("./models/test.pth")
```
⚠️ Warning: load_learner (from fastai) requires all your custom code be in the exact same place as when exporting your Learner (the main script, or the module you imported it from).
```
test_probas, test_targets, test_preds = learn.get_X_preds(X_test, with_decoded=True)
test_probas, test_targets, test_preds
test_probas2, test_targets2, test_preds2 = learn.get_X_preds(X_test, y_test, with_decoded=True) # This test fails on torch==1.10.0
test_probas2, test_targets2, test_preds2
test_probas3, test_targets3, test_preds3, test_losses3 = learn.get_X_preds(X_test, y_test, with_loss=True, with_decoded=True)
test_probas3, test_targets3, test_preds3, test_losses3
from fastcore.test import test_eq
test_eq(test_probas, test_probas2)
test_eq(test_preds, test_preds2)
test_eq(test_probas, test_probas3)
test_eq(test_preds, test_preds3)
#hide
from tsai.imports import create_scripts
from tsai.export import get_nb_name
nb_name = get_nb_name()
create_scripts(nb_name);
```
| true |
code
| 0.498474 | null | null | null | null |
|
# [deplacy](https://koichiyasuoka.github.io/deplacy/)을 사용한 문법 분석
## [Camphr-Udify](https://camphr.readthedocs.io/en/latest/notes/udify.html)로 분석
```
!pip install deplacy camphr 'unofficial-udify>=0.3.0' en-udify@https://github.com/PKSHATechnology-Research/camphr_models/releases/download/0.7.0/en_udify-0.7.tar.gz
import pkg_resources,imp
imp.reload(pkg_resources)
import spacy
nlp=spacy.load("en_udify")
doc=nlp("홍시 맛이 나서 홍시라 생각한다.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## [UDPipe 2](http://ufal.mff.cuni.cz/udpipe/2)로 분석
```
!pip install deplacy
def nlp(t):
import urllib.request,urllib.parse,json
with urllib.request.urlopen("https://lindat.mff.cuni.cz/services/udpipe/api/process?model=ko_gsd&tokenizer&tagger&parser&data="+urllib.parse.quote(t)) as r:
return json.loads(r.read())["result"]
doc=nlp("홍시 맛이 나서 홍시라 생각한다.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## [Trankit](https://github.com/nlp-uoregon/trankit)로 분석
```
!pip install deplacy trankit transformers
import trankit
nlp=trankit.Pipeline("korean")
doc=nlp("홍시 맛이 나서 홍시라 생각한다.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## [spaCy-jPTDP](https://github.com/KoichiYasuoka/spaCy-jPTDP)로 분석
```
!pip install deplacy spacy_jptdp
import spacy_jptdp
nlp=spacy_jptdp.load("ko_gsd")
doc=nlp("홍시 맛이 나서 홍시라 생각한다.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## [Turku-neural-parser-pipeline](https://turkunlp.org/Turku-neural-parser-pipeline/)로 분석
```
!pip install deplacy ufal.udpipe configargparse 'tensorflow<2' torch==0.4.1 torchtext==0.3.1 torchvision==0.2.1
!test -d Turku-neural-parser-pipeline || git clone --depth=1 https://github.com/TurkuNLP/Turku-neural-parser-pipeline
!cd Turku-neural-parser-pipeline && git submodule update --init --recursive && test -d models_ko_gsd || python fetch_models.py ko_gsd
import sys,subprocess
nlp=lambda t:subprocess.run([sys.executable,"full_pipeline_stream.py","--gpu","-1","--conf","models_ko_gsd/pipelines.yaml"],cwd="Turku-neural-parser-pipeline",input=t,encoding="utf-8",stdout=subprocess.PIPE).stdout
doc=nlp("홍시 맛이 나서 홍시라 생각한다.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## [spacy-udpipe](https://github.com/TakeLab/spacy-udpipe)로 분석
```
!pip install deplacy spacy-udpipe
import spacy_udpipe
spacy_udpipe.download("ko-gsd")
nlp=spacy_udpipe.load("ko-gsd")
doc=nlp("홍시 맛이 나서 홍시라 생각한다.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## [NLP-Cube](https://github.com/Adobe/NLP-Cube)로 분석
```
!pip install deplacy nlpcube
from cube.api import Cube
nlp=Cube()
nlp.load("ko")
doc=nlp("홍시 맛이 나서 홍시라 생각한다.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## [spaCy-COMBO](https://github.com/KoichiYasuoka/spaCy-COMBO)로 분석
```
!pip install deplacy spacy_combo
import spacy_combo
nlp=spacy_combo.load("ko_gsd")
doc=nlp("홍시 맛이 나서 홍시라 생각한다.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## [Stanza](https://stanfordnlp.github.io/stanza)로 분석
```
!pip install deplacy stanza
import stanza
stanza.download("ko")
nlp=stanza.Pipeline("ko")
doc=nlp("홍시 맛이 나서 홍시라 생각한다.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
| true |
code
| 0.401365 | null | null | null | null |
|
# Lightweight Networks and MobileNet
We have seen that complex networks require significant computational resources, such as GPU, for training, and also for fast inference. However, it turns out that a model with significanly smaller number of parameters in most cases can still be trained to perform resonably well. In other words, increase in the model complexity typically results in small (non-proportional) increase in the model performance.
We have observed this in the beginning of the module when training MNIST digit classification. The accuracy of simple dense model was not significanly worse than that of a powerful CNN. Increasing the number of CNN layers and/or number of neurons in the classifier allowed us to gain a few percents of accuracy at most.
This leads us to the idea that we can experiment with Lightweight network architectures in order to train faster models. This is especially important if we want to be able to execute our models on mobile devices.
This module will rely on the Cats and Dogs dataset that we have downloaded in the previous unit. First we will make sure that the dataset is available.
```
import torch
import torch.nn as nn
import torchvision
import matplotlib.pyplot as plt
from torchinfo import summary
import os
from pytorchcv import train, display_dataset, train_long, load_cats_dogs_dataset, validate, common_transform
if not os.path.exists('data/kagglecatsanddogs_3367a.zip'):
!wget -P data -q http://download.microsoft.com/download/3/E/1/3E1C3F21-ECDB-4869-8368-6DEBA77B919F/kagglecatsanddogs_3367a.zip
dataset, train_loader, test_loader = load_cats_dogs_dataset()
```
## MobileNet
In the previous unit, we have seen **ResNet** architecture for image classification. More lightweight analog of ResNet is **MobileNet**, which uses so-called *Inverted Residual Blocks*. Let's load pre-trained mobilenet and see how it works:
```
model = torch.hub.load('pytorch/vision:v0.6.0', 'mobilenet_v2', pretrained=True)
model.eval()
print(model)
```
Let's apply the model to our dataset and make sure that it works.
```
sample_image = dataset[0][0].unsqueeze(0)
res = model(sample_image)
print(res[0].argmax())
```
**Exercise:** Compare the number of parameters in MobileNet and full-scale ResNet model.
## Using MobileNet for Transfer Learning
Now let's perform the same transfer learning process as in previous unit, but using MobileNet. First of all, let's freeze all parameters of the model:
```
for x in model.parameters():
x.requires_grad = False
```
Then, replace the final classifier. We also transfer the model to our default training device (GPU or CPU):
```
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model.classifier = nn.Linear(1280,2)
model = model.to(device)
summary(model,input_size=(1,3,244,244))
```
Now let's do the actual training:
```
train_long(model,train_loader,test_loader,loss_fn=torch.nn.CrossEntropyLoss(),epochs=1,print_freq=90)
```
## Takeaway
Notice that MobileNet results in almost the same accuracy as VGG-16, and just slightly lower than full-scale ResNet.
The main advantage of small models, such as MobileNet or ResNet-18 is that they can be used on mobile devices. [Here](https://pytorch.org/mobile/android/) is official example of using ResNet-18 on Android device, and [here](https://heartbeat.fritz.ai/pytorch-mobile-image-classification-on-android-5c0cfb774c5b) is similar example using MobileNet.
| true |
code
| 0.671928 | null | null | null | null |
|
# AutoEncoders
---
The following code was created by Aymeric Damien. You can find some of his code in <a href="https://github.com/aymericdamien">here</a>. We made some modifications for us to import the datasets to Jupyter Notebooks.
Let's call our imports and make the MNIST data available to use.
```
#from __future__ import division, print_function, absolute_import
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
```
Now, let's give the parameters that are going to be used by our NN.
```
learning_rate = 0.01
training_epochs = 20
batch_size = 256
display_step = 1
examples_to_show = 10
# Network Parameters
n_hidden_1 = 256 # 1st layer num features
n_hidden_2 = 128 # 2nd layer num features
n_input = 784 # MNIST data input (img shape: 28*28)
# tf Graph input (only pictures)
X = tf.placeholder("float", [None, n_input])
weights = {
'encoder_h1': tf.Variable(tf.random_normal([n_input, n_hidden_1])),
'encoder_h2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])),
'decoder_h1': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_1])),
'decoder_h2': tf.Variable(tf.random_normal([n_hidden_1, n_input])),
}
biases = {
'encoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
'encoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
'decoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
'decoder_b2': tf.Variable(tf.random_normal([n_input])),
}
```
Now we need to create our encoder. For this, we are going to use sigmoidal functions. Sigmoidal functions delivers great results with this type of network. This is due to having a good derivative that is well-suited to backpropagation. We can create our encoder using the sigmoidal function like this:
```
# Building the encoder
def encoder(x):
# Encoder first layer with sigmoid activation #1
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['encoder_h1']), biases['encoder_b1']))
# Encoder second layer with sigmoid activation #2
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['encoder_h2']), biases['encoder_b2']))
return layer_2
```
And the decoder:
You can see that the layer_1 in the encoder is the layer_2 in the decoder and vice-versa.
```
# Building the decoder
def decoder(x):
# Decoder first layer with sigmoid activation #1
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['decoder_h1']),biases['decoder_b1']))
# Decoder second layer with sigmoid activation #2
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['decoder_h2']), biases['decoder_b2']))
return layer_2
```
Let's construct our model.
In the variable <code>cost</code> we have the loss function and in the <code>optimizer</code> variable we have our gradient used for backpropagation.
```
# Construct model
encoder_op = encoder(X)
decoder_op = decoder(encoder_op)
# Reconstructed Images
y_pred = decoder_op
# Targets (Labels) are the input data.
y_true = X
# Define loss and optimizer, minimize the squared error
cost = tf.reduce_mean(tf.pow(y_true - y_pred, 2))
optimizer = tf.train.RMSPropOptimizer(learning_rate).minimize(cost)
# Initializing the variables
init = tf.global_variables_initializer()
```
For training we will run for 20 epochs.
```
# Launch the graph
# Using InteractiveSession (more convenient while using Notebooks)
sess = tf.InteractiveSession()
sess.run(init)
total_batch = int(mnist.train.num_examples / batch_size)
# Training cycle
for epoch in range(training_epochs):
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# Run optimization op (backprop) and cost op (to get loss value)
_, c = sess.run([optimizer, cost], feed_dict={X: batch_xs})
# Display logs per epoch step
if epoch % display_step == 0:
print("Epoch:", '%04d' % (epoch+1),
"cost=", "{:.9f}".format(c))
print("Optimization Finished!")
```
Now, let's apply encoder and decoder for our tests.
```
# Applying encode and decode over test set
encode_decode = sess.run(
y_pred, feed_dict={X: mnist.test.images[:examples_to_show]})
```
Let's simply visualize our graphs!
```
# Compare original images with their reconstructions
f, a = plt.subplots(2, 10, figsize=(10, 2))
for i in range(examples_to_show):
a[0][i].imshow(np.reshape(mnist.test.images[i], (28, 28)))
a[1][i].imshow(np.reshape(encode_decode[i], (28, 28)))
```
As you can see, the reconstructions were successful. It can be seen that some noise were added to the image.
## Thanks for reading :)
Created by [Saeed Aghabozorgi](https://www.linkedin.com/in/saeedaghabozorgi/) and modified by [Tarun Kamboj](https://www.linkedin.com/in/kambojtarun/).
| true |
code
| 0.745552 | null | null | null | null |
|
# Torch Hub Detection Inference Tutorial
In this tutorial you'll learn:
- how to load a pretrained detection model using Torch Hub
- run inference to detect actions in a demo video
## NOTE:
At the moment tutorial only works if ran on local clone from the directory `pytorchvideo/tutorials/video_detection_example`
### Install and Import modules
If `torch`, `torchvision`, `cv2` and `pytorchvideo` are not installed, run the following cell:
```
try:
import torch
except ModuleNotFoundError:
!pip install torch torchvision
import os
import sys
import torch
try:
import cv2
except ModuleNotFoundError:
!pip install opencv-python
if torch.__version__=='1.6.0+cu101' and sys.platform.startswith('linux'):
!pip install pytorchvideo
else:
need_pytorchvideo=False
try:
# Running notebook locally
import pytorchvideo
except ModuleNotFoundError:
need_pytorchvideo=True
if need_pytorchvideo:
# Install from GitHub
!pip install "git+https://github.com/facebookresearch/pytorchvideo.git"
from functools import partial
import numpy as np
import cv2
import torch
import detectron2
from detectron2.config import get_cfg
from detectron2 import model_zoo
from detectron2.engine import DefaultPredictor
import pytorchvideo
from pytorchvideo.transforms.functional import (
uniform_temporal_subsample,
short_side_scale_with_boxes,
clip_boxes_to_image,
)
from torchvision.transforms._functional_video import normalize
from pytorchvideo.data.ava import AvaLabeledVideoFramePaths
from pytorchvideo.models.hub import slow_r50_detection # Another option is slowfast_r50_detection
from visualization import VideoVisualizer
```
## Load Model using Torch Hub API
PyTorchVideo provides several pretrained models through Torch Hub. Available models are described in [model zoo documentation.](https://github.com/facebookresearch/pytorchvideo/blob/main/docs/source/model_zoo.md)
Here we are selecting the slow_r50_detection model which was trained using a 4x16 setting on the Kinetics 400 dataset and
fine tuned on AVA V2.2 actions dataset.
NOTE: to run on GPU in Google Colab, in the menu bar selet: Runtime -> Change runtime type -> Harware Accelerator -> GPU
```
device = 'cuda' # or 'cpu'
video_model = slow_r50_detection(True) # Another option is slowfast_r50_detection
video_model = video_model.eval().to(device)
```
## Load an off-the-shelf Detectron2 object detector
We use the object detector to detect bounding boxes for the people.
These bounding boxes later feed into our video action detection model.
For more details, please refer to the Detectron2's object detection tutorials.
To install Detectron2, please follow the instructions mentioned [here](https://github.com/facebookresearch/detectron2/blob/main/INSTALL.md)
```
cfg = get_cfg()
cfg.merge_from_file(model_zoo.get_config_file("COCO-Detection/faster_rcnn_R_50_FPN_3x.yaml"))
cfg.MODEL.ROI_HEADS.SCORE_THRESH_TEST = 0.55 # set threshold for this model
cfg.MODEL.WEIGHTS = model_zoo.get_checkpoint_url("COCO-Detection/faster_rcnn_R_50_FPN_3x.yaml")
predictor = DefaultPredictor(cfg)
# This method takes in an image and generates the bounding boxes for people in the image.
def get_person_bboxes(inp_img, predictor):
predictions = predictor(inp_img.cpu().detach().numpy())['instances'].to('cpu')
boxes = predictions.pred_boxes if predictions.has("pred_boxes") else None
scores = predictions.scores if predictions.has("scores") else None
classes = np.array(predictions.pred_classes.tolist() if predictions.has("pred_classes") else None)
predicted_boxes = boxes[np.logical_and(classes==0, scores>0.75 )].tensor.cpu() # only person
return predicted_boxes
```
## Define the transformations for the input required by the model
Before passing the video and bounding boxes into the model we need to apply some input transforms and sample a clip of the correct frame rate in the clip.
Here, below we define a method that can pre-process the clip and bounding boxes. It generates inputs accordingly for both Slow (Resnet) and SlowFast models depending on the parameterization of the variable `slow_fast_alpha`.
```
def ava_inference_transform(
clip,
boxes,
num_frames = 4, #if using slowfast_r50_detection, change this to 32
crop_size = 256,
data_mean = [0.45, 0.45, 0.45],
data_std = [0.225, 0.225, 0.225],
slow_fast_alpha = None, #if using slowfast_r50_detection, change this to 4
):
boxes = np.array(boxes)
ori_boxes = boxes.copy()
# Image [0, 255] -> [0, 1].
clip = uniform_temporal_subsample(clip, num_frames)
clip = clip.float()
clip = clip / 255.0
height, width = clip.shape[2], clip.shape[3]
# The format of boxes is [x1, y1, x2, y2]. The input boxes are in the
# range of [0, width] for x and [0,height] for y
boxes = clip_boxes_to_image(boxes, height, width)
# Resize short side to crop_size. Non-local and STRG uses 256.
clip, boxes = short_side_scale_with_boxes(
clip,
size=crop_size,
boxes=boxes,
)
# Normalize images by mean and std.
clip = normalize(
clip,
np.array(data_mean, dtype=np.float32),
np.array(data_std, dtype=np.float32),
)
boxes = clip_boxes_to_image(
boxes, clip.shape[2], clip.shape[3]
)
# Incase of slowfast, generate both pathways
if slow_fast_alpha is not None:
fast_pathway = clip
# Perform temporal sampling from the fast pathway.
slow_pathway = torch.index_select(
clip,
1,
torch.linspace(
0, clip.shape[1] - 1, clip.shape[1] // slow_fast_alpha
).long(),
)
clip = [slow_pathway, fast_pathway]
return clip, torch.from_numpy(boxes), ori_boxes
```
## Setup
Download the id to label mapping for the AVA V2.2 dataset on which the Torch Hub models were finetuned.
This will be used to get the category label names from the predicted class ids.
Create a visualizer to visualize and plot the results(labels + bounding boxes).
```
!wget https://dl.fbaipublicfiles.com/pytorchvideo/data/class_names/ava_action_list.pbtxt
# Create an id to label name mapping
label_map, allowed_class_ids = AvaLabeledVideoFramePaths.read_label_map('ava_action_list.pbtxt')
# Create a video visualizer that can plot bounding boxes and visualize actions on bboxes.
video_visualizer = VideoVisualizer(81, label_map, top_k=3, mode="thres",thres=0.5)
```
## Load an example video
We get an opensourced video off the web from WikiMedia.
```
!wget https://dl.fbaipublicfiles.com/pytorchvideo/projects/theatre.webm
# Load the video
encoded_vid = pytorchvideo.data.encoded_video.EncodedVideo.from_path('theatre.webm')
print('Completed loading encoded video.')
```
## Generate bounding boxes and action predictions for a 10 second clip in the video.
```
# Video predictions are generated at an internal of 1 sec from 90 seconds to 100 seconds in the video.
time_stamp_range = range(90,100) # time stamps in video for which clip is sampled.
clip_duration = 1.0 # Duration of clip used for each inference step.
gif_imgs = []
for time_stamp in time_stamp_range:
print("Generating predictions for time stamp: {} sec".format(time_stamp))
# Generate clip around the designated time stamps
inp_imgs = encoded_vid.get_clip(
time_stamp - clip_duration/2.0, # start second
time_stamp + clip_duration/2.0 # end second
)
inp_imgs = inp_imgs['video']
# Generate people bbox predictions using Detectron2's off the self pre-trained predictor
# We use the the middle image in each clip to generate the bounding boxes.
inp_img = inp_imgs[:,inp_imgs.shape[1]//2,:,:]
inp_img = inp_img.permute(1,2,0)
# Predicted boxes are of the form List[(x_1, y_1, x_2, y_2)]
predicted_boxes = get_person_bboxes(inp_img, predictor)
if len(predicted_boxes) == 0:
print("Skipping clip no frames detected at time stamp: ", time_stamp)
continue
# Preprocess clip and bounding boxes for video action recognition.
inputs, inp_boxes, _ = ava_inference_transform(inp_imgs, predicted_boxes.numpy())
# Prepend data sample id for each bounding box.
# For more details refere to the RoIAlign in Detectron2
inp_boxes = torch.cat([torch.zeros(inp_boxes.shape[0],1), inp_boxes], dim=1)
# Generate actions predictions for the bounding boxes in the clip.
# The model here takes in the pre-processed video clip and the detected bounding boxes.
if isinstance(inputs, list):
inputs = [inp.unsqueeze(0).to(device) for inp in inputs]
else:
inputs = inputs.unsqueeze(0).to(device)
preds = video_model(inputs, inp_boxes.to(device))
preds= preds.to('cpu')
# The model is trained on AVA and AVA labels are 1 indexed so, prepend 0 to convert to 0 index.
preds = torch.cat([torch.zeros(preds.shape[0],1), preds], dim=1)
# Plot predictions on the video and save for later visualization.
inp_imgs = inp_imgs.permute(1,2,3,0)
inp_imgs = inp_imgs/255.0
out_img_pred = video_visualizer.draw_clip_range(inp_imgs, preds, predicted_boxes)
gif_imgs += out_img_pred
print("Finished generating predictions.")
```
## Save predictions as video
The generated video consists of bounding boxes with predicted actions for each bounding box.
```
height, width = gif_imgs[0].shape[0], gif_imgs[0].shape[1]
vide_save_path = 'output_detections.mp4'
video = cv2.VideoWriter(vide_save_path,cv2.VideoWriter_fourcc(*'DIVX'), 7, (width,height))
for image in gif_imgs:
img = (255*image).astype(np.uint8)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
video.write(img)
video.release()
print('Predictions are saved to the video file: ', vide_save_path)
```
| true |
code
| 0.584686 | null | null | null | null |
|
# Generador Unix
Utilizando el generador UNIX de números aleatorios, pero con los coeficientes del generador Visual Basic, programe una serie de 60 números aleatorios en hoja de cálculo, verificando que, a igual semilla corresponde igual serie.
Utilice como “Blanco” una serie del mismo tamaño generada con una macro en Visual Basic for Apps con la misma semilla (NOTA: las series no darán los mismos valores, aunque usen la misma semilla porque los algoritmos son diferentes)
- 1) Demuestre que con semillas aleatorias esa serie no se repite.
- 2) Utilizando la prueba de Chi cuadrado demuestre que se trata de una serie uniforme
- 3) Haga las dos pruebas anteriores para la serie “VBA”
- 4) Conclusiones
_Obtener conclusiones, por ejemplo, calcular el promedio y la desviación estándar de ambas
muestras y hacer análisis de varianza para determinar si las medias son iguales o no._
Datos para construir el generador:
- m = 2^24
- a = 1140671485
- b = 12820163
```
import numpy as np
from scipy.stats import chi2
from random import randint
import matplotlib.pyplot as plt
from scipy.stats import norm
np.set_printoptions(formatter={'float': lambda x: "{0:0.20f}".format(x)})
a = 1140671485
b = 12820163
m = 2**24
def semillar(X,tantos):
semillas = np.random.rand(X, tantos)
semillas.dtype = np.float64
r = np.zeros((X, tantos))
r.dtype = np.float64
for j in range(0,tantos):
oldSeed = np.random.randint(0,m)
for i in range(0,X):
newSeed = (a*oldSeed+b) % m
oldSeed = newSeed
semillas[i,j] = newSeed
r[i,j] = semillas[i,j] / m
return r
def agrupar(N,Q):
g = np.zeros((N,Q.shape[1]))
incremento = 1.0/np.float64(N)
for i in range(0,ensayos):
for j in range(0,serie):
aux = 0
for k in range(0,N):
aux += incremento
if Q[j,i] <= aux and Q[j,i] > (aux-incremento):
g[k,i] += 1
return g
def chiCuadrado(r):
chi = np.zeros((divIn,r.shape[1]))
FE = (serie/np.float64(divIn))
for i in range(0,r.shape[1]):
for j in range(0,divIn):
chi[j,i] = ((FE-r[j,i])**2)/FE
return chi.sum(0)
```
# El programa
```
serie = 60
ensayos = 5000
resultados = semillar(serie,ensayos)
' divIn = np.int(np.sqrt(serie).round()) '
divIn = 10
grupos = agrupar(divIn,resultados)
resultados.shape
```
# Pruebas
## Medias
```
av = resultados.mean(0).mean()
print 'Media:',av
print 'Error:', (0.5-av)
```
## Evaluar Varianza y Desviacion
```
print 'Varianza media:',resultados.var(0).mean()
print 'Desviacion media:',resultados.std(0).mean()
```
## Evaluar Chi
La prueba Chi-Cuadrada en lugar de medir la diferencia de cada punto entre la muestra y la desviación verdadera, checa la desviación del valor esperado.
n
X2 =∑ (Oi−Ei)^2/Ei
i
Donde n es el número de intervalos de clase (ejemplo: Oi es el número observado en la clase i, y Ei es el número esperado en cada clase i , y n es el número de clases. Para una distribución uniforme, Ei , el número en cada clase esta dado por;
* Ei = N / n
_Para clases igualmente espaciadas, donde N es el número total de observaciones. Puede ser mostrado que la distribución de la muestra Chi-Cuadrada esta aproximadamente a la distribución Chi-Cuadrada con n-1 grados de libertad._
```
p=0.95
gradosDeLibertad = divIn-1
print 'Chi2 Observado | Inverso de Chi2'
print ' {0:0.05f} | {1:0.09f} '.format(chiCuadrado(grupos).mean(),chi2.ppf(p, gradosDeLibertad))
print'\nConfianza(%):',p
print 'Grados de Libertad:',gradosDeLibertad
```
**Debido a que X2calculada < que el valor de X2(0.95,9) de la tabla, la hipótesis Nula de que no existe diferencia entre la distribución de la muestra y la distribución uniforme se Acepta.**
_ el estadístico chi-cuadrado cuantifica qué tanto varía la distribución observada de conteos con respecto a la distribución hipotética._
Chi Inversa me dice para una distribución chi-cuadrado de k grados de libertad, cual es el valor de x que deja a su izquierda una probabilidad p.
```
x = np.linspace(0, serie, serie)
obtenido = resultados[:,np.random.randint(0,ensayos)]*serie
fig,ax = plt.subplots(1,1)
obtenido.sort()
linestyles = ['--', '-.']
deg_of_freedom = divIn-1
comparar = [obtenido,x]
for comp, ls in zip(comparar, linestyles):
ax.plot(comp, chi2.pdf(comp, deg_of_freedom), linestyle=ls, label=r'$df=%i$' % deg_of_freedom)
plt.xlim(0, serie)
plt.ylim(0, 0.15)
plt.axvline(x=chi2.ppf(p, gradosDeLibertad),linestyle='-.',color='orange')
plt.xlabel('$\chi^2$')
plt.ylabel(r'$f(\chi^2)$')
plt.title(r'$\chi^2\ \mathrm{Distribution}$')
plt.legend()
plt.show()
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
mediaDeGrupos = grupos[:,:].mean(axis=1)
plt.hist(resultados[:,np.random.randint(0,ensayos)])
mm = serie*ensayos
plt.plot(np.repeat(6,serie), linewidth=2)
plt.xlabel('Cantidad')
plt.ylabel('Grupos')
plt.title('Histograma')
plt.axis([0, 1, 0, 12])
plt.grid(True)
plt.show()
plt.plot(mediaDeGrupos,'ro')
plt.plot(np.repeat(6,divIn), linewidth=2, color='red')
plt.show()
```
## EXPORTAR
```
import pandas as pd
df = pd.DataFrame(resultados)
df.to_csv("exportarPython.csv",sep=';',header=None)
```
| true |
code
| 0.304972 | null | null | null | null |
|
## 2. Multi Layer Perceptron
### 1) import modules
```
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
from modules import multi_layer_perceptron
```
### 2) define placeholder for INPUT & LABELS
```
INPUT = tf.placeholder(tf.float32, [None, 28*28])
LABELS = tf.placeholder(tf.int32, [None])
```
### 3) define mlp model with multi_layer_perceptron function
<img src="./images/mlp.png" alt="slp model" width=1000 align="left"/>
```
# def multi_layer_perceptron(input=None, output_dim=None):
# input_dim = input.shape[1].value
# # your code start here
# return output
prediction = multi_layer_perceptron(INPUT, output_dim=10)
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(
labels=LABELS, logits=prediction
)
cost = tf.reduce_mean(cross_entropy)
optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
```
### 4) load data
```
mnist = input_data.read_data_sets("./data/", one_hot=True)
```
### 5) start training
#### - set training parameters : batch size, learning rate, total loop
```
BATCH_SIZE = 100
LEARNING_RATE = 0.01
TOTAL_LOOP = 10000
```
- arrA = [[0,0,0,0,1],[0,1,0,0,0]]
- np.where(arrA) => ([0,1], [4,1])
- ref) https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.where.html?highlight=numpy%20where#numpy.where
```
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for loop in range(1, TOTAL_LOOP + 1):
train_images, train_labels = mnist.train \
.next_batch(BATCH_SIZE)
train_labels = np.where(train_labels)[1]
_, loss = sess.run(
[optimizer, cost],
feed_dict={
INPUT: train_images,
LABELS: train_labels
}
)
if loop % 500 == 0 or loop == 0:
print("loop: %05d,"%(loop), "loss:", loss)
print("Training Finished! (loss : " + str(loss) + ")")
```
### 6) test performance
- test image shape: (100, 784)
- test label shape: (100, 10)
- arrB = [[0, 1, 2],[3, 4, 5]]
- np.argmax(arrB) => 5
- np.argmax(arrB, axis=0) => [1, 1, 1]
- np.argmax(arrB, axis=1) => [2, 2]
- ref) https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.argmax.html
```
TEST_SAMPLE_SIZE = 100
TEST_NUMBER = 5
accuracy_save = dict()
for number in range(1, 1+TEST_NUMBER):
test_images, test_labels = mnist.test \
.next_batch(TEST_SAMPLE_SIZE)
pred_result = sess.run(
prediction,
feed_dict={INPUTtest performance: test_images}
)
pred_number = np.argmax(pred_result, axis=1) # 100x1
label_number = np.where(test_labels)[1] #100x1
accuracy_save[number] = np.sum(pred_number == label_number)
print("Accuracy:", accuracy_save)
print("Total mean Accuracy:",
np.mean(list(accuracy_save.values()))
)
```
| true |
code
| 0.665383 | null | null | null | null |
|
# Chapter 8
## Question 10
Using boosting to predict `Salary` in the `Hitters` data set
```
import statsmodels.api as sm
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import sklearn.model_selection
import sklearn.ensemble
import sklearn.tree
import sklearn.metrics
import sklearn.neighbors
from collections import namedtuple
from tqdm import tqdm_notebook
sns.set(style="whitegrid")
hitters = sm.datasets.get_rdataset("Hitters", "ISLR").data
hitters.head()
print(hitters.dtypes)
for column in ["League", "Division", "NewLeague"]:
print(hitters[column].value_counts())
print()
```
### (a) Remove the observations for whom the salary information is unknown, and then log-transform the salaries
```
hitters = hitters.dropna(subset=["Salary"])
hitters["LogSalary"] = np.log(hitters["Salary"])
```
### (b) Creating a training set consisting of the first 200 observations, and a test set consisting of the remaining observations
```
# I'm not doing this, I'll use test_train_split instead
X = hitters.drop(columns=["Salary", "LogSalary"])
y = hitters.LogSalary
# Encode categoricals
for col in ["League", "Division", "NewLeague"]:
X = pd.concat([X, pd.get_dummies(X[col], prefix=col, drop_first=True)],axis=1).drop(columns=col)
X_train, X_test, y_train, y_test = sklearn.model_selection.train_test_split(X, y, test_size=len(hitters)-200)
```
### (c) Perform boosting on the training set with 1,000 trees for a range of values of the shrinkage parameter $\lambda$. Produce a plot of shrinkage against training MSE.
```
DataPoint = namedtuple('DataPoint', 'shrinkage_lambda, train_mse, test_mse')
data = []
for shrinkage_lambda in tqdm_notebook(np.linspace(0.001, 3, 100)):
boost_regressor = sklearn.ensemble.AdaBoostRegressor(base_estimator=sklearn.tree.DecisionTreeRegressor(max_depth=3),
n_estimators=1000,
learning_rate=shrinkage_lambda
)
boost_regressor.fit(X_train, y_train)
y_pred_train = boost_regressor.predict(X_train)
training_mse = sklearn.metrics.mean_squared_error(y_train, y_pred_train)
y_pred_test = boost_regressor.predict(X_test)
test_mse = sklearn.metrics.mean_squared_error(y_test, y_pred_test)
data.append(DataPoint(shrinkage_lambda, training_mse, test_mse))
```
### (d) Produce a plot of shrinkage vs test set MSE
```
lambdas = [x.shrinkage_lambda for x in data]
train_mses = [x.train_mse for x in data]
test_mses = [x.test_mse for x in data]
plt.plot(lambdas, train_mses)
plt.show()
plt.plot(lambdas, test_mses)
plt.show()
```
### (e) Compare the test MSE of boosting to the test set MSE resulting from two of the regression approaches in Chapters 3 and 6
```
parameters = {'base_estimator__max_depth': range(1,4),
'n_estimators': [100,1000,10000],
'learning_rate': np.linspace(0.001,1,100)
}
tree = sklearn.tree.DecisionTreeRegressor()
boosted_regressor = sklearn.ensemble.AdaBoostRegressor(base_estimator=tree)
clf = sklearn.model_selection.GridSearchCV(boosted_regressor, parameters, n_jobs=4, cv=5)
clf.fit(X=X_train, y=y_train)
best_tree = clf.best_estimator_
print (clf.best_score_, clf.best_params_)
# Chapter 3: Linear Regression and KNN
boosted_tree_test_mse = sklearn.metrics.mean_squared_error(y_test, best_tree.predict(X_test))
linear_regression = sklearn.linear_model.LinearRegression()
linear_regression.fit(X_train,y_train)
y_pred = linear_regression.predict(X_test)
linear_regression_test_mse = sklearn.metrics.mean_squared_error(y_test, y_pred)
knn_model = sklearn.neighbors.KNeighborsRegressor(n_neighbors=5)
knn_model.fit(X_train, y_train) # reshape required to cast the training data to a 2d array
y_pred = knn_model.predict(X_test)
knn_test_mse = sklearn.metrics.mean_squared_error(y_test, y_pred)
# Chapter 6: Ridge Regression/Lasso
# Use the LassoCV
lasso_model = sklearn.linear_model.LassoLarsCV(cv=5, max_iter=1e6)
lasso_model.fit(X_train,y_train) # Don't really need to separate the data as we are using CV
y_pred = lasso_model.predict(X_test)
lasso_test_mse = sklearn.metrics.mean_squared_error(y_test, y_pred)
ridge_regression = sklearn.linear_model.RidgeCV(cv=5)
ridge_regression.fit(X_train,y_train) # Don't really need to separate the data as we are using CV
y_pred = ridge_regression.predict(X_test)
ridge_test_mse = sklearn.metrics.mean_squared_error(y_test, y_pred)
print(f"Boosting: {boosted_tree_test_mse:.2f}")
print(f"Linear Regression: {linear_regression_test_mse:.2f}")
print(f"KNN: {knn_test_mse:.2f}")
print(f"Lasso: {lasso_test_mse:.2f}")
print(f"Ridge Regression: {ridge_test_mse:.2f}")
```
### (f) Which variables appear to be the most important predictors in the boosted model?
```
def getFeatureImportance(random_forest, X):
"""Given a trained classifier, plot the feature importance"""
importances = random_forest.feature_importances_
std = np.std([tree.feature_importances_ for tree in random_forest.estimators_],
axis=0)
indices = np.argsort(importances)[::-1]
text_indices = [X.columns[i] for i in indices]
# Print the feature ranking
print("Feature ranking:")
for f in range(X.shape[1]):
print(f"{f+1}. {text_indices[f]}: {importances[indices[f]] :.2f}")
# Plot the feature importances of the forest
plt.figure()
plt.title("Feature importances")
plt.bar(range(X.shape[1]), importances[indices],
color="r", yerr=std[indices], align="center")
plt.xticks(range(X.shape[1]), text_indices, rotation=90)
plt.xlim([-1, X.shape[1]])
plt.show()
getFeatureImportance(best_tree, X)
```
### (g) Now apply bagging to the training set. What is the test set MSE for this approach?
```
# A random forest, when all predictors are consider, is equivalent to using bagging
parameters = {'max_depth': range(1,10),
'n_estimators': [100,1000,10000],
'max_leaf_nodes': [5,10,50,100,500]
}
random_forest = sklearn.ensemble.RandomForestRegressor(max_features=None)
random_forest_cv = sklearn.model_selection.GridSearchCV(random_forest, parameters, n_jobs=4, cv=5)
random_forest_cv.fit(X=X_train, y=y_train)
best_random_forest = random_forest_cv.best_estimator_
print (random_forest_cv.best_score_, random_forest_cv.best_params_)
y_pred = random_forest_cv.predict(X_test)
bagging_test_mse = sklearn.metrics.mean_squared_error(y_test, y_pred)
print(f"Bagging: {bagging_test_mse:.2f}")
```
| true |
code
| 0.652989 | null | null | null | null |
|
# Homework 07
### Preparation...
Run this code from the lecture to be ready for the exercises below!
```
import glob
import os.path
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets, linear_model, ensemble, neural_network
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
from pathlib import Path
CONFIG_FILE = '../entsoe-data.config'
if not os.path.exists(CONFIG_FILE):
download_dir = input('Path to ENTSO-E data folder: ')
if not os.path.isdir(download_dir):
raise RuntimeError(f'Invalid download_dir, please run cell again: {download_dir}')
with open(CONFIG_FILE, 'w') as f:
f.write(download_dir)
else:
with open(CONFIG_FILE) as f:
download_dir = f.read()
# Clear the output after this cell if you want to aovid having your path in the notebook (or execute it twice)!
def read_single_csv_entso_e(file):
return pd.read_csv(file, sep='\t', encoding='utf-16', parse_dates=["DateTime"])
def load_complete_entso_e_data(directory):
pattern = Path(directory) / '*.csv'
files = glob.glob(str(pattern))
if not files:
raise ValueError(f"No files found when searching in {pattern}, wrong directory?")
print(f'Concatenating {len(files)} csv files...')
each_csv_file = [read_single_csv_entso_e(file) for file in files]
data = pd.concat(each_csv_file, ignore_index=True)
data = data.sort_values(by=["AreaName", "DateTime"])
data = data.set_index("DateTime")
print("Loading done.")
return data
power_demand = load_complete_entso_e_data(download_dir)
def get_hourly_country_data(data, country):
ret_data = data[data["AreaName"] == country].interpolate()
#ret_data = ret_data.set_index("DateTime")
ret_data = ret_data.resample("1h").mean().interpolate()
return ret_data
power_demand_at_hourly = get_hourly_country_data(power_demand, "Austria")["2015-01-01":"2019-12-31"]
```
## Exercise 1
Explain the following terms:
**Input feature:** < your explanation goes here >
**Output feature:** < your explanation goes here >
**Fit a function to data:** < your explanation goes here >
**Training data:** < your explanation goes here >
**Test data:** < your explanation goes here >
## Exercise 2
In lecture07 we created a plot of the ratio of actual load and predicted load for Austria step by step (Exercise 04). Now put all of this together in one function which takes one parameter `country` as input and calculates and plots the figure of Exercise 04 for this country! The model should be trained on 2015-2019 data and then you should predict for 2020 and compare it to observations. Also do a training/test split and print the R2 for both datasets.
Apply the function to the following countries and show the results in one plot: Austria, Germany, Switzerland, Italy, Spain, Sweden, United Kingdom.
(1) Print the country name. Get the data for the specific country using ```get_hourly_country_data``` from the lecture and extract two periods, i.e 2015-2019 and 2020 in two separate dataframes.
(2) Define X (the input features, i.e. the indicators for time) and Y (i.e. the output feature, the electricity load). Observe that for training, we use the period 2015-2019.
(3) Do a train/test split
(4) Fit the input features to the output feature using a ```RandomForestRegressor```
(5) Predict the output with the training data and the test data and compute the R^2 for both!
(6) Print the R^2.
(7) Create a new variable ```X_2020``` which contains the input features for the year 2020.
(8) Predict with your model the load for 2020.
(9) Assign your prediction back to the dataframe in a new column and calculate the monthly mean for prediction and for observed load. You might need to copy the dataframe first by doing something like `power_demand_hourly = power_demand_hourly.copy()` (otherwise it might be just a slice of the complete time range and then you can't add a column for some rows only).
(10) Plot the ratio of load and prediction. With ```label=country```, you can add a label to your plot for making a legend.
(11) Execute the function for the following countries: Austria, Germany, Switzerland, Italy, Spain, Sweden, United Kingdom.
(12) After calling the functions, use ```plt.legend()``` to show a legend.
## Exercise 3
Answer the following questions:
(1) Which country had the strongest decline in electricity consumption?
< your answer goes here >
(2) For which country does the fit work best?
< your answer goes here >
(3) Where is the difference of R2 between training data and test data the largest? What does that mean?
< your answer goes here >
(4) Look into the data of the country with the largest difference in the R2 of the training and the test data. Can you explain what is happening there? Might this effect our model?
< your answer goes here >
## Exercise 4
The difference between model prediction and actual observation may help understanding how people behaved during the lockdown. In this exercise, you should come up with your own hypothesis of how people behaved and how this affected power consumption. You may, e.g., look into demand on different weekdays or in different hours. Once you have a hypothesis and a theory, why this hypothesis may be valid, test it with the model: is your hypothesis covered by what you observe in the load data?
## Exercise 5
Download ERA5 temperature data for the next lecture.
First install necessary dependencies `xarray` and `cdsapi`:
```
conda install --yes xarray
conda install --yes -c conda-forge cdsapi
```
The [Copernicus Climate Data Store](https://cds.climate.copernicus.eu/) provides [reanalysis climate data](https://cds.climate.copernicus.eu/cdsapp#!/search?type=dataset&keywords=((%20%22Product%20type:%20Reanalysis%22%20))). We are going to download [ERA5](https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=form) data and use the [temperature 2m above ground values](https://apps.ecmwf.int/codes/grib/param-db?id=167).
Register for the CDS API and install the API key by following [this guide](https://cds.climate.copernicus.eu/api-how-to). You don't need to run `pip install cdsapi`, this has been done in the cell above already using conda.
```
import cdsapi
c = cdsapi.Client()
# Add the path to the lecture repository here:
PATH_TO_LECTURE_REPO = '../..'
if not os.path.isdir(Path(PATH_TO_LECTURE_REPO) / 'lecture00-introduction'):
raise RuntimeError(f"Wrong path to lecture repository: PATH_TO_LECTURE_REPO = {PATH_TO_LECTURE_REPO}")
```
We'll download data from 2015 to 2020 in a bounding box which covers all countries we used so far for our analysis.
To make the download a bit faster, we'll use a [0.5° grid](https://confluence.ecmwf.int/display/CKB/ERA5%3A+Web+API+to+CDS+API) instead of the 0.1° grid. This will download approximately 500MB. The download might take a couple of hours, because the data is prepared on their servers before it can be downloaded.
```
filename = Path(PATH_TO_LECTURE_REPO) / 'data' / 'temperatures_era5.nc'
north, west, south, east = 70.,-13.5, 35.5, 24.5
c.retrieve(
'reanalysis-era5-land',
{
'format': 'netcdf',
'variable': '2m_temperature',
'area': [
north, west, south, east
],
'grid': [0.5, 0.5], # grid in 0.5deg steps in longitude/latitude
'day': [f"{day:02d}" for day in range(1, 32)],
'time': [f"{hour:02d}:00" for hour in range(24)],
'month': [f"{month:02d}" for month in range(1, 13)],
'year': [str(year) for year in range(2015, 2021)],
},
f"{filename}.part")
# this prevents you from accidentally using broken files:
os.rename(f"{filename}.part", filename)
```
## Exercise 6
Load the file downloaded in exercise 3 and plot the temperature for one location. This is also a test if the download was successful. To load the file import the library `xarray`. Typically it is imported by using `import xarray as xr`. Then load the file using the command `xr.load_dataset(filename)`. Check the type of the return value. Then select the data variable `t2m` (temperature at 2m), select the values for `longitude=16.5` and `latitude=48` by using `temperatures_dataset.t2m.sel(longitude=16.5, latitude=48.)`. Then plot the result by calling `.plot()` on the resulting object.
Does the result look reasonable?
| true |
code
| 0.566978 | null | null | null | null |
|
<h1 align="center">PROGRAMACIÓN DE COMPUTADORES </h1>
<h2 align="center">UNIVERSIDAD EAFIT</h2>
<h3 align="center">MEDELLÍN - COLOMBIA </h3>
<h2 align="center">Sesión 12 - Ecosistema Python - Matplotlib</h2>
## Instructor:
> <strong> *Carlos Alberto Álvarez Henao, I.C. Ph.D.* </strong>
## Matplotlib
> Primero hay qué instalar el paquete [matplotlib](https://anaconda.org/conda-forge/matplotlib)
> - Estandar de facto de visualización en Python
> - Pretende ser similar a las funciones de visualización del Matlab
En Jupyter es necesario activar la opción inline para viusalizar las gráficas en el notebook

```
%matplotlib inline
```
> Ahora es necesario importar todos los paquetes necesarios
```
import numpy as np
import matplotlib.pyplot as plt
```
> La biblioteca matplotlib es gigantesca y es difícil hacerse una idea global de todas sus posibilidades en una primera toma de contacto. Es recomendable tener a mano la documentación y la galería:
```
from IPython.display import HTML
HTML('<iframe src="http://matplotlib.org/gallery.html#pylab_examples" width="800" height="600"></iframe>')
```
> Si hacemos clic en cualquiera de las imágenes, accedemos al código fuente que la ha generado
```
HTML('<iframe src="http://matplotlib.org/examples/pylab_examples/annotation_demo.html" width="800" height="600"></iframe>')
```
### Interfaz pyplot
> La interfaz *pyplot* proporciona una serie de funciones que operan sobre un estado global.
> - No especificamos sobre qué gráfica o ejes estamos actuando.
> - Es una forma rápida y cómoda de crear gráficas pero perdemos parte del control.
> - El paquete pyplot se suele importar bajo el alias *plt*, de modo que todas las funciones se acceden a través de *plt.$<funcion>$*.
> - La función más básica es la función plot:
```
plt.plot([0, 0.1, 0.2, 0.5], [1, -1, 0.5, 2])
#GRAFICA SENO
# coding=utf-8
# Carga los módulos necesarios
import scipy as sp
import matplotlib.pyplot as plt
# Crea el arreglo x de cero a cien con cien puntos
x = sp.linspace(0, 10, 100)
# Crea el arreglo y con la función indicada
y = sp.sin(x)
# Crea una figura
plt.figure()
# imprime la figura
plt.plot(x,y)
# Muestra en pantalla
plt.show()
#GRAFICA SENO - en repl.it
import scipy as sp
import matplotlib.pyplot as plt
# Crea el arreglo x de cero a cien con cien puntos
x = sp.linspace(0, 10, 100)
# Crea el arreglo y con la función indicada
y = sp.sin(x)
# Crea una figura
#plt.figure()
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111)
# imprime la figura
plt.plot(x,y)
# Muestra en pantalla
fig.savefig('seno.png')
```
> La función *plot* recibe una sola lista (si queremos especificar los valores y) o dos listas (si especificamos $x$ e $y$).
> - Naturalmente si especificamos dos listas ambas tienen que tener la misma longitud.
> La tarea más habitual a la hora de trabajar con *matplotlib* es representar una función.
> - Lo que tendremos que hacer es definir un dominio y evaluarla en dicho dominio. Por ejemplo:
$$f(x)=e^{-x^2}$$
```
def f(x):
return np.exp(-x ** 2)
a = f(2)
print(a)
plt.plot(2,f(2))
```
> Definimos el dominio con la función *np.linspace*, que crea un vector de puntos equiespaciados:
```
x = np.linspace(-1, 5, num=100)
x
```
> Y representamos la función:
```
plt.plot(x, f(x), label="Función f(x)")
plt.xlabel("Eje $x$")
plt.ylabel("$f(x)$")
plt.legend()
plt.title("Función $f(x)=e^{-x^2}$")
```
### Personalización
> La función *plot* acepta una serie de argumentos para personalizar el aspecto de la función.
> - Con una letra podemos especificar el color, y con un símbolo el tipo de línea.
```
plt.plot(x, f(x), 'g-')
plt.plot(x, 1 - f(x), 'b--')
```
> Esto en realidad son códigos abreviados, que se corresponden con argumentos de la función *plot*:
```
#colorcito = 'green'
plt.plot(x, f(x), color='black', linestyle='', marker='o')
plt.plot(x, 1 - f(x), c='g', ls='--')
```
> La lista de posibles argumentos y abreviaturas está disponible en la documentación de la función *plot* la podrás encontrar en este [enlace](http://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.plot).
### Otro tipo de gráficas
> La función *scatter* muestra una nube de puntos, con posibilidad de variar también el tamaño y el color.
```
N = 100
x = np.random.randn(N)
y = np.random.randn(N)
plt.scatter(x, y)
```
> Con *s* y *c* podemos modificar el tamaño y el color respectivamente.
> - Para el color, a cada valor numérico se le asigna un color a través de un mapa de colores; ese mapa se puede cambiar con el argumento *cmap*. Esa correspondencia se puede visualizar llamando a la función *colorbar*.
```
s = 50 + 50 * np.random.randn(N)
c = np.random.randn(N)
plt.scatter(x, y, s=s, c=c, cmap=plt.cm.Blues)
plt.colorbar()
plt.scatter(x, y, s=s, c=c, cmap=plt.cm.Oranges)
plt.colorbar()
```
> *matplotlib* trae por defecto muchos mapas de colores. En las *SciPy Lecture Notes* dan una lista de todos ellos:

> La función *contour* se utiliza para visualizar las curvas de nivel de funciones de dos variables y está muy ligada a la función *np.meshgrid*. Veamos un ejemplo:
$$f(x,y) = cos(x) + sin^2(y)$$
```
def f(x, y):
return np.cos(x) + np.sin(y) ** 2
x = np.linspace(-2, 2)
y = np.linspace(-2, 2)
xx, yy = np.meshgrid(x, y)
plt.contour(xx, yy, f(xx, yy))
plt.colorbar()
```
> La función *contourf* es casi idéntica pero rellena el espacio entre niveles.
> - Podemos especificar manualmente estos niveles usando el cuarto argumento:
```
zz = f(xx, yy)
plt.contourf(xx, yy, zz, np.linspace(-0.5, 2.0),cmap=plt.cm.rainbow)
plt.colorbar()
```
### Interfaz Orientada a Objetos
```
x = np.linspace(-1, 5, num=50)
x
def f(x):
return np.exp(-x ** 2)
f(x)
fig, axes = plt.subplots()
axes.plot(x,f(x),'ro', label='Función f(x)')
axes.set_xlim(-1,4)
axes.set_ylim(0,1)
fig.savefig('Grafica1.png')
```
> Ahora usaremos la función *subplots* para crear una figura con varios sistemas de ejes.
```
fig, axes = plt.subplots(2,2, sharey=True)
axes[0].plot(x,f(x))
axes[0].set_xlabel('Eje x0')
axes[1].plot(x,-f(x),'r')
axes[1].set_xlabel('Eje x1')
axes[2].plot(x,1-f(x),'r')
axes[2].set_xlabel('Eje x2')
x = np.random.rand(100)
y = np.random.rand(100)
s = 200*np.random.randn(100)
c = np.random.randn(100)
plt.scatter(x,y,s,c,cmap=plt.cm.seismic)
```
$$g(x,y) = cos(x) + sin^2(y)$$
```
x = np.linspace(-2,2)
y = np.linspace(-2,2)
xx,yy = np.meshgrid(x,y)
def g(x,y):
return np.cos(x) + np.sin(y)**2
zz = g(xx,yy)
fig, axes = plt.subplots()
axes.contourf(xx,yy,zz, np.linspace(-1,1),cmap=plt.cm.autumn)
```
### Ejemplo con datos reales
```
!type temperaturas.csv
datos = np.loadtxt("temperaturas.csv",usecols=(1,2,3),skiprows=1,delimiter=",")
fig, axes = plt.subplots()
x = np.arange(len(datos[:,1]))
temp_media = (datos[:,1] + datos[:,2]) / 2
axes.plot(x,datos[:,1],'r')
axes.plot(x,datos[:,2],'b')
axes.plot(x,temp_media,'k')
```
| true |
code
| 0.455138 | null | null | null | null |
|
# Optimizing Performance Using Numba & Cython
## Numba & Cython: What are they?
At a high level, Numba and Cython are both modules that make your Python code run faster. This means we can have the quick prototyping and iteration that Python is known for, while getting the speed we expect from programs written in C. This is great--we can have our cake and eat it too!
## Use Case: Cholesky Decomposition
Matrix computations are a standard benchmark for speed. In that vein, we'll be examining the execution time of various implementations of Cholesky Decomposition, a method of matrix decomposition that we used in a previous homework assignment:
* A pure Python implementation
* A Numba-fied implementation
* A Cython-ized implementation
* The provided SciPy implementation
We'll begin with a pure Python implementation and work our way towards the Numba-fied and Cython-ized versions. Then, we'll see how those fare against SciPy.
## Some mathematical formalism:
This isn't too important for implementing a way of calculating the Cholesky decomposition, but it might provide some intuition. Feel free to skip ahead to the next section if you don't want to deal with the linear algebra details.
Formally, the Cholesky decomposition (factorization) is the decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. There a lot of terms here that might be foreign if you've never taken a course in linear algebra before, so I'll try to break them down:
1. A square matrix $A$ is said to be Hermitian if for every entry $a_{i,j}$ in $A$, it's true that $a_{i,j} = \overline{a}_{j,i}$, where $\overline{z}$ denotes the complex conjugate of $z$.
- The complex conjugate of a complex number $z = a + bi\,$ is defined to be $\overline{z} := a - bi$.
- Symmetric, real, square matrices are Hermitian
2. A Hermitian matrix $A$ is said to be positive-definite if the scalar $\overline{z} A z$ is real and positive for all non-zero column vectors $z$ of complex numbers.
3. A lower triangle matrix is a matrix $L$ of the form $$\begin{bmatrix}\ell_{11} & 0 & \cdots & 0 \\ \ell_{21} & \ell_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & 0 \\ \ell_{n1} & \ell_{n2} & \cdots & \ell_{nn}\end{bmatrix}$$
So, given a symmetric, positive-definite matrix $A$, the Cholesky decomposition of $A$ gives us a lower triangular matrix $L$ such that
$$
A = \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}
=
\begin{bmatrix}
\ell_{11} & 0 \cdots & 0\\
\ell_{21} & \ell_{22} \cdots & 0\\
\vdots & \vdots & \ddots & 0\\
\ell_{n1} & \ell_{n2} & \cdots & \ell_{nn}
\end{bmatrix}
\begin{bmatrix}
\overline{\ell}_{11} & \overline{\ell}_{21} & \cdots & \overline{\ell}_{n1} \\
0 & \overline{\ell}_{22} & \cdots & \overline{\ell}_{n2}\\
\vdots & \vdots & \ddots & \vdots\\
0 & 0 & \cdots & \overline{\ell}_{nn}
\end{bmatrix}
= L\overline{L}^T
$$
## The Cholesky-Banachiewicz & Cholesky-Crout Algorithms
###### (Wikipedia)
Let $A$ be a real, symmetric, positive-definite matrix. Then, the Cholesky factor $L$ of $A$ is the lower triangular matrix such that $A = LL^T$ and
$$
L_{ii} = \sqrt{A_{ii} - \sum_{k=1}^{i-1}L_{i,k}^2}
\\
L_{ij} = \frac{1}{L_{jj}}\left(A_{ij} - \sum_{k=1}^{j-1}L_{ik}L_{jk}\right) \;\;\; \text{for $i > j$}
$$
This means that we can compute $L_{ij}$ if we know the entries to the left and above.
- The Cholesky-Banachiewicz algorithm starts from the upper left corner of the matrix $L$ and proceeds to calculate the matrix row by row.
- The Cholesky-Crout algorithm starts from the upper left corner of the matrix $L$ and proceeds to calculate the matrix column by column.
Now we can move on to implementation.
```
def cholesky_banachiewicz_pure(A):
n = len(A)
L = [[0.0] * n for _ in xrange(n)]
for i in xrange(n):
for j in xrange(i + 1): # Build row i
temp = A[i][j] - sum(L[i][k] * L[j][k] for k in xrange(j))
L[i][j] = temp**0.5 if i == j else temp / L[j][j]
return L
def cholesky_crout_pure(A):
n = len(A)
L = [[0.0] * n for _ in xrange(n)]
for j in xrange(n):
for i in xrange(j, n): # Build column i
temp = A[i][j] - sum(L[i][k] * L[j][k] for k in xrange(j))
L[i][j] = temp**0.5 if i == j else temp / L[j][j]
return L
```
Let's consider a small example just to verify that our implementation is working as intended.
```
import scipy
import scipy.linalg
A = [[6, 3, 4, 8], [3, 6, 5, 1], [4, 5, 10, 7], [8, 1, 7, 25]]
A_array = scipy.array(A)
L_banachiewicz = cholesky_banachiewicz_pure(A)
L_crout = cholesky_crout_pure(A)
L_scipy = scipy.linalg.cholesky(A_array, lower=True).tolist()
assert L_banachiewicz == L_crout == L_scipy
print "Looks good!"
```
Using the ``timeit`` module, let's write a small function that'll let us profile our various implementations:
```
import timeit
def profile(func, n=100000):
def profiled_func(*args, **kwargs):
total = 0.0
worst = 0.0
best = 999999.999 # a sufficiently large amount of time
for _ in xrange(n):
start_time = timeit.default_timer()
func(*args, **kwargs)
end_time = timeit.default_timer()
duration = end_time - start_time
if duration > worst:
worst = duration
if duration < best:
best = duration
total += duration
avg = total / n
print "%s:" % (func.__name__)
print " average execution time = %f" % avg
print " fastest execution time = %f" % best
print " slowest execution time = %f" % worst
return profiled_func
```
Alternatively, we could make use of the ``%timeit`` line magic:
```
%timeit -r 10 cholesky_banachiewicz_pure(A)
```
For the sake of clarity, however, we'll be using our small ``profile`` function to benchmark our code for the rest of the tutorial.
```
profile(cholesky_banachiewicz_pure)(A)
profile(cholesky_crout_pure)(A)
profile(scipy.linalg.cholesky)(A_array, lower=True)
```
It looks like the SciPy implementation is a few microseconds faster than our pure Python implementation. As the matrices get larger, so does the difference in execution time between pure Python and SciPy. To illustrate, I've included some graphs of what the execution time looks like as the size of $A$ grows:

Let's see how these performance graphs change when we optimize our code using Numba.
```
from numba import jit
import numpy as np
@jit
def cholesky_banachiewicz_numba(A):
n = len(A)
L = np.zeros(A.shape)
for i in xrange(n):
for j in xrange(i + 1):
temp = A[i,j]
for k in xrange(j):
temp -= L[i,k] * L[j,k]
L[i,j] = temp**0.5 if i == j else temp / L[j,j]
return L
@jit
def cholesky_crout_numba(A):
n = len(A)
L = np.zeros(A.shape)
for j in xrange(n):
for i in xrange(j, n):
temp = A[i,j]
for k in xrange(j):
temp -= L[i,k] * L[j,k]
L[i,j] = temp**0.5 if i == j else temp / L[j,j]
return L
profile(cholesky_banachiewicz_numba)(A_array)
profile(cholesky_crout_numba)(A_array)
profile(scipy.linalg.cholesky)(A_array, lower=True)
```
Now we're beating SciPy's implementation by a longshot. That's great! But wait, our code has changed. Why? Numba only accelerates code that uses scalars or (N-dimensional) arrays. You can't use built-in types like ``list`` or ``dict`` or your own custom classes, you can't allocate new arrays in accelerated code, and you can't even use recursion. This means that Numba is only useful in certain cases.
Let's see how the performance changes as we increase the size of the matrix:

For additional information, examples, and documentation, check out the [Numba](http://numba.pydata.org/) website. In general though, to Numba-fy your code, apply the ``@jit`` decorator, remove built-in types and custom classes, translate recursive functions to iterative ones, and don't alloacate new arrays if possible.
## The Cython Language
###### (Cython docs)
Cython is a programming language that makes writing C extensions for the Python language as easy as Python itself. It aims to become a superset of the Python language which gives it high-level, object-oriented, functional, and dynamic programming. Its main feature on top of these is support for optional static type declarations as part of the language. The source code gets translated into optimized C/C++ code and compiled as Python extension modules. This allows for both very fast program execution and tight integration with external C libraries, while keeping up the high programmer productivity for which the Python language is well known.
Using Cython in IPython notebooks is fairly straightforward. First, we load the Cython extension within our notebook:
```
%load_ext Cython
```
Now, we can use the cell magic ``%%cython`` to compile our original pure Python solution in the next cell:
```
%%cython
def cholesky_banachiewicz_cython_v1(A):
n = len(A)
L = [[0.0] * n for _ in xrange(n)]
for i in xrange(n):
for j in xrange(i + 1):
temp = A[i][j] - sum(L[i][k] * L[j][k] for k in xrange(j))
L[i][j] = temp**0.5 if i == j else temp / L[j][j]
return L
def cholesky_crout_cython_v1(A):
n = len(A)
L = [[0.0] * n for _ in xrange(n)]
for j in xrange(n):
for i in xrange(j, n):
temp = A[i][j] - sum(L[i][k] * L[j][k] for k in xrange(j))
L[i][j] = temp**0.5 if i == j else temp / L[j][j]
return L
profile(cholesky_banachiewicz_cython_v1)(A)
profile(cholesky_crout_cython_v1)(A)
profile(scipy.linalg.cholesky)(A_array, lower=True)
```
Notice how we only needed to use the ``%%cython`` cell magic to gain this speedup. Unlike with Numba, we didn't need to make any changes to our code to see improvements; however, the speedup we get from Cython isn't quite as good as the one we get from Numba. In fact, this approach yields almost no improvement for small matrices, and can actually worsen our performance as the dimensions of our input grows:



Not all hope is lost for Cython, though! We can do better using what are called *typed memoryviews* and learning a little bit more about the Cython language.
#### C vs. Python Functions/Variables in Cython
In Cython, we can declare both C variables/functions and Python variables/functions. To declare a C variable or function, we use the ``cdef`` keyword with type definitions. Python variables and functions can be declared just as they are in Python. If we wanted to declare integers ``i, j, k`` and floats ``f, g[42], *h`` as C variables, we would do the following
``` cython
cdef int i, j, k
cdef float f, g[42], *h
```
C functions written in Cython, like C variables, are declared with the ``cdef`` keyword. C functions in Cython can take in either Python objects or C values as arguments, and can return either Python objects or C values. The scope of C functions written is Cython is limited, however, to the module in which it was written: "Within a Cython module, Python functions and C functions can call each other freely, but only Python functions can be called from outside the module interpreted by Python code. So any functions that you want to "export" from your Cython module must be declared as Python functions using ``def``."
To learn more about the differences between C functions and Python functions in Cython, check out [Cython Language Basics](http://cython.readthedocs.io/en/latest/src/userguide/language_basics.html).
#### Buffers and MemoryViews in Python
Before we continue, let's take a moment to consider how Python does operations on things like Strings, DataFrames, and Series. These objects (except for DataFrames and Series when inplace operations are applied) are immutable. To perform calculations and transformations on them require that we first make a copy of the object and then apply our operations. Whenever we index into a String, DataFrame, or Series by slicing, we're making a copy of the original object. This is why you'll notice that your program runs a lot slower when you, for example, define an empty DataFrame and iteratively insert all the rows one-by-one, than when you use a mutable class (like a dictionary) to iteratively build your object *and then* convert it to a DataFrame.
Python objects implemented in C can export a group of functions called the "buffer interface." These functions can be used by an object to expose its data in a raw byte-oriented format. Clients of the object can use the buffer interface to access the object data directly, without needing to copy it first. Since the release of Python 2.7, MemoryViews and Buffers provide an efficient way to deal with the general copying behavior when dealing with objects like Strings, DataFrames, and Series. A MemoryView is just like a buffer, except you can also write to it, not just read.
To learn more about MemoryViews in Python 2.7, check out the [documentation](https://docs.python.org/2/c-api/buffer.html).
#### Typed MemoryViews in Cython
From the Cython documentation page on [Typed MemoryViews](http://cython.readthedocs.io/en/latest/src/userguide/memoryviews.html): "Typed MemoryViews allow efficient access to memory buffers, such as those underlying NumPy arrasys, without incurring any Python overhead." Here are some examples of using typed MemoryViews in Cython (taken from the documentation):
```cython
# Create a complete view on a one-dimensional int buffer:
cdef int[:] view1d = oneD_obj
# A complete 3D view:
cdef int[:, :, :] view3D = threeD_obj
```
Using Typed MemoryViews in our Cython code will provide the compiler more information about the desired behavior, enabling it to make further optimizations at compile-time.
Armed with this information, we can now create an improved version of our Cython implementation:
```
%%cython
import numpy as np
def cholesky_banachiewicz_cython_v2(long[:, :] A):
cdef int i, j, k
cdef int n = len(A)
cdef double[:, :] L = np.zeros(shape=(n, n))
for i in xrange(n):
for j in xrange(i + 1):
temp = A[i][j] - sum(L[i][k] * L[j][k] for k in xrange(j))
L[i][j] = temp**0.5 if i == j else temp / L[j][j]
return np.asarray(L)
def cholesky_crout_cython_v2(long[:, :] A):
cdef int i, j, k
cdef int n = len(A)
cdef double[:, :] L = np.zeros(shape=(n, n))
for j in xrange(n):
for i in xrange(j, n):
temp = A[i][j] - sum(L[i][k] * L[j][k] for k in xrange(j))
L[i][j] = temp**0.5 if i == j else temp / L[j][j]
return np.asarray(L)
profile(cholesky_banachiewicz_cython_v2)(A_array)
profile(cholesky_crout_cython_v2)(A_array)
profile(scipy.linalg.cholesky)(A_array, lower=True)
```
Now, the performance graphs look a little different:



We managed to dramatically improve our performance relative to our ``_cython_v1`` implementations; however, we didn't beat out Numba or SciPy. In any case, though, the difference between our two Cython implementations should provide sufficient evidence to convince you that simply using the ``%%cython`` magic isn't sufficient to make full use of Cython.
Using Cython in your terminal takes a little more work, but [this](http://cython.readthedocs.io/en/latest/src/quickstart/build.html) should show you how to get up and running.
## Conclusion
First and foremost, we should walk away from this being reassured in the efficiency of the existing SciPy implementations. Unless you're tackling something very specific, it's almost always a good idea to use the SciPy implementation if it's available to you.
However, what do we do when we don't have SciPy available to us, or it's not exactly what we need? That's where Numba and Cython come in. Due to the limitations of Numba (e.g., no lists, dicts, recursion, custom classes, etc.), it's not always the appropriate solution. In the cases where we can't use Numba, we can use Cython, which allows us to gain some noticeable speedups in comparison to a pure Python implementation.
We've also seen that Cython's relative generalizability comes at a cost: it takes significantly more effort on behalf of the coder to reach Numba or SciPy-like levels of efficiency. At a certain point, the amount of effort spent optimizing a Cython function might be better spent writing an actual C implementation with considerations being made to memory layout and caching.
| true |
code
| 0.42322 | null | null | null | null |
|
# Tanzanian Ministry of Water Dataset Modeling
**Import libraries**
```
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import KNNImputer, IterativeImputer
from sklearn.model_selection import RandomizedSearchCV
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier, AdaBoostClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
import plotly.express as px
import plotly.io as pio
pio.renderers.default = "notebook_connected"
```
**Import datasets**
```
y = pd.read_csv('../assets/data/dependent_vars.csv')
X = pd.read_csv('../assets/data/independent_vars.csv')
X_test = pd.read_csv('../assets/data/independent_test.csv')
SF = pd.read_csv('../assets/data/SubmissionFormat.csv')
```
**Creating a baseline model**
```
y['status_group'].value_counts(normalize=True)
```
**Create training, validation, and final test datasets**
```
X_train, X_val, y_train, y_val = train_test_split(
X, y, test_size=0.25, random_state=42)
```
**TMW analysis pipeline**
```
def data_preprocesser(X, y):
# Transforming Target
y.drop('id', axis=1, inplace=True)
le = LabelEncoder()
y = le.fit_transform(y)
print(le.classes_)
y = pd.DataFrame(y, columns=['status_group'])
# Transfroming Features
# also dropping permit and public metting due to feature importance
drop_features = ['extraction_type', 'extraction_type_group', 'waterpoint_type_group',
'source', 'source_type', 'quantity_group', 'water_quality', 'payment_type',
'management', 'region', 'district_code', 'num_private', 'wpt_name', 'ward',
'recorded_by', 'funder', 'installer', 'subvillage', 'scheme_management',
'permit', 'public_meeting', 'scheme_name']
X.drop(drop_features, axis=1, inplace=True)
# revealing the nan values
X.replace(0, np.nan, inplace=True)
X.replace(-2.000000e-08, np.nan, inplace=True)
X.replace('unknown', np.nan, inplace=True)
# Impoting numeric features
numeric_features = ['amount_tsh', 'gps_height', 'longitude', 'latitude',
'region_code', 'population', 'construction_year']
imputer = KNNImputer(n_neighbors=5)
X[numeric_features] = imputer.fit_transform(X[numeric_features])
# Imputing Categorical variables
categorical_features = ['basin', 'lga', 'extraction_type_class', 'management_group',
'payment', 'quality_group', 'quantity', 'source_class', 'waterpoint_type']
# Label encoding with a trick to keep nan values
le = LabelEncoder()
X[categorical_features] = X[categorical_features].apply(lambda series: pd.Series(
le.fit_transform(series[series.notnull()]),
index=series[series.notnull()].index
))
imputer = IterativeImputer()
X[categorical_features] = imputer.fit_transform(X[categorical_features])
# Feature Engineering DateTime
X['date_recorded'] = pd.to_datetime(X['date_recorded'], infer_datetime_format=True)
X['year_recorded'] = X['date_recorded'].dt.year
X['month_rec'] = X['date_recorded'].dt.month
X['day_rec'] = X['date_recorded'].dt.day
days_in_a_month = 31 # can potentially be done better (28, 30, 31)
months_in_a_year = 12
# Sin
X['sin_day'] = np.sin((X.day_rec-1)*(2*np.pi/days_in_a_month))
X['sin_month'] = np.sin((X.month_rec-1)*(2*np.pi/months_in_a_year))
# Cosine
X['cos_day'] = np.cos((X.day_rec-1)*(2*np.pi/days_in_a_month))
X['cos_month'] = np.cos((X.month_rec-1)*(2*np.pi/months_in_a_year))
# Engineering years in service
X['years_in_service'] = X['year_recorded'] - X['construction_year']
# Dropping unneeded features
X.drop(['id'], axis=1, inplace=True)
X.drop('date_recorded', axis=1, inplace=True)
X.drop('construction_year', axis=1, inplace=True)
X.drop('year_recorded', axis=1, inplace=True)
X.drop('month_rec', axis=1, inplace=True)
X.drop('day_rec', axis=1, inplace=True)
return X, y
```
**Processing data for modeling**
```
X_train, y_train = data_preprocesser(X_train, y_train)
X_val, y_val = data_preprocesser(X_val, y_val)
```
### Hyper perameter tunening
**Decision Tree**
Tuned Decision Tree Parameters: {'splitter': 'best', 'min_samples_leaf': 3, 'max_leaf_nodes': None, 'max_features': None, 'max_depth': 21, 'criterion': 'entropy'}
Best score is 0.7624469693152618
```
# Parameter Distrubutions
param_dist = {'criterion': ['gini', 'entropy'],
'splitter': ['best', 'random'],
'max_depth': [*range(2, 100, 5), None],
'min_samples_leaf': [*range(2, 10), None],
'max_features': ['auto', 'sqrt', 'log2', None],
'max_leaf_nodes': [*range(2, 10, 1), None]
}
model = DecisionTreeClassifier()
model_cv = RandomizedSearchCV(model, param_dist, cv=100)
# Fit it to the data
model_cv.fit(X_train, y_train)
# Print the tuned parameters and score
print("Tuned Decision Tree Parameters: {}".format(model_cv.best_params_))
print("Best score is {}".format(model_cv.best_score_))
```
**Random Forest**
Tuned Random Forest Parameters: {'warm_start': False, 'n_jobs': 2, 'n_estimators': 31, 'max_samples': None, 'max_features': 'sqrt', 'criterion': 'entropy'}
Best score is 0.8004041613493289
```
param_dist = {'n_estimators': [*range(1, 100, 5), None],
'criterion': ['gini', 'entropy'],
'max_features': ['auto', 'sqrt', 'log2'],
'n_jobs': [*range(0, 5, 1), None],
'warm_start': [True, False],
'max_samples': [2, 4, 6, 8, 10, None]
}
model = RandomForestClassifier()
model_cv = RandomizedSearchCV(model, param_dist, cv=20)
# Fit it to the data
model_cv.fit(X_train, y_train)
# Print the tuned parameters and score
print("Tuned Random Forest Parameters: {}".format(model_cv.best_params_))
print("Best score is {}".format(model_cv.best_score_))
```
**Logistic Regression**
Tuned Logistic Regression Parameters: {'penalty': 'l2'}
Best score is 0.594702581369248
```
model = LogisticRegression()
model_cv = RandomizedSearchCV(model, param_dist, cv=10)
# Fit it to the data
model_cv.fit(X_train, y_train)
# Print the tuned parameters and score
print("Tuned Logistic Regression Parameters: {}".format(model_cv.best_params_))
print("Best score is {}".format(model_cv.best_score_))
```
**ada_boost**
Tuned Logistic Regression Parameters: {'n_estimators': 11, 'learning_rate': 1.5, 'algorithm': 'SAMME.R'}
Best score is 0.6995735129068462
```
param_dist = {'n_estimators': [*range(1, 100, 5), None],
'learning_rate': [0.5, 1.0, 1.5, 2.0, 2.5],
'algorithm': ['SAMME', 'SAMME.R']
}
model = AdaBoostClassifier()
model_cv = RandomizedSearchCV(model, param_dist, cv=10)
# Fit it to the data
model_cv.fit(X_train, y_train)
# Print the tuned parameters and score
print("Tuned adaboost Parameters: {}".format(model_cv.best_params_))
print("Best score is {}".format(model_cv.best_score_))
```
**Gradient Boost**
Tuned Gradient Boost Parameters: {'n_estimators': 150, 'learning_rate': 0.5}
Best score is 0.7760718294051626
```
param_dist = {
'learning_rate': [0.5, 1.0, 1.5],
'n_estimators': [*range(50, 250, 50), None],
}
model = GradientBoostingClassifier()
model_cv = RandomizedSearchCV(model, param_dist, cv=10)
# Fit it to the data
model_cv.fit(X_train, y_train)
# Print the tuned parameters and score
print("Tuned Gradient Boost Parameters: {}".format(model_cv.best_params_))
print("Best score is {}".format(model_cv.best_score_))
```
**Final fit and analysis on random forest model**
```
# Initiat the model
model = RandomForestClassifier(warm_start=False, n_jobs=2, n_estimators=200, max_samples=None, max_features='sqrt', criterion='entropy')
# Fit the model
model.fit(X_train,y_train)
# Accuracy score
print("model score: %.3f" % model.score(X_val, y_val))
```
**Feature importance**
```
rfdtmportances = pd.DataFrame(model.feature_importances_, X_train.columns, columns=['value'])
rfdtmportances = pd.DataFrame(model.feature_importances_, X_train.columns, columns=['value'])
rf_importances = pd.DataFrame(model.feature_importances_, X_train.columns, columns=['value'])
rf_importances.reset_index(inplace=True)
rf_importances = rf_importances.sort_values(by='value', ascending=True)
fig = px.bar(y=rf_importances['index'], x=rf_importances['value'], width=600, height=1000, title="Random Forest Feature Importance")
fig.update_xaxes(range=[0, 0.5])
fig.show()
```
**Graphing confusion matrix**
```
# Plot the decision matrix
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1,1,figsize=(8,8))
plot_confusion_matrix(model, X_val, y_val,
display_labels=['functional', 'functional needs repair', 'non-functional'],
cmap=plt.cm.Blues, ax=ax)
ax.set_title('Confusion Matrix: Digits decision tree model')
plt.plot();
roc_yval = y_val.copy()
roc_xval = X_val.copy()
```
**ROC AUC Score**
```
from sklearn.metrics import roc_curve, roc_auc_score
from sklearn.model_selection import train_test_split
#predicting the data
y_prob_pred = model.predict_proba(roc_xval)
#roc auc score
roc_auc_score(roc_yval, y_prob_pred, multi_class='ovr')
```
**Ploting ROC Curve**
```
# roc curve for classes
fpr = {}
tpr = {}
thresh ={}
n_class = 3
for i in range(n_class):
fpr[i], tpr[i], thresh[i] = roc_curve(y_val, y_prob_pred[:,i], pos_label=i)
# plotting
plt.plot(fpr[0], tpr[0], linestyle='--',color='orange', label='Class 0 vs Rest')
plt.plot(fpr[1], tpr[1], linestyle='--',color='green', label='Class 1 vs Rest')
plt.plot(fpr[2], tpr[2], linestyle='--',color='blue', label='Class 2 vs Rest')
plt.title('Multiclass ROC curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive rate')
plt.legend(loc='best')
plt.savefig('Multiclass ROC',dpi=300);
```
**Submitting to DataDriven**
```
X_test, _ = data_preprocesser(X_test, y)
SF['status_group'] = model.predict(X_test)
SF.replace(0, 'functional', inplace=True)
SF.replace(1, 'functional needs repair', inplace=True)
SF.replace(2, 'non functional', inplace=True)
SF.to_csv('TMW_Predicted.csv', index=False)
```
**Joblibing (pickling) model for use in web-app**
```
pkl_features = ['gps_height', 'longitude', 'latitude', 'quantity', 'years_in_service']
pkl_X = X_train[pkl_features]
pkl_y = y_train
pkl_X.to_csv('pkl_X.csv')
pkl_y.to_csv('pkl_y.csv')
# Initiat the model
model = RandomForestClassifier(warm_start=False, n_jobs=2, n_estimators=10, max_samples=None, max_features='sqrt', criterion='entropy')
# Fit the model
model.fit(pkl_X, pkl_y)
from joblib import dump, load
dump(model, 'TMWRandomForest.joblib', compress=True)
```
| true |
code
| 0.491212 | null | null | null | null |
|
*This notebook is part of course materials for CS 345: Machine Learning Foundations and Practice at Colorado State University.
Original versions were created by Ben Sattelberg and Asa Ben-Hur.
The content is availabe [on GitHub](https://github.com/asabenhur/CS345).*
*The text is released under the [CC BY-SA license](https://creativecommons.org/licenses/by-sa/4.0/), and code is released under the [MIT license](https://opensource.org/licenses/MIT).*
<img style="padding: 10px; float:right;" alt="CC-BY-SA icon.svg in public domain" src="https://upload.wikimedia.org/wikipedia/commons/d/d0/CC-BY-SA_icon.svg" width="125">
<a href="https://colab.research.google.com/github//asabenhur/CS345/blob/master/notebooks/module08_03_neural_networks_mnist.ipynb">
<img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/>
</a>
```
%autosave 0
%matplotlib inline
import numpy as np
import keras
import matplotlib.pyplot as plt
```
# Neural Networks
### Preface: enabling GPUs on google colab
Until now we ran our neural networks on a CPU. If you are running this notebook on google colab, you are in luck - google colab will allow you to run your code on a GPU. Enabling a GPU is very simple: All you need to do is navigate to Edit→Notebook Settings and select GPU from the Hardware Accelerator drop-down.
This [colab notebook](https://colab.research.google.com/notebooks/gpu.ipynb) has instructions for verifying that you are using a GPU and see the resulting speedup.
## The MNIST dataset
In the previous notebooks we used Keras to solve toy problems and built some understanding of how the networks are solving those problems. In this notebook, we'll look at the real (but still relatively easy) problem of handwritten digit recognition. We will be using the MNIST (modified National Institute of Standards and Technology) database which has images taken from a NIST database of handwritten digits and modified by Yann Lecun, Corinna Cortes, and Christopher J.C. Burges to be more easily used in machine learning.
The first thing we need to do is to load the dataset. Fortunately, Keras does this work for us:
```
# This will download an 11.5 MB file to ~/.keras/datasets/
(X_train, y_train), (X_test, y_test) = keras.datasets.mnist.load_data()
```
Let's get some information about the dataset:
```
print(X_train.shape, y_train.shape)
print(min(y_train), max(y_train))
```
This tells that we have 60,000 input images, each of which is 28x28 pixels. The labels are, unsuprisingly for a database of digits, the numbers 0 through 9, corresponding to which digit the image represents. Now let's look at the test set:
```
print(X_test.shape)
print(y_test.shape)
```
Here we have 10,000 samples with the same format as the training set.
Let's look at one of the images:
```
fig, ax = plt.subplots(1,1,figsize=(6,6))
im = ax.imshow(X_train[0, :, :].reshape(28,28), cmap='Greys')
ax.set_title(y_train[0])
cbar = fig.colorbar(im)
cbar.set_ticks([0, 128, 255])
ax.set_xticks([0, 14, 27])
ax.set_yticks([0, 14, 27]);
```
Here we can see that the image is a grayscale 28x28 image with pixel values between 0 and 255. We can also look at a few other images in the dataset:
```
fig, axes = plt.subplots(5, 5, figsize=(10,10))
for i in range(5):
for j in range(5):
axes[i,j].imshow(X_train[i*5 + j, :, :].reshape(28,28), cmap='Greys')
axes[i,j].set_title(y_train[i*5+j])
axes[i,j].axis('off')
```
There are a few things we want to do to the input data before we use it. The first is to convert it to 32 bit floats:
```
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
```
We also want to change the range of the data from integers between 0 and 255 to numbers between 0 and 1 to help with training:
```
X_train /= 255
X_test /= 255
```
The last step, which is less obvious, is to reshape the actual data to have an extra dimension:
```
X_train = X_train.reshape(-1, 28, 28, 1)
X_test = X_test.reshape(-1, 28, 28, 1)
```
This dimension corresponds to the number of "channels" in the image. This data is grayscale, but color images are typically stored in RGB (red, green, blue) format, where there the three channels describe the amount of red, green, and blue at each pixel. Keras is designed to handle images as a native data format without needing to "flatten" the images into vectors as a preprocessing step.
We will also convert the `y_train` and `y_test` to a one-hot encoding:
```
y_train_one_hot = keras.utils.to_categorical(y_train, 10)
y_test_one_hot = keras.utils.to_categorical(y_test, 10)
```
The first experiment we will do with this dataset is to test a simple linear model to get a baseline for how good we can expect our models to be. We will use Keras for this, and simply not have any hidden layers in our network.
In addition to the accuracy on the training set, we want to keep track of the accuracy on the testing set. One way to do this with Keras is with a callback function that keeps track of the accuracy on the testing set as we progress through it. It isn't necessary to understand the code here, but it is good to be aware of the goal of this structure.
```
# Structure based on https://github.com/keras-team/keras/issues/2548
class EvaluateCallback(keras.callbacks.Callback):
def __init__(self, test_data):
self.test_data = test_data
def on_epoch_end(self, epoch, logs):
x, y = self.test_data
loss, acc = self.model.evaluate(x, y, verbose=0)
if 'test loss' not in logs:
logs['test loss'] = []
logs['test acc'] = []
logs['test loss'] += [loss]
logs['test acc'] += [acc]
print('Testing loss: {}, acc: {}\n'.format(round(loss, 4), round(acc, 4)))
```
We can now train our model. One layer to notice is the ```Flatten()``` layer. This layer converts the data from a 28x28x1 dimensional image to a 784=28\*28\*1 dimensional vector.
```
linear_model = keras.Sequential()
linear_model.add(keras.layers.Flatten())
linear_model.add(keras.layers.Dense(10, activation='softmax'))
loss_fn = keras.losses.CategoricalCrossentropy()
opt = keras.optimizers.Adam()
linear_model.compile(loss=loss_fn, optimizer=opt, metrics=['accuracy'])
linear_history = linear_model.fit(X_train, y_train_one_hot,
batch_size=100, epochs=20,
verbose=1, callbacks=[EvaluateCallback((X_test, y_test_one_hot))])
print('Final loss: {}, test accuracy: {}'.format(*map(lambda x: round(x, 4), linear_model.evaluate(X_test, y_test_one_hot, verbose=0))))
```
We can look at the summary of this model - the main thing to note here is the number of parameters:
```
linear_model.summary()
```
We can also look at the accuracy over the epochs of the network:
```
plt.plot(linear_history.history['accuracy'], label='Train')
plt.plot(linear_history.history['test acc'], label='Test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
plt.ylim([0.85, 1]);
```
We can see that even a simple linear classifier gets about 92% accuracy. MNIST is commonly used as a tutorial dataset, and one of the reasons for that is that basically anything will be successful on it. The dataset is also solved - methods exist that do better than human accuracy and will reach around 99.9% accuracy (i.e 10 samples out of the 10,000 misclassified).
## An MNIST network
Now let's train a more interesting neural network on this problem. We'll start with a single hidden layer with 128 nodes:
```
network = keras.Sequential()
network.add(keras.layers.Flatten())
network.add(keras.layers.Dense(100, activation='relu'))
network.add(keras.layers.Dense(10, activation='softmax'))
loss_fn = keras.losses.CategoricalCrossentropy()
opt = keras.optimizers.Adam()
network.compile(loss=loss_fn, optimizer=opt, metrics=['accuracy'])
history = network.fit(X_train, y_train_one_hot, batch_size=100,
epochs=20, verbose=1,
callbacks=[EvaluateCallback((X_test, keras.utils.to_categorical(y_test, 10)))])
print('Final loss: {}, test accuracy: {}'.format(*map(lambda x: round(x, 4), network.evaluate(X_test, y_test_one_hot, verbose=0))))
```
The total number of parameters for this network is more than an order of magnitude higher than the linear model. However, it does improve on the linear model's accuracy from 92% to about 97.5%.
```
network.summary()
```
The network also reaches nearly 100% accuracy on the training set, and continues improving on the training set after it plateaus in accuracy on the test set. This is a sign that the network has found a solution to and that further training can potentially *reduce* the accuracy through overfitting.
```
plt.plot(history.history['accuracy'], label='Train')
plt.plot(history.history['test acc'], label='Test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
plt.ylim([0.85, 1]);
```
Since there's the potential to overfit, and a large number of parameters, simply increasing the depth or the width of this network could potentially lead to issues. Instead of going that route, we will use a different kind of layer in our next notebook that works well for images and introduce convolutional networks, which have become the standard architecture for image data.
For reference, and to convince ourselves that we obtained good accuracy with our neural network let's try random forests:
```
X_train_flat = X_train.reshape(-1, 784)
X_test_flat = X_test.reshape(-1, 784)
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=500)
rf.fit(X_train_flat, y_train);
from sklearn.metrics import accuracy_score
y_pred = rf.predict(X_test_flat)
accuracy_score(y_pred, y_test)
```
### Comments
There are major issues in using feed-forward neural networks for image classification:
* Fully connected networks can have very large numbers of parameters with increasing image sizes. Consider for example images of size 228x228x3, which is standard in this field. Using the network architecture we have here would result in 228\*228\*3\*100 parameters from the input to the hidden layer - about 15,000,000. This network would also not be successful - we would need to significantly increase the width and depth, compounding the issue. It is likely that billions of parameters would be necessary to achieve good accuracy.
* If we take an image that represents the number seven, and shift the seven over a few pixels, we would expect it to still be classified as a seven. However, fully connected networks are not able to represent this invariance.
Some of these concerns apply to other standard machine learning approaches as well.
Convolutional networks which are introduced next, address these shortcomings, and have led to major improvements in accuracy in image classification tasks. Their success has led to a renaissance of the field of neural networks.
| true |
code
| 0.760512 | null | null | null | null |
|
# Enter State Farm
```
from __future__ import division, print_function
%matplotlib inline
#path = "data/state/"
path = "data/state/sample/"
from importlib import reload # Python 3
import utils; reload(utils)
from utils import *
from IPython.display import FileLink
batch_size=64
```
## Setup batches
```
batches = get_batches(path+'train', batch_size=batch_size)
val_batches = get_batches(path+'valid', batch_size=batch_size*2, shuffle=False)
steps_per_epoch = int(np.ceil(batches.samples/batch_size))
validation_steps = int(np.ceil(val_batches.samples/(batch_size*2)))
(val_classes, trn_classes, val_labels, trn_labels,
val_filenames, filenames, test_filenames) = get_classes(path)
```
Rather than using batches, we could just import all the data into an array to save some processing time. (In most examples I'm using the batches, however - just because that's how I happened to start out.)
```
trn = get_data(path+'train')
val = get_data(path+'valid')
save_array(path+'results/val.dat', val)
save_array(path+'results/trn.dat', trn)
val = load_array(path+'results/val.dat')
trn = load_array(path+'results/trn.dat')
```
## Re-run sample experiments on full dataset
We should find that everything that worked on the sample (see statefarm-sample.ipynb), works on the full dataset too. Only better! Because now we have more data. So let's see how they go - the models in this section are exact copies of the sample notebook models.
### Single conv layer
```
def conv1(batches):
model = Sequential([
BatchNormalization(axis=1, input_shape=(3,224,224)),
Conv2D(32,(3,3), activation='relu'),
BatchNormalization(axis=1),
MaxPooling2D((3,3)),
Conv2D(64,(3,3), activation='relu'),
BatchNormalization(axis=1),
MaxPooling2D((3,3)),
Flatten(),
Dense(200, activation='relu'),
BatchNormalization(),
Dense(10, activation='softmax')
])
model.compile(Adam(lr=1e-4), loss='categorical_crossentropy', metrics=['accuracy'])
model.fit_generator(batches, steps_per_epoch, epochs=2, validation_data=val_batches,
validation_steps=validation_steps)
model.optimizer.lr = 0.001
model.fit_generator(batches, steps_per_epoch, epochs=4, validation_data=val_batches,
validation_steps=validation_steps)
return model
model = conv1(batches)
```
Interestingly, with no regularization or augmentation we're getting some reasonable results from our simple convolutional model. So with augmentation, we hopefully will see some very good results.
### Data augmentation
```
gen_t = image.ImageDataGenerator(rotation_range=15, height_shift_range=0.05,
shear_range=0.1, channel_shift_range=20, width_shift_range=0.1)
batches = get_batches(path+'train', gen_t, batch_size=batch_size)
model = conv1(batches)
model.optimizer.lr = 0.0001
model.fit_generator(batches, steps_per_epoch, epochs=15, validation_data=val_batches,
validation_steps=validation_steps)
```
I'm shocked by *how* good these results are! We're regularly seeing 75-80% accuracy on the validation set, which puts us into the top third or better of the competition. With such a simple model and no dropout or semi-supervised learning, this really speaks to the power of this approach to data augmentation.
### Four conv/pooling pairs + dropout
Unfortunately, the results are still very unstable - the validation accuracy jumps from epoch to epoch. Perhaps a deeper model with some dropout would help.
```
gen_t = image.ImageDataGenerator(rotation_range=15, height_shift_range=0.05,
shear_range=0.1, channel_shift_range=20, width_shift_range=0.1)
batches = get_batches(path+'train', gen_t, batch_size=batch_size)
model = Sequential([
BatchNormalization(axis=1, input_shape=(3,224,224)),
Conv2D(32,(3,3), activation='relu'),
BatchNormalization(axis=1),
MaxPooling2D(),
Conv2D(64,(3,3), activation='relu'),
BatchNormalization(axis=1),
MaxPooling2D(),
Conv2D(128,(3,3), activation='relu'),
BatchNormalization(axis=1),
MaxPooling2D(),
Flatten(),
Dense(200, activation='relu'),
BatchNormalization(),
Dropout(0.5),
Dense(200, activation='relu'),
BatchNormalization(),
Dropout(0.5),
Dense(10, activation='softmax')
])
model.compile(Adam(lr=10e-5), loss='categorical_crossentropy', metrics=['accuracy'])
model.fit_generator(batches, steps_per_epoch, epochs=2, validation_data=val_batches,
validation_steps=validation_steps)
model.optimizer.lr=0.001
model.fit_generator(batches, steps_per_epoch, epochs=10, validation_data=val_batches,
validation_steps=validation_steps)
model.optimizer.lr=0.00001
model.fit_generator(batches, steps_per_epoch, epochs=10, validation_data=val_batches,
validation_steps=validation_steps)
```
This is looking quite a bit better - the accuracy is similar, but the stability is higher. There's still some way to go however...
### Imagenet conv features
Since we have so little data, and it is similar to imagenet images (full color photos), using pre-trained VGG weights is likely to be helpful - in fact it seems likely that we won't need to fine-tune the convolutional layer weights much, if at all. So we can pre-compute the output of the last convolutional layer, as we did in lesson 3 when we experimented with dropout. (However this means that we can't use full data augmentation, since we can't pre-compute something that changes every image.)
```
vgg = Vgg16()
model=vgg.model
last_conv_idx = [i for i,l in enumerate(model.layers) if type(l) is Convolution2D][-1]
conv_layers = model.layers[:last_conv_idx+1]
conv_model = Sequential(conv_layers)
(val_classes, trn_classes, val_labels, trn_labels,
val_filenames, filenames, test_filenames) = get_classes(path)
test_batches = get_batches(path+'test', batch_size=batch_size*2, shuffle=False)
conv_feat = conv_model.predict_generator(batches, int(np.ceil(batches.samples/batch_size)))
conv_val_feat = conv_model.predict_generator(val_batches, int(np.ceil(val_batches.samples/(batch_size*2))))
conv_test_feat = conv_model.predict_generator(test_batches, int(np.ceil(test_batches.samples/(batch_size*2))))
save_array(path+'results/conv_val_feat.dat', conv_val_feat)
save_array(path+'results/conv_test_feat.dat', conv_test_feat)
save_array(path+'results/conv_feat.dat', conv_feat)
conv_feat = load_array(path+'results/conv_feat.dat')
conv_val_feat = load_array(path+'results/conv_val_feat.dat')
conv_val_feat.shape
```
### Batchnorm dense layers on pretrained conv layers
Since we've pre-computed the output of the last convolutional layer, we need to create a network that takes that as input, and predicts our 10 classes. Let's try using a simplified version of VGG's dense layers.
```
def get_bn_layers(p):
return [
MaxPooling2D(input_shape=conv_layers[-1].output_shape[1:]),
Flatten(),
Dropout(p/2),
Dense(128, activation='relu'),
BatchNormalization(),
Dropout(p/2),
Dense(128, activation='relu'),
BatchNormalization(),
Dropout(p),
Dense(10, activation='softmax')
]
p=0.8
bn_model = Sequential(get_bn_layers(p))
bn_model.compile(Adam(lr=0.001), loss='categorical_crossentropy', metrics=['accuracy'])
bn_model.fit(conv_feat, trn_labels, batch_size=batch_size, epochs=1,
validation_data=(conv_val_feat, val_labels))
bn_model.optimizer.lr=0.01
bn_model.fit(conv_feat, trn_labels, batch_size=batch_size, epochs=2,
validation_data=(conv_val_feat, val_labels))
bn_model.save_weights(path+'models/conv8.h5')
```
Looking good! Let's try pre-computing 5 epochs worth of augmented data, so we can experiment with combining dropout and augmentation on the pre-trained model.
### Pre-computed data augmentation + dropout
We'll use our usual data augmentation parameters:
```
gen_t = image.ImageDataGenerator(rotation_range=15, height_shift_range=0.05,
shear_range=0.1, channel_shift_range=20, width_shift_range=0.1)
da_batches = get_batches(path+'train', gen_t, batch_size=batch_size, shuffle=False)
```
We use those to create a dataset of convolutional features 5x bigger than the training set.
```
da_conv_feat = conv_model.predict_generator(da_batches, 5*int(np.ceil((da_batches.samples)/(batch_size))), workers=3)
save_array(path+'results/da_conv_feat2.dat', da_conv_feat)
da_conv_feat = load_array(path+'results/da_conv_feat2.dat')
```
Let's include the real training data as well in its non-augmented form.
```
da_conv_feat = np.concatenate([da_conv_feat, conv_feat])
```
Since we've now got a dataset 6x bigger than before, we'll need to copy our labels 6 times too.
```
da_trn_labels = np.concatenate([trn_labels]*6)
```
Based on some experiments the previous model works well, with bigger dense layers.
```
def get_bn_da_layers(p):
return [
MaxPooling2D(input_shape=conv_layers[-1].output_shape[1:]),
Flatten(),
Dropout(p),
Dense(256, activation='relu'),
BatchNormalization(),
Dropout(p),
Dense(256, activation='relu'),
BatchNormalization(),
Dropout(p),
Dense(10, activation='softmax')
]
p=0.8
bn_model = Sequential(get_bn_da_layers(p))
bn_model.compile(Adam(lr=0.001), loss='categorical_crossentropy', metrics=['accuracy'])
```
Now we can train the model as usual, with pre-computed augmented data.
```
bn_model.fit(da_conv_feat, da_trn_labels, batch_size=batch_size, epochs=1,
validation_data=(conv_val_feat, val_labels))
bn_model.optimizer.lr=0.01
bn_model.fit(da_conv_feat, da_trn_labels, batch_size=batch_size, epochs=4,
validation_data=(conv_val_feat, val_labels))
bn_model.optimizer.lr=0.0001
bn_model.fit(da_conv_feat, da_trn_labels, batch_size=batch_size, epochs=4,
validation_data=(conv_val_feat, val_labels))
```
Looks good - let's save those weights.
```
bn_model.save_weights(path+'models/da_conv8_1.h5')
```
### Pseudo labeling
We're going to try using a combination of [pseudo labeling](http://deeplearning.net/wp-content/uploads/2013/03/pseudo_label_final.pdf) and [knowledge distillation](https://arxiv.org/abs/1503.02531) to allow us to use unlabeled data (i.e. do semi-supervised learning). For our initial experiment we'll use the validation set as the unlabeled data, so that we can see that it is working without using the test set. At a later date we'll try using the test set.
To do this, we simply calculate the predictions of our model...
```
val_pseudo = bn_model.predict(conv_val_feat, batch_size=batch_size)
```
...concatenate them with our training labels...
```
comb_pseudo = np.concatenate([da_trn_labels, val_pseudo])
comb_feat = np.concatenate([da_conv_feat, conv_val_feat])
```
...and fine-tune our model using that data.
```
bn_model.load_weights(path+'models/da_conv8_1.h5')
bn_model.fit(comb_feat, comb_pseudo, batch_size=batch_size, epochs=1,
validation_data=(conv_val_feat, val_labels))
bn_model.fit(comb_feat, comb_pseudo, batch_size=batch_size, epochs=4,
validation_data=(conv_val_feat, val_labels))
bn_model.optimizer.lr=0.00001
bn_model.fit(comb_feat, comb_pseudo, batch_size=batch_size, epochs=4,
validation_data=(conv_val_feat, val_labels))
```
That's a distinct improvement - even although the validation set isn't very big. This looks encouraging for when we try this on the test set.
```
bn_model.save_weights(path+'models/bn-ps8.h5')
```
### Submit
We'll find a good clipping amount using the validation set, prior to submitting.
```
def do_clip(arr, mx): return np.clip(arr, (1-mx)/9, mx)
val_preds = bn_model.predict(conv_val_feat, batch_size=batch_size*2)
np.mean(keras.metrics.categorical_crossentropy(val_labels, do_clip(val_preds, 0.93)).eval())
conv_test_feat = load_array(path+'results/conv_test_feat.dat')
preds = bn_model.predict(conv_test_feat, batch_size=batch_size*2)
subm = do_clip(preds,0.93)
subm_name = path+'results/subm.gz'
classes = sorted(batches.class_indices, key=batches.class_indices.get)
submission = pd.DataFrame(subm, columns=classes)
submission.insert(0, 'img', [a[4:] for a in test_filenames])
submission.head()
submission.to_csv(subm_name, index=False, compression='gzip')
FileLink(subm_name)
```
This gets 0.534 on the leaderboard.
## The "things that didn't really work" section
You can safely ignore everything from here on, because they didn't really help.
### Finetune some conv layers too
```
#for l in get_bn_layers(p): conv_model.add(l) # this choice would give a weight shape error
for l in get_bn_da_layers(p): conv_model.add(l) # ... so probably this is the right one
for l1,l2 in zip(bn_model.layers, conv_model.layers[last_conv_idx+1:]):
l2.set_weights(l1.get_weights())
for l in conv_model.layers: l.trainable =False
for l in conv_model.layers[last_conv_idx+1:]: l.trainable =True
comb = np.concatenate([trn, val])
# not knowing what the experiment was about, added this to avoid a shape match error with comb using gen_t.flow
comb_pseudo = np.concatenate([trn_labels, val_pseudo])
gen_t = image.ImageDataGenerator(rotation_range=8, height_shift_range=0.04,
shear_range=0.03, channel_shift_range=10, width_shift_range=0.08)
batches = gen_t.flow(comb, comb_pseudo, batch_size=batch_size)
val_batches = get_batches(path+'valid', batch_size=batch_size*2, shuffle=False)
conv_model.compile(Adam(lr=0.00001), loss='categorical_crossentropy', metrics=['accuracy'])
conv_model.fit_generator(batches, steps_per_epoch, epochs=1, validation_data=val_batches,
validation_steps=validation_steps)
conv_model.optimizer.lr = 0.0001
conv_model.fit_generator(batches, steps_per_epoch, epochs=3, validation_data=val_batches,
validation_steps=validation_steps)
for l in conv_model.layers[16:]: l.trainable =True
#- added compile instruction in order to avoid Keras 2.1 warning message
conv_model.compile(Adam(), loss='categorical_crossentropy', metrics=['accuracy'])
conv_model.optimizer.lr = 0.00001
conv_model.fit_generator(batches, steps_per_epoch, epochs=8, validation_data=val_batches,
validation_steps=validation_steps)
conv_model.save_weights(path+'models/conv8_ps.h5')
#conv_model.load_weights(path+'models/conv8_da.h5') # conv8_da.h5 was not saved in this notebook
val_pseudo = conv_model.predict(val, batch_size=batch_size*2)
save_array(path+'models/pseudo8_da.dat', val_pseudo)
```
### Ensembling
```
drivers_ds = pd.read_csv(path+'driver_imgs_list.csv')
drivers_ds.head()
img2driver = drivers_ds.set_index('img')['subject'].to_dict()
driver2imgs = {k: g["img"].tolist()
for k,g in drivers_ds[['subject', 'img']].groupby("subject")}
# It seems this function is not used in this notebook
def get_idx(driver_list):
return [i for i,f in enumerate(filenames) if img2driver[f[3:]] in driver_list]
# drivers = driver2imgs.keys() # Python 2
drivers = list(driver2imgs) # Python 3
rnd_drivers = np.random.permutation(drivers)
ds1 = rnd_drivers[:len(rnd_drivers)//2]
ds2 = rnd_drivers[len(rnd_drivers)//2:]
# The following cells seem to require some preparation code not included in this notebook
models=[fit_conv([d]) for d in drivers]
models=[m for m in models if m is not None]
all_preds = np.stack([m.predict(conv_test_feat, batch_size=128) for m in models])
avg_preds = all_preds.mean(axis=0)
avg_preds = avg_preds/np.expand_dims(avg_preds.sum(axis=1), 1)
keras.metrics.categorical_crossentropy(val_labels, np.clip(avg_val_preds,0.01,0.99)).eval()
keras.metrics.categorical_accuracy(val_labels, np.clip(avg_val_preds,0.01,0.99)).eval()
```
| true |
code
| 0.758913 | null | null | null | null |
|
```
import sys
sys.path.append("functions/")
from datastore import DataStore
from searchgrid import SearchGrid
from crossvalidate import CrossValidate
from sklearn.dummy import DummyClassifier
from sklearn.metrics import f1_score
from sklearn.metrics import roc_auc_score
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import balanced_accuracy_score
from sampleddatastore import SampledDataStore
```
First, we will load up our predefined functions for loading the data and running the model.
Due to the high class imbalance, F1 score is a much better metric to use than just accuracy (since 99% of the data belongs to class 0). We will also have ROC-AUC for comparison.
We fetch the true positives, false positives and false negatives to calculate the f1 score across all folds rather than using the builtin functionality. This is because the averaged f1 score returned by Sklearn is slighly biased for imbalanced class problems (for cross validation). This doesn't matter when evaluating the test set. All the relevant functions are in their respective python files (same folder as the notebook).
Reference: https://www.hpl.hp.com/techreports/2009/HPL-2009-359.pdf
```
#Load object for CrossValidation
crossvalidate = CrossValidate()
#Load object for GridSearchCV
GridSpace = SearchGrid()
```
Let's establish a baseline model that simply predicts the minority class:
```
classifier = DummyClassifier(strategy="constant", constant=1)
crossvalidate.setClassifier(classifier)
crossvalidate.run()
f1, roc = crossvalidate.getMetrics().getScores()
print(f"F1 score is: {f1}")
print(f"ROC-AUC is: {roc}")
```
A good model is one that can perform better than the baseline, in terms of F1 Score. Anything below is worse than a model that simply predicts minority class.
Note that 0.5 ROC-AUC score indicates that it's a random classifier.
```
classifier = LogisticRegression()
crossvalidate.setClassifier(classifier)
crossvalidate.run()
f1, roc = crossvalidate.getMetrics().getScores()
print(f"F1 score is: {f1}")
print(f"ROC-AUC is: {roc}")
```
Looks like it's slightly better than a random classifier; this means that our model is learning some relationships for the underlying data, albeit small.
The low score is to expected, especially given the class imbalance. Let's try using the class weight functionality that assigns weights to each class based on their frequency.
```
classifier = LogisticRegression(class_weight='balanced')
crossvalidate.setClassifier(classifier)
crossvalidate.run()
f1, roc = crossvalidate.getMetrics().getScores()
print(f"F1 score is: {f1}")
print(f"ROC-AUC is: {roc}")
```
Looks like the balanced class weight performs worse in terms of f1 score (probably because it results in a lot more false positives).
Let's test different parameters using GridSearchCV. We will be using our custom objects.
```
parameters = {'class_weight':[{0:1,1:1}, {0:1,1:10}, {0:1,1:100}, {0:10,1:1}]}
GridSpace.setGridParameters(parameters)
GridSpace.setClassifier(LogisticRegression())
GridSpace.run()
parameters, scores = GridSpace.getMetrics().getBestResults()
f1 = scores[0]
roc = scores[1]
print(f"F1 score is: {f1}")
print(f"ROC-AUC is: {roc}")
print(f"Best Parameters: {parameters}")
```
We are making progress, but can we do even better?
Adjusting the weights were not enough, we will have to try different sampling techniques. Imbalanced-learn library will come in handy here.
We will start with RandomOverSampler to duplicates records from the minority class. We will use a sampling ratio of 0.1 (i.e. increasing gilded class to ~10%).
Read more: https://imbalanced-learn.readthedocs.io/en/stable/over_sampling.html#a-practical-guide
```
SampledDataStore = SampledDataStore()
SampledDataStore.initializeSamplers()
#Using RandomOverSampler to duplicate records belonging to class 1 (gilded)
random = SampledDataStore.getRandomSampled
X_resampled, y_resampled = random()
classifier = LogisticRegression(class_weight={0: 1, 1: 10})
crossvalidate.getDataStore().setxTrain(X_resampled)
crossvalidate.getDataStore().setyTrain(y_resampled)
crossvalidate.setClassifier(classifier)
crossvalidate.run()
f1, roc = crossvalidate.getMetrics().getScores()
print("Random Over Sampling:")
print(f"F1 score is: {f1}")
print(f"ROC-AUC is: {roc}")
crossvalidate.getDataStore().revertToOriginal()
```
We can also generate new samples with SMOTE and ADASYN based on existing samples. We will keep the sampling ratio the same for comparison.
```
smote = SampledDataStore.getSMOTESampled
ada = SampledDataStore.getADASYNSampled
samplers = [smote, ada]
sampler_names = ["SMOTE", "ADASYN"]
for i in range(len(samplers)):
X_resampled, y_resampled = samplers[i]()
crossvalidate.getDataStore().setxTrain(X_resampled)
crossvalidate.getDataStore().setyTrain(y_resampled)
classifier = LogisticRegression(class_weight={0: 1, 1: 10})
crossvalidate.setClassifier(classifier)
crossvalidate.run()
f1, roc = crossvalidate.getMetrics().getScores()
print(f"{sampler_names[i]}: ")
print(f"F1 score is: {f1}")
print(f"ROC-AUC is: {roc}")
print("\n")
crossvalidate.getDataStore().revertToOriginal()
```
Imbalanced learn also recommends combining oversampling with undersampling the majority class.
Ref: https://imbalanced-learn.readthedocs.io/en/stable/auto_examples/combine/plot_comparison_combine.html
SMOTE can generate noisy samples (ex: when classes cannot be well separated), undersampling allows to clean the noisy data.
```
smote_tomek = SampledDataStore.getSMOTETOMEKSampled
smote_enn = SampledDataStore.getSMOTEENNSampled
samplers = [smote_tomek, smote_enn]
sampler_names = ["SMOTE TOMEK", "SMOTE ENN"]
for i in range(len(samplers)):
X_resampled, y_resampled = samplers[i]()
crossvalidate.getDataStore().setxTrain(X_resampled)
crossvalidate.getDataStore().setyTrain(y_resampled)
classifier = LogisticRegression(class_weight={0: 1, 1: 10})
crossvalidate.setClassifier(classifier)
crossvalidate.run()
f1, roc = crossvalidate.getMetrics().getScores()
print(f"{sampler_names[i]}: ")
print(f"F1 score is: {f1}")
print(f"ROC-AUC is: {roc}")
print("\n")
crossvalidate.getDataStore().revertToOriginal()
```
SMOTE, SMOTEENN and RandomOverSampler produces the best results so far. Let's evaluate those them on our test set.
```
random = SampledDataStore.getRandomSampled
smote = SampledDataStore.getSMOTESampled
smote_enn = SampledDataStore.getSMOTEENNSampled
samplers = [random, smote, smote_enn]
sampler_names = ["Random OverSampler", "SMOTE", "SMOTE ENN"]
classifier = LogisticRegression()
for i in range(len(samplers)):
parameters = {'class_weight':[{0:1,1:10}]}
X_resampled, y_resampled = samplers[i]()
GridSpace.getDataStore().setxTrain(X_resampled)
GridSpace.getDataStore().setyTrain(y_resampled)
GridSpace.setGridParameters(parameters)
GridSpace.setClassifier(classifier)
grid = GridSpace.run()
y_preds = grid.predict(GridSpace.getDataStore().getxTest())
print(f"{sampler_names[i]} on test set:")
print(f"F1 score: {f1_score(GridSpace.getDataStore().getyTest(), y_preds)}")
print(f"ROC_AUC score: {roc_auc_score(GridSpace.getDataStore().getyTest(), y_preds)}")
print(f"Balanced accuracy score: {balanced_accuracy_score(GridSpace.getDataStore().getyTest(), y_preds)}")
print("\n")
GridSpace.getDataStore().revertToOriginal()
```
Logistic regression predicts the class probabilities for each sample and decides class based on a threshold (default: 0.5). We can also check if a different threshold value produces better results.
Ref: https://machinelearningmastery.com/threshold-moving-for-imbalanced-classification/
Let's define the relevant functions first.
```
import numpy as np
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegressionCV
def trainAndgetProbabilities(xTrain, yTrain, xTest):
rskf = RepeatedStratifiedKFold(n_splits=10, n_repeats=2, random_state=42)
model = LogisticRegressionCV(cv=rskf, class_weight=[{0: 1, 1: 10}])
model.fit(xTrain, yTrain)
return model.predict_proba(xTest)[:,1]
def convert_probs(probs, threshold):
return (probs >= threshold).astype('int')
from datastore import DataStore
Data = DataStore()
random = SampledDataStore.getRandomSampled
smote = SampledDataStore.getSMOTESampled
smote_enn = SampledDataStore.getSMOTEENNSampled
samplers = [random, smote, smote_enn]
sampler_names = ["Random Oversampling", "SMOTE", "SMOTE ENN"]
thresholds = np.arange(0, 1, 0.001)
for i in range(len(samplers)):
X_resampled, y_resampled = samplers[i]()
probs = trainAndgetProbabilities(X_resampled, y_resampled, Data.getxTest())
f1_scores = [f1_score(Data.getyTest(), convert_probs(probs, t)) for t in thresholds]
roc_scores = [roc_auc_score(Data.getyTest(), convert_probs(probs, t)) for t in thresholds]
maxf1Index = np.argmax(f1_scores)
maxrocIndex = np.argmax(roc_scores)
print(f"\n{sampler_names[i]} on test set:")
print("Maxiziming F1 Score:")
print(f"Threshold: {thresholds[maxf1Index]}, F1 Score: {f1_scores[maxf1Index]}, ROC AUC: {roc_scores[maxf1Index]}")
print("Maxiziming ROC-AUC Score:")
print(f"Threshold: {thresholds[maxrocIndex]}, F1 Score: {f1_scores[maxrocIndex]}, ROC AUC: {roc_scores[maxrocIndex]}")
```
Better, but not ideal. The difference in ROC_AUC score points to the problem; The higher threshold value causes the model to predict smaller number of samples to be positive (true positive or false positive), resulting in lower ROC AUC and a higher F1 score.
Overall, our results are better than the baseline model, but not ideal. Perhaps, we can achieve better results with a more complex (non-linear) model. Let's try SVM next.
| true |
code
| 0.374076 | null | null | null | null |
|
# Rank Classification using BERT on Amazon Review dataset
## Introduction
In this tutorial, you learn how to train a rank classification model using [Transfer Learning](https://en.wikipedia.org/wiki/Transfer_learning). We will use a pretrained DistilBert model to train on the Amazon review dataset.
## About the dataset and model
[Amazon Customer Review dataset](https://s3.amazonaws.com/amazon-reviews-pds/readme.html) consists of all different valid reviews from amazon.com. We will use the "Digital_software" category that consists of 102k valid reviews. As for the pre-trained model, use the DistilBERT[[1]](https://arxiv.org/abs/1910.01108) model. It's a light-weight BERT model already trained on [Wikipedia text corpora](https://en.wikipedia.org/wiki/List_of_text_corpora), a much larger dataset consisting of over millions text. The DistilBERT served as a base layer and we will add some more classification layers to output as rankings (1 - 5).
<img src="https://djl-ai.s3.amazonaws.com/resources/images/amazon_review.png" width="500">
<center>Amazon Review example</center>
We will use review body as our data input and ranking as label.
## Pre-requisites
This tutorial assumes you have the following knowledge. Follow the READMEs and tutorials if you are not familiar with:
1. How to setup and run [Java Kernel in Jupyter Notebook](https://github.com/deepjavalibrary/djl/blob/master/jupyter/README.md)
2. Basic components of Deep Java Library, and how to [train your first model](https://github.com/deepjavalibrary/djl/blob/master/jupyter/tutorial/02_train_your_first_model.ipynb).
## Getting started
Load the Deep Java Libarary and its dependencies from Maven. In here, you can choose between MXNet or PyTorch. MXNet is enabled by default. You can uncomment PyTorch dependencies and comment MXNet ones to switch to PyTorch.
```
// %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
%maven ai.djl:api:0.15.0
%maven ai.djl:basicdataset:0.15.0
%maven org.slf4j:slf4j-simple:1.7.32
%maven ai.djl.mxnet:mxnet-model-zoo:0.15.0
// PyTorch
// %maven ai.djl.pytorch:pytorch-model-zoo:0.15.0
```
Now let's import the necessary modules:
```
import ai.djl.*;
import ai.djl.basicdataset.tabular.*;
import ai.djl.basicdataset.utils.*;
import ai.djl.engine.*;
import ai.djl.inference.*;
import ai.djl.metric.*;
import ai.djl.modality.*;
import ai.djl.modality.nlp.*;
import ai.djl.modality.nlp.bert.*;
import ai.djl.ndarray.*;
import ai.djl.ndarray.types.*;
import ai.djl.nn.*;
import ai.djl.nn.core.*;
import ai.djl.nn.norm.*;
import ai.djl.repository.zoo.*;
import ai.djl.training.*;
import ai.djl.training.dataset.*;
import ai.djl.training.evaluator.*;
import ai.djl.training.listener.*;
import ai.djl.training.loss.*;
import ai.djl.training.util.*;
import ai.djl.translate.*;
import java.io.*;
import java.nio.file.*;
import java.util.*;
import org.apache.commons.csv.*;
System.out.println("You are using: " + Engine.getInstance().getEngineName() + " Engine");
```
## Prepare Dataset
First step is to prepare the dataset for training. Since the original data was in TSV format, we can use CSVDataset to be the dataset container. We will also need to specify how do we want to preprocess the raw data. For BERT model, the input data are required to be tokenized and mapped into indices based on the inputs. In DJL, we defined an interface called Fearurizer, it is designed to allow user customize operation on each selected row/column of a dataset. In our case, we would like to clean and tokenize our sentencies. So let's try to implement it to deal with customer review sentencies.
```
final class BertFeaturizer implements CsvDataset.Featurizer {
private final BertFullTokenizer tokenizer;
private final int maxLength; // the cut-off length
public BertFeaturizer(BertFullTokenizer tokenizer, int maxLength) {
this.tokenizer = tokenizer;
this.maxLength = maxLength;
}
/** {@inheritDoc} */
@Override
public void featurize(DynamicBuffer buf, String input) {
Vocabulary vocab = tokenizer.getVocabulary();
// convert sentence to tokens (toLowerCase for uncased model)
List<String> tokens = tokenizer.tokenize(input.toLowerCase());
// trim the tokens to maxLength
tokens = tokens.size() > maxLength ? tokens.subList(0, maxLength) : tokens;
// BERT embedding convention "[CLS] Your Sentence [SEP]"
buf.put(vocab.getIndex("[CLS]"));
tokens.forEach(token -> buf.put(vocab.getIndex(token)));
buf.put(vocab.getIndex("[SEP]"));
}
}
```
Once we got this part done, we can apply the `BertFeaturizer` into our Dataset. We take `review_body` column and apply the Featurizer. We also pick `star_rating` as our label set. Since we go for batch input, we need to tell the dataset to pad our data if it is less than the `maxLength` we defined. `PaddingStackBatchifier` will do the work for you.
```
CsvDataset getDataset(int batchSize, BertFullTokenizer tokenizer, int maxLength, int limit) {
String amazonReview =
"https://s3.amazonaws.com/amazon-reviews-pds/tsv/amazon_reviews_us_Digital_Software_v1_00.tsv.gz";
float paddingToken = tokenizer.getVocabulary().getIndex("[PAD]");
return CsvDataset.builder()
.optCsvUrl(amazonReview) // load from Url
.setCsvFormat(CSVFormat.TDF.withQuote(null).withHeader()) // Setting TSV loading format
.setSampling(batchSize, true) // make sample size and random access
.optLimit(limit)
.addFeature(
new CsvDataset.Feature(
"review_body", new BertFeaturizer(tokenizer, maxLength)))
.addLabel(
new CsvDataset.Feature(
"star_rating", (buf, data) -> buf.put(Float.parseFloat(data) - 1.0f)))
.optDataBatchifier(
PaddingStackBatchifier.builder()
.optIncludeValidLengths(false)
.addPad(0, 0, (m) -> m.ones(new Shape(1)).mul(paddingToken))
.build()) // define how to pad dataset to a fix length
.build();
}
```
## Construct your model
We will load our pretrained model and prepare the classification. First construct the `criteria` to specify where to load the embedding (DistiledBERT), then call `loadModel` to download that embedding with pre-trained weights. Since this model is built without classification layer, we need to add a classification layer to the end of the model and train it. After you are done modifying the block, set it back to model using `setBlock`.
### Load the word embedding
We will download our word embedding and load it to memory (this may take a while)
```
// MXNet base model
String modelUrls = "https://resources.djl.ai/test-models/distilbert.zip";
if ("PyTorch".equals(Engine.getInstance().getEngineName())) {
modelUrls = "https://resources.djl.ai/test-models/traced_distilbert_wikipedia_uncased.zip";
}
Criteria<NDList, NDList> criteria = Criteria.builder()
.optApplication(Application.NLP.WORD_EMBEDDING)
.setTypes(NDList.class, NDList.class)
.optModelUrls(modelUrls)
.optProgress(new ProgressBar())
.build();
ZooModel<NDList, NDList> embedding = criteria.loadModel();
```
### Create classification layers
Then let's build a simple MLP layer to classify the ranks. We set the output of last FullyConnected (Linear) layer to 5 to get the predictions for star 1 to 5. Then all we need to do is to load the block into the model. Before applying the classification layer, we also need to add text embedding to the front. In our case, we just create a Lambda function that do the followings:
1. batch_data (batch size, token indices) -> batch_data + max_length (size of the token indices)
2. generate embedding
```
Predictor<NDList, NDList> embedder = embedding.newPredictor();
Block classifier = new SequentialBlock()
// text embedding layer
.add(
ndList -> {
NDArray data = ndList.singletonOrThrow();
NDList inputs = new NDList();
long batchSize = data.getShape().get(0);
float maxLength = data.getShape().get(1);
if ("PyTorch".equals(Engine.getInstance().getEngineName())) {
inputs.add(data.toType(DataType.INT64, false));
inputs.add(data.getManager().full(data.getShape(), 1, DataType.INT64));
inputs.add(data.getManager().arange(maxLength)
.toType(DataType.INT64, false)
.broadcast(data.getShape()));
} else {
inputs.add(data);
inputs.add(data.getManager().full(new Shape(batchSize), maxLength));
}
// run embedding
try {
return embedder.predict(inputs);
} catch (TranslateException e) {
throw new IllegalArgumentException("embedding error", e);
}
})
// classification layer
.add(Linear.builder().setUnits(768).build()) // pre classifier
.add(Activation::relu)
.add(Dropout.builder().optRate(0.2f).build())
.add(Linear.builder().setUnits(5).build()) // 5 star rating
.addSingleton(nd -> nd.get(":,0")); // Take [CLS] as the head
Model model = Model.newInstance("AmazonReviewRatingClassification");
model.setBlock(classifier);
```
## Start Training
Finally, we can start building our training pipeline to train the model.
### Creating Training and Testing dataset
Firstly, we need to create a voabulary that is used to map token to index such as "hello" to 1121 (1121 is the index of "hello" in dictionary). Then we simply feed the vocabulary to the tokenizer that used to tokenize the sentence. Finally, we just need to split the dataset based on the ratio.
Note: we set the cut-off length to 64 which means only the first 64 tokens from the review will be used. You can increase this value to achieve better accuracy.
```
// Prepare the vocabulary
DefaultVocabulary vocabulary = DefaultVocabulary.builder()
.addFromTextFile(embedding.getArtifact("vocab.txt"))
.optUnknownToken("[UNK]")
.build();
// Prepare dataset
int maxTokenLength = 64; // cutoff tokens length
int batchSize = 8;
int limit = Integer.MAX_VALUE;
// int limit = 512; // uncomment for quick testing
BertFullTokenizer tokenizer = new BertFullTokenizer(vocabulary, true);
CsvDataset amazonReviewDataset = getDataset(batchSize, tokenizer, maxTokenLength, limit);
// split data with 7:3 train:valid ratio
RandomAccessDataset[] datasets = amazonReviewDataset.randomSplit(7, 3);
RandomAccessDataset trainingSet = datasets[0];
RandomAccessDataset validationSet = datasets[1];
```
### Setup Trainer and training config
Then, we need to setup our trainer. We set up the accuracy and loss function. The model training logs will be saved to `build/modlel`.
```
SaveModelTrainingListener listener = new SaveModelTrainingListener("build/model");
listener.setSaveModelCallback(
trainer -> {
TrainingResult result = trainer.getTrainingResult();
Model model = trainer.getModel();
// track for accuracy and loss
float accuracy = result.getValidateEvaluation("Accuracy");
model.setProperty("Accuracy", String.format("%.5f", accuracy));
model.setProperty("Loss", String.format("%.5f", result.getValidateLoss()));
});
DefaultTrainingConfig config = new DefaultTrainingConfig(Loss.softmaxCrossEntropyLoss()) // loss type
.addEvaluator(new Accuracy())
.optDevices(Engine.getInstance().getDevices(1)) // train using single GPU
.addTrainingListeners(TrainingListener.Defaults.logging("build/model"))
.addTrainingListeners(listener);
```
### Start training
We will start our training process. Training on GPU will takes approximately 10 mins. For CPU, it will take more than 2 hours to finish.
```
int epoch = 2;
Trainer trainer = model.newTrainer(config);
trainer.setMetrics(new Metrics());
Shape encoderInputShape = new Shape(batchSize, maxTokenLength);
// initialize trainer with proper input shape
trainer.initialize(encoderInputShape);
EasyTrain.fit(trainer, epoch, trainingSet, validationSet);
System.out.println(trainer.getTrainingResult());
```
### Save the model
```
model.save(Paths.get("build/model"), "amazon-review.param");
```
## Verify the model
We can create a predictor from the model to run inference on our customized dataset. Firstly, we can create a `Translator` for the model to do preprocessing and post processing. Similar to what we have done before, we need to tokenize the input sentence and get the output ranking.
```
class MyTranslator implements Translator<String, Classifications> {
private BertFullTokenizer tokenizer;
private Vocabulary vocab;
private List<String> ranks;
public MyTranslator(BertFullTokenizer tokenizer) {
this.tokenizer = tokenizer;
vocab = tokenizer.getVocabulary();
ranks = Arrays.asList("1", "2", "3", "4", "5");
}
@Override
public Batchifier getBatchifier() { return Batchifier.STACK; }
@Override
public NDList processInput(TranslatorContext ctx, String input) {
List<String> tokens = tokenizer.tokenize(input);
float[] indices = new float[tokens.size() + 2];
indices[0] = vocab.getIndex("[CLS]");
for (int i = 0; i < tokens.size(); i++) {
indices[i+1] = vocab.getIndex(tokens.get(i));
}
indices[indices.length - 1] = vocab.getIndex("[SEP]");
return new NDList(ctx.getNDManager().create(indices));
}
@Override
public Classifications processOutput(TranslatorContext ctx, NDList list) {
return new Classifications(ranks, list.singletonOrThrow().softmax(0));
}
}
```
Finally, we can create a `Predictor` to run the inference. Let's try with a random customer review:
```
String review = "It works great, but it takes too long to update itself and slows the system";
Predictor<String, Classifications> predictor = model.newPredictor(new MyTranslator(tokenizer));
predictor.predict(review)
```
| true |
code
| 0.820577 | null | null | null | null |
|
# Resample Data
## Pandas Resample
You've learned about bucketing to different periods of time like Months. Let's see how it's done. We'll start with an example series of days.
```
import numpy as np
import pandas as pd
dates = pd.date_range('10/10/2018', periods=11, freq='D')
close_prices = np.arange(len(dates))
close = pd.Series(close_prices, dates)
close
```
Let's say we want to bucket these days into 3 day periods. To do that, we'll use the [DataFrame.resample](https://pandas.pydata.org/pandas-docs/version/0.21/generated/pandas.DataFrame.resample.html) function. The first parameter in this function is a string called `rule`, which is a representation of how to resample the data. This string representation is made using an offset alias. You can find a list of them [here](http://pandas.pydata.org/pandas-docs/stable/timeseries.html#offset-aliases). To create 3 day periods, we'll set `rule` to "3D".
```
close.resample('3D')
```
This returns a `DatetimeIndexResampler` object. It's an intermediate object similar to the `GroupBy` object. Just like group by, it breaks the original data into groups. That means, we'll have to apply an operation to these groups. Let's make it simple and get the first element from each group.
```
close.resample('3D').first()
```
You might notice that this is the same as `.iloc[::3]`
```
close.iloc[::3]
```
So, why use the `resample` function instead of `.iloc[::3]` or the `groupby` function?
The `resample` function shines when handling time and/or date specific tasks. In fact, you can't use this function if the index isn't a [time-related class](https://pandas.pydata.org/pandas-docs/version/0.21/timeseries.html#overview).
```
try:
# Attempt resample on a series without a time index
pd.Series(close_prices).resample('W')
except TypeError:
print('It threw a TypeError.')
else:
print('It worked.')
```
One of the resampling tasks it can help with is resampling on periods, like weeks. Let's resample `close` from it's days frequency to weeks. We'll use the "W" offset allies, which stands for Weeks.
```
pd.DataFrame({
'days': close,
'weeks': close.resample('W').first()})
```
The weeks offset considers the start of a week on a Monday. Since 2018-10-10 is a Wednesday, the first group only looks at the first 5 items. There are offsets that handle more complicated problems like filtering for Holidays. For now, we'll only worry about resampling for days, weeks, months, quarters, and years. The frequency you want the data to be in, will depend on how often you'll be trading. If you're making trade decisions based on reports that come out at the end of the year, we might only care about a frequency of years or months.
## OHLC
Now that you've seen how Pandas resamples time series data, we can apply this to Open, High, Low, and Close (OHLC). Pandas provides the [`Resampler.ohlc`](https://pandas.pydata.org/pandas-docs/version/0.21.0/generated/pandas.core.resample.Resampler.ohlc.html#pandas.core.resample.Resampler.ohlc) function will convert any resampling frequency to OHLC data. Let's get the Weekly OHLC.
```
close.resample('W').ohlc()
```
Can you spot a potential problem with that? It has to do with resampling data that has already been resampled.
We're getting the OHLC from close data. If we want OHLC data from already resampled data, we should resample the first price from the open data, resample the highest price from the high data, etc..
To get the weekly closing prices from `close`, you can use the [`Resampler.last`](https://pandas.pydata.org/pandas-docs/version/0.21.0/generated/pandas.core.resample.Resampler.last.html#pandas.core.resample.Resampler.last) function.
```
close.resample('W').last()
```
## Quiz
Implement `days_to_weeks` function to resample OHLC price data to weekly OHLC price data. You find find more Resampler functions [here](https://pandas.pydata.org/pandas-docs/version/0.21.0/api.html#id44) for calculating high and low prices.
```
import quiz_tests
def days_to_weeks(open_prices, high_prices, low_prices, close_prices):
"""Converts daily OHLC prices to weekly OHLC prices.
Parameters
----------
open_prices : DataFrame
Daily open prices for each ticker and date
high_prices : DataFrame
Daily high prices for each ticker and date
low_prices : DataFrame
Daily low prices for each ticker and date
close_prices : DataFrame
Daily close prices for each ticker and date
Returns
-------
open_prices_weekly : DataFrame
Weekly open prices for each ticker and date
high_prices_weekly : DataFrame
Weekly high prices for each ticker and date
low_prices_weekly : DataFrame
Weekly low prices for each ticker and date
close_prices_weekly : DataFrame
Weekly close prices for each ticker and date
"""
open_prices_weekly = open_prices.resample('W').first()
high_prices_weekly = high_prices.resample('W').max()
low_prices_weekly = low_prices.resample('W').min()
close_prices_weekly = close_prices.resample('W').last()
return open_prices_weekly, high_prices_weekly, low_prices_weekly, close_prices_weekly
quiz_tests.test_days_to_weeks(days_to_weeks)
```
## Quiz Solution
If you're having trouble, you can check out the quiz solution [here](resample_data_solution.ipynb).
| true |
code
| 0.638976 | null | null | null | null |
|
# Linear Support Vector Regressor with PowerTransformer
This Code template is for the Classification task using Support Vector Regressor (SVR) based on the Support Vector Machine algorithm with Power Transformer as Feature Transformation Technique in a pipeline.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.preprocessing import PowerTransformer
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from imblearn.over_sampling import RandomOverSampler
from sklearn.svm import LinearSVR
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path=""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_values
target=''
```
### Data fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)#performing datasplitting
```
### Model
Support vector machines (SVMs) are a set of supervised learning methods used for classification, regression and outliers detection.
A Support Vector Machine is a discriminative classifier formally defined by a separating hyperplane. In other terms, for a given known/labelled data points, the SVM outputs an appropriate hyperplane that classifies the inputted new cases based on the hyperplane. In 2-Dimensional space, this hyperplane is a line separating a plane into two segments where each class or group occupied on either side.
LinearSVR is similar to SVR with kernel=’linear’. It has more flexibility in the choice of tuning parameters and is suited for large samples.
#### Model Tuning Parameters
1. epsilon : float, default=0.0
> Epsilon parameter in the epsilon-insensitive loss function.
2. loss : {‘epsilon_insensitive’, ‘squared_epsilon_insensitive’}, default=’epsilon_insensitive’
> Specifies the loss function. ‘hinge’ is the standard SVM loss (used e.g. by the SVC class) while ‘squared_hinge’ is the square of the hinge loss. The combination of penalty='l1' and loss='hinge' is not supported.
3. C : float, default=1.0
> Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive.
4. tol : float, default=1e-4
> Tolerance for stopping criteria.
5. dual : bool, default=True
> Select the algorithm to either solve the dual or primal optimization problem. Prefer dual=False when n_samples > n_features.
####Feature Transformation
PowerTransformer applies a power transform featurewise to make data more Gaussian-like.
Power transforms are a family of parametric, monotonic transformations that are applied to make data more Gaussian-like. This is useful for modeling issues related to heteroscedasticity (non-constant variance), or other situations where normality is desired.
For more information... [click here](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PowerTransformer.html)
```
model=make_pipeline(PowerTransformer(),LinearSVR())
model.fit(x_train, y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
> **score**: The **score** function returns the coefficient of determination <code>R<sup>2</sup></code> of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
plt.figure(figsize=(14,10))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(x_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator:Anu Rithiga B , Github: [Profile](https://github.com/iamgrootsh7)
| true |
code
| 0.513546 | null | null | null | null |
|
<div align="center">
<h1><img width="30" src="https://madewithml.com/static/images/rounded_logo.png"> <a href="https://madewithml.com/">Made With ML</a></h1>
Applied ML · MLOps · Production
<br>
Join 30K+ developers in learning how to responsibly <a href="https://madewithml.com/about/">deliver value</a> with ML.
<br>
</div>
<br>
<div align="center">
<a target="_blank" href="https://newsletter.madewithml.com"><img src="https://img.shields.io/badge/Subscribe-30K-brightgreen"></a>
<a target="_blank" href="https://github.com/GokuMohandas/MadeWithML"><img src="https://img.shields.io/github/stars/GokuMohandas/MadeWithML.svg?style=social&label=Star"></a>
<a target="_blank" href="https://www.linkedin.com/in/goku"><img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
<a target="_blank" href="https://twitter.com/GokuMohandas"><img src="https://img.shields.io/twitter/follow/GokuMohandas.svg?label=Follow&style=social"></a>
<br>
🔥 Among the <a href="https://github.com/topics/deep-learning" target="_blank">top ML</a> repositories on GitHub
</div>
<br>
<hr>
# Attention
In this lesson we will learn how to incorporate attention mechanisms to create more context-aware representations.
<div align="left">
<a target="_blank" href="https://madewithml.com/courses/foundations/attention/"><img src="https://img.shields.io/badge/📖 Read-blog post-9cf"></a>
<a href="https://github.com/GokuMohandas/MadeWithML/blob/main/notebooks/14_Attention.ipynb" role="button"><img src="https://img.shields.io/static/v1?label=&message=View%20On%20GitHub&color=586069&logo=github&labelColor=2f363d"></a>
<a href="https://colab.research.google.com/github/GokuMohandas/MadeWithML/blob/main/notebooks/14_Attention.ipynb"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"></a>
</div>
# Overview
In the <a target="_blank" href="https://madewithml.com/courses/foundations/recurrent-neural-networks/">RNN lesson</a>, we were constrained to using the representation at the very end but what if we could give contextual weight to each encoded input ($h_i$) when making our prediction? This is also preferred because it can help mitigate the vanishing gradient issue which stems from processing very long sequences.
Below is attention applied to the outputs from an RNN. In theory, the outputs can come from anywhere where we want to learn how to weight amongst them but since we're working with the context of an RNN from the previous lesson , we'll continue with that.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/attention/attention.png" width="500">
</div>
$ \alpha = softmax(W_{attn}h) $
$c_t = \sum_{i=1}^{n} \alpha_{t,i}h_i $
*where*:
* $ h $ = RNN outputs (or any group of outputs you want to attend to) $\in \mathbb{R}^{NXMXH}$ ($N$ is the batch size, $M$ is the max sequence length in the batch, $H$ is the hidden dim)
* $ \alpha_{t,i} $ = alignment function for output $ y_t $ using input $ h_i $ (we also concatenate other useful representations with $h_i$ here). In our case, this would be the attention value to attribute to each input $h_i$.
* $W_{attn}$ = attention weights to learn $\in \mathbb{R}^{HX1}$. We can also apply activations functions, transformations, etc. here
* $c_t$ = context vector that accounts for the different inputs with attention. We can pass this context vector to downstream processes.
* **Objective:** At it's core, attention is about learning how to weigh a group of encoded representations to produce a context-aware representation to use for downstream tasks. This is done by learning a set of attention weights and then using softmax to create attention values that sum to 1.
* **Advantages:**
* Learn how to account for the appropriate encoded representations regardless of position.
* **Disadvantages:**
* Another compute step that involves learning weights.
* **Miscellaneous:**
* Several state-of-the-art approaches extend on basic attention to deliver highly context-aware representations (ex. self-attention).
# Set up
```
import numpy as np
import pandas as pd
import random
import torch
import torch.nn as nn
SEED = 1234
def set_seeds(seed=1234):
"""Set seeds for reproducibility."""
np.random.seed(seed)
random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed) # multi-GPU# Set seeds for reproducibility
set_seeds(seed=SEED)
# Set seeds for reproducibility
set_seeds(seed=SEED)
# Set device
cuda = True
device = torch.device('cuda' if (
torch.cuda.is_available() and cuda) else 'cpu')
torch.set_default_tensor_type('torch.FloatTensor')
if device.type == 'cuda':
torch.set_default_tensor_type('torch.cuda.FloatTensor')
print (device)
```
## Load data
We will download the [AG News dataset](http://www.di.unipi.it/~gulli/AG_corpus_of_news_articles.html), which consists of 120K text samples from 4 unique classes (`Business`, `Sci/Tech`, `Sports`, `World`)
```
import numpy as np
import pandas as pd
import re
import urllib
# Load data
url = "https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/datasets/news.csv"
df = pd.read_csv(url, header=0) # load
df = df.sample(frac=1).reset_index(drop=True) # shuffle
df.head()
```
## Preprocessing
We're going to clean up our input data first by doing operations such as lower text, removing stop (filler) words, filters using regular expressions, etc.
```
import nltk
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
import re
nltk.download('stopwords')
STOPWORDS = stopwords.words('english')
print (STOPWORDS[:5])
porter = PorterStemmer()
def preprocess(text, stopwords=STOPWORDS):
"""Conditional preprocessing on our text unique to our task."""
# Lower
text = text.lower()
# Remove stopwords
pattern = re.compile(r'\b(' + r'|'.join(stopwords) + r')\b\s*')
text = pattern.sub('', text)
# Remove words in paranthesis
text = re.sub(r'\([^)]*\)', '', text)
# Spacing and filters
text = re.sub(r"([-;;.,!?<=>])", r" \1 ", text)
text = re.sub('[^A-Za-z0-9]+', ' ', text) # remove non alphanumeric chars
text = re.sub(' +', ' ', text) # remove multiple spaces
text = text.strip()
return text
# Sample
text = "Great week for the NYSE!"
preprocess(text=text)
# Apply to dataframe
preprocessed_df = df.copy()
preprocessed_df.title = preprocessed_df.title.apply(preprocess)
print (f"{df.title.values[0]}\n\n{preprocessed_df.title.values[0]}")
```
## Split data
```
import collections
from sklearn.model_selection import train_test_split
TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15
def train_val_test_split(X, y, train_size):
"""Split dataset into data splits."""
X_train, X_, y_train, y_ = train_test_split(X, y, train_size=TRAIN_SIZE, stratify=y)
X_val, X_test, y_val, y_test = train_test_split(X_, y_, train_size=0.5, stratify=y_)
return X_train, X_val, X_test, y_train, y_val, y_test
# Data
X = preprocessed_df["title"].values
y = preprocessed_df["category"].values
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X=X, y=y, train_size=TRAIN_SIZE)
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"Sample point: {X_train[0]} → {y_train[0]}")
```
## LabelEncoder
Next we'll define a `LabelEncoder` to encode our text labels into unique indices
```
import itertools
class LabelEncoder(object):
"""Label encoder for tag labels."""
def __init__(self, class_to_index={}):
self.class_to_index = class_to_index
self.index_to_class = {v: k for k, v in self.class_to_index.items()}
self.classes = list(self.class_to_index.keys())
def __len__(self):
return len(self.class_to_index)
def __str__(self):
return f"<LabelEncoder(num_classes={len(self)})>"
def fit(self, y):
classes = np.unique(y)
for i, class_ in enumerate(classes):
self.class_to_index[class_] = i
self.index_to_class = {v: k for k, v in self.class_to_index.items()}
self.classes = list(self.class_to_index.keys())
return self
def encode(self, y):
encoded = np.zeros((len(y)), dtype=int)
for i, item in enumerate(y):
encoded[i] = self.class_to_index[item]
return encoded
def decode(self, y):
classes = []
for i, item in enumerate(y):
classes.append(self.index_to_class[item])
return classes
def save(self, fp):
with open(fp, 'w') as fp:
contents = {'class_to_index': self.class_to_index}
json.dump(contents, fp, indent=4, sort_keys=False)
@classmethod
def load(cls, fp):
with open(fp, 'r') as fp:
kwargs = json.load(fp=fp)
return cls(**kwargs)
# Encode
label_encoder = LabelEncoder()
label_encoder.fit(y_train)
NUM_CLASSES = len(label_encoder)
label_encoder.class_to_index
# Convert labels to tokens
print (f"y_train[0]: {y_train[0]}")
y_train = label_encoder.encode(y_train)
y_val = label_encoder.encode(y_val)
y_test = label_encoder.encode(y_test)
print (f"y_train[0]: {y_train[0]}")
# Class weights
counts = np.bincount(y_train)
class_weights = {i: 1.0/count for i, count in enumerate(counts)}
print (f"counts: {counts}\nweights: {class_weights}")
```
## Tokenizer
We'll define a `Tokenizer` to convert our text input data into token indices.
```
import json
from collections import Counter
from more_itertools import take
class Tokenizer(object):
def __init__(self, char_level, num_tokens=None,
pad_token='<PAD>', oov_token='<UNK>',
token_to_index=None):
self.char_level = char_level
self.separator = '' if self.char_level else ' '
if num_tokens: num_tokens -= 2 # pad + unk tokens
self.num_tokens = num_tokens
self.pad_token = pad_token
self.oov_token = oov_token
if not token_to_index:
token_to_index = {pad_token: 0, oov_token: 1}
self.token_to_index = token_to_index
self.index_to_token = {v: k for k, v in self.token_to_index.items()}
def __len__(self):
return len(self.token_to_index)
def __str__(self):
return f"<Tokenizer(num_tokens={len(self)})>"
def fit_on_texts(self, texts):
if not self.char_level:
texts = [text.split(" ") for text in texts]
all_tokens = [token for text in texts for token in text]
counts = Counter(all_tokens).most_common(self.num_tokens)
self.min_token_freq = counts[-1][1]
for token, count in counts:
index = len(self)
self.token_to_index[token] = index
self.index_to_token[index] = token
return self
def texts_to_sequences(self, texts):
sequences = []
for text in texts:
if not self.char_level:
text = text.split(' ')
sequence = []
for token in text:
sequence.append(self.token_to_index.get(
token, self.token_to_index[self.oov_token]))
sequences.append(np.asarray(sequence))
return sequences
def sequences_to_texts(self, sequences):
texts = []
for sequence in sequences:
text = []
for index in sequence:
text.append(self.index_to_token.get(index, self.oov_token))
texts.append(self.separator.join([token for token in text]))
return texts
def save(self, fp):
with open(fp, 'w') as fp:
contents = {
'char_level': self.char_level,
'oov_token': self.oov_token,
'token_to_index': self.token_to_index
}
json.dump(contents, fp, indent=4, sort_keys=False)
@classmethod
def load(cls, fp):
with open(fp, 'r') as fp:
kwargs = json.load(fp=fp)
return cls(**kwargs)
# Tokenize
tokenizer = Tokenizer(char_level=False, num_tokens=5000)
tokenizer.fit_on_texts(texts=X_train)
VOCAB_SIZE = len(tokenizer)
print (tokenizer)
# Sample of tokens
print (take(5, tokenizer.token_to_index.items()))
print (f"least freq token's freq: {tokenizer.min_token_freq}") # use this to adjust num_tokens
# Convert texts to sequences of indices
X_train = tokenizer.texts_to_sequences(X_train)
X_val = tokenizer.texts_to_sequences(X_val)
X_test = tokenizer.texts_to_sequences(X_test)
preprocessed_text = tokenizer.sequences_to_texts([X_train[0]])[0]
print ("Text to indices:\n"
f" (preprocessed) → {preprocessed_text}\n"
f" (tokenized) → {X_train[0]}")
```
## Padding
We'll need to do 2D padding to our tokenized text.
```
def pad_sequences(sequences, max_seq_len=0):
"""Pad sequences to max length in sequence."""
max_seq_len = max(max_seq_len, max(len(sequence) for sequence in sequences))
padded_sequences = np.zeros((len(sequences), max_seq_len))
for i, sequence in enumerate(sequences):
padded_sequences[i][:len(sequence)] = sequence
return padded_sequences
# 2D sequences
padded = pad_sequences(X_train[0:3])
print (padded.shape)
print (padded)
```
## Datasets
We're going to create Datasets and DataLoaders to be able to efficiently create batches with our data splits.
```
class Dataset(torch.utils.data.Dataset):
def __init__(self, X, y):
self.X = X
self.y = y
def __len__(self):
return len(self.y)
def __str__(self):
return f"<Dataset(N={len(self)})>"
def __getitem__(self, index):
X = self.X[index]
y = self.y[index]
return [X, len(X), y]
def collate_fn(self, batch):
"""Processing on a batch."""
# Get inputs
batch = np.array(batch, dtype=object)
X = batch[:, 0]
seq_lens = batch[:, 1]
y = np.stack(batch[:, 2], axis=0)
# Pad inputs
X = pad_sequences(sequences=X)
# Cast
X = torch.LongTensor(X.astype(np.int32))
seq_lens = torch.LongTensor(seq_lens.astype(np.int32))
y = torch.LongTensor(y.astype(np.int32))
return X, seq_lens, y
def create_dataloader(self, batch_size, shuffle=False, drop_last=False):
return torch.utils.data.DataLoader(
dataset=self, batch_size=batch_size, collate_fn=self.collate_fn,
shuffle=shuffle, drop_last=drop_last, pin_memory=True)
# Create datasets
train_dataset = Dataset(X=X_train, y=y_train)
val_dataset = Dataset(X=X_val, y=y_val)
test_dataset = Dataset(X=X_test, y=y_test)
print ("Datasets:\n"
f" Train dataset:{train_dataset.__str__()}\n"
f" Val dataset: {val_dataset.__str__()}\n"
f" Test dataset: {test_dataset.__str__()}\n"
"Sample point:\n"
f" X: {train_dataset[0][0]}\n"
f" seq_len: {train_dataset[0][1]}\n"
f" y: {train_dataset[0][2]}")
# Create dataloaders
batch_size = 64
train_dataloader = train_dataset.create_dataloader(
batch_size=batch_size)
val_dataloader = val_dataset.create_dataloader(
batch_size=batch_size)
test_dataloader = test_dataset.create_dataloader(
batch_size=batch_size)
batch_X, batch_seq_lens, batch_y = next(iter(train_dataloader))
print ("Sample batch:\n"
f" X: {list(batch_X.size())}\n"
f" seq_lens: {list(batch_seq_lens.size())}\n"
f" y: {list(batch_y.size())}\n"
"Sample point:\n"
f" X: {batch_X[0]}\n"
f" seq_len: {batch_seq_lens[0]}\n"
f" y: {batch_y[0]}")
```
## Trainer
Let's create the `Trainer` class that we'll use to facilitate training for our experiments.
```
class Trainer(object):
def __init__(self, model, device, loss_fn=None, optimizer=None, scheduler=None):
# Set params
self.model = model
self.device = device
self.loss_fn = loss_fn
self.optimizer = optimizer
self.scheduler = scheduler
def train_step(self, dataloader):
"""Train step."""
# Set model to train mode
self.model.train()
loss = 0.0
# Iterate over train batches
for i, batch in enumerate(dataloader):
# Step
batch = [item.to(self.device) for item in batch] # Set device
inputs, targets = batch[:-1], batch[-1]
self.optimizer.zero_grad() # Reset gradients
z = self.model(inputs) # Forward pass
J = self.loss_fn(z, targets) # Define loss
J.backward() # Backward pass
self.optimizer.step() # Update weights
# Cumulative Metrics
loss += (J.detach().item() - loss) / (i + 1)
return loss
def eval_step(self, dataloader):
"""Validation or test step."""
# Set model to eval mode
self.model.eval()
loss = 0.0
y_trues, y_probs = [], []
# Iterate over val batches
with torch.no_grad():
for i, batch in enumerate(dataloader):
# Step
batch = [item.to(self.device) for item in batch] # Set device
inputs, y_true = batch[:-1], batch[-1]
z = self.model(inputs) # Forward pass
J = self.loss_fn(z, y_true).item()
# Cumulative Metrics
loss += (J - loss) / (i + 1)
# Store outputs
y_prob = torch.sigmoid(z).cpu().numpy()
y_probs.extend(y_prob)
y_trues.extend(y_true.cpu().numpy())
return loss, np.vstack(y_trues), np.vstack(y_probs)
def predict_step(self, dataloader):
"""Prediction step."""
# Set model to eval mode
self.model.eval()
y_probs = []
# Iterate over val batches
with torch.no_grad():
for i, batch in enumerate(dataloader):
# Forward pass w/ inputs
inputs, targets = batch[:-1], batch[-1]
y_prob = self.model(inputs, apply_softmax=True)
# Store outputs
y_probs.extend(y_prob)
return np.vstack(y_probs)
def train(self, num_epochs, patience, train_dataloader, val_dataloader):
best_val_loss = np.inf
for epoch in range(num_epochs):
# Steps
train_loss = self.train_step(dataloader=train_dataloader)
val_loss, _, _ = self.eval_step(dataloader=val_dataloader)
self.scheduler.step(val_loss)
# Early stopping
if val_loss < best_val_loss:
best_val_loss = val_loss
best_model = self.model
_patience = patience # reset _patience
else:
_patience -= 1
if not _patience: # 0
print("Stopping early!")
break
# Logging
print(
f"Epoch: {epoch+1} | "
f"train_loss: {train_loss:.5f}, "
f"val_loss: {val_loss:.5f}, "
f"lr: {self.optimizer.param_groups[0]['lr']:.2E}, "
f"_patience: {_patience}"
)
return best_model
```
# Attention
Attention applied to the outputs from an RNN. In theory, the outputs can come from anywhere where we want to learn how to weight amongst them but since we're working with the context of an RNN from the previous lesson , we'll continue with that.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/attention/attention.png" width="500">
</div>
$ \alpha = softmax(W_{attn}h) $
$c_t = \sum_{i=1}^{n} \alpha_{t,i}h_i $
*where*:
* $ h $ = RNN outputs (or any group of outputs you want to attend to) $\in \mathbb{R}^{NXMXH}$ ($N$ is the batch size, $M$ is the max length of each sequence in the batch, $H$ is the hidden dim)
* $ \alpha_{t,i} $ = alignment function for output $ y_t $ using input $ h_i $ (we also concatenate other useful representations with $h_i$ here). In our case, this would be the attention value to attribute to each input $h_i$.
* $W_{attn}$ = attention weights to learn $\in \mathbb{R}^{HX1}$. We can also apply activations functions, transformations, etc. here
* $c_t$ = context vector that accounts for the different inputs with attention. We can pass this context vector to downstream processes.
```
import torch.nn.functional as F
```
The RNN will create an encoded representation for each word in our input resulting in a stacked vector that has dimensions $NXMXH$, where N is the # of samples in the batch, M is the max sequence length in the batch, and H is the number of hidden units in the RNN.
```
BATCH_SIZE = 64
SEQ_LEN = 8
EMBEDDING_DIM = 100
RNN_HIDDEN_DIM = 128
# Embed
x = torch.rand((BATCH_SIZE, SEQ_LEN, EMBEDDING_DIM))
# Encode
rnn = nn.RNN(EMBEDDING_DIM, RNN_HIDDEN_DIM, batch_first=True)
out, h_n = rnn(x) # h_n is the last hidden state
print ("out: ", out.shape)
print ("h_n: ", h_n.shape)
# Attend
attn = nn.Linear(RNN_HIDDEN_DIM, 1)
e = attn(out)
attn_vals = F.softmax(e.squeeze(2), dim=1)
c = torch.bmm(attn_vals.unsqueeze(1), out).squeeze(1)
print ("e: ", e.shape)
print ("attn_vals: ", attn_vals.shape)
print ("attn_vals[0]: ", attn_vals[0])
print ("sum(attn_vals[0]): ", sum(attn_vals[0]))
print ("c: ", c.shape)
# Predict
fc1 = nn.Linear(RNN_HIDDEN_DIM, NUM_CLASSES)
output = F.softmax(fc1(c), dim=1)
print ("output: ", output.shape)
```
> In a many-to-many task such as machine translation, our attentional interface will also account for the encoded representation of token in the output as well (via concatenation) so we can know which encoded inputs to attend to based on the encoded output we're focusing on. For more on this, be sure to explore <a target="_blank" href="https://arxiv.org/abs/1409.0473">Bahdanau's attention paper</a>.
## Model
Now let's create our RNN based model but with the addition of the attention layer on top of the RNN's outputs.
```
RNN_HIDDEN_DIM = 128
DROPOUT_P = 0.1
HIDDEN_DIM = 100
class RNN(nn.Module):
def __init__(self, embedding_dim, vocab_size, rnn_hidden_dim,
hidden_dim, dropout_p, num_classes, padding_idx=0):
super(RNN, self).__init__()
# Initialize embeddings
self.embeddings = nn.Embedding(
embedding_dim=embedding_dim, num_embeddings=vocab_size,
padding_idx=padding_idx)
# RNN
self.rnn = nn.RNN(embedding_dim, rnn_hidden_dim, batch_first=True)
# Attention
self.attn = nn.Linear(rnn_hidden_dim, 1)
# FC weights
self.dropout = nn.Dropout(dropout_p)
self.fc1 = nn.Linear(rnn_hidden_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def forward(self, inputs, apply_softmax=False):
# Embed
x_in, seq_lens = inputs
x_in = self.embeddings(x_in)
# Encode
out, h_n = self.rnn(x_in)
# Attend
e = self.attn(out)
attn_vals = F.softmax(e.squeeze(2), dim=1)
c = torch.bmm(attn_vals.unsqueeze(1), out).squeeze(1)
# Predict
z = self.fc1(c)
z = self.dropout(z)
y_pred = self.fc2(z)
if apply_softmax:
y_pred = F.softmax(y_pred, dim=1)
return y_pred
# Simple RNN cell
model = RNN(
embedding_dim=EMBEDDING_DIM, vocab_size=VOCAB_SIZE,
rnn_hidden_dim=RNN_HIDDEN_DIM, hidden_dim=HIDDEN_DIM,
dropout_p=DROPOUT_P, num_classes=NUM_CLASSES)
model = model.to(device) # set device
print (model.named_parameters)
```
## Training
```
from torch.optim import Adam
NUM_LAYERS = 1
LEARNING_RATE = 1e-4
PATIENCE = 10
NUM_EPOCHS = 50
# Define Loss
class_weights_tensor = torch.Tensor(list(class_weights.values())).to(device)
loss_fn = nn.CrossEntropyLoss(weight=class_weights_tensor)
# Define optimizer & scheduler
optimizer = Adam(model.parameters(), lr=LEARNING_RATE)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(
optimizer, mode='min', factor=0.1, patience=3)
# Trainer module
trainer = Trainer(
model=model, device=device, loss_fn=loss_fn,
optimizer=optimizer, scheduler=scheduler)
# Train
best_model = trainer.train(
NUM_EPOCHS, PATIENCE, train_dataloader, val_dataloader)
```
## Evaluation
```
import json
from sklearn.metrics import precision_recall_fscore_support
def get_performance(y_true, y_pred, classes):
"""Per-class performance metrics."""
# Performance
performance = {"overall": {}, "class": {}}
# Overall performance
metrics = precision_recall_fscore_support(y_true, y_pred, average="weighted")
performance["overall"]["precision"] = metrics[0]
performance["overall"]["recall"] = metrics[1]
performance["overall"]["f1"] = metrics[2]
performance["overall"]["num_samples"] = np.float64(len(y_true))
# Per-class performance
metrics = precision_recall_fscore_support(y_true, y_pred, average=None)
for i in range(len(classes)):
performance["class"][classes[i]] = {
"precision": metrics[0][i],
"recall": metrics[1][i],
"f1": metrics[2][i],
"num_samples": np.float64(metrics[3][i]),
}
return performance
# Get predictions
test_loss, y_true, y_prob = trainer.eval_step(dataloader=test_dataloader)
y_pred = np.argmax(y_prob, axis=1)
# Determine performance
performance = get_performance(
y_true=y_test, y_pred=y_pred, classes=label_encoder.classes)
print (json.dumps(performance['overall'], indent=2))
# Save artifacts
from pathlib import Path
dir = Path("rnn")
dir.mkdir(parents=True, exist_ok=True)
label_encoder.save(fp=Path(dir, "label_encoder.json"))
tokenizer.save(fp=Path(dir, "tokenizer.json"))
torch.save(best_model.state_dict(), Path(dir, "model.pt"))
with open(Path(dir, "performance.json"), "w") as fp:
json.dump(performance, indent=2, sort_keys=False, fp=fp)
```
## Inference
```
def get_probability_distribution(y_prob, classes):
"""Create a dict of class probabilities from an array."""
results = {}
for i, class_ in enumerate(classes):
results[class_] = np.float64(y_prob[i])
sorted_results = {k: v for k, v in sorted(
results.items(), key=lambda item: item[1], reverse=True)}
return sorted_results
# Load artifacts
device = torch.device("cpu")
label_encoder = LabelEncoder.load(fp=Path(dir, "label_encoder.json"))
tokenizer = Tokenizer.load(fp=Path(dir, "tokenizer.json"))
model = RNN(
embedding_dim=EMBEDDING_DIM, vocab_size=VOCAB_SIZE,
rnn_hidden_dim=RNN_HIDDEN_DIM, hidden_dim=HIDDEN_DIM,
dropout_p=DROPOUT_P, num_classes=NUM_CLASSES)
model.load_state_dict(torch.load(Path(dir, "model.pt"), map_location=device))
model.to(device)
# Initialize trainer
trainer = Trainer(model=model, device=device)
# Dataloader
text = "The final tennis tournament starts next week."
X = tokenizer.texts_to_sequences([preprocess(text)])
print (tokenizer.sequences_to_texts(X))
y_filler = label_encoder.encode([label_encoder.classes[0]]*len(X))
dataset = Dataset(X=X, y=y_filler)
dataloader = dataset.create_dataloader(batch_size=batch_size)
# Inference
y_prob = trainer.predict_step(dataloader)
y_pred = np.argmax(y_prob, axis=1)
label_encoder.decode(y_pred)
# Class distributions
prob_dist = get_probability_distribution(y_prob=y_prob[0], classes=label_encoder.classes)
print (json.dumps(prob_dist, indent=2))
```
# Interpretability
Let's use the attention values to see which encoded tokens were most useful in predicting the appropriate label.
```
import collections
import seaborn as sns
class InterpretAttn(nn.Module):
def __init__(self, embedding_dim, vocab_size, rnn_hidden_dim,
hidden_dim, dropout_p, num_classes, padding_idx=0):
super(InterpretAttn, self).__init__()
# Initialize embeddings
self.embeddings = nn.Embedding(
embedding_dim=embedding_dim, num_embeddings=vocab_size,
padding_idx=padding_idx)
# RNN
self.rnn = nn.RNN(embedding_dim, rnn_hidden_dim, batch_first=True)
# Attention
self.attn = nn.Linear(rnn_hidden_dim, 1)
# FC weights
self.dropout = nn.Dropout(dropout_p)
self.fc1 = nn.Linear(rnn_hidden_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def forward(self, inputs, apply_softmax=False):
# Embed
x_in, seq_lens = inputs
x_in = self.embeddings(x_in)
# Encode
out, h_n = self.rnn(x_in)
# Attend
e = self.attn(out) # could add optional activation function (ex. tanh)
attn_vals = F.softmax(e.squeeze(2), dim=1)
return attn_vals
# Initialize model
interpretable_model = InterpretAttn(
embedding_dim=EMBEDDING_DIM, vocab_size=VOCAB_SIZE,
rnn_hidden_dim=RNN_HIDDEN_DIM, hidden_dim=HIDDEN_DIM,
dropout_p=DROPOUT_P, num_classes=NUM_CLASSES)
interpretable_model.load_state_dict(torch.load(Path(dir, "model.pt"), map_location=device))
interpretable_model.to(device)
# Initialize trainer
interpretable_trainer = Trainer(model=interpretable_model, device=device)
# Get attention values
attn_vals = interpretable_trainer.predict_step(dataloader)
print (attn_vals.shape) # (N, max_seq_len)
# Visualize a bi-gram filter's outputs
sns.set(rc={"figure.figsize":(10, 1)})
tokens = tokenizer.sequences_to_texts(X)[0].split(' ')
sns.heatmap(attn_vals, xticklabels=tokens)
```
The word `tennis` was attended to the most to result in the `Sports` label.
# Types of attention
We'll briefly look at the different types of attention and when to use each them.
## Soft (global) attention
Soft attention the type of attention we've implemented so far, where we attend to all encoded inputs when creating our context vector.
- **advantages**: we always have the ability to attend to all inputs in case something we saw much earlier/ see later are crucial for determing the output.
- **disadvantages**: if our input sequence is very long, this can lead to expensive compute.
## Hard attention
Hard attention is focusing on a specific set of the encoded inputs at each time step.
- **advantages**: we can save a lot of compute on long sequences by only focusing on a local patch each time.
- **disadvantages**: non-differentiable and so we need to use more complex techniques (variance reduction, reinforcement learning, etc.) to train.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/attention/soft_attention.png" width="700">
</div>
<div align="left">
<small><a href="https://arxiv.org/abs/1502.03044" target="_blank">Show, Attend and Tell: Neural Image Caption Generation with Visual Attention</a></small>
</div>
## Local attention
[Local attention](https://arxiv.org/abs/1508.04025) blends the advantages of soft and hard attention. It involves learning an aligned position vector and empirically determining a local window of encoded inputs to attend to.
- **advantages**: apply attention to a local patch of inputs yet remain differentiable.
- **disadvantages**: need to determine the alignment vector for each output but it's a worthwhile trade off to determine the right window of inputs to attend to in order to avoid attending to all of them.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/attention/local_attention.png" width="700">
</div>
<div align="left">
<small><a href="https://arxiv.org/abs/1508.04025" target="_blank">Effective Approaches to Attention-based Neural Machine Translation
</a></small>
</div>
## Self-attention
We can also use attention within the encoded input sequence to create a weighted representation that based on the similarity between input pairs. This will allow us to create rich representations of the input sequence that are aware of the relationships between each other. For example, in the image below you can see that when composing the representation of the token "its", this specific attention head will be incorporating signal from the token "Law" (it's learned that "its" is referring to the "Law").
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/attention/self_attention.png" width="300">
</div>
<div align="left">
<small><a href="https://arxiv.org/abs/1706.03762" target="_blank">Attention Is All You Need</a></small>
</div>
# Transformers
Transformers are a very popular architecture that leverage and extend the concept of self-attention to create very useful representations of our input data for a downstream task.
## Scaled dot-product attention
The most popular type of self-attention is scaled dot-product attention from the widely-cited [Attention is all you need](https://arxiv.org/abs/1706.03762) paper. This type of attention involves projecting our encoded input sequences onto three matrices, queries (Q), keys (K) and values (V), whose weights we learn.
$ inputs \in \mathbb{R}^{NXMXH} $ ($N$ = batch size, $M$ = sequence length, $H$ = hidden dim)
$ Q = XW_q $ where $ W_q \in \mathbb{R}^{HXd_q} $
$ K = XW_k $ where $ W_k \in \mathbb{R}^{HXd_k} $
$ V = XW_v $ where $ W_v \in \mathbb{R}^{HXd_v} $
$ attention (Q, K, V) = softmax( \frac{Q K^{T}}{\sqrt{d_k}} )V \in \mathbb{R}^{MXd_v} $
## Multi-head attention
Instead of applying self-attention only once across the entire encoded input, we can also separate the input and apply self-attention in parallel (heads) to each input section and concatenate them. This allows the different head to learn unique representations while maintaining the complexity since we split the input into smaller subspaces.
$ MultiHead(Q, K, V) = concat({head}_1, ..., {head}_{h})W_O $
* ${head}_i = attention(Q_i, K_i, V_i) $
* $h$ = # of self-attention heads
* $W_O \in \mathbb{R}^{hd_vXH} $
* $H$ = hidden dim. (or dimension of the model $d_{model}$)
## Positional encoding
With self-attention, we aren't able to account for the sequential position of our input tokens. To address this, we can use positional encoding to create a representation of the location of each token with respect to the entire sequence. This can either be learned (with weights) or we can use a fixed function that can better extend to create positional encoding for lengths during inference that were not observed during training.
$ PE_{(pos,2i)} = sin({pos}/{10000^{2i/H}}) $
$ PE_{(pos,2i+1)} = cos({pos}/{10000^{2i/H}}) $
where:
* $pos$ = position of the token $(1...M)$
* $i$ = hidden dim $(1..H)$
This effectively allows us to represent each token's relative position using a fixed function for very large sequences. And because we've constrained the positional encodings to have the same dimensions as our encoded inputs, we can simply concatenate them before feeding them into the multi-head attention heads.
## Architecture
And here's how it all fits together! It's an end-to-end architecture that creates these contextual representations and uses an encoder-decoder architecture to predict the outcomes (one-to-one, many-to-one, many-to-many, etc.) Due to the complexity of the architecture, they require massive amounts of data for training without overfitting, however, they can be leveraged as pretrained models to finetune with smaller datasets that are similar to the larger set it was initially trained on.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/attention/transformer.png" width="800">
</div>
<div align="left">
<small><a href="https://arxiv.org/abs/1706.03762" target="_blank">Attention Is All You Need</a></small>
</div>
> We're not going to the implement the Transformer [from scratch](https://nlp.seas.harvard.edu/2018/04/03/attention.html) but we will use the[ Hugging Face library](https://github.com/huggingface/transformers) to do so in the [baselines](https://madewithml.com/courses/mlops/baselines/#transformers-w-contextual-embeddings) lesson!
| true |
code
| 0.648077 | null | null | null | null |
|
# Exploring violations related to farming activity
To run this notebook, load SDWIS csv data files into the folder ``../../../data/sdwis/SDWIS``
```
import os
import numpy as np
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
STATE_CODE = 'VT'
DATA_DIR = '../../../../data'
SDWIS_DIR = os.path.join(DATA_DIR, 'sdwis')
# These contaminants are typically associated with farming activity.
FARM_CONTAMINANTS = [
'ALACHLOR ESA',
'Atrazine',
'Carbofuran',
'2,4-D',
'Dalapon',
'1,2-Dibromo-3-chloropropane',
'Dinoseb',
'Diquat',
'Endothall',
'Glyphosate',
'Lindane',
'Methoxychlor',
'Nitrate',
'Nitrite',
'Oxamyl',
'Picloram',
'Simazine',
'Toxaphene',
'2,4,5-TP'
]
# Label data with full year, e.g., 2012 for 01-JUL-12
def get_year_from_mmddyy_series(ser, last_year_in_2000s=pd.Timestamp('now').year):
"""
Expected input will be in the form 01-JUL-12.
Output will be the year of the data.
Assumes years will never be greater than current year.
"""
last_two_digits_year_cutoff = int(str(last_year_in_2000s)[-2:])
# calculate last two digits of year
return_series = ser.str.split('-').str[2].astype(int)
# add first two digits
return_series += (
+ (2000*(return_series <= last_two_digits_year_cutoff))
+ (1900*(return_series > last_two_digits_year_cutoff))
)
return return_series
def print_water_system_violations(water_system_df, viol_df):
viol_df = viol_df.merge(water_system_df, left_on='VIOLATION.PWSID', right_on='WATER_SYSTEM.PWSID')
print('# water systems: ' + str(water_system_df.shape[0]))
print('# violations: ' + str(viol_df.shape[0]))
print('# reporting violations: ' \
+ str(viol_df[viol_df['VIOLATION.VIOLATION_CATEGORY_CODE'] == 'MR'].shape[0]))
print('# health violations: ' \
+ str(viol_df[viol_df['VIOLATION.IS_HEALTH_BASED_IND'] == 'Y'].shape[0]))
# read input files
viol = pd.read_csv(os.path.join(SDWIS_DIR, 'VIOLATION.csv'),
sep=',',
dtype={'VIOLATION.CONTAMINANT_CODE': np.str},
low_memory=False)
ws = pd.read_csv(os.path.join(SDWIS_DIR, 'WATER_SYSTEM.csv'),
low_memory=False)
wsf = pd.read_csv(os.path.join(SDWIS_DIR, 'WATER_SYSTEM_FACILITY.csv'),
low_memory=False)
# this file currently only contains entries for VT, can be expanded to include other states
# source: https://www.nass.usda.gov/Quick_Stats/CDQT/chapter/2/table/1/state/VT/county/027
farms = pd.read_csv(os.path.join(DATA_DIR, 'usda/farm_operations.csv'))
contaminants = pd.read_csv(os.path.join(SDWIS_DIR, 'contaminant-codes.csv'),
sep=',',
dtype={'CODE': np.str})
last_two_digits_current_year = int(str(pd.Timestamp('now').year)[-2:])
viol['VIOLATION.YEAR'] = get_year_from_mmddyy_series(viol['VIOLATION.COMPL_PER_BEGIN_DATE'])
# violations in 2017
viol_2017 = viol[viol['VIOLATION.YEAR'] == 2017]
viol_2017.head()
# Filter only to systems in Vermont
ws = ws.loc[
(
ws['WATER_SYSTEM.PRIMACY_AGENCY_CODE'] == STATE_CODE)
& (ws['WATER_SYSTEM.PWS_ACTIVITY_CODE'] == 'A')
]
farms = farms.drop(['state_fips', 'county_code', 'commodity', 'domain_category'], axis=1)
farms['county'] = farms['county'].str.capitalize()
farms.head()
farms[['county', '2017']].plot.bar(x='county', y='2017')
viol_2017_county = pd.merge(viol_2017, ws, left_on='VIOLATION.PWSID', \
right_on='WATER_SYSTEM.PWSID')
viol_2017_county = viol_2017_county[['VIOLATION.PWSID', 'VIOLATION.CONTAMINANT_CODE', 'WATER_SYSTEM.COUNTIES_SERVED']]
viol_2017_county.head()
viol_2017_county_contaminant = pd.merge(viol_2017_county, contaminants, \
left_on='VIOLATION.CONTAMINANT_CODE', \
right_on='CODE')
viol_2017_county_contaminant_subset = viol_2017_county_contaminant[['VIOLATION.PWSID', \
'NAME', \
'WATER_SYSTEM.COUNTIES_SERVED']]
viol_2017_county_contaminant_subset.head()
viol_2017_county_contaminant_subset = viol_2017_county_contaminant_subset.loc[
viol_2017_county_contaminant_subset['NAME'].isin(pd.Series(FARM_CONTAMINANTS).str.upper())
]
```
## Possible farm-related contaminant violations by county
```
viol_2017_county_contaminant_subset.groupby(['WATER_SYSTEM.COUNTIES_SERVED', 'NAME'])\
.size().unstack().plot.bar(stacked=True)
plt.title('Safe drinking water violations by county\nand contaminant in Vermont (2017)')
plt.xlabel('County')
plt.ylabel('Number of violations')
plt.show()
```
| true |
code
| 0.463505 | null | null | null | null |
|
```
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import scipy.stats as stats
%config InlineBackend.figure_format = 'retina'
az.style.use('arviz-darkgrid')
```
#### Code 2.1
```
ways = np.array([0, 3, 8, 9, 0])
ways / ways.sum()
```
#### Code 2.2
$$Pr(w \mid n, p) = \frac{n!}{w!(n − w)!} p^w (1 − p)^{n−w}$$
The probability of observing six W’s in nine tosses—under a value of p=0.5
```
stats.binom.pmf(6, n=9, p=0.5)
```
#### Code 2.3 and 2.5
Computing the posterior using a grid approximation.
In the book the following code is not inside a function, but this way is easier to play with different parameters
```
def posterior_grid_approx(grid_points=5, success=6, tosses=9):
"""
"""
# define grid
p_grid = np.linspace(0, 1, grid_points)
# define prior
prior = np.repeat(5, grid_points) # uniform
#prior = (p_grid >= 0.5).astype(int) # truncated
#prior = np.exp(- 5 * abs(p_grid - 0.5)) # double exp
# compute likelihood at each point in the grid
likelihood = stats.binom.pmf(success, tosses, p_grid)
# compute product of likelihood and prior
unstd_posterior = likelihood * prior
# standardize the posterior, so it sums to 1
posterior = unstd_posterior / unstd_posterior.sum()
return p_grid, posterior
```
#### Code 2.3
```
points = 20
w, n = 6, 9
p_grid, posterior = posterior_grid_approx(points, w, n)
plt.plot(p_grid, posterior, 'o-', label=f'success = {w}\ntosses = {n}')
plt.xlabel('probability of water', fontsize=14)
plt.ylabel('posterior probability', fontsize=14)
plt.title(f'{points} points')
plt.legend(loc=0);
```
#### Code 2.6
Computing the posterior using the quadratic aproximation
```
data = np.repeat((0, 1), (3, 6))
with pm.Model() as normal_aproximation:
p = pm.Uniform('p', 0, 1)
w = pm.Binomial('w', n=len(data), p=p, observed=data.sum())
mean_q = pm.find_MAP()
std_q = ((1/pm.find_hessian(mean_q, vars=[p]))**0.5)[0]
mean_q['p'], std_q
norm = stats.norm(mean_q, std_q)
prob = .89
z = stats.norm.ppf([(1-prob)/2, (1+prob)/2])
pi = mean_q['p'] + std_q * z
pi
```
#### Code 2.7
```
# analytical calculation
w, n = 6, 9
x = np.linspace(0, 1, 100)
plt.plot(x, stats.beta.pdf(x , w+1, n-w+1),
label='True posterior')
# quadratic approximation
plt.plot(x, stats.norm.pdf(x, mean_q['p'], std_q),
label='Quadratic approximation')
plt.legend(loc=0, fontsize=13)
plt.title(f'n = {n}', fontsize=14)
plt.xlabel('Proportion water', fontsize=14)
plt.ylabel('Density', fontsize=14);
import platform
import sys
import IPython
import matplotlib
import scipy
print("""This notebook was created using:\nPython {}\nIPython {}\nPyMC {}\nArviZ {}\nNumPy {}\nSciPy {}\nMatplotlib {}\n""".format(sys.version[:5], IPython.__version__, pm.__version__, az.__version__, np.__version__, scipy.__version__, matplotlib.__version__))
```
| true |
code
| 0.699473 | null | null | null | null |
|
# Final Prediction Model and Results
Now that we have evaluated our model, we can use all the data and build a model to predict values of the future. In this case, we predict Electricity Consumption and Generation in year 2020 in Germany.
## Import Libraries
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import time
from matplotlib.dates import date2num
%matplotlib inline
sns.set_style('darkgrid')
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.preprocessing import sequence
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Input, LSTM
from tensorflow.keras.losses import mean_squared_error
from tensorflow.keras.models import Model
from tensorflow.keras.models import load_model
import h5py
```
## Load Data
```
consumption= pd.read_pickle('../Data_Cleaned/consumption_ready_for_forcast.pkl')
generation= pd.read_pickle('../Data_Cleaned/generation_ready_for_forcast.pkl')
```
## Batch Size and Timesteps
```
# defining the batch size and timesteps
batch_size = 64
timesteps=24*7
```
## Prepare Prediction Indexes
```
idx= pd.date_range(start='2020-01-01 00:00:00',end='2020-12-31 23:00:00',freq='H')
con_idx= pd.DataFrame(index=idx,data={consumption.columns.values[0]:0})
gen_idx= pd.DataFrame(index=idx,data={generation.columns.values[0]:0})
consumption_full= pd.concat([consumption,con_idx])
generation_full= pd.concat([generation,gen_idx])
```
## Prepare Train Set
```
# Function to calculate training size regarding batch_size
def get_train_length(dataset, timesteps, batch_size):
# substract pred_percent to be excluded from training, reserved for predset
length = len(dataset)-2.1*timesteps
train_length_values = []
for x in range(int(length) - 200,int(length)):
modulo=x%batch_size
if (modulo == 0):
train_length_values.append(x)
return (max(train_length_values))
length = get_train_length(consumption, timesteps, batch_size)
upper_train = length + timesteps*2
print('\nDatasets length:',len(consumption))
print('Last divisible index:', upper_train)
print('Train Sets length:', length,'\n')
# Set y_train variable for consumption df
consumption_train_df = consumption[0:upper_train]
consumption_y_train = consumption_train_df.iloc[:,].values
print('\nTraining Sets Shapes after Adding Timesteps:', consumption_y_train.shape)
# Set y_train variable for generation df
generation_train_df = generation[0:upper_train]
generation_y_train = generation_train_df.iloc[:,].values
```
## Feature Scaling
```
#scale between 0 and 1. the weights are esier to find.
sc_con = MinMaxScaler(feature_range = (0, 1))
sc_gen = MinMaxScaler(feature_range = (0, 1))
consumption_y_train_scaled = sc_con.fit_transform(np.float64(consumption_y_train))
generation_y_train_scaled = sc_gen.fit_transform(np.float64(generation_y_train))
```
## Creating a data structure with n timesteps
```
# Empty Lists to store X_train and y_train
consumption_X_train_matrix = []
consumption_y_train_matrix = []
# Creating a data structure with n timesteps
for i in range(timesteps, length + timesteps):
#create X_train matrix
#24*7 items per array (timestep)
consumption_X_train_matrix.append(consumption_y_train_scaled[i-timesteps:i,0])
#create Y_train matrix
#24*7 items per array (timestep)
consumption_y_train_matrix.append(consumption_y_train_scaled[i:i+timesteps,0])
# reapeat all of these steps fot generation dataframe
generation_X_train_matrix = []
generation_y_train_matrix = []
for i in range(timesteps, length + timesteps):
generation_X_train_matrix.append(generation_y_train_scaled[i-timesteps:i,0])
generation_y_train_matrix.append(generation_y_train_scaled[i:i+timesteps,0])
# Check shape
print()
print('X_train sets shape:', np.array(consumption_X_train_matrix).shape)
print('y_train sets shape:', np.array(consumption_y_train_matrix).shape)
print()
```
## Reshape
```
# Turn list into numpy array
consumption_X_train_matrix = np.array(consumption_X_train_matrix)
consumption_y_train_matrix = np.array(consumption_y_train_matrix)
# reshape arrays
consumption_X_train_reshaped = np.reshape(consumption_X_train_matrix,
(consumption_X_train_matrix.shape[0],
consumption_X_train_matrix.shape[1], 1))
consumption_y_train_reshaped = np.reshape(consumption_y_train_matrix,
(consumption_y_train_matrix.shape[0],
consumption_y_train_matrix.shape[1], 1))
# Repeat the same stes for generatin dataframe
generation_X_train_matrix = np.array(generation_X_train_matrix)
generation_y_train_matrix = np.array(generation_y_train_matrix)
generation_X_train_reshaped = np.reshape(generation_X_train_matrix,
(generation_X_train_matrix.shape[0],
generation_X_train_matrix.shape[1], 1))
generation_y_train_reshaped = np.reshape(generation_y_train_matrix,
(generation_y_train_matrix.shape[0],
generation_y_train_matrix.shape[1], 1))
# Check shapes
print()
print('X_train sets shape:', generation_X_train_reshaped.shape)
print('y_train sets shape:', generation_y_train_reshaped.shape)
print()
```
## Building the LSTM
```
# Initialising the LSTM Model with MSE Loss-Function
# Using Functional API, each layer output is the input of next layer
# Input
inputs = Input(batch_shape=(batch_size,timesteps,1))
# Layer 1: LSTM
lstm_1 = LSTM(12,
activation='tanh',
recurrent_activation='sigmoid',
stateful=True,
return_sequences=True)(inputs)
# Layer 2: LSTM
lstm_2 = LSTM(12,
activation='tanh',
recurrent_activation='sigmoid',
stateful=True,
return_sequences=True)(lstm_1)
# Output
output = Dense(units = 1)(lstm_2)
# Sticking all layers into a Model
regressor = Model(inputs=inputs, outputs = output)
#adam is fast starting off and then gets slower and more precise
regressor.compile(optimizer='adam', loss = mean_squared_error)
# Check the model summary
regressor.summary()
```
## Run LSTM
We run the code on the cloud.
```python
epochs = 5
# start time
start=time.time()
#Statefull
for i in range(epochs):
print("\nEpoch: " + str(i))
#run through all data but the cell, hidden state are used for the next batch.
regressor.fit(consumption_X_train_reshaped, consumption_y_train_reshaped,
shuffle=False, epochs = 1, batch_size = batch_size)
#resets only the states but the weights, cell and hidden are kept.
regressor.reset_states()
# duration of training the model
duration=time.time()-start
```
**Load Models**:
```
# Model is trained with a batch size of 128 and 10 epochs
regressor_con = load_model(filepath="../Models/LSTM_Model_Consumption_128.h5")
# Model is trained with a batch size of 128 and 10 epochs
regressor_gen = load_model(filepath="../Models/LSTM_Model_Generation_128.h5")
```
## Prepare Prediction Function
```
def predict_lstm(dataframe, lstm_model, scaler, batch_size, timesteps):
"""
This function forcast next values in a timeserie dataframe
based on a LSTM modelbatch_size. The predicted values start
from last timestamp index plus time interval
Total Number of predicted values is: batch_size*periods
INPUT:
dataframe: type pandas dataframe
a dataframe with timestamps as index and a metric
lstm_model: type Keras LSTM training Model
It has to be already trained
scaler: type sklearn scaker
It hase to be already fitted. It is used for
transform and inverse transform
batch_size: type int
batch_size with which the model is trained
(also number of sequences)
timesteps: type int
number of values in a batch (or sequence)
periods: type int
number of periods that should be predicted
OUTPUT:
numpy array of shape 1 and size batch_size*periods
containg predicted values
"""
# subsetting
df_pred= dataframe[-(batch_size+timesteps):]
df_pred_set=np.float64(df_pred)
# scaling
X_pred_scaled = scaler.fit_transform(df_pred_set)
# creating input data
X_pred_matrix = []
for i in range(batch_size):
X_pred_matrix.append(X_pred_scaled[i:i+timesteps, 0])
# turn list into array
X_pred_matrix = np.array(X_pred_matrix)
# reshaping
X_pred_reshaped = np.reshape(X_pred_matrix, (X_pred_matrix.shape[0], X_pred_matrix.shape[1], 1))
# prediction
y_hat= lstm_model.predict(X_pred_reshaped, batch_size=batch_size)
# reshaping
y_hat = np.reshape(y_hat, (y_hat.shape[0], y_hat.shape[1]))
# inverse transform
y_hat = scaler.inverse_transform(y_hat)
# creating y_pred data
y_pred = []
for i in range(batch_size):
y_pred = np.append(y_pred, y_hat[i,-1])
return y_pred
```
## Results
**Electricity Consumption:**
```
final_pred_con= predict_lstm(dataframe=consumption, lstm_model=regressor_con,
scaler=sc_con, batch_size=128, timesteps=timesteps)
# Visualising the results
x_index_pred= pd.date_range(consumption.index[-1],freq='H',periods=129)[1:]
fig= plt.figure(figsize=(15,5))
ax = fig.add_subplot(111)
plt.plot(consumption[-256:], color = 'blue', label = 'Real Values')
plt.plot(x_index_pred,final_pred_con, color = 'red', label = 'Predicted Values')
plt.title("\nGermany's Electricity Consumption Forcast using LSTM\n",
fontsize=20 ,fontweight='bold')
ax.xaxis.set_major_locator(plt.IndexLocator(base=2, offset=0))
plt.xlabel('')
plt.ylabel('Electricity Unit [MWh]', fontsize=15)
plt.legend()
plt.show()
```
**Electricity Generation:**
```
final_pred_gen= predict_lstm(dataframe=consumption, lstm_model=regressor_gen,
scaler=sc_gen, batch_size=128, timesteps=timesteps)
# Visualising the results
x_index_pred= pd.date_range(generation.index[-1],freq='H',periods=129)[1:]
fig= plt.figure(figsize=(15,5))
ax = fig.add_subplot(111)
plt.plot(generation[-256:], color = 'blue', label = 'Real Values')
plt.plot(x_index_pred,final_pred_gen, color = 'red', label = 'Predicted Values')
plt.title("\nGermany's Electricity Generation Forcast using LSTM\n",
fontsize=20 ,fontweight='bold')
ax.xaxis.set_major_locator(plt.IndexLocator(base=2, offset=0))
plt.xlabel('')
plt.ylabel('Electricity Unit [MWh]', fontsize=15)
plt.legend()
plt.show()
```
| true |
code
| 0.514156 | null | null | null | null |
|
# Binary Image Denoising
#### *Jiaolong Xu (GitHub ID: [Jiaolong](https://github.com/Jiaolong))*
#### This notebook is written during GSoC 2014. Thanks Shell Hu and Thoralf Klein for taking time to help me on this project!
This notebook illustrates how to use shogun structured output learning framework for binary images denoising. The task is defined as a pairwise factor graph model with [Graph cuts](http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CGraphCut.html) inference, where model parameters are learned by SOSVM using a [SGD solver](http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CStochasticSOSVM.html).
## Introduction
This notebook illustrates how to use shogun structured output learning framework for binary images denoising. I recommend [1] for a nice introduction of structured learning and prediction in computer vision. One of the founding publications on the topic of learning structured models might be [4]. In the following, I will give an explicit example of structured output prediction for binary image denoising.
Given a noise black/withe image $\textbf{x}$ of size $m \times n$, the task of denoising is to predicted the original binary image $\textbf{y}$. We flatten the image into a long vector $\textbf{y} = [y_0, \dots, y_{m\times n}]$, where $y_i \in \{0, 1\}$ is the value for pixel $i$. In this work, we aim to learn a model from a bunch of noise input images and their ground truth binary images, i.e., supervised learning. One may think about learning a binary classifier for each pixel. It has several drawbacks. First, we may not care about classifying every single pixel completely correct, i.e., if we misclassify a single pixel, this is not as bad as misclassify a whole image. Second, we lose all context, e.g., pairwise pixels (one pixel and its neighbore). The structured predition here is to predict an entire binary image $\textbf{y}$ or a grid graph of $m \times n$. Here, the output space $\mathcal{Y}$ is all possible binary images of size $m \times n$. It can be formulated as following:
$$
\hat{\textbf{y}} = \underset{\textbf{y} \in \mathcal{Y}}{\operatorname{argmax}} f(\textbf{x},\textbf{y}), (1)
$$
where $f(\textbf{x},\textbf{y})$ is the compitibility function, measures how well $\textbf{y}$ fits $\textbf{x}$. There are basically three challenges in doing structured learning and prediction:
- Choosing a parametric form of $f(\textbf{x},\textbf{y})$
- solving $\underset{\textbf{y} \in \mathcal{Y}}{\operatorname{argmax}} f(\textbf{x},\textbf{y})$
- learning parameters for $f(\textbf{x},\textbf{y})$ to minimize a loss
In this work, our parameters are pairwise and unary potentials and they can be written as:
$$
f(\textbf{x},\textbf{y}) = \sum_i \textbf{w}_i'\phi_i(\textbf{x}) + \sum_{i,j} \textbf{w}_{ij}'\phi_{ij}(\textbf{x}), (2)
$$
where $\textbf{w}_i$ and $\textbf{w}_{ij}$ are unary and pairwise parameters, $\phi_i(\textbf{x})$ and $\phi_{ij}(\textbf{x})$ are unary and pairwise features respectively. Equation (2) is a linear function and can be written as a dot product of a global parameter $\textbf{w}$ and joint feature vector $\Phi(\textbf{x},\textbf{y})$, i.e., $f(\textbf{x},\textbf{y}) = \textbf{w}'\Phi(\textbf{x}, \textbf{y})$. The global parameter $\textbf{w}$ is a collection of unary and pairwise parameters. The joint feature $\Phi(\textbf{x}, \textbf{y})$ maps local features, e.g., pixel values from each location, to the corresponding location of the global feature vector according to $\textbf{y}$. In factor graph model, parameters are associated with a set of factor types.
As said before, the output space $\mathcal{Y}$ is usually finite but very large. In our case, it is all possible binary images of size $m \times n$. Finding ${\operatorname{argmax}}$ in such a large space by exhaustive search is not practical. To do the maximization over $\textbf{y}$ efficiently, the most popular tool is using energy functions or conditional random fields (CRFs). In this work, we implemented Graph cuts [5] for efficient inference. We also implemented max-product LP relaxation inference and tree max-product inference. However, the later is limited to tree-struct graph while for image denosing, we use grid graph.
The parameters are learned by regularized risk minimization, where the risk defined by user provided loss function $\Delta(\mathbf{y},\mathbf{\hat{y}})$. We use the Hamming loss in this experiment. The empirical risk is defined in terms of the surrogate hinge loss $\mathcal{L}_i(\mathbf{w}) = \max_{\mathbf{y} \in \mathcal{Y}} \Delta(\mathbf{y}_i,\mathbf{y}) - \mathbf{w}' [\Phi(\mathbf{x}_i,\mathbf{y}_i) - \Phi(\mathbf{x}_i,\mathbf{y})]$. The training objective is given by
$$
\min_{\mathbf{w}} \frac{\lambda}{2} ||\mathbf{w}||^2 + \frac{1}{N} \sum_{i=1}^N \mathcal{L}_i(\mathbf{w}). (3)
$$
## Create binary denoising dataset
```
import os
SHOGUN_DATA_DIR=os.getenv('SHOGUN_DATA_DIR', '../../../data')
import numpy as np
import numpy.random
```
We dfine an Example class for the training and testing examples.
```
class Example:
""" Example class.
Member variables:
id: id of the example
im_bw: original binary image
im_noise: original image with noise
feats: feature for each pixel
labels: binary labels of each pixel
"""
def __init__(self, id, im_bw, im_noise, feats, labels):
self.id = id
self.im_bw = im_bw
self.im_noise = im_noise
self.feature = feats
self.labels = labels
```
In the following, we create a toy dataset. Similar to [2], we make random noisy images, then smooth them to make the true (discrete) output values.
```
import scipy.ndimage
# generate random binary images
im_size = np.array([50, 50], np.int32)
num_images = 30
ims_bw = []
for i in range(num_images):
im_rand = np.random.random_sample(im_size)
im_bw = np.round(scipy.ndimage.gaussian_filter(im_rand, sigma=3))
ims_bw.append(im_bw)
```
Next, noises are added to the binary images. We apply the same strategy as in [3], the noisy images are generated as $z_i = x_i(1-t_i^n) + (1-x_i)t_i^n$, where $x_i$ is the true binary label, and $t_i \in [0,1]$ is a random value. Here, $n \in (1, \infty)$ is the noise level, where lower values correspond to more noise.
In this experiment, we use only two features as unary features: a constant of $1$ and the noisy input value at the pixel, i.e., $\textbf{u}(i) = [z_i, 1]$.
```
# define noisy level
noise_level = 2
# initialize an empty list
example_list = []
for i in range(len(ims_bw)):
im_bw = ims_bw[i]
# add noise to the binary image
t = np.random.random_sample(im_bw.shape)
im_noise = im_bw*(1-t**noise_level) + (1-im_bw)*(t**noise_level)
# create 2-d unary features
c1 = np.ravel(im_noise)
c2 = np.ones(im_noise.size, np.int32)
feats = np.column_stack([c1, c2])
# we use pixel-level labels
# so just flatten the original binary image into a vector
labels = np.ravel(im_bw)
example = Example(i, im_bw, im_noise, feats, labels)
example_list.append(example)
```
Now we creat a function to visualize our examples.
```
import matplotlib.pyplot as plt
%matplotlib inline
def plot_example(example):
""" Plot example."""
fig, plots = plt.subplots(1, 2, figsize=(12, 4))
plots[0].matshow(example.im_bw, cmap=plt.get_cmap('Greys'))
plots[0].set_title('Binary image')
plots[1].matshow(example.im_noise, cmap=plt.get_cmap('Greys'))
plots[1].set_title('Noise image')
for p in plots:
p.set_xticks(())
p.set_yticks(())
plt.show()
# plot an example
plot_example(example_list[9])
```
## Build Factor Graph Model
```
from shogun import Factor, TableFactorType, FactorGraph
from shogun import FactorGraphObservation, FactorGraphLabels, FactorGraphFeatures
from shogun import FactorGraphModel, GRAPH_CUT, LP_RELAXATION
from shogun import MAPInference
```
We define a 'make_grid_edges' function to compute the indeces of the pairwise pixels. we use grid graph with neighborhood size of $4$ in our experiment.
```
def make_grid_edges(grid_w, grid_h, neighborhood=4):
""" Create grid edge lists.
Args:
grid_w: width of the grid
grid_h: height of the grid
neigborhood: neigborhood of the node (4 or 8)
Returns:
edge list of the grid graph
"""
if neighborhood not in [4, 8]:
raise ValueError("neighborhood can only be '4' or '8', got %s" % repr(neighborhood))
inds = np.arange(grid_w * grid_h).reshape([grid_w, grid_h])
inds = inds.astype(np.int64)
right = np.c_[inds[:, :-1].ravel(), inds[:, 1:].ravel()]
down = np.c_[inds[:-1, :].ravel(), inds[1:, :].ravel()]
edges = [right, down]
if neighborhood == 8:
upright = np.c_[inds[1:, :-1].ravel(), inds[:-1, 1:].ravel()]
downright = np.c_[inds[:-1, :-1].ravel(), inds[1:, 1:].ravel()]
edges.extend([upright, downright])
return np.vstack(edges)
# in this experiment, we use fixed image size
im_w = example_list[0].im_bw.shape[1]
im_h = example_list[0].im_bw.shape[0]
# we compute the indeces of the pairwise nodes
edge_list = make_grid_edges(im_w, im_h)
```
For binary denosing, we define two types of factors:
- unary factor: the unary factor type is used to define unary potentials that captures the the appearance likelyhood of each pixel. We use very simple unary feature in this experiment, the pixel value and a constant value $1$. As we use binary label, thus the size of the unary parameter is $4$.
- pairwise factor: the pairwise factor type is used to define pairwise potentials between each pair of pixels. There features of the pairwise factors are constant $1$ and there are no additional edge features. For the pairwise factors, there are $2 \times 2$ parameters.
Putting all parameters together, the global parameter vector $\mathbf{w}$ has length $8$.
```
def define_factor_type(num_status, dim_feat):
""" Define factor type.
Args:
num_status: number of status.
dim_feat: dimention of the unary node feature
Returns:
ftype_unary: unary factor type
ftype_pair: pairwise factor type
"""
# unary, type id = 0
cards_u = np.array([num_status], np.int32) # cardinalities
w_u = np.zeros(num_status*dim_feat, np.float64)
ftype_unary = TableFactorType(0, cards_u, w_u)
# pairwise, type id = 1
cards_p = np.array([num_status, num_status], np.int32)
w_p = np.zeros(num_status*num_status, np.float64)
ftype_pair = TableFactorType(1, cards_p, w_p)
return ftype_unary, ftype_pair
# define factor types
ftype_unary, ftype_pair = define_factor_type(num_status=2, dim_feat=2)
def prepare_factor_graph_model(example_list, ftype_unary, ftype_pair, edge_list, num_status = 2, dim_feat = 2):
""" Prepare factor graph model data.
Args:
example_list: the examples
num_status: number of status
dim_feat: dimention of the unary features
"""
num_samples = len(example_list)
# Initialize factor graph features and labels
feats_fg = FactorGraphFeatures(num_samples)
labels_fg = FactorGraphLabels(num_samples)
# Interate over all the examples
for i in range(num_samples):
example = example_list[i]
feats = example.feature
num_var = feats.shape[0]
dim_feat = feats.shape[1]
# Initialize factor graph
cards = np.array([num_status]*num_var, np.int32) # cardinalities
fg = FactorGraph(cards)
# add unary
for u in range(num_var):
data_u = np.array(feats[u,:], np.float64)
inds_u = np.array([u], np.int32)
factor_u = Factor(ftype_unary, inds_u, data_u)
fg.add_factor(factor_u)
# add pairwise
for p in range(edge_list.shape[0]):
data_p = np.array([1.0], np.float64)
inds_p = np.array(edge_list[p,:], np.int32)
factor_p = Factor(ftype_pair, inds_p, data_p)
fg.add_factor(factor_p)
# add factor graph feature
feats_fg.add_sample(fg)
# add factor graph label
labels = example.labels.astype(np.int32)
assert(labels.shape[0] == num_var)
loss_weight = np.array([1.0/num_var]*num_var)
f_obs = FactorGraphObservation(labels, loss_weight)
labels_fg.add_label(f_obs)
return feats_fg, labels_fg
```
We split the samples into training and testing sets. The features and labels are converted for factor graph model.
```
num_train_samples = 10
examples_train = example_list[:num_train_samples]
examples_test = example_list[num_train_samples:]
# create features and labels for factor graph mode
(feats_train, labels_train) = prepare_factor_graph_model(examples_train, ftype_unary, ftype_pair, edge_list)
(feats_test, labels_test) = prepare_factor_graph_model(examples_test, ftype_unary, ftype_pair, edge_list)
```
In this experiment, we use [Graph cuts](http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CGraphCut.html) as approximate inference algorithm, i.e., solve Eq. (1). Please refer to [4] for a comprehensive understanding.
```
# inference algorithm
infer_alg = GRAPH_CUT
#infer_alg = LP_RELAXATION
# create model and register factor types
model = FactorGraphModel(feats_train, labels_train, infer_alg)
model.add_factor_type(ftype_unary)
model.add_factor_type(ftype_pair)
```
## Learning parameter with structured output SVM
We apply (<a href="http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CStochasticSOSVM.html">StochasticSOSVM</a>) to learn the parameter $\textbf{w}$.
```
from shogun import StochasticSOSVM
import time
# Training with Stocastic Gradient Descent
sgd = StochasticSOSVM(model, labels_train, True, True)
sgd.put('num_iter', 300)
sgd.put('lambda', 0.0001)
# train
t0 = time.time()
sgd.train()
t1 = time.time()
w_sgd = sgd.get_w()
print( "SGD took", t1 - t0, "seconds.")
def evaluation(labels_pr, labels_gt, model):
""" Evaluation
Args:
labels_pr: predicted label
labels_gt: ground truth label
model: factor graph model
Returns:
ave_loss: average loss
"""
num_train_samples = labels_pr.get_num_labels()
acc_loss = 0.0
ave_loss = 0.0
for i in range(num_train_samples):
y_pred = labels_pr.get_label(i)
y_truth = labels_gt.get_label(i)
acc_loss = acc_loss + model.delta_loss(y_truth, y_pred)
ave_loss = acc_loss / num_train_samples
return ave_loss
# training error
labels_train_pr = sgd.apply()
ave_loss = evaluation(labels_train_pr, labels_train, model)
print('SGD: Average training error is %.4f' % ave_loss)
def plot_primal_trainError(sosvm, name = 'SGD'):
""" Plot primal objective values and training errors."""
primal_val = sosvm.get_helper().get_primal_values()
train_err = sosvm.get_helper().get_train_errors()
fig, plots = plt.subplots(1, 2, figsize=(12,4))
# primal vs passes
plots[0].plot(range(primal_val.size), primal_val, label=name)
plots[0].set_xlabel('effecitve passes')
plots[0].set_ylabel('primal objective')
plots[0].set_title('whole training progress')
plots[0].legend(loc=1)
plots[0].grid(True)
# training error vs passes
plots[1].plot(range(train_err.size), train_err, label=name)
plots[1].set_xlabel('effecitve passes')
plots[1].set_ylabel('training error')
plots[1].set_title('effective passes')
plots[1].legend(loc=1)
plots[1].grid(True)
# plot primal objective values and training errors at each pass
plot_primal_trainError(sgd)
```
## Testing results
```
# Testing error
sgd.set_features(feats_test)
sgd.set_labels(labels_test)
labels_test_pr = sgd.apply()
ave_loss = evaluation(labels_test_pr, labels_test, model)
print('SGD: Average testing error is %.4f' % ave_loss)
def plot_results(example, y_pred):
""" Plot example."""
im_pred = y_pred.reshape(example.im_bw.shape)
fig, plots = plt.subplots(1, 3, figsize=(12, 4))
plots[0].matshow(example.im_noise, cmap=plt.get_cmap('Greys'))
plots[0].set_title('noise input')
plots[1].matshow(example.im_bw, cmap=plt.get_cmap('Greys'))
plots[1].set_title('ground truth labels')
plots[2].matshow(im_pred, cmap=plt.get_cmap('Greys'))
plots[2].set_title('predicted labels')
for p in plots:
p.set_xticks(())
p.set_yticks(())
plt.show()
import matplotlib.pyplot as plt
%matplotlib inline
# plot one example
i = 8
# get predicted output
y_pred = FactorGraphObservation.obtain_from_generic(labels_test_pr.get_label(i)).get_data()
# plot results
plot_results(examples_test[i], y_pred)
def plot_results_more(examples, labels_pred, num_samples=10):
""" Plot example."""
fig, plots = plt.subplots(num_samples, 3, figsize=(12, 4*num_samples))
for i in range(num_samples):
example = examples[i]
# get predicted output
y_pred = FactorGraphObservation.obtain_from_generic(labels_pred.get_label(i)).get_data()
im_pred = y_pred.reshape(example.im_bw.shape)
plots[i][0].matshow(example.im_noise, cmap=plt.get_cmap('Greys'))
plots[i][0].set_title('noise input')
plots[i][0].set_xticks(())
plots[i][0].set_yticks(())
plots[i][1].matshow(example.im_bw, cmap=plt.get_cmap('Greys'))
plots[i][1].set_title('ground truth labels')
plots[i][1].set_xticks(())
plots[i][1].set_yticks(())
plots[i][2].matshow(im_pred, cmap=plt.get_cmap('Greys'))
plots[i][2].set_title('predicted labels')
plots[i][2].set_xticks(())
plots[i][2].set_yticks(())
plt.show()
plot_results_more(examples_test, labels_test_pr, num_samples=5)
```
## Reference
[1] Nowozin, S., & Lampert, C. H. Structured learning and prediction in computer vision. Foundations and Trends® in Computer Graphics and Vision, 6(3–4), 185-365, 2011.
[2] http://users.cecs.anu.edu.au/~jdomke/JGMT/
[3] Justin Domke, Learning Graphical Model Parameters with Approximate Marginal Inference, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 10, pp. 2454-2467, 2013.
[4] Tsochantaridis, I., Hofmann, T., Joachims, T., Altun, Y., Support Vector Machine Learning for Interdependent and Structured Ouput Spaces, ICML 2004.
[5] Boykov, Y., Veksler, O., & Zabih, R. Fast approximate energy minimization via graph cuts. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 23(11), 1222-1239, 2001.
| true |
code
| 0.796114 | null | null | null | null |
|
# Converting RMarkdown files to SoS notebooks
* **Difficulty level**: easy
* **Time need to lean**: 10 minutes or less
* **Key points**:
* `sos convert file.Rmd file.ipynb` converts a Rmarkdown file to SoS notebook. A `markdown` kernel is used to render markdown text with in-line expressions.
* `sos convert file.Rmd file.ipynb --execute` executes the resulting SoS notebook
* `sos convert file.Rmd file.html --execute --template` converts a R markdown file to SoS notebook, executes it, and converts the resulting notebook to HTML format
The RMarkdown format is a markdown format with embedded R expressions and code blocks, and is extremely popular for R users. SoS Notebook provides an utility to convert Rmarkdown files to a SoS Notebook with command
```
sos convert input.Rmd output.ipynb
```
with the option to execute the resulting notebook
```
sos convert input.Rmd output.ipynb --execute
```
Example files and commands:
* [Example Rmd file](../media/example.Rmd) copied from [jeromyanglim/example-r-markdown.rmd](https://gist.github.com/jeromyanglim/2716336)
* [Converted ipynb file](../media/example.ipynb) generated by command
```
sos convert example.Rmd example.ipynb
```
* [Executed version of the notebook](../media/executed.ipynb) generated by command
```
sos convert example.Rmd executed.ipynb --execute
```
or
```
sos convert example.ipynb executed.ipynb --execute
```
from the converted notebook.
* [Export HTML file using template `sos-report-toc-v2`](../media/example.html) generated by command
```
sos convert example.Rmd example.html --execute --template sos-report-toc-v2
```
or
```
sos convert example.ipynb example.html --execute --template sos-report-toc-v2
```
or
```
sos convert executed.ipynb example.html --template sos-report-toc-v2
```
if we start from the intermediate results.
## Converting R Markdown to SoS Notebook
Although there are already a number of Rmd to Jupyter converters (e.g. [notedown](https://github.com/aaren/notedown), [RMD-to-Jupyter](https://github.com/lecy/RMD-to-Jupyter) (uses rpy2)), they lack support for some of the Rmakdown features due to limitations of the Jupyter notebook platform. Fortunately, SoS Notebook, especially its Jupyter Lab extension addresses most of the limitations and offers an almost perfect conversion from R markdown to Jupyter notebook.
The first Rmarkdown feature that is difficult to convert is its inline expressions, which are R expressions embedded in markdown texts. Jupyter cannot handle embedded expressions in its markdown cells because markdown cells are handled in its frontend and does not interact with the computing kernel. SoS Notebook addresses this problem with the use of a [markdown kernel](https://github.com/vatlab/markdown-kernel), which is essentially a markdown kernel
For example, the following Rmarkdown text
```
I counted `r sum(c(1,2,3))` blue cars on the highway.
```
is converted to a markdown cell that is evaluated in a R kernel as follows
```
%expand `r ` --in R
I counted `r sum(c(1,2,3))` blue cars on the highway.
```
The second Rmarkdown feature is its support for multiple languages, which allows it to have [code blocks in a number of langauges](https://bookdown.org/yihui/rmarkdown/language-engines.html). A Jupyter notebook with an `ir` kernel can only evaluate R scripts, but a SoS Notebook is able to include multiple kernels in one notebook.
For example, code blocks such as
```{python}
def f(x):
return x + 2
f(2)
```
and
```{r engine="python"}
def f(x):
return x + 2
f(2)
```
are converted to cells with approprivate kernels such as
```
def f(x):
return x + 2
f(2)
```
The last feature that is not properly supported are options such as `echo=FALSE` and `include=FALSE` for Rmarkdown code blocks. There were no corresponding features for classic Jupyter Notebook but Jupyter Lab supports hiding of input and/or output of cells. Using these features, code blocks such as the following are converted as collapsed input and/or outputs,
```{r echo=FALSE}
arr <- rnorm(5)
cat(arr)
```
```
arr <- rnorm(5)
cat(arr)
```
A related problem is that `jupyter nbconvert` does not respect the collasping status of cells and renders input and output of all cells. SoS Notebook addresses this problem by providing templates that honor the show/hide status of cells. For example, template `sos-report-toc-v2` outputs all cells but hides collapsed inputs and outputs by default. The hidden content could be displayed by selecting a dropdown box to the top right corner of the document.
## Option `--execute`
Rmarkdown files do not contain outputs from inline expressions and code blocks so `output.ipynb` generated from command
```
sos convert input.Rmd output.ipynb
```
only contains inputs. To obtain a notebook with embedded output, you can add option `--execute` to the `convert` command
```
sos convert input.Rmd output.ipynb --execute
```
This command will convert `input.Rmd` to a SoS notebook, executes it to generate the resulting `output.ipynb`. It is basically a shortcut for commands
```
sos convert input.Rmd tmp_output.ipynb
papermill --engine sos temp_output.ipynb output.ipynb
rm -f temp_output.ipynb
```
## Generate a HTML report from a Rmarkdown file
Command
```
sos convert input.Rmd output.html --execute
```
convert `file.Rmd` to a SoS notebook, executes it, and generates a HTML report using specified template. It is basically a shortcut for commands
```
sos convert input.Rmd temp_output.ipynb
papermill --engine sos temp_output.ipynb temp_executed.ipynb
sos convert temp_executed.ipynb output.html
rm -rf temp_output.ipynb temp_executed.ipynb
```
Note that SoS provides a few templates to generate reports that hides input and/or outputs of code blocks, corresponding to `echo=FALSE`, `include=FALSE` options of Rmd code blocks. You can specify the use of templates with options such as `--template sos-report-toc-v2`. You can see a list of templates provided by SoS [here](magic_convert.html).
| true |
code
| 0.745198 | null | null | null | null |
|
# Visualization
PySwarms implements tools for visualizing the behavior of your swarm. These are built on top of `matplotlib`, thus rendering charts that are easy to use and highly-customizable.
In this example, we will demonstrate three plotting methods available on PySwarms:
- `plot_cost_history`: for plotting the cost history of a swarm given a matrix
- `plot_contour`: for plotting swarm trajectories of a 2D-swarm in two-dimensional space
- `plot_surface`: for plotting swarm trajectories of a 2D-swarm in three-dimensional space
```
# Import modules
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import Image
# Import PySwarms
import pyswarms as ps
from pyswarms.utils.functions import single_obj as fx
from pyswarms.utils.plotters import (plot_cost_history, plot_contour, plot_surface)
```
The first step is to create an optimizer. Here, we're going to use Global-best PSO to find the minima of a sphere function. As usual, we simply create an instance of its class `pyswarms.single.GlobalBestPSO` by passing the required parameters that we will use. Then, we'll call the `optimize()` method for 100 iterations.
```
options = {'c1':0.5, 'c2':0.3, 'w':0.9}
optimizer = ps.single.GlobalBestPSO(n_particles=50, dimensions=2, options=options)
cost, pos = optimizer.optimize(fx.sphere, iters=100)
```
## Plotting the cost history
To plot the cost history, we simply obtain the `cost_history` from the `optimizer` class and pass it to the `cost_history` function. Furthermore, this method also accepts a keyword argument `**kwargs` similar to `matplotlib`. This enables us to further customize various artists and elements in the plot. In addition, we can obtain the following histories from the same class:
- mean_neighbor_history: average local best history of all neighbors throughout optimization
- mean_pbest_history: average personal best of the particles throughout optimization
```
plot_cost_history(cost_history=optimizer.cost_history)
plt.show()
```
## Animating swarms
The `plotters` module offers two methods to perform animation, `plot_contour()` and `plot_surface()`. As its name suggests, these methods plot the particles in a 2-D or 3-D space.
Each animation method returns a `matplotlib.animation.Animation` class that still needs to be animated by a `Writer` class (thus necessitating the installation of a writer module). For the proceeding examples, we will convert the animations into a JS script. In such case, we need to invoke some extra methods to do just that.
Lastly, it would be nice to add meshes in our swarm to plot the sphere function. This enables us to visually recognize where the particles are with respect to our objective function. We can accomplish that using the `Mesher` class.
```
from pyswarms.utils.plotters.formatters import Mesher
# Initialize mesher with sphere function
m = Mesher(func=fx.sphere)
```
There are different formatters available in the `pyswarms.utils.plotters.formatters` module to customize your plots and visualizations. Aside from `Mesher`, there is a `Designer` class for customizing font sizes, figure sizes, etc. and an `Animator` class to set delays and repeats during animation.
### Plotting in 2-D space
We can obtain the swarm's position history using the `pos_history` attribute from the `optimizer` instance. To plot a 2D-contour, simply pass this together with the `Mesher` to the `plot_contour()` function. In addition, we can also mark the global minima of the sphere function, `(0,0)`, to visualize the swarm's "target".
```
%%capture
# Make animation
animation = plot_contour(pos_history=optimizer.pos_history,
mesher=m,
mark=(0,0))
# Enables us to view it in a Jupyter notebook
animation.save('plot0.gif', writer='imagemagick', fps=10)
Image(url='plot0.gif')
```
### Plotting in 3-D space
To plot in 3D space, we need a position-fitness matrix with shape `(iterations, n_particles, 3)`. The first two columns indicate the x-y position of the particles, while the third column is the fitness of that given position. You need to set this up on your own, but we have provided a helper function to compute this automatically
```
# Obtain a position-fitness matrix using the Mesher.compute_history_3d()
# method. It requires a cost history obtainable from the optimizer class
pos_history_3d = m.compute_history_3d(optimizer.pos_history)
# Make a designer and set the x,y,z limits to (-1,1), (-1,1) and (-0.1,1) respectively
from pyswarms.utils.plotters.formatters import Designer
d = Designer(limits=[(-1,1), (-1,1), (-0.1,1)], label=['x-axis', 'y-axis', 'z-axis'])
%%capture
# Make animation
animation3d = plot_surface(pos_history=pos_history_3d, # Use the cost_history we computed
mesher=m, designer=d, # Customizations
mark=(0,0,0)) # Mark minima
animation3d.save('plot1.gif', writer='imagemagick', fps=10)
Image(url='plot1.gif')
```
| true |
code
| 0.66769 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import pyqg
year = 24*60*60*360.
# Set up a model which will run for 20 years and start averaging after 10 years.
# There are lots of parameters that can be specified as keyword arguments
# but we are just using the defaults.
m = pyqg.QGModel(tmax=20*year, twrite=10000, tavestart=10*year)
# run it
m.run()
```
## Example of plots
## The QG potential vorticities in physical space
```
q1 = m.q[0] + m.Qy[0]*m.y
q2 = m.q[1] + m.Qy[1]*m.y
X, Y = m.x/1e3, m.y/1e3 # give units in km
pv_factor = 1.e4
factor_s = str('%1.1e') %pv_factor
fig = plt.figure(figsize=(16.,5.))
ax1 = fig.add_subplot(121)
cf1 = ax1.contourf(X, Y, pv_factor*q1, 12, cmap='RdBu_r')
cb1 = fig.colorbar(cf1)
cb1.ax.text(.0,1.05,factor_s,rotation=0)
ax1.set_xlabel('x [km]')
ax1.set_ylabel('y [km]')
ax1.set_title('Layer 1 QGPV')
ax2 = fig.add_subplot(122)
cf2 = ax2.contourf(X, Y, pv_factor*q2, 12, cmap='RdBu_r')
cb2 = fig.colorbar(cf2)
ax2.set_title('Layer 2 QGPV')
cb2.ax.text(.0,1.05,factor_s,rotation=0)
ax2.set_xlabel('x [km]')
ax2.set_ylabel('y [km]')
```
## KE spectra and Energy budget
```
# some spectral plots
KE1spec = m.get_diagnostic('KEspec')[0].sum(axis=0) # note that this is misleading for anisotrphic flows...
KE2spec = m.get_diagnostic('KEspec')[1].sum(axis=0) # we should sum azimuthaly, and plot as a functions of kappa
# factor ebud
ebud_factor = 1.e4
ebud_factor_s= str('%1.1e') %ebud_factor
# inertial range
ir = np.r_[10:20]
fig = plt.figure(figsize=(16.,7.))
ax1 = fig.add_subplot(121)
ax1.loglog( m.kk, KE1spec, '.-' )
ax1.loglog( m.kk, KE2spec, '.-' )
ax1.loglog( m.kk[10:20], 2*(m.kk[ir]**-3) *
KE1spec[ir].mean() / (m.kk[ir]**-3).mean(),
'0.5')
ax1.set_ylim([1e-9,1e-3])
ax1.set_xlim([m.kk.min(), m.kk.max()])
ax1.grid()
ax1.legend(['upper layer','lower layer', r'$k^{-3}$'],
loc='lower left')
ax1.set_xlabel(r'k (m$^{-1})$')
ax1.set_title('Kinetic Energy Spectrum')
# the spectral energy budget
ebud = [ -m.get_diagnostic('APEgenspec').sum(axis=0),
-m.get_diagnostic('APEflux').sum(axis=0),
-m.get_diagnostic('KEflux').sum(axis=0),
-m.rek*m.del2*m.get_diagnostic('KEspec')[1].sum(axis=0)*m.M**2 ]
ebud.append(-np.vstack(ebud).sum(axis=0))
ebud_labels = ['APE gen','APE flux','KE flux','Diss.','Resid.']
ax2 = fig.add_subplot(122)
[ax2.semilogx(m.kk, term) for term in ebud]
ax2.legend(ebud_labels, loc='upper right')
ax2.grid()
ax2.set_xlim([m.kk.min(), m.kk.max()])
ax1.set_xlabel(r'k (m$^{-1})$')
ax2.ticklabel_format(axis='y',style = 'sci', scilimits=(-2,2))
ax2.set_title(r' Spectral Energy Budget')
ax2.set_xlabel(r'k (m$^{-1})$')
```
| true |
code
| 0.619126 | null | null | null | null |
|
## Mergesort
Implement mergesort.
### Approach
Mergesort is a divide-and-conquer algorithm. We divide the array into two sub-arrays, recursively call the function and pass in the two halves, until each sub-array has one element. Since each sub-array has only one element, they are all sorted. We then merge each sub-array until we form a sorted array.
The merge function will be used to merge two sorted halves.
```
def merge_sort(array, left, right):
if left < right:
mid = (left + (right - 1)) // 2 # same as ((left + right) // 2) but avoids overflow for large left
merge_sort(array, left, mid)
merge_sort(array, mid + 1, right)
merge(array, left, mid, right)
return array
def merge(array, left, mid, right):
n1 = mid - left + 1
n2 = right - mid
# create temp arrays
left_array = [0] * n1
right_array = [0] * n2
# copy the data to the temp arrays
for i in range(0, n1):
left_array[i] = array[left + i]
for j in range(0, n2):
right_array[j] = array[mid + 1 + j]
# merge the temp arrays into one array
i = 0 # index for arr1
j = 0 # index for arr2
k = left # index for the final array
while i < n1 and j < n2:
if left_array[i] <= right_array[j]:
array[k] = left_array[i]
i += 1
else:
array[k] = right_array[j]
j += 1
k += 1
# copy remaining elements of left array if any
while i < n1:
array[k] = left_array[i]
i += 1
k += 1
# copy remaining elements of right array if any
while j < n2:
array[k] = right_array[j]
j += 1
k += 1
A = [2, 4, 1, 6, 0, 3]
n = len(A)
merge_sort(A, 0, n - 1)
```
## Bottom-up approach
We can implement merge-sort iteratively in a bottom-up manner.
We start by sorting all sub-arrays of size 1, then we merge them into sub-arrays of two elements. We perform successive merges until the array is completely sorted.
```
def merge(A, temp, frm, mid, to):
k = frm
i = frm
j = mid + 1
while i <= mid and j <= to:
if A[i] <= A[j]:
temp[k] = A[i]
i += 1
else:
temp[k] = A[j]
j += 1
k += 1
# copy remaining elements
while i < len(A) and i <= mid:
temp[k] = A[i]
i += 1
k += 1
# no need to copy second half ...
# copy back original list to reflect sorted order
for i in range(frm, to + 1):
A[i] = temp[i]
def mergeSort(array):
left = 0
right = len(array) - 1
temp = array.copy()
m = 1
while m <= right - left:
for i in range(left, right, 2 * m):
frm = i
mid = i + m - 1
to = min(i + 2 * m - 1, right)
merge(A, temp, frm, mid, to)
m = 2 * m
return array
A = [5, -4, 3, 2, 1]
mergeSort(A)
```
| true |
code
| 0.387227 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/anjali0503/Internship-Projects/blob/main/Iris_ML_DTC.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## ***ANJALI RAMLOLARAKH PANDEY***
**TSF GRIP SPARKS FOUNDATION**
Prediction using Decision Tree Algorithm
## TASK:06
'Create the Decision Tree classifier and visualize it graphically.'
```
#Import dependencies
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
data=pd.read_csv('Iris.csv') #Reading dataset
data
X = data.drop(['Id', 'Species'], axis=1)
y = data['Species']
print(X.shape)
print(y.shape)
#Splitting dataset into testing and training
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=5)
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
#Accuracy of model
score = tree_clf.score(X_test, y_test)
accuracy=score*100
print("score:",score)
print("Accuracy",accuracy)
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
#Defining function - print_score to calculate test and train score
def print_score(clf, X_train, y_train, X_test, y_test, train=True):
if train:
pred = clf.predict(X_train)
clf_report = pd.DataFrame(classification_report(y_train, pred, output_dict=True))
print("Train Result:\n================================================")
print(f"Accuracy Score: {accuracy_score(y_train, pred) * 100:.2f}%")
print("_______________________________________________")
print(f"CLASSIFICATION REPORT:\n{clf_report}")
print("_______________________________________________")
print(f"Confusion Matrix: \n {confusion_matrix(y_train, pred)}\n")
elif train==False:
pred = clf.predict(X_test)
clf_report = pd.DataFrame(classification_report(y_test, pred, output_dict=True))
print("Test Result:\n================================================")
print(f"Accuracy Score: {accuracy_score(y_test, pred) * 100:.2f}%")
print("_______________________________________________")
print(f"CLASSIFICATION REPORT:\n{clf_report}")
print("_______________________________________________")
print(f"Confusion Matrix: \n {confusion_matrix(y_test, pred)}\n")
#Evaluating model by checking accuracy of testing and training model
from sklearn.tree import DecisionTreeClassifier
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)
print_score(tree_clf, X_train, y_train, X_test, y_test, train=True)
print_score(tree_clf, X_train, y_train, X_test, y_test, train=False)
#Storing results in a table
test_score = accuracy_score(y_test, tree_clf.predict(X_test)) * 100
train_score = accuracy_score(y_train, tree_clf.predict(X_train)) * 100
results_df = pd.DataFrame(data=[["Decision Tree Classifier", train_score, test_score]],
columns=['Model', 'Training Accuracy %', 'Testing Accuracy %'])
results_df = results_df.append(results_df, ignore_index=True)
results_df
```
| true |
code
| 0.31076 | null | null | null | null |
|
```
%matplotlib inline
```
`Learn the Basics <intro.html>`_ ||
`Quickstart <quickstart_tutorial.html>`_ ||
`Tensors <tensorqs_tutorial.html>`_ ||
**Datasets & DataLoaders** ||
`Transforms <transforms_tutorial.html>`_ ||
`Build Model <buildmodel_tutorial.html>`_ ||
`Autograd <autogradqs_tutorial.html>`_ ||
`Optimization <optimization_tutorial.html>`_ ||
`Save & Load Model <saveloadrun_tutorial.html>`_
Datasets & Dataloaders
===================
Code for processing data samples can get messy and hard to maintain; we ideally want our dataset code
to be decoupled from our model training code for better readability and modularity.
PyTorch provides two data primitives: ``torch.utils.data.DataLoader`` and ``torch.utils.data.Dataset``
that allow you to use pre-loaded datasets as well as your own data.
``Dataset`` stores the samples and their corresponding labels, and ``DataLoader`` wraps an iterable around
the ``Dataset`` to enable easy access to the samples.
PyTorch domain libraries provide a number of pre-loaded datasets (such as FashionMNIST) that
subclass ``torch.utils.data.Dataset`` and implement functions specific to the particular data.
They can be used to prototype and benchmark your model. You can find them
here: `Image Datasets <https://pytorch.org/vision/stable/datasets.html>`_,
`Text Datasets <https://pytorch.org/text/stable/datasets.html>`_, and
`Audio Datasets <https://pytorch.org/audio/stable/datasets.html>`_
Loading a Dataset
-------------------
Here is an example of how to load the `Fashion-MNIST <https://research.zalando.com/project/fashion_mnist/fashion_mnist/>`_ dataset from TorchVision.
Fashion-MNIST is a dataset of Zalando’s article images consisting of 60,000 training examples and 10,000 test examples.
Each example comprises a 28×28 grayscale image and an associated label from one of 10 classes.
We load the `FashionMNIST Dataset <https://pytorch.org/vision/stable/datasets.html#fashion-mnist>`_ with the following parameters:
- ``root`` is the path where the train/test data is stored,
- ``train`` specifies training or test dataset,
- ``download=True`` downloads the data from the internet if it's not available at ``root``.
- ``transform`` and ``target_transform`` specify the feature and label transformations
```
import torch
from torch.utils.data import Dataset
from torchvision import datasets
from torchvision.transforms import ToTensor
import matplotlib.pyplot as plt
training_data = datasets.FashionMNIST(
root="data",
train=True,
download=True,
transform=ToTensor()
)
test_data = datasets.FashionMNIST(
root="data",
train=False,
download=True,
transform=ToTensor()
)
```
Iterating and Visualizing the Dataset
-----------------
We can index ``Datasets`` manually like a list: ``training_data[index]``.
We use ``matplotlib`` to visualize some samples in our training data.
```
labels_map = {
0: "T-Shirt",
1: "Trouser",
2: "Pullover",
3: "Dress",
4: "Coat",
5: "Sandal",
6: "Shirt",
7: "Sneaker",
8: "Bag",
9: "Ankle Boot",
}
figure = plt.figure(figsize=(8, 8))
cols, rows = 3, 3
for i in range(1, cols * rows + 1):
sample_idx = torch.randint(len(training_data), size=(1,)).item()
img, label = training_data[sample_idx]
figure.add_subplot(rows, cols, i)
plt.title(labels_map[label])
plt.axis("off")
plt.imshow(img.squeeze(), cmap="gray")
plt.show()
type(training_data)
img.shape, label
```
..
.. figure:: /_static/img/basics/fashion_mnist.png
:alt: fashion_mnist
--------------
Creating a Custom Dataset for your files
---------------------------------------------------
A custom Dataset class must implement three functions: `__init__`, `__len__`, and `__getitem__`.
Take a look at this implementation; the FashionMNIST images are stored
in a directory ``img_dir``, and their labels are stored separately in a CSV file ``annotations_file``.
In the next sections, we'll break down what's happening in each of these functions.
```
import os
import pandas as pd
from torchvision.io import read_image
class CustomImageDataset(Dataset):
def __init__(self, annotations_file, img_dir, transform=None, target_transform=None):
self.img_labels = pd.read_csv(annotations_file)
self.img_dir = img_dir
self.transform = transform
self.target_transform = target_transform
def __len__(self):
return len(self.img_labels)
def __getitem__(self, idx):
img_path = os.path.join(self.img_dir, self.img_labels.iloc[idx, 0])
image = read_image(img_path)
label = self.img_labels.iloc[idx, 1]
if self.transform:
image = self.transform(image)
if self.target_transform:
label = self.target_transform(label)
return image, label
```
__init__
^^^^^^^^^^^^^^^^^^^^
The __init__ function is run once when instantiating the Dataset object. We initialize
the directory containing the images, the annotations file, and both transforms (covered
in more detail in the next section).
The labels.csv file looks like: ::
tshirt1.jpg, 0
tshirt2.jpg, 0
......
ankleboot999.jpg, 9
```
def __init__(self, annotations_file, img_dir, transform=None, target_transform=None):
self.img_labels = pd.read_csv(annotations_file)
self.img_dir = img_dir
self.transform = transform
self.target_transform = target_transform
```
__len__
^^^^^^^^^^^^^^^^^^^^
The __len__ function returns the number of samples in our dataset.
Example:
```
def __len__(self):
return len(self.img_labels)
```
__getitem__
^^^^^^^^^^^^^^^^^^^^
The __getitem__ function loads and returns a sample from the dataset at the given index ``idx``.
Based on the index, it identifies the image's location on disk, converts that to a tensor using ``read_image``, retrieves the
corresponding label from the csv data in ``self.img_labels``, calls the transform functions on them (if applicable), and returns the
tensor image and corresponding label in a tuple.
```
def __getitem__(self, idx):
img_path = os.path.join(self.img_dir, self.img_labels.iloc[idx, 0])
image = read_image(img_path)
label = self.img_labels.iloc[idx, 1]
if self.transform:
image = self.transform(image)
if self.target_transform:
label = self.target_transform(label)
return image, label
```
--------------
Preparing your data for training with DataLoaders
-------------------------------------------------
The ``Dataset`` retrieves our dataset's features and labels one sample at a time. While training a model, we typically want to
pass samples in "minibatches", reshuffle the data at every epoch to reduce model overfitting, and use Python's ``multiprocessing`` to
speed up data retrieval.
``DataLoader`` is an iterable that abstracts this complexity for us in an easy API.
```
from torch.utils.data import DataLoader
train_dataloader = DataLoader(training_data, batch_size=64, shuffle=True)
test_dataloader = DataLoader(test_data, batch_size=64, shuffle=True)
```
Iterate through the DataLoader
--------------------------
We have loaded that dataset into the ``Dataloader`` and can iterate through the dataset as needed.
Each iteration below returns a batch of ``train_features`` and ``train_labels`` (containing ``batch_size=64`` features and labels respectively).
Because we specified ``shuffle=True``, after we iterate over all batches the data is shuffled (for finer-grained control over
the data loading order, take a look at `Samplers <https://pytorch.org/docs/stable/data.html#data-loading-order-and-sampler>`_).
```
# Display image and label.
train_features, train_labels = next(iter(train_dataloader))
print(f"Feature batch shape: {train_features.size()}")
print(f"Labels batch shape: {train_labels.size()}")
img = train_features[0].squeeze()
label = train_labels[0]
plt.imshow(img, cmap="gray")
plt.show()
print(f"Label: {label}")
```
--------------
Further Reading
--------------
- `torch.utils.data API <https://pytorch.org/docs/stable/data.html>`_
| true |
code
| 0.665791 | null | null | null | null |
|
# V0.1.6 - System Identification Using Adaptative Filters
Example created by Wilson Rocha Lacerda Junior
## Generating 1 input 1 output sample data
The data is generated by simulating the following model:
$y_k = 0.2y_{k-1} + 0.1y_{k-1}x_{k-1} + 0.9x_{k-1} + e_{k}$
If *colored_noise* is set to True:
$e_{k} = 0.8\nu_{k-1} + \nu_{k}$
where $x$ is a uniformly distributed random variable and $\nu$ is a gaussian distributed variable with $\mu=0$ and $\sigma=0.1$
In the next example we will generate a data with 1000 samples with white noise and selecting 90% of the data to train the model.
```
pip install sysidentpy
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sysidentpy.polynomial_basis import PolynomialNarmax
from sysidentpy.metrics import root_relative_squared_error
from sysidentpy.utils.generate_data import get_miso_data, get_siso_data
from sysidentpy.parameter_estimation import Estimators
x_train, x_valid, y_train, y_valid = get_siso_data(n=1000,
colored_noise=False,
sigma=0.001,
train_percentage=90)
```
One can create a model object and access the Adaptative Filters available in SysIdentPy individually. If you want to build a regressor matrix and estimate the parameters using only the Adaptative Filter method (not applying FROLS + ERR algorithm), follow the steps bellow.
```
model = PolynomialNarmax()
psi = model.build_information_matrix(x_train, y_train, xlag=2, ylag=1, non_degree=2) # creating the regressor matrix
pd.DataFrame(psi).head()
[regressor_code, max_lag] = model.regressor_space(2, 2, 1, 1)
regressor_code # the entire regressor space is our input in this case. But you can define specific subsets to use as an input
model.final_model = regressor_code # defines the model representation
model.psi = psi
```
Here we are using the Affine Least Mean Squares method, but you can use any of the methods available on SysIdentPy
- Least Mean Squares (LMS)
- Affine LMS
- LMS Sign Error
- Normalized LMS
- Normalized LSM Sign Error
- LSM Sign Regressor
- Normalized LMS Sign Regressor
- LMS Sign-Sign
- Normalized LMS Sign-Sign
- Normalized LMS Leaky
- LMS Leaky
- LMS Mixed Norm
- LMS Fourth
Also, you can use:
- Least Squares (LS)
- Total LS
- Recursive LS
## Building the model
```
model.theta = Estimators(mu=0.01).affine_least_mean_squares(model.psi, y_train[1:, 0].reshape(-1, 1))
```
## Simulating the model
```
yhat = model.predict(x_valid, y_valid)
rrse = root_relative_squared_error(y_valid, yhat)
print(rrse)
model.n_terms = 10 # the number of terms we selected (necessary in the 'results' methods)
model.err = model.n_terms*[0] # just to use the `results` method
results = pd.DataFrame(model.results(err_precision=8,
dtype='dec'),
columns=['Regressors', 'Parameters', 'ERR'])
print(results)
ee, ex, extras, lam = model.residuals(x_valid, y_valid, yhat)
model.plot_result(y_valid, yhat, ee, ex)
```
## Final code
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sysidentpy.polynomial_basis import PolynomialNarmax
from sysidentpy.metrics import root_relative_squared_error
from sysidentpy.utils.generate_data import get_miso_data, get_siso_data
from sysidentpy.parameter_estimation import Estimators
x_train, x_valid, y_train, y_valid = get_siso_data(n=1000,
colored_noise=False,
sigma=0.001,
train_percentage=90)
model = PolynomialNarmax()
psi = model.build_information_matrix(x_train, y_train, xlag=2, ylag=1, non_degree=2) # creating the regressor matrix
[regressor_code, max_lag] = model.regressor_space(2, 2, 1, 1)
regressor_code # the entire regressor space is our input in this case. But you can define specific subsets to use as an input
model.final_model = regressor_code # defines the model representation
model.psi = psi
model.theta = Estimators(mu=0.01).affine_least_mean_squares(model.psi, y_train[1:, 0].reshape(-1, 1))
yhat = model.predict(x_valid, y_valid)
rrse = root_relative_squared_error(y_valid, yhat)
print(rrse)
model.n_terms = 10 # the number of terms we selected (necessary in the 'results' methods)
model.err = model.n_terms*[0] # just to use the `results` method
results = pd.DataFrame(model.results(err_precision=8,
dtype='dec'),
columns=['Regressors', 'Parameters', 'ERR'])
print(results)
ee, ex, extras, lam = model.residuals(x_valid, y_valid, yhat)
model.plot_result(y_valid, yhat, ee, ex)
```
| true |
code
| 0.683921 | null | null | null | null |
|
```
%matplotlib inline
import matplotlib.pyplot as plt
from keras.layers import Input, Dense, Convolution2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras import regularizers
import numpy as np
```
### Reference :
* Blog : building autoencoders in keras : https://blog.keras.io/building-autoencoders-in-keras.html
### Load market data from Quandl
```
import quandl # pip install quandl
import pandas as pd
def qData(tick='XLU'):
# GOOG/NYSE_XLU.4
# WIKI/MSFT.4
qtck = "GOOG/NYSE_"+tick+".4"
return quandl.get(qtck,
start_date="2003-01-01",
end_date="2016-12-31",
collapse="daily")
'''TICKERS = ['MSFT','JPM','INTC','DOW','KO',
'MCD','CAT','WMT','MMM','AXP',
'BA','GE','XOM','PG','JNJ']'''
TICKERS = ['XLU','XLF','XLK','XLY','XLV','XLB','XLE','XLP','XLI']
try:
D.keys()
except:
print('create empty Quandl cache')
D = {}
for tckr in TICKERS:
if not(tckr in D.keys()):
print(tckr)
qdt = qData(tckr)
qdt.rename(columns={'Close': tckr}, inplace = True)
D[tckr] = qdt
for tck in D.keys():
assert(D[tck].keys() == [tck])
for tck in D.keys():
print(D[tck].shape)
J = D[TICKERS[0]].join(D[TICKERS[1]])
for tck in TICKERS[2:]:
J = J.join(D[tck])
J.head(5)
J.isnull().sum()
J2 = J.fillna(method='ffill')
#J2[J['WMT'].isnull()]
LogDiffJ = J2.apply(np.log).diff(periods=1, axis=0)
LogDiffJ.drop(LogDiffJ.index[0:1], inplace=True)
print LogDiffJ.shape
MktData = LogDiffJ.as_matrix(columns=None) # as numpy.array
print MktData.shape
np.random.shuffle(MktData)
split_index = 3000
x_train = MktData[0:split_index,:]*100
x_test = MktData[split_index:,:]*100
np.std(x_train, axis=0)
```
## Linear auto-encoder : like PCA
### We get a linear model by removing activation functions
```
original_dim = 9
# this is the size of our encoded representations
encoding_dim = 3
# this is our input placeholder
input_data = Input(shape=(original_dim,))
if True: # no sparsity constraint
encoded = Dense(encoding_dim, activation=None)(input_data)
else:
encoded = Dense(encoding_dim, activation=None,
activity_regularizer=regularizers.activity_l1(10e-5))(input_data)
# "decoded" is the lossy reconstruction of the input
decoded = Dense(original_dim, activation=None)(encoded)
# this model maps an input to its reconstruction
autoencoder = Model(inputs=input_data, outputs=decoded)
# this model maps an input to its encoded representation
encoder = Model(inputs=input_data, outputs=encoded)
# create a placeholder for an encoded (32-dimensional) input
encoded_input = Input(shape=(encoding_dim,))
# retrieve the last layer of the autoencoder model
decoder_layer = autoencoder.layers[-1]
# create the decoder model
decoder = Model(inputs=encoded_input, outputs=decoder_layer(encoded_input))
# train autoencoder to reconstruct Stock returns
# use L2 loss
autoencoder.compile(optimizer='adadelta', loss='mean_squared_error')
autoencoder.fit(x_train, x_train,
epochs=50,
batch_size=128,
shuffle=True,
validation_data=(x_test, x_test))
# encode and decode some digits
# note that we take them from the *test* set
encoded_data = encoder.predict(x_test)
decoded_data = decoder.predict(encoded_data)
for i in range(original_dim):
print i, np.corrcoef(x_test[:,i].T, decoded_data[:,i].T)[0,1]
decoding_error = x_test - decoded_data
for i in range(original_dim):
print i, np.corrcoef(decoded_data[:,i].T, decoding_error[:,i].T)[0,1]
```
| true |
code
| 0.422683 | null | null | null | null |
|
If you're opening this Notebook on colab, you will probably need to install 🤗 Transformers and 🤗 Datasets. Uncomment the following cell and run it.
```
#! pip install datasets transformers[sentencepiece] sacrebleu
```
If you're opening this notebook locally, make sure your environment has an install from the last version of those libraries.
To be able to share your model with the community and generate results like the one shown in the picture below via the inference API, there are a few more steps to follow.
First you have to store your authentication token from the Hugging Face website (sign up [here](https://huggingface.co/join) if you haven't already!) then execute the following cell and input your username and password:
```
from huggingface_hub import notebook_login
notebook_login()
```
Then you need to install Git-LFS. Uncomment the following instructions:
```
# !apt install git-lfs
```
Make sure your version of Transformers is at least 4.11.0 since the functionality was introduced in that version:
```
import transformers
print(transformers.__version__)
```
You can find a script version of this notebook to fine-tune your model in a distributed fashion using multiple GPUs or TPUs [here](https://github.com/huggingface/transformers/tree/master/examples/seq2seq).
# Fine-tuning a model on a translation task
In this notebook, we will see how to fine-tune one of the [🤗 Transformers](https://github.com/huggingface/transformers) model for a translation task. We will use the [WMT dataset](http://www.statmt.org/wmt16/), a machine translation dataset composed from a collection of various sources, including news commentaries and parliament proceedings.

We will see how to easily load the dataset for this task using 🤗 Datasets and how to fine-tune a model on it using the `Trainer` API.
```
model_checkpoint = "Helsinki-NLP/opus-mt-en-ro"
```
This notebook is built to run with any model checkpoint from the [Model Hub](https://huggingface.co/models) as long as that model has a sequence-to-sequence version in the Transformers library. Here we picked the [`Helsinki-NLP/opus-mt-en-ro`](https://huggingface.co/Helsinki-NLP/opus-mt-en-ro) checkpoint.
## Loading the dataset
We will use the [🤗 Datasets](https://github.com/huggingface/datasets) library to download the data and get the metric we need to use for evaluation (to compare our model to the benchmark). This can be easily done with the functions `load_dataset` and `load_metric`. We use the English/Romanian part of the WMT dataset here.
```
from datasets import load_dataset, load_metric
raw_datasets = load_dataset("wmt16", "ro-en")
metric = load_metric("sacrebleu")
```
The `dataset` object itself is [`DatasetDict`](https://huggingface.co/docs/datasets/package_reference/main_classes.html#datasetdict), which contains one key for the training, validation and test set:
```
raw_datasets
```
To access an actual element, you need to select a split first, then give an index:
```
raw_datasets["train"][0]
```
To get a sense of what the data looks like, the following function will show some examples picked randomly in the dataset.
```
import datasets
import random
import pandas as pd
from IPython.display import display, HTML
def show_random_elements(dataset, num_examples=5):
assert num_examples <= len(dataset), "Can't pick more elements than there are in the dataset."
picks = []
for _ in range(num_examples):
pick = random.randint(0, len(dataset)-1)
while pick in picks:
pick = random.randint(0, len(dataset)-1)
picks.append(pick)
df = pd.DataFrame(dataset[picks])
for column, typ in dataset.features.items():
if isinstance(typ, datasets.ClassLabel):
df[column] = df[column].transform(lambda i: typ.names[i])
display(HTML(df.to_html()))
show_random_elements(raw_datasets["train"])
```
The metric is an instance of [`datasets.Metric`](https://huggingface.co/docs/datasets/package_reference/main_classes.html#datasets.Metric):
```
metric
```
You can call its `compute` method with your predictions and labels, which need to be list of decoded strings (list of list for the labels):
```
fake_preds = ["hello there", "general kenobi"]
fake_labels = [["hello there"], ["general kenobi"]]
metric.compute(predictions=fake_preds, references=fake_labels)
```
## Preprocessing the data
Before we can feed those texts to our model, we need to preprocess them. This is done by a 🤗 Transformers `Tokenizer` which will (as the name indicates) tokenize the inputs (including converting the tokens to their corresponding IDs in the pretrained vocabulary) and put it in a format the model expects, as well as generate the other inputs that model requires.
To do all of this, we instantiate our tokenizer with the `AutoTokenizer.from_pretrained` method, which will ensure:
- we get a tokenizer that corresponds to the model architecture we want to use,
- we download the vocabulary used when pretraining this specific checkpoint.
That vocabulary will be cached, so it's not downloaded again the next time we run the cell.
```
from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained(model_checkpoint)
```
For the mBART tokenizer (like we have here), we need to set the source and target languages (so the texts are preprocessed properly). You can check the language codes [here](https://huggingface.co/facebook/mbart-large-cc25) if you are using this notebook on a different pairs of languages.
```
if "mbart" in model_checkpoint:
tokenizer.src_lang = "en-XX"
tokenizer.tgt_lang = "ro-RO"
```
By default, the call above will use one of the fast tokenizers (backed by Rust) from the 🤗 Tokenizers library.
You can directly call this tokenizer on one sentence or a pair of sentences:
```
tokenizer("Hello, this one sentence!")
```
Depending on the model you selected, you will see different keys in the dictionary returned by the cell above. They don't matter much for what we're doing here (just know they are required by the model we will instantiate later), you can learn more about them in [this tutorial](https://huggingface.co/transformers/preprocessing.html) if you're interested.
Instead of one sentence, we can pass along a list of sentences:
```
tokenizer(["Hello, this one sentence!", "This is another sentence."])
```
To prepare the targets for our model, we need to tokenize them inside the `as_target_tokenizer` context manager. This will make sure the tokenizer uses the special tokens corresponding to the targets:
```
with tokenizer.as_target_tokenizer():
print(tokenizer(["Hello, this one sentence!", "This is another sentence."]))
```
If you are using one of the five T5 checkpoints that require a special prefix to put before the inputs, you should adapt the following cell.
```
if model_checkpoint in ["t5-small", "t5-base", "t5-larg", "t5-3b", "t5-11b"]:
prefix = "translate English to Romanian: "
else:
prefix = ""
```
We can then write the function that will preprocess our samples. We just feed them to the `tokenizer` with the argument `truncation=True`. This will ensure that an input longer that what the model selected can handle will be truncated to the maximum length accepted by the model. The padding will be dealt with later on (in a data collator) so we pad examples to the longest length in the batch and not the whole dataset.
```
max_input_length = 128
max_target_length = 128
source_lang = "en"
target_lang = "ro"
def preprocess_function(examples):
inputs = [prefix + ex[source_lang] for ex in examples["translation"]]
targets = [ex[target_lang] for ex in examples["translation"]]
model_inputs = tokenizer(inputs, max_length=max_input_length, truncation=True)
# Setup the tokenizer for targets
with tokenizer.as_target_tokenizer():
labels = tokenizer(targets, max_length=max_target_length, truncation=True)
model_inputs["labels"] = labels["input_ids"]
return model_inputs
```
This function works with one or several examples. In the case of several examples, the tokenizer will return a list of lists for each key:
```
preprocess_function(raw_datasets['train'][:2])
```
To apply this function on all the pairs of sentences in our dataset, we just use the `map` method of our `dataset` object we created earlier. This will apply the function on all the elements of all the splits in `dataset`, so our training, validation and testing data will be preprocessed in one single command.
```
tokenized_datasets = raw_datasets.map(preprocess_function, batched=True)
```
Even better, the results are automatically cached by the 🤗 Datasets library to avoid spending time on this step the next time you run your notebook. The 🤗 Datasets library is normally smart enough to detect when the function you pass to map has changed (and thus requires to not use the cache data). For instance, it will properly detect if you change the task in the first cell and rerun the notebook. 🤗 Datasets warns you when it uses cached files, you can pass `load_from_cache_file=False` in the call to `map` to not use the cached files and force the preprocessing to be applied again.
Note that we passed `batched=True` to encode the texts by batches together. This is to leverage the full benefit of the fast tokenizer we loaded earlier, which will use multi-threading to treat the texts in a batch concurrently.
## Fine-tuning the model
Now that our data is ready, we can download the pretrained model and fine-tune it. Since our task is of the sequence-to-sequence kind, we use the `AutoModelForSeq2SeqLM` class. Like with the tokenizer, the `from_pretrained` method will download and cache the model for us.
```
from transformers import AutoModelForSeq2SeqLM, DataCollatorForSeq2Seq, Seq2SeqTrainingArguments, Seq2SeqTrainer
model = AutoModelForSeq2SeqLM.from_pretrained(model_checkpoint)
```
Note that we don't get a warning like in our classification example. This means we used all the weights of the pretrained model and there is no randomly initialized head in this case.
To instantiate a `Seq2SeqTrainer`, we will need to define three more things. The most important is the [`Seq2SeqTrainingArguments`](https://huggingface.co/transformers/main_classes/trainer.html#transformers.Seq2SeqTrainingArguments), which is a class that contains all the attributes to customize the training. It requires one folder name, which will be used to save the checkpoints of the model, and all other arguments are optional:
```
batch_size = 16
model_name = model_checkpoint.split("/")[-1]
args = Seq2SeqTrainingArguments(
f"{model_name}-finetuned-{source_lang}-to-{target_lang}",
evaluation_strategy = "epoch",
learning_rate=2e-5,
per_device_train_batch_size=batch_size,
per_device_eval_batch_size=batch_size,
weight_decay=0.01,
save_total_limit=3,
num_train_epochs=1,
predict_with_generate=True,
fp16=True,
push_to_hub=True,
)
```
Here we set the evaluation to be done at the end of each epoch, tweak the learning rate, use the `batch_size` defined at the top of the cell and customize the weight decay. Since the `Seq2SeqTrainer` will save the model regularly and our dataset is quite large, we tell it to make three saves maximum. Lastly, we use the `predict_with_generate` option (to properly generate summaries) and activate mixed precision training (to go a bit faster).
The last argument to setup everything so we can push the model to the [Hub](https://huggingface.co/models) regularly during training. Remove it if you didn't follow the installation steps at the top of the notebook. If you want to save your model locally in a name that is different than the name of the repository it will be pushed, or if you want to push your model under an organization and not your name space, use the `hub_model_id` argument to set the repo name (it needs to be the full name, including your namespace: for instance `"sgugger/marian-finetuned-en-to-ro"` or `"huggingface/marian-finetuned-en-to-ro"`).
Then, we need a special kind of data collator, which will not only pad the inputs to the maximum length in the batch, but also the labels:
```
data_collator = DataCollatorForSeq2Seq(tokenizer, model=model)
```
The last thing to define for our `Seq2SeqTrainer` is how to compute the metrics from the predictions. We need to define a function for this, which will just use the `metric` we loaded earlier, and we have to do a bit of pre-processing to decode the predictions into texts:
```
import numpy as np
def postprocess_text(preds, labels):
preds = [pred.strip() for pred in preds]
labels = [[label.strip()] for label in labels]
return preds, labels
def compute_metrics(eval_preds):
preds, labels = eval_preds
if isinstance(preds, tuple):
preds = preds[0]
decoded_preds = tokenizer.batch_decode(preds, skip_special_tokens=True)
# Replace -100 in the labels as we can't decode them.
labels = np.where(labels != -100, labels, tokenizer.pad_token_id)
decoded_labels = tokenizer.batch_decode(labels, skip_special_tokens=True)
# Some simple post-processing
decoded_preds, decoded_labels = postprocess_text(decoded_preds, decoded_labels)
result = metric.compute(predictions=decoded_preds, references=decoded_labels)
result = {"bleu": result["score"]}
prediction_lens = [np.count_nonzero(pred != tokenizer.pad_token_id) for pred in preds]
result["gen_len"] = np.mean(prediction_lens)
result = {k: round(v, 4) for k, v in result.items()}
return result
```
Then we just need to pass all of this along with our datasets to the `Seq2SeqTrainer`:
```
trainer = Seq2SeqTrainer(
model,
args,
train_dataset=tokenized_datasets["train"],
eval_dataset=tokenized_datasets["validation"],
data_collator=data_collator,
tokenizer=tokenizer,
compute_metrics=compute_metrics
)
```
We can now finetune our model by just calling the `train` method:
```
trainer.train()
```
You can now upload the result of the training to the Hub, just execute this instruction:
```
trainer.push_to_hub()
```
You can now share this model with all your friends, family, favorite pets: they can all load it with the identifier `"your-username/the-name-you-picked"` so for instance:
```python
from transformers import AutoModelForSeq2SeqLM
model = AutoModelForSeq2SeqLM.from_pretrained("sgugger/my-awesome-model")
```
| true |
code
| 0.59355 | null | null | null | null |
|
**Loading Data and creating benchmark model**
```
# Defining the path to the Github repository
file_url = 'https://raw.githubusercontent.com/PacktWorkshops/The-Data-Science-Workshop/master/Chapter17/Datasets/bank-full.csv'
# Loading data using pandas
import pandas as pd
bankData = pd.read_csv(file_url,sep=";")
bankData.head()
# Removing the target variable
Y = bankData.pop('y')
from sklearn.model_selection import train_test_split
# Splitting the data into train and test sets
X_train, X_test, y_train, y_test = train_test_split(bankData, Y, test_size=0.3, random_state=123)
# Using pipeline to transform categorical variable and numeric variables
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, OneHotEncoder
categorical_transformer = Pipeline(steps=[('onehot', OneHotEncoder(handle_unknown='ignore'))])
numeric_transformer = Pipeline(steps=[('scaler', StandardScaler())])
# Defining data types for numeric and categorical features
numeric_features = bankData.select_dtypes(include=['int64', 'float64']).columns
categorical_features = bankData.select_dtypes(include=['object']).columns
# Defining preprocessor
from sklearn.compose import ColumnTransformer
preprocessor = ColumnTransformer(
transformers=[
('num', numeric_transformer, numeric_features),
('cat', categorical_transformer, categorical_features)])
# Defining the estimator for processing and classification
from sklearn.linear_model import LogisticRegression
estimator = Pipeline(steps=[('preprocessor', preprocessor),
('classifier',LogisticRegression(random_state=123))])
# Fit the estimator on the training set
estimator.fit(X_train, y_train)
print("model score: %.2f" % estimator.score(X_test, y_test))
# Predict on the test set
pred = estimator.predict(X_test)
# Generating classification report
from sklearn.metrics import classification_report
print(classification_report(pred,y_test))
```
**Establishing entities and relationship**
```
# Creating the Ids for Demographic Entity
bankData['custID'] = bankData.index.values
bankData['custID'] = 'cust' + bankData['custID'].astype(str)
# Creating AssetId
bankData['AssetId'] = 0
bankData.loc[bankData.housing == 'yes','AssetId']= 1
# Creating LoanId
bankData['LoanId'] = 0
bankData.loc[bankData.loan == 'yes','LoanId']= 1
# Creating Financial behaviour ID
bankData['FinbehId'] = 0
bankData.loc[bankData.default == 'yes','FinbehId']= 1
# Importing necessary libraries
import featuretools as ft
import numpy as np
# creating the entity set 'Bankentities'
Bankentities = ft.EntitySet(id = 'Bank')
# Mapping a dataframe to the entityset to form the parent entity
Bankentities.entity_from_dataframe(entity_id = 'Demographic Data', dataframe = bankData, index = 'custID')
# Mapping to parent entity and setting the relationship
Bankentities.normalize_entity(base_entity_id='Demographic Data', new_entity_id='Assets', index = 'AssetId',
additional_variables = ['housing'])
Bankentities.normalize_entity(base_entity_id='Demographic Data', new_entity_id='Liability', index = 'LoanId',
additional_variables = ['loan'])
Bankentities.normalize_entity(base_entity_id='Demographic Data', new_entity_id='FinBehaviour', index = 'FinbehId',
additional_variables = ['default'])
```
**Feature Engineering**
```
# Creating aggregation and transformation primitives
aggPrimitives=[
'std', 'min', 'max', 'mean',
'last', 'count'
]
tranPrimitives=[
'percentile',
'subtract', 'divide']
# Defining the new set of features
feature_set, feature_names = ft.dfs(entityset=Bankentities,
target_entity = 'Demographic Data',
agg_primitives=aggPrimitives,
trans_primitives=tranPrimitives,
max_depth = 2,
verbose = 1,
n_jobs = 1)
# Reindexing the feature_set
feature_set = feature_set.reindex(index=bankData['custID'])
feature_set = feature_set.reset_index()
# Displaying the feature set
feature_set.shape
```
**Cleaning na values and infinity values**
```
# Dropping all Ids
X = feature_set[feature_set.columns[~feature_set.columns.str.contains(
'custID|AssetId|LoanId|FinbehId')]]
# Replacing all columns with infinity with nan
X = X.replace([np.inf, -np.inf], np.nan)
# Dropping all columns with nan
X = X.dropna(axis=1, how='any')
X.shape
```
**Modelling phase**
```
# Splitting train and test sets
from sklearn.model_selection import train_test_split
# Splitting the data into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=123)
# Creating the preprocessing pipeline
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, OneHotEncoder
categorical_transformer = Pipeline(steps=[('onehot', OneHotEncoder(handle_unknown='ignore'))])
numeric_transformer = Pipeline(steps=[('scaler', StandardScaler())])
numeric_features = X.select_dtypes(include=['int64', 'float64']).columns
categorical_features = X.select_dtypes(include=['object']).columns
from sklearn.compose import ColumnTransformer
preprocessor = ColumnTransformer(
transformers=[
('num', numeric_transformer, numeric_features),
('cat', categorical_transformer, categorical_features)])
# Creating the estimator function and fitting the training set
estimator = Pipeline(steps=[('preprocessor', preprocessor),
('classifier',LogisticRegression(random_state=123))])
estimator.fit(X_train, y_train)
print("model score: %.2f" % estimator.score(X_test, y_test))
# Predicting on the test set
pred = estimator.predict(X_test)
# Generating the classification report
from sklearn.metrics import classification_report
print(classification_report(pred,y_test))
```
| true |
code
| 0.628778 | null | null | null | null |
|
```
import cvxopt
import numpy as np
import matplotlib.pyplot as plt
import sys
sys.path.append('../../pyutils')
import metrics
```
# Introduction
The predictor $G(X)$ takes values in a discrete set $\mathbb{G}$. The input space is divided into a collection regions labeled according to their clasification.
The boundaries of these regions are called decisions boundaries, and they are linear for linear methods
## Example 1
Example of $K$ classes with discriminant function:
$$\delta_k(x) = \beta_{k0} + \beta_k^Tx$$
The assigned class is the one with the biggest value for $\delta_k$.
The decision boundary between class $k$ and $l$ is the set of points for wich $\delta_k(x) = \delta_l(x)$.
That is the hyperplane defined by $\{x: (\beta_{k0} - \beta_{l0}) + (\beta_k - \beta_l)^Tx = 0 \}$.
Methods that model the posterior probabilities $P(G = k | X = x)$ are also in this class.
If $\delta_k(x)$ or $P(G = k | X = x)$ is linear in $x$, then the decision boundaries will be linear.
## Example 2
Example of 2 classes with posterior probabilities:
$$P(G = 1 | X = x) = \frac{\exp(\beta_0 + \beta^Tx)}{1 + \exp(\beta_0 + \beta^Tx)}$$
$$P(G = 2 | X = x) = \frac{1}{1 + \exp(\beta_0 + \beta^Tx)}$$
The decision boundary is the set of points for which the log-odds are zero:
$$\log(\frac{p}{1-p}) = 0$$
$$\log \frac{P(G = 1 | X = x)}{P(G = 2 | X = x)} = \beta_0 + \beta^Tx$$
Thus the decision boundary is an hyperplane defined by $\{x | \beta_0 + \beta^Tx = 0\}$.
Linear logistic regression and linear discriminant analysis have linear log-odds.
Another solution is to explicitely model linear boundaries between the classes.
# Linear Regression of an Indicator Matrix
The output is a vector $y \in \mathbb{R}^{K}$, with $K$ the number of classes.
If the example belong to classs $k$, $y_j = 1_{j=k}$.
For a training set of size $N$, the output matrix is $Y \in \mathbb{R}^{N*K}$.
The parameters are fitted using any multiple outputs linear classification methods for $X$ and $Y$, eg normal equations:
$$\hat{B} = (X^TX)^{-1} X^TY$$.
Classify an example:
$$\hat{y} = x^T \hat{B}$$
$$\hat{G}(x) = \arg \max_{k \in \mathbb{G}} \hat{y}_k$$
Regression gives an expectation of conditional expectation.
$$y_k = \mathbb{E}(y_k | X = x) = P(G = k | X = x)$$
```
def gen_toy_class(N, noise=0.001):
X = 2.8 * np.random.randn(N, 4)**1 + 4.67
v1 = 1.5*X[:, 0] + 2.3*X[:, 1] - 0.3*X[:, 2] + 4.5 + noise*np.random.randn(len(X))
v2 = 1.7*X[:, 0] + 0.4*X[:, 1] + 2.3*X[:, 2] - 3.7 + noise*np.random.randn(len(X))
v3 = -0.6*X[:, 0] + 5.8*X[:, 1] - 1.3*X[:, 2] + 0.1 + noise*np.random.randn(len(X))
V = np.vstack((v1, v2, v3)).T
g = np.argmax(V, axis=1)
return X, g
def label2onehot(g, nclasses):
Y = np.zeros((len(g), nclasses))
Y[np.arange(len(g)), g] = 1
return Y
def onehot2labels(Y):
return np.argmax(Y, axis=1)
def add_col1(X):
return np.append(np.ones((len(X),1)), X, axis=1)
#Example with 3 classes
X, g = gen_toy_class(117, noise=1e-3)
Y = label2onehot(g, 3)
X2 = add_col1(X)
B = np.linalg.inv(X2.T @ X2) @ X2.T @ Y
Y_preds = X2 @ B
preds = onehot2labels(Y_preds)
print('error:', np.mean((Y - Y_preds)**2))
print('acc:', np.mean(g == preds))
def gen_toy_bin(N, noise=0.001):
X = 2.8 * np.random.randn(100000, 4)**2 + 4.67
v = 1.5*X[:, 0] + 2.3*X[:, 1] - 4.7*X[:, 2] + 4.5 + noise*np.random.randn(len(X))
m = v.mean()
X = X[:N]
g = (v[:N] > m).astype(np.int)
return X, g
#Binary example
X, g = gen_toy_bin(117000, noise=0)
Y = label2onehot(g, 2)
X2 = add_col1(X)
B = np.linalg.inv(X2.T @ X2) @ X2.T @ Y
Y_preds = X2 @ B
preds = onehot2labels(Y_preds)
print('error:', np.mean((Y - Y_preds)**2))
print('acc:', np.mean(g == preds))
```
$y_k$ doesn't belong like a probability. Even though $\sum_{k \in \mathbb{G}} y_k = 1$, $y_k$ might be negative or greater than $1$.
Another approch is to construct a target $t_k$ for each class, with $t_k$ $k$-th columns of $I_K$.
Obervations are $y_i = t_k$ if $g_i = k$.
We fit the least-squares criterion:
$$\hat{B} = \arg \min_{B} \sum_{i=1}^N ||y_i - x_i^TB||^2$$
Classify an example:
$$\hat{G}(x) = \arg \min_{k} ||x_i^T\hat{B} - t_k||^2$$
Actually, this model yields exactly the same results than the previous ones.
This model doesn't work well when $K \geq 3$. Because of the rigid nature of regression, classes can be masked by others.
A general rule is that with $K \geq 3$ classes, polynomials terms up to degree $K - 1$ might be needed to solve them.
Masking usually occurs for large $K$ and small $p$.
Other methods like logistic regression and linear distriminant analysis doesn't suffer from masking
# Linear Discriminant Analysis
According to Bayes theorem:
$$P(G = k | X = x) = \frac{P(X = x | G = k) P(G = k)}{P(X)}$$
$$P(G = k | X = x) = \frac{P(X = x | G = k) P(G = k)}{\sum_{l=1}^K P(X = x | G = l) P(G = l)}$$
Let $\pi_k$ the prior probability of class $k$: $\pi_k = P(G = k)$.
Let $f_k(x)$ the class-condisional density of $X$ in class $G = k$: $P(X \in T | G = k) = \int_T f_k(x)dx$.
Thus, the posterior probability is:
$$P(G = k | X = x) = \frac{f_k(x) \pi_k}{\sum_{l=1}^K f_l(x) \pi_l}$$
Each density class is represented as a multivariate Gaussian:
$$f_k(x) = \frac{\exp(-\frac{1}{2} (x-\mu_k)^T \Sigma^{-1} (x - \mu_k) )}{\sqrt{(2\pi)^p |\Sigma|}}$$
with:
- $\Sigma \in \mathbb{R}^{p*p}$ covariance matrix shared by all class densities.
- $\mu_k \in \mathbb{R}^p$ the mean vector for class density $k$.
- $|\Sigma| = \det(\Sigma)$
$$\log \frac{P(G = k | X = x)}{P(G = l | X = x)} = \log \frac{\pi_k}{\pi_l} - \frac{1}{2}(\mu_k + \mu_l)^T\Sigma^{-1}(\mu_k - \mu_l) + x^T \Sigma^{-1}(\mu_k - \mu_l)$$.
The log-odds function is linear in $x$, so the decision boundaries are linear.
The decision rule can be described with linear descriminant functions:
$$\delta_k(x) = x^T \Sigma^{-1} \mu_k - \frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k + \log \pi_k$$
$$G(x) = \arg \max_k \delta_k(x)$$
The parameters are estimated from the training data:
$$\hat{\pi}_k = \frac{N_k}{N}$$
$$\hat{\mu}_k = \frac{\sum_{g_i = k} x_i}{N_k}$$
$$\hat{\Sigma} = \frac{\sum_{k=1}^K \sum_{g_i = k} (x_i - \mu_k)(x_i - \mu_k)^T}{N - K}$$
```
#Example with 3 classes
def lda(X, g, K):
N = X.shape[0]
p = X.shape[1]
pis = []
mus = []
cov = np.zeros((p, p))
for k in range(K):
nk = np.sum(g == k)
pi = nk / N
mu = np.zeros((p,))
for i in range(N):
if g[i] == k:
mu += X[i]
mu /= nk
pis.append(pi)
mus.append(mu)
for i in range(N):
cov += np.outer(X[i] - mus[g[i]], X[i] - mus[g[i]])
cov /= (N - K)
icov = np.linalg.inv(cov)
B = np.empty((p, K))
intercept = np.empty((K,))
for k in range(K):
B[:, k] = icov @ mus[k]
intercept[k] = - 1/2 * (mus[k] @ icov @ mus[k]) + np.log(pis[k])
return B, intercept
X, g = gen_toy_class(11700, noise=1e-5)
B, intercept = lda(X, g, 3)
Y_preds = X @ B + intercept
preds = np.argmax(Y_preds, axis=1)
print('acc:', np.mean(g == preds))
```
## Quadratic Discriminant Analysis
If each $f_k(x)$ as it's own covariance marix $\Sigma_k$, the logs-odd function and the distriminant functions became quadratic:
$$\delta_l(x) = - \frac{1}{2} \log | \Sigma_k| - \frac{1}{2} (x - \mu_k)^T \Sigma_k^{-1} (x - \mu_k) + \log \pi_k$$
When $p$ large, QDA causes a dramatic increase in the number of parameters.
There is little difference between LDA applied to dataset augmented with polynomials of degree $2$, and QDA.
For QDA, the estimates of $\pi_k$ and $u_k$ stays the same, and the estimate of $\Sigma_k$ is:
$$\hat{\Sigma}_k = \frac{\sum_{g_i = k} (x_i - \mu_k)(x_i - \mu_k)^T}{N_k - 1}$$
```
#Example with 3 classes
def qda(X, g, K):
N = X.shape[0]
p = X.shape[1]
pis = []
mus = []
dcovs = []
icovs = []
for k in range(K):
nk = np.sum(g == k)
pi = nk / N
mu = np.zeros((p,))
for i in range(N):
if g[i] == k:
mu += X[i]
mu /= nk
cov = np.zeros((p, p))
for i in range(N):
if g[i] == k:
cov += np.outer(X[i] - mu, X[i] - mu)
cov /= (nk - 1)
pis.append(pi)
mus.append(mu)
dcovs.append(-1/2 * np.log(np.linalg.det(cov)))
icovs.append(np.linalg.inv(cov))
return pis, mus, dcovs, icovs
def qda_pred(x, pis, mus, dcovs, icovs):
K = len(pis)
y = np.empty((K,))
for k in range(K):
qt = -1/2 * (x - mus[k]) @ icovs[k] @ (x - mus[k])
y[k] = dcovs[k] + qt + np.log(pis[k])
return np.argmax(y)
X, g = gen_toy_class(11700, noise=1e-5)
pis, mus, dcovs, icovs = qda(X, g, 3)
preds = np.empty((len(X),))
for i in range(len(X)):
preds[i] = qda_pred(X[i], pis, mus, dcovs, icovs)
print('acc:', np.mean(g == preds))
```
## Regularized Discriminant Analysis
RDA is a oompromise between LDA and QDA, allowing to shrink the separate covariances of QDA toward a common covariance as in LDA.
$$\hat{\Sigma}_k(\alpha) = \alpha \hat{\Sigma}_k + (1 - \alpha) \hat{\Sigma}$$
with $\alpha$ hyperparameter that allows a continuum of models between LDA and QDA.
Another modificatio allows $\hat{\Sigma}$ to be shunk toward a scalar covariance:
$$\hat{\Sigma}(\gamma) = \gamma \hat{\Sigma} + (1 - \gamma) \hat{\sigma}^2I$$
## Computations for LDA
Computations can be simplified by diagonalization of $\Sigma$.
For QDA:
$$\hat{\Sigma}_k = U_k D_k U^T_k$$
$$(x - \hat{\mu}_k)^T\Sigma^{-1}_k (x - \hat{\mu}_k) = [U_k^T(x - \hat{\mu}_k)]^T D^{-1}_k [U_k^T(x - \hat{\mu}_k)]$$
$$log |\Sigma_k| = \sum_l log d_{kl}$$
For LDA, we can project the data into a space where the common covariance estimate is $I$:
$$\hat{\Sigma} = UDU^T$$
$$X^* \leftarrow X D^{-\frac{1}{2}}U^T$$
## Reduced-Rank LDA
The $K$ centroids in $p$-dimensional input space lie in an affine subspace of dimension $\leq K - 1$. We might just as well project $X*$ onto this centroid-spanning subpace $H_{K-1}$.
We can also project $X*$ into a subspace $H_L$ for $L \leq K$, where the projected centroids were spread out as much as possible in terms of variance.
### Algorithm
- Compute matrix of class centroids $M \in \mathbb{R}^{K*p}$
$$M_k = \frac{1}{N_k} \sum_{g_i = k} x_i$$
- Compute within class covariance matrix $W \in \mathbb{R}^{p*p}$
$$W = \sum_{k=1}^K \sum_{g_i = k} (x_i - M_k) (x_i - M_k)^T$$
- Compute $M^* = MW^{-\frac{1}{2}}$, $M^* \in \mathbb{R}^{K*p}$
$$P_W^T W P_W = D_W$$
$$W^{-\frac{1}{2}} = P_W D^{-\frac{1}{2}}P_W^T$$
- Compute between class covariance matrix $B^*$ of $M^*$, $B^* \in \mathbb{R}^{p*p}$
$$\mu = \frac{1}{K} \sum_{k=1}^K M_k^*$$
$$B^* = \sum_{k=1}^K N_k (M^*_k - \mu) (M^*_k - \mu)^T$$
- Diagionalize $B^*$: $B^* = V^* D_B V^{*T}$
- Project the data:
$$v_l = W^{-\frac{1}{2}}v_l^*, \space v_l^* \in \mathbb{R}^p$$
$$z_l = Xv_l, \space z_l \in \mathbb{R}^n$$
### Fisher Method
This is a different method, that gives the same results.
Fisher LDA looks for a projection $Z = a^TX$ such that the between-class variance is maximized relative to the within-class variance.
Let $B$ and $W$ respectively the between-class and the within-class variance of $X$. Note than $T = B + W$ with $T$ the covariance matrix of $X$, ignoring class information.
The between-class and within-class variance of $Z$ are respectively $a^TBa$ and $a^TWa$.
The objective is:
$$\max_a \frac{a^TBa}{a^TWa}$$
$a$ is the eigeinvector corresponding to the largest eigeinvalue of $W^{-1}B$
### Algorithm
- Compute matrix of class centroids $M \in \mathbb{R}^{K*p}$
$$M_k = \frac{1}{N_k} \sum_{g_i = k} x_i$$
- Compute within class covariance matrix $W \in \mathbb{R}^{p*p}$
$$W = \sum_{k=1}^K \sum_{g_i = k} (x_i - M_k) (x_i - M_k)^T$$
- Compute between class covariance matrix $B \in \mathbb{R}^{p*p}$
$$\mu = \frac{1}{K} \sum_{k=1}^K M_k$$
$$B = \sum_{k=1}^K N_k (M_k - \mu) (M_k - \mu)^T$$
- Diagionalize $W^{-1}B$:
$$W^{-1}B = V D V^T$$
- Project the data:
$$z_l = Xv_l, \space z_l \in \mathbb{R}^N$$
$$Z = XV_L, \space Z \in \mathbb{R}^{N*L}$$
with $V_L$ columns the $L$ eigenvectors corresponding to the largest eigeinvalues of $W^{-1}B$
```
N = 11700
K = 3
X, g = gen_toy_class(N, noise=1e-5)
p = X.shape[1]
#1) Compute class centroids M
M = np.zeros((K, p))
for k in range(K):
nk = np.sum(g == k)
for i in range(N):
if g[i] == k:
M[k] += X[i]
M[k] /= nk
#2) Compute within-class covariance W
W = np.zeros((p, p))
for i in range(N):
W += np.outer(X[i] - M[g[i]], X[i] - M[g[i]])
#3) Compute between class covariance B
mu = np.mean(M, axis=0)
B = np.zeros((p, p))
for k in range(K):
nk = np.sum(g == k)
B += nk * np.outer(M[k] - mu, M[k] - mu)
#4) Diagonalize W^-1B
d, V = np.linalg.eig(np.linalg.inv(W) @ B)
#5) Project the data
Vr = V[:, :2]
Z = X @ Vr
#6) Make predictions
MZ = M @ Vr
preds = np.empty((N,)).astype(np.int)
for i in range(N):
min_k = None
min_dist = float('inf')
for k in range(K):
d = (Z[i] - MZ[k]) @ (Z[i] - MZ[k])
if d < min_dist:
min_k = k
min_dist = d
preds[i] = min_k
print('acc:', np.mean(g == preds))
```
# Logistic Regression
The model is defined by the log-odds of the posterior probabilities.
$$\log \frac{P(G = k | X = x)}{P(G = K | X = x)} = \beta_{k0} + \beta_{k}^T x, \space k=1\text{...}K-1$$
It can be deduced that:
$$P(G = k | X = x) = \frac{\exp (\beta_{k0} + \beta_{k}^T x)}{1 + \sum_{l=1}^{K-1} \exp (\beta_{l0} + \beta_{l}^T x)}, \space k=1\text{...}K-1$$
$$P(G = K | X = x) = \frac{1}{1 + \sum_{l=1}^{K-1} \exp (\beta_{l0} + \beta_{l}^T x)}$$
The log-likelihood for $N$ observations is:
$$l(\theta) = \sum_{i=1}^N \log P(G=g_i | X = x_i; \theta)$$
Let's focus on the cases with $K = 2$, with a response $y_i$ with $y_i = 1$ when $g_i = 1$ and $y_1 = 0$ when $g_i = 2$
$$l(\beta) = \sum_{i=1}^N y_i \log p(x_i) + (1 - y_i) \log(1 - p(x_i))$$
$$\text{with } p(x_i) = P(G=1|X=x) = \frac{\exp(\beta^Tx)}{1 + \exp(\beta^Tx)}$$
$$l(\beta) = \sum_{i=1}^N y_i \beta^Tx_i - \log(1 + \exp(\beta^Tx_i))$$
In order to maximize the log-likelihood, we solve:
$$\frac{\partial l(\beta)}{\partial \beta} = 0$$
$$\frac{\partial l(\beta)}{\partial \beta} = \sum_{i=1}^N x_i(y_i - p(x_i))$$
This can be solved using the Newton-Raphson algorithm, with second-derivates:
$$\frac{\partial^2 l(\beta)}{\partial \beta \partial \beta^T} = - \sum_{i=1}^N x_ix_i^T p(x_i)(1-p(x_i))$$
The update is:
$$\beta \leftarrow \beta - (\frac{\partial^2 l(\beta)}{\partial \beta \partial \beta^T})^{-1} \frac{\partial l(\beta)}{\partial \beta}$$
It can be rewritten in matrix form as:
$$\frac{\partial l(\beta)}{\partial \beta} = X^T(y-p)$$
$$\frac{\partial^2 l(\beta)}{\partial \beta \partial \beta^T} = - X^TWX$$
with:
- $X \in \mathbb{R}^{N * p}$ the matrix of features
- $p \in \mathbb{R}^N$ the vector of predictions
- $y \in \mathbb{R}^N$ the vector of labels
- $W \in \mathbb{R}^{N*N}$ diagonal matrix: $W_{ii} = p_i(1-p_i)$
The update became
$$\beta \leftarrow \beta + (X^TWX)^{-1}X^T (y - p)$$
$$\beta \leftarrow (X^TWX)^{-1}X^T Wz$$
$$\text{with } z = X \beta + W^{-1} (y-p)$$
So the update is equivalent to solving a weigthed least square problem with output $z$:
$$\beta \leftarrow \arg \min_\beta (z - X\beta)^TW(z - X\beta)$$
```
X, y = gen_toy_bin(117, noise=1e-5)
def logreg(X, y):
n = X.shape[0]
p = X.shape[1]
#works a lot better when init at 0
beta = np.zeros((p,))
#beta = np.random.randn(p)
for i in range(5):
p = np.exp(X @ beta) / (1 + np.exp(X @ beta))
l = np.sum(y * np.log(p) + (1 - y) * np.log(1 - p))
W = np.diag(p * (1-p))
#IRLS update
z = X @ beta + np.linalg.inv(W) @ (y - p)
beta = np.linalg.inv(X.T @ W @ X) @ X.T @ W @ z
'''
#newton update
g = X.T @ (y - p)
H = - X.T @ W @ X
beta = beta - np.linalg.inv(H) @ g
'''
print('loss:', l)
return beta
Xc = np.mean(X, axis=0, keepdims=True)
Xs = np.std(X, axis=0, keepdims=True)
X2 = (X - Xc) / Xs
beta = logreg(X2, y)
y_hat = np.exp(X2 @ beta) / (1 + np.exp(X2 @ beta))
preds = np.round(y_hat).astype(np.int)
print('beta:', beta)
print('acc:', np.mean(y == preds))
```
## LDA vs Logistic Regression
Both models have a linear logs-odd properties with exactly the same form.
But the parameters are estimated in a completely different way.
Logistic regression maximames the conditional likelihood and totaly ignores $P(X)$.
LDA maximixes the log-likelihood on the joint density $P(X,G)$. It assumes that $P(X)$ comes from a mixture of gaussians. This restriction add more informations and helps reduce variance.
In theory, if the model is Gaussian, LDA should get better results. But LDA is not robust to outliers, and Logistic regressions makes no assumption about the model data.
In pratice, logistic regression is safer and more robust than LDA, but they both often tend to give silimar results.
# Separating Hyperplanes
An hyperplane or affine set $L$ is defined by the equation:
$$\beta_0 + \beta^Tx = 0, \space \beta_0 \in \mathbb{R}, \beta, x \in \mathbb{R}^p$$
$$x_0 \in L \implies \beta^Tx_0 = - \beta_0$$
$$x_1, x_2 \in L \implies \beta^T(x_1 - x_2) = 0$$
$\beta$ is a vector normal to the surface of $L$
The signed distance from any $x$ to $L$ is given by:
$$\frac{1}{||\beta||}(\beta^Tx + \beta_0)$$
positive if $x$ on the side of the hyperplane directed by $\beta$, negative if $x$ on the other side.
We can use an hyperplane to perform a binary classification
- if $x^T\beta + \beta_0 > 0$, $x$ is on the side of the hyperplane directed by $\beta$
- if $x^T\beta + \beta_0 < 0$, $x$ is on the other side of the hyperplane
- if $x^T\beta + \beta_0 = 0$, $x$ belongs to the hyperplane
Let $X \in \mathbb{R}^{n*p}$
$$
\hat{y_i} =
\begin{cases}
1 & \text{if } x_i^T\beta + \beta_0 > 0\\
-1 & \text{otherwise}
\end{cases}
$$
The goal is to find an hyperplanes that correctly separate all examples of the data set
```
b = np.array([2, 1])
b0 = 3
def plot_data(b, b0, X, y):
#bo + b1x1 + b2x2 = 0 => x2 = -b1/b2*x1 - b0/b2
x1 = np.linspace(np.min(X[:,0]) - 10, np.max(X[:,0]) + 10, 1000)
plt.plot(x1, -b[0]/b[1]*x1 -b0/b[1])
b10 = b / np.linalg.norm(b) * 10
plt.plot([0, b10[0]], [-b0/b[1], b10[1]-b0/b[1]], c='y')
for i in range(len(X)):
plt.scatter(X[i][0], X[i][1], c=('r' if y[i] == 1 else 'g'))
plt.axis('equal')
plt.grid()
plt.show()
X = np.array([
[10, 1],
[4, 2],
[-2, -1]
])
y = np.array([
1,
1,
-1
])
plot_data(b, b0, X, y)
preds = np.sign(X @ b + b0)
print(metrics.tdist(preds, y))
def sep_dist(x):
return (x @ b + b0) / np.linalg.norm(b)
for i in range(len(X)):
print(sep_dist(X[i]))
def perceptron(X, y, lr, nepochs):
b = np.random.randn(2)
b0 = np.random.randn()
def get_loss():
loss = 0
for i in range(len(X)):
v = X[i] @ b + b0
if np.sign(v) != y[i]:
loss -= y[i] * v
return loss
print('epoch -1: loss = {}'.format(get_loss()))
for epoch in range(nepochs):
for i in range(len(X)):
v = X[i] @ b + b0
if np.sign(v) != y[i]:
b += lr * y[i] * X[i]
b0 += lr * y[i]
print('epoch {}: loss = {}'.format(epoch, get_loss()))
break
return b, b0
b, b0 = perceptron(X, y, 1, 10)
plot_data(b, b0, X, y)
```
## Optimal Separating Hyperplanes
An optimal separating hyperplane separates correctly the 2 classes and maximizes the distance between the hyperplane and the closest point
$$\max_{\beta, \beta_0} M$$
$$\text{subject to } \frac{1}{||\beta||} y_i(x_i^T\beta + \beta_0) \geq M, i=1,\text{...},N$$
- $M$ is the minimum distance between the hyperplane and every point of $X$.
- $\frac{1}{||\beta||} y_i(x_i^T\beta + \beta_0)$ is the distance between $x_i$ and the hyperplane. It's possitive if correctly classified, negative otherwhise
- Let's fix $||\beta|| = \frac{1}{M}$. The problem becames:
$$\min_{\beta, \beta_0} \frac{1}{2} ||\beta||^2$$
$$\text{subject to } y_i(x_i^T\beta + \beta_0) \geq 1, i=1,\text{...},N$$
Using the Lagrangian, the problem is turned into an unconstrained one:
$$L_P(\beta, \beta_0, \alpha) = \frac{1}{2} ||\beta||^2 - \sum_{i=1}^N \alpha_i [y_i(x_i^T\beta + \beta_0) - 1]$$
$$\min_{\beta, \beta_0} \max_{\alpha, \alpha_i \geq 0} L_P(\beta, \beta_0, \alpha)$$
Instead of solving the primal, we solve the dual, that gaves the same result:
$$\min_{\beta, \beta_0} \max_{\alpha, \alpha_i \geq 0} L_P(\beta, \beta_0, \alpha) = \max_{\alpha, \alpha_i \geq 0} \min_{\beta, \beta_0} L_P(\beta, \beta_0, \alpha)$$
The solution of the primal $\min_{\beta, \beta_0} \max_{\alpha, \alpha_i \geq 0} L_P(\beta, \beta_0, \alpha)$ is the same than the solution of the dual $\max_{\alpha, \alpha_i \geq 0} \min_{\beta, \beta_0} L_P(\beta, \beta_0, \alpha)$ because the KKT conditions are satisfied.
Solving $\frac{\partial L_P(\beta, \beta_0, \alpha)}{\partial \beta} = 0$, we get:
$$\beta = \sum_{i=1}^N \alpha_i y_i x_i$$
Solving $\frac{\partial L_P(\beta, \beta_0, \alpha)}{\partial \beta_0} = 0$, we get:
$$\sum_{i=1}^N \alpha_i y_i = 0$$
Remplacing on the original equation, we get:
$$L_D(\alpha) = \sum_{i=1}^N\alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{k=1}^N \alpha_i \alpha_k y_i y_k x_i^Tx_k$$
The problem became:
$$\max_{\alpha} L_D(\alpha)$$
$$\text{s.t. } \alpha_i \geq 0 \space i=1,\text{...}, N$$
$$\text{s.t. } \sum_{i=1}^N \alpha_i y_i = 0$$
Another condition is satisfied:
$$\alpha_i[y_i(x_i^T\beta + \beta_0) - 1] = 0 \space i = 1,\text{...},N$$
- $\alpha_i > 0$: $y_i(x_i^T\beta + \beta_0) = 1$, which means $x_i$ is on the boundary of the slab
- $\alpha_i =0$: $y_i(x_i^T\beta + \beta_0) > 1$, which means $x_i$ is outside of the slab
$\beta$ is defined in terms of a linear combination of the support points $x_i$ (where $\alpha_i > 0$).
$\beta_0$ is obtained by solving $y_i(x_i^T + \beta_0) = 1$ for any support points.
Predictions are made using:
$$\hat{G}(x) = \text{sign}(x^T\hat{\beta} + \hat{\beta_0})$$
We now convert the problem into a standard quadradic programming problem:
Let $H \in \mathbb{R}^{N*N}$: $H_{ij} = y_i y_j x_i^Tx_j$
The problem became:
$$\max_{\alpha} 1^T\alpha - \frac{1}{2} \alpha^TH\alpha$$
$$\text{s.t. } \alpha_i \geq 0$$
$$\text{s.t. } y^T \alpha = 0$$
We reverse the sign and turn it into a minimization:
$$\min_{\alpha} \frac{1}{2} \alpha^TH\alpha - 1^T\alpha$$
$$\text{s.t. } - \alpha_i \leq 0$$
$$\text{s.t. } y^T \alpha = 0$$
We can compute the parameters:
$$\beta = (y \odot \alpha) X$$
$$\beta_0 = y_i - x_i \beta, \space \forall i: \alpha_i > 0$$
```
np.random.seed(18)
N = 25
P = 2
X1 = np.random.randn(int(N/2), P) * 2 - 3.4
X2 = np.random.randn(int(N/2), P) * (-2) + 4.2
X = np.concatenate((X1, X2), axis=0)
rb = np.random.randn(P)
rb0 = np.random.randn()
y = np.sign(X @ rb + rb0)
plot_data(rb, rb0, X, y)
def svm_hard(X, y):
n, p = X.shape
X = X.astype(np.double)
y = y.astype(np.double)
H = (y.reshape(-1, 1)*X @ (y.reshape(-1, 1)*X).T)
P = cvxopt.matrix(H)
q = cvxopt.matrix(-np.ones((n, 1)))
G = cvxopt.matrix(-np.eye(n))
h = cvxopt.matrix(np.zeros((n,)))
A = cvxopt.matrix(y.reshape(1, -1))
b = cvxopt.matrix(np.zeros((1,)))
cvxopt.solvers.options['show_progress'] = False
cvxopt.solvers.options['abstol'] = 1e-10
cvxopt.solvers.options['reltol'] = 1e-10
cvxopt.solvers.options['feastol'] = 1e-10
sol = cvxopt.solvers.qp(P, q, G, h, A, b)
alpha = np.array(sol['x']).flatten()
beta = (y * alpha) @ X
S = (alpha > 1e-4)
beta0 = y[S] - (X[S] @ beta)
beta0 = np.mean(beta0)
return alpha, beta, beta0
alpha, beta, beta0 = svm_hard(X, y)
plot_data(beta, beta0, X, y)
def plot_data_support(b, b0, X, y):
#bo + b1x1 + b2x2 = 0 => x2 = -b1/b2*x1 - b0/b2
x1 = np.linspace(np.min(X[:,0]) - 10, np.max(X[:,0]) + 10, 1000)
plt.plot(x1, -b[0]/b[1]*x1 -b0/b[1])
plt.plot(x1, (1 - b0 - b[0] * x1)/b[1], c='orange')
plt.plot(x1, (-1 - b0 - b[0] * x1)/b[1], c='orange')
b10 = b / np.linalg.norm(b) * 10
plt.plot([0, b10[0]], [-b0/b[1], b10[1]-b0/b[1]], c='y')
for i in range(len(X)):
plt.scatter(X[i][0], X[i][1], c=('r' if y[i] == 1 else 'g'))
plt.axis('equal')
plt.grid()
plt.show()
plot_data_support(beta, beta0, X, y)
S = (alpha > 1e-4)
S_idxs = np.arange(len(X))[S]
S_vecs = X[S_idxs]
S_nc = np.array([
np.sum(y[S_idxs] == -1),
np.sum(y[S_idxs] == +1),
])
y_pred = np.sign(X @ beta + beta0)
acc = np.average(y == y_pred)
print('beta:', beta)
print('beta_0:', beta0)
print('Indices of support vectors:', S_idxs)
print('Support vectors:', S_vecs)
print('Number of support vectors for each class:', S_nc)
print('Accuracy:', acc)
#Comparing with sklearn
from sklearn.svm import SVC
clf = SVC(C = 1e10, kernel = 'linear')
clf.fit(X, y)
y_pred = clf.predict(X)
acc = np.average(y == y_pred)
print('beta:', clf.coef_)
print('beta_0:', clf.intercept_)
print('Indices of support vectors:', clf.support_)
print('Support vectors:', clf.support_vectors_)
print('Number of support vectors for each class:', clf.n_support_)
print('Accuracy:', acc)
```
| true |
code
| 0.355929 | null | null | null | null |
|
```
# import numpy as np
# import pandas as pd
# import matplotlib.pyplot as plt
# from laspy.file import File
# from pickle import dump, load
# import torch
# import torch.nn as nn
# import torch.nn.functional as F
# import torch.optim as optim
# import torch.utils.data as udata
# from torch.autograd import Variable
# from sklearn.preprocessing import MinMaxScaler
# %matplotlib inline
import argparse
import logging
import sys
import matplotlib.pyplot as plt
import numpy as np
import torch
import torchvision
import torch.nn.functional as F
from torch.utils.tensorboard import SummaryWriter
from utils import data
import models, utils
import pandas as pd
from laspy.file import File
from pickle import dump, load
import torch.nn as nn
import torch.optim as optim
import torch.utils.data as udata
from torch.autograd import Variable
from sklearn.preprocessing import MinMaxScaler
%matplotlib inline
```
### Inputs
```
# Training Data parameters
scan_line_gap_break = 7000 # threshold over which scan_gap indicates a new scan line
min_pt_count = 1700 # in a scan line, otherwise line not used
max_pt_count = 2000 # in a scan line, otherwise line not used
seq_len = 100
num_scan_lines = 150 # to use as training set
val_split = 0.2
# LSTM Model parameters
hidden_size = 100 # hidden features
num_layers = 2 # Default is 1, 2 is a stacked LSTM
output_dim = 3 # x,y,z
# Training parameters
num_epochs = 500
learning_rate = 0.01
# gpu or cpu
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
```
### Load the data
first_return_df has been processed in the following ways:
* Removed outliers outside of [0.01,0.99] percentile range
* Normalized xyz values to [0,1]
* Mapped each point to a scan line index
```
first_return_df = pd.read_pickle("../../Data/parking_lot/first_returns_modified_164239.pkl")
# Note: x_scaled, y_scaled, and z_scaled MUST be the first 3 features
feature_list = [
'x_scaled',
'y_scaled',
'z_scaled',
# 'scan_line_idx',
# 'scan_angle_deg',
# 'abs_scan_angle_deg'
]
```
## Mask the Data
```
# miss_pts_before is the count of missing points before the point in question (scan gap / 5 -1)
first_return_df['miss_pts_before'] = round((first_return_df['scan_gap']/-5)-1)
first_return_df['miss_pts_before'] = [max(0,pt) for pt in first_return_df['miss_pts_before']]
# Add 'mask' column, set to one by default
first_return_df['mask'] = [1]*first_return_df.shape[0]
def add_missing_pts(first_return_df):
# Create a series with the indices of points after gaps and the number of missing points (max of 5)
miss_pt_ser = first_return_df[(first_return_df['miss_pts_before']>0)&\
(first_return_df['miss_pts_before']<6)]['miss_pts_before']
# miss_pts_arr is an array of zeros that is the dimensions [num_missing_pts,cols_in_df]
miss_pts_arr = np.zeros([int(miss_pt_ser.sum()),first_return_df.shape[1]])
# Create empty series to collect the indices of the missing points
indices = np.ones(int(miss_pt_ser.sum()))
# Fill in the indices, such that they all slot in in order before the index
i=0
for index, row in zip(miss_pt_ser.index,miss_pt_ser):
new_indices = index + np.arange(row)/row-1+.01
indices[i:i+int(row)] = new_indices
i+=int(row)
# Create a Dataframe of the indices and miss_pts_arr
miss_pts_df = pd.DataFrame(miss_pts_arr,index=indices,columns = first_return_df.columns)
miss_pts_df['mask'] = [0]*miss_pts_df.shape[0]
# Fill scan fields with NaN so we can interpolate them
for col in ['scan_angle','scan_angle_deg']:
miss_pts_df[col] = [np.NaN]*miss_pts_df.shape[0]
# Concatenate first_return_df and new df
full_df = first_return_df.append(miss_pts_df, ignore_index=False)
# Resort so that the missing points are interspersed, and then reset the index
full_df = full_df.sort_index().reset_index(drop=True)
return full_df
first_return_df = add_missing_pts(first_return_df)
first_return_df[['scan_angle','scan_angle_deg']] = first_return_df[['scan_angle','scan_angle_deg']].interpolate()
first_return_df['abs_scan_angle_deg'] = abs(first_return_df['scan_angle_deg'])
first_return_df.iloc[9780:9790]
```
#### 2) Extract tensor of scan lines
```
# Number of points per scan line
scan_line_pt_count = first_return_df.groupby('scan_line_idx').count()['gps_time']
# Identify the indices for points at end of scan lines
scan_break_idx = first_return_df[(first_return_df['scan_gap']>scan_line_gap_break)].index
# Create Tensor
line_count = ((scan_line_pt_count>min_pt_count)&(scan_line_pt_count<max_pt_count)).sum()
scan_line_tensor = torch.randn([line_count,min_pt_count,len(feature_list)])
# Collect the scan lines longer than min_pt_count
# For each, collect the first min_pt_count points
i=0
for line,count in enumerate(scan_line_pt_count):
if (count>min_pt_count)&(count<max_pt_count):
try:
line_idx = scan_break_idx[line-1]
scan_line_tensor[i,:,:] = torch.Tensor(first_return_df.iloc\
[line_idx:line_idx+min_pt_count][feature_list].values)
i+=1
except RuntimeError:
print("line: ",line)
print("line_idx: ",line_idx)
```
Note: Setting all features to [0,1] overvalues the z coordinate in MSE Loss.
```
def min_max_tensor(tensor):
# Function takes a 3-D tensor, performs minmax scaling to [0,1] along the third dimension.
# First 2 dimensions are flattened
a,b,c = tensor.shape
# Flatten first two dimensions
flat_tensor = tensor.view(-1,c)
sc = MinMaxScaler()
flat_norm_tensor = sc.fit_transform(flat_tensor)
# Reshape to original
output = flat_norm_tensor.reshape([a,b,c])
return torch.Tensor(output), sc
scan_line_tensor_norm, sc = min_max_tensor(scan_line_tensor)
```
#### 3) Generate the data
```
def sliding_windows(data, seq_length, line_num, x, y):
for i in range(len(data)-seq_length):
# Index considers previous lines
idx = i+line_num*(min_pt_count-seq_length)
_x = data[i:(i+seq_length)]
_y = data[i+seq_length,:3] # Assumes xyz are the first 3 features in scan_line_tensor
x[idx,:,:] = _x
y[idx,:,:] = _y
return x,y
def generate_samples(data,min_pt_count,seq_len,num_scan_lines,val_split,starting_line=1000):
'''
Function generates training and validation samples for predicting the next point in the sequence.
Inputs:
data: 3-Tensor with dimensions: i) the number of viable scan lines in the flight pass,
ii) the minimum number of points in the scan line,
iii) 3 (xyz, or feature count)
'''
# Create generic x and y tensors
x = torch.ones([(min_pt_count-seq_len)*num_scan_lines,seq_len,len(feature_list)])
y = torch.ones([(min_pt_count-seq_len)*num_scan_lines,1,3])
i=0
# Cycle through the number of scan lines requested, starting somewhere in the middle
for line_idx in range(starting_line,starting_line+num_scan_lines):
x,y = sliding_windows(data[line_idx,:,:],seq_len,line_idx-starting_line, x, y)
x_train,y_train,x_val,y_val = train_val_split(x,y,val_split)
return x_train,y_train,x_val,y_val
def train_val_split(x,y,val_split):
# Training/Validation split
# For now, we'll do the last part of the dataset as validation...shouldn't matter?
train_val_split_idx = int(x.shape[0]*(1-val_split))
x_train = x[:train_val_split_idx,:,:]
x_val = x[train_val_split_idx:,:,:]
y_train = y[:train_val_split_idx,:,:]
y_val = y[train_val_split_idx:,:,:]
return x_train,y_train,x_val,y_val
x_train,y_train,x_val,y_val = generate_samples(scan_line_tensor_norm,min_pt_count,seq_len,num_scan_lines,val_split)
```
### 2: Train the model
Borrowing a lot of code from here: https://github.com/spdin/time-series-prediction-lstm-pytorch/blob/master/Time_Series_Prediction_with_LSTM_Using_PyTorch.ipynb
#### 1) Define the model
```
class LSTM(nn.Module):
def __init__(self, output_dim, input_size, hidden_size, num_layers, seq_len):
super(LSTM, self).__init__()
# output_dim = 3: X,Y,Z
self.output_dim = output_dim
self.num_layers = num_layers
# inputs_size = 3: X,Y,Z (could be larger in the future if we add features here)
self.input_size = input_size
# Not sure what to do here, larger than input size?
self.hidden_size = hidden_size
# Passes from above
self.seq_len = seq_len
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size,
num_layers=num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, output_dim)
def forward(self, x):
self.lstm.flatten_parameters()
h_0 = Variable(torch.zeros(
self.num_layers, x.size(0), self.hidden_size)).to(device)
c_0 = Variable(torch.zeros(
self.num_layers, x.size(0), self.hidden_size)).to(device)
# Propagate input through LSTM
ula, (h_out, _) = self.lstm(x, (h_0, c_0))
# In case multiple LSTM layers are used, this predicts using only the last layer
h_out = h_out.view(num_layers,-1, self.hidden_size)
out = self.fc(h_out[-1,:,:])
return out
# Define a loss function that weights the loss according to coordinate ranges (xmax-xmin, ymax-ymin, zmax-zmin)
def weighted_MSELoss(pred,true,sc):
'''Assumes that x,y,z are the first 3 features in sc scaler'''
ranges = torch.Tensor(sc.data_max_[:3]-sc.data_min_[:3])
raw_loss = torch.zeros(3,dtype=float)
crit = torch.nn.MSELoss()
for i in range(3):
raw_loss[i] = crit(pred[:,:,i], true[:,:,i])
return (ranges * raw_loss).sum()
def calculate_loss(lstm,x,y,ltype='Training'):
# Training loss
y_pred = lstm(x).detach().to('cpu')
loss = weighted_MSELoss(y_pred.unsqueeze(1), y,sc)
print("{} Loss: {:.4f}".format(ltype,loss))
return loss
class LidarLstmDataset(udata.Dataset):
def __init__(self, x, y):
super(LidarLstmDataset, self).__init__()
self.x = x
self.y = y
def __len__(self):
return self.x.shape[0]
def __getitem__(self,index):
return self.x[index],self.y[index]
```
#### 2) Train the model
```
batch_loss,vl = [],[]
lstm_local = LSTM(output_dim, len(feature_list), hidden_size, num_layers, seq_len)
lstm = lstm_local.to(device)
# Create the dataloader
train_dataset = LidarLstmDataset(x_train,y_train)
val_dataset = LidarLstmDataset(x_val,y_val)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=1024, num_workers=4, shuffle=True)
valid_loader = torch.utils.data.DataLoader(val_dataset, batch_size=1, num_workers=4, shuffle=False)
# criterion = torch.nn.MSELoss() # mean-squared error for regression
optimizer = torch.optim.Adam(lstm.parameters(), lr=learning_rate)
# Scheduler to reduce the learning rate
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 50, gamma=0.5)
# Train the model
for epoch in range(num_epochs):
for x,y in train_loader:
print(x.shape)
outputs = lstm(x.to(device))
optimizer.zero_grad()
# obtain the loss function
loss = weighted_MSELoss(outputs.unsqueeze(1), y.to(device),sc)
loss.backward()
optimizer.step()
batch_loss.append(loss)
print("Epoch: %d, Training batch loss: %1.5f\n" % (epoch, loss.item()))
scheduler.step()
if epoch % 5 == 0:
print("*"*30)
val = calculate_loss(lstm,x_val.to(device),y_val,'Validation')
print("*"*30)
vl.append(val)
for x,y in train_loader:
print(x.shape)
# Print loss plot
plt.subplot(2,1,1)
plt.plot(20*np.arange(len(batch_loss)-10),tl[10:],label='Training')
plt.xlabel("Batch")
plt.ylabel("Weighted MSE")
plt.subplot(2,1,2)
plt.plot(20*np.arange(len(vl)-10),vl[10:],'+',label='Validation')
plt.xlabel("Epoch")
plt.ylabel("Weighted MSE")
plt.legend()
```
#### 3) Evaluate the model
```
#Load the model
dir_name = '8_31_20/'
run_descriptor = 'seq_len_100_hidden_size_100'
scaler = load(open("models/"+dir_name+"SCALER_"+run_descriptor+".pkl",'rb'))
lstm = load(open("models/"+dir_name+run_descriptor+".pkl",'rb'))
def print_results(x,y,lstm,sc,sample_num,transform=False):
markersize,fontsize=12,14
if transform:
in_seq = sc.inverse_transform(x[sample_num])
pred_norm = (lstm(x[sample_num].unsqueeze(0).to(device)).view(-1,3).detach())
pred_point = pred_norm.to('cpu')*(sc.data_max_[:3]-sc.data_min_[:3])+sc.data_min_[:3]
true_point = y[sample_num]*(sc.data_max_[:3]-sc.data_min_[:3])+sc.data_min_[:3]
else:
in_seq = x[sample_num]
pred_point = (lstm(x[sample_num].unsqueeze(0).to(device)).view(-1,3).detach()).to('cpu')
true_point = y[sample_num]
plt.figure(figsize=[12,12])
plt.subplot(2,1,1)
plt.plot(in_seq[:,0],in_seq[:,1],'x',label='sequence')
plt.plot(pred_point[0,0],pred_point[0,1],'ro',markersize=markersize,label='Prediction')
plt.plot(true_point[0,0],true_point[0,1],'go',markersize=markersize,label='True')
plt.xlabel("X",fontsize=fontsize)
plt.ylabel("Y",fontsize=fontsize)
plt.xticks(fontsize=fontsize)
plt.yticks(fontsize=fontsize)
plt.legend(fontsize=fontsize)
plt.subplot(2,1,2)
plt.plot(in_seq[:,0],in_seq[:,2],'x',label='sequence')
plt.plot(pred_point[0,0],pred_point[0,2],'ro',markersize=markersize,label='Prediction')
plt.plot(true_point[0,0],true_point[0,2],'go',markersize=markersize,label='True')
plt.xlabel("X",fontsize=fontsize)
plt.ylabel("Z",fontsize=fontsize)
plt.xticks(fontsize=fontsize)
plt.yticks(fontsize=fontsize)
plt.legend(fontsize=fontsize)
plt.show()
for i in range(4120,4125):
print_results(x_train,y_train,lstm,scaler,i)
```
## Save the model
```
import os
import json
dir_name = '8_31_20/'
run_descriptor = 'seq_len_100_hidden_size_100'
os.mkdir('models/'+dir_name)
class Args(object):
def __init__(self):
self.scan_line_gap_break = scan_line_gap_break
self.min_pt_count = min_pt_count
self.max_pt_count = max_pt_count
self.seq_len = seq_len
self.num_scan_lines = num_scan_lines
self.val_split = val_split
self.hidden_size = hidden_size
self.num_layers = num_layers
self.output_dim = output_dim
self.num_epochs = num_epochs
self.learning_rate = learning_rate
args=Args()
# Save the scaler
dump(lstm, open('models/'+dir_name+run_descriptor+'.pkl','wb'))
dump(sc, open('models/'+dir_name+'SCALER_'+run_descriptor+'.pkl', 'wb'))
dump(args, open('models/'+dir_name+'args_'+run_descriptor+'.pkl', 'wb'))
with open('models/'+dir_name+'args_'+run_descriptor+'.json', 'w') as json_file:
json.dump(json.dumps(args.__dict__), json_file)
```
### Create .pts file of predictions
Include the actual and the predicted, indicated with a binary flag
```
def create_pts_file(y_val,x_val,lstm,sc):
y_val_reinflate = np.concatenate((y_val[:,0,:]*(sc.data_max_[:3]-sc.data_min_[:3]) \
+sc.data_min_[:3],np.zeros((y_val.shape[0],1))),axis=1)
out_df = pd.DataFrame(np.array(y_val_reinflate[:,:]),columns=['x','y','z','class'])
pred_norm = (lstm(x_val).view(-1,3).detach())
pred_reinflate = pred_norm*(sc.data_max_[:3]-sc.data_min_[:3])+sc.data_min_[:3]
pred_arr = np.concatenate((pred_reinflate,np.ones((pred_reinflate.shape[0],1))),axis=1)
out_df = out_df.append(pd.DataFrame(pred_arr,columns = out_df.columns)).reset_index(drop=True)
return out_df
out_df = create_pts_file(y_val,x_val,lstm,sc)
out_df.to_csv("output_test.pts")
```
### Data Prep
Already done, but this removes outliers and adds scan_line_idx to the first_return_df
```
# Adj GPS Time: Set both timestamps to zero for the first record
def adjust_time(df,time_field):
# Function adds adj_gps_time to points or pulse dataframe, set to zero at the minimum timestamp.
df['adj_gps_time'] = df[time_field] - df[time_field].min()
return df
def label_returns(las_df):
'''
Parses the flag_byte into number of returns and return number, adds these fields to las_df.
Input - las_df - dataframe from .laz or .lz file
Output - first_return_df - only the first return points from las_df.
- las_df - input dataframe with num_returns and return_num fields added
'''
las_df['num_returns'] = np.floor(las_df['flag_byte']/16).astype(int)
las_df['return_num'] = las_df['flag_byte']%16
first_return_df = las_df[las_df['return_num']==1]
first_return_df = first_return_df.reset_index(drop=True)
return first_return_df, las_df
def pull_first_scan_gap(df):
# Separate return num, only keep the first returns, add scan_gap, sort
df['num_returns'] = np.floor(df['flag_byte']/16).astype(int)
df['return_num'] = df['flag_byte']%16
first_return_wall = df[df['return_num']==1]
# Outliers
# Remove outliers outside of [.01,.99] percentiles
a = first_return_wall[['x_scaled','y_scaled','z_scaled']].quantile([.01,.99])
first_return_wall = first_return_wall[(first_return_wall['x_scaled']>a.iloc[0]['x_scaled'])&\
(first_return_wall['x_scaled']<a.iloc[1]['x_scaled'])&\
(first_return_wall['y_scaled']>a.iloc[0]['y_scaled'])&\
(first_return_wall['y_scaled']<a.iloc[1]['y_scaled'])&\
(first_return_wall['z_scaled']>a.iloc[0]['z_scaled'])&\
(first_return_wall['z_scaled']<a.iloc[1]['z_scaled'])]
first_return_wall.sort_values(by=['gps_time'],inplace=True)
first_return_wall.reset_index(inplace=True)
first_return_wall.loc[1:,'scan_gap'] = [first_return_wall.loc[i+1,'scan_angle'] - first_return_wall.loc[i,'scan_angle'] for i in range(first_return_wall.shape[0]-1)]
first_return_wall.loc[0,'scan_gap'] = 0
first_return_wall['scan_angle_deg'] = first_return_wall['scan_angle']*.006
return first_return_wall
# Load LAS points
las_df = pd.read_hdf("../../Data/parking_lot/las_points_164239.lz")
# Separate out the first returns only
las_df = adjust_time(las_df,'gps_time')
# Sort records by timestamp
las_df.sort_values(by=['adj_gps_time'],inplace=True)
# TO DO: consider only last returns?
# First returns only
first_return_df = pull_first_scan_gap(las_df)
# # Identify the indices for points at end of scan lines
scan_break_idx = first_return_df[(first_return_df['scan_gap']>scan_line_gap_break)].index
# # Concat adds index 0 as 0th scan line
_right = pd.DataFrame(data=range(1,len(scan_break_idx)+1),index=scan_break_idx,columns=['scan_line_idx'])
right = pd.concat([pd.DataFrame(data=[0],index=[0],columns=['scan_line_idx']),_right])
first_return_df = pd.merge_asof(first_return_df,right,left_index=True,right_index=True,direction='backward')
```
| true |
code
| 0.500488 | null | null | null | null |
|
```
# This cell is added by sphinx-gallery
!pip install mrsimulator --quiet
%matplotlib inline
import mrsimulator
print(f'You are using mrsimulator v{mrsimulator.__version__}')
```
# MCl₂.2D₂O, ²H (I=1) Shifting-d echo
²H (I=1) 2D NMR CSA-Quad 1st order correlation spectrum simulation.
The following is a static shifting-*d* echo NMR correlation simulation of
$\text{MCl}_2\cdot 2\text{D}_2\text{O}$ crystalline solid, where
$M \in [\text{Cu}, \text{Ni}, \text{Co}, \text{Fe}, \text{Mn}]$. The tensor
parameters for the simulation and the corresponding spectrum are reported by
Walder `et al.` [#f1]_.
```
import matplotlib.pyplot as plt
from mrsimulator import Simulator, SpinSystem, Site
from mrsimulator.methods import Method2D
from mrsimulator import signal_processing as sp
```
Generate the site and spin system objects.
```
site_Ni = Site(
isotope="2H",
isotropic_chemical_shift=-97, # in ppm
shielding_symmetric={
"zeta": -551, # in ppm
"eta": 0.12,
"alpha": 62 * 3.14159 / 180, # in rads
"beta": 114 * 3.14159 / 180, # in rads
"gamma": 171 * 3.14159 / 180, # in rads
},
quadrupolar={"Cq": 77.2e3, "eta": 0.9}, # Cq in Hz
)
site_Cu = Site(
isotope="2H",
isotropic_chemical_shift=51, # in ppm
shielding_symmetric={
"zeta": 146, # in ppm
"eta": 0.84,
"alpha": 95 * 3.14159 / 180, # in rads
"beta": 90 * 3.14159 / 180, # in rads
"gamma": 0 * 3.14159 / 180, # in rads
},
quadrupolar={"Cq": 118.2e3, "eta": 0.86}, # Cq in Hz
)
site_Co = Site(
isotope="2H",
isotropic_chemical_shift=215, # in ppm
shielding_symmetric={
"zeta": -1310, # in ppm
"eta": 0.23,
"alpha": 180 * 3.14159 / 180, # in rads
"beta": 90 * 3.14159 / 180, # in rads
"gamma": 90 * 3.14159 / 180, # in rads
},
quadrupolar={"Cq": 114.6e3, "eta": 0.95}, # Cq in Hz
)
site_Fe = Site(
isotope="2H",
isotropic_chemical_shift=101, # in ppm
shielding_symmetric={
"zeta": -1187, # in ppm
"eta": 0.4,
"alpha": 122 * 3.14159 / 180, # in rads
"beta": 90 * 3.14159 / 180, # in rads
"gamma": 90 * 3.14159 / 180, # in rads
},
quadrupolar={"Cq": 114.2e3, "eta": 0.98}, # Cq in Hz
)
site_Mn = Site(
isotope="2H",
isotropic_chemical_shift=145, # in ppm
shielding_symmetric={
"zeta": -1236, # in ppm
"eta": 0.23,
"alpha": 136 * 3.14159 / 180, # in rads
"beta": 90 * 3.14159 / 180, # in rads
"gamma": 90 * 3.14159 / 180, # in rads
},
quadrupolar={"Cq": 1.114e5, "eta": 1.0}, # Cq in Hz
)
spin_systems = [
SpinSystem(sites=[s], name=f"{n}Cl$_2$.2D$_2$O")
for s, n in zip(
[site_Ni, site_Cu, site_Co, site_Fe, site_Mn], ["Ni", "Cu", "Co", "Fe", "Mn"]
)
]
```
Use the generic 2D method, `Method2D`, to generate a shifting-d echo method. The
reported shifting-d 2D sequence is a correlation of the shielding frequencies to the
first-order quadrupolar frequencies. Here, we create a correlation method using the
:attr:`~mrsimulator.method.event.freq_contrib` attribute, which acts as a switch
for including the frequency contributions from interaction during the event.
In the following method, we assign the ``["Quad1_2"]`` and
``["Shielding1_0", "Shielding1_2"]`` as the value to the ``freq_contrib`` key. The
*Quad1_2* is an enumeration for selecting the first-order second-rank quadrupolar
frequency contributions. *Shielding1_0* and *Shielding1_2* are enumerations for
the first-order shielding with zeroth and second-rank tensor contributions,
respectively. See `freq_contrib_api` for details.
```
shifting_d = Method2D(
name="Shifting-d",
channels=["2H"],
magnetic_flux_density=9.395, # in T
spectral_dimensions=[
{
"count": 512,
"spectral_width": 2.5e5, # in Hz
"label": "Quadrupolar frequency",
"events": [
{
"rotor_frequency": 0,
"transition_query": {"P": [-1]},
"freq_contrib": ["Quad1_2"],
}
],
},
{
"count": 256,
"spectral_width": 2e5, # in Hz
"reference_offset": 2e4, # in Hz
"label": "Paramagnetic shift",
"events": [
{
"rotor_frequency": 0,
"transition_query": {"P": [-1]},
"freq_contrib": ["Shielding1_0", "Shielding1_2"],
}
],
},
],
)
# A graphical representation of the method object.
plt.figure(figsize=(5, 2.5))
shifting_d.plot()
plt.show()
```
Create the Simulator object, add the method and spin system objects, and
run the simulation.
```
sim = Simulator(spin_systems=spin_systems, methods=[shifting_d])
# Configure the simulator object. For non-coincidental tensors, set the value of the
# `integration_volume` attribute to `hemisphere`.
sim.config.integration_volume = "hemisphere"
sim.config.decompose_spectrum = "spin_system" # simulate spectra per spin system
sim.run()
```
Add post-simulation signal processing.
```
data = sim.methods[0].simulation
processor = sp.SignalProcessor(
operations=[
# Gaussian convolution along both dimensions.
sp.IFFT(dim_index=(0, 1)),
sp.apodization.Gaussian(FWHM="9 kHz", dim_index=0), # along dimension 0
sp.apodization.Gaussian(FWHM="9 kHz", dim_index=1), # along dimension 1
sp.FFT(dim_index=(0, 1)),
]
)
processed_data = processor.apply_operations(data=data).real
```
The plot of the simulation. Because we configured the simulator object to simulate
spectrum per spin system, the following data is a CSDM object containing five
simulations (dependent variables). Let's visualize the first data corresponding to
$\text{NiCl}_2\cdot 2 \text{D}_2\text{O}$.
```
data_Ni = data.split()[0]
plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
cb = ax.imshow(data_Ni / data_Ni.max(), aspect="auto", cmap="gist_ncar_r")
plt.title(None)
plt.colorbar(cb)
plt.tight_layout()
plt.show()
```
The plot of the simulation after signal processing.
```
proc_data_Ni = processed_data.split()[0]
plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
cb = ax.imshow(proc_data_Ni / proc_data_Ni.max(), cmap="gist_ncar_r", aspect="auto")
plt.title(None)
plt.colorbar(cb)
plt.tight_layout()
plt.show()
```
Let's plot all the simulated datasets.
```
fig, ax = plt.subplots(
2, 5, sharex=True, sharey=True, figsize=(12, 5.5), subplot_kw={"projection": "csdm"}
)
for i, data_obj in enumerate([data, processed_data]):
for j, datum in enumerate(data_obj.split()):
ax[i, j].imshow(datum / datum.max(), aspect="auto", cmap="gist_ncar_r")
ax[i, j].invert_xaxis()
ax[i, j].invert_yaxis()
plt.tight_layout()
plt.show()
```
.. [#f1] Walder B.J, Patterson A.M., Baltisberger J.H, and Grandinetti P.J
Hydrogen motional disorder in crystalline iron group chloride dihydrates
spectroscopy, J. Chem. Phys. (2018) **149**, 084503.
`DOI: 10.1063/1.5037151 <https://doi.org/10.1063/1.5037151>`_
| true |
code
| 0.747149 | null | null | null | null |
|
# Performative Prediction: A Case Study in Strategic Classification
This notebook replicates the main experiments in [Performative Prediction](https://arxiv.org/abs/2002.06673):
- Juan C. Perdomo, Tijana Zrnic, Celestine Mendler-Dünner, Moritz Hardt. "Performative Prediction." arXiv preprint 2002.06673, 2020.
Strategic classification is a two-player game between an institution which deploys a classifier and agents who selectively adapt their features in order to improve their outcomes. This process is "performative" in the sense that the classifier deployed by the institution *causes* a change in the distribution of the target variable.
We use WhyNot to explore when repeatedly retraining the classifier on the new distributions *converges* to a stable point. For more details and theoretical calculations, see the original paper.
```
%load_ext autoreload
%autoreload 2
import matplotlib.pyplot as plt
import numpy as np
import whynot as wn
import whynot.gym as gym
import scripts.utils as utils
%matplotlib inline
```
## Setting up the strategic classification environment
We use the [credit simulator](https://whynot.readthedocs.io/en/latest/simulators.html#credit-simulator), which is a strategic classification simulator based on the Kaggle [*Give Me Some Credit* dataset](https://www.kaggle.com/c/GiveMeSomeCredit).
```
env = gym.make('Credit-v0')
env.seed(1)
```
## Training a baseline logistic regression classifier
The state of the environment is a dataset consisting of (1) financial features of individuals, e.g. `DebtRatio`, and (2) a binary label indicating whether an individual experienced financial distress in the subsequent two years.
```
base_dataset = env.initial_state.values()
base_features, base_labels = base_dataset["features"], base_dataset["labels"]
num_agents, num_features = base_features.shape
print(f"The dataset has {num_agents} agents and {num_features} features.")
```
Fit a logistic regression model to the data
```
l2_penalty = 1.0 / num_agents
baseline_theta = utils.fit_logistic_regression(base_features, base_labels, l2_penalty)
baseline_acc = ((base_features.dot(baseline_theta) > 0) == base_labels).mean()
print(f"Baseline logistic regresion model accuracy: {100 * baseline_acc:.2f}%")
```
## Running repeated risk minimization
Using the credit environment, we simulate repeated retraining of the logistic regression model in response to
strategic distribution shift. We perform `num_iters` rounds. In each round:
1. We train an logistic regression classifier on the current set of features
2. The classifier is deployed via `env.step(theta)`
3. In the environment, individuals react strategically to the deployed classifier, and the environment returns a new set of fetaures for the next round.
The parameter `epsilon` changes the strength of the strategic response. Higher values of epsilon correspond to proportionally more strategic distribution shift. Each run is warm-started with the `baseline_theta` classifier computed without strategic response.
```
def repeated_risk_minimization(base_theta, epsilon, num_steps):
"""Run repeated risk minimization for num_iters steps"""
env.config.epsilon = epsilon
env.config.l2_penalty = l2_penalty
env.reset()
# Track loss and accuracy before/after updating model on new distribution
loss_start, loss_end, acc_start, acc_end, theta_gap = [], [], [], [], []
# Warm-start with baseline classifier
theta = np.copy(base_theta)
for step in range(num_steps):
# Deploy classifier and observe strategic response
observation, _, _, _ = env.step(theta)
features_strat, labels = observation["features"], observation["labels"]
# Evaluate loss and accuracy on the new distribution
loss_start.append(
utils.evaluate_logistic_loss(features_strat, labels, theta, l2_penalty))
acc_start.append(
((features_strat.dot(theta) > 0) == labels).mean()
)
# Learn a new model on the induced distribution
theta_new = utils.fit_logistic_regression(features_strat, labels, l2_penalty,
theta_init=np.copy(theta))
# Evaluate loss and accuracy on the strategic distribution after training
loss_end.append(
utils.evaluate_logistic_loss(features_strat, labels, theta_new, l2_penalty)
)
acc_end.append(
((features_strat.dot(theta_new) > 0) == labels).mean()
)
# Track distance between iterates
theta_gap.append(np.linalg.norm(theta_new - theta))
theta = np.copy(theta_new)
return loss_start, loss_end, acc_start, acc_end, theta_gap
epsilon_list = [1, 80, 150, 1000]
num_iters = 25
loss_starts, acc_starts, loss_ends, acc_ends, theta_gaps = [], [], [], [], []
for epsilon_idx, epsilon in enumerate(epsilon_list):
print(f"Running retraining for epsilon {epsilon:.2f}")
loss_start, loss_end, acc_start, acc_end, theta_gap = repeated_risk_minimization(
baseline_theta, epsilon, num_iters)
loss_starts.append(loss_start)
loss_ends.append(loss_end)
acc_starts.append(acc_start)
acc_ends.append(acc_end)
theta_gaps.append(theta_gap)
```
## Visualizing the results
We visualize the perfromative risk during the repeated risk minimization procedure. We plot the risk at the beginning and at the end of each round, connecting the two values with a blue line and indicating change in risk due to strategic distribution shift with a dashed green line.
```
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(16, 12))
for idx, epsilon in enumerate(epsilon_list):
ax = axes[idx // 2][idx % 2]
offset = 0.8
ax.set_title(f"Performative Risk, $\epsilon$={epsilon}", fontsize=20)
for i in range(2, num_iters):
ax.plot([i,i + offset],[loss_starts[idx][i], loss_ends[idx][i]],'b*-')
if i < num_iters - 1:
ax.plot([i + offset, i + 1],[loss_ends[idx][i], loss_starts[idx][i + 1]],'g--')
ax.set_xlabel("Step", fontsize=16)
ax.set_ylabel("Loss", fontsize=16)
ax.set_yscale('log')
plt.subplots_adjust(hspace=0.25)
```
The performative risk is a surrogate for the underlying metric we care about, accuracy. We can similarly plot accuracy during retraining.
```
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(16, 12))
for idx, epsilon in enumerate(epsilon_list):
ax = axes[idx // 2][idx % 2]
offset = 0.8
ax.set_title(f"Performative Accuracy, $\epsilon$={epsilon}", fontsize=20)
for i in range(2, num_iters):
ax.plot([i,i + offset],[acc_starts[idx][i], acc_ends[idx][i]],'b*-')
if i < num_iters - 1:
ax.plot([i + offset, i + 1],[acc_ends[idx][i], acc_starts[idx][i + 1]],'g--')
ax.set_xlabel("Step", fontsize=16)
ax.set_ylabel("Accuracy", fontsize=16)
ax.set_ylim([0.5, 0.75])
plt.subplots_adjust(hspace=0.25)
```
Finally, we plot the distance between consecutive iterates. This is the quantity bounded by the theorems in Performative Prediction, which shows that repeated risk minimization *converges in domain* to a stable point.
```
processed_theta_gaps = [[x for x in tg if x != 0.0] for tg in theta_gaps]
_, ax = plt.subplots(figsize=(10, 8))
for idx, (gaps, eps) in enumerate(zip(processed_theta_gaps, epsilon_list)):
label = '$\\varepsilon$ = {}'.format(eps)
if idx == 0:
ax.semilogy(gaps, label=label, linewidth=3, alpha=1,
markevery=[-1], marker='*', linestyle=(0, (1, 1)))
elif idx == 1:
ax.semilogy(gaps, label=label, linewidth=3, alpha=1,
markevery=[-1], marker='*', linestyle='solid')
else:
ax.semilogy(gaps, label=label, linewidth=3)
ax.set_title("Convergence in Domain for Repeated Risk Minimization", fontsize=18)
ax.set_xlabel('Iteration $t$',fontsize=18)
ax.set_ylabel(r'Distance Between Iterates: $\|\theta_{t+1} - \theta_{t}\|_2 $', fontsize=14)
ax.tick_params(labelsize=18)
plt.legend(fontsize=18)
```
| true |
code
| 0.696771 | null | null | null | null |
|
# Modeling and Simulation in Python
Case study.
Copyright 2017 Allen Downey
License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
```
# Configure Jupyter so figures appear in the notebook
%matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
%config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import functions from the modsim.py module
from modsim import *
```
### Unrolling
Let's simulate a kitten unrolling toilet paper. As reference material, see [this video](http://modsimpy.com/kitten).
The interactions of the kitten and the paper roll are complex. To keep things simple, let's assume that the kitten pulls down on the free end of the roll with constant force. Also, we will neglect the friction between the roll and the axle.

This figure shows the paper roll with $r$, $F$, and $\tau$. As a vector quantity, the direction of $\tau$ is into the page, but we only care about its magnitude for now.
We'll start by loading the units we need.
```
radian = UNITS.radian
m = UNITS.meter
s = UNITS.second
kg = UNITS.kilogram
N = UNITS.newton
```
And a few more parameters in the `Params` object.
```
params = Params(Rmin = 0.02 * m,
Rmax = 0.055 * m,
Mcore = 15e-3 * kg,
Mroll = 215e-3 * kg,
L = 47 * m,
tension = 2e-4 * N,
t_end = 120 * s)
```
`make_system` computes `rho_h`, which we'll need to compute moment of inertia, and `k`, which we'll use to compute `r`.
```
def make_system(params):
"""Make a system object.
params: Params with Rmin, Rmax, Mcore, Mroll,
L, tension, and t_end
returns: System with init, k, rho_h, Rmin, Rmax,
Mcore, Mroll, ts
"""
unpack(params)
init = State(theta = 0 * radian,
omega = 0 * radian/s,
y = L)
area = pi * (Rmax**2 - Rmin**2)
rho_h = Mroll / area
k = (Rmax**2 - Rmin**2) / 2 / L / radian
return System(init=init, k=k, rho_h=rho_h,
Rmin=Rmin, Rmax=Rmax,
Mcore=Mcore, Mroll=Mroll,
t_end=t_end)
```
Testing `make_system`
```
system = make_system(params)
system.init
```
Here's how we compute `I` as a function of `r`:
```
def moment_of_inertia(r, system):
"""Moment of inertia for a roll of toilet paper.
r: current radius of roll in meters
system: System object with Mcore, rho, Rmin, Rmax
returns: moment of inertia in kg m**2
"""
unpack(system)
Icore = Mcore * Rmin**2
Iroll = pi * rho_h / 2 * (r**4 - Rmin**4)
return Icore + Iroll
```
When `r` is `Rmin`, `I` is small.
```
moment_of_inertia(system.Rmin, system)
```
As `r` increases, so does `I`.
```
moment_of_inertia(system.Rmax, system)
```
## Exercises
Write a slope function we can use to simulate this system. Here are some suggestions and hints:
* `r` is no longer part of the `State` object. Instead, we compute `r` at each time step, based on the current value of `y`, using
$y = \frac{1}{2k} (r^2 - R_{min}^2)$
* Angular velocity, `omega`, is no longer constant. Instead, we compute torque, `tau`, and angular acceleration, `alpha`, at each time step.
* I changed the definition of `theta` so positive values correspond to clockwise rotation, so `dydt = -r * omega`; that is, positive values of `omega` yield decreasing values of `y`, the amount of paper still on the roll.
* Your slope function should return `omega`, `alpha`, and `dydt`, which are the derivatives of `theta`, `omega`, and `y`, respectively.
* Because `r` changes over time, we have to compute moment of inertia, `I`, at each time step.
That last point might be more of a problem than I have made it seem. In the same way that $F = m a$ only applies when $m$ is constant, $\tau = I \alpha$ only applies when $I$ is constant. When $I$ varies, we usually have to use a more general version of Newton's law. However, I believe that in this example, mass and moment of inertia vary together in a way that makes the simple approach work out. Not all of my collegues are convinced.
```
# Solution
def slope_func(state, t, system):
"""Computes the derivatives of the state variables.
state: State object with theta, omega, y
t: time
system: System object with Rmin, k, Mcore, rho_h, tension
returns: sequence of derivatives
"""
theta, omega, y = state
unpack(system)
r = sqrt(2*k*y + Rmin**2)
I = moment_of_inertia(r, system)
tau = r * tension
alpha = tau / I
dydt = -r * omega
return omega, alpha, dydt
```
Test `slope_func` with the initial conditions.
```
# Solution
slope_func(system.init, 0*s, system)
```
Run the simulation.
```
# Solution
results, details = run_ode_solver(system, slope_func, max_step=10*s)
details
```
And look at the results.
```
results.tail()
```
Check the results to see if they seem plausible:
* The final value of `theta` should be about 220 radians.
* The final value of `omega` should be near 4 radians/second, which is less one revolution per second, so that seems plausible.
* The final value of `y` should be about 35 meters of paper left on the roll, which means the kitten pulls off 12 meters in two minutes. That doesn't seem impossible, although it is based on a level of consistency and focus that is unlikely in a kitten.
* Angular velocity, `omega`, should increase almost linearly at first, as constant force yields almost constant torque. Then, as the radius decreases, the lever arm decreases, yielding lower torque, but moment of inertia decreases even more, yielding higher angular acceleration.
Plot `theta`
```
def plot_theta(results):
plot(results.theta, color='C0', label='theta')
decorate(xlabel='Time (s)',
ylabel='Angle (rad)')
plot_theta(results)
```
Plot `omega`
```
def plot_omega(results):
plot(results.omega, color='C2', label='omega')
decorate(xlabel='Time (s)',
ylabel='Angular velocity (rad/s)')
plot_omega(results)
```
Plot `y`
```
def plot_y(results):
plot(results.y, color='C1', label='y')
decorate(xlabel='Time (s)',
ylabel='Length (m)')
plot_y(results)
```
| true |
code
| 0.772144 | null | null | null | null |
|
Use this utlity to update the returns and std_dev fields within investment-options.csv
```
%%javascript
IPython.OutputArea.prototype._should_scroll = function(lines) {
return false;
}
# imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
import brownbear as bb
# format price data
pd.options.display.float_format = '{:0.2f}'.format
%matplotlib inline
# set size of inline plots
'''note: rcParams can't be in same cell as import matplotlib
or %matplotlib inline
%matplotlib notebook: will lead to interactive plots embedded within
the notebook, you can zoom and resize the figure
%matplotlib inline: only draw static images in the notebook
'''
plt.rcParams["figure.figsize"] = (10, 7)
```
Globals
```
# set refresh_timeseries=True to download timeseries. Otherwise /symbol-cache is used.
refresh_timeseries = True
# read in dow30.csv
dow30 = pd.read_csv('dow30.csv')
# remove the exchange from the beginning of the symbol
def _symbol(row):
return row['Symbol'].split(':')[-1].strip()
dow30['Symbol'] = dow30.apply(_symbol, axis=1)
dow30.drop(columns=['Exchange', 'Date added', 'Notes', 'Index weighting'], inplace=True)
dow30.rename(columns={'Symbol': 'Symbol',
'Company':'Description',
'Industry':'Asset Class'}, inplace=True)
dow30.set_index("Symbol", inplace=True)
dow30
# read in gics-2-asset-class.csv
gics2asset_class = pd.read_csv('gics-2-asset-class.csv', skip_blank_lines=True, comment='#')
gics2asset_class.set_index("GICS", inplace=True)
gics2asset_class = gics2asset_class['Asset Class'].to_dict()
gics2asset_class
# map dow30 GICS sectors to brownbear defined asset classes
def _asset_class(row):
return gics2asset_class[row['Asset Class']]
dow30['Asset Class'] = dow30.apply(_asset_class, axis=1)
# yahoo finance uses '-' where '.' is used in symbol names
dow30.index = dow30.index.str.replace('.', '-')
dow30
# make symbols list
symbols = list(dow30.index)
#symbols
# get the timeseries for the symbols and compile into a single csv
bb.fetch_timeseries(symbols, refresh=refresh_timeseries)
bb.compile_timeseries(symbols)
# read symbols timeseries into a dataframe
df = pd.read_csv('symbols-timeseries.csv', skip_blank_lines=True, comment='#')
df.set_index("Date", inplace=True)
df
# sample symbol
symbol = 'MMM'
annual_returns = bb.annualize_returns(df, timeperiod='daily', years=1)
annual_returns[symbol]
# calculate annualized returns
annual_returns_1mo = bb.annualize_returns(df, timeperiod='daily', years=1/12)
annual_returns_3mo = bb.annualize_returns(df, timeperiod='daily', years=3/12)
annual_returns_1yr = bb.annualize_returns(df, timeperiod='daily', years=1)
annual_returns_3yr = bb.annualize_returns(df, timeperiod='daily', years=3)
annual_returns_5yr = bb.annualize_returns(df, timeperiod='daily', years=5)
# calculate volatility
daily_returns = df.pct_change()
years = bb.TRADING_DAYS_PER_MONTH / bb.TRADING_DAYS_PER_YEAR
vola = bb.annualized_standard_deviation(daily_returns, timeperiod='daily', years=years)
vola[symbol]
# calculate downside volatility
ds_vola = bb.annualized_standard_deviation(daily_returns, timeperiod='daily', years=years, downside=True)
ds_vola[symbol]
# resample df on a monthly basis
df.index = pd.to_datetime(df.index)
monthly = df.resample('M').ffill()
bb.print_full(monthly[symbol])
# calculate monthly returns
monthly_returns = monthly.pct_change()
monthly_returns[symbol]
# calculate standard deviation
std_dev = bb.annualized_standard_deviation(monthly_returns, timeperiod='monthly', years=3)
std_dev[symbol]
# read investment-options-header.csv
lines = []
with open('investment-options-in.csv', 'r') as f:
lines = [line.strip() for line in f]
lines
# for each symbol, write out the 1 Yr, 3 Yr, 5 Yr, and std dev
out = lines.copy()
for i, (index, row) in enumerate(dow30.iterrows()):
symbol = index
description = row['Description']
asset_class = row['Asset Class']
ret_1mo = annual_returns_1mo[symbol]
ret_3mo = annual_returns_3mo[symbol]
ret_1yr = annual_returns_1yr[symbol]
ret_3yr = annual_returns_3yr[symbol]
ret_5yr = annual_returns_5yr[symbol]
if np.isnan(ret_3yr): ret_3yr = ret_1yr
if np.isnan(ret_5yr): ret_5yr = ret_3yr
_vola = vola[symbol]*100
_ds_vola = ds_vola[symbol]*100
sd = std_dev[symbol]*100
out.append(
'"{}","{}","{}","{:0.2f}","{:0.2f}","{:0.2f}","{:0.2f}","{:0.2f}","{:0.2f}","{:0.2f}","{:0.2f}"'
.format(symbol, description, asset_class,
ret_1mo, ret_3mo, ret_1yr, ret_3yr, ret_5yr, _vola, _ds_vola, sd))
# write out asset-classes.csv
with open('investment-options.csv', 'w') as f:
for line in out:
f.write(line + '\n')
```
| true |
code
| 0.48499 | null | null | null | null |
|
**Data Description**
age: The person's age in years
sex: The person's sex (1 = male, 0 = female)
cp: The chest pain experienced (Value 1: typical angina, Value 2: atypical angina, Value 3: non-anginal pain, Value 4: asymptomatic)
trestbps: The person's resting blood pressure (mm Hg on admission to the hospital)
chol: The person's cholesterol measurement in mg/dl
fbs: The person's fasting blood sugar (> 120 mg/dl, 1 = true; 0 = false)
restecg: Resting electrocardiographic measurement (0 = normal, 1 = having ST-T wave abnormality, 2 = showing probable or definite left ventricular hypertrophy by Estes' criteria)
thalach: The person's maximum heart rate achieved
exang: Exercise induced angina (1 = yes; 0 = no)
oldpeak: ST depression induced by exercise relative to rest ('ST' relates to positions on the ECG plot. See more here)
slope: the slope of the peak exercise ST segment (Value 1: upsloping, Value 2: flat, Value 3: downsloping)
ca: The number of major vessels (0-3)
thal: A blood disorder called thalassemia (3 = normal; 6 = fixed defect; 7 = reversable defect)
target: Heart disease (0 = no, 1 = yes)
```
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
df = pd.read_csv('heart.csv')
df.head()
df.shape
import pandas_profiling as ppl
profile = ppl.ProfileReport(df)
profile
```
Check for null values in the dataset. No needed as pandas_profiling has already done this job
```
df.isnull().sum().sort_values(ascending=False)
```
Now , Check for the Correlation in the data.
```
plt.figure(figsize=(12,10))
sns.heatmap(df.corr(),cmap='viridis',annot=True)
```
**Check the Correlation of features with the target variable.**
```
df.corr()['target'].sort_values(ascending=False)
```
The following plot shows the Distribution of Age. This Graph tells that the highest number of people suffering from heart diseases are in the age group of 55-65 years.
```
sns.set_style('whitegrid')
plt.figure(figsize=(10,5))
sns.distplot(df['age'],color='cyan',kde=False)
```
### Now , Let's Look at target. It is such a quite balanced with almost equal number of both classes
```
sns.countplot(df['target'],palette='rainbow')
```
## It's time to do some other plots.
```
plt.figure(figsize=(10,7))
sns.boxplot(df['target'], df['trestbps'],hue=df['sex'], palette = 'viridis')
sns.countplot(x='target',hue='sex',data=df)
sns.boxplot(x='target',y='age',hue='sex',data=df)
```
### The following function changes int-type categorical columns to object-type to perform OneHotEncoding (using pd.get_dummies). If we don't change them to object-type,after performing OneHotEncoding the values remains same.So that's why we changed them to object-type. Then we append the categorical column into categories .
```
categories = []
def categorical(df):
for column in df.drop('target',axis=1).columns :
if len(df[column].value_counts()) <10 and df[column].dtype != 'object': # and df[column].dtype != 'object' is no needed.
df[column] = df[column].astype('object')
categories.append(column)
return df
df = categorical(df)
categories
df.head()
df.info()
```
### Creating Dummy Variables for those categorical columns. Make sure that drop_first = True to avoid "Dummy Variable Trap".
```
onehot = pd.get_dummies(df[categories],drop_first = True)
onehot
df.drop(categories,axis=1,inplace=True) # Removing those categorical columns
df
y = df['target']
df.drop('target',axis=1,inplace=True)
df = pd.concat([df,onehot],axis=1)
df.head()
X = df.values
X.shape
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size = 0.2, random_state=0)
X_train.shape,X_test.shape
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train[:,0:5] = sc.fit_transform(X_train[:,0:5])
X_test[:,0:5] = sc.transform(X_test[:,0:5])
from sklearn.ensemble import RandomForestClassifier,VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from xgboost import XGBClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import confusion_matrix,accuracy_score,classification_report
rf = RandomForestClassifier()
rf.fit(X_train,y_train)
predictions = rf.predict(X_test)
confusion_matrix(y_test,predictions)
```
# Hyperparameter Tuning Starts...!
## Tuning Random Forest
```
n_estimators = [200,300,400,500,600,700]
max_depth = range(1,12)
criterions = ['gini', 'entropy']
parameters = {'n_estimators':n_estimators,
'max_depth':max_depth,
'criterion': criterions
}
grid = GridSearchCV(estimator=RandomForestClassifier(max_features='auto',n_jobs=-1),
param_grid=parameters,
cv=5,
verbose=1,
n_jobs = -1)
grid.fit(X_train,y_train)
rf_grid = grid.best_estimator_
rf_grid.fit(X_train,y_train)
predictions = rf_grid.predict(X_test)
confusion_matrix(y_test,predictions)
```
## Let's look at some important features...!
```
feature_importances = pd.DataFrame(rf_grid.feature_importances_,
index=df.columns,
columns=['importance'])
feature_importances.sort_values(by='importance', ascending=False)
```
## Tuning Logistic Regression
```
C_vals = [0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,2,3,3.2,3.6,
4,5,6,7,8,9,10]
penalties = ['l1','l2']
solvers = ['liblinear', 'sag','lbfgs']
parameters = {'penalty': penalties, 'C': C_vals, 'solver':solvers}
grid = GridSearchCV(estimator=LogisticRegression(),
param_grid=parameters,
scoring='accuracy',
cv=5,
verbose=1,
n_jobs=-1)
grid.fit(X_train,y_train)
lr_grid = grid.best_estimator_
lr_grid.fit(X_train,y_train)
predictions = lr_grid.predict(X_test)
confusion_matrix(y_test,predictions)
```
## Tuning SVM
```
C = [0.01, 0.1, 1,1.2,1.5,2,2.5,3,3.2,3.5,4]
gamma = [0.0001,0.001,0.005, 0.01, 0.1, 1]
parameters = {'C': C, 'gamma' : gamma}
grid = GridSearchCV(estimator=SVC(kernel = 'rbf', probability=True),
param_grid=parameters,
scoring='accuracy',
verbose=1,
cv=5,
n_jobs=-1)
grid.fit(X_train,y_train)
svm_grid = grid.best_estimator_
svm_grid.fit(X_train,y_train)
predictions = svm_grid.predict(X_test)
confusion_matrix(y_test,predictions)
feature_importances = pd.DataFrame(rf_grid.feature_importances_,
index=df.columns,
columns=['importance'])
feature_importances.sort_values(by='importance', ascending=False)
```
## Tuning Bagging Classifier
```
from sklearn.ensemble import BaggingClassifier
n_estimators = [200,300,330,370,400,430,470,500,600,700]
parameters = {'n_estimators':n_estimators}
grid = GridSearchCV(BaggingClassifier(base_estimator= None),
param_grid=parameters,
cv=5,verbose=1,
n_jobs = -1)
grid.fit(X_train,y_train)
bag_grid = grid.best_estimator_
bag_grid.fit(X_train,y_train)
predictions = bag_grid.predict(X_test)
confusion_matrix(y_test,predictions)
```
## Tuning XGBClassifier
```
base_score = [0.1,0.3,0.5,0.7,0.9]
max_depth = range(4,15)
learning_rate = [0.01,0.1,0.2,0.3,0.4]
gamma = [0.001,0.01,0.1,0.3,0.5]
parameters = {'base_score':base_score,
'max_depth':max_depth,
'learning_rate': learning_rate,
'gamma':gamma
}
grid = GridSearchCV(estimator=XGBClassifier(n_jobs=-1),
param_grid=parameters,
cv=5,
verbose=1,
n_jobs = -1)
grid.fit(X_train,y_train)
xgb_grid = grid.best_estimator_
xgb_grid.fit(X_train,y_train)
predictions = xgb_grid.predict(X_test)
confusion_matrix(y_test,predictions)
```
## Now, Combine all of them using Voting Classifier...!
```
vot_clf = VotingClassifier(estimators=[('rf',rf_grid),
('lr',lr_grid),
('svc',svm_grid),
('bag',bag_grid),
('xgb',xgb_grid)], voting='hard')
vot_clf.fit(X_train,y_train)
predictions = vot_clf.predict(X_test)
confusion_matrix(y_test,predictions)
vot_clf.score(X_test,y_test)
rf_grid.score(X_test,y_test)
bag_grid.score(X_test,y_test)
xgb_grid.score(X_test,y_test)
```
### Let's use Artificial Neural Network (ANN) ...!
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense,Dropout
from tensorflow.keras.callbacks import EarlyStopping
model = Sequential()
model.add(Dense(units=30,activation = 'relu' ,input_shape=(22,)))
model.add(Dropout(0.2))
model.add(Dense(units=15,activation = 'relu'))
model.add(Dropout(0.2))
model.add(Dense(units=7,activation = 'relu'))
model.add(Dropout(0.2))
model.add(Dense(units=1,activation = 'sigmoid'))
model.compile(optimizer = 'adam',loss='binary_crossentropy',metrics=['accuracy'])
early_stop = EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=5)
history = model.fit(x=X_train,
y=y_train,
epochs=200,
validation_data=(X_test, y_test),
verbose=1,
callbacks=[early_stop]
)
predictions = model.predict(X_test)
predictions = [1 if i>0.5 else 0 for i in predictions]
confusion_matrix(y_test,predictions)
```
## Tuning ANN Using GridSearch ....!
```
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
from tensorflow.keras.layers import BatchNormalization
```
### Create a function to build our ANN model.
### Keras provides a wrapper class KerasClassifier that allows us to use our deep learning models with scikit-learn, this is especially useful when you want to tune hyperparameters using scikit-learn's RandomizedSearchCV or GridSearchCV.
```
def build_model(layers,dropout_rate=0):
model = Sequential()
for i,nodes in enumerate(layers):
if i==0:
model.add(Dense(nodes,activation='relu',input_dim=X_train.shape[1]))
else :
model.add(Dense(nodes,activation='relu'))
model.add(BatchNormalization())
if dropout_rate:
model.add(Dropout(dropout_rate))
model.add(Dense(1,activation='sigmoid'))
model.compile(optimizer='adam',loss='binary_crossentropy',metrics=['accuracy'])
return model
model = KerasClassifier(build_fn=build_model,verbose=0)
```
### Define the parameters when we fit our ANN except X and y , such as epochs,callbacks etc.
```
early_stop = EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=5)
callbacks = [early_stop]
fit_parameters = {'callbacks': callbacks,
'epochs': 200,
'validation_data' : (X_test,y_test),
'verbose' : 0}
```
### Define some of the Hyperparameters of our model.
```
layers = [(15,1),(20,10,1),(30,15,7,1)]
parameters = dict(layers=layers,dropout_rate=[0,0.1,0.2,0.3],batch_size=[32,64,128,256])
grid = GridSearchCV(estimator=model,
param_grid=parameters,
cv=5,
verbose=1,
n_jobs=-1)
```
### To fit the fit_params we have to do "**fit_params"
```
grid.fit(X_train,y_train,**fit_parameters)
predictions = grid.predict(X_test)
confusion_matrix(y_test,predictions)
```
### I had used grid for every tuned model.But Below grid has the tuned ANN model because it is the latest one.
```
all_models = [rf_grid,
lr_grid,
svm_grid,
bag_grid,
xgb_grid,
vot_clf,
grid]
c = {}
for i in all_models :
a = i.predict(X_test)
b = accuracy_score(y_test,a)
c[i] = b
c
```
## Final Prediction !!!
```
predictions = (max(c,key=c.get)).predict(X_test)
confusion_matrix(y_test,predictions)
print(classification_report(y_test,predictions))
```
## Save and Load the Model
```
import pickle
```
### I saved the vot_clf model because ANN or any Deep Learning model can be saved in the h5 file format.
```
filename = 'model.pkl'
pickle.dump(vot_clf, open(filename, 'wb'))
loaded_model = pickle.load(open(filename, 'rb'))
predictions = loaded_model.predict(X_test)
confusion_matrix(y_test,predictions)
```
| true |
code
| 0.431045 | null | null | null | null |
|
```
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12,8)
import numpy as np
import tensorflow as tf
import keras
import pandas as pd
from keras_tqdm import TQDMNotebookCallback
from keras.preprocessing.sequence import pad_sequences
def data_generator(batch_size, tfrecord, start_frac=0, end_frac=1):
'''
Shuffles the Audioset training data and returns a generator of training data and boolean laughter labels
batch_size: batch size for each set of training data and labels
tfrecord: filestring of the tfrecord file to train on
start_frac: the starting point of the data set to use, as a fraction of total record length (used for CV)
end_frac: the ending point of the data set to use, as a fraction of total record length (used for CV)
'''
max_len=10
records = list(tf.python_io.tf_record_iterator(tfrecord))
records = records[int(start_frac*len(records)):int(end_frac*len(records))]
rec_len = len(records)
shuffle = np.random.permutation(range(rec_len))
num_batches = rec_len//batch_size - 1
j = 0
laugh_labels = [16, 17, 18, 19, 20, 21]
while True:
X = []
y = []
for idx in shuffle[j*batch_size:(j+1)*batch_size]:
example = records[idx]
tf_seq_example = tf.train.SequenceExample.FromString(example)
example_label = list(np.asarray(tf_seq_example.context.feature['labels'].int64_list.value))
laugh_bin = any((True for x in example_label if x in laugh_labels))
y.append(laugh_bin)
n_frames = len(tf_seq_example.feature_lists.feature_list['audio_embedding'].feature)
audio_frame = []
for i in range(n_frames):
audio_frame.append(np.frombuffer(tf_seq_example.feature_lists.feature_list['audio_embedding'].
feature[i].bytes_list.value[0],np.uint8).astype(np.float32))
pad = [np.zeros([128], np.float32) for i in range(max_len-n_frames)]
audio_frame += pad
X.append(audio_frame)
j += 1
if j >= num_batches:
shuffle = np.random.permutation(range(rec_len))
j = 0
X = np.array(X)
yield X, np.array(y)
```
### Logistic Regression
```
from keras.models import Sequential
from keras.layers import Dense, BatchNormalization, Flatten
lr_model = Sequential()
# lr_model.add(keras.Input((None, 128)))
lr_model.add(BatchNormalization(input_shape=(10, 128)))
lr_model.add(Flatten())
lr_model.add(Dense(1, activation='sigmoid'))
# try using different optimizers and different optimizer configs
lr_model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
batch_size=32
CV_frac = 0.1
train_gen = data_generator(batch_size,'../Data/bal_laugh_speech_subset.tfrecord', 0, 1-CV_frac)
val_gen = data_generator(128,'../Data/bal_laugh_speech_subset.tfrecord', 1-CV_frac, 1)
rec_len = 18768
lr_h = lr_model.fit_generator(train_gen,steps_per_epoch=int(rec_len*(1-CV_frac))//batch_size, epochs=100,
validation_data=val_gen, validation_steps=int(rec_len*CV_frac)//128,
verbose=0, callbacks=[TQDMNotebookCallback()])
plt.plot(lr_h.history['acc'], label='train_acc')
plt.plot(lr_h.history['val_acc'], label='val_acc')
plt.legend()
lr_model.save('../Models/LogisticRegression_100Epochs.h5')
```
### Single Layer LSTM
```
from keras.models import Sequential
from keras.layers import Dense, BatchNormalization, Dropout
from keras.layers import LSTM
from keras import regularizers
lstm_model = Sequential()
lstm_model.add(BatchNormalization(input_shape=(None, 128)))
lstm_model.add(Dropout(0.5))
lstm_model.add(LSTM(128, activation='relu',
kernel_regularizer=regularizers.l2(0.01),
activity_regularizer=regularizers.l2(0.01)))
lstm_model.add(Dense(1, activation='sigmoid'))
# try using different optimizers and different optimizer configs
lstm_model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
batch_size=32
CV_frac = 0.1
train_gen = data_generator(batch_size,'../Data/bal_laugh_speech_subset.tfrecord', 0, 1-CV_frac)
val_gen = data_generator(128,'../Data/bal_laugh_speech_subset.tfrecord', 1-CV_frac, 1)
rec_len = 18768
lstm_h = lstm_model.fit_generator(train_gen,steps_per_epoch=int(rec_len*(1-CV_frac))//batch_size, epochs=100,
validation_data=val_gen, validation_steps=int(rec_len*CV_frac)//128,
verbose=0, callbacks=[TQDMNotebookCallback()])
plt.plot(lstm_h.history['acc'], label='train_acc')
plt.plot(lstm_h.history['val_acc'], label='val_acc')
plt.legend()
lstm_model.save('../Models/LSTM_SingleLayer_100Epochs.h5')
```
### 3 Layer LSTM
```
from keras.models import Sequential
from keras.layers import Dense, BatchNormalization, Dropout
from keras.layers import LSTM
from keras import regularizers
lstm3_model = Sequential()
lstm3_model.add(BatchNormalization(input_shape=(None, 128)))
lstm3_model.add(Dropout(0.5))
lstm3_model.add(LSTM(64, activation='relu',
kernel_regularizer=regularizers.l2(0.01),
activity_regularizer=regularizers.l2(0.01),
return_sequences=True))
lstm3_model.add(BatchNormalization())
lstm3_model.add(Dropout(0.5))
lstm3_model.add(LSTM(64, activation='relu',
kernel_regularizer=regularizers.l2(0.01),
activity_regularizer=regularizers.l2(0.01),
return_sequences=True))
lstm3_model.add(BatchNormalization())
lstm3_model.add(Dropout(0.5))
lstm3_model.add(LSTM(64, activation='relu',
kernel_regularizer=regularizers.l2(0.01),
activity_regularizer=regularizers.l2(0.01)))
lstm3_model.add(Dense(1, activation='sigmoid'))
# try using different optimizers and different optimizer configs
lstm3_model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
batch_size=32
CV_frac = 0.1
train_gen = data_generator(batch_size,'../Data/bal_laugh_speech_subset.tfrecord', 0, 1-CV_frac)
val_gen = data_generator(128,'../Data/bal_laugh_speech_subset.tfrecord', 1-CV_frac, 1)
rec_len = 18768
lstm3_h = lstm3_model.fit_generator(train_gen,steps_per_epoch=int(rec_len*(1-CV_frac))//batch_size, epochs=100,
validation_data=val_gen, validation_steps=int(rec_len*CV_frac)//128,
verbose=0, callbacks=[TQDMNotebookCallback()])
plt.plot(lstm3_h.history['acc'], label='train_acc')
plt.plot(lstm3_h.history['val_acc'], label='val_acc')
plt.legend()
lstm3_model.save('../Models/LSTM_ThreeLayer_100Epochs.h5')
keras.__version__
```
| true |
code
| 0.718483 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/dinesh110598/Spin_glass_NN/blob/master/main.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Classifying Bimodal triangular EA lattices
The Hamiltonian for the EA model on a 2d triangular lattice with spins {S}:
$ H = \displaystyle\sum_{<i,j>} J_{ij}(p).S_iS_j$ where \<ij\> denotes nearest neighbour positions on a triangular lattice and $J_{ij}(p)$ takes values +1 and -1 with probabilities p and 1-p respectively. We'll consider only the values of p between 0.5 and 1 throughout this notebook.
## Classification between p=0.5 and p=0.7
In this subsection, we will supply a convolutional neural network (CNN) with properly labelled samples for p=0.5 and p=0.7, over multiple realisations of couplings $J_{ij}$ in each category. Later, we'll analyse the network's output for intermediate values of p. Following this, we'll look at 2 point correlation functions of these lattices for the same values and compare the variation of correlation functions with that of neural network output.
### Imports and dependecies
```
import math
import numpy as np
import cupy as cp
import tensorflow.keras as tfk
import tensorflow as tf
import matplotlib.pyplot as plt
from google.colab import drive
from google.colab import output
drive.mount('/content/drive', force_remount=True)
folder_path = "/content/drive/My Drive/Project Presentations/Spin_glass_phase_classification/"
```
I've written Numba CUDA kernels (functions that perform calculations inside GPUs using CUDA) for simulating MCMC and parallel tempering algorithms for triangular EA model, in a seperate python file. Let's import the file and its contents inside this notebook:
```
!curl -o TriEA_kernels.py https://raw.githubusercontent.com/dinesh110598/Spin_glass_NN/master/TriEA_kernels.py
from TriEA_kernels import *
!nvidia-smi -L
```
### Data generating function
Let's write a function that uses the imported kernels to generate our training data:
```
#Jnn = cp.random.choice ([-1,1], (1,48,48,3),
#p=[1.0, 0.]).astype(np.float32)
def generate_train_data (train_len, prob, lat_len=48, m=100):
shape = (lat_len, lat_len)
n_ens = train_len//m
spin = cp.random.choice ([1,-1], (train_len,)+shape).astype(np.int8)
seed = cp.random.randint (-10000,10000, size=(train_len,)+shape,
dtype=np.int32)
Jnn = cp.random.choice ([-1,1], (n_ens,)+shape+(3,),
p=[1-prob, prob]).astype(np.float32)
energy = cp.zeros ((n_ens,m), np.float32)
tpb = (1,8,8)
bpg = (train_len, lat_len//8, lat_len//8)
perm = cp.arange (0, train_len, dtype=np.int32)
temp = 0.5
T = cp.full ((n_ens,m), 0.5, np.float32)
for _ in range (3000):
update_red [bpg,tpb] (spin, seed, T, Jnn, perm)
update_blue [bpg,tpb] (spin, seed, T, Jnn, perm)
update_green [bpg,tpb] (spin, seed, T, Jnn, perm)
calc_energy [math.ceil(train_len/64),64] (spin, energy, Jnn)
spin = 0.5*cp.asnumpy (spin)
#return cp.asnumpy (energy)
return spin[...,np.newaxis]#Additional axis required for conv2d layer
energy = generate_train_data (1000, 0.5)
np.sort(energy[0]/(48**2))
```
Let's generate training data for p=0.5 and concatenate with that of p=0.7, with corresponding labels 0 and 1 respectively:
```
t_lattice = generate_train_data (8000, 0.8)
t_label = np.zeros (8000, np.int32)
t_lattice = np.concatenate ([t_lattice, generate_train_data (8000,0.9)])
t_label = np.concatenate ([t_label, np.ones (8000, np.int32)])
output.eval_js('new Audio("https://upload.wikimedia.org/wikipedia/commons/0/05/Beep-09.ogg").play()')
```
Let's gather our numpy data in a single tf.data dataset
```
train_data = tf.data.Dataset.from_tensor_slices ((t_lattice,t_label))
train_data = train_data.shuffle (buffer_size=16000)
```
Splitting the dataset into training and validation datasets:
```
val_data = train_data.take (4000)
train_data = train_data.skip (4000)
val_data = val_data.batch (8)
train_data = train_data.batch (8)
```
### Neural network initialization and training:
```
brain = tfk. Sequential([
tfk.layers.Conv2D(64, (2,2), activation='relu', input_shape = (48,48,1)),
tfk.layers.MaxPool2D (),
tfk.layers.Conv2D(64, (2,2), activation='relu'),
tfk.layers.Flatten(),
tfk.layers.Dense(64, activation='relu'),
tfk.layers.Dropout(0.3),
tfk.layers.Dense(2, activation='softmax')
])
brain.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
hist = brain.fit (train_data, epochs=1, validation_data=val_data)
brain.save (folder_path+"EA_8_9.h5")
```
### Neural network predictions for intermediate values
```
datax = []
lattice = []
p = 0.5
while (p < 0.601):
lattice.append (generate_train_data (2000, p))
datax.append (p)
p += 0.01
lattice = np.concatenate (lattice)
output.eval_js('new Audio("https://upload.wikimedia.org/wikipedia/commons/0/05/Beep-09.ogg").play()')
brain = tfk.models.load_model (folder_path+"EA_7_8.h5")
predictions = brain.predict (lattice[10000:16000])
predictions.shape
datax = np.arange (0.7, 0.801, 0.02)
datay = []
for i in range (len(datax)):
datay.append (predictions[1000*i:1000*(i+1),0].mean())
plt.plot (datax, datay)
plt.grid()
```
### Correlation functions for intermediate values
Let's calculate 2 point correlation functions with distance, averaged over both translations and the three rotations possible on a triangular lattice, using the below expression:
$$ C_2(r) = \frac{<S(x).S(x+r)>_x}{<S(x)^2>_x-<S(x)>^2_x} $$ which assumes translational invariance between averaging over x as opposed to x+r, and that $<S_x>=0$ for all x. The assumptions are perfectly valid for Edwards Anderson model with periodic boundary conditions.
On that note, we'll import a scipy library function pearsonr that'd help us calculate correlation between data without getting our hands dirty:
```
from scipy.stats import pearsonr
```
We'll sample Jnn's from appropriate distributions for each p:
```
Jnn = []
p = 0.5
while (p < 0.9001):
Jnn.append (np.random.choice ([-1,1], (100,48,48,3), p=[1-p,p]))
p += 0.02
Jnn = np.concatenate (Jnn)
Jnn = cp.asarray (Jnn)
```
We've made changes to the previous generating function to run this:
```
def generate_train_data (train_len, lat_len=48, m=10):
shape = (lat_len, lat_len)
n_ens = train_len//m
spin = cp.random.choice ([1,-1], (train_len,)+shape).astype(np.int8)
seed = cp.random.randint (-10000,10000, size=(train_len,)+shape,
dtype=np.int32)
#Jnn = cp.random.choice ([-1,1], (n_ens,)+shape+(3,),
#p=[1-prob, prob]).astype(np.float32)
energy = cp.zeros ((n_ens,m), np.float32)
tpb = (1,8,8)
bpg = (train_len, lat_len//8, lat_len//8)
perm = cp.arange (0, train_len, dtype=np.int32)
temp = 0.5
T = cp.full ((n_ens,m), 0.5, np.float32)
for _ in range (3000):
update_red [bpg,tpb] (spin, seed, T, Jnn, perm)
update_blue [bpg,tpb] (spin, seed, T, Jnn, perm)
update_green [bpg,tpb] (spin, seed, T, Jnn, perm)
calc_energy [math.ceil(train_len/64),64] (spin, energy, Jnn)
spin = 0.5*cp.asnumpy (spin)
#return cp.asnumpy (energy)
return spin[...,np.newaxis]#Additional axis required for conv2d layer
lattice = generate_train_data (Jnn.shape[0]*10)
np.save (folder_path+"Training Data/TriEAlattice.npy", lattice)
TriEA = []
for i in range (21):
TriEA.append (lattice[1000*i:1000*(i+1)])
corr = np.zeros ((21,3,20,24,24), np.float32)
for n in range (21):
for r1 in range (24):
for r2 in range (24):
x1 = np.ravel (TriEA[n][:,r1,r2,:])
for r in range (1,21):
x2 = np.ravel (TriEA[n][:,r1+r,r2,:])
val, _ = pearsonr (x1,x2)
corr [n,0,r-1,r1,r2] = (val)
x2 = np.ravel(TriEA[n][:,r1+int(r-(r%2)*(-1**r2))//2,
r2+r,:])
val, _ = pearsonr (x1,x2)
corr [n,1,r-1,r1,r2] = (val)
x2 = np.ravel(TriEA[n][:,r1-int(r+(r%2)*(-1**r2))//2,
r2+r,:])
val, _ = pearsonr (x1,x2)
corr [n,2,r-1,r1,r2] = (val)
corr = np.mean (corr, axis=(1,3,4))
corr2 = np.zeros ((3,20,24,24), np.float32)
for r1 in range (24):
for r2 in range (24):
x1 = np.ravel (TriEA2[:,r1,r2,:])
for r in range (1,21):
x2 = np.ravel (TriEA2[:,r1+r,r2,:])
val, _ = pearsonr (x1,x2)
corr2 [0,r-1,r1,r2] = (val)
x2 = np.ravel(TriEA2[:,r1+int(r-(r%2)*(-1**r2))//2,
r2+r,:])
val, _ = pearsonr (x1,x2)
corr2 [1,r-1,r1,r2] = (val)
x2 = np.ravel(TriEA2[:,r1-int(r+(r%2)*(-1**r2))//2,
r2+r,:])
val, _ = pearsonr (x1,x2)
corr2 [2,r-1,r1,r2] = (val)
corr2 = np.mean (corr2, axis=(0,2,3))
corr3 = np.zeros ((3,20,24,24), np.float32)
for r1 in range (24):
for r2 in range (24):
x1 = np.ravel (TriEA3[:,r1,r2,:])
for r in range (1,21):
x2 = np.ravel (TriEA3[:,r1+r,r2,:])
val, _ = pearsonr (x1,x2)
corr3 [0,r-1,r1,r2] = (val)
x2 = np.ravel(TriEA3[:,r1+int(r-(r%2)*(-1**r2))//2,
r2+r,:])
val, _ = pearsonr (x1,x2)
corr3 [1,r-1,r1,r2] = (val)
x2 = np.ravel(TriEA3[:,r1-int(r+(r%2)*(-1**r2))//2,
r2+r,:])
val, _ = pearsonr (x1,x2)
corr3 [2,r-1,r1,r2] = (val)
corr3 = np.mean (corr3, axis=(0,2,3))
output.eval_js('new Audio("https://upload.wikimedia.org/wikipedia/commons/0/05/Beep-09.ogg").play()')
_, ax = plt.subplots()
ax.plot (range(1,21), list(corr1), label='p = 0.50')
ax.plot (range(1,21), list(corr2), label='p = 0.52')
ax.plot (range(1,21), list(corr3), label='p = 0.54')
ax.legend (loc= 'upper right' )
ax.grid ()
plt.show ()
_, ax = plt.subplots()
ax.plot (range(1,21), list(corr1), label='p = 0.56')
ax.plot (range(1,21), list(corr2), label='p = 0.58')
ax.plot (range(1,21), list(corr3), label='p = 0.60')
ax.legend (loc= 'upper right' )
ax.grid ()
plt.show ()
_, ax = plt.subplots()
ax.plot (range(1,21), list(corr[3]), label='p = 0.56')
ax.plot (range(1,21), list(corr[5]), label='p = 0.60')
ax.plot (range(1,21), list(corr[7]), label='p = 0.64')
ax.plot (range(1,21), list(corr[9]), label='p = 0.68')
ax.legend (loc= 'upper right' )
ax.grid ()
plt.show ()
param = (corr[:,0])
probs = np.arange (0.5, 0.91, 0.02)
plt.plot (probs, param)
plt.xlabel ("p")
plt.ylabel ("")
plt.grid ()
mags = np.mean(t_lattice, axis=(2,3,4))
mags = np.abs (mags)
mags = np.mean (mags, axis=1)
mags
plt.plot (np.arange (0.4, 0.61, 0.02, float), mags)
```
# Bimodal EA lattice temperature evolution
```
import math
import numpy as np
import cupy as cp
import tensorflow.keras as tfk
import tensorflow as tf
import matplotlib.pyplot as plt
from numba import cuda
```
## Fixed couplings
Let's fix our couplings and broadcast the same to the entire ensemble:
```
Jnn = cp.random.choice ([-1,1], (48,48,2))
Jnn = cp.broadcast_to (Jnn, (10,48,48,2))
@cuda.jit
def update_sq (spin, seed, T, J_nn, is_black, perm):
m = T.shape[1]
z, x, y = cuda.grid (3)
z = perm[z]
n = int(math.floor (z / m))
l = z % m
p, q = x % 3, y % 2
def random_uniform ():
seed[z, x, y] = np.int32((seed[z ,x, y]*1664525 + 1013904223) % 2**31)
return seed[z, x, y] / (2**31)
def bvc (x):
if x == spin.shape[1]:
x = 0
return x
def sum_nn(): # This adds spins of six neighbours instead of 4 subject to
#many constraints characteristic of triangular lattices
value = 0.
value += J_nn[n,x,y,0]*spin[z, bvc(x+1), y]
value += J_nn[n,x,y,1]*spin[z, x, bvc(y+1)]
value += J_nn[n,x-1,y,0]*spin[z, x-1, y]
value += J_nn[n,x,y-1,1]*spin[z, x-1, y]
return value
def calc():
probs = random_uniform()
if (probs < math.exp(2*spin[z, x, y]*sum_nn()/T[n,l])):
spin[z, x, y] *= np.int8(-1)
if is_black==True:
if (p == 0 and q == 0) or (p == 1 and q == 1):
calc()
else:
if (p == 0 and q == 1) or (p == 1 and q == 0):
calc()
@cuda.jit
def calc_energy_sq (spin, energy, J_nn):
z = cuda.grid (1)
n = int(math.floor (z / energy.shape[1]))
l = z % energy.shape[1]
def bvc (x):
if x == spin.shape[1]:
x = 0
return x
def sum_nn_part(x, y, z): # This adds spins of six neighbours instead of 4 subject to
#many constraints characteristic of triangular lattices
value = 0.
value += J_nn[n,x,y,0]*spin[z, bvc(x+1), y]
value += J_nn[n,x,y,1]*spin[z, x, bvc(y+1)]
return value
ener = 0
if z < spin.shape[0]:
for x in range (spin.shape[1]):
for y in range (spin.shape[2]):
ener += spin[z,x,y]*sum_nn_part(x,y,z)
energy[n,l] = ener
@cuda.jit
def parallel_temper2 (T, seed, energy, perm):
z = cuda.grid(1)
m = T.shape[1]//2
n = int(math.floor (z/m))
l = z % m #Takes values between 0 and m//2
if z < seed.shape[0]//2:
rand_n = 0 if np.float32(seed[n, 0, 0]/2**31) < 0.5 else 1
ptr = 2*l + rand_n
z = 2*z + rand_n
if ptr < energy.shape[0]-1:
val0 = perm[z]
val1 = perm[z+1]
e0 = energy[n,ptr]
e1 = energy[n,ptr+1]
rand_unif = np.float32(seed[z, 1, 0] / 2**31)
arg = (e0 - e1)*((1./T[n,ptr]) - (1./T[n,ptr+1]))
if (arg < 0):
if rand_unif < math.exp(arg):
perm[z] = val1
perm[z+1] = val0
else:
perm[z] = val1
perm[z+1] = val0
def generate_train_data (train_len, prob, lat_len=48, m=100):
shape = (lat_len, lat_len)
n_ens = train_len//m
spin = cp.random.choice ([1,-1], (train_len,)+shape).astype(np.int8)
seed = cp.random.randint (-10000,10000, size=(train_len,)+shape,
dtype=np.int32)
#Jnn = cp.random.choice ([-1,1], (n_ens,)+shape+(3,),
#p=[1-prob, prob]).astype(np.float32)
energy = cp.zeros ((n_ens,m), np.float32)
tpb = (1,8,8)
bpg = (train_len, lat_len//8, lat_len//8)
perm = cp.arange (0, train_len, dtype=np.int32)
T = cp.linspace (0.5, 4.0, m, dtype=np.float32)
T = cp.broadcast_to (T, (n_ens,m))
for _ in range (500):
for _ in range (4):
update_sq [bpg,tpb] (spin, seed, T, Jnn, True, perm)
update_sq [bpg,tpb] (spin, seed, T, Jnn, True, perm)
calc_energy_sq [math.ceil(train_len/64),64] (spin, energy, Jnn)
parallel_temper2 [math.ceil(train_len/128),64] (T, seed, energy, perm)
T = cp.full ((n_ens,m), 0.5, np.float32)
for _ in range (2000):
update_sq [bpg,tpb] (spin, seed, T, Jnn, True, perm)
update_sq [bpg,tpb] (spin, seed, T, Jnn, True, perm)
calc_energy_sq [math.ceil(train_len/64),64] (spin, energy, Jnn)
spin = 0.5*cp.asnumpy (spin)
return cp.asnumpy (energy)
energy = generate_train_data (1000, 0.5)
np.sort(energy[0])
val = cp.asarray (True)
val == False
```
| true |
code
| 0.524029 | null | null | null | null |
|
[](https://colab.research.google.com/github/huggingface/education-toolkit/blob/main/02_ml-demos-with-gradio.ipynb)
💡 **Welcome!**
We’ve assembled a toolkit that university instructors and organizers can use to easily prepare labs, homework, or classes. The content is designed in a self-contained way such that it can easily be incorporated into the existing curriculum. This content is free and uses widely known Open Source technologies (`transformers`, `gradio`, etc).
Alternatively, you can request for someone on the Hugging Face team to run the tutorials for your class via the [ML demo.cratization tour](https://huggingface2.notion.site/ML-Demo-cratization-tour-with-66847a294abd4e9785e85663f5239652) initiative!
You can find all the tutorials and resources we’ve assembled [here](https://huggingface2.notion.site/Education-Toolkit-7b4a9a9d65ee4a6eb16178ec2a4f3599).
# Tutorial: Build and Host Machine Learning Demos with Gradio ⚡ & Hugging Face 🤗
**Learning goals:** The goal of this tutorial is to learn How To
1. Build a quick demo for your machine learning model in Python using the `gradio` library
2. Host the demos for free with Hugging Face Spaces
3. Add your demo to the Hugging Face org for your class or conference. This includes:
* A setup step for instructors (or conference organizers)
* Upload instructions for students (or conference participants)
**Duration**: 20-40
minutes
**Prerequisites:** Knowledge of Python and basic familiarity with machine learning
**Author**: [Abubakar Abid](https://twitter.com/abidlabs) (feel free to ping me with any questions about this tutorial)
All of these steps can be done for free! All you need is an Internet browser and a place where you can write Python 👩💻
## Why Demos?
**Demos** of machine learning models are an increasingly important part of machine learning _courses_ and _conferences_. Demos allow:
* model developers to easily **present** their work to a wide audience
* increase **reproducibility** of machine learning research
* diverse users to more easily **identify and debug** failure points of models
As a quick example of what we would like to build, check out the [Keras Org on Hugging Face](https://huggingface.co/keras-io), which includes a description card and a collection of Models and Spaces built by Keras community. Any Space can be opened in your browser and you can use the model immediately, as shown here:

## 1. Build Quick ML Demos in Python Using the Gradio Library
`gradio` is a handy Python library that lets you build web demos simply by specifying the list of input and output **components** expected by your machine learning model.
What do I mean by input and output components? Gradio comes with a bunch of predefined components for different kinds of machine learning models. Here are some examples:
* For an **image classifier**, the expected input type is an `Image` and the output type is a `Label`.
* For a **speech recognition model**, the expected input component is an `Microphone` (which lets users record from the browser) or `Audio` (which lets users drag-and-drop audio files), while the output type is `Text`.
* For a **question answering model**, we expect **2 inputs**: [`Text`, `Text`], one textbox for the paragraph and one for the question, and the output type is a single `Text` corresponding to the answer.
You get the idea... (for all of the supported components, [see the docs](https://gradio.app/docs/))
In addition to the input and output types, Gradio expects a third parameter, which is the prediction function itself. This parameter can be ***any* regular Python function** that takes in parameter(s) corresponding to the input component(s) and returns value(s) corresponding to the output component(s)
Enough words. Let's see some code!
```
# First, install Gradio
!pip install --quiet gradio
import numpy as np
def sepia(image):
sepia_filter = np.array(
[[0.393, 0.769, 0.189],
[0.349, 0.686, 0.168],
[0.272, 0.534, 0.131]]
)
sepia_img = image.dot(sepia_filter.T)
sepia_img /= sepia_img.max()
return sepia_img
import gradio as gr
# Write 1 line of Python to create a simple GUI
gr.Interface(fn=sepia, inputs="image", outputs="image").launch();
```
Running the code above should produce a simple GUI inside this notebook allowing you to type example inputs and see the output returned by your function.
Notice that we define an `Interface` using the 3 ingredients mentioned earlier:
* A function
* Input component(s)
* Output component(s)
This is a simple example for images, but the same principle holds true for any other kind of data type. For example, here is an interface that generates a musical tone when provided a few different parameters (the specific code inside `generate_tone()` is not important for the purpose of this tutorial):
```
import numpy as np
import gradio as gr
def generate_tone(note, octave, duration):
sampling_rate = 48000
a4_freq, tones_from_a4 = 440, 12 * (octave - 4) + (note - 9)
frequency = a4_freq * 2 ** (tones_from_a4 / 12)
audio = np.linspace(0, int(duration), int(duration) * sampling_rate)
audio = (20000 * np.sin(audio * (2 * np.pi * frequency))).astype(np.int16)
return sampling_rate, audio
gr.Interface(
generate_tone,
[
gr.Dropdown(["C", "C#", "D", "D#", "E", "F", "F#", "G", "G#", "A", "A#", "B"], type="index"),
gr.Slider(4, 6, step=1),
gr.Number(value=1, label="Duration in seconds"),
],
"audio",
title="Generate a Musical Tone!"
).launch()
```
**Challenge #1**: build a Gradio demo that takes in an image and returns the same image *flipped upside down* in less than 10 lines of Python code.
There are a lot more examples you can try in Gradio's [getting started page](https://gradio.app/getting_started/), which cover additional features such as:
* Adding example inputs
* Adding _state_ (e.g. for chatbots)
* Sharing demos easily using one parameter called `share` (<-- this is pretty cool 😎)
It is especially easy to demo a `transformers` model from Hugging Face's Model Hub, using the special `gr.Interface.load` method.
Let's try a text-to-speech model built by Facebook:
```
import gradio as gr
gr.Interface.load("huggingface/facebook/fastspeech2-en-ljspeech").launch();
```
Here is the code to build a demo for [GPT-J](https://huggingface.co/EleutherAI/gpt-j-6B), a large language model & add a couple of examples inputs:
```
import gradio as gr
examples = [["The Moon's orbit around Earth has"], ["There once was a pineapple"]]
gr.Interface.load("huggingface/EleutherAI/gpt-j-6B", examples=examples).launch();
```
**Challenge #2**: Go to the [Hugging Face Model Hub](https://huggingface.co/models), and pick a model that performs one of the other tasks supported in the `transformers` library (other than the two you just saw: text generation or text-to-speech). Create a Gradio demo for that model using `gr.Interface.load`.
## 2. Host the Demo (for free) on Hugging Face Spaces
Once you made a Gradio demo, you can host it permanently on Hugging Spaces very easily:
Here are the steps to that (shown in the GIF below):
A. First, create a Hugging Face account if you do not already have one, by visiting https://huggingface.co/ and clicking "Sign Up"
B. Once you are logged in, click on your profile picture and then click on "New Space" underneath it to get to this page: https://huggingface.co/new-space
C. Give your Space a name and a license. Select "Gradio" as the Space SDK, and then choose "Public" if you are fine with everyone accessing your Space and the underlying code
D. Then you will find a page that provides you instructions on how to upload your files into the Git repository for that Space. You may also need to add a `requirements.txt` file to specify any Python package dependencies.
E. Once you have pushed your files, that's it! Spaces will automatically build your Gradio demo allowing you to share it with anyone, anywhere!
You can even embed your Gradio demo on any website -- in a blog, a portfolio page, or even in a colab notebook, like I've done with a Pictionary sketch recognition model below:
```
from IPython.display import IFrame
IFrame(src='https://hf.space/gradioiframe/abidlabs/Draw/+', width=1000, height=800)
```
**Challenge #3**: Upload your Gradio demo to Hugging Face Spaces and get a permanent URL for it. Share the permanent URL with someone (a colleague, a collaborator, a friend, a user, etc.) -- what kind of feedback do you get on your machine learning model?
## 3. Add your demo to the Hugging Face org for your class or conference
#### **Setup** (for instructors or conference organizers)
A. First, create a Hugging Face account if you do not already have one, by visiting https://huggingface.co/ and clicking "Sign Up"
B. Once you are logged in, click on your profile picture and then click on "New Organization" underneath it to get to this page: https://huggingface.co/organizations/new
C. Fill out the information for your class or conference. We recommend creating a separate organization each time that a class is taught (for example, "Stanford-CS236g-20222") and for each year of the conference.
D. Your organization will be created and now now users will be able request adding themselves to your organizations by visiting the organization page.
E. Optionally, you can change the settings by clicking on the "Organization settings" button. Typically, for classes and conferences, you will want to navigate to `Settings > Members` and set the "Default role for new members" to be "write", which allows them to submit Spaces but not change the settings.
#### For students or conference participants
A. Ask your instructor / coneference organizer for the link to the Organization page if you do not already have it
B. Visit the Organization page and click "Request to join this org" button, if you are not yet part of the org.
C. Then, once you have been approved to join the organization (and built your Gradio Demo and uploaded it to Spaces -- see Sections 1 and 2), then simply go to your Space and go to `Settings > Rename or transfer this space` and then select the organization name under `New owner`. Click the button and the Space will now be added to your class or conference Space!
| true |
code
| 0.482734 | null | null | null | null |
|
# Time Domain and Gating
## Intro
This notebooks demonstrates how to use [scikit-rf](www.scikit-rf.org) for time-domain analysis and gating. A quick example is given first, followed by a more detailed explanation.
S-parameters are measured in the frequency domain, but can be analyzed in time domain if you like. In many cases, measurements are not made down to DC. This implies that the time-domain transform is not complete, but it can be very useful non-theless. A major application of time-domain analysis is to use *gating* to isolate a single response in space. More information about the details of time domain analysis see [1].
References
* [1] Agilent Time Domain Analysis Using a Network Analyzer (Application Note 1287-12) [pdf](http://cp.literature.agilent.com/litweb/pdf/5989-5723EN.pdf)
## Quick Example
```
import skrf as rf
%matplotlib inline
rf.stylely()
from pylab import *
# load data for the waveguide to CPW probe
probe = rf.Network('../metrology/oneport_tiered_calibration/probe.s2p')
# we will focus on s11
s11 = probe.s11
# time-gate the first largest reflection
s11_gated = s11.time_gate(center=0, span=.2)
s11_gated.name='gated probe'
# plot frequency and time-domain s-parameters
figure(figsize=(8,4))
subplot(121)
s11.plot_s_db()
s11_gated.plot_s_db()
title('Frequency Domain')
subplot(122)
s11.plot_s_db_time()
s11_gated.plot_s_db_time()
title('Time Domain')
tight_layout()
```
## Interpreting Time Domain
Out DUT in this example is a waveguide-to-CPW probe, that was measured in [this other example](./oneport_tiered_calibration/One Port Tiered Calibration.ipynb).
```
# load data for the waveguide to CPW probe
probe = rf.Network('../metrology/oneport_tiered_calibration/probe.s2p')
probe
```
Note there are two time-domain plotting functions in scikit-rf:
* `Network.plot_s_db_time()`
* `Network.plot_s_time_db()`
The difference is that the former, `plot_s_db_time()`, employs windowing before plotting to enhance impluse resolution. Windowing will be discussed in a bit, but for now we just use `plot_s_db_time()`.
Plotting all four s-parameters of the probe in both frequency and time-domain.
```
# plot frequency and time-domain s-parameters
figure(figsize=(8,4))
subplot(121)
probe.plot_s_db()
title('Frequency Domain')
subplot(122)
probe.plot_s_db_time()
title('Time Domain')
tight_layout()
```
Focusing on the reflection coefficient from the waveguide port (s11), you can see there is an interference pattern present.
```
probe.plot_s_db(0,0)
title('Reflection Coefficient From \nWaveguide Port')
```
This ripple is evidence of several discrete reflections. Plotting s11 in the time-domain allows us to see where, or *when*, these reflections occur.
```
probe_s11 = probe.s11
probe_s11.plot_s_db_time(0,0)
title('Reflection Coefficient From \nWaveguide Port, Time Domain')
ylim(-100,0)
```
From this plot we can see two dominant reflections;
* one at $t=0$ns (the test-port)
* and another at $t=.2$ns (who knows?).
## Gating The Reflection of Interest
To isolate the reflection from the waveguide port, we can use time-gating. This can be done by using the method `Network.time_gate()`, and provide it an appropriate center and span (in ns). To see the effects of the gate, both the original and gated reponse are compared.
```
probe_s11_gated = probe_s11.time_gate(center=0, span=.2)
probe_s11_gated.name='gated probe'
s11.plot_s_db_time()
s11_gated.plot_s_db_time()
```
Next, compare both responses in frequency domain to see the effect of the gate.
```
s11.plot_s_db()
s11_gated.plot_s_db()
```
### Auto-gate
The time-gating method in `skrf` has an auto-gating feature which can also be used to gate the largest reflection. When no gate parameters are provided, `time_gate()` does the following:
1. find the two largest peaks
* center the gate on the tallest peak
* set span to distance between two tallest peaks
You may want to plot the gated network in time-domain to see what the determined gate shape looks like.
```
title('Waveguide Interface of Probe')
s11.plot_s_db(label='original')
s11.time_gate().plot_s_db(label='autogated') #autogate on the fly
```
Might see how the autogate does on the other proben interface,
```
title('Other Interface of Probe')
probe.s22.plot_s_db()
probe.s22.time_gate().plot_s_db()
```
## Determining Distance
To make time-domain useful as a diagnostic tool, one would like to convert the x-axis to distance. This requires knowledge of the propagation velocity in the device. **skrf** provides some transmission-line models in the module [skrf.media](http://scikit-rf.readthedocs.org/en/latest/reference/media/index.html), which can be used for this.
**However...**
For dispersive media, such as rectangular waveguide, the phase velocity is a function of frequency, and transforming time to distance is not straightforward. As an approximation, you can normalize the x-axis to the speed of light.
Alternativly, you can simulate the a known device and compare the two time domain responses. This allows you to attribute quantatative meaning to the axes. For example, you could create an ideal delayed load as shown below. Note: the magnitude of a response *behind* a large impulse doesn not have meaningful units.
```
from skrf.media import RectangularWaveguide
# create a rectangular waveguide media to gererate a theoretical network
wr1p5 = RectangularWaveguide(frequency=probe.frequency,
a=15*rf.mil,z0=1)
# create an ideal delayed load, parameters are adjusted until the
# theoretical response agrees with the measurement
theory = wr1p5.delay_load(Gamma0=rf.db_2_mag(-20),
d=2.4, unit='cm')
probe.plot_s_db_time(0,0, label = 'Measurement')
theory.plot_s_db_time(label='-20dB @ 2.4cm from test-port')
ylim(-100,0)
```
This plot demonstrates a few important points:
* the theortical delayed load is not a perfect impulse in time. This is due to the dispersion in waveguide.
* the peak of the magnitude in time domain is not identical to that specified, also due to disperison (and windowing).
## What the hell is Windowing?
The `'plot_s_db_time()'` function does a few things.
1. windows the s-parameters.
* converts to time domain
* takes magnitude component, convert to dB
* calculates time-axis s
* plots
A word about step 1: **windowing**. A FFT represents a signal with a basis of periodic signals (sinusoids). If your frequency response is not periodic, which in general it isnt, taking a FFT will introduces artifacts in the time-domain results. To minimize these effects, the frequency response is *windowed*. This makes the frequency response more periodic by tapering off the band-edges.
Windowing is just applied to improve the plot appearance,d it does not affect the original network.
In skrf this can be done explicitly using the `'windowed()'` function. By default this function uses the hamming window, but can be adjusted through arguments. The result of windowing is show below.
```
probe_w = probe.windowed()
probe.plot_s_db(0,0, label = 'Original')
probe_w.plot_s_db(0,0, label = 'Windowed')
```
Comparing the two time-domain plotting functions, we can see the difference between windowed and not.
```
probe.plot_s_time_db(0,0, label = 'Original')
probe_w.plot_s_time_db(0,0, label = 'Windowed')
```
| true |
code
| 0.616301 | null | null | null | null |
|
# 第2章 最小二乗法:機械学習理論の第一歩
## 「02-square_error.py」の解説
ITエンジニアための機械学習理論入門「第2章 最小二乗法:機械学習理論の第一歩」で使用しているサンプルコード「02-square_error.py」の解説です。
※ 解説用にコードの内容は少し変更しています。
### データ数 N=10 の場合
はじめに必要なモジュールをインポートしておきます。
関数 normal は、正規分布に従う乱数を生成するために利用します。
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pandas import Series, DataFrame
from numpy.random import normal
import matplotlib
matplotlib.rcParams['font.size'] = 12
```
正弦関数に正規分布のノイズを載せたデータセットを生成する関数を定義します。
これは、0≦x≦1 の区間を等分した num 個の点 x に対して、対応する y の値を生成します。
```
# データセット {x_n,y_n} (n=1...num) を用意
def create_dataset(num):
dataset = DataFrame(columns=['x', 'y'])
for i in range(num):
x = float(i)/float(num-1)
y = np.sin(2*np.pi*x) + normal(scale=0.3)
dataset = dataset.append(Series([x, y], index=['x', 'y']),
ignore_index=True)
return dataset
```
例として、10個のデータをトレーニングセットとして生成します。
```
N=10 # サンプルを取得する位置 x の個数
train_set = create_dataset(N)
train_set
```
x と y の値のリストは、train_set.x と train_set.y で取得できます。
グラフ上にプロットすると次のようになります。
```
plt.scatter(train_set.x, train_set.y, marker='o', color='blue')
```
このデータに対して、最小二乗法でフィッティングした m 次多項式を決定する関数を用意します。
引数 dataset と m にトレーニングセットと多項式の次数を代入すると、多項式に対応する関数 f(x) のオブジェクトが返ります。
```
# 最小二乗法で解を求める
def resolve(dataset, m):
t = dataset.y
phi = DataFrame()
for i in range(0, m+1):
p = dataset.x**i
p.name="x**%d" % i
phi = pd.concat([phi, p], axis=1)
tmp = np.linalg.inv(np.dot(phi.T, phi))
ws = np.dot(np.dot(tmp, phi.T), t)
def f(x):
y = 0
for i, w in enumerate(ws):
y += w * (x ** i)
return y
return f
```
また、得られた関数 f(x) に対して、トレーニングセットに対する平方根平均二乗誤差(RMS)を求める関数を用意します。
```
# 平方根平均二乗誤差(Root mean square error)を計算
def rms_error(dataset, f):
err = 0.0
for index, line in dataset.iterrows():
x, y = line.x, line.y
err += 0.5 * (y - f(x))**2
return np.sqrt(2 * err / len(dataset))
```
これらを用いて、結果をグラフに可視化する関数が次になります。
```
def show_result(subplot, train_set, m):
f = resolve(train_set, m)
subplot.set_xlim(-0.05, 1.05)
subplot.set_ylim(-1.5, 1.5)
subplot.set_title("M=%d" % m, fontsize=10)
# トレーニングセットを表示
subplot.scatter(train_set.x, train_set.y, marker='o',
color='blue', label=None)
# 真の曲線を表示
linex = np.linspace(0, 1, 101)
liney = np.sin(2*np.pi*linex)
subplot.plot(linex, liney, color='green', linestyle='--')
# 多項式近似の曲線を表示
linex = np.linspace(0, 1, 101)
liney = f(linex)
label = "E(RMS)=%.2f" % rms_error(train_set, f)
subplot.plot(linex, liney, color='red', label=label)
subplot.legend(loc=1, fontsize=10)
```
先ほど生成したトレーニングセットを用いて、0, 1, 3, 9次多項式(定数関数)でフィッティングした結果を表示します。
```
fig = plt.figure(figsize=(10, 7))
for i, m in enumerate([0, 1, 3, 9]):
subplot = fig.add_subplot(2, 2, i+1)
show_result(subplot, train_set, m)
```
多項式の次数が上がるにつれてデータポイントの近くを通るようになり、平方根平均二乗誤差が減少していることがわかります。
ここで、トレーニングセットとテストセットに対する平方根平均二乗誤差の変化を確認します。
多項式の次数を0〜10に変化させながら、平方根平均二乗誤差のグラフを描く関数を用意します。
```
# トレーニングセットとテストセットでの誤差の変化を表示
def show_rms_trend(train_set, test_set):
df = DataFrame(columns=['Training set', 'Test set'])
for m in range(0,10): # 多項式の次数
f = resolve(train_set, m)
train_error = rms_error(train_set, f)
test_error = rms_error(test_set, f)
df = df.append(
Series([train_error, test_error],
index=['Training set','Test set']),
ignore_index=True)
df.plot(title='RMS Error', style=['-','--'], grid=True,
xticks=range(0, 10), figsize=(8, 5), ylim=(0, 0.9))
```
トレーニングセットとは独立に生成したテストセットを用意します。
```
test_set = create_dataset(N)
test_set
```
多項式の次数を0〜10に変化させながら、トレーニングセットとテストセットに対する平方根平均二条誤差を計算して、結果をグラフ表示します。
```
show_rms_trend(train_set, test_set)
```
次数が3を超えるとテストセットに対する誤差が減少しなくなることがわかります。
### データ数 N=100 の場合
同じ計算をデータ数を増やして実施してみます。
N=100 でトレーニングセットとテストセットを用意します。
```
N=100 # サンプルを取得する位置 x の個数
train_set = create_dataset(N)
test_set = create_dataset(N)
```
最小二乗法でフィッティングした結果を表示します。
```
fig = plt.figure(figsize=(10, 7))
for i, m in enumerate([0, 1, 3, 9]):
subplot = fig.add_subplot(2, 2, i+1)
show_result(subplot, train_set, m)
```
多項式の次数があがってもオーバーフィッティングが発生しにくくなっていることがわかります。
トレーニングセットとテストセットに対する平方根平均二乗誤差の変化を表示します。
```
show_rms_trend(train_set, test_set)
```
次数が3を超えると平方根平均二乗誤差が約0.3で一定になります。これは、このデータが本質的に±0.3程度の誤差を持っている事を示します。
| true |
code
| 0.411702 | null | null | null | null |
|
```
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Dense
from tensorflow.keras.preprocessing.text import Tokenizer
sentences = ['I love my dog', 'I love my cat']
tokenizer = Tokenizer(num_words = 100)
tokenizer.fit_on_texts(sentences)
word_index = tokenizer.word_index
print(word_index)
sentences = ['I love my dog', 'I love my cat',
'you love my dog!', 'do you think my dog is amazing']
tokenizer = Tokenizer(num_words = 100, oov_token = "<OOV>")
tokenizer.fit_on_texts(sentences)
word_index = tokenizer.word_index
sequences = tokenizer.texts_to_sequences(sentences)
print(word_index)
print(sequences)
```
# Padding
```
padded = pad_sequences(sequences,maxlen=6,truncating=trunc_type)
padded
```
# Embedding
show difference degree from similarity
```
#IMDB
import tensorflow_datasets as tfds
from tensorflow.keras.preprocessing.sequence import pad_sequences
padded = pad_sequences(sequences, padding='post',
truncating='post', maxlen=5)
print(padded)
imdb, info = tfds.load("imdb_reviews", with_info=True, as_supervised=True)
import numpy as np
# data are tensors foramt
train_data, test_data = imdb['train'], imdb['test']
training_sentences = []
trainging_labels = []
testing_sentences =[]
testing_labels = []
for s,l in train_data:
training_sentences.append(str(s.numpy()))
trainging_labels.append(l.numpy())
for s,l in test_data:
testing_sentences.append(str(s.numpy()))
testing_labels.append(l.numpy())
training_labels_final = np.array(trainging_labels)
testing_labels_final = np.array(testing_labels)
#Hyper parameters
vocab_size = 10000
embedding_dim = 16
max_length = 100
trunc_type = 'post'
oov_tok = '<OOV>'
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
tokenizer = Tokenizer(num_words=vocab_size, oov_token=oov_tok)
tokenizer.fit_on_texts(training_sentences)
word_index = tokenizer.word_index
sequences = tokenizer.texts_to_sequences(training_sentences)
padded = pad_sequences(sequences,maxlen=max_length,truncating=trunc_type)
testing_sentences = tokenizer.texts_to_sequences(testing_sentences)
testing_padded = pad_sequences(testing_sentences, maxlen=max_length)
reverse_word_index = dict([(value,key) for (key,value) in word_index.items()])
def decode_review(text):
return ' '.join([reverse_word_index.get(i, '?') for i in text])
print(decode_review(padded[1]))
print(training_sentences[1])
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.GlobalAveragePooling1D(),#Flatten(), #
tf.keras.layers.Dense(6, activation='relu'),
tf.keras.layers.Dense(1,activation='sigmoid')
])
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
model.summary()
num_epochs = 15
history = model.fit(padded, training_labels_final, epochs=num_epochs, validation_data=(testing_padded, testing_labels_final))
import matplotlib.pyplot as plt
def plot_graphs(history, string):
plt.plot(history.history[string])
plt.plot(history.history['val_'+string])
plt.xlabel("Epochs")
plt.ylabel(string)
plt.legend([string, 'val_'+string])
plt.show()
plot_graphs(history, 'accuracy')
plot_graphs(history, 'loss')
model.save("NlpModel.h5")
```
# LSTM
```
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(embedding_dim, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(8)),
tf.keras.layers.Dense(embedding_dim, activation='relu'),
tf.keras.layers.Dense(1,activation='sigmoid')
])
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
model.summary()
num_epochs = 15
history = model.fit(padded, training_labels_final, epochs=num_epochs, validation_data=(testing_padded, testing_labels_final))
plot_graphs(history, 'accuracy')
plot_graphs(history, 'loss')
#Layer 0 is the Embedding layer
e = model.layers[0]
weights = e.get_weights()[0]
print(weights.shape)
```
## cnn
```
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Conv1D(128,5, activation='relu'),
tf.keras.layers.GlobalAveragePooling1D(),#Flatten(), #
tf.keras.layers.Dense(embedding_dim, activation='relu'),
tf.keras.layers.Dense(1,activation='sigmoid')
])
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
model.summary()
```
# Using predifine token
```
num_epochs = 15
history = model.fit(padded, training_labels_final, epochs=num_epochs, validation_data=(testing_padded, testing_labels_final))
plot_graphs(history, 'accuracy')
plot_graphs(history, 'loss')
import tensorflow_datasets as tfds
imdb, info = tfds.load("imdb_reviews/subwords8k", with_info=True, as_supervised=True)
tokenizer = info.features['text'].encoder
```
| true |
code
| 0.69333 | null | null | null | null |
|
# TensorFlow Fold Quick Start
TensorFlow Fold is a library for turning complicated Python data structures into TensorFlow Tensors.
```
# boilerplate
import random
import tensorflow as tf
sess = tf.InteractiveSession()
import tensorflow_fold as td
```
The basic elements of Fold are *blocks*. We'll start with some blocks that work on simple data types.
```
scalar_block = td.Scalar()
vector3_block = td.Vector(3)
```
Blocks are functions with associated input and output types.
```
def block_info(block):
print("%s: %s -> %s" % (block, block.input_type, block.output_type))
block_info(scalar_block)
block_info(vector3_block)
```
We can use `eval()` to see what a block does with its input:
```
scalar_block.eval(42)
vector3_block.eval([1,2,3])
```
Not very exciting. We can compose simple blocks together with `Record`, like so:
```
record_block = td.Record({'foo': scalar_block, 'bar': vector3_block})
block_info(record_block)
```
We can see that Fold's type system is a bit richer than vanilla TF; we have tuple types! Running a record block does what you'd expect:
```
record_block.eval({'foo': 1, 'bar': [5, 7, 9]})
```
One useful thing you can do with blocks is wire them up to create pipelines using the `>>` operator, which performs function composition. For example, we can take our tuple two tensors and compose it with `Concat`, like so:
```
record2vec_block = record_block >> td.Concat()
record2vec_block.eval({'foo': 1, 'bar': [5, 7, 9]})
```
Note that because Python dicts are unordered, Fold always sorts the outputs of a record block by dictionary key. If you want preserve order you can construct a Record block from an OrderedDict.
The whole point of Fold is to get your data into TensorFlow; the `Function` block lets you convert a TITO (Tensors On, Tensors Out) function to a block:
```
negative_block = record2vec_block >> td.Function(tf.negative)
negative_block.eval({'foo': 1, 'bar': [5, 7, 9]})
```
This is all very cute, but where's the beef? Things start to get interesting when our inputs contain sequences of indeterminate length. The `Map` block comes in handy here:
```
map_scalars_block = td.Map(td.Scalar())
```
There's no TF type for sequences of indeterminate length, but Fold has one:
```
block_info(map_scalars_block)
```
Right, but you've done the TF [RNN Tutorial](https://www.tensorflow.org/tutorials/recurrent/) and even poked at [seq-to-seq](https://www.tensorflow.org/tutorials/seq2seq/). You're a wizard with [dynamic rnns](https://www.tensorflow.org/api_docs/python/nn/recurrent_neural_networks#dynamic_rnn). What does Fold offer?
Well, how about jagged arrays?
```
jagged_block = td.Map(td.Map(td.Scalar()))
block_info(jagged_block)
```
The Fold type system is fully compositional; any block you can create can be composed with `Map` to create a sequence, or `Record` to create a tuple, or both to create sequences of tuples or tuples of sequences:
```
seq_of_tuples_block = td.Map(td.Record({'foo': td.Scalar(), 'bar': td.Scalar()}))
seq_of_tuples_block.eval([{'foo': 1, 'bar': 2}, {'foo': 3, 'bar': 4}])
tuple_of_seqs_block = td.Record({'foo': td.Map(td.Scalar()), 'bar': td.Map(td.Scalar())})
tuple_of_seqs_block.eval({'foo': range(3), 'bar': range(7)})
```
Most of the time, you'll eventually want to get one or more tensors out of your sequence, for wiring up to your particular learning task. Fold has a bunch of built-in reduction functions for this that do more or less what you'd expect:
```
((td.Map(td.Scalar()) >> td.Sum()).eval(range(10)),
(td.Map(td.Scalar()) >> td.Min()).eval(range(10)),
(td.Map(td.Scalar()) >> td.Max()).eval(range(10)))
```
The general form of such functions is `Reduce`:
```
(td.Map(td.Scalar()) >> td.Reduce(td.Function(tf.multiply))).eval(range(1,10))
```
If the order of operations is important, you should use `Fold` instead of `Reduce` (but if you can use `Reduce` you should, because it will be faster):
```
((td.Map(td.Scalar()) >> td.Fold(td.Function(tf.divide), tf.ones([]))).eval(range(1,5)),
(td.Map(td.Scalar()) >> td.Reduce(td.Function(tf.divide), tf.ones([]))).eval(range(1,5))) # bad, not associative!
```
Now, let's do some learning! This is the part where "magic" happens; if you want a deeper understanding of what's happening here you might want to jump right to our more formal [blocks tutorial](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/blocks.md) or learn more about [running blocks in TensorFlow](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/running.md)
```
def reduce_net_block():
net_block = td.Concat() >> td.FC(20) >> td.FC(1, activation=None) >> td.Function(lambda xs: tf.squeeze(xs, axis=1))
return td.Map(td.Scalar()) >> td.Reduce(net_block)
```
The `reduce_net_block` function creates a block (`net_block` that contains a two-layer fully connected (FC) network that takes a pair of scalar tensors as input and produces a scalar tensor as output. This network gets applied in a binary tree to reduce a sequence of scalar tensors to a single scalar tensor.
One thing to notice here is that we are calling [`tf.squeeze`](https://www.tensorflow.org/versions/r1.0/api_docs/python/array_ops/shapes_and_shaping#squeeze) with `axis=1`, even though the Fold output type of `td.FC(1, activation=None)` (and hence the input type of the enclosing `Function` block) is a `TensorType` with shape `(1)`). This is because all Fold blocks actually run on TF tensors with an implicit leading batch dimension, which enables execution via [*dynamic batching*](https://openreview.net/pdf?id=ryrGawqex). It is important to bear this in mind when creating `Function` blocks that wrap functions that are not applied elementwise.
```
def random_example(fn):
length = random.randrange(1, 10)
data = [random.uniform(0,1) for _ in range(length)]
result = fn(data)
return data, result
```
The `random_example` function generates training data consisting of `(example, fn(example)` pairs, where `example` is a random list of numbers, e.g.:
```
random_example(sum)
random_example(min)
def train(fn, batch_size=100):
net_block = reduce_net_block()
compiler = td.Compiler.create((net_block, td.Scalar()))
y, y_ = compiler.output_tensors
loss = tf.nn.l2_loss(y - y_)
train = tf.train.AdamOptimizer().minimize(loss)
sess.run(tf.global_variables_initializer())
validation_fd = compiler.build_feed_dict(random_example(fn) for _ in range(1000))
for i in range(2000):
sess.run(train, compiler.build_feed_dict(random_example(fn) for _ in range(batch_size)))
if i % 100 == 0:
print(i, sess.run(loss, validation_fd))
return net_block
```
Now we're going to train a neural network to approximate a reduction function of our choosing. Calling `eval()` repeatedly is super-slow and cannot exploit batch-wise parallelism, so we create a [`Compiler`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#compiler). See our page on [running blocks in TensorFlow](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/running.md) for more on Compilers and how to use them effectively.
```
sum_block = train(sum)
sum_block.eval([1, 1])
```
Breaking news; deep neural network learns to calculate 1 + 1!!!!
Of course we've done something a little sneaky here by constructing a model that can only represent associative functions and then training it to compute an associative function. The technical term for being sneaky in machine learning is [inductive bias](https://en.wikipedia.org/wiki/Inductive_bias).
```
min_block = train(min)
min_block.eval([2, -1, 4])
```
Oh noes! What went wrong? Note that we trained our network to compute `min` on positive numbers; negative numbers are outside of it's input distribution.
```
min_block.eval([0.3, 0.2, 0.9])
```
Well, that's better. What happens if you train the network on negative numbers as well as on positives? What if you only train on short lists and then evaluate the net on long ones? What if you used a `Fold` block instead of a `Reduce`? ... Happy Folding!
| true |
code
| 0.653376 | null | null | null | null |
|
### This is a simple/fast tutorial for creating experiments
```
from scheduling_functions import *
from scheduling_algorithms import *
import numpy as np
import sys
import copy
from random import sample, randint, seed
from math import isclose, ceil, floor
from statistics import mean
from decimal import *
from fractions import *
import matplotlib.pyplot as plt
from operator import add
```
## General instructions/restrictions
1. Usually job instances are denoted by J_something. They are python dictionaries in which every element is a tuple (job_weight, release_time, deadline). By convention we will refer to the job that arrives at time t as the job with id (key in the dictionary representation) t+1.
2. __Job weights should be integers >=0__.
3. The robustness parameter epsilon should be rational, e.g. epsilon = Fraction(1,10). Most internal operations in the scheduling libraries use the __fraction module__ to avoid errors due to arithmetic precision.
4. To create a job instance easily, use the job_instance_creation function, the inputs should be a weights list, and D. The i-th element of the weights list (ws[i-1]) represents the job which is released at time i-1.
5. To create a bounded random walk as described in the paper, use random_walk_creation
6. The functions __AVR_energy_ratio__, __OA_energy_ratio__, __BKP_energy_ratio__ and __LAS_energy_ratio__ take as input a job instance as described before and give as output the competitive ratios of the respective algorithms.
```
#creates a bounded random walk:
def random_walk_creation(num_jobs, step_size, random_seed, m, M):
seed(random_seed)
ws = [0]*num_jobs
ws[0] = randint(m,M)
steps = [randint(-step_size,step_size) for i in range(1,num_jobs)]
for i in range(1, num_jobs):
ws[i] = ws[i-1] + steps[i-1]
ws[i] = min(ws[i], M)
ws[i] = max(ws[i], m)
return ws
#creates a job instance given a list of weights and T
def job_instance_creation(ws, T):
# dictionary: key --> job id
# value --> (weight, release time , deadline)
J = {}
job_id = 1
i = 0
for job_weight in ws:
J[job_id] = (job_weight , i, i+T)
i+=1
job_id+=1
return J
#returns the energy ratio AVR_energy/Optimal_energy
def AVR_energy_ratio(_J, alpha):
J = copy.deepcopy(_J)
#speed list of average rate
AVR_speed_list = Avg_rate(J)
#energy consumption of AVR
energy_AVR = compute_energy(AVR_speed_list, alpha)
J = copy.deepcopy(_J)
#speed list of the optimal schedule
optimal_alg_speed_list, _ = Optimal_Alg(J)
#energy consumption of the optimal schedule
energy_optimal = compute_energy(optimal_alg_speed_list, alpha)
return float(energy_AVR)/energy_optimal
#returns the energy ratio OA_energy/Optimal_energy
def OA_energy_ratio(_J, alpha):
J = copy.deepcopy(_J)
#speed list of Optimal Available
OA_speed_list = OptimalOnline(J)
#energy consumption of Optimal Available
energy_OA = sum([s**alpha for s in OA_speed_list])
J = copy.deepcopy(_J)
#speed list of the optimal schedule
optimal_alg_speed_list, _ = Optimal_Alg(J)
#energy consumption of the optimal schedule
energy_optimal = compute_energy(optimal_alg_speed_list, alpha)
return float(energy_OA)/energy_optimal
#returns the energy ratio BKP_energy/Optimal_energy
def BKP_energy_ratio(_J, granularity, alpha):
J = copy.deepcopy(_J)
#energy consumption of the BKP algorithm
energy_BKP = BKP_alg(J, granularity, alpha)
J = copy.deepcopy(_J)
#speed list of the optimal schedule
optimal_alg_speed_list, _ = Optimal_Alg(J)
#energy consumption of the optimal schedule
energy_optimal = compute_energy(optimal_alg_speed_list, alpha)
return float(energy_BKP)/energy_optimal
#returns the energy ratio LAS_energy/Optimal_energy
def LAS_energy_ratio(_J_true, _J_pred, epsilon, alpha, dt):
#compute energy of LAS algorithm
J_true = copy.deepcopy(_J_true)
J_pred = copy.deepcopy(_J_pred)
speed_sol = LAS(J_pred, J_true, epsilon, dt, alpha)
energy_LAS = sum([s**alpha for s in speed_sol])*dt
#compute speedlist and energu consumption of the optimal schedule of the true instance
J_true = copy.deepcopy(_J_true)
J_pred = copy.deepcopy(_J_pred)
optimal_alg_speed_list, _ = Optimal_Alg(J_true)
energy_optimal = compute_energy(optimal_alg_speed_list, alpha)
return float(energy_LAS)/energy_optimal
```
### First experiment
#### parameters setting
```
num_jobs = 80
D = 10
alpha = 3
epsilon = Fraction(1,20)
dt = 0.01
bkp_granularity = 0.25
```
#### we create a random ground truth instance
```
w_min = 10
w_max = 100
w_true = [randint(w_min,w_max) for _ in range(0,num_jobs)]
J_true = job_instance_creation(w_true, D)
```
#### we create a very accurate predictor by adding pointwise a small integer error between [-3,3]
```
s = 3
error = [randint(-s,s) for _ in range(0,num_jobs)]
w_pred = list(map(add,w_true, error))
J_pred = job_instance_creation(w_pred, D)
```
#### now we will calculate the competitive ratio of the online algorithms AVR, OA and BKP
```
AVR = AVR_energy_ratio(J_true, alpha)
print("AVR competitive ratio: ", AVR)
OA = OA_energy_ratio(J_true, alpha)
print("OA competitive ratio: ", OA)
BKP = BKP_energy_ratio(J_true, bkp_granularity, alpha)
print("BKP competitive ratio: ", BKP)
```
#### now we will calculate the competitive ratio of LAS algorithm with $\epsilon = 1/20$
```
LAS_ratio = LAS_energy_ratio(J_true, J_pred, epsilon, alpha, dt)
print("LAS competitive ratio: ", LAS_ratio)
```
#### we will repeat the experiment by using a perfect predictor and LAS algorithm with $\epsilon = 1/20$
```
LAS_ratio = LAS_energy_ratio(J_true, J_true, epsilon, alpha, dt)
print("LAS competitive ratio: ", LAS_ratio)
```
### Second experiment
#### we will create an instance which mimics a bounded random walk and an accurate predictor
```
M = 100
m = 10
random_seed = 10
step_size = 10
s = 10
w_true = random_walk_creation(num_jobs, step_size, random_seed, m, M)
J_true = job_instance_creation(w_true, D)
error = [randint(-s,s) for _ in range(0,num_jobs)]
w_pred = list(map(add,w_true, error))
J_pred = job_instance_creation(w_pred, D)
```
#### we will plot the weights of the true and the predicted instance
```
x = range(0, num_jobs)
plt.plot(x, w_true, label = "True instance")
plt.plot(x, w_pred, label = "Predicted instance")
plt.legend(loc="upper left")
plt.show()
```
#### performance of LAS with $\epsilon = 1/20$
```
LAS_ratio = LAS_energy_ratio(J_true, J_pred, epsilon, alpha, dt)
print("LAS competitive ratio: ", LAS_ratio)
```
| true |
code
| 0.653099 | null | null | null | null |
|
# About this Notebook
---
**Bayesian Gaussian CP decomposition** (or **BGCP** for short) is a type of Bayesian tensor decomposition that achieves state-of-the-art results on challenging the missing data imputation problem. In the following, we will discuss:
- What the Bayesian Gaussian CP decomposition is.
- How to implement BGCP mainly using Python `numpy` with high efficiency.
- How to make imputations with real-world spatiotemporal datasets.
If you want to understand BGCP and its modeling tricks in detail, our paper is for you:
> Xinyu Chen, Zhaocheng He, Lijun Sun (2019). **A Bayesian tensor decomposition approach for spatiotemporal traffic data imputation**. Transportation Research Part C: Emerging Technologies, 98: 73-84. [[**data**](https://doi.org/10.5281/zenodo.1205228)] [[**Matlab code**](https://github.com/lijunsun/bgcp_imputation)]
## Quick Run
This notebook is publicly available for any usage at our data imputation project. Please click [**transdim - GitHub**](https://github.com/xinychen/transdim).
We start by importing the necessary dependencies. We will make use of `numpy` and `scipy`.
```
import numpy as np
from numpy.random import multivariate_normal as mvnrnd
from scipy.stats import wishart
from numpy.linalg import inv as inv
```
# Part 1: Matrix Computation Concepts
## 1) Kronecker product
- **Definition**:
Given two matrices $A\in\mathbb{R}^{m_1\times n_1}$ and $B\in\mathbb{R}^{m_2\times n_2}$, then, the **Kronecker product** between these two matrices is defined as
$$A\otimes B=\left[ \begin{array}{cccc} a_{11}B & a_{12}B & \cdots & a_{1m_2}B \\ a_{21}B & a_{22}B & \cdots & a_{2m_2}B \\ \vdots & \vdots & \ddots & \vdots \\ a_{m_11}B & a_{m_12}B & \cdots & a_{m_1m_2}B \\ \end{array} \right]$$
where the symbol $\otimes$ denotes Kronecker product, and the size of resulted $A\otimes B$ is $(m_1m_2)\times (n_1n_2)$ (i.e., $m_1\times m_2$ columns and $n_1\times n_2$ rows).
- **Example**:
If $A=\left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \\ \end{array} \right]$ and $B=\left[ \begin{array}{ccc} 5 & 6 & 7\\ 8 & 9 & 10 \\ \end{array} \right]$, then, we have
$$A\otimes B=\left[ \begin{array}{cc} 1\times \left[ \begin{array}{ccc} 5 & 6 & 7\\ 8 & 9 & 10\\ \end{array} \right] & 2\times \left[ \begin{array}{ccc} 5 & 6 & 7\\ 8 & 9 & 10\\ \end{array} \right] \\ 3\times \left[ \begin{array}{ccc} 5 & 6 & 7\\ 8 & 9 & 10\\ \end{array} \right] & 4\times \left[ \begin{array}{ccc} 5 & 6 & 7\\ 8 & 9 & 10\\ \end{array} \right] \\ \end{array} \right]$$
$$=\left[ \begin{array}{cccccc} 5 & 6 & 7 & 10 & 12 & 14 \\ 8 & 9 & 10 & 16 & 18 & 20 \\ 15 & 18 & 21 & 20 & 24 & 28 \\ 24 & 27 & 30 & 32 & 36 & 40 \\ \end{array} \right]\in\mathbb{R}^{4\times 6}.$$
## 2) Khatri-Rao product (`kr_prod`)
- **Definition**:
Given two matrices $A=\left( \boldsymbol{a}_1,\boldsymbol{a}_2,...,\boldsymbol{a}_r \right)\in\mathbb{R}^{m\times r}$ and $B=\left( \boldsymbol{b}_1,\boldsymbol{b}_2,...,\boldsymbol{b}_r \right)\in\mathbb{R}^{n\times r}$ with same number of columns, then, the **Khatri-Rao product** (or **column-wise Kronecker product**) between $A$ and $B$ is given as follows,
$$A\odot B=\left( \boldsymbol{a}_1\otimes \boldsymbol{b}_1,\boldsymbol{a}_2\otimes \boldsymbol{b}_2,...,\boldsymbol{a}_r\otimes \boldsymbol{b}_r \right)\in\mathbb{R}^{(mn)\times r},$$
where the symbol $\odot$ denotes Khatri-Rao product, and $\otimes$ denotes Kronecker product.
- **Example**:
If $A=\left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \\ \end{array} \right]=\left( \boldsymbol{a}_1,\boldsymbol{a}_2 \right) $ and $B=\left[ \begin{array}{cc} 5 & 6 \\ 7 & 8 \\ 9 & 10 \\ \end{array} \right]=\left( \boldsymbol{b}_1,\boldsymbol{b}_2 \right) $, then, we have
$$A\odot B=\left( \boldsymbol{a}_1\otimes \boldsymbol{b}_1,\boldsymbol{a}_2\otimes \boldsymbol{b}_2 \right) $$
$$=\left[ \begin{array}{cc} \left[ \begin{array}{c} 1 \\ 3 \\ \end{array} \right]\otimes \left[ \begin{array}{c} 5 \\ 7 \\ 9 \\ \end{array} \right] & \left[ \begin{array}{c} 2 \\ 4 \\ \end{array} \right]\otimes \left[ \begin{array}{c} 6 \\ 8 \\ 10 \\ \end{array} \right] \\ \end{array} \right]$$
$$=\left[ \begin{array}{cc} 5 & 12 \\ 7 & 16 \\ 9 & 20 \\ 15 & 24 \\ 21 & 32 \\ 27 & 40 \\ \end{array} \right]\in\mathbb{R}^{6\times 2}.$$
```
def kr_prod(a, b):
return np.einsum('ir, jr -> ijr', a, b).reshape(a.shape[0] * b.shape[0], -1)
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8], [9, 10]])
print(kr_prod(A, B))
```
## 3) CP decomposition
### CP Combination (`cp_combine`)
- **Definition**:
The CP decomposition factorizes a tensor into a sum of outer products of vectors. For example, for a third-order tensor $\mathcal{Y}\in\mathbb{R}^{m\times n\times f}$, the CP decomposition can be written as
$$\hat{\mathcal{Y}}=\sum_{s=1}^{r}\boldsymbol{u}_{s}\circ\boldsymbol{v}_{s}\circ\boldsymbol{x}_{s},$$
or element-wise,
$$\hat{y}_{ijt}=\sum_{s=1}^{r}u_{is}v_{js}x_{ts},\forall (i,j,t),$$
where vectors $\boldsymbol{u}_{s}\in\mathbb{R}^{m},\boldsymbol{v}_{s}\in\mathbb{R}^{n},\boldsymbol{x}_{s}\in\mathbb{R}^{f}$ are columns of factor matrices $U\in\mathbb{R}^{m\times r},V\in\mathbb{R}^{n\times r},X\in\mathbb{R}^{f\times r}$, respectively. The symbol $\circ$ denotes vector outer product.
- **Example**:
Given matrices $U=\left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \\ \end{array} \right]\in\mathbb{R}^{2\times 2}$, $V=\left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{array} \right]\in\mathbb{R}^{3\times 2}$ and $X=\left[ \begin{array}{cc} 1 & 5 \\ 2 & 6 \\ 3 & 7 \\ 4 & 8 \\ \end{array} \right]\in\mathbb{R}^{4\times 2}$, then if $\hat{\mathcal{Y}}=\sum_{s=1}^{r}\boldsymbol{u}_{s}\circ\boldsymbol{v}_{s}\circ\boldsymbol{x}_{s}$, then, we have
$$\hat{Y}_1=\hat{\mathcal{Y}}(:,:,1)=\left[ \begin{array}{ccc} 31 & 42 & 65 \\ 63 & 86 & 135 \\ \end{array} \right],$$
$$\hat{Y}_2=\hat{\mathcal{Y}}(:,:,2)=\left[ \begin{array}{ccc} 38 & 52 & 82 \\ 78 & 108 & 174 \\ \end{array} \right],$$
$$\hat{Y}_3=\hat{\mathcal{Y}}(:,:,3)=\left[ \begin{array}{ccc} 45 & 62 & 99 \\ 93 & 130 & 213 \\ \end{array} \right],$$
$$\hat{Y}_4=\hat{\mathcal{Y}}(:,:,4)=\left[ \begin{array}{ccc} 52 & 72 & 116 \\ 108 & 152 & 252 \\ \end{array} \right].$$
```
def cp_combine(U, V, X):
return np.einsum('is, js, ts -> ijt', U, V, X)
U = np.array([[1, 2], [3, 4]])
V = np.array([[1, 3], [2, 4], [5, 6]])
X = np.array([[1, 5], [2, 6], [3, 7], [4, 8]])
print(cp_combine(U, V, X))
print()
print('tensor size:')
print(cp_combine(U, V, X).shape)
```
## 4) Tensor Unfolding (`ten2mat`)
Using numpy reshape to perform 3rd rank tensor unfold operation. [[**link**](https://stackoverflow.com/questions/49970141/using-numpy-reshape-to-perform-3rd-rank-tensor-unfold-operation)]
```
def ten2mat(tensor, mode):
return np.reshape(np.moveaxis(tensor, mode, 0), (tensor.shape[mode], -1), order = 'F')
X = np.array([[[1, 2, 3, 4], [3, 4, 5, 6]],
[[5, 6, 7, 8], [7, 8, 9, 10]],
[[9, 10, 11, 12], [11, 12, 13, 14]]])
print('tensor size:')
print(X.shape)
print('original tensor:')
print(X)
print()
print('(1) mode-1 tensor unfolding:')
print(ten2mat(X, 0))
print()
print('(2) mode-2 tensor unfolding:')
print(ten2mat(X, 1))
print()
print('(3) mode-3 tensor unfolding:')
print(ten2mat(X, 2))
```
## 5) Computing Covariance Matrix (`cov_mat`)
For any matrix $X\in\mathbb{R}^{m\times n}$, `cov_mat` can return a $n\times n$ covariance matrix for special use in the following.
```
def cov_mat(mat):
dim1, dim2 = mat.shape
new_mat = np.zeros((dim2, dim2))
mat_bar = np.mean(mat, axis = 0)
for i in range(dim1):
new_mat += np.einsum('i, j -> ij', mat[i, :] - mat_bar, mat[i, :] - mat_bar)
return new_mat
```
# Part 2: Bayesian Gaussian CP decomposition (BGCP)
## 1) Model Description
#### Gaussian assumption
Given a matrix $\mathcal{Y}\in\mathbb{R}^{m\times n\times f}$ which suffers from missing values, then the factorization can be applied to reconstruct the missing values within $\mathcal{Y}$ by
$$y_{ijt}\sim\mathcal{N}\left(\sum_{s=1}^{r}u_{is} v_{js} x_{ts},\tau^{-1}\right),\forall (i,j,t),$$
where vectors $\boldsymbol{u}_{s}\in\mathbb{R}^{m},\boldsymbol{v}_{s}\in\mathbb{R}^{n},\boldsymbol{x}_{s}\in\mathbb{R}^{f}$ are columns of latent factor matrices, and $u_{is},v_{js},x_{ts}$ are their elements. The precision term $\tau$ is an inverse of Gaussian variance.
#### Bayesian framework
Based on the Gaussian assumption over tensor elements $y_{ijt},(i,j,t)\in\Omega$ (where $\Omega$ is a index set indicating observed tensor elements), the conjugate priors of model parameters (i.e., latent factors and precision term) and hyperparameters are given as
$$\boldsymbol{u}_{i}\sim\mathcal{N}\left(\boldsymbol{\mu}_{u},\Lambda_{u}^{-1}\right),\forall i,$$
$$\boldsymbol{v}_{j}\sim\mathcal{N}\left(\boldsymbol{\mu}_{v},\Lambda_{v}^{-1}\right),\forall j,$$
$$\boldsymbol{x}_{t}\sim\mathcal{N}\left(\boldsymbol{\mu}_{x},\Lambda_{x}^{-1}\right),\forall t,$$
$$\tau\sim\text{Gamma}\left(a_0,b_0\right),$$
$$\boldsymbol{\mu}_{u}\sim\mathcal{N}\left(\boldsymbol{\mu}_0,\left(\beta_0\Lambda_u\right)^{-1}\right),\Lambda_u\sim\mathcal{W}\left(W_0,\nu_0\right),$$
$$\boldsymbol{\mu}_{v}\sim\mathcal{N}\left(\boldsymbol{\mu}_0,\left(\beta_0\Lambda_v\right)^{-1}\right),\Lambda_v\sim\mathcal{W}\left(W_0,\nu_0\right),$$
$$\boldsymbol{\mu}_{x}\sim\mathcal{N}\left(\boldsymbol{\mu}_0,\left(\beta_0\Lambda_x\right)^{-1}\right),\Lambda_x\sim\mathcal{W}\left(W_0,\nu_0\right).$$
## 2) Posterior Inference
In the following, we will apply Gibbs sampling to implement our Bayesian inference for the matrix factorization task.
#### - Sampling latent factors $\boldsymbol{u}_{i},i\in\left\{1,2,...,m\right\}$
Draw $\boldsymbol{u}_{i}\sim\mathcal{N}\left(\boldsymbol{\mu}_i^{*},(\Lambda_{i}^{*})^{-1}\right)$ with following parameters:
$$\boldsymbol{\mu}_{i}^{*}=\left(\Lambda_{i}^{*}\right)^{-1}\left\{\tau\sum_{j,t:(i,j,t)\in\Omega}y_{ijt}\left(\boldsymbol{v}_{j}\circledast\boldsymbol{x}_{t}\right)+\Lambda_u\boldsymbol{\mu}_u\right\},$$
$$\Lambda_{i}^{*}=\tau\sum_{j,t:(i,j,t)\in\Omega}\left(\boldsymbol{v}_{j}\circledast\boldsymbol{x}_{t}\right)\left(\boldsymbol{v}_{j}\circledast\boldsymbol{x}_{t}\right)^{T}+\Lambda_u.$$
#### - Sampling latent factors $\boldsymbol{v}_{j},j\in\left\{1,2,...,n\right\}$
Draw $\boldsymbol{v}_{j}\sim\mathcal{N}\left(\boldsymbol{\mu}_j^{*},(\Lambda_{j}^{*})^{-1}\right)$ with following parameters:
$$\boldsymbol{\mu}_{j}^{*}=\left(\Lambda_{j}^{*}\right)^{-1}\left\{\tau\sum_{i,t:(i,j,t)\in\Omega}y_{ijt}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{x}_{t}\right)+\Lambda_v\boldsymbol{\mu}_v\right\}$$
$$\Lambda_{j}^{*}=\tau\sum_{i,t:(i,j,t)\in\Omega}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{x}_{t}\right)\left(\boldsymbol{u}_{i}\circledast\boldsymbol{x}_{t}\right)^{T}+\Lambda_v.$$
#### - Sampling latent factors $\boldsymbol{x}_{t},t\in\left\{1,2,...,f\right\}$
Draw $\boldsymbol{x}_{t}\sim\mathcal{N}\left(\boldsymbol{\mu}_t^{*},(\Lambda_{t}^{*})^{-1}\right)$ with following parameters:
$$\boldsymbol{\mu}_{t}^{*}=\left(\Lambda_{t}^{*}\right)^{-1}\left\{\tau\sum_{i,j:(i,j,t)\in\Omega}y_{ijt}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)+\Lambda_x\boldsymbol{\mu}_x\right\}$$
$$\Lambda_{t}^{*}=\tau\sum_{i,j:(i,j,t)\in\Omega}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)^{T}+\Lambda_x.$$
#### - Sampling precision term $\tau$
Draw $\tau\in\text{Gamma}\left(a^{*},b^{*}\right)$ with following parameters:
$$a^{*}=a_0+\frac{1}{2}|\Omega|,~b^{*}=b_0+\frac{1}{2}\sum_{(i,j,t)\in\Omega}\left(y_{ijt}-\sum_{s=1}^{r}u_{is}v_{js}x_{ts}\right)^2.$$
#### - Sampling hyperparameters $\left(\boldsymbol{\mu}_{u},\Lambda_{u}\right)$
Draw
- $\Lambda_{u}\sim\mathcal{W}\left(W_u^{*},\nu_u^{*}\right)$
- $\boldsymbol{\mu}_{u}\sim\mathcal{N}\left(\boldsymbol{\mu}_{u}^{*},\left(\beta_u^{*}\Lambda_u\right)^{-1}\right)$
with following parameters:
$$\boldsymbol{\mu}_{u}^{*}=\frac{m\boldsymbol{\bar{u}}+\beta_0\boldsymbol{\mu}_0}{m+\beta_0},~\beta_u^{*}=m+\beta_0,~\nu_u^{*}=m+\nu_0,$$
$$\left(W_u^{*}\right)^{-1}=W_0^{-1}+mS_u+\frac{m\beta_0}{m+\beta_0}\left(\boldsymbol{\bar{u}}-\boldsymbol{\mu}_0\right)\left(\boldsymbol{\bar{u}}-\boldsymbol{\mu}_0\right)^T,$$
where $\boldsymbol{\bar{u}}=\sum_{i=1}^{m}\boldsymbol{u}_{i},~S_u=\frac{1}{m}\sum_{i=1}^{m}\left(\boldsymbol{u}_{i}-\boldsymbol{\bar{u}}\right)\left(\boldsymbol{u}_{i}-\boldsymbol{\bar{u}}\right)^T$.
#### - Sampling hyperparameters $\left(\boldsymbol{\mu}_{v},\Lambda_{v}\right)$
Draw
- $\Lambda_{v}\sim\mathcal{W}\left(W_v^{*},\nu_v^{*}\right)$
- $\boldsymbol{\mu}_{v}\sim\mathcal{N}\left(\boldsymbol{\mu}_{v}^{*},\left(\beta_v^{*}\Lambda_v\right)^{-1}\right)$
with following parameters:
$$\boldsymbol{\mu}_{v}^{*}=\frac{n\boldsymbol{\bar{v}}+\beta_0\boldsymbol{\mu}_0}{n+\beta_0},~\beta_v^{*}=n+\beta_0,~\nu_v^{*}=n+\nu_0,$$
$$\left(W_v^{*}\right)^{-1}=W_0^{-1}+nS_v+\frac{n\beta_0}{n+\beta_0}\left(\boldsymbol{\bar{v}}-\boldsymbol{\mu}_0\right)\left(\boldsymbol{\bar{v}}-\boldsymbol{\mu}_0\right)^T,$$
where $\boldsymbol{\bar{v}}=\sum_{j=1}^{n}\boldsymbol{v}_{j},~S_v=\frac{1}{n}\sum_{j=1}^{n}\left(\boldsymbol{v}_{j}-\boldsymbol{\bar{v}}\right)\left(\boldsymbol{v}_{j}-\boldsymbol{\bar{v}}\right)^T$.
#### - Sampling hyperparameters $\left(\boldsymbol{\mu}_{x},\Lambda_{x}\right)$
Draw
- $\Lambda_{x}\sim\mathcal{W}\left(W_x^{*},\nu_x^{*}\right)$
- $\boldsymbol{\mu}_{x}\sim\mathcal{N}\left(\boldsymbol{\mu}_{x}^{*},\left(\beta_x^{*}\Lambda_x\right)^{-1}\right)$
with following parameters:
$$\boldsymbol{\mu}_{x}^{*}=\frac{f\boldsymbol{\bar{x}}+\beta_0\boldsymbol{\mu}_0}{f+\beta_0},~\beta_x^{*}=f+\beta_0,~\nu_x^{*}=f+\nu_0,$$
$$\left(W_x^{*}\right)^{-1}=W_0^{-1}+fS_x+\frac{f\beta_0}{f+\beta_0}\left(\boldsymbol{\bar{x}}-\boldsymbol{\mu}_0\right)\left(\boldsymbol{\bar{x}}-\boldsymbol{\mu}_0\right)^T,$$
where $\boldsymbol{\bar{x}}=\sum_{t=1}^{f}\boldsymbol{x}_{t},~S_x=\frac{1}{f}\sum_{t=1}^{f}\left(\boldsymbol{x}_{t}-\boldsymbol{\bar{x}}\right)\left(\boldsymbol{x}_{t}-\boldsymbol{\bar{x}}\right)^T$.
```
def BGCP(dense_tensor, sparse_tensor, init, rank, maxiter1, maxiter2):
"""Bayesian Gaussian CP (BGCP) decomposition."""
dim1, dim2, dim3 = sparse_tensor.shape
binary_tensor = np.zeros((dim1, dim2, dim3))
dim = np.array([dim1, dim2, dim3])
pos = np.where((dense_tensor != 0) & (sparse_tensor == 0))
position = np.where(sparse_tensor != 0)
binary_tensor[position] = 1
U = init["U"]
V = init["V"]
X = init["X"]
beta0 = 1
nu0 = rank
mu0 = np.zeros((rank))
W0 = np.eye(rank)
tau = 1
alpha = 1e-6
beta = 1e-6
U_plus = np.zeros((dim1, rank))
V_plus = np.zeros((dim2, rank))
X_plus = np.zeros((dim3, rank))
tensor_hat_plus = np.zeros((dim1, dim2, dim3))
for iters in range(maxiter1):
for order in range(dim.shape[0]):
if order == 0:
mat = U.copy()
elif order == 1:
mat = V.copy()
else:
mat = X.copy()
mat_bar = np.mean(mat, axis = 0)
var_mu_hyper = (dim[order] * mat_bar + beta0 * mu0)/(dim[order] + beta0)
var_W_hyper = inv(inv(W0) + cov_mat(mat) + dim[order] * beta0/(dim[order] + beta0)
* np.outer(mat_bar - mu0, mat_bar - mu0))
var_Lambda_hyper = wishart(df = dim[order] + nu0, scale = var_W_hyper, seed = None).rvs()
var_mu_hyper = mvnrnd(var_mu_hyper, inv((dim[order] + beta0) * var_Lambda_hyper))
if order == 0:
var1 = kr_prod(X, V).T
elif order == 1:
var1 = kr_prod(X, U).T
else:
var1 = kr_prod(V, U).T
var2 = kr_prod(var1, var1)
var3 = (tau * np.matmul(var2, ten2mat(binary_tensor, order).T).reshape([rank, rank, dim[order]])
+ np.dstack([var_Lambda_hyper] * dim[order]))
var4 = (tau * np.matmul(var1, ten2mat(sparse_tensor, order).T)
+ np.dstack([np.matmul(var_Lambda_hyper, var_mu_hyper)] * dim[order])[0, :, :])
for i in range(dim[order]):
var_Lambda = var3[ :, :, i]
inv_var_Lambda = inv((var_Lambda + var_Lambda.T)/2)
vec = mvnrnd(np.matmul(inv_var_Lambda, var4[:, i]), inv_var_Lambda)
if order == 0:
U[i, :] = vec.copy()
elif order == 1:
V[i, :] = vec.copy()
else:
X[i, :] = vec.copy()
if iters + 1 > maxiter1 - maxiter2:
U_plus += U
V_plus += V
X_plus += X
tensor_hat = cp_combine(U, V, X)
if iters + 1 > maxiter1 - maxiter2:
tensor_hat_plus += tensor_hat
rmse = np.sqrt(np.sum((dense_tensor[pos] - tensor_hat[pos]) ** 2)/dense_tensor[pos].shape[0])
var_alpha = alpha + 0.5 * sparse_tensor[position].shape[0]
error = sparse_tensor - tensor_hat
var_beta = beta + 0.5 * np.sum(error[position] ** 2)
tau = np.random.gamma(var_alpha, 1/var_beta)
if (iters + 1) % 200 == 0 and iters < maxiter1 - maxiter2:
print('Iter: {}'.format(iters + 1))
print('RMSE: {:.6}'.format(rmse))
print()
U = U_plus/maxiter2
V = V_plus/maxiter2
X = X_plus/maxiter2
tensor_hat = tensor_hat_plus/maxiter2
final_mape = np.sum(np.abs(dense_tensor[pos] - tensor_hat[pos])/dense_tensor[pos])/dense_tensor[pos].shape[0]
final_rmse = np.sqrt(np.sum((dense_tensor[pos] - tensor_hat[pos]) ** 2)/dense_tensor[pos].shape[0])
print('Final MAPE: {:.6}'.format(final_mape))
print('Final RMSE: {:.6}'.format(final_rmse))
print()
```
# Part 3: Data Organization
## 1) Matrix Structure
We consider a dataset of $m$ discrete time series $\boldsymbol{y}_{i}\in\mathbb{R}^{f},i\in\left\{1,2,...,m\right\}$. The time series may have missing elements. We express spatio-temporal dataset as a matrix $Y\in\mathbb{R}^{m\times f}$ with $m$ rows (e.g., locations) and $f$ columns (e.g., discrete time intervals),
$$Y=\left[ \begin{array}{cccc} y_{11} & y_{12} & \cdots & y_{1f} \\ y_{21} & y_{22} & \cdots & y_{2f} \\ \vdots & \vdots & \ddots & \vdots \\ y_{m1} & y_{m2} & \cdots & y_{mf} \\ \end{array} \right]\in\mathbb{R}^{m\times f}.$$
## 2) Tensor Structure
We consider a dataset of $m$ discrete time series $\boldsymbol{y}_{i}\in\mathbb{R}^{nf},i\in\left\{1,2,...,m\right\}$. The time series may have missing elements. We partition each time series into intervals of predifined length $f$. We express each partitioned time series as a matrix $Y_{i}$ with $n$ rows (e.g., days) and $f$ columns (e.g., discrete time intervals per day),
$$Y_{i}=\left[ \begin{array}{cccc} y_{11} & y_{12} & \cdots & y_{1f} \\ y_{21} & y_{22} & \cdots & y_{2f} \\ \vdots & \vdots & \ddots & \vdots \\ y_{n1} & y_{n2} & \cdots & y_{nf} \\ \end{array} \right]\in\mathbb{R}^{n\times f},i=1,2,...,m,$$
therefore, the resulting structure is a tensor $\mathcal{Y}\in\mathbb{R}^{m\times n\times f}$.
**How to transform a data set into something we can use for time series imputation?**
# Part 4: Experiments on Guangzhou Data Set
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Guangzhou-data-set/tensor.mat')
dense_tensor = tensor['tensor']
random_matrix = scipy.io.loadmat('../datasets/Guangzhou-data-set/random_matrix.mat')
random_matrix = random_matrix['random_matrix']
random_tensor = scipy.io.loadmat('../datasets/Guangzhou-data-set/random_tensor.mat')
random_tensor = random_tensor['random_tensor']
missing_rate = 0.4
# =============================================================================
### Random missing (RM) scenario:
# binary_tensor = np.round(random_tensor + 0.5 - missing_rate)
# =============================================================================
# =============================================================================
### Non-random missing (NM) scenario:
binary_tensor = np.zeros(dense_tensor.shape)
for i1 in range(dense_tensor.shape[0]):
for i2 in range(dense_tensor.shape[1]):
binary_tensor[i1, i2, :] = np.round(random_matrix[i1, i2] + 0.5 - missing_rate)
# =============================================================================
sparse_tensor = np.multiply(dense_tensor, binary_tensor)
```
**Question**: Given only the partially observed data $\mathcal{Y}\in\mathbb{R}^{m\times n\times f}$, how can we impute the unknown missing values?
The main influential factors for such imputation model are:
- `rank`.
- `maxiter1`.
- `maxiter2`.
```
import time
start = time.time()
dim1, dim2, dim3 = sparse_tensor.shape
rank = 10
init = {"U": 0.1 * np.random.rand(dim1, rank),
"V": 0.1 * np.random.rand(dim2, rank),
"X": 0.1 * np.random.rand(dim3, rank)}
maxiter1 = 1100
maxiter2 = 100
BGCP(dense_tensor, sparse_tensor, init, rank, maxiter1, maxiter2)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Experiment results** of missing data imputation using Bayesian Gaussian CP decomposition (BGCP):
| scenario |`rank`|`maxiter1`|`maxiter2`| mape | rmse |
|:----------|-----:|---------:|---------:|-----------:|----------:|
|**20%, RM**| 80 | 1100 | 100 | **0.0828** | **3.5729**|
|**40%, RM**| 80 | 1100 | 100 | **0.0829** | **3.5869**|
|**20%, NM**| 10 | 1100 | 100 | **0.1023** | **4.2756**|
|**40%, NM**| 10 | 1100 | 100 | **0.1023** | **4.3214**|
# Part 5: Experiments on Birmingham Data Set
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Birmingham-data-set/tensor.mat')
dense_tensor = tensor['tensor']
random_matrix = scipy.io.loadmat('../datasets/Birmingham-data-set/random_matrix.mat')
random_matrix = random_matrix['random_matrix']
random_tensor = scipy.io.loadmat('../datasets/Birmingham-data-set/random_tensor.mat')
random_tensor = random_tensor['random_tensor']
missing_rate = 0.1
# =============================================================================
### Random missing (RM) scenario:
binary_tensor = np.round(random_tensor + 0.5 - missing_rate)
# =============================================================================
# =============================================================================
### Non-random missing (NM) scenario:
# binary_tensor = np.zeros(dense_tensor.shape)
# for i1 in range(dense_tensor.shape[0]):
# for i2 in range(dense_tensor.shape[1]):
# binary_tensor[i1,i2,:] = np.round(random_matrix[i1,i2] + 0.5 - missing_rate)
# =============================================================================
sparse_tensor = np.multiply(dense_tensor, binary_tensor)
import time
start = time.time()
dim1, dim2, dim3 = sparse_tensor.shape
rank = 30
init = {"U": 0.1 * np.random.rand(dim1, rank),
"V": 0.1 * np.random.rand(dim2, rank),
"X": 0.1 * np.random.rand(dim3, rank)}
maxiter1 = 1100
maxiter2 = 100
BGCP(dense_tensor, sparse_tensor, init, rank, maxiter1, maxiter2)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Experiment results** of missing data imputation using Bayesian Gaussian CP decomposition (BGCP):
| scenario |`rank`|`maxiter1`|`maxiter2`| mape | rmse |
|:----------|-----:|---------:|---------:|-----------:|----------:|
|**10%, RM**| 30 | 1100 | 100 | **0.0650** |**19.6926**|
|**30%, RM**| 30 | 1100 | 100 | **0.0623** | **19.982**|
|**10%, NM**| 10 | 1100 | 100 | **0.1364** |**43.1498**|
|**30%, NM**| 10 | 1100 | 100 | **0.1593** |**57.0697**|
# Part 6: Experiments on Hangzhou Data Set
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Hangzhou-data-set/tensor.mat')
dense_tensor = tensor['tensor']
random_matrix = scipy.io.loadmat('../datasets/Hangzhou-data-set/random_matrix.mat')
random_matrix = random_matrix['random_matrix']
random_tensor = scipy.io.loadmat('../datasets/Hangzhou-data-set/random_tensor.mat')
random_tensor = random_tensor['random_tensor']
missing_rate = 0.4
# =============================================================================
### Random missing (RM) scenario:
binary_tensor = np.round(random_tensor + 0.5 - missing_rate)
# =============================================================================
# =============================================================================
### Non-random missing (NM) scenario:
# binary_tensor = np.zeros(dense_tensor.shape)
# for i1 in range(dense_tensor.shape[0]):
# for i2 in range(dense_tensor.shape[1]):
# binary_tensor[i1, i2, :] = np.round(random_matrix[i1, i2] + 0.5 - missing_rate)
# =============================================================================
sparse_tensor = np.multiply(dense_tensor, binary_tensor)
import time
start = time.time()
dim1, dim2, dim3 = sparse_tensor.shape
rank = 50
init = {"U": 0.1 * np.random.rand(dim1, rank),
"V": 0.1 * np.random.rand(dim2, rank),
"X": 0.1 * np.random.rand(dim3, rank)}
maxiter1 = 1100
maxiter2 = 100
BGCP(dense_tensor, sparse_tensor, init, rank, maxiter1, maxiter2)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Experiment results** of missing data imputation using Bayesian Gaussian CP decomposition (BGCP):
| scenario |`rank`|`maxiter1`|`maxiter2`| mape | rmse |
|:----------|-----:|---------:|---------:|-----------:|----------:|
|**20%, RM**| 50 | 1100 | 100 | **0.1901**|**41.1558**|
|**40%, RM**| 50 | 1100 | 100 | **0.1959**|**32.7057**|
|**20%, NM**| 10 | 1100 | 100 | **0.2557**|**35.9867**|
|**40%, NM**| 10 | 1100 | 100 | **0.2437**|**49.6438**|
# Part 7: Experiments on New York Data Set
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/NYC-data-set/tensor.mat')
dense_tensor = tensor['tensor']
rm_tensor = scipy.io.loadmat('../datasets/NYC-data-set/rm_tensor.mat')
rm_tensor = rm_tensor['rm_tensor']
nm_tensor = scipy.io.loadmat('../datasets/NYC-data-set/nm_tensor.mat')
nm_tensor = nm_tensor['nm_tensor']
missing_rate = 0.3
# =============================================================================
### Random missing (RM) scenario
### Set the RM scenario by:
binary_tensor = np.round(rm_tensor + 0.5 - missing_rate)
# =============================================================================
# =============================================================================
### Non-random missing (NM) scenario
### Set the NM scenario by:
# binary_tensor = np.zeros(dense_tensor.shape)
# for i1 in range(dense_tensor.shape[0]):
# for i2 in range(dense_tensor.shape[1]):
# for i3 in range(61):
# binary_tensor[i1, i2, i3 * 24 : (i3 + 1) * 24] = np.round(nm_tensor[i1, i2, i3] + 0.5 - missing_rate)
# =============================================================================
sparse_tensor = np.multiply(dense_tensor, binary_tensor)
import time
start = time.time()
dim1, dim2, dim3 = sparse_tensor.shape
rank = 30
init = {"U": 0.1 * np.random.rand(dim1, rank),
"V": 0.1 * np.random.rand(dim2, rank),
"X": 0.1 * np.random.rand(dim3, rank)}
maxiter1 = 1100
maxiter2 = 100
BGCP(dense_tensor, sparse_tensor, init, rank, maxiter1, maxiter2)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Experiment results** of missing data imputation using Bayesian Gaussian CP decomposition (BGCP):
| scenario |`rank`|`maxiter1`|`maxiter2`| mape | rmse |
|:----------|-----:|---------:|---------:|-----------:|----------:|
|**10%, RM**| 30 | 1100 | 100 | **0.5202** | **4.7106**|
|**30%, RM**| 30 | 1100 | 100 | **0.5252** | **4.8218**|
|**10%, NM**| 30 | 1100 | 100 | **0.5295** | **4.7879**|
|**30%, NM**| 30 | 1100 | 100 | **0.5282** | **4.8664**|
# Part 8: Experiments on Seattle Data Set
```
import pandas as pd
dense_mat = pd.read_csv('../datasets/Seattle-data-set/mat.csv', index_col = 0)
RM_mat = pd.read_csv('../datasets/Seattle-data-set/RM_mat.csv', index_col = 0)
NM_mat = pd.read_csv('../datasets/Seattle-data-set/NM_mat.csv', index_col = 0)
dense_mat = dense_mat.values
RM_mat = RM_mat.values
NM_mat = NM_mat.values
dense_tensor = dense_mat.reshape([dense_mat.shape[0], 28, 288])
missing_rate = 0.2
# =============================================================================
### Random missing (RM) scenario
### Set the RM scenario by:
# binary_tensor = np.round(RM_mat.reshape([RM_mat.shape[0], 28, 288]) + 0.5 - missing_rate)
# =============================================================================
# =============================================================================
### Non-random missing (NM) scenario
### Set the NM scenario by:
binary_tensor = np.zeros((dense_mat.shape[0], 28, 288))
for i1 in range(binary_tensor.shape[0]):
for i2 in range(binary_tensor.shape[1]):
binary_tensor[i1, i2, :] = np.round(NM_mat[i1, i2] + 0.5 - missing_rate)
# =============================================================================
sparse_tensor = np.multiply(dense_tensor, binary_tensor)
import time
start = time.time()
dim1, dim2, dim3 = sparse_tensor.shape
rank = 10
init = {"U": 0.1 * np.random.rand(dim1, rank),
"V": 0.1 * np.random.rand(dim2, rank),
"X": 0.1 * np.random.rand(dim3, rank)}
maxiter1 = 1100
maxiter2 = 100
BGCP(dense_tensor, sparse_tensor, init, rank, maxiter1, maxiter2)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Experiment results** of missing data imputation using Bayesian Gaussian CP decomposition (BGCP):
| scenario |`rank`|`maxiter1`|`maxiter2`| mape | rmse |
|:----------|-----:|---------:|---------:|-----------:|----------:|
|**20%, RM**| 50 | 1100 | 100 | **0.0745** | **4.50**|
|**40%, RM**| 50 | 1100 | 100 | **0.0758** | **4.54**|
|**20%, NM**| 10 | 1100 | 100 | **0.0993** | **5.65**|
|**40%, NM**| 10 | 1100 | 100 | **0.0994** | **5.68**|
| true |
code
| 0.551815 | null | null | null | null |
|
# 基于U-Net卷积神经网络实现宠物图像分割
**作者:** [PaddlePaddle](https://github.com/PaddlePaddle)<br>
**日期:** 2021.10<br>
**摘要:** 本示例教程使用U-Net实现图像分割。
## 一、简要介绍
在计算机视觉领域,图像分割指的是将数字图像细分为多个图像子区域的过程。图像分割的目的是简化或改变图像的表示形式,使得图像更容易理解和分析。图像分割通常用于定位图像中的物体和边界(线,曲线等)。更精确的,图像分割是对图像中的每个像素加标签的一个过程,这一过程使得具有相同标签的像素具有某种共同视觉特性。图像分割的领域非常多,无人车、地块检测、表计识别等等。
本示例简要介绍如何通过飞桨开源框架,实现图像分割。这里采用了一个在图像分割领域比较熟知的U-Net网络结构,是一个基于FCN做改进后的一个深度学习网络,包含下采样(编码器,特征提取)和上采样(解码器,分辨率还原)两个阶段,因模型结构比较像U型而命名为U-Net。
## 二、环境设置
导入一些比较基础常用的模块,确认自己的飞桨版本。
```
import os
import io
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image as PilImage
import paddle
from paddle.nn import functional as F
paddle.__version__
```
## 三、数据集
### 3.1 数据集下载
本案例使用Oxford-IIIT Pet数据集,官网:https://www.robots.ox.ac.uk/~vgg/data/pets 。
数据集统计如下:

数据集包含两个压缩文件:
1. 原图:https://www.robots.ox.ac.uk/~vgg/data/pets/data/images.tar.gz
2. 分割图像:https://www.robots.ox.ac.uk/~vgg/data/pets/data/annotations.tar.gz
```
!wget http://www.robots.ox.ac.uk/~vgg/data/pets/data/images.tar.gz
!wget http://www.robots.ox.ac.uk/~vgg/data/pets/data/annotations.tar.gz
!tar -xf images.tar.gz
!tar -xf annotations.tar.gz
```
### 3.2 数据集概览
首先先看看下载到磁盘上的文件结构是什么样,来了解一下数据集。
1. 首先看一下images.tar.gz这个压缩包,该文件解压后得到一个images目录,这个目录比较简单,里面直接放的是用类名和序号命名好的图片文件,每个图片是对应的宠物照片。
```bash
.
├── samoyed_7.jpg
├── ......
└── samoyed_81.jpg
```
2. 然后在看下annotations.tar.gz,文件解压后的目录里面包含以下内容,目录中的README文件将每个目录和文件做了比较详细的介绍,可以通过README来查看每个目录文件的说明。
```bash
.
├── README
├── list.txt
├── test.txt
├── trainval.txt
├── trimaps
│ ├── Abyssinian_1.png
│ ├── Abyssinian_10.png
│ ├── ......
│ └── yorkshire_terrier_99.png
└── xmls
├── Abyssinian_1.xml
├── Abyssinian_10.xml
├── ......
└── yorkshire_terrier_190.xml
```
本次主要使用到images和annotations/trimaps两个目录,即原图和三元图像文件,前者作为训练的输入数据,后者是对应的标签数据。
来看看这个数据集提供了多少个训练样本。
```
IMAGE_SIZE = (160, 160)
train_images_path = "images/"
label_images_path = "annotations/trimaps/"
image_count = len([os.path.join(train_images_path, image_name)
for image_name in os.listdir(train_images_path)
if image_name.endswith('.jpg')])
print("用于训练的图片样本数量:", image_count)
# 对数据集进行处理,划分训练集、测试集
def _sort_images(image_dir, image_type):
"""
对文件夹内的图像进行按照文件名排序
"""
files = []
for image_name in os.listdir(image_dir):
if image_name.endswith('.{}'.format(image_type)) \
and not image_name.startswith('.'):
files.append(os.path.join(image_dir, image_name))
return sorted(files)
def write_file(mode, images, labels):
with open('./{}.txt'.format(mode), 'w') as f:
for i in range(len(images)):
f.write('{}\t{}\n'.format(images[i], labels[i]))
"""
由于所有文件都是散落在文件夹中,在训练时需要使用的是数据集和标签对应的数据关系,
所以第一步是对原始的数据集进行整理,得到数据集和标签两个数组,分别一一对应。
这样可以在使用的时候能够很方便的找到原始数据和标签的对应关系,否则对于原有的文件夹图片数据无法直接应用。
在这里是用了一个非常简单的方法,按照文件名称进行排序。
因为刚好数据和标签的文件名是按照这个逻辑制作的,名字都一样,只有扩展名不一样。
"""
images = _sort_images(train_images_path, 'jpg')
labels = _sort_images(label_images_path, 'png')
eval_num = int(image_count * 0.15)
write_file('train', images[:-eval_num], labels[:-eval_num])
write_file('test', images[-eval_num:], labels[-eval_num:])
write_file('predict', images[-eval_num:], labels[-eval_num:])
```
### 3.3 PetDataSet数据集抽样展示
划分好数据集之后,来查验一下数据集是否符合预期,通过划分的配置文件读取图片路径后再加载图片数据来用matplotlib进行展示,这里要注意的是对于分割的标签文件因为是1通道的灰度图片,需要在使用imshow接口时注意下传参cmap='gray'。
```
with open('./train.txt', 'r') as f:
i = 0
for line in f.readlines():
image_path, label_path = line.strip().split('\t')
image = np.array(PilImage.open(image_path))
label = np.array(PilImage.open(label_path))
if i > 2:
break
# 进行图片的展示
plt.figure()
plt.subplot(1,2,1),
plt.title('Train Image')
plt.imshow(image.astype('uint8'))
plt.axis('off')
plt.subplot(1,2,2),
plt.title('Label')
plt.imshow(label.astype('uint8'), cmap='gray')
plt.axis('off')
plt.show()
i = i + 1
```
### 3.4 数据集类定义
飞桨(PaddlePaddle)数据集加载方案是统一使用Dataset(数据集定义) + DataLoader(多进程数据集加载)。
首先进行数据集的定义,数据集定义主要是实现一个新的Dataset类,继承父类paddle.io.Dataset,并实现父类中以下两个抽象方法,`__getitem__`和`__len__`:
```python
class MyDataset(Dataset):
def __init__(self):
...
# 每次迭代时返回数据和对应的标签
def __getitem__(self, idx):
return x, y
# 返回整个数据集的总数
def __len__(self):
return count(samples)
```
在数据集内部可以结合图像数据预处理相关API进行图像的预处理(改变大小、反转、调整格式等)。
由于加载进来的图像不一定都符合自己的需求,举个例子,已下载的这些图片里面就会有RGBA格式的图片,这个时候图片就不符合所需3通道的需求,需要进行图片的格式转换,那么这里直接实现了一个通用的图片读取接口,确保读取出来的图片都是满足需求。
另外图片加载出来的默认shape是HWC,这个时候要看看是否满足后面训练的需要,如果Layer的默认格式和这个不是符合的情况下,需要看下Layer有没有参数可以进行格式调整。不过如果layer较多的话,还是直接调整原数据Shape比较好,否则每个layer都要做参数设置,如果有遗漏就会导致训练出错,那么在本案例中是直接对数据源的shape做了统一调整,从HWC转换成了CHW,因为飞桨的卷积等API的默认输入格式为CHW,这样处理方便后续模型训练。
```
import random
from paddle.io import Dataset
from paddle.vision.transforms import transforms as T
class PetDataset(Dataset):
"""
数据集定义
"""
def __init__(self, mode='train'):
"""
构造函数
"""
self.image_size = IMAGE_SIZE
self.mode = mode.lower()
assert self.mode in ['train', 'test', 'predict'], \
"mode should be 'train' or 'test' or 'predict', but got {}".format(self.mode)
self.train_images = []
self.label_images = []
with open('./{}.txt'.format(self.mode), 'r') as f:
for line in f.readlines():
image, label = line.strip().split('\t')
self.train_images.append(image)
self.label_images.append(label)
def _load_img(self, path, color_mode='rgb', transforms=[]):
"""
统一的图像处理接口封装,用于规整图像大小和通道
"""
with open(path, 'rb') as f:
img = PilImage.open(io.BytesIO(f.read()))
if color_mode == 'grayscale':
# if image is not already an 8-bit, 16-bit or 32-bit grayscale image
# convert it to an 8-bit grayscale image.
if img.mode not in ('L', 'I;16', 'I'):
img = img.convert('L')
elif color_mode == 'rgba':
if img.mode != 'RGBA':
img = img.convert('RGBA')
elif color_mode == 'rgb':
if img.mode != 'RGB':
img = img.convert('RGB')
else:
raise ValueError('color_mode must be "grayscale", "rgb", or "rgba"')
return T.Compose([
T.Resize(self.image_size)
] + transforms)(img)
def __getitem__(self, idx):
"""
返回 image, label
"""
train_image = self._load_img(self.train_images[idx],
transforms=[
T.Transpose(),
T.Normalize(mean=127.5, std=127.5)
]) # 加载原始图像
label_image = self._load_img(self.label_images[idx],
color_mode='grayscale',
transforms=[T.Grayscale()]) # 加载Label图像
# 返回image, label
train_image = np.array(train_image, dtype='float32')
label_image = np.array(label_image, dtype='int64')
return train_image, label_image
def __len__(self):
"""
返回数据集总数
"""
return len(self.train_images)
```
## 四、模型组网
U-Net是一个U型网络结构,可以看做两个大的阶段,图像先经过Encoder编码器进行下采样得到高级语义特征图,再经过Decoder解码器上采样将特征图恢复到原图片的分辨率。
### 4.1 定义SeparableConv2D接口
为了减少卷积操作中的训练参数来提升性能,是继承paddle.nn.Layer自定义了一个SeparableConv2D Layer类,整个过程是把`filter_size * filter_size * num_filters`的Conv2D操作拆解为两个子Conv2D,先对输入数据的每个通道使用`filter_size * filter_size * 1`的卷积核进行计算,输入输出通道数目相同,之后在使用`1 * 1 * num_filters`的卷积核计算。
```
from paddle.nn import functional as F
class SeparableConv2D(paddle.nn.Layer):
def __init__(self,
in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=None,
weight_attr=None,
bias_attr=None,
data_format="NCHW"):
super(SeparableConv2D, self).__init__()
self._padding = padding
self._stride = stride
self._dilation = dilation
self._in_channels = in_channels
self._data_format = data_format
# 第一次卷积参数,没有偏置参数
filter_shape = [in_channels, 1] + self.convert_to_list(kernel_size, 2, 'kernel_size')
self.weight_conv = self.create_parameter(shape=filter_shape, attr=weight_attr)
# 第二次卷积参数
filter_shape = [out_channels, in_channels] + self.convert_to_list(1, 2, 'kernel_size')
self.weight_pointwise = self.create_parameter(shape=filter_shape, attr=weight_attr)
self.bias_pointwise = self.create_parameter(shape=[out_channels],
attr=bias_attr,
is_bias=True)
def convert_to_list(self, value, n, name, dtype=np.int):
if isinstance(value, dtype):
return [value, ] * n
else:
try:
value_list = list(value)
except TypeError:
raise ValueError("The " + name +
"'s type must be list or tuple. Received: " + str(
value))
if len(value_list) != n:
raise ValueError("The " + name + "'s length must be " + str(n) +
". Received: " + str(value))
for single_value in value_list:
try:
dtype(single_value)
except (ValueError, TypeError):
raise ValueError(
"The " + name + "'s type must be a list or tuple of " + str(
n) + " " + str(dtype) + " . Received: " + str(
value) + " "
"including element " + str(single_value) + " of type" + " "
+ str(type(single_value)))
return value_list
def forward(self, inputs):
conv_out = F.conv2d(inputs,
self.weight_conv,
padding=self._padding,
stride=self._stride,
dilation=self._dilation,
groups=self._in_channels,
data_format=self._data_format)
out = F.conv2d(conv_out,
self.weight_pointwise,
bias=self.bias_pointwise,
padding=0,
stride=1,
dilation=1,
groups=1,
data_format=self._data_format)
return out
```
### 4.2 定义Encoder编码器
将网络结构中的Encoder下采样过程进行了一个Layer封装,方便后续调用,减少代码编写,下采样是有一个模型逐渐向下画曲线的一个过程,这个过程中是不断的重复一个单元结构将通道数不断增加,形状不断缩小,并且引入残差网络结构,将这些都抽象出来进行统一封装。
```
class Encoder(paddle.nn.Layer):
def __init__(self, in_channels, out_channels):
super(Encoder, self).__init__()
self.relus = paddle.nn.LayerList(
[paddle.nn.ReLU() for i in range(2)])
self.separable_conv_01 = SeparableConv2D(in_channels,
out_channels,
kernel_size=3,
padding='same')
self.bns = paddle.nn.LayerList(
[paddle.nn.BatchNorm2D(out_channels) for i in range(2)])
self.separable_conv_02 = SeparableConv2D(out_channels,
out_channels,
kernel_size=3,
padding='same')
self.pool = paddle.nn.MaxPool2D(kernel_size=3, stride=2, padding=1)
self.residual_conv = paddle.nn.Conv2D(in_channels,
out_channels,
kernel_size=1,
stride=2,
padding='same')
def forward(self, inputs):
previous_block_activation = inputs
y = self.relus[0](inputs)
y = self.separable_conv_01(y)
y = self.bns[0](y)
y = self.relus[1](y)
y = self.separable_conv_02(y)
y = self.bns[1](y)
y = self.pool(y)
residual = self.residual_conv(previous_block_activation)
y = paddle.add(y, residual)
return y
```
### 4.3 定义Decoder解码器
在通道数达到最大得到高级语义特征图后,网络结构会开始进行decode操作,进行上采样,通道数逐渐减小,对应图片尺寸逐步增加,直至恢复到原图像大小,那么这个过程里面也是通过不断的重复相同结构的残差网络完成,也是为了减少代码编写,将这个过程定义一个Layer来放到模型组网中使用。
```
class Decoder(paddle.nn.Layer):
def __init__(self, in_channels, out_channels):
super(Decoder, self).__init__()
self.relus = paddle.nn.LayerList(
[paddle.nn.ReLU() for i in range(2)])
self.conv_transpose_01 = paddle.nn.Conv2DTranspose(in_channels,
out_channels,
kernel_size=3,
padding=1)
self.conv_transpose_02 = paddle.nn.Conv2DTranspose(out_channels,
out_channels,
kernel_size=3,
padding=1)
self.bns = paddle.nn.LayerList(
[paddle.nn.BatchNorm2D(out_channels) for i in range(2)]
)
self.upsamples = paddle.nn.LayerList(
[paddle.nn.Upsample(scale_factor=2.0) for i in range(2)]
)
self.residual_conv = paddle.nn.Conv2D(in_channels,
out_channels,
kernel_size=1,
padding='same')
def forward(self, inputs):
previous_block_activation = inputs
y = self.relus[0](inputs)
y = self.conv_transpose_01(y)
y = self.bns[0](y)
y = self.relus[1](y)
y = self.conv_transpose_02(y)
y = self.bns[1](y)
y = self.upsamples[0](y)
residual = self.upsamples[1](previous_block_activation)
residual = self.residual_conv(residual)
y = paddle.add(y, residual)
return y
```
### 4.4 训练模型组网
按照U型网络结构格式进行整体的网络结构搭建,三次下采样,四次上采样。
```
class PetNet(paddle.nn.Layer):
def __init__(self, num_classes):
super(PetNet, self).__init__()
self.conv_1 = paddle.nn.Conv2D(3, 32,
kernel_size=3,
stride=2,
padding='same')
self.bn = paddle.nn.BatchNorm2D(32)
self.relu = paddle.nn.ReLU()
in_channels = 32
self.encoders = []
self.encoder_list = [64, 128, 256]
self.decoder_list = [256, 128, 64, 32]
# 根据下采样个数和配置循环定义子Layer,避免重复写一样的程序
for out_channels in self.encoder_list:
block = self.add_sublayer('encoder_{}'.format(out_channels),
Encoder(in_channels, out_channels))
self.encoders.append(block)
in_channels = out_channels
self.decoders = []
# 根据上采样个数和配置循环定义子Layer,避免重复写一样的程序
for out_channels in self.decoder_list:
block = self.add_sublayer('decoder_{}'.format(out_channels),
Decoder(in_channels, out_channels))
self.decoders.append(block)
in_channels = out_channels
self.output_conv = paddle.nn.Conv2D(in_channels,
num_classes,
kernel_size=3,
padding='same')
def forward(self, inputs):
y = self.conv_1(inputs)
y = self.bn(y)
y = self.relu(y)
for encoder in self.encoders:
y = encoder(y)
for decoder in self.decoders:
y = decoder(y)
y = self.output_conv(y)
return y
```
### 4.5 模型可视化
调用飞桨提供的summary接口对组建好的模型进行可视化,方便进行模型结构和参数信息的查看和确认。
```
num_classes = 4
network = PetNet(num_classes)
model = paddle.Model(network)
model.summary((-1, 3,) + IMAGE_SIZE)
```
## 五、模型训练
### 5.1 启动模型训练
使用模型代码进行Model实例生成,使用prepare接口定义优化器、损失函数和评价指标等信息,用于后续训练使用。在所有初步配置完成后,调用fit接口开启训练执行过程,调用fit时只需要将前面定义好的训练数据集、测试数据集、训练轮次(Epoch)和批次大小(batch_size)配置好即可。
```
train_dataset = PetDataset(mode='train') # 训练数据集
val_dataset = PetDataset(mode='test') # 验证数据集
optim = paddle.optimizer.RMSProp(learning_rate=0.001,
rho=0.9,
momentum=0.0,
epsilon=1e-07,
centered=False,
parameters=model.parameters())
model.prepare(optim, paddle.nn.CrossEntropyLoss(axis=1))
model.fit(train_dataset,
val_dataset,
epochs=15,
batch_size=32,
verbose=1)
```
## 六、模型预测
### 6.1 预测数据集准备和预测
继续使用PetDataset来实例化待预测使用的数据集。这里为了方便没有在另外准备预测数据,复用了评估数据。
可以直接使用model.predict接口来对数据集进行预测操作,只需要将预测数据集传递到接口内即可。
```
predict_dataset = PetDataset(mode='predict')
predict_results = model.predict(predict_dataset)
```
### 6.2 预测结果可视化
从预测数据集中抽3个动物来看看预测的效果,展示一下原图、标签图和预测结果。
```
plt.figure(figsize=(10, 10))
i = 0
mask_idx = 0
with open('./predict.txt', 'r') as f:
for line in f.readlines():
image_path, label_path = line.strip().split('\t')
resize_t = T.Compose([
T.Resize(IMAGE_SIZE)
])
image = resize_t(PilImage.open(image_path))
label = resize_t(PilImage.open(label_path))
image = np.array(image).astype('uint8')
label = np.array(label).astype('uint8')
if i > 8:
break
plt.subplot(3, 3, i + 1)
plt.imshow(image)
plt.title('Input Image')
plt.axis("off")
plt.subplot(3, 3, i + 2)
plt.imshow(label, cmap='gray')
plt.title('Label')
plt.axis("off")
# 模型只有一个输出,所以通过predict_results[0]来取出1000个预测的结果
# 映射原始图片的index来取出预测结果,提取mask进行展示
data = predict_results[0][mask_idx][0].transpose((1, 2, 0))
mask = np.argmax(data, axis=-1)
plt.subplot(3, 3, i + 3)
plt.imshow(mask.astype('uint8'), cmap='gray')
plt.title('Predict')
plt.axis("off")
i += 3
mask_idx += 1
plt.show()
```
| true |
code
| 0.367526 | null | null | null | null |
|
```
#Import required packages
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
import ipdb # deb
# Getting the data ready
# Generate train dummy data for 1000 Students and dummy test
# for 500
#Columns :Age, Hours of Study &Avg Previous test scores
np.random.seed(2018) #Setting seed for reproducibility
train_data, test_data = np.random.random((1000, 3)), np.random.random((500, 3))
#Generate dummy results for 1000 students : Whether Passed (1)
# or Failed (0)
labels = np.random.randint(2, size=(1000, 2))
#Defining the model structure with the required layers,
# of neurons, activation function and optimizers
model = Sequential()
model.add(Dense(5, input_dim=3, activation='relu'))
model.add(Dense(4, activation='relu'))
model.add(Dense(2, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
#Train the model and make predictions
model.fit(train_data, labels, epochs=10, batch_size=32)
#Make predictions from the trained model
predictions = model.predict(test_data)
predictions[:10]
```
## Train, Test and validation
```
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
# Generate dummy training dataset
np.random.seed(2019)
x_train = np.random.random((6000,10))
y_train = np.random.randint(2, size=(6000, 1))
# Generate dummy validation dataset
x_val = np.random.random((2000,10))
y_val = np.random.randint(2, size=(2000, 1))
# Generate dummy test dataset
x_test = np.random.random((2000,10))
y_test = np.random.randint(2, size=(2000, 1))
#Define the model architecture
model = Sequential()
model.add(Dense(64, input_dim=10,activation = "relu")) #Layer 1
model.add(Dense(32,activation = "relu")) #Layer 2
model.add(Dense(16,activation = "relu")) #Layer 3
model.add(Dense(8,activation = "relu")) #Layer 4
model.add(Dense(4,activation = "relu")) #Layer 5
model.add(Dense(1,activation = "sigmoid")) #Output Layer
#Configure the model
model.compile(optimizer='Adam',loss='binary_crossentropy',
metrics=['accuracy'])
#Train the model
model.fit(x_train, y_train, batch_size=64, epochs=3,
validation_data=(x_val,y_val))
print(model.metrics_names)
print(model.evaluate(x_test,y_test))
#Make predictions on the test dataset and print the first 10
predictions
pred = model.predict(x_test)
pred[:10]
```
# Boston House Prices dataset
```
from keras.datasets import boston_housing
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
(x_train, y_train), (x_test, y_test) = boston_housing.load_data()
#Explore the data structure using basic python commands
print("Type of the Dataset:",type(y_train))
print("Shape of training data :",x_train.shape)
print("Shape of training labels :",y_train.shape)
print("Shape of testing data :",type(x_test))
print("Shape of testing labels :",y_test.shape)
```
Column Name Description :
- **CriM** per capita crime rate by town
- **Zn** proportion of residential land zoned for lots over 25,000 sq. ft.
- **inDUs** proportion of nonretail business acres per town
- **Chas** Charles river dummy variable (= 1 if tract bounds river; 0 otherwise)
- **noX** nitric oxide concentration (parts per 10 million)
- **rM** average number of rooms per dwelling
- **aGe** proportion of owner-occupied units built prior to 1940
- **Dis** weighted distances to five Boston employment centers
- **raD** index of accessibility to radial highways
- **taX** full-value property tax rate per $\$10,000$
- **ptratio** pupil-teacher ratio by town
- **B** $1000(Bk – 0.63)^2$, where Bk is the proportion of blacks by town
- **Lstat** \% lower status of the population
- **MeDV** median value of owner-occupied homes in $\$1000's$
```
x_train[:5,:]
```
It a good idea, to split the training data in training set and validation set.
```
# Extract the last 100 rows from the training
# data to create the validation datasets.
x_val = x_train[300:,]
y_val = y_train[300:,]
#Define the model architecture
model = Sequential()
model.add(Dense(13, input_dim=13, kernel_initializer='normal',
activation='relu'))
model.add(Dense(6, kernel_initializer='normal',
activation='relu'))
model.add(Dense(1, kernel_initializer='normal'))
# Compile model
model.compile(loss='mean_squared_error', optimizer='adam',
metrics=['mean_absolute_percentage_error'])
#Train the model
model.fit(x_train, y_train, batch_size=32, epochs=3,
validation_data=(x_val,y_val))
```
We have created a simple two-hidden-layer model for the regression use case. We have chosen _MAPE_ as the metric. Generally, this is not the best metric to choose for studying model performance, but its advantage is simplicity in terms of comprehending the results. It gives a simple percentage value for the error, say $10\%$ error. So, if you know the average range of your prediction, you can easily estimate what the predictions are going to look like
```
results = model.evaluate(x_test, y_test)
for i in range(len(model.metrics_names)):
print(model.metrics_names[i]," : ", results[i])
```
We can see that __MAPE__ is around $96\%$, which is actually not a great number to have for model performance. This would translate into our model predictions at around $96\%$ error. So, in general, if a house was priced at $10K$, our model would have predicted $\approx20K$.
```
#Train the model
model.fit(x_train, y_train, batch_size=32, epochs=30,
validation_data=(x_val,y_val))
```
# Regression
## Rossmann Store sales dataset
Rossmann is one of the largest drugstore chains in Germany, with
operations across Europe. As of 2018, they have well over 3,900 stores in
Europe with an annual turnover of 9 billion euros. Our task is to predict the
sales for a few identified stores on a given day.
### Data fields
Most of the fields are self-explanatory. The following are descriptions for those that aren't.
- **Id** - an Id that represents a (Store, Date) duple within the test set
- **Store** - a unique Id for each store
- **Sales** - the turnover for any given day (this is what you are predicting)
- **Customers** - the number of customers on a given day
- **Open** - an indicator for whether the store was open: 0 = closed, 1 = open
- **StateHoliday** - indicates a state holiday. Normally all stores, with few exceptions, are closed on state holidays. Note that all schools are closed on public holidays and weekends. a = public holiday, b = Easter holiday, c = Christmas, 0 = None
- **SchoolHoliday** - indicates if the (Store, Date) was affected by the closure of public schools
- **StoreType** - differentiates between 4 different store models: a, b, c, d
- **Assortment** - describes an assortment level: a = basic, b = extra, c = extended
- **CompetitionDistance** - distance in meters to the nearest competitor store
- **CompetitionOpenSince[Month/Year]** - gives the approximate year and month of the time the nearest competitor was opened
- **Promo** - indicates whether a store is running a promo on that day
- **Promo2** - Promo2 is a continuing and consecutive promotion for some stores: 0 = store is not participating, 1 = store is participating
- **Promo2Since[Year/Week]** - describes the year and calendar week when the store started participating in Promo2
- **PromoInterval** - describes the consecutive intervals Promo2 is started, naming the months the promotion is started anew. E.g. "Feb,May,Aug,Nov" means each round starts in February, May, August, November of any given year for that store
```
import pandas as pd
import numpy as np
df = pd.read_csv("./data/Rossmann Store Sales/train.csv")
print("Shape of the Dataset:",df.shape)
#the head method displays the first 5 rows of the data
df.head(5)
store = pd.read_csv("./data/Rossmann Store Sales/store.csv")
print("Shape of the Dataset:",store.shape)
#Display the first 5 rows of data using the head method of pandas dataframe
store.head(5)
```
To have all the data points together, we need to create one single
dataframe with the store and promotion features. We can achieve this by
joining the two dataframes on the ‘store’ column, which represents the
store ID. Pandas provides a ‘merge’ function that is analogous to the join
statement in SQL. We can perform left, right, inner, and full outer joins on
one or more dataframes using one or more columns as the joining key.
```
df_new = df.merge(store,on=["Store"], how="inner")
print(df_new.shape)
df_new.tail()
print("Distinct number of Stores :", len(df_new["Store"].unique()))
print("Distinct number of Days :", len(df_new["Date"].unique()))
print("Average daily sales of all stores : ",round(df_new["Sales"].mean(),2))
df_new.dtypes
df_new["DayOfWeek"].value_counts()
```
Let’s create additional features that will help our model learn patterns
better. We will create the week number, month, day, quarter, and year as
features from the date variable. Similarly, since we are already creating
time-related features, we can add a new feature based on climate and
seasons. Considering that the stores are in Europe, we can refer to the
standard season cycles and create a new season feature with values of
Spring, Summer, Fall, and Winter. Pandas provides easy-to-use functions
to extract date-related features; the season-related feature can be created
with a simple ‘if else’ equivalent convention.
```
#We can extract all date properties from a datetime datatype
df_new['Date'] = pd.to_datetime(df_new['Date'], infer_datetime_format=True)
df_new["Month"] = df_new["Date"].dt.month
df_new["Quarter"] = df_new["Date"].dt.quarter
df_new["Year"] = df_new["Date"].dt.year
df_new["Day"] = df_new["Date"].dt.day
df_new["Week"] = df_new["Date"].dt.week
df_new["Season"] = np.where(df_new["Month"].isin([3,4,5]),"Spring",
np.where(df_new["Month"].isin([6,7,8]),"Summer",
np.where(df_new["Month"].isin([9,10,11]),"Fall",
np.where(df_new["Month"].isin([12,1,2]),"Winter","None"))))
df_new[["Date","Year","Month","Day","Week","Quarter","Season"]].head()
#Import matplotlib, python most popular data visualizing library
import matplotlib.pyplot as plt
%matplotlib inline
#Create a histogram to study the Daily Sales for the stores
plt.figure(figsize=(15,8))
plt.hist(df_new["Sales"])
plt.title("Histogram for Store Sales")
plt.xlabel("bins")
plt.xlabel("Frequency")
plt.show()
```
The histogram helps us understand the distribution of the data at a
high level. From the preceding plot, we can see that the data range is from
0 to 40,000, but there is barely any data after 20,000. This indicates that
most of the stores have sales in the range 0–20,000, and just a few stores
have sales greater than 20,000. It might be worthwhile to remove these
outliers, as it helps the model learn better.
```
#Use the histogram function provided by the Pandas object
#The function returns a cross-tab histogram plot for all numeric columns in the data
df_new.hist(figsize=(20,15))
```
Let’s have a look at the number of missing data points in each column
(if any) in its associated percentage form.
```
df_new.isnull().sum()/df_new.shape[0] * 100
```
We can see that Promo2SinceWeek,
Promo2SinceYear, PromoInterval, CompetitionOpenSinceMonth, and
CompetitionOpenSinceYear have over 30% null values. This is a big
loss and there is nothing much we can do to fix this. As a rule of thumb,
if there is a loss of anything between 0% and 10%, we can make a few
attempts to fill the missing points and use the feature. But, 30% technically
becomes beyond the usable range. On the other hand, we can see
CompetitionDistance has around 0.25% missing values. This would much easier to handle and fix.
```
#Replace nulls with the mode
df_new["CompetitionDistance"]=df_new["CompetitionDistance"].fillna(df_new["CompetitionDistance"].mode()[0])
#Double check if we still see nulls for the column
df_new["CompetitionDistance"].isnull().sum()/df_new.shape[0] * 100
```
The best way to study a categorical
variable is to study the impact on the target variable from its individual
classes. We can do this by plotting the mean sales across different values of
the classes in the feature. To accomplish this, we can leverage “seaborn,”
another powerful and easy-to-use Python visualization library, similar to
matplotlib but providing much more beautiful visuals.
```
import seaborn as sns #Seaborn is another powerful visualization library for Python
sns.set(style="whitegrid")
#Create the bar plot for Average Sales across different Seasons
ax = sns.barplot(x="Season", y="Sales", data=df_new)
#Create the bar plot for Average Sales across different Assortments
ax = sns.barplot(x="Assortment", y="Sales", data=df_new)
#Create the bar plot for Average Sales across different Store Types
ax = sns.barplot(x="StoreType", y="Sales", data=df_new)
```
As you can see, the seaborn package has internally calculated the
average sales across its classes for the provided categorical column and
displayed a beautiful bar plot showcasing the relationship with our
target variable. We can change the aggregation function to a different
one if required; this can be changed by using the ‘estimator’ parameter
within the barplot function. Sales across seasons barely seem to
differ; however, there seems to be an increasing trend for sales across
assortments. Stores with assortment “b” generally have the highest sales.
Store type also shows a unique relationship with sales across store types.
We can see fairly higher sales for “b” store types also. However, before we
conclude our observations, there is one more sanity check required to
validate these hypotheses. What if the number of stores in the different
types mentioned in the preceding is disproportionate or skewed?
In such a scenario, our observation might be flawed. To cement our
understanding about the observation, we can simply check the number
of data points across each category using the same barplot function with
one additional parameter setting. We will use a new aggregation function
to showcase the counts as the metric for bar charts. The following code
snippet visualizes the bar plots for the same set of categorical variables
we studied earlier, albeit for counts.
```
ax = sns.barplot(x="Season", y="Sales", data=df_new, estimator=np.size)
ax = sns.barplot(x="Assortment", y="Sales", data=df_new, estimator=np.size)
ax = sns.barplot(x="StoreType", y="Sales", data=df_new, estimator=np.size)
```
we will start with treating Season, Assortment, Month,
Year, Quarter, DayOfWeek, and StoreType in one-hot encoded form and
keep aside Day, Week, and Store as continuous for the time being. We will
revisit this after we build a few models and study their performance.
To transform a categorical column into a one-hot encoded version,
Python provides the preprocessing module in the sklearn package with
rich and easy-to-use functions. The following code snippet engineers the
training dataframe into the final required form for model development.
```
# Define a variable for each type of feature
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OneHotEncoder
target = ["Sales"]
numeric_columns = ["Customers","Open","Promo","Promo2",
"StateHoliday","SchoolHoliday","CompetitionDistance"]
categorical_columns = ["DayOfWeek","Quarter","Month","Year",
"StoreType","Assortment","Season"] # note that we left aside (Day, Week, and Store)
# Define a function that will intake the raw dataframe and the
# column name and return a one hot encoded DF
def create_ohe(df, col):
le = LabelEncoder()
a = le.fit_transform(df_new[col]).reshape(-1,1) #; ipdb.set_trace()
ohe = OneHotEncoder(sparse=False)
column_names = [col+ "_"+ str(i) for i in le.classes_]
return(pd.DataFrame(ohe.fit_transform(a),columns =column_names))
# Since the above function converts the column, one at a time
# We create a loop to create the final dataset with all features
temp = df_new[numeric_columns]
for column in categorical_columns:
temp_df = create_ohe(df_new, column)
temp = pd.concat([temp,temp_df], axis=1)
print("Shape of Data:",temp.shape)
print("Distinct Datatypes:",temp.dtypes.unique())
print(temp.columns[temp.dtypes=="object"])
temp["StateHoliday"].unique()
```
The feature seems to have incorrect values. Ideally, StateHoliday
should have either a 0 or 1 as the possible values to indicate whether it is a
holiday or not. Let’s repair the feature by replacing all values of “a,” “b,” and
“c” with 1 and the rest with 0, therefore converting the variable as numeric.
```
temp["StateHoliday"]= np.where(temp["StateHoliday"]== '0',0,1)
# One last check of the data type
temp.dtypes.unique()
```
Spliting data
```
from sklearn.model_selection import train_test_split
#Create train and test dataset with an 80:20 split
x_train, x_test, y_train, y_test = train_test_split(
temp, df_new[target],test_size=0.2,random_state=2018)
#Further divide training dataset into train and validation
# dataset with an 90:10 split
x_train, x_val, y_train, y_val = train_test_split(
x_train, y_train,test_size=0.1,random_state=2018)
#Check the sizes of all newly created datasets
print("Shape of x_train:",x_train.shape)
print("Shape of x_val:",x_val.shape)
print("Shape of x_test:",x_test.shape)
print("Shape of y_train:",y_train.shape)
print("Shape of y_val:",y_val.shape)
print("Shape of y_test:",y_test.shape)
```
### Defining Model
For a regression model, if we assume the mean value of sales in the
training dataset to be the prediction for all samples in the test dataset, we
would have a basic benchmark score. The DL model should at least score
better than this score to be considered as useful.
```
#calculate the average score of the train dataset
mean_sales = y_train.mean()
print("Average Sales :",mean_sales)
```
Now, if we assume the average sales as the prediction for all samples in
the test dataset, what does the MAE metric look like?
```
#Calculate the Mean Absolute Error on the test dataset
print("MAE for Test Data : ",abs(y_test - mean_sales).mean()[0])
```
So, our baseline performance is 2,883.58.
If our DL model doesn’t deliver results better (i.e., lower) than the
baseline score, then it would barely add any value.
## Designing the DNN
Here are a few guidelines.
- **Rule 1: Start with small architectures.**
In the case of DNNs, it is always advised to start with a single-layer network with around
100–300 neurons. Train the network and measure
performance using the defined metrics (while
defining the baseline score). If the results are not
encouraging, try adding one more layer with the
same number of neurons and repeating the process.
- __Rule 2: When small architectures (with two layers)__
fail, increase the size.
When the results from small networks are not
great, you need to increase the number of neurons
in layers by three to five times (i.e., around 1,000
neurons in each layer). Also, increase regularization
(to be covered in depth in Chapter 5) to 0.3, 0.4,
or 0.5 for both layers and repeat the process for
training and performance measurement.
- **Rule 3: When larger networks with two layers fail, go deeper.**
Try increasing the depth of the network with more
and more layers while maintaining regularization with
dropout layers (if required) after each dense (or your
selected layer) with a dropout rate between 0.2 and 0.5.
- **Rule 4: When larger and deeper networks also fail, go even larger and even deeper.**
In case large networks with ~1000 neurons and five
or six layers also don’t give the desired performance,
try increasing the width and depth of the network.
Try adding layers with 8,000–10,000 neurons per
layer and a dropout of 0.6 to 0.8.
- **Rule 5: When everything fails, revisit the data.**
If all the aforementioned rules fail, revisit the
data for improved feature engineering and
normalization, and then you will need to try other
ML alternatives.
```
#Create Deep Neural Network Architecture
from keras.models import Sequential
from keras.layers import Dense, Dropout
model = Sequential()
model.add(Dense(150,input_dim = 44,activation="relu"))
#The input_dim =44, since the width of the training data=44 (refer data engg section)
model.add(Dense(1,activation = "linear"))
#Configure the model
model.compile(optimizer='adam',loss="mean_absolute_error",
metrics=["mean_absolute_error"])
#Train the model
model.fit(x_train.values,y_train.values, validation_data=
(x_val,y_val),epochs=10,batch_size=64)
#Use the model's evaluate method to predict and evaluate the test datasets
result = model.evaluate(x_test.values,y_test.values) # ,value to moove from data set to array
#Print the results
for i in range(len(model.metrics_names)):
print("Metric ",model.metrics_names[i],":",str(round(result[i],2)))
```
(Mean) 2883.587604303127 vs 685.43 (DNN)
### Improoving model
In the following network, we have added two more layers with similar
numbers of neurons. We will update our loss function to mean squared
error instead of MAE. Let’s train the network and have a look at the
performance on the test dataset.
```
model = Sequential()
model.add(Dense(150,input_dim = 44,activation="relu"))
model.add(Dense(150,activation="relu"))
model.add(Dense(150,activation="relu"))
model.add(Dense(1,activation = "linear"))
model.compile(optimizer='adam',
loss="mean_squared_error",
metrics=["mean_absolute_error"])
history = model.fit(x_train,y_train, validation_data=(x_val, y_val),
epochs=10, batch_size=64)
result = model.evaluate(x_test,y_test)
for i in range(len(model.metrics_names)):
print("Metric ",model.metrics_names[i],":",str(round(result[i],2)))
```
Let’s try a couple of more experiments to see if we can expect further
improved performance. We can develop another deeper model with five
hidden layers having 150 neurons each. In this case, we have increased the
number of epochs from 10 to 15. This would therefore increase computation.
```
model = Sequential()
model.add(Dense(150,input_dim = 44,activation="relu"))
model.add(Dense(150,activation="relu"))
model.add(Dense(150,activation="relu"))
model.add(Dense(150,activation="relu"))
model.add(Dense(150,activation="relu"))
model.add(Dense(1,activation = "linear"))
model.compile(optimizer='adam',
loss="mean_squared_error",
metrics=["mean_absolute_error"])
model.fit(x_train, y_train, validation_data=(x_val,y_val),
epochs=15, batch_size=64)
result = model.evaluate(x_test,y_test)
for i in range(len(model.metrics_names)):
print("Metric ",model.metrics_names[i],":",str(round(result[i],2)))
```
## Increasing the Number of Neurons
```
model = Sequential()
model.add(Dense(350,input_dim = 44,activation="relu"))
model.add(Dense(350,activation="relu"))
model.add(Dense(1,activation = "linear"))
model.compile(optimizer='adam',
loss="mean_squared_error",
metrics=["mean_absolute_error"])
model.fit(x_train,y_train,
validation_data=(x_val,y_val),
epochs=15,batch_size=64)
result = model.evaluate(x_test,y_test)
for i in range(len(model.metrics_names)):
print("Metric ",model.metrics_names[i],":", str(round(result[i],2)))
```
We can see quite a bit of improvement when we use an architecture
that was built with a higher number of neurons. This was a considerable
improvement for the model. Let us now try deeper models for the same
architecture. Additionally, we add a new [optional] configuration to the
model to record the history of various metrics during the training process.
This can be done by adding the callbacks parameter, as shown in the
following example. We can use the history, post training, to visualize and
understand the model’s learning curve.
```
from keras.callbacks import History
history = History()
model = Sequential()
model.add(Dense(350,input_dim = 44,activation="relu"))
model.add(Dense(350,activation="relu"))
model.add(Dense(350,activation="relu"))
model.add(Dense(350,activation="relu"))
model.add(Dense(350,activation="relu"))
model.add(Dense(1,activation = "linear"))
model.compile(optimizer='adam',
loss="mean_squared_error",
metrics=["mean_absolute_error"])
model.fit(x_train,y_train, validation_data=(x_val,y_val),
epochs=15, batch_size=64, callbacks=[history])
result = model.evaluate(x_test,y_test)
for i in range(len(model.metrics_names)):
print("Metric ",model.metrics_names[i],":",str(round(result[i],2)))
```
## Plotting the Loss Metric Across Epochs
```
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title("Model's Training & Validation loss across epochs")
plt.ylabel('Loss')
plt.xlabel('Epochs')
plt.legend(['Train', 'Validation'], loc='upper right')
plt.show()
```
### Testing the Model Manually
```
#Manually predicting from the model, instead of using model's
# evaluate function
y_test["Prediction"] = model.predict(x_test)
y_test.columns = ["Actual Sales","Predicted Sales"]
print(y_test.head(10))
from sklearn.metrics import mean_squared_error, mean_absolute_error
print("MSE :",mean_squared_error(y_test["Actual Sales"].values,y_test["Predicted Sales"].values))
print("MAE :",mean_absolute_error(y_test["Actual Sales"].values,y_test["Predicted Sales"].values))
```
# Hyperparameters in DL
We will then look
at various approaches for selecting the right set of hyperparameters for a
## Number of Neurons in a Layer
Generally,
a simple rule of thumb for selecting the number of neurons in the first
layer is to refer to the number of input dimensions. If the final number of
input dimensions in a given training dataset (this includes the one-hot encoded features also) is x, we should use at least the closest number to 2x
in the power of 2. Let’s say you have 100 input dimensions in your training
dataset: preferably start with 2 × 100 = 200, and take the closest power of 2,
so 256. It is good to have the number of neurons in the power of 2, as it
helps the computation of the network to be faster. Also, good choices for
the number of neurons would be 8, 16, 32, 64, 128, 256, 512, 1024, and so
on. Based on the number of input dimensions, take the number closest to
2 times the size. So, when you have 300 input dimensions, try using 512
neurons.
## Number of Layers
It is true that just adding a few more layers will generally increase the
performance, at least marginally. But the problem is that with an increased
number of layers, the training time and computation increase significantly.
Moreover, you would need a higher number of epochs to see promising
results. Not using deeper networks is not an always an option; in cases
when you have to, try using a few best practices.
In case you are using a very large network, say more than 20 layers,
try using a tapering size architecture (i.e., gradually reduce the number
of neurons in each layer as the depth increases). So, if you are using an
architecture of 30 layers with 512 neurons in each layer, try reducing the
number of neurons in the layers slowly. An improved architecture would
be with the first 8 layers having 512 neurons, the next 8 with 256, the next
8 with 128, and so on. For the last hidden layer (not the output layer), try
keeping the number of neurons to at least around 30–40% of the input size.
Alternatively, if you are using wider networks (i.e., not reducing the
number of neurons in the lower layers), always use L2 regularization or
dropout layers with a drop rate of around 30%. The chances of overfitting
are highly reduced.
## Weight Initialization
Initializing the weights for your network also has a tremendous impact
on the overall performance. A good weight initialization technique not
only speeds up the training process but also circumvents deadlocks in
the model training process. By default, the Keras framework uses glorot
uniform initialization, also called Xavier uniform initialization, but this can be changed as per your needs. We can initialize the weights for a layer
using the kernel initializer parameter as well as bias using a bias initializer.
Other popular options to select are ‘He Normal’ and ‘He Uniform’
initialization and ‘lecun normal’ and ‘lecun uniform’ initialization.
There are quite a few other options available in Keras too, but the
aforementioned choices are the most popular.
```
from keras import Sequential
from keras.layers import Dense
model = Sequential()
model.add(Dense(64,activation="relu", input_dim = 32, kernel_
initializer = "random_uniform",bias_initializer = "zeros"))
model.add(Dense(1,activation="sigmoid"))
```
## Batch Size
Using a moderate batch size always helps achieve a smoother learning
process for the model. A batch size of 32 or 64, irrespective of the dataset
size and the number of samples, will deliver a smooth learning curve in
most cases. Even in scenarios where your hardware environment has
large RAM memory to accommodate a bigger batch size, I would still
recommend staying with a batch size of 32 or 64.
## Dropout
In addition to L1 and L2 regularization, there is another popular technique
in DL to reduce overfitting. This technique is to use a dropout mechanism.
In this method, the model arbitrarily drops or deactivates a few neurons
for a layer during each iteration
The following code snippet showcases dropout added to the dense
hidden layer. The parameter value of 0.25 indicates the dropout rate
(i.e., the percentage of the neurons to be dropped).
```
from keras import Sequential
from keras.layers.core import Dropout, Dense
model = Sequential()
model.add(Dense(100, input_dim= 50, activation='relu'))
model.add(Dropout(0.25))
model.add(Dense(1,activation="linear"))
```
| true |
code
| 0.658912 | null | null | null | null |
|
```
%matplotlib inline
```
# Classifier Chain
Example of using classifier chain on a multilabel dataset.
For this example we will use the `yeast
<https://www.openml.org/d/40597>`_ dataset which contains
2417 datapoints each with 103 features and 14 possible labels. Each
data point has at least one label. As a baseline we first train a logistic
regression classifier for each of the 14 labels. To evaluate the performance of
these classifiers we predict on a held-out test set and calculate the
`jaccard score <jaccard_similarity_score>` for each sample.
Next we create 10 classifier chains. Each classifier chain contains a
logistic regression model for each of the 14 labels. The models in each
chain are ordered randomly. In addition to the 103 features in the dataset,
each model gets the predictions of the preceding models in the chain as
features (note that by default at training time each model gets the true
labels as features). These additional features allow each chain to exploit
correlations among the classes. The Jaccard similarity score for each chain
tends to be greater than that of the set independent logistic models.
Because the models in each chain are arranged randomly there is significant
variation in performance among the chains. Presumably there is an optimal
ordering of the classes in a chain that will yield the best performance.
However we do not know that ordering a priori. Instead we can construct an
voting ensemble of classifier chains by averaging the binary predictions of
the chains and apply a threshold of 0.5. The Jaccard similarity score of the
ensemble is greater than that of the independent models and tends to exceed
the score of each chain in the ensemble (although this is not guaranteed
with randomly ordered chains).
```
# Author: Adam Kleczewski
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.multioutput import ClassifierChain
from sklearn.model_selection import train_test_split
from sklearn.multiclass import OneVsRestClassifier
from sklearn.metrics import jaccard_score
from sklearn.linear_model import LogisticRegression
print(__doc__)
# Load a multi-label dataset from https://www.openml.org/d/40597
X, Y = fetch_openml('yeast', version=4, return_X_y=True)
Y = Y == 'TRUE'
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.2,
random_state=0)
# Fit an independent logistic regression model for each class using the
# OneVsRestClassifier wrapper.
base_lr = LogisticRegression()
ovr = OneVsRestClassifier(base_lr)
ovr.fit(X_train, Y_train)
Y_pred_ovr = ovr.predict(X_test)
ovr_jaccard_score = jaccard_score(Y_test, Y_pred_ovr, average='samples')
# Fit an ensemble of logistic regression classifier chains and take the
# take the average prediction of all the chains.
chains = [ClassifierChain(base_lr, order='random', random_state=i)
for i in range(10)]
for chain in chains:
chain.fit(X_train, Y_train)
Y_pred_chains = np.array([chain.predict(X_test) for chain in
chains])
chain_jaccard_scores = [jaccard_score(Y_test, Y_pred_chain >= .5,
average='samples')
for Y_pred_chain in Y_pred_chains]
Y_pred_ensemble = Y_pred_chains.mean(axis=0)
ensemble_jaccard_score = jaccard_score(Y_test,
Y_pred_ensemble >= .5,
average='samples')
model_scores = [ovr_jaccard_score] + chain_jaccard_scores
model_scores.append(ensemble_jaccard_score)
model_names = ('Independent',
'Chain 1',
'Chain 2',
'Chain 3',
'Chain 4',
'Chain 5',
'Chain 6',
'Chain 7',
'Chain 8',
'Chain 9',
'Chain 10',
'Ensemble')
x_pos = np.arange(len(model_names))
# Plot the Jaccard similarity scores for the independent model, each of the
# chains, and the ensemble (note that the vertical axis on this plot does
# not begin at 0).
fig, ax = plt.subplots(figsize=(7, 4))
ax.grid(True)
ax.set_title('Classifier Chain Ensemble Performance Comparison')
ax.set_xticks(x_pos)
ax.set_xticklabels(model_names, rotation='vertical')
ax.set_ylabel('Jaccard Similarity Score')
ax.set_ylim([min(model_scores) * .9, max(model_scores) * 1.1])
colors = ['r'] + ['b'] * len(chain_jaccard_scores) + ['g']
ax.bar(x_pos, model_scores, alpha=0.5, color=colors)
plt.tight_layout()
plt.show()
```
| true |
code
| 0.761439 | null | null | null | null |
|
<table>
<tr align=left><td><img align=left src="./images/CC-BY.png">
<td>Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved MIT license. (c) Marc Spiegelman</td>
</table>
```
%matplotlib inline
import numpy
import matplotlib.pyplot as plt
```
# Plotting Bifurcations
**GOAL:** Find where $f(x,r) = 0$ and label the stable and unstable branches.
A bifurcation diagram provides information on how the fixed points of a dynamical system $f(x,r)=0$ vary as a function of the control parameter $r$
Here we write a snazzy little python function to extract the zero contour and label it with respect to whether it is a stable branch with ($\partial f/\partial x < 0$) or an unstable branch ($\partial f/\partial x > 0 $)
```
def bifurcation_plot(f,f_x,r,x,rlabel='r'):
""" produce a bifurcation diagram for a function f(r,x) given
f and its partial derivative f_x(r,x) over a domain given by numpy arrays r and x
f(r,x) : RHS function of autonomous ode dx/dt = f(r,x)
f_x(r,x): partial derivative of f with respect to x
r : numpy array giving r coordinates of domain
x : numpy array giving x coordinates of domain
rlabel : string for x axis parameter label
"""
# set up a mesh grid and extract the 0 level set of f
R,X = numpy.meshgrid(r,x)
plt.figure()
CS = plt.contour(R,X,f(R,X),[0],colors='k')
plt.clf()
c0 = CS.collections[0]
# for each path in the contour extract vertices and mask by the sign of df/dx
for path in c0.get_paths():
vertices = path.vertices
vr = vertices[:,0]
vx = vertices[:,1]
mask = numpy.sign(f_x(vr,vx))
stable = mask < 0.
unstable = mask > 0.
# plot the stable and unstable branches for each path
plt.plot(vr[stable],vx[stable],'b')
plt.hold(True)
plt.plot(vr[unstable],vx[unstable],'b--')
plt.xlabel('parameter {0}'.format(rlabel))
plt.ylabel('x')
plt.legend(('stable','unstable'),loc='best')
plt.xlim(r[0],r[-1])
plt.ylim(x[0],x[-1])
```
### Example #1: Saddle node bifurcation
consider the problem
$$ f(r,x) = r + x^2$$
and we will define $f$ and $\partial f/\partial x$ using inlined python lambda functions
```
f = lambda r,x: r + x*x
f_x = lambda r,x: 2.*x
x = numpy.linspace(-4,4,100)
r = numpy.linspace(-4,4,100)
bifurcation_plot(f,f_x,r,x)
```
### Example #2: Logistic equation with constant harvesting
$$ dx/dt = x(1-x) - h $$
```
f = lambda h,x: x*(1-x) - h
f_x = lambda h,x: 1. - 2.*x
x = numpy.linspace(0,1.,100)
h = numpy.linspace(0,.5,100)
bifurcation_plot(f,f_x,h,x,rlabel='h')
```
### Example #3: transcritical bifurcation
$$f(r,x) = rx - x^2$$
```
f = lambda r,x: r*x - x*x
f_x = lambda r,x: r - 2.*x
x = numpy.linspace(-1.,1.,100)
r = numpy.linspace(-1.,1.,100)
bifurcation_plot(f,f_x,r,x)
```
### Example #4 super-critical pitchfork bifurcation
$$f(r,x) = rx - x^3$$
```
f = lambda r,x: r*x - x**3
f_x = lambda r,x: r - 3.*x**2
x = numpy.linspace(-1.,1.,100)
r = numpy.linspace(-1.,1.,100)
bifurcation_plot(f,f_x,r,x)
```
##### Example #4 sub-critical pitchfork bifurcation
$$f(r,x) = rx + x^3$$
```
f = lambda r,x: r*x + x**3
f_x = lambda r,x: r + 3.*x**2
x = numpy.linspace(-1.,1.,100)
r = numpy.linspace(-1.,1.,100)
bifurcation_plot(f,f_x,r,x)
```
### Example #6 subcritical pitchfork bifurcation with stabilization
$$f(r,x) = rx + x^3 - x^5 $$
```
f = lambda r,x: r*x + x**3 - x**5
f_x = lambda r,x: r + 3.*x**2 -5.*x**4
x = numpy.linspace(-2.,2.,100)
r = numpy.linspace(-.5,.5,100)
bifurcation_plot(f,f_x,r,x)
```
FIXME: this plot needs to mask out the spurious stable branch which is a plotting error
And now you can play with your own function
```
f = lambda r,x: # < your function here >
f_x = lambda r,x: # < your derivative here >
# Adjust your domain and resolution
x = numpy.linspace(-10.,10.,100)
r = numpy.linspace(-10.,10.,100)
#plot and pray (and watch out for glitches)
bifurcation_plot(f,f_x,r,x)
```
| true |
code
| 0.626696 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content-dl/blob/main/tutorials/W2D1_ConvnetsAndRecurrentNeuralNetworks/student/W2D1_Tutorial2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a> <a href="https://kaggle.com/kernels/welcome?src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content-dl/main/tutorials/W2D1_ConvnetsAndRecurrentNeuralNetworks/student/W2D1_Tutorial2.ipynb" target="_parent"><img src="https://kaggle.com/static/images/open-in-kaggle.svg" alt="Open in Kaggle"/></a>
# Tutorial 2: Introduction to RNNs
**Week 2, Day 1: Convnets And Recurrent Neural Networks**
**By Neuromatch Academy**
__Content creators:__ Dawn McKnight, Richard Gerum, Cassidy Pirlot, Rohan Saha, Liam Peet-Pare, Saeed Najafi, Alona Fyshe
__Content reviewers:__ Saeed Salehi, Lily Cheng, Yu-Fang Yang, Polina Turishcheva, Nina Kudryashova, Kelson Shilling-Scrivo
__Content editors:__ Nina Kudryashova
__Production editors:__ Anmol Gupta, Spiros Chavlis
*Based on material from:* Konrad Kording, Hmrishav Bandyopadhyay, Rahul Shekhar, Tejas Srivastava
**Our 2021 Sponsors, including Presenting Sponsor Facebook Reality Labs**
<p align='center'><img src='https://github.com/NeuromatchAcademy/widgets/blob/master/sponsors.png?raw=True'/></p>
---
# Tutorial Objectives
At the end of this tutorial, we will be able to:
- Understand the structure of a Recurrent Neural Network (RNN)
- Build a simple RNN model
```
# @title Tutorial slides
# @markdown These are the slides for the videos in this tutorial
# @markdown If you want to download locally the slides, click [here](https://osf.io/5asx2/download)
from IPython.display import IFrame
IFrame(src=f"https://mfr.ca-1.osf.io/render?url=https://osf.io/5asx2/?direct%26mode=render%26action=download%26mode=render", width=854, height=480)
```
---
# Setup
```
# @title Install dependencies
!pip install livelossplot --quiet
!pip install unidecode
!pip install git+https://github.com/NeuromatchAcademy/evaltools --quiet
from evaltools.airtable import AirtableForm
# generate airtable form
atform = AirtableForm('appn7VdPRseSoMXEG','W2D1_T2','https://portal.neuromatchacademy.org/api/redirect/to/351ca652-13d8-4e31-be28-30153d03e639')
# Imports
import time
import math
import torch
import string
import random
import unidecode
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
from tqdm.notebook import tqdm
# @title Figure settings
import ipywidgets as widgets # interactive display
%config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/content-creation/main/nma.mplstyle")
plt.rcParams["mpl_toolkits.legacy_colorbar"] = False
import warnings
warnings.filterwarnings("ignore", category=UserWarning, module="matplotlib")
# @title Helper functions
# https://github.com/spro/char-rnn.pytorch
def read_file(filename):
file = unidecode.unidecode(open(filename).read())
return file, len(file)
# Turning a string into a tensor
def char_tensor(string):
tensor = torch.zeros(len(string)).long()
for c in range(len(string)):
try:
tensor[c] = all_characters.index(string[c])
except:
continue
return tensor
# Readable time elapsed
def time_since(since):
s = time.time() - since
m = math.floor(s / 60)
s -= m * 60
out = f"{m}min {s}sec"
return out
def generate(decoder, prime_str='A', predict_len=100, temperature=0.8,
device='cpu'):
hidden = decoder.init_hidden(1)
prime_input = char_tensor(prime_str).unsqueeze(0)
hidden = hidden.to(device)
prime_input = prime_input.to(device)
predicted = prime_str
# Use priming string to "build up" hidden state
for p in range(len(prime_str) - 1):
_, hidden = decoder(prime_input[:,p], hidden)
inp = prime_input[:,-1]
for p in range(predict_len):
output, hidden = decoder(inp, hidden)
# Sample from the network as a multinomial distribution
output_dist = output.data.view(-1).div(temperature).exp()
top_i = torch.multinomial(output_dist, 1)[0]
# Add predicted character to string and use as next input
predicted_char = all_characters[top_i]
predicted += predicted_char
inp = char_tensor(predicted_char).unsqueeze(0)
inp = inp.to(device)
return predicted
# @title Set random seed
# @markdown Executing `set_seed(seed=seed)` you are setting the seed
# for DL its critical to set the random seed so that students can have a
# baseline to compare their results to expected results.
# Read more here: https://pytorch.org/docs/stable/notes/randomness.html
# Call `set_seed` function in the exercises to ensure reproducibility.
import random
import torch
def set_seed(seed=None, seed_torch=True):
if seed is None:
seed = np.random.choice(2 ** 32)
random.seed(seed)
np.random.seed(seed)
if seed_torch:
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
print(f'Random seed {seed} has been set.')
# In case that `DataLoader` is used
def seed_worker(worker_id):
worker_seed = torch.initial_seed() % 2**32
np.random.seed(worker_seed)
random.seed(worker_seed)
#@title Set device (GPU or CPU). Execute `set_device()`
# especially if torch modules used.
# inform the user if the notebook uses GPU or CPU.
def set_device():
device = "cuda" if torch.cuda.is_available() else "cpu"
if device != "cuda":
print("WARNING: For this notebook to perform best, "
"if possible, in the menu under `Runtime` -> "
"`Change runtime type.` select `GPU` ")
else:
print("GPU is enabled in this notebook.")
return device
SEED = 2021
set_seed(seed=SEED)
DEVICE = set_device()
```
---
# Section 1: Recurrent Neural Networks (RNNs)
*Time estimate: ~20mins*
```
# @title Video 1: RNNs
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1L44y1m7PP", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"PsZjS125lLs", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add event to airtable
atform.add_event('Video 1: RNNs')
display(out)
```
RNNs are compact models that operate over timeseries, and have the ability to remember past input. They also save parameters by using the same weights at every time step. If you've heard of Transformers, those models don't have this kind of temporal weight sharing, and so they are *much* larger.
The code below is adapted from [this github repository](https://github.com/spro/char-rnn.pytorch).
```
# RNN
# https://github.com/spro/char-rnn.pytorch
class CharRNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size,
model="gru", n_layers=1):
"""
input_size: int
Size of the input layer.
hidden_size: int
Size of the hidden layers.
output_size: int
Size of the output layer.
model: string
`model` can take the values "gru", "rnn", "lstm". Default is "gru".
n_layers: int
Number of layers
"""
super(CharRNN, self).__init__()
self.model = model.lower()
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.n_layers = n_layers
self.encoder = nn.Embedding(input_size, hidden_size)
if self.model == "gru":
self.rnn = nn.GRU(hidden_size, hidden_size, n_layers)
elif self.model == "lstm":
self.rnn = nn.LSTM(hidden_size, hidden_size, n_layers)
elif self.model == "rnn":
self.rnn = nn.RNN(hidden_size, hidden_size, n_layers)
self.decoder = nn.Linear(hidden_size, output_size)
def forward(self, input, hidden):
batch_size = input.size(0)
encoded = self.encoder(input)
output, hidden = self.rnn(encoded.reshape(1, batch_size, -1), hidden)
output = self.decoder(output.reshape(batch_size, -1))
return output, hidden
def init_hidden(self, batch_size):
if self.model == "lstm":
return (torch.zeros(self.n_layers, batch_size, self.hidden_size), torch.zeros(self.n_layers, batch_size, self.hidden_size))
return torch.zeros(self.n_layers, batch_size, self.hidden_size)
```
This next section of code takes care of training the RNN on several of Mark Twain's books. In this short section, we won't dive into the code, but you'll get to learn a lot more about RNNs in a few days! For now, we are just going to observe the training process.
```
# @title Run Me to get the data
import requests
url = 'https://raw.githubusercontent.com/NeuromatchAcademy/course-content-dl/main/tutorials/W2D1_ConvnetsAndRecurrentNeuralNetworks/static/twain.txt'
r = requests.get(url, stream=True)
with open('twain.txt', 'wb') as fd:
fd.write(r.content)
```
One cool thing about RNNs is that they can be used to _generate_ language based on what the network sees during training. As the network makes predictions, instead of confirming of those predictions are correct against some training text, we just feed them back into the model as the next observed token. Starting from a random vector for the hidden state, we can generate many original sentences! And what the network generates will reflect the text it was trained on.
```
# https://github.com/spro/char-rnn.pytorch
def random_training_set(file, file_len, chunk_len, batch_size,
device='cpu', seed=0):
random.seed(seed)
inp = torch.LongTensor(batch_size, chunk_len).to(device)
target = torch.LongTensor(batch_size, chunk_len).to(device)
for bi in range(batch_size):
start_index = random.randint(0, file_len - chunk_len - 1)
end_index = start_index + chunk_len + 1
chunk = file[start_index:end_index]
inp[bi] = char_tensor(chunk[:-1])
target[bi] = char_tensor(chunk[1:])
return inp, target, chunk_len, batch_size, device
def train(decoder, criterion, inp, target, chunk_len, batch_size, device):
hidden = decoder.init_hidden(batch_size)
decoder.zero_grad()
loss = 0
for c in range(chunk_len):
output, hidden = decoder(inp[:, c].to(device), hidden.to(device))
loss += criterion(output.reshape(batch_size, -1), target[:,c])
loss.backward()
decoder_optimizer.step()
return loss.item() / chunk_len
```
First, let's load the text file, and define the model and its hyperparameters.
```
# Reading and un-unicode-encoding data
all_characters = string.printable
n_characters = len(all_characters)
# load the text file
file, file_len = read_file('twain.txt')
# Hyperparams
batch_size = 50
chunk_len = 200
model = "rnn" # other options: `lstm`, `gru`
n_layers = 2
hidden_size = 200
learning_rate = 0.01
# Define the model, optimizer, and the loss criterion
decoder = CharRNN(n_characters, hidden_size, n_characters,
model=model, n_layers=n_layers)
decoder.to(DEVICE)
decoder_optimizer = torch.optim.Adagrad(decoder.parameters(), lr=learning_rate)
criterion = nn.CrossEntropyLoss()
```
Let's try it! Run the code below. As the network trains, it will output samples of generated text every 25 epochs. Notice that as the training progresses, the model learns to spell short words, then learns to string some words together, and eventually can produce meaningful sentences (sometimes)! Keep in mind that this is a relatively small network, and doesn't employ some of the cool things you'll learn about later in the week (e.g., LSTMs, though you can change that in the code below by changing the value of the `model` variable if you wish!)
After running the model, and observing the output, get together with your pod, and talk about what you noticed during training. Did your network produce anything interesting? Did it produce anything characteristic of Twain?
**Note:** training for the full 2000 epochs is likely to take a while, so you may need to stop it before it finishes. If you have time left, set `n_epochs` to 2000 below.
```
n_epochs = 1000 # initial was set to 2000
print_every = 50 # frequency of printing the outputs
start = time.time()
all_losses = []
loss_avg = 0
print(f"Training for {n_epochs} epochs...\n")
for epoch in tqdm(range(1, n_epochs + 1), position=0, leave=True):
loss = train(decoder, criterion,
*random_training_set(file, file_len, chunk_len, batch_size,
device=DEVICE, seed=epoch))
loss_avg += loss
if epoch % print_every == 0:
print(f"[{time_since(start)} {epoch/n_epochs * 100}%) {loss:.4f}]")
print(f"{generate(decoder, prime_str='Wh', predict_len=150, device=DEVICE)}")
```
Now you can generate more examples using a trained model. Recall that `generate` takes the mentioned below arguments to work:
```python
generate(decoder, prime_str='A', predict_len=100, temperature=0.8, device='cpu')
```
Try it by yourself
```
print(f"{generate(decoder, prime_str='Wh', predict_len=100, device=DEVICE)}\n")
```
---
# Section 2: Power consumption in Deep Learning
*Time estimate: ~20mins*
Training NN models can be incredibly costly, both in actual money but also in power consumption.
```
# @title Video 2: Carbon Footprint of AI
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1My4y1j7HJ", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"as6C334LmRs", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add event to airtable
atform.add_event('Video 2: Carbon Footprint of AI')
display(out)
```
Take a few moments to chat with your pod about the following points:
* Which societal costs of training do you find most compelling?
* When is training an AI model worth the cost? Who should make that decision?
* Should there be additional taxes on energy costs for compute centers?
## Exercise 2: Calculate the carbon footprint that your pod generated today.
You can use this [online calculator](https://mlco2.github.io/impact/#compute).
```
# @title Student Response
from ipywidgets import widgets
text=widgets.Textarea(
value='Type your answer here and click on `Submit!`',
placeholder='Type something',
description='',
disabled=False
)
button = widgets.Button(description="Submit!")
display(text,button)
def on_button_clicked(b):
atform.add_answer('q1', text.value)
print("Submission successful!")
button.on_click(on_button_clicked)
```
---
# Summary
What a day! We've learned a lot! The basics of CNNs and RNNs, and how changes to architecture that allow models to parameter share can greatly reduce the size of the model. We learned about convolution and pooling, as well as the basic idea behind RNNs. To wrap up we thought about the impact of training large NN models.
```
# @title Airtable Submission Link
from IPython import display as IPydisplay
IPydisplay.HTML(
f"""
<div>
<a href= "{atform.url()}" target="_blank">
<img src="https://github.com/NeuromatchAcademy/course-content-dl/blob/main/tutorials/static/SurveyButton.png?raw=1"
alt="button link end of day Survey" style="width:410px"></a>
</div>""" )
```
| true |
code
| 0.801819 | null | null | null | null |
|
<!--NAVIGATION-->
< [OPTIONAL - More about interact](02.01-OPTIONAL-More-About-Interact.ipynb) | [Contents](00.00-index.ipynb) | [Widgets in the core ipywidgets package](04.00-widget-list.ipynb) >
# Simple Widget Introduction
## O que são widgets?
Widgets são objetos python que têm uma representação no navegador, geralmente como um controle como `slider`, `textbox`, etc.
## Para que eles podem ser usados?
Você pode usar widgets para construir **interactive GUIs** para seus notebooks.
Você também pode usar widgets para **sincronizar informações com e sem estado** entre Python e JavaScript.
## Usando widgets
Para usar o framework de widget, você precisa importar `ipywidgets`.
```
import ipywidgets as widgets
```
### repr
Os widgets têm seu próprio display `repr`, o que permite que eles sejam exibidos usando a estrutura de exibição do IPython. Construindo e retornando um `IntSlider` que exibe automaticamente o widget (como visto abaixo). Os widgets são exibidos dentro da área de saída abaixo da célula de código. Limpar a saída da célula também removerá o widget.
```
widgets.IntSlider()
```
### display()
Você também pode exibir explicitamente o widget usando `display(...)`.
```
from IPython.display import display
w = widgets.IntSlider()
display(w)
```
### Múltiplas chamadas `display()`
Se você exibir o mesmo widget duas vezes, as instâncias exibidas no frontend permanecerão sincronizadas entre si. Tente arrastar o `slider` abaixo e observe o controle deslizante acima.
```
display(w)
```
## Por que exibir o mesmo widget duas vezes funciona?
Os widgets são representados no back-end por um único objeto. Cada vez que um widget é exibido, uma nova representação desse mesmo objeto é criada no frontend. Essas representações são chamadas de `views`.

## Propriedades Widget
Todos os widgets IPython compartilham um esquema de nomenclatura semelhante. Para ler o valor de um widget, você pode consultar a propriedade `value`.
```
w = widgets.IntSlider()
display(w)
w.value
```
Da mesma forma, para definir o valor de um widget, você pode definir sua propriedade `value`.
```
w.value = 100
```
### keys
Além de `valor`, a maioria dos widgets compartilham` keys`, `description` e` disabled`. Para ver toda a lista de propriedades sincronizadas e com estado de qualquer widget específico, você pode consultar a propriedade `keys`. Geralmente, você não deve interagir com propriedades que começam com um sublinhado.
```
w.keys
```
### Abreviação para definir os valores iniciais das propriedades do widget
Ao criar um widget, você pode definir alguns ou todos os valores iniciais desse widget, definindo-os como argumentos de palavra-chave no construtor do widget (conforme visto abaixo).
```
widgets.Text(value='Hello World!', disabled=True)
```
## Linkar dois widgets semelhantes
Se você precisar exibir o mesmo valor de duas maneiras diferentes, terá que usar dois widgets diferentes. Em vez de tentar sincronizar manualmente os valores dos dois widgets, você pode usar a função `link` ou` jslink` para vincular duas propriedades (a diferença entre elas é discutida no [Widget Events](08.00-Widget_Events.ipynb)). Veja abaixo, os valores de dois widgets estão vinculados.
```
slider = widgets.FloatSlider(
value=7.5,
min=5.0,
max=10.0,
step=0.1,
description='Input:',
)
# Criar `text box` para ter o valor do `slider`
text = widgets.FloatText(description='Value')
# Linkar o valor do `slider` com o valor do `text box`
widgets.link((slider, 'value'), (text, 'value'))
# Colocar eles em uma caixa vertical
widgets.VBox([slider, text])
```
### Desvincular widgets
Desvincular os widgets é simples. Tudo que você precisa fazer é chamar `.unlink` no objeto de link. Tente alterar um dos widgets acima após desvincular para ver se eles podem ser alterados de forma independente.
```
# mylink.unlink()
```
## `observe` mudanças no valor de um widget
Quase todos os widgets podem ser observados quanto a mudanças em seu valor que acionam uma chamada para uma função. O exemplo abaixo é o `slider` do primeiro bloco de notas do tutorial.
O widget `HTML` abaixo do `slider` exibe o quadrado do número.
```
slider = widgets.FloatSlider(
value=7.5,
min=5.0,
max=10.0,
step=0.1,
description='Input:',
)
# Cria uma área de texto não editável para exibir o quadrado de valor
square_display = widgets.HTML(description="Square: ", value='{}'.format(slider.value**2))
# Crie uma função para atualizar o valor do square_display quando o `slider` mudar
def update_square_display(change):
square_display.value = '{}'.format(change.new**2)
slider.observe(update_square_display, names='value')
# Coloque-os em uma caixa vertical
widgets.VBox([slider, square_display])
```
<!--NAVIGATION-->
< [OPTIONAL - More about interact](02.01-OPTIONAL-More-About-Interact.ipynb) | [Contents](00.00-index.ipynb) | [Widgets in the core ipywidgets package](04.00-widget-list.ipynb) >
| true |
code
| 0.299835 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.